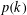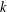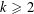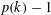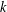Let 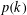$p(k)$ denote the partition function of 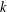$k$. For each 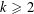$k\geqslant 2$, we describe a list of 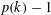$p(k)-1$ quasirandom properties that a 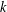$k$-uniform hypergraph can have. Our work connects previous notions on linear hypergraph quasirandomness by Kohayakawa, Rödl, and Skokan, and by Conlon, Hàn, Person, and Schacht, and the spectral approach of Friedman and Wigderson. For each of the quasirandom properties that is described, we define the largest and the second largest eigenvalues. We show that a hypergraph satisfies these quasirandom properties if and only if it has a large spectral gap. This answers a question of Conlon, Hàn, Person, and Schacht. Our work can be viewed as a partial extension to hypergraphs of the seminal spectral results of Chung, Graham, and Wilson for graphs.

Let $K$ be the quotient field of a Dedekind domain $R$. We characterize the $R$-orders $\Lambda$ in a separable $K$-algebra for which every $R$-projective $\Lambda$-module decomposes into $\Lambda$-lattices. Butler, Campbell and Kovács have recently shown that the latter holds for the integral group ring of a cyclic group of prime order, as well as for lattice-finite orders over a complete discrete valuation domain.