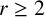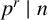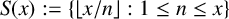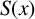DISTRIBUTION OF r-FREE INTEGERS OVER A FLOOR FUNCTION SET

Abstract

For a positive integer $r\geq 2$, a natural number n is r-free if there is no prime p such that $p^r\mid n$. Asymptotic formulae for the distribution of r-free integers in the floor function set $S(x):=\{\lfloor x/ n \rfloor :1\leq n\leq x\}$ are derived. The first formula uses an estimate for elements of $S(x)$ belonging to arithmetic progressions. The other, more refined, formula makes use of an exponent pair and the Riemann hypothesis.

1 Introduction and results

Let $\lfloor t \rfloor $ be the integral part of $t\in \mathbb {R}$ and let r be a fixed integer $\geq 2$ . A positive integer n is called r-free if in its canonical prime representation, each exponent is $<r$ ; a 2-free integer is also called square-free. Let $\mu _r$ be the characteristic function of the r-free integers. There is considerable research on the distribution of r-free integers over certain special sets, such as the set of integer parts, the Beatty sequence $\lfloor \alpha n+\beta \rfloor $ , [1, 8, 9, 19] and the Piatetski-Shapiro sequence $\lfloor n^c \rfloor $ , [5–7, 13–15, 17, 18, 21]. In 2019, Bordellés et al. [4] established an asymptotic formula for a sum of the form

$$ \begin{align*} \sum_{n\leq x}f\bigg( \bigg\lfloor\frac{x}{n}\bigg\rfloor \bigg), \end{align*} $$

where f is an arithmetic function subject to some growth condition, and applied it in particular to Euler’s totient function. It is thus natural to consider such a sum for various other functions. For example, in [3], Bordellés proved that

(1.1) $$ \begin{align} S_{\mu_2}(x)=x\sum_{n=1}^\infty \frac{\mu_2(n)}{n(n+1)}+O(x^{1919/4268+\epsilon}), \end{align} $$

where $\mu _2(n)$ is the characteristic function of the set of square-free numbers. Later, Liu et al. [12] improved the O-term in (1.1) to $O(x^{2/5+\epsilon })$ . In 2022, Stucky [16] generalised the sum in (1.1) to the case of r-free integers and showed that for $r\geq 3,$

$$ \begin{align*} S_{\mu_r}(x)=\sum_{n=1}^\infty \frac{\mu_r(n)}{n(n+1)}x+O(x^{\theta_r}),\quad \theta_r:=\frac{r+1}{3r+1}, \end{align*} $$

where $\mu _r(n)$ is the characteristic function of the set of r-free numbers. Very recently, Heyman [10] considered the floor function set

(1.2) $$ \begin{align} S(x):=\bigg\{\bigg\lfloor \frac{x}{n} \bigg\rfloor :1\leq n\leq x\bigg\} \end{align} $$

and studied the number of primes in $S(x)$ . Our objective here is to investigate how the r-free integers are distributed over the set $S(x)$ , that is, to ask for an asymptotic estimate for the function

(1.3) $$ \begin{align} T_{\mu_r}(x):=\sum_{m\in S(x)}\mu_r(m). \end{align} $$

There first arises the question whether the sum (1.3) is identical or related to the sum

(1.4) $$ \begin{align} S_{\mu_r}(x):=\sum_{n\leq x}\mu_r\bigg( \bigg\lfloor\frac{x}{n}\bigg\rfloor \bigg). \end{align} $$

To answer this question, we rewrite the sum (1.3) as

$$ \begin{align*} T_{\mu_r}(x)=\sum_{\substack{m\leq x\\ \exists n\in \mathbb{N} \text{ such that }\lfloor x/n \rfloor=m}}\mu_r(m). \end{align*} $$

Observe that each argument appears once in the sum (1.3), but usually appears several times in the sum (1.4), as seen in the following example. Taking $x=20$ and $r=2$ , for the sum (1.4), we get

$$ \begin{align*} &S_{\mu_2}(20)=\sum_{n\leq 20}\mu_2\bigg( \bigg\lfloor\frac{20}{n}\bigg\rfloor \bigg)\\ &=\mu_2(20)+\mu_2(10)+\mu_2(6)+\mu_2(5)+\mu_2(4)+\mu_2(3)+\mu_2(2)+\mu_2(2)+\mu_2(2)+\mu_2(2)\\ &\quad +\mu_2(1)+\mu_2(1)+\mu_2(1)+\mu_2(1)+\mu_2(1)+\mu_2(1)+\mu_2(1)+\mu_2(1)+\mu_2(1)+\mu_2(1)\\ &=\mu_2(20)+\mu_2(10)+\mu_2(6)+\mu_2(5)+\mu_2(4)+\mu_2(3)+4\mu_2(2)+10\mu_2(1)=18, \end{align*} $$

while for the sum (1.3), we get $S(20)=\{\lfloor {20}/{n} \rfloor :1\leq n\leq 20\}=\{1, 2, 3, 4, 5, 6, 10, 20\}$ and

$$ \begin{align*} T_{\mu_2}(20)&=\sum_{m\in S(20)}\mu_2(m) \\ &=\mu_2(20)+\mu_2(10)+\mu_2(6)+\mu_2(5)+\mu_2(4)+\mu_2(3)+\mu_2(2)+\mu_2(1) =6. \end{align*} $$

Our first main result is proved using the following estimate of Yu and Wu [20].

Lemma 1.1 [20].

Let $x\in \mathbb {R},\ x>0$ , let $q, a\in \mathbb {Z}$ such that $0\leq a<q\leq x^{1/4}\log ^{-3/2} x$ and let $S(x)$ be as defined in (1.2). Then,

$$ \begin{align*} \sum_{\substack{n\in S(x)\\ n \, \equiv\, a\ ({\mathrm{mod }}\, q)}}1=\frac{2x^{1/2}}{q }+ O \bigg(\frac{x^{1/3}}{q^{1/3}}\log x\bigg). \end{align*} $$

Remark 1.2. For real large x, let $S(x)$ be as defined in (1.2). We shall need the estimate $\lvert {S(x)}\rvert =O(x^{1/2})$ in our proofs. To verify this, note that for $n\in \{1,2,\ldots \lfloor x\rfloor \}$ :

• • if $\lfloor x/n \rfloor =1$ , then $n\leq x$ ;

• • if $\lfloor x/n \rfloor =2$ , then $n\leq x/2$ ;

  ⋮

• • if $\lfloor x/n \rfloor =\lfloor x^{1/2}\rfloor $ , then $n< x^{1/2}$ .

It follows that for $n<x^{1/2}$ , the function $\lfloor x/n\rfloor $ takes at most $\lfloor x^{1/2}\rfloor $ distinct integral values. However, if $n\geq x^{1/2}$ , the function $\lfloor x/n\rfloor \leq x^{1/2}$ can then take at most $\lfloor x^{1/2}\rfloor $ integral values. Thus, $\lvert {S(x)}\rvert \leq 2\lfloor x^{1/2}\rfloor =O(x^{1/2})$ .

Our first theorem reads as follows.

Theorem 1.3. Let $S(x)$ and $T_{\mu _r}$ be as defined in (1.2) and (1.3). Then,

$$ \begin{align*} T_{\mu_r}(x)=\frac{2x^{1/2}}{\zeta(r)}+\begin{cases} O(x^{3/8}\log^{3/4} x) & \text{for } r=2, \\ O(x^{1/3}\log x) & \text{for } r\geq3.\\ \end{cases} \end{align*} $$

Regarding our second main result, very recently, Zhang [22] improved the results of Bordellés (1.1), Stuctky [16] and Liu et al. [12] by proving using the exponent pair method, that

$$ \begin{align*} S_{\mu_r}(x)=x\sum_{n=1}^\infty \frac{\mu_r(n)}{n(n+1)}+\begin{cases} O(x^{11/29}\log^{2} x) & \text{for } r=2, \\ O(x^{1/3}\log^2 x) & \text{for } r=3,\\ O(x^{1/3}\log x), & \text{for } r\geq 3. \end{cases} \end{align*} $$

We use the same idea as in [22] to give another formula, which, in the case $r=2$ , is slightly weaker than that in Theorem 1.3.

Theorem 1.4. For an exponent pair $(\kappa ,\lambda )$ such that ${1}/{2}<{\lambda }/{(1+\kappa )}$ , we have

$$ \begin{align*} T_{\mu_r}(x)=\frac{2x^{1/2}}{\zeta(r)}+\begin{cases} O( x^{1/4+\lambda/4(1+\kappa)}(\log x)^{3/2-3\lambda/2(1+\kappa)}) & \text{for } r=2, \\ O(x^{1/3}\log x) & \text{for } r\geq3. \end{cases} \end{align*} $$

We note in passing that a result better than that in Theorem 1.4 for the case $r=2$ can be derived, assuming the Riemann hypothesis, by taking the exponent pair $(\kappa , \lambda )=(2/7, 4/7)$ to get

$$ \begin{align*} T_{\mu_2}(x)=\frac{2x^{1/2}}{\zeta(2)}+ O( x^{13/36}(\log x)^{1/6} ). \end{align*} $$

Under the Riemann hypothesis, we can omit the restriction on the exponent pair $(\kappa ,\lambda )$ such that ${1}/{2}<{\lambda }/{(1+\kappa )}$ and obtain the following result.

Theorem 1.5. Assume the Riemann hypothesis. For an exponent pair $(\kappa ,\lambda )$ such that ${1}/{4}<{\lambda }/{(1+\kappa )}$ , we have

$$ \begin{align*} T_{\mu_2}(x)=\frac{2x^{1/2}}{\zeta(2)}+ O( x^{1/4+\lambda/4(1+\kappa)}(\log x)^{3/2-3\lambda/2(1+\kappa)}). \end{align*} $$

2 Proofs

Proof of Theorem 1.3.

Since $\mu _r(n)$ is the characteristic function of the set of r-free numbers, by the well-known identity $\mu _r(n)=\sum _{d^r\mid n}\mu (d)$ , we have

$$ \begin{align*} T_{\mu_r}(x)&=\sum_{n\in S(x)}\mu_r(n)=\sum_{n\in S(x)}\sum_{d^r\mid n}\mu(d) =\sum_{d\leq x^{1/r}}\mu(d)\sum_{\substack{n\in S(x)\\ n \, \equiv\, {0\, \textrm{(mod} \; d^r\textrm{)}} }}1\\ &=\sum_{d\leq x^{1/4r}\log^{-3/2r} x}\mu(d)\sum_{\substack{n\in S(x)\\ n \, \equiv\, {0\, \textrm{(mod} \; d^r\textrm{)}} }}1+\sum_{ x^{1/4r}\log^{-3/2r} x< d\leq x^{1/r}}\mu(d)\sum_{\substack{n\in S(x)\\ n \, \equiv\, {0\, \textrm{(mod} \; d^r\textrm{)}} }}1. \end{align*} $$

Using Lemma 1.1 to compute the first sum, we have

$$ \begin{align*} \sum_{d\leq x^{1/4r}\log^{-3/2r} x}\mu(d)\sum_{\substack{n\in S(x)\\ n \, \equiv\, {0\, \textrm{(mod} \; d^r\textrm{)}} }}1 & =\sum_{d\leq x^{1/4r}\log^{-3/2r} x}\mu(d)\bigg(\frac{2x^{1/2}}{d^r }+ O \bigg(\frac{x^{1/3}}{d^{r/3}}\log x\bigg)\bigg)\\ &=\frac{2x^{1/2}}{\zeta(r)}+\begin{cases} O(x^{3/8}\log^{3/4} x) & \text{for } r=2, \\ O(x^{1/3}\log x) & \text{for } r\geq3. \end{cases} \end{align*} $$

By the remark preceding the statement of Theorem 1.3, we have $\lvert {S(x)}\rvert =O(x^{1/2})$ and so the second sum is bounded by

$$ \begin{align*} \sum_{ x^{1/4r}\log^{-3/2r} x< d\leq x^{1/r}}\mu(d)\sum_{\substack{n\in S(x)\\ n \, \equiv\, {0\, \textrm{(mod} \; d^2\textrm{)}} }}1&=O\bigg(x^{1/2}\sum_{ x^{1/4r}\log^{-3/2r} x< d\leq x^{1/r}}\frac{1}{ d^2}\bigg)\\ &=\begin{cases} O(x^{3/8}\log^{3/4} x) & \text{for } r=2, \\ O(x^{1/4}\log^{1/2} x) & \text{for } r\geq3, \end{cases} \end{align*} $$

which completes the proof of Theorem 1.3.

Proof of Theorem 1.4.

In view of [11, (14.23)],

$$ \begin{align*}\mu_r(n)=\sum_{d\mid n}g(d),\quad\text{where } g(d)=\begin{cases} \mu(\ell) & \text{if } d=\ell^r,\ \text{for some } \ell\in \mathbb{N}, \\ 0 & \text{otherwise.} \end{cases}\end{align*} $$

From the definition of $g(d)$ ,

(2.1) $$ \begin{align} \sum_{d\leq x}\lvert{g(d)}\rvert=\begin{cases} O(x^{1/2}) & \text{if } r=2, \\ O(x^{1/3}) & \text{if } r\geq 3. \end{cases} \end{align} $$

Let $(\kappa ,\lambda )$ be an exponent pair such that ${1}/{2}<{\lambda }/{(1+\kappa )}\ (< 1)$ . Trivially, from (2.1),

(2.2) $$ \begin{align} \sum_{d\leq x}\lvert{g(d)}\rvert=O(x^{{\lambda}/{(1+\kappa)}}). \end{align} $$

For $x>1$ ,

$$ \begin{align*} \sum_{n\in S(x)}\mu_r(n)&=\sum_{n\in S(x)}\sum_{d\mid n}g(d)=\sum_{d\leq x}g(d)\sum_{\substack{n\in S(x)\\ n \, \equiv\, {0\, \textrm{(mod} \; d\textrm{)}}} }1\\ &=\sum_{d\leq x^{1/4}\log^{-3/2} x}g(d)\sum_{\substack{n\in S(x)\\ n \, \equiv\, {0\, \textrm{(mod} \; d\textrm{)}}} }1+\sum_{ x^{1/4}\log^{-3/2} x< d\leq x}g(d)\sum_{\substack{n\in S(x)\\ n \, \equiv\, {0\, \textrm{(mod} \; d\textrm{)}} }}1. \end{align*} $$

We use Lemma 1.1 to compute the first sum. We have

$$ \begin{align*} \sum_{d\leq x^{1/4}\log^{-3/2} x} g(d)\sum_{\substack{n\in S(x)\\ n \, \equiv\, {0\, \textrm{(mod} \; d\textrm{)}} }}1&=\sum_{d\leq x^{1/4}\log^{-3/2} x}g(d)\bigg(\frac{2x^{1/2}}{d }+ O \bigg(\frac{x^{1/3}}{d^{1/3}}\log x\bigg)\bigg)\\ &=2x^{1/2}\sum_{d\leq x^{1/4}\log^{-3/2} x}\frac{g(d)}{d }+O\bigg(x^{1/3}\log x\sum_{d\leq x^{1/4}\log^{-3/2} x} \frac{\lvert{g(d)}\rvert}{d^{1/3} }\bigg). \end{align*} $$

Denote the first and the second sums on the right-hand side by $\Sigma _1$ and $\Sigma _2$ , respectively. Using partial summation (or Abel’s identity [2, Theorem 4.2]) and (2.2),

$$ \begin{align*} \sum_{d\leq x^{1/4}\log^{-3/2} x}\frac{g(d)}{d }&=\sum_{d=1}^\infty \frac{g(d)}{d }-\sum_{d> x^{1/4}\log^{-3/2} x}\frac{g(d)}{d } =\sum_{d=1}^\infty \frac{g(d)}{d }+O \bigg(\sum_{d> x^{1/4}\log^{-3/2} x}\frac{\lvert{g(d)}\rvert}{d }\bigg) \\ &=\sum_{d=1}^\infty \frac{g(d)}{d }+O( x^{-1/4+\lambda/4(1+\kappa)}(\log x)^{3/2-3\lambda/2(1+\kappa)} ) \end{align*} $$

and so

$$ \begin{align*} \Sigma_1=2x^{1/2}\sum_{d=1}^\infty \frac{g(d)}{d }+O( x^{1/4+\lambda/4(1+\kappa)}(\log x)^{3/2-3\lambda/2(1+\kappa)} ). \end{align*} $$

Again from (2.2), by Abel’s identity,

$$ \begin{align*} \sum_{d\leq x^{1/4}\log^{-3/2} x}\frac{\lvert{g(d)}\rvert}{d^{1/3} }\ll x^{-1/12+\lambda/4(1+\kappa)}(\log x)^{1/2-3\lambda/2(1+\kappa)} \end{align*} $$

and so

$$ \begin{align*} \Sigma_2=O( x^{1/4+\lambda/4(1+\kappa)}(\log x)^{3/2-3\lambda/2(1+\kappa)} ). \end{align*} $$

Then,

$$ \begin{align*} \sum_{d\leq x^{1/4}\log^{-3/2} x}g(d)\sum_{\substack{n\in S(x)\\ n \, \equiv\, {0\, \textrm{(mod} \; d\textrm{)}}} }1=2x^{1/2}\sum_{d=1}^\infty \frac{g(d)}{d }+O( x^{1/4+\lambda/4(1+\kappa)}(\log x)^{3/2-3\lambda/2(1+\kappa)} ). \end{align*} $$

Next, we bound the second sum. Using $\lvert {S(x)}\rvert =O(x^{1/2})$ ,

$$ \begin{align*} \sum_{ x^{1/4}\log^{-3/2} x< d\leq x}g(d)\sum_{\substack{n\in S(x)\\ n \, \equiv\, {0\, \textrm{(mod} \; d\textrm{)}}} }1=O\bigg(x^{1/2}\sum_{ x^{1/4}\log^{-3/2} x< d\leq x}\frac{\lvert{g(d)}\rvert}{d}\bigg). \end{align*} $$

By Abel’s identity and (2.2), we arrive at

$$ \begin{align*} x^{1/2}\sum_{ x^{1/4}\log^{-3/2} x< d\leq x}\frac{\lvert{g(d)}\rvert}{d}\ll x^{1/4+\lambda/4(1+\kappa)}(\log x)^{3/2-3\lambda/2(1+\kappa)}, \end{align*} $$

and Theorem 1.4 follows.

Proof of Theorem 1.5.

The proof is the same as the proof of Theorem 1.4. We assume the Riemann hypothesis. Thus, we can replace (2.1) by

(2.3) $$ \begin{align} \sum_{d\leq x}\lvert{g(d)}\rvert=O(x^{{1}/{4}+\epsilon}). \end{align} $$

Using (2.3), we choose the exponent pairs $(\kappa ,\lambda )$ such that ${1}/{4}<{\lambda }/{(1+\kappa )}$ . The result follows.