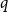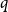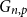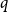1. Introduction
This paper concerns hypergraphs, and throughout we allow our hypergraphs to have repeated edges. If
![]() $A$
is a set of vertices of a hypergraph
$A$
is a set of vertices of a hypergraph
![]() $\mathcal{H}$
, we define the degree of
$\mathcal{H}$
, we define the degree of
![]() $A$
to be the number of edges of
$A$
to be the number of edges of
![]() $\mathcal{H}$
containing
$\mathcal{H}$
containing
![]() $A$
, and we denote this quantity by
$A$
, and we denote this quantity by
![]() $d_{\mathcal{H}}(A)$
, or simply by
$d_{\mathcal{H}}(A)$
, or simply by
![]() $d(A)$
if
$d(A)$
if
![]() $\mathcal{H}$
is understood. We say that a hypergraph
$\mathcal{H}$
is understood. We say that a hypergraph
![]() $\mathcal{H}$
is
$\mathcal{H}$
is
![]() $q$
-spread if it is non-empty and if
$q$
-spread if it is non-empty and if
![]() $d(A)\le q^{|A|}|\mathcal{H}|$
for all sets of vertices
$d(A)\le q^{|A|}|\mathcal{H}|$
for all sets of vertices
![]() $A$
. A hypergraph is said to be
$A$
. A hypergraph is said to be
![]() $r$
-bounded if each of its edges have size at most
$r$
-bounded if each of its edges have size at most
![]() $r$
and it is
$r$
and it is
![]() $r$
-uniform if all of its edges have size exactly
$r$
-uniform if all of its edges have size exactly
![]() $r$
.
$r$
.
The notion of
![]() $q$
-spread hypergraphs was introduced by Alweiss, Lovett, Wu, and Zhang [Reference Alweiss, Lovett, Wu and Zhang2] where it was a key ingredient in their groundbreaking work which significantly improved upon the bounds on the largest size of a set system that contains no sunflower. Their method was refined by Frankston, Kahn, Narayanan, and Park [Reference Frankston, Kahn, Narayanan and Park4] who proved the following.
$q$
-spread hypergraphs was introduced by Alweiss, Lovett, Wu, and Zhang [Reference Alweiss, Lovett, Wu and Zhang2] where it was a key ingredient in their groundbreaking work which significantly improved upon the bounds on the largest size of a set system that contains no sunflower. Their method was refined by Frankston, Kahn, Narayanan, and Park [Reference Frankston, Kahn, Narayanan and Park4] who proved the following.
Theorem 1.1 ([Reference Frankston, Kahn, Narayanan and Park4]). There exists an absolute constant
![]() $K_0$
such that the following holds. Let
$K_0$
such that the following holds. Let
![]() $\mathcal{H}$
be an
$\mathcal{H}$
be an
![]() $r$
-bounded
$r$
-bounded
![]() $q$
-spread hypergraph on
$q$
-spread hypergraph on
![]() $V$
. If
$V$
. If
![]() $W$
is a set of size
$W$
is a set of size
![]() $K_0 (\log r) q |V|$
chosen uniformly at random from
$K_0 (\log r) q |V|$
chosen uniformly at random from
![]() $V$
, then
$V$
, then
![]() $W$
contains an edge of
$W$
contains an edge of
![]() $\mathcal{H}$
with probability tending to 1 as
$\mathcal{H}$
with probability tending to 1 as
![]() $r$
tends towards infinity.
$r$
tends towards infinity.
This theorem was used in [Reference Frankston, Kahn, Narayanan and Park4] to prove a number of remarkable results. In particular it resolved a conjecture of Talagrand, and it also gave a much simpler solution to Shamir’s problem, which had originally been solved by Johansson, Kahn, and Vu [Reference Johansson, Kahn and Vu6].
Kahn, Narayanan, and Park [Reference Kahn, Narayanan and Park7] used a variant of the method from [Reference Frankston, Kahn, Narayanan and Park4] to show that for certain
![]() $q$
-spread hypergraphs, the conclusion of Theorem 1.1 holds for random sets
$q$
-spread hypergraphs, the conclusion of Theorem 1.1 holds for random sets
![]() $W$
of size only
$W$
of size only
![]() $C q |V|$
. They used this to determine the threshold for when a square of a Hamiltonian cycle appears in the random graph
$C q |V|$
. They used this to determine the threshold for when a square of a Hamiltonian cycle appears in the random graph
![]() $G_{n,p}$
, which was a long-standing open problem.
$G_{n,p}$
, which was a long-standing open problem.
In a talk, Narayanan asked if there was a “smoother” definition of spread hypergraphs which interpolated between
![]() $q$
-spread hypergraphs and hypergraphs like those in [Reference Kahn, Narayanan and Park7] where the
$q$
-spread hypergraphs and hypergraphs like those in [Reference Kahn, Narayanan and Park7] where the
![]() $\log r$
term of Theorem 1.1 can be dropped. The aim of this paper is to provide such a definition.
$\log r$
term of Theorem 1.1 can be dropped. The aim of this paper is to provide such a definition.
Definition 1.2. Let
![]() $0\lt q\le 1$
be a real number and
$0\lt q\le 1$
be a real number and
![]() $r_1\gt \cdots \gt r_\ell$
positive integers. We say that a hypergraph
$r_1\gt \cdots \gt r_\ell$
positive integers. We say that a hypergraph
![]() $\mathcal{H}$
on
$\mathcal{H}$
on
![]() $V$
is
$V$
is
![]() $(q;\;r_1,\ldots,r_\ell )$
-spread if
$(q;\;r_1,\ldots,r_\ell )$
-spread if
![]() $\mathcal{H}$
is non-empty,
$\mathcal{H}$
is non-empty,
![]() $r_1$
-bounded, and if for all
$r_1$
-bounded, and if for all
![]() $A\subseteq V$
with
$A\subseteq V$
with
![]() $d(A)\gt 0$
and
$d(A)\gt 0$
and
![]() $r_{i}\ge |A|\ge r_{i+1}$
for some
$r_{i}\ge |A|\ge r_{i+1}$
for some
![]() $1\le i\lt \ell$
, we have for all
$1\le i\lt \ell$
, we have for all
![]() $j\ge r_{i+1}$
that
$j\ge r_{i+1}$
that
Roughly speaking, this condition says that every set
![]() $A$
of
$A$
of
![]() $r_i$
vertices intersects few edges of
$r_i$
vertices intersects few edges of
![]() $\mathcal{H}$
in more than
$\mathcal{H}$
in more than
![]() $r_{i+1}$
vertices.
$r_{i+1}$
vertices.
As a warm-up, we show how this definition relates to the definition of being
![]() $q$
-spread.
$q$
-spread.
Proposition 1.3. We have the following.
-
(a) If
 $\mathcal{H}$
is
$\mathcal{H}$
is
 $(q;\;r_1,\ldots,r_\ell,1)$
-spread, then it is
$(q;\;r_1,\ldots,r_\ell,1)$
-spread, then it is
 $q$
-spread.
$q$
-spread.
-
(b) If
 $\mathcal{H}$
is
$\mathcal{H}$
is
 $q$
-spread and
$q$
-spread and
 $r_1$
-bounded, then it is
$r_1$
-bounded, then it is
 $(4q;\;r_1,\ldots,r_\ell )$
-spread for any sequence of integers
$(4q;\;r_1,\ldots,r_\ell )$
-spread for any sequence of integers
 $r_i$
satisfying
$r_i$
satisfying
 $r_i\gt r_{i+1}\ge \frac{1}{2} r_i$
.
$r_i\gt r_{i+1}\ge \frac{1}{2} r_i$
.
Proof. For (a), assume
![]() $\mathcal{H}$
is
$\mathcal{H}$
is
![]() $(q;\;r_1,\ldots,r_\ell,1)$
-spread and let
$(q;\;r_1,\ldots,r_\ell,1)$
-spread and let
![]() $r_{\ell +1}=1$
. Let
$r_{\ell +1}=1$
. Let
![]() $A$
be a set of vertices of
$A$
be a set of vertices of
![]() $\mathcal{H}$
. If
$\mathcal{H}$
. If
![]() $A=\emptyset$
, then
$A=\emptyset$
, then
![]() $d(A)=|\mathcal{H}|=q^{|A|}|\mathcal{H}|$
, so we can assume
$d(A)=|\mathcal{H}|=q^{|A|}|\mathcal{H}|$
, so we can assume
![]() $A$
is non-empty. If
$A$
is non-empty. If
![]() $d(A)=0$
, then trivially
$d(A)=0$
, then trivially
![]() $d(A)\le q^{|A|}|\mathcal{H}|$
, so we can assume
$d(A)\le q^{|A|}|\mathcal{H}|$
, so we can assume
![]() $d(A)\gt 0$
. This means
$d(A)\gt 0$
. This means
![]() $|A|\le r_1$
since in particular
$|A|\le r_1$
since in particular
![]() $\mathcal{H}$
is
$\mathcal{H}$
is
![]() $r_1$
-bounded. Thus, there exists an integer
$r_1$
-bounded. Thus, there exists an integer
![]() $1\le i\le \ell$
such that
$1\le i\le \ell$
such that
![]() $r_i\ge |A|\ge r_{i+1}$
, so the hypothesis that
$r_i\ge |A|\ge r_{i+1}$
, so the hypothesis that
![]() $\mathcal{H}$
is
$\mathcal{H}$
is
![]() $(q;\;r_1,\ldots,r_\ell,1)$
-spread and
$(q;\;r_1,\ldots,r_\ell,1)$
-spread and
![]() $d(A)\gt 0$
implies
$d(A)\gt 0$
implies
proving that
![]() $\mathcal{H}$
is
$\mathcal{H}$
is
![]() $q$
-spread.
$q$
-spread.
For (b), assume
![]() $\mathcal{H}$
is
$\mathcal{H}$
is
![]() $q$
-spread and
$q$
-spread and
![]() $r_1$
-bounded. If
$r_1$
-bounded. If
![]() $A$
is any set of vertices of
$A$
is any set of vertices of
![]() $\mathcal{H}$
, then for all
$\mathcal{H}$
, then for all
![]() $j\ge \frac{1}{2} |A|$
we have
$j\ge \frac{1}{2} |A|$
we have
In particular, if
![]() $r_i\ge |A|\ge r_{i+1}$
, then this bound holds for any
$r_i\ge |A|\ge r_{i+1}$
, then this bound holds for any
![]() $j\ge r_{i+1}$
since
$j\ge r_{i+1}$
since
![]() $r_{i+1}\ge \frac{1}{2} r_i\ge \frac{1}{2} |A|$
. We conclude that
$r_{i+1}\ge \frac{1}{2} r_i\ge \frac{1}{2} |A|$
. We conclude that
![]() $\mathcal{H}$
is
$\mathcal{H}$
is
![]() $(4q;\;r_1,\ldots,r_\ell )$
-spread.
$(4q;\;r_1,\ldots,r_\ell )$
-spread.
We now state our main result for uniform hypergraphs, which says that a random set of size
![]() $C\ell q |V|$
will contain an edge of an
$C\ell q |V|$
will contain an edge of an
![]() $r_1$
-uniform
$r_1$
-uniform
![]() $(q;\;r_1,\ldots,r_\ell,1)$
-spread hypergraph with high probability as
$(q;\;r_1,\ldots,r_\ell,1)$
-spread hypergraph with high probability as
![]() $C\ell$
tends towards infinity. An analogous result can be proven for non-uniform hypergraphs, but for ease of presentation we defer this result to Section 3.
$C\ell$
tends towards infinity. An analogous result can be proven for non-uniform hypergraphs, but for ease of presentation we defer this result to Section 3.
Theorem 1.4.
There exists an absolute constant
![]() $K_0$
such that the following holds. Let
$K_0$
such that the following holds. Let
![]() $\mathcal{H}$
be an
$\mathcal{H}$
be an
![]() $r_1$
-uniform
$r_1$
-uniform
![]() $(q;\;r_1,\ldots,r_\ell,1)$
-spread hypergraph on
$(q;\;r_1,\ldots,r_\ell,1)$
-spread hypergraph on
![]() $V$
. If
$V$
. If
![]() $W$
is a set of size
$W$
is a set of size
![]() $C\ell q|V|$
chosen uniformly at random from
$C\ell q|V|$
chosen uniformly at random from
![]() $V$
with
$V$
with
![]() $C\ge K_0$
, then
$C\ge K_0$
, then
We note that Theorem 1.4 with
![]() $\ell =\Theta (\log r)$
together with Proposition 1.3(b) implies Theorem 1.1 for uniform
$\ell =\Theta (\log r)$
together with Proposition 1.3(b) implies Theorem 1.1 for uniform
![]() $\mathcal{H}$
. In [Reference Kahn, Narayanan and Park7], it is implicitly proven that the hypergraph
$\mathcal{H}$
. In [Reference Kahn, Narayanan and Park7], it is implicitly proven that the hypergraph
![]() $\mathcal{H}$
encoding squares of Hamiltonian cycles is a
$\mathcal{H}$
encoding squares of Hamiltonian cycles is a
![]() $(2n)$
-uniform
$(2n)$
-uniform
![]() $(Cn^{-1/2};2n,C_0n^{1/2},1)$
-spread hypergraph for some appropriate constants
$(Cn^{-1/2};2n,C_0n^{1/2},1)$
-spread hypergraph for some appropriate constants
![]() $C,C_0$
, so the
$C,C_0$
, so the
![]() $\ell =2$
case of Theorem 1.4 suffices to prove the main result of [Reference Kahn, Narayanan and Park7]. Thus, at least in the uniform case, Theorem 1.4 provides an interpolation between the results of [Reference Frankston, Kahn, Narayanan and Park4, Reference Kahn, Narayanan and Park7]. Theorem 1.4 can also be used to recover results from very recent work of Espuny Díaz and Person [Reference Espuny Díaz and Person3] who extended the results of [Reference Kahn, Narayanan and Park7] to other spanning subgraphsFootnote
1
of
$\ell =2$
case of Theorem 1.4 suffices to prove the main result of [Reference Kahn, Narayanan and Park7]. Thus, at least in the uniform case, Theorem 1.4 provides an interpolation between the results of [Reference Frankston, Kahn, Narayanan and Park4, Reference Kahn, Narayanan and Park7]. Theorem 1.4 can also be used to recover results from very recent work of Espuny Díaz and Person [Reference Espuny Díaz and Person3] who extended the results of [Reference Kahn, Narayanan and Park7] to other spanning subgraphsFootnote
1
of
![]() $G_{n,p}$
.
$G_{n,p}$
.
2. Proof of Theorem 1.4
Our approach borrows heavily from Kahn, Narayanan, and Park [Reference Kahn, Narayanan and Park7]. We break our proof into three parts: the main reduction lemma, auxiliary lemmas to deal with some special cases, and a final subsection proving the theorem.
2.1. The main lemma
We briefly sketch our approach for proving Theorem 1.4. Let
![]() $\mathcal{H}$
be a hypergraph with vertex set
$\mathcal{H}$
be a hypergraph with vertex set
![]() $V$
. We first choose a random set
$V$
. We first choose a random set
![]() $W_1\subseteq V$
of size roughly
$W_1\subseteq V$
of size roughly
![]() $q|V|$
. If
$q|V|$
. If
![]() $W_1$
contains an edge of
$W_1$
contains an edge of
![]() $\mathcal{H}$
then we would be done, but most likely we will need to try and add in an additional random set
$\mathcal{H}$
then we would be done, but most likely we will need to try and add in an additional random set
![]() $W_2$
of size
$W_2$
of size
![]() $q|V|$
and repeat the process. In total then we are interested in finding the smallest
$q|V|$
and repeat the process. In total then we are interested in finding the smallest
![]() $I$
such that
$I$
such that
![]() $W_1\cup \cdots \cup W_I$
contains an edge of
$W_1\cup \cdots \cup W_I$
contains an edge of
![]() $\mathcal{H}$
with relatively high probability. One way to guarantee that
$\mathcal{H}$
with relatively high probability. One way to guarantee that
![]() $I$
is small would be if we had
$I$
is small would be if we had
![]() $|S\setminus W_1|$
small for most
$|S\setminus W_1|$
small for most
![]() $S\in \mathcal{H}$
(i.e., most vertices of most edges
$S\in \mathcal{H}$
(i.e., most vertices of most edges
![]() $S\in \mathcal{H}$
are covered by
$S\in \mathcal{H}$
are covered by
![]() $W_1$
), and then that
$W_1$
), and then that
![]() $W_2$
covered most of the vertices of most
$W_2$
covered most of the vertices of most
![]() $S\setminus W_1$
, and so on.
$S\setminus W_1$
, and so on.
The condition that, say,
![]() $|S\setminus W_1|$
is small for most
$|S\setminus W_1|$
is small for most
![]() $S\in \mathcal{H}$
turns out to be too strong a condition to impose. However, if
$S\in \mathcal{H}$
turns out to be too strong a condition to impose. However, if
![]() $\mathcal{H}$
is sufficiently spread, then we can guarantee a weaker result: for most
$\mathcal{H}$
is sufficiently spread, then we can guarantee a weaker result: for most
![]() $S\in \mathcal{H}$
, there is an
$S\in \mathcal{H}$
, there is an
![]() $S'\subseteq S\cup W_1$
such that
$S'\subseteq S\cup W_1$
such that
![]() $|S'\setminus W_1|$
is small. We can then discard
$|S'\setminus W_1|$
is small. We can then discard
![]() $S$
and focus only on
$S$
and focus only on
![]() $S'$
, and by iterating this repeatedly we obtain the desired result.
$S'$
, and by iterating this repeatedly we obtain the desired result.
To be more precise, given a hypergraph
![]() $\mathcal{H}$
, we say that a pair of sets
$\mathcal{H}$
, we say that a pair of sets
![]() $(S,W)$
is
$(S,W)$
is
![]() $k$
-good if there exists
$k$
-good if there exists
![]() $S'\in \mathcal{H}$
such that
$S'\in \mathcal{H}$
such that
![]() $S'\subseteq S\cup W$
and
$S'\subseteq S\cup W$
and
![]() $|S'\setminus W|\le k$
, and we say that the pair is
$|S'\setminus W|\le k$
, and we say that the pair is
![]() $k$
-bad otherwise. We note for later that if
$k$
-bad otherwise. We note for later that if
![]() $(S,W)$
is
$(S,W)$
is
![]() $k$
-bad with
$k$
-bad with
![]() $S\cup W=Z$
, then
$S\cup W=Z$
, then
![]() $(S,Z\setminus S)$
is also
$(S,Z\setminus S)$
is also
![]() $k$
-bad.
$k$
-bad.
The next lemma shows that
![]() $(q;\;r,k)$
-spread hypergraphs have few
$(q;\;r,k)$
-spread hypergraphs have few
![]() $k$
-bad pairs with
$k$
-bad pairs with
![]() $S\in \mathcal{H}$
and
$S\in \mathcal{H}$
and
![]() $W$
a set of size roughly
$W$
a set of size roughly
![]() $q|V|$
. In the lemma statement we adopt the notation that
$q|V|$
. In the lemma statement we adopt the notation that
![]() $\left(\substack{V\\[5pt] m}\right)$
is the set of subsets of
$\left(\substack{V\\[5pt] m}\right)$
is the set of subsets of
![]() $V$
of size
$V$
of size
![]() $m$
.
$m$
.
Lemma 2.1.
Let
![]() $\mathcal{H}$
be an
$\mathcal{H}$
be an
![]() $r$
-uniform
$r$
-uniform
![]() $n$
-vertex hypergraph on
$n$
-vertex hypergraph on
![]() $V$
which is
$V$
which is
![]() $(q;\;r,k)$
-spread. Let
$(q;\;r,k)$
-spread. Let
![]() $C\ge 4$
and define
$C\ge 4$
and define
![]() $p=Cq$
. If
$p=Cq$
. If
![]() $pn\ge 2r$
and
$pn\ge 2r$
and
![]() $p\le \frac{1}{2}$
, then
$p\le \frac{1}{2}$
, then
Proof. Throughout this lemma, we make frequent use of the identity
which follows from the simple combinatorial identity
![]() $\left(\substack{a\\[4pt] b}\right)\left(\substack{b\\[4pt] c}\right)=\left(\substack{a\\[4pt] c}\right)\left(\substack{a-c\\[4pt] b-c}\right)$
.
$\left(\substack{a\\[4pt] b}\right)\left(\substack{b\\[4pt] c}\right)=\left(\substack{a\\[4pt] c}\right)\left(\substack{a-c\\[4pt] b-c}\right)$
.
For
![]() $t\le r$
, define
$t\le r$
, define
Observe that the quantity we wish to bound is
![]() $\sum _{t} |{\mathcal{B}}_{t}|$
, so it suffices to bound each term of this sum. From now on, we fix some
$\sum _{t} |{\mathcal{B}}_{t}|$
, so it suffices to bound each term of this sum. From now on, we fix some
![]() $t$
and define
$t$
and define
At this point, we need to count the number of elements in
![]() ${\mathcal{B}}_t$
, and there are several natural approaches that could be used. One way would be to first pick any
${\mathcal{B}}_t$
, and there are several natural approaches that could be used. One way would be to first pick any
![]() $S\in \mathcal{H}$
and then count how many
$S\in \mathcal{H}$
and then count how many
![]() $W$
satisfy
$W$
satisfy
![]() $(S,W)\in{\mathcal{B}}_{t}$
. Another approach would be to pick any set
$(S,W)\in{\mathcal{B}}_{t}$
. Another approach would be to pick any set
![]() $Z$
of size
$Z$
of size
![]() $r+w$
(which will be the size of
$r+w$
(which will be the size of
![]() $S\cup W$
since
$S\cup W$
since
![]() $|S\cap W|=t$
) and then bound how many
$|S\cap W|=t$
) and then bound how many
![]() $S,W\subseteq Z$
have
$S,W\subseteq Z$
have
![]() $(S,W)\in{\mathcal{B}}_{t}$
. For some pairs, the first approach is more efficient, and for others the second is. In particular, the second approach will be more effective whenever
$(S,W)\in{\mathcal{B}}_{t}$
. For some pairs, the first approach is more efficient, and for others the second is. In particular, the second approach will be more effective whenever
![]() $Z=S\cup W$
contains few elements of
$Z=S\cup W$
contains few elements of
![]() ${\mathcal{B}}_{t}$
.
${\mathcal{B}}_{t}$
.
With this in mind, we say that a set
![]() $Z$
is pathological if
$Z$
is pathological if
where
and we say that
![]() $Z$
is non-pathological otherwise. We say that a pair
$Z$
is non-pathological otherwise. We say that a pair
![]() $(S,W)$
is pathological if the set
$(S,W)$
is pathological if the set
![]() $S\cup W$
is pathological and that
$S\cup W$
is pathological and that
![]() $(S,W)$
is non-pathological otherwise.
$(S,W)$
is non-pathological otherwise.
Claim 2.2.
The number of
![]() $(S,W)\in{\mathcal{B}}_{t}$
which are non-pathological is at most
$(S,W)\in{\mathcal{B}}_{t}$
which are non-pathological is at most
Proof. We identify each of the non-pathological pairs
![]() $(S,W)$
by specifying
$(S,W)$
by specifying
![]() $S\cup W$
, then
$S\cup W$
, then
![]() $S$
, then
$S$
, then
![]() $S\cap W$
.
$S\cap W$
.
Observe that
![]() $S\cup W$
is a non-pathological set of size
$S\cup W$
is a non-pathological set of size
![]() $r+w$
, and in particular there are at most
$r+w$
, and in particular there are at most
![]() $\left(\substack{n\\[4pt] r+w}\right)$
ways to make this first choice. Fix such a non-pathological set
$\left(\substack{n\\[4pt] r+w}\right)$
ways to make this first choice. Fix such a non-pathological set
![]() $Z$
of size
$Z$
of size
![]() $r+w$
. As noted before the statement of Lemma 2.1, if
$r+w$
. As noted before the statement of Lemma 2.1, if
![]() $(S,W)$
is
$(S,W)$
is
![]() $k$
-bad with
$k$
-bad with
![]() $S\cup W= Z$
, then
$S\cup W= Z$
, then
![]() $(S,Z\setminus S)$
is also
$(S,Z\setminus S)$
is also
![]() $k$
-bad. Because
$k$
-bad. Because
![]() $Z$
is non-pathological, there are at most
$Z$
is non-pathological, there are at most
![]() $N$
choices for
$N$
choices for
![]() $S$
such that
$S$
such that
![]() $(S,Z\setminus S)$
is
$(S,Z\setminus S)$
is
![]() $k$
-bad. Given
$k$
-bad. Given
![]() $S$
, there are at most
$S$
, there are at most
![]() $\left(\substack{r\\[4pt] t}\right)$
choices for
$\left(\substack{r\\[4pt] t}\right)$
choices for
![]() $S\cap W$
. Multiplying the number of choices at each step gives the stated result.
$S\cap W$
. Multiplying the number of choices at each step gives the stated result.
Claim 2.3.
The number of
![]() $(S,W)\in{\mathcal{B}}_{t}$
which are pathological is at most
$(S,W)\in{\mathcal{B}}_{t}$
which are pathological is at most
Proof. We identify these pairs by first specifying
![]() $S\in \mathcal{H}$
, then
$S\in \mathcal{H}$
, then
![]() $S\cap W$
, then
$S\cap W$
, then
![]() $W\setminus S$
.
$W\setminus S$
.
Note that
![]() $S$
and
$S$
and
![]() $S\cap W$
can be specified in at most
$S\cap W$
can be specified in at most
![]() $|\mathcal{H}|\cdot\left(\substack{r\\[4pt] t}\right)$
ways, and from now on we fix such a choice of
$|\mathcal{H}|\cdot\left(\substack{r\\[4pt] t}\right)$
ways, and from now on we fix such a choice of
![]() $S$
and
$S$
and
![]() $S\cap W$
. It remains to specify
$S\cap W$
. It remains to specify
![]() $W\setminus S$
, which will be some element of
$W\setminus S$
, which will be some element of
![]() $\left(\substack{V \setminus S\\[4pt] w}\right)$
. Thus it suffices to count the number of
$\left(\substack{V \setminus S\\[4pt] w}\right)$
. Thus it suffices to count the number of
![]() $W'\in{\left(\substack{V \setminus S\\[4pt] w}\right)}$
such that
$W'\in{\left(\substack{V \setminus S\\[4pt] w}\right)}$
such that
![]() $(S,W')$
is both
$(S,W')$
is both
![]() $k$
-bad and pathological.
$k$
-bad and pathological.
For
![]() $W'\in{\left(\substack{V\setminus S\\[4pt] w}\right)}$
, define
$W'\in{\left(\substack{V\setminus S\\[4pt] w}\right)}$
, define
Observe that if
![]() $(S,W')$
is
$(S,W')$
is
![]() $k$
-bad, then every edge
$k$
-bad, then every edge
![]() $S'\subseteq S\cup W'$
has
$S'\subseteq S\cup W'$
has
![]() $|S'\cap S|\ge k$
(since
$|S'\cap S|\ge k$
(since
![]() $|S'\cap S|\ge |S'\setminus W'|$
), so the
$|S'\cap S|\ge |S'\setminus W'|$
), so the
![]() $W'$
we wish to count satisfy
$W'$
we wish to count satisfy
If
![]() $(S,W')$
is pathological, then this latter set has size at least
$(S,W')$
is pathological, then this latter set has size at least
![]() $N$
. In total, if
$N$
. In total, if
![]() ${\textbf{W}}'$
is chosen uniformly at random from
${\textbf{W}}'$
is chosen uniformly at random from
![]() $\left(\substack{V \setminus S\\[4pt] w}\right)$
, then
$\left(\substack{V \setminus S\\[4pt] w}\right)$
, then
where this last step used Markov’s inequality. It remains to upper bound
![]() ${\mathbb{E}}[{\mathcal{S}}({\textbf{W}}')]$
.
${\mathbb{E}}[{\mathcal{S}}({\textbf{W}}')]$
.
Let
and observe that for any
![]() $S'$
with
$S'$
with
![]() $|S\cap S'|=j$
, the number of
$|S\cap S'|=j$
, the number of
![]() $W'\in{\left(\substack{V \setminus S\\[4pt] w}\right)}$
with
$W'\in{\left(\substack{V \setminus S\\[4pt] w}\right)}$
with
![]() $S'\subseteq S\cup W'$
is exactly
$S'\subseteq S\cup W'$
is exactly
![]() $\left(\substack{n-2r+j\\[4pt] w-r+j}\right)$
. With this we see that
$\left(\substack{n-2r+j\\[4pt] w-r+j}\right)$
. With this we see that
 \begin{align}{\mathbb{E}}[{\mathcal{S}}({\textbf{W}}')]=\sum _{j\ge k} m_j(S) \frac{\left(\substack{n-2r+j\\[4pt] w-r+j}\right)}{{\left(\substack{n-r\\[4pt] w}\right)}}&=\sum _{j\ge k} m_j(S) \frac{\left(\substack{w\\[4pt] r-j}\right)}{{\left(\substack{n-r\\[4pt] r-j}\right)}}=\frac{{\left(\substack{r+w\\[4pt] r}\right)}}{{\left(\substack{n\\[4pt] r}\right)}}\sum _{j\ge k} m_j(S) \frac{{\left(\substack{w\\[4pt] r-j}\right)}}{{\left(\substack{n-r\\[4pt] r-j}\right)}}\cdot \frac{{\left(\substack{n\\[4pt] r+w}\right)}}{{\left(\substack{n-r\\[4pt] w}\right)}}. \end{align}
\begin{align}{\mathbb{E}}[{\mathcal{S}}({\textbf{W}}')]=\sum _{j\ge k} m_j(S) \frac{\left(\substack{n-2r+j\\[4pt] w-r+j}\right)}{{\left(\substack{n-r\\[4pt] w}\right)}}&=\sum _{j\ge k} m_j(S) \frac{\left(\substack{w\\[4pt] r-j}\right)}{{\left(\substack{n-r\\[4pt] r-j}\right)}}=\frac{{\left(\substack{r+w\\[4pt] r}\right)}}{{\left(\substack{n\\[4pt] r}\right)}}\sum _{j\ge k} m_j(S) \frac{{\left(\substack{w\\[4pt] r-j}\right)}}{{\left(\substack{n-r\\[4pt] r-j}\right)}}\cdot \frac{{\left(\substack{n\\[4pt] r+w}\right)}}{{\left(\substack{n-r\\[4pt] w}\right)}}. \end{align}
Because
![]() $\mathcal{H}$
is
$\mathcal{H}$
is
![]() $(q;\;r,k)$
-spread, we have for each
$(q;\;r,k)$
-spread, we have for each
![]() $j\ge k$
in the sum that
$j\ge k$
in the sum that
For integers
![]() $x,y$
, define the falling factorial
$x,y$
, define the falling factorial
![]() $(x)_y\;:\!=\;x(x-1)\cdots (x-y+1)$
. With this we have
$(x)_y\;:\!=\;x(x-1)\cdots (x-y+1)$
. With this we have
 \begin{align} \frac{{\left(\substack{w\\[4pt] r-j}\right)}}{{\left(\substack{n-r\\[4pt] r-j}\right)}}\cdot \frac{{\left(\substack{n\\[4pt] r+w}\right)}}{{\left(\substack{n-r\\[4pt] w}\right)}}&=\frac{(w)_{r-j}}{(n-r)_{r-j}}\cdot \frac{(n)_{r}}{(r+w)_r}\le \left (\frac{w}{n-r}\right )^{r-j}\cdot \left (\frac{n-r}{w}\right )^r=\left (\frac{w}{n-r}\right )^{-j}\le (Cq/2)^{-j}, \end{align}
\begin{align} \frac{{\left(\substack{w\\[4pt] r-j}\right)}}{{\left(\substack{n-r\\[4pt] r-j}\right)}}\cdot \frac{{\left(\substack{n\\[4pt] r+w}\right)}}{{\left(\substack{n-r\\[4pt] w}\right)}}&=\frac{(w)_{r-j}}{(n-r)_{r-j}}\cdot \frac{(n)_{r}}{(r+w)_r}\le \left (\frac{w}{n-r}\right )^{r-j}\cdot \left (\frac{n-r}{w}\right )^r=\left (\frac{w}{n-r}\right )^{-j}\le (Cq/2)^{-j}, \end{align}
where the first inequality used
![]() $w\le pn\le \frac{1}{2} n\le n-r$
, and the second inequality used
$w\le pn\le \frac{1}{2} n\le n-r$
, and the second inequality used
Combining (2), (3), and (4) shows that
 \begin{equation*}{\mathbb {E}}[{\mathcal {S}}({\textbf {W}}')]\le \frac {{\left(\substack{r+w\\[4pt] r}\right)}}{{\left(\substack{n\\[4pt] r}\right)}} |\mathcal {H}|(C/2)^{-k}\cdot \sum _{j\ge k} (C/2)^{k-j}\le \frac {{\left(\substack{r+w\\[4pt] r}\right)}}{{\left(\substack{n\\[4pt] r}\right)}} |\mathcal {H}|(C/2)^{-k}\cdot 2,\end{equation*}
\begin{equation*}{\mathbb {E}}[{\mathcal {S}}({\textbf {W}}')]\le \frac {{\left(\substack{r+w\\[4pt] r}\right)}}{{\left(\substack{n\\[4pt] r}\right)}} |\mathcal {H}|(C/2)^{-k}\cdot \sum _{j\ge k} (C/2)^{k-j}\le \frac {{\left(\substack{r+w\\[4pt] r}\right)}}{{\left(\substack{n\\[4pt] r}\right)}} |\mathcal {H}|(C/2)^{-k}\cdot 2,\end{equation*}
where this last step used
![]() $C\ge 4$
. Plugging this into (1) shows that the number of
$C\ge 4$
. Plugging this into (1) shows that the number of
![]() $W'\in{\left(\substack{V \setminus S\\[4pt] w}\right)}$
such that
$W'\in{\left(\substack{V \setminus S\\[4pt] w}\right)}$
such that
![]() $(S,W')$
is
$(S,W')$
is
![]() $k$
-bad and pathological is at most
$k$
-bad and pathological is at most
 \begin{equation*} 2(C/2)^{-k} |\mathcal {H}|\frac {{\left(\substack{r+w\\[4pt] r}\right)}}{{\left(\substack{n\\[4pt] r}\right)} N}\cdot {\left(\substack{n-r\\[4pt] w}\right)}= 2(C/2)^{-k/2}\cdot {\left(\substack{n-r\\[4pt] w}\right)}.\end{equation*}
\begin{equation*} 2(C/2)^{-k} |\mathcal {H}|\frac {{\left(\substack{r+w\\[4pt] r}\right)}}{{\left(\substack{n\\[4pt] r}\right)} N}\cdot {\left(\substack{n-r\\[4pt] w}\right)}= 2(C/2)^{-k/2}\cdot {\left(\substack{n-r\\[4pt] w}\right)}.\end{equation*}
Combining this with the fact that there were
![]() $|\mathcal{H}|\cdot{\left(\substack{r\\[4pt] t}\right)}$
ways of choosing
$|\mathcal{H}|\cdot{\left(\substack{r\\[4pt] t}\right)}$
ways of choosing
![]() $S$
and
$S$
and
![]() $S\cap W$
gives the claim.
$S\cap W$
gives the claim.
In total,
![]() $|{\mathcal{B}}_{t}|$
is at most the sum of the bounds from these two claims. Using this and
$|{\mathcal{B}}_{t}|$
is at most the sum of the bounds from these two claims. Using this and
![]() $w=pn-t$
implies
$w=pn-t$
implies
 \begin{align*} \sum _{t\le r}|{\mathcal{B}}_{t}|&\le \sum _{t\le r} 3 (C/2)^{-k/2} |\mathcal{H}|{\left(\substack{r\\[4pt] t}\right)}{\left(\substack{n-r\\[4pt] pn-t}\right)}\\&= 3 (C/2)^{-k/2}|\mathcal{H}|{\left(\substack{n\\[4pt] pn}\right)}, \end{align*}
\begin{align*} \sum _{t\le r}|{\mathcal{B}}_{t}|&\le \sum _{t\le r} 3 (C/2)^{-k/2} |\mathcal{H}|{\left(\substack{r\\[4pt] t}\right)}{\left(\substack{n-r\\[4pt] pn-t}\right)}\\&= 3 (C/2)^{-k/2}|\mathcal{H}|{\left(\substack{n\\[4pt] pn}\right)}, \end{align*}
giving the desired result.
2.2. Auxiliary lemmas
To prove Theorem 1.4, we need to consider two special cases. The first is when
![]() $\mathcal{H}$
is
$\mathcal{H}$
is
![]() $r$
-uniform with
$r$
-uniform with
![]() $r$
relatively small. In this case, the following lemma gives effective bounds.
$r$
relatively small. In this case, the following lemma gives effective bounds.
Lemma 2.4 ([Reference Frankston, Kahn, Narayanan and Park4] Corollary 4.2). Let
![]() $\mathcal{H}$
be a
$\mathcal{H}$
be a
![]() $q$
-spread
$q$
-spread
![]() $r$
-bounded hypergraph on
$r$
-bounded hypergraph on
![]() $V$
and let
$V$
and let
![]() $\alpha \in (0,1)$
satisfy
$\alpha \in (0,1)$
satisfy
![]() $\alpha \ge 2rq$
. If
$\alpha \ge 2rq$
. If
![]() $W$
is a set of size
$W$
is a set of size
![]() $\alpha |V|$
chosen uniformly at random from
$\alpha |V|$
chosen uniformly at random from
![]() $V$
, then the probability that
$V$
, then the probability that
![]() $W$
does not contain an element of
$W$
does not contain an element of
![]() $\mathcal{H}$
is at most
$\mathcal{H}$
is at most
The other special case we consider is the following.
Lemma 2.5.
Let
![]() $\mathcal{H}$
be an
$\mathcal{H}$
be an
![]() $r$
-uniform
$r$
-uniform
![]() $(q;\;r,1)$
-spread hypergraph on
$(q;\;r,1)$
-spread hypergraph on
![]() $V$
and
$V$
and
![]() $\alpha \in (0,1)$
such that
$\alpha \in (0,1)$
such that
![]() $\alpha \ge 4q$
. If
$\alpha \ge 4q$
. If
![]() $W$
is a set of size
$W$
is a set of size
![]() $\alpha |V|$
chosen uniformly at random from
$\alpha |V|$
chosen uniformly at random from
![]() $V$
, then the probability that
$V$
, then the probability that
![]() $W$
does not contain an edge of
$W$
does not contain an edge of
![]() $\mathcal{H}$
is at most
$\mathcal{H}$
is at most
Proof. Let
![]() $W'$
be a random set of
$W'$
be a random set of
![]() $V$
obtained by including each vertex independently and with probability
$V$
obtained by including each vertex independently and with probability
![]() $\alpha/2$
. Let
$\alpha/2$
. Let
![]() $X=|\{S\in \mathcal{H}\;:\; S\subseteq W'\}|$
and define
$X=|\{S\in \mathcal{H}\;:\; S\subseteq W'\}|$
and define
![]() $m_j(S)$
to be the number of
$m_j(S)$
to be the number of
![]() $S'\in \mathcal{H}$
with
$S'\in \mathcal{H}$
with
![]() $|S\cap S'|=j$
. Note that
$|S\cap S'|=j$
. Note that
![]() ${\mathbb{E}}[X]=(\alpha/2)^r|\mathcal{H}|$
and that
${\mathbb{E}}[X]=(\alpha/2)^r|\mathcal{H}|$
and that
 \begin{align*} \text{Var}(X)&\le (\alpha/2)^{2r}\sum _{S,S'\in \mathcal{H},\ S\cap S'\ne \emptyset } (\alpha/2)^{-|S\cap S'|} =(\alpha/2)^{2r}\sum _{S\in \mathcal{H}}\sum _{j=1}^r (\alpha/2)^{-j} \cdot m_j(S)\\ &\le (\alpha/2)^{2r}\sum _{S\in \mathcal{H}}\sum _{j=1}^r (\alpha/2)^{-j} \cdot q^j |\mathcal{H}| =(\alpha/2)^{2r}\sum _{j=1}^r (\alpha/2q)^{-j} |\mathcal{H}|^2\\&={\mathbb{E}}[X]^2 (\alpha/2q)^{-1} \sum _{j=1}^{r} (\alpha/2q)^{1-j}\le 4{\mathbb{E}}[X]^2 q\alpha ^{-1}, \end{align*}
\begin{align*} \text{Var}(X)&\le (\alpha/2)^{2r}\sum _{S,S'\in \mathcal{H},\ S\cap S'\ne \emptyset } (\alpha/2)^{-|S\cap S'|} =(\alpha/2)^{2r}\sum _{S\in \mathcal{H}}\sum _{j=1}^r (\alpha/2)^{-j} \cdot m_j(S)\\ &\le (\alpha/2)^{2r}\sum _{S\in \mathcal{H}}\sum _{j=1}^r (\alpha/2)^{-j} \cdot q^j |\mathcal{H}| =(\alpha/2)^{2r}\sum _{j=1}^r (\alpha/2q)^{-j} |\mathcal{H}|^2\\&={\mathbb{E}}[X]^2 (\alpha/2q)^{-1} \sum _{j=1}^{r} (\alpha/2q)^{1-j}\le 4{\mathbb{E}}[X]^2 q\alpha ^{-1}, \end{align*}
where the second inequality used that
![]() $\mathcal{H}$
being
$\mathcal{H}$
being
![]() $(q;\;r,1)$
-spread implies
$(q;\;r,1)$
-spread implies
![]() $m_j(S)\le q^j |\mathcal{H}|$
for all
$m_j(S)\le q^j |\mathcal{H}|$
for all
![]() $S\in \mathcal{H}$
and
$S\in \mathcal{H}$
and
![]() $j\ge 1$
, and the last inequality used
$j\ge 1$
, and the last inequality used
![]() $\alpha/2q\ge 2$
. By Chebyshev’s inequality we have
$\alpha/2q\ge 2$
. By Chebyshev’s inequality we have
Lastly, observe that
By the Chernoff bound (see for example [Reference Alon and Spencer1]) we have
![]() ${\mathbb{P}}[|W'|\gt \alpha |V|]\le 2e^{-\alpha |V|/4}$
. Note that
${\mathbb{P}}[|W'|\gt \alpha |V|]\le 2e^{-\alpha |V|/4}$
. Note that
![]() $W'$
contains an edge of
$W'$
contains an edge of
![]() $\mathcal{H}$
precisely when
$\mathcal{H}$
precisely when
![]() $X\gt 0$
, so the result follows from our analysis above.
$X\gt 0$
, so the result follows from our analysis above.
We conclude this subsection with a small observation.
Lemma 2.6.
If
![]() $\mathcal{H}$
is an
$\mathcal{H}$
is an
![]() $r_1$
-uniform
$r_1$
-uniform
![]() $(q;\;r_1,\ldots,r_\ell )$
-spread hypergraph on
$(q;\;r_1,\ldots,r_\ell )$
-spread hypergraph on
![]() $V$
, then
$V$
, then
![]() $r_1\le eq|V|$
.
$r_1\le eq|V|$
.
Proof. Let
![]() $m=\max _{S\in \mathcal{H}} d(S)$
, i.e. this is the maximum multiplicity of any edge in
$m=\max _{S\in \mathcal{H}} d(S)$
, i.e. this is the maximum multiplicity of any edge in
![]() $\mathcal{H}$
. Then for any
$\mathcal{H}$
. Then for any
![]() $S\in \mathcal{H}$
with
$S\in \mathcal{H}$
with
![]() $d(S)=m$
, we have
$d(S)=m$
, we have
proving the result.
2.3. Putting the pieces together
We now prove a technical version of Theorem 1.4 with more explicit quantitative bounds. Theorem 1.4 will follow shortly (but not immediately) after proving this.
Theorem 2.7.
Let
![]() $\mathcal{H}$
be an
$\mathcal{H}$
be an
![]() $r_1$
-uniform
$r_1$
-uniform
![]() $(q;\;r_1,\ldots,r_\ell,1)$
-spread hypergraph on
$(q;\;r_1,\ldots,r_\ell,1)$
-spread hypergraph on
![]() $V$
and let
$V$
and let
![]() $C\ge 8$
. If
$C\ge 8$
. If
![]() $W$
is a set of size
$W$
is a set of size
![]() $2C\ell q|V|$
chosen uniformly at random from
$2C\ell q|V|$
chosen uniformly at random from
![]() $V$
, then
$V$
, then
and for any
![]() $i$
with
$i$
with
![]() $4r_i\le C\ell$
we have
$4r_i\le C\ell$
we have
Proof. Define
![]() $p\;:\!=\;Cq$
and
$p\;:\!=\;Cq$
and
![]() $n\;:\!=\;|V|$
. We can assume
$n\;:\!=\;|V|$
. We can assume
![]() $p\le \frac{1}{2}$
, as otherwise the result is trivial (since the set
$p\le \frac{1}{2}$
, as otherwise the result is trivial (since the set
![]() $W$
in the hypothesis of the theorem has size at least
$W$
in the hypothesis of the theorem has size at least
![]() $|V|$
). Let
$|V|$
). Let
![]() $W_1,\ldots W_{\ell -1}$
be chosen independently and uniformly at random from
$W_1,\ldots W_{\ell -1}$
be chosen independently and uniformly at random from
![]() $\left(\substack{V\\[4pt] pn}\right)$
. Throughout this proof we let
$\left(\substack{V\\[4pt] pn}\right)$
. Throughout this proof we let
![]() $r_{\ell +1}=1$
.
$r_{\ell +1}=1$
.
Let
![]() $\mathcal{H}_1=\mathcal{H}$
and let
$\mathcal{H}_1=\mathcal{H}$
and let
![]() $\phi _1 \;:\; \mathcal{H}_1\to \mathcal{H}$
be the identity map. Inductively assume we have defined
$\phi _1 \;:\; \mathcal{H}_1\to \mathcal{H}$
be the identity map. Inductively assume we have defined
![]() $\mathcal{H}_i$
and
$\mathcal{H}_i$
and
![]() $\phi _i \;:\; \mathcal{H}_i\to \mathcal{H}$
for some
$\phi _i \;:\; \mathcal{H}_i\to \mathcal{H}$
for some
![]() $1\le i\lt \ell$
. Let
$1\le i\lt \ell$
. Let
![]() $\mathcal{H'}_{\!\!i}\subseteq \mathcal{H}_i$
be all the edges
$\mathcal{H'}_{\!\!i}\subseteq \mathcal{H}_i$
be all the edges
![]() $S\in \mathcal{H}_i$
such that
$S\in \mathcal{H}_i$
such that
![]() $(S,W_{i})$
is
$(S,W_{i})$
is
![]() $r_{i+1}$
-good with respect to
$r_{i+1}$
-good with respect to
![]() $\mathcal{H}_{i}$
. Thus for each
$\mathcal{H}_{i}$
. Thus for each
![]() $S\in \mathcal{H'}_{\!\!i}$
, there exists an
$S\in \mathcal{H'}_{\!\!i}$
, there exists an
![]() $S'\in \mathcal{H}_i$
such that
$S'\in \mathcal{H}_i$
such that
![]() $S'\subseteq S\cup W_i$
and
$S'\subseteq S\cup W_i$
and
![]() $|S'\setminus W_i|\le r_{i+1}$
. Choose such an
$|S'\setminus W_i|\le r_{i+1}$
. Choose such an
![]() $S'$
for each
$S'$
for each
![]() $S\in \mathcal{H'}_{\!\!i}$
and let
$S\in \mathcal{H'}_{\!\!i}$
and let
![]() $A_S$
be any subset of
$A_S$
be any subset of
![]() $S$
of size exactly
$S$
of size exactly
![]() $r_{i+1}$
that contains
$r_{i+1}$
that contains
![]() $S'\setminus W_i$
(noting that
$S'\setminus W_i$
(noting that
![]() $S'\setminus W_i\subseteq S$
since
$S'\setminus W_i\subseteq S$
since
![]() $S'\subseteq S\cup W_i$
). Finally, define
$S'\subseteq S\cup W_i$
). Finally, define
![]() $\mathcal{H}_{i+1}=\{A_S\;:\; S\in \mathcal{H'}_{\!\!i}\}$
and
$\mathcal{H}_{i+1}=\{A_S\;:\; S\in \mathcal{H'}_{\!\!i}\}$
and
![]() $\phi _{i+1}\;:\;\mathcal{H}_{i+1}\to \mathcal{H}$
by
$\phi _{i+1}\;:\;\mathcal{H}_{i+1}\to \mathcal{H}$
by
![]() $\phi _{i+1}(A_S)=\phi _i(S)$
.
$\phi _{i+1}(A_S)=\phi _i(S)$
.
Intuitively,
![]() $\phi _i(A)$
is meant to correspond to the “original” edge
$\phi _i(A)$
is meant to correspond to the “original” edge
![]() $S\in \mathcal{H}$
which generated
$S\in \mathcal{H}$
which generated
![]() $A$
. More precisely, we have the following.
$A$
. More precisely, we have the following.
Claim 2.8.
For
![]() $i\le \ell$
, the maps
$i\le \ell$
, the maps
![]() $\phi _i$
are injective and
$\phi _i$
are injective and
![]() $A\subseteq \phi _i(A)$
for all
$A\subseteq \phi _i(A)$
for all
![]() $A\in \mathcal{H}_i$
.
$A\in \mathcal{H}_i$
.
Proof. This claim trivially holds for
![]() $i=1$
. Inductively assume the result has been proved for
$i=1$
. Inductively assume the result has been proved for
![]() $1,\ldots,i$
. Observe that in the process of generating
$1,\ldots,i$
. Observe that in the process of generating
![]() ${\mathcal{H}}_{i+1}$
, we have implicitly defined a bijection
${\mathcal{H}}_{i+1}$
, we have implicitly defined a bijection
![]() $\psi \;:\;\mathcal{H'}_{\!\!i}\to \mathcal{H}_{i+1}$
through the correspondence
$\psi \;:\;\mathcal{H'}_{\!\!i}\to \mathcal{H}_{i+1}$
through the correspondence
![]() $\psi (S)=A_S$
.
$\psi (S)=A_S$
.
By construction of
![]() $\phi _{i+1}$
, we have
$\phi _{i+1}$
, we have
![]() $\phi _{i+1}(A)=\phi _i(\psi ^{-1}(A))$
, so
$\phi _{i+1}(A)=\phi _i(\psi ^{-1}(A))$
, so
![]() $\phi _{i+1}$
is injective since
$\phi _{i+1}$
is injective since
![]() $\phi _i$
was inductively assumed to be injective and
$\phi _i$
was inductively assumed to be injective and
![]() $\psi$
is a bijection. Also by construction we have
$\psi$
is a bijection. Also by construction we have
![]() $A\subseteq \psi ^{-1}(A)$
, and by the inductive hypothesis we have
$A\subseteq \psi ^{-1}(A)$
, and by the inductive hypothesis we have
![]() $\psi ^{-1}(A)\subseteq \phi _i(\psi ^{-1}(A))=\phi _{i+1}(A)$
. This completes the proof.
$\psi ^{-1}(A)\subseteq \phi _i(\psi ^{-1}(A))=\phi _{i+1}(A)$
. This completes the proof.
For
![]() $i\lt \ell$
, we say that
$i\lt \ell$
, we say that
![]() $W_i$
is successful if
$W_i$
is successful if
![]() $|\mathcal{H}_{i+1}|\ge (1-\frac{1}{2\ell })|\mathcal{H}_{i}|$
. Note that
$|\mathcal{H}_{i+1}|\ge (1-\frac{1}{2\ell })|\mathcal{H}_{i}|$
. Note that
![]() $|\mathcal{H}_{i+1}|=|\mathcal{H}_{i}'|$
, so this is equivalent to saying that the number of
$|\mathcal{H}_{i+1}|=|\mathcal{H}_{i}'|$
, so this is equivalent to saying that the number of
![]() $r_{i+1}$
-bad pairs
$r_{i+1}$
-bad pairs
![]() $(S,W_i)$
with
$(S,W_i)$
with
![]() $S\in \mathcal{H}_{i}$
is at most
$S\in \mathcal{H}_{i}$
is at most
![]() $\frac{1}{2\ell }|\mathcal{H}_{i}|$
.
$\frac{1}{2\ell }|\mathcal{H}_{i}|$
.
Claim 2.9.
For
![]() $i\le \ell$
, if
$i\le \ell$
, if
![]() $W_1,\ldots,W_{i-1}$
are successful, then
$W_1,\ldots,W_{i-1}$
are successful, then
![]() $\mathcal{H}_i$
is
$\mathcal{H}_i$
is
![]() $(2q;\;r_i,\ldots,r_{\ell },1)$
-spread.
$(2q;\;r_i,\ldots,r_{\ell },1)$
-spread.
Proof. For a hypergraph
![]() $\mathcal{H}'$
, we let
$\mathcal{H}'$
, we let
![]() $M_j(A;\;\mathcal{H}')$
denote the number of edges of
$M_j(A;\;\mathcal{H}')$
denote the number of edges of
![]() $\mathcal{H}'$
intersecting
$\mathcal{H}'$
intersecting
![]() $A$
in at least
$A$
in at least
![]() $j$
vertices. By Claim 2.8, if
$j$
vertices. By Claim 2.8, if
![]() $\{A_1,\ldots,A_t\}$
are the set of edges of
$\{A_1,\ldots,A_t\}$
are the set of edges of
![]() $\mathcal{H}_i$
which intersect some set
$\mathcal{H}_i$
which intersect some set
![]() $A$
in at least
$A$
in at least
![]() $j$
vertices, then
$j$
vertices, then
![]() $\{\phi _i(A_1),\ldots,\phi _i(A_t)\}$
is a set of
$\{\phi _i(A_1),\ldots,\phi _i(A_t)\}$
is a set of
![]() $t$
distinct edges of
$t$
distinct edges of
![]() $\mathcal{H}$
intersecting
$\mathcal{H}$
intersecting
![]() $A$
in at least
$A$
in at least
![]() $j$
vertices. Thus for all sets
$j$
vertices. Thus for all sets
![]() $A$
and integers
$A$
and integers
![]() $j$
we have
$j$
we have
![]() $M_j(A;\;\mathcal{H}_i)\le M_j(A;\;\mathcal{H})$
.
$M_j(A;\;\mathcal{H}_i)\le M_j(A;\;\mathcal{H})$
.
If
![]() $A$
is contained in an edge
$A$
is contained in an edge
![]() $A'$
of
$A'$
of
![]() $\mathcal{H}_i$
, then by Claim 2.8
$\mathcal{H}_i$
, then by Claim 2.8
![]() $A$
is contained in the edge
$A$
is contained in the edge
![]() $\phi _i(A')$
of
$\phi _i(A')$
of
![]() $\mathcal{H}$
. Thus
$\mathcal{H}$
. Thus
![]() $d_{{\mathcal{H}}_i}(A)\gt 0$
implies
$d_{{\mathcal{H}}_i}(A)\gt 0$
implies
![]() $d_{{\mathcal{H}}}(A)\gt 0$
. By assumption of
$d_{{\mathcal{H}}}(A)\gt 0$
. By assumption of
![]() $\mathcal{H}$
being
$\mathcal{H}$
being
![]() $(q;\;r_1,\ldots,r_\ell,1)$
-spread, if
$(q;\;r_1,\ldots,r_\ell,1)$
-spread, if
![]() $A$
is a set with
$A$
is a set with
![]() $r_{i'}\ge |A|\ge r_{i'+1}$
for some integer
$r_{i'}\ge |A|\ge r_{i'+1}$
for some integer
![]() $i'$
such that
$i'$
such that
![]() $d_{\mathcal{H}_i}(A)\gt 0$
, and if
$d_{\mathcal{H}_i}(A)\gt 0$
, and if
![]() $j$
is an integer satisfying
$j$
is an integer satisfying
![]() $j\ge r_{i'+1}$
, then our previous observations imply
$j\ge r_{i'+1}$
, then our previous observations imply
Because each of
![]() $W_1,\ldots,W_{i-1}$
were successful, we have
$W_1,\ldots,W_{i-1}$
were successful, we have
where in this last step we used that
![]() $(1-1/(2x))^x$
is an increasing function for
$(1-1/(2x))^x$
is an increasing function for
![]() $x\ge 1$
. Plugging
$x\ge 1$
. Plugging
![]() $|\mathcal{H}|\le 2|\mathcal{H}_i|$
into (7) shows that
$|\mathcal{H}|\le 2|\mathcal{H}_i|$
into (7) shows that
![]() $\mathcal{H}_i$
is
$\mathcal{H}_i$
is
![]() $(2q;\;r_i,\ldots,r_{\ell },1)$
-spread as desired.
$(2q;\;r_i,\ldots,r_{\ell },1)$
-spread as desired.
Claim 2.10.
For
![]() $i\lt \ell$
,
$i\lt \ell$
,
Proof. By construction
![]() $\mathcal{H}_i$
is
$\mathcal{H}_i$
is
![]() $r_i$
-uniform. Conditional on
$r_i$
-uniform. Conditional on
![]() $W_1,\ldots,W_{i-1}$
being successful, Claim 2.9 implies that
$W_1,\ldots,W_{i-1}$
being successful, Claim 2.9 implies that
![]() $\mathcal{H}_{i}$
is in particular
$\mathcal{H}_{i}$
is in particular
![]() $(2q;\;r_{i},r_{i+1})$
-spread. By hypothesis we have
$(2q;\;r_{i},r_{i+1})$
-spread. By hypothesis we have
![]() $p\le \frac{1}{2}$
and
$p\le \frac{1}{2}$
and
![]() $C/2\ge 4$
, and by Lemma 2.6 applied to
$C/2\ge 4$
, and by Lemma 2.6 applied to
![]() $\mathcal{H}$
we have
$\mathcal{H}$
we have
![]() $2r_i\le pn$
since
$2r_i\le pn$
since
![]() $C\ge 2e$
. Thus we can apply Lemma 2.1 to
$C\ge 2e$
. Thus we can apply Lemma 2.1 to
![]() $\mathcal{H}_i$
(using
$\mathcal{H}_i$
(using
![]() $C/2$
instead of
$C/2$
instead of
![]() $C$
), which shows that the expected number of
$C$
), which shows that the expected number of
![]() $r_{i+1}$
-bad pairs
$r_{i+1}$
-bad pairs
![]() $(S,W_i)$
is at most
$(S,W_i)$
is at most
![]() $3(C/4)^{-r_{i+1}/2}|\mathcal{H}_i|$
. By Markov’s inequality, the probability of there being more than
$3(C/4)^{-r_{i+1}/2}|\mathcal{H}_i|$
. By Markov’s inequality, the probability of there being more than
![]() $\frac{1}{2\ell } |\mathcal{H}_i|$
total
$\frac{1}{2\ell } |\mathcal{H}_i|$
total
![]() $r_{i+1}$
-bad pairs is at most
$r_{i+1}$
-bad pairs is at most
![]() $6\ell (C/4)^{-r_{i+1}/2}$
, giving the result.
$6\ell (C/4)^{-r_{i+1}/2}$
, giving the result.
We are now ready to prove the result. Let
![]() $W$
and
$W$
and
![]() $W'$
be sets of size
$W'$
be sets of size
![]() $2\ell pn$
and
$2\ell pn$
and
![]() $\ell pn$
chosen uniformly at random from
$\ell pn$
chosen uniformly at random from
![]() $V$
. Observe that for any
$V$
. Observe that for any
![]() $1\le i\le \ell$
, the probability of
$1\le i\le \ell$
, the probability of
![]() $W$
containing an edge of
$W$
containing an edge of
![]() $\mathcal{H}$
is at least the probability of
$\mathcal{H}$
is at least the probability of
![]() $W_1\cup \cdots \cup W_{i-1} \cup W'$
containing an edge of
$W_1\cup \cdots \cup W_{i-1} \cup W'$
containing an edge of
![]() $\mathcal{H}$
, and this is at least the probability that
$\mathcal{H}$
, and this is at least the probability that
![]() $W'$
contains an edge of
$W'$
contains an edge of
![]() $\mathcal{H}_{i}$
(since every edge of
$\mathcal{H}_{i}$
(since every edge of
![]() $\mathcal{H}_i$
is an edge of
$\mathcal{H}_i$
is an edge of
![]() $\mathcal{H}$
after removing vertices that are in
$\mathcal{H}$
after removing vertices that are in
![]() $W_1\cup \cdots \cup W_{i-1}$
), so it suffices to show that this latter probability is large for some
$W_1\cup \cdots \cup W_{i-1}$
), so it suffices to show that this latter probability is large for some
![]() $i$
.
$i$
.
By Proposition 1.3(a) and Claim 2.9, the hypergraph
![]() $\mathcal{H}_{i}$
will be
$\mathcal{H}_{i}$
will be
![]() $(2q)$
-spread if
$(2q)$
-spread if
![]() $W_1,\ldots,W_{i-1}$
are all successful. If
$W_1,\ldots,W_{i-1}$
are all successful. If
![]() $i$
is such that
$i$
is such that
![]() $C\ell \ge 4r_i$
, then by Claim 2.10 and Lemma 2.4 the probability that
$C\ell \ge 4r_i$
, then by Claim 2.10 and Lemma 2.4 the probability that
![]() $W_1,\ldots,W_{i-1}$
are all successful and
$W_1,\ldots,W_{i-1}$
are all successful and
![]() $W'$
contains an edge of
$W'$
contains an edge of
![]() $\mathcal{H}_i$
is at least
$\mathcal{H}_i$
is at least
giving (6).
Alternatively, the probability that
![]() $W'$
contains an edge of
$W'$
contains an edge of
![]() $\mathcal{H}_{\ell }$
can be computed using Lemma 2.5, which gives that the probability of success is at least
$\mathcal{H}_{\ell }$
can be computed using Lemma 2.5, which gives that the probability of success is at least
Using
![]() $qn\ge e^{-1}r_1\ge 1/3$
from Lemma 2.6 together with
$qn\ge e^{-1}r_1\ge 1/3$
from Lemma 2.6 together with
![]() $e^{-x}\le x^{-1}$
gives (5) as desired.
$e^{-x}\le x^{-1}$
gives (5) as desired.
We now use this to prove Theorem 1.4.
Proof of Theorem
1.4. There exists a large constant
![]() $K'$
such that ifFootnote
2
$K'$
such that ifFootnote
2
![]() $r_\ell \ge K' \log (\ell +1)$
, then the result follows from (5). If this does not hold and if
$r_\ell \ge K' \log (\ell +1)$
, then the result follows from (5). If this does not hold and if
![]() $r_1\gt K'\log (\ell +1)$
, then there exists some
$r_1\gt K'\log (\ell +1)$
, then there exists some
![]() $I\ge 2$
such that
$I\ge 2$
such that
![]() $r_{I-1}\gt K'\log (\ell +1)\ge r_I$
. If
$r_{I-1}\gt K'\log (\ell +1)\ge r_I$
. If
![]() $r_I=K'\log (\ell +1)$
, then the result follows from (6) with
$r_I=K'\log (\ell +1)$
, then the result follows from (6) with
![]() $i=I$
provided
$i=I$
provided
![]() $C$
is sufficiently large in terms of
$C$
is sufficiently large in terms of
![]() $K'$
. Otherwise we define a new sequence of integers
$K'$
. Otherwise we define a new sequence of integers
![]() $r'_1,\ldots,r'_{\ell +1}$
with
$r'_1,\ldots,r'_{\ell +1}$
with
![]() $r'_i=r_i$
for
$r'_i=r_i$
for
![]() $i\lt I$
,
$i\lt I$
,
![]() $r'_I=K'\log (\ell +1)$
, and
$r'_I=K'\log (\ell +1)$
, and
![]() $r'_i=r_{i-1}$
for
$r'_i=r_{i-1}$
for
![]() $i\gt I$
. It is not hard to see that
$i\gt I$
. It is not hard to see that
![]() $\mathcal{H}$
is
$\mathcal{H}$
is
![]() $(q;\;r_1',\ldots,r'_{\ell +1},1)$
-spread, so the result followsFootnote
3
from (6) with
$(q;\;r_1',\ldots,r'_{\ell +1},1)$
-spread, so the result followsFootnote
3
from (6) with
![]() $i=I$
.
$i=I$
.
It remains to deal with the case
![]() $r_1\le K'\log (\ell +1)$
. Because
$r_1\le K'\log (\ell +1)$
. Because
![]() $\ell \le r_1$
, this can only hold if
$\ell \le r_1$
, this can only hold if
![]() $r_1\le K''$
for some large constant
$r_1\le K''$
for some large constant
![]() $K''$
. In this case we can apply Lemma 2.4 to give the desired result by choosing
$K''$
. In this case we can apply Lemma 2.4 to give the desired result by choosing
![]() $K_0$
sufficiently large in terms of
$K_0$
sufficiently large in terms of
![]() $K''$
.
$K''$
.
3. Concluding remarks
With a very similar proof one can prove the following non-uniform analog of Theorem 1.4.
Theorem 3.1.
Let
![]() $\mathcal{H}$
be a
$\mathcal{H}$
be a
![]() $(q;\;r_1,\ldots,r_\ell,1)$
-spread hypergraph on
$(q;\;r_1,\ldots,r_\ell,1)$
-spread hypergraph on
![]() $V$
and define
$V$
and define
![]() $s=\min _{S\in \mathcal{H}}|S|$
. Assume that there exists a
$s=\min _{S\in \mathcal{H}}|S|$
. Assume that there exists a
![]() $K$
such that
$K$
such that
![]() $r_1\le K q|V|$
, and such that for all
$r_1\le K q|V|$
, and such that for all
![]() $i$
with
$i$
with
![]() $r_{i}\gt s$
we have
$r_{i}\gt s$
we have
![]() $\log r_i\le K r_{i+1}$
. Then there exists a constant
$\log r_i\le K r_{i+1}$
. Then there exists a constant
![]() $K_0$
depending only on
$K_0$
depending only on
![]() $K$
such that if
$K$
such that if
![]() $r_\ell \le \max \{s,K_0\log (\ell +1)\}$
and
$r_\ell \le \max \{s,K_0\log (\ell +1)\}$
and
![]() $C\ge K_0$
, then a set
$C\ge K_0$
, then a set
![]() $W$
of size
$W$
of size
![]() $C\ell q|V|$
chosen uniformly at random from
$C\ell q|V|$
chosen uniformly at random from
![]() $V$
satisfies
$V$
satisfies
Observe that if
![]() $\mathcal{H}$
is
$\mathcal{H}$
is
![]() $r_1$
-uniform then this reduces to Theorem 1.4 with the additional constraint that
$r_1$
-uniform then this reduces to Theorem 1.4 with the additional constraint that
![]() $r_1\le Kq|V|$
for some
$r_1\le Kq|V|$
for some
![]() $K$
. By Lemma 2.6, this extra condition is always satisfied for uniform hypergraphs with
$K$
. By Lemma 2.6, this extra condition is always satisfied for uniform hypergraphs with
![]() $K=e$
. We note that Theorem 3.1 together with Proposition 1.3(b) implies Theorem 1.1. We briefly describe the details on how to prove this.
$K=e$
. We note that Theorem 3.1 together with Proposition 1.3(b) implies Theorem 1.1. We briefly describe the details on how to prove this.
Sketch of Proof. We first adjust the statement and proof of Lemma 2.1 to allow
![]() $\mathcal{H}$
to be
$\mathcal{H}$
to be
![]() $r$
-bounded. To do this, we partition
$r$
-bounded. To do this, we partition
![]() $\mathcal{H}$
into the uniform hypergraphs
$\mathcal{H}$
into the uniform hypergraphs
![]() $\mathcal{H}_{r'}=\{S\in \mathcal{H}\;:\;|S|=r'\}$
, and word for word the exact same proofFootnote
4
as before shows that the number of
$\mathcal{H}_{r'}=\{S\in \mathcal{H}\;:\;|S|=r'\}$
, and word for word the exact same proofFootnote
4
as before shows that the number of
![]() $k$
-bad pairs using
$k$
-bad pairs using
![]() $S\in \mathcal{H}_{r'}$
is at most
$S\in \mathcal{H}_{r'}$
is at most
![]() $3 (C/2)^{-k/2}|\mathcal{H}|{\left(\substack{n\\[4pt] pn}\right)}$
. We then add these bounds over all
$3 (C/2)^{-k/2}|\mathcal{H}|{\left(\substack{n\\[4pt] pn}\right)}$
. We then add these bounds over all
![]() $r'$
to get the same bound as in Lemma 2.1 multiplied by an extra factor of
$r'$
to get the same bound as in Lemma 2.1 multiplied by an extra factor of
![]() $r$
. With regards to the other lemmas, one no longer needs Lemma 2.6 due to the
$r$
. With regards to the other lemmas, one no longer needs Lemma 2.6 due to the
![]() $r_1\le K q|V|$
hypothesis, and Lemmas 2.4 and 2.5 are fine as is (in particular, Lemma 2.5 still requires
$r_1\le K q|V|$
hypothesis, and Lemmas 2.4 and 2.5 are fine as is (in particular, Lemma 2.5 still requires
![]() $\mathcal{H}$
to be uniform).
$\mathcal{H}$
to be uniform).
For the main part of the proof, instead of choosing
![]() $A_S$
to be a subset of
$A_S$
to be a subset of
![]() $S$
of size exactly
$S$
of size exactly
![]() $r_i$
, we choose it to have size at most
$r_i$
, we choose it to have size at most
![]() $r_i$
and at least
$r_i$
and at least
![]() $\min \{r_i,s\}$
. With this
$\min \{r_i,s\}$
. With this
![]() $\mathcal{H}_i$
will be uniform if
$\mathcal{H}_i$
will be uniform if
![]() $r_i\le s$
, and otherwise when we apply the non-uniform version of Lemma 2.1 our error term will have an extra factor of
$r_i\le s$
, and otherwise when we apply the non-uniform version of Lemma 2.1 our error term will have an extra factor of
![]() $r_i\le e^{Kr_{i+1}}$
, with this inequality holding by our hypothesis for
$r_i\le e^{Kr_{i+1}}$
, with this inequality holding by our hypothesis for
![]() $r_i\gt s$
. This term will be insignificant compared to
$r_i\gt s$
. This term will be insignificant compared to
![]() $(C/2)^{-r_{i+1}/2}$
provided
$(C/2)^{-r_{i+1}/2}$
provided
![]() $C$
is large in terms of
$C$
is large in terms of
![]() $K$
.
$K$
.
If
![]() $r_\ell \le K' \log (\ell +1)$
for some large
$r_\ell \le K' \log (\ell +1)$
for some large
![]() $K'$
depending on
$K'$
depending on
![]() $K$
, then as in the proof of Theorem 1.4 we can assume
$K$
, then as in the proof of Theorem 1.4 we can assume
![]() $r_I=K'\log (\ell +1)$
for some
$r_I=K'\log (\ell +1)$
for some
![]() $I$
and conclude the result as before. Otherwise
$I$
and conclude the result as before. Otherwise
![]() $r_\ell \le s$
by hypothesis, so
$r_\ell \le s$
by hypothesis, so
![]() $\mathcal{H}_\ell$
will be uniform and we can apply Lemma 2.5 to conclude the result.
$\mathcal{H}_\ell$
will be uniform and we can apply Lemma 2.5 to conclude the result.
Another extension can be made by not requiring the same “level of spreadness” throughout
![]() $\mathcal{H}$
.
$\mathcal{H}$
.
Definition 3.2. Let
![]() $0\lt q_1,\ldots,q_{\ell -1}\le 1$
be real numbers and
$0\lt q_1,\ldots,q_{\ell -1}\le 1$
be real numbers and
![]() $r_1\gt \cdots \gt r_\ell$
positive integers. We say that a hypergraph
$r_1\gt \cdots \gt r_\ell$
positive integers. We say that a hypergraph
![]() $\mathcal{H}$
on
$\mathcal{H}$
on
![]() $V$
is
$V$
is
![]() $(q_1,\ldots,q_{\ell -1};\;r_1,\ldots,r_\ell )$
-spread if
$(q_1,\ldots,q_{\ell -1};\;r_1,\ldots,r_\ell )$
-spread if
![]() $\mathcal{H}$
is non-empty,
$\mathcal{H}$
is non-empty,
![]() $r_1$
-bounded, and if for all
$r_1$
-bounded, and if for all
![]() $A\subseteq V$
with
$A\subseteq V$
with
![]() $d(A)\gt 0$
and
$d(A)\gt 0$
and
![]() $r_{i}\ge |A|\ge r_{i+1}$
for some
$r_{i}\ge |A|\ge r_{i+1}$
for some
![]() $1\le i\lt \ell$
, we have for all
$1\le i\lt \ell$
, we have for all
![]() $j\ge r_{i+1}$
that
$j\ge r_{i+1}$
that
Different levels of spread was also considered in [Reference Alweiss, Lovett, Wu and Zhang2]. Here, one can prove the following.
Theorem 3.3.
Let
![]() $\mathcal{H}$
be a
$\mathcal{H}$
be a
![]() $(q_1,\ldots,q_{\ell };\; r_1,\ldots,r_\ell,1)$
-spread hypergraph on
$(q_1,\ldots,q_{\ell };\; r_1,\ldots,r_\ell,1)$
-spread hypergraph on
![]() $V$
and define
$V$
and define
![]() $s=\min _{S\in \mathcal{H}}|S|$
. Assume that there exists a
$s=\min _{S\in \mathcal{H}}|S|$
. Assume that there exists a
![]() $K$
such that for all
$K$
such that for all
![]() $i$
we have
$i$
we have
![]() $r_i\le K q_i|V|$
, and that for all
$r_i\le K q_i|V|$
, and that for all
![]() $i$
with
$i$
with
![]() $r_{i}\gt s$
we have
$r_{i}\gt s$
we have
![]() $\log r_i\le K r_{i+1}$
. Then there exists a constant
$\log r_i\le K r_{i+1}$
. Then there exists a constant
![]() $K_0$
depending only on
$K_0$
depending only on
![]() $K$
such that if
$K$
such that if
![]() $r_\ell \le \max \{s,K_0\log (\ell +1)\}$
and if
$r_\ell \le \max \{s,K_0\log (\ell +1)\}$
and if
![]() $C\ge K_0$
, then a set
$C\ge K_0$
, then a set
![]() $W$
of size
$W$
of size
![]() $C\sum q_i|V|$
chosen uniformly at random from
$C\sum q_i|V|$
chosen uniformly at random from
![]() $V$
satisfies
$V$
satisfies
where
![]() $L\;:\!=\;\sum _i q_i/\max _i q_i$
.
$L\;:\!=\;\sum _i q_i/\max _i q_i$
.
Note that
![]() $\sum q_i\le \ell \max q_i$
, so we have
$\sum q_i\le \ell \max q_i$
, so we have
![]() $L\le \ell$
with equality if
$L\le \ell$
with equality if
![]() $q_i=q_j$
for all
$q_i=q_j$
for all
![]() $i,j$
.
$i,j$
.
Sketch of Proof. We now choose our random sets
![]() $W_i$
to have sizes
$W_i$
to have sizes
![]() $Cq_i|V|$
and
$Cq_i|V|$
and
![]() $W'$
to have size
$W'$
to have size
![]() $C\sum q_i |V|=C(L\cdot \max q_i)|V|$
. With this any of the
$C\sum q_i |V|=C(L\cdot \max q_i)|V|$
. With this any of the
![]() $\mathcal{H}_i$
could be at worst
$\mathcal{H}_i$
could be at worst
![]() $(2\max q_i)$
-spread if each
$(2\max q_i)$
-spread if each
![]() $\mathcal{H}_{i'}$
was successful, so in this case when we apply Lemma 2.4 with
$\mathcal{H}_{i'}$
was successful, so in this case when we apply Lemma 2.4 with
![]() $W'$
we end up getting a probability of roughly
$W'$
we end up getting a probability of roughly
![]() $1-e^{-CL/r_i}$
of containing an edge. From this quantity, we should subtract roughly
$1-e^{-CL/r_i}$
of containing an edge. From this quantity, we should subtract roughly
![]() $\ell ^2 C^{-r_i}$
, since this is the probability that some
$\ell ^2 C^{-r_i}$
, since this is the probability that some
![]() $\mathcal{H}_{i'}$
is unsuccessful. If
$\mathcal{H}_{i'}$
is unsuccessful. If
![]() $r_i=K'\log (\ell +1)$
for some large constant
$r_i=K'\log (\ell +1)$
for some large constant
![]() $K'$
then this gives the desired bound. Otherwise by using the same logic as in the proof of Theorem 1.4 we can assume
$K'$
then this gives the desired bound. Otherwise by using the same logic as in the proof of Theorem 1.4 we can assume
![]() $r_\ell \gt K'\log (\ell +1)$
and apply Lemma 2.5 to
$r_\ell \gt K'\log (\ell +1)$
and apply Lemma 2.5 to
![]() $\mathcal{H}_\ell$
to get a probability of roughly
$\mathcal{H}_\ell$
to get a probability of roughly
![]() $1-(CL)^{-1}$
, which also gives the result after subtracting
$1-(CL)^{-1}$
, which also gives the result after subtracting
![]() $\ell ^2 C^{-r_\ell }$
to account for some
$\ell ^2 C^{-r_\ell }$
to account for some
![]() $\mathcal{H}_{i'}$
being unsuccessful.
$\mathcal{H}_{i'}$
being unsuccessful.
Lastly, we note that Frieze and Marbach [Reference Frieze and Marbach5] recently developed a variant of Theorem 1.1 for rainbow structures in hypergraphs. We suspect that straightforward generalizations of our proofs and those of [Reference Frieze and Marbach5] should give an analog of Theorem 1.4 (as well as Theorems 3.1 and 3.3) for the rainbow setting.
Acknowledgments
We thank Bhargav Narayanan for looking over an earlier draft.