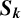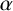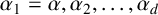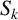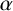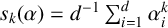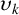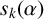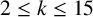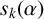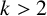1 Introduction
Let
![]() $\alpha $
be a totally positive algebraic integer of degree d, that is, its conjugates
$\alpha $
be a totally positive algebraic integer of degree d, that is, its conjugates
![]() $\alpha _1=\alpha , \alpha _2, \ldots , \alpha _d$
are all positive real numbers, while its minimal polynomial is
$\alpha _1=\alpha , \alpha _2, \ldots , \alpha _d$
are all positive real numbers, while its minimal polynomial is
![]() $P(x)=a_0x^{d}+a_1x^{d-1}+\cdots +a_{d-1}x+a_d$
, where
$P(x)=a_0x^{d}+a_1x^{d-1}+\cdots +a_{d-1}x+a_d$
, where
![]() $a_0=1$
and
$a_0=1$
and
![]() $a_i \in \mathbb {Z}$
(
$a_i \in \mathbb {Z}$
(
![]() $1\leq i\leq d$
). For
$1\leq i\leq d$
). For
![]() $k>0$
, we define the
$k>0$
, we define the
![]() $S_k$
-measure of
$S_k$
-measure of
![]() $\alpha $
by
$\alpha $
by
 $$ \begin{align*} S_k(\alpha)=S_k(P)=\sum_{i=1}^{d}\alpha_i^k, \end{align*} $$
$$ \begin{align*} S_k(\alpha)=S_k(P)=\sum_{i=1}^{d}\alpha_i^k, \end{align*} $$
and the absolute
![]() $S_k$
-measure of
$S_k$
-measure of
![]() $\alpha $
by
$\alpha $
by
![]() $s_k(\alpha )=s_k(P)=S_k(\alpha )/d$
. It follows from the arithmetic–geometric inequality that
$s_k(\alpha )=s_k(P)=S_k(\alpha )/d$
. It follows from the arithmetic–geometric inequality that
![]() $s_k(\alpha )>1$
unless
$s_k(\alpha )>1$
unless
![]() $\alpha =1$
. Let
$\alpha =1$
. Let
![]() $\mathcal {T}_k$
be the spectrum of
$\mathcal {T}_k$
be the spectrum of
![]() $s_k(\alpha )$
, that is,
$s_k(\alpha )$
, that is,
1.1 The absolute trace of totally positive algebraic integers
When
![]() $k=1$
,
$k=1$
,
![]() $S_1(\alpha )=\mathrm {Tr}(\alpha )$
is the usual trace of
$S_1(\alpha )=\mathrm {Tr}(\alpha )$
is the usual trace of
![]() $\alpha $
and
$\alpha $
and
![]() $\mathrm {tr}(\alpha )=\mathrm {Tr}(\alpha )/d$
denotes the absolute trace of
$\mathrm {tr}(\alpha )=\mathrm {Tr}(\alpha )/d$
denotes the absolute trace of
![]() $\alpha $
. The Schur–Siegel–Smyth trace problem [Reference Borwein3] is to find the smallest limit point of
$\alpha $
. The Schur–Siegel–Smyth trace problem [Reference Borwein3] is to find the smallest limit point of
![]() $\mathcal {T}_1$
. That is, given
$\mathcal {T}_1$
. That is, given
![]() $\rho <2$
, show that all but finitely many totally positive algebraic integers
$\rho <2$
, show that all but finitely many totally positive algebraic integers
![]() $\alpha $
satisfy
$\alpha $
satisfy
![]() $\mathrm {tr}(\alpha )>\rho $
.
$\mathrm {tr}(\alpha )>\rho $
.
One way of trying to solve this problem is to study the lower bound of
![]() $\mathrm {tr}(\alpha )$
. Schur [Reference Schur17] solved this for
$\mathrm {tr}(\alpha )$
. Schur [Reference Schur17] solved this for
![]() $\rho ={{\kern-2pt}\sqrt {e}}$
with an exceptional polynomial
$\rho ={{\kern-2pt}\sqrt {e}}$
with an exceptional polynomial
![]() $P_3$
(all the exceptional polynomials denoted by
$P_3$
(all the exceptional polynomials denoted by
![]() $P_j$
in this paper can be found in Table 2). Siegel [Reference Siegel18] solved it for
$P_j$
in this paper can be found in Table 2). Siegel [Reference Siegel18] solved it for
![]() $\rho =1.7336\ldots $
with another exceptional polynomial
$\rho =1.7336\ldots $
with another exceptional polynomial
![]() $P_7$
. Smyth [Reference Smyth20] solved it for
$P_7$
. Smyth [Reference Smyth20] solved it for
![]() $\rho =1.7719\ldots $
with two new exceptional polynomials
$\rho =1.7719\ldots $
with two new exceptional polynomials
![]() $P_{9}$
and
$P_{9}$
and
![]() $P_{10}$
. The method of explicit auxiliary functions established by Smyth [Reference Smyth20] has been used by many authors to study this problem, but no more exceptional polynomials have been found. In [Reference Wang, Wu and Wu22], the authors solved it for
$P_{10}$
. The method of explicit auxiliary functions established by Smyth [Reference Smyth20] has been used by many authors to study this problem, but no more exceptional polynomials have been found. In [Reference Wang, Wu and Wu22], the authors solved it for
![]() $\rho =1.793145\ldots .$
$\rho =1.793145\ldots .$
On the other hand, Serre [Reference Aguirre, Peral, McKee and Smyth1] showed that the method of Smyth [Reference Smyth20] does not produce such a value for any
![]() $\rho $
larger than
$\rho $
larger than
![]() $1.8983021\ldots .$
Applying this result, Smith [Reference Smith19] recently proved that the smallest limit point of
$1.8983021\ldots .$
Applying this result, Smith [Reference Smith19] recently proved that the smallest limit point of
![]() $\mathcal {T}_1$
is less than
$\mathcal {T}_1$
is less than
![]() $1.8984$
, and his ongoing computational work suggests that it could be decreased to
$1.8984$
, and his ongoing computational work suggests that it could be decreased to
![]() $1.81$
.
$1.81$
.
1.2 The lower bounds of
 $s_k(\alpha )$
for integers
$s_k(\alpha )$
for integers
 $k\geq 2$
$k\geq 2$
More generally, no exact value of the smallest limit point of
![]() $\mathcal {T}_k$
is known for any
$\mathcal {T}_k$
is known for any
![]() $k>0$
. Studying its lower and upper bounds is closely related to the study of the spectrum
$k>0$
. Studying its lower and upper bounds is closely related to the study of the spectrum
![]() $\mathcal {M}_p$
of the measure defined by
$\mathcal {M}_p$
of the measure defined by
 $$ \begin{align*} M_p(\alpha)=\bigg(\frac{1}{d}\sum_{i=1}^{d}|\alpha_i|^p \bigg)^{1/p} \end{align*} $$
$$ \begin{align*} M_p(\alpha)=\bigg(\frac{1}{d}\sum_{i=1}^{d}|\alpha_i|^p \bigg)^{1/p} \end{align*} $$
for
![]() $p>0$
, where
$p>0$
, where
![]() $\alpha $
varies over all totally real algebraic integers (all of whose conjugates are real numbers) of degree d, because
$\alpha $
varies over all totally real algebraic integers (all of whose conjugates are real numbers) of degree d, because
![]() $(M_{2p}(\alpha ))^2=(s_p(\alpha ^2))^{1/{p}}$
for
$(M_{2p}(\alpha ))^2=(s_p(\alpha ^2))^{1/{p}}$
for
![]() $\alpha $
totally real. Smyth [Reference Smyth21] carried out a detailed analysis of
$\alpha $
totally real. Smyth [Reference Smyth21] carried out a detailed analysis of
![]() $\mathcal {M}_p$
. His results can be used to analyse the structure of
$\mathcal {M}_p$
. His results can be used to analyse the structure of
![]() $\mathcal {T}_k$
. For instance, it follows from [Reference Smyth21] that the set
$\mathcal {T}_k$
. For instance, it follows from [Reference Smyth21] that the set
![]() $\mathcal {T}_2$
consists of five isolated points
$\mathcal {T}_2$
consists of five isolated points
![]() $s_2(P_1),s_2(P_3),s_2(P_7)$
,
$s_2(P_1),s_2(P_3),s_2(P_7)$
,
![]() $s_2(P_{12}),s_2(P_{13})$
in the interval
$s_2(P_{12}),s_2(P_{13})$
in the interval
![]() $(1,\upsilon _2)$
(where
$(1,\upsilon _2)$
(where
![]() $\upsilon _2=5.19610\ldots $
), is everywhere dense in
$\upsilon _2=5.19610\ldots $
), is everywhere dense in
![]() $(6, \infty )$
and is undetermined in
$(6, \infty )$
and is undetermined in
![]() $(\upsilon _2,6)$
; and the set
$(\upsilon _2,6)$
; and the set
![]() $\mathcal {T}_3$
consists of four isolated points
$\mathcal {T}_3$
consists of four isolated points
![]() $s_3(P_1),s_3(P_3),s_3(P_7),s_3(P_{12})$
in
$s_3(P_1),s_3(P_3),s_3(P_7),s_3(P_{12})$
in
![]() $(1,\upsilon _3)$
(where
$(1,\upsilon _3)$
(where
![]() $\upsilon _3=16.26481\ldots $
), is everywhere dense in
$\upsilon _3=16.26481\ldots $
), is everywhere dense in
![]() $(20, \infty )$
and is undetermined in
$(20, \infty )$
and is undetermined in
![]() $(\upsilon _3,20)$
. Similar results for
$(\upsilon _3,20)$
. Similar results for
![]() $\mathcal {T}_k$
for
$\mathcal {T}_k$
for
![]() $k=4,5,6,9,12,15$
can also be deduced from [Reference Smyth21]. Moreover, It follows that the upper bound for the limit point of
$k=4,5,6,9,12,15$
can also be deduced from [Reference Smyth21]. Moreover, It follows that the upper bound for the limit point of
![]() $\mathcal {T}_k$
for each
$\mathcal {T}_k$
for each
![]() $k>1$
is
$k>1$
is
![]() $D(k)=d(2k)^{2k}$
, where
$D(k)=d(2k)^{2k}$
, where
![]() $d(p)=\lim _{n\rightarrow \infty }M_p(2\cos ({2\pi }/{n}))$
for
$d(p)=\lim _{n\rightarrow \infty }M_p(2\cos ({2\pi }/{n}))$
for
![]() $p>2$
.
$p>2$
.
In [Reference Liang and Wu11], Liang and Wu improved the value of
![]() $\upsilon _2$
to
$\upsilon _2$
to
![]() $5.31935\ldots ,$
the value of
$5.31935\ldots ,$
the value of
![]() $\upsilon _3$
to
$\upsilon _3$
to
![]() $17.56765\ldots ,$
and found a new isolated point
$17.56765\ldots ,$
and found a new isolated point
![]() $s_2(P_{10})$
in
$s_2(P_{10})$
in
![]() $(1,\upsilon _2)$
and three new isolated points
$(1,\upsilon _2)$
and three new isolated points
![]() $s_3(P_{13}),s_3(P_{14}),s_3(P_{15})$
in
$s_3(P_{13}),s_3(P_{14}),s_3(P_{15})$
in
![]() $(1,\upsilon _3)$
. In [Reference Flammang9], Flammang improved the value of
$(1,\upsilon _3)$
. In [Reference Flammang9], Flammang improved the value of
![]() $\upsilon _2$
to
$\upsilon _2$
to
![]() $5.32176\ldots .$
She also showed that the method of auxiliary functions does not give a value for any
$5.32176\ldots .$
She also showed that the method of auxiliary functions does not give a value for any
![]() $\upsilon _2$
larger than
$\upsilon _2$
larger than
![]() $5.895237\ldots .$
This result, combined with [Reference Smith19, Corollary 5.5], can be used to show that the smallest limit point of
$5.895237\ldots .$
This result, combined with [Reference Smith19, Corollary 5.5], can be used to show that the smallest limit point of
![]() $\mathcal {T}_2$
is less than
$\mathcal {T}_2$
is less than
![]() $5.8953$
. In [Reference Flammang8], Flammang improved the value of
$5.8953$
. In [Reference Flammang8], Flammang improved the value of
![]() $\upsilon _3$
to
$\upsilon _3$
to
![]() $17.56827\ldots .$
$17.56827\ldots .$
In this work, we compute lower bounds
![]() $\upsilon _k$
for
$\upsilon _k$
for
![]() $s_k(\alpha )$
for each integer in the range
$s_k(\alpha )$
for each integer in the range
![]() $2\leq k \leq 15$
, and go further to study the results for integers
$2\leq k \leq 15$
, and go further to study the results for integers
![]() $k>15$
. Then we derive lower bounds for
$k>15$
. Then we derive lower bounds for
![]() $s_k(\alpha )$
for all real numbers
$s_k(\alpha )$
for all real numbers
![]() $k>2$
.
$k>2$
.
Theorem 1.1. If
![]() $\alpha \neq 1$
is a totally positive algebraic integer, then for each integer in the range
$\alpha \neq 1$
is a totally positive algebraic integer, then for each integer in the range
![]() $2\leq k\leq 15$
we have
$2\leq k\leq 15$
we have
![]() $s_k(\alpha ) \geq \upsilon _k$
with finitely many exceptions, where
$s_k(\alpha ) \geq \upsilon _k$
with finitely many exceptions, where
![]() $\upsilon _2,\ldots ,\upsilon _{15}$
are given in Table 1.
$\upsilon _2,\ldots ,\upsilon _{15}$
are given in Table 1.
Table 1 The values of
![]() $\upsilon _k,\upsilon ^{\prime }_k$
and indices of exceptional polynomials in Theorem 1.1.
$\upsilon _k,\upsilon ^{\prime }_k$
and indices of exceptional polynomials in Theorem 1.1.

If
![]() $s_k(\alpha )<\upsilon _k$
, that is,
$s_k(\alpha )<\upsilon _k$
, that is,
![]() $\alpha $
is an exception, then
$\alpha $
is an exception, then
![]() $s_k(\alpha )$
is an isolated point in
$s_k(\alpha )$
is an isolated point in
![]() $\mathcal {T}_k$
. The exceptional polynomials, whose indices are listed in Table 1, can be read off from Table 2. In Table 1, the values
$\mathcal {T}_k$
. The exceptional polynomials, whose indices are listed in Table 1, can be read off from Table 2. In Table 1, the values
![]() $\upsilon ^{\prime }_k$
denote the previous results [Reference Flammang8, Reference Flammang9, Reference Smyth21] for the lower bounds of
$\upsilon ^{\prime }_k$
denote the previous results [Reference Flammang8, Reference Flammang9, Reference Smyth21] for the lower bounds of
![]() $s_k(\alpha )$
. The exceptional polynomials with underlined indices are found from previous research. The polynomials marked with asterisks in Table 2 will appear later in this paper as the predicted exceptional polynomials for
$s_k(\alpha )$
. The exceptional polynomials with underlined indices are found from previous research. The polynomials marked with asterisks in Table 2 will appear later in this paper as the predicted exceptional polynomials for
![]() $k>15$
.
$k>15$
.
We observe the staircase distribution of the exceptional polynomials in Table 1 and propose the following conjecture.
Conjecture 1.2. For an algebraic integer
![]() $\alpha $
, if
$\alpha $
, if
![]() $s_k(\alpha )$
is an isolated point in
$s_k(\alpha )$
is an isolated point in
![]() $\mathcal {T}_k$
for
$\mathcal {T}_k$
for
![]() $k>2$
, then
$k>2$
, then
![]() $s_{k+1}(\alpha )$
is also an isolated point in
$s_{k+1}(\alpha )$
is also an isolated point in
![]() $\mathcal {T}_{k+1}$
.
$\mathcal {T}_{k+1}$
.
Let
![]() $\omega _k=\upsilon _k^{1/k}$
. We give a function
$\omega _k=\upsilon _k^{1/k}$
. We give a function
![]() $g(x)$
to approximate the values of
$g(x)$
to approximate the values of
![]() $\omega _k$
for
$\omega _k$
for
![]() ${2\leq k \leq 15}$
, and to predict the behaviour of
${2\leq k \leq 15}$
, and to predict the behaviour of
![]() $\upsilon _k$
for integers
$\upsilon _k$
for integers
![]() $k>15$
:
$k>15$
:
 $$ \begin{align*} g(x)=1+u_0\bigg(\frac{\log(u_1\log(x))}{u_2\log(x)}\bigg)^{2/x} \end{align*} $$
$$ \begin{align*} g(x)=1+u_0\bigg(\frac{\log(u_1\log(x))}{u_2\log(x)}\bigg)^{2/x} \end{align*} $$
for
![]() $x\geq 2$
, where the parameters
$x\geq 2$
, where the parameters
![]() $u_0=2.96$
,
$u_0=2.96$
,
![]() $u_1=4.22$
and
$u_1=4.22$
and
![]() $u_2=3.51$
are optimised according to the values of
$u_2=3.51$
are optimised according to the values of
![]() $\upsilon _k$
for integers
$\upsilon _k$
for integers
![]() $2\leq k \leq 15$
.
$2\leq k \leq 15$
.
Proposition 1.3. If
![]() $\alpha \neq 1$
is a totally positive algebraic integer, then for each integer in the range
$\alpha \neq 1$
is a totally positive algebraic integer, then for each integer in the range
![]() $2\leq k\leq 15$
, with finitely many exceptions, we have
$2\leq k\leq 15$
, with finitely many exceptions, we have
![]() $s_k(\alpha )\geq g^k(k).$
$s_k(\alpha )\geq g^k(k).$
Conjecture 1.4. If
![]() $\alpha \neq 1$
is a totally positive algebraic integer, then for all integers
$\alpha \neq 1$
is a totally positive algebraic integer, then for all integers
![]() $k>15$
, with finitely many exceptions, we have
$k>15$
, with finitely many exceptions, we have
![]() $s_k(\alpha )\geq g^k(k).$
$s_k(\alpha )\geq g^k(k).$
With Conjecture 1.4, for each integer
![]() $k>15$
, we give an estimate of
$k>15$
, we give an estimate of
![]() $\upsilon _k$
with
$\upsilon _k$
with
![]() $g^k(k)$
and some of the exceptions satisfying
$g^k(k)$
and some of the exceptions satisfying
![]() $s_k(\alpha )< g^k(k)$
. For instance, for
$s_k(\alpha )< g^k(k)$
. For instance, for
![]() $16\leq k \leq 25 $
, we list in Table 3 the values of
$16\leq k \leq 25 $
, we list in Table 3 the values of
![]() $g^k(k)$
and indices of the polynomials
$g^k(k)$
and indices of the polynomials
![]() $P_j$
satisfying
$P_j$
satisfying
![]() $s_k(P_j)< g^k(k)$
. Note that all these polynomials conform to Conjecture 1.2.
$s_k(P_j)< g^k(k)$
. Note that all these polynomials conform to Conjecture 1.2.
Table 2 The exceptional polynomials
![]() $P_j$
.
$P_j$
.

Table 3 The values of
![]() $g^k(k)$
and polynomials with
$g^k(k)$
and polynomials with
![]() $s_k(P_j)<g^k(k)$
for
$s_k(P_j)<g^k(k)$
for
![]() $16\leq k \leq 25$
.
$16\leq k \leq 25$
.

Let
![]() $d'(k)=D(k)^{1/k}$
. In Figure 1, the behaviours of
$d'(k)=D(k)^{1/k}$
. In Figure 1, the behaviours of
![]() $\omega _k$
,
$\omega _k$
,
![]() $g(k)$
and
$g(k)$
and
![]() $d'(k)$
are represented graphically. One can prove that
$d'(k)$
are represented graphically. One can prove that
![]() $g(k)$
tends to
$g(k)$
tends to
![]() $1+u_0$
as k tends to infinity. Although this bound is not very sharp for k sufficiently large, it gives an explicit approximate expression of
$1+u_0$
as k tends to infinity. Although this bound is not very sharp for k sufficiently large, it gives an explicit approximate expression of
![]() $\upsilon _k$
for the first time. The values of
$\upsilon _k$
for the first time. The values of
![]() $u_0, u_1$
and
$u_0, u_1$
and
![]() $u_2$
in
$u_2$
in
![]() $g(x)$
can be modified if the results on
$g(x)$
can be modified if the results on
![]() $\upsilon _k$
for integers
$\upsilon _k$
for integers
![]() $2\leq k \leq 15$
are improved.
$2\leq k \leq 15$
are improved.

Figure 1 The values of
![]() $\omega _k$
for
$\omega _k$
for
![]() $2\leq k\leq 15$
and the asymptotic behaviour of
$2\leq k\leq 15$
and the asymptotic behaviour of
![]() $g(k)$
and
$g(k)$
and
![]() $d'(k)$
for
$d'(k)$
for
![]() $k>0$
.
$k>0$
.
1.3 The lower bounds of
 $s_k(\alpha )$
for all real numbers
$s_k(\alpha )$
for all real numbers
 $k>2$
$k>2$
As an application of Theorem 1.1, we give the corresponding results for the lower bounds of
![]() $s_k(\alpha )$
for all
$s_k(\alpha )$
for all
![]() $k>2$
, which supersede the results in [Reference Smyth21].
$k>2$
, which supersede the results in [Reference Smyth21].
Corollary 1.5. If
![]() $\alpha \neq 1$
is a totally positive algebraic integer, then for all real numbers
$\alpha \neq 1$
is a totally positive algebraic integer, then for all real numbers
![]() $k>2$
we have
$k>2$
we have
![]() $s_k(\alpha )>\upsilon _{[k]}$
, with finitely many exceptions.
$s_k(\alpha )>\upsilon _{[k]}$
, with finitely many exceptions.
The values of
![]() $\upsilon _{[k]}$
(where
$\upsilon _{[k]}$
(where
![]() ${[k]}$
is the integer part of k) in Corollary 1.5 are read off from Table 1, and the isolated points of
${[k]}$
is the integer part of k) in Corollary 1.5 are read off from Table 1, and the isolated points of
![]() $\mathcal {T}_k$
in
$\mathcal {T}_k$
in
![]() $(1,\upsilon _{[k]})$
are found with the aid of Table 1 (for more details see [Reference Smyth21]). For instance, for
$(1,\upsilon _{[k]})$
are found with the aid of Table 1 (for more details see [Reference Smyth21]). For instance, for
![]() $k=3.5$
, there are two elements
$k=3.5$
, there are two elements
![]() $s_{3.5}(P_1)\text { and }s_{3.5}(P_3)$
of
$s_{3.5}(P_1)\text { and }s_{3.5}(P_3)$
of
![]() $\mathcal {T}_{3.5}$
in
$\mathcal {T}_{3.5}$
in
![]() $(1, 17.6201)$
. The proof of Corollary 1.5 refers to the proof of [Reference Smyth21, Theorem 2].
$(1, 17.6201)$
. The proof of Corollary 1.5 refers to the proof of [Reference Smyth21, Theorem 2].
This paper is organised as follows. In Section 2 we explain how to use the explicit auxiliary functions to compute the lower bounds of
![]() $s_k(\alpha )$
for totally positive algebraic integers, and give the relation between the auxiliary function and integer transfinite diameter. In Section 3 we show our improvement in finding polynomials used in the explicit auxiliary functions. In Section 4, we give some numerical results.
$s_k(\alpha )$
for totally positive algebraic integers, and give the relation between the auxiliary function and integer transfinite diameter. In Section 3 we show our improvement in finding polynomials used in the explicit auxiliary functions. In Section 4, we give some numerical results.
2 The method of auxiliary functions
2.1 The explicit auxiliary function
Auxiliary functions of this type have been used by many authors for the computation of different measures of totally positive algebraic integers. We take
 $$ \begin{align} f(x,\mathbf{c})=\psi(x)-\sum_{j=1}^J c_{j}{\log|Q_{j}(x)|} \quad\mbox{for } x\in I, \end{align} $$
$$ \begin{align} f(x,\mathbf{c})=\psi(x)-\sum_{j=1}^J c_{j}{\log|Q_{j}(x)|} \quad\mbox{for } x\in I, \end{align} $$
where
![]() $\mathbf {c}=(c_1,c_2,\ldots ,c_J)$
, the
$\mathbf {c}=(c_1,c_2,\ldots ,c_J)$
, the
![]() $c_{j}$
are positive real numbers, the
$c_{j}$
are positive real numbers, the
![]() $Q_{j}$
are nonzero polynomials in
$Q_{j}$
are nonzero polynomials in
![]() $\mathbb {Z}[x]$
and I is a real interval. For instance, if
$\mathbb {Z}[x]$
and I is a real interval. For instance, if
![]() $\psi (x)=\log (x+1)$
, the auxiliary function (2.1) can be applied for the lower bound of the absolute length
$\psi (x)=\log (x+1)$
, the auxiliary function (2.1) can be applied for the lower bound of the absolute length
![]() $R(\alpha )=L(\alpha )^{1/d}$
, where
$R(\alpha )=L(\alpha )^{1/d}$
, where
![]() $L(\alpha )=\sum _{i=0}^{d}|a_i|$
(for more details, see [Reference Flammang5, Reference Flammang6, Reference Mu and Wu14]); and
$L(\alpha )=\sum _{i=0}^{d}|a_i|$
(for more details, see [Reference Flammang5, Reference Flammang6, Reference Mu and Wu14]); and
![]() $\psi (x)=\log (\max \{1,x\})$
for the lower bound of the absolute Mahler measure
$\psi (x)=\log (\max \{1,x\})$
for the lower bound of the absolute Mahler measure
![]() $\Omega (\alpha )=M(\alpha )^{1/d}$
, where
$\Omega (\alpha )=M(\alpha )^{1/d}$
, where
![]() $M(\alpha )=|a_0|\prod _{i=1}^d \max (1,|\alpha _i|)$
(for more details, see [Reference Flammang5, Reference Flammang7, Reference Mu and Wu14]).
$M(\alpha )=|a_0|\prod _{i=1}^d \max (1,|\alpha _i|)$
(for more details, see [Reference Flammang5, Reference Flammang7, Reference Mu and Wu14]).
To prove Theorem 1, we take
![]() $\psi (x)=x^k$
and
$\psi (x)=x^k$
and
![]() $I=(0,+\infty )$
(see [Reference Flammang9, Reference Mossinghoff, Rhin and Wu13, Reference Rhin and Wu15, Reference Wu24]) for each integer in the range
$I=(0,+\infty )$
(see [Reference Flammang9, Reference Mossinghoff, Rhin and Wu13, Reference Rhin and Wu15, Reference Wu24]) for each integer in the range
![]() $2\leq k\leq 15$
. That is,
$2\leq k\leq 15$
. That is,
 $$ \begin{align} f_k(x,\mathbf{c})=x^k-\sum_{j=1}^J c_{j}{\log|Q_{j}(x)|} \quad\mbox{for } x>0. \end{align} $$
$$ \begin{align} f_k(x,\mathbf{c})=x^k-\sum_{j=1}^J c_{j}{\log|Q_{j}(x)|} \quad\mbox{for } x>0. \end{align} $$
Let
![]() $m_k$
be the minimum of
$m_k$
be the minimum of
![]() $f_k(x,\mathbf {c})$
for
$f_k(x,\mathbf {c})$
for
![]() $x>0$
. Then
$x>0$
. Then
![]() $\sum _{i=1}^df_k(\alpha _i,\mathbf {c}) \geq d m_k ,$
that is,
$\sum _{i=1}^df_k(\alpha _i,\mathbf {c}) \geq d m_k ,$
that is,
 $$ \begin{align*} S_k(\alpha)\geq d m_k + \sum_{j=1}^J c_{j}{\log|{\text {Res}}(P,Q_j)|}, \end{align*} $$
$$ \begin{align*} S_k(\alpha)\geq d m_k + \sum_{j=1}^J c_{j}{\log|{\text {Res}}(P,Q_j)|}, \end{align*} $$
where
![]() ${\text {Res}}(P,Q_{j})=\prod _{i=1}^dQ_{j}(\alpha _i)$
is the resultant of P and
${\text {Res}}(P,Q_{j})=\prod _{i=1}^dQ_{j}(\alpha _i)$
is the resultant of P and
![]() $Q_{j}$
. If P does not divide any
$Q_{j}$
. If P does not divide any
![]() $Q_{j}$
, it follows that
$Q_{j}$
, it follows that
![]() ${\text {Res}}(P,Q_{j})$
is a nonzero integer for all
${\text {Res}}(P,Q_{j})$
is a nonzero integer for all
![]() $1\leq j\leq J$
and
$1\leq j\leq J$
and
![]() $s_k(\alpha )\geq m_k.$
Hence we have to solve an optimisation problem to determine
$s_k(\alpha )\geq m_k.$
Hence we have to solve an optimisation problem to determine
2.2 The relation between the auxiliary function and integer transfinite diameter
Let K be a compact subset of
![]() $\mathbb {C}$
. If
$\mathbb {C}$
. If
![]() $\phi $
is a positive function defined on K, the
$\phi $
is a positive function defined on K, the
![]() $\phi $
-generalised integer transfinite diameter [Reference Amoroso2] of K is defined by
$\phi $
-generalised integer transfinite diameter [Reference Amoroso2] of K is defined by
 $$ \begin{align*} t_{\mathbb{Z}, \ \phi}(K)=\liminf_{\substack{h\geq 1 \\ h\rightarrow \infty}} \inf_{\substack{H\in \mathbb{Z}[x] \\ \deg H=h}} \sup_{x\in K} (|H(x)|^{1/h}\phi (x)). \end{align*} $$
$$ \begin{align*} t_{\mathbb{Z}, \ \phi}(K)=\liminf_{\substack{h\geq 1 \\ h\rightarrow \infty}} \inf_{\substack{H\in \mathbb{Z}[x] \\ \deg H=h}} \sup_{x\in K} (|H(x)|^{1/h}\phi (x)). \end{align*} $$
In the auxiliary function (2.1), if we replace the positive real constants
![]() $c_j$
by rational numbers for
$c_j$
by rational numbers for
![]() $1\leq j\leq J$
, we obtain
$1\leq j\leq J$
, we obtain
where the polynomial
![]() $H\in \mathbb {Z}[x]$
is of degree h and t is a positive real number. We want to determine a function
$H\in \mathbb {Z}[x]$
is of degree h and t is a positive real number. We want to determine a function
![]() $f(x,\mathbf {c})$
whose minimum m in I is as large as possible. Thus we need to seek a polynomial
$f(x,\mathbf {c})$
whose minimum m in I is as large as possible. Thus we need to seek a polynomial
![]() $H \in \mathbb Z [x]$
such that
$H \in \mathbb Z [x]$
such that
Now, if we suppose that t is fixed, say
![]() $t=1$
, we need to get an effective upper bound on the weighted integer transfinite diameter with the weight
$t=1$
, we need to get an effective upper bound on the weighted integer transfinite diameter with the weight
![]() $\phi (x)=e^{-\psi (x)}$
and the compact set
$\phi (x)=e^{-\psi (x)}$
and the compact set
![]() $K=I$
. It is sufficient to find an explicit polynomial
$K=I$
. It is sufficient to find an explicit polynomial
![]() $H\in \mathbb {Z}[x]$
and then use the sequence of the successive powers of H.
$H\in \mathbb {Z}[x]$
and then use the sequence of the successive powers of H.
3 Finding polynomials used in auxiliary functions
3.1 An improvement in the application of the LLL algorithm
The main point is to make a good choice of the polynomials to be used in the explicit auxiliary functions. In 2003, based on the LLL algorithm (the lattice reduction algorithm) [Reference Lenstra, Lenstra and Lovász10], the third author [Reference Wu23] developed an algorithm to search the polynomials in (2.1) systematically. Before that, the polynomials were found heuristically. In 2009, Flammang [Reference Flammang4] developed an algorithm called the recursive algorithm on the basis of the method in [Reference Wu23].
With the third author’s algorithm [Reference Wu23], we consider the auxiliary function (2.1). We start with the polynomial x, get the best
![]() $c_1$
and take
$c_1$
and take
![]() $t=c_1$
. Supposing that we have some polynomials
$t=c_1$
. Supposing that we have some polynomials
![]() $Q_1,Q_2,\ldots ,Q_J$
, we optimise the numbers
$Q_1,Q_2,\ldots ,Q_J$
, we optimise the numbers
![]() $c_1,c_2,\ldots ,c_J$
with the semi-infinite linear programming method that was introduced into number theory by Smyth [Reference Smyth21]. This gives us a new number t and we continue by induction to get
$c_1,c_2,\ldots ,c_J$
with the semi-infinite linear programming method that was introduced into number theory by Smyth [Reference Smyth21]. This gives us a new number t and we continue by induction to get
![]() $J + 1$
polynomials. That is, we have
$J + 1$
polynomials. That is, we have
 $$ \begin{align*} F=\prod_{j=1}^J Q_j^{c_j} \end{align*} $$
$$ \begin{align*} F=\prod_{j=1}^J Q_j^{c_j} \end{align*} $$
of degree t (for noninteger t, we can multiply it by a large enough integer to make it integral), and we seek a polynomial
![]() $Q \in \mathbb {Z}[x]$
of degree q such that
$Q \in \mathbb {Z}[x]$
of degree q such that
We want the quantity
![]() $\sup _{x\in I}|F(x)Q(x)|e^{-\psi (x)(t+q)}$
as small as possible. We apply the LLL algorithm to the linear forms
$\sup _{x\in I}|F(x)Q(x)|e^{-\psi (x)(t+q)}$
as small as possible. We apply the LLL algorithm to the linear forms
The
![]() $x_i$
are control points in the interval I, chosen as the points where the function f has local minima.
$x_i$
are control points in the interval I, chosen as the points where the function f has local minima.
The LLL algorithm tends to give polynomials of small degree with small Euclidean norm, which are always ‘good’ candidates for the set
![]() $\{Q_1,Q_2,\ldots ,Q_J\}$
. But sometimes we need polynomials with larger degree, which is a challenge to the previous method. Besides, as the absolute value of
$\{Q_1,Q_2,\ldots ,Q_J\}$
. But sometimes we need polynomials with larger degree, which is a challenge to the previous method. Besides, as the absolute value of
![]() $\psi (x)$
in I increases, it becomes intractable to search for
$\psi (x)$
in I increases, it becomes intractable to search for
![]() $Q_j$
with the LLL algorithm. This requires an improvement in the application of the LLL algorithm.
$Q_j$
with the LLL algorithm. This requires an improvement in the application of the LLL algorithm.
In the auxiliary function (2.2), we observe that some irreducible polynomials with small absolute
![]() $S_k$
-measure always appear repeatedly as factors of polynomials given by the LLL algorithm, and tend to have high powers. To make the LLL algorithm produce more factors that differ from the existing polynomials
$S_k$
-measure always appear repeatedly as factors of polynomials given by the LLL algorithm, and tend to have high powers. To make the LLL algorithm produce more factors that differ from the existing polynomials
![]() $Q_j$
, we introduce the perturbations
$Q_j$
, we introduce the perturbations
![]() $\delta _0,\delta _1,\ldots ,\delta _J$
, where
$\delta _0,\delta _1,\ldots ,\delta _J$
, where
![]() $\delta _j\geq 0$
are real numbers. That is, let
$\delta _j\geq 0$
are real numbers. That is, let
 $$ \begin{align*} \mathcal{F}=\prod_{j=1}^J Q_j^{c_j+\delta_j} \end{align*} $$
$$ \begin{align*} \mathcal{F}=\prod_{j=1}^J Q_j^{c_j+\delta_j} \end{align*} $$
be of degree
![]() $t'$
. We apply the LLL algorithm to the linear forms
$t'$
. We apply the LLL algorithm to the linear forms
in the interval
![]() $I_0=(0,A)$
, where A is large enough.
$I_0=(0,A)$
, where A is large enough.
For different sets
![]() $\{\delta _0,\delta _1,\delta _2,\ldots ,\delta _J\}$
, the LLL algorithm will produce some different polynomials. The
$\{\delta _0,\delta _1,\delta _2,\ldots ,\delta _J\}$
, the LLL algorithm will produce some different polynomials. The
![]() $\delta _j \ (\,j=0,\ldots ,J)$
are chosen so that the LLL algorithm gives ‘good’ polynomials. We note that for a fixed k in (3.1), in the set
$\delta _j \ (\,j=0,\ldots ,J)$
are chosen so that the LLL algorithm gives ‘good’ polynomials. We note that for a fixed k in (3.1), in the set
![]() $\{\delta _0,\delta _1,\ldots ,\delta _J\}$
that gives ‘good’ polynomials, there are only a small number of nonzero elements, the corresponding
$\{\delta _0,\delta _1,\ldots ,\delta _J\}$
that gives ‘good’ polynomials, there are only a small number of nonzero elements, the corresponding
![]() $Q_j$
to which always have small absolute
$Q_j$
to which always have small absolute
![]() $S_k$
-measure. In fact, for
$S_k$
-measure. In fact, for
![]() $k\geq 2$
, all the perturbations of exceptional polynomials
$k\geq 2$
, all the perturbations of exceptional polynomials
![]() $P_j$
are nonzero.
$P_j$
are nonzero.
In the program applying the LLL algorithm, we make some modifications so that it produces a large number of candidates for
![]() $Q_j$
in less time. This improvement in the application of the LLL algorithm helps us improve the lower bounds of
$Q_j$
in less time. This improvement in the application of the LLL algorithm helps us improve the lower bounds of
![]() $s_k(\alpha )$
. It can be used to find polynomials for any explicit auxiliary function with the form (2.1).
$s_k(\alpha )$
. It can be used to find polynomials for any explicit auxiliary function with the form (2.1).
3.2 The Kronecker polynomials
Since all the exceptional polynomials should be used in the auxiliary functions, we analyse the characteristics of the known exceptions. That may help us find more candidates for the set
![]() $\{Q_1,Q_2,\ldots ,Q_J\}$
.
$\{Q_1,Q_2,\ldots ,Q_J\}$
.
It is clear that the absolute
![]() $S_k$
-measure of a totally positive algebraic integer is related to the distribution of its conjugates. An important measure of an algebraic integer
$S_k$
-measure of a totally positive algebraic integer is related to the distribution of its conjugates. An important measure of an algebraic integer
![]() $\alpha $
associated with its conjugates is
$\alpha $
associated with its conjugates is
![]() , the house of
, the house of
![]() $\alpha $
. We observe that all the known exceptions for
$\alpha $
. We observe that all the known exceptions for
![]() $2\leq k\leq 15$
satisfy
$2\leq k\leq 15$
satisfy
![]() . This is an extension of the observations of McAuley [Reference McAuley12] and Smyth [Reference Smyth21]. In fact, for fixed
. This is an extension of the observations of McAuley [Reference McAuley12] and Smyth [Reference Smyth21]. In fact, for fixed
![]() $\alpha $
,
$\alpha $
,
![]() $s_k(\alpha )^{1/k}$
is an increasing function of k [Reference Smyth21], and
$s_k(\alpha )^{1/k}$
is an increasing function of k [Reference Smyth21], and
![]() $s_k(\alpha )^{1/k}$
tends to
$s_k(\alpha )^{1/k}$
tends to
![]() as k tends to infinity [Reference McAuley12]. Note that
as k tends to infinity [Reference McAuley12]. Note that
![]() $d'(k)$
tends to
$d'(k)$
tends to
![]() $4$
as k tends to infinity. This suggests that the minimal polynomials of totally positive algebraic integers with
$4$
as k tends to infinity. This suggests that the minimal polynomials of totally positive algebraic integers with
![]() may be useful in the auxiliary function (2.2).
may be useful in the auxiliary function (2.2).
Kronecker showed that the polynomials whose zeros all lie in
![]() $[0,4]$
are precisely
$[0,4]$
are precisely
 $$ \begin{align*} K_m=\mathop{\prod}\limits_{\substack{(l,m)=1\\ 0\leq l\leq {m}/{2}}}\bigg(x-\bigg(2+2\cos\frac{2\pi l}{m}\bigg)\bigg) \end{align*} $$
$$ \begin{align*} K_m=\mathop{\prod}\limits_{\substack{(l,m)=1\\ 0\leq l\leq {m}/{2}}}\bigg(x-\bigg(2+2\cos\frac{2\pi l}{m}\bigg)\bigg) \end{align*} $$
(the so-called Kronecker polynomials [Reference Robinson16]) for every positive integer m. A cyclotomic polynomial
![]() $\Phi _n(z)$
of degree
$\Phi _n(z)$
of degree
![]() $\varphi (n)$
(where
$\varphi (n)$
(where
![]() $\varphi (n)$
is the Euler function) produces a Kronecker polynomial of degree
$\varphi (n)$
is the Euler function) produces a Kronecker polynomial of degree
![]() $\varphi (n)/2$
by the change of variable
$\varphi (n)/2$
by the change of variable
![]() $x=z+1/z+2$
. This transformation produces
$x=z+1/z+2$
. This transformation produces
![]() $158$
Kronecker polynomials of degree less than or equal to
$158$
Kronecker polynomials of degree less than or equal to
![]() $40$
. We test them in the auxiliary function (2.2) for each integer
$40$
. We test them in the auxiliary function (2.2) for each integer
![]() $2\leq k\leq 15$
, and reserve the ones with nonzero
$2\leq k\leq 15$
, and reserve the ones with nonzero
![]() $c_j$
. This idea is very effective, especially for k relatively large. We give the number of the Kronecker polynomials used in our calculation in Table 4 in the following section.
$c_j$
. This idea is very effective, especially for k relatively large. We give the number of the Kronecker polynomials used in our calculation in Table 4 in the following section.
Table 4 Values of
![]() $l_k,m_k,n_k$
and
$l_k,m_k,n_k$
and
![]() for
for
![]() $2\leq k\leq 15$
.
$2\leq k\leq 15$
.

4 Numerical results and analyses
When k is large enough, the computation of
![]() $\upsilon _k$
becomes intractable, so we stop at
$\upsilon _k$
becomes intractable, so we stop at
![]() $k=16$
. Thanks to the improvement in the application of the LLL algorithm, we find a large number of irreducible polynomials used in the auxiliary function (2.2). For instance, we find
$k=16$
. Thanks to the improvement in the application of the LLL algorithm, we find a large number of irreducible polynomials used in the auxiliary function (2.2). For instance, we find
![]() $72$
new polynomials for
$72$
new polynomials for
![]() $k=2$
,
$k=2$
,
![]() $60$
new polynomials for
$60$
new polynomials for
![]() $k=3$
, and improve the values of
$k=3$
, and improve the values of
![]() $\upsilon _2$
and
$\upsilon _2$
and
![]() $\upsilon _3$
. Besides, for k relatively large, the Kronecker polynomials mentioned in Section 3.2 work very well. The number of all the different irreducible polynomials used in (2.2) is
$\upsilon _3$
. Besides, for k relatively large, the Kronecker polynomials mentioned in Section 3.2 work very well. The number of all the different irreducible polynomials used in (2.2) is
![]() $490$
(available from the corresponding author).
$490$
(available from the corresponding author).
In Table 4, for each integer in the range
![]() $2\leq k\leq 15$
, we give the number
$2\leq k\leq 15$
, we give the number
![]() $l_k$
of irreducible polynomials used for computing
$l_k$
of irreducible polynomials used for computing
![]() $\upsilon _k$
. Among them are
$\upsilon _k$
. Among them are
![]() $m_k$
monic irreducible polynomials with all zeros positive (the so-called totally positive polynomials) and
$m_k$
monic irreducible polynomials with all zeros positive (the so-called totally positive polynomials) and
![]() $n_k$
Kronecker polynomials. The biggest house of the
$n_k$
Kronecker polynomials. The biggest house of the
![]() $m_k$
totally positive polynomials is denoted by
$m_k$
totally positive polynomials is denoted by
![]() . With increasing k, the proportion of totally positive polynomials and that of Kronecker polynomials increase, while the biggest house of the available totally positive polynomials decreases. It is an interesting question whether all the available totally positive polynomials used in the auxiliary function (2.2) should be Kronecker polynomials to compute the lower bounds of
. With increasing k, the proportion of totally positive polynomials and that of Kronecker polynomials increase, while the biggest house of the available totally positive polynomials decreases. It is an interesting question whether all the available totally positive polynomials used in the auxiliary function (2.2) should be Kronecker polynomials to compute the lower bounds of
![]() $s_k(\alpha )$
for k large enough. It is also interesting to investigate the relation between the house and the absolute
$s_k(\alpha )$
for k large enough. It is also interesting to investigate the relation between the house and the absolute
![]() $S_k$
-measure of totally positive algebraic integers.
$S_k$
-measure of totally positive algebraic integers.
If
![]() $k>0$
is a real number, lower bounds
$k>0$
is a real number, lower bounds
![]() $\upsilon _k$
of
$\upsilon _k$
of
![]() $s_k(\alpha )$
can also be calculated. For example, for
$s_k(\alpha )$
can also be calculated. For example, for
![]() $k=2.5$
, using
$k=2.5$
, using
![]() $114$
irreducible polynomials found by the improved algorithm, we improve the previous result
$114$
irreducible polynomials found by the improved algorithm, we improve the previous result
![]() $\upsilon _{2.5}=9.0509$
(with isolated points
$\upsilon _{2.5}=9.0509$
(with isolated points
![]() $s_{2.5}(P_1),s_{2.5}(P_3),s_{2.5}(P_7),s_{2.5}(P_{12})$
in
$s_{2.5}(P_1),s_{2.5}(P_3),s_{2.5}(P_7),s_{2.5}(P_{12})$
in
![]() $(1,\upsilon _{2.5})$
) [Reference Smyth21] to
$(1,\upsilon _{2.5})$
) [Reference Smyth21] to
![]() $\upsilon _{2.5}=9.6101$
and find two new isolated points
$\upsilon _{2.5}=9.6101$
and find two new isolated points
![]() $s_{2.5}(P_{13})$
and
$s_{2.5}(P_{13})$
and
![]() $s_{2.5}(P_{14})$
. Theoretically, all the results in [Reference Smyth21] on the lower bounds of
$s_{2.5}(P_{14})$
. Theoretically, all the results in [Reference Smyth21] on the lower bounds of
![]() $s_k(\alpha )$
for
$s_k(\alpha )$
for
![]() $k>0$
can be improved with our method.
$k>0$
can be improved with our method.
All the computations are done using the Pascal programming language and Pari/GP.
Acknowledgement
We are very much indebted to Professor Georges Rhin for his valuable help.