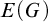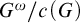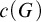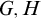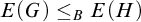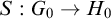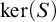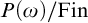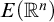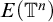1 Introduction
A topological space is Polish if it is separable and completely metrizable. For more details in descriptive set theory, we refer to [Reference Kechris13]. It is an important application of descriptive set theory to study equivalence relations by using Borel reducibility. Given two Borel equivalence relations E and F on Polish spaces X and Y, respectively, recall that E is Borel reducible to F, denoted
![]() $E\leq _B F$
, if there exists a Borel map
$E\leq _B F$
, if there exists a Borel map
![]() $\theta :X\rightarrow Y$
such that for all
$\theta :X\rightarrow Y$
such that for all
![]() $x,y\in X$
,
$x,y\in X$
,
We denote
![]() $E\sim _B F$
if both
$E\sim _B F$
if both
![]() $E\leq _B F$
and
$E\leq _B F$
and
![]() $F\leq _B E$
, and denote
$F\leq _B E$
, and denote
![]() $E<_B F$
if
$E<_B F$
if
![]() $E\leq _B F$
and
$E\leq _B F$
and
![]() $F\nleq _B E$
. We refer to [Reference Gao7] for background on Borel reducibility.
$F\nleq _B E$
. We refer to [Reference Gao7] for background on Borel reducibility.
Polish groups are important tools in the research on Borel reducibility. A topological group is Polish if its topology is Polish. For a Polish group G, the authors [Reference Ding and Zheng5] defined an equivalence relation
![]() $E(G)$
on
$E(G)$
on
![]() $G^{\omega }$
by
$G^{\omega }$
by
for
![]() $x,y\in G^{\omega }$
. We say that
$x,y\in G^{\omega }$
. We say that
![]() $E(G)$
is the equivalence relation induced by G. Indeed,
$E(G)$
is the equivalence relation induced by G. Indeed,
![]() $E(G)$
is the right coset equivalence relation
$E(G)$
is the right coset equivalence relation
![]() $G^{\omega }/c(G)$
, where
$G^{\omega }/c(G)$
, where
![]() $c(G)$
is the group of all convergent sequences in G.
$c(G)$
is the group of all convergent sequences in G.
In this article, we focus on equivalence relations induced by locally compact abelian Polish groups. Some interesting results have been found in some special cases. For instance, for
![]() $c_0,e_0,c_1,e_1\in {\mathbb {N}}$
,
$c_0,e_0,c_1,e_1\in {\mathbb {N}}$
,
![]() $E({\mathbb {R}}^{c_0}\times {\mathbb {T}}^{e_0})\le _BE({\mathbb {R}}^{c_1}\times {\mathbb {T}}^{e_1})$
iff
$E({\mathbb {R}}^{c_0}\times {\mathbb {T}}^{e_0})\le _BE({\mathbb {R}}^{c_1}\times {\mathbb {T}}^{e_1})$
iff
![]() $e_0\le e_1$
and
$e_0\le e_1$
and
![]() $c_0+e_0\le c_1+e_1$
(cf. [Reference Ding and Zheng5, Theorem 6.19]).
$c_0+e_0\le c_1+e_1$
(cf. [Reference Ding and Zheng5, Theorem 6.19]).
Given a group G, the identity element of G is denoted by
![]() $1_G$
. If G is a topological group, the connected component of
$1_G$
. If G is a topological group, the connected component of
![]() $1_G$
in G is denoted by
$1_G$
in G is denoted by
![]() $G_0$
. Recall that a Polish group G is non-archimedean if it has a neighborhood base of
$G_0$
. Recall that a Polish group G is non-archimedean if it has a neighborhood base of
![]() $1_G$
consisting of open subgroups.
$1_G$
consisting of open subgroups.
Theorem 1.1. Let G and H be two locally compact abelian Polish groups. If
![]() $E(G)\leq _B E(H)$
, then there is a continuous homomorphism
$E(G)\leq _B E(H)$
, then there is a continuous homomorphism
![]() $S:G_0\rightarrow H_0$
such that
$S:G_0\rightarrow H_0$
such that
![]() $\ker (S)$
is non-archimedean.
$\ker (S)$
is non-archimedean.
By restricting attention to compact connected abelian Polish groups, we prove the following theorem.
Theorem 1.2 (Rigid Theorem).
Let G be a compact connected abelian Polish group and let H be a locally compact abelian Polish group. Then
![]() $E(G)\leq _B E(H)$
iff there is a continuous homomorphism
$E(G)\leq _B E(H)$
iff there is a continuous homomorphism
![]() $S:G\rightarrow H$
such that
$S:G\rightarrow H$
such that
![]() $\ker (S)$
is non-archimedean.
$\ker (S)$
is non-archimedean.
For every normal space X, denoted by
![]() $\dim (X)$
the covering dimension of X, where
$\dim (X)$
the covering dimension of X, where
![]() $\dim (X)$
is an integer
$\dim (X)$
is an integer
![]() $\ge -1$
or the “infinite number
$\ge -1$
or the “infinite number
![]() $\infty $
.” Let G be an abelian topological group. The topological group Hom
$\infty $
.” Let G be an abelian topological group. The topological group Hom
![]() $(G,{\mathbb {T}})$
is called the dual group of G, denoted by
$(G,{\mathbb {T}})$
is called the dual group of G, denoted by
![]() $\widehat {G}$
(see Section 4). For any finite dimensional compact abelian Polish group G,
$\widehat {G}$
(see Section 4). For any finite dimensional compact abelian Polish group G,
![]() $\dim (G)=\mathrm {rank}(\widehat {G})$
, the torsion-free rank of
$\dim (G)=\mathrm {rank}(\widehat {G})$
, the torsion-free rank of
![]() $\widehat G$
(cf. Lemma 8.13 and Corollary 8.26 of [Reference Hofmann and Morris11]). We say G is n-dimensional if
$\widehat G$
(cf. Lemma 8.13 and Corollary 8.26 of [Reference Hofmann and Morris11]). We say G is n-dimensional if
![]() $\dim (G)=n$
for some integer n, or infinite dimensional if
$\dim (G)=n$
for some integer n, or infinite dimensional if
![]() $\dim (G)$
is infinite.
$\dim (G)$
is infinite.
Recall that
![]() ${\mathbb {T}}$
is the multiplicative group of all complex numbers with modulus
${\mathbb {T}}$
is the multiplicative group of all complex numbers with modulus
![]() $1$
. For finite dimensional compact abelian Polish groups, we obtain the following results.
$1$
. For finite dimensional compact abelian Polish groups, we obtain the following results.
Theorem 1.3. Let
![]() $G,H$
be locally compact abelian Polish groups.
$G,H$
be locally compact abelian Polish groups.
-
(1) If G is non-archimedean, then
 $E(G)\leq _B E_0^{\omega }$
.
$E(G)\leq _B E_0^{\omega }$
. -
(2) If G is not non-archimedean, then
 $E({\mathbb {R}})\leq _B E(G)$
.
$E({\mathbb {R}})\leq _B E(G)$
. -
(3) If G is not non-archimedean and
 $G_0$
is open, then
$G_0$
is open, then
 $E(G)\sim _B E(G_0)$
.
$E(G)\sim _B E(G_0)$
. -
(4) If n is a positive integer, then
 $E({\mathbb {T}}^n)\leq _B E(G)$
iff
$E({\mathbb {T}}^n)\leq _B E(G)$
iff
 ${\mathbb {T}}^n$
embeds in G.
${\mathbb {T}}^n$
embeds in G. -
(5) If n is a positive integer and G is compact, then G is n-dimensional iff
 $E({\mathbb {R}}^n)<_B E(G)\leq _B E({\mathbb {T}}^n)$
.
$E({\mathbb {R}}^n)<_B E(G)\leq _B E({\mathbb {T}}^n)$
.
Let
![]() $\mathcal {P}$
denote the set of all primes. For
$\mathcal {P}$
denote the set of all primes. For
![]() $P,Q\in \mathcal P^{\omega }$
,
$P,Q\in \mathcal P^{\omega }$
,
![]() $Q\preceq P$
means that there is a co-finite subset A of
$Q\preceq P$
means that there is a co-finite subset A of
![]() $\omega $
and an injection
$\omega $
and an injection
![]() $f:A\to \omega $
such that
$f:A\to \omega $
such that
![]() $Q(n)=P(f(n))$
for each
$Q(n)=P(f(n))$
for each
![]() $n\in A$
.
$n\in A$
.
For
![]() $P\in \mathcal {P}^{\omega }$
, we consider the closed subgroup of
$P\in \mathcal {P}^{\omega }$
, we consider the closed subgroup of
![]() ${\mathbb {T}}^{\omega }$
, named P-adic solenoid,
${\mathbb {T}}^{\omega }$
, named P-adic solenoid,
![]() $\Sigma _P=\{g\in {\mathbb {T}}^{\omega }:\forall l\,(g(l)=g(l+1)^{P(l)})\}$
(cf. [Reference Gumerov8]).
$\Sigma _P=\{g\in {\mathbb {T}}^{\omega }:\forall l\,(g(l)=g(l+1)^{P(l)})\}$
(cf. [Reference Gumerov8]).
Theorem 1.4. Let P and Q be in
![]() $\mathcal {P}^{\omega }$
. Then
$\mathcal {P}^{\omega }$
. Then
![]() $E(\Sigma _P)\leq _B E(\Sigma _Q)$
iff
$E(\Sigma _P)\leq _B E(\Sigma _Q)$
iff
![]() $Q\preceq P$
.
$Q\preceq P$
.
The partially ordered set
![]() $P(\omega )/\mbox {Fin}$
is so complicated that every Boolean algebra of size
$P(\omega )/\mbox {Fin}$
is so complicated that every Boolean algebra of size
![]() $\le \omega _1$
embeds into it (see [Reference Bella, Dow, Hart, Hrusak, van Mill and Ursino2]). We usually express that some classes of Borel equivalence relations are extremely complicated under the order of Borel reducibility by showing that
$\le \omega _1$
embeds into it (see [Reference Bella, Dow, Hart, Hrusak, van Mill and Ursino2]). We usually express that some classes of Borel equivalence relations are extremely complicated under the order of Borel reducibility by showing that
![]() $P(\omega )/\mbox {Fin}$
embeds into them. For instance, Louveau–Velickovic [Reference Louveau and Velickovic14] and Yin [Reference Yin18] showed that
$P(\omega )/\mbox {Fin}$
embeds into them. For instance, Louveau–Velickovic [Reference Louveau and Velickovic14] and Yin [Reference Yin18] showed that
![]() $P(\omega )/\mbox {Fin}$
embeds into both LV-equalities and Borel equivalence relations between
$P(\omega )/\mbox {Fin}$
embeds into both LV-equalities and Borel equivalence relations between
![]() $\ell _p$
and
$\ell _p$
and
![]() $\ell _q$
, respectively. As an application, we prove that, the partially ordered set
$\ell _q$
, respectively. As an application, we prove that, the partially ordered set
![]() $P(\omega )/\mbox {Fin}$
embeds into the partially ordered set of all
$P(\omega )/\mbox {Fin}$
embeds into the partially ordered set of all
![]() $E(G)$
’s under the ordering of Borel reducibility.
$E(G)$
’s under the ordering of Borel reducibility.
Theorem 1.5. Let
![]() $n\in \mathbb {N}^+$
. Then for
$n\in \mathbb {N}^+$
. Then for
![]() $A\subseteq \omega $
, there is an n-dimensional compact connected abelian Polish group
$A\subseteq \omega $
, there is an n-dimensional compact connected abelian Polish group
![]() $G_A$
such that
$G_A$
such that
![]() $E({\mathbb {R}}^n)<_B E(G_A)<_B E({\mathbb {T}}^n)$
and for
$E({\mathbb {R}}^n)<_B E(G_A)<_B E({\mathbb {T}}^n)$
and for
![]() $A,B\subseteq \omega $
, we have
$A,B\subseteq \omega $
, we have
We also get a sufficient and necessary condition concerning dual groups.
Theorem 1.6 (Dual Rigid Theorem).
Let G be a compact connected abelian Polish group and let H be a locally compact abelian Polish group. Then
![]() $E(G)\leq _B E(H)$
iff there is a continuous homomorphism
$E(G)\leq _B E(H)$
iff there is a continuous homomorphism
![]() $S^*:\widehat {H}\to \widehat {G}$
such that
$S^*:\widehat {H}\to \widehat {G}$
such that
![]() $\widehat {G}/\mathrm {im}(S^*)$
is a torsion group.
$\widehat {G}/\mathrm {im}(S^*)$
is a torsion group.
Notation convention
In this article, the addition operation of any subgroup of
![]() ${\mathbb {R}}^n$
is denoted by
${\mathbb {R}}^n$
is denoted by
![]() $+$
and its identity element is denoted by
$+$
and its identity element is denoted by
![]() $0$
. Unless otherwise specified, for abstract abelian topological groups G, we still use multiplicative notation to express the group operation, and use
$0$
. Unless otherwise specified, for abstract abelian topological groups G, we still use multiplicative notation to express the group operation, and use
![]() $1_G$
to express the identity element of G, since we often consider subgroups of
$1_G$
to express the identity element of G, since we often consider subgroups of
![]() ${\mathbb {T}}^{\omega }$
.
${\mathbb {T}}^{\omega }$
.
This article is organized as follows: In Section 2, we prove Theorems 1.1–1.3. In Section 3, we consider P-adic solenoids and prove Theorems 1.4 and 1.5. Finally, In Section 4, we consider dual groups and prove Theorem 1.6.
2 Locally compact abelian Polish groups
Definition 2.1 [Reference Ding and Zheng5, Definition 6.1].
Let G be a Polish group. We define equivalence relation
![]() $E_*(G)$
on
$E_*(G)$
on
![]() $G^{\omega }$
as, for
$G^{\omega }$
as, for
![]() $x,y\in G^{\omega }$
,
$x,y\in G^{\omega }$
,
The following is an easy but important observation.
Proposition 2.2. Let G be a Polish group. Then
![]() $E(G)\sim _B E_*(G)$
.
$E(G)\sim _B E_*(G)$
.
Proof To see that
![]() $E(G)\leq _B E_*(G)$
, for
$E(G)\leq _B E_*(G)$
, for
![]() $x\in G^{\omega }$
, we define
$x\in G^{\omega }$
, we define
![]() $\theta (x)\in G^{\omega }$
as
$\theta (x)\in G^{\omega }$
as
 $$ \begin{align*}\theta(x)(n)=\left\{\begin{array}{ll}x(0), & n=0,\cr x(n-1)^{-1}x(n), & n>0.\end{array} \right.\end{align*} $$
$$ \begin{align*}\theta(x)(n)=\left\{\begin{array}{ll}x(0), & n=0,\cr x(n-1)^{-1}x(n), & n>0.\end{array} \right.\end{align*} $$
Then
![]() $\theta $
witnesses that
$\theta $
witnesses that
![]() $E(G)\leq _B E_*(G)$
.
$E(G)\leq _B E_*(G)$
.
To show the converse, for
![]() $x\in G^{\omega }$
, we define
$x\in G^{\omega }$
, we define
![]() $\vartheta (x)\in G^{\omega }$
as
$\vartheta (x)\in G^{\omega }$
as
Then
![]() $\vartheta $
witnesses that
$\vartheta $
witnesses that
![]() $E_*(G)\leq _B E(G)$
.
$E_*(G)\leq _B E(G)$
.
In this article, we focus on abelian Polish groups. For abelian Polish groups G, it is more convenient to take
![]() $E_*(G)$
as research object than
$E_*(G)$
as research object than
![]() $E(G)$
.
$E(G)$
.
Some reducibility results are obtained in [Reference Ding and Zheng5]. Since we will use them again and again in this article, for the convenience of readers, we list them as follows.
Proposition 2.3 [Reference Ding and Zheng5, Proposition 3.4].
Let
![]() $G,H$
be two Polish groups. If G is topologically isomorphic to a closed subgroup of H, then
$G,H$
be two Polish groups. If G is topologically isomorphic to a closed subgroup of H, then
![]() $E(G)\le _BE(H)$
.
$E(G)\le _BE(H)$
.
A metric d on a group G is called two-sided invariant if
![]() $d(ghl,gkl)=d(h,k)$
for all
$d(ghl,gkl)=d(h,k)$
for all
![]() $g,h,k,l\in G$
. We say that a Polish group G is TSI if it admits a compatible two-sided invariant metric. Any abelian Polish group is TSI (cf. [Reference Gao7, Exercise 2.1.4]).
$g,h,k,l\in G$
. We say that a Polish group G is TSI if it admits a compatible two-sided invariant metric. Any abelian Polish group is TSI (cf. [Reference Gao7, Exercise 2.1.4]).
Lemma 2.4 [Reference Ding and Zheng5, Theorem 6.5].
Let
![]() $G,H,K$
be three TSI Polish groups. Suppose
$G,H,K$
be three TSI Polish groups. Suppose
![]() $\psi :G\to H$
and
$\psi :G\to H$
and
![]() $\varphi :H\to K$
are continuous homomorphisms with
$\varphi :H\to K$
are continuous homomorphisms with
![]() $\varphi (\psi (G))=K$
such that
$\varphi (\psi (G))=K$
such that
![]() $\ker (\varphi \circ \psi )$
is non-archimedean. If the interval
$\ker (\varphi \circ \psi )$
is non-archimedean. If the interval
![]() $[0,1]$
embeds into H, then
$[0,1]$
embeds into H, then
![]() $E(G)\le _BE(H)$
.
$E(G)\le _BE(H)$
.
Lemma 2.5 [Reference Ding and Zheng5, Theorem 6.13].
Let
![]() $G,H$
be TSI Polish groups such that H is locally compact. If
$G,H$
be TSI Polish groups such that H is locally compact. If
![]() $E(G)\le _BE(H)$
, then there exist an open normal subgroup
$E(G)\le _BE(H)$
, then there exist an open normal subgroup
![]() $G_c$
of G and a continuous map
$G_c$
of G and a continuous map
![]() $S:G_c\to H$
with
$S:G_c\to H$
with
![]() $S(1_G)=1_H$
such that, for
$S(1_G)=1_H$
such that, for
![]() $x,y\in G_c^{\omega }$
, if
$x,y\in G_c^{\omega }$
, if
![]() $\lim _nx(n)y(n)^{-1}=1_G$
, then
$\lim _nx(n)y(n)^{-1}=1_G$
, then
where
![]() $S(x)(n)=S(x(n)),S(y)(n)=S(y(n))$
for each
$S(x)(n)=S(x(n)),S(y)(n)=S(y(n))$
for each
![]() $n\in \omega $
.
$n\in \omega $
.
In particular, if
![]() $G=G_c$
and the interval
$G=G_c$
and the interval
![]() $[0,1]$
embeds in H, then the converse is also true.
$[0,1]$
embeds in H, then the converse is also true.
Remark 2.6. Since
![]() $G_c$
in the preceding lemma is an open subgroup, it is also closed. So
$G_c$
in the preceding lemma is an open subgroup, it is also closed. So
![]() $G_0\subseteq G_c$
as it is connected. Since S is continuous, we have
$G_0\subseteq G_c$
as it is connected. Since S is continuous, we have
![]() $S(G_0)\subseteq H_0$
. Moreover, for all
$S(G_0)\subseteq H_0$
. Moreover, for all
![]() $x,y\in G_0^{\omega }$
, if
$x,y\in G_0^{\omega }$
, if
![]() $\lim _nx(n)y(n)^{-1}=1_G$
, we have
$\lim _nx(n)y(n)^{-1}=1_G$
, we have
The next lemma plays the key role in the proof of Theorem 2.8.
Lemma 2.7. Let G and H be two abelian Polish groups such that:
-
(1) H is locally compact,
-
(2)
 $H_0\subseteq {\mathbb {R}}^{\omega }\times {\mathbb {T}}^{\omega }$
,
$H_0\subseteq {\mathbb {R}}^{\omega }\times {\mathbb {T}}^{\omega }$
, -
(3) there is a nonzero continuous homomorphism
 $f:{\mathbb {R}}^m\rightarrow G$
for some
$f:{\mathbb {R}}^m\rightarrow G$
for some
 $m\in {\mathbb {N}}^+$
.
$m\in {\mathbb {N}}^+$
.
If
![]() $E_*(G)\leq _B E_*(H)$
, then there is a continuous map
$E_*(G)\leq _B E_*(H)$
, then there is a continuous map
![]() $S:G_0\rightarrow H_0$
such that the map S restricted on
$S:G_0\rightarrow H_0$
such that the map S restricted on
![]() $f({\mathbb {R}}^m)$
is a homomorphism to
$f({\mathbb {R}}^m)$
is a homomorphism to
![]() $H_0$
.
$H_0$
.
Proof First, from Remark 2.6, we can obtain a continuous map
![]() $S:G_0\rightarrow H_0$
with
$S:G_0\rightarrow H_0$
with
![]() $S(1_{G_0})=1_{H_0}$
such that, for
$S(1_{G_0})=1_{H_0}$
such that, for
![]() $x,y\in G_0^{\omega }$
, if
$x,y\in G_0^{\omega }$
, if
![]() $\lim _nx(n)y(n)^{-1}=1_{G_0}$
, then
$\lim _nx(n)y(n)^{-1}=1_{G_0}$
, then
where
![]() $S(x)(n)=S(x(n)),S(y)(n)=S(y(n))$
for each
$S(x)(n)=S(x(n)),S(y)(n)=S(y(n))$
for each
![]() $n\in \omega $
.
$n\in \omega $
.
Since
![]() $H_0\subseteq {\mathbb {R}}^{\omega }\times {\mathbb {T}}^{\omega }$
, without loss of generality we may assume that
$H_0\subseteq {\mathbb {R}}^{\omega }\times {\mathbb {T}}^{\omega }$
, without loss of generality we may assume that
![]() $h(2k)\in {\mathbb {R}}$
and
$h(2k)\in {\mathbb {R}}$
and
![]() $h(2k+1)\in {\mathbb {T}}$
for all
$h(2k+1)\in {\mathbb {T}}$
for all
![]() $h\in H_0.$
For
$h\in H_0.$
For
![]() $k\in \omega $
, we define continuous homomorphisms
$k\in \omega $
, we define continuous homomorphisms
![]() $\phi ^{2k}:H_0\rightarrow {\mathbb {R}}$
and
$\phi ^{2k}:H_0\rightarrow {\mathbb {R}}$
and
![]() $\phi ^{2k+1}:H_0\rightarrow {\mathbb {T}}$
by
$\phi ^{2k+1}:H_0\rightarrow {\mathbb {T}}$
by
![]() $\phi ^j(h)=h(j)$
.
$\phi ^j(h)=h(j)$
.
Now fix
![]() $g_0,g_1\in f({\mathbb {R}}^m)$
and find
$g_0,g_1\in f({\mathbb {R}}^m)$
and find
![]() $a_0,a_1\in {\mathbb {R}}^m$
such that
$a_0,a_1\in {\mathbb {R}}^m$
such that
![]() $f(a_0)=g_0$
and
$f(a_0)=g_0$
and
![]() ${f(a_1)=g_1}$
. For
${f(a_1)=g_1}$
. For
![]() $t\in [0,1]$
and
$t\in [0,1]$
and
![]() $l\in \{1,2\}$
, define
$l\in \{1,2\}$
, define
![]() $a^l(t)\in {\mathbb {R}}^m$
as
$a^l(t)\in {\mathbb {R}}^m$
as
 $$ \begin{align*}a^l(t)=\left\{\begin{array}{ll}a_0+t(a_1-a_0), & l=1,\cr t(a_0+a_1), & l=2.\end{array} \right.\end{align*} $$
$$ \begin{align*}a^l(t)=\left\{\begin{array}{ll}a_0+t(a_1-a_0), & l=1,\cr t(a_0+a_1), & l=2.\end{array} \right.\end{align*} $$
By the following claim, we can easily construct a continuous function
![]() $F^l_j:[0,1]\rightarrow {\mathbb {R}}$
for each
$F^l_j:[0,1]\rightarrow {\mathbb {R}}$
for each
![]() $l\in \{1,2\}$
and
$l\in \{1,2\}$
and
![]() $k\in \omega $
such that
$k\in \omega $
such that
The nontrivial part of the construction, i.e.,
![]() $j=2k+1$
, follows from a more general claim.
$j=2k+1$
, follows from a more general claim.
Claim 1. Given a continuous function
![]() $\gamma :[0,1]\rightarrow {\mathbb {T}}$
and
$\gamma :[0,1]\rightarrow {\mathbb {T}}$
and
![]() $t_0\in [0,1]$
with
$t_0\in [0,1]$
with
![]() $\exp (\mathrm {i} s_0)=\gamma (t_0)$
for some
$\exp (\mathrm {i} s_0)=\gamma (t_0)$
for some
![]() $s_0\in {\mathbb {R}}$
, there exists a continuous function
$s_0\in {\mathbb {R}}$
, there exists a continuous function
![]() $\widetilde {\gamma }:[0,1]\rightarrow {\mathbb {R}}$
such that
$\widetilde {\gamma }:[0,1]\rightarrow {\mathbb {R}}$
such that
![]() $\exp (\mathrm {i}\widetilde {\gamma }(t))=\gamma (t)$
and
$\exp (\mathrm {i}\widetilde {\gamma }(t))=\gamma (t)$
and
![]() $\widetilde {\gamma }(t_0)=s_0$
.
$\widetilde {\gamma }(t_0)=s_0$
.
Proof Note that the map
![]() $t\mapsto \exp (\mathrm {i} t)$
is a covering map from
$t\mapsto \exp (\mathrm {i} t)$
is a covering map from
![]() ${\mathbb {R}}$
to
${\mathbb {R}}$
to
![]() ${\mathbb {T}}$
, and the interval
${\mathbb {T}}$
, and the interval
![]() $[0,1]$
is simply connected (see Definitions A2.1 and Proposition A2.8 of [Reference Hofmann and Morris11]). So such a
$[0,1]$
is simply connected (see Definitions A2.1 and Proposition A2.8 of [Reference Hofmann and Morris11]). So such a
![]() $\widetilde {\gamma }$
exists (cf. [Reference Hofmann and Morris11, Definition A2.6]).
$\widetilde {\gamma }$
exists (cf. [Reference Hofmann and Morris11, Definition A2.6]).
For the convenience of readers, we briefly explain the construction of
![]() $\widetilde {\gamma }$
. Since the map
$\widetilde {\gamma }$
. Since the map
![]() $t\mapsto \exp (it)$
is a local homeomorphism, by the continuity of
$t\mapsto \exp (it)$
is a local homeomorphism, by the continuity of
![]() $\gamma $
, for each
$\gamma $
, for each
![]() $u\in [0,1]$
, there is an open interval
$u\in [0,1]$
, there is an open interval
![]() $J_u$
containing u and a continuous function
$J_u$
containing u and a continuous function
![]() $\widetilde {\gamma _u}:J_u\cap [0,1]\to {\mathbb {R}}$
such that
$\widetilde {\gamma _u}:J_u\cap [0,1]\to {\mathbb {R}}$
such that
![]() $\sup _{t,t'\in J_u\cap [0,1]}|\gamma (t)-\gamma (t')|<\frac {1}{2}$
and
$\sup _{t,t'\in J_u\cap [0,1]}|\gamma (t)-\gamma (t')|<\frac {1}{2}$
and
![]() $\exp (\mathrm { i}\widetilde {\gamma _u}(t))=\gamma (t)$
for
$\exp (\mathrm { i}\widetilde {\gamma _u}(t))=\gamma (t)$
for
![]() $t\in J_u\cap [0,1]$
. Note that
$t\in J_u\cap [0,1]$
. Note that
![]() $\exp (\mathrm {i}(\widetilde {\gamma _u}(t)+2p\pi ))=\exp (\mathrm {i}\widetilde {\gamma _u}(t))$
for each
$\exp (\mathrm {i}(\widetilde {\gamma _u}(t)+2p\pi ))=\exp (\mathrm {i}\widetilde {\gamma _u}(t))$
for each
![]() $p\in {\mathbb {Z}}$
. By the compactness of
$p\in {\mathbb {Z}}$
. By the compactness of
![]() $[0,1]$
, there are
$[0,1]$
, there are
![]() $u_0,u_1,\dots ,u_q\in [0,1]$
such that
$u_0,u_1,\dots ,u_q\in [0,1]$
such that
![]() $[0,1]\subseteq \bigcup _{0\leq i\leq q} J_{u_i}$
. We can find
$[0,1]\subseteq \bigcup _{0\leq i\leq q} J_{u_i}$
. We can find
![]() $0=p_0,p_1,\dots ,p_q\in \mathbb {Z}$
such that for each
$0=p_0,p_1,\dots ,p_q\in \mathbb {Z}$
such that for each
![]() $t\in J_{u_i}\cap J_{u_j}\cap [0,1]$
, we have
$t\in J_{u_i}\cap J_{u_j}\cap [0,1]$
, we have
![]() $\widetilde {\gamma _{u_i}}(t)+2p_i\pi =\widetilde {\gamma _{u_j}}(t)+2p_j\pi $
. Then for
$\widetilde {\gamma _{u_i}}(t)+2p_i\pi =\widetilde {\gamma _{u_j}}(t)+2p_j\pi $
. Then for
![]() $t\in [0,1]\cap J_{u_i}$
, let
$t\in [0,1]\cap J_{u_i}$
, let
![]() $\widetilde \gamma '(t)=\widetilde {\gamma _{u_i}}(t)+2p_i\pi $
. In the end, we put
$\widetilde \gamma '(t)=\widetilde {\gamma _{u_i}}(t)+2p_i\pi $
. In the end, we put
![]() $\widetilde {\gamma }(t)=\widetilde \gamma '(t)-\widetilde \gamma '(t_0)+s_0$
. It is obvious that
$\widetilde {\gamma }(t)=\widetilde \gamma '(t)-\widetilde \gamma '(t_0)+s_0$
. It is obvious that
![]() $\exp (\mathrm {i}\widetilde {\gamma }(t))=\gamma (t)$
and
$\exp (\mathrm {i}\widetilde {\gamma }(t))=\gamma (t)$
and
![]() $\widetilde {\gamma }(t_0)=s_0$
.
$\widetilde {\gamma }(t_0)=s_0$
.
Note that
![]() $S(f(a^2(0)))=1_H$
. We can assume that
$S(f(a^2(0)))=1_H$
. We can assume that
![]() $F^2_j(0)=0$
for each j.
$F^2_j(0)=0$
for each j.
Next we claim that
![]() $F^l_j$
are linear functions.
$F^l_j$
are linear functions.
Claim 2.
![]() $F^l_j(t)=F^l_j(0)+t(F^l_j(1)-F^l_j(0))$
for
$F^l_j(t)=F^l_j(0)+t(F^l_j(1)-F^l_j(0))$
for
![]() $t\in [0,1]$
.
$t\in [0,1]$
.
Proof We only verify the claim for
![]() $l=1$
. It is similar for
$l=1$
. It is similar for
![]() $l=2$
.
$l=2$
.
Fix
![]() $j_0\in \omega $
. Define
$j_0\in \omega $
. Define
![]() $\gamma :[0,1]\to {\mathbb {R}}$
as
$\gamma :[0,1]\to {\mathbb {R}}$
as
![]() $\gamma (t)=F^1_{j_0}(t)-F^1_{j_0}(0)-t(F^1_{j_0}(1)-F^1_{j_0}(0))$
. Note that
$\gamma (t)=F^1_{j_0}(t)-F^1_{j_0}(0)-t(F^1_{j_0}(1)-F^1_{j_0}(0))$
. Note that
![]() $\gamma $
is continuous and
$\gamma $
is continuous and
![]() $\gamma (0)=\gamma (1)=0$
. We only need to prove that
$\gamma (0)=\gamma (1)=0$
. We only need to prove that
![]() $\gamma (t)=0$
for all
$\gamma (t)=0$
for all
![]() $t\in (0,1)$
.
$t\in (0,1)$
.
If not, without loss of generality we may assume that
![]() $\gamma (t_0)>0$
for some
$\gamma (t_0)>0$
for some
![]() $t_0\in (0,1)$
. Similar to the proof of [Reference Ding and Zheng5, Lemma 6.17], we can find
$t_0\in (0,1)$
. Similar to the proof of [Reference Ding and Zheng5, Lemma 6.17], we can find
![]() $0<\xi _0<\xi _1<\xi _2<\cdots <\xi <1$
such that
$0<\xi _0<\xi _1<\xi _2<\cdots <\xi <1$
such that
![]() $\gamma (\xi _k)=\frac {k+1}{k+2}\gamma (t_0)$
for each
$\gamma (\xi _k)=\frac {k+1}{k+2}\gamma (t_0)$
for each
![]() $k\in \omega $
, and
$k\in \omega $
, and
![]() $1>\zeta _0>\zeta _1>\zeta _2>\cdots >\zeta >0, K\in \omega $
such that, for
$1>\zeta _0>\zeta _1>\zeta _2>\cdots >\zeta >0, K\in \omega $
such that, for
![]() $k\ge K$
, we have
$k\ge K$
, we have
![]() $\lim _k \xi _k=\xi $
,
$\lim _k \xi _k=\xi $
,
![]() $\lim _k \zeta _k=\zeta $
,
$\lim _k \zeta _k=\zeta $
,
![]() $\gamma (\xi )=\gamma (t_0)$
, and
$\gamma (\xi )=\gamma (t_0)$
, and
![]() $\gamma (\zeta )>\gamma (\zeta _k)$
for each k.
$\gamma (\zeta )>\gamma (\zeta _k)$
for each k.
Note that
![]() $f:{\mathbb {R}}^m\rightarrow G$
is a nonzero continuous homomorphism. For
$f:{\mathbb {R}}^m\rightarrow G$
is a nonzero continuous homomorphism. For
![]() $p\in \omega $
, we set
$p\in \omega $
, we set
 $$ \begin{align*}x(p)=\left\{\begin{array}{ll}f(a^1(\xi)), & p=2k,\cr f(a^1(\zeta)), & p=2k+1,\end{array} \right.\quad y(p)=\left\{\begin{array}{ll}f(a^1(\xi_k)), & p=2k,\cr f(a^1(\zeta_k)), & p=2k+1.\end{array} \right.\end{align*} $$
$$ \begin{align*}x(p)=\left\{\begin{array}{ll}f(a^1(\xi)), & p=2k,\cr f(a^1(\zeta)), & p=2k+1,\end{array} \right.\quad y(p)=\left\{\begin{array}{ll}f(a^1(\xi_k)), & p=2k,\cr f(a^1(\zeta_k)), & p=2k+1.\end{array} \right.\end{align*} $$
From the alternating series test, the following series:
is convergent. Then
 $$ \begin{align*}\begin{array}{ll} &x(0)x(1)\dots x(2k)y(2k)^{-1}\dots y(1)^{-1}y(0)^{-1} \cr =&x(0)y(0)^{-1}x(1)y(1)^{-1}\dots x(2k)y(2k)^{-1}\cr =&f(((\xi-\xi_0)+(\zeta-\zeta_0)+\cdots+(\xi-\xi_k))(a_1-a_0)).\cr \end{array}\end{align*} $$
$$ \begin{align*}\begin{array}{ll} &x(0)x(1)\dots x(2k)y(2k)^{-1}\dots y(1)^{-1}y(0)^{-1} \cr =&x(0)y(0)^{-1}x(1)y(1)^{-1}\dots x(2k)y(2k)^{-1}\cr =&f(((\xi-\xi_0)+(\zeta-\zeta_0)+\cdots+(\xi-\xi_k))(a_1-a_0)).\cr \end{array}\end{align*} $$
Since f is continuous and
![]() $\lim _p x(p)y(p)^{-1}=1_G$
, we have
$\lim _p x(p)y(p)^{-1}=1_G$
, we have
![]() $xE_*(G)y$
. And hence, by Remark 2.6, we have
$xE_*(G)y$
. And hence, by Remark 2.6, we have
![]() $S(x)E_*(H)S(y)$
.
$S(x)E_*(H)S(y)$
.
On the other hand, we have
 $$ \begin{align*}\sum_k(\gamma(\xi)-\gamma(\xi_k)+\gamma(\zeta)-\gamma(\zeta_k))\ge\sum_k(\gamma(\xi)-\gamma(\xi_k))=\sum_k\frac{\gamma(t_0)}{k+2}=\infty.\end{align*} $$
$$ \begin{align*}\sum_k(\gamma(\xi)-\gamma(\xi_k)+\gamma(\zeta)-\gamma(\zeta_k))\ge\sum_k(\gamma(\xi)-\gamma(\xi_k))=\sum_k\frac{\gamma(t_0)}{k+2}=\infty.\end{align*} $$
Note that
 $$ \begin{align*}\begin{array}{ll} &F^1_{j_0}(\xi)-F^1_{j_0}(\xi_k)+F^1_{j_0}(\zeta)-F^1_{j_0}(\zeta_k)\cr =&\gamma(\xi)-\gamma(\xi_k)+\gamma(\zeta)-\gamma(\zeta_k)+(\xi-\xi_k+\zeta-\zeta_k)(F^1_{j_0}(1)-F^1_{j_0}(0)).\cr \end{array}\end{align*} $$
$$ \begin{align*}\begin{array}{ll} &F^1_{j_0}(\xi)-F^1_{j_0}(\xi_k)+F^1_{j_0}(\zeta)-F^1_{j_0}(\zeta_k)\cr =&\gamma(\xi)-\gamma(\xi_k)+\gamma(\zeta)-\gamma(\zeta_k)+(\xi-\xi_k+\zeta-\zeta_k)(F^1_{j_0}(1)-F^1_{j_0}(0)).\cr \end{array}\end{align*} $$
If
![]() $j_0=2i$
, then
$j_0=2i$
, then
 $$ \begin{align*}\begin{array}{ll} &\phi^{2i}(S(x(0))S(x(1))\dots S(x(2k))S(y(2k))^{-1}\dots S(y(1))^{-1}S(y(0))^{-1})\cr =&F^1_{j_0}(\xi)-F^1_{j_0}(\xi_0)+F^1_{j_0}(\zeta)-F^1_{j_0}(\zeta_0)+\cdots+F^1_{j_0}(\xi)-F^1_{j_0}(\xi_k).\cr \end{array}\end{align*} $$
$$ \begin{align*}\begin{array}{ll} &\phi^{2i}(S(x(0))S(x(1))\dots S(x(2k))S(y(2k))^{-1}\dots S(y(1))^{-1}S(y(0))^{-1})\cr =&F^1_{j_0}(\xi)-F^1_{j_0}(\xi_0)+F^1_{j_0}(\zeta)-F^1_{j_0}(\zeta_0)+\cdots+F^1_{j_0}(\xi)-F^1_{j_0}(\xi_k).\cr \end{array}\end{align*} $$
Thus
![]() $S(x)E_*(H)S(y)$
fails. We get a contradiction. If
$S(x)E_*(H)S(y)$
fails. We get a contradiction. If
![]() $j_0=2i+1$
, following similar arguments, we can also get a contradiction. This complete the proof of the claim.
$j_0=2i+1$
, following similar arguments, we can also get a contradiction. This complete the proof of the claim.
Now by Claim 2 and
![]() $F^2_j(0)=0$
, we know that
$F^2_j(0)=0$
, we know that
By comparing equation
![]() $(*)$
before Claim 1, it follows that
$(*)$
before Claim 1, it follows that
Since
![]() $a^1(1/2)=a^2(1/2)$
, we have
$a^1(1/2)=a^2(1/2)$
, we have
![]() $S(g_0)S(g_1)=S(g_0g_1)$
.
$S(g_0)S(g_1)=S(g_0g_1)$
.
So, the map
![]() $S:f({\mathbb {R}}^m)\rightarrow H_0$
is a continuous homomorphism.
$S:f({\mathbb {R}}^m)\rightarrow H_0$
is a continuous homomorphism.
Let us recall the structure of Hausdorff locally compact abelian groups. Let G be a Hausdorff locally compact abelian group, then G is topologically isomorphic to the group
![]() ${\mathbb {R}}^n\times H$
, where H is a locally compact abelian group containing a compact open subgroup (cf. [Reference Hewitt and Ross10, Theorem 24.30]). Moreover, if G is also connected, then it is a direct product of a compact connected abelian group K and the group
${\mathbb {R}}^n\times H$
, where H is a locally compact abelian group containing a compact open subgroup (cf. [Reference Hewitt and Ross10, Theorem 24.30]). Moreover, if G is also connected, then it is a direct product of a compact connected abelian group K and the group
![]() ${\mathbb {R}}^n$
(cf. [Reference Hewitt and Ross10, Theorem 9.14]). Any locally compact connected metrizable abelian group can be embedded as a closed subgroup of
${\mathbb {R}}^n$
(cf. [Reference Hewitt and Ross10, Theorem 9.14]). Any locally compact connected metrizable abelian group can be embedded as a closed subgroup of
![]() ${\mathbb {R}}^n\times {\mathbb {T}}^{\omega }$
. In particular, all compact metrizable abelian groups can be embedded in
${\mathbb {R}}^n\times {\mathbb {T}}^{\omega }$
. In particular, all compact metrizable abelian groups can be embedded in
![]() ${\mathbb {T}}^{\omega }$
(see page 119 of [Reference Armacost1]). G is said to be solenoidal if there is a continuous homomorphism
${\mathbb {T}}^{\omega }$
(see page 119 of [Reference Armacost1]). G is said to be solenoidal if there is a continuous homomorphism
![]() $f: \ {\mathbb {R}}\rightarrow G$
such that
$f: \ {\mathbb {R}}\rightarrow G$
such that
![]() $f({\mathbb {R}})$
is dense in G (see [Reference Hewitt and Ross10, (9.2)]). It is well known that a compact metrizable abelian group is solenoidal iff it is connected (see page 13 and Proposition 5.16 of [Reference Armacost1]). Thus for each locally compact connected metrizable abelian group G, there is a continuous homomorphism
$f({\mathbb {R}})$
is dense in G (see [Reference Hewitt and Ross10, (9.2)]). It is well known that a compact metrizable abelian group is solenoidal iff it is connected (see page 13 and Proposition 5.16 of [Reference Armacost1]). Thus for each locally compact connected metrizable abelian group G, there is a continuous homomorphism
![]() $f: \ {\mathbb {R}}^m \rightarrow G$
which satisfies
$f: \ {\mathbb {R}}^m \rightarrow G$
which satisfies
![]() $\overline {f({\mathbb {R}}^m)}=G$
. For more details on locally compact abelian groups, we refer to [Reference Armacost1, Reference Hewitt and Ross10].
$\overline {f({\mathbb {R}}^m)}=G$
. For more details on locally compact abelian groups, we refer to [Reference Armacost1, Reference Hewitt and Ross10].
By applying Lemma 2.7 for locally compact abelian Polish groups, we get the following result.
Theorem 2.8. Let G and H be two locally compact abelian Polish groups. If
![]() $E(G)\leq _B E(H)$
, then there is a continuous homomorphism
$E(G)\leq _B E(H)$
, then there is a continuous homomorphism
![]() $S:G_0\rightarrow H_0$
such that
$S:G_0\rightarrow H_0$
such that
![]() $\ker (S)$
is non-archimedean.
$\ker (S)$
is non-archimedean.
Proof If
![]() $E(G)\leq _B E(H)$
, then
$E(G)\leq _B E(H)$
, then
![]() $E_*(G)\leq _B E_*(H)$
. Without loss of generality we may assume that
$E_*(G)\leq _B E_*(H)$
. Without loss of generality we may assume that
![]() $G_0$
is nontrivial. First note that
$G_0$
is nontrivial. First note that
![]() $H_0$
can be embedded into
$H_0$
can be embedded into
![]() ${\mathbb {R}}^n\times {\mathbb {T}}^{\omega }$
. Thus we may assume without loss of generality that
${\mathbb {R}}^n\times {\mathbb {T}}^{\omega }$
. Thus we may assume without loss of generality that
![]() $H_0\subseteq {\mathbb {R}}^{\omega }\times {\mathbb {T}}^{\omega }$
. Let f be a continuous homomorphism from
$H_0\subseteq {\mathbb {R}}^{\omega }\times {\mathbb {T}}^{\omega }$
. Let f be a continuous homomorphism from
![]() ${\mathbb {R}}^m$
to
${\mathbb {R}}^m$
to
![]() $G_0$
with
$G_0$
with
![]() $\overline {f({\mathbb {R}}^m)}=G_0$
. Then by Lemma 2.7 there exists a continuous map
$\overline {f({\mathbb {R}}^m)}=G_0$
. Then by Lemma 2.7 there exists a continuous map
![]() $S:G_0\rightarrow H_0$
such that the map S restricted on
$S:G_0\rightarrow H_0$
such that the map S restricted on
![]() $f({\mathbb {R}}^m)$
is a homomorphism to
$f({\mathbb {R}}^m)$
is a homomorphism to
![]() $H_0$
. Since
$H_0$
. Since
![]() $f({\mathbb {R}}^m)$
is dense in
$f({\mathbb {R}}^m)$
is dense in
![]() $G_0$
, we see that S is a homomorphism from
$G_0$
, we see that S is a homomorphism from
![]() $G_0$
to
$G_0$
to
![]() $H_0$
.
$H_0$
.
Then we only need to check that
![]() $\ker (S)$
is non-archimedean. Assume toward a contradiction that
$\ker (S)$
is non-archimedean. Assume toward a contradiction that
![]() $\ker (S)$
is not non-archimedean.
$\ker (S)$
is not non-archimedean.
Note that
![]() $\ker (S)$
is an abelian Polish group. Fix a compatible two-sided invariant metric on
$\ker (S)$
is an abelian Polish group. Fix a compatible two-sided invariant metric on
![]() $\ker (S)$
. Let
$\ker (S)$
. Let
![]() $V_k\subseteq \ker (S),\,k\in \omega $
be an open symmetric neighborhood base of
$V_k\subseteq \ker (S),\,k\in \omega $
be an open symmetric neighborhood base of
![]() $1_{\ker (S)}=1_G$
with
$1_{\ker (S)}=1_G$
with
![]() $\lim _k{\mathrm {diam}\,}(V_k)=0$
. Then there exists a
$\lim _k{\mathrm {diam}\,}(V_k)=0$
. Then there exists a
![]() $k_0\in \omega $
such that
$k_0\in \omega $
such that
![]() $V_{k_0}$
does not contain any open subgroup of
$V_{k_0}$
does not contain any open subgroup of
![]() $\ker (S)$
. Since
$\ker (S)$
. Since
![]() $V_k$
is symmetric,
$V_k$
is symmetric,
![]() $\bigcup _m V_k^m$
is an open subgroup of
$\bigcup _m V_k^m$
is an open subgroup of
![]() $\ker (S)$
, so
$\ker (S)$
, so
![]() $\bigcup _m V_k^m\nsubseteq V_{k_0}$
for each k. Thus we can find an
$\bigcup _m V_k^m\nsubseteq V_{k_0}$
for each k. Thus we can find an
![]() $m_k\in \omega $
and
$m_k\in \omega $
and
![]() $g_{k,0},\dots ,g_{k,m_k-1}\in V_k$
such that
$g_{k,0},\dots ,g_{k,m_k-1}\in V_k$
such that
![]() $g_{k,0}g_{k,1}\ldots g_{k,m_k-1}\notin V_{k_0}$
.
$g_{k,0}g_{k,1}\ldots g_{k,m_k-1}\notin V_{k_0}$
.
Denote
![]() $M_{-1}=0$
and
$M_{-1}=0$
and
![]() $M_k=m_0+m_1+\dots +m_k$
for
$M_k=m_0+m_1+\dots +m_k$
for
![]() $k\in \omega $
. Now for
$k\in \omega $
. Now for
![]() $n\in \omega $
, define
$n\in \omega $
, define
 $$ \begin{align*}x(n)=\left\{\begin{array}{ll}g_{k,j}, &n=M_{k-1}+j,0\leq j<m_k,\cr 1_G, & \mbox{otherwise.}\end{array} \right.\end{align*} $$
$$ \begin{align*}x(n)=\left\{\begin{array}{ll}g_{k,j}, &n=M_{k-1}+j,0\leq j<m_k,\cr 1_G, & \mbox{otherwise.}\end{array} \right.\end{align*} $$
Therefore
![]() $xE_*(G)1_{G^{\omega }}$
fails. Note that we have
$xE_*(G)1_{G^{\omega }}$
fails. Note that we have
![]() $\lim _nx(n)=1_G$
and
$\lim _nx(n)=1_G$
and
![]() $S(x(n))=1_H$
for each n. So it is trivial that
$S(x(n))=1_H$
for each n. So it is trivial that
![]() $S(x)E_*(H_0)S(1_{G^{\omega }})$
, where
$S(x)E_*(H_0)S(1_{G^{\omega }})$
, where
![]() $S(x)(n)=S(x(n))$
, contradicting Lemma 2.5.
$S(x)(n)=S(x(n))$
, contradicting Lemma 2.5.
In particular, if G is compact connected, then the converse of Theorem 2.8 is also true.
Theorem 2.9 (Rigid Theorem).
Let G be a compact connected abelian Polish group and let H be a locally compact abelian Polish group. Then
![]() $E(G)\leq _B E(H)$
iff there is a continuous homomorphism
$E(G)\leq _B E(H)$
iff there is a continuous homomorphism
![]() $S:G\rightarrow H$
such that
$S:G\rightarrow H$
such that
![]() $\ker (S)$
is non-archimedean.
$\ker (S)$
is non-archimedean.
Proof Let S be a continuous homomorphism from G to H such that
![]() $\ker (S)$
is non-archimedean. Since G is compact,
$\ker (S)$
is non-archimedean. Since G is compact,
![]() $S(G)$
is a compact, thus closed subgroup of H. So we have
$S(G)$
is a compact, thus closed subgroup of H. So we have
![]() $E(S(G))\le _BE(H)$
.
$E(S(G))\le _BE(H)$
.
Note that
![]() $S(G)$
is also a compact connected abelian Polish group. Let f be a continuous homomorphism
$S(G)$
is also a compact connected abelian Polish group. Let f be a continuous homomorphism
![]() $f:{\mathbb {R}}\rightarrow S(G)$
such that
$f:{\mathbb {R}}\rightarrow S(G)$
such that
![]() $\overline {f({\mathbb {R}})}=S(G)$
. Then
$\overline {f({\mathbb {R}})}=S(G)$
. Then
![]() $\ker (f)$
is a proper closed subgroup of
$\ker (f)$
is a proper closed subgroup of
![]() ${\mathbb {R}}$
. Hence
${\mathbb {R}}$
. Hence
![]() $\ker (f)$
is a discrete group. This gives that the interval
$\ker (f)$
is a discrete group. This gives that the interval
![]() $[0,1]$
embeds in
$[0,1]$
embeds in
![]() $S(G)$
. Then by Lemma 2.4, we get that
$S(G)$
. Then by Lemma 2.4, we get that
![]() $E(G)\leq _B E(S(G))\le _BE(H)$
.
$E(G)\leq _B E(S(G))\le _BE(H)$
.
On the other hand, if
![]() $E(G)\le _BE(H)$
, by Theorem 2.8, there is a continuous homomorphism
$E(G)\le _BE(H)$
, by Theorem 2.8, there is a continuous homomorphism
![]() $S:G_0\to H_0$
such that
$S:G_0\to H_0$
such that
![]() $\ker (S)$
is non-archimedean. Since G is connected, we have
$\ker (S)$
is non-archimedean. Since G is connected, we have
![]() $G=G_0$
.
$G=G_0$
.
Corollary 2.10. Let G be a compact connected abelian Polish group and let H be a locally compact abelian Polish group. Suppose
![]() $H_0\cong {\mathbb {R}}^n\times K$
, where K is a compact connected abelian group. Then
$H_0\cong {\mathbb {R}}^n\times K$
, where K is a compact connected abelian group. Then
![]() $E(G)\le _BE(H)$
iff
$E(G)\le _BE(H)$
iff
![]() $E(G)\le _BE(K)$
.
$E(G)\le _BE(K)$
.
Proof
![]() $(\Leftarrow )$
part is trivial, since
$(\Leftarrow )$
part is trivial, since
![]() $E(K)\le _BE(H_0)\le _BE(H)$
.
$E(K)\le _BE(H_0)\le _BE(H)$
.
![]() $(\Rightarrow )$
. If
$(\Rightarrow )$
. If
![]() $E(G)\le _BE(H)$
, then there exists a continuous homomorphism
$E(G)\le _BE(H)$
, then there exists a continuous homomorphism
![]() $S:G\to H$
such that
$S:G\to H$
such that
![]() $\ker (S)$
is non-archimedean. So
$\ker (S)$
is non-archimedean. So
![]() $S(G)$
is a connected compact subgroup of H, thus
$S(G)$
is a connected compact subgroup of H, thus
![]() $S(G)\subseteq H_0$
. Without loss of generality, we assume that
$S(G)\subseteq H_0$
. Without loss of generality, we assume that
![]() $H_0={\mathbb {R}}^n\times K$
. Let
$H_0={\mathbb {R}}^n\times K$
. Let
![]() $\pi :H_0\to {\mathbb {R}}^n$
and
$\pi :H_0\to {\mathbb {R}}^n$
and
![]() $\pi _K:H_0\to K$
be canonical projections. Then
$\pi _K:H_0\to K$
be canonical projections. Then
![]() $\pi (S(G))$
is a compact subgroup of
$\pi (S(G))$
is a compact subgroup of
![]() ${\mathbb {R}}^n$
, so
${\mathbb {R}}^n$
, so
![]() $\pi (S(G))=\{0\}$
. It follows that
$\pi (S(G))=\{0\}$
. It follows that
![]() $\ker (\pi _K\circ S)=\ker (S)$
. Applying Theorem 2.9 on
$\ker (\pi _K\circ S)=\ker (S)$
. Applying Theorem 2.9 on
![]() $\pi _K\circ S:G\to K$
, we have
$\pi _K\circ S:G\to K$
, we have
![]() $E(G)\le _BE(K)$
.
$E(G)\le _BE(K)$
.
Recall that a topological group G is totally disconnected if
![]() $G_0=\{1_G\}$
. For any locally compact abelian Polish group, it is totally disconnected iff it is non-archimedean (cf. [Reference Hofmann and Morris11, Theorem 1.34]).
$G_0=\{1_G\}$
. For any locally compact abelian Polish group, it is totally disconnected iff it is non-archimedean (cf. [Reference Hofmann and Morris11, Theorem 1.34]).
For every normal space X, denoted by
![]() $\dim (X)$
the covering dimension of X, where
$\dim (X)$
the covering dimension of X, where
![]() $\dim (X)$
is an integer
$\dim (X)$
is an integer
![]() $\ge\ -1$
or the “infinite number
$\ge\ -1$
or the “infinite number
![]() $\infty $
.” We omit the definition of covering dimension since it is very complicated (see page 54 of [Reference Engelking6]). We recall the following useful facts concerning compact abelian group G:
$\infty $
.” We omit the definition of covering dimension since it is very complicated (see page 54 of [Reference Engelking6]). We recall the following useful facts concerning compact abelian group G:
![]() $\dim (G)=n<\infty $
iff G has a totally disconnected closed subgroup
$\dim (G)=n<\infty $
iff G has a totally disconnected closed subgroup
![]() $\Delta $
such that
$\Delta $
such that
![]() $G/\Delta \cong {\mathbb {T}}^n$
iff there is a compact totally disconnected subgroup N of G and a continuous surjective homomorphism
$G/\Delta \cong {\mathbb {T}}^n$
iff there is a compact totally disconnected subgroup N of G and a continuous surjective homomorphism
![]() $\varphi :N\times {\mathbb {R}}^n\rightarrow G$
which has a discrete kernel (see Theorem 8.22 and Corollary 8.26 of [Reference Hofmann and Morris11]). In this case, we say that G is finite dimensional (cf. [Reference Hofmann and Morris11, Definitions 8.23]). Clearly,
$\varphi :N\times {\mathbb {R}}^n\rightarrow G$
which has a discrete kernel (see Theorem 8.22 and Corollary 8.26 of [Reference Hofmann and Morris11]). In this case, we say that G is finite dimensional (cf. [Reference Hofmann and Morris11, Definitions 8.23]). Clearly,
![]() $\dim (G)=0$
iff G is totally disconnected. For more details on compact abelian groups, see [Reference Hofmann and Morris11].
$\dim (G)=0$
iff G is totally disconnected. For more details on compact abelian groups, see [Reference Hofmann and Morris11].
Now we recall two equivalence relations
![]() $E_0^{\omega }$
and
$E_0^{\omega }$
and
![]() $E(M;0)$
(see [Reference Ding4, Definition 3.2]). The equivalence relation
$E(M;0)$
(see [Reference Ding4, Definition 3.2]). The equivalence relation
![]() $E_0^{\omega }$
on
$E_0^{\omega }$
on
![]() $2^{\omega \times \omega }$
defined by
$2^{\omega \times \omega }$
defined by
Fix a metric space M. The equivalence relation
![]() $E(M;0)$
on
$E(M;0)$
on
![]() $M^{\omega }$
defined by
$M^{\omega }$
defined by
From the above discussions, we can establish the following theorem.
Theorem 2.11. Let
![]() $G,H$
be locally compact abelian Polish groups.
$G,H$
be locally compact abelian Polish groups.
-
(1) If G is non-archimedean, then
 $E(G)\leq _B E_0^{\omega }$
.
$E(G)\leq _B E_0^{\omega }$
. -
(2) If G is not non-archimedean, then
 $E({\mathbb {R}})\leq _B E(G)$
.
$E({\mathbb {R}})\leq _B E(G)$
. -
(3) If G is not non-archimedean and
 $G_0$
is open, then
$G_0$
is open, then
 $E(G)\sim _B E(G_0)$
.
$E(G)\sim _B E(G_0)$
. -
(4) If n is a positive integer, then
 $E({\mathbb {T}}^n)\leq _B E(G)$
iff
$E({\mathbb {T}}^n)\leq _B E(G)$
iff
 ${\mathbb {T}}^n$
embeds in G.
${\mathbb {T}}^n$
embeds in G. -
(5) If n is a positive integer and G is compact, then G is n-dimensional iff
 $E({\mathbb {R}}^n)<_B E(G)\leq _B E({\mathbb {T}}^n)$
.
$E({\mathbb {R}}^n)<_B E(G)\leq _B E({\mathbb {T}}^n)$
.
Proof (1) It follows from [Reference Ding and Zheng5, Theorem 3.5(3)].
(2) Note that G is not totally disconnected (cf. [Reference Hofmann and Morris11, Theorem 1.34]), so
![]() $G_0$
contains at least two points. We have
$G_0$
contains at least two points. We have
![]() $G_0\cong {\mathbb {R}}^n\times K$
, where K is a compact connected abelian group. If
$G_0\cong {\mathbb {R}}^n\times K$
, where K is a compact connected abelian group. If
![]() $n>0$
, it is trivial that
$n>0$
, it is trivial that
![]() $E({\mathbb {R}})\le _BE(G)$
. By Proposition 2.3,
$E({\mathbb {R}})\le _BE(G)$
. By Proposition 2.3,
![]() $E(K)\le _BE(G_0)\le _BE(G)$
. Thus we may assume that G is compact connected and
$E(K)\le _BE(G_0)\le _BE(G)$
. Thus we may assume that G is compact connected and
![]() $G\subseteq {\mathbb {T}}^{\omega }$
. Note that there is a continuous homomorphism
$G\subseteq {\mathbb {T}}^{\omega }$
. Note that there is a continuous homomorphism
![]() $f: \ {\mathbb {R}}\rightarrow G$
such that
$f: \ {\mathbb {R}}\rightarrow G$
such that
![]() ${\overline {f({\mathbb {R}})}=G}$
. For
${\overline {f({\mathbb {R}})}=G}$
. For
![]() $g\in G\subseteq {\mathbb {T}}^{\omega }$
and
$g\in G\subseteq {\mathbb {T}}^{\omega }$
and
![]() $p\in \omega $
, let
$p\in \omega $
, let
![]() $\phi _p(g)=g(p)$
. Since G contains at least two points, we can find
$\phi _p(g)=g(p)$
. Since G contains at least two points, we can find
![]() ${p_0}\in \omega $
such that
${p_0}\in \omega $
such that
![]() $\phi _{p_0}(f({\mathbb {R}}))\ne \{1_{\mathbb {T}}\}$
, so
$\phi _{p_0}(f({\mathbb {R}}))\ne \{1_{\mathbb {T}}\}$
, so
![]() $\phi _{p_0}(f({\mathbb {R}}))={\mathbb {T}}$
. By [Reference Hofmann and Morris11, Corollary 8.24], the interval
$\phi _{p_0}(f({\mathbb {R}}))={\mathbb {T}}$
. By [Reference Hofmann and Morris11, Corollary 8.24], the interval
![]() $[0,1]$
embeds in G. Then by Lemma 2.4, we have
$[0,1]$
embeds in G. Then by Lemma 2.4, we have
![]() $E({\mathbb {R}})\le _BE(G)$
.
$E({\mathbb {R}})\le _BE(G)$
.
(3) By [Reference Hewitt and Ross10, Section 24.45], we have
![]() $G\cong G_0\times G/G_0$
. Since
$G\cong G_0\times G/G_0$
. Since
![]() $G_0$
is open,
$G_0$
is open,
![]() $G/G_0$
is countable and discrete. By [Reference Ding and Zheng5, Corollary 3.6], this implies that
$G/G_0$
is countable and discrete. By [Reference Ding and Zheng5, Corollary 3.6], this implies that
![]() $E(G_0\times G/G_0)\sim _B E(G_0)$
and thus
$E(G_0\times G/G_0)\sim _B E(G_0)$
and thus
![]() $E(G)\sim _B E(G_0)$
.
$E(G)\sim _B E(G_0)$
.
(4) The “if” part follows Proposition 2.3. Assume that
![]() $E({\mathbb {T}}^n)\le _BE(G)$
. By Theorem 2.8 and [Reference Gao7, Corollary 2.3.4], there is a closed subgroup
$E({\mathbb {T}}^n)\le _BE(G)$
. By Theorem 2.8 and [Reference Gao7, Corollary 2.3.4], there is a closed subgroup
![]() $\Delta $
of
$\Delta $
of
![]() ${\mathbb {T}}^n$
such that the group
${\mathbb {T}}^n$
such that the group
![]() ${\mathbb {T}}^n/\Delta $
can be embedded in G, where
${\mathbb {T}}^n/\Delta $
can be embedded in G, where
![]() $\Delta $
is non-archimedean. It is obvious that
$\Delta $
is non-archimedean. It is obvious that
![]() ${\mathbb {T}}^n/\Delta $
is a locally connected, connected and compact abelian Polish group. By [Reference Armacost1, Proposition 8.17],
${\mathbb {T}}^n/\Delta $
is a locally connected, connected and compact abelian Polish group. By [Reference Armacost1, Proposition 8.17],
![]() ${\mathbb {T}}^n/\Delta \cong {\mathbb {T}}^n$
.
${\mathbb {T}}^n/\Delta \cong {\mathbb {T}}^n$
.
(5) If
![]() $n=\dim (G)$
, then we have
$n=\dim (G)$
, then we have
![]() $(N\times {\mathbb {R}}^n)/\Delta _1\cong G$
and
$(N\times {\mathbb {R}}^n)/\Delta _1\cong G$
and
![]() $G/\Delta _2\cong {\mathbb {T}}^n$
, where
$G/\Delta _2\cong {\mathbb {T}}^n$
, where
![]() $N,\Delta _1$
, and
$N,\Delta _1$
, and
![]() $\Delta _2$
are totally disconnected, and hence are non-archimedean. Then Proposition 2.3 and Lemma 2.4 imply that
$\Delta _2$
are totally disconnected, and hence are non-archimedean. Then Proposition 2.3 and Lemma 2.4 imply that
So we only need to show that
![]() $E(G)\nleq _B E({\mathbb {R}}^n)$
. To see this, assume toward a contradiction that
$E(G)\nleq _B E({\mathbb {R}}^n)$
. To see this, assume toward a contradiction that
![]() $E(G)\leq _B E({\mathbb {R}}^n)$
. By Theorem 2.8, there exists a continuous homomorphism
$E(G)\leq _B E({\mathbb {R}}^n)$
. By Theorem 2.8, there exists a continuous homomorphism
![]() $S:G_0\rightarrow {\mathbb {R}}^n$
such that
$S:G_0\rightarrow {\mathbb {R}}^n$
such that
![]() $\ker (S)$
is non-archimedean. Note that
$\ker (S)$
is non-archimedean. Note that
![]() ${\mathbb {R}}^n$
has no nontrivial compact connected subgroup. So this implies that
${\mathbb {R}}^n$
has no nontrivial compact connected subgroup. So this implies that
![]() $S(G_0)=\{0\}$
, contradicting that
$S(G_0)=\{0\}$
, contradicting that
![]() $\ker (S)$
is non-archimedean.
$\ker (S)$
is non-archimedean.
On the other hand, suppose
![]() $E({\mathbb {R}}^n)<_B E(G)\leq _B E({\mathbb {T}}^n)$
. Let
$E({\mathbb {R}}^n)<_B E(G)\leq _B E({\mathbb {T}}^n)$
. Let
![]() $m=\dim (G)$
. By (1) we have
$m=\dim (G)$
. By (1) we have
![]() $m>0$
. Assume for contradiction that
$m>0$
. Assume for contradiction that
![]() $m=\infty $
, then there exists a continuous homomorphism
$m=\infty $
, then there exists a continuous homomorphism
![]() $S:G_0\rightarrow {\mathbb {T}}^n$
such that
$S:G_0\rightarrow {\mathbb {T}}^n$
such that
![]() $\ker (S)$
is non-archimedean. Then we have
$\ker (S)$
is non-archimedean. Then we have
![]() $\dim (G_0/\ker (S))=\infty $
, and hence
$\dim (G_0/\ker (S))=\infty $
, and hence
![]() $[0,1]^{\omega }$
embeds into
$[0,1]^{\omega }$
embeds into
![]() $G_0/\ker (S)$
(cf. [Reference Hofmann and Morris11, Corollary 8.24]). By [Reference Gao7, Corollary 2.3.4], S induces an embedding from
$G_0/\ker (S)$
(cf. [Reference Hofmann and Morris11, Corollary 8.24]). By [Reference Gao7, Corollary 2.3.4], S induces an embedding from
![]() $G_0/\ker (S)$
to
$G_0/\ker (S)$
to
![]() ${\mathbb {T}}^n$
. So
${\mathbb {T}}^n$
. So
![]() $[0,1]^{\omega }$
embeds into
$[0,1]^{\omega }$
embeds into
![]() ${\mathbb {T}}^n$
, contradicting that n is finite. Therefore, we have
${\mathbb {T}}^n$
, contradicting that n is finite. Therefore, we have
![]() $0<m<\infty $
, and hence
$0<m<\infty $
, and hence
![]() $E({\mathbb {R}}^m)<_BE(G)\le _BE({\mathbb {T}}^m)$
. Then [Reference Ding and Zheng5, Theorem 6.19] gives
$E({\mathbb {R}}^m)<_BE(G)\le _BE({\mathbb {T}}^m)$
. Then [Reference Ding and Zheng5, Theorem 6.19] gives
![]() $m=n$
.
$m=n$
.
Remark 2.12. Let G and H be two locally compact abelian Polish groups. Suppose that
![]() $G_0$
is an open subgroup of G, and that
$G_0$
is an open subgroup of G, and that
![]() $G_0$
is compact or
$G_0$
is compact or
![]() $G_0\cong {\mathbb {R}}$
. Then Theorems 2.8, 2.9, and 2.11(2),(3) imply that
$G_0\cong {\mathbb {R}}$
. Then Theorems 2.8, 2.9, and 2.11(2),(3) imply that
![]() $E(G)\leq _B E(H)$
iff there is a continuous homomorphism
$E(G)\leq _B E(H)$
iff there is a continuous homomorphism
![]() $S:G_0\rightarrow H_0$
such that
$S:G_0\rightarrow H_0$
such that
![]() $\ker (S)$
is non-archimedean. This generalizes Rigid Theorem, i.e., Theorem 2.9. We don’t know whether this can be generalized to all locally compact abelian Polish groups.
$\ker (S)$
is non-archimedean. This generalizes Rigid Theorem, i.e., Theorem 2.9. We don’t know whether this can be generalized to all locally compact abelian Polish groups.
Question 2.13. Does the converse of Theorem 2.8 hold for all locally compact abelian Polish groups?
Question 2.14. Let G be a locally compact abelian Polish group. If G is not non-archimedean, does
![]() $E(G)\sim _B E(G_0)$
?
$E(G)\sim _B E(G_0)$
?
3 P-adic solenoids
Let
![]() $P=(P(0),P(1),\dots )$
be a sequence of integers greater than
$P=(P(0),P(1),\dots )$
be a sequence of integers greater than
![]() $1$
. Recall that the P-adic solenoid
$1$
. Recall that the P-adic solenoid
![]() $S_P$
is defined by
$S_P$
is defined by
In particular, if for each i,
![]() $P(i)$
is a prime number, then the P-adic solenoid is denoted by
$P(i)$
is a prime number, then the P-adic solenoid is denoted by
![]() $\Sigma _P$
(cf. [Reference Gumerov8]). Let
$\Sigma _P$
(cf. [Reference Gumerov8]). Let
![]() $\mathcal {P}$
denote the set of all primes. The group
$\mathcal {P}$
denote the set of all primes. The group
![]() $S_P$
is topologically isomorphic to
$S_P$
is topologically isomorphic to
![]() $\Sigma _{P'}$
for some
$\Sigma _{P'}$
for some
![]() $P'\in \mathcal {P}^{\omega }$
satisfying that
$P'\in \mathcal {P}^{\omega }$
satisfying that
![]() $P(l)=P'(i_l)\ldots P'(i_{l+1}-1)$
, where
$P(l)=P'(i_l)\ldots P'(i_{l+1}-1)$
, where
![]() $0=i_0<i_1<\cdots <i_l<\cdots $
. For example, we have
$0=i_0<i_1<\cdots <i_l<\cdots $
. For example, we have
![]() $S_{(4,6,8,9,\dots ,9,\dots )}\cong \Sigma _{(2,2,2,3,2,2,2,3,3,\dots ,3,3,\dots )}$
.
$S_{(4,6,8,9,\dots ,9,\dots )}\cong \Sigma _{(2,2,2,3,2,2,2,3,3,\dots ,3,3,\dots )}$
.
It is well known that, the group
![]() $\Sigma _P$
is a compact connected abelian group which is neither locally connected (cf. [Reference Gumerov8]), nor arcwise connected (see [Reference Armacost1, Theorem 8.27]). Every nontrivial proper closed subgroup H of a P-adic solenoid is totally disconnected (cf. [Reference Kadri12, Proposition 2.7]), and thus H is non-archimedean. Clearly,
$\Sigma _P$
is a compact connected abelian group which is neither locally connected (cf. [Reference Gumerov8]), nor arcwise connected (see [Reference Armacost1, Theorem 8.27]). Every nontrivial proper closed subgroup H of a P-adic solenoid is totally disconnected (cf. [Reference Kadri12, Proposition 2.7]), and thus H is non-archimedean. Clearly,
![]() $\Sigma _P$
is a
$\Sigma _P$
is a
![]() $1$
-dimensional and metrizable group.
$1$
-dimensional and metrizable group.
Denote
![]() $\Omega =\{{\mathbb {R}},{\mathbb {T}},\Sigma _P:P\in \mathcal {P}^{\omega }\}$
.
$\Omega =\{{\mathbb {R}},{\mathbb {T}},\Sigma _P:P\in \mathcal {P}^{\omega }\}$
.
Lemma 3.1. Let
![]() $m,n\in {\mathbb {N}}^+$
and let
$m,n\in {\mathbb {N}}^+$
and let
![]() $G_1, G_2,\dots ,G_m,H_1,H_2\dots ,H_n\in \Omega $
. Then the following are equivalent:
$G_1, G_2,\dots ,G_m,H_1,H_2\dots ,H_n\in \Omega $
. Then the following are equivalent:
-
(1)
 $E(G_1\times G_2\times \dots \times G_m)\leq _B E(H_1\times H_2\times \dots \times H_n)$
.
$E(G_1\times G_2\times \dots \times G_m)\leq _B E(H_1\times H_2\times \dots \times H_n)$
. -
(2) There is a injective map
 $\theta ^*:\{1,2,\dots ,m\}\rightarrow \{1,2,\dots ,n\}$
such that
$\theta ^*:\{1,2,\dots ,m\}\rightarrow \{1,2,\dots ,n\}$
such that
 $E(G_i)\leq _B E(H_{\theta ^*(i)})$
for
$E(G_i)\leq _B E(H_{\theta ^*(i)})$
for
 $1\leq i\le m$
.
$1\leq i\le m$
.
In particular,
![]() $E(G_1^m)\leq _B E(H_1^n)$
iff
$E(G_1^m)\leq _B E(H_1^n)$
iff
![]() $m\le n$
and
$m\le n$
and
![]() $E(G_1)\leq _B E(H_1)$
.
$E(G_1)\leq _B E(H_1)$
.
Proof
![]() $(2)\Rightarrow (1)$
is obvious. We only prove
$(2)\Rightarrow (1)$
is obvious. We only prove
![]() $(1)\Rightarrow (2)$
.
$(1)\Rightarrow (2)$
.
Denote
![]() $G=G_1\times G_2\times \dots \times G_m$
and
$G=G_1\times G_2\times \dots \times G_m$
and
![]() $H=H_1\times H_2\times \dots \times H_n$
. For
$H=H_1\times H_2\times \dots \times H_n$
. For
![]() $1\leq i\le m$
, let
$1\leq i\le m$
, let
![]() $e^i$
be the canonical injection of
$e^i$
be the canonical injection of
![]() $G_i$
into
$G_i$
into
![]() $G_1 \times \cdots \times G_m$
, i.e.,
$G_1 \times \cdots \times G_m$
, i.e.,
![]() $e^i(g)=(1_{G_1},\dots ,1_{G_{i-1}},g,1_{G_{i+1}},\dots ,1_{G_m})$
.
$e^i(g)=(1_{G_1},\dots ,1_{G_{i-1}},g,1_{G_{i+1}},\dots ,1_{G_m})$
.
Suppose
![]() $E(G)\le _B E(H)$
. Since G and H are both connected, by Theorem 2.8, there is a continuous homomorphism
$E(G)\le _B E(H)$
. Since G and H are both connected, by Theorem 2.8, there is a continuous homomorphism
![]() $S:G\rightarrow H$
such that
$S:G\rightarrow H$
such that
![]() $\ker (S)$
is non-archimedean. For each
$\ker (S)$
is non-archimedean. For each
![]() $1\leq j\le n$
, let
$1\leq j\le n$
, let
![]() $\pi _{j}$
be the canonical projection from H onto
$\pi _{j}$
be the canonical projection from H onto
![]() $H_j$
.
$H_j$
.
Note that, except for
![]() ${\mathbb {R}}$
, all groups in
${\mathbb {R}}$
, all groups in
![]() $\Omega $
are compact. By rearranging, we may assume that there is an
$\Omega $
are compact. By rearranging, we may assume that there is an
![]() $i_0\le m$
such that,
$i_0\le m$
such that,
![]() $G_i$
is compact for
$G_i$
is compact for
![]() $1\le i\le i_0$
, and
$1\le i\le i_0$
, and
![]() $G_i={\mathbb {R}}$
for
$G_i={\mathbb {R}}$
for
![]() $i_0<i\le m$
.
$i_0<i\le m$
.
For any
![]() $1\leq i\le i_0$
, since
$1\leq i\le i_0$
, since
![]() $\ker (S)$
is non-archimedean, there exists j satisfying that
$\ker (S)$
is non-archimedean, there exists j satisfying that
![]() $\pi _{j}(S(e^i(G_i)))\not =\{1_{H_j}\}$
. Note that
$\pi _{j}(S(e^i(G_i)))\not =\{1_{H_j}\}$
. Note that
![]() $H_j$
has no nontrivial proper connected compact subgroup. It follows that
$H_j$
has no nontrivial proper connected compact subgroup. It follows that
![]() $\pi _{j}(S(e^i(G_i)))=H_j$
. Now we construct a bipartite graph
$\pi _{j}(S(e^i(G_i)))=H_j$
. Now we construct a bipartite graph
![]() $G[X,Y]$
as follows. Let
$G[X,Y]$
as follows. Let
![]() $X=\{G_1,G_2,\dots ,G_{i_0}\}$
,
$X=\{G_1,G_2,\dots ,G_{i_0}\}$
,
For
![]() $G_i\in X$
and
$G_i\in X$
and
![]() $H_j\in Y$
, we put an edge between
$H_j\in Y$
, we put an edge between
![]() $G_i$
and
$G_i$
and
![]() $H_j$
if
$H_j$
if
![]() $\pi _{j}(S(e^i(G_i)))=H_j$
. Given
$\pi _{j}(S(e^i(G_i)))=H_j$
. Given
![]() $K\subseteq X$
, we denote the set of all neighbors of the vertices in K by
$K\subseteq X$
, we denote the set of all neighbors of the vertices in K by
![]() $N(K)$
.
$N(K)$
.
Next we show that
![]() $\left |N(K)\right |\geq \left |K\right |$
for all
$\left |N(K)\right |\geq \left |K\right |$
for all
![]() $K\subseteq X$
. Given
$K\subseteq X$
. Given
![]() $K\subseteq X$
, denote
$K\subseteq X$
, denote
Then the restriction of S on
![]() $G^{K}$
is a continuous homomorphism to
$G^{K}$
is a continuous homomorphism to
![]() $H^{N(K)}$
. By Theorem 2.9,
$H^{N(K)}$
. By Theorem 2.9,
![]() $E(G^{K})\le _B E(H^{N(K)})$
. Again by Theorem 2.11(5), this implies
$E(G^{K})\le _B E(H^{N(K)})$
. Again by Theorem 2.11(5), this implies
![]() $E({\mathbb {R}}^{\left |K\right |})\leq _B E({\mathbb {T}}^{\left |N(K)\right |})$
. Then [Reference Ding and Zheng5, Theorem 6.19] gives
$E({\mathbb {R}}^{\left |K\right |})\leq _B E({\mathbb {T}}^{\left |N(K)\right |})$
. Then [Reference Ding and Zheng5, Theorem 6.19] gives
![]() $\left |N(K)\right |\geq \left |K\right |$
.
$\left |N(K)\right |\geq \left |K\right |$
.
By Hall’s theorem (cf. [Reference Bondy and Murty3, Theorem 16.4]), there is a injective map
![]() $\theta ^*:\{1,2,\dots ,i_0\}\rightarrow \{1,2,\dots ,n\}$
such that
$\theta ^*:\{1,2,\dots ,i_0\}\rightarrow \{1,2,\dots ,n\}$
such that
![]() $\pi _{\theta ^*(i)}(S(e^i(G_i)))=H_{\theta ^*(i)}$
. Since every proper closed subgroup of
$\pi _{\theta ^*(i)}(S(e^i(G_i)))=H_{\theta ^*(i)}$
. Since every proper closed subgroup of
![]() $G_i$
is non-archimedean, from Theorem 2.9, we have
$G_i$
is non-archimedean, from Theorem 2.9, we have
![]() $E(G_i)\le _BE(H_{\theta ^*(i)})$
.
$E(G_i)\le _BE(H_{\theta ^*(i)})$
.
In the end, since
![]() $\dim (G)=m$
and
$\dim (G)=m$
and
![]() $\dim (H)=n$
, by Theorem 2.11(5), we have
$\dim (H)=n$
, by Theorem 2.11(5), we have
![]() $E({\mathbb {R}}^m)\le _BE({\mathbb {T}}^n)$
. So
$E({\mathbb {R}}^m)\le _BE({\mathbb {T}}^n)$
. So
![]() $m\le n$
. Since
$m\le n$
. Since
![]() $E({\mathbb {R}})\le _BE(H_j)$
for each j, we can trivially extend
$E({\mathbb {R}})\le _BE(H_j)$
for each j, we can trivially extend
![]() $\theta ^*$
to an injection from
$\theta ^*$
to an injection from
![]() $\{1,2,\dots ,m\}$
to
$\{1,2,\dots ,m\}$
to
![]() $\{1,2,\dots ,n\}$
such that
$\{1,2,\dots ,n\}$
such that
![]() $E(G_i)\le _BE(H_{\theta ^*(i)})$
for each i.
$E(G_i)\le _BE(H_{\theta ^*(i)})$
for each i.
Let P and Q be in
![]() $\mathcal {P}^{\omega }$
. We write
$\mathcal {P}^{\omega }$
. We write
![]() $Q\preceq P$
provided there is a co-finite subset A of
$Q\preceq P$
provided there is a co-finite subset A of
![]() $\omega $
and an injection
$\omega $
and an injection
![]() $f:A\to \omega $
such that
$f:A\to \omega $
such that
![]() $Q(n)=P(f(n))$
for each
$Q(n)=P(f(n))$
for each
![]() $n\in A$
(for more details, see [Reference Gumerov8, Reference Gutek9, Reference Prajs16]).
$n\in A$
(for more details, see [Reference Gumerov8, Reference Gutek9, Reference Prajs16]).
Lemma 3.2 (folklore).
Let P and Q be in
![]() $\mathcal {P}^{\omega }$
. Then the following are equivalent:
$\mathcal {P}^{\omega }$
. Then the following are equivalent:
-
(1) There is a nonzero continuous homomorphism
 $f:\Sigma _P\rightarrow \Sigma _Q$
.
$f:\Sigma _P\rightarrow \Sigma _Q$
. -
(2) There is a surjective continuous homomorphism
 $g:\Sigma _P\rightarrow \Sigma _Q$
.
$g:\Sigma _P\rightarrow \Sigma _Q$
. -
(3) There is a surjective continuous map
 $h:\Sigma _P\rightarrow \Sigma _Q$
.
$h:\Sigma _P\rightarrow \Sigma _Q$
. -
(4)
 $Q\preceq P$
.
$Q\preceq P$
.
Proof
![]() $(2)\Rightarrow (1)$
and
$(2)\Rightarrow (1)$
and
![]() $(2)\Rightarrow (3)$
are obvious.
$(2)\Rightarrow (3)$
are obvious.
![]() $(1)\Rightarrow (2)$
follows immediately from the fact that each nontrivial proper closed subgroup of a P-adic solenoid is totally disconnected. The equivalence of
$(1)\Rightarrow (2)$
follows immediately from the fact that each nontrivial proper closed subgroup of a P-adic solenoid is totally disconnected. The equivalence of
![]() $(3)$
and
$(3)$
and
![]() $(4)$
follows from [Reference Prajs16, Theorem 4.4].
$(4)$
follows from [Reference Prajs16, Theorem 4.4].
It remains to show
![]() $(3)\Rightarrow (1)$
. Let h be a surjective continuous map from
$(3)\Rightarrow (1)$
. Let h be a surjective continuous map from
![]() $\Sigma _P$
to
$\Sigma _P$
to
![]() $\Sigma _Q$
. Without loss of generality assume that
$\Sigma _Q$
. Without loss of generality assume that
![]() $h(1_{\Sigma _P})=1_{\Sigma _Q}$
. Then there exists a continuous homomorphism
$h(1_{\Sigma _P})=1_{\Sigma _Q}$
. Then there exists a continuous homomorphism
![]() $f:\Sigma _P\rightarrow \Sigma _Q$
such that h is homotopic to f (cf. [Reference Scheffer17, Corollary 2]). Since
$f:\Sigma _P\rightarrow \Sigma _Q$
such that h is homotopic to f (cf. [Reference Scheffer17, Corollary 2]). Since
![]() $\Sigma _Q$
is not arcwise connected,
$\Sigma _Q$
is not arcwise connected,
![]() $\ker (f)\ne \Sigma _P$
.
$\ker (f)\ne \Sigma _P$
.
Theorem 3.3. Let P and Q be in
![]() $\mathcal {P}^{\omega }$
. Then
$\mathcal {P}^{\omega }$
. Then
![]() $E(\Sigma _P)\leq _B E(\Sigma _Q)$
iff
$E(\Sigma _P)\leq _B E(\Sigma _Q)$
iff
![]() $Q\preceq P$
iff there is a nonzero continuous homomorphism
$Q\preceq P$
iff there is a nonzero continuous homomorphism
![]() $f:\Sigma _P\rightarrow \Sigma _Q$
.
$f:\Sigma _P\rightarrow \Sigma _Q$
.
Proof Note that every nontrivial proper closed subgroup of
![]() $\Sigma _P$
is non-archimedean. Then this follows from Theorem 2.9 and Lemma 3.2.
$\Sigma _P$
is non-archimedean. Then this follows from Theorem 2.9 and Lemma 3.2.
Let
![]() $\mathrm {Fin}$
denote the set of all finite subsets of
$\mathrm {Fin}$
denote the set of all finite subsets of
![]() $\omega $
. For
$\omega $
. For
![]() $A,B\subseteq \omega $
, we use
$A,B\subseteq \omega $
, we use
![]() $A\subseteq ^* B$
to denote
$A\subseteq ^* B$
to denote
![]() $A\setminus B\in \mathrm {Fin}$
.
$A\setminus B\in \mathrm {Fin}$
.
We prove that, for
![]() $n\in {\mathbb {N}}^+$
, the partially ordered set
$n\in {\mathbb {N}}^+$
, the partially ordered set
![]() $P(\omega )/\mathrm {Fin}$
can be embedded into Borel equivalence relations between
$P(\omega )/\mathrm {Fin}$
can be embedded into Borel equivalence relations between
![]() $E({\mathbb {R}}^n)$
and
$E({\mathbb {R}}^n)$
and
![]() $E({\mathbb {T}}^n)$
.
$E({\mathbb {T}}^n)$
.
Lemma 3.4. Let P be in
![]() $\mathcal {P}^{\omega }$
. Then
$\mathcal {P}^{\omega }$
. Then
![]() $E({\mathbb {R}})<_B E(\Sigma _P)<_B E({\mathbb {T}})$
.
$E({\mathbb {R}})<_B E(\Sigma _P)<_B E({\mathbb {T}})$
.
Proof By Theorem 2.11(5), we have that
![]() $E({\mathbb {R}})<_B E(\Sigma _P)\leq _B E({\mathbb {T}})$
.
$E({\mathbb {R}})<_B E(\Sigma _P)\leq _B E({\mathbb {T}})$
.
Assume toward a contradiction that
![]() $E({\mathbb {T}})\leq _B E(\Sigma _P)$
. From Theorem 2.11(4),
$E({\mathbb {T}})\leq _B E(\Sigma _P)$
. From Theorem 2.11(4),
![]() ${\mathbb {T}}$
embeds in
${\mathbb {T}}$
embeds in
![]() $\Sigma _P$
. This is impossible, since
$\Sigma _P$
. This is impossible, since
![]() $\Sigma _P$
is not arcwise connected and every proper closed subgroup of
$\Sigma _P$
is not arcwise connected and every proper closed subgroup of
![]() $\Sigma _P$
is non-archimedean.
$\Sigma _P$
is non-archimedean.
For
![]() $P\in \mathcal {P}^{\omega }$
and
$P\in \mathcal {P}^{\omega }$
and
![]() $\gamma \in \mathcal {P}$
, we define
$\gamma \in \mathcal {P}$
, we define
![]() $t^{P}(\gamma )\in \omega \cup \{\omega \}$
as
$t^{P}(\gamma )\in \omega \cup \{\omega \}$
as
 $$ \begin{align*}t^{P}(\gamma)=\left\{\begin{array}{ll} \omega, & \exists^{\infty} j\in\omega\,(P(j)=\gamma),\cr \left|\{j:P(j)=\gamma\}\right|, & \mbox{otherwise.}\end{array} \right.\end{align*} $$
$$ \begin{align*}t^{P}(\gamma)=\left\{\begin{array}{ll} \omega, & \exists^{\infty} j\in\omega\,(P(j)=\gamma),\cr \left|\{j:P(j)=\gamma\}\right|, & \mbox{otherwise.}\end{array} \right.\end{align*} $$
Given
![]() $P,Q\in \mathcal {P}^{\omega }$
, denote
$P,Q\in \mathcal {P}^{\omega }$
, denote
From the definition of
![]() $Q\preceq P$
, we can easily see that
$Q\preceq P$
, we can easily see that
Lemma 3.5. Let
![]() $P,Q\in \mathcal {P}^{\omega }$
with
$P,Q\in \mathcal {P}^{\omega }$
with
![]() $E(\Sigma _Q)\leq _B E(\Sigma _P)$
. Suppose that
$E(\Sigma _Q)\leq _B E(\Sigma _P)$
. Suppose that
![]() $D(P,Q)$
is infinite. Then for
$D(P,Q)$
is infinite. Then for
![]() $A\subseteq \omega $
, there is a group
$A\subseteq \omega $
, there is a group
![]() $\Sigma _{P_A}$
such that
$\Sigma _{P_A}$
such that
![]() $E(\Sigma _Q)<_B E(\Sigma _{P_A})<_B E(\Sigma _P)$
and for
$E(\Sigma _Q)<_B E(\Sigma _{P_A})<_B E(\Sigma _P)$
and for
![]() $A,B\subseteq \omega $
, we have
$A,B\subseteq \omega $
, we have
Proof Enumerate
![]() $D(P,Q)$
as
$D(P,Q)$
as
![]() $d_0<d_1<d_2<\dots $
. Let
$d_0<d_1<d_2<\dots $
. Let
![]() $P_0^*\in \mathcal {P}^{\omega }$
such that
$P_0^*\in \mathcal {P}^{\omega }$
such that
![]() $P_0^*(i)=d_{3i}$
for all
$P_0^*(i)=d_{3i}$
for all
![]() $i\in \omega $
.
$i\in \omega $
.
For
![]() $L,M\in \mathcal {P}^{\omega }$
, we define an element
$L,M\in \mathcal {P}^{\omega }$
, we define an element
![]() $L\oplus M\in \mathcal {P}^{\omega }$
as
$L\oplus M\in \mathcal {P}^{\omega }$
as
 $$ \begin{align*}(L\oplus M)(n)=\left\{\begin{array}{ll}L(k), & n=2k,\cr M(k), & n=2k+1.\end{array} \right.\end{align*} $$
$$ \begin{align*}(L\oplus M)(n)=\left\{\begin{array}{ll}L(k), & n=2k,\cr M(k), & n=2k+1.\end{array} \right.\end{align*} $$
It is clear that
 $$ \begin{align*}t^{L\oplus M}(\gamma)=\left\{\begin{array}{ll}\omega,& t^L(\gamma)=\omega\mbox{ or }t^M(\gamma)=\omega,\cr t^L(\gamma)+t^M(\gamma),& \mbox{otherwise.}\end{array} \right.\end{align*} $$
$$ \begin{align*}t^{L\oplus M}(\gamma)=\left\{\begin{array}{ll}\omega,& t^L(\gamma)=\omega\mbox{ or }t^M(\gamma)=\omega,\cr t^L(\gamma)+t^M(\gamma),& \mbox{otherwise.}\end{array} \right.\end{align*} $$
Given a set
![]() $A\subseteq \omega $
, define
$A\subseteq \omega $
, define
![]() $P_A\in \mathcal {P}^{\omega }$
as follows. If
$P_A\in \mathcal {P}^{\omega }$
as follows. If
![]() $\omega \setminus A$
is finite, put
$\omega \setminus A$
is finite, put
![]() $P_A=P_0^*\oplus P$
. Then
$P_A=P_0^*\oplus P$
. Then
 $$ \begin{align*}t^{P_A}(\gamma)=\left\{\begin{array}{ll}t^P(\gamma)+1, & \gamma=d_{3i},i\in\omega,\cr t^P(\gamma), & \mbox{otherwise.}\end{array} \right.\end{align*} $$
$$ \begin{align*}t^{P_A}(\gamma)=\left\{\begin{array}{ll}t^P(\gamma)+1, & \gamma=d_{3i},i\in\omega,\cr t^P(\gamma), & \mbox{otherwise.}\end{array} \right.\end{align*} $$
If
![]() $\omega \setminus A$
is infinite, enumerate it as
$\omega \setminus A$
is infinite, enumerate it as
![]() $a_0<a_1<a_2<\ldots $
. Define
$a_0<a_1<a_2<\ldots $
. Define
![]() $P_A^*\in \mathcal {P}^{\omega }$
as
$P_A^*\in \mathcal {P}^{\omega }$
as
![]() $P_A^*(j)=d_{1+3a_j}$
for
$P_A^*(j)=d_{1+3a_j}$
for
![]() $j\in \omega $
, and put
$j\in \omega $
, and put
![]() $P_A=P_A^*\oplus (P_0^*\oplus P)$
. Then
$P_A=P_A^*\oplus (P_0^*\oplus P)$
. Then
 $$ \begin{align*}t^{P_A}(\gamma)=\left\{\begin{array}{ll}t^P(\gamma)+1, & (\gamma=d_{3i},i\in\omega)\mbox{ or }(\gamma=d_{1+3a},a\in(\omega\setminus A)),\cr t^P(\gamma), & \mbox{otherwise.}\end{array} \right.\end{align*} $$
$$ \begin{align*}t^{P_A}(\gamma)=\left\{\begin{array}{ll}t^P(\gamma)+1, & (\gamma=d_{3i},i\in\omega)\mbox{ or }(\gamma=d_{1+3a},a\in(\omega\setminus A)),\cr t^P(\gamma), & \mbox{otherwise.}\end{array} \right.\end{align*} $$
Next we show that
![]() $E(\Sigma _Q)<_B E(\Sigma _{P_A})<_B E(\Sigma _P)$
for all
$E(\Sigma _Q)<_B E(\Sigma _{P_A})<_B E(\Sigma _P)$
for all
![]() $A\subseteq \omega $
.
$A\subseteq \omega $
.
First, since
![]() $t^P(\gamma )\le t^{P_A}(\gamma )$
for all
$t^P(\gamma )\le t^{P_A}(\gamma )$
for all
![]() $\gamma \in \mathcal P$
, we have
$\gamma \in \mathcal P$
, we have
![]() $D(P_A,P)=\emptyset $
. So
$D(P_A,P)=\emptyset $
. So
![]() $P\preceq P_A$
, and hence
$P\preceq P_A$
, and hence
![]() $E(\Sigma _{P_A})\le _B E(\Sigma _P)$
.
$E(\Sigma _{P_A})\le _B E(\Sigma _P)$
.
Since
![]() $E(\Sigma _Q)\leq _B E(\Sigma _P)$
, by Theorem 3.3, we have
$E(\Sigma _Q)\leq _B E(\Sigma _P)$
, by Theorem 3.3, we have
![]() $P\preceq Q$
, and hence
$P\preceq Q$
, and hence
Note that
![]() $t^{P_A}(\gamma )=t^P(\gamma )+1$
only occurs when
$t^{P_A}(\gamma )=t^P(\gamma )+1$
only occurs when
![]() $t^Q(\gamma )>t^P(\gamma )$
holds, in which case we always have
$t^Q(\gamma )>t^P(\gamma )$
holds, in which case we always have
![]() $\gamma \notin D(Q,P_A)$
. So we have
$\gamma \notin D(Q,P_A)$
. So we have
![]() $D(Q,P_A)=D(Q,P)$
and
$D(Q,P_A)=D(Q,P)$
and
![]() $t^{P_A}(\gamma )=t^P(\gamma )$
for all
$t^{P_A}(\gamma )=t^P(\gamma )$
for all
![]() $\gamma \in D(Q,P_A)$
. This gives
$\gamma \in D(Q,P_A)$
. This gives
![]() $E(\Sigma _Q)\leq _B E(\Sigma _{P_A})$
.
$E(\Sigma _Q)\leq _B E(\Sigma _{P_A})$
.
Since
![]() $d_{3i}\in D(P,P_A)$
for
$d_{3i}\in D(P,P_A)$
for
![]() $i\in \omega $
,
$i\in \omega $
,
![]() $D(P,P_A)$
is infinite, so
$D(P,P_A)$
is infinite, so
![]() $E(\Sigma _P)\not \le _B E(\Sigma _{P_A})$
. Similarly, since
$E(\Sigma _P)\not \le _B E(\Sigma _{P_A})$
. Similarly, since
![]() $t^{P_A}(d_{2+3i})=t^P(d_{2+3i})<t^Q(d_{2+3i})$
, we have
$t^{P_A}(d_{2+3i})=t^P(d_{2+3i})<t^Q(d_{2+3i})$
, we have
![]() $d_{2+3i}\in D(P_A,Q)$
for
$d_{2+3i}\in D(P_A,Q)$
for
![]() $i\in \omega $
, so
$i\in \omega $
, so
![]() $E(\Sigma _{P_A})\not \le _B E(\Sigma _Q)$
.
$E(\Sigma _{P_A})\not \le _B E(\Sigma _Q)$
.
Given
![]() $A,B\subseteq \omega $
, note that
$A,B\subseteq \omega $
, note that
![]() $A\subseteq ^* B$
iff
$A\subseteq ^* B$
iff
![]() $(\omega \setminus B)\setminus (\omega \setminus A)=(A\setminus B)$
is finite. We will check that
$(\omega \setminus B)\setminus (\omega \setminus A)=(A\setminus B)$
is finite. We will check that
![]() $A\subseteq ^* B$
iff
$A\subseteq ^* B$
iff
![]() $P_B\preceq P_A$
. We consider four cases as follows: (1) If both
$P_B\preceq P_A$
. We consider four cases as follows: (1) If both
![]() $\omega \setminus A$
and
$\omega \setminus A$
and
![]() $\omega \setminus B$
are finite, then we have
$\omega \setminus B$
are finite, then we have
![]() $A\subseteq ^* B$
and
$A\subseteq ^* B$
and
![]() $P_A=P_B=P_0^*\oplus P$
. (2) If
$P_A=P_B=P_0^*\oplus P$
. (2) If
![]() $\omega \setminus A$
is infinite and
$\omega \setminus A$
is infinite and
![]() $\omega \setminus B$
is finite, then we have
$\omega \setminus B$
is finite, then we have
![]() $A\subseteq ^* B$
and
$A\subseteq ^* B$
and
![]() $P_B=P_0^*\oplus P\preceq P_A^*\oplus (P_0^*\oplus P)=P_A$
, since
$P_B=P_0^*\oplus P\preceq P_A^*\oplus (P_0^*\oplus P)=P_A$
, since
![]() $t^{P_B}(\gamma )\le t^{P_A}(\gamma )$
for all
$t^{P_B}(\gamma )\le t^{P_A}(\gamma )$
for all
![]() $\gamma \in \mathcal P$
. (3) If
$\gamma \in \mathcal P$
. (3) If
![]() $\omega \setminus A$
is finite and
$\omega \setminus A$
is finite and
![]() $\omega \setminus B$
is infinite, then
$\omega \setminus B$
is infinite, then
![]() $A\not \subseteq ^* B$
and
$A\not \subseteq ^* B$
and
![]() $P_B=P_B^*\oplus (P_0^*\oplus P)\not \preceq P_0^*\oplus P=P_A$
, since
$P_B=P_B^*\oplus (P_0^*\oplus P)\not \preceq P_0^*\oplus P=P_A$
, since
![]() $t^{P_A}(d_{1+3b})<t^{P_B}(d_{1+3b})$
for
$t^{P_A}(d_{1+3b})<t^{P_B}(d_{1+3b})$
for
![]() $b\in (\omega \setminus B)$
. (4) If both
$b\in (\omega \setminus B)$
. (4) If both
![]() $\omega \setminus A$
and
$\omega \setminus A$
and
![]() $\omega \setminus B$
are infinite, then
$\omega \setminus B$
are infinite, then
![]() $t^{P_A}(\gamma )<t^{P_B}(\gamma )$
iff
$t^{P_A}(\gamma )<t^{P_B}(\gamma )$
iff
![]() $\gamma =d_{1+3b}$
for some
$\gamma =d_{1+3b}$
for some
![]() $b\in (\omega \setminus B)\setminus (\omega \setminus A)=(A\setminus B)$
. Moreover,
$b\in (\omega \setminus B)\setminus (\omega \setminus A)=(A\setminus B)$
. Moreover,
![]() $t^{P_B}(d_{1+3b})=t^P(d_{1+3b})+1=t^{P_A}(d_{1+3b})+1$
for all
$t^{P_B}(d_{1+3b})=t^P(d_{1+3b})+1=t^{P_A}(d_{1+3b})+1$
for all
![]() $b\in (A\setminus B)$
. So
$b\in (A\setminus B)$
. So
 $$ \begin{align*}\sum_{\gamma\in D(P_A,P_B)}(t^{P_B}(\gamma)-t^{P_A}(\gamma))=|A\setminus B|,\end{align*} $$
$$ \begin{align*}\sum_{\gamma\in D(P_A,P_B)}(t^{P_B}(\gamma)-t^{P_A}(\gamma))=|A\setminus B|,\end{align*} $$
and hence
![]() $A\subseteq ^* B$
iff
$A\subseteq ^* B$
iff
![]() $P_B\preceq P_A$
.
$P_B\preceq P_A$
.
Again by Theorem 3.3, we have
![]() $A\subseteq ^* B$
iff
$A\subseteq ^* B$
iff
![]() $E(\Sigma _{P_A})\le _B E(\Sigma _{P_B})$
.
$E(\Sigma _{P_A})\le _B E(\Sigma _{P_B})$
.
Theorem 3.6. Let
![]() $n\in \mathbb {N}^+$
. Then for
$n\in \mathbb {N}^+$
. Then for
![]() $A\subseteq \omega $
, there is an n-dimensional compact connected abelian Polish group
$A\subseteq \omega $
, there is an n-dimensional compact connected abelian Polish group
![]() $G_A$
such that
$G_A$
such that
![]() $E({\mathbb {R}}^n)<_B E(G_A)<_B E({\mathbb {T}}^n)$
and for
$E({\mathbb {R}}^n)<_B E(G_A)<_B E({\mathbb {T}}^n)$
and for
![]() $A,B\subseteq \omega $
, we have
$A,B\subseteq \omega $
, we have
4 Dual groups
Let G and H be two abelian topological groups. Denote the class of all continuous homomorphisms of G to H by
![]() $\mathrm {Hom}(G,H)$
, which is an abelian group under pointwise addition. We always equip Hom
$\mathrm {Hom}(G,H)$
, which is an abelian group under pointwise addition. We always equip Hom
![]() $(G,H)$
with compact-open topology. The abelian topological group Hom
$(G,H)$
with compact-open topology. The abelian topological group Hom
![]() $(G,{\mathbb {T}})$
is called the dual group of G, denoted by
$(G,{\mathbb {T}})$
is called the dual group of G, denoted by
![]() $\widehat {G}$
(cf. [Reference Hofmann and Morris11, Definition 7.4]).
$\widehat {G}$
(cf. [Reference Hofmann and Morris11, Definition 7.4]).
Let
![]() $(A,+)$
be an abelian group whose identity element denoted by
$(A,+)$
be an abelian group whose identity element denoted by
![]() $0_A$
. We say that
$0_A$
. We say that
![]() $(A,+)$
is a torsion group if each element of A is finite order. We say that
$(A,+)$
is a torsion group if each element of A is finite order. We say that
![]() $(A,+)$
is torsion-free if
$(A,+)$
is torsion-free if
![]() $n\cdot g\neq 0_A$
for all
$n\cdot g\neq 0_A$
for all
![]() $g\in A$
with
$g\in A$
with
![]() $g\neq 0_A$
and
$g\neq 0_A$
and
![]() $n\in {\mathbb {N}}^+$
. A subset X of A is free if any equation
$n\in {\mathbb {N}}^+$
. A subset X of A is free if any equation
![]() $\sum _{x\in X} n_x\cdot x=0_A$
implies
$\sum _{x\in X} n_x\cdot x=0_A$
implies
![]() $n_x=0$
for all
$n_x=0$
for all
![]() $x\in X$
. The torsion-free rank of A, written rank
$x\in X$
. The torsion-free rank of A, written rank
![]() $(A)$
, is the cardinal number (uniquely determined) of any maximal free subset of A.
$(A)$
, is the cardinal number (uniquely determined) of any maximal free subset of A.
Each Hausdorff locally compact abelian group G is reflexive, thus it is topologically isomorphic to the double dual group
![]() $\widehat {\widehat {G}}$
(cf. [Reference Hofmann and Morris11, Theorem 7.63]). A Hausdorff locally compact abelian group is compact and metrizable iff its dual group is a countable discrete group (cf. Proposition 7.5(i) and Theorem 8.45 of [Reference Hofmann and Morris11]). Let G be a Hausdorff compact abelian group, then G is connected iff
$\widehat {\widehat {G}}$
(cf. [Reference Hofmann and Morris11, Theorem 7.63]). A Hausdorff locally compact abelian group is compact and metrizable iff its dual group is a countable discrete group (cf. Proposition 7.5(i) and Theorem 8.45 of [Reference Hofmann and Morris11]). Let G be a Hausdorff compact abelian group, then G is connected iff
![]() $\widehat {G}$
is torsion-free; and G is totally disconnected iff
$\widehat {G}$
is torsion-free; and G is totally disconnected iff
![]() $\widehat G$
is torsion (cf. [Reference Hofmann and Morris11, Corollary 8.5]). For any finite dimensional compact abelian Polish group G, the covering dimension of A is equal to rank
$\widehat G$
is torsion (cf. [Reference Hofmann and Morris11, Corollary 8.5]). For any finite dimensional compact abelian Polish group G, the covering dimension of A is equal to rank
![]() $(\widehat {G})$
(cf. Lemma 8.13 and Corollary 8.26 of [Reference Hofmann and Morris11]).
$(\widehat {G})$
(cf. Lemma 8.13 and Corollary 8.26 of [Reference Hofmann and Morris11]).
If H is a subset of an abelian topological group G, then the subgroup
is called the annihilator of H in
![]() $\widehat {G}$
(cf. [Reference Hofmann and Morris11, Definition 7.12]).
$\widehat {G}$
(cf. [Reference Hofmann and Morris11, Definition 7.12]).
Now we focus on compact connected abelian Polish groups.
Theorem 4.1 (Dual Rigid Theorem).
Let G be a compact connected abelian Polish group and let H be a locally compact abelian Polish group. Then
![]() $E(G)\leq _B E(H)$
iff there is a continuous homomorphism
$E(G)\leq _B E(H)$
iff there is a continuous homomorphism
![]() $S^*:\widehat {H}\to \widehat {G}$
such that
$S^*:\widehat {H}\to \widehat {G}$
such that
![]() $\widehat {G}/\mathrm {im}(S^*)$
is a torsion group.
$\widehat {G}/\mathrm {im}(S^*)$
is a torsion group.
Proof
![]() $(\Rightarrow )$
. We assume that
$(\Rightarrow )$
. We assume that
![]() $E(G)\leq _B E(H)$
. By Theorem 2.8, there is a continuous homomorphism
$E(G)\leq _B E(H)$
. By Theorem 2.8, there is a continuous homomorphism
![]() $S:G\rightarrow H$
such that
$S:G\rightarrow H$
such that
![]() $\ker (S)$
is non-archimedean. This implies that there is a homomorphism
$\ker (S)$
is non-archimedean. This implies that there is a homomorphism
![]() $S^*$
from
$S^*$
from
![]() $\widehat {H}$
to
$\widehat {H}$
to
![]() $\widehat {G}$
such that
$\widehat {G}$
such that
![]() $\ker (S)\cong {\mathrm {im}(S^*)}^{\perp }$
(cf. [Reference Armacost1, P.22 and P.23(a)]). By [Reference Hofmann and Morris11, Lemma 7.13(ii)], we have that
$\ker (S)\cong {\mathrm {im}(S^*)}^{\perp }$
(cf. [Reference Armacost1, P.22 and P.23(a)]). By [Reference Hofmann and Morris11, Lemma 7.13(ii)], we have that
![]() $\ker (S)\cong (\widehat {G}/\mathrm {im}(S^*))^{\widehat {}}$
, and hence
$\ker (S)\cong (\widehat {G}/\mathrm {im}(S^*))^{\widehat {}}$
, and hence
![]() $\widehat {\ker (S)}\cong \widehat {G}/\mathrm {im}(S^*)$
. Since
$\widehat {\ker (S)}\cong \widehat {G}/\mathrm {im}(S^*)$
. Since
![]() $\ker (S)$
is non-archimedean, thus is totally disconnected, so
$\ker (S)$
is non-archimedean, thus is totally disconnected, so
![]() $\widehat {G}/\mathrm {im}(S^*)$
is a torsion group.
$\widehat {G}/\mathrm {im}(S^*)$
is a torsion group.
![]() $(\Leftarrow )$
. Since
$(\Leftarrow )$
. Since
![]() $G\cong {\widehat {\widehat {G}}}$
and
$G\cong {\widehat {\widehat {G}}}$
and
![]() $H\cong \widehat {\widehat {H}}$
, we can define
$H\cong \widehat {\widehat {H}}$
, we can define
![]() $S:G\to H$
via
$S:G\to H$
via
![]() $(S^*)^*:{\widehat {\widehat G}}\to {\widehat {\widehat H}}$
(cf. [Reference Hewitt and Ross10, (24.41)]). Then the similar arguments as the preceding paragraph give the desired result.
$(S^*)^*:{\widehat {\widehat G}}\to {\widehat {\widehat H}}$
(cf. [Reference Hewitt and Ross10, (24.41)]). Then the similar arguments as the preceding paragraph give the desired result.
Corollary 4.2. Let G be a compact connected abelian Polish group and let H be a locally compact abelian Polish group. If
![]() $E(G)\leq _B E(H)$
, then there is a nonzero continuous homomorphism
$E(G)\leq _B E(H)$
, then there is a nonzero continuous homomorphism
![]() $S^*:\widehat {H}\to \widehat {G}$
.
$S^*:\widehat {H}\to \widehat {G}$
.
Proof It follows from Theorem 4.1 and that
![]() $\widehat {G}$
is non-torsion.
$\widehat {G}$
is non-torsion.
Example 4.3.
![]() $\widehat {\mathbb {T}}\cong {\mathbb {Z}}$
(cf. [Reference Hewitt and Ross10, Examples 23.27(a)]). Fix a
$\widehat {\mathbb {T}}\cong {\mathbb {Z}}$
(cf. [Reference Hewitt and Ross10, Examples 23.27(a)]). Fix a
![]() $P\in \mathcal {P}^{\omega }$
, then
$P\in \mathcal {P}^{\omega }$
, then
![]() $\widehat {\Sigma _P}\cong \left \{\frac {m}{P(0)P(1)\dots P(n)}:m\in {\mathbb {Z}},n\in {\mathbb {N}}\right \}$
(see [Reference Hewitt and Ross10, (25.3)]). In view of Corollary 4.2, we get
$\widehat {\Sigma _P}\cong \left \{\frac {m}{P(0)P(1)\dots P(n)}:m\in {\mathbb {Z}},n\in {\mathbb {N}}\right \}$
(see [Reference Hewitt and Ross10, (25.3)]). In view of Corollary 4.2, we get
![]() $E({\mathbb {T}})\nleq _B E(\Sigma _P)$
again.
$E({\mathbb {T}})\nleq _B E(\Sigma _P)$
again.
Recall that
![]() $\widehat {{\mathbb {Q}}}\cong S_{(2,3,4,5,6,\dots )}$
(see [Reference Hewitt and Ross10, (25.4)]). We have the following.
$\widehat {{\mathbb {Q}}}\cong S_{(2,3,4,5,6,\dots )}$
(see [Reference Hewitt and Ross10, (25.4)]). We have the following.
Corollary 4.4. Let G be an n-dimensional compact abelian Polish group with
![]() $n\in {\mathbb {N}}^+$
. Then
$n\in {\mathbb {N}}^+$
. Then
![]() $E((\widehat {{\mathbb {Q}}})^n)\leq _B E(G)$
.
$E((\widehat {{\mathbb {Q}}})^n)\leq _B E(G)$
.
Proof By [Reference Hofmann and Morris11, Theorem 8.22(4)],
![]() $G_0\cong (\widehat {{\mathbb {Q}}})^n/\Delta $
, where
$G_0\cong (\widehat {{\mathbb {Q}}})^n/\Delta $
, where
![]() $\Delta $
is a compact totally disconnected subgroup of
$\Delta $
is a compact totally disconnected subgroup of
![]() $(\widehat {{\mathbb {Q}}})^n$
. Again by Theorem 2.9, this means that
$(\widehat {{\mathbb {Q}}})^n$
. Again by Theorem 2.9, this means that
![]() $E((\widehat {{\mathbb {Q}}})^n)\leq _B E(G_0)$
, and thus
$E((\widehat {{\mathbb {Q}}})^n)\leq _B E(G_0)$
, and thus
![]() $E((\widehat {{\mathbb {Q}}})^n)\leq _B E(G)$
.
$E((\widehat {{\mathbb {Q}}})^n)\leq _B E(G)$
.
From the arguments above, if
![]() $\Gamma $
is a countable discrete torsion-free abelian group, then
$\Gamma $
is a countable discrete torsion-free abelian group, then
![]() $\widehat {\Gamma }$
is a compact connected abelian Polish group.
$\widehat {\Gamma }$
is a compact connected abelian Polish group.
Remark 4.5. Let G be a compact connected Polish group with
![]() $E({\mathbb {R}}^n)\le _BE(G)\le _BE({\mathbb {T}}^n)$
for some
$E({\mathbb {R}}^n)\le _BE(G)\le _BE({\mathbb {T}}^n)$
for some
![]() $n>0$
. By Theorem 2.11(5),
$n>0$
. By Theorem 2.11(5),
![]() $\dim (G){\kern-1pt}={\kern-1pt}n$
, so
$\dim (G){\kern-1pt}={\kern-1pt}n$
, so
![]() $\mathrm {rank}(\widehat G){\kern-1pt}={\kern-1pt}n$
. Thus
$\mathrm {rank}(\widehat G){\kern-1pt}={\kern-1pt}n$
. Thus
![]() $\widehat G$
is isomorphic to a subgroup of
$\widehat G$
is isomorphic to a subgroup of
![]() $\mathbb Q^n$
(cf. [Reference Gao7, Exercise 13.4.3]). In particular, if
$\mathbb Q^n$
(cf. [Reference Gao7, Exercise 13.4.3]). In particular, if
![]() $n=1$
, we have either
$n=1$
, we have either
![]() $G\cong {\mathbb {T}}$
or there exists a
$G\cong {\mathbb {T}}$
or there exists a
![]() $P\in \mathcal P^{\omega }$
such that
$P\in \mathcal P^{\omega }$
such that
![]() $G\cong \Sigma _P$
.
$G\cong \Sigma _P$
.
The following proposition shows that, if
![]() $n>1$
, the structure of G can be more complicated.
$n>1$
, the structure of G can be more complicated.
Proposition 4.6. There is a
![]() $2$
-dimensional compact connected Polish group G such that
$2$
-dimensional compact connected Polish group G such that
![]() $E(G)\nleq _B E(\Sigma _{P_0}\times \Sigma _{P_1}\times \dots \times \Sigma _{P_n})$
for
$E(G)\nleq _B E(\Sigma _{P_0}\times \Sigma _{P_1}\times \dots \times \Sigma _{P_n})$
for
![]() $n\in {\mathbb {N}}$
and each
$n\in {\mathbb {N}}$
and each
![]() $P_i\in \mathcal {P}^{\omega }$
. Moreover, if
$P_i\in \mathcal {P}^{\omega }$
. Moreover, if
![]() $\left |\{i\in \omega :P(i)=2\}\right |<\infty $
, then
$\left |\{i\in \omega :P(i)=2\}\right |<\infty $
, then
![]() $E(\Sigma _{P})\nleq _B E(G)$
.
$E(\Sigma _{P})\nleq _B E(G)$
.
Proof Pontryagin has constructed a countable torsion-free abelian group
![]() $\Gamma \subseteq {\mathbb {Q}}^2$
whose rank is two (cf. [Reference Pontrjagin15, Example 2]). Then
$\Gamma \subseteq {\mathbb {Q}}^2$
whose rank is two (cf. [Reference Pontrjagin15, Example 2]). Then
![]() $\widehat {\Gamma }$
is a
$\widehat {\Gamma }$
is a
![]() $2$
-dimensional compact connected abelian Polish group. The group
$2$
-dimensional compact connected abelian Polish group. The group
![]() $\Gamma $
defined by its generators
$\Gamma $
defined by its generators
![]() $\eta ,\xi _i,(i=0,1,2\dots )$
and relations,
$\eta ,\xi _i,(i=0,1,2\dots )$
and relations,
where
![]() $i\in \omega $
and
$i\in \omega $
and
![]() $k_i\in {\mathbb {N}}^+$
such that
$k_i\in {\mathbb {N}}^+$
such that
![]() $\sup \{k_i:i\in \omega \}=\infty $
.
$\sup \{k_i:i\in \omega \}=\infty $
.
Put
![]() $G=\widehat {\Gamma }$
. We claim that
$G=\widehat {\Gamma }$
. We claim that
![]() $E(G)\nleq _B E(\Sigma _{P_0}\times \Sigma _{P_1}\times \dots \times \Sigma _{P_n})$
. Otherwise, by Corollary 4.2 and [Reference Hewitt and Ross10, Theorem 23.18], there exists
$E(G)\nleq _B E(\Sigma _{P_0}\times \Sigma _{P_1}\times \dots \times \Sigma _{P_n})$
. Otherwise, by Corollary 4.2 and [Reference Hewitt and Ross10, Theorem 23.18], there exists
![]() $i\leq n$
such that there is a nonzero continuous homomorphism f from
$i\leq n$
such that there is a nonzero continuous homomorphism f from
![]() $\widehat {\Sigma _{P_i}}$
to
$\widehat {\Sigma _{P_i}}$
to
![]() $\widehat {G}$
. Note that for any
$\widehat {G}$
. Note that for any
![]() $a\in \ \widehat {\Sigma _{P_i}}$
, there are infinitely many positive integers n such that the equation
$a\in \ \widehat {\Sigma _{P_i}}$
, there are infinitely many positive integers n such that the equation
![]() $nx=a$
has a solution. But any element in
$nx=a$
has a solution. But any element in
![]() $\Gamma $
does not admit such property. This implies that
$\Gamma $
does not admit such property. This implies that
![]() $f(\widehat {\Sigma _{P_i}})=\{1_{\Gamma }\}$
contradicting that f is a nonzero homomorphism.
$f(\widehat {\Sigma _{P_i}})=\{1_{\Gamma }\}$
contradicting that f is a nonzero homomorphism.
Now assume that
![]() $E(\Sigma _{P})\leq _B E(G)$
for some
$E(\Sigma _{P})\leq _B E(G)$
for some
![]() $P\in \mathcal P^{\omega }$
. We show that
$P\in \mathcal P^{\omega }$
. We show that
![]() $\{i\in \omega :P(i)=2\}$
is infinite. By Corollary 4.2, there is a nonzero homomorphism f from
$\{i\in \omega :P(i)=2\}$
is infinite. By Corollary 4.2, there is a nonzero homomorphism f from
![]() $\widehat {G}$
to
$\widehat {G}$
to
![]() $\widehat {\Sigma _{P}}$
. Without loss of generality we may assume
$\widehat {\Sigma _{P}}$
. Without loss of generality we may assume
![]() $\widehat {G}=\Gamma $
and
$\widehat {G}=\Gamma $
and
![]() $\widehat {\Sigma _P}=\left \{\frac {m}{P(0)P(1)\dots P(n)}:m\in {\mathbb {Z}},n\in {\mathbb {N}}\right \}\subseteq {\mathbb {Q}}$
. From
$\widehat {\Sigma _P}=\left \{\frac {m}{P(0)P(1)\dots P(n)}:m\in {\mathbb {Z}},n\in {\mathbb {N}}\right \}\subseteq {\mathbb {Q}}$
. From
![]() $(**)$
, a straightforward calculation shows that
$(**)$
, a straightforward calculation shows that
So we have
Note that
![]() $\lim _i2^{-(k_1+k_2+\dots +k_i)}f(\xi _0)=0$
and
$\lim _i2^{-(k_1+k_2+\dots +k_i)}f(\xi _0)=0$
and
This implies that
![]() $\lim _if(\xi _i)=0$
.
$\lim _if(\xi _i)=0$
.
Let
![]() $f(\xi _0)=a/b$
and
$f(\xi _0)=a/b$
and
![]() $f(\eta )=c/d$
for some integers
$f(\eta )=c/d$
for some integers
![]() $a,b,c,d$
with
$a,b,c,d$
with
![]() $c,d>0$
. Note that
$c,d>0$
. Note that
![]() $2^{k_{i+1}}f(\xi _{i+1})=f(\xi _i)+f(\eta )$
. Since f is a nonzero homomorphism, there can be at most one
$2^{k_{i+1}}f(\xi _{i+1})=f(\xi _i)+f(\eta )$
. Since f is a nonzero homomorphism, there can be at most one
![]() $f(\xi _i)=0$
. For large enough i, we have
$f(\xi _i)=0$
. For large enough i, we have
![]() $f(\xi _i)\ne 0$
. So there exist integers
$f(\xi _i)\ne 0$
. So there exist integers
![]() $m_i,m^{\prime }_i,c',d',l_i$
with
$m_i,m^{\prime }_i,c',d',l_i$
with
![]() $m_i,m^{\prime }_i\ne 0$
and
$m_i,m^{\prime }_i\ne 0$
and
![]() $c',d'>0$
such that
$c',d'>0$
such that
where
![]() $m^{\prime }_i$
and
$m^{\prime }_i$
and
![]() $2^{l_i}c'd'$
are coprime and
$2^{l_i}c'd'$
are coprime and
![]() $c'|c$
,
$c'|c$
,
![]() $d'|d$
. It follows that
$d'|d$
. It follows that
So
![]() $l_i\to \infty $
as
$l_i\to \infty $
as
![]() $i\to \infty $
, and hence
$i\to \infty $
, and hence
![]() $\{i\in \omega :P(i)=2\}$
is infinite.
$\{i\in \omega :P(i)=2\}$
is infinite.
Acknowledgements
The authors would like to thank the anonymous referee for helpful comments and suggestions.
Funding
This research is partially supported by the National Natural Science Foundation of China (Grant No. 11725103).