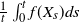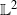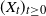An ergodic theorem for asymptotically periodic time-inhomogeneous Markov processes, with application to quasi-stationarity with moving boundaries

Abstract

This paper deals with ergodic theorems for particular time-inhomogeneous Markov processes, whose time-inhomogeneity is asymptotically periodic. Under a Lyapunov/minorization condition, it is shown that, for any measurable bounded function f, the time average $\frac{1}{t} \int_0^t f(X_s)ds$ converges in $\mathbb{L}^2$ towards a limiting distribution, starting from any initial distribution for the process $(X_t)_{t \geq 0}$ . This convergence can be improved to an almost sure convergence under an additional assumption on the initial measure. This result is then applied to show the existence of a quasi-ergodic distribution for processes absorbed by an asymptotically periodic moving boundary, satisfying a conditional Doeblin condition.

1. Notation

Throughout, we shall use the following notation:

• $\mathbb{N} = \{1,2, \ldots, \}$ and $\mathbb{Z}_+ = \{0\} \cup \mathbb{N}$ .

• $\mathcal{M}_1(E)$ denotes the space of the probability measures whose support is included in E.

• $\mathcal{B}(E)$ denotes the set of the measurable bounded functions defined on E.

• $\mathcal{B}_1(E)$ denotes the set of the measurable functions f defined on E such that $\|f\|_\infty \leq 1$ .

• For all $\mu \in \mathcal{M}_1(E)$ and $p \in \mathbb{N}$ , $\mathbb{L}^p(\mu)$ denotes the set of the measurable functions $f \;:\; E \mapsto \mathbb{R}$ such that $\int_E |f(x)|^p \mu(dx) < + \infty$ .

• For any $\mu \in \mathcal{M}_1(E)$ and $f \in \mathbb{L}^1(\mu)$ , we define

  \begin{equation*}\mu(f) \;:\!=\; \int_E f(x) \mu(dx).\end{equation*}

• For any positive function $\psi$ ,

  \begin{equation*}\mathcal{M}_1(\psi) \;:\!=\; \{\mu \in \mathcal{M}_1(E) \;:\; \mu(\psi) < + \infty\}.\end{equation*}

• Id denotes the identity operator.

2. Introduction

In general, an ergodic theorem for a Markov process $(X_t)_{t \geq 0}$ and probability measure $\pi$ refers to the almost sure convergence

(1) \begin{equation} \frac{1}{t} \int_0^t f(X_s)ds \underset{t \to \infty}{\longrightarrow} \pi(f),\;\;\;\;\forall f \in \mathbb{L}^1(\pi). \end{equation}

In the time-homogeneous setting, such an ergodic theorem holds for positive Harris-recurrent Markov processes with the limiting distribution $\pi$ corresponding to an invariant measure for the underlying Markov process. For time-inhomogeneous Markov processes, such a result does not hold in general (in particular the notion of invariant measure is in general not well-defined), except for specific types of time-inhomogeneity such as periodic time-inhomogeneous Markov processes, defined as time-inhomogeneous Markov processes for which there exists $\gamma > 0$ such that, for any $s \leq t$ , $k \in \mathbb{Z}_+$ , and x,

(2) \begin{equation}\mathbb{P}[X_t \in \cdot | X_s = x] = \mathbb{P}[X_{t+k\gamma} \in \cdot | X_{s+k \gamma} = x].\end{equation}

In other words, a time-inhomogeneous Markov process is periodic when the transition law between any times s and t remains unchanged when the time interval [s, t] is shifted by a multiple of the period $\gamma$ . In particular, this implies that, for any $s \in [0,\gamma)$ , the Markov chain $(X_{s+n \gamma})_{n \in \mathbb{Z}_+}$ is time-homogeneous. This fact allowed Höpfner et al. (in [20, 21, 22]) to show that, if the skeleton Markov chain $(X_{n \gamma})_{n \in \mathbb{Z}_+}$ is Harris-recurrent, then the chains $(X_{s + n \gamma})_{n \in \mathbb{Z}_+}$ , for all $s \in [0,\gamma)$ , are also Harris-recurrent and

\begin{equation*}\frac{1}{t} \int_0^t f(X_s)ds \underset{t \to \infty}{\longrightarrow} \frac{1}{\gamma} \int_0^\gamma \pi_s(f)ds,\;\;\;\;\text{almost surely, from any initial measure,}\end{equation*}

where $\pi_s$ is the invariant measure for $(X_{s+n \gamma})_{n \in \mathbb{Z}_+}$ .

This paper aims to prove a similar result for time-inhomogeneous Markov processes said to be asymptotically periodic. Roughly speaking (a precise definition will be explicitly given later), an asymptotically periodic Markov process is such that, given a time interval $T \geq 0$ , its transition law on the interval $[s,s+T]$ is asymptotically ‘close to’ the transition law, on the same interval, of a periodic time-inhomogeneous Markov process called an auxiliary Markov process, when $s \to \infty$ . This definition is very similar to the notion of asymptotic homogenization, defined as follows in [1, Subsection 3.3]. A time-inhomogeneous Markov process $(X_t)_{t \geq 0}$ is said to be asymptotically homogeneous if there exists a time-homogeneous Markovian semigroup $(Q_t)_{t \geq 0}$ such that, for all $s \geq 0$ ,

(3) \begin{equation}\lim_{t \to \infty} \sup_{x} \left\| \mathbb{P}[X_{t+s} \in \cdot | X_t = x] - \delta_x Q_s\right\|_{TV} = 0,\end{equation}

where, for two positive measures with finite mass $\mu_1$ and $\mu_2$ , $\| \mu_1 - \mu_2\|_{TV}$ is the total variation distance between $\mu_1$ and $\mu_2$ :

(4) \begin{equation}\| \mu_1 - \mu_2\|_{TV} \;:\!=\; \sup_{f \in \mathcal{B}_1(E)} |\mu_1(f) - \mu_2(f)|.\end{equation}

In particular, it is well known (see [1, Theorem 3.11]) that, under this and suitable additional conditions, an asymptotically homogeneous Markov process converges towards a probability measure which is invariant for $(Q_t)_{t \geq 0}$ . It is similarly expected that an asymptotically periodic process has the same asymptotic properties as a periodic Markov process; in particular an ergodic theorem holds for the asymptotically periodic process.

The main result of this paper provides for an asymptotically periodic Markov process to satisfy

(5) $${1 \over t}\int_0^t f ({X_s})ds\mathrel{\mathop{\kern0pt\longrightarrow} \limits_{t \to \infty }^{{\mathbb{L}^2}({\mathbb{P}_{0,\mu }})}} {1 \over \gamma }\int_0^\gamma {{\beta _s}} (f)ds,\;\;\;\;\forall f \in {\cal B}(E),\forall \mu \in {{\cal M}_1}(E),$$

where $\mathbb{P}_{0,\mu}$ is a probability measure under which $X_0 \sim \mu$ , and where $\beta_s$ is the limiting distribution of the skeleton Markov chain $(X_{s+n \gamma})_{n \in \mathbb{Z}_+}$ , if it satisfies a Lyapunov-type condition and a local Doeblin condition (defined further in Section 3), and is such that its auxiliary process satisfies a Lyapunov/minorization condition.

Furthermore, this convergence result holds almost surely if a Lyapunov function of the process $(X_t)_{t \geq 0}$ , denoted by $\psi$ , is integrable with respect to the initial measure:

\begin{equation*}\frac{1}{t} \int_0^t f(X_s)ds \underset{t \to \infty}{\overset{\mathbb{P}_{0,\mu}\text{-almost surely}}{\longrightarrow}} \frac{1}{\gamma} \int_0^\gamma \beta_s(f) ds,\;\;\;\;\forall \mu \in \mathcal{M}_1(\psi).\end{equation*}

This will be more precisely stated and proved in Section 3.

The main motivation of this paper is then to deal with quasi-stationarity with moving boundaries, that is, the study of asymptotic properties for the process X, conditioned not to reach some moving subset of the state space. In particular, such a study is motivated by models such as those presented in [3], which studies Brownian particles absorbed by cells whose volume may vary over time.

Quasi-stationarity with moving boundaries has been studied in particular in [24, 25], where a ‘conditional ergodic theorem’ (see further the definition of a quasi-ergodic distribution) has been shown when the absorbing boundaries move periodically. In this paper, we show that a similar result holds when the boundary is asymptotically periodic, assuming that the process satisfies a conditional Doeblin condition (see Assumption (A′)). This will be dealt with in Section 4.

The paper will be concluded by using these results in two examples: an ergodic theorem for an asymptotically periodic Ornstein–Uhlenbeck process, and the existence of a unique quasi-ergodic distribution for a Brownian motion confined between two symmetric asymptotically periodic functions.

3. Ergodic theorem for asymptotically periodic time-inhomogeneous semigroup.

Asymptotic periodicity: the definition. Let $(E,{\mathcal E})$ be a measurable space. Consider $\{(E_t, {\mathcal E}_t)_{t \geq 0}, (P_{s,t})_{s \leq t}\}$ a Markovian time-inhomogeneous semigroup, giving a family of measurable subspaces of $(E, {\mathcal E})$ , denoted by $(E_t, {\mathcal E}_t)_{t \geq 0}$ , and a family of linear operator $(P_{s,t})_{s \leq t}$ , with $P_{s,t} \;:\; \mathcal{B}(E_t) \to \mathcal{B}(E_s)$ , satisfying for any $r \leq s \leq t$ ,

\begin{equation*}P_{s,s} = \text{Id},\;\;\;\;\;\;\;\;P_{s,t}\mathbb{1}_{E_t} = \mathbb{1}_{E_s},\;\;\;\;\;\;\;\;P_{r,s}P_{s,t} = P_{r,t}.\end{equation*}

In particular, associated to $\{(E_t, {\mathcal E}_t)_{t \geq 0}, (P_{s,t})_{s \leq t}\}$ is a Markov process $(X_t)_{t \geq 0}$ and a family of probability measures $(\mathbb{P}_{s,x})_{s \geq 0, x \in E_s}$ such that, for any $s \leq t$ , $x \in E_s$ , and $A \in {\mathcal E}_t$ ,

\begin{equation*}\mathbb{P}_{s,x}[X_t \in A] = P_{s,t}\mathbb{1}_{A}(x).\end{equation*}

We denote by $\mathbb{P}_{s,\mu} \;:\!=\; \int_{E_s} \mathbb{P}_{s,x} \mu(dx)$ any probability measure $\mu$ supported on $E_s$ . We also denote by $\mathbb{E}_{s,x}$ and $\mathbb{E}_{s,\mu}$ the expectations associated to $\mathbb{P}_{s,x}$ and $\mathbb{P}_{s,\mu}$ respectively. Finally, the following notation will be used for $\mu \in \mathcal{M}_1(E_s)$ , $s \leq t$ , and $f \in \mathcal{B}(E_t)$ :

\begin{equation*}\mu P_{s,t} f \;:\!=\; \mathbb{E}_{s,\mu}[f(X_t)],\;\;\;\;\;\;\mu P_{s,t} \;:\!=\; \mathbb{P}_{s,\mu}[X_t \in \cdot].\end{equation*}

The periodicity of a time-inhomogeneous semigroup is defined as follows. We say a semigroup $\{(F_t, {\mathcal F}_t)_{t \geq 0},(Q_{s,t})_{s \leq t}\}$ is $\gamma$ -periodic (for $\gamma > 0$ ) if, for any $s \leq t$ ,

\begin{equation*}(F_t, {\mathcal F}_t) = (F_{t+k\gamma}, {\mathcal F}_{t+k\gamma}),\;\;\;\;Q_{s,t} = Q_{s+k \gamma,t+k\gamma},\;\;\;\;\forall k \in \mathbb{Z}_+.\end{equation*}

It is now possible to define an asymptotically periodic semigroup.

Definition 1. (Asymptotically periodic semigroups.) A time-inhomogeneous semigroup $\{(E_t, {\mathcal E}_t)_{t \geq 0},(P_{s,t})_{s \leq t}\}$ is said to be asymptotically periodic if (for some $\gamma > 0$ ) there exist a $\gamma$ -periodic semigroup $\{(F_t, {\mathcal F}_t)_{t \geq 0},(Q_{s,t})_{s \leq t}\}$ and two families of functions $(\psi_s)_{s \geq 0}$ and $(\tilde{\psi}_s)_{s \geq 0}$ such that $\tilde{\psi}_{s+\gamma} = \tilde{\psi}_s$ for all $s \geq 0$ , and for any $s \in [0, \gamma)$ , the following hold:

1. 1. $\bigcup_{k=0}^\infty \bigcap_{l \geq k} E_{s+l\gamma} \cap F_s \ne \emptyset$ .

2. 2. There exists $x_s \in \bigcup_{k=0}^\infty \bigcap_{l \geq k} E_{s+l\gamma} \cap F_s$ such that, for any $n \in \mathbb{Z}_+$ ,

   (6) \begin{equation} \|\delta_{x_s} P_{s+k \gamma, s+(k+n)\gamma}[\psi_{s+(k+n)\gamma} \times \cdot] - \delta_{x_s} Q_{s, s + n \gamma}[\tilde{\psi}_{s} \times \cdot]\|_{TV} \underset{k \to \infty}{\longrightarrow} 0.\end{equation}

The semigroup $\{(F_t, {\mathcal F}_t)_{t \geq 0},(Q_{s,t})_{s \leq t}\}$ is then called the auxiliary semigroup of $(P_{s,t})_{s \leq t}$ .

When $\psi_s = \tilde{\psi}_s = \mathbb{1}$ for all $s \geq 0$ , we say that the semigroup $(P_{s,t})_{s \leq t}$ is asymptotically periodic in total variation. By extension, we will say that the process $(X_t)_{t \geq 0}$ is asymptotically periodic (in total variation) if the associated semigroup $\{(E_t, {\mathcal E}_t)_{t \geq 0},(P_{s,t})_{s \leq t}\}$ is asymptotically periodic (in total variation).

In what follows, the functions $(\psi_s)_{s \geq 0}$ and $(\tilde{\psi}_s)_{s \in [0,\gamma)}$ will play the role of Lyapunov functions (that is to say, satisfying Assumption 1(ii) below) for the semigroups $(P_{s,t})_{s \leq t}$ and $(Q_{s,t})_{s \leq t}$ , respectively. The introduction of these functions in the definition of asymptotically periodic semigroups will allow us to establish an ergodic theorem for processes satisfying the Lyapunov/minorization conditions stated below.

Lyapunov/minorization conditions. The main assumption of Theorem 1, which will be provided later, will be that the asymptotically periodic Markov process satisfies the following assumption.

Assumption 1. There exist $t_1 \geq 0$ , $n_0 \in \mathbb{N}$ , $c > 0$ , $\theta \in (0,1)$ , a family of measurable sets $(K_t)_{t \geq 0}$ such that $K_t \subset E_t$ for all $t \geq 0$ , a family of probability measures $\left(\nu_{s}\right)_{s \geq 0}$ on $(K_{s})_{s \geq 0}$ , and a family of functions $(\psi_s)_{s \geq 0}$ , all lower-bounded by 1, such that the following hold:

1. (i) For any $s \geq 0$ , $x \in K_s$ , and $n \geq n_0$ ,

   \begin{equation*}\delta_x P_{s,s+n t_1} \geq c \nu_{s+nt_1}.\end{equation*}

2. (ii) For any $s \geq 0$ ,

   \begin{equation*}P_{s,s+t_1} \psi_{s+t_1} \leq \theta \psi_s + C \mathbb{1}_{K_s}.\end{equation*}

3. (iii) For any $s \geq 0$ and $t \in [0,t_1)$ ,

   \begin{equation*}P_{s,s+t} \psi_{s+t} \leq C \psi_s.\end{equation*}

When a semigroup $(P_{s,t})_{s \leq t}$ satisfies Assumption 1 as stated above, we will say that the functions $(\psi_s)_{s \geq 0}$ are Lyapunov functions for the semigroup $(P_{s,t})_{s \leq t}$ . In particular, under (ii) and (iii), it is easy to prove that for any $s \leq t$ ,

(7) \begin{equation} P_{s,t} \psi_t \leq C \bigg(1 + \frac{C}{1-\theta}\bigg) \psi_s. \end{equation}

We remark in particular that Assumption 1 implies an exponential weak ergodicity in $\psi_t$ -distance; that is, we have the existence of two constants $C' > 0$ and $\kappa > 0$ such that, for all $s \leq t$ and for all probability measures $\mu_1, \mu_2 \in \mathcal{M}_1(E_s)$ ,

(8) \begin{equation} \| \mu_1 P_{s,t} - \mu_2 P_{s,t} \|_{\psi_t} \leq C' [\mu_1(\psi_s) + \mu_2(\psi_s)] e^{-\kappa (t-s)}, \end{equation}

where, for a given function $\psi$ , $\| \mu - \nu \|_\psi$ is the $\psi$ -distance, defined to be

\begin{equation*}\| \mu - \nu \|_{\psi} \;:\!=\; \sup_{|f| \leq \psi} \left| \mu(f) - \nu(f) \right|,\;\;\;\;\forall \mu, \nu \in \mathcal{M}_1(\psi).\end{equation*}

In particular, when $\psi = \mathbb{1}$ for all $t \geq 0$ , the $\psi$ -distance is the total variation distance. If we have weak ergodicity (8) in the time-homogeneous setting (see in particular [15]), the proof of [15, Theorem 1.3] can be adapted to a general time-inhomogeneous framework (see for example [6, Subsection 9.5]).

The main theorem and proof. The main result of this paper is the following.

Theorem 1. Let $\{ (E_t, {\mathcal E}_t)_{t \geq 0},(P_{s,t})_{s \leq t}, (X_t)_{t \geq 0}, (\mathbb{P}_{s,x})_{s \geq 0, x \in E_s}\}$ be an asymptotically $\gamma$ -periodic time-inhomogeneous Markov process, with $\gamma > 0$ , and denote by $\{(F_t, {\mathcal F}_t)_{t \geq 0},(Q_{s,t})_{s \leq t}\}$ its periodic auxiliary semigroup. Also, denote by $(\psi_s)_{s \geq 0}$ and $(\tilde{\psi}_s)_{s \geq 0}$ the two families of functions as defined in Definition 1. Assume moreover the following:

1. 1. The semigroups $(P_{s,t})_{s \leq t}$ and $(Q_{s,t})_{s \leq t}$ satisfy Assumption 1, with $(\psi_s)_{s \geq 0}$ and $(\tilde{\psi}_s)_{s \geq 0}$ respectively as Lyapunov functions.

2. 2. For any $s \in [0,\gamma)$ , $(\psi_{s+n \gamma})_{n \in \mathbb{Z}_+}$ converges pointwise to $\tilde{\psi}_s$ .

Then, for any $\mu \in \mathcal{M}_1(E_0)$ such that $\mu(\psi_0) < + \infty$ ,

(9) \begin{equation} \Bigg\|\frac{1}{t} \int_0^t \mu P_{0,s}[\psi_s \times \cdot] ds - \frac{1}{\gamma} \int_0^\gamma \beta_{\gamma} Q_{0,s}\big[\tilde{\psi}_s \times \cdot\big] ds \Bigg\|_{TV} \underset{t \to \infty}{{\longrightarrow}} 0, \end{equation}

where $\beta_\gamma \in \mathcal{M}_1(F_0)$ is the unique invariant probability measure of the skeleton semigroup $(Q_{0,n \gamma})_{n \in \mathbb{Z}_+}$ satisfying $\beta_\gamma(\tilde{\psi}_0) < + \infty$ . Moreover, for any $f \in \mathcal{B}(E)$ we have the following:

1. 1. For any $\mu \in \mathcal{M}_1(E_0)$ ,

   (10) \begin{equation} \mathbb{E}_{0,\mu}\!\left[\Bigg|\frac{1}{t} \int_0^t f(X_s)ds - \frac{1}{\gamma} \int_0^\gamma \beta_\gamma Q_{0,s}f ds\Bigg|^2\right] \underset{t \to \infty}{\longrightarrow} 0.\end{equation}

2. 2. If moreover $\mu(\psi_0) < + \infty$ , then

   (11) \begin{equation}\frac{1}{t} \int_0^t f(X_s) ds \underset{t \to \infty}{\longrightarrow} \frac{1}{\gamma} \int_0^\gamma \beta_\gamma Q_{0,s}f ds,\;\;\;\;\mathbb{P}_{0,\mu}\textit{-almost surely.}\end{equation}

Remark 1. When Assumption 1 holds for $K_s = E_s$ for any s, the condition (i) in Assumption 1 implies the Doeblin condition.

Doeblin condition. There exist $t_0 \geq 0$ , $c > 0$ , and a family of probability measures $(\nu_t)_{t \geq 0}$ on $(E_t)_{t \geq 0}$ such that, for any $s \geq 0$ and $x \in E_s$ ,

(12) \begin{equation} \delta_x P_{s,s+t_0} \geq c \nu_{s+t_0}.\end{equation}

In fact, if we assume that Assumption 1(i) holds for $K_s = E_s$ , the Doeblin condition holds if we set $t_0 \;:\!=\; n_0 t_1$ . Conversely, the Doeblin condition implies the conditions (i), (ii), and (iii) with $K_s = E_s$ and $\psi_s = \mathbb{1}_{E_s}$ for all $s \geq 0$ , so that these conditions are equivalent. In fact, (ii) and (iii) straightforwardly hold true for $(K_s)_{s \geq 0} = (E_s)_{s \geq 0}$ , $(\psi_s)_{s \geq 0} = (\mathbb{1}_{E_s})_{s \geq 0}$ , $C = 1$ , any $\theta \in (0,1)$ , and any $t_1 \geq 0$ . If we set $t_1 = t_0$ and $n_0 = 1$ , the Doeblin condition implies that, for any $s \in [0,t_1)$ ,

\begin{equation*}\delta_x P_{s,s+t_1} \geq c \nu_{s+t_1},\;\;\;\;\forall x \in E_s.\end{equation*}

Integrating this inequality over $\mu \in \mathcal{M}_1(E_s)$ , one obtains

\begin{equation*}\mu P_{s,s+t_1} \geq c \nu_{s+t_1},\;\;\;\;\forall s \in [0,t_1), \ \forall \mu \in \mathcal{M}_1(E_s).\end{equation*}

Then, by the Markov property, for all $s \in [0,t_1)$ , $x \in E_s$ , and $n \in \mathbb{N}$ , we have

\begin{equation*}\delta_x P_{s,s+nt_1} = (\delta_x P_{s,s+(n-1)t_1})P_{s + (n-1)t_1, s + nt_1} \geq c \nu_{s+nt_1},\end{equation*}

which is (i).

Theorem 1 then implies the following corollary.

Corollary 1. Let $(X_t)_{t \geq 0}$ be asymptotically $\gamma$ -periodic in total variation distance. If $(X_t)_{t \geq 0}$ and its auxiliary semigroup satisfy a Doeblin condition, then the convergence (10) is improved to

\begin{equation*} \sup_{\mu \in \mathcal{M}_1(E_0)} \sup_{f \in \mathcal{B}_1(E)} \mathbb{E}_{0,\mu}\left[\Bigg|\frac{1}{t} \int_0^t f(X_s)ds - \frac{1}{\gamma} \int_0^\gamma \beta_\gamma Q_{0,s}f ds\Bigg|^2\right] \underset{t \to \infty}{\longrightarrow} 0.\end{equation*}

Moreover, the almost sure convergence (11) holds for any initial measure $\mu$ .

Remark 2. We also note that, if the convergence (6) holds for all

\begin{equation*}x \in \bigcup_{k=0}^\infty \bigcap_{l \geq k} E_{s+l \gamma} \cap F_s,\end{equation*}

then this implies (6) and therefore the pointwise convergence of $(\psi_{s+n \gamma})_{n \in \mathbb{Z}_+}$ to $\tilde{\psi}_s$ (by taking $n = 0$ in (6)).

Proof of Theorem 1. The proof is divided into five steps.

First step. Since the auxiliary semigroup $(Q_{s,t})_{s \leq t}$ satisfies Assumption 1 with $(\tilde{\psi}_s)_{s \geq 0}$ as Lyapunov functions, the time-homogeneous semigroup $(Q_{0,n\gamma})_{n \in \mathbb{Z}_+}$ satisfies Assumptions 1 and 2 of [15], which we now recall (using our notation).

Assumption 2. ([15, Assumption 1].) There exist $V \;:\; F_0 \to [0,+\infty)$ , $n_1 \in \mathbb{N}$ , and constants $K \geq 0$ and $\kappa \in (0,1)$ such that

\begin{equation*}Q_{0,n_1\gamma} V \leq \kappa V + K.\end{equation*}

Assumption 3. ([15, Assumption 2].) There exist a constant $\alpha \in (0,1)$ and a probability measure $\nu$ such that

\begin{equation*}\inf_{x \in \mathcal{C}_R} \delta_x Q_{0,n_1\gamma} \geq \alpha \nu(\cdot),\end{equation*}

with $\mathcal{C}_R \;:\!=\; \{x \in F_0 \;:\; V(x) \leq R \}$ for some $R > 2 K/(1-\kappa)$ , where $n_1$ , K, and $\kappa$ are the constants from Assumption 2.

In fact, since $(Q_{s,t})_{s \leq t}$ satisfies (ii) and (iii) of Assumption 1, there exist $C > 0$ , $\theta \in (0,1)$ , $t_1 \geq 0$ , and $(K_s)_{s \geq 0}$ such that

(13) \begin{equation}Q_{s,s+t_1} \tilde{\psi}_{s+t_1} \leq \theta \tilde{\psi}_s + C \mathbb{1}_{K_s},\;\;\;\;\forall s \geq 0,\end{equation}

and

\begin{equation*}Q_{s,s+t}\tilde{\psi}_{s+t} \leq C \tilde{\psi}_s,\;\;\;\;\forall s \geq 0, \forall t \in [0,t_1).\end{equation*}

We let $n_2 \in \mathbb{N}$ be such that $\theta^{n_2} C \bigl(1 + \frac{C}{1-\theta}\bigl) < 1$ . By (13) and recalling that $\tilde{\psi}_t = \tilde{\psi}_{t+\gamma}$ for all $t \geq 0$ , one has for any $s \geq 0$ and $n \in \mathbb{N}$ ,

(14) \begin{equation}Q_{s,s+nt_1}\tilde{\psi}_{s+nt_1} \leq \theta^n \tilde{\psi}_s + \frac{C}{1 - \theta}.\end{equation}

Thus, for all $n_1 \geq \lceil \frac{n_2t_1}{\gamma} \rceil$ ,

\begin{align*}Q_{0,n_1\gamma}\tilde{\psi}_0 &= Q_{0,n_1 \gamma - n_2t_1} Q_{n_1 \gamma - n_2t_1, n_1 \gamma} \tilde{\psi}_{n_1 \gamma}\\[5pt] &\leq \theta^{n_2} Q_{0,n_1 \gamma -n_2t_1} \tilde{\psi}_{n_1\gamma-n_2t_1} + \frac{C}{1-\theta}\\[5pt] &\leq \theta^{n_2}C\bigg(1 + \frac{C}{1-\theta}\bigg) \tilde{\psi}_0 + \frac{C}{1 - \theta},\end{align*}

where we successively used the semigroup property of $(Q_{s,t})_{s \leq t}$ , (14), and (7) applied to $(Q_{s,t})_{s \leq t}$ . Hence one has Assumption 2 by setting $V = \tilde{\psi}_0$ , $\kappa \;:\!=\; \theta^{n_2}C\bigl(1 + \frac{C}{1-\theta}\bigl)$ , and $K \;:\!=\; \frac{C}{1 - \theta}$ .

We now prove Assumption 3. To this end, we introduce a Markov process $(Y_t)_{t \geq 0}$ and a family of probability measures $(\hat{\mathbb{P}}_{s,x})_{s \geq 0, x \in F_s}$ such that

\begin{equation*}\hat{\mathbb{P}}_{s,x}(Y_t \in A) = Q_{s,t}\mathbb{1}_A(x),\;\;\;\;\forall s \leq t,\ x \in F_s,\ A \in {\mathcal F}_t.\end{equation*}

In what follows, for all $s \geq 0$ and $x \in F_s$ , we will use the notation $\hat{\mathbb{E}}_{s,x}$ for the expectation associated to $\hat{\mathbb{P}}_{s,x}$ . Moreover, we define

\begin{equation*}T_K \;:\!=\; \inf\!\big\{n \in \mathbb{Z}_+ \;:\; Y_{n t_1} \in K_{nt_1}\big\}.\end{equation*}

Then, using (13) recursively, for all $k \in \mathbb{N}$ , $R > 0$ , and $x \in \mathcal{C}_R$ (recalling that $\mathcal{C}_R$ is defined in the statement of Assumption 3), we have

\begin{align*}\hat{\mathbb{E}}_{0,x}\big[\tilde{\psi}_{kt_1}(Y_{kt_1})\mathbb{1}_{T_K > k}\big] &= \hat{\mathbb{E}}_{0,x}\big[\mathbb{1}_{T_K > k-1} \hat{\mathbb{E}}_{(k-1)t_1,Y_{(k-1)t_1}}\big(\tilde{\psi}_{kt_1}(Y_{kt_1})\mathbb{1}_{T_K > k}\big)\big] \\[5pt] &\leq \theta \hat{\mathbb{E}}_{0,x}\big[\tilde{\psi}_{(k-1)t_1}(Y_{(k-1)t_1})\mathbb{1}_{T_K > k-1}\big] \leq \theta^{k} \tilde{\psi}_0(x) \leq R \theta^k.\end{align*}

Since $\tilde{\psi}_{kt_1} \geq 1$ for all $k \in \mathbb{Z}_+$ , we have that for all $x \in \mathcal{C}_R$ , for all $k \in \mathbb{Z}_+$ ,

\begin{equation*}\hat{\mathbb{P}}_{0,x}(T_K > k) \leq R \theta^k.\end{equation*}

In particular, there exists $k_0 \geq n_0$ such that, for all $k \geq k_0 - n_0$ ,

\begin{equation*}\hat{\mathbb{P}}_{0,x}(T_K > k) \leq \frac{1}{2}.\end{equation*}

Hence, for all $x \in \mathcal{C}_R$ ,

\begin{align*}\delta_x Q_{0,k_0t_1} = \hat{\mathbb{P}}_{0,x}\big(Y_{k_0t_1} \in \cdot\big) \geq &\sum_{i=0}^{k_0-n_0} \hat{\mathbb{E}}_{0,x}\big(\mathbb{1}_{T_K = i} \hat{\mathbb{P}}_{it_1,Y_{it_1}}\big(Y_{k_0t_1} \in \cdot\big)\big) \\[5pt] &\geq c \sum_{i=0}^{k_0-n_0} \hat{\mathbb{E}}_{0,x}\big(\mathbb{1}_{T_K = i}\big) \times \nu_{k_0t_1} \\[5pt] &= c \hat{\mathbb{P}}_{0,x}\big(T_K \leq k_0 - n_0\big) \nu_{k_0t_1} \\[5pt] &\geq \frac{c}{2} \nu_{k_0t_1}.\end{align*}

Hence, for all $n_1 \geq \bigl\lceil \frac{k_0t_1}{\gamma} \bigl\rceil$ , for all $x \in \mathcal{C}_R$ ,

\begin{equation*}\delta_x Q_{0,k_0t_1}Q_{k_0t_1,n_1\gamma} \geq \frac{c}{2} \nu_{k_0t_1} Q_{k_0t_1, n_1 \gamma}.\end{equation*}

Thus, Assumption 3 is satisfied if we take $n_1 \;:\!=\; \bigl\lceil \frac{n_2 t_1}{\gamma}\bigl\rceil \lor \bigl\lceil \frac{k_0t_1}{\gamma} \bigl\rceil$ , $\alpha \;:\!=\; \frac{c}{2}$ , and $\nu(\cdot) \;:\!=\; \nu_{k_0t_1} Q_{k_0t_1,n_1\gamma}$ .

Then, by [15, Theorem 1.2], Assumptions 2 and 3 imply that $Q_{0,n_1 \gamma}$ admits a unique invariant probability measure $\beta_\gamma$ . Furthermore, there exist constants $C > 0$ and $\delta \in (0,1)$ such that, for all $\mu \in \mathcal{M}_1(F_0)$ ,

(15) \begin{equation}\| \mu Q_{0,nn_1\gamma} - \beta_\gamma\|_{\tilde{\psi}_0} \leq C \mu(\tilde{\psi}_0) \delta^n.\end{equation}

Since $\beta_\gamma$ is the unique invariant probability measure of $Q_{0,n_1 \gamma}$ , and noting that $\beta_\gamma Q_{0,\gamma}$ is invariant for $Q_{0,n_1 \gamma}$ , we deduce that $\beta_\gamma$ is the unique invariant probability measure for $Q_{0,\gamma}$ , and by (15), for all $\mu$ such that $\mu(\tilde{\psi}_0) < + \infty$ ,

\begin{equation*}\|\mu Q_{0,n\gamma} - \beta_\gamma\|_{\tilde{\psi}_0} \underset{n \to \infty}{\longrightarrow} 0.\end{equation*}

Now, for any $s \geq 0$ , note that $\delta_x Q_{s,\lceil \frac{s}{\gamma} \rceil \gamma} \tilde{\psi}_0 < + \infty$ for all $x \in F_s$ (this is a consequence of (7) applied to the semigroup $(Q_{s,t})_{s \leq t}$ ), and therefore, taking $\mu = \delta_x Q_{s,\lceil \frac{s}{\gamma} \rceil \gamma}$ in the above convergence,

\begin{equation*}\|\delta_x Q_{s,n\gamma} - \beta_\gamma\|_{\tilde{\psi}_0} \underset{n \to \infty}{\longrightarrow} 0\end{equation*}

for all $x \in F_s$ . Hence, since $Q_{n\gamma, n \gamma +s}\tilde{\psi}_s \leq C \bigl(1 + \frac{C}{1-\theta}\bigl) \tilde{\psi}_{n \gamma}$ by (7), we conclude from the above convergence that

(16) \begin{equation} \| \delta_{x} Q_{s,s+n\gamma} - \beta_\gamma Q_{0,s} \|_{\tilde{\psi}_s} \leq C \bigg(1 + \frac{C}{1-\theta}\bigg) \|\delta_x Q_{s,n\gamma} - \beta_\gamma\|_{\tilde{\psi}_0} \underset{n \to \infty}{\longrightarrow} 0.\end{equation}

Moreover, $\beta_\gamma(\tilde{\psi}_0) < + \infty$ .

Second step. The first part of this step (up to the equality (20)) is inspired by the proof of [1, Theorem 3.11].

We fix $s \in [0,\gamma]$ . Without loss of generality, we assume that $\bigcap_{l \geq 0} E_{s+l \gamma} \cap F_s \ne \emptyset$ . Then, by Definition 1, there exists $x_s \in \bigcap_{l \geq 0} E_{s+l \gamma} \cap F_s$ such that for any $n \geq 0$ ,

\begin{equation*} \big\|\delta_{x_s} P_{s+k \gamma, s+(k+n)\gamma}[\psi_{s+(k+n)\gamma} \times \cdot] - \delta_{x_s} Q_{s, s + n \gamma}\big[\tilde{\psi}_{s} \times \cdot\big]\big\|_{TV} \underset{k \to \infty}{\longrightarrow} 0,\end{equation*}

which implies by (16) that

(17) \begin{equation} \lim_{n \to \infty} \lim_{k \to \infty} \big\|\delta_{x_s} P_{s+k \gamma, s+(k+n)\gamma}[\psi_{s+(k+n)\gamma} \times \cdot] - \beta_\gamma Q_{0,s}\big[\tilde{\psi}_s \times \cdot\big] \big\|_{TV} = 0.\end{equation}

Then, by the Markov property, (8), and (7), one obtains that, for any $k,n \in \mathbb{N}$ and $x \in \bigcap_{l \geq 0} E_{s+l \gamma}$ ,

(18) \begin{align} \|\delta_{x} & P_{s,s+(k+n)\gamma} - \delta_{x} P_{s+k\gamma, s+(k+n)\gamma} \|_{\psi_{s+(k+n)\gamma}} \notag \\[5pt] & \qquad = \|\left(\delta_{x} P_{s,s+k \gamma} \right) P_{s+k\gamma,s+(k+n)\gamma} - \delta_{x} P_{s+k\gamma, s+(k+n)\gamma} \|_{\psi_{s+(k+n)\gamma}} \notag \\[5pt] & \qquad \leq C' [P_{s,s+k \gamma} \psi_{s+k \gamma}(x) + \psi_{s+k \gamma}(x)] e^{- \kappa \gamma n} \notag \\[5pt] & \qquad \leq C''[\psi_s(x) + \psi_{s+k \gamma}(x)] e^{-\kappa \gamma n},\end{align}

where $C'' \;:\!=\; C' \bigl(C \bigl(1 + \frac{C}{1-\theta}\bigl) \lor 1\bigl)$ . Then, for any $k,n \in \mathbb{N}$ ,

(19) \begin{align} \| \delta_{x_s} P_{s,s+(k+n)\gamma}[\psi_{s+(k+n)\gamma} \times \cdot] - \beta_\gamma Q_{0,s} [\tilde{\psi}_{s} \times \cdot] \|_{TV} \end{align}

\begin{align*} \leq C''[\psi_s(x) + \psi_{s+k \gamma}(x)] e^{-\kappa \gamma n} +\big\|\delta_{x_s} P_{s+k \gamma, s+(k+n)\gamma}[\psi_{s+(k+n)\gamma} \times \cdot] - \beta_\gamma Q_{0,s}\big[\tilde{\psi}_s \times \cdot\big] \big\|_{TV}, \end{align*}

which by (17) and the pointwise convergence of $(\psi_{s+k \gamma})_{k \in \mathbb{Z}_+}$ implies that

(20) \begin{align} \lim_{n \to \infty} &\big\| \delta_{x_s} P_{s,s+n\gamma}[\psi_{s+n\gamma} \times \cdot] - \beta_\gamma Q_{0,s}\big[\tilde{\psi}_s \times \cdot\big] \big\|_{TV} \notag \\[5pt] & = \lim_{n \to \infty} \limsup_{k \to \infty} \| \delta_{x_s} P_{s,s+(k+n)\gamma}[\psi_{s+(k+n)\gamma} \times \cdot] - \beta_\gamma Q_{0,s} \big[\tilde{\psi}_{s} \times \cdot\big] \big\|_{TV} \notag \\[5pt] & = 0.\end{align}

The weak ergodicity (8) implies therefore that the previous convergence actually holds for any initial distribution $\mu \in \mathcal{M}_1(E_0)$ satisfying $\mu(\psi_0) < + \infty$ , so that

(21) \begin{equation} \big\| \mu P_{0,s+n \gamma}[\psi_{s+n \gamma} \times \cdot] - \beta_\gamma Q_{0,s}\big[\tilde{\psi}_s \times \cdot\big] \big\|_{TV} \underset{n \to \infty}{\longrightarrow} 0.\end{equation}

Since

\begin{equation*}\big\|\mu P_{0,s+n\gamma}[\psi_{s+n\gamma} \times \cdot] - \beta_\gamma Q_{0,s}\big[\tilde{\psi}_s \times \cdot\big]\big\|_{TV} \leq 2\end{equation*}

for all $\mu \in \mathcal{M}_1(E_0)$ , $s \geq 0$ , and $n \in \mathbb{Z}_+$ , (21) and Lebesgue’s dominated convergence theorem imply that

\begin{equation*}\frac{1}{\gamma} \int_0^\gamma \big\|\mu P_{0,s+n\gamma}[\psi_{s+n\gamma} \times \cdot] - \beta_\gamma Q_{0,s}\big[\tilde{\psi}_s \times \cdot\big]\big\|_{TV}ds \underset{n \to \infty}{\longrightarrow} 0,\end{equation*}

which implies that

\begin{equation*}\bigg\|\frac{1}{\gamma}\int_0^\gamma \mu P_{0,s+n\gamma}[\psi_{s+n \gamma} \times \cdot]ds - \frac{1}{\gamma} \int_0^\gamma \beta_\gamma Q_{0,s}\big[\tilde{\psi}_{s} \times \cdot\big] ds \bigg\|_{TV} \underset{n \to \infty}{\longrightarrow} 0.\end{equation*}

By Cesaro’s lemma, this allows us to conclude that, for any $\mu \in \mathcal{M}_1(E_0)$ such that $\mu(\psi_0) < + \infty$ ,

\begin{align*} \bigg\|\frac{1}{t} \int_0^t &\mu P_{0,s} [\psi_{s} \times \cdot] ds - \frac{1}{\gamma} \int_0^\gamma \beta_\gamma Q_{0,s} \big[\tilde{\psi}_{s} \times \cdot\big] ds \bigg\|_{TV} \\[5pt] & \leq \frac{1}{\lfloor \frac{t}{\gamma} \rfloor} \sum_{k=0}^{\lfloor \frac{t}{\gamma} \rfloor}\bigg\|\frac{1}{\gamma}\int_0^\gamma \mu P_{0,s+k\gamma}[\psi_{s+k \gamma} \times \cdot]ds - \frac{1}{\gamma} \int_0^\gamma \beta_\gamma Q_{0,s}\big[\tilde{\psi}_{s} \times \cdot\big] ds \bigg\|_{TV} \\[5pt] & \quad\qquad\qquad\qquad\qquad\qquad\qquad\qquad + \Bigg\|\frac{1}{t} \int_{\lfloor \frac{t}{\gamma} \rfloor \gamma}^t \mu P_{0,s}[\psi_{s} \times \cdot] ds\Bigg\|_{TV}\underset{t \to \infty}{\longrightarrow} 0,\end{align*}

which concludes the proof of (9) .

Third step. In the same manner, we now prove that, for any $\mu \in \mathcal{M}_1(E_0)$ such that $\mu(\psi_0) < + \infty$ ,

(22) \begin{equation} \bigg\|\frac{1}{t} \int_0^t \mu P_{0,s} ds - \frac{1}{\gamma} \int_0^\gamma \beta_\gamma Q_{0,s} ds \bigg\|_{TV} \underset{t \to \infty}{\longrightarrow} 0.\end{equation}

In fact, for any function f bounded by 1 and $\mu \in \mathcal{M}_1(E_0)$ such that $\mu(\psi_0) < + \infty$ ,

\begin{align*}&\bigg| \mu P_{0,s+n \gamma}\bigg[\psi_{s+n\gamma} \times \frac{f}{\psi_{s+n \gamma}}\bigg] - \beta_\gamma Q_{0,s}\bigg[\tilde{\psi}_s \times \frac{f}{\tilde{\psi}_s}\bigg]\bigg| \\[5pt] & \leq \bigg| \mu P_{0,s+n \gamma}\bigg[\psi_{s+n\gamma} \times \frac{f}{\psi_{s+n \gamma}}\bigg] - \beta_\gamma Q_{0,s}\bigg[\tilde{\psi}_s \times \frac{f}{{\psi}_{s+n\gamma}}\bigg]\bigg| + \bigg| \beta_\gamma Q_{0,s}\bigg[\tilde{\psi}_s \times \frac{f}{{\psi}_{s+n\gamma}}\bigg] \\[5pt] & \quad - \beta_\gamma Q_{0,s}\bigg[\tilde{\psi}_s \times \frac{f}{\tilde{\psi}_s}\bigg]\bigg| \\[5pt] & \leq \bigg\| \mu P_{0,s+n \gamma}[\psi_{s+n \gamma} \times \cdot] - \beta_\gamma Q_{0,s}\big[\tilde{\psi}_s \times \cdot\big] \bigg\|_{TV} + \bigg| \beta_\gamma Q_{0,s}\bigg[\tilde{\psi}_s \times \frac{f}{{\psi}_{s+n\gamma}}\bigg] \\[5pt] & \quad - \beta_\gamma Q_{0,s}\bigg[\tilde{\psi}_s \times \frac{f}{\tilde{\psi}_s}\bigg]\bigg|.\end{align*}

We now remark that, since $\psi_{s+n \gamma} \geq 1$ for any s and $n \in \mathbb{Z}_+$ , one has that

\begin{equation*}\bigg| \frac{\tilde{\psi}_s}{\psi_{s+n \gamma}} - 1 \bigg| \leq 1 + \tilde{\psi}_s.\end{equation*}

Since $(\psi_{s + n \gamma})_{n \in \mathbb{Z}_+}$ converges pointwise towards $\tilde{\psi}_s$ and $\beta_\gamma Q_{0,s} \tilde{\psi}_s < + \infty$ , Lebesgue’s dominated convergence theorem implies

\begin{equation*}\sup_{f \in \mathcal{B}_1(E)} \bigg| \beta_\gamma Q_{0,s}\bigg[\tilde{\psi}_s \times \frac{f}{{\psi}_{s+n\gamma}}\bigg] - \beta_\gamma Q_{0,s}\bigg[\tilde{\psi}_s \times \frac{f}{\tilde{\psi}_s}\bigg]\bigg| \underset{n \to \infty}{\longrightarrow} 0.\end{equation*}

Then, using (21), one has

\begin{equation*} \left\| \mu P_{0,s+n \gamma} - \beta_\gamma Q_{0,s} \right\|_{TV} \underset{n \to \infty}{\longrightarrow} 0,\end{equation*}

which allows us to conclude (22), using the same argument as in the first step.

Fourth step. In order to show the $\mathbb{L}^2$ -ergodic theorem, we let $f \in \mathcal{B}(E)$ . For any $x \in E_0$ and $t \geq 0$ ,

\begin{align*} \mathbb{E}_{0,x}&\Bigg[\bigg|\frac{1}{t} \int_0^t f(X_s)ds - \mathbb{E}_{0,x}\bigg[\frac{1}{t} \int_0^t f(X_s)ds\bigg] \bigg|^2\Bigg] \\[5pt] & = \frac{2}{t^2} \int_0^t \int_s^t (\mathbb{E}_{0,x}[f(X_s)f(X_u)] - \mathbb{E}_{0,x}[f(X_s)]\mathbb{E}_{0,x}[f(X_u)])du\,ds\\[5pt] & = \frac{2}{t^2} \int_0^t \int_s^t \mathbb{E}_{0,x}[f(X_s)(f(X_u) - \mathbb{E}_{0,x}[f(X_u)])]du\,ds\\[5pt] & = \frac{2}{t^2} \int_0^t \int_s^t \mathbb{E}_{0,x}[f(X_s)(\mathbb{E}_{s,X_s}[f(X_u)] - \mathbb{E}_{s,\delta_x P_{0,s}}[f(X_u)])]du\,ds,\end{align*}

where the Markov property was used in the last line. By (8) (weak ergodicity) and (7), one obtains for any $s \leq t$

(23) \begin{equation} \big|\mathbb{E}_{s,X_s}[f(X_t)] - \mathbb{E}_{s,\delta_x P_{0,s}}[f(X_t)]\big| \leq C'' \|f\|_\infty [\psi_s(X_s) + \psi_0(x)] e^{- \kappa (t-s)},\;\;\;\;\mathbb{P}_{0,x}\text{-almost surely,}\end{equation}

where C ′ was defined in the first part. As a result, for any $x \in E_0$ and $t \geq 0$ ,

\begin{align*} \mathbb{E}_{0,x} &\Bigg[\bigg|\frac{1}{t} \int_0^t f(X_s)ds - \mathbb{E}_{0,x}\bigg[\frac{1}{t} \int_0^t f(X_s)ds\bigg] \bigg|^2\Bigg] \\[5pt] &\leq \frac{2C''\|f\|_\infty}{t^2} \int_0^t \int_s^t \mathbb{E}_{0,x}[|f(X_s)|(\psi_s(X_s)+\psi_0(x))] e^{-\kappa(u-s)}du\,ds \\[5pt] &= \frac{2C''\|f\|_\infty}{t^2} \int_0^t \mathbb{E}_{0,x}[|f(X_s)|(\psi_s(X_s)+\psi_0(x))] e^{\kappa s} \frac{e^{-\kappa s} - e^{- \kappa t}}{\kappa}ds \\[5pt] &= \frac{2C''\|f\|_\infty}{\kappa t} \times \mathbb{E}_{0,x}\bigg[\frac{1}{t} \int_0^t |f(X_s)|(\psi_s(X_s) + \psi_0(x))ds\bigg] \\[5pt] & \quad - \frac{2C''\|f\|_\infty e^{-\kappa t}}{\kappa t^2} \int_0^t e^{\kappa s} \mathbb{E}_{0,x}[|f(X_s)|(\psi_s(X_s)+\psi_0(x))]ds.\end{align*}

Then, by (9), there exists a constant $\tilde{C} > 0$ such that, for any $x \in E_0$ , when $t \to \infty$ ,

(24) \begin{align} & \mathbb{E}_{0,x}\Bigg[\bigg|\frac{1}{t} \int_0^t f(X_s)ds - \mathbb{E}_{0,x}\bigg[\frac{1}{t} \int_0^t f(X_s)ds\bigg] \bigg|^2\Bigg] \leq \frac{\tilde{C} \|f\|_{\infty} \psi_0(x)}{t} \nonumber \\[5pt] & \quad \times \frac{1}{\gamma} \int_0^\gamma \beta_\gamma Q_{0,s}\big[|f|\tilde{\psi}_s\big] ds + o\bigg(\frac{1}{t}\bigg).\end{align}

Since $f \in \mathcal{B}(E)$ and by definition of the total variation distance, (22) implies that, for all $x \in E_0$ ,

\begin{equation*}\bigg| \frac{1}{t} \int_0^t P_{0,s}f(x) - \frac{1}{\gamma} \int_0^\gamma \beta_\gamma Q_{0,s} f ds \bigg| \leq \|f\|_\infty \bigg\|\frac{1}{t} \int_0^t \delta_x P_{0,s} ds - \frac{1}{\gamma} \int_0^\gamma \beta_\gamma Q_{0,s} ds \bigg\|_{TV} \underset{t \to \infty}{\longrightarrow} 0.\end{equation*}

Then, using (22), one deduces that for any $x \in E_0$ and bounded function f,

\begin{align*}& \mathbb{E}_{0,x}\Bigg[\bigg|\frac{1}{t} \int_0^t f(X_s)ds - \frac{1}{\gamma} \int_0^\gamma \beta_\gamma Q_{0,s} f ds \bigg|^2\Bigg] \\[5pt] & \leq 2 \Bigg(\mathbb{E}_{0,x}\Bigg[\!\bigg(\frac{1}{t} \int_0^t f(X_s)ds - \frac{1}{t} \int_0^t P_{0,s}f(x)\!\bigg)^2\Bigg] + \left| \frac{1}{t} \int_0^t P_{0,s}f(x) - \frac{1}{\gamma} \int_0^\gamma \beta_\gamma Q_{0,s} f ds \right|^2\Bigg) \!\underset{t \to \infty}{\longrightarrow} \!0.\end{align*}

The convergence for any probability measure $\mu \in \mathcal{M}_1(E_0)$ comes from Lebesgue’s dominated convergence theorem.

Fifth step. We now fix nonnegative $f \in \mathcal{B}(E)$ , and $\mu \in \mathcal{M}_1(E_0)$ satisfying $\mu(\psi_0) < + \infty$ . The following proof is inspired by the proof of [26, Theorem 12].

Since $\mu(\psi_0) < + \infty$ , the inequality (24) implies that there exists a finite constant $C_{f,\mu} \in (0,\infty)$ such that, for t large enough,

\begin{equation*}\mathbb{E}_{0,\mu}\Bigg[\bigg|\frac{1}{t} \int_0^t f(X_s)ds - \mathbb{E}_{0,\mu}\bigg[\frac{1}{t} \int_0^t f(X_s)ds\bigg] \bigg|^2\Bigg] \leq \frac{C_{f,\mu}}{t}.\end{equation*}

Then, for n large enough,

\begin{equation*}\mathbb{E}_{0,\mu}\Bigg[\Bigg|\frac{1}{n^2} \int_0^{n^2} f(X_s)ds - \mathbb{E}_{0,\mu}\Bigg[\frac{1}{n^2} \int_0^{n^2} f(X_s)ds\Bigg] \Bigg|^2\Bigg] \leq \frac{C_{f,\mu}}{n^2}.\end{equation*}

Then, by Chebyshev’s inequality and the Borel–Cantelli lemma, this last inequality implies that

\begin{equation*}\Bigg|\frac{1}{n^2} \int_0^{n^2} f(X_s)ds - \mathbb{E}_{0,\mu}\Bigg[\frac{1}{n^2} \int_0^{n^2} f(X_s)ds\Bigg] \Bigg| \underset{n \to \infty}{{\longrightarrow}} 0,\;\;\;\;\mathbb{P}_{0,\mu}\text{-almost surely.}\end{equation*}

One thereby obtains by the convergence (22) that

(25) \begin{equation}\frac{1}{n^2} \int_0^{n^2} f(X_s)ds \underset{n \to \infty}{{\longrightarrow}} \frac{1}{\gamma} \int_0^\gamma \beta_\gamma Q_{0,s} f ds,\;\;\;\;\mathbb{P}_{0,\mu}\text{-almost surely.}\end{equation}

Since the nonnegativity of f is assumed, this implies that for any $t > 0$ we have

\begin{equation*}\int_0^{\lfloor \sqrt{t} \rfloor^2} f(X_s)ds \leq \int_0^t f(X_s)ds \leq \int_0^{\lceil \sqrt{t} \rceil^2} f(X_s)ds.\end{equation*}

These inequalities and (25) then give that

\begin{equation*}\frac{1}{t} \int_0^t f(X_s)ds \;\underset{t \to \infty}{{\longrightarrow}}\; \frac{1}{\gamma} \int_0^\gamma \beta_\gamma Q_{0,s} f ds,\;\;\;\;\mathbb{P}_{0,\mu}\text{-almost surely.}\end{equation*}

In order to conclude that the result holds for any bounded measurable function f, it is enough to decompose $f = f_+ - f_-$ with $f_+ \;:\!=\; f \lor 0$ and $f_- = (\!-\!f) \lor 0$ and apply the above convergence to $f_+$ and $f_-$ . This concludes the proof of Theorem 1.

Proof of corollary 1. We remark as in the previous proof that, if $\|f\|_\infty \leq 1$ and $\psi_s = \mathbb{1}$ , an upper bound for the inequality (24) can be obtained, which does not depend on f and x. Likewise, the convergence (21) holds uniformly in the initial measure thanks to (23).

Remark 3. The proof of Theorem 1, as written above, does not allow us to deal with semigroups satisfying a Doeblin condition with time-dependent constant $c_s$ , that is, such that there exist $t_0 \geq 0$ and a family of probability measure $(\nu_t)_{t \geq 0}$ on $(E_t)_{t \geq 0}$ such that, for all $s \geq 0$ and $x \in E_s$ ,

\begin{equation*}\delta_x P_{s,s+t_0} \geq c_{s+t_0} \nu_{s+t_0}.\end{equation*}

In fact, under the condition written above, we can show (see for example the proof of the formula (2.7) of [9, Theorem 2.1]) that, for all $s \leq t$ and $\mu_1, \mu_2 \in \mathcal{M}_1(E_s)$ ,

\begin{equation*}\| \mu_1 P_{s,t} - \mu_2 P_{s,t} \|_{TV} \leq 2 \prod_{k=0}^{\left \lfloor \frac{t-s}{t_0} \right \rfloor-1} (1-c_{t-k t_0}).\end{equation*}

Hence, by this last inequality with $\mu_1 = \delta_x P_{s,s+k\gamma}$ , $\mu_2 = \delta_x$ , replacing s by $s+k\gamma$ and t by $s+(k+n)\gamma$ , one obtains

\begin{equation*}\|\delta_x P_{s,s+(k+n)\gamma} - \delta_x P_{s+k\gamma,s+(k+n)\gamma}\|_{TV} \leq 2 \prod_{l=0}^{\big\lfloor \frac{n\gamma}{t_0}\big\rfloor-1} (1-c_{s+(k+n)\gamma-lt_0}),\end{equation*}

which replaces the inequality (18) in the proof of Theorem 1. Plugging this last inequality into the formula (19), one obtains

\begin{equation*}\| \delta_{x} P_{s,s+(k+n)\gamma} - {\beta}_{\gamma} Q_{0,s} \|_{TV} \leq 2 \prod_{l=0}^{\left \lfloor \frac{n \gamma}{t_0} \right \rfloor-1} (1-c_{s + (k+n)\gamma-l t_0}) + \| \delta_{x} P_{s+k\gamma, s+(k+n)\gamma} - \beta_\gamma Q_{0,s} \|_{TV}.\end{equation*}

Hence, we see that we cannot conclude a similar result when $c_s \longrightarrow 0$ as $s \to + \infty$ , since, for n fixed,

\begin{equation*}\limsup_{k \to \infty} \prod_{l=0}^{\left \lfloor \frac{n \gamma}{t_0} \right \rfloor-1} (1-c_{s+(k+n)\gamma-l t_0}) = 1.\end{equation*}

4. Application to quasi-stationarity with moving boundaries

In this section, $(X_t)_{t \geq 0}$ is assumed to be a time-homogeneous Markov process. We consider a family of measurable subsets $(A_t)_{t \geq 0}$ of E, and define the hitting time

\begin{equation*}\tau_A \;:\!=\; \inf\{t \geq 0 \;:\; X_t \in A_t\}.\end{equation*}

For all $s \leq t$ , denote by ${\mathcal F}_{s,t}$ the $\sigma$ -field generated by the family $(X_u)_{s \leq u \leq t}$ , with ${\mathcal F}_t \;:\!=\; {\mathcal F}_{0,t}$ . Assume that $\tau_A$ is a stopping time with respect to the filtration $({\mathcal F}_{t})_{t \geq 0}$ . Assume also that for any $x \not \in A_0$ ,

\begin{equation*}\mathbb{P}_{0,x}[\tau_A < + \infty] = 1 \;\;\;\;\;\;\text{ and }\;\;\;\;\;\; \mathbb{P}_{0,x}[\tau_A > t] > 0,\;\;\forall t \geq 0.\end{equation*}

We will be interested in a notion of quasi-stationarity with moving boundaries, which studies the asymptotic behavior of the Markov process $(X_t)_{t \geq 0}$ conditioned not to hit $(A_t)_{t \geq 0}$ up to the time t. For non-moving boundaries ( $A_t = A_0$ for any $t \geq 0$ ), the quasi-limiting distribution is defined as a probability measure $\alpha$ such that, for at least one initial measure $\mu$ and for all measurable subsets $\mathcal{A} \subset E$ ,

\begin{equation*}\mathbb{P}_{0,\mu}[X_t \in \mathcal{A} | \tau_A > t] \underset{t \to \infty}{\longrightarrow} \alpha(\mathcal{A}).\end{equation*}

Such a definition is equivalent (still in the non-moving framework) to the notion of quasi-stationary distribution, defined as a probability measure $\alpha$ such that, for any $t \geq 0$ ,

(26) \begin{equation}\mathbb{P}_{0,\alpha}[X_t \in \cdot | \tau_A > t] = \alpha.\end{equation}

If quasi-limiting and quasi-stationary distributions are in general well-defined for time-homogeneous Markov processes and non-moving boundaries (see [11, 23] for a general overview of the theory of quasi-stationarity), these notions are nevertheless not well-defined for time-inhomogeneous Markov processes or moving boundaries, for which they are no longer equivalent. In particular, under reasonable assumptions on irreducibility, it was shown in [24] that the notion of quasi-stationary distribution as defined by (26) is not well-defined for time-homogeneous Markov processes absorbed by moving boundaries.

Another asymptotic notion to study is the quasi-ergodic distribution, related to a conditional version of the ergodic theorem and usually defined as follows.

Definition 2. A probability measure $\beta$ is a quasi-ergodic distribution if, for some initial measure $\mu \in \mathcal{M}_1(E \setminus A_0)$ and for any bounded continuous function f,

\begin{equation*}\mathbb{E}_{0,\mu}\bigg[\frac{1}{t} \int_0^t f(X_s)ds \bigg| \tau_A > t\bigg] \underset{t \to \infty}{\longrightarrow} \beta(f).\end{equation*}

In the time-homogeneous setting (in particular for non-moving boundaries), this notion has been extensively studied (see for example [2, 8, 10, 12, 13, 16–18, 24]). In the ‘moving boundaries’ framework, the existence of quasi-ergodic distributions has been dealt with in [24] for Markov chains on finite state spaces absorbed by periodic boundaries, and in [25] for processes satisfying a Champagnat–Villemonais condition (see Assumption (A′) below) absorbed by converging or periodic boundaries. In this last paper, the existence of the quasi-ergodic distribution is dealt with through the following inequality (see [25, Theorem 1]), which holds for any initial state x, $s \leq t$ , and for some constants $C, \gamma > 0$ independent of x, s, and t:

\begin{equation*}\|\mathbb{P}_{0,x}(X_s \in \cdot | \tau_A > t) - \mathbb{Q}_{0,x}(X_s \in \cdot)\|_{TV} \leq C e^{-\gamma (t-s)},\end{equation*}

where the family of probability measures $(\mathbb{Q}_{s,x})_{s \geq 0, x \in E_s}$ is defined by

\begin{equation*}\mathbb{Q}_{s,x}[\Gamma] \;:\!=\; \lim_{T \to \infty} \mathbb{P}_{s,x}[\Gamma | \tau_A > T],\;\;\;\;\forall s \leq t,\ x \in E \setminus A_s,\ \Gamma \in {\mathcal F}_{s,t}.\end{equation*}

Moreover, by [9, Proposition 3.1], there exists a family of positive bounded functions $(\eta_t)_{t \geq 0}$ defined in such a way that, for all $s \leq t$ and $x \in E_s$ ,

\begin{equation*}\mathbb{E}_{s,x}(\eta_t(X_t)\mathbb{1}_{\tau_A > t}) = \eta_s(x).\end{equation*}

Then we can show (this is actually shown in [9]) that

\begin{equation*}\mathbb{Q}_{s,x}(\Gamma) = \mathbb{E}_{s,x}\bigg(\mathbb{1}_{\Gamma, \tau_A > t} \frac{\eta_t(X_t)}{\eta_s(x)}\bigg)\end{equation*}

and that, for all $\mu \in \mathcal{M}_1(E_0)$ ,

\begin{equation*}\|\mathbb{P}_{0,\mu}(X_s \in \cdot | \tau_A > t) - \mathbb{Q}_{0,\eta_0*\mu}(X_s \in \cdot)\|_{TV} \leq C e^{-\gamma (t-s)},\end{equation*}

where

\begin{equation*}\eta_0 * \mu(dx) \;:\!=\; \frac{\eta_0(x)\mu(dx)}{\mu(\eta_0)}.\end{equation*}

By the triangle inequality, one has

(27) \begin{equation}\bigg\|\frac{1}{t} \int_0^t \mathbb{P}_{0,\mu}[X_s \in \cdot | \tau_A > t]ds - \frac{1}{t} \int_0^t \mathbb{Q}_{0,\eta_0 * \mu}[X_s \in \cdot]ds \bigg\|_{TV} \leq \frac{C}{\gamma t},\;\;\;\;\forall t > 0.\end{equation}

In particular, the inequality (27) implies that there exists a quasi-ergodic distribution $\beta$ for the process $(X_t)_{t \geq 0}$ absorbed by $(A_t)_{t \geq 0}$ if and only if there exist some probability measures $\mu \in \mathcal{M}_1(E_0)$ such that $\frac{1}{t} \int_0^t \mathbb{Q}_{0,\eta_0 * \mu}[X_s \in \cdot]ds$ converges weakly to $\beta$ , when t goes to infinity. In other words, under Assumption (A′), the existence of a quasi-ergodic distribution for the absorbed process is equivalent to the law of large numbers for its Q-process.

We now state Assumption (A′).

Assumption 4. There exists a family of probability measures $(\nu_t)_{t \geq 0}$ , defined on $E \setminus A_t$ for each t, such that the following hold:

(A′1) There exist $t_0 \geq 0$ and $c_1 > 0$ such that

\begin{equation*}\mathbb{P}_{s,x}[X_{s+t_0} \in \cdot | \tau_A > s + t_0] \geq c_1 \nu_{s+t_0},\;\;\;\;\forall s \geq 0,\ \forall x \in E \setminus A_s.\end{equation*}

(A′2) There exists $c_2 > 0$ such that

\begin{equation*}\mathbb{P}_{s,\nu_s}[\tau_A > t] \geq c_2 \mathbb{P}_{s,x}[\tau_A > t],\;\;\;\;\forall s \leq t,\ \forall x \in E \setminus A_s.\end{equation*}

In what follows, we say that the pair $\{(X_t)_{t \geq 0}, (A_t)_{t \geq 0}\}$ satisfies Assumption (A′) when the assumption holds for the Markov process $(X_t)_{t \geq 0}$ considered as absorbed by the moving boundary $(A_t)_{t \geq 0}$ .

The condition (A′1) is a conditional version of the Doeblin condition (12), and (A′2) is a Harnack-like inequality on the probabilities of surviving, necessary to deal with the conditioning. They are equivalent to the set of conditions presented in [1, Definition 2.2], when the non-conservative semigroup is sub-Markovian. In the time-homogeneous framework, we obtain the Champagnat–Villemonais condition defined in [5] (see Assumption (A)), shown as being equivalent to the exponential uniform convergence to quasi-stationarity in total variation.

In [25], the existence of a unique quasi-ergodic distribution is proved only for converging or periodic boundaries. However, we can expect such a result on existence (and uniqueness) for other kinds of movement for the boundary. Hence, the aim of this section is to extend the results on the existence of quasi-ergodic distributions obtained in [25] to Markov processes absorbed by asymptotically periodic moving boundaries.

Now let us state the following theorem.

Theorem 2. Assume that there exists a $\gamma$ -periodic sequence of subsets $(B_t)_{t \geq 0}$ such that, for any $s \in [0,\gamma)$ ,

\begin{equation*}E'_{\!\!s} \;:\!=\; E \setminus \bigcap_{k \in \mathbb{Z}_+} \bigcup_{l \geq k} A_{s+l \gamma} \cup B_s \ne \emptyset,\end{equation*}

and there exists $x_s \in E_s$ such that, for any $n \leq N$ ,

(28) \begin{equation} \|\mathbb{P}_{s+k \gamma, x_s}[X_{s+(k+n)\gamma} \in \cdot, \tau_A > s+(k+N)\gamma] - \mathbb{P}_{s, x_s}[X_{s+n\gamma} \in \cdot, \tau_B > s+N\gamma]\|_{TV} \underset{k \to \infty}{\longrightarrow} 0.\end{equation}

Assume also that Assumption (A′) is satisfied by the pairs $\{(X_t)_{t \geq 0}, (A_t)_{t \geq 0}\}$ and $\{(X_t)_{t \geq 0}, (B_t)_{t \geq 0}\}$ .

Then there exists a probability measure $\beta \in \mathcal{M}_1(E)$ such that

(29) \begin{equation}\sup_{\mu \in \mathcal{M}_1(E \setminus A_0)} \sup_{f \in \mathcal{B}_1(E)} \mathbb{E}_{0,\mu}\Bigg[ \bigg| \frac{1}{t} \int_0^t f(X_s)ds - \beta(f) \bigg|^2 \Bigg| \tau_A > t\Bigg] \underset{t \to \infty}{\longrightarrow} 0.\end{equation}

Remark 4. Observe that the condition (28) implies that, for any $n \in \mathbb{Z}_+$ ,

\begin{equation*}\mathbb{P}_{s+k \gamma,x_s}[\tau_A > s +(k+n) \gamma] \underset{k \to \infty}{\longrightarrow} \mathbb{P}_{s,x_s}[\tau_B > s + n \gamma].\end{equation*}

Under the additional condition $B_t \subset A_t$ for all $t \geq 0$ , these two conditions are equivalent, since for all $n \leq N$ ,

\begin{align*} & \|\mathbb{P}_{s+k \gamma, x_s}[X_{s+(k+n)\gamma} \in \cdot, \tau_A > s+(k+N)\gamma] - \mathbb{P}_{s, x_s}[X_{s+n\gamma} \in \cdot, \tau_B > s+N\gamma]\|_{TV} \\[5pt] & \qquad\qquad = \|\mathbb{P}_{s+k\gamma,x_s}[X_{s+(k+n)\gamma} \in \cdot, \tau_B \leq s+(k+N) \gamma < \tau_A] \|_{TV} \\[5pt] & \qquad\qquad\qquad\qquad \leq \mathbb{P}_{s+k\gamma,x_s}[\tau_B \leq s+(k+N) \gamma< \tau_A] \\[5pt] & \qquad\qquad\qquad\qquad\qquad = |\mathbb{P}_{s+k \gamma, x_s}[\tau_A > s+(k+N)\gamma] - \mathbb{P}_{s, x_s}[\tau_B > s+N\gamma]|,\end{align*}

where we used the periodicity of $(B_t)_{t \geq 0}$ , writing

\begin{equation*}\mathbb{P}_{s, x_s}[X_{s+n\gamma} \in \cdot, \tau_B > s+N\gamma] = \mathbb{P}_{s+k\gamma, x_s}[X_{s+(k+n)\gamma} \in \cdot, \tau_B > s+(k+N)\gamma]\end{equation*}

for all $k \in \mathbb{Z}_+$ . This implies the following corollary.

Corollary 2. Assume that there exists a $\gamma$ -periodic sequence of subsets $(B_t)_{t \geq 0}$ , with $B_t \subset A_t$ for all $t \geq 0$ , such that, for any $s \in [0,\gamma)$ , there exists $x_s \in E'_{\!\!s}$ such that, for any $n \leq N$ ,

\begin{equation*}\mathbb{P}_{s+k \gamma,x_s}[\tau_A > s +(k+n) \gamma] \underset{k \to \infty}{\longrightarrow} \mathbb{P}_{s,x_s}[\tau_B > s + n \gamma].\end{equation*}

Assume also that Assumption (A′) is satisfied by $\{(X_t)_{t \geq 0}, (A_t)_{t \geq 0}\}$ and $\{(X_t)_{t \geq 0}, (B_t)_{t \geq 0}\}$ .

Then there exists $\beta \in \mathcal{M}_1(E)$ such that (29) holds.

Proof of theorem 2. Since $\{(X_t)_{t \geq 0}, (B_t)_{t \geq 0}\}$ satisfies Assumption (A′) and $(B_t)_{t \geq 0}$ is a periodic boundary, we already know by [25, Theorem 2] that, for any initial distribution $\mu$ , $t \mapsto \frac{1}{t} \int_0^t \mathbb{P}_{0,\mu}[X_s \in \cdot | \tau_B > t]ds$ converges weakly to a quasi-ergodic distribution $\beta$ .

The main idea of this proof is to apply Corollary 1. Since $\{(X_t)_{t \geq 0}, (A_t)_{t \geq 0}\}$ and $\{(X_t)_{t \geq 0}, (B_t)_{t \geq 0}\}$ satisfy Assumption (A′), [25, Theorem 1] implies that there exist two families of probability measures $\big(\mathbb{Q}^A_{s,x}\big)_{s \geq 0, x \in E \setminus A_s}$ and $\big(\mathbb{Q}^B_{s,x}\big)_{s \geq 0, x \in E \setminus B_s}$ such that, for any $s \leq t$ , $x \in E \setminus A_s$ , $y \in E \setminus B_s$ , and $\Gamma \in {\mathcal F}_{s,t}$ ,

\begin{equation*}\mathbb{Q}_{s,x}^A[\Gamma] = \lim_{T \to \infty} \mathbb{P}_{s,x}[\Gamma | \tau_A > T] \;\;\text{ and } \;\;\mathbb{Q}_{s,y}^B[\Gamma] = \lim_{T \to \infty} \mathbb{P}_{s,y}[\Gamma | \tau_B > T].\end{equation*}

In particular, the quasi-ergodic distribution $\beta$ is the limit of $t \mapsto \frac{1}{t} \int_0^t \mathbb{Q}^B_{0, \mu}[X_s \in \cdot]ds$ , when t goes to infinity (see [25, Theorem 5]). Also, by [25, Theorem 1], there exist constants $C > 0$ and $\kappa > 0$ such that, for any $s \leq t \leq T$ , for any $x \in E \setminus A_{s}$ ,

\begin{equation*}\big\| \mathbb{Q}^A_{s,x}[X_t \in \cdot] - \mathbb{P}_{s, x}[X_{t} \in \cdot | \tau_A > T] \big\|_{TV} \leq C e^{-\kappa (T-t)},\end{equation*}

and for any $x \in E \setminus B_s$ ,

\begin{equation*}\big\| \mathbb{Q}^B_{s,x}[X_{t} \in \cdot] - \mathbb{P}_{s, x}[X_{t} \in \cdot | \tau_B > T] \big\|_{TV} \leq C e^{-\kappa (T-t)}.\end{equation*}

Moreover, for any $s \leq t \leq T$ and $x \in E'_{\!\!s}$ ,

(30) \begin{align}\| \mathbb{P}_{s,x}&[X_{t} \in \cdot | \tau_A > T] - \mathbb{P}_{s,x}[X_{t} \in \cdot | \tau_B > T] \|_{TV} \notag \\[5pt] &=\bigg\| \frac{\mathbb{P}_{s,x}[X_{t} \in \cdot, \tau_A > T]}{\mathbb{P}_{s,x}[\tau_A > T]} - \frac{\mathbb{P}_{s,x}[X_{t} \in \cdot, \tau_B > T]}{\mathbb{P}_{s,x}[\tau_B > T]} \bigg\|_{TV} \notag \\[5pt] &= \bigg\| \frac{\mathbb{P}_{s,x}(\tau_B > T)}{\mathbb{P}_{s,x}(\tau_A > T)}\frac{\mathbb{P}_{s,x}[X_{t} \in \cdot, \tau_A > T]}{\mathbb{P}_{s,x}[\tau_B > T]} - \frac{\mathbb{P}_{s,x}[X_{t} \in \cdot, \tau_B > T]}{\mathbb{P}_{s,x}[\tau_B > T]} \bigg\|_{TV} \notag \\[5pt] &\leq \bigg\| \frac{\mathbb{P}_{s,x}(\tau_B > T)}{\mathbb{P}_{s,x}(\tau_A > T)}\frac{\mathbb{P}_{s,x}[X_{t} \in \cdot, \tau_A > T]}{\mathbb{P}_{s,x}[\tau_B > T]} - \frac{\mathbb{P}_{s,x}[X_{t} \in \cdot, \tau_A > T]}{\mathbb{P}_{s,x}[\tau_B > T]} \bigg\|_{TV} \notag \\[5pt] &\;\;\;\;\;\;+ \bigg\| \frac{\mathbb{P}_{s,x}[X_{t} \in \cdot, \tau_A > T]}{\mathbb{P}_{s,x}[\tau_B > T]} - \frac{\mathbb{P}_{s,x}[X_{t} \in \cdot, \tau_B > T]}{\mathbb{P}_{s,x}[\tau_B > T]} \bigg\|_{TV} \notag \\[5pt] &\leq \frac{|\mathbb{P}_{s,x}(\tau_B > T) - \mathbb{P}_{s,x}(\tau_A > T)|}{\mathbb{P}_{s,x}(\tau_B > T)} + \frac{\|\mathbb{P}_{s,x}[X_t \in \cdot, \tau_A > T] - \mathbb{P}_{s,x}[X_t \in \cdot, \tau_B > T]\|_{TV}}{\mathbb{P}_{s,x}[\tau_B > T]} \notag \\[5pt] &\leq 2 \frac{\|\mathbb{P}_{s,x}[X_t \in \cdot, \tau_A > T] - \mathbb{P}_{s,x}[X_t \in \cdot, \tau_B > T]\|_{TV}}{\mathbb{P}_{s,x}[\tau_B > T]},\end{align}

since

\begin{equation*}|\mathbb{P}_{s,x}(\tau_B > T) - \mathbb{P}_{s,x}(\tau_A > T)| \leq \|\mathbb{P}_{s,x}[X_t \in \cdot, \tau_A > T] - \mathbb{P}_{s,x}[X_t \in \cdot, \tau_B > T]\|_{TV}.\end{equation*}

Then we obtain, for any $s \leq t \leq T$ and $x \in E'_{\!\!s}$ ,

(31) \begin{align} \bigl\|\mathbb{Q}_{s,x}^A[X_{t} \in \cdot] &- \mathbb{Q}_{s,x}^B[X_{t} \in \cdot] \bigl\|_{TV} \nonumber \\[5pt] &\leq 2 C e^{-\kappa (T - t)} + 2 \frac{\|\mathbb{P}_{s,x}[X_t \in \cdot, \tau_A > T] - \mathbb{P}_{s,x}[X_t \in \cdot, \tau_B > T]\|_{TV}}{\mathbb{P}_{s,x}[\tau_B > T]}.\end{align}

The condition (28) implies the existence of $x_s \in E_s$ such that, for any $n \leq N$ , for all $k \in \mathbb{Z}_+$ ,

\begin{equation*}\lim_{k \to \infty} \|\mathbb{P}_{s+k \gamma, x_s}[X_{s+(k+n)\gamma} \in \cdot, \tau_A > s+(k+N)\gamma] - \mathbb{P}_{s, x_s}[X_{s+n\gamma} \in \cdot, \tau_B > s+N\gamma]\|_{TV} = 0,\end{equation*}

which implies by (31) that, for any $n \leq N$ ,

\begin{equation*}\limsup_{k \to \infty} \bigl\|\mathbb{Q}_{s+k\gamma,x_s}^A[X_{s+(k+n)\gamma} \in \cdot] - \mathbb{Q}_{s+k\gamma,x_s}^B[X_{s+(k+n)\gamma} \in \cdot] \bigl\|_{TV} \leq 2Ce^{-\kappa \gamma (N-n)}.\end{equation*}

Now, letting $N \to \infty$ , for any $n \in \mathbb{Z}_+$ we have

\begin{align*}\lim_{k \to \infty} & \bigl\|\mathbb{Q}_{s+k\gamma,x_s}^A[X_{s+(k+n)\gamma} \in \cdot] - \mathbb{Q}_{s+k\gamma,x_s}^B[X_{s+(k+n)\gamma} \in \cdot] \bigl\|_{TV}\\[5pt] &= \lim_{k \to \infty} \bigl\| \mathbb{Q}_{s+k\gamma,x_s}^A(X_{s+(k+n)\gamma}\in \cdot)-\mathbb{Q}_{s,x_s}^B(X_{s+n\gamma}\in \cdot)\bigl\|_{TV}\\[5pt] &= 0.\end{align*}

In other words, the semigroup $\big(Q^A_{s,t}\big)_{s \leq t}$ defined by

\begin{equation*}Q_{s,t}^Af(x) \;:\!=\; \mathbb{E}_{s,x}^{\mathbb{Q}^A}(f(X_t)),\;\;\;\;\forall s \leq t,\ \forall f \in \mathcal{B}(E \setminus A_t),\ \forall x \in E \setminus A_s,\end{equation*}

is asymptotically periodic (according to Definition 1, with $\psi_s = \tilde{\psi}_s = 1$ for all $s \geq 0$ ), associated to the auxiliary semigroup $\big(Q^B_{s,t}\big)_{s \leq t}$ defined by

\begin{equation*}Q_{s,t}^Bf(x) \;:\!=\; \mathbb{E}_{s,x}^{\mathbb{Q}^B}(f(X_t)),\;\;\;\;\forall s \leq t,\ \forall f \in \mathcal{B}(E \setminus B_t),\ \forall x \in E \setminus B_s.\end{equation*}

Moreover, since Assumption (A′) is satisfied for $\{(X_t)_{t \geq 0}, (A_t)_{t \geq 0}\}$ and $\{(X_t)_{t \geq 0}, (B_t)_{t \geq 0}\}$ , the Doeblin condition holds for these two Q-processes. As a matter of fact, by the Markov property, for all $s \leq t \leq T$ and $x \in E \setminus A_s$ ,

(32) \begin{align} \mathbb{P}_{s,x}(X_t \in \cdot | \tau_A > T) &= \mathbb{E}_{s,x}\bigg[\mathbb{1}_{X_t \in \cdot, \tau_A > t} \frac{\mathbb{P}_{t,X_t}(\tau_A > T)}{\mathbb{P}_{s,x}(\tau_A > T)}\bigg] \notag \\[5pt] &= \mathbb{E}_{s,x}\bigg[\frac{\mathbb{1}_{X_t \in \cdot, \tau_A > t}}{\mathbb{P}_{s,x}(\tau_A > t)} \frac{\mathbb{P}_{t,X_t}(\tau_A > T)}{\mathbb{P}_{t,\phi_{t,s}(\delta_x)}(\tau_A > T)}\bigg] \notag \\[5pt] &= \mathbb{E}_{s,x}\bigg[\mathbb{1}_{X_t \in \cdot} \frac{\mathbb{P}_{t,X_t}(\tau_A > T)}{\mathbb{P}_{t,\phi_{t,s}(\delta_x)}(\tau_A > T)} \bigg| \tau_A > t\bigg], \end{align}

where, for all $s \leq t$ and $\mu \in \mathcal{M}_1(E_s)$ , $\phi_{t,s}(\mu) \;:\!=\; \mathbb{P}_{s,\mu}(X_t \in \cdot | \tau_A > t)$ . By (A′1), for any $s \geq 0$ , $T \geq s+t_0$ , $x \in E \setminus A_s$ , and measurable set $\mathcal{A}$ ,

\begin{equation*}\mathbb{E}_{s,x}\bigg[\mathbb{1}_{X_{s+t_0} \in \mathcal{A}} \frac{\mathbb{P}_{s+t_0,X_{s+t_0}}(\tau_A > T)}{\mathbb{P}_{s+t_0,\phi_{s+t_0,s}(\delta_x)}(\tau_A > T)} \bigg| \tau_A > s+t_0\bigg] \geq c_1 \int_{\mathcal{A}} \nu_{s+t_0}(dy) \frac{\mathbb{P}_{s+t_0,y}(\tau_A > T)}{\mathbb{P}_{s+t_0,\phi_{s+t_0,s}(\delta_x)}(\tau_A > T)};\end{equation*}

that is, by (32),

\begin{equation*}\mathbb{P}_{s,x}(X_{s+t_0} \in \mathcal{A} | \tau_A > T) \geq c_1 \int_{\mathcal{A}} \nu_{s+t_0}(dy) \frac{\mathbb{P}_{s+t_0,y}(\tau_A > T)}{\mathbb{P}_{s+t_0,\phi_{s+t_0,s}(\delta_x)}(\tau_A > T)}.\end{equation*}

Letting $T \to \infty$ in this last inequality and using [9, Proposition 3.1], for any $s \geq 0$ , $x \in E \setminus A_s$ , and measurable set $\mathcal{A}$ ,

\begin{equation*}\mathbb{Q}_{s,x}^A(X_{s+t_0} \in \mathcal{A}) \geq c_1 \int_\mathcal{A} \nu_{s+t_0}(dy) \frac{\eta_{s+t_0}(y)}{\phi_{s+t_0,s}(\delta_x)(\eta_{s+t_0})}.\end{equation*}

The measure

\begin{equation*}\mathcal{A} \mapsto \int_\mathcal{A} \nu_{s+t_0}(dy) \frac{\eta_{s+t_0}(y)}{\phi_{s+t_0,s}(\delta_x)(\eta_{s+t_0})}\end{equation*}

is then a positive measure whose mass is bounded below by $c_2$ , by (A′2), since for all $s \geq 0$ and $T \geq s + t_0$ ,

\begin{equation*}\int_{E \setminus A_{s+t_0}} \nu_{s+t_0}(dy) \frac{\mathbb{P}_{t,y}(\tau_A > T)}{\mathbb{P}_{t,\phi_{t,s}(\delta_x)}(\tau_A > T)} \geq c_2.\end{equation*}

This proves a Doeblin condition for the semigroup $\big(Q_{s,t}^A\big)_{s \leq t}$ . The same reasoning also applies to prove a Doeblin condition for the semigroup $\big(Q_{s,t}^B\big)_{s \leq t}$ . Then, using (27) followed by Corollary 1, we have

\begin{align*}\lim_{t \to \infty} \frac{1}{t} \int_0^t \mathbb{P}_{0,\mu}[X_s \in \cdot | \tau_A > t]ds &= \lim_{t \to \infty} \frac{1}{t} \int_0^t \mathbb{Q}_{0,\eta_0*\mu}^A(X_s \in \cdot)ds\\[5pt] &= \lim_{t \to \infty} \frac{1}{t} \int_0^t \mathbb{Q}^B_{0,\eta_0*\mu}[X_s \in \cdot]ds = \beta,\end{align*}

where the limits refer to convergence in total variation and hold uniformly in the initial measure.

For any $\mu \in \mathcal{M}_1(E \setminus A_0)$ , $f \in \mathcal{B}_1(E)$ , and $t \geq 0$ ,

\begin{equation*}\mathbb{E}_{0,\mu}\Bigg[\bigg| \frac{1}{t} \int_0^t f(X_s)ds \bigg|^2\Bigg| \tau_A > t\Bigg] = \frac{2}{t^2} \int_0^t \int_s^t \mathbb{E}_{0,\mu}[f(X_s)f(X_u) | \tau_A > t]du\,ds.\end{equation*}

Then, by [25, Theorem 1], for any $s \leq u \leq t$ , for any $\mu \in \mathcal{M}_1(E \setminus A_0)$ and $f \in \mathcal{B}(E)$ ,

\begin{equation*}\Big| \mathbb{E}_{0,\mu}[f(X_s)f(X_u) | \tau_A > t] - \mathbb{E}^{\mathbb{Q}^A}_{0,\eta_0*\mu}[f(X_s)f(X_u)]\Big| \leq C \|f\|_\infty e^{-\kappa (t-u)},\end{equation*}

where the expectation $\mathbb{E}^{\mathbb{Q}^A}_{0,\eta_0*\mu}$ is associated to the probability measure $\mathbb{Q}_{0,\eta_0*\mu}^A$ . Hence, for any $\mu \in \mathcal{M}_1(E \setminus A_0)$ , $f \in \mathcal{B}_1(E)$ , and $t > 0$ ,

\begin{align*} & \Bigg| \mathbb{E}_{0,\mu}\Bigg[\bigg| \frac{1}{t} \int_0^t f(X_s)ds - \beta(f) \bigg|^2\Bigg| \tau_A > t\Bigg] - \mathbb{E}_{0,\eta_0*\mu}^{\mathbb{Q}^A}\Bigg[\bigg| \frac{1}{t} \int_0^t f(X_s)ds - \beta(f) \bigg|^2\Bigg] \Bigg| \\[5pt] & \qquad \leq \frac{4C}{t^2} \int_0^t \int_s^t e^{-\kappa(t-u)}du\,ds \\[5pt] & \qquad \leq \frac{4C}{\kappa t} - \frac{4C (1 - e^{-\kappa t})}{\kappa^2 t^2}.\end{align*}

Moreover, since $\big(Q^A_{s,t}\big)_{s \leq t}$ is asymptotically periodic in total variation and satisfies the Doeblin condition, like $\big(Q^B_{s,t}\big)_{s \leq t}$ , Corollary 1 implies that

\begin{equation*}\sup_{\mu \in \mathcal{M}_1(E \setminus A_0)} \sup_{f \in \mathcal{B}_1(E)} \mathbb{E}_{0,\eta_0*\mu}^{\mathbb{Q}^A}\Bigg[\bigg| \frac{1}{t} \int_0^t f(X_s)ds - \beta(f) \bigg|^2\Bigg] \underset{t \to \infty}{\longrightarrow} 0.\end{equation*}

Then

\begin{equation*}\sup_{\mu \in \mathcal{M}_1(E \setminus A_0)} \sup_{f \in \mathcal{B}_1(E)} \mathbb{E}_{0,\mu}\Bigg[\bigg| \frac{1}{t} \int_0^t f(X_s)ds - \beta(f) \bigg|^2\Bigg| \tau_A > t\Bigg] \underset{t \to \infty}{\longrightarrow} 0.\end{equation*}

Remark 5. It seems that Assumption (A′) can be weakened by a conditional version of Assumption 1. In particular, such conditions can be derived from Assumption (F) in [6], as will be shown later in the paper [4], currently in preparation.

5. Examples

5.1. Asymptotically periodic Ornstein–Uhlenbeck processes

Let $(X_t)_{t \geq 0}$ be a time-inhomogeneous diffusion process on $\mathbb{R}$ satisfying the stochastic differential equation

\begin{equation*}dX_t = dW_t - \lambda(t) X_t dt,\end{equation*}

where $(W_t)_{t \geq 0}$ is a one-dimensional Brownian motion and $\lambda \;:\; [0, \infty) \to [0, \infty)$ is a function such that

\begin{equation*}\sup_{t \geq 0} |\lambda(t)| < + \infty\end{equation*}

and such that there exists $\gamma > 0$ such that

\begin{equation*}\inf_{s \geq 0} \int_s^{s+\gamma} \lambda(u)du > 0.\end{equation*}

By Itô’s lemma, for any $s \leq t$ ,

\begin{equation*}X_t = e^{-\int_s^t \lambda(u)du}\bigg[X_s + \int_s^t e^{\int_s^u \lambda(v)dv} dW_u\bigg].\end{equation*}

In particular, denoting by $(P_{s,t})_{s \leq t}$ the semigroup associated to $(X_t)_{t \geq 0}$ , for any $f \in \mathcal{B}(\mathbb{R})$ , $t \geq 0$ , and $x \in \mathbb{R}$ ,

\begin{equation*}P_{s,t}f(x) = \mathbb{E}\!\left[f\!\left(e^{-\int_s^t \lambda(u)du}x + e^{-\int_s^t \lambda(u)du} \sqrt{\int_s^t e^{2\int_s^u \lambda(v)dv}du} \times \mathcal{N}(0,1)\right)\right],\end{equation*}

where $\mathcal{N}(0,1)$ denotes a standard Gaussian variable.

Theorem 3. Assume that there exists a $\gamma$ -periodic function g, bounded on $\mathbb{R}$ , such that $\lambda \sim_{t \to \infty} g$ . Then the assumptions of Theorem 1 hold.

Proof. In our case, the auxiliary semigroup $(Q_{s,t})_{s \leq t}$ of Definition 1 will be defined as follows: for any $f \in \mathcal{B}(\mathbb{R})$ , $t \geq 0$ , and $x \in \mathbb{R}$ ,

\begin{equation*}Q_{s,t}f(x) = \mathbb{E}\left[f\left(e^{-\int_s^t g(u)du}x + e^{-\int_s^t g(u)du} \sqrt{\int_s^t e^{2\int_s^u g(v)dv}du} \times \mathcal{N}(0,1)\right)\right].\end{equation*}

In particular, the semigroup $(Q_{s,t})_{s \leq t}$ is associated to the process $(Y_t)_{t \geq 0}$ following

\begin{equation*}dY_t = dW_t - g(t) Y_t dt.\end{equation*}

We first remark that the function $\psi \;:\; x \mapsto 1 + x^2$ is a Lyapunov function for $(P_{s,t})_{s \leq t}$ and $(Q_{s,t})_{s \leq t}$ . In fact, for any $s \geq 0$ and $x \in \mathbb{R}$ ,

\begin{align*} P_{s,s+\gamma} \psi(x) &= 1 + e^{-2 \int_s^{s+\gamma} \lambda(u)du}x^2 + e^{-2\int_s^{s+\gamma} \lambda(u)du} \int_s^{s+\gamma} e^{2\int_s^u \lambda(v)dv}du \\[5pt] &= e^{-2\int_s^{s+\gamma} \lambda(u)du} \psi(x) + 1 - e^{-2\int_s^{s+\gamma} \lambda(u)du} + e^{-2\int_s^{s+\gamma} \lambda(u)du} \int_s^{s+\gamma} e^{2\int_s^u \lambda(v)dv}du \\[5pt] &\leq e^{-2 \gamma c_{\inf}} \psi(x) + C,\end{align*}

where $C \in (0,+\infty)$ and $c_{\inf} \;:\!=\; \inf_{t \geq 0} \frac{1}{\gamma} \int_t^{t+\gamma}\lambda(u)du > 0$ . Taking $\theta \in (e^{-2 \gamma c_{\inf}},1)$ , there exists a compact set K such that, for any $s \geq 0$ ,

\begin{equation*}P_{s,s+\gamma} \psi(x) \leq \theta \psi(x) + C \mathbb{1}_K(x).\end{equation*}

Moreover, for any $s \geq 0$ and $t \in [0, \gamma)$ , the function $P_{s,s+t}\psi/\psi$ is upper-bounded uniformly in s and t. It remains therefore to prove Assumption 1(i) for $(P_{s,t})_{s \leq t}$ , which is a consequence of the following lemma.

Lemma 1. For any $a,b_{-},b_{+} > 0$ , define the subset $\mathcal{C}(a,b_{-},b_{+}) \subset \mathcal{M}_1(\mathbb{R})$ as

\begin{equation*}\mathcal{C}(a,b_{-},b_{+}) \;:\!=\; \{ \mathcal{N}(m,\sigma) \;:\; m \in [\!-\!a,a], \sigma \in [b_{-},b_{+}]\}.\end{equation*}

Then, for any $a,b_{-},b_{+} > 0$ , there exist a probability measure $\nu$ and a constant $c > 0$ such that, for any $\mu \in \mathcal{C}(a,b_{-},b_{+})$ ,

\begin{equation*}\mu \geq c \nu.\end{equation*}

The proof of this lemma is postponed until after the end of this proof.

Since $\lambda \sim_{t \to \infty} g$ and these two functions are bounded on $\mathbb{R}_+$ , Lebesgue’s dominated convergence theorem implies that, for all $s \leq t$ ,

\begin{equation*}\bigg| \int_{s+k\gamma}^{t+k\gamma} \lambda(u)du - \int_s^{t} g(u)du\bigg| \underset{k \to \infty}{\longrightarrow} 0.\end{equation*}

In the same way, for all $s \leq t$ ,

\begin{equation*}\int_{s+k\gamma}^{t+k\gamma} e^{2\int_{s+k\gamma}^u \lambda(v)dv}du \underset{k \to \infty}{\longrightarrow} \int_s^{t} e^{2\int_s^u g(v)dv}du.\end{equation*}

Hence, for any $s \leq t$ ,

\begin{equation*}e^{-\int_{s+k\gamma}^{t+k\gamma} \lambda(u)du} \underset{k \to \infty}{\longrightarrow} e^{-\int_s^{t} g(u)du},\end{equation*}

and

\begin{equation*}e^{-\int_{s+k \gamma}^{t+k\gamma} \lambda(u)du} \sqrt{\int_{s+k\gamma}^{t+k\gamma} e^{2\int_{s+k\gamma}^u \lambda(v)dv}du} \underset{k \to \infty}{\longrightarrow} e^{-\int_s^{t} g(u)du} \sqrt{\int_s^{t} e^{2\int_s^u g(v)dv}du}.\end{equation*}

Using [14, Theorem 1.3], for any $x \in \mathbb{R}$ ,

(33) \begin{equation}\| \delta_x P_{s+k\gamma, t+k\gamma} - \delta_x Q_{s+k\gamma, t+k\gamma} \|_{TV} \underset{k \to \infty}{\longrightarrow} 0.\end{equation}

To deduce the convergence in $\psi$ -distance, we will draw inspiration from the proof of [19, Lemma 3.1]. Since the variances are uniformly bounded in k (for $s \leq t$ fixed), there exists $H > 0$ such that, for any $k \in \mathbb{N}$ and $s \leq t$ ,

(34) \begin{equation}\delta_x P_{s+k\gamma, t+k\gamma}\big[\psi^2\big] \leq H\;\;\text{ and }\;\;\delta_x Q_{s, t}\big[\psi^2\big] \leq H.\end{equation}

Since $\lim_{|x| \to \infty} \frac{\psi(x)}{\psi^2(x)} = 0$ , for any $\epsilon > 0$ there exists $l_\epsilon > 0$ such that, for any function f such that $|f| \leq \psi$ and for any $|x| \geq l_\epsilon$ ,

\begin{equation*}|f(x)| \leq \frac{\epsilon \psi(x)^2}{H}.\end{equation*}

Combining this with (34), and letting $K_\epsilon \;:\!=\; [\!-\!l_\epsilon, l_\epsilon]$ , we find that for any $k \in \mathbb{Z}_+$ , f such that $|f| \leq \psi$ , and $x \in \mathbb{R}$ ,

\begin{equation*}\delta_x P_{s+k \gamma, t+k\gamma}[f \mathbb{1}_{K_\epsilon^c}] \leq \epsilon\;\;\text{ and }\;\;\delta_x Q_{s, t}[f \mathbb{1}_{K_\epsilon^c}] \leq \epsilon.\end{equation*}

Then, for any $k \in \mathbb{Z}_+$ and f such that $|f| \leq \psi$ ,

(35) \begin{align} | \delta_x P_{s+k \gamma, t+k\gamma}f - \delta_x Q_{s, t}f| &\leq 2 \epsilon + | \delta_x P_{s+k \gamma, t+k\gamma}[f \mathbb{1}_{K_\epsilon}] - \delta_x Q_{s, t}[f \mathbb{1}_{K_\epsilon}]| \end{align}

(36) \begin{align} & \qquad\qquad\qquad\qquad\qquad \leq 2 \epsilon + (1+l_\epsilon^2) \| \delta_x P_{s+k\gamma, t+k\gamma} - \delta_x Q_{s, t} \|_{TV}. \end{align}

Hence, (33) implies that, for k large enough, for any f bounded by $\psi$ ,

(37) \begin{align} | \delta_x P_{s+k \gamma, t+k\gamma}f - \delta_x Q_{s, t}f| &\leq 3 \epsilon,\end{align}

implying that

\begin{equation*}\| \delta_x P_{s+k \gamma, t+k\gamma} - \delta_x Q_{s, t} \|_{\psi} \underset{k \to \infty}{\longrightarrow} 0.\end{equation*}

We now prove Lemma 1.

Proof of Lemma 1. Defining

\begin{equation*}f_\nu(x) \;:\!=\; e^{-\frac{(x-a)^2}{2 {b_-}^2}} \land e^{-\frac{(x+a)^2}{2 {b_-}^2}},\end{equation*}

we conclude easily that, for any $m \in [\!-\!a,a]$ and $\sigma \geq b_-$ , for any $x \in \mathbb{R}$ ,

\begin{equation*}e^{-\frac{(x-m)^2}{2 \sigma^2}} \geq f_\nu(x).\end{equation*}

Imposing moreover that $\sigma \leq b_+$ , one has

\begin{equation*}\frac{1}{\sqrt{2 \pi} \sigma} e^{-\frac{(x-m)^2}{2 \sigma^2}} \geq \frac{1}{\sqrt{2 \pi} b_+} f_\nu(x),\end{equation*}

which concludes the proof.

5.2. Quasi-ergodic distribution for Brownian motion absorbed by an asymptotically periodic moving boundary

Let $(W_t)_{t \geq 0}$ be a one-dimensional Brownian motion, and let h be a $\mathcal{C}^1$ -function such that

\begin{equation*}h_{\min} \;:\!=\; \inf_{t \geq 0} h(t) > 0\;\;\;\;\text{ and }\;\;\;\;h_{\max} \;:\!=\; \sup_{t \geq 0} h(t) < + \infty.\end{equation*}

We assume also that

\begin{equation*}-\infty < \inf_{t \geq 0} h'(t) \leq \sup_{t \geq 0} h'(t) < + \infty.\end{equation*}

Define

\begin{equation*}\tau_h \;:\!=\; \inf\{t \geq 0 \;:\; |W_t| \geq h(t)\}.\end{equation*}

Since h is continuous, the hitting time $\tau_h$ is a stopping time with respect to the natural filtration of $(W_t)_{t \geq 0}$ . Moreover, since $\sup_{t \geq 0} h(t) < + \infty$ and $\inf_{t \geq 0} h(t) > 0$ ,

\begin{equation*}\mathbb{P}_{s,x}[\tau_h < + \infty] = 1 \;\;\text{ and }\;\; \mathbb{P}_{s,x}[\tau_h > t] > 0,\;\;\;\;\forall s \leq t,\ \forall x \in [\!-\!h(s),h(s)].\end{equation*}

The main assumption on the function h is the existence of a $\gamma$ -periodic function g such that $h(t) \leq g(t)$ , for any $t \geq 0$ , and such that

\begin{equation*}h \sim_{t \to \infty} g \;\;\text{and}\;\;h' \sim_{t \to \infty} g'.\end{equation*}

Similarly to $\tau_h$ , define

\begin{equation*}\tau_g \;:\!=\; \inf\{t \geq 0 \;:\; |W_t| = g(t)\}.\end{equation*}

Finally, let us assume that there exists $n_0 \in \mathbb{N}$ such that, for any $s \geq 0$ ,

(38) \begin{equation} \inf \{ u \geq s \;:\; h(u) = \inf_{t \geq s} h(t)\} - s \leq n_0 \gamma.\end{equation}

This condition says that there exists $n_0 \in \mathbb{N}$ such that, for any time $s \geq 0$ , the infimum of the function h on the domain $[s, + \infty)$ is reached on the subset $[s, s + n_0 \gamma]$ .

We first prove the following proposition.

Proposition 1. The Markov process $(W_{t})_{t \geq 0}$ , considered as absorbed by h or by g, satisfies Assumption (A′).

Proof. In what follows, we will prove Assumption (A′) with respect to the absorbing function h. The proof can easily be adapted for the function g.

• Proof of (A′1). Define $\mathcal{T} \;:\!=\; \{s \geq 0 \;:\; h(s) = \inf_{t \geq s} h(t)\}$ . The condition (38) implies that this set contains an infinity of times.

In what follows, the following notation is needed: for any $z \in \mathbb{R}$ , define $\tau_z$ as

\begin{equation*}\tau_z \;:\!=\; \inf\{t \geq 0 \;:\; |W_t| = z\}.\end{equation*}

Also, let us state that, since the Brownian motion absorbed at $\{-1,1\}$ satisfies Assumption (A) of [5] at any time (see [7]), it follows that, for a given $t_0 > 0$ , there exist $c > 0$ and $\nu \in \mathcal{M}_1((\!-\!1,1))$ such that, for any $x \in (\!-\!1,1)$ ,

(39) \begin{equation} \mathbb{P}_{0,x}\bigg[W_{\frac{t_0}{h_{\max}^2} \land t_0} \in \cdot \bigg| \tau_1 > \frac{t_0}{h_{\max}^2} \land t_0\bigg] \geq c \nu.\end{equation}

Moreover, in relation to the proof of [7, Section 5.1], the probability measure $\nu$ can be expressed as

(40) \begin{equation} \nu = \frac{1}{2}\left(\mathbb{P}_{0,1-\epsilon}[W_{t_2} \in \cdot | \tau_1 > t_2] + \mathbb{P}_{0,-1+\epsilon}[W_{t_2} \in \cdot | \tau_1 > t_2]\right),\end{equation}

for some $0 < t_2 < \frac{t_0}{h_{\max}^2} \land t_0$ and $\epsilon \in (0,1)$ .

The following lemma is very important for the next part of the argument.

Lemma 2. For all $z \in [h_{\min},h_{max}]$ ,

\begin{equation*}\mathbb{P}_{0,x}[W_{u} \in \cdot | \tau_z > u] \geq c \nu_z,\;\;\;\;\forall x \in (\!-\!z,z),\ \forall u \geq t_0,\end{equation*}

where $t_0$ is as previously mentioned, $c > 0$ is the same constant as in (39), and

\begin{equation*}\nu_z(f) = \int_{(\!-\!1,1)} f(z x) \nu(dx),\end{equation*}

with $\nu \in \mathcal{M}_1((\!-\!1,1))$ defined in (40).

The proof of this lemma is postponed until after the current proof.

Let $s \in \mathcal{T}$ . Then, for all $x \in (\!-\!h(s),h(s))$ and $t \geq 0$ ,

\begin{equation*}\mathbb{P}_{s,x}[W_{s+t} \in \cdot | \tau_{h} > s+t] \geq \frac{ \mathbb{P}_{s,x}[\tau_{h(s)} > s+t]}{\mathbb{P}_{s,x}[\tau_h > s+t]} \mathbb{P}_{s,x}[W_{s+t} \in \cdot | \tau_{h(s)} > s+t].\end{equation*}

By Lemma 2, for all $x \in (\!-\!h(s),h(s))$ and $t \geq t_0$ ,

\begin{equation*}\mathbb{P}_{s,x}[W_{s+t} \in \cdot | \tau_{h(s)} > s+t] \geq c \nu_{h(s)},\end{equation*}

which implies that, for any $t \in [t_0, t_0 + n_0 \gamma]$ ,

(41) \begin{align} \mathbb{P}_{s,x}[W_{s+t} \in \cdot | \tau_h > s+t] &\geq \frac{ \mathbb{P}_{s,x}[\tau_{h(s)} > s+t]}{\mathbb{P}_{s,x}[\tau_h > s+t]} c \nu_{h(s)} \notag \\[5pt] &\geq \frac{ \mathbb{P}_{s,x}[\tau_{h(s)} > s+t_0+n_0 \gamma]}{\mathbb{P}_{s,x}[\tau_h > s+t_0]} c \nu_{h(s)}.\end{align}

Let us introduce the process $X^h$ defined by, for all $t \geq 0$ ,

\begin{equation*}X^h_t \;:\!=\; \frac{W_t}{h(t)}.\end{equation*}

By Itô’s formula, for any $t \geq 0$ ,

\begin{equation*}X^h_t = X^h_0 + \int_0^t \frac{dW_s}{h(s)} - \int_0^t \frac{h'(s)}{h(s)} X^h_s ds.\end{equation*}

Define

\begin{equation*}\big(M^h_t\big)_{t \geq 0} \;:\!=\; \bigg(\int_0^t \frac{1}{h(s)}dW_s\bigg)_{t \geq 0}.\end{equation*}

By the Dubins–Schwarz theorem, it is well known that the process $M^h$ has the same law as

\begin{equation*}\bigg(W_{\int_0^t \frac{1}{h^2(s)}ds}\bigg)_{t \geq 0}.\end{equation*}

Then, defining

\begin{equation*}I^h(s) \;:\!=\; \int_0^s \frac{1}{h^2(u)}du\end{equation*}

and, for any $s \leq t$ and for any trajectory w,

(42) \begin{align} {\mathcal E}_{s,t}^h(w) \;:\!=\; \sqrt{\frac{h(t)}{h(s)}} \exp\bigg(& -\frac{1}{2} \bigg[h'(t)h(t) w_{I^h(t)}^2 - h'(s)h(s) w_{I^h(s)}^2 \end{align}

(43) \begin{align} & \qquad\qquad\qquad\qquad\qquad + \int_{s}^{t} w_{I^h(u)}^2[(h'(u))^2 - [h(u)h'(u)]']du\bigg]\bigg), \end{align}

Girsanov’s theorem implies that, for all $x \in (\!-\!h(s),h(s))$ ,

(44) \begin{equation}\mathbb{P}_{s,x}[\tau_h > s+t_0] = \mathbb{E}_{I^h(s),\frac{x}{h(s)}}\bigg[{\mathcal E}_{s,s+t_0}^h(W) \mathbb{1}_{\tau_1 > \int_0^{s+t_0} \frac{1}{h^2(u)} du}\bigg].\end{equation}

On the event

\begin{equation*}\bigg\{\tau_1 > \int_0^{s+t_0} \frac{1}{h^2(u)} du\bigg\},\end{equation*}

and since h and h ′ are bounded on $\mathbb{R}_+$ , the random variable ${\mathcal E}_{s,s+t_0}^h(W)$ is almost surely bounded by a constant $C > 0$ , uniformly in s, such that for all $x \in (\!-\!h(s),h(s))$ ,

(45) \begin{equation}\mathbb{E}_{I^h(s),\frac{x}{h(s)}}\bigg[{\mathcal E}_{s,s+t_0}^h(W) \mathbb{1}_{\tau_1 > \int_0^{s+t_0} \frac{1}{h^2(u)} du}\bigg] \leq C \mathbb{P}_{0,\frac{x}{h(s)}}\bigg[\tau_1 > \int_s^{s+t_0} \frac{1}{h^2(u)} du\bigg].\end{equation}

Since $h(t) \geq h(s)$ for all $t \geq s$ (since $s \in \mathcal{T}$ ),

\begin{equation*}I^h(s+t_0) - I^h(s) \leq \frac{t_0}{h(s)^2}.\end{equation*}

By the scaling property of the Brownian motion and by the Markov property, one has for all $x \in (\!-\!h(s),h(s))$

\begin{align*}\mathbb{P}_{s,x}[\tau_{h(s)} > s+t_0] &= \mathbb{P}_{0,x}[\tau_{h(s)} > t_0] \\[5pt] &= \mathbb{P}_{0,\frac{x}{h(s)}}\bigg[\tau_1 > \frac{t_0}{h^2(s)}\bigg] \\[5pt] &= \mathbb{E}_{0,\frac{x}{h(s)}}\bigg[\mathbb{1}_{\tau_1 > \int_s^{s+t_0} \frac{1}{h^2(u)}du} \mathbb{P}_{0,W_{ \int_s^{s+t_0} \frac{1}{h^2(u)}du}}\bigg[\tau_1 > \frac{t_0}{h^2(s)} - \int_s^{s+t_0} \frac{1}{h^2(s)}ds\bigg]\bigg] \\[5pt] &= \mathbb{P}_{0,\frac{x}{h(s)}}\bigg[\tau_1 > \int_s^{s+t_0} \frac{1}{h^2(u)} du\bigg] \\[5pt] & \quad \mathbb{P}_{0,\phi_{I^h(s+t_0) - I^h(s)}(\delta_x)}\bigg[\tau_1 > \frac{t_0}{h^2(s)} - \int_s^{s+t_0} \frac{1}{h^2(u)}du\bigg],\end{align*}

where, for any initial distribution $\mu$ and any $t \geq 0$ ,

\begin{equation*}\phi_{t}(\mu) \;:\!=\; \mathbb{P}_{0,\mu}[W_t \in \cdot | \tau_1 > t].\end{equation*}

The family $(\phi_t)_{t \geq 0}$ satisfies the equality $\phi_t \circ \phi_s = \phi_{t+s}$ for all $s,t \geq 0$ . By this property, and using that

\begin{equation*}I^h(s+t_0) - I^h(s) \geq \frac{t_0}{h_{\max}^2}\end{equation*}

for any $s \geq 0$ , the minorization (39) implies that, for all $s \geq 0$ and $x \in (\!-\!1,1)$ ,

\begin{equation*}\phi_{I^h(s+t_0) - I^h(s)}(\delta_x) \geq c \nu.\end{equation*}

Hence, by this minorization, and using that h is upper-bounded and lower-bounded positively on $\mathbb{R}_+$ , one has for all $x \in (\!-\!1,1)$

\begin{align*}\mathbb{P}_{0,\phi_{I^h(s+t_0)-I^h(s)}(\delta_x)} &\bigg[\tau_1 > \frac{t_0}{h^2(s)} - \int_s^{s+t_0} \frac{1}{h^2(u)}du\bigg]\\[5pt] &\geq c \mathbb{P}_{0,\nu}\bigg[\tau_1 > \inf_{s \geq 0} \bigg\{\frac{t_0}{h^2(s)} - \int_s^{s+t_0} \frac{1}{h^2(u)}du\bigg\}\bigg];\end{align*}

that is to say,

\begin{equation*}\frac{\mathbb{P}_{s,x}[\tau_{h(s)} > s+t_0]}{\mathbb{P}_{0,\frac{x}{h(s)}}\bigl[\tau_1 > \int_s^{s+t_0} \frac{1}{h^2(u)} du\bigl]} \geq c \mathbb{P}_{0,\nu}\bigg[\tau_1 > \inf_{s \geq 0} \bigg\{\frac{\gamma}{h^2(s)} - \int_s^{s+t_0} \frac{1}{h^2(u)}du\bigg\}\bigg].\end{equation*}

In other words, we have just shown that, for all $x \in (\!-\!h(s),h(s))$ ,

(46) \begin{equation} \frac{ \mathbb{P}_{s,x}[\tau_{h(s)} > s+t_0]}{\mathbb{P}_{s,x}[\tau_h > s+t_0]} \geq \frac{c}{C} \mathbb{P}_{0,\nu}\bigg[\tau_1 > \inf_{s \geq 0} \bigg\{\frac{t_0}{h^2(s)} - \int_s^{s+t_0} \frac{1}{h^2(u)}du\bigg\}\bigg] > 0.\end{equation}

Moreover, by Lemma 2 and the scaling property of the Brownian motion, for all $x \in (\!-\!h(s),h(s))$ ,

(47) \begin{align}\frac{\mathbb{P}_{s,x}[\tau_{h(s)} > s + t_0 + n_0 \gamma]}{\mathbb{P}_{s,x}[\tau_{h(s)} > s+ t_0]} &= \mathbb{P}_{0,\mathbb{P}_{0,x}[W_{t_0} \in \cdot | \tau_{h(s)} > t_0]}[\tau_{h(s)} > n_0 \gamma] \notag \\[5pt] &\geq c \mathbb{P}_{0,\nu_{h(s)}}[\tau_{h(s)} > n_0 \gamma] \notag \\[5pt] &= c \int_{(\!-\!1,1)} \nu(dy) \mathbb{P}_{h(s)y}[\tau_{h(s)} > n_0 \gamma] \notag\\[5pt] &\geq c \mathbb{P}_{0,\nu}\Bigg[\tau_1 > \frac{n_0 \gamma}{h_{\min}^2}\Bigg] > 0.\end{align}

Thus, combining (41), (46), and (47), for any $x \in (\!-\!h(s),h(s))$ and any $t \in [t_0, t_0 + n_0 \gamma]$ ,

(48) \begin{equation}\mathbb{P}_{s,x}[W_{s+t} \in \cdot | \tau_h > s+t] \geq c_1 \nu_{h(s)},\end{equation}

where

\begin{equation*}c_1 \;:\!=\; c \mathbb{P}_{0,\nu}\bigg[\tau_1 > \frac{n_0 \gamma}{h_{\max}^2}\bigg] \times \frac{c}{C} \mathbb{P}_{0,\nu}\bigg[\tau_1 > \inf_{s \geq 0} \bigg\{\frac{\gamma}{h^2(s)} - \int_s^{s+\gamma} \frac{1}{h^2(u)}du\bigg\}\bigg] c.\end{equation*}

We recall that the Doeblin condition (48) has, for now, been obtained only for $s \in \mathcal{T}$ . Consider now $s \not \in \mathcal{T}$ . Then, by the condition (38), there exists $s_1 \in \mathcal{T}$ such that $s < s_1 \leq s + n_0 \gamma$ . The Markov property and (48) therefore imply that, for any $x \in (\!-\!h(s),h(s))$ ,

\begin{equation*}\mathbb{P}_{s,x}[W_{s+t_0 + n_0 \gamma} \in \cdot | \tau_h > s+t_0 + n_0 \gamma] = \mathbb{P}_{s_1,\phi_{s_1,s}}[W_{s+t_0 + n_0 \gamma} \in \cdot | \tau_h > s+t_0 + n_0\gamma] \geq c_1 \nu_{h(s_1)},\end{equation*}

where, for all $s \leq t$ and $\mu \in \mathcal{M}_1((\!-\!h(s),h(s)))$ ,

\begin{equation*}\phi_{t,s}(\mu) \;:\!=\; \mathbb{P}_{s,\mu}[W_t \in \cdot | \tau_h > t].\end{equation*}

This concludes the proof of (A′1).

• Proof of (A′2). Since $(W_t)_{t \geq 0}$ is a Brownian motion, note that for any $s \leq t$ ,

  \begin{equation*}\sup_{x \in (\!-\!1,1)} \mathbb{P}_{s,x}[\tau_h > t] = \mathbb{P}_{s,0}[\tau_h > t].\end{equation*}
  Also, for any $a \in (0,h(s))$ ,
  \begin{equation*}\inf_{[\!-\!a,a]}\mathbb{P}_{s,x}[\tau_h > t] = \mathbb{P}_{s,a}[\tau_h > t].\end{equation*}
  Thus, by the Markov property, and using that the function $s \mapsto \mathbb{P}_{s,0}[\tau_g > t]$ is non-decreasing on [0, t] (for all $t \geq 0$ ), one has, for any $s \leq t$ ,
  (49) \begin{align} \mathbb{P}_{s,a}[\tau_h > t] \geq \mathbb{E}_{s,a}[\mathbb{1}_{\tau_0 < s+\gamma < \tau_h} \mathbb{P}_{\tau_0,0}[\tau_h > t]] \geq \mathbb{P}_{s,a}[\tau_0 < s+\gamma < \tau_h] \mathbb{P}_{s,0}[\tau_h > t].\end{align}
  Defining $a \;:\!=\; \frac{h_{\min}}{h_{\max}}$ , by Lemma 2 and taking $s_1 \;:\!=\; \inf\{u \geq s \;:\; u \in \mathcal{T}\}$ , one obtains that, for all $s \leq t$ ,
  \begin{align*}\mathbb{P}_{s,\nu_{h(s_1)}}[\tau_h > t] &= \int_{(\!-\!1,1)} \nu(dx) \mathbb{P}_{s,h(s_1)x}[\tau_h > t] \\[5pt] &\geq \nu([\!-\!a,a]) \mathbb{P}_{s,h(s_1)a}[\tau_h > t] \\[5pt] & \geq \nu([\!-\!a,a]) \mathbb{P}_{0,h_{\min}}[\tau_0 < \gamma < \tau_h] \sup_{x \in (\!-\!h(s),h(s))} \mathbb{P}_{s,x}[\tau_h > t].\end{align*}
  This concludes the proof, since, using (40), one has $\nu([\!-\!a,a]) > 0$ .

We now prove Lemma 2.

Proof of Lemma 2. This result comes from the scaling property of a Brownian motion. In fact, for any $z \in [h_{\min},h_{\max}]$ , $x \in (\!-\!z,z)$ , and $t \geq 0$ , and for any measurable bounded function f,

\begin{align*} \mathbb{E}_{0,x}[f(W_t) | \tau_z > t] &= \mathbb{E}_{0,x}\bigg[f\bigg(z \times \frac{1}{z}W_{z^2 \frac{t}{z^2}}\bigg) \bigg| \tau_z > t\bigg] \\[5pt] &= \mathbb{E}_{0,\frac{x}{z}}\bigg[f\bigg(z \times W_{\frac{t}{z^2}}\bigg) \bigg| \tau_1 > \frac{t}{z^2}\bigg].\end{align*}

Then the minorization (39) implies that for any $x \in (\!-\!1,1)$ ,

\begin{equation*}\mathbb{P}_{0,x}\bigg[W_{\frac{t_0}{h_{\max}^2}} \in \cdot \bigg| \tau_1 > \frac{t_0}{h_{\max}^2}\bigg] \geq c \nu.\end{equation*}

This inequality holds for any time greater than $\frac{t_0}{h_{\max}^2}$ . In particular, for any $z \in [h_{\min},h_{\max}]$ and $x \in (\!-\!1,1)$ ,

\begin{equation*}\mathbb{P}_{0,x}\bigg[W_{\frac{t_0}{z^2}} \in \cdot \bigg| \tau_1 > \frac{t_0}{z^2}\bigg] \geq c \nu.\end{equation*}

Then, for any $z \in [a,b]$ , f positive and measurable, and $x \in (\!-\!z,z)$ ,

\begin{equation*}\mathbb{E}_{0,x}[f(W_{t_0}) | \tau_z > t_0] \geq c \nu_z\left(f\right),\end{equation*}

where $\nu_z(f) \;:\!=\; \int_E f(z \times x)\nu(dx)$ . This completes the proof of Lemma 2.

We now conclude the section by stating and proving the following result.

Theorem 4. For any $s \leq t$ , $n \in \mathbb{N}$ , and any $x \in \mathbb{R}$ ,

\begin{equation*}\mathbb{P}_{s+k \gamma, x}[\tau_h \leq t+k \gamma < \tau_g] \underset{k \to \infty}{\longrightarrow} 0.\end{equation*}

In particular, Corollary 2 holds for $(W_t)_{t \geq 0}$ absorbed by h.

Proof. Recalling (43), by the Markov property for the Brownian motion, one has, for any $k,n \in \mathbb{N}$ and any $x \in \mathbb{R}$ ,

\begin{align*} \mathbb{P}_{s+k\gamma,x}[\tau_h > t+k\gamma] &= \sqrt{\frac{h(t+k\gamma)}{h(s+k \gamma)}} \mathbb{E}_{0,x}\bigg[\exp\bigg(-\frac{1}{2} \mathcal{A}^h_{s,t,k}(W) \bigg) \mathbb{1}_{\tau_1 > I^h(t+k\gamma) - I^h(s+k \gamma)}\bigg], \end{align*}

where, for any trajectory $w = (w_u)_{u \geq 0}$ ,

\begin{align*} \mathcal{A}_{s,t,k}^h(w) =h'(t+k\gamma)h(t+k\gamma) w_{I^h(t+k\gamma) - I^h(s+k \gamma)}^2 - h'(s+k \gamma)h(s+k \gamma) w_0^2 \\[5pt] + \int_{0}^{t-s} w_{I^h(u+s+k\gamma) - I^h(s+k \gamma)}^2[(h'(u+s+k\gamma))^2 - [h(u+s+k \gamma)h'(u+s+k\gamma)]']du.\end{align*}

Since $h \sim_{t \to \infty} g$ , one has for any $s,t \in [0, \gamma]$

\begin{equation*}\sqrt{\frac{h(t+k\gamma)}{h(s+k \gamma)}} \underset{k \to \infty}{\longrightarrow} \sqrt{\frac{g(t)}{g(s)}}.\end{equation*}

For the same reasons, and using that the function h is bounded on $[s+k \gamma, t+k\gamma]$ for all $s \leq t$ , Lebesgue’s dominated convergence theorem implies that

\begin{equation*}I^h(t+k\gamma) - I^h(s+k\gamma) \underset{k \to \infty}{\longrightarrow} I^g(t) - I^g(s)\end{equation*}

for all $s \leq t \in [0,\gamma]$ . Moreover, since $h \sim_{t \to \infty} g$ and $h' \sim_{t \to \infty} g'$ , one has for all trajectories $w = (w_u)_{u \geq 0}$ and $s \leq t \in [0,\gamma]$

\begin{equation*} \mathcal{A}_{s,t,k}^h(w) \underset{k \to \infty}{\longrightarrow} g'(t)g(t) w_{I^g(t) - I^g(s)}^2 - g'(s)g(s)w_0^2 + \int_{s}^{t} w_{I^g(u)}^2[(g'(u))^2 - [g(u)g'(u)]']du.\end{equation*}

Since the random variable

\begin{equation*}\exp\bigg(-\frac{1}{2} \mathcal{A}^h_{s,t,k}(W) \bigg) \mathbb{1}_{\tau_1 > I^h(t+k\gamma) - I^h(s+k \gamma)}\end{equation*}

is bounded almost surely, Lebesgue’s dominated convergence theorem implies that

\begin{equation*}\mathbb{P}_{s+k \gamma, x}[\tau_h > t+k \gamma] \underset{k \to \infty}{\longrightarrow} \mathbb{P}_{s,x}[\tau_g > t],\end{equation*}

which concludes the proof.