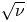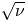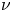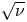1. Introduction
Recent stellarator optimization efforts (Landreman & Sengupta Reference Landreman and Sengupta2018, Reference Landreman and Sengupta2019; Landreman Reference Landreman2019; Landreman, Sengupta & Plunk Reference Landreman, Sengupta and Plunk2019; Plunk et al. Reference Plunk, Landreman, Sengupta and Helander2019) extending the earlier near magnetic axis formalism of Garren & Boozer (Reference Garren and Boozer1991a,Reference Garren and Boozerb) demonstrate that many optimized nearly quasisymmetric and/or omnigenous (Boozer Reference Boozer1983; Nührenberg & Zille Reference Nührenberg and Zille1988; Cary & Shasharina Reference Cary and Shasharina1997a,Reference Cary and Shasharinab; Parra et al. Reference Parra, Calvo, Helander and Landreman2015) configurations are possible and can be efficiently constructed. For an exactly quasisymmetric (QS) magnetic flux surface in a stellarator a drift kinetic canonical angular momentum (Boozer Reference Boozer1983; Landreman & Catto Reference Landreman and Catto2011) exists that is a constant of the motion as in a tokamak. Optimized nearly QS stellarators provide good collisional confinement for the background ions and electrons (Beidler et al. Reference Beidler, Allmaier, Isaev, Kaslov, Kernbichler, Leitold, Maaβberg, Mikkelsen, Murakami, Schmidt, Spong, Tribaldos and Wakasa2011; Landreman & Sengupta Reference Landreman and Sengupta2019). However, the alpha particles produced by fusion must also be well confined so that most of their energy heats the background plasma before they are lost by collisional radial heat transport. As this is a more difficult task, collisional radial transport at low collisionality in nearly optimized QS stellarators remains a focus of magnetic fusion efforts (Gates et al. Reference Gates, Boozer, Brown, Breslau, Curreli, Landreman, Lazerson, Lore, Mynick, Neilson, Pomphrey, Xanthopoulos and Zolfaghari2017; Henneberg et al. Reference Henneberg, Drevlak, Nührenberg, Beidler, Turkin, Loizu and Helander2019), with a proxy sometimes used in place of full collisional treatments (Bader et al. Reference Bader, Drevlak, Anderson, Faber, Hegna, Likin, Schmitt and Talmadge2019; Velasco et al. Reference Velasco, Calvo, Mulas, Sánchez, Parra and Cappa2021) to reduce computational costs. Importantly, recent work by Landreman & Paul (Reference Landreman and Paul2022) demonstrates that quasiaxisymmetric (QAS) and quasihelically symmetric (QHS) configurations with excellent collisionless alpha confinement are within reach.
Here, earlier work on weakly collisional superbanana (or resonant) plateau and $\sqrt \nu$![]() alpha particle transport (Catto Reference Catto2019b) is extended to retain magnetic shear, where $\nu$
alpha particle transport (Catto Reference Catto2019b) is extended to retain magnetic shear, where $\nu$![]() is the pitch angle scattering collision frequency for the trapped alphas. Superbanana plateau transport occurs when the tangential drift vanishes so the alphas encounter a drift resonance. The definition of tangential drift is such that there is no parallel streaming along the tangential drift direction within a flux surface. The resonance enhances the transport caused by any small radial drift departure from quasisymmetry. Because the trapped alpha response must vanish at the passing velocity space boundary,$\sqrt \nu$
is the pitch angle scattering collision frequency for the trapped alphas. Superbanana plateau transport occurs when the tangential drift vanishes so the alphas encounter a drift resonance. The definition of tangential drift is such that there is no parallel streaming along the tangential drift direction within a flux surface. The resonance enhances the transport caused by any small radial drift departure from quasisymmetry. Because the trapped alpha response must vanish at the passing velocity space boundary,$\sqrt \nu$![]() transport also arises as a result of the same symmetry breaking radial drift. Even though shear is often weak to modest in a stellarator, it is shown to enter the results in a sensitive way. Indeed, shear can result in a merging of the superbanana plateau (Galeev et al. Reference Galeev, Sagdeev, Furth and Rosenbluth1969; Shaing Reference Shaing2015) and $\sqrt \nu$
transport also arises as a result of the same symmetry breaking radial drift. Even though shear is often weak to modest in a stellarator, it is shown to enter the results in a sensitive way. Indeed, shear can result in a merging of the superbanana plateau (Galeev et al. Reference Galeev, Sagdeev, Furth and Rosenbluth1969; Shaing Reference Shaing2015) and $\sqrt \nu$![]() (Galeev et al. Reference Galeev, Sagdeev, Furth and Rosenbluth1969; Ho & Kulsrud Reference Ho and Kulsrud1987) transport regimes. The sensitivity arises because shear alters the location in velocity space of the sign change in the tangential drift frequency. The reversal of the tangential drift is responsible for the resonant alphas associated with the superbanana or resonant plateau transport. Depending on the details of the QS stellarator configuration, shear can move the resonance closer to the trapped--passing boundary, where the vanishing of the passing response provides the boundary condition for $\sqrt \nu$
(Galeev et al. Reference Galeev, Sagdeev, Furth and Rosenbluth1969; Ho & Kulsrud Reference Ho and Kulsrud1987) transport regimes. The sensitivity arises because shear alters the location in velocity space of the sign change in the tangential drift frequency. The reversal of the tangential drift is responsible for the resonant alphas associated with the superbanana or resonant plateau transport. Depending on the details of the QS stellarator configuration, shear can move the resonance closer to the trapped--passing boundary, where the vanishing of the passing response provides the boundary condition for $\sqrt \nu$![]() transport. It is this feature that causes the merging of the two regimes and allows the two separate regimes to be treated as a single merged regime close to the trapped--passing boundary. The key new aspect of the work presented here is a method for treating the merging of these two regimes in a unified manner. The narrow collisional boundary layer treatment demonstrates that superbanana plateau transport need not dominate over $\sqrt \nu$
transport. It is this feature that causes the merging of the two regimes and allows the two separate regimes to be treated as a single merged regime close to the trapped--passing boundary. The key new aspect of the work presented here is a method for treating the merging of these two regimes in a unified manner. The narrow collisional boundary layer treatment demonstrates that superbanana plateau transport need not dominate over $\sqrt \nu$![]() regime transport (Beidler et al. Reference Beidler, Allmaier, Isaev, Kaslov, Kernbichler, Leitold, Maaβberg, Mikkelsen, Murakami, Schmidt, Spong, Tribaldos and Wakasa2011; Calvo et al. Reference Calvo, Parra, Velasco and Alonso2017). Depending on the details of the QS configuration, the shear is typically restricted in sign to justify the narrow boundary layer assumption employed here. The sensitivity to shear arises when it causes the resonant alphas to be so close to the passing boundary that the pitch angle variation of the drift becomes strong enough to reduce the number of resonant alphas.
regime transport (Beidler et al. Reference Beidler, Allmaier, Isaev, Kaslov, Kernbichler, Leitold, Maaβberg, Mikkelsen, Murakami, Schmidt, Spong, Tribaldos and Wakasa2011; Calvo et al. Reference Calvo, Parra, Velasco and Alonso2017). Depending on the details of the QS configuration, the shear is typically restricted in sign to justify the narrow boundary layer assumption employed here. The sensitivity to shear arises when it causes the resonant alphas to be so close to the passing boundary that the pitch angle variation of the drift becomes strong enough to reduce the number of resonant alphas.
The narrow boundary layer treatment also allows the formulation of a quasilinear (QL) treatment whereby the radial transport of the alphas alters the background alpha distribution function. This QL equation indicates that a substantial departure from QS is needed for radial transport to modify the unperturbed alpha distribution function from its usual isotropic form.
The details of the treatments in the sections that follow are somewhat involved kinetic theory calculations with the added complication of stellarator geometry. Consequently, it is useful to keep in mind that the departure from QS only matters in the radial drift. Unperturbed QS alpha trajectories are used everywhere else. In addition, the full alpha collision operator with electron and ion drag and pitch angle scattering by the background ions matters for determining the unperturbed distribution function. However, radial transport introduces velocity space anisotropy, thereby requiring the retention of pitch angle scattering off the background ions to resolve narrow boundary layers associated with the perturbed alpha distribution function.
The superbanana or resonant plateau regime is particularly interesting since it occurs because the tangential drift vanishes, thereby allowing a drift resonance to occur. The occurrence of this resonant plateau behaviour is similar to the effect of the small parallel velocity particles that are responsible for the usual plateau regime of neoclassical transport in a tokamak. Indeed, the superbanana plateau radial diffusivity is independent of collision frequency even though the process responsible for the transport is collisional. To understand how this happens its diffusivity can be estimated by considering the tangential magnetic drift frequency ${\omega _\alpha }$![]() and the radial drift speed ${V_r}$
and the radial drift speed ${V_r}$![]() . In a large aspect ratio torus the QS tangential magnetic drift is of order ${\omega _\alpha }\sim qv_0^2/{\varOmega _0}Rr$
. In a large aspect ratio torus the QS tangential magnetic drift is of order ${\omega _\alpha }\sim qv_0^2/{\varOmega _0}Rr$![]() , with ${v_0}$
, with ${v_0}$![]() the alpha birth speed, ${\varOmega _0}$
the alpha birth speed, ${\varOmega _0}$![]() the on axis alpha gyrofrequency, R and r the major and minor radii and q the safety factor. The radial drift due to a departure from QS is of order ${V_r}\sim \delta qv_0^2/{\varOmega _0}r$
the on axis alpha gyrofrequency, R and r the major and minor radii and q the safety factor. The radial drift due to a departure from QS is of order ${V_r}\sim \delta qv_0^2/{\varOmega _0}r$![]() , where $\delta \ll \varepsilon = r/R$
, where $\delta \ll \varepsilon = r/R$![]() is the error or QS breaking magnetic field amplitude normalized by the on axis magnetic field (Calvo et al. Reference Calvo, Parra, Velasco and Alonso2013, Reference Calvo, Parra, Alonso and Velasco2014a,Reference Calvo, Parra, Velasco and Alonsob). Diffusive collisions result in a narrow boundary layer of dimensionless width ${w_{sbp}}$
is the error or QS breaking magnetic field amplitude normalized by the on axis magnetic field (Calvo et al. Reference Calvo, Parra, Velasco and Alonso2013, Reference Calvo, Parra, Alonso and Velasco2014a,Reference Calvo, Parra, Velasco and Alonsob). Diffusive collisions result in a narrow boundary layer of dimensionless width ${w_{sbp}}$![]() in pitch angle such that the effective collision frequency in the superbanana plateau regime is ${\nu _{sbp}}\sim \nu /w_{sbp}^2$
in pitch angle such that the effective collision frequency in the superbanana plateau regime is ${\nu _{sbp}}\sim \nu /w_{sbp}^2$![]() , with $\nu$
, with $\nu$![]() the effective collision frequency for pitch angle scattering of the trapped alphas by the background ions. A resonance occurs because the tangential drift vanishes at some pitch angle with collisions resulting in a spread out drift resonance with an effective width given by ${\omega _\alpha }{w_{sbp}}$
the effective collision frequency for pitch angle scattering of the trapped alphas by the background ions. A resonance occurs because the tangential drift vanishes at some pitch angle with collisions resulting in a spread out drift resonance with an effective width given by ${\omega _\alpha }{w_{sbp}}$![]() . Balancing the effective drift and collisions $\textrm{(}{\omega _\alpha }{w_{sbp}}\sim {\nu _{sbp}}\textrm{)}$
. Balancing the effective drift and collisions $\textrm{(}{\omega _\alpha }{w_{sbp}}\sim {\nu _{sbp}}\textrm{)}$![]() gives the dimensionless width (Catto & Tolman Reference Catto and Tolman2021) to be ${w_{sbp}}\sim {\textrm{(}\nu /{\omega _\alpha }\textrm{)}^{1/3}} \ll 1$
gives the dimensionless width (Catto & Tolman Reference Catto and Tolman2021) to be ${w_{sbp}}\sim {\textrm{(}\nu /{\omega _\alpha }\textrm{)}^{1/3}} \ll 1$![]() , and thereby an enhanced collision frequency of ${\nu _{sbp}}\sim \nu /w_{sbp}^2 \gg \nu \sim {\nu _{\alpha i}}/\varepsilon$
, and thereby an enhanced collision frequency of ${\nu _{sbp}}\sim \nu /w_{sbp}^2 \gg \nu \sim {\nu _{\alpha i}}/\varepsilon$![]() , where ${\nu _{\alpha i}}$
, where ${\nu _{\alpha i}}$![]() is the pitch angle scattering frequency of the alphas by the background ions. The resulting radial step size is then $\Delta = {V_r}{\kern 1pt} \textrm{/}{\nu _{sbp}}$
is the pitch angle scattering frequency of the alphas by the background ions. The resulting radial step size is then $\Delta = {V_r}{\kern 1pt} \textrm{/}{\nu _{sbp}}$![]() . Only the trapped particles in the narrow collisional boundary layer contribute to transport. Defining the inverse aspect ratio as $\varepsilon = r/R$
. Only the trapped particles in the narrow collisional boundary layer contribute to transport. Defining the inverse aspect ratio as $\varepsilon = r/R$![]() , then this fraction is ${w_{sbp}}{\varepsilon ^{1/2}}$
, then this fraction is ${w_{sbp}}{\varepsilon ^{1/2}}$![]() . Consequently, the diffusivity is seen to be independent of the collision frequency and given by
. Consequently, the diffusivity is seen to be independent of the collision frequency and given by
due to a cancelation between the boundary layer trapped fraction and the effective collision frequency. In some QAS and QHS configurations it will be shown that magnetic shear can reduce ${w_{sbp}}$![]() by a factor that increases exponentially with shear. These configurations are the ones of interest here and for them the superbanana plateau diffusivity is reduced to
by a factor that increases exponentially with shear. These configurations are the ones of interest here and for them the superbanana plateau diffusivity is reduced to
as the shear reduction factor $\gamma$![]() is large. The reduction occurs because very few barely trapped alphas are able to resonate with the drift once the drift varies strongly with pitch angle very near the trapped--passing boundary.
is large. The reduction occurs because very few barely trapped alphas are able to resonate with the drift once the drift varies strongly with pitch angle very near the trapped--passing boundary.
The estimate for the $\sqrt \nu$![]() regime is a bit more straightforward to obtain since the tangential drift ${\omega _\alpha }$
regime is a bit more straightforward to obtain since the tangential drift ${\omega _\alpha }$![]() does not vanish so the effective collision frequency is ${\nu _{\sqrt \nu }}\sim \nu /w_{\sqrt \nu }^2$
does not vanish so the effective collision frequency is ${\nu _{\sqrt \nu }}\sim \nu /w_{\sqrt \nu }^2$![]() . The dimensionless width ${w_{\sqrt \nu }}$
. The dimensionless width ${w_{\sqrt \nu }}$![]() is found from ${\omega _\alpha }\sim \nu /w_{\sqrt \nu }^2$
is found from ${\omega _\alpha }\sim \nu /w_{\sqrt \nu }^2$![]() to be ${w_{\sqrt \nu }}\sim {(\nu /{\omega _\alpha })^{1/2}} \ll 1$
to be ${w_{\sqrt \nu }}\sim {(\nu /{\omega _\alpha })^{1/2}} \ll 1$![]() . In this case, the trapped fraction in the narrow boundary layer is ${w_{\sqrt \nu }}{\varepsilon ^{1/2}}$
. In this case, the trapped fraction in the narrow boundary layer is ${w_{\sqrt \nu }}{\varepsilon ^{1/2}}$![]() , and results in the smaller diffusivity of
, and results in the smaller diffusivity of
Magnetic shear will be shown to have little effect on this estimate, but as the shear reduction factor is large ${D_{sbp}} \gg {D_{\sqrt \nu }}$![]() may no longer hold.
may no longer hold.
Results very similar to the preceding will be recovered in the merged regime treatment by assuming that radial transport does not modify the unperturbed distribution function significantly.
The sections that follow begin by introducing notation and briefly presenting some background for general stellarators in § 2 and QS stellarators in § 3. In § 4 an average over the tangential angle variable $\alpha$![]() is introduced and used to obtain the energy and particle balance equations with radial transport retained. Section 5 uses the $\alpha$
is introduced and used to obtain the energy and particle balance equations with radial transport retained. Section 5 uses the $\alpha$![]() average to derive the QL equation for the unperturbed distribution function and the linearized equation for the perturbed distribution function. Simplification of the linearized kinetic equation for a narrow boundary layer is performed in § 6 and, except for the retention of finite drift effects to retain magnetic shear, is similar to the procedure used by Catto (Reference Catto2019b). A unified solution of the merged superbanana plateau and $\sqrt \nu$
average to derive the QL equation for the unperturbed distribution function and the linearized equation for the perturbed distribution function. Simplification of the linearized kinetic equation for a narrow boundary layer is performed in § 6 and, except for the retention of finite drift effects to retain magnetic shear, is similar to the procedure used by Catto (Reference Catto2019b). A unified solution of the merged superbanana plateau and $\sqrt \nu$![]() regime is presented in § 7. Section 8 derives the QL velocity space dependent radial diffusivity needed to complete the derivation of the full QL equation for the unperturbed distribution function. In § 9 the alpha particle energy diffusivity is evaluated for the merged superbanana plateau and $\sqrt \nu$
regime is presented in § 7. Section 8 derives the QL velocity space dependent radial diffusivity needed to complete the derivation of the full QL equation for the unperturbed distribution function. In § 9 the alpha particle energy diffusivity is evaluated for the merged superbanana plateau and $\sqrt \nu$![]() regime by using the usual slowing down tail alpha distribution function. The results indicate that magnetic shear in some QS configurations can be used to reduce superbanana plateau transport below the $\sqrt \nu$
regime by using the usual slowing down tail alpha distribution function. The results indicate that magnetic shear in some QS configurations can be used to reduce superbanana plateau transport below the $\sqrt \nu$![]() transport level. The last section summarizes and discusses the results.
transport level. The last section summarizes and discusses the results.
2. General stellarator properties
A general stellarator magnetic field depends on the poloidal flux function ${\psi _p}$![]() , and the poloidal and toroidal angles $\vartheta$
, and the poloidal and toroidal angles $\vartheta$![]() and $\zeta$
and $\zeta$![]() , respectively. Introducing the angle variable
, respectively. Introducing the angle variable
the Boozer (Reference Boozer1981) and Clebsch representations for a general stellarator magnetic field are
with $\boldsymbol{B}\boldsymbol{\cdot }\boldsymbol{\nabla }{\psi _p}{\kern 1pt} = 0 = \boldsymbol{B}\boldsymbol{\cdot }\boldsymbol{\nabla }\alpha$![]() , q the safety factor and $\not{\iota }$
, q the safety factor and $\not{\iota }$![]() the rotational transform flux functions, and
the rotational transform flux functions, and
The coefficients I and G are flux functions and related to the toroidal current enclosed by a magnetic field line or flux surface
and the poloidal current outside the flux surface

In the preceding, unlike in usual stellarator notation, I is used with $\boldsymbol{\nabla }\zeta$![]() to more closely conform to tokamak notation.
to more closely conform to tokamak notation.
3. Quasisymmetric stellarator properties
The magnetic field $B = |\boldsymbol{B}|$![]() of a QS stellarator depends on the flux and is periodic in a single angle variable
of a QS stellarator depends on the flux and is periodic in a single angle variable
where $M \ge 0$![]() and $N \ge 0$
and $N \ge 0$![]() with N = 0 and M = 1 for a tokamak. On a QS flux surface a point on a constant B contour closes on itself after $\vartheta$
with N = 0 and M = 1 for a tokamak. On a QS flux surface a point on a constant B contour closes on itself after $\vartheta$![]() increases by $2\pi N$
increases by $2\pi N$![]() and $\zeta$
and $\zeta$![]() increases by $2\pi M$
increases by $2\pi M$![]() . Defining the helical magnetic flux function (Boozer Reference Boozer1983; Landreman & Catto Reference Landreman and Catto2011) as
. Defining the helical magnetic flux function (Boozer Reference Boozer1983; Landreman & Catto Reference Landreman and Catto2011) as
with the poloidal flux function ${\psi _p}$![]() and toroidal flux function ${\psi _t}$
and toroidal flux function ${\psi _t}$![]() related by
related by
then
The special case of M = 0 is often referred to as quasi-poloidal symmetry (QPS), the N = 0 case is referred to as quasi-axisymmetry (QAS includes, but is not limited to, strict axisymmetry), and the general $N \ne 0 \ne M$![]() case is referred to as quasi-hleical symmetry (QHS). The preceding imply that the Boozer (Reference Boozer1981) representations for a QS stellarator magnetic field may also be written as
case is referred to as quasi-hleical symmetry (QHS). The preceding imply that the Boozer (Reference Boozer1981) representations for a QS stellarator magnetic field may also be written as
with ${K_p} = (M - qN){K_h}$![]()
and
In terms of $\alpha$![]() and $\eta$
and $\eta$![]()
and
For fixed $\alpha$![]() , $\eta$
, $\eta$![]() changes by $2\pi$
changes by $2\pi$![]() when $\vartheta \to \vartheta + 2\mathrm{\pi }/(M - qN)$
when $\vartheta \to \vartheta + 2\mathrm{\pi }/(M - qN)$![]() and $\zeta \to \zeta + 2\mathrm{\pi }q/ (M - qN)$
and $\zeta \to \zeta + 2\mathrm{\pi }q/ (M - qN)$![]() .
.
In a QS stellarator the drift kinetic canonical angular momentum constant of the motion (Boozer Reference Boozer1983; see Appendix A of Landreman & Catto Reference Landreman and Catto2011) is
where $\varOmega = ZeB/{M_\alpha }c$![]() and
and
with Z the alpha charge number, ${M_\alpha }$![]() the alpha mass, e the charge on a proton and c the speed of light. As in a tokamak, the drift kinetic angular momentum in ${\psi _h},\vartheta ,\zeta$
the alpha mass, e the charge on a proton and c the speed of light. As in a tokamak, the drift kinetic angular momentum in ${\psi _h},\vartheta ,\zeta$![]() variables satisfies
variables satisfies
where the combined magnetic and electric drifts used are
in magnetic moment, $\mu = v_ \bot ^2/2B$![]() , and total energy variables
, and total energy variables
for which $v_{||}^2 = 2(E - Ze\varPhi /{M_\alpha } - \mu B)$![]() , with $\varPhi$
, with $\varPhi$![]() the electrostatic potential. The parallel component of the last form of ${\boldsymbol{v}_d}$
the electrostatic potential. The parallel component of the last form of ${\boldsymbol{v}_d}$![]() is negligible compared with parallel streaming so ${\boldsymbol{v}_d} \simeq {\varOmega ^{ - 1}}{v_{||}}{\nabla _ \bot }{\kern 1pt} \times ({v_{||}}\boldsymbol{b})$
is negligible compared with parallel streaming so ${\boldsymbol{v}_d} \simeq {\varOmega ^{ - 1}}{v_{||}}{\nabla _ \bot }{\kern 1pt} \times ({v_{||}}\boldsymbol{b})$![]() may be employed.
may be employed.
4. Alpha transport for nearly QS stellarators
In E, $\mu$![]() and $\varphi$
and $\varphi$![]() (= gyrophase) velocity space variables the drift kinetic equation for alpha particles is simply
(= gyrophase) velocity space variables the drift kinetic equation for alpha particles is simply
where the flux function $S = {n_T}{n_D}{\langle \sigma v\rangle _{DT}}$![]() is the birth rate of the alphas born isotropically in velocity space at the birth speed ${v_0}$
is the birth rate of the alphas born isotropically in velocity space at the birth speed ${v_0}$![]() , and
, and
is the collision operator retaining electron and ion drag and pitch angle scattering by ions, with

the slowing down time, ${v_c}$![]() the critical speed defined by
the critical speed defined by

and ${\tau _s}{v^3}v_\lambda ^{ - 3}$![]() the pitch angle scattering time, where
the pitch angle scattering time, where

The electron temperature ${T_e}$![]() and the electron and ion densities ${n_e}$
and the electron and ion densities ${n_e}$![]() and ${n_i}$
and ${n_i}$![]() are taken to be flux functions and quasineutrality $({n_e} \simeq {\Sigma _i}{Z_i}{n_i})$
are taken to be flux functions and quasineutrality $({n_e} \simeq {\Sigma _i}{Z_i}{n_i})$![]() is employed. The masses of the background ions and electrons are ${M_i}$
is employed. The masses of the background ions and electrons are ${M_i}$![]() and ${m_e}$
and ${m_e}$![]() , respectively, and ${Z_i}$
, respectively, and ${Z_i}$![]() is the charge number of the ions with ${\Sigma _i}$
is the charge number of the ions with ${\Sigma _i}$![]() denoting a sum over all background ion species. The alpha particle collision operator is obtained by expanding unlike collision operators for ${v_i} \ll {v_\lambda }{\kern 1pt} \sim {v_c}\ll {v_0} \ll {v_e}$
denoting a sum over all background ion species. The alpha particle collision operator is obtained by expanding unlike collision operators for ${v_i} \ll {v_\lambda }{\kern 1pt} \sim {v_c}\ll {v_0} \ll {v_e}$![]() , making energy scattering of alphas by ions and electrons small because ${v^2} \gg v_i^2 = 2{T_i}/{M_i}$
, making energy scattering of alphas by ions and electrons small because ${v^2} \gg v_i^2 = 2{T_i}/{M_i}$![]() and ${v^2} \ll v_e^2 = 2{T_e}/{m_e}$
and ${v^2} \ll v_e^2 = 2{T_e}/{m_e}$![]() , respectively.
, respectively.
In an imperfect stellarator B, and therefore ${v_{||}}$![]() , depends on $\alpha$
, depends on $\alpha$![]() as well as $\eta$
as well as $\eta$![]() and the flux. Using $\alpha$
and the flux. Using $\alpha$![]() and $\eta$
and $\eta$![]() from (3.8) and (3.9) in the Boozer form of (3.5) along with (3.4) and (3.6) gives
from (3.8) and (3.9) in the Boozer form of (3.5) along with (3.4) and (3.6) gives

In the final form of (4.6), the last term proportional $\partial /{\kern 1pt} \partial \alpha$![]() is the drive term that arises from the lack of QS and the first term proportional to $\boldsymbol{b}\boldsymbol{\cdot }\boldsymbol{\nabla }$
is the drive term that arises from the lack of QS and the first term proportional to $\boldsymbol{b}\boldsymbol{\cdot }\boldsymbol{\nabla }$![]() is the neoclassical drive term. As the departure from QS is assumed small, the QS trajectories may be used to evaluate all other terms in the drift kinetic equation. Consequently, departures from QS must be retained in the radial drift, while unperturbed QS trajectories are employed elsewhere.
is the neoclassical drive term. As the departure from QS is assumed small, the QS trajectories may be used to evaluate all other terms in the drift kinetic equation. Consequently, departures from QS must be retained in the radial drift, while unperturbed QS trajectories are employed elsewhere.
As the departure from QS is assumed small, the lowestorder alpha distribution function ${f_0}$![]() cannot depend on $\alpha$
cannot depend on $\alpha$![]() . Consequently,
. Consequently,
with ${f_0} \gg {f_1}$![]() . Then, compared with parallel streaming, the radial and tangential drifts are small and the source term and collisions are weak, giving to lowest order
. Then, compared with parallel streaming, the radial and tangential drifts are small and the source term and collisions are weak, giving to lowest order
Therefore, for small departures from QS, $\partial {f_0}/\partial \eta = 0$![]() as well as $\partial {f_0}/\partial \alpha = 0$
as well as $\partial {f_0}/\partial \alpha = 0$![]() , leading to
, leading to
with no dependence on $\sigma$![]() as the alphas are born isotropically.
as the alphas are born isotropically.
Going to next order by retaining $\partial {f_1}/\partial {\psi _p}$![]() to allow radial transport to modify ${f_0}$
to allow radial transport to modify ${f_0}$![]() , the kinetic equation becomes
, the kinetic equation becomes

where the alternate form on the far right follows by using
and $C\{ {f_0} + {f_1}\} = C\{ {f_0}\} + C\{ {f_1}\}$![]() . The usual slowing down distribution function
. The usual slowing down distribution function
with H the Heaviside step function, satisfies $4\mathrm{\pi }{v^2}C\{ {f_0}\} + S\delta (v - {v_0}) = 0$![]() . However, strong radial losses in (4.10) cause a departure from the isotropic behaviour of (4.12).
. However, strong radial losses in (4.10) cause a departure from the isotropic behaviour of (4.12).
The right most form of the drift kinetic operator is convenient for forming flux surface averaged moments. To do so, use ${d^3}v \to 2\mathrm{\pi }{\sum _\sigma }BdEd\mu /|{v_{||}}|= 2\mathrm{\pi }{\sum _\sigma }B{v^2}dvd\lambda /{B_0}|\xi |$![]() , with ${\sum _\sigma }$
, with ${\sum _\sigma }$![]() a reminder to sum over both signs of $\sigma = {v_{||}}/|{v_{||}}|$
a reminder to sum over both signs of $\sigma = {v_{||}}/|{v_{||}}|$![]() , $\xi = {v_{||}}/v$
, $\xi = {v_{||}}/v$![]() , $\lambda = 2\mu {B_0}/{v^2}$
, $\lambda = 2\mu {B_0}/{v^2}$![]() , and the flux surface average of an arbitrary function A as defined by
, and the flux surface average of an arbitrary function A as defined by
where $\textrm{d}\eta \,\textrm{d}\alpha = (M - qN)\,\textrm{d}\vartheta \,\textrm{d}\zeta$![]() . Then allowing for a collisional loss sink L at small speeds where the alphas become ash due to ion drag, the continuity equation leads to the expected result that radial particle loss reduces the amount of ash
. Then allowing for a collisional loss sink L at small speeds where the alphas become ash due to ion drag, the continuity equation leads to the expected result that radial particle loss reduces the amount of ash
where $V^{\prime} = \oint {\textrm{d}\vartheta \,\textrm{d}\zeta /\boldsymbol{B}\boldsymbol{\cdot }\boldsymbol{\nabla }\vartheta }$![]() , (3.13), $\langle \int {{d^3}v} {f_0}{\boldsymbol{v}_d}\boldsymbol{\cdot }\boldsymbol{\nabla }{\psi _p}\rangle = \langle {\varOmega ^{ - 1}}\int {{d^3}v} {v_{||}}\boldsymbol{\nabla }\boldsymbol{\cdot }({f_0}{v_{||}}\boldsymbol{b} \times \boldsymbol{\nabla }{\psi _p})\rangle = 0$
, (3.13), $\langle \int {{d^3}v} {f_0}{\boldsymbol{v}_d}\boldsymbol{\cdot }\boldsymbol{\nabla }{\psi _p}\rangle = \langle {\varOmega ^{ - 1}}\int {{d^3}v} {v_{||}}\boldsymbol{\nabla }\boldsymbol{\cdot }({f_0}{v_{||}}\boldsymbol{b} \times \boldsymbol{\nabla }{\psi _p})\rangle = 0$![]() and
and
are employed. The loss into a small velocity space sphere about the origin is
where ${\nabla _v} \cdot (\boldsymbol{v}{v^{ - 3}}f)\mathop \to \limits_{v \to 0} - 4\mathrm{\pi }\delta (\boldsymbol{v})f(\psi ,v = 0)$![]() . In the absence of alpha transport loss L = S as all the alphas become ash.
. In the absence of alpha transport loss L = S as all the alphas become ash.
A related, but more important, result holds for energy conservation
with E the alpha energy loss to the background ions and electrons
To avoid severe depletion, radial alpha energy losses must be kept small compared with ${M_\alpha }v_0^2S/{\kern 1pt} 2$![]() .
.
5. Quasilinear theory for nearly QS stellarators
Quasilinear theory allows the unperturbed distribution to be altered if the radial transport is large. To obtain this QL feature the form of the drift kinetic equation must be simplified further. To do so it is necessary to introduce the $\alpha$![]() average of an arbitrary function A as
average of an arbitrary function A as

where the integration on a fixed flux surface is over a closed loop on a constant B contour that closes back on itself when $\vartheta \to \vartheta + 2\mathrm{\pi }N$![]() and $\zeta {\kern 1pt} \to \zeta + 2\mathrm{\pi }M$
and $\zeta {\kern 1pt} \to \zeta + 2\mathrm{\pi }M$![]() (causing $\alpha \to \alpha + 2\mathrm{\pi }(M - qN)$
(causing $\alpha \to \alpha + 2\mathrm{\pi }(M - qN)$![]() ). Such B contours exist by definition for a QS magnetic field.
). Such B contours exist by definition for a QS magnetic field.
The drive term (4.6) in the kinetic equation is the sum of two contributions
with
the usual QS neoclassical drive term, and
the drive term due to the departure from QS. Therefore, ${f_1}$![]() is written as the sum of the neoclassical (nc) and non-QS (im) contributions
is written as the sum of the neoclassical (nc) and non-QS (im) contributions
with $f_1^{nc} \equiv {\langle {f_1}\rangle _\alpha }$![]() and ${\langle f_1^{im}\rangle _\alpha }{\kern 1pt} = 0$
and ${\langle f_1^{im}\rangle _\alpha }{\kern 1pt} = 0$![]() . Then the neoclassical portion satisfies
. Then the neoclassical portion satisfies
where $\partial f_1^{nc}/\partial \alpha = 0$![]() and the ${\boldsymbol{v}_d}\boldsymbol{\cdot }\boldsymbol{\nabla }\eta \partial f_1^{nc}/\partial \eta$
and the ${\boldsymbol{v}_d}\boldsymbol{\cdot }\boldsymbol{\nabla }\eta \partial f_1^{nc}/\partial \eta$![]() term is ignored as negligible. The solution to the neoclassical equation for alphas in a QS stellarator does not involve any resonant particles and can be obtained from Hsu et al. (Reference Hsu, Catto and Sigmar1990) and Catto (Reference Catto2018) using the isomorphism of stellarators with tokamaks (Boozer Reference Boozer1983; Landreman & Catto Reference Landreman and Catto2011). It is of no concern here.
term is ignored as negligible. The solution to the neoclassical equation for alphas in a QS stellarator does not involve any resonant particles and can be obtained from Hsu et al. (Reference Hsu, Catto and Sigmar1990) and Catto (Reference Catto2018) using the isomorphism of stellarators with tokamaks (Boozer Reference Boozer1983; Landreman & Catto Reference Landreman and Catto2011). It is of no concern here.
Subtracting the neoclassical equation from the full equation and continuing to keep $\partial {f_1}/\partial {\psi _h}$![]() , leaves
, leaves
where the ash sink is implicit as ${\nabla _v}\,{\cdot}\, (\boldsymbol{v}{v^{ - 3}}{f_0})\mathop \to \limits_{v \to 0} - 4\mathrm{\pi }\delta (\boldsymbol{v}){f_0}(\psi ,v \,{=}\, 0)$![]() and ${\int d^3v\delta(\boldsymbol{v})=1}$
and ${\int d^3v\delta(\boldsymbol{v})=1}$![]() . Departures from a QS magnetic field are assumed to satisfy stellarator symmetry. Upon Fourier decomposition they may be written as proportional to $\cos (m\vartheta - n\zeta )$
. Departures from a QS magnetic field are assumed to satisfy stellarator symmetry. Upon Fourier decomposition they may be written as proportional to $\cos (m\vartheta - n\zeta )$![]() with $m \ne M$
with $m \ne M$![]() and $n \ne N$
and $n \ne N$![]() . As a result, the non-QS drive terms are proportional to $\sin (m\vartheta - n\zeta )$
. As a result, the non-QS drive terms are proportional to $\sin (m\vartheta - n\zeta )$![]() , where
, where
Then $f_1^{im}$![]() is the portion of ${f_1}$
is the portion of ${f_1}$![]() periodic in $\alpha$
periodic in $\alpha$![]() such that ${\langle f_1^{im}\rangle _\alpha } = 0$
such that ${\langle f_1^{im}\rangle _\alpha } = 0$![]() , ${\langle \partial f_1^{im}/\partial \alpha \rangle _\alpha } = 0$
, ${\langle \partial f_1^{im}/\partial \alpha \rangle _\alpha } = 0$![]() and ${\langle {\boldsymbol{v}_d}\boldsymbol{\cdot }\boldsymbol{\nabla }\psi { {_h} |_{im}}/{v_{||}}\boldsymbol{b}\boldsymbol{\cdot }\boldsymbol{\nabla }\eta \rangle _\alpha } = 0$
and ${\langle {\boldsymbol{v}_d}\boldsymbol{\cdot }\boldsymbol{\nabla }\psi { {_h} |_{im}}/{v_{||}}\boldsymbol{b}\boldsymbol{\cdot }\boldsymbol{\nabla }\eta \rangle _\alpha } = 0$![]() (recall $\boldsymbol{b}\boldsymbol{\cdot }\boldsymbol{\nabla }\eta \propto B$
(recall $\boldsymbol{b}\boldsymbol{\cdot }\boldsymbol{\nabla }\eta \propto B$![]() ). Consequently, writing out the divergence on the left of (5.7) in ${\psi _h},\eta ,\alpha$
). Consequently, writing out the divergence on the left of (5.7) in ${\psi _h},\eta ,\alpha$![]() variables, dividing by ${v_{||}}\boldsymbol{b}\boldsymbol{\cdot }\boldsymbol{\nabla }\eta$
variables, dividing by ${v_{||}}\boldsymbol{b}\boldsymbol{\cdot }\boldsymbol{\nabla }\eta$![]() , and averaging over $\alpha$
, and averaging over $\alpha$![]() as in (5.1), leaves
as in (5.1), leaves

where for narrow collisional boundary layers ${\langle {B^{ - 1}}v_{||}^{ - 1}C\{ f_1^{im}\} \rangle _\alpha } \simeq {B^{ - 1}}v_{||}^{ - 1}C\{ {\langle f_1^{im}\rangle _\alpha }\} = 0$![]() is assumed.
is assumed.
A final simplification follows by integrating $\eta$![]() over a full bounce for the trapped and over a fixed $\alpha$
over a full bounce for the trapped and over a fixed $\alpha$![]() path for which $\eta$
path for which $\eta$![]() changes by $2\pi$
changes by $2\pi$![]() for the passing. Periodicity in $\eta$
for the passing. Periodicity in $\eta$![]() is then used to obtain the QL equation to evaluate ${f_0}$
is then used to obtain the QL equation to evaluate ${f_0}$![]() once the solution $f_1^{im}$
once the solution $f_1^{im}$![]() is found, namely,
is found, namely,

The subscript on the integral is a reminder that it is performed at fixed $\alpha$![]() . This QL equation for ${f_0}$
. This QL equation for ${f_0}$![]() implies that depletion due to strong ${\psi _p}$
implies that depletion due to strong ${\psi _p}$![]() variation of $f_1^{im}{\boldsymbol{v}_d}\boldsymbol{\cdot }\boldsymbol{\nabla }\psi { {_p} |_{im}}$
variation of $f_1^{im}{\boldsymbol{v}_d}\boldsymbol{\cdot }\boldsymbol{\nabla }\psi { {_p} |_{im}}$![]() caused by $\alpha$
caused by $\alpha$![]() variation can alter the alpha distribution function for large enough departures from QS. The radial transport term on the left must remain unimportant to control alpha particle losses in a stellarator.
variation can alter the alpha distribution function for large enough departures from QS. The radial transport term on the left must remain unimportant to control alpha particle losses in a stellarator.
Subtracting the $\alpha$![]() average of (5.7) from the full equation yields the $f_1^{im}$
average of (5.7) from the full equation yields the $f_1^{im}$![]() equation
equation

where $\partial f_1^{nc}/\partial {\psi _h} \ll \partial {f_0}/\partial {\psi _h}$![]() is assumed. In a standard QL treatment the terms on the right side of this equation are ignored. The neglect corresponds to an assumption that the departure from QS is small. Therefore, only the remaining linear equation,
is assumed. In a standard QL treatment the terms on the right side of this equation are ignored. The neglect corresponds to an assumption that the departure from QS is small. Therefore, only the remaining linear equation,
is to be solved. The passing alphas trace out flux surfaces and, as ${v_{||}}\boldsymbol{b}\boldsymbol{\cdot }\boldsymbol{\nabla }f_1^{im}{\kern 1pt} \gg {\boldsymbol{v}_d}\boldsymbol{\cdot }\boldsymbol{\nabla }f_1^{im} \gg C\{ f_1^{im}\}$![]() for all passing particles, little to no transport occurs. The trapped alphas are unable to trace out flux surfaces. Moreover, the tangential drift in a flux surface is known to change sign at some pitch angle. Consequently, it is these trapped alphas that give the dominant contribution to the radial transport. Therefore, the next task is to further simplify this kinetic equation for the trapped alphas by using the unperturbed QS trajectories on the left side based on the approximations already outlined.
for all passing particles, little to no transport occurs. The trapped alphas are unable to trace out flux surfaces. Moreover, the tangential drift in a flux surface is known to change sign at some pitch angle. Consequently, it is these trapped alphas that give the dominant contribution to the radial transport. Therefore, the next task is to further simplify this kinetic equation for the trapped alphas by using the unperturbed QS trajectories on the left side based on the approximations already outlined.
6. Formulation of the linearized drift kinetic equation for nearly QS stellarators
As the unperturbed QS trajectories are adequate on the left side, $({v_{||}}\boldsymbol{b} + {\boldsymbol{v}_d})\boldsymbol{\cdot }\boldsymbol{\nabla }{\psi _ \ast } = 0$![]() is used there. Then, to retain radial drift departures from QS it is convenient to use the variables ${\psi _ \ast }$
is used there. Then, to retain radial drift departures from QS it is convenient to use the variables ${\psi _ \ast }$![]() , $\eta$
, $\eta$![]() and
and
along with E and $\mu$![]() , with ${q_ \ast } = {q_ \ast }({\psi _ \ast })$
, with ${q_ \ast } = {q_ \ast }({\psi _ \ast })$![]() , $q = q({\psi _h})$
, $q = q({\psi _h})$![]() and $\textrm{d}{\psi _h} = (M - qN)\,\textrm{d}{\psi _p}$
and $\textrm{d}{\psi _h} = (M - qN)\,\textrm{d}{\psi _p}$![]() . Using (3.12)
. Using (3.12)

where magnetic shear effects are retained (unlike Catto Reference Catto2019b), and ${q_ \ast }{\boldsymbol{v}_d}\boldsymbol{\cdot }\boldsymbol{\nabla }\vartheta \simeq q{\boldsymbol{v}_d}\boldsymbol{\cdot }\boldsymbol{\nabla }\vartheta$![]() and
and
are employed. Using ${\alpha _ \ast }$![]() instead of $\alpha$
instead of $\alpha$![]() removes the awkward secular term $\vartheta {\boldsymbol{v}_d}\boldsymbol{\cdot }\boldsymbol{\nabla }q \ne 0$
removes the awkward secular term $\vartheta {\boldsymbol{v}_d}\boldsymbol{\cdot }\boldsymbol{\nabla }q \ne 0$![]() as $\vartheta ({v_{||}}\boldsymbol{b} + {\boldsymbol{v}_d})\boldsymbol{\cdot }\boldsymbol{\nabla }{q_ \ast } = 0$
as $\vartheta ({v_{||}}\boldsymbol{b} + {\boldsymbol{v}_d})\boldsymbol{\cdot }\boldsymbol{\nabla }{q_ \ast } = 0$![]() in ${\omega _\alpha }$
in ${\omega _\alpha }$![]() . Consequently, the drift kinetic equation for the trapped alphas with finite orbit effects retained becomes
. Consequently, the drift kinetic equation for the trapped alphas with finite orbit effects retained becomes
where the drift correction to the streaming term is neglected as small and now
For alphas the electrostatic potential is unimportant and it is convenient to introduce the pitch angle variable
with
so that
As the drive term due to the departure from QS is small and parallel streaming dominates the left side of the equation, to lowest order $\partial f_1^{im}/\partial \eta = 0$![]() . Letting $f_1^{im} = \bar{f}_1^{im} + \tilde{f}_1^{im}$
. Letting $f_1^{im} = \bar{f}_1^{im} + \tilde{f}_1^{im}$![]() with $\partial \bar{f}_1^{im}/\partial \eta = 0$
with $\partial \bar{f}_1^{im}/\partial \eta = 0$![]() and $f_1^{im}({\psi _p},\alpha ,v,\lambda ) \gg \tilde{f}_1^{im}$
and $f_1^{im}({\psi _p},\alpha ,v,\lambda ) \gg \tilde{f}_1^{im}$![]() , the next order equation is
, the next order equation is
where the distinction between ${\alpha _ \ast }$![]() and $\alpha$
and $\alpha$![]() no longer matters to the requisite order, collisions are weak and ${v_{||}}\boldsymbol{b}\boldsymbol{\cdot }\boldsymbol{\nabla }\eta \gg {\omega _\alpha }$
no longer matters to the requisite order, collisions are weak and ${v_{||}}\boldsymbol{b}\boldsymbol{\cdot }\boldsymbol{\nabla }\eta \gg {\omega _\alpha }$![]() is assumed.
is assumed.
To annihilate the streaming term integration along the characteristics associated with the alpha trajectories at fixed $\alpha$![]() is employed by defining the total trajectory derivatives using
is employed by defining the total trajectory derivatives using
with $\eta (\tau = 0) = \eta$![]() and $\eta ({\tau _0}) = 0$
and $\eta ({\tau _0}) = 0$![]() at the closed minimum B contour of the lowest order QS magnetic field (recall that unperturbed QS trajectories are being used on the left side of the kinetic equation). Transit or bounce averaging over a full bounce for the trapped alphas leads to the reduced kinetic equation
at the closed minimum B contour of the lowest order QS magnetic field (recall that unperturbed QS trajectories are being used on the left side of the kinetic equation). Transit or bounce averaging over a full bounce for the trapped alphas leads to the reduced kinetic equation
where $qI \gg G$![]() is employed and the transit average subscript is a reminder to hold $\alpha$
is employed and the transit average subscript is a reminder to hold $\alpha$![]() fixed. The usual superbanana plateau resonance and $\sqrt \nu$
fixed. The usual superbanana plateau resonance and $\sqrt \nu$![]() behaviour occurs for the trapped when $\oint_\alpha {\textrm{d}\tau {\omega _\alpha }}$
behaviour occurs for the trapped when $\oint_\alpha {\textrm{d}\tau {\omega _\alpha }}$![]() changes sign and near the passing boundary, respectively. Consequently, trapped particle contributions to transport will always occur.
changes sign and near the passing boundary, respectively. Consequently, trapped particle contributions to transport will always occur.
From here on the focus is on evaluating the superbanana plateau and $\sqrt \nu$![]() transport for the trapped alphas. To proceed analytically it is convenient to assume a large aspect ratio stellarator by using the approximations ${B_t} \simeq {B_0}$
transport for the trapped alphas. To proceed analytically it is convenient to assume a large aspect ratio stellarator by using the approximations ${B_t} \simeq {B_0}$![]() and $I \simeq R{B_0}$
and $I \simeq R{B_0}$![]() , where ${B_0}$
, where ${B_0}$![]() is a constant equal to the lowestorder toroidal magnetic field while the constant R is the nominal major radius. Then, to lowest order, ${\psi _t}{\kern 1pt} \simeq {B_0}a(r)$
is a constant equal to the lowestorder toroidal magnetic field while the constant R is the nominal major radius. Then, to lowest order, ${\psi _t}{\kern 1pt} \simeq {B_0}a(r)$![]() , where a = a(r) is the area enclosed by the flux surface labelled by r, and $\partial /{\kern 1pt} \partial {\psi _p} = q\partial /\partial {\psi _t} \simeq (q/{B_0}a^{\prime})\partial /\partial r$
, where a = a(r) is the area enclosed by the flux surface labelled by r, and $\partial /{\kern 1pt} \partial {\psi _p} = q\partial /\partial {\psi _t} \simeq (q/{B_0}a^{\prime})\partial /\partial r$![]() with $a^{\prime} = \textrm{d}a/\textrm{d}r\sim r$
with $a^{\prime} = \textrm{d}a/\textrm{d}r\sim r$![]() and ${a^2}\sim {r^2}$
and ${a^2}\sim {r^2}$![]() . Using $G/{\kern 1pt} qI \ll 1$
. Using $G/{\kern 1pt} qI \ll 1$![]() , $NG \ll MI$
, $NG \ll MI$![]() and ${\varOmega _0} \equiv Ze{B_0}/{M_\alpha }c$
and ${\varOmega _0} \equiv Ze{B_0}/{M_\alpha }c$![]() ,
,

Continuing to assume large aspect ratio by taking

with $1 \gg \varepsilon \simeq r/{\kern 1pt} R \gg \delta _m^n$![]() , and $\sum$
, and $\sum$![]() denoting the sums over $n \ne N \ge 0$
denoting the sums over $n \ne N \ge 0$![]() and $m \ne M \ge 0$
and $m \ne M \ge 0$![]() (n = N and $m \ne M$
(n = N and $m \ne M$![]() or $n \ne N$
or $n \ne N$![]() and m = M represent field departures from QS). Then
and m = M represent field departures from QS). Then

For the unperturbed QS trajectories using $B \simeq {B_0}(1 - \varepsilon \cos \eta )$![]() gives
gives
with the magnetic shear defined as
To evaluate the transit averages it is convenient to define
and use the QS trapped results by letting $\sin (\eta /2) = \kappa \sin x$![]() to find
to find

and

where ${\kappa ^2} = [1 - (1 - \varepsilon )\lambda ]/{\kern 1pt} 2\varepsilon \lambda$![]() . Then $\boldsymbol{b}\boldsymbol{\cdot }\boldsymbol{\nabla }\eta \simeq (M - qN)/qR$
. Then $\boldsymbol{b}\boldsymbol{\cdot }\boldsymbol{\nabla }\eta \simeq (M - qN)/qR$![]() leads to $\oint_t {\textrm{d}\tau \xi } \simeq 2\mathrm{\pi }qR/|M - qN|v$
leads to $\oint_t {\textrm{d}\tau \xi } \simeq 2\mathrm{\pi }qR/|M - qN|v$![]() ,
,
and

In the absence of shear and a radial electric field a superbanana plateau resonance $(\oint_\alpha \textrm{d} \tau {\omega _\alpha } = 0)$![]() occurs at 2E = K (Shaing, Sabbagh & Chu Reference Shaing, Sabbagh and Chu2009; Catto Reference Catto2019b), corresponding to ${\kappa ^2} \simeq 0.83$
occurs at 2E = K (Shaing, Sabbagh & Chu Reference Shaing, Sabbagh and Chu2009; Catto Reference Catto2019b), corresponding to ${\kappa ^2} \simeq 0.83$![]() . In a tokamak, s > 0 moves the resonance closer to the trapped--passing boundary. Stellarators tend to have weaker shear but can have s > 0 or s < 0. Shear is unimportant in QPS stellarators (M = 0), while for QAS and QHS stellarators the limiting forms of the trapped tangential drift follow from
. In a tokamak, s > 0 moves the resonance closer to the trapped--passing boundary. Stellarators tend to have weaker shear but can have s > 0 or s < 0. Shear is unimportant in QPS stellarators (M = 0), while for QAS and QHS stellarators the limiting forms of the trapped tangential drift follow from

Magnetic shear tends to be weak or modest in a stellarator, keeping q between any lower rational surfaces (M ~ 1 ~ N). A deeply trapped ${\kappa ^2} \ll 1$![]() resonance is less likely as it requires $4sM/(qN - M) \gg 1$
resonance is less likely as it requires $4sM/(qN - M) \gg 1$![]() and often M = 1 (Landreman & Paul Reference Landreman and Paul2022). More importantly, the resonance as ${\kappa ^2} \to 1$
and often M = 1 (Landreman & Paul Reference Landreman and Paul2022). More importantly, the resonance as ${\kappa ^2} \to 1$![]() is exponentially sensitive to even modest shear and leads to shear reduction factor $\gamma$
is exponentially sensitive to even modest shear and leads to shear reduction factor $\gamma$![]() to be introduced in the next section that also appears in (1.2). It is these barely trapped alphas that give a superbanana plateau resonance when
to be introduced in the next section that also appears in (1.2). It is these barely trapped alphas that give a superbanana plateau resonance when
although (6.24) is less accurate for s = 0. To keep $1 - \kappa _{res}^2 \ll 1$![]() requires either s > 0 for M > qN, or s < 0 for M < qN. In addition, as $sM/(M - qN) > 0$
requires either s > 0 for M > qN, or s < 0 for M < qN. In addition, as $sM/(M - qN) > 0$![]() increases the resonance moves even closer to the passing boundary, merging the superbanana plateau and $\sqrt \nu$
increases the resonance moves even closer to the passing boundary, merging the superbanana plateau and $\sqrt \nu$![]() transport regimes. The behaviour when the two regions merge is the focus of much of the remaining sections, with only QAS (with N = 0 and s > 0) and QHS stellarators (with $sM/(M - qN) > 0$
transport regimes. The behaviour when the two regions merge is the focus of much of the remaining sections, with only QAS (with N = 0 and s > 0) and QHS stellarators (with $sM/(M - qN) > 0$![]() ) of interest as the resonance for QPS stellarators is insensitive to shear. These are two QS configurations recently shown by Landreman & Paul (Reference Landreman and Paul2022) to offer the possibility of good alpha confinement.
) of interest as the resonance for QPS stellarators is insensitive to shear. These are two QS configurations recently shown by Landreman & Paul (Reference Landreman and Paul2022) to offer the possibility of good alpha confinement.
The form of the kinetic equation for the trapped alphas suggests a solution of the form
where $\partial h_m^n/\partial \eta = 0$![]() , which leads to
, which leads to
Next, the solution of (6.26) is given when the superbanana plateau and $\sqrt \nu$![]() regimes merge.
regimes merge.
7. Merged solution for the trapped alphas in nearly QS stellarators
In the presence of shear, superbanana plateau and $\sqrt \nu$![]() transport collisions only matter in narrow layers near the trapped--passing boundary. Consequently, in (6.26)
transport collisions only matter in narrow layers near the trapped--passing boundary. Consequently, in (6.26)
where $\partial {\bar{\omega }_\alpha }/\partial \lambda = (\partial {\kappa ^2}{\kern 1pt} /\partial \lambda )\partial {\bar{\omega }_\alpha }/\partial {\kappa ^2}\mathop \to \limits_{\kappa \to 1} - q{v^2}[1$![]() $+ 2sM/(M - qN)]/4{\varOmega _0}a^{\prime}r(1 - {\kappa ^2})\ell {n^2} (4/\sqrt {1 - {\kappa ^2}} )$
$+ 2sM/(M - qN)]/4{\varOmega _0}a^{\prime}r(1 - {\kappa ^2})\ell {n^2} (4/\sqrt {1 - {\kappa ^2}} )$![]() is responsible for the sensitivity to magnetic shear that enters via the shear reduction factor
is responsible for the sensitivity to magnetic shear that enters via the shear reduction factor
As only pitch angle scattering need be retained in the collision operator in (6.26),
gives

In addition, the phase factor in the drive term of (6.26), which enters as
can be taken to be approximately equal to one as long as $2\mathrm{\pi }(m - qn)/(M - qN)<1$![]() . Keeping $\varTheta$
. Keeping $\varTheta$![]() allows the recovery of ripple modifications in a tokamak (M = 1, N = 0, $n \gg 1\sim m$
allows the recovery of ripple modifications in a tokamak (M = 1, N = 0, $n \gg 1\sim m$![]() ).
).
Using the preceding simplifies (6.26) to

To consider the merged trapped regime it is convenient to first rewrite the kinetic equation by introducing the new variable
to obtain
where
and
As $\varsigma \to 0$![]() , $h_m^n \to - iV/W$
, $h_m^n \to - iV/W$![]() , provided $\ell n(1/{\kern 1pt} \varsigma ) \gg \ell n(\gamma )$
, provided $\ell n(1/{\kern 1pt} \varsigma ) \gg \ell n(\gamma )$![]() . However, a solution is required that vanishes at the trapped--passing boundary. An approximate matched asymptotic solution in $\sqrt \nu$
. However, a solution is required that vanishes at the trapped--passing boundary. An approximate matched asymptotic solution in $\sqrt \nu$![]() regime is given by (Catto Reference Catto2019a)
regime is given by (Catto Reference Catto2019a)
with the upper (lower) sign for W > 0 (W < 0) and where the $\sqrt \nu$![]() boundary layer width is
boundary layer width is
To carefully capture the preceding features in a merged superbanana plateau and $\sqrt \nu$![]() evaluation and demonstrate that the two contributions are additive, an expansion in the vicinity of $\gamma \varsigma = 1$
evaluation and demonstrate that the two contributions are additive, an expansion in the vicinity of $\gamma \varsigma = 1$![]() is employed by writing $\ell n(\gamma {\kern 1pt} \varsigma ) \simeq (\gamma {\kern 1pt} \varsigma - 1) + \cdots$
is employed by writing $\ell n(\gamma {\kern 1pt} \varsigma ) \simeq (\gamma {\kern 1pt} \varsigma - 1) + \cdots$![]() to be able to consider ${\kappa ^2} \simeq 1 - 16/\gamma$
to be able to consider ${\kappa ^2} \simeq 1 - 16/\gamma$![]() close to one when $\gamma \gg 1$
close to one when $\gamma \gg 1$![]() . Then letting $x = \gamma {\kern 1pt} \varsigma$
. Then letting $x = \gamma {\kern 1pt} \varsigma$![]() the kinetic equation can be approximated by
the kinetic equation can be approximated by
This merged limit is the situation of interest and $x = \gamma \varsigma \sim 1$![]() implies that $\varsigma = (1 - {\kappa ^2})/16\sim 1/\gamma$
implies that $\varsigma = (1 - {\kappa ^2})/16\sim 1/\gamma$![]() , giving $\partial {\bar{\omega }_\alpha }/\partial \lambda \mathop \to \limits_{\kappa \to 1} - q{v^2}\gamma /64{\varOmega _0}a^{\prime}r\ell n(\gamma )\sim {\bar{\omega }_\alpha }\gamma /\varepsilon \ell n(\gamma )\sim {\bar{\omega }_\alpha }\gamma /{\kern 1pt} \varepsilon$
, giving $\partial {\bar{\omega }_\alpha }/\partial \lambda \mathop \to \limits_{\kappa \to 1} - q{v^2}\gamma /64{\varOmega _0}a^{\prime}r\ell n(\gamma )\sim {\bar{\omega }_\alpha }\gamma /\varepsilon \ell n(\gamma )\sim {\bar{\omega }_\alpha }\gamma /{\kern 1pt} \varepsilon$![]() , as used to obtain estimate (1.2). Using this estimate for the merged case for which the superbanana plateau boundary layer extends to the trapped--passing boundary gives $C\{ h_m^n\} \sim \nu h_m^n/w_{sbp}^2\sim {\bar{\omega }_\alpha }\gamma {\varepsilon ^{ - 1}}{w_{sbp}}h_m^n$
, as used to obtain estimate (1.2). Using this estimate for the merged case for which the superbanana plateau boundary layer extends to the trapped--passing boundary gives $C\{ h_m^n\} \sim \nu h_m^n/w_{sbp}^2\sim {\bar{\omega }_\alpha }\gamma {\varepsilon ^{ - 1}}{w_{sbp}}h_m^n$![]() , and a width ${w_{sbp}}\sim {(\nu /\gamma {\omega _\alpha })^{1/3}} \ll 1$
, and a width ${w_{sbp}}\sim {(\nu /\gamma {\omega _\alpha })^{1/3}} \ll 1$![]() , where $\nu \sim v_\lambda ^3/\varepsilon v_0^3{\tau _s}\sim {\nu _{\alpha i}}/\varepsilon$
, where $\nu \sim v_\lambda ^3/\varepsilon v_0^3{\tau _s}\sim {\nu _{\alpha i}}/\varepsilon$![]() is the effective pitch angle scattering frequency of the trapped alphas with the background ions. This width becomes narrower than the $\sqrt \nu$
is the effective pitch angle scattering frequency of the trapped alphas with the background ions. This width becomes narrower than the $\sqrt \nu$![]() boundary layer width ${w_{\sqrt \nu }}\sim {(\nu /{\omega _\alpha })^{1/2}} \ll 1$
boundary layer width ${w_{\sqrt \nu }}\sim {(\nu /{\omega _\alpha })^{1/2}} \ll 1$![]() when shear becomes strong, that is when $\gamma > {({\omega _\alpha }/\nu )^{1/2}}$
when shear becomes strong, that is when $\gamma > {({\omega _\alpha }/\nu )^{1/2}}$![]() .
.
Letting

with the upper (lower) sign for W > 0 (W < 0) and ${w_{sbp}}$![]() the superbanana plateau boundary layer width, more precisely defined as
the superbanana plateau boundary layer width, more precisely defined as
leads to the Su & Oberman (Reference Su and Oberman1968) form

As $W\sim {\omega _\alpha }/\nu$![]() , this more precise definition of ${w_{sbp}}$
, this more precise definition of ${w_{sbp}}$![]() is consistent with the rougher estimates. The superbanana plateau solution is
is consistent with the rougher estimates. The superbanana plateau solution is
The resonance $\gamma \varsigma = x = 1$![]() remains near the trapped--passing boundary as long as $16/{\kern 1pt} \gamma \ll 1$
remains near the trapped--passing boundary as long as $16/{\kern 1pt} \gamma \ll 1$![]() , a condition that is marginally satisfied even for s = 0. Using (7.12) and (7.15) gives
, a condition that is marginally satisfied even for s = 0. Using (7.12) and (7.15) gives
indicating ${w_{sbp}}$![]() will become smaller than ${w_{\sqrt \nu }}$
will become smaller than ${w_{\sqrt \nu }}$![]() as the shear becomes stronger.
as the shear becomes stronger.
To estimate the magnetic shear level at which the narrow boundary layer treatment fails consider a D-T plasma with ${v_0} \simeq 1.3 \times {10^9}\;\textrm{cm}\;{\sec ^{ - 1}}$![]() , R = 10 m, B = 10 T, T = 10 keV and ${n_e} = {10^{14}}\;\textrm{c}{\textrm{m}^{ - 3}}$
, R = 10 m, B = 10 T, T = 10 keV and ${n_e} = {10^{14}}\;\textrm{c}{\textrm{m}^{ - 3}}$![]() , to find ${\tau _s} \simeq 0.6\;\sec$
, to find ${\tau _s} \simeq 0.6\;\sec$![]() , ${\rho _0} \simeq 1\;cm$
, ${\rho _0} \simeq 1\;cm$![]() , ${v_0}{\tau _s}/R\sim {10^6}$
, ${v_0}{\tau _s}/R\sim {10^6}$![]() , $R/{\rho _0}\sim {10^3}$
, $R/{\rho _0}\sim {10^3}$![]() , R/a = 10 and ${v_0}/{v_\lambda }\sim 3$
, R/a = 10 and ${v_0}/{v_\lambda }\sim 3$![]() . These parameters give $|W|\sim {10^6}$
. These parameters give $|W|\sim {10^6}$![]() if $\textrm{|}(nM - mN)/(M - qN)\textrm{|}\sim 1$
if $\textrm{|}(nM - mN)/(M - qN)\textrm{|}\sim 1$![]() , indicating that, for $\gamma \sim {10^3}$
, indicating that, for $\gamma \sim {10^3}$![]() , the boundary layers are of comparable width. For the modest shear $(0 < sM/(M - qN)< 1)$
, the boundary layers are of comparable width. For the modest shear $(0 < sM/(M - qN)< 1)$![]() case of interest here, ${w_{\sqrt \nu }}< {w_{sbp}} \ll 1$
case of interest here, ${w_{\sqrt \nu }}< {w_{sbp}} \ll 1$![]() . Once $\gamma \gg |W{|^{1/2}}$
. Once $\gamma \gg |W{|^{1/2}}$![]() , the superbanana plateau regime gives negligible transport.
, the superbanana plateau regime gives negligible transport.
The merged regime solution about to be presented is valid when $1 \ll \gamma \ll {({\omega _\alpha }/\nu )^{1/2}}$![]() . It is obtained by adding the appropriate homogeneous solution to the Su & Oberman (Reference Su and Oberman1968) form to make the total solution vanish at the trapped--passing boundary. To do so it is convenient to consider
. It is obtained by adding the appropriate homogeneous solution to the Su & Oberman (Reference Su and Oberman1968) form to make the total solution vanish at the trapped--passing boundary. To do so it is convenient to consider
then the merged solution is given by
with
A particular solution to this inhomogeneous Airy equation is the Su & Oberman form,
For the homogenous solutions it is convenient to use Airy functions by letting y = iz to obtain
Then the convenient homogenous solutions are $Ai(y)$![]() and $Ai(y\,{\textrm{e}^{ - \textrm{i}2\mathrm{\pi }/3}})$
and $Ai(y\,{\textrm{e}^{ - \textrm{i}2\mathrm{\pi }/3}})$![]() for large z > 0 (upper sign) and $Ai(y)$
for large z > 0 (upper sign) and $Ai(y)$![]() and $Ai(y\,{\textrm{e}^{\textrm{i}2\mathrm{\pi }/3}})$
and $Ai(y\,{\textrm{e}^{\textrm{i}2\mathrm{\pi }/3}})$![]() for z < 0 with -z large (lower sign) (Abramowitz & Stegun Reference Abramowitz and Stegun1964). Asymptotically these give
for z < 0 with -z large (lower sign) (Abramowitz & Stegun Reference Abramowitz and Stegun1964). Asymptotically these give
while for z > 0 with $\textrm{|}z\textrm{|} \gg 1$![]()
and for z < 0 with $\textrm{|}z\textrm{|} \gg 1$![]()
Consequently, the solution vanishing for the barely trapped alphas is
where the constant a is determined by the need to satisfy $\varUpsilon (z ={\mp} 1/u) = 0$![]() at the trapped--passing boundary. Hence, once the two regimes merge
at the trapped--passing boundary. Hence, once the two regimes merge
is the solution from which the QL diffusivity and alpha heat flux can be evaluated, with ${\varUpsilon _{\sqrt \nu }}(z)$![]() the homogenous contribution needed to satisfy the trapped--passing boundary condition. The solution $\varUpsilon$
the homogenous contribution needed to satisfy the trapped--passing boundary condition. The solution $\varUpsilon$![]() in figure 1 shows the ${\varUpsilon _{\sqrt \nu }}$
in figure 1 shows the ${\varUpsilon _{\sqrt \nu }}$![]() contribution from the truncated tail nearer $\kappa = 1$
contribution from the truncated tail nearer $\kappa = 1$![]() is small and the larger ${\varUpsilon _{SO}}$
is small and the larger ${\varUpsilon _{SO}}$![]() feature moves toward the trapped--passing boundary and narrows as $\gamma$
feature moves toward the trapped--passing boundary and narrows as $\gamma$![]() increases.
increases.

Figure 1. The solution for $\varUpsilon$![]() given by (7.28) is plotted for various values of the shear reduction factor $\gamma$
given by (7.28) is plotted for various values of the shear reduction factor $\gamma$![]() . The ${\varUpsilon _{\sqrt \nu }}$
. The ${\varUpsilon _{\sqrt \nu }}$![]() contribution from the truncated tail is small and nearer $\kappa = 1$
contribution from the truncated tail is small and nearer $\kappa = 1$![]() , while the larger ${\varUpsilon _{SO}}$
, while the larger ${\varUpsilon _{SO}}$![]() feature moves toward the trapped--passing boundary and narrows as $\gamma$
feature moves toward the trapped--passing boundary and narrows as $\gamma$![]() increases.
increases.
8. The QL alpha diffusivity in nearly QS stellarators
At large aspect ratio the QL equation (5.10) for ${f_0}$![]() becomes
becomes

where the sink term is contained in $v_c^3\int {{d^3}v{v^{ - 2}}\partial {f_0}} /\partial v\mathop \to \limits_{v \to 0} - 4\mathrm{\pi }v_c^3{f_0}(\psi ,v = 0)$![]() .
.
To evaluate the diffusivity in the QL equation for ${f_0}$![]() and the alpha energy flux, the remaining angle integral is performed by first using $\lambda \simeq 1$
and the alpha energy flux, the remaining angle integral is performed by first using $\lambda \simeq 1$![]() and
and
to find

where only $m\vartheta - n\zeta$![]() in $\chi ^{\prime} = m^{\prime}\vartheta - n^{\prime}\zeta$
in $\chi ^{\prime} = m^{\prime}\vartheta - n^{\prime}\zeta$![]() contributes.
contributes.
Inserting $h_m^n$![]() with $u = \gamma {w_{sbp}}$
with $u = \gamma {w_{sbp}}$![]() , (8.3) becomes
, (8.3) becomes

The delta function behaviour of ${\varUpsilon _{SO}}$![]() occurs upon integration over pitch angle $\lambda$
occurs upon integration over pitch angle $\lambda$![]() (Catto & Tolman Reference Catto and Tolman2021). Using
(Catto & Tolman Reference Catto and Tolman2021). Using
with $\textrm{d}\lambda \simeq{-} 2\varepsilon \,\textrm{d}{\kappa ^2}$![]() and $\gamma \,\textrm{d}{\kappa ^2} \simeq{-} 16u\,\textrm{d}z$
and $\gamma \,\textrm{d}{\kappa ^2} \simeq{-} 16u\,\textrm{d}z$![]() gives
gives

due to the superbanana or resonant plateau contribution.
Using $\partial /{\kern 1pt} \partial {\psi _p} \simeq (q/{B_0}a^{\prime})\partial /\partial r$![]() and $\varepsilon \simeq r/R$
and $\varepsilon \simeq r/R$![]() , and defining the spatial diffusivity
, and defining the spatial diffusivity

the QL equation (5.10) becomes

where ${{\oint_\alpha {\textrm{d}\eta \xi } } / {\oint_\alpha {\textrm{d}\eta {\xi ^{ - 1}}} }} = 2\varepsilon [E(\kappa ) - (1 - {\kappa ^2})K(\kappa )]/K(\kappa )$![]() and $\oint_\alpha {\textrm{d}\eta {\xi ^{ - 1}}} \propto {\varepsilon ^{ - 1/2}}$
and $\oint_\alpha {\textrm{d}\eta {\xi ^{ - 1}}} \propto {\varepsilon ^{ - 1/2}}$![]() .
.
In addition to retaining alpha birth and slowing down (including the ash sink) on the left, the preceding QL equation retains the radial loss of alphas on the right. The strong dependence of the spatial diffusivity on pitch angle allows pitch angle scattering to enter on the left side of (8.8). Notice that $D \propto {v^2}$![]() implies that radial loss becomes negligible at low speed where ${f_0}$
implies that radial loss becomes negligible at low speed where ${f_0}$![]() becomes isotropic.
becomes isotropic.
Negative definite entropy production is associated with both the radial transport and pitch angle scattering terms as multiplying by $\ell n{f_0}|{\oint_t {\textrm{d}\eta {\xi^{ - 1}}} } |$![]() and integrating over velocity space and cross section $\textrm{d}a \simeq \textrm{d}ra^{\prime}$
and integrating over velocity space and cross section $\textrm{d}a \simeq \textrm{d}ra^{\prime}$![]() out to some reference flux surface label ${r_0}$
out to some reference flux surface label ${r_0}$![]() leads to the expression
leads to the expression

The entropy production is associated with the alphas attempting to remove radial and pitch angle gradients to become the slowing down distribution function of (4.12) as implied by the remaining source and drag terms in (8.8).
9. The QL alpha heat flux in nearly QS stellarators
The heat flux evaluation involves performing velocity space integrals in addition to the angle integral evaluated in the last section. Rewriting

where $\oint {\textrm{d}\eta } = 2\mathrm{\pi }$![]() . To simplify further recall that the superbanana plateau resonance is at $\gamma \varsigma = 1$
. To simplify further recall that the superbanana plateau resonance is at $\gamma \varsigma = 1$![]() , and the $\sqrt \nu$
, and the $\sqrt \nu$![]() boundary layer width estimate from (7.11) is $\varsigma = (1 - {\kappa ^2}){\kern 1pt} /16\sim {W^{ - 1/2}}$
boundary layer width estimate from (7.11) is $\varsigma = (1 - {\kappa ^2}){\kern 1pt} /16\sim {W^{ - 1/2}}$![]() , while the superbanana plateau boundary layer width estimate is $\varsigma = (1 - {\kappa ^2})/16\sim {\gamma ^{ - 1}}$
, while the superbanana plateau boundary layer width estimate is $\varsigma = (1 - {\kappa ^2})/16\sim {\gamma ^{ - 1}}$![]() . As these small $\varsigma$
. As these small $\varsigma$![]() are very close to the trapped--passing boundary they imply
are very close to the trapped--passing boundary they imply

where
Moreover, the barely trapped $(\kappa \to 1)$![]() evaluation in Appendix A of Catto (Reference Catto2019b) suggests
evaluation in Appendix A of Catto (Reference Catto2019b) suggests

then $|\varTheta {|^2} \to 1$![]() as required for $|(qn - m)/(M - qN)|\ll 1$
as required for $|(qn - m)/(M - qN)|\ll 1$![]() , but $|\varTheta {|^2} < 1$
, but $|\varTheta {|^2} < 1$![]() otherwise. When $|(qn - m)/(M - qN)|\gg 1$
otherwise. When $|(qn - m)/(M - qN)|\gg 1$![]() the rapid oscillation of the $\varTheta$
the rapid oscillation of the $\varTheta$![]() phase factor in (7.5) cannot be ignored as it acts to reduce the effective step size of a trapped alpha (for a tokamak N = 0, M = 1 and $n \gg m\sim 1$
phase factor in (7.5) cannot be ignored as it acts to reduce the effective step size of a trapped alpha (for a tokamak N = 0, M = 1 and $n \gg m\sim 1$![]() ). Using the preceding approximations indicates the pitch angle dependence of ${\kern 1pt} |\varTheta {|^2}$
). Using the preceding approximations indicates the pitch angle dependence of ${\kern 1pt} |\varTheta {|^2}$![]() and $\oint_t {\textrm{d}\eta {\xi ^{ - 1}}}$
and $\oint_t {\textrm{d}\eta {\xi ^{ - 1}}}$![]() only enters logarithmically and suggests writing
only enters logarithmically and suggests writing

where defining ${w_{\sqrt \nu }} = 1/{(2|W|)^{1/2}}$![]() leads to $u = \gamma {w_{sbp}}{\kern 1pt} = {\gamma ^{2/3}}w_{\sqrt \nu }^{2/3}$
leads to $u = \gamma {w_{sbp}}{\kern 1pt} = {\gamma ^{2/3}}w_{\sqrt \nu }^{2/3}$![]() . The ${\varUpsilon _{SO}}$
. The ${\varUpsilon _{SO}}$![]() term has already been evaluated in (8.6). For the ${\varUpsilon _{\sqrt \nu }}$
term has already been evaluated in (8.6). For the ${\varUpsilon _{\sqrt \nu }}$![]() term only the large z limit is required giving
term only the large z limit is required giving

Using the $u \ll 1$![]() asymptotic forms (Abramowitz & Stegun Reference Abramowitz and Stegun1964)
asymptotic forms (Abramowitz & Stegun Reference Abramowitz and Stegun1964)
and

leads to

Therefore, using ${\varUpsilon _{SO}}({\mp} 1/u) \simeq{\mp} iu$![]() ,
,

and

Amazingly, ${u^{3/2}} = \gamma /\sqrt {2|W|} \propto \tau _s^{ - 1/2}$![]() , and is just the $\sqrt \nu$
, and is just the $\sqrt \nu$![]() regime contribution. Consequently, the merged procedure formulated here has the virtue of recovering both the $\sqrt \nu$
regime contribution. Consequently, the merged procedure formulated here has the virtue of recovering both the $\sqrt \nu$![]() and superbanana plateau regimes in a unified and additive manner when $u \ll 1$
and superbanana plateau regimes in a unified and additive manner when $u \ll 1$![]() . Only the $u \ll 1$
. Only the $u \ll 1$![]() limit is considered here. Once $\gamma \gg \sqrt {2|W|}$
limit is considered here. Once $\gamma \gg \sqrt {2|W|}$![]() is satisfied, presumably $\sqrt \nu$
is satisfied, presumably $\sqrt \nu$![]() transport will dominate since so few trapped alphas experience the tangential drift resonance.
transport will dominate since so few trapped alphas experience the tangential drift resonance.
Inserting the preceding results into the heat flux leads to

Then using the approximation that near the birth speed ${v^3}\partial {f_0}/\partial r \simeq {(4\mathrm{\pi })^{ - 1}}\partial (S{\tau _s})/\partial r$![]() ,
,

where for the slowing down distribution the alpha density is ${n_\alpha } \simeq S{\tau _s}\ell n({v_0}/{v_c})$![]() . Importantly, in the presence of magnetic shear with $sM/(qN - M) > 0$
. Importantly, in the presence of magnetic shear with $sM/(qN - M) > 0$![]() , superbanana plateau transport no longer dominates over $\sqrt \nu$
, superbanana plateau transport no longer dominates over $\sqrt \nu$![]() regime transport when $\gamma \to W_0^{1/2}\sim {({\omega _\alpha }/\nu )^{1/2}}$
regime transport when $\gamma \to W_0^{1/2}\sim {({\omega _\alpha }/\nu )^{1/2}}$![]() as suggested by the estimate of (7.18). The merged solution found here fails in this limit, but by then superbanana plateau transport is expected to be as small or smaller than $\sqrt \nu$
as suggested by the estimate of (7.18). The merged solution found here fails in this limit, but by then superbanana plateau transport is expected to be as small or smaller than $\sqrt \nu$![]() transport.
transport.
The preceding leads to the heat transport as being the sum of the superbanana plateau and $\sqrt \nu$![]() heat diffusivities (${D_{sbp}}$
heat diffusivities (${D_{sbp}}$![]() and ${D_{\sqrt \nu }}$
and ${D_{\sqrt \nu }}$![]() , respectively)
, respectively)

and

where in some stellarator cases ${\kern 1pt} |\varTheta |_{sbp}^2 \simeq 1$![]() and ${\kern 1pt} |\varTheta |_{\sqrt \nu }^2 \simeq 1$
and ${\kern 1pt} |\varTheta |_{\sqrt \nu }^2 \simeq 1$![]() may be adequate approximations in
may be adequate approximations in

The preceding results retain magnetic shear for $sM/(qN - M) > 0$![]() with $\gamma \equiv {\textrm{e}^{4 + 8sM/(M - qN)}} \gg 1$
with $\gamma \equiv {\textrm{e}^{4 + 8sM/(M - qN)}} \gg 1$![]() and confirm the estimates in the Introduction of
and confirm the estimates in the Introduction of
and
The general expressions (9.14) and (9.15) indicate that shear can significantly reduce superbanana plateau transport but has little effect on $\sqrt \nu$![]() regime transport. As $\gamma \equiv {\textrm{e}^{4 + 8sM/(M - qN)}}$
regime transport. As $\gamma \equiv {\textrm{e}^{4 + 8sM/(M - qN)}}$![]() increases the superbanana plateau boundary layer narrows and the diffusivity is strongly reduced because of the rapid variation the transit average tangential drift as seen in (7.1) and noted there. As a result, fewer trapped alphas are able participate in the drift resonance, thereby reducing the transport. The shear at the edge of a tokamak means that superbanana transport is unlikely to ever be of concern, and the small ripple makes $\sqrt \nu$
increases the superbanana plateau boundary layer narrows and the diffusivity is strongly reduced because of the rapid variation the transit average tangential drift as seen in (7.1) and noted there. As a result, fewer trapped alphas are able participate in the drift resonance, thereby reducing the transport. The shear at the edge of a tokamak means that superbanana transport is unlikely to ever be of concern, and the small ripple makes $\sqrt \nu$![]() transport weak as well (Catto Reference Catto2019a). The $\sqrt \varepsilon$
transport weak as well (Catto Reference Catto2019a). The $\sqrt \varepsilon$![]() and q factors found here are consistent with the shearless limit (Catto Reference Catto2019b). However, the result here is larger, presumably because the barely trapped asymptotic limits of the elliptic integrals are used here to treat finite shear. This last approximation works well for finite shear, but is less accurate in the absence of shear.
and q factors found here are consistent with the shearless limit (Catto Reference Catto2019b). However, the result here is larger, presumably because the barely trapped asymptotic limits of the elliptic integrals are used here to treat finite shear. This last approximation works well for finite shear, but is less accurate in the absence of shear.
The superbanana plateau diffusivity can be rewritten in an alternate approximate form. Using the resonance condition $\kappa _{res}^2 = 1 - 16/{\kern 1pt} \gamma$![]() in ${\kappa ^2} = [1 - (1 - \varepsilon )\lambda ]/{\kern 1pt} 2\varepsilon \lambda$
in ${\kappa ^2} = [1 - (1 - \varepsilon )\lambda ]/{\kern 1pt} 2\varepsilon \lambda$![]() gives the resonant pitch angle to be
gives the resonant pitch angle to be
Then taking advantage of the implicit delta function in $Re \varUpsilon$![]() by letting
by letting
this result is used to obtain an approximate superbanana plateau D for the QL operator (8.8) of the form

where $|\varTheta {|^2} \simeq 1$![]() is also assumed. In this form collisions no longer appear even though the derivation is based on a collisional boundary layer treatment. The diffusivity can also be rewritten using $\delta (\lambda - {\lambda _{res}}) = \delta (\kappa - {\kappa _{res}})/{\kern 1pt} 4\varepsilon$
is also assumed. In this form collisions no longer appear even though the derivation is based on a collisional boundary layer treatment. The diffusivity can also be rewritten using $\delta (\lambda - {\lambda _{res}}) = \delta (\kappa - {\kappa _{res}})/{\kern 1pt} 4\varepsilon$![]() since $\textrm{d}\lambda \simeq{-} 4\varepsilon \,\textrm{d}\kappa$
since $\textrm{d}\lambda \simeq{-} 4\varepsilon \,\textrm{d}\kappa$![]() . The absence of an explicit collisional dependence is characteristic of resonant plateau regime behaviour to lowest order.
. The absence of an explicit collisional dependence is characteristic of resonant plateau regime behaviour to lowest order.
The strong pitch angle dependence of the diffusivity ${D_{sbp}}$![]() means that ignoring the $\lambda$
means that ignoring the $\lambda$![]() dependence of ${f_0}$
dependence of ${f_0}$![]() when evaluating the evaluation of the radial heat transport is not justified for large departures from QS.
when evaluating the evaluation of the radial heat transport is not justified for large departures from QS.
10. Discussion
Superbanana plateau and $\sqrt \nu$![]() transport of alpha particles in a nearly QS, large aspect ratio stellarator, having a sheared magnetic field with $sM/(M - qN) > 0$
transport of alpha particles in a nearly QS, large aspect ratio stellarator, having a sheared magnetic field with $sM/(M - qN) > 0$![]() is evaluated by solving a kinetic equation retaining both processes in the same narrow collisional boundary layer. The radial superbanana plateau alpha energy flux is reduced by magnetic shear s satisfying $sM/(M - qN) > 0$
is evaluated by solving a kinetic equation retaining both processes in the same narrow collisional boundary layer. The radial superbanana plateau alpha energy flux is reduced by magnetic shear s satisfying $sM/(M - qN) > 0$![]() , with M and N the integers associated with the toroidal and poloidal variation of the QS field, respectively, for the QS angle variable $\eta = M\vartheta - N\zeta$
, with M and N the integers associated with the toroidal and poloidal variation of the QS field, respectively, for the QS angle variable $\eta = M\vartheta - N\zeta$![]() (for which a B contour closes on itself after a $2\mathrm{\pi }N$
(for which a B contour closes on itself after a $2\mathrm{\pi }N$![]() change in $\vartheta$
change in $\vartheta$![]() and a $2\mathrm{\pi }M$
and a $2\mathrm{\pi }M$![]() change in $\zeta$
change in $\zeta$![]() ). As $M \ge 0$
). As $M \ge 0$![]() and $N \ge 0$
and $N \ge 0$![]() the shear in a QHS stellarator needs to be positive for M > qN and negative for M < qN. In a QAS stellarator (N = 0) the shear must be positive. In a QPS stellarator (M = 0) shear has no significant effect. The corresponding superbanana plateau and $\sqrt \nu$
the shear in a QHS stellarator needs to be positive for M > qN and negative for M < qN. In a QAS stellarator (N = 0) the shear must be positive. In a QPS stellarator (M = 0) shear has no significant effect. The corresponding superbanana plateau and $\sqrt \nu$![]() energy diffusivities are given by (9.14) and (9.15), respectively, for a slowing down tail alpha distribution function, with the alpha energy balance equation given by (9.16). The key new result is the significant reduction of superbanana plateau transport due to magnetic shear for the cases just enumerated. Shear acts to move the tangential drift resonance of the alphas very close to the trapped--passing boundary where the strong pitch angle variation of the drift reduces the number of alphas that are able to resonate, thereby reducing the transport. Even at modest shear levels it is possible to substantially reduce superbanana plateau transport. Although the solution presented here fails in this limit, it suggests that superbanana plateau transport will become as small or smaller than $\sqrt \nu$
energy diffusivities are given by (9.14) and (9.15), respectively, for a slowing down tail alpha distribution function, with the alpha energy balance equation given by (9.16). The key new result is the significant reduction of superbanana plateau transport due to magnetic shear for the cases just enumerated. Shear acts to move the tangential drift resonance of the alphas very close to the trapped--passing boundary where the strong pitch angle variation of the drift reduces the number of alphas that are able to resonate, thereby reducing the transport. Even at modest shear levels it is possible to substantially reduce superbanana plateau transport. Although the solution presented here fails in this limit, it suggests that superbanana plateau transport will become as small or smaller than $\sqrt \nu$![]() transport at rather modest shear. Similar behaviour is expected for the background ions when the superbanana plateau and $\sqrt \nu$
transport at rather modest shear. Similar behaviour is expected for the background ions when the superbanana plateau and $\sqrt \nu$![]() regimes merge.
regimes merge.
In addition, a QL description of radial alpha particle transport is derived to find (8.8) with the QL diffusivity given by (8.7). The QL formulation demonstrates how transport acts to deplete the resonant pitch angle and thereby introduce a pitch angle modification to the usual isotropic slowing down tail alpha distribution.
As the departure from QS becomes smaller and smaller, the perturbed radial drift term in the kinetic equation (5.12) can no longer be ignored. Once it matters collisional detrapping and retrapping in the wells due to imperfect QS is expected to lead to transport becoming linear in the collision frequency due to collisional changes in the second adiabatic invariant. In this superbanana regime the collision operator acts to place a constraint on how the constants of the drift motion and the first and second adiabatic invariant dependences are allowed to change the non-Maxwellian features (Hazeltine & Catto Reference Hazeltine and Catto1981; Shaing Reference Shaing2015; d'Herbemont et al. Reference D'herbemont, Parra, Calvo and Velasco2022). The stellarator case is discussed in detail in this last reference for background ions.
The alpha particle case differs from the background ion case because the magnetic tangential drift matters rather than the tangential $\boldsymbol{E} \times \boldsymbol{B}$![]() drift. Accounting for this difference allows an estimate of when a superbanana plateau regime treatment is expected to remain a valid description. As the trapped alphas drift radially at speed ${V_r}\sim \delta {\omega _\alpha }R$
drift. Accounting for this difference allows an estimate of when a superbanana plateau regime treatment is expected to remain a valid description. As the trapped alphas drift radially at speed ${V_r}\sim \delta {\omega _\alpha }R$![]() into a different magnetic field the pitch angle of the turning point of the trapped, $\lambda = {B_0}/B$
into a different magnetic field the pitch angle of the turning point of the trapped, $\lambda = {B_0}/B$![]() , does not change, but the bounce points change by $\Delta r/{\kern 1pt} R\sim \Delta B/{B_0}$
, does not change, but the bounce points change by $\Delta r/{\kern 1pt} R\sim \Delta B/{B_0}$![]() thereby shifting the trapped--passing boundary $\lambda = 1{\kern 1pt} /(1 + \varepsilon )$
thereby shifting the trapped--passing boundary $\lambda = 1{\kern 1pt} /(1 + \varepsilon )$![]() by $\Delta \lambda \sim \Delta r/R$
by $\Delta \lambda \sim \Delta r/R$![]() relative to the drift reversal layer location. Consequently, the nonlinear or finite orbit radial drift term neglected in (5.12) enters once this boundary change becomes comparable to the boundary layer width, $\Delta \lambda \sim {w_{sbp}}\sim \Delta r/R$
relative to the drift reversal layer location. Consequently, the nonlinear or finite orbit radial drift term neglected in (5.12) enters once this boundary change becomes comparable to the boundary layer width, $\Delta \lambda \sim {w_{sbp}}\sim \Delta r/R$![]() . Therefore, the radial and tangential drift terms will compete once
. Therefore, the radial and tangential drift terms will compete once
where $\partial f_1^{im}/\partial r\sim f_1^{im}/{w_{sbp}}R$![]() and recall that expanding about drift reversal layer near the trapped--passing boundary gives the estimate ${\omega _\alpha } \to \gamma {\omega _\alpha }{w_{sbp}}$
and recall that expanding about drift reversal layer near the trapped--passing boundary gives the estimate ${\omega _\alpha } \to \gamma {\omega _\alpha }{w_{sbp}}$![]() . As a result, a superbanana plateau treatment for the alphas using unperturbed trajectories assumes
. As a result, a superbanana plateau treatment for the alphas using unperturbed trajectories assumes

where shear enters through $\gamma$![]() . For the numbers given below (7.18) this requires highly optimized fields with $\delta < {10^{ - 3}}$
. For the numbers given below (7.18) this requires highly optimized fields with $\delta < {10^{ - 3}}$![]() for s = 0 (for which ${\gamma ^{1/3}}\sim 4$
for s = 0 (for which ${\gamma ^{1/3}}\sim 4$![]() ). When ${sM/(M - qN) > 0}$
). When ${sM/(M - qN) > 0}$![]() this requirement is relaxed, while for $sM/(M - qN) < 0$
this requirement is relaxed, while for $sM/(M - qN) < 0$![]() it is more stringent (and the description here begins to fail as $\gamma {\kern 1pt} \to 1$
it is more stringent (and the description here begins to fail as $\gamma {\kern 1pt} \to 1$![]() ). In addition, to the preceding, $\partial f_1^{im}/\partial r< \partial {f_0}/\partial r$
). In addition, to the preceding, $\partial f_1^{im}/\partial r< \partial {f_0}/\partial r$![]() , requires $f_1^{im}/{f_0}\sim {w_{sbp}}/\varepsilon \ll 1$
, requires $f_1^{im}/{f_0}\sim {w_{sbp}}/\varepsilon \ll 1$![]() . Combining this with (10.2) leads to the restriction
. Combining this with (10.2) leads to the restriction
further confirming that $\delta /\varepsilon \ll 1$![]() is required.
is required.
Based on the QL (8.8), ${\tau _s}{D_{sbp}}/{a^2}$![]() must be small to avoid superbanana plateau transport from becoming a concern. For $|\varTheta |_{sbp}^2|{\kern 1pt} mN - nM|/|M - qN|\sim 1$
must be small to avoid superbanana plateau transport from becoming a concern. For $|\varTheta |_{sbp}^2|{\kern 1pt} mN - nM|/|M - qN|\sim 1$![]() , (9.14) gives the estimate of (1.2), namely ${D_{sbp}}\sim {\delta ^2}qv_0^2/\gamma {\varepsilon ^{1/2}}{\Omega _o}\sim {\delta ^2}{\omega _\alpha }Ra/\gamma {\varepsilon ^{1/2}}$
, (9.14) gives the estimate of (1.2), namely ${D_{sbp}}\sim {\delta ^2}qv_0^2/\gamma {\varepsilon ^{1/2}}{\Omega _o}\sim {\delta ^2}{\omega _\alpha }Ra/\gamma {\varepsilon ^{1/2}}$![]() . Using it with the preceding estimate $\delta < \gamma w_{sbp}^2$
. Using it with the preceding estimate $\delta < \gamma w_{sbp}^2$![]() and $r\sim a$
and $r\sim a$![]() , leads to an estimate of the condition for small alpha loss while the transport still remains in the superbanana plateau regime
, leads to an estimate of the condition for small alpha loss while the transport still remains in the superbanana plateau regime

As $\nu {\tau _s}/{\gamma ^{1/2}} \ll 1$![]() , as long as ${(\delta /\varepsilon )^{1/2}} \ll 1$
, as long as ${(\delta /\varepsilon )^{1/2}} \ll 1$![]() , then for any reasonable aspect ratio it seems likely that superbanana plateau alpha transport will remain small. In particular, for $\delta \sim {10^{ - 3}}$
, then for any reasonable aspect ratio it seems likely that superbanana plateau alpha transport will remain small. In particular, for $\delta \sim {10^{ - 3}}$![]() and $\varepsilon \sim 0.1$
and $\varepsilon \sim 0.1$![]() , large alpha losses are unlikely to be an issue as long as shear is favourable or unimportant. Indeed, as superbanana plateau transport is always expected to be larger that superbanana transport, well optimized stellarators are expected to provide adequate alpha confinement as long as magnetic shear is weak or favourable.
, large alpha losses are unlikely to be an issue as long as shear is favourable or unimportant. Indeed, as superbanana plateau transport is always expected to be larger that superbanana transport, well optimized stellarators are expected to provide adequate alpha confinement as long as magnetic shear is weak or favourable.
Acknowledgements
The United States Government retains a non-exclusive, paid-up, irrevocable, worldwide license to publish or reproduce the published form of this manuscript, or allow others to do so, for United States Government purposes.
Editor Per Helander thanks the referees for their advice in evaluating this article.
Declaration of interests
The authors report no conflict of interest.
Funding
This work was supported by the U.S. Department of Energy under contract numbers DE-FG02-91ER-54109 and DE-AC02-09CH11466, research at the Institute for Advanced Study was supported by the W. M. Keck Foundation Fund, and research at the Flatiron Institute is supported by the Simons Foundation.