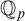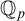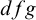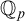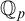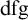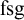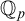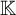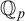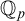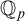1 Introduction
In the recent years there has been growing interest in the interaction between topological dynamics and model theory. This approach was introduced by Newelski [Reference Newelski22], then developed in a number of papers, including [Reference Chernikov and Simon4, Reference Jagiella15, Reference Pillay27, Reference Pillay and Yao28, Reference Yao and Long38], and now called definable topological dynamics. Definable topological dynamics studies the action of a group G definable in a structure M on its type space
![]() $S_G(M)$
and tries to link the invariants suggested by topological dynamics (e.g., enveloping semigroups, minimal subflows, Ellis groups, …) with model-theoretic invariants.
$S_G(M)$
and tries to link the invariants suggested by topological dynamics (e.g., enveloping semigroups, minimal subflows, Ellis groups, …) with model-theoretic invariants.
This framework allows us to generalize stable group theory to some unstable groups with tame behaviour. Under the assumption that the theory T has
![]() ${\mathrm {NIP}}$
, the class of definably amenable groups is a reasonable choice for the class of stable-like groups in
${\mathrm {NIP}}$
, the class of definably amenable groups is a reasonable choice for the class of stable-like groups in
![]() ${\mathrm {NIP}}$
context since Newelski’s conjecture [Reference Newelski22] holds. Namely, the smallest type-definable subgroup of G of bounded-index, written
${\mathrm {NIP}}$
context since Newelski’s conjecture [Reference Newelski22] holds. Namely, the smallest type-definable subgroup of G of bounded-index, written
![]() $G^{00}$
, exists and
$G^{00}$
, exists and
![]() $G/G^{00}$
is isomorphic to its Ellis group (see [Reference Chernikov and Simon4]). In the stable case, this coincides with the space (group) of generic types of G.
$G/G^{00}$
is isomorphic to its Ellis group (see [Reference Chernikov and Simon4]). In the stable case, this coincides with the space (group) of generic types of G.
We will now be assuming that our ambient theory T is
![]() ${\mathrm {NIP}}$
.
${\mathrm {NIP}}$
.
As generic types may not always exist in the
![]() ${\mathrm {NIP}}$
environment, other notions were introduced to describe the generic-like formulas and types. The notion of f-generic was first introduced in [Reference Hrushovski and Pillay13] and then slightly modified in [Reference Chernikov and Simon4]. We let
${\mathrm {NIP}}$
environment, other notions were introduced to describe the generic-like formulas and types. The notion of f-generic was first introduced in [Reference Hrushovski and Pillay13] and then slightly modified in [Reference Chernikov and Simon4]. We let
![]() $\mathbb {M}$
be a so-called “monster” model (of whatever complete theory we are working with). Recall that this means that
$\mathbb {M}$
be a so-called “monster” model (of whatever complete theory we are working with). Recall that this means that
![]() $\mathbb {M}$
is
$\mathbb {M}$
is
![]() $\kappa $
-saturated and
$\kappa $
-saturated and
![]() $\kappa $
-strongly homogeneous for some suitably large
$\kappa $
-strongly homogeneous for some suitably large
![]() $\kappa $
. If the reader is willing to make some set-theoretic assumptions, they can just take
$\kappa $
. If the reader is willing to make some set-theoretic assumptions, they can just take
![]() $\mathbb {M}$
to be
$\mathbb {M}$
to be
![]() $\kappa $
-saturated and of cardinality
$\kappa $
-saturated and of cardinality
![]() $\kappa $
for suitable
$\kappa $
for suitable
![]() $\kappa $
. Let G be a group definable in
$\kappa $
. Let G be a group definable in
![]() $\mathbb {M}$
. A definable subset (or formula)
$\mathbb {M}$
. A definable subset (or formula)
![]() $X\subseteq G$
(definable over M) is said to be f-generic if for every
$X\subseteq G$
(definable over M) is said to be f-generic if for every
![]() $g\in G$
, the left translate
$g\in G$
, the left translate
![]() $gX$
does not fork over M. A global type
$gX$
does not fork over M. A global type
![]() $p\in S_G(\mathbb {M})$
is f-generic if every formula in p is f-generic. A global f-generic type p is strongly f-generic if every G-translate of p does not fork over a fixed small submodel M (equivalently by
$p\in S_G(\mathbb {M})$
is f-generic if every formula in p is f-generic. A global f-generic type p is strongly f-generic if every G-translate of p does not fork over a fixed small submodel M (equivalently by
![]() ${\mathrm {NIP}}$
is invariant under automorphisms fixing M).
${\mathrm {NIP}}$
is invariant under automorphisms fixing M).
One of the nice observations in [Reference Chernikov and Simon4] was that an
![]() ${\mathrm {NIP}}$
group is definably amenable if and only if it admits a global strongly f-generic type. Now there are two extreme case for a global strongly f-generic type p in
${\mathrm {NIP}}$
group is definably amenable if and only if it admits a global strongly f-generic type. Now there are two extreme case for a global strongly f-generic type p in
![]() ${\mathrm {NIP}}$
environment:
${\mathrm {NIP}}$
environment:
-
(i) p (as well as every left translate) is finitely satisfiable in some fixed small model M. In this case p is actually generic, meaning that for every formula
 $\phi $
in p, finitely many translates of
$\phi $
in p, finitely many translates of
 $\phi $
cover G. We call p a finitely satisfiable generic, abbreviated as
$\phi $
cover G. We call p a finitely satisfiable generic, abbreviated as
 $fsg$
.
$fsg$
. -
(ii) p (so also all its translates) is definable over some fixed small model M, and we call p a definable f-generic, abbreviated as
 $dfg$
.
$dfg$
.
A definable group G is said to be an
![]() $\operatorname {\mathrm {fsg}}$
group if it admits a global
$\operatorname {\mathrm {fsg}}$
group if it admits a global
![]() $\operatorname {\mathrm {fsg}}$
type, and a
$\operatorname {\mathrm {fsg}}$
type, and a
![]() $\mathrm {dfg}$
group if it admits a global
$\mathrm {dfg}$
group if it admits a global
![]() $\mathrm {dfg}$
type.
$\mathrm {dfg}$
type.
In [Reference Hrushovski, Peterzil and Pillay11], Hrushovski, Peterzil, and Pillay proved that
![]() $\operatorname {\mathrm {fsg}}$
groups coincide with definably compact groups in o-minimal expansions of real closed field. Moreover, in [Reference Onshuus and Pillay23], Onshuus and Pillay proved that it is also true for groups definable in
$\operatorname {\mathrm {fsg}}$
groups coincide with definably compact groups in o-minimal expansions of real closed field. Moreover, in [Reference Onshuus and Pillay23], Onshuus and Pillay proved that it is also true for groups definable in
![]() ${{\mathbb {Q}}_p}$
. The above results say that the model-theoretic concept of
${{\mathbb {Q}}_p}$
. The above results say that the model-theoretic concept of
![]() $\operatorname {\mathrm {fsg}}$
is able to describe the topological concept of “compactness” in o-minimal and p-adic context.
$\operatorname {\mathrm {fsg}}$
is able to describe the topological concept of “compactness” in o-minimal and p-adic context.
On the other hand, putting various results together, we know that for definably connected groups definable in o-minimal expansions of
![]() $RCF$
, torsion-free is equivalent to being
$RCF$
, torsion-free is equivalent to being
![]() $\mathrm {dfg}$
. Here are some details. The left implies right direction is precisely Proposition 4.7 in [Reference Conversano and Pillay6]. For the right implies left direction: The proof of Lemma 1.15 in [Reference Pillay and Yao28] shows that if G is
$\mathrm {dfg}$
. Here are some details. The left implies right direction is precisely Proposition 4.7 in [Reference Conversano and Pillay6]. For the right implies left direction: The proof of Lemma 1.15 in [Reference Pillay and Yao28] shows that if G is
![]() $\mathrm {dfg}$
, then there is a
$\mathrm {dfg}$
, then there is a
![]() $G^{0}$
-invariant definable type, so by connectedness there is a G-invariant definable type p. Now we know G to be definably amenable, so by Propositions 2.6 and 4.6 of [Reference Conversano and Pillay6], there is a normal definable torsion-free (solvable) subgroup H of G such that
$G^{0}$
-invariant definable type, so by connectedness there is a G-invariant definable type p. Now we know G to be definably amenable, so by Propositions 2.6 and 4.6 of [Reference Conversano and Pillay6], there is a normal definable torsion-free (solvable) subgroup H of G such that
![]() $G/H$
is definably compact (and definably connected). We claim that
$G/H$
is definably compact (and definably connected). We claim that
![]() $G/H$
is trivial, which will show that
$G/H$
is trivial, which will show that
![]() $G = H$
is torsion-free. Assuming
$G = H$
is torsion-free. Assuming
![]() $G/H$
nontrivial, p gives rise to a
$G/H$
nontrivial, p gives rise to a
![]() $G/H$
-invariant type
$G/H$
-invariant type
![]() $p/H$
of
$p/H$
of
![]() $G/H$
, which implies that
$G/H$
, which implies that
![]() $(G/H)^{00} = G/H$
, a contradiction to definable compactness of
$(G/H)^{00} = G/H$
, a contradiction to definable compactness of
![]() $G/H$
(for example, to the truth of Pillay’s conjecture).
$G/H$
(for example, to the truth of Pillay’s conjecture).
Since torsion-free means “totally non-definably compact” for groups definable in o-minimal expansions of
![]() $RCF$
this translates into
$RCF$
this translates into
![]() $\mathrm {dfg}$
meaning “totally non
$\mathrm {dfg}$
meaning “totally non
![]() $\operatorname {\mathrm {fsg}}$
” in the o-minimal context. This observation is also witnessed by the following:
$\operatorname {\mathrm {fsg}}$
” in the o-minimal context. This observation is also witnessed by the following:
Fact 1.1 [Reference Simon34].
![]() $\operatorname {\mathrm {Th}}({{\mathbb {Q}}_p})$
and o-minimal theories are distal.
$\operatorname {\mathrm {Th}}({{\mathbb {Q}}_p})$
and o-minimal theories are distal.
Note that distality of a theory implies that no global types can be both definable and finitely satisfiable (in a small model), and in fact such types are weakly orthogonal.
Anyway it is natural to ask what happens in the p-adic context. We will be working with
![]() $\operatorname {\mathrm {Th}}({{\mathbb {Q}}_p})$
in the ring language and we will actually be restricting ourselves to groups definable in or over the standard model
$\operatorname {\mathrm {Th}}({{\mathbb {Q}}_p})$
in the ring language and we will actually be restricting ourselves to groups definable in or over the standard model
![]() ${{\mathbb {Q}}_p}$
.
${{\mathbb {Q}}_p}$
.
Question 1. Are
![]() $\mathrm {dfg}$
groups exactly “totally noncompact” groups in this p-adic context?
$\mathrm {dfg}$
groups exactly “totally noncompact” groups in this p-adic context?
The aim of the paper is to answer this question. Our first result is a structure theorem for
![]() $\mathrm {dfg}$
groups over
$\mathrm {dfg}$
groups over
![]() ${{\mathbb {Q}}_p}$
, which gives a positive answer to Question 1.
${{\mathbb {Q}}_p}$
, which gives a positive answer to Question 1.
Theorem 1. Let G be a group definable over
![]() ${{\mathbb {Q}}_p}$
with
${{\mathbb {Q}}_p}$
with
![]() $\mathrm {dfg}$
, then there is a normal sequence
$\mathrm {dfg}$
, then there is a normal sequence
where the
![]() $G_{i}$
are definable over
$G_{i}$
are definable over
![]() ${{\mathbb {Q}}_p}$
, and such that
${{\mathbb {Q}}_p}$
, and such that
![]() $G_0$
is finite,
$G_0$
is finite,
![]() $G_n$
is a finite index subgroup of G, and each
$G_n$
is a finite index subgroup of G, and each
![]() $G_{i+1}/G_i$
is definably (over
$G_{i+1}/G_i$
is definably (over
![]() ${{\mathbb {Q}}_p}$
) isomorphic to either the additive group
${{\mathbb {Q}}_p}$
) isomorphic to either the additive group
![]() ${\mathbb {G}}_a$
, or a finite index subgroup of the multiplicative group
${\mathbb {G}}_a$
, or a finite index subgroup of the multiplicative group
![]() ${\mathbb {G}}_m$
.
${\mathbb {G}}_m$
.
Recall that if G is a definable group in a structure M, then by definition a type in
![]() $S_{G}(M)$
is almost periodic if the closure of its G-orbit is a minimal G-invariant closed subset of
$S_{G}(M)$
is almost periodic if the closure of its G-orbit is a minimal G-invariant closed subset of
![]() $S_{G}(M)$
. In the following, the ambient model M is assumed to be saturated. The following conjecture was raised in [Reference Pillay and Yao28].
$S_{G}(M)$
. In the following, the ambient model M is assumed to be saturated. The following conjecture was raised in [Reference Pillay and Yao28].
Conjecture 1. Let G be a
![]() $\mathrm {dfg}$
group definable in an
$\mathrm {dfg}$
group definable in an
![]() ${\mathrm {NIP}}$
structure. Then any global f-generic type is almost periodic.
${\mathrm {NIP}}$
structure. Then any global f-generic type is almost periodic.
The following theorem gives a positive answer to Conjecture 1 in the p-adic case. The proof makes use of a recent result in [Reference Yao37].
Theorem 2. Suppose that G is a
![]() $\mathrm {dfg}$
group definable over
$\mathrm {dfg}$
group definable over
![]() ${{\mathbb {Q}}_p}$
, then every global f-generic type of G is almost periodic.
${{\mathbb {Q}}_p}$
, then every global f-generic type of G is almost periodic.
The paper is organized as follows. In the rest of this introduction we will recall precise notation, definitions, and results from earlier papers, relevant to our results. In Section 2.1, we will prove some general results for
![]() $\mathrm {dfg}$
and
$\mathrm {dfg}$
and
![]() $\operatorname {\mathrm {fsg}}$
groups. In Section 2.2, we will characterise the one-dimensional
$\operatorname {\mathrm {fsg}}$
groups. In Section 2.2, we will characterise the one-dimensional
![]() $\mathrm {dfg}$
groups definable over
$\mathrm {dfg}$
groups definable over
![]() ${{\mathbb {Q}}_p}$
. Section 2.3 contains the key lemmas of the paper, where we proved that every algebraic group containing an open
${{\mathbb {Q}}_p}$
. Section 2.3 contains the key lemmas of the paper, where we proved that every algebraic group containing an open
![]() $\mathrm {dfg}$
subgroup is trigonalizable. In Section 2.4, we prove a structure theorem for an arbitrary
$\mathrm {dfg}$
subgroup is trigonalizable. In Section 2.4, we prove a structure theorem for an arbitrary
![]() $\mathrm {dfg}$
group definable over
$\mathrm {dfg}$
group definable over
![]() ${{\mathbb {Q}}_p}$
, showing that every
${{\mathbb {Q}}_p}$
, showing that every
![]() $\mathrm {dfg}$
group is virtually trigonalizable over
$\mathrm {dfg}$
group is virtually trigonalizable over
![]() ${{\mathbb {Q}}_p}$
, and concluding that every global f-generic type of a
${{\mathbb {Q}}_p}$
, and concluding that every global f-generic type of a
![]() $\mathrm {dfg}$
group is almost periodic.
$\mathrm {dfg}$
group is almost periodic.
1.1 Notations
We will assume a basic knowledge of model theory. Good references are [Reference Marker19] and [Reference Poizat31]. Let T be a complete theory in a language L and let
![]() $\mathbb {M}$
be the monster model, in which every type over a small subset
$\mathbb {M}$
be the monster model, in which every type over a small subset
![]() $A\subset \mathbb {M}$
is realized, where “small” means
$A\subset \mathbb {M}$
is realized, where “small” means
![]() $|A|<|\mathbb {M}|$
. We will assume T to be
$|A|<|\mathbb {M}|$
. We will assume T to be
![]() $1$
-sorted. By
$1$
-sorted. By
![]() $x,y,z$
we mean finite tuples of variables, and
$x,y,z$
we mean finite tuples of variables, and
![]() $a,b,c\in \mathbb {M}$
finite tuples from
$a,b,c\in \mathbb {M}$
finite tuples from
![]() $\mathbb {M}$
. For a subset A of
$\mathbb {M}$
. For a subset A of
![]() $\mathbb {M}$
,
$\mathbb {M}$
,
![]() $L_{A}$
is the language obtained from L by adjoining constants for elements of A. As a rule, by a formula we will mean an
$L_{A}$
is the language obtained from L by adjoining constants for elements of A. As a rule, by a formula we will mean an
![]() $L_{\mathbb {M}}$
-formula (unless otherwise stated). For an arbitrary elementary submodel M of
$L_{\mathbb {M}}$
-formula (unless otherwise stated). For an arbitrary elementary submodel M of
![]() $\mathbb {M}$
and an
$\mathbb {M}$
and an
![]() $L_M$
-formula
$L_M$
-formula
![]() $\phi (x)$
,
$\phi (x)$
,
![]() $\phi (M)$
denotes the definable subset of
$\phi (M)$
denotes the definable subset of
![]() $M^{|x|}$
defined by
$M^{|x|}$
defined by
![]() $\phi $
, and a set
$\phi $
, and a set
![]() $X\subseteq M^n$
is definable if there is an
$X\subseteq M^n$
is definable if there is an
![]() $L_M$
-formula
$L_M$
-formula
![]() $\phi (x)$
such that
$\phi (x)$
such that
![]() $X=\phi (M)$
. If
$X=\phi (M)$
. If
![]() $\bar X\subseteq \mathbb {M}^n$
is definable, defined with parameters from M, then
$\bar X\subseteq \mathbb {M}^n$
is definable, defined with parameters from M, then
![]() $\bar X(M)$
will denote
$\bar X(M)$
will denote
![]() $\bar X\cap M^n$
, the realizations from M, which is clearly a definable subset of
$\bar X\cap M^n$
, the realizations from M, which is clearly a definable subset of
![]() $M^n$
. Suppose that
$M^n$
. Suppose that
![]() $X\subseteq \mathbb {M}^n$
is a definable set, defined with parameters from M, then we write
$X\subseteq \mathbb {M}^n$
is a definable set, defined with parameters from M, then we write
![]() $S_X(M)$
for the space of complete types concentrating on X. We use freely basic notions of model theory such as definable type, heir, coheir, …. The book [Reference Poizat31] is a possible source.
$S_X(M)$
for the space of complete types concentrating on X. We use freely basic notions of model theory such as definable type, heir, coheir, …. The book [Reference Poizat31] is a possible source.
We will be distinguishing in the current paper, between definable and interpretable. So by a definable set in the saturated structure
![]() $\mathbb {M}$
we mean a subset of
$\mathbb {M}$
we mean a subset of
![]() $\mathbb {M}^{n}$
defined by a formula with parameters.
$\mathbb {M}^{n}$
defined by a formula with parameters.
1.2 Topological dynamics
Our reference for (abstract) topological dynamics is [Reference Auslander1].
Given a (Hausdorff) topological group G, by a G-flow we mean a continuous action
![]() $G\times X\to X$
of G on a compact (Hausdorff) topological space X. We sometimes write the flow as
$G\times X\to X$
of G on a compact (Hausdorff) topological space X. We sometimes write the flow as
![]() $(X,G)$
. Often it is assumed that there is a dense orbit, and a G-flow
$(X,G)$
. Often it is assumed that there is a dense orbit, and a G-flow
![]() $(X,G)$
with a distinguished point
$(X,G)$
with a distinguished point
![]() $x\in X$
whose orbit is dense is called a G-ambit (although we will not make much use of this notation).
$x\in X$
whose orbit is dense is called a G-ambit (although we will not make much use of this notation).
In spite of p-adic algebraic groups being nondiscrete topological groups, we will be treating them as discrete groups so as to have their actions on type spaces being continuous. So in this background section we may assume G to be a discrete group, in which case a G-flow is simply an action of G by homeomorphisms on a compact space X.
By a subflow of
![]() $(X,G)$
we mean a nonempty closed G-invariant nonempty subspace Y of X (together with the action of G on Y).
$(X,G)$
we mean a nonempty closed G-invariant nonempty subspace Y of X (together with the action of G on Y).
![]() $(X,G)$
will always have minimal subflows. A point
$(X,G)$
will always have minimal subflows. A point
![]() $x\in X$
is almost periodic if the closure of its orbit is a minimal subflow.
$x\in X$
is almost periodic if the closure of its orbit is a minimal subflow.
Let
![]() $(X,G)$
and
$(X,G)$
and
![]() $(Y,G)$
be flows (with the same acting group). A homomorphism from X to Y is a continuous map
$(Y,G)$
be flows (with the same acting group). A homomorphism from X to Y is a continuous map
![]() $f: X\longrightarrow Y$
such that
$f: X\longrightarrow Y$
such that
![]() $f(gx)=gf(x)$
for all
$f(gx)=gf(x)$
for all
![]() $g\in G$
and
$g\in G$
and
![]() $x\in X$
.
$x\in X$
.
Fact 1.2. Let
![]() $(X,G)$
and
$(X,G)$
and
![]() $(Y,G)$
be flows,
$(Y,G)$
be flows,
![]() $f: X\longrightarrow Y$
a homomorphism. Then:
$f: X\longrightarrow Y$
a homomorphism. Then:
-
(i) If
 $X_0$
is a minimal subflow of X, then
$X_0$
is a minimal subflow of X, then
 $Y_0=f(X_0)$
is a minimal subflow of Y.
$Y_0=f(X_0)$
is a minimal subflow of Y. -
(ii) If Y is a minimal flow, then f is onto.
1.3 Definably amenable groups
Let T be any first-order theory, let
![]() $\mathbb {M}\models T$
be a very saturated model, and let G be a group
$\mathbb {M}\models T$
be a very saturated model, and let G be a group
![]() $\emptyset $
-definable in
$\emptyset $
-definable in
![]() $\mathbb {M}$
defined by the formula
$\mathbb {M}$
defined by the formula
![]() $G(x)$
. For any
$G(x)$
. For any
![]() $M\prec \mathbb {M}$
,
$M\prec \mathbb {M}$
,
![]() $G(M)=\{g\in M^n| g\in G\}$
is a subgroup of G. By
$G(M)=\{g\in M^n| g\in G\}$
is a subgroup of G. By
![]() $S_G(M)$
we mean the space of all complete types over M concentrating on
$S_G(M)$
we mean the space of all complete types over M concentrating on
![]() $G(x)$
. It is easy to see that
$G(x)$
. It is easy to see that
![]() $S_G(M)$
together with the type of the identity element is a
$S_G(M)$
together with the type of the identity element is a
![]() $G(M)$
-ambit, taking the dense orbit to be
$G(M)$
-ambit, taking the dense orbit to be
![]() $\{\operatorname {\mathrm {tp}}(g/M)|\ g\in G(M)\}$
. From now on, we will, throughout this paper, assume that every formula
$\{\operatorname {\mathrm {tp}}(g/M)|\ g\in G(M)\}$
. From now on, we will, throughout this paper, assume that every formula
![]() $\phi (x)\in L_{\mathbb {M}}$
, with parameters in
$\phi (x)\in L_{\mathbb {M}}$
, with parameters in
![]() $\mathbb {M}$
, is contained in
$\mathbb {M}$
, is contained in
![]() $G(x)$
, namely, the subset
$G(x)$
, namely, the subset
![]() $\phi (\mathbb {M})$
defined by
$\phi (\mathbb {M})$
defined by
![]() $\phi $
is contained in G. Suppose that
$\phi $
is contained in G. Suppose that
![]() $\phi \in L_M$
and
$\phi \in L_M$
and
![]() $g\in G(M)$
, then the left translate
$g\in G(M)$
, then the left translate
![]() $g\phi (x)$
is defined to be
$g\phi (x)$
is defined to be
![]() $\phi (g^{-1}x)$
. It is easy to check that
$\phi (g^{-1}x)$
. It is easy to check that
![]() $(g\phi )(M)=gX$
with
$(g\phi )(M)=gX$
with
![]() $X=\phi (M)$
.
$X=\phi (M)$
.
Definition 1.3. Let the notation be as above.
-
• A definable subset
 $X\subseteq G$
is generic if finitely many left translates of X cover G. Namely, there are
$X\subseteq G$
is generic if finitely many left translates of X cover G. Namely, there are
 $g_1,\dots ,g_n\in G$
such that
$g_1,\dots ,g_n\in G$
such that
 $G=\cup _{_{1\leq i\leq n}} g_iX$
.
$G=\cup _{_{1\leq i\leq n}} g_iX$
. -
• A definable subset
 $X\subseteq G$
is weakly generic if there is a non-generic definable subset
$X\subseteq G$
is weakly generic if there is a non-generic definable subset
 $Y\subseteq G$
such that
$Y\subseteq G$
such that
 $X\cup Y$
is generic.
$X\cup Y$
is generic. -
• A definable subset
 $X\subseteq G$
is f-generic if for some/any model M over which X is defined and any
$X\subseteq G$
is f-generic if for some/any model M over which X is defined and any
 $g\in G$
,
$g\in G$
,
 $gX$
does not divide over M. Namely, for any M-indiscernible sequence
$gX$
does not divide over M. Namely, for any M-indiscernible sequence
 $(g_i:i< \omega )$
, with
$(g_i:i< \omega )$
, with
 $g=g_0$
,
$g=g_0$
,
 $\{g_iX: i<\omega \}$
is consistent.
$\{g_iX: i<\omega \}$
is consistent. -
• A formula
 $\phi (x)$
is generic if the definable set
$\phi (x)$
is generic if the definable set
 $\phi (\mathbb {M})$
is generic. Similarly for weakly generic and f-generic formulas.
$\phi (\mathbb {M})$
is generic. Similarly for weakly generic and f-generic formulas. -
• A type
 $p\in S_G(M)$
is generic if every formula
$p\in S_G(M)$
is generic if every formula
 $\phi (x)\in p$
is generic. Similarly for weakly generic and f-generic types.
$\phi (x)\in p$
is generic. Similarly for weakly generic and f-generic types. -
• A type
 $p\in S_G(M)$
is almost periodic if p is an almost periodic point of the
$p\in S_G(M)$
is almost periodic if p is an almost periodic point of the
 $G(M)$
-flow
$G(M)$
-flow
 $S_G(M)$
.
$S_G(M)$
. -
• A global type
 $p\in S_G(\mathbb {M})$
is strongly f-generic over a small model M if every left
$p\in S_G(\mathbb {M})$
is strongly f-generic over a small model M if every left
 $G(\mathbb {M})$
-translate of p does not fork over M. A global type
$G(\mathbb {M})$
-translate of p does not fork over M. A global type
 $p\in S_G(\mathbb {M})$
is strongly f-generic if it is strongly f-generic over some small model.
$p\in S_G(\mathbb {M})$
is strongly f-generic if it is strongly f-generic over some small model.
Fact 1.4 [Reference Newelski22].
Let
![]() $AP\subseteq S_G(M)$
be the space of almost periodic types, and
$AP\subseteq S_G(M)$
be the space of almost periodic types, and
![]() $WG\subseteq S_G(M)$
the space of weakly generic types. Then
$WG\subseteq S_G(M)$
the space of weakly generic types. Then
![]() $WG=\operatorname {\mathrm {cl}}(AP)$
.
$WG=\operatorname {\mathrm {cl}}(AP)$
.
Recall that a type definable over A subgroup
![]() $H\leq G$
has bounded index if
$H\leq G$
has bounded index if
![]() $|G/H|<2^{|T|+|A|}$
. For groups definable in
$|G/H|<2^{|T|+|A|}$
. For groups definable in
![]() ${\mathrm {NIP}}$
structures, the smallest type-definable subgroup
${\mathrm {NIP}}$
structures, the smallest type-definable subgroup
![]() $G^{00}$
exists (see [Reference Hrushovski, Peterzil and Pillay11]). Namely, the intersection of all type-definable subgroups of bounded index still has bounded index. We call
$G^{00}$
exists (see [Reference Hrushovski, Peterzil and Pillay11]). Namely, the intersection of all type-definable subgroups of bounded index still has bounded index. We call
![]() $G^{00}$
the type-definable connected component of G. Another model theoretic invariant is
$G^{00}$
the type-definable connected component of G. Another model theoretic invariant is
![]() $G^0$
, called the definable-connected component of G, which is the intersection of all definable subgroups of G of finite index. Clearly,
$G^0$
, called the definable-connected component of G, which is the intersection of all definable subgroups of G of finite index. Clearly,
![]() $G^{00}\leq G^0$
.
$G^{00}\leq G^0$
.
Recall also that a Keisler measure over M on X, with X a definable subset of
![]() $M^n$
, is a finitely additive probability measure on the Boolean algebra of M-definable subsets of X. When we take the monster model, i.e.,
$M^n$
, is a finitely additive probability measure on the Boolean algebra of M-definable subsets of X. When we take the monster model, i.e.,
![]() $M=\mathbb {M}$
, we call it a global Keisler measure. A definable group G is said to be definably amenable if it admits a global (left) G-invariant Keisler measure.
$M=\mathbb {M}$
, we call it a global Keisler measure. A definable group G is said to be definably amenable if it admits a global (left) G-invariant Keisler measure.
The following facts will be used later.
Fact 1.5 [Reference Chernikov and Simon4].
Let G be a group definable in a saturated
![]() ${\mathrm {NIP}}$
structure
${\mathrm {NIP}}$
structure
![]() $\mathbb {M}$
. Then:
$\mathbb {M}$
. Then:
-
(i) G is definably amenable if and only if it admits a global type
 $p\in S_G(\mathbb {M})$
with bounded G-orbit.
$p\in S_G(\mathbb {M})$
with bounded G-orbit. -
(ii) G is definably amenable if and only if it admits a strongly f-generic type.
Moreover,
Fact 1.6 [Reference Chernikov and Simon4].
Let G be a definably amenable group definable in a saturated
![]() ${\mathrm {NIP}}$
structure
${\mathrm {NIP}}$
structure
![]() $\mathbb {M}$
. Then:
$\mathbb {M}$
. Then:
-
(i) Weakly generic definable subsets, formulas, and types coincide with f-generic definable subsets, formulas, and types, respectively.
-
(ii)
 $p\in S_G(\mathbb {M})$
is f-generic if and only if it has bounded G-orbit.
$p\in S_G(\mathbb {M})$
is f-generic if and only if it has bounded G-orbit. -
(iii)
 $p\in S_G(\mathbb {M})$
is f-generic if and only if it is
$p\in S_G(\mathbb {M})$
is f-generic if and only if it is
 $G^{00}$
-invariant.
$G^{00}$
-invariant. -
(iv) The type-definable subgroup H fixing a global f-generic type is exactly
 $G^{00}$
.
$G^{00}$
. -
(v)
 $G/G^{00}$
is isomorphic to the Ellis group of
$G/G^{00}$
is isomorphic to the Ellis group of
 $S_G(M)$
for any
$S_G(M)$
for any
 $M\prec \mathbb {M}$
.
$M\prec \mathbb {M}$
.
Note that in the context of Fact 1.6, if p is global f-generic type which is either definable over, or finitely satisfiable in, a small model, then p will be strongly f-generic (because of parts (iii) or (iv)).
Remark 1.7. Fact 1.6(v) gives a positive answer to the so-called Ellis group conjecture. The equality between
![]() $G/G^{00}$
and the Ellis group, under possibly additional assumptions, was suggested first by Newelski [Reference Newelski22] in Question 5.5 and Problem 5.6. A precise formulation under an assumption of
$G/G^{00}$
and the Ellis group, under possibly additional assumptions, was suggested first by Newelski [Reference Newelski22] in Question 5.5 and Problem 5.6. A precise formulation under an assumption of
![]() ${\mathrm {NIP}}$
and definable amenability was made by Pillay [Reference Pillay27]. This makes it reasonable to consider definably amenable groups as the “stable-like” groups in
${\mathrm {NIP}}$
and definable amenability was made by Pillay [Reference Pillay27]. This makes it reasonable to consider definably amenable groups as the “stable-like” groups in
![]() ${\mathrm {NIP}}$
environment.
${\mathrm {NIP}}$
environment.
1.4 Groups definable in
 $({{\mathbb {Q}}_p},+,\times , 0,1)$
$({{\mathbb {Q}}_p},+,\times , 0,1)$
We will be referring a lot to the comprehensive survey in [Reference Belair2] for the basic model theory of the p-adic field
![]() ${{\mathbb {Q}}_p}$
. A key point is Macintyre’s theorem [Reference Macintyre18] that
${{\mathbb {Q}}_p}$
. A key point is Macintyre’s theorem [Reference Macintyre18] that
![]() $\operatorname {\mathrm {Th}}({{\mathbb {Q}}_p},+,\times , 0,1)$
has quantifier elimination in the language where we add predicates
$\operatorname {\mathrm {Th}}({{\mathbb {Q}}_p},+,\times , 0,1)$
has quantifier elimination in the language where we add predicates
![]() $P_n(x)$
for the nth powers for each
$P_n(x)$
for the nth powers for each
![]() $n\in \mathbb {N}^+$
. The valuation is quantifier-free definable in this expanded language, in particular is definable in the language of rings (see Section 3.2 of [Reference Belair2]). Let us give some notation we will be using. M denotes the structure
$n\in \mathbb {N}^+$
. The valuation is quantifier-free definable in this expanded language, in particular is definable in the language of rings (see Section 3.2 of [Reference Belair2]). Let us give some notation we will be using. M denotes the structure
![]() $({{\mathbb {Q}}_p},+,\times , 0,1)$
,
$({{\mathbb {Q}}_p},+,\times , 0,1)$
,
![]() ${{\mathbb {Q}}_p}^{*}={{\mathbb {Q}}_p}\backslash \{0\}$
is the multiplicative group and
${{\mathbb {Q}}_p}^{*}={{\mathbb {Q}}_p}\backslash \{0\}$
is the multiplicative group and
![]() $\mathbb {Z}$
is the ordered additive group of integers, the value group of
$\mathbb {Z}$
is the ordered additive group of integers, the value group of
![]() ${{\mathbb {Q}}_p}$
. The group homomorphism
${{\mathbb {Q}}_p}$
. The group homomorphism
![]() $\nu : {{\mathbb {Q}}_p}^{*}\longrightarrow \mathbb {Z}$
is the valuation map. The valuation map
$\nu : {{\mathbb {Q}}_p}^{*}\longrightarrow \mathbb {Z}$
is the valuation map. The valuation map
![]() $\nu $
induces an absolute valuation
$\nu $
induces an absolute valuation
![]() $|\ \ |$
on
$|\ \ |$
on
![]() ${{\mathbb {Q}}_p}$
: for each
${{\mathbb {Q}}_p}$
: for each
![]() $x\in {{\mathbb {Q}}_p}$
,
$x\in {{\mathbb {Q}}_p}$
,
![]() $|x|=p^{-\nu (x)}$
if
$|x|=p^{-\nu (x)}$
if
![]() $x\neq 0$
and
$x\neq 0$
and
![]() $|x|=0$
otherwise. The absolute valuation makes the p-adic field
$|x|=0$
otherwise. The absolute valuation makes the p-adic field
![]() ${{\mathbb {Q}}_p}$
into a locally compact topological field, with basis given by the sets
${{\mathbb {Q}}_p}$
into a locally compact topological field, with basis given by the sets
![]() $\nu (x-a)\geq n$
for
$\nu (x-a)\geq n$
for
![]() $a\in {{\mathbb {Q}}_p}$
and
$a\in {{\mathbb {Q}}_p}$
and
![]() $n\in \mathbb {Z}$
. The ring of p-adic integers (valuation ring)
$n\in \mathbb {Z}$
. The ring of p-adic integers (valuation ring)
is of course a definable subset of
![]() ${{\mathbb {Q}}_p}$
. We can add new predicates
${{\mathbb {Q}}_p}$
. We can add new predicates
![]() ${\cal O}(x)$
for the valuation ring and
${\cal O}(x)$
for the valuation ring and
![]() ${\cal O}^{\times }(x)$
for the elements with valuation
${\cal O}^{\times }(x)$
for the elements with valuation
![]() $0$
. So
$0$
. So
![]() ${\cal O}(M)={\cal O}({{\mathbb {Q}}_p})={\mathbb {Z}}_p$
and
${\cal O}(M)={\cal O}({{\mathbb {Q}}_p})={\mathbb {Z}}_p$
and
![]() ${\cal O}^{\times }(M)={\cal O}^{\times }({{\mathbb {Q}}_p})=\{x\in {{\mathbb {Q}}_p}| \nu (x)=0\}$
.
${\cal O}^{\times }(M)={\cal O}^{\times }({{\mathbb {Q}}_p})=\{x\in {{\mathbb {Q}}_p}| \nu (x)=0\}$
.
It is convenient to refer to Section 3 of [Reference Pillay25] for various notions such as definable p-adic analytic manifold and definable p-adic analytic group. (One can also consult [Reference Onshuus and Pillay23].) In the background are the notions of dimension of definable (with parameters) sets in the structure
![]() $M = ({{\mathbb {Q}}_p},+,\times , 0,1)$
as well as theorems on p-adic cell decomposition and definable functions, which are due to van den Dries and Scowcroft [Reference Dries and Scowcroft9]. But we mention here a few details: For X a definable set in M, say
$M = ({{\mathbb {Q}}_p},+,\times , 0,1)$
as well as theorems on p-adic cell decomposition and definable functions, which are due to van den Dries and Scowcroft [Reference Dries and Scowcroft9]. But we mention here a few details: For X a definable set in M, say
![]() $X\subseteq {{\mathbb {Q}}_p}^{n}$
,
$X\subseteq {{\mathbb {Q}}_p}^{n}$
,
![]() $\dim (X)$
is the greatest
$\dim (X)$
is the greatest
![]() $k\leq n$
such that some projection on
$k\leq n$
such that some projection on
![]() ${{\mathbb {Q}}_p}^{k}$
contains an open set. An n-dimensional definable p-adic analytic manifold is a topological space with a covering by finitely many open sets each homeomorphic to an open definable (in M) subset of
${{\mathbb {Q}}_p}^{k}$
contains an open set. An n-dimensional definable p-adic analytic manifold is a topological space with a covering by finitely many open sets each homeomorphic to an open definable (in M) subset of
![]() ${{\mathbb {Q}}_p}^{n}$
such that the transition maps are definable and analytic. See [Reference Serre32] for analytic functions over complete fields. A definable p-adic analytic group is a definable p-adic analytic manifold equipped with a group structure which is definable and analytic when read in the appropriate charts. Such a definable p-adic analytic group is a definable group in M and Lemma 3.8 of [Reference Pillay25] says that conversely any group G definable in M can be definably equipped with the structure of a definable p-adic analytic group.
${{\mathbb {Q}}_p}^{n}$
such that the transition maps are definable and analytic. See [Reference Serre32] for analytic functions over complete fields. A definable p-adic analytic group is a definable p-adic analytic manifold equipped with a group structure which is definable and analytic when read in the appropriate charts. Such a definable p-adic analytic group is a definable group in M and Lemma 3.8 of [Reference Pillay25] says that conversely any group G definable in M can be definably equipped with the structure of a definable p-adic analytic group.
In the current paper we will really be concerned with groups G definable in the structure
![]() $M = ({{\mathbb {Q}}_p},+,\times , 0,1)$
. However, the various notions introduced in the previous section depend on an ambient saturated model. So we let
$M = ({{\mathbb {Q}}_p},+,\times , 0,1)$
. However, the various notions introduced in the previous section depend on an ambient saturated model. So we let
![]() $\mathbb {M}$
denote a very saturated elementary extension
$\mathbb {M}$
denote a very saturated elementary extension
![]() $(\mathbb {K}, +, \times , 0, 1)$
of M. We also let
$(\mathbb {K}, +, \times , 0, 1)$
of M. We also let
![]() $N=(K,+,\times , 0)\prec \mathbb {M}$
be an elementary extension of M. So K and
$N=(K,+,\times , 0)\prec \mathbb {M}$
be an elementary extension of M. So K and
![]() $\mathbb {K}$
are p-adically closed fields. The dimension of definable sets is defined as before, but can also be defined in terms of the underlying algebraic closure relation, which coincides with field-theoretic algebraic closure: assuming X is definable over a finite set A, then
$\mathbb {K}$
are p-adically closed fields. The dimension of definable sets is defined as before, but can also be defined in terms of the underlying algebraic closure relation, which coincides with field-theoretic algebraic closure: assuming X is definable over a finite set A, then
![]() $\dim (X)$
can be described as the maximum of
$\dim (X)$
can be described as the maximum of
![]() $\dim ({\bar a}/A)$
as
$\dim ({\bar a}/A)$
as
![]() ${\bar a}$
ranges over points of X. We have the notion of a “definable
${\bar a}$
ranges over points of X. We have the notion of a “definable
![]() $C^{k}$
-manifold in N (or over K),” a topological space with a finite covering by open sets each homeomorphic to an open definable subset of
$C^{k}$
-manifold in N (or over K),” a topological space with a finite covering by open sets each homeomorphic to an open definable subset of
![]() $K^{n}$
(fixed n) with transition maps definable and
$K^{n}$
(fixed n) with transition maps definable and
![]() $C^{k}$
. Either adapting the methods of [Reference Pillay25] or by transfer from the case
$C^{k}$
. Either adapting the methods of [Reference Pillay25] or by transfer from the case
![]() $K = {{\mathbb {Q}}_p}$
, one sees that for any group G definable in N and for any
$K = {{\mathbb {Q}}_p}$
, one sees that for any group G definable in N and for any
![]() $k<\omega $
, G can be definably equipped with the structure of a definable
$k<\omega $
, G can be definably equipped with the structure of a definable
![]() $C^{k}$
-manifold in N with respect to which the group structure is
$C^{k}$
-manifold in N with respect to which the group structure is
![]() $C^{k}$
. In contrast with the analogous situation for real closed fields, it seems not to be known whether we can also do it for
$C^{k}$
. In contrast with the analogous situation for real closed fields, it seems not to be known whether we can also do it for
![]() $k = \infty $
. On the other hand if G is defined with parameters from
$k = \infty $
. On the other hand if G is defined with parameters from
![]() ${{\mathbb {Q}}_p}$
, then
${{\mathbb {Q}}_p}$
, then
![]() $G({{\mathbb {Q}}_p})$
is as in the previous paragraph, and so the definable analytic manifold and group structure on
$G({{\mathbb {Q}}_p})$
is as in the previous paragraph, and so the definable analytic manifold and group structure on
![]() $G({{\mathbb {Q}}_p})$
DOES give rise to a definable
$G({{\mathbb {Q}}_p})$
DOES give rise to a definable
![]() $C^{\infty }$
-structure on G with respect to which the group operation is
$C^{\infty }$
-structure on G with respect to which the group operation is
![]() $C^{\infty }$
.
$C^{\infty }$
.
Recall from [Reference Onshuus and Pillay23] that a definable manifold X over K is definably compact, if for any definable continuous function
![]() $f : {\cal O}(K) \backslash \{0\} \longrightarrow X$
, the limit
$f : {\cal O}(K) \backslash \{0\} \longrightarrow X$
, the limit
![]() $\displaystyle \lim _{x \to 0}f(x)$
exists in X. Definable compactness agrees with compactness if K is
$\displaystyle \lim _{x \to 0}f(x)$
exists in X. Definable compactness agrees with compactness if K is
![]() ${{\mathbb {Q}}_p}$
. A definable subset of
${{\mathbb {Q}}_p}$
. A definable subset of
![]() $K^n$
with the induced topology is definably compact if and only if it is closed and bounded.
$K^n$
with the induced topology is definably compact if and only if it is closed and bounded.
Let G be a group definable in N with parameters from
![]() ${{\mathbb {Q}}_p}$
. As remarked above
${{\mathbb {Q}}_p}$
. As remarked above
![]() $G({{\mathbb {Q}}_p})$
has (definably in M) the structure of a p-adic analytic (Lie) group, and as such has an open compact subgroup, which must be definable in M. It follows that G has a
$G({{\mathbb {Q}}_p})$
has (definably in M) the structure of a p-adic analytic (Lie) group, and as such has an open compact subgroup, which must be definable in M. It follows that G has a
![]() ${{\mathbb {Q}}_p}$
-definable subgroup C with
${{\mathbb {Q}}_p}$
-definable subgroup C with
![]() $\dim (C) = \dim (G)$
and
$\dim (C) = \dim (G)$
and
![]() $C({{\mathbb {Q}}_p})$
is compact (and C definably compact).
$C({{\mathbb {Q}}_p})$
is compact (and C definably compact).
Let C be a group definable in N over
![]() ${{\mathbb {Q}}_p}$
which is (with its definable manifold topology) definably compact. Then
${{\mathbb {Q}}_p}$
which is (with its definable manifold topology) definably compact. Then
![]() $C({{\mathbb {Q}}_p})$
is compact. We have the standard part map
$C({{\mathbb {Q}}_p})$
is compact. We have the standard part map
![]() $st: C\longrightarrow C({{\mathbb {Q}}_p})$
. The kernel of
$st: C\longrightarrow C({{\mathbb {Q}}_p})$
. The kernel of
![]() $st$
is precisely the group of infinitesimals of C and coincides with the intersection of all
$st$
is precisely the group of infinitesimals of C and coincides with the intersection of all
![]() ${{\mathbb {Q}}_p}$
-definable subgroups of C of finite index. This is elaborated on in the following fact.
${{\mathbb {Q}}_p}$
-definable subgroups of C of finite index. This is elaborated on in the following fact.
Fact 1.8. Let C be a group definable in
![]() $\mathbb {M}$
over
$\mathbb {M}$
over
![]() ${{\mathbb {Q}}_p}$
.
${{\mathbb {Q}}_p}$
.
-
(i) If C definably compact, then
 $C^{00}=C^0$
coincides with
$C^{00}=C^0$
coincides with
 $\ker (st)$
, and
$\ker (st)$
, and
 $st$
induces a homeomorphism between
$st$
induces a homeomorphism between
 $C/C^{0}$
(with its logic topology) and the p-adic Lie group
$C/C^{0}$
(with its logic topology) and the p-adic Lie group
 $C({{\mathbb {Q}}_p})$
.
$C({{\mathbb {Q}}_p})$
. -
(ii) C is definably compact iff C has
 $\operatorname {\mathrm {fsg}}$
.
$\operatorname {\mathrm {fsg}}$
.
Proof For (i) see Corollary 2.4 of [Reference Onshuus and Pillay23].
The left implies right direction of (ii) is Corollary 2.3(iv) of [Reference Onshuus and Pillay23]. The right to left direction (easy direction) does not appear explicitly in [Reference Onshuus and Pillay23], but appears in somewhat greater generality in Proposition 3.1 of [Reference Johnson16]
Fact 1.9 [Reference Pillay and Yao29].
If G is a one-dimensional group definable over
![]() ${{\mathbb {Q}}_p}$
, then G is abelian-by-finite, hence definably amenable.
${{\mathbb {Q}}_p}$
, then G is abelian-by-finite, hence definably amenable.
1.5 Definable groups and quotient groups
We will try to give some coherent notation regarding definable groups and algebraic groups. Our underlying first-order theory is
![]() $\operatorname {\mathrm {Th}}({{\mathbb {Q}}_p})$
in the ring language (or in the Macintyre language, a definitional expansion). As in Section 1.4, M denotes the standard model,
$\operatorname {\mathrm {Th}}({{\mathbb {Q}}_p})$
in the ring language (or in the Macintyre language, a definitional expansion). As in Section 1.4, M denotes the standard model,
![]() $\mathbb {M}$
a “monster model,” and
$\mathbb {M}$
a “monster model,” and
![]() $N\prec \mathbb {M}$
a not necessarily saturated elementary extension of M. When we speak of a group definable
$N\prec \mathbb {M}$
a not necessarily saturated elementary extension of M. When we speak of a group definable
![]() $in \ M$
, N, or
$in \ M$
, N, or
![]() $\mathbb {M}$
, we mean the obvious thing. When we speak of a group G definable
$\mathbb {M}$
, we mean the obvious thing. When we speak of a group G definable
![]() $over$
$over$
![]() ${{\mathbb {Q}}_p}$
(for example) we typically mean a group definable in
${{\mathbb {Q}}_p}$
(for example) we typically mean a group definable in
![]() $\mathbb {M}$
defined with parameters from
$\mathbb {M}$
defined with parameters from
![]() ${{\mathbb {Q}}_p}$
. In this case
${{\mathbb {Q}}_p}$
. In this case
![]() $G({{\mathbb {Q}}_p})$
denotes the group definable in
$G({{\mathbb {Q}}_p})$
denotes the group definable in
![]() ${{\mathbb {Q}}_p}$
by the same formulas defining G in
${{\mathbb {Q}}_p}$
by the same formulas defining G in
![]() $\mathbb {M}$
. On the other hand if for example G is a group definable
$\mathbb {M}$
. On the other hand if for example G is a group definable
![]() $in \ {{\mathbb {Q}}_p}$
then we can consider the groups definable in N or
$in \ {{\mathbb {Q}}_p}$
then we can consider the groups definable in N or
![]() $\mathbb {M}$
by the same formulas, which we may refer to as
$\mathbb {M}$
by the same formulas, which we may refer to as
![]() $G(K)$
,
$G(K)$
,
![]() $G(\mathbb {K})$
, or
$G(\mathbb {K})$
, or
![]() $G(N)$
,
$G(N)$
,
![]() $G(\mathbb {M})$
. In general, when we speak of a definable object (set, or group) we mean a definable object in the monster model
$G(\mathbb {M})$
. In general, when we speak of a definable object (set, or group) we mean a definable object in the monster model
![]() $\mathbb {M}$
of
$\mathbb {M}$
of
![]() $\operatorname {\mathrm {Th}}({{\mathbb {Q}}_p})$
. As mentioned in Section 1.4 we are mainly interested in groups definable in the standard model M, but we will need information about their interpretations in
$\operatorname {\mathrm {Th}}({{\mathbb {Q}}_p})$
. As mentioned in Section 1.4 we are mainly interested in groups definable in the standard model M, but we will need information about their interpretations in
![]() $\mathbb {M}$
. Let us again emphasize that we distinguish between definable and interpretable (definable in
$\mathbb {M}$
. Let us again emphasize that we distinguish between definable and interpretable (definable in
![]() $\mathbb {K}^{\text {eq}}$
) and our groups will be definable.
$\mathbb {K}^{\text {eq}}$
) and our groups will be definable.
The usual mathematical notation for algebraic groups is to consider an algebraic group G over a field K as something like a functor which takes a field L containing K to the group
![]() $G(L)$
. Alternatively, one can identify G with
$G(L)$
. Alternatively, one can identify G with
![]() $G(L)$
for a given algebraically closed field containing K, where the variety structure as well as the group structure are given by data (polynomial equations, transition maps, morphisms) over K. (See [Reference Pillay and Bouscaren26] for more details on this and the later discussion of algebraic varieties and groups over algebraically closed fields.) With this notation the algebraic groups we will consider will be over
$G(L)$
for a given algebraically closed field containing K, where the variety structure as well as the group structure are given by data (polynomial equations, transition maps, morphisms) over K. (See [Reference Pillay and Bouscaren26] for more details on this and the later discussion of algebraic varieties and groups over algebraically closed fields.) With this notation the algebraic groups we will consider will be over
![]() ${{\mathbb {Q}}_p}$
and we will consider their groups
${{\mathbb {Q}}_p}$
and we will consider their groups
![]() $G({{\mathbb {Q}}_p})$
and
$G({{\mathbb {Q}}_p})$
and
![]() $G(\mathbb {K})$
of
$G(\mathbb {K})$
of
![]() ${{\mathbb {Q}}_p}$
-points, and
${{\mathbb {Q}}_p}$
-points, and
![]() $\mathbb {K}$
-points. Of course the latter will be also definable groups in the structures M,
$\mathbb {K}$
-points. Of course the latter will be also definable groups in the structures M,
![]() $\mathbb {M}$
, respectively, in the earlier sense, but essentially just quantifier-free definable in the ring language.
$\mathbb {M}$
, respectively, in the earlier sense, but essentially just quantifier-free definable in the ring language.
So in this paper we will slightly modify notation, by defining a p-adic algebraic group to be the group
![]() $G({{\mathbb {Q}}_p})$
of
$G({{\mathbb {Q}}_p})$
of
![]() ${{\mathbb {Q}}_p}$
-points of an algebraic group G over
${{\mathbb {Q}}_p}$
-points of an algebraic group G over
![]() ${{\mathbb {Q}}_p}$
. When G is a linear algebraic group over
${{\mathbb {Q}}_p}$
. When G is a linear algebraic group over
![]() ${{\mathbb {Q}}_p}$
, then
${{\mathbb {Q}}_p}$
, then
![]() $G({{\mathbb {Q}}_p})$
will simply be a subgroup of some
$G({{\mathbb {Q}}_p})$
will simply be a subgroup of some
![]() $GL_{n}({{\mathbb {Q}}_p})$
defined by a finite system of polynomial equations over
$GL_{n}({{\mathbb {Q}}_p})$
defined by a finite system of polynomial equations over
![]() ${{\mathbb {Q}}_p}$
. So a p-adic algebraic group is a special case of a group definable in M. As above we denote by
${{\mathbb {Q}}_p}$
. So a p-adic algebraic group is a special case of a group definable in M. As above we denote by
![]() $G(\mathbb {K})$
the group of
$G(\mathbb {K})$
the group of
![]() $\mathbb {K}$
-points of G, which is consistent with our earlier notation regarding definable groups.
$\mathbb {K}$
-points of G, which is consistent with our earlier notation regarding definable groups.
We now just want to observe that the quotient of a p-adic algebraic group by a p-adic algebraic subgroup can be seen as a definable (rather than just interpretable) set in M: So we are given algebraic groups
![]() $G, H$
over
$G, H$
over
![]() ${{\mathbb {Q}}_p}$
such that
${{\mathbb {Q}}_p}$
such that
![]() $H({{\mathbb {Q}}_p})$
is a subgroup of
$H({{\mathbb {Q}}_p})$
is a subgroup of
![]() $G({{\mathbb {Q}}_p})$
. We assume G to be connected as an algebraic group. Let L be an algebraically closed field containing
$G({{\mathbb {Q}}_p})$
. We assume G to be connected as an algebraic group. Let L be an algebraically closed field containing
![]() ${{\mathbb {Q}}_p}$
such as
${{\mathbb {Q}}_p}$
such as
![]() ${{\mathbb {Q}}_p}^{alg}$
. Then
${{\mathbb {Q}}_p}^{alg}$
. Then
![]() $H(L)$
is a subgroup of
$H(L)$
is a subgroup of
![]() $G(L)$
. But then by elimination of imaginaries in
$G(L)$
. But then by elimination of imaginaries in
![]() $ACF$
together with a theorem of Weil,
$ACF$
together with a theorem of Weil,
![]() $G(L)/H(L)$
is, in the structure
$G(L)/H(L)$
is, in the structure
![]() $(L,+,\times )$
, definably isomorphic over
$(L,+,\times )$
, definably isomorphic over
![]() ${{\mathbb {Q}}_p}$
to an algebraic variety
${{\mathbb {Q}}_p}$
to an algebraic variety
![]() $X(L)$
over
$X(L)$
over
![]() ${{\mathbb {Q}}_p}$
, which is a homogeneous space for
${{\mathbb {Q}}_p}$
, which is a homogeneous space for
![]() $G(L)$
all defined over
$G(L)$
all defined over
![]() ${{\mathbb {Q}}_p}$
. Namely we have a surjective morphism
${{\mathbb {Q}}_p}$
. Namely we have a surjective morphism
![]() $f:G(L) \to X(L)$
defined over
$f:G(L) \to X(L)$
defined over
![]() ${{\mathbb {Q}}_p}$
, constant on cosets of
${{\mathbb {Q}}_p}$
, constant on cosets of
![]() $H(L)$
in
$H(L)$
in
![]() $G(L)$
and inducing a bijection between
$G(L)$
and inducing a bijection between
![]() $G(L)/H(L)$
and
$G(L)/H(L)$
and
![]() $X(L)$
. Restricting f to
$X(L)$
. Restricting f to
![]() $G({{\mathbb {Q}}_p})$
gives a definable (in M) bijection between
$G({{\mathbb {Q}}_p})$
gives a definable (in M) bijection between
![]() $G({{\mathbb {Q}}_p})/H({{\mathbb {Q}}_p})$
and a subset Y of
$G({{\mathbb {Q}}_p})/H({{\mathbb {Q}}_p})$
and a subset Y of
![]() $X({{\mathbb {Q}}_p})$
which is definable in M and can be seen, by dimension reasons, to be an open subset of the p-adic manifold
$X({{\mathbb {Q}}_p})$
which is definable in M and can be seen, by dimension reasons, to be an open subset of the p-adic manifold
![]() $X({{\mathbb {Q}}_p})$
, so a p-adic manifold itself. In the case where
$X({{\mathbb {Q}}_p})$
, so a p-adic manifold itself. In the case where
![]() $H({{\mathbb {Q}}_p})$
is normal in
$H({{\mathbb {Q}}_p})$
is normal in
![]() $G({{\mathbb {Q}}_p})$
, then Y becomes an open subgroup of the p-adic algebraic group
$G({{\mathbb {Q}}_p})$
, then Y becomes an open subgroup of the p-adic algebraic group
![]() $X({{\mathbb {Q}}_p})$
.
$X({{\mathbb {Q}}_p})$
.
2 Main results
2.1
 $\operatorname {\mathrm {fsg}}$
groups and
$\operatorname {\mathrm {fsg}}$
groups and
 $\mathrm {dfg}$
groups over
$\mathrm {dfg}$
groups over
 ${{\mathbb {Q}}_p}$
${{\mathbb {Q}}_p}$
Fact 2.1. Let G be a group definable in
![]() $\mathbb {M}$
over
$\mathbb {M}$
over
![]() ${{\mathbb {Q}}_p}$
and suppose G to be definably amenable. Then there is an algebraic group H over
${{\mathbb {Q}}_p}$
and suppose G to be definably amenable. Then there is an algebraic group H over
![]() ${{\mathbb {Q}}_p}$
and a finite-to-one
${{\mathbb {Q}}_p}$
and a finite-to-one
![]() ${{\mathbb {Q}}_p}$
-definable group homomorphism from
${{\mathbb {Q}}_p}$
-definable group homomorphism from
![]() $G^{00}$
to
$G^{00}$
to
![]() $H(\mathbb {K})$
.
$H(\mathbb {K})$
.
Explanation. This follows from Theorem 2.19 of [Reference Montenegro, Onshuus and Simon21], making use of the proof of Corollary 2.22 of [Reference Montenegro, Onshuus and Simon21].
Lemma 2.2. Let G be a definably amenable group over
![]() ${{\mathbb {Q}}_p}$
such that
${{\mathbb {Q}}_p}$
such that
![]() $G^{00}=G^{0}$
. Then there is a
$G^{00}=G^{0}$
. Then there is a
![]() ${{\mathbb {Q}}_p}$
-definable subgroup
${{\mathbb {Q}}_p}$
-definable subgroup
![]() $A\leq G({{\mathbb {Q}}_p})$
of finite index and a finite normal subgroup
$A\leq G({{\mathbb {Q}}_p})$
of finite index and a finite normal subgroup
![]() $A_0\subseteq A$
such that
$A_0\subseteq A$
such that
![]() $A/A_0$
is
$A/A_0$
is
![]() ${{\mathbb {Q}}_p}$
-definably isomorphic to an open subgroup of a p-adic algebraic group.
${{\mathbb {Q}}_p}$
-definably isomorphic to an open subgroup of a p-adic algebraic group.
Proof By Fact 2.1, there is an algebraic group H over
![]() ${{\mathbb {Q}}_p}$
and a definable over
${{\mathbb {Q}}_p}$
and a definable over
![]() ${{\mathbb {Q}}_p}$
finite-to-one group homomorphism from
${{\mathbb {Q}}_p}$
finite-to-one group homomorphism from
![]() $G^{00}$
to
$G^{00}$
to
![]() $H(\mathbb {K})$
. Since
$H(\mathbb {K})$
. Since
![]() $G^{00}=G^{0}$
, by compactness, there is a
$G^{00}=G^{0}$
, by compactness, there is a
![]() ${{\mathbb {Q}}_p}$
-definable finite index subgroup
${{\mathbb {Q}}_p}$
-definable finite index subgroup
![]() $A\leq G$
and a
$A\leq G$
and a
![]() ${{\mathbb {Q}}_p}$
-definable finite-to-one group homomorphism f from
${{\mathbb {Q}}_p}$
-definable finite-to-one group homomorphism f from
![]() $A({{\mathbb {Q}}_p})$
to
$A({{\mathbb {Q}}_p})$
to
![]() $H({{\mathbb {Q}}_p})$
. Let
$H({{\mathbb {Q}}_p})$
. Let
![]() $H_0({{\mathbb {Q}}_p})$
be the Zariski closure of
$H_0({{\mathbb {Q}}_p})$
be the Zariski closure of
![]() $\operatorname {\mathrm {im}}(f)$
in
$\operatorname {\mathrm {im}}(f)$
in
![]() $H({{\mathbb {Q}}_p})$
, then
$H({{\mathbb {Q}}_p})$
, then
![]() $H_0({{\mathbb {Q}}_p})$
is a p-adic algebraic group. By Remark 2.13 of [Reference Hrushovski and Pillay12],
$H_0({{\mathbb {Q}}_p})$
is a p-adic algebraic group. By Remark 2.13 of [Reference Hrushovski and Pillay12],
![]() $\dim (\operatorname {\mathrm {im}}(f))=\dim (H_0({{\mathbb {Q}}_p}))$
. By the topological definition of dimension
$\dim (\operatorname {\mathrm {im}}(f))=\dim (H_0({{\mathbb {Q}}_p}))$
. By the topological definition of dimension
![]() $\operatorname {\mathrm {im}}(f)$
has interior in
$\operatorname {\mathrm {im}}(f)$
has interior in
![]() $H_{0}({{\mathbb {Q}}_p})$
, hence
$H_{0}({{\mathbb {Q}}_p})$
, hence
![]() $\operatorname {\mathrm {im}}(f)$
, being a subgroup, is open in
$\operatorname {\mathrm {im}}(f)$
, being a subgroup, is open in
![]() $H_{0}({{\mathbb {Q}}_p})$
.
$H_{0}({{\mathbb {Q}}_p})$
.
Fact 2.3 [Reference Pillay and Yao28].
Assuming
![]() ${\mathrm {NIP}}$
. If a definable group G has
${\mathrm {NIP}}$
. If a definable group G has
![]() $\mathrm {dfg}$
, then
$\mathrm {dfg}$
, then
![]() $G^{00}=G^{0}$
.
$G^{00}=G^{0}$
.
Corollary 2.4. Let G be a group definable over
![]() ${{\mathbb {Q}}_p}$
which is either
${{\mathbb {Q}}_p}$
which is either
![]() $\operatorname {\mathrm {fsg}}$
or
$\operatorname {\mathrm {fsg}}$
or
![]() $\mathrm {dfg}$
. Then there is a finite index
$\mathrm {dfg}$
. Then there is a finite index
![]() ${{\mathbb {Q}}_p}$
-definable subgroup
${{\mathbb {Q}}_p}$
-definable subgroup
![]() $A\leq G({{\mathbb {Q}}_p})$
and a finite normal subgroup
$A\leq G({{\mathbb {Q}}_p})$
and a finite normal subgroup
![]() $A_0\subseteq A$
such that
$A_0\subseteq A$
such that
![]() $A/A_0$
is
$A/A_0$
is
![]() ${{\mathbb {Q}}_p}$
-definably isomorphic to an open subgroup of a p-adic algebraic group.
${{\mathbb {Q}}_p}$
-definably isomorphic to an open subgroup of a p-adic algebraic group.
2.2 One-dimensional
 $\mathrm {dfg}$
groups over
$\mathrm {dfg}$
groups over
 ${{\mathbb {Q}}_p}$
${{\mathbb {Q}}_p}$
Recall that the dp-rank of a partial type
![]() $\pi (x)$
over A is
$\pi (x)$
over A is
![]() $\geq \kappa $
if there are
$\geq \kappa $
if there are
![]() $a\models \pi (x)$
and
$a\models \pi (x)$
and
![]() $\kappa $
sequences
$\kappa $
sequences
![]() $(I_i,i<\kappa )$
mutually indiscernible over A and none of which is indiscernible over
$(I_i,i<\kappa )$
mutually indiscernible over A and none of which is indiscernible over
![]() $Aa$
. Dp-minimal theories are theories in which all nonalgebraic
$Aa$
. Dp-minimal theories are theories in which all nonalgebraic
![]() $1$
-types have dp-rank
$1$
-types have dp-rank
![]() $1$
. Every dp-minimal theory has
$1$
. Every dp-minimal theory has
![]() ${\mathrm {NIP}}$
.
${\mathrm {NIP}}$
.
Fact 2.5 [Reference Dolich, Goodrick and Lippel7].
![]() $\operatorname {\mathrm {Th}}({{\mathbb {Q}}_p})$
is dp-minimal.
$\operatorname {\mathrm {Th}}({{\mathbb {Q}}_p})$
is dp-minimal.
Fact 2.6 [Reference Simon35].
Assume that T has
![]() ${\mathrm {NIP}}$
. Let
${\mathrm {NIP}}$
. Let
![]() $N\models T$
be a small model. If p is an N-invariant global type of dp-rank
$N\models T$
be a small model. If p is an N-invariant global type of dp-rank
![]() $1$
, then p is either finitely satisfiable in N or definable over N.
$1$
, then p is either finitely satisfiable in N or definable over N.
Fact 2.7 [Reference Simon35].
Assume that T is dp-minimal, and
![]() $\operatorname {\mathrm {acl}}$
satisfies exchange. Then dp-rank coincides with the
$\operatorname {\mathrm {acl}}$
satisfies exchange. Then dp-rank coincides with the
![]() $\operatorname {\mathrm {acl}}$
-dimension.
$\operatorname {\mathrm {acl}}$
-dimension.
Fact 2.8 [Reference Hrushovski and Pillay13].
If T has
![]() ${\mathrm {NIP}}$
then a global complete type does not fork over a small submodel M iff it is M-invariant.
${\mathrm {NIP}}$
then a global complete type does not fork over a small submodel M iff it is M-invariant.
Lemma 2.9. Let G be a
![]() ${{\mathbb {Q}}_p}$
-definable group of dimension
${{\mathbb {Q}}_p}$
-definable group of dimension
![]() $1$
. Then G is either
$1$
. Then G is either
![]() $\mathrm {dfg}$
or
$\mathrm {dfg}$
or
![]() $\operatorname {\mathrm {fsg}}$
.
$\operatorname {\mathrm {fsg}}$
.
Proof By Fact 1.9, G is definably amenable. By Fact 1.6, G admits a strongly f-generic type. Let
![]() $p\in S_G(\mathbb {K})$
be a global strongly f-generic type. There is a small submodel M such that every left translate of p does not fork over M, and hence M-invariant by Fact 2.8. By Facts 2.5 and 2.6, p is either definable over M or finitely satisfiable in M. So G is either
$p\in S_G(\mathbb {K})$
be a global strongly f-generic type. There is a small submodel M such that every left translate of p does not fork over M, and hence M-invariant by Fact 2.8. By Facts 2.5 and 2.6, p is either definable over M or finitely satisfiable in M. So G is either
![]() $\mathrm {dfg}$
or
$\mathrm {dfg}$
or
![]() $\operatorname {\mathrm {fsg}}$
.
$\operatorname {\mathrm {fsg}}$
.
Recall the notion of generically stable type from [Reference Hrushovski and Pillay13]: a global type p is generically stable if it is both definable and finitely satisfiable in some small model.
Fact 2.10 [Reference Simon34].
Let
![]() $p\in S(\mathbb {K})$
be a non-algebraic global type. Then p is not generically stable.
$p\in S(\mathbb {K})$
be a non-algebraic global type. Then p is not generically stable.
Corollary 2.11. If G is an infinite
![]() ${{\mathbb {Q}}_p}$
-definable group which has
${{\mathbb {Q}}_p}$
-definable group which has
![]() $\mathrm {dfg}$
then G is NOT definably compact.
$\mathrm {dfg}$
then G is NOT definably compact.
Proof Suppose for a contradiction (using Fact 1.8) that G were both
![]() $\mathrm {dfg}$
and
$\mathrm {dfg}$
and
![]() $\operatorname {\mathrm {fsg}}$
. Let p be a global definable (strongly) f-generic type. By [Reference Hrushovski, Pillay and Simon14] p is generic, namely every formula in p is generic. By Proposition 4.2 of [Reference Hrushovski, Peterzil and Pillay11], p (and all its translates) are finitely satisfiable in a small model. So p is generically stable, which contradicts Fact 2.10. This proves the corollary.
$\operatorname {\mathrm {fsg}}$
. Let p be a global definable (strongly) f-generic type. By [Reference Hrushovski, Pillay and Simon14] p is generic, namely every formula in p is generic. By Proposition 4.2 of [Reference Hrushovski, Peterzil and Pillay11], p (and all its translates) are finitely satisfiable in a small model. So p is generically stable, which contradicts Fact 2.10. This proves the corollary.
The following is from [Reference Penazzi, Pillay and Yao24]. Part (a) is Lemma 2.1 there, part (b)(i) is contained in Proposition 2.3 there, and part (b)(ii) in Proposition 2.4. Let us emphasize that the data in items (ii) and (iii) of part (a) determine complete types over M as is proved in [Reference Penazzi, Pillay and Yao24].
Fact 2.12.
-
(a) The complete
 $1$
-types over M (or
$1$
-types over M (or
 ${{\mathbb {Q}}_p}$
) are precisely the following:
${{\mathbb {Q}}_p}$
) are precisely the following:-
(i) The realized types
 $\operatorname {\mathrm {tp}}(a/M)$
for each
$\operatorname {\mathrm {tp}}(a/M)$
for each
 $a\in {{\mathbb {Q}}_p}$
.
$a\in {{\mathbb {Q}}_p}$
. -
(ii) For each
 $a\in {{\mathbb {Q}}_p}$
and coset C of
$a\in {{\mathbb {Q}}_p}$
and coset C of
 $(\mathbb {K}^{*})^0$
, the type
$(\mathbb {K}^{*})^0$
, the type
 $p_{a,C}$
saying that x is infinitesimally close to a (i.e.,
$p_{a,C}$
saying that x is infinitesimally close to a (i.e.,
 $\nu (x-a)>n$
for each
$\nu (x-a)>n$
for each
 $n\in \mathbb {N}$
), and
$n\in \mathbb {N}$
), and
 $(x-a)\in C$
.
$(x-a)\in C$
. -
(iii) For each coset C as above the type
 $p_{\infty , C}$
saying that
$p_{\infty , C}$
saying that
 $x\in C$
and
$x\in C$
and
 $\nu (x)<n$
for all
$\nu (x)<n$
for all
 $n\in \mathbb {Z}$
.
$n\in \mathbb {Z}$
.
-
- (b)
-
(i) A global type of
 ${\mathbb {G}}_a(\mathbb {K})$
is (strongly) f-generic iff it is an heir of some
${\mathbb {G}}_a(\mathbb {K})$
is (strongly) f-generic iff it is an heir of some
 $p_{\infty , C}$
.
$p_{\infty , C}$
. -
(ii) A global type of
 ${\mathbb {G}}_m(\mathbb {K})$
is (strongly) f-generic iff it is an heir of some
${\mathbb {G}}_m(\mathbb {K})$
is (strongly) f-generic iff it is an heir of some
 $p_{\infty , C}$
or
$p_{\infty , C}$
or
 $p_{_{0,C}}$
.
$p_{_{0,C}}$
.
-
Part (ii) of the next remark is precisely Remark 2.2(ii) from [Reference Penazzi, Pillay and Yao24].
Remark 2.13.
-
(i) Let
 $q(x)\in S_1(\mathbb {K})$
be a
$q(x)\in S_1(\mathbb {K})$
be a
 $\emptyset $
-definable
$\emptyset $
-definable
 $1$
-type. By Fact 2.12, we see that if q is NOT infinitesimally close to any point of
$1$
-type. By Fact 2.12, we see that if q is NOT infinitesimally close to any point of
 ${{\mathbb {Q}}_p}$
over
${{\mathbb {Q}}_p}$
over
 ${{\mathbb {Q}}_p}$
, then q is a global heir of some
${{\mathbb {Q}}_p}$
, then q is a global heir of some
 $p_{\infty , C}$
.
$p_{\infty , C}$
. -
(ii) Conversely, any global complete
 $1$
-type extending the partial type
$1$
-type extending the partial type
 $\nu (x)<\Gamma $
is an heir of some
$\nu (x)<\Gamma $
is an heir of some
 $p_{\infty , C}$
, and hence definable over
$p_{\infty , C}$
, and hence definable over
 ${{\mathbb {Q}}_p}$
.
${{\mathbb {Q}}_p}$
.
Lemma 2.14. Suppose that G is a one-dimensional group definable over
![]() ${{\mathbb {Q}}_p}$
. Let
${{\mathbb {Q}}_p}$
. Let
![]() $f: {\mathbb {Z}}_p\backslash \{0\}\longrightarrow G({{\mathbb {Q}}_p})$
be a definable continuous function such that
$f: {\mathbb {Z}}_p\backslash \{0\}\longrightarrow G({{\mathbb {Q}}_p})$
be a definable continuous function such that
![]() $\displaystyle \lim _{x \to 0}f(x)\notin G({{\mathbb {Q}}_p})$
, and
$\displaystyle \lim _{x \to 0}f(x)\notin G({{\mathbb {Q}}_p})$
, and
![]() $\alpha \in \bar {\mathbb {K}}\succ {\mathbb {K}}$
such that
$\alpha \in \bar {\mathbb {K}}\succ {\mathbb {K}}$
such that
![]() $\alpha \neq 0$
and
$\alpha \neq 0$
and
![]() $\nu (\alpha )>\Gamma $
. Then
$\nu (\alpha )>\Gamma $
. Then
![]() $\operatorname {\mathrm {tp}}(f(\alpha )/{\mathbb {K}})$
is a global definable f-generic type of G.
$\operatorname {\mathrm {tp}}(f(\alpha )/{\mathbb {K}})$
is a global definable f-generic type of G.
Proof First let us check that the notation in the statement of the lemma makes sense. First the continuity of f is meant with respect to the p-adic topology on
![]() ${\mathbb {Z}}_p$
and the definable p-adic analytic group topology on
${\mathbb {Z}}_p$
and the definable p-adic analytic group topology on
![]() $G({{\mathbb {Q}}_p})$
from Section 1.4. For any elementary extension
$G({{\mathbb {Q}}_p})$
from Section 1.4. For any elementary extension
![]() $N = (K,+,\times ,0)$
of
$N = (K,+,\times ,0)$
of
![]() $M = ({{\mathbb {Q}}_p},+,\times ,0)$
,
$M = ({{\mathbb {Q}}_p},+,\times ,0)$
,
![]() $f(K)$
is a continuous definable over
$f(K)$
is a continuous definable over
![]() ${{\mathbb {Q}}_p}$
function from
${{\mathbb {Q}}_p}$
function from
![]() ${\cal O}\setminus \{0\}$
to
${\cal O}\setminus \{0\}$
to
![]() $G(K)$
, which we may also write as just f. So for
$G(K)$
, which we may also write as just f. So for
![]() $\alpha \in \bar {\mathbb {K}}\succ \mathbb {K}$
, nonzero such that
$\alpha \in \bar {\mathbb {K}}\succ \mathbb {K}$
, nonzero such that
![]() $\nu (\alpha )>\Gamma $
,
$\nu (\alpha )>\Gamma $
,
![]() $f(\alpha ) \in G(\bar {\mathbb {K}})$
.
$f(\alpha ) \in G(\bar {\mathbb {K}})$
.
Note that
![]() $\operatorname {\mathrm {tp}}(\alpha /\mathbb {K})$
is
$\operatorname {\mathrm {tp}}(\alpha /\mathbb {K})$
is
![]() $\emptyset $
-definable. Since
$\emptyset $
-definable. Since
![]() $\displaystyle \lim _{x \to 0}f(x)\notin G({{\mathbb {Q}}_p})$
,
$\displaystyle \lim _{x \to 0}f(x)\notin G({{\mathbb {Q}}_p})$
,
![]() $f(\alpha )$
is not infinitesimally close (over
$f(\alpha )$
is not infinitesimally close (over
![]() ${{\mathbb {Q}}_p}$
) to any point of
${{\mathbb {Q}}_p}$
) to any point of
![]() $G({{\mathbb {Q}}_p})$
. Moreover, since
$G({{\mathbb {Q}}_p})$
. Moreover, since
![]() $G({{\mathbb {Q}}_p})$
has a definable manifold structure, for any
$G({{\mathbb {Q}}_p})$
has a definable manifold structure, for any
![]() $g\in G({{\mathbb {Q}}_p})$
,
$g\in G({{\mathbb {Q}}_p})$
,
![]() $gf(\alpha )$
is not infinitesimally close to any point of
$gf(\alpha )$
is not infinitesimally close to any point of
![]() $G({{\mathbb {Q}}_p})$
over
$G({{\mathbb {Q}}_p})$
over
![]() ${{\mathbb {Q}}_p}$
.
${{\mathbb {Q}}_p}$
.
By Lemma 2.2, let
![]() $H({{\mathbb {Q}}_p})$
be a one-dimensional algebraic group,
$H({{\mathbb {Q}}_p})$
be a one-dimensional algebraic group,
![]() $ U({{\mathbb {Q}}_p})\leq G({{\mathbb {Q}}_p})$
a
$ U({{\mathbb {Q}}_p})\leq G({{\mathbb {Q}}_p})$
a
![]() ${{\mathbb {Q}}_p}$
-definable subgroup of finite index, and
${{\mathbb {Q}}_p}$
-definable subgroup of finite index, and
![]() $\pi :U({{\mathbb {Q}}_p})\longrightarrow H({{\mathbb {Q}}_p})$
a definable finite-to-one homomorphism. Let
$\pi :U({{\mathbb {Q}}_p})\longrightarrow H({{\mathbb {Q}}_p})$
a definable finite-to-one homomorphism. Let
![]() $V({{\mathbb {Q}}_p})=\pi (U({{\mathbb {Q}}_p}))$
. Since
$V({{\mathbb {Q}}_p})=\pi (U({{\mathbb {Q}}_p}))$
. Since
![]() $U({{\mathbb {Q}}_p})$
is generic, we may assume that
$U({{\mathbb {Q}}_p})$
is generic, we may assume that
![]() $f(\alpha )\in U(\bar {\mathbb {K}})$
. Let
$f(\alpha )\in U(\bar {\mathbb {K}})$
. Let
![]() $\beta =\pi (f(\alpha ))$
. Then, for any
$\beta =\pi (f(\alpha ))$
. Then, for any
![]() $g\in V({{\mathbb {Q}}_p})$
,
$g\in V({{\mathbb {Q}}_p})$
,
![]() $g\beta $
is not infinitesimally close to any point of
$g\beta $
is not infinitesimally close to any point of
![]() $V({{\mathbb {Q}}_p})$
over
$V({{\mathbb {Q}}_p})$
over
![]() ${{\mathbb {Q}}_p}$
.
${{\mathbb {Q}}_p}$
.
Claim.
![]() $\beta $
is not infinitesimally close to any point of
$\beta $
is not infinitesimally close to any point of
![]() $H({{\mathbb {Q}}_p})$
.
$H({{\mathbb {Q}}_p})$
.
Proof As any open subgroup is clopen, we see that
![]() $V({{\mathbb {Q}}_p})$
is a clopen subgroup of
$V({{\mathbb {Q}}_p})$
is a clopen subgroup of
![]() $H({{\mathbb {Q}}_p})$
. Now suppose for a contradiction that
$H({{\mathbb {Q}}_p})$
. Now suppose for a contradiction that
![]() $\beta $
is infinitesimally close to
$\beta $
is infinitesimally close to
![]() $h\in H({{\mathbb {Q}}_p})$
over
$h\in H({{\mathbb {Q}}_p})$
over
![]() ${{\mathbb {Q}}_p}$
, then
${{\mathbb {Q}}_p}$
, then
![]() $h\in \operatorname {\mathrm {cl}}(V({{\mathbb {Q}}_p}))=V({{\mathbb {Q}}_p})$
. A contradiction.
$h\in \operatorname {\mathrm {cl}}(V({{\mathbb {Q}}_p}))=V({{\mathbb {Q}}_p})$
. A contradiction.
Now
![]() $H({{\mathbb {Q}}_p})$
is a p-adic algebraic group (as defined in Section 1.5). So
$H({{\mathbb {Q}}_p})$
is a p-adic algebraic group (as defined in Section 1.5). So
![]() $H({{\mathbb {Q}}_p})$
is definably isomorphic to
$H({{\mathbb {Q}}_p})$
is definably isomorphic to
![]() $({{\mathbb {Q}}_p},+)$
, or
$({{\mathbb {Q}}_p},+)$
, or
![]() $({{\mathbb {Q}}_p}^{*},\times )$
, or a definably compact group
$({{\mathbb {Q}}_p}^{*},\times )$
, or a definably compact group
![]() $C({{\mathbb {Q}}_p})$
(which is either an anisotropic group or an elliptic curve). But any point in
$C({{\mathbb {Q}}_p})$
(which is either an anisotropic group or an elliptic curve). But any point in
![]() $C(\bar {\mathbb {K}})$
is infinitesimally close to its standard part in
$C(\bar {\mathbb {K}})$
is infinitesimally close to its standard part in
![]() $C({{\mathbb {Q}}_p})$
over
$C({{\mathbb {Q}}_p})$
over
![]() ${{\mathbb {Q}}_p}$
. So
${{\mathbb {Q}}_p}$
. So
![]() $H({{\mathbb {Q}}_p})$
is isomorphic to
$H({{\mathbb {Q}}_p})$
is isomorphic to
![]() $({{\mathbb {Q}}_p},+)$
, or
$({{\mathbb {Q}}_p},+)$
, or
![]() $({{\mathbb {Q}}_p}^{*},\times )$
.
$({{\mathbb {Q}}_p}^{*},\times )$
.
As
![]() $\beta $
is not infinitesimally close to any point of
$\beta $
is not infinitesimally close to any point of
![]() $H({{\mathbb {Q}}_p})$
, and
$H({{\mathbb {Q}}_p})$
, and
![]() $\operatorname {\mathrm {tp}}(\beta /\mathbb {K})$
is definable over
$\operatorname {\mathrm {tp}}(\beta /\mathbb {K})$
is definable over
![]() $\emptyset $
, we conclude by Remark 2.13 and Fact 2.12 that
$\emptyset $
, we conclude by Remark 2.13 and Fact 2.12 that
![]() $tp(\beta /\mathbb {K})$
is the heir of some
$tp(\beta /\mathbb {K})$
is the heir of some
![]() $p_{\infty ,C}$
in the case
$p_{\infty ,C}$
in the case
![]() $H = ({{\mathbb {Q}}_p},+)$
, and the heir of some
$H = ({{\mathbb {Q}}_p},+)$
, and the heir of some
![]() $p_{\infty ,C}$
or some
$p_{\infty ,C}$
or some
![]() $p_{0,\mathbb {C}}$
in the case that
$p_{0,\mathbb {C}}$
in the case that
![]() $H = ({{\mathbb {Q}}_p}^{*},\times )$
. Either way
$H = ({{\mathbb {Q}}_p}^{*},\times )$
. Either way
![]() $tp(\beta /\mathbb {K})$
is a global definable (strong) f-generic of H. So the
$tp(\beta /\mathbb {K})$
is a global definable (strong) f-generic of H. So the
![]() $V(\mathbb {K})$
-orbit of
$V(\mathbb {K})$
-orbit of
![]() $\operatorname {\mathrm {tp}}(\beta /\mathbb {K})$
is bounded. Since
$\operatorname {\mathrm {tp}}(\beta /\mathbb {K})$
is bounded. Since
![]() $\pi : U(\mathbb {K})\longrightarrow V(\mathbb {K})$
is a finite-to-one homomorphism, the
$\pi : U(\mathbb {K})\longrightarrow V(\mathbb {K})$
is a finite-to-one homomorphism, the
![]() $U(\mathbb {K})$
-orbit of
$U(\mathbb {K})$
-orbit of
![]() $\operatorname {\mathrm {tp}}(f(\alpha )/\mathbb {K})$
is bounded. This implies that
$\operatorname {\mathrm {tp}}(f(\alpha )/\mathbb {K})$
is bounded. This implies that
![]() $\operatorname {\mathrm {tp}}(f(\alpha )/\mathbb {K})$
is a global f-generic type of G.
$\operatorname {\mathrm {tp}}(f(\alpha )/\mathbb {K})$
is a global f-generic type of G.
Proposition 2.15. Let G be a one-dimensional
![]() ${{\mathbb {Q}}_p}$
-definable group. If
${{\mathbb {Q}}_p}$
-definable group. If
![]() $H\subseteq G$
is an open
$H\subseteq G$
is an open
![]() $\mathrm {dfg}$
subgroup of G definable over
$\mathrm {dfg}$
subgroup of G definable over
![]() ${{\mathbb {Q}}_p}$
, then H has finite index in G.
${{\mathbb {Q}}_p}$
, then H has finite index in G.
Proof By Corollary 2.11, there is a definable continuous function
![]() $f: {\mathbb {Z}}_p\backslash \{0\}\rightarrow H({{\mathbb {Q}}_p})$
such that
$f: {\mathbb {Z}}_p\backslash \{0\}\rightarrow H({{\mathbb {Q}}_p})$
such that
![]() $\displaystyle \lim _{x \to 0}f(x)\notin H({{\mathbb {Q}}_p})$
. Moreover, we claim the following.
$\displaystyle \lim _{x \to 0}f(x)\notin H({{\mathbb {Q}}_p})$
. Moreover, we claim the following.
Claim. There is a definable continuous function
![]() $f: {\mathbb {Z}}_p\backslash \{0\}\rightarrow H({{\mathbb {Q}}_p})$
such that
$f: {\mathbb {Z}}_p\backslash \{0\}\rightarrow H({{\mathbb {Q}}_p})$
such that
![]() $\displaystyle \lim _{x \to 0}f(x)\notin G({{\mathbb {Q}}_p})$
.
$\displaystyle \lim _{x \to 0}f(x)\notin G({{\mathbb {Q}}_p})$
.
Proof Suppose NOT. Then
![]() $H({{\mathbb {Q}}_p})=\operatorname {\mathrm {cl}}(H({{\mathbb {Q}}_p}))$
is definably compact. This contradicts Corollary 2.11.
$H({{\mathbb {Q}}_p})=\operatorname {\mathrm {cl}}(H({{\mathbb {Q}}_p}))$
is definably compact. This contradicts Corollary 2.11.
Let f be a definable continuous function
![]() $f: {\mathbb {Z}}_p\backslash \{0\}\rightarrow H({{\mathbb {Q}}_p})$
such that
$f: {\mathbb {Z}}_p\backslash \{0\}\rightarrow H({{\mathbb {Q}}_p})$
such that
![]() $\displaystyle \lim _{x \to 0}f(x)\notin G({{\mathbb {Q}}_p})$
, and
$\displaystyle \lim _{x \to 0}f(x)\notin G({{\mathbb {Q}}_p})$
, and
![]() $\alpha \in \bar {\mathbb {K}}\succ \mathbb {K}$
such that
$\alpha \in \bar {\mathbb {K}}\succ \mathbb {K}$
such that
![]() $v(\alpha )>\Gamma $
. By Lemma 2.14,
$v(\alpha )>\Gamma $
. By Lemma 2.14,
![]() $\operatorname {\mathrm {tp}}(f(\alpha )/\mathbb {K})$
is a global definable f-generic type of both G and H. Now
$\operatorname {\mathrm {tp}}(f(\alpha )/\mathbb {K})$
is a global definable f-generic type of both G and H. Now
![]() $\operatorname {\mathrm {tp}}(f(\alpha )/\mathbb {K})\in S_H(\mathbb {K})$
is
$\operatorname {\mathrm {tp}}(f(\alpha )/\mathbb {K})\in S_H(\mathbb {K})$
is
![]() $G^{00}$
-invariant. So
$G^{00}$
-invariant. So
![]() $G^{00}\subseteq H$
. By compactness, H has finite index.
$G^{00}\subseteq H$
. By compactness, H has finite index.
Corollary 2.16. Let G be a one-dimensional
![]() $\mathrm {dfg}$
group definable over
$\mathrm {dfg}$
group definable over
![]() ${{\mathbb {Q}}_p}$
. Then
${{\mathbb {Q}}_p}$
. Then
![]() $G^{00}=\cap _{n\in \mathbb {N}^+}nG$
.
$G^{00}=\cap _{n\in \mathbb {N}^+}nG$
.
Proof By Fact 1.9, we may assume that G is commutative. Consider the map
![]() $f_n: G\longrightarrow nG$
given by
$f_n: G\longrightarrow nG$
given by
![]() $x\mapsto nx$
. Let
$x\mapsto nx$
. Let
![]() $\operatorname {\mathrm {tp}}(\alpha /\mathbb {K})\in S_G(\mathbb {K})$
be a definable f-generic type. Then there is a small submodel
$\operatorname {\mathrm {tp}}(\alpha /\mathbb {K})\in S_G(\mathbb {K})$
be a definable f-generic type. Then there is a small submodel
![]() $M\prec \mathbb {K}$
such that every left
$M\prec \mathbb {K}$
such that every left
![]() $nG$
-translate of
$nG$
-translate of
![]() $\operatorname {\mathrm {tp}}(n\alpha /\mathbb {K})$
is definable over M. So
$\operatorname {\mathrm {tp}}(n\alpha /\mathbb {K})$
is definable over M. So
![]() $nG$
is a
$nG$
is a
![]() $\mathrm {dfg}$
group. By Proposition 2.15,
$\mathrm {dfg}$
group. By Proposition 2.15,
![]() $nG$
has finite index for each
$nG$
has finite index for each
![]() $n\in \mathbb {N}^+$
. On the other hand, if
$n\in \mathbb {N}^+$
. On the other hand, if
![]() $H\leq G$
is a definable subgroup of index n with
$H\leq G$
is a definable subgroup of index n with
![]() $n\in \mathbb {N}^+$
, then
$n\in \mathbb {N}^+$
, then
![]() $nG\leq H$
. So
$nG\leq H$
. So
![]() $G^{0}=\cap _{n\in \mathbb {N}^+}nG$
. By Fact 2.3, we have
$G^{0}=\cap _{n\in \mathbb {N}^+}nG$
. By Fact 2.3, we have
![]() $G^{00}=\cap _{n\in \mathbb {N}^+}nG$
as required.
$G^{00}=\cap _{n\in \mathbb {N}^+}nG$
as required.
Recall that a definable group is definably connected if it has no proper finite index definable subgroups. We will call a definable group G is definably totally disconnected if every finite index definable subgroup of G is NOT definably connected. Namely, a definably totally disconnected group has no minimal finite index definable subgroups.
Note that
![]() ${\mathbb {G}}_a(\mathbb {K})$
is definably connected since
${\mathbb {G}}_a(\mathbb {K})$
is definably connected since
![]() ${\mathbb {G}}_a(\mathbb {K})^0={\mathbb {G}}_a(\mathbb {K})$
, while
${\mathbb {G}}_a(\mathbb {K})^0={\mathbb {G}}_a(\mathbb {K})$
, while
![]() ${\mathbb {G}}_m(\mathbb {K})$
is definably totally disconnected since
${\mathbb {G}}_m(\mathbb {K})$
is definably totally disconnected since
![]() ${\mathbb {G}}_m(\mathbb {K})^0=\bigcap _{n\in \mathbb {N}^+}P_n(\mathbb {K}^{*})$
(see [Reference Penazzi, Pillay and Yao24]).
${\mathbb {G}}_m(\mathbb {K})^0=\bigcap _{n\in \mathbb {N}^+}P_n(\mathbb {K}^{*})$
(see [Reference Penazzi, Pillay and Yao24]).
Proposition 2.17. Let G be a one-dimensional
![]() $\mathrm {dfg}$
group definable over
$\mathrm {dfg}$
group definable over
![]() ${{\mathbb {Q}}_p}$
.
${{\mathbb {Q}}_p}$
.
-
1. If
 $G({{\mathbb {Q}}_p})$
is definably connected, then there is a finite normal subgroup
$G({{\mathbb {Q}}_p})$
is definably connected, then there is a finite normal subgroup
 $A_0$
such that
$A_0$
such that
 $G({{\mathbb {Q}}_p})/A_0$
is definably isomorphic to
$G({{\mathbb {Q}}_p})/A_0$
is definably isomorphic to
 $({{\mathbb {Q}}_p},+)$
.
$({{\mathbb {Q}}_p},+)$
. -
2. If
 $G({{\mathbb {Q}}_p})$
is definably totally disconnected, then there is a definable subgroup
$G({{\mathbb {Q}}_p})$
is definably totally disconnected, then there is a definable subgroup
 $A\leq G$
of finite index, and a finite normal subgroup
$A\leq G$
of finite index, and a finite normal subgroup
 $A_0\leq A({{\mathbb {Q}}_p})$
such that
$A_0\leq A({{\mathbb {Q}}_p})$
such that
 $A({{\mathbb {Q}}_p})/A_0$
is definably isomorphic to
$A({{\mathbb {Q}}_p})/A_0$
is definably isomorphic to
 $(P_n({{\mathbb {Q}}_p}^{*}),\times ).$
$(P_n({{\mathbb {Q}}_p}^{*}),\times ).$
Proof By Lemma 2.2, there are a one-dimensional algebraic group H and a definable finite-to-one group homomorphism f from
![]() $A({{\mathbb {Q}}_p})$
to
$A({{\mathbb {Q}}_p})$
to
![]() $H({{\mathbb {Q}}_p})$
, where
$H({{\mathbb {Q}}_p})$
, where
![]() $A\leq G$
is a finite index subgroup definable over
$A\leq G$
is a finite index subgroup definable over
![]() ${{\mathbb {Q}}_p}$
. Clearly, A has
${{\mathbb {Q}}_p}$
. Clearly, A has
![]() $\mathrm {dfg}$
. Let
$\mathrm {dfg}$
. Let
![]() $\operatorname {\mathrm {tp}}(\alpha /\mathbb {K})$
be a global definable f-generic type of A. Then
$\operatorname {\mathrm {tp}}(\alpha /\mathbb {K})$
be a global definable f-generic type of A. Then
![]() $\operatorname {\mathrm {tp}}(f(\alpha )/\mathbb {K})$
is also a global definable f-generic type of
$\operatorname {\mathrm {tp}}(f(\alpha )/\mathbb {K})$
is also a global definable f-generic type of
![]() $\operatorname {\mathrm {im}}(f)$
. As
$\operatorname {\mathrm {im}}(f)$
. As
![]() $\operatorname {\mathrm {im}}(f)$
has
$\operatorname {\mathrm {im}}(f)$
has
![]() $\mathrm {dfg}$
,
$\mathrm {dfg}$
,
![]() $\operatorname {\mathrm {im}}(f)\leq H$
has finite index by Proposition 2.15. So
$\operatorname {\mathrm {im}}(f)\leq H$
has finite index by Proposition 2.15. So
![]() $H({{\mathbb {Q}}_p})$
is
$H({{\mathbb {Q}}_p})$
is
![]() $\mathrm {dfg}$
, and hence is either
$\mathrm {dfg}$
, and hence is either
![]() $({{\mathbb {Q}}_p},+)$
or
$({{\mathbb {Q}}_p},+)$
or
![]() $({{\mathbb {Q}}_p}^{*},\times )$
.
$({{\mathbb {Q}}_p}^{*},\times )$
.
If
![]() $G({{\mathbb {Q}}_p})$
is definably connected. Then
$G({{\mathbb {Q}}_p})$
is definably connected. Then
![]() $\operatorname {\mathrm {im}}(f)$
is definably connected. So
$\operatorname {\mathrm {im}}(f)$
is definably connected. So
![]() $H({{\mathbb {Q}}_p})$
has to be
$H({{\mathbb {Q}}_p})$
has to be
![]() $({{\mathbb {Q}}_p},+)$
, and hence is
$({{\mathbb {Q}}_p},+)$
, and hence is
![]() $\operatorname {\mathrm {im}}(f)$
.
$\operatorname {\mathrm {im}}(f)$
.
If
![]() $G({{\mathbb {Q}}_p})$
is totally disconnected, then
$G({{\mathbb {Q}}_p})$
is totally disconnected, then
![]() $\operatorname {\mathrm {im}}(f)$
is also totally disconnected. So
$\operatorname {\mathrm {im}}(f)$
is also totally disconnected. So
![]() $H({{\mathbb {Q}}_p})$
has to be
$H({{\mathbb {Q}}_p})$
has to be
![]() $({{\mathbb {Q}}_p}^{*},\times )$
, and hence
$({{\mathbb {Q}}_p}^{*},\times )$
, and hence
![]() $\operatorname {\mathrm {im}}(f)$
contains
$\operatorname {\mathrm {im}}(f)$
contains
![]() $(P_n({{\mathbb {Q}}_p}^{*}),\times )$
for some n. Replace
$(P_n({{\mathbb {Q}}_p}^{*}),\times )$
for some n. Replace
![]() $A({{\mathbb {Q}}_p})$
by
$A({{\mathbb {Q}}_p})$
by
![]() $f^{-1}(P_n({{\mathbb {Q}}_p}^{*}))$
if necessary.
$f^{-1}(P_n({{\mathbb {Q}}_p}^{*}))$
if necessary.
2.3 Algebraic groups with open
 $\mathrm {dfg}$
subgroups
$\mathrm {dfg}$
subgroups
The following will be used later:
Fact 2.18 [Reference Onshuus and Pillay23].
Let
![]() $X\subseteq \mathbb {K}^n$
be open, definable and defined over
$X\subseteq \mathbb {K}^n$
be open, definable and defined over
![]() ${{\mathbb {Q}}_p}$
. Let
${{\mathbb {Q}}_p}$
. Let
![]() $X=Y_1\cup Y_2$
, where the
$X=Y_1\cup Y_2$
, where the
![]() $Y_i$
are definable in
$Y_i$
are definable in
![]() $\mathbb {K}$
. Then one of the
$\mathbb {K}$
. Then one of the
![]() $Y_i$
contains an open
$Y_i$
contains an open
![]() ${{\mathbb {Q}}_p}$
-definable subset.
${{\mathbb {Q}}_p}$
-definable subset.
Lemma 2.19. Let H be an algebraic group over
![]() ${{\mathbb {Q}}_p}$
, and G an open
${{\mathbb {Q}}_p}$
, and G an open
![]() ${{\mathbb {Q}}_p}$
-definable
${{\mathbb {Q}}_p}$
-definable
![]() $\mathrm {dfg}$
subgroup of
$\mathrm {dfg}$
subgroup of
![]() $H(\mathbb {K})$
. Suppose A is an algebraic subgroup of H, also defined over
$H(\mathbb {K})$
. Suppose A is an algebraic subgroup of H, also defined over
![]() ${{\mathbb {Q}}_p}$
. Let
${{\mathbb {Q}}_p}$
. Let
![]() $G/A(\mathbb {K})$
be the set of cosets
$G/A(\mathbb {K})$
be the set of cosets
![]() $g/A(\mathbb {K})$
for
$g/A(\mathbb {K})$
for
![]() $g\in G$
. Then
$g\in G$
. Then
![]() $G/A(\mathbb {K})$
infinite implies
$G/A(\mathbb {K})$
infinite implies
![]() $G/A(\mathbb {K})$
is not definably compact (equivalently
$G/A(\mathbb {K})$
is not definably compact (equivalently
![]() $G({{\mathbb {Q}}_p})/A({{\mathbb {Q}}_p})$
is not compact.)
$G({{\mathbb {Q}}_p})/A({{\mathbb {Q}}_p})$
is not compact.)
Proof We start with some explanations, partly suggested by the referee. First the quotient space
![]() $H({{\mathbb {Q}}_p})/A({{\mathbb {Q}}_p})$
(a homogeneous space for
$H({{\mathbb {Q}}_p})/A({{\mathbb {Q}}_p})$
(a homogeneous space for
![]() $H({{\mathbb {Q}}_p})$
) can be viewed as a definable (rather than interpretable) set in M, and moreover a definable p-adic manifold. This is by the last paragraph of Section 1.5. So
$H({{\mathbb {Q}}_p})$
) can be viewed as a definable (rather than interpretable) set in M, and moreover a definable p-adic manifold. This is by the last paragraph of Section 1.5. So
![]() $G({{\mathbb {Q}}_p})/A({{\mathbb {Q}}_p})$
, as defined in the statement of the lemma will be a definable submanifold of
$G({{\mathbb {Q}}_p})/A({{\mathbb {Q}}_p})$
, as defined in the statement of the lemma will be a definable submanifold of
![]() $H({{\mathbb {Q}}_p})/A({{\mathbb {Q}}_p})$
, and a homogeneous space for
$H({{\mathbb {Q}}_p})/A({{\mathbb {Q}}_p})$
, and a homogeneous space for
![]() $G({{\mathbb {Q}}_p})$
, and we call it
$G({{\mathbb {Q}}_p})$
, and we call it
![]() $C({{\mathbb {Q}}_p})$
. So
$C({{\mathbb {Q}}_p})$
. So
![]() $C = C(\mathbb {K})$
is a definable (over
$C = C(\mathbb {K})$
is a definable (over
![]() ${{\mathbb {Q}}_p}$
) manifold in the sense of Section 1.4, and also a homogeneous space for
${{\mathbb {Q}}_p}$
) manifold in the sense of Section 1.4, and also a homogeneous space for
![]() $G = G(\mathbb {K})$
. Note also that the lemma we are proving is a natural generalization of Corollary 2.11 to homogeneous spaces (transitive flows).
$G = G(\mathbb {K})$
. Note also that the lemma we are proving is a natural generalization of Corollary 2.11 to homogeneous spaces (transitive flows).
Let
![]() $\pi : G\to C$
be the natural
$\pi : G\to C$
be the natural
![]() ${{\mathbb {Q}}_p}$
-definable projection map.
${{\mathbb {Q}}_p}$
-definable projection map.
So we have the action of
![]() $G = G(\mathbb {M})$
on
$G = G(\mathbb {M})$
on
![]() $C = C(\mathbb {M})$
and hence also an action on the type space
$C = C(\mathbb {M})$
and hence also an action on the type space
![]() $S_{C}(\mathbb {M})$
of global types concentrating on C. We will call a definable subset X of C generic if finitely many G-translates of X cover C, and likewise a type
$S_{C}(\mathbb {M})$
of global types concentrating on C. We will call a definable subset X of C generic if finitely many G-translates of X cover C, and likewise a type
![]() $p\in S_{C}(\mathbb {M})$
generic if all formulas in p are generic.
$p\in S_{C}(\mathbb {M})$
generic if all formulas in p are generic.
We first show that for any
![]() ${{\mathbb {Q}}_p}$
-definable open subset
${{\mathbb {Q}}_p}$
-definable open subset
![]() $O(\mathbb {M})$
of
$O(\mathbb {M})$
of
![]() $G(\mathbb {M})$
,
$G(\mathbb {M})$
,
![]() $\pi (O(\mathbb {M}))$
contains a
$\pi (O(\mathbb {M}))$
contains a
![]() ${{\mathbb {Q}}_p}$
-definable open subset of
${{\mathbb {Q}}_p}$
-definable open subset of
![]() $C(\mathbb {M})$
. Take
$C(\mathbb {M})$
. Take
![]() $g\in O(\mathbb {M})$
such that
$g\in O(\mathbb {M})$
such that
![]() $\dim (g/{{\mathbb {Q}}_p})=\dim (G)$
, then we have
$\dim (g/{{\mathbb {Q}}_p})=\dim (G)$
, then we have
![]() $g\in \pi ^{-1}(\pi (g))$
and
$g\in \pi ^{-1}(\pi (g))$
and
So
![]() $\dim (g/{{\mathbb {Q}}_p},\pi (g))\leq \dim (A)$
, and thus
$\dim (g/{{\mathbb {Q}}_p},\pi (g))\leq \dim (A)$
, and thus
As
![]() $\pi (g)\in \pi (O(\mathbb {M}))$
, we see that
$\pi (g)\in \pi (O(\mathbb {M}))$
, we see that
So
![]() $\pi (O(\mathbb {M}))$
contains a
$\pi (O(\mathbb {M}))$
contains a
![]() ${{\mathbb {Q}}_p}$
-definable open subset of
${{\mathbb {Q}}_p}$
-definable open subset of
![]() $C(\mathbb {M})$
as required.
$C(\mathbb {M})$
as required.
Now suppose for a contradiction that
![]() $C({{\mathbb {Q}}_p})$
is definably compact and infinite. Then
$C({{\mathbb {Q}}_p})$
is definably compact and infinite. Then
![]() $C({{\mathbb {Q}}_p})$
is compact as a topological space (as mentioned earlier, definable compactness and compactness agree for definable p-adic manifolds).
$C({{\mathbb {Q}}_p})$
is compact as a topological space (as mentioned earlier, definable compactness and compactness agree for definable p-adic manifolds).
Claim.
![]() $S_C(\mathbb {M})$
has a generic type which is moreover finitely satisfiable in
$S_C(\mathbb {M})$
has a generic type which is moreover finitely satisfiable in
![]() ${{\mathbb {Q}}_p}$
(i.e., in
${{\mathbb {Q}}_p}$
(i.e., in
![]() $C({{\mathbb {Q}}_p})$
).
$C({{\mathbb {Q}}_p})$
).
Proof Let
![]() $p(x)$
be any type in
$p(x)$
be any type in
![]() $S_{C}(M)$
which contains only open definable sets, and let
$S_{C}(M)$
which contains only open definable sets, and let
![]() $p'(x)\in S_{C}(\mathbb {M})$
be a coheir of p. We will show that
$p'(x)\in S_{C}(\mathbb {M})$
be a coheir of p. We will show that
![]() $p'$
is a generic type of
$p'$
is a generic type of
![]() $S_{C}(\mathbb {M})$
as defined above. So let X be a definable set in
$S_{C}(\mathbb {M})$
as defined above. So let X be a definable set in
![]() $p'$
. By definability of types over
$p'$
. By definability of types over
![]() ${{\mathbb {Q}}_p}$
,
${{\mathbb {Q}}_p}$
,
![]() $X\cap C({{\mathbb {Q}}_p}) = Y$
is a definable set in the structure M. Note that Y has interior in the sense of the space
$X\cap C({{\mathbb {Q}}_p}) = Y$
is a definable set in the structure M. Note that Y has interior in the sense of the space
![]() $C({{\mathbb {Q}}_p})$
, because otherwise
$C({{\mathbb {Q}}_p})$
, because otherwise
![]() $Y\notin p$
, so
$Y\notin p$
, so
![]() $X\wedge \neg (Y(\mathbb {M}))\in p'$
, but the latter definable set does not meet
$X\wedge \neg (Y(\mathbb {M}))\in p'$
, but the latter definable set does not meet
![]() $C({{\mathbb {Q}}_p})$
, contradicting
$C({{\mathbb {Q}}_p})$
, contradicting
![]() $p'$
being finitely satisfiable in M. We have shown that Y has interior in
$p'$
being finitely satisfiable in M. We have shown that Y has interior in
![]() $C({{\mathbb {Q}}_p})$
. It follows that
$C({{\mathbb {Q}}_p})$
. It follows that
![]() $Y(\mathbb {M})$
contains a
$Y(\mathbb {M})$
contains a
![]() ${{\mathbb {Q}}_p}$
-definable open set.
${{\mathbb {Q}}_p}$
-definable open set.
Now consider
![]() $Y(\mathbb {M}) = (X\cap Y(\mathbb {M})) \cup ((\neg X)\cap Y(\mathbb {M}))$
. Note that
$Y(\mathbb {M}) = (X\cap Y(\mathbb {M})) \cup ((\neg X)\cap Y(\mathbb {M}))$
. Note that
![]() $(\neg (X)\cap Y(\mathbb {M}))\cap C({{\mathbb {Q}}_p})) = \emptyset $
so in particular does not contain any
$(\neg (X)\cap Y(\mathbb {M}))\cap C({{\mathbb {Q}}_p})) = \emptyset $
so in particular does not contain any
![]() ${{\mathbb {Q}}_p}$
-definable open set. It follows from Fact 2.18 that
${{\mathbb {Q}}_p}$
-definable open set. It follows from Fact 2.18 that
![]() $X\cap Y(\mathbb {M})$
contains a
$X\cap Y(\mathbb {M})$
contains a
![]() ${{\mathbb {Q}}_p}$
-definable open set, so in particular, X contains a
${{\mathbb {Q}}_p}$
-definable open set, so in particular, X contains a
![]() ${{\mathbb {Q}}_p}$
-definable open set Z. As
${{\mathbb {Q}}_p}$
-definable open set Z. As
![]() $C({{\mathbb {Q}}_p})$
is compact, finitely many
$C({{\mathbb {Q}}_p})$
is compact, finitely many
![]() $G({{\mathbb {Q}}_p})$
translates of
$G({{\mathbb {Q}}_p})$
translates of
![]() $Z({{\mathbb {Q}}_p})$
cover
$Z({{\mathbb {Q}}_p})$
cover
![]() $C({{\mathbb {Q}}_p})$
. So finitely many G-translates of Z cover C, so finitely many G-translates of X cover C. So X is generic, and as X was an arbitrary definable set in
$C({{\mathbb {Q}}_p})$
. So finitely many G-translates of Z cover C, so finitely many G-translates of X cover C. So X is generic, and as X was an arbitrary definable set in
![]() $p'$
we have shown that
$p'$
we have shown that
![]() $p'$
is generic. This completes the proof of the claim.
$p'$
is generic. This completes the proof of the claim.
Let us now complete the proof of the lemma. Note that we have a
![]() $G(\mathbb {M})$
-flow map from
$G(\mathbb {M})$
-flow map from
![]() $(G(\mathbb {M}), S_{G}(\mathbb {M}))$
to
$(G(\mathbb {M}), S_{G}(\mathbb {M}))$
to
![]() $(G(\mathbb {M}), S_{C}(\mathbb {M}))$
induced by
$(G(\mathbb {M}), S_{C}(\mathbb {M}))$
induced by
![]() $\pi $
. By our assumptions, let
$\pi $
. By our assumptions, let
![]() $r\in S_{G}(\mathbb {M})$
be a definable f-generic type. By Lemma 1.15 of [Reference Pillay and Yao28] (and its proof) the orbit
$r\in S_{G}(\mathbb {M})$
be a definable f-generic type. By Lemma 1.15 of [Reference Pillay and Yao28] (and its proof) the orbit
![]() $(G(\mathbb {M})\cdot r)$
is closed, hence a minimal subflow of
$(G(\mathbb {M})\cdot r)$
is closed, hence a minimal subflow of
![]() $S_{G}(\mathbb {M})$
. Then
$S_{G}(\mathbb {M})$
. Then
![]() $\pi (G(\mathbb {M})\cdot r)$
is a minimal subflow of
$\pi (G(\mathbb {M})\cdot r)$
is a minimal subflow of
![]() $S_{C}(\mathbb {M})$
. But
$S_{C}(\mathbb {M})$
. But
![]() $S_{C}(\mathbb {M})$
has generic types, by the claim, hence as is well-known (see [Reference Newelski22]) has a unique minimal subflow. By the claim, let
$S_{C}(\mathbb {M})$
has generic types, by the claim, hence as is well-known (see [Reference Newelski22]) has a unique minimal subflow. By the claim, let
![]() $p\in S_{C}(\mathbb {M})$
be generic and finitely satisfiable in
$p\in S_{C}(\mathbb {M})$
be generic and finitely satisfiable in
![]() $C({{\mathbb {Q}}_p})$
. But then p is of the form
$C({{\mathbb {Q}}_p})$
. But then p is of the form
![]() $\pi (q)$
for some
$\pi (q)$
for some
![]() $q\in G(\mathbb {M})\cdot r$
. As q is definable, so is
$q\in G(\mathbb {M})\cdot r$
. As q is definable, so is
![]() $\pi (q) = p$
. Then p is both definable and finitely satisfiable, which contradicts distality.
$\pi (q) = p$
. Then p is both definable and finitely satisfiable, which contradicts distality.
Remark 2.20. Note that if G and H are definable groups, and G has
![]() $\mathrm {dfg}$
, and
$\mathrm {dfg}$
, and
![]() $f: G\longrightarrow H$
is a definable onto homomorphism, then H has
$f: G\longrightarrow H$
is a definable onto homomorphism, then H has
![]() $\mathrm {dfg}$
.
$\mathrm {dfg}$
.
At this point we will need some of the basic theory of linear algebraic groups. The notation in the literature (such as [Reference Milne20]) for (linear) algebraic groups over a field k is consistent with our notation from Section 1.5 where
![]() $k = {{\mathbb {Q}}_p}$
. See Chapter 14 of [Reference Milne20] for the notions of unipotent elements in a linear algebraic group G and unipotent algebraic subgroups G. An algebraic group G over
$k = {{\mathbb {Q}}_p}$
. See Chapter 14 of [Reference Milne20] for the notions of unipotent elements in a linear algebraic group G and unipotent algebraic subgroups G. An algebraic group G over
![]() ${{\mathbb {Q}}_p}$
is trigonalizable over
${{\mathbb {Q}}_p}$
is trigonalizable over
![]() ${{\mathbb {Q}}_p}$
if it is isomorphic over
${{\mathbb {Q}}_p}$
if it is isomorphic over
![]() ${{\mathbb {Q}}_p}$
to a group of upper triangular matrices in some
${{\mathbb {Q}}_p}$
to a group of upper triangular matrices in some
![]() $GL_{n}$
. An algebraic torus over
$GL_{n}$
. An algebraic torus over
![]() ${{\mathbb {Q}}_p}$
is split over
${{\mathbb {Q}}_p}$
is split over
![]() ${{\mathbb {Q}}_p}$
if it is isomorphic over
${{\mathbb {Q}}_p}$
if it is isomorphic over
![]() ${{\mathbb {Q}}_p}$
to a product of copies of the multiplicative group. A connected linear solvable algebraic group G over
${{\mathbb {Q}}_p}$
to a product of copies of the multiplicative group. A connected linear solvable algebraic group G over
![]() ${{\mathbb {Q}}_p}$
is split over
${{\mathbb {Q}}_p}$
is split over
![]() ${{\mathbb {Q}}_p}$
if G admits a subnormal series of algebraic subgroups over
${{\mathbb {Q}}_p}$
if G admits a subnormal series of algebraic subgroups over
![]() ${{\mathbb {Q}}_p}$
whose quotients are isomorphic over
${{\mathbb {Q}}_p}$
whose quotients are isomorphic over
![]() ${{\mathbb {Q}}_p}$
to the additive or multiplicative group. A connected semisimple algebraic group G over
${{\mathbb {Q}}_p}$
to the additive or multiplicative group. A connected semisimple algebraic group G over
![]() ${{\mathbb {Q}}_p}$
is said to be isotropic if contains a nontrivial
${{\mathbb {Q}}_p}$
is said to be isotropic if contains a nontrivial
![]() ${{\mathbb {Q}}_p}$
-split algebraic torus defined over
${{\mathbb {Q}}_p}$
-split algebraic torus defined over
![]() ${{\mathbb {Q}}_p}$
. Let G be a reductive algebraic group over
${{\mathbb {Q}}_p}$
. Let G be a reductive algebraic group over
![]() ${{\mathbb {Q}}_p}$
. A parabolic subgroup is a connected subgroup P of G such that the quotient variety
${{\mathbb {Q}}_p}$
. A parabolic subgroup is a connected subgroup P of G such that the quotient variety
![]() $G/P$
is complete.
$G/P$
is complete.
We summarise the various facts from the literature that we need (specialized to the case
![]() $k = {{\mathbb {Q}}_p}$
).
$k = {{\mathbb {Q}}_p}$
).
Fact 2.21.
-
(i) (See Theorem 16.33 of [Reference Milne20]) Let G be a connected linear solvable algebraic group over
 ${{\mathbb {Q}}_p}$
. Then G has a maximal unipotent algebraic subgroup,
${{\mathbb {Q}}_p}$
. Then G has a maximal unipotent algebraic subgroup,
 $G_{u}$
which is normal and over
$G_{u}$
which is normal and over
 ${{\mathbb {Q}}_p}$
and
${{\mathbb {Q}}_p}$
and
 $G/G_{u}$
is an algebraic torus (over
$G/G_{u}$
is an algebraic torus (over
 ${{\mathbb {Q}}_p}$
).
${{\mathbb {Q}}_p}$
). -
(ii) (See Proposition 16.52 of [Reference Milne20]) Any connected solvable linear algebraic group over
 ${{\mathbb {Q}}_p}$
which is split over
${{\mathbb {Q}}_p}$
which is split over
 ${{\mathbb {Q}}_p}$
is trigonalizable over
${{\mathbb {Q}}_p}$
is trigonalizable over
 ${{\mathbb {Q}}_p}$
.
${{\mathbb {Q}}_p}$
. -
(iii) (See Corollaire 4.17 of [Reference Borel and Tits3]) Let G be a (connected) semisimple algebraic group over
 ${{\mathbb {Q}}_p}$
. Then G is
${{\mathbb {Q}}_p}$
. Then G is
 ${{\mathbb {Q}}_p}$
-isotropic if and only if G has a proper parabolic subgroup P defined over
${{\mathbb {Q}}_p}$
-isotropic if and only if G has a proper parabolic subgroup P defined over
 ${{\mathbb {Q}}_p}$
.
${{\mathbb {Q}}_p}$
. -
(iv) (Theorem 3.1 of [Reference Platonov and Rapinchuk30]) Suppose G is a connected semisimple algebraic group over
 ${{\mathbb {Q}}_p}$
which is not
${{\mathbb {Q}}_p}$
which is not
 ${{\mathbb {Q}}_p}$
-isotropic. Then
${{\mathbb {Q}}_p}$
-isotropic. Then
 $G({{\mathbb {Q}}_p})$
is compact.
$G({{\mathbb {Q}}_p})$
is compact.
Proposition 2.22. Let H be a connected (not necessarily linear) algebraic group over
![]() ${{\mathbb {Q}}_p}$
. Suppose that
${{\mathbb {Q}}_p}$
. Suppose that
![]() $H(\mathbb {M})$
contains an open
$H(\mathbb {M})$
contains an open
![]() ${{\mathbb {Q}}_p}$
-definable
${{\mathbb {Q}}_p}$
-definable
![]() $\mathrm {dfg}$
subgroup G, then H is linear, solvable, and the algebraic torus
$\mathrm {dfg}$
subgroup G, then H is linear, solvable, and the algebraic torus
![]() $H/H_{u}$
(from part (i) of the fact above) splits over
$H/H_{u}$
(from part (i) of the fact above) splits over
![]() ${{\mathbb {Q}}_p}$
.
${{\mathbb {Q}}_p}$
.
Proof The algebraic group H admits a short exact sequence of connected algebraic groups over
![]() ${{\mathbb {Q}}_p}$
${{\mathbb {Q}}_p}$
with L a linear algebraic, and A an abelian variety. Now
![]() $G({{\mathbb {Q}}_p})/L({{\mathbb {Q}}_p})$
definably over
$G({{\mathbb {Q}}_p})/L({{\mathbb {Q}}_p})$
definably over
![]() ${{\mathbb {Q}}_p}$
embeds in
${{\mathbb {Q}}_p}$
embeds in
![]() $A({{\mathbb {Q}}_p})$
which is compact, so
$A({{\mathbb {Q}}_p})$
which is compact, so
![]() $G({{\mathbb {Q}}_p})/L({{\mathbb {Q}}_p})$
is compact so definably compact. If A is nontrivial, then
$G({{\mathbb {Q}}_p})/L({{\mathbb {Q}}_p})$
is compact so definably compact. If A is nontrivial, then
![]() $\dim (L) < \dim (H)$
, so as
$\dim (L) < \dim (H)$
, so as
![]() $G({{\mathbb {Q}}_p})$
is open in
$G({{\mathbb {Q}}_p})$
is open in
![]() $H({{\mathbb {Q}}_p})$
,
$H({{\mathbb {Q}}_p})$
,
![]() $G({{\mathbb {Q}}_p})/L({{\mathbb {Q}}_p})$
is infinite. By Lemma 2.19 this implies that
$G({{\mathbb {Q}}_p})/L({{\mathbb {Q}}_p})$
is infinite. By Lemma 2.19 this implies that
![]() $G({{\mathbb {Q}}_p})/L({{\mathbb {Q}}_p})$
is not definably compact, so not compact, a contradiction. So A is trivial and hence H is linear.
$G({{\mathbb {Q}}_p})/L({{\mathbb {Q}}_p})$
is not definably compact, so not compact, a contradiction. So A is trivial and hence H is linear.
Let
![]() $R = \operatorname {\mathrm {rad}}(H)$
be the solvable radical of H, the maximal connected normal solvable algebraic subgroup of H, which is automatically defined over
$R = \operatorname {\mathrm {rad}}(H)$
be the solvable radical of H, the maximal connected normal solvable algebraic subgroup of H, which is automatically defined over
![]() ${{\mathbb {Q}}_p}$
. Let S be the quotient
${{\mathbb {Q}}_p}$
. Let S be the quotient
![]() $H/R$
a connected semisimple algebraic group over
$H/R$
a connected semisimple algebraic group over
![]() ${{\mathbb {Q}}_p}$
. We want to show that S is trivial, so H will be solvable, as desired. Suppose for a contradiction that S is nontrivial.
${{\mathbb {Q}}_p}$
. We want to show that S is trivial, so H will be solvable, as desired. Suppose for a contradiction that S is nontrivial.
As in the statement of Lemma 2.19, we define
![]() $G/R(\mathbb {K})$
to be the set of cosets
$G/R(\mathbb {K})$
to be the set of cosets
![]() $g/R(\mathbb {K})$
in
$g/R(\mathbb {K})$
in
![]() $H(\mathbb {K})/R(\mathbb {K})$
for
$H(\mathbb {K})/R(\mathbb {K})$
for
![]() $g\in G$
, which (as R is normal in H and G an open
$g\in G$
, which (as R is normal in H and G an open
![]() $\mathrm {dfg}$
subgroup of
$\mathrm {dfg}$
subgroup of
![]() $H(\mathbb {K})$
) is an open
$H(\mathbb {K})$
) is an open
![]() ${{\mathbb {Q}}_p}$
-definable
${{\mathbb {Q}}_p}$
-definable
![]() $\mathrm {dfg}$
subgroup of
$\mathrm {dfg}$
subgroup of
![]() $S(\mathbb {K})$
. As
$S(\mathbb {K})$
. As
![]() $G/R(\mathbb {K})$
is infinite, by Lemma 2.19
$G/R(\mathbb {K})$
is infinite, by Lemma 2.19
![]() $G/R(\mathbb {K})$
is not definably compact, so
$G/R(\mathbb {K})$
is not definably compact, so
![]() $G({{\mathbb {Q}}_p})/R({{\mathbb {Q}}_p})$
is not compact. But the latter is a closed subgroup of
$G({{\mathbb {Q}}_p})/R({{\mathbb {Q}}_p})$
is not compact. But the latter is a closed subgroup of
![]() $S({{\mathbb {Q}}_p})$
, whereby
$S({{\mathbb {Q}}_p})$
, whereby
![]() $S({{\mathbb {Q}}_p})$
is not compact. By Fact 2.21(iv), S is
$S({{\mathbb {Q}}_p})$
is not compact. By Fact 2.21(iv), S is
![]() ${{\mathbb {Q}}_p}$
-isotropic. So by Fact 2.21(iii), S has a proper parabolic subgroup P defined over
${{\mathbb {Q}}_p}$
-isotropic. So by Fact 2.21(iii), S has a proper parabolic subgroup P defined over
![]() ${{\mathbb {Q}}_p}$
. As
${{\mathbb {Q}}_p}$
. As
![]() $S/P$
is a complete variety defined over
$S/P$
is a complete variety defined over
![]() ${{\mathbb {Q}}_p}$
,
${{\mathbb {Q}}_p}$
,
![]() $(S/P)({{\mathbb {Q}}_p})$
is compact, so
$(S/P)({{\mathbb {Q}}_p})$
is compact, so
![]() $(S/P)(\mathbb {K})$
is definably compact. Let X be the image of G (or of
$(S/P)(\mathbb {K})$
is definably compact. Let X be the image of G (or of
![]() $G/R(\mathbb {K})$
) in
$G/R(\mathbb {K})$
) in
![]() $(S/P)(\mathbb {K})$
. Then X is also definably compact, again contradicting Lemma 2.19. This contradiction proves that S was trivial, and so
$(S/P)(\mathbb {K})$
. Then X is also definably compact, again contradicting Lemma 2.19. This contradiction proves that S was trivial, and so
![]() $H = R$
is solvable.
$H = R$
is solvable.
We finally have to prove that the toric part
![]() $T = H/H_{u}$
of H splits over
$T = H/H_{u}$
of H splits over
![]() ${{\mathbb {Q}}_p}$
. T is an algebraic torus defined over
${{\mathbb {Q}}_p}$
. T is an algebraic torus defined over
![]() ${{\mathbb {Q}}_p}$
, and by page 53 of [Reference Platonov and Rapinchuk30] for example, T is an almost direct product of tori
${{\mathbb {Q}}_p}$
, and by page 53 of [Reference Platonov and Rapinchuk30] for example, T is an almost direct product of tori
![]() $T_{1}$
,
$T_{1}$
,
![]() $T_{2}$
defined over
$T_{2}$
defined over
![]() ${{\mathbb {Q}}_p}$
where
${{\mathbb {Q}}_p}$
where
![]() $T_{1}$
is
$T_{1}$
is
![]() ${{\mathbb {Q}}_p}$
-split and
${{\mathbb {Q}}_p}$
-split and
![]() $T_{2}$
has no nontrivial split subtorus over
$T_{2}$
has no nontrivial split subtorus over
![]() ${{\mathbb {Q}}_p}$
. We have to show that
${{\mathbb {Q}}_p}$
. We have to show that
![]() $T_{2}$
is trivial. Otherwise
$T_{2}$
is trivial. Otherwise
![]() $T_{2}$
is nontrivial, and by Theorem 3.1 of [Reference Platonov and Rapinchuk30]
$T_{2}$
is nontrivial, and by Theorem 3.1 of [Reference Platonov and Rapinchuk30]
![]() $T_{2}({{\mathbb {Q}}_p})$
is compact so
$T_{2}({{\mathbb {Q}}_p})$
is compact so
![]() $T_{2}(\mathbb {K})$
is definably compact. Now H has a proper normal algebraic subgroup
$T_{2}(\mathbb {K})$
is definably compact. Now H has a proper normal algebraic subgroup
![]() $H_{1}$
defined over
$H_{1}$
defined over
![]() ${{\mathbb {Q}}_p}$
(namely the preimage of
${{\mathbb {Q}}_p}$
(namely the preimage of
![]() $T_{1}$
under the homomorphism
$T_{1}$
under the homomorphism
![]() $H \to H/H_{u}$
) such that the quotient
$H \to H/H_{u}$
) such that the quotient
![]() $H/H_{1} = T_{2}$
. But by Lemma 2.19, as usual the image of G in
$H/H_{1} = T_{2}$
. But by Lemma 2.19, as usual the image of G in
![]() $(H/H_{1}(\mathbb {K})$
is infinite and not definably compact, a contradiction. This completes the proof of the proposition.
$(H/H_{1}(\mathbb {K})$
is infinite and not definably compact, a contradiction. This completes the proof of the proposition.
Corollary 2.23. Let H be a connected algebraic group over
![]() ${{\mathbb {Q}}_p}$
. If
${{\mathbb {Q}}_p}$
. If
![]() $H(\mathbb {K})$
contains an open
$H(\mathbb {K})$
contains an open
![]() ${{\mathbb {Q}}_p}$
-definable
${{\mathbb {Q}}_p}$
-definable
![]() $\mathrm {dfg}$
subgroup G say, then H is trigonalizable over
$\mathrm {dfg}$
subgroup G say, then H is trigonalizable over
![]() ${{\mathbb {Q}}_p}$
.
${{\mathbb {Q}}_p}$
.
Proof By the previous proposition H is linear, solvable, and
![]() $H/H_{u}$
is a
$H/H_{u}$
is a
![]() ${{\mathbb {Q}}_p}$
-split torus. As we are in characteristic
${{\mathbb {Q}}_p}$
-split torus. As we are in characteristic
![]() $0$
the unipotent part
$0$
the unipotent part
![]() $H_{u}$
of H is split (i.e., admits a subnormal series of algebraic subgroups over
$H_{u}$
of H is split (i.e., admits a subnormal series of algebraic subgroups over
![]() ${{\mathbb {Q}}_p}$
whose quotients are isomorphic over
${{\mathbb {Q}}_p}$
whose quotients are isomorphic over
![]() ${{\mathbb {Q}}_p}$
to the additive group). Hence H itself is a
${{\mathbb {Q}}_p}$
to the additive group). Hence H itself is a
![]() ${{\mathbb {Q}}_p}$
-split solvable group over
${{\mathbb {Q}}_p}$
-split solvable group over
![]() ${{\mathbb {Q}}_p}$
. By Fact 2.21(ii), H is trigonalizable over
${{\mathbb {Q}}_p}$
. By Fact 2.21(ii), H is trigonalizable over
![]() ${{\mathbb {Q}}_p}$
.
${{\mathbb {Q}}_p}$
.
2.4
 $\mathrm {dfg}$
Groups and f-generic types
$\mathrm {dfg}$
Groups and f-generic types
Let A, B, C be definable groups, defined over
![]() ${{\mathbb {Q}}_p}$
, such that
${{\mathbb {Q}}_p}$
, such that
![]() $A\leq B$
and
$A\leq B$
and
![]() $\pi : B\longrightarrow C$
is
$\pi : B\longrightarrow C$
is
![]() ${{\mathbb {Q}}_p}$
-definable, such that, moreover,
${{\mathbb {Q}}_p}$
-definable, such that, moreover,
is a short exact sequence, where
![]() $i: A\longrightarrow B$
is the inclusion map. Since
$i: A\longrightarrow B$
is the inclusion map. Since
![]() $\operatorname {\mathrm {Th}}({{\mathbb {Q}}_p})$
has definable Skolem functions (see [Reference Dries8]), let
$\operatorname {\mathrm {Th}}({{\mathbb {Q}}_p})$
has definable Skolem functions (see [Reference Dries8]), let
![]() $f: C\longrightarrow B$
be a
$f: C\longrightarrow B$
be a
![]() ${{\mathbb {Q}}_p}$
-definable section of
${{\mathbb {Q}}_p}$
-definable section of
![]() $\pi $
. Every element b of B can be written uniquely as
$\pi $
. Every element b of B can be written uniquely as
![]() $af(\pi (b))$
for some
$af(\pi (b))$
for some
![]() $a\in A$
.
$a\in A$
.
We will be freely using Facts 1.5 and 1.6 in the following.
Lemma 2.24. Fix notation as above. Suppose that B is definably amenable, then both A and C are definably amenable. Moreover if
![]() $b\in B(\bar {\mathbb {M}})$
is such that
$b\in B(\bar {\mathbb {M}})$
is such that
![]() $\operatorname {\mathrm {tp}}(b/\mathbb {M})$
is an f-generic type, then both
$\operatorname {\mathrm {tp}}(b/\mathbb {M})$
is an f-generic type, then both
![]() $\operatorname {\mathrm {tp}}(\pi (b)/\mathbb {M})$
and
$\operatorname {\mathrm {tp}}(\pi (b)/\mathbb {M})$
and
![]() $\operatorname {\mathrm {tp}}(a/\mathbb {M})$
are f-generic types of C and A, respectively.
$\operatorname {\mathrm {tp}}(a/\mathbb {M})$
are f-generic types of C and A, respectively.
Proof Since
![]() $\operatorname {\mathrm {tp}}(b/\mathbb {M})$
is
$\operatorname {\mathrm {tp}}(b/\mathbb {M})$
is
![]() $B^{00}$
-invariant, we see that
$B^{00}$
-invariant, we see that
![]() $\operatorname {\mathrm {tp}}(\pi (b)/\mathbb {M})$
is
$\operatorname {\mathrm {tp}}(\pi (b)/\mathbb {M})$
is
![]() $\pi (B^{00})$
-invariant, so C is definably amenable and
$\pi (B^{00})$
-invariant, so C is definably amenable and
![]() $\operatorname {\mathrm {tp}}(\pi (b)/\mathbb {M})$
is an f-generic type of C.
$\operatorname {\mathrm {tp}}(\pi (b)/\mathbb {M})$
is an f-generic type of C.
Let
![]() $\eta : B\rightarrow A$
be the function given by
$\eta : B\rightarrow A$
be the function given by
![]() $\eta (x)=x\cdot f(\pi (x))^{-1}$
, then
$\eta (x)=x\cdot f(\pi (x))^{-1}$
, then
![]() $a=\eta (b)$
. For each
$a=\eta (b)$
. For each
![]() $a_0\in A$
, we have
$a_0\in A$
, we have
Since
![]() $\operatorname {\mathrm {tp}}(b/\mathbb {M})$
is f-generic, we see that
$\operatorname {\mathrm {tp}}(b/\mathbb {M})$
is f-generic, we see that
is bounded. So the A-orbit of
![]() $\operatorname {\mathrm {tp}}(a/\mathbb {M})$
$\operatorname {\mathrm {tp}}(a/\mathbb {M})$
is bounded. We conclude that A is definably amenable and
![]() $\operatorname {\mathrm {tp}}(a/\mathbb {M})$
is an f-generic type of C.
$\operatorname {\mathrm {tp}}(a/\mathbb {M})$
is an f-generic type of C.
Lemma 2.25. Let the notation be as above. Suppose that B has
![]() $\mathrm {dfg}$
. Then both A and C have
$\mathrm {dfg}$
. Then both A and C have
![]() $\mathrm {dfg}$
.
$\mathrm {dfg}$
.
Proof Let
![]() $\operatorname {\mathrm {tp}}(b/\mathbb {M})$
be a global f-generic type definable over some small model
$\operatorname {\mathrm {tp}}(b/\mathbb {M})$
be a global f-generic type definable over some small model
![]() $M_0$
. Then, by Lemma 2.24, we see that both
$M_0$
. Then, by Lemma 2.24, we see that both
![]() $\operatorname {\mathrm {tp}}(\pi (b)/\mathbb {M})$
and
$\operatorname {\mathrm {tp}}(\pi (b)/\mathbb {M})$
and
![]() $\operatorname {\mathrm {tp}}(a/\mathbb {M})$
are f-generic types of C and A, respectively.
$\operatorname {\mathrm {tp}}(a/\mathbb {M})$
are f-generic types of C and A, respectively.
Assume that
![]() $M_0$
contains the parameters of
$M_0$
contains the parameters of
![]() $A,B,C$
and
$A,B,C$
and
![]() $\pi $
, then
$\pi $
, then
![]() $a,\pi (b)\in \operatorname {\mathrm {dcl}}(M_0,b)$
, we see that
$a,\pi (b)\in \operatorname {\mathrm {dcl}}(M_0,b)$
, we see that
![]() $\operatorname {\mathrm {tp}}(\pi (b)/\mathbb {M})$
and
$\operatorname {\mathrm {tp}}(\pi (b)/\mathbb {M})$
and
![]() $\operatorname {\mathrm {tp}}(a/\mathbb {M})$
are definable over
$\operatorname {\mathrm {tp}}(a/\mathbb {M})$
are definable over
![]() $M_0$
, and hence
$M_0$
, and hence
![]() $\mathrm {dfg}$
types of C and A, respectively. This concludes the proof that A and C have
$\mathrm {dfg}$
types of C and A, respectively. This concludes the proof that A and C have
![]() $\mathrm {dfg}$
.
$\mathrm {dfg}$
.
Remark 2.26. Let
![]() $A,B$
be algebraic groups over
$A,B$
be algebraic groups over
![]() ${{\mathbb {Q}}_p}$
such that A is a subgroup of B, and
${{\mathbb {Q}}_p}$
such that A is a subgroup of B, and
![]() $B(\mathbb {K})$
is
$B(\mathbb {K})$
is
![]() $\mathrm {dfg}$
. Since the coset space
$\mathrm {dfg}$
. Since the coset space
![]() $(B/A)(\mathbb {K})$
is definable, a similar argument to the proof of Lemma 2.25 shows that
$(B/A)(\mathbb {K})$
is definable, a similar argument to the proof of Lemma 2.25 shows that
![]() $A(\mathbb {K})$
is also
$A(\mathbb {K})$
is also
![]() $\mathrm {dfg}$
.
$\mathrm {dfg}$
.
Proposition 2.27. Let H be an algebraic group over
![]() ${{\mathbb {Q}}_p}$
and G an open
${{\mathbb {Q}}_p}$
and G an open
![]() $\mathrm {dfg}$
subgroup of
$\mathrm {dfg}$
subgroup of
![]() $H(\mathbb {K})$
definable over
$H(\mathbb {K})$
definable over
![]() ${{\mathbb {Q}}_p}$
. Then G has finite index in
${{\mathbb {Q}}_p}$
. Then G has finite index in
![]() $H(\mathbb {K}).$
$H(\mathbb {K}).$
Proof The proof is by induction on
![]() $\dim (H)$
. The statement holds for
$\dim (H)$
. The statement holds for
![]() $\dim (H)=1$
by Proposition 2.15.
$\dim (H)=1$
by Proposition 2.15.
Now assume that
![]() $\dim (H)>1$
.
$\dim (H)>1$
.
By Corollary 2.23, H is trigonalizable over
![]() ${{\mathbb {Q}}_p}$
, and hence there is a short exact sequence of algebraic groups over
${{\mathbb {Q}}_p}$
, and hence there is a short exact sequence of algebraic groups over
![]() ${{\mathbb {Q}}_p}$
${{\mathbb {Q}}_p}$
where A a one-dimensional algebraic group central in H, and C an algebraic group of dimension
![]() $\dim (H)-1$
. Then we have an induced short exact sequence:
$\dim (H)-1$
. Then we have an induced short exact sequence:
By Lemma 2.25, we see that both
![]() $A(\mathbb {K})\cap G$
and
$A(\mathbb {K})\cap G$
and
![]() $\pi (G)$
are open
$\pi (G)$
are open
![]() $\mathrm {dfg}$
subgroups of
$\mathrm {dfg}$
subgroups of
![]() $A(\mathbb {K})$
and
$A(\mathbb {K})$
and
![]() $C(\mathbb {K})$
, respectively. By induction hypothesis, both
$C(\mathbb {K})$
, respectively. By induction hypothesis, both
![]() $A(\mathbb {K})\cap G$
and
$A(\mathbb {K})\cap G$
and
![]() $\pi (G)$
have finite index in
$\pi (G)$
have finite index in
![]() $A(\mathbb {K})$
and
$A(\mathbb {K})$
and
![]() $C(\mathbb {K})$
, respectively. This concludes that G has finite index in
$C(\mathbb {K})$
, respectively. This concludes that G has finite index in
![]() $H(\mathbb {K})$
.
$H(\mathbb {K})$
.
Corollary 2.28. Suppose that
![]() $G_1\leq G_2$
are
$G_1\leq G_2$
are
![]() $\mathrm {dfg}$
groups definable over
$\mathrm {dfg}$
groups definable over
![]() ${{\mathbb {Q}}_p}$
. If
${{\mathbb {Q}}_p}$
. If
![]() $\dim (G_1)=\dim (G_2)$
, then
$\dim (G_1)=\dim (G_2)$
, then
![]() $G_1$
has finite index in
$G_1$
has finite index in
![]() $G_{2}$
.
$G_{2}$
.
Proof By Corollary 2.4, there are a finite index subgroup A of
![]() $G_{2}$
and a finite normal subgroup
$G_{2}$
and a finite normal subgroup
![]() $A_0$
of A, with both A and
$A_0$
of A, with both A and
![]() $A_{0}$
definable over
$A_{0}$
definable over
![]() ${{\mathbb {Q}}_p}$
, and such that
${{\mathbb {Q}}_p}$
, and such that
![]() $A/A_0$
is
$A/A_0$
is
![]() ${{\mathbb {Q}}_p}$
-definably isomorphic to an open subgroup of
${{\mathbb {Q}}_p}$
-definably isomorphic to an open subgroup of
![]() $H(\mathbb {K})$
for some algebraic group H defined over
$H(\mathbb {K})$
for some algebraic group H defined over
![]() ${{\mathbb {Q}}_p}$
. Let
${{\mathbb {Q}}_p}$
. Let
![]() $f: A\longrightarrow H(\mathbb {K})$
be the finite-to-one homomorphism with
$f: A\longrightarrow H(\mathbb {K})$
be the finite-to-one homomorphism with
![]() $\ker (f)=A_0$
as in Fact 2.1. By Proposition 2.27,
$\ker (f)=A_0$
as in Fact 2.1. By Proposition 2.27,
![]() $\operatorname {\mathrm {im}}(f)$
has finite index in
$\operatorname {\mathrm {im}}(f)$
has finite index in
![]() $H({{\mathbb {Q}}_p})$
. As
$H({{\mathbb {Q}}_p})$
. As
![]() $G_1\cap A$
has finite index in
$G_1\cap A$
has finite index in
![]() $G_1$
, we see that
$G_1$
, we see that
![]() $G_1\cap A$
has
$G_1\cap A$
has
![]() $\mathrm {dfg}$
. So the image
$\mathrm {dfg}$
. So the image
![]() $f(G_1\cap A)$
is an open
$f(G_1\cap A)$
is an open
![]() $\mathrm {dfg}$
subgroup of
$\mathrm {dfg}$
subgroup of
![]() $H(\mathbb {K})$
, and hence has finite index in
$H(\mathbb {K})$
, and hence has finite index in
![]() $H(\mathbb {K})$
by Proposition 2.27. It follows easily that
$H(\mathbb {K})$
by Proposition 2.27. It follows easily that
![]() $G_{1}$
has finite index in
$G_{1}$
has finite index in
![]() $G_{2}$
.
$G_{2}$
.
A generalization of Corollary 2.28 has been proved in [Reference Guerrero and Johnson10, Corollary 4.4].
We now prove the following two structure theorems for
![]() $\mathrm {dfg}$
groups using Proposition 2.27:
$\mathrm {dfg}$
groups using Proposition 2.27:
Theorem 2.29. Let G be an open
![]() $\mathrm {dfg} \ {{\mathbb {Q}}_p}$
-definable subgroup of
$\mathrm {dfg} \ {{\mathbb {Q}}_p}$
-definable subgroup of
![]() $H(\mathbb {K})$
where H is an algebraic group defined over
$H(\mathbb {K})$
where H is an algebraic group defined over
![]() ${{\mathbb {Q}}_p}$
. Then there is a normal sequence
${{\mathbb {Q}}_p}$
. Then there is a normal sequence
such that each
![]() $G_{i}$
is definable over
$G_{i}$
is definable over
![]() ${{\mathbb {Q}}_p}$
and each
${{\mathbb {Q}}_p}$
and each
![]() $G_{i+1}/G_i$
is definably over
$G_{i+1}/G_i$
is definably over
![]() ${{\mathbb {Q}}_p}$
isomorphic to a one-dimensional
${{\mathbb {Q}}_p}$
isomorphic to a one-dimensional
![]() $\mathrm {dfg}$
group.
$\mathrm {dfg}$
group.
Proof Induction on
![]() $\dim (G)$
. Clearly, the statement is trivial if
$\dim (G)$
. Clearly, the statement is trivial if
![]() $\dim (G)=1$
. Now assume that
$\dim (G)=1$
. Now assume that
![]() $\dim (G)>1$
. As we showed in Proposition 2.27, there is a short exact sequence
$\dim (G)>1$
. As we showed in Proposition 2.27, there is a short exact sequence
with A a one-dimensional algebraic group central in H, and C an algebraic group of dimension
![]() $\dim (H)-1$
, where everything is over
$\dim (H)-1$
, where everything is over
![]() ${{\mathbb {Q}}_p}.$
Both
${{\mathbb {Q}}_p}.$
Both
![]() $A(\mathbb {K})\cap G$
and
$A(\mathbb {K})\cap G$
and
![]() $\pi (G)$
are open
$\pi (G)$
are open
![]() $\mathrm {dfg}$
subgroups of
$\mathrm {dfg}$
subgroups of
![]() $A(\mathbb {K})$
and
$A(\mathbb {K})$
and
![]() $C(\mathbb {K})$
, respectively. By induction hypothesis, there is a normal sequence
$C(\mathbb {K})$
, respectively. By induction hypothesis, there is a normal sequence
such that each
![]() $D_{i+1}/D_i$
is definably isomorphic to a one-dimensional
$D_{i+1}/D_i$
is definably isomorphic to a one-dimensional
![]() $\mathrm {dfg}$
group over
$\mathrm {dfg}$
group over
![]() ${{\mathbb {Q}}_p}$
. It is easy to see that the normal sequence
${{\mathbb {Q}}_p}$
. It is easy to see that the normal sequence
meets our requirements.
Theorem 2.30. Let G be a group definable over
![]() ${{\mathbb {Q}}_p}$
with
${{\mathbb {Q}}_p}$
with
![]() $\mathrm {dfg}$
. Then there is a normal sequence
$\mathrm {dfg}$
. Then there is a normal sequence
of
![]() ${{\mathbb {Q}}_p}$
-definable groups, such that
${{\mathbb {Q}}_p}$
-definable groups, such that
![]() $G_0$
is finite,
$G_0$
is finite,
![]() $G_n$
is a finite index subgroup of G, and
$G_n$
is a finite index subgroup of G, and
![]() $G_{i+1}/G_i$
is isomorphic to a one-dimensional
$G_{i+1}/G_i$
is isomorphic to a one-dimensional
![]() $\mathrm {dfg}$
group over
$\mathrm {dfg}$
group over
![]() ${{\mathbb {Q}}_p}$
.
${{\mathbb {Q}}_p}$
.
Proof By Corollary 2.4, there is a finite index subgroup
![]() $A_{1}\leq G$
and a finite normal subgroup
$A_{1}\leq G$
and a finite normal subgroup
![]() $A_0\subseteq A$
, all
$A_0\subseteq A$
, all
![]() ${{\mathbb {Q}}_p}$
-definable, such that
${{\mathbb {Q}}_p}$
-definable, such that
![]() $A_1/A_0$
is
$A_1/A_0$
is
![]() ${{\mathbb {Q}}_p}$
-definably isomorphic to an open subgroup of
${{\mathbb {Q}}_p}$
-definably isomorphic to an open subgroup of
![]() $H(\mathbb {K})$
for H some (connected) algebraic group defined over
$H(\mathbb {K})$
for H some (connected) algebraic group defined over
![]() ${{\mathbb {Q}}_p}$
. Let
${{\mathbb {Q}}_p}$
. Let
![]() $f: A_1\longrightarrow H(\mathbb {K})$
be the finite-to-one homomorphism with
$f: A_1\longrightarrow H(\mathbb {K})$
be the finite-to-one homomorphism with
![]() $\ker (f)=A_0$
as in Fact 2.1. By Proposition 2.27,
$\ker (f)=A_0$
as in Fact 2.1. By Proposition 2.27,
![]() $\operatorname {\mathrm {im}}(f)$
has finite index in
$\operatorname {\mathrm {im}}(f)$
has finite index in
![]() $H(\mathbb {K})$
. Moreover H is trigonalizable over
$H(\mathbb {K})$
. Moreover H is trigonalizable over
![]() ${{\mathbb {Q}}_p}$
by Proposition 2.22.
${{\mathbb {Q}}_p}$
by Proposition 2.22.
Clearly, the statement is trivial if
![]() $\dim (G)=1$
. Now assume that
$\dim (G)=1$
. Now assume that
![]() $\dim (G)>1$
. As we showed in Proposition 2.27, there is a short exact sequence
$\dim (G)>1$
. As we showed in Proposition 2.27, there is a short exact sequence
with A a one-dimensional algebraic group central in H, and C an algebraic group of dimension
![]() $\dim (H)-1$
, all defined over
$\dim (H)-1$
, all defined over
![]() ${{\mathbb {Q}}_p}$
. Both
${{\mathbb {Q}}_p}$
. Both
![]() $A(\mathbb {K})\cap \operatorname {\mathrm {im}}(f)$
and
$A(\mathbb {K})\cap \operatorname {\mathrm {im}}(f)$
and
![]() $\pi (\operatorname {\mathrm {im}}(f))$
are open
$\pi (\operatorname {\mathrm {im}}(f))$
are open
![]() $\mathrm {dfg}$
subgroups of
$\mathrm {dfg}$
subgroups of
![]() $A(\mathbb {K})$
and
$A(\mathbb {K})$
and
![]() $C(\mathbb {K})$
, respectively. By Theorem 2.29, there is a normal sequence
$C(\mathbb {K})$
, respectively. By Theorem 2.29, there is a normal sequence
such that each
![]() $D_{i+1}/D_i$
is definably isomorphic to a one-dimensional
$D_{i+1}/D_i$
is definably isomorphic to a one-dimensional
![]() $\mathrm {dfg}$
group over
$\mathrm {dfg}$
group over
![]() ${{\mathbb {Q}}_p}$
. Let
${{\mathbb {Q}}_p}$
. Let
![]() $E_i=\pi ^{-1}(D_i)\cap \operatorname {\mathrm {im}} (f).$
It is easy to see that
$E_i=\pi ^{-1}(D_i)\cap \operatorname {\mathrm {im}} (f).$
It is easy to see that
![]() $D_i=\pi (E_i)$
, thus
$D_i=\pi (E_i)$
, thus
![]() $E_i/(A(\mathbb {K})\cap \operatorname {\mathrm {im}}(f))\cong D_i$
. So
$E_i/(A(\mathbb {K})\cap \operatorname {\mathrm {im}}(f))\cong D_i$
. So
is definably isomorphic to a one-dimensional
![]() $\mathrm {dfg}$
group over
$\mathrm {dfg}$
group over
![]() ${{\mathbb {Q}}_p}$
. We conclude that
${{\mathbb {Q}}_p}$
. We conclude that
is a normal sequence such that
![]() $ E_0=A(\mathbb {K})\cap \operatorname {\mathrm {im}}(f)$
and each
$ E_0=A(\mathbb {K})\cap \operatorname {\mathrm {im}}(f)$
and each
![]() $E_{i+1}/E_i$
is definably isomorphic to a one-dimensional
$E_{i+1}/E_i$
is definably isomorphic to a one-dimensional
![]() $\mathrm {dfg}$
group over
$\mathrm {dfg}$
group over
![]() ${{\mathbb {Q}}_p}$
. Let
${{\mathbb {Q}}_p}$
. Let
![]() $G_0=A_0$
and
$G_0=A_0$
and
![]() $G_{i+1}=f^{-1}(E_i)$
, we see that the normal sequence
$G_{i+1}=f^{-1}(E_i)$
, we see that the normal sequence
satisfies our requirement.
Finally we answer the Conjecture 1 in the p-adic case, making use of the following.
Fact 2.31 [Reference Yao37].
Let H be a trigonalizable algebraic group over
![]() ${{\mathbb {Q}}_p}$
. Then every global complete f-generic type of
${{\mathbb {Q}}_p}$
. Then every global complete f-generic type of
![]() $H(\mathbb {K})$
is almost periodic.
$H(\mathbb {K})$
is almost periodic.
By Proposition 2.27 and Fact 2.31, we easily conclude the following.
Theorem 2.32. Suppose that G is a
![]() $\mathrm {dfg}$
group over
$\mathrm {dfg}$
group over
![]() ${{\mathbb {Q}}_p}$
. Then every global complete f-generic type of G is almost periodic.
${{\mathbb {Q}}_p}$
. Then every global complete f-generic type of G is almost periodic.
Acknowledgements
The authors would like to thank the referee for carefully reading our paper and offering detailed comments, which have been very helpful for us as we revise the paper.
Funding
The first author was supported by the NSF grants DMS-1665035, DMS-1760212, and DMS-2054271. The second author was supported by The National Social Science Fund of China (Grant No. 20CZX050).