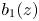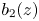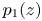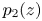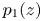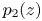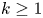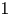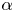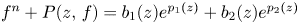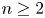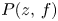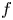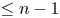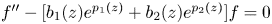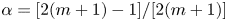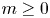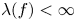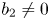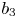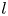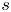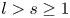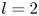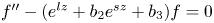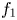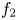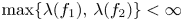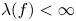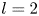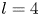On the oscillation of certain second-order linear differential equations

Abstract

This paper consists of three parts: First, letting $b_1(z)$, $b_2(z)$, $p_1(z)$ and $p_2(z)$ be nonzero polynomials such that $p_1(z)$ and $p_2(z)$ have the same degree $k\geq 1$ and distinct leading coefficients $1$ and $\alpha$, respectively, we solve entire solutions of the Tumura–Clunie type differential equation $f^{n}+P(z,\,f)=b_1(z)e^{p_1(z)}+b_2(z)e^{p_2(z)}$, where $n\geq 2$ is an integer, $P(z,\,f)$ is a differential polynomial in $f$ of degree $\leq n-1$ with coefficients having polynomial growth. Second, we study the oscillation of the second-order differential equation $f''-[b_1(z)e^{p_1(z)}+b_2(z)e^{p_2(z)}]f=0$ and prove that $\alpha =[2(m+1)-1]/[2(m+1)]$ for some integer $m\geq 0$ if this equation admits a nontrivial solution such that $\lambda (f)<\infty$. This partially answers a question of Ishizaki. Finally, letting $b_2\not =0$ and $b_3$ be constants and $l$ and $s$ be relatively prime integers such that $l> s\geq 1$, we prove that $l=2$ if the equation $f''-(e^{lz}+b_2e^{sz}+b_3)f=0$ admits two linearly independent solutions $f_1$ and $f_2$ such that $\max \{\lambda (f_1),\,\lambda (f_2)\}<\infty$. In particular, we precisely characterize all solutions such that $\lambda (f)<\infty$ when $l=2$ and $l=4$.

1. Introduction

In the last several decades, the growth and value distribution of meromorphic solutions of complex differential equations have attracted much interest; see [23] and references therein. One of the main tools in this subject is Nevanlinna theory; see, e.g., [14, 23] for the standard notation and basic results of Nevanlinna theory. Bank and Laine [2, 3] initiated the study on the oscillation of the second-order linear differential equation

(1.1)\begin{equation} f''+A(z)f=0, \end{equation}

where $A(z)$ is an entire function. It is well-known that all solutions of equation (1.1) are entire. For an entire function $f$, denote by $\sigma (f)$ the order of $f$ which is defined as

\[ \sigma(f)=\limsup_{r\to\infty}\frac{\log T(r,f)}{\log r}=\limsup_{r\to\infty}\frac{\log\log M(r,f)}{\log r}, \]

where $M(r,\,f)$ is the maximum modulus of $f$ on the circle $|z|=r$. When $A$ is transcendental, an application of the lemma on the logarithmic derivative easily yields that all nontrivial solutions of (1.1) satisfy $\sigma (f)=\infty$. Denote by $\lambda (f)$ the exponent of convergence of zeros of $f$ which is defined as

\[ \lambda(f)=\limsup_{r\to\infty}\frac{\log n(r,f)}{\log r}, \]

where $n(r,\,f)$ denotes the number of zeros of $f$ in the disc $\{z: |z|< r\}$. Concerning the zero distribution of solutions of equation (1.1), Bank and Laine [2, 3] proved: Let $f_1$ and $f_2$ be two linearly independent solutions of (1.1). If $\sigma (A)$ is not an integer, then $\max \{\lambda (f_1),\,\lambda (f_2)\}\geq \sigma (A)$; if $\sigma (A)<1/2$, then $\max \{\lambda (f_1),\,\lambda (f_2)\}=\infty$. Later, Shen [29] and Rossi [28] relaxed the condition $\sigma (A)<1/2$ to the case $\sigma (A)=1/2$. Based on these results, Bank and Laine conjectured that $\max \{\lambda (f_1),\,\lambda (f_2)\}=\infty$ whenever $\sigma (A)$ is not an integer. This conjecture is known as the Bank–Laine conjecture and has attracted much interest; see the surveys [13, 24] and references therein. Recently, this conjecture was disproved by Bergweiler and Eremenko [7, 8]. They constructed counterexamples for the coefficient $A$ such that $\sigma (A)$ is not an integer and equation (1.1) admits two linearly independent solutions such that $\max \{\lambda (f_1),\,\lambda (f_2)\}<\infty$. In particular, one of the solutions is free of zeros. In their constructions, they used the solutions of (1.1) with $A$ being a polynomial of $e^z$ of degree 2, namely $A(z)=a_1e^{2z}+a_2e^z+a_3$ with certain coefficients $a_1$, $a_2$ and $a_3$.

On the other hand, it is natural to give explicit solutions of (1.1) such that $\lambda (f)<\infty$ when $A$ is a periodic entire function of the form

(1.2)\begin{equation} A(z)=B(e^z), \quad B(\zeta)=b_{{-}k}\zeta^{{-}k}+\cdots+b_0+\cdots+b_l\zeta^{l}, \quad b_{{-}k}b_l\not=0. \end{equation}

For such solutions, a remarkable result in [4, 9] states that there exist complex constants $c$, $c_j$ and a polynomial $P(z)$ with simple roots only such that if $l$ is an odd positive integer, then

(1.3)\begin{equation} f=P(e^{z/2})\exp\left(\sum_{j=0}^{l}c_je^{(l-j)z/2}+cz\right), \end{equation}

where $c_j=0$ whenever $j$ is even; while if $l$ is an even positive integer, then

(1.4)\begin{equation} f=P(e^{z})\exp\left(\sum_{j=0}^{l/2}c_je^{(l/2-j)z}+cz\right). \end{equation}

However, it seems difficult to determine explicitly $c_j$ and also the polynomial $P(z)$ in the above two expressions and, until now, they are only known in some special cases. For example, Bank and Laine [4] gave a precise characterization of all nontrivial solutions such that $\lambda (f)<\infty$ of (1.1) when $A(z)=e^{z}-b$ for some constant $b$; see also [23, theorem 5.22]. Bank and Laine [4] also characterized entire solutions such that $\lambda (f)<\infty$ of equation (1.1) when $A(z)=-(1/4)e^{-2z}+(1/2)e^{-z}+b$ for some constant $b$. For these two coefficients, Chiang and Ismail [10] expressed all solutions of (1.1) in terms of some special functions and give a complete characterization of the zero distribution of these solutions.

In [1], Bank developed a method to find entire solutions such that $\lambda (f)<\infty$ of equation (1.1), but the manipulation of this method seems complicated. One of the main purposes of this paper is to give a more precise description of the oscillation of equation (1.1) when $A(z)$ contains two exponential terms, i.e.,

(1.5)\begin{equation} A(z)=B(e^z), \quad B(\zeta)=b_{{-}k}\zeta^{{-}k}+b_0+b_l\zeta^{l}, \quad b_{{-}k}b_l\not=0, \end{equation}

or

(1.6)\begin{equation} A(z)=B(e^z), \quad B(\zeta)=b_0+b_{s}\zeta^{s}+b_l\zeta^{l}, \quad b_sb_l\not=0. \end{equation}

In particular, this provides a different approach from that in [10] and also leads to a complete characterization of all solutions such that $\lambda (f)<\infty$ of (1.1) when $A(z)$ is an arbitrary polynomial in $e^z$ of degree $2$; see theorem 4.4 in § 4. This work is a continuation of [33], where the present author found all nontrivial solutions such that $\lambda (f)< k$ of the differential equation

(1.7)\begin{equation} f''-\left[b_1(z)e^{p_1(z)}+b_2(z)e^{p_2(z)}+b_3(z)\right]f=0, \end{equation}

where $b_1(z)$, $b_2(z)$ and $b_3(z)$ are three polynomials such that $b_1(z)b_2(z)\not \equiv 0$ and $p_1(z)$ and $p_2(z)$ are two polynomials of the same degree $k\geq 1$ with distinct leading coefficients $1$ and $\alpha$, respectively.

Theorem 1.1 see [33]

Let $b_1$, $b_2$ and $b_3$ be polynomials such that $b_1b_2\not \equiv 0$ and $p_1$, $p_2$ be two polynomials of degree $k\geq 1$ with distinct leading coefficients $1$ and $\alpha$, respectively, and $p_1(0)=p_2(0)=0$. Suppose that (1.7) admits a nontrivial solution such that $\lambda (f)< k$. Then $\alpha =1/2$ or $\alpha =3/4$. Moreover,

1. (1) if $\alpha =1/2,$ then $p_2=p_1/2,$ $f=\kappa e^{h},$ where $\kappa$ is a polynomial with simple roots only and $h$ satisfies $h'=\gamma _1e^{p_1/2}+\gamma$ with $\gamma _1$ and $\gamma$ being two polynomials such that $\gamma _1^2=b_1$, $2\gamma _1\gamma +\gamma _1'+\gamma _1p_1'/2+2\kappa '/\kappa \gamma _1=b_2$ and $\gamma ^2+\gamma '+2\gamma \kappa '/\kappa +\kappa ''/\kappa =b_3$;

2. (2) if $\alpha =3/4,$ then $p_1=z,$ $p_2=3z/4$ and $f=e^{h},$ where $h$ satisfies $h'=-4c^2e^{z/2}+ce^{z/4}-1/8$ and $A=-(16c^2e^{z}-8c^3e^{3z/4}+1/64),$ where $c$ is a nonzero constant.

The proof of theorem 1.1 is based on a development of the Tumura–Clunie method; see [14, chapter 4]. Define a differential polynomial $P(z,\,g)$ in $g$ to be a finite sum of monomials in $g$ and its derivatives of the form $P(z,\,g)=\sum _{l=1}^{m}a_{l}g^{n_{l0}}(g')^{n_{l1}}\cdots (g^{(s)})^{n_{ls}}$, where $n_{l0},\,\cdots,\,n_{ls}\in \mathbb {N}$ and the coefficients $a_l$ are meromorphic functions of order less than $\sigma (g)$. Define the degree of $P(z,\,g)$ to be the greatest integer of $d_l:=\sum _{t=0}^sn_{lt}$, $l=1,\,\cdots,\,m$, and denote it by $\deg _g(P(z,\,g))$. Consider the equation

(1.8)\begin{equation} g^n+P(z,g)=b_1e^{p_1}+b_2e^{p_2}, \end{equation}

where $n\geq 2$ and $P(z,\,g)$ is a differential polynomial in $g$ of degree $\leq n-1$ with meromorphic functions of order less than $k$ as coefficients. If equation (1.7) admits an entire solution such that $\lambda (f)< k$, then equation (1.7) reduces to an equation of the form in (1.8) with $n=2$. It is shown in [33, theorem 2.1] that if equation (1.8) admits an entire solution, then either $\alpha =-1$ or $\alpha$ is positive rational number and in either case $g$ is a linear combination of certain exponential functions plus some function of order less than $k$. However, to solve entire solutions of (1.7) such that $\lambda (f)<\infty$, [33, theorem 2.1] fails to work since in this case the coefficients of $P(z,\,g)$ shall contain some logarithmic derivatives which have order no less than $k$.

The remainder of this paper is organized in the following way. Denote by $\mathcal {R}$ the set of rational functions and by $\mathcal {L}$ the set of functions $a(z)$ such that $a(z)=h^{(l)}(z)/h(z)$, $l\geq 1$, for some meromorphic function $h(z)$ of finite order, respectively. In § 2, we further develop the Tumura–Clunie method by solving entire solutions of equation (1.8), where $P(z,\,g)$ is now a differential polynomial in $g$ with coefficients that are combinations of functions in the set $\mathcal {S}=\mathcal {R}\cup \mathcal {L}$. For equation (1.8) with such coefficients, we can also write the entire solution as a linear combination of exponential functions with certain constant coefficients, but unlike in [33, theorem 2.1], it is impossible to determine whether $\alpha$ is a rational number; see theorem 2.1. In § 3, we apply our results on equation (1.8) to study the oscillation of equation (1.7) and prove that $\alpha =[2(m+1)-1]/[2(m+1)$] for some integer $m\geq 0$ provided that equation (1.7) with $b_3\equiv 0$ admits a nontrivial solution such that $\lambda (f)<\infty$; see theorem 3.1. This gives a partial answer to a question of Ishizaki [19]. In § 4, we consider the equation $f''-(b_1e^{lz}+b_2e^{sz}+b_3)f=0$, where $l,\,s$ are relatively prime integers such that $l>s\geq 1$ and $b_i$ are constants such that $b_1b_2\not =0$. We prove that $l=2$ if this equation admits two linearly independent solutions $f_1$ and $f_2$ such that $\max \{\lambda (f_1),\,\lambda (f_2)\}<\infty$. In particular, when $l=2$ or $l=4$, we determine the polynomial $P(z)$ and the coefficients $c_j$ and $c$ in (1.4) precisely. Finally, in § 5, we give some remarks on our results.

2. Tumura–clunie differential equations

Let $b_1(z)$ and $b_2(z)$ be two nonzero polynomials and $p_1(z)$ and $p_2(z)$ be two polynomials of the same degree $k\geq 1$ with distinct leading coefficients $1$ and $\alpha$, respectively, and $p_1(0)=p_2(0)=0$. Without loss of generality, we may suppose that $0<|\alpha |\leq 1$. In this section, we solve entire solutions of the differential equation

(2.1)\begin{equation} f^n+P(z,f)=b_1e^{p_1}+b_2e^{p_2}, \end{equation}

where $n\geq 2$ and $P(z,\,f)$ is a differential polynomial in $f$ of degree $\leq n-1$ with coefficients being combinations of functions in $\mathcal {S}$. In the following, a differential polynomial in $f$ will always have coefficients which are combinations of functions in $\mathcal {S}$ and thus we will omit mentioning this from now on.

To state our results, we first set up some notation: Let $p(z)$ be a polynomial of degree $k\geq 1$. We write $p(z)=(a+ib)z^{k}+q(z)$, where $a,\,b$ are real and $a+ib\not =0$ and $q(z)$ is a polynomial of degree at most $k-1$. Denote

(2.2)\begin{equation} \delta(p,\theta)=a\cos k\theta-b\sin k\theta, \quad \theta\in[0,2\pi). \end{equation}

Then on the ray $z=re^{i\theta }$, $r\geq 0$, from [6] (or [23, lemma 5.14]) we know that:

1. 1. if $\delta (p,\,\theta )>0$, then there exists an $r_0=r_0(\theta )$ such that $\log |e^{p(z)}|$ is increasing on $[r_0,\,\infty )$ and $|e^{p(z)}|\geq e^{\delta (p,\theta )r^{n}/2}$ there;

2. 2. if $\delta (p,\,\theta )<0$, then there exists an $r_0=r_0(\theta )$ such that $\log |e^{p(z)}|$ is decreasing on $[r_0,\,\infty )$ and $|e^{p(z)}|\leq e^{\delta (p,\theta )r^{n}/2}$ there.

Let $\theta _1,\, \theta _2,\, \cdots,\, \theta _{2k}\in [0,\,2\pi )$ be such that $\delta (p,\,\theta _j)=0$, $j=1,\,2,\,\cdots,\,2k$. We may suppose that $\theta _1< \pi$ and $\theta _j=\theta _1+(j-1)\pi /k$. Denoting $\theta _{2k+1}=\theta _1+2\pi$, then $\theta _1$, $\theta _2$, $\cdots$, $\theta _{2k}$ divides the complex plane $\mathbb {C}$ into $2k$ sectors $S_j$, namely

(2.3)\begin{equation} S_j=\left\{re^{i\theta}:\, 0\leq r<\infty, \quad \theta_j< \theta<\theta_{j+1}\right\}, \quad j=1,2,\cdots,2k. \end{equation}

Throughout this paper, we let $\epsilon >0$ be an arbitrary constant. We also denote

(2.4)\begin{equation} S_{j,\epsilon}=\left\{re^{i\theta}:\, 0\leq r<\infty, \quad \theta_j+\epsilon<\theta<\theta_{j+1}-\epsilon\right\}, \quad j=1,2,\cdots,2k. \end{equation}

Denote by $\overline {S}_j$ and $\overline {S}_{j,\epsilon }$ the closure of $S_j$ and $S_{j,\epsilon }$, respectively. For $p_1$ in (2.1), we choose $\theta _1=-\pi /(2k)$ and thus $\delta (p_1,\,\theta )>0$ in the sectors $S_j$ when $j$ is odd, and $\delta (p_1,\,\theta )<0$ in the sectors $S_j$ when $j$ is even. Denote by $J_1$ and $J_2$ the subsets of odd and even integers in the set $J=\{1,\,2\cdots,\,2k\}$, respectively, i.e., $J_1=\{1,\,3,\,\cdots,\,2k-1\}$ and $J_2=\{2,\,4,\,\cdots,\,2k\}$. We prove the following

Theorem 2.1 Let $n\geq 2$ be an integer and $P(z,\,f)$ be a differential polynomial in $f$ of degree $\leq {n-1}$. Suppose that (2.1) admits an entire solution $f$. Then $\alpha$ is real. Moreover,

1. (1) if $-1\leq \alpha <0,$ then $f=\gamma _1e^{p_1/n}+\gamma _2e^{p_2/n}+\eta,$ where $\gamma _1,$ $\gamma _2$ are two polynomials such that $\gamma _1^n=b_1,$ $\gamma _2^n=b_2$ and $\eta$ is an entire function such that $\eta =(\mu _{1,j}-1)\gamma _1e^{p_1/n}+(\mu _{2,j}-1)\gamma _2e^{p_2/n}+\eta _j,$ where $\mu _{1,j}$ and $\mu _{2,j}$ are the $n$-th roots of $1$ such that $\mu _{1,j}=1$ when $j\in \{1\}\cup J_2$ and $\mu _{2,j}=1$ when $j\in \{2\}\cup J_1,$ and there is an integer $N$ such that $|\eta _j|=O(r^N)$ uniformly in $\overline {S}_{j,\epsilon };$ in particular, when $k=1,$ $\eta$ is a polynomial;

2. (2) if $0<\alpha <1,$ letting $m$ be the smallest integer such that $\alpha \leq [(m+1)n-1]/[(m+1)n],$ then $f=\gamma _1\sum _{j=0}^mc_j(b_2/b_1)^je^{[jn(\alpha -1)+1]p_1/n}+\eta$, where $\gamma _1$ is a polynomial such that $\gamma _1^n=b_1$ and $c_0,$ $\cdots,$ $c_m$ are constants such that $c_0^{n}=1$ when $m=0,$ and $c_0^{n}=nc_0^{n-1}c_1=1$ when $m=1$, and $c_0^{n}=nc_0^{n-1}c_1=1$ and $\sum _{\substack {j_0+\cdots +j_m=n,\\ j_1+\cdots +mj_m=k_0}}\frac {n!}{j_0!j_1!\cdots j_m!}c_0^{j_0}c_1^{j_1}\cdots c_m^{j_m}=0,$ $k_0=2,\,\cdots,\,m,$ when $m\geq 2,$ and $\eta$ is a meromorphic function with at most finitely many poles such that $\eta =\gamma _1\sum _{l=0}^m(\mu _j-1)c_{j}(b_2/b_1)^je^{[jn(\alpha -1)+1]p_1/n}+\eta _{j},$ where $\mu _j$ are the $n$-th roots of $1$ such that $\mu _j=1$ when $j\in \{1\}\cup J_2,$ and there is an integer $N$ such that $|\eta _j|=O(r^N)$ uniformly in $\overline {S}_{j,\epsilon };$ moreover, we have $p_2=\alpha p_1$ when $m\geq 1;$ in particular, when $k=1,$ $\eta$ is a rational function.

In theorem 2.1, if all coefficients of the monomials in $P(z,\,f)$ of degree $n-1$ are rational functions, then we may use the method in the proof of [33, theorem 2.1] to show that $\eta$ is a polynomial or a rational function. We also remark that, by using the method in the proof of theorem 2.1 for the case $-1\leq \alpha <0$ together with the method in [34], we may extend [33, theorem 2.1] to the case $P(z,\,f)$ is a delay–differential polynomial in $f$ with meromorphic functions of order less than $k$ as coefficients; see [34] for the definition of a delay–differential polynomial.

As in the proof of theorems [34, theorem 1.1] and [33, theorem 2.1], we also start from analysing first-order linear differential equation $f'-uf=w$, where $u$ is a nonzero polynomial and $w$ is a meromorphic function with at most finitely many poles. Let $p(z)$ be a primitive function of $u$ and suppose that $\deg (p(z))=k\geq 1$. If $f$ is meromorphic, then there is a rational function $v(z)$ such that $v(z)\to 0$ as $z\to \infty$ and $h(z)=f(z)-v(z)$ is entire. It follows that $f(z)=h(z)+v(z)$ and $h$ satisfies $h'-uh=w-(v'-uv)$ and $w-(v'-uv)$ is an entire function. By elementary integration, the meromorphic solutions of $f'-uf=w$ are $f=ce^{p(z)}+H(z)$, where

(2.5)\begin{equation} H(z)=e^{p(z)}\int_0^{z}w(t) e^{{-}p(t)}\,{\rm d}t. \end{equation}

To study the growth behaviour of this function, a useful tool is the Phragmén–Lindelöf theorem (see [18, theorem 7.3]): Let $f(z)$ be an analytic function, regular in a region $D$ between two straight lines making an angle $\pi /\tau _1$ at the origin, and on the lines themselves. Suppose that $|f(z)|\leq M$ on the line, and that, as $r\to \infty$ $|f(z)|=O(e^{r^{\tau _2}})$, where $\tau _2<\tau _1$, uniformly in the angle. Then actually $|f(z)|\leq M$ holds throughout the region. Moreover, if $f(z)\to c_1$ and $f(z)\to c_2$ as $z\to \infty$ along the two lines, respectively, then $c_1=c_2$ and $f(z)\to c_1$ uniformly as $z\to \infty$ in $D$. Using the Phragmén–Lindelöf theorem, the present author proved the following

Lemma 2.2 see [33, 34]

Let $p(z)$ be a polynomial with degree $k\geq 1$ and $w$ be a nonzero polynomial. Then there is an integer $N$ such that for each $S_j$ where $\delta (p,\,\theta )>0$, there is a constant $a_j$ such that $|H(re^{i\theta })-a_je^{p(re^{i\theta })}|= O(r^N)$ uniformly in $\overline {S}_{j,\epsilon }$, and for each $S_j$ where $\delta (p,\,\theta )<0$ and any constant $a$, $|H(re^{i\theta })-ae^{p(re^{i\theta })}|= O(r^N)$ uniformly in $\overline {S}_{j,\epsilon }$.

Most arguments we use below are the same as that in the proof of [33, theorem 2.1]. We also first introduce the definition of $R$–set: An $R$–set in the complex plane is a countable union of discs whose radii have finite sum. Let $f(z)$ be an entire solution of (2.1). We denote the union of all $R$–sets associated with $f(z)$ and each coefficient of $P(z,\,f)$ by $\tilde {R}$ from now on. In the proof of theorem 2.1, after taking the derivatives on both sides of equation (2.1), there may be some new coefficients appearing in the resulting equations. We will always assume that $\tilde {R}$ also contains those $R$-sets associated with these new coefficients.

As in the proof of [33, theorem 2.1], we first reduce (2.1) into a non-homogeneous linear differential equation with rational coefficients. Now, with all coefficients of $P(z,\,f)$ being combinations of functions in $\mathcal {S}$, the key lemma for this aim is the following

Lemma 2.3 Under the assumptions of theorem 2.1 , $\sigma (f)=k$ and $\alpha$ is real. Moreover, for any $\theta \in [0,\,2\pi )$ such that the ray $z=re^{i\theta }$ meets finitely discs in $\tilde {R},$

1. (1) when $-1\!\leq\! \alpha <0,$ if $\delta (p_1,\,\theta )\!>\!0,$ then $|f(re^{i\theta })^n|=(1+o(1)) |b_1(re^{i\theta })e^{p_1(re^{i\theta })}|,$ $r\to \infty ;$ if $\delta (p_2,\,\theta )>0,$ then $|f(re^{i\theta })^n|=(1+o(1))|b_2(re^{i\theta })e^{p_2(re^{i\theta })}|,$ $r\to \infty ;$

2. (2) when $0<\alpha <1,$ if $\delta (p_1,\,\theta )>0,$ then $|f(re^{i\theta })^n|=(1+o(1)) |b_1(re^{i\theta })e^{p_1(re^{i\theta })}|,$ $r\to \infty ;$ if $\delta (p_1,\,\theta )<0,$ then there is an integer $N$ such that $|f(re^{i\theta })|\leq r^N$ for all large $r$.

Proof of lemma 2.3. Since $\alpha \not =1$, then by Steinmetz's result [30] for exponential polynomials, we have $T(r,\,b_1e^{p_1}+b_2e^{p_2})=K(1+o(1))r^k$ for some nonzero constant $K$ depending only on $\alpha$. Recall that the coefficients of equation (2.1) are combinations of functions in $\mathcal {S}$. By the lemma on the logarithmic derivative, we deduce from equation (2.1) that

(2.6)\begin{equation} \begin{aligned} T\left(r,b_1e^{p_1}+b_2e^{p_2}\right) & =m\left(r,b_1e^{p_1}+b_2e^{p_2}\right)\\ & =m\left(r,f^n+P(z,f)\right)\leq nm(r,f)+O(\log r). \end{aligned} \end{equation}

Therefore, $f$ is transcendental and $T(r,\,f)\geq K_1 r^k$ for some positive constant $K_1$. On the other hand, by the lemma on the logarithmic derivative we also have from equation (2.1) that

(2.7)\begin{equation} \begin{aligned} nT(r,f) & =T\left(r,f^n\right)=m\left(r,f^n\right)=m\left(r,b_1e^{p_1}+b_2e^{p_2}-P(z,f)\right)\\ & \leq m\left(r,b_1e^{p_1}+b_2e^{p_2}\right)+m\left(r,P(z,f)\right)+O(1)\\ & \leq K(1+o(1))r^k+(n-1)m(r,f)+O(\log r), \end{aligned} \end{equation}

which yields that $T(r,\,f)\leq K_2 r^k$ for some positive constant $K_2$. This together with $T(r,\,f)\geq K_1 r^k$ yields $\sigma (f)=k$. Then by definition of $\mathcal {S}$ and looking at the proof of [33, theorem 2.1], we see that $\alpha$ is real. Now, $-1\leq \alpha <0$ or $0<\alpha <1$.

Recall that $\theta _1=-\pi /(2k)$ and from (2.2) that $\delta (p_1,\,\theta )=\cos k\theta$ and $\delta (p_2,\,\theta )=\alpha \cos k\theta$. When $\alpha <0$, we see that $\delta (p_1,\,\theta )$ and $\delta (p_2,\,\theta )$ have opposite signs for each $\theta$ in the sectors $S_j$ defined in (2.3) for $p_1$ and $\delta (p_1,\,\theta )>0$ for $\theta$ in the sectors $S_{j}$ where $j\in J_1$; when $\alpha >0$, we see that $\delta (p_1,\,\theta )>0$ and $\delta (p_2,\,\theta )>0$ simultaneously for each $\theta$ in the sectors $S_{j}$ where $j\in J_1$ and $\delta (p_1,\,\theta )<0$ and $\delta (p_2,\,\theta )<0$ simultaneously for each $\theta$ in the sectors $S_{j}$ where $j\in J_2$. Then we see that the assertion (1) and the assertion (2) for the case that $\delta (p_1,\,\theta )>0$ can be obtained by directly following the proof of [34, lemma 2.5].

Now we consider the growth behaviour of $f(z)$ along the ray $z=re^{i\theta }$ such that $\delta (p_1,\,\theta )<0$ when $0<\alpha <1$. Let $\varepsilon >0$ be given. By [12, corollary 1], there exists a constant $r_0=r_0(\theta )>1$ such that for all $z$ on the ray $z=re^{i\theta }$ which does not meet $\tilde {R}$ when $r\geq r_0$, and for all positive integers $j$,

(2.8)\begin{equation} \left|\frac{f^{(j)}(re^{i\theta})}{f(re^{i\theta})}\right|\leq r^{j(k-1+\varepsilon)}. \end{equation}

Since all coefficients of $P(z,\,f)$ are combinations of functions in $\mathcal {S}$, then for each coefficient of $P(z,\,f)$, say $a_l$, by [12, corollary 1], we also have, along the ray $z=re^{i\theta }$, that

(2.9)\begin{equation} \left|a_l(re^{i\theta})\right|\leq r^{M}, \end{equation}

for sufficiently large $r$ and some large integer $M$. Recalling from the introduction that $P(z,\,f)=\sum ^{m}_{l=1}a_{l}f^{n_{l0}}(f')^{n_{l1}}\cdots (f^{(s)})^{n_{ls}}$, where $m$ is an integer and $n_{l0}+n_{l1}+\cdots n_{ls}\leq n-1$, we may write

(2.10)\begin{equation} P(z,f)=\sum^{m}_{l=1}\hat{a}_{l}f^{n_{l0}+n_{l1}+\cdots+n_{ls}}, \end{equation}

with the new coefficients $\hat {a}_l=a_l(f'/f)^{n_{l1}}\cdots (f^{(s)}/f)^{n_{ls}}$, where $n_{l0},\,\cdots,\,n_{ls}$ are nonnegative integers. Note that the greatest order of the derivatives of $f$ in $P(z,\,f)$ is equal to $s\geq 0$. Suppose now that $|f(r_je^{i\theta })|\geq r_j^{N}$ for some infinite sequence $z_j=r_je^{i\theta }$ and some large $N\geq M+s(k-1+\varepsilon )$. Then, from (2.1), (2.8), (2.9) and (2.10) we have

(2.11)\begin{equation} \begin{aligned} & \left|b_1(r_je^{i\theta})e^{p_1(r_je^{i\theta})}+b_2(r_je^{i\theta})e^{p_2(r_je^{i\theta})}\right|\\ & \quad=\left|f(r_je^{i\theta})^n\right|\left|1+\frac{P(r_je^{i\theta},f(r_je^{i\theta}))}{f(r_je^{i\theta})^n}\right|\geq(1-o(1))r^{nN}, \end{aligned} \end{equation}

which is impossible when $r_j$ is large since $b_1(r_je^{i\theta })e^{p_1(r_je^{i\theta })}+b_2(r_je^{i\theta })e^{p_2(r_je^{i\theta })}\to 0$ as $z_j\to \infty$. Therefore, along the ray $z=re^{i\theta }$ such that $\delta (p_1,\,\theta )<0$ we must have $|f(re^{i\theta })|\leq r^{N}$ for all large $r$ and some integer $N$. Thus our second assertion follows.

Now we begin to prove theorem 2.1.

Proof of theorem 2.1. For simplicity, we denote $P=P(z,\,f)$. By taking the derivatives on both sides of (2.1) and eliminating $e^{p_2}$ and $e^{p_1}$ from (2.1) and the resulting equation, respectively, we get the following two equations:

(2.12)\begin{align} b_2B_2f^n-nb_2f^{n-1}f'+b_2B_2 P-b_2P'& =A_1{e^{p_1}}, \end{align}

(2.13)\begin{align} b_1B_1f^n-nb_1f^{n-1}f'+b_1B_1 P-b_1P'& ={-}A_1{e^{p_2}}, \end{align}

where $B_1=b_1'/b_1+p_1'$, $B_2=b_2'/b_2+p_2'$ and $A_1=b_1b_2(B_2-B_1)$. Note that $B_1B_2A_1\not \equiv 0$. By differentiating on both sides of (2.12) and then eliminating $e^{p_1}$ from (2.12) and the resulting equation, we get

(2.14)\begin{equation} h_1 f^n+h_2f^{n-1}f'+h_3f^{n-2}(f')^2+h_4f^{n-1}f''+P_1=0, \end{equation}

where $h_1=b_2B_2(A_1'+p_1'A_1)-(b_2B_2)'A_1$, $h_2=-n b_2A_1(p_1'+p_2')-nb_2A_1'$, $h_3=n(n-1)b_2A_1$, $h_4=nb_2A_1$, and $P_1=(A_1'+p_1'A_1)(b_2B_2P-b_2P')-A_1(b_2B_2P-b_2P')'$ is a differential polynomial in $f$ of degree $\leq n-1$. By lemma 2.3 and our assumption, $\alpha$ is a nonzero real number such that $-1\leq \alpha < 1$. Below we consider the two cases where $-1\leq \alpha < 0$ and $0<\alpha <1$, respectively.

Case 1: $-1\leq \alpha < 0$. We multiply both sides of equations (2.12) and (2.13) and obtain

(2.15)\begin{equation} g_1 f^{2n}+g_2f^{2n-1}f'+g_3f^{2n-2}(f')^2+P_2={-}A_1^2e^{p_1+p_2}, \end{equation}

where $g_1=b_1b_2B_1B_2$, $g_2=-nb_1b_2(B_1+B_2)$, $g_3=n^2b_1b_2$ and $P_2=b_1b_2(B_2f^n-nf^{n-1}f')(B_1P-P')+b_1b_2(B_1f^n-nf^{n-1}f')$ $(B_2P-P')+b_1b_2(B_1P-P')(B_2P-P')$ is a differential polynomial in $f$ of degree $\leq 2n-1$. By eliminating $(f')^2$ from (2.14) and (2.15), we get

(2.16)\begin{equation} f^{2n-1}\left[(g_3h_1-h_3g_1)f+(g_3h_2-h_3g_2)f'+g_3h_4f''\right]+P_3=h_3A_1^2e^{p_1+p_2}, \end{equation}

where $P_3=g_3f^nP_1-h_3P_2$ is a differential polynomial in $f$ of degree $\leq 2n-1$. For simplicity, we denote

(2.17)\begin{equation} \varphi=\frac{h_3A_1^2}{g_3h_4}\frac{e^{p_1+p_2}}{f^{2n-1}}-\frac{1}{g_3h_4}\frac{P_3}{f^{2n-1}}. \end{equation}

Recalling $B_1=b_1'/b_1+p_1'$ and $B_2=b_2'/b_2+p_2'$, we get from equation (2.16) that

(2.18)\begin{equation} f''+H_1f'+H_2f=\varphi, \end{equation}

where

(2.19)\begin{equation} \begin{aligned} H_1 & =\frac{h_2}{h_4}-\frac{g_2h_3}{g_3h_4}={-}\left[\frac{1}{n}(p_1'+p_2')-\frac{n-1}{n}\left(\frac{b_1'}{b_1}+\frac{b_2'}{b_2}\right)+\frac{A_1'}{A_1}\right],\\ H_2 & =\frac{h_1}{h_4}-\frac{g_1h_3}{g_3h_4}=\frac{1}{n}\left[B_2\left(\frac{A_1'}{A_1}-\frac{b_1'}{b_1}\right)-\frac{(b_2B_2)'}{b_2}\right]+\frac{1}{n^2}B_1B_2. \end{aligned} \end{equation}

Now we prove that $\varphi$ is a rational function. Recall that $b_1,\,b_2,\,p_1,\,p_2$ are all polynomials and $B_1=b_1'/b_1+p_1'$, $B_2=b_2'/b_2+p_2'$ and $A_1=b_1b_2(B_2-B_1)$. Since $f$ is entire, we see that $\varphi$ has only finitely many poles. By lemma 2.3, $\sigma (f)=k$. By the lemma on the logarithmic derivative, we deduce from (2.18) that

(2.20)\begin{equation} T(r,\varphi)=m(r,\varphi)+O(\log r)\leq m(r,f)+O(\log r)=T(r,f)+O(\log r). \end{equation}

Therefore, $\sigma (\varphi )\leq k$. Now let $\theta \in [0,\,2\pi )$ be such that $\delta (p_1,\,\theta )\not =0$ and $z=re^{i\theta }$ is a ray that meets only finitely discs in $\tilde {R}$. Since $\alpha <0$, then by lemma 2.3 (1) we see that in both cases that $\delta (p_1,\,\theta )>0$ and $\delta (p_1,\,\theta )<0$ we always have $|e^{p_1(re^{i\theta })+p_2(re^{i\theta })}/f(re^{i\theta })^{2n-1}|\to 0$ as $r\to \infty$ along the ray $z=re^{i\theta }$. Together with [12, corollary 1] we see from (2.17) that there is some integer $N$ such that $|\varphi (re^{i\theta })|\leq r^{N}$ for all large $r$. Then by the Phragmén–Lindelöf theorem we see that $|\varphi |\leq r^{N}$ uniformly in each $\overline {S}_{j,\epsilon }$, $j=1,\,2,\,\cdots,\,2k$, for some integer $N=N(j)$. Since $\epsilon$ can be arbitrarily small, then by the Phragmén–Lindelöf theorem again we conclude that $\varphi$ is a rational function. From now on we fix one large $N$.

Recall that $B_2=b_2'/b_2+p_2'$. Denote $F_1=f'-(B_1/n)f$. Then by simple computations we obtain from (2.18) that

(2.21)\begin{equation} F_1'-\left(\frac{1}{n}p_2'-\frac{b_1'}{b_1}-\frac{n-1}{n}\frac{b_2'}{b_2}+\frac{A_1'}{A_1}\right)F_1=\varphi. \end{equation}

Denote $\xi _1=p_2'/n-b_1'/b_1-(n-1)b_2'/nb_2+A_1'/A_1$. Then the general solution of the homogeneous equation $F_1'-\xi _1 F_1=0$ is defined on a finite-sheeted Riemann surface and is of the form $F_1=C_2b_2^{1/n}A_1/(b_1b_2)e^{p_2/n}$, where $C_2$ is a constant and $b_2^{1/n}$ is in general an algebraic function (see [21] for the theory of algebroid functions). Suppose that $\Gamma _2$ is a particular solution of $F_1'-\xi _1F_1=\varphi$. We may write the meromorphic solution of this equation as $F_1=C_2b_2^{1/n}A_1/(b_1b_2)e^{p_2/n}+\Gamma _2$. By an elementary series expansion analysis around the zeros of $b_2$, we conclude that $\Gamma _2/b_2^{1/n}$ is a meromorphic function. This implies that $b_2$ is an $n$-square of some polynomial. Then by lemma 2.2 we integrate the equation (2.21) along the ray $z=re^{i\theta }$ in $S_2$ such that $\delta (p_2,\,\theta )>0$ and obtain

(2.22)\begin{equation} F_1=f'-\frac{1}{n}B_1f=\frac{c_2}{n}\frac{b_2^{1/n}A_1}{b_1b_2}e^{p_2/n}+\Gamma_2, \end{equation}

where

(2.23)\begin{equation} \Gamma_2=\frac{A_1b_2^{1/n}}{b_1b_2}e^{p_2/n}\int_{0}^{z} e^{{-}p_2/n}\frac{b_1b_2}{A_1b_2^{1/n}} \varphi \,{\rm d}t-a_{2,2}\frac{A_1b_2^{1/n}}{b_1b_2}e^{p_2/n}, \end{equation}

where $a_{2,2}=a_{2,2}(\theta )$ is a constant such that $|\Gamma _2|=O(r^N)$ along the ray $z=re^{i\theta }$ in $S_2$. Now, for $z\in S_{j,\epsilon }$ where $j\in J_2$, we have $\delta (p_2,\,\theta )>0$ and so $\Gamma _2=(c_2d_{2,j}/n)b_2^{1/n}A_1/(b_1b_2)e^{p_2/n}+\gamma _{2,j}$, where $d_{2,j}$ are some constants related to a sector $S_{j,\epsilon }$ and $|\gamma _{2,j}|=O(r^N)$ uniformly in $\overline {S}_{j,\epsilon }$. Of course, for $j=2$, we have $d_{2,2}=0$. Furthermore, $|\Gamma _2|=O(r^N)$ uniformly in $\overline {S}_{j,\epsilon }$ where $j\in J_1$. We then define $d_{2,j}=0$ for $j\in J_1$.

Similarly, denoting that $\xi _2=p_1'/n-b_2'/b_2-(n-1)b_1'/nb_1+A_1'/A_1$ we also have $F_2'-\xi _2F_2=\varphi$ and it follows by integration that $F_2=-(c_1/n)b_1^{1/n}A_1/(b_1b_2)e^{p_1/n}+\Gamma _1$, where $\Gamma _1=-(c_1d_{1,j}/n)b_1^{1/n}A_1/(b_1b_2)e^{p_1/n}+\gamma _{1,j}$, where $d_{l,j}$ are some constants related to a sector $S_{j,\epsilon }$ and $|\gamma _{1,j}|=O(r^N)$ uniformly in $\overline {S}_{j,\epsilon }$ for $j\in J_1$. Of course, for $j=1$, we have $d_{1,1}=0$. Furthermore, $|\Gamma _1|=O(r^N)$ uniformly in $\overline {S}_{j,\epsilon }$ where $j\in J_2$. We then define $d_{1,j}=0$ for $j\in J_2$.

Denoting $B=n/(B_2-B_1)$, we have $f=B(F_1-F_2)$. Together with the relation $A_1=b_1b_2(B_2-B_1)$, we have $f=c_1b_1^{1/n}e^{p_1/n}+c_2b_2^{1/n}e^{p_2/n}+\eta$ with an entire function $\eta =B(\Gamma _2-\Gamma _1)$. We see that $\eta =c_2d_{2,j}b_2^{1/n}e^{p_2/n}+B(\gamma _{2,j}-\gamma _{1,j})$ when $j\in J_1$ and $\eta =c_1d_{1,j}b_1^{1/n}e^{p_1/n}+B(\gamma _{2,j}-\gamma _{1,j})$ when $j\in J_2$.

Now we determine $d_{1,j}$ and $d_{2,j}$. By [12, corollary 1], we may suppose that along the ray $z=re^{i\theta }$ we have $|f^{(j)}(re^{i\theta })/f(re^{i\theta })|=r^{j(k-1+\varepsilon )}$ for all $j>0$ for all sufficiently large $r$ and thus write $P$ in the form in (2.10) with the new coefficients $\hat {a}_l=a_l(f'/f)^{n_{l1}}\cdots (f^{(s)}/f)^{n_{ls}}$, where $n_{l1},\,\cdots,\,n_{ls}$ are nonnegative integers. For simplicity, denote $D_{1,j}=c_1+c_1d_{1,j}$. By substituting $f=c_1b_1^{1/n}e^{p_1/n}+c_2b_2^{1/n}e^{p_2/n}+\eta$ into (2.1), we obtain, for $z=re^{i\theta }$ for a $\theta$ in $S_j$ and $j\in J_1$,

(2.24)\begin{equation} \begin{aligned} & \left(D_{1,j}^n-1\right)b_1e^{p_1}+\sum_{k_0=1}^{n-1}\binom{n}{k_0}\left(D_{1,j}b_1^{1/n}\right)^{n-k_0}(c_2b_2^{1/n})^{k_0}e^{[(n-k_0)p_1+k_0p_2]/n}\\ & \quad+(c_2^n-1)b_2e^{p_2}+\sum_{s=1}^{n}\sum_{k_s=0}^{n-s}\alpha_{s,k_s}e^{[(n-s-k_s)p_1+k_sp_2]/n}=0, \end{aligned} \end{equation}

where $\alpha _{s,k_s}$, $s=1,\,\cdots,\,n$, $k_s=0,\,\cdots,\,n-s$, are functions satisfying $|\alpha _{s,k_s}(re^{i\theta })|=O(r^N)$ along the ray $z=re^{i\theta }$. By letting $r\to \infty$ along the above ray $z=re^{i\theta }$ such that $\delta (p_1,\,\theta )>0$ and comparing the growth on both sides of the above equation we conclude that $c_1^n(1+d_{1,j})^n=1$. Since $d_{1,1}=0$, we have $c_1^n=1$ and $d_{1,j}=\mu _{1,j}-1$ for some $\mu _{1,j}$ such that $\mu _{1,j}^n=1$. Similarly, we can prove that $d_{2,j}=\mu _{2,j}-1$ for some $\mu _{2,j}$ such that $\mu _{2,j}^n=1$. In particular, when $k=1$, since $d_{1,1}=d_{2,2}=0$ and $|\eta _j|=O(r^N)$ uniformly in the sectors $\overline {S}_{j,\epsilon }$, $j=1,\,2$ and since $\epsilon$ can be arbitrarily small, by the Phragmén–Lindelöf theorem we conclude that $\eta$ is a polynomial. Thus our first assertion follows.

Case 2: $0<\alpha <1$.

As in the proof of [33, theorem 2.1], we first define some functions in the following way: We let $m$ be the smallest integer such that $\alpha \leq [(m+1)n-1]/[(m+1)n]$ and ${\iota _0,\,\cdots,\,\iota _m}$ be a finite sequence of functions such that

(2.25)\begin{equation} \begin{aligned} \iota_0 & =\frac{A_1}{nb_1},\\ \iota_j & =({-}1)^{j}\left(\frac{A_1}{nb_1}\right)^{j+1}(jn-1)\cdots(n-1), \quad j=1,2,\cdots,m. \end{aligned} \end{equation}

Recall that $B_1=b_1'/b_1+p_1'$. We also let ${\kappa _0,\,\cdots,\,\kappa _m}$ be a finite sequence of functions defined in the following way:

(2.26)\begin{equation} \begin{aligned} \kappa_0 & =\frac{1}{n}\frac{b_1'}{b_1}+\frac{1}{n}p_1',\\ \kappa_j & =\frac{\iota_{j-1}'}{\iota_{j-1}}-\frac{jn-1}{n}\frac{b_1'}{b_1}+\left[j(\alpha-1)+\frac{1}{n}\right]p_1', \quad j=1,2,\cdots,m. \end{aligned} \end{equation}

Then we define $m+1$ functions $G_0$, $G_1$, $\cdots$, $G_m$ in the way that $G_0=f'-\kappa _0f$, $G_{1}=G_{0}'-\kappa _1G_{0}$, $\cdots$, $G_{m}=G_{m-1}'-\kappa _mG_{m-1}$. Now we have equation (2.13) and it follows that

(2.27)\begin{equation} G_0=f'-\kappa_0f=\iota_0\frac{{e^{p_2}}}{f^{n-1}}+W_0, \end{equation}

where $W_0=-(B_1P-P')/(nf^{n-1})$. Moreover, when $m\geq 1$, by simple computations we obtain

\begin{align*} G_1& =G_0'-\kappa_1G_0=\iota_1\frac{e^{2p_2}}{f^{2n-1}}+W_1,\\ W_1& =W'_0-\kappa_1W_0-(n-1)\iota_0\frac{e^{p_2}}{f^n}W_0, \end{align*}

and by induction we obtain

(2.28)\begin{align} G_{j}& =G_{j-1}'-\kappa_jG_{j-1}=\iota_j\frac{e^{(j+1)p_2}}{f^{(j+1)n-1}}+W_{j}, \quad j=1,\cdots,m, \end{align}

(2.29)\begin{align} W_{j}& =W'_{j-1}-\kappa_jW_{j-1}-(jn-1)\iota_{j-1}\frac{e^{jp_2}}{f^{jn}}W_0, \quad j=1,\cdots,m. \end{align}

For an integer $l\geq 0$, by elementary computations it is easy to show that $W_0^{(l)}=W_{0l}/f^{n+l-1}$, where $W_{0l}=W_{0l}(z,\,f)$ is a differential polynomial in $f$ of degree $\leq n+l-1$, and also that $(e^{p_2}/f^{n})^{(l)}=e^{p_2}W_{1l}/f^{n+l}$, where $W_{1l}=W_{1l}(z,\,f)$ is a differential polynomial in $f$ of degree $\leq n+l$. We see that $W_j$, $1\leq j\leq m$, is formulated in terms of $W_0$ and $e^{p_2}/f^{n}$ and their derivatives. We may write

(2.30)\begin{equation} G_m=\iota_m\frac{e^{(m+1)p_2}}{f^{(m+1)n-1}}+F(W_0,e^{p_2}/f^{n}), \end{equation}

where $F(W_0,\,e^{p_2}/f^{n})$ is a combination of $W_0$ and $e^{p_2}/f^{n}$ and their derivatives with functions being combinations of functions in $\mathcal {S}$. Moreover, from the recursion formula $G_j=G_{j-1}'-\kappa _jG_{j-1}$, $j\geq 1$, and $G_0=f'-\kappa _0f$, we easily deduce that $f$ satisfies the linear differential equation

(2.31)\begin{equation} f^{(m+1)}-\hat{t}_{m}f^{(m)}+\cdots+({-}1)^{m+1}\hat{t}_0f=G_m, \end{equation}

where $\hat {t}_m$, $\hat {t}_{m-1}$, $\cdots$, $\hat {t}_0$ are functions formulated in terms of $\kappa _0$, $\cdots$, $\kappa _m$ and their derivatives.

Now we prove that $G_m$ is a rational function. Recall that $b_1,\,b_2,\,p_1,\,p_2$ are all polynomials. Since $f$ is entire, then by the definitions of $\kappa _0$ and $\kappa _j$ in (2.26), we see that $G_m$ has only finitely many poles. With an application of the lemma on the logarithmic derivative as in previous case, we deduce from (2.31) that $\sigma (G_m)\leq \sigma (f)=k$. Now let $\theta \in [0,\,2\pi )$ be such that $\delta (p_1,\,\theta )\not =0$ and $z=re^{i\theta }$ be a ray that meets only finitely may discs in $\tilde {R}$. By [12, corollary 1] and lemma 2.3 (2), we see from (2.31) that there is some integer $N$ such that $|G_m(re^{i\theta })|\leq r^{N}$ for all large $r$ along the ray $z=re^{i\theta }$ such that $\delta (p_1,\,\theta )<0$. On the other hand, by lemma 2.3 (2) there is some integer $N$ such that

1. (1) if $\alpha <[(m+1)n-1]/[(m+1)n]$, then $|e^{(m+1)p_2(re^{i\theta })}/f(re^{i\theta })^{(m+1)n-1}|\to 0$ as $r\to \infty$ along the ray $z=re^{i\theta }$ such that $\delta (p_1,\,\theta )>0$;

2. (2) if $\alpha =[(m+1)n-1]/[(m+1)n]$, then $|e^{(m+1)p_2(re^{i\theta })}/f(re^{i\theta })^{(m+1)n-1}|\leq e^{Nr^{k-1}}$ for all large $r$ along the ray $z=re^{i\theta }$ such that $\delta (p_1,\,\theta )>0$.

Note that $e^{p_2(re^{i\theta })}/f(re^{i\theta })^{n}\to 0$ as $r\to \infty$ along the ray $z=re^{i\theta }$ such that $\delta (p_1,\,\theta )>0$. In case (1), together with [12, corollary 1] we see from (2.30) that $|G_m(re^{i\theta })|\leq r^{N}$ for all large $r$ and thus by the Phragmén–Lindelöf theorem we see that $|G_m|\leq r^{N}$ uniformly in each $\overline {S}_{j,\epsilon }$, $j\in J_2$, for some integer $N=N(j)$; in case (2), together with [12, corollary 1] we see from (2.30) that $|G_m(re^{i\theta })|\leq e^{Nr^{k-1}}$ for all large $r$ and, since the set of rays $z=re^{i\theta }$ meeting infinitely many discs in $\tilde {R}$ has zero linear measure, then by the Phragmén–Lindelöf theorem we see that $|G_m|\leq e^{Nr^{k-1}}$ uniformly in each $\overline {S}_{j,\epsilon }$, $j\in J_2$, for some integer $N=N(j)$. Since $\epsilon$ can be arbitrarily small, then in either case of (1) and (2) by the Phragmén–Lindelöf theorem again we conclude that $G_m$ is a rational function. From now on we fix one large $N$.

We denote $D_0=b_1^{1/n}$ and $D_j=\iota _{j-1}b_1^{-j}b_1^{1/n}$, $j=1,\,\cdots,\,m$. Now we choose one $\theta$ such that $\delta (p_1,\,\theta )>0$ and let $z=re^{i\theta }\in S_1$. Let $t_0=1/n$, $t_1=(\alpha -1)+1/n$, $\cdots$, $t_m=m(\alpha -1)+1/n$. Similarly as in the proof of [33, theorem 2.1], we may use lemma 2.2 to integrate the recursion formulas $G_j=G_{j-1}'-\kappa _jG_{j-1}$ from $j=m$ to $j=1$ along the above ray $z=re^{i\theta }$ such that $\delta (p_1,\,\theta )>0$ inductively and finally integrating $G_0=f'-\kappa _0f$ along this ray $z=re^{i\theta }$ to obtain

(2.32)\begin{equation} f=b_1^{1/n}\sum_{i=0}^mc_i\left(\frac{b_2}{b_1}\right)^ie^{t_ip_1}+H_0, \end{equation}

where $c_0$, $\cdots$, $c_m$ are constants and

(2.33)\begin{equation} H_{0}=b_1^{1/n}e^{t_0p_1}\int_{0}^{z}b_1^{{-}1/n}e^{{-}t_0p_1}H_1ds-a_{0}b_1^{1/n}e^{t_0p_1}, \end{equation}

where $a_0=a_{0}(\theta )$ is a constant such that $|H_0|=O(r^N)$ along the ray $z=re^{i\theta }$.

As is shown in the proof of [33, theorem 2.1], $b_1$ is an $n$-square of some polynomial and we may write the entire solution of (2.1) as $f=\gamma _1\sum _{j=0}^mc_j(b_2/b_1)^je^{t_jp_1}+\eta$, where $\gamma _1$ is a polynomial such that $\gamma _1^n=b_1$ and $\eta$ is a meromorphic function with at most finitely many poles. Then we can integrate $G_j=G_{j-1}'-\kappa _jG_{j-1}$ from $j=m$ to $j=1$ inductively and finally integrate $G_0=f'-\kappa _0f$ to obtain that $H_0$ is a meromorphic function with at most finitely many poles. We choose $\eta =H_0$. Recall that along the ray $z=re^{i\theta }$ such that $\delta (p_1,\,\theta )>0$ and $z=re^{i\theta }\in S_1$, we have $|H_0|=O(r^N)$. Denote $g=b_1^{1/n}\sum _{i=0}^mc_i(b_2/b_1)^ie^{t_ip_1}$. Then

(2.34)\begin{equation} g^n=b_1\sum_{k_0=0}^{mn}C_{k_0}\left(\frac{b_2}{b_1}\right)^{k_0}e^{(k_0t-k_0+1)p_1}, \end{equation}

where

(2.35)\begin{equation} C_{k_0}=\sum_{\substack{j_0+\cdots+j_m=n,\\j_1+\cdots+mj_m=k_0}}\frac{n!}{j_0!j_1!\cdots j_m!}c_0^{j_0}c_1^{j_1}\cdots c_m^{j_m}, \quad k_0=0,1,\cdots,mn. \end{equation}

By [12, corollary 1], we may suppose that along the ray $z=re^{i\theta }$ we have $|f(re^{i\theta })^{(j)}/f(re^{i\theta })|=r^{j(k-1+\varepsilon )}$ for all $j>0$ and all sufficiently large $r$. By writing $P$ in the form in (2.10) with the new coefficients $\hat {a}_l=a_l(f'/f)^{n_{l1}}\cdots (f^{(s)}/f)^{n_{ls}}$, where $n_{l1},\,\cdots,\,n_{ls}$ are nonnegative integers, and using [12, corollary 1], we see that each term in $P(z,\,f)$ of degree $n-j$, $1\leq j\leq n-1$, equals a linear combination of exponential functions of the form $e^{[nk_{j}(\alpha -1)+n-j]p_1/n}$, $0\leq k_{j}\leq (n-j)m$, with coefficients $\beta _j$ having polynomial growth along the ray $z=re^{i\theta }$. Therefore, by substituting $f=g+H_0$ into (2.1) we obtain by the same arguments in the proof of [33, theorem 2.1] that $c_0^n=1$ when $m=0$, and $c_0^{n}=1$, $nc_0^{n-1}c_1=1$ and $p_2=\alpha p_1$ when $m=1$ and further that $C_{k_0}\equiv 0$ for all $2\leq k_0\leq m$ when $m\geq 2$.

Now, $b_1^{1/n}$ denotes a polynomial. By the definition of $\iota _j$ and $D_j$, we see that $D_j$ are rational functions. Recall that $G_m$ is a rational function. By lemma 2.2 and looking at the calculations to obtain $H_0$ in (2.33), we have, for $z\in S_{j,\epsilon }$, $j\in J_1$, such that $\delta (p_1,\,\theta )>0$, $H_0=\gamma _1\sum _{l=0}^md_{l,j}(b_2/b_1)^je^{t_jp_1}+\eta _{j}$, where $d_{l,j}$, $l=0,\,\cdots,\,m$, are some constants related to a sector $S_{j,\epsilon }$ and $|\eta _j|=O(r^N)$ uniformly in $\overline {S}_{j,\epsilon }$, $j\in J_1$. Of course, for $j=1$, we have $d_{l,1}=0$ for all $l$. Since $c_0^{n}=1$ when $m=0$, $c_0^{n}=nc_0^{n-1}c_1=1$ when $m=1$, and $c_0^{n}=nc_0^{n-1}c_1=1$ and $C_{k_0}=0$ for all $2\leq k_0\leq m$ when $m\geq 2$, then by simple computations, we deduce that $c_j=s_jc_0$ for some nonzero rational numbers $s_j$, $j=0,\,1,\,\cdots,\,m$. Therefore, by considering the growth of $f$ along the ray $z=re^{i\theta }$ such that $z\in S_{j,\epsilon }$, $j\in J_1$, as for the ray $z=re^{i\theta }\in S_1$, we have $(c_0+d_{0,j})^n=1$ when $m=0$, $(c_0+d_{0,j})^n=n(c_0+d_{0,j})^{n-1}(c_1+d_{1,j})=1$ when $m=1$ and further that $\hat {C}_{k_0}=\sum _{\substack {j_0+\cdots +j_m=n,\\j_1+\cdots +mj_m=k_0}}\frac {n!}{j_0!j_1!\cdots j_m!}(c_0+d_{0,j})^{j_0}(c_1+d_{1,j})^{j_1}\cdots (c_m+d_{m,j})^{j_m}=0$ for $k_0=2,\,\cdots,\,m$ when $m\geq 2$. Therefore, for each $j\in J_1$, there is a $\mu _j$ satisfying $\mu _j^n=1$ such that $c_l+a_{l,j}=\mu _j c_l$ for all $l$. Note that $\mu _{1}=1$. Also, we have $|\eta |=O(r^N)$ uniformly in the sectors $\overline {S}_{j,\epsilon }$, $j\in J_2$. In conclusion, we may write $\eta =\gamma _1\sum _{l=0}^m(\mu _j-1)c_{j}(b_2/b_1)^je^{[jn(\alpha -1)+1]p_1/n}+\eta _{j}$, where $\mu _j$ are the $n$-th roots of $1$ such that $\mu _j=1$, $j=\{1\}\cup \in J_2$, and $|\eta _j|=O(r^N)$ uniformly in the sector $\overline {S}_{j,\epsilon }$. In particular, when $k=1$, since $\epsilon$ can be arbitrarily small, then by the Phragmén–Lindelöf theorem we conclude that $\eta$ is a rational function. This completes the proof.

3. An oscillation question of Ishizaki

Let $b_1(z)$, $b_2(z)$ and $b_3(z)$ be three polynomials such that $b_1b_2\not \equiv 0$ and $p_1(z)$ and $p_2(z)$ be two polynomials of the same degree $k\geq 1$ with distinct leading coefficients $1$ and $\alpha$, respectively, and $p_1(0)=p_2(0)=0$. In this section, we use theorem 2.1 to investigate the oscillation of the second-order linear differential equation:

(3.1)\begin{equation} f''-\left[b_1(z)e^{p_1(z)}+b_2(z)e^{p_2(z)}+b_3(z)\right]f=0. \end{equation}

There have been several results about the oscillation of equation (3.1) and recently second-order linear differential equations with exponential polynomials are taken into more consideration in [15, 16]. The results of Bank, Laine and langely [5], Ishizaki and Kazuya [20] and Ishizaki [19] can be summarized as follows:

1. (1) if $\alpha$ is non-real, then all nontrivial solutions of (3.1) satisfy $\lambda (f)=\infty$;

2. (2) if $\alpha$ is negative, then all nontrivial solutions of (3.1) satisfy $\lambda (f)=\infty$;

3. (3) if $0<\alpha <1/2$ or if $b_3\equiv 0$ and $3/4<\alpha <1$, then all nontrivial solutions of (3.1) satisfy $\lambda (f)\geq k$.

Theorem 1.1 shows that the condition $b_3\equiv 0$ in the third result can be removed. Ishizaki [19] asked if the third result $\lambda (f)\geq k$ above can be replaced by $\lambda (f)=\infty$. With theorem 2.1 at our disposal, we are able to answer this question partially. We prove the following

Theorem 3.1 Let $0<\alpha <1$ and $m$ be the smallest integer such that $\alpha \leq [2(m+1) -1]/[2(m+1)]$. Suppose that $b_3\equiv 0$ in (3.1). If (3.1) admits a nontrivial solution $f$ such that $\lambda (f)<\infty,$ then $\alpha =[2(m+1)-1]/[2(m+1)]$ and $p_2=\alpha p_1$.

We will mainly use the techniques in [6] (see also [23, theorem 5.7]) to prove theorem 3.1. Since $\alpha$ is a positive number, we have $\int _{1}^{\infty }r|A(re^{i\theta })|dr<\infty$ along the ray $z=re^{i\theta }$ such that $\delta (p_1,\,\theta )<0$. The following lemma can be proved similarly as in [23, lemma 5.16] by using Gronwall's lemma (see [23, p. 86]).

Lemma 3.2 Under the assumptions of theorem 3.1, all solutions of equation (3.1) satisfy $|f(re^{i\theta })|=O(r)$ as $r\to \infty$ along the ray $z=re^{i\theta }$ such that $\delta (p_1,\,\theta )<0$.

Now we begin to prove theorem 3.1.

Proof of theorem 3.1. Let $f$ be a nontrivial solution of equation (3.1) such that $\lambda (f)<\infty$. By Hadamard's factorization theorem we may write $f=\kappa e^{h}$, where $h$ is an entire function and $\kappa$ is the canonical product from the zeros of $f$ satisfying $\rho (\kappa )=\lambda (\kappa )<\infty$. Denoting $g=h'$, then from (3.1) we have

(3.2)\begin{equation} g^2+g'+2\frac{\kappa'}{\kappa}g+\frac{\kappa''}{\kappa}=b_1(z)e^{p_1(z)}+b_2(z)e^{p_2(z)}. \end{equation}

Below we consider the two cases where $0<\alpha \leq 1/2$ and $(2m-1)/(2m)< \alpha \leq [2(m+1)-1]/[2(m+1)]$, $m\geq 1$, respectively.

Case 1: $0<\alpha \leq 1/2$.

By theorem 2.1, we may write $g=\gamma _1e^{p_1/2}+\eta$, where $\gamma _1$ is a polynomial such that $\gamma _1^2=b_1$ and $\eta$ is an entire function such that $|\eta |=O(r^N)$ uniformly in $\overline {S}_{1,\epsilon }$ and $\overline {S}_{2,\epsilon }$. By substituting this expression into equation (3.2), we obtain

(3.3)\begin{equation} 2\gamma_1\left(\frac{\kappa'}{\kappa}+\frac{1}{2}\frac{\gamma_1'}{\gamma_1}+\frac{p_1'}{4}+\eta\right)e^{p_1/2}-b_2e^{p_2}+\frac{\kappa''}{\kappa}+2\eta\frac{\kappa'}{\kappa}+\eta^2+\eta'=0. \end{equation}

Suppose that $0<\alpha <1/2$. We define

(3.4)\begin{equation} w=\kappa \gamma_1^{1/2}e^{p_1/4+\int_{z_0}^{z} \eta \,{\rm d}t}, \end{equation}

where $z_0$ is chosen so that $|z_0|$ is large. Then $w$ is analytic outside a finite disc centred at $0$ and satisfy

(3.5)\begin{equation} \frac{w'}{w}=\frac{\kappa'}{\kappa}+\frac{1}{2}\frac{\gamma_1'}{\gamma_1}+\frac{p_1'}{4}+\eta. \end{equation}

Dividing by $2\gamma _1e^{p_1/2}$ on both sides of equation (3.3) and then considering the growth of $w'/w$ along the ray $z=re^{i(\theta _2-\epsilon )}$ such that $w$ has no zero around the neighbourhood of the ray $z=re^{i(\theta _2-\epsilon )}$, we have by [12, corollary 1] that $|w'(re^{i\theta })/w(re^{i\theta })|=O(r^{-2})$ as $r\to \infty$. By integration, we obtain that $w(re^{i(\theta _2-\epsilon )})\to a$ as $r\to \infty$ along the ray $z=re^{i(\theta _2-\epsilon )}$ for some nonzero constant $a=a(\theta _2,\,\epsilon )$. On the other hand, by applying lemma 3.2 to equation (3.1) we have $|f(re^{i(\theta _2+\epsilon )})|=O(r)$ along the ray $z=re^{i(\theta _2+\epsilon )}$. Recalling that $f=\kappa e^{h}$ and $g=h'=\gamma _1e^{p_1/2}+\eta$, we may write

(3.6)\begin{equation} w=fe^{{-}h}\gamma_1^{1/2}e^{p_1/4+\int \eta dz}=f\gamma_1^{1/2}e^{p_1/4-\int_{z_0}^z \gamma_1e^{p_1/2}\,{\rm d}t}. \end{equation}

Since $\delta (p_1,\,\theta _2+\epsilon )<0$ and thus along the ray $z=re^{i(\theta _2+\epsilon )}$ we have $\int _{z_0}^z \gamma _1e^{p_1/2}\,{\rm d}t\to c$ for some constant $c=c(\theta _2,\,\epsilon )$, we see from (3.6) that $w$ defined in (3.4) satisfies $w(re^{i(\theta +\epsilon )})\to 0$ as $r\to \infty$. Denote

(3.7)\begin{equation} S_{\epsilon}=\{re^{i\theta}:\theta_2-\epsilon\leq \theta\leq \theta_2+\epsilon\}. \end{equation}

By choosing $\epsilon$ to be small and applying the Phragmén–Lindelöf theorem to $w$ defined in (3.4) in the sector in (3.7), we get $a=0$, a contradiction. Therefore, we must have $\alpha =1/2$ when $b_3\equiv 0$.

Now, if $k=1$, then obviously $p_2=p_1/2$ since we have assumed $p_1(0)=p_2(0)=0$. If $k>1$, then by theorem 2.1 we have $g=\mu _j\gamma _1e^{p_1/2}+\eta _j$, where $\mu _j^n=1$, $\gamma _1$ is a polynomial such that $\gamma _1^2=b_1$ and $\eta _j$ is an entire function such that $|\eta _j|=O(r^N)$ uniformly in $\overline {S}_{j,\epsilon }$. Note that $\eta _j$ has finite order. Denoting $p_3=p_2-p_1/2$, we rewrite equation (3.3) as

(3.8)\begin{equation} \left[b_2e^{p_3}-2\mu_j\gamma_1\left(\frac{\kappa'}{\kappa}+\frac{1}{2}\frac{\gamma_1'}{\gamma_1}+\frac{p_1'}{4}+\eta_j\right)\right]e^{p_1/2}=\frac{\kappa''}{\kappa}+2\eta_j\frac{\kappa'}{\kappa}+\eta_j^2+\eta_j'. \end{equation}

If $p_2\not \equiv p_1/2$, then $p_3$ is a nonconstant polynomial such that $\deg (p_3)\leq \deg (p_2)-1$. By the definition of $S_j$ in (2.3), we may choose a $\theta \in [0,\,2\pi )$ so that the ray $z=re^{i\theta }$ meets only finitely discs in $\tilde {R}$ and also that $\log |e^{p_1/2}|$ and $\log |e^{p_2-p_1/2}|$ both increase along the ray $z=re^{i\theta }$. By [12, corollary 1] we see that $\kappa '/\kappa +\gamma _1'/2\gamma _1+p_1'/4+\eta _j$ and $\kappa ''/\kappa +2\eta _j\kappa '/\kappa +\eta _j^2+\eta _j'-b_3$ both have polynomial growth along the ray $z=re^{i\theta }$. Then by comparing the growth on both sides of equation (3.8) along the ray $z=re^{i\theta }$, we get a contradiction. Therefore, we must have $p_2\equiv p_1/2$ when $\alpha =1/2$.

Case 2: $(2m-1)/(2m)<\alpha \leq [2(m+1)-1]/[2(m+1)]$, $m\geq 1$.

In this case, by theorem 2.1 we already have $p_2=\alpha p_1$ and we may write $g=\gamma _1\sum _{j=0}^mc_j(b_2/b_1)^je^{[2j(\alpha -1)+1]p_1/2}+\eta$, where $m\geq 1$, $\gamma _1$ is a polynomial such that $\gamma _1^2=b_1$ and $\eta$ is a mermorphic function with at most finitely many poles such that $|\eta |=O(r^N)$ uniformly in $\overline {S}_{1,\epsilon }$ and $\overline {S}_{2,\epsilon }$. By substituting this expression into equation (3.2), we obtain

(3.9)\begin{equation} \begin{aligned} & 2\gamma_1\sum_{j=0}^mc_j\left(\frac{b_2}{b_1}\right)^{j}\left[\frac{\kappa'}{\kappa}+\frac{1}{2}\frac{\gamma_1'}{\gamma_1}+j\frac{(b_2/b_1)'}{b_2/b_1}+\frac{2j(\alpha-1)+1}{4}p_1'+\eta\right]e^{L_jp_1}\\ & \gamma_1^2\sum_{k_0=m+1}^{2m}C_{k_0}\left(\frac{b_2}{b_1}\right)^{k_0}e^{M_{k_0}p_1}+\frac{\kappa''}{\kappa}+2\eta\frac{\kappa'}{\kappa}+\eta^2+\eta'=0, \end{aligned} \end{equation}

where $L_j=[2j(\alpha -1)+1]/2$, $M_{k_0}=k_0\alpha -k_0+1$ and the coefficients $C_{k_0}=\sum _{\substack {j_0+\cdots +j_m=2,\\j_1+\cdots +mj_m=k_0}}\frac {2!}{j_0!j_1!\cdots j_m!}c_0^{j_0}c_1^{j_1}\cdots c_m^{j_m}$, $k_0=m+1,\,\cdots,\,2\,m$. Suppose that $\alpha <[2(m+1)-1]/2(m+1)$. Then, for $k_0=m+1+j$, $j=0,\,1,\,\cdots,\,m-1$, we have $L_{j+1}< k_0\alpha -\alpha +1< L_j$. As in previous case, we also define the function $w$ in (3.4), where $z_0$ is chosen so that $|z_0|$ is large and $w$ is analytic outside a finite disc centred at $0$. It follows that $w'/w$ has the form in (3.5). Similarly as in previous case, we first divide by $2c_0\gamma _1e^{p_1/2}$ on both sides of equation (3.9) and conclude that $w(re^{i(\theta _2-\epsilon )})\to a$ as $r\to \infty$ along the ray $z=re^{i(\theta _2-\epsilon )}$ for some nonzero constant $a=a(\theta _2,\,\epsilon )$; then we use the expression $g=h'=\gamma _1\sum _{j=0}^mc_j(b_2/b_1)^je^{[2j(\alpha -1)+1]p_1/2}+\eta$ to derive from (3.4) that $w(re^{i(\theta +\epsilon )})\to 0$ as $r\to \infty$ along the ray $z=re^{i(\theta _2+\epsilon )}$. An application of the Phragmén–Lindelöf theorem to $w$ in the sector in (3.7) then yields a contradiction. We omit those details. Therefore, we must have $\alpha =[2(m+1)-1]/2(m+1)$. We complete the proof.

4. Equation (1.1) with periodic coefficients in (1.6)

As mentioned in the introduction, all nontrivial solutions of the second-order linear differential equation $f''+(e^z-b)f=0$ such that $\lambda (f)<\infty$ are given explicit expressions. In this section we solve nontrivial solutions such that $\lambda (f)<\infty$ of the second-order linear differential equation:

(4.1)\begin{equation} f''-\left(e^{lz}+b_2e^{sz}+b_3\right)f=0, \end{equation}

where $l$ and $s$ are relatively prime integers such that $l>s\geq 1$, $b_2$ and $b_3$ are constants and $b_2\not =0$. We remark that by using the method in [25], we may prove that all nontrivial solutions of equation (4.1) satisfy $\lambda (f)=\infty$ when $b_3$ is replaced by a nonconstant polynomial.

Suppose that equation (4.1) admits a nontrivial solution such that $\lambda (f)<\infty$. Then $f$ has the form in (1.3) or (1.4). Also, we may write $f=\kappa e^{h}$, where $h$ is an entire function and $\kappa$ is the canonical product from the zeros of $f$ satisfying $\sigma (\kappa )=\lambda (\kappa )<\infty$. Thus we may suppose that $\kappa$ equals a polynomial in $e^{z/2}$ or $e^{z}$ and $h'$ equals a polynomial in $e^{z/2}$ or $e^{z}$. By denoting $g=h'$, from (4.1) we have

(4.2)\begin{equation} g^2+g'+2\frac{\kappa'}{\kappa}g+\frac{\kappa''}{\kappa}=e^{lz}+b_2e^{sz}+b_3. \end{equation}

By theorem 2.1, we may determine the coefficients $c_j$ in (1.3) or (1.4) from equation (4.2). Our main result is the following

Theorem 4.1 Let $b_2$ and $b_3$ be constants such that $b_2\not =0$ and $l,$ $s$ be relatively prime integers such that $l>s\geq 1$. Suppose that (4.1) admits two linearly independent solutions $f_1$ and $f_2$ such that $\max \{\lambda (f_1),\,\lambda (f_2)\}<\infty$. Then $s=1$ and $l=2$.

Recall the following well-known result due to Wittich [32]. We say that a function $f$ is subnormal if $\limsup _{r\to \infty } \log T(r,\,f)/r=0$. This lemma gives the form of subnormal solutions of second-order linear differential equations with certain periodic functions as coefficients.

Lemma 4.2 Let $P(z)$ and $Q(z)$ be polynomials in $z$ and not both constants. If $w\not \equiv 0$ is a subnormal solution of equation

(4.3)\begin{equation} w''+P(e^z)w'+Q(e^z)w=0, \end{equation}

then $w$ must have the form $w=e^{cz}(a_0+a_1e^{z}+\cdots +a_ke^{kz})$, where $k\geq 0$ is an integer and $c$, $a_0$, $\cdots$, $a_k$ are constants with $a_0\not =0$ and $a_k\not =0$. Moreover, we have $c^2+cP(0)+Q(0)=0$.

Proof of lemma 4.2. By Wittich [32], we have $w=e^{cz}(a_0+a_1e^{z}+\cdots +a_ke^{kz})$. By taking the derivatives of $w$ and then dividing $w'$ and $w''$ by $w$, respectively, we get

(4.4)\begin{align} \frac{w'}{w}& =\frac{\sum_{j=0}^k(c+j)a_je^{jz}}{\sum_{j=0}^ka_je^{jz}}, \end{align}

(4.5)\begin{align} \frac{w''}{w}& =\frac{\sum_{j=0}^k(c^2+2jc+j^2)a_je^{jz}}{\sum_{j=0}^ka_je^{jz}}. \end{align}

We write equation (4.3) as $Q(e^z)=-w''/w-P(e^z)w'/w$. Since $w$ is of finite order, then an application of the lemma on the logarithmic derivative yields $\deg (Q(z))m(r,\,e^z)\leq \deg (P(z))m(r,\,e^z)+O(\log r)$, i.e., $[\deg (Q(z))-\deg (P(z))]T(r,\,e^z)\leq O(\log r)$. Therefore, $\deg (Q(z))\leq \deg (P(z))$ and thus $P(z)$ is nonconstant. Together with equations (4.4) and (4.5), we rewrite equation (4.3) as

(4.6)\begin{equation} \frac{\sum_{j=0}^k(c^2+2jc+j^2)a_je^{jz}}{\sum_{j=0}^ka_je^{jz}}+\frac{\sum_{j=0}^k(c+j)a_je^{jz}}{\sum_{j=0}^ka_je^{jz}}P(e^z)+Q(e^z)=0. \end{equation}

Since along a ray $z=re^{i\theta }$ such that $\cos \theta <0$, we have $e^{z}\to 0$ as $r\to \infty$, then by letting $r\to \infty$ along the ray $z=re^{i\theta }$, we obtain from equation (4.6) that $c^2+cP(0)+Q(0)=0$. This completes the proof.

Unlike in § 2 and 3 where Nevanlinna theory plays the central role in proving theorems 2.1 and 3.1, the proof of theorem 4.1 will, however, mainly rely on the Lommel transformation for the generalized Bessel equation:

(4.7)\begin{equation} x^2y''+xy'+\left(\sum_{{-}n'}^nd_jx^{j}\right)y=0. \end{equation}

Recall the Bessel equation: $x^2y''+xy'+(x^2-\nu ^2)y=0$, where $\nu$ is a nonzero constant. Lommel [26] and Pearson [27] independently (see also [31]) studied the following transformation given by:

(4.8)\begin{equation} x=\alpha t^{\beta}, \quad y(x)=t^{\gamma}u(t), \end{equation}

where $\alpha$, $\beta$ and $\gamma$ are constants and applied to the Bessel equation. By using the above transformation to equation (4.7) and by computing the derivatives of $x$ and $y$, we get

(4.9)\begin{equation} t^2u''(t)+(2\gamma+1)tu'(t)+\left(\gamma^2+\beta^2\sum_{{-}n'}^n\alpha^jd_jt^{\beta j}\right)=0. \end{equation}

A further change of variable such that

(4.10)\begin{equation} t=e^{pz}, \quad f(z)=u(t), \end{equation}

leads to an equation of the form

(4.11)\begin{equation} f''+2\gamma pf'+p^2\left(\gamma^2+\beta^2\sum_{{-}n'}^n\alpha^jd_je^{\beta pjz}\right)=0. \end{equation}

In the case of equation (4.1), by Lommel's transformation we have

(4.12)\begin{equation} x^2y''+xy'-\left(d_1x^{l}+d_2x^{s}+d_3\right)y=0, \end{equation}

where $d_1$, $d_2$ and $d_3$ are some constants. By comparing the coefficients of equation (4.1) and (4.11), we deduce that $2\gamma p=0$, $\beta p=1$, $\alpha ^{l}d_1=1$, $\alpha ^{s}d_2=b_2$ and $d_3=b_3$. Further, for equation (4.12), it is well-known that the transformation $y=x^{-1/2}u$ leads to an equation of the form

(4.13)\begin{equation} u''-\left[\frac{1}{\alpha^{l}}x^{l-2}+\frac{b_2}{\alpha^{s}}x^{s-2}+\left(b_3-\frac{1}{4}\right)\frac{1}{x^2}\right]u=0. \end{equation}

In the case $l=4$, it has been shown by Chiang and Yu [11] that there is a full correspondence between solutions of (4.1) such that $\lambda (f)<\infty$ and Liouvillian solutions of (4.13). The only possible singular point of equation (4.13) is $x=0$. Concerning the local solutions around a singular point of a second-order linear differential equation, we have the following elementary lemma 4.3; see [17] or in [23, lemma 6.6].

Lemma 4.3 [17, 23]

Suppose that $h$ is analytic in $|z|< R,$ $R>0,$ and consider the differential equation

(4.14)\begin{equation} u''+\frac{h(z)}{z^2}u=0 \end{equation}

in the disc $|z|< R$. Let $\rho _1$ and $\rho _2$ be the roots of

(4.15)\begin{equation} \rho(\rho-1)+h(0)=0. \end{equation}

Denote by $D=D(r)$ the slit disc $D:=\{z:|z|< r\}\setminus \{t \ | \ 0\leq t< r\}$. Then

1. (1) if $\rho _1-\rho _2\in \mathbb {Z}\setminus \{0\}$, then equation (4.14) admits in some slit disc $D=D(r)$, $r\leq R$, two linearly independent solutions $u_1$ and $u_2$ of the form:

   (4.16)\begin{equation} \begin{aligned} u_1(z) & =z^{\rho_1}\sum_{i=0}^{\infty}a_iz^i, \quad a_0\not=0, \\ u_2(z) & =u_1(z)d\log z+z^{\rho_2}\sum_{i=0}^{\infty}b_iz^i, \end{aligned} \end{equation}
   where $d=0$ or $d=1$;

2. (2) if $\rho _1-\rho _2\not \in \mathbb {Z},$ then equation (4.14) admits in some slit disc $D=D(r),$ $r\leq R,$ two linearly independent solutions $u_1$ and $u_2$ of the form:

   (4.17)\begin{equation} \begin{aligned} u_1(z) & =z^{\rho_1}\sum_{i=0}^{\infty}a_iz^i, \quad a_0\not=0, \\ u_2(z) & =z^{\rho_2}\sum_{i=0}^{\infty}b_iz^i, \quad b_0\not=0; \end{aligned} \end{equation}

3. (3) if $\rho _1-\rho _2=0,$ then equation (4.14) admits in some slit disc $D=D(r),$ $r\leq R,$ two linearly independent solutions $u_1$ and $u_2$ of the form:

   (4.18)\begin{equation} \begin{aligned} u_1(z) & =z^{\rho_1}\sum_{i=0}^{\infty}a_iz^i, \quad a_0\not=0, \\ u_2(z) & =u_1(z)\log z+z^{\rho_2}\sum_{i=0}^{\infty}b_iz^i. \end{aligned} \end{equation}

For the solution $u_2$ in (4.16), if $d=0$, then from the proof of [23, lemma 6.6] we know that $b_0\not =0$.

Now, by elementary theory of ordinary differential equation (see [17]), lemma 4.3 shows that equation (4.13) admits two linearly independent solutions $u_1$ and $u_2$ in the broken plane $\mathbb {C}^{-}=\mathbb {C}\setminus \{x \ | \ 0\leq x<\infty \}$. When $p=1$ in (4.10), by the Lommel transformation and analytic continuation principle, the general solution of (4.1) is thus given by

(4.19)\begin{equation} f=(\alpha e^{z})^{{-}1/2}[E_1u_1(\alpha e^{z})+E_2u_2(\alpha e^{z})], \end{equation}

where $E_1$ and $E_2$ are two arbitrary constants. Note that the above solution is independent from the choice of the branches of $u_1$ and $u_2$ in lemma 4.3. This is the key observation for the proof of theorem 4.1.

Now we begin to prove theorem 4.1.

Proof of theorem 4.1. We first suppose that $f$ is a nontrivial solution such that $\lambda (f)<\infty$ of equation (4.1) and use the expressions in (1.3) and (1.4) to write $f(z)=\Psi (x)=x^{c}\psi (x)e^{\chi (x)}$, where $x=e^{z/h}$, $h=1$ or $h=2$. From the proof of [11, theorem 1.2], we know that in the broken plane $\mathbb {C}^{-}$ equation (4.13) admits a solution of the form

(4.20)\begin{equation} u=\exp\left(\int \omega {\rm d}x\right), \end{equation}

where $\omega :=\chi '+\psi '/\psi +(2hc+1)/(2x)$ is rational function in the complex plane $\mathbb {C}$. By using Kovacic's algorithm in [22] and giving the same discussions as in the proof of [11, theorem 3.1] to equation (4.13) for the two cases $b_3\not =1/4$ and $b_3=1/4$, respectively, we conclude that $l$ must be even. It follows that $f$ has the form in (1.4) and thus $p=1$ in (4.10) and $\alpha =1$ in (4.8). We write $f=\kappa e^{h}$, where $\kappa$ and $h'$ are both polynomials in $\zeta =e^z$ such that $\kappa (0)\not =0$. We may also write $f=\kappa _ce^{h_c}$, where $\kappa _c=\kappa e^{cz}$ and $h_c'=h'-c$. Then, denoting $g_c=h_c'$, we have from (4.1) that

(4.21)\begin{equation} g_c^2+g'_c+2\frac{\kappa'_c}{\kappa_c}g_c+\frac{\kappa''_c}{\kappa_c}=e^{lz}+b_2e^{sz}+b_3. \end{equation}

By lemma 4.2 and the expression in (1.4), we see that the constant $c$ in (1.4) satisfies $c^2=b_3$.

Now, for the solution in (4.19), by lemma 4.3 we have $\rho _1+\rho _2=1$ and $\rho _1\rho _2=1/4-b_3$, which yield $(\rho _1-\rho _2)^2=4b_3$. Then $\rho _1-\rho _2=-2c$ and it follows that $\rho _1=(1-2c)/2$ and $\rho _2=(1+2c)/2$. Thus the solutions in (4.19) can be written as

(4.22)\begin{equation} f=(e^{z})^{c}\left[\left(E_1+E_2d\log e^z\right)(e^{z})^{{-}2c}\sum_{j=0}^{\infty}a_j(e^{z})^{j}+E_2\sum_{j=0}^{\infty}b_j(e^{z})^{j}\right], \end{equation}

when $\rho _1-\rho _2\not =0$, or

(4.23)\begin{equation} f=\left(E_1+E_2\log e^z\right)\sum_{j=0}^{\infty}a_j(e^{z})^{j}+E_2\sum_{j=0}^{\infty}b_j(e^{z})^{j}, \end{equation}

when $\rho _1-\rho _2=0$. Note that $d=0$ in (4.22) when $\rho _1-\rho _2$ is not an integer. On the other hand, for the solution $f=\kappa e^{h}$, we may write the expression in (1.4) in the form $f=e^{cz}\sum _{j=0}^{\infty }d_je^{jz}$. By comparing this series with the one in (4.22) or in (4.23), we conclude that the logarithmic term in $u_2$ does not occur. This implies that $d=0$ or $E_2=0$ in (4.22) and $E_2=0$ in (4.23) when $f=\kappa e^{h}$.

With these preparations, we now suppose that $f_1$ and $f_2$ are two linearly independent solutions of (4.1) such that $\max \{\lambda (f_1),\,\lambda (f_2)\}<\infty$. We write $l=2(m+1)$ for some integer $m\geq 0$ and also write $s=2(m+1)-t$ for some integer $t\geq 1$.

Let $q$ be the smallest integer such that $s/l\leq [2(q+1)-1]/[2(q+1)]$. Since $l$ and $s$ are relatively prime, we see that the equality holds only when $q=m$. For each of $f_1$ and $f_2$, denoted by $f$, we may write $f=\kappa _ce^{h_c}$, where $\kappa _c=\kappa e^{cz}$. Then, denoting $g_c=h_c'$, we have equation (4.21). By theorem 2.1, $g_c=h_c'=\sum _{j=0}^{q}c_je^{(m+1-jt)z}$, where $c_0,\,c_1,\,\cdots,\,c_q$ are constants such that $c_0^2=1$ and $c_1,\,\cdots,\,c_q$ satisfy certain relations. In both of the two cases where $q=1$ and $q\geq 2$, we have $2c_0c_1=b_2$ and, by simple computations, that,

(4.24)\begin{equation} c_j=\frac{t_jc_1^{j}}{({-}2c_0)^{j-1}}, \quad j=1,\cdots,q, \end{equation}

where $t_j$ are positive integers such that $t_1<\cdots < t_q$, and further that

(4.25)\begin{equation} C_{q+j}=\sum_{\substack{j_0+\cdots+j_q=2,\\j_1+\cdots+qj_q=q+j}}\frac{2}{j_0!\cdots j_q!}c_0^{j_0}\cdots c_q^{j_q}=\frac{T_{q+j}c_1^{q+j}}{({-}2c_0)^{q+j-2}}, \quad j=1,\cdots,q, \end{equation}

where $T_{q+j}$ are positive integers such that $T_{q+1}<\cdots < T_{2q}$. By substituting $g_c=\sum _{j=0}^{q}c_je^{(m+1-jt)z}$ into (4.21) together with theorem 2.1, we get

(4.26)\begin{equation} \frac{\kappa_c''}{\kappa_c}+2c_0e^{(m+1)z}\frac{\kappa_c'}{\kappa_c}+c_0(m+1)e^{(m+1)z}-b_2e^{sz}-b_3=0, \end{equation}

when $q=0$, and

(4.27)\begin{equation} \begin{aligned} & \frac{\kappa_c''}{\kappa_c}+2\left(\sum_{j=0}^{q}c_je^{(m+1-jt)z}\right)\frac{\kappa_c'}{\kappa_c}-b_3\\ & \quad+\sum_{j=0}^{q}\left[C_{k_j}e^{[m+1-(q+1)t]z}+(m+1-jt)c_j\right]e^{(m+1-jt)z}=0, \end{aligned} \end{equation}

when $q\geq 1$, where $C_{k_j}=C_{q+1+j}$ and $C_{2q+1}=0$. By substituting equations (4.4) and (4.5) for $\kappa _{c}=e^{cz}(\sum _{i=1}^ka_ie^{iz})$, $a_0a_k\not =0$, into (4.26) or (4.27) and noting that $b_3=c^2$, we finally get

(4.28)\begin{equation} \sum_{i=0}^k\left[(2ic+i^2)a_ie^{iz}+c_0(2c+2i+m+1)a_ie^{(m+1+i)z}-b_2a_ie^{(i+s)z}\right]=0, \end{equation}

when $q=0$, and

(4.29)\begin{equation} \begin{aligned} & \sum_{i=0}^k(2ic+i^2)a_ie^{iz}+2\left(\sum_{i=0}^k(c+i)a_ie^{iz}\right)\left(\sum_{j=0}^{q}c_je^{(m+1-jt)z}\right)\\ & \quad+\left(\sum_{i=0}^ka_ie^{iz}\right)\left\{\sum_{j=0}^{q}[C_{k_j}e^{[m+1-(q+1)t]z}+(m+1-jt)c_j]e^{(m+1-jt)z}\right\}=0, \end{aligned} \end{equation}

when $q\geq 1$. Note that the inequality $(2q-1)/(2q)< s/l\leq [2(q+1)-1]/[2(q+1)]$ implies $qt< m+1\leq (q+1)t$, where the equality holds when $q=m$. The left-hand side of equations (4.28) and (4.29) are polynomials in $e^{z}$ of degree $k+m+1$ and thus all coefficients of these two polynomials vanish. When $s=2(m+1)-t<2m+1$, we have $q< m$ and $t\geq 2$. By looking at the highest-degree term in the resulting polynomial and noting that $a_k\not =0$, we find

(4.30)\begin{equation} m+2c+2k+1=0. \end{equation}

Similarly, when $s=2m+1$, we have $q=m$ and $t=1$ and find

(4.31)\begin{equation} C_{m+1}+(m+2c+2k+1)c_0=0. \end{equation}

Let $c_+$ or $c_{-}$ be any square root of $b_3$. We may write $f_1=\kappa _{1c}e^{h_{1c}}$ and $f_2=\kappa _{2c}e^{h_{2c}}$, where $\kappa _{1c}=\kappa _1e^{c_+z}$ and $\kappa _{2c}=\kappa _2e^{c_{-}z}$ and $\kappa _{1}$ and $\kappa _{2}$ are two polynomials in $e^z$ of degrees $k_1$ and $k_2$, respectively. Moreover, $h_{1c}$ satisfies $h_{1c}'=\sum _{j=0}^{q}c_je^{(m+1-jt)z}$. Since $c_0^2=1$ and since $2c_0c_1=b_2$ when $q\ge 1$, we easily deduce from (4.24) that $h_{2c}=\pm h_{1c}$. Recall the elementary Wronskian determinant: $f_1'f_2-f_1f_2'=D$, where $D$ is a nonzero constant (see [23]). Then we have $(f_1/f_2)'=D/f_2^2$. If $h_{2c}=h_{1c}$, then $f_1/f_2$ is of finite order while $f_1^2$ is of infinite order, a contradiction. Therefore, $h_{2c}=-h_{1c}$. We may suppose that $c_+=c$. When $s<2m+1$, from (4.30) we deduce that $c_+=c_{-}=c$, which implies that $-2c=m+1+2k_1$ is a positive integer and hence $k_1=k_2$; when $s=2m+1$, using (4.25) and the relation $2c_0c_1=b_2$ we deduce from (4.31) that $c_++c_{-}+m+1+k_1+k_2=0$, which implies that $c_+=c_{-}=c$ and hence $-2c=m+1+k_1+k_2$ is a positive integer. Now $\rho _1-\rho _2=-2c$ is a positive integer. Together with (4.19) and previous preparations, we conclude that equation (4.13) admits in the broken plane $\mathbb {C}^{-}$ two linearly independent solutions of the form $u_1=x^{\rho _1}v_1$ and $u_2=x^{\rho _2}v_2$, where $v_1$ and $v_2$ are two entire functions such that $v_1(0)\not =0$ and $v_2(0)\not =0$, so that

(4.32)\begin{equation} \begin{aligned} f_1 & =x^{c}\kappa_{11}e^{h_{11}}=x^{{-}1/2}\left(D_1x^{\rho_1}v_1+D_2x^{\rho_2}v_2\right),\\ f_2 & =x^{c}\kappa_{12}e^{{-}h_{11}}=x^{{-}1/2}\left(D_3x^{\rho_1}v_1+D_4x^{\rho_2}v_2\right), \end{aligned} \end{equation}

where $D_j$ are constants, $h_{11}=\sum _{j=0}^{q}\frac {c_j}{m+1-jt}x^{m+1-jt}$, and $\kappa _{11}$ and $\kappa _{12}$ are two polynomials of degrees $k_1$ and $k_2$, respectively, such that $\kappa _{11}(0)\not =0$ and $\kappa _{12}(0)\not =0$. Noting $\rho _1=(1-2c)/2$ and $\rho _2=(1+2c)/2$, we see from (4.22) that $D_2D_4\not =0$. Obviously, $E:=D_1D_4-D_2D_3\not =0$. From equation (4.32) we get

(4.33)\begin{equation} u_1=x^{\rho_1}v_1=\frac{1}{E}x^{1/2}x^{c}\left(D_4\kappa_{11}e^{h_{11}}-D_2\kappa_{12}e^{{-}h_{11}}\right). \end{equation}

Since $v_1$ is an entire function with $v_1(0)\not =0$, we see from (4.33) that the function $w:=D_4\kappa _{11}e^{2h_{11}}-D_2\kappa _{12}$ has a zero of order $-2c$ at the point $z=0$ and so $w(0)=w'(0)=\cdots =w^{(-2c-1)}(0)=0$. Denote

(4.34)\begin{equation} \begin{aligned} \kappa_{11} & =a_{1,0}+a_{1,1}x+\cdots+a_{1,k_1}x^{k_1},\\ \kappa_{12} & =a_{2,0}+a_{2,1}x+\cdots+a_{2,k_2}x^{k_2}, \end{aligned} \end{equation}

where $a_{1,0},\,a_{2,0},\,a_{1,k_1},\,a_{1,k_2}\not =0$. $w(0)=0$ implies that $D_4a_{1,0}=D_2a_{2,0}$. Supposing that $a_{1,0}=a_{2,0}=1$, we have $D_4=D_2$. Below we consider the case when $m\geq 1$.

Consider first the case when $s/l<1/2$. Since $m\geq 1$, by theorem 1.1 and (4.30), we see that $k_1=k_2\geq 1$. Now $w^{(m+1)}(0)=0$ implies that $a_{1,m+1}+2(m!)c_0=a_{2,m+1}$. Here $a_{1,m+1}=0$ if $m+1>k_1$ and so is for $a_{2,m+1}$. Obviously, $m+1\leq k_1$. For each of $f_1$ and $f_2$, denoted by $f$, we may write $f=\kappa _ce^{h_c}$. Then we have equation (4.28). Note that $1\leq s=2(m+1)-t\leq m$. The left-hand side of equation (4.28) is a polynomial in $e^{z}$ of degree $m+1+k$ and thus all coefficients of this polynomial vanish. Denoting $a_{-m-1}=\cdots =a_{-2}=a_{-1}=0$ and $a_{k+1}=\cdots =a_{k+m}=0$, we obtain from equation (4.28) that $c_0(2c+2k+m+1)a_k=0$, which yields (4.30), and

(4.35)\begin{equation} c_0(2c+2i-m-1)a_{i-m-1}=b_2a_{i-s}-(2ic+i^2)a_{i}, \quad i=0,\cdots,k+m. \end{equation}

By substituting $2c=-2k-m-1$ into the equations in (4.35) we get

(4.36)\begin{equation} 2c_0(k-i+m+1)a_{i-m-1}={-}b_2a_{i-s}+(2ic+i^2)a_i, \quad i=0,\cdots,k+m. \end{equation}

Since $1\leq s\leq m$, by letting $i=1,\,2,\,\cdots,\,m$, we see that $a_1/a_0=K_1$, $\cdots$, $a_m/a_0=K_m$ for some constants $K_1,\,\cdots,\,K_m$ independent from $c_0$. Then by letting $i=m+1$ in (4.36) together with the relation $a_{1,m+1}+2(m!)c_0=a_{2,m+1}$, we get $2k_1/(m+1)(2c+m+1)+2(m!)=-2k_2/(m+1)(2c+m+1)$. Since $k_1=k_2$ and $-2c=2k_1+m+1$, we get $(m+1)!=1$, which is impossible when $m\geq 1$.

Consider next the case when $s/l>1/2$ and $s<2m+1$. Now $qt< m+1< (q+1)t$ for some integer $1\leq q< m$. Recalling that $s=2(m+1)-t$ and $l$ and $s$ are relatively prime, we see that $t\geq 3$ is an odd integer. Denoting each of $f_1$ and $f_2$ by $f$, we may write $f=\kappa _ce^{h_c}$. Then we have equation (4.29). Denote $M=m+1-qt$ for simplicity. Since $-2c=2k+m+1$ and $C_{2q+1}=0$ and $C_{2q}=c_q^2$, then by looking at the coefficient of the term $e^{Mz}$ on the left-hand side of equation (4.29), we find $M(2c+M)a_M+2ca_0c_q+Ma_0c_q=0$, which gives $a_0c_q+Ma_M=0$. Recall that the function $w:=D_4\kappa _{11}e^{2h_{11}}-D_2\kappa _{12}$ has a zero of order $-2c$ at the point $z=0$. Then $w^{(M)}(0)=0$ implies that $a_{1,M}+2(M-1)!c_q=a_{2,M}$. Using equation (4.24) together with $2c_0c_1=b_2$ and $a_0c_q+Ma_M=0$, we get $M!=1$, which implies that $M=1$. It follows that $m=qt$. By looking at the coefficient of the term $e^{2z}$ on the left-hand side of equation (4.29), we find $2(2c+2)a_2+2(c+1)a_1c_q+a_0c_q^2+a_1c_q=0$, which together with $a_1=-a_0c_q$ yields $2a_2=a_0c_q^2$. Then by looking at the coefficient of the term $e^{3z}$ on the left-hand side of equation (4.29), we find $3(2c+3)a_3+2(c+2)a_2c_q+a_2c_q+a_1c_q^2=0$, i.e., $(2c+3)(6a_3+c_q^3)=0$ and thus $6a_3+c_q^3=0$. Now $w^{(3)}(0)=0$ implies that $a_{1,3}+6a_{1,2}c_q+12a_{1,1}c_q^2+8c_q^3=a_{2,3}$, which together with the relation $a_1=-a_0c_q$ and $2a_2=a_0c_q^2$ gives $a_{1,3}-c_q^3=a_{2,3}$. Then using equation (4.24) together with $2c_0c_1=b_2$ and $c_q^3+6a_3=0$, we get $c_q^3=0$, a contradiction to (4.24).

Finally, we consider the case when $s=2m+1$. Recall that $q=m$ and $t=1$ in (4.29). In this case, if $k_1=k_2$, then using (4.25) and the relation $2c_0c_1=b_2$ we get from (4.31) that $C_{m+1}=0$, a contradiction. Therefore, without loss of generality, we may suppose that $k_1>k_2\geq 0$. If $k_2=0$, then by theorem 1.1 have $2c+1=0$, which is impossible since $-2c=m+1+k_1+k_2$. Therefore, $k_2>0$. Note that $C_{2m}=c_m^2$. Since $-2c=m+1+k_1+k_2$, then by looking at the coefficient of the terms $e^z$ and $e^{2z}$ in equation (4.29), respectively, we find $a_{1}+a_{0}c_m=0$ and $2(2c+2)a_2+(2c+3)c_ma_1+[c_m^2+(2c+2)c_{m-1}]a_0=0$ and so $2a_2-c_m^2a_0+c_{m-1}a_0=0$. Recall that the function $w:=D_4\kappa _{11}e^{2h_{11}}-D_2\kappa _{12}$ has a zero of order $-2c$ at the point $z=0$. Now $w''(0)=0$ implies that $a_{1,2}+4a_{1,1}c_m+4c_{m-1}+4c_m^2=a_{2,2}$. Using equation (4.24) together with $2c_0c_1=b_2$, we get $-c_{m-1}/2+4c_{m-1}=c_{m-1}/2$, which yields $c_{m-1}=0$, a contradiction to (4.24).

From the above reasoning, we conclude that $l=2$. We complete the proof.

In the rest of this section, we use theorem 2.1 to determine precisely all nontrivial solutions such that $\lambda (f)<\infty$ of equation (4.1) for the case $l=2$ and $l=4$.

Theorem 4.4 Let $b_1$, $b_2$ and $b_3$ be constants such that $b_1b_2\not =0$ and $s$ and $l$ be relatively prime integers such that $1\leq s< l\leq 4$. Suppose that (4.1) admits a nontrivial solution $f$ such that $\lambda (f)<\infty$. Then

1. (1) if $s=1$ and $l=2,$ then $f=\kappa e^{h},$ $\kappa =\sum _{i=-1}^ka_ie^{iz}$ and $h=c_0e^{z}+cz,$ where $k\geq 0$ is an integer, $c_0$ and $c$ are constants such that $c_0^2=1,$ $2c_0(c+k)+c_0=b_2$ and $c^2=b_3,$ and $a_{-1},$ $a_0,$ $\cdots,$ $a_k$ are constants such that $a_0a_k\not =0,$ $a_{-1}=0$ and

   (4.37)\begin{equation} 2c_0(k+1-i)a_{i-1}=(2ic+i^2)a_i, \quad i=0,1,\cdots,k; \end{equation}

2. (2) if $s=1$ and $l=4,$ then $f=\kappa e^{h},$ $\kappa =\sum _{i=-2}^{k+1}a_ie^{iz}$ and $h=(c_0/2)e^{2z}+cz,$ where $k\geq 1$ is an integer, $c_0$ and $c$ are constants such that $c_0^2=1,$ $2c+2k+2=0$ and $c^2=b_3,$ and $a_{-2},$ $a_{-1},$ $a_0,$ $\cdots,$ $a_{k+1}$ are constants such that $a_0a_k\not =0,$ $a_{-2}=a_{-1}=a_{k+1}=0$ and

   (4.38)\begin{equation} 2c_0(k-i+2)a_{i-2}={-}b_2a_{i-1}+(2ic+i^2)a_i, \quad i=0,1,\cdots,k+1; \end{equation}

3. (3) if $s=3$ and $l=4,$ then $f=\kappa e^{h},$ $\kappa =\sum _{i=-2}^{k+1}a_ie^{iz}$ and $h=(c_0/2)e^{2z}+c_1e^{z}+cz,$ where $k\geq 0$ is an integer, $c_0$, $c_1$ and $c$ are constants such that $c_0^2=1,$ $2c_0c_1=b_2,$ $c^2=b_3$ and $c_1^2+(2+2c+2k)c_0=0$, and $a_{-2},$ $a_{-1},$ $a_0,$ $\cdots,$ $a_{k+1}$ are constants such that $a_0a_k\not =0,$ $a_{-2}=a_{-1}=a_{k+1}=0$ and

   (4.39)\begin{equation} (2k-2i+4)c_0a_{i-2}=(2c+2i-1)c_1a_{i-1}+(2ic+i^2)a_{i}, \quad i=0,\cdots,k+1. \end{equation}

For the convenience to write the recursive formulas in (4.37)–(4.39), we have introduced some extra coefficients $a_{-2}$, $a_{-1}$, $a_{k+1}$, which are all equal to $0$.

When $s=1$ and $l=4$, since $a_0\not =0$ and $a_{k}\not =0$ and $2c+2k+2=0$, the recursive formulas in (4.38) yield a polynomial equation $P(b_2)=0$ with respect to $b_2$ with coefficients formulated in terms of $c_0$ and $k$. For example, when $k=1$, we have $0=-b_2a_{0}+(2c+1)a_1$ and $2c_0a_{0}=-b_2a_{1}$, which together with the equation $2c+4=0$ yield $b_2^2-6c_0=0$, etc.

When $s=3$ and $l=4$, if $2c+1\not =0$, then we may solve from the first $k+1$ equations in (4.39) that $a_{k-1}=P(c)a_k$ for some polynomial $P(c)$ with respect to $c$ with coefficients formulated in terms of $c_0$ and $c_1$. By combining this equation with the equation $2c_0a_{k-1}=(2c+k)c_1a_{k}$ together with the relation $c_1^2+(2+2c+2k) c_0=0$ we may obtain a polynomial equation $P(t)=0$ with respect to $t=2c$ with coefficients independent from $c_0$ and $c_1$. For example, when $k=1$, we have $0=(2c+1)(c_1a_{0}+a_{1})$ and $2c_0a_{0}=(2c+3)c_1a_{1}$, which yield $P(t)=(t+2)(t+5)=0$ and thus $2c=-2$ or $2c=-5$, etc.

Proof of theorem 4.4. Suppose that $f$ is a nontrivial solution such that $\lambda (f)<\infty$ of equation (4.1). Following the proof of theorem 4.1, we may write $f=\kappa _c e^{h_c}$, where $\kappa _c=\kappa e^{cz}$ and $g_{c}=h_{c}'$ and then from (4.1) we get equation (4.21). Below we consider three cases: (1) $s=1$ and $l=2$; (2) $s=1$ and $l=4$; (3) $s=3$ and $l=4$.

For the first two cases $s=1$ and $l=2$ or $s=1$ and $s=4$, we have $\kappa _c=e^{cz}(\sum _{i=0}^ka_ie^{iz})$ and $h_c=[c_0/(m+1)]e^{(m+1)z}$, where $m=0$ or $m=1$ and $c_0$ is a constant such that $c_0^2=1$. Moreover, if $m=1$, then by theorem 1.1 we see $k\geq 1$. From the proof of theorem 4.1, we have equations (4.26) and (4.28) with $s=1$. When $l=2$, since the left-hand side of equation (4.28) is a polynomial in $e^{z}$ of degree $1+k$, all coefficients of this polynomial vanish. Therefore, denoting $a_{-1}=0$, we obtain from equation (4.28) that $[2c_0(c+k)+c_0-b_2]a_k=0$ and

(4.40)\begin{equation} [2c_0(c+i-1)+c_0-b_2]a_{i-1}+(2ic+i^2)a_i=0, \quad i=0,1,\cdots,k. \end{equation}

Since $a_k\not =0$, we have $2c_0(c+k)+c_0-b_2=0$ and then obtain the recursive formulas in (4.37) by substituting $2c_0c+c_0-b_2=-2c_0k$ into the equations in (4.40). When $m=1$, we have the recursive formulas in (4.36) with $s=1$. Denoting $a_{-2}=a_{-1}=0$ and $a_{k+1}=0$, we have the recursive formulas in (4.38).

When $s=3$ and $l=4$, we have $\kappa _c=e^{cz}(\sum _{i=0}^ka_ie^{iz})$ and $h_c=(c_0/2)e^{2z}+c_1e^{z}$, where $c_0$, $c_1$ are two constants such that $c_0^{2}=1$, $2c_0c_1=b_2$. From the proof of theorem 4.1, we get equation (4.29) with $q=m=1$. Similarly as in previous cases, denoting $a_{-2}=a_{-1}=a_{k+1}=0$, we finally get the recursive formulas in (4.39). We omit those details.

By theorem 4.4, we may give a different formulation from the results in [10, theorem 1.6].

Corollary 4.5 Let $s=1$ and $l=2$. Then equation (4.1) admits two linearly independent solutions $f_1$ and $f_2$ such that $\max \{\lambda (f_1),\,\lambda (f_2)\}<\infty$ if and only if there are two distinct nonnegative integers $k_1,\,k_2$ such that $b_2=\pm (k_1-k_2)$ and $4b_3=(k_1+k_2+1)^2$. In particular, it is possible that $\min \{\lambda (f_1),\,\lambda (f_2)\}=0$.

Proof of corollary 4.5. Let $f_1$ and $f_2$ be two linearly independent solutions of equation (4.1) such that $\max \{\lambda (f_1),\,\lambda (f_2)\}<\infty$. Let $c_+$ or $c_{-}$ be any square-root of $b_3$. By theorem 4.4, we may write $f_1=\kappa _{1}e^{h_{1}}$ and $f_2=\kappa _{2}e^{h_{2}}$, where $h_{1}=c_0e^{z}+c_+z$ and $c_0$ is a constant such that $c_0^2=1$, $h_{2}=\pm c_0e^{z}+c_{-}z$, $\kappa _{1}$ and $\kappa _2$ are two polynomials in $e^z$ of degrees $k_1$ and $k_2$, respectively. From the proof of theorem 4.1 we know that $h_{2}=-c_0e^{z}+c_{-}z$. Since $2c_0(c_++k_1)+c_0=-2c_0(c_{-}+k_2)-c_0=b_2$, we see that $c_+=c_{-}$ for otherwise we have $1+k_1+k_2=0$, which is impossible. Letting $c_+=c_{-}=c$, then we have $2c+k_{1}+k_{2}+1=0$ and it follows that $b_2=c_0(k_1-k_2)$. Since $b_2\not =0$ and $b_3=c^2$, we have $k_1\not =k_2$ and $4b_3=(k_1+k_2+1)^2$.

Conversely, we let $k_1$ and $k_2$ be two nonnegative integers such that $2c+k_{1}+k_{2}+1=0$, where $c$ satisfies $c^2=b_3$. We first define $f_1=\kappa _1e^{h_1}$, where $\kappa _1=\sum _{i=-1}^{k_1}a_ie^{iz}$, $h_{1}=c_0e^{z}+cz$, $k_1\geq 0$ is an integer, $c_0$ satisfies $c_0^2=1$ and $c_0[2(c+k_1)+1]=b_2$, and $a_{-1}$, $a_0$, $\cdots$, $a_k$ are constants such that $a_{-1}=0$ and

(4.41)\begin{equation} 2c_0(k_1+1-i)a_{i-1}=(2ic+i^2)a_i, \quad i=0,1,\cdots,k_1. \end{equation}

Also, we define $f_2=\kappa _2 e^{h_2}$, where $\kappa _2=\sum _{i=-1}^{k_2}\hat {a}_ie^{iz}$ and $h_2=-c_0e^{z}+cz$, $k_2\geq 0$ is an integer, $c_0$ satisfies $c_0^2=1$ and $-c_0[2(c+k_2)+1]=b_2$, and $\hat {a}_{-1}$, $\hat {a}_0$, $\cdots$, $\hat {a}_k$ are constants such that $\hat {a}_{-1}=0$ and

(4.42)\begin{equation} -2c_0(k_2+1-i)\hat{a}_{i-1}=(2ic+i^2)\hat{a}_i, \quad i=0,1,\cdots,k_2. \end{equation}

Then by theorem 4.4 we see that $f_1$ and $f_2$ are two linearly independent solutions of (4.1) such that $\max \{\lambda (f_1),\,\lambda (f_2)\}<\infty$. Obviously, we may choose one of $k_1$ and $k_2$ to be zero and thus $\min \{\lambda (f_1),\,\lambda (f_2)\}=0$. We complete the proof.

5. Concluding remarks

The oscillation of certain second-order linear differential equation (1.1) are investigated in this paper. If equation (1.1) with $A(z)$ being a linear combination of two exponential type functions admits a nontrivial solution such that $\lambda (f)<\infty$, by Hadamard's factorization theorem we obtain a Tumura–Clunie type differential equation with coefficients being combinations of functions in $\mathcal {S}$. In § 2, we give the form of entire solutions of the Tumura–Clunie type differential equations. As an application, in § 3 we give a partial answer to an oscillation question concerning equation (3.1) proposed by Ishizaki [19]. In § 4, we consider equation (1.1) for the case $A(z)=e^{lz}+b_2e^{sz}+b_3$, where $l$ and $s$ are two relatively prime integers and $b_2,\,b_3$ are constants such that $b_2\not =0$. The general form of solutions such that $\lambda (f)<\infty$ are known. If there are two linearly independent such solutions, we prove that the only possible case is when $l=2$.

By doing straightforward computations, we precisely characterize all solutions such that $\lambda (f)<\infty$ of equation (4.1) for the two cases $l=2$ and $l=4$. Unfortunately, we are unable to include or exclude other possibilities. Although, by using theorems 3.1 and 4.1 together with lemma 4.2, when $l\not =2,\,4$, we may also obtain some recursive formulas as in (4.37), (4.38) and (4.39) for the solutions such that $\lambda (f)<\infty$, it is difficult to verify the existence of $b_2$ and $b_3$ satisfying these recursive formulas. We conjecture that equation (4.1) can admit a nontrivial solution $f$ such that $\lambda (f)<\infty$ only when $l=2$ or $l=4$. We will study this conjecture further.