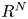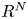1. Introduction
Recently, a great attention has been focussed on the study of inhomogeneous fractional nonlinear Schrödinger equation

where $m>0$![]() and $\varepsilon >0$
and $\varepsilon >0$![]() are real physical constants, $\sigma$
are real physical constants, $\sigma$![]() and $\gamma$
and $\gamma$![]() are real constants, $1< p<\frac {N+2\alpha }{(N-2\alpha )_+}$
are real constants, $1< p<\frac {N+2\alpha }{(N-2\alpha )_+}$![]() , and this equation comes from various physical contexts in the description of nonlinear waves such as propagation of a laser beam and plasma waves. When $\sigma =2$
, and this equation comes from various physical contexts in the description of nonlinear waves such as propagation of a laser beam and plasma waves. When $\sigma =2$![]() , the potential term is often called the harmonic potential and occurs in the condensed states. When $\alpha =1$
, the potential term is often called the harmonic potential and occurs in the condensed states. When $\alpha =1$![]() , there is a strong physical background related to the study of (1.1) and one may prefer to the papers [Reference Byeon and Wang3, Reference Smets, Su and Willem34, Reference Zhang37]. When $\sigma =0=\gamma$
, there is a strong physical background related to the study of (1.1) and one may prefer to the papers [Reference Byeon and Wang3, Reference Smets, Su and Willem34, Reference Zhang37]. When $\sigma =0=\gamma$![]() , to understand the ground state of (1.1) (see proposition 3.1 in [Reference Frank, Lenzmann and Silvestre14] or [Reference Saanouni33]), one may use the well-known fractional Gagliardo–Nirenberg inequality that for some $\theta \in (0,1)$
, to understand the ground state of (1.1) (see proposition 3.1 in [Reference Frank, Lenzmann and Silvestre14] or [Reference Saanouni33]), one may use the well-known fractional Gagliardo–Nirenberg inequality that for some $\theta \in (0,1)$![]() such that $\frac 1{q}=\frac 12-\frac {\theta \alpha }{N}$
such that $\frac 1{q}=\frac 12-\frac {\theta \alpha }{N}$![]() , it holds that
, it holds that
(see proposition A.3 in [Reference Tao35]). When $\sigma =-1$![]() , a new fractional Gagliardo–Nirenberg inequality has been obtained in [Reference Li and Ma20] to prove the existence of the ground state. In the above papers, the Schwartz symmetrization method (so called re-arrangement argument) has been used. However, for $\sigma >0$
, a new fractional Gagliardo–Nirenberg inequality has been obtained in [Reference Li and Ma20] to prove the existence of the ground state. In the above papers, the Schwartz symmetrization method (so called re-arrangement argument) has been used. However, for $\sigma >0$![]() and $m>0$
and $m>0$![]() , one can not directly use the re-arrangement argument to get the ground state to (1.1). The natural question is if one may get the ground state in broad class of the powers $\sigma,\gamma >0$
, one can not directly use the re-arrangement argument to get the ground state to (1.1). The natural question is if one may get the ground state in broad class of the powers $\sigma,\gamma >0$![]() without using re-arrangement argument, which is one subject of this paper. In [Reference Ma25], the author has found the ground state in the case when $\sigma =2$
without using re-arrangement argument, which is one subject of this paper. In [Reference Ma25], the author has found the ground state in the case when $\sigma =2$![]() and $\alpha \in \left (\frac 12,\frac {N}{2}\right )$
and $\alpha \in \left (\frac 12,\frac {N}{2}\right )$![]() by restricting the working space to the class of radially functions. In case when $m=0$
by restricting the working space to the class of radially functions. In case when $m=0$![]() , the ground states have been obtained [Reference Ma26]. The range of $\alpha$
, the ground states have been obtained [Reference Ma26]. The range of $\alpha$![]() also plays a crucial role in the existence result of ground states. In this paper, we first set up a new fractional interpolation inequality related to (1.1) and prove that the best constant in the new inequality can be obtained by a radially measurable solution function. We then get the ground states of the fractional Schrödinger equation on the whole space. For $\alpha \in (0,\frac 12]$
also plays a crucial role in the existence result of ground states. In this paper, we first set up a new fractional interpolation inequality related to (1.1) and prove that the best constant in the new inequality can be obtained by a radially measurable solution function. We then get the ground states of the fractional Schrödinger equation on the whole space. For $\alpha \in (0,\frac 12]$![]() , the power of the nonlinearity will be restricted into $p\in \left (1,\frac {N}{N-\alpha }\right )$
, the power of the nonlinearity will be restricted into $p\in \left (1,\frac {N}{N-\alpha }\right )$![]() and the compactness result about radially symmetric functions obtained by Lions [Reference Lions23] will be used. Even in this case, we need to have more conditions about $\gamma$
and the compactness result about radially symmetric functions obtained by Lions [Reference Lions23] will be used. Even in this case, we need to have more conditions about $\gamma$![]() and $\sigma$
and $\sigma$![]() . The precise results will be stated (see theorems 1.2 and 1.3 below) after we briefly report some related results obtained by others. In the recent very interesting paper [Reference Ao, Chan, Delatorre, Fontelos, Gonzalez and Wei2], the authors have introduced the ODE approach to nonlinear equations with the fractional Laplacian and their approach may be useful to the problem (1.1).
. The precise results will be stated (see theorems 1.2 and 1.3 below) after we briefly report some related results obtained by others. In the recent very interesting paper [Reference Ao, Chan, Delatorre, Fontelos, Gonzalez and Wei2], the authors have introduced the ODE approach to nonlinear equations with the fractional Laplacian and their approach may be useful to the problem (1.1).
In [Reference Chen and Guo5], for $\alpha =1$![]() in (1.1), Chen and Guo have given a criterion for the global existence of solutions of the corresponding Cauchy problem for an inhomogeneous nonlinear Schrödinger equation with harmonic potential:
in (1.1), Chen and Guo have given a criterion for the global existence of solutions of the corresponding Cauchy problem for an inhomogeneous nonlinear Schrödinger equation with harmonic potential:

with radial initial data
Their result may be stated as the following. Let $b>0, N>1+\frac {b}{2},1+\frac {4+2b}{N}< p<\frac {N+2}{N-2}+\frac {2b}{N-1}$![]() $(1+\frac {4+2b}{N}< p<\infty, if N\leq 2), A=\frac {N(p-1)-2b}{2},B=\frac {2(p-1)-(N(p-1)-2b)}{2}$
$(1+\frac {4+2b}{N}< p<\infty, if N\leq 2), A=\frac {N(p-1)-2b}{2},B=\frac {2(p-1)-(N(p-1)-2b)}{2}$![]() and let $V(\lambda )=\left (\frac {A-2}{p+1-A}\right )^\frac{A-2}{2B}||Q||^\frac{p-1}{B}_{L^{2}}\lambda ^{-\frac {A-2}{2B}}$
and let $V(\lambda )=\left (\frac {A-2}{p+1-A}\right )^\frac{A-2}{2B}||Q||^\frac{p-1}{B}_{L^{2}}\lambda ^{-\frac {A-2}{2B}}$![]() , where $Q$
, where $Q$![]() is the ground state solution to the equation
is the ground state solution to the equation
Define $\mathscr {S}=\{\phi \in \widetilde {\Sigma }:||\phi ||_{L^{2}}< V(||\nabla \phi ||^{2}_{L^{2}}+||x\phi ||^{2}_{L^{2}})\}$![]() . If $\varphi _0\in \mathscr {S}$
. If $\varphi _0\in \mathscr {S}$![]() , then the corresponding solution to (1.2) is global in time and uniformly bounded in $\widetilde {\Sigma }$
, then the corresponding solution to (1.2) is global in time and uniformly bounded in $\widetilde {\Sigma }$![]() . Furthermore, $\mathscr {S}$
. Furthermore, $\mathscr {S}$![]() is unbounded in $\widetilde {\Sigma }$
is unbounded in $\widetilde {\Sigma }$![]() . The proof relies on a Gagliardo–Nirenberg inequality with best constant and an energy method. Moreover, a similar result holds true for the critical power $p=1+\frac {4+2b}{N}$
. The proof relies on a Gagliardo–Nirenberg inequality with best constant and an energy method. Moreover, a similar result holds true for the critical power $p=1+\frac {4+2b}{N}$![]() , where the assumption $\varphi _0\in \mathscr {S}$
, where the assumption $\varphi _0\in \mathscr {S}$![]() is replaced with $\varphi _0\in \widetilde {\Sigma }$
is replaced with $\varphi _0\in \widetilde {\Sigma }$![]() and $||\varphi _0||_{L^{2}}<||Q||_{L^{2}}$
and $||\varphi _0||_{L^{2}}<||Q||_{L^{2}}$![]() . In addition, this criterion is sharp in the following sense. For any $\lambda >0$
. In addition, this criterion is sharp in the following sense. For any $\lambda >0$![]() and $c\in \mathbb {C}$
and $c\in \mathbb {C}$![]() with $|c|\geq 1$
with $|c|\geq 1$![]() , if $\varphi _0(x)= c\lambda ^{\frac {N}{2}}Q(\lambda x)$
, if $\varphi _0(x)= c\lambda ^{\frac {N}{2}}Q(\lambda x)$![]() , then $\varphi _0\in \widetilde {\Sigma }, ||\varphi _0||_{L^{2}}\geq ||Q||_{L^{2}}$
, then $\varphi _0\in \widetilde {\Sigma }, ||\varphi _0||_{L^{2}}\geq ||Q||_{L^{2}}$![]() and the corresponding solution to (1.2) blows up in finite time. See also [Reference Li, Wang and Zeng21, Reference Smets, Su and Willem34] for related results. For $\sigma =-s$
and the corresponding solution to (1.2) blows up in finite time. See also [Reference Li, Wang and Zeng21, Reference Smets, Su and Willem34] for related results. For $\sigma =-s$![]() and $\gamma =-t$
and $\gamma =-t$![]() with $0\leq t<2s$
with $0\leq t<2s$![]() , via a detailed study of a fractional version Hardy–Sobolev–Maz'ya inequality, with particular attention to the optimality of the constants involved, Mallick [Reference Mallick28] has studied the existence of positive solutions of the nonlinear equation involving fractional powers of the Laplacian with cylindrical potentials. Moreover, he has also considered the symmetric and asymptotic properties of the positive solution. The study of the problem (1.1) is also closely related to weighted Hardy type inequalities [Reference Frank and Seiringer13, Reference Li and Ma20]. See also [Reference Chhetri and Girg7, Reference Cho, Hwang, Kwon and Lee9, Reference Hajaiej, Molica Bisci and Vilasi15–Reference Le Coz19, Reference Luo and Zhang24, Reference Moroz and Van Schaftingen29, Reference Paul and Santra32] for related results of nonlocal problems.
, via a detailed study of a fractional version Hardy–Sobolev–Maz'ya inequality, with particular attention to the optimality of the constants involved, Mallick [Reference Mallick28] has studied the existence of positive solutions of the nonlinear equation involving fractional powers of the Laplacian with cylindrical potentials. Moreover, he has also considered the symmetric and asymptotic properties of the positive solution. The study of the problem (1.1) is also closely related to weighted Hardy type inequalities [Reference Frank and Seiringer13, Reference Li and Ma20]. See also [Reference Chhetri and Girg7, Reference Cho, Hwang, Kwon and Lee9, Reference Hajaiej, Molica Bisci and Vilasi15–Reference Le Coz19, Reference Luo and Zhang24, Reference Moroz and Van Schaftingen29, Reference Paul and Santra32] for related results of nonlocal problems.
We use the following notations: $A\lesssim B$![]() denotes an estimate of the form $A\leqslant CB$
denotes an estimate of the form $A\leqslant CB$![]() for some absolute constant $C>0$
for some absolute constant $C>0$![]() ; for $q\geq 1$
; for $q\geq 1$![]() , $L^{q}:=L^{q}({R}^{N})$
, $L^{q}:=L^{q}({R}^{N})$![]() is the Lebesgue space endowed with the usual norm $\|\,\cdot \,\|_q:=\|\,\cdot \,\|_{L^{q}}$
is the Lebesgue space endowed with the usual norm $\|\,\cdot \,\|_q:=\|\,\cdot \,\|_{L^{q}}$![]() ; $\|\,\cdot \,\|:=\|\,\cdot \,\|_2$
; $\|\,\cdot \,\|:=\|\,\cdot \,\|_2$![]() , and $\|(-\Delta )^\frac{\alpha }{2}\cdot \|=\|\cdot \|_{\dot H^{\alpha }}$
, and $\|(-\Delta )^\frac{\alpha }{2}\cdot \|=\|\cdot \|_{\dot H^{\alpha }}$![]() . We also use the brief notation that $\int \cdot {\rm d}\kern0.06em x:=\int _{R^{N}} \cdot {\rm d}\kern0.06em x$
. We also use the brief notation that $\int \cdot {\rm d}\kern0.06em x:=\int _{R^{N}} \cdot {\rm d}\kern0.06em x$![]() .
.
Recall that for $s\in (0,1)$![]() , the fractional Hilbert space $H^{s}=H^{s}(R^{N})$
, the fractional Hilbert space $H^{s}=H^{s}(R^{N})$![]() is defined by [Reference Adams1, Reference Chen, Li and Ma6, Reference Di Nezza, Palatucci and Valdinoci11, Reference Dyda, Ihnatsyeva and Vähäkangas12, Reference Musina and Nazarov30]
is defined by [Reference Adams1, Reference Chen, Li and Ma6, Reference Di Nezza, Palatucci and Valdinoci11, Reference Dyda, Ihnatsyeva and Vähäkangas12, Reference Musina and Nazarov30]
where $\mathcal {F}(u)$![]() denotes the Fourier transformation of $u$
denotes the Fourier transformation of $u$![]() , with norm
, with norm

We also denote by
We introduce, for $\sigma \in (0,2)$![]() , $\alpha \in (0,1)$
, $\alpha \in (0,1)$![]() , a fractional Sobolev space $D^{\alpha }$
, a fractional Sobolev space $D^{\alpha }$![]() with the norm
with the norm
such that under this norm $D^{\alpha }$![]() is the completion of $C_0^{\infty }(R^{N})$
is the completion of $C_0^{\infty }(R^{N})$![]() . We also let $\dot H^{\alpha }$
. We also let $\dot H^{\alpha }$![]() be the completion of $C_0^{\infty }(R^{N})$
be the completion of $C_0^{\infty }(R^{N})$![]() under the usual norm $\|(-\Delta )^\frac\alpha 2 u\|$
under the usual norm $\|(-\Delta )^\frac\alpha 2 u\|$![]() . For $\alpha >1$
. For $\alpha >1$![]() , we may use Fourier transform to define $H^{\alpha }$
, we may use Fourier transform to define $H^{\alpha }$![]() and we refer to [Reference Cho and Ozawa8]. Then we may define $D^{\alpha }$
and we refer to [Reference Cho and Ozawa8]. Then we may define $D^{\alpha }$![]() as above.
as above.
For $Z$![]() being any space of functions on $R^{N}$
being any space of functions on $R^{N}$![]() , we denote by $Z_{rd}$
, we denote by $Z_{rd}$![]() the space of radial functions in $Z$
the space of radial functions in $Z$![]() . Here and hereafter, we denote, for $\phi \in D_{rd}^{\alpha },$
. Here and hereafter, we denote, for $\phi \in D_{rd}^{\alpha },$![]() the mass and energy functionals for (1.1):
the mass and energy functionals for (1.1):
and
where the integration is over the whole space $R^{N}$![]() . We remark that the ground state to (1.1) may be considered as the mountain pass critical point of the energy functional $E(\cdot )$
. We remark that the ground state to (1.1) may be considered as the mountain pass critical point of the energy functional $E(\cdot )$![]() on the working space $D_{rd}^{\alpha }$
on the working space $D_{rd}^{\alpha }$![]() [Reference Costa10].
[Reference Costa10].
We define the functional
on the space $D_{rd}^{\alpha }$![]() , where
, where
where $\theta =\frac {N+\sigma -\frac {2N+2\gamma }{p+1}}{2\alpha +\sigma }$![]() .
.
We now consider the minimization problem
There is no previous result about this problem with $\sigma >0$![]() . We now set up the interpolation inequality as below.
. We now set up the interpolation inequality as below.
Proposition 1.1
(1). Let $\alpha \in (0,\frac 12]$
 , $1< p<\frac {N}{N-\alpha }$
, $1< p<\frac {N}{N-\alpha }$ , $\gamma '=\frac {\gamma }{p+1}>0$
, $\gamma '=\frac {\gamma }{p+1}>0$ , and $\sigma >0$
, and $\sigma >0$ with $\frac {2\alpha }{(1-p)N+\alpha (p+1)}\gamma \leq \sigma$
with $\frac {2\alpha }{(1-p)N+\alpha (p+1)}\gamma \leq \sigma$ . Then
\[ \||x|^{\gamma'}u\|_{p+1}\lesssim\||x|^{\frac\sigma 2}u\|^{1-\theta}\|u\|_{\dot H^{\alpha}}^{\theta}, \]for any $u\in D_{rd}^{\alpha }({R^{N}})$
. Then
\[ \||x|^{\gamma'}u\|_{p+1}\lesssim\||x|^{\frac\sigma 2}u\|^{1-\theta}\|u\|_{\dot H^{\alpha}}^{\theta}, \]for any $u\in D_{rd}^{\alpha }({R^{N}})$
 .
.(2). Let $\alpha \in \left (\frac 12,\frac {N}{2}\right )$
 , $\frac {N+2\gamma -2\alpha -4\sigma }{N-2\alpha }\leq p\leq \frac {2(N+\gamma )}{N-2\alpha }-1$
, $\frac {N+2\gamma -2\alpha -4\sigma }{N-2\alpha }\leq p\leq \frac {2(N+\gamma )}{N-2\alpha }-1$ , and $\theta :=\frac {N+\sigma -\frac {2N}{p+1}-2\gamma '}{2\alpha +\sigma }.$
, and $\theta :=\frac {N+\sigma -\frac {2N}{p+1}-2\gamma '}{2\alpha +\sigma }.$ Then
\[ \||x|^{\gamma'}u\|_{p+1}\lesssim\||x|^{\frac\sigma 2}u\|^{1-\theta}\|u\|_{\dot H^{\alpha}}^{\theta}, \]for any $u\in D_{rd}^{\alpha }({R^{N}})$
Then
\[ \||x|^{\gamma'}u\|_{p+1}\lesssim\||x|^{\frac\sigma 2}u\|^{1-\theta}\|u\|_{\dot H^{\alpha}}^{\theta}, \]for any $u\in D_{rd}^{\alpha }({R^{N}})$
 .
.
For $\alpha \in (0,1)$![]() , a more general result than proposition 1.1 is proven in theorem 1.1 in [Reference Nguyen and Squassina31]. Since we have different purpose, we shall present a simpler and direct proof of proposition 1.1 for completeness. We now explain why $\theta$
, a more general result than proposition 1.1 is proven in theorem 1.1 in [Reference Nguyen and Squassina31]. Since we have different purpose, we shall present a simpler and direct proof of proposition 1.1 for completeness. We now explain why $\theta$![]() can be chosen in this way. So we do the dimension analysis. Note that for $p>1$
can be chosen in this way. So we do the dimension analysis. Note that for $p>1$![]() , $\gamma '\geq 0$
, $\gamma '\geq 0$![]() , $a>0,b>0$
, $a>0,b>0$![]() , we let the scaling $\psi = u_{a,b}:= au\left (\frac {x}{b}\right )$
, we let the scaling $\psi = u_{a,b}:= au\left (\frac {x}{b}\right )$![]() with $\frac {x}{b}=z$
with $\frac {x}{b}=z$![]() :
:

Note that for $p=1$![]() and $\gamma '=\frac \sigma 2$
and $\gamma '=\frac \sigma 2$![]() , we have
, we have
We also have
If proposition 1.1 is true, then for any constant $c$![]() , we have
, we have
By this we have
which implies that
Then we get
which implies that
As the consequences, we may obtain some of our main results (and the very new part is when $\alpha \in \left (0,\frac 12\right ]$![]() , which has not been treated before).
, which has not been treated before).
Theorem 1.2 Let $\gamma \geq 0$![]() . Assume (1) $\alpha \in (0,\frac 12]$
. Assume (1) $\alpha \in (0,\frac 12]$![]() , $1< p<\frac {N}{N-\alpha }$
, $1< p<\frac {N}{N-\alpha }$![]() , and $\frac {2\alpha }{(1-p)N+\alpha (p+1)} \gamma \leq \sigma$
, and $\frac {2\alpha }{(1-p)N+\alpha (p+1)} \gamma \leq \sigma$![]() ; or (2) $\alpha \in \left (\frac 12,\frac {N}{2}\right )$
; or (2) $\alpha \in \left (\frac 12,\frac {N}{2}\right )$![]() , and $\frac {2\gamma +2\alpha -N-4\sigma }{N-2\alpha }\leq p\leq \frac {2(N+\gamma )}{N-2\alpha }-1$
, and $\frac {2\gamma +2\alpha -N-4\sigma }{N-2\alpha }\leq p\leq \frac {2(N+\gamma )}{N-2\alpha }-1$![]() . We have three conclusions below.
. We have three conclusions below.
(1). There exists a positive constant $C(N,p,\gamma,\alpha )$
 , such that for any $u\in D^{\alpha }_{rd}$
, such that for any $u\in D^{\alpha }_{rd}$ , it holds
(1.4)\begin{equation} \int|x|^{\gamma}|u|^{1+p}\,{\rm d}\kern0.06em x\leq C(N,p,\gamma,\alpha)\||x|^\frac{\sigma}{2}u\|^{A}\|u\|_{\dot H^{\alpha}}^{B}. \end{equation}
, it holds
(1.4)\begin{equation} \int|x|^{\gamma}|u|^{1+p}\,{\rm d}\kern0.06em x\leq C(N,p,\gamma,\alpha)\||x|^\frac{\sigma}{2}u\|^{A}\|u\|_{\dot H^{\alpha}}^{B}. \end{equation}
(2). Moreover, if $\frac {2\gamma +2\alpha -N-4\sigma }{N-2\alpha }< p< \frac {2(N+\gamma )}{N-2\alpha }-1$
 , then the minimization problem
(1.5)\begin{equation} \beta:=\inf\left\{J(u),\quad u\in D^{\alpha}_{rd}\right\} \end{equation}is attained in some $\psi \in D^{\alpha }_{rd}$
, then the minimization problem
(1.5)\begin{equation} \beta:=\inf\left\{J(u),\quad u\in D^{\alpha}_{rd}\right\} \end{equation}is attained in some $\psi \in D^{\alpha }_{rd}$
 (that is, $\beta =(\int |x|^{\gamma }|\psi |^{p+1}\,{\rm d}\kern0.06em x)^{-1}$
(that is, $\beta =(\int |x|^{\gamma }|\psi |^{p+1}\,{\rm d}\kern0.06em x)^{-1}$ , $\||x|^\frac{\sigma }{2}\psi \|=\|\psi \|_{\dot H^{\alpha }}=1$
, $\||x|^\frac{\sigma }{2}\psi \|=\|\psi \|_{\dot H^{\alpha }}=1$ ) and $\psi$
) and $\psi$ satisfies
(1.6)\begin{equation} B(-\Delta)^{\alpha}\psi+A|x|^{\sigma}\psi-\beta(p+1)|x|^{\gamma}\psi|\psi|^{p-1}=0. \end{equation}
satisfies
(1.6)\begin{equation} B(-\Delta)^{\alpha}\psi+A|x|^{\sigma}\psi-\beta(p+1)|x|^{\gamma}\psi|\psi|^{p-1}=0. \end{equation}
(3). Furthermore,
(1.7)\begin{equation} C(N,p,\gamma,\alpha)=\frac{1+p}{{A}}\left(\frac AB\right)^{\frac{B}2}\|\phi\|^{-(p-1)}, \end{equation}where $\phi$
 is a ground state solution to the following equation on $R^{N}$
is a ground state solution to the following equation on $R^{N}$ :
(1.8)\begin{equation} (-\Delta)^{\alpha} \phi +|x|^{\sigma}\phi -|x|^{\gamma}\phi|\phi|^{p-1}=0 ,\quad 0\neq \phi \in D^{\alpha}_{rd}. \end{equation}
:
(1.8)\begin{equation} (-\Delta)^{\alpha} \phi +|x|^{\sigma}\phi -|x|^{\gamma}\phi|\phi|^{p-1}=0 ,\quad 0\neq \phi \in D^{\alpha}_{rd}. \end{equation}
Using this proposition, we shall prove that there is a ground state of (1.9) below.
Theorem 1.3 Take $\epsilon =1$![]() , $\gamma \geq 0$
, $\gamma \geq 0$![]() , $\frac 12<\alpha <\frac N2$
, $\frac 12<\alpha <\frac N2$![]() , and $\frac {2\gamma +2\alpha -N-4\sigma }{N-2\alpha }\leq p\leq \frac {2(N+\gamma )}{N-2\alpha }-1$
, and $\frac {2\gamma +2\alpha -N-4\sigma }{N-2\alpha }\leq p\leq \frac {2(N+\gamma )}{N-2\alpha }-1$![]() . Then, there is a ground state solution to (1.1) in the following meaning
. Then, there is a ground state solution to (1.1) in the following meaning
To prove the result above, we need to set up a compactness result, which is parallel to the classical Sobolev injection (see [Reference Chen and Guo5, Reference Lions23]). We state here such result in case $\frac 12<\alpha <\frac N2$![]() .
.
Lemma 1.4 Let $\gamma \geq 0$![]() , $\frac 12<\alpha <\frac N2$
, $\frac 12<\alpha <\frac N2$![]() , and $\frac {2\gamma +2\alpha -N-4\sigma }{N-2\alpha }\leq p\leq \frac {2(N+\gamma )}{N-2\alpha }-1$
, and $\frac {2\gamma +2\alpha -N-4\sigma }{N-2\alpha }\leq p\leq \frac {2(N+\gamma )}{N-2\alpha }-1$![]() . Then, the following injection
. Then, the following injection
is compact, and we may simply write $\Sigma :=L^{p+1}(|x|^{\gamma }\,{\rm d}\kern0.06em x)$![]() .
.
We may also show the existence of other standing states to (1.1) in the following way. We now define on $D^{\alpha }_{rd}$![]() the action for (1.1) by
the action for (1.1) by
and let $Q(u)=< S'(u),u>$![]() . Set
. Set
and
It is clear that when restricted on $M$![]() , the action $S$
, the action $S$![]() is simplified to
is simplified to
where $a=\left (\frac 12-\frac {1}{p+1}\right )$![]() . Hence $m_0\geq 0$
. Hence $m_0\geq 0$![]() .
.
We shall show in next section that
Lemma 1.5 $m_0=\inf \{S(u),u\in {M}\}>0.$![]()
The proof of lemma 1.5 replies on theorem 1.2 and this result will play an important role in the argument of theorem 1.6 below.
Then, we can show the following result about the existence of standing waves and their orbital stability for (1.1).
Theorem 1.6 Take $\varepsilon =1, \gamma \geq 0$![]() , $\alpha \in \left (\frac 12,\frac N2\right )$
, $\alpha \in \left (\frac 12,\frac N2\right )$![]() , and $\frac {2\gamma +2\alpha -N-4\sigma }{N-2\alpha }\leq p\leq \frac {2(N+\gamma )}{N-2\alpha }-1$
, and $\frac {2\gamma +2\alpha -N-4\sigma }{N-2\alpha }\leq p\leq \frac {2(N+\gamma )}{N-2\alpha }-1$![]() . We have the following conclusions.
. We have the following conclusions.
(1) There is a standing wave solution to (1.1) in the following sense
\[ (-\Delta)^{\alpha}\phi+|x|^{\sigma}\phi+\phi-|x|^{\gamma}\phi|\phi|^{p-1}=0,\ 0\neq\phi\in D^{\alpha}_{rd},\ m_0=S(\phi). \]
(2) Let $B_1=(1-\theta _0)(q+1)+\frac {2\gamma }{N-2\alpha }$
 , where $q+1=p+1-\frac {2\gamma }{N-2\alpha }$
, where $q+1=p+1-\frac {2\gamma }{N-2\alpha }$ and $\theta _0=\frac {N}{\alpha }\left (\frac 12-\frac 1{q+1}\right )$
and $\theta _0=\frac {N}{\alpha }\left (\frac 12-\frac 1{q+1}\right )$ . For $B_1<2$
. For $B_1<2$ , this standing wave is orbitally stable.
, this standing wave is orbitally stable.
As usual, in the orbitally stable part, we always suppose that the global existence of solutions to (1.1) with initial datum near to the standing waves.
The rest of the paper is organized as follows. In §2, we prove lemmas 1.4 and 1.5. We recall some useful inequalities and some tools like compactness result needed in the sequel. In §3, we prove proposition 1.1. In §4, we prove theorem 1.2. We prove theorem 1.3 in § 5. We establish the existence of standing states of (1.1) and the orbital stability in §6. Thus, we prove theorem 1.6 in the last section.
2. Preliminary results
In this section, we collect some well-known facts about properties about radially symmetric function on $R^{N}$![]() . An estimate similar to Strauss's inequality [Reference Strauss36] in the fractional case is as follows [Reference Cho and Ozawa8]:
. An estimate similar to Strauss's inequality [Reference Strauss36] in the fractional case is as follows [Reference Cho and Ozawa8]:
Lemma 2.1 Let $N\geq 2$![]() and $\frac 12<\alpha <\frac N2$
and $\frac 12<\alpha <\frac N2$![]() . Then, for any $u\in \dot H_{rd}^{\alpha }(R^{N})$
. Then, for any $u\in \dot H_{rd}^{\alpha }(R^{N})$![]() ,
,
where

and $\Gamma$![]() is the Gamma function.
is the Gamma function.
To facilitate the proofs of our latter results, we show that $\|u\|_{D^{\alpha }}$![]() is stronger than $\|u\|_{H^{\alpha }}$
is stronger than $\|u\|_{H^{\alpha }}$![]() .
.
Proposition 2.2 Fix $\alpha >0$![]() . There exists a uniform constant $c_1>0$
. There exists a uniform constant $c_1>0$![]() depending only on $\alpha$
depending only on $\alpha$![]() and $n$
and $n$![]() such that
such that
for any $u\in D_{rd}^{\alpha }$![]() .
.
Proof. We argue by contradiction. Assume that (2.12) is not true. Then there exists a sequence $(u_j)$![]() in $D_{rd}^{\alpha }$
in $D_{rd}^{\alpha }$![]() such that $\|u_j\|_{H^{\alpha }}=1, \|u_j\|_{D^{\alpha }}\rightarrow 0$
such that $\|u_j\|_{H^{\alpha }}=1, \|u_j\|_{D^{\alpha }}\rightarrow 0$![]() . We may assume that $u_j \rightarrow u$
. We may assume that $u_j \rightarrow u$![]() in $L^{2}_{loc}$
in $L^{2}_{loc}$![]() , $u_j \rightarrow u \ a.e.$
, $u_j \rightarrow u \ a.e.$![]() , $(-\Delta )^\frac\alpha 2 u_j \rightarrow 0$
, $(-\Delta )^\frac\alpha 2 u_j \rightarrow 0$![]() in $L^{2}$
in $L^{2}$![]() . Since
. Since
we have
For any $R>0$![]() , we know that $\|{u_j}\|^{2}_{L^{2}}=\|u_j\|^{2}_{L^{2}(B_R)}+\|u_j\|^{2}_{L^{2}(B^{c}_R)}$
, we know that $\|{u_j}\|^{2}_{L^{2}}=\|u_j\|^{2}_{L^{2}(B_R)}+\|u_j\|^{2}_{L^{2}(B^{c}_R)}$![]() and
and
This implies that $u=0$![]() almost everywhere and
almost everywhere and
By the local compactness imbedding theorem we conclude that $\|{u_j}\|_{L^{2}_{loc}}\rightarrow 0.$![]() Then we have $\|u_j\|^{2}_{L^{2}(B_R)}+\|u_j\|^{2}_{L^{2}(B^{c}_R)}= \circ (1)$
Then we have $\|u_j\|^{2}_{L^{2}(B_R)}+\|u_j\|^{2}_{L^{2}(B^{c}_R)}= \circ (1)$![]() , which leads to a contradiction with the equality (2.13). This completes the proof.
, which leads to a contradiction with the equality (2.13). This completes the proof.
Taking into account proposition 2.2, we get $D_{rd}^{\alpha } \hookrightarrow H^{\alpha } \hookrightarrow L^{q}$![]() for any $q\in \left [2,\frac {2N}{N-2\alpha }\right ]$
for any $q\in \left [2,\frac {2N}{N-2\alpha }\right ]$![]() .
.
Lemma 2.3 Let $N\geq 2$![]() , $p\in (1,\infty )$
, $p\in (1,\infty )$![]() and $\alpha \in (0,1)$
and $\alpha \in (0,1)$![]() . Then $D_{rd}^{\alpha } \hookrightarrow H^{\alpha } \hookrightarrow L^{q}$
. Then $D_{rd}^{\alpha } \hookrightarrow H^{\alpha } \hookrightarrow L^{q}$![]() for any $q\in \left [2,\frac {2N}{N-2\alpha }\right ]$
for any $q\in \left [2,\frac {2N}{N-2\alpha }\right ]$![]() .
.
This result will be useful in the proof of theorem 1.2.
We may prove lemma 1.4 by using the imbedding $D_{rd}^{\alpha } \hookrightarrow H^{\alpha }$![]() . However, we prefer to give a direct proof below.
. However, we prefer to give a direct proof below.
Proof. (Proof of lemma 1.4). Recall that
which is a Banach space endowed with the norm

We divide the proof into three steps. Take ${(u_j)}$![]() a bounded sequence of ${D_{rd}^{\alpha }}$
a bounded sequence of ${D_{rd}^{\alpha }}$![]() and let $\varepsilon >0$
and let $\varepsilon >0$![]() . We may assume that $u_j$
. We may assume that $u_j$![]() converges weakly in $D_{rd}^{\alpha }$
converges weakly in $D_{rd}^{\alpha }$![]() and almost everywhere to zero. We write
and almost everywhere to zero. We write

We should only concern $\gamma > 0$![]() . Lemma 2.1 will play an important role below.
. Lemma 2.1 will play an important role below.
Step I. We consider the integral in the region $|x|\leq \varepsilon.$![]()
Since $|u(x)|\lesssim |x|^{\alpha -\frac {N}{2}}\|(-\Delta )^{\frac {\alpha }{2}} u\|$![]() for $x\neq 0$
for $x\neq 0$![]() and $\gamma +\left (\alpha -\frac {N}{2}\right )(p+1)+N > 0$
and $\gamma +\left (\alpha -\frac {N}{2}\right )(p+1)+N > 0$![]() , that is,
, that is,
we have

as $\epsilon \to 0$![]() .
.
Step II. We consider the integral in the region $O_\epsilon :=\{\varepsilon \leq |x|\leq \frac {1}{\varepsilon }\}.$![]()
Since $\int _{O_\epsilon }|u_j|^{2}dx\rightarrow 0$![]() and $|x|^{2\sigma }$
and $|x|^{2\sigma }$![]() is bounded in $O_\epsilon$
is bounded in $O_\epsilon$![]() , we obtain
, we obtain
Then,

as $j$![]() tends to infinity.
tends to infinity.
Step III. We consider the integral in the region $|x|\geq \frac {1}{\varepsilon }.$![]()
For $\gamma <(p-1)\left (\frac {N}{2}-\alpha \right )+2\sigma$![]() , we have
, we have

as $\epsilon \to 0$![]() . Thus, the proof is completed.
. Thus, the proof is completed.
We now give the proof of lemma 1.5.
Proof. By theorem 1.2, for $u\in {M}$![]() , we have
, we have

and then

Hence,

which implies that

3. Proof of proposition 1.1
We now prove proposition 1.1 via arguing by contradiction.
Proof. (proposition 1.1). We prove the result by dividing $\alpha$![]() into two cases: case (1): $\alpha \in (0,1/2]$
into two cases: case (1): $\alpha \in (0,1/2]$![]() and case (2): $\alpha \in (1/2,N/2)$
and case (2): $\alpha \in (1/2,N/2)$![]() .
.
Case (1): In this case we have
If the conclusion of proposition 1.1 is not true, up to a scaling, there exists a sequence $(u_j)\subset D_{rd}^{\alpha }$![]() such that $\||x|^{\frac {\gamma }{p+1}} u_j\|_{L^{p+1}}=1$
such that $\||x|^{\frac {\gamma }{p+1}} u_j\|_{L^{p+1}}=1$![]() , $\|(-\Delta )^{\frac {\alpha }{2}}u_j\|_{L^{2}}=1$
, $\|(-\Delta )^{\frac {\alpha }{2}}u_j\|_{L^{2}}=1$![]() , and
, and
By $D_{rd}^{\alpha } \hookrightarrow H^{\alpha }$![]() , we may assume that $\|u_j\|_{H^{\alpha }}\leq C$
, we may assume that $\|u_j\|_{H^{\alpha }}\leq C$![]() for some constant $C>0$
for some constant $C>0$![]() . So for any $\epsilon >0$
. So for any $\epsilon >0$![]() , we have $\||x|^{\frac {\gamma }{p+1}}u_j\|_{L^{p+1}(|x|\leq 1/\epsilon )}\rightarrow 0$
, we have $\||x|^{\frac {\gamma }{p+1}}u_j\|_{L^{p+1}(|x|\leq 1/\epsilon )}\rightarrow 0$![]() . Let $\lambda =\frac {\frac {2N}{N-\alpha }-2p}{\frac {2N}{N-\alpha }-(p+1)}$
. Let $\lambda =\frac {\frac {2N}{N-\alpha }-2p}{\frac {2N}{N-\alpha }-(p+1)}$![]() . Let $B^{R}=\{|x|\geq R\}$
. Let $B^{R}=\{|x|\geq R\}$![]() for $R=1/\epsilon$
for $R=1/\epsilon$![]() . Then, applying Cauchy–Schwartz inequality for $u=u_j$
. Then, applying Cauchy–Schwartz inequality for $u=u_j$![]() and omitting the integration domain for moment,
and omitting the integration domain for moment,

Note that $2p=\lambda (p+1)+(1-\lambda )\frac {2N}{N-\alpha }$![]() ,
,
which is bounded by
and further bounded by
In the last step we have used the assumption that
which is equivalent to $(2\gamma -\sigma )\lambda ^{-1}\leq \gamma$![]() .
.
Combining all these together, we get for some uniform constant $C>0$![]() ,
,

which gives a contradiction to the assumption that
Case (2): Again we argue by contradiction and take the sequence $(u_j)$![]() as above. Note that
as above. Note that
Let $q+1=p+1-\frac {2\gamma }{N-2\alpha }$![]() , By lemma 2.1, we know that
, By lemma 2.1, we know that
Using the well-known fractional Gagliardo–Nirenberg inequality (proposition A.3 in [Reference Tao35]) that
where $\theta _0=\frac {N}{\alpha }\left (\frac 12-\frac 1{q+1}\right )$![]() , we get
, we get
That is,
However,
For any $\varepsilon > 0$![]() small, $\|u_j\|_{L^{2}(B_\varepsilon )}\rightarrow \|u\|_{L^{2}(B_\varepsilon )}= \circ (\varepsilon )$
small, $\|u_j\|_{L^{2}(B_\varepsilon )}\rightarrow \|u\|_{L^{2}(B_\varepsilon )}= \circ (\varepsilon )$![]() . Then
. Then
which lead to a contradiction with (3.16) that $\|u_j\|_{L^{2}}\geq c$![]() .
.
4. Proof of theorem 1.2
The proofs of theorem 1.2 in the two groups of assumptions are almost the same. So we present the full proof only in case $\alpha \in (1/2,N/2)$![]() (but in case (1), we need to use the compactness result theorem II.1 of [Reference Lions23]). We divide the proof into three parts.
(but in case (1), we need to use the compactness result theorem II.1 of [Reference Lions23]). We divide the proof into three parts.
A. Proof of the interpolation inequality (1.4):
First, using lemma 2.1, we get

Now, thanks to lemma 1.1, it yields

The proof of (1.4) is complete.
B. Proof of the equation (1.6):
Recall that $\beta =\frac {1}{C(N, p,\gamma,\alpha )}$![]() and
and
on $D_{rd}^{\alpha }$![]() , where
, where
where $\theta =\frac {N+\sigma -\frac {2N+2\gamma }{p+1}}{2\alpha +\sigma }$![]() .
.
Using the definition of $\beta$![]() in (1.5), there exists a sequence $(u_j)$
in (1.5), there exists a sequence $(u_j)$![]() in $D^{\alpha }_{rd}$
in $D^{\alpha }_{rd}$![]() such that $J(u_j)\rightarrow \beta.$
such that $J(u_j)\rightarrow \beta.$![]() Denoting for $a_j, b_j>0$
Denoting for $a_j, b_j>0$![]() such that
such that
Let $v_j={u_j}_{a_jb_j}$![]() , $J(u_j)=J(v_j)$
, $J(u_j)=J(v_j)$![]() and $\|v_j\|_{\dot H^{\alpha }}=1, \||x|^{\frac {\sigma }{2}}v_j\|=1.$
and $\|v_j\|_{\dot H^{\alpha }}=1, \||x|^{\frac {\sigma }{2}}v_j\|=1.$![]()
It follows that
Then we may assume that $v_j\rightarrow v$![]() a.e., $v_j\rightharpoonup v$
a.e., $v_j\rightharpoonup v$![]() in $D^{\alpha }_{rd}$
in $D^{\alpha }_{rd}$![]() .
.
Since the injection $D_{rd}^{\alpha }\hookrightarrow L^{p+1}(|x|^{\gamma }\,{\rm d}\kern0.06em x)$![]() is compact (by lemma 1.4), we obtain
is compact (by lemma 1.4), we obtain
which means that
Hence
The minimizer $\psi :=v$![]() satisfies the Euler–Lagrange equation,
satisfies the Euler–Lagrange equation,
Since
we have from
that for any $\eta \in D^{\alpha }_{rd}$![]() ,
,
That is, $\psi$![]() satisfies
satisfies
in the weak sense, i.e., $\psi$![]() satisfies (1.6) in the weak sense.
satisfies (1.6) in the weak sense.
C. Proof of the equation (1.7):
We use the scaling property of the functional $J$![]() . By the fact that
. By the fact that
letting

and $\psi =\phi ^{a,b}:=a\phi (bx)$![]() , we have
, we have
It follows that
Since
we get
which is the desired equation (1.7). The proof is complete.
5. Proof of theorem 1.3
The plan of proving theorem 1.3 is to use the Nehari method (see [Reference Costa10, Reference Ma25, Reference Ma26]). We denote by $X:=D_{rd}^{\alpha }$![]() .
.
Proof. We now consider the existence of the ground state $\phi$![]() , that is, it is the positive solution with minimal energy to
, that is, it is the positive solution with minimal energy to
For this, we let
Note that
We define the Nehari functional
We define the Nehari manifold by
Define
the depth of the potential well.
Claim 1: $d>0.$![]()
For $u\in \mathcal {N}_{rd}$![]() , via a use of proposition 1.1 (2) we have
, via a use of proposition 1.1 (2) we have

Since $A+B>2$![]() , we obtain $\|u\|_X\geq c>0$
, we obtain $\|u\|_X\geq c>0$![]() for some uniform constant $c>0$
for some uniform constant $c>0$![]() . It follows that for $u\in \mathcal {N}_{rd}$
. It follows that for $u\in \mathcal {N}_{rd}$![]() ,
,
which implies that
Claim 2: There exists $u\in \mathcal {N}_{rd},$![]() such that $d=K(u)$
such that $d=K(u)$![]() .
.
To prove this, we may take a minimizing sequence $(u_j)\subset \mathcal {N}_{rd}, K(u_j)\rightarrow d.$![]() By this we may assume $\|u_j\|_X \leq c$
By this we may assume $\|u_j\|_X \leq c$![]() for some uniform constant $c>0$
for some uniform constant $c>0$![]() . Then using lemma 1.4, there exists a subsequence, still denoted by $(u_j)$
. Then using lemma 1.4, there exists a subsequence, still denoted by $(u_j)$![]() with the weak limit $u\in X$
with the weak limit $u\in X$![]() such that $u_j\rightarrow u\ a.e.$
such that $u_j\rightarrow u\ a.e.$![]() and $u_j\rightarrow u$
and $u_j\rightarrow u$![]() in $L^{p+1}(|x|^{\gamma }\,{\rm d}\kern0.06em x).$
in $L^{p+1}(|x|^{\gamma }\,{\rm d}\kern0.06em x).$![]()
On one hand,
On the other hand,
According to $K(u_j)\rightarrow d,$![]() we get
we get
Then $u\neq 0$![]() and $N(u)\leq 0.$
and $N(u)\leq 0.$![]()
If $N(u)<0$![]() and
and
for $t>0$![]() small, then we have $N(t_cu)=0$
small, then we have $N(t_cu)=0$![]() for some $t_c\in (0,1)$
for some $t_c\in (0,1)$![]() . Then $t_cu\in \mathcal {N}_{rd}$
. Then $t_cu\in \mathcal {N}_{rd}$![]() and $K(t_cu)\geq d$
and $K(t_cu)\geq d$![]() . However, by direct computation, we have
. However, by direct computation, we have
It is absurd. Then $N(u)=0$![]() and $K(u)=d$
and $K(u)=d$![]() , which implies that $u$
, which implies that $u$![]() is a minimizer of $K$
is a minimizer of $K$![]() on $\mathcal {N}_{rd}$
on $\mathcal {N}_{rd}$![]() . Then we have $J'(u)= 0$
. Then we have $J'(u)= 0$![]() in the sense that for any $\varphi \in C_0^{\infty } (R^{n})\bigcap D_{rd}^{\alpha },$
in the sense that for any $\varphi \in C_0^{\infty } (R^{n})\bigcap D_{rd}^{\alpha },$![]()
This implies that $u$![]() is a nontrivial ground state as desired.
is a nontrivial ground state as desired.
Using the argument we may also get similar conclusion for the case when $\alpha \in (0,1/2]$![]() , $1< p<\frac {N}{N-\alpha }$
, $1< p<\frac {N}{N-\alpha }$![]() , and $\frac {2\alpha }{(1-p)N+\alpha (p+1)}\gamma \leq \sigma$
, and $\frac {2\alpha }{(1-p)N+\alpha (p+1)}\gamma \leq \sigma$![]() .
.
6. Proof of theorem 1.6
The argument in the proof of proposition 1.1 can be used to prove the following interesting interpolation result.
Lemma 6.1 Let $\alpha \in (1/2,N/2)$![]() . There is a uniform constant $C$
. There is a uniform constant $C$![]() such that for any $u\in H_{rd}^{\alpha }$
such that for any $u\in H_{rd}^{\alpha }$![]() ,
,
where $A_1=\theta _0(q+1)$![]() , $B_1=(1-\theta _0)(q+1)+\frac {2\gamma }{N-2\alpha }$
, $B_1=(1-\theta _0)(q+1)+\frac {2\gamma }{N-2\alpha }$![]() , $q+1=p+1-\frac {2\gamma }{N-2\alpha }$
, $q+1=p+1-\frac {2\gamma }{N-2\alpha }$![]() and $\theta _0=\frac {N}{\alpha }\left (\frac 12-\frac 1{q+1}\right )$
and $\theta _0=\frac {N}{\alpha }\left (\frac 12-\frac 1{q+1}\right )$![]() .
.
Proof. Let $u\in H_{rd}^{\alpha }$![]() . Note that
. Note that
By lemma 2.1, we know that for $x\not =0$![]() ,
,
Then we have
Using the well-known fractional Gagliardo–Nirenberg inequality (proposition A.3 in [Reference Tao35]) that
for any $u\in H^{\alpha }$![]() , where $\theta _0=\frac {N}{\alpha }\left (\frac 12-\frac 1{q+1}\right )$
, where $\theta _0=\frac {N}{\alpha }\left (\frac 12-\frac 1{q+1}\right )$![]() . Then we have
. Then we have
This completes the proof.
This result improves the power $\alpha \in (0,1)$![]() in theorem 2.1 (1) [Reference Saanouni33] to $\alpha \in \left (1,\frac {N}{2}\right )$
in theorem 2.1 (1) [Reference Saanouni33] to $\alpha \in \left (1,\frac {N}{2}\right )$![]() .
.
The proof of theorem 1.6 is now given below.
Proof. To consider the existence of the ground state $\phi$![]() , we take a minimizing sequence $(u_i)\in {M}, u_i\neq 0, S(u_i)\to m_0,$
, we take a minimizing sequence $(u_i)\in {M}, u_i\neq 0, S(u_i)\to m_0,$![]() and we may assume
and we may assume

This implies that $(u_i)\subset D_{rd}^{\alpha }$![]() is bounded. From the compact imbedding theorem, $D_{rd}^{\alpha }\hookrightarrow \Sigma$
is bounded. From the compact imbedding theorem, $D_{rd}^{\alpha }\hookrightarrow \Sigma$![]() . We may choose a sequence $(u_i)$
. We may choose a sequence $(u_i)$![]() such that $u_i\to u\in D_{rd}^{\alpha }$
such that $u_i\to u\in D_{rd}^{\alpha }$![]() weakly and almost everywhere, and
weakly and almost everywhere, and
Then,
By this, we have $u\in D_{rd}^{\alpha }, u\neq 0$![]() . In the following, we prove $u\in {M},$
. In the following, we prove $u\in {M},$![]() and then $S(u)=m_0$
and then $S(u)=m_0$![]() , that is, $u$
, that is, $u$![]() is the standing wave by the convergence of $(u_i)$
is the standing wave by the convergence of $(u_i)$![]() . First, we have
. First, we have

that is, $Q(u)\leq 0.$![]() If $Q(u)<0,$
If $Q(u)<0,$![]() then for $\lambda \in (0,1),$
then for $\lambda \in (0,1),$![]()

By this, for $\lambda >0$![]() small, $Q(\lambda u)>0$
small, $Q(\lambda u)>0$![]() . Using the intermediate value theorem, we have $\lambda _0\in (0,1),\ Q(\lambda _0 u)=0,\ i.e.\ \lambda _0 u\in {M},$
. Using the intermediate value theorem, we have $\lambda _0\in (0,1),\ Q(\lambda _0 u)=0,\ i.e.\ \lambda _0 u\in {M},$![]() it implies $S(\lambda _0 u)\geq m_0.$
it implies $S(\lambda _0 u)\geq m_0.$![]() Note that
Note that

a contradiction. Then $Q(u)=0,\ i.e.\ u\in {M}.$![]()
Next, we prove the stability of standing wave and the idea is similar to [Reference Cazenave4] (see also [Reference Saanouni33]). Suppose there exists a sequence $(u^{0}_n)\in D_{rd}^{\alpha }$![]() such that for positive real numbers $(t_n)$
such that for positive real numbers $(t_n)$![]() and $\varepsilon _0>0$
and $\varepsilon _0>0$![]() , where for some $T^{*}\in (0, \infty ]$
, where for some $T^{*}\in (0, \infty ]$![]() , $u_n\in C([0,T^{*}),D_{rd}^{\alpha })$
, $u_n\in C([0,T^{*}),D_{rd}^{\alpha })$![]() is the solution to (1.1) when taking $n\to \infty$
is the solution to (1.1) when taking $n\to \infty$![]() ,
,
Denote $\phi _n:=u_n(t_n)$![]() . Since $\phi$
. Since $\phi$![]() is a ground state to (1.1), we have $S(\phi )=m_0, ||\phi ||=q>0$
is a ground state to (1.1), we have $S(\phi )=m_0, ||\phi ||=q>0$![]() . Then
. Then
By theorem 1.2, $\int |x|^{\gamma }|u_n-\phi |^{p+1}\,{\rm d}\kern0.06em x\leq ||u_n-\phi ||_{D_{rd}^{\alpha }}^{p+1}\to 0$![]() , and using the mass conservation, $||u_n(t_n)||=||u_n^{0}||\to ||\phi ||.$
, and using the mass conservation, $||u_n(t_n)||=||u_n^{0}||\to ||\phi ||.$![]() By (6.17) and proposition 2.2, we have
By (6.17) and proposition 2.2, we have
If $\phi _n\to \phi \in D_{rd}^{\alpha }$![]() , then
, then
which is a contradiction. Then we need only to prove that $(\phi _n)$![]() is relatively compact in $D_{rd}^{\alpha }$
is relatively compact in $D_{rd}^{\alpha }$![]() such that
such that
The latter is
For large $n$![]() , and $\varepsilon >0,$
, and $\varepsilon >0,$![]() using lemma 6.1 and proposition 2.2,
using lemma 6.1 and proposition 2.2,

Since $B_1<2$![]() , it follows that $\phi _n$
, it follows that $\phi _n$![]() is bounded in $\dot H^{\alpha }$
is bounded in $\dot H^{\alpha }$![]() . This then implies that the term $\int |x|^{\gamma }|\phi _n|^{p+1}dx$
. This then implies that the term $\int |x|^{\gamma }|\phi _n|^{p+1}dx$![]() is bounded. Going back to (6.18), we then know that $\phi _n$
is bounded. Going back to (6.18), we then know that $\phi _n$![]() is bounded in $D_{rd}^{\alpha }$
is bounded in $D_{rd}^{\alpha }$![]() . This completes the proof.
. This completes the proof.
We remark that in [Reference Ma and Zhang27] the authors have proved existence results about ground states of related nonlinear problems with drifting term and the existence of related principal eigen-functions. We believe that related results there may be true for the fractional cases.
Acknowledgments
The authors thank the unknown referee for useful suggestions, especially for pointing out the reference [Reference Nguyen and Squassina31]. The research of Li Ma is partially supported by the National Natural Science Foundation of China No. 11771124 and a research grant from USTB, China.