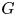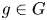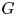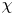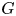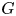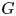1. Introduction
Throughout this paper, $G$![]() is a finite group, $Z(G)$
is a finite group, $Z(G)$![]() is the centre of $G$
is the centre of $G$![]() and ${\rm Fit}(G)$
and ${\rm Fit}(G)$![]() is the fitting subgroup of $G$
is the fitting subgroup of $G$![]() . For $x,\,y \in G$
. For $x,\,y \in G$![]() , $x^{y}=y^{-1}xy$
, $x^{y}=y^{-1}xy$![]() . For $a \in G$
. For $a \in G$![]() , $o(a)$
, $o(a)$![]() is the order of $a$
is the order of $a$![]() , $cl_{G}(a)$
, $cl_{G}(a)$![]() is the conjugacy class in $G$
is the conjugacy class in $G$![]() containing $a$
containing $a$![]() and $C_G(a)$
and $C_G(a)$![]() denotes the centralizer of $a$
denotes the centralizer of $a$![]() in $G$
in $G$![]() . Let ${\rm Irr}(G)$
. Let ${\rm Irr}(G)$![]() denote the set of the irreducible characters of $G$
denote the set of the irreducible characters of $G$![]() . For a normal subgroup $N$
. For a normal subgroup $N$![]() of $G$
of $G$![]() and $\theta \in {\rm Irr}(N)$
and $\theta \in {\rm Irr}(N)$![]() , let $I_G(\theta )$
, let $I_G(\theta )$![]() denote the inertia group of $\theta$
denote the inertia group of $\theta$![]() in $G$
in $G$![]() and let ${\rm Irr}(G|\theta )$
and let ${\rm Irr}(G|\theta )$![]() be the set of the irreducible constituents of the induced character $\theta ^{G}$
be the set of the irreducible constituents of the induced character $\theta ^{G}$![]() . An element $g \in G$
. An element $g \in G$![]() is called vanishing in $G$
is called vanishing in $G$![]() if there is a character $\chi \in {\rm Irr}(G)$
if there is a character $\chi \in {\rm Irr}(G)$![]() such that $\chi (g)=0$
such that $\chi (g)=0$![]() , otherwise, $g$
, otherwise, $g$![]() is non-vanishing in $G$
is non-vanishing in $G$![]() . We denote by ${ \rm Van} (G)$
. We denote by ${ \rm Van} (G)$![]() the set of the vanishing elements of $G$
the set of the vanishing elements of $G$![]() . The size of a conjugacy class of $G$
. The size of a conjugacy class of $G$![]() containing a vanishing element is called a vanishing conjugacy class size of $G$
containing a vanishing element is called a vanishing conjugacy class size of $G$![]() .
.
For a prime $p$![]() , the set of Sylow $p$
, the set of Sylow $p$![]() -subgroups of $G$
-subgroups of $G$![]() is denoted by ${\rm Syl}_p(G)$
is denoted by ${\rm Syl}_p(G)$![]() . Let $\pi (G)$
. Let $\pi (G)$![]() be the set of prime divisors of $|G|$
be the set of prime divisors of $|G|$![]() . For a prime $r$
. For a prime $r$![]() and natural numbers $a$
and natural numbers $a$![]() and $b$
and $b$![]() , $|a|_r$
, $|a|_r$![]() is the $r$
is the $r$![]() -part of $a$
-part of $a$![]() , $|a|_{r'}=a/|a|_r$
, $|a|_{r'}=a/|a|_r$![]() and, ${\rm gcd}(a,\,b)$
and, ${\rm gcd}(a,\,b)$![]() and ${\rm lcm}(a,\,b)$
and ${\rm lcm}(a,\,b)$![]() are the greatest common divisor and the lowest common multiple of $a$
are the greatest common divisor and the lowest common multiple of $a$![]() and $b$
and $b$![]() , respectively. For integers $a$
, respectively. For integers $a$![]() and $n$
and $n$![]() with $|a|>1$
with $|a|>1$![]() and $n\geq 1$
and $n\geq 1$![]() , the primitive prime divisor of $a^{n}-1$
, the primitive prime divisor of $a^{n}-1$![]() is a prime $l$
is a prime $l$![]() such that $l \mid (a^{n}-1)$
such that $l \mid (a^{n}-1)$![]() and $l \nmid (a^{i}-1)$
and $l \nmid (a^{i}-1)$![]() , for $1 \leq i < n$
, for $1 \leq i < n$![]() . Put $Z_n(a) =\{l:l{\rm ~is~a~primitive~\ prime~\ divisor\ ~of\ ~}a^{n}-1\}\cup \{2^{m}\}$
. Put $Z_n(a) =\{l:l{\rm ~is~a~primitive~\ prime~\ divisor\ ~of\ ~}a^{n}-1\}\cup \{2^{m}\}$![]() , where if either $n=1$
, where if either $n=1$![]() and $a \equiv 1~ ({\rm mod}~ 4)$
and $a \equiv 1~ ({\rm mod}~ 4)$![]() or $n=2$
or $n=2$![]() and $a \equiv -1~ ({\rm mod}~ 4)$
and $a \equiv -1~ ({\rm mod}~ 4)$![]() , then $m=1$
, then $m=1$![]() . Otherwise, $m=0$
. Otherwise, $m=0$![]() . Note that $Z_n(a) \neq \{1\}$
. Note that $Z_n(a) \neq \{1\}$![]() , unless $(a,\,n) \in \{(2,\,1),\, (2,\, 6),\,(-2,\,2),\,(-2,\,3),\,(3,\,1),\,(-3,\,2)\}$
, unless $(a,\,n) \in \{(2,\,1),\, (2,\, 6),\,(-2,\,2),\,(-2,\,3),\,(3,\,1),\,(-3,\,2)\}$![]() , by [Reference Feit8].
, by [Reference Feit8].
In [Reference Bianchi, Camina, Lewis and Pacifici2], Bianchi, Camina, Lewis and Pacifici classify the finite super-solvable groups with one vanishing conjugacy class size and put forward a problem on the solvability of the groups with one vanishing conjugacy class size. In this paper, we prove that:
Theorem A If $G$![]() is a finite group with exactly one vanishing conjugacy class size, then $G$
is a finite group with exactly one vanishing conjugacy class size, then $G$![]() is solvable.
is solvable.
In this paper, we say that $G$![]() satisfies $(*)$
satisfies $(*)$![]() when all vanishing conjugacy classes of $G$
when all vanishing conjugacy classes of $G$![]() have equal sizes.
have equal sizes.
2. Some useful lemmas and propositions
For convenience, this section is organized in the following four subsections.
2.1 On the order of elements and Hall subgroups of some finite groups
Lemma 2.1 Let $l\geq 7$![]() be an integer and $S$
be an integer and $S$![]() be a finite non-abelian simple group.
be a finite non-abelian simple group.
(i) Then, there are at least two prime numbers $r$
 and $t$
and $t$ such that $l/2 \leq r< t \leq l$
such that $l/2 \leq r< t \leq l$ .
.(ii) If $r$
 and $t$
and $t$ are as in (i), then ${\rm Alt}_l$
are as in (i), then ${\rm Alt}_l$ and ${\rm Sym}_l$
and ${\rm Sym}_l$ contains no element of order $tr$
contains no element of order $tr$ .
.(iii) For the triple $(S,\,t,\,r)$
 given in tables I and II , $S$
given in tables I and II , $S$ contains no element of order $tr$
contains no element of order $tr$ .
.(iv) $S$
 contains no nilpotent Hall $2'$
contains no nilpotent Hall $2'$ -subgroup. Moreover, if $S$
-subgroup. Moreover, if $S$ is isomorphic to ${\rm Suz}{\rm,\,} {\rm Co}_3$
is isomorphic to ${\rm Suz}{\rm,\,} {\rm Co}_3$ or ${\rm Alt}_l,$
or ${\rm Alt}_l,$ then $S$
then $S$ contains no nilpotent Hall $(\pi (S)-\{2,\,3\})$
contains no nilpotent Hall $(\pi (S)-\{2,\,3\})$ -subgroup.
-subgroup.
TABLE 1. Orders of some vanishing elements in finite simple groups of lie type (![]() $q=p^{k}$)
$q=p^{k}$)

TABLE 2. Orders of some vanishing elements in some finite simple groups

Proof. (i) and (iii) follow from [Reference Kondratev and Mazurov15, lemma 1] and [Reference Vasiliev and Vdovin17], respectively and (ii) is straightforward. Working towards a contradiction, let $H$![]() be a nilpotent $2$
be a nilpotent $2$![]() -complement of $S$
-complement of $S$![]() . Let $t \in \pi (S)-\{2\}$
. Let $t \in \pi (S)-\{2\}$![]() , $T \in {\rm Syl}_t(H)$
, $T \in {\rm Syl}_t(H)$![]() and $1 \neq x \in Z(T)$
and $1 \neq x \in Z(T)$![]() . Then, $|cl_S(x)|$
. Then, $|cl_S(x)|$![]() is a power of $2$
is a power of $2$![]() , contradicting Burnside's theorem [Reference Huppert11, 15.2]. Obviously, ${\rm Alt}_l$
, contradicting Burnside's theorem [Reference Huppert11, 15.2]. Obviously, ${\rm Alt}_l$![]() contains no nilpotent Hall $(\pi (S)-\{2,\,3\})$
contains no nilpotent Hall $(\pi (S)-\{2,\,3\})$![]() -subgroup and also, by [Reference Conway, Curtis, Norton, Parker and Wilson4], ${\rm Suz}$
-subgroup and also, by [Reference Conway, Curtis, Norton, Parker and Wilson4], ${\rm Suz}$![]() and ${\rm Co}_3$
and ${\rm Co}_3$![]() contain no nilpotent Hall $(\pi (S)-\{2,\,3\})$
contain no nilpotent Hall $(\pi (S)-\{2,\,3\})$![]() -subgroup. So, (iv) follows.
-subgroup. So, (iv) follows.
Lemma 2.2 [Reference Kurzweil and Stellmacher16, 8.2.8]
For a prime $p,$![]() let $P$
let $P$![]() be a $p$
be a $p$![]() -group and $Q$
-group and $Q$![]() be a $p'$
be a $p'$![]() -group. If $P \times Q$
-group. If $P \times Q$![]() acts on a $p$
acts on a $p$![]() -group $G$
-group $G$![]() such that $C_G(P) \leq C_G(Q),$
such that $C_G(P) \leq C_G(Q),$![]() then $Q$
then $Q$![]() acts trivially on $G$
acts trivially on $G$![]() .
.
2.2 The conjugacy classes and centralizers of elements
Lemma 2.3 Let $N$![]() be a normal subgroup of $G$
be a normal subgroup of $G$![]() , $t \in \pi (G)$
, $t \in \pi (G)$![]() and $x,\,y\in G$
and $x,\,y\in G$![]() .
.
(i) If $gcd(o(x),\,o(y)) = 1$
 and $xy=yx,$
and $xy=yx,$ then $C_G(xy) =C_G(x)\cap C_G(y) \leq C_G(x)$
then $C_G(xy) =C_G(x)\cap C_G(y) \leq C_G(x)$ .
.(ii) $|C_G(x)|_t$
 divides $|N|_t|C_{G/N}(xN)|_t$
divides $|N|_t|C_{G/N}(xN)|_t$ and $|cl_{G/N}(xN)|$
and $|cl_{G/N}(xN)|$ divides $|cl_G(x)|$
divides $|cl_G(x)|$ .
.(iii) If ${\rm gcd}(o(xN),\,o(yN)) = 1$
 and $N \neq yN \in C_{G/N}(xN),$
and $N \neq yN \in C_{G/N}(xN),$ then there exist $x_1,\,y_1\in G$
then there exist $x_1,\,y_1\in G$ such that $xN=x_1N,$
such that $xN=x_1N,$ $o(xN)=o(x_1),$
$o(xN)=o(x_1),$ $yN=y_1N,$
$yN=y_1N,$ $o(yN) =o(y_1)$
$o(yN) =o(y_1)$ and $y_1\in C_G(x_1)$
and $y_1\in C_G(x_1)$ .
.(iv) Let $\emptyset \neq \pi \subseteq \pi (N)$
 . If $2 \not \in \pi$
. If $2 \not \in \pi$ and for every $\pi$
and for every $\pi$ -element $x \in N-Z(N),$
-element $x \in N-Z(N),$ $|cl_G(x)| = m,$
$|cl_G(x)| = m,$ for some integer $m,$
for some integer $m,$ then $N$
then $N$ has nilpotent Hall $\pi$
has nilpotent Hall $\pi$ -subgroups.
-subgroups.(v) Let $A$
 and $M$
and $M$ be subgroups of $G$
be subgroups of $G$ . If $N \leq M$
. If $N \leq M$ and ${\rm gcd}(|A|,\,|N|)=1,$
and ${\rm gcd}(|A|,\,|N|)=1,$ then $C_{M/N}(AN/N)=C_M(A)N/N$
then $C_{M/N}(AN/N)=C_M(A)N/N$ and $|C_M(A)|=|C_N(A)||C_{M/N}(AN/N)|$
and $|C_M(A)|=|C_N(A)||C_{M/N}(AN/N)|$ .
.(vi) Let $A$
 be a $t'$
be a $t'$ -group of automorphisms of an abelian $t$
-group of automorphisms of an abelian $t$ -group $T$
-group $T$ . Then, $T=C_T(A) \times [T,\,A]$
. Then, $T=C_T(A) \times [T,\,A]$ .
.
Proof. The proof of (i) is straightforward. For proving (ii), let $T_1 \in {\rm Syl}_t(C_G(x))$![]() . Then, $T_1N/N\leq C_G(x)N/N \leq C_{G/N}(xN)$
. Then, $T_1N/N\leq C_G(x)N/N \leq C_{G/N}(xN)$![]() . Thus, $|T_1/(T_1\cap N)| \mid |C_{G/N}(xN)|$
. Thus, $|T_1/(T_1\cap N)| \mid |C_{G/N}(xN)|$![]() . So, $|C_G(x)|_t=|T_1|$
. So, $|C_G(x)|_t=|T_1|$![]() divides $|N|_t|C_{G/N}(xN)|_t$
divides $|N|_t|C_{G/N}(xN)|_t$![]() . The remaining claim of (ii) is straightforward. Also, (iii) and (iv) are taken from [Reference Ahanjideh1, lemma 2.5(iv) and theorem 1.1]. Finally, (v) and (vi) follow from [Reference Casolo, Dolfi and Jabara3, lemma 2.7] and [Reference Gorenstein9, lemma 5.2.3].
. The remaining claim of (ii) is straightforward. Also, (iii) and (iv) are taken from [Reference Ahanjideh1, lemma 2.5(iv) and theorem 1.1]. Finally, (v) and (vi) follow from [Reference Casolo, Dolfi and Jabara3, lemma 2.7] and [Reference Gorenstein9, lemma 5.2.3].
The following corollary follows immediately from lemma 2.3(v).
Corollary 2.4 Let $\{1\}=L_0\leq L_1 \leq \cdots \leq L_t=L$![]() be a chief series of a finite group $L$
be a chief series of a finite group $L$![]() such that $L_{t-1}$
such that $L_{t-1}$![]() is a $p$
is a $p$![]() -group, for some prime $p$
-group, for some prime $p$![]() . If $B$
. If $B$![]() is a subgroup of $L$
is a subgroup of $L$![]() such that $p \nmid |B|,$
such that $p \nmid |B|,$![]() then $|C_L(B)|=|C_{L_1}(B)||C_{L_2/L_1}(BL_1/L_1)|\cdots |C_{L_t/L_{t-1}}(BL_{t-1}/L_{t-1})|.$
then $|C_L(B)|=|C_{L_1}(B)||C_{L_2/L_1}(BL_1/L_1)|\cdots |C_{L_t/L_{t-1}}(BL_{t-1}/L_{t-1})|.$![]()
Lemma 2.5 Let $p \in \pi (G)$![]() and let $N$
and let $N$![]() be a Hall $p'$
be a Hall $p'$![]() -subgroup of ${\rm Fit}(G)$
-subgroup of ${\rm Fit}(G)$![]() . If for every $x \in G -{\rm Fit}(G),$
. If for every $x \in G -{\rm Fit}(G),$![]() $|cl_G(x)|=m$
$|cl_G(x)|=m$![]() , for some positive integer $m,$
, for some positive integer $m,$![]() then for every $x \in G - {\rm Fit}(G),$
then for every $x \in G - {\rm Fit}(G),$![]() $|cl_{G/N}(xN)|_p=|m|_p$
$|cl_{G/N}(xN)|_p=|m|_p$![]() .
.
Proof. Let $x \in G - {\rm Fit}(G)$![]() and $P$
and $P$![]() be a $p$
be a $p$![]() -subgroup of $G$
-subgroup of $G$![]() such that $PN/N \in {\rm Syl}_p(C_{G/N}(xN))$
such that $PN/N \in {\rm Syl}_p(C_{G/N}(xN))$![]() . Then, $xN \in C_{G/N}(PN/N)$
. Then, $xN \in C_{G/N}(PN/N)$![]() . By lemma 2.3(v), $C_{G/N}(PN/N) =C_G(P)N/N.$
. By lemma 2.3(v), $C_{G/N}(PN/N) =C_G(P)N/N.$![]() So, $x=yn$
So, $x=yn$![]() , for some $y \in C_G(P)$
, for some $y \in C_G(P)$![]() and $n \in N$
and $n \in N$![]() . As, $N \leq {\rm Fit}(G)$
. As, $N \leq {\rm Fit}(G)$![]() and $x\not \in {\rm Fit}(G)$
and $x\not \in {\rm Fit}(G)$![]() , $y \not \in {\rm Fit}(G)$
, $y \not \in {\rm Fit}(G)$![]() . Hence, $|cl_G(y)|=m$
. Hence, $|cl_G(y)|=m$![]() . Since $P \leq C_G(y)$
. Since $P \leq C_G(y)$![]() , $|m|_p=|cl_G(y)|_p \leq |G|_p/|P|.$
, $|m|_p=|cl_G(y)|_p \leq |G|_p/|P|.$![]() So, $|cl_{G/N}(xN)|_p=|G/N|_p/|C_{G/N}(xN)|_p$
So, $|cl_{G/N}(xN)|_p=|G/N|_p/|C_{G/N}(xN)|_p$![]() $=|G/N|_p/|PN/N|=|G|_p/|P| \geq |m|_p$
$=|G/N|_p/|PN/N|=|G|_p/|P| \geq |m|_p$![]() . By lemma 2.3(ii), $|cl_{G/N}(xN)|_p \leq | m|_p$
. By lemma 2.3(ii), $|cl_{G/N}(xN)|_p \leq | m|_p$![]() . Hence, $|cl_{G/N}(xN)|_p = | m|_p$
. Hence, $|cl_{G/N}(xN)|_p = | m|_p$![]() .
.
Lemma 2.6 Suppose that $N \unlhd G$![]() is a $p$
is a $p$![]() -group, for some prime $p$
-group, for some prime $p$![]() and $G/N$
and $G/N$![]() is a non-abelian simple group such that the order of the Schur multiplier of $G/N$
is a non-abelian simple group such that the order of the Schur multiplier of $G/N$![]() is not divisible by $p$
is not divisible by $p$![]() . Let $\{1\}=M_0 \leq M_1 \leq \cdots \leq M_t=N \leq G$
. Let $\{1\}=M_0 \leq M_1 \leq \cdots \leq M_t=N \leq G$![]() be a chief series of $G$
be a chief series of $G$![]() . If $M_i/M_{i-1} \leq Z(G/M_{i-1}),$
. If $M_i/M_{i-1} \leq Z(G/M_{i-1}),$![]() for every $i \in \{1,\,\ldots,\,t\},$
for every $i \in \{1,\,\ldots,\,t\},$![]() then $G=N \times L,$
then $G=N \times L,$![]() for some subgroup $L$
for some subgroup $L$![]() of $G$
of $G$![]() .
.
Proof. Let $i$![]() be the smallest number such that $0 \leq i \leq t$
be the smallest number such that $0 \leq i \leq t$![]() and $G/M_i = N/M_i \times M/M_i$
and $G/M_i = N/M_i \times M/M_i$![]() , for some subgroup $M_i \leq M \unlhd G$
, for some subgroup $M_i \leq M \unlhd G$![]() . Then, $M/M_i \cong G/N$
. Then, $M/M_i \cong G/N$![]() . Working towards a contradiction, let $i>0$
. Working towards a contradiction, let $i>0$![]() . Then, $(M/M_{i-1})' \not \leq M_i/M_{i-1}$
. Then, $(M/M_{i-1})' \not \leq M_i/M_{i-1}$![]() , because $M/M_i$
, because $M/M_i$![]() is non-abelian. So, $\{M_i/M_{i-1}\} \neq \frac {(M/M_{i-1})' M_i/M_{i-1}}{M_i/M_{i-1}} \unlhd \frac {M/M_{i-1}}{M_i/M_{i-1}} \cong M/M_{i} \cong G/N .$
is non-abelian. So, $\{M_i/M_{i-1}\} \neq \frac {(M/M_{i-1})' M_i/M_{i-1}}{M_i/M_{i-1}} \unlhd \frac {M/M_{i-1}}{M_i/M_{i-1}} \cong M/M_{i} \cong G/N .$![]() Thus, $\frac {(M/M_{i-1})' M_i/M_{i-1}}{M_i/M_{i-1}}= \frac {M/M_{i-1}}{M_i/M_{i-1}}$
Thus, $\frac {(M/M_{i-1})' M_i/M_{i-1}}{M_i/M_{i-1}}= \frac {M/M_{i-1}}{M_i/M_{i-1}}$![]() . Since $M_{i}/M_{i-1}$
. Since $M_{i}/M_{i-1}$![]() is a minimal normal subgroup of $G/M_{i-1}$
is a minimal normal subgroup of $G/M_{i-1}$![]() , $(M/M_{i-1})'\cap M_i/M_{i-1}=M_i/M_{i-1}$
, $(M/M_{i-1})'\cap M_i/M_{i-1}=M_i/M_{i-1}$![]() or $\{M_{i-1}\}$
or $\{M_{i-1}\}$![]() . Therefore, either $(M/M_{i-1})'=M/M_{i-1}$
. Therefore, either $(M/M_{i-1})'=M/M_{i-1}$![]() or $M /M_{i-1}=(M/M_{i-1})' \times M_i/M_{i-1}$
or $M /M_{i-1}=(M/M_{i-1})' \times M_i/M_{i-1}$![]() . In the former case, since $M_i/M_{i-1} \leq Z(M/M_{i-1})$
. In the former case, since $M_i/M_{i-1} \leq Z(M/M_{i-1})$![]() and $M/M_i \cong G/N$
and $M/M_i \cong G/N$![]() , we get that $|M_i/M_{i-1}|$
, we get that $|M_i/M_{i-1}|$![]() divides the order of the Schur multiplier of $G/N$
divides the order of the Schur multiplier of $G/N$![]() , a contradiction, because $M_i/M_{i-1}$
, a contradiction, because $M_i/M_{i-1}$![]() is a $p$
is a $p$![]() -group. In the latter case, regarding $M/M_{i-1} \cap N/M_{i-1}=M_i/M_{i-1}$
-group. In the latter case, regarding $M/M_{i-1} \cap N/M_{i-1}=M_i/M_{i-1}$![]() , we have $(M/M_{i-1})' \cap N/M_{i-1}=(M/M_{i-1})' \cap M_{i}/M_{i-1}=\{M_{i-1}\}$
, we have $(M/M_{i-1})' \cap N/M_{i-1}=(M/M_{i-1})' \cap M_{i}/M_{i-1}=\{M_{i-1}\}$![]() . Also, $(M/M_{i-1})' \cong G/N$
. Also, $(M/M_{i-1})' \cong G/N$![]() , hence $|G/M_{i-1}|=|G/N||N/M_{i-1}|=|(M/M_{i-1})'||N/M_{i-1}|$
, hence $|G/M_{i-1}|=|G/N||N/M_{i-1}|=|(M/M_{i-1})'||N/M_{i-1}|$![]() . Consequently, $G/M_{i-1}=(M/M_{i-1})' \times N/M_{i-1},$
. Consequently, $G/M_{i-1}=(M/M_{i-1})' \times N/M_{i-1},$![]() a contradiction with minimality of $i$
a contradiction with minimality of $i$![]() . Therefore, $i=0$
. Therefore, $i=0$![]() . Now, the lemma follows.
. Now, the lemma follows.
Lemma 2.7 Let $N$![]() be a normal $3$
be a normal $3$![]() -subgroup of $G$
-subgroup of $G$![]() such that $G/N \cong {\rm Alt}_5$
such that $G/N \cong {\rm Alt}_5$![]() . If $P \in {\rm Syl}_2(G)$
. If $P \in {\rm Syl}_2(G)$![]() and $M$
and $M$![]() is a minimal normal subgroup of $G$
is a minimal normal subgroup of $G$![]() such that $M \leq N$
such that $M \leq N$![]() , then:
, then:
(i) $P =\{1,\,x,\,y,\,xy\}$
 such that $o(x)=o(y)=o(xy)=2;$
such that $o(x)=o(y)=o(xy)=2;$
(ii) $M \leq Z(N)$
 and $M$
and $M$ is an elementary abelian $3$
is an elementary abelian $3$ -group. Also, either $M \leq Z(G)$
-group. Also, either $M \leq Z(G)$ or $M=C_M(P) \times C_T(x) \times C_T(y) \times C_T(xy),$
or $M=C_M(P) \times C_T(x) \times C_T(y) \times C_T(xy),$ where $T=[P,\,M];$
where $T=[P,\,M];$
(iii) $N_G(P)$
 contains a $3$
contains a $3$ -element $\sigma$
-element $\sigma$ such that $\sigma \not \in N,$
such that $\sigma \not \in N,$ $x^{\sigma }=y,$
$x^{\sigma }=y,$ $y^{\sigma }=xy$
$y^{\sigma }=xy$ and $(xy)^{\sigma }=x$
and $(xy)^{\sigma }=x$ . In particular, $C_T(x)^{\sigma }=C_T(y),$
. In particular, $C_T(x)^{\sigma }=C_T(y),$ $C_T(y)^{\sigma }=C_T(xy)$
$C_T(y)^{\sigma }=C_T(xy)$ and $C_T(xy)^{\sigma }=C_T(x);$
and $C_T(xy)^{\sigma }=C_T(x);$
(iv) for every $t \in P- \{1\}$
 , $u \in P - \{1,\,t\}$
, $u \in P - \{1,\,t\}$ and $1 \neq n \in C_T(t),$
and $1 \neq n \in C_T(t),$ we have $n^{u}=n^{2}$
we have $n^{u}=n^{2}$ .
.
Proof. (i) follows immediately from the facts that $P=P/(P\cap N) \cong PN/N \in {\rm Syl}_2(G/N)$![]() and $G/N \cong {\rm Alt}_5$
and $G/N \cong {\rm Alt}_5$![]() . Since $N$
. Since $N$![]() is a $3$
is a $3$![]() -group and $M \unlhd N$
-group and $M \unlhd N$![]() , $Z(N) \cap M \neq \{1\}$
, $Z(N) \cap M \neq \{1\}$![]() . Hence, we get from minimality of $M$
. Hence, we get from minimality of $M$![]() that $M \cap Z(N) =M$
that $M \cap Z(N) =M$![]() . Consequently, $M \leq Z(N)$
. Consequently, $M \leq Z(N)$![]() . Now, let $M \not \leq Z(G)$
. Now, let $M \not \leq Z(G)$![]() . Since $M \unlhd G$
. Since $M \unlhd G$![]() , $P$
, $P$![]() acts on $M$
acts on $M$![]() . By lemma 2.3(vi), $M=C_M(P) \times T$
. By lemma 2.3(vi), $M=C_M(P) \times T$![]() , where $T=[M,\,P]$
, where $T=[M,\,P]$![]() . If $T=\{1\}$
. If $T=\{1\}$![]() , then $M=C_M(P)$
, then $M=C_M(P)$![]() . So $N,\,P \leq C_G(M)$
. So $N,\,P \leq C_G(M)$![]() . Therefore, $\{N\} \neq PN/N \leq C_G(M)/N \trianglelefteq G/N \cong {\rm Alt}_5$
. Therefore, $\{N\} \neq PN/N \leq C_G(M)/N \trianglelefteq G/N \cong {\rm Alt}_5$![]() . By simplicity of $G/N$
. By simplicity of $G/N$![]() , $C_G(M)=G$
, $C_G(M)=G$![]() , a contradiction with $M \not \leq Z(G)$
, a contradiction with $M \not \leq Z(G)$![]() . This guarantees that $T \neq \{1\}$
. This guarantees that $T \neq \{1\}$![]() . We observe that $P$
. We observe that $P$![]() acts on $T$
acts on $T$![]() by conjugation and $C_T(x) \times C_T(y) \times C_T(xy) \leq T$
by conjugation and $C_T(x) \times C_T(y) \times C_T(xy) \leq T$![]() . Taking into account the fact that ${\rm gcd}(|P|,\,|T|)=1$
. Taking into account the fact that ${\rm gcd}(|P|,\,|T|)=1$![]() , Maschke's theorem yields the existence of a $P$
, Maschke's theorem yields the existence of a $P$![]() -invariant subgroup $T_1$
-invariant subgroup $T_1$![]() of $T$
of $T$![]() such that $T=C_T(x) \times C_T(y) \times C_T(xy) \times T_1$
such that $T=C_T(x) \times C_T(y) \times C_T(xy) \times T_1$![]() . If $T_1 \neq \{1\}$
. If $T_1 \neq \{1\}$![]() , then since $(C_T(x) \times C_T(y) \times C_T(xy)) \cap T_1 =\{1\}$
, then since $(C_T(x) \times C_T(y) \times C_T(xy)) \cap T_1 =\{1\}$![]() , we get that $P$
, we get that $P$![]() acts fixed point freely on $T_1$
acts fixed point freely on $T_1$![]() . Hence, $P$
. Hence, $P$![]() is cyclic, a contradiction. This shows that $T_1=\{1\}$
is cyclic, a contradiction. This shows that $T_1=\{1\}$![]() and $M=C_M(P) \times C_T(x) \times C_T(y) \times C_T(xy)$
and $M=C_M(P) \times C_T(x) \times C_T(y) \times C_T(xy)$![]() , as needed in (ii).
, as needed in (ii).
Since $G/N \cong {\rm Alt}_5$![]() and $PN/N \in {\rm Syl}_2(G/N)$
and $PN/N \in {\rm Syl}_2(G/N)$![]() , we get that $N_G(P)N/N =N_{G/N}(PN/N)$
, we get that $N_G(P)N/N =N_{G/N}(PN/N)$![]() is a non-abelian group of order $12$
is a non-abelian group of order $12$![]() . Thus, $N_G(P)$
. Thus, $N_G(P)$![]() contains a $3$
contains a $3$![]() -element $\sigma$
-element $\sigma$![]() such that $\sigma \not \in N \cup C_G(P)$
such that $\sigma \not \in N \cup C_G(P)$![]() . Hence, $\sigma$
. Hence, $\sigma$![]() permutes the elements of $P-\{1\}$
permutes the elements of $P-\{1\}$![]() . Without loss of generality, we can assume that $x^{\sigma }=y$
. Without loss of generality, we can assume that $x^{\sigma }=y$![]() , $y^{\sigma }=xy$
, $y^{\sigma }=xy$![]() and $(xy)^{\sigma }=x$
and $(xy)^{\sigma }=x$![]() . As $\sigma \in N_G(P)$
. As $\sigma \in N_G(P)$![]() , we can see $T^{\sigma }=T$
, we can see $T^{\sigma }=T$![]() . Hence, (iii) follows.
. Hence, (iii) follows.
Finally, suppose that $t \in P- \{1\}$![]() and $u \in P- \{1,\,t\}$
and $u \in P- \{1,\,t\}$![]() . Let $1\neq n \in C_T(t)$
. Let $1\neq n \in C_T(t)$![]() . Note that $n^{u} \in C_{T^{u}}(t^{u})=C_T(t)$
. Note that $n^{u} \in C_{T^{u}}(t^{u})=C_T(t)$![]() and regarding $o(u)=2$
and regarding $o(u)=2$![]() , $(n^{u}n)^{u}=n^{u}n$
, $(n^{u}n)^{u}=n^{u}n$![]() . Thus, $n^{u}n \in C_T(t) \cap C_T(u)=C_T(P)=C_M(P) \cap T=\{1\}$
. Thus, $n^{u}n \in C_T(t) \cap C_T(u)=C_T(P)=C_M(P) \cap T=\{1\}$![]() . This gives $n^{u}n=1$
. This gives $n^{u}n=1$![]() . Since $T \leq M$
. Since $T \leq M$![]() , $o(n)=3$
, $o(n)=3$![]() . It follows that $n^{u}=n^{2}$
. It follows that $n^{u}=n^{2}$![]() , as desired in (iv).
, as desired in (iv).
Proposition 2.8 Suppose that $N$![]() is a normal subgroup of $G$
is a normal subgroup of $G$![]() which is a $3$
which is a $3$![]() -group and $G/N \cong {\rm Alt}_5$
-group and $G/N \cong {\rm Alt}_5$![]() . Let $P \in {\rm Syl}_2(G)$
. Let $P \in {\rm Syl}_2(G)$![]() , $x_5 \in G-N$
, $x_5 \in G-N$![]() be of order $5$
be of order $5$![]() and let $\{1\}=M_0 \leq M_1 \leq \cdots \leq M_t=N \leq G$
and let $\{1\}=M_0 \leq M_1 \leq \cdots \leq M_t=N \leq G$![]() be a chief series of $G$
be a chief series of $G$![]() . If for every $y \in G - N,$
. If for every $y \in G - N,$![]() $|cl_G(y)|_3=3^{e},$
$|cl_G(y)|_3=3^{e},$![]() for some positive integer $e$
for some positive integer $e$![]() , then for every $1 \neq x \in P$
, then for every $1 \neq x \in P$![]() , there is an $1 \leq i \leq t$
, there is an $1 \leq i \leq t$![]() such that $M_i/M_{i-1} \not \leq Z(G/M_{i-1})$
such that $M_i/M_{i-1} \not \leq Z(G/M_{i-1})$![]() and $|C_{M_i /M_{i-1}}(x_5M_{i-1})| \geq |C_{M_i /M_{i-1}}(xM_{i-1})|$
and $|C_{M_i /M_{i-1}}(x_5M_{i-1})| \geq |C_{M_i /M_{i-1}}(xM_{i-1})|$![]() .
.
Proof. Set $\mathfrak {A}=\{1\leq i \leq t: |C_{M_i/M_{i-1}}(x_5M_{i-1})| \geq |C_{M_i/M_{i-1}}(x_2M_{i-1})|\}$![]() , for some $1\neq x_2 \in P$
, for some $1\neq x_2 \in P$![]() . Since $G/N \cong {\rm Alt}_5$
. Since $G/N \cong {\rm Alt}_5$![]() , $|C_{G/N}(x_5N)|_3=|C_{G/N}(x_2N)|_3=1$
, $|C_{G/N}(x_5N)|_3=|C_{G/N}(x_2N)|_3=1$![]() . So, corollary 2.4 yields that $\mathfrak {A} \neq \emptyset$
. So, corollary 2.4 yields that $\mathfrak {A} \neq \emptyset$![]() . Working towards a contradiction, let for every $i \in \mathfrak {A}$
. Working towards a contradiction, let for every $i \in \mathfrak {A}$![]() , $M_i /M_{i-1} \leq Z(G/M_{i-1})$
, $M_i /M_{i-1} \leq Z(G/M_{i-1})$![]() , which gives that $C_{M_i/M_{i-1}}(x_5M_{i-1})=M_i/M_{i-1}=C_{M_i/M_{i-1}}(x_2M_{i-1})$
, which gives that $C_{M_i/M_{i-1}}(x_5M_{i-1})=M_i/M_{i-1}=C_{M_i/M_{i-1}}(x_2M_{i-1})$![]() . If there exists an integer $i \in \{1,\,\ldots,\,t\}\!-\!\mathfrak {A}$
. If there exists an integer $i \in \{1,\,\ldots,\,t\}\!-\!\mathfrak {A}$![]() , then $|C_{M_i/M_{i-1}} (x_5M_{i-1})|<|C_{M_i/M_{i-1}}(x_2M_{i-1})|$
, then $|C_{M_i/M_{i-1}} (x_5M_{i-1})|<|C_{M_i/M_{i-1}}(x_2M_{i-1})|$![]() . Hence, corollary 2.4 forces $|C_G(x_5)|_3< |C_G(x_2)|_3$
. Hence, corollary 2.4 forces $|C_G(x_5)|_3< |C_G(x_2)|_3$![]() , a contradiction. Therefore, $\mathfrak {A} =\{1,\,\ldots,\,t\}$
, a contradiction. Therefore, $\mathfrak {A} =\{1,\,\ldots,\,t\}$![]() . So, for every $i \in \{1,\,\ldots,\,t\}$
. So, for every $i \in \{1,\,\ldots,\,t\}$![]() , $M_i /M_{i-1} \leq Z(G/M_{i-1})$
, $M_i /M_{i-1} \leq Z(G/M_{i-1})$![]() . By lemma 2.6, $G = M \times N$
. By lemma 2.6, $G = M \times N$![]() , where $M \cong {\rm Alt}_5$
, where $M \cong {\rm Alt}_5$![]() . Let $x_3 \in M$
. Let $x_3 \in M$![]() be of order $3$
be of order $3$![]() . Then, $x_3 \in G - N$
. Then, $x_3 \in G - N$![]() and $3^{e}=|cl_G(x_3)|_3=1$
and $3^{e}=|cl_G(x_3)|_3=1$![]() . Hence, $|cl_G(x_5)|_3 =1$
. Hence, $|cl_G(x_5)|_3 =1$![]() . By lemma 2.3(v), $3 \mid |C_{G/N}(x_5N)|$
. By lemma 2.3(v), $3 \mid |C_{G/N}(x_5N)|$![]() , a contradiction, because $G/N\cong {\rm Alt}_5$
, a contradiction, because $G/N\cong {\rm Alt}_5$![]() . Thus, there is an $i \in \mathfrak {A}$
. Thus, there is an $i \in \mathfrak {A}$![]() such that $M_i/M_{i-1} \not \leq Z(G/M_{i-1})$
such that $M_i/M_{i-1} \not \leq Z(G/M_{i-1})$![]() , as wanted.
, as wanted.
2.3 The conjugacy class sizes of elements outside a normal subgroup
Let $N \lhd G$![]() and $G=N \cup (\cup _{i}H_i)$
and $G=N \cup (\cup _{i}H_i)$![]() , where $H_i < G$
, where $H_i < G$![]() are subgroups satisfying $H_i \cap H_j \subseteq N$
are subgroups satisfying $H_i \cap H_j \subseteq N$![]() when $i \neq j$
when $i \neq j$![]() . Then, $G$
. Then, $G$![]() is said to be partitioned relative to $N$
is said to be partitioned relative to $N$![]() (see [Reference Isaacs13, definition 1]).
(see [Reference Isaacs13, definition 1]).
Lemma 2.9 [Reference Isaacs13, proposition 4]
Suppose that $N \lhd G,$![]() $G$
$G$![]() is partitioned relative to $N$
is partitioned relative to $N$![]() and $G/N$
and $G/N$![]() is abelian. Let $p$
is abelian. Let $p$![]() be a prime divisor of $[G:N]$
be a prime divisor of $[G:N]$![]() and a Sylow $p$
and a Sylow $p$![]() -subgroup of $G$
-subgroup of $G$![]() be normal in $G$
be normal in $G$![]() . Then, $G/N$
. Then, $G/N$![]() is an elementary abelian $p$
is an elementary abelian $p$![]() -group.
-group.
Now, we prove proposition 2.10 which is a key tool in the proof of theorem A.
Proposition 2.10 For an integer $m>1,$![]() let $G_m =\{g \in G: |cl_G(g)|=m\}$
let $G_m =\{g \in G: |cl_G(g)|=m\}$![]() . Let $N$
. Let $N$![]() be a normal subgroup of $G$
be a normal subgroup of $G$![]() and $\overline {G}= G/N$
and $\overline {G}= G/N$![]() . Suppose that $\overline {x}$
. Suppose that $\overline {x}$![]() is the image of an element $x$
is the image of an element $x$![]() of $G$
of $G$![]() in $\overline {G}$
in $\overline {G}$![]() and $r$
and $r$![]() is a divisor of $o(\bar {x})$
is a divisor of $o(\bar {x})$![]() such that $o(\bar {x})/r$
such that $o(\bar {x})/r$![]() is not prime. If for every $\bar {y} \in \langle \bar {x}\rangle$
is not prime. If for every $\bar {y} \in \langle \bar {x}\rangle$![]() with $o(\bar {y}) \nmid r,$
with $o(\bar {y}) \nmid r,$![]() ${y} \in G_m,$
${y} \in G_m,$![]() then for every prime divisor $p$
then for every prime divisor $p$![]() of $o(\bar {x})/r$
of $o(\bar {x})/r$![]() , we have:
, we have:
(i) the Sylow $p$
 -subgroups of $N$
-subgroups of $N$ are abelian and $C_G(x)$
are abelian and $C_G(x)$ contains a Sylow $p$
contains a Sylow $p$ -subgroup of $N;$
-subgroup of $N;$
(ii) $|N|_p|o(\bar {x})|_p \mid |C_G(x)|$
 .
.
Proof. Let $p$![]() be a prime divisor of $o(\bar {x})/r$
be a prime divisor of $o(\bar {x})/r$![]() and $P \in {\rm Syl}_p(N)$
and $P \in {\rm Syl}_p(N)$![]() . By the Frattini argument, $G=NN_G(P)$
. By the Frattini argument, $G=NN_G(P)$![]() . Thus, $x=nx'$
. Thus, $x=nx'$![]() , for some $n \in N$
, for some $n \in N$![]() and $x' \in N_G(P)$
and $x' \in N_G(P)$![]() . First suppose that $n=1$
. First suppose that $n=1$![]() . Then, $x \in N_G(P)$
. Then, $x \in N_G(P)$![]() . Set $T=\langle P,\,x\rangle$
. Set $T=\langle P,\,x\rangle$![]() . For every $y \in T-\langle T \cap N,\, x^{o(\bar {x})/r}\rangle$
. For every $y \in T-\langle T \cap N,\, x^{o(\bar {x})/r}\rangle$![]() , let $C_y =C_T(C_G(y))$
, let $C_y =C_T(C_G(y))$![]() . If $z \in T-\langle T \cap N,\, x^{o(\bar {x})/r}\rangle$
. If $z \in T-\langle T \cap N,\, x^{o(\bar {x})/r}\rangle$![]() , then there exist an element $n \in T \cap N$
, then there exist an element $n \in T \cap N$![]() and an integer $\alpha$
and an integer $\alpha$![]() such that $1 \leq \alpha < o(\bar {x})$
such that $1 \leq \alpha < o(\bar {x})$![]() and $z=n x^{\alpha }$
and $z=n x^{\alpha }$![]() . Taking into account the facts that every element of $\langle \bar {x} \rangle$
. Taking into account the facts that every element of $\langle \bar {x} \rangle$![]() whose order divides $r$
whose order divides $r$![]() lies in $\langle \bar {x}^{o(\bar {x})/r} \rangle$
lies in $\langle \bar {x}^{o(\bar {x})/r} \rangle$![]() and $\bar {x}^{\alpha }=\bar {z}\not \in \langle \bar {x}^{o(\bar {x})/r} \rangle$
and $\bar {x}^{\alpha }=\bar {z}\not \in \langle \bar {x}^{o(\bar {x})/r} \rangle$![]() , we get that $o(\bar {x}^{\alpha }) \nmid r$
, we get that $o(\bar {x}^{\alpha }) \nmid r$![]() and the assumption yields that $z \in G_m$
and the assumption yields that $z \in G_m$![]() . Hence, $T-\langle T \cap N,\, x^{o(\bar {x})/r}\rangle \subseteq G_m$
. Hence, $T-\langle T \cap N,\, x^{o(\bar {x})/r}\rangle \subseteq G_m$![]() . Thus, for every $u,\,v \in T-\langle T \cap N,\, x^{o(\bar {x})/r}\rangle$
. Thus, for every $u,\,v \in T-\langle T \cap N,\, x^{o(\bar {x})/r}\rangle$![]() , $|C_G(u)|=|C_G(v)|$
, $|C_G(u)|=|C_G(v)|$![]() . If there exists an element $w \in (C_u \cap C_v)-(\langle T \cap N,\, x^{o(\bar {x})/r}\rangle )$
. If there exists an element $w \in (C_u \cap C_v)-(\langle T \cap N,\, x^{o(\bar {x})/r}\rangle )$![]() , then $C_G(u),\,C_G(v) \leq C_G(w)$
, then $C_G(u),\,C_G(v) \leq C_G(w)$![]() . On the other hand, $w \in T-\langle T \cap N,\, x^{o(\bar {x})/r} \rangle$
. On the other hand, $w \in T-\langle T \cap N,\, x^{o(\bar {x})/r} \rangle$![]() . Hence, $w \in G_m$
. Hence, $w \in G_m$![]() . So, $|C_G(w)|=|C_G(u)|=|C_G(v)|$
. So, $|C_G(w)|=|C_G(u)|=|C_G(v)|$![]() . Therefore, $C_G(u)=C_G(w)=C_G(v)$
. Therefore, $C_G(u)=C_G(w)=C_G(v)$![]() . Consequently, $C_u=C_v$
. Consequently, $C_u=C_v$![]() . Now, we claim that $T$
. Now, we claim that $T$![]() is abelian. If not, then for every $y \in T-\langle T \cap N,\, x^{o(\bar {x})/r}\rangle$
is abelian. If not, then for every $y \in T-\langle T \cap N,\, x^{o(\bar {x})/r}\rangle$![]() , $C_y \neq T$
, $C_y \neq T$![]() , because $C_y \leq Z(C_G(y))$
, because $C_y \leq Z(C_G(y))$![]() is abelian. This yields that $T$
is abelian. This yields that $T$![]() is partitioned relative to $\langle T \cap N,\, x^{o(\bar {x})/r}\rangle$
is partitioned relative to $\langle T \cap N,\, x^{o(\bar {x})/r}\rangle$![]() . Since $P \leq T \cap N$
. Since $P \leq T \cap N$![]() , $T/\langle T \cap N,\, x^{o(\bar {x})/r}\rangle \leq \langle x\langle T \cap N,\, x^{o(\bar {x})/r}\rangle \rangle$
, $T/\langle T \cap N,\, x^{o(\bar {x})/r}\rangle \leq \langle x\langle T \cap N,\, x^{o(\bar {x})/r}\rangle \rangle$![]() , which is abelian. Consequently, $T/\langle T \cap N,\, x^{o(\bar {x})/r}\rangle$
, which is abelian. Consequently, $T/\langle T \cap N,\, x^{o(\bar {x})/r}\rangle$![]() is abelian. Also, $x \in N_G(P)$
is abelian. Also, $x \in N_G(P)$![]() and hence, $T \leq N_G(P)$
and hence, $T \leq N_G(P)$![]() . Thus, a Sylow $p$
. Thus, a Sylow $p$![]() -subgroup of $T$
-subgroup of $T$![]() is normal in $T$
is normal in $T$![]() . By lemma 2.9, $T/\langle T \cap N,\, x^{o(\bar {x})/r}\rangle$
. By lemma 2.9, $T/\langle T \cap N,\, x^{o(\bar {x})/r}\rangle$![]() is an elementary abelian $p$
is an elementary abelian $p$![]() -group. This forces $o(\bar {x})/r$
-group. This forces $o(\bar {x})/r$![]() to be prime, a contradiction. Therefore, $T$
to be prime, a contradiction. Therefore, $T$![]() is abelian. Thus, $P$
is abelian. Thus, $P$![]() is abelian and $x \in C_G(P)$
is abelian and $x \in C_G(P)$![]() , as desired in (i). Now let $n \neq 1$
, as desired in (i). Now let $n \neq 1$![]() . Set $T_1=\langle P,\,x'\rangle$
. Set $T_1=\langle P,\,x'\rangle$![]() and $H=\langle x',\, N \rangle$
and $H=\langle x',\, N \rangle$![]() . Since $\bar {x}=\bar {x}'$
. Since $\bar {x}=\bar {x}'$![]() , substituting $x$
, substituting $x$![]() with $x'$
with $x'$![]() in the above argument shows that $T_1$
in the above argument shows that $T_1$![]() is abelian. Also, $T_1$
is abelian. Also, $T_1$![]() contains a Sylow $p$
contains a Sylow $p$![]() -subgroup of $H$
-subgroup of $H$![]() . Hence, the Sylow $p$
. Hence, the Sylow $p$![]() -subgroups of $H$
-subgroups of $H$![]() are abelian. On the other hand, $x=x'n$
are abelian. On the other hand, $x=x'n$![]() for some $n\in N$
for some $n\in N$![]() . Thus, $H=\langle x,\, N \rangle$
. Thus, $H=\langle x,\, N \rangle$![]() . Note that $p \mid o(\bar {x})$
. Note that $p \mid o(\bar {x})$![]() . Let $x_p$
. Let $x_p$![]() be the $p$
be the $p$![]() -part of $x$
-part of $x$![]() . Then, $C_G(x_p)$
. Then, $C_G(x_p)$![]() contains a Sylow $p$
contains a Sylow $p$![]() -subgroup of $N$
-subgroup of $N$![]() . By our assumption, $x,\,x_p \in G_m$
. By our assumption, $x,\,x_p \in G_m$![]() and since, $C_G(x) \leq C_G(x_p)$
and since, $C_G(x) \leq C_G(x_p)$![]() , we have $C_G(x) =C_G(x_p)$
, we have $C_G(x) =C_G(x_p)$![]() . Therefore, $C_G(x)$
. Therefore, $C_G(x)$![]() contains a Sylow $p$
contains a Sylow $p$![]() -subgroup of $N$
-subgroup of $N$![]() . So, (i) follows. By (i), there exists a $P \in {\rm Syl}_p(N)$
. So, (i) follows. By (i), there exists a $P \in {\rm Syl}_p(N)$![]() such that $T=\langle P,\,x\rangle$
such that $T=\langle P,\,x\rangle$![]() is abelian. Hence, $T \leq C_G(x)$
is abelian. Hence, $T \leq C_G(x)$![]() . Therefore, $|T|_p=|N|_p|o(\bar {x})|_p \mid |C_G(x)|$
. Therefore, $|T|_p=|N|_p|o(\bar {x})|_p \mid |C_G(x)|$![]() , as desired in (ii).
, as desired in (ii).
2.4 Vanishing and non-vanishing elements
A $\chi \in {\rm Irr}(G)$![]() is said to have $q$
is said to have $q$![]() -defect zero for some prime $q$
-defect zero for some prime $q$![]() , if $q\nmid |G|/\chi (1)$
, if $q\nmid |G|/\chi (1)$![]() .
.
Lemma 2.11 [Reference Granville and Ono10, corollary 2]
Let $G$![]() be non-abelian simple and $q \in \pi (G)$
be non-abelian simple and $q \in \pi (G)$![]() . Then, $G$
. Then, $G$![]() has an irreducible character of $q$
has an irreducible character of $q$![]() -defect zero unless one of the following holds:
-defect zero unless one of the following holds:
(a) the prime $q$
 is $2$
is $2$ and $G$
and $G$ is isomorphic to ${\rm M}_{12},\, {\rm M}_{22},\, {\rm M}_{24},\, {\rm J}_2,\, {\rm HS},\, {\rm Ru},\, {\rm Co}_1$
is isomorphic to ${\rm M}_{12},\, {\rm M}_{22},\, {\rm M}_{24},\, {\rm J}_2,\, {\rm HS},\, {\rm Ru},\, {\rm Co}_1$ or ${\rm BM}$
or ${\rm BM}$ .
.(b) $q\in \{2,\,3\}$
 and $G$
and $G$ is isomorphic to ${\rm Suz},\, {\rm Co}_3$
is isomorphic to ${\rm Suz},\, {\rm Co}_3$ or ${\rm Alt}_n$
or ${\rm Alt}_n$ for some $n \geq 7$
for some $n \geq 7$ .
.
Lemma 2.12 Let $N$![]() be a normal subgroup of $G$
be a normal subgroup of $G$![]() and $p \in \pi (N)$
and $p \in \pi (N)$![]() . Suppose that $N \cong S_1 \times \cdots \times S_l,$
. Suppose that $N \cong S_1 \times \cdots \times S_l,$![]() where every $S_i$
where every $S_i$![]() is isomorphic to the non-abelian simple group $S$
is isomorphic to the non-abelian simple group $S$![]() .
.
(a) If $S$
 has an irreducible character of $p$
has an irreducible character of $p$ -defect zero, then every element of $N$
-defect zero, then every element of $N$ of order divisible by $p$
of order divisible by $p$ is a vanishing element of $G$
is a vanishing element of $G$ .
.(b) Let the triple $(S,\,r,\,t)$
 be as in lemma 2.1(i), and tables I and II. If $u \in \{t,\,r\},$
be as in lemma 2.1(i), and tables I and II. If $u \in \{t,\,r\},$ then for every $x \in N$
then for every $x \in N$ with $u \mid o(x),$
with $u \mid o(x),$ $x \in {\rm Van}(G)$
$x \in {\rm Van}(G)$ .
.
Proof. By our assumption, every $S_i$![]() has an irreducible character $\theta _i$
has an irreducible character $\theta _i$![]() of $p$
of $p$![]() -defect zero, because $S_i \cong S$
-defect zero, because $S_i \cong S$![]() . Thus, $\theta _1 \times \cdots \times \theta _l \in {\rm Irr}(N)$
. Thus, $\theta _1 \times \cdots \times \theta _l \in {\rm Irr}(N)$![]() is of $p$
is of $p$![]() -defect zero. So, (a) follows from [Reference Dolfi, Pacifici, Sanus and Spiga7, lemma 2.7]. Also, (b) can be concluded from lemma 2.11 and (a).
-defect zero. So, (a) follows from [Reference Dolfi, Pacifici, Sanus and Spiga7, lemma 2.7]. Also, (b) can be concluded from lemma 2.11 and (a).
In lemma 2.13, we have brought some known results:
Lemma 2.13 Let $M$![]() and $N$
and $N$![]() be normal subgroups of $G$
be normal subgroups of $G$![]() , $g \in G$
, $g \in G$![]() and let $p$
and let $p$![]() be a prime.
be a prime.
(i) [Reference Dolfi, Navarro, Pacifici, Sanus and Tiep5] If $g \not \in {\rm Fit}(G)$
 is non-vanishing in $G,$
is non-vanishing in $G,$ then ${\rm gcd}(6,\,o(g{\rm Fit}(G)))\neq 1$
then ${\rm gcd}(6,\,o(g{\rm Fit}(G)))\neq 1$ .
.(ii) [Reference Dolfi, Pacifici, Sanus and Spiga7, lemma 2.1] If $gN \in {\rm Van}(G/N),$
 then $gN \subseteq {\rm Van}(G)$
then $gN \subseteq {\rm Van}(G)$ .
.(iii) [Reference Dolfi, Pacifici, Sanus and Spiga7, proposition 2.5] If $M \cap N = \{1\},$
 then $({\rm Van}(G)\cap M)N \subseteq {\rm Van}(G)$
then $({\rm Van}(G)\cap M)N \subseteq {\rm Van}(G)$ .
.(iv) [Reference Dolfi, Pacifici, Sanus and Spiga7, lemma 2.4] Let $M \leq N \leq G$
 such that ${\rm gcd}(|M|,\,|N/M|)=1$
such that ${\rm gcd}(|M|,\,|N/M|)=1$ and $M$
and $M$ is nilpotent. If $C_N(M) \leq M$
is nilpotent. If $C_N(M) \leq M$ and $N/M$
and $N/M$ is abelian, then $N- M \subseteq {\rm Van}(G)$
is abelian, then $N- M \subseteq {\rm Van}(G)$ .
.(v) [Reference Dolfi, Pacifici, Sanus and Spiga7, lemma 5.1] If $N\neq \{1\}$
 is a $p$
is a $p$ -group and $G/N \cong {\rm Alt}_7,$
-group and $G/N \cong {\rm Alt}_7,$ then there are distinct primes $q_1,\,q_2 \in \pi ({\rm Alt}_7)-\{p\}$
then there are distinct primes $q_1,\,q_2 \in \pi ({\rm Alt}_7)-\{p\}$ and $q_i$
and $q_i$ -elements $x_iN \in {\rm Van}(G/N)$
-elements $x_iN \in {\rm Van}(G/N)$ such that $C_N(x_1),\,C_N(x_2)\neq \{1\}$
such that $C_N(x_1),\,C_N(x_2)\neq \{1\}$ .
.(vi) [Reference Isaacs, Navarro and Wolf14, lemma 2.3] Let $x$
 be a non-vanishing element in $G$
be a non-vanishing element in $G$ . Then, $x$
. Then, $x$ fixes some member of each orbit of the action of $G$
fixes some member of each orbit of the action of $G$ on ${\rm Irr}(N)$
on ${\rm Irr}(N)$ .
.
Now, we follow the ideas in the proof of [Reference Dolfi, Navarro, Pacifici, Sanus and Tiep5, theorem A] to prove a new fact about non-vanishing elements of a group lying in its normal solvable subgroup:
Proposition 2.14 Let $N \ne \{1\}$![]() be a normal solvable subgroup of $G$
be a normal solvable subgroup of $G$![]() and, let $x \in N$
and, let $x \in N$![]() be non-vanishing in $G$
be non-vanishing in $G$![]() . If $o(x{\rm Fit}(G))$
. If $o(x{\rm Fit}(G))$![]() is odd in $G/{\rm Fit}(G),$
is odd in $G/{\rm Fit}(G),$![]() then $x \in {\rm Fit}(G)$
then $x \in {\rm Fit}(G)$![]() .
.
Proof. The proof is by induction on $|G|$![]() . For every non-trivial normal subgroup $M$
. For every non-trivial normal subgroup $M$![]() of $G$
of $G$![]() , $NM/M$
, $NM/M$![]() is normal in $G/M$
is normal in $G/M$![]() and since $NM/M \cong N/(N\cap M)$
and since $NM/M \cong N/(N\cap M)$![]() , $NM/M$
, $NM/M$![]() is solvable. By induction, for every $\{1\} \neq M \unlhd G$
is solvable. By induction, for every $\{1\} \neq M \unlhd G$![]() , we get that $xM \in {\rm Fit}(G/M)$
, we get that $xM \in {\rm Fit}(G/M)$![]() . Now as mentioned in the proof of [Reference Dolfi, Navarro, Pacifici, Sanus and Tiep5, theorem A], one of the following cases occurs:
. Now as mentioned in the proof of [Reference Dolfi, Navarro, Pacifici, Sanus and Tiep5, theorem A], one of the following cases occurs:
Case 1. Let $M_1 \neq M_2$![]() be minimal normal subgroups of $G$
be minimal normal subgroups of $G$![]() . Then, the function $\phi : G \rightarrow \hat {G} = G/M_1 \times G/M_2$
. Then, the function $\phi : G \rightarrow \hat {G} = G/M_1 \times G/M_2$![]() , defined by $\phi (g) = (gM_1,\, gM_2)$
, defined by $\phi (g) = (gM_1,\, gM_2)$![]() for $g \in G$
for $g \in G$![]() , is an injective homomorphism. By induction, $\phi (x) \in {\rm Fit}(G/M_1)\times {\rm Fit}(G/M_2) = {\rm Fit}(\hat {G} )$
, is an injective homomorphism. By induction, $\phi (x) \in {\rm Fit}(G/M_1)\times {\rm Fit}(G/M_2) = {\rm Fit}(\hat {G} )$![]() . So, $\phi (x) \in \phi (G) \cap {\rm Fit}(\hat {G} ) \leq {\rm Fit}(\phi (G))$
. So, $\phi (x) \in \phi (G) \cap {\rm Fit}(\hat {G} ) \leq {\rm Fit}(\phi (G))$![]() . Since $\phi$
. Since $\phi$![]() induces an isomorphism between $G$
induces an isomorphism between $G$![]() and $\phi (G)$
and $\phi (G)$![]() , we get that $x \in {\rm Fit}(G)$
, we get that $x \in {\rm Fit}(G)$![]() , as wanted.
, as wanted.
Case 2. Assume that $G$![]() has the unique minimal normal subgroup $M$
has the unique minimal normal subgroup $M$![]() . By our assumption on $N$
. By our assumption on $N$![]() , $M\leq N$
, $M\leq N$![]() . Hence, $M \leq {\rm Fit}(G)$
. Hence, $M \leq {\rm Fit}(G)$![]() . Let $\Phi (G)$
. Let $\Phi (G)$![]() denote the Frattini subgroup of $G$
denote the Frattini subgroup of $G$![]() . If $\Phi (G) \neq \{1\}$
. If $\Phi (G) \neq \{1\}$![]() , then $x \Phi (G) \in {\rm Fit}(G/\Phi (G))$
, then $x \Phi (G) \in {\rm Fit}(G/\Phi (G))$![]() , by induction. However, ${\rm Fit}(G/\Phi (G))={\rm Fit}(G)/\Phi (G)$
, by induction. However, ${\rm Fit}(G/\Phi (G))={\rm Fit}(G)/\Phi (G)$![]() . So, $x \in {\rm Fit}(G)$
. So, $x \in {\rm Fit}(G)$![]() , as wanted. Now let $\Phi (G)=\{1\}$
, as wanted. Now let $\Phi (G)=\{1\}$![]() and $x\not \in M$
and $x\not \in M$![]() . By [Reference Huppert12, III, lemma 4.4], $M$
. By [Reference Huppert12, III, lemma 4.4], $M$![]() has a complement as $H$
has a complement as $H$![]() in $G$
in $G$![]() , because $M \unlhd G$
, because $M \unlhd G$![]() is abelian. Since $C_H(M) \unlhd G$
is abelian. Since $C_H(M) \unlhd G$![]() , the uniqueness of $M$
, the uniqueness of $M$![]() forces $C_H(M) =\{1\}$
forces $C_H(M) =\{1\}$![]() . So, $C_G(M)=M$
. So, $C_G(M)=M$![]() . Let $V$
. Let $V$![]() be the group of the irreducible characters of $M$
be the group of the irreducible characters of $M$![]() . We can check that $V$
. We can check that $V$![]() is a faithful and irreducible $G/M$
is a faithful and irreducible $G/M$![]() -module. On the other hand, by lemma 2.13(vi), $xM$
-module. On the other hand, by lemma 2.13(vi), $xM$![]() fixes some element of each orbit of $G/M$
fixes some element of each orbit of $G/M$![]() on $V$
on $V$![]() and by induction, $xM \in {\rm Fit}(G/M)$
and by induction, $xM \in {\rm Fit}(G/M)$![]() . So, [Reference Isaacs, Navarro and Wolf14, theorem 4.2] forces $x^{2} \in M$
. So, [Reference Isaacs, Navarro and Wolf14, theorem 4.2] forces $x^{2} \in M$![]() . Since $M \leq {\rm Fit}(G)$
. Since $M \leq {\rm Fit}(G)$![]() , $x^{2} \in {\rm Fit}(G)$
, $x^{2} \in {\rm Fit}(G)$![]() . However, $o(x{\rm Fit}(G))$
. However, $o(x{\rm Fit}(G))$![]() is odd. Hence, $x \in {\rm Fit(G)}$
is odd. Hence, $x \in {\rm Fit(G)}$![]() , as desired.
, as desired.
Lemma 2.15 Let $N \unlhd G$![]() be a $p$
be a $p$![]() -group, for some prime $p$
-group, for some prime $p$![]() and $G/N$
and $G/N$![]() be non-abelian simple. If $M$
be non-abelian simple. If $M$![]() is a minimal normal subgroup of $G$
is a minimal normal subgroup of $G$![]() such that $M \leq N$
such that $M \leq N$![]() and $\chi \in {\rm Irr}(M)-\{1_M\},$
and $\chi \in {\rm Irr}(M)-\{1_M\},$![]() then (i) $M \leq Z(N)$
then (i) $M \leq Z(N)$![]() and (ii) if $I_G(\chi )=G,$
and (ii) if $I_G(\chi )=G,$![]() then $M \leq Z(G)$
then $M \leq Z(G)$![]() .
.
Proof. Since $M \unlhd N$![]() and $N$
and $N$![]() is a $p$
is a $p$![]() -group, $\{1\} \neq M \cap Z(N) \unlhd G$
-group, $\{1\} \neq M \cap Z(N) \unlhd G$![]() . As $M$
. As $M$![]() is a minimal normal subgroup of $G$
is a minimal normal subgroup of $G$![]() , $M \cap Z(N) =M$
, $M \cap Z(N) =M$![]() . So, (i) follows. If $I_G(\chi )=G$
. So, (i) follows. If $I_G(\chi )=G$![]() , then it is easy to see that $M$
, then it is easy to see that $M$![]() is a cyclic group of order $p$
is a cyclic group of order $p$![]() . By (i), $M \leq Z(N)$
. By (i), $M \leq Z(N)$![]() . Therefore, $\frac {G/N}{C_G(M)/N}\cong G/C_G(M)=N_G(M)/C_G(M)\lesssim {\rm Aut}(M)$
. Therefore, $\frac {G/N}{C_G(M)/N}\cong G/C_G(M)=N_G(M)/C_G(M)\lesssim {\rm Aut}(M)$![]() is cyclic. Hence, $G/N =C_G(M)/N$
is cyclic. Hence, $G/N =C_G(M)/N$![]() . Consequently, $C_G(M)=G$
. Consequently, $C_G(M)=G$![]() , so $M \leq Z(G)$
, so $M \leq Z(G)$![]() , as wanted in (ii).
, as wanted in (ii).
Proposition 2.16 Let $N$![]() be a normal subgroup of $G$
be a normal subgroup of $G$![]() which is a $7$
which is a $7$![]() -group and $G/N \cong {\rm Alt}_7$
-group and $G/N \cong {\rm Alt}_7$![]() . If $M$
. If $M$![]() is a minimal normal subgroup of $G$
is a minimal normal subgroup of $G$![]() such that $M \leq N$
such that $M \leq N$![]() and $M \not \leq Z(G),$
and $M \not \leq Z(G),$![]() then for every $x \in G- N$
then for every $x \in G- N$![]() of order $3$
of order $3$![]() or $6,$
or $6,$![]() $x \in {\rm Van}(G)$
$x \in {\rm Van}(G)$![]() .
.
Proof. Let $P \in {\rm Syl}_7(G)$![]() and $1_M=\lambda _1,\,\ldots,\,\lambda _t$
and $1_M=\lambda _1,\,\ldots,\,\lambda _t$![]() be the representatives of the action of $P$
be the representatives of the action of $P$![]() on ${\rm Irr}(M)$
on ${\rm Irr}(M)$![]() . If $\mathcal {O}_i$
. If $\mathcal {O}_i$![]() is the $P$
is the $P$![]() -orbit of $\lambda _i$
-orbit of $\lambda _i$![]() , then $1+\Sigma _{i=2}^{t}|\mathcal {O}_i|\lambda _i(1)^{2}=\Sigma _{\lambda \in {\rm Irr}(M)}\lambda (1)^{2}=|M| \equiv _7 0$
, then $1+\Sigma _{i=2}^{t}|\mathcal {O}_i|\lambda _i(1)^{2}=\Sigma _{\lambda \in {\rm Irr}(M)}\lambda (1)^{2}=|M| \equiv _7 0$![]() . Thus, there exists an $i >1$
. Thus, there exists an $i >1$![]() such that $7 \nmid |\mathcal {O}_i|=[P:I_P(\lambda _i)]$
such that $7 \nmid |\mathcal {O}_i|=[P:I_P(\lambda _i)]$![]() . Therefore, $|\mathcal {O}_i|=1$
. Therefore, $|\mathcal {O}_i|=1$![]() and hence $P \leq I_G(\lambda _i)$
and hence $P \leq I_G(\lambda _i)$![]() . On the other hand, $M \leq Z(N)$
. On the other hand, $M \leq Z(N)$![]() , by lemma 2.15(i). So, $N \leq I_G(\lambda _i)$
, by lemma 2.15(i). So, $N \leq I_G(\lambda _i)$![]() . This yields that $\{N\} \neq PN/N \leq I_G(\lambda _i)/N \leq G/N \cong {\rm Alt}_7$
. This yields that $\{N\} \neq PN/N \leq I_G(\lambda _i)/N \leq G/N \cong {\rm Alt}_7$![]() . Lemma 2.15(ii) shows that $I_G(\lambda _i)/N < G/N \cong {\rm Alt}_7$
. Lemma 2.15(ii) shows that $I_G(\lambda _i)/N < G/N \cong {\rm Alt}_7$![]() . Note that the only maximal subgroup of ${\rm Alt}_7$
. Note that the only maximal subgroup of ${\rm Alt}_7$![]() whose order is divisible by $7$
whose order is divisible by $7$![]() is isomorphic to $PSL_2(7)$
is isomorphic to $PSL_2(7)$![]() . This signifies that
. This signifies that
So, $I_{G}(\lambda _i)/N$![]() does not contain any element of order $6$
does not contain any element of order $6$![]() and neither does $I_{G}(\lambda _i)$
and neither does $I_{G}(\lambda _i)$![]() . It follows from lemma 2.13(vi) that every element of $G$
. It follows from lemma 2.13(vi) that every element of $G$![]() of order $6$
of order $6$![]() is vanishing in $G$
is vanishing in $G$![]() .
.
Now, let $\phi$![]() be a group isomorphism from $G/N$
be a group isomorphism from $G/N$![]() to ${\rm Alt}_7$
to ${\rm Alt}_7$![]() . It is known that ${\rm Alt}_7$
. It is known that ${\rm Alt}_7$![]() contains exactly two conjugacy classes containing $3$
contains exactly two conjugacy classes containing $3$![]() -elements. Let $\phi (x_3N)$
-elements. Let $\phi (x_3N)$![]() and $\phi (y_3N)$
and $\phi (y_3N)$![]() be the representatives of these classes, for some $x_3N,\,y_3 N\in G/N$
be the representatives of these classes, for some $x_3N,\,y_3 N\in G/N$![]() of orders $3$
of orders $3$![]() . Since $N$
. Since $N$![]() is a $7$
is a $7$![]() -group, we can assume that $o(x_3)=o(y_3)=3$
-group, we can assume that $o(x_3)=o(y_3)=3$![]() . By [Reference Conway, Curtis, Norton, Parker and Wilson4], we can assume that $\phi (x_3N) \in {\rm Van}({\rm Alt}_7)$
. By [Reference Conway, Curtis, Norton, Parker and Wilson4], we can assume that $\phi (x_3N) \in {\rm Van}({\rm Alt}_7)$![]() , $\phi (x_3N)$
, $\phi (x_3N)$![]() normalizes some Sylow $7$
normalizes some Sylow $7$![]() -subgroup of ${\rm Alt}_7$
-subgroup of ${\rm Alt}_7$![]() and $\phi (y_3N)$
and $\phi (y_3N)$![]() does not normalize any Sylow $7$
does not normalize any Sylow $7$![]() -subgroup of ${\rm Alt}_7$
-subgroup of ${\rm Alt}_7$![]() . So,
. So,
$x_3N$![]() normalizes some Sylow $7$
normalizes some Sylow $7$![]() -subgroup of $G/N$
-subgroup of $G/N$![]() and $y_3 N$
and $y_3 N$![]() does not normalize any Sylow $7$
does not normalize any Sylow $7$![]() -subgroup of $G/N$
-subgroup of $G/N$![]() . By (2.1), $I_G(\lambda _i)/N$
. By (2.1), $I_G(\lambda _i)/N$![]() is isomorphic to a subgroup of $PSL_2(7)$
is isomorphic to a subgroup of $PSL_2(7)$![]() . However, $PSL_2(7)$
. However, $PSL_2(7)$![]() has only one conjugacy class containing $3$
has only one conjugacy class containing $3$![]() -elements and every element of this class normalizes some Sylow $7$
-elements and every element of this class normalizes some Sylow $7$![]() -subgroup of $PSL_2(7)$
-subgroup of $PSL_2(7)$![]() . Note that a Sylow $7$
. Note that a Sylow $7$![]() -subgroup of $I_G(\lambda _i)/N$
-subgroup of $I_G(\lambda _i)/N$![]() is a Sylow $7$
is a Sylow $7$![]() -subgroup of $G/N$
-subgroup of $G/N$![]() . This shows that no conjugate of $y_3N$
. This shows that no conjugate of $y_3N$![]() lies in $I_G(\lambda _i)/N$
lies in $I_G(\lambda _i)/N$![]() and if $I_G(\lambda _i)/N$
and if $I_G(\lambda _i)/N$![]() contains a $3$
contains a $3$![]() -element $uN$
-element $uN$![]() , then $uN \in cl_{G/N}(x_3N)$
, then $uN \in cl_{G/N}(x_3N)$![]() . This yields that no conjugate of $y_3$
. This yields that no conjugate of $y_3$![]() lies in $I_G(\lambda _i)$
lies in $I_G(\lambda _i)$![]() . Thus, for every $3$
. Thus, for every $3$![]() -element $w \in G$
-element $w \in G$![]() , either $wN \in cl_{G/N}(x_3N)$
, either $wN \in cl_{G/N}(x_3N)$![]() or no conjugate of $w$
or no conjugate of $w$![]() lies in $I_G(\lambda _i)$
lies in $I_G(\lambda _i)$![]() . In the former case, (2.2) and lemma 2.13(ii) show that $w \in {\rm Van}(G)$
. In the former case, (2.2) and lemma 2.13(ii) show that $w \in {\rm Van}(G)$![]() . In the latter case, $w \in {\rm Van}(G)$
. In the latter case, $w \in {\rm Van}(G)$![]() , by lemma 2.13(vi). Now, the proposition follows.
, by lemma 2.13(vi). Now, the proposition follows.
Proposition 2.17 Suppose that $N$![]() is a normal $3$
is a normal $3$![]() -subgroup of $G$
-subgroup of $G$![]() such that $G/N \cong {\rm Alt}_5$
such that $G/N \cong {\rm Alt}_5$![]() . Let $Q \in {\rm Syl}_5(G)$
. Let $Q \in {\rm Syl}_5(G)$![]() and $M$
and $M$![]() be a minimal normal subgroup of $G$
be a minimal normal subgroup of $G$![]() such that $M \leq N$
such that $M \leq N$![]() . If $M \not \leq Z(G),$
. If $M \not \leq Z(G),$![]() then one of the following holds:
then one of the following holds:
(i) there exist an element $1 \neq n \in C_M(Q)$
 and a character $\psi \in {\rm Irr}(G)$
and a character $\psi \in {\rm Irr}(G)$ such that $\psi (n)=0;$
such that $\psi (n)=0;$
(ii) $N_G(Q)$
 contains a non-trivial $2$
contains a non-trivial $2$ -element $x$
-element $x$ such that $|C_M(Q)| < |C_M(x)|$
such that $|C_M(Q)| < |C_M(x)|$ .
.
Proof. Since $|Q|=5$![]() , there is an element $x_5 \in G - N$
, there is an element $x_5 \in G - N$![]() such that $o(x_5)=5$
such that $o(x_5)=5$![]() and $Q=\langle x_5 \rangle$
and $Q=\langle x_5 \rangle$![]() . Also, regarding $G/N \cong {\rm Alt}_5$
. Also, regarding $G/N \cong {\rm Alt}_5$![]() , we get that $N_{G/N}(QN/N) =N_G(Q)N/N$
, we get that $N_{G/N}(QN/N) =N_G(Q)N/N$![]() is a dihedral group of order $10$
is a dihedral group of order $10$![]() . Thus, $N_G(Q)$
. Thus, $N_G(Q)$![]() contains an element $x$
contains an element $x$![]() such that $o(x)=2$
such that $o(x)=2$![]() and $x \not \in N\cup C_G(Q)$
and $x \not \in N\cup C_G(Q)$![]() . Let $P \in {\rm Syl}_2(G)$
. Let $P \in {\rm Syl}_2(G)$![]() such that $x \in P$
such that $x \in P$![]() . By lemma 2.7 (i,iii), $P = \{1,\,x,\,y,\,xy\}$
. By lemma 2.7 (i,iii), $P = \{1,\,x,\,y,\,xy\}$![]() such that $o(y)=o(xy)=2$
such that $o(y)=o(xy)=2$![]() and there is a $3$
and there is a $3$![]() -element $\sigma \in N_G(P) - N$
-element $\sigma \in N_G(P) - N$![]() such that $x^{\sigma }=y,\,~ y^{\sigma }=xy,\,~(xy)^{\sigma }=x.$
such that $x^{\sigma }=y,\,~ y^{\sigma }=xy,\,~(xy)^{\sigma }=x.$![]() Put $\bar {G}=G/N$
Put $\bar {G}=G/N$![]() and for every $H \leq G$
and for every $H \leq G$![]() and $g \in G$
and $g \in G$![]() , let $\bar {H}=HN/N$
, let $\bar {H}=HN/N$![]() and $\bar {g}$
and $\bar {g}$![]() denote the image of $g$
denote the image of $g$![]() in $\bar {G}$
in $\bar {G}$![]() . As $\bar {G} \cong {\rm Alt}_5$
. As $\bar {G} \cong {\rm Alt}_5$![]() , we observe that
, we observe that
Since $\bar {G} \cong {\rm Alt}_5$![]() , $(2~5)(3~4) \in N_{{\rm Alt}_5}(\langle (1~2~3~4~5)\rangle )$
, $(2~5)(3~4) \in N_{{\rm Alt}_5}(\langle (1~2~3~4~5)\rangle )$![]() , $U=\langle (2~5)(3~4),\, (2~3)(4~5) \rangle \in {\rm Syl}_2({\rm Alt}_5)$
, $U=\langle (2~5)(3~4),\, (2~3)(4~5) \rangle \in {\rm Syl}_2({\rm Alt}_5)$![]() and $(2~3~4) \in N_{{\rm Alt}_5}(U)$
and $(2~3~4) \in N_{{\rm Alt}_5}(U)$![]() , there exists a group isomorphism $\phi$
, there exists a group isomorphism $\phi$![]() from $\bar {G}$
from $\bar {G}$![]() to ${\rm Alt}_5$
to ${\rm Alt}_5$![]() which sends $\bar {x}_5$
which sends $\bar {x}_5$![]() to $(1~2~3~4~5)$
to $(1~2~3~4~5)$![]() , $\bar {x}$
, $\bar {x}$![]() to $(2~5)(3~4)$
to $(2~5)(3~4)$![]() , $\bar {y}$
, $\bar {y}$![]() to $(2~3)(4~5)$
to $(2~3)(4~5)$![]() and $\bar {\sigma }$
and $\bar {\sigma }$![]() to $(2~3~4)$
to $(2~3~4)$![]() . Let $\bar {u} \in \langle \bar {x}_5\rangle \bar {P}$
. Let $\bar {u} \in \langle \bar {x}_5\rangle \bar {P}$![]() . If $o(\bar {u})=t \in \{2,\,3,\,5\}$
. If $o(\bar {u})=t \in \{2,\,3,\,5\}$![]() , then $o(\phi (\bar {u}))=t$
, then $o(\phi (\bar {u}))=t$![]() . So, considering the $t$
. So, considering the $t$![]() -elements of ${\rm Alt}_5$
-elements of ${\rm Alt}_5$![]() lying in $\phi (\langle \bar {x}_5\rangle \bar {P})$
lying in $\phi (\langle \bar {x}_5\rangle \bar {P})$![]() shows that if $t=2$
shows that if $t=2$![]() , then $\phi (\bar {u}) \in N_{{\rm Alt}_5}(\langle (1~2~3~4~5)\rangle ) - \langle (1~2~3~4~5)\rangle =N_{\phi (\bar {G})}(\langle \phi (\bar {x}_5)\rangle ) - \langle \phi (\bar {x}_5)\rangle$
, then $\phi (\bar {u}) \in N_{{\rm Alt}_5}(\langle (1~2~3~4~5)\rangle ) - \langle (1~2~3~4~5)\rangle =N_{\phi (\bar {G})}(\langle \phi (\bar {x}_5)\rangle ) - \langle \phi (\bar {x}_5)\rangle$![]() or $\phi (\bar {u}) \in \{(2~3)(4~5),\,(2~4)(3~5)\}=\{\phi (\bar {y}),\,\phi (\bar {x}\bar {y})\}$
or $\phi (\bar {u}) \in \{(2~3)(4~5),\,(2~4)(3~5)\}=\{\phi (\bar {y}),\,\phi (\bar {x}\bar {y})\}$![]() , if $t=3$
, if $t=3$![]() , then $\phi (\bar {u}) \in \{(1~2~4),\,(1~5~3),\,(1~3~2),\,(1~4~5)\}$
, then $\phi (\bar {u}) \in \{(1~2~4),\,(1~5~3),\,(1~3~2),\,(1~4~5)\}$![]() and if $t=5$
and if $t=5$![]() , then $\phi (\bar {u}) \in \langle (1~2~3~4~5)\rangle =\langle \phi (\bar {x}_5)\rangle$
, then $\phi (\bar {u}) \in \langle (1~2~3~4~5)\rangle =\langle \phi (\bar {x}_5)\rangle$![]() or $\phi (\bar {u}) \in \{(1~3~4~2~5),\,(1~4~3~5~2),\,(1~2~5~4~3),\,(1~5~2~3~4)\}$
or $\phi (\bar {u}) \in \{(1~3~4~2~5),\,(1~4~3~5~2),\,(1~2~5~4~3),\,(1~5~2~3~4)\}$![]() . Thus, if $t=3$
. Thus, if $t=3$![]() , then $\phi (\bar {u}^{-1}) \in$
, then $\phi (\bar {u}^{-1}) \in$![]() $\{ (1\; 4\; 2) = \phi (\bar{x}_5^3 \bar{x}{\bar{\sigma }}^2),{\mkern 1mu} (1\; 3\; 5) = \phi (\bar{x}_5^2 \bar{y}{\bar{\sigma }}^2),{\mkern 1mu} (1\; 2\; 3)$
$\{ (1\; 4\; 2) = \phi (\bar{x}_5^3 \bar{x}{\bar{\sigma }}^2),{\mkern 1mu} (1\; 3\; 5) = \phi (\bar{x}_5^2 \bar{y}{\bar{\sigma }}^2),{\mkern 1mu} (1\; 2\; 3)$![]() $_5^4 \bar{\sigma })\}$
$_5^4 \bar{\sigma })\}$![]() . Hence, $\bar {u}^{-1} \in \{\bar {x}_5^{3}\bar {x}\bar { \sigma }^{2},\,\bar {x}_5^{2}\bar {y}\bar { \sigma }^{2},\,\bar {x}_5\bar {y}\bar { \sigma },\,\bar {x}_5^{4}\bar { \sigma }\}$
. Hence, $\bar {u}^{-1} \in \{\bar {x}_5^{3}\bar {x}\bar { \sigma }^{2},\,\bar {x}_5^{2}\bar {y}\bar { \sigma }^{2},\,\bar {x}_5\bar {y}\bar { \sigma },\,\bar {x}_5^{4}\bar { \sigma }\}$![]() . Consequently, $\bar {u}^{-1} \not \in \langle \bar {x}_5\rangle \bar {P}$
. Consequently, $\bar {u}^{-1} \not \in \langle \bar {x}_5\rangle \bar {P}$![]() . Similarly, if $t=5$
. Similarly, if $t=5$![]() , then either $\bar {u}^{-1} \not \in \langle \bar {x}_5\rangle \bar {P}$
, then either $\bar {u}^{-1} \not \in \langle \bar {x}_5\rangle \bar {P}$![]() or $\bar {u} \in \langle \bar {x}_5\rangle$
or $\bar {u} \in \langle \bar {x}_5\rangle$![]() . In addition, we get that
. In addition, we get that

On the other hand, by lemma 2.7(ii,iii),
where $T=[M,\,P]$![]() . If $C_T(x) =\{1\}$
. If $C_T(x) =\{1\}$![]() , then (2.6) shows that $C_T(y)=C_T(xy)=\{1\}$
, then (2.6) shows that $C_T(y)=C_T(xy)=\{1\}$![]() . Thus, $M=C_M(P)$
. Thus, $M=C_M(P)$![]() . So, $P \leq C_G(M)$
. So, $P \leq C_G(M)$![]() . However, $N \leq C_G(M)$
. However, $N \leq C_G(M)$![]() , by lemma 2.15(i). Hence, $\{\bar {1}\} \neq \bar {P} \leq C_G(M)/N \unlhd G/N=\phi ^{-1}({\rm Alt}_5)$
, by lemma 2.15(i). Hence, $\{\bar {1}\} \neq \bar {P} \leq C_G(M)/N \unlhd G/N=\phi ^{-1}({\rm Alt}_5)$![]() . Therefore, $C_G(M)=G$
. Therefore, $C_G(M)=G$![]() , because $G/N$
, because $G/N$![]() is simple. Consequently, $M \leq Z(G)$
is simple. Consequently, $M \leq Z(G)$![]() , a contradiction. Thus, $C_T(x) \neq \{1\}$
, a contradiction. Thus, $C_T(x) \neq \{1\}$![]() . By our assumption, $M$
. By our assumption, $M$![]() is an elementary abelian $3$
is an elementary abelian $3$![]() -group, so is $C_T(x)$
-group, so is $C_T(x)$![]() . Hence, there exist subgroups $A_1,\, \ldots,\, A_t$
. Hence, there exist subgroups $A_1,\, \ldots,\, A_t$![]() of $C_T(x)$
of $C_T(x)$![]() such that $|A_1|=\cdots =|A_t|=3$
such that $|A_1|=\cdots =|A_t|=3$![]() and
and
where $B_i=A_i^{\sigma }$![]() and $C_i=A_i^{\sigma ^{2}}$
and $C_i=A_i^{\sigma ^{2}}$![]() , for every $1\leq i \leq t$
, for every $1\leq i \leq t$![]() , by (2.6). Let $n\in M$
, by (2.6). Let $n\in M$![]() . By (2.5),
. By (2.5),
where $n_1 \in C_M(P)$![]() , $n_2 \in C_T(x)$
, $n_2 \in C_T(x)$![]() , $n_3 \in C_T(y)$
, $n_3 \in C_T(y)$![]() and $n_4 \in C_T(xy)$
and $n_4 \in C_T(xy)$![]() . Also, by (2.7),
. Also, by (2.7),
where for every $1\leq i \leq t$![]() , $n_{2i} \in A_i$
, $n_{2i} \in A_i$![]() , $n_{3i} \in B_i$
, $n_{3i} \in B_i$![]() and $n_{4i} \in C_i$
and $n_{4i} \in C_i$![]() .
.
If $C_M(x_5)=\{1\}$![]() , then $|C_M(x)| \geq |C_T(x)|>1=|C_M(x_5)|$
, then $|C_M(x)| \geq |C_T(x)|>1=|C_M(x_5)|$![]() . So, (ii) follows. Next, let $1 \neq n \in C_M(x_5)$
. So, (ii) follows. Next, let $1 \neq n \in C_M(x_5)$![]() . For every $1 \leq i \leq 5$
. For every $1 \leq i \leq 5$![]() , (2.8) and lemma 2.7(iii,iv) yield that
, (2.8) and lemma 2.7(iii,iv) yield that

Let check one of the above equalities in details. For instance, $n^{x_5^{i}xy\sigma }= (x_5^{i}xy\sigma )^{-1}n(x_5^{i}xy\sigma )=((xy)^{-1}((x_5^{i})^{-1}nx_5^{i})xy)^{\sigma }= ((xy)^{-1}nxy)^{\sigma }$![]() $=(n_1n_2^{2}n_3^{2}n_4)^{\sigma } = n_1^{\sigma } n_4^{\sigma }(n_2^{2})^{\sigma }(n_3^{2})^{\sigma }$
$=(n_1n_2^{2}n_3^{2}n_4)^{\sigma } = n_1^{\sigma } n_4^{\sigma }(n_2^{2})^{\sigma }(n_3^{2})^{\sigma }$![]() . Similarly, we can check the other ones. Note that
. Similarly, we can check the other ones. Note that
by (2.7). We continue the proof in the following cases:
Case 1. Assume that $n_2=n_3=n_4=1$![]() . Then, $n=n_1 \in C_M(P)$
. Then, $n=n_1 \in C_M(P)$![]() . Regarding the facts that $n \in C_M( x_5)$
. Regarding the facts that $n \in C_M( x_5)$![]() and $M \leq Z(N)$
and $M \leq Z(N)$![]() , we have $P,\, \langle x_5\rangle,\,N \leq G_G(n)$
, we have $P,\, \langle x_5\rangle,\,N \leq G_G(n)$![]() . Therefore, $\bar {P},\,\langle \bar {x}_5\rangle \leq C_G(n)/N \leq G/N=\phi ^{-1}({\rm Alt}_5)$
. Therefore, $\bar {P},\,\langle \bar {x}_5\rangle \leq C_G(n)/N \leq G/N=\phi ^{-1}({\rm Alt}_5)$![]() . Since the only subgroup of ${\rm Alt}_5$
. Since the only subgroup of ${\rm Alt}_5$![]() whose order is divisible by $20$
whose order is divisible by $20$![]() is ${\rm Alt}_5$
is ${\rm Alt}_5$![]() , we get that $C_G(n)/N=G/N$
, we get that $C_G(n)/N=G/N$![]() . Thus, $C_G(n)=G$
. Thus, $C_G(n)=G$![]() . Consequently, $n \in Z(G)$
. Consequently, $n \in Z(G)$![]() . Therefore, $M=\langle n\rangle \leq Z(G)$
. Therefore, $M=\langle n\rangle \leq Z(G)$![]() , a contradiction.
, a contradiction.
Case 2. Assume that $n_{2i} \neq 1$![]() , for some $1 \leq i \leq t$
, for some $1 \leq i \leq t$![]() . Without loss of generality, let $i=1$
. Without loss of generality, let $i=1$![]() . Since $x \in N_G(\langle x_5\rangle )$
. Since $x \in N_G(\langle x_5\rangle )$![]() and $n \in C_M(x_5)$
and $n \in C_M(x_5)$![]() , we have $n^{x} \in C_M(\langle x_5\rangle )^{x}=C_M(\langle x_5\rangle )=C_M(x_5)$
, we have $n^{x} \in C_M(\langle x_5\rangle )^{x}=C_M(\langle x_5\rangle )=C_M(x_5)$![]() . By lemma 2.7(iv), $n_3^{x}=n_3^{2}$
. By lemma 2.7(iv), $n_3^{x}=n_3^{2}$![]() and $n_4^{x}=n_4^{2}$
and $n_4^{x}=n_4^{2}$![]() . Thus, $(n^{x})_{31}=n_{31}^{2}$
. Thus, $(n^{x})_{31}=n_{31}^{2}$![]() and $(n^{x})_{41}=n_{41}^{2}$
and $(n^{x})_{41}=n_{41}^{2}$![]() . Also, $n_2^{x}=n_2$
. Also, $n_2^{x}=n_2$![]() , because $n_2 \in C_T(x)$
, because $n_2 \in C_T(x)$![]() . Hence, $(nn^{x})_{21}=(n_{21})^{2} \neq 1$
. Hence, $(nn^{x})_{21}=(n_{21})^{2} \neq 1$![]() , $(nn^{x})_{31}=n_{31}(n_{31})^{2} = 1$
, $(nn^{x})_{31}=n_{31}(n_{31})^{2} = 1$![]() and $(nn^{x})_{41}=n_{41}(n_{41})^{2} = 1$
and $(nn^{x})_{41}=n_{41}(n_{41})^{2} = 1$![]() , because $M$
, because $M$![]() is an elementary abelian $3$
is an elementary abelian $3$![]() -group and $n_{21},\,n_{31},\,n_{41} \in M$
-group and $n_{21},\,n_{31},\,n_{41} \in M$![]() . As $1 \neq nn^{x} \in C_M(x_5)$
. As $1 \neq nn^{x} \in C_M(x_5)$![]() , by substituting $n$
, by substituting $n$![]() with $nn^{x}$
with $nn^{x}$![]() , we can assume that $n_{31}=n_{41}=1$
, we can assume that $n_{31}=n_{41}=1$![]() . Set $\chi = 1_{C_{M}(P)} \times 1_{C_T(x)} \times (\theta _3 \times 1_{B_2} \times \cdots \times 1_{B_t})\times (\theta _4 \times 1_{C_2}\times \cdots \times 1_{C_t}),\,$
. Set $\chi = 1_{C_{M}(P)} \times 1_{C_T(x)} \times (\theta _3 \times 1_{B_2} \times \cdots \times 1_{B_t})\times (\theta _4 \times 1_{C_2}\times \cdots \times 1_{C_t}),\,$![]() where $\theta _3 \in {\rm Irr}(B_1)-\{1_{B_1}\}$
where $\theta _3 \in {\rm Irr}(B_1)-\{1_{B_1}\}$![]() , $\theta _4 \in {\rm Irr}(C_1)-\{1_{C_1}\}$
, $\theta _4 \in {\rm Irr}(C_1)-\{1_{C_1}\}$![]() and $\theta _4(m^{\sigma })=\theta _3(m^{2})$
and $\theta _4(m^{\sigma })=\theta _3(m^{2})$![]() , for every $m \in B_1$
, for every $m \in B_1$![]() . Then, $1_M \neq \chi \in {\rm Irr}(M)$
. Then, $1_M \neq \chi \in {\rm Irr}(M)$![]() . As $M \leq Z(N)$
. As $M \leq Z(N)$![]() , $N \leq I_G(\chi )$
, $N \leq I_G(\chi )$![]() . Let $u \in I_{G}(\chi )- N$
. Let $u \in I_{G}(\chi )- N$![]() . Then $\bar {u} \in \bar {G}$
. Then $\bar {u} \in \bar {G}$![]() . By (2.3), $\bar {u}=\bar {x}_5^{i}\bar {x}^{j}\bar {y}^{k}\bar {\sigma }^{l}$
. By (2.3), $\bar {u}=\bar {x}_5^{i}\bar {x}^{j}\bar {y}^{k}\bar {\sigma }^{l}$![]() , for some non-negative integers $i,\,j,\,k$
, for some non-negative integers $i,\,j,\,k$![]() and $l$
and $l$![]() . Working towards a contradiction, let $l \neq 0$
. Working towards a contradiction, let $l \neq 0$![]() . Since $o(\phi (\bar {\sigma }))=3$
. Since $o(\phi (\bar {\sigma }))=3$![]() , $o(\bar {\sigma })=3$
, $o(\bar {\sigma })=3$![]() and hence, we can assume that $l \in \{1,\,2\}$
and hence, we can assume that $l \in \{1,\,2\}$![]() . Also, $j,\,k \in \{0,\,1\}$
. Also, $j,\,k \in \{0,\,1\}$![]() . Regarding $u \in I_{G}(\chi )$
. Regarding $u \in I_{G}(\chi )$![]() , $u^{-1} \in I_G(\chi )$
, $u^{-1} \in I_G(\chi )$![]() . Therefore, $\chi ^{u^{-1}}(n)=\chi (n)$
. Therefore, $\chi ^{u^{-1}}(n)=\chi (n)$![]() . Also, $n \in M \leq Z(N)$
. Also, $n \in M \leq Z(N)$![]() . By (2.10), $\chi ^{u^{-1}}(n) = \chi (u^{-1}nu)= \chi ({\sigma ^{-l}(n_1n_2^{2^{k}}n_3^{2^{j}}n_4^{2^{|j-k|}})\sigma ^{l}})$
. By (2.10), $\chi ^{u^{-1}}(n) = \chi (u^{-1}nu)= \chi ({\sigma ^{-l}(n_1n_2^{2^{k}}n_3^{2^{j}}n_4^{2^{|j-k|}})\sigma ^{l}})$![]() , so
, so

It follows that either $l=1$![]() and $\chi ^{u^{-1}}(n)=\theta _3((n_{21}^{2^{k}})^{\sigma })\theta _4((n_{31}^{2^{j}})^{\sigma })$
and $\chi ^{u^{-1}}(n)=\theta _3((n_{21}^{2^{k}})^{\sigma })\theta _4((n_{31}^{2^{j}})^{\sigma })$![]() or $l=2$
or $l=2$![]() and $\chi ^{u^{-1}}(n)=\theta _3((n_{41}^{2^{|j-k|}})^{\sigma ^{2}})\theta _4((n_{21}^{2^{k}})^{\sigma ^{2}})$
and $\chi ^{u^{-1}}(n)=\theta _3((n_{41}^{2^{|j-k|}})^{\sigma ^{2}})\theta _4((n_{21}^{2^{k}})^{\sigma ^{2}})$![]() . Since $n_{31}=n_{41}=1$
. Since $n_{31}=n_{41}=1$![]() , $n_{21} \neq 1$
, $n_{21} \neq 1$![]() and $\theta _4((n_{21}^{2^{k}})^{\sigma ^{2}})=\theta _3(((n_{21}^{2^{k}})^{\sigma })^{2})$
and $\theta _4((n_{21}^{2^{k}})^{\sigma ^{2}})=\theta _3(((n_{21}^{2^{k}})^{\sigma })^{2})$![]() , we have $\chi ^{u^{-1}}(n)=\theta _3((n_{21}^{2^{k}})^{\sigma })^{l} \neq 1$
, we have $\chi ^{u^{-1}}(n)=\theta _3((n_{21}^{2^{k}})^{\sigma })^{l} \neq 1$![]() . However, $\chi (n)=\theta _3(n_{31})\theta _4(n_{41})=1$
. However, $\chi (n)=\theta _3(n_{31})\theta _4(n_{41})=1$![]() , a contradiction. This forces $\bar {u} \in \langle \bar {x}_5\rangle \bar {P}$
, a contradiction. This forces $\bar {u} \in \langle \bar {x}_5\rangle \bar {P}$![]() . Consequently,
. Consequently,
Also, for $1 \neq \gamma \in B_1$![]() and $1 \neq \beta \in C_1$
and $1 \neq \beta \in C_1$![]() , $\chi ^{xy}(\gamma )=\chi ^{x}(\gamma )=\chi (\gamma ^{2})=\theta _3(\gamma ^{2}) \neq \theta _3(\gamma )=\chi (\gamma )$
, $\chi ^{xy}(\gamma )=\chi ^{x}(\gamma )=\chi (\gamma ^{2})=\theta _3(\gamma ^{2}) \neq \theta _3(\gamma )=\chi (\gamma )$![]() and $\chi ^{y}(\beta )=\chi (\beta ^{2})=\theta _4(\beta ^{2}) \neq \theta _4(\beta )=\chi (\beta )$
and $\chi ^{y}(\beta )=\chi (\beta ^{2})=\theta _4(\beta ^{2}) \neq \theta _4(\beta )=\chi (\beta )$![]() . Therefore,
. Therefore,
Now, assume that $u \in I_G(\chi )$![]() . Then, $\bar {u},\,\bar {u}^{-1} \in I_G(\chi )/N$
. Then, $\bar {u},\,\bar {u}^{-1} \in I_G(\chi )/N$![]() . So, in view of (2.4), (2.13) and (2.14), one of the following sub-cases holds:
. So, in view of (2.4), (2.13) and (2.14), one of the following sub-cases holds:
Sub-case a. Assume that $o(\bar {u})=2$![]() . If $4$
. If $4$![]() or $5 \mid |I_G(\chi )/N|$
or $5 \mid |I_G(\chi )/N|$![]() , then taking the elements mentioned in (2.4) into account, we conclude that $I_G(\chi )/N=\bar {P}$
, then taking the elements mentioned in (2.4) into account, we conclude that $I_G(\chi )/N=\bar {P}$![]() or $I_G(\chi )/N=N_{\bar {G}}(\langle \bar {x}_5\rangle )=\langle \bar {x}_5\rangle \langle \bar {x}\rangle$
or $I_G(\chi )/N=N_{\bar {G}}(\langle \bar {x}_5\rangle )=\langle \bar {x}_5\rangle \langle \bar {x}\rangle$![]() , contradicting (2.14). Thus, $|I_G(\chi )/N|=o(\bar {u})=2$
, contradicting (2.14). Thus, $|I_G(\chi )/N|=o(\bar {u})=2$![]() and $\bar {u} \in \{\bar {x}_5^{i}\bar {x} :1\leq i \leq 5\}$
and $\bar {u} \in \{\bar {x}_5^{i}\bar {x} :1\leq i \leq 5\}$![]() . So, $\mathcal {B}=\{(x_5^{j}y^{l}\sigma ^{k})^{-1}: 1\leq j\leq 5,\, 0 \leq l \leq 1 ~{\rm and}~ 0\leq k \leq 2\}$
. So, $\mathcal {B}=\{(x_5^{j}y^{l}\sigma ^{k})^{-1}: 1\leq j\leq 5,\, 0 \leq l \leq 1 ~{\rm and}~ 0\leq k \leq 2\}$![]() is a transversal set of $I_G(\chi )$
is a transversal set of $I_G(\chi )$![]() in $G$
in $G$![]() . Hence, for every $\psi \in {\rm Irr}(G|\chi )$
. Hence, for every $\psi \in {\rm Irr}(G|\chi )$![]() , $\psi (n)= e\Sigma _{g \in \mathcal {B}} \chi (n^{g^{-1}})=e\Sigma _{i=1}^{5}[\chi (n^{(x_5^{i})})+\chi (n^{(x_5^{i}\sigma )})+\chi (n^{(x_5^{i}\sigma ^{2})})]+e\Sigma _{i=1}^{5}[\chi (n^{(x_5^{i}y)})]$
, $\psi (n)= e\Sigma _{g \in \mathcal {B}} \chi (n^{g^{-1}})=e\Sigma _{i=1}^{5}[\chi (n^{(x_5^{i})})+\chi (n^{(x_5^{i}\sigma )})+\chi (n^{(x_5^{i}\sigma ^{2})})]+e\Sigma _{i=1}^{5}[\chi (n^{(x_5^{i}y)})]$![]() $+\chi (n^{(x_5^{i}y\sigma )})+\chi (n^{(x_5^{i}y\sigma ^{2})})]$
$+\chi (n^{(x_5^{i}y\sigma )})+\chi (n^{(x_5^{i}y\sigma ^{2})})]$![]() , for some positive integer $e$
, for some positive integer $e$![]() . By (2.10), $\psi (n)= e\Sigma _{i=1}^{5}[ \chi (n)+\chi (n_1^{\sigma }n_4^{\sigma }n_2^{\sigma }n_3^{\sigma })+ \chi (n_1^{\sigma ^{2}}n_3^{\sigma ^{2}}n_4^{\sigma ^{2}}n_2^{\sigma ^{2}})]$
. By (2.10), $\psi (n)= e\Sigma _{i=1}^{5}[ \chi (n)+\chi (n_1^{\sigma }n_4^{\sigma }n_2^{\sigma }n_3^{\sigma })+ \chi (n_1^{\sigma ^{2}}n_3^{\sigma ^{2}}n_4^{\sigma ^{2}}n_2^{\sigma ^{2}})]$![]() $~+~e\Sigma _{i=1}^{5}[ \chi (n_1n_2^{2}n_3n_4^{2})+\chi (n_1(n_4^{2})^{\sigma } (n_2^{2})^{\sigma }n_3^{\sigma })+ \chi (n_1n_3^{\sigma ^{2}} (n_4^{2})^{\sigma ^{2}} (n_2^{2})^{\sigma ^{2}})]$
$~+~e\Sigma _{i=1}^{5}[ \chi (n_1n_2^{2}n_3n_4^{2})+\chi (n_1(n_4^{2})^{\sigma } (n_2^{2})^{\sigma }n_3^{\sigma })+ \chi (n_1n_3^{\sigma ^{2}} (n_4^{2})^{\sigma ^{2}} (n_2^{2})^{\sigma ^{2}})]$![]() . Thus, $\psi (n) ~=~e\Sigma _{i=1}^{5}[ 1+ \theta _3((n_{21})^{\sigma }) \theta _4 ((n_{31})^{\sigma }) +\theta _3((n_{41})^{\sigma ^{2}}) \theta _4((n_{21})^{\sigma ^{2}})] +e\Sigma _{i=1}^{5}[ \theta _3(n_{31}) ]$
. Thus, $\psi (n) ~=~e\Sigma _{i=1}^{5}[ 1+ \theta _3((n_{21})^{\sigma }) \theta _4 ((n_{31})^{\sigma }) +\theta _3((n_{41})^{\sigma ^{2}}) \theta _4((n_{21})^{\sigma ^{2}})] +e\Sigma _{i=1}^{5}[ \theta _3(n_{31}) ]$![]() $\theta _4(n_{41}^{2})+\theta _3((n_{21}^{2})^{\sigma })\theta _4((n_{31})^{\sigma }) +\theta _3((n_{41}^{2})^{\sigma ^{2}})]$
$\theta _4(n_{41}^{2})+\theta _3((n_{21}^{2})^{\sigma })\theta _4((n_{31})^{\sigma }) +\theta _3((n_{41}^{2})^{\sigma ^{2}})]$![]() $\theta _4((n_{21}^{2})^{\sigma ^{2}})]=5e[2( 1+\theta _3((n_{21})^{\sigma }) +\theta _3(((n_{21})^{\sigma })^{2}))]$
$\theta _4((n_{21}^{2})^{\sigma ^{2}})]=5e[2( 1+\theta _3((n_{21})^{\sigma }) +\theta _3(((n_{21})^{\sigma })^{2}))]$![]() . Note that $n_{21} \neq 1$
. Note that $n_{21} \neq 1$![]() . Therefore, $\theta _3((n_{21})^{\sigma })\neq 1$
. Therefore, $\theta _3((n_{21})^{\sigma })\neq 1$![]() is a primitive $3$
is a primitive $3$![]() rd root of unitary. Hence,
rd root of unitary. Hence,
It follows that $\psi (n)=0$![]() , as wanted in (i).
, as wanted in (i).
Sub-case b. Assume that $I_G(\chi ) / N \leq \langle \bar {x}_5\rangle$![]() . So, either $I_G(\chi ) / N = \langle \bar {x}_5\rangle$
. So, either $I_G(\chi ) / N = \langle \bar {x}_5\rangle$![]() or $I_G(\chi )=N$
or $I_G(\chi )=N$![]() . If $I_G(\chi )/N=\langle \bar {x}_5\rangle$
. If $I_G(\chi )/N=\langle \bar {x}_5\rangle$![]() , let $b=1$
, let $b=1$![]() and if $I_G(\chi )=N$
and if $I_G(\chi )=N$![]() , let $b=5$
, let $b=5$![]() . So, $\mathcal {B}=\{(x_5^{i}x^{j}y^{k}\sigma ^{l})^{-1} : 0 \leq i \leq b-1,\,j,\,k \in \{0,\,1\},\,l\in \{0,\,1,\,2\}\}$
. So, $\mathcal {B}=\{(x_5^{i}x^{j}y^{k}\sigma ^{l})^{-1} : 0 \leq i \leq b-1,\,j,\,k \in \{0,\,1\},\,l\in \{0,\,1,\,2\}\}$![]() is a transversal set of $I_G(\chi )$
is a transversal set of $I_G(\chi )$![]() in $G$
in $G$![]() . Hence, for every $\psi \in {\rm Irr}(G|\chi )$
. Hence, for every $\psi \in {\rm Irr}(G|\chi )$![]() , $\psi (n)=e\Sigma _{g \in \mathcal {B}} \chi ^{g}(n)= e\Sigma _{i=0}^{b-1}[\chi (n^{x_5^{i}})+\chi (n^{x_5^{i}\sigma })+\chi (n^{x_5^{i}\sigma ^{2}})] $
, $\psi (n)=e\Sigma _{g \in \mathcal {B}} \chi ^{g}(n)= e\Sigma _{i=0}^{b-1}[\chi (n^{x_5^{i}})+\chi (n^{x_5^{i}\sigma })+\chi (n^{x_5^{i}\sigma ^{2}})] $![]() $ +~ e\Sigma _{i=0}^{b-1}[\chi (n^{x_5^{i}x})+\chi (n^{x_5^{i}x\sigma })+\chi (n^{x_5^{i}x\sigma ^{2}})]$
$ +~ e\Sigma _{i=0}^{b-1}[\chi (n^{x_5^{i}x})+\chi (n^{x_5^{i}x\sigma })+\chi (n^{x_5^{i}x\sigma ^{2}})]$![]() $+~ e\Sigma _{i=0}^{b-1}[\chi (n^{x_5^{i}y})+\chi (n^{x_5^{i}y\sigma })+\chi (n^{x_5^{i}y\sigma ^{2}})] + e\Sigma _{i=0}^{b-1}[\chi (n^{x_5^{i}xy})]$
$+~ e\Sigma _{i=0}^{b-1}[\chi (n^{x_5^{i}y})+\chi (n^{x_5^{i}y\sigma })+\chi (n^{x_5^{i}y\sigma ^{2}})] + e\Sigma _{i=0}^{b-1}[\chi (n^{x_5^{i}xy})]$![]() $+\chi (n^{x_5^{i}xy\sigma })+\chi (n^{x_5^{i}xy\sigma ^{2}})]$
$+\chi (n^{x_5^{i}xy\sigma })+\chi (n^{x_5^{i}xy\sigma ^{2}})]$![]() , for some positive integer $e$
, for some positive integer $e$![]() . By (2.10) and (2.15), we can check at once that $\psi (n)= 4be[1+\theta _3(n_{21}^{\sigma })+\theta _3(n_{21}^{\sigma })^{2} ] =0$
. By (2.10) and (2.15), we can check at once that $\psi (n)= 4be[1+\theta _3(n_{21}^{\sigma })+\theta _3(n_{21}^{\sigma })^{2} ] =0$![]() , as wanted in (i).
, as wanted in (i).
Case 3. Assume that $n_2=1$![]() and there exists an $1 \leq i \leq t$
and there exists an $1 \leq i \leq t$![]() such that $n_{3i} \neq 1$
such that $n_{3i} \neq 1$![]() and $n_{4i}=1$
and $n_{4i}=1$![]() . Without loss of generality, let $i=1$
. Without loss of generality, let $i=1$![]() and set $\chi = 1_{C_{M}(P)} \times (\theta _2 \times 1_{A_2} \times \cdots \times 1_{A_t}) \times 1_{C_T(y)}\times (\theta _4 \times 1_{C_2}\times \cdots \times 1_{C_t}),\,$
and set $\chi = 1_{C_{M}(P)} \times (\theta _2 \times 1_{A_2} \times \cdots \times 1_{A_t}) \times 1_{C_T(y)}\times (\theta _4 \times 1_{C_2}\times \cdots \times 1_{C_t}),\,$![]() where $\theta _2 \in {\rm Irr}(A_1)-\{1_{A_1}\}$
where $\theta _2 \in {\rm Irr}(A_1)-\{1_{A_1}\}$![]() , $\theta _4 \in {\rm Irr}(C_1)-\{1_{C_1}\}$
, $\theta _4 \in {\rm Irr}(C_1)-\{1_{C_1}\}$![]() and $\theta _4(m^{\sigma ^{2}})=\theta _2(m^{2})$
and $\theta _4(m^{\sigma ^{2}})=\theta _2(m^{2})$![]() , for every $m \in A_1$
, for every $m \in A_1$![]() . Also, if $n_2=1$
. Also, if $n_2=1$![]() and there exists an $1 \leq i \leq t$
and there exists an $1 \leq i \leq t$![]() such that $n_{4i} \neq 1$
such that $n_{4i} \neq 1$![]() and $n_{3i}=1$
and $n_{3i}=1$![]() , then without loss of generality, let $i=1$
, then without loss of generality, let $i=1$![]() and set $\chi = 1_{C_{M}(P)} \times (\theta _2 \times 1_{A_2} \times \cdots \times 1_{A_t}) \times (\theta _3 \times 1_{B_2}\times \cdots \times 1_{B_t}) \times 1_{C_T(xy)} ,\,$
and set $\chi = 1_{C_{M}(P)} \times (\theta _2 \times 1_{A_2} \times \cdots \times 1_{A_t}) \times (\theta _3 \times 1_{B_2}\times \cdots \times 1_{B_t}) \times 1_{C_T(xy)} ,\,$![]() where $\theta _2 \in {\rm Irr}(A_1)-\{1_{A_1}\}$
where $\theta _2 \in {\rm Irr}(A_1)-\{1_{A_1}\}$![]() , $\theta _3 \in {\rm Irr}(B_1)-\{1_{B_1}\}$
, $\theta _3 \in {\rm Irr}(B_1)-\{1_{B_1}\}$![]() and $\theta _3(m^{\sigma })=\theta _2(m^{2})$
and $\theta _3(m^{\sigma })=\theta _2(m^{2})$![]() , for every $m \in A_1$
, for every $m \in A_1$![]() . Then, $1_M \neq \chi \in {\rm Irr}(M)$
. Then, $1_M \neq \chi \in {\rm Irr}(M)$![]() and arguing by analogy as Case 2 shows that for every $\psi \in {\rm Irr}(G|\chi )$
and arguing by analogy as Case 2 shows that for every $\psi \in {\rm Irr}(G|\chi )$![]() , $\psi (n)=0$
, $\psi (n)=0$![]() , as wanted in (i).
, as wanted in (i).
Case 4. Assume that $C_M(x_5)$![]() does not contain any element satisfying cases 1–3. Let $\alpha,\, \beta \in C_M(x_5)$
does not contain any element satisfying cases 1–3. Let $\alpha,\, \beta \in C_M(x_5)$![]() . By (2.8), $\alpha =\alpha _1\alpha _2\alpha _3\alpha _4$
. By (2.8), $\alpha =\alpha _1\alpha _2\alpha _3\alpha _4$![]() and $\beta =\beta _1\beta _2\beta _3\beta _4$
and $\beta =\beta _1\beta _2\beta _3\beta _4$![]() , where $\alpha _1,\,\beta _1 \in C_M(P)$
, where $\alpha _1,\,\beta _1 \in C_M(P)$![]() , $\alpha _2,\,\beta _2 \in C_T(x)$
, $\alpha _2,\,\beta _2 \in C_T(x)$![]() , $\alpha _3,\,\beta _3 \in C_T(y)$
, $\alpha _3,\,\beta _3 \in C_T(y)$![]() and $\alpha _4,\,\beta _4 \in C_T(xy)$
and $\alpha _4,\,\beta _4 \in C_T(xy)$![]() are uniquely determined. (2.9) shows that for every $j \in \{2,\,3,\,4\}$
are uniquely determined. (2.9) shows that for every $j \in \{2,\,3,\,4\}$![]() , $\alpha _j=\alpha _{j1} \ldots \alpha _{jt}$
, $\alpha _j=\alpha _{j1} \ldots \alpha _{jt}$![]() and $\beta _j=\beta _{j1} \ldots \beta _{jt}$
and $\beta _j=\beta _{j1} \ldots \beta _{jt}$![]() , where for every $1\leq i \leq t$
, where for every $1\leq i \leq t$![]() , $\alpha _{2i},\,\beta _{2i} \in A_i$
, $\alpha _{2i},\,\beta _{2i} \in A_i$![]() , $\alpha _{3i},\,\beta _{3i} \in B_i$
, $\alpha _{3i},\,\beta _{3i} \in B_i$![]() and $\alpha _{4i},\,\beta _{4i} \in C_i$
and $\alpha _{4i},\,\beta _{4i} \in C_i$![]() . By our assumption, $\alpha _2=\beta _2=1$
. By our assumption, $\alpha _2=\beta _2=1$![]() , $\alpha _3,\,\beta _3,\,\alpha _4,\,\beta _4 \neq 1$
, $\alpha _3,\,\beta _3,\,\alpha _4,\,\beta _4 \neq 1$![]() and for every $1 \leq i \leq t$
and for every $1 \leq i \leq t$![]() , $\alpha _{3i} \neq 1$
, $\alpha _{3i} \neq 1$![]() if and only if $\alpha _{4i} \neq 1$
if and only if $\alpha _{4i} \neq 1$![]() . Also, $\beta _{3i} \neq 1$
. Also, $\beta _{3i} \neq 1$![]() if and only if $\beta _{4i} \neq 1$
if and only if $\beta _{4i} \neq 1$![]() . If $\alpha _{3i}=\beta _{3i}\neq 1$
. If $\alpha _{3i}=\beta _{3i}\neq 1$![]() and $\alpha _{4i}=\beta _{4i}^{2}\neq 1$
and $\alpha _{4i}=\beta _{4i}^{2}\neq 1$![]() , for some $1\leq i \leq t$
, for some $1\leq i \leq t$![]() , then $(\alpha \beta )_{3i}=\alpha _{3i} \beta _{3i}=\alpha _{3i}^{2} \neq 1$
, then $(\alpha \beta )_{3i}=\alpha _{3i} \beta _{3i}=\alpha _{3i}^{2} \neq 1$![]() and $(\alpha \beta )_{4i}=\alpha _{4i} \beta _{4i}=\alpha _{4i}^{3}= 1$
and $(\alpha \beta )_{4i}=\alpha _{4i} \beta _{4i}=\alpha _{4i}^{3}= 1$![]() . However, $\alpha \beta \in C_M(x_5)$
. However, $\alpha \beta \in C_M(x_5)$![]() . So, $\alpha \beta$
. So, $\alpha \beta$![]() satisfies the assumption of case 3, a contradiction. This shows that for an element $\alpha \in C_M(x_5)$
satisfies the assumption of case 3, a contradiction. This shows that for an element $\alpha \in C_M(x_5)$![]() and an integer $1 \leq i \leq t$
and an integer $1 \leq i \leq t$![]() , if $\alpha _{3i}\neq 1$
, if $\alpha _{3i}\neq 1$![]() , then $\alpha _{4i} \neq 1$
, then $\alpha _{4i} \neq 1$![]() and
and
Now, working towards a contradiction, let $\alpha _1\neq 1$![]() . Then, since $x \in N_{G}(\langle x_5\rangle )$
. Then, since $x \in N_{G}(\langle x_5\rangle )$![]() , $\alpha ^{x} \in C_M({x}_5)^{x}=C_M(x_5)$
, $\alpha ^{x} \in C_M({x}_5)^{x}=C_M(x_5)$![]() . By lemma 2.7(iv), $\alpha ^{x}=\alpha _1\alpha _2\alpha _3^{2}\alpha _4^{2}$
. By lemma 2.7(iv), $\alpha ^{x}=\alpha _1\alpha _2\alpha _3^{2}\alpha _4^{2}$![]() . Thus, $\alpha \alpha ^{x}=\alpha _1^{2}\alpha _2^{2}\alpha _3^{3}\alpha _4^{3}$
. Thus, $\alpha \alpha ^{x}=\alpha _1^{2}\alpha _2^{2}\alpha _3^{3}\alpha _4^{3}$![]() . Note that $\alpha _2=1$
. Note that $\alpha _2=1$![]() and $o(\alpha _3)=o(\alpha _4)=3$
and $o(\alpha _3)=o(\alpha _4)=3$![]() . Therefore, $1 \neq \alpha \alpha ^{x}=\alpha _1^{2} \in C_M(P)$
. Therefore, $1 \neq \alpha \alpha ^{x}=\alpha _1^{2} \in C_M(P)$![]() . On the other hand, $\alpha,\, \alpha ^{x}\in C_M(x_5)$
. On the other hand, $\alpha,\, \alpha ^{x}\in C_M(x_5)$![]() . So, $1 \neq \alpha ^{x}\alpha =\alpha _1^{2} \in C_M(x_5) \cap C_M(P)$
. So, $1 \neq \alpha ^{x}\alpha =\alpha _1^{2} \in C_M(x_5) \cap C_M(P)$![]() , which is a contradiction with case 1. This shows that for every $\alpha \in C_M(x_5)$
, which is a contradiction with case 1. This shows that for every $\alpha \in C_M(x_5)$![]() , $\alpha _1=1$
, $\alpha _1=1$![]() . It follows from (2.16) that $|C_M(x_5)|\leq |C_T(y)|$
. It follows from (2.16) that $|C_M(x_5)|\leq |C_T(y)|$![]() . If $C_M(P) \neq \{1\}$
. If $C_M(P) \neq \{1\}$![]() , then we get that $|C_M(x_5)| < |C_M(P)||C_T(y)|=|C_M(P)||C_T(x)|=|C_M(x)|$
, then we get that $|C_M(x_5)| < |C_M(P)||C_T(y)|=|C_M(P)||C_T(x)|=|C_M(x)|$![]() , so (ii) follows. Next, let $C_M(P)=\{1\}$
, so (ii) follows. Next, let $C_M(P)=\{1\}$![]() . Then, $T=M=C_M(x) \times C_M(y) \times C_M(xy)$
. Then, $T=M=C_M(x) \times C_M(y) \times C_M(xy)$![]() and $|C_M(x_5)| \leq |C_T(y)|=|C_M(y)|=|C_M(x)|$
and $|C_M(x_5)| \leq |C_T(y)|=|C_M(y)|=|C_M(x)|$![]() , by (2.16). If $|C_M(x_5)| <|C_M(x)|$
, by (2.16). If $|C_M(x_5)| <|C_M(x)|$![]() , then (ii) follows. Otherwise, $|C_M(x_5)|=|C_M(x)|$
, then (ii) follows. Otherwise, $|C_M(x_5)|=|C_M(x)|$![]() . If $|C_M(x)|=3$
. If $|C_M(x)|=3$![]() , then $|M|=27$
, then $|M|=27$![]() and $|[M,\,\langle x_5\rangle ]|=9$
and $|[M,\,\langle x_5\rangle ]|=9$![]() . However, $\langle x_5\rangle$
. However, $\langle x_5\rangle$![]() acts fixed point freely on $[M,\,\langle x_5\rangle ]$
acts fixed point freely on $[M,\,\langle x_5\rangle ]$![]() . So, $5 \mid |[M,\,\langle x_5\rangle ]|-1=8$
. So, $5 \mid |[M,\,\langle x_5\rangle ]|-1=8$![]() , which is impossible. This forces $|C_M(x)| \geq 9$
, which is impossible. This forces $|C_M(x)| \geq 9$![]() . Consequently, $t \geq 2$
. Consequently, $t \geq 2$![]() ($t$
($t$![]() was fixed in (2.7)). Since $|C_M(x_5)|=|C_M(x)|=|C_M(y)|$
was fixed in (2.7)). Since $|C_M(x_5)|=|C_M(x)|=|C_M(y)|$![]() , we get from (2.16) that for every $1 \leq i \leq t$
, we get from (2.16) that for every $1 \leq i \leq t$![]() and $m \in B_i$
and $m \in B_i$![]() , there exists an element $\alpha \in C_M(x_5)$
, there exists an element $\alpha \in C_M(x_5)$![]() such that $\alpha _{3i}=m$
such that $\alpha _{3i}=m$![]() . So, for $1 \neq n \in C_M(x_5)$
. So, for $1 \neq n \in C_M(x_5)$![]() , we can assume that $n_{31},\,n_{32} \neq 1$
, we can assume that $n_{31},\,n_{32} \neq 1$![]() . Consequently, $n_{41},\,n_{42} \neq 1$
. Consequently, $n_{41},\,n_{42} \neq 1$![]() . As was mentioned above, $n_2=1$
. As was mentioned above, $n_2=1$![]() . Set $\chi = 1_{C_{M}(x)} \times (\theta _3 \times \theta _3'\times 1_{B_3} \times \cdots \times 1_{B_t}) \times (\theta _4 \times \theta _4' \times 1_{C_3}\times \cdots \times 1_{C_t}),\,$
. Set $\chi = 1_{C_{M}(x)} \times (\theta _3 \times \theta _3'\times 1_{B_3} \times \cdots \times 1_{B_t}) \times (\theta _4 \times \theta _4' \times 1_{C_3}\times \cdots \times 1_{C_t}),\,$![]() where $\theta _3 \in {\rm Irr}(B_1)-\{1_{B_1}\}$
where $\theta _3 \in {\rm Irr}(B_1)-\{1_{B_1}\}$![]() , $\theta _3' \in {\rm Irr}(B_2)-\{1_{B_2}\}$
, $\theta _3' \in {\rm Irr}(B_2)-\{1_{B_2}\}$![]() , $\theta _4\in {\rm Irr}(C_1)-\{1_{C_1}\}$
, $\theta _4\in {\rm Irr}(C_1)-\{1_{C_1}\}$![]() and $\theta _4' \in {\rm Irr}(C_2)-\{1_{C_2}\}$
and $\theta _4' \in {\rm Irr}(C_2)-\{1_{C_2}\}$![]() such that $\theta _3'(n_{32})=\theta _3(n_{31})^{2}$
such that $\theta _3'(n_{32})=\theta _3(n_{31})^{2}$![]() and $\theta _4'(n_{42})=\theta _4(n_{41})^{2}$
and $\theta _4'(n_{42})=\theta _4(n_{41})^{2}$![]() . Moreover, suppose that $\theta _4(n_{41})=\theta _3(n_{31})$
. Moreover, suppose that $\theta _4(n_{41})=\theta _3(n_{31})$![]() . Then, $1_{M}\neq \chi \in {\rm Irr}(M)$
. Then, $1_{M}\neq \chi \in {\rm Irr}(M)$![]() . Note that $n_{31}$
. Note that $n_{31}$![]() and $n_{32}$
and $n_{32}$![]() are generators of $B_1$
are generators of $B_1$![]() and $B_2$
and $B_2$![]() , respectively. Also, $n_{41}$
, respectively. Also, $n_{41}$![]() and $n_{42}$
and $n_{42}$![]() are generators of $C_1$
are generators of $C_1$![]() and $C_2$
and $C_2$![]() , respectively.
, respectively.
In the following, we first assume that $(n_{31}^{\sigma },\, n_{32}^{\sigma }) =(n_{41},\,n_{42})$![]() or $(n_{31}^{\sigma },\, n_{32}^{\sigma }) =(n_{41}^{2},\,n_{42}^{2})$
or $(n_{31}^{\sigma },\, n_{32}^{\sigma }) =(n_{41}^{2},\,n_{42}^{2})$![]() . If $(n_{31}^{\sigma },\, n_{32}^{\sigma }) =(n_{41},\,n_{42})$
. If $(n_{31}^{\sigma },\, n_{32}^{\sigma }) =(n_{41},\,n_{42})$![]() , let $u=1$
, let $u=1$![]() and otherwise let $u=2$
and otherwise let $u=2$![]() . We note that $N \leq I_G(\chi )$
. We note that $N \leq I_G(\chi )$![]() . By (2.10), we can check that for every $g\in G$
. By (2.10), we can check that for every $g\in G$![]() , $\chi (n^{g})=1$
, $\chi (n^{g})=1$![]() , for instance, $\chi (n^{x_5^{i}x\sigma ^{2}})= \chi ((n_3^{2})^{\sigma ^{2}}(n_4^{2})^{\sigma ^{2}}n_2^{\sigma ^{2}})= [\theta _3((n_{41}^{2})^{\sigma ^{2}})\theta _3'((n_{42}^{2})^{\sigma ^{2}})] [\theta _4(1)\theta _4'(1)]=\theta _3(n_{31})^{6u}=1$
, for instance, $\chi (n^{x_5^{i}x\sigma ^{2}})= \chi ((n_3^{2})^{\sigma ^{2}}(n_4^{2})^{\sigma ^{2}}n_2^{\sigma ^{2}})= [\theta _3((n_{41}^{2})^{\sigma ^{2}})\theta _3'((n_{42}^{2})^{\sigma ^{2}})] [\theta _4(1)\theta _4'(1)]=\theta _3(n_{31})^{6u}=1$![]() . So, for every $\psi \in {\rm Irr}(G|\chi )$
. So, for every $\psi \in {\rm Irr}(G|\chi )$![]() , $\psi (n) =\psi (1)$
, $\psi (n) =\psi (1)$![]() . Therefore, $1 \neq n \in {\rm ker}\psi \cap M$
. Therefore, $1 \neq n \in {\rm ker}\psi \cap M$![]() . Thus, $\{1\} \neq M \cap {\rm ker}\psi \unlhd G$
. Thus, $\{1\} \neq M \cap {\rm ker}\psi \unlhd G$![]() . Since $M$
. Since $M$![]() is a minimal normal subgroup of $G$
is a minimal normal subgroup of $G$![]() , $M \cap {\rm ker}\psi =M$
, $M \cap {\rm ker}\psi =M$![]() . Therefore, $\psi _M =\psi (1)1_M$
. Therefore, $\psi _M =\psi (1)1_M$![]() , a contradiction.
, a contradiction.
Next, suppose that $(n_{31}^{\sigma },\,n_{32}^{\sigma }) \in \{(n_{41},\,n_{42}^{2}),\,(n_{41}^{2},\,n_{42})\}$![]() . If $u=x_5^{i}x^{j}y^{k}\sigma ^{l} h \in I_G(\chi )$
. If $u=x_5^{i}x^{j}y^{k}\sigma ^{l} h \in I_G(\chi )$![]() , where $h \in N$
, where $h \in N$![]() , $i \in \{1,\,\ldots,\,5\}$
, $i \in \{1,\,\ldots,\,5\}$![]() , $j,\,k \in \{0,\,1\}$
, $j,\,k \in \{0,\,1\}$![]() and $l \in \{1,\,2\}$
and $l \in \{1,\,2\}$![]() , then $u^{-1} \in I_G(\chi )$
, then $u^{-1} \in I_G(\chi )$![]() and we get from (2.12) that if $l=1$
and we get from (2.12) that if $l=1$![]() , then $\chi ^{u^{-1}}(n)\in \{(\theta _4(n_{41})^{2})^{2^{j}},\,(\theta _4(n_{41}))^{2^{j}}\}$
, then $\chi ^{u^{-1}}(n)\in \{(\theta _4(n_{41})^{2})^{2^{j}},\,(\theta _4(n_{41}))^{2^{j}}\}$![]() and if $l=2$
and if $l=2$![]() , then $\chi ^{u^{-1}}(n)\in \{(\theta _3(n_{31})^{2})^{2^{|j-k|}},\,(\theta _3(n_{31}))^{2^{|j-k|}}\}$
, then $\chi ^{u^{-1}}(n)\in \{(\theta _3(n_{31})^{2})^{2^{|j-k|}},\,(\theta _3(n_{31}))^{2^{|j-k|}}\}$![]() . Hence, $\chi ^{u^{-1}}(n) \neq 1$
. Hence, $\chi ^{u^{-1}}(n) \neq 1$![]() . However, $\chi (n)=1$
. However, $\chi (n)=1$![]() , a contradiction. Consequently, $\bar {u} \in \langle \bar {x}_5\rangle \bar {P}$
, a contradiction. Consequently, $\bar {u} \in \langle \bar {x}_5\rangle \bar {P}$![]() . Therefore, $I_G(\chi )/N \subseteq \langle \bar {x}_5\rangle \bar {P}.$
. Therefore, $I_G(\chi )/N \subseteq \langle \bar {x}_5\rangle \bar {P}.$![]() Let $\beta =n_{41} \in C_1-\{1\}$
Let $\beta =n_{41} \in C_1-\{1\}$![]() . By lemma 2.7(iv), $\chi (\beta )=\theta _4(n_{41})$
. By lemma 2.7(iv), $\chi (\beta )=\theta _4(n_{41})$![]() , $\chi ^{x^{-1}}(\beta )=\chi (\beta ^{x})=\chi (\beta ^{2})=\theta _4(n_{41})^{2}$
, $\chi ^{x^{-1}}(\beta )=\chi (\beta ^{x})=\chi (\beta ^{2})=\theta _4(n_{41})^{2}$![]() and $\chi ^{y^{-1}}(\beta )=\chi (\beta ^{y})=\chi (\beta ^{2})=\theta _4(n_{41})^{2}$
and $\chi ^{y^{-1}}(\beta )=\chi (\beta ^{y})=\chi (\beta ^{2})=\theta _4(n_{41})^{2}$![]() . Since $n_{41} \neq 1$
. Since $n_{41} \neq 1$![]() , $\theta _4(n_{41})^{2} \neq \theta _4(n_{41})$
, $\theta _4(n_{41})^{2} \neq \theta _4(n_{41})$![]() . Consequently, $\chi ^{x^{-1}},\,\chi ^{y^{-1}} \neq \chi$
. Consequently, $\chi ^{x^{-1}},\,\chi ^{y^{-1}} \neq \chi$![]() . Hence, $x,\,y \not \in I_G(\chi ).$
. Hence, $x,\,y \not \in I_G(\chi ).$![]() By (2.16) and since $|C_M(y)|=|C_M(x_5)|$
By (2.16) and since $|C_M(y)|=|C_M(x_5)|$![]() , we can assume that there exists an element $\alpha \in C_M(x_5)$
, we can assume that there exists an element $\alpha \in C_M(x_5)$![]() such that $\alpha _2=1$
such that $\alpha _2=1$![]() , $\alpha _{31}=n_{31}\neq 1$
, $\alpha _{31}=n_{31}\neq 1$![]() and for every $j \in \{2,\,\ldots,\,t\}$
and for every $j \in \{2,\,\ldots,\,t\}$![]() , $\alpha _{3j}=1$
, $\alpha _{3j}=1$![]() . Then, (2.16) guarantees that $\alpha _{41}=n_{41} \neq 1$
. Then, (2.16) guarantees that $\alpha _{41}=n_{41} \neq 1$![]() and for every $j\in \{2,\,\ldots,\,t\}$
and for every $j\in \{2,\,\ldots,\,t\}$![]() , $\alpha _{4j}=1$
, $\alpha _{4j}=1$![]() . However, $\chi (\alpha )=\theta _3(\alpha _{31})\theta _4(\alpha _{41})=\theta _3(n_{31})\theta _4(n_{41})= \theta _3(n_{31})^{2}$
. However, $\chi (\alpha )=\theta _3(\alpha _{31})\theta _4(\alpha _{41})=\theta _3(n_{31})\theta _4(n_{41})= \theta _3(n_{31})^{2}$![]() and $\chi ^{(x_5^{i}x)^{-1}}(\alpha )=\chi (\alpha ^{x_5^{i}x})=\chi (\alpha _2\alpha _3^{2}\alpha _4^{2})= \theta _3(\alpha _{31}^{2})\theta _4(\alpha _{41}^{2})=\theta _3(n_{31})^{4}=\theta _3(n_{31})$
and $\chi ^{(x_5^{i}x)^{-1}}(\alpha )=\chi (\alpha ^{x_5^{i}x})=\chi (\alpha _2\alpha _3^{2}\alpha _4^{2})= \theta _3(\alpha _{31}^{2})\theta _4(\alpha _{41}^{2})=\theta _3(n_{31})^{4}=\theta _3(n_{31})$![]() . Since $\theta _3(n_{31}) \neq 1$
. Since $\theta _3(n_{31}) \neq 1$![]() , $\chi ^{(x_5^{i}x)^{-1}}(\alpha ) \neq \chi (\alpha )$
, $\chi ^{(x_5^{i}x)^{-1}}(\alpha ) \neq \chi (\alpha )$![]() . This shows that $x_5^{i}x \not \in I_G(\chi )$
. This shows that $x_5^{i}x \not \in I_G(\chi )$![]() . Taking the elements mentioned in (2.4) into account, we conclude that $I_G(\chi ) / N \leq \langle \bar {x}_5\rangle$
. Taking the elements mentioned in (2.4) into account, we conclude that $I_G(\chi ) / N \leq \langle \bar {x}_5\rangle$![]() . So, either $I_G(\chi ) / N = \langle \bar {x}_5\rangle$
. So, either $I_G(\chi ) / N = \langle \bar {x}_5\rangle$![]() or $I_G(\chi )=N$
or $I_G(\chi )=N$![]() . If $I_G(\chi )/N=\langle \bar {x}_5\rangle$
. If $I_G(\chi )/N=\langle \bar {x}_5\rangle$![]() , let $b=1$
, let $b=1$![]() and if $I_G(\chi )=N$
and if $I_G(\chi )=N$![]() , let $b=5$
, let $b=5$![]() . So, $\mathcal {B}=\{(x_5^{i}x^{j}y^{k}\sigma ^{l})^{-1} : 0 \leq i \leq b-1,\,j,\,k \in \{0,\,1\},\,l\in \{0,\,1,\,2\}\}$
. So, $\mathcal {B}=\{(x_5^{i}x^{j}y^{k}\sigma ^{l})^{-1} : 0 \leq i \leq b-1,\,j,\,k \in \{0,\,1\},\,l\in \{0,\,1,\,2\}\}$![]() is a transversal set of $I_G(\chi )$
is a transversal set of $I_G(\chi )$![]() in $G$
in $G$![]() . Hence, for every $\psi \in {\rm Irr}(G|\chi )$
. Hence, for every $\psi \in {\rm Irr}(G|\chi )$![]() , $\psi (n)=e\Sigma _{g \in \mathcal {B}} \chi ^{g}(n)= e\Sigma _{i=0}^{b-1}[\chi (n^{x_5^{i}})+\chi (n^{x_5^{i}\sigma })+\chi (n^{x_5^{i}\sigma ^{2}})]$
, $\psi (n)=e\Sigma _{g \in \mathcal {B}} \chi ^{g}(n)= e\Sigma _{i=0}^{b-1}[\chi (n^{x_5^{i}})+\chi (n^{x_5^{i}\sigma })+\chi (n^{x_5^{i}\sigma ^{2}})]$![]() $ + e\Sigma _{i=0}^{b-1}[\chi (n^{x_5^{i}x})+\chi (n^{x_5^{i}x\sigma })+\chi (n^{x_5^{i}x\sigma ^{2}})] + e\Sigma _{i=0}^{b-1}[\chi (n^{x_5^{i}y})+\chi (n^{x_5^{i}y\sigma })+\chi (n^{x_5^{i}y\sigma ^{2}})]$
$ + e\Sigma _{i=0}^{b-1}[\chi (n^{x_5^{i}x})+\chi (n^{x_5^{i}x\sigma })+\chi (n^{x_5^{i}x\sigma ^{2}})] + e\Sigma _{i=0}^{b-1}[\chi (n^{x_5^{i}y})+\chi (n^{x_5^{i}y\sigma })+\chi (n^{x_5^{i}y\sigma ^{2}})]$![]() $+ e\Sigma _{i=0}^{b-1}[\chi (n^{x_5^{i}xy})+\chi (n^{x_5^{i}xy\sigma })+\chi (n^{x_5^{i}xy\sigma ^{2}})]$
$+ e\Sigma _{i=0}^{b-1}[\chi (n^{x_5^{i}xy})+\chi (n^{x_5^{i}xy\sigma })+\chi (n^{x_5^{i}xy\sigma ^{2}})]$![]() , for some positive integer $e$
, for some positive integer $e$![]() . We note that $\chi (n_2n_3n_4)=\chi (n_2n_3^{2}n_4^{2})=\chi (n_2^{2}n_3n_4^{2})=\chi (n_2^{2}n_3^{2}n_4)=1$
. We note that $\chi (n_2n_3n_4)=\chi (n_2n_3^{2}n_4^{2})=\chi (n_2^{2}n_3n_4^{2})=\chi (n_2^{2}n_3^{2}n_4)=1$![]() . Thus, if $(n_{31}^{\sigma },\,n_{32}^{\sigma })=(n_{41},\,n_{42}^{2})$
. Thus, if $(n_{31}^{\sigma },\,n_{32}^{\sigma })=(n_{41},\,n_{42}^{2})$![]() , then by (2.10), $\psi (n) =e\Sigma _{i=0}^{b-1}[1+ \theta _3(n_{31})^{2}+\theta _3(n_{31})^{2}] + e\Sigma _{i=0}^{b-1}[1+ \theta _3(n_{31})$
, then by (2.10), $\psi (n) =e\Sigma _{i=0}^{b-1}[1+ \theta _3(n_{31})^{2}+\theta _3(n_{31})^{2}] + e\Sigma _{i=0}^{b-1}[1+ \theta _3(n_{31})$![]() $\theta _3(n_{31})] + e\Sigma _{i=0}^{b-1}[1+\theta _3(n_{31})+ \theta _3(n_{31})^{2} ] +e\Sigma _{i=0}^{b-1} [1+ \theta _3(n_{31})^{2}$
$\theta _3(n_{31})] + e\Sigma _{i=0}^{b-1}[1+\theta _3(n_{31})+ \theta _3(n_{31})^{2} ] +e\Sigma _{i=0}^{b-1} [1+ \theta _3(n_{31})^{2}$![]() $+ \theta _3(n_{31})] = 4be(1+\theta _3(n_{31})+\theta _3(n_{31})^{2}).$
$+ \theta _3(n_{31})] = 4be(1+\theta _3(n_{31})+\theta _3(n_{31})^{2}).$![]() Also, if $(n_{31}^{\sigma },\,n_{32}^{\sigma })=(n_{41}^{2},\,n_{42})$
Also, if $(n_{31}^{\sigma },\,n_{32}^{\sigma })=(n_{41}^{2},\,n_{42})$![]() , then similarly $\psi (n)= 4be(1+\theta _3(n_{31})+\theta _3(n_{31})^{2}).$
, then similarly $\psi (n)= 4be(1+\theta _3(n_{31})+\theta _3(n_{31})^{2}).$![]() However, $n_{31} \neq 1$
However, $n_{31} \neq 1$![]() . So, $o(\theta _3(n_{31}))=3$
. So, $o(\theta _3(n_{31}))=3$![]() . Therefore, $1 \neq \theta _3(n_{31})$
. Therefore, $1 \neq \theta _3(n_{31})$![]() is a primitive third root of unitary. It follows that $(\theta _3(n_{31}))^{2}+\theta _3(n_{31})+1=0$
is a primitive third root of unitary. It follows that $(\theta _3(n_{31}))^{2}+\theta _3(n_{31})+1=0$![]() . Thus, we get that $\psi (n)=4be(1+\theta _3(n_{31})+\theta _3(n_{31})^{2})=0,\,$
. Thus, we get that $\psi (n)=4be(1+\theta _3(n_{31})+\theta _3(n_{31})^{2})=0,\,$![]() as desired in (i). Now, the proof is complete.
as desired in (i). Now, the proof is complete.
3. Proof of theorem A
Now, we are going to prove theorem A. Working towards a contradiction, suppose that $G$![]() is non-solvable. Let $M$
is non-solvable. Let $M$![]() be the maximal normal solvable subgroup of $G$
be the maximal normal solvable subgroup of $G$![]() and let $N/M$
and let $N/M$![]() be a minimal normal subgroup of $G/M$
be a minimal normal subgroup of $G/M$![]() . Then, ${\rm Fit}(G)={\rm Fit}(M)$
. Then, ${\rm Fit}(G)={\rm Fit}(M)$![]() and $N/M=S_1/M \times \cdots \times S_t/M$
and $N/M=S_1/M \times \cdots \times S_t/M$![]() such that $S_1/M ,\, \ldots,\, S_t/M$
such that $S_1/M ,\, \ldots,\, S_t/M$![]() are isomorphic to a fixed non-abelian simple group $S$
are isomorphic to a fixed non-abelian simple group $S$![]() . Let $\alpha$
. Let $\alpha$![]() be the size of vanishing classes of $G$
be the size of vanishing classes of $G$![]() . Set $G_{\alpha }=\{g \in G: |cl_G(g)|=\alpha \}$
. Set $G_{\alpha }=\{g \in G: |cl_G(g)|=\alpha \}$![]() . By $(*)$
. By $(*)$![]() , ${\rm Van}(G) \subseteq G_{\alpha }$
, ${\rm Van}(G) \subseteq G_{\alpha }$![]() . We are going to complete the proof in the following steps:
. We are going to complete the proof in the following steps:
Step 1. $t=1$![]() .
.
Proof. Working towards a contradiction, let $t \neq 1$![]() . Let $\pi _1 \subseteq \pi (S)$
. Let $\pi _1 \subseteq \pi (S)$![]() such that if $S$
such that if $S$![]() is one of the groups mentioned in lemma 2.11(b), then $\pi _1=\{2,\,3\}$
is one of the groups mentioned in lemma 2.11(b), then $\pi _1=\{2,\,3\}$![]() and otherwise, $\pi _1=\{2\}$
and otherwise, $\pi _1=\{2\}$![]() . Fix $\pi =\pi (S) - \pi _1$
. Fix $\pi =\pi (S) - \pi _1$![]() . Let $p,\,q \in \pi$
. Let $p,\,q \in \pi$![]() be distinct. Suppose that $i ,\, j \in \{1,\,\ldots,\,t\}$
be distinct. Suppose that $i ,\, j \in \{1,\,\ldots,\,t\}$![]() and $i \neq j$
and $i \neq j$![]() . Then, for every non-trivial $p$
. Then, for every non-trivial $p$![]() -element $xM \in S_i/M$
-element $xM \in S_i/M$![]() and $q$
and $q$![]() -element $yM \in S_j/M$
-element $yM \in S_j/M$![]() , $xM,\,yM,\,xyM \in {\rm Van}(G/M)$
, $xM,\,yM,\,xyM \in {\rm Van}(G/M)$![]() , by lemmas 2.11 and 2.12(a). Thus, $xM,\,yM,\,xyM \subseteq {\rm Van}(G)\subseteq G_{\alpha }$
, by lemmas 2.11 and 2.12(a). Thus, $xM,\,yM,\,xyM \subseteq {\rm Van}(G)\subseteq G_{\alpha }$![]() , by lemma 2.13(ii). So, for every $m \in M$
, by lemma 2.13(ii). So, for every $m \in M$![]() , proposition 2.10 shows that $C_G(xym)$
, proposition 2.10 shows that $C_G(xym)$![]() contains a Sylow $p$
contains a Sylow $p$![]() -subgroup and a Sylow $q$
-subgroup and a Sylow $q$![]() -subgroup of $M$
-subgroup of $M$![]() , which are abelian. Let $P \in {\rm Syl}_p({\rm Fit}(G))$
, which are abelian. Let $P \in {\rm Syl}_p({\rm Fit}(G))$![]() and $Q \in {\rm Syl}_q({\rm Fit}(G))$
and $Q \in {\rm Syl}_q({\rm Fit}(G))$![]() . Since ${\rm Fit}(G) \leq M$
. Since ${\rm Fit}(G) \leq M$![]() , we get that
, we get that
Thus, $P,\,Q \leq Z(M)$![]() . Let $F_0$
. Let $F_0$![]() be a Hall $\pi$
be a Hall $\pi$![]() -subgroup of ${\rm Fit}(G)$
-subgroup of ${\rm Fit}(G)$![]() . Since $p$
. Since $p$![]() is an arbitrary element of $\pi$
is an arbitrary element of $\pi$![]() , we get that $F_0 \leq Z(M)$
, we get that $F_0 \leq Z(M)$![]() . By lemma 2.3(iii), there exist a $p$
. By lemma 2.3(iii), there exist a $p$![]() -element $x_1 \in N - M$
-element $x_1 \in N - M$![]() , a $q$
, a $q$![]() -element $y_1 \in N - M$
-element $y_1 \in N - M$![]() and $m_1,\,m_1',\,m'' \in M$
and $m_1,\,m_1',\,m'' \in M$![]() such that $x_1y_1=y_1x_1$
such that $x_1y_1=y_1x_1$![]() , $xm_1=x_1$
, $xm_1=x_1$![]() , $ym_1'=y_1$
, $ym_1'=y_1$![]() and $xym''=x_1y_1$
and $xym''=x_1y_1$![]() . Lemma 2.3(i) and (3.1) yield that $P,\,Q \leq C_G(xym'')=C_G(x_1y_1) = C_G(x_1) \cap C_G(y_1)$
. Lemma 2.3(i) and (3.1) yield that $P,\,Q \leq C_G(xym'')=C_G(x_1y_1) = C_G(x_1) \cap C_G(y_1)$![]() . So $P,\,Q \leq C_G(x),\,C_G(y)$
. So $P,\,Q \leq C_G(x),\,C_G(y)$![]() , because $P,\,Q \leq Z(M)$
, because $P,\,Q \leq Z(M)$![]() , $xm_1=x_1$
, $xm_1=x_1$![]() and $ym_1'=y_1$
and $ym_1'=y_1$![]() . However, $p,\,q \in \pi$
. However, $p,\,q \in \pi$![]() and $i,\,j \in \{1,\,\ldots,\,t\}$
and $i,\,j \in \{1,\,\ldots,\,t\}$![]() are arbitrary. Thus, for every $r \in \pi$
are arbitrary. Thus, for every $r \in \pi$![]() and every $r$
and every $r$![]() -element $z \in N - M$
-element $z \in N - M$![]() , $F_0 \leq C_G(z)$
, $F_0 \leq C_G(z)$![]() . Hence, lemma 2.3(i) forces the $\pi$
. Hence, lemma 2.3(i) forces the $\pi$![]() -elements of $N- M$
-elements of $N- M$![]() to centralize $F_0$
to centralize $F_0$![]() . Next, let $zM$
. Next, let $zM$![]() be a $\pi _1$
be a $\pi _1$![]() -element of $S_i/M$
-element of $S_i/M$![]() . By lemma 2.3(iii), there exist a $q$
. By lemma 2.3(iii), there exist a $q$![]() -element $y_2 \in N - M$
-element $y_2 \in N - M$![]() , a $\pi _1$
, a $\pi _1$![]() -element $z_1 \in N- M$
-element $z_1 \in N- M$![]() and $u,\,u' \in M$
and $u,\,u' \in M$![]() such that $zu=z_1$
such that $zu=z_1$![]() , $yu'=y_2$
, $yu'=y_2$![]() and $y_2z_1=z_1y_2$
and $y_2z_1=z_1y_2$![]() . By lemmas 2.11, 2.12(a) and 2.13(ii), $z_1y_2,\,y_2 \in {\rm Van}(G) \subseteq G_{\alpha }$
. By lemmas 2.11, 2.12(a) and 2.13(ii), $z_1y_2,\,y_2 \in {\rm Van}(G) \subseteq G_{\alpha }$![]() . Therefore, $C_G(y_2) =C_G(y_2z_1) \leq C_G(z_1)$
. Therefore, $C_G(y_2) =C_G(y_2z_1) \leq C_G(z_1)$![]() , by lemma 2.3(i). Consequently, $F_0 \leq C_G(z_1)$
, by lemma 2.3(i). Consequently, $F_0 \leq C_G(z_1)$![]() . However, $F_0 \leq Z(M)$
. However, $F_0 \leq Z(M)$![]() and $zu=z_1$
and $zu=z_1$![]() . So, $F_0 \leq C_G(z)$
. So, $F_0 \leq C_G(z)$![]() . Since $i \in \{1,\,\ldots,\,t\}$
. Since $i \in \{1,\,\ldots,\,t\}$![]() is arbitrary, we have that $\pi _1$
is arbitrary, we have that $\pi _1$![]() -elements of $N - M$
-elements of $N - M$![]() centralize $F_0$
centralize $F_0$![]() . Thus, $F_0 \leq Z(N)$
. Thus, $F_0 \leq Z(N)$![]() . On the other hand, every $\pi$
. On the other hand, every $\pi$![]() -element $w \in N-{\rm Fit}(G)$
-element $w \in N-{\rm Fit}(G)$![]() is vanishing in $G$
is vanishing in $G$![]() , by lemma 2.12(a) and proposition 2.14. Therefore, $|cl_G(w)|=\alpha$
, by lemma 2.12(a) and proposition 2.14. Therefore, $|cl_G(w)|=\alpha$![]() . It follows from lemma 2.3(iv) that $N$
. It follows from lemma 2.3(iv) that $N$![]() contains a nilpotent Hall $\pi$
contains a nilpotent Hall $\pi$![]() -subgroup, so does $N/M$
-subgroup, so does $N/M$![]() , contradicting lemma 2.1(iv).
, contradicting lemma 2.1(iv).
Step 2. $C_{G/M}(N/M)=\{M\}$![]() .
.
Proof. Working towards a contradiction, let $C_{G/M}(N/M) \neq \{M\}$![]() and let $C/M$
and let $C/M$![]() be a minimal normal subgroup of $G/M$
be a minimal normal subgroup of $G/M$![]() such that $C/M \leq C_{G/M}(N/M)$
such that $C/M \leq C_{G/M}(N/M)$![]() . By step 1, $N/M$
. By step 1, $N/M$![]() and $C/M$
and $C/M$![]() are isomorphic to the simple groups $S_1$
are isomorphic to the simple groups $S_1$![]() and $S_2$
and $S_2$![]() , respectively. Let $p \in \pi (S_1)-\pi _1$
, respectively. Let $p \in \pi (S_1)-\pi _1$![]() and $p \neq q \in \pi (S_2)-\pi _2$
and $p \neq q \in \pi (S_2)-\pi _2$![]() , where for $i \in \{1,\,2\}$
, where for $i \in \{1,\,2\}$![]() , if $S_i$
, if $S_i$![]() is one of the groups mentioned in lemma 2.11(b), then $\pi _i=\{2,\,3\}$
is one of the groups mentioned in lemma 2.11(b), then $\pi _i=\{2,\,3\}$![]() and otherwise, $\pi _i=\{2\}$
and otherwise, $\pi _i=\{2\}$![]() . If $\pi _1\cup \pi _2=\{2,\,3\}$
. If $\pi _1\cup \pi _2=\{2,\,3\}$![]() , then without loss of generality, we can assume that $\pi _1=\{2,\,3\}$
, then without loss of generality, we can assume that $\pi _1=\{2,\,3\}$![]() . Set $\pi =\pi (N/M)-\pi _1$
. Set $\pi =\pi (N/M)-\pi _1$![]() . Let $M \neq xM \in N/M$
. Let $M \neq xM \in N/M$![]() be a $p$
be a $p$![]() -element and $M \neq yM \in C/M$
-element and $M \neq yM \in C/M$![]() be a $q$
be a $q$![]() -element. Then, lemmas 2.11, 2.12(a) and 2.13(ii) guarantee that $xM,\,yM,\,xyM \subseteq {\rm Van}(G)\subseteq G_{\alpha }$
-element. Then, lemmas 2.11, 2.12(a) and 2.13(ii) guarantee that $xM,\,yM,\,xyM \subseteq {\rm Van}(G)\subseteq G_{\alpha }$![]() . Thus, for every $m \in M$
. Thus, for every $m \in M$![]() , proposition 2.10 shows that $C_G(xym)$
, proposition 2.10 shows that $C_G(xym)$![]() contains an abelian Sylow $p$
contains an abelian Sylow $p$![]() -subgroup and an abelian Sylow $q$
-subgroup and an abelian Sylow $q$![]() -subgroup of $M$
-subgroup of $M$![]() . Let $P \in {\rm Syl}_p({\rm Fit}(G))$
. Let $P \in {\rm Syl}_p({\rm Fit}(G))$![]() and $Q \in {\rm Syl}_q({\rm Fit}(G))$
and $Q \in {\rm Syl}_q({\rm Fit}(G))$![]() . Since ${\rm Fit}(G) \leq M$
. Since ${\rm Fit}(G) \leq M$![]() , we get that
, we get that
Thus, $P,\,Q \leq Z(M)$![]() . Let $F_0$
. Let $F_0$![]() be a Hall $\pi$
be a Hall $\pi$![]() -subgroup of ${\rm Fit}(G)$
-subgroup of ${\rm Fit}(G)$![]() . Since $p$
. Since $p$![]() is an arbitrary element of $\pi$
is an arbitrary element of $\pi$![]() , we get that $F_0 \leq Z(M)$
, we get that $F_0 \leq Z(M)$![]() . By lemma 2.3(iii), there exist a $p$
. By lemma 2.3(iii), there exist a $p$![]() -element $x_1 \in N - M$
-element $x_1 \in N - M$![]() , a $q$
, a $q$![]() -element $y_1 \in C - M$
-element $y_1 \in C - M$![]() and $m_1,\,m_1',\,m'' \in M$
and $m_1,\,m_1',\,m'' \in M$![]() such that $x_1y_1=y_1x_1$
such that $x_1y_1=y_1x_1$![]() , $xm_1=x_1$
, $xm_1=x_1$![]() , $ym_1'=y_1$
, $ym_1'=y_1$![]() and $xym''=x_1y_1$
and $xym''=x_1y_1$![]() . Hence, lemma 2.3(i) and (3.2) give that $P,\,Q \leq C_G(xym'')=C_G(x_1y_1) = C_G(x_1) \cap C_G(y_1)$
. Hence, lemma 2.3(i) and (3.2) give that $P,\,Q \leq C_G(xym'')=C_G(x_1y_1) = C_G(x_1) \cap C_G(y_1)$![]() . So $P,\,Q \leq C_G(y),\, C_G(x)$
. So $P,\,Q \leq C_G(y),\, C_G(x)$![]() , because $P,\,Q \leq Z(M)$
, because $P,\,Q \leq Z(M)$![]() , $xm_1=x_1$
, $xm_1=x_1$![]() and $ym_1'=y_1$
and $ym_1'=y_1$![]() . Since $p \in \pi$
. Since $p \in \pi$![]() is arbitrary, we get that $F_0 \leq C_G(y)$
is arbitrary, we get that $F_0 \leq C_G(y)$![]() . Consequently, $F_0 \leq C_G(y_1)$
. Consequently, $F_0 \leq C_G(y_1)$![]() . However, $x_1y_1,\,x_1,\,y_1 \in {\rm Van}(G) \subseteq G_{\alpha }$
. However, $x_1y_1,\,x_1,\,y_1 \in {\rm Van}(G) \subseteq G_{\alpha }$![]() . Thus, $|C_G(x_1)|=|C_G(x_1y_1)|=|C_G(y_1)|$
. Thus, $|C_G(x_1)|=|C_G(x_1y_1)|=|C_G(y_1)|$![]() . It follows from lemma 2.3(i) that $F_0 \leq C_G(y_1)=C_G(x_1y_1)=C_G(x_1)$
. It follows from lemma 2.3(i) that $F_0 \leq C_G(y_1)=C_G(x_1y_1)=C_G(x_1)$![]() . Since $F_0 \leq Z(M)$
. Since $F_0 \leq Z(M)$![]() and $xm_1=x_1$
and $xm_1=x_1$![]() , we get that $F_0 \leq C_G(x)$
, we get that $F_0 \leq C_G(x)$![]() . Regarding the fact that $p \in \pi$
. Regarding the fact that $p \in \pi$![]() is arbitrary, we conclude that the $\pi$
is arbitrary, we conclude that the $\pi$![]() -elements of $N - M$
-elements of $N - M$![]() centralize $F_0$
centralize $F_0$![]() . Now, let $M \neq zM$
. Now, let $M \neq zM$![]() be a $\pi '$
be a $\pi '$![]() -element of $N/M$
-element of $N/M$![]() . Without loss of generality, we can assume that $q \not \in \pi (S_1) - \pi$
. Without loss of generality, we can assume that $q \not \in \pi (S_1) - \pi$![]() . By lemmas 2.11, 2.12(a) and 2.13(ii,iii), $yM,\,yzM \subseteq {\rm Van}(G)$
. By lemmas 2.11, 2.12(a) and 2.13(ii,iii), $yM,\,yzM \subseteq {\rm Van}(G)$![]() . On the other hand, lemma 2.3(iii) forces to exist a $q$
. On the other hand, lemma 2.3(iii) forces to exist a $q$![]() -element $y_2 \in C - M$
-element $y_2 \in C - M$![]() , a $\pi '$
, a $\pi '$![]() -element $z_1 \in N - M$
-element $z_1 \in N - M$![]() and $u,\,u' \in M$
and $u,\,u' \in M$![]() such that $y_2z_1=z_1y_2$
such that $y_2z_1=z_1y_2$![]() , $zu=z_1$
, $zu=z_1$![]() and $yu'=y_2$
and $yu'=y_2$![]() . Then, $y_2,\,y_2z_1 \in {\rm Van}(G) \subseteq G_{\alpha }$
. Then, $y_2,\,y_2z_1 \in {\rm Van}(G) \subseteq G_{\alpha }$![]() . Thus $|C_G(y_2z_1)|=|C_G(y_2)|$
. Thus $|C_G(y_2z_1)|=|C_G(y_2)|$![]() . So, lemma 2.3(i) guarantees that $C_G(y_2) =C_G(y_2z_1) \leq C_G(z_1)$
. So, lemma 2.3(i) guarantees that $C_G(y_2) =C_G(y_2z_1) \leq C_G(z_1)$![]() . As, $F_0 \leq C_G(y),\,Z(M)$
. As, $F_0 \leq C_G(y),\,Z(M)$![]() and $yu'=y_2$
and $yu'=y_2$![]() , we have $F_0 \leq C_G(y_2) \leq C_G(z_1)$
, we have $F_0 \leq C_G(y_2) \leq C_G(z_1)$![]() . However, $zu=z_1$
. However, $zu=z_1$![]() and $F_0 \leq Z(M)$
and $F_0 \leq Z(M)$![]() . Hence, $F_0 \leq C_G(z)$
. Hence, $F_0 \leq C_G(z)$![]() . This forces $F_0 \leq Z(N)$
. This forces $F_0 \leq Z(N)$![]() . On the other hand, every $\pi$
. On the other hand, every $\pi$![]() -element $w \in N-{\rm Fit}(G)$
-element $w \in N-{\rm Fit}(G)$![]() is vanishing in $G$
is vanishing in $G$![]() , by lemmas 2.11, 2.12(a) and 2.13(ii), and proposition 2.14. Therefore, $|cl_G(w)|=\alpha$
, by lemmas 2.11, 2.12(a) and 2.13(ii), and proposition 2.14. Therefore, $|cl_G(w)|=\alpha$![]() . So, lemma 2.3(iv) yields that $N$
. So, lemma 2.3(iv) yields that $N$![]() contains a nilpotent Hall $\pi$
contains a nilpotent Hall $\pi$![]() -subgroup, so does $N/M$
-subgroup, so does $N/M$![]() . This is a contradiction with lemma 2.1(iv).
. This is a contradiction with lemma 2.1(iv).
Step 3. $G/M \cong {\rm Alt}_5$![]() or ${\rm Alt}_7$
or ${\rm Alt}_7$![]() .
.
Proof. By steps 1 and 2, $N/M\cong S$![]() is non-abelian simple and $G/M \lesssim {\rm Aut}(N/M)$
is non-abelian simple and $G/M \lesssim {\rm Aut}(N/M)$![]() . Fix $\bar {N}=N/M$
. Fix $\bar {N}=N/M$![]() and $\bar {G}=G/M$
and $\bar {G}=G/M$![]() . For $x \in G$
. For $x \in G$![]() , let $\bar {x}$
, let $\bar {x}$![]() be the image of $x$
be the image of $x$![]() in $\bar {G}$
in $\bar {G}$![]() .
.
a. Let $S \not \cong {\rm Alt}_5,\,M_{22}$![]() and let either $(S,\,r,\,m,\,t)$
and let either $(S,\,r,\,m,\,t)$![]() be as in tables I and II or $S \cong {\rm Alt}_{l}$
be as in tables I and II or $S \cong {\rm Alt}_{l}$![]() , where $8 \leq l \leq 10$
, where $8 \leq l \leq 10$![]() , and $(r,\,m,\,t)=(5,\,15,\,7)$
, and $(r,\,m,\,t)=(5,\,15,\,7)$![]() . Then, $\bar {N}$
. Then, $\bar {N}$![]() contains an element $\bar {x}$
contains an element $\bar {x}$![]() of order $m$
of order $m$![]() . By lemmas 2.11 and 2.12(a), for every $1 \leq i < m$
. By lemmas 2.11 and 2.12(a), for every $1 \leq i < m$![]() , $\bar {x}^{i} \in {\rm Van}(\bar {G})$
, $\bar {x}^{i} \in {\rm Van}(\bar {G})$![]() . If $S \cong {\rm Alt}_l$
. If $S \cong {\rm Alt}_l$![]() , where $8 \leq l \leq 10$
, where $8 \leq l \leq 10$![]() , then we apply [Reference Conway, Curtis, Norton, Parker and Wilson4] for the previous conclusion. Consequently, $x^{i} \in {\rm Van}(G)$
, then we apply [Reference Conway, Curtis, Norton, Parker and Wilson4] for the previous conclusion. Consequently, $x^{i} \in {\rm Van}(G)$![]() , by lemma 2.13(ii). Since ${\rm Van}(G) \subseteq G_{\alpha }$
, by lemma 2.13(ii). Since ${\rm Van}(G) \subseteq G_{\alpha }$![]() , $m$
, $m$![]() is a composite number and $r \mid m$
is a composite number and $r \mid m$![]() , proposition 2.10(ii) shows that $|M|_r|o(\bar {x})|_r \mid |C_G(x)|$
, proposition 2.10(ii) shows that $|M|_r|o(\bar {x})|_r \mid |C_G(x)|$![]() . So, for every $z \in {\rm Van}({G})$
. So, for every $z \in {\rm Van}({G})$![]() , $|M|_r|o(\bar {x})|_r \mid |C_G(z)|$
, $|M|_r|o(\bar {x})|_r \mid |C_G(z)|$![]() . On the other hand, ${\rm Van}(\bar {G})$
. On the other hand, ${\rm Van}(\bar {G})$![]() contains an element $\bar {y}$
contains an element $\bar {y}$![]() of order $t$
of order $t$![]() , by lemma 2.12(b). Lemma 2.13(ii) guarantees that $y \in {\rm Van}({G})$
, by lemma 2.12(b). Lemma 2.13(ii) guarantees that $y \in {\rm Van}({G})$![]() . Hence, $|M|_r|o(\bar {x})|_r \mid |C_G(y)|$
. Hence, $|M|_r|o(\bar {x})|_r \mid |C_G(y)|$![]() . Thus, lemma 2.3(ii) forces $r \mid |C_{\bar {G}}(\bar {y})|$
. Thus, lemma 2.3(ii) forces $r \mid |C_{\bar {G}}(\bar {y})|$![]() . Therefore, $\bar {G}$
. Therefore, $\bar {G}$![]() contains an element $\bar {z}$
contains an element $\bar {z}$![]() of order $rt$
of order $rt$![]() . By lemma 2.12(b), for every $1 \leq i < tr$
. By lemma 2.12(b), for every $1 \leq i < tr$![]() , $\bar {z}^{i} \in {\rm Van}(\bar {G})$
, $\bar {z}^{i} \in {\rm Van}(\bar {G})$![]() . Consequently, $|M|_t|o(\bar {z})|_t \mid |C_G(z)|$
. Consequently, $|M|_t|o(\bar {z})|_t \mid |C_G(z)|$![]() , by lemma 2.13(ii) and proposition 2.10(ii). It follows from $(*)$
, by lemma 2.13(ii) and proposition 2.10(ii). It follows from $(*)$![]() that $|M|_t|o(\bar {z})|_t \mid |C_G(x)|$
that $|M|_t|o(\bar {z})|_t \mid |C_G(x)|$![]() . In view of lemma 2.3(ii), $t \mid |C_{\bar {G}}(\bar {x})|$
. In view of lemma 2.3(ii), $t \mid |C_{\bar {G}}(\bar {x})|$![]() . However, $t \nmid |{\rm Out}(S)|$
. However, $t \nmid |{\rm Out}(S)|$![]() . So, $t \mid |C_{\bar {N}}(\bar {x})|$
. So, $t \mid |C_{\bar {N}}(\bar {x})|$![]() , contradicting lemma 2.1(iii).
, contradicting lemma 2.1(iii).
b. Assume that $S \cong {\rm Alt}_l$![]() , where $l > 11$
, where $l > 11$![]() . Suppose that $m=35$
. Suppose that $m=35$![]() and $r$
and $r$![]() and $t$
and $t$![]() are as in lemma 2.1(i). Then, $\bar {N}$
are as in lemma 2.1(i). Then, $\bar {N}$![]() contains an element $\bar {x}$
contains an element $\bar {x}$![]() of order $m$
of order $m$![]() . By lemmas 2.11 and 2.12(a), for every $1 \leq i < m$
. By lemmas 2.11 and 2.12(a), for every $1 \leq i < m$![]() , $\bar {x}^{i} \in {\rm Van}(\bar {G})$
, $\bar {x}^{i} \in {\rm Van}(\bar {G})$![]() . Lemma 2.13(ii) yields $x^{i} \in {\rm Van}(G)$
. Lemma 2.13(ii) yields $x^{i} \in {\rm Van}(G)$![]() . Since ${\rm Van}(G) \subseteq G_{\alpha }$
. Since ${\rm Van}(G) \subseteq G_{\alpha }$![]() , $m$
, $m$![]() is a composite number and $7 \mid m$
is a composite number and $7 \mid m$![]() , proposition 2.10(ii) shows that $|M|_7|o(\bar {x})|_7 \mid |C_G(x)|$
, proposition 2.10(ii) shows that $|M|_7|o(\bar {x})|_7 \mid |C_G(x)|$![]() . So, for every $z \in {\rm Van}({G})$
. So, for every $z \in {\rm Van}({G})$![]() , $|M|_7|o(\bar {x})|_7 \mid |C_G(z)|$
, $|M|_7|o(\bar {x})|_7 \mid |C_G(z)|$![]() . On the other hand, ${\rm Van}(\bar {G})$
. On the other hand, ${\rm Van}(\bar {G})$![]() contains an element $\bar {y}$
contains an element $\bar {y}$![]() of order $t$
of order $t$![]() , by lemma 2.12(b). Lemma 2.13(ii) forces $y \in {\rm Van}({G})$
, by lemma 2.12(b). Lemma 2.13(ii) forces $y \in {\rm Van}({G})$![]() . Hence, $|M|_7|o(\bar {x})|_7\mid |C_G(y)|$
. Hence, $|M|_7|o(\bar {x})|_7\mid |C_G(y)|$![]() . Lemma 2.3(ii) implies that $7 \mid |C_{\bar {G}}(\bar {y})|$
. Lemma 2.3(ii) implies that $7 \mid |C_{\bar {G}}(\bar {y})|$![]() . Therefore, $\bar {G}$
. Therefore, $\bar {G}$![]() contains an element $\bar {z}$
contains an element $\bar {z}$![]() of order $7t$
of order $7t$![]() . By lemma 2.12(b), for every $1 \leq i < 7t$
. By lemma 2.12(b), for every $1 \leq i < 7t$![]() , $\bar {z}^{i} \in {\rm Van}(\bar {G})$
, $\bar {z}^{i} \in {\rm Van}(\bar {G})$![]() . So, $|M|_t|o(\bar {z})|_t \mid |C_G(z)|$
. So, $|M|_t|o(\bar {z})|_t \mid |C_G(z)|$![]() , by lemma 2.13(ii) and proposition 2.10(ii). Thus, $|M|_t|o(\bar {z})|_t \mid |C_G(u)|$
, by lemma 2.13(ii) and proposition 2.10(ii). Thus, $|M|_t|o(\bar {z})|_t \mid |C_G(u)|$![]() , for every $u \in {\rm Van}(G)$
, for every $u \in {\rm Van}(G)$![]() . Also, lemma 2.12(b) forces ${\rm Van}(\bar {G}) \cap \bar {N}$
. Also, lemma 2.12(b) forces ${\rm Van}(\bar {G}) \cap \bar {N}$![]() to contain an element $\bar {w}$
to contain an element $\bar {w}$![]() of order $r$
of order $r$![]() . Hence, $t \mid |C_{\bar {G}}(\bar {w})|$
. Hence, $t \mid |C_{\bar {G}}(\bar {w})|$![]() , by lemmas 2.3(ii) and 2.13(ii). However, $t \nmid |{\rm Out}(S)|$
, by lemmas 2.3(ii) and 2.13(ii). However, $t \nmid |{\rm Out}(S)|$![]() . So, $t \mid |C_{\bar {N}}(\bar {w})|$
. So, $t \mid |C_{\bar {N}}(\bar {w})|$![]() , contradicting lemma 2.1(ii).
, contradicting lemma 2.1(ii).
c. Let $S \cong {M}_{22}$![]() or ${\rm Alt}_{11}$
or ${\rm Alt}_{11}$![]() , $m=8$
, $m=8$![]() and let $t=11$
and let $t=11$![]() . [Reference Conway, Curtis, Norton, Parker and Wilson4] implies that $\bar {N}$
. [Reference Conway, Curtis, Norton, Parker and Wilson4] implies that $\bar {N}$![]() contains an element $\bar {x}$
contains an element $\bar {x}$![]() of order $m$
of order $m$![]() such that for every $1 \leq i < 4$
such that for every $1 \leq i < 4$![]() , $\bar {x}^{i} \in {\rm Van}(\bar {G})$
, $\bar {x}^{i} \in {\rm Van}(\bar {G})$![]() . Consequently, ${x}^{i} \in {\rm Van}({G})$
. Consequently, ${x}^{i} \in {\rm Van}({G})$![]() , by lemma 2.13(ii). So, proposition 2.10(ii) shows that $2|M|_2 \mid |C_G(x)|$
, by lemma 2.13(ii). So, proposition 2.10(ii) shows that $2|M|_2 \mid |C_G(x)|$![]() . Hence, $(*)$
. Hence, $(*)$![]() forces $2|M|_2 \mid |C_G(z)|$
forces $2|M|_2 \mid |C_G(z)|$![]() , for every $z \in {\rm Van}({G})$
, for every $z \in {\rm Van}({G})$![]() . On the other hand, ${\rm Van}(\bar {G})$
. On the other hand, ${\rm Van}(\bar {G})$![]() contains an element $\bar {y}$
contains an element $\bar {y}$![]() of order $t$
of order $t$![]() , by lemma 2.12(b). By lemma 2.13(ii), $y \in {\rm Van}({G})$
, by lemma 2.12(b). By lemma 2.13(ii), $y \in {\rm Van}({G})$![]() and hence, $2|M|_2\mid |C_G(y)|$
and hence, $2|M|_2\mid |C_G(y)|$![]() . Thus, lemma 2.3(ii) implies that $2 \mid |C_{\bar {G}}(\bar {y})|$
. Thus, lemma 2.3(ii) implies that $2 \mid |C_{\bar {G}}(\bar {y})|$![]() . This shows that ${\rm Aut}(S)$
. This shows that ${\rm Aut}(S)$![]() contains an element of order $2t=22$
contains an element of order $2t=22$![]() , which is a contradiction, by considering [Reference Conway, Curtis, Norton, Parker and Wilson4].
, which is a contradiction, by considering [Reference Conway, Curtis, Norton, Parker and Wilson4].
The above cases show that $N/M \cong {\rm Alt}_5$![]() or ${\rm Alt}_7$
or ${\rm Alt}_7$![]() . By step 2, $C_{G/M}(N/M)=\{M\}$
. By step 2, $C_{G/M}(N/M)=\{M\}$![]() . Thus, $G/M \lesssim {\rm Aut}(N/M)$
. Thus, $G/M \lesssim {\rm Aut}(N/M)$![]() . Working towards a contradiction, let $G/M \neq N/M$
. Working towards a contradiction, let $G/M \neq N/M$![]() . Then, $G/M \cong {\rm Sym}_7$
. Then, $G/M \cong {\rm Sym}_7$![]() or ${\rm Sym}_5$
or ${\rm Sym}_5$![]() . If $\bar {G}\cong {\rm Sym}_7$
. If $\bar {G}\cong {\rm Sym}_7$![]() , let $(r,\,t,\,d)=(5,\,7,\,10)$
, let $(r,\,t,\,d)=(5,\,7,\,10)$![]() and if $\bar {G} \cong {\rm Sym}_5$
and if $\bar {G} \cong {\rm Sym}_5$![]() , let $(r,\,t,\,d)=(3,\,5,\,6)$
, let $(r,\,t,\,d)=(3,\,5,\,6)$![]() . [Reference Conway, Curtis, Norton, Parker and Wilson4] guarantees that ${\rm Van}(\bar {G})$
. [Reference Conway, Curtis, Norton, Parker and Wilson4] guarantees that ${\rm Van}(\bar {G})$![]() contains an element $\bar {x}$
contains an element $\bar {x}$![]() of order $d$
of order $d$![]() such that for every $1 \leq i < d$
such that for every $1 \leq i < d$![]() , $\bar {x}^{i} \in {\rm Van}(\bar {G})$
, $\bar {x}^{i} \in {\rm Van}(\bar {G})$![]() . Since ${\rm Van}(G) \subseteq G_{\alpha }$
. Since ${\rm Van}(G) \subseteq G_{\alpha }$![]() , $d$
, $d$![]() is a composite number and $r \mid d$
is a composite number and $r \mid d$![]() , proposition 2.10(ii) shows that $|M|_r|o(\bar {x})|_r \mid |C_G(x)|$
, proposition 2.10(ii) shows that $|M|_r|o(\bar {x})|_r \mid |C_G(x)|$![]() . So for every $z \in {\rm Van}({G})$
. So for every $z \in {\rm Van}({G})$![]() , $|M|_r|o(\bar {x})|_r \mid |C_G(z)|$
, $|M|_r|o(\bar {x})|_r \mid |C_G(z)|$![]() . On the other hand, ${\rm Van}(\bar {G})$
. On the other hand, ${\rm Van}(\bar {G})$![]() contains an element $\bar {y}$
contains an element $\bar {y}$![]() of order $t$
of order $t$![]() , by lemma 2.12(b). Lemma 2.13(ii) yields that $y \in {\rm Van}({G})$
, by lemma 2.12(b). Lemma 2.13(ii) yields that $y \in {\rm Van}({G})$![]() . Hence, $|M|_r|o(\bar {x})|_r \mid |C_G(y)|$
. Hence, $|M|_r|o(\bar {x})|_r \mid |C_G(y)|$![]() . Thus, lemma 2.3(ii) forces $r \mid |C_{\bar {G}}(\bar {y})|$
. Thus, lemma 2.3(ii) forces $r \mid |C_{\bar {G}}(\bar {y})|$![]() . Therefore, $\bar {G}$
. Therefore, $\bar {G}$![]() contains an element $\bar {z}$
contains an element $\bar {z}$![]() of order $rt$
of order $rt$![]() , which is a contradiction, regarding the orders of elements of $\bar {G}$
, which is a contradiction, regarding the orders of elements of $\bar {G}$![]() . This shows that $G/M=N/M$
. This shows that $G/M=N/M$![]() . Thus, $G/M \cong {\rm Alt}_5$
. Thus, $G/M \cong {\rm Alt}_5$![]() or ${\rm Alt}_7$
or ${\rm Alt}_7$![]() .
.
Step 4. $\pi (M/{\rm Fit}(G)) \subseteq \{2\}$![]() .
.
Proof. By step 3, $G/M \cong {\rm Alt}_5$![]() or ${\rm Alt}_7$
or ${\rm Alt}_7$![]() . It is worth mentioning that by [Reference Conway, Curtis, Norton, Parker and Wilson4],
. It is worth mentioning that by [Reference Conway, Curtis, Norton, Parker and Wilson4],
Fix $F_0=\{1\}$![]() and for $1 \leq i \leq n$
and for $1 \leq i \leq n$![]() , let $F_i/F_{i-1}={\rm Fit}(G/F_{i-1})$
, let $F_i/F_{i-1}={\rm Fit}(G/F_{i-1})$![]() such that $F_n=M$
such that $F_n=M$![]() . Let $P \in {\rm Syl}_2(M)$
. Let $P \in {\rm Syl}_2(M)$![]() . Working towards a contradiction, suppose that $\pi (M/F_1)\not \subseteq \{2\}$
. Working towards a contradiction, suppose that $\pi (M/F_1)\not \subseteq \{2\}$![]() . Then, one of the following cases occurs:
. Then, one of the following cases occurs:
Case 1. Let $\pi (F_n/F_{n-1})=\{2\}$![]() . Since by our assumption $\pi (M/F_1) \not \subseteq \{2\}$
. Since by our assumption $\pi (M/F_1) \not \subseteq \{2\}$![]() , we have $n \geq 3$
, we have $n \geq 3$![]() and obviously, $\pi (F_{n-1}/F_{n-2}) \neq \{2\}$
and obviously, $\pi (F_{n-1}/F_{n-2}) \neq \{2\}$![]() . Set $W = (P \cap F_{n-1})F_{n-2}$
. Set $W = (P \cap F_{n-1})F_{n-2}$![]() . Then, $W \trianglelefteq G$
. Then, $W \trianglelefteq G$![]() , $\{W\} \neq F_{n-1}/W \trianglelefteq G/W$
, $\{W\} \neq F_{n-1}/W \trianglelefteq G/W$![]() is nilpotent and $\{W\} \neq Z/W \trianglelefteq G/W$
is nilpotent and $\{W\} \neq Z/W \trianglelefteq G/W$![]() , where $F_{n-1} \leq Z$
, where $F_{n-1} \leq Z$![]() and $Z/F_{n-1}=Z(M/F_{n-1})$
and $Z/F_{n-1}=Z(M/F_{n-1})$![]() . Also, $Z/F_{n-1} \leq M/F_{n-1}$
. Also, $Z/F_{n-1} \leq M/F_{n-1}$![]() is a $2$
is a $2$![]() -group and ${\rm gcd}(|F_{n-1}/W|,\,2)=1$
-group and ${\rm gcd}(|F_{n-1}/W|,\,2)=1$![]() . Let $C/W=C_{Z/W}(F_{n-1}/W)$
. Let $C/W=C_{Z/W}(F_{n-1}/W)$![]() . If $W \neq y W \in C/W$
. If $W \neq y W \in C/W$![]() , then for every $W\neq xW \in F_{n-1}/W$
, then for every $W\neq xW \in F_{n-1}/W$![]() , there is an element $w \in W$
, there is an element $w \in W$![]() such that
such that
We can assume that $xF_{n-2}$![]() is a $2'$
is a $2'$![]() -element. Since $W/F_{n-2}$
-element. Since $W/F_{n-2}$![]() is a $2$
is a $2$![]() -group, $o(wF_{n-2})$
-group, $o(wF_{n-2})$![]() is a power of $2$
is a power of $2$![]() . Also, $wF_{n-2},\,xF_{n-2} \in F_{n-1}/F_{n-2}$
. Also, $wF_{n-2},\,xF_{n-2} \in F_{n-1}/F_{n-2}$![]() and $F_{n-1}/F_{n-2}$
and $F_{n-1}/F_{n-2}$![]() is nilpotent. So, $xwF_{n-2}=wxF_{n-2}$
is nilpotent. So, $xwF_{n-2}=wxF_{n-2}$![]() . By (3.4), $o(xF_{n-2})={\rm lcm}(o(xF_{n-2}),\,o(wF_{n-2}))$
. By (3.4), $o(xF_{n-2})={\rm lcm}(o(xF_{n-2}),\,o(wF_{n-2}))$![]() . Thus, $wF_{n-2}=F_{n-2}$
. Thus, $wF_{n-2}=F_{n-2}$![]() . Consequently, $yF_{n-2} \in C_{G/F_{n-2}}(xF_{n-2})$
. Consequently, $yF_{n-2} \in C_{G/F_{n-2}}(xF_{n-2})$![]() . So, $yF_{n-2} \in C_{G/F_{n-2}}(O_{2'}(F_{n-1}/F_{n-2}))$
. So, $yF_{n-2} \in C_{G/F_{n-2}}(O_{2'}(F_{n-1}/F_{n-2}))$![]() . However, $C/F_{n-2} \leq Z/F_{n-2}$
. However, $C/F_{n-2} \leq Z/F_{n-2}$![]() . Therefore, $O_{2'}(C/F_{n-2}) \leq O_{2'}(F_{n-1}/F_{n-2})$
. Therefore, $O_{2'}(C/F_{n-2}) \leq O_{2'}(F_{n-1}/F_{n-2})$![]() is nilpotent. Thus, $C/F_{n-2}=O_2(C/F_{n-2}) \times O_{2'}(C/F_{n-2})$
is nilpotent. Thus, $C/F_{n-2}=O_2(C/F_{n-2}) \times O_{2'}(C/F_{n-2})$![]() is nilpotent. Hence, $C/F_{n-2} \leq {\rm Fit}(G/F_{n-2})=F_{n-1}/F_{n-2}$
is nilpotent. Hence, $C/F_{n-2} \leq {\rm Fit}(G/F_{n-2})=F_{n-1}/F_{n-2}$![]() . So, $C_{Z/W}(F_{n-1}/W)=C/W \leq F_{n-1}/W$
. So, $C_{Z/W}(F_{n-1}/W)=C/W \leq F_{n-1}/W$![]() . By lemma 2.13(ii,iv), $Z -F_{n-1} \subseteq {\rm Van}(G)$
. By lemma 2.13(ii,iv), $Z -F_{n-1} \subseteq {\rm Van}(G)$![]() . Now, let $s \in \pi (F_{n-1}/F_{n-2})-\{2\}$
. Now, let $s \in \pi (F_{n-1}/F_{n-2})-\{2\}$![]() . Then, $(P \cap Z)/(P \cap F_{n-1})$
. Then, $(P \cap Z)/(P \cap F_{n-1})$![]() acts on a Sylow $s$
acts on a Sylow $s$![]() -subgroup of $F_{n-1}/F_{n-2}$
-subgroup of $F_{n-1}/F_{n-2}$![]() , by conjugation and one of the following sub-cases occurs:
, by conjugation and one of the following sub-cases occurs:
a. Let the action of $(P \cap Z)/(P \cap F_{n-1})$![]() on a Sylow $s$
on a Sylow $s$![]() -subgroup of $F_{n-1}/F_{n-2}$
-subgroup of $F_{n-1}/F_{n-2}$![]() be fixed point freely. Then, $(P \cap Z)/(P \cap F_{n-1}) \cong (P\cap Z)F_{n-1}/F_{n-1}=Z/F_{n-1}$
be fixed point freely. Then, $(P \cap Z)/(P \cap F_{n-1}) \cong (P\cap Z)F_{n-1}/F_{n-1}=Z/F_{n-1}$![]() is a cyclic $2$
is a cyclic $2$![]() -group, because $Z/F_{n-1}$
-group, because $Z/F_{n-1}$![]() is abelian. Hence, $Z/F_{n-1}$
is abelian. Hence, $Z/F_{n-1}$![]() contains a subgroup $\langle z_1 F_{n-1}\rangle$
contains a subgroup $\langle z_1 F_{n-1}\rangle$![]() of order $2$
of order $2$![]() , which is normal in $G/F_{n-1}$
, which is normal in $G/F_{n-1}$![]() . Obviously, $C_{G/F_{n-1}}(\langle z_1 F_{n-1}\rangle )=G/F_{n-1}$
. Obviously, $C_{G/F_{n-1}}(\langle z_1 F_{n-1}\rangle )=G/F_{n-1}$![]() . Thus, there is an element $xF_{n-1} \in C_{G/F_{n-1}}(\langle z_1 F_{n-1}\rangle )$
. Thus, there is an element $xF_{n-1} \in C_{G/F_{n-1}}(\langle z_1 F_{n-1}\rangle )$![]() of order $5$
of order $5$![]() , so $o(xz_1F_{n-1})=10$
, so $o(xz_1F_{n-1})=10$![]() . By lemma 2.13(i,ii) and since $Z- F_{n-1} \subseteq {\rm Van}(G)$
. By lemma 2.13(i,ii) and since $Z- F_{n-1} \subseteq {\rm Van}(G)$![]() , $z_1,\,x,\,xz_1\in {\rm Van}(G)\subseteq G_{\alpha }$
, $z_1,\,x,\,xz_1\in {\rm Van}(G)\subseteq G_{\alpha }$![]() . Hence, proposition 2.10 shows that $|F_{n-1}|_5 |o(xz_1F_{n-1})|_5 \mid |C_G(xz_1)|$
. Hence, proposition 2.10 shows that $|F_{n-1}|_5 |o(xz_1F_{n-1})|_5 \mid |C_G(xz_1)|$![]() . So, for every $h \in {\rm Van}(G)$
. So, for every $h \in {\rm Van}(G)$![]() , $5|F_{n-1}|_5 \mid |C_G(h)|$
, $5|F_{n-1}|_5 \mid |C_G(h)|$![]() . If $G/M \cong {\rm Alt}_5$
. If $G/M \cong {\rm Alt}_5$![]() , let $p=3$
, let $p=3$![]() and otherwise, let $p=7$
and otherwise, let $p=7$![]() . Suppose that $y$
. Suppose that $y$![]() is a $p$
is a $p$![]() -element of $G- M$
-element of $G- M$![]() . By (3.3) and lemma 2.13(ii), $y \in {\rm Van}(G)$
. By (3.3) and lemma 2.13(ii), $y \in {\rm Van}(G)$![]() . Thus, $5|F_{n-1}|_5 \mid |C_G(y)|$
. Thus, $5|F_{n-1}|_5 \mid |C_G(y)|$![]() . Since $\pi (M/F_{n-1})=\{2\}$
. Since $\pi (M/F_{n-1})=\{2\}$![]() , lemma 2.3(ii) forces $5 \mid |C_{G/M}(yM)|$
, lemma 2.3(ii) forces $5 \mid |C_{G/M}(yM)|$![]() , which is impossible.
, which is impossible.
b. Assume that there exist a $2$![]() -element $z \in (Z\cap P)- F_{n-1}$
-element $z \in (Z\cap P)- F_{n-1}$![]() and an $s$
and an $s$![]() -element $y \in F_{n-1} - F_{n-2}$
-element $y \in F_{n-1} - F_{n-2}$![]() such that $yF_{n-2} \in C_{G/F_{n-2}}(z F_{n-2})$
such that $yF_{n-2} \in C_{G/F_{n-2}}(z F_{n-2})$![]() . We can assume by lemma 2.3(iii) that $z\in C_G(y)$
. We can assume by lemma 2.3(iii) that $z\in C_G(y)$![]() , and by proposition 2.14, $y \in {\rm Van}(G)$
, and by proposition 2.14, $y \in {\rm Van}(G)$![]() . As stated before, $Z - F_{n-1} \subseteq {\rm Van}(G)$
. As stated before, $Z - F_{n-1} \subseteq {\rm Van}(G)$![]() , so $z,\,zy \in {\rm Van}(G)$
, so $z,\,zy \in {\rm Van}(G)$![]() . Thus, $zy$
. Thus, $zy$![]() satisfies the assumption of proposition 2.10. Let $H_{n-1}/F_{n-2}$
satisfies the assumption of proposition 2.10. Let $H_{n-1}/F_{n-2}$![]() be a Hall $s'$
be a Hall $s'$![]() -subgroup of $F_{n-1}/F_{n-2}$
-subgroup of $F_{n-1}/F_{n-2}$![]() . Then, $H_{n-1} \unlhd G$
. Then, $H_{n-1} \unlhd G$![]() and proposition 2.10 shows that $|H_{n-1}|_s |o(yzH_{n-1})|_s \mid |C_G(yz)|$
and proposition 2.10 shows that $|H_{n-1}|_s |o(yzH_{n-1})|_s \mid |C_G(yz)|$![]() . It follows that for every $h \in {\rm Van}(G)$
. It follows that for every $h \in {\rm Van}(G)$![]() , $s|H_{n-1}|_s \mid |C_G(h)|$
, $s|H_{n-1}|_s \mid |C_G(h)|$![]() . If $G/M \cong {\rm Alt}_5$
. If $G/M \cong {\rm Alt}_5$![]() , let $r \in \{3,\,5\}-\{s\}$
, let $r \in \{3,\,5\}-\{s\}$![]() and $p \in \{3,\,5\}-\{r\}$
and $p \in \{3,\,5\}-\{r\}$![]() and if $G/M \cong {\rm Alt}_7$
and if $G/M \cong {\rm Alt}_7$![]() , let $r \in \{5,\,7\}-\{s\}$
, let $r \in \{5,\,7\}-\{s\}$![]() and $p \in \{5,\,7\}-\{r\}$
and $p \in \{5,\,7\}-\{r\}$![]() . Let $w$
. Let $w$![]() be an $r$
be an $r$![]() -element of $G- M$
-element of $G- M$![]() . By (3.3) and lemma 2.13(ii), $wM\subseteq {\rm Van}(G)$
. By (3.3) and lemma 2.13(ii), $wM\subseteq {\rm Van}(G)$![]() . Thus $s|H_{n-1}|_s \mid |C_G(w)|$
. Thus $s|H_{n-1}|_s \mid |C_G(w)|$![]() . So, there exists an $s$
. So, there exists an $s$![]() -element $w' \in G - H_{n-1}$
-element $w' \in G - H_{n-1}$![]() such that $w'H_{n-1} \in C_{G/H_{n-1}}(wH_{n-1})$
such that $w'H_{n-1} \in C_{G/H_{n-1}}(wH_{n-1})$![]() . However, $|C_{G/M}(wM)|=r$
. However, $|C_{G/M}(wM)|=r$![]() . Hence, $w'\in M- H_{n-1}$
. Hence, $w'\in M- H_{n-1}$![]() . Then, $w,\,w',\,ww' \in {\rm Van}(G)$
. Then, $w,\,w',\,ww' \in {\rm Van}(G)$![]() , by proposition 2.14 and lemma 2.13(ii). So, proposition 2.10 shows that $r|H_{n-1}|_r \mid |C_G(ww')|$
, by proposition 2.14 and lemma 2.13(ii). So, proposition 2.10 shows that $r|H_{n-1}|_r \mid |C_G(ww')|$![]() . Consequently, for every $h \in {\rm Van}(G)$
. Consequently, for every $h \in {\rm Van}(G)$![]() , $r |H_{n-1}|_r \mid |C_G(h)|$
, $r |H_{n-1}|_r \mid |C_G(h)|$![]() . Assume that $v$
. Assume that $v$![]() is a $p$
is a $p$![]() -element of $G- M$
-element of $G- M$![]() . By (3.3) and lemma 2.13(ii), $v \in {\rm Van}(G)$
. By (3.3) and lemma 2.13(ii), $v \in {\rm Van}(G)$![]() . Thus, $r|H_{n-1}|_r \mid |C_G(v)|$
. Thus, $r|H_{n-1}|_r \mid |C_G(v)|$![]() . Note that $\pi (M/H_{n-1})=\{2,\,s\}$
. Note that $\pi (M/H_{n-1})=\{2,\,s\}$![]() . By lemma 2.3(ii), $r \mid |C_{G/M}(vM)|$
. By lemma 2.3(ii), $r \mid |C_{G/M}(vM)|$![]() , which is impossible.
, which is impossible.
Case 2. Let $2 \neq s \in \pi (F_n/F_{n-1})$![]() . Assume that $S/F_{n-1} \in {\rm Syl}_s(M/F_{n-1})$
. Assume that $S/F_{n-1} \in {\rm Syl}_s(M/F_{n-1})$![]() , $L/F_{n-1}$
, $L/F_{n-1}$![]() is a Hall $s'$
is a Hall $s'$![]() -subgroup of $M/F_{n-1}$
-subgroup of $M/F_{n-1}$![]() and $H/F_{n-1}=Z(S/F_{n-1})$
and $H/F_{n-1}=Z(S/F_{n-1})$![]() . First, let $G/M \cong {\rm Alt}_5$
. First, let $G/M \cong {\rm Alt}_5$![]() and $p=2$
and $p=2$![]() . Then, $G/M$
. Then, $G/M$![]() acts on $H/F_{n-1}$
acts on $H/F_{n-1}$![]() . This action is not fixed point freely, because the Sylow $2$
. This action is not fixed point freely, because the Sylow $2$![]() -subgroups of $G/M$
-subgroups of $G/M$![]() are abelian and non-cyclic. Thus, there exists a $2$
are abelian and non-cyclic. Thus, there exists a $2$![]() -element $M \neq xM \in G/M$
-element $M \neq xM \in G/M$![]() such that $C_{H/F_{n-1}}(xF_{n-1})\neq \{F_{n-1}\}$
such that $C_{H/F_{n-1}}(xF_{n-1})\neq \{F_{n-1}\}$![]() . Let $F_{n-1} \neq yF_{n-1} \in C_{H/F_{n-1}}(xF_{n-1})$
. Let $F_{n-1} \neq yF_{n-1} \in C_{H/F_{n-1}}(xF_{n-1})$![]() . Since $s \neq 2$
. Since $s \neq 2$![]() , (3.3), lemma 2.13(ii) and proposition 2.14 force $x,\,y,\,xy \in {\rm Van}(G)$
, (3.3), lemma 2.13(ii) and proposition 2.14 force $x,\,y,\,xy \in {\rm Van}(G)$![]() . So, $xy$
. So, $xy$![]() satisfies the assumption of proposition 2.10. Next, let $G/M \cong {\rm Alt}_7$
satisfies the assumption of proposition 2.10. Next, let $G/M \cong {\rm Alt}_7$![]() . By lemma 2.13(v), ${\rm Van}(G/M)$
. By lemma 2.13(v), ${\rm Van}(G/M)$![]() contains a $p$
contains a $p$![]() -element $xM$
-element $xM$![]() such that $C_{M/L}(xL) \neq \{L\}$
such that $C_{M/L}(xL) \neq \{L\}$![]() and $p \in \pi (G/M) - \{2,\,s\}$
and $p \in \pi (G/M) - \{2,\,s\}$![]() . Let $L \neq yL \in C_{M/L}(xL)$
. Let $L \neq yL \in C_{M/L}(xL)$![]() . We can assume that $o(y)$
. We can assume that $o(y)$![]() is a power of $s$
is a power of $s$![]() . Then, $x,\,y,\,xy \in {\rm Van}(G)$
. Then, $x,\,y,\,xy \in {\rm Van}(G)$![]() , by lemma 2.13(ii) and proposition 2.14. Consequently, $xy$
, by lemma 2.13(ii) and proposition 2.14. Consequently, $xy$![]() satisfies the assumption of proposition 2.10. In both cases, proposition 2.10 shows that $|L|_p |o(xyL) |_p \mid |C_G(xy)|$
satisfies the assumption of proposition 2.10. In both cases, proposition 2.10 shows that $|L|_p |o(xyL) |_p \mid |C_G(xy)|$![]() . So, for every $h \in {\rm Van}(G)$
. So, for every $h \in {\rm Van}(G)$![]() , $p|L|_p \mid |C_G(h)|$
, $p|L|_p \mid |C_G(h)|$![]() . Let $zM \in G/M$
. Let $zM \in G/M$![]() be of order $r$
be of order $r$![]() , where if $G/M \cong {\rm Alt}_5$
, where if $G/M \cong {\rm Alt}_5$![]() , $r=5$
, $r=5$![]() and otherwise, $r \in \{5,\,7\}-\{p\}$
and otherwise, $r \in \{5,\,7\}-\{p\}$![]() . By (3.3) and lemma 2.13(ii), $z \in {\rm Van}(G)$
. By (3.3) and lemma 2.13(ii), $z \in {\rm Van}(G)$![]() . Thus, $p|L|_p \mid |C_G(z)|$
. Thus, $p|L|_p \mid |C_G(z)|$![]() . As, $p \nmid |M/L|$
. As, $p \nmid |M/L|$![]() , lemma 2.3(ii) yields $p \mid |C_{G/M}(zM)|$
, lemma 2.3(ii) yields $p \mid |C_{G/M}(zM)|$![]() , which is impossible.
, which is impossible.
These contradictions show that $\pi (M/{\rm Fit}(G)) \subseteq \{2\}$![]() .
.
Step 5. $\pi (G/M) -\{2\} \subseteq \pi ({\rm Fit}(G))$![]() .
.
Proof. By steps 3 and 4, $\pi (M/{\rm Fit}(G)) \subseteq \{2\}$![]() and $G/M \cong {\rm Alt}_5$
and $G/M \cong {\rm Alt}_5$![]() or ${\rm Alt}_7$
or ${\rm Alt}_7$![]() . Let $p \in \pi (G/M)-\{2\}$
. Let $p \in \pi (G/M)-\{2\}$![]() . Then, there are the elements $xM,\,yM \in {\rm Van}(G/M)$
. Then, there are the elements $xM,\,yM \in {\rm Van}(G/M)$![]() such that $|G_{G/M}(xM)|_p=|G/M|_p$
such that $|G_{G/M}(xM)|_p=|G/M|_p$![]() and $p \nmid |C_{G/M}(yM)|$
and $p \nmid |C_{G/M}(yM)|$![]() . By lemma 2.13(ii), $x,\,y \in {\rm Van}(G)$
. By lemma 2.13(ii), $x,\,y \in {\rm Van}(G)$![]() . So, $(*)$
. So, $(*)$![]() , corollary 2.4 and lemma 2.3(ii) force $p \mid |C_G(x)|$
, corollary 2.4 and lemma 2.3(ii) force $p \mid |C_G(x)|$![]() and $|C_G(x)|_p=|C_G(y)|_p \mid |M|_p|C_{G/M}(yM)|_p=|{\rm Fit}(G)|_p$
and $|C_G(x)|_p=|C_G(y)|_p \mid |M|_p|C_{G/M}(yM)|_p=|{\rm Fit}(G)|_p$![]() , because $p \neq 2$
, because $p \neq 2$![]() . Therefore, $p \mid |{\rm Fit}(G)|$
. Therefore, $p \mid |{\rm Fit}(G)|$![]() , as desired.
, as desired.
Step 6. $M={\rm Fit}(G)$![]() .
.
Proof. By steps 3 and 4, $\pi (M/{\rm Fit}(G)) \subseteq \{2\}$![]() and $G/M \cong {\rm Alt}_5$
and $G/M \cong {\rm Alt}_5$![]() or ${\rm Alt}_7$
or ${\rm Alt}_7$![]() . Working towards a contradiction, suppose that $M \neq {\rm Fit}(G)$
. Working towards a contradiction, suppose that $M \neq {\rm Fit}(G)$![]() . Let $P \in {\rm Syl}_2(M)$
. Let $P \in {\rm Syl}_2(M)$![]() . Set $P_1=P \cap {\rm Fit}(G)$
. Set $P_1=P \cap {\rm Fit}(G)$![]() and assume that $Z/{\rm Fit}(G)$
and assume that $Z/{\rm Fit}(G)$![]() is the maximal normal abelian subgroup of $G/{\rm Fit}(G)$
is the maximal normal abelian subgroup of $G/{\rm Fit}(G)$![]() such that $Z \leq M$
such that $Z \leq M$![]() . Then, $P_1 \in {\rm Syl}_2({\rm Fit}(G))$
. Then, $P_1 \in {\rm Syl}_2({\rm Fit}(G))$![]() , $Z(M/{\rm Fit}(G)) \leq Z/{\rm Fit}(G)$
, $Z(M/{\rm Fit}(G)) \leq Z/{\rm Fit}(G)$![]() and $Z/{\rm Fit}(G)$
and $Z/{\rm Fit}(G)$![]() is a $2$
is a $2$![]() -group. By step 5, $\pi (G/M)-\{2\} \subseteq \pi ({\rm Fit}(G))$
-group. By step 5, $\pi (G/M)-\{2\} \subseteq \pi ({\rm Fit}(G))$![]() . Hence, ${\rm Fit}(G)/P_1$
. Hence, ${\rm Fit}(G)/P_1$![]() is a non-trivial Hall $2'$
is a non-trivial Hall $2'$![]() -subgroup of $M/P_1$
-subgroup of $M/P_1$![]() that is nilpotent and normal in $G/P_1$
that is nilpotent and normal in $G/P_1$![]() . If $xP_1 \in C_{M/P_1}({\rm Fit}(G)/P_1),\,$
. If $xP_1 \in C_{M/P_1}({\rm Fit}(G)/P_1),\,$![]() then $[x,\,{\rm Fit}(G)]\subseteq P_1$
then $[x,\,{\rm Fit}(G)]\subseteq P_1$![]() . So, for every $2'$
. So, for every $2'$![]() -element $f \in {\rm Fit}(G)$
-element $f \in {\rm Fit}(G)$![]() , there exists an element $g \in P_1$
, there exists an element $g \in P_1$![]() such that $xfx^{-1}f^{-1} =g$
such that $xfx^{-1}f^{-1} =g$![]() . Hence, $xfx^{-1} =gf$
. Hence, $xfx^{-1} =gf$![]() . However, ${\rm Fit}(G)$
. However, ${\rm Fit}(G)$![]() is nilpotent and $P_1 \leq {\rm Fit}(G)$
is nilpotent and $P_1 \leq {\rm Fit}(G)$![]() . Therefore, $o(f)={\rm lcm}(o(f),\,o(g))$
. Therefore, $o(f)={\rm lcm}(o(f),\,o(g))$![]() . This forces $g=1$
. This forces $g=1$![]() . Thus, $x \in C_M(O_{2'}({\rm Fit}(G))).$
. Thus, $x \in C_M(O_{2'}({\rm Fit}(G))).$![]() Since $M/{\rm Fit}(G)$
Since $M/{\rm Fit}(G)$![]() is a $2$
is a $2$![]() -group, we have $x=x_1x_2=x_2x_1$
-group, we have $x=x_1x_2=x_2x_1$![]() such that $x_1 \in M$
such that $x_1 \in M$![]() is a $2$
is a $2$![]() -element and $x_2 \in {\rm Fit}(G)$
-element and $x_2 \in {\rm Fit}(G)$![]() is a $2'$
is a $2'$![]() -element. Let $Q_1 \in {\rm Syl}_2(C_M(O_{2'}({\rm Fit}(G)))$
-element. Let $Q_1 \in {\rm Syl}_2(C_M(O_{2'}({\rm Fit}(G)))$![]() such that $x_1 \in Q_1$
such that $x_1 \in Q_1$![]() . Then, $P_1 \leq Q_1$
. Then, $P_1 \leq Q_1$![]() and $Q_1 {\rm Fit}(G)= Q_1 \times O_{2'}({\rm Fit}(G))$
and $Q_1 {\rm Fit}(G)= Q_1 \times O_{2'}({\rm Fit}(G))$![]() is a nilpotent subgroup of $G$
is a nilpotent subgroup of $G$![]() . However, $Q_1{\rm Fit}(G)/{\rm Fit}(G)=C_M(O_{2'}({\rm Fit}(G)){\rm Fit}(G)/{\rm Fit}(G) \unlhd G/ {\rm Fit}(G)$
. However, $Q_1{\rm Fit}(G)/{\rm Fit}(G)=C_M(O_{2'}({\rm Fit}(G)){\rm Fit}(G)/{\rm Fit}(G) \unlhd G/ {\rm Fit}(G)$![]() . Consequently, $Q_1 \times O_{2'}({\rm Fit}(G))=Q_1 {\rm Fit}(G) \unlhd G$
. Consequently, $Q_1 \times O_{2'}({\rm Fit}(G))=Q_1 {\rm Fit}(G) \unlhd G$![]() . Therefore, ${\rm Fit}(G)= O_{2'}({\rm Fit}(G)) \times P_1 \leq O_{2'}({\rm Fit}(G)) \times Q_1 \leq {\rm Fit}(G)$
. Therefore, ${\rm Fit}(G)= O_{2'}({\rm Fit}(G)) \times P_1 \leq O_{2'}({\rm Fit}(G)) \times Q_1 \leq {\rm Fit}(G)$![]() . This yields that $O_{2'}({\rm Fit}(G)) \times Q_1 = {\rm Fit}(G)$
. This yields that $O_{2'}({\rm Fit}(G)) \times Q_1 = {\rm Fit}(G)$![]() , so $Q_1=P_1$
, so $Q_1=P_1$![]() . Thus, $x_1\in P_1$
. Thus, $x_1\in P_1$![]() . As $x=x_1x_2$
. As $x=x_1x_2$![]() and $x_2 \in {\rm Fit}(G)$
and $x_2 \in {\rm Fit}(G)$![]() , we get $x \in {\rm Fit}(G)$
, we get $x \in {\rm Fit}(G)$![]() . Thus,
. Thus,
Hence, $C_{Z/P_1}({\rm Fit}(G)/P_1) \leq {\rm Fit}(G)/P_1.$![]() By lemma 2.13(iv,ii).
By lemma 2.13(iv,ii).
In the following, we first assume that $G/M \cong {\rm Alt}_7$![]() and $Z=M$
and $Z=M$![]() . We observe that $G/M$
. We observe that $G/M$![]() acts on $Z/{\rm Fit}(G)$
acts on $Z/{\rm Fit}(G)$![]() , by conjugation. Hence, there are an odd prime $q$
, by conjugation. Hence, there are an odd prime $q$![]() , a $q$
, a $q$![]() -element $yM \in {\rm Van}(G/M)$
-element $yM \in {\rm Van}(G/M)$![]() and an element ${\rm Fit}(G)\neq x{\rm Fit}(G) \in Z/{\rm Fit}(G)$
and an element ${\rm Fit}(G)\neq x{\rm Fit}(G) \in Z/{\rm Fit}(G)$![]() such that $y{\rm Fit}(G) \in C_{G/{\rm Fit}(G)}(x{\rm Fit}(G))$
such that $y{\rm Fit}(G) \in C_{G/{\rm Fit}(G)}(x{\rm Fit}(G))$![]() , by lemma 2.13(v). Therefore, $x,\,y,\,xy \in {\rm Van}(G)$
, by lemma 2.13(v). Therefore, $x,\,y,\,xy \in {\rm Van}(G)$![]() . So, proposition 2.10 shows that $|{\rm Fit}(G)|_q |o(xy{\rm Fit}(G))|_q \mid |C_G(xy)|$
. So, proposition 2.10 shows that $|{\rm Fit}(G)|_q |o(xy{\rm Fit}(G))|_q \mid |C_G(xy)|$![]() . It follows that for every $h \in {\rm Van}(G)$
. It follows that for every $h \in {\rm Van}(G)$![]() , $q|{\rm Fit}(G)|_q \mid |C_G(h)|$
, $q|{\rm Fit}(G)|_q \mid |C_G(h)|$![]() . Let $p \in \{5,\,7\}- \{q\}$
. Let $p \in \{5,\,7\}- \{q\}$![]() . Suppose that $z$
. Suppose that $z$![]() is a $p$
is a $p$![]() -element of $G-M$
-element of $G-M$![]() . By lemma 2.13(i), $z \in {\rm Van}(G)$
. By lemma 2.13(i), $z \in {\rm Van}(G)$![]() . Thus, $q|{\rm Fit}(G)|_q \mid |C_G(z)|$
. Thus, $q|{\rm Fit}(G)|_q \mid |C_G(z)|$![]() . Regarding $\pi (M/{\rm Fit}(G))=\{2\}$
. Regarding $\pi (M/{\rm Fit}(G))=\{2\}$![]() , we get that $q\mid |C_{G/M}(zM)|$
, we get that $q\mid |C_{G/M}(zM)|$![]() , which is impossible.
, which is impossible.
Now, let $G/M \cong {\rm Alt}_5$![]() , $Z=M$
, $Z=M$![]() and a Sylow $2$
and a Sylow $2$![]() -subgroup of ${G}/{{\rm Fit}}(G)$
-subgroup of ${G}/{{\rm Fit}}(G)$![]() is abelian. Then, for every $2$
is abelian. Then, for every $2$![]() -element ${x}_2 \in {G} - {Z}$
-element ${x}_2 \in {G} - {Z}$![]() , $x_2{\rm Fit}(G) \in C_{G/{\rm Fit}(G)}(Z/{\rm Fit}(G))$
, $x_2{\rm Fit}(G) \in C_{G/{\rm Fit}(G)}(Z/{\rm Fit}(G))$![]() . Set $C/{\rm Fit}(G) = C_{G/{\rm Fit}(G)}(Z/{\rm Fit}(G)) .$
. Set $C/{\rm Fit}(G) = C_{G/{\rm Fit}(G)}(Z/{\rm Fit}(G)) .$![]() So, $x_2 \in C - Z$
So, $x_2 \in C - Z$![]() . Therefore, $Z \neq x_2Z \in C/Z\trianglelefteq G/Z =G/M \cong {\rm Alt}_5$
. Therefore, $Z \neq x_2Z \in C/Z\trianglelefteq G/Z =G/M \cong {\rm Alt}_5$![]() . This forces $C/Z=G/Z$
. This forces $C/Z=G/Z$![]() , consequently, $C=G$
, consequently, $C=G$![]() . Thus, $C_{G/{\rm Fit}(G)}(Z/{\rm Fit}(G))=G/{\rm Fit}(G)$
. Thus, $C_{G/{\rm Fit}(G)}(Z/{\rm Fit}(G))=G/{\rm Fit}(G)$![]() . Hence, $G/{\rm Fit}(G)$
. Hence, $G/{\rm Fit}(G)$![]() contains an element $x{\rm Fit}(G)$
contains an element $x{\rm Fit}(G)$![]() of order $6$
of order $6$![]() such that $x^{2} \in G - M$
such that $x^{2} \in G - M$![]() and $x^{3} \in Z- {\rm Fit}(G)$
and $x^{3} \in Z- {\rm Fit}(G)$![]() . Since $M \neq xM,\, x^{2}M \in G/M \cong {\rm Alt}_5$
. Since $M \neq xM,\, x^{2}M \in G/M \cong {\rm Alt}_5$![]() , $xM,\,x^{2}M \in {\rm Van}(G/M)$
, $xM,\,x^{2}M \in {\rm Van}(G/M)$![]() . By lemma 2.13(ii), $x^{2},\,x \in {\rm Van}(G)$
. By lemma 2.13(ii), $x^{2},\,x \in {\rm Van}(G)$![]() . Also, (3.6) shows that $x^{3} \in {\rm Van}(G)$
. Also, (3.6) shows that $x^{3} \in {\rm Van}(G)$![]() . So, proposition 2.10 shows that $3|{\rm Fit}(G)|_3 \mid | C_G(x)|$
. So, proposition 2.10 shows that $3|{\rm Fit}(G)|_3 \mid | C_G(x)|$![]() . Regarding $[G:{\rm Fit}(G)]_3 = 3$
. Regarding $[G:{\rm Fit}(G)]_3 = 3$![]() , we get that that $|G|_3 \mid |C_G(x)|$
, we get that that $|G|_3 \mid |C_G(x)|$![]() . Hence, $|cl_G(x)|_3=1$
. Hence, $|cl_G(x)|_3=1$![]() . Since $x \in {\rm Van}(G)$
. Since $x \in {\rm Van}(G)$![]() , $(*)$
, $(*)$![]() forces $3$
forces $3$![]() not to divide the vanishing conjugacy class sizes of $G$
not to divide the vanishing conjugacy class sizes of $G$![]() . It follows from [Reference Dolfi, Pacifici and Sanus6, theorem A] that $G$
. It follows from [Reference Dolfi, Pacifici and Sanus6, theorem A] that $G$![]() has a normal $3$
has a normal $3$![]() -complement, which is impossible.
-complement, which is impossible.
Then, suppose that $M \neq Z$![]() , $Z/{\rm Fit}(G)$
, $Z/{\rm Fit}(G)$![]() is an elementary abelian $2$
is an elementary abelian $2$![]() -group and $G/M \cong {\rm Alt}_5$
-group and $G/M \cong {\rm Alt}_5$![]() or ${\rm Alt}_7$
or ${\rm Alt}_7$![]() . Assume that $L/Z$
. Assume that $L/Z$![]() is a chief factor of $G$
is a chief factor of $G$![]() such that $L \leq M$
such that $L \leq M$![]() . If $o(u{\rm Fit}(G))=2$
. If $o(u{\rm Fit}(G))=2$![]() , for every $u{\rm Fit}(G) \in L/{\rm Fit}(G)$
, for every $u{\rm Fit}(G) \in L/{\rm Fit}(G)$![]() , then $L/{\rm Fit}(G)$
, then $L/{\rm Fit}(G)$![]() is abelian, contradicting our assumption on $Z$
is abelian, contradicting our assumption on $Z$![]() . So, $L/{\rm Fit}(G)$
. So, $L/{\rm Fit}(G)$![]() contains an element $u{\rm Fit}(G)$
contains an element $u{\rm Fit}(G)$![]() of order $4$
of order $4$![]() . Since $Z/{\rm Fit}(G)$
. Since $Z/{\rm Fit}(G)$![]() and $L/Z$
and $L/Z$![]() are elementary abelian $2$
are elementary abelian $2$![]() -groups, $u \in L - Z$
-groups, $u \in L - Z$![]() and ${\rm Fit}(G)\neq u^{2} {\rm Fit}(G) \in Z/{\rm Fit}(G)$
and ${\rm Fit}(G)\neq u^{2} {\rm Fit}(G) \in Z/{\rm Fit}(G)$![]() . In the following, set $\bar {G}=G/P_1$
. In the following, set $\bar {G}=G/P_1$![]() and, for every $H \leq G$
and, for every $H \leq G$![]() and $x \in G$
and $x \in G$![]() , let $\bar {H}=HP_1/P_1$
, let $\bar {H}=HP_1/P_1$![]() and $\bar {x}$
and $\bar {x}$![]() be the image of $x$
be the image of $x$![]() in $\bar {G}$
in $\bar {G}$![]() . Since $|\bar {{\rm Fit}}(G)|$
. Since $|\bar {{\rm Fit}}(G)|$![]() is odd, we can assume that $o(\bar {u})=4$
is odd, we can assume that $o(\bar {u})=4$![]() and $\bar {u}^{2} \in \bar {Z}- \bar {{\rm Fit}}(G)$
and $\bar {u}^{2} \in \bar {Z}- \bar {{\rm Fit}}(G)$![]() . Let $\{\bar {1}\}=\bar {N}_0 \leq \cdots \leq \bar {N}_t =\bar {{\rm Fit}}(G) \leq \bar {G}$
. Let $\{\bar {1}\}=\bar {N}_0 \leq \cdots \leq \bar {N}_t =\bar {{\rm Fit}}(G) \leq \bar {G}$![]() be a normal series of $\bar {G}$
be a normal series of $\bar {G}$![]() such that for every $1\leq i \leq t$
such that for every $1\leq i \leq t$![]() , $\bar {N}_i/\bar {N}_{i-1}$
, $\bar {N}_i/\bar {N}_{i-1}$![]() is a chief factor of $\bar {G}$
is a chief factor of $\bar {G}$![]() . Suppose that $i$
. Suppose that $i$![]() is the smallest number such that $0\leq i \leq t$
is the smallest number such that $0\leq i \leq t$![]() and
and
By (3.5), $i\neq 0$![]() . Working towards a contradiction, let
. Working towards a contradiction, let
Assume that $\bar {n}\bar {N}_{i-1} \in \bar {{\rm Fit}}(G)/\bar {N}_{i-1}$![]() is arbitrary. If $\bar {n} \in \bar {N}_i$
is arbitrary. If $\bar {n} \in \bar {N}_i$![]() , then (3.8) forces $\bar {n} \bar {N}_{i-1}\in C_{\bar {M}/\bar {N}_{i-1}}(\bar {u}^{2}\bar {N}_{i-1}).$
, then (3.8) forces $\bar {n} \bar {N}_{i-1}\in C_{\bar {M}/\bar {N}_{i-1}}(\bar {u}^{2}\bar {N}_{i-1}).$![]() Next, let $\bar {n} \not \in \bar {N}_{i}$
Next, let $\bar {n} \not \in \bar {N}_{i}$![]() . By (3.7), $[\bar {n},\,\bar {u}^{2}]\in \bar {N}_i$
. By (3.7), $[\bar {n},\,\bar {u}^{2}]\in \bar {N}_i$![]() . So, there is an element $\bar {m} \in \bar {N}_i$
. So, there is an element $\bar {m} \in \bar {N}_i$![]() such that $[\bar {n},\,\bar {u}^{2}]=\bar {m}$
such that $[\bar {n},\,\bar {u}^{2}]=\bar {m}$![]() . Thus, ${\bar {n}}(\bar {u}^{2}){\bar {n}}^{-1} \bar {N}_{i-1}=\bar {m}\bar {u}^{2}\bar {N}_{i-1}$
. Thus, ${\bar {n}}(\bar {u}^{2}){\bar {n}}^{-1} \bar {N}_{i-1}=\bar {m}\bar {u}^{2}\bar {N}_{i-1}$![]() . By (3.8), $\bar {m}\bar {u}^{2}\bar {N}_{i-1}=\bar {u}^{2}\bar {m}\bar {N}_{i-1}$
. By (3.8), $\bar {m}\bar {u}^{2}\bar {N}_{i-1}=\bar {u}^{2}\bar {m}\bar {N}_{i-1}$![]() . Since $\bar {u}^{2}\bar {N}_{i-1}$
. Since $\bar {u}^{2}\bar {N}_{i-1}$![]() is a $2$
is a $2$![]() -element and $\bar {m}\bar {N}_{i-1} \in \bar {{\rm Fit}}(G)/\bar {N}_{i-1}$
-element and $\bar {m}\bar {N}_{i-1} \in \bar {{\rm Fit}}(G)/\bar {N}_{i-1}$![]() , which is a $2'$
, which is a $2'$![]() -group, we get that $\bar {m}\bar {N}_{i-1}=\bar {N}_{i-1}$
-group, we get that $\bar {m}\bar {N}_{i-1}=\bar {N}_{i-1}$![]() . Consequently, $\bar {n} \bar {N}_{i-1}\in C_{\bar {M}/\bar {N}_{i-1}}(\bar {u}^{2}\bar {N}_{i-1})$
. Consequently, $\bar {n} \bar {N}_{i-1}\in C_{\bar {M}/\bar {N}_{i-1}}(\bar {u}^{2}\bar {N}_{i-1})$![]() , for every $\bar {n} \bar {N}_{i-1} \in {\bar {\rm Fit}}(G)/\bar {N}_{i-1}$
, for every $\bar {n} \bar {N}_{i-1} \in {\bar {\rm Fit}}(G)/\bar {N}_{i-1}$![]() . Therefore, ${\bar {\rm Fit}}(G)/ \bar {N}_{i-1} \leq C_{\bar {M}/\bar {N}_{i-1}}(\bar {u}^{2}\bar {N}_{i-1})$
. Therefore, ${\bar {\rm Fit}}(G)/ \bar {N}_{i-1} \leq C_{\bar {M}/\bar {N}_{i-1}}(\bar {u}^{2}\bar {N}_{i-1})$![]() . Hence, $\bar {u}^{2}\bar {N}_{i-1} \in C_{\bar {M}/\bar {N}_{i-1}}({\bar {\rm Fit}}(G)/\bar {N}_{i-1})$
. Hence, $\bar {u}^{2}\bar {N}_{i-1} \in C_{\bar {M}/\bar {N}_{i-1}}({\bar {\rm Fit}}(G)/\bar {N}_{i-1})$![]() , contradicting our assumption on $i$
, contradicting our assumption on $i$![]() . So,
. So,
Since $\{\bar {N}_{i-1}\} \neq Z({\bar {\rm Fit}}(G)/\bar {N}_{i-1} ) \cap \bar {N}_i/\bar {N}_{i-1}\unlhd \bar {G}/\bar {N}_{i-1}$![]() and $\bar {N}_i/\bar {N}_{i-1}$
and $\bar {N}_i/\bar {N}_{i-1}$![]() is a chief factor of $\bar {G}$
is a chief factor of $\bar {G}$![]() , $Z({\bar {\rm Fit}}(G)/\bar {N}_{i-1} ) \cap \bar {N}_i/\bar {N}_{i-1}=\bar {N}_i/\bar {N}_{i-1}$
, $Z({\bar {\rm Fit}}(G)/\bar {N}_{i-1} ) \cap \bar {N}_i/\bar {N}_{i-1}=\bar {N}_i/\bar {N}_{i-1}$![]() . So, $\bar {N}_i/\bar {N}_{i-1} \leq Z({\bar {\rm Fit}}(G)/\bar {N}_{i-1} )$
. So, $\bar {N}_i/\bar {N}_{i-1} \leq Z({\bar {\rm Fit}}(G)/\bar {N}_{i-1} )$![]() . Therefore, ${\bar {\rm Fit}}(G)/\bar {N}_{i-1} \leq C_{\bar {Z}/\bar {N}_{i-1}}(\bar {N}_i/\bar {N}_{i-1})$
. Therefore, ${\bar {\rm Fit}}(G)/\bar {N}_{i-1} \leq C_{\bar {Z}/\bar {N}_{i-1}}(\bar {N}_i/\bar {N}_{i-1})$![]() . As $Z/{\rm Fit}(G)$
. As $Z/{\rm Fit}(G)$![]() is abelian, we get that $(\bar {Z}/\bar {N}_{i-1}){C_{\bar {G}/\bar {N}_{i-1}}(\bar {N}_i/\bar {N}_{i-1})}/ {C_{\bar {G}/\bar {N}_{i-1}}(\bar {N}_i/\bar {N}_{i-1})}$
is abelian, we get that $(\bar {Z}/\bar {N}_{i-1}){C_{\bar {G}/\bar {N}_{i-1}}(\bar {N}_i/\bar {N}_{i-1})}/ {C_{\bar {G}/\bar {N}_{i-1}}(\bar {N}_i/\bar {N}_{i-1})}$![]() is abelian. Hence, [Reference Dolfi, Pacifici, Sanus and Spiga7, the proof of lemma 2.3] yields the existence of a character $\lambda \in {\rm Irr}(\bar {N}_i/\bar {N}_{i-1})$
is abelian. Hence, [Reference Dolfi, Pacifici, Sanus and Spiga7, the proof of lemma 2.3] yields the existence of a character $\lambda \in {\rm Irr}(\bar {N}_i/\bar {N}_{i-1})$![]() such that
such that
If there exists an element $\bar {g}\bar {N}_{i-1} \in \bar {G}/\bar {N}_{i-1}$![]() such that $\bar {u}^{\bar {g}}\bar {N}_{i-1} \in I_{\bar {G}/\bar {N}_{i-1}}(\lambda )$
such that $\bar {u}^{\bar {g}}\bar {N}_{i-1} \in I_{\bar {G}/\bar {N}_{i-1}}(\lambda )$![]() , then $(\bar {u}^{2})^{\bar {g}}\bar {N}_{i-1} \in I_{\bar {Z}/\bar {N}_{i-1}}(\lambda ) .$
, then $(\bar {u}^{2})^{\bar {g}}\bar {N}_{i-1} \in I_{\bar {Z}/\bar {N}_{i-1}}(\lambda ) .$![]() Thus, since by (3.10), $I_{\bar {Z}/\bar {N}_{i-1}}(\lambda )=C_{\bar {Z}/\bar {N}_{i-1}}(\bar {N}_i/\bar {N}_{i-1}) \unlhd \bar {G}/\bar {N}_{i-1}$
Thus, since by (3.10), $I_{\bar {Z}/\bar {N}_{i-1}}(\lambda )=C_{\bar {Z}/\bar {N}_{i-1}}(\bar {N}_i/\bar {N}_{i-1}) \unlhd \bar {G}/\bar {N}_{i-1}$![]() , we get that $(\bar {u}^{2})\bar {N}_{i-1} \in C_{\bar {Z}/\bar {N}_{i-1}}(\bar {N}_i/\bar {N}_{i-1})$
, we get that $(\bar {u}^{2})\bar {N}_{i-1} \in C_{\bar {Z}/\bar {N}_{i-1}}(\bar {N}_i/\bar {N}_{i-1})$![]() , which is a contradiction with (3.9). This shows that no conjugate of $\bar {u}^{2}\bar {N}_{i-1}$
, which is a contradiction with (3.9). This shows that no conjugate of $\bar {u}^{2}\bar {N}_{i-1}$![]() and no conjugate of $\bar {u}\bar {N}_{i-1}$
and no conjugate of $\bar {u}\bar {N}_{i-1}$![]() fix $\lambda$
fix $\lambda$![]() . So, lemma 2.13(vi) implies that $\bar {u}\bar {N}_{i-1},\,\bar {u}^{2}\bar {N}_{i-1} \in {\rm Van}(\bar {G}/\bar {N}_{i-1})$
. So, lemma 2.13(vi) implies that $\bar {u}\bar {N}_{i-1},\,\bar {u}^{2}\bar {N}_{i-1} \in {\rm Van}(\bar {G}/\bar {N}_{i-1})$![]() and by lemma 2.13(ii),
and by lemma 2.13(ii),
Also, if ${Z}/{{\rm Fit}}(G)$![]() is not an elementary abelian $2$
is not an elementary abelian $2$![]() -group, then there exists an element ${u} \in {Z} - {{\rm Fit}}(G)$
-group, then there exists an element ${u} \in {Z} - {{\rm Fit}}(G)$![]() such that $o({u}{\rm Fit}(G))=4$
such that $o({u}{\rm Fit}(G))=4$![]() . So, (3.6) shows that
. So, (3.6) shows that
Next, suppose that $G/M \cong {\rm Alt}_5$![]() , $Z=M$
, $Z=M$![]() and a Sylow $2$
and a Sylow $2$![]() -subgroup of ${G}/{{\rm Fit}}(G)$
-subgroup of ${G}/{{\rm Fit}}(G)$![]() is not abelian. Then, there exists a $2$
is not abelian. Then, there exists a $2$![]() -element ${u} \in {G} - {Z}=G-M$
-element ${u} \in {G} - {Z}=G-M$![]() such that $o({u}{{\rm Fit}}(G))=4$
such that $o({u}{{\rm Fit}}(G))=4$![]() and ${{\rm Fit}}(G) \neq {u}^{2}{{\rm Fit}}(G) \in {Z}/{{\rm Fit}}(G)$
and ${{\rm Fit}}(G) \neq {u}^{2}{{\rm Fit}}(G) \in {Z}/{{\rm Fit}}(G)$![]() . Since ${u}{M} \in {G}/{M} \cong {\rm Alt}_5$
. Since ${u}{M} \in {G}/{M} \cong {\rm Alt}_5$![]() , we have ${u}{M} \in {\rm Van}({G}/{M})$
, we have ${u}{M} \in {\rm Van}({G}/{M})$![]() . We conclude from lemma 2.13(ii) and (3.6) that
. We conclude from lemma 2.13(ii) and (3.6) that
Nevertheless, if $Z \neq M$![]() or $G/M \cong {\rm Alt}_5$
or $G/M \cong {\rm Alt}_5$![]() , $Z=M$
, $Z=M$![]() and a Sylow $2$
and a Sylow $2$![]() -subgroup of ${G}/{{\rm Fit}}(G)$
-subgroup of ${G}/{{\rm Fit}}(G)$![]() is not abelian, then $(*)$
is not abelian, then $(*)$![]() , (3.11), (3.12) and (3.13) yield that there is an element ${u} \in {\rm Van}(G)$
, (3.11), (3.12) and (3.13) yield that there is an element ${u} \in {\rm Van}(G)$![]() such that ${u}^{2} \in {\rm Van}(G)$
such that ${u}^{2} \in {\rm Van}(G)$![]() , $o({u}{\rm Fit}(G))=4$
, $o({u}{\rm Fit}(G))=4$![]() and $|cl_G(u)|=|cl_G(u^{2})|$
and $|cl_G(u)|=|cl_G(u^{2})|$![]() . Hence, proposition 2.10 shows that $4|{\rm Fit}(G)|_2 \mid |C_G(u)|$
. Hence, proposition 2.10 shows that $4|{\rm Fit}(G)|_2 \mid |C_G(u)|$![]() . Consequently, $4|{\rm Fit}(G)|_2 \mid |C_G(w)|$
. Consequently, $4|{\rm Fit}(G)|_2 \mid |C_G(w)|$![]() , for every $w \in {\rm Van}(G)$
, for every $w \in {\rm Van}(G)$![]() . If $x_5 \in G - {\rm Fit}(G)$
. If $x_5 \in G - {\rm Fit}(G)$![]() is a $5$
is a $5$![]() -element, then $M \neq x_5M$
-element, then $M \neq x_5M$![]() is a $5$
is a $5$![]() -element of $G/M$
-element of $G/M$![]() . However, $G/M \cong {\rm Alt}_5$
. However, $G/M \cong {\rm Alt}_5$![]() or ${\rm Alt}_7$
or ${\rm Alt}_7$![]() . Thus, $x_5M \in {\rm Van}(G/M)$
. Thus, $x_5M \in {\rm Van}(G/M)$![]() . By lemma 2.13(ii), $x_5M \subseteq {\rm Van}(G)$
. By lemma 2.13(ii), $x_5M \subseteq {\rm Van}(G)$![]() . Therefore, $4|{\rm Fit}(G)|_2 \mid |C_G(x_5)|$
. Therefore, $4|{\rm Fit}(G)|_2 \mid |C_G(x_5)|$![]() . As, $|C_{G/M}(x_5M)|_2=1$
. As, $|C_{G/M}(x_5M)|_2=1$![]() , $x_5M$
, $x_5M$![]() contains a $\{2,\,5\}$
contains a $\{2,\,5\}$![]() -element $y$
-element $y$![]() such that $o(y{\rm Fit}(G))=10$
such that $o(y{\rm Fit}(G))=10$![]() , $y_5 \in x_5M$
, $y_5 \in x_5M$![]() and $y_2 \in M - {\rm Fit}(G)$
and $y_2 \in M - {\rm Fit}(G)$![]() , where $y_2$
, where $y_2$![]() and $y_5$
and $y_5$![]() are the $2$
are the $2$![]() -part and the $5$
-part and the $5$![]() -part of $y$
-part of $y$![]() , respectively. As mentioned above, $y_5,\,y \in {\rm Van}(G)$
, respectively. As mentioned above, $y_5,\,y \in {\rm Van}(G)$![]() and $y_2 \in M - {\rm Fit}(G)$
and $y_2 \in M - {\rm Fit}(G)$![]() . Thus, $|C_G(y)|=|C_G(y_5)|$
. Thus, $|C_G(y)|=|C_G(y_5)|$![]() . By lemma 2.3(i),
. By lemma 2.3(i),
On the other hand, if $P_5 \in {\rm Syl}_5({\rm Fit}(G))$![]() , then since $5 \in \pi ({\rm Fit}(G))$
, then since $5 \in \pi ({\rm Fit}(G))$![]() , $P_5 \neq \{1\}$
, $P_5 \neq \{1\}$![]() and $\langle y\rangle = \langle y_2\rangle \times \langle y_5\rangle$
and $\langle y\rangle = \langle y_2\rangle \times \langle y_5\rangle$![]() acts on $P_5$
acts on $P_5$![]() , by conjugation. By (3.14), $C_{P_5}(y_5) \leq C_{P_5}(y_2)$
, by conjugation. By (3.14), $C_{P_5}(y_5) \leq C_{P_5}(y_2)$![]() . It follows from lemma 2.2 that $y_2 \in C_G(P_5).$
. It follows from lemma 2.2 that $y_2 \in C_G(P_5).$![]() Fix $A:=C_G(P_5)$
Fix $A:=C_G(P_5)$![]() . Then, $1\neq y_2 \in (A - {\rm Fit}(G)) \cap M$
. Then, $1\neq y_2 \in (A - {\rm Fit}(G)) \cap M$![]() . Hence, ${\rm Fit}(G) < (AP_5 \cap M) \trianglelefteq G$
. Hence, ${\rm Fit}(G) < (AP_5 \cap M) \trianglelefteq G$![]() . Thus, $\{{\rm Fit}(G)\} \neq (AP_5\cap M)/{\rm Fit}(G) \trianglelefteq G/{\rm Fit}(G)$
. Thus, $\{{\rm Fit}(G)\} \neq (AP_5\cap M)/{\rm Fit}(G) \trianglelefteq G/{\rm Fit}(G)$![]() . Let $B/{\rm Fit}(G)$
. Let $B/{\rm Fit}(G)$![]() be a minimal normal subgroup of $G/{\rm Fit}(G)$
be a minimal normal subgroup of $G/{\rm Fit}(G)$![]() such that $B \leq (AP_5\cap M)$
such that $B \leq (AP_5\cap M)$![]() . Then, $\bar {B}/\bar {{\rm Fit}}(G)$
. Then, $\bar {B}/\bar {{\rm Fit}}(G)$![]() is abelian. By (3.5) and lemma 2.13(iv),
is abelian. By (3.5) and lemma 2.13(iv),
Obviously, there exists an element $g \in B \cap A$![]() such that $g \not \in {\rm Fit}(G)$
such that $g \not \in {\rm Fit}(G)$![]() . Since $\bar {g} \in \bar {B} - {\bar {\rm Fit}}(G)$
. Since $\bar {g} \in \bar {B} - {\bar {\rm Fit}}(G)$![]() , we get from (3.15) and lemma 2.13(ii) that $g \in {\rm Van}(G)$
, we get from (3.15) and lemma 2.13(ii) that $g \in {\rm Van}(G)$![]() . However, $g \in A=C_G(P_5)$
. However, $g \in A=C_G(P_5)$![]() and $[G:P_5]_5=5$
and $[G:P_5]_5=5$![]() . It follows that $|cl_G(g)|_5 \leq 5$
. It follows that $|cl_G(g)|_5 \leq 5$![]() . So, $|cl_G(w)|_5 \leq 5$
. So, $|cl_G(w)|_5 \leq 5$![]() , for every $w \in {\rm Van}(G)$
, for every $w \in {\rm Van}(G)$![]() . Let $x_2 \in G - M$
. Let $x_2 \in G - M$![]() be a $p$
be a $p$![]() -element, where if $G/M \cong {\rm Alt}_5$
-element, where if $G/M \cong {\rm Alt}_5$![]() , then $p=2$
, then $p=2$![]() and otherwise, $p=7$
and otherwise, $p=7$![]() . Then, $x_2 M \in {\rm Van}({G}/M)$
. Then, $x_2 M \in {\rm Van}({G}/M)$![]() . By lemma 2.13(ii), $x_2 \in {\rm Van}(G)$
. By lemma 2.13(ii), $x_2 \in {\rm Van}(G)$![]() . So, $|P_5| \mid |C_G(x_2)|$
. So, $|P_5| \mid |C_G(x_2)|$![]() . We have $|cl_{G/M}(x_2M)|_5=1$
. We have $|cl_{G/M}(x_2M)|_5=1$![]() and $M/{\rm Fit}(G)$
and $M/{\rm Fit}(G)$![]() is a $2$
is a $2$![]() -group. Thus, corollary 2.4 forces $P_5 \leq C_G(x_2)$
-group. Thus, corollary 2.4 forces $P_5 \leq C_G(x_2)$![]() . Therefore, $x_2 \in C_G(P_5)$
. Therefore, $x_2 \in C_G(P_5)$![]() . This yields that $M \neq x_2M \in C_G(P_5)M/M \trianglelefteq G/M \cong {\rm Alt}_5$
. This yields that $M \neq x_2M \in C_G(P_5)M/M \trianglelefteq G/M \cong {\rm Alt}_5$![]() or ${\rm Alt}_7$
or ${\rm Alt}_7$![]() . Since $G/M$
. Since $G/M$![]() is simple, $C_G(P_5)M/M =G/M$
is simple, $C_G(P_5)M/M =G/M$![]() . Consequently, $C_G(P_5)M=G$
. Consequently, $C_G(P_5)M=G$![]() . Thus, $C_G(P_5)$
. Thus, $C_G(P_5)$![]() contains a $5$
contains a $5$![]() -element $x_5$
-element $x_5$![]() such that $x_5 \not \in M$
such that $x_5 \not \in M$![]() . So, $M \neq x_5M \in G/M$
. So, $M \neq x_5M \in G/M$![]() . It follows that $x_5M \in {\rm Van}(G/M)$
. It follows that $x_5M \in {\rm Van}(G/M)$![]() . By lemma 2.13(ii), $x_5 \in {\rm Van}(G)$
. By lemma 2.13(ii), $x_5 \in {\rm Van}(G)$![]() . Also, $P_5 \langle x_5\rangle \leq C_G(x_5)$
. Also, $P_5 \langle x_5\rangle \leq C_G(x_5)$![]() . So, $5\nmid |cl_G(x_5)|$
. So, $5\nmid |cl_G(x_5)|$![]() . Hence, $(*)$
. Hence, $(*)$![]() forces $5$
forces $5$![]() not to divide the vanishing conjugacy class sizes of $G$
not to divide the vanishing conjugacy class sizes of $G$![]() . It follows from [Reference Dolfi, Pacifici and Sanus6, theorem A] that $G$
. It follows from [Reference Dolfi, Pacifici and Sanus6, theorem A] that $G$![]() has a normal $5$
has a normal $5$![]() -complement, which is impossible.
-complement, which is impossible.
This shows that $M={\rm Fit}(G)$![]() , as wanted.
, as wanted.
Step 7. We get the final contradiction.
Proof. By step 6, $G/{\rm Fit}(G) \cong {\rm Alt}_5$![]() or ${\rm Alt}_7$
or ${\rm Alt}_7$![]() . First, let $G/{\rm Fit}(G) \cong {\rm Alt}_5$
. First, let $G/{\rm Fit}(G) \cong {\rm Alt}_5$![]() . Then, for every $x \in G - {\rm Fit}(G)$
. Then, for every $x \in G - {\rm Fit}(G)$![]() , ${\rm Fit}(G) \neq x{\rm Fit}(G) \in G/{\rm Fit}(G) \cong {\rm Alt}_5$
, ${\rm Fit}(G) \neq x{\rm Fit}(G) \in G/{\rm Fit}(G) \cong {\rm Alt}_5$![]() . So, $x{\rm Fit}(G) \in {\rm Van}(G/{\rm Fit}(G))$
. So, $x{\rm Fit}(G) \in {\rm Van}(G/{\rm Fit}(G))$![]() . By lemma 2.13(ii), $x \in {\rm Van}(G)$
. By lemma 2.13(ii), $x \in {\rm Van}(G)$![]() . By step 5, $3,\,5 \in \pi ({\rm Fit}(G))$
. By step 5, $3,\,5 \in \pi ({\rm Fit}(G))$![]() . Let $E$
. Let $E$![]() be a Hall $3'$
be a Hall $3'$![]() -subgroup of ${\rm Fit}(G)$
-subgroup of ${\rm Fit}(G)$![]() . Set $\tilde {G}=G/E$
. Set $\tilde {G}=G/E$![]() and, for every $H \leq G$
and, for every $H \leq G$![]() and $x \in G$
and $x \in G$![]() , let $\tilde {{H}}=HE/E$
, let $\tilde {{H}}=HE/E$![]() and $\tilde {{x}}$
and $\tilde {{x}}$![]() be the image of $x$
be the image of $x$![]() in $\tilde {{G}}$
in $\tilde {{G}}$![]() . Then, $\tilde {{\rm Fit}}(G)$
. Then, $\tilde {{\rm Fit}}(G)$![]() is a $3$
is a $3$![]() -group and lemma 2.5 shows that for every $\tilde {1} \neq \tilde {x} \in \tilde {G} - \tilde {{\rm Fit}}(G)$
-group and lemma 2.5 shows that for every $\tilde {1} \neq \tilde {x} \in \tilde {G} - \tilde {{\rm Fit}}(G)$![]() , $|cl_{\tilde {G}}(\tilde {x})|_3=3^{e}$
, $|cl_{\tilde {G}}(\tilde {x})|_3=3^{e}$![]() , for some positive integer $e$
, for some positive integer $e$![]() . Let $\tilde {x}_5 \in \tilde {G}- \tilde {{\rm Fit}}(G)$
. Let $\tilde {x}_5 \in \tilde {G}- \tilde {{\rm Fit}}(G)$![]() be of order $5$
be of order $5$![]() and let $\{\tilde {1}\}=\tilde {M}_0 \leq \tilde {M}_1 \leq \cdots \leq \tilde {M}_t=\tilde {{\rm Fit}}(G) \leq \tilde {G}$
and let $\{\tilde {1}\}=\tilde {M}_0 \leq \tilde {M}_1 \leq \cdots \leq \tilde {M}_t=\tilde {{\rm Fit}}(G) \leq \tilde {G}$![]() be a chief series of $\tilde {G}$
be a chief series of $\tilde {G}$![]() . By proposition 2.8, there is an $1 \leq i \leq t$
. By proposition 2.8, there is an $1 \leq i \leq t$![]() such that $\tilde {M}_i/\tilde {M}_{i-1} \not \leq Z(\tilde {G}/\tilde {M}_{i-1})$
such that $\tilde {M}_i/\tilde {M}_{i-1} \not \leq Z(\tilde {G}/\tilde {M}_{i-1})$![]() and $|C_{\tilde {M}_i /\tilde {M}_{i-1}}(\tilde {x}_5\tilde {M}_{i-1})| \geq |C_{\tilde {M}_i /\tilde {M}_{i-1}}(\tilde {x}\tilde {M}_{i-1})|$
and $|C_{\tilde {M}_i /\tilde {M}_{i-1}}(\tilde {x}_5\tilde {M}_{i-1})| \geq |C_{\tilde {M}_i /\tilde {M}_{i-1}}(\tilde {x}\tilde {M}_{i-1})|$![]() , for some $2$
, for some $2$![]() -element $\tilde {M}_{i-1} \neq \tilde {x}\tilde {M}_{i-1} \in N_{\tilde {G}/\tilde {M}_{i-1}}(\langle \tilde {x}_5\tilde {M}_{i-1}\rangle )$
-element $\tilde {M}_{i-1} \neq \tilde {x}\tilde {M}_{i-1} \in N_{\tilde {G}/\tilde {M}_{i-1}}(\langle \tilde {x}_5\tilde {M}_{i-1}\rangle )$![]() . Hence, proposition 2.17 implies the existence of a non-trivial element $\tilde {n}\tilde {M}_{i-1} \in C_{\tilde {M}_i /\tilde {M}_{i-1}}(\tilde {x}_5\tilde {M}_{i-1})$
. Hence, proposition 2.17 implies the existence of a non-trivial element $\tilde {n}\tilde {M}_{i-1} \in C_{\tilde {M}_i /\tilde {M}_{i-1}}(\tilde {x}_5\tilde {M}_{i-1})$![]() and a character $\psi \in {\rm Irr}(\tilde {G}/\tilde {M}_{i-1})$
and a character $\psi \in {\rm Irr}(\tilde {G}/\tilde {M}_{i-1})$![]() such that $\psi (\tilde {n}\tilde {M}_{i-1})=0$
such that $\psi (\tilde {n}\tilde {M}_{i-1})=0$![]() . So, $\tilde {n}\tilde {M}_{i-1} \in {\rm Van}(\tilde {G}/\tilde {M}_{i-1})$
. So, $\tilde {n}\tilde {M}_{i-1} \in {\rm Van}(\tilde {G}/\tilde {M}_{i-1})$![]() . By lemma 2.13(ii), $n \in nM_{i-1} \subseteq {\rm Van}(G)$
. By lemma 2.13(ii), $n \in nM_{i-1} \subseteq {\rm Van}(G)$![]() . Since $3 \nmid |E|$
. Since $3 \nmid |E|$![]() and $\tilde {M}_i$
and $\tilde {M}_i$![]() is a $3$
is a $3$![]() -group, we can assume that $n$
-group, we can assume that $n$![]() is a $3$
is a $3$![]() -element. Thus, $E \leq C_G(n)$
-element. Thus, $E \leq C_G(n)$![]() , because $n \in {\rm Fit}(G)$
, because $n \in {\rm Fit}(G)$![]() , $E \leq {\rm Fit}(G)$
, $E \leq {\rm Fit}(G)$![]() is a $3'$
is a $3'$![]() -group and ${\rm Fit}(G)$
-group and ${\rm Fit}(G)$![]() is nilpotent. We note that $|G/E|_5=|G/{\rm Fit}(G)|_5 =|{\rm Alt}_5|_5=5$
is nilpotent. We note that $|G/E|_5=|G/{\rm Fit}(G)|_5 =|{\rm Alt}_5|_5=5$![]() . Therefore, $|cl_G(n)|_5 \leq |G/E|_5=5$
. Therefore, $|cl_G(n)|_5 \leq |G/E|_5=5$![]() . Hence,
. Hence,
Let $x_3 \in G- {\rm Fit}(G)$![]() be a $3$
be a $3$![]() -element. Then, $|C_{G/{\rm Fit}(G)}(x_3{\rm Fit}(G))|_5=1$
-element. Then, $|C_{G/{\rm Fit}(G)}(x_3{\rm Fit}(G))|_5=1$![]() . By (3.16) and corollary 2.4, $|C_{{\rm Fit}(G)}(x_3)|_5=|{\rm Fit}(G)|_5$
. By (3.16) and corollary 2.4, $|C_{{\rm Fit}(G)}(x_3)|_5=|{\rm Fit}(G)|_5$![]() . So, $P_5 \leq C_{{\rm Fit}(G)}(x_3)$
. So, $P_5 \leq C_{{\rm Fit}(G)}(x_3)$![]() , where $P_5 \in {\rm Syl}_5({\rm Fit}(G))$
, where $P_5 \in {\rm Syl}_5({\rm Fit}(G))$![]() . Thus, $x_3 \in P_5C_G(P_5) -{\rm Fit}(G)$
. Thus, $x_3 \in P_5C_G(P_5) -{\rm Fit}(G)$![]() . This yields that $\{{\rm Fit}(G)\} \neq P_5C_G(P_5)/{\rm Fit}(G)\trianglelefteq G/ {\rm Fit}(G)$
. This yields that $\{{\rm Fit}(G)\} \neq P_5C_G(P_5)/{\rm Fit}(G)\trianglelefteq G/ {\rm Fit}(G)$![]() . However, $G/{\rm Fit}(G) \cong {\rm Alt}_5$
. However, $G/{\rm Fit}(G) \cong {\rm Alt}_5$![]() is simple. Therefore, $P_5C_G(P_5)/{\rm Fit}(G)=G/{\rm Fit}(G)$
is simple. Therefore, $P_5C_G(P_5)/{\rm Fit}(G)=G/{\rm Fit}(G)$![]() . Hence, $P_5C_G(P_5)=G$
. Hence, $P_5C_G(P_5)=G$![]() . This guarantees the existence of a $5$
. This guarantees the existence of a $5$![]() -element $y_5 \in C_G(P_5) - {\rm Fit}(G)$
-element $y_5 \in C_G(P_5) - {\rm Fit}(G)$![]() . Then, $y_5 \in {\rm Van}(G)$
. Then, $y_5 \in {\rm Van}(G)$![]() . Also, $P_5\langle y_5\rangle \leq C_G(y_5)$
. Also, $P_5\langle y_5\rangle \leq C_G(y_5)$![]() . This signifies that $5|P_5| \mid |C_G(y_5)|$
. This signifies that $5|P_5| \mid |C_G(y_5)|$![]() . Taking into account the fact that $[G:P_5]_5=5$
. Taking into account the fact that $[G:P_5]_5=5$![]() , we get that $|G|_5 \mid |C_G(y_5)|$
, we get that $|G|_5 \mid |C_G(y_5)|$![]() . Therefore, $5 \nmid |cl_G(y_5)|$
. Therefore, $5 \nmid |cl_G(y_5)|$![]() . So, $(*)$
. So, $(*)$![]() forces $5$
forces $5$![]() not to divide any vanishing conjugacy class size of $G$
not to divide any vanishing conjugacy class size of $G$![]() . It follows from [Reference Dolfi, Pacifici and Sanus6, theorem A] that $G$
. It follows from [Reference Dolfi, Pacifici and Sanus6, theorem A] that $G$![]() has a normal $5$
has a normal $5$![]() -complement, which is impossible.
-complement, which is impossible.
Next, let $G/{\rm Fit}(G) \cong {\rm Alt}_7$![]() . By step 5, $3,\,5,\,7 \in \pi ({\rm Fit}(G))$
. By step 5, $3,\,5,\,7 \in \pi ({\rm Fit}(G))$![]() . Let $F$
. Let $F$![]() be a Hall $7'$
be a Hall $7'$![]() -subgroup of ${\rm Fit}(G)$
-subgroup of ${\rm Fit}(G)$![]() . Set $\bar {G}=G/F$
. Set $\bar {G}=G/F$![]() and, for every $H \leq G$
and, for every $H \leq G$![]() and $x \in G$
and $x \in G$![]() , let $\bar {H}=HF/F$
, let $\bar {H}=HF/F$![]() and $\bar {x}$
and $\bar {x}$![]() be the image of $x$
be the image of $x$![]() in $\bar {G}$
in $\bar {G}$![]() . Then, ${\bar {\rm Fit}}(G) \unlhd \bar {G}$
. Then, ${\bar {\rm Fit}}(G) \unlhd \bar {G}$![]() is a $7$
is a $7$![]() -group and $\bar {G}/{\bar {\rm Fit}}(G) \cong G/{\rm Fit}(G) \cong {\rm Alt}_7$
-group and $\bar {G}/{\bar {\rm Fit}}(G) \cong G/{\rm Fit}(G) \cong {\rm Alt}_7$![]() . Suppose that $\{\bar {1}\}=\bar {N}_0 \leq \cdots \leq \bar {N}_t ={\bar {\rm Fit}}(G) \leq \bar {G}$
. Suppose that $\{\bar {1}\}=\bar {N}_0 \leq \cdots \leq \bar {N}_t ={\bar {\rm Fit}}(G) \leq \bar {G}$![]() is a chief series of $\bar {G}$
is a chief series of $\bar {G}$![]() . Assume that for every $i \in \{1,\,\ldots,\,t\}$
. Assume that for every $i \in \{1,\,\ldots,\,t\}$![]() , $\bar {N}_i /\bar {N}_{i-1} \leq Z(\bar {G}/\bar {N}_{i-1})$
, $\bar {N}_i /\bar {N}_{i-1} \leq Z(\bar {G}/\bar {N}_{i-1})$![]() . By lemma 2.6, $\bar {G} =\bar {L} \times {\bar {\rm Fit}}(G)$
. By lemma 2.6, $\bar {G} =\bar {L} \times {\bar {\rm Fit}}(G)$![]() , where $\bar {L} \cong {\rm Alt}_7$
, where $\bar {L} \cong {\rm Alt}_7$![]() . Let $x \in L - F$
. Let $x \in L - F$![]() be a $7$
be a $7$![]() -element. Then, ${\bar {\rm Fit}}(G)\langle \bar {x}\rangle \leq C_{\bar {G}}(\bar {x})$
-element. Then, ${\bar {\rm Fit}}(G)\langle \bar {x}\rangle \leq C_{\bar {G}}(\bar {x})$![]() . However, $[G:{\rm Fit}(G)]_7=7$
. However, $[G:{\rm Fit}(G)]_7=7$![]() . Thus, $|\bar {G}|_7 \mid |C_{\bar {G}}(\bar {x})|$
. Thus, $|\bar {G}|_7 \mid |C_{\bar {G}}(\bar {x})|$![]() . Since ${\rm gcd}(|F|,\,7)=1$
. Since ${\rm gcd}(|F|,\,7)=1$![]() and $x$
and $x$![]() is a $7$
is a $7$![]() -element, we get from lemma 2.3(v) that $C_{\bar {G}}(\bar {x})=C_G(x)F/F\cong C_G(x)/C_F(x)$
-element, we get from lemma 2.3(v) that $C_{\bar {G}}(\bar {x})=C_G(x)F/F\cong C_G(x)/C_F(x)$![]() . Thus, $|G|_7=|\bar {G}|_7 \mid |C_G(x)|$
. Thus, $|G|_7=|\bar {G}|_7 \mid |C_G(x)|$![]() . Therefore, $7 \nmid |cl_{{G}}({x})|$
. Therefore, $7 \nmid |cl_{{G}}({x})|$![]() . However, $\bar {1} \neq \bar {x} \in \bar {L}$
. However, $\bar {1} \neq \bar {x} \in \bar {L}$![]() is a $7$
is a $7$![]() -element and $\bar {L} \cong {\rm Alt}_7$
-element and $\bar {L} \cong {\rm Alt}_7$![]() . Hence, $\bar {x} \in {\rm Van}(\bar {G})$
. Hence, $\bar {x} \in {\rm Van}(\bar {G})$![]() . By lemma 2.13(ii), $x \in {\rm Van}(G)$
. By lemma 2.13(ii), $x \in {\rm Van}(G)$![]() . So, $7$
. So, $7$![]() does not divide the vanishing conjugacy class sizes of $G$
does not divide the vanishing conjugacy class sizes of $G$![]() . Hence, [Reference Dolfi, Pacifici and Sanus6, theorem A] implies that $G$
. Hence, [Reference Dolfi, Pacifici and Sanus6, theorem A] implies that $G$![]() has a normal $7$
has a normal $7$![]() -complement, which is impossible. This guarantees the existence of an element $i \in \{1,\,\ldots,\,t\}$
-complement, which is impossible. This guarantees the existence of an element $i \in \{1,\,\ldots,\,t\}$![]() such that $\bar {N}_i/\bar {N}_{i-1} \not \leq Z(\bar {G}/\bar {N}_{i-1})$
such that $\bar {N}_i/\bar {N}_{i-1} \not \leq Z(\bar {G}/\bar {N}_{i-1})$![]() . Let $y \in G$
. Let $y \in G$![]() be a $\{2,\,3\}$
be a $\{2,\,3\}$![]() -element such that $\bar {y}{\bar {\rm Fit}}(G) \in \bar {G}/{\bar {\rm Fit}}(G)$
-element such that $\bar {y}{\bar {\rm Fit}}(G) \in \bar {G}/{\bar {\rm Fit}}(G)$![]() is of order $6$
is of order $6$![]() . Let $y_2$
. Let $y_2$![]() and $y_3$
and $y_3$![]() be the $2$
be the $2$![]() -part and the $3$
-part and the $3$![]() -part of $y$
-part of $y$![]() , respectively. Then, $y_2 \not \in {\rm Fit}(G)$
, respectively. Then, $y_2 \not \in {\rm Fit}(G)$![]() and $o(\bar {y}_3{\bar {\rm Fit}}(G))=3$
and $o(\bar {y}_3{\bar {\rm Fit}}(G))=3$![]() . It follows from proposition 2.16 that $\bar {y}\bar {N}_{i-1},\,\bar {y}_3\bar {N}_{i-1} \in {\rm Van}(\bar {G}/\bar {N}_{i-1})$
. It follows from proposition 2.16 that $\bar {y}\bar {N}_{i-1},\,\bar {y}_3\bar {N}_{i-1} \in {\rm Van}(\bar {G}/\bar {N}_{i-1})$![]() . By lemma 2.13(ii), $y,\,y_3 \in {\rm Van}(G)$
. By lemma 2.13(ii), $y,\,y_3 \in {\rm Van}(G)$![]() . Thus, $|C_G(y)|=|C_G(y_3)|$
. Thus, $|C_G(y)|=|C_G(y_3)|$![]() , by $(*)$
, by $(*)$![]() . By lemma 2.3(i),
. By lemma 2.3(i),
Also, $3 \mid |{\rm Fit}(G)|$![]() . So, $\langle y\rangle =\langle y_3\rangle \times \langle y_2\rangle$
. So, $\langle y\rangle =\langle y_3\rangle \times \langle y_2\rangle$![]() acts on $P_3$
acts on $P_3$![]() , where $\{1\} \neq P_3\in {\rm Syl}_3({\rm Fit}(G)).$
, where $\{1\} \neq P_3\in {\rm Syl}_3({\rm Fit}(G)).$![]() By (3.17), $C_{P_3}(y_3) \leq C_{P_3}(y_2)$
By (3.17), $C_{P_3}(y_3) \leq C_{P_3}(y_2)$![]() . It follows from lemma 2.2 that $y_2 \in C_G(P_3).$
. It follows from lemma 2.2 that $y_2 \in C_G(P_3).$![]() Then, $y_2 \in C_G(P_3) - {\rm Fit}(G)$
Then, $y_2 \in C_G(P_3) - {\rm Fit}(G)$![]() . This yields that ${\rm Fit}(G) \neq y_2{\rm Fit}(G) \in C_G(P_3)P_3/{\rm Fit}(G) \unlhd G/ {\rm Fit}(G) \cong {\rm Alt}_7$
. This yields that ${\rm Fit}(G) \neq y_2{\rm Fit}(G) \in C_G(P_3)P_3/{\rm Fit}(G) \unlhd G/ {\rm Fit}(G) \cong {\rm Alt}_7$![]() . Since $G/{\rm Fit}(G)$
. Since $G/{\rm Fit}(G)$![]() is simple, $C_G(P_3)P_3/{\rm Fit}(G) =G/{\rm Fit}(G)$
is simple, $C_G(P_3)P_3/{\rm Fit}(G) =G/{\rm Fit}(G)$![]() . Consequently, $G=C_G(P_3)P_3$
. Consequently, $G=C_G(P_3)P_3$![]() . Thus, $C_G(P_3)$
. Thus, $C_G(P_3)$![]() contains a $3$
contains a $3$![]() -element $x_3$
-element $x_3$![]() such that $x_3 \not \in {\rm Fit}(G)$
such that $x_3 \not \in {\rm Fit}(G)$![]() . By proposition 2.16, $\bar {x}_3\bar {N}_{i-1} \in {\rm Van}(\bar {G}/\bar {N}_{i-1} )$
. By proposition 2.16, $\bar {x}_3\bar {N}_{i-1} \in {\rm Van}(\bar {G}/\bar {N}_{i-1} )$![]() . It follows from lemma 2.13(ii) that $x_3 \in {\rm Van}(G)$
. It follows from lemma 2.13(ii) that $x_3 \in {\rm Van}(G)$![]() . Also, $P_3 \langle x_3\rangle \leq C_G(x_3)$
. Also, $P_3 \langle x_3\rangle \leq C_G(x_3)$![]() . So, $|cl_G(x_3)|_3 \leq 3$
. So, $|cl_G(x_3)|_3 \leq 3$![]() . Hence, $(*)$
. Hence, $(*)$![]() forces $3^{2}$
forces $3^{2}$![]() not to divide the vanishing conjugacy class sizes of $G$
not to divide the vanishing conjugacy class sizes of $G$![]() . Let $x_5 \in G - {\rm Fit}(G)$
. Let $x_5 \in G - {\rm Fit}(G)$![]() be a $5$
be a $5$![]() -element. Since $G/{\rm Fit}(G) \cong {\rm Alt}_7$
-element. Since $G/{\rm Fit}(G) \cong {\rm Alt}_7$![]() , $x_5 {\rm Fit}(G) \in {\rm Van}(G/{\rm Fit}(G))$
, $x_5 {\rm Fit}(G) \in {\rm Van}(G/{\rm Fit}(G))$![]() . By lemma 2.13(ii), $x_5 \in {\rm Van}(G)$
. By lemma 2.13(ii), $x_5 \in {\rm Van}(G)$![]() . Thus, $3^{2} \nmid |cl_G(x_5)|$
. Thus, $3^{2} \nmid |cl_G(x_5)|$![]() . However, $[G:{\rm Fit}(G)]_3=3^{2}$
. However, $[G:{\rm Fit}(G)]_3=3^{2}$![]() . So, corollary 2.4 forces $3 \mid |C_{G/{\rm Fit}(G)}(x_5{\rm Fit}(G))|$
. So, corollary 2.4 forces $3 \mid |C_{G/{\rm Fit}(G)}(x_5{\rm Fit}(G))|$![]() , which is impossible, because $G/{\rm Fit}(G) \cong {\rm Alt}_7$
, which is impossible, because $G/{\rm Fit}(G) \cong {\rm Alt}_7$![]() .
.
The above steps show that $G$![]() is solvable. Now, the proof of theorem A is complete.
is solvable. Now, the proof of theorem A is complete.
Acknowledgements
The author expresses her gratitude to Professor Silvio Dolfi for the helpful discussions. Also, the author thanks the referee for careful reading and several useful comments.