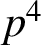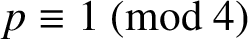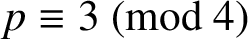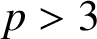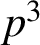1 Introduction
In his first letter to Hardy in 1913, Ramanujan mentioned the following formula (see [Reference Berndt and Rankin1, page 25, (2)]):
 $$ \begin{align} \sum_{k=0}^\infty(8k+1)\frac{(\frac{1}{4})_k^4}{k!^4} =\frac{2\sqrt{2}}{\sqrt{\pi}\,\Gamma(\frac 34)^2}. \end{align} $$
$$ \begin{align} \sum_{k=0}^\infty(8k+1)\frac{(\frac{1}{4})_k^4}{k!^4} =\frac{2\sqrt{2}}{\sqrt{\pi}\,\Gamma(\frac 34)^2}. \end{align} $$
Here
![]() $(a)_n=a(a+1)\cdots (a+n-1)$
is the rising factorial and
$(a)_n=a(a+1)\cdots (a+n-1)$
is the rising factorial and
![]() $\Gamma (x) $
is the Gamma function. Ramanujan did not give a proof of (1.1) and the first proof was given by Hardy [Reference Hardy7]. In 1997, Van Hamme [Reference Van Hamme12] conjectured 13 p-adic analogues of Ramanujan’s series, including
$\Gamma (x) $
is the Gamma function. Ramanujan did not give a proof of (1.1) and the first proof was given by Hardy [Reference Hardy7]. In 1997, Van Hamme [Reference Van Hamme12] conjectured 13 p-adic analogues of Ramanujan’s series, including
 $$ \begin{align} &\sum_{k=0}^{(p-1)/4}(8k+1)\frac{(\frac{1}{4})_k^4}{k!^4} \equiv p\frac{\Gamma_p(\frac 12)\Gamma_p(\frac 14)}{\Gamma_p(\frac 34)} \pmod{p^3} \quad\text{for}\ p\equiv 1 \pmod 4 \end{align} $$
$$ \begin{align} &\sum_{k=0}^{(p-1)/4}(8k+1)\frac{(\frac{1}{4})_k^4}{k!^4} \equiv p\frac{\Gamma_p(\frac 12)\Gamma_p(\frac 14)}{\Gamma_p(\frac 34)} \pmod{p^3} \quad\text{for}\ p\equiv 1 \pmod 4 \end{align} $$
(marked (G.2) in Van Hamme’s list). Here and throughout the paper, p always denotes an odd prime and
![]() $\Gamma _p(x)$
stands for Morita’s p-adic Gamma function [Reference Morita10]. Swisher [Reference Swisher11] and He [Reference He8] independently showed that (1.2) holds modulo the stronger power
$\Gamma _p(x)$
stands for Morita’s p-adic Gamma function [Reference Morita10]. Swisher [Reference Swisher11] and He [Reference He8] independently showed that (1.2) holds modulo the stronger power
![]() $p^4$
.
$p^4$
.
We shall give a generalisation of (1.2): for
![]() $p\equiv 1 \pmod 4$
and
$p\equiv 1 \pmod 4$
and
![]() $0\leqslant s\leqslant (p-1)/4$
,
$0\leqslant s\leqslant (p-1)/4$
,
 $$ \begin{align} \sum_{k=s}^{(p-1)/4} (8k+1)\frac{(\frac{1}{4})_{k-s}(\frac{1}{4})_{k+s}(\frac{1}{4})_k^2} {(k-s)!(k+s)!k!^2} \equiv (p+4s)\frac{(\frac{1}{4})_s^2(\frac{1}{4})_{(p-1)/4+s} (\frac{1}{2})_{(p-1)/4-s}} {s!^2(1)_{(p-1)/4+s}(\frac{1}{4})_{(p-1)/4-s}} \pmod{p^3}. \end{align} $$
$$ \begin{align} \sum_{k=s}^{(p-1)/4} (8k+1)\frac{(\frac{1}{4})_{k-s}(\frac{1}{4})_{k+s}(\frac{1}{4})_k^2} {(k-s)!(k+s)!k!^2} \equiv (p+4s)\frac{(\frac{1}{4})_s^2(\frac{1}{4})_{(p-1)/4+s} (\frac{1}{2})_{(p-1)/4-s}} {s!^2(1)_{(p-1)/4+s}(\frac{1}{4})_{(p-1)/4-s}} \pmod{p^3}. \end{align} $$
When
![]() $s=0$
, the right-hand side of (1.3) reduces to
$s=0$
, the right-hand side of (1.3) reduces to
 $p(\tfrac 12)_{(p-1)/4}/(1)_{(p-1)/4}$
, which is congruent to the right-hand side of (1.2) modulo
$p(\tfrac 12)_{(p-1)/4}/(1)_{(p-1)/4}$
, which is congruent to the right-hand side of (1.2) modulo
![]() $p^3$
(see [Reference Liu and Wang9]). Thus, the supercongruence (1.3) is indeed a generalisation of (1.2). A similar extension of the (A.2) supercongruence of Van Hamme was recently given by Guo [Reference Guo3].
$p^3$
(see [Reference Liu and Wang9]). Thus, the supercongruence (1.3) is indeed a generalisation of (1.2). A similar extension of the (A.2) supercongruence of Van Hamme was recently given by Guo [Reference Guo3].
We shall prove (1.3) by establishing the following q-supercongruence.
Theorem 1.1. Let
![]() $n\equiv 1\pmod 4$
be an integer greater than
$n\equiv 1\pmod 4$
be an integer greater than
![]() $1$
and let
$1$
and let
![]() $0\leqslant s\leqslant(n-1)/4$
. Then
$0\leqslant s\leqslant(n-1)/4$
. Then
 $$ \begin{align} &\sum_{k=s}^{(n-1)/4} [8k+1]\frac{(q;q^4)_{k-s}(q;q^4)_{k+s}(q;q^4)_k^2} {(q^4;q^4)_{k-s}(q^4;q^4)_{k+s}(q^4;q^4)_k^2} q^{2k} \notag\\[6pt] &\quad\equiv [n+4s] \frac{(q;q^4)_s^2(q;q^4)_{(n-1)/4+s} (q^2;q^4)_{(n-1)/4-s}} {(q^4;q^4)_s^2(q^4;q^4)_{(n-1)/4+s}(q;q^4)_{(n-1)/4-s}} q^{3s+(1-n)/4} \pmod{\Phi_n(q)^3}. \end{align} $$
$$ \begin{align} &\sum_{k=s}^{(n-1)/4} [8k+1]\frac{(q;q^4)_{k-s}(q;q^4)_{k+s}(q;q^4)_k^2} {(q^4;q^4)_{k-s}(q^4;q^4)_{k+s}(q^4;q^4)_k^2} q^{2k} \notag\\[6pt] &\quad\equiv [n+4s] \frac{(q;q^4)_s^2(q;q^4)_{(n-1)/4+s} (q^2;q^4)_{(n-1)/4-s}} {(q^4;q^4)_s^2(q^4;q^4)_{(n-1)/4+s}(q;q^4)_{(n-1)/4-s}} q^{3s+(1-n)/4} \pmod{\Phi_n(q)^3}. \end{align} $$
Here we need to be familiar with the standard q-notation. The q-shifted factorial is defined by
![]() $(a;q)_0=1$
and
$(a;q)_0=1$
and
![]() $(a;q)_n=(1-a)(1-aq)\cdots (1-aq^{n-1})$
for any positive integer n. The q-integer is defined as
$(a;q)_n=(1-a)(1-aq)\cdots (1-aq^{n-1})$
for any positive integer n. The q-integer is defined as
![]() $[n]=(1-q^n)/(1-q)$
and
$[n]=(1-q^n)/(1-q)$
and
![]() $\Phi _n(q)$
denotes the nth cyclotomic polynomial, which can be written as
$\Phi _n(q)$
denotes the nth cyclotomic polynomial, which can be written as
 $$ \begin{align*} \Phi_n(q)=\prod_{\substack{1\leqslant k\leqslant n\\ \gcd(k,n)=1}}(q-\zeta^k), \end{align*} $$
$$ \begin{align*} \Phi_n(q)=\prod_{\substack{1\leqslant k\leqslant n\\ \gcd(k,n)=1}}(q-\zeta^k), \end{align*} $$
where
![]() $\zeta $
is a primitive nth root of unity.
$\zeta $
is a primitive nth root of unity.
It is easy to see that (1.3) follows from (1.4) by taking
![]() $n=p$
and
$n=p$
and
![]() $q\to 1$
. The
$q\to 1$
. The
![]() $s=0$
case of (1.4) was given by Liu and Wang [Reference Liu and Wang9] and can also be deduced from [Reference Guo and Schlosser5, Theorem 4.3].
$s=0$
case of (1.4) was given by Liu and Wang [Reference Liu and Wang9] and can also be deduced from [Reference Guo and Schlosser5, Theorem 4.3].
Swisher [Reference Swisher11, (3)] gave the following extension of Van Hamme’s (G.2) supercongruence: for
![]() $p\equiv 3 \pmod 4$
and
$p\equiv 3 \pmod 4$
and
![]() $p>3$
,
$p>3$
,
 $$ \begin{align} &\sum_{k=0}^{(3p-1)/4}(8k+1)\frac{(\frac{1}{4})_k^4}{k!^4} \equiv -\frac{3p^2\Gamma_p(\frac 12)\Gamma_p(\frac 14)}{2\Gamma_p(\frac 34)} \pmod{p^4}. \end{align} $$
$$ \begin{align} &\sum_{k=0}^{(3p-1)/4}(8k+1)\frac{(\frac{1}{4})_k^4}{k!^4} \equiv -\frac{3p^2\Gamma_p(\frac 12)\Gamma_p(\frac 14)}{2\Gamma_p(\frac 34)} \pmod{p^4}. \end{align} $$
(The negative sign was missing in Swisher’s original supercongruence.)
We shall give a new generalisation of (1.5) modulo
![]() $p^3$
as follows: for
$p^3$
as follows: for
![]() $p\equiv 3\pmod {4}$
and
$p\equiv 3\pmod {4}$
and
![]() $0\leqslant s\leqslant (p-3)/4$
,
$0\leqslant s\leqslant (p-3)/4$
,
 $$ \begin{align} \sum_{k=s}^{(3p-1)/4} (8k+1)\frac{(\frac{1}{4})_{k-s}(\frac{1}{4})_{k+s}(\frac{1}{4})_k^2} {(k-s)!(k+s)!k!^2} \equiv (3p+4s)\frac{(\frac{1}{4})_s^2(\frac{1}{4})_{(3p-1)/4+s} (\frac{1}{2})_{(3p-1)/4-s}} {s!^2(1)_{(3p-1)/4+s}(\frac{1}{4})_{(3p-1)/4-s}} \pmod{p^3}. \end{align} $$
$$ \begin{align} \sum_{k=s}^{(3p-1)/4} (8k+1)\frac{(\frac{1}{4})_{k-s}(\frac{1}{4})_{k+s}(\frac{1}{4})_k^2} {(k-s)!(k+s)!k!^2} \equiv (3p+4s)\frac{(\frac{1}{4})_s^2(\frac{1}{4})_{(3p-1)/4+s} (\frac{1}{2})_{(3p-1)/4-s}} {s!^2(1)_{(3p-1)/4+s}(\frac{1}{4})_{(3p-1)/4-s}} \pmod{p^3}. \end{align} $$
When
![]() $s=0$
, the right-hand side of (1.6) reduces to
$s=0$
, the right-hand side of (1.6) reduces to
 $3p(\tfrac 12)_{(3p-1)/4}/(1)_{(3p-1)/4}$
, which is easily seen to be congruent to the right-hand side of (1.5) modulo
$3p(\tfrac 12)_{(3p-1)/4}/(1)_{(3p-1)/4}$
, which is easily seen to be congruent to the right-hand side of (1.5) modulo
![]() $p^3$
. Thus, the supercongruence (1.6) can be deemed a generalisation of the modulo
$p^3$
. Thus, the supercongruence (1.6) can be deemed a generalisation of the modulo
![]() $p^3$
case of (1.5). A result of Guo and Schlosser [Reference Guo and Schlosser5, Corollary 1.2 with
$p^3$
case of (1.5). A result of Guo and Schlosser [Reference Guo and Schlosser5, Corollary 1.2 with
![]() $d = 4$
and
$d = 4$
and
![]() $q\to 1$
] implies that (1.6) is even true modulo
$q\to 1$
] implies that (1.6) is even true modulo
![]() $p^4$
for
$p^4$
for
![]() $s=0$
. However, numerical evaluation indicates that (1.6) is not true modulo
$s=0$
. However, numerical evaluation indicates that (1.6) is not true modulo
![]() $p^4$
for general s.
$p^4$
for general s.
In the same way as before, we shall prove (1.6) via the following q-supercongruence.
Theorem 1.2. Let
![]() $n\equiv 3\pmod 4$
be a positive integer and let
$n\equiv 3\pmod 4$
be a positive integer and let
![]() $0\leqslant s\leqslant (n-3)/4$
. Then
$0\leqslant s\leqslant (n-3)/4$
. Then
 $$ \begin{align} &\sum_{k=s}^{(3n-1)/4} [8k+1]\frac{(q;q^4)_{k-s}(q;q^4)_{k+s}(q;q^4)_k^2} {(q^4;q^4)_{k-s}(q^4;q^4)_{k+s}(q^4;q^4)_k^2} q^{2k} \notag\\[6pt] &\quad\equiv [3n+4s] \frac{(q;q^4)_s^2(q;q^4)_{(3n-1)/4+s} (q^2;q^4)_{(3n-1)/4-s}} {(q^4;q^4)_s^2(q^4;q^4)_{(3n-1)/4+s}(q;q^4)_{(3n-1)/4-s}} q^{3s+(1-3n)/4} \pmod{\Phi_n(q)^3}. \end{align} $$
$$ \begin{align} &\sum_{k=s}^{(3n-1)/4} [8k+1]\frac{(q;q^4)_{k-s}(q;q^4)_{k+s}(q;q^4)_k^2} {(q^4;q^4)_{k-s}(q^4;q^4)_{k+s}(q^4;q^4)_k^2} q^{2k} \notag\\[6pt] &\quad\equiv [3n+4s] \frac{(q;q^4)_s^2(q;q^4)_{(3n-1)/4+s} (q^2;q^4)_{(3n-1)/4-s}} {(q^4;q^4)_s^2(q^4;q^4)_{(3n-1)/4+s}(q;q^4)_{(3n-1)/4-s}} q^{3s+(1-3n)/4} \pmod{\Phi_n(q)^3}. \end{align} $$
Our proof of Theorems 1.1 and 1.2 will use the powerful method of ‘creative microscoping’, which was devised by Guo and Zudilin [Reference Guo and Zudilin6].
2 Proof of Theorem 1.1
We require the following easily proved q-congruence, which was first given by Guo and Schlosser [Reference Guo and Schlosser4, Lemma 3].
Lemma 2.1. Let d, m and n be positive integers with
![]() $m\leqslant n-1$
and
$m\leqslant n-1$
and
![]() $dm\equiv -1\pmod {n}$
. Then, for
$dm\equiv -1\pmod {n}$
. Then, for
![]() $0\leqslant k\leqslant m$
,
$0\leqslant k\leqslant m$
,
 $$ \begin{align*} \frac{(aq;q^d)_{m-k}}{(q^d/a;q^d)_{m-k}} \equiv (-a)^{m-2k}\frac{(aq;q^d)_k}{(q^d/a;q^d)_k} q^{m(dm-d+2)/2+(d-1)k} \pmod{\Phi_n(q)}. \end{align*} $$
$$ \begin{align*} \frac{(aq;q^d)_{m-k}}{(q^d/a;q^d)_{m-k}} \equiv (-a)^{m-2k}\frac{(aq;q^d)_k}{(q^d/a;q^d)_k} q^{m(dm-d+2)/2+(d-1)k} \pmod{\Phi_n(q)}. \end{align*} $$
Following Gasper and Rahman’s monograph [Reference Gasper and Rahman2], the basic hypergeometric series
![]() $_{r+1}\phi _r$
is defined as
$_{r+1}\phi _r$
is defined as
 $$ \begin{align*}_{r+1}\phi_{r}\bigg[\begin{array}{@{}c@{}} a_1,a_2,\ldots,a_{r+1}\\[6pt] b_1,b_2,\ldots,b_{r} \end{array};q,\, z \bigg] =\sum_{k=0}^{\infty}\frac{(a_1;q)_k(a_2;q)_k\cdots(a_{r+1};q)_k } {(q;q)_k(b_1;q)_k\cdots(b_{r};q)_k}z^k. \end{align*} $$
$$ \begin{align*}_{r+1}\phi_{r}\bigg[\begin{array}{@{}c@{}} a_1,a_2,\ldots,a_{r+1}\\[6pt] b_1,b_2,\ldots,b_{r} \end{array};q,\, z \bigg] =\sum_{k=0}^{\infty}\frac{(a_1;q)_k(a_2;q)_k\cdots(a_{r+1};q)_k } {(q;q)_k(b_1;q)_k\cdots(b_{r};q)_k}z^k. \end{align*} $$
Jackson’s
![]() ${}_6\phi _5$
summation (see [Reference Gasper and Rahman2, Appendix (II.21)]) can be stated as follows:
${}_6\phi _5$
summation (see [Reference Gasper and Rahman2, Appendix (II.21)]) can be stated as follows:
 $$ \begin{align} _6\phi_5 \bigg[\begin{array}{@{}c@{}} a,\, qa^{1/2},\, -qa^{1/2},\, b,\, c,\, q^{-n} \\[6pt] a^{1/2},\, -a^{1/2},\, aq/b,\, aq/c,\, aq^{n+1}\end{array};q,\,\frac{aq^{n+1}}{bc} \bigg] =\frac{(aq;q)_n (aq/bc;q)_n}{(aq/b;q)_n(aq/c;q)_n}. \end{align} $$
$$ \begin{align} _6\phi_5 \bigg[\begin{array}{@{}c@{}} a,\, qa^{1/2},\, -qa^{1/2},\, b,\, c,\, q^{-n} \\[6pt] a^{1/2},\, -a^{1/2},\, aq/b,\, aq/c,\, aq^{n+1}\end{array};q,\,\frac{aq^{n+1}}{bc} \bigg] =\frac{(aq;q)_n (aq/bc;q)_n}{(aq/b;q)_n(aq/c;q)_n}. \end{align} $$
To prove Theorem 1.1, we first establish the following result.
Theorem 2.2. Let
![]() $n\equiv 1\pmod 4$
be an integer greater than
$n\equiv 1\pmod 4$
be an integer greater than
![]() $1$
. Let
$1$
. Let
![]() $0\leqslant s\leqslant (n-1)/4$
and let a be an indeterminate. Then, modulo
$0\leqslant s\leqslant (n-1)/4$
and let a be an indeterminate. Then, modulo
![]() $\Phi _n(q)(1-aq^n)(a-q^n)$
,
$\Phi _n(q)(1-aq^n)(a-q^n)$
,
 $$ \begin{align} &\sum_{k=s}^{(n-1)/4} [8k+1]\frac{(aq;q^4)_k(q/a;q^4)_k (q;q^4)_{k-s}(q;q^4)_{k+s} } {(aq^4;q^4)_k(q^4/a;q^4)_k(q^4;q^4)_{k-s}(q^4;q^4)_{k+s}}q^{2k} \notag\\[6pt] &\quad\equiv [n+4s] \frac{(aq;q^4)_{s}(q/a;q^4)_{s}(q;q^4)_{(n-1)/4+s} (q^2;q^4)_{(n-1)/4-s}} {(aq^4;q^4)_{s}(q^4/a;q^4)_{s}(q^4;q^4)_{(n-1)/4+s}(q;q^4)_{(n-1)/4-s}} q^{3s+(1-n)/4}. \end{align} $$
$$ \begin{align} &\sum_{k=s}^{(n-1)/4} [8k+1]\frac{(aq;q^4)_k(q/a;q^4)_k (q;q^4)_{k-s}(q;q^4)_{k+s} } {(aq^4;q^4)_k(q^4/a;q^4)_k(q^4;q^4)_{k-s}(q^4;q^4)_{k+s}}q^{2k} \notag\\[6pt] &\quad\equiv [n+4s] \frac{(aq;q^4)_{s}(q/a;q^4)_{s}(q;q^4)_{(n-1)/4+s} (q^2;q^4)_{(n-1)/4-s}} {(aq^4;q^4)_{s}(q^4/a;q^4)_{s}(q^4;q^4)_{(n-1)/4+s}(q;q^4)_{(n-1)/4-s}} q^{3s+(1-n)/4}. \end{align} $$
Proof. For
![]() $a=q^{-n}$
or
$a=q^{-n}$
or
![]() $a=q^{n}$
, the left-hand side of (2.2) is equal to
$a=q^{n}$
, the left-hand side of (2.2) is equal to
 $$ \begin{align} &\sum_{k=s}^{(n-1)/4} [8k+1]\frac{(q^{1-n};q^4)_k(q^{1+n};q^4)_k (q;q^4)_{k-s}(q;q^4)_{k+s} } {(q^{4-n};q^4)_k(q^{4+n};q^4)_k(q^4;q^4)_{k-s}(q^4;q^4)_{k+s}}q^{2k} \notag\\[6pt] &\quad=\sum_{k=0}^{(n-1)/4-s} [8k+8s+1]\frac{(q^{1-n};q^4)_{k+s}(q^{1+n};q^4)_{k+s} (q;q^4)_{k}(q;q^4)_{k+2s} } {(q^{4-n};q^4)_{k+s}(q^{4+n};q^4)_{k+s}(q^4;q^4)_{k}(q^4;q^4)_{k+2s}}q^{2k+2s} \notag\\[6pt] &\quad=[8s+1] \frac{(q^{1-n};q^4)_{s}(q^{1+n};q^4)_{s} (q;q^4)_{2s} } {(q^{4-n};q^4)_{s}(q^{4+n};q^4)_{s}(q^4;q^4)_{2s}} q^{2s}\notag\\[6pt] &\quad\quad\times {}_{6}\phi_{5}\!\left[\begin{array}{@{}cccccccc@{}} q^{1+8s},&\!\! q^{\frac{9}{2}+4s},&\!\! -q^{\frac{9}{2}+4s}, &\!\! q, &\!\! q^{1+n+4s}, &\!\! q^{1-n+4s} \\[8pt] &\!\! q^{\frac{1}{2}+4s}, &\!\! -q^{\frac{1}{2}+4s}, &\!\! q^{4+8s}, &\!\! q^{4-n+4s}, &\!\! q^{4+n+4s} \end{array}\!\!;q^4, q^2 \right]. \end{align} $$
$$ \begin{align} &\sum_{k=s}^{(n-1)/4} [8k+1]\frac{(q^{1-n};q^4)_k(q^{1+n};q^4)_k (q;q^4)_{k-s}(q;q^4)_{k+s} } {(q^{4-n};q^4)_k(q^{4+n};q^4)_k(q^4;q^4)_{k-s}(q^4;q^4)_{k+s}}q^{2k} \notag\\[6pt] &\quad=\sum_{k=0}^{(n-1)/4-s} [8k+8s+1]\frac{(q^{1-n};q^4)_{k+s}(q^{1+n};q^4)_{k+s} (q;q^4)_{k}(q;q^4)_{k+2s} } {(q^{4-n};q^4)_{k+s}(q^{4+n};q^4)_{k+s}(q^4;q^4)_{k}(q^4;q^4)_{k+2s}}q^{2k+2s} \notag\\[6pt] &\quad=[8s+1] \frac{(q^{1-n};q^4)_{s}(q^{1+n};q^4)_{s} (q;q^4)_{2s} } {(q^{4-n};q^4)_{s}(q^{4+n};q^4)_{s}(q^4;q^4)_{2s}} q^{2s}\notag\\[6pt] &\quad\quad\times {}_{6}\phi_{5}\!\left[\begin{array}{@{}cccccccc@{}} q^{1+8s},&\!\! q^{\frac{9}{2}+4s},&\!\! -q^{\frac{9}{2}+4s}, &\!\! q, &\!\! q^{1+n+4s}, &\!\! q^{1-n+4s} \\[8pt] &\!\! q^{\frac{1}{2}+4s}, &\!\! -q^{\frac{1}{2}+4s}, &\!\! q^{4+8s}, &\!\! q^{4-n+4s}, &\!\! q^{4+n+4s} \end{array}\!\!;q^4, q^2 \right]. \end{align} $$
Letting
![]() $q\mapsto q^4$
,
$q\mapsto q^4$
,
![]() $a=q^{1+8s}$
,
$a=q^{1+8s}$
,
![]() $b=q$
,
$b=q$
,
![]() $c= q^{1+n+4s}$
and
$c= q^{1+n+4s}$
and
![]() $n\mapsto (n-1)/4-s$
in (2.1), one sees that the right-hand side of (2.3) can be simplified as
$n\mapsto (n-1)/4-s$
in (2.1), one sees that the right-hand side of (2.3) can be simplified as
 $$ \begin{align*} &q^{2s}[8s+1] \frac{(q^{1-n};q^4)_{s}(q^{1+n};q^4)_{s} (q;q^4)_{2s} } {(q^{4-n};q^4)_{s}(q^{4+n};q^4)_{s}(q^4;q^4)_{2s}} \frac{(q^{5+8s};q^4)_{(n-1)/4-s} (q^{3-n+4s};q^4)_{(n-1)/4-s}}{(q^{4+8s};q^4)_{(n-1)/4-s}(q^{4-n+4s};q^4)_{(n-1)/4-s}} \\[6pt] &\quad=[n+4s]\frac{(q^{1-n};q^4)_{s}(q^{1+n};q^4)_{s} } {(q^{4-n};q^4)_{s}(q^{4+n};q^4)_{s}} \frac{(q;q^4)_{(n-1)/4+s} (q^{3-n+4s};q^4)_{(n-1)/4-s}}{(q^4;q^4)_{(n-1)/4+s}(q^{4-n+4s};q^4)_{(n-1)/4-s}} q^{2s}\\[6pt] &\quad=[n+4s]\frac{(q^{1-n};q^4)_{s}(q^{1+n};q^4)_{s} } {(q^{4-n};q^4)_{s}(q^{4+n};q^4)_{s}} \frac{(q;q^4)_{(n-1)/4+s} (q^2;q^4)_{(n-1)/4-s}}{(q^4;q^4)_{(n-1)/4+s}(q;q^4)_{(n-1)/4-s}} q^{3s+(1-n)/4}. \end{align*} $$
$$ \begin{align*} &q^{2s}[8s+1] \frac{(q^{1-n};q^4)_{s}(q^{1+n};q^4)_{s} (q;q^4)_{2s} } {(q^{4-n};q^4)_{s}(q^{4+n};q^4)_{s}(q^4;q^4)_{2s}} \frac{(q^{5+8s};q^4)_{(n-1)/4-s} (q^{3-n+4s};q^4)_{(n-1)/4-s}}{(q^{4+8s};q^4)_{(n-1)/4-s}(q^{4-n+4s};q^4)_{(n-1)/4-s}} \\[6pt] &\quad=[n+4s]\frac{(q^{1-n};q^4)_{s}(q^{1+n};q^4)_{s} } {(q^{4-n};q^4)_{s}(q^{4+n};q^4)_{s}} \frac{(q;q^4)_{(n-1)/4+s} (q^{3-n+4s};q^4)_{(n-1)/4-s}}{(q^4;q^4)_{(n-1)/4+s}(q^{4-n+4s};q^4)_{(n-1)/4-s}} q^{2s}\\[6pt] &\quad=[n+4s]\frac{(q^{1-n};q^4)_{s}(q^{1+n};q^4)_{s} } {(q^{4-n};q^4)_{s}(q^{4+n};q^4)_{s}} \frac{(q;q^4)_{(n-1)/4+s} (q^2;q^4)_{(n-1)/4-s}}{(q^4;q^4)_{(n-1)/4+s}(q;q^4)_{(n-1)/4-s}} q^{3s+(1-n)/4}. \end{align*} $$
Thus, we have proved that (2.2) is true modulo
![]() $1-aq^n$
and
$1-aq^n$
and
![]() $a-q^n$
.
$a-q^n$
.
Since
![]() $n\equiv 1\pmod {4}$
, letting
$n\equiv 1\pmod {4}$
, letting
![]() $d=4$
and
$d=4$
and
![]() $m=(n-1)/4$
in Lemma 2.1, we obtain
$m=(n-1)/4$
in Lemma 2.1, we obtain
 $$ \begin{align} \frac{(aq;q^4)_{m-k}}{(q^4/a;q^d)_{m-k}} \equiv (-a)^{m-2k}\frac{(aq;q^4)_k}{(q^4/a;q^d)_k} q^{m(2m-1)+3k} \pmod{\Phi_n(q)} \end{align} $$
$$ \begin{align} \frac{(aq;q^4)_{m-k}}{(q^4/a;q^d)_{m-k}} \equiv (-a)^{m-2k}\frac{(aq;q^4)_k}{(q^4/a;q^d)_k} q^{m(2m-1)+3k} \pmod{\Phi_n(q)} \end{align} $$
for
![]() $0\leqslant k\leqslant m$
. Using this q-congruence, we can easily verify the following congruence, for
$0\leqslant k\leqslant m$
. Using this q-congruence, we can easily verify the following congruence, for
![]() $m=(n-1)/4$
and
$m=(n-1)/4$
and
![]() $s\leqslant k\leqslant m-s$
,
$s\leqslant k\leqslant m-s$
,
 $$ \begin{align} &[8(m-k)+1]\frac{(aq;q^4)_{m-k}(q/a;q^4)_{m-k} (q;q^4)_{m-k-s}(q;q^4)_{m-k+s} } {(aq^4;q^4)_{m-k}(q^4/a;q^4)_{m-k}(q^4;q^4)_{m-k-s}(q^4;q^4)_{m-k+s}} q^{2m-2k} \notag\\[6pt] &\quad\equiv -[8k+1]\frac{(aq;q^4)_k(q/a;q^4)_k (q;q^4)_{k-s}(q;q^4)_{k+s} } {(aq^4;q^4)_k(q^4/a;q^4)_k(q^4;q^4)_{k-s}(q^4;q^4)_{k+s} } q^{2k} \pmod{\Phi_n(q)}. \end{align} $$
$$ \begin{align} &[8(m-k)+1]\frac{(aq;q^4)_{m-k}(q/a;q^4)_{m-k} (q;q^4)_{m-k-s}(q;q^4)_{m-k+s} } {(aq^4;q^4)_{m-k}(q^4/a;q^4)_{m-k}(q^4;q^4)_{m-k-s}(q^4;q^4)_{m-k+s}} q^{2m-2k} \notag\\[6pt] &\quad\equiv -[8k+1]\frac{(aq;q^4)_k(q/a;q^4)_k (q;q^4)_{k-s}(q;q^4)_{k+s} } {(aq^4;q^4)_k(q^4/a;q^4)_k(q^4;q^4)_{k-s}(q^4;q^4)_{k+s} } q^{2k} \pmod{\Phi_n(q)}. \end{align} $$
Moreover, for
![]() $(n-1)/4-s<k\leqslant (n-1)/4$
, the summand indexed k on the left-hand side of (2.2) is congruent to
$(n-1)/4-s<k\leqslant (n-1)/4$
, the summand indexed k on the left-hand side of (2.2) is congruent to
![]() $0$
modulo
$0$
modulo
![]() $\Phi _n(q)$
because
$\Phi _n(q)$
because
![]() $k+s>(n-1)/4$
and
$k+s>(n-1)/4$
and
![]() $(q;q^4)_{k+s}$
in the numerator incorporates the factor
$(q;q^4)_{k+s}$
in the numerator incorporates the factor
![]() $1-q^n$
. This means that the left-hand side of (2.2) is congruent to
$1-q^n$
. This means that the left-hand side of (2.2) is congruent to
![]() $0$
modulo
$0$
modulo
![]() $\Phi _n(q)$
. Since
$\Phi _n(q)$
. Since
 $$ \begin{align*}[n+4s](q;q^4)_{(n-1)/4+s}=[n](q;q^4)_{(n-1)/4}(q^{n+4};q^4)_s\equiv 0\pmod{\Phi_n(q)}\end{align*} $$
$$ \begin{align*}[n+4s](q;q^4)_{(n-1)/4+s}=[n](q;q^4)_{(n-1)/4}(q^{n+4};q^4)_s\equiv 0\pmod{\Phi_n(q)}\end{align*} $$
for
![]() $n>1$
, we conclude that (2.2) is also true modulo
$n>1$
, we conclude that (2.2) is also true modulo
![]() $\Phi _n(q)$
. Noting that the polynomials
$\Phi _n(q)$
. Noting that the polynomials
![]() $1-aq^n$
,
$1-aq^n$
,
![]() $a-q^n$
and
$a-q^n$
and
![]() $\Phi _n(q)$
are pairwise relatively prime, we complete the proof of the theorem.
$\Phi _n(q)$
are pairwise relatively prime, we complete the proof of the theorem.
3 Proof of Theorem 1.2
The proof is similar to that of Theorem 1.1. We first establish the following parametric generalisation of Theorem 1.2.
Theorem 3.1. Let
![]() $n\equiv 3\pmod 4$
be a positive integer. Let
$n\equiv 3\pmod 4$
be a positive integer. Let
![]() $0\leqslant s\leqslant (n-3)/4$
and let a be an indeterminate. Then, modulo
$0\leqslant s\leqslant (n-3)/4$
and let a be an indeterminate. Then, modulo
![]() $\Phi _n(q)(1-aq^{3n})(a-q^{3n})$
,
$\Phi _n(q)(1-aq^{3n})(a-q^{3n})$
,
 $$ \begin{align} &\sum_{k=s}^{(3n-1)/4} [8k+1]\frac{(aq;q^4)_k(q/a;q^4)_k (q;q^4)_{k-s}(q;q^4)_{k+s} } {(aq^4;q^4)_k(q^4/a;q^4)_k(q^4;q^4)_{k-s}(q^4;q^4)_{k+s}}q^{2k} \notag\\[6pt] &\quad\equiv [n+4s] \frac{(aq;q^4)_{s}(q/a;q^4)_{s}(q;q^4)_{(3n-1)/4+s} (q^2;q^4)_{(3n-1)/4-s}} {(aq^4;q^4)_{s}(q^4/a;q^4)_{s}(q^4;q^4)_{(3n-1)/4+s}(q;q^4)_{(3n-1)/4-s}} q^{3s+(1-3n)/4}. \end{align} $$
$$ \begin{align} &\sum_{k=s}^{(3n-1)/4} [8k+1]\frac{(aq;q^4)_k(q/a;q^4)_k (q;q^4)_{k-s}(q;q^4)_{k+s} } {(aq^4;q^4)_k(q^4/a;q^4)_k(q^4;q^4)_{k-s}(q^4;q^4)_{k+s}}q^{2k} \notag\\[6pt] &\quad\equiv [n+4s] \frac{(aq;q^4)_{s}(q/a;q^4)_{s}(q;q^4)_{(3n-1)/4+s} (q^2;q^4)_{(3n-1)/4-s}} {(aq^4;q^4)_{s}(q^4/a;q^4)_{s}(q^4;q^4)_{(3n-1)/4+s}(q;q^4)_{(3n-1)/4-s}} q^{3s+(1-3n)/4}. \end{align} $$
Proof. For
![]() $a=q^{-3n}$
or
$a=q^{-3n}$
or
![]() $a=q^{3n}$
, the left-hand side of (3.1) is equal to
$a=q^{3n}$
, the left-hand side of (3.1) is equal to
 $$ \begin{align} &\sum_{k=s}^{(3n-1)/4} [8k+1]\frac{(q^{1-3n};q^4)_k(q^{1+3n};q^4)_k (q;q^4)_{k-s}(q;q^4)_{k+s} } {(q^{4-3n};q^4)_k(q^{4+3n};q^4)_k(q^4;q^4)_{k-s}(q^4;q^4)_{k+s}}q^{2k} \notag\\[6pt] &\quad=[8s+1] \frac{(q^{1-3n};q^4)_{s}(q^{1+3n};q^4)_{s} (q;q^4)_{2s} } {(q^{4-3n};q^4)_{s}(q^{4+3n};q^4)_{s}(q^4;q^4)_{2s}} q^{2s}\notag\\[6pt] &\quad\quad\times {}_{6}\phi_{5}\!\left[\begin{array}{@{}cccccccc@{}} q^{1+8s},&\!\! q^{\frac{9}{2}+4s},&\!\! -q^{\frac{9}{2}+4s}, &\!\! q, &\!\! q^{1+3n+4s}, &\!\! q^{1-3n+4s} \\[6pt] &\!\! q^{\frac{1}{2}+4s}, &\!\! -q^{\frac{1}{2}+4s}, &\!\! q^{4+8s}, &\!\! q^{4-3n+4s}, &\!\! q^{4+3n+4s} \end{array}\!\!;q^4, q^2 \right]. \end{align} $$
$$ \begin{align} &\sum_{k=s}^{(3n-1)/4} [8k+1]\frac{(q^{1-3n};q^4)_k(q^{1+3n};q^4)_k (q;q^4)_{k-s}(q;q^4)_{k+s} } {(q^{4-3n};q^4)_k(q^{4+3n};q^4)_k(q^4;q^4)_{k-s}(q^4;q^4)_{k+s}}q^{2k} \notag\\[6pt] &\quad=[8s+1] \frac{(q^{1-3n};q^4)_{s}(q^{1+3n};q^4)_{s} (q;q^4)_{2s} } {(q^{4-3n};q^4)_{s}(q^{4+3n};q^4)_{s}(q^4;q^4)_{2s}} q^{2s}\notag\\[6pt] &\quad\quad\times {}_{6}\phi_{5}\!\left[\begin{array}{@{}cccccccc@{}} q^{1+8s},&\!\! q^{\frac{9}{2}+4s},&\!\! -q^{\frac{9}{2}+4s}, &\!\! q, &\!\! q^{1+3n+4s}, &\!\! q^{1-3n+4s} \\[6pt] &\!\! q^{\frac{1}{2}+4s}, &\!\! -q^{\frac{1}{2}+4s}, &\!\! q^{4+8s}, &\!\! q^{4-3n+4s}, &\!\! q^{4+3n+4s} \end{array}\!\!;q^4, q^2 \right]. \end{align} $$
Letting
![]() $q\mapsto q^4$
,
$q\mapsto q^4$
,
![]() $a=q^{1+8s}$
,
$a=q^{1+8s}$
,
![]() $b=q$
,
$b=q$
,
![]() $c= q^{1+3n+4s}$
and
$c= q^{1+3n+4s}$
and
![]() $n\mapsto (3n-1)/4-s$
in (2.1), one sees that the right-hand side of (3.2) may be written as
$n\mapsto (3n-1)/4-s$
in (2.1), one sees that the right-hand side of (3.2) may be written as
 $$ \begin{align*} &q^{2s}[8s+1] \frac{(q^{1-3n};q^4)_{s}(q^{1+3n};q^4)_{s} (q;q^4)_{2s} } {(q^{4-3n};q^4)_{s}(q^{4+3n};q^4)_{s}(q^4;q^4)_{2s}} \frac{(q^{5+8s};q^4)_{(3n-1)/4-s} (q^{3-3n+4s};q^4)_{(3n-1)/4-s}}{(q^{4+8s};q^4)_{(3n-1)/4-s}(q^{4-3n+4s};q^4)_{(3n-1)/4-s}} \\[6pt] &=[3n+4s]\frac{(q^{1-3n};q^4)_{s}(q^{1+3n};q^4)_{s} } {(q^{4-3n};q^4)_{s}(q^{4+3n};q^4)_{s}} \frac{(q;q^4)_{(3n-1)/4+s} (q^2;q^4)_{(3n-1)/4-s}}{(q^4;q^4)_{(3n-1)/4+s}(q;q^4)_{(3n-1)/4-s}} q^{3s+(1-3n)/4}. \end{align*} $$
$$ \begin{align*} &q^{2s}[8s+1] \frac{(q^{1-3n};q^4)_{s}(q^{1+3n};q^4)_{s} (q;q^4)_{2s} } {(q^{4-3n};q^4)_{s}(q^{4+3n};q^4)_{s}(q^4;q^4)_{2s}} \frac{(q^{5+8s};q^4)_{(3n-1)/4-s} (q^{3-3n+4s};q^4)_{(3n-1)/4-s}}{(q^{4+8s};q^4)_{(3n-1)/4-s}(q^{4-3n+4s};q^4)_{(3n-1)/4-s}} \\[6pt] &=[3n+4s]\frac{(q^{1-3n};q^4)_{s}(q^{1+3n};q^4)_{s} } {(q^{4-3n};q^4)_{s}(q^{4+3n};q^4)_{s}} \frac{(q;q^4)_{(3n-1)/4+s} (q^2;q^4)_{(3n-1)/4-s}}{(q^4;q^4)_{(3n-1)/4+s}(q;q^4)_{(3n-1)/4-s}} q^{3s+(1-3n)/4}. \end{align*} $$
This proves that (2.2) holds modulo
![]() $1-aq^{3n}$
and
$1-aq^{3n}$
and
![]() $a-q^{3n}$
.
$a-q^{3n}$
.
Since
![]() $n\equiv 3\pmod {4}$
, letting
$n\equiv 3\pmod {4}$
, letting
![]() $d=4$
and
$d=4$
and
![]() $m=(3n-1)/4$
in Lemma 2.1, we again obtain (2.4) for
$m=(3n-1)/4$
in Lemma 2.1, we again obtain (2.4) for
![]() $0\leqslant k\leqslant m$
. Applying this q-congruence, we can check (2.5) for
$0\leqslant k\leqslant m$
. Applying this q-congruence, we can check (2.5) for
![]() $m=(3n-1)/4$
and
$m=(3n-1)/4$
and
![]() $s\leqslant k\leqslant m-s$
. For
$s\leqslant k\leqslant m-s$
. For
![]() $(3n-1)/4-s<k\leqslant (3n-1)/4$
, the summand indexed k on the left-hand side of (3.1) is congruent to
$(3n-1)/4-s<k\leqslant (3n-1)/4$
, the summand indexed k on the left-hand side of (3.1) is congruent to
![]() $0$
modulo
$0$
modulo
![]() $\Phi _n(q)$
because
$\Phi _n(q)$
because
![]() $k+s>(3n-1)/4$
and
$k+s>(3n-1)/4$
and
![]() $(q;q^4)_{k+s}$
has the factor
$(q;q^4)_{k+s}$
has the factor
![]() $1-q^{3n}$
. This implies that the left-hand side of (3.1) is congruent to
$1-q^{3n}$
. This implies that the left-hand side of (3.1) is congruent to
![]() $0$
modulo
$0$
modulo
![]() $\Phi _n(q)$
. Since
$\Phi _n(q)$
. Since
 $$ \begin{align*}[3n+4s](q;q^4)_{(3n-1)/4+s}=[3n](q;q^4)_{(3n-1)/4}(q^{3n+4};q^4)_s\equiv 0\pmod{\Phi_n(q)},\end{align*} $$
$$ \begin{align*}[3n+4s](q;q^4)_{(3n-1)/4+s}=[3n](q;q^4)_{(3n-1)/4}(q^{3n+4};q^4)_s\equiv 0\pmod{\Phi_n(q)},\end{align*} $$
we conclude that (3.1) is also true modulo
![]() $\Phi _n(q)$
.
$\Phi _n(q)$
.
4 An open problem
We believe that the following conjecture is true.
The above conjecture is clearly true for
![]() $s=0$
(see [Reference Guo and Schlosser5, Reference Liu and Wang9]). Numerical computation indicates that both sides of (1.4) (or (1.7)) should be congruent to
$s=0$
(see [Reference Guo and Schlosser5, Reference Liu and Wang9]). Numerical computation indicates that both sides of (1.4) (or (1.7)) should be congruent to
![]() $0$
modulo
$0$
modulo
![]() $[n]$
. However, it seems difficult to confirm this. The technique of proving a q-congruence modulo
$[n]$
. However, it seems difficult to confirm this. The technique of proving a q-congruence modulo
![]() $[n]$
introduced in [Reference Guo and Zudilin6] does not work here, because of the additional parameter s.
$[n]$
introduced in [Reference Guo and Zudilin6] does not work here, because of the additional parameter s.