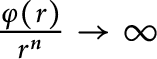1 Introduction and notation
For a domain
![]() $D \subset \mathbb C$
, we denote by
$D \subset \mathbb C$
, we denote by
![]() $H(D)$
and
$H(D)$
and
![]() $M(D)$
the spaces of holomorphic and meromorphic functions on D, respectively, and further set
$M(D)$
the spaces of holomorphic and meromorphic functions on D, respectively, and further set
![]() $M_{\infty }(D) := M(D) \cup \{f_{\infty }|_{D}\}$
, where
$M_{\infty }(D) := M(D) \cup \{f_{\infty }|_{D}\}$
, where
![]() $f_{\infty } \equiv \infty $
. Given two functions f and g defined on D, we say that g avoids f on D, if
$f_{\infty } \equiv \infty $
. Given two functions f and g defined on D, we say that g avoids f on D, if
![]() $g(z) \neq f(z)$
for every
$g(z) \neq f(z)$
for every
![]() $z \in D$
. A function f is called unavoidable with respect to
$z \in D$
. A function f is called unavoidable with respect to
![]() $A \subset M_{\infty }(D)$
, if there is no
$A \subset M_{\infty }(D)$
, if there is no
![]() $g \in A$
that avoids f on D. Furthermore, we say that a family F of functions is unavoidable with respect to
$g \in A$
that avoids f on D. Furthermore, we say that a family F of functions is unavoidable with respect to
![]() $A \subset M_{\infty }(D)$
, if there is no
$A \subset M_{\infty }(D)$
, if there is no
![]() $g \in A$
that avoids every function
$g \in A$
that avoids every function
![]() $f \in F$
on D, that is, if for every
$f \in F$
on D, that is, if for every
![]() $g \in A$
, there exists
$g \in A$
, there exists
![]() $f \in F$
such that the equation
$f \in F$
such that the equation
![]() $g(z) = f(z)$
has at least one solution in D (including the possibility that both functions take the value
$g(z) = f(z)$
has at least one solution in D (including the possibility that both functions take the value
![]() $\infty $
).
$\infty $
).
Unavoidable families seem to first have been investigated by Rubel and Yang [Reference Rubel and Yang12], who proved that for two functions
![]() $f_{1}$
and
$f_{1}$
and
![]() $f_{2} \in M(\mathbb C)$
, the family
$f_{2} \in M(\mathbb C)$
, the family
![]() $\{f_{1}, f_{2}\}$
is never unavoidable with respect to
$\{f_{1}, f_{2}\}$
is never unavoidable with respect to
![]() $M(\mathbb C)$
. On the other hand, they also showed that any family consisting of three polynomials
$M(\mathbb C)$
. On the other hand, they also showed that any family consisting of three polynomials
![]() $p_{1}, p_{2}$
, and
$p_{1}, p_{2}$
, and
![]() $p_{3}$
, such that
$p_{3}$
, such that
![]() $p_{1} - p_{2}$
and
$p_{1} - p_{2}$
and
![]() $p_{2} - p_{3}$
are not both constant, is unavoidable with respect to
$p_{2} - p_{3}$
are not both constant, is unavoidable with respect to
![]() $M(\mathbb C)$
. Thus, the minimum cardinality of a family
$M(\mathbb C)$
. Thus, the minimum cardinality of a family
![]() $F \subset M(\mathbb C)$
that is unavoidable with respect to
$F \subset M(\mathbb C)$
that is unavoidable with respect to
![]() $M(\mathbb C)$
is 3. Hayman and Rubel [Reference Hayman and Rubel5] considered similar questions for general domains
$M(\mathbb C)$
is 3. Hayman and Rubel [Reference Hayman and Rubel5] considered similar questions for general domains
![]() $D \subset \mathbb C$
and proved that a family
$D \subset \mathbb C$
and proved that a family
![]() $F \subset M(D)$
consisting of two functions cannot be unavoidable with respect to
$F \subset M(D)$
consisting of two functions cannot be unavoidable with respect to
![]() $M(D)$
. In the other direction, it is shown in [Reference Hayman and Rubel5] that there exists a function
$M(D)$
. In the other direction, it is shown in [Reference Hayman and Rubel5] that there exists a function
![]() $f \in H(D)$
, such that for every function
$f \in H(D)$
, such that for every function
![]() $g \in M(D)$
, at least one of the three equations
$g \in M(D)$
, at least one of the three equations
![]() $g(z) = f(z), g(z) = -f(z)$
, and
$g(z) = f(z), g(z) = -f(z)$
, and
![]() $g(z) = \infty $
has infinitely many solutions in D. In particular, it follows that the family
$g(z) = \infty $
has infinitely many solutions in D. In particular, it follows that the family
![]() $\{f, - f, f_{\infty }|_{D}\}$
is unavoidable with respect to
$\{f, - f, f_{\infty }|_{D}\}$
is unavoidable with respect to
![]() $M_{\infty }(D)$
. Note that a result from [Reference Lappan7] shows that if
$M_{\infty }(D)$
. Note that a result from [Reference Lappan7] shows that if
![]() $F \subset M_{\infty }(D)$
is a family of three functions that is unavoidable with respect to
$F \subset M_{\infty }(D)$
is a family of three functions that is unavoidable with respect to
![]() $M_{\infty }(D)$
, the three functions cannot avoid each other on D. The aforementioned result from [Reference Hayman and Rubel5] also implies that the family
$M_{\infty }(D)$
, the three functions cannot avoid each other on D. The aforementioned result from [Reference Hayman and Rubel5] also implies that the family
![]() $\{f, -f\}$
is unavoidable with respect to the set of meromorphic functions in D that have at most finitely many poles. In particular,
$\{f, -f\}$
is unavoidable with respect to the set of meromorphic functions in D that have at most finitely many poles. In particular,
![]() $\{f, -f\}$
is unavoidable with respect to
$\{f, -f\}$
is unavoidable with respect to
![]() $H(D)$
, and because for a function
$H(D)$
, and because for a function
![]() $g \in H(D)$
, the function
$g \in H(D)$
, the function
![]() $g + 1 \in H(D)$
avoids g on D, it follows that the minimum cardinality of a family
$g + 1 \in H(D)$
avoids g on D, it follows that the minimum cardinality of a family
![]() $F \subset H(D)$
that is unavoidable with respect to
$F \subset H(D)$
that is unavoidable with respect to
![]() $H(D)$
is 2. Again, according to [Reference Lappan7], the two functions cannot avoid each other on D in this case. We further mention some results from [Reference Logvinenko9], where unavoidable families of rational functions are investigated. For example, it is shown that the minimum cardinality of a family of rational functions, that no rational function can avoid on
$H(D)$
is 2. Again, according to [Reference Lappan7], the two functions cannot avoid each other on D in this case. We further mention some results from [Reference Logvinenko9], where unavoidable families of rational functions are investigated. For example, it is shown that the minimum cardinality of a family of rational functions, that no rational function can avoid on
![]() $\mathbb C$
, is 2. On the other hand, given two rational functions
$\mathbb C$
, is 2. On the other hand, given two rational functions
![]() $r_{1}$
and
$r_{1}$
and
![]() $r_{2}$
, and a bounded domain
$r_{2}$
, and a bounded domain
![]() $D \subset \mathbb C$
, there is a rational function that avoids both
$D \subset \mathbb C$
, there is a rational function that avoids both
![]() $r_{1}$
and
$r_{1}$
and
![]() $r_{2}$
on D. Finally, for any domain
$r_{2}$
on D. Finally, for any domain
![]() $D \subset \mathbb C$
, there exist two rational functions
$D \subset \mathbb C$
, there exist two rational functions
![]() $r_{1}$
and
$r_{1}$
and
![]() $r_{2}$
, such that
$r_{2}$
, such that
![]() $\{r_{1}|_{D},r_{2}|_{D}\}$
is unavoidable with respect to
$\{r_{1}|_{D},r_{2}|_{D}\}$
is unavoidable with respect to
![]() $H(D)$
; hence,
$H(D)$
; hence,
![]() $\{r_{1}|_{D},r_{2}|_{D}, f_{\infty }|_{D}\}$
is unavoidable with respect to
$\{r_{1}|_{D},r_{2}|_{D}, f_{\infty }|_{D}\}$
is unavoidable with respect to
![]() $M_{\infty }(D)$
.
$M_{\infty }(D)$
.
The abovementioned results show, in particular, that no single function
![]() $f \in M(D)$
is unavoidable with respect to
$f \in M(D)$
is unavoidable with respect to
![]() $M_{\infty }(D)$
. However, a result of Lappan [Reference Lappan8] shows that for every simply connected domain
$M_{\infty }(D)$
. However, a result of Lappan [Reference Lappan8] shows that for every simply connected domain
![]() $D \subset \mathbb C$
, there exists a continuous function on D that is unavoidable with respect to
$D \subset \mathbb C$
, there exists a continuous function on D that is unavoidable with respect to
![]() $M_{\infty }(D)$
. In a previous paper [Reference Lappan7], the same author constructed a function continuous on the unit disk
$M_{\infty }(D)$
. In a previous paper [Reference Lappan7], the same author constructed a function continuous on the unit disk
![]() $\mathbb D$
, which is unavoidable with respect to
$\mathbb D$
, which is unavoidable with respect to
![]() $H(\mathbb D)$
. In a similar vein, there may exist single functions
$H(\mathbb D)$
. In a similar vein, there may exist single functions
![]() $f \in M(D)$
that are unavoidable with respect to certain subsets of
$f \in M(D)$
that are unavoidable with respect to certain subsets of
![]() $M_{\infty }(D)$
. For example, in [Reference Lappan, Begehr, Gilbert and Wong6], it was proved that there exists a function
$M_{\infty }(D)$
. For example, in [Reference Lappan, Begehr, Gilbert and Wong6], it was proved that there exists a function
![]() $f \in M(\mathbb D)$
that is unavoidable with respect to the set of all normal functions in
$f \in M(\mathbb D)$
that is unavoidable with respect to the set of all normal functions in
![]() $M(\mathbb D)$
, and a corresponding result for
$M(\mathbb D)$
, and a corresponding result for
![]() $H(\mathbb D)$
is also given.
$H(\mathbb D)$
is also given.
In this note, we prove further results on unavoidable families of meromorphic functions. We give new examples of families of cardinality 3 that are unavoidable with respect to
![]() $M_{\infty }(\mathbb C)$
and further construct families containing less than three functions that are unavoidable with respect to certain subsets of
$M_{\infty }(\mathbb C)$
and further construct families containing less than three functions that are unavoidable with respect to certain subsets of
![]() $M_{\infty }(\mathbb C)$
.
$M_{\infty }(\mathbb C)$
.
2 Unavoidable functions and zero–one sets
Let
![]() $(a_{n})$
and
$(a_{n})$
and
![]() $(b_{n})$
be two (finite or infinite) disjoint sequences of complex numbers having no finite limit point. We say that
$(b_{n})$
be two (finite or infinite) disjoint sequences of complex numbers having no finite limit point. We say that
![]() $((a_{n}),(b_{n}))$
is a zero–one set, if there exists an entire function, whose zeros are exactly given by
$((a_{n}),(b_{n}))$
is a zero–one set, if there exists an entire function, whose zeros are exactly given by
![]() $(a_{n})$
and whose ones are exactly given by
$(a_{n})$
and whose ones are exactly given by
![]() $(b_{n})$
, where multiple occurrences of elements
$(b_{n})$
, where multiple occurrences of elements
![]() $a_{n}$
and
$a_{n}$
and
![]() $b_{n}$
correspond to zeros and ones of the corresponding multiplicity. This notation was introduced in [Reference Rubel and Yang12], where it was shown that given sequences
$b_{n}$
correspond to zeros and ones of the corresponding multiplicity. This notation was introduced in [Reference Rubel and Yang12], where it was shown that given sequences
![]() $(a_{n})$
and
$(a_{n})$
and
![]() $(b_{n})$
, the set
$(b_{n})$
, the set
![]() $((a_{n}),(b_{n}))$
is not, in general, a zero–one set. More precisely, [Reference Rubel and Yang12, Theorem 1] states that given any infinite sequence
$((a_{n}),(b_{n}))$
is not, in general, a zero–one set. More precisely, [Reference Rubel and Yang12, Theorem 1] states that given any infinite sequence
![]() $(a_{n})$
in
$(a_{n})$
in
![]() $\mathbb C$
without a finite limit point, there exists an infinite disjoint discrete sequence
$\mathbb C$
without a finite limit point, there exists an infinite disjoint discrete sequence
![]() $(b_{n})$
, such that
$(b_{n})$
, such that
![]() $((a_{n}),(b_{n}))$
is not a zero–one set. For further results related to zero–one sets, we refer the reader, for example, to [Reference Ozawa10, Reference Ozawa11, Reference Winkler14].
$((a_{n}),(b_{n}))$
is not a zero–one set. For further results related to zero–one sets, we refer the reader, for example, to [Reference Ozawa10, Reference Ozawa11, Reference Winkler14].
In the following, we show how the existence of sequences
![]() $(a_{n})$
and
$(a_{n})$
and
![]() $(b_{n})$
, such that
$(b_{n})$
, such that
![]() $((a_{n}),(b_{n}))$
is not a zero–one set, can be used to obtain unavoidable functions. Note that we always assume that
$((a_{n}),(b_{n}))$
is not a zero–one set, can be used to obtain unavoidable functions. Note that we always assume that
![]() $(a_{n})$
and
$(a_{n})$
and
![]() $(b_{n})$
are disjoint and have no finite limit point.
$(b_{n})$
are disjoint and have no finite limit point.
Proposition 1 Let be given sequences
![]() $(a_{n})$
and
$(a_{n})$
and
![]() $(b_{n})$
in
$(b_{n})$
in
![]() $\mathbb C$
such that
$\mathbb C$
such that
![]() $((a_{n}),(b_{n}))$
is not a zero–one set. Consider a function
$((a_{n}),(b_{n}))$
is not a zero–one set. Consider a function
![]() $f \in H(\mathbb C)$
whose zeros are exactly given by
$f \in H(\mathbb C)$
whose zeros are exactly given by
![]() $(a_{n})$
. Then, f is unavoidable with respect to the set of entire functions whose zeros are exactly given by
$(a_{n})$
. Then, f is unavoidable with respect to the set of entire functions whose zeros are exactly given by
![]() $(b_{n})$
.
$(b_{n})$
.
Proof Assuming that the statement is not correct, there exists a function
![]() $g \in H(\mathbb C)$
whose zeros are exactly given by
$g \in H(\mathbb C)$
whose zeros are exactly given by
![]() $(b_{n})$
such that
$(b_{n})$
such that
![]() $f(z) \neq g(z)$
for every
$f(z) \neq g(z)$
for every
![]() $z \in \mathbb C$
. Then,
$z \in \mathbb C$
. Then,
![]() $f(z) - g(z) \neq 0$
, for all
$f(z) - g(z) \neq 0$
, for all
![]() $z \in \mathbb C$
, and the function
$z \in \mathbb C$
, and the function
 $$ \begin{align*}F(z) := \frac{f(z)}{f(z) - g(z)}\end{align*} $$
$$ \begin{align*}F(z) := \frac{f(z)}{f(z) - g(z)}\end{align*} $$
is an entire function, whose zeros are exactly given by
![]() $(a_{n})$
and whose ones are exactly given by
$(a_{n})$
and whose ones are exactly given by
![]() $(b_{n})$
. This contradicts the assumption that
$(b_{n})$
. This contradicts the assumption that
![]() $((a_{n}),(b_{n}))$
is not a zero–one set.▪
$((a_{n}),(b_{n}))$
is not a zero–one set.▪
To give an example, we recall that a classic result states that for two distinct rays
![]() $L_{0}$
and
$L_{0}$
and
![]() $L_{1}$
emanating from the origin, there is no transcendental entire function for which all zeros lie on
$L_{1}$
emanating from the origin, there is no transcendental entire function for which all zeros lie on
![]() $L_{0}$
and all ones lie on
$L_{0}$
and all ones lie on
![]() $L_{1}$
, while any (nonconstant) polynomial having this property is of degree 1 (e.g., [Reference Bergweiler and Eremenko1, Reference Bergweiler, Eremenko and Hinkkanen2]). Hence, given two sequences
$L_{1}$
, while any (nonconstant) polynomial having this property is of degree 1 (e.g., [Reference Bergweiler and Eremenko1, Reference Bergweiler, Eremenko and Hinkkanen2]). Hence, given two sequences
![]() $(a_{n}) \subset L_{0}$
and
$(a_{n}) \subset L_{0}$
and
![]() $(b_{n}) \subset L_{1}$
having no finite limit point and such that
$(b_{n}) \subset L_{1}$
having no finite limit point and such that
![]() $(a_{n})$
has at least two elements, the set
$(a_{n})$
has at least two elements, the set
![]() $((a_{n}),(b_{n}))$
is not a zero–one set. Thus, if f is an entire function having at least two zeros and all whose zeros lie on a ray
$((a_{n}),(b_{n}))$
is not a zero–one set. Thus, if f is an entire function having at least two zeros and all whose zeros lie on a ray
![]() $L_{0}$
, we infer from Proposition 1 that f is unavoidable with respect to any entire function, all whose zeros are located on a ray that is different from
$L_{0}$
, we infer from Proposition 1 that f is unavoidable with respect to any entire function, all whose zeros are located on a ray that is different from
![]() $L_{0}$
.
$L_{0}$
.
Using a similar idea as in Proposition 1, we obtain the following result that gives examples of families
![]() $F \subset M(\mathbb C)$
of cardinality 3 that are unavoidable with respect to
$F \subset M(\mathbb C)$
of cardinality 3 that are unavoidable with respect to
![]() $M_{\infty }(\mathbb C)$
.
$M_{\infty }(\mathbb C)$
.
Theorem 1 Let be given sequences
![]() $(a_{n})$
and
$(a_{n})$
and
![]() $(b_{n})$
in
$(b_{n})$
in
![]() $\mathbb C$
such that
$\mathbb C$
such that
![]() $((a_{n}),(b_{n}))$
is not a zero–one set. Consider functions
$((a_{n}),(b_{n}))$
is not a zero–one set. Consider functions
![]() $f_{1}$
and
$f_{1}$
and
![]() $f_{2} \in H(\mathbb C)$
, whose zeros are exactly given by
$f_{2} \in H(\mathbb C)$
, whose zeros are exactly given by
![]() $(a_{n})$
and
$(a_{n})$
and
![]() $(b_{n})$
, respectively. Then, the family
$(b_{n})$
, respectively. Then, the family
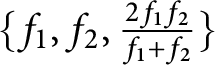 $\{f_{1}, f_{2}, \frac {2f_{1} f_{2}}{f_{1} + f_{2}}\}$
is unavoidable with respect to
$\{f_{1}, f_{2}, \frac {2f_{1} f_{2}}{f_{1} + f_{2}}\}$
is unavoidable with respect to
![]() $M_{\infty }(\mathbb C)$
.
$M_{\infty }(\mathbb C)$
.
Proof Let be given functions
![]() $f_{1}$
and
$f_{1}$
and
![]() $f_{2} \in H(\mathbb C)$
, such that the zeros of
$f_{2} \in H(\mathbb C)$
, such that the zeros of
![]() $f_{1}$
are exactly given by
$f_{1}$
are exactly given by
![]() $(a_{n})$
and the zeros of
$(a_{n})$
and the zeros of
![]() $f_{2}$
are exactly given by
$f_{2}$
are exactly given by
![]() $(b_{n})$
. Let further
$(b_{n})$
. Let further
![]() $g \in M(\mathbb C)$
, and suppose that g avoids both
$g \in M(\mathbb C)$
, and suppose that g avoids both
![]() $f_{1}$
and
$f_{1}$
and
![]() $f_{2}$
in
$f_{2}$
in
![]() $\mathbb C$
. Then,
$\mathbb C$
. Then,
![]() $g(z) - f_{1}(z) \neq 0$
and
$g(z) - f_{1}(z) \neq 0$
and
![]() $g(z) - f_{2}(z) \neq 0$
, for every
$g(z) - f_{2}(z) \neq 0$
, for every
![]() $z \in \mathbb C$
; in particular, g and
$z \in \mathbb C$
; in particular, g and
![]() $f_{1}$
, as well as g and
$f_{1}$
, as well as g and
![]() $f_{2}$
, have no common zeros. Consider now the function
$f_{2}$
, have no common zeros. Consider now the function
 $$ \begin{align} F(z) := \frac{f_{1}(z) (g(z) - f_{2}(z))}{f_{1}(z) (g(z) - f_{2}(z)) + f_{2}(z) (g(z) - f_{1}(z))}. \end{align} $$
$$ \begin{align} F(z) := \frac{f_{1}(z) (g(z) - f_{2}(z))}{f_{1}(z) (g(z) - f_{2}(z)) + f_{2}(z) (g(z) - f_{1}(z))}. \end{align} $$
It follows from the assumptions that the zeros of F are exactly given by
![]() $(a_{n})$
, whereas its ones are exactly given by
$(a_{n})$
, whereas its ones are exactly given by
![]() $(b_{n})$
. Because
$(b_{n})$
. Because
![]() $((a_{n}),(b_{n}))$
is not a zero–one set, we must have
$((a_{n}),(b_{n}))$
is not a zero–one set, we must have
![]() $F \in M(\mathbb C) \,\backslash\, H(\mathbb C)$
. Thus, F must have at least one pole, implying that there exists
$F \in M(\mathbb C) \,\backslash\, H(\mathbb C)$
. Thus, F must have at least one pole, implying that there exists
![]() $z_{0} \in \mathbb C$
such that
$z_{0} \in \mathbb C$
such that
![]() $f_{1}(z_{0}) (g(z_{0}) - f_{2}(z_{0})) + f_{2}(z_{0}) (g(z_{0}) - f_{1}(z_{0})) = 0$
. It follows
$f_{1}(z_{0}) (g(z_{0}) - f_{2}(z_{0})) + f_{2}(z_{0}) (g(z_{0}) - f_{1}(z_{0})) = 0$
. It follows
and because
![]() $f_{1}$
and
$f_{1}$
and
![]() $f_{2}$
have no common zeros, we obtain
$f_{2}$
have no common zeros, we obtain
 $$ \begin{align*}g(z_{0}) = \frac{2 f_{1}(z_{0}) f_{2}(z_{0})}{f_{1}(z_{0}) + f_{2}(z_{0})}.\end{align*} $$
$$ \begin{align*}g(z_{0}) = \frac{2 f_{1}(z_{0}) f_{2}(z_{0})}{f_{1}(z_{0}) + f_{2}(z_{0})}.\end{align*} $$
Hence, if the function
![]() $g \in M(\mathbb C)$
avoids
$g \in M(\mathbb C)$
avoids
![]() $f_{1}$
and
$f_{1}$
and
![]() $f_{2}$
, it cannot avoid
$f_{2}$
, it cannot avoid
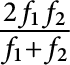 $\frac {2f_{1} f_{2}}{f_{1} + f_{2}}$
, and the family
$\frac {2f_{1} f_{2}}{f_{1} + f_{2}}$
, and the family
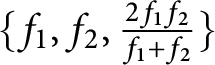 $\{f_{1}, f_{2}, \frac {2f_{1} f_{2}}{f_{1} + f_{2}}\}$
is unavoidable with respect to
$\{f_{1}, f_{2}, \frac {2f_{1} f_{2}}{f_{1} + f_{2}}\}$
is unavoidable with respect to
![]() $M(\mathbb C)$
. By Proposition 1, the functions
$M(\mathbb C)$
. By Proposition 1, the functions
![]() $f_{1}$
and
$f_{1}$
and
![]() $-f_{2}$
cannot avoid each other, and because they further have no common zeros, there exists
$-f_{2}$
cannot avoid each other, and because they further have no common zeros, there exists
![]() $z_{1} \in \mathbb C$
with
$z_{1} \in \mathbb C$
with
![]() $f_{1}(z_{1}) + f_{2}(z_{1}) = 0$
and
$f_{1}(z_{1}) + f_{2}(z_{1}) = 0$
and
![]() $f_{1}(z_{1}) \neq 0 \neq f_{2}(z_{1})$
. Thus,
$f_{1}(z_{1}) \neq 0 \neq f_{2}(z_{1})$
. Thus,
![]() $z_{1}$
is a pole of
$z_{1}$
is a pole of
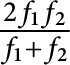 $\frac {2f_{1} f_{2}}{f_{1} + f_{2}}$
, so that the family
$\frac {2f_{1} f_{2}}{f_{1} + f_{2}}$
, so that the family
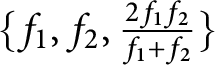 $\{f_{1}, f_{2}, \frac {2f_{1} f_{2}}{f_{1} + f_{2}}\}$
is unavoidable with respect to
$\{f_{1}, f_{2}, \frac {2f_{1} f_{2}}{f_{1} + f_{2}}\}$
is unavoidable with respect to
![]() $M_{\infty }(\mathbb C)$
.▪
$M_{\infty }(\mathbb C)$
.▪
Remark If, in (1), we consider the function
 $$ \begin{align*}F(z) := \frac{f_{1}(z) (g(z) - f_{1}(z))}{f_{1}(z) (g(z) - f_{1}(z)) + f_{2}(z) (g(z) - f_{2}(z))},\end{align*} $$
$$ \begin{align*}F(z) := \frac{f_{1}(z) (g(z) - f_{1}(z))}{f_{1}(z) (g(z) - f_{1}(z)) + f_{2}(z) (g(z) - f_{2}(z))},\end{align*} $$
we obtain that the family
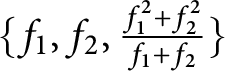 $\{f_{1}, f_{2}, \frac {f_{1}^{2} + f_{2}^{2}}{f_{1} + f_{2}}\}$
is unavoidable with respect to
$\{f_{1}, f_{2}, \frac {f_{1}^{2} + f_{2}^{2}}{f_{1} + f_{2}}\}$
is unavoidable with respect to
![]() $M_{\infty }(\mathbb C)$
. Indeed, in this case, there exists
$M_{\infty }(\mathbb C)$
. Indeed, in this case, there exists
![]() $z_{0} \in \mathbb C$
such that
$z_{0} \in \mathbb C$
such that
![]() $f_{1}(z_{0}) (g(z_{0}) - f_{1}(z_{0})) + f_{2}(z_{0}) (g(z_{0}) - f_{2}(z_{0})) = 0$
, and hence
$f_{1}(z_{0}) (g(z_{0}) - f_{1}(z_{0})) + f_{2}(z_{0}) (g(z_{0}) - f_{2}(z_{0})) = 0$
, and hence
Because
![]() $f_{1}$
and
$f_{1}$
and
![]() $f_{2}$
have no common zeros, it follows
$f_{2}$
have no common zeros, it follows
 $$ \begin{align*}g(z_{0}) = \frac{f_{1}^{2}(z_{0}) + f_{2}^{2}(z_{0})}{f_{1}(z_{0}) + f_{2}(z_{0})}.\end{align*} $$
$$ \begin{align*}g(z_{0}) = \frac{f_{1}^{2}(z_{0}) + f_{2}^{2}(z_{0})}{f_{1}(z_{0}) + f_{2}(z_{0})}.\end{align*} $$
3 Unavoidable functions with multiple zeros and poles
In the following, we will use some standard terminology from Nevanlinna Theory (e.g., [Reference Gol’dberg and Ostrovskii3, Reference Hayman4, Reference Yang15]), that is, for a nonconstant function
![]() $f \in M(\mathbb C)$
, a value
$f \in M(\mathbb C)$
, a value
![]() $a \in \mathbb C_{\infty } := \mathbb C \cup \{\infty \}$
and
$a \in \mathbb C_{\infty } := \mathbb C \cup \{\infty \}$
and
![]() $r \geq 0$
, we denote by
$r \geq 0$
, we denote by
![]() $n(r,a,f)$
and
$n(r,a,f)$
and
![]() $\overline {n}(r,a,f)$
the number of a-points (counting multiplicity) and of distinct a-points of f, respectively, in
$\overline {n}(r,a,f)$
the number of a-points (counting multiplicity) and of distinct a-points of f, respectively, in
![]() $\{z: \left |z\right | \leq r\}$
. The corresponding integrated counting functions will be denoted by
$\{z: \left |z\right | \leq r\}$
. The corresponding integrated counting functions will be denoted by
![]() $N(r,a,f)$
and
$N(r,a,f)$
and
![]() $\overline {N}(r,a,f)$
, respectively. We write
$\overline {N}(r,a,f)$
, respectively. We write
![]() $T(r,f)$
for the characteristic function of f, and we recall that the deficiency
$T(r,f)$
for the characteristic function of f, and we recall that the deficiency
![]() $\delta (a,f)$
and the branching index
$\delta (a,f)$
and the branching index
![]() $\Theta (a,f)$
of a are defined by
$\Theta (a,f)$
of a are defined by
 $$ \begin{align*} \delta(a,f) = 1 - \limsup_{r \to \infty} \frac{N(r,a,f)}{T(r,f)} \qquad \text{and} \qquad \Theta(a,f) = 1 - \limsup_{r \to \infty} \frac{\overline{N}(r,a,f)}{T(r,f)}. \end{align*} $$
$$ \begin{align*} \delta(a,f) = 1 - \limsup_{r \to \infty} \frac{N(r,a,f)}{T(r,f)} \qquad \text{and} \qquad \Theta(a,f) = 1 - \limsup_{r \to \infty} \frac{\overline{N}(r,a,f)}{T(r,f)}. \end{align*} $$
Note that
![]() $\delta (a,f) \leq \Theta (a,f)$
, and it is a consequence of the Second Fundamental Theorem that
$\delta (a,f) \leq \Theta (a,f)$
, and it is a consequence of the Second Fundamental Theorem that
![]() $\sum _{a \in \mathbb C_{\infty }} \Theta (a, f) \leq 2$
.
$\sum _{a \in \mathbb C_{\infty }} \Theta (a, f) \leq 2$
.
As mentioned in the introduction, a result from [Reference Hayman and Rubel5] states the existence of an entire function f, such that for every
![]() $g \in M(\mathbb C)$
having at most finitely many poles, at least one of the two equations
$g \in M(\mathbb C)$
having at most finitely many poles, at least one of the two equations
![]() $g(z) = f(z)$
and
$g(z) = f(z)$
and
![]() $g(z) = -f(z)$
has infinitely many solutions in
$g(z) = -f(z)$
has infinitely many solutions in
![]() $\mathbb C$
. Using similar ideas as in [Reference Hayman and Rubel5], we show the following result.
$\mathbb C$
. Using similar ideas as in [Reference Hayman and Rubel5], we show the following result.
Theorem 2 Let
![]() $f \in M(\mathbb C)$
have infinitely many zeros, of which at most finitely many are simple. Suppose further that
$f \in M(\mathbb C)$
have infinitely many zeros, of which at most finitely many are simple. Suppose further that
![]() $g \in M(\mathbb C)$
has at most finitely many simple poles. Then, at least one of the two equations
$g \in M(\mathbb C)$
has at most finitely many simple poles. Then, at least one of the two equations
![]() $g(z) = f(z)$
and
$g(z) = f(z)$
and
![]() $g(z) = -f(z)$
has infinitely many solutions in
$g(z) = -f(z)$
has infinitely many solutions in
![]() $\mathbb C$
. In particular, the family
$\mathbb C$
. In particular, the family
![]() $\{f, -f\}$
is unavoidable with respect to the set of meromorphic functions having at most finitely many simple poles.
$\{f, -f\}$
is unavoidable with respect to the set of meromorphic functions having at most finitely many simple poles.
Proof Suppose that
![]() $f \in M(\mathbb C)$
has infinitely many zeros, of which at most finitely many are simple. Assuming that the statement is not correct, there exists a function
$f \in M(\mathbb C)$
has infinitely many zeros, of which at most finitely many are simple. Assuming that the statement is not correct, there exists a function
![]() $g \in M(\mathbb C)$
that has at most finitely many simple poles, such that both equations
$g \in M(\mathbb C)$
that has at most finitely many simple poles, such that both equations
![]() $g(z) = f(z)$
and
$g(z) = f(z)$
and
![]() $g(z) = -f(z)$
have at most finitely many solutions in
$g(z) = -f(z)$
have at most finitely many solutions in
![]() $\mathbb C$
. In particular, f and g then have at most finitely many common zeros, and it follows from the assumptions that the function
$\mathbb C$
. In particular, f and g then have at most finitely many common zeros, and it follows from the assumptions that the function
 $$ \begin{align*}F(z) = \frac{f(z)}{g(z)}\end{align*} $$
$$ \begin{align*}F(z) = \frac{f(z)}{g(z)}\end{align*} $$
has infinitely many zeros, of which at most finitely many are simple. Using the First Fundamental Theorem, this implies
 $$ \begin{align*}\overline{N}\left(r,0, F \right) \leq \frac{1}{2} \, N\left(r,0, F \right) + \mathcal{O}(1) \leq \frac{1}{2} \, T\left(r, F \right) + \mathcal{O}(1),\end{align*} $$
$$ \begin{align*}\overline{N}\left(r,0, F \right) \leq \frac{1}{2} \, N\left(r,0, F \right) + \mathcal{O}(1) \leq \frac{1}{2} \, T\left(r, F \right) + \mathcal{O}(1),\end{align*} $$
and hence
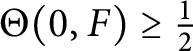 $\Theta (0, F) \geq \frac {1}{2}$
. Furthermore, it follows that the equations
$\Theta (0, F) \geq \frac {1}{2}$
. Furthermore, it follows that the equations
![]() $F(z) = 1$
and
$F(z) = 1$
and
![]() $F(z) = -1$
have at most finitely many roots, so that we obtain
$F(z) = -1$
have at most finitely many roots, so that we obtain
![]() $\Theta (1, F) = 1$
and
$\Theta (1, F) = 1$
and
![]() $\Theta (-1, F) = 1$
, because F is transcendental. Finally,
$\Theta (-1, F) = 1$
, because F is transcendental. Finally,
![]() $\Theta (0, F) + \Theta (1, F) + \Theta (-1, F)> 2$
, in contradiction to the Second Fundamental Theorem.▪
$\Theta (0, F) + \Theta (1, F) + \Theta (-1, F)> 2$
, in contradiction to the Second Fundamental Theorem.▪
Remark As previously mentioned, it was shown in [Reference Rubel and Yang12] that a family consisting of two meromorphic functions is never unavoidable with respect to
![]() $M(\mathbb C)$
. In particular, given
$M(\mathbb C)$
. In particular, given
![]() $f \in M(\mathbb C)$
, there exists
$f \in M(\mathbb C)$
, there exists
![]() $g \in M(\mathbb C)$
such that
$g \in M(\mathbb C)$
such that
![]() $g(z) \neq f(z)$
and
$g(z) \neq f(z)$
and
![]() $g(z) \neq -f(z)$
, for every
$g(z) \neq -f(z)$
, for every
![]() $z \in \mathbb C$
. It follows from the above theorem that if f has infinitely many zeros, of which at most finitely many are simple, then such a function g necessarily has infinitely many simple poles.
$z \in \mathbb C$
. It follows from the above theorem that if f has infinitely many zeros, of which at most finitely many are simple, then such a function g necessarily has infinitely many simple poles.
The following is an immediate consequence of Theorem 2.
Corollary 1 Let
![]() $f \in M(\mathbb C)$
have infinitely many zeros, of which at most finitely many are simple. Let further
$f \in M(\mathbb C)$
have infinitely many zeros, of which at most finitely many are simple. Let further
![]() $g \in M(\mathbb C)$
and
$g \in M(\mathbb C)$
and
![]() $n, m \in \mathbb N$
with
$n, m \in \mathbb N$
with
![]() $m \geq 2$
be given. Then, the following hold:
$m \geq 2$
be given. Then, the following hold:
-
(i) At least one of the two equations
 $g^{(n)}(z) = f(z)$
and
$g^{(n)}(z) = f(z)$
and
 $g^{(n)}(z) = -f(z)$
has infinitely many solutions in
$g^{(n)}(z) = -f(z)$
has infinitely many solutions in
 $\mathbb C$
.
$\mathbb C$
. -
(ii) At least one of the two equations
 $g^{m}(z) = f(z)$
and
$g^{m}(z) = f(z)$
and
 $g^{m}(z) = -f(z)$
has infinitely many solutions in
$g^{m}(z) = -f(z)$
has infinitely many solutions in
 $\mathbb C$
.
$\mathbb C$
.
In particular, for every
![]() $n, m \in \mathbb N$
with
$n, m \in \mathbb N$
with
![]() $m \geq 2$
, the family
$m \geq 2$
, the family
![]() $\{f, -f\}$
is unavoidable with respect to the sets
$\{f, -f\}$
is unavoidable with respect to the sets
![]() $\{g^{(n)}: g \in M(\mathbb C)\}$
and
$\{g^{(n)}: g \in M(\mathbb C)\}$
and
![]() $\{g^{m}: g \in M(\mathbb C)\}$
.
$\{g^{m}: g \in M(\mathbb C)\}$
.
If we make stronger assumptions on the zeros and poles, we can also obtain single functions
![]() $f \in M(\mathbb C)$
that are unavoidable with respect to certain subsets of
$f \in M(\mathbb C)$
that are unavoidable with respect to certain subsets of
![]() $M(\mathbb C)$
.
$M(\mathbb C)$
.
Proposition 2 Let
![]() $f \in M(\mathbb C)$
be a meromorphic function having infinitely many zeros and poles, at most finitely many of which have multiplicity less than 3. If
$f \in M(\mathbb C)$
be a meromorphic function having infinitely many zeros and poles, at most finitely many of which have multiplicity less than 3. If
![]() $g \in M(\mathbb C)$
has at most finitely many zeros and poles with multiplicity less than 3, the equation
$g \in M(\mathbb C)$
has at most finitely many zeros and poles with multiplicity less than 3, the equation
![]() $g(z) = f(z)$
has infinitely many solutions in
$g(z) = f(z)$
has infinitely many solutions in
![]() $\mathbb C$
.
$\mathbb C$
.
Proof Let be given a function
![]() $f \in M(\mathbb C)$
having infinitely many zeros and poles, at most finitely many of which have multiplicity less than 3. Assuming that the statement does not hold, there exists a function
$f \in M(\mathbb C)$
having infinitely many zeros and poles, at most finitely many of which have multiplicity less than 3. Assuming that the statement does not hold, there exists a function
![]() $g \in M(\mathbb C)$
that has at most finitely many zeros and poles with multiplicity less than 3, such that the equation
$g \in M(\mathbb C)$
that has at most finitely many zeros and poles with multiplicity less than 3, such that the equation
![]() $g(z) = f(z)$
has at most finitely many solutions in
$g(z) = f(z)$
has at most finitely many solutions in
![]() $\mathbb C$
. In particular, f and g then have at most finitely many common zeros and poles, so that the function
$\mathbb C$
. In particular, f and g then have at most finitely many common zeros and poles, so that the function
 $$ \begin{align*}F(z) = \frac{f(z)}{g(z)}\end{align*} $$
$$ \begin{align*}F(z) = \frac{f(z)}{g(z)}\end{align*} $$
has infinitely many zeros and poles, at most finitely many of which have multiplicity less than 3. As before, this implies
 $$ \begin{align*}\overline{N}\left(r,0, F \right) \leq \frac{1}{3} \, N\left(r,0, F \right) + \mathcal{O}(1) \leq \frac{1}{3} \, T\left(r, F \right) + \mathcal{O}(1),\end{align*} $$
$$ \begin{align*}\overline{N}\left(r,0, F \right) \leq \frac{1}{3} \, N\left(r,0, F \right) + \mathcal{O}(1) \leq \frac{1}{3} \, T\left(r, F \right) + \mathcal{O}(1),\end{align*} $$
and hence
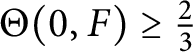 $\Theta (0, F) \geq \frac {2}{3}$
. A similar argumentation gives
$\Theta (0, F) \geq \frac {2}{3}$
. A similar argumentation gives
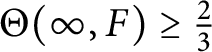 $\Theta (\infty , F) \geq \frac {2}{3}$
, and because F is a transcendental function taking at most finitely many times the value
$\Theta (\infty , F) \geq \frac {2}{3}$
, and because F is a transcendental function taking at most finitely many times the value
![]() $1$
, we further have
$1$
, we further have
![]() $\Theta (1, F) = 1$
. Hence,
$\Theta (1, F) = 1$
. Hence,
![]() $\Theta (0, F) + \Theta (1, F) + \Theta (\infty , F)> 2$
, in contradiction to the Second Fundamental Theorem.▪
$\Theta (0, F) + \Theta (1, F) + \Theta (\infty , F)> 2$
, in contradiction to the Second Fundamental Theorem.▪
Corollary 2 Let
![]() $f \in M(\mathbb C)$
have infinitely many zeros and poles, and consider
$f \in M(\mathbb C)$
have infinitely many zeros and poles, and consider
![]() $g \in M(\mathbb C)$
. Then, for every
$g \in M(\mathbb C)$
. Then, for every
![]() $n, m \in \mathbb N$
with
$n, m \in \mathbb N$
with
![]() $n, m \geq 3$
, the equation
$n, m \geq 3$
, the equation
![]() $g^{n}(z) = f^{m}(z)$
has infinitely many solutions in
$g^{n}(z) = f^{m}(z)$
has infinitely many solutions in
![]() $\mathbb C$
.
$\mathbb C$
.
Note that it follows from Theorem 2 that if
![]() $f \in M(\mathbb C)$
has infinitely many zeros, then for
$f \in M(\mathbb C)$
has infinitely many zeros, then for
![]() $g \in M(\mathbb C)$
and every
$g \in M(\mathbb C)$
and every
![]() $n, m \in \mathbb N$
with
$n, m \in \mathbb N$
with
![]() $n, m \geq 2$
, at least one of the two equations
$n, m \geq 2$
, at least one of the two equations
![]() $g^{n}(z) = f^{m}(z)$
and
$g^{n}(z) = f^{m}(z)$
and
![]() $g^{n}(z) = -f^{m}(z)$
has infinitely many solutions in
$g^{n}(z) = -f^{m}(z)$
has infinitely many solutions in
![]() $\mathbb C$
.
$\mathbb C$
.
It is easily seen that similar results can be obtained for entire functions.
Proposition 3 Let
![]() $f \in H(\mathbb C)$
be an entire function having infinitely many zeros, at most finitely many of which have multiplicity less than 3. If
$f \in H(\mathbb C)$
be an entire function having infinitely many zeros, at most finitely many of which have multiplicity less than 3. If
![]() $g \in H(\mathbb C)$
has at most finitely many simple zeros, the equation
$g \in H(\mathbb C)$
has at most finitely many simple zeros, the equation
![]() $g(z) = f(z)$
has infinitely many solutions in
$g(z) = f(z)$
has infinitely many solutions in
![]() $\mathbb C$
.
$\mathbb C$
.
Indeed, assuming that the statement does not hold, there exists a function
![]() $g \in H(\mathbb C)$
that has at most finitely many simple zeros, such that the equation
$g \in H(\mathbb C)$
that has at most finitely many simple zeros, such that the equation
![]() $g(z) = f(z)$
has at most finitely many solutions in
$g(z) = f(z)$
has at most finitely many solutions in
![]() $\mathbb C$
. The function
$\mathbb C$
. The function
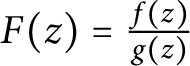 $F(z) = \frac {f(z)}{g(z)}$
is then transcendental, and it follows as before that
$F(z) = \frac {f(z)}{g(z)}$
is then transcendental, and it follows as before that
 $\Theta (F,0) \geq \frac {2}{3}$
,
$\Theta (F,0) \geq \frac {2}{3}$
,
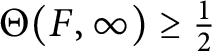 $\Theta (F,\infty ) \geq \frac {1}{2}$
and
$\Theta (F,\infty ) \geq \frac {1}{2}$
and
![]() $\Theta (F,1) = 1$
, which leads to a contradiction.
$\Theta (F,1) = 1$
, which leads to a contradiction.
Corollary 3 Let
![]() $f \in H(\mathbb C)$
have infinitely many zeros, and consider
$f \in H(\mathbb C)$
have infinitely many zeros, and consider
![]() $g \in H(\mathbb C)$
. Then, for every
$g \in H(\mathbb C)$
. Then, for every
![]() $n, m \in \mathbb N$
with
$n, m \in \mathbb N$
with
![]() $n \geq 2$
and
$n \geq 2$
and
![]() $m \geq 3$
, the equation
$m \geq 3$
, the equation
![]() $g^{n}(z) = f^{m}(z)$
has infinitely many solutions in
$g^{n}(z) = f^{m}(z)$
has infinitely many solutions in
![]() $\mathbb C$
.
$\mathbb C$
.
In the following, we will show the existence of meromorphic functions that are unavoidable with respect to functions in
![]() $M(\mathbb C)$
whose number of zeros and poles are bounded in some sense. We therefore introduce the following notation. Given a continuous increasing function
$M(\mathbb C)$
whose number of zeros and poles are bounded in some sense. We therefore introduce the following notation. Given a continuous increasing function
![]() $\varphi : [0,\infty ) \to [1,\infty )$
with
$\varphi : [0,\infty ) \to [1,\infty )$
with
![]() $\varphi (r) \to \infty $
for
$\varphi (r) \to \infty $
for
![]() $r \to \infty $
, we denote by
$r \to \infty $
, we denote by
![]() $M_{\varphi }(\mathbb C)$
the set of all functions
$M_{\varphi }(\mathbb C)$
the set of all functions
![]() $f \in M(\mathbb C)$
such that
$f \in M(\mathbb C)$
such that
![]() $n(r,0,f) = \mathcal {O}(\varphi (r))$
and
$n(r,0,f) = \mathcal {O}(\varphi (r))$
and
![]() $n(r,\infty ,f) = \mathcal {O}(\varphi (r))$
. Our result will be an immediate consequence of the following more general statement.
$n(r,\infty ,f) = \mathcal {O}(\varphi (r))$
. Our result will be an immediate consequence of the following more general statement.
Theorem 3 Let be given a continuous increasing function
![]() $\varphi : [0,\infty ) \to [1,\infty )$
with
$\varphi : [0,\infty ) \to [1,\infty )$
with
![]() $\varphi (r) \to \infty $
for
$\varphi (r) \to \infty $
for
![]() $r \to \infty $
. There exists a function
$r \to \infty $
. There exists a function
![]() $f \in M(\mathbb C)$
, such that for every function
$f \in M(\mathbb C)$
, such that for every function
![]() $g \in M_{\varphi }(\mathbb C)$
, we have
$g \in M_{\varphi }(\mathbb C)$
, we have
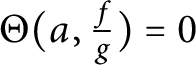 $\Theta (a, \frac {f}{g}) = 0$
for every
$\Theta (a, \frac {f}{g}) = 0$
for every
![]() $a \in \mathbb C \,\backslash\,\{0\}$
.
$a \in \mathbb C \,\backslash\,\{0\}$
.
Proof Because
![]() $M_{\varphi _{1}}(\mathbb C) \subset M_{\varphi _{2}}(\mathbb C)$
if
$M_{\varphi _{1}}(\mathbb C) \subset M_{\varphi _{2}}(\mathbb C)$
if
![]() $\varphi _{1}(r) \leq \varphi _{2}(r)$
for
$\varphi _{1}(r) \leq \varphi _{2}(r)$
for
![]() $r \in [0,\infty )$
, we may assume that
$r \in [0,\infty )$
, we may assume that
![]() $r \leq \varphi (r)$
for
$r \leq \varphi (r)$
for
![]() $r \in [0,\infty )$
. We shall show that any function
$r \in [0,\infty )$
. We shall show that any function
![]() $f \in M(\mathbb C)$
with “sufficiently few” distinct zeros and poles, but “sufficiently many” zeros and poles (counting multiplicity) has the claimed property. We therefore consider a function
$f \in M(\mathbb C)$
with “sufficiently few” distinct zeros and poles, but “sufficiently many” zeros and poles (counting multiplicity) has the claimed property. We therefore consider a function
![]() $f_{1} \in H(\mathbb C)$
such that for every
$f_{1} \in H(\mathbb C)$
such that for every
![]() $n \in \mathbb N$
, the function
$n \in \mathbb N$
, the function
![]() $f_{1}$
has a zero at
$f_{1}$
has a zero at
![]() $z = n$
with multiplicity
$z = n$
with multiplicity
![]() $[\varphi (n + 2)]!$
and
$[\varphi (n + 2)]!$
and
![]() $f_{1}(z) \neq 0$
for
$f_{1}(z) \neq 0$
for
![]() $z \in \mathbb C \,\backslash\, \mathbb N$
, where, here and in the following, we denote by
$z \in \mathbb C \,\backslash\, \mathbb N$
, where, here and in the following, we denote by
![]() $[r]$
the integer part of the real number r. We then define
$[r]$
the integer part of the real number r. We then define
![]() $f_{2}(z) := f_{1}(-z)$
and set
$f_{2}(z) := f_{1}(-z)$
and set
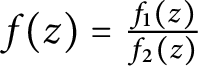 $f(z) = \frac {f_{1}(z)}{f_{2}(z)}$
. We claim that f satisfies the statement of the theorem.
$f(z) = \frac {f_{1}(z)}{f_{2}(z)}$
. We claim that f satisfies the statement of the theorem.
Let therefore
![]() $g \in M_{\varphi }(\mathbb C)$
be given. There exist
$g \in M_{\varphi }(\mathbb C)$
be given. There exist
![]() $g_{1}$
and
$g_{1}$
and
![]() $g_{2} \in H(\mathbb C)$
, such that
$g_{2} \in H(\mathbb C)$
, such that
![]() $g_{1}$
and
$g_{1}$
and
![]() $g_{2}$
have no common zeros and such that
$g_{2}$
have no common zeros and such that
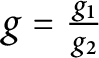 $g = \frac {g_{1}}{g_{2}}$
. Because
$g = \frac {g_{1}}{g_{2}}$
. Because
![]() $g \in M_{\varphi }(\mathbb C)$
, we have
$g \in M_{\varphi }(\mathbb C)$
, we have
![]() $n(r,0,g_{1}) = \mathcal {O}(\varphi (r))$
and
$n(r,0,g_{1}) = \mathcal {O}(\varphi (r))$
and
![]() $n(r,0,g_{2}) = \mathcal {O}(\varphi (r))$
, and considering the function
$n(r,0,g_{2}) = \mathcal {O}(\varphi (r))$
, and considering the function
 $$ \begin{align*} F(z) := \frac{f(z)}{g(z)} = \frac{f_{1}(z)}{f_{2}(z)} \, \frac{g_{2}(z)}{g_{1}(z)}, \end{align*} $$
$$ \begin{align*} F(z) := \frac{f(z)}{g(z)} = \frac{f_{1}(z)}{f_{2}(z)} \, \frac{g_{2}(z)}{g_{1}(z)}, \end{align*} $$
we obtain for
![]() $r> 0$
sufficiently large
$r> 0$
sufficiently large
where
![]() $c_{1}> 0$
and
$c_{1}> 0$
and
![]() $c_{2}> 0$
are suitable constants. Moreover, for
$c_{2}> 0$
are suitable constants. Moreover, for
![]() $r> 0$
sufficiently large, we have
$r> 0$
sufficiently large, we have
 $$ \begin{align} n\left(r,0, F\right) \kern1pt{\geq}\kern1pt n(r,0, f_{1}) \kern1.2pt{-}\kern1.2pt n(r,0,g_{1}) \kern1pt{\geq} \sum_{i=3}^{[r] + 2} [\varphi(i)]! \kern1.2pt{-}\kern1.2pt c_{3} \, \varphi(r) \kern1pt{\geq} \sum_{i=3}^{[r] + 1} [\varphi(i)]!\kern1pt{>}\kern1pt [\varphi([r] \kern1pt{+}\kern1pt 1)\!]! \end{align} $$
$$ \begin{align} n\left(r,0, F\right) \kern1pt{\geq}\kern1pt n(r,0, f_{1}) \kern1.2pt{-}\kern1.2pt n(r,0,g_{1}) \kern1pt{\geq} \sum_{i=3}^{[r] + 2} [\varphi(i)]! \kern1.2pt{-}\kern1.2pt c_{3} \, \varphi(r) \kern1pt{\geq} \sum_{i=3}^{[r] + 1} [\varphi(i)]!\kern1pt{>}\kern1pt [\varphi([r] \kern1pt{+}\kern1pt 1)\!]! \end{align} $$
for a suitable constant
![]() $c_{3}> 0$
.
$c_{3}> 0$
.
Let now
![]() $\varepsilon> 0$
be given. Then, there exists
$\varepsilon> 0$
be given. Then, there exists
![]() $k \in \mathbb N$
such that
$k \in \mathbb N$
such that
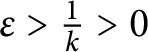 $\varepsilon> \frac {1}{k} > 0$
, and from (2) and (3), we obtain that there exists
$\varepsilon> \frac {1}{k} > 0$
, and from (2) and (3), we obtain that there exists
![]() $R_{k}> 0$
, such that for
$R_{k}> 0$
, such that for
![]() $r> R_{k}$
, we have
$r> R_{k}$
, we have
 $$ \begin{align*}\overline{n}\left(r,0, F \right) \leq \frac{1}{k} \, n\left(r,0, F \right),\end{align*} $$
$$ \begin{align*}\overline{n}\left(r,0, F \right) \leq \frac{1}{k} \, n\left(r,0, F \right),\end{align*} $$
which, using the First Fundamental Theorem, implies
 $$ \begin{align*}\overline{N}\left(r,0, F \right) \leq \frac{1}{k} \, N\left(r,0, F \right) + \mathcal{O}(1) \leq \frac{1}{k} \, T\left(r,F \right) + \mathcal{O}(1).\end{align*} $$
$$ \begin{align*}\overline{N}\left(r,0, F \right) \leq \frac{1}{k} \, N\left(r,0, F \right) + \mathcal{O}(1) \leq \frac{1}{k} \, T\left(r,F \right) + \mathcal{O}(1).\end{align*} $$
This finally yields
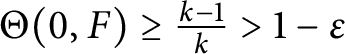 $\Theta (0,F) \geq \frac {k-1}{k}> 1 - \varepsilon $
, and thus
$\Theta (0,F) \geq \frac {k-1}{k}> 1 - \varepsilon $
, and thus
![]() $\Theta (0,F) = 1$
.
$\Theta (0,F) = 1$
.
By a similar argumentation, we obtain that
![]() $\Theta (\infty ,F) = 1$
; hence,
$\Theta (\infty ,F) = 1$
; hence,
![]() $\Theta (\infty ,F) + \Theta (0,F) = 2$
, so that
$\Theta (\infty ,F) + \Theta (0,F) = 2$
, so that
![]() $\Theta (a,F) = 0$
for every
$\Theta (a,F) = 0$
for every
![]() $a \in \mathbb C \,\backslash\, \{0\}$
by the Second Fundamental Theorem.▪
$a \in \mathbb C \,\backslash\, \{0\}$
by the Second Fundamental Theorem.▪
Corollary 4 Let be given a continuous increasing function
![]() $\varphi : [0,\infty ) \to [1,\infty )$
with
$\varphi : [0,\infty ) \to [1,\infty )$
with
![]() $\varphi (r) \to \infty $
for
$\varphi (r) \to \infty $
for
![]() $r \to \infty $
. There exists a function
$r \to \infty $
. There exists a function
![]() $f \in M(\mathbb C)$
, such that for every function
$f \in M(\mathbb C)$
, such that for every function
![]() $g \in M_{\varphi }(\mathbb C) \cup \{0, f_{\infty }\}$
, the equation
$g \in M_{\varphi }(\mathbb C) \cup \{0, f_{\infty }\}$
, the equation
![]() $g(z) = f(z)$
has infinitely many solutions in
$g(z) = f(z)$
has infinitely many solutions in
![]() $\mathbb C$
. In particular, f is unavoidable with respect to
$\mathbb C$
. In particular, f is unavoidable with respect to
![]() $M_{\varphi }(\mathbb C) \cup \{0, f_{\infty }\}$
.
$M_{\varphi }(\mathbb C) \cup \{0, f_{\infty }\}$
.
It is easily seen that the function f from the proof of Theorem 3 satisfies the requirement, for, assuming this is not the case, there exists a function
![]() $g \in M_{\varphi }(\mathbb C) \cup \{0, f_{\infty }\}$
such that the equation
$g \in M_{\varphi }(\mathbb C) \cup \{0, f_{\infty }\}$
such that the equation
![]() $g(z) = f(z)$
has at most finitely many solutions in
$g(z) = f(z)$
has at most finitely many solutions in
![]() $\mathbb C$
. Because f has infinitely many zeros and poles, we have that
$\mathbb C$
. Because f has infinitely many zeros and poles, we have that
![]() $g \in M_{\varphi }(\mathbb C)$
, and the function
$g \in M_{\varphi }(\mathbb C)$
, and the function
![]() $\frac {f}{g}$
takes at most finitely many times the value
$\frac {f}{g}$
takes at most finitely many times the value
![]() $1$
. Because
$1$
. Because
![]() $\frac {f}{g}$
is transcendental, this implies
$\frac {f}{g}$
is transcendental, this implies
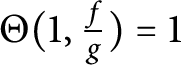 $\Theta (1, \frac {f}{g}) = 1$
, which is in contradiction to Theorem 3.
$\Theta (1, \frac {f}{g}) = 1$
, which is in contradiction to Theorem 3.
Remark
-
(i) Note that if the function
 $\varphi $
is such that for every
$\varphi $
is such that for every
 $n \in \mathbb N$
, we have
$n \in \mathbb N$
, we have
 $\frac {\varphi (r)}{r^{n}} \to \infty $
for
$\frac {\varphi (r)}{r^{n}} \to \infty $
for
 $r \to \infty $
, the set
$r \to \infty $
, the set
 $M_{\varphi }(\mathbb C)$
contains every meromorphic function g of the form
$M_{\varphi }(\mathbb C)$
contains every meromorphic function g of the form
 $g = g_{1} \, e^{g_{2}}$
, where
$g = g_{1} \, e^{g_{2}}$
, where
 $g_{1} \in M(\mathbb C)$
is of finite order of growth and
$g_{1} \in M(\mathbb C)$
is of finite order of growth and
 $g_{2} \in H(\mathbb C)$
.
$g_{2} \in H(\mathbb C)$
. -
(ii) We further mention that it is a consequence of a generalization of the Second Fundamental Theorem (e.g., [Reference Hayman4, Theorem 2.5]) that given a function
 $f \in M(\mathbb C)$
and three functions
$f \in M(\mathbb C)$
and three functions
 $g_{1},g_{2}$
, and
$g_{1},g_{2}$
, and
 $g_{3} \in M(\mathbb C)$
that are “small” with respect to f, that is, functions satisfying
$g_{3} \in M(\mathbb C)$
that are “small” with respect to f, that is, functions satisfying
 $T(r,g_{i}) = o(T(r,f))$
for
$T(r,g_{i}) = o(T(r,f))$
for
 $r \to \infty $
, at least one of the three equations
$r \to \infty $
, at least one of the three equations
 $g_{1}(z) = f(z)$
,
$g_{1}(z) = f(z)$
,
 $g_{2}(z) = f(z)$
, and
$g_{2}(z) = f(z)$
, and
 $g_{3}(z) = f(z)$
has infinitely many solutions in
$g_{3}(z) = f(z)$
has infinitely many solutions in
 $\mathbb C$
. Hence, a meromorphic function can avoid at most two small functions; in particular, a meromorphic function of infinite order can avoid at most two functions of finite order. Moreover, it follows from the deficiency relation for small functions (e.g., [Reference Yang15, p. 41]) that if
$\mathbb C$
. Hence, a meromorphic function can avoid at most two small functions; in particular, a meromorphic function of infinite order can avoid at most two functions of finite order. Moreover, it follows from the deficiency relation for small functions (e.g., [Reference Yang15, p. 41]) that if
 $f \in M(\mathbb C)$
is a function that takes every value
$f \in M(\mathbb C)$
is a function that takes every value
 $a \in \mathbb C_{\infty }$
infinitely many times and satisfies
$a \in \mathbb C_{\infty }$
infinitely many times and satisfies
 $\sum _{a \in \mathbb C_{\infty }} \delta (a,f) = 2$
, the equation
$\sum _{a \in \mathbb C_{\infty }} \delta (a,f) = 2$
, the equation
 $g(z) = f(z)$
has infinitely many solutions in
$g(z) = f(z)$
has infinitely many solutions in
 $\mathbb C$
for every function
$\mathbb C$
for every function
 $g \in M(\mathbb C)$
that is small with respect to f. In particular, such a function f is unavoidable with respect to the set of small functions.
$g \in M(\mathbb C)$
that is small with respect to f. In particular, such a function f is unavoidable with respect to the set of small functions.
4 No
 $f \in M(\mathbb C)$
is unavoidable with respect to
$f \in M(\mathbb C)$
is unavoidable with respect to
 $H(\mathbb C)$
$H(\mathbb C)$
In the other direction, we have the following result.
Theorem 4 Given
![]() $f \in M(\mathbb C)$
, there exists a function
$f \in M(\mathbb C)$
, there exists a function
![]() $g \in H(\mathbb C)$
that avoids f on
$g \in H(\mathbb C)$
that avoids f on
![]() $\mathbb C$
. In particular, no
$\mathbb C$
. In particular, no
![]() $f \in M(\mathbb C)$
is unavoidable with respect to
$f \in M(\mathbb C)$
is unavoidable with respect to
![]() $H(\mathbb C)$
.
$H(\mathbb C)$
.
Proof Let
![]() $f \in M(\mathbb C)$
be given. Then, there exist entire functions
$f \in M(\mathbb C)$
be given. Then, there exist entire functions
![]() $f_{1}$
and
$f_{1}$
and
![]() $f_{2}$
that have no common zeros such that
$f_{2}$
that have no common zeros such that
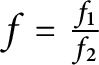 $f = \frac {f_{1}}{f_{2}}$
. Denote by A the set of zeros of
$f = \frac {f_{1}}{f_{2}}$
. Denote by A the set of zeros of
![]() $f_{2}$
, and denote the order of a zero
$f_{2}$
, and denote the order of a zero
![]() $a \in A$
by
$a \in A$
by
![]() $p_{a}$
. We can assume that
$p_{a}$
. We can assume that
![]() $A \neq \emptyset $
, because otherwise f is entire and the function
$A \neq \emptyset $
, because otherwise f is entire and the function
![]() $g = f + 1$
avoids f on
$g = f + 1$
avoids f on
![]() $\mathbb C$
. Because
$\mathbb C$
. Because
![]() $f_{1}$
and
$f_{1}$
and
![]() $f_{2}$
have no common zeros, for every
$f_{2}$
have no common zeros, for every
![]() $a \in A$
, there exists
$a \in A$
, there exists
![]() $\varepsilon _{a}> 0$
such that
$\varepsilon _{a}> 0$
such that
![]() $f_{1}(z) \neq 0$
in
$f_{1}(z) \neq 0$
in
![]() $D_{a} := \{z: \left |z - a\right | < \varepsilon _{a}\}$
. Hence, for every
$D_{a} := \{z: \left |z - a\right | < \varepsilon _{a}\}$
. Hence, for every
![]() $a \in A$
, there exists a function
$a \in A$
, there exists a function
![]() $g_{a} \in H(D_{a})$
such that
$g_{a} \in H(D_{a})$
such that
![]() $e^{g_{a}(z)} = f_{1}(z)$
holds for every
$e^{g_{a}(z)} = f_{1}(z)$
holds for every
![]() $z \in D_{a}$
. For
$z \in D_{a}$
. For
![]() $a \in A$
and
$a \in A$
and
![]() $z \in D_{a}$
, we have the expansion
$z \in D_{a}$
, we have the expansion
 $$ \begin{align*}g_{a}(z) = \sum_{n = 0}^{\infty} c_{n}^{(a)} (z - a)^{n} = \sum_{n = 0}^{p_{a} - 1} c_{n}^{(a)} (z - a)^{n} + \sum_{n = p_{a}}^{\infty} c_{n}^{(a)} (z - a)^{n}.\end{align*} $$
$$ \begin{align*}g_{a}(z) = \sum_{n = 0}^{\infty} c_{n}^{(a)} (z - a)^{n} = \sum_{n = 0}^{p_{a} - 1} c_{n}^{(a)} (z - a)^{n} + \sum_{n = p_{a}}^{\infty} c_{n}^{(a)} (z - a)^{n}.\end{align*} $$
According to a classic interpolation result (e.g., [Reference Rudin13, p. 304]), there exists a function
![]() $\varphi \in H(\mathbb C)$
that has, at every
$\varphi \in H(\mathbb C)$
that has, at every
![]() $a \in A$
, the same power series development up to
$a \in A$
, the same power series development up to
![]() $(z - a)^{p_{a} - 1}$
as
$(z - a)^{p_{a} - 1}$
as
![]() $g_{a}$
. Hence, for every
$g_{a}$
. Hence, for every
![]() $a \in A$
and
$a \in A$
and
![]() $z \in D_{a}$
, we obtain
$z \in D_{a}$
, we obtain
 $$ \begin{align*} \begin{split} \varphi(z) &= \sum_{n = 0}^{p_{a} - 1} c_{n}^{(a)} (z - a)^{n} + \sum_{n = p_{a}}^{\infty} d_{n}^{(a)} (z - a)^{n} \\ &= g_{a}(z) + \sum_{n = p_{a}}^{\infty} (d_{n}^{(a)} - c_{n}^{(a)}) (z - a)^{n} \\ &= g_{a}(z) + Q_{a}(z), \end{split} \end{align*} $$
$$ \begin{align*} \begin{split} \varphi(z) &= \sum_{n = 0}^{p_{a} - 1} c_{n}^{(a)} (z - a)^{n} + \sum_{n = p_{a}}^{\infty} d_{n}^{(a)} (z - a)^{n} \\ &= g_{a}(z) + \sum_{n = p_{a}}^{\infty} (d_{n}^{(a)} - c_{n}^{(a)}) (z - a)^{n} \\ &= g_{a}(z) + Q_{a}(z), \end{split} \end{align*} $$
where
![]() $Q_{a}$
has a zero of order
$Q_{a}$
has a zero of order
![]() $p_{a}$
at the point a. Thus,
$p_{a}$
at the point a. Thus,
![]() $e^{\varphi (z)} = f_{1}(z) \, e^{Q_{a}(z)}$
for
$e^{\varphi (z)} = f_{1}(z) \, e^{Q_{a}(z)}$
for
![]() $a \in A$
and
$a \in A$
and
![]() $z \in D_{a}$
, so that the function
$z \in D_{a}$
, so that the function
![]() $f_{1} - e^{\varphi }$
has a zero of order
$f_{1} - e^{\varphi }$
has a zero of order
![]() $p_{a}$
at the point a. It follows that the function
$p_{a}$
at the point a. It follows that the function
 $$ \begin{align*}g(z) := \frac{f_{1}(z) - e^{\varphi(z)}}{f_{2}(z)}\end{align*} $$
$$ \begin{align*}g(z) := \frac{f_{1}(z) - e^{\varphi(z)}}{f_{2}(z)}\end{align*} $$
is entire, and because
 $$ \begin{align*}f(z) - g(z) = \frac{f_{1}(z)}{f_{2}(z)} - \frac{f_{1}(z) - e^{\varphi(z)}}{f_{2}(z)} = \frac{e^{\varphi(z)}}{f_{2}(z)}\end{align*} $$
$$ \begin{align*}f(z) - g(z) = \frac{f_{1}(z)}{f_{2}(z)} - \frac{f_{1}(z) - e^{\varphi(z)}}{f_{2}(z)} = \frac{e^{\varphi(z)}}{f_{2}(z)}\end{align*} $$
is zero-free, the function g avoids f on
![]() $\mathbb C$
.▪
$\mathbb C$
.▪
Remark
-
(i) Because the interpolation result we use in the proof also holds for arbitrary domains
 $D \subset \mathbb C$
, it follows that the result also holds in this case; hence, no
$D \subset \mathbb C$
, it follows that the result also holds in this case; hence, no
 $f \in M(D)$
is unavoidable with respect to
$f \in M(D)$
is unavoidable with respect to
 $H(D)$
. In [Reference Lappan7], it is shown that there exists a continuous function f on
$H(D)$
. In [Reference Lappan7], it is shown that there exists a continuous function f on
 $\mathbb D$
that is unavoidable with respect to
$\mathbb D$
that is unavoidable with respect to
 $H(\mathbb D)$
. Theorem 4 shows that there exists no
$H(\mathbb D)$
. Theorem 4 shows that there exists no
 $f \in M(\mathbb D)$
with such a property.
$f \in M(\mathbb D)$
with such a property. -
(ii) As stated in the introduction, results from [Reference Hayman and Rubel5, Reference Rubel and Yang12] show that given
 $f_{1}$
and
$f_{1}$
and
 $f_{2} \in M(\mathbb C)$
, there exists
$f_{2} \in M(\mathbb C)$
, there exists
 $g \in M(\mathbb C)$
that avoids both
$g \in M(\mathbb C)$
that avoids both
 $f_{1}$
and
$f_{1}$
and
 $f_{2}$
on
$f_{2}$
on
 $\mathbb C$
. The proof given in [Reference Hayman and Rubel5, Reference Rubel and Yang12] does, however, not directly apply in case that
$\mathbb C$
. The proof given in [Reference Hayman and Rubel5, Reference Rubel and Yang12] does, however, not directly apply in case that
 $f_{1} = f_{\infty }$
or
$f_{1} = f_{\infty }$
or
 $f_{2} = f_{\infty }$
, from which Theorem 4 would immediately follow. Nevertheless, we use similar ideas in our proof of Theorem 4.
$f_{2} = f_{\infty }$
, from which Theorem 4 would immediately follow. Nevertheless, we use similar ideas in our proof of Theorem 4.