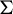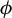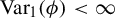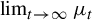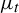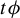1 Introduction
Consider X a metric space and let
![]() $(X,T)$
be a dynamical system. The thermodynamic formalism studies the existence, uniqueness and properties of T-invariant probability measures that maximize the value
$(X,T)$
be a dynamical system. The thermodynamic formalism studies the existence, uniqueness and properties of T-invariant probability measures that maximize the value
![]() $h(\mu )+\int \phi \mathop{\mathrm {d}}\nolimits \mu $
, where
$h(\mu )+\int \phi \mathop{\mathrm {d}}\nolimits \mu $
, where
![]() $h(\mu )$
is the metric entropy, whose measures are widely known in the mathematical literature as equilibrium states. In this paper, we consider
$h(\mu )$
is the metric entropy, whose measures are widely known in the mathematical literature as equilibrium states. In this paper, we consider
![]() $(X, T)$
as a countable Markov shift and
$(X, T)$
as a countable Markov shift and
![]() $\phi : X \to \mathbb {R}$
as a continuous potential. Several properties about these observables have been studied using the so-called Ruelle operator and variational principles. In particular, in both the context of finite Markov shifts and countable Markov shifts, the notions of pressure, recurrence and transience were presented to guarantee the existence and uniqueness, see for instance [Reference Baraviera, Leplaideur and Lopes1, Reference Gurevich13, Reference Mauldin and Urbański20, Reference Sarig24].
$\phi : X \to \mathbb {R}$
as a continuous potential. Several properties about these observables have been studied using the so-called Ruelle operator and variational principles. In particular, in both the context of finite Markov shifts and countable Markov shifts, the notions of pressure, recurrence and transience were presented to guarantee the existence and uniqueness, see for instance [Reference Baraviera, Leplaideur and Lopes1, Reference Gurevich13, Reference Mauldin and Urbański20, Reference Sarig24].
For any
![]() $t\geq 1$
, we denote by
$t\geq 1$
, we denote by
![]() $\mu _t$
the equilibrium state associated to the potential
$\mu _t$
the equilibrium state associated to the potential
![]() $t\phi $
. An interesting problem in ergodic optimization is to study the weak
$t\phi $
. An interesting problem in ergodic optimization is to study the weak
![]() $^\star $
accumulation points at infinity of the family
$^\star $
accumulation points at infinity of the family
![]() $(\mu _t)_{t\geq 1}$
. The foregoing occurs because those accumulation points, also called in the mathematical literature as ground states, usually result in maximizing measures for the potential
$(\mu _t)_{t\geq 1}$
. The foregoing occurs because those accumulation points, also called in the mathematical literature as ground states, usually result in maximizing measures for the potential
![]() $\phi $
, that is, those measures are the ones giving greater mass to the potential
$\phi $
, that is, those measures are the ones giving greater mass to the potential
![]() $\phi $
on the set of all the T-invariant probability measures. In addition, the entropy of the ground states usually exhibits interesting properties among the entropies of all the maximizing measures for the potential
$\phi $
on the set of all the T-invariant probability measures. In addition, the entropy of the ground states usually exhibits interesting properties among the entropies of all the maximizing measures for the potential
![]() $\phi $
. Actually, the fact that these accumulation points usually become maximizing measures for the system shows an interesting connection between thermodynamic formalism and ergodic optimization.
$\phi $
. Actually, the fact that these accumulation points usually become maximizing measures for the system shows an interesting connection between thermodynamic formalism and ergodic optimization.
From the point of view of statistical mechanics, the equilibrium state
![]() $\mu _t$
describes the equilibrium of the system whose interactions are given by the potential
$\mu _t$
describes the equilibrium of the system whose interactions are given by the potential
![]() $\phi $
at temperature
$\phi $
at temperature
![]() $1/t$
. Thus, the existence of accumulation points of the sequence
$1/t$
. Thus, the existence of accumulation points of the sequence
![]() $(\mu _t)_{t\geq 1}$
is associated with the freezing of the system. Because of that, the accumulation points when
$(\mu _t)_{t\geq 1}$
is associated with the freezing of the system. Because of that, the accumulation points when
![]() $t\to \infty $
are also known as zero-temperature limits. A first study about limits at zero temperature in the setting of countable Markov shifts was developed by Coelho in [Reference Coelho-Filho10]. In fact, in that work, the properties of the pressure associated to the potential
$t\to \infty $
are also known as zero-temperature limits. A first study about limits at zero temperature in the setting of countable Markov shifts was developed by Coelho in [Reference Coelho-Filho10]. In fact, in that work, the properties of the pressure associated to the potential
![]() $t\phi $
were studied as well as a version of the central limit theorem in the context of aperiodic finite Markov shifts, also known as topologically mixing shifts of finite type.
$t\phi $
were studied as well as a version of the central limit theorem in the context of aperiodic finite Markov shifts, also known as topologically mixing shifts of finite type.
When
![]() $(X, T)$
is a finite Markov shift, the existence of ground states follows as an immediate consequence of the compactness of the set of Borel probability measures on X. However, the uniqueness of the accumulation point at zero temperature was studied in the setting of locally constant potentials in [Reference Brémont6, Reference Chazottes, Gambaudo and Ugalde8, Reference Leplaideur18] assuming transitivity on the dynamics. It is important to mention that Chazottes and Hochman in [Reference Chazottes and Hochman9] reported an example where the existence of the limit at zero temperature of the equilibrium state fails when the potential is not locally constant. Another interesting example of the existence of more than one accumulation point at zero temperature in the setting of the so-called XY models was presented in [Reference van Enter and Ruszel28]. When the alphabet is countable infinite, seminal works about the existence of accumulation points at zero temperature were performed considering the well-known finitely irreducible condition, which is a strong assumption on the combinatorics of the shift X that allowed the generalization of several of the main results of the thermodynamic formalism in the countable Markov shifts context, see for instance [Reference Jenkinson, Mauldin and Urbański15, Reference Kempton17, Reference Mauldin and Urbański20]. Actually, in [Reference Jenkinson, Mauldin and Urbański15], the existence of ground states was proved in the setting of summable potentials. Moreover, the uniqueness was obtained in [Reference Kempton17] assuming the so-called big images and preimages property (BIP) condition on X, in the setting of locally constant potentials. Later, in [Reference Freire and Vargas12], the existence of accumulation points at zero temperature was shown under the hypothesis of transitivity. Also, in [Reference Souza and Vargas27], the existence of weak
$(X, T)$
is a finite Markov shift, the existence of ground states follows as an immediate consequence of the compactness of the set of Borel probability measures on X. However, the uniqueness of the accumulation point at zero temperature was studied in the setting of locally constant potentials in [Reference Brémont6, Reference Chazottes, Gambaudo and Ugalde8, Reference Leplaideur18] assuming transitivity on the dynamics. It is important to mention that Chazottes and Hochman in [Reference Chazottes and Hochman9] reported an example where the existence of the limit at zero temperature of the equilibrium state fails when the potential is not locally constant. Another interesting example of the existence of more than one accumulation point at zero temperature in the setting of the so-called XY models was presented in [Reference van Enter and Ruszel28]. When the alphabet is countable infinite, seminal works about the existence of accumulation points at zero temperature were performed considering the well-known finitely irreducible condition, which is a strong assumption on the combinatorics of the shift X that allowed the generalization of several of the main results of the thermodynamic formalism in the countable Markov shifts context, see for instance [Reference Jenkinson, Mauldin and Urbański15, Reference Kempton17, Reference Mauldin and Urbański20]. Actually, in [Reference Jenkinson, Mauldin and Urbański15], the existence of ground states was proved in the setting of summable potentials. Moreover, the uniqueness was obtained in [Reference Kempton17] assuming the so-called big images and preimages property (BIP) condition on X, in the setting of locally constant potentials. Later, in [Reference Freire and Vargas12], the existence of accumulation points at zero temperature was shown under the hypothesis of transitivity. Also, in [Reference Souza and Vargas27], the existence of weak
![]() $^\star $
accumulation points at zero temperature was proved for a wider class of positive recurrent potentials defined on topologically transitive countable Markov shifts satisfying suitable conditions. However, in [Reference Lopes and Vargas19], conditions were presented to guarantee the existence of ground states in a wider class of linear dynamical systems defined on Banach spaces of infinite dimension.
$^\star $
accumulation points at zero temperature was proved for a wider class of positive recurrent potentials defined on topologically transitive countable Markov shifts satisfying suitable conditions. However, in [Reference Lopes and Vargas19], conditions were presented to guarantee the existence of ground states in a wider class of linear dynamical systems defined on Banach spaces of infinite dimension.
In this paper, we prove the uniqueness of the accumulation point at infinity of the family of equilibrium states
![]() $(\mu _t)_{t\geq 1}$
assuming that the potential
$(\mu _t)_{t\geq 1}$
assuming that the potential
![]() $\phi $
has bounded variations and finite Gurevich pressure. The above serve as a generalization of the results presented in [Reference Kempton17] to the case of topologically transitive countable Markov shifts. To do that, we show that the equilibrium states can be expressed as stationary Markov measures, see [Reference Gurevich13] for details. In addition, we use an approximation of the topologically transitive countable Markov shift by finite Markov subshifts, in a similar way as in [Reference Kempton17], with the aim of obtaining an approximation of the unique accumulation point at zero temperature of the family
$\phi $
has bounded variations and finite Gurevich pressure. The above serve as a generalization of the results presented in [Reference Kempton17] to the case of topologically transitive countable Markov shifts. To do that, we show that the equilibrium states can be expressed as stationary Markov measures, see [Reference Gurevich13] for details. In addition, we use an approximation of the topologically transitive countable Markov shift by finite Markov subshifts, in a similar way as in [Reference Kempton17], with the aim of obtaining an approximation of the unique accumulation point at zero temperature of the family
![]() $(\mu _t)_{t\geq 1}$
by the ones obtained in the setting of finite Markov subshifts. It is important to mention that we assume uniqueness of the accumulation point at zero temperature in the compact context, which was actually proved in [Reference Brémont6, Reference Chazottes, Gambaudo and Ugalde8, Reference Leplaideur18]. Additionally, we present some examples where the uniqueness of the accumulation point is guaranteed assuming weaker conditions on the potential
$(\mu _t)_{t\geq 1}$
by the ones obtained in the setting of finite Markov subshifts. It is important to mention that we assume uniqueness of the accumulation point at zero temperature in the compact context, which was actually proved in [Reference Brémont6, Reference Chazottes, Gambaudo and Ugalde8, Reference Leplaideur18]. Additionally, we present some examples where the uniqueness of the accumulation point is guaranteed assuming weaker conditions on the potential
![]() $\phi $
.
$\phi $
.
The paper is organized as follows. In §2, we introduce some definitions on thermodynamic formalism in the setting of countable Markov shifts and recall some previously known results. In §3, we study the accumulation points of the family of equilibrium states
![]() $(\mu _t)_{t\geq 1}$
at infinity and we prove the existence of the zero-temperature limit of equilibrium states on topologically transitive countable Markov shifts. Finally, in §4, we present two examples of the zero-temperature limit of the equilibrium state on the renewal shift.
$(\mu _t)_{t\geq 1}$
at infinity and we prove the existence of the zero-temperature limit of equilibrium states on topologically transitive countable Markov shifts. Finally, in §4, we present two examples of the zero-temperature limit of the equilibrium state on the renewal shift.
2 Preliminaries
Let S be a countable set of states (when
![]() $|S|=\infty $
, let us consider
$|S|=\infty $
, let us consider
![]() $S=\mathbb {N}$
). Assume that
$S=\mathbb {N}$
). Assume that
![]() $A=(A(i,j))_{S\times S}$
is a square matrix of zeroes and ones with no columns or rows whose entries are all zeroes. Fix the set
$A=(A(i,j))_{S\times S}$
is a square matrix of zeroes and ones with no columns or rows whose entries are all zeroes. Fix the set
![]() $\mathbb {N}_0 = \mathbb {N}\cup \{0\}$
. The countable Markov shift is the set of all the sequences allowed by the matrix A, that is,
$\mathbb {N}_0 = \mathbb {N}\cup \{0\}$
. The countable Markov shift is the set of all the sequences allowed by the matrix A, that is,
equipped with the topology generated by the collection of cylinders
where
![]() $x_i\in S$
, for every
$x_i\in S$
, for every
![]() $0\leq i\leq n-1$
, and the shift map (to be defined below) acting on it. The sigma-algebra considered on
$0\leq i\leq n-1$
, and the shift map (to be defined below) acting on it. The sigma-algebra considered on
![]() $\Sigma $
is the smallest one containing all the cylinders, that is, the Borel
$\Sigma $
is the smallest one containing all the cylinders, that is, the Borel
![]() $\sigma $
-algebra. In the case where the set of states S is finite, the shift
$\sigma $
-algebra. In the case where the set of states S is finite, the shift
![]() $\Sigma $
is known as a finite Markov shift. A path of length n, denoted by
$\Sigma $
is known as a finite Markov shift. A path of length n, denoted by
![]() $\underline {\gamma }=x_0x_1\!\ldots x_{n}$
, is an element of
$\underline {\gamma }=x_0x_1\!\ldots x_{n}$
, is an element of
![]() $S^{n+1}$
satisfying
$S^{n+1}$
satisfying
![]() $[x_0x_1\ldots x_{n}]\neq \emptyset $
and we say that the path
$[x_0x_1\ldots x_{n}]\neq \emptyset $
and we say that the path
![]() $\underline {\gamma }$
passes from
$\underline {\gamma }$
passes from
![]() $x_0$
to
$x_0$
to
![]() $x_n$
through the states
$x_n$
through the states
![]() $x_1$
, …,
$x_1$
, …,
![]() $x_{n-1}$
. The set of paths of length n is denoted by
$x_{n-1}$
. The set of paths of length n is denoted by
![]() $\mathcal {P}_n(\Sigma )$
and we denote the set of paths on
$\mathcal {P}_n(\Sigma )$
and we denote the set of paths on
![]() $\Sigma $
by
$\Sigma $
by
![]() $\mathcal {P}(\Sigma ):=\bigcup _{n\geq 1}\mathcal {P}_n(\Sigma )$
. As usual, the function
$\mathcal {P}(\Sigma ):=\bigcup _{n\geq 1}\mathcal {P}_n(\Sigma )$
. As usual, the function
![]() $\sigma :\Sigma \to \Sigma $
defined by
$\sigma :\Sigma \to \Sigma $
defined by
![]() $(\sigma x)_i=x_{i+1}$
, for every
$(\sigma x)_i=x_{i+1}$
, for every
![]() $i\in \mathbb {N}_0$
, is called the shift map.
$i\in \mathbb {N}_0$
, is called the shift map.
The countable Markov shift
![]() $\Sigma $
is topologically transitive if for every
$\Sigma $
is topologically transitive if for every
![]() $a,b\in S$
, there is a path connecting a and b, and it is topologically mixing if there exists
$a,b\in S$
, there is a path connecting a and b, and it is topologically mixing if there exists
![]() $N\in \mathbb {N}$
such that there is a path of length n connecting a and b, for all
$N\in \mathbb {N}$
such that there is a path of length n connecting a and b, for all
![]() $n\geq N$
. Also, we say that
$n\geq N$
. Also, we say that
![]() $\Sigma $
satisfies the BIP if there are
$\Sigma $
satisfies the BIP if there are
![]() $b_1,b_2,\ldots ,b_N\in S$
such that, for all
$b_1,b_2,\ldots ,b_N\in S$
such that, for all
![]() $a\in S$
, there exists
$a\in S$
, there exists
![]() $1\leq i,j\leq N$
such that
$1\leq i,j\leq N$
such that
![]() $A(a,b_i)=A(b_j,a)=1$
.
$A(a,b_i)=A(b_j,a)=1$
.
Throughout the paper, we call potential a continuous function
![]() $\phi :\Sigma \to \mathbb {R}$
determining the interactions on the lattice (that is, the one used to define the Ruelle operator). For each
$\phi :\Sigma \to \mathbb {R}$
determining the interactions on the lattice (that is, the one used to define the Ruelle operator). For each
![]() $n\geq 1$
, we define
$n\geq 1$
, we define
![]() $S_n\phi (x):=\sum _{i=0}^{n-1}\phi (\sigma ^i(x))$
as the nth ergodic sum and the nth variation of
$S_n\phi (x):=\sum _{i=0}^{n-1}\phi (\sigma ^i(x))$
as the nth ergodic sum and the nth variation of
![]() $\phi $
as
$\phi $
as
We say that
![]() $\phi $
has bounded variations if
$\phi $
has bounded variations if
 $$ \begin{align*}\overline{\mathop{\mathrm{Var}}\nolimits}(\phi):=\sum_{n= 1}^{\infty}\mathop{\mathrm{Var}}\nolimits_n(\phi)<\infty,\end{align*} $$
$$ \begin{align*}\overline{\mathop{\mathrm{Var}}\nolimits}(\phi):=\sum_{n= 1}^{\infty}\mathop{\mathrm{Var}}\nolimits_n(\phi)<\infty,\end{align*} $$
and has summable variations if
![]() $\sum _{n= 2}^{\infty }\mathop {\mathrm {Var}}\nolimits _n(\phi )<\infty $
. Also,
$\sum _{n= 2}^{\infty }\mathop {\mathrm {Var}}\nolimits _n(\phi )<\infty $
. Also,
![]() $\phi $
is a locally constant if there exists an
$\phi $
is a locally constant if there exists an
![]() $n\in \mathbb {N}$
such that
$n\in \mathbb {N}$
such that
![]() $\mathop {\mathrm {Var}}\nolimits _n(\phi )=0$
. However, we say that
$\mathop {\mathrm {Var}}\nolimits _n(\phi )=0$
. However, we say that
![]() $\phi $
is a summable potential if it satisfies
$\phi $
is a summable potential if it satisfies
where
![]() $\sup (\phi |_{[i]}):=\sup \{\phi (x): x\in [i]\}$
, for every
$\sup (\phi |_{[i]}):=\sup \{\phi (x): x\in [i]\}$
, for every
![]() $i\in \mathbb {N}$
. The so-called summability condition becomes important here, because it allows to guarantee a suitable behaviour of the Gurevich pressure, also allows to have a uniform control on the tails of the measures belonging to the family
$i\in \mathbb {N}$
. The so-called summability condition becomes important here, because it allows to guarantee a suitable behaviour of the Gurevich pressure, also allows to have a uniform control on the tails of the measures belonging to the family
![]() $(\mu _{t})_{t\geq 1}$
and implies the existence of maximizing measures for the potential
$(\mu _{t})_{t\geq 1}$
and implies the existence of maximizing measures for the potential
![]() $\phi $
(see for instance [Reference Bissacot and Freire3, Reference Jenkinson, Mauldin and Urbański15]).
$\phi $
(see for instance [Reference Bissacot and Freire3, Reference Jenkinson, Mauldin and Urbański15]).
Throughout the paper,
![]() $\mathcal {M}(\Sigma )$
denotes the set of Borel probability measures on
$\mathcal {M}(\Sigma )$
denotes the set of Borel probability measures on
![]() $\Sigma $
,
$\Sigma $
,
![]() $\mathcal {M}_{\sigma }(\Sigma )$
the set of
$\mathcal {M}_{\sigma }(\Sigma )$
the set of
![]() $\sigma $
-invariant Borel probability measures on
$\sigma $
-invariant Borel probability measures on
![]() $\Sigma $
and
$\Sigma $
and
![]() $\mathcal {M}_{\mathrm {erg}}(\Sigma )$
the set of Borel ergodic probability measures on
$\mathcal {M}_{\mathrm {erg}}(\Sigma )$
the set of Borel ergodic probability measures on
![]() $\Sigma $
. For any
$\Sigma $
. For any
![]() $\mu \in \mathcal {M}(\Sigma )$
, we use the following notation:
$\mu \in \mathcal {M}(\Sigma )$
, we use the following notation:
For every
![]() $\nu \in \mathcal {M}_{\sigma }(\Sigma )$
, the metric pressure is defined by the following quantity:
$\nu \in \mathcal {M}_{\sigma }(\Sigma )$
, the metric pressure is defined by the following quantity:
where
![]() $h(\nu )$
is the metric entropy associated to measure
$h(\nu )$
is the metric entropy associated to measure
![]() $\nu $
(see [Reference Sarig24, Reference Sarig23]). The thermodynamic formalism studies the existence and properties of measures
$\nu $
(see [Reference Sarig24, Reference Sarig23]). The thermodynamic formalism studies the existence and properties of measures
![]() $\nu \in \mathcal {M}_{\sigma }(\Sigma )$
that maximize the value of the metric pressure defined in equation (2.1). Note that the sum at the right side of equation (2.1) is not always well defined, the foregoing occurs because the potential
$\nu \in \mathcal {M}_{\sigma }(\Sigma )$
that maximize the value of the metric pressure defined in equation (2.1). Note that the sum at the right side of equation (2.1) is not always well defined, the foregoing occurs because the potential
![]() $\phi $
may not be
$\phi $
may not be
![]() $\nu $
-integrable or it could even happen that
$\nu $
-integrable or it could even happen that
![]() $h(\nu )=+\infty $
and
$h(\nu )=+\infty $
and
![]() $\nu (\phi )=-\infty $
. By the above, the usual definition of topological pressure in the setting of countable Markov shifts is given by
$\nu (\phi )=-\infty $
. By the above, the usual definition of topological pressure in the setting of countable Markov shifts is given by
However, the Gurevich pressure of
![]() $\phi $
is defined by
$\phi $
is defined by
where
![]() . It is well known that
. It is well known that
![]() $P_G(\phi )$
is independent of the choice of
$P_G(\phi )$
is independent of the choice of
![]() $a\in \mathbb {N}$
when the countable Markov shift
$a\in \mathbb {N}$
when the countable Markov shift
![]() $\Sigma $
is topologically transitive. Moreover, under the assumptions above,
$\Sigma $
is topologically transitive. Moreover, under the assumptions above,
![]() $-\infty < P_G(\phi )\leq \infty $
. Actually, Sarig in [Reference Sarig24] showed that for a topologically mixing countable Markov shift
$-\infty < P_G(\phi )\leq \infty $
. Actually, Sarig in [Reference Sarig24] showed that for a topologically mixing countable Markov shift
![]() $\Sigma $
and a potential
$\Sigma $
and a potential
![]() $\phi $
with summable variations and
$\phi $
with summable variations and
![]() $\sup \phi <\infty $
, the Gurevich pressure satisfies the variational principle and thus
$\sup \phi <\infty $
, the Gurevich pressure satisfies the variational principle and thus
Furthermore, an analogous result in the setting of topologically transitive countable Markov shifts was presented in [Reference Buzzi and Sarig7].
A measure
![]() $\mu \in \mathcal {M}_{\sigma }(\Sigma )$
is an equilibrium state associated to the potential
$\mu \in \mathcal {M}_{\sigma }(\Sigma )$
is an equilibrium state associated to the potential
![]() $\phi $
if the supremum of equation (2.2) is attained for
$\phi $
if the supremum of equation (2.2) is attained for
![]() $\mu $
, that is, when it satisfies
$\mu $
, that is, when it satisfies
We say that a potential
![]() $\phi $
is recurrent if
$\phi $
is recurrent if
For every
![]() $n\geq 1$
and
$n\geq 1$
and
![]() $a\in S$
, let
$a\in S$
, let
where
and
![]() $\inf \emptyset :=\infty $
(with
$\inf \emptyset :=\infty $
(with
![]() $0\cdot \infty :=0$
). Fix some
$0\cdot \infty :=0$
). Fix some
![]() $a\in S$
. We say that a recurrent potential
$a\in S$
. We say that a recurrent potential
![]() $\phi $
is positive recurrent if
$\phi $
is positive recurrent if
In the case where the above series diverges, the potential
![]() $\phi $
is called null recurrent. It is important to point out that when
$\phi $
is called null recurrent. It is important to point out that when
![]() $\Sigma $
is topologically transitive, all modes of recurrence defined above are independent of the choice of
$\Sigma $
is topologically transitive, all modes of recurrence defined above are independent of the choice of
![]() $a\in S$
. We refer the reader to [Reference Sarig23] for details. Also, when
$a\in S$
. We refer the reader to [Reference Sarig23] for details. Also, when
![]() $|S|<\infty $
, we have that any potential
$|S|<\infty $
, we have that any potential
![]() $\phi $
is positive recurrent. The positive recurrent potentials have an important role in the setting in which we are interested in, because they are the ones with an equilibrium state associated to them, as we describe below.
$\phi $
is positive recurrent. The positive recurrent potentials have an important role in the setting in which we are interested in, because they are the ones with an equilibrium state associated to them, as we describe below.
A well-known tool in thermodynamic formalism useful to find equilibrium states is the so-called Ruelle operator, which is defined in the setting of countable Markov shifts by the following equation:
 $$ \begin{align} L_{\phi}f(x):=\sum_{\sigma(y)=x}\mathop{\mathrm{exp}}\nolimits({\phi(y)})f(y). \end{align} $$
$$ \begin{align} L_{\phi}f(x):=\sum_{\sigma(y)=x}\mathop{\mathrm{exp}}\nolimits({\phi(y)})f(y). \end{align} $$
When
![]() $|S|<\infty $
, the Markov shift
$|S|<\infty $
, the Markov shift
![]() $\Sigma $
is a compact metric space, the Ruelle operator is well defined on the space of functions
$\Sigma $
is a compact metric space, the Ruelle operator is well defined on the space of functions
![]() $C(\Sigma )$
and we have the famous Ruelle’s Perron–Frobenius theorem, which guarantees the existence of a main eigenvalue with the associated eigenfunctions to the Ruelle operator and eigenmeasures for the dual of the Ruelle operator, see [Reference Bowen5, Reference Ruelle22] for complete details. In general, for countable Markov shifts with
$C(\Sigma )$
and we have the famous Ruelle’s Perron–Frobenius theorem, which guarantees the existence of a main eigenvalue with the associated eigenfunctions to the Ruelle operator and eigenmeasures for the dual of the Ruelle operator, see [Reference Bowen5, Reference Ruelle22] for complete details. In general, for countable Markov shifts with
![]() $|S|=\mathbb {N}$
, the series in equation (2.6) can be infinite. However, in [Reference Cyr11, Reference Mauldin and Urbański20, Reference Sarig24, Reference Shwartz26], one can find different types of regularity that can be considered, both on the countable Markov shift
$|S|=\mathbb {N}$
, the series in equation (2.6) can be infinite. However, in [Reference Cyr11, Reference Mauldin and Urbański20, Reference Sarig24, Reference Shwartz26], one can find different types of regularity that can be considered, both on the countable Markov shift
![]() $\Sigma $
and on the potential
$\Sigma $
and on the potential
![]() $\phi :\Sigma \to \mathbb {R}$
, to have the Ruelle operator in equation (2.6) well defined and obtain an analogous result to the so-called Ruelle’s Perron–Frobenius theorem.
$\phi :\Sigma \to \mathbb {R}$
, to have the Ruelle operator in equation (2.6) well defined and obtain an analogous result to the so-called Ruelle’s Perron–Frobenius theorem.
For positive recurrent potentials
![]() $\phi $
with
$\phi $
with
![]() $P_G(\phi ) < \infty $
, O. Sarig showed that there exists a
$P_G(\phi ) < \infty $
, O. Sarig showed that there exists a
![]() $\phi $
-conformal sigma-finite measure
$\phi $
-conformal sigma-finite measure
![]() $\nu $
, that is, a finite Borel measure satisfying
$\nu $
, that is, a finite Borel measure satisfying
Here the identity in equation (2.7) is denoted by
![]() $L_{\phi }^{*}\nu =\unicode{x3bb} \nu $
(see Theorem
$L_{\phi }^{*}\nu =\unicode{x3bb} \nu $
(see Theorem
![]() $4.9$
in [Reference Sarig23]).
$4.9$
in [Reference Sarig23]).
In the context of topologically transitive countable Markov shifts, for any potential
![]() $\phi $
bounded from above, with summable variations and finite Gurevich pressure, there is at most one equilibrium state and, in the case where the existence is guaranteed, the equilibrium state is given by
$\phi $
bounded from above, with summable variations and finite Gurevich pressure, there is at most one equilibrium state and, in the case where the existence is guaranteed, the equilibrium state is given by
![]() $\mathop {\mathrm{d}}\nolimits \mu = h\mathop {\mathrm {d}}\nolimits \nu $
, where h is the main eigenfunction of
$\mathop {\mathrm{d}}\nolimits \mu = h\mathop {\mathrm {d}}\nolimits \nu $
, where h is the main eigenfunction of
![]() $L_\phi $
, that is,
$L_\phi $
, that is,
![]() $L_{\phi }h=\mathop {\mathrm {exp}}\nolimits (P_G(\phi ))h$
, and
$L_{\phi }h=\mathop {\mathrm {exp}}\nolimits (P_G(\phi ))h$
, and
![]() $\nu $
is a sigma-finite measure such that
$\nu $
is a sigma-finite measure such that
![]() $L_{\phi }^{*}\nu =\mathop {\mathrm {exp}}\nolimits (P_G(\phi ))\nu $
(for more details, see Theorems
$L_{\phi }^{*}\nu =\mathop {\mathrm {exp}}\nolimits (P_G(\phi ))\nu $
(for more details, see Theorems
![]() $1.1$
and
$1.1$
and
![]() $1.2$
in [Reference Buzzi and Sarig7]).
$1.2$
in [Reference Buzzi and Sarig7]).
Remark 2.1. The hypotheses that we assume throughout the paper to prove the existence of the zero-temperature limit are the following: we consider
![]() $\Sigma $
as a topologically transitive countable Markov shift and
$\Sigma $
as a topologically transitive countable Markov shift and
![]() $\phi :\Sigma \to \mathbb {R}$
as a summable potential such that
$\phi :\Sigma \to \mathbb {R}$
as a summable potential such that
![]() ${\overline {\mathop {\mathrm {Var}}\nolimits }}(\phi )<\infty $
and
${\overline {\mathop {\mathrm {Var}}\nolimits }}(\phi )<\infty $
and
![]() $P_G(\phi )<\infty $
. Under these hypotheses, Theorem
$P_G(\phi )<\infty $
. Under these hypotheses, Theorem
![]() $1.1$
from [Reference Buzzi and Sarig7] assures that the Gurevich pressure satisfies the variational principle in equation (2.4). Moreover, by Theorem
$1.1$
from [Reference Buzzi and Sarig7] assures that the Gurevich pressure satisfies the variational principle in equation (2.4). Moreover, by Theorem
![]() $1$
from [Reference Freire and Vargas12], we have that
$1$
from [Reference Freire and Vargas12], we have that
for every
![]() $t\geq 1$
, where
$t\geq 1$
, where
![]() $\mu _{t}$
is the unique equilibrium state associated to the potential
$\mu _{t}$
is the unique equilibrium state associated to the potential
![]() $t\phi $
. In addition, the existence of accumulation points at infinity for the family
$t\phi $
. In addition, the existence of accumulation points at infinity for the family
![]() $(\mu _{t})_{t\geq 1}$
is also guaranteed. It is important to point out that we will additionally assume in Theorem 3.1 that
$(\mu _{t})_{t\geq 1}$
is also guaranteed. It is important to point out that we will additionally assume in Theorem 3.1 that
![]() $\phi $
is a locally constant potential.
$\phi $
is a locally constant potential.
Let us define
A measure
![]() $\mu \in \mathcal {M}_{\sigma }(\Sigma )$
is called
$\mu \in \mathcal {M}_{\sigma }(\Sigma )$
is called
![]() $\phi $
-maximizing if
$\phi $
-maximizing if
![]() $\alpha (\phi )=\mu (\phi )$
. We denote by
$\alpha (\phi )=\mu (\phi )$
. We denote by
![]() $\mathcal {M}_{\mathrm{max}}(\phi )$
the set of
$\mathcal {M}_{\mathrm{max}}(\phi )$
the set of
![]() $\phi $
-maximizing measures.
$\phi $
-maximizing measures.
In the setting of finite Markov shifts, it is widely known that the existence of maximizing measures is a direct consequence of the compactness of the subshift. Nevertheless, in the non-compact approach, that is, when the alphabet S is countable infinite, one requires additional conditions on the regularity of the potential. Indeed, in Theorem
![]() $1$
of [Reference Bissacot and Freire3], the authors proposed conditions on the potential
$1$
of [Reference Bissacot and Freire3], the authors proposed conditions on the potential
![]() $\phi $
that guarantee the existence of such a kind of measure. To be specific, they proved that any coercive potential with bounded variations has a maximizing measure supported on a finite Markov shift
$\phi $
that guarantee the existence of such a kind of measure. To be specific, they proved that any coercive potential with bounded variations has a maximizing measure supported on a finite Markov shift
![]() $\Sigma _I$
, where
$\Sigma _I$
, where
![]() $I\subset \mathbb {N}$
is a finite set such that
$I\subset \mathbb {N}$
is a finite set such that
![]() $(\Sigma _I,\sigma )$
is a topologically transitive countable Markov shift. Actually, the class of potentials satisfying the so-called coercive property considered in [Reference Bissacot and Freire3] strictly contains the class of summable potentials. For instance, the potential
$(\Sigma _I,\sigma )$
is a topologically transitive countable Markov shift. Actually, the class of potentials satisfying the so-called coercive property considered in [Reference Bissacot and Freire3] strictly contains the class of summable potentials. For instance, the potential
![]() $\phi (x) := -\log (x_0)$
is coercive, but it is not a summable one.
$\phi (x) := -\log (x_0)$
is coercive, but it is not a summable one.
Let
![]() $\mathrm {Per}_p(\Sigma )$
be the set of points
$\mathrm {Per}_p(\Sigma )$
be the set of points
![]() $x\in \Sigma $
such that
$x\in \Sigma $
such that
![]() $\sigma ^p(x)=x$
and consider
$\sigma ^p(x)=x$
and consider
![]() $\mathrm {Per}(\Sigma ):=\bigcup _{p\geq 1}\mathrm {Per}_p(\Sigma )$
. For every
$\mathrm {Per}(\Sigma ):=\bigcup _{p\geq 1}\mathrm {Per}_p(\Sigma )$
. For every
![]() $x\in \Sigma $
, define
$x\in \Sigma $
, define
![]() $\alpha (\phi ,x):=\limsup _{n\to \infty }({1}/{n})S_n\phi (x)$
. So, when
$\alpha (\phi ,x):=\limsup _{n\to \infty }({1}/{n})S_n\phi (x)$
. So, when
![]() $x\in \mathrm {Per}(\Sigma )$
, it follows that
$x\in \mathrm {Per}(\Sigma )$
, it follows that
![]() $\alpha (\phi ,x) = ({1}/{p})S_p\phi (x)$
, where p is the period of x (that is, the minimum
$\alpha (\phi ,x) = ({1}/{p})S_p\phi (x)$
, where p is the period of x (that is, the minimum
![]() $p \in \mathbb {N}$
such that
$p \in \mathbb {N}$
such that
![]() $\sigma ^p(x)=x$
). Denote by
$\sigma ^p(x)=x$
). Denote by
![]() $\mathcal {M}_{\mathrm {per}}(\Sigma )$
the set of periodic probability measures on
$\mathcal {M}_{\mathrm {per}}(\Sigma )$
the set of periodic probability measures on
![]() $\Sigma $
, that is, those supported on periodic orbits. Since
$\Sigma $
, that is, those supported on periodic orbits. Since
by the ergodic decomposition theorem, we have
![]() $\alpha (\phi )=\sup \{\alpha (\phi ,x): x\in Per(\Sigma )\}$
(see for instance [Reference Bissacot and Freire3]). This last identity will be used later in Example 4.2.
$\alpha (\phi )=\sup \{\alpha (\phi ,x): x\in Per(\Sigma )\}$
(see for instance [Reference Bissacot and Freire3]). This last identity will be used later in Example 4.2.
3 Zero-temperature limits on topologically transitive countable Markov shifts
As we already said in the previous section, for any
![]() $t\geq 1$
, there is a unique equilibrium state
$t\geq 1$
, there is a unique equilibrium state
![]() $\mu _{t}\in \mathcal {M}_{\sigma }(\Sigma )$
associated to the potential
$\mu _{t}\in \mathcal {M}_{\sigma }(\Sigma )$
associated to the potential
![]() $t\phi $
. Moreover, by [Reference Freire and Vargas12], the family of equilibrium states
$t\phi $
. Moreover, by [Reference Freire and Vargas12], the family of equilibrium states
![]() $(\mu _{t})_{t\geq 1}$
has weak
$(\mu _{t})_{t\geq 1}$
has weak
![]() $^\star $
accumulation points at
$^\star $
accumulation points at
![]() $t\to \infty $
. In addition, Theorem 3.1, which is the main result of this paper, states that there is at most one of those accumulation points for
$t\to \infty $
. In addition, Theorem 3.1, which is the main result of this paper, states that there is at most one of those accumulation points for
![]() $(\mu _{t})_{t\geq 1}$
when
$(\mu _{t})_{t\geq 1}$
when
![]() $\phi $
is a locally constant potential, that is, there is
$\phi $
is a locally constant potential, that is, there is
![]() $n \in \mathbb {N}$
such that
$n \in \mathbb {N}$
such that
![]() $\phi =\phi (x_0 \ldots x_{n-1})$
. The statement of the result is the following.
$\phi =\phi (x_0 \ldots x_{n-1})$
. The statement of the result is the following.
Theorem 3.1. Let
![]() $\Sigma $
be a topologically transitive countable Markov shift and let
$\Sigma $
be a topologically transitive countable Markov shift and let
![]() $\phi :\Sigma \to \mathbb {R}$
be a summable locally constant potential such that
$\phi :\Sigma \to \mathbb {R}$
be a summable locally constant potential such that
![]() ${\mathop {\mathrm{Var}}\nolimits }_1(\phi )<\infty $
and
${\mathop {\mathrm{Var}}\nolimits }_1(\phi )<\infty $
and
![]() ${P_G(\phi )<\infty }$
. Then, the limit
${P_G(\phi )<\infty }$
. Then, the limit
![]() $\lim _{t\to \infty }\mu _t$
exists in the weak
$\lim _{t\to \infty }\mu _t$
exists in the weak
![]() $^\star $
topology, where
$^\star $
topology, where
![]() $\mu _{t}\in \mathcal {M}_{\sigma }(\Sigma )$
is the unique equilibrium state associated to the potential
$\mu _{t}\in \mathcal {M}_{\sigma }(\Sigma )$
is the unique equilibrium state associated to the potential
![]() $t\phi $
, for
$t\phi $
, for
![]() $t\geq 1$
. Furthermore, the limit measure
$t\geq 1$
. Furthermore, the limit measure
![]() $\mu _\infty $
is
$\mu _\infty $
is
![]() $\phi $
-maximizing.
$\phi $
-maximizing.
The main idea to prove the above theorem is to obtain an approximation of the weak
![]() $^\star $
accumulation points at
$^\star $
accumulation points at
![]() $\infty $
of the family
$\infty $
of the family
![]() $(\mu _t)_{t\geq 1}$
by the unique accumulation point at
$(\mu _t)_{t\geq 1}$
by the unique accumulation point at
![]() $\infty $
of a family of equilibrium states
$\infty $
of a family of equilibrium states
![]() $(\vartheta _{t})_{t\geq 1}$
defined on a suitable finite Markov shift
$(\vartheta _{t})_{t\geq 1}$
defined on a suitable finite Markov shift
![]() $\Sigma '$
, which guarantees uniqueness in the non-compact context. Here we use a similar technique to that in [Reference Kempton17] guaranteeing that in our setting, any equilibrium state can be expressed as a stationary Markov measure and that expression can be used to obtain the desired approximation.
$\Sigma '$
, which guarantees uniqueness in the non-compact context. Here we use a similar technique to that in [Reference Kempton17] guaranteeing that in our setting, any equilibrium state can be expressed as a stationary Markov measure and that expression can be used to obtain the desired approximation.
Our first goal here is to characterize the behaviour of those accumulation points and the asymptotic behaviour of the map
![]() $t \mapsto P_G(t\phi )$
. To do that, next we present a lemma that will be useful to state and prove Proposition 3.1, which assures that every weak
$t \mapsto P_G(t\phi )$
. To do that, next we present a lemma that will be useful to state and prove Proposition 3.1, which assures that every weak
![]() $^\star $
accumulation point at
$^\star $
accumulation point at
![]() $\infty $
of the family
$\infty $
of the family
![]() $(\mu _{t})_{t\geq 1}$
is a maximizing measure for the potential
$(\mu _{t})_{t\geq 1}$
is a maximizing measure for the potential
![]() $\phi $
. The following lemma is already a well-known result in the matter of countable Markov shifts satisfying the BIP condition, for details see [Reference Bissacot, Mengue and Pérez4], and its validity basically depends on the existence of equilibrium states
$\phi $
. The following lemma is already a well-known result in the matter of countable Markov shifts satisfying the BIP condition, for details see [Reference Bissacot, Mengue and Pérez4], and its validity basically depends on the existence of equilibrium states
![]() $\mu _t$
, for each
$\mu _t$
, for each
![]() $t\geq 1$
. Since, the existence of each one of the
$t\geq 1$
. Since, the existence of each one of the
![]() $\mu _t$
states is guaranteed in the topologically transitive context (see [Reference Freire and Vargas12]), here, we expect to obtain something similar to the result in [Reference Bissacot, Mengue and Pérez4]. The statement of the lemma is the following.
$\mu _t$
states is guaranteed in the topologically transitive context (see [Reference Freire and Vargas12]), here, we expect to obtain something similar to the result in [Reference Bissacot, Mengue and Pérez4]. The statement of the lemma is the following.
Lemma 3.2. Given
![]() $t \geq 1$
, assume that
$t \geq 1$
, assume that
![]() $\mu _t\in \mathcal {M}_{\sigma }(\Sigma )$
is an equilibrium state associated to the potential
$\mu _t\in \mathcal {M}_{\sigma }(\Sigma )$
is an equilibrium state associated to the potential
![]() $t\phi $
. Then:
$t\phi $
. Then:
-
(i) the family
 $\{h(\mu _t)\}_{t\geq 1}$
is decreasing;
$\{h(\mu _t)\}_{t\geq 1}$
is decreasing; -
(ii)
 $\lim \nolimits _{t\to \infty }({P_G(t\phi )}/{t})=\alpha (\phi )$
.
$\lim \nolimits _{t\to \infty }({P_G(t\phi )}/{t})=\alpha (\phi )$
.
Proof. A similar procedure to that in Lemma
![]() $9$
from [Reference Bissacot, Mengue and Pérez4] shows that the family
$9$
from [Reference Bissacot, Mengue and Pérez4] shows that the family
![]() $\{\mu _{t}(\phi )\}_{t\geq 1}$
is increasing. Fix
$\{\mu _{t}(\phi )\}_{t\geq 1}$
is increasing. Fix
![]() $1\leq t_1<t_2$
. Since
$1\leq t_1<t_2$
. Since
![]() $\mu _1\in \mathcal {M}_{\sigma }(\Sigma )$
is an equilibrium state for the potential
$\mu _1\in \mathcal {M}_{\sigma }(\Sigma )$
is an equilibrium state for the potential
![]() $t_1\phi $
, we have
$t_1\phi $
, we have
Note that by the variational principle in equation (2.4), we have
![]() $P_G(t_1\phi )> h(\mu _{t_2})+t_1\mu _{t_2}(\phi )$
. Hence, replacing in equation (3.1), we obtain
$P_G(t_1\phi )> h(\mu _{t_2})+t_1\mu _{t_2}(\phi )$
. Hence, replacing in equation (3.1), we obtain
As
![]() $\mu _{t_2}(\phi )-\mu _{t_1}(\phi )> 0$
, so
$\mu _{t_2}(\phi )-\mu _{t_1}(\phi )> 0$
, so
![]() $h(\mu _{t_1})> h(\mu _{t_2})$
and thus the family
$h(\mu _{t_1})> h(\mu _{t_2})$
and thus the family
![]() $\{h(\mu _t)\}_{t\geq 1}$
is decreasing.
$\{h(\mu _t)\}_{t\geq 1}$
is decreasing.
Now we will prove item (ii). Note that
![]() $|\mathcal {M}_{\mathrm{max}}(\phi )|\neq \emptyset $
, see Theorem
$|\mathcal {M}_{\mathrm{max}}(\phi )|\neq \emptyset $
, see Theorem
![]() $1$
from [Reference Bissacot and Freire3]. Let
$1$
from [Reference Bissacot and Freire3]. Let
![]() $\nu \in \mathcal {M}_{\mathrm{max}}(\phi )$
and
$\nu \in \mathcal {M}_{\mathrm{max}}(\phi )$
and
![]() $t\geq 1$
, then by the variational principle of equation (2.4), we have
$t\geq 1$
, then by the variational principle of equation (2.4), we have
Later,
However, the map
![]() $t\mapsto P_G(t{\phi })-t\alpha (\phi )$
is decreasing in
$t\mapsto P_G(t{\phi })-t\alpha (\phi )$
is decreasing in
![]() $[1,\infty )$
, see [Reference Bissacot, Mengue and Pérez4]. Therefore,
$[1,\infty )$
, see [Reference Bissacot, Mengue and Pérez4]. Therefore,
![]() $0\leq P_G(t{\phi })-t\alpha (\phi )\leq P_G({\phi })-\alpha (\phi )<\infty $
for every
$0\leq P_G(t{\phi })-t\alpha (\phi )\leq P_G({\phi })-\alpha (\phi )<\infty $
for every
![]() $t \geq 1$
, so
$t \geq 1$
, so
Proposition 3.1. Every weak
![]() $^\star $
accumulation point at
$^\star $
accumulation point at
![]() $\infty $
of the family of equilibrium states
$\infty $
of the family of equilibrium states
![]() $(\mu _{t})_{t\geq 1}$
belongs to the set
$(\mu _{t})_{t\geq 1}$
belongs to the set
![]() $\mathcal {M}_{\mathrm{max}}(\phi )$
.
$\mathcal {M}_{\mathrm{max}}(\phi )$
.
Proof. Consider some arbitrary accumulation point
![]() $\mu _{\infty }\in \mathcal {M}_{\sigma }(\Sigma )$
of the family
$\mu _{\infty }\in \mathcal {M}_{\sigma }(\Sigma )$
of the family
![]() $(\mu _{t})_{t\geq 1}$
. It is enough to verify that
$(\mu _{t})_{t\geq 1}$
. It is enough to verify that
Indeed, since that map
![]() $\mu \mapsto \mu (\phi )$
, from
$\mu \mapsto \mu (\phi )$
, from
![]() $\mathcal {M}_{\sigma }(\Sigma )$
into
$\mathcal {M}_{\sigma }(\Sigma )$
into
![]() $[0, \infty )$
, is upper semi-continuous in the weak
$[0, \infty )$
, is upper semi-continuous in the weak
![]() $^\star $
topology, see Lemma
$^\star $
topology, see Lemma
![]() $1$
in [Reference Jenkinson, Mauldin and Urbański15], we have
$1$
in [Reference Jenkinson, Mauldin and Urbański15], we have
However, by variational principle, for each
![]() $t\geq 1$
, we have
$t\geq 1$
, we have
Now, taking the
![]() $\limsup $
in the last equality, since
$\limsup $
in the last equality, since
![]() $(h(\mu _t))_{t\geq 1}$
is bounded from above (see Lemma 3.2), we obtain that
$(h(\mu _t))_{t\geq 1}$
is bounded from above (see Lemma 3.2), we obtain that
An important condition necessary to prove the convergence in the weak
![]() $^\star $
topology of the family of equilibrium states
$^\star $
topology of the family of equilibrium states
![]() $(\mu _t)_{t\geq 1}$
at
$(\mu _t)_{t\geq 1}$
at
![]() $\infty $
is to show that the potential
$\infty $
is to show that the potential
![]() $t\phi $
is positively recurrent for each
$t\phi $
is positively recurrent for each
![]() $t\geq 1$
. That statement is verified in the following proposition.
$t\geq 1$
. That statement is verified in the following proposition.
Proposition 3.2. For every
![]() $t\geq 1$
, the potential
$t\geq 1$
, the potential
![]() $t\phi $
is positive recurrent.
$t\phi $
is positive recurrent.
Proof. Note that the potential
![]() $\phi $
is positive recurrent. Theorem 1 in [Reference Freire and Vargas12] guarantees that for every
$\phi $
is positive recurrent. Theorem 1 in [Reference Freire and Vargas12] guarantees that for every
![]() $t>1$
, there is a unique equilibrium state
$t>1$
, there is a unique equilibrium state
![]() $\mu _{t}$
associated to potential
$\mu _{t}$
associated to potential
![]() $t\phi $
, so by Theorem
$t\phi $
, so by Theorem
![]() $1.2$
in [Reference Buzzi and Sarig7], the potential
$1.2$
in [Reference Buzzi and Sarig7], the potential
![]() $t\phi $
is positive recurrent, for every
$t\phi $
is positive recurrent, for every
![]() $t>1$
.
$t>1$
.
Remark 3.3. Under the same hypotheses of the previous lemma, but assuming that
![]() $\Sigma $
is a finitely primitive countable Markov shift, Morris showed in [Reference Morris21] that
$\Sigma $
is a finitely primitive countable Markov shift, Morris showed in [Reference Morris21] that
where
![]() $\mu _{\infty }\in \mathcal {M}_{\sigma }(\Sigma )$
is some accumulation point of the family of equilibrium states
$\mu _{\infty }\in \mathcal {M}_{\sigma }(\Sigma )$
is some accumulation point of the family of equilibrium states
![]() $(\mu _t)_{t\geq 1}$
. Actually, Freire and Vargas in [Reference Freire and Vargas12] obtained an extension of equation (3.5) for the setting of topologically transitive countable Markov shifts.
$(\mu _t)_{t\geq 1}$
. Actually, Freire and Vargas in [Reference Freire and Vargas12] obtained an extension of equation (3.5) for the setting of topologically transitive countable Markov shifts.
We say the two potentials
![]() $\phi $
and
$\phi $
and
![]() $\psi $
are cohomologous when there is
$\psi $
are cohomologous when there is
![]() $\eta $
such that
$\eta $
such that
![]() $\phi = \psi + \eta - \eta \circ \sigma $
. It is not difficult to check that cohomology between potentials is an equivalence relation preserving equilibrium states and maximizing measures.
$\phi = \psi + \eta - \eta \circ \sigma $
. It is not difficult to check that cohomology between potentials is an equivalence relation preserving equilibrium states and maximizing measures.
Since there is an equilibrium measure associated with the potential
![]() $\phi $
, we have that there is a potential
$\phi $
, we have that there is a potential
![]() $\widetilde {\phi }$
cohomologous to
$\widetilde {\phi }$
cohomologous to
![]() $\phi $
, such that
$\phi $
, such that
![]() $\widetilde {\phi }\leq \alpha (\phi )$
, see [Reference Jenkinson, Mauldin and Urbański16]. The potential
$\widetilde {\phi }\leq \alpha (\phi )$
, see [Reference Jenkinson, Mauldin and Urbański16]. The potential
![]() $\widetilde {\phi }-\alpha (\phi )$
is called normalized potential. So, for ease of computation, from now on, we consider the normalization
$\widetilde {\phi }-\alpha (\phi )$
is called normalized potential. So, for ease of computation, from now on, we consider the normalization
![]() $\widetilde {\phi } - \alpha (\phi )$
of the potential
$\widetilde {\phi } - \alpha (\phi )$
of the potential
![]() $\phi $
and, to not overload the notation, we will denote the normalized one simply by
$\phi $
and, to not overload the notation, we will denote the normalized one simply by
![]() $\phi $
.
$\phi $
.
Proposition 3.3. The following properties are satisfied:
-
(i)
 $P_G(t\phi )\geq 0$
, for every
$P_G(t\phi )\geq 0$
, for every
 $t\geq 1$
;
$t\geq 1$
; -
(ii) the function
 $t\mapsto P_G(t\phi )$
is decreasing;
$t\mapsto P_G(t\phi )$
is decreasing; -
(iii)
 $\lim \nolimits _{t\to \infty }P_{G}(t\phi )=h(\mu _{\infty })$
, where
$\lim \nolimits _{t\to \infty }P_{G}(t\phi )=h(\mu _{\infty })$
, where
 $\mu _{\infty }\in \mathcal {M}_{\mathrm{max}}(\Sigma )$
is a weak
$\mu _{\infty }\in \mathcal {M}_{\mathrm{max}}(\Sigma )$
is a weak
 $^\star $
accumulation point at
$^\star $
accumulation point at
 $\infty $
for the family of equilibrium states
$\infty $
for the family of equilibrium states
 $(\mu _{t})_{t\geq 1}$
.
$(\mu _{t})_{t\geq 1}$
.
Proof. The proofs of items (i) and (ii) are obtained directly from Lemma 3.2. Now we proceed to check item (iii). Let
![]() $\{t_k\}_{k\in \mathbb {N}}$
be an increasing sequence of numbers greater than one converging to infinity such that
$\{t_k\}_{k\in \mathbb {N}}$
be an increasing sequence of numbers greater than one converging to infinity such that
![]() $\mu _{t_k}\to \mu _{\infty }$
as
$\mu _{t_k}\to \mu _{\infty }$
as
![]() $k\to \infty $
in the weak
$k\to \infty $
in the weak
![]() $^\star $
topology. Note that
$^\star $
topology. Note that
![]() $\lim _{k\to \infty }\mu _{t_k}(\phi )=0$
, see Proposition 3.1. So, by Theorem 2 in [Reference Freire and Vargas12], we obtain
$\lim _{k\to \infty }\mu _{t_k}(\phi )=0$
, see Proposition 3.1. So, by Theorem 2 in [Reference Freire and Vargas12], we obtain
 $$ \begin{align*} h(\mu_{\infty})&=\limsup_{k\to\infty}h(\mu_{t_k})\\[3pt] &=\limsup_{k\to\infty}(P_G(t_{k}\phi)-t_{k}\cdot\mu_{t_k}(\phi))\\[3pt] &\geq\limsup_{k\to\infty}(P_G(t_k\phi)-\mu_{t_k}(\phi))\\[3pt] &=\lim_{k\to\infty}P_G(t_k\phi)-\liminf_{k\to\infty}\mu_{t_k}(\phi)\\[3pt] &=\lim_{t\to\infty}P_G(t\phi). \end{align*} $$
$$ \begin{align*} h(\mu_{\infty})&=\limsup_{k\to\infty}h(\mu_{t_k})\\[3pt] &=\limsup_{k\to\infty}(P_G(t_{k}\phi)-t_{k}\cdot\mu_{t_k}(\phi))\\[3pt] &\geq\limsup_{k\to\infty}(P_G(t_k\phi)-\mu_{t_k}(\phi))\\[3pt] &=\lim_{k\to\infty}P_G(t_k\phi)-\liminf_{k\to\infty}\mu_{t_k}(\phi)\\[3pt] &=\lim_{t\to\infty}P_G(t\phi). \end{align*} $$
However,
![]() $P_G(t\phi )\geq h(\mu _{\infty }) + t\mu _{\infty }(\phi ) = h(\mu _{\infty })$
. Therefore,
$P_G(t\phi )\geq h(\mu _{\infty }) + t\mu _{\infty }(\phi ) = h(\mu _{\infty })$
. Therefore,
![]() $\lim \nolimits _{t\to \infty } P_{G}(t\phi ) = h(\mu _{\infty })$
.
$\lim \nolimits _{t\to \infty } P_{G}(t\phi ) = h(\mu _{\infty })$
.
3.1 Existence of the zero-temperature limit for locally constant potentials
From now on, we consider locally constant potentials
![]() $\phi : \Sigma \to \mathbb {R}$
, that is, we assume that there exists
$\phi : \Sigma \to \mathbb {R}$
, that is, we assume that there exists
![]() $n \in \mathbb {N}_0$
such that
$n \in \mathbb {N}_0$
such that
![]() $\phi (x) = \phi (x_0 \ldots x_{n-1})$
for any
$\phi (x) = \phi (x_0 \ldots x_{n-1})$
for any
![]() $x \in \Sigma $
. We also consider the normalization
$x \in \Sigma $
. We also consider the normalization
![]() $\widetilde {\phi } - \alpha (\phi )$
of the potential
$\widetilde {\phi } - \alpha (\phi )$
of the potential
![]() $\phi $
such that
$\phi $
such that
![]() $\widetilde {\phi } \leq \alpha (\phi )$
. As stated above, the normalized potential will be denoted also by
$\widetilde {\phi } \leq \alpha (\phi )$
. As stated above, the normalized potential will be denoted also by
![]() $\phi $
(see [Reference Jenkinson, Mauldin and Urbański16] for details). In fact, without loss of generality, we can assume
$\phi $
(see [Reference Jenkinson, Mauldin and Urbański16] for details). In fact, without loss of generality, we can assume
![]() $\phi $
as a Markov potential as well, that is,
$\phi $
as a Markov potential as well, that is,
![]() $\phi (x)=\phi (x_0 x_1)$
. This is true because we can recode the Markov shift
$\phi (x)=\phi (x_0 x_1)$
. This is true because we can recode the Markov shift
![]() $\Sigma $
to guarantee that any word of length
$\Sigma $
to guarantee that any word of length
![]() $r+1$
can be written as a word of length
$r+1$
can be written as a word of length
![]() $2$
in the new codification (we refer the reader to [Reference Chazottes, Gambaudo and Ugalde8] for details).
$2$
in the new codification (we refer the reader to [Reference Chazottes, Gambaudo and Ugalde8] for details).
By [Reference Sarig24], we have that the potential
![]() $\phi (x) = \phi (x_0 x_1)$
has an associated equilibrium state
$\phi (x) = \phi (x_0 x_1)$
has an associated equilibrium state
![]() $\mu \in \mathcal {M}_{\sigma }(\Sigma )$
because it is positive recurrent, see Lemma 3.9. So the Ruelle operator
$\mu \in \mathcal {M}_{\sigma }(\Sigma )$
because it is positive recurrent, see Lemma 3.9. So the Ruelle operator
![]() $L_\phi $
is well defined on the space of bounded continuous functions. In particular, for any function of the form
$L_\phi $
is well defined on the space of bounded continuous functions. In particular, for any function of the form
![]() $\psi (x)= \psi (x_0)$
, we have
$\psi (x)= \psi (x_0)$
, we have
 $$ \begin{align} L_\phi (\psi)(x) = L_\phi (\psi)(x_0) = \sum_{\substack{a\in S\\ A(a, x_0)=1}}\mathop{\mathrm{exp}}\nolimits({\phi(ax_0)})\psi(a). \end{align} $$
$$ \begin{align} L_\phi (\psi)(x) = L_\phi (\psi)(x_0) = \sum_{\substack{a\in S\\ A(a, x_0)=1}}\mathop{\mathrm{exp}}\nolimits({\phi(ax_0)})\psi(a). \end{align} $$
From Theorem
![]() $1.2$
in [Reference Buzzi and Sarig7], it follows that the operator
$1.2$
in [Reference Buzzi and Sarig7], it follows that the operator
![]() $L_{\phi }$
has a strictly positive eigenfunction h,
$L_{\phi }$
has a strictly positive eigenfunction h,
![]() $L_{\phi }h=\unicode{x3bb} h$
, where
$L_{\phi }h=\unicode{x3bb} h$
, where
![]() $\unicode{x3bb} =\mathop {\mathrm {exp}}\nolimits (P_G(\phi ))$
and by equation (3.6), we have
$\unicode{x3bb} =\mathop {\mathrm {exp}}\nolimits (P_G(\phi ))$
and by equation (3.6), we have
![]() $h(x)=h(x_0)$
. In this case, we also can define the transpose of the Ruelle operator,
$h(x)=h(x_0)$
. In this case, we also can define the transpose of the Ruelle operator,
![]() $L^\intercal _{\phi },$
calculated in a function
$L^\intercal _{\phi },$
calculated in a function
![]() $\psi (x)= \psi (x_0)$
as
$\psi (x)= \psi (x_0)$
as
 $$ \begin{align*} L^\intercal_\phi (\psi)(x) = L^\intercal_\phi (\psi)(x_0) = \sum_{\substack{a\in S \\ A(x_0 a)=1}}\mathop{\mathrm{exp}}\nolimits({\phi(x_0a)})\psi(a). \end{align*} $$
$$ \begin{align*} L^\intercal_\phi (\psi)(x) = L^\intercal_\phi (\psi)(x_0) = \sum_{\substack{a\in S \\ A(x_0 a)=1}}\mathop{\mathrm{exp}}\nolimits({\phi(x_0a)})\psi(a). \end{align*} $$
It is not difficult to check that the operator
![]() $L^\intercal _\phi $
has a strictly positive eigenfunction
$L^\intercal _\phi $
has a strictly positive eigenfunction
![]() $h^\intercal $
, satisfying
$h^\intercal $
, satisfying
![]() $L^\intercal _\phi (h^\intercal ) = \unicode{x3bb} h^\intercal $
and
$L^\intercal _\phi (h^\intercal ) = \unicode{x3bb} h^\intercal $
and
![]() $h^\intercal (x) = h^\intercal (x_0)$
, where
$h^\intercal (x) = h^\intercal (x_0)$
, where
![]() $\unicode{x3bb} $
is the main eigenvalue of the operator
$\unicode{x3bb} $
is the main eigenvalue of the operator
![]() $L_\phi $
and
$L_\phi $
and
![]() $\sum _{a \in S}h(a)h^\intercal (a) = 1$
. A detailed proof about this claim can be found in [Reference Gurevich13].
$\sum _{a \in S}h(a)h^\intercal (a) = 1$
. A detailed proof about this claim can be found in [Reference Gurevich13].
Remark 3.4. Theorem C in [Reference Gurevich13] states that the equilibrium state
![]() $\mu $
is unique and it is a stationary Markov measure given by the formula:
$\mu $
is unique and it is a stationary Markov measure given by the formula:
where
![]() $\pi (a)=h(a)h^\intercal (a)>0$
for all
$\pi (a)=h(a)h^\intercal (a)>0$
for all
![]() $a \in S$
is the stationary probability measure. Moreover, here h,
$a \in S$
is the stationary probability measure. Moreover, here h,
![]() $h^\intercal $
are the main eigenfunctions of the previously indicated operators
$h^\intercal $
are the main eigenfunctions of the previously indicated operators
![]() $L_\phi $
and
$L_\phi $
and
![]() $L^\intercal _\phi $
, respectively. The explicit form for the transition probabilities is given by
$L^\intercal _\phi $
, respectively. The explicit form for the transition probabilities is given by
Here, it is convenient to define a measure
![]() $\widehat {\mu }_t\in \mathcal {M}_{\sigma }(\widehat {\Sigma })$
on the bilateral countable Markov shift
$\widehat {\mu }_t\in \mathcal {M}_{\sigma }(\widehat {\Sigma })$
on the bilateral countable Markov shift
![]() $\widehat {\Sigma } := \{x \in S^{\mathbb {Z}}: A(x_i, x_{i+1})=1,\; \text { for all } i \in \mathbb {Z}\}$
, associated to the potential
$\widehat {\Sigma } := \{x \in S^{\mathbb {Z}}: A(x_i, x_{i+1})=1,\; \text { for all } i \in \mathbb {Z}\}$
, associated to the potential
![]() $t\widehat {\phi }((x_i)_{i \in \mathbb {Z}}) = t\phi (x_0x_1)$
, given by
$t\widehat {\phi }((x_i)_{i \in \mathbb {Z}}) = t\phi (x_0x_1)$
, given by
![]() $\widehat {\mu }_t([x_mx_{m-1}\ldots x_n]) = \mu _t([x^{\prime }_0x^{\prime }_1\ldots x^{\prime }_{n-m}])$
,
$\widehat {\mu }_t([x_mx_{m-1}\ldots x_n]) = \mu _t([x^{\prime }_0x^{\prime }_1\ldots x^{\prime }_{n-m}])$
,
![]() $m, n \in \mathbb {Z}$
and
$m, n \in \mathbb {Z}$
and
![]() $m \leq n$
, where
$m \leq n$
, where
![]() $x^{\prime }_0 =x_m,\ldots , x^{\prime }_{n-m}=x_n$
. The measure
$x^{\prime }_0 =x_m,\ldots , x^{\prime }_{n-m}=x_n$
. The measure
![]() $\widehat {\mu }_t$
is invariant under the bilateral shift map and convergence of the family
$\widehat {\mu }_t$
is invariant under the bilateral shift map and convergence of the family
![]() $(\widehat {\mu }_t)_{t\geq 1}$
implies the convergence of the family
$(\widehat {\mu }_t)_{t\geq 1}$
implies the convergence of the family
![]() $(\mu _t)_{t\geq 1}$
.
$(\mu _t)_{t\geq 1}$
.
To facilitate the computations that appear below, we will use the measures
![]() $\widehat {\mu }_t$
defined on the bilateral countable Markov shift
$\widehat {\mu }_t$
defined on the bilateral countable Markov shift
![]() $\widehat {\Sigma }$
instead of the measures
$\widehat {\Sigma }$
instead of the measures
![]() $\mu _t$
defined on the unilateral one
$\mu _t$
defined on the unilateral one
![]() $\Sigma $
. Trying to not overload the notation, hereafter, we will denote the bilateral countable Markov shift by
$\Sigma $
. Trying to not overload the notation, hereafter, we will denote the bilateral countable Markov shift by
![]() $\Sigma $
, we will use the notation
$\Sigma $
, we will use the notation
![]() $\mu _t$
for its corresponding equilibrium states and we will denote by
$\mu _t$
for its corresponding equilibrium states and we will denote by
![]() $\sigma $
the map given by
$\sigma $
the map given by
![]() $(\sigma x)_i = x_{i+1}$
for any
$(\sigma x)_i = x_{i+1}$
for any
![]() $i \in \mathbb {Z}$
.
$i \in \mathbb {Z}$
.
Also, to simplify our notation, for each path
![]() $\underline {\gamma }=x_0x_1\ldots x_n$
, we use
$\underline {\gamma }=x_0x_1\ldots x_n$
, we use
![]() $l(\underline {\gamma })$
to denote its length and
$l(\underline {\gamma })$
to denote its length and
![]() $\phi (\underline {\gamma }):=S_n\phi (x)$
,
$\phi (\underline {\gamma }):=S_n\phi (x)$
,
![]() $x\in [\underline {\gamma }]$
. Since
$x\in [\underline {\gamma }]$
. Since
![]() $\phi $
is a Markov potential, it follows that
$\phi $
is a Markov potential, it follows that
![]() $\phi (\underline {\gamma })$
is constant on each
$\phi (\underline {\gamma })$
is constant on each
![]() $x\in [\underline {\gamma }]$
, so this notation is not ambiguous. Similarly, for any probability measure
$x\in [\underline {\gamma }]$
, so this notation is not ambiguous. Similarly, for any probability measure
![]() $\mu \in \mathcal {M}_{\sigma }(\Sigma )$
, we write
$\mu \in \mathcal {M}_{\sigma }(\Sigma )$
, we write
![]() $\mu (\underline {\gamma }):=\mu ([\underline {\gamma }])$
. Now, for a typical path
$\mu (\underline {\gamma }):=\mu ([\underline {\gamma }])$
. Now, for a typical path
![]() $\underline {\gamma }=x_0x_1\ldots x_n \in \mathcal {P}(\Sigma )$
, from equations (3.7) and (3.8) of Remark 3.4, we have
$\underline {\gamma }=x_0x_1\ldots x_n \in \mathcal {P}(\Sigma )$
, from equations (3.7) and (3.8) of Remark 3.4, we have
 $$ \begin{align} \mu_t(\underline{\gamma})&=\pi(x_0)\prod_{k=0}^{n-1}\frac{h(x_{k+1})}{ h(x_k)}\mathop{\mathrm{exp}}\nolimits(t\phi(x_kx_{k+1})-P_G(t \phi))\nonumber\\[5pt] &=\pi(x_0) \frac{h(x_{n})}{ h(x_0)}\mathop{\mathrm{exp}}\nolimits(t\phi(\underline{\gamma})-nP_G(t \phi)). \end{align} $$
$$ \begin{align} \mu_t(\underline{\gamma})&=\pi(x_0)\prod_{k=0}^{n-1}\frac{h(x_{k+1})}{ h(x_k)}\mathop{\mathrm{exp}}\nolimits(t\phi(x_kx_{k+1})-P_G(t \phi))\nonumber\\[5pt] &=\pi(x_0) \frac{h(x_{n})}{ h(x_0)}\mathop{\mathrm{exp}}\nolimits(t\phi(\underline{\gamma})-nP_G(t \phi)). \end{align} $$
Obviously
![]() $\pi (x_0)=\mu _t(x_0)>0$
, when
$\pi (x_0)=\mu _t(x_0)>0$
, when
![]() $\underline {\gamma }$
is a loop, that is,
$\underline {\gamma }$
is a loop, that is,
![]() $x_0=x_n$
, we have
$x_0=x_n$
, we have
![]() $h(x_0)=h(x_n)$
and consequently
$h(x_0)=h(x_n)$
and consequently
This identity was deduced by Kempton in a more restrictive case (see [Reference Kempton17]). In fact, the positive recurrence of the potential
![]() $t \phi $
and the topologically transitive condition of the Markov shift
$t \phi $
and the topologically transitive condition of the Markov shift
![]() $\Sigma $
are necessary and sufficient conditions to get equation (3.10) (see Theorems C and D from [Reference Gurevich13] for more details).
$\Sigma $
are necessary and sufficient conditions to get equation (3.10) (see Theorems C and D from [Reference Gurevich13] for more details).
Notice that by the notation introduced earlier, we have that
for every
![]() $t\geq 1$
. Therefore, for any loop
$t\geq 1$
. Therefore, for any loop
![]() $\underline {\gamma }=x_0x_1\ldots x_n$
satisfying
$\underline {\gamma }=x_0x_1\ldots x_n$
satisfying
![]() $x_0=x_n$
, equation (3.10) can be re-written into the form
$x_0=x_n$
, equation (3.10) can be re-written into the form
 $$ \begin{align} \frac{\mu_{t}(\underline{\gamma})}{\mu_{t}([x_0])}= \mathop{\mathrm{exp}}\nolimits((t\phi-P_G(t \phi))(\underline{\gamma})). \end{align} $$
$$ \begin{align} \frac{\mu_{t}(\underline{\gamma})}{\mu_{t}([x_0])}= \mathop{\mathrm{exp}}\nolimits((t\phi-P_G(t \phi))(\underline{\gamma})). \end{align} $$
However, by Theorem
![]() $1$
from [Reference Bissacot and Freire3], there exists a finite set
$1$
from [Reference Bissacot and Freire3], there exists a finite set
![]() $I\subset \mathbb {N}$
such that any
$I\subset \mathbb {N}$
such that any
![]() $\phi $
-maximizing measure
$\phi $
-maximizing measure
![]() $\mu \in \mathcal {M}_{\sigma }(\Sigma )$
satisfies
$\mu \in \mathcal {M}_{\sigma }(\Sigma )$
satisfies
![]() $\sup (\mu ) \subset \Sigma _I$
. From now on, the finite set I will denote the set given for this theorem.
$\sup (\mu ) \subset \Sigma _I$
. From now on, the finite set I will denote the set given for this theorem.
Remark 3.5. Since
![]() $\phi $
is a coercive potential, by Lemma
$\phi $
is a coercive potential, by Lemma
![]() $2$
in [Reference Bissacot and Freire3], there exists
$2$
in [Reference Bissacot and Freire3], there exists
![]() $d>0$
such that
$d>0$
such that
![]() $\sup \phi |_{[i]}<-d$
, for every
$\sup \phi |_{[i]}<-d$
, for every
![]() $i\notin I$
, where
$i\notin I$
, where
![]() $\sup \phi |_{[i]}:=\sup \{\phi (x): x\in [i]\}$
.
$\sup \phi |_{[i]}:=\sup \{\phi (x): x\in [i]\}$
.
By Proposition 3.1, we have that any weak
![]() $^\star $
accumulation point
$^\star $
accumulation point
![]() $\mu _\infty $
of the family of equilibrium states
$\mu _\infty $
of the family of equilibrium states
![]() $(\mu _t)_{t\geq 1}$
is a maximizing measure supported on
$(\mu _t)_{t\geq 1}$
is a maximizing measure supported on
![]() $\bigcup _{i \in I}[i]$
. As a consequence, the existence of the limit
$\bigcup _{i \in I}[i]$
. As a consequence, the existence of the limit
![]() $\lim _{t \to \infty }\mu _t$
in the weak
$\lim _{t \to \infty }\mu _t$
in the weak
![]() $^\star $
topology is equivalent to showing existence of the limit
$^\star $
topology is equivalent to showing existence of the limit
![]() $\lim _{t\to \infty }\mu _t[a]$
for all
$\lim _{t\to \infty }\mu _t[a]$
for all
![]() $a\in I$
(see for instance [Reference Kempton17]). Because of that, it is enough to check the convergence of the ratios
$a\in I$
(see for instance [Reference Kempton17]). Because of that, it is enough to check the convergence of the ratios
![]() $\lim _{t\to \infty }({\mu _{t}([b])}/{\mu _{t}([a])})$
, for all
$\lim _{t\to \infty }({\mu _{t}([b])}/{\mu _{t}([a])})$
, for all
![]() $a,b\in I$
, to show the convergence of
$a,b\in I$
, to show the convergence of
![]() $(\mu _t)_{t\geq 1}$
in the weak
$(\mu _t)_{t\geq 1}$
in the weak
![]() $^\star $
topology. In fact, the limit of the ratios can even be infinite.
$^\star $
topology. In fact, the limit of the ratios can even be infinite.
From now on, let us fix
![]() $a,b \in I$
. We define
$a,b \in I$
. We define
Clearly,
![]() $\Sigma (a)$
is
$\Sigma (a)$
is
![]() $\sigma $
-invariant. For every
$\sigma $
-invariant. For every
![]() $t \geq 1$
, the potential
$t \geq 1$
, the potential
![]() $t \phi $
is positive recurrent, see Lemma 3.2, so that
$t \phi $
is positive recurrent, see Lemma 3.2, so that
![]() $\mu _{t}\in \mathcal {M}_{\sigma }(\Sigma )$
is an ergodic measure and moreover
$\mu _{t}\in \mathcal {M}_{\sigma }(\Sigma )$
is an ergodic measure and moreover
![]() $\mu _{t}(\Sigma (a))=1$
, for all
$\mu _{t}(\Sigma (a))=1$
, for all
![]() $t\geq 1$
. Then we have that
$t\geq 1$
. Then we have that
![]() $\mu _{t}([b])=\mu _{t}(\Sigma (a)\cap [b])$
, for every
$\mu _{t}([b])=\mu _{t}(\Sigma (a)\cap [b])$
, for every
![]() $b \in I$
.
$b \in I$
.
Let
![]() $\Gamma (a)$
denote the set of paths
$\Gamma (a)$
denote the set of paths
![]() $\underline {\gamma }=x_0x_1\ldots x_n$
,
$\underline {\gamma }=x_0x_1\ldots x_n$
,
![]() $n\geq 1$
, such that
$n\geq 1$
, such that
![]() $x_j=a$
if and only if
$x_j=a$
if and only if
![]() $j\in \{0,n\}$
. Since
$j\in \{0,n\}$
. Since
![]() $\Gamma (a)$
is countable (because it is a countable union of countable sets), this allows to write them as
$\Gamma (a)$
is countable (because it is a countable union of countable sets), this allows to write them as
![]() $\Gamma (a)=\{\underline {\gamma _i}\}_{i=1}^{\infty }$
, where every
$\Gamma (a)=\{\underline {\gamma _i}\}_{i=1}^{\infty }$
, where every
![]() $\underline {\gamma }_i\in \Gamma (a)$
for
$\underline {\gamma }_i\in \Gamma (a)$
for
![]() $i\in \mathbb {N}$
. Notice that
$i\in \mathbb {N}$
. Notice that
![]() $\Sigma (a)$
can be split as
$\Sigma (a)$
can be split as
 $$ \begin{align*}\Sigma(a)=\bigcup_{i=1}^{\infty}\bigcup_{k=1}^{l(\underline{\gamma}_i)}\sigma^k[\underline{\gamma}_i],\end{align*} $$
$$ \begin{align*}\Sigma(a)=\bigcup_{i=1}^{\infty}\bigcup_{k=1}^{l(\underline{\gamma}_i)}\sigma^k[\underline{\gamma}_i],\end{align*} $$
and so,
 $$ \begin{align} \Sigma(a)\cap[b]=\bigcup_{i=1}^{\infty}\bigcup_{k=1}^{l(\underline{\gamma}_i)}\sigma^k[\underline{\gamma}_i]\cap[b]. \end{align} $$
$$ \begin{align} \Sigma(a)\cap[b]=\bigcup_{i=1}^{\infty}\bigcup_{k=1}^{l(\underline{\gamma}_i)}\sigma^k[\underline{\gamma}_i]\cap[b]. \end{align} $$
For any loop
![]() $\underline {\gamma }_i \in \Gamma (a)$
, let
$\underline {\gamma }_i \in \Gamma (a)$
, let
![]() $N(b,\underline {\gamma }_i)$
be the number of occurrences of the symbol b within the loop
$N(b,\underline {\gamma }_i)$
be the number of occurrences of the symbol b within the loop
![]() $\underline {\gamma }_i$
, note that
$\underline {\gamma }_i$
, note that
![]() .
.
Fix
![]() $t\geq 1$
, recalling that
$t\geq 1$
, recalling that
![]() $\mu _{t}([b])=\mu _{t}(\Sigma (a)\cap [b])$
and
$\mu _{t}([b])=\mu _{t}(\Sigma (a)\cap [b])$
and
![]() $\mu _t$
is invariant by the action of the bilateral shift
$\mu _t$
is invariant by the action of the bilateral shift
![]() $\sigma $
. From equation (3.12), we see that
$\sigma $
. From equation (3.12), we see that

 $$ \begin{align} &\hspace{-19pt}=\sum_{i=1}^{\infty}\mu_{t}(\underline{\gamma}_i)N(b,\underline{\gamma}_i). \end{align} $$
$$ \begin{align} &\hspace{-19pt}=\sum_{i=1}^{\infty}\mu_{t}(\underline{\gamma}_i)N(b,\underline{\gamma}_i). \end{align} $$
From equation (3.11), we know that for any closed loop
![]() $\underline {\gamma }_i\in \Gamma (a)$
,
$\underline {\gamma }_i\in \Gamma (a)$
,
so
 $$ \begin{align} \mu_{t}([b])&=\sum_{i=1}^{\infty}\mu_{t}([a])\mathop{\mathrm{exp}}\nolimits((t\phi-P_{G}(t\phi))(\underline{\gamma}_i))N(b,\underline{\gamma}_i) \end{align} $$
$$ \begin{align} \mu_{t}([b])&=\sum_{i=1}^{\infty}\mu_{t}([a])\mathop{\mathrm{exp}}\nolimits((t\phi-P_{G}(t\phi))(\underline{\gamma}_i))N(b,\underline{\gamma}_i) \end{align} $$
and hence
 $$ \begin{align} \frac{\mu_{t}([b])}{\mu_{t}([a])}=\sum_{i=1}^{\infty}\mathop{\mathrm{exp}}\nolimits((t\phi-P_{G}(t\phi))(\underline{\gamma}_i))N(b,\underline{\gamma}_i). \end{align} $$
$$ \begin{align} \frac{\mu_{t}([b])}{\mu_{t}([a])}=\sum_{i=1}^{\infty}\mathop{\mathrm{exp}}\nolimits((t\phi-P_{G}(t\phi))(\underline{\gamma}_i))N(b,\underline{\gamma}_i). \end{align} $$
Actually, the finiteness of
![]() ${\mu _{t}([b])}/{\mu _{t}([a])}$
, for all
${\mu _{t}([b])}/{\mu _{t}([a])}$
, for all
![]() $t \geq 1$
, is guaranteed by the positive recurrence of the potential
$t \geq 1$
, is guaranteed by the positive recurrence of the potential
![]() $t \phi $
(see for instance [Reference Sarig24]).
$t \phi $
(see for instance [Reference Sarig24]).
Those closed loops
![]() $\underline {\gamma }_i\in \Gamma (a)$
which do not pass through of the symbol b have no relevance at the right-hand of equation (3.17), because
$\underline {\gamma }_i\in \Gamma (a)$
which do not pass through of the symbol b have no relevance at the right-hand of equation (3.17), because
![]() $N(b,\underline {\gamma }_i)=0$
. In this case, equation (3.17) is equivalent to
$N(b,\underline {\gamma }_i)=0$
. In this case, equation (3.17) is equivalent to

where
![]() if
if
![]() $N(b,\underline {\gamma }_i)=m$
and otherwise
$N(b,\underline {\gamma }_i)=m$
and otherwise
![]() .
.
Definition 3.1. Let
![]() $a,b\in I$
. We say that
$a,b\in I$
. We say that
![]() $\underline {\gamma }=x_0\ldots x_n$
,
$\underline {\gamma }=x_0\ldots x_n$
,
![]() $n \geq 1$
, is a main path in
$n \geq 1$
, is a main path in
![]() $\Sigma $
that starts at i and ends at j, where
$\Sigma $
that starts at i and ends at j, where
![]() $i,j\in \{a,b\}$
if and only if
$i,j\in \{a,b\}$
if and only if
![]() $x_0=i$
,
$x_0=i$
,
![]() $x_n=j$
and
$x_n=j$
and
![]() $x_m\notin \{a,b\}$
for
$x_m\notin \{a,b\}$
for
![]() $m\in \{1,2,\ldots ,n-1\}$
. This means that the symbols
$m\in \{1,2,\ldots ,n-1\}$
. This means that the symbols
![]() $a,b$
do not appear in the middle of the path
$a,b$
do not appear in the middle of the path
![]() $\underline {\gamma }$
. We will denote by
$\underline {\gamma }$
. We will denote by
![]() $\{\underline {\gamma }: i\to j\}$
the set of all the main paths that start at i and end at j.
$\{\underline {\gamma }: i\to j\}$
the set of all the main paths that start at i and end at j.
Note that
![]() $\{\underline {\gamma }: a\to a\}$
and
$\{\underline {\gamma }: a\to a\}$
and
![]() $\Gamma (a)$
do not represent the same set. The foregoing is true because
$\Gamma (a)$
do not represent the same set. The foregoing is true because
![]() $\Gamma (a)$
contains paths with the symbol b while
$\Gamma (a)$
contains paths with the symbol b while
![]() $\{\underline {\gamma }: a\to a\}$
does not. For
$\{\underline {\gamma }: a\to a\}$
does not. For
![]() $\widetilde {\Sigma }$
, a topologically transitive
$\widetilde {\Sigma }$
, a topologically transitive
![]() $\sigma -$
invariant subset of the Markov shift
$\sigma -$
invariant subset of the Markov shift
![]() $\Sigma $
, we use the notation
$\Sigma $
, we use the notation
![]() $\{\underline {\gamma }: i\to j\in \mathcal {P}(\widetilde {\Sigma })\}$
to indicate that each main path that starts at i and ends at j is a path of
$\{\underline {\gamma }: i\to j\in \mathcal {P}(\widetilde {\Sigma })\}$
to indicate that each main path that starts at i and ends at j is a path of
![]() $\widetilde {\Sigma }$
(remember that
$\widetilde {\Sigma }$
(remember that
![]() $\mathcal {P}(\widetilde {\Sigma })$
denotes the set of paths in
$\mathcal {P}(\widetilde {\Sigma })$
denotes the set of paths in
![]() $\widetilde {\Sigma }$
).
$\widetilde {\Sigma }$
).
For every
![]() $i,j \in \{a,b\}$
, we define
$i,j \in \{a,b\}$
, we define
 $$ \begin{align} p_{ij}^{t}:=\sum_{\underline{\gamma} \in\{\underline{\gamma}: i\to j\}}\mathop{\mathrm{exp}}\nolimits((t\phi-P_{G}(t\phi))(\underline{\gamma})). \end{align} $$
$$ \begin{align} p_{ij}^{t}:=\sum_{\underline{\gamma} \in\{\underline{\gamma}: i\to j\}}\mathop{\mathrm{exp}}\nolimits((t\phi-P_{G}(t\phi))(\underline{\gamma})). \end{align} $$
Note from equation (3.11) that
![]() $p_{ii}^{t}<1$
, for every
$p_{ii}^{t}<1$
, for every
![]() $i\in I$
. Indeed, the probability, with respect to
$i\in I$
. Indeed, the probability, with respect to
![]() $\mu _{t}$
, that a path from i returns to i eventually is one, so from equations (3.11) and (3.19), we observe that it can be split into
$\mu _{t}$
, that a path from i returns to i eventually is one, so from equations (3.11) and (3.19), we observe that it can be split into
![]() $p_{ii}^{t}$
, the probability that a path from i returns to i without passing through j, where
$p_{ii}^{t}$
, the probability that a path from i returns to i without passing through j, where
![]() $j\neq i$
, and
$j\neq i$
, and
![]() $p_{ij}^{t}(\sum _{n\geq 1}(p_{jj}^{t})^n)p_{ji}^{t}$
, the probability that a path from i returns to i passing through j at least once. Therefore,
$p_{ij}^{t}(\sum _{n\geq 1}(p_{jj}^{t})^n)p_{ji}^{t}$
, the probability that a path from i returns to i passing through j at least once. Therefore,
Recalling that
![]() $t \phi $
is a Markov potential, for all
$t \phi $
is a Markov potential, for all
![]() $m\in \mathbb {N}$
, we get from equation (3.19),
$m\in \mathbb {N}$
, we get from equation (3.19),

Therefore, from equation (3.18), we obtain
 $$ \begin{align} \frac{\mu_{t}([b])}{\mu_{t}([a])}=\sum_{m=1}^{\infty}m p^t_{ab}(p_{bb}^t)^{m-1}p^t_{ba}=\frac{p^t_{ab}p^t_{ba}}{(1-p^t_{bb})^2}. \end{align} $$
$$ \begin{align} \frac{\mu_{t}([b])}{\mu_{t}([a])}=\sum_{m=1}^{\infty}m p^t_{ab}(p_{bb}^t)^{m-1}p^t_{ba}=\frac{p^t_{ab}p^t_{ba}}{(1-p^t_{bb})^2}. \end{align} $$
By inverting the roles of a and b, we get
![]() ${\mu _{t}([a])}/{\mu _{t}([b])}={p^t_{ba}p^t_{ab}}/{(1-p^t_{aa})^2}$
and combining both expressions, we conclude
${\mu _{t}([a])}/{\mu _{t}([b])}={p^t_{ba}p^t_{ab}}/{(1-p^t_{aa})^2}$
and combining both expressions, we conclude
 $$ \begin{align} \frac{\mu_{t}([b])}{\mu_{t}([a])}=\frac{1-p_{aa}^t}{1-p_{bb}^t}. \end{align} $$
$$ \begin{align} \frac{\mu_{t}([b])}{\mu_{t}([a])}=\frac{1-p_{aa}^t}{1-p_{bb}^t}. \end{align} $$
Therefore, proving the convergence of the equilibrium states
![]() $(\mu _t)_{t\geq 1}$
,
$(\mu _t)_{t\geq 1}$
,
![]() $\lim _{t\to \infty }\mu _{t}$
reduces to showing the existence of
$\lim _{t\to \infty }\mu _{t}$
reduces to showing the existence of
![]() $\lim _{t\to \infty }({1-p_{aa}^t})/({1-p_{bb}^t})$
for all
$\lim _{t\to \infty }({1-p_{aa}^t})/({1-p_{bb}^t})$
for all
![]() $a,b\in I$
.
$a,b\in I$
.
It is well known that in the setting of finite Markov shifts, the existence of the limit at zero temperature is satisfied for families of equilibrium states associated to Markov potentials. Below, we present a definition of a suitable collection of finite Markov shifts contained in
![]() $\Sigma $
which are useful to approximate the unique accumulation point of the family
$\Sigma $
which are useful to approximate the unique accumulation point of the family
![]() $(\mu _t)_{t\geq 1}$
in the weak
$(\mu _t)_{t\geq 1}$
in the weak
![]() $^\star $
topology.
$^\star $
topology.
Definition 3.2. Let
![]() $\Sigma $
be a topologically transitive countable Markov shift,
$\Sigma $
be a topologically transitive countable Markov shift,
![]() $\phi :\Sigma \to \mathbb {R}$
be a Markov potential
$\phi :\Sigma \to \mathbb {R}$
be a Markov potential
![]() $\phi (x)=\phi (x_0x_1)$
and let
$\phi (x)=\phi (x_0x_1)$
and let
![]() $c\in (0, \infty )$
. We denote by
$c\in (0, \infty )$
. We denote by
![]() $\Sigma _{-c}$
a minimal topologically transitive subshift of
$\Sigma _{-c}$
a minimal topologically transitive subshift of
![]() $\Sigma $
that contains all the symbols
$\Sigma $
that contains all the symbols
![]() $i\in \mathbb {N}$
such that
$i\in \mathbb {N}$
such that
![]() $\sup \phi |_{[i]}\geq -c$
.
$\sup \phi |_{[i]}\geq -c$
.
Remark 3.6. In Definition 3.2, minimal is understood in the sense that any other topologically transitive subshift strictly contained in
![]() $\Sigma _{-c}$
does not exist that includes all the symbols
$\Sigma _{-c}$
does not exist that includes all the symbols
![]() $i \in \mathbb {N}$
satisfying
$i \in \mathbb {N}$
satisfying
![]() $\sup \phi |_{[i]}\geq -c$
.
$\sup \phi |_{[i]}\geq -c$
.
By summability,
![]() $\Sigma _{-c}$
is a finite Markov shift when c is large enough. Furthermore, for any
$\Sigma _{-c}$
is a finite Markov shift when c is large enough. Furthermore, for any
![]() $c \leq c^{\prime }$
, it is possible to find
$c \leq c^{\prime }$
, it is possible to find
![]() $\Sigma _{-c^{\prime }}$
satisfying Definition 3.2 such that
$\Sigma _{-c^{\prime }}$
satisfying Definition 3.2 such that
![]() $\Sigma _{-c} \subset \Sigma _{-c^{\prime }}$
. In the following, the key argument to prove the existence of the zero-temperature limit of equilibrium states on topologically transitive countable Markov shifts is the construction of an appropriate finite Markov subshift (which remains fixed for all
$\Sigma _{-c} \subset \Sigma _{-c^{\prime }}$
. In the following, the key argument to prove the existence of the zero-temperature limit of equilibrium states on topologically transitive countable Markov shifts is the construction of an appropriate finite Markov subshift (which remains fixed for all
![]() $t\geq 1$
), whose equilibrium states approximate those defined on the countable Markov shift
$t\geq 1$
), whose equilibrium states approximate those defined on the countable Markov shift
![]() $\Sigma $
.
$\Sigma $
.
For every
![]() $a,b\in I$
, we will denote by
$a,b\in I$
, we will denote by
![]() $\underline {\gamma _a^b}$
the shortest path connecting a to b. From the construction, we immediately get that
$\underline {\gamma _a^b}$
the shortest path connecting a to b. From the construction, we immediately get that
![]() $\underline {\gamma _a^b}$
contains the symbols a and b only at the ends, so that
$\underline {\gamma _a^b}$
contains the symbols a and b only at the ends, so that
![]() $\underline {\gamma _a^b} \in \{ \underline {\gamma }: a \rightarrow b \}$
. This path always exists because
$\underline {\gamma _a^b} \in \{ \underline {\gamma }: a \rightarrow b \}$
. This path always exists because
![]() $\Sigma $
is topologically transitive which allows to guarantee that any pair of symbols can be linked by a finite path. We denote
$\Sigma $
is topologically transitive which allows to guarantee that any pair of symbols can be linked by a finite path. We denote
![]() $\underline {\gamma _a^b}\underline {\gamma _b^a}$
the concatenation of the paths
$\underline {\gamma _a^b}\underline {\gamma _b^a}$
the concatenation of the paths
![]() $\underline {\gamma _a^b}$
with
$\underline {\gamma _a^b}$
with
![]() $\underline {\gamma _b^a}$
. With this, we have that there is always a loop that passes through a and b. We now consider the set
$\underline {\gamma _b^a}$
. With this, we have that there is always a loop that passes through a and b. We now consider the set
which is a non-empty and finite set. In addition, for each pair
![]() $a,b\in I$
and each non-empty finite set of symbols
$a,b\in I$
and each non-empty finite set of symbols
![]() $J\subset I$
, consider
$J\subset I$
, consider
![]() $\underline {\gamma _a^b}(J)$
as the shortest path connecting a to b and avoiding in the middle any symbol belonging to J, the foregoing, in the case where there is at least a path satisfying those conditions. We define the set of all the paths between a and b avoiding some subset of I as
$\underline {\gamma _a^b}(J)$
as the shortest path connecting a to b and avoiding in the middle any symbol belonging to J, the foregoing, in the case where there is at least a path satisfying those conditions. We define the set of all the paths between a and b avoiding some subset of I as
Finally, we fix
where
![]() $d>0$
was given in Remark 3.5. The above construction leads us to the following proposition.
$d>0$
was given in Remark 3.5. The above construction leads us to the following proposition.
Proposition 3.4. Let
![]() $N\in \mathbb {N}$
,
$N\in \mathbb {N}$
,
![]() $C \geq 0$
and
$C \geq 0$
and
![]() $c>0$
as in equations (3.24), (3.25) and (3.26), respectively. Then, for every
$c>0$
as in equations (3.24), (3.25) and (3.26), respectively. Then, for every
![]() $a,b\in I$
, we have:
$a,b\in I$
, we have:
-
(i) there exists a loop
 $\underline {\gamma }\in \mathcal {P}(\Sigma )$
connecting a to b such that
$\underline {\gamma }\in \mathcal {P}(\Sigma )$
connecting a to b such that
 $\phi (\underline {\gamma })\geq -C$
and
$\phi (\underline {\gamma })\geq -C$
and
 $l(\underline {\gamma })\leq N$
;
$l(\underline {\gamma })\leq N$
; -
(ii) if there exists a loop
 $\underline {\gamma }$
connecting a to a and avoiding the set symbols of
$\underline {\gamma }$
connecting a to a and avoiding the set symbols of
 $J\subset I$
, then
$J\subset I$
, then
 $\phi (\underline {\gamma })\geq -C$
and
$\phi (\underline {\gamma })\geq -C$
and
 $l(\underline {\gamma })\leq N$
.
$l(\underline {\gamma })\leq N$
.
Also, each symbol of I belongs to the symbols of the topologically transitive finite Markov shift
![]() $\Sigma _{-c}$
, that is,
$\Sigma _{-c}$
, that is,
![]() $\Sigma _I\subset \Sigma _{-c}$
.
$\Sigma _I\subset \Sigma _{-c}$
.
Proof. Note that items (i) and (ii) are a direct consequence of equations (3.24), (3.25) and (3.26). Furthermore, fixing
![]() $i, j\in I$
, it follows that
$i, j\in I$
, it follows that
so, by Definition 3.2, we have
![]() $\Sigma _I\subset \Sigma _{-c}$
.
$\Sigma _I\subset \Sigma _{-c}$
.
The main difference here between the BIP case and the topologically transitive case is the following: in the BIP case, we are able to link a and b using only symbols of the finite set
![]() $\{b_1, b_2, \ldots , b_N\}$
and, thus, the length of the path is at most N. However, in the topologically transitive setting, we are only able to guarantee the existence of a finite path linking a and b, but we do not have any control on the length of the paths. Despite this, the finiteness of the set I makes it possible to build a compact subshift as in Proposition 3.4.
$\{b_1, b_2, \ldots , b_N\}$
and, thus, the length of the path is at most N. However, in the topologically transitive setting, we are only able to guarantee the existence of a finite path linking a and b, but we do not have any control on the length of the paths. Despite this, the finiteness of the set I makes it possible to build a compact subshift as in Proposition 3.4.
Fix the topologically transitive finite Markov shift
![]() $\Sigma ^{\prime }:=\Sigma _{-7c}$
, note that
$\Sigma ^{\prime }:=\Sigma _{-7c}$
, note that
![]() $\Sigma _I\subset \Sigma _{-c}\subset \Sigma ^{\prime }\subset \Sigma $
. For the subshift
$\Sigma _I\subset \Sigma _{-c}\subset \Sigma ^{\prime }\subset \Sigma $
. For the subshift
![]() $\Sigma ^{\prime }$
, we will denote by
$\Sigma ^{\prime }$
, we will denote by
![]() $\vartheta _{t}$
the equilibrium state associated with the potential
$\vartheta _{t}$
the equilibrium state associated with the potential
![]() $t\phi $
restricted to
$t\phi $
restricted to
![]() $\Sigma ^{\prime }$
(this will be denoted by
$\Sigma ^{\prime }$
(this will be denoted by
![]() $t\phi |_{\Sigma ^{\prime }}$
), and
$t\phi |_{\Sigma ^{\prime }}$
), and
![]() $Q(t\phi ) \leq P_G(t \phi )$
is the topological pressure of the potential
$Q(t\phi ) \leq P_G(t \phi )$
is the topological pressure of the potential
![]() $t\phi |_{\Sigma ^{\prime }}$
.
$t\phi |_{\Sigma ^{\prime }}$
.
For every
![]() $i,j\in \{a,b\}$
and
$i,j\in \{a,b\}$
and
![]() $t\geq 1$
, we define
$t\geq 1$
, we define
 $$ \begin{align} q_{ij}^{t}:=\sum_{\{\underline{\gamma} :i\to j\in\mathcal{P}(\Sigma^{\prime})\}}\mathop{\mathrm{exp}}\nolimits((t\phi-Q(t\phi))(\underline{\gamma})), \end{align} $$
$$ \begin{align} q_{ij}^{t}:=\sum_{\{\underline{\gamma} :i\to j\in\mathcal{P}(\Sigma^{\prime})\}}\mathop{\mathrm{exp}}\nolimits((t\phi-Q(t\phi))(\underline{\gamma})), \end{align} $$
where
![]() $\{\underline {\gamma }: i\to j\in \mathcal {P}(\Sigma ^{\prime })\}$
is the set of paths in
$\{\underline {\gamma }: i\to j\in \mathcal {P}(\Sigma ^{\prime })\}$
is the set of paths in
![]() $\Sigma ^{\prime }$
that connect i to j and such that do not have an intermediate occurrence of neither a nor b. Similarly to equation (3.23), we see that
$\Sigma ^{\prime }$
that connect i to j and such that do not have an intermediate occurrence of neither a nor b. Similarly to equation (3.23), we see that
 $$ \begin{align} \frac{\vartheta_{t}([b])}{\vartheta_{t}([a])}=\frac{1-q_{aa}^{t}}{1-q_{bb}^{t}}, \end{align} $$
$$ \begin{align} \frac{\vartheta_{t}([b])}{\vartheta_{t}([a])}=\frac{1-q_{aa}^{t}}{1-q_{bb}^{t}}, \end{align} $$
for each
![]() $a,b\in I$
. Since
$a,b\in I$
. Since
![]() $\Sigma '$
is a finite Markov shift, we have an existence of the limit
$\Sigma '$
is a finite Markov shift, we have an existence of the limit
![]() $\lim _{t\to \infty }({\vartheta _{t}([b])}/{\vartheta _{t}([a])})$
for any
$\lim _{t\to \infty }({\vartheta _{t}([b])}/{\vartheta _{t}([a])})$
for any
![]() $a,b\in I$
, see [Reference Brémont6, Reference Chazottes, Gambaudo and Ugalde8, Reference Leplaideur18] for details.
$a,b\in I$
, see [Reference Brémont6, Reference Chazottes, Gambaudo and Ugalde8, Reference Leplaideur18] for details.
Next, we will show the following equality:
for each
![]() $a,b\in I$
. Since, we have an existence of the limit in the right side of the equation above (see for instance [Reference Brémont6, Reference Chazottes, Gambaudo and Ugalde8, Reference Leplaideur18]), by Proposition 3.1, it follows that equation (3.29) guarantees the main theorem of this work (that is, Theorem 3.1).
$a,b\in I$
. Since, we have an existence of the limit in the right side of the equation above (see for instance [Reference Brémont6, Reference Chazottes, Gambaudo and Ugalde8, Reference Leplaideur18]), by Proposition 3.1, it follows that equation (3.29) guarantees the main theorem of this work (that is, Theorem 3.1).
So, by equations (3.23) and (3.28), it is only necessary to prove the following:
 $$ \begin{align} \lim_{t\to\infty}\frac{1-p_{aa}^{t}}{1-p_{bb}^{t}}=\lim_{t\to\infty}\frac{1-q_{aa}^{t}}{1-q_{bb}^{t}}. \end{align} $$
$$ \begin{align} \lim_{t\to\infty}\frac{1-p_{aa}^{t}}{1-p_{bb}^{t}}=\lim_{t\to\infty}\frac{1-q_{aa}^{t}}{1-q_{bb}^{t}}. \end{align} $$
To study the asymptotic behaviour of
![]() $1-p_{aa}^{t}$
and
$1-p_{aa}^{t}$
and
![]() $1-q_{aa}^{t}$
, we will use item (i) of Proposition 3.4 to find their lower bounds. Now we will find a lower bound for
$1-q_{aa}^{t}$
, we will use item (i) of Proposition 3.4 to find their lower bounds. Now we will find a lower bound for
![]() $1-p_{aa}^{t}$
. Fix
$1-p_{aa}^{t}$
. Fix
![]() $a,b\in I$
and
$a,b\in I$
and
![]() $t\geq 1$
. By Proposition 3.4, the concatenation
$t\geq 1$
. By Proposition 3.4, the concatenation
![]() $\underline {\gamma _a^b\gamma _b^a}$
is a path from a to a passing though b with length at most N satisfying
$\underline {\gamma _a^b\gamma _b^a}$
is a path from a to a passing though b with length at most N satisfying
![]() $\phi (\underline {\gamma _a^b\gamma _b^a}) \geq -C$
, thus
$\phi (\underline {\gamma _a^b\gamma _b^a}) \geq -C$
, thus
Therefore, from equations (3.20) and (3.31), we obtain the lower bound
Obviously, the same argument gives us lower bounds for
![]() $1-p_{bb}^{t}$
,
$1-p_{bb}^{t}$
,
![]() $1-q_{aa}^{t}$
and
$1-q_{aa}^{t}$
and
![]() $1-q_{bb}^{t}$
.
$1-q_{bb}^{t}$
.
To continue analysing the asymptotic behaviour of
![]() $({1-p_{aa}^{t}})/({1-p_{bb}^{t}})$
and
$({1-p_{aa}^{t}})/({1-p_{bb}^{t}})$
and
![]() $({1-q_{aa}^{t}})/({1-q_{bb}^{t}})$
, we introduce the terms:
$({1-q_{aa}^{t}})/({1-q_{bb}^{t}})$
, we introduce the terms:
 $$ \begin{align} r_{ij}^{t}=\sum_{\{\underline{\gamma}: i\to j\in\mathcal{P}(\Sigma^{\prime})\}}\mathop{\mathrm{exp}}\nolimits(t\phi-P_G(t\phi))(\underline{\gamma}), \end{align} $$
$$ \begin{align} r_{ij}^{t}=\sum_{\{\underline{\gamma}: i\to j\in\mathcal{P}(\Sigma^{\prime})\}}\mathop{\mathrm{exp}}\nolimits(t\phi-P_G(t\phi))(\underline{\gamma}), \end{align} $$
for each
![]() $i,j\in \{a,b\}$
. It can be observed that
$i,j\in \{a,b\}$
. It can be observed that
![]() $r_{ij}^{t}\leq p_{ij}^{t}$
and
$r_{ij}^{t}\leq p_{ij}^{t}$
and
![]() $r_{ij}^{t}\leq q_{ij}^{t}$
. Note that
$r_{ij}^{t}\leq q_{ij}^{t}$
. Note that
![]() $r_{ij}^{t}$
is obtained by taking the sum only on the main paths in
$r_{ij}^{t}$
is obtained by taking the sum only on the main paths in
![]() $\Sigma ^{\prime }$
, while
$\Sigma ^{\prime }$
, while
![]() $p_{ij}^{t}$
considers all the main paths of
$p_{ij}^{t}$
considers all the main paths of
![]() $\Sigma $
. Later, in Lemma 3.9, we will show that for each
$\Sigma $
. Later, in Lemma 3.9, we will show that for each
![]() $a\in I$
fixed, the value of
$a\in I$
fixed, the value of
![]() $r_{aa}^{t}$
is close to
$r_{aa}^{t}$
is close to
![]() $p_{aa}^{t}$
and
$p_{aa}^{t}$
and
![]() $q_{aa}^{t}$
for t large enough.
$q_{aa}^{t}$
for t large enough.
The main tool to prove equation (3.30) is Lemma 3.9; in fact, Lemmas 3.7 and 3.8 allow us to prove this lemma. The aforementioned results are the same as those obtained by T. Kempton for countable Markov shifts satisfying the BIP condition and the proofs are similar, which can be found in [Reference Kempton17]. This is due to Proposition 3.4 and because the Gurevich pressure on topologically transitive countable Markov shifts has a similar behaviour to the one observed in the case of countable Markov shifts satisfying the BIP condition. This was proved in Proposition 3.3.
For each main path
![]() $\underline {\gamma }\in \{\underline {\gamma }:a\to a\}$
, we write
$\underline {\gamma }\in \{\underline {\gamma }:a\to a\}$
, we write
![]() $n(\underline {\gamma })$
to denote the number of times that a symbol of I appears in
$n(\underline {\gamma })$
to denote the number of times that a symbol of I appears in
![]() $\underline {\gamma }$
without taking into account the symbols that appear at the end. So, when
$\underline {\gamma }$
without taking into account the symbols that appear at the end. So, when
![]() $n(\underline {\gamma })=n$
, these symbols of I can be labelled as
$n(\underline {\gamma })=n$
, these symbols of I can be labelled as
![]() $i_0,i_1,i_2,\ldots ,i_{n+1}$
with the convention
$i_0,i_1,i_2,\ldots ,i_{n+1}$
with the convention
![]() $i_0=i_{n+1}=a$
. We denote by
$i_0=i_{n+1}=a$
. We denote by
![]() $X_{aa}^n$
all those main paths satisfying
$X_{aa}^n$
all those main paths satisfying
![]() $n(\underline {\gamma })=n$
. From the definition of a main path, we necessarily have
$n(\underline {\gamma })=n$
. From the definition of a main path, we necessarily have
![]() $i_k \neq \{a,b\}$
,
$i_k \neq \{a,b\}$
,
![]() $1 \leq k \leq n$
. By calling
$1 \leq k \leq n$
. By calling
![]() $X_{aa}^n$
the collection of main paths such that
$X_{aa}^n$
the collection of main paths such that
![]() $n(\underline {\gamma })=n$
, we get
$n(\underline {\gamma })=n$
, we get
 $$ \begin{align} p_{aa}^{t}=\sum_{n=0}^{\infty}p_{aa}^{t}(n), \end{align} $$
$$ \begin{align} p_{aa}^{t}=\sum_{n=0}^{\infty}p_{aa}^{t}(n), \end{align} $$
where
 $$ \begin{align} p_{aa}^{t}(n)=\sum_{i_0,\ldots,i_{n+1}\in X_{aa}^n}\prod_{k=0}^{n}\bigg(\sum_{\{\underline{\gamma}:i_k\hookrightarrow i_{k+1}\in\mathcal{P}(\Sigma)\}}\mathop{\mathrm{exp}}\nolimits(t\phi-P_G(t\phi))(\underline{\gamma})\bigg). \end{align} $$
$$ \begin{align} p_{aa}^{t}(n)=\sum_{i_0,\ldots,i_{n+1}\in X_{aa}^n}\prod_{k=0}^{n}\bigg(\sum_{\{\underline{\gamma}:i_k\hookrightarrow i_{k+1}\in\mathcal{P}(\Sigma)\}}\mathop{\mathrm{exp}}\nolimits(t\phi-P_G(t\phi))(\underline{\gamma})\bigg). \end{align} $$
Note that for every
![]() $n\geq 0$
, the terms
$n\geq 0$
, the terms
![]() $p^t_{aa}(n)$
are of the form
$p^t_{aa}(n)$
are of the form
![]() $\mathop {\mathrm {exp}}\nolimits (t\phi -P_G(t\phi ))(\underline {\gamma })$
, where
$\mathop {\mathrm {exp}}\nolimits (t\phi -P_G(t\phi ))(\underline {\gamma })$
, where
![]() $\underline {\gamma }\in \mathcal {P}(\Sigma )$
such that
$\underline {\gamma }\in \mathcal {P}(\Sigma )$
such that
![]() $n(\underline {\gamma })=n$
. The following lemma gives a lower bound for
$n(\underline {\gamma })=n$
. The following lemma gives a lower bound for
![]() $p_{aa}^{t}(n)$
, for every
$p_{aa}^{t}(n)$
, for every
![]() $a\in I$
.
$a\in I$
.
Lemma 3.7. For every
![]() $r\in \mathbb {N}_0$
and
$r\in \mathbb {N}_0$
and
![]() $r|I|\leq n < (r+1)|I|$
, we have that
$r|I|\leq n < (r+1)|I|$
, we have that
Similarly to equations (3.34), (3.35), we now define
![]() $r_{aa}^{t}=\sum _{n=0}^{\infty }r_{aa}^{t}(n)$
, where
$r_{aa}^{t}=\sum _{n=0}^{\infty }r_{aa}^{t}(n)$
, where
 $$ \begin{align*}r_{aa}^{t}(n):=\sum_{i_0,\ldots,i_{n+1}\in X_{aa}^n}\prod_{k=0}^{n}\bigg(\sum_{\{\underline{\gamma}:i_k\hookrightarrow i_{k+1}\in\mathcal{P}(\Sigma^{\prime})\}}\mathop{\mathrm{exp}}\nolimits(t\phi-P_G(t\phi))(\underline{\gamma})\bigg).\end{align*} $$
$$ \begin{align*}r_{aa}^{t}(n):=\sum_{i_0,\ldots,i_{n+1}\in X_{aa}^n}\prod_{k=0}^{n}\bigg(\sum_{\{\underline{\gamma}:i_k\hookrightarrow i_{k+1}\in\mathcal{P}(\Sigma^{\prime})\}}\mathop{\mathrm{exp}}\nolimits(t\phi-P_G(t\phi))(\underline{\gamma})\bigg).\end{align*} $$
By calling
 $$ \begin{align*}\epsilon(n):=\frac{p_{aa}^{t}(n)}{r_{aa}^{t}(n)},\end{align*} $$
$$ \begin{align*}\epsilon(n):=\frac{p_{aa}^{t}(n)}{r_{aa}^{t}(n)},\end{align*} $$
it can be checked that
 $$ \begin{align*}0\leq p_{aa}^{t}-r_{aa}^{t}=\sum_{n=0}^{\infty}p_{aa}^{t}(n)\bigg(1-\frac{1}{\epsilon(n)}\bigg).\end{align*} $$
$$ \begin{align*}0\leq p_{aa}^{t}-r_{aa}^{t}=\sum_{n=0}^{\infty}p_{aa}^{t}(n)\bigg(1-\frac{1}{\epsilon(n)}\bigg).\end{align*} $$
Lemma 3.8. There exists
![]() $T>0$
and
$T>0$
and
![]() $K_1$
such that for all
$K_1$
such that for all
![]() $t>T$
, the following hold.
$t>T$
, the following hold.
-
(i) For each
 $0 \leq n<|I|-1$
, the following inequality holds:
$0 \leq n<|I|-1$
, the following inequality holds:  $$ \begin{align*}\epsilon(n)\leq 1+K_1\mathop{\mathrm{exp}}\nolimits(-5Ct).\end{align*} $$
$$ \begin{align*}\epsilon(n)\leq 1+K_1\mathop{\mathrm{exp}}\nolimits(-5Ct).\end{align*} $$
-
(ii) For each
 $r\geq 1$
and
$r\geq 1$
and
 $r|I|\leq n < (r+1)|I|$
, the following statement is satisfied:
$r|I|\leq n < (r+1)|I|$
, the following statement is satisfied:  $$ \begin{align*}\epsilon(n)\leq (1+K_1\mathop{\mathrm{exp}}\nolimits(-5Ct))^r.\end{align*} $$
$$ \begin{align*}\epsilon(n)\leq (1+K_1\mathop{\mathrm{exp}}\nolimits(-5Ct))^r.\end{align*} $$
Proof. From Proposition 3.3(ii) and Theorem 2 from [Reference Freire and Vargas12], the Gurevich pressure
![]() $P_{G}(t\phi )$
decreases to
$P_{G}(t\phi )$
decreases to
![]() $h_{\mathrm{max}}$
. So, there exists
$h_{\mathrm{max}}$
. So, there exists
![]() $T>0$
such that
$T>0$
such that
where d was given in Remark 3.5, also
Therefore,
and thus the difference between the pressure
![]() $P_G(t\phi )$
and
$P_G(t\phi )$
and
![]() $P_G(T\phi )$
can be controlled, for
$P_G(T\phi )$
can be controlled, for
![]() $t\gg 0$
. Let
$t\gg 0$
. Let
![]() $i_k,i_{k+1}\in I$
be arbitrary. Consider a path
$i_k,i_{k+1}\in I$
be arbitrary. Consider a path
![]() $\underline {\gamma }=i_kx_1 \ldots x_{m-1}i_{k+1}:i_k\hookrightarrow i_{k+1}\in \mathcal {P}(\Sigma \setminus \Sigma ^{\prime })$
, that is,
$\underline {\gamma }=i_kx_1 \ldots x_{m-1}i_{k+1}:i_k\hookrightarrow i_{k+1}\in \mathcal {P}(\Sigma \setminus \Sigma ^{\prime })$
, that is,
![]() $x_n \notin I$
for all
$x_n \notin I$
for all
![]() $1 \leq n \leq m-1$
and at least one symbol
$1 \leq n \leq m-1$
and at least one symbol
![]() $x_n$
,
$x_n$
,
![]() $n=1,2,\ldots ,m-1$
does not belongs to the alphabet associated to the finite Markov shift
$n=1,2,\ldots ,m-1$
does not belongs to the alphabet associated to the finite Markov shift
![]() $\Sigma ^{\prime }$
. From Remark 3.5, we have
$\Sigma ^{\prime }$
. From Remark 3.5, we have
![]() $\phi (i_k x_1)\leq 0$
,
$\phi (i_k x_1)\leq 0$
,
![]() $\phi (x_n x_{n+1})<-d$
for
$\phi (x_n x_{n+1})<-d$
for
![]() $n=1,\ldots ,m-2$
and
$n=1,\ldots ,m-2$
and
![]() $\phi (x_{m-1}i_{k+1})<-d$
, because
$\phi (x_{m-1}i_{k+1})<-d$
, because
![]() $x_n\notin I$
for
$x_n\notin I$
for
![]() $n=1,\ldots ,m-1$
. Moreover, since
$n=1,\ldots ,m-1$
. Moreover, since
![]() $\underline {\gamma }\in \mathcal {P}(\Sigma \setminus \Sigma ^{\prime })$
, there exists some
$\underline {\gamma }\in \mathcal {P}(\Sigma \setminus \Sigma ^{\prime })$
, there exists some
![]() $j\in \{1,2,\ldots ,m-1\}$
such that
$j\in \{1,2,\ldots ,m-1\}$
such that
![]() $\phi (x_j x_{j+1})<-7c$
and consequently
$\phi (x_j x_{j+1})<-7c$
and consequently
In addition, from equation (3.36), we have
![]() $P_{G}(T\phi )-P_{G}(t\phi ) \leq d \leq (t-T)d$
for
$P_{G}(T\phi )-P_{G}(t\phi ) \leq d \leq (t-T)d$
for
![]() $t\geq T+1$
, so that
$t\geq T+1$
, so that
 $$ \begin{align} (t\phi-P_{G}(t\phi))(\underline{\gamma})-(T\phi-P_{G}(T\phi))(\underline{\gamma})&=((t-T)\phi-P_{G}(t\phi)+P_{G}(T\phi))(\underline{\gamma})\nonumber\\ &=m(P_{G}(T\phi)-P_{G}(t\phi))+(t-T)\phi(\underline{\gamma})\nonumber\\ &\leq(t-T)md+(t-T)(-d(m-2)-7c)\nonumber\\ &=(t-T)(2d-7c)\nonumber\\ &\leq-7C(t-T). \end{align} $$
$$ \begin{align} (t\phi-P_{G}(t\phi))(\underline{\gamma})-(T\phi-P_{G}(T\phi))(\underline{\gamma})&=((t-T)\phi-P_{G}(t\phi)+P_{G}(T\phi))(\underline{\gamma})\nonumber\\ &=m(P_{G}(T\phi)-P_{G}(t\phi))+(t-T)\phi(\underline{\gamma})\nonumber\\ &\leq(t-T)md+(t-T)(-d(m-2)-7c)\nonumber\\ &=(t-T)(2d-7c)\nonumber\\ &\leq-7C(t-T). \end{align} $$
We now fix the constant:
 $$ \begin{align} K:=\mathop{\mathrm{exp}}\nolimits(7CT)\max_{i_k,i_{k+1}\in I}\sum_{\underline{\gamma}:i_k\hookrightarrow i_{k+1}\in\mathcal{P}(\Sigma\setminus\Sigma^{\prime})}\mathop{\mathrm{exp}}\nolimits((T\phi-P_{G}(T\phi))(\underline{\gamma})), \end{align} $$
$$ \begin{align} K:=\mathop{\mathrm{exp}}\nolimits(7CT)\max_{i_k,i_{k+1}\in I}\sum_{\underline{\gamma}:i_k\hookrightarrow i_{k+1}\in\mathcal{P}(\Sigma\setminus\Sigma^{\prime})}\mathop{\mathrm{exp}}\nolimits((T\phi-P_{G}(T\phi))(\underline{\gamma})), \end{align} $$
note that
![]() $K<\infty $
, because
$K<\infty $
, because
![]() ${\sum _{\underline {\gamma }:i_k\hookrightarrow i_{k+1}\in \mathcal {P}(\Sigma \setminus \Sigma ^{\prime })}\mathop {\mathrm {exp}}\nolimits ((T\phi -P_{G}(T\phi ))(\underline {\gamma }))\leq p_{i_ki_{k+1}}^T<\infty }$
. From equation (3.37), we have for
${\sum _{\underline {\gamma }:i_k\hookrightarrow i_{k+1}\in \mathcal {P}(\Sigma \setminus \Sigma ^{\prime })}\mathop {\mathrm {exp}}\nolimits ((T\phi -P_{G}(T\phi ))(\underline {\gamma }))\leq p_{i_ki_{k+1}}^T<\infty }$
. From equation (3.37), we have for
![]() $t\geq T+1$
,
$t\geq T+1$
,
so that
 $$ \begin{align*} &\sum_{\underline{\gamma}:i_k\hookrightarrow i_{k+1}\in\mathcal{P}(\Sigma\setminus\Sigma^{\prime})}\mathop{\mathrm{exp}}\nolimits((t\phi-P_{G}(t\phi))(\underline{\gamma}))\\ &\ \ \ \ \leq \mathop{\mathrm{exp}}\nolimits(-7Ct+7CT) \sum_{\underline{\gamma}:i_k\hookrightarrow i_{k+1}\in\mathcal{P}(\Sigma\setminus\Sigma^{\prime})}\mathop{\mathrm{exp}}\nolimits(((T\phi-P_{G}(T\phi))(\underline{\gamma}))\\ &\ \ \ \ \leq \mathop{\mathrm{exp}}\nolimits(-7Ct)K. \end{align*} $$
$$ \begin{align*} &\sum_{\underline{\gamma}:i_k\hookrightarrow i_{k+1}\in\mathcal{P}(\Sigma\setminus\Sigma^{\prime})}\mathop{\mathrm{exp}}\nolimits((t\phi-P_{G}(t\phi))(\underline{\gamma}))\\ &\ \ \ \ \leq \mathop{\mathrm{exp}}\nolimits(-7Ct+7CT) \sum_{\underline{\gamma}:i_k\hookrightarrow i_{k+1}\in\mathcal{P}(\Sigma\setminus\Sigma^{\prime})}\mathop{\mathrm{exp}}\nolimits(((T\phi-P_{G}(T\phi))(\underline{\gamma}))\\ &\ \ \ \ \leq \mathop{\mathrm{exp}}\nolimits(-7Ct)K. \end{align*} $$
The proof continues following the same steps as [Reference Kempton17] to obtain items (i) and (ii).
Due to Lemmas 3.7 and 3.8, the following lemma is obtained.
Lemma 3.9. There exists
![]() $T>0$
and
$T>0$
and
![]() $0<M<\infty $
such that for each pair
$0<M<\infty $
such that for each pair
![]() $a,b\in I$
and for all
$a,b\in I$
and for all
![]() $t>T$
:
$t>T$
:
-
(i)
 $p_{aa}^{t}\leq r_{aa}^{t}+ M\mathop {\mathrm {exp}}\nolimits (-3Ct);$
$p_{aa}^{t}\leq r_{aa}^{t}+ M\mathop {\mathrm {exp}}\nolimits (-3Ct);$
-
(ii)
 $p_{ab}^{t}p_{ba}^{t}\leq r_{ab}^{t}r_{ba}^{t}+ M\mathop {\mathrm {exp}}\nolimits (-3Ct).$
$p_{ab}^{t}p_{ba}^{t}\leq r_{ab}^{t}r_{ba}^{t}+ M\mathop {\mathrm {exp}}\nolimits (-3Ct).$
We write
![]() $a(t)\sim b(t)$
to express that
$a(t)\sim b(t)$
to express that
As a consequence of the previous lemma, one can obtain that
for every
![]() $a\in I$
, see [Reference Kempton17] for complete details.
$a\in I$
, see [Reference Kempton17] for complete details.
Finally, from equation (3.39), we have that
 $$ \begin{align*}\frac{\mu_t([b])}{\mu_t([a])}=\frac{1-p_{aa}^{t}}{1-p_{bb}^{t}}\sim\frac{1-r_{aa}^{t}}{1-r_{bb}^{t}}\sim\frac{1-q_{aa}^{t}}{1-q_{bb}^{t}}=\frac{\vartheta_{t}([b])}{\vartheta_{t}([a])}.\end{align*} $$
$$ \begin{align*}\frac{\mu_t([b])}{\mu_t([a])}=\frac{1-p_{aa}^{t}}{1-p_{bb}^{t}}\sim\frac{1-r_{aa}^{t}}{1-r_{bb}^{t}}\sim\frac{1-q_{aa}^{t}}{1-q_{bb}^{t}}=\frac{\vartheta_{t}([b])}{\vartheta_{t}([a])}.\end{align*} $$
Therefore,
since that
![]() $\lim _{t\to \infty }({\vartheta _{t}([b])}/{\vartheta _{t}([a])})$
exists for all
$\lim _{t\to \infty }({\vartheta _{t}([b])}/{\vartheta _{t}([a])})$
exists for all
![]() $a,b\in I$
, we finally have that
$a,b\in I$
, we finally have that
![]() $\lim _{t\to \infty }\mu _t$
exists in the weak
$\lim _{t\to \infty }\mu _t$
exists in the weak
![]() $^\star $
topology.
$^\star $
topology.

Figure 1 Renewal shift.
4 Examples on the renewal shift
Throughout this section, we present some examples where there is selection at zero temperature for the family of equilibrium states
![]() $(\mu _t)_{t\geq }$
, that is, where the limit
$(\mu _t)_{t\geq }$
, that is, where the limit
![]() $\lim _{t \to \infty }\mu _t$
exists in the weak
$\lim _{t \to \infty }\mu _t$
exists in the weak
![]() $^\star $
topology. In fact, those examples are given in the context of the so-called renewal shifts (to be defined below), when the potentials do not necessarily satisfy the conditions stated in Theorem 3.1.
$^\star $
topology. In fact, those examples are given in the context of the so-called renewal shifts (to be defined below), when the potentials do not necessarily satisfy the conditions stated in Theorem 3.1.
The renewal shift is the countable Markov shift whose transition matrix
![]() $(A(i,j))_{\mathbb {N}\times \mathbb {N}}$
has entries
$(A(i,j))_{\mathbb {N}\times \mathbb {N}}$
has entries
![]() $A(1,1),A(1,i)$
, and
$A(1,1),A(1,i)$
, and
![]() $A(i,i-1)$
are equal to
$A(i,i-1)$
are equal to
![]() $1$
for every
$1$
for every
![]() $i>1$
, and the other entries are equal to
$i>1$
, and the other entries are equal to
![]() $0$
. Note that the renewal shift is topologically mixing and does not satisfy the BIP property (see Figure 1).
$0$
. Note that the renewal shift is topologically mixing and does not satisfy the BIP property (see Figure 1).
In this subsection, we will present two examples of the zero-temperature limit of equilibrium states on the renewal shift. Example 4.1 is for the potential
![]() $\phi (x)=-x_0$
. Note that this potential satisfies the hypotheses of Theorem 3.1. However, Example 4.2 is for the potential
$\phi (x)=-x_0$
. Note that this potential satisfies the hypotheses of Theorem 3.1. However, Example 4.2 is for the potential
![]() $\phi (x)=x_0-x_1$
, which is not a summable potential; however, it has zero temperature limits for its associated equilibrium states.
$\phi (x)=x_0-x_1$
, which is not a summable potential; however, it has zero temperature limits for its associated equilibrium states.
In a renewal shift with
![]() $\phi :\Sigma \to \mathbb {R}$
a weakly Hölder continuous function such that
$\phi :\Sigma \to \mathbb {R}$
a weakly Hölder continuous function such that
![]() $\sup \phi <\infty $
, Sarig [Reference Sarig25] showed that there exists
$\sup \phi <\infty $
, Sarig [Reference Sarig25] showed that there exists
![]() $t_c>0$
and a unique equilibrium state
$t_c>0$
and a unique equilibrium state
![]() $\mu _t\in \mathcal {M}_{\sigma }(\Sigma )$
associated to the potential
$\mu _t\in \mathcal {M}_{\sigma }(\Sigma )$
associated to the potential
![]() $t\phi $
, for
$t\phi $
, for
![]() $t\in (0,t_c)$
. In that same context, Iommi [Reference Iommi14] showed that if
$t\in (0,t_c)$
. In that same context, Iommi [Reference Iommi14] showed that if
![]() $t_c=\infty $
, then the set of
$t_c=\infty $
, then the set of
![]() $\phi $
-maximizing
$\phi $
-maximizing
![]() $\mathcal {M}_{\mathrm{max}}(\phi )\neq \emptyset $
, otherwise there is no maximizing measure associated to potential
$\mathcal {M}_{\mathrm{max}}(\phi )\neq \emptyset $
, otherwise there is no maximizing measure associated to potential
![]() $\phi $
.
$\phi $
.
Example 4.1. Consider the renewal shift
![]() $\Sigma $
and a potential
$\Sigma $
and a potential
![]() $\phi :\Sigma \to \mathbb {R}$
given by
$\phi :\Sigma \to \mathbb {R}$
given by
We will show that
![]() $\lim _{t\to \infty }\mu _{t}$
exists and is a maximizing measure, where
$\lim _{t\to \infty }\mu _{t}$
exists and is a maximizing measure, where
![]() $\mu _{t}$
is the equilibrium state associated to potential
$\mu _{t}$
is the equilibrium state associated to potential
![]() $t\phi $
. Also,
$t\phi $
. Also,
![]() $\lim _{t\to \infty }\mu _{t}([a])=0$
, for all
$\lim _{t\to \infty }\mu _{t}([a])=0$
, for all
![]() $a\geq 2$
.
$a\geq 2$
.
Note that
![]() $\phi $
is a summable potential with
$\phi $
is a summable potential with
![]() $\overline {\mathop {\mathrm {Var}}\nolimits }(\phi )=0$
. Also,
$\overline {\mathop {\mathrm {Var}}\nolimits }(\phi )=0$
. Also,
So, by Theorem 1 in [Reference Freire and Vargas12], the family
![]() $(\mu _{t})_{t\geq 1}$
of equilibrium states associated to potential
$(\mu _{t})_{t\geq 1}$
of equilibrium states associated to potential
![]() $t\phi $
have accumulation points. To verify the statement of the previous example, we need the following affirmations to hold.
$t\phi $
have accumulation points. To verify the statement of the previous example, we need the following affirmations to hold.
Affirmation 1. For
![]() $a,n\in \mathbb {N}$
, we have
$a,n\in \mathbb {N}$
, we have
Proof. Let
![]() $a,n\in \mathbb {N}$
. It can be verified that
$a,n\in \mathbb {N}$
. It can be verified that
for all
![]() $x\in [a]$
. Let us integrate that expression with respect to
$x\in [a]$
. Let us integrate that expression with respect to
![]() $\nu _t$
, which is the eigenmeasure of the dual of the Ruelle operator, that is,
$\nu _t$
, which is the eigenmeasure of the dual of the Ruelle operator, that is,
![]() $L_{t\phi }^{*}\nu _t=\mathop {\mathrm {exp}}\nolimits (P_G(t\phi ))\nu _t$
. So, we obtain
$L_{t\phi }^{*}\nu _t=\mathop {\mathrm {exp}}\nolimits (P_G(t\phi ))\nu _t$
. So, we obtain

Affirmation 2. For any
![]() $a\in \mathbb {N}$
, there is a constant
$a\in \mathbb {N}$
, there is a constant
![]() $C=\mathop {\mathrm {exp}}\nolimits (-{(a-1)(a+2)}/{2})$
such that
$C=\mathop {\mathrm {exp}}\nolimits (-{(a-1)(a+2)}/{2})$
such that
where
![]() $x\in [a]$
.
$x\in [a]$
.
Proof. Fix
![]() $x\in [a]$
. We define the application bijective:
$x\in [a]$
. We define the application bijective:
 $$ \begin{align*}\begin{array}{llll} \theta \ : & \!\{y\in[1]:~ \sigma ^{n}(y)=x\} & \!\longrightarrow & \! \{z\in[1]: \sigma ^{n+a-1}(z)=z,z_n=a\} \\ &\! y=1,y_1,\ldots ,y_{n-1},x_0^{\infty} & \! \longmapsto & \! z=\overline{1,y_1,\ldots ,y_{n-1},a,(a-1),\ldots ,2}_{\mathrm{per}}. \end{array}\end{align*} $$
$$ \begin{align*}\begin{array}{llll} \theta \ : & \!\{y\in[1]:~ \sigma ^{n}(y)=x\} & \!\longrightarrow & \! \{z\in[1]: \sigma ^{n+a-1}(z)=z,z_n=a\} \\ &\! y=1,y_1,\ldots ,y_{n-1},x_0^{\infty} & \! \longmapsto & \! z=\overline{1,y_1,\ldots ,y_{n-1},a,(a-1),\ldots ,2}_{\mathrm{per}}. \end{array}\end{align*} $$
Note that for every
![]() $y\in \text {Dom}(\theta )$
,
$y\in \text {Dom}(\theta )$
,
![]() $S_n\phi (y)-S_{n+a-1}\phi (\theta (y))= -{(a-1)(a+2)}/{2}$
. So,
$S_n\phi (y)-S_{n+a-1}\phi (\theta (y))= -{(a-1)(a+2)}/{2}$
. So,

Affirmation 3. For
![]() $a\in \mathbb {N}$
, we have
$a\in \mathbb {N}$
, we have
 $$ \begin{align*}\nu_{t}([a])=\mathop{\mathrm{exp}}\nolimits\bigg(-\frac{(a+2)(a-1)}{2}t-(a-1)P_G(t\phi)\bigg)\nu_{t}([1]).\end{align*} $$
$$ \begin{align*}\nu_{t}([a])=\mathop{\mathrm{exp}}\nolimits\bigg(-\frac{(a+2)(a-1)}{2}t-(a-1)P_G(t\phi)\bigg)\nu_{t}([1]).\end{align*} $$
Proof. Fix
![]() $t\geq 1$
. By the generalized Ruelle’s Perron–Frobenius theorem (see Theorem 4.9 in [Reference Sarig23]), there is an eigenmeasure
$t\geq 1$
. By the generalized Ruelle’s Perron–Frobenius theorem (see Theorem 4.9 in [Reference Sarig23]), there is an eigenmeasure
![]() $\nu _{t}$
such that
$\nu _{t}$
such that
Let
![]() $a\geq 2$
. Consider
$a\geq 2$
. Consider
. Substituting in equation (4.1), we have

So,
using equation (4.2) recursively follows the statement.
Note that the potential
![]() $t\phi $
is positive recurrent, for every
$t\phi $
is positive recurrent, for every
![]() $t\geq 1$
. Consider
$t\geq 1$
. Consider
![]() $a\geq 1$
, then by the generalized Ruelle’s Perron–Frobenius theorem, we have
$a\geq 1$
, then by the generalized Ruelle’s Perron–Frobenius theorem, we have

where in the third line, the Affirmations 1 and 2 were used. Later, by Affirmation 3, we have
Therefore,
We will show that
![]() $(\mu _{t})_{t\geq 1}$
has only one accumulation point and this is
$(\mu _{t})_{t\geq 1}$
has only one accumulation point and this is
![]() $\delta _{\overline {1}}\in \mathcal {M}_{\sigma }(\Sigma )$
, where this measure is the one supported at the point
$\delta _{\overline {1}}\in \mathcal {M}_{\sigma }(\Sigma )$
, where this measure is the one supported at the point
![]() $\overline {1}=111\ldots 1\ldots \in \Sigma $
. Consider
$\overline {1}=111\ldots 1\ldots \in \Sigma $
. Consider
![]() $\mu _{\infty }\in \mathcal {M}_{\sigma }(\Sigma )$
an arbitrary accumulation point of
$\mu _{\infty }\in \mathcal {M}_{\sigma }(\Sigma )$
an arbitrary accumulation point of
![]() $(\mu _{t})_{t\geq 1}$
. Note that it is enough to show that
$(\mu _{t})_{t\geq 1}$
. Note that it is enough to show that
![]() $\mu _{\infty }=\delta _{\overline {1}}$
. From equation (4.3), we have that
$\mu _{\infty }=\delta _{\overline {1}}$
. From equation (4.3), we have that
![]() $\mu _{\infty }([a])=0$
, for all
$\mu _{\infty }([a])=0$
, for all
![]() $a\geq 2$
, and hence
$a\geq 2$
, and hence
![]() $\mu _{\infty }([1])=1$
. Since the measure
$\mu _{\infty }([1])=1$
. Since the measure
![]() $\mu _{\infty }$
is
$\mu _{\infty }$
is
![]() $\sigma $
-invariant, then
$\sigma $
-invariant, then
so, from equation (4.3) and the fact that
![]() $[1]=\bigcup _{i\geq 1}[1i]$
, we have that
$[1]=\bigcup _{i\geq 1}[1i]$
, we have that
![]() $\mu _{\infty }([1a])=0$
, for all
$\mu _{\infty }([1a])=0$
, for all
![]() $a\geq 2$
. Similarly, we obtain that
$a\geq 2$
. Similarly, we obtain that
So, since
![]() $\mu _{\infty }([1])=1$
, we have
$\mu _{\infty }([1])=1$
, we have
where
![]() $1\ldots 1$
is a word of arbitrary size composed only of the symbol one. To show that
$1\ldots 1$
is a word of arbitrary size composed only of the symbol one. To show that
![]() $\mu _{\infty }=\delta _{\overline {1}}$
, it suffices to show that
$\mu _{\infty }=\delta _{\overline {1}}$
, it suffices to show that
Note that for every
![]() $a\geq 2$
and
$a\geq 2$
and
![]() $\underline {\omega }\in \mathcal {W}$
such that
$\underline {\omega }\in \mathcal {W}$
such that
![]() $[\underline {\omega }]\cap [a]\neq \emptyset $
, we have that equation (4.6) is satisfied. Also, from equations (4.4) and (4.5), for every
$[\underline {\omega }]\cap [a]\neq \emptyset $
, we have that equation (4.6) is satisfied. Also, from equations (4.4) and (4.5), for every
![]() $[\underline {\omega }]\cap [1]\neq \emptyset $
, we have that equation (4.6) is satisfied. Therefore,
$[\underline {\omega }]\cap [1]\neq \emptyset $
, we have that equation (4.6) is satisfied. Therefore,
![]() $\lim _{t\to \infty }\mu _{t}=\delta _{\overline {1}}$
. Also, Proposition 3.1 ensures that
$\lim _{t\to \infty }\mu _{t}=\delta _{\overline {1}}$
. Also, Proposition 3.1 ensures that
![]() $\delta _{\overline {1}}\in \mathcal {M}_{\mathrm{max}}(\phi )$
.
$\delta _{\overline {1}}\in \mathcal {M}_{\mathrm{max}}(\phi )$
.
Example 4.2. Consider the renewal shift
![]() $\Sigma $
and the potential
$\Sigma $
and the potential
![]() $\phi :\Sigma \to \mathbb {R}$
given by
$\phi :\Sigma \to \mathbb {R}$
given by
We will show that
![]() $\lim _{t\to \infty }\mu _{t}$
exists and it is a
$\lim _{t\to \infty }\mu _{t}$
exists and it is a
![]() $\phi $
-maximizing measure, where
$\phi $
-maximizing measure, where
![]() $\mu _{t}\in \mathcal {M}_{\sigma }(\Sigma )$
is the equilibrium state associated to potential
$\mu _{t}\in \mathcal {M}_{\sigma }(\Sigma )$
is the equilibrium state associated to potential
![]() $t\phi $
, for every
$t\phi $
, for every
![]() $t\geq 1$
. Also,
$t\geq 1$
. Also,
![]() $\lim _{t\to \infty }\mu _{t} ([a])>0$
, for every
$\lim _{t\to \infty }\mu _{t} ([a])>0$
, for every
![]() $a\in \mathbb {N}$
.
$a\in \mathbb {N}$
.
Note that
![]() $\phi $
is a weakly Hölder continuous potential with
$\phi $
is a weakly Hölder continuous potential with
![]() $\mathop {\mathrm{Var}}\nolimits _1(\phi )=+\infty $
and
$\mathop {\mathrm{Var}}\nolimits _1(\phi )=+\infty $
and
![]() ${\sup \phi <\infty }$
. Also
${\sup \phi <\infty }$
. Also
![]() $t_c=\infty $
. Next, by Theorem 5 in [Reference Sarig25], we know that the equilibrium state
$t_c=\infty $
. Next, by Theorem 5 in [Reference Sarig25], we know that the equilibrium state
![]() $\mu _{t}\in \mathcal {M}_{\sigma }(\Sigma )$
associated with the potential
$\mu _{t}\in \mathcal {M}_{\sigma }(\Sigma )$
associated with the potential
![]() $t\phi $
exists, for every
$t\phi $
exists, for every
![]() $t\geq 1$
, and hence
$t\geq 1$
, and hence
![]() $\mathcal {M}_{\mathrm{max}}(\phi )\neq \emptyset $
, see Theorem 1.1 in [Reference Iommi14]. Fix
$\mathcal {M}_{\mathrm{max}}(\phi )\neq \emptyset $
, see Theorem 1.1 in [Reference Iommi14]. Fix
![]() $t\geq 1$
, and notice that the Gurevich pressure of
$t\geq 1$
, and notice that the Gurevich pressure of
![]() $P_G(t\phi )$
is constant,
$P_G(t\phi )$
is constant,
![]() $P_G(t\phi )=\log 2$
(see [Reference Beltrán, Bissacot and Endo2]). Also,
$P_G(t\phi )=\log 2$
(see [Reference Beltrán, Bissacot and Endo2]). Also,
![]() $\alpha (\phi )=0$
, and
$\alpha (\phi )=0$
, and
![]() $|\mathcal {M}_{\mathrm{max}}(\phi )|=\infty $
, because of the fact that for every
$|\mathcal {M}_{\mathrm{max}}(\phi )|=\infty $
, because of the fact that for every
![]() $x\in Per(\Sigma )$
such that
$x\in Per(\Sigma )$
such that
![]() $\sigma ^nx=x$
, we have
$\sigma ^nx=x$
, we have
![]() $S_n\phi (x)=0$
.
$S_n\phi (x)=0$
.
However, let
![]() $\underline {\omega }\in \mathcal {W}_m$
, such that
$\underline {\omega }\in \mathcal {W}_m$
, such that
![]() $\underline {\omega }\subset [a]$
, then
$\underline {\omega }\subset [a]$
, then

So, for any cylinder
![]() $\underline {\omega }$
, we have that
$\underline {\omega }$
, we have that
![]() $\mu _{t}([\underline {\omega }])$
does not depend on t. Since
$\mu _{t}([\underline {\omega }])$
does not depend on t. Since
![]() $\underline {\omega }$
was arbitrary, we have that
$\underline {\omega }$
was arbitrary, we have that
![]() $(\mu _{t})_{t\geq 1}$
is a singleton which we will denote by
$(\mu _{t})_{t\geq 1}$
is a singleton which we will denote by
![]() $\mu _{\infty }\in \mathcal {M}_{\sigma }(\Sigma )$
. By Proposition 3.3(iii),
$\mu _{\infty }\in \mathcal {M}_{\sigma }(\Sigma )$
. By Proposition 3.3(iii),
![]() $h(\mu _{\infty })=\log 2$
. So, by the variational principle, we have
$h(\mu _{\infty })=\log 2$
. So, by the variational principle, we have
and thus
![]() $\mu _{\infty }(\phi )=0$
. Therefore,
$\mu _{\infty }(\phi )=0$
. Therefore,
![]() $\mu _{\infty }$
is a
$\mu _{\infty }$
is a
![]() $\phi $
-maximizing measure. If we consider
$\phi $
-maximizing measure. If we consider
![]() $\underline {\omega }=a$
in equation (4.7), we have
$\underline {\omega }=a$
in equation (4.7), we have
![]() $\mu _{\infty }([a])={1}/{2^a}$
.
$\mu _{\infty }([a])={1}/{2^a}$
.
Note that from Example 4.2, we have the existence of the zero temperature limit of equilibrium states in more general conditions than Theorem 3.1.
Acknowledgements
The authors would like to thank the anonymous referee for his comments, suggestions and corrections, which have helped us to improve the paper. V.V. would to thank to the Foundation for Science and Technology (FCT) Project UIDP/00144/2020 and the Francisco José de Caldas Fund (FFJC) Process 80740-628-2020 for the financial support during part of the development of this paper. C.M. thanks CONACYT Mexico for financial support through Ciencia de Frontera (Ciencia Básica) Project No. A1-S-15528. J.L. and E.B. would to thank to the fellow program Fondo Postdoctorado Universidad Católica del Norte No 0001, 2020.