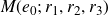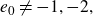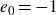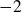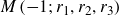1. Introduction
Seifert fibered 3-manifolds not carrying fillable contact structures have been singled out by Lecuona and Lisca [ Reference Lecuona and Lisca9 ]; they call them manifolds of special type. In this paper, we are interested in exactly which contact structures on small Seifert fibered spaces are fillable. For the surgery presentation of the underlying manifold see Figure 1.
Tight contact structures on small Seifert fibered spaces
![]() $M(e_0;\,r_1,r_2,r_3)$
where
$M(e_0;\,r_1,r_2,r_3)$
where
![]() $e_0\in{\mathbb{Z}}$
and
$e_0\in{\mathbb{Z}}$
and
![]() $r_i\in{\mathbb{Q}}\cap(0,1),$
are completely classified [
Reference Ghiggini, Lisca and Stipsicz5
,
Reference Wu19
] whenever
$r_i\in{\mathbb{Q}}\cap(0,1),$
are completely classified [
Reference Ghiggini, Lisca and Stipsicz5
,
Reference Wu19
] whenever
![]() $e_0\neq -1$
or
$e_0\neq -1$
or
![]() $-2$
; they are all given by Legendrian surgery on the standard Stein fillable
$-2$
; they are all given by Legendrian surgery on the standard Stein fillable
![]() $S^3$
or
$S^3$
or
![]() $S^1\times S^2$
, and hence they are also Stein fillable. Generally, there are essentially two types of tight contact structures on
$S^1\times S^2$
, and hence they are also Stein fillable. Generally, there are essentially two types of tight contact structures on
![]() $M(e_0;\,r_1,r_2,r_3)$
, distinguished by the maximal twisting of the regular fiber; that is, the maximal difference between the contact framing and the fibration framing within the smooth isotopy class of the fiber. The negative twisting structures are related to the transverse contact structures, and they are expected to be all at least symplectically fillable (see [
Reference Ghiggini4
,
Reference Ghiggini and Van Horn–Morris7
,
Reference Tosun17
] for some partial results). On the other hand, the zero-twisting tight contact structures exist only when
$M(e_0;\,r_1,r_2,r_3)$
, distinguished by the maximal twisting of the regular fiber; that is, the maximal difference between the contact framing and the fibration framing within the smooth isotopy class of the fiber. The negative twisting structures are related to the transverse contact structures, and they are expected to be all at least symplectically fillable (see [
Reference Ghiggini4
,
Reference Ghiggini and Van Horn–Morris7
,
Reference Tosun17
] for some partial results). On the other hand, the zero-twisting tight contact structures exist only when
![]() $e_0\geq-1$
; in the only unsettled case, for
$e_0\geq-1$
; in the only unsettled case, for
![]() $M\left({-}1;\,r_1,r_2,r_3\right)$
, they share a common contact surgery description [
Reference Lisca and Stipsicz10
] and are conjecturally [
Reference Stipsicz16
] characterised by non-vanishing of the Ozsváth–Szabó contact invariant
$M\left({-}1;\,r_1,r_2,r_3\right)$
, they share a common contact surgery description [
Reference Lisca and Stipsicz10
] and are conjecturally [
Reference Stipsicz16
] characterised by non-vanishing of the Ozsváth–Szabó contact invariant
![]() $c(M,\xi)\in\widehat{HF}({-}M,\mathbf t_\xi)$
; in the particular case of L-spaces this covers all tight structures and it has been confirmed in [
Reference Matkovič13
].
$c(M,\xi)\in\widehat{HF}({-}M,\mathbf t_\xi)$
; in the particular case of L-spaces this covers all tight structures and it has been confirmed in [
Reference Matkovič13
].
Zero-twisting tight contact structures on
![]() $M\left({-}1;\,r_1,r_2,r_3\right)$
are all described by contact surgery diagrams of Figure 2, as shown by Lisca and Stipsicz in [
Reference Lisca and Stipsicz10
]. Recall that such a diagram gives a family of contact structures, whose elements can be specified by replacing each contact
$M\left({-}1;\,r_1,r_2,r_3\right)$
are all described by contact surgery diagrams of Figure 2, as shown by Lisca and Stipsicz in [
Reference Lisca and Stipsicz10
]. Recall that such a diagram gives a family of contact structures, whose elements can be specified by replacing each contact
![]() $-{1}/{r_i}$
-surgery with a Legendrian surgery along a chain
$-{1}/{r_i}$
-surgery with a Legendrian surgery along a chain
![]() $L_i$
– called a leg – of unknots
$L_i$
– called a leg – of unknots
![]() $v_i^j$
whose Thurston–Bennequin invariants are determined by the continued fraction expansion of
$v_i^j$
whose Thurston–Bennequin invariants are determined by the continued fraction expansion of
 \begin{equation*}-\frac{1}{r_i}=-a^0_i-\frac{1}{\ddots-\frac{1}{-a^{k_i}_i}}=\left[a^0_i,\ldots,a^{k_i}_i\right],\ a^j_i\geq 2,\end{equation*}
\begin{equation*}-\frac{1}{r_i}=-a^0_i-\frac{1}{\ddots-\frac{1}{-a^{k_i}_i}}=\left[a^0_i,\ldots,a^{k_i}_i\right],\ a^j_i\geq 2,\end{equation*}
as
 \begin{equation*}\begin{array}{l}\mathrm{tb}_i^0=-a_i^0 \text{ for the leading unknot of } L_i \text{ and}\\[3pt] \mathrm{tb}_i^j=-a_i^j+1 \text{ for } j>0, \end{array}\end{equation*}
\begin{equation*}\begin{array}{l}\mathrm{tb}_i^0=-a_i^0 \text{ for the leading unknot of } L_i \text{ and}\\[3pt] \mathrm{tb}_i^j=-a_i^j+1 \text{ for } j>0, \end{array}\end{equation*}
and rotation numbers are chosen arbitrarily in

Fig. 1. Small Sefert fibered space
![]() $M\left(e_0;\,r_1,r_2,r_3\right)$
.
$M\left(e_0;\,r_1,r_2,r_3\right)$
.

Fig. 2. Contact structures on
![]() $M\left({-}1;\,r_1,r_2,r_3\right)$
.
$M\left({-}1;\,r_1,r_2,r_3\right)$
.
These structures are all supported by planar open books (see Subsection 2·1); but in contrast to contact structures on small Seifert spaces with
![]() $e_0\neq -1$
, not all tight ones are Stein fillable. With the aid of a theorem of Wendl [
Reference Wendl18
] (evoked as Theorem 2·6), we see that the non-Stein fillable structures are not fillable at all. Lecuona and Lisca [
Reference Lecuona and Lisca9
] showed that, when
$e_0\neq -1$
, not all tight ones are Stein fillable. With the aid of a theorem of Wendl [
Reference Wendl18
] (evoked as Theorem 2·6), we see that the non-Stein fillable structures are not fillable at all. Lecuona and Lisca [
Reference Lecuona and Lisca9
] showed that, when
![]() $M\left({-}1;\,r_1,r_2,r_3\right)$
is an L-space and
$M\left({-}1;\,r_1,r_2,r_3\right)$
is an L-space and
![]() $r_i+r_j<1$
for all pairs i,j, topology (the diagonalisation argument) prevents existence of Stein fillings; though, we know from the classification of Lisca and Stipsicz [
Reference Lisca and Stipsicz11
] that many of these manifolds actually admit tight structures. Another concrete example of a tight non-fillable structure was given by Ghiggini, Lisca and Stipsicz in [
Reference Ghiggini, Lisca and Stipsicz6
] on
$r_i+r_j<1$
for all pairs i,j, topology (the diagonalisation argument) prevents existence of Stein fillings; though, we know from the classification of Lisca and Stipsicz [
Reference Lisca and Stipsicz11
] that many of these manifolds actually admit tight structures. Another concrete example of a tight non-fillable structure was given by Ghiggini, Lisca and Stipsicz in [
Reference Ghiggini, Lisca and Stipsicz6
] on
![]() $M({-}1;\, {1}/{2}, {1}/{2}, {1}/{p})$
; while Plamenevskaya and Van Horn-Morris [
Reference Plamenevskaya and Van Horn–Morris14
] later obtained that when
$M({-}1;\, {1}/{2}, {1}/{2}, {1}/{p})$
; while Plamenevskaya and Van Horn-Morris [
Reference Plamenevskaya and Van Horn–Morris14
] later obtained that when
![]() $r_1\geq ({p-1})/{p}, r_2\geq {1}/{2}$
and
$r_1\geq ({p-1})/{p}, r_2\geq {1}/{2}$
and
![]() $r_3\geq {1}/{p}$
, all tight structures are also fillable. However, although all (possibly) tight structures admit common surgery presentation, the fillability of these structures has never been systematically analysed; the only manifolds for which the fillability of all tight structures has been understood are the ones which do not admit fillable structures and some for which all tight structures are also fillable.
$r_3\geq {1}/{p}$
, all tight structures are also fillable. However, although all (possibly) tight structures admit common surgery presentation, the fillability of these structures has never been systematically analysed; the only manifolds for which the fillability of all tight structures has been understood are the ones which do not admit fillable structures and some for which all tight structures are also fillable.
Here, we show that all fillable zero-twisting structures on
![]() $M\left({-}1;\,r_1,r_2,r_3\right)$
arise as Legendrian surgeries on the tight
$M\left({-}1;\,r_1,r_2,r_3\right)$
arise as Legendrian surgeries on the tight
![]() $S^1\times S^2$
. For L-spaces this covers all fillable structures, and hence implies the result of Lecuona and Lisca. More specifically, we show that fillability of a given surgery presentation is completely decided on specific sublinks representing
$S^1\times S^2$
. For L-spaces this covers all fillable structures, and hence implies the result of Lecuona and Lisca. More specifically, we show that fillability of a given surgery presentation is completely decided on specific sublinks representing
![]() $S^1\times S^2$
, whose tightness is in turn met by a unique choice of rotation numbers for this sublink.
$S^1\times S^2$
, whose tightness is in turn met by a unique choice of rotation numbers for this sublink.
First notice that, whenever
![]() $r_i+r_j\geq 1$
there exists a truncated continued fraction
$r_i+r_j\geq 1$
there exists a truncated continued fraction
![]() $- {1}/{s_i}=\left[a^0_i,\dots,a^{m_i}_i\right]<\left[a^0_i,\dots,a^{k_i}_i\right]=- {1}/{r_i}$
with
$- {1}/{s_i}=\left[a^0_i,\dots,a^{m_i}_i\right]<\left[a^0_i,\dots,a^{k_i}_i\right]=- {1}/{r_i}$
with
![]() $m_i\leq k_i$
, and for
$m_i\leq k_i$
, and for
![]() $r_j$
alike, such that
$r_j$
alike, such that
![]() $s_i+s_j=1$
(see [
Reference Lecuona and Lisca9
, lemma 3·2]). We will call any subdiagram of the contact surgery diagram in Figure 2 which consists of the two unstabilized unknots with
$s_i+s_j=1$
(see [
Reference Lecuona and Lisca9
, lemma 3·2]). We will call any subdiagram of the contact surgery diagram in Figure 2 which consists of the two unstabilized unknots with
![]() $+1$
-coefficient and two truncated legs, representing rational numbers
$+1$
-coefficient and two truncated legs, representing rational numbers
![]() $- {1}/{s_i}$
such that
$- {1}/{s_i}$
such that
![]() $s_i\leq r_i, s_j\leq r_j$
and
$s_i\leq r_i, s_j\leq r_j$
and
![]() $s_i+s_j=1$
, a circular sublink.
$s_i+s_j=1$
, a circular sublink.
Additionally, we will say that a Legendrian knot is fully positive if all its stabilisations are positive (for the unknot, this means
![]() $\mathrm{rot}=-(\mathrm{tb}+1)$
). When all the knots forming a leg are fully positive, the leg will be said to be positive. Analogously, we define a fully negative Legendrian knot and a negative leg. Now, a circular sublink whose one leg is positive and the other one negative will be referred to as a balanced sublink. With the terminology set we can state our result.
$\mathrm{rot}=-(\mathrm{tb}+1)$
). When all the knots forming a leg are fully positive, the leg will be said to be positive. Analogously, we define a fully negative Legendrian knot and a negative leg. Now, a circular sublink whose one leg is positive and the other one negative will be referred to as a balanced sublink. With the terminology set we can state our result.
Theorem 1·1. Assume that a contact structure
![]() $\xi$
on
$\xi$
on
![]() $M\left({-}1;\,r_1,r_2,r_3\right)$
is given by some surgery diagram of Figure 2. Then
$M\left({-}1;\,r_1,r_2,r_3\right)$
is given by some surgery diagram of Figure 2. Then
![]() $\xi$
is fillable if and only if the surgery presentation contains a balanced sublink.
$\xi$
is fillable if and only if the surgery presentation contains a balanced sublink.
As explained above, the theorem covers all zero-twisting tight structures on Seifert manifolds
![]() $M\left({-}1;\,r_1,r_2,r_3\right)$
and all tight contact structures when the underlying manifold is also an L-space. Additionally, when
$M\left({-}1;\,r_1,r_2,r_3\right)$
and all tight contact structures when the underlying manifold is also an L-space. Additionally, when
![]() $r_3=0$
(equivalently, when there is no surgery along
$r_3=0$
(equivalently, when there is no surgery along
![]() $L_3$
) and
$L_3$
) and
![]() $r_1+r_2=1$
we have the following.
$r_1+r_2=1$
we have the following.
Proposition 1·2. A contact surgery diagram as in Figure 2 describes the tight contact
![]() $S^1\times S^2$
if and only if it equals some balanced link.
$S^1\times S^2$
if and only if it equals some balanced link.
Our results are obtained by analysing monodromy factorisations of associated planar open books. The main new idea is the use of perspectives (see Section 4): by simultaneously looking at the planar page as a disk-with-holes with different outer boundaries, we extend the applicability of both the standard monodromy substitutions and the obstructions for positive factorisations due to Plamenevskaya and Van Horn–Morris [ Reference Plamenevskaya and Van Horn–Morris14 ].
Overview. In Section 2, we recall how to associate open books to the given surgery presentations, and present the main properties of planar monodromies. The proof of Theorem 1·1 is split between the following sections. In Section 3, we show that surgery along any balanced link indeed gives the fillable
![]() $S^1\times S^2$
. In Section 4, we obtain negative results by obstructing positive factorisation of monodromy in the abelianisation of the mapping class group of the planar page.
$S^1\times S^2$
. In Section 4, we obtain negative results by obstructing positive factorisation of monodromy in the abelianisation of the mapping class group of the planar page.
2. Open book presentation
2·1. Planar open book from the contact surgery presentation
In [ Reference Lisca and Stipsicz10 , theorem 1·5], Lisca and Stipsicz proved that contact structures of Figure 2 are planar; indeed, from a Legendrian surgery diagram as in Figure 2, one can construct a supporting open book with planar pages as follows. Look at Figure 3 top for the corresponding illustration.

Fig. 3. Illustration of our notation conventions on an example:
![]() $\mathrm{tb}_1=({-}2,-2,-1)$
and
$\mathrm{tb}_1=({-}2,-2,-1)$
and
![]() $\mathrm{rot}_1=(1,1,0)$
,
$\mathrm{rot}_1=(1,1,0)$
,
![]() $\mathrm{tb}_2=({-}2,-2)$
and
$\mathrm{tb}_2=({-}2,-2)$
and
![]() $\mathrm{rot}_2=(1,-1)$
,
$\mathrm{rot}_2=(1,-1)$
,
![]() $\mathrm{tb}_3=({-}3,-2)$
and
$\mathrm{tb}_3=({-}3,-2)$
and
![]() $\mathrm{rot}_3=({-}2,-1).$
In gray are boundary components of the punctured disk. The full curves correspond to positive Dehn twists, the boundary twists of the stabilisation holes are black, the
$\mathrm{rot}_3=({-}2,-1).$
In gray are boundary components of the punctured disk. The full curves correspond to positive Dehn twists, the boundary twists of the stabilisation holes are black, the
![]() $T_1$
-twists are blue, the
$T_1$
-twists are blue, the
![]() $T_2$
-twists orange and the
$T_2$
-twists orange and the
![]() $T_3$
-twists green. The dashed curve represents the negative Dehn twist N. The page is shown in two perspectives: with initial outer boundary (top) and with outer boundary in one
$T_3$
-twists green. The dashed curve represents the negative Dehn twist N. The page is shown in two perspectives: with initial outer boundary (top) and with outer boundary in one
![]() $\nu^0_3$
-hole (bottom).
$\nu^0_3$
-hole (bottom).
One
![]() $+1$
-surgery along an unknot with
$+1$
-surgery along an unknot with
![]() $\mathrm{tb}=-1$
is presented by an annulus with identity monodromy, the other
$\mathrm{tb}=-1$
is presented by an annulus with identity monodromy, the other
![]() $+1$
-surgery manifests itself in a negative Dehn twist along its core.
$+1$
-surgery manifests itself in a negative Dehn twist along its core.
Notation 2·1. Write
![]() $\pi^{\text{in}}$
and
$\pi^{\text{in}}$
and
![]() $\nu^{\text{out}}$
for the inner and the outer boundary of the annulus. Additionally, write N for the curve which supports the negative Dehn twist and, abusing the notation, also for the negative Dehn twist itself.
$\nu^{\text{out}}$
for the inner and the outer boundary of the annulus. Additionally, write N for the curve which supports the negative Dehn twist and, abusing the notation, also for the negative Dehn twist itself.
Every other unknot contributes a positive Dehn twist on a stabilised annulus. Concretely, we insert a hole, encircled by one boundary-parallel positive Dehn twist, for every stabilisation of every unknot in the surgery diagram; the stabilisation holes which correspond to positive stabilisations lie between the inner boundary
![]() $\pi^{\text{in}}$
of the annulus and its core N, the negative ones between N and the outer boundary
$\pi^{\text{in}}$
of the annulus and its core N, the negative ones between N and the outer boundary
![]() $\nu^{\text{out}}$
.
$\nu^{\text{out}}$
.
Notation 2·2. Denote by
![]() $\nu^j_i$
and
$\nu^j_i$
and
![]() $\pi^j_i$
any of the stabilisation holes which correspond to negative and positive stabilisations, respectively, of the unknot
$\pi^j_i$
any of the stabilisation holes which correspond to negative and positive stabilisations, respectively, of the unknot
![]() $v_i^j$
. When grouped into certain types, we use
$v_i^j$
. When grouped into certain types, we use
![]() $\nu_i$
for any of
$\nu_i$
for any of
![]() $\cup_{j}\nu^j_i$
, similarly
$\cup_{j}\nu^j_i$
, similarly
![]() $\nu^{\geq j}_i$
for any of
$\nu^{\geq j}_i$
for any of
![]() $\cup_{y\geq j}\nu^y_i$
, and
$\cup_{y\geq j}\nu^y_i$
, and
![]() $\nu$
to denote any of
$\nu$
to denote any of
![]() $\nu^{\text{out}}\cup\nu_i$
; the notation for the
$\nu^{\text{out}}\cup\nu_i$
; the notation for the
![]() $\pi$
-type holes is analogous. Note that, since the names of holes (equivalently, boundary components) are chosen as common names, we will refer to a single (not specified) hole with the given name
$\pi$
-type holes is analogous. Note that, since the names of holes (equivalently, boundary components) are chosen as common names, we will refer to a single (not specified) hole with the given name
![]() $\chi$
as a
$\chi$
as a
![]() $\chi$
-hole.
$\chi$
-hole.
Remark 2·3. Using
![]() $|\cdot |$
for the number of respective holes, we see that
$|\cdot |$
for the number of respective holes, we see that
![]() $2+|\nu^j_i|+|\pi^j_i|$
equals
$2+|\nu^j_i|+|\pi^j_i|$
equals
![]() $a^j_i$
for
$a^j_i$
for
![]() $j>0$
and
$j>0$
and
![]() $a^0_i+1$
for
$a^0_i+1$
for
![]() $j=0$
,
$j=0$
,
![]() $-1-|\nu^j_i|-|\pi^j_i|=\mathrm{tb}^j_i$
and
$-1-|\nu^j_i|-|\pi^j_i|=\mathrm{tb}^j_i$
and
![]() $|\pi^j_i|-|\nu^j_i|=\mathrm{rot}^j_i$
.
$|\pi^j_i|-|\nu^j_i|=\mathrm{rot}^j_i$
.
The positive Dehn twists corresponding to the Legendrian surgeries along
![]() $v_i^j$
are formed successively along the legs: From the leading unknot
$v_i^j$
are formed successively along the legs: From the leading unknot
![]() $v^0_i$
of each leg we get a positive Dehn twist along a push-off of the core N modified by encircling an additional
$v^0_i$
of each leg we get a positive Dehn twist along a push-off of the core N modified by encircling an additional
![]() $\nu_i^0$
-hole for each negative stabilisation, and avoiding a
$\nu_i^0$
-hole for each negative stabilisation, and avoiding a
![]() $\pi_i^0$
-hole for each positive stabilisation. The twists corresponding to the subsequent unknots
$\pi_i^0$
-hole for each positive stabilisation. The twists corresponding to the subsequent unknots
![]() $v_i^j$
in each leg are then obtained from a push-off of the twist corresponding to the preceding unknot
$v_i^j$
in each leg are then obtained from a push-off of the twist corresponding to the preceding unknot
![]() $v_i^{j-1}$
modified so that it additionally encircles all
$v_i^{j-1}$
modified so that it additionally encircles all
![]() $\nu_i^j$
-holes and avoids all
$\nu_i^j$
-holes and avoids all
![]() $\pi_i^j$
-holes.
$\pi_i^j$
-holes.
Notation 2·4. Denote
![]() $T_i^j$
the curve which corresponds to the unknot
$T_i^j$
the curve which corresponds to the unknot
![]() $v_i^j$
. From the construction in the preceding paragraph, we see that
$v_i^j$
. From the construction in the preceding paragraph, we see that
![]() $T_i^j$
encircles exactly
$T_i^j$
encircles exactly
![]() $\pi^{\text{in}}$
, all
$\pi^{\text{in}}$
, all
![]() $\pi_l$
for
$\pi_l$
for
![]() $l\neq i$
,
$l\neq i$
,
![]() $\pi_i^{>j}$
and
$\pi_i^{>j}$
and
![]() $\nu_i^{\leq j}$
$\nu_i^{\leq j}$
![]() $\big($
and so, it does not encircle exactly
$\big($
and so, it does not encircle exactly
![]() $\pi_i^{\leq j}$
,
$\pi_i^{\leq j}$
,
![]() $\nu_l$
for
$\nu_l$
for
![]() $l\neq i$
and
$l\neq i$
and
![]() $\nu_i^{>j}\big)$
. Abusing the notation, we will use
$\nu_i^{>j}\big)$
. Abusing the notation, we will use
![]() $T_i^j$
also for the corresponding positive Dehn twist. As in the case of holes, we will need also common names such as
$T_i^j$
also for the corresponding positive Dehn twist. As in the case of holes, we will need also common names such as
![]() $T_i=\cup_j T_i^j$
, referring to any single one of them as a
$T_i=\cup_j T_i^j$
, referring to any single one of them as a
![]() $T_i$
-twist or curve.
$T_i$
-twist or curve.
Remark 2·5. The unknots
![]() $T_i^j$
and
$T_i^j$
and
![]() $v_i^j$
are not exactly the same; while
$v_i^j$
are not exactly the same; while
![]() $v_i^j$
with fixed i form a chain
$v_i^j$
with fixed i form a chain
![]() $L_i$
, the corresponding
$L_i$
, the corresponding
![]() $T_i^j$
give the rolled-up diagram of
$T_i^j$
give the rolled-up diagram of
![]() $L_i$
(as described in [
Reference Schöberger15
]). Anyway, since the Legendrian push-off and the meridian of a Legendrian knot are Legendrian isotopic after we perform
$L_i$
(as described in [
Reference Schöberger15
]). Anyway, since the Legendrian push-off and the meridian of a Legendrian knot are Legendrian isotopic after we perform
![]() $-1$
-surgery on the original knot [
Reference Ding and Geiges2
], the two presentations give the same contact manifold.
$-1$
-surgery on the original knot [
Reference Ding and Geiges2
], the two presentations give the same contact manifold.
All together, the associated open book has as a page the punctured disk with one more hole than the number of stabilisations of all unknots in the surgery presentation, and the monodromy (up to conjugation) is given as a product of the negative Dehn twist N, positive Dehn twists
![]() $T_i^j$
for all j for all i and a single positive boundary twist along all boundary components except
$T_i^j$
for all j for all i and a single positive boundary twist along all boundary components except
![]() $\pi^{\text{in}}$
and
$\pi^{\text{in}}$
and
![]() $\nu^{\text{out}}$
.
$\nu^{\text{out}}$
.
2·2. Planar monodromy
Since our contact structures are all planar, the following theorem of Wendl ensures that to prove non-fillability it suffices to study positive factorisations of the given monodromy.
Theorem 2·6. [ Reference Wendl18 , corollary 2] A planar contact manifold is strongly symplectically fillable if and only if it is Stein fillable if and only if every supporting planar open book has monodromy isotopic to a product of positive Dehn twists.
Let us briefly review the characteristic features of the abelianised planar mapping classes, as used by Plamenevskaya and Van Horn–Morris in [ Reference Plamenevskaya and Van Horn–Morris14 ].
The mapping class group of a planar surface (in the presentation of Margalit and McCammond [
Reference Margalit and McCammond12
]) is described (geometrically) on a disk,
![]() $\mathbf D_n$
, with n holes arranged in the roots of unity. The group
$\mathbf D_n$
, with n holes arranged in the roots of unity. The group
![]() $\mathrm{Map}\ \mathbf{D}_n$
is generated by all convex Dehn twists (that is, the twists whose core is the boundary of the convex hull of a set of holes), and factored by commutators of disjoint twists and all lantern relations. Then, up to conjugation we have the following.
$\mathrm{Map}\ \mathbf{D}_n$
is generated by all convex Dehn twists (that is, the twists whose core is the boundary of the convex hull of a set of holes), and factored by commutators of disjoint twists and all lantern relations. Then, up to conjugation we have the following.
Lemma 2·7. A Dehn twist as an element of
![]() $\mathrm{AbMap}\ \mathbf{D}_n$
is determined by the set of holes it encircles.
$\mathrm{AbMap}\ \mathbf{D}_n$
is determined by the set of holes it encircles.
Furthermore, any mapping class
![]() $\phi$
factors into a product of Dehn twists. We can then define the single and pairwise multiplicities,
$\phi$
factors into a product of Dehn twists. We can then define the single and pairwise multiplicities,
![]() $m_\alpha(\phi)$
and
$m_\alpha(\phi)$
and
![]() $m_{\alpha\beta}(\phi)$
, as the number of twists (counted with signs) in a factorisation of the extension of
$m_{\alpha\beta}(\phi)$
, as the number of twists (counted with signs) in a factorisation of the extension of
![]() $\phi$
to the disk with all but one hole
$\phi$
to the disk with all but one hole
![]() $\alpha$
, or a pair of holes
$\alpha$
, or a pair of holes
![]() $\alpha$
and
$\alpha$
and
![]() $\beta$
, capped off. It is shown in [
Reference Plamenevskaya and Van Horn–Morris14
] that these numbers are independent of factorisation and that they contain a complete homological information about
$\beta$
, capped off. It is shown in [
Reference Plamenevskaya and Van Horn–Morris14
] that these numbers are independent of factorisation and that they contain a complete homological information about
![]() $\phi$
.
$\phi$
.
Lemma 2·8. [
Reference Plamenevskaya and Van Horn–Morris14
, p. 2084] A mapping class
![]() $\phi$
as an element of
$\phi$
as an element of
![]() $\mathrm{AbMap}\ \mathbf{D}_n$
is uniquely determined by a collection of multiplicities
$\mathrm{AbMap}\ \mathbf{D}_n$
is uniquely determined by a collection of multiplicities
![]() $\left\{m_\alpha(\phi),m_{\alpha\beta}(\phi)\right\}$
.
$\left\{m_\alpha(\phi),m_{\alpha\beta}(\phi)\right\}$
.
In particular, in a positive factorisation, the number of non-boundary twists around every hole is bounded from above by the number (counted with signs) of all twists encircling this hole in any given presentation.
In the following, we will make extensive use of an iterated lantern relation, also known as a daisy relation, which we state in the lemma below and illustrate in Figure 4.

Fig. 4. Daisy relation.
Lemma 2·9. [
Reference Plamenevskaya and Van Horn–Morris14
, lemma 3·5] In the mapping class group of the disk with
![]() $k+2$
holes, the positive Dehn twists
$k+2$
holes, the positive Dehn twists
![]() $B, B_0,B_1,\dots, B_{k+1}$
and
$B, B_0,B_1,\dots, B_{k+1}$
and
![]() $A_1,\dots,A_{k+1},C$
, as denoted in Figure 4, satisfy the relation
$A_1,\dots,A_{k+1},C$
, as denoted in Figure 4, satisfy the relation
Remark 2·10. The daisy relation of the disk with
![]() $k+2$
holes exactly describes the rational blow-down along
$k+2$
holes exactly describes the rational blow-down along
![]() $L\left((k+1)^2,k\right)$
, as monodromy substitution for the Lefschetz fibration [
Reference Endo, Mark and Van Horn-Morris3
].
$L\left((k+1)^2,k\right)$
, as monodromy substitution for the Lefschetz fibration [
Reference Endo, Mark and Van Horn-Morris3
].
3. Surgery links of tight
 $S^1\times S^2$
$S^1\times S^2$
Lemma 3·1. The contact surgery presentation given by a circular link smoothly describes
![]() $S^1\times S^2$
.
$S^1\times S^2$
.
Proof. The circular link smoothly consists of four
![]() $-1$
-linked unknots with framing coefficients
$-1$
-linked unknots with framing coefficients
![]() $0,0,-({s_1+1})/{s_1},-({s_2+1})/{s_2}$
for some
$0,0,-({s_1+1})/{s_1},-({s_2+1})/{s_2}$
for some
![]() $s_1+s_2=1$
. Switching to integral coefficients, we have the legs
$s_1+s_2=1$
. Switching to integral coefficients, we have the legs
![]() $L_1$
and
$L_1$
and
![]() $L_2$
in place of rational framed unknots, with surgery coefficients
$L_2$
in place of rational framed unknots, with surgery coefficients
![]() $\left({-}a_i^0-1,-a_i^1,\dots,-a_i^{m_i}\right)$
where
$\left({-}a_i^0-1,-a_i^1,\dots,-a_i^{m_i}\right)$
where
![]() $- {1}/{s_i}=\left[a^0_i,\dots,a^{m_i}_i\right]$
for
$- {1}/{s_i}=\left[a^0_i,\dots,a^{m_i}_i\right]$
for
![]() $i=1,2$
. Blowing-up once at the linking point (followed by a blow-down of the two
$i=1,2$
. Blowing-up once at the linking point (followed by a blow-down of the two
![]() $(+1)$
-framed meridians of the thus-added curve), we obtain a chain of unknots with coefficients
$(+1)$
-framed meridians of the thus-added curve), we obtain a chain of unknots with coefficients
![]() $\left({-}a^{m_1}_1,\dots,-a^0_1,-1,-a^0_2,\dots,-a^{m_2}_2\right)$
. Since
$\left({-}a^{m_1}_1,\dots,-a^0_1,-1,-a^0_2,\dots,-a^{m_2}_2\right)$
. Since
![]() $\left[a^{m_1}_1,\dots,a^0_1,1,a^0_2,\dots,a^{m_2}_2\right]=0$
, this chain can be successively blown-down, starting from the middle
$\left[a^{m_1}_1,\dots,a^0_1,1,a^0_2,\dots,a^{m_2}_2\right]=0$
, this chain can be successively blown-down, starting from the middle
![]() $-1$
-framed unknot, until it reduces to a 0-framed unknot.
$-1$
-framed unknot, until it reduces to a 0-framed unknot.
Remark 3·2. Notice that, after the blow-up the two legs of a circular link become dual to each other (that is, they describe a lens space and its orientation reversal). Explicitly, the coefficients of the two are related as follows (here,
![]() $-2^{\times b}$
means a chain of b-many unknots with framing
$-2^{\times b}$
means a chain of b-many unknots with framing
![]() $-2$
):
$-2$
):
 \begin{equation*}\begin{array}{l@{\quad}l@{\quad}l@{\quad}c@{\quad}c@{\quad}c@{\quad}c}L^{\prime}_1&:&\big({-}b_1-2,&-2^{\times b_2},& -b_3-3,&\dots,&-2^{\times b_m}\text{ or }-b_m-2\big)\\[3pt] L^{\prime}_2&:&\big({-}2^{\times b_1},&-b_2-3,&-2^{\times b_3},&\dots,& -b_m-2\text{ or }-2^{\times b_m}\big)\end{array}.\end{equation*}
\begin{equation*}\begin{array}{l@{\quad}l@{\quad}l@{\quad}c@{\quad}c@{\quad}c@{\quad}c}L^{\prime}_1&:&\big({-}b_1-2,&-2^{\times b_2},& -b_3-3,&\dots,&-2^{\times b_m}\text{ or }-b_m-2\big)\\[3pt] L^{\prime}_2&:&\big({-}2^{\times b_1},&-b_2-3,&-2^{\times b_3},&\dots,& -b_m-2\text{ or }-2^{\times b_m}\big)\end{array}.\end{equation*}
Hence, since the legs are affected by the blow-up only at the leading unknots, the smooth surgery coefficients of the original legs correlate as:
 \begin{equation*}\begin{array}{l@{\quad}l@{\quad}l@{\quad}c@{\quad}c@{\quad}c@{\quad}c}L_1&:&\big({-}b_1-3,&-2^{\times b_2},& -b_3-3,&\dots,&-2^{\times b_m}\text{ or }-b_m-2\big)\\[3pt] L_2&:&\big({-}3,-2^{\times (b_1-1)},&-b_2-3,&-2^{\times b_3},&\dots,& -b_m-2\text{ or }-2^{\times b_m}\big)\end{array}.\end{equation*}
\begin{equation*}\begin{array}{l@{\quad}l@{\quad}l@{\quad}c@{\quad}c@{\quad}c@{\quad}c}L_1&:&\big({-}b_1-3,&-2^{\times b_2},& -b_3-3,&\dots,&-2^{\times b_m}\text{ or }-b_m-2\big)\\[3pt] L_2&:&\big({-}3,-2^{\times (b_1-1)},&-b_2-3,&-2^{\times b_3},&\dots,& -b_m-2\text{ or }-2^{\times b_m}\big)\end{array}.\end{equation*}
Proposition 3·3. The contact surgery presentation given by a balanced link corresponds to the tight
![]() $S^1\times S^2$
.
$S^1\times S^2$
.
Proof. We prove that the presented contact manifold is Stein fillable by describing a concrete positive factorisation of the associated monodromy.
Since a balanced link is circular, we can write out the smooth surgery coefficients of its two legs as in Remark 3·2:
 \begin{equation*}\begin{array}{l@{\quad}l@{\quad}l@{\quad}c@{\quad}c@{\quad}c@{\quad}c}L_1&:&\big({-}b_1-3,&-2^{\times b_2},& -b_3-3,&\dots,&-2^{\times b_m}\text{ or }-b_m-2\big)\\[3pt] L_2&:&\big({-}3,-2^{\times (b_1-1)},&-b_2-3,&-2^{\times b_3},&\dots,& -b_m-2\text{ or }-2^{\times b_m}\big)\end{array}\end{equation*}
\begin{equation*}\begin{array}{l@{\quad}l@{\quad}l@{\quad}c@{\quad}c@{\quad}c@{\quad}c}L_1&:&\big({-}b_1-3,&-2^{\times b_2},& -b_3-3,&\dots,&-2^{\times b_m}\text{ or }-b_m-2\big)\\[3pt] L_2&:&\big({-}3,-2^{\times (b_1-1)},&-b_2-3,&-2^{\times b_3},&\dots,& -b_m-2\text{ or }-2^{\times b_m}\big)\end{array}\end{equation*}
for some
![]() $b_i\geq 0$
. Without loss of generality, we choose
$b_i\geq 0$
. Without loss of generality, we choose
![]() $L_1$
to be negative and
$L_1$
to be negative and
![]() $L_2$
positive.
$L_2$
positive.
Recall from Section 2·1 that the associated monodromy factorises into a product of the negative Dehn twist N, the positive Dehn twist
![]() $T_i^j$
for every unknot
$T_i^j$
for every unknot
![]() $v_i^j$
and the positive boundary twists of stabilisation holes. In the case of a balanced link with
$v_i^j$
and the positive boundary twists of stabilisation holes. In the case of a balanced link with
![]() $L_1$
negative and
$L_1$
negative and
![]() $L_2$
positive, we have only
$L_2$
positive, we have only
![]() $\nu_1$
- and
$\nu_1$
- and
![]() $\pi_2$
-stabilisation holes, all
$\pi_2$
-stabilisation holes, all
![]() $T_1$
-curves lie outside N, while all
$T_1$
-curves lie outside N, while all
![]() $T_2$
-curves lie inside. We can rewrite this monodromy by repeated use of the daisy relation as follows; look also at the example given by Figure 5.
$T_2$
-curves lie inside. We can rewrite this monodromy by repeated use of the daisy relation as follows; look also at the example given by Figure 5.

Fig. 5. Example of positive factorisation:
![]() $\mathrm{tb}_1=({-}3,-2)$
with
$\mathrm{tb}_1=({-}3,-2)$
with
![]() $\mathrm{rot}_1=({-}2,-1)$
and
$\mathrm{rot}_1=({-}2,-1)$
and
![]() $\mathrm{tb}_2=({-}2,-2,-1)$
with
$\mathrm{tb}_2=({-}2,-2,-1)$
with
![]() $\mathrm{rot}_2=(1,1,0)$
. On the first and the last picture the page is presented as a punctured disk with outer boundary in
$\mathrm{rot}_2=(1,1,0)$
. On the first and the last picture the page is presented as a punctured disk with outer boundary in
![]() $\nu^{\text{out}}$
and one of
$\nu^{\text{out}}$
and one of
![]() $\nu^0_1$
, respectively. Intermediate steps are presented as punctured spheres. In each row, the twists involved in a single application of the daisy relation are highlighted in orange.
$\nu^0_1$
, respectively. Intermediate steps are presented as punctured spheres. In each row, the twists involved in a single application of the daisy relation are highlighted in orange.
For the ease of notation, we write
![]() $v(b_\ell)$
for the unknot with the surgery coefficient
$v(b_\ell)$
for the unknot with the surgery coefficient
![]() $-b_\ell-3$
for
$-b_\ell-3$
for
![]() $\ell<m$
and
$\ell<m$
and
![]() $-b_m-2$
for
$-b_m-2$
for
![]() $\ell=m$
. So, in our general notation
$\ell=m$
. So, in our general notation
![]() $v(b_\ell)$
equals
$v(b_\ell)$
equals
![]() $v_1^{\left(\sum_{l=1}^{\ell'}b_{2l}\right)+\ell'}$
for odd
$v_1^{\left(\sum_{l=1}^{\ell'}b_{2l}\right)+\ell'}$
for odd
![]() $\ell=2\ell'+1$
and
$\ell=2\ell'+1$
and
![]() $v_2^{\left(\sum_{l=1}^{\ell'}b_{2l-1}\right)+\ell'-1}$
for even
$v_2^{\left(\sum_{l=1}^{\ell'}b_{2l-1}\right)+\ell'-1}$
for even
![]() $\ell=2\ell'$
. We attune the notation for twists and stabilisation holes, so that the twist
$\ell=2\ell'$
. We attune the notation for twists and stabilisation holes, so that the twist
![]() $T(b_\ell)$
corresponds to the unknot
$T(b_\ell)$
corresponds to the unknot
![]() $v(b_\ell)$
, and the holes
$v(b_\ell)$
, and the holes
![]() $\nu(b_\ell)$
or
$\nu(b_\ell)$
or
![]() $\pi(b_\ell)$
correspond to its stabilisations.
$\pi(b_\ell)$
correspond to its stabilisations.
Throughout, we imagine the page as a disk with the outer boundary in one of the
![]() $\nu(b_1)$
-holes; this hole (and its boundary parallel twist) will not be considered a stabilisation hole and hence, we change its notation to
$\nu(b_1)$
-holes; this hole (and its boundary parallel twist) will not be considered a stabilisation hole and hence, we change its notation to
![]() $\delta$
. Then, all the
$\delta$
. Then, all the
![]() $T_1$
-curves encircle
$T_1$
-curves encircle
![]() $\nu^{\text{out}}$
, and all the
$\nu^{\text{out}}$
, and all the
![]() $T_2$
-curves encircle
$T_2$
-curves encircle
![]() $\pi^{\text{in}}$
. The new twists which arise by applying lantern relations, will be described by the subset of holes they encircle on the disk bounded by
$\pi^{\text{in}}$
. The new twists which arise by applying lantern relations, will be described by the subset of holes they encircle on the disk bounded by
![]() $\delta$
.
$\delta$
.
To obtain a positive factorisation, we will need m applications of the daisy relation. It will be alternately applied from inside, involving some
![]() $T_2$
-twists, and from outside, involving some
$T_2$
-twists, and from outside, involving some
![]() $T_1$
-twists.
$T_1$
-twists.
For the zeroth application of the daisy relation (from inside), we consider:
-
(i) the first
 $b_1$
parallel
$b_1$
parallel
 $T_2$
-twists;
$T_2$
-twists; -
(ii) the boundary twists of
 $b_1$
of the
$b_1$
of the
 $\nu(b_1)$
-holes (note that the only non-considered
$\nu(b_1)$
-holes (note that the only non-considered
 $\nu(b_1)$
-hole we set as the outer boundary);
$\nu(b_1)$
-hole we set as the outer boundary); -
(iii) the boundary twist of the
 $\pi_2^0$
-hole;
$\pi_2^0$
-hole; -
(iv) the negative Dehn twist N.
The daisy relation (Lemma 2·9), for which the
![]() $T_2$
-twists take the role of
$T_2$
-twists take the role of
![]() $B_0$
, the stabilisation holes the role of
$B_0$
, the stabilisation holes the role of
![]() $B_1,\dots,B_{b_1+1}$
and N the role of
$B_1,\dots,B_{b_1+1}$
and N the role of
![]() $\left(A_{b_1+1}\right)^{-1}$
, results in:
$\left(A_{b_1+1}\right)^{-1}$
, results in:
-
(i) a new negative twist
 $N_0$
around
$N_0$
around
 $\left\{\pi^{\text{in}}\cup\pi_2\cup\nu(b_1)\right\}$
, playing the role of
$\left\{\pi^{\text{in}}\cup\pi_2\cup\nu(b_1)\right\}$
, playing the role of
 $(B)^{-1}$
, while we eliminate the negative twist N;
$(B)^{-1}$
, while we eliminate the negative twist N; -
(ii) a new positive twist
 $D_0$
around all considered stabilisation holes
$D_0$
around all considered stabilisation holes
 $\left\{\pi_2^0\cup\nu(b_1)\right\}$
, playing the role of C;
$\left\{\pi_2^0\cup\nu(b_1)\right\}$
, playing the role of C; -
(iii) new positive twists in role of
 $A_1,\dots,A_{b_1}$
, which we will not keep track of because they remain unchanged in the continuation.
$A_1,\dots,A_{b_1}$
, which we will not keep track of because they remain unchanged in the continuation.
For the first application of the daisy relation (from outside), we consider:
-
(i) the positive Dehn twist
 $T(b_1)=T_1^0$
and all its parallel
$T(b_1)=T_1^0$
and all its parallel
 $T_1$
-twists; all together there are
$T_1$
-twists; all together there are
 $b_2+1$
of them;
$b_2+1$
of them; -
(ii) the boundary twists of all
 $b_2+1$
of
$b_2+1$
of
 $\pi(b_2)$
-holes;
$\pi(b_2)$
-holes; -
(iii) the positive Dehn twist
 $D_0$
.
$D_0$
.
We apply the daisy relation on them, so that the
![]() $T_1$
-twists take the role of
$T_1$
-twists take the role of
![]() $B_0$
and the stabilisation holes together with
$B_0$
and the stabilisation holes together with
![]() $D_0$
the role of
$D_0$
the role of
![]() $B_1,\dots,B_{b_2+2}$
. This results in:
$B_1,\dots,B_{b_2+2}$
. This results in:
-
(i) a new negative twist
 $N^{\prime}_1$
around
$N^{\prime}_1$
around
 $\left\{\nu^{\text{out}}\cup\nu_1\cup\pi_2^0\cup\pi(b_2)\right\}$
, playing the role of
$\left\{\nu^{\text{out}}\cup\nu_1\cup\pi_2^0\cup\pi(b_2)\right\}$
, playing the role of
 $(B)^{-1}$
;
$(B)^{-1}$
; -
(ii) a new positive twist
 $D_1$
around
$D_1$
around
 $\left\{\pi_2^0\cup\nu(b_1)\cup\pi\left(b_2\right)\right\}$
, playing the role of C, while we eliminate the positive twist
$\left\{\pi_2^0\cup\nu(b_1)\cup\pi\left(b_2\right)\right\}$
, playing the role of C, while we eliminate the positive twist
 $D_0$
;
$D_0$
; -
(iii) new positive twists in role of
 $A_1,\dots,A_{b_2+2}$
, which we will again not keep track of.
$A_1,\dots,A_{b_2+2}$
, which we will again not keep track of.
We continue by alternately applying the daisy relation from inside and from outside. The
![]() $\ell{\text{th}}$
application involves
$\ell{\text{th}}$
application involves
![]() $T(b_\ell)$
and all its parallel twists, along with the stabilisation holes of the unknot
$T(b_\ell)$
and all its parallel twists, along with the stabilisation holes of the unknot
![]() $v(b_{\ell+1})$
. From inside (for the even applications
$v(b_{\ell+1})$
. From inside (for the even applications
![]() $\ell=2\ell'$
),
$\ell=2\ell'$
),
![]() $T(b_\ell)$
and its parallels are
$T(b_\ell)$
and its parallels are
![]() $T_2$
-twists and the stabilisation holes are
$T_2$
-twists and the stabilisation holes are
![]() $\nu(b_{\ell+1})$
-holes; the daisy relation affects also
$\nu(b_{\ell+1})$
-holes; the daisy relation affects also
![]() $N_{\ell-2}$
and
$N_{\ell-2}$
and
![]() $D_{\ell-1}$
which get cancelled and replaced by enlarged curves
$D_{\ell-1}$
which get cancelled and replaced by enlarged curves
![]() $N_\ell$
and
$N_\ell$
and
![]() $D_\ell$
, additionally encircling
$D_\ell$
, additionally encircling
![]() $\nu(b_{\ell+1})$
-holes. From outside (for the odd applications
$\nu(b_{\ell+1})$
-holes. From outside (for the odd applications
![]() $\ell=2\ell'+1$
),
$\ell=2\ell'+1$
),
![]() $T(b_\ell)$
and its parallels are
$T(b_\ell)$
and its parallels are
![]() $T_1$
-twists and the stabilisation holes are
$T_1$
-twists and the stabilisation holes are
![]() $\pi(b_{\ell+1})$
-holes; the daisy relation affects also
$\pi(b_{\ell+1})$
-holes; the daisy relation affects also
![]() $N^{\prime}_{\ell-2}$
and
$N^{\prime}_{\ell-2}$
and
![]() $D_{\ell-1}$
which get cancelled and replaced by enlarged curves
$D_{\ell-1}$
which get cancelled and replaced by enlarged curves
![]() $N^{\prime}_\ell$
and
$N^{\prime}_\ell$
and
![]() $D_\ell$
, additionally encircling
$D_\ell$
, additionally encircling
![]() $\pi(b_{\ell+1})$
-holes. So, after the
$\pi(b_{\ell+1})$
-holes. So, after the
![]() $\ell{\text{th}}$
application of the daisy relation, the twists contain:
$\ell{\text{th}}$
application of the daisy relation, the twists contain:
 \begin{equation*}\begin{array}{l@{\quad}l} \ell=2\ell': & D_\ell =\left\{\pi^0_2\cup\nu(b_1)\cup\pi(b_2)\cup\cdots\cup\pi(b_{\ell})\cup\nu(b_{\ell+1})\right\} \\[8pt] & N_\ell =\left\{\pi^{\text{in}}\cup\pi_2\cup\nu(b_1)\cup\dots\cup\nu(b_{\ell+1})\right\} \\[12pt] \ell=2\ell'+1: & D_\ell =\left\{\pi^0_2\cup\nu(b_1)\cup\pi(b_2)\cup\cdots\cup\nu(b_{\ell})\cup\pi(b_{\ell+1})\right\} \\[8pt] & N^{\prime}_\ell =\left\{\nu^{\text{out}}\cup\nu_1\cup\pi_2^0\cup\pi(b_2)\cup\dots\cup\pi(b_{\ell+1})\right\}\!. \end{array}\end{equation*}
\begin{equation*}\begin{array}{l@{\quad}l} \ell=2\ell': & D_\ell =\left\{\pi^0_2\cup\nu(b_1)\cup\pi(b_2)\cup\cdots\cup\pi(b_{\ell})\cup\nu(b_{\ell+1})\right\} \\[8pt] & N_\ell =\left\{\pi^{\text{in}}\cup\pi_2\cup\nu(b_1)\cup\dots\cup\nu(b_{\ell+1})\right\} \\[12pt] \ell=2\ell'+1: & D_\ell =\left\{\pi^0_2\cup\nu(b_1)\cup\pi(b_2)\cup\cdots\cup\nu(b_{\ell})\cup\pi(b_{\ell+1})\right\} \\[8pt] & N^{\prime}_\ell =\left\{\nu^{\text{out}}\cup\nu_1\cup\pi_2^0\cup\pi(b_2)\cup\dots\cup\pi(b_{\ell+1})\right\}\!. \end{array}\end{equation*}
Note that, as in the first two applications which we have explicitly described above, the T-twists always take the role of
![]() $B_0$
, the stabilisation holes together with
$B_0$
, the stabilisation holes together with
![]() $D_{\ell-1}$
the role of
$D_{\ell-1}$
the role of
![]() $B_1,\dots,B_{b_{\ell+1}+2}$
, and
$B_1,\dots,B_{b_{\ell+1}+2}$
, and
![]() $N_{\ell-2}$
or
$N_{\ell-2}$
or
![]() $N^{\prime}_{\ell-2}$
the role of
$N^{\prime}_{\ell-2}$
the role of
![]() $\left(A_{b_{\ell+1}+2}\right)^{-1}$
; while for the resulting twists,
$\left(A_{b_{\ell+1}+2}\right)^{-1}$
; while for the resulting twists,
![]() $D_\ell$
takes the role of C and
$D_\ell$
takes the role of C and
![]() $N_\ell$
or
$N_\ell$
or
![]() $N^{\prime}_\ell$
the role of
$N^{\prime}_\ell$
the role of
![]() $(B)^{-1}$
. Note also that,
$(B)^{-1}$
. Note also that,
![]() $N_\ell$
exists only for even
$N_\ell$
exists only for even
![]() $\ell$
and
$\ell$
and
![]() $N^{\prime}_\ell$
only for odd
$N^{\prime}_\ell$
only for odd
![]() $\ell$
, either of them remaining untouched by the
$\ell$
, either of them remaining untouched by the
![]() $(\ell+1){\text{th}}$
application of the daisy relation.
$(\ell+1){\text{th}}$
application of the daisy relation.
Finally, in the last, the
![]() $(m-1){\text{th}}$
, application of the daisy relation, there are
$(m-1){\text{th}}$
, application of the daisy relation, there are
![]() $b_m+1$
parallel twists
$b_m+1$
parallel twists
![]() $T\left(b_{m-1}\right)$
, but there are only
$T\left(b_{m-1}\right)$
, but there are only
![]() $b_m$
stabilisation holes of
$b_m$
stabilisation holes of
![]() $v(b_m)$
, so together with
$v(b_m)$
, so together with
![]() $D_{m-2}$
only
$D_{m-2}$
only
![]() $b_m+1$
twists in role of
$b_m+1$
twists in role of
![]() $B_i$
for
$B_i$
for
![]() $ i>0$
. Hence, we involve as an additional
$ i>0$
. Hence, we involve as an additional
![]() $B_i$
, the twist
$B_i$
, the twist
![]() $T\left(b_m\right)$
, which in our perspective appears as the boundary twist around
$T\left(b_m\right)$
, which in our perspective appears as the boundary twist around
![]() $\nu^{\text{out}}$
when m odd and around
$\nu^{\text{out}}$
when m odd and around
![]() $\pi^{\text{in}}$
when m even. So, after we apply the daisy relation, the twist
$\pi^{\text{in}}$
when m even. So, after we apply the daisy relation, the twist
![]() $D_{m-1}$
encircles:
$D_{m-1}$
encircles:
 \begin{equation*}\begin{array}{l@{\quad}l} D_{m-1} =\left\{\pi^0_2\cup\nu(b_1)\cup\pi(b_2)\cup\cdots\cup\pi(b_{m-1})\cup\nu(b_{m})\cup\nu^{\text{out}}\right\} & \text{for odd } m, \\ & \\ D_{m-1} =\left\{\pi^0_2\cup\nu(b_1)\cup\pi(b_2)\cup\cdots\cup\nu(b_{m-1})\cup\pi(b_{m})\cup\pi^{\text{in}}\right\} & \text{for even } m. \\\end{array}\end{equation*}
\begin{equation*}\begin{array}{l@{\quad}l} D_{m-1} =\left\{\pi^0_2\cup\nu(b_1)\cup\pi(b_2)\cup\cdots\cup\pi(b_{m-1})\cup\nu(b_{m})\cup\nu^{\text{out}}\right\} & \text{for odd } m, \\ & \\ D_{m-1} =\left\{\pi^0_2\cup\nu(b_1)\cup\pi(b_2)\cup\cdots\cup\nu(b_{m-1})\cup\pi(b_{m})\cup\pi^{\text{in}}\right\} & \text{for even } m. \\\end{array}\end{equation*}
It exactly agrees with
![]() $N^{\prime}_{m-2}$
for odd m and
$N^{\prime}_{m-2}$
for odd m and
![]() $N_{m-2}$
for even m, and hence the corresponding negative twist gets cancelled by
$N_{m-2}$
for even m, and hence the corresponding negative twist gets cancelled by
![]() $D_{m-1}$
. The other negative twist,
$D_{m-1}$
. The other negative twist,
![]() $N_{m-1}$
when m odd and
$N_{m-1}$
when m odd and
![]() $N^{\prime}_{m-1}$
when m even, encircles all the holes and it cancels with the positive Dehn twist along the outer boundary
$N^{\prime}_{m-1}$
when m even, encircles all the holes and it cancels with the positive Dehn twist along the outer boundary
![]() $\delta$
.
$\delta$
.
4. Obstructing positive factorisations
When there is no balanced sublink of the surgery presentation, we show that the contact manifold of Figure 2 cannot be fillable.
Proposition 4·1. When the contact surgery presentation of Figure 2 does not contain a balanced sublink, the corresponding monodromy does not admit any positive factorisation.
The rest of the section is devoted to the proof of Proposition 4·1. First, we recall that the oppositely stabilised leading unknots are needed already for tightness (Proposition 4·2). Then, after setting up some further conventions and notation, we undertake a systematic analysis of possible positive factorisations of the monodromy
![]() $\phi$
as being read from the surgery presentation, obtaining eventually that the factorisation cannot exist in the absence of a balanced sublink. First, we study how possible positive factorisations behave with respect to the
$\phi$
as being read from the surgery presentation, obtaining eventually that the factorisation cannot exist in the absence of a balanced sublink. First, we study how possible positive factorisations behave with respect to the
![]() $\pi$
-holes (Lemmas 4·3–4·4). Then, we specify particular properties of the twists which encircle
$\pi$
-holes (Lemmas 4·3–4·4). Then, we specify particular properties of the twists which encircle
![]() $\nu$
-holes (Lemmas 4·6–4·8). Finally, we obtain that (the lifts of) the factorisations as characterised among the
$\nu$
-holes (Lemmas 4·6–4·8). Finally, we obtain that (the lifts of) the factorisations as characterised among the
![]() $\pi$
-holes can fulfill the above list of properties only when there is a balanced sublink (Lemmas 4·11–4·15).
$\pi$
-holes can fulfill the above list of properties only when there is a balanced sublink (Lemmas 4·11–4·15).
Necessary condition for tightness
We can argue via convex surface theory that some surgery configurations are always overtwisted.
Proposition 4·2. Necessarily for tightness, the presentation admits a leg with fully negative leading unknot and a leg with fully positive leading unknot.
Proof. The absence of a pair of fully oppositely stabilized leading unknots is a very special case of the overtwistedness conditions given in [ Reference Matkovič13 , section 5].
Due to Proposition 4·2, we may, up to an overall orientation of the surgery link, assume that there is only one leg, say
![]() $L_3$
, whose leading unknot is fully negative. Notice that since
$L_3$
, whose leading unknot is fully negative. Notice that since
![]() $\mathrm{tb}_3^0=-a_3^0\leq -2$
, the leading unknot always admits a negative stabilisation, and so, there is at least one
$\mathrm{tb}_3^0=-a_3^0\leq -2$
, the leading unknot always admits a negative stabilisation, and so, there is at least one
![]() $\nu_3^0$
-hole.
$\nu_3^0$
-hole.
Conventions and notation
Throughout the proof, we try to build a positive factorisation of the monodromy
![]() $\phi$
only on the level of abelianization. Abusing the notation, all mapping classes and their factorizations are considered as elements of AbMap. In particular, we are interested in Dehn twists only up to conjugation, and we freely choose the order of Dehn twist factors. Note that we reserve the capital Greek letters to denote specific factorizations, in contrast to the maps as a whole.
$\phi$
only on the level of abelianization. Abusing the notation, all mapping classes and their factorizations are considered as elements of AbMap. In particular, we are interested in Dehn twists only up to conjugation, and we freely choose the order of Dehn twist factors. Note that we reserve the capital Greek letters to denote specific factorizations, in contrast to the maps as a whole.
It will be essential to look at a planar page of the open book from different perspectives, by which we mean a diffeomorphism of the page where a fixed boundary component becomes the outer boundary of the disk; see Figure 3 for illustration. Our preferred perspective will be the punctured disk obtained by setting one of the
![]() $\nu^0_3$
-holes to be the outer boundary; call it
$\nu^0_3$
-holes to be the outer boundary; call it
![]() $\mathbf D$
. As already in the proof of Proposition 3·3, this
$\mathbf D$
. As already in the proof of Proposition 3·3, this
![]() $\nu^0_3$
-hole (and its boundary parallel twist) will not be considered a stabilisation hole and hence, we change its notation to
$\nu^0_3$
-hole (and its boundary parallel twist) will not be considered a stabilisation hole and hence, we change its notation to
![]() $\delta$
; so, whenever we consider (any subset of) the
$\delta$
; so, whenever we consider (any subset of) the
![]() $\nu$
-holes or twists,
$\nu$
-holes or twists,
![]() $\delta$
is not included. When some of the holes in
$\delta$
is not included. When some of the holes in
![]() $\mathbf D$
are capped off, we denote this by putting the remaining holes in the index; for example, the notation
$\mathbf D$
are capped off, we denote this by putting the remaining holes in the index; for example, the notation
![]() $\mathbf D_\chi$
means the page
$\mathbf D_\chi$
means the page
![]() $\mathbf D$
with all but the
$\mathbf D$
with all but the
![]() $\chi$
-holes capped off, and
$\chi$
-holes capped off, and
![]() $\mathbf D$
is equal to
$\mathbf D$
is equal to
![]() $\mathbf D_{\pi\cup\nu}$
.
$\mathbf D_{\pi\cup\nu}$
.
In arguments, we will interchangeably use two other perspectives on the (possibly capped-off) disk
![]() $\mathbf D$
: the initial with
$\mathbf D$
: the initial with
![]() $\nu^{\text{out}}$
as the outer boundary of the disk, and the turned-over with
$\nu^{\text{out}}$
as the outer boundary of the disk, and the turned-over with
![]() $\pi^{\text{in}}$
as the outer boundary. For example,
$\pi^{\text{in}}$
as the outer boundary. For example,
![]() $\mathbf D$
in the initial perspective is just the page as described in Subsection 2·1,
$\mathbf D$
in the initial perspective is just the page as described in Subsection 2·1,
![]() $\mathbf D_{\pi}$
cannot be given in the initial perspective because
$\mathbf D_{\pi}$
cannot be given in the initial perspective because
![]() $\nu^{\text{out}}$
is capped-off, and
$\nu^{\text{out}}$
is capped-off, and
![]() $\mathbf D_\pi$
in the turned-over perspective is a disk with outer boundary
$\mathbf D_\pi$
in the turned-over perspective is a disk with outer boundary
![]() $\pi^{\text{in}}$
and holes
$\pi^{\text{in}}$
and holes
![]() $\delta$
and
$\delta$
and
![]() $\pi_i$
for all i. The (collections of) twists or holes, which are taken one to another by the diffeomorphism which changes perspectives, will be denoted by the same names regardless the perspective.
$\pi_i$
for all i. The (collections of) twists or holes, which are taken one to another by the diffeomorphism which changes perspectives, will be denoted by the same names regardless the perspective.
The (single and pairwise) multiplicities with respect to each perspective will be denoted by capital M in
![]() $\mathbf D$
, by m for the initial disk, and by m
′ for the turned-over one. According to Lemma 2·8, these numbers are independent of factorisation; however, when we wish to emphasize from which factorization the multiplicity was read, we put the factorization in the parenthesis, for example
$\mathbf D$
, by m for the initial disk, and by m
′ for the turned-over one. According to Lemma 2·8, these numbers are independent of factorisation; however, when we wish to emphasize from which factorization the multiplicity was read, we put the factorization in the parenthesis, for example
![]() $M(\Psi)$
.
$M(\Psi)$
.
Let
![]() $\Phi$
denote the original factorisation of the monodromy
$\Phi$
denote the original factorisation of the monodromy
![]() $\phi$
as being read from the surgery presentation. We recall from Section 2·1 that
$\phi$
as being read from the surgery presentation. We recall from Section 2·1 that
![]() $\Phi=N\cdot\prod_{i,j}T_i^j\cdot D_\partial$
where N is the negative twist representing one
$\Phi=N\cdot\prod_{i,j}T_i^j\cdot D_\partial$
where N is the negative twist representing one
![]() $+1$
-surgery, the positive twists
$+1$
-surgery, the positive twists
![]() $T_i^j$
correspond to
$T_i^j$
correspond to
![]() $-1$
-surgeries on
$-1$
-surgeries on
![]() $v_i^j$
, and
$v_i^j$
, and
![]() $D_\partial$
is a boundary twist about all but two,
$D_\partial$
is a boundary twist about all but two,
![]() $\nu^{\text{out}}$
and
$\nu^{\text{out}}$
and
![]() $\pi^{\text{in}}$
, boundary components.
$\pi^{\text{in}}$
, boundary components.
Positive factorisations and
![]() $\pi$
-holes
$\pi$
-holes
To begin with, let us study how positive factorisations can possibly behave with respect to the
![]() $\pi$
-holes.
$\pi$
-holes.
Lemma 4·3. By capping off all the
![]() $\nu$
-holes, we descend from
$\nu$
-holes, we descend from
![]() $\mathrm{AbMap} \mathbf D_{\pi\cup\nu}$
to
$\mathrm{AbMap} \mathbf D_{\pi\cup\nu}$
to
![]() $\mathrm{AbMap} \mathbf D_{\pi}$
, sending
$\mathrm{AbMap} \mathbf D_{\pi}$
, sending
![]() $\phi$
to
$\phi$
to
![]() $\overline{\phi}$
. This maps the given factorisation
$\overline{\phi}$
. This maps the given factorisation
![]() $\Phi$
to
$\Phi$
to
![]() $\overline\Phi$
, which is a composition
$\overline\Phi$
, which is a composition
![]() $\overline{\Phi}_1\overline{\Phi}_2\overline{\Phi}_3$
with
$\overline{\Phi}_1\overline{\Phi}_2\overline{\Phi}_3$
with
![]() $\overline{\Phi}_i$
being a product of the
$\overline{\Phi}_i$
being a product of the
![]() $\overline T_i$
-twists and the boundary twists around the
$\overline T_i$
-twists and the boundary twists around the
![]() $\pi_i$
-holes. Every positive factorisation
$\pi_i$
-holes. Every positive factorisation
![]() $\overline\Psi$
of
$\overline\Psi$
of
![]() $\overline\phi$
splits into subfactorizations
$\overline\phi$
splits into subfactorizations
![]() $\overline\Psi=\overline{\Psi}_1\overline{\Psi}_2\overline{\Psi}_3$
so that
$\overline\Psi=\overline{\Psi}_1\overline{\Psi}_2\overline{\Psi}_3$
so that
![]() $\overline{\Psi}_i$
and
$\overline{\Psi}_i$
and
![]() $\overline{\Phi}_i$
describe the same element
$\overline{\Phi}_i$
describe the same element
![]() $\overline{\phi}_i$
in
$\overline{\phi}_i$
in
![]() $\mathrm{AbMap}\ \mathbf{D}_{\pi}$
.
$\mathrm{AbMap}\ \mathbf{D}_{\pi}$
.
Proof. The
![]() $\overline\Phi$
itself presents a positive factorisation of the extended monodromy
$\overline\Phi$
itself presents a positive factorisation of the extended monodromy
![]() $\overline\phi$
. Indeed, the only negative twist of
$\overline\phi$
. Indeed, the only negative twist of
![]() $\Phi$
cancels with the boundary twist of
$\Phi$
cancels with the boundary twist of
![]() $\delta$
after we have capped-off the
$\delta$
after we have capped-off the
![]() $\nu$
-holes. By construction,
$\nu$
-holes. By construction,
![]() $\overline\Phi$
factors into a product of
$\overline\Phi$
factors into a product of
![]() $\overline T_i^j$
, the extended
$\overline T_i^j$
, the extended
![]() $T_i^j$
, for every j for every i and the boundary twists of
$T_i^j$
, for every j for every i and the boundary twists of
![]() $\pi_i$
-holes for all i; we define
$\pi_i$
-holes for all i; we define
![]() $\overline\Phi_i$
to be the product of all
$\overline\Phi_i$
to be the product of all
![]() $\overline T_i$
-twists and the boundary twists of
$\overline T_i$
-twists and the boundary twists of
![]() $\pi_i$
-holes. We will show that, in the turned-over perspective, the only hole which appears in more than one factor
$\pi_i$
-holes. We will show that, in the turned-over perspective, the only hole which appears in more than one factor
![]() $\overline\Phi_i$
is the hole
$\overline\Phi_i$
is the hole
![]() $\delta$
. This together with Lemma 2·8 will allow us to see that every positive factorisation splits into three factors, completely determined by m
′-multiplicities of
$\delta$
. This together with Lemma 2·8 will allow us to see that every positive factorisation splits into three factors, completely determined by m
′-multiplicities of
![]() $\overline\Phi_i$
.
$\overline\Phi_i$
.
So, let us first compute the multiplicities from
![]() $\overline\Phi$
. Set
$\overline\Phi$
. Set
![]() $\pi^{\text{in}}$
as the outer boundary and consider the capped-off page
$\pi^{\text{in}}$
as the outer boundary and consider the capped-off page
![]() $\mathbf D_\pi$
in the turned-over perspective. Here, no
$\mathbf D_\pi$
in the turned-over perspective. Here, no
![]() $\pi_i$
-hole is encircled together with any
$\pi_i$
-hole is encircled together with any
![]() $\pi_j$
-hole for
$\pi_j$
-hole for
![]() $i\neq j$
, in symbols
$i\neq j$
, in symbols
![]() $m^{\prime}_{\pi_i\pi_j}=0$
, and
$m^{\prime}_{\pi_i\pi_j}=0$
, and
![]() $\delta$
is in at most
$\delta$
is in at most
![]() $m^{\prime}_{\delta}=k_1+k_2+2$
twists. Indeed, the factors of
$m^{\prime}_{\delta}=k_1+k_2+2$
twists. Indeed, the factors of
![]() $\overline\Phi$
all arise from the factorisation
$\overline\Phi$
all arise from the factorisation
![]() $\Phi$
, and by construction in Subsection 2·1, in the initial perspective each twist of
$\Phi$
, and by construction in Subsection 2·1, in the initial perspective each twist of
![]() $\Phi$
which contains
$\Phi$
which contains
![]() $\pi^{\text{in}}$
skips
$\pi^{\text{in}}$
skips
![]() $\pi_i$
-holes for one i only, and among the twists containing
$\pi_i$
-holes for one i only, and among the twists containing
![]() $\pi^{\text{in}}$
all
$\pi^{\text{in}}$
all
![]() $T_1$
- and
$T_1$
- and
![]() $T_2$
-twists avoid
$T_2$
-twists avoid
![]() $\delta$
. On the other hand, the pairwise multiplicity of
$\delta$
. On the other hand, the pairwise multiplicity of
![]() $\delta$
with
$\delta$
with
![]() $\pi^0_i$
in the turned-over perspective is exactly
$\pi^0_i$
in the turned-over perspective is exactly
![]() $m^{\prime}_{\delta\pi^0_i}=k_i+1$
. So, there are exactly
$m^{\prime}_{\delta\pi^0_i}=k_i+1$
. So, there are exactly
![]() $k_i+1$
twists encircling
$k_i+1$
twists encircling
![]() $\delta$
together with only
$\delta$
together with only
![]() $\pi_i$
-holes. Again, this follows by construction as all the twists of
$\pi_i$
-holes. Again, this follows by construction as all the twists of
![]() $\Phi$
(in the initial perspective) which avoid any of the
$\Phi$
(in the initial perspective) which avoid any of the
![]() $\pi_i$
-holes, avoid also
$\pi_i$
-holes, avoid also
![]() $\pi^0_i$
.
$\pi^0_i$
.
But, according to Lemma 2·8, the multiplicities are independent of factoriation. Therefore, in the turned-over perspective no positive factorisation admits any twist encircling
![]() $\pi_i$
and
$\pi_i$
and
![]() $\pi_j$
together, and we can consider the whole (abelianised) monodromy
$\pi_j$
together, and we can consider the whole (abelianised) monodromy
![]() $\overline\phi$
as a product of three monodromies
$\overline\phi$
as a product of three monodromies
![]() $\overline\phi_i$
, uniquely determined by m
′-multiplicities: the single and pairwise multiplicities of
$\overline\phi_i$
, uniquely determined by m
′-multiplicities: the single and pairwise multiplicities of
![]() $\pi_i$
-holes are non-zero only in
$\pi_i$
-holes are non-zero only in
![]() $\overline\phi_i$
, and the twists around
$\overline\phi_i$
, and the twists around
![]() $\delta$
are distributed so that pairwise multiplicity of
$\delta$
are distributed so that pairwise multiplicity of
![]() $\delta$
with the
$\delta$
with the
![]() $\pi_i^0$
-holes is
$\pi_i^0$
-holes is
![]() $k_1+1,k_2+1$
, and 0, respectively. In other words, any positive factorisation splits as
$k_1+1,k_2+1$
, and 0, respectively. In other words, any positive factorisation splits as
![]() $\overline{\Psi}_1\overline{\Psi}_2\overline{\Psi}_3$
with
$\overline{\Psi}_1\overline{\Psi}_2\overline{\Psi}_3$
with
![]() $\overline\Psi_i$
describing
$\overline\Psi_i$
describing
![]() $\overline\phi_i$
.
$\overline\phi_i$
.
For
![]() $\overline{\phi}_i\in\mathrm{AbMap}\ \mathbf{D}_{\pi}$
when
$\overline{\phi}_i\in\mathrm{AbMap}\ \mathbf{D}_{\pi}$
when
![]() $i=1$
or 2, let us write out the given factorisation
$i=1$
or 2, let us write out the given factorisation
![]() $\overline{\Phi}_i$
as
$\overline{\Phi}_i$
as
![]() $F^0_i\cdots F^{l_i}_i$
and the arbitrary positive factorization
$F^0_i\cdots F^{l_i}_i$
and the arbitrary positive factorization
![]() $\overline{\Psi}_i$
as
$\overline{\Psi}_i$
as
![]() $P^0_i\cdots P^{l^{\prime}_i}_i$
. We order the Dehn twist factors so that viewed in
$P^0_i\cdots P^{l^{\prime}_i}_i$
. We order the Dehn twist factors so that viewed in
![]() $\mathbf D_{\pi}$
the ones encircling
$\mathbf D_{\pi}$
the ones encircling
![]() $\pi^{\text{in}}$
come first and in the decreasing order of the number of holes they encircle. For
$\pi^{\text{in}}$
come first and in the decreasing order of the number of holes they encircle. For
![]() $\overline{\Phi}_i$
the first
$\overline{\Phi}_i$
the first
![]() $k_i+1$
twists
$k_i+1$
twists
![]() $F^0_i,\dots,F^{k_i}_i$
are then exactly equal to
$F^0_i,\dots,F^{k_i}_i$
are then exactly equal to
![]() $\overline T^0_i,\dots,\overline T^{k_i}_i$
, and they are followed by the boundary twists of
$\overline T^0_i,\dots,\overline T^{k_i}_i$
, and they are followed by the boundary twists of
![]() $\pi_i$
-holes. For any positive factorisation
$\pi_i$
-holes. For any positive factorisation
![]() $\overline\Psi_i$
we see (using Lemma 2·8) that its length
$\overline\Psi_i$
we see (using Lemma 2·8) that its length
![]() $l^{\prime}_i+1$
is at least the length of the corresponding leg,
$l^{\prime}_i+1$
is at least the length of the corresponding leg,
![]() $k_i+1$
(because
$k_i+1$
(because
![]() $m^{\prime}_{\delta\pi^0_i}=k_i+1$
), and that
$m^{\prime}_{\delta\pi^0_i}=k_i+1$
), and that
![]() $\pi^{\text{in}}$
is contained exactly in its first
$\pi^{\text{in}}$
is contained exactly in its first
![]() $k_i+1$
twists
$k_i+1$
twists
![]() $P^0_i,\ldots, P^{k_i}_i$
(because
$P^0_i,\ldots, P^{k_i}_i$
(because
![]() $M_{\pi^{\text{in}}}=m^{\prime}_{\delta}=k_1+k_2+2$
).
$M_{\pi^{\text{in}}}=m^{\prime}_{\delta}=k_1+k_2+2$
).
Moreover, if the factorisation
![]() $\overline{\Psi}_i$
is not equal to
$\overline{\Psi}_i$
is not equal to
![]() $\overline{\Phi}_i$
, all of the first
$\overline{\Phi}_i$
, all of the first
![]() $k_i+1$
twists cannot be the same. Because if they were, the pairwise multiplicities among
$k_i+1$
twists cannot be the same. Because if they were, the pairwise multiplicities among
![]() $\pi_i$
-holes in the turned-over perspective of the product
$\pi_i$
-holes in the turned-over perspective of the product
![]() $\prod_{j=0}^{k_i}P_i^j$
would be already equal to the pairwise multiplicities of
$\prod_{j=0}^{k_i}P_i^j$
would be already equal to the pairwise multiplicities of
![]() $\overline\Phi_i$
, requiring that the rest of the twists were boundary-parallel, and so the factorisation
$\overline\Phi_i$
, requiring that the rest of the twists were boundary-parallel, and so the factorisation
![]() $\overline\Psi_i$
would agree with
$\overline\Psi_i$
would agree with
![]() $\overline\Phi_i$
.
$\overline\Phi_i$
.
Lemma 4·4. When the factorisation
![]() $\overline{\Psi}_i$
does not agree with
$\overline{\Psi}_i$
does not agree with
![]() $\overline{\Phi}_i$
, denote the first index on which they differ by
$\overline{\Phi}_i$
, denote the first index on which they differ by
![]() $x_i\,:\!=\,\min\left\{j;\,F^j_i\neq P^j_i\right\} \leq k_i$
. Then, the holes in
$x_i\,:\!=\,\min\left\{j;\,F^j_i\neq P^j_i\right\} \leq k_i$
. Then, the holes in
![]() $\mathbf D_\pi$
encircled by
$\mathbf D_\pi$
encircled by
![]() $P^{x_i}_i$
constitute a strict subset of the holes encircled by
$P^{x_i}_i$
constitute a strict subset of the holes encircled by
![]() $F^{x_i}_i$
, and no
$F^{x_i}_i$
, and no
![]() $\pi_i$
-hole outside of
$\pi_i$
-hole outside of
![]() $F^{x_i}_i$
is encircled by any non-boundary twist
$F^{x_i}_i$
is encircled by any non-boundary twist
![]() $P^j_i$
for
$P^j_i$
for
![]() $j\geq x_i$
.
$j\geq x_i$
.
Proof. Look at the capped-off page
![]() $\mathbf D_\pi$
in the turned-over perspective, with
$\mathbf D_\pi$
in the turned-over perspective, with
![]() $\pi^{\text{in}}$
as the outer boundary. Encircling
$\pi^{\text{in}}$
as the outer boundary. Encircling
![]() $\pi^{\text{in}}$
in the preferred perspective
$\pi^{\text{in}}$
in the preferred perspective
![]() $\mathbf D_\pi$
exactly corresponds to encircling
$\mathbf D_\pi$
exactly corresponds to encircling
![]() $\delta$
in the turned-over perspective. Furthermore, for the twists containing
$\delta$
in the turned-over perspective. Furthermore, for the twists containing
![]() $\pi^{\text{in}}$
in
$\pi^{\text{in}}$
in
![]() $\mathbf D_\pi$
the subset relation for encircled holes turns when viewed in the turned-over perspective.
$\mathbf D_\pi$
the subset relation for encircled holes turns when viewed in the turned-over perspective.
Now, if in the turned-over perspective
![]() $P^{x_i}_i$
did not encircle some hole
$P^{x_i}_i$
did not encircle some hole
![]() $\chi$
encircled in
$\chi$
encircled in
![]() $F^{x_i}_i$
, the pairwise multiplicity of
$F^{x_i}_i$
, the pairwise multiplicity of
![]() $\chi$
with
$\chi$
with
![]() $\delta$
in
$\delta$
in
![]() $\overline\Psi_i$
would be strictly smaller than in
$\overline\Psi_i$
would be strictly smaller than in
![]() $\overline\Phi_i$
, in symbols
$\overline\Phi_i$
, in symbols
![]() $m^{\prime}_{\chi\delta}\left(\overline\Psi_i\right)<m^{\prime}_{\chi\delta}\left(\overline\Phi_i\right)$
. Indeed, the number of twists encircling
$m^{\prime}_{\chi\delta}\left(\overline\Psi_i\right)<m^{\prime}_{\chi\delta}\left(\overline\Phi_i\right)$
. Indeed, the number of twists encircling
![]() $\delta$
is fixed and equal to
$\delta$
is fixed and equal to
![]() $k_i+1$
, and
$k_i+1$
, and
![]() $F^j_i$
for
$F^j_i$
for
![]() $j\geq x_i$
all encircle
$j\geq x_i$
all encircle
![]() $\chi$
, while
$\chi$
, while
![]() $F^j_i$
for
$F^j_i$
for
![]() $j<x_i$
encircles
$j<x_i$
encircles
![]() $\chi$
if and only if
$\chi$
if and only if
![]() $P^j_i$
does.
$P^j_i$
does.
Finally, as in the preferred perspective
![]() $\mathbf D$
the pairwise M-multiplicities of holes out of
$\mathbf D$
the pairwise M-multiplicities of holes out of
![]() $F^{x_i}_i$
with any other
$F^{x_i}_i$
with any other
![]() $\pi$
-hole are exactly as many as there are twists from
$\pi$
-hole are exactly as many as there are twists from
![]() $\left\{P^j_i=F^j_i;\,j<x_i\right\}$
around them, neither can be encircled together with any other
$\left\{P^j_i=F^j_i;\,j<x_i\right\}$
around them, neither can be encircled together with any other
![]() $\pi$
-hole additionally.
$\pi$
-hole additionally.
Properties of the twists encircling
![]() $\nu$
-holes
$\nu$
-holes
Having understood positive factorisations among the
![]() $\pi$
-holes, the problem of finding a positive factorisation reduces to whether any factorisation
$\pi$
-holes, the problem of finding a positive factorisation reduces to whether any factorisation
![]() $\overline{\Psi}$
(maybe
$\overline{\Psi}$
(maybe
![]() $\overline\Phi$
) of
$\overline\Phi$
) of
![]() $\overline\phi\in\mathrm{AbMap} \mathbf D_\pi$
can be lifted to a positive factorisation of
$\overline\phi\in\mathrm{AbMap} \mathbf D_\pi$
can be lifted to a positive factorisation of
![]() $\phi\in\mathrm{AbMap} \mathbf D$
.
$\phi\in\mathrm{AbMap} \mathbf D$
.
In the following, we investigate possible lifts of the twists in
![]() $\overline\Psi$
. In particular, we notice that the multiplicities put some restraints on the lifted twists, culminating in a list of properties satisfied by any positive factorisation.
$\overline\Psi$
. In particular, we notice that the multiplicities put some restraints on the lifted twists, culminating in a list of properties satisfied by any positive factorisation.
Notation 4·5. Let
![]() $n_i$
be the index of the first unknot on the leg
$n_i$
be the index of the first unknot on the leg
![]() $L_i$
whose stabilisations are not all of the same sign as the stabilisations of its leading unknot; when the leading unknot admits positive and negative stabilisations, we choose
$L_i$
whose stabilisations are not all of the same sign as the stabilisations of its leading unknot; when the leading unknot admits positive and negative stabilisations, we choose
![]() $n_i=0$
, and when all stabilisations on
$n_i=0$
, and when all stabilisations on
![]() $L_i$
are of the same sign, we set
$L_i$
are of the same sign, we set
![]() $n_i=k_i+1$
.
$n_i=k_i+1$
.
Lemma 4·6. Looking at
![]() $\mathbf D$
in the preferred perspective, in any positive factorisation of
$\mathbf D$
in the preferred perspective, in any positive factorisation of
![]() $\phi$
lifting
$\phi$
lifting
![]() $\overline\Psi$
, there are at least
$\overline\Psi$
, there are at least
![]() $k_i-n_i+1$
twists among
$k_i-n_i+1$
twists among
![]() $\left\{P^{0}_i,\dots,P^{k_i}_i\right\}$
for
$\left\{P^{0}_i,\dots,P^{k_i}_i\right\}$
for
![]() $i=1$
and 2, which lift to the twists which additionally encircle only
$i=1$
and 2, which lift to the twists which additionally encircle only
![]() $\nu_i$
-holes. They all encircle
$\nu_i$
-holes. They all encircle
![]() $\pi^{\text{in}}$
and avoid
$\pi^{\text{in}}$
and avoid
![]() $\pi^k_i$
for
$\pi^k_i$
for
![]() $k\leq n_i$
; in particular, for
$k\leq n_i$
; in particular, for
![]() $\overline\Phi_i$
these are exactly
$\overline\Phi_i$
these are exactly
![]() $\left\{F_i^{n_i},\dots,F_i^{k_i}\right\}$
.
$\left\{F_i^{n_i},\dots,F_i^{k_i}\right\}$
.
Proof. Because of Lemma 2·8, throughout the proof the multiplicities computed from
![]() $\Phi$
give us information about any positive factorisation.
$\Phi$
give us information about any positive factorisation.
Recall now that on the disk with the initial outer boundary all the multiplicities
![]() $m_{\nu_i\nu_j}=0$
for
$m_{\nu_i\nu_j}=0$
for
![]() $i\neq j$
. In
$i\neq j$
. In
![]() $\mathbf D$
, this means that whenever some
$\mathbf D$
, this means that whenever some
![]() $\nu_i$
is encircled together with any of
$\nu_i$
is encircled together with any of
![]() $\nu_j$
, the twist needs to contain also the initial outer boundary, the hole
$\nu_j$
, the twist needs to contain also the initial outer boundary, the hole
![]() $\nu^{\text{out}}$
. On the other hand, for any
$\nu^{\text{out}}$
. On the other hand, for any
![]() $\nu_1$
or
$\nu_1$
or
![]() $\nu_2$
the pairwise multiplicity with
$\nu_2$
the pairwise multiplicity with
![]() $\pi^{\text{in}}$
in
$\pi^{\text{in}}$
in
![]() $\mathbf D$
,
$\mathbf D$
,
![]() $M_{\pi^{\text{in}}\nu_1}$
or
$M_{\pi^{\text{in}}\nu_1}$
or
![]() $M_{\pi^{\text{in}}\nu_2}$
, is greater than
$M_{\pi^{\text{in}}\nu_2}$
, is greater than
![]() $M_{\pi^{\text{in}}\nu^{\text{out}}}=1$
; precisely, for a
$M_{\pi^{\text{in}}\nu^{\text{out}}}=1$
; precisely, for a
![]() $\nu^j_i$
-hole the multiplicity is exactly
$\nu^j_i$
-hole the multiplicity is exactly
![]() $M_{\pi^{\text{in}}\nu^j_i}=k_i-j+2$
. Indeed, in
$M_{\pi^{\text{in}}\nu^j_i}=k_i-j+2$
. Indeed, in
![]() $\Phi$
there is a single twist around both
$\Phi$
there is a single twist around both
![]() $\pi^{\text{in}}$
and
$\pi^{\text{in}}$
and
![]() $\nu^{\text{out}}$
(which is the boundary twist of the outer boundary
$\nu^{\text{out}}$
(which is the boundary twist of the outer boundary
![]() $\delta$
), while
$\delta$
), while
![]() $\nu^j_i$
are encircled together with
$\nu^j_i$
are encircled together with
![]() $\pi^{\text{in}}$
also by the
$\pi^{\text{in}}$
also by the
![]() $T^k_i$
-twists for
$T^k_i$
-twists for
![]() $k\geq j$
(there are
$k\geq j$
(there are
![]() $k_i+1-j$
of them). Thus, when there is some negative stabilisation on
$k_i+1-j$
of them). Thus, when there is some negative stabilisation on
![]() $L_i$
(at least)
$L_i$
(at least)
![]() $k_i-n_i+1$
Dehn twists which contain
$k_i-n_i+1$
Dehn twists which contain
![]() $\pi^{\text{in}}$
need to lift to twists which additionally include only the
$\pi^{\text{in}}$
need to lift to twists which additionally include only the
![]() $\nu_i$
-holes.
$\nu_i$
-holes.
Moreover, as on the initial disk the multiplicities equal
![]() $m_{\pi^k_i\nu_i}=0$
for
$m_{\pi^k_i\nu_i}=0$
for
![]() $k\leq n_i$
, the
$k\leq n_i$
, the
![]() $k_i-n_i+1$
twists mentioned above avoid all
$k_i-n_i+1$
twists mentioned above avoid all
![]() $\pi^k_i$
for
$\pi^k_i$
for
![]() $k\leq n_i$
. In case of
$k\leq n_i$
. In case of
![]() $\overline\Phi_i$
these are exactly
$\overline\Phi_i$
these are exactly
![]() $\left\{F_i^{n_i},\dots,F_i^{k_i}\right\}$
.
$\left\{F_i^{n_i},\dots,F_i^{k_i}\right\}$
.
Lemma 4·7. Looking at
![]() $\mathbf D$
in the preferred perspective, in any positive factorisation of
$\mathbf D$
in the preferred perspective, in any positive factorisation of
![]() $\phi$
lifting
$\phi$
lifting
![]() $\overline\Psi$
, the lifts of twists from
$\overline\Psi$
, the lifts of twists from
![]() $\overline\Psi_3$
do not encircle any of
$\overline\Psi_3$
do not encircle any of
![]() $\nu^k_3$
for
$\nu^k_3$
for
![]() $k\leq n_3$
. Furthermore, around
$k\leq n_3$
. Furthermore, around
![]() $\nu^{\text{out}}$
and each
$\nu^{\text{out}}$
and each
![]() $\nu^k_3$
for
$\nu^k_3$
for
![]() $k>n_3$
, there are at least as many lifts of twists from
$k>n_3$
, there are at least as many lifts of twists from
![]() $\overline\Psi_3$
as there are
$\overline\Psi_3$
as there are
![]() $T_3$
-twists around the same hole in the original factorisation.
$T_3$
-twists around the same hole in the original factorisation.
Proof. Again, because of Lemma 2·8, throughout the proof the multiplicities computed from
![]() $\Phi$
give us information about any positive factorisation.
$\Phi$
give us information about any positive factorisation.
Viewed in the turned-over perspective, the multiplicities equal
![]() $m^{\prime}_{\nu^k_3\pi_3}=0$
for
$m^{\prime}_{\nu^k_3\pi_3}=0$
for
![]() $k\leq n_3$
. Hence, whenever in the preferred perspective
$k\leq n_3$
. Hence, whenever in the preferred perspective
![]() $\mathbf D$
such
$\mathbf D$
such
![]() $\nu^k_3$
is encircled together with any
$\nu^k_3$
is encircled together with any
![]() $\pi_3$
, the twist contains also
$\pi_3$
, the twist contains also
![]() $\pi^{\text{in}}$
. But since no twist in
$\pi^{\text{in}}$
. But since no twist in
![]() $\overline\Psi_3$
contains
$\overline\Psi_3$
contains
![]() $\pi^{\text{in}}$
in
$\pi^{\text{in}}$
in
![]() $\mathbf D$
, their lifts necessarily avoid all
$\mathbf D$
, their lifts necessarily avoid all
![]() $\nu^k_3$
for
$\nu^k_3$
for
![]() $k\leq n_3$
.
$k\leq n_3$
.
Moreover, the pairwise multiplicities equal
![]() $M_{\nu^j_3\pi^k_3}=1+j-k$
for
$M_{\nu^j_3\pi^k_3}=1+j-k$
for
![]() $j>k\geq n_3$
, while
$j>k\geq n_3$
, while
![]() $M_{\nu^j_3\pi^{\text{in}}}=1$
. Indeed, in the factorisation
$M_{\nu^j_3\pi^{\text{in}}}=1$
. Indeed, in the factorisation
![]() $\Phi$
seen in
$\Phi$
seen in
![]() $\mathbf D$
, the only twist which encircles
$\mathbf D$
, the only twist which encircles
![]() $\pi^{\text{in}}$
with any
$\pi^{\text{in}}$
with any
![]() $\nu_3$
is
$\nu_3$
is
![]() $\delta$
. On the other hand, by construction from Subsection 2·1, if a non-boundary twist encircles
$\delta$
. On the other hand, by construction from Subsection 2·1, if a non-boundary twist encircles
![]() $\nu_3$
-hole in the initial perspective, it is a
$\nu_3$
-hole in the initial perspective, it is a
![]() $T_3$
-twist; concretely, a
$T_3$
-twist; concretely, a
![]() $T_3^y$
encircles all
$T_3^y$
encircles all
![]() $\nu_3^j$
for
$\nu_3^j$
for
![]() $j\leq y$
and does not encircle exactly
$j\leq y$
and does not encircle exactly
![]() $\pi_3^k$
for
$\pi_3^k$
for
![]() $k\leq y$
. In the preferred perspective then
$k\leq y$
. In the preferred perspective then
![]() $T_3^y$
encircles all
$T_3^y$
encircles all
![]() $\nu_3^j$
for
$\nu_3^j$
for
![]() $j>y$
and all
$j>y$
and all
![]() $\pi_3^k$
for
$\pi_3^k$
for
![]() $k\leq y$
; so, the twists that encircle
$k\leq y$
; so, the twists that encircle
![]() $\nu^j_3$
and
$\nu^j_3$
and
![]() $\pi^k_3$
together are
$\pi^k_3$
together are
![]() $\delta$
and
$\delta$
and
![]() $j-k$
of
$j-k$
of
![]() $T_3$
-twists.
$T_3$
-twists.
Hence, since all twists in
![]() $\overline\Psi_1$
and
$\overline\Psi_1$
and
![]() $\overline\Psi_2$
which contain any (hence all)
$\overline\Psi_2$
which contain any (hence all)
![]() $\pi_3$
-hole contain also
$\pi_3$
-hole contain also
![]() $\pi^{\text{in}}$
, all but one twists which contain a
$\pi^{\text{in}}$
, all but one twists which contain a
![]() $\nu_3$
-hole together with some
$\nu_3$
-hole together with some
![]() $\pi_3$
need to arise as lifts of twists in
$\pi_3$
need to arise as lifts of twists in
![]() $\overline\Psi_3$
; for
$\overline\Psi_3$
; for
![]() $\nu^j_3$
, there are
$\nu^j_3$
, there are
![]() $j-n_3$
of them, which is exactly the number of
$j-n_3$
of them, which is exactly the number of
![]() $T_3$
-twists around
$T_3$
-twists around
![]() $\nu^j_3$
.
$\nu^j_3$
.
Proposition 4·8. Properties of a positive factorisation of
![]() $\phi$
concerning the holes
$\phi$
concerning the holes
![]() $\nu^{\text{out}}\cup\nu_3$
in
$\nu^{\text{out}}\cup\nu_3$
in
![]() $\mathbf D$
:
$\mathbf D$
:
-
(i) the pairwise multiplicity of each
 $\nu^{\text{out}}\cup\nu_3$
with any of
$\nu^{\text{out}}\cup\nu_3$
with any of
 $\pi^{\text{in}}\cup\pi_1\cup\pi_2$
is one, and with the
$\pi^{\text{in}}\cup\pi_1\cup\pi_2$
is one, and with the
 $\pi_3$
-holes the multiplicities equal
$\pi_3$
-holes the multiplicities equal
 $M_{\nu^j_3\pi^k_3}=\max\{1,1+j-k\}$
;
$M_{\nu^j_3\pi^k_3}=\max\{1,1+j-k\}$
; -
(ii) each of
 $\nu^j_3$
-holes is encircled by at most
$\nu^j_3$
-holes is encircled by at most
 $j+2$
non-boundary Dehn twists,
$j+2$
non-boundary Dehn twists,
 $\nu^{\text{out}}$
by at most
$\nu^{\text{out}}$
by at most
 $k_3+2$
;
$k_3+2$
; -
(iii) the pairwise multiplicity of each
 $\nu^j_3$
with any
$\nu^j_3$
with any
 $\nu^{\geq j}_3$
is exactly
$\nu^{\geq j}_3$
is exactly
 $j+1$
;
$j+1$
; -
(iv) lifts of
 $k_i-n_i+1$
twists among
$k_i-n_i+1$
twists among
 $\left\{P^{0}_i,\dots,P^{k_i}_i\right\}$
for
$\left\{P^{0}_i,\dots,P^{k_i}_i\right\}$
for
 $i=1,2$
never encircle any of
$i=1,2$
never encircle any of
 $\nu^{\text{out}}\cup\nu_3$
;
$\nu^{\text{out}}\cup\nu_3$
; -
(v) for every
 $\nu^{\text{out}}\cup\nu_3$
there is exactly one twist which encircles it together with any (and hence all) of
$\nu^{\text{out}}\cup\nu_3$
there is exactly one twist which encircles it together with any (and hence all) of
 $\pi_3$
, and is not a lift of a twist from
$\pi_3$
, and is not a lift of a twist from
 $\overline\Psi_3$
. There is no lift of twists from
$\overline\Psi_3$
. There is no lift of twists from
 $\overline\Psi_3$
around any
$\overline\Psi_3$
around any
 $\nu^j_3$
with
$\nu^j_3$
with
 $j\leq n_3$
, there are at least
$j\leq n_3$
, there are at least
 $j-n_3$
of them around
$j-n_3$
of them around
 $\nu^j_3$
with
$\nu^j_3$
with
 $j>n_3$
, and at least
$j>n_3$
, and at least
 $k_3-n_3+1$
around
$k_3-n_3+1$
around
 $\nu^{\text{out}}$
.
$\nu^{\text{out}}$
.
Proof. Properties (i)–(iii) are obtained by counting twists in the original factorisation
![]() $\Phi$
(and applying Lemma 2·8): for (i), we see that the only twist encircling any of
$\Phi$
(and applying Lemma 2·8): for (i), we see that the only twist encircling any of
![]() $\nu^{\text{out}}\cup\nu_3$
with any of
$\nu^{\text{out}}\cup\nu_3$
with any of
![]() $\pi^{\text{in}}\cup\pi_1\cup\pi_2$
is
$\pi^{\text{in}}\cup\pi_1\cup\pi_2$
is
![]() $\delta$
, while the multiplicity
$\delta$
, while the multiplicity
![]() $M_{\nu^j_3\pi^k_3}$
has been computed in the previous proof. For (ii), the multiplicity
$M_{\nu^j_3\pi^k_3}$
has been computed in the previous proof. For (ii), the multiplicity
![]() $M_{\nu_3^j}$
counts
$M_{\nu_3^j}$
counts
![]() $T_3^y$
for
$T_3^y$
for
![]() $j>y$
, the boundary twist and
$j>y$
, the boundary twist and
![]() $\delta$
, while
$\delta$
, while
![]() $M_{\nu^{\text{out}}}$
counts all
$M_{\nu^{\text{out}}}$
counts all
![]() $T_3$
and
$T_3$
and
![]() $\delta$
. For (iii), the twists that encircle
$\delta$
. For (iii), the twists that encircle
![]() $\nu^j_3$
with any
$\nu^j_3$
with any
![]() $\nu^{\geq j}_3$
are only
$\nu^{\geq j}_3$
are only
![]() $T_3^y$
for
$T_3^y$
for
![]() $j>y$
. Property (iv) restates Lemma 4·6, and property (v) restates Lemma 4·7.
$j>y$
. Property (iv) restates Lemma 4·6, and property (v) restates Lemma 4·7.
Taking the properties (i) and (v), we see that for each
![]() $\nu^{\text{out}}\cup\nu_3$
the twists in
$\nu^{\text{out}}\cup\nu_3$
the twists in
![]() $\overline\Psi_1\cup\overline\Psi_2$
whose lifts encircle that hole, regarded as the sets of holes they encircle, form a partition of
$\overline\Psi_1\cup\overline\Psi_2$
whose lifts encircle that hole, regarded as the sets of holes they encircle, form a partition of
![]() $\pi$
-holes (and the remaining
$\pi$
-holes (and the remaining
![]() $j-k$
twists encircling
$j-k$
twists encircling
![]() $\nu^j_3$
together with
$\nu^j_3$
together with
![]() $\pi^k_3$
come from
$\pi^k_3$
come from
![]() $\overline\Psi_3$
). Furthermore, according to the property (ii) there is a bound on the number of parts – that is, twists – such a partition can consist of. Finally, property (iii) specifies how the partitions associated to different
$\overline\Psi_3$
). Furthermore, according to the property (ii) there is a bound on the number of parts – that is, twists – such a partition can consist of. Finally, property (iii) specifies how the partitions associated to different
![]() $\nu_3$
-holes interact.
$\nu_3$
-holes interact.
Definition 4·9. Let a
![]() $\overline\Psi$
-partition be a set of twists from
$\overline\Psi$
-partition be a set of twists from
![]() $\overline\Psi_1\cup\overline\Psi_2$
which – as the sets of holes they encircle – partition the
$\overline\Psi_1\cup\overline\Psi_2$
which – as the sets of holes they encircle – partition the
![]() $\pi$
-holes. The equal twists of different partitions are referred to as shared.
$\pi$
-holes. The equal twists of different partitions are referred to as shared.
As noticed above, in a positive factorisation every
![]() $\nu_3$
-hole
$\nu_3$
-hole
![]() $\chi$
defines a
$\chi$
defines a
![]() $\overline\Psi$
-partition; we will call it a
$\overline\Psi$
-partition; we will call it a
![]() $\overline\Psi$
-partition associated to
$\overline\Psi$
-partition associated to
![]() $\chi$
.
$\chi$
.
Lifting positive factorisations from
![]() $\mathbf D_\pi$
to
$\mathbf D_\pi$
to
![]() $\mathbf D$
$\mathbf D$
We proceed successively, focusing on
![]() $\nu^j_3$
for j in
$\nu^j_3$
for j in
![]() $0,1,\dots,k_3+1$
; here, we denote
$0,1,\dots,k_3+1$
; here, we denote
![]() $\nu^{k_3+1}_3\,:\!=\,\nu^{\text{out}}$
. Let
$\nu^{k_3+1}_3\,:\!=\,\nu^{\text{out}}$
. Let
![]() $\{j_l\}$
be a subsequence such that
$\{j_l\}$
be a subsequence such that
![]() $\big|\nu^{j_l}_3\big|\neq 0$
$\big|\nu^{j_l}_3\big|\neq 0$
![]() $\big($
note that we have renamed the outer boundary of
$\big($
note that we have renamed the outer boundary of
![]() $\mathbf D$
to
$\mathbf D$
to
![]() $\delta$
, so it is not counted in
$\delta$
, so it is not counted in
![]() $\big|\nu^0_3\big|\big)$
. Formally, we set
$\big|\nu^0_3\big|\big)$
. Formally, we set
 \begin{equation*}\begin{array}{l}j_0=-1 \\[4pt] j_l\,:\!=\,\min\left\{j;\,j>j_{l-1}\text{ and }|\nu^j_3|\geq1\right\}. \end{array} \end{equation*}
\begin{equation*}\begin{array}{l}j_0=-1 \\[4pt] j_l\,:\!=\,\min\left\{j;\,j>j_{l-1}\text{ and }|\nu^j_3|\geq1\right\}. \end{array} \end{equation*}
Definition 4·10. We will refer to the subsequence counter as the level. We will say that
![]() $\overline\Psi$
lifts over
$\overline\Psi$
lifts over
![]() $\nu_3^{\leq j_\ell}$
if the twists in
$\nu_3^{\leq j_\ell}$
if the twists in
![]() $\overline\Psi$
can be lifted to
$\overline\Psi$
can be lifted to
![]() $\mathrm{AbMap} \mathbf D_{\pi\cup\nu^{\leq {j_\ell}}_3}$
so that the factorisation satisfies the properties of Proposition 4·8.
$\mathrm{AbMap} \mathbf D_{\pi\cup\nu^{\leq {j_\ell}}_3}$
so that the factorisation satisfies the properties of Proposition 4·8.
Note that to have a positive factorisation, it is necessary that some positive factorisation
![]() $\overline\Psi$
lifts over all
$\overline\Psi$
lifts over all
![]() $\nu_3\cup\nu^{\text{out}}$
.
$\nu_3\cup\nu^{\text{out}}$
.
Lemma 4·11. If
![]() $\overline\Psi$
lifts over
$\overline\Psi$
lifts over
![]() $\nu_3\cup\nu^{\text{out}}$
, the
$\nu_3\cup\nu^{\text{out}}$
, the
![]() $\overline\Psi$
-partitions associated to every
$\overline\Psi$
-partitions associated to every
![]() $\nu_3$
-hole and to
$\nu_3$
-hole and to
![]() $\nu^{\text{out}}$
are all built of twists from the same
$\nu^{\text{out}}$
are all built of twists from the same
![]() $\overline\Psi_i$
for either
$\overline\Psi_i$
for either
![]() $i=1$
or 2. Furthermore, every
$i=1$
or 2. Furthermore, every
![]() $\overline\Psi_i$
-partition consists of a single twist
$\overline\Psi_i$
-partition consists of a single twist
![]() $P_i^K$
with
$P_i^K$
with
![]() $K\leq k_i$
and some
$K\leq k_i$
and some
![]() $P_i^k$
with
$P_i^k$
with
![]() $k>k_i$
which partition
$k>k_i$
which partition
![]() $\pi_i$
-holes not encircled by
$\pi_i$
-holes not encircled by
![]() $P_i^K$
; the latter are necessary shared by all
$P_i^K$
; the latter are necessary shared by all
![]() $\nu_3\cup\nu^{\text{out}}$
.
$\nu_3\cup\nu^{\text{out}}$
.
Proof. As observed under Proposition 4·8, the set of all twists from
![]() $\overline\Psi_1\cup\overline\Psi_2$
whose lifts encircle a
$\overline\Psi_1\cup\overline\Psi_2$
whose lifts encircle a
![]() $\nu^{\text{out}}\cup\nu_3$
-hole forms a partition of the
$\nu^{\text{out}}\cup\nu_3$
-hole forms a partition of the
![]() $\pi$
-holes. Since every partition needs a twist which contains
$\pi$
-holes. Since every partition needs a twist which contains
![]() $\pi^{\text{in}}$
, every
$\pi^{\text{in}}$
, every
![]() $\overline\Psi$
-partition consists of a twist
$\overline\Psi$
-partition consists of a twist
![]() $P^K_i$
with
$P^K_i$
with
![]() $K\leq k_i$
for either
$K\leq k_i$
for either
![]() $i=1$
or 2, and some twists covering all
$i=1$
or 2, and some twists covering all
![]() $\pi_i$
-holes which are not encircled by
$\pi_i$
-holes which are not encircled by
![]() $P^K_i$
. Now, we separate three cases:
$P^K_i$
. Now, we separate three cases:
-
(a) if all partitions have more than
 $j_1+2$
parts, the property (ii) of Proposition 4·8 can never be satisfied and there is no positive factorisation;
$j_1+2$
parts, the property (ii) of Proposition 4·8 can never be satisfied and there is no positive factorisation; -
(b) if there is a partition of exactly
 $j_1+2$
parts,
$j_1+2$
parts,
 $j_1+1$
of them are necessarily shared by partitions associated to all
$j_1+1$
of them are necessarily shared by partitions associated to all
 $\nu_3\cup\nu^{\text{out}}$
, to fulfill the property (iii) of Proposition 4·8. Since for any i,j the difference between
$\nu_3\cup\nu^{\text{out}}$
, to fulfill the property (iii) of Proposition 4·8. Since for any i,j the difference between
 $M_{\pi^j_i}$
and
$M_{\pi^j_i}$
and
 $M_{\pi^{\text{in}} \pi_i^j}$
is one, around each
$M_{\pi^{\text{in}} \pi_i^j}$
is one, around each
 $\pi$
-hole there can be only one twist which does not encircle
$\pi$
-hole there can be only one twist which does not encircle
 $\pi^{\text{in}}$
. Therefore, the twists other than
$\pi^{\text{in}}$
. Therefore, the twists other than
 $P^K_i$
with
$P^K_i$
with
 $K\leq k_i$
are always shared by all
$K\leq k_i$
are always shared by all
 $\nu_3\cup\nu^{\text{out}}$
, and by Lemma 4·3 all of them belong to
$\nu_3\cup\nu^{\text{out}}$
, and by Lemma 4·3 all of them belong to
 $\overline\Psi_i$
. Moreover, the
$\overline\Psi_i$
. Moreover, the
 $\overline\Psi$
-partitions associated to different
$\overline\Psi$
-partitions associated to different
 $\nu^{j}_3$
-holes come from different partitioning of holes contained in
$\nu^{j}_3$
-holes come from different partitioning of holes contained in
 $P^K_i$
, which is possible only by
$P^K_i$
, which is possible only by
 $\overline\Psi_i$
-twists;
$\overline\Psi_i$
-twists; -
(c) if there is a partition of less than
 $j_1+2$
parts, we can lift all its defining twists over all
$j_1+2$
parts, we can lift all its defining twists over all
 $\nu^{\text{out}}\cup\nu_3$
. Indeed, this choice – after we complete the factorisation by lifts of the twists from
$\nu^{\text{out}}\cup\nu_3$
. Indeed, this choice – after we complete the factorisation by lifts of the twists from
 $\overline\Psi_3$
and some twists which do not contain any
$\overline\Psi_3$
and some twists which do not contain any
 $\pi$
-holes – satisfies all properties of Proposition 4·8, and the partition obviously come from a single
$\pi$
-holes – satisfies all properties of Proposition 4·8, and the partition obviously come from a single
 $\overline\Psi_i$
.
$\overline\Psi_i$
.
From the above proof we see that, in case (a) the factorisation
![]() $\overline\Psi$
does not lift over
$\overline\Psi$
does not lift over
![]() $\nu_3^{j_1}$
and hence there is no positive factorisation lifting
$\nu_3^{j_1}$
and hence there is no positive factorisation lifting
![]() $\overline\Psi$
, while in case (c) the factorisation
$\overline\Psi$
, while in case (c) the factorisation
![]() $\overline\Psi$
lifts over
$\overline\Psi$
lifts over
![]() $\nu_3\cup\nu^{\text{out}}$
and there is no obstruction for positive factorisation in terms of Proposition 4·8. In fact, we will see in Lemma 4·15 that the case (c) happens only in the presence of a balanced link. In case (b) the factorisation
$\nu_3\cup\nu^{\text{out}}$
and there is no obstruction for positive factorisation in terms of Proposition 4·8. In fact, we will see in Lemma 4·15 that the case (c) happens only in the presence of a balanced link. In case (b) the factorisation
![]() $\overline\Psi$
lifts over
$\overline\Psi$
lifts over
![]() $\nu_3^{j_1}$
and in this case, we continue by repeating a similar analysis for the holes
$\nu_3^{j_1}$
and in this case, we continue by repeating a similar analysis for the holes
![]() $\nu_3^{j_l}$
with
$\nu_3^{j_l}$
with
![]() $l>1$
.
$l>1$
.
We first notice that, when looking for obstructions of positive factorisation, it suffices to examine one particular factorisation of
![]() $\overline\phi$
, namely
$\overline\phi$
, namely
![]() $\overline\Phi$
.
$\overline\Phi$
.
Notation 4·12. We name the truncated continued fraction which corresponds to the maximal fully positive (for
![]() $i=1,2$
) or maximal fully negative (for
$i=1,2$
) or maximal fully negative (for
![]() $i=3$
) truncation of the leg
$i=3$
) truncation of the leg
![]() $L_i$
, by
$L_i$
, by
![]() $- {1}/{q_i}\,:\!=\,[a^0_i,\dots,a^{n_i-1}_i]$
, or
$- {1}/{q_i}\,:\!=\,[a^0_i,\dots,a^{n_i-1}_i]$
, or
![]() $-{1}/{q_i}\,:\!=\,-\infty$
when
$-{1}/{q_i}\,:\!=\,-\infty$
when
![]() $n_i=0$
.
$n_i=0$
.
Lemma 4·13. Assume that the legs are ordered so that
![]() $-{1}/{q_1}\geq - {1}/{q_2}$
. If any positive factorisation
$-{1}/{q_1}\geq - {1}/{q_2}$
. If any positive factorisation
![]() $\overline\Psi_i$
of either
$\overline\Psi_i$
of either
![]() $\overline\phi_1$
or
$\overline\phi_1$
or
![]() $\overline\phi_2$
lifts over
$\overline\phi_2$
lifts over
![]() $\nu^{\leq j}_3$
, so does
$\nu^{\leq j}_3$
, so does
![]() $\overline\Phi_1$
.
$\overline\Phi_1$
.
Proof. Suppose we are lifting
![]() $\overline\Psi_i$
which differs from
$\overline\Psi_i$
which differs from
![]() $\overline\Phi_i$
. At each level l we are looking for partitions of the least possible parts among the partitions not associated to any
$\overline\Phi_i$
. At each level l we are looking for partitions of the least possible parts among the partitions not associated to any
![]() $\nu_3^{<j_l}$
. From Lemma 4·11 it follows that the partitions associated to
$\nu_3^{<j_l}$
. From Lemma 4·11 it follows that the partitions associated to
![]() $\nu_3^{j_l}$
-holes are built from the partitions associated to
$\nu_3^{j_l}$
-holes are built from the partitions associated to
![]() $\nu_3^{j_{l-1}}$
-holes by splitting the twist which contains
$\nu_3^{j_{l-1}}$
-holes by splitting the twist which contains
![]() $\pi^{\text{in}}$
. This means that the twists
$\pi^{\text{in}}$
. This means that the twists
![]() $P^k_i$
for
$P^k_i$
for
![]() $k\leq k_i$
are taken as parts of the successive partitions in order of increasing k. Since – according to Lemma 4·4 – the holes out of
$k\leq k_i$
are taken as parts of the successive partitions in order of increasing k. Since – according to Lemma 4·4 – the holes out of
![]() $F^{x_i}_i$
for
$F^{x_i}_i$
for
![]() $x_i=\min\left\{k;\,P^k_i\neq F^k_i\right\}$
are encircled in any positive factorisation
$x_i=\min\left\{k;\,P^k_i\neq F^k_i\right\}$
are encircled in any positive factorisation
![]() $\overline\Psi_i$
only by the twists which agree with some twists in
$\overline\Psi_i$
only by the twists which agree with some twists in
![]() $\overline\Phi_i$
, the first
$\overline\Phi_i$
, the first
![]() $x_i$
of the
$x_i$
of the
![]() $\overline\Psi_i$
-partitions agree with the
$\overline\Psi_i$
-partitions agree with the
![]() $\overline\Phi_i$
-partitions; they are composed of a twist
$\overline\Phi_i$
-partitions; they are composed of a twist
![]() $P^k_i=F^k_i$
for
$P^k_i=F^k_i$
for
![]() $k< x_i$
and the boundary twists of the holes out of
$k< x_i$
and the boundary twists of the holes out of
![]() $P^k_i$
, and the two factorisations lift simultaneously. But, once, at the level
$P^k_i$
, and the two factorisations lift simultaneously. But, once, at the level
![]() $\ell$
, we associate to a
$\ell$
, we associate to a
![]() $\nu_3^{j_\ell}$
a
$\nu_3^{j_\ell}$
a
![]() $\overline\Psi_i$
-partition which involves a twist
$\overline\Psi_i$
-partition which involves a twist
![]() $P^{x_i}_i\neq F^{x_i}_i$
, Lemma 4·4 tells us that using
$P^{x_i}_i\neq F^{x_i}_i$
, Lemma 4·4 tells us that using
![]() $\overline\Phi_i$
there is at least one more partition of at least one less part which we could associate to
$\overline\Phi_i$
there is at least one more partition of at least one less part which we could associate to
![]() $\nu_3^{j_\ell}$
. This is because
$\nu_3^{j_\ell}$
. This is because
![]() $P_i^{x_i}$
encircles strictly less holes than
$P_i^{x_i}$
encircles strictly less holes than
![]() $F_i^{x_i}$
does, and the other
$F_i^{x_i}$
does, and the other
![]() $\overline\Psi_i$
-twists forming the partition are necessary boundary parallel. Now, since by assumption
$\overline\Psi_i$
-twists forming the partition are necessary boundary parallel. Now, since by assumption
![]() $\overline\Psi_i$
lifts over
$\overline\Psi_i$
lifts over
![]() $\nu^{\leq j_\ell}_3$
, this existing
$\nu^{\leq j_\ell}_3$
, this existing
![]() $\overline\Phi_i$
-partition has less than
$\overline\Phi_i$
-partition has less than
![]() $j_\ell+2$
parts, and can be associated to all
$j_\ell+2$
parts, and can be associated to all
![]() $\nu^{\geq j_\ell}_3$
, fulfilling the properties of Proposition 4·8.
$\nu^{\geq j_\ell}_3$
, fulfilling the properties of Proposition 4·8.
Combining Lemma 4·11 with Lemma 4·6 (which says that lifts of
![]() $F_i^{n_i},\dots,F_i^{k_i}$
for
$F_i^{n_i},\dots,F_i^{k_i}$
for
![]() $i=1$
or 2 do not encircle
$i=1$
or 2 do not encircle
![]() $\nu_3$
-holes), we see that every
$\nu_3$
-holes), we see that every
![]() $\overline\Phi_i$
-partition consists of a single
$\overline\Phi_i$
-partition consists of a single
![]() $F^K_i$
-twist with
$F^K_i$
-twist with
![]() $K<n_i$
and the boundary twists of the holes out of
$K<n_i$
and the boundary twists of the holes out of
![]() $F^K_i$
. Recall that
$F^K_i$
. Recall that
![]() $F^k_i$
are exactly the extensions of
$F^k_i$
are exactly the extensions of
![]() $T^k_i$
to
$T^k_i$
to
![]() $\mathbf D_\pi$
, denoted
$\mathbf D_\pi$
, denoted
![]() $\overline T_i^k$
. Now, comparing
$\overline T_i^k$
. Now, comparing
![]() $\overline\Phi_1$
to
$\overline\Phi_1$
to
![]() $\overline\Phi_2$
, the inequality
$\overline\Phi_2$
, the inequality
![]() $- {1}/{q_1}\geq - {1}/{q_2}$
means that at the first index in which the two continued fractions disagree, the coefficient
$- {1}/{q_1}\geq - {1}/{q_2}$
means that at the first index in which the two continued fractions disagree, the coefficient
![]() $a^k_1$
is smaller than
$a^k_1$
is smaller than
![]() $a^k_2$
(see for example [
Reference Cox, Little and Schenck1
] for the basic calculus of continued fractions). Hence, the corresponding
$a^k_2$
(see for example [
Reference Cox, Little and Schenck1
] for the basic calculus of continued fractions). Hence, the corresponding
![]() $\overline T^k_1$
-twist avoids less
$\overline T^k_1$
-twist avoids less
![]() $\pi$
-holes than
$\pi$
-holes than
![]() $\overline T^k_2$
does, and the
$\overline T^k_2$
does, and the
![]() $(k+1)^{\text{th}}$
$(k+1)^{\text{th}}$
![]() $\overline\Phi_1$
-partition has less parts than the
$\overline\Phi_1$
-partition has less parts than the
![]() $(k+1){\text{th}}$
$(k+1){\text{th}}$
![]() $\overline\Phi_2$
-partition, while the first k partitions have the same number of parts. The same argument as in the conclusion of the previous paragraph now shows that once
$\overline\Phi_2$
-partition, while the first k partitions have the same number of parts. The same argument as in the conclusion of the previous paragraph now shows that once
![]() $\overline\Phi_2$
lifts also
$\overline\Phi_2$
lifts also
![]() $\overline\Phi_1$
does.
$\overline\Phi_1$
does.
Lemma 4·13 essentially means that, when looking for obstructions of positive factorisation, we can focus only on
![]() $\overline\Phi$
among
$\overline\Phi$
among
![]() $\overline\phi$
-factorisations. Moreover, once we number the legs so that
$\overline\phi$
-factorisations. Moreover, once we number the legs so that
![]() $- {1}/{q_1}\geq - {1}/{q_2}$
, it suffices to check whether
$- {1}/{q_1}\geq - {1}/{q_2}$
, it suffices to check whether
![]() $\overline\Phi_1$
lifts over
$\overline\Phi_1$
lifts over
![]() $\nu^{\leq j_l}_3$
for all levels l. If it does not, then no positive factorisation
$\nu^{\leq j_l}_3$
for all levels l. If it does not, then no positive factorisation
![]() $\overline\Psi_i$
of either
$\overline\Psi_i$
of either
![]() $\overline\phi_1$
or
$\overline\phi_1$
or
![]() $\overline\phi_2$
does (Lemma 4·13). Hence, also
$\overline\phi_2$
does (Lemma 4·13). Hence, also
![]() $\overline\Psi$
cannot lift to a positive factorisation of
$\overline\Psi$
cannot lift to a positive factorisation of
![]() $\phi$
(Lemma 4·11).
$\phi$
(Lemma 4·11).
Definition 4·14. If two sets of twists from
![]() $\overline\Psi_1\cup\overline\Psi_2$
define set-wise the same partition, then, since the twists of the two sets need to be parallel or equal, we say that the two
$\overline\Psi_1\cup\overline\Psi_2$
define set-wise the same partition, then, since the twists of the two sets need to be parallel or equal, we say that the two
![]() $\overline\Psi$
-partitions are parallel.
$\overline\Psi$
-partitions are parallel.
Lemma 4·15. Assume that
![]() $\overline\Phi_1$
lifts over
$\overline\Phi_1$
lifts over
![]() $\nu_3^{<j_\ell}$
and that no
$\nu_3^{<j_\ell}$
and that no
![]() $\overline\Phi_1$
-partition associated to
$\overline\Phi_1$
-partition associated to
![]() $\nu_3^{<j_\ell}$
could be extended over
$\nu_3^{<j_\ell}$
could be extended over
![]() $\nu_3^{\geq j_\ell}$
. At the
$\nu_3^{\geq j_\ell}$
. At the
![]() $\ell{\text{th}}$
level when
$\ell{\text{th}}$
level when
![]() $j_\ell< n_3$
(where we consider
$j_\ell< n_3$
(where we consider
![]() $n_3=k_3+1$
if there is no positive stabilisation on
$n_3=k_3+1$
if there is no positive stabilisation on
![]() $L_3$
) one of the following happens:
$L_3$
) one of the following happens:
-
(A) if there is no
 $\overline\Phi_1$
-partition into less than
$\overline\Phi_1$
-partition into less than
 $j_\ell+2$
parts which has not been associated to some
$j_\ell+2$
parts which has not been associated to some
 $\nu_3^{<j_\ell}$
, and there are less than
$\nu_3^{<j_\ell}$
, and there are less than
 $\big|\nu^{j_\ell}_3\big|$
of parallel
$\big|\nu^{j_\ell}_3\big|$
of parallel
 $\overline\Phi_1$
-partitions into
$\overline\Phi_1$
-partitions into
 $j_\ell+2$
parts, there is no positive factorisation of
$j_\ell+2$
parts, there is no positive factorisation of
 $\phi$
.
$\phi$
. -
(B) if there is no
 $\overline\Phi_1$
-partition into less than
$\overline\Phi_1$
-partition into less than
 $j_\ell+2$
parts which has not been associated to some
$j_\ell+2$
parts which has not been associated to some
 $\nu_3^{<j_\ell}$
, and there are at least
$\nu_3^{<j_\ell}$
, and there are at least
 $\big|\nu^{j_\ell}_3\big|$
of parallel
$\big|\nu^{j_\ell}_3\big|$
of parallel
 $\overline\Phi_1$
-partitions into
$\overline\Phi_1$
-partitions into
 $j_\ell+2$
parts, the factorisation
$j_\ell+2$
parts, the factorisation
 $\overline\Phi$
lifts over
$\overline\Phi$
lifts over
 $\nu_3^{\leq j_\ell}$
and there are truncations of the legs
$\nu_3^{\leq j_\ell}$
and there are truncations of the legs
 $L_1$
and
$L_1$
and
 $L_3$
which are related as either: or:
$L_3$
which are related as either: or: \begin{equation*}\begin{array}{l@{\quad}l@{\quad}l@{\quad}c@{\quad}c@{\quad}c@{\quad}c}L_3^{(\ell)}&:&\big({-}a_3^{j_1},&-2^{\times (j_2-j_1-1)},& -a_3^{j_2},&\dots,&-a_3^{j_\ell}\big)\\[8pt] L_1^{(\ell)}&:&\Big({-}3,-2^{\times \big(a_3^{j_1}-4\big)},&-j_2+j_1-2,&-2^{\times \big(a_3^{j_2}-3\big)},&\dots,& -2^{\times (a_3^{j_\ell}-3)}\Big)\end{array}\end{equation*}
\begin{equation*}\begin{array}{l@{\quad}l@{\quad}l@{\quad}c@{\quad}c@{\quad}c@{\quad}c}L_3^{(\ell)}&:&\big({-}a_3^{j_1},&-2^{\times (j_2-j_1-1)},& -a_3^{j_2},&\dots,&-a_3^{j_\ell}\big)\\[8pt] L_1^{(\ell)}&:&\Big({-}3,-2^{\times \big(a_3^{j_1}-4\big)},&-j_2+j_1-2,&-2^{\times \big(a_3^{j_2}-3\big)},&\dots,& -2^{\times (a_3^{j_\ell}-3)}\Big)\end{array}\end{equation*}
 \begin{equation*}\begin{array}{l@{\quad}l@{\quad}l@{\quad}c@{\quad}c@{\quad}c@{\quad}c}L_3^{(\ell)}&:&\big({-}3,-2^{\times (j_1-1)},&-a_3^{j_1},&-2^{\times (j_2-j_1-1)},&\dots,&-a_3^{j_\ell}\big)\\[8pt] L_1^{(\ell)}&:&\Big({-}j_1-3,&-2^{\times \big(a_3^{j_1}-3\big)}&-j_2+j_1-2,&\dots,& -2^{\times \big(a_3^{j_\ell}-3\big)}\Big).\end{array}\end{equation*}
\begin{equation*}\begin{array}{l@{\quad}l@{\quad}l@{\quad}c@{\quad}c@{\quad}c@{\quad}c}L_3^{(\ell)}&:&\big({-}3,-2^{\times (j_1-1)},&-a_3^{j_1},&-2^{\times (j_2-j_1-1)},&\dots,&-a_3^{j_\ell}\big)\\[8pt] L_1^{(\ell)}&:&\Big({-}j_1-3,&-2^{\times \big(a_3^{j_1}-3\big)}&-j_2+j_1-2,&\dots,& -2^{\times \big(a_3^{j_\ell}-3\big)}\Big).\end{array}\end{equation*}
-
(C) if there is a
 $\overline\Phi_1$
-partition into less than
$\overline\Phi_1$
-partition into less than
 $j_\ell+2$
parts, the factorisation
$j_\ell+2$
parts, the factorisation
 $\overline\Phi$
lifts over all
$\overline\Phi$
lifts over all
 $\nu_3\cup\nu^{\text{out}}$
, but the surgery presentation contains a balanced sublink.
$\nu_3\cup\nu^{\text{out}}$
, but the surgery presentation contains a balanced sublink.
Proof. The assumption means that
![]() $\overline\Phi_1$
falls under (B) for all levels up to the
$\overline\Phi_1$
falls under (B) for all levels up to the
![]() $\ell{\text{th}}$
.
$\ell{\text{th}}$
.
At the
![]() $\ell{\text{th}}$
level, if (A) there are only partitions of more than
$\ell{\text{th}}$
level, if (A) there are only partitions of more than
![]() $j_\ell+2$
twists or there are less than
$j_\ell+2$
twists or there are less than
![]() $\big|\nu^{j_\ell}_3\big|$
of
$\big|\nu^{j_\ell}_3\big|$
of
![]() $j_\ell+2$
-part partitions, there is no positive factorisation; because we cannot satisfy property (i) and property (ii) of Proposition 4·8 simultaneously.
$j_\ell+2$
-part partitions, there is no positive factorisation; because we cannot satisfy property (i) and property (ii) of Proposition 4·8 simultaneously.
On the other hand, the conditions of (B) allow us to obtain a positive factorisation in
![]() $\mathbf D_{\pi\cup\nu_3^{\leq j_\ell}}$
, but these conditions also prescribe how the truncations of legs are related. Indeed,
$\mathbf D_{\pi\cup\nu_3^{\leq j_\ell}}$
, but these conditions also prescribe how the truncations of legs are related. Indeed,
![]() $j_l$
always gives the index of an unknot on
$j_l$
always gives the index of an unknot on
![]() $L_3$
with surgery coefficient less than
$L_3$
with surgery coefficient less than
![]() $-2$
,
$-2$
,
![]() $j_l-j_{l-1}$
counts the number of parallel twists, which is one more than the number of unknots with coefficient
$j_l-j_{l-1}$
counts the number of parallel twists, which is one more than the number of unknots with coefficient
![]() $-2$
preceding the unknot
$-2$
preceding the unknot
![]() $v^{j_l}_3$
; so, the corresponding part of
$v^{j_l}_3$
; so, the corresponding part of
![]() $L_3$
looks like
$L_3$
looks like
The fact that the conditions of (B) are satisfied for the levels up to
![]() $\ell{\text{th}}$
means that the number of separated holes in the partitions associated to
$\ell{\text{th}}$
means that the number of separated holes in the partitions associated to
![]() $\nu_3^{j_l}$
compared to the partitions associated to
$\nu_3^{j_l}$
compared to the partitions associated to
![]() $\nu_3^{j_{l-1}}$
is exactly
$\nu_3^{j_{l-1}}$
is exactly
![]() $j_l-j_{l-1}$
(because there are no partitions of less than
$j_l-j_{l-1}$
(because there are no partitions of less than
![]() $j_l+2$
parts, there exists
$j_l+2$
parts, there exists
![]() $j_l+2$
-part partition, and previous partitions have
$j_l+2$
-part partition, and previous partitions have
![]() $j_{l-1}+2$
parts), which on
$j_{l-1}+2$
parts), which on
![]() $L_1$
corresponds to an unknot of coefficient
$L_1$
corresponds to an unknot of coefficient
![]() $-j_l+j_{l-1}-2$
, which is followed by exactly
$-j_l+j_{l-1}-2$
, which is followed by exactly
![]() $\big|\nu^{j_l}_3\big|-1$
of unknots with coefficient
$\big|\nu^{j_l}_3\big|-1$
of unknots with coefficient
![]() $-2$
(because there is at least
$-2$
(because there is at least
![]() $\big|\nu^{j_l}_3\big|$
partitions into
$\big|\nu^{j_l}_3\big|$
partitions into
![]() $j_l+2$
parts at the
$j_l+2$
parts at the
![]() $l{\text{th}}$
level, and there is no
$l{\text{th}}$
level, and there is no
![]() $j_l+2$
-part partition at the
$j_l+2$
-part partition at the
![]() $(l+1){\text{th}}$
level). The corresponding part of
$(l+1){\text{th}}$
level). The corresponding part of
![]() $L_1$
looks like
$L_1$
looks like
Finally, the condition (C) at the
![]() $\ell{\text{th}}$
level requires that the coefficients at the
$\ell{\text{th}}$
level requires that the coefficients at the
![]() $\ell{\text{th}}$
truncation of
$\ell{\text{th}}$
truncation of
![]() $L_3$
and
$L_3$
and
![]() $L_1$
are related differently as in (B): We have
$L_1$
are related differently as in (B): We have
![]() $j_\ell-j_{\ell-1}$
parallel twists (so,
$j_\ell-j_{\ell-1}$
parallel twists (so,
![]() $j_\ell-j_{\ell-1}-1$
of unknots with coefficient
$j_\ell-j_{\ell-1}-1$
of unknots with coefficient
![]() $-2$
on
$-2$
on
![]() $L_3$
) but we leave out less than
$L_3$
) but we leave out less than
![]() $j_\ell-j_{\ell-1}$
holes by the next
$j_\ell-j_{\ell-1}$
holes by the next
![]() $\overline T_{1}$
-curve (the coefficient of the corresponding unknot is at least
$\overline T_{1}$
-curve (the coefficient of the corresponding unknot is at least
![]() $-j_\ell+j_{\ell-1}-1$
). Since
$-j_\ell+j_{\ell-1}-1$
). Since
![]() $j_\ell< n_3$
(hence, the preceding unknots of coefficient
$j_\ell< n_3$
(hence, the preceding unknots of coefficient
![]() $-2$
are at the indices lower than
$-2$
are at the indices lower than
![]() $n_3$
) and since according to Lemma 4·6 only the twists
$n_3$
) and since according to Lemma 4·6 only the twists
![]() $\overline T_1^0,\dots,\overline T^{n_1-1}_1$
form
$\overline T_1^0,\dots,\overline T^{n_1-1}_1$
form
![]() $\overline\Phi_1$
-partitions associated to any
$\overline\Phi_1$
-partitions associated to any
![]() $\nu_3$
(hence, the unknot of coefficient greater than
$\nu_3$
(hence, the unknot of coefficient greater than
![]() $-j_\ell+j_{\ell-1}-2$
is at the index lower than
$-j_\ell+j_{\ell-1}-2$
is at the index lower than
![]() $n_1$
), the two truncated chains correspond to the rational numbers smaller than or equal to
$n_1$
), the two truncated chains correspond to the rational numbers smaller than or equal to
![]() $- {1}/{q_3}$
and
$- {1}/{q_3}$
and
![]() $-{1}/{q_1}$
, respectively. Comparing to Remark 3·2, we see that
$-{1}/{q_1}$
, respectively. Comparing to Remark 3·2, we see that
![]() $q_3$
and
$q_3$
and
![]() $q_1$
add up to at least 1.
$q_1$
add up to at least 1.
Proof of Proposition 4·1. The process of lifting
![]() $\overline\Phi$
over
$\overline\Phi$
over
![]() $\nu_3$
-holes eventually stops as we run into an obstruction for positive factorisation, (A) of Lemma 4·15, or we leave the assumed conditions, (C) of Lemma 4·15, if not before when we hit the
$\nu_3$
-holes eventually stops as we run into an obstruction for positive factorisation, (A) of Lemma 4·15, or we leave the assumed conditions, (C) of Lemma 4·15, if not before when we hit the
![]() $n_3$
-level (the
$n_3$
-level (the
![]() $(k_3+1)$
-level if there is no positive stabilisation on
$(k_3+1)$
-level if there is no positive stabilisation on
![]() $L_3$
). In the latter case, when (B) of Lemma 4·15 is fulfilled by all levels
$L_3$
). In the latter case, when (B) of Lemma 4·15 is fulfilled by all levels
![]() $j_l< n_3$
, we look at the possibilities of encircling
$j_l< n_3$
, we look at the possibilities of encircling
![]() $\nu^{\text{out}}$
. In order for a positive factorisation to exist, the properties (ii) and (v) of Proposition 4·8 require that there is another
$\nu^{\text{out}}$
. In order for a positive factorisation to exist, the properties (ii) and (v) of Proposition 4·8 require that there is another
![]() $\overline\Phi$
-partition of at most
$\overline\Phi$
-partition of at most
![]() $n_3+1$
parts which has not been associated to any
$n_3+1$
parts which has not been associated to any
![]() $\nu_3^{\leq j_\ell}$
where
$\nu_3^{\leq j_\ell}$
where
![]() $\ell=\max\big\{l;\,j_l<n_3\big\}$
. But, the existence of such a partition would, as in the last paragraph of the previous proof, imply that there is a balanced sublink in the surgery presentation. Indeed, there would be
$\ell=\max\big\{l;\,j_l<n_3\big\}$
. But, the existence of such a partition would, as in the last paragraph of the previous proof, imply that there is a balanced sublink in the surgery presentation. Indeed, there would be
![]() $n_3-j_\ell-1$
of unknots with coefficient
$n_3-j_\ell-1$
of unknots with coefficient
![]() $-2$
preceding
$-2$
preceding
![]() $v^{n_3}_3$
on
$v^{n_3}_3$
on
![]() $L_3$
, and the corresponding unknot on the truncated
$L_3$
, and the corresponding unknot on the truncated
![]() $L_1$
would have coefficient at least
$L_1$
would have coefficient at least
![]() $-n_3+j_\ell-1$
, meaning by Remark 3·2 that
$-n_3+j_\ell-1$
, meaning by Remark 3·2 that
![]() $q_3+q_1\geq 1$
.
$q_3+q_1\geq 1$
.
Proof of Theorem 1·1 and Proposition 1·2. Joining Proposition 3·3 and Proposition 4·1 we obtain the theorem, and the proposition should be read as its special case.
Indeed, Legendrian surgeries on the tight
![]() $S^1\times S^2$
, given by a balanced link (as in Proposition 3·3), give Stein fillable structures. On the other hand, in the absence of the balanced sublink, Proposition 4·1 tells us that the associated planar monodromy do not admit positive factorisation and hence, because of the Wendl’s theorem (Theorem 2·6), the presented contact manifold do not admit any Stein filling.
$S^1\times S^2$
, given by a balanced link (as in Proposition 3·3), give Stein fillable structures. On the other hand, in the absence of the balanced sublink, Proposition 4·1 tells us that the associated planar monodromy do not admit positive factorisation and hence, because of the Wendl’s theorem (Theorem 2·6), the presented contact manifold do not admit any Stein filling.
Acknowledgement
I thank András Stipsicz, Alberto Cavallo and the referee for their interest and the valuable comments on an early draft of this paper. My research has been supported by the NKFIH Grant Élvonal (Frontier) KKP 126683 and by the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (grant agreement No 674978).