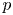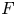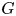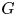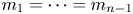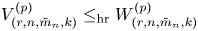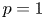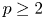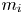1. Introduction
In the last two decades, a great attention has been put on stochastic orderings of order statistics and other ordered random variables. In another direction, such random variables can be embedded in the concept of generalized order statistics (GOS), introduced by Kamps [Reference Kamps16], as a general framework for models of ordered random variables. Since then, the researchers attempt to obtain their results for ordered data into the model of GOS.
Let ![]() $X$ and
$X$ and ![]() $Y$ be two nonnegative variables with absolutely continuous cumulative distribution functions (cdfs)
$Y$ be two nonnegative variables with absolutely continuous cumulative distribution functions (cdfs) ![]() $F$ and
$F$ and ![]() $G$, survival functions (sfs)
$G$, survival functions (sfs) ![]() $\bar {F}=1-F$ and
$\bar {F}=1-F$ and ![]() $\bar {G}=1-G$, and probability density functions (pdfs)
$\bar {G}=1-G$, and probability density functions (pdfs) ![]() $f$ and
$f$ and ![]() $g$, respectively, in which
$g$, respectively, in which ![]() $F^{-1}(0)=G^{-1}(0)$ (
$F^{-1}(0)=G^{-1}(0)$ (![]() $F^{-1}$ is the right continuous inverse of
$F^{-1}$ is the right continuous inverse of ![]() $F$). Let
$F$). Let ![]() $h_X=f/\bar F$ and
$h_X=f/\bar F$ and ![]() $h_Y=g/\bar G$ denote the hazard rate functions of
$h_Y=g/\bar G$ denote the hazard rate functions of ![]() $X$ and
$X$ and ![]() $Y$, respectively.
$Y$, respectively.
The random variables ![]() $X_{(r,n,\tilde {m}_n,k)}$,
$X_{(r,n,\tilde {m}_n,k)}$, ![]() $r=1,2,\ldots,n$, arising from independent and identically distributed random variables, are referred to as GOS if their joint density function is given by
$r=1,2,\ldots,n$, arising from independent and identically distributed random variables, are referred to as GOS if their joint density function is given by
 $$\mathbf{f}({x_1},\ldots,{x_n})= k\left(\prod_{j=1}^{n-1}{\gamma_{(j,n,\tilde{m}_n,k)}}\right) \left(\prod_{i=1}^{n-1} [\bar F{(x_i)}]^{m_i}f(x_i)\right)[\bar F{(x_n)}]^{k-1}f(x_n),$$
$$\mathbf{f}({x_1},\ldots,{x_n})= k\left(\prod_{j=1}^{n-1}{\gamma_{(j,n,\tilde{m}_n,k)}}\right) \left(\prod_{i=1}^{n-1} [\bar F{(x_i)}]^{m_i}f(x_i)\right)[\bar F{(x_n)}]^{k-1}f(x_n),$$for all ![]() $F^{-1}(0)< x_1\leq x_2 \leq \cdots \leq x_n < F^{-1}(1-)$, where
$F^{-1}(0)< x_1\leq x_2 \leq \cdots \leq x_n < F^{-1}(1-)$, where ![]() $n \in \mathbb {N}$,
$n \in \mathbb {N}$, ![]() $k>0$, and
$k>0$, and ![]() $m_1,\ldots,m_{n-1}\in \mathbb {R}$ are such that
$m_1,\ldots,m_{n-1}\in \mathbb {R}$ are such that ![]() ${\gamma _{(i,n,\tilde {m}_n,k)}}=k+n-i+\sum _{j=i}^{n-1}{m_j}\geq 1$ for all
${\gamma _{(i,n,\tilde {m}_n,k)}}=k+n-i+\sum _{j=i}^{n-1}{m_j}\geq 1$ for all ![]() $i\in \{1,\ldots,n-1\}$, and
$i\in \{1,\ldots,n-1\}$, and ![]() $\tilde {m}_n=(m_1,\ldots,m_{n-1})$ if
$\tilde {m}_n=(m_1,\ldots,m_{n-1})$ if ![]() $n\geq 2$ (
$n\geq 2$ (![]() $\tilde {m}_n\in \mathbb {R}$ is arbitrary if
$\tilde {m}_n\in \mathbb {R}$ is arbitrary if ![]() $n=1$). Indeed, special choices of parameters
$n=1$). Indeed, special choices of parameters ![]() $k$ and
$k$ and ![]() $m_i$ correspond to some well-known submodels such as order statistics, record values, and sequential order statistics. We refer the readers to Table 1 of Kamps [Reference Kamps17] for complete information on various submodels.
$m_i$ correspond to some well-known submodels such as order statistics, record values, and sequential order statistics. We refer the readers to Table 1 of Kamps [Reference Kamps17] for complete information on various submodels.
Throughout this paper, we shall use the word increasing (decreasing) for nondecreasing (nonincreasing). Furthermore, ratios are supposed to be well defined whenever they are used. We say that ![]() $X$ is smaller than
$X$ is smaller than ![]() $Y$ in the
$Y$ in the
• likelihood ratio order (denoted by
 $X\leq _{{\rm lr}} Y$) if
$X\leq _{{\rm lr}} Y$) if  $g(x)/f(x)$ is increasing in
$g(x)/f(x)$ is increasing in  $x$;
$x$;• hazard rate order (denoted by
 $X\leq _{{\rm hr}} Y$) if
$X\leq _{{\rm hr}} Y$) if  $\bar {G}(x)/\bar {F}(x)$ is increasing in
$\bar {G}(x)/\bar {F}(x)$ is increasing in  $x$ or, equivalently,
$x$ or, equivalently,  $h_Y(x)\leq h_X(x)$.
$h_Y(x)\leq h_X(x)$.
It is well-known that ![]() $X\leq _{{\rm lr}} Y \Rightarrow X\leq _{{\rm hr}} Y$ (cf. [Reference Shaked and Shanthikumar23]). We say that
$X\leq _{{\rm lr}} Y \Rightarrow X\leq _{{\rm hr}} Y$ (cf. [Reference Shaked and Shanthikumar23]). We say that ![]() $X$ is DFR (decreasing failure rate) if
$X$ is DFR (decreasing failure rate) if ![]() $\bar F$ is logconvex in
$\bar F$ is logconvex in ![]() $x\in \mathbb {R_+}$ or, equivalently,
$x\in \mathbb {R_+}$ or, equivalently, ![]() $\bar F(x+\epsilon )/\bar F(x)$ is an increasing function of
$\bar F(x+\epsilon )/\bar F(x)$ is an increasing function of ![]() $x$ for each fixed
$x$ for each fixed ![]() $\epsilon >0$.
$\epsilon >0$.
Let ![]() $Y_{(r,n,\tilde {m}_n,k)}$,
$Y_{(r,n,\tilde {m}_n,k)}$, ![]() $r=1,\ldots,n$, be GOS based on
$r=1,\ldots,n$, be GOS based on ![]() $G$. We denote the
$G$. We denote the ![]() $p$-spacings of GOS from
$p$-spacings of GOS from ![]() $F$ and
$F$ and ![]() $G$ by
$G$ by ![]() $V_{(r,n,\tilde {m}_n,k)}^{(p)}=X_{(r+p-1,n,\tilde {m}_n,k)}-X_{(r-1,n,\tilde {m}_n,k)}$ and
$V_{(r,n,\tilde {m}_n,k)}^{(p)}=X_{(r+p-1,n,\tilde {m}_n,k)}-X_{(r-1,n,\tilde {m}_n,k)}$ and ![]() $W_{(r,n,\tilde {m}_n,k)}^{(p)}=Y_{(r+p-1,n,\tilde {m}_n,k)}-Y_{(r-1,n,\tilde {m}_n,k)}$, for
$W_{(r,n,\tilde {m}_n,k)}^{(p)}=Y_{(r+p-1,n,\tilde {m}_n,k)}-Y_{(r-1,n,\tilde {m}_n,k)}$, for ![]() $2\leq r \leq n-p+1$ and
$2\leq r \leq n-p+1$ and ![]() $p\geq 1$, respectively.
$p\geq 1$, respectively.
For one-sample problem of ![]() $p$-spacings, some stochastic properties of order statistics and GOS have been studied by several authors such as Misra and van der Meulen [Reference Misra and van der Meulen21], Hu and Zhuang [Reference Hu and Zhuang13,Reference Hu and Zhuang14], Xie and Hu [Reference Xie and Hu25], and Alimohammadi et al. [Reference Alimohammadi, Esna-Ashari and Navarro4]. For two-sample problem of
$p$-spacings, some stochastic properties of order statistics and GOS have been studied by several authors such as Misra and van der Meulen [Reference Misra and van der Meulen21], Hu and Zhuang [Reference Hu and Zhuang13,Reference Hu and Zhuang14], Xie and Hu [Reference Xie and Hu25], and Alimohammadi et al. [Reference Alimohammadi, Esna-Ashari and Navarro4]. For two-sample problem of ![]() $p$-spacings, a study of stochastic comparisons was initiated by Kochar [Reference Kochar20]. He investigated the usual stochastic, hazard rate, and likelihood ratio orderings of order statistics for
$p$-spacings, a study of stochastic comparisons was initiated by Kochar [Reference Kochar20]. He investigated the usual stochastic, hazard rate, and likelihood ratio orderings of order statistics for ![]() $p=1$. Franco et al. [Reference Franco, Ruiz and Ruiz12] studied the usual stochastic, hazard rate, and dispersive orderings of GOS under the condition
$p=1$. Franco et al. [Reference Franco, Ruiz and Ruiz12] studied the usual stochastic, hazard rate, and dispersive orderings of GOS under the condition ![]() $m_1=m_2=\cdots =m_{n-1}$. Then, without this condition, Belzunce et al. [Reference Belzunce, Mercader and Ruiz7] gave the usual stochastic and likelihood ratio orderings of GOS for
$m_1=m_2=\cdots =m_{n-1}$. Then, without this condition, Belzunce et al. [Reference Belzunce, Mercader and Ruiz7] gave the usual stochastic and likelihood ratio orderings of GOS for ![]() $p=1$. Finally, in an interesting article, Hu and Zhuang [Reference Hu and Zhuang15] established the likelihood ratio ordering of GOS for any
$p=1$. Finally, in an interesting article, Hu and Zhuang [Reference Hu and Zhuang15] established the likelihood ratio ordering of GOS for any ![]() $p\geq 1$ and the hazard rate ordering of GOS for
$p\geq 1$ and the hazard rate ordering of GOS for ![]() $p=1$ under the condition
$p=1$ under the condition ![]() $m_1=m_2=\cdots =m_{n-1}$ and left the case
$m_1=m_2=\cdots =m_{n-1}$ and left the case ![]() $p\geq 2$ as an open problem. In particular, they proved
$p\geq 2$ as an open problem. In particular, they proved
provided that any one of the following conditions is satisfied:
i.
 $m_i\geq 0$
$m_i\geq 0$  $\forall i$,
$\forall i$,  $X\leq _{{\rm lr}} Y$, and
$X\leq _{{\rm lr}} Y$, and  $X$ or
$X$ or  $Y$ is DFR;
$Y$ is DFR;ii.
 $-1\leq m_i < 0$
$-1\leq m_i < 0$  $\forall i$,
$\forall i$,  $X\leq _{{\rm hr}} Y$,
$X\leq _{{\rm hr}} Y$,  $h_Y(x)/h_X(x)$ is increasing in
$h_Y(x)/h_X(x)$ is increasing in  $x$, and
$x$, and  $X$ or
$X$ or  $Y$ is DFR;
$Y$ is DFR;
and said that whether this ordering holds for ![]() $p\geq 2$ under the same assumptions as those of above. In this article, we first answer to this open problem in the affirmative without the condition
$p\geq 2$ under the same assumptions as those of above. In this article, we first answer to this open problem in the affirmative without the condition ![]() $m_1=m_2=\cdots =m_{n-1}$. Finally, the applications of this result are demonstrated for sequential systems, progressive Type-II censored order statistics with arbitrary censoring schemes and record values.
$m_1=m_2=\cdots =m_{n-1}$. Finally, the applications of this result are demonstrated for sequential systems, progressive Type-II censored order statistics with arbitrary censoring schemes and record values.
2. Preliminaries
There exist several representations for the marginal density functions of GOS (see, e.g., [Reference Cramer and Kamps10,Reference Kamps16]). Cramer et al. [Reference Cramer, Kamps and Rychlik11] obtained the expression
where ![]() $c_{r-1}=\prod _{i=1}^{r}\gamma _i$,
$c_{r-1}=\prod _{i=1}^{r}\gamma _i$, ![]() $r=1,\ldots,n$,
$r=1,\ldots,n$, ![]() $\gamma _n=k$, and
$\gamma _n=k$, and ![]() $\xi _{r}$ is a particular Meijer's
$\xi _{r}$ is a particular Meijer's ![]() $G$-function. For the joint pdf of
$G$-function. For the joint pdf of ![]() $X_{(r,n,\tilde {m}_n,k)}$ and
$X_{(r,n,\tilde {m}_n,k)}$ and ![]() $X_{(s,n,\tilde {m}_n,k)}$,
$X_{(s,n,\tilde {m}_n,k)}$, ![]() $1\leq r< s \leq n$, Tavangar and Asadi [Reference Tavangar and Asadi24] established the expression
$1\leq r< s \leq n$, Tavangar and Asadi [Reference Tavangar and Asadi24] established the expression
 \begin{align} & f_{X_{(r,n,\tilde{m}_n,k)},X_{(s,n,\tilde{m}_n,k)}}(x_1,x_2)=c_{s-1}[\bar F{(x_1)}]^{\gamma_r-\gamma_s-1}\xi_{r}(F(x_1))\nonumber\\ & \quad \times {[\bar F{(x_2)}]^{\gamma_s-1}}\psi_{s-r-1}\left(\frac{\bar F{(x_2)}}{\bar F{(x_1)}}\right)f(x_1)f(x_2),\quad x_1< x_2, \end{align}
\begin{align} & f_{X_{(r,n,\tilde{m}_n,k)},X_{(s,n,\tilde{m}_n,k)}}(x_1,x_2)=c_{s-1}[\bar F{(x_1)}]^{\gamma_r-\gamma_s-1}\xi_{r}(F(x_1))\nonumber\\ & \quad \times {[\bar F{(x_2)}]^{\gamma_s-1}}\psi_{s-r-1}\left(\frac{\bar F{(x_2)}}{\bar F{(x_1)}}\right)f(x_1)f(x_2),\quad x_1< x_2, \end{align}(zero elsewhere), where ![]() $\psi _{0}(t)= 1$,
$\psi _{0}(t)= 1$, ![]() $\psi _{1}(t)=\delta _{m_{r+1}}(1-t)$,
$\psi _{1}(t)=\delta _{m_{r+1}}(1-t)$,
 $$\psi_{\alpha}(t)=\int_t^1\int_{u_{\alpha-1}}^1\ldots \int_{u_2}^1 \delta_{m_{r+1}}(1-u_{1})\prod_{i=1}^{\alpha-1}{u_i}^{m_{r+i+1}}\,du_1\ldots d{u_{\alpha-2}}\,d{u_{\alpha-1}}, \quad 0\leq t \leq 1,\ \alpha =2,3,\ldots,$$
$$\psi_{\alpha}(t)=\int_t^1\int_{u_{\alpha-1}}^1\ldots \int_{u_2}^1 \delta_{m_{r+1}}(1-u_{1})\prod_{i=1}^{\alpha-1}{u_i}^{m_{r+i+1}}\,du_1\ldots d{u_{\alpha-2}}\,d{u_{\alpha-1}}, \quad 0\leq t \leq 1,\ \alpha =2,3,\ldots,$$and
 $$\delta_{m}(t)=\begin{cases} \dfrac{1}{m+1}(1-{(1-t)^{m+1}}), & m\neq{-}1\\ - {\ln(1-t)}, & m={-}1 \end{cases} ,\quad t\in(0,1).$$
$$\delta_{m}(t)=\begin{cases} \dfrac{1}{m+1}(1-{(1-t)^{m+1}}), & m\neq{-}1\\ - {\ln(1-t)}, & m={-}1 \end{cases} ,\quad t\in(0,1).$$According to Lemmas 2.1 and 3.1 of Alimohammadi and Alamatsaz [Reference Alimohammadi and Alamatsaz1], we have the following recursive formulas:
and
Some convexity properties of the function ![]() $\xi _{r}$ and GOS have been studied by Cramer et al. [Reference Cramer, Kamps and Rychlik11] and Alimohammadi et al. [Reference Alimohammadi, Alamatsaz and Cramer2,Reference Alimohammadi, Alamatsaz and Cramer3].
$\xi _{r}$ and GOS have been studied by Cramer et al. [Reference Cramer, Kamps and Rychlik11] and Alimohammadi et al. [Reference Alimohammadi, Alamatsaz and Cramer2,Reference Alimohammadi, Alamatsaz and Cramer3].
Now, substituting ![]() $r$ with
$r$ with ![]() $r-1$ and
$r-1$ and ![]() $s$ with
$s$ with ![]() $r+p-1$ in (2) and after some calculations, for
$r+p-1$ in (2) and after some calculations, for ![]() $2\leq r \leq n-p+1$, we obtain
$2\leq r \leq n-p+1$, we obtain
 \begin{align} f_{V_{(r,n,\tilde{m}_n,k)}^{(p)}}(x)& =c_{r+p-2}\int_{0}^{+\infty} {[\bar F{(x+u)}]^{\gamma_{r+p-1}-1}}\psi_{p-1}\left(\frac{\bar F{(x+u)}}{\bar F{(u)}}\right)f(x+u)\nonumber\\ & \quad \times {[\bar F{(u)}]^{\gamma_{r-1}-\gamma_{r+p-1}-1}}\xi_{r-1}(F(u))f(u)\,du,\quad x\geq 0, \end{align}
\begin{align} f_{V_{(r,n,\tilde{m}_n,k)}^{(p)}}(x)& =c_{r+p-2}\int_{0}^{+\infty} {[\bar F{(x+u)}]^{\gamma_{r+p-1}-1}}\psi_{p-1}\left(\frac{\bar F{(x+u)}}{\bar F{(u)}}\right)f(x+u)\nonumber\\ & \quad \times {[\bar F{(u)}]^{\gamma_{r-1}-\gamma_{r+p-1}-1}}\xi_{r-1}(F(u))f(u)\,du,\quad x\geq 0, \end{align}where, according to (4) for ![]() $r-1$,
$r-1$,
 \begin{equation} \psi_{p-1}\left(\frac{\bar F{(x+u)}}{\bar F{(u)}}\right)=\int_{{\bar F{(x+u)}}/{\bar F{(u)}}}^1 \psi_{p-2}(u)u^{m_{r+p-2}}\,du,\quad 2\leq p \leq n-r+1, \end{equation}
\begin{equation} \psi_{p-1}\left(\frac{\bar F{(x+u)}}{\bar F{(u)}}\right)=\int_{{\bar F{(x+u)}}/{\bar F{(u)}}}^1 \psi_{p-2}(u)u^{m_{r+p-2}}\,du,\quad 2\leq p \leq n-r+1, \end{equation}with ![]() $\psi _{0}(t)= 1$ and, for
$\psi _{0}(t)= 1$ and, for ![]() $r=1$, we have
$r=1$, we have ![]() $f_{V_{(1,n,\tilde {m}_n,k)}^{(p)}}(x)=f_{X_{(r+p-1,n,\tilde {m}_n,k)}}(x)$. Also, for
$f_{V_{(1,n,\tilde {m}_n,k)}^{(p)}}(x)=f_{X_{(r+p-1,n,\tilde {m}_n,k)}}(x)$. Also, for ![]() $2\leq r \leq n-p+1$, from (5) we arrive at
$2\leq r \leq n-p+1$, from (5) we arrive at
 \begin{align} \bar{F}_{V_{(r,n,\tilde{m}_n,k)}^{(p)}}(x)& =c_{r+p-2}\int_{0}^{+\infty} {[\bar F{(x+u)}]^{\gamma_{r+p-1}}}\left[\int_{0}^{1} z^{\gamma_{r+p-1}-1} \psi_{p-1}\left(z\cdot \left(\frac{\bar F{(x+u)}}{\bar F{(u)}}\right)\right)dz\right]\nonumber\\ & \quad \times {[\bar F{(u)}]^{\gamma_{r-1}-\gamma_{r+p-1}-1}}\xi_{r-1}(F(u))f(u)\,du,\quad x\geq 0. \end{align}
\begin{align} \bar{F}_{V_{(r,n,\tilde{m}_n,k)}^{(p)}}(x)& =c_{r+p-2}\int_{0}^{+\infty} {[\bar F{(x+u)}]^{\gamma_{r+p-1}}}\left[\int_{0}^{1} z^{\gamma_{r+p-1}-1} \psi_{p-1}\left(z\cdot \left(\frac{\bar F{(x+u)}}{\bar F{(u)}}\right)\right)dz\right]\nonumber\\ & \quad \times {[\bar F{(u)}]^{\gamma_{r-1}-\gamma_{r+p-1}-1}}\xi_{r-1}(F(u))f(u)\,du,\quad x\geq 0. \end{align}Now, we recall the following definition about the very useful concept of total positivity (cf. [Reference Karlin19]).
Definition 2.1 Let ![]() $\mathcal {X}$ and
$\mathcal {X}$ and ![]() $\mathcal {Y}$ be subsets of the real line
$\mathcal {Y}$ be subsets of the real line ![]() $\mathbb {R}$. A function
$\mathbb {R}$. A function ![]() $\lambda : \mathcal {X}\times \mathcal {Y} \rightarrow \mathbb {R}$ is said to be totally positive of order 2
$\lambda : \mathcal {X}\times \mathcal {Y} \rightarrow \mathbb {R}$ is said to be totally positive of order 2 ![]() $(TP_2)$ (reverse regular of order 2
$(TP_2)$ (reverse regular of order 2 ![]() $(RR_2)$) if
$(RR_2)$) if
for all ![]() $x_1\leq x_2$ in
$x_1\leq x_2$ in ![]() $\mathcal {X}$ and all
$\mathcal {X}$ and all ![]() $y_1\leq y_2$ in
$y_1\leq y_2$ in ![]() $\mathcal {Y}$.
$\mathcal {Y}$.
Note that the ![]() $TP_2$
$TP_2$ ![]() $(RR_2)$ property is equivalent to
$(RR_2)$ property is equivalent to ![]() $\lambda (x_2,y)/\lambda (x_1,y)$ is increasing (decreasing) in
$\lambda (x_2,y)/\lambda (x_1,y)$ is increasing (decreasing) in ![]() $y$ when
$y$ when ![]() $x_1 \leq x_2$, whenever this ratio exists. Also, note that the product of two
$x_1 \leq x_2$, whenever this ratio exists. Also, note that the product of two ![]() $TP_2$ (
$TP_2$ (![]() $RR_2$) functions is
$RR_2$) functions is ![]() $TP_2$ (
$TP_2$ (![]() $RR_2$). Moreover, if
$RR_2$). Moreover, if ![]() $\lambda (x,y)$ is
$\lambda (x,y)$ is ![]() $TP_2$ (
$TP_2$ (![]() $RR_2$) in
$RR_2$) in ![]() $(x,y)$, then
$(x,y)$, then ![]() $\lambda _1(x)\lambda (x,y)\lambda _2(y)$ is
$\lambda _1(x)\lambda (x,y)\lambda _2(y)$ is ![]() $TP_2$ (
$TP_2$ (![]() $RR_2$) in
$RR_2$) in ![]() $(x,y)$ when
$(x,y)$ when ![]() $\lambda _1$ and
$\lambda _1$ and ![]() $\lambda _2$ are two nonnegative functions (cf. [Reference Karlin19]).
$\lambda _2$ are two nonnegative functions (cf. [Reference Karlin19]).
The lemma below, due to Misra and van der Meulen [Reference Misra and van der Meulen21], is often used in establishing the monotonicity of a fraction in which the numerator and denominator are integrals or summations.
Lemma 2.2 Assume that ![]() $\Theta$ is a subset of the real line
$\Theta$ is a subset of the real line ![]() $\mathbb {R}$, and let U be a nonnegative random variable having a cdf belonging to the family
$\mathbb {R}$, and let U be a nonnegative random variable having a cdf belonging to the family ![]() $\mathcal {P}=\{\Xi (\cdot \,|\,\theta ),\theta \in \Theta \}$ which satisfies that, for
$\mathcal {P}=\{\Xi (\cdot \,|\,\theta ),\theta \in \Theta \}$ which satisfies that, for ![]() $\theta _1, \theta _2 \in \Theta$,
$\theta _1, \theta _2 \in \Theta$,
Let ![]() $\phi (u,\theta )$ be a real-valued function defined on
$\phi (u,\theta )$ be a real-valued function defined on ![]() $\mathbb {R}\times \Theta$, which is measurable in u for each
$\mathbb {R}\times \Theta$, which is measurable in u for each ![]() $\theta$ such that
$\theta$ such that ![]() $E_\theta [\phi (U,\theta )]$ exists. Then,
$E_\theta [\phi (U,\theta )]$ exists. Then, ![]() $E_\theta [\phi (U,\theta )]$ is
$E_\theta [\phi (U,\theta )]$ is
(i) increasing in
 $\theta$, if
$\theta$, if  $\phi (u,\theta )$ is increasing in
$\phi (u,\theta )$ is increasing in  $\theta$ and increasing (decreasing) in
$\theta$ and increasing (decreasing) in  $u$;
$u$;(ii) decreasing in
 $\theta$, if
$\theta$, if  $\phi (u,\theta )$ is decreasing in
$\phi (u,\theta )$ is decreasing in  $\theta$ and decreasing (increasing) in
$\theta$ and decreasing (increasing) in  $u$.
$u$.
3. Main result
Now, we are ready to resolve the mentioned problem.
Theorem 3.1 Let ![]() ${X_{(r,n,\tilde {m}_n,k)}}$ and
${X_{(r,n,\tilde {m}_n,k)}}$ and ![]() ${Y_{(r,n,\tilde {m}_n,k)}}$,
${Y_{(r,n,\tilde {m}_n,k)}}$, ![]() $r=1,\ldots,n$, be GOSs based on absolutely continuous cdfs
$r=1,\ldots,n$, be GOSs based on absolutely continuous cdfs ![]() $F$ and
$F$ and ![]() $G$, respectively. Then, for all
$G$, respectively. Then, for all ![]() $2\leq r \leq n-p+1$ and all
$2\leq r \leq n-p+1$ and all ![]() $p\geq 1$,
$p\geq 1$,
provided that any one of the following conditions is satisfied:
(i)
 $m_i\geq 0$
$m_i\geq 0$  $\forall i$,
$\forall i$,  $X\leq _{{\rm lr}} Y$, and
$X\leq _{{\rm lr}} Y$, and  $X$ or
$X$ or  $Y$ is DFR;
$Y$ is DFR;(ii)
 $-1\leq m_i < 0$
$-1\leq m_i < 0$  $\forall i$,
$\forall i$,  $X\leq _{{\rm hr}} Y$,
$X\leq _{{\rm hr}} Y$,  $h_Y(x)/h_X(x)$ is increasing in
$h_Y(x)/h_X(x)$ is increasing in  $x$, and
$x$, and  $X$ or
$X$ or  $Y$ is DFR.
$Y$ is DFR.
Proof. First note that by changing variable ![]() $z=\bar {F}(t)/\bar {F}(x+u)$ in (7), we have
$z=\bar {F}(t)/\bar {F}(x+u)$ in (7), we have
 \begin{align} \bar{F}_{V_{(r,n,\tilde{m}_n,k)}^{(p)}}(x)& =c_{r+p-2}\int_{0}^{+\infty} \left[\int_{x+u}^{+\infty} [\bar F{(t)}]^{\gamma_{r+p-1}-1} \psi_{p-1}\left(\frac{\bar F{(t)}}{\bar F{(u)}}\right)f(t)\,dt\right]\nonumber\\ & \quad \times {[\bar F{(u)}]^{\gamma_{r-1}-\gamma_{r+p-1}-1}}\xi_{r-1}(F(u))f(u)\,du. \end{align}
\begin{align} \bar{F}_{V_{(r,n,\tilde{m}_n,k)}^{(p)}}(x)& =c_{r+p-2}\int_{0}^{+\infty} \left[\int_{x+u}^{+\infty} [\bar F{(t)}]^{\gamma_{r+p-1}-1} \psi_{p-1}\left(\frac{\bar F{(t)}}{\bar F{(u)}}\right)f(t)\,dt\right]\nonumber\\ & \quad \times {[\bar F{(u)}]^{\gamma_{r-1}-\gamma_{r+p-1}-1}}\xi_{r-1}(F(u))f(u)\,du. \end{align}We give the proof for the case ![]() $p \geq 2$ while the case
$p \geq 2$ while the case ![]() $p=1$ can be proved in an analogous and simpler manner (because some terms will be vanished for
$p=1$ can be proved in an analogous and simpler manner (because some terms will be vanished for ![]() $p=1$). Assume that
$p=1$). Assume that ![]() $X$ is DFR. Let's define
$X$ is DFR. Let's define
 $$\phi_2(t,x,u)= \left[\frac{\bar G{(u)}}{\bar F{(u)}}\right]^{\gamma_{r+p-1}-1} \frac{\psi_{p-1}\left(\frac{\bar G{(t)}}{\bar G{(u)}}\right)}{\psi_{p-1}\left(\frac{\bar F{(t)}}{\bar F{(u)}}\right)}\frac{g(u)}{f(u)}.$$
$$\phi_2(t,x,u)= \left[\frac{\bar G{(u)}}{\bar F{(u)}}\right]^{\gamma_{r+p-1}-1} \frac{\psi_{p-1}\left(\frac{\bar G{(t)}}{\bar G{(u)}}\right)}{\psi_{p-1}\left(\frac{\bar F{(t)}}{\bar F{(u)}}\right)}\frac{g(u)}{f(u)}.$$From (9), we have
 $$\frac{\bar{F}_{W_{(r,n,\tilde{m}_n,k)}^{(p)}}(x)}{\bar{F}_{V_{(r,n,\tilde{m}_n,k)}^{(p)}}(x)} =E[\phi_1(U,x)],$$
$$\frac{\bar{F}_{W_{(r,n,\tilde{m}_n,k)}^{(p)}}(x)}{\bar{F}_{V_{(r,n,\tilde{m}_n,k)}^{(p)}}(x)} =E[\phi_1(U,x)],$$where
 \begin{align} \phi_1(u,x)& = E[\phi_2(T,x,u)]\left[\frac{\bar G{(u)}}{\bar F{(u)}}\right]^{\gamma_{r-1}-\gamma_{r+p-1}-1} \frac{\xi_{r-1}(G(u))}{\xi_{r-1}(F(u))}\frac{g(u)}{f(u)} \nonumber\\ & =\left(\left[\frac{\bar G{(u)}}{\bar F{(u)}}\right]^{m_{r-1}}\frac{g(u)}{f(u)}\right) \left(\frac{\xi_{r-1}(G(u))}{\xi_{r-1}(F(u))}\right) \left(E[\phi_2(T,x,u)]\cdot \left[\frac{\bar G{(u)}}{\bar F{(u)}}\right]^{\sum_{j=r}^{r+p-2}(m_{j}+1)}\right) \end{align}
\begin{align} \phi_1(u,x)& = E[\phi_2(T,x,u)]\left[\frac{\bar G{(u)}}{\bar F{(u)}}\right]^{\gamma_{r-1}-\gamma_{r+p-1}-1} \frac{\xi_{r-1}(G(u))}{\xi_{r-1}(F(u))}\frac{g(u)}{f(u)} \nonumber\\ & =\left(\left[\frac{\bar G{(u)}}{\bar F{(u)}}\right]^{m_{r-1}}\frac{g(u)}{f(u)}\right) \left(\frac{\xi_{r-1}(G(u))}{\xi_{r-1}(F(u))}\right) \left(E[\phi_2(T,x,u)]\cdot \left[\frac{\bar G{(u)}}{\bar F{(u)}}\right]^{\sum_{j=r}^{r+p-2}(m_{j}+1)}\right) \end{align} \begin{align} & =\left(\left[\frac{\bar G{(u)}}{\bar F{(u)}}\right]^{m_{r-1}+1} \frac{h_Y(u)}{h_X(u)}\right) \left(\frac{\xi_{r-1}(G(u))}{\xi_{r-1}(F(u))}\right) \left(E[\phi_2(T,x,u)]\cdot \left[\frac{\bar G{(u)}}{\bar F{(u)}}\right]^{\sum_{j=r}^{r+p-2}(m_{j}+1)}\right), \end{align}
\begin{align} & =\left(\left[\frac{\bar G{(u)}}{\bar F{(u)}}\right]^{m_{r-1}+1} \frac{h_Y(u)}{h_X(u)}\right) \left(\frac{\xi_{r-1}(G(u))}{\xi_{r-1}(F(u))}\right) \left(E[\phi_2(T,x,u)]\cdot \left[\frac{\bar G{(u)}}{\bar F{(u)}}\right]^{\sum_{j=r}^{r+p-2}(m_{j}+1)}\right), \end{align}![]() $U$ and
$U$ and ![]() $T$ are nonnegative random variables having the respective cdfs belonging to the families
$T$ are nonnegative random variables having the respective cdfs belonging to the families ![]() $\mathcal {P}_1=\{\mathcal {U}(\cdot \,|\,x),x \in \mathbb {R_+}\}$ and
$\mathcal {P}_1=\{\mathcal {U}(\cdot \,|\,x),x \in \mathbb {R_+}\}$ and ![]() $\mathcal {P}_2=\{\mathcal {T}(\cdot \,|\,x,u),x,u \in \mathbb {R_+}\}$ with the respective pdfs
$\mathcal {P}_2=\{\mathcal {T}(\cdot \,|\,x,u),x,u \in \mathbb {R_+}\}$ with the respective pdfs
 \begin{align*} l_1(u\,|\,x)& =c_1(x)I_{\{0 \leq u \}}\left[\int_{x+u}^{+\infty} [\bar F{(t)}]^{\gamma_{r+p-1}-1} \psi_{p-1}\left(\frac{\bar F{(t)}}{\bar F{(u)}}\right)f(t)\,dt\right]\nonumber\\ & \quad \times {[\bar F{(u)}]^{\gamma_{r-1}-\gamma_{r+p-1}-1}}\xi_{r-1}(F(u))f(u) \end{align*}
\begin{align*} l_1(u\,|\,x)& =c_1(x)I_{\{0 \leq u \}}\left[\int_{x+u}^{+\infty} [\bar F{(t)}]^{\gamma_{r+p-1}-1} \psi_{p-1}\left(\frac{\bar F{(t)}}{\bar F{(u)}}\right)f(t)\,dt\right]\nonumber\\ & \quad \times {[\bar F{(u)}]^{\gamma_{r-1}-\gamma_{r+p-1}-1}}\xi_{r-1}(F(u))f(u) \end{align*}and
in which
 $$c_1(x)=\left[\int_{0}^{+\infty} \left[\int_{x+u}^{+\infty} [\bar F{(t)}]^{\gamma_{r+p-1}-1} \psi_{p-1}\left(\frac{\bar F{(t)}}{\bar F{(u)}}\right)f(t)\,dt\right]{[\bar F{(u)}]^{\gamma_{r-1}-\gamma_{r+p-1}-1}}\xi_{r-1}(F(u))f(u)\,du\right]^{{-}1}$$
$$c_1(x)=\left[\int_{0}^{+\infty} \left[\int_{x+u}^{+\infty} [\bar F{(t)}]^{\gamma_{r+p-1}-1} \psi_{p-1}\left(\frac{\bar F{(t)}}{\bar F{(u)}}\right)f(t)\,dt\right]{[\bar F{(u)}]^{\gamma_{r-1}-\gamma_{r+p-1}-1}}\xi_{r-1}(F(u))f(u)\,du\right]^{{-}1}$$and
 $$c_2(x,u)=\left[\int_{x+u}^{+\infty} [\bar F{(t)}]^{\gamma_{r+p-1}-1} \psi_{p-1}\left(\frac{\bar F{(t)}}{\bar F{(u)}}\right)f(t)\,dt\right]^{{-}1}$$
$$c_2(x,u)=\left[\int_{x+u}^{+\infty} [\bar F{(t)}]^{\gamma_{r+p-1}-1} \psi_{p-1}\left(\frac{\bar F{(t)}}{\bar F{(u)}}\right)f(t)\,dt\right]^{{-}1}$$are the normalizing constants and ![]() $I_A$ is the indicator function.
$I_A$ is the indicator function.
Now, we show that ![]() $\phi _1(u,x)$ is increasing in
$\phi _1(u,x)$ is increasing in ![]() $u$ and
$u$ and ![]() $x$ in either (10) and (11).
$x$ in either (10) and (11).
The first parentheses is increasing in ![]() $u$: It is obvious according to the conditions (i) and (ii) of theorem.
$u$: It is obvious according to the conditions (i) and (ii) of theorem.
The second parentheses is increasing in ![]() $u$: We prove it by induction on
$u$: We prove it by induction on ![]() $r$. It is clearly valid for
$r$. It is clearly valid for ![]() $r=2$. For
$r=2$. For ![]() $r\geq 3$, let us assume that
$r\geq 3$, let us assume that ![]() $\xi _{j-1}(G(u))/\xi _{j-1}(F(u))$ is increasing in
$\xi _{j-1}(G(u))/\xi _{j-1}(F(u))$ is increasing in ![]() $u$ for
$u$ for ![]() $j=3,\ldots,r-1$. According to (3), we then have
$j=3,\ldots,r-1$. According to (3), we then have
 \begin{align} & \frac{d}{du}\left(\frac{\xi_{r-1}(G(u))}{\xi_{r-1}(F(u))}\right)\geq 0\nonumber\\ \iff & g(u) \xi_{r-2}(G(u))(\bar G(u))^{m_{r-2}}\cdot \xi_{r-1}(F(u)) \geq f(u) \xi_{r-2}(F(u))(\bar F(u))^{m_{r-2}}\cdot \xi_{r-1}(G(u))\nonumber\\ \iff & \frac{g(u)}{f(u)} \frac{ {\xi}_{r-2}(G(u))}{ {\xi}_{r-2}(F(u))}\left(\frac{\bar G(u)}{\bar F(u)}\right)^{m_{r-2}} \geq \frac{\xi_{r-1}(G(u))}{\xi_{r-1}(F(u))}. \end{align}
\begin{align} & \frac{d}{du}\left(\frac{\xi_{r-1}(G(u))}{\xi_{r-1}(F(u))}\right)\geq 0\nonumber\\ \iff & g(u) \xi_{r-2}(G(u))(\bar G(u))^{m_{r-2}}\cdot \xi_{r-1}(F(u)) \geq f(u) \xi_{r-2}(F(u))(\bar F(u))^{m_{r-2}}\cdot \xi_{r-1}(G(u))\nonumber\\ \iff & \frac{g(u)}{f(u)} \frac{ {\xi}_{r-2}(G(u))}{ {\xi}_{r-2}(F(u))}\left(\frac{\bar G(u)}{\bar F(u)}\right)^{m_{r-2}} \geq \frac{\xi_{r-1}(G(u))}{\xi_{r-1}(F(u))}. \end{align}Let us define
Then, we have the right-hand side of (12) to be
 \begin{align*} \frac{\xi_{r-1}(G(u))}{\xi_{r-1}(F(u))}& =\frac{\int_{F^{{-}1}(0)}^{1} {\xi}_{r-2}(G(z))(\bar G(z))^{m_{r-2}}g(z)\,dz-\int_{u}^{1} {\xi}_{r-2}(G(z))(\bar G(z))^{m_{r-2}}g(z)\,dz}{\int_{F^{{-}1}(0)}^{1} {\xi}_{r-2}(F(z))(\bar F(z))^{m_{r-2}}f(z)\,dz-\int_{u}^{1} {\xi}_{r-2}(F(z))(\bar F(z))^{m_{r-2}}f(z)\,dz}\\ & =\frac{\nu_1(u)-\nu_1(F^{{-}1}(0))}{\nu_2(u)-\nu_2(F^{{-}1}(0))}. \end{align*}
\begin{align*} \frac{\xi_{r-1}(G(u))}{\xi_{r-1}(F(u))}& =\frac{\int_{F^{{-}1}(0)}^{1} {\xi}_{r-2}(G(z))(\bar G(z))^{m_{r-2}}g(z)\,dz-\int_{u}^{1} {\xi}_{r-2}(G(z))(\bar G(z))^{m_{r-2}}g(z)\,dz}{\int_{F^{{-}1}(0)}^{1} {\xi}_{r-2}(F(z))(\bar F(z))^{m_{r-2}}f(z)\,dz-\int_{u}^{1} {\xi}_{r-2}(F(z))(\bar F(z))^{m_{r-2}}f(z)\,dz}\\ & =\frac{\nu_1(u)-\nu_1(F^{{-}1}(0))}{\nu_2(u)-\nu_2(F^{{-}1}(0))}. \end{align*}Because of the integral form of ![]() $\nu _1(x)$ and
$\nu _1(x)$ and ![]() $\nu _2(x)$, they are continuous on
$\nu _2(x)$, they are continuous on ![]() $x \in [F^{-1}(0),u]$ and differentiable on
$x \in [F^{-1}(0),u]$ and differentiable on ![]() $x \in (F^{-1}(0),u)$. Also, we have
$x \in (F^{-1}(0),u)$. Also, we have ![]() $\nu _2'(x)\neq 0$ for all
$\nu _2'(x)\neq 0$ for all ![]() $x \in (F^{-1}(0),u)$. Because we consider the pdfs on their support and if
$x \in (F^{-1}(0),u)$. Because we consider the pdfs on their support and if ![]() $X$ is DFR, then its support is
$X$ is DFR, then its support is ![]() $(F^{-1}(0),\infty )$ with finite
$(F^{-1}(0),\infty )$ with finite ![]() $F^{-1}(0)$ (cf. [Reference Block, Savits and Singh8]) and, thus, we have
$F^{-1}(0)$ (cf. [Reference Block, Savits and Singh8]) and, thus, we have ![]() $(F^{-1}(0),u) \subset (F^{-1}(0),\infty )$. So, according to Cauchy's mean value theorem, there exists some
$(F^{-1}(0),u) \subset (F^{-1}(0),\infty )$. So, according to Cauchy's mean value theorem, there exists some ![]() $\theta \in (F^{-1}(0),u)$ such that
$\theta \in (F^{-1}(0),u)$ such that
Also, we have
 $$\frac{\nu_1'(\theta)}{\nu_2'(\theta)}=\frac{g(\theta)}{f(\theta)} \frac{ {\xi}_{r-2}(G(\theta))}{ {\xi}_{r-2}(F(\theta))}\left(\frac{\bar G(\theta)}{\bar F(\theta)}\right)^{m_{r-2}}=\frac{h_Y(\theta)}{h_X(\theta)} \frac{ {\xi}_{r-2}(G(\theta))}{ {\xi}_{r-2}(F(\theta))}\left(\frac{\bar G(\theta)}{\bar F(\theta)}\right)^{m_{r-2}+1}.$$
$$\frac{\nu_1'(\theta)}{\nu_2'(\theta)}=\frac{g(\theta)}{f(\theta)} \frac{ {\xi}_{r-2}(G(\theta))}{ {\xi}_{r-2}(F(\theta))}\left(\frac{\bar G(\theta)}{\bar F(\theta)}\right)^{m_{r-2}}=\frac{h_Y(\theta)}{h_X(\theta)} \frac{ {\xi}_{r-2}(G(\theta))}{ {\xi}_{r-2}(F(\theta))}\left(\frac{\bar G(\theta)}{\bar F(\theta)}\right)^{m_{r-2}+1}.$$Now, as ![]() $\theta \leq u$ and according to the conditions (i) and (ii) of theorem, respectively
$\theta \leq u$ and according to the conditions (i) and (ii) of theorem, respectively ![]() $({g(u)}/{f(u)}) (c{\bar G(u)}/{\bar F(u)})^{m_{r-2}}$ and
$({g(u)}/{f(u)}) (c{\bar G(u)}/{\bar F(u)})^{m_{r-2}}$ and ![]() $({h_Y(u)}/{h_X(u)}) ({\bar G(u)}/{\bar F(u)})^{m_{r-2}+1}$ is increasing in
$({h_Y(u)}/{h_X(u)}) ({\bar G(u)}/{\bar F(u)})^{m_{r-2}+1}$ is increasing in ![]() $u$, the right-hand side of (12) becomes less than or equal to the left-hand side by induction.
$u$, the right-hand side of (12) becomes less than or equal to the left-hand side by induction.
The third parentheses is increasing in ![]() $u$: We first prove that
$u$: We first prove that
 \begin{equation} \frac{\psi_{p-1}\left(\frac{\bar G{(t)}}{\bar G{(u)}}\right)}{\psi_{p-1}\left(\frac{\bar F{(t)}}{\bar F{(u)}}\right)}\cdot \left[\frac{\bar G{(u)}}{\bar F{(u)}}\right]^{\sum_{j=r}^{r+p-2}(m_{j}+1)} \end{equation}
\begin{equation} \frac{\psi_{p-1}\left(\frac{\bar G{(t)}}{\bar G{(u)}}\right)}{\psi_{p-1}\left(\frac{\bar F{(t)}}{\bar F{(u)}}\right)}\cdot \left[\frac{\bar G{(u)}}{\bar F{(u)}}\right]^{\sum_{j=r}^{r+p-2}(m_{j}+1)} \end{equation}is increasing in ![]() $u$ by induction on
$u$ by induction on ![]() $p$. For
$p$. For ![]() $p=2$, from (6) we have
$p=2$, from (6) we have
 $$\frac{\psi_{1}\left(\frac{\bar G{(t)}}{\bar G{(u)}}\right)}{\psi_{1}\left(\frac{\bar F{(t)}}{\bar F{(u)}}\right)}\cdot \left[\frac{\bar G{(u)}}{\bar F{(u)}}\right]^{m_r+1} = \frac{\int_{u}^{t} \! (\bar G(z))^{m_{r}}g(z)\,dz}{\int_{u}^{t} (\bar F(z))^{m_{r}}f(z)\,dz} =E[\phi_3(Z,t,u)],$$
$$\frac{\psi_{1}\left(\frac{\bar G{(t)}}{\bar G{(u)}}\right)}{\psi_{1}\left(\frac{\bar F{(t)}}{\bar F{(u)}}\right)}\cdot \left[\frac{\bar G{(u)}}{\bar F{(u)}}\right]^{m_r+1} = \frac{\int_{u}^{t} \! (\bar G(z))^{m_{r}}g(z)\,dz}{\int_{u}^{t} (\bar F(z))^{m_{r}}f(z)\,dz} =E[\phi_3(Z,t,u)],$$where
 \begin{align*} \phi_3(z,t,u)& =\left[\frac{\bar G{(z)}}{\bar F{(z)}}\right]^{m_{r}} \frac{g(z)}{f(z)}\\ & =\left[\frac{\bar G{(z)}}{\bar F{(z)}}\right]^{m_{r}+1} \frac{h_Y(z)}{h_X(z)}, \end{align*}
\begin{align*} \phi_3(z,t,u)& =\left[\frac{\bar G{(z)}}{\bar F{(z)}}\right]^{m_{r}} \frac{g(z)}{f(z)}\\ & =\left[\frac{\bar G{(z)}}{\bar F{(z)}}\right]^{m_{r}+1} \frac{h_Y(z)}{h_X(z)}, \end{align*}and ![]() $Z$ is a nonnegative random variable having the cdf belonging to the family
$Z$ is a nonnegative random variable having the cdf belonging to the family ![]() $\mathcal {P}_3=\{\mathcal {Z}(\cdot \,|\,t,u),t,u \in \mathbb {R_+}\}$ with the pdf
$\mathcal {P}_3=\{\mathcal {Z}(\cdot \,|\,t,u),t,u \in \mathbb {R_+}\}$ with the pdf
in which ![]() $c_3(t,u)$ is the normalizing constant. According to the conditions (i) and (ii) of theorem,
$c_3(t,u)$ is the normalizing constant. According to the conditions (i) and (ii) of theorem, ![]() $\phi _3(z,t,u)$ is increasing in
$\phi _3(z,t,u)$ is increasing in ![]() $z$. Also, it is constant with respect to
$z$. Also, it is constant with respect to ![]() $u$. Since,
$u$. Since, ![]() $I_{\{u \leq z \leq t\}}$ is
$I_{\{u \leq z \leq t\}}$ is ![]() $TP_2$ in
$TP_2$ in ![]() $(z,u)$, we have
$(z,u)$, we have ![]() $\mathcal {Z}(\cdot \,|\,t, u_1) \leq _{{\rm lr}} \mathcal {Z}(\cdot \,|\,t, u_2)$ for
$\mathcal {Z}(\cdot \,|\,t, u_1) \leq _{{\rm lr}} \mathcal {Z}(\cdot \,|\,t, u_2)$ for ![]() $u_1 \leq u_2$. Now, part (i) of Lemma 2.2 implies that
$u_1 \leq u_2$. Now, part (i) of Lemma 2.2 implies that ![]() $E[\phi _3(Z,t,u)]$ is increasing in
$E[\phi _3(Z,t,u)]$ is increasing in ![]() $u$. By the same manner and according to
$u$. By the same manner and according to
 \begin{align*} & \frac{\psi_{p-1}\left(\frac{\bar G{(t)}}{\bar G{(u)}}\right)}{\psi_{p-1}\left(\frac{\bar F{(t)}}{\bar F{(u)}}\right)}\cdot \left[\frac{\bar G{(u)}}{\bar F{(u)}}\right]^{\sum_{j=r}^{r+p-2}(m_{j}+1)}\nonumber\\ & \quad =\frac{\int_{u}^{t} \psi_{p-2}\left(\frac{\bar G{(z)}}{\bar G{(u)}}\right)(\bar G(u))^{\sum_{j=r}^{r+p-3}(m_{j}+1)}(\bar G(z))^{m_{r+p-2}}g(z)\,dz}{\int_{u}^{t} \psi_{p-2}\left(\frac{\bar F{(z)}}{\bar F{(u)}}\right)(\bar F(u))^{\sum_{j=r}^{r+p-3}(m_{j}+1)}(\bar F(z))^{m_{r+p-2}}f(z)\,dz}, \end{align*}
\begin{align*} & \frac{\psi_{p-1}\left(\frac{\bar G{(t)}}{\bar G{(u)}}\right)}{\psi_{p-1}\left(\frac{\bar F{(t)}}{\bar F{(u)}}\right)}\cdot \left[\frac{\bar G{(u)}}{\bar F{(u)}}\right]^{\sum_{j=r}^{r+p-2}(m_{j}+1)}\nonumber\\ & \quad =\frac{\int_{u}^{t} \psi_{p-2}\left(\frac{\bar G{(z)}}{\bar G{(u)}}\right)(\bar G(u))^{\sum_{j=r}^{r+p-3}(m_{j}+1)}(\bar G(z))^{m_{r+p-2}}g(z)\,dz}{\int_{u}^{t} \psi_{p-2}\left(\frac{\bar F{(z)}}{\bar F{(u)}}\right)(\bar F(u))^{\sum_{j=r}^{r+p-3}(m_{j}+1)}(\bar F(z))^{m_{r+p-2}}f(z)\,dz}, \end{align*}the term in (13) is increasing in ![]() $u$ by induction.
$u$ by induction.
Then, since ![]() $X$ is DFR and
$X$ is DFR and ![]() $I_{\{x+u \leq t \}}$ is
$I_{\{x+u \leq t \}}$ is ![]() $TP_2$ in
$TP_2$ in ![]() $(t,u)$, one can similarly see that
$(t,u)$, one can similarly see that ![]() $\mathcal {T}(\cdot \,|\,x,u_1) \leq _{{\rm lr}} \mathcal {T}(\cdot \,|\,x,u_2)$ for
$\mathcal {T}(\cdot \,|\,x,u_1) \leq _{{\rm lr}} \mathcal {T}(\cdot \,|\,x,u_2)$ for ![]() $u_1 \leq u_2$. Thus, part (i) of Lemma 2.2 implies that the third parentheses is increasing in
$u_1 \leq u_2$. Thus, part (i) of Lemma 2.2 implies that the third parentheses is increasing in ![]() $u$.
$u$.
The third parentheses is increasing in ![]() $x$: Similar to the previous step, we can show that
$x$: Similar to the previous step, we can show that ![]() ${\psi _{p-1}({\bar G{(t)}}/{\bar G{(u)}})}/{\psi _{p-1}({\bar F{(t)}}/{\bar F{(u)}})}$ is increasing in
${\psi _{p-1}({\bar G{(t)}}/{\bar G{(u)}})}/{\psi _{p-1}({\bar F{(t)}}/{\bar F{(u)}})}$ is increasing in ![]() $t$ and
$t$ and ![]() $\mathcal {T}(\cdot \,|\,x_1,u) \leq _{{\rm lr}} \mathcal {T}(\cdot \,|\,x_2,u)$ for
$\mathcal {T}(\cdot \,|\,x_1,u) \leq _{{\rm lr}} \mathcal {T}(\cdot \,|\,x_2,u)$ for ![]() $x_1 \leq x_2$. Again, part (i) of Lemma 2.2 implies that
$x_1 \leq x_2$. Again, part (i) of Lemma 2.2 implies that ![]() $E[\phi _2(T,x,u)]$ is increasing in
$E[\phi _2(T,x,u)]$ is increasing in ![]() $x$.
$x$.
Finally, since ![]() $\mathcal {U}(\cdot \,|\,x_1) \leq _{{\rm lr}} \mathcal {U}(\cdot \,|\,x_2)$ for
$\mathcal {U}(\cdot \,|\,x_1) \leq _{{\rm lr}} \mathcal {U}(\cdot \,|\,x_2)$ for ![]() $x_1 \leq x_2$, part (i) of Lemma 2.2 implies that
$x_1 \leq x_2$, part (i) of Lemma 2.2 implies that ![]() $E[\phi _1(U,x)]$ is increasing in
$E[\phi _1(U,x)]$ is increasing in ![]() $x$.
$x$.
For the case that ![]() $Y$ is DFR, analogously one can see that
$Y$ is DFR, analogously one can see that ![]() ${\bar {F}_{V_{(r,n,\tilde {m}_n,k)}^{(p)}}(x)}/{\bar {F}_{W_{(r,n,\tilde {m}_n,k)}^{(p)}}(x)}$ is decreasing in
${\bar {F}_{V_{(r,n,\tilde {m}_n,k)}^{(p)}}(x)}/{\bar {F}_{W_{(r,n,\tilde {m}_n,k)}^{(p)}}(x)}$ is decreasing in ![]() $x$ by part (ii) of Lemma 2.2. Therefore, the proof is completed. □
$x$ by part (ii) of Lemma 2.2. Therefore, the proof is completed. □
It is worthwhile mentioning that there are two crucial points in resolving this problem. The first one is the choosing an appropriate change of variable in the structure of ![]() $\bar {F}_{V_{(r,n,\tilde {m}_n,k)}^{(p)}}(x)$. The second one is the noting that
$\bar {F}_{V_{(r,n,\tilde {m}_n,k)}^{(p)}}(x)$. The second one is the noting that ![]() ${\psi _{p-1}({\bar G{(t)}}/{\bar G{(u)}})}/{\psi _{p-1}({\bar F{(t)}}/{\bar F{(u)}})}$ is not increasing in
${\psi _{p-1}({\bar G{(t)}}/{\bar G{(u)}})}/{\psi _{p-1}({\bar F{(t)}}/{\bar F{(u)}})}$ is not increasing in ![]() $u$ on its own (while it is increasing in
$u$ on its own (while it is increasing in ![]() $t$), and thus, it is needed to borrow some increasing terms from the other parts to make it increasing.
$t$), and thus, it is needed to borrow some increasing terms from the other parts to make it increasing.
Remark 3.2 By a similar approach, one can see that all results and all corollaries of Hu and Zhuang [Reference Hu and Zhuang15] are now valid for any ![]() $p\geq 1$ and for unequal
$p\geq 1$ and for unequal ![]() $m_i$'s.
$m_i$'s.
4. Applications in submodels
The hazard rate of spacings is an important measure for studying lifetime random variables in reliability theory and survival analysis. According to the previous findings, one could compare the simple spacings of ordered random variables in terms of the hazard rate ordering. But, now, one can do that for ![]() $p$-spacings. Here, we present the applications for three useful submodels and the other ones can be considered similarly.
$p$-spacings. Here, we present the applications for three useful submodels and the other ones can be considered similarly.
4.1. Sequential  $(n-r+1)$-out-of-
$(n-r+1)$-out-of- $n$ systems
$n$ systems
In this system (in which contains the ordinary ![]() $(n-r+1)$-out-of-
$(n-r+1)$-out-of-![]() $n$ systems), successive failure times of components are observed which are called sequential order statistics (SOS). The system collapses after the
$n$ systems), successive failure times of components are observed which are called sequential order statistics (SOS). The system collapses after the ![]() $r$th failure so that the
$r$th failure so that the ![]() $r$th SOS describes the system lifetime. After the failure of the
$r$th SOS describes the system lifetime. After the failure of the ![]() $i$th component, the distribution of the lifetimes of the remaining components in the system is adjusted by a parameter
$i$th component, the distribution of the lifetimes of the remaining components in the system is adjusted by a parameter ![]() $\alpha _i$ (cf. [Reference Cramer and Kamps9]). This reflects both a damage caused by the previous failures and a higher load imposed on the remaining components leading possibly to shorter residual life. SOS under proportional hazard rates are included in GOS (cf. [Reference Kamps16,Reference Kamps17]). Indeed, the specific choice of distribution functions
$\alpha _i$ (cf. [Reference Cramer and Kamps9]). This reflects both a damage caused by the previous failures and a higher load imposed on the remaining components leading possibly to shorter residual life. SOS under proportional hazard rates are included in GOS (cf. [Reference Kamps16,Reference Kamps17]). Indeed, the specific choice of distribution functions
with a cdf ![]() $F$ and positive real numbers
$F$ and positive real numbers ![]() $\alpha _1,\ldots,\alpha _n$ leads to the model of GOS with parameters
$\alpha _1,\ldots,\alpha _n$ leads to the model of GOS with parameters ![]() $k=\alpha _n$,
$k=\alpha _n$, ![]() $m_i=(n-i+1)\alpha _i-(n-i)\alpha _{i+1}-1$,
$m_i=(n-i+1)\alpha _i-(n-i)\alpha _{i+1}-1$, ![]() $i=1,\ldots,n-1$, and hence,
$i=1,\ldots,n-1$, and hence, ![]() $\gamma _i=(n-i+1)\alpha _i$,
$\gamma _i=(n-i+1)\alpha _i$, ![]() $i=1,\ldots,n$, (
$i=1,\ldots,n$, (![]() $\alpha _1=\cdots =\alpha _n=1$ leads to the ordinary
$\alpha _1=\cdots =\alpha _n=1$ leads to the ordinary ![]() $(n-r+1)$-out-of-
$(n-r+1)$-out-of-![]() $n$ systems). The main result of the paper enables us to compare the
$n$ systems). The main result of the paper enables us to compare the ![]() $p$-spacings of failures of components in two different sequential systems in hazard ratio orders. Let
$p$-spacings of failures of components in two different sequential systems in hazard ratio orders. Let ![]() $V^{{\rm SOS}}_{(r,n,\tilde {\alpha })}$ and
$V^{{\rm SOS}}_{(r,n,\tilde {\alpha })}$ and ![]() $W^{{\rm SOS}}_{(r,n,\tilde {\alpha })}$ represent the
$W^{{\rm SOS}}_{(r,n,\tilde {\alpha })}$ represent the ![]() $p$-spacings of two sequential systems when the components have the lifetime distributions
$p$-spacings of two sequential systems when the components have the lifetime distributions ![]() $F$ and
$F$ and ![]() $G$, respectively. Then, we have
$G$, respectively. Then, we have
provided that the corresponding conditions in Theorem 3.1 are satisfied.
4.2. Progressive Type-II censored order statistics
A progressively censored life test involves ![]() $N$ items with i.i.d. lifetimes placed simultaneously on test. At the time of the
$N$ items with i.i.d. lifetimes placed simultaneously on test. At the time of the ![]() $i$th failure (
$i$th failure (![]() $i=1,\ldots,n$),
$i=1,\ldots,n$), ![]() $R_i$ surviving units are randomly withdrawn from the test. Progressively Type-II censored order statistics (PCOS) arising from such a reliability experiment correspond to GOS with parameters
$R_i$ surviving units are randomly withdrawn from the test. Progressively Type-II censored order statistics (PCOS) arising from such a reliability experiment correspond to GOS with parameters ![]() $m_i = R_i \in \mathbb {N}_0$,
$m_i = R_i \in \mathbb {N}_0$, ![]() $i=1,\ldots,n-1$, and
$i=1,\ldots,n-1$, and ![]() $k = R_n + 1$. The vector
$k = R_n + 1$. The vector ![]() $\tilde {R}=(R_1,\ldots, R_n)$ is called censoring plan (cf. [Reference Balakrishnan and Cramer5], Section 3.2). Our result can be applied to compare the hazard rate of
$\tilde {R}=(R_1,\ldots, R_n)$ is called censoring plan (cf. [Reference Balakrishnan and Cramer5], Section 3.2). Our result can be applied to compare the hazard rate of ![]() $p$-spacings of failures in two life tests when the components have different lifetime distributions. Let
$p$-spacings of failures in two life tests when the components have different lifetime distributions. Let ![]() $V^{{\rm PCOS}}_{(r,n,\tilde {R})}$ and
$V^{{\rm PCOS}}_{(r,n,\tilde {R})}$ and ![]() $W^{{\rm PCOS}}_{(r,n,\tilde {R})}$ represent the
$W^{{\rm PCOS}}_{(r,n,\tilde {R})}$ represent the ![]() $p$-spacings of PCOS with item lifetime distributions
$p$-spacings of PCOS with item lifetime distributions ![]() $F$ and
$F$ and ![]() $G$, respectively. If the conditions in part (i) of Theorem 3.1 are satisfied, we then have
$G$, respectively. If the conditions in part (i) of Theorem 3.1 are satisfied, we then have
4.3. Record values
Record values are defined as a model of successive extremes in a sequence of i.i.d. random variables. Pellerey et al. [Reference Pellerey, Shaked and Zinn22] and Belzunce et al. [Reference Belzunce, Lillo, Ruiz and Shaked6] investigated the inter-epoch intervals of nonhomogeneous Poisson processes, which can be regarded as spacings of record values. Choosing ![]() $m_1=\cdots =m_{n-1}=-1$, GOS can be viewed as record values (cf. [Reference Kamps16,Reference Kamps17]). Now, one can compare the
$m_1=\cdots =m_{n-1}=-1$, GOS can be viewed as record values (cf. [Reference Kamps16,Reference Kamps17]). Now, one can compare the ![]() $p$-spacings of record values arising from different distributions in hazard ratio orders. Let
$p$-spacings of record values arising from different distributions in hazard ratio orders. Let ![]() $V^{*}_{(1)},~V^{*}_{(2)},\ldots$ and
$V^{*}_{(1)},~V^{*}_{(2)},\ldots$ and ![]() $W^{*}_{(1)},~W^{*}_{(2)},\ldots$ represent the
$W^{*}_{(1)},~W^{*}_{(2)},\ldots$ represent the ![]() $p$-spacings of record values based on
$p$-spacings of record values based on ![]() $F$ and
$F$ and ![]() $G$, respectively. If the conditions in part (ii) of Theorem 3.1 are satisfied, we then have
$G$, respectively. If the conditions in part (ii) of Theorem 3.1 are satisfied, we then have
Acknowledgment
The author is grateful to the reviewers for several constructive comments which lead to an improved version of the manuscript.