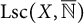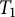The Cuntz semigroup of unital commutative AI-algebras

Abstract

We provide an abstract characterization for the Cuntz semigroup of unital commutative AI-algebras, as well as a characterization for abstract Cuntz semigroups of the form $\operatorname {\mathrm {Lsc}} (X,\overline {\mathbb {N}})$ for some $T_1$-space X. In our investigations, we also uncover new properties that the Cuntz semigroup of all AI-algebras satisfies.

1 Introduction

The celebrated Effros-Handelman-Shen theorem [11, Theorem 2.2] characterizes when a countable ordered abelian group G is order isomorphic to the ordered $K_0$ -group of an approximately finite-dimensional (AF) $\mathrm{C}^*$ -algebra. More explicitly, it states that G is unperforated and has the Riesz interpolation property if and only if G is order isomorphic to the $K_0$ -group of such a $\mathrm {C}^*$ -algebra.

In analogy to the definition of an AF-algebra, a $\mathrm {C}^*$ -algebra A is said to be an AI-algebra if A is $*$ -isomorphic to an inductive limit whose building blocks have the form $C[0,1]\otimes F_n$ with $F_n$ finite-dimensional for every n. In the unital commutative setting, an AI-algebra is of the form $C(X)$ , with X homeomorphic to an inverse limit of (possibly increasing) finite disjoint unions of unit intervals.

In this paper, we use the Cuntz semigroup of a $\mathrm {C}^*$ -algebra, a refinement of $K_0$ introduced by Cuntz in [10] and used successfully in the classification of not necessarily simple $\mathrm {C}^*$ -algebras (see, for example, [7, 8, 19, 21]). We provide an abstract characterization for the Cuntz semigroup of unital commutative AI-algebras and introduce new properties that the Cuntz semigroup of every AI-algebra satisfies. This settles the range problem for the Cuntz semigroup of this class of commutative $\mathrm {C}^*$ -algebras; the corresponding problem in the setting of general AI-algebras was posed during the 2018 mini-workshop on the Cuntz semigroup in Houston, and is studied in [25].

Abstracting some of the properties that the Cuntz semigroup of a $\mathrm {C}^*$ -algebra always satisfies, the subcategory $\operatorname {\mathrm {Cu}}$ of partially ordered monoids was introduced in [9]. This subcategory, whose objects are often called $\mathrm {Cu}$ -semigroups, contains the Cuntz semigroup of all $\mathrm {C}^*$ -algebras, and has been studied extensively in [1, 3, 4, 5], among others. A relevant family in $\operatorname {\mathrm {Cu}}$ is that of countably based $\mathrm {Cu}$ -semigroups satisfying (O5) (see Paragraph 2.3), which contains the Cuntz semigroups of all separable $\mathrm {C}^*$ -algebras (see [2, 22]).

The range problem for this class of algebras consists of finding a list of properties that a $\mathrm {Cu}$ -semigroup S satisfies if and only if S is $\operatorname {\mathrm {Cu}}$ -isomorphic to the Cuntz semigroup of a unital commutative AI-algebra. In order to do this, we first investigate when a compact metric space X is such that $C(X)$ is an AI-algebra, that is to say, we analyze when X is homeomorphic to an inverse limit of finite disjoint unions of unit intervals. To this end, and in analogy to the definition of a chainable continuum (see, for example, [17, Chapter 12]), we introduce almost chainable and generalized arc-like spaces (see Definitions 3.4 and 3.7, respectively). We prove the following theorem.

Theorem 1.1 (3.15)

Let X be a compact metric space. The following are equivalent:

1. (i) X is almost chainable.

2. (ii) X is a generalized arc-like space.

3. (iii) X is an inverse limit of finite disjoint copies of unit intervals.

4. (iv) $C(X)$ is an AI-algebra.

The dimension of the spaces appearing in Theorem 1.1 is at most one, and in this case the Cuntz semigroup of $C(X)$ is isomorphic to the semigroup $\operatorname {\mathrm {Lsc}} (X,\overline {\mathbb {N}})$ of lower semicontinuous functions from X to $\{ 0,1,\ldots ,\infty \}$ (see, e.g., [20]). Thus, the next step in our approach is to characterize those $\mathrm {Cu}$ -semigroups of the form $\operatorname {\mathrm {Lsc}} (X,\overline {\mathbb {N}})$ for some $T_1$ -space X. In Section 4, we define the notion of an $\operatorname {\mathrm {Lsc}}$ -like $\mathrm {Cu}$ -semigroup. Given such a semigroup S, we prove in Section 5 that S has an associated $T_1$ -topological space $X_S$ (Paragraph 5.1) and that many properties defined for $\mathrm {Cu}$ -semigroups have a topological counterpart whenever the semigroup is $\operatorname {\mathrm {Lsc}}$ -like (see Proposition 5.6). For example, an $\operatorname {\mathrm {Lsc}}$ -like $\mathrm {Cu}$ -semigroup S has a compact order unit (in the sense of Paragraph 2.3) if and only if $X_S$ is countably compact. In Theorem 6.4, we show that S is $\operatorname {\mathrm {Lsc}}$ -like if and only if it is $\operatorname {\mathrm {Cu}}$ -isomorphic to $\operatorname {\mathrm {Lsc}} (X_S,\overline {\mathbb {N}} )$ .

Using this characterization, together with the notion of covering dimension for $\mathrm {Cu}$ -semigroups introduced in [23], we obtain the following result.

Theorem 1.2 (6.5)

Let S be a $\mathrm {Cu}$ -semigroup satisfying (O5), and let $n\in \mathbb {N}\cup \{ \infty \}$ . Then, S is $\operatorname {\mathrm {Cu}}$ -isomorphic to $\operatorname {\mathrm {Lsc}} (X,\overline {\mathbb {N}} )$ with X a compact metric space such that $\dim (X)= n$ if and only if S is $\operatorname {\mathrm {Lsc}}$ -like, countably based, has a compact order unit, and $\dim (S)=n$ .

In particular, a $\mathrm {Cu}$ -semigroup S is $\operatorname {\mathrm {Cu}}$ -isomorphic to the Cuntz semigroup of the $\mathrm {C}^*$ -algebra $C(X)$ with X compact metric and $\dim (X)\leq 1$ if and only if S is $\operatorname {\mathrm {Lsc}}$ -like, countably based, satisfies (O5), has a compact order unit, and $\dim (S)\leq 1$ .

With these results at hand, we introduce in Section 7 notions of chainability for $\mathrm {Cu}$ -semigroups. These conditions aim at modeling, at the level of abstract Cuntz semigroups, the concepts of cover and chain for a topological space. We prove the following theorem.

Theorem 1.3 (7.11)

Let S be a $\mathrm {Cu}$ -semigroup. Then, S is $\operatorname {\mathrm {Cu}}$ -isomorphic to the Cuntz semigroup of a unital commutative AI-algebra if and only if S is countably based, $\operatorname {\mathrm {Lsc}}$ -like, weakly chainable, has a compact order unit, and satisfies (O5).

Finally, in Section 8, we generalize some of the properties used in Theorem 7.11 and show that these generalizations are satisfied for the Cuntz semigroup of every AI-algebra (see Theorem 8.7).

In [25], we continue the study of Cuntz semigroups of AI-algebras and develop tools toward a similar characterization of Theorem 7.11 in the general case.

2 Preliminaries

Given a $\mathrm {C}^*$ -algebra A and two positive elements $a,b\in A$ , recall that a is Cuntz subequivalent to b, and write $a\precsim b$ , if there exists a sequence $(r_n)_n$ in A such that $a=\lim _n r_n b r_n^*$ . Moreover, if $a\precsim b$ and $b\precsim a$ , we say that a and b are Cuntz equivalent, in symbols $a\sim b$ .

The Cuntz semigroup of A, denoted by $\operatorname {\mathrm {Cu}} (A)$ , is defined as the quotient $(A\otimes \mathcal {K})_+/{\sim }$ , where we denote by $[a]$ the class of an element $a\in (A\otimes \mathcal {K})_+$ . Equipped with the order induced by $\precsim $ and the addition induced by , the Cuntz semigroup becomes a positively ordered monoid (see [9, 10]).

2.1 Given two elements $x,y$ in a partially ordered set, we say that x is way-below y, and write $x\ll y$ , if for every increasing sequence $(z_n)_n$ whose supremum exists and is greater than or equal to y there exists $n\in \mathbb {N}$ such that $x\leq z_n$ .

In [9], it was shown that the Cuntz semigroup S of every $\mathrm {C}^*$ -algebra always satisfies the following properties:

1. (O1) Every increasing sequence in S has a supremum.

2. (O2) Every element in S can be written as the supremum of a $\ll $ -increasing sequence.

3. (O3) For every $x'\ll x$ and $y'\ll y$ , we have $x'+y'\ll x+y$ .

4. (O4) For every pair of increasing sequences $(x_n)_n$ and $(y_n)_n$ , we have $\sup _n x_n +\sup _n y_n = \sup _n (x_n+y_n)_n$ .

2.2 In a more abstract setting, we say that a positively ordered monoid is a $\mathrm {Cu}$ -semigroup if it satisfies (O1)–(O4).

We also say that a map between two $\mathrm {Cu}$ -semigroups is a $\mathrm {Cu}$ -morphism if it is a positively ordered monoid morphism that preserves suprema of increasing sequences and the way-below relation. As proved in [9], every *-homomorphism $\varphi $ between $\mathrm {C}^*$ -algebras induces a $\mathrm {Cu}$ -morphism $\operatorname {\mathrm {Cu}} (\varphi )$ between their Cuntz semigroups.

Thus, one can consider the subcategory $\operatorname {\mathrm {Cu}}$ of the category of positively ordered monoid as the category with $\mathrm {Cu}$ -semigroups and $\mathrm {Cu}$ -morphisms as its objects and morphisms, respectively. By the results from [9], the assignment $\operatorname {\mathrm {Cu}}\colon C^*\to \operatorname {\mathrm {Cu}}$ is functorial.

Moreover, we know from [3, Corollary 3.2.9] that the category $\operatorname {\mathrm {Cu}}$ has arbitrary inductive limits and that the functor $\operatorname {\mathrm {Cu}}$ is arbitrarily continuous (see also [9]).

2.3 A $\mathrm {Cu}$ -semigroup is said to have weak cancelation if $x\ll y$ whenever $x+z\ll y+z$ for some element z. Given a compact element z, that is, an element such that $z\ll z$ , weak cancelation implies that $x\leq y$ whenever $x+z\leq y+z$ . Stable rank one $\mathrm {C}^*$ -algebras have weakly cancellative Cuntz semigroups by [22, Theorem 4.3].

It was also proved in [22] that the Cuntz semigroup of a $\mathrm {C}^*$ -algebra always satisfies the following property: for every $x'\ll x\leq z$ , there exists c such that

$$\begin{align*}x'+c\leq z\leq x+c. \end{align*}$$

Moreover, it was shown in [3, Proposition 4.6] that a stronger property termed (O5) was also satisfied in the Cuntz semigroup of any $\mathrm {C}^*$ -algebra:

1. (O5) Given $x'\ll x$ , $y'\ll y$ and $x+y\leq z$ , there exists an element c such that $y'\ll c$ and $x'+c\leq z\leq x+c$ .

Under the assumption of weak cancelation, (O5) and the weaker property from [22] coincide.

We will say that a $\mathrm {Cu}$ -semigroup is countably based if there exists a countable subset such that every element in the semigroup can be written as the supremum of an increasing sequence of elements in the subset. It follows from [2, Lemma 1.3] that Cuntz semigroups of separable $\mathrm {C}^*$ -algebras are countably based.

2.4 Recall that a $\mathrm {C}^*$ -algebra A is an AI-algebra if it is *-isomorphic to an inductive limit of the form $\lim _n C[0,1]\otimes F_n$ with $F_n$ finite-dimensional for every n.

By [24], every unital commutative AI-algebra is *-isomorphic to an inductive limit of the form

with $n_{i}\leq n_{i+1}$ for each i and where all the homomorphisms are in standard form. That is to say, for every i, we have

$$ \begin{align*} \pi_{j,i+1}\varphi_{i+1,i}(f_{1},\ldots ,f_{n_{i}}) = f_{r}\sigma_{j,i}, \end{align*} $$

where $\pi _{j,i+1}\colon C([0,1])^{n_{i+1}}\rightarrow C([0,1])$ is the jth projection map, $\sigma _{j,i}\colon [0,1]\rightarrow [0,1]$ is a continuous function, and $r\leq n_{i}$ .

Thus, every unital commutative AI-algebra is isomorphic to $C(X)$ , where X is an inverse limit of (possibly increasing) finite disjoint unions of unit intervals. Conversely, it is easy to see that $C(X)$ is an AI-algebra for such an inverse limit X.

Since the space X above will always have dimension at most one, we know by [20, Theorem 1.1] that $\operatorname {\mathrm {Cu}} (C(X))\cong \operatorname {\mathrm {Lsc}} (X,\overline {\mathbb {N}})$ .

Moreover, note that, with the above notation, if there exists some i such that $n_{i}=n_{j}$ for every $j\geq i$ , we can write $A\cong \oplus _{k=1}^{n_{i}} C(X_{k})$ with $X_{k}$ an inverse limit of unit intervals.

3 Chainable and almost chainable spaces

In this section, we will prove that a compact metric space X is homeomorphic to an inverse limit of finite disjoint copies of unit intervals (i.e., $C(X)$ is an AI-algebra) if and only if X satisfies an abstract property, which we call almost chainability (see Theorem 3.15). This is done in analogy to [17, Chapter 12], where it is shown that a continuum is homeomorphic to the inverse limit of unit intervals if and only if it is chainable, as defined below.

3.1 Recall that a compactum is a compact metric space, and that a continuum is a connected compactum. As in [17, Chapter 12], a chain in a continuum X will be a finite nonempty indexed collection $C=\{C_{1},\ldots , C_{k}\}$ of open subsets of X such that

$$\begin{align*}C_{i}\cap C_{j}\neq\emptyset \text{ if and only if }\vert i-j\vert\leq 1. \end{align*}$$

The mesh of a chain $C=\{C_{1},\ldots , C_{k}\}$ , in symbols $\operatorname {\mathrm {mesh}} (C)$ , is defined as

$$\begin{align*}\operatorname{\mathrm{mesh}} (C)=\max\{ \operatorname{\mathrm{diam}} (C_{i})\}. \end{align*}$$

A chain of mesh less than $\epsilon $ is called an $\epsilon $ -chain.

Following [17, Chapter 12], one can now define chainable continua.

Definition 3.1 A continuum X is said to be chainable if for every positive $\epsilon $ there exists an $\epsilon $ -chain covering X.

We will say that a compactum is piecewise chainable if it can be written as the finite disjoint union of closed chainable subspaces.

Chainability may also be defined in a general setting, and one can check that the previous and following definitions coincide whenever X is a continuum (see Lemma 3.5).

Definition 3.2 A topological space X is said to be topologically chainable if any finite open cover of X can be refined by a chain, that is, an open cover $C_{1},\ldots ,C_{k}$ such that $C_{i}\cap C_{j}\neq \emptyset $ if and only if $\vert i-j\vert \leq 1$ .

Remark 3.2 Note that both of the abovementioned definitions imply that the dimension of the space is at most one, and that the space is connected whenever it is compact.

The following proposition shows why we consider chainable continua. More on chainable spaces can be found in [17, Chapter 12].

Proposition 3.3 A compactum is an inverse limit of unit intervals if and only if it is chainable.

Proof Let X be the inverse limit of unit intervals. Since the unit interval is compact and connected, X is connected and, consequently, a continuum.

If X is degenerate (i.e., a point), it is clearly chainable, so we may assume otherwise.

If X is nondegenerate, then [17, Theorems 12.11 and 12.19] and the comments following Theorem 12.19 of [17] imply that X is chainable.

Conversely, if X is chainable, it can either be degenerate (in which case we are done) or nondegenerate. By [17, Theorem 12.11], a nondegenerate chainable continuum is an inverse limit of unit intervals, so the result follows.

Definition 3.3 A unital AI-algebra A will be said to be block stable if it is isomorphic to $C(X)$ with X a compact metric piecewise chainable space, that is, if $A\cong \oplus _{k=1}^{n}C(X_{k})$ with $X_{k}$ a chainable continuum for each k.

3.1 Generalized arc-like spaces

We now generalize the previous results and characterize the topological spaces arising from unital commutative AI-algebras in terms of a weaker property.

3.4 Let X be a compactum. In analogy with the definition of chains, an almost chain in X will be a finite nonempty indexed collection $C=\{ C_{1},\ldots , C_{k} \}$ of open subsets of X such that

$$\begin{align*}C_{i}\cap C_{j}= \emptyset \text{ whenever } \vert i-j\vert \geq 2. \end{align*}$$

The mesh of an almost chain will be $\operatorname {\mathrm {mesh}} (C)=\max \{\operatorname {\mathrm {diam}} (C_{i}) \}$ , and an almost chain of mesh less than $\epsilon $ will be called an $\epsilon $ -almost chain.

Definition 3.4 A compact metric space X will be said to be almost chainable if, for every $\epsilon>0$ , there exists an $\epsilon $ -almost chain covering X.

Definition 3.5 A topological space X will be said to be topologically almost chainable if any finite open cover of X can be refined by an almost chain, that is, an open refinement $C_{1},\ldots ,C_{k}$ such that $C_{i}\cap C_{j}= \emptyset $ whenever $\vert i-j\vert \geq 2$ .

Lemma 3.5 Definitions 3.4 and 3.5 coincide whenever X is a compact metric space.

The same proof can be applied to chainability and topological chainability.

Proof If X is topologically almost chainable, let $\epsilon>0$ and take an open cover of $\epsilon $ -balls in X. Since X is compact, there exist finitely many points $x_{1},\ldots ,x_{n}$ such that their $\epsilon $ -balls cover X.

By topological almost chainability, this finite open cover can be refined by open subsets $C_{1},\ldots ,C_{k}$ such that $C_{i}\cap C_{j}=\emptyset $ whenever $\vert i-j\vert \geq 2$ . Since $C_{i}$ is contained in some $\epsilon $ -ball, it follows that $C_{1},\ldots ,C_{k}$ is an $\epsilon $ -almost chain.

Conversely, assume that X is almost chainable and take a (finite) open cover $U_{1},\ldots ,U_{n}$ .

Since X is a compact metric space, the cover has a nonzero Lebesgue number $\delta $ . That is, every subset of X having diameter less than $\delta $ is contained in some $U_{j}$ .

Set $\epsilon <\delta $ and consider an $\epsilon $ -almost chain $C=\{ C_{1},\ldots ,C_{k} \}$ covering X. Since $\operatorname {\mathrm {diam}} (C_{i})\leq \epsilon <\delta $ for every i, it follows that each $C_{i}$ is contained in some $U_{j}$ . Consequently, $C_{1},\ldots ,C_{k}$ is an open refinement of $U_{1},\ldots , U_{n}$ with the required property.

We now define the notion of $(\epsilon , \delta )$ -maps and generalized arc-like spaces. This is done in analogy with [17, Theorem 12.11].

Recall that a continuous map $f\colon X\rightarrow Y$ is an $\epsilon $ -map if $\operatorname {\mathrm {diam}} (f^{-1}( y) )\leq \epsilon $ for every $y\in Y$ , where $\operatorname {\mathrm {diam}} (\emptyset )=0$ by definition.

Definition 3.6 Let $X,Y$ be metric spaces. Given $\epsilon ,\delta>0$ , we will say that a continuous map $f\colon X\rightarrow Y$ is an $(\epsilon , \delta )$ -map if $\operatorname {\mathrm {diam}} (f^{-1}(Z))< \epsilon $ for every $Z\subseteq Y$ with $\operatorname {\mathrm {diam}} (Z)<\delta $ .

Recall also that a continuum X is arc-like if, for every $\epsilon>0$ , there exists an $\epsilon $ -map from X onto $[0,1]$ (see [17, Definition 2.12]).

Definition 3.7 A compactum X is said to be a generalized arc-like space if, for every $\epsilon>0$ , there exists $\delta>0$ and an $(\epsilon ,\delta )$ -map $f\colon X\rightarrow I_{1}\sqcup \cdots \sqcup I_{n}$ with $I_{j}=[0,1]$ for each j.

Remark 3.6 Given a finite disjoint union of unit intervals $I_{1}\sqcup \cdots \sqcup I_{n}$ and some $\delta>0$ , one can clearly construct a $(\delta , \delta ')$ -map $r\colon I_{1}\sqcup \cdots \sqcup I_{n}\rightarrow [0,1]$ (by simply rescaling $I_{1}\sqcup \cdots \sqcup I_{n}$ until it fits in $[0,1]$ ).

Thus, a compactum X is a generalized arc-like space if and only if, for every $\epsilon>0$ , there exists an $(\epsilon ,\delta )$ -map $f\colon X\rightarrow [0,1]$ for some $\delta>0$ .

Lemma 3.7 Inverse limits of finite disjoint unions of unit intervals are generalized arc-like spaces.

Proof Let X be an inverse limit of finite disjoint unions of unit intervals, and let $( [0,1]\sqcup \cdots \sqcup [0,1] ,f_{i,j} )$ be its associated inverse system.

Recall that the metric on X is defined to be

$$\begin{align*}\text{d}((x_{i})_{i=1}^{\infty} , (y_{i})_{i=1}^{\infty})=\sum_{i=1}^{\infty} \frac{1}{2^{i}} \frac{\text{d}_{i}(x_{i},y_{i})}{1+\text{d}_{i}(x_{i},y_{i})}, \end{align*}$$

where $\text {d}_{i}$ is the distance in the ith component of the inverse system.

Moreover, recall that the distance between two points $x,y$ in $[0,1]\sqcup \cdots \sqcup [0,1]$ is either the usual distance if $x,y$ belong to the same connected component or $2$ if they do not.

Given $\epsilon>0$ , let n be such that $\sum _{i> n} 2/2^{i}<\epsilon /2$ .

Then, since for every fixed n the maps $f_{i,n}$ are uniformly continuous for every $i\leq n$ , there exists $\delta>0$ such that

$$\begin{align*}\text{d}_{i}(f_{i,n}(x),f_{i,n}(y))\leq\epsilon /2n \end{align*}$$

whenever $\text {d}_{n}(x,y)\leq \delta $ .

Let $\pi _{n}\colon X\rightarrow [0,1]\sqcup \cdots \sqcup [0,1]$ be the nth canonical projection map, and take $Z\subseteq \pi _{n}(X)$ with $\operatorname {\mathrm {diam}}_{n} (Z)\leq \delta $ ,

Take $x,y\in \pi _{n}^{-1}(Z)$ . Then, we have

$$\begin{align*}\text{d}(x,y)=\sum_{i=1}^{n} \frac{1}{2^{i}}\frac{\text{d}_i(f_{i,n}(x_{n}),f_{i,n}(y_{n}))}{1+ \text{d}_i(f_{i,n}(x_{n}),f_{i,n}(y_{n}))} + \sum_{i>n}\!\frac{1}{2^{i}} \frac{\text{d}_{i}(x_{i},y_{i})}{1+\text{d}_{i}(x_{i},y_{i})}\leq n\frac{\epsilon}{2n} + \sum_{i>n}\!\frac{1}{2^{i}} 2\leq \epsilon , \end{align*}$$

since any pair of elements is at distance at most $2$ .

This shows that $\operatorname {\mathrm {diam}} (\pi _{n}^{-1}(Z)) \leq \epsilon $ , and so $\pi _{n}$ is an $(\epsilon ,\delta )$ -map, as required.

Proposition 3.8 A compactum X is a generalized arc-like space if and only if it is almost chainable.

Proof We follow the proof of [17, Theorem 12.11] while making some minor adjustments.

Assume first that X is almost chainable and take $\epsilon>0$ . Let C be an $\epsilon /2$ -almost chain covering X, and decompose it as $C=C_{1}\sqcup \cdots \sqcup C_{r}$ with

$$\begin{align*}C_{1}=\{ C_{i,1} \}_{i} ,\ldots , C_{r}=\{ C_{i,r} \}_{i} \end{align*}$$

$\epsilon /2$ -chains in X. Note that, for any $i,l$ we have $C_{i,j}\cap C_{l,k}=\emptyset $ whenever $j\neq k$ and

$$\begin{align*}X=\bigsqcup_{j} \bigcup_{i} C_{i,j}, \end{align*}$$

because C covers X.

Take $s\leq r$ . If $\vert C_{s}\vert \leq 2$ , consider the map $f_{s}\colon \cup _{i} C_{i,s}\rightarrow [0,1]$ sending every element to $0$ . Note that $\operatorname {\mathrm {diam}} (f_{s}^{-1}(Z))<\epsilon $ whenever $\operatorname {\mathrm {diam}} (Z)<1$ .

If $\vert C_{s}\vert \geq 3$ , use the techniques in [17, Theorem 12.11] to obtain an $(\epsilon ,\delta _{s})$ -map $f_{s}\colon \cup _{i} C_{i,s}\rightarrow [0,1]$ .

Now, define $f=f_{1}\sqcup \cdots \sqcup f_{r}\colon X\rightarrow I_{1}\sqcup \cdots \sqcup I_{r}$ , where $I_{l}=[0,1]$ for every l. Note that this is clearly continuous.

Setting $\delta < \min \{1, \delta _{s}\}$ , one gets that, if the diameter of $Z\subseteq I_{1}\sqcup \cdots \sqcup I_{r}$ is less than $\delta $ , Z is a subset of some $I_{l}$ (since the distance between disjoint components is $2$ ).

This implies that $f^{-1}(Z)=f^{-1}_{l}(Z)$ has diameter at most $\epsilon $ , as required.

Conversely, if X is a generalized arc-like, then given any $\epsilon $ there exists $\delta $ with $f\colon X\rightarrow I_{1}\sqcup \cdots \sqcup I_{r}$ an $(\epsilon ,\delta )$ -map.

For each $I_{l}$ , consider a $\delta $ -chain $C_{l}$ . The inverse image of these chains through f gives the desired $\epsilon $ -almost chain for X.

Corollary 3.9 Inverse limits of disjoint unions of unit intervals are almost chainable. In particular, each connected component is arc-like.

Proof This follows from our previous two results. Note, however, that only one implication of Proposition 3.8 has been used.

We will now show that the converse of Corollary 3.9 also holds, thus obtaining a characterization of inverse limits of finite disjoint copies of unit intervals (see Theorem 3.15).

We first recall the following result from [13], even though this particular formulation is from [24, Lemma 2.14, p. 184].

Lemma 3.10 Let C be a closed nonempty subset of $[0,1]$ , and let $\epsilon>0$ . Then, there exist a subset $Y\subseteq C$ which is a finite disjoint union of closed intervals (possibly degenerate) and a map $\alpha \colon C\rightarrow Y$ such that $\alpha (y)=y$ for every $y\in Y$ and $\vert \alpha (x)-x\vert <\epsilon $ for every $x\in C$ .

Remark 3.11 With the previous notation, note that $\alpha $ is an onto $2 \epsilon $ -map from C to Y.

Indeed, for any $y\in Y$ and for any $x\in C$ with $\alpha (x)=y$ , we must have $\vert x-y\vert <\epsilon $ . Since $y\in \alpha ^{-1}(y)$ , it follows that $\operatorname {\mathrm {diam}} (\alpha ^{-1}(y))\leq \operatorname {\mathrm {diam}} (B_{\epsilon }(y))<2 \epsilon $ .

From now on, by a closed interval, we will mean a possibly degenerate closed interval (that is to say, either a point or a nondegenerate closed interval).

3.12 Given any $(\epsilon ,\delta )$ -map $f\colon X\rightarrow [0,1]$ , consider the induced onto $\epsilon $ -map $f\colon X\rightarrow \text {Im}(f)$ .

Since X is compact, so is $\text {Im}(f)$ . Using Lemma 3.10, we can find an onto $\delta $ -map $\alpha \colon \text {Im}(f)\rightarrow Y$ with Y the finite disjoint union of closed intervals and, consequently, we get an onto $\epsilon $ -map $\alpha f\colon X\rightarrow Y$ .

This shows that given any generalized arc-like compactum X (equivalently, any almost chainable compactum, by Proposition 3.8) and any $\epsilon>0$ , there exists an onto $\epsilon $ -map $f\colon X\rightarrow Y$ with Y a finite disjoint union of closed intervals. Indeed, given any $\epsilon>0$ , we know by Definition 3.7 and Remark 3.6 that there exists an $(\epsilon ,\delta )$ -map $f\colon X\to Y$ . The conclusion now follows from the previous argument.

Using Paragraph 3.12, we will see that $C(X)$ is a commutative AI-algebra for any generalized arc-like compactum X. Since we already know that X is almost chainable whenever $C(X)$ is an AI-algebra (see Corollary 3.9), this will show that X is almost chainable if and only if $C(X)$ is a commutative AI-algebra.

The following lemma is a natural generalization of [17, Lemma 12.17]. We follow both the structure and the notation of the proof of said lemma.

Lemma 3.13 Let X be a compactum, let $g_{1}\colon X\rightarrow Y_{1}$ be an onto continuous map with $Y_{1}$ a finite disjoint union of closed intervals, and let $\eta>0$ .

Then, there exists $\epsilon>0$ such that, for any onto $\epsilon $ -map $g_{2}\colon X\rightarrow Y_{2}$ with $Y_{2}$ a finite disjoint union of closed intervals, there exists a continuous map $\varphi \colon Y_{2}\rightarrow Y_{1}$ such that $\vert g_{1}(x)-\varphi g_{2}(x)\vert <\eta $ for every $x\in X$ .

Proof First, write

$$\begin{align*}Y_{1} = J_{1}\sqcup\cdots\sqcup J_{n_{1}}\sqcup \{q_{1}\}\sqcup\cdots\sqcup\{ q_{m_{1}} \} \end{align*}$$

with $J_{k}$ closed nondegenerate intervals for every k.

Fix $m\in \mathbb {N}$ such that $1/m<\eta /2$ and define $s_{i}=i/m$ for every $0\leq i\leq m$ . Since $g_{1}$ is uniformly continuous, there exists some $\gamma>0$ such that $\operatorname {\mathrm {diam}} (g_{1}(A))<1/m$ whenever $\operatorname {\mathrm {diam}} (A)<\gamma $ .

Set $\epsilon =\gamma /2$ and fix an onto $\epsilon $ -map $g_{2}\colon X\rightarrow Y_{2}$ as in the statement of the lemma. Recall that there exists $\delta>0$ such that $\operatorname {\mathrm {diam}} (g_{2}^{-1}(Z) )<2\epsilon =\gamma $ whenever $\operatorname {\mathrm {diam}} (Z)<\delta $ .

Now, fix $n\in \mathbb {N}$ such that $1/n<\delta /2$ and define $t_{j}=j/n$ for every $0\leq j\leq n$ .

As before, write $Y_{2}$ as

$$\begin{align*}Y_{2} = I_{1}\sqcup\cdots\sqcup I_{n_{2}}\sqcup \{p_{1}\}\sqcup\cdots\sqcup\{ p_{m_{2}} \} \end{align*}$$

with $I_{l}$ closed nondegenerate intervals for every l.

For each $l,k$ , consider the subsets

$$\begin{align*}\begin{aligned} A_{1}^{k} &= [s_{0},s_{1}) \, ,\, A_{i}^{k} = (s_{i-1},s_{i+1})\, ,\, A_{m}^{k} = (s_{m-1},s_{m}] \subseteq J_{k}, \\ B_{1}^{l} &= [t_{0},t_{1}) \, ,\, B_{j}^{l} = (t_{j-1},t_{j+1})\, ,\, B_{n}^{l} = (t_{n-1},t_{n}] \subseteq I_{l}. \end{aligned} \end{align*}$$

By construction, we know that $\operatorname {\mathrm {diam}} (B_{j}^{l})< \delta $ for every fixed $j,l$ . This implies that $\operatorname {\mathrm {diam}} ( g_{2}^{-1}(B_{j}^{l}))< \gamma $ and, consequently,

$$\begin{align*}g_{1} ( g_{2}^{-1} (B_{j}^{l}) )\subseteq A_{i}^{k}\,\text{ or }\, g_{1} ( g_{2}^{-1} (B_{j}^{l}) )\subseteq \{ q_{r'}\} \end{align*}$$

for some $i,k,r'$ . Here, we have taken m large enough so that the distance between the connected components of $Y_{1}$ is greater than $1/m$ .

Note that, by the same argument, we also have that for every $r\leq m_{2}$ there exist $i,k$ with $g_{1} ( g_{2}^{-1} (p_{r}) )\subseteq A_{i}^{k}$ or $g_{1} ( g_{2}^{-1} (p_{r}) )\subseteq \{ q_{r'}\}$ for some $r'$ .

Moreover, since for every fixed l and every j we have $B^{l}_{j}\cap B^{l}_{j+1}\neq \emptyset $ , we get

$$\begin{align*}\emptyset \neq g_{1}(g_{2}^{-1}(B^{l}_{j}))\cap g_{1}(g_{2}^{-1}(B^{l}_{j+1})) \end{align*}$$

because $g_{2}$ is onto.

It follows that, for every fixed l, the sets $g_{1}(g_{2}^{-1}(B_{j}^{l}))$ belong to the same connected component of $Y_{1}$ for every j. Thus, for every l, there either exists k such that $g_{1}(g_{2}^{-1}(I_{l}))\subseteq J_{k}$ or there exists $r'$ such that $g_{1}(g_{2}^{-1}(I_{l}))=\{q_{r'}\}$ .

Given a connected component Y of $Y_{2}$ , we define the map $\varphi _{Y}\colon Y\to Y_{1}$ as follows:

If $g_{1}(g_{2}^{-1}(Y))=\{ q_{r'}\}$ for some $r'$ , define $\varphi _{Y}\colon Y\to \{ q_{r'}\}$ as the constant map.

Else, there exists some k such that $g_{1}(g_{2}^{-1}(Y))\subseteq J_{k}$ . If Y is degenerate, we can find $A_{i}^{k}\subseteq J_{k}$ such that $g_{1}(g_{2}^{-1}(Y))\subseteq A_{i}^{k}$ for some $i,k$ . Define $\varphi _{Y}\colon Y\to A_{i}^{k}\subseteq J_{k}$ as the constant map $\varphi _{Y}\equiv s_{i}$ .

Finally, if Y is nondegenerate, it is of the form $Y=I_{l}$ . Then, for every j, fix $i(j)$ such that $g_{1}(g_{2}^{-1}(B_{j}^{l}))\subseteq A_{i(j)}^{k}$ , and recall that

$$\begin{align*}\emptyset \neq g_{1}(g_{2}^{-1}(B^{l}_{j}))\cap g_{1}(g_{2}^{-1}(B^{l}_{j+1})) \end{align*}$$

for every j. This shows that $\vert i(j)-i(j+1)\vert \leq 1$ .

Define $\varphi _{I_{l}}\colon I_{l}\rightarrow J_{k}$ as $\varphi _{I_{l}}(t_{j})=s_{i(j)}$ and extend it linearly.

Let $\varphi :=\varphi _{I_{1}}\sqcup \cdots \sqcup \varphi _{I_{n_{2}}}\sqcup \varphi _{p_{1}}\sqcup \cdots \sqcup \varphi _{p_{m_{2}}}\colon Y_{2}\rightarrow Y_{1}$ , which is clearly continuous. We will now see that $\vert g_{1}(x)-\varphi g_{2}(x)\vert <\eta $ .

Thus, let $x\in X$ and let $B\subseteq Y_{2}$ such that $g_{2}(x)\in B$ with B being either $B^{l}_{j}$ for some $l,j$ or $\{ p_{r}\}$ for some r. Note that $g_{1}(x)\in g_{1}(g_{2}^{-1}(B))$ .

Thus, if $g_{1}(g_{2}^{-1}(B))=\{ q_{r'}\}$ for some $r'$ , we have $g_{1}(x)=q_{r'}$ and, consequently,

$$\begin{align*}\vert g_{1}(x)-\varphi g_{2}(x)\vert = \vert q_{r'}-q_{r'}\vert =0 \end{align*}$$

by the definition of $\varphi $ .

Finally, if $g_{1}(g_{2}^{-1}(B))\subseteq A^{k}_{i}$ , we have that $g_{1}(x)\in A^{k}_{i}$ . Therefore, one gets $\vert g_{1}(x)-s_{i}\vert <1/m$ . There are now two different situations:

If $B=\{ p_{r}\}$ for some r, we have defined $\varphi _{p_{r}}$ as the constant map $s_{i}$ . Thus, one gets

$$\begin{align*}\vert g_{1}(x)-\varphi g_{2}(x)\vert = \vert g_{1}(x)-s_{i}\vert <1/m<\eta /2. \end{align*}$$

Else, if $B=B^{l}_{j}$ for some l and j, let $i(j)$ be the previously fixed integer such that $g_{1}(g_{2}^{-1}(B))\subseteq A^{k}_{i(j)}$ .

Then, since $g_{2}(x)\in B$ , we either have $t_{j-1}\leq g_{2}(x)\leq t_{j}$ or $t_{j}\leq g_{2}(x)\leq t_{j+1}$ . This implies that $\varphi (g_{2}(x))$ is either between $s_{i(j-1)}$ and $s_{i(j)}$ or between $s_{i(j)}$ and $s_{i(j+1)}$ .

Since $\vert i(j)-i(j+1)\vert \leq 1$ , the triangle inequality implies that

$$\begin{align*}\vert g_{1}(x)-\varphi g_{2}(x)\vert \leq \vert g_{1}(x)-s_{i(j)} \vert + \vert s_{i(j)}-\varphi g_{2}(x)\vert \leq 2/m<\eta, \end{align*}$$

as required.

In order to prove our next result, we will need the following proposition, a proof of which can be found in [17, Proposition 12.18].

Proposition 3.14 Let $(X,d)$ be a compactum, and let $Y= \varprojlim (Y_{i},f_{i})$ be an inverse limit of compacta $(Y_{i},d_{i})$ with $f_i\colon Y_{i+1}\to Y_i$ .

Assume that there exist two sequences of strictly positive real numbers $(\delta _{i})$ , $(\epsilon _{i})$ with $\lim \epsilon _{i}=0$ and a family of onto $\epsilon _{i}$ -maps $g_{i}\colon X\rightarrow Y_{i}$ such that the following conditions hold:

1. (i) For every pair $i<j$ , we have $\operatorname {\mathrm {diam}} (f_{i,j}(A))\leq \delta _{i}/2^{j-i}$ for any $A\subseteq Y_{j}$ with $\operatorname {\mathrm {diam}} (A)\leq \delta _{j}$ .

2. (ii) $d_{i}( g_{i}(x),g_{i}(y) )>2\delta _{i}$ whenever $d(x,y)\geq 2\epsilon _{i}$ .

3. (iii) $d_{i}(g_{i},f_{i}g_{i+1})\leq \delta _{i}/2$ .

Then, $X\cong Y$ .

We summarize our results in the following.

Theorem 3.15 Let X be a compactum. The following are equivalent:

1. (i) X is almost chainable.

2. (ii) X is a generalized arc-like space.

3. (iii) X is homeomorphic to an inverse limit of finite disjoint copies of unit intervals.

4. (iv) $C(X)$ is an AI-algebra.

Proof Conditions (i) and (ii) are equivalent by Proposition 3.8, whereas (iii) is equivalent to (iv) by the arguments in Paragraph 2.4. Furthermore, that (iii) implies (i) follows from Corollary 3.9. Thus, we are left to prove that (i) implies (iii).

Let X be an almost chainable compactum. Then, for every $\epsilon>0$ , there exists an onto $\epsilon $ -map $f\colon X\rightarrow Y$ with Y a finite disjoint union of closed intervals.

As in [17, Theorem 12.19], we will inductively construct sequences of maps and real numbers satisfying the conditions of Proposition 3.14. We give the proof here for the sake of completeness, although the only difference with the original proof is that we replace $[0,1]$ with Y.

Let $0<\epsilon _{1}\leq 1$ , and consider an onto $\epsilon _{1}$ -map $g_{1}$ from X to a finite disjoint union of closed intervals $Y_{1}$ .

Note that, in particular, we must have $g_{1}(x)\neq g_{1}(y)$ whenever $d(x,y)\geq 2 \epsilon _{1}$ . By compactness of X, this implies that there exists some $\delta _{1}>0$ such that $\vert g_{1}(x)-g_{1}(y)\vert>2\delta _{1} $ whenever $d(x,y)\geq 2\epsilon _{1}$ .

Setting $\eta =\delta _{1}/2$ , let $\epsilon>0$ be as in our previous lemma and set $\epsilon _{2}=\min \{ 1/2,\epsilon \}$ . Then, let $g_{2}\colon X\rightarrow Y_{2}$ be an onto $\epsilon _{2}$ -map given by the almost chainability of X.

By our choice of $\epsilon _{2}$ , there exists some $f_{1}\colon Y_{2}\rightarrow Y_{1}$ such that

$$\begin{align*}\vert g_{1}(x)-f_{1}g_{2}(x) \vert <\eta=\delta_{1}/2 \end{align*}$$

for every $x\in X$ .

As before, there exists $\delta _{2}>0$ such that $\vert g_{2}(x)-g_{2}(y)\vert>2\delta _{2} $ whenever $d(x,y)\geq 2\epsilon _{2}$ . Furthermore, by the uniform continuity of $f_{1}$ , we can choose $\delta _{2}>0$ so that $\operatorname {\mathrm {diam}} (f_{1}(A))\leq \eta $ whenever $\operatorname {\mathrm {diam}} (A)\leq \delta _{2}$ .

This shows that $g_1, g_2$ satisfy conditions (i)–(iii) of Proposition 3.14.

Proceeding as in [17, Theorem 12.19], one can now inductively find $\epsilon _{i},\delta _{i}>0$ and maps $g_{i}\colon X\rightarrow Y_{i}$ , $f_{i}\colon Y_{i+1}\rightarrow Y_{i}$ satisfying conditions (i)–(iii) of Proposition 3.14.

Applying Proposition 3.14, we have $X\cong \lim (Y_{k},f_{k})$ with $Y_{k}$ finite disjoint unions of closed intervals. Clearly, this implies that $C(X)$ is an AI-algebra, as required.

4 Lsc-like Cu-semigroups

In this section, we introduce $\operatorname {\mathrm {Lsc}}$ -like $\mathrm {Cu}$ -semigroups (Definition 4.3) and prove some of their main properties. As we shall prove in Theorem 6.4, such $\mathrm {Cu}$ -semigroups are exactly those that are $\operatorname {\mathrm {Cu}}$ -isomorphic to the $\mathrm {Cu}$ -semigroup of lower-semicontinuous functions $\operatorname {\mathrm {Lsc}} (X,\overline {\mathbb {N}} )$ for some $T_{1}$ topological space.

Using Lemma 4.18, we also prove that the semigroup $\operatorname {\mathrm {Lsc}} (X,\overline {\mathbb {N}})$ is a $\mathrm {Cu}$ -semigroup whenever X is compact and metric (see Corollary 4.19).

Definition 4.1 A $\mathrm {Cu}$ -semigroup S will be called distributively lattice ordered if S is a distributive lattice such that, given any pair of elements $x,y\in S$ , we have $x+y=(x\vee y) + (x\wedge y)$ .

We will say that a distributively lattice ordered $\mathrm {Cu}$ -semigroup is complete if suprema of arbitrary sets exist.

Remark 4.1 Given two increasing sequences $(x_{n})_{n}$ and $(y_{n})_{n}$ in a complete distributively lattice ordered $\operatorname {\mathrm {Cu}}$ -semigroup, we have that $(\sup _{n} x_{n})\vee (\sup _{n} y_{n})= \sup _{n} (x_{n}\vee y_{n})$ .

Indeed, by definition, we know that $\sup _{n} x_{n}=\vee _{n=1}^{\infty } x_{n}$ and the equality

$$\begin{align*}(\vee_{n=1}^{\infty} x_{n})\vee (\vee_{n=1}^{\infty} y_{n})= \vee_{n=1}^{\infty} (x_{n}\vee y_{n}) \end{align*}$$

holds in any complete lattice.

Throughout the paper, we will say that a sum of finitely many indexed elements $x_{1}+\cdots +x_{n}$ is ordered if the sequence $(x_{i})_{i=1}^{n}$ is increasing or decreasing.

Lemma 4.2 Let S be a distributively lattice ordered $\operatorname {\mathrm {Cu}}$ -semigroup. Given two finite decreasing sequences $(x_{i})_{i=1}^{m}, (y_{i})_{i=1}^{m}$ , the following equality holds:

$$\begin{align*}\sum_{i=1}^{m} (x_{i}+y_{i})=\sum_{i=1}^{2m} \vee_{j=0}^{m}(x_{j}\wedge y_{i-j}), \end{align*}$$

where, on the right-hand side, $x_{i}\wedge y_{k}=x_{i}$ , and $x_{k}\wedge y_{i} =y_{i}$ whenever $k\leq m$ and $y_{k}=x_{k}=0$ whenever $k>m$ .

Note that the sum on the right-hand side is decreasingly ordered.

Proof This is a generalization of the equality $x+y=(x\vee y) + (x\wedge y)$ and is proved by induction.

Remark 4.3 Given any finite sum $x_{1}+\cdots +x_{n}$ , we can apply Lemma 4.2 iteratively (first to $x_{1}+x_{2}$ , then to $((x_{1}\vee x_{2}) +(x_{1}\wedge x_{2}))+x_{3}$ , etc.) to obtain an ordered sum.

Therefore, every sum in a distributively lattice ordered semigroup can be written as an ordered sum.

Definition 4.2 Let S be a $\mathrm {Cu}$ -semigroup, and let H be a subset of S. We say that H is topological if, given two finite increasing sequences $(x_{i})_{i=1}^{m}, (y_{i})_{i=1}^{m}$ in H, we have

$$ \begin{align*} \sum_{i=1}^{m} x_{i}\leq \sum_{i=1}^{m} y_{i} \end{align*} $$

if and only if $x_{i}\leq y_{i}$ for every i.

Similar notions to that of topological order appear in other contexts, such as in [6, Definition 4.1].

Given any element r in partially ordered set P, we denote by $\downarrow r$ the set $\{s\in P\mid s\leq r\}$ (see, for example, [14, Definition O-1.3]).

Notation 4.4 Given a $\mathrm {Cu}$ -semigroup S and an element $y\in S$ , we write $\infty y:=\sup _n ny$ . Furthermore, if S has a greatest element, we denote it by $\infty $ .

Definition 4.3 A $\mathrm {Cu}$ -semigroup S will be said to be $Lsc$ -like if it is a complete distributively lattice ordered $\mathrm {Cu}$ -semigroup such that the following conditions hold:

1. (C1) For every pair of idempotent elements $y,z$ in S, $y\geq z$ if and only if

   $$\begin{align*}&\{ x<\infty \mid x \text{ maximal idempotent},\, x\geq y \}\\ &\quad \subseteq \{ x<\infty \mid x \text{ maximal idempotent},\, x\geq z \}. \end{align*}$$

2. (C2) There exists a topological subset of the form $\downarrow e$ such that the finite sums of elements in $\downarrow e$ are sup-dense in S.

The following example justifies our terminology.

Example 4.5 Any $\mathrm {Cu}$ -semigroup of the form $\operatorname {\mathrm {Lsc}} (X,\overline {\mathbb {N}} )$ with X a $T_{1}$ -space is $\operatorname {\mathrm {Lsc}}$ -like. Indeed, $\operatorname {\mathrm {Lsc}} (X,\overline {\mathbb {N}} )$ is clearly a complete distributively lattice ordered semigroup.

Furthermore, the maximal idempotent elements $s<\infty $ are of the form $s=\infty \chi _{X\setminus \{ x \}}$ , and given any pair of elements $\infty f=\infty \chi _{\text {supp}(f)}$ and $\infty g=\infty \chi _{\text {supp}(g)}$ , we know that $\infty \chi _{\text {supp}(f)}\leq \infty \chi _{\text {supp}(g)}$ if and only if $\text {supp}(f)\subseteq \text {supp}(g)$ . That is, if and only if for every $x\in X$ such that $\text {supp}(g)\subseteq X\setminus \{ x\}$ we have $\text {supp}(f)\subseteq X\setminus \{ x\}$ . This shows that $\operatorname {\mathrm {Lsc}} (X,\overline {\mathbb {N}} )$ satisfies (C1).

To see (C2), consider the subset $\downarrow 1$ . One can see that the order is topological, and it clearly generates a semigroup that is dense in $\operatorname {\mathrm {Lsc}} (X,\overline {\mathbb {N}} )$ .

Recall that by an order unit we mean an element e such that $x\leq \infty e$ for every $x\in S$ .

Remark 4.6 Let S be an $\operatorname {\mathrm {Lsc}}$ -like $\mathrm {Cu}$ -semigroup. Since the semigroup generated by $\downarrow e$ is dense in S, e is an order unit.

Furthermore, let f be another order unit, and let $(f_{m})_{m}$ be an increasing sequence of ordered finite sums of elements below e such that $f=\sup _{m} f_{m}$ (the sums can be assumed to be ordered by Remark 4.3). Write $f_{m}=\sum _{i=1}^{r_{m}}g_{i,m}$ with $e\geq g_{i,m}\geq g_{i+1,m}$ for each $i< r_{m}$ .

Moreover, consider a $\ll $ -increasing $(e_{n})_{n}$ whose supremum is e.

Then, since $e\leq \infty f$ , one has that for every $n\in \mathbb {N}$ there exist some $k,m\in \mathbb {N}$ with $e_{n}\leq kf_{m}=\sum _{i=1}^{r_{m}} kg_{i,m}$ . Thus, since the order in $\downarrow e$ is topological and $\sum _{i=1}^{r_{m}} kg_{i,m}$ is an ordered sum of elements below e (the first k greatest elements are $g_{1,m}$ , the next k are $g_{2,m}$ , etc.), it follows that $e_{n}\leq g_{1,m}\leq f$ .

This shows $e\leq f$ and, consequently, e is the least order unit of S.

4.7 Note that an $\operatorname {\mathrm {Lsc}}$ -like $\mathrm {Cu}$ -semigroup S has no maximal idempotent elements $x<\infty $ if and only if $S= \{ 0\}$ . Indeed, if S has no maximal idempotents, then every idempotent z satisfies $z\leq 0$ by condition (C1). This implies that every idempotent element is zero and, since for every $s\in S$ the element $\infty s$ is idempotent and $\infty s\geq s$ , we get $s=0$ for every s, as desired. The converse is trivial.

Similarly, an element $s\in S$ satisfies $\infty s=\infty $ if and only if there are no maximal idempotents $x<\infty $ with $\infty s\leq x$ .

Lemma 4.8 Let S be an $\operatorname {\mathrm {Lsc}}$ -like $\mathrm {Cu}$ -semigroup, and let $y\leq ne$ , where e is the least order unit of S and $n\in \mathbb {N}$ . Then, y can be written as an ordered sum of at most n nonzero terms in $\downarrow e$ .

Proof Write y as $y=\sup _{r} y_{r}$ , where each $y_{r}$ is a finite ordered sum of elements in $\downarrow e$ (see Lemma 4.2 and Remark 4.3).

As $y_{r}\leq ne$ for each r and $\downarrow e$ is topological, each $y_{r}$ has at most n nonzero summands.

Furthermore, since $y_{r}\leq y_{r+1}$ , the kth summands of $(y_{r})_{r}$ form an increasing sequence for every k.

Taking their suprema, this shows that y is an ordered sum of at most n elements in $\downarrow e$ .

Corollary 4.9 Let S be an $\operatorname {\mathrm {Lsc}}$ -like $\mathrm {Cu}$ -semigroup. Given $y_{1},\ldots ,y_{n}\in S$ such that $y_{1}+\cdots +y_{n}\geq s$ for some $s\leq e$ , we have $y_{1}\vee \cdots \vee y_{n}\geq s$ .

Proof Take any $s'\ll s$ , and let $y^{\prime }_{i}\ll y_{i}$ be such that $y^{\prime }_{1}+\cdots +y^{\prime }_{n}\geq s'$ . Since $\infty e\geq y_{1}+\cdots + y_{n}\gg y^{\prime }_{1}+\cdots +y^{\prime }_{n}$ , there exists some $k\in \mathbb {N}$ such that $ke\geq y^{\prime }_{1}+\cdots +y^{\prime }_{n}$ .

By Lemma 4.8, each $y^{\prime }_{i}$ can be written as an ordered sum of at most k elements below e. That is, we can write $y^{\prime }_{i}=\sum _{j=1}^{k} y_{j,i}$ with $e\geq y_{j,i}\geq y_{j+1,i}$ for each $j<k$ .

Applying Lemma 4.2 iteratively, we have that $y^{\prime }_{1}+\cdots +y^{\prime }_{n}$ can be written as a finite ordered sum of elements below e, and that the greatest summand of the sum is $y_{1,1}\vee \cdots \vee y_{1,n}$ .

Since the order in $\downarrow e$ is topological, we get $y_{1,1}\vee \cdots \vee y_{1,n}\geq s'$ . It follows that

$$\begin{align*}s'\leq y_{1,1}\vee\cdots \vee y_{1,n}\leq y^{\prime}_{1}\vee\cdots\vee y^{\prime}_{n}\leq y_{1}\vee\cdots \vee y_{n}. \end{align*}$$

Since this holds for every $s'\ll s$ , we have $s\leq y_{1}\vee \cdots \vee y_{n}$ as required.

The next two lemmas will be of particular importance when working with the induced topology of an $\operatorname {\mathrm {Lsc}}$ -like $\mathrm {Cu}$ -semigroup (see Paragraph 5.1). In particular, Lemma 4.11 gives an alternative version of (C1) in Definition 4.3.

Lemma 4.10 Let S be an $\operatorname {\mathrm {Lsc}}$ -like $\mathrm {Cu}$ -semigroup with least order unit e, and let $x\in S$ . Then, $\infty x=\infty (x\wedge e)$ and $(\infty x)\wedge e=x\wedge e$ .

In particular, if $x<\infty $ is a maximal idempotent, we must have $x\wedge e\neq e$ .

Proof By Lemma 4.8 and condition (C2) in Definition 4.3, x can be written as the supremum of finite ordered sums of elements in $\downarrow e$ . Moreover, using that the order in $\downarrow e$ is topological, it follows that the sequence formed by the greatest element of each ordered sum is increasing. Let $x'$ be the supremum of such a sequence.

Then, it is clear that $\infty x=\infty x'$ and $x\wedge e=x'$ . Therefore, we have

$$\begin{align*}\infty x=\infty x' = \infty (x\wedge e), \,\,\,\text{ and }\,\,\, (\infty x)\wedge e = (\infty x')\wedge e = x'=x\wedge e, \end{align*}$$

as desired.

Lemma 4.11 Let S be an $\operatorname {\mathrm {Lsc}}$ -like $\mathrm {Cu}$ -semigroup with least order unit e. Let $y,z\leq e$ . If $z\leq x$ for every maximal element $x<e$ such that $y\leq x$ , then $z\leq y$ .

Proof If there are no maximal idempotent elements $x<\infty $ , we know that $S=\{ 0\}$ , so we may assume otherwise.

We claim that the maximal idempotent elements $x<\infty $ are precisely the elements $\infty s$ with $s<e$ maximal.

To see this, let $x<\infty $ be a maximal idempotent and take $s=x\wedge e$ . By Lemma 4.10, we have $\infty s= \infty (x\wedge e)=\infty x=x$ . Let us check that s is maximal, and thus take $t\in S$ with $s\leq t\leq e$ .

By maximality of x, we either have $\infty t=\infty $ or $\infty t=x$ . Using Lemma 4.10 once again, it follows that we have $t= (\infty t)\wedge e=\infty \wedge e = e$ or $t=x\wedge e=s$ , as required.

Conversely, let $s<e$ be maximal and consider the element $\infty s=\sup _{n} ns$ . Let $(s_k)_k$ be a $\ll $ -increasing sequence with supremum s.

Given an idempotent element x such that $\infty s\leq x\leq \infty $ , we know by Lemma 4.8 that there exists a $\ll $ -increasing sequence $(x_{m})_m$ with supremum x such that each $x_m$ can be written as a finite increasing sum of elements in $\downarrow e$ .

Let $(m_k)_k$ be an increasing sequence of integers such that $ks_{k}\leq x_{m_{k}}$ for every k.

Using that $\downarrow e$ is topological, each $s_{k}$ is less than or equal to each of the first k summands of $x_{m_{k}}$ . As in the proof of Lemma 4.10, note that the largest summands of each sum form an increasing sequence of elements below e. Letting $x'$ be the supremum of this sequence, we get $s\leq x'\leq e$ .

By maximality of s, we either have $s=x'$ or $x'=e$ . Thus, it follows from Lemma 4.10 that $\infty s= x$ or $x=\infty x'=\infty $ . This proves that $\infty s$ is a maximal idempotent, as desired.

A similar argument shows that for any $y,z\leq e$ we have $y\leq z\leq e$ if and only if $\infty y\leq \infty z$ . Consequently, if $z\leq s$ for every maximal element $s<e$ such that $y\leq s$ , we know that $\infty z\leq \infty y$ . Taking the infimum with e, one gets $z=(\infty z)\wedge e\leq (\infty y)\wedge e=y$ , as required.

Remark 4.12 Note that the previous lemma implies that $y<e$ if and only if there exists a maximal element $x<e$ with $y\leq x$ .

Recall that a complete lattice $(P,\leq )$ is said to be a complete Heyting algebra if, for every element $s\in P$ and every subset $T\subseteq P$ , the following holds:

$$\begin{align*}s\wedge (\vee_{t\in T} t)=\vee_{t\in T}(s\wedge t). \end{align*}$$

Lemma 4.13 Let S be an $\operatorname {\mathrm {Lsc}}$ -like $\mathrm {Cu}$ -semigroup with least order unit e. The subset $\downarrow e\subseteq S$ is a complete Heyting algebra.

Proof By definition, we have to see that for every subset $T\subseteq \downarrow e$ , one has $s\wedge (\vee _{t\in T} t)=\vee _{t\in T}(s\wedge t)$ for every $s\in \downarrow e$ . Thus, let $x<e$ be maximal with $x\geq \vee _{t\in T}(s\wedge t)$ , which happens if and only if $x\geq s\wedge t$ for every $t\in T$ . Since $x\neq e$ and $x\vee x\geq x\vee (s\wedge t)=(x\vee s)\wedge (x\vee t)$ , we either have $x\vee s=x$ or $x\vee t=x$ (since otherwise both of these unions would be equal to e and then $x\geq e$ , a contradiction).

If $x= x\vee s \geq s$ , we have $x\geq s\wedge (\vee _{t\in T} t)$ . Else, $x\geq t$ for each $t\in T$ , so we also get $x\geq s\wedge (\vee _{t\in T} t)$ .

By Lemma 4.11, this shows that $s\wedge (\vee _{t\in T} t)\leq \vee _{t\in T}(s\wedge t)$ .

The other inequality holds in any lattice.

Let S be a $\mathrm {Cu}$ -semigroup, and let $y,z\in S$ be a pair of elements such that $y\leq z$ . We say that an element u is the almost complement of z by y if, for every $x\in S$ , we have $x+y\leq z$ if and only if $x\leq u$ . If it exists, the almost complement is unique, and we denote by $y\setminus z$ .

Given a $\mathrm {Cu}$ -semigroup S where every pair of elements has a supremum, we say that S is sup-semilattice ordered if for every $x,y,z\in S$ we have $x+(y\vee z)=(x+y) \vee (x+z)$ .

A natural question to ask about $\operatorname {\mathrm {Lsc}}$ -like $\mathrm {Cu}$ -semigroups is if they satisfy such a property. This is indeed the case.

Lemma 4.14 Let S be an $\operatorname {\mathrm {Lsc}}$ -like $\mathrm {Cu}$ -semigroup, and let e be its least order unit. Given $y\leq z$ with $y\leq ne$ for some n, the almost complement $y\setminus z$ exists.

In particular, given $x,y,z\in S$ , we have $x+ (y\vee z)=(x+y)\vee (x+z)$ .

Proof We will construct our almost complement $y\setminus z$ in three steps.

Step 1. Let e be the least order unit of S and assume that $y\leq z\leq e$ . Then, consider the subset $T:=\{ x\in S\mid y+x\leq z \}$ and, since arbitrary suprema exist in S, we define

$$\begin{align*}y\setminus z :=\vee \{ x\in S\mid y+x\leq z \} = \vee_{x\in T}x. \end{align*}$$

Furthermore, note that, for $x\in T$ , $y+x=(y\vee x)+(y\wedge x)$ and, as $z\leq e$ and $\downarrow e$ is topological, we have $y\vee x\leq z$ and $y\wedge x=0$ .

Using that $\downarrow e$ is a complete Heyting algebra, we get $(\vee _{x\in T}x)\vee y=\vee _{x\in T} (x\vee y)\leq z$ and $(\vee _{x\in T}x)\wedge y=\vee _{x\in T}(x\wedge y)=0$ . Consequently, we get

$$\begin{align*}y+(y\setminus z)=y\vee (y\setminus z)+y\wedge (y\setminus z)=y\vee (y\setminus z)\leq z. \end{align*}$$

This shows that $x\leq y\setminus z$ if and only if $y+x\leq z$ .

Step 2. Now, given any pair of elements $y\leq z\leq ne$ for some $n\in \mathbb {N}$ , write them as finite ordered sums of elements in $\downarrow e$ , say $y=\sum _{i=1}^{n} y_{i}$ and $z=\sum _{j=1}^{n} z_{j}$ .

Since $\downarrow e$ is topological, $y_{i}\leq z_{i}\leq e$ for every i, so we can define $y\setminus z:=\sum _{i=1}^{n} y_{i}\setminus z_{i}$ .

Note that, given any element x such that $y+x\leq z\leq ne$ , we have $x\leq ne$ and so, by Lemma 4.8, x can be written as a finite ordered sum $\sum _{i=1}^{n} x_{i}$ with $x_i\leq e$ for every i. Moreover, we also have

$$\begin{align*}\sum_{i=1}^{n} y_{i}\vee x_{i}\leq y+x\leq \sum_{i=1}^{n} z_{i} \end{align*}$$

and so $y_{i}\vee x_{i}\leq z_{i}$ , which happens if and only if $x_{i}\leq y_{i}\setminus z_{i}$ .

This shows that $x+y\leq z\leq ne$ for some n if and only if $x\leq y\setminus z$ .

Step 3. Given $y\leq z\wedge ne$ for some n, we have that $y\leq z\wedge me$ for every $m\geq n$ .

Thus, we can consider the element $y\setminus (z\wedge me)$ . Furthermore, it is easy to check that $y\setminus (z\wedge me)\leq y\setminus (z\wedge (m+1)e)$ for every m. We define $y\setminus z:=\sup _{m} y\setminus (z\wedge me)$ , which has the required property.

Finally, to see that $x+ (y\vee z)=(x+y)\vee (x+z)$ for any given $x,y,z$ , note that “ $\geq $ ” is clear. To prove “ $\leq $ ,” let $x'\ll x$ and let s be such that $x'+(y\vee z)\leq s$ .

Since $x'\ll x\leq \infty e$ , there exists some n with $x'\leq ne$ , so we can consider the element $x'\setminus s$ .

Thus, we know that $x'+(y\vee z)\leq s$ holds if and only if $y\vee z\leq x'\setminus s$ , which in turn holds if and only if $x'+y,x'+z\leq s$ . Consequently, we get

$$\begin{align*}x'+(y\vee z)=(x'+y) \vee (x'+z). \end{align*}$$

Since the equality holds for every $x'\ll x$ , it also holds for x.

Lemma 4.15 Let S be an $\operatorname {\mathrm {Lsc}}$ -like $\mathrm {Cu}$ -semigroup with least order unit e, and let $x,y,z\leq e$ with $x+y\leq x+z$ . Then, $y\leq z$ .

Proof First, note that $y\leq x\vee y\leq x\vee z$ . Indeed, since $x,y,z\leq e$ and we know that $x+y=(x\vee y)+(x\wedge y)$ and $x+z=(x\vee z) +(x\wedge z)$ , we have that $(x\vee y)+ (x\wedge y)\leq (x\vee z) +(x\wedge z)$ .

Since the right- and left-hand sides of the previous inequality are ordered sums of elements below e, we can use that the order in $\downarrow e$ is topological to get $x\vee y\leq x\vee z$ , as desired.

Therefore, the sum $(z\vee x)+y$ is ordered, as we have $y\leq z\vee x$ .

Using Lemma 4.14 at the first and third steps, the inequality $x+y\leq x+z$ at the second step, and that S is distributively lattice ordered at the last step, one obtains

$$\begin{align*}\begin{aligned} (z\vee x) +y &= (y+z)\vee (y+x) \leq (y+z)\vee (z+x) = z+(y\vee x)\\ &=(z\vee y\vee x) + z\wedge (y\vee x). \end{aligned} \end{align*}$$

Using once again that the order in $\downarrow e$ is topological, it follows that $y\leq z\wedge (y\vee x)\leq z$ , as required.

By extending the previous proof, one can check that whenever $y,z\in S$ and $x\leq ne$ for some n, the same cancelation property holds. In particular, it follows that every $\operatorname {\mathrm {Lsc}}$ -like $\mathrm {Cu}$ -semigroup has weak cancelation.

Remark 4.16 Using the previous form of cancelation and the equality

$$\begin{align*}\begin{aligned} ((x+y)\vee (x+z)) + (x+(y\wedge z))&=x+y+x+z\\ &=((x+y)\vee (x+z)) + ((x+y)\wedge (x+z)), \end{aligned} \end{align*}$$

one can check that S is inf-semilattice ordered, that is to say, $x+y\wedge z=(x+y)\wedge (x+z)$ for every $x,y,z$ (see [1]). For elements $x,y,z\leq ne$ for some n, note that this simply follows by canceling the term $((x+y)\vee (x+z))$ .

Using that every element in S is the supremum of a $\ll $ -increasing sequence of finite sums of elements below e, one can then prove that the equality $x+(y\wedge z)=(x+y)\wedge (x+z)$ is always satisfied.

As one might expect, having a topological order also affects the way below relation.

Lemma 4.17 Let S be an $\operatorname {\mathrm {Lsc}}$ -like $\mathrm {Cu}$ -semigroup with least order unit e. If $y,z,y',z'\leq e$ are such that

$$\begin{align*}y+z\ll y' +z' \end{align*}$$

with $y\geq z$ and $y'\geq z'$ , we have that $y\ll y'$ and $z\ll z'$ .

The same holds for any pair of finite sums (i.e., with more than two summands).

Proof Write $y'=\sup _{n} y^{\prime }_{n}$ and $z'=\sup _{n} z^{\prime }_{n}$ with $(y^{\prime }_{n})_{n}$ and $(z^{\prime }_{n})_{n}$ $\ll $ -increasing. Since $y+z\ll y' +z'$ , we have $y+z\leq y^{\prime }_{n}+z^{\prime }_{n}$ for some n.

Moreover, as we have that $z^{\prime }_{n}\ll z'\leq y'$ , there exists a k such that $z^{\prime }_{n}\leq y^{\prime }_{k}$ . This implies that

$$\begin{align*}y+z\leq y^{\prime}_{n}+z^{\prime}_{n}\leq y^{\prime}_{\max\{n,k\} }+z^{\prime}_{n}, \end{align*}$$

and, since the order is topological, we obtain $y\leq y^{\prime }_{\max \{n,k\} }\ll y'$ and $z\leq z^{\prime }_{n}\ll z'$ .

Even though the following lemma is probably well known, we prove it here for the sake of completeness. For second countable finite-dimensional compact Hausdorff spaces, it follows from a much more general result that $\operatorname {\mathrm {Lsc}} (X,\overline {\mathbb {N}} )\in \operatorname {\mathrm {Cu}}$ (see [2, Theorem 5.15]). As a consequence of Lemma 4.18, we will have that $\operatorname {\mathrm {Lsc}} (X,\overline {\mathbb {N}} )$ is a $\mathrm {Cu}$ -semigroup whenever X is a compact metric space (see Corollary 4.19). Recently, this result has been further generalized by Elliott and Im (see [12, Proposition 1.16]).

Given $f\in \operatorname {\mathrm {Lsc}} (X,\overline {\mathbb {N}} )$ and $n\in \mathbb {N}$ , we write $\{ f\geq n\}$ to denote the open set $f^{-1}([n,\infty ])$ . For an open set $U\subseteq X$ , we denote by $\chi _U$ the indicator function of U.

Lemma 4.18 For any topological space X and any pair $f,g\in \operatorname {\mathrm {Lsc}} (X,\overline {\mathbb {N}} )$ , one has $f\ll g$ if and only if

$$\begin{align*}\chi_{\{ f\geq n\}}\ll \chi_{\{ g\geq n\}} \text{ for every }n \text{ and } \sup (f)<\infty. \end{align*}$$

Proof First, let us assume that $f\ll g$ . Fix $n\in \mathbb {N}$ and consider an increasing sequence $(h_{k})_{k}$ such that

$$\begin{align*}\chi_{\{ g\geq n\}}\leq \sup_{k} h_{k}, \end{align*}$$

which happens if and only if $\chi _{\{ g\geq n\}}\leq \chi _{\cup _{k}\text {supp}(h_{k})}$ .

Define the increasing sequence of functions

$$\begin{align*}G_{k}:= (n-1) + \chi_{\text{supp}(h_{k})} \sum_{r=0}^{\infty }\chi_{\{ g\geq n+r\}}, \end{align*}$$

and note that $g\leq \sup _{k}G_{k}$ .

Since $f\ll g$ , we get that $f\leq G_{k}$ for some k and, consequently,

$$\begin{align*}\{f\geq n\} \subseteq \{G_{k}\geq n\}=\text{supp}(h_{k})\cap \{g\geq n\}\subseteq \text{supp}(h_{k}). \end{align*}$$

This in turn implies $\chi _{\{f\geq n\}}\leq \chi _{\text {supp}(h_{k})}\leq h_{k}$ , so it follows that $\chi _{\{f\geq n\}}\ll \chi _{\{g\geq n\}}$ . That $\sup (f)<\infty $ is clear.

Conversely, if $\sup (f)<\infty $ , we know that $f=\sum _{i=1}^{m} \chi _{\{ f\geq i \}}$ for some $m<\infty $ . Furthermore, given an increasing sequence $(h_{k})_{k}$ with $g\leq \sup _{k}h_{k}$ , it follows that

$$\begin{align*}\{g\geq n\}\subseteq \bigcup_{k} \{h_{k}\geq n\}, \end{align*}$$

so $\chi _{\{ g\geq n\}}\leq \sup _{k}\chi _{\{h_{k}\geq n\}}$ . Since $\chi _{\{ f\geq n\}}\ll \chi _{\{ g\geq n\}}$ for every n, we get that for each i there exists an integer $k_{i}$ with

$$\begin{align*}\chi_{\{ f\geq i\}}\leq\chi_{\{ h_{k_{i}}\geq i\}}. \end{align*}$$

Taking $k=\max _{i=1,\ldots ,m}\{k_{i}\}$ , we have

$$\begin{align*}f\leq \sum_{i=1}^{m} \chi_{\{ h_{k}\geq i\}}\leq h_{k}, \end{align*}$$

as desired.

Corollary 4.19 Let X be a compact metric space. Then $\operatorname {\mathrm {Lsc}} (X,\overline {\mathbb {N}} )$ is a $\mathrm {Cu}$ -semigroup with pointwise order and addition.

Proof Axioms (O1) and (O4) are always satisfied in $\operatorname {\mathrm {Lsc}} (X,\overline {\mathbb {N}} )$ , so we only need to prove (O2) and (O3).

Let $U,V$ be open subsets of X, and note that $\chi _U\ll \chi _V$ if and only if U is compactly contained in V. Indeed, if $\chi _U\ll \chi _V$ , we can write V as a countable increasing union of open sets $V_n$ such that $V_n$ is compactly contained in $V_{n+1}$ for every n. Thus, one gets $\chi _U\ll \sup _n \chi _{V_n}$ , which implies that U is contained in $V_n$ for some n. Conversely, if $\overline {U}\subseteq V$ and $(W_n)_n$ is an increasing sequence of open sets with $V=\cup _n W_n$ , it is clear that $U\subseteq W_n$ for some n. This shows $\chi _U\ll \chi _V$ , as required.

In particular, it follows that every indicator function can be written as the supremum of a $\ll $ -increasing sequence. Since every element in $S=\operatorname {\mathrm {Lsc}} (X,\overline {\mathbb {N}} )$ is the supremum of finite sums of indicator functions, one can check that S satisfies (O2).

Now, let $f'\ll f$ and $g'\ll g$ in S, which by Lemma 4.18 implies that $\sup (f),\sup (g)<m\leq \infty $ and $\{ f'\geq n \}, \{ g'\geq n\}$ are compactly contained in $\{ f\geq n \}, \{ g\geq n\}$ , respectively. Thus, we have

$$\begin{align*}\bigcup_{k=0}^{m}\overline{(\{ f'\geq k \}\cap\{ g'\geq n-k \})} \subseteq \bigcup_{k=0}^{m}(\{ f\geq k \}\cap\{ g\geq n-k \}) \end{align*}$$

for every $n\leq \sup (f)+\sup (g)$ , where note that the left-hand side is equal to $\overline {\{ f'+g'\geq n\}}$ and the right-hand side is contained in $\{f+g\geq n\}$ . By Lemma 4.18, we have $f'+g'\ll f+g$ , which shows that S satisfies (O3).

5 The topological space of an Lsc-like Cu-semigroup

In this section, we associate with each $\operatorname {\mathrm {Lsc}}$ -like $\mathrm {Cu}$ -semigroup S a topological space $X_S$ . In Proposition 5.3, we prove some of the properties that such a topological space must satisfy and, using these, we show that $\operatorname {\mathrm {Lsc}} (X_S,\overline {\mathbb {N}} )$ is always a $\mathrm {Cu}$ -semigroup (see Theorem 5.9). In Theorem 6.4, we will see that S and $\operatorname {\mathrm {Lsc}} (X_S,\overline {\mathbb {N}} )$ are in fact $\operatorname {\mathrm {Cu}}$ -isomorphic.

We also introduce notions for $\mathrm {Cu}$ -semigroups that have a topological equivalent when the semigroup is $\operatorname {\mathrm {Lsc}}$ -like. More explicitly, given an $\operatorname {\mathrm {Lsc}}$ -like $\mathrm {Cu}$ -semigroup S, we characterize when $X_{S}$ is second countable, normal, and metric in terms of algebraic properties of S (see Proposition 5.6).

5.1 Let S be an $\operatorname {\mathrm {Lsc}}$ -like $\mathrm {Cu}$ -semigroup with least order unit e. The topological space $X_S$ of S is defined as

$$\begin{align*}X_{S}:=\{ x\in S\mid x<e \text{ maximal} \}, \end{align*}$$

with closed subsets

$$\begin{align*}C_{y}:=\{ x\in X_{S}\mid x\geq y\}, \quad y\leq e. \end{align*}$$

We check that this is indeed a topology for $X_{S}$ .

Lemma 5.2 Let S be an $\operatorname {\mathrm {Lsc}}$ -like $\mathrm {Cu}$ -semigroup. Then, $\{X_S\setminus C_y \mid y\leq e\}$ is a $T_1$ -topology for $X_{S}$ .

Proof First, note that $C_{0}=X_S$ and that $C_{e}=\emptyset $ . Moreover, $C_{x}=\{ x\}$ for every $x\in X_S$ . Thus, our topology is $T_1$ .

To see that arbitrary intersections of $C_{y}$ ’s are of the form $C_{z}$ for some $z\leq e$ , simply note that

$$\begin{align*}\bigcap_{i} C_{y_{i}} = C_{\vee_{i}y_{i}}. \end{align*}$$

Furthermore, one also has that

$$\begin{align*}\bigcup_{i=1}^{n} C_{y_{i}} = C_{\wedge_{i=1}^{n}y_{i}}. \end{align*}$$

Indeed, given $x\in X_S$ with $x\geq \wedge _{i=1}^{n}y_{i}$ , we have

$$\begin{align*}x= x\vee x \geq x\vee (\wedge_{i=1}^{n}y_{i})=(x\vee y_{1})\wedge \cdots\wedge (x\vee y_{n}). \end{align*}$$

Since x is maximal, for each i, we either have $x\vee y_{i}=x$ or $x\vee y_{i}=e$ .

However, note that the previous inequality implies that we cannot have $x\vee y_{i}=e$ for every i, so $x=x\vee y_{j}\geq y_{j}$ for some j.

The other inclusion is clear.

Retaining the above notation, for every $y\leq e$ , we will denote by $U_y$ its associated open subset. That is, $U_y=X\setminus C_y$ .

We list some properties of these sets. Recall that, for every pair of elements $y\leq z\leq e$ , the element $y\setminus z$ denotes the almost complement of z by y, as constructed in Lemma 4.14.

Proposition 5.3 Let S be an $\operatorname {\mathrm {Lsc}}$ -like $\mathrm {Cu}$ -semigroup with least order unit e. Then:

1. (i) For every $y,z\leq e$ , $C_{y}\subseteq C_{z}$ if and only if $y\geq z$ .

2. (ii) For every $y\leq e$ , $U_y = \{x\in X_{S}\mid y\vee x=e\}$ .

3. (iii) Given $y,z\leq e$ such that $U_{y}\subseteq C_{z}$ , we have $y\wedge z=0$ .

4. (iv) The closure of $U_{y}$ , denoted by $\overline {U_{y}}$ , is $C_{y\setminus e}$ for every $y\leq e$ .

5. (v) Given $y\leq e$ , we have $\operatorname {\mathrm {Int}} (C_{y})=X_S\setminus \overline {(X_S\setminus C_{y})}=U_{y\setminus e}$ , where $\operatorname {\mathrm {Int}} (C_{y})$ stands for the interior of $C_y$ .

6. (vi) For every $y,z\leq e$ , $C_{y}\subseteq U_{z}$ if and only if $y\vee z=e$ .

Proof To see (i), recall that, by definition, $C_{y}\subseteq C_{z}$ if and only if $x\geq z$ for every $x\geq y$ with $x<e$ maximal. Using Lemma 4.11, we see that this is equivalent to $y\geq z$ .

For (ii), let $y\leq e$ and take $x<e$ be maximal. Thus, we have $x\leq y\vee x\leq e$ . Since x is maximal, we either have $x=y\vee x\geq y$ (i.e., $x\in C_{y}$ ) or $y\vee x=e$ . Thus, $U_{y}= \{ x\in X_S: y\vee x=e \}$ .

To prove (iii), let us assume, for the sake of contradiction, that $y\wedge z\neq 0$ . Then, $U_{y\wedge z}$ is nonempty and we can consider a maximal element $x\in U_{y\wedge z}$ .

By (ii), we have $x\vee (y\wedge z)=e$ . Thus, one gets $x\vee y=e$ and, consequently, $x\geq z$ from our assumption that $U_y \subseteq C_z$ . However, we also have

$$\begin{align*}e= x\vee (y\wedge z) = (x\vee y)\wedge (x\vee z) = e\wedge x=x, \end{align*}$$

which is a contradiction, as required.

Let us now prove (iv) and, consequently, (v). First, note that, if $y\vee x=e$ , we have

$$\begin{align*}y+x=(y\vee x) + (y\wedge x)\geq e\geq y\setminus e +y. \end{align*}$$

Canceling y (see Lemma 4.15), we have that $x\geq y\setminus e$ . This shows $U_{y}\subseteq C_{y\setminus e}$ .

Conversely, let z be such that $U_{y}\subseteq C_{z}$ . By (iii), we know that this implies $y\wedge z=0$ and, consequently, $y+z\leq e$ . Thus, $z\leq y\setminus e$ or, equivalently, $C_{y\setminus e}\subseteq C_{z}$ .

Finally, for (vi), assume first that $C_{y}\subseteq U_{z}$ . Furthermore, assume for the sake of contradiction that $y\vee z\neq e$ . Then, there exists $x\in X_{S}$ with $x\geq y\vee z$ . This implies $x\geq y$ and, consequently, $x\vee z=e$ from $C_y\subseteq U_z$ . However, we have

$$\begin{align*}x = x\vee y\vee z \geq x\vee z=e, \end{align*}$$

which is a contradiction.

Conversely, if $y\vee z=e$ , take $x\geq y$ , which implies that $x\vee z\geq y\vee z=e$ . In particular, $x\in U_{z}$ .

Example 5.4 Let X be a $T_{1}$ topological space. Recall from Example 4.5 that $S=\operatorname {\mathrm {Lsc}} (X, \overline {\mathbb {N}} )$ is an $\operatorname {\mathrm {Lsc}}$ -like $\mathrm {Cu}$ -semigroup with least order unit $1$ . Then, the topological space of S is homeomorphic to X.

Indeed, note that the maximal elements below $1$ are the characteristic functions $\chi _{X\setminus \{ x \}}$ . Thus, we have

$$\begin{align*}X_{S} =\{ \chi_{X\setminus\{ x \}}\mid x\in X \} \end{align*}$$

and

$$\begin{align*}\begin{aligned} U_{\chi_{\mathcal{U}}} &= X_{S}\setminus C_{\chi_{\mathcal{U}}}= X_{S}\setminus\{ \chi_{X\setminus\{ x \}} \mid \chi_{X\setminus\{ x \}}\geq \chi_{\mathcal{U}} \}\\ &= X_{S}\setminus\{ \chi_{X\setminus\{ x \}}\mid x\in X\setminus\mathcal{U} \} = \{ \chi_{X\setminus\{ x \}}\mid x\in\mathcal{U} \} \end{aligned} \end{align*}$$

for every open subset $\mathcal {U}\subseteq X$ .

It should now be clear that $\varphi \colon X_{S}\rightarrow X$ defined as $\chi _{X\setminus \{ x \}}\mapsto x$ is a homeomorphism between X and $X_{S}$ .

The following characterizes compact containment under certain conditions.

Lemma 5.5 Let S be an $\operatorname {\mathrm {Lsc}}$ -like $\mathrm {Cu}$ -semigroup with least order unit e. Assume that e is compact and that S satisfies (O5). Then $X_S$ is normal.

Furthermore, given $y,z\leq e$ , we have $\overline {U_{y}}\subseteq U_{z}$ if and only if $y\ll z$ .

Proof Let $x,y<e$ be two elements such that $C_{x}\cap C_{y}=C_{e}=\emptyset $ . In terms of the elements in S, this is equivalent to $x+y\geq e\gg e$ . Then, we can take $x'\ll x$ and $y'\ll y$ such that $x'+y'\gg e$ .

Using (O5), there exist $c,d\leq e$ such that

$$\begin{align*}x'+c\leq e\leq x+c, \quad y'+d\leq e\leq y+d. \end{align*}$$

Consequently, we also have $x'+c+y'+d\leq e+e$ with $x'+y'\gg e$ . Since every $\operatorname {\mathrm {Lsc}}$ -like $\mathrm {Cu}$ -semigroup has weak cancelation, it follows that $c+d\leq e$ .

Since our order is topological, we get $c\wedge d=0$ , $x\vee c= e$ , and $y\vee d=e$ .

Using the properties listed in Proposition 5.3, the previous inequalities imply that $C_{x}\subseteq U_{c}$ , $C_{y}\subseteq U_{d}$ , and $U_{c}\cap U_{d}= U_{c\wedge d}=\emptyset $ . Thus, $X_{S}$ is normal.

Now, let $y,z\leq e$ and assume that $\overline {U_{y}}\subseteq U_{z}$ , which by (iv) in Proposition 5.3 happens if and only if $(y\setminus e)\vee z=e$ . Furthermore, since $y\setminus e + z\geq e$ , we have $y\setminus e + z\geq e\gg e\geq y\setminus e + y$ . As elements below e have cancelation (see Lemma 4.15), one gets $z\gg y$ .

Conversely, assume that $e\geq z\gg y$ . Then, by (O5), there exists an element x such that $y+x\leq e$ and $e\leq z+x$ .

From the first inequality, it follows that $x\leq y\setminus e$ , so $e\leq z+x\leq z+y\setminus e$ as required.

In Proposition 5.6, we study notions for $\mathrm {Cu}$ -semigroups that have a topological equivalent when the semigroup is $\operatorname {\mathrm {Lsc}}$ -like. Recall from Paragraph 2.3 that a $\mathrm {Cu}$ -semigroup is said to be countably based if it has a countable sup-dense subset.

Definition 5.1 We say that an inf-semilattice ordered $\mathrm {Cu}$ -semigroup S is normal if there exists an order unit $z\in S$ such that, whenever $x+ y\geq z$ for some $x,y\in S$ , there exist $s,t\in S$ with

$$\begin{align*}x+ s\geq z, \quad y+ t\geq z, \quad s\wedge t=0. \end{align*}$$

Proposition 5.6 Let S be an $\operatorname {\mathrm {Lsc}}$ -like $\mathrm {Cu}$ -semigroup, and let $X_S$ be its associated topological space. Then:

1. (i) $X_{S}$ is second countable if and only if S is countably based.

2. (ii) $X_{S}$ is countably compact if and only if S has a compact order unit.

3. (iii) $X_S$ is normal if and only if S is normal.

4. (iv) $X_{S}$ is a metric space whenever S is countably based and normal.

5. (v) $X_S$ is a compact metric space whenever S is countably based, has a compact order unit, and satisfies (O5).

Proof Let $e\in S$ be the least order unit of S. To show (i), assume first that S is countably based with a countable basis B, and let $\sum '(\downarrow e)$ denote the set of finite sums of elements in $\downarrow e$ . Naturally, the set $B':=B\cap \sum '(\downarrow e)$ is also a countable basis for S.

Given an open set $U_{y}$ with $y\leq e$ , write $y=\sup _{n} y_{n}$ with $y_{n}\in B'$ . We have $\cup _{n} U_{y_{n}} = U_{y}$ , and so $X_{S}$ is second countable.

Conversely, assume that $X_{S}$ is second countable with basis $C=\{U_{z_{n}}\}_{n}$ . Note that the family $C'$ consisting of all the finite unions of sets in C is also countable.

Then, any open subset $U_{y}$ can be written as the countable union of increasing open subsets $U_{z^{\prime }_{n}}$ of $C'$ . We know that this is equivalent to $y=\sup _{n}z^{\prime }_{n}$ . This implies that the set $\sum ' \{ z^{\prime }_{n}\}_{n}$ of finite sums from $\{ z^{\prime }_n\}_n$ is a countable basis for $\sum ' (\downarrow e)$ and, since $\sum ' (\downarrow e)$ is dense in S, $\sum ' \{ z^{\prime }_{n}\}_{n}$ is a countable basis for S.

To prove (ii), note that it is easy to check that $e\in S$ is compact if and only if $X_{S}$ is countably compact. Therefore, we are left to prove that, if there exists a compact order unit in S, then e must also be compact.

To see this, let p be a compact order unit in S, which implies that $p\leq ne$ for some $n\in \mathbb {N}$ . Since we know that p can be written as a finite ordered sum of elements below e, there exist $m\in \mathbb {N} $ and elements $q_{m}\leq \cdots \leq q_{1}\leq e$ such that $p=q_{1}+\cdots +q_{m}$ .

By weak cancelation applied to $q_1+\cdots +q_m\ll q_1+\cdots +q_m$ , the element $q_{1}$ is compact and satisfies $\infty q_{1}=\infty p=\infty $ . Thus, $q_{1}$ is a compact order unit with $e\geq q_{1}$ . By minimality of e, one gets $e=q_{1}$ compact as required.

Let us now show (iii). First, assume that S is normal, and let z be the associated order unit. Let $C_x , C_y$ be closed subsets of $X_S$ with $x,y\leq e$ , and recall that $C_{x}, C_{y}$ are disjoint if and only if $x\vee y=e$ .

Since e is an order unit, we have $\infty x + \infty y= \infty \geq z$ . Thus, we get $s,t$ such that $\infty x +s\geq z$ , $\infty y +t\geq z$ , and $s\wedge t=0$ . As $z\geq e$ , we know by Corollary 4.9 that $\infty x\vee s\geq e$ and $\infty y\vee t\geq e$ .

Since $x,y\leq e$ , taking the infimum with e and using Lemma 4.10, we have $e=(\infty x\wedge e)\vee (s\wedge e)=x\vee (s\wedge e)$ , $y\vee (t\wedge e)=e$ , and $(s\wedge e)\wedge (t\wedge e)=0$ . By (vi) in Proposition 5.3, it follows that $C_{x}\subseteq U_{s\wedge e}$ , $C_{y}\subseteq U_{t\wedge e}$ , and $U_{s\wedge e}\cap U_{t\wedge e}=\emptyset $ . This implies that $X_{S}$ is normal.

Conversely, if $X_{S}$ is normal, it is easy to see that S is normal by setting $z=e$ in the definition of normality.

To prove (iv), we have that $X_{S}$ is second countable and normal by (i) and (iii), and that $C_{x}=\{x \}$ for any $x\in X_{S}$ . Thus, points are closed in our topology, so $X_{S}$ is Hausdorff. We can now use Urysohn’s metrization theorem to conclude that $X_{S}$ is metric (see, e.g., [16, Theorem 34.1]).

For (v), note that $e\ll e$ . Thus, Lemma 5.5 implies that $X_S$ is normal. Following the arguments above, one gets that $X_S$ is metric. Moreover, we also know that $X_S$ is second countable and countably compact by (i) and (ii) above. Thus, $X_S$ is compact.

We will now show that $\operatorname {\mathrm {Lsc}} (X_{S},\overline {\mathbb {N}} )$ is a $\mathrm {Cu}$ -semigroup with the usual way-below relation for every $\operatorname {\mathrm {Lsc}}$ -like $\mathrm {Cu}$ -semigroup S. Note that (O1) and (O4) are always satisfied, so we are left to prove (O2) and (O3).

Lemma 5.7 Let S be an $\operatorname {\mathrm {Lsc}}$ -like $\mathrm {Cu}$ -semigroup with least order unit e. Given $y,z\leq e$ , we have $\chi _{U_{y}}\ll \chi _{U_{z}}$ in $\operatorname {\mathrm {Lsc}} (X_{S},\overline {\mathbb {N}} )$ if and only if $y\ll z$ in S.

Proof Assume $y\ll z$ , and let $(f_{n})_{n}$ be an increasing sequence in $\operatorname {\mathrm {Lsc}} (X_{S},\overline {\mathbb {N}} )$ such that $\chi _{U_{z}}\leq \sup _{n} f_{n}$ . In particular, note that this holds if and only if $\chi _{U_{z}}\leq \chi _{\cup _{n} \text {supp}(f_{n})}$ or, equivalently, if

$$\begin{align*}\bigcap_{n}(X_S\setminus\text{supp}(f_{n})) \subseteq C_{z}.\\[-9pt] \end{align*}$$

Denote by $z_{n}$ the elements in $\downarrow e$ with $C_{z_{n}}=X_S\setminus \text {supp}(f_{n})$ . Given that $\text {supp}(f_{n})\subseteq \text {supp}(f_{n+1})$ , (i) in Proposition 5.3 implies that $z_{n}$ is increasing.

Using the proof of Lemma 5.2 in the first step, we can rewrite the previous inclusion as

$$\begin{align*}C_{\sup_{n}(z_{n})} = \bigcap_{n} C_{z_n}\subseteq C_{z}.\\[-9pt] \end{align*}$$

Applying (i) in Proposition 5.3 once again, one gets $z\leq \sup _{n}(z_{n})$ and, consequently, $y\leq z_{n}$ for some n. This implies that $U_{y}\subseteq U_{z_{n}}$ or, equivalently, that $\chi _{U_{y}}\leq \chi _{U_{z_{n}}}= \chi _{\text {supp}(f_{n})}\leq f_{n}$ . This shows $\chi _{U_{y}}\ll \chi _{U_{z}}$ .

Now, let $y,z\leq e$ be such that $\chi _{U_{y}}\ll \chi _{U_{z}}$ , and consider an increasing sequence $(h_{n})_{n}$ in S such that $z\leq \sup _{n}(h_{n})$ . Note that, by taking $z\wedge h_{n}$ instead of $h_{n}$ , we can assume $h_{n}\leq e$ for every n.

Applying again (the proof of) Lemma 5.2, one gets

$$\begin{align*}\bigcap_{n} C_{h_{n}}=C_{\sup_{n}(h_{n})}\subseteq C_{z}, \end{align*}$$

and, consequently, we have $\sup _{n}\chi _{U_{h_{n}}}\geq \chi _{U_{z}}$ since $\chi _{U_{y}}\ll \chi _{U_{z}}$ , there exists some n with $\chi _{U_{y}}\leq \chi _{U_{h_{n}}}$ ; i.e., $C_{h_n}\subseteq C_y$ .

Using (i) in Proposition 5.3 one last time, one sees that $y\leq h_{n}$ as required.

Proposition 5.8 Let S be a $\mathrm {Cu}$ -semigroup. If S is $\operatorname {\mathrm {Lsc}}$ -like, then $\operatorname {\mathrm {Lsc}} (X_{S},\overline {\mathbb {N}} )$ satisfies (O2).

Proof Take $f\in \operatorname {\mathrm {Lsc}} (X_{S},\overline {\mathbb {N}} )$ , and let $(y_{i})_{i}$ be the sequence on $\downarrow e$ such that

$$\begin{align*}\{f\geq i\} = U_{y_{i}}, \end{align*}$$

where recall that the sequence is decreasing as a consequence of (i) in Proposition 5.3.

Since S satisfies (O2), we have $y_{i}=\sup _{n} y_{i,n}$ with $y_{i,n}\ll y_{i,n+1}$ for every n.

For every fixed k, we have

$$\begin{align*}y_{1}\geq\cdots\geq y_{k}\gg y_{k,n} \text{ for all }n. \end{align*}$$

Thus, for every i, one can choose inductively $n_{i,k}$ with $k\geq i$ such that

$$\begin{align*}y_{i,n_{i,k}}\ll y_{i,n_{i,k+1}}, \,\,\,\text{ and }\,\,\, y_{1,n_{1,k}}\geq\cdots\geq y_{k,n_{k,k}}. \end{align*}$$

Indeed, we begin by setting $n_{1,1}=1$ (i.e., $y_{1,n_{1,1}}=y_{1,1}$ ). Then, assuming that we have defined $n_{i,k}$ for every $i,k\leq m-1$ (and $k\geq i$ ) for some fixed m, we set $n_{m,m}=1$ , that is, $y_{m,n_{m,m}}=y_{m,1}$ . We then set $n_{m-1,m}$ large enough so that $y_{m-1,n_{m-1,m}}\geq y_{m,n_{m,m}}$ and $n_{m-1,m}\geq n_{m-1,m-1}$ . Similarly, we set $n_{m-2,m}\geq n_{m-2,m-1}$ such that $y_{m-2,n_{m-2,m}}\geq y_{m-1,n_{m-1,m}}$ and define $n_{i,m}$ for every $i\leq m-2$ in the same fashion.

Now, consider the sums $f_{k}=\sum _{i=1}^{k} \chi _{U_{y_{i,n_{i,k}}}}$ , which are ordered by construction. Thus, one has $U_{y_{i,n_{i,k}}}=\{ f_k\geq i\}$ for every i. Since $y_{i,n_{i,k}}\ll y_{i,n_{i,k+1}}$ for every i, it follows from Lemmas 4.18 and 5.7 that

$$\begin{align*}f_{k}=\sum_{i=1}^{k} \chi_{U_{y_{i,n_{i,k}}}}\ll \sum_{i=1}^{k} \chi_{U_{y_{i,n_{i,k+1}}}} \leq f_{k+1}. \end{align*}$$

It is now easy to check that $\sup _{k} f_{k}=f$ .

Theorem 5.9 Let S be a $\mathrm {Cu}$ -semigroup. If S is $\operatorname {\mathrm {Lsc}}$ -like, the monoid $\operatorname {\mathrm {Lsc}} (X_{S},\overline {\mathbb {N}} )$ is a $\mathrm {Cu}$ -semigroup.

Proof Note that the semigroup $\operatorname {\mathrm {Lsc}} (X_S ,\overline {\mathbb {N}} )$ always satisfies (O1) and (O4). Moreover, we already know that (O2) is also satisfied by Proposition 5.8. Thus, we are left to prove (O3).

Let $f\ll f'$ and $g\ll g'$ . By Lemma 4.18, this implies that

$$\begin{align*}\chi_{\{ f\geq i\}} \ll \chi_{\{ f'\geq i\}}\,\,\,\text{ and }\,\,\, \chi_{\{ g\geq i\}} \ll \chi_{\{ g'\geq i\}} \end{align*}$$

for every i. We also know that there exists $m<\infty $ such that $\sup (f),\sup (g)\leq m$ .

Let $y_{i},y^{\prime }_{i},z_{i}$ , and $z^{\prime }_{i}$ be elements in $\downarrow e$ such that

$$\begin{align*}U_{y_{i}}= \{ f\geq i\},\quad U_{y^{\prime}_{i}}= \{ f'\geq i\},\quad U_{z_{i}}= \{ g\geq i\},\,\,\,\text{ and }\,\,\, U_{z^{\prime}_{i}}= \{ g'\geq i\}. \end{align*}$$

By Lemma 5.7, we have $y_{i}\ll y^{\prime }_{i}$ and $z_{i}\ll z^{\prime }_{i}$ for every i and, since S satisfies (O3), one gets

$$\begin{align*}\sum_{i=1}^{m} (y_{i}+z_{i}) \ll \sum_{i=1}^{m} (y^{\prime}_{i}+z^{\prime}_{i}). \end{align*}$$

By Lemma 4.2, these sums can be rewritten as

$$\begin{align*}\sum_{i=1}^{2m} \vee_{j=0}^{m}(y_{j}\wedge z_{i-j}) \ll \sum_{i=1}^{2m} \vee_{j=0}^{m}(y^{\prime}_{j}\wedge z^{\prime}_{i-j}) \end{align*}$$

and, since both the right- and left-hand sides of the previous inequality are ordered, we can use Lemma 4.17 to obtain

$$\begin{align*}\vee_{j=0}^{m}(y_{j}\wedge z_{i-j}) \ll \vee_{j=0}^{m}(y^{\prime}_{j}\wedge z^{\prime}_{i-j}) \end{align*}$$

for every i.

Note that

$$\begin{align*}\{ f+g\geq i \} = \bigcup_{j=0}^{m}(\{ f\geq j \}\cap\{ g\geq i-j \}), \end{align*}$$

so, by the equalities in the proof of Lemma 5.2, one gets

$$\begin{align*}X_S\setminus\{ f+g\geq i \} &= \bigcap_{j=0}^{m} ((X_S\setminus \{ f\geq j \})\cup (X_S\setminus\{ g\geq i-j \})) = \bigcap_{j=0}^{m} (C_{y_{j}\wedge z_{i-j}})\\ &= C_{\vee_{j=0}^{m}(y_{j}\wedge z_{i-j})} \end{align*}$$

and, consequently, $\chi _{\{ f+g\geq i \}} = \chi _{U_{\vee _{j=0}^{m}(y_{j}\wedge z_{i-j})}}$ .

The same argument also shows that $\chi _{\{ f'+g'\geq i \}}\geq \chi _{ U_{\vee _{j=0}^{m}(y^{\prime }_{j}\wedge z^{\prime }_{i-j})}}$ .

By using Lemma 5.7, we get $\chi _{\{ f+g\geq i \}}\ll \chi _{\{ f'+g'\geq i \}}$ for every i. Lemma 4.18 then implies that $f+g\ll f'+g'$ , as desired.

6 An abstract characterization of Lsc(X,N)

In this section, we prove that every $\operatorname {\mathrm {Lsc}}$ -like $\mathrm {Cu}$ -semigroup S is $\operatorname {\mathrm {Cu}}$ -isomorphic to the semigroup of lower-semicontinuous functions $ \operatorname {\mathrm {Lsc}}(X_{S},\overline {\mathbb {N}} )$ (see Theorem 6.4). To do so, we first define a map $\varphi '\colon \operatorname {\mathrm {Lsc}}(X_{S},\overline {\mathbb {N}} )_{fs} \rightarrow S$ , where $\operatorname {\mathrm {Lsc}} (X_{S},\overline {\mathbb {N}} )_{fs}$ is the subsemigroup of functions with finite supremum.

We then extend this map to a $\mathrm {Cu}$ -morphism $\varphi \colon \operatorname {\mathrm {Lsc}} (X_{S},\overline {\mathbb {N}} ) \rightarrow S$ . Finally, the following (probably well-known) lemma will be used to complete the proof.

Lemma 6.1 Let $S,H$ be $\mathrm {Cu}$ -semigroups, and let $\varphi \colon S\rightarrow H$ be a $\mathrm {Cu}$ -morphism such that:

1. (i) $\varphi $ is an order embedding on a basis of S.

2. (ii) $\varphi (S)$ is a basis for H.

Then, $\varphi $ is a $\operatorname {\mathrm {Cu}}$ -isomorphism

Proof It is easy to see that $\varphi $ is a global order embedding.

To prove surjectivity, let $h\in H$ . Since $\varphi (S)$ is a basis for H, we can write $h=\sup _{n} \varphi (s_{n})$ for some $s_{n}\in S$ . Furthermore, as we know that $\varphi $ is an order embedding, the sequence $(s_{n})_{n}$ is increasing in S, so $\sup _{n} \varphi (s_{n})=\varphi (s)$ for $s=\sup _{n} s_{n}$ .

Definition 6.1 Let S be an $\operatorname {\mathrm {Lsc}}$ -like $\mathrm {Cu}$ -semigroup. Given $f\in \operatorname {\mathrm {Lsc}} (X_{S},\overline {\mathbb {N}} )_{fs}$ , there exists $m<\infty $ such that we can write

$$\begin{align*}f=\sum_{i=1}^{m} \chi_{\{ f\geq i \}}.\\[-9pt] \end{align*}$$

We define the map $\varphi '\colon \operatorname {\mathrm {Lsc}} (X_{S},\overline {\mathbb {N}} )_{fs}\rightarrow S$ as $\varphi '(f)=\sum _{i=1}^{m}z_{i}$ , where $\{ f\geq i \}=U_{z_{i}}$ .

Lemma 6.2 $\varphi '$ is a positively ordered monoid morphism and an order embedding.

Proof Let $f=\sum _{i=1}^{m} \chi _{U_{z_{i}}}$ as above and take $g=\sum _{j=1}^{n} \chi _{U_{y_{j}}}$ . We will first prove by induction on m that $\varphi ' (f+g)=\varphi '(f)+\varphi '(g)$ .

For $m=1$ , f is simply $\chi _{U_{z}}$ for some open subset $U_{z}$ . Since $\operatorname {\mathrm {Lsc}} (X_{S},\overline {\mathbb {N}} )$ is distributively lattice ordered and $0\leq 0\leq \cdots \leq 0\leq f$ is an increasing sequence, we can apply Lemma 4.2 to get

$$\begin{align*}f + \sum_{j=1}^{n} \chi_{U_{y_{j}}} = \chi_{U_{z}\cup U_{y_{1}}} + \chi_{(U_{z}\cap U_{y_{1}})\cup U_{y_{2}} } + \cdots + \chi_{U_{z}\cap (\cap_{j} U_{y_{j}})}.\\[-9pt] \end{align*}$$

Applying $\varphi '$ and the equalities in the proof of Lemma 5.2 at the first step, and Lemma 4.2 at the second step, one gets

$$\begin{align*}\begin{aligned} \varphi'(f+g) &= (z\vee y_{1}) + ((z\wedge y_{1})\vee y_{2}) + \cdots + (z\wedge y_{1}\wedge\cdots\wedge y_{n})\\ &=z+(y_{1}+\cdots +y_{n}) = \varphi'(f)+ \varphi'(g). \end{aligned} \end{align*}$$

Now, fix any finite m and assume that the result has been proved for any $k\leq m-1$ . Then, using the induction hypothesis at the second step, and the case $m=1$ at the third and fourth steps, we have

$$\begin{align*}\begin{aligned} \varphi '(f+g) &= \varphi' ( (f-\chi_{U_{z_{m}}}) + (g+\chi_{U_{z_{m}}}) ) = \varphi' ( f-\chi_{U_{z_{m}}}) + \varphi' (g+\chi_{U_{z_{m}}})\\ &= \varphi' ( f-\chi_{U_{z_{m}}}) + \varphi' (g) + \varphi' (\chi_{U_{z_{m}}})= \varphi' ( f-\chi_{U_{z_{m}}}+\chi_{U_{z_{m}}}) + \varphi' (g)\\ &= \varphi' (f) + \varphi' (g), \end{aligned} \end{align*}$$

as desired.

Note that this could have also been proved using Lemma 4.2.

To see that $\varphi '$ is an order embedding, let $f\leq g$ in $\operatorname {\mathrm {Lsc}} (X_{S},\overline {\mathbb {N}} )_{fs}$ and note that $f\leq g$ if and only if $\{ f\geq i\}\subseteq \{ g\geq i\}$ for every i. Let $z_i, y_i\in S$ be such that $U_{z_i}=\{ f\geq i\}$ and $U_{y_i}=\{ g\geq i\}$

By (i) in Proposition 5.3, $U_{z_i}\subseteq U_{y_i}$ if and only if $z_{i}\leq y_{i}$ for every i. Furthermore, note that the sequences $(z_{i})_{i=1}^{m},(y_{i})_{i=1}^{m}$ are both decreasing. Since we have a topological order, $z_{i}\leq y_{i}$ for every i if and only if

$$\begin{align*}\sum_{i=1}^{m} z_{i}\leq \sum_{i=1}^{m} y_{i}, \end{align*}$$

where note that the right- and left-hand sides correspond to $\varphi '(f)$ and $\varphi '(g)$ , respectively.

Using $\varphi '$ , one can now construct a $\operatorname {\mathrm {Cu}}$ -isomorphism.

Theorem 6.3 Let S be an $\operatorname {\mathrm {Lsc}}$ -like $\mathrm {Cu}$ -semigroup. Then, the $\mathrm {Cu}$ -morphism $\varphi '$ extends to a $\operatorname {\mathrm {Cu}}$ -isomorphism.

Proof We will need the following claims.

Claim 1 Let $(f_{n})_{n}$ and $(g_{n})_{n}$ be two $\ll $ -increasing sequences with the same supremum in $\operatorname {\mathrm {Lsc}} (X_S ,\overline {\mathbb {N}} )$ . Then, $\sup _{n}\varphi '(f_{n})=\sup _{n}\varphi '(g_{n})$ .

Since $(f_{n})_{n}$ and $(g_{n})_{n}$ have the same supremum, we know that for every n there exist $k,m$ such that $f_{n}\leq g_{m}$ and $g_{n}\leq f_{k}$ .

Applying $\varphi '$ , we get

$$\begin{align*}\varphi'(f_{n})\leq \varphi'(g_{m})\leq \sup_{m}\varphi'(g_{m}),\,\,\,\text{ and }\,\,\, \varphi'(g_{n})\leq \varphi'(f_{k})\leq \sup_{k}\varphi'(f_{k}), \end{align*}$$

and so $\sup _{k}\varphi '(f_{k})=\sup _{m}\varphi '(g_{m})$ as desired.

By Claim 1, we can define the map $\varphi \colon \operatorname {\mathrm {Lsc}} (X_{S},\overline {\mathbb {N}} )\rightarrow S$ as $\varphi (f)=\sup _{n}\varphi '(f_{n})$ , where $(f_{n})_{n}$ is a $\ll $ -increasing sequence with supremum f. We will see that $\varphi $ is a $\mathrm {Cu}$ -morphism that extends $\varphi '$ and that it satisfies the conditions in Lemma 6.1 (i.e., $\varphi $ is a $\operatorname {\mathrm {Cu}}$ -isomorphism).

Claim 2 Let $(f_{n})_{n}$ be an increasing sequence in $\operatorname {\mathrm {Lsc}} (X_{S},\overline {\mathbb {N}} )_{fs}$ with supremum $f=\sup f_n\in \operatorname {\mathrm {Lsc}} (X_{S},\overline {\mathbb {N}} )_{fs}$ . Then, we have $\varphi '(f)=\sup _{n}\varphi '(f_{n})$ .

To prove the claim, let $f_{n}=\chi _{U_{z_{n}}}$ for every n, and recall that $\sup _{n}\chi _{U_{z_{n}}}=\chi _{U_{\sup _{n}(z_{n})}}$ . This is equivalent to

$$\begin{align*}\varphi'(\sup_{n}f_{n})=\sup_{n}(z_{n})=\sup_{n}\varphi'(f_{n}). \end{align*}$$

Now, given any increasing sequence as in the statement of the lemma with supremum f, we know that $\sup (f)<\infty $ , say $\sup (f)=m\in \mathbb {N}$ .

Thus, given $U_{i,n}=\{f_{n}\geq i\}$ for $1\leq i\leq m$ , we can write

$$\begin{align*}f_{n}=\sum_{i=1}^{m} \chi_{U_{i,n}} \end{align*}$$

with some possibly empty $U_{i,n}$ ’s.

We have

$$\begin{align*}f=\sup_{n} (f_{n})=\sum_{i=1}^{m} \chi_{\cup_{n}U_{i,n}}, \end{align*}$$

where $\cup _{n}U_{i,n}=\{ f\geq i\}$ .

Using that $\varphi '$ preserves suprema of indicator functions, we have

$$\begin{align*}\varphi'(f)= \sum_{i=1}^{m} \varphi'(\chi_{\cup_{n}U_{i,n}})= \sup_{n}\varphi'(\sum_{i=1}^{m}\chi_{U_{i,n}})=\sup_{n}\varphi'(f_{n}), \end{align*}$$

as required.

Since $\varphi '$ preserves addition and S is a $\operatorname {\mathrm {Cu}}$ -semigroup, it is clear that $\varphi $ also preserves addition. Note that the proof of Claim 2 also shows that $\varphi $ extends $\varphi '$ and that $\varphi $ is order-preserving.

To see that $\varphi $ preserves suprema, let $\varphi (f)=\sup _{n}\varphi '(f_{n})$ with $(f_{n})_{n} \ \ll $ -increasing with supremum f and consider an increasing sequence $(g_{n})_{n}$ whose supremum is also f.

Then, for every n, there exists an m with $f_{n}\leq g_{m}$ and, consequently, $\varphi '(f_{n})=\varphi (f_{n})\leq \varphi (g_{m})$ . It follows that $\varphi (f)=\sup _{n}\varphi '(f_{n})\leq \sup _{m}\varphi (g_{m})$ .

On the other hand, $f\geq g_{m}$ for every m, so $\varphi (f)=\sup _{m}\varphi (g_{m})$ .

Now, let $f,g\in \operatorname {\mathrm {Lsc}} (X_{S},\overline {\mathbb {N}} )$ be such that $f \ll g$ . Then, we know by Lemma 4.18 that this happens if and only if

$$\begin{align*}\chi_{\{ f\geq i\}}\ll \chi_{\{ g\geq i\}} \text{ for every } i \,\,\,\text{ and }\,\,\, \sup (f)=m<\infty. \end{align*}$$

Letting $y_i, z_i\in S$ such that $U_{y_{i}}= \{ f\geq i\}$ and $U_{z_{i}}= \{ g\geq i\}$ , we know that

$$\begin{align*}\varphi(f)=\varphi'(f)= y_{1}+\cdots +y_{m}\ll z_{1}+\cdots +z_{m}\leq \sup_{n}\sum_{i=1}^{n} z_{i}=\varphi(g). \end{align*}$$

Finally, note that the image of $\varphi $ is clearly dense in S, since $\varphi '$ is surjective on $\downarrow e$ . Furthermore, $\varphi $ is an order embedding in $\operatorname {\mathrm {Lsc}} (X_{S},\overline {\mathbb {N}} )_{fs}$ , since $\varphi $ coincides with $\varphi '$ in this basis of $\operatorname {\mathrm {Lsc}} (X_{S},\overline {\mathbb {N}} )$ .

Thus, since the conditions in Lemma 6.1 are satisfied, it follows that $\varphi $ is a $\operatorname {\mathrm {Cu}}$ -isomorphism.

Theorem 6.4 Let S be a $\operatorname {\mathrm {Cu}}$ -semigroup. Then, S is $\operatorname {\mathrm {Lsc}}$ -like if and only if S is $\operatorname {\mathrm {Cu}}$ -isomorphic to $\operatorname {\mathrm {Lsc}} (X,\overline {\mathbb {N}} )$ for a $T_{1}$ topological space X.

Proof We already know that $\operatorname {\mathrm {Lsc}} (X,\overline {\mathbb {N}} )$ is $\operatorname {\mathrm {Lsc}} $ -like whenever it is a $\mathrm {Cu}$ -semigroup (see Example 4.5), and the converse follows from Theorem 6.3.

In [23], a notion of covering dimension for $\mathrm {Cu}$ -semigroups is introduced. This dimension satisfies many of the expected permanence properties [23, Proposition 3.10], and is related to other dimensions, such as the nuclear dimension of $\mathrm {C}^*$ -algebras [23, Theorem 4.1] and the Lebesgue covering dimension (see [23, Proposition 4.3 and Corollary 4.4]).

Using such a notion, one can prove the following.

Theorem 6.5 Let S be a $\mathrm {Cu}$ -semigroup satisfying (O5), and let $n\in \mathbb {N}\cup \{ \infty \}$ . Then, S is $\operatorname {\mathrm {Cu}}$ -isomorphic to $\operatorname {\mathrm {Lsc}} (X,\overline {\mathbb {N}} )$ with X a compact metric space such that $\dim (X)= n$ if and only if S is $\operatorname {\mathrm {Lsc}}$ -like, countably based, has a compact order unit, and $\dim (S)=n$ .

In particular, a $\mathrm {Cu}$ -semigroup S is $\operatorname {\mathrm {Cu}}$ -isomorphic to the Cuntz semigroup of $C(X)$ with X compact metric and $\dim (X)\leq 1$ if and only if S is $\operatorname {\mathrm {Lsc}}$ -like, countably based, satisfies (O5), has a compact order unit, and $\dim (S)\leq 1$ .

Proof The forward implication follows from Examples 4.5 and 5.4, Proposition 5.6, and [23, Corollary 4.4].

To prove the converse, use Theorem 6.4 and (v) in Proposition 5.6 to deduce that $S\cong \operatorname {\mathrm {Lsc}} (X_S ,\overline {\mathbb {N}} )$ with $X_S$ compact metric. Then, it follows from [23, Corollary 4.4] that $\dim (X_S)=\dim (S)=n$ , as required.

Now, assume that S is $\operatorname {\mathrm {Cu}}$ -isomorphic to the Cuntz semigroup of $C(X)$ with X compact metric and $\dim (X)\leq 1$ . By [20, Theorem 1.1] we know that $\operatorname {\mathrm {Cu}} (C(X))\cong \operatorname {\mathrm {Lsc}} (X,\overline {\mathbb {N}} )$ . In particular, S satisfies (O5) (e.g., [22]).

Thus, it now follows from our previous argument that S is $\operatorname {\mathrm {Lsc}}$ -like, countably based, satisfies (O5), has a compact order unit, and $\dim (S)\leq 1$ .

Conversely, if S satisfies the list of properties in the second part of the statement, note that $S\cong \operatorname {\mathrm {Lsc}} (X_S ,\overline {\mathbb {N}} )$ with $\dim (X_S)\leq 1$ again by Theorem 6.4. Using [20, Theorem 1.1] a second time, it follows that $\operatorname {\mathrm {Lsc}} (X_S ,\overline {\mathbb {N}} )\cong \operatorname {\mathrm {Cu}} (C(X_S))$ , as desired.

7 Chain conditions and the Cuntz semigroup of commutative AI-algebras

In this section, we introduce the notions of piecewise chainable and weakly chainable $\mathrm {Cu}$ -semigroups and prove that, together with some additional properties, these notions give a characterization of when S is $\operatorname {\mathrm {Cu}}$ -isomorphic to the Cuntz semigroup of a unital commutative block stable AI-algebra and a unital commutative AI-algebra, respectively (see Theorems 7.4 and 7.11).

We also show that the Cuntz semigroup of any AI-algebra is weakly chainable, thus uncovering a new property that the Cuntz semigroup of any AI-algebra satisfies (see Corollary 7.9).

We first prove the following categorical proposition, which summarizes the results of the above sections. We denote by $\mathrm {Top}$ the category of topological spaces, and by $\mathcal {T}_{1}^{\operatorname {\mathrm {Cu}}}$ the subcategory of $\mathrm {Top}$ whose objects X are the $T_1$ spaces such that $\operatorname {\mathrm {Lsc}} (X,\overline {\mathbb {N}} )\in \operatorname {\mathrm {Cu}}$ . Note that, by Corollary 4.19, this includes all compact, metric spaces.

Proposition 7.1 Let $\operatorname {\mathrm {Lsc}}$ be the subcategory of $\operatorname {\mathrm {Cu}}$ consisting of $\operatorname {\mathrm {Lsc}}$ -like $\mathrm {Cu}$ -semigroups.

There exists a faithful and essentially surjective contravariant functor $T\colon \mathcal {T}_{1}^{\operatorname {\mathrm {Cu}}}\to \operatorname {\mathrm {Lsc}}$ that is full on isomorphisms.

Proof For every topological space $X\in \mathcal {T}_{1}^{\operatorname {\mathrm {Cu}}}$ , define $T(X)=\operatorname {\mathrm {Lsc}} (X,\overline {\mathbb {N}} )$ .

Furthermore, given any continuous map $f\colon X\to Y$ , set $T(f)\colon \operatorname {\mathrm {Lsc}} (Y,\overline {\mathbb {N}} )\to \operatorname {\mathrm {Lsc}} (X,\overline {\mathbb {N}} )$ as the unique $\operatorname {\mathrm {Cu}}$ -morphism such that $T(f)(\chi _{U})=\chi _{f^{-1}(U)}$ for every open subset U of Y.

Note that, given $f\colon X\to Y$ and $g\colon Y\to Z$ in $\mathcal {T}_{1}^{\operatorname {\mathrm {Cu}}}$ , we have

$$\begin{align*}T(g\circ f)(\chi_{U})=\chi_{(g\circ f)^{-1}(U)}=\chi_{f^{-1}g^{-1}(U)}=(T(f)\circ T(g))(\chi_{U}). \end{align*}$$

Thus, T is a contravariant functor, which is clearly faithful by construction.

Moreover, we know by Theorem 6.4 that for every $\operatorname {\mathrm {Lsc}}$ -like $\mathrm {Cu}$ -semigroup S there exists a $T_{1}$ -space $X_{S}$ with $S\cong \operatorname {\mathrm {Lsc}} (X_{S},\overline {\mathbb {N}} )$ . Therefore, T is essentially surjective.

Now, let $\varphi \colon S\to T$ be a $\operatorname {\mathrm {Cu}}$ -isomorphism of $\operatorname {\mathrm {Lsc}}$ -like $\mathrm {Cu}$ -semigroups. Using Theorem 6.4, we get a $\operatorname {\mathrm {Cu}}$ -isomorphism of the form $\phi \colon \operatorname {\mathrm {Lsc}} (X_{S},\overline {\mathbb {N}} )\to \operatorname {\mathrm {Lsc}} (X_{T},\overline {\mathbb {N}} )$ .

Since $\phi (1)= 1$ , indicator functions must map to indicator functions. Since $\phi $ is a $\operatorname {\mathrm {Cu}}$ -isomorphism, maximal elements below $1$ must map to maximal elements below $1$ . More explicitly, for every $x\in X_{S}$ , there exists $y\in X_{T}$ such that $\phi (\chi _{X_{S}\setminus \{ x\}})=\chi _{X_{T}\setminus \{ y\}}$ .

We define the map $f\colon X_{T}\to X_{S}$ as $y\mapsto x$ , which is bijective because $\phi $ is a $\operatorname {\mathrm {Cu}}$ -isomorphism.

To see that it is continuous, let U be an open subset of $X_{S}$ and let $V\subseteq X_{T}$ be such that $\phi (\chi _{U})=\chi _{V}$ . Then, given $y\in X_{T}$ , we have that $y\in V$ if and only if

$$\begin{align*}1\leq \chi_{X_{T}\setminus\{ y\}}+\chi_{V}= \phi (\chi_{X_{S}\setminus\{ f(y)\}}+\chi_{U}). \end{align*}$$

Since $\phi $ is a $\operatorname {\mathrm {Cu}}$ -isomorphism, this in turn holds if and only if $(X_{S}\setminus \{ f(y)\})\cup U=X_{S}$ or, equivalently, if $f(y)\in U$ .

This shows that $f^{-1}(U)=V$ and, consequently, that f is continuous.

Finally, let $V\subseteq X_{T}$ be open. Since $\phi $ is an isomorphism, there exists some open subset $U\subseteq X_{S}$ such that $\chi _{V}=\phi (\chi _{U})$ .

By the argument above, one has $V=f^{-1}(U)$ and, since f is bijective, it follows that $f(V)=f(f^{-1}(U))=U$ . This shows that f is open.

Thus, f is a homeomorphism between $X_{S}$ and $X_{T}$ , as required.

We now introduce chainable and piecewise chainable inf-semilattice ordered $\mathrm {Cu}$ -semigroups.

Definition 7.1 Let S be an inf-semilattice ordered $\mathrm {Cu}$ -semigroup. An element $x\in S$ is said to be chainable if for every sum $y_{1}+\cdots +y_{n}\geq x$ , there exist elements $z_{1},\cdots ,z_{m}$ such that:

1. (i) For every i, there exists some k with $z_{i}\leq y_{k}$ .

2. (ii) $z_{i}\wedge z_{j}\neq 0$ if and only if $\vert i-j \vert \leq 1$ .

3. (iii) $z_{1}+\cdots +z_{m}\geq x$ .

S will be called chainable if it has a chainable order unit.

Moreover, we will say that S is piecewise chainable if there exist chainable elements $s_{1},\ldots ,s_{n}$ such that $s_{1}+\cdots +s_{n}$ is an order unit and $s_{i}\wedge s_{j}=0$ whenever $i\neq j$ .

Lemma 7.2 Given an $\operatorname {\mathrm {Lsc}}$ -like $\mathrm {Cu}$ -semigroup S with least order unit e and an element $y\leq e$ , $U_{y}$ is topologically chainable if and only if y is chainable.

In particular, S is chainable if and only if $X_{S}$ is topologically chainable.

Proof If y is chainable, take a finite cover $U_{y_{1}}\cup \cdots \cup U_{y_{n}}=U_{y}$ . We have that $y=y_{1}\vee \cdots \vee y_{n}\leq y_{1}+\cdots +y_{n}$ . Thus, applying the chainability of y, one gets elements $z_{1}, \ldots , z_{m}$ such that for every i there exists k with $z_{i}\leq y_{k}\leq y$ . This shows that $z_1\vee \cdots \vee z_m\leq y$ .

By Corollary 4.9 and (iii) in Definition 7.1, we have $z_{1}\vee \cdots \vee z_{m}\geq y$ and, consequently, $z_1\vee \cdots \vee z_m= y$ . This shows that $U_{z_{1}},\ldots , U_{z_{m}}$ is a cover for $U_y$ .

Using the equalities in the proof of Lemma 5.2 and conditions (i)–(iii) in Definition 7.1, one sees that $U_{z_{1}},\ldots , U_{z_{m}}$ is a chain that refines our original cover in the sense of Definition 3.1.

Conversely, if $U_{y}$ is topologically chainable and we have a sum $y_{1}+\cdots +y_{n}\geq y$ , we can apply Corollary 4.9 once again to obtain

$$\begin{align*}(y_{1}\wedge y)\vee\cdots \vee (y_{n}\wedge y)=y. \end{align*}$$

This shows that $U_{y_{1}\wedge y}\cup \cdots \cup U_{y_{n}\wedge y}=U_y$ , and we can use the chainability of $U_{y}$ to obtain a chain refining this cover. Using Lemma 5.2, it is easy to check that the elements below e corresponding to the open subsets of the chain satisfy conditions (i)–(iii) in Definition 7.1.

In particular, the previous argument shows that e is chainable whenever $X_{S}$ is topologically chainable. By definition, this implies that S is chainable.

Conversely, if S is chainable, we have a chainable order unit s. Let us now show that e is also chainable, which by the above arguments will imply that $U_e=X_{S}$ is topologically chainable.

Thus, let $y_1+\cdots +y_n\geq e$ , which by Corollary 4.9 implies that $y_1\vee \cdots \vee y_n\geq e$ . Since s is an order unit, one has

$$\begin{align*}\infty y_1\vee\cdots\vee \infty y_n\geq \infty e = \infty = \infty s\geq s. \end{align*}$$

Using that s is chainable, we obtain elements $z_1,\ldots ,z_m$ satisfying (i)–(iii) in Definition 7.1. In particular, since for every i there exists k with $z_i\leq \infty y_k$ , one can use Lemma 4.10 in the second step to get

$$\begin{align*}z_i\wedge e\leq (\infty y_k)\wedge e= y_k\wedge e\leq y_k. \end{align*}$$

Furthermore, since e is the least order unit in S and $z_1+\cdots +z_m\geq s\geq e$ , it follows from Corollary 4.9 that $z_1\vee \cdots \vee z_m\geq e$ . Taking the infimum by e and using Corollary 4.9 once again, we get $z_1\wedge e+\cdots +z_m\wedge e\geq e$ .

This shows that the elements $z_i\wedge e$ satisfy conditions (i)–(iii) in Definition 7.1 for $y_1\vee \cdots \vee y_n\geq e$ , as desired.

Lemma 7.3 A countably based $\operatorname {\mathrm {Lsc}}$ -like $\mathrm {Cu}$ -semigroup S with a compact order unit is piecewise chainable if and only if $X_{S}$ is.

Proof If $X_{S}$ is piecewise chainable, there exist chainable components $Y_{1},\ldots , Y_{n}$ such that $X_{S}=Y_{1}\sqcup \cdots \sqcup Y_{n}$ . Since chainability implies connectedness (whenever the space is compact), there is a finite number of connected components, and so these are clopen.

By Lemma 7.2, the disjoint chainable components correspond to disjoint chainable elements, so S is piecewise chainable by definition.

Conversely, if S is piecewise chainable, each element $s_{i}$ in the definition of chainable corresponds to a chainable open subset of $X_{S}$ , which is disjoint from the other chainable open subsets by construction.

Theorem 7.4 Let S be a $\mathrm {Cu}$ -semigroup. Then, S is $\operatorname {\mathrm {Cu}}$ -isomorphic to the Cuntz semigroup of a unital block stable commutative AI-algebra if and only if S is countably based, $\operatorname {\mathrm {Lsc}}$ -like, piecewise chainable, has a compact order unit, and satisfies (O5).

Proof Let S be $\operatorname {\mathrm {Cu}}$ -isomorphic to the Cuntz semigroup of a unital commutative block stable AI-algebra. Then, we know from [20, Theorem 1.1] and Definition 3.3 that $S\cong \operatorname {\mathrm {Lsc}} (X,\overline {\mathbb {N}})$ with X a compact, metric, piecewise chainable space. In particular, S satisfies (O5), has a compact order unit, is countably based, and is $\operatorname {\mathrm {Lsc}}$ -like. Using Lemma 7.3, it also follows that S is piecewise chainable.

Conversely, assume that S satisfies all the conditions in the list. By Theorem 6.4 and (v) in Proposition 5.6, we have $S\cong \operatorname {\mathrm {Lsc}} (X,\overline {\mathbb {N}} )$ with X a compact metric space.

Then, it follows from Example 5.4 and Lemma 7.3 that X is piecewise chainable. In particular, it has dimension less than or equal to one by Remark 3.2. Thus, $\operatorname {\mathrm {Cu}} (C(X))\cong \operatorname {\mathrm {Lsc}} (X,\overline {\mathbb {N}} )$ by [20, Theorem 1.1], so S is isomorphic to the Cuntz semigroup of a unital commutative block stable AI-algebra.

We now define weak chainability for any $\mathrm {Cu}$ -semigroup and prove that every $\mathrm {Cu}$ -semigroup of an AI-algebra satisfies such a condition. Moreover, we also show that an $\operatorname {\mathrm {Lsc}}$ -like $\mathrm {Cu}$ -semigroup is weakly chainable if and only if its associated space is almost chainable.

Given two elements $x,y$ in a $\mathrm {Cu}$ -semigroup, we write $x\propto y$ if there exists $n\in \mathbb {N}$ with $x\leq ny$ .

Definition 7.2 We will say that a $\mathrm {Cu}$ -semigroup S is weakly chainable, or that it satisfies the weak chainability condition if, for any $x,y,y_{1},\ldots ,y_{n}$ such that

$$\begin{align*}x\ll y\ll y_1+\cdots +y_n, \end{align*}$$

there exist $x', z_{1},\ldots ,z_{m}\in S$ such that $x'\leq y$ , $x\propto x'$ and:

1. (i) For any i, there exists j such that $z_{i}\leq y_{j}$ .

2. (ii) $z_{i}+z_{j}\leq x'$ whenever $\vert i-j\vert \geq 2$ .

3. (iii) $z_{1}+\cdots +z_{m}\geq x'$ .

Lemma 7.5 Let X be a compact metric space. Then, $\operatorname {\mathrm {Lsc}} (X,\overline {\mathbb {N}} )$ is weakly chainable if and only if X is almost chainable.

Proof First, recall that $S=\operatorname {\mathrm {Lsc}} (X,\overline {\mathbb {N}} )$ is a $\mathrm {Cu}$ -semigroup whenever X is compact and metric by Corollary 4.19. Furthermore, also recall from Example 4.5 that S is an $\operatorname {\mathrm {Lsc}}$ -like $\mathrm {Cu}$ -semigroup with least order unit $1$ , and that $X\cong X_S$ by Example 5.4.

Now, assume that S is weakly chainable, and let $U_{y_1},\ldots , U_{y_n}$ be a cover of $X_S$ . Then, the elements $y_1,\ldots ,y_n\leq 1$ satisfy $y_1\vee \cdots \vee y_n\geq 1$ and, consequently, $y_1+\cdots +y_n\geq 1$ .

Set $x=y=1$ , and apply Definition 7.2 to obtain elements $x',z_1,\ldots ,z_m$ satisfying the conditions in the definition. Note that, since $x'$ satisfies $x'\leq 1\leq kx'$ for some $k\in \mathbb {N}$ , it follows from the second inequality that $x'\geq 1$ and, therefore, $x'=1$ . Let $U_{z_1},\ldots ,U_{z_m}$ be the open subsets of $X_S$ corresponding to $z_1,\ldots ,z_m$ , respectively. Using (i)–(iii) in Definition 7.2, it is easy to see that such sets form an almost chain refining the original cover. This implies that $X_S$ is almost chainable and, since $X\cong X_S$ , so is X.

Conversely, assume that X is almost chainable and let $x,y,y_{1},\ldots ,y_{n}\in S$ be as in Definition 7.2. Set $x'=x\wedge 1$ . Then, we know by Corollary 4.9 that $y_{1}\vee \cdots \vee y_{n}\geq y\gg x'$ . Taking the infimum with $1$ , one has $(y_{1}\wedge 1)\vee \cdots \vee (y_{n}\wedge 1)\gg x'$ .

Moreover, note that $x'$ satisfies $x'\leq y$ and $x\propto x'$ . Since X is compact, metric, and almost chainable, we know by Remark 3.2 that its dimension is less than $2$ . This implies by [20, Theorem 1.1] that $\operatorname {\mathrm {Cu}} (C(X))\cong \operatorname {\mathrm {Lsc}} (X,\overline {\mathbb {N}})$ and, in particular, that S satisfies (O5).

Thus, by the proof of Lemmas 5.2 and 5.5, $(y_{1}\wedge 1)\vee \cdots \vee (y_{n}\wedge 1)\gg x'$ corresponds to a cover $\overline {U_{x'}}\subseteq U_{y_{1}}\cup \cdots \cup U_{y_{n}}$ . In particular, the open sets $X\setminus \overline {U_{x'}},U_{y_{1}},\ldots , U_{y_{n}}$ form a cover of X and, since X is almost chainable, there exists an almost chain $C_{1},\ldots , C_{m}$ covering X and refining $X\setminus \overline {U_{x'}},U_{y_{1}},\ldots , U_{y_{n}}$ .

Now, take the almost chain $C_{1}\cap U_{x'},\ldots , C_{m}\cap U_{x'}$ , which clearly covers $U_{x'}$ . For each i, let $z_{i}\in S$ be the associated element to $C_{i}\cap U_{x'}$ . These elements satisfy the desired conditions in Definition 7.2.

Indeed, to see condition (ii), note that $z_i\leq x'$ for every i, so it follows that $z_i+z_j\leq x'$ if and only if $z_i\wedge z_j=0$ . By the proof of Lemma 5.2, this is equivalent to $(C_{i}\cap U_{x'})\cap (C_{i}\cap U_{x'})=\emptyset $ . Since $\{C_{i}\cap U_{x'}\}_{i}$ is an almost chain, this condition is satisfied.

Conditions (i) and (iii) follow similarly using that $\{C_{i}\cap U_{x'}\}_{i}$ is a cover of $U_{x'}$ refining $\{U_{y_{j}}\}_{j}$ .

Using Remark 3.2, one gets the following result.

Corollary 7.6 Given X compact, metric, and connected, the $\mathrm {Cu}$ -semigroup $\operatorname {\mathrm {Lsc}} (X,\overline {\mathbb {N}} )$ is weakly chainable if and only if X is chainable.

It would be interesting to know whether a general $\operatorname {\mathrm {Lsc}}$ -like $\mathrm {Cu}$ -semigroup S is weakly chainable if $X_S$ is almost chainable.

Lemma 7.7 Given two weakly chainable $\mathrm {Cu}$ -semigroups S and T, their direct sum $S\oplus T$ is also weakly chainable.

Proof Take $x,y,y_{1},\ldots , y_{n}\in S\oplus T$ as in Definition 7.2. Write $x=(x_{1},x_{2})$ , $y=(y_{1},y_{2})$ , and $y_{j}= (y_{j,1},y_{j,2})$ with $x_{1},y_{1},y_{j,1}\in S$ and $x_{2},y_{2},y_{j,2}\in T$ .

Since S and T are weakly chainable, one gets elements $x^{\prime }_{1}$ , $z_{1,1}$ , $\ldots $ , $z_{m,1}\in S$ and $x^{\prime }_{2}$ , $z_{1,2}$ , $\ldots $ , $z_{m',2}\in T$ satisfying the conditions in Definition 7.2. Define $x'=(x^{\prime }_{1},x^{\prime }_{2})$ and note that $x'\leq y$ and that there exists some $k\in \mathbb {N}$ with $x\leq kx'$ .

Now, set $z_{i}=(z_{i,1},0)$ for $i\leq m$ and $z_{i}=(0,z_{i-m+1,2})$ for $i> m$ . We have that

$$\begin{align*}\begin{aligned} z_{1}+\cdots +z_{m+m'-1}&= ((z_{1,1},0)+\cdots +(z_{m,1},0)) + ((0,z_{1,2})+\cdots +(0,z_{m',2}))\\ &\geq (x^{\prime}_{1},0) + (0,x^{\prime}_{2})=x'. \end{aligned} \end{align*}$$

As expected, we also get that for every i there exists a j such that $z_{i}\leq (y_{j,1},0)\leq y_{j}$ or $z_{i}\leq (0,y_{j,2})\leq y_{j}$ .

Now, take $z_{i},z_{j}$ with $\vert i-j\vert \geq 2$ . If $i,j\leq m$ , we have $z_{i}+z_{j}\leq (x^{\prime }_{1},0)\leq x'$ . Similarly, $z_{i}+z_{j}\leq (0,x^{\prime }_{2})\leq x'$ whenever $i,j> m$ .

Moreover, if $i\leq m$ and $j>m$ , we know that $z_{i}=(z_{i,1},0)\leq (x^{\prime }_{1},0)$ and $z_{j}=(0,z_{j-m+1,2})\leq (0,x^{\prime }_{2})$ . This implies $z_{i}+z_{j}\leq (x^{\prime }_{1},0) + (0,x^{\prime }_{2})=x'$ .

Since $z_{1},\ldots , z_{m+m'-1}$ satisfy all the required properties, S satisfies the weak chainability condition.

Proposition 7.8 Let $S=\lim _n S_n$ be a sequential inductive limit of $\mathrm {Cu}$ -semigroups. Assume that $S_n$ is weakly chainable for each n. Then, S is also weakly chainable.

Proof Let $S=\lim S_{n}$ with $S_{n}$ weakly chainable for every n. Given an element $x\in S_n$ , let us denote its image through the canonical map $S_n\to S$ by $[x]$ .

Let $x,y,y_{1},\ldots ,y_{n}\in S$ be as in Definition 7.2. Then, let $m\in \mathbb {N}$ be such that there exist elements $u, v$ , and $v_j$ in $S_m$ with $[v_j]\ll y_j$ ,

$$\begin{align*}x\ll [u]\ll [v]\ll y\ll [v_1]+\cdots +[v_n]\ll y_1+\cdots +y_n, \end{align*}$$

and $u\ll v\ll v_1+\cdots +v_n$ .

Since $S_{m}$ is weakly chainable, we obtain elements $u', z_{1},\ldots ,z_{m}\in S_{m}$ satisfying the conditions in Definition 7.2. We have:

1. (i) $u'\leq v , u\leq ku'$ for some $k\in \mathbb {N}$ . This implies $ [ u' ]\leq [ v ]\leq y$ and $x\leq [ u ]\leq k [ u' ]$ .

2. (ii) For any i, there exists j such that $z_{i}\leq v_{j}$ , which shows that $[ z_{i} ]\leq [ v_{j} ] \leq y_j$ .

3. (iii) $z_{i}+z_{j}\leq u'$ whenever $\vert i-j\vert \geq 2$ . Consequently, $[ z_{i} ] + [ z_{j} ]\leq [ u' ]$ whenever $\vert i-j\vert \geq 2$ .

Since $z_{1}+\cdots +z_{m}\geq u'$ , one also gets $ [u']\leq [z_{1}]+\cdots + [z_{m}]$ . Thus, S is weakly chainable, as desired.

Corollary 7.9 The Cuntz semigroup of any AI-algebra is weakly chainable.

Example 7.10 The $\mathrm {Cu}$ -semigroups $\operatorname {\mathrm {Lsc}} (\mathbb {T},\overline {\mathbb {N}} )$ and $\operatorname {\mathrm {Lsc}} ([0,1]^{2},\overline {\mathbb {N}} )$ do not satisfy the weak chainability condition.

Indeed, this follows clearly from Corollary 7.6, as $\mathbb {T}$ and $[0,1]^{2}$ are not chainable continua.

Using the results developed thus far, one can now use an analogous proof to that of Theorem 7.4 to prove the following theorem.

Theorem 7.11 Let S be a $\mathrm {Cu}$ -semigroup. Then, S is $\operatorname {\mathrm {Cu}}$ -isomorphic to the Cuntz semigroup of a unital commutative AI-algebra if and only if S is countably based, $\operatorname {\mathrm {Lsc}}$ -like, weakly chainable, has a compact order unit, and satisfies (O5).

8 New properties of the Cuntz semigroup of an AI-algebra

Inspired by the abstract characterization obtained above, in this section, we introduce properties that are satisfied by the Cuntz semigroups of all AI-algebras and that are not satisfied by other well-known $\operatorname {\mathrm {Cu}}$ -semigroups. In Definition 7.2, we have already introduced one such property, which is not satisfied by $\operatorname {\mathrm {Lsc}} (\mathbb {T},\overline {\mathbb {N}} )$ (see Example 7.10). We now introduce the conditions of $\mathrm {Cu}$ -semigroups with refinable sums and almost ordered sums, and show that the Cuntz semigroups of all AI-algebras satisfy these properties. We also prove that Z, the Cuntz semigroup of the Jiang–Su algebra $\mathcal {Z}$ , does not have refinable sums (see Example 8.2).

Definition 8.1 We say that a $\mathrm {Cu}$ -semigroup S has refinable sums if, given a finite $\ll $ -increasing sequence

$$\begin{align*}x_{1}\ll \cdots\ll x_{n} \end{align*}$$

and elements $x^{\prime }_{1},\ldots ,x^{\prime }_{n}$ such that $x_{i}\propto x^{\prime }_{i}$ for every i, there exist finite decreasing sequences $(y_{j}^{i})_{j=1}^{l}$ such that:

1. (i) $x^{\prime }_{i+1}\geq y_{1}^{i}$ for every i.

2. (ii) $y_{j}^{i}\ll y_{j}^{i+1}$ for every i and j.

3. (iii) $x_{i}\ll y_{1}^{i}+\cdots +y_{l}^{i} \ll x_{i+1}$ .

Example 8.1 Any $\mathrm {Cu}$ -semigroup S of the form $\operatorname {\mathrm {Lsc}} (X,\overline {\mathbb {N}} )$ has refinable sums.

To see this, let $x_{i},x^{\prime }_{i}$ as in Definition 8.1, and let $\tilde {x_{i}}$ be such that

$$\begin{align*}x_{1}\ll \tilde{x}_{1} \ll x_{2}\ll \tilde{x}_{2} \ll x_{3}\ll \cdots\ll x_{n}. \end{align*}$$

Since $\tilde {x}_{i}\in S_{\ll }$ for each i, they can all be written as ordered finite sum of elements below one. Furthermore, by possibly adding some zeros, we may assume that all $\tilde {x}_{i}$ ’s have the same amount of summands. That is to say, we have

$$\begin{align*}x_{1}\ll \tilde{x}_{1}=y_{1}^{1}+\cdots +y_{l}^{1} \ll x_{2}\ll \tilde{x}_{2}=y_{1}^{2}+\cdots +y_{l}^{2} \ll x_{3}\ll\cdots\ll x_{n}. \end{align*}$$

Thus, we know by Lemma 4.17 that $y_{j}^{i}\ll y_{j}^{i+1}$ for every $i,j$ . Moreover, since we have $\tilde {x}_{i}\ll x_{i+1}\propto x_{i+1}'$ , one can find $x^{\prime \prime }_{i+1}\ll x^{\prime }_{i+1}$ such that $\tilde {x}_{i}\propto x^{\prime \prime }_{i+1}$ .

Since $x^{\prime \prime }_{i+1}\in S_{\ll }$ , we have that $\tilde {x}_{i}\propto x^{\prime \prime }_{i+1}\propto x^{\prime \prime }_{i+1}\wedge 1$ . Applying the topological order in S, we obtain $y_{1}^{i}\leq x^{\prime \prime }_{i+1}\wedge 1\leq x^{\prime }_{i+1}$ , as required.

Example 8.2 Let $Z=(0,\infty ]\sqcup \mathbb {N}$ , and denote by $n^\natural \in (0,\infty ]$ the associated element to $n\in \mathbb {N}$ . Order and addition in Z are defined normally in each component, and given $x\in (0,\infty ]$ and $n\in \mathbb {N}$ , we set $x\leq n$ if and only if $x\leq n^\natural $ in $(0,\infty ]$ ; $n\leq x$ if and only if $n^\natural <x$ ; and $x+n=x+n^\natural $ . It was proved in [18, Theorem 3.1] that Z is $\operatorname {\mathrm {Cu}}$ -isomorphic to the Cuntz semigroup of the Jiang–Su algebra $\mathcal {Z}$ , as defined in [15].

We claim that Z does not have refinable sums. Indeed, assume for the sake of contradiction that it does, and consider the elements $x_1=x_1'=x_2=1$ and $x_2'=0.5$ in Z. These satisfy

$$\begin{align*}x_1\ll x_2,\quad x_1 \propto x_1', \,\,\,\text{ and }\,\,\, x_2\propto x_2'. \end{align*}$$

Thus, applying Definition 8.1, we obtain a finite decreasing sequence $(y^{1}_j)_{j=1}^l$ such that

$$\begin{align*}1=x_1\ll y_{1}^{1}+\cdots +y_{l}^{1}\ll x_2=1. \end{align*}$$

Since $(y^{1}_j)_{j=1}^l$ is decreasing, one must have $y_{1}^{1}=1$ and $y_{i}^{1}=0$ whenever $i\geq 2$ . However, it follows from (i) in Definition 8.1 that

$$\begin{align*}1=y_{1}^{1}\leq x_2'= 0.5, \end{align*}$$

which is a clear contradiction.

Proposition 8.3 Let S be a $\mathrm {Cu}$ -semigroup that can be written as a sequential inductive limit $\lim S_{k}$ of $\mathrm {Cu}$ -semigroups $S_{k}$ that have refinable sums. Then, S also has refinable sums.

Proof Let $S=\lim S_{k}$ where each $S_{k}$ has refinable sums. As in the proof of Proposition 7.8, let us denote the image through the canonical map $S_k\to S$ of an element $x\in S_k$ by $[x]$ .

Let $x_{1},\ldots , x_{n}$ and $x^{\prime }_{1},\ldots , x^{\prime }_{n}$ be elements in S as in Definition 8.1. Let $k\in \mathbb {N}$ such that, for every $i\leq n-1$ , there exist elements $u_{2i-1},u_{2i},v_{2i-1},v_{2i}\in S_k$ satisfying

$$\begin{align*}x_{i}\ll [u_{2i-1}] \ll [u_{2i}] \ll x_{i+1},\quad [v_{2i}]\leq x_{i+1}', \end{align*}$$

and

$$\begin{align*}u_{1}\ll\cdots\ll u_{2n-2},\,\,\,\text{ and }\,\,\, u_{i}\propto v_{i}. \end{align*}$$

Since $S_{k}$ has refinable sums, we obtain decreasing sequences $(y_{j}^{i})_{j=1}^{l}$ for $i\leq 2n-2$ satisfying the properties of Definition 8.1. In particular, we get

$$\begin{align*}x_{i}\ll [u_{2i-1}]\ll [y_{1}^{2i-1}]+\cdots +[y_{1}^{2i-1}]\ll [u_{2i}] \ll x_{i+1}, \end{align*}$$

and $[y_{1}^{2i-1}]\leq [v_{i+1}]\leq x^{\prime }_{i+1}$ .

It follows that S has refinable sums.

Definition 8.2 A $\mathrm {Cu}$ -semigroup S is said to have almost ordered sums if for any finite set of elements $x_{1},\ldots ,x_{n}$ in S there exist elements $y_{j,i}$ in S such that

$$\begin{align*}x_{1}+\cdots +x_{n}=\sup_{i} (y_{1,i}+\cdots +y_{n,i}) \end{align*}$$

and such that:

1. (i) $y_{1,i}\geq \cdots \geq y_{n,i}$ .

2. (ii) $(y_{n,i})_{i}$ is increasing and bounded by $x_{1},\ldots ,x_{n}$ .

3. (iii) If $x'\ll x_{j_{1}},\ldots ,x_{j_{r}}\leq z$ for $j_{1},\ldots ,j_{r}$ pairwise different, we have $x'\leq y_{r,i}$ and $y_{n+1-r,i}\leq z$ for every sufficiently large i.

Example 8.4 If S is a distributively lattice ordered $\mathrm {Cu}$ -semigroup, S has almost ordered sums. This applies, in particular, to $\mathrm {Cu}$ -semigroups such that $S\cong \operatorname {\mathrm {Lsc}} (X,\overline {\mathbb {N}} )$ for some X.

Indeed, given $x_{1},\ldots ,x_{n}$ , set

$$\begin{align*}y_{1,i} &= x_{1}\vee\cdots\vee x_{n},\quad y_{2,i} = (x_{1}\wedge x_{2})\vee \cdots\vee (x_{n-1}\wedge x_{n}),\quad \ldots ,\,\,\,\text{ and }\\ y_{n,i} &=x_{1}\wedge\cdots\wedge x_{n}, \end{align*}$$

for every i, and note that by Lemma 4.2 we have

$$\begin{align*}x_{1}+\cdots +x_{n}=y_{1,i}+\cdots +y_{n,i}. \end{align*}$$

This implies that S has almost ordered sums.

Example 8.5 Let $Z'=Z\cup \{ 1"\}$ with $1"$ a compact element not comparable with $1$ such that $1+x=1"+x$ for every $x\in Z\setminus \{ 0\}$ and $k1"=k$ for every $k\in \mathbb {N}$ . Then, $Z'$ does not have almost ordered sums.

To see this, consider the sum $1+1"$ and assume, for the sake of contradiction, that $Z'$ has refinable sums. Then, there exist elements $y_{1,i},y_{2,i}$ such that $1+1"= \sup _{i}y_{1,i}+y_{2,i}$ .

Since $1+1"=2$ is compact, for every sufficiently large i, we have $1+1"= y_{1,i}+y_{2,i}$ .

This implies that $y_{1,i}=2$ and $y_{2,i}=0$ , since we know that $1,1"\leq y_{1,i}$ and that $1$ , $1"$ are not comparable.

However, we also have $1,1"\leq 1.5$ , so we get $2=y_{1,i}\leq 1.5$ , a contradiction.

Proposition 8.6 Sequential inductive limits of distributively lattice ordered $\mathrm {Cu}$ -semigroups have almost ordered sums.

Proof Let $S=\lim _{k} (S_{k},\varphi _{k+1,k})$ be the inductive limit of distributively lattice ordered $\mathrm {Cu}$ -semigroups $S_{k}$ . As before, given an element $x\in S_k$ , let us denote its image through the canonical map $S_k\to S$ by $[x]$ .

Let $x_{1},\ldots ,x_{n}$ be elements in S. One can check that there exists an increasing sequence of integers $(k_{l})$ and elements take $x_{1}^{l},\ldots ,x_{n}^{l}\in S_{k_{l}}$ such that $([x_{j}^{l}])_{l}$ are $\ll $ -increasing sequences in S with suprema $x_{j}$ for every $j\leq n$ , in such a way that $\varphi _{k_{l+1},k_{l}}(x_{j}^{l})\ll x_{j}^{l+1}$ for every j and l.

Since each $S_{k}$ is distributively lattice ordered, for every l, there exist elements $y_{1}^{l},\ldots ,y_{n}^{l}$ in $S_{k_{l}}$ with

$$\begin{align*}x_{1}^{l}+\cdots +x_{n}^{l}=y_{1}^{l}+\cdots +y_{n}^{l}, \end{align*}$$

satisfying the properties of Definition 8.2 (see Example 8.4). This implies, in particular, $\sup _{l}([y_{1}^{l}]+\cdots + [y_{n}^{l}])=x_{1}+\cdots +x_{n}$ .

We will now check that the elements $[y_{1}^{l}],\ldots , [y_{n}^{l}]$ satisfy conditions (i)–(iii) in Definition 8.2.

By construction, one has $y_{1}^{l}\geq \cdots \geq y_{n}^{l}$ for every l, so condition (i) is satisfied. For condition (ii), let $l\in \mathbb {N}$ . Then, applying condition (ii) in $S_{k_{l}}$ , we have

$$\begin{align*}\varphi_{k_{l+1},k_{l}} (y_{n}^{l}) \leq \varphi_{k_{l+1},k_{l}}(x_{1}^{l}), \ldots , \varphi_{k_{l+1},k_{l}}(x_{n}^{l})\ll x_{1}^{l+1},\ldots, x_{n}^{l+1}, \end{align*}$$

and, by condition (iii) in $S_{k_{l+1}}$ , we get $\varphi _{k_{l+1},k_{l}} (y_{n}^{l})\leq y_{n}^{l+1}$ . It follows that condition (ii) is satisfied.

To prove (iii), take $x',z\in S$ such that $x'\ll x_{j_{1}}, \ldots ,x_{j_{r}}\leq z$ for some pairwise different $j_{1},\ldots ,j_{r}\leq n$ . For a large enough l, there exist u such that

$$\begin{align*}u\ll x_{j_{1}}^{l},\ldots ,x_{j_{r}}^{l} \end{align*}$$

and $x'\ll [u]$ in S.

This implies that, for every $l'\geq l$ , one has

$$\begin{align*}\varphi_{k_{l'},k_{l}}(u)\ll \varphi_{k_{l'},k_{l}}(x_{j_{1}}^{l})+\cdots + \varphi_{k_{l'},k_{l}}(x_{j_{r}}^{l}) \end{align*}$$

in $S_{k_{l'}}$ .

Consequently, we have $\varphi _{k_{l'},k_{l}}(u)\leq d_{r}^{l'}$ and so $x\ll [u]\ll [d_{r}^{l'}]$ in S for every $l'\geq l$ . Furthermore, since $x_{j_{1}}, \ldots ,x_{j_{r}}\leq z$ , for every l, there exists some $z_{l}\in S_{k_{l}}$ with $[z_{l}]\ll z$ and

$$\begin{align*}x_{j_{1}}^{l},\ldots ,x_{j_{r}}^{l}\leq z_{l}. \end{align*}$$

Therefore, one gets $y_{n+1-r}^{l}\leq z_{l}$ . This implies $[y_{n+1-r}^{l}]\leq [z_{l}]\ll z$ for every l, as required.

Theorem 8.7 Let A be an AI-algebra. Then, its Cuntz semigroup $\operatorname {\mathrm {Cu}} (A)$ is weakly chainable and has refinable sums and almost ordered sums.

Proof The Cuntz semigroup $\operatorname {\mathrm {Cu}} (A)$ is weakly chainable by Corollary 7.9. Furthermore, using the same arguments as in Lemma 7.7, it is easy to see that finite direct sums of $\mathrm {Cu}$ -semigroups having refinable sums or almost ordered sums have refinable sums or almost ordered sums, respectively. Thus, it follows from Example 8.1 and Proposition 8.3 that S has refinable sums.

By Example 8.4 and Proposition 8.6, $\operatorname {\mathrm {Cu}} (A)$ also has almost ordered sums.