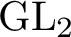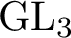1. Introduction
Let
![]() $\mathbf{F}_{q}$
be the finite field with q elements. Let
$\mathbf{F}_{q}$
be the finite field with q elements. Let
![]() $F=\mathbf{F}_{q}(\!(\epsilon )\!)$
be the field of Laurent series with coefficients in
$F=\mathbf{F}_{q}(\!(\epsilon )\!)$
be the field of Laurent series with coefficients in
![]() $\mathbf{F}_{q}$
,
$\mathbf{F}_{q}$
,
![]() $\mathcal {O}=\mathbf{F}_{q}[\![\epsilon ]\!]$
the ring of integers of F, and
$\mathcal {O}=\mathbf{F}_{q}[\![\epsilon ]\!]$
the ring of integers of F, and
![]() $\mathfrak {p}=\epsilon \mathbf{F}_{q}[\![\epsilon ]\!]$
the maximal ideal of
$\mathfrak {p}=\epsilon \mathbf{F}_{q}[\![\epsilon ]\!]$
the maximal ideal of
![]() $\mathcal {O}$
. We fix an algebraic closure
$\mathcal {O}$
. We fix an algebraic closure
![]() $\overline {\mathbf{F}}_{q}$
of
$\overline {\mathbf{F}}_{q}$
of
![]() $\mathbf{F}_{q}$
and also a compatible separable algebraic closure
$\mathbf{F}_{q}$
and also a compatible separable algebraic closure
![]() $\overline {F}$
of F. Let
$\overline {F}$
of F. Let
 $\mathrm{val}:\overline {F}^{\times }\to \textbf {Q}$
be the discrete valuation normalized by
$\mathrm{val}:\overline {F}^{\times }\to \textbf {Q}$
be the discrete valuation normalized by
![]() $\mathrm{val}(\epsilon )=1$
.
$\mathrm{val}(\epsilon )=1$
.
Let G be a connected split reductive algebraic group over
![]() $\mathbf{F}_{q}$
, and assume that
$\mathbf{F}_{q}$
, and assume that
![]() $\text {char}\left (\mathbf{F}_{q}\right )>\lvert W\rvert $
, W being the Weyl group of G. Let
$\text {char}\left (\mathbf{F}_{q}\right )>\lvert W\rvert $
, W being the Weyl group of G. Let
![]() $G_{F}$
be the base change of G to F. Let T be a maximal torus of
$G_{F}$
be the base change of G to F. Let T be a maximal torus of
![]() $G_{F}$
. We make the assumption that the splitting field of T is totally ramified over F. Let
$G_{F}$
. We make the assumption that the splitting field of T is totally ramified over F. Let
![]() $S\subset T$
be the maximal F-split subtorus of T, and let
$S\subset T$
be the maximal F-split subtorus of T, and let
![]() $M_{0}=Z_{G_{F}}(S)$
be the centralizer of S in
$M_{0}=Z_{G_{F}}(S)$
be the centralizer of S in
![]() $G_{F}$
; then
$G_{F}$
; then
![]() $M_{0}$
is a Levi subgroup of
$M_{0}$
is a Levi subgroup of
![]() $G_{F}$
and T is elliptic in
$G_{F}$
and T is elliptic in
![]() $M_{0}$
. Given an algebraic group, we use the Gothic letter to denote its Lie algebra.
$M_{0}$
. Given an algebraic group, we use the Gothic letter to denote its Lie algebra.
Let
![]() $\gamma \in \mathfrak {t}(F)$
be a regular element, elliptic in
$\gamma \in \mathfrak {t}(F)$
be a regular element, elliptic in
![]() $\mathfrak {m}_{0}(F)$
. Let
$\mathfrak {m}_{0}(F)$
. Let
![]() $\mathcal {L}(M_{0})$
be the set of Levi subgroups of G containing
$\mathcal {L}(M_{0})$
be the set of Levi subgroups of G containing
![]() $M_{0}$
. For
$M_{0}$
. For
![]() $M\in \mathcal {L}(M_{0})$
, consider Arthur’s weighted orbital integral
$M\in \mathcal {L}(M_{0})$
, consider Arthur’s weighted orbital integral

where
![]() is the characteristic function of the lattice
is the characteristic function of the lattice
![]() $\mathfrak {g}(\mathcal {O})$
in
$\mathfrak {g}(\mathcal {O})$
in
![]() $\mathfrak {g}(F)$
,
$\mathfrak {g}(F)$
,
![]() $\textrm {v}_{M}(g)$
is Arthur’s weight factor, and
$\textrm {v}_{M}(g)$
is Arthur’s weight factor, and
![]() $dg$
and
$dg$
and
![]() $dt$
are Haar measures on
$dt$
are Haar measures on
![]() $G(F)$
and
$G(F)$
and
![]() $T(F)$
, respectively. One of our main results states that it can be expressed in terms of the number of rational points of the fundamental domains
$T(F)$
, respectively. One of our main results states that it can be expressed in terms of the number of rational points of the fundamental domains
 $F_{\gamma }^{L}$
of the affine Springer fiber
$F_{\gamma }^{L}$
of the affine Springer fiber
 $\mathscr {X}_{\gamma }^{L}$
,
$\mathscr {X}_{\gamma }^{L}$
,
![]() $L\in \mathcal {L}(M_{0})$
. The main idea is to count the number of rational points of the truncated affine Springer fibers in two different ways: by the Arthur–Kottwitz reduction and by the Harder–Narasimhan reduction.
$L\in \mathcal {L}(M_{0})$
. The main idea is to count the number of rational points of the truncated affine Springer fibers in two different ways: by the Arthur–Kottwitz reduction and by the Harder–Narasimhan reduction.
Before entering into the details of our approach, we give examples of results that can be obtained in this way. The calculations for the group
![]() $G=\textrm {GL}_{2}$
are easy; the results are summarized in Theorems 5.1 and 5.2. But for the group
$G=\textrm {GL}_{2}$
are easy; the results are summarized in Theorems 5.1 and 5.2. But for the group
![]() $G=\textrm {GL}_{3}$
, the calculations are already quite nontrivial. There are three cases to deal with: the element
$G=\textrm {GL}_{3}$
, the calculations are already quite nontrivial. There are three cases to deal with: the element
![]() $\gamma $
can be split, mixed, or elliptic. When
$\gamma $
can be split, mixed, or elliptic. When
![]() $\gamma $
is split, we can find a set of simple roots
$\gamma $
is split, we can find a set of simple roots
![]() $\{\alpha _{1},\alpha _{2}\}$
in the root system
$\{\alpha _{1},\alpha _{2}\}$
in the root system
![]() $\Phi (G,T)$
of G with respect to T such that
$\Phi (G,T)$
of G with respect to T such that
We call
![]() $(n_{1},n_{2})=(\mathrm{val}(\alpha _{1}(\gamma )), \mathrm{val}(\alpha _{2}(\gamma )))$
the root valuation of
$(n_{1},n_{2})=(\mathrm{val}(\alpha _{1}(\gamma )), \mathrm{val}(\alpha _{2}(\gamma )))$
the root valuation of
![]() $\gamma $
.
$\gamma $
.
Theorem 1.1. Let
![]() $G=\textrm {GL}_{3}$
and T the maximal torus of diagonal matrices. Let
$G=\textrm {GL}_{3}$
and T the maximal torus of diagonal matrices. Let
![]() $\gamma \in \mathfrak {t}(\mathcal {O})$
be a regular element with root valuation
$\gamma \in \mathfrak {t}(\mathcal {O})$
be a regular element with root valuation
![]() $(n_{1},n_{2})\in \textbf{N}^{2}$
, with
$(n_{1},n_{2})\in \textbf{N}^{2}$
, with
![]() $n_{1}\leq n_{2}$
. Up to an explicit volume factor, we have
$n_{1}\leq n_{2}$
. Up to an explicit volume factor, we have
 $$ \begin{align*} J_{T}(\gamma)\doteq\sum_{i=1}^{n_{1}}i\left(q^{2i-1}+q^{2i-2}\right) +\sum_{i=n_{1}+n_{2}}^{2n_{1}+n_{2}-1} (4n_{1}+2n_{2}-4i-3)q^{i} +\left(n_{1}^{2}+2n_{1}n_{2}\right)q^{2n_{1}+n_{2}}. \end{align*} $$
$$ \begin{align*} J_{T}(\gamma)\doteq\sum_{i=1}^{n_{1}}i\left(q^{2i-1}+q^{2i-2}\right) +\sum_{i=n_{1}+n_{2}}^{2n_{1}+n_{2}-1} (4n_{1}+2n_{2}-4i-3)q^{i} +\left(n_{1}^{2}+2n_{1}n_{2}\right)q^{2n_{1}+n_{2}}. \end{align*} $$
For
![]() $\alpha \in \Phi (G,T)$
, let
$\alpha \in \Phi (G,T)$
, let
![]() $M_{\alpha }$
be the unique Levi subgroup containing T with root system
$M_{\alpha }$
be the unique Levi subgroup containing T with root system
![]() $\{\pm \alpha \}$
; then, up to an explicit volume factor,
$\{\pm \alpha \}$
; then, up to an explicit volume factor,
 $$ \begin{align*} J_{M_{\alpha_{1}}}(\gamma)=J_{M_{\alpha_{1}+\alpha_{2}}}(\gamma)&\doteq(n_{1}+n_{2})q^{2n_{1}+n_{2}}-q^{n_{1}+n_{2}}\left(1+q+\dotsb+q^{n_{1}-1}\right)\\ & \quad -q^{2n_{1}}\left(1+q+\dotsb+q^{n_{2}-1}\right) \end{align*} $$
$$ \begin{align*} J_{M_{\alpha_{1}}}(\gamma)=J_{M_{\alpha_{1}+\alpha_{2}}}(\gamma)&\doteq(n_{1}+n_{2})q^{2n_{1}+n_{2}}-q^{n_{1}+n_{2}}\left(1+q+\dotsb+q^{n_{1}-1}\right)\\ & \quad -q^{2n_{1}}\left(1+q+\dotsb+q^{n_{2}-1}\right) \end{align*} $$
and
 $$ \begin{align*} J_{M_{\alpha_{2}}}(\gamma)\doteq 2n_{1}q^{2n_{1}+n_{2}}-2q^{n_{1}+n_{2}}\left(1+q+\dotsb+q^{n_{1}-1}\right). \end{align*} $$
$$ \begin{align*} J_{M_{\alpha_{2}}}(\gamma)\doteq 2n_{1}q^{2n_{1}+n_{2}}-2q^{n_{1}+n_{2}}\left(1+q+\dotsb+q^{n_{1}-1}\right). \end{align*} $$
When
![]() $\gamma $
is mixed – that is, T is isomorphic to
$\gamma $
is mixed – that is, T is isomorphic to
![]() $F^{\times }\times \textrm {Res}_{E_{2}/F}E_{2}^{\times }$
, where
$F^{\times }\times \textrm {Res}_{E_{2}/F}E_{2}^{\times }$
, where
 $E_{2}=\mathbf{F}_{q}((\epsilon ^{\frac {1}{2}}))$
is the unique totally ramified extension of F of degree
$E_{2}=\mathbf{F}_{q}((\epsilon ^{\frac {1}{2}}))$
is the unique totally ramified extension of F of degree
![]() $2$
– it can be conjugate to a matrix of the form
$2$
– it can be conjugate to a matrix of the form
 $$ \begin{align} \gamma=\begin{bmatrix} a&&\\ &&b\\&b\epsilon& \end{bmatrix}. \end{align} $$
$$ \begin{align} \gamma=\begin{bmatrix} a&&\\ &&b\\&b\epsilon& \end{bmatrix}. \end{align} $$
Let
![]() $m=\mathrm{val}(a)$
and
$m=\mathrm{val}(a)$
and
![]() $n=\mathrm{val}(b)$
; then we have the following:
$n=\mathrm{val}(b)$
; then we have the following:
Theorem 1.2. Let
![]() $G=\textrm {GL}_{3}$
and let
$G=\textrm {GL}_{3}$
and let
![]() $\gamma $
be a matrix in the form of equation (1.2). When
$\gamma $
be a matrix in the form of equation (1.2). When
![]() $\mathrm{val}(a)=m\leq n$
, up to an explicit volume factor,
$\mathrm{val}(a)=m\leq n$
, up to an explicit volume factor,
 $$ \begin{align*} J_{M_{0}}(\gamma)\doteq 2mq^{2m+n}+\sum_{j=m+n+1}^{2m+n-1}2(j-m-n)q^{j} -\sum_{j=0}^{2m-1}\left(\left\lfloor \frac{j}{2} \right\rfloor+1\right) q^{j}. \end{align*} $$
$$ \begin{align*} J_{M_{0}}(\gamma)\doteq 2mq^{2m+n}+\sum_{j=m+n+1}^{2m+n-1}2(j-m-n)q^{j} -\sum_{j=0}^{2m-1}\left(\left\lfloor \frac{j}{2} \right\rfloor+1\right) q^{j}. \end{align*} $$
Similarly, when
![]() $\mathrm{val}(a)=m> n$
, up to an explicit volume factor,
$\mathrm{val}(a)=m> n$
, up to an explicit volume factor,
 $$ \begin{align*} J_{M_{0}}(\gamma)\doteq (2n+1)q^{3n+1}+\sum_{j=2n+1}^{3n}(2j-4n-1)q^{j}-\sum_{j=0}^{2n}\left(\left\lfloor \frac{j}{2} \right\rfloor+1\right) q^{j}, \end{align*} $$
$$ \begin{align*} J_{M_{0}}(\gamma)\doteq (2n+1)q^{3n+1}+\sum_{j=2n+1}^{3n}(2j-4n-1)q^{j}-\sum_{j=0}^{2n}\left(\left\lfloor \frac{j}{2} \right\rfloor+1\right) q^{j}, \end{align*} $$
where
![]() $\lfloor x\rfloor $
denotes the maximal integer less than or equal to x.
$\lfloor x\rfloor $
denotes the maximal integer less than or equal to x.
When
![]() $\gamma $
is anisotropic, Arthur’s weighted orbital integral is just the orbital integral, and the result was essentially obtained by Goresky, Kottwitz, and MacPherson [Reference Goresky, Kottwitz and MacPherson16]. See Theorems 8.1 and 8.2 for the counting result.
$\gamma $
is anisotropic, Arthur’s weighted orbital integral is just the orbital integral, and the result was essentially obtained by Goresky, Kottwitz, and MacPherson [Reference Goresky, Kottwitz and MacPherson16]. See Theorems 8.1 and 8.2 for the counting result.
Now we explain our approach to calculating Arthur’s weighted orbital integrals using the geometry of the affine Springer fibers. For simplicity, we restrict to
![]() $J_{M_{0}}(\gamma )$
. The affine Springer fiber
$J_{M_{0}}(\gamma )$
. The affine Springer fiber
![]() $\mathscr {X}_{\gamma }$
is the closed subscheme of the affine Grassmannian
$\mathscr {X}_{\gamma }$
is the closed subscheme of the affine Grassmannian
![]() $\mathscr {X}=G(F)/G(\mathcal {O})$
defined by the equation
$\mathscr {X}=G(F)/G(\mathcal {O})$
defined by the equation
 $$ \begin{align*} \mathscr{X}_{\gamma}=\left\{g\in G(F)/G(\mathcal{O}) \mid \textrm{Ad}\left(g^{-1}\right)\gamma \in \mathfrak{g}(\mathcal{O})\right\}. \end{align*} $$
$$ \begin{align*} \mathscr{X}_{\gamma}=\left\{g\in G(F)/G(\mathcal{O}) \mid \textrm{Ad}\left(g^{-1}\right)\gamma \in \mathfrak{g}(\mathcal{O})\right\}. \end{align*} $$
They can be used to geometrize Arthur’s weighted orbital integrals. The group
![]() $T(F)$
acts on
$T(F)$
acts on
![]() $\mathscr {X}_{\gamma }$
by left translation. For
$\mathscr {X}_{\gamma }$
by left translation. For
![]() $\mu \in X_{*}(S)$
, we write
$\mu \in X_{*}(S)$
, we write
![]() $\epsilon ^{\mu }$
for
$\epsilon ^{\mu }$
for
![]() $\mu (\epsilon )\in S(F)$
. The map
$\mu (\epsilon )\in S(F)$
. The map
![]() $\mu \to \epsilon ^{\mu }$
identifies
$\mu \to \epsilon ^{\mu }$
identifies
![]() $X_{*}(S)$
with a subgroup of
$X_{*}(S)$
with a subgroup of
![]() $S(F)\subset T(F)$
, which we denote by
$S(F)\subset T(F)$
, which we denote by
![]() $\Lambda $
. It acts freely on
$\Lambda $
. It acts freely on
![]() $\mathscr {X}_{\gamma }$
, and the quotient
$\mathscr {X}_{\gamma }$
, and the quotient
![]() $\Lambda \backslash \mathscr {X}_{\gamma }$
is a projective scheme of finite type over
$\Lambda \backslash \mathscr {X}_{\gamma }$
is a projective scheme of finite type over
![]() $\mathbf{F}_{q}$
(see [Reference Kottwitz17, §3]). A simple reformulation shows that
$\mathbf{F}_{q}$
(see [Reference Kottwitz17, §3]). A simple reformulation shows that

where
![]() $[g]$
denotes the point
$[g]$
denotes the point
![]() $gG(\mathcal {O})\in \mathscr {X}$
and c is a volume factor.
$gG(\mathcal {O})\in \mathscr {X}$
and c is a volume factor.
But this expression does not facilitate the calculations of Arthur’s weighted orbital integral. We have to proceed in an indirect way. Let
 $\xi \in \mathfrak {a}_{M_{0}}^{G}$
be a generic element (for the definition of
$\xi \in \mathfrak {a}_{M_{0}}^{G}$
be a generic element (for the definition of
 $\mathfrak {a}_{M_{0}}^{G}$
, see §1.1). Chaudouard and Laumon [Reference Chen8] introduce a variant of the weighted orbital integral
$\mathfrak {a}_{M_{0}}^{G}$
, see §1.1). Chaudouard and Laumon [Reference Chen8] introduce a variant of the weighted orbital integral

with a slightly different weight factor
 $\mathrm{w}_{M_{0}}^{\xi }(g)$
. The two weight factors are closely related to each other. When G is semisimple, Chaudouard and Laumon show that
$\mathrm{w}_{M_{0}}^{\xi }(g)$
. The two weight factors are closely related to each other. When G is semisimple, Chaudouard and Laumon show that
 $$ \begin{align*} J_{M_{0}}(\gamma)=\text{vol}\left(\mathfrak{a}_{M_{0}}/X_{*}(M_{0})\right)\cdot J_{M_{0}}^{\xi}(\gamma). \end{align*} $$
$$ \begin{align*} J_{M_{0}}(\gamma)=\text{vol}\left(\mathfrak{a}_{M_{0}}/X_{*}(M_{0})\right)\cdot J_{M_{0}}^{\xi}(\gamma). \end{align*} $$
The variant
 $J_{M_{0}}^{\xi }(\gamma )$
has a better geometric interpretation. In fact, we can introduce a notion of
$J_{M_{0}}^{\xi }(\gamma )$
has a better geometric interpretation. In fact, we can introduce a notion of
![]() $\xi $
-stability on the affine Springer fiber
$\xi $
-stability on the affine Springer fiber
![]() $\mathscr {X}_{\gamma }$
and show that
$\mathscr {X}_{\gamma }$
and show that
 $$ \begin{align*} J_{M_{0}}^{\xi}(\gamma)=\mathrm{vol}_{dt}\left(T(F)^{1}\right)^{-1}\cdot\left\lvert\mathscr{X}_{\gamma}^{\xi}\left(\mathbf{F}_{q}\right)\right\rvert.\end{align*} $$
$$ \begin{align*} J_{M_{0}}^{\xi}(\gamma)=\mathrm{vol}_{dt}\left(T(F)^{1}\right)^{-1}\cdot\left\lvert\mathscr{X}_{\gamma}^{\xi}\left(\mathbf{F}_{q}\right)\right\rvert.\end{align*} $$
The advantage of this variant is clear: it is a plain count rather than a weighted count. Moreover, we can use the Harder–Narasimhan reduction to get
 $\left \lvert \mathscr {X}_{\gamma }^{\xi }\left (\mathbf{F}_{q}\right )\right \rvert $
recursively from
$\left \lvert \mathscr {X}_{\gamma }^{\xi }\left (\mathbf{F}_{q}\right )\right \rvert $
recursively from
![]() $\left \lvert \mathscr {X}_{\gamma }\left (\mathbf{F}_{q}\right )\right \rvert $
, if only the latter is finite. Unfortunately this is not the case, as can be seen from the fact that the free abelian group
$\left \lvert \mathscr {X}_{\gamma }\left (\mathbf{F}_{q}\right )\right \rvert $
, if only the latter is finite. Unfortunately this is not the case, as can be seen from the fact that the free abelian group
![]() $\Lambda $
acts freely on
$\Lambda $
acts freely on
![]() $\mathscr {X}_{\gamma }$
.
$\mathscr {X}_{\gamma }$
.
Let
![]() $\Pi $
be a positive
$\Pi $
be a positive
![]() $(G,M_{0})$
-orthogonal family. We can introduce a truncation
$(G,M_{0})$
-orthogonal family. We can introduce a truncation
![]() $\mathscr {X}_{\gamma }(\Pi )$
to overcome the finiteness issue. When
$\mathscr {X}_{\gamma }(\Pi )$
to overcome the finiteness issue. When
![]() $\Pi $
is sufficiently regular, we can reduce the calculation of the rational points on
$\Pi $
is sufficiently regular, we can reduce the calculation of the rational points on
![]() $\mathscr {X}_{\gamma }(\Pi )$
to that of the fundamental domains
$\mathscr {X}_{\gamma }(\Pi )$
to that of the fundamental domains
 $F_{\gamma }^{L}$
, by the Arthur–Kottwitz reduction. Recall that the fundamental domain
$F_{\gamma }^{L}$
, by the Arthur–Kottwitz reduction. Recall that the fundamental domain
![]() $F_{\gamma }$
is introduced in [Reference Chaudouard and Laumon11] to play the role of an irreducible component of
$F_{\gamma }$
is introduced in [Reference Chaudouard and Laumon11] to play the role of an irreducible component of
![]() $\mathscr {X}_{\gamma }$
. (All the irreducible components of
$\mathscr {X}_{\gamma }$
. (All the irreducible components of
![]() $\mathscr {X}_{\gamma }$
are isomorphic, because
$\mathscr {X}_{\gamma }$
are isomorphic, because
![]() $T(F)$
acts transitively on a dense open subscheme of it.) The Arthur–Kottwitz reduction is a construction that decomposes
$T(F)$
acts transitively on a dense open subscheme of it.) The Arthur–Kottwitz reduction is a construction that decomposes
![]() $\mathscr {X}_{\gamma }(\Pi )$
into locally closed subschemes, which are iterated affine fibrations over the fundamental domains
$\mathscr {X}_{\gamma }(\Pi )$
into locally closed subschemes, which are iterated affine fibrations over the fundamental domains
 $F_{\gamma }^{L}$
,
$F_{\gamma }^{L}$
,
![]() $L\in \mathcal {L}(M_{0})$
. The counting result is summarized in Corollary 3.7. In particular, it shows that
$L\in \mathcal {L}(M_{0})$
. The counting result is summarized in Corollary 3.7. In particular, it shows that
![]() $\mathscr {X}_{\gamma }(\Pi )$
depends quasi-polynomially on the truncation parameter.
$\mathscr {X}_{\gamma }(\Pi )$
depends quasi-polynomially on the truncation parameter.
On the other hand, the Harder–Narasimhan reduction does not behave well on
![]() $\mathscr {X}_{\gamma }(\Pi )$
. In fact, near the boundary, the Harder–Narasimhan strata are generally not affine fibrations over truncations of
$\mathscr {X}_{\gamma }(\Pi )$
. In fact, near the boundary, the Harder–Narasimhan strata are generally not affine fibrations over truncations of
 $\mathscr {X}_{\gamma }^{L,\,\xi ^{L}}$
. To overcome this difficulty, we cut
$\mathscr {X}_{\gamma }^{L,\,\xi ^{L}}$
. To overcome this difficulty, we cut
![]() $\mathscr {X}_{\gamma }(\Pi )$
into two parts: the tail and the main body. Roughly speaking, the tail is the union of the ‘boundary irreducible components’ of
$\mathscr {X}_{\gamma }(\Pi )$
into two parts: the tail and the main body. Roughly speaking, the tail is the union of the ‘boundary irreducible components’ of
![]() $\mathscr {X}_{\gamma }(\Pi )$
, and the main body is its complement. The Harder–Narasimhan reduction works well on the main body, and we can use it to count the number of rational points. The result is summarized in Theorem 4.8; it can be expressed in terms of
$\mathscr {X}_{\gamma }(\Pi )$
, and the main body is its complement. The Harder–Narasimhan reduction works well on the main body, and we can use it to count the number of rational points. The result is summarized in Theorem 4.8; it can be expressed in terms of
 $\lvert \mathscr {X}_{\gamma }^{L,\xi ^{L}}(\mathbf{F}_{q})\rvert $
,
$\lvert \mathscr {X}_{\gamma }^{L,\xi ^{L}}(\mathbf{F}_{q})\rvert $
,
![]() $L\in \mathcal {L}(M_{0})$
. Counting points on the tail proceeds by the Arthur–Kottwitz reduction, and can be expressed in terms of
$L\in \mathcal {L}(M_{0})$
. Counting points on the tail proceeds by the Arthur–Kottwitz reduction, and can be expressed in terms of
 $\lvert F_{\gamma }^{L}(\mathbf{F}_{q})\rvert $
s. But we are not able to obtain an explicit expression; we get a recursion.
$\lvert F_{\gamma }^{L}(\mathbf{F}_{q})\rvert $
s. But we are not able to obtain an explicit expression; we get a recursion.
These two different approaches to counting rational points on
![]() $\mathscr {X}_{\gamma }(\Pi )$
give us a recursive equation that involves the
$\mathscr {X}_{\gamma }(\Pi )$
give us a recursive equation that involves the
 $\lvert F_{\gamma }^{L}(\mathbf{F}_{q})\rvert $
s and the
$\lvert F_{\gamma }^{L}(\mathbf{F}_{q})\rvert $
s and the
 $\lvert \mathscr {X}_{\gamma }^{L,\xi ^{L}}(\mathbf{F}_{q})\rvert $
s. Solving it, we can express the latter in terms of the former. The problem of calculating
$\lvert \mathscr {X}_{\gamma }^{L,\xi ^{L}}(\mathbf{F}_{q})\rvert $
s. Solving it, we can express the latter in terms of the former. The problem of calculating
![]() $J_{M_{0}}(\gamma )$
is thus reduced to counting points on
$J_{M_{0}}(\gamma )$
is thus reduced to counting points on
![]() $F_{\gamma }$
.
$F_{\gamma }$
.
The geometry of
![]() $F_{\gamma }$
is simpler than that of
$F_{\gamma }$
is simpler than that of
 $\mathscr {X}_{\gamma }^{\xi }$
: Goresky, Kottwitz, and MacPherson [Reference Goresky, Kottwitz and MacPherson14] have conjectured that the cohomology of
$\mathscr {X}_{\gamma }^{\xi }$
: Goresky, Kottwitz, and MacPherson [Reference Goresky, Kottwitz and MacPherson14] have conjectured that the cohomology of
![]() $\mathscr {X}_{\gamma }$
is pure in the sense of Deligne. As we have shown in [Reference Chaudouard and Laumon11], this is equivalent to the cohomological purity of
$\mathscr {X}_{\gamma }$
is pure in the sense of Deligne. As we have shown in [Reference Chaudouard and Laumon11], this is equivalent to the cohomological purity of
![]() $F_{\gamma }$
. In fact, it is even expected that
$F_{\gamma }$
. In fact, it is even expected that
![]() $F_{\gamma }$
admits a Hessenberg paving. (This notion was introduced by Goresky, Kottwitz, and MacPherson [Reference Goresky, Kottwitz and MacPherson16].) On the contrary,
$F_{\gamma }$
admits a Hessenberg paving. (This notion was introduced by Goresky, Kottwitz, and MacPherson [Reference Goresky, Kottwitz and MacPherson16].) On the contrary,
 $\mathscr {X}_{\gamma }^{\xi }$
is generally not cohomologically pure, as one can see in case
$\mathscr {X}_{\gamma }^{\xi }$
is generally not cohomologically pure, as one can see in case
![]() $G=\textrm {SL}_{2}$
or from the appearance of a minus sign in the counting-points result of Theorems 6.6, 6.10, and 6.14. Although one can still look at the quotient
$G=\textrm {SL}_{2}$
or from the appearance of a minus sign in the counting-points result of Theorems 6.6, 6.10, and 6.14. Although one can still look at the quotient
 $\mathscr {X}_{\gamma }^{\xi }/A_{M_{0}}$
, where
$\mathscr {X}_{\gamma }^{\xi }/A_{M_{0}}$
, where
![]() $A_{M_{0}}$
is the maximal F-split torus of the center of
$A_{M_{0}}$
is the maximal F-split torus of the center of
![]() $M_{0}$
, it is clear that the quotient no longer admits a torus action, and hence it has much less structure to explore than
$M_{0}$
, it is clear that the quotient no longer admits a torus action, and hence it has much less structure to explore than
![]() $F_{\gamma }$
.
$F_{\gamma }$
.
When the torus T splits, we make a conjecture on the Poincaré polynomial of
![]() $F_{\gamma }$
[Reference Chaudouard and Laumon12], assuming the cohomological purity of
$F_{\gamma }$
[Reference Chaudouard and Laumon12], assuming the cohomological purity of
![]() $F_{\gamma }$
. This gives a conjectural expression for
$F_{\gamma }$
. This gives a conjectural expression for
![]() $\left \lvert F_{\gamma }\left (\mathbf{F}_{q}\right )\right \rvert $
. We reproduce it here for the convenience of the reader. Following Chaudouard and Laumon [Reference Chen7], under the purity assumption the cohomology of
$\left \lvert F_{\gamma }\left (\mathbf{F}_{q}\right )\right \rvert $
. We reproduce it here for the convenience of the reader. Following Chaudouard and Laumon [Reference Chen7], under the purity assumption the cohomology of
![]() $F_{\gamma }$
can be expressed in terms of its
$F_{\gamma }$
can be expressed in terms of its
![]() $1$
-skeleton under the T-action. Indeed, the T-equivariant cohomology
$1$
-skeleton under the T-action. Indeed, the T-equivariant cohomology
 $H_{T}^{*}\left (F_{\gamma },\overline {\textbf {Q}}_{\ell }\right )$
Footnote
1
will then be a free
$H_{T}^{*}\left (F_{\gamma },\overline {\textbf {Q}}_{\ell }\right )$
Footnote
1
will then be a free
![]() $H_{T}^{*}(\text {pt}, \overline {\textbf {Q}}_{\ell })$
-algebra, and we have
$H_{T}^{*}(\text {pt}, \overline {\textbf {Q}}_{\ell })$
-algebra, and we have
 $$ \begin{align} H^{*}\left(F_{\gamma},\overline{\textbf{Q}}_{\ell}\right)=H^{*}_{T}\left(F_{\gamma},\overline{\textbf{Q}}_{\ell}\right)\otimes_{H^{*}_{T}\left(\text{pt},\overline{\textbf{Q}}_{\ell}\right)}\overline{\textbf{Q}}_{\ell}. \end{align} $$
$$ \begin{align} H^{*}\left(F_{\gamma},\overline{\textbf{Q}}_{\ell}\right)=H^{*}_{T}\left(F_{\gamma},\overline{\textbf{Q}}_{\ell}\right)\otimes_{H^{*}_{T}\left(\text{pt},\overline{\textbf{Q}}_{\ell}\right)}\overline{\textbf{Q}}_{\ell}. \end{align} $$
The torus T acts on
![]() $F_{\gamma }$
with finitely many fixed points, but the
$F_{\gamma }$
with finitely many fixed points, but the
![]() $1$
-dimensional T-orbits form a higher-dimensional variety which we denote by
$1$
-dimensional T-orbits form a higher-dimensional variety which we denote by
 $F_{\gamma }^{T,1}$
. The bigger torus
$F_{\gamma }^{T,1}$
. The bigger torus
![]() $\widetilde {T}=T\times \mathbb {G}_{m}$
, where
$\widetilde {T}=T\times \mathbb {G}_{m}$
, where
![]() $\mathbb {G}_{m}$
is the rotational torus, acts on
$\mathbb {G}_{m}$
is the rotational torus, acts on
 $F_{\gamma }^{T,1}$
with finitely many
$F_{\gamma }^{T,1}$
with finitely many
![]() $1$
-dimensional
$1$
-dimensional
![]() $\widetilde {T}$
-orbits; let
$\widetilde {T}$
-orbits; let
 $F_{\gamma }^{\widetilde {T},1}$
be their union. Let
$F_{\gamma }^{\widetilde {T},1}$
be their union. Let
 $F_{\gamma }^{\widetilde {T}}$
be the set of
$F_{\gamma }^{\widetilde {T}}$
be the set of
![]() $\widetilde {T}$
-fixed points on
$\widetilde {T}$
-fixed points on
![]() $F_{\gamma }$
, and let
$F_{\gamma }$
, and let
 $$ \begin{align} H^{*}_{\widetilde{T}}\left(F_{\gamma},\overline{\textbf{Q}}_{\ell}\right):=H^{*}_{T}\left(F_{\gamma},\overline{\textbf{Q}}_{\ell}\right)\otimes_{H^{*}_{T}\left(\text{pt},\overline{\textbf{Q}}_{\ell}\right)}H^{*}_{\widetilde{T}}\left(\text{pt},\overline{\textbf{Q}}_{\ell}\right). \end{align} $$
$$ \begin{align} H^{*}_{\widetilde{T}}\left(F_{\gamma},\overline{\textbf{Q}}_{\ell}\right):=H^{*}_{T}\left(F_{\gamma},\overline{\textbf{Q}}_{\ell}\right)\otimes_{H^{*}_{T}\left(\text{pt},\overline{\textbf{Q}}_{\ell}\right)}H^{*}_{\widetilde{T}}\left(\text{pt},\overline{\textbf{Q}}_{\ell}\right). \end{align} $$
Then the localization theorem of Goresky, Kottwitz, and MacPherson [Reference Goresky, Kottwitz and MacPherson13] implies an exact sequence of equivariant cohomology
 $$ \begin{align} 0\to H_{\widetilde{T}}^{*}\left(F_{\gamma},\overline{\textbf{Q}}_{\ell}\right)\to H^{*}_{\widetilde{T}}\left(F_{\gamma}^{\widetilde{T}},\overline{\textbf{Q}}_{\ell}\right)\to H^{*}_{\widetilde{T}}\left(F_{\gamma}^{\widetilde{T},1},F_{\gamma}^{\widetilde{T}};\overline{\textbf{Q}}_{\ell}\right). \end{align} $$
$$ \begin{align} 0\to H_{\widetilde{T}}^{*}\left(F_{\gamma},\overline{\textbf{Q}}_{\ell}\right)\to H^{*}_{\widetilde{T}}\left(F_{\gamma}^{\widetilde{T}},\overline{\textbf{Q}}_{\ell}\right)\to H^{*}_{\widetilde{T}}\left(F_{\gamma}^{\widetilde{T},1},F_{\gamma}^{\widetilde{T}};\overline{\textbf{Q}}_{\ell}\right). \end{align} $$
Let
![]() $\Gamma $
be the graph with vertices
$\Gamma $
be the graph with vertices
 $F_{\gamma }^{\widetilde {T}}$
and edges
$F_{\gamma }^{\widetilde {T}}$
and edges
 $F_{\gamma }^{\widetilde {T},1}$
. Two vertices are linked by an edge if and only if they lie on the closure of the corresponding
$F_{\gamma }^{\widetilde {T},1}$
. Two vertices are linked by an edge if and only if they lie on the closure of the corresponding
![]() $1$
-dimensional
$1$
-dimensional
![]() $\widetilde {T}$
-orbit. We call it the moment graph of
$\widetilde {T}$
-orbit. We call it the moment graph of
![]() $F_{\gamma }$
with respect to the action of
$F_{\gamma }$
with respect to the action of
![]() $\widetilde {T}$
. The foregoing result implies that the information about the cohomology of
$\widetilde {T}$
. The foregoing result implies that the information about the cohomology of
![]() $F_{\gamma }$
is encoded in
$F_{\gamma }$
is encoded in
![]() $\Gamma $
. A direct calculation of the cohomology via formulas (1.4), (1.5), and (1.6) turns out to be very hard, and we look for a combinatorial way to get around it.
$\Gamma $
. A direct calculation of the cohomology via formulas (1.4), (1.5), and (1.6) turns out to be very hard, and we look for a combinatorial way to get around it.
Let
![]() $\mathfrak {o}$
be a total order among the vertices of the graph
$\mathfrak {o}$
be a total order among the vertices of the graph
![]() $\Gamma $
; it will serve as the paving order. We associate to it an acyclic oriented graph
$\Gamma $
; it will serve as the paving order. We associate to it an acyclic oriented graph
![]() $(\Gamma , \mathfrak {o})$
such that the source of each arrow is greater than its target with respect to
$(\Gamma , \mathfrak {o})$
such that the source of each arrow is greater than its target with respect to
![]() $\mathfrak {o}$
. For
$\mathfrak {o}$
. For
![]() $v\in \Gamma $
, denote by
$v\in \Gamma $
, denote by
![]() $n^{\mathfrak {o}}_{v}$
the number of arrows having source v.
$n^{\mathfrak {o}}_{v}$
the number of arrows having source v.
Definition 1.1. The formal Betti number
![]() $b^{\mathfrak {o}}_{2i}$
associated to the order
$b^{\mathfrak {o}}_{2i}$
associated to the order
![]() $\mathfrak {o}$
is defined as
$\mathfrak {o}$
is defined as
We call
 $$ \begin{align*} P^{\mathfrak{o}}(t)=\sum_{i}b_{2i}^{\mathfrak{o}}t^{2i} \end{align*} $$
$$ \begin{align*} P^{\mathfrak{o}}(t)=\sum_{i}b_{2i}^{\mathfrak{o}}t^{2i} \end{align*} $$
the formal Poincaré polynomial associated to the order
![]() $\mathfrak {o}$
.
$\mathfrak {o}$
.
Definition 1.2. For
![]() $P_{1}(t),P_{2}(t)\in \textbf {Z}[t]$
, we say that
$P_{1}(t),P_{2}(t)\in \textbf {Z}[t]$
, we say that
![]() $P_{1}(t)< P_{2}(t)$
if the leading coefficient of
$P_{1}(t)< P_{2}(t)$
if the leading coefficient of
![]() $P_{2}(t)-P_{1}(t)$
is positive.
$P_{2}(t)-P_{1}(t)$
is positive.
Conjecture 1.1. Let
![]() $P(t)$
be the Poincaré polynomial of
$P(t)$
be the Poincaré polynomial of
![]() $F_{\gamma }$
. Then
$F_{\gamma }$
. Then
 $$ \begin{align*} P(t)=\min_{\mathfrak{o}}\left\{P^{\mathfrak{o}}(t)\right\}, \end{align*} $$
$$ \begin{align*} P(t)=\min_{\mathfrak{o}}\left\{P^{\mathfrak{o}}(t)\right\}, \end{align*} $$
where
![]() $\mathfrak {o}$
runs through all the total orders among the vertices of
$\mathfrak {o}$
runs through all the total orders among the vertices of
![]() $\Gamma $
.
$\Gamma $
.
The conjecture can be thought of as a kind of Morse inequality; it has been verified in a lot of examples. For the group
![]() $G=\textrm {GL}_{2}$
and
$G=\textrm {GL}_{2}$
and
![]() $\gamma =\textrm {diag}(\gamma _{1},\gamma _{2})$
, with
$\gamma =\textrm {diag}(\gamma _{1},\gamma _{2})$
, with
![]() $\gamma _{1},\gamma _{2}\in F$
and
$\gamma _{1},\gamma _{2}\in F$
and
![]() $\mathrm{val}(\gamma _{1}-\gamma _{2})=n\in \textbf {N}$
, the moment graph of
$\mathrm{val}(\gamma _{1}-\gamma _{2})=n\in \textbf {N}$
, the moment graph of
![]() $F_{\gamma }$
contains
$F_{\gamma }$
contains
![]() $n+1$
vertices, which are pairwise connected by an edge. It is clear that the conjecture holds in this case. In general, the moment graph of
$n+1$
vertices, which are pairwise connected by an edge. It is clear that the conjecture holds in this case. In general, the moment graph of
![]() $F_{\gamma }$
is easy to describe, and we have an algorithm to find an order
$F_{\gamma }$
is easy to describe, and we have an algorithm to find an order
![]() $\mathfrak {o}$
which conjecturally should attain the minimum. Although we are not able to prove both conjectures at the moment, they have been very helpful in constructing affine pavings of
$\mathfrak {o}$
which conjecturally should attain the minimum. Although we are not able to prove both conjectures at the moment, they have been very helpful in constructing affine pavings of
![]() $F_{\gamma }$
in concrete examples.
$F_{\gamma }$
in concrete examples.
Under the purity assumption, Conjecture 1.1 implies a point-counting result for
![]() $F_{\gamma }$
. Indeed, the formulas (1.4), (1.5), and (1.6) are
$F_{\gamma }$
. Indeed, the formulas (1.4), (1.5), and (1.6) are
 $\textrm {Gal}\left (\overline {\mathbf{F}}_{q}/\mathbf{F}_{q}\right )$
-equivariant, and the Frobenius endomorphism acts on
$\textrm {Gal}\left (\overline {\mathbf{F}}_{q}/\mathbf{F}_{q}\right )$
-equivariant, and the Frobenius endomorphism acts on
 $H^{2i}_{\widetilde {T}}(F_{\gamma }^{\widetilde {T}},\overline {\textbf {Q}}_{\ell })$
by
$H^{2i}_{\widetilde {T}}(F_{\gamma }^{\widetilde {T}},\overline {\textbf {Q}}_{\ell })$
by
![]() $q^{i}$
(the odd-degree cohomologies vanish), and hence it acts on
$q^{i}$
(the odd-degree cohomologies vanish), and hence it acts on
 $H^{*}\left (F_{\gamma },\overline {\textbf {Q}}_{\ell }\right )$
in the same way and so
$H^{*}\left (F_{\gamma },\overline {\textbf {Q}}_{\ell }\right )$
in the same way and so
 $$ \begin{align*} \left\lvert F_{\gamma}\left(\mathbf{F}_{q}\right)\right\rvert=\min_{\mathfrak{o}}\left\{P^{\mathfrak{o}}(q^{1/2})\right\}. \end{align*} $$
$$ \begin{align*} \left\lvert F_{\gamma}\left(\mathbf{F}_{q}\right)\right\rvert=\min_{\mathfrak{o}}\left\{P^{\mathfrak{o}}(q^{1/2})\right\}. \end{align*} $$
Together with the recurrence relation between
 $\left \lvert \mathscr {X}_{\gamma }^{\xi }\left (\mathbf{F}_{q}\right )\right \rvert $
and
$\left \lvert \mathscr {X}_{\gamma }^{\xi }\left (\mathbf{F}_{q}\right )\right \rvert $
and
![]() $\left \lvert F_{\gamma }\left (\mathbf{F}_{q}\right )\right \rvert $
, it gives a conjectural complete answer to the calculation of Arthur’s weighted orbital integrals in the split case.
$\left \lvert F_{\gamma }\left (\mathbf{F}_{q}\right )\right \rvert $
, it gives a conjectural complete answer to the calculation of Arthur’s weighted orbital integrals in the split case.
1.1. Notation
We fix a split maximal torus A of G over
![]() $\mathbf{F}_{q}$
. Without loss of generality, we suppose that
$\mathbf{F}_{q}$
. Without loss of generality, we suppose that
![]() $A\subset M_{0}$
. Let
$A\subset M_{0}$
. Let
![]() $\Phi =\Phi (G,A)$
be the root system of G with respect to A and let W be the Weyl group of G with respect to A. For any subgroup H of G which is stable under the conjugation of A, we write
$\Phi =\Phi (G,A)$
be the root system of G with respect to A and let W be the Weyl group of G with respect to A. For any subgroup H of G which is stable under the conjugation of A, we write
![]() $\Phi (H,A)$
for the roots appearing in
$\Phi (H,A)$
for the roots appearing in
![]() $\textrm {Lie}(H)$
. We fix a Borel subgroup
$\textrm {Lie}(H)$
. We fix a Borel subgroup
![]() $B_{0}$
of G containing A. Let
$B_{0}$
of G containing A. Let
![]() $\Delta =\{\alpha _{1},\dotsc ,\alpha _{r}\}$
be the set of simple roots with respect to
$\Delta =\{\alpha _{1},\dotsc ,\alpha _{r}\}$
be the set of simple roots with respect to
![]() $B_{0}$
and let
$B_{0}$
and let
![]() $\{\varpi _{i}\}_{i=1}^{r}$
be the corresponding fundamental weights. For an element
$\{\varpi _{i}\}_{i=1}^{r}$
be the corresponding fundamental weights. For an element
![]() $\alpha \in \Delta $
, we have a unique maximal parabolic subgroup
$\alpha \in \Delta $
, we have a unique maximal parabolic subgroup
![]() $P_{\alpha }$
of G containing
$P_{\alpha }$
of G containing
![]() $B_{0}$
such that
$B_{0}$
such that
![]() $\Phi \left (N_{P_{\alpha }},A\right )\cap \Delta =\{\alpha \}$
, where
$\Phi \left (N_{P_{\alpha }},A\right )\cap \Delta =\{\alpha \}$
, where
![]() $N_{P_{\alpha }}$
is the unipotent radical of
$N_{P_{\alpha }}$
is the unipotent radical of
![]() $P_{\alpha }$
. This gives a bijective correspondence between the simple roots in
$P_{\alpha }$
. This gives a bijective correspondence between the simple roots in
![]() $\Delta $
and the maximal parabolic subgroups of G containing
$\Delta $
and the maximal parabolic subgroups of G containing
![]() $B_{0}$
. Any semistandard maximal parabolic subgroup P of G is conjugate to certain
$B_{0}$
. Any semistandard maximal parabolic subgroup P of G is conjugate to certain
![]() $P_{\alpha }$
by an element
$P_{\alpha }$
by an element
![]() $w\in W$
; when the element
$w\in W$
; when the element
![]() $w\varpi _{\alpha }$
does not depend on the choice of w, we denote it by
$w\varpi _{\alpha }$
does not depend on the choice of w, we denote it by
![]() $\varpi _{P}$
.
$\varpi _{P}$
.
We use the
![]() $(G,M)$
notation of Arthur. Let
$(G,M)$
notation of Arthur. Let
![]() $\mathcal {F}(A)$
be the set of parabolic subgroups of G containing A and let
$\mathcal {F}(A)$
be the set of parabolic subgroups of G containing A and let
![]() $\mathcal {L}(A)$
be the set of Levi subgroups of G containing A. For every
$\mathcal {L}(A)$
be the set of Levi subgroups of G containing A. For every
![]() $M\in \mathcal {L}(A)$
, we denote by
$M\in \mathcal {L}(A)$
, we denote by
![]() $\mathcal {P}(M)$
the set of parabolic subgroups of G whose Levi factor is M, by
$\mathcal {P}(M)$
the set of parabolic subgroups of G whose Levi factor is M, by
![]() $\mathcal {L}(M)$
the set of Levi subgroups of G containing M, and by
$\mathcal {L}(M)$
the set of Levi subgroups of G containing M, and by
![]() $\mathcal {F}(M)$
the set of parabolic subgroups of G containing M. For
$\mathcal {F}(M)$
the set of parabolic subgroups of G containing M. For
![]() $P\in \mathcal {P}(M)$
, we denote by
$P\in \mathcal {P}(M)$
, we denote by
![]() $P^{-}\in \mathcal {P}(M)$
the opposite of P with respect to M.
$P^{-}\in \mathcal {P}(M)$
the opposite of P with respect to M.
Let
![]() $X^*(M)=\textrm {Hom}(M, \mathbb {G}_m)$
and
$X^*(M)=\textrm {Hom}(M, \mathbb {G}_m)$
and
![]() $X_{*}(M)=\textrm {Hom}(X^{*}(M), \textbf {Z})$
. Let
$X_{*}(M)=\textrm {Hom}(X^{*}(M), \textbf {Z})$
. Let
![]() $\mathfrak {a}_M^{*}=X^*(M)\otimes \textbf {R}$
and
$\mathfrak {a}_M^{*}=X^*(M)\otimes \textbf {R}$
and
![]() $\mathfrak {a}_M=X_{*}(M)\otimes \textbf {R}$
. The restriction
$\mathfrak {a}_M=X_{*}(M)\otimes \textbf {R}$
. The restriction
![]() $X^{*}(M)\to X^{*}(A)$
induces an injection
$X^{*}(M)\to X^{*}(A)$
induces an injection
![]() $\mathfrak {a}_{M}^{*}\hookrightarrow \mathfrak {a}_{A}^{*}$
. Let
$\mathfrak {a}_{M}^{*}\hookrightarrow \mathfrak {a}_{A}^{*}$
. Let
 $\left (\mathfrak {a}_{A}^{M}\right )^{*}$
be the subspace of
$\left (\mathfrak {a}_{A}^{M}\right )^{*}$
be the subspace of
![]() $\mathfrak {a}_{A}^{*}$
generated by
$\mathfrak {a}_{A}^{*}$
generated by
![]() $\Phi (M,A)$
. We have the decomposition in direct sums
$\Phi (M,A)$
. We have the decomposition in direct sums
 $$ \begin{align*} \mathfrak{a}_{A}^{*}=\left(\mathfrak{a}_{A}^{M}\right)^{*}\oplus \mathfrak{a}_{M}^{*}. \end{align*} $$
$$ \begin{align*} \mathfrak{a}_{A}^{*}=\left(\mathfrak{a}_{A}^{M}\right)^{*}\oplus \mathfrak{a}_{M}^{*}. \end{align*} $$
The canonical pairing
![]() $ X_{*}(A)\times X^{*}(A)\to \textbf {Z} $
can be extended bilinearly to
$ X_{*}(A)\times X^{*}(A)\to \textbf {Z} $
can be extended bilinearly to
![]() $\mathfrak {a}_{A}\times \mathfrak {a}_{A}^{*}\to \textbf {R}$
. For
$\mathfrak {a}_{A}\times \mathfrak {a}_{A}^{*}\to \textbf {R}$
. For
![]() $M\in \mathcal {L}(A)$
, we can embed
$M\in \mathcal {L}(A)$
, we can embed
![]() $\mathfrak {a}_{M}$
in
$\mathfrak {a}_{M}$
in
![]() $\mathfrak {a}_{A}$
as the orthogonal subspace to
$\mathfrak {a}_{A}$
as the orthogonal subspace to
 $\left (\mathfrak {a}_{A}^{M}\right )^{*}$
. Let
$\left (\mathfrak {a}_{A}^{M}\right )^{*}$
. Let
![]() $\mathfrak {a}_{A}^{M}\subset \mathfrak {a}_{A}$
be the subspace orthogonal to
$\mathfrak {a}_{A}^{M}\subset \mathfrak {a}_{A}$
be the subspace orthogonal to
![]() $\mathfrak {a}_{M}^{*}$
. We have the dual decomposition
$\mathfrak {a}_{M}^{*}$
. We have the dual decomposition
Let
![]() $\pi _{M},\pi ^{M}$
be the projections to the two factors. More generally, for
$\pi _{M},\pi ^{M}$
be the projections to the two factors. More generally, for
![]() $L,M\in \mathcal {F}(A),M\subset L$
, we also have a decomposition
$L,M\in \mathcal {F}(A),M\subset L$
, we also have a decomposition
Let
![]() $\pi _{M,L},\pi _{M}^{L}$
be the projections to the two factors. If the context is clear, we also simplify them to
$\pi _{M,L},\pi _{M}^{L}$
be the projections to the two factors. If the context is clear, we also simplify them to
![]() $\pi _{L},\pi ^{L}$
.
$\pi _{L},\pi ^{L}$
.
We identify
![]() $X_{*}(A)$
with
$X_{*}(A)$
with
![]() $A(F)/A(\mathcal {O})$
by sending
$A(F)/A(\mathcal {O})$
by sending
![]() $\chi $
to
$\chi $
to
![]() $\chi (\epsilon )$
. With this identification, the canonical surjection
$\chi (\epsilon )$
. With this identification, the canonical surjection
![]() $A(F)\to A(F)/A(\mathcal {O})$
can be viewed as
$A(F)\to A(F)/A(\mathcal {O})$
can be viewed as
We use
![]() $\Lambda _{G}$
to denote the quotient of
$\Lambda _{G}$
to denote the quotient of
![]() $X_{*}(A)$
by the coroot lattice of G (the subgroup of
$X_{*}(A)$
by the coroot lattice of G (the subgroup of
![]() $X_{*}(A)$
generated by the coroots of A in G). It is independent of the choice of A; this is the algebraic fundamental group introduced by Borovoi [Reference Borovoi6]. According to Kottwitz [Reference Kottwitz18], we have a canonical homomorphism
$X_{*}(A)$
generated by the coroots of A in G). It is independent of the choice of A; this is the algebraic fundamental group introduced by Borovoi [Reference Borovoi6]. According to Kottwitz [Reference Kottwitz18], we have a canonical homomorphism
which is characterized by the following properties: it is trivial on the image of
![]() $G_{\text {sc}}(F)$
in
$G_{\text {sc}}(F)$
in
![]() $G(F)$
(
$G(F)$
(
![]() $G_{\text {sc}}$
is the simply connected cover of the derived group of G), and its restriction to
$G_{\text {sc}}$
is the simply connected cover of the derived group of G), and its restriction to
![]() $A(F)$
coincides with the composition of formula (1.7) with the projection of
$A(F)$
coincides with the composition of formula (1.7) with the projection of
![]() $X_{*}(A)$
to
$X_{*}(A)$
to
![]() $\Lambda _{G}$
. Since the morphism (1.8) is trivial on
$\Lambda _{G}$
. Since the morphism (1.8) is trivial on
![]() $G(\mathcal {O})$
, it descends to a map
$G(\mathcal {O})$
, it descends to a map
whose fibers are the connected components of
![]() $\mathscr {X}$
. For
$\mathscr {X}$
. For
![]() $\mu \in \Lambda _{G}$
, we denote the connected component
$\mu \in \Lambda _{G}$
, we denote the connected component
 $\nu _{G}^{-1}(\mu )$
by
$\nu _{G}^{-1}(\mu )$
by
![]() $\mathscr {X}^{\mu }$
.
$\mathscr {X}^{\mu }$
.
Finally, we suppose that
![]() $\gamma \in \mathfrak {t}(\mathcal {O})$
satisfies
$\gamma \in \mathfrak {t}(\mathcal {O})$
satisfies
![]() $\gamma \equiv 0 \mod \epsilon $
, to avoid unnecessary complications.
$\gamma \equiv 0 \mod \epsilon $
, to avoid unnecessary complications.
2. (Weighted) orbital integrals and the affine Springer fibers
We recall briefly the geometrization of the (weighted) orbital integrals using the affine Springer fibers. We fix a regular element
![]() $\gamma \in \mathfrak {t}(\mathcal {O})$
as in the introduction. Let
$\gamma \in \mathfrak {t}(\mathcal {O})$
as in the introduction. Let
![]() $P_{0}=M_{0}N_{0}$
be the unique element in
$P_{0}=M_{0}N_{0}$
be the unique element in
![]() $\mathcal {P}(M_{0})$
which contains
$\mathcal {P}(M_{0})$
which contains
![]() $B_{0}$
.
$B_{0}$
.
2.1. Orbital integrals
We begin by fixing the Haar measures. Let
![]() $dg$
be the Haar measure on
$dg$
be the Haar measure on
![]() $G(F)$
normalized by the condition
$G(F)$
normalized by the condition
 $\textrm {vol}_{dg}\big (G(\mathcal {O})\big )=1$
. For the group
$\textrm {vol}_{dg}\big (G(\mathcal {O})\big )=1$
. For the group
![]() $T(F)$
, the definition is more involved, as there is no natural
$T(F)$
, the definition is more involved, as there is no natural
![]() $\mathcal {O}$
-structure on T. Let
$\mathcal {O}$
-structure on T. Let
![]() $F^{\text {ur}}=\overline {\mathbf{F}}_{q}(\!(\epsilon )\!)$
; it is the completion of the maximal unramified extension of F. Let
$F^{\text {ur}}=\overline {\mathbf{F}}_{q}(\!(\epsilon )\!)$
; it is the completion of the maximal unramified extension of F. Let
![]() $\sigma $
be the Frobenius automorphism of both
$\sigma $
be the Frobenius automorphism of both
![]() $\overline {\mathbf{F}}_{q}/\mathbf{F}_{q}$
and
$\overline {\mathbf{F}}_{q}/\mathbf{F}_{q}$
and
![]() $F^{\text {ur}}/F$
. We fix a separable algebraic closure
$F^{\text {ur}}/F$
. We fix a separable algebraic closure
![]() $\overline {F^{\text {ur}}}$
of
$\overline {F^{\text {ur}}}$
of
![]() $F^{\text {ur}}$
and let
$F^{\text {ur}}$
and let
 $I_{F}=\textrm {Gal}\left (\overline {F^{\text {ur}}}/F^{\text {ur}}\right )$
– this is the inertia subgroup of
$I_{F}=\textrm {Gal}\left (\overline {F^{\text {ur}}}/F^{\text {ur}}\right )$
– this is the inertia subgroup of
 $\Gamma =\textrm {Gal}\left (\overline {F}/F\right )$
. According to Kottwitz [Reference Kazhdan and Lusztig19, §7.6], we have an exact sequence
$\Gamma =\textrm {Gal}\left (\overline {F}/F\right )$
. According to Kottwitz [Reference Kazhdan and Lusztig19, §7.6], we have an exact sequence
which implies another exact sequence if we take the
![]() $\langle \sigma \rangle $
-invariants:
$\langle \sigma \rangle $
-invariants:
 $$ \begin{align} 1\to T(F)_{1}\to T(F) \xrightarrow{w_{T}} \left(X_{*}(T)_{I_{F}}\right)^{\langle \sigma \rangle}\to 1, \end{align} $$
$$ \begin{align} 1\to T(F)_{1}\to T(F) \xrightarrow{w_{T}} \left(X_{*}(T)_{I_{F}}\right)^{\langle \sigma \rangle}\to 1, \end{align} $$
with
![]() $T(F)_{1}:=T(F)\cap T(F^{\text {ur}})_{1}$
. We fix the Haar measure
$T(F)_{1}:=T(F)\cap T(F^{\text {ur}})_{1}$
. We fix the Haar measure
![]() $dt$
on
$dt$
on
![]() $T(F)$
by setting
$T(F)$
by setting
 $\textrm {vol}_{dt}\big (T(F)_{1}\big )=1$
. The group
$\textrm {vol}_{dt}\big (T(F)_{1}\big )=1$
. The group
![]() $\Lambda $
is discrete and cocompact in
$\Lambda $
is discrete and cocompact in
![]() $T(F)$
. The volume of the quotient
$T(F)$
. The volume of the quotient
![]() $\Lambda \backslash T(F)$
is calculated in [Reference Goresky, Kottwitz and MacPherson14, §15.3]:
$\Lambda \backslash T(F)$
is calculated in [Reference Goresky, Kottwitz and MacPherson14, §15.3]:
 $$ \begin{align*} \mathrm{vol}_{dt}\big(\Lambda\backslash T(F)\big)=\frac{\left\lvert\text{coker}[X_{*}(S)_{\Gamma}\to X_{*}(T)_{\Gamma}]\right\rvert}{\left\lvert\ker[X_{*}(S)_{\Gamma}\to X_{*}(T)_{\Gamma}]\right\rvert}. \end{align*} $$
$$ \begin{align*} \mathrm{vol}_{dt}\big(\Lambda\backslash T(F)\big)=\frac{\left\lvert\text{coker}[X_{*}(S)_{\Gamma}\to X_{*}(T)_{\Gamma}]\right\rvert}{\left\lvert\ker[X_{*}(S)_{\Gamma}\to X_{*}(T)_{\Gamma}]\right\rvert}. \end{align*} $$
Consider the orbital integral

It can be interpreted as counting points on the affine Springer fiber:
Proposition 2.1 Goresky, Kottwitz, MacPherson [Reference Goresky, Kottwitz and MacPherson14]
 $$ \begin{align*} I_{\gamma}^{G}=\frac{\left\lvert\ker[X_{*}(S)_{\Gamma}\to X_{*}(T)_{\Gamma}]\right\rvert}{\left\lvert\text{coker}[X_{*}(S)_{\Gamma}\to X_{*}(T)_{\Gamma}]\right\rvert}\cdot\left\lvert\Lambda\backslash \left(\mathscr{X}_{\gamma}\left(\mathbf{F}_{q}\right)\right)\right\rvert. \end{align*} $$
$$ \begin{align*} I_{\gamma}^{G}=\frac{\left\lvert\ker[X_{*}(S)_{\Gamma}\to X_{*}(T)_{\Gamma}]\right\rvert}{\left\lvert\text{coker}[X_{*}(S)_{\Gamma}\to X_{*}(T)_{\Gamma}]\right\rvert}\cdot\left\lvert\Lambda\backslash \left(\mathscr{X}_{\gamma}\left(\mathbf{F}_{q}\right)\right)\right\rvert. \end{align*} $$
The
![]() $T(F)$
-action on
$T(F)$
-action on
![]() $\mathscr {X}_{\gamma }$
can be exploited to further simplify the computations. Let
$\mathscr {X}_{\gamma }$
can be exploited to further simplify the computations. Let
![]() $\mathscr {X}_{\gamma }^{\mathrm{reg}}$
be the open subscheme of
$\mathscr {X}_{\gamma }^{\mathrm{reg}}$
be the open subscheme of
![]() $\mathscr {X}_{\gamma }$
consisting of the points
$\mathscr {X}_{\gamma }$
consisting of the points
![]() $[g]\in \mathscr {X}_{\gamma }$
such that the image of
$[g]\in \mathscr {X}_{\gamma }$
such that the image of
 $\textrm {Ad}\left (g^{-1}\right )\gamma $
under the reduction
$\textrm {Ad}\left (g^{-1}\right )\gamma $
under the reduction
![]() $\mathfrak {g}(\mathcal {O})\to \mathfrak {g}$
is regular nilpotent.
$\mathfrak {g}(\mathcal {O})\to \mathfrak {g}$
is regular nilpotent.
Proposition 2.2 Bezrukavnikov [Reference Bezrukavnikov5]
The group
![]() $T(F)$
acts transitively on
$T(F)$
acts transitively on
![]() $\mathscr {X}_{\gamma }^{\mathrm{reg}}$
.
$\mathscr {X}_{\gamma }^{\mathrm{reg}}$
.
Proposition 2.3 Ngô [Reference Ngô20, Proposition 3.10.1]
The open subscheme
![]() $\mathscr {X}_{\gamma }^{\mathrm{reg}}$
is dense in
$\mathscr {X}_{\gamma }^{\mathrm{reg}}$
is dense in
![]() $\mathscr {X}_{\gamma }$
.
$\mathscr {X}_{\gamma }$
.
Consequently, all the irreducible components of
![]() $\mathscr {X}_{\gamma }$
are isomorphic to each other, and they are parametrized by
$\mathscr {X}_{\gamma }$
are isomorphic to each other, and they are parametrized by
![]() $\pi _{0}(T(F))$
. In particular, all the connected components of
$\pi _{0}(T(F))$
. In particular, all the connected components of
![]() $\mathscr {X}_{\gamma }$
are isomorphic and can be translated to each other under the
$\mathscr {X}_{\gamma }$
are isomorphic and can be translated to each other under the
![]() $T(F)$
-action. In calculating the orbital integral (2.3), we can thus restrict to the central connected component of
$T(F)$
-action. In calculating the orbital integral (2.3), we can thus restrict to the central connected component of
![]() $\mathscr {X}_{\gamma }$
, which often simplifies calculations.
$\mathscr {X}_{\gamma }$
, which often simplifies calculations.
The calculation of
![]() $I_{\gamma }^{G}$
can be reduced to that of
$I_{\gamma }^{G}$
can be reduced to that of
 $I_{\gamma }^{M_{0}}$
; it dates back at least to Harish-Chandra that
$I_{\gamma }^{M_{0}}$
; it dates back at least to Harish-Chandra that
 $$ \begin{align} I_{\gamma}^{G} =q^{\frac{1}{2}\mathrm{val}\left(\det\left(\mathrm{ad}(\gamma)\mid\mathfrak{g}_{F}/\mathfrak{m}_{0,F}\right)\right)}\cdot I_{\gamma}^{M_{0}}. \end{align} $$
$$ \begin{align} I_{\gamma}^{G} =q^{\frac{1}{2}\mathrm{val}\left(\det\left(\mathrm{ad}(\gamma)\mid\mathfrak{g}_{F}/\mathfrak{m}_{0,F}\right)\right)}\cdot I_{\gamma}^{M_{0}}. \end{align} $$
Geometrically, this is a reflection of the existence of an affine fibration
 $f_{P}:\mathscr {X}_{\gamma }\to \mathscr {X}_{\gamma }^{M_{0}}$
for each
$f_{P}:\mathscr {X}_{\gamma }\to \mathscr {X}_{\gamma }^{M_{0}}$
for each
![]() $P\in \mathcal {P}(M_{0})$
. Recall that for
$P\in \mathcal {P}(M_{0})$
. Recall that for
![]() $Q=LN_{Q}\in \mathcal {F}(A)$
, we have the retraction
$Q=LN_{Q}\in \mathcal {F}(A)$
, we have the retraction
which sends
![]() $[g]=gK$
to
$[g]=gK$
to
![]() $[h]:=hL(\mathcal {O})$
, where
$[h]:=hL(\mathcal {O})$
, where
![]() $g=nhk, n\in N_{Q}(F), h\in L(F), k\in K$
, is the Iwasawa decomposition. We want to point out that the retraction
$g=nhk, n\in N_{Q}(F), h\in L(F), k\in K$
, is the Iwasawa decomposition. We want to point out that the retraction
![]() $f_{Q}$
is not a morphism between ind-
$f_{Q}$
is not a morphism between ind-
![]() $\mathbf{F}_{q}$
-schemes, but its restriction to the inverse image of each connected component of
$\mathbf{F}_{q}$
-schemes, but its restriction to the inverse image of each connected component of
![]() $\mathscr {X}^{L}$
,
$\mathscr {X}^{L}$
,
 $$ \begin{align*} f_{Q}:f_{Q}^{-1}\left(\mathscr{X}^{L,\nu}\right)\to \mathscr{X}^{L,\nu},\qquad \nu\in \Lambda_{L}, \end{align*} $$
$$ \begin{align*} f_{Q}:f_{Q}^{-1}\left(\mathscr{X}^{L,\nu}\right)\to \mathscr{X}^{L,\nu},\qquad \nu\in \Lambda_{L}, \end{align*} $$
is actually a morphism over
![]() $\mathbf{F}_{q}$
between ind-
$\mathbf{F}_{q}$
between ind-
![]() $\mathbf{F}_{q}$
-schemes. Moreover, these retractions satisfy the obvious transitivity property.
$\mathbf{F}_{q}$
-schemes. Moreover, these retractions satisfy the obvious transitivity property.
Restricted to the affine Springer fibers, the retraction
![]() $f_{Q}$
sends
$f_{Q}$
sends
![]() $\mathscr {X}_{\gamma }$
to
$\mathscr {X}_{\gamma }$
to
 $\mathscr {X}_{\gamma }^{L}$
. To see this, for
$\mathscr {X}_{\gamma }^{L}$
. To see this, for
![]() $[g]\in \mathscr {X}_{\gamma }$
, let
$[g]\in \mathscr {X}_{\gamma }$
, let
![]() $g=nhk$
be the Iwasawa decomposition as before. We can write
$g=nhk$
be the Iwasawa decomposition as before. We can write
![]() $g=hn'k$
, with
$g=hn'k$
, with
![]() $n'=h^{-1}nh\in N_{Q}(F)$
. Now that
$n'=h^{-1}nh\in N_{Q}(F)$
. Now that
 $\textrm {Ad}\left (h^{-1}\right )\gamma \in \mathfrak {l}(F)$
, we have
$\textrm {Ad}\left (h^{-1}\right )\gamma \in \mathfrak {l}(F)$
, we have
 $$ \begin{align*} \textrm{Ad}\left(n^{\prime -1}\right)\textrm{Ad}\left(h^{-1}\right)\gamma=\textrm{Ad}\left(h^{-1}\right)\gamma+n'' \end{align*} $$
$$ \begin{align*} \textrm{Ad}\left(n^{\prime -1}\right)\textrm{Ad}\left(h^{-1}\right)\gamma=\textrm{Ad}\left(h^{-1}\right)\gamma+n'' \end{align*} $$
for some
![]() $n''\in \mathfrak {n}_{Q}(F)$
. This implies that
$n''\in \mathfrak {n}_{Q}(F)$
. This implies that
which means that
 $f_{Q}([g])=[h]\in \mathscr {X}_{\gamma }^{L}$
.
$f_{Q}([g])=[h]\in \mathscr {X}_{\gamma }^{L}$
.
Proposition 2.4 Kazhdan and Lusztig [Reference Kottwitz17, §5, Proposition 1]
For any
![]() $\nu \in \Lambda _{L}$
, the retraction
$\nu \in \Lambda _{L}$
, the retraction
 $$ \begin{align*} f_{Q}:\mathscr{X}_{\gamma}\cap f_{Q}^{-1}\left(\mathscr{X}_{\gamma}^{L,\nu}\right)\to \mathscr{X}_{\gamma}^{L,\nu} \end{align*} $$
$$ \begin{align*} f_{Q}:\mathscr{X}_{\gamma}\cap f_{Q}^{-1}\left(\mathscr{X}_{\gamma}^{L,\nu}\right)\to \mathscr{X}_{\gamma}^{L,\nu} \end{align*} $$
is an iterated affine fibration over
![]() $\mathbf{F}_{q}$
of relative dimension
$\mathbf{F}_{q}$
of relative dimension
![]() $ \mathrm{val}(\det (\mathrm{ad}(\gamma )\mid \mathfrak {n}_{Q}(F))). $
$ \mathrm{val}(\det (\mathrm{ad}(\gamma )\mid \mathfrak {n}_{Q}(F))). $
The reader can also consult [Reference Chaudouard and Laumon11, Proposition 3.2] for a proof.
2.2. Arthur’s weighted orbital integral
2.2.1. The weight factor
 $\textrm {v}_{M}$
$\textrm {v}_{M}$
Set
![]() $M\in \mathcal {L}(M_{0})$
. Roughly speaking, the weight factor
$M\in \mathcal {L}(M_{0})$
. Roughly speaking, the weight factor
![]() $\textrm {v}_{M}(g)$
is the volume of a polytope in
$\textrm {v}_{M}(g)$
is the volume of a polytope in
![]() $\mathfrak {a}_{M}$
generated by the point
$\mathfrak {a}_{M}$
generated by the point
![]() $[g]\in \mathscr {X}$
. Let
$[g]\in \mathscr {X}$
. Let
![]() $H_{M}: M(F)\to \mathfrak {a}_{M}$
be the unique mapFootnote
2
satisfying
$H_{M}: M(F)\to \mathfrak {a}_{M}$
be the unique mapFootnote
2
satisfying
Notice that it is a group homomorphism. Moreover, it is invariant under the right K-action, so it induces a map from
![]() $\mathscr {X}^{M}$
to
$\mathscr {X}^{M}$
to
![]() $\mathfrak {a}_{M}$
, still denoted by
$\mathfrak {a}_{M}$
, still denoted by
![]() $H_{M}$
. For
$H_{M}$
. For
![]() $P=MN\in \mathcal {F}(A)$
, let
$P=MN\in \mathcal {F}(A)$
, let
![]() $H_{P}:\mathscr {X}\to \mathfrak {a}_{M}$
be the composition
$H_{P}:\mathscr {X}\to \mathfrak {a}_{M}$
be the composition
 $$ \begin{align*} H_{P}:\mathscr{X}\xrightarrow{f_{P}}\mathscr{X}^{M}\xrightarrow{H_{M}}\mathfrak{a}_{M}. \end{align*} $$
$$ \begin{align*} H_{P}:\mathscr{X}\xrightarrow{f_{P}}\mathscr{X}^{M}\xrightarrow{H_{M}}\mathfrak{a}_{M}. \end{align*} $$
As shown in [Reference Chen7, Lemma 6.1], the map
![]() $H_{M}$
is constant on each connected component of
$H_{M}$
is constant on each connected component of
![]() $\mathscr {X}^{M}$
, so it has a factorization
$\mathscr {X}^{M}$
, so it has a factorization
![]() $ H_{M}:\mathscr {X}^{M}\xrightarrow {\nu _{M}}\Lambda _{M}\to \mathfrak {a}_{M}$
. A simple calculation of the restriction of the map to
$ H_{M}:\mathscr {X}^{M}\xrightarrow {\nu _{M}}\Lambda _{M}\to \mathfrak {a}_{M}$
. A simple calculation of the restriction of the map to
![]() $\mathscr {X}^{A}\subset \mathscr {X}^{M}$
shows that the map
$\mathscr {X}^{A}\subset \mathscr {X}^{M}$
shows that the map
![]() $\Lambda _{M}\to \mathfrak {a}_{M}$
is just the one induced from the natural inclusion
$\Lambda _{M}\to \mathfrak {a}_{M}$
is just the one induced from the natural inclusion
![]() $X_{*}(A)\hookrightarrow \mathfrak {a}_{A}= X_{*}(A)\otimes \textbf {R}$
. Hence
$X_{*}(A)\hookrightarrow \mathfrak {a}_{A}= X_{*}(A)\otimes \textbf {R}$
. Hence
![]() $H_{P}$
is also the composition
$H_{P}$
is also the composition
 $$ \begin{align*} H_{P}:\mathscr{X}\xrightarrow{f_{P}}\mathscr{X}^{M}\xrightarrow{\nu_{M}}\Lambda_{M}\to \mathfrak{a}_{M}. \end{align*} $$
$$ \begin{align*} H_{P}:\mathscr{X}\xrightarrow{f_{P}}\mathscr{X}^{M}\xrightarrow{\nu_{M}}\Lambda_{M}\to \mathfrak{a}_{M}. \end{align*} $$
The map
![]() $H_{P}$
has the following remarkable property. There is a notion of adjacency among the parabolic subgroups in
$H_{P}$
has the following remarkable property. There is a notion of adjacency among the parabolic subgroups in
![]() $\mathcal {P}(M)$
: two parabolic subgroups
$\mathcal {P}(M)$
: two parabolic subgroups
![]() $P_{1}=MN_{1}, P_{2}=MN_{2}\in \mathcal {P}(M)$
are said to be adjacent if both of them are contained in a parabolic subgroup
$P_{1}=MN_{1}, P_{2}=MN_{2}\in \mathcal {P}(M)$
are said to be adjacent if both of them are contained in a parabolic subgroup
![]() $Q=LN_{Q}$
such that
$Q=LN_{Q}$
such that
![]() $L\supset M$
and
$L\supset M$
and
![]() $\textrm {rk}(L)=\textrm {rk}(M)+1$
. Given such an adjacent pair, we define an element
$\textrm {rk}(L)=\textrm {rk}(M)+1$
. Given such an adjacent pair, we define an element
![]() $\beta _{P_{1},P_{2}}\in \Lambda _{M}$
in the following way: consider the collection of elements in
$\beta _{P_{1},P_{2}}\in \Lambda _{M}$
in the following way: consider the collection of elements in
![]() $\Lambda _{M}$
obtained from coroots of A in
$\Lambda _{M}$
obtained from coroots of A in
![]() $\mathfrak {n}_{1}\cap \mathfrak {n}_{2}^{-}$
. We define
$\mathfrak {n}_{1}\cap \mathfrak {n}_{2}^{-}$
. We define
![]() $\beta _{P_{1},P_{2}}$
to be the minimal element in this collection – that is, all the other elements are positive integral multiples of it. Note that
$\beta _{P_{1},P_{2}}$
to be the minimal element in this collection – that is, all the other elements are positive integral multiples of it. Note that
![]() $\beta _{P_{2},P_{1}}=-\beta _{P_{1},P_{2}}$
, and if
$\beta _{P_{2},P_{1}}=-\beta _{P_{1},P_{2}}$
, and if
![]() $M=A$
, then
$M=A$
, then
![]() $\beta _{P_{1},P_{2}}$
is the unique coroot which is positive for
$\beta _{P_{1},P_{2}}$
is the unique coroot which is positive for
![]() $P_{1}$
and negative for
$P_{1}$
and negative for
![]() $P_{2}$
. We also denote its image in
$P_{2}$
. We also denote its image in
![]() $\mathfrak {a}_{M}$
by
$\mathfrak {a}_{M}$
by
![]() $\beta _{P_{1},P_{2}}$
if no confusion is caused.
$\beta _{P_{1},P_{2}}$
if no confusion is caused.
Proposition 2.5 Arthur [Reference Arthur1, Lemma 3.6]
Let
![]() $P_{1}, P_{2}\in \mathcal {P}(M)$
be two adjacent parabolic subgroups. For any
$P_{1}, P_{2}\in \mathcal {P}(M)$
be two adjacent parabolic subgroups. For any
![]() $x\in \mathscr {X}$
, we have
$x\in \mathscr {X}$
, we have
with
![]() $n(x, P_{1}, P_{2})\in \textbf {Z}_{\geq 0}$
.
$n(x, P_{1}, P_{2})\in \textbf {Z}_{\geq 0}$
.
The reader can consult [Reference Chaudouard and Laumon11, Proposition 2.1] for a proof. For any point
![]() $x\in \mathscr {X}$
, we write
$x\in \mathscr {X}$
, we write
![]() $\mathrm{Ec}_{M}(x)$
for the convex hull in
$\mathrm{Ec}_{M}(x)$
for the convex hull in
![]() $\mathfrak {a}_{M}$
of the
$\mathfrak {a}_{M}$
of the
![]() $H_{P}(x), P\in \mathcal {P}(M)$
. For any
$H_{P}(x), P\in \mathcal {P}(M)$
. For any
![]() $Q\in \mathcal {F}(M)$
, we denote by
$Q\in \mathcal {F}(M)$
, we denote by
 $\mathrm{Ec}_{M}^{Q}(x)$
the face of
$\mathrm{Ec}_{M}^{Q}(x)$
the face of
![]() $\mathrm{Ec}_{M}(x)$
whose vertices are
$\mathrm{Ec}_{M}(x)$
whose vertices are
![]() $H_{P}(x), P\in \mathcal {P}(M), P\subset Q$
. When
$H_{P}(x), P\in \mathcal {P}(M), P\subset Q$
. When
![]() $M=A$
, we omit the subscript A to simplify the notation.
$M=A$
, we omit the subscript A to simplify the notation.
To define the volume, we need to choose a Lebesgue measure on
![]() $\mathfrak {a}_{M}^{G}$
. We fix a W-invariant inner product
$\mathfrak {a}_{M}^{G}$
. We fix a W-invariant inner product
![]() $\langle \cdot ,\cdot \rangle $
on the vector space
$\langle \cdot ,\cdot \rangle $
on the vector space
![]() $\mathfrak {a}_{A}^{G}$
. Notice that
$\mathfrak {a}_{A}^{G}$
. Notice that
![]() $\mathfrak {a}_{A}^{M}$
and
$\mathfrak {a}_{A}^{M}$
and
![]() $\mathfrak {a}_{M}$
are orthogonal to each other with respect to the inner product for any
$\mathfrak {a}_{M}$
are orthogonal to each other with respect to the inner product for any
![]() $M\in \mathcal {L}(A)$
. We fix a Lebesgue measure on
$M\in \mathcal {L}(A)$
. We fix a Lebesgue measure on
![]() $\mathfrak {a}_{M}^{G}$
normalized by the condition that the lattice generated by the orthonormal bases in
$\mathfrak {a}_{M}^{G}$
normalized by the condition that the lattice generated by the orthonormal bases in
![]() $\mathfrak {a}_{M}^{G}$
has covolume
$\mathfrak {a}_{M}^{G}$
has covolume
![]() $1$
.
$1$
.
The weight factor
![]() $\textrm {v}_{M}(g)$
is the volume of the projection
$\textrm {v}_{M}(g)$
is the volume of the projection
 $\pi _{M}^{G}\big (\mathrm{Ec}_{M}(g)\big )\subset \mathfrak {a}_{M}^{G}$
. We have to pass to
$\pi _{M}^{G}\big (\mathrm{Ec}_{M}(g)\big )\subset \mathfrak {a}_{M}^{G}$
. We have to pass to
![]() $\mathfrak {a}_{M}^{G}$
because the polytope
$\mathfrak {a}_{M}^{G}$
because the polytope
![]() $\mathrm{Ec}_{M}(g)$
will lie in a hyperplane of
$\mathrm{Ec}_{M}(g)$
will lie in a hyperplane of
![]() $\mathfrak {a}_{M}$
if G has nontrivial connected center. The weight factor
$\mathfrak {a}_{M}$
if G has nontrivial connected center. The weight factor
![]() $\textrm {v}_{M}(g)$
has the following invariance properties: it is invariant under the right action of K – that is,
$\textrm {v}_{M}(g)$
has the following invariance properties: it is invariant under the right action of K – that is,
This is evident from the definition of
![]() $\textrm {v}_{M}(g)$
. It is not so evident, but also true, that
$\textrm {v}_{M}(g)$
. It is not so evident, but also true, that
Indeed, for any
![]() $P\in \mathcal {P}(M)$
, we have
$P\in \mathcal {P}(M)$
, we have
![]() $ f_{P}(mg)=mf_{P}(g). $
As
$ f_{P}(mg)=mf_{P}(g). $
As
![]() $H_{M}$
is a group homomorphism, this implies
$H_{M}$
is a group homomorphism, this implies
so
![]() $ \mathrm{Ec}_{M}(mg)$
is just the translation of
$ \mathrm{Ec}_{M}(mg)$
is just the translation of
![]() $\mathrm{Ec}_{M}(g)$
by
$\mathrm{Ec}_{M}(g)$
by
![]() $H_{M}(m). $
In particular, they have the same volume.
$H_{M}(m). $
In particular, they have the same volume.
Similar to Proposition 2.1, we can interpret Arthur’s weighted orbital integral as

That is, it is a weighted count of the rational points on the affine Springer fiber. Notice also that
 $J_{G}(\gamma )=I_{\gamma }^{G}$
, as
$J_{G}(\gamma )=I_{\gamma }^{G}$
, as
![]() $\textrm {v}_{G}(g)=1$
for all
$\textrm {v}_{G}(g)=1$
for all
![]() $g\in G(F)$
.
$g\in G(F)$
.
2.2.2. A variant
In their work on the weighted fundamental lemma [Reference Chen8], Chaudouard and Laumon introduce a variant of the weighted orbital integral.
Assume that G is semisimple and let
![]() $\xi \in \mathfrak {a}_{M}$
be a generic element. For
$\xi \in \mathfrak {a}_{M}$
be a generic element. For
![]() $g\in G(F)$
, they introduce the weight factor
$g\in G(F)$
, they introduce the weight factor
 $$ \begin{align*} \textrm{w}_{M}^{\xi}(g)=\left\lvert\{\lambda\in X_{*}(M)\mid \lambda+\xi\in \textrm{Ec}_{M}(g)\}\right\rvert. \end{align*} $$
$$ \begin{align*} \textrm{w}_{M}^{\xi}(g)=\left\lvert\{\lambda\in X_{*}(M)\mid \lambda+\xi\in \textrm{Ec}_{M}(g)\}\right\rvert. \end{align*} $$
It is the number of integral points in the polytope
![]() $\mathrm{Ec}_{M}(g)-\xi $
. Similar to
$\mathrm{Ec}_{M}(g)-\xi $
. Similar to
![]() $\textrm {v}_{M}(g)$
, the weight factor
$\textrm {v}_{M}(g)$
, the weight factor
 $\mathrm{w}_{M}^{\xi }(g)$
is invariant under the right K-action and the left
$\mathrm{w}_{M}^{\xi }(g)$
is invariant under the right K-action and the left
![]() $M(F)$
-action. In particular, it descends to a function on
$M(F)$
-action. In particular, it descends to a function on
![]() $\mathscr {X}$
. Consider the following weighted orbital integral:
$\mathscr {X}$
. Consider the following weighted orbital integral:

Remark 2.1. For a general reductive algebraic group G,
![]() $\xi \in \mathfrak {a}_{M}^{G}$
, as
$\xi \in \mathfrak {a}_{M}^{G}$
, as
![]() $G(F)=M(F)\cdot G_{\text {der}}(F)$
, we can define the weight factor
$G(F)=M(F)\cdot G_{\text {der}}(F)$
, we can define the weight factor
 $\mathrm{w}_{M}^{\xi }$
uniquely by requiring it to be invariant under the left
$\mathrm{w}_{M}^{\xi }$
uniquely by requiring it to be invariant under the left
![]() $M(F)$
-action and the right K-action, and that as a function on
$M(F)$
-action and the right K-action, and that as a function on
![]() $\mathscr {X}$
its restriction to
$\mathscr {X}$
its restriction to
![]() $\mathscr {X}^{G_{\text {der}}}$
coincide with the given definition for
$\mathscr {X}^{G_{\text {der}}}$
coincide with the given definition for
![]() $G_{\text {der}}$
. In other words, for generic
$G_{\text {der}}$
. In other words, for generic
![]() $\xi \in \mathfrak {a}_{M}^{G}$
, we define
$\xi \in \mathfrak {a}_{M}^{G}$
, we define
 $$ \begin{align*} \textrm{w}_{M}^{\xi}(g)=\left\lvert\left\{\lambda\in X_{*}\left(M_{G_{\text{der}}}\right)\mid \lambda+\xi\in \pi_{M}^{G}(\textrm{Ec}_{M}(g))\right\}\right\rvert, \end{align*} $$
$$ \begin{align*} \textrm{w}_{M}^{\xi}(g)=\left\lvert\left\{\lambda\in X_{*}\left(M_{G_{\text{der}}}\right)\mid \lambda+\xi\in \pi_{M}^{G}(\textrm{Ec}_{M}(g))\right\}\right\rvert, \end{align*} $$
where
![]() $M_{G_{\text {der}}}=M\cap G_{\text {der}}$
. Notice that the weight factor
$M_{G_{\text {der}}}=M\cap G_{\text {der}}$
. Notice that the weight factor
![]() $\textrm {v}_{M}$
satisfies these conditions as well, and this justifies our definition in the general case.
$\textrm {v}_{M}$
satisfies these conditions as well, and this justifies our definition in the general case.
The variant
 $J_{M}^{\xi }(\gamma )$
has a better geometric interpretation.
$J_{M}^{\xi }(\gamma )$
has a better geometric interpretation.
Lemma 2.6. Let
![]() $T(F)^{1}=T(F)\cap \ker \left (H_{M_{0}}\right )$
. Then it is of finite volume and we have an exact sequence
$T(F)^{1}=T(F)\cap \ker \left (H_{M_{0}}\right )$
. Then it is of finite volume and we have an exact sequence
 $$ \begin{align*} 1\to T(F)^{1}\to T(F)\xrightarrow{H_{M_{0}}} X_{*}(M_{0})\to 1. \end{align*} $$
$$ \begin{align*} 1\to T(F)^{1}\to T(F)\xrightarrow{H_{M_{0}}} X_{*}(M_{0})\to 1. \end{align*} $$
Proof. The first assertion is due to the fact that T is anisotropic modulo the center of
![]() $M_{0}$
. For the second assertion, only the surjectivity is nontrivial. Recall that we have the exact sequence
$M_{0}$
. For the second assertion, only the surjectivity is nontrivial. Recall that we have the exact sequence
 $$ \begin{align*} 1\to T(F)_{1}\to T(F)\xrightarrow{w_{T}} \left(X_{*}(T)_{I_{F}}\right)^{\langle \sigma\rangle}\to 1, \end{align*} $$
$$ \begin{align*} 1\to T(F)_{1}\to T(F)\xrightarrow{w_{T}} \left(X_{*}(T)_{I_{F}}\right)^{\langle \sigma\rangle}\to 1, \end{align*} $$
and that the map
![]() $w_{T}$
is defined via a map
$w_{T}$
is defined via a map
 $v_{T}: T(F^{\text {ur}})\to \textrm {Hom}\left (X^{*}(T)^{I_{F}},\textbf {Z}\right )$
, similar to the definition of
$v_{T}: T(F^{\text {ur}})\to \textrm {Hom}\left (X^{*}(T)^{I_{F}},\textbf {Z}\right )$
, similar to the definition of
![]() $H_{M_{0}}$
. Hence the morphism
$H_{M_{0}}$
. Hence the morphism
![]() $H_{M_{0}}$
factors through
$H_{M_{0}}$
factors through
![]() $w_{T}$
, and the surjectivity results from those of
$w_{T}$
, and the surjectivity results from those of
![]() $w_{T}$
and the homomorphism
$w_{T}$
and the homomorphism
 $$ \begin{align*} \left(X_{*}(T)_{I_{F}}\right)^{\langle \sigma\rangle}=X_{*}(T)_{I_{F}}\to \textrm{Hom}(X^{*}(M_{0}),\textbf{Z})=X_{*}(M_{0}). \end{align*} $$
$$ \begin{align*} \left(X_{*}(T)_{I_{F}}\right)^{\langle \sigma\rangle}=X_{*}(T)_{I_{F}}\to \textrm{Hom}(X^{*}(M_{0}),\textbf{Z})=X_{*}(M_{0}). \end{align*} $$
As a consequence, let
![]() $T(F)_{M}^{1}=T(F)\cap \,\ker (H_{M})$
and let
$T(F)_{M}^{1}=T(F)\cap \,\ker (H_{M})$
and let
![]() $\Lambda ^{H_{M}}=\Lambda \cap \,\ker (H_{M})$
. Then the quotient
$\Lambda ^{H_{M}}=\Lambda \cap \,\ker (H_{M})$
. Then the quotient
![]() $\Lambda ^{H_{M}}\backslash T(F)_{M}^{1}$
is of finite volume and we have an exact sequence
$\Lambda ^{H_{M}}\backslash T(F)_{M}^{1}$
is of finite volume and we have an exact sequence
 $$ \begin{align*} 1\to T(F)_{M}^{1}\to T(F)\xrightarrow{H_{M}} X_{*}(M)\to 1. \end{align*} $$
$$ \begin{align*} 1\to T(F)_{M}^{1}\to T(F)\xrightarrow{H_{M}} X_{*}(M)\to 1. \end{align*} $$
Proposition 2.7. We have the equality
 $$ \begin{align*} J_{M}^{\xi}(\gamma)=\mathrm{vol}_{dt}\left(\Lambda^{H_{M}}\backslash T(F)_{M}^{1}\right)^{-1}\cdot \left\lvert\Lambda^{H_{M}}\backslash \left\{[g]\in \mathscr{X}_{\gamma}\left(\mathbf{F}_{q}\right)\mid \xi\in \text{Ec}_{M}(g)\right\}\right\rvert. \end{align*} $$
$$ \begin{align*} J_{M}^{\xi}(\gamma)=\mathrm{vol}_{dt}\left(\Lambda^{H_{M}}\backslash T(F)_{M}^{1}\right)^{-1}\cdot \left\lvert\Lambda^{H_{M}}\backslash \left\{[g]\in \mathscr{X}_{\gamma}\left(\mathbf{F}_{q}\right)\mid \xi\in \text{Ec}_{M}(g)\right\}\right\rvert. \end{align*} $$
In particular,
 $$ \begin{align*} J_{M_{0}}^{\xi}(\gamma)=\mathrm{vol}_{dt}\left(T(F)^{1}\right)^{-1}\cdot \left\lvert\left\{[g]\in \mathscr{X}_{\gamma}\left(\mathbf{F}_{q}\right)\mid \xi\in \mathrm{Ec}_{M_{0}}(g)\right\}\right\rvert. \end{align*} $$
$$ \begin{align*} J_{M_{0}}^{\xi}(\gamma)=\mathrm{vol}_{dt}\left(T(F)^{1}\right)^{-1}\cdot \left\lvert\left\{[g]\in \mathscr{X}_{\gamma}\left(\mathbf{F}_{q}\right)\mid \xi\in \mathrm{Ec}_{M_{0}}(g)\right\}\right\rvert. \end{align*} $$
Proof. Let
be the characteristic function of
![]() $\mathrm{Ec}_{M}(g)$
. As
$\mathrm{Ec}_{M}(g)$
. As
we have

Now we can rewrite

In particular,
 $J_{M}^{\xi }(\gamma )$
is a plain count of a subset of
$J_{M}^{\xi }(\gamma )$
is a plain count of a subset of
![]() $\mathscr {X}_{\gamma }\left (\mathbf{F}_{q}\right )$
. In §4.1, we will see that the condition
$\mathscr {X}_{\gamma }\left (\mathbf{F}_{q}\right )$
. In §4.1, we will see that the condition
![]() $\xi \in \mathrm{Ec}_{M}(g)$
behaves as a stability condition. (We believe that it is in fact a stability condition in the sense of Mumford.) In particular, there is a Harder–Narasimhan-type decomposition of
$\xi \in \mathrm{Ec}_{M}(g)$
behaves as a stability condition. (We believe that it is in fact a stability condition in the sense of Mumford.) In particular, there is a Harder–Narasimhan-type decomposition of
![]() $\mathscr {X}_{\gamma }$
associated with it.
$\mathscr {X}_{\gamma }$
associated with it.
Remark 2.2. It is time to explain why we have imposed the assumption that T is totally ramified over F. Without it, the Frobenius
 $\sigma \in \textrm {Gal}\left (\overline {\mathbf{F}}_{q}/\mathbf{F}_{q}\right )$
acts nontrivially on
$\sigma \in \textrm {Gal}\left (\overline {\mathbf{F}}_{q}/\mathbf{F}_{q}\right )$
acts nontrivially on
![]() $X_{*}(T)_{I_{F}}$
, and the morphism
$X_{*}(T)_{I_{F}}$
, and the morphism
![]() $T(F)\to X_{*}(M_{0})$
in Lemma 2.6 might fail to be surjective. (Indeed, it does fail for T an unramified maximal torus in
$T(F)\to X_{*}(M_{0})$
in Lemma 2.6 might fail to be surjective. (Indeed, it does fail for T an unramified maximal torus in
![]() $\textrm {GL}_{n}$
.) As a consequence, the interpretation of
$\textrm {GL}_{n}$
.) As a consequence, the interpretation of
 $J_{M}^{\xi }(\gamma )$
as in Proposition 2.7 no longer holds.
$J_{M}^{\xi }(\gamma )$
as in Proposition 2.7 no longer holds.
For completeness, we compute the volume factors in Proposition 2.7. We have the exact sequence
 $$ \begin{align*} 1\to \Lambda^{H_{M}}\to T(F)_{M}^{1}\to \Lambda\backslash T(F) \xrightarrow{H_{M}} X_{*}(M)/H_{M}(\Lambda)\to 1. \end{align*} $$
$$ \begin{align*} 1\to \Lambda^{H_{M}}\to T(F)_{M}^{1}\to \Lambda\backslash T(F) \xrightarrow{H_{M}} X_{*}(M)/H_{M}(\Lambda)\to 1. \end{align*} $$
Because
![]() $\Lambda $
is of finite index in
$\Lambda $
is of finite index in
![]() $X_{*}(M_{0})$
and the morphism
$X_{*}(M_{0})$
and the morphism
![]() $X_{*}(M_{0})\to X_{*}(M)$
is surjective, the quotient
$X_{*}(M_{0})\to X_{*}(M)$
is surjective, the quotient
![]() $X_{*}(M)/H_{M}(\Lambda )$
is finite, and so
$X_{*}(M)/H_{M}(\Lambda )$
is finite, and so
 $$ \begin{align} \mathrm{vol}_{dt}\left(\Lambda^{H_{M}}\backslash T(F)_{M}^{1}\right) &= \mathrm{vol}_{dt}\left( \Lambda\backslash T(F) \right)\cdot \left\lvert X_{*}(M)/H_{M}(\Lambda)\right\rvert^{-1} \nonumber\\ &= \frac{\left\lvert\text{coker}[X_{*}(S)_{\Gamma}\to X_{*}(T)_{\Gamma}]\right\rvert}{\left\lvert\ker[X_{*}(S)_{\Gamma}\to X_{*}(T)_{\Gamma}]\right\rvert\cdot \left\lvert X_{*}(M)/H_{M}(X_{*}(S))\right\rvert}. \end{align} $$
$$ \begin{align} \mathrm{vol}_{dt}\left(\Lambda^{H_{M}}\backslash T(F)_{M}^{1}\right) &= \mathrm{vol}_{dt}\left( \Lambda\backslash T(F) \right)\cdot \left\lvert X_{*}(M)/H_{M}(\Lambda)\right\rvert^{-1} \nonumber\\ &= \frac{\left\lvert\text{coker}[X_{*}(S)_{\Gamma}\to X_{*}(T)_{\Gamma}]\right\rvert}{\left\lvert\ker[X_{*}(S)_{\Gamma}\to X_{*}(T)_{\Gamma}]\right\rvert\cdot \left\lvert X_{*}(M)/H_{M}(X_{*}(S))\right\rvert}. \end{align} $$
2.2.3. Comparison of weighted orbital integrals
The weight factors
![]() $\textrm {v}_{M}$
and
$\textrm {v}_{M}$
and
 $\mathrm{w}_{M}^{\xi }$
are closely related, so we can compare the associated weighted orbital integrals.
$\mathrm{w}_{M}^{\xi }$
are closely related, so we can compare the associated weighted orbital integrals.
Theorem 2.8 Chaudouard and Laumon [Reference Chen8]
We have the equality
 $$ \begin{align*} J_{M}(\gamma)= \mathrm{vol}\left(\mathfrak{a}_{M}/X_{*}(M)\right) \cdot J_{M}^{\xi}(\gamma). \end{align*} $$
$$ \begin{align*} J_{M}(\gamma)= \mathrm{vol}\left(\mathfrak{a}_{M}/X_{*}(M)\right) \cdot J_{M}^{\xi}(\gamma). \end{align*} $$
Remark 2.3. For a general reductive algebraic group G, with the definition of
 $\mathrm{w}_{M}^{\xi }$
as explained in Remark 2.1, the comparison theorem becomes
$\mathrm{w}_{M}^{\xi }$
as explained in Remark 2.1, the comparison theorem becomes
 $$ \begin{align*} J_{M}(\gamma)= \mathrm{vol}\left(\mathfrak{a}_{M_{G_{\text{der}}}}^{G_{\text{der}}}\middle/X_{*}\left(M_{G_{\text{der}}}\right)\right) \cdot J_{M}^{\xi}(\gamma), \end{align*} $$
$$ \begin{align*} J_{M}(\gamma)= \mathrm{vol}\left(\mathfrak{a}_{M_{G_{\text{der}}}}^{G_{\text{der}}}\middle/X_{*}\left(M_{G_{\text{der}}}\right)\right) \cdot J_{M}^{\xi}(\gamma), \end{align*} $$
as can be seen from the proof below.
Chaudouard and Laumon work over the ring of adèles, but their proof carries over to the local setting. We reproduce their proof here, but to simplify the exposition, we assume moreover that G is simply connected. The key is to rewrite the convex polytope
![]() $\mathrm{Ec}_{M}(g)$
as alternating differences of translations of cones. We need some notation. For
$\mathrm{Ec}_{M}(g)$
as alternating differences of translations of cones. We need some notation. For
![]() $P=MN_{P}\in \mathcal {F}(A)$
, take a Borel subgroup
$P=MN_{P}\in \mathcal {F}(A)$
, take a Borel subgroup
![]() $B\in \mathcal {P}(A)$
contained in P. Let
$B\in \mathcal {P}(A)$
contained in P. Let
![]() $\Delta _{B}$
be the simple roots of
$\Delta _{B}$
be the simple roots of
![]() $\Phi (G,A)$
with respect to B, and let
$\Phi (G,A)$
with respect to B, and let
![]() $\Delta _{B,P}=\Delta _{B}\cap \Phi (N_{P},A)$
and
$\Delta _{B,P}=\Delta _{B}\cap \Phi (N_{P},A)$
and
 $\Delta _{B, P}^{\vee }$
be the associated coroots. The restriction
$\Delta _{B, P}^{\vee }$
be the associated coroots. The restriction
![]() $X^{*}(A)\to X^{*}(A_{M})$
induces a bijection from
$X^{*}(A)\to X^{*}(A_{M})$
induces a bijection from
![]() $\Delta _{B,P}$
to a subset of
$\Delta _{B,P}$
to a subset of
![]() $X^{*}(A_{M})$
denoted
$X^{*}(A_{M})$
denoted
![]() $\Delta _{P}$
. Similarly, the projection
$\Delta _{P}$
. Similarly, the projection
![]() $\mathfrak {a}_{A}\to \mathfrak {a}_{M}$
induces a bijection from
$\mathfrak {a}_{A}\to \mathfrak {a}_{M}$
induces a bijection from
 $\Delta _{B,P}^{\vee }$
to a subset
$\Delta _{B,P}^{\vee }$
to a subset
![]() $\Delta _{P}^{\vee }$
. Obviously, the definition of
$\Delta _{P}^{\vee }$
. Obviously, the definition of
![]() $\Delta _{P}$
and
$\Delta _{P}$
and
![]() $\Delta _{P}^{\vee }$
is independent of the choice of B. Moreover, they form bases of
$\Delta _{P}^{\vee }$
is independent of the choice of B. Moreover, they form bases of
![]() $\mathfrak {a}_{M}^{*}$
and
$\mathfrak {a}_{M}^{*}$
and
![]() $\mathfrak {a}_{M}$
, respectively. Let
$\mathfrak {a}_{M}$
, respectively. Let
![]() $(\varpi _{\alpha })_{\alpha \in \Delta _{P}}$
be the basis of
$(\varpi _{\alpha })_{\alpha \in \Delta _{P}}$
be the basis of
![]() $\mathfrak {a}_{M}^{*}$
dual to
$\mathfrak {a}_{M}^{*}$
dual to
![]() $\Delta _{P}^{\vee }$
.
$\Delta _{P}^{\vee }$
.
For a generic element
![]() $\lambda \in \mathfrak {a}_{M}^{*}$
, let
$\lambda \in \mathfrak {a}_{M}^{*}$
, let
and let
![]() $\varphi _{P}^{\lambda }$
be the characteristic function of the cone
$\varphi _{P}^{\lambda }$
be the characteristic function of the cone
 $$ \begin{align*} \left\{a\in \mathfrak{a}_{M}\mid \varpi_{\alpha}(a)>0,\ \forall \alpha\in \Delta_{P}^{\lambda};\varpi_{\alpha}(a)\leq 0,\ \forall \alpha\in \Delta_{P}\backslash \Delta_{P}^{\lambda}\right\}. \end{align*} $$
$$ \begin{align*} \left\{a\in \mathfrak{a}_{M}\mid \varpi_{\alpha}(a)>0,\ \forall \alpha\in \Delta_{P}^{\lambda};\varpi_{\alpha}(a)\leq 0,\ \forall \alpha\in \Delta_{P}\backslash \Delta_{P}^{\lambda}\right\}. \end{align*} $$
According to Arthur [Reference Arthur3], the characteristic function of the convex polytope
![]() $\mathrm{Ec}_{M}(g)$
is equal to the function
$\mathrm{Ec}_{M}(g)$
is equal to the function
 $$ \begin{align*} a\in \mathfrak{a}_{M}\longmapsto \sum_{P\in \mathcal{P}(M)} (-1)^{\left\lvert\Delta_{P}^{\lambda}\right\rvert}\varphi_{P}^{\lambda}(-H_{P}(g)+a). \end{align*} $$
$$ \begin{align*} a\in \mathfrak{a}_{M}\longmapsto \sum_{P\in \mathcal{P}(M)} (-1)^{\left\lvert\Delta_{P}^{\lambda}\right\rvert}\varphi_{P}^{\lambda}(-H_{P}(g)+a). \end{align*} $$
The proof is best illustrated by [Reference Arthur4, Figure 11.1, p. 63]. It relies on the combinatorial identity
 $$ \begin{align*} \sum_{F\subset S} (-1)^{\lvert F\rvert}=\begin{cases} 1&\text{if } S=\emptyset,\\ 0 &\text{otherwise}, \end{cases} \end{align*} $$
$$ \begin{align*} \sum_{F\subset S} (-1)^{\lvert F\rvert}=\begin{cases} 1&\text{if } S=\emptyset,\\ 0 &\text{otherwise}, \end{cases} \end{align*} $$
for any finite set S. Now we can rewrite
 $$ \begin{align} \textrm{w}_{M}^{\xi}(g) &= \sum_{\chi\in X_{*}(M)}\sum_{P\in \mathcal{P}(M)}(-1)^{\left\lvert\Delta_{P}^{\lambda}\right\rvert} \varphi^{\lambda}_{P}(-H_{P}(g)+\chi+\xi), \end{align} $$
$$ \begin{align} \textrm{w}_{M}^{\xi}(g) &= \sum_{\chi\in X_{*}(M)}\sum_{P\in \mathcal{P}(M)}(-1)^{\left\lvert\Delta_{P}^{\lambda}\right\rvert} \varphi^{\lambda}_{P}(-H_{P}(g)+\chi+\xi), \end{align} $$
 $$ \begin{align} \textrm{v}_{M}(g) &= \int_{\mathfrak{a}_{M}} \sum_{P\in \mathcal{P}(M)} (-1)^{\left\lvert\Delta_{P}^{\lambda}\right\rvert}\varphi_{P}^{\lambda}(-H_{P}(g)+a)da. \end{align} $$
$$ \begin{align} \textrm{v}_{M}(g) &= \int_{\mathfrak{a}_{M}} \sum_{P\in \mathcal{P}(M)} (-1)^{\left\lvert\Delta_{P}^{\lambda}\right\rvert}\varphi_{P}^{\lambda}(-H_{P}(g)+a)da. \end{align} $$
We introduce an extra exponential factor to treat the infinite sum in equation (2.6):
 $$ \begin{align*} S_{P}(\lambda)=\sum_{\chi\in X_{*}(M)} \varphi^{\lambda}_{P}(-H_{P}(g)+\chi+\xi)e^{\langle\lambda,\chi\rangle}. \end{align*} $$
$$ \begin{align*} S_{P}(\lambda)=\sum_{\chi\in X_{*}(M)} \varphi^{\lambda}_{P}(-H_{P}(g)+\chi+\xi)e^{\langle\lambda,\chi\rangle}. \end{align*} $$
The series converges absolutely for generic
![]() $\lambda $
, and hence
$\lambda $
, and hence
 $$ \begin{align*} \textrm{w}_{M}^{\xi}(g)=\lim_{\lambda\to 0}\sum_{P\in \mathcal{P}(M)}(-1)^{\left\lvert\Delta_{P}^{\lambda}\right\rvert} S_{P}(\lambda), \end{align*} $$
$$ \begin{align*} \textrm{w}_{M}^{\xi}(g)=\lim_{\lambda\to 0}\sum_{P\in \mathcal{P}(M)}(-1)^{\left\lvert\Delta_{P}^{\lambda}\right\rvert} S_{P}(\lambda), \end{align*} $$
where the limit is taken for generic
![]() $\lambda \in \mathfrak {a}_{M}^{*}$
.
$\lambda \in \mathfrak {a}_{M}^{*}$
.
We can calculate
![]() $S_{P}(\lambda )$
explicitly. Let
$S_{P}(\lambda )$
explicitly. Let
![]() $\xi =[\xi ]_{P}+\{\xi \}_{P}$
, with
$\xi =[\xi ]_{P}+\{\xi \}_{P}$
, with
![]() $[\xi ]_{P}\in X_{*}(M)$
and
$[\xi ]_{P}\in X_{*}(M)$
and
 $\{\xi \}_{P}=\sum _{\alpha \in \Delta _{P}}r_{\alpha }\alpha ^{\vee }$
for some
$\{\xi \}_{P}=\sum _{\alpha \in \Delta _{P}}r_{\alpha }\alpha ^{\vee }$
for some
![]() $0< r_{\alpha }<1$
. After a simple change of variables, we get
$0< r_{\alpha }<1$
. After a simple change of variables, we get
 $$ \begin{align*} S_{P}(\lambda)&= e^{\left\langle \lambda, H_{P}(g)-[\xi]_{P} \right\rangle} \sum_{\chi\in X_{*}(M)} \varphi_{P}^{\lambda}(\chi+\{\xi\}_{P})e^{\langle\lambda,\chi\rangle}\\ &= e^{\left\langle \lambda, H_{P}(g)-[\xi]_{P} \right\rangle} \sum_{(m_{\alpha})_{\alpha\in \Delta_{P}}} e^{\left\langle\lambda,\sum_{\alpha}m_{\alpha}\alpha^{\vee}\right\rangle}, \end{align*} $$
$$ \begin{align*} S_{P}(\lambda)&= e^{\left\langle \lambda, H_{P}(g)-[\xi]_{P} \right\rangle} \sum_{\chi\in X_{*}(M)} \varphi_{P}^{\lambda}(\chi+\{\xi\}_{P})e^{\langle\lambda,\chi\rangle}\\ &= e^{\left\langle \lambda, H_{P}(g)-[\xi]_{P} \right\rangle} \sum_{(m_{\alpha})_{\alpha\in \Delta_{P}}} e^{\left\langle\lambda,\sum_{\alpha}m_{\alpha}\alpha^{\vee}\right\rangle}, \end{align*} $$
where
![]() $(m_{\alpha })_{\alpha \in \Delta _{P}}$
runs over the integers satisfying
$(m_{\alpha })_{\alpha \in \Delta _{P}}$
runs over the integers satisfying
![]() $m_{\alpha }\geq 0$
for
$m_{\alpha }\geq 0$
for
![]() $\alpha \in \Delta _{P}^{\lambda }$
and
$\alpha \in \Delta _{P}^{\lambda }$
and
![]() $m_{\alpha }\leq -1$
for
$m_{\alpha }\leq -1$
for
![]() $\alpha \in \Delta _{P}\backslash \Delta _{P}^{\lambda }$
. The geometric series can be calculated to be
$\alpha \in \Delta _{P}\backslash \Delta _{P}^{\lambda }$
. The geometric series can be calculated to be
 $$ \begin{align*} S_{P}(\lambda)=(-1)^{\left\lvert\Delta_{P}^{\lambda}\right\rvert}e^{\left\langle \lambda, H_{P}(g)-[\xi]_{P} \right \rangle}\prod_{\alpha\in \Delta_{P}}\frac{1}{e^{\left\langle\lambda,\alpha^{\vee}\right\rangle}-1}. \end{align*} $$
$$ \begin{align*} S_{P}(\lambda)=(-1)^{\left\lvert\Delta_{P}^{\lambda}\right\rvert}e^{\left\langle \lambda, H_{P}(g)-[\xi]_{P} \right \rangle}\prod_{\alpha\in \Delta_{P}}\frac{1}{e^{\left\langle\lambda,\alpha^{\vee}\right\rangle}-1}. \end{align*} $$
Let
 $\textrm {c}_{P}(\lambda )=\prod _{\alpha \in \Delta _{P}} \left (e^{\left \langle \lambda ,\alpha ^{\vee }\right \rangle }-1\right )$
. Taking everything together, we get
$\textrm {c}_{P}(\lambda )=\prod _{\alpha \in \Delta _{P}} \left (e^{\left \langle \lambda ,\alpha ^{\vee }\right \rangle }-1\right )$
. Taking everything together, we get
 $$ \begin{align} \textrm{w}_{M}^{\xi}(g)= \lim_{\lambda\to 0} \sum_{P\in \mathcal{P}(M)} \textrm{c}_{P}(\lambda)^{-1}e^{\left\langle \lambda, H_{P}(g)-[\xi]_{P} \right\rangle}. \end{align} $$
$$ \begin{align} \textrm{w}_{M}^{\xi}(g)= \lim_{\lambda\to 0} \sum_{P\in \mathcal{P}(M)} \textrm{c}_{P}(\lambda)^{-1}e^{\left\langle \lambda, H_{P}(g)-[\xi]_{P} \right\rangle}. \end{align} $$
Similarly, we can rewrite equation (2.7) as
 $$ \begin{align*} \textrm{v}_{M}(g) &= \lim_{\lambda\to 0} \int_{\mathfrak{a}_{M}} \sum_{P\in \mathcal{P}(M)} (-1)^{\left\lvert\Delta_{P}^{\lambda}\right\rvert}\varphi_{P}^{\lambda}(-H_{P}(g)+a) e^{\langle \lambda,a \rangle} da \\ &= \lim_{\lambda\to 0} \sum_{P\in \mathcal{P}(M)} (-1)^{\left\lvert\Delta_{P}^{\lambda}\right\rvert} \int_{\mathfrak{a}_{M}} \varphi_{P}^{\lambda}(-H_{P}(g)+a) e^{\langle \lambda,a \rangle} da \\ &= \lim_{\lambda\to 0} \sum_{P\in \mathcal{P}(M)} e^{\left\langle \lambda,H_{P}(g) \right\rangle}\cdot \mathrm{vol}\left(\mathfrak{a}_{M}/X_{*}(M)\right)\prod_{\alpha\in \Delta_{P}} \left\langle \lambda,\alpha^{\vee}\right\rangle^{-1}. \end{align*} $$
$$ \begin{align*} \textrm{v}_{M}(g) &= \lim_{\lambda\to 0} \int_{\mathfrak{a}_{M}} \sum_{P\in \mathcal{P}(M)} (-1)^{\left\lvert\Delta_{P}^{\lambda}\right\rvert}\varphi_{P}^{\lambda}(-H_{P}(g)+a) e^{\langle \lambda,a \rangle} da \\ &= \lim_{\lambda\to 0} \sum_{P\in \mathcal{P}(M)} (-1)^{\left\lvert\Delta_{P}^{\lambda}\right\rvert} \int_{\mathfrak{a}_{M}} \varphi_{P}^{\lambda}(-H_{P}(g)+a) e^{\langle \lambda,a \rangle} da \\ &= \lim_{\lambda\to 0} \sum_{P\in \mathcal{P}(M)} e^{\left\langle \lambda,H_{P}(g) \right\rangle}\cdot \mathrm{vol}\left(\mathfrak{a}_{M}/X_{*}(M)\right)\prod_{\alpha\in \Delta_{P}} \left\langle \lambda,\alpha^{\vee}\right\rangle^{-1}. \end{align*} $$
Letting
 $\textrm {d}_{P}(\lambda )=\textrm {vol}\left (\mathfrak {a}_{M}/X_{*}(M)\right )^{-1}\prod _{\alpha \in \Delta _{P}} \left \langle \lambda ,\alpha ^{\vee }\right \rangle $
, we get
$\textrm {d}_{P}(\lambda )=\textrm {vol}\left (\mathfrak {a}_{M}/X_{*}(M)\right )^{-1}\prod _{\alpha \in \Delta _{P}} \left \langle \lambda ,\alpha ^{\vee }\right \rangle $
, we get
 $$ \begin{align} \textrm{v}_{M}(g)=\lim_{\lambda\to 0} \sum_{P\in \mathcal{P}(M)} \textrm{d}_{P}(\lambda)^{-1}\cdot e^{\left\langle \lambda,H_{P}(g) \right \rangle}. \end{align} $$
$$ \begin{align} \textrm{v}_{M}(g)=\lim_{\lambda\to 0} \sum_{P\in \mathcal{P}(M)} \textrm{d}_{P}(\lambda)^{-1}\cdot e^{\left\langle \lambda,H_{P}(g) \right \rangle}. \end{align} $$
To deal with limits of the form in equations (2.8) and (2.9) systematically, we need Arthur’s notion of a
![]() $(G,M)$
-family [Reference Arthur2]. It is a family of smooth functions
$(G,M)$
-family [Reference Arthur2]. It is a family of smooth functions
![]() $(\textrm {r}_{P}(\lambda ))_{P\in \mathcal {P}(M)}$
on
$(\textrm {r}_{P}(\lambda ))_{P\in \mathcal {P}(M)}$
on
![]() $\mathfrak {a}_{M}^{*}$
which satisfy, for any adjacent parabolic subgroups
$\mathfrak {a}_{M}^{*}$
which satisfy, for any adjacent parabolic subgroups
![]() $(P,P')$
, the property that
$(P,P')$
, the property that
![]() $\textrm {r}_{P}(\lambda )=\textrm {r}_{P'}(\lambda )$
for any
$\textrm {r}_{P}(\lambda )=\textrm {r}_{P'}(\lambda )$
for any
![]() $\lambda $
on the hyperplane defined by the unique coroot in
$\lambda $
on the hyperplane defined by the unique coroot in
![]() $\Delta _{P}^{\vee }\cap \left (-\Delta _{P'}^{\vee }\right )$
. For any such family, we define
$\Delta _{P}^{\vee }\cap \left (-\Delta _{P'}^{\vee }\right )$
. For any such family, we define
 $$ \begin{align*} \textrm{r}_{M}(\lambda)=\sum_{P\in \mathcal{P}(M)} \textrm{d}_{P}(\lambda)^{-1} \textrm{r}_{P}(\lambda), \end{align*} $$
$$ \begin{align*} \textrm{r}_{M}(\lambda)=\sum_{P\in \mathcal{P}(M)} \textrm{d}_{P}(\lambda)^{-1} \textrm{r}_{P}(\lambda), \end{align*} $$
for generic
![]() $\lambda \in \mathfrak {a}_{M}^{*}$
. Arthur has shown in [Reference Arthur2] that the function extends smoothly over all
$\lambda \in \mathfrak {a}_{M}^{*}$
. Arthur has shown in [Reference Arthur2] that the function extends smoothly over all
![]() $\mathfrak {a}_{M}^{*}$
. Let
$\mathfrak {a}_{M}^{*}$
. Let
 $$ \begin{align*} \textrm{r}_{M}=\lim_{\lambda\to 0} \textrm{r}_{M}(\lambda). \end{align*} $$
$$ \begin{align*} \textrm{r}_{M}=\lim_{\lambda\to 0} \textrm{r}_{M}(\lambda). \end{align*} $$
It generalizes equation (2.9). Indeed, the functions
 $$ \begin{align*} \textrm{v}_{P}(\lambda, g)=e^{\left\langle \lambda,H_{P}(g) \right\rangle},\qquad P\in \mathcal{P}(M), \end{align*} $$
$$ \begin{align*} \textrm{v}_{P}(\lambda, g)=e^{\left\langle \lambda,H_{P}(g) \right\rangle},\qquad P\in \mathcal{P}(M), \end{align*} $$
form a
![]() $(G,M)$
-family, and the resulting
$(G,M)$
-family, and the resulting
![]() $\textrm {v}_{M}(g)$
is exactly Arthur’s weight factor. From this point of view, we call
$\textrm {v}_{M}(g)$
is exactly Arthur’s weight factor. From this point of view, we call
![]() $\textrm {r}_{M}$
the volume of the
$\textrm {r}_{M}$
the volume of the
![]() $(G,M)$
-family
$(G,M)$
-family
![]() $(\textrm {r}_{P}(\lambda ))_{P\in \mathcal {P}(M)}$
.
$(\textrm {r}_{P}(\lambda ))_{P\in \mathcal {P}(M)}$
.
Notice that the summands in equations (2.8) and (2.9) differ by a factor
 $$ \begin{align*} \textrm{w}_{P}(\lambda,\xi)=\frac{\textrm{d}_{P}(\lambda)}{\textrm{c}_{P}(\lambda)}e^{-\left\langle \lambda,[\xi]_{P} \right\rangle}, \end{align*} $$
$$ \begin{align*} \textrm{w}_{P}(\lambda,\xi)=\frac{\textrm{d}_{P}(\lambda)}{\textrm{c}_{P}(\lambda)}e^{-\left\langle \lambda,[\xi]_{P} \right\rangle}, \end{align*} $$
and that they form a
![]() $(G,M)$
-family. Letting
$(G,M)$
-family. Letting
![]() $\mathrm{w}_{P}(\lambda ,g,\xi )=\textrm {v}_{P}(\lambda ,g)\mathrm{w}_{P}(\lambda ,\xi )$
,
$\mathrm{w}_{P}(\lambda ,g,\xi )=\textrm {v}_{P}(\lambda ,g)\mathrm{w}_{P}(\lambda ,\xi )$
,
![]() $P\in \mathcal {P}(M)$
, they form a
$P\in \mathcal {P}(M)$
, they form a
![]() $(G,M)$
-family and equation (2.8) can be rewritten as
$(G,M)$
-family and equation (2.8) can be rewritten as
 $$ \begin{align} \textrm{w}_{M}^{\xi}(g)=\textrm{w}_{M}(g,\xi). \end{align} $$
$$ \begin{align} \textrm{w}_{M}^{\xi}(g)=\textrm{w}_{M}(g,\xi). \end{align} $$
In other words, we have expressed the lattice point-counting weight factor
 $\mathrm{w}_{M}^{\xi }(g)$
as the volume of the product of two
$\mathrm{w}_{M}^{\xi }(g)$
as the volume of the product of two
![]() $(G,M)$
-families.
$(G,M)$
-families.
We need a result of Arthur on the volume of the product of two
![]() $(G,M)$
-families. Let
$(G,M)$
-families. Let
![]() $\{\textrm {r}_{P}(\lambda )\}_{P\in \mathcal {P}(M)}$
and
$\{\textrm {r}_{P}(\lambda )\}_{P\in \mathcal {P}(M)}$
and
![]() $\{\mathrm{s}_{P}(\lambda )\}_{P\in \mathcal {P}(M)}$
be two
$\{\mathrm{s}_{P}(\lambda )\}_{P\in \mathcal {P}(M)}$
be two
![]() $(G,M)$
-families. For
$(G,M)$
-families. For
![]() $Q=LN_{Q}\in \mathcal {F}(M)$
, let
$Q=LN_{Q}\in \mathcal {F}(M)$
, let
 $$ \begin{align*} \textrm{r}_{R}^{Q}(\lambda)=\textrm{r}_{RN_{Q}}(\lambda), \qquad \forall R\in \mathcal{P}^{L}(M). \end{align*} $$
$$ \begin{align*} \textrm{r}_{R}^{Q}(\lambda)=\textrm{r}_{RN_{Q}}(\lambda), \qquad \forall R\in \mathcal{P}^{L}(M). \end{align*} $$
It is easy to see that
 $\textrm {r}_{R}^{Q}(\lambda )$
,
$\textrm {r}_{R}^{Q}(\lambda )$
,
![]() $R\in \mathcal {P}^{L}(M)$
, form an
$R\in \mathcal {P}^{L}(M)$
, form an
![]() $(L,M)$
-family. The function
$(L,M)$
-family. The function
 $\textrm {r}_{M}^{Q}(\lambda )$
and the volume
$\textrm {r}_{M}^{Q}(\lambda )$
and the volume
![]() $\textrm {r}_{M}^{Q}$
are defined in a similar way. From the
$\textrm {r}_{M}^{Q}$
are defined in a similar way. From the
![]() $(G,M)$
-family
$(G,M)$
-family
![]() $\{\mathrm{s}_{P}(\lambda )\}_{P\in \mathcal {P}(M)}$
, Arthur has defined a smooth function
$\{\mathrm{s}_{P}(\lambda )\}_{P\in \mathcal {P}(M)}$
, Arthur has defined a smooth function
 $\mathrm{s}_{Q}'(\lambda )$
on
$\mathrm{s}_{Q}'(\lambda )$
on
![]() $\mathfrak {a}_{Q}^{*}$
. The definition is quite involved, and we refer the reader to [Reference Arthur2, §6]. Let
$\mathfrak {a}_{Q}^{*}$
. The definition is quite involved, and we refer the reader to [Reference Arthur2, §6]. Let
 $\mathrm{s}_{Q}'=\mathrm{s}_{Q}'(0)$
.
$\mathrm{s}_{Q}'=\mathrm{s}_{Q}'(0)$
.
Lemma 2.9 Arthur [Reference Arthur2, Lemma 6.3 and Corollary 6.4]
Let
![]() $\{\textrm {r}_{P}(\lambda )\}_{P\in \mathcal {P}(M)}$
and
$\{\textrm {r}_{P}(\lambda )\}_{P\in \mathcal {P}(M)}$
and
![]() $\{\mathrm{s}_{P}(\lambda )\}_{P\in \mathcal {P}(M)}$
be two
$\{\mathrm{s}_{P}(\lambda )\}_{P\in \mathcal {P}(M)}$
be two
![]() $(G,M)$
-families, and let
$(G,M)$
-families, and let
![]() $\textrm {r}\cdot \mathrm{s}$
be their product. Then for any
$\textrm {r}\cdot \mathrm{s}$
be their product. Then for any
![]() $\lambda \in \mathfrak {a}_{M}^{*}$
, we have
$\lambda \in \mathfrak {a}_{M}^{*}$
, we have
 $$ \begin{align*} (\textrm{r}\cdot \textrm{s})_{M}(\lambda)=\sum_{Q\in \mathcal{F}(M)}\textrm{r}_{M}^{Q}(\lambda)\textrm{s}_{Q}'(\lambda). \end{align*} $$
$$ \begin{align*} (\textrm{r}\cdot \textrm{s})_{M}(\lambda)=\sum_{Q\in \mathcal{F}(M)}\textrm{r}_{M}^{Q}(\lambda)\textrm{s}_{Q}'(\lambda). \end{align*} $$
In particular,
 $$ \begin{align*} \textrm{s}_{M}(\lambda)=\sum_{P\in \mathcal{P}(M)}\textrm{s}_{P}'(\lambda). \end{align*} $$
$$ \begin{align*} \textrm{s}_{M}(\lambda)=\sum_{P\in \mathcal{P}(M)}\textrm{s}_{P}'(\lambda). \end{align*} $$
In our situation, this implies
 $$ \begin{align} \textrm{w}_{M}^{\xi}(g)=\big(\textrm{v}(g)\cdot \textrm{w}(\xi)\big)(0)=\sum_{Q\in \mathcal{F}(M)}\textrm{v}_{M}^{Q}(g)\textrm{w}_{Q}'(\xi) \end{align} $$
$$ \begin{align} \textrm{w}_{M}^{\xi}(g)=\big(\textrm{v}(g)\cdot \textrm{w}(\xi)\big)(0)=\sum_{Q\in \mathcal{F}(M)}\textrm{v}_{M}^{Q}(g)\textrm{w}_{Q}'(\xi) \end{align} $$
and
 $$ \begin{align} \textrm{w}_{M}(\xi)=\sum_{P\in \mathcal{P}(M)}\textrm{w}_{P}'(\xi). \end{align} $$
$$ \begin{align} \textrm{w}_{M}(\xi)=\sum_{P\in \mathcal{P}(M)}\textrm{w}_{P}'(\xi). \end{align} $$
Similar results hold for Levi subgroups L containing M:
 $$ \begin{align} \textrm{w}_{L}^{\xi_{L}}(g)&=\sum_{R\in \mathcal{F}(L)}\textrm{v}_{L}^{R}(g)\textrm{w}_{R}'(\xi_{L}), \end{align} $$
$$ \begin{align} \textrm{w}_{L}^{\xi_{L}}(g)&=\sum_{R\in \mathcal{F}(L)}\textrm{v}_{L}^{R}(g)\textrm{w}_{R}'(\xi_{L}), \end{align} $$
 $$ \begin{align} \textrm{w}_{L}(\xi_{L})&=\sum_{Q\in \mathcal{P}(L)}\textrm{w}_{Q}'(\xi_{L}), \end{align} $$
$$ \begin{align} \textrm{w}_{L}(\xi_{L})&=\sum_{Q\in \mathcal{P}(L)}\textrm{w}_{Q}'(\xi_{L}), \end{align} $$
with
![]() $\mathrm{w}_{R}'(\xi _{L})$
deduced from the
$\mathrm{w}_{R}'(\xi _{L})$
deduced from the
![]() $(G,L)$
-family
$(G,L)$
-family
 $$ \begin{align*} \textrm{w}_{Q}(\lambda,\xi_{L})=\frac{\textrm{d}_{Q}(\lambda)}{\textrm{c}_{Q}(\lambda)}e^{-\left\langle \lambda,[\xi_{L}]_{Q} \right\rangle}, \qquad \forall Q\in \mathcal{P}(L). \end{align*} $$
$$ \begin{align*} \textrm{w}_{Q}(\lambda,\xi_{L})=\frac{\textrm{d}_{Q}(\lambda)}{\textrm{c}_{Q}(\lambda)}e^{-\left\langle \lambda,[\xi_{L}]_{Q} \right\rangle}, \qquad \forall Q\in \mathcal{P}(L). \end{align*} $$
Setting
![]() $g=e\in G$
in equation (2.13), and noting that
$g=e\in G$
in equation (2.13), and noting that
 $$ \begin{align*} \textrm{v}_{L}^{R}(e)= \begin{cases} 1 & \text{if } R\in \mathcal{P}(L),\\ 0 & \text{otherwise}, \end{cases} \end{align*} $$
$$ \begin{align*} \textrm{v}_{L}^{R}(e)= \begin{cases} 1 & \text{if } R\in \mathcal{P}(L),\\ 0 & \text{otherwise}, \end{cases} \end{align*} $$
we get
 $$ \begin{align} \textrm{w}_{L}^{\xi_{L}}(e)=\sum_{Q\in \mathcal{P}(L)} \textrm{w}_{Q}'(\xi_{L})=\textrm{w}_{L}(\xi_{L}), \end{align} $$
$$ \begin{align} \textrm{w}_{L}^{\xi_{L}}(e)=\sum_{Q\in \mathcal{P}(L)} \textrm{w}_{Q}'(\xi_{L})=\textrm{w}_{L}(\xi_{L}), \end{align} $$
where the second equality is just equation (2.14).
Lemma 2.10.
 $$ \begin{align*} \sum_{Q\in \mathcal{P}(L)} \textrm{w}_{Q}'(\xi) =\frac{\mathrm{vol}\left(\mathfrak{a}_{L}/X_{*}(L)\right)}{\mathrm{vol}\left(\mathfrak{a}_{M}/X_{*}(M)\right)}\cdot \textrm{w}_{L}^{\xi_{L}}(e)= \begin{cases} \mathrm{vol}\left(\mathfrak{a}_{M}/X_{*}(M)\right)^{-1} & \text{if } L=G,\\ 0 &\text{otherwise}. \end{cases} \end{align*} $$
$$ \begin{align*} \sum_{Q\in \mathcal{P}(L)} \textrm{w}_{Q}'(\xi) =\frac{\mathrm{vol}\left(\mathfrak{a}_{L}/X_{*}(L)\right)}{\mathrm{vol}\left(\mathfrak{a}_{M}/X_{*}(M)\right)}\cdot \textrm{w}_{L}^{\xi_{L}}(e)= \begin{cases} \mathrm{vol}\left(\mathfrak{a}_{M}/X_{*}(M)\right)^{-1} & \text{if } L=G,\\ 0 &\text{otherwise}. \end{cases} \end{align*} $$
Proof. Recall that given a
![]() $(G,M)$
-family
$(G,M)$
-family
![]() $\{\mathrm{s}_{P}(\lambda )\}_{P\in \mathcal {P}(M)}$
, we can define a
$\{\mathrm{s}_{P}(\lambda )\}_{P\in \mathcal {P}(M)}$
, we can define a
![]() $(G,L)$
-family by setting
$(G,L)$
-family by setting
for any
![]() $P\in \mathcal {P}(M)$
,
$P\in \mathcal {P}(M)$
,
![]() $P\subset Q$
. Moreover, the function
$P\subset Q$
. Moreover, the function
 $\mathrm{s}_{Q}'(\lambda )$
deduced from the
$\mathrm{s}_{Q}'(\lambda )$
deduced from the
![]() $(G,M)$
-family
$(G,M)$
-family
![]() $\{\mathrm{s}_{P}(\lambda )\}_{P\in \mathcal {P}(M)}$
is the same as that from the
$\{\mathrm{s}_{P}(\lambda )\}_{P\in \mathcal {P}(M)}$
is the same as that from the
![]() $(G,L)$
-family
$(G,L)$
-family
![]() $\{\mathrm{s}_{Q}(\lambda )\}_{Q\in \mathcal {P}(L)}$
, by [Reference Arthur2, formula 6.3]. In this way, we get the
$\{\mathrm{s}_{Q}(\lambda )\}_{Q\in \mathcal {P}(L)}$
, by [Reference Arthur2, formula 6.3]. In this way, we get the
![]() $(G,L)$
-family
$(G,L)$
-family
![]() $\{\mathrm{w}_{Q}(\lambda ,\xi )\}_{Q\in \mathcal {P}(L)}$
and the equality
$\{\mathrm{w}_{Q}(\lambda ,\xi )\}_{Q\in \mathcal {P}(L)}$
and the equality
 $$ \begin{align*} \sum_{Q\in \mathcal{P}(L)}\textrm{w}_{Q}'(\xi)=\textrm{w}_{L}(\xi)=\lim_{\lambda\to 0} \sum_{Q\in \mathcal{P}(L)} \textrm{d}_{Q}(\lambda)^{-1}\cdot \frac{\textrm{d}_{P}(\lambda)}{\textrm{c}_{P}(\lambda)}\cdot e^{-\left\langle \lambda,[\xi]_{P} \right \rangle}, \end{align*} $$
$$ \begin{align*} \sum_{Q\in \mathcal{P}(L)}\textrm{w}_{Q}'(\xi)=\textrm{w}_{L}(\xi)=\lim_{\lambda\to 0} \sum_{Q\in \mathcal{P}(L)} \textrm{d}_{Q}(\lambda)^{-1}\cdot \frac{\textrm{d}_{P}(\lambda)}{\textrm{c}_{P}(\lambda)}\cdot e^{-\left\langle \lambda,[\xi]_{P} \right \rangle}, \end{align*} $$
by the second assertion of Lemma 2.9, where for each
![]() $Q\in \mathcal {P}(L)$
we take
$Q\in \mathcal {P}(L)$
we take
![]() $P\in \mathcal {P}(M)$
,
$P\in \mathcal {P}(M)$
,
![]() $P\subset Q$
, and the limit is taken for
$P\subset Q$
, and the limit is taken for
![]() $\lambda \in \mathfrak {a}_{L}^{*}$
generic. Now that
$\lambda \in \mathfrak {a}_{L}^{*}$
generic. Now that
 $$ \begin{align*} \frac{\textrm{d}_{P}(\lambda)}{\textrm{c}_{P}(\lambda)} =\frac{\mathrm{vol}\left(\mathfrak{a}_{L}/X_{*}(L)\right)}{\mathrm{vol}\left(\mathfrak{a}_{M}/X_{*}(M)\right)}\cdot \frac{\textrm{d}_{Q}(\lambda)}{\textrm{c}_{Q}(\lambda)} \end{align*} $$
$$ \begin{align*} \frac{\textrm{d}_{P}(\lambda)}{\textrm{c}_{P}(\lambda)} =\frac{\mathrm{vol}\left(\mathfrak{a}_{L}/X_{*}(L)\right)}{\mathrm{vol}\left(\mathfrak{a}_{M}/X_{*}(M)\right)}\cdot \frac{\textrm{d}_{Q}(\lambda)}{\textrm{c}_{Q}(\lambda)} \end{align*} $$
and
![]() $\langle \lambda ,[\xi ]_{P} \rangle =\langle \lambda ,[\xi _{L}]_{Q} \rangle $
for any
$\langle \lambda ,[\xi ]_{P} \rangle =\langle \lambda ,[\xi _{L}]_{Q} \rangle $
for any
![]() $\lambda \in \mathfrak {a}_{L}^{*}$
, we get
$\lambda \in \mathfrak {a}_{L}^{*}$
, we get
 $$ \begin{align*} \sum_{Q\in \mathcal{P}(L)}\textrm{w}_{Q}'(\xi)=\frac{\mathrm{vol}\left(\mathfrak{a}_{L}/X_{*}(L)\right)}{\mathrm{vol}\left(\mathfrak{a}_{M}/X_{*}(M)\right)}\cdot \textrm{w}_{L}(\xi_{L}) =\frac{\mathrm{vol}\left(\mathfrak{a}_{L}/X_{*}(L)\right)}{\mathrm{vol}\left(\mathfrak{a}_{M}/X_{*}(M)\right)}\cdot \textrm{w}_{L}^{\xi_{L}}(e), \end{align*} $$
$$ \begin{align*} \sum_{Q\in \mathcal{P}(L)}\textrm{w}_{Q}'(\xi)=\frac{\mathrm{vol}\left(\mathfrak{a}_{L}/X_{*}(L)\right)}{\mathrm{vol}\left(\mathfrak{a}_{M}/X_{*}(M)\right)}\cdot \textrm{w}_{L}(\xi_{L}) =\frac{\mathrm{vol}\left(\mathfrak{a}_{L}/X_{*}(L)\right)}{\mathrm{vol}\left(\mathfrak{a}_{M}/X_{*}(M)\right)}\cdot \textrm{w}_{L}^{\xi_{L}}(e), \end{align*} $$
where the last equality follows from equation (2.15).
By equation (2.11), we can rewrite
 $J_{M}^{\xi }(\gamma )$
as
$J_{M}^{\xi }(\gamma )$
as

As
 $\textrm {v}_{M}^{Q}$
is also left
$\textrm {v}_{M}^{Q}$
is also left
![]() $T(F)$
-invariant, we can define
$T(F)$
-invariant, we can define

Let
![]() $Q=LN_{Q}$
be the standard Levi decomposition. Let
$Q=LN_{Q}$
be the standard Levi decomposition. Let
![]() $dl$
be the Haar measure on
$dl$
be the Haar measure on
![]() $L(F)$
normalized by
$L(F)$
normalized by
![]() $\textrm {vol}_{dl}(L(\mathcal {O}))=1$
and let
$\textrm {vol}_{dl}(L(\mathcal {O}))=1$
and let
![]() $dn $
be the Haar measure on
$dn $
be the Haar measure on
![]() $N_{Q}(F)$
normalized by
$N_{Q}(F)$
normalized by
![]() $\textrm {vol}_{dn}\left (N_{Q}(\mathcal {O})\right )=1$
. Using Iwasawa decomposition, we can rewrite
$\textrm {vol}_{dn}\left (N_{Q}(\mathcal {O})\right )=1$
. Using Iwasawa decomposition, we can rewrite
 $J_{M}^{Q}(\gamma )$
as
$J_{M}^{Q}(\gamma )$
as

where in the second and third lines we have used the equalities
 $\textrm {v}_{M}^{Q}(nlk)=\textrm {v}_{M}^{Q}(l)$
and
$\textrm {v}_{M}^{Q}(nlk)=\textrm {v}_{M}^{Q}(l)$
and
 $\textrm {v}_{M}^{Q}(l)=\textrm {v}_{M}^{L}(l)$
respectively, which follow directly from definitions. Notice that
$\textrm {v}_{M}^{Q}(l)=\textrm {v}_{M}^{L}(l)$
respectively, which follow directly from definitions. Notice that

where the last equality follows from Proposition 2.4. Continuing the calculation of equation (2.16), we get

Combining all the foregoing calculations, we get
 $$ \begin{align*} J_{M}^{\xi}(\gamma) &= \sum_{L\in \mathcal{L}(M)}\sum_{Q\in \mathcal{P}(L)} J_{M}^{Q}(\gamma) \cdot \textrm{w}_{Q}'(\xi)=\sum_{L\in \mathcal{L}(M)}\sum_{Q\in \mathcal{P}(L)}q^{\mathrm{val}\left(\det\left(\mathrm{ad}\gamma\mid\mathfrak{n}_{Q,F}\right)\right)} J_{M}^{L}(\gamma) \cdot \textrm{w}_{Q}'(\xi)\\ &= \sum_{L\in \mathcal{L}(M)}q^{\frac{1}{2}\mathrm{val}\left(\det\left(\mathrm{ad}\gamma\mid\mathfrak{g}_{F}/\mathfrak{l}_{F}\right)\right)} J_{M}^{L}(\gamma) \sum_{Q\in \mathcal{P}(L)}\textrm{w}_{Q}'(\xi)\\ &= {\mathrm{vol}\left(\mathfrak{a}_{M}/X_{*}(M)\right)}^{-1} \cdot J_{M}(\gamma), \end{align*} $$
$$ \begin{align*} J_{M}^{\xi}(\gamma) &= \sum_{L\in \mathcal{L}(M)}\sum_{Q\in \mathcal{P}(L)} J_{M}^{Q}(\gamma) \cdot \textrm{w}_{Q}'(\xi)=\sum_{L\in \mathcal{L}(M)}\sum_{Q\in \mathcal{P}(L)}q^{\mathrm{val}\left(\det\left(\mathrm{ad}\gamma\mid\mathfrak{n}_{Q,F}\right)\right)} J_{M}^{L}(\gamma) \cdot \textrm{w}_{Q}'(\xi)\\ &= \sum_{L\in \mathcal{L}(M)}q^{\frac{1}{2}\mathrm{val}\left(\det\left(\mathrm{ad}\gamma\mid\mathfrak{g}_{F}/\mathfrak{l}_{F}\right)\right)} J_{M}^{L}(\gamma) \sum_{Q\in \mathcal{P}(L)}\textrm{w}_{Q}'(\xi)\\ &= {\mathrm{vol}\left(\mathfrak{a}_{M}/X_{*}(M)\right)}^{-1} \cdot J_{M}(\gamma), \end{align*} $$
where the last equality follows from Lemma 2.10. This finishes the proof of Theorem 2.8.
3. Counting points by Arthur–Kottwitz reduction
From now on, we will assume that
![]() $G_{\text {der}}$
is simply connected. The general case can be reduced to this one by focusing on each connected component. This extra assumption gives some technical convenience – for example,
$G_{\text {der}}$
is simply connected. The general case can be reduced to this one by focusing on each connected component. This extra assumption gives some technical convenience – for example,
![]() $M_{0,\text {der}}$
will be simply connected,
$M_{0,\text {der}}$
will be simply connected,
![]() $\Lambda _{M_{0}}$
will be torsion-free, and we get an inclusion
$\Lambda _{M_{0}}$
will be torsion-free, and we get an inclusion
![]() $\Lambda _{M_{0}}\hookrightarrow \mathfrak {a}_{M_{0}}$
. Moreover, we have
$\Lambda _{M_{0}}\hookrightarrow \mathfrak {a}_{M_{0}}$
. Moreover, we have
![]() $X_{*}(M_{0})=\Lambda _{M_{0}}$
, according to [Reference Chen8, Lemma 11.6.1].
$X_{*}(M_{0})=\Lambda _{M_{0}}$
, according to [Reference Chen8, Lemma 11.6.1].
Fix
![]() $M\in \mathcal {L}(M_{0})$
and let
$M\in \mathcal {L}(M_{0})$
and let
![]() $\Pi $
be a sufficiently regular positive
$\Pi $
be a sufficiently regular positive
![]() $(G,M)$
-orthogonal family. We count the number of points on
$(G,M)$
-orthogonal family. We count the number of points on
 $\Lambda ^{H_{M}}\backslash \mathscr {X}_{\gamma }^{\nu _{0}}(\Pi )$
,
$\Lambda ^{H_{M}}\backslash \mathscr {X}_{\gamma }^{\nu _{0}}(\Pi )$
,
![]() $\nu _{0}\in \Lambda _{G}$
. Generalizing our previous work [Reference Chaudouard and Laumon11], we show that it can be reduced to counting points on the intermediate fundamental domains
$\nu _{0}\in \Lambda _{G}$
. Generalizing our previous work [Reference Chaudouard and Laumon11], we show that it can be reduced to counting points on the intermediate fundamental domains
 $F_{\gamma }^{L,M}$
,
$F_{\gamma }^{L,M}$
,
![]() $L\in \mathcal {L}(M)$
, and the counting result depends quasi-polynomially on the truncation parameter. Moreover, counting points on
$L\in \mathcal {L}(M)$
, and the counting result depends quasi-polynomially on the truncation parameter. Moreover, counting points on
 $\Lambda ^{H_{M}}\backslash F_{\gamma }^{L,M}$
can be further reduced to counting points on the fundamental domains
$\Lambda ^{H_{M}}\backslash F_{\gamma }^{L,M}$
can be further reduced to counting points on the fundamental domains
 $F_{\gamma }^{M'}$
for some
$F_{\gamma }^{M'}$
for some
![]() $M'\in \mathcal {L}(M_{0})$
‘transversal’ to M.
$M'\in \mathcal {L}(M_{0})$
‘transversal’ to M.
3.1. Truncations on the affine Grassmannian
Recall the following definition of Arthur [Reference Arthur1], which is a formalization of the orthogonal properties in Proposition 2.5:
Definition 3.1. A family
![]() $\Pi =(\lambda _{P})_{P\in \mathcal {P}(M)}$
of elements in
$\Pi =(\lambda _{P})_{P\in \mathcal {P}(M)}$
of elements in
![]() $\mathfrak {a}_{M}^{G}$
is called a positive
$\mathfrak {a}_{M}^{G}$
is called a positive
![]() $(G,M)$
-orthogonal family if it satisfies
$(G,M)$
-orthogonal family if it satisfies
 $$ \begin{align*} \lambda_{P_{1}}-\lambda_{P_{2}}=n_{P_{1},P_{2}}\cdot \pi_{M}^{G}\left(\beta_{P_{1},P_{2}}\right), \qquad \text{with } n_{P_{1},P_{2}}\in \textbf{R}_{\geq 0}, \end{align*} $$
$$ \begin{align*} \lambda_{P_{1}}-\lambda_{P_{2}}=n_{P_{1},P_{2}}\cdot \pi_{M}^{G}\left(\beta_{P_{1},P_{2}}\right), \qquad \text{with } n_{P_{1},P_{2}}\in \textbf{R}_{\geq 0}, \end{align*} $$
for any two adjacent parabolic subgroups
![]() $P_{1}, P_{2}\in \mathcal {P}(M)$
.
$P_{1}, P_{2}\in \mathcal {P}(M)$
.
Given such a positive
![]() $(G,M)$
-orthogonal family, we will denote again by
$(G,M)$
-orthogonal family, we will denote again by
![]() $\Pi $
the convex hull of the
$\Pi $
the convex hull of the
![]() $\lambda _{P}$
s. For
$\lambda _{P}$
s. For
![]() $Q=LN_{Q}\in \mathcal {F}(M)$
, parallel to
$Q=LN_{Q}\in \mathcal {F}(M)$
, parallel to
 $\mathrm{Ec}_{M}^{Q}(x)$
, we denote by
$\mathrm{Ec}_{M}^{Q}(x)$
, we denote by
![]() $\Pi ^{Q}$
the face of
$\Pi ^{Q}$
the face of
![]() $\Pi $
whose vertices are
$\Pi $
whose vertices are
![]() $\lambda _{P}$
,
$\lambda _{P}$
,
![]() $P\in \mathcal {P}(M), P\subset Q$
. With the projection
$P\in \mathcal {P}(M), P\subset Q$
. With the projection
![]() $\pi _{M}^{L}$
, it can be seen as a positive
$\pi _{M}^{L}$
, it can be seen as a positive
![]() $(L,M)$
-orthogonal family. This sets up a bijection between the set
$(L,M)$
-orthogonal family. This sets up a bijection between the set
![]() $\mathcal {F}(M)$
and the set of the faces of
$\mathcal {F}(M)$
and the set of the faces of
![]() $\Pi $
. Moreover, we denote by
$\Pi $
. Moreover, we denote by
![]() $\lambda _{Q}$
or
$\lambda _{Q}$
or
![]() $\lambda _{Q}(\Pi )$
the element
$\lambda _{Q}(\Pi )$
the element
![]() $\pi _{M,L}\left (\lambda _{P'}\right )$
for any
$\pi _{M,L}\left (\lambda _{P'}\right )$
for any
![]() $P'\in \mathcal {P}(M), P'\subset Q$
. One can show that
$P'\in \mathcal {P}(M), P'\subset Q$
. One can show that
 $\left (\lambda _{Q}(\Pi )\right )_{Q\in \mathcal {P}(L)}$
forms a positive
$\left (\lambda _{Q}(\Pi )\right )_{Q\in \mathcal {P}(L)}$
forms a positive
![]() $(G,L)$
-orthogonal family. Later on, we also use the notation
$(G,L)$
-orthogonal family. Later on, we also use the notation
![]() $(\lambda _{\bar {w}})_{\bar {w}\in W/W_{M}}$
for
$(\lambda _{\bar {w}})_{\bar {w}\in W/W_{M}}$
for
![]() $(\lambda _{\bar {w}\cdot P})_{\bar {w}\in W/W_{M}}$
, and we use the notation
$(\lambda _{\bar {w}\cdot P})_{\bar {w}\in W/W_{M}}$
, and we use the notation
![]() $\lambda _{w}(\Pi )$
or
$\lambda _{w}(\Pi )$
or
![]() $\lambda _{w\cdot P}(\Pi )$
to indicate the vertex of
$\lambda _{w\cdot P}(\Pi )$
to indicate the vertex of
![]() $\Pi $
indexed by
$\Pi $
indexed by
![]() $w\cdot P$
.
$w\cdot P$
.
Following Chaudouard and Laumon [Reference Chen7], we define the truncated affine Grassmannian
![]() $\mathscr {X}(\Pi )$
to be
$\mathscr {X}(\Pi )$
to be
 $$ \begin{align*} \mathscr{X}(\Pi)=\left\{x\in \mathscr{X} \mid \pi_{M}^{G}(\textrm{Ec}_{M}(x))\subset \Pi\right\}. \end{align*} $$
$$ \begin{align*} \mathscr{X}(\Pi)=\left\{x\in \mathscr{X} \mid \pi_{M}^{G}(\textrm{Ec}_{M}(x))\subset \Pi\right\}. \end{align*} $$
We want to point out that its connected components are also parametrized by
![]() $\Lambda _{G}$
, but they are not isomorphic in general. However, there is periodicity in the connected components: let
$\Lambda _{G}$
, but they are not isomorphic in general. However, there is periodicity in the connected components: let
![]() $G^{\mathrm{ad}}$
be the adjoint group of G and let
$G^{\mathrm{ad}}$
be the adjoint group of G and let
![]() $c_{G}:\Lambda _{G}\to \Lambda _{G^{\mathrm{ad}}}$
be the projection induced by the natural projection
$c_{G}:\Lambda _{G}\to \Lambda _{G^{\mathrm{ad}}}$
be the projection induced by the natural projection
![]() $T\to T/Z_{G}$
. For
$T\to T/Z_{G}$
. For
![]() $\nu ,\nu '\in \Lambda _{G}$
, we have
$\nu ,\nu '\in \Lambda _{G}$
, we have
 $$ \begin{align*} \mathscr{X}^{\nu}(\Pi)=\mathscr{X}^{\nu'}(\Pi), \qquad \text{if } c_{G}(\nu)=c_{G}(\nu'), \end{align*} $$
$$ \begin{align*} \mathscr{X}^{\nu}(\Pi)=\mathscr{X}^{\nu'}(\Pi), \qquad \text{if } c_{G}(\nu)=c_{G}(\nu'), \end{align*} $$
because they can be translated to each other by elements in
![]() $Z_{G}(F)$
.
$Z_{G}(F)$
.
For a regular element
![]() $\gamma \in \mathfrak {t}(\mathcal {O})$
, we can truncate the affine Springer fiber
$\gamma \in \mathfrak {t}(\mathcal {O})$
, we can truncate the affine Springer fiber
![]() $\mathscr {X}_{\gamma }$
similarly by defining
$\mathscr {X}_{\gamma }$
similarly by defining
and the same observation on the connected components of
![]() $\mathscr {X}(\Pi )$
holds also for
$\mathscr {X}(\Pi )$
holds also for
![]() $\mathscr {X}_{\gamma }(\Pi )$
.
$\mathscr {X}_{\gamma }(\Pi )$
.
3.2. The intermediate fundamental domain
We generalize our construction of the fundamental domain
![]() $F_{\gamma }$
in [Reference Chaudouard and Laumon11].Footnote
3
$F_{\gamma }$
in [Reference Chaudouard and Laumon11].Footnote
3
Let
![]() $P_{1}=MN_{1}$
and
$P_{1}=MN_{1}$
and
![]() $P_{2}=MN_{2}\in \mathcal {P}(M)$
be two adjacent parabolic subgroups. Let
$P_{2}=MN_{2}\in \mathcal {P}(M)$
be two adjacent parabolic subgroups. Let
![]() $m_{\alpha }$
be the unique positive integer such that the image of
$m_{\alpha }$
be the unique positive integer such that the image of
![]() $\alpha ^{\vee }$
in
$\alpha ^{\vee }$
in
![]() $\Lambda _{M}$
is equal to
$\Lambda _{M}$
is equal to
![]() $m_{\alpha }\cdot \beta _{P_{1},P_{2}}$
, and let
$m_{\alpha }\cdot \beta _{P_{1},P_{2}}$
, and let
 $$ \begin{align*} n(\gamma, P_{1},P_{2})=\sum_{\alpha\in \Phi\left(N_{1}, T_{\overline{F}}\right)\cap \Phi\left(N_{2}^{-}, T_{\overline{F}}\right)} \mathrm{val}(\alpha(\gamma))\cdot m_{\alpha}. \end{align*} $$
$$ \begin{align*} n(\gamma, P_{1},P_{2})=\sum_{\alpha\in \Phi\left(N_{1}, T_{\overline{F}}\right)\cap \Phi\left(N_{2}^{-}, T_{\overline{F}}\right)} \mathrm{val}(\alpha(\gamma))\cdot m_{\alpha}. \end{align*} $$
It can be verified that
![]() $n(\gamma , P_{1},P_{2})$
is an integer.
$n(\gamma , P_{1},P_{2})$
is an integer.
Proposition 3.1 Goresky-Kottwitz-MacPherson, [Reference Goresky, Kottwitz and MacPherson15]
Set
![]() $x\in \mathscr {X}_{\gamma }$
.
$x\in \mathscr {X}_{\gamma }$
.
-
(1) For any two adjacent parabolic subgroups
 $P_{1}, P_{2}\in \mathcal {P}(M)$
, we have
$P_{1}, P_{2}\in \mathcal {P}(M)$
, we have  $$ \begin{align*} n(x,P_{1},P_{2})\leq n(\gamma,P_{1},P_{2}). \end{align*} $$
$$ \begin{align*} n(x,P_{1},P_{2})\leq n(\gamma,P_{1},P_{2}). \end{align*} $$
-
(2) The point x is regular in
 $\mathscr {X}_{\gamma }$
if and only if the following two conditions hold:
$\mathscr {X}_{\gamma }$
if and only if the following two conditions hold:-
(a) The point
 $f_{P}(x)$
is regular in
$f_{P}(x)$
is regular in
 $\mathscr {X}^{M}_{\gamma }$
for all
$\mathscr {X}^{M}_{\gamma }$
for all
 $P\in \mathcal {P}(M)$
.
$P\in \mathcal {P}(M)$
. -
(b) For any two adjacent parabolic subgroups
 $P_{1}, P_{2}$
in
$P_{1}, P_{2}$
in
 $\mathcal {P}(M)$
, one has
$\mathcal {P}(M)$
, one has  $$ \begin{align*} n(x,P_{1},P_{2})=n(\gamma,P_{1},P_{2}). \end{align*} $$
$$ \begin{align*} n(x,P_{1},P_{2})=n(\gamma,P_{1},P_{2}). \end{align*} $$
-
Notice that although Goresky, Kottwitz, and MacPherson work over the field
![]() $F=\textbf {C}(\!(\epsilon )\!)$
, their proof works for any field
$F=\textbf {C}(\!(\epsilon )\!)$
, their proof works for any field
![]() $F=k(\!(\epsilon )\!)$
with
$F=k(\!(\epsilon )\!)$
with
![]() $\text {char}(k)>\lvert W\rvert $
. Their result motivates our definition:
$\text {char}(k)>\lvert W\rvert $
. Their result motivates our definition:
Definition 3.2. Take a regular point
![]() $x_{0}\in \mathscr {X}_{\gamma }^{\mathrm{reg}}$
. Let
$x_{0}\in \mathscr {X}_{\gamma }^{\mathrm{reg}}$
. Let
 $$ \begin{align*} F_{\gamma}^{G,M}=\left\{x\in \mathscr{X}_{\gamma}\mid \textrm{Ec}_{M}(x)\subset \textrm{Ec}_{M}(x_{0}), \ \nu_{G}(x)=\nu_{G}(x_{0})\right\}. \end{align*} $$
$$ \begin{align*} F_{\gamma}^{G,M}=\left\{x\in \mathscr{X}_{\gamma}\mid \textrm{Ec}_{M}(x)\subset \textrm{Ec}_{M}(x_{0}), \ \nu_{G}(x)=\nu_{G}(x_{0})\right\}. \end{align*} $$
We call it an intermediate fundamental domain of
![]() $\mathscr {X}_{\gamma }$
with respect to M.
$\mathscr {X}_{\gamma }$
with respect to M.
We should have used the notation
 $F_{\gamma ,x_{0}}^{G,M}$
to indicate the dependence on
$F_{\gamma ,x_{0}}^{G,M}$
to indicate the dependence on
![]() $x_{0}$
, but they are isomorphic to each other for any choice of the regular point
$x_{0}$
, but they are isomorphic to each other for any choice of the regular point
![]() $x_{0}$
. Indeed, for any two regular points
$x_{0}$
. Indeed, for any two regular points
![]() $x_{1},x_{2}$
, we can find
$x_{1},x_{2}$
, we can find
![]() $t\in T(F)$
such that
$t\in T(F)$
such that
![]() $x_{1}=t\cdot x_{2}$
. Now that
$x_{1}=t\cdot x_{2}$
. Now that
![]() $\mathrm{Ec}_{M}(tx)=\mathrm{Ec}_{M}(x)+H_{M}(t), \ \forall x\in \mathscr {X}$
, the intermediate fundamental domain given by
$\mathrm{Ec}_{M}(tx)=\mathrm{Ec}_{M}(x)+H_{M}(t), \ \forall x\in \mathscr {X}$
, the intermediate fundamental domain given by
![]() $x_{1}$
is just the translation by t of that given by
$x_{1}$
is just the translation by t of that given by
![]() $x_{2}$
. Notice that for
$x_{2}$
. Notice that for
![]() $M=M_{0}$
, we recover the fundamental domain
$M=M_{0}$
, we recover the fundamental domain
![]() $F_{\gamma }$
. For simplicity, we assume that
$F_{\gamma }$
. For simplicity, we assume that
![]() $\nu _{G}(x_{0})=0$
.
$\nu _{G}(x_{0})=0$
.
Unlike the fundamental domain, the intermediate
 $F_{\gamma }^{G,M}$
is no longer of finite type for
$F_{\gamma }^{G,M}$
is no longer of finite type for
![]() $M\supsetneq M_{0}$
. Nonetheless, we have the following:
$M\supsetneq M_{0}$
. Nonetheless, we have the following:
Proposition 3.2. The free discrete abelian group
![]() $\Lambda ^{H_{M}}$
acts freely on
$\Lambda ^{H_{M}}$
acts freely on
 $F_{\gamma }^{G,M}$
, and the quotient
$F_{\gamma }^{G,M}$
, and the quotient
 $\Lambda ^{H_{M}}\backslash F_{\gamma }^{G,M}$
is of finite type.
$\Lambda ^{H_{M}}\backslash F_{\gamma }^{G,M}$
is of finite type.
Proof. Recall that
![]() $\Lambda ^{H_{M}}=\Lambda \cap \ker (H_{M})$
by definition, and hence it preserves
$\Lambda ^{H_{M}}=\Lambda \cap \ker (H_{M})$
by definition, and hence it preserves
 $F_{\gamma }^{G,M}$
because left translation by
$F_{\gamma }^{G,M}$
because left translation by
![]() $m\in \ker (H_{M})$
does not change the polytope
$m\in \ker (H_{M})$
does not change the polytope
![]() $\mathrm{Ec}_{M}(x)$
, due to the property
$\mathrm{Ec}_{M}(x)$
, due to the property
For the finiteness issue, let
 $\Lambda _{M_{0}}^{H_{M}}\subset \Lambda _{M_{0}}$
be the kernel of the natural projection
$\Lambda _{M_{0}}^{H_{M}}\subset \Lambda _{M_{0}}$
be the kernel of the natural projection
![]() $\Lambda _{M_{0}}\to \Lambda _{M}$
. By definition, we have
$\Lambda _{M_{0}}\to \Lambda _{M}$
. By definition, we have
 $$ \begin{align*} \pi_{M_{0},M}^{-1}(\textrm{Ec}_{M}(x_{0}))=\bigcup_{\nu\in \Lambda_{M_{0}}^{H_{M}}}\left(\nu+\textrm{Ec}_{M_{0}}(x_{0})\right), \end{align*} $$
$$ \begin{align*} \pi_{M_{0},M}^{-1}(\textrm{Ec}_{M}(x_{0}))=\bigcup_{\nu\in \Lambda_{M_{0}}^{H_{M}}}\left(\nu+\textrm{Ec}_{M_{0}}(x_{0})\right), \end{align*} $$
which implies that
 $$ \begin{align*} F_{\gamma}^{G,M}=\bigcup_{\nu\in \Lambda_{M_{0}}^{H_{M}}}\mathscr{X}_{\gamma}^{0}\left(\nu+\textrm{Ec}_{M_{0}}(x_{0})\right). \end{align*} $$
$$ \begin{align*} F_{\gamma}^{G,M}=\bigcup_{\nu\in \Lambda_{M_{0}}^{H_{M}}}\mathscr{X}_{\gamma}^{0}\left(\nu+\textrm{Ec}_{M_{0}}(x_{0})\right). \end{align*} $$
Now that
![]() $\Lambda \cong X_{*}(S)$
and
$\Lambda \cong X_{*}(S)$
and
![]() $X_{*}(S)\hookrightarrow \Lambda _{M_{0}}$
is of finite index, the quotient
$X_{*}(S)\hookrightarrow \Lambda _{M_{0}}$
is of finite index, the quotient
 $\Lambda ^{H_{M}}\backslash \Lambda _{M_{0}}^{H_{M}}$
is of finite cardinality. Hence the quotient
$\Lambda ^{H_{M}}\backslash \Lambda _{M_{0}}^{H_{M}}$
is of finite cardinality. Hence the quotient
 $\Lambda ^{H_{M}}\backslash F_{\gamma }^{G,M}$
is dominated by the union of finitely many translations of
$\Lambda ^{H_{M}}\backslash F_{\gamma }^{G,M}$
is dominated by the union of finitely many translations of
![]() $F_{\gamma }$
under the natural projection
$F_{\gamma }$
under the natural projection
 $F_{\gamma }^{G,M}\to \Lambda ^{H_{M}}\backslash F_{\gamma }^{G,M}$
. As
$F_{\gamma }^{G,M}\to \Lambda ^{H_{M}}\backslash F_{\gamma }^{G,M}$
. As
![]() $F_{\gamma }$
is of finite type, so is the quotient
$F_{\gamma }$
is of finite type, so is the quotient
 $\Lambda ^{H_{M}}\backslash F_{\gamma }^{G,M}$
.
$\Lambda ^{H_{M}}\backslash F_{\gamma }^{G,M}$
.
A similar proof applies to the following:
Proposition 3.3. Let
![]() $\Pi $
be a regular positive
$\Pi $
be a regular positive
![]() $(G,M)$
-orthogonal family. For any
$(G,M)$
-orthogonal family. For any
![]() $\nu \in \Lambda _{G}$
, the free discrete abelian group
$\nu \in \Lambda _{G}$
, the free discrete abelian group
![]() $\Lambda ^{H_{M}}$
acts freely on
$\Lambda ^{H_{M}}$
acts freely on
![]() $\mathscr {X}_{\gamma }^{\nu }(\Pi )$
, and the quotient
$\mathscr {X}_{\gamma }^{\nu }(\Pi )$
, and the quotient
 $\Lambda ^{H_{M}}\backslash \mathscr {X}_{\gamma }^{\nu }(\Pi )$
is of finite type. In particular,
$\Lambda ^{H_{M}}\backslash \mathscr {X}_{\gamma }^{\nu }(\Pi )$
is of finite type. In particular,
 $$ \begin{align*} \left\lvert\left(\Lambda^{H_{M}}\middle\backslash \mathscr{X}_{\gamma}^{\nu}(\Pi)\right)\left(\mathbf{F}_{q}\right)\right\rvert<\infty. \end{align*} $$
$$ \begin{align*} \left\lvert\left(\Lambda^{H_{M}}\middle\backslash \mathscr{X}_{\gamma}^{\nu}(\Pi)\right)\left(\mathbf{F}_{q}\right)\right\rvert<\infty. \end{align*} $$
Remark 3.1. In the definition of the (weighted) orbital integral, we are concerned more about analogues of
 $\Lambda ^{H_{M}}\backslash \left (\mathscr {X}_{\gamma }^{\nu }(\Pi )\left (\mathbf{F}_{q}\right )\right )$
, but notice that there is bijection between
$\Lambda ^{H_{M}}\backslash \left (\mathscr {X}_{\gamma }^{\nu }(\Pi )\left (\mathbf{F}_{q}\right )\right )$
, but notice that there is bijection between
 $$ \begin{align*} \left(\Lambda^{H_{M}}\middle\backslash \mathscr{X}_{\gamma}^{\nu}(\Pi)\right)\left(\mathbf{F}_{q}\right)\qquad \text{and} \qquad\Lambda^{H_{M}}\backslash \left(\mathscr{X}_{\gamma}^{\nu}(\Pi)\left(\mathbf{F}_{q}\right)\right), \end{align*} $$
$$ \begin{align*} \left(\Lambda^{H_{M}}\middle\backslash \mathscr{X}_{\gamma}^{\nu}(\Pi)\right)\left(\mathbf{F}_{q}\right)\qquad \text{and} \qquad\Lambda^{H_{M}}\backslash \left(\mathscr{X}_{\gamma}^{\nu}(\Pi)\left(\mathbf{F}_{q}\right)\right), \end{align*} $$
because
![]() $\Lambda ^{H_{M}}$
acts freely on
$\Lambda ^{H_{M}}$
acts freely on
![]() $\mathscr {X}_{\gamma }^{\nu }(\Pi )$
and the Galois group
$\mathscr {X}_{\gamma }^{\nu }(\Pi )$
and the Galois group
 $\textrm {Gal}\left (\overline {\mathbf{F}}_{q}/\mathbf{F}_{q}\right )$
acts trivially on
$\textrm {Gal}\left (\overline {\mathbf{F}}_{q}/\mathbf{F}_{q}\right )$
acts trivially on
![]() $\Lambda ^{H_{M}}$
. We will decompose the scheme
$\Lambda ^{H_{M}}$
. We will decompose the scheme
 $\Lambda ^{H_{M}}\backslash \mathscr {X}_{\gamma }^{\nu }(\Pi )$
in different ways, and the bijection given here implies that we can deduce equality of rational points over
$\Lambda ^{H_{M}}\backslash \mathscr {X}_{\gamma }^{\nu }(\Pi )$
in different ways, and the bijection given here implies that we can deduce equality of rational points over
![]() $\mathbf{F}_{q}$
from the decomposition of schemes.
$\mathbf{F}_{q}$
from the decomposition of schemes.
In the following, we simplify the notation
![]() $\mathrm{Ec}_{M}(x_{0})$
to
$\mathrm{Ec}_{M}(x_{0})$
to
 $\Sigma _{\gamma }^{G,M}$
. For
$\Sigma _{\gamma }^{G,M}$
. For
![]() $\nu \in \Lambda _{G}$
, let
$\nu \in \Lambda _{G}$
, let
 $$ \begin{align*} F_{\gamma}^{G,M, \nu}:=\mathscr{X}_{\gamma}^{\nu}\left(\Sigma_{\gamma}^{G,M}\right). \end{align*} $$
$$ \begin{align*} F_{\gamma}^{G,M, \nu}:=\mathscr{X}_{\gamma}^{\nu}\left(\Sigma_{\gamma}^{G,M}\right). \end{align*} $$
As we have explained before, it depends only on the class
![]() $c_{G}(\nu )\in \Lambda _{G^{\mathrm{ad}}}$
. For
$c_{G}(\nu )\in \Lambda _{G^{\mathrm{ad}}}$
. For
![]() $M=M_{0}$
, we simplify
$M=M_{0}$
, we simplify
 $\Sigma _{\gamma }^{G,M_{0}}$
to
$\Sigma _{\gamma }^{G,M_{0}}$
to
![]() $\Sigma _{\gamma }$
and
$\Sigma _{\gamma }$
and
 $F_{\gamma }^{G,M_{0}, \nu }$
to
$F_{\gamma }^{G,M_{0}, \nu }$
to
![]() $F_{\gamma }^{\nu }$
.
$F_{\gamma }^{\nu }$
.
3.3. The Arthur–Kottwitz reduction
Recall that we can reduce the geometry of
![]() $\mathscr {X}_{\gamma }$
to that of its fundamental domain by the Arthur–Kottwitz reduction [Reference Chaudouard and Laumon11]. The construction can be generalized to our current setting.
$\mathscr {X}_{\gamma }$
to that of its fundamental domain by the Arthur–Kottwitz reduction [Reference Chaudouard and Laumon11]. The construction can be generalized to our current setting.
Let
![]() $Q_{0}$
be the unique parabolic subgroup in
$Q_{0}$
be the unique parabolic subgroup in
![]() $\mathcal {P}(M)$
which contains
$\mathcal {P}(M)$
which contains
![]() $P_{0}$
. Let
$P_{0}$
. Let
![]() $\varsigma \in \mathfrak {a}_{M}^{G}$
be such that
$\varsigma \in \mathfrak {a}_{M}^{G}$
be such that
![]() $\alpha (\varsigma )$
is positive but almost equal to
$\alpha (\varsigma )$
is positive but almost equal to
![]() $0$
for any
$0$
for any
![]() $\alpha \in \Delta _{Q_{0}}$
. Let
$\alpha \in \Delta _{Q_{0}}$
. Let
![]() $D_{M}=(\lambda _{P})_{P\in \mathcal {P}(M)}$
be the
$D_{M}=(\lambda _{P})_{P\in \mathcal {P}(M)}$
be the
![]() $(G,M)$
-orthogonal family given by
$(G,M)$
-orthogonal family given by
where
![]() $w\in W$
is any element satisfying
$w\in W$
is any element satisfying
![]() $P=w\cdot Q_{0}$
. For
$P=w\cdot Q_{0}$
. For
![]() $Q=LN_{Q}\in \mathcal {F}(M)$
, define
$Q=LN_{Q}\in \mathcal {F}(M)$
, define
 $R^{G,M}_{Q}$
to be the subset of
$R^{G,M}_{Q}$
to be the subset of
![]() $ \mathfrak {a}_{M}^{G}$
satisfying the conditions
$ \mathfrak {a}_{M}^{G}$
satisfying the conditions
 $$ \begin{align*} \pi_{M}^{L}(a)&\subset D_{M}^{Q},\\ \alpha\left(\pi_{M,L}(a)\right)&\geq \alpha\left(\pi_{M,L}\left(\lambda_{Q}\right)\right),\qquad \forall \alpha\in \Delta_{Q}. \end{align*} $$
$$ \begin{align*} \pi_{M}^{L}(a)&\subset D_{M}^{Q},\\ \alpha\left(\pi_{M,L}(a)\right)&\geq \alpha\left(\pi_{M,L}\left(\lambda_{Q}\right)\right),\qquad \forall \alpha\in \Delta_{Q}. \end{align*} $$
This gives us a partition which dates back at least to Arthur [Reference Arthur3]:
 $$ \begin{align} \mathfrak{a}_{M}^{G}=\bigcup_{Q\in \mathcal{F}(M)} R^{G,M}_{Q}. \end{align} $$
$$ \begin{align} \mathfrak{a}_{M}^{G}=\bigcup_{Q\in \mathcal{F}(M)} R^{G,M}_{Q}. \end{align} $$
It induces a disjoint partition of
![]() $\Lambda _{M}$
via the map
$\Lambda _{M}$
via the map
![]() $\Lambda _{M}\to \mathfrak {a}_{M}^{G}$
, as we have perturbed
$\Lambda _{M}\to \mathfrak {a}_{M}^{G}$
, as we have perturbed
![]() $(H_{P}(x_{0}))_{P\in \mathcal {P}(M)}$
with
$(H_{P}(x_{0}))_{P\in \mathcal {P}(M)}$
with
![]() $\varsigma $
. Figure 1 gives an illustration of the partition for the group
$\varsigma $
. Figure 1 gives an illustration of the partition for the group
![]() $\textrm {GL}_{3}$
and
$\textrm {GL}_{3}$
and
![]() $M_{0}=T=A$
.
$M_{0}=T=A$
.

Figure 1 Partition of
![]() $\mathfrak {a}_{A}^{G}$
for
$\mathfrak {a}_{A}^{G}$
for
![]() $\textrm {GL}_{3}$
.
$\textrm {GL}_{3}$
.
Similar to [Reference Chaudouard and Laumon11, Lemma 3.1], we have the following result due to Proposition 3.1:
Lemma 3.4. For any
![]() $x\in \mathscr {X}_{\gamma }$
, there exists a unique
$x\in \mathscr {X}_{\gamma }$
, there exists a unique
![]() $Q\in \mathcal {F}(M)$
such that
$Q\in \mathcal {F}(M)$
such that
 $$ \begin{align*} \pi_{M}^{G}\left(\textrm{Ec}_{M}^{Q}(x)\right)\subset R^{G,M}_{Q}. \end{align*} $$
$$ \begin{align*} \pi_{M}^{G}\left(\textrm{Ec}_{M}^{Q}(x)\right)\subset R^{G,M}_{Q}. \end{align*} $$
The referee has suggested an equivalent form of the lemma, which is much easier to understand and to prove: let
 $\mathfrak {a}_{M}^{G}=\bigcup _{Q\in \mathcal {F}(M)} R^{\prime }_{Q}$
be the partition attached to the positive
$\mathfrak {a}_{M}^{G}=\bigcup _{Q\in \mathcal {F}(M)} R^{\prime }_{Q}$
be the partition attached to the positive
![]() $(G,M)$
-orthogonal family
$(G,M)$
-orthogonal family
![]() $(H_{P}(x_{0})-H_{P}(x)+w\cdot \varsigma )_{P\in \mathcal {P}(M)}$
, then the statement is equivalent to the existence of a unique
$(H_{P}(x_{0})-H_{P}(x)+w\cdot \varsigma )_{P\in \mathcal {P}(M)}$
, then the statement is equivalent to the existence of a unique
![]() $Q\in \mathcal {F}(M)$
such that
$Q\in \mathcal {F}(M)$
such that
 $0\in R^{\prime }_{Q}$
. Here the positiveness of the
$0\in R^{\prime }_{Q}$
. Here the positiveness of the
![]() $(G,M)$
-orthogonal family is due to Proposition 3.1. Let
$(G,M)$
-orthogonal family is due to Proposition 3.1. Let
 $$ \begin{align*} S_{Q}^{G,M}:=\left\{x\in \mathscr{X}_{\gamma}\mid \pi_{M}^{G}\left(\textrm{Ec}_{M}^{Q}(x)\right)\subset R_{Q}^{G,M}\right\}. \end{align*} $$
$$ \begin{align*} S_{Q}^{G,M}:=\left\{x\in \mathscr{X}_{\gamma}\mid \pi_{M}^{G}\left(\textrm{Ec}_{M}^{Q}(x)\right)\subset R_{Q}^{G,M}\right\}. \end{align*} $$
We thus get a disjoint partition
 $$ \begin{align} \mathscr{X}_{\gamma}=\mathscr{X}_{\gamma}(D_{M})\cup\bigcup_{\substack{Q\in \mathcal{F}(M)\\Q\neq G}}S^{G,M}_{Q}. \end{align} $$
$$ \begin{align} \mathscr{X}_{\gamma}=\mathscr{X}_{\gamma}(D_{M})\cup\bigcup_{\substack{Q\in \mathcal{F}(M)\\Q\neq G}}S^{G,M}_{Q}. \end{align} $$
For each parabolic subgroup
![]() $Q=LN_{Q}\in \mathcal {F}(M)$
, consider the restriction of the retraction
$Q=LN_{Q}\in \mathcal {F}(M)$
, consider the restriction of the retraction
![]() $f_{Q}: \mathscr {X}\to \mathscr {X}^{L}$
to
$f_{Q}: \mathscr {X}\to \mathscr {X}^{L}$
to
 $S^{G,M}_{Q}$
; its image is
$S^{G,M}_{Q}$
; its image is
 $S^{G,M}_{Q}\cap \mathscr {X}_{\gamma }^{L}$
. Recall that the connected components of
$S^{G,M}_{Q}\cap \mathscr {X}_{\gamma }^{L}$
. Recall that the connected components of
 $\mathscr {X}_{\gamma }^{L}$
are fibers of the map
$\mathscr {X}_{\gamma }^{L}$
are fibers of the map
 $\nu _{L}:\mathscr {X}_{\gamma }^{L}\to \Lambda _{L}$
. For
$\nu _{L}:\mathscr {X}_{\gamma }^{L}\to \Lambda _{L}$
. For
![]() $\nu \in \Lambda _{L}$
, let
$\nu \in \Lambda _{L}$
, let
 $\mathscr {X}_{\gamma }^{L,\nu }$
be its fiber at
$\mathscr {X}_{\gamma }^{L,\nu }$
be its fiber at
![]() $\nu $
. Letting
$\nu $
. Letting
 $$ \begin{align*} S_{Q}^{G,M,\nu}=S_{Q}^{G,M}\cap f_{Q}^{-1}\left(\mathscr{X}_{\gamma}^{L,\nu}\right), \end{align*} $$
$$ \begin{align*} S_{Q}^{G,M,\nu}=S_{Q}^{G,M}\cap f_{Q}^{-1}\left(\mathscr{X}_{\gamma}^{L,\nu}\right), \end{align*} $$
we have
 $$ \begin{align*} S_{Q}^{G,M,\nu}\cap \mathscr{X}_{\gamma}^{L,\nu}=\mathscr{X}_{\gamma}^{L,\nu}\left(D_{M}^{Q}\right). \end{align*} $$
$$ \begin{align*} S_{Q}^{G,M,\nu}\cap \mathscr{X}_{\gamma}^{L,\nu}=\mathscr{X}_{\gamma}^{L,\nu}\left(D_{M}^{Q}\right). \end{align*} $$
Proposition 3.5. The strata
 $S_{Q}^{G,M,\nu }$
are locally closed subschemes of
$S_{Q}^{G,M,\nu }$
are locally closed subschemes of
![]() $\mathscr {X}_{\gamma }$
, and the retraction
$\mathscr {X}_{\gamma }$
, and the retraction
 $f_{Q}: S_{Q}^{G,M,\nu }\to \mathscr {X}_{\gamma }^{L,\nu }\left (D_{M}^{Q}\right )$
is an iterated affine fibration over
$f_{Q}: S_{Q}^{G,M,\nu }\to \mathscr {X}_{\gamma }^{L,\nu }\left (D_{M}^{Q}\right )$
is an iterated affine fibration over
![]() $\mathbf{F}_{q}$
of dimension
$\mathbf{F}_{q}$
of dimension
Indeed, by the bound on
![]() $\mathrm{Ec}_{M}(x)$
given by Proposition 3.1, we get
$\mathrm{Ec}_{M}(x)$
given by Proposition 3.1, we get
 $$ \begin{align*} S_{Q}^{G,M,\nu}=\mathscr{X}_{\gamma}\cap f_{Q}^{-1}\left(\mathscr{X}_{\gamma}^{L,\nu}\left(D_{M}^{Q}\right)\right). \end{align*} $$
$$ \begin{align*} S_{Q}^{G,M,\nu}=\mathscr{X}_{\gamma}\cap f_{Q}^{-1}\left(\mathscr{X}_{\gamma}^{L,\nu}\left(D_{M}^{Q}\right)\right). \end{align*} $$
It is an iterated affine fibration over
 $\mathscr {X}_{\gamma }^{L,\nu }\left (D_{M}^{Q}\right )$
by Proposition 2.4.
$\mathscr {X}_{\gamma }^{L,\nu }\left (D_{M}^{Q}\right )$
by Proposition 2.4.
The decomposition (3.3) can thus be refined to
 $$ \begin{align} \mathscr{X}_{\gamma}=\mathscr{X}_{\gamma}(D_{M})\cup \bigcup_{\substack{Q=LN_{Q}\in \mathcal{F}(M)\\ Q\neq G}}\bigcup_{\nu\in \Lambda_{L}\cap \pi_{L}\left(R^{G,M}_{Q}\right)} S_{Q}^{G,M,\nu}, \end{align} $$
$$ \begin{align} \mathscr{X}_{\gamma}=\mathscr{X}_{\gamma}(D_{M})\cup \bigcup_{\substack{Q=LN_{Q}\in \mathcal{F}(M)\\ Q\neq G}}\bigcup_{\nu\in \Lambda_{L}\cap \pi_{L}\left(R^{G,M}_{Q}\right)} S_{Q}^{G,M,\nu}, \end{align} $$
where we have loosely used
 $\Lambda _{L}\cap \pi _{L}\left (R_{Q}^{G,M}\right )$
to mean elements in
$\Lambda _{L}\cap \pi _{L}\left (R_{Q}^{G,M}\right )$
to mean elements in
![]() $\Lambda _{L}$
whose projection to
$\Lambda _{L}$
whose projection to
![]() $\mathfrak {a}_{L}^{G}$
lies in
$\mathfrak {a}_{L}^{G}$
lies in
 $\pi _{L}\left (R_{Q}^{G,M}\right )$
. Similar notations will be used later on. The decomposition (3.4) will also be called the Arthur–Kottwitz reduction. Notice that the stratum
$\pi _{L}\left (R_{Q}^{G,M}\right )$
. Similar notations will be used later on. The decomposition (3.4) will also be called the Arthur–Kottwitz reduction. Notice that the stratum
 $S_{Q}^{G,M,\nu }$
is an iterated affine fibration over
$S_{Q}^{G,M,\nu }$
is an iterated affine fibration over
 $\mathscr {X}_{\gamma }^{L,\nu }\left (D_{M}^{Q}\right )=F_{\gamma }^{L,M,\nu }$
, and the latter is related to
$\mathscr {X}_{\gamma }^{L,\nu }\left (D_{M}^{Q}\right )=F_{\gamma }^{L,M,\nu }$
, and the latter is related to
 $F_{\gamma }^{L,M}$
again by the Arthur–Kottwitz reduction, similar to what is explained in [Reference Chaudouard and Laumon11, Lemma 3.4].
$F_{\gamma }^{L,M}$
again by the Arthur–Kottwitz reduction, similar to what is explained in [Reference Chaudouard and Laumon11, Lemma 3.4].
As in [Reference Chaudouard and Laumon11], the existence of Arthur–Kottwitz reduction implies the following:
Corollary 3.6. For any
![]() $\gamma \in \mathfrak {t}(\mathcal {O})$
, suppose that
$\gamma \in \mathfrak {t}(\mathcal {O})$
, suppose that
 $F_{\gamma }^{L,M}$
is cohomologically pure for any proper Levi subgroup
$F_{\gamma }^{L,M}$
is cohomologically pure for any proper Levi subgroup
![]() $L\in \mathcal {L}(M)$
. Then
$L\in \mathcal {L}(M)$
. Then
![]() $\mathscr {X}_{\gamma }$
is cohomologically pure if and only if
$\mathscr {X}_{\gamma }$
is cohomologically pure if and only if
 $F_{\gamma }^{G,M}$
is.
$F_{\gamma }^{G,M}$
is.
We can restrict the Arthur–Kottwitz reduction to the truncated affine Springer fibers. A positive
![]() $(G,M)$
-orthogonal family
$(G,M)$
-orthogonal family
![]() $\Pi =(\mu _{P})_{P\in \mathcal {P}(M)}$
is said to be regular with respect to
$\Pi =(\mu _{P})_{P\in \mathcal {P}(M)}$
is said to be regular with respect to
![]() $D_{M}$
if
$D_{M}$
if
 $\mu _{P}\in R^{G,M}_{P}, \ \forall P\in \mathcal {P}(M)$
. In this case, each
$\mu _{P}\in R^{G,M}_{P}, \ \forall P\in \mathcal {P}(M)$
. In this case, each
 $S_{Q}^{G,M,\nu }$
is either contained in
$S_{Q}^{G,M,\nu }$
is either contained in
![]() $\mathscr {X}_{\gamma }^{\nu }(\Pi )$
or disjoint from it. So we have
$\mathscr {X}_{\gamma }^{\nu }(\Pi )$
or disjoint from it. So we have
 $$ \begin{align} \mathscr{X}_{\gamma}(\Pi)=\mathscr{X}_{\gamma}(D_{M})\cup \bigcup_{\substack{Q=LN_{Q}\in \mathcal{F}(M)\\ Q\neq G}}\bigcup_{\substack{\nu\in \Lambda_{L}\cap \pi_{L}\left(R^{G,M}_{Q}\right) \\ \cap \pi_{L}(\Pi)}} S_{Q}^{G,M,\nu}. \end{align} $$
$$ \begin{align} \mathscr{X}_{\gamma}(\Pi)=\mathscr{X}_{\gamma}(D_{M})\cup \bigcup_{\substack{Q=LN_{Q}\in \mathcal{F}(M)\\ Q\neq G}}\bigcup_{\substack{\nu\in \Lambda_{L}\cap \pi_{L}\left(R^{G,M}_{Q}\right) \\ \cap \pi_{L}(\Pi)}} S_{Q}^{G,M,\nu}. \end{align} $$
The reduction can be further restricted to each connected component of
![]() $\mathscr {X}_{\gamma }(\Pi )$
:
$\mathscr {X}_{\gamma }(\Pi )$
:
 $$ \begin{align} \mathscr{X}_{\gamma}^{\nu_{0}}(\Pi)=\mathscr{X}_{\gamma}^{\nu_{0}}(D_{M})\cup \bigcup_{\substack{Q=LN_{Q}\in \mathcal{F}(M)\\ Q\neq G}}\bigcup_{\substack{\nu\in \Lambda^{\nu_{0}}_{L}\cap \pi_{L}\left(R^{G,M}_{Q}\right) \\ \cap \pi_{L}(\Pi)}} S_{Q}^{G,M, \nu}. \end{align} $$
$$ \begin{align} \mathscr{X}_{\gamma}^{\nu_{0}}(\Pi)=\mathscr{X}_{\gamma}^{\nu_{0}}(D_{M})\cup \bigcup_{\substack{Q=LN_{Q}\in \mathcal{F}(M)\\ Q\neq G}}\bigcup_{\substack{\nu\in \Lambda^{\nu_{0}}_{L}\cap \pi_{L}\left(R^{G,M}_{Q}\right) \\ \cap \pi_{L}(\Pi)}} S_{Q}^{G,M, \nu}. \end{align} $$
As we have explained, left translation by elements in
![]() $\ker (H_{M})$
does not change the polytope
$\ker (H_{M})$
does not change the polytope
![]() $\mathrm{Ec}_{M}(x)$
, and hence the group
$\mathrm{Ec}_{M}(x)$
, and hence the group
![]() $\Lambda ^{H_{M}}$
acts on each item of equation (3.6). Now that we have finiteness results – Propositions 3.2 and 3.3, combined with Proposition 3.5 and the periodicity of
$\Lambda ^{H_{M}}$
acts on each item of equation (3.6). Now that we have finiteness results – Propositions 3.2 and 3.3, combined with Proposition 3.5 and the periodicity of
 $F_{\gamma }^{L,M,\nu }$
in
$F_{\gamma }^{L,M,\nu }$
in
![]() $\nu \in \Lambda _{L}$
– equation (3.6) implies equality of counting points:
$\nu \in \Lambda _{L}$
– equation (3.6) implies equality of counting points:
Corollary 3.7. We have the equality
 $$ \begin{align*} \left\lvert\left(\Lambda^{H_{M}}\middle\backslash\mathscr{X}_{\gamma}^{\nu_{0}}(\Pi)\right)\left(\mathbf{F}_{q}\right)\right\rvert &= \left\lvert\left(\Lambda^{H_{M}}\middle\backslash F_{\gamma}^{G,M,\nu_{0}}\right)\left(\mathbf{F}_{q}\right)\right\rvert+\sum_{\substack{Q=LN_{Q}\in \mathcal{F}(M)\\Q\neq G}}\sum_{\mu\in \Lambda_{L^{\mathrm{ad}}}} q^{\mathrm{val}\left(\det\left(\mathrm{ad}\gamma\mid\mathfrak{n}_{Q,F}\right)\right)} \\ & \quad \cdot \left\lvert\left(\Lambda^{H_{M}}\middle\backslash F_{\gamma}^{L,M,\mu}\right)\left(\mathbf{F}_{q}\right)\right\rvert\cdot \left\lvert\Lambda^{\nu_{0}}_{L}\cap \pi_{L}\left(R_{Q}^{G,M}\right)\cap \pi_{L}(\Pi)\cap c_{L}^{-1}(\mu)\right\rvert. \end{align*} $$
$$ \begin{align*} \left\lvert\left(\Lambda^{H_{M}}\middle\backslash\mathscr{X}_{\gamma}^{\nu_{0}}(\Pi)\right)\left(\mathbf{F}_{q}\right)\right\rvert &= \left\lvert\left(\Lambda^{H_{M}}\middle\backslash F_{\gamma}^{G,M,\nu_{0}}\right)\left(\mathbf{F}_{q}\right)\right\rvert+\sum_{\substack{Q=LN_{Q}\in \mathcal{F}(M)\\Q\neq G}}\sum_{\mu\in \Lambda_{L^{\mathrm{ad}}}} q^{\mathrm{val}\left(\det\left(\mathrm{ad}\gamma\mid\mathfrak{n}_{Q,F}\right)\right)} \\ & \quad \cdot \left\lvert\left(\Lambda^{H_{M}}\middle\backslash F_{\gamma}^{L,M,\mu}\right)\left(\mathbf{F}_{q}\right)\right\rvert\cdot \left\lvert\Lambda^{\nu_{0}}_{L}\cap \pi_{L}\left(R_{Q}^{G,M}\right)\cap \pi_{L}(\Pi)\cap c_{L}^{-1}(\mu)\right\rvert. \end{align*} $$
Notice that the term
 $\left \lvert \Lambda ^{\nu _{0}}_{L}\cap \pi _{L}\left (R_{Q}^{G,M}\right )\cap \pi _{L}(\Pi )\cap c_{L}^{-1}(\mu )\right \rvert $
counts the number of lattice points in a polytope. Well-known techniques from toric geometry tells us that the counting result depends quasi-polynomially on the size of the polytope.
$\left \lvert \Lambda ^{\nu _{0}}_{L}\cap \pi _{L}\left (R_{Q}^{G,M}\right )\cap \pi _{L}(\Pi )\cap c_{L}^{-1}(\mu )\right \rvert $
counts the number of lattice points in a polytope. Well-known techniques from toric geometry tells us that the counting result depends quasi-polynomially on the size of the polytope.
Remark 3.2. As the foregoing constructions rely ultimately on the bound of
![]() $\mathrm{Ec}_{M}(x)$
given by Proposition 3.1, they continue to work if we replace
$\mathrm{Ec}_{M}(x)$
given by Proposition 3.1, they continue to work if we replace
 $\Sigma _{\gamma }^{G,M}$
from the beginning by any integral positive
$\Sigma _{\gamma }^{G,M}$
from the beginning by any integral positive
![]() $(G,M)$
-orthogonal family
$(G,M)$
-orthogonal family
![]() $\Sigma $
which satisfies
$\Sigma $
which satisfies
for any two adjacent parabolic subgroups
![]() $P_{1},P_{2}\in \mathcal {P}(M)$
. The resulting decomposition will also be called the Arthur–Kottwitz reduction.
$P_{1},P_{2}\in \mathcal {P}(M)$
. The resulting decomposition will also be called the Arthur–Kottwitz reduction.
3.4. Counting points on the intermediate fundamental domains
Although the intermediate fundamental domains
 $F_{\gamma }^{G,M}$
look like something new, it turns out that counting points of
$F_{\gamma }^{G,M}$
look like something new, it turns out that counting points of
 $\Lambda ^{H_{M}}\backslash F_{\gamma }^{G,M}$
can be reduced to counting points of the fundamental domains.
$\Lambda ^{H_{M}}\backslash F_{\gamma }^{G,M}$
can be reduced to counting points of the fundamental domains.
As explained in the proof of Proposition 3.2, we have
 $$ \begin{align*} \pi_{M_{0},M}^{-1}\left(\Sigma_{\gamma}^{G,M}\right)=\bigcup_{\nu\in \Lambda_{M_{0}}^{H_{M}}}\left(\nu+\Sigma_{\gamma}\right) \end{align*} $$
$$ \begin{align*} \pi_{M_{0},M}^{-1}\left(\Sigma_{\gamma}^{G,M}\right)=\bigcup_{\nu\in \Lambda_{M_{0}}^{H_{M}}}\left(\nu+\Sigma_{\gamma}\right) \end{align*} $$
and
 $$ \begin{align*} F_{\gamma}^{G,M}=\bigcup_{\nu\in \Lambda_{M_{0}}^{H_{M}}}\mathscr{X}_{\gamma}^{0}\left(\nu+\Sigma_{\gamma}\right). \end{align*} $$
$$ \begin{align*} F_{\gamma}^{G,M}=\bigcup_{\nu\in \Lambda_{M_{0}}^{H_{M}}}\mathscr{X}_{\gamma}^{0}\left(\nu+\Sigma_{\gamma}\right). \end{align*} $$
Let
![]() $P_{0}^{M}=P_{0}\cap M$
, and let
$P_{0}^{M}=P_{0}\cap M$
, and let
 $\beta _{1}^{\vee },\dotsc ,\beta _{r'}^{\vee }\in \Lambda _{M_{0}}^{H_{M}}$
be a basis of
$\beta _{1}^{\vee },\dotsc ,\beta _{r'}^{\vee }\in \Lambda _{M_{0}}^{H_{M}}$
be a basis of
 $\mathfrak {a}_{M_{0}}^{M}$
which is positive with respect to
$\mathfrak {a}_{M_{0}}^{M}$
which is positive with respect to
![]() $P_{0}^{M}$
. For
$P_{0}^{M}$
. For
 $\mu _{1},\mu _{2}\in \Lambda _{M_{0}}^{H_{M}}$
, we say that
$\mu _{1},\mu _{2}\in \Lambda _{M_{0}}^{H_{M}}$
, we say that
![]() $\mu _{1}\preccurlyeq _{P_{0}^{M}} \mu _{2}$
if
$\mu _{1}\preccurlyeq _{P_{0}^{M}} \mu _{2}$
if
![]() $\mu _{2}-\mu _{1}$
is a linear combination of
$\mu _{2}-\mu _{1}$
is a linear combination of
![]() $\beta _{i}^{\vee }$
s with positive coefficients. This defines a partial order
$\beta _{i}^{\vee }$
s with positive coefficients. This defines a partial order
![]() $\preccurlyeq _{P_{0}^{M}}$
on
$\preccurlyeq _{P_{0}^{M}}$
on
 $\Lambda _{M_{0}}^{H_{M}}$
. For
$\Lambda _{M_{0}}^{H_{M}}$
. For
 $\mu \in \Lambda _{M_{0}}^{H_{M}}$
, define
$\mu \in \Lambda _{M_{0}}^{H_{M}}$
, define
 $$ \begin{align*} \Lambda_{M_{0},\preccurlyeq \mu}^{H_{M}}:=\left\{\nu\in \Lambda_{M_{0}}^{H_{M}}\mid \nu\preccurlyeq_{P_{0}^{M}} \mu\right\} \qquad \text{and} \qquad \Pi_{\gamma,\preccurlyeq \mu}^{G,M}:=\bigcup_{\nu\in \Lambda_{M_{0},\preccurlyeq \mu}^{H_{M}}}\left(\nu+\Sigma_{\gamma}\right). \end{align*} $$
$$ \begin{align*} \Lambda_{M_{0},\preccurlyeq \mu}^{H_{M}}:=\left\{\nu\in \Lambda_{M_{0}}^{H_{M}}\mid \nu\preccurlyeq_{P_{0}^{M}} \mu\right\} \qquad \text{and} \qquad \Pi_{\gamma,\preccurlyeq \mu}^{G,M}:=\bigcup_{\nu\in \Lambda_{M_{0},\preccurlyeq \mu}^{H_{M}}}\left(\nu+\Sigma_{\gamma}\right). \end{align*} $$
Then
 $\Pi _{\gamma ,\preccurlyeq \mu }^{G,M}$
is a semi-infinite polytope in
$\Pi _{\gamma ,\preccurlyeq \mu }^{G,M}$
is a semi-infinite polytope in
 $\mathfrak {a}_{M_{0}}^{G}$
and
$\mathfrak {a}_{M_{0}}^{G}$
and
 $\Lambda _{M_{0},\preccurlyeq \mu }^{H_{M}}$
is the integral points in it. Similar definitions hold for
$\Lambda _{M_{0},\preccurlyeq \mu }^{H_{M}}$
is the integral points in it. Similar definitions hold for
 $\Lambda _{M_{0},\prec \mu }^{H_{M}}$
and
$\Lambda _{M_{0},\prec \mu }^{H_{M}}$
and
 $\Pi _{\gamma ,\prec \mu }^{G,M}$
. But notice that
$\Pi _{\gamma ,\prec \mu }^{G,M}$
. But notice that
 $\Pi _{\gamma ,\prec \mu }^{G,M}$
is not a semi-infinite polytope: it is the union of finitely many semi-infinite polytopes of the form
$\Pi _{\gamma ,\prec \mu }^{G,M}$
is not a semi-infinite polytope: it is the union of finitely many semi-infinite polytopes of the form
 $\Pi _{\gamma ,\preccurlyeq \mu '}^{G,M}$
,
$\Pi _{\gamma ,\preccurlyeq \mu '}^{G,M}$
,
 $\mu '\in \Lambda _{M_{0}}^{H_{M}}$
. Define
$\mu '\in \Lambda _{M_{0}}^{H_{M}}$
. Define
 $$ \begin{align*} F_{\gamma,\preccurlyeq \mu}^{G,M}:=\mathscr{X}_{\gamma}^{0}\left(\Pi_{\gamma,\preccurlyeq \mu}^{G,M}\right) =\bigcup_{\nu\in \Lambda_{M_{0},\preccurlyeq \mu}^{H_{M}}}\mathscr{X}_{\gamma}^{0}\left(\nu+\Sigma_{\gamma}\right) \end{align*} $$
$$ \begin{align*} F_{\gamma,\preccurlyeq \mu}^{G,M}:=\mathscr{X}_{\gamma}^{0}\left(\Pi_{\gamma,\preccurlyeq \mu}^{G,M}\right) =\bigcup_{\nu\in \Lambda_{M_{0},\preccurlyeq \mu}^{H_{M}}}\mathscr{X}_{\gamma}^{0}\left(\nu+\Sigma_{\gamma}\right) \end{align*} $$
and similarly
 $$ \begin{align*} F_{\gamma,\prec \mu}^{G,M}:=\bigcup_{\nu\in \Lambda_{M_{0},\prec \mu}^{H_{M}}}\mathscr{X}_{\gamma}^{0}\left(\nu+\Sigma_{\gamma}\right). \end{align*} $$
$$ \begin{align*} F_{\gamma,\prec \mu}^{G,M}:=\bigcup_{\nu\in \Lambda_{M_{0},\prec \mu}^{H_{M}}}\mathscr{X}_{\gamma}^{0}\left(\nu+\Sigma_{\gamma}\right). \end{align*} $$
It is the union of finitely many
 $F_{\gamma ,\preccurlyeq \mu '}^{G,M}$
,
$F_{\gamma ,\preccurlyeq \mu '}^{G,M}$
,
 $\mu '\in \Lambda _{M_{0}}^{H_{M}}$
. Define
$\mu '\in \Lambda _{M_{0}}^{H_{M}}$
. Define
 $$ \begin{align*} F_{\gamma,\mu}^{G,M}:=F_{\gamma,\preccurlyeq \mu}^{G,M}\Big\backslash F_{\gamma,\prec \mu}^{G,M}. \end{align*} $$
$$ \begin{align*} F_{\gamma,\mu}^{G,M}:=F_{\gamma,\preccurlyeq \mu}^{G,M}\Big\backslash F_{\gamma,\prec \mu}^{G,M}. \end{align*} $$
Being a difference of closed subschemes,
 $F_{\gamma ,\mu }^{G,M}$
is locally closed in
$F_{\gamma ,\mu }^{G,M}$
is locally closed in
 $\mathscr {X}_{\gamma }^{0}$
. As
$\mathscr {X}_{\gamma }^{0}$
. As
 $F_{\gamma ,\preccurlyeq \mu }^{G,M}$
is semi-infinite unions of translations of the fundamental domains, they are all isomorphic, and similarly for
$F_{\gamma ,\preccurlyeq \mu }^{G,M}$
is semi-infinite unions of translations of the fundamental domains, they are all isomorphic, and similarly for
 $F_{\gamma ,\prec \mu }^{G,M}$
. Hence
$F_{\gamma ,\prec \mu }^{G,M}$
. Hence
 $F_{\gamma ,\mu }^{G,M}$
are all isomorphic. Moreover,
$F_{\gamma ,\mu }^{G,M}$
are all isomorphic. Moreover,
 $$ \begin{align*} F_{\gamma,\preccurlyeq \mu}^{G,M}=\bigsqcup_{\nu\in \Lambda_{M_{0},\preccurlyeq \mu}^{H_{M}}} F_{\gamma,\nu}^{G,M} \end{align*} $$
$$ \begin{align*} F_{\gamma,\preccurlyeq \mu}^{G,M}=\bigsqcup_{\nu\in \Lambda_{M_{0},\preccurlyeq \mu}^{H_{M}}} F_{\gamma,\nu}^{G,M} \end{align*} $$
by induction, and
 $$ \begin{align*} F_{\gamma}^{G,M}=\lim_{\mu\to \infty} F_{\gamma,\preccurlyeq \mu}^{G,M}=\bigsqcup_{\nu\in \Lambda_{M_{0}}^{H_{M}}} F_{\gamma,\nu}^{G,M}. \end{align*} $$
$$ \begin{align*} F_{\gamma}^{G,M}=\lim_{\mu\to \infty} F_{\gamma,\preccurlyeq \mu}^{G,M}=\bigsqcup_{\nu\in \Lambda_{M_{0}}^{H_{M}}} F_{\gamma,\nu}^{G,M}. \end{align*} $$
From all these we conclude the following:
Proposition 3.8.
 $F_{\gamma ,\mu }^{G,M}$
is isomorphic to each other for all
$F_{\gamma ,\mu }^{G,M}$
is isomorphic to each other for all
 $\mu \in \Lambda _{M_{0}}^{H_{M}}$
. In particular,
$\mu \in \Lambda _{M_{0}}^{H_{M}}$
. In particular,
 $$ \begin{align*} \left\lvert\left(\Lambda^{H_{M}}\middle\backslash F_{\gamma}^{G,M}\right)\left(\mathbf{F}_{q}\right)\right\rvert=\left\lvert\Lambda^{H_{M}}\middle\backslash \Lambda_{M_{0}}^{H_{M}}\right\rvert\cdot \left\lvert F_{\gamma,\mu}^{G,M}\left(\mathbf{F}_{q}\right)\right\rvert. \end{align*} $$
$$ \begin{align*} \left\lvert\left(\Lambda^{H_{M}}\middle\backslash F_{\gamma}^{G,M}\right)\left(\mathbf{F}_{q}\right)\right\rvert=\left\lvert\Lambda^{H_{M}}\middle\backslash \Lambda_{M_{0}}^{H_{M}}\right\rvert\cdot \left\lvert F_{\gamma,\mu}^{G,M}\left(\mathbf{F}_{q}\right)\right\rvert. \end{align*} $$
Counting points on
 $F_{\gamma ,\mu }^{G,M}$
can be reduced to the fundamental domains via a process similar to the Arthur–Kottwitz reduction. To begin with, notice that
$F_{\gamma ,\mu }^{G,M}$
can be reduced to the fundamental domains via a process similar to the Arthur–Kottwitz reduction. To begin with, notice that
 $\Pi _{\gamma ,\preccurlyeq \mu }^{G,M}$
is bounded only in directions that are positive with respect to
$\Pi _{\gamma ,\preccurlyeq \mu }^{G,M}$
is bounded only in directions that are positive with respect to
![]() $P_{0}^{M}$
. Indeed, its vertices are indexed by
$P_{0}^{M}$
. Indeed, its vertices are indexed by
![]() $P\in \mathcal {P}(M_{0})$
satisfying
$P\in \mathcal {P}(M_{0})$
satisfying
![]() $P\cap M=P_{0}^{M}$
, and its faces by
$P\cap M=P_{0}^{M}$
, and its faces by
![]() $Q\in \mathcal {F}(M_{0})$
such that
$Q\in \mathcal {F}(M_{0})$
such that
![]() $Q\cap M\supset P_{0}^{M}$
. Then we define a semi-infinite polytope
$Q\cap M\supset P_{0}^{M}$
. Then we define a semi-infinite polytope
 $\Pi _{\gamma ,\preccurlyeq \mu ^{-}}^{G,M}$
which is a translation of
$\Pi _{\gamma ,\preccurlyeq \mu ^{-}}^{G,M}$
which is a translation of
 $\Pi _{\gamma ,\preccurlyeq \mu }^{G,M}$
: let
$\Pi _{\gamma ,\preccurlyeq \mu }^{G,M}$
: let
![]() $\Delta ^{M}$
be the set of simple roots in
$\Delta ^{M}$
be the set of simple roots in
![]() $\Phi (M,A)$
with respect to
$\Phi (M,A)$
with respect to
![]() $B_{0}\cap M$
, and let
$B_{0}\cap M$
, and let
 $\Delta ^{M}_{P_{0}^{M}}=\Delta ^{M}\cap \Phi \left (N_{P_{0}^{M}},A\right )$
, with
$\Delta ^{M}_{P_{0}^{M}}=\Delta ^{M}\cap \Phi \left (N_{P_{0}^{M}},A\right )$
, with
![]() $N_{P_{0}^{M}}$
the unipotent radical of
$N_{P_{0}^{M}}$
the unipotent radical of
![]() $P_{0}^{M}$
. For
$P_{0}^{M}$
. For
 $\alpha \in \Delta ^{M}_{P_{0}^{M}}$
, let
$\alpha \in \Delta ^{M}_{P_{0}^{M}}$
, let
![]() $\left \{\omega _{\alpha }^{\vee }\right \}$
be the corresponding fundamental coweights. Let
$\left \{\omega _{\alpha }^{\vee }\right \}$
be the corresponding fundamental coweights. Let
 $$ \begin{align} \mu^{-}=\mu-\pi_{2}\left(\textstyle\sum_{\alpha\in \Delta^{M}_{P_{0}^{M}}}\omega_{\alpha}^{\vee}\right), \end{align} $$
$$ \begin{align} \mu^{-}=\mu-\pi_{2}\left(\textstyle\sum_{\alpha\in \Delta^{M}_{P_{0}^{M}}}\omega_{\alpha}^{\vee}\right), \end{align} $$
where
![]() $\pi _{2}$
is the projection to the second factor in the orthogonal decomposition
$\pi _{2}$
is the projection to the second factor in the orthogonal decomposition
 $\mathfrak {a}_{A}^{G}=\mathfrak {a}_{A}^{M_{0}}\oplus \mathfrak {a}_{M_{0}}^{M}\oplus \mathfrak {a}_{M}^{G}$
. Then
$\mathfrak {a}_{A}^{G}=\mathfrak {a}_{A}^{M_{0}}\oplus \mathfrak {a}_{M_{0}}^{M}\oplus \mathfrak {a}_{M}^{G}$
. Then
 $\Pi _{\gamma ,\preccurlyeq \mu ^{-}}^{G,M}$
is a translation of
$\Pi _{\gamma ,\preccurlyeq \mu ^{-}}^{G,M}$
is a translation of
 $\Pi _{\gamma ,\preccurlyeq \mu }^{G,M}$
by the same vector. Now let
$\Pi _{\gamma ,\preccurlyeq \mu }^{G,M}$
by the same vector. Now let
 $\varsigma \in \mathfrak {a}_{M_{0}}^{G}$
be a generic element such that
$\varsigma \in \mathfrak {a}_{M_{0}}^{G}$
be a generic element such that
![]() $\alpha (\varsigma )$
is positive but almost equal to
$\alpha (\varsigma )$
is positive but almost equal to
![]() $0$
for any
$0$
for any
![]() $\alpha \in \Delta _{P_{0}}$
. We perturb the semi-infinite polytope
$\alpha \in \Delta _{P_{0}}$
. We perturb the semi-infinite polytope
 $\Pi _{\gamma ,\preccurlyeq \mu ^{-}}^{G,M}$
to a similar one
$\Pi _{\gamma ,\preccurlyeq \mu ^{-}}^{G,M}$
to a similar one
![]() $\Pi '$
, with vertices
$\Pi '$
, with vertices
 $$ \begin{align*} \lambda_{P}(\Pi')=\lambda_{P}\left(\Pi_{\gamma,\preccurlyeq \mu^{-}}^{G,M}\right)+w\cdot \varsigma, \qquad \forall P\in \mathcal{P}(M_{0}), \ P\cap M=P_{0}^{M}, \end{align*} $$
$$ \begin{align*} \lambda_{P}(\Pi')=\lambda_{P}\left(\Pi_{\gamma,\preccurlyeq \mu^{-}}^{G,M}\right)+w\cdot \varsigma, \qquad \forall P\in \mathcal{P}(M_{0}), \ P\cap M=P_{0}^{M}, \end{align*} $$
where
![]() $w\in W$
is any element satisfying
$w\in W$
is any element satisfying
![]() $P=w\cdot P_{0}$
. Both
$P=w\cdot P_{0}$
. Both
 $\Pi _{\gamma ,\preccurlyeq \mu }^{G,M}$
and
$\Pi _{\gamma ,\preccurlyeq \mu }^{G,M}$
and
![]() $\Pi '$
can be seen as limits of positive
$\Pi '$
can be seen as limits of positive
![]() $(G,M_{0})$
-orthogonal families containing
$(G,M_{0})$
-orthogonal families containing
![]() $\Sigma _{\gamma }$
, hence we can apply an analogue of the Arthur–Kottwitz reduction to get a decomposition of the complement
$\Sigma _{\gamma }$
, hence we can apply an analogue of the Arthur–Kottwitz reduction to get a decomposition of the complement
 $\mathscr {X}_{\gamma }^{0}\left (\Pi _{\gamma ,\preccurlyeq \mu }^{G,M}\right )\Big \backslash \mathscr {X}_{\gamma }^{0}(\Pi ')$
. For
$\mathscr {X}_{\gamma }^{0}\left (\Pi _{\gamma ,\preccurlyeq \mu }^{G,M}\right )\Big \backslash \mathscr {X}_{\gamma }^{0}(\Pi ')$
. For
![]() $Q=LN_{Q}\in \mathcal {F}(M_0)$
satisfying
$Q=LN_{Q}\in \mathcal {F}(M_0)$
satisfying
![]() $Q\cap M\supset P_{0}^{M}$
, define
$Q\cap M\supset P_{0}^{M}$
, define
![]() $R_{\Pi ',Q}$
to be the subset of
$R_{\Pi ',Q}$
to be the subset of
 $ \mathfrak {a}_{M_0}^{G}$
satisfying conditions
$ \mathfrak {a}_{M_0}^{G}$
satisfying conditions
 $$ \begin{align*} \pi_{M_{0}}^{L}(a)&\subset {\Pi'}^{Q},\\ \alpha\left(\pi_{M_{0},L}(a)\right)&\geq \alpha\left(\pi_{M_{0},L}\left(\lambda_{Q}(\Pi')\right)\right),\qquad \forall \alpha\in \Delta_{Q}. \end{align*} $$
$$ \begin{align*} \pi_{M_{0}}^{L}(a)&\subset {\Pi'}^{Q},\\ \alpha\left(\pi_{M_{0},L}(a)\right)&\geq \alpha\left(\pi_{M_{0},L}\left(\lambda_{Q}(\Pi')\right)\right),\qquad \forall \alpha\in \Delta_{Q}. \end{align*} $$
This gives us a partition
 $$ \begin{align} \mathfrak{a}_{M_0}^{G}=\Pi'\cup \bigcup_{\substack{Q\in \mathcal{F}\left(M_0\right), Q\neq G\\ Q\cap M\supset P_{0}^{M}}} R_{\Pi',Q}. \end{align} $$
$$ \begin{align} \mathfrak{a}_{M_0}^{G}=\Pi'\cup \bigcup_{\substack{Q\in \mathcal{F}\left(M_0\right), Q\neq G\\ Q\cap M\supset P_{0}^{M}}} R_{\Pi',Q}. \end{align} $$
It induces a disjoint partition of
![]() $\Lambda _{M_{0}}$
. For
$\Lambda _{M_{0}}$
. For
![]() $G=\textrm {GL}_{3}$
,
$G=\textrm {GL}_{3}$
,
![]() $\gamma $
split, and
$\gamma $
split, and
![]() $M=M_{\alpha _{12}}$
, we get Figure 2.
$M=M_{\alpha _{12}}$
, we get Figure 2.

Figure 2 Arthur–Kottwitz reduction for
 $\Pi _{\gamma ,\preccurlyeq \mu }^{G,M}$
.
$\Pi _{\gamma ,\preccurlyeq \mu }^{G,M}$
.
Running the same construction as in §3.3, for
![]() $Q=LN_{Q}\in \mathcal {F}(M_0)$
,
$Q=LN_{Q}\in \mathcal {F}(M_0)$
,
![]() $Q\neq G$
and
$Q\neq G$
and
![]() $Q\cap M\supset P_{0}^{M}$
, define
$Q\cap M\supset P_{0}^{M}$
, define
 $$ \begin{align*} S_{\Pi',Q}:=\left\{x\in \mathscr{X}_{\gamma}\mid \pi_{M_{0}}^{G}\left(\textrm{Ec}_{M_{0}}^{Q}(x)\right)\subset R_{\Pi', Q}\right\}, \end{align*} $$
$$ \begin{align*} S_{\Pi',Q}:=\left\{x\in \mathscr{X}_{\gamma}\mid \pi_{M_{0}}^{G}\left(\textrm{Ec}_{M_{0}}^{Q}(x)\right)\subset R_{\Pi', Q}\right\}, \end{align*} $$
and let
 $$ \begin{align*} S_{\Pi',Q}^{\nu}=S_{\Pi',Q}\cap f_{Q}^{-1}\left(\mathscr{X}_{\gamma}^{L,\nu}\right),\qquad \forall \nu\in \Lambda_{L}. \end{align*} $$
$$ \begin{align*} S_{\Pi',Q}^{\nu}=S_{\Pi',Q}\cap f_{Q}^{-1}\left(\mathscr{X}_{\gamma}^{L,\nu}\right),\qquad \forall \nu\in \Lambda_{L}. \end{align*} $$
We get a disjoint partition
 $$ \begin{align} \mathscr{X}_{\gamma}^{0}\left(\Pi_{\gamma,\preccurlyeq \mu}^{G,M}\right) = \mathscr{X}_{\gamma}^{0}(\Pi')\cup \bigcup_{\substack{Q\in \mathcal{F}\left(M_0\right),Q\neq G\\ Q\cap M\supset P_{0}^{M}}}\bigcup_{\substack{\nu\in \Lambda^{0}_{L}\cap \pi_{L}\left(R_{\Pi',Q}\right) \\ \cap \pi_{L}\left(\Pi_{\gamma,\preccurlyeq \mu}^{G,M}\right)}} S_{\Pi', Q}^{\nu}. \end{align} $$
$$ \begin{align} \mathscr{X}_{\gamma}^{0}\left(\Pi_{\gamma,\preccurlyeq \mu}^{G,M}\right) = \mathscr{X}_{\gamma}^{0}(\Pi')\cup \bigcup_{\substack{Q\in \mathcal{F}\left(M_0\right),Q\neq G\\ Q\cap M\supset P_{0}^{M}}}\bigcup_{\substack{\nu\in \Lambda^{0}_{L}\cap \pi_{L}\left(R_{\Pi',Q}\right) \\ \cap \pi_{L}\left(\Pi_{\gamma,\preccurlyeq \mu}^{G,M}\right)}} S_{\Pi', Q}^{\nu}. \end{align} $$
The strata
![]() $S_{\Pi ', Q}^{\nu }$
are locally closed subschemes of
$S_{\Pi ', Q}^{\nu }$
are locally closed subschemes of
![]() $\mathscr {X}_{\gamma }$
, and the retraction
$\mathscr {X}_{\gamma }$
, and the retraction
 $f_{Q}: S_{\Pi ',Q}^{\nu }\to \mathscr {X}_{\gamma }^{L,\nu }(\Pi ^{'Q})$
is an iterated affine fibration over
$f_{Q}: S_{\Pi ',Q}^{\nu }\to \mathscr {X}_{\gamma }^{L,\nu }(\Pi ^{'Q})$
is an iterated affine fibration over
![]() $\mathbf{F}_{q}$
of dimension
$\mathbf{F}_{q}$
of dimension
![]() $ \mathrm{val}\left (\det \left (\mathrm{ad}\left (\gamma \mid \mathfrak {n}_{Q,F}\right )\right )\right ). $
$ \mathrm{val}\left (\det \left (\mathrm{ad}\left (\gamma \mid \mathfrak {n}_{Q,F}\right )\right )\right ). $
Proposition 3.9. We have the equality
 $$ \begin{align*} F_{\gamma,\mu}^{G,M}=\bigcup_{\substack{Q\in \mathcal{F}\left(M_0\right),Q\neq G\\ Q\cap M=P_{0}^{M}}}\bigcup_{\substack{\nu\in \Lambda^{0}_{L}\cap \pi_{L}\left(R_{\Pi',Q}\right) \\ \cap \pi_{L}\left(\Pi_{\gamma,\preccurlyeq \mu}^{G,M}\right)}} S_{\Pi', Q}^{\nu}. \end{align*} $$
$$ \begin{align*} F_{\gamma,\mu}^{G,M}=\bigcup_{\substack{Q\in \mathcal{F}\left(M_0\right),Q\neq G\\ Q\cap M=P_{0}^{M}}}\bigcup_{\substack{\nu\in \Lambda^{0}_{L}\cap \pi_{L}\left(R_{\Pi',Q}\right) \\ \cap \pi_{L}\left(\Pi_{\gamma,\preccurlyeq \mu}^{G,M}\right)}} S_{\Pi', Q}^{\nu}. \end{align*} $$
Moreover, the index set
 $\Lambda ^{0}_{L}\cap \pi _{L}\left (R_{\Pi ',Q}\right ) \cap \pi _{L}\left (\Pi _{\gamma ,\preccurlyeq \mu }^{G,M}\right )$
consists of at most one element, and is nonempty if and only if Q is not contained in any
$\Lambda ^{0}_{L}\cap \pi _{L}\left (R_{\Pi ',Q}\right ) \cap \pi _{L}\left (\Pi _{\gamma ,\preccurlyeq \mu }^{G,M}\right )$
consists of at most one element, and is nonempty if and only if Q is not contained in any
![]() $Q'\in \mathcal {F}(M)$
.
$Q'\in \mathcal {F}(M)$
.
Proof. For the first assertion, by construction, the points
 $x\in F_{\gamma ,\,\mu }^{G,M}$
are characterized by the property
$x\in F_{\gamma ,\,\mu }^{G,M}$
are characterized by the property
 $$ \begin{align*} \textrm{Ec}_{M_{0}}^{Q}(x)\subset \left(\mu+\Sigma_{\gamma}\right)^{Q} \end{align*} $$
$$ \begin{align*} \textrm{Ec}_{M_{0}}^{Q}(x)\subset \left(\mu+\Sigma_{\gamma}\right)^{Q} \end{align*} $$
for some
![]() $Q\in \mathcal {F}(M_0)$
,
$Q\in \mathcal {F}(M_0)$
,
![]() $Q\neq G, Q\cap M=P_{0}^{M}$
. Since this is also the property characterizing points on the right-hand side of the equality, we get the equality as claimed. The second assertion follows from the observation that
$Q\neq G, Q\cap M=P_{0}^{M}$
. Since this is also the property characterizing points on the right-hand side of the equality, we get the equality as claimed. The second assertion follows from the observation that
![]() $\Pi '$
is a slight expansion of
$\Pi '$
is a slight expansion of
 $\Pi _{\gamma ,\preccurlyeq \mu ^{-}}^{G,M}$
, and hence the regions
$\Pi _{\gamma ,\preccurlyeq \mu ^{-}}^{G,M}$
, and hence the regions
![]() $R_{\Pi ',Q}$
, Q contained in some maximal parabolic subgroup in
$R_{\Pi ',Q}$
, Q contained in some maximal parabolic subgroup in
![]() $\mathcal {F}(M)$
, contain no elements in
$\mathcal {F}(M)$
, contain no elements in
 $\Lambda _{L}^{0}\cap \pi _{L}\left (\Pi _{\gamma ,\preccurlyeq \mu }^{G,M}\right )$
.
$\Lambda _{L}^{0}\cap \pi _{L}\left (\Pi _{\gamma ,\preccurlyeq \mu }^{G,M}\right )$
.
If the index set
 $\Lambda ^{0}_{L}\cap \pi _{L}\left (R_{\Pi ',Q}\right ) \cap \pi _{L}\left (\Pi _{\gamma ,\preccurlyeq \mu }^{G,M}\right )$
is nonempty, we denote by
$\Lambda ^{0}_{L}\cap \pi _{L}\left (R_{\Pi ',Q}\right ) \cap \pi _{L}\left (\Pi _{\gamma ,\preccurlyeq \mu }^{G,M}\right )$
is nonempty, we denote by
![]() $\nu _{Q}$
the unique element in it. Let
$\nu _{Q}$
the unique element in it. Let
![]() $\mu _{Q}\in \Lambda _{L}^{0}$
be the unique element such that
$\mu _{Q}\in \Lambda _{L}^{0}$
be the unique element such that
![]() $\alpha \left (\mu _{Q}\right )=1$
for all
$\alpha \left (\mu _{Q}\right )=1$
for all
![]() $\alpha \in \Delta _{Q}$
; then we have
$\alpha \in \Delta _{Q}$
; then we have
 $$ \begin{align*} \mathscr{X}_{\gamma}^{L,\nu_{Q}}\left(\Pi^{'Q}\right)\cong F_{\gamma}^{L,\mu_{Q}}. \end{align*} $$
$$ \begin{align*} \mathscr{X}_{\gamma}^{L,\nu_{Q}}\left(\Pi^{'Q}\right)\cong F_{\gamma}^{L,\mu_{Q}}. \end{align*} $$
Combining with the fact that
 $$ \begin{align*} f_{Q}: S_{\Pi',Q}^{\nu_{Q}}\to \mathscr{X}_{\gamma}^{L,\nu_{Q}}\left(\Pi^{'Q}\right) \end{align*} $$
$$ \begin{align*} f_{Q}: S_{\Pi',Q}^{\nu_{Q}}\to \mathscr{X}_{\gamma}^{L,\nu_{Q}}\left(\Pi^{'Q}\right) \end{align*} $$
is an iterated affine fibration, we get the following:
Corollary 3.10. For
![]() $M\in \mathcal {L}(M_{0})$
,
$M\in \mathcal {L}(M_{0})$
,
![]() $M\neq M_{0}$
, we have the equality
$M\neq M_{0}$
, we have the equality
 $$ \begin{align*} \left\lvert F_{\gamma,\mu}^{G,M}\left(\mathbf{F}_{q}\right)\right\rvert= \sum_{\substack{Q=LN_{Q}\in \mathcal{F}\left(M_0\right),Q\neq G\\ \text{satisfying }(*)}} q^{\frac{1}{2}\mathrm{val}\left(\det\left(\mathrm{ad}\gamma\mid\mathfrak{g}_{F}/\mathfrak{l}_{F}\right)\right)}\cdot \left\lvert F_{\gamma}^{L,\mu_{Q}}\left(\mathbf{F}_{q}\right)\right\rvert, \end{align*} $$
$$ \begin{align*} \left\lvert F_{\gamma,\mu}^{G,M}\left(\mathbf{F}_{q}\right)\right\rvert= \sum_{\substack{Q=LN_{Q}\in \mathcal{F}\left(M_0\right),Q\neq G\\ \text{satisfying }(*)}} q^{\frac{1}{2}\mathrm{val}\left(\det\left(\mathrm{ad}\gamma\mid\mathfrak{g}_{F}/\mathfrak{l}_{F}\right)\right)}\cdot \left\lvert F_{\gamma}^{L,\mu_{Q}}\left(\mathbf{F}_{q}\right)\right\rvert, \end{align*} $$
where
![]() $(*)$
refers to the condition that
$(*)$
refers to the condition that
![]() $Q\cap M=P_{0}^{M}$
and
$Q\cap M=P_{0}^{M}$
and
![]() $Q\nsubseteq Q', \forall Q'\in \mathcal {F}(M)$
.
$Q\nsubseteq Q', \forall Q'\in \mathcal {F}(M)$
.
Notice that the equation does not involve the fundamental domain
![]() $F_{\gamma }$
. Together with Corollary 3.7 and Proposition 3.8, we get an expression of
$F_{\gamma }$
. Together with Corollary 3.7 and Proposition 3.8, we get an expression of
 $\left \lvert \left (\Lambda ^{H_{M}}\middle \backslash \mathscr {X}_{\gamma }^{\nu _{0}}(\Pi )\right )\left (\mathbf{F}_{q}\right )\right \rvert $
in terms of
$\left \lvert \left (\Lambda ^{H_{M}}\middle \backslash \mathscr {X}_{\gamma }^{\nu _{0}}(\Pi )\right )\left (\mathbf{F}_{q}\right )\right \rvert $
in terms of
 $\left \lvert F_{\gamma }^{L,\mu _{Q}}\left (\mathbf{F}_{q}\right )\right \rvert $
,
$\left \lvert F_{\gamma }^{L,\mu _{Q}}\left (\mathbf{F}_{q}\right )\right \rvert $
,
![]() $L\in \mathcal {L}(M_{0}), L\neq G$
. Recalling that counting points on
$L\in \mathcal {L}(M_{0}), L\neq G$
. Recalling that counting points on
 $F_{\gamma }^{L,\mu _{Q}}$
can be reduced to counting points on
$F_{\gamma }^{L,\mu _{Q}}$
can be reduced to counting points on
 $F_{\gamma }^{L'}$
,
$F_{\gamma }^{L'}$
,
![]() $L'\in \mathcal {L}(M_{0}), L'\subset L$
, by the Arthur–Kottwitz reduction we get an expression of
$L'\in \mathcal {L}(M_{0}), L'\subset L$
, by the Arthur–Kottwitz reduction we get an expression of
 $\left \lvert \left (\Lambda ^{H_{M}}\middle \backslash \mathscr {X}_{\gamma }^{\nu _{0}}(\Pi )\right )\left (\mathbf{F}_{q}\right )\right \rvert $
in terms of
$\left \lvert \left (\Lambda ^{H_{M}}\middle \backslash \mathscr {X}_{\gamma }^{\nu _{0}}(\Pi )\right )\left (\mathbf{F}_{q}\right )\right \rvert $
in terms of
 $\left \lvert F_{\gamma }^{L'}\left (\mathbf{F}_{q}\right )\right \rvert $
,
$\left \lvert F_{\gamma }^{L'}\left (\mathbf{F}_{q}\right )\right \rvert $
,
![]() $L'\in \mathcal {L}(M_{0})$
.
$L'\in \mathcal {L}(M_{0})$
.
4. Counting points by Harder–Narasimhan reduction
The number of points
 $\left \lvert \left (\Lambda ^{H_{M}}\middle \backslash \mathscr {X}_{\gamma }^{\nu _{0}}(\Pi )\right )\left (\mathbf{F}_{q}\right )\right \rvert $
,
$\left \lvert \left (\Lambda ^{H_{M}}\middle \backslash \mathscr {X}_{\gamma }^{\nu _{0}}(\Pi )\right )\left (\mathbf{F}_{q}\right )\right \rvert $
,
![]() $\nu _{0}\in \Lambda _{G}$
, can also be counted by the Harder–Narasimhan reduction. Comparison with results from the last section gives us a recursive relation between Arthur’s weighted orbital integrals and the number of rational points on the fundamental domains.
$\nu _{0}\in \Lambda _{G}$
, can also be counted by the Harder–Narasimhan reduction. Comparison with results from the last section gives us a recursive relation between Arthur’s weighted orbital integrals and the number of rational points on the fundamental domains.
4.1. Harder–Narasimhan reduction on the affine Springer fibers
We have introduced a notion of
![]() $\xi $
-stability on the affine Grassmannian and constructed the associated Harder–Narasimhan reduction in [Reference Chen10]. In this section, we generalize it to a broader setup. The following lemma is an analogue of [Reference Chen8, Proposition 5.6.1]. Let S be an affine
$\xi $
-stability on the affine Grassmannian and constructed the associated Harder–Narasimhan reduction in [Reference Chen10]. In this section, we generalize it to a broader setup. The following lemma is an analogue of [Reference Chen8, Proposition 5.6.1]. Let S be an affine
![]() $\mathbf{F}_{q}$
-scheme and set
$\mathbf{F}_{q}$
-scheme and set
![]() $x\in \mathscr {X}(S)$
. For every point
$x\in \mathscr {X}(S)$
. For every point
![]() $s\in S$
, let
$s\in S$
, let
![]() $x_{s}\in \mathscr {X}(k(s))$
be the base change of x to the residue field
$x_{s}\in \mathscr {X}(k(s))$
be the base change of x to the residue field
![]() $k(s)$
of S at s. Let
$k(s)$
of S at s. Let
![]() $\mathcal {C}_{x}$
be the map on S which sends every point
$\mathcal {C}_{x}$
be the map on S which sends every point
![]() $s\in S$
to the convex polytope
$s\in S$
to the convex polytope
![]() $\mathrm{Ec}(x_{s})$
.
$\mathrm{Ec}(x_{s})$
.
Lemma 4.1. Suppose that S is noetherian. The map
![]() $\mathcal {C}_{x}$
from S to the set of convex polytopes in
$\mathcal {C}_{x}$
from S to the set of convex polytopes in
![]() $\mathfrak {a}_{A}^{G}$
ordered by inclusion is lower semicontinuous. In other words, for any convex polytope
$\mathfrak {a}_{A}^{G}$
ordered by inclusion is lower semicontinuous. In other words, for any convex polytope
![]() $\Xi $
, the set
$\Xi $
, the set
is open.
Proof. To begin with, we show that
![]() $\mathcal {C}_{x}$
is constructible and takes only finitely many values. Passing to the irreducible components of S, we can suppose that S is irreducible. Let
$\mathcal {C}_{x}$
is constructible and takes only finitely many values. Passing to the irreducible components of S, we can suppose that S is irreducible. Let
![]() $\eta $
be the generic point of S, and let
$\eta $
be the generic point of S, and let
 $g_{\eta }\in G\big (k(\eta )(\!(\epsilon )\!)\big )$
be a representative of
$g_{\eta }\in G\big (k(\eta )(\!(\epsilon )\!)\big )$
be a representative of
![]() $x_{\eta }$
. For
$x_{\eta }$
. For
![]() $B=AN\in \mathcal {P}(A)$
, we have the Iwasawa decomposition
$B=AN\in \mathcal {P}(A)$
, we have the Iwasawa decomposition
where
 $n_{\eta }\in N\big (k(\eta )(\!(\epsilon )\!)\big )$
,
$n_{\eta }\in N\big (k(\eta )(\!(\epsilon )\!)\big )$
,
 $a_{\eta }\in A\big (k(\eta )(\!(\epsilon )\!)\big )$
, and
$a_{\eta }\in A\big (k(\eta )(\!(\epsilon )\!)\big )$
, and
 $k_{\eta }\in G\big (k(\eta )[\![\epsilon ]\!]\big )$
. Because
$k_{\eta }\in G\big (k(\eta )[\![\epsilon ]\!]\big )$
. Because
![]() $\eta $
is the generic point and the map
$\eta $
is the generic point and the map
![]() $\nu _{A}:\mathscr {X}^{A}\to X_{*}(A)$
is essentially the valuation map, there exists an open subscheme U of S such that
$\nu _{A}:\mathscr {X}^{A}\to X_{*}(A)$
is essentially the valuation map, there exists an open subscheme U of S such that
![]() $H_{B}(x_{s})=\nu _{A}\left (a_{\eta }\right )$
for any
$H_{B}(x_{s})=\nu _{A}\left (a_{\eta }\right )$
for any
![]() $x\in U$
. As
$x\in U$
. As
![]() $\mathrm{Ec}(x_{s})$
is the convex hull of
$\mathrm{Ec}(x_{s})$
is the convex hull of
![]() $H_{B}(x_{s})$
,
$H_{B}(x_{s})$
,
![]() $B\in \mathcal {P}(A)$
, the map
$B\in \mathcal {P}(A)$
, the map
![]() $\mathcal {C}_{x}$
takes the constant value
$\mathcal {C}_{x}$
takes the constant value
![]() $\mathrm{Ec}\left (x_{\eta }\right )$
on the intersection of all such open subschemes U. This proves the constructibility of
$\mathrm{Ec}\left (x_{\eta }\right )$
on the intersection of all such open subschemes U. This proves the constructibility of
![]() $\mathcal {C}_{x}$
. By noetherian induction, the map
$\mathcal {C}_{x}$
. By noetherian induction, the map
![]() $\mathcal {C}_{x}$
takes only finitely many values.
$\mathcal {C}_{x}$
takes only finitely many values.
To finish the proof, we only need to show that the map
![]() $\mathcal {C}_{x}$
decreases under specialization. In other words, let S be the spectrum of a discrete valuation ring and let s be its special point and
$\mathcal {C}_{x}$
decreases under specialization. In other words, let S be the spectrum of a discrete valuation ring and let s be its special point and
![]() $\eta $
its generic point. Then
$\eta $
its generic point. Then
This is equivalent to the assertion that
where
![]() $\prec _{B}$
is the order on
$\prec _{B}$
is the order on
![]() $X_{*}(A)$
such that
$X_{*}(A)$
such that
![]() $\mu _{1}\prec _{B}\mu _{2}$
if and only if
$\mu _{1}\prec _{B}\mu _{2}$
if and only if
![]() $ \mu _{2}-\mu _{1}$
is a positive linear combination of positive coroots with respect to B.
$ \mu _{2}-\mu _{1}$
is a positive linear combination of positive coroots with respect to B.
Let
![]() $\mu =f_{B}\left (x_{\eta }\right )\in X_{*}(A)$
. By definition, we have
$\mu =f_{B}\left (x_{\eta }\right )\in X_{*}(A)$
. By definition, we have
where
![]() $U_{B}$
is the unipotent radical of B. So
$U_{B}$
is the unipotent radical of B. So
 $$ \begin{align*} x_{s}\in \overline{x_{\eta}}\subset \overline{U_{B}(\!(\epsilon)\!)\epsilon^{\mu}G[\![\epsilon]\!]/G[\![\epsilon]\!]}=\bigcup_{\substack{\lambda\in X_{*}(A)\\ \lambda\prec_{B}\mu}} U_{B}(\!(\epsilon)\!)\epsilon^{\lambda}G[\![\epsilon]\!]/G[\![\epsilon]\!], \end{align*} $$
$$ \begin{align*} x_{s}\in \overline{x_{\eta}}\subset \overline{U_{B}(\!(\epsilon)\!)\epsilon^{\mu}G[\![\epsilon]\!]/G[\![\epsilon]\!]}=\bigcup_{\substack{\lambda\in X_{*}(A)\\ \lambda\prec_{B}\mu}} U_{B}(\!(\epsilon)\!)\epsilon^{\lambda}G[\![\epsilon]\!]/G[\![\epsilon]\!], \end{align*} $$
which implies the relation (4.1).
Definition 4.1. Let
![]() $\xi \in \mathfrak {a}_{M}^{G}$
be a generic element. A point
$\xi \in \mathfrak {a}_{M}^{G}$
be a generic element. A point
![]() $x\in \mathscr {X}$
is said to be
$x\in \mathscr {X}$
is said to be
![]() $\xi $
-stable if the polytope
$\xi $
-stable if the polytope
 $\pi ^{G}\big (\mathrm{Ec}_{M}(x)\big )$
contains
$\pi ^{G}\big (\mathrm{Ec}_{M}(x)\big )$
contains
![]() $\xi $
.
$\xi $
.
As
![]() $\mathrm{Ec}_{M}(x)=\pi _{M}(\mathrm{Ec}(x))$
, the subset
$\mathrm{Ec}_{M}(x)=\pi _{M}(\mathrm{Ec}(x))$
, the subset
 $$ \begin{align*} \mathscr{X}^{\xi}=\left\{x\in \mathscr{X}\mid \xi\in \pi^{G}(\textrm{Ec}_{M}(x))\right\} \end{align*} $$
$$ \begin{align*} \mathscr{X}^{\xi}=\left\{x\in \mathscr{X}\mid \xi\in \pi^{G}(\textrm{Ec}_{M}(x))\right\} \end{align*} $$
is an open sub-ind-
![]() $\mathbf{F}_{q}$
-scheme of
$\mathbf{F}_{q}$
-scheme of
![]() $\mathscr {X}$
by Lemma 4.1. This being shown, all the other constructions of [Reference Chen10] generalize.
$\mathscr {X}$
by Lemma 4.1. This being shown, all the other constructions of [Reference Chen10] generalize.
Remark 4.1. When
![]() $M=A$
, we recover the
$M=A$
, we recover the
![]() $\xi $
-stability of [Reference Chen10]. In that work, we prove that the notion of
$\xi $
-stability of [Reference Chen10]. In that work, we prove that the notion of
![]() $\xi $
-stability coincides with the notion of stability for a twisted action of A on
$\xi $
-stability coincides with the notion of stability for a twisted action of A on
![]() $\mathscr {X}$
. We believe that this holds also in the current setting, with the torus
$\mathscr {X}$
. We believe that this holds also in the current setting, with the torus
![]() $A_{M}$
playing the role of A. If this holds, we can conclude that the quotient
$A_{M}$
playing the role of A. If this holds, we can conclude that the quotient
![]() $\mathscr {X}^{\xi }/A_{M}$
exists as an ind-
$\mathscr {X}^{\xi }/A_{M}$
exists as an ind-
![]() $\mathbf{F}_{q}$
-scheme.
$\mathbf{F}_{q}$
-scheme.
Harder–Narasimhan reduction works as well in this setting. For
![]() $Q=LN_{Q}\in \mathcal {F}(M)$
, let
$Q=LN_{Q}\in \mathcal {F}(M)$
, let
![]() $\Phi _Q(G,L)$
be the image of
$\Phi _Q(G,L)$
be the image of
![]() $\Phi \left (N_{Q},A\right )$
in
$\Phi \left (N_{Q},A\right )$
in
 $\left (\mathfrak {a}_L^G\right )^{*}$
. For any point
$\left (\mathfrak {a}_L^G\right )^{*}$
. For any point
![]() $a\in \mathfrak {a}_L^G$
, we define a cone in
$a\in \mathfrak {a}_L^G$
, we define a cone in
![]() $\mathfrak {a}_L^G$
,
$\mathfrak {a}_L^G$
,
 $$ \begin{align*} D_Q(a)=\left\{y\in\mathfrak{a}_L^G\mid \alpha(y-a)\geq 0, \ \forall \alpha\in \Phi_Q(G,L)\right\}. \end{align*} $$
$$ \begin{align*} D_Q(a)=\left\{y\in\mathfrak{a}_L^G\mid \alpha(y-a)\geq 0, \ \forall \alpha\in \Phi_Q(G,L)\right\}. \end{align*} $$
Definition 4.2. For any geometric point
![]() $x\in \mathscr {X}$
, we define a semicylinder
$x\in \mathscr {X}$
, we define a semicylinder
![]() $C_Q(x)$
in
$C_Q(x)$
in
![]() $\mathfrak {a}_{M}^G$
by
$\mathfrak {a}_{M}^G$
by
 $$ \begin{align*} C_Q(x)=\pi_{M}^{L,-1}\left(\textrm{Ec}_{M}^{L}\left(f_{Q}(x)\right)\right)\cap \pi_{M,L}^{-1}\left(D_Q\left(H_{Q}(x)\right)\right). \end{align*} $$
$$ \begin{align*} C_Q(x)=\pi_{M}^{L,-1}\left(\textrm{Ec}_{M}^{L}\left(f_{Q}(x)\right)\right)\cap \pi_{M,L}^{-1}\left(D_Q\left(H_{Q}(x)\right)\right). \end{align*} $$
By definition, we get a partition
 $$ \begin{align*} \mathfrak{a}_{M}^{G}=\pi^{G}(\textrm{Ec}_{M}(x))\cup\bigcup_{\substack{Q\in \mathcal{F}(M)\\Q\neq G}}C_Q(x), \end{align*} $$
$$ \begin{align*} \mathfrak{a}_{M}^{G}=\pi^{G}(\textrm{Ec}_{M}(x))\cup\bigcup_{\substack{Q\in \mathcal{F}(M)\\Q\neq G}}C_Q(x), \end{align*} $$
for which the interior of any two parts does not intersect. The picture is similar to Figure 1. Hence for any
![]() $x\notin \mathscr {X}^{\xi }$
, there exists a unique parabolic subgroup
$x\notin \mathscr {X}^{\xi }$
, there exists a unique parabolic subgroup
![]() $Q\in \mathcal {F}(M)$
such that
$Q\in \mathcal {F}(M)$
such that
![]() $\xi \in C_Q(x)$
, as
$\xi \in C_Q(x)$
, as
![]() $\xi $
is generic. In this case,
$\xi $
is generic. In this case,
![]() $f_Q(x)\in \mathscr {X}^L$
is
$f_Q(x)\in \mathscr {X}^L$
is
![]() $\xi ^{L}$
-stable, where
$\xi ^{L}$
-stable, where
![]() $\xi ^{L}=\pi _{M}^{L}(\xi )\in \mathfrak {a}_{M}^L$
. Let
$\xi ^{L}=\pi _{M}^{L}(\xi )\in \mathfrak {a}_{M}^L$
. Let
We have the decomposition of the affine Grassmannian
 $$ \begin{align} \mathscr{X}=\mathscr{X}^{\xi}\sqcup \bigsqcup_{\substack{Q\in \mathcal{F}(M)\\Q\neq G}}X_Q. \end{align} $$
$$ \begin{align} \mathscr{X}=\mathscr{X}^{\xi}\sqcup \bigsqcup_{\substack{Q\in \mathcal{F}(M)\\Q\neq G}}X_Q. \end{align} $$
For
![]() $Q\in \mathcal {P}(L)$
, let
$Q\in \mathcal {P}(L)$
, let
![]() $Q^{-}$
be the parabolic subgroup opposite to Q with respect to L. Let
$Q^{-}$
be the parabolic subgroup opposite to Q with respect to L. Let
 $\Lambda ^{\xi }_{L,Q}=\left (\pi _{L}^{G}\right )^{-1}\left (D_{Q^{-}}(\xi _{L})\right )\cap \Lambda _{L}$
, we have the disjoint partition
$\Lambda ^{\xi }_{L,Q}=\left (\pi _{L}^{G}\right )^{-1}\left (D_{Q^{-}}(\xi _{L})\right )\cap \Lambda _{L}$
, we have the disjoint partition
 $$ \begin{align*} \Lambda_L=\bigsqcup_{Q\in \mathcal{P}(L)}\Lambda^{\xi}_{L,Q}. \end{align*} $$
$$ \begin{align*} \Lambda_L=\bigsqcup_{Q\in \mathcal{P}(L)}\Lambda^{\xi}_{L,Q}. \end{align*} $$
For
![]() $\lambda \in \Lambda _{L}$
, let
$\lambda \in \Lambda _{L}$
, let
![]() $ \mathscr {X}^{L,\lambda ,\xi ^L}=\mathscr {X}^{L,\xi ^L}\cap \mathscr {X}^{L,\lambda }. $
The stratum
$ \mathscr {X}^{L,\lambda ,\xi ^L}=\mathscr {X}^{L,\xi ^L}\cap \mathscr {X}^{L,\lambda }. $
The stratum
![]() $X_{Q}$
can be further decomposed into
$X_{Q}$
can be further decomposed into
![]() $N_{Q}(\!(\epsilon )\!)$
-orbits
$N_{Q}(\!(\epsilon )\!)$
-orbits
 $$ \begin{align*} X_{Q}=\bigsqcup_{\lambda\in \Lambda^{\xi}_{L,Q}} N_{Q}(\!(\epsilon)\!)\mathscr{X}^{L,\lambda,\xi^{L}}. \end{align*} $$
$$ \begin{align*} X_{Q}=\bigsqcup_{\lambda\in \Lambda^{\xi}_{L,Q}} N_{Q}(\!(\epsilon)\!)\mathscr{X}^{L,\lambda,\xi^{L}}. \end{align*} $$
Each orbit is locally closed in
![]() $\mathscr {X}$
, and they are infinite-dimensional homogeneous affine fibrations on
$\mathscr {X}$
, and they are infinite-dimensional homogeneous affine fibrations on
![]() $\mathscr {X}^{L,\lambda ,\xi ^{L}}$
under the retraction
$\mathscr {X}^{L,\lambda ,\xi ^{L}}$
under the retraction
![]() $f_{Q}$
. The foregoing discussions can be summarized as follows:
$f_{Q}$
. The foregoing discussions can be summarized as follows:
Theorem 4.2. The affine Grassmannian can be decomposed as
 $$ \begin{align*} \mathscr{X}=\mathscr{X}^{\xi}\sqcup \bigsqcup_{\substack{Q=LN_{Q}\in \mathcal{F}(M)\\ Q\neq G}}\bigsqcup_{\lambda\in \Lambda^{\xi}_{L,Q}} N_{Q}(\!(\epsilon)\!)\mathscr{X}^{L,\lambda,\xi^{L}}. \end{align*} $$
$$ \begin{align*} \mathscr{X}=\mathscr{X}^{\xi}\sqcup \bigsqcup_{\substack{Q=LN_{Q}\in \mathcal{F}(M)\\ Q\neq G}}\bigsqcup_{\lambda\in \Lambda^{\xi}_{L,Q}} N_{Q}(\!(\epsilon)\!)\mathscr{X}^{L,\lambda,\xi^{L}}. \end{align*} $$
Each stratum
 $N_{Q}(\!(\epsilon )\!)\mathscr {X}^{L,\lambda ,\xi ^{L}}$
is an infinite-dimensional homogeneous affine fibration over
$N_{Q}(\!(\epsilon )\!)\mathscr {X}^{L,\lambda ,\xi ^{L}}$
is an infinite-dimensional homogeneous affine fibration over
![]() $\mathscr {X}^{L,\lambda ,\xi ^{L}}$
.
$\mathscr {X}^{L,\lambda ,\xi ^{L}}$
.
Now that
![]() $\gamma \in \mathfrak {m}(F)$
, we can restrict these constructions to
$\gamma \in \mathfrak {m}(F)$
, we can restrict these constructions to
![]() $\mathscr {X}_{\gamma }$
. Let
$\mathscr {X}_{\gamma }$
. Let
 $\mathscr {X}_{\gamma }^{\xi }=\mathscr {X}_{\gamma }\cap \mathscr {X}^{\xi }$
; it is an open subscheme of
$\mathscr {X}_{\gamma }^{\xi }=\mathscr {X}_{\gamma }\cap \mathscr {X}^{\xi }$
; it is an open subscheme of
![]() $\mathscr {X}_{\gamma }$
. As
$\mathscr {X}_{\gamma }$
. As
 $T(F)\xrightarrow {H_{M}} X_{*}(M)$
is surjective, the connected components of
$T(F)\xrightarrow {H_{M}} X_{*}(M)$
is surjective, the connected components of
 $\mathscr {X}_{\gamma }^{\xi }$
can be translated to each other by elements of
$\mathscr {X}_{\gamma }^{\xi }$
can be translated to each other by elements of
![]() $T(F)$
. Moreover, for different choices of generic element
$T(F)$
. Moreover, for different choices of generic element
![]() $\xi $
,
$\xi $
,
![]() $\xi '\in \mathfrak {a}_{M}^{G}$
, the corresponding
$\xi '\in \mathfrak {a}_{M}^{G}$
, the corresponding
 $\mathscr {X}_{\gamma }^{\xi },\mathscr {X}_{\gamma }^{\xi '}$
can be translated to each other by elements of
$\mathscr {X}_{\gamma }^{\xi },\mathscr {X}_{\gamma }^{\xi '}$
can be translated to each other by elements of
![]() $T(F)$
. Hence
$T(F)$
. Hence
 $\mathscr {X}_{\gamma }^{\xi }$
does not depend on the choice of
$\mathscr {X}_{\gamma }^{\xi }$
does not depend on the choice of
![]() $\xi $
.
$\xi $
.
The Harder–Narasimhan reduction restricts to
 $$ \begin{align} \mathscr{X}_{\gamma}=\mathscr{X}_{\gamma}^{\xi}\sqcup \bigsqcup_{\substack{Q=LN_{Q}\in \mathcal{F}(M)\\ Q\neq G}}\bigsqcup_{\lambda\in \Lambda^{\xi}_{L,Q}}\left(\mathscr{X}_{\gamma}\cap N_{Q}(\!(\epsilon)\!)\mathscr{X}_{\gamma}^{L,\lambda,\xi^{L}}\right). \end{align} $$
$$ \begin{align} \mathscr{X}_{\gamma}=\mathscr{X}_{\gamma}^{\xi}\sqcup \bigsqcup_{\substack{Q=LN_{Q}\in \mathcal{F}(M)\\ Q\neq G}}\bigsqcup_{\lambda\in \Lambda^{\xi}_{L,Q}}\left(\mathscr{X}_{\gamma}\cap N_{Q}(\!(\epsilon)\!)\mathscr{X}_{\gamma}^{L,\lambda,\xi^{L}}\right). \end{align} $$
By Proposition 2.4, the retraction
 $$ \begin{align*} f_{Q}:\mathscr{X}_{\gamma}\cap N_{Q}(\!(\epsilon)\!)\mathscr{X}_{\gamma}^{L,\lambda,\xi^{L}}\to \mathscr{X}_{\gamma}^{L,\lambda,\xi^{L}} \end{align*} $$
$$ \begin{align*} f_{Q}:\mathscr{X}_{\gamma}\cap N_{Q}(\!(\epsilon)\!)\mathscr{X}_{\gamma}^{L,\lambda,\xi^{L}}\to \mathscr{X}_{\gamma}^{L,\lambda,\xi^{L}} \end{align*} $$
is an iterated affine fibration over
![]() $\mathbf{F}_{q}$
of relative dimension
$\mathbf{F}_{q}$
of relative dimension
![]() $ \mathrm{val}\left (\det \left (\mathrm{ad}(\gamma )\mid \mathfrak {n}_{Q}(F)\right )\right ). $
$ \mathrm{val}\left (\det \left (\mathrm{ad}(\gamma )\mid \mathfrak {n}_{Q}(F)\right )\right ). $
Coming back to the weighted orbital integrals, with the definition for general reductive algebraic groups as explained in Remark 2.1, Proposition 2.7 can be reformulated as follows:
Proposition 4.3. Let
![]() $\xi \in \mathfrak {a}_{M}^{G}$
be a generic element. Then
$\xi \in \mathfrak {a}_{M}^{G}$
be a generic element. Then
 $$ \begin{align*} J_{M}^{\xi}(\gamma)=\mathrm{vol}_{dt}\left(\Lambda^{H_{M}}\middle\backslash T(F)_{M}^{1}\right)^{-1}\cdot \left\lvert\Lambda^{H_{M}}\middle\backslash \left(\left(\mathscr{X}^{G_{\text{der}}}\cap\mathscr{X}_{\gamma}^{\xi}\right)\left(\mathbf{F}_{q}\right)\right)\right\rvert. \end{align*} $$
$$ \begin{align*} J_{M}^{\xi}(\gamma)=\mathrm{vol}_{dt}\left(\Lambda^{H_{M}}\middle\backslash T(F)_{M}^{1}\right)^{-1}\cdot \left\lvert\Lambda^{H_{M}}\middle\backslash \left(\left(\mathscr{X}^{G_{\text{der}}}\cap\mathscr{X}_{\gamma}^{\xi}\right)\left(\mathbf{F}_{q}\right)\right)\right\rvert. \end{align*} $$
In particular, let
 $\xi _{0}\in \mathfrak {a}_{M_{0}}^{G}$
be a generic element. Then
$\xi _{0}\in \mathfrak {a}_{M_{0}}^{G}$
be a generic element. Then
 $$ \begin{align*} J_{M_{0}}^{\xi_{0}}(\gamma)=\mathrm{vol}_{dt}\left(T(F)^{1}\right)^{-1}\cdot \left\lvert\left(\mathscr{X}^{G_{\text{der}}}\cap\mathscr{X}_{\gamma}^{\xi}\right)\left(\mathbf{F}_{q}\right)\right\rvert. \end{align*} $$
$$ \begin{align*} J_{M_{0}}^{\xi_{0}}(\gamma)=\mathrm{vol}_{dt}\left(T(F)^{1}\right)^{-1}\cdot \left\lvert\left(\mathscr{X}^{G_{\text{der}}}\cap\mathscr{X}_{\gamma}^{\xi}\right)\left(\mathbf{F}_{q}\right)\right\rvert. \end{align*} $$
Proof. When G is semisimple, the proposition is a reformulation of Proposition 2.7. The complexity arises when G has nontrivial connected center.
As T is totally ramified over F, with the exact sequence (2.2) we see that the morphism
![]() $T(F)\xrightarrow {\nu _{G}} \Lambda _{G}$
is surjective, hence
$T(F)\xrightarrow {\nu _{G}} \Lambda _{G}$
is surjective, hence
![]() $G(F)=T(F)G_{\text {der}}(F)$
, and so
$G(F)=T(F)G_{\text {der}}(F)$
, and so

with
![]() $T_{G_{\text {der}}}=T\cap G_{\text {der}}$
and
$T_{G_{\text {der}}}=T\cap G_{\text {der}}$
and
![]() $M_{G_{\text {der}}}=M\cap G_{\text {der}}$
. Following calculations in Proposition 2.7, we get a result similar to what we claim, with
$M_{G_{\text {der}}}=M\cap G_{\text {der}}$
. Following calculations in Proposition 2.7, we get a result similar to what we claim, with
![]() $\Lambda ^{H_{M}}$
replaced by
$\Lambda ^{H_{M}}$
replaced by
 $\Lambda \cap G_{\text {der}}(F)\cap \ker \left (H_{M_{G_{\text {der}}}}\right )$
and
$\Lambda \cap G_{\text {der}}(F)\cap \ker \left (H_{M_{G_{\text {der}}}}\right )$
and
![]() $T(F)_{M}^{1}$
replaced by
$T(F)_{M}^{1}$
replaced by
 $T_{G_{\text {der}}}(F)_{M_{G_{\text {der}}}}^{1}$
. Noting that
$T_{G_{\text {der}}}(F)_{M_{G_{\text {der}}}}^{1}$
. Noting that
![]() $\ker (H_{M})=M_{\text {der}}(F)\cdot M(\mathcal {O})$
by [Reference Chen7, Lemma 6.1], we have
$\ker (H_{M})=M_{\text {der}}(F)\cdot M(\mathcal {O})$
by [Reference Chen7, Lemma 6.1], we have
 $$ \begin{align*} \Lambda\cap G_{\text{der}}(F)\cap \ker\left(H_{M_{G_{\text{der}}}}\right)=\Lambda\cap \ker(H_{M})=\Lambda^{H_{M}} \end{align*} $$
$$ \begin{align*} \Lambda\cap G_{\text{der}}(F)\cap \ker\left(H_{M_{G_{\text{der}}}}\right)=\Lambda\cap \ker(H_{M})=\Lambda^{H_{M}} \end{align*} $$
and
 $$ \begin{align*} T_{G_{\text{der}}}(F)_{M_{G_{\text{der}}}}^{1}=T(F)\cap G_{\text{der}}(F)\cap \ker\left(H_{M_{G_{\text{der}}}}\right)=T(F)\cap \ker(H_{M})=T(F)_{M}^{1}, \end{align*} $$
$$ \begin{align*} T_{G_{\text{der}}}(F)_{M_{G_{\text{der}}}}^{1}=T(F)\cap G_{\text{der}}(F)\cap \ker\left(H_{M_{G_{\text{der}}}}\right)=T(F)\cap \ker(H_{M})=T(F)_{M}^{1}, \end{align*} $$
and the proposition is proved.
The volume factors have been calculated in equation (2.5).
4.2. Harder–Narasimhan reduction for the truncated affine Springer fibers
In contrast to the Arthur–Kottwitz reduction, the Harder–Narasimhan reduction does not work well on the truncated affine Springer fiber
![]() $\mathscr {X}_{\gamma }(\Pi )$
. We need to cut it into two parts, the tail and the main body. The Harder–Narasimhan reduction works well on the main body, and we can handle the tail with the Arthur–Kottwitz reduction.
$\mathscr {X}_{\gamma }(\Pi )$
. We need to cut it into two parts, the tail and the main body. The Harder–Narasimhan reduction works well on the main body, and we can handle the tail with the Arthur–Kottwitz reduction.
For
![]() $Q\in \mathcal {F}(M)$
,
$Q\in \mathcal {F}(M)$
,
![]() $Q\neq G$
, we define the positive
$Q\neq G$
, we define the positive
![]() $(G,M)$
-orthogonal family
$(G,M)$
-orthogonal family
![]() $ E_{Q}(\Pi ) $
, which as a polytope is the union of the translations
$ E_{Q}(\Pi ) $
, which as a polytope is the union of the translations
 $\pi ^{G}\left (\Sigma _{\gamma }^{G,M}+\lambda \right )$
,
$\pi ^{G}\left (\Sigma _{\gamma }^{G,M}+\lambda \right )$
,
![]() $\lambda \in \Lambda _{M}$
, such that
$\lambda \in \Lambda _{M}$
, such that
 $ \pi ^{G}\left (\Sigma _{\gamma }^{G,M}+\lambda \right )^{Q}\subset \Pi ^{Q}. $
Let
$ \pi ^{G}\left (\Sigma _{\gamma }^{G,M}+\lambda \right )^{Q}\subset \Pi ^{Q}. $
Let
 $$ \begin{align*} {}^{t}\mathscr{X}_{\gamma}(\Pi)=\bigcup_{\substack{Q\in \mathcal{F}(M)\\ Q\neq G}}\mathscr{X}_{\gamma}\left(E_{Q}(\Pi)\right), \qquad {}^{m}\mathscr{X}_{\gamma}(\Pi)=\mathscr{X}_{\gamma}(\Pi)\backslash {}^{t}\mathscr{X}_{\gamma}(\Pi). \end{align*} $$
$$ \begin{align*} {}^{t}\mathscr{X}_{\gamma}(\Pi)=\bigcup_{\substack{Q\in \mathcal{F}(M)\\ Q\neq G}}\mathscr{X}_{\gamma}\left(E_{Q}(\Pi)\right), \qquad {}^{m}\mathscr{X}_{\gamma}(\Pi)=\mathscr{X}_{\gamma}(\Pi)\backslash {}^{t}\mathscr{X}_{\gamma}(\Pi). \end{align*} $$
We call them the tail and the main body of
![]() $\mathscr {X}_{\gamma }(\Pi )$
, and they are respectively closed and open subschemes of
$\mathscr {X}_{\gamma }(\Pi )$
, and they are respectively closed and open subschemes of
![]() $\mathscr {X}_{\gamma }(\Pi )$
. Figure 3 gives an example of
$\mathscr {X}_{\gamma }(\Pi )$
. Figure 3 gives an example of
![]() $E_{Q}(\Pi )$
for the group
$E_{Q}(\Pi )$
for the group
![]() $G=\textrm {GL}_{3}$
when
$G=\textrm {GL}_{3}$
when
![]() $M=A$
.
$M=A$
.

Figure 3
![]() $E_{Q}(\mathrm{I{\kern0.5pt}I})$
for
$E_{Q}(\mathrm{I{\kern0.5pt}I})$
for
![]() $\textrm {GL}_{3}$
when
$\textrm {GL}_{3}$
when
![]() $M_{0}=A$
.
$M_{0}=A$
.
Before proceeding, we make precise the condition of
![]() $\Pi $
being sufficiently regular. We would like it to satisfy the following conditions:
$\Pi $
being sufficiently regular. We would like it to satisfy the following conditions:
-
(1)
 $\Pi $
is
$\Pi $
is
 $\Sigma _{\gamma }$
-regular.
$\Sigma _{\gamma }$
-regular. -
(2) For all
 $P,Q\in \mathcal {F}(M)$
,
$P,Q\in \mathcal {F}(M)$
,
 $E_{P}(\Pi )\cap E_{Q}(\Pi )=E_{P\cap Q}(\Pi )$
.
$E_{P}(\Pi )\cap E_{Q}(\Pi )=E_{P\cap Q}(\Pi )$
. -
(3) The complement
 $\Pi \backslash \bigcup _{\substack {Q\in \mathcal {F}(M)\\ Q\neq G}}E_{Q}(\Pi )$
is a polytope associated to a positive
$\Pi \backslash \bigcup _{\substack {Q\in \mathcal {F}(M)\\ Q\neq G}}E_{Q}(\Pi )$
is a polytope associated to a positive
 $(G,M)$
-orthogonal family; let
$(G,M)$
-orthogonal family; let
 $\Pi _{0}$
be a slight shrinking of it (the definition is similar to equation (3.1), with plus sign replaced by a minus). We require that
$\Pi _{0}$
be a slight shrinking of it (the definition is similar to equation (3.1), with plus sign replaced by a minus). We require that
 $\Pi _{0}$
be sufficiently large: for all
$\Pi _{0}$
be sufficiently large: for all
 $Q=LN_{Q}\in \mathcal {F}(M)$
, the face
$Q=LN_{Q}\in \mathcal {F}(M)$
, the face
 $\Pi _{0}^{Q}$
contains the translations of
$\Pi _{0}^{Q}$
contains the translations of
 $\Sigma _{\gamma }^{Q}$
in
$\Sigma _{\gamma }^{Q}$
in
 $\mathfrak {a}_{M}^{L}$
which have
$\mathfrak {a}_{M}^{L}$
which have
 $\xi ^{L}$
as one of their vertices.
$\xi ^{L}$
as one of their vertices.
Remark 4.2. As
![]() $\Pi _{0}$
is convex, condition (3) implies that for any
$\Pi _{0}$
is convex, condition (3) implies that for any
 $\nu \in \Lambda _{L,Q}^{\xi }\cap \pi _{L}(\Pi _{0})$
, the intersection
$\nu \in \Lambda _{L,Q}^{\xi }\cap \pi _{L}(\Pi _{0})$
, the intersection
 $\Pi _{0}\cap \pi _{M_{0},L}^{-1}(\nu )$
contains translations of
$\Pi _{0}\cap \pi _{M_{0},L}^{-1}(\nu )$
contains translations of
 $\Sigma _{\gamma }^{Q}$
in the hyperplane
$\Sigma _{\gamma }^{Q}$
in the hyperplane
 $\pi _{M_{0},L}^{-1}(\nu )$
which have
$\pi _{M_{0},L}^{-1}(\nu )$
which have
![]() $\xi ^{L}$
as one of their vertices. By the definition of
$\xi ^{L}$
as one of their vertices. By the definition of
![]() $\xi $
-stability, this implies
$\xi $
-stability, this implies
 $$ \begin{align*} \mathscr{X}_{\gamma}^{L,\nu,\xi^{L}}\subset \mathscr{X}_{\gamma}^{L,\nu}\left(\Pi_{0}\cap \pi_{M_{0},L}^{-1}(\nu)\right),\qquad \forall \nu\in \Lambda_{L,Q}^{\xi}\cap \pi_{L}(\Pi_{0}). \end{align*} $$
$$ \begin{align*} \mathscr{X}_{\gamma}^{L,\nu,\xi^{L}}\subset \mathscr{X}_{\gamma}^{L,\nu}\left(\Pi_{0}\cap \pi_{M_{0},L}^{-1}(\nu)\right),\qquad \forall \nu\in \Lambda_{L,Q}^{\xi}\cap \pi_{L}(\Pi_{0}). \end{align*} $$
Actually, this is the reason to impose condition (3).
4.2.1. The main body
By definition, a Harder–Narasimhan stratum
 $$ \begin{align*} N_{Q}(\!(\epsilon )\!)\mathscr {X}_{\gamma }^{L,\nu ,\xi ^{L}}\cap \mathscr {X}_{\gamma },\ \nu \in \Lambda _{L,Q}^{\xi }, \end{align*} $$
$$ \begin{align*} N_{Q}(\!(\epsilon )\!)\mathscr {X}_{\gamma }^{L,\nu ,\xi ^{L}}\cap \mathscr {X}_{\gamma },\ \nu \in \Lambda _{L,Q}^{\xi }, \end{align*} $$
intersects nontrivially with
![]() $\mathscr {X}_{\gamma }(\Pi )$
if and only if
$\mathscr {X}_{\gamma }(\Pi )$
if and only if
 $\nu \in \Lambda _{L,Q}^{\xi }\cap \pi _{L}(\Pi )$
. So, after restriction, the Harder–Narasimhan reduction becomes
$\nu \in \Lambda _{L,Q}^{\xi }\cap \pi _{L}(\Pi )$
. So, after restriction, the Harder–Narasimhan reduction becomes
 $$ \begin{align*} \mathscr{X}_{\gamma}(\Pi)=\mathscr{X}_{\gamma}^{\xi}\sqcup \bigsqcup_{\substack{Q=LN_{Q}\in \mathcal{F}(M)\\ Q\neq G}}\bigsqcup_{\lambda\in \Lambda^{\xi}_{L,Q}\cap \pi_{L}(\Pi)}\left(\mathscr{X}_{\gamma}(\Pi)\cap N_{Q}(\!(\epsilon)\!)\mathscr{X}_{\gamma}^{L,\lambda,\xi^{L}}\right). \end{align*} $$
$$ \begin{align*} \mathscr{X}_{\gamma}(\Pi)=\mathscr{X}_{\gamma}^{\xi}\sqcup \bigsqcup_{\substack{Q=LN_{Q}\in \mathcal{F}(M)\\ Q\neq G}}\bigsqcup_{\lambda\in \Lambda^{\xi}_{L,Q}\cap \pi_{L}(\Pi)}\left(\mathscr{X}_{\gamma}(\Pi)\cap N_{Q}(\!(\epsilon)\!)\mathscr{X}_{\gamma}^{L,\lambda,\xi^{L}}\right). \end{align*} $$
The problem is that the retraction
 $$ \begin{align*} f_{Q}: \mathscr{X}_{\gamma}(\Pi)\cap N_{Q}(\!(\epsilon)\!)\mathscr{X}_{\gamma}^{L,\lambda,\xi^{L}} \to \mathscr{X}_{\gamma}^{L,\lambda,\xi^{L}} \end{align*} $$
$$ \begin{align*} f_{Q}: \mathscr{X}_{\gamma}(\Pi)\cap N_{Q}(\!(\epsilon)\!)\mathscr{X}_{\gamma}^{L,\lambda,\xi^{L}} \to \mathscr{X}_{\gamma}^{L,\lambda,\xi^{L}} \end{align*} $$
is not necessarily an iterated affine fibration. This problem disappears on the main body
![]() ${}^{m}\mathscr {X}_{\gamma }(\Pi )$
. We begin by analyzing the polytope
${}^{m}\mathscr {X}_{\gamma }(\Pi )$
. We begin by analyzing the polytope
![]() $\mathrm{Ec}(x)$
,
$\mathrm{Ec}(x)$
,
![]() $x\in \mathscr {X}_{\gamma }(\Pi )$
.
$x\in \mathscr {X}_{\gamma }(\Pi )$
.
Lemma 4.4. For
![]() $x\in \mathscr {X}_{\gamma }(\Pi )$
, suppose that
$x\in \mathscr {X}_{\gamma }(\Pi )$
, suppose that
 $$ \begin{align*} \pi^{G}(\textrm{Ec}_{M}(x))\subset \bigcup_{\substack{Q\in \mathcal{F}(M)\\ Q\neq G}} E_{Q}(\Pi). \end{align*} $$
$$ \begin{align*} \pi^{G}(\textrm{Ec}_{M}(x))\subset \bigcup_{\substack{Q\in \mathcal{F}(M)\\ Q\neq G}} E_{Q}(\Pi). \end{align*} $$
Then
![]() $\pi ^{G}(\mathrm{Ec}_{M}(x))\subset E_{Q}(\Pi )$
for some
$\pi ^{G}(\mathrm{Ec}_{M}(x))\subset E_{Q}(\Pi )$
for some
![]() $Q\in \mathcal {F}(M),\,Q\neq G$
.
$Q\in \mathcal {F}(M),\,Q\neq G$
.
Proof. By Proposition 3.1, it is enough to prove the lemma for
![]() $x\in \mathscr {X}_{\gamma }^{\mathrm{reg}}$
. In this case, the polytope
$x\in \mathscr {X}_{\gamma }^{\mathrm{reg}}$
. In this case, the polytope
![]() $\pi ^{G}(\mathrm{Ec}_{M}(x))$
is a translation of
$\pi ^{G}(\mathrm{Ec}_{M}(x))$
is a translation of
 $\Sigma _{\gamma }^{G,M}$
. As
$\Sigma _{\gamma }^{G,M}$
. As
 $\bigcup _{\substack {Q\in \mathcal {F}(M)\\ Q\neq G}} E_{Q}(\Pi )$
is the union of translations of
$\bigcup _{\substack {Q\in \mathcal {F}(M)\\ Q\neq G}} E_{Q}(\Pi )$
is the union of translations of
 $\Sigma _{\gamma }^{G,M}$
along the facets of
$\Sigma _{\gamma }^{G,M}$
along the facets of
![]() $\Pi $
, there must be a maximal parabolic subgroup
$\Pi $
, there must be a maximal parabolic subgroup
![]() $Q\in \mathcal {F}(M)_{\max }$
such that
$Q\in \mathcal {F}(M)_{\max }$
such that
 $\pi ^{G}(\mathrm{Ec}_{M}^{Q}(x))\subset \Pi ^{Q}$
. By definition, this means that
$\pi ^{G}(\mathrm{Ec}_{M}^{Q}(x))\subset \Pi ^{Q}$
. By definition, this means that
![]() $\pi ^{G}(\mathrm{Ec}_{M}(x))\subset E_{Q}(\Pi )$
.
$\pi ^{G}(\mathrm{Ec}_{M}(x))\subset E_{Q}(\Pi )$
.
Lemma 4.5. Let
![]() $Q=LN\in \mathcal {F}(M)$
,
$Q=LN\in \mathcal {F}(M)$
,
 $\nu \in \Lambda _{L,Q}^{\xi }$
. Suppose that
$\nu \in \Lambda _{L,Q}^{\xi }$
. Suppose that
 $$ \begin{align*} {}^{m}\mathscr{X}_{\gamma}(\Pi)\cap N(\!(\epsilon)\!)\mathscr{X}_{\gamma}^{L,\nu}\neq \emptyset. \end{align*} $$
$$ \begin{align*} {}^{m}\mathscr{X}_{\gamma}(\Pi)\cap N(\!(\epsilon)\!)\mathscr{X}_{\gamma}^{L,\nu}\neq \emptyset. \end{align*} $$
Then
 $\nu \in \Lambda _{L,Q}^{\xi }\cap \pi _{L}(\Pi _{0})$
.
$\nu \in \Lambda _{L,Q}^{\xi }\cap \pi _{L}(\Pi _{0})$
.
Proof. We only need to show that
![]() $\nu \in \pi _{L}(\Pi _{0})$
. Set
$\nu \in \pi _{L}(\Pi _{0})$
. Set
 $x\in {}^{m}\mathscr {X}_{\gamma }(\Pi )\cap N(\!(\epsilon )\!)\mathscr {X}_{\gamma }^{L,\nu }$
. As
$x\in {}^{m}\mathscr {X}_{\gamma }(\Pi )\cap N(\!(\epsilon )\!)\mathscr {X}_{\gamma }^{L,\nu }$
. As
![]() $x\in {}^{m}\mathscr {X}_{\gamma }(\Pi )$
, we have
$x\in {}^{m}\mathscr {X}_{\gamma }(\Pi )$
, we have
 $$ \begin{align*} \pi^{G}(\textrm{Ec}_{M}(x))\nsubseteq E_{Q'}(\Pi),\qquad \forall Q'\in \mathcal{F}(M), \ Q'\neq G. \end{align*} $$
$$ \begin{align*} \pi^{G}(\textrm{Ec}_{M}(x))\nsubseteq E_{Q'}(\Pi),\qquad \forall Q'\in \mathcal{F}(M), \ Q'\neq G. \end{align*} $$
By Lemma 4.4, this is equivalent to
 $$ \begin{align} \pi^{G}(\textrm{Ec}_{M}(x))\nsubseteq \bigcup_{\substack{Q'\in \mathcal{F}(M)\\Q'\neq G}}E_{Q'}(\Pi). \end{align} $$
$$ \begin{align} \pi^{G}(\textrm{Ec}_{M}(x))\nsubseteq \bigcup_{\substack{Q'\in \mathcal{F}(M)\\Q'\neq G}}E_{Q'}(\Pi). \end{align} $$
Suppose that
![]() $\nu \notin \pi _{L}(\Pi _{0})$
. Then
$\nu \notin \pi _{L}(\Pi _{0})$
. Then
![]() $\nu \in \pi _{L}\left (E_{Q_{0}}(\Pi )\right )$
for some
$\nu \in \pi _{L}\left (E_{Q_{0}}(\Pi )\right )$
for some
![]() $Q_{0}\in \mathcal {F}(M), Q_{0}\supset L$
. As
$Q_{0}\in \mathcal {F}(M), Q_{0}\supset L$
. As
 $\nu \in \Lambda _{L,Q}^{\xi }$
, the parabolic subgroup
$\nu \in \Lambda _{L,Q}^{\xi }$
, the parabolic subgroup
![]() $Q_{0}$
needs to satisfy
$Q_{0}$
needs to satisfy
![]() $Q_{0}\supset Q^{-}$
. Now that
$Q_{0}\supset Q^{-}$
. Now that
 $x\in N(\!(\epsilon )\!)\mathscr {X}_{\gamma }^{L,\nu }$
and
$x\in N(\!(\epsilon )\!)\mathscr {X}_{\gamma }^{L,\nu }$
and
![]() $\mathrm{Ec}_{L}(x)$
is a positive
$\mathrm{Ec}_{L}(x)$
is a positive
![]() $(G,L)$
-orthogonal family, we have
$(G,L)$
-orthogonal family, we have
As
![]() $Q_{0}\supset Q^{-}$
, this implies that
$Q_{0}\supset Q^{-}$
, this implies that
Hence
![]() $\pi _{L}(\mathrm{Ec}_{M}(x))\subset \pi _{L}\left (E_{Q_{0}}(\Pi )\right )$
, so
$\pi _{L}(\mathrm{Ec}_{M}(x))\subset \pi _{L}\left (E_{Q_{0}}(\Pi )\right )$
, so
 $$ \begin{align*} \textrm{Ec}_{M}(x)\subset \pi_{L}^{-1}\left(\pi_{L}\left(E_{Q_{0}}(\Pi)\right)\right)\subset\bigcup_{\substack{Q'\subset \mathcal{F}(M),Q'\neq G\\Q'\cap Q_{0}\neq \emptyset}} E_{Q'}(\Pi). \end{align*} $$
$$ \begin{align*} \textrm{Ec}_{M}(x)\subset \pi_{L}^{-1}\left(\pi_{L}\left(E_{Q_{0}}(\Pi)\right)\right)\subset\bigcup_{\substack{Q'\subset \mathcal{F}(M),Q'\neq G\\Q'\cap Q_{0}\neq \emptyset}} E_{Q'}(\Pi). \end{align*} $$
This is in contradiction to the relation (4.4), hence
![]() $\nu $
must lie in
$\nu $
must lie in
![]() $\pi _{L}(\Pi _{0})$
.
$\pi _{L}(\Pi _{0})$
.
Restricting the Harder–Narasimhan reduction (4.3) to the main part
![]() ${}^{m}\mathscr {X}_{\gamma }(\Pi )$
, we have
${}^{m}\mathscr {X}_{\gamma }(\Pi )$
, we have
 $$ \begin{align*} {}^{m}\mathscr{X}_{\gamma}(\Pi)=\mathscr{X}_{\gamma}^{\xi}\sqcup \bigsqcup_{\substack{Q=LN_{Q}\in \mathcal{F}(M)\\ Q\neq G}}\bigsqcup_{\lambda\in \Lambda^{\xi}_{L,Q}\cap \pi_{L}(\Pi_{0})} \left({}^{m}\mathscr{X}_{\gamma}(\Pi)\cap N_{Q}(\!(\epsilon)\!)\mathscr{X}_{\gamma}^{L,\lambda,\xi^{L}}\right). \end{align*} $$
$$ \begin{align*} {}^{m}\mathscr{X}_{\gamma}(\Pi)=\mathscr{X}_{\gamma}^{\xi}\sqcup \bigsqcup_{\substack{Q=LN_{Q}\in \mathcal{F}(M)\\ Q\neq G}}\bigsqcup_{\lambda\in \Lambda^{\xi}_{L,Q}\cap \pi_{L}(\Pi_{0})} \left({}^{m}\mathscr{X}_{\gamma}(\Pi)\cap N_{Q}(\!(\epsilon)\!)\mathscr{X}_{\gamma}^{L,\lambda,\xi^{L}}\right). \end{align*} $$
The retraction
![]() $f_{Q}$
behaves much better on the stratum
$f_{Q}$
behaves much better on the stratum
 ${}^{m}\mathscr {X}_{\gamma }(\Pi )\cap N_{Q}(\!(\epsilon )\!)\mathscr {X}_{\gamma }^{L,\lambda ,\xi ^{L}}$
:
${}^{m}\mathscr {X}_{\gamma }(\Pi )\cap N_{Q}(\!(\epsilon )\!)\mathscr {X}_{\gamma }^{L,\lambda ,\xi ^{L}}$
:
Proposition 4.6. Let
![]() $Q=LN_{Q}\in \mathcal {F}(M)$
,
$Q=LN_{Q}\in \mathcal {F}(M)$
,
 $\nu \in \Lambda _{L,Q}^{\xi }\cap \pi _{L}(\Pi _{0})$
. We have
$\nu \in \Lambda _{L,Q}^{\xi }\cap \pi _{L}(\Pi _{0})$
. We have
 $$ \begin{align*} {}^{m}\mathscr{X}_{\gamma}(\Pi)\cap N_{Q}(\!(\epsilon)\!)\mathscr{X}_{\gamma}^{L,\nu,\xi^{L}}=\mathscr{X}_{\gamma}\cap N_{Q}(\!(\epsilon)\!)\mathscr{X}_{\gamma}^{L,\nu,\xi^{L}}. \end{align*} $$
$$ \begin{align*} {}^{m}\mathscr{X}_{\gamma}(\Pi)\cap N_{Q}(\!(\epsilon)\!)\mathscr{X}_{\gamma}^{L,\nu,\xi^{L}}=\mathscr{X}_{\gamma}\cap N_{Q}(\!(\epsilon)\!)\mathscr{X}_{\gamma}^{L,\nu,\xi^{L}}. \end{align*} $$
Hence the retraction
 $$ \begin{align*} f_{Q}: {}^{m}\mathscr{X}_{\gamma}(\Pi)\cap N_{Q}(\!(\epsilon)\!)\mathscr{X}_{\gamma}^{L,\nu,\xi^{L}}\to \mathscr{X}_{\gamma}^{L,\nu,\xi^{L}} \end{align*} $$
$$ \begin{align*} f_{Q}: {}^{m}\mathscr{X}_{\gamma}(\Pi)\cap N_{Q}(\!(\epsilon)\!)\mathscr{X}_{\gamma}^{L,\nu,\xi^{L}}\to \mathscr{X}_{\gamma}^{L,\nu,\xi^{L}} \end{align*} $$
is an iterated affine fibration over
![]() $\mathbf{F}_{q}$
.
$\mathbf{F}_{q}$
.
Proof. Notice that the second assertion is the corollary of the first one, as follows from Proposition 2.4. It is thus enough to show the first one. In particular, it is enough to show
 $$ \begin{align*} \mathscr{X}_{\gamma}\cap N_{Q}(\!(\epsilon)\!)\mathscr{X}_{\gamma}^{L,\nu,\xi^{L}}\subset {}^{m}\mathscr{X}_{\gamma}(\Pi)\cap N_{Q}(\!(\epsilon)\!)\mathscr{X}_{\gamma}^{L,\nu,\xi^{L}}, \end{align*} $$
$$ \begin{align*} \mathscr{X}_{\gamma}\cap N_{Q}(\!(\epsilon)\!)\mathscr{X}_{\gamma}^{L,\nu,\xi^{L}}\subset {}^{m}\mathscr{X}_{\gamma}(\Pi)\cap N_{Q}(\!(\epsilon)\!)\mathscr{X}_{\gamma}^{L,\nu,\xi^{L}}, \end{align*} $$
as the inclusion in the other direction is obvious.
Let
 $x\in \mathscr {X}_{\gamma }\cap N_{Q}(\!(\epsilon )\!)\mathscr {X}_{\gamma }^{L,\nu ,\xi ^{L}}$
. We claim that
$x\in \mathscr {X}_{\gamma }\cap N_{Q}(\!(\epsilon )\!)\mathscr {X}_{\gamma }^{L,\nu ,\xi ^{L}}$
. We claim that
![]() $\mathrm{Ec}_{M}(x)\subset \Pi $
. According to Remark 4.2, condition (3) of
$\mathrm{Ec}_{M}(x)\subset \Pi $
. According to Remark 4.2, condition (3) of
![]() $\Pi $
being sufficiently regular implies
$\Pi $
being sufficiently regular implies
 $$ \begin{align} \textrm{Ec}_{M}^{L}\left(f_{Q}(x)\right)\subset \Pi_{0}\cap \pi_{L}^{-1}(\nu), \end{align} $$
$$ \begin{align} \textrm{Ec}_{M}^{L}\left(f_{Q}(x)\right)\subset \Pi_{0}\cap \pi_{L}^{-1}(\nu), \end{align} $$
because
 $f_{Q}(x)\in \mathscr {X}_{\gamma }^{L,\nu ,\xi ^{L}}$
. This implies that
$f_{Q}(x)\in \mathscr {X}_{\gamma }^{L,\nu ,\xi ^{L}}$
. This implies that
![]() $\mathrm{Ec}_{M}(x)\subset \Pi $
by Proposition 3.1, because of the inclusion
$\mathrm{Ec}_{M}(x)\subset \Pi $
by Proposition 3.1, because of the inclusion
 $$ \begin{align*} \bigcup_{\substack{\lambda\in \Lambda_{M}\\ \text{satisfying }(*)}}\left(\lambda+\Sigma_{\gamma}^{G,M}\right)\subset \Pi, \end{align*} $$
$$ \begin{align*} \bigcup_{\substack{\lambda\in \Lambda_{M}\\ \text{satisfying }(*)}}\left(\lambda+\Sigma_{\gamma}^{G,M}\right)\subset \Pi, \end{align*} $$
where the condition
![]() $(*)$
refers to
$(*)$
refers to
 $$ \begin{align*} \left(\lambda+\Sigma_{\gamma}^{G,M}\right)\cap \Pi_{0}\neq \emptyset. \end{align*} $$
$$ \begin{align*} \left(\lambda+\Sigma_{\gamma}^{G,M}\right)\cap \Pi_{0}\neq \emptyset. \end{align*} $$
The inclusion (4.5) also implies that
 $$ \begin{align*} \textrm{Ec}_{M}(x)\nsubseteq \bigcup_{\substack{Q\in \mathcal{F}(M)\\Q\neq G}}E_{Q}(\Pi). \end{align*} $$
$$ \begin{align*} \textrm{Ec}_{M}(x)\nsubseteq \bigcup_{\substack{Q\in \mathcal{F}(M)\\Q\neq G}}E_{Q}(\Pi). \end{align*} $$
So
![]() $x\in {}^{m}\mathscr {X}_{\gamma }(\Pi )$
, and the proof is concluded.
$x\in {}^{m}\mathscr {X}_{\gamma }(\Pi )$
, and the proof is concluded.
We summarize the foregoing discussions in a proposition.
Proposition 4.7. The main body has a decomposition
 $$ \begin{align*} {}^{m}\mathscr{X}_{\gamma}(\Pi)=\mathscr{X}_{\gamma}^{\xi}\sqcup \bigsqcup_{\substack{Q=LN_{Q}\in \mathcal{F}(M)\\ Q\neq G}}\bigsqcup_{\lambda\in \Lambda^{\xi}_{L,Q}\cap \pi_{L}\left(\Pi_{0}\right)} \left({}^{m}\mathscr{X}_{\gamma}(\Pi)\cap N_{Q}(\!(\epsilon)\!)\mathscr{X}_{\gamma}^{L,\lambda,\xi^{L}}\right), \end{align*} $$
$$ \begin{align*} {}^{m}\mathscr{X}_{\gamma}(\Pi)=\mathscr{X}_{\gamma}^{\xi}\sqcup \bigsqcup_{\substack{Q=LN_{Q}\in \mathcal{F}(M)\\ Q\neq G}}\bigsqcup_{\lambda\in \Lambda^{\xi}_{L,Q}\cap \pi_{L}\left(\Pi_{0}\right)} \left({}^{m}\mathscr{X}_{\gamma}(\Pi)\cap N_{Q}(\!(\epsilon)\!)\mathscr{X}_{\gamma}^{L,\lambda,\xi^{L}}\right), \end{align*} $$
and the retraction
![]() $f_{Q}$
on each stratum
$f_{Q}$
on each stratum
 $$ \begin{align*} f_{Q}: {}^{m}\mathscr{X}_{\gamma}(\Pi)\cap N_{Q}(\!(\epsilon)\!)\mathscr{X}_{\gamma}^{L,\nu,\xi^{L}}\to \mathscr{X}_{\gamma}^{L,\nu,\xi^{L}} \end{align*} $$
$$ \begin{align*} f_{Q}: {}^{m}\mathscr{X}_{\gamma}(\Pi)\cap N_{Q}(\!(\epsilon)\!)\mathscr{X}_{\gamma}^{L,\nu,\xi^{L}}\to \mathscr{X}_{\gamma}^{L,\nu,\xi^{L}} \end{align*} $$
is an iterated affine fibration over
![]() $\mathbf{F}_{q}$
of dimension
$\mathbf{F}_{q}$
of dimension
![]() $ \mathrm{val}\left (\det \left (\mathrm{ad}(\gamma )\mid \mathfrak {n}_{Q,F}\right )\right ). $
$ \mathrm{val}\left (\det \left (\mathrm{ad}(\gamma )\mid \mathfrak {n}_{Q,F}\right )\right ). $
Of course, we can restrict the decomposition to each connected component
![]() ${}^{m}\mathscr {X}_{\gamma }^{\nu _{0}}(\Pi )$
,
${}^{m}\mathscr {X}_{\gamma }^{\nu _{0}}(\Pi )$
,
![]() $\nu _{0}\in \Lambda _{G}$
. Let
$\nu _{0}\in \Lambda _{G}$
. Let
 $\Lambda _{L,Q}^{\nu _{0},\xi }=\Lambda _{L,Q}^{\xi }\cap \Lambda _{L}^{\nu _{0}}$
. The decomposition implies
$\Lambda _{L,Q}^{\nu _{0},\xi }=\Lambda _{L,Q}^{\xi }\cap \Lambda _{L}^{\nu _{0}}$
. The decomposition implies
 $$ \begin{align*} &\left\lvert\left(\Lambda^{H_{M}}\middle\backslash {}^{m}\mathscr{X}_{\gamma}^{\nu_{0}}(\Pi)\right)\left(\mathbf{F}_{q}\right)\right\rvert\\ & \quad = \left\lvert\left(\Lambda^{H_{M}}\middle\backslash\mathscr{X}_{\gamma}^{\nu_{0},\xi}\right)\left(\mathbf{F}_{q}\right)\right\vert+\sum_{\substack{Q=LN_{Q}\in \mathcal{F}(M)\\ Q\neq G}}\sum_{\lambda\in \Lambda^{\nu_{0},\xi}_{L,Q}\cap \pi_{L}\left(\Pi_{0}\right)} q^{\frac{1}{2}\mathrm{val}\left(\det\left(\mathrm{ad}(\gamma)\mid \mathfrak{g}_{F}/\mathfrak{l}_{F}\right)\right)} \nonumber \\ &\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\quad\quad \cdot \left\lvert\left(\Lambda^{H_{M}}\middle\backslash\mathscr{X}^{L,\lambda,\xi^{L}}_{\gamma}\right)\left(\mathbf{F}_{q}\right)\right\rvert \\ & \quad = \left\lvert\left(\Lambda^{H_{M}}\middle\backslash\mathscr{X}_{\gamma}^{0,\xi}\right)\left(\mathbf{F}_{q}\right)\right\rvert +\sum_{\substack{Q=LN_{Q}\in \mathcal{F}(M)\\ Q\neq G}} q^{\frac{1}{2}\mathrm{val}\left(\det\left(\mathrm{ad} \gamma\mid\mathfrak{g}_{F}/\mathfrak{l}_{F}\right)\right)}\cdot \left\lvert\left(\Lambda^{H_{M}}\middle\backslash\mathscr{X}^{L,0,\xi^{L}}_{\gamma}\right)\left(\mathbf{F}_{q}\right)\right\rvert\nonumber \\ &\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\quad\quad \cdot \left\lvert\Lambda^{\nu_{0},\xi}_{L,Q}\cap \pi_{L}(\Pi_{0})\right\rvert \\ & \quad = \left\lvert\left(\Lambda^{H_{M}}\middle\backslash\mathscr{X}_{\gamma}^{0,\xi}\right)\left(\mathbf{F}_{q}\right)\right\vert +\sum_{\substack{L\in \mathcal{L}(M)\\ L\neq G}} q^{\frac{1}{2}\mathrm{val}\left(\det\left(\mathrm{ad} \gamma\mid\mathfrak{g}_{F}/\mathfrak{l}_{F}\right)\right)}\cdot \left\lvert\left(\Lambda^{H_{M}}\middle\backslash\mathscr{X}^{L,0,\xi^{L}}_{\gamma}\right)\left(\mathbf{F}_{q}\right)\right\rvert\nonumber \\ &\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\quad\quad \cdot\sum_{Q\in \mathcal{P}(L)} \left\lvert\Lambda^{\nu_{0},\xi}_{L,Q}\cap \pi_{L}(\Pi_{0})\right\rvert \\ & \quad = \left\lvert\left(\Lambda^{H_{M}}\middle\backslash\mathscr{X}_{\gamma}^{0,\xi}\right)\left(\mathbf{F}_{q}\right)\right\rvert +\sum_{\substack{L\in \mathcal{L}(M)\\ L\neq G}} q^{\frac{1}{2}\mathrm{val}\left(\det\left(\mathrm{ad} \gamma\mid\mathfrak{g}_{F}/\mathfrak{l}_{F}\right)\right)}\cdot \left\lvert\left(\Lambda^{H_{M}}\middle\backslash\mathscr{X}^{L,0,\xi^{L}}_{\gamma}\right)\left(\mathbf{F}_{q}\right)\right\rvert\nonumber \\ &\qquad\qquad\qquad\qquad\qquad\qquad\qquad\quad \cdot\left\lvert\Lambda^{\nu_{0}}_{L}\cap \pi_{L}(\Pi_{0})\right\rvert. \end{align*} $$
$$ \begin{align*} &\left\lvert\left(\Lambda^{H_{M}}\middle\backslash {}^{m}\mathscr{X}_{\gamma}^{\nu_{0}}(\Pi)\right)\left(\mathbf{F}_{q}\right)\right\rvert\\ & \quad = \left\lvert\left(\Lambda^{H_{M}}\middle\backslash\mathscr{X}_{\gamma}^{\nu_{0},\xi}\right)\left(\mathbf{F}_{q}\right)\right\vert+\sum_{\substack{Q=LN_{Q}\in \mathcal{F}(M)\\ Q\neq G}}\sum_{\lambda\in \Lambda^{\nu_{0},\xi}_{L,Q}\cap \pi_{L}\left(\Pi_{0}\right)} q^{\frac{1}{2}\mathrm{val}\left(\det\left(\mathrm{ad}(\gamma)\mid \mathfrak{g}_{F}/\mathfrak{l}_{F}\right)\right)} \nonumber \\ &\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\quad\quad \cdot \left\lvert\left(\Lambda^{H_{M}}\middle\backslash\mathscr{X}^{L,\lambda,\xi^{L}}_{\gamma}\right)\left(\mathbf{F}_{q}\right)\right\rvert \\ & \quad = \left\lvert\left(\Lambda^{H_{M}}\middle\backslash\mathscr{X}_{\gamma}^{0,\xi}\right)\left(\mathbf{F}_{q}\right)\right\rvert +\sum_{\substack{Q=LN_{Q}\in \mathcal{F}(M)\\ Q\neq G}} q^{\frac{1}{2}\mathrm{val}\left(\det\left(\mathrm{ad} \gamma\mid\mathfrak{g}_{F}/\mathfrak{l}_{F}\right)\right)}\cdot \left\lvert\left(\Lambda^{H_{M}}\middle\backslash\mathscr{X}^{L,0,\xi^{L}}_{\gamma}\right)\left(\mathbf{F}_{q}\right)\right\rvert\nonumber \\ &\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\quad\quad \cdot \left\lvert\Lambda^{\nu_{0},\xi}_{L,Q}\cap \pi_{L}(\Pi_{0})\right\rvert \\ & \quad = \left\lvert\left(\Lambda^{H_{M}}\middle\backslash\mathscr{X}_{\gamma}^{0,\xi}\right)\left(\mathbf{F}_{q}\right)\right\vert +\sum_{\substack{L\in \mathcal{L}(M)\\ L\neq G}} q^{\frac{1}{2}\mathrm{val}\left(\det\left(\mathrm{ad} \gamma\mid\mathfrak{g}_{F}/\mathfrak{l}_{F}\right)\right)}\cdot \left\lvert\left(\Lambda^{H_{M}}\middle\backslash\mathscr{X}^{L,0,\xi^{L}}_{\gamma}\right)\left(\mathbf{F}_{q}\right)\right\rvert\nonumber \\ &\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\quad\quad \cdot\sum_{Q\in \mathcal{P}(L)} \left\lvert\Lambda^{\nu_{0},\xi}_{L,Q}\cap \pi_{L}(\Pi_{0})\right\rvert \\ & \quad = \left\lvert\left(\Lambda^{H_{M}}\middle\backslash\mathscr{X}_{\gamma}^{0,\xi}\right)\left(\mathbf{F}_{q}\right)\right\rvert +\sum_{\substack{L\in \mathcal{L}(M)\\ L\neq G}} q^{\frac{1}{2}\mathrm{val}\left(\det\left(\mathrm{ad} \gamma\mid\mathfrak{g}_{F}/\mathfrak{l}_{F}\right)\right)}\cdot \left\lvert\left(\Lambda^{H_{M}}\middle\backslash\mathscr{X}^{L,0,\xi^{L}}_{\gamma}\right)\left(\mathbf{F}_{q}\right)\right\rvert\nonumber \\ &\qquad\qquad\qquad\qquad\qquad\qquad\qquad\quad \cdot\left\lvert\Lambda^{\nu_{0}}_{L}\cap \pi_{L}(\Pi_{0})\right\rvert. \end{align*} $$
Here for the second equality we have used the fact that all the connected components of
 $\mathscr {X}_{\gamma }^{L,\xi _{L}}$
are isomorphic. Moreover, the last term in the equation counts the number of lattice points in a polytope; it can be calculated effectively with methods from toric geometry. The following theorem summarizes:
$\mathscr {X}_{\gamma }^{L,\xi _{L}}$
are isomorphic. Moreover, the last term in the equation counts the number of lattice points in a polytope; it can be calculated effectively with methods from toric geometry. The following theorem summarizes:
Theorem 4.8. For any
![]() $\nu _{0}\in \Lambda _{G}$
, the number of rational points on the main body is
$\nu _{0}\in \Lambda _{G}$
, the number of rational points on the main body is
 $$ \begin{align*} \left\lvert\left(\Lambda^{H_{M}}\middle\backslash {}^{m}\mathscr{X}_{\gamma}^{\nu_{0}}(\Pi)\right)\left(\mathbf{F}_{q}\right)\right\rvert&=\left\lvert\left(\Lambda^{H_{M}}\middle\backslash\mathscr{X}_{\gamma}^{0,\xi}\right)\left(\mathbf{F}_{q}\right)\right\rvert +\sum_{\substack{L\in \mathcal{L}(M)\\ L\neq G}} q^{\frac{1}{2}\mathrm{val}\left(\det\left(\mathrm{ad} \gamma\mid\mathfrak{g}_{F}/\mathfrak{l}_{F}\right)\right)}\\ & \qquad \cdot \left\lvert\left(\Lambda^{H_{M}}\middle\backslash\mathscr{X}^{L,0,\xi^{L}}_{\gamma}\right)\left(\mathbf{F}_{q}\right)\right\rvert\cdot\left\lvert\Lambda^{\nu_{0}}_{L}\cap \pi_{L}(\Pi_{0})\right\rvert. \end{align*} $$
$$ \begin{align*} \left\lvert\left(\Lambda^{H_{M}}\middle\backslash {}^{m}\mathscr{X}_{\gamma}^{\nu_{0}}(\Pi)\right)\left(\mathbf{F}_{q}\right)\right\rvert&=\left\lvert\left(\Lambda^{H_{M}}\middle\backslash\mathscr{X}_{\gamma}^{0,\xi}\right)\left(\mathbf{F}_{q}\right)\right\rvert +\sum_{\substack{L\in \mathcal{L}(M)\\ L\neq G}} q^{\frac{1}{2}\mathrm{val}\left(\det\left(\mathrm{ad} \gamma\mid\mathfrak{g}_{F}/\mathfrak{l}_{F}\right)\right)}\\ & \qquad \cdot \left\lvert\left(\Lambda^{H_{M}}\middle\backslash\mathscr{X}^{L,0,\xi^{L}}_{\gamma}\right)\left(\mathbf{F}_{q}\right)\right\rvert\cdot\left\lvert\Lambda^{\nu_{0}}_{L}\cap \pi_{L}(\Pi_{0})\right\rvert. \end{align*} $$
4.2.2. The tail
As the polytope
![]() $\Pi $
satisfies
$\Pi $
satisfies
by the inclusion-exclusion principle we have
 $$ \begin{align} \left\lvert\left(\Lambda^{H_{M}}\middle\backslash {}^{t}\mathscr{X}_{\gamma}^{\nu_{0}}(\Pi)\right)\left(\mathbf{F}_{q}\right)\right\rvert=\sum_{\substack{Q\in \mathcal{F}(M)\\ Q\neq G}} (-1)^{\textrm{rk}(G)-\textrm{rk}(Q)-1}\left\lvert\left(\Lambda^{H_{M}}\middle\backslash \mathscr{X}_{\gamma}^{\nu_{0}}\left(E_{Q}(\Pi)\right)\right)\left(\mathbf{F}_{q}\right)\right\rvert, \end{align} $$
$$ \begin{align} \left\lvert\left(\Lambda^{H_{M}}\middle\backslash {}^{t}\mathscr{X}_{\gamma}^{\nu_{0}}(\Pi)\right)\left(\mathbf{F}_{q}\right)\right\rvert=\sum_{\substack{Q\in \mathcal{F}(M)\\ Q\neq G}} (-1)^{\textrm{rk}(G)-\textrm{rk}(Q)-1}\left\lvert\left(\Lambda^{H_{M}}\middle\backslash \mathscr{X}_{\gamma}^{\nu_{0}}\left(E_{Q}(\Pi)\right)\right)\left(\mathbf{F}_{q}\right)\right\rvert, \end{align} $$
where the notation
![]() $\textrm {rk}$
means the semisimple rank. Although the polytope
$\textrm {rk}$
means the semisimple rank. Although the polytope
![]() $E_{Q}(\Pi )$
is not
$E_{Q}(\Pi )$
is not
 $\Sigma _{\gamma }^{G,M}$
-regular, we can use the general Arthur–Kottwitz reduction, as explained in Remark 3.2, repeatedly to decompose
$\Sigma _{\gamma }^{G,M}$
-regular, we can use the general Arthur–Kottwitz reduction, as explained in Remark 3.2, repeatedly to decompose
![]() $\mathscr {X}_{\gamma }\left (E_{Q}(\Pi )\right )$
into locally closed subschemes which are iterated affine fibrations over
$\mathscr {X}_{\gamma }\left (E_{Q}(\Pi )\right )$
into locally closed subschemes which are iterated affine fibrations over
 $F_{\gamma }^{L, M}$
,
$F_{\gamma }^{L, M}$
,
![]() $L\in \mathcal {L}(M)$
. This gives a formula for
$L\in \mathcal {L}(M)$
. This gives a formula for
 $\left \lvert \left (\Lambda ^{H_{M}}\middle \backslash \mathscr {X}_{\gamma }^{\nu _{0}}\left (E_{Q}(\Pi )\right )\right )\left (\mathbf{F}_{q}\right )\right \rvert $
in terms of the
$\left \lvert \left (\Lambda ^{H_{M}}\middle \backslash \mathscr {X}_{\gamma }^{\nu _{0}}\left (E_{Q}(\Pi )\right )\right )\left (\mathbf{F}_{q}\right )\right \rvert $
in terms of the
 $\left \lvert \left (\Lambda ^{H_{M}}\middle \backslash F_{\gamma }^{L,M}\right )\left (\mathbf{F}_{q}\right )\right \rvert $
s, which can be further reduced to counting points on the fundamental domains by Proposition 3.8 and Corollary 3.10. This process applies to a large family of truncated affine Springer fibers.
$\left \lvert \left (\Lambda ^{H_{M}}\middle \backslash F_{\gamma }^{L,M}\right )\left (\mathbf{F}_{q}\right )\right \rvert $
s, which can be further reduced to counting points on the fundamental domains by Proposition 3.8 and Corollary 3.10. This process applies to a large family of truncated affine Springer fibers.
We introduce a family of operators on the set of all positive
![]() $(G,M)$
-orthogonal families. Recall that
$(G,M)$
-orthogonal families. Recall that
![]() $Q_{0}=MU_{0}$
is the unique parabolic subgroup in
$Q_{0}=MU_{0}$
is the unique parabolic subgroup in
![]() $\mathcal {P}(M)$
which contains
$\mathcal {P}(M)$
which contains
![]() $P_{0}$
. For
$P_{0}$
. For
![]() $L\in \mathcal {L}(M)$
, let
$L\in \mathcal {L}(M)$
, let
![]() $Q_{0}^{L}=Q_{0}\cap L$
. For a positive
$Q_{0}^{L}=Q_{0}\cap L$
. For a positive
![]() $(L,M)$
-orthogonal family, we say that two faces of it are conjugate if their associated parabolic subgroups are conjugate to each other by the Weyl group
$(L,M)$
-orthogonal family, we say that two faces of it are conjugate if their associated parabolic subgroups are conjugate to each other by the Weyl group
![]() $W_{L}/W_{M}$
. In particular, the edges of the polytope are parametrized by minimal elements in
$W_{L}/W_{M}$
. In particular, the edges of the polytope are parametrized by minimal elements in
![]() $\mathcal {F}^{L}(M)\backslash \{M\}$
. An edge is said to be of type
$\mathcal {F}^{L}(M)\backslash \{M\}$
. An edge is said to be of type
 $\alpha \in \Delta _{A_{M}}^{Q_{0}^{L}}:=\Phi (L,A)\cap \Phi (U_{0},A)\cap \Delta $
if it is conjugate to the edge having vertices
$\alpha \in \Delta _{A_{M}}^{Q_{0}^{L}}:=\Phi (L,A)\cap \Phi (U_{0},A)\cap \Delta $
if it is conjugate to the edge having vertices
![]() $\lambda _{Q^{L}_{0}},\lambda _{s_{\alpha }Q^{L}_{0}}$
, where
$\lambda _{Q^{L}_{0}},\lambda _{s_{\alpha }Q^{L}_{0}}$
, where
![]() $s_{\alpha }$
is the simple reflection associated to
$s_{\alpha }$
is the simple reflection associated to
![]() $\alpha $
. Let
$\alpha $
. Let
 $A_{M,\alpha }^{G,L}$
be the operator on the set of positive
$A_{M,\alpha }^{G,L}$
be the operator on the set of positive
![]() $(G,M)$
-orthogonal families defined as follows: as a polytope, it increases by
$(G,M)$
-orthogonal families defined as follows: as a polytope, it increases by
![]() $1$
the length of all the edges whose images in
$1$
the length of all the edges whose images in
![]() $\mathfrak {a}_{M}^{L}$
under the projection
$\mathfrak {a}_{M}^{L}$
under the projection
![]() $\pi _{M}^{L}$
are of type
$\pi _{M}^{L}$
are of type
![]() $\alpha $
, and keeps the lengths of all the others invariant. To check that it actually sends a positive
$\alpha $
, and keeps the lengths of all the others invariant. To check that it actually sends a positive
![]() $(G,M)$
-orthogonal family to another one, it suffices to verify for the faces of dimension
$(G,M)$
-orthogonal family to another one, it suffices to verify for the faces of dimension
![]() $2$
, but this is clear. Then we set the vertex
$2$
, but this is clear. Then we set the vertex
 $$ \begin{align*} \lambda_{Q_{0}}\left(A_{M,\alpha}^{G,L}(\Pi)\right)=\lambda_{Q_{0}}(\Pi)+\frac{1}{2}\pi_{M}\left(\varpi_{\alpha}^{\vee}\right), \end{align*} $$
$$ \begin{align*} \lambda_{Q_{0}}\left(A_{M,\alpha}^{G,L}(\Pi)\right)=\lambda_{Q_{0}}(\Pi)+\frac{1}{2}\pi_{M}\left(\varpi_{\alpha}^{\vee}\right), \end{align*} $$
to make
 $A_{M,\alpha }^{G,L}(\Pi )$
symmetric with respect to
$A_{M,\alpha }^{G,L}(\Pi )$
symmetric with respect to
![]() $\Pi $
. Here
$\Pi $
. Here
![]() $\varpi _{\alpha }^{\vee }$
is the fundamental coweight corresponding to
$\varpi _{\alpha }^{\vee }$
is the fundamental coweight corresponding to
![]() $\alpha $
. By definition, we see that the operators
$\alpha $
. By definition, we see that the operators
 $A_{M,\alpha }^{G,L}$
commute with each other. When
$A_{M,\alpha }^{G,L}$
commute with each other. When
![]() $G=L$
, we simplify the notation
$G=L$
, we simplify the notation
 $A_{M,\alpha }^{G,G}$
to
$A_{M,\alpha }^{G,G}$
to
 $A_{M,\alpha }^{G}$
.
$A_{M,\alpha }^{G}$
.
Given a tuple of nonnegative integers
![]() $\underline {n}=(n_{\alpha })$
,
$\underline {n}=(n_{\alpha })$
,
 $\alpha \in \Delta _{A_{M}}^{Q_{0}^{L}}$
, let
$\alpha \in \Delta _{A_{M}}^{Q_{0}^{L}}$
, let
 $$ \begin{align} \Sigma_{\gamma}^{\underline{n}} =\prod_{\alpha\in \Delta_{A_{M}}^{Q_{0}^{L}}}\left(A_{M,\alpha}^{G,L}\right)^{n_{\alpha}}\left(\Sigma_{\gamma}\right). \end{align} $$
$$ \begin{align} \Sigma_{\gamma}^{\underline{n}} =\prod_{\alpha\in \Delta_{A_{M}}^{Q_{0}^{L}}}\left(A_{M,\alpha}^{G,L}\right)^{n_{\alpha}}\left(\Sigma_{\gamma}\right). \end{align} $$
It is easy to see that the polytopes
![]() $E_{Q}(\Pi )$
can be made by iterating this process. For
$E_{Q}(\Pi )$
can be made by iterating this process. For
 $\alpha \in \Delta _{A_{M}}^{Q_{0}^{L}}$
, let
$\alpha \in \Delta _{A_{M}}^{Q_{0}^{L}}$
, let
![]() $1_{\alpha }$
be the tuple taking value
$1_{\alpha }$
be the tuple taking value
![]() $1$
at
$1$
at
![]() $\alpha $
and
$\alpha $
and
![]() $0$
otherwhere. By Remark 3.2, the Arthur–Kottwitz reduction works for the complement
$0$
otherwhere. By Remark 3.2, the Arthur–Kottwitz reduction works for the complement
 $\mathscr {X}_{\gamma }\left (\Sigma _{\gamma }^{\underline {n}+1_{\alpha }}\right ) \Big \backslash \mathscr {X}_{\gamma }\left (\Sigma _{\gamma }^{\underline {n}}\right )$
. The process is completely the same as explained in §3.3, so we do not repeat it here. The resulting strata are iterated affine fibrations over truncated affine Springer fibers of the form
$\mathscr {X}_{\gamma }\left (\Sigma _{\gamma }^{\underline {n}+1_{\alpha }}\right ) \Big \backslash \mathscr {X}_{\gamma }\left (\Sigma _{\gamma }^{\underline {n}}\right )$
. The process is completely the same as explained in §3.3, so we do not repeat it here. The resulting strata are iterated affine fibrations over truncated affine Springer fibers of the form
 $\mathscr {X}_{\gamma }^{L,\nu '}\left (\Sigma _{\gamma }^{L,(\underline {n}')}\right )$
,
$\mathscr {X}_{\gamma }^{L,\nu '}\left (\Sigma _{\gamma }^{L,(\underline {n}')}\right )$
,
![]() $L\in \mathcal {L}(M),\nu '\in \Lambda _{L}$
. Iterating this process,
$L\in \mathcal {L}(M),\nu '\in \Lambda _{L}$
. Iterating this process,
 $\mathscr {X}_{\gamma }\left (\Sigma _{\gamma }^{\underline {n}}\right )$
can be decomposed as a disjoint union of locally closed subschemes, which are iterated affine fibrations over
$\mathscr {X}_{\gamma }\left (\Sigma _{\gamma }^{\underline {n}}\right )$
can be decomposed as a disjoint union of locally closed subschemes, which are iterated affine fibrations over
 $F_{\gamma }^{L,M,\mu }$
,
$F_{\gamma }^{L,M,\mu }$
,
![]() $L\in \mathcal {L}(M),\mu \in \Lambda _{L}$
. In particular, counting points on
$L\in \mathcal {L}(M),\mu \in \Lambda _{L}$
. In particular, counting points on
 $\Lambda ^{H_{M}}\big \backslash \mathscr {X}_{\gamma }\left (\Sigma _{\gamma }^{\underline {n}}\right )$
can be reduced to counting points on
$\Lambda ^{H_{M}}\big \backslash \mathscr {X}_{\gamma }\left (\Sigma _{\gamma }^{\underline {n}}\right )$
can be reduced to counting points on
 $\Lambda ^{H_{M}}\big \backslash F_{\gamma }^{L,M,\mu }$
, which can be further reduced to counting points on the fundamental domains
$\Lambda ^{H_{M}}\big \backslash F_{\gamma }^{L,M,\mu }$
, which can be further reduced to counting points on the fundamental domains
 $F_{\gamma }^{L'}$
,
$F_{\gamma }^{L'}$
,
![]() $L'\in \mathcal {L}(M_{0}),$
as we have explained in §3.2. This process applies to counting points on
$L'\in \mathcal {L}(M_{0}),$
as we have explained in §3.2. This process applies to counting points on
 $ \Lambda ^{H_{M}}\big \backslash \mathscr {X}_{\gamma }^{\nu _{0}}\left (E_{Q}(\Pi )\right ). $
By equation (4.6), it gives an expression of
$ \Lambda ^{H_{M}}\big \backslash \mathscr {X}_{\gamma }^{\nu _{0}}\left (E_{Q}(\Pi )\right ). $
By equation (4.6), it gives an expression of
 $\left \lvert \left (\Lambda ^{H_{M}}\middle \backslash {}^{t}\mathscr {X}_{\gamma }^{\nu _{0}}(\Pi )\right )\left (\mathbf{F}_{q}\right )\right \rvert $
in terms of
$\left \lvert \left (\Lambda ^{H_{M}}\middle \backslash {}^{t}\mathscr {X}_{\gamma }^{\nu _{0}}(\Pi )\right )\left (\mathbf{F}_{q}\right )\right \rvert $
in terms of
 $\left \lvert F_{\gamma }^{L}\left (\mathbf{F}_{q}\right )\right \rvert $
,
$\left \lvert F_{\gamma }^{L}\left (\mathbf{F}_{q}\right )\right \rvert $
,
![]() $L\in \mathcal {L}(M_{0})$
.
$L\in \mathcal {L}(M_{0})$
.
4.3. Application to Arthur’s weighted orbital integral
By Theorem 2.8 and Proposition 4.3, Arthur’s weighted orbital integral
![]() $J_{M}(\gamma )$
calculates essentially
$J_{M}(\gamma )$
calculates essentially
 $\left \lvert \left (\Lambda ^{H_{M}}\middle \backslash \mathscr {X}_{\gamma }^{0,\xi }\right )\left (\mathbf{F}_{q}\right )\right \rvert $
, as
$\left \lvert \left (\Lambda ^{H_{M}}\middle \backslash \mathscr {X}_{\gamma }^{0,\xi }\right )\left (\mathbf{F}_{q}\right )\right \rvert $
, as
 $\mathscr {X}^{G_{\text {der}}}\cap \mathscr {X}_{\gamma }^{\xi }$
is the union of
$\mathscr {X}^{G_{\text {der}}}\cap \mathscr {X}_{\gamma }^{\xi }$
is the union of
![]() $\left \lvert \Lambda _{G_{\text {der}}}\right \rvert $
-copies of
$\left \lvert \Lambda _{G_{\text {der}}}\right \rvert $
-copies of
 $\mathscr {X}_{\gamma }^{0,\xi }$
. The two approaches in §3 and §4 to calculating
$\mathscr {X}_{\gamma }^{0,\xi }$
. The two approaches in §3 and §4 to calculating
 $\left \lvert \left (\Lambda ^{H_{M}}\middle \backslash \mathscr {X}_{\gamma }^{0}(\Pi )\right )\left (\mathbf{F}_{q}\right )\right \rvert $
give us a recurrence relation involving
$\left \lvert \left (\Lambda ^{H_{M}}\middle \backslash \mathscr {X}_{\gamma }^{0}(\Pi )\right )\left (\mathbf{F}_{q}\right )\right \rvert $
give us a recurrence relation involving
 $\left \lvert \left (\Lambda ^{H_{M}}\middle \backslash F_{\gamma }^{L, M,\mu }\right )\left (\mathbf{F}_{q}\right )\right \rvert $
and
$\left \lvert \left (\Lambda ^{H_{M}}\middle \backslash F_{\gamma }^{L, M,\mu }\right )\left (\mathbf{F}_{q}\right )\right \rvert $
and
 $\left \lvert \left (\Lambda ^{H_{M}} \big\backslash \mathscr {X}_{\gamma }^{L,0,\xi ^{L}}\right )\left (\mathbf{F}_{q}\right )\right \rvert $
, for
$\left \lvert \left (\Lambda ^{H_{M}} \big\backslash \mathscr {X}_{\gamma }^{L,0,\xi ^{L}}\right )\left (\mathbf{F}_{q}\right )\right \rvert $
, for
![]() $L\in \mathcal {L}(M), \mu \in \Lambda _{L^{\mathrm{ad}}}$
. If we are able to solve this recurrence relation, we will get an expression for
$L\in \mathcal {L}(M), \mu \in \Lambda _{L^{\mathrm{ad}}}$
. If we are able to solve this recurrence relation, we will get an expression for
 $\left \lvert \left (\Lambda ^{H_{M}}\middle \backslash \mathscr {X}_{\gamma }^{0,\xi }\right )\left (\mathbf{F}_{q}\right )\right \rvert $
in terms of
$\left \lvert \left (\Lambda ^{H_{M}}\middle \backslash \mathscr {X}_{\gamma }^{0,\xi }\right )\left (\mathbf{F}_{q}\right )\right \rvert $
in terms of
 $\left \lvert \left (\Lambda ^{H_{M}}\middle \backslash F_{\gamma }^{L, M,\mu }\right )\left (\mathbf{F}_{q}\right )\right \rvert $
s, which can be further reduced to counting points on fundamental domains, as explained in §3.2.
$\left \lvert \left (\Lambda ^{H_{M}}\middle \backslash F_{\gamma }^{L, M,\mu }\right )\left (\mathbf{F}_{q}\right )\right \rvert $
s, which can be further reduced to counting points on fundamental domains, as explained in §3.2.
5. Calculations for the group
 $\textrm {GL}_{2}$
$\textrm {GL}_{2}$
Let
![]() $G=\textrm {GL}_{2}$
and let
$G=\textrm {GL}_{2}$
and let
![]() $\gamma \in \mathfrak {gl}_{2}(F)$
be a regular semisimple integral element. Assume that
$\gamma \in \mathfrak {gl}_{2}(F)$
be a regular semisimple integral element. Assume that
![]() $\text {char}(k)>2$
and the splitting field of
$\text {char}(k)>2$
and the splitting field of
![]() $\gamma $
is totally ramified over F. The torus T is isomorphic either to
$\gamma $
is totally ramified over F. The torus T is isomorphic either to
![]() $F^{\times }\times F^{\times }$
or to
$F^{\times }\times F^{\times }$
or to
![]() $\textrm {Res}_{E/F}E^{\times }$
, where E is a separable totally ramified field extension over F of degree
$\textrm {Res}_{E/F}E^{\times }$
, where E is a separable totally ramified field extension over F of degree
![]() $2$
. We call elements
$2$
. We call elements
![]() $\gamma $
in these cases split and anisotropic, respectively.
$\gamma $
in these cases split and anisotropic, respectively.
5.1. Split elements
We can take T to be the maximal torus of G of the diagonal matrices and
![]() $\gamma \in \mathfrak {t}(\mathcal {O})$
a regular element. Let
$\gamma \in \mathfrak {t}(\mathcal {O})$
a regular element. Let
which we call the root valuation of
![]() $\gamma $
. The dimension of the affine Springer fiber
$\gamma $
. The dimension of the affine Springer fiber
![]() $\mathscr {X}_{\gamma }$
is known to be
$\mathscr {X}_{\gamma }$
is known to be
In the remainder of this section, we assume that
![]() $n\geq 1$
, as the case
$n\geq 1$
, as the case
![]() $n=0$
reduces to the group
$n=0$
reduces to the group
![]() $\textrm {GL}_{1}$
. Recall that we have calculated
$\textrm {GL}_{1}$
. Recall that we have calculated
![]() $F_{\gamma }$
in [Reference Chaudouard and Laumon11]. Let
$F_{\gamma }$
in [Reference Chaudouard and Laumon11]. Let
![]() $X_{*}(T)\cong \textbf {Z}^{2}$
be the usual identification, set
$X_{*}(T)\cong \textbf {Z}^{2}$
be the usual identification, set
![]() $(n,0)\in \textbf {Z}^{2}$
, and let
$(n,0)\in \textbf {Z}^{2}$
, and let
 $$ \begin{align*} \textrm{Sch}(n,0)=\overline{K \begin{pmatrix}\epsilon^{n}&\\ &1\end{pmatrix}K/K}. \end{align*} $$
$$ \begin{align*} \textrm{Sch}(n,0)=\overline{K \begin{pmatrix}\epsilon^{n}&\\ &1\end{pmatrix}K/K}. \end{align*} $$
We have
![]() $F_{\gamma }\cong \textrm {Sch}(n,0)$
, and its number of rational points is
$F_{\gamma }\cong \textrm {Sch}(n,0)$
, and its number of rational points is
 $$ \begin{align*} \left\lvert F_{\gamma}\left(\mathbf{F}_{q}\right)\right\rvert=\sum_{i=0}^{n}q^{i} \end{align*} $$
$$ \begin{align*} \left\lvert F_{\gamma}\left(\mathbf{F}_{q}\right)\right\rvert=\sum_{i=0}^{n}q^{i} \end{align*} $$
by the Bruhat–Tits decomposition of
![]() $\textrm {Sch}(n,0)$
. As
$\textrm {Sch}(n,0)$
. As
![]() $\Lambda _{\textrm {PGL}_{2}}=\textbf {Z}/2$
,
$\Lambda _{\textrm {PGL}_{2}}=\textbf {Z}/2$
,
![]() $F_{\gamma }$
has only one variant
$F_{\gamma }$
has only one variant
![]() $F_{\gamma }^{1}$
; we can calculate its number of rational points to be
$F_{\gamma }^{1}$
; we can calculate its number of rational points to be
 $$ \begin{align*} F_{\gamma}^{1}\left(\mathbf{F}_{q}\right)=\sum_{i=0}^{n-1}q^{i}. \end{align*} $$
$$ \begin{align*} F_{\gamma}^{1}\left(\mathbf{F}_{q}\right)=\sum_{i=0}^{n-1}q^{i}. \end{align*} $$
Set
![]() $a\in \textbf {N}$
and let
$a\in \textbf {N}$
and let
![]() $\Pi $
be the positive
$\Pi $
be the positive
![]() $(G,T)$
-orthogonal family defined by
$(G,T)$
-orthogonal family defined by
Assume that
![]() $a\gg 0$
. Then
$a\gg 0$
. Then
![]() $\Pi $
is sufficiently regular in the sense of §4.2. We can easily calculate
$\Pi $
is sufficiently regular in the sense of §4.2. We can easily calculate
 $$ \begin{align*} Q_{\gamma}^{0}(a):=\left\lvert\mathscr{X}_{\gamma}^{0}(\Pi)\left(\mathbf{F}_{q}\right)\right\rvert=\sum_{i=0}^{n}q^{i}+2q^{n}a, \end{align*} $$
$$ \begin{align*} Q_{\gamma}^{0}(a):=\left\lvert\mathscr{X}_{\gamma}^{0}(\Pi)\left(\mathbf{F}_{q}\right)\right\rvert=\sum_{i=0}^{n}q^{i}+2q^{n}a, \end{align*} $$
by the Arthur–Kottwitz reduction. We see that
 $Q_{\gamma }^{0}(a)$
is polynomial in a. By Theorem 4.8, we have
$Q_{\gamma }^{0}(a)$
is polynomial in a. By Theorem 4.8, we have
 $$ \begin{align*} \left\lvert {}^{m}\mathscr{X}_{\gamma}^{0}(\Pi)\left(\mathbf{F}_{q}\right)\right\rvert=\left\lvert \mathscr{X}_{\gamma}^{0,\xi}\left(\mathbf{F}_{q}\right)\right\rvert+[2a-(n+1)]q^{n}. \end{align*} $$
$$ \begin{align*} \left\lvert {}^{m}\mathscr{X}_{\gamma}^{0}(\Pi)\left(\mathbf{F}_{q}\right)\right\rvert=\left\lvert \mathscr{X}_{\gamma}^{0,\xi}\left(\mathbf{F}_{q}\right)\right\rvert+[2a-(n+1)]q^{n}. \end{align*} $$
The tail is the disjoint union of two fundamental domains, so its number of rational points is
 $$ \begin{align*} \left\lvert {}^{t}\mathscr{X}_{\gamma}^{0}(\Pi)\left(\mathbf{F}_{q}\right)\right\rvert=2\sum_{i=0}^{n}q^{i}. \end{align*} $$
$$ \begin{align*} \left\lvert {}^{t}\mathscr{X}_{\gamma}^{0}(\Pi)\left(\mathbf{F}_{q}\right)\right\rvert=2\sum_{i=0}^{n}q^{i}. \end{align*} $$
Because
 $$ \begin{align*} \left\lvert \mathscr{X}_{\gamma}^{0}(\Pi)\left(\mathbf{F}_{q}\right)\right\rvert=\left\lvert {}^{m}\mathscr{X}_{\gamma}^{0}(\Pi)\left(\mathbf{F}_{q}\right)\right\rvert+\left\lvert {}^{t}\mathscr{X}_{\gamma}^{0}(\Pi)\left(\mathbf{F}_{q}\right)\right\rvert, \end{align*} $$
$$ \begin{align*} \left\lvert \mathscr{X}_{\gamma}^{0}(\Pi)\left(\mathbf{F}_{q}\right)\right\rvert=\left\lvert {}^{m}\mathscr{X}_{\gamma}^{0}(\Pi)\left(\mathbf{F}_{q}\right)\right\rvert+\left\lvert {}^{t}\mathscr{X}_{\gamma}^{0}(\Pi)\left(\mathbf{F}_{q}\right)\right\rvert, \end{align*} $$
we get the equation
 $$ \begin{align*} \sum_{i=0}^{n}q^{i}+2aq^{n}=\left\lvert \mathscr{X}_{\gamma}^{0,\xi}\left(\mathbf{F}_{q}\right)\right\rvert+[2a-(n+1)]q^{n}+2\sum_{i=0}^{n}q^{i}. \end{align*} $$
$$ \begin{align*} \sum_{i=0}^{n}q^{i}+2aq^{n}=\left\lvert \mathscr{X}_{\gamma}^{0,\xi}\left(\mathbf{F}_{q}\right)\right\rvert+[2a-(n+1)]q^{n}+2\sum_{i=0}^{n}q^{i}. \end{align*} $$
Solving it, we get
 $$ \begin{align} \left\lvert\mathscr{X}_{\gamma}^{0,\xi}\left(\mathbf{F}_{q}\right)\right\rvert=nq^{n}-\sum_{i=0}^{n-1}q^{i}. \end{align} $$
$$ \begin{align} \left\lvert\mathscr{X}_{\gamma}^{0,\xi}\left(\mathbf{F}_{q}\right)\right\rvert=nq^{n}-\sum_{i=0}^{n-1}q^{i}. \end{align} $$
Now that
![]() $T(F)^{1}=T(\mathcal {O})=T(F)_{1}$
has volume
$T(F)^{1}=T(\mathcal {O})=T(F)_{1}$
has volume
![]() $1$
, by Proposition 4.3 we have
$1$
, by Proposition 4.3 we have
 $$ \begin{align*} J_{T}^{\xi}(\gamma)=\left\lvert\mathscr{X}_{\gamma}^{0,\xi}\left(\mathbf{F}_{q}\right)\right\rvert=nq^{n}-\sum_{i=0}^{n-1}q^{i}. \end{align*} $$
$$ \begin{align*} J_{T}^{\xi}(\gamma)=\left\lvert\mathscr{X}_{\gamma}^{0,\xi}\left(\mathbf{F}_{q}\right)\right\rvert=nq^{n}-\sum_{i=0}^{n-1}q^{i}. \end{align*} $$
On the other hand, we can use equation (2.4) to easily calculate the orbital integral
 $$ \begin{align*} I^{G}_{\gamma}=q^{n}. \end{align*} $$
$$ \begin{align*} I^{G}_{\gamma}=q^{n}. \end{align*} $$
Combined with Theorem 2.8, the foregoing calculations can be summarized as follows:
Theorem 5.1. Let
![]() $\gamma \in \mathfrak {gl}_{2}(F)$
be a regular semisimple integral element of root valuation n. It has orbital integral
$\gamma \in \mathfrak {gl}_{2}(F)$
be a regular semisimple integral element of root valuation n. It has orbital integral
 $ I^{G}_{\gamma }=q^{n}. $
The number of rational points on
$ I^{G}_{\gamma }=q^{n}. $
The number of rational points on
 $\mathscr {X}_{\gamma }^{0}(\Pi )$
is
$\mathscr {X}_{\gamma }^{0}(\Pi )$
is
 $$ \begin{align*} \left\lvert\mathscr{X}_{\gamma}^{0}(\Pi)\left(\mathbf{F}_{q}\right)\right\rvert=\sum_{i=0}^{n}q^{i}+2aq^{n}, \end{align*} $$
$$ \begin{align*} \left\lvert\mathscr{X}_{\gamma}^{0}(\Pi)\left(\mathbf{F}_{q}\right)\right\rvert=\sum_{i=0}^{n}q^{i}+2aq^{n}, \end{align*} $$
and Arthur’s weighted orbital integral
![]() $J_{T}(\gamma )$
equals
$J_{T}(\gamma )$
equals
 $$ \begin{align*} J_{T}(\gamma)=\mathrm{vol}\left(\mathfrak{a}_{T_{\textrm{SL}_{2}}}^{\textrm{SL}_{2}}\middle/X_{*}\left(T_{\textrm{SL}_{2}}\right)\right)\cdot \left[nq^{n}-\sum_{i=0}^{n-1}q^{i}\right]. \end{align*} $$
$$ \begin{align*} J_{T}(\gamma)=\mathrm{vol}\left(\mathfrak{a}_{T_{\textrm{SL}_{2}}}^{\textrm{SL}_{2}}\middle/X_{*}\left(T_{\textrm{SL}_{2}}\right)\right)\cdot \left[nq^{n}-\sum_{i=0}^{n-1}q^{i}\right]. \end{align*} $$
5.2. Anisotropic elements
In this case,
 $E=\mathbf{F}_{q} (\! (\epsilon ^{\frac {1}{2}} )\! )$
. Suppose that
$E=\mathbf{F}_{q} (\! (\epsilon ^{\frac {1}{2}} )\! )$
. Suppose that
 $\gamma =a+ b\epsilon ^{\frac {1}{2}}$
under the isomorphism
$\gamma =a+ b\epsilon ^{\frac {1}{2}}$
under the isomorphism
![]() $Z_{G(F)}(\gamma )\cong \textrm {Res}_{E/F}E^{\times }$
, with
$Z_{G(F)}(\gamma )\cong \textrm {Res}_{E/F}E^{\times }$
, with
![]() $a,b\in \mathcal {O}$
. Under the basis
$a,b\in \mathcal {O}$
. Under the basis
 $\left \{\epsilon ^{\frac {1}{2}},1\right \}$
of E over
$\left \{\epsilon ^{\frac {1}{2}},1\right \}$
of E over
![]() $\mathbf{F}_{q}(\!(\epsilon )\!)$
, the element
$\mathbf{F}_{q}(\!(\epsilon )\!)$
, the element
![]() $\gamma $
is of the form
$\gamma $
is of the form
 $$ \begin{align*} \gamma=\begin{bmatrix} a&b\\ b\epsilon&a \end{bmatrix}. \end{align*} $$
$$ \begin{align*} \gamma=\begin{bmatrix} a&b\\ b\epsilon&a \end{bmatrix}. \end{align*} $$
It is clear that the affine Springer fibers
![]() $\mathscr {X}_{\gamma }$
and
$\mathscr {X}_{\gamma }$
and
![]() $\mathscr {X}_{-a+\gamma }$
are isomorphic, so we can assume that
$\mathscr {X}_{-a+\gamma }$
are isomorphic, so we can assume that
![]() $a=0$
. Let
$a=0$
. Let
![]() $b=b_{0}\epsilon ^{n}$
,
$b=b_{0}\epsilon ^{n}$
,
![]() $b_{0}\in \mathcal {O}^{\times }$
. We can write
$b_{0}\in \mathcal {O}^{\times }$
. We can write
 $$ \begin{align} \gamma=\begin{bmatrix} &b_{0}\epsilon^{n}\\ b_{0}\epsilon^{n+1}& \end{bmatrix}. \end{align} $$
$$ \begin{align} \gamma=\begin{bmatrix} &b_{0}\epsilon^{n}\\ b_{0}\epsilon^{n+1}& \end{bmatrix}. \end{align} $$
Put in this form, it has been shown by Goresky, Kottwitz, and MacPherson [Reference Goresky, Kottwitz and MacPherson16] that
![]() $\mathscr {X}_{\gamma }$
admits an affine paving which is induced by the standard Bruhat–Tits decomposition of the affine Grassmannian. More precisely, let I be the standard Iwahori subgroup – that is, it is the preimage of
$\mathscr {X}_{\gamma }$
admits an affine paving which is induced by the standard Bruhat–Tits decomposition of the affine Grassmannian. More precisely, let I be the standard Iwahori subgroup – that is, it is the preimage of
![]() $B_{0}$
under the reduction
$B_{0}$
under the reduction
![]() $G(\mathcal {O})\to G$
. Then
$G(\mathcal {O})\to G$
. Then
 $$ \begin{align*} \mathscr{X}_{\gamma}=\bigsqcup_{\left(a_{1},a_{2}\right)\in \textbf{Z}^{2}} \mathscr{X}_{\gamma}\cap I\begin{pmatrix} \epsilon^{a_{1}}&\\ &\epsilon^{a_{2}} \end{pmatrix}K/K, \end{align*} $$
$$ \begin{align*} \mathscr{X}_{\gamma}=\bigsqcup_{\left(a_{1},a_{2}\right)\in \textbf{Z}^{2}} \mathscr{X}_{\gamma}\cap I\begin{pmatrix} \epsilon^{a_{1}}&\\ &\epsilon^{a_{2}} \end{pmatrix}K/K, \end{align*} $$
and each intersection, denoted
![]() $S_{\textbf {a}}$
, is isomorphic to a standard affine space. We calculate that
$S_{\textbf {a}}$
, is isomorphic to a standard affine space. We calculate that
![]() $S_{\textbf {a}}$
is not empty if and only if
$S_{\textbf {a}}$
is not empty if and only if
and that
 $$ \begin{align*} \dim(S_{\textbf{a}})= \begin{cases} a_{1}-a_{2} &\text{if } a_{1}\geq a_{2},\\ a_{2}-a_{1}-1 &\text{if } a_{1}< a_{2}. \end{cases} \end{align*} $$
$$ \begin{align*} \dim(S_{\textbf{a}})= \begin{cases} a_{1}-a_{2} &\text{if } a_{1}\geq a_{2},\\ a_{2}-a_{1}-1 &\text{if } a_{1}< a_{2}. \end{cases} \end{align*} $$
Notice that this is also the dimension of
 $I\begin {pmatrix} \epsilon ^{a_{1}}&\\ &\epsilon ^{a_{2}} \end {pmatrix}K/K$
, so they must be the same. Summarizing the foregoing calculations, and noting that
$I\begin {pmatrix} \epsilon ^{a_{1}}&\\ &\epsilon ^{a_{2}} \end {pmatrix}K/K$
, so they must be the same. Summarizing the foregoing calculations, and noting that
![]() $T(F)^{1}=T(\mathcal {O})=T(F)_{1}$
has volume
$T(F)^{1}=T(\mathcal {O})=T(F)_{1}$
has volume
![]() $1$
, we get the following:
$1$
, we get the following:
Theorem 5.2. Let
![]() $\gamma $
be matrix (5.2). For
$\gamma $
be matrix (5.2). For
![]() $(a_{1},a_{2})\in \textbf {Z}^{2}$
, we have
$(a_{1},a_{2})\in \textbf {Z}^{2}$
, we have
 $$ \begin{align*} \mathscr{X}_{\gamma}\cap I \begin{pmatrix} \epsilon^{a_{1}}&\\ &\epsilon^{a_{2}} \end{pmatrix} K/K= \begin{cases} I \begin{pmatrix} \epsilon^{a_{1}}&\\ &\epsilon^{a_{2}} \end{pmatrix} K/K &\text{if } -(n+1)\leq a_{1}- a_{2}\leq n,\\ \emptyset &\text{if not}. \end{cases} \end{align*} $$
$$ \begin{align*} \mathscr{X}_{\gamma}\cap I \begin{pmatrix} \epsilon^{a_{1}}&\\ &\epsilon^{a_{2}} \end{pmatrix} K/K= \begin{cases} I \begin{pmatrix} \epsilon^{a_{1}}&\\ &\epsilon^{a_{2}} \end{pmatrix} K/K &\text{if } -(n+1)\leq a_{1}- a_{2}\leq n,\\ \emptyset &\text{if not}. \end{cases} \end{align*} $$
As a corollary, we have
 $$ \begin{align*} J_{G}(\gamma)=I^{G}_{\gamma}=\left\lvert F_{\gamma}\left(\mathbf{F}_{q}\right)\right\rvert=\sum_{i=0}^{n} q^{i}. \end{align*} $$
$$ \begin{align*} J_{G}(\gamma)=I^{G}_{\gamma}=\left\lvert F_{\gamma}\left(\mathbf{F}_{q}\right)\right\rvert=\sum_{i=0}^{n} q^{i}. \end{align*} $$
6. Calculations for
 $\textrm {GL}_{3}$
-split case
$\textrm {GL}_{3}$
-split case
Let
![]() $G=\textrm {GL}_{3}$
and let
$G=\textrm {GL}_{3}$
and let
![]() $\gamma \in \mathfrak {gl}_{3}(F)$
be a regular semisimple integral element. Assume that
$\gamma \in \mathfrak {gl}_{3}(F)$
be a regular semisimple integral element. Assume that
![]() $\text {char}(k)>3$
and the splitting field of
$\text {char}(k)>3$
and the splitting field of
![]() $\gamma $
is totally ramified over F. The torus T is isomorphic to either
$\gamma $
is totally ramified over F. The torus T is isomorphic to either
![]() $F^{\times }\times F^{\times }\times F^{\times }$
or
$F^{\times }\times F^{\times }\times F^{\times }$
or
![]() $F^{\times }\times \textrm {Res}_{E_{2}/F}E_{2}^{\times }$
or
$F^{\times }\times \textrm {Res}_{E_{2}/F}E_{2}^{\times }$
or
![]() $\textrm {Res}_{E_{3}/F}E_{3}^{\times }$
, where
$\textrm {Res}_{E_{3}/F}E_{3}^{\times }$
, where
![]() $E_{2}, E_{3}$
are separable totally ramified field extensions over F of degree
$E_{2}, E_{3}$
are separable totally ramified field extensions over F of degree
![]() $2$
and
$2$
and
![]() $3$
, respectively. We call elements
$3$
, respectively. We call elements
![]() $\gamma $
in these cases split, mixed, and anisotropic respectively. Notice that in all these cases,
$\gamma $
in these cases split, mixed, and anisotropic respectively. Notice that in all these cases,
![]() $T(F)^{1}=T(\mathcal {O})=T(F)_{1}$
has volume
$T(F)^{1}=T(\mathcal {O})=T(F)_{1}$
has volume
![]() $1$
; hence by Proposition 4.3 we have
$1$
; hence by Proposition 4.3 we have
 $$ \begin{align*} J_{M}^{\xi}(\gamma)=\left\lvert\mathscr{X}_{\gamma}^{0,\xi}\left(\mathbf{F}_{q}\right)\right\rvert, \end{align*} $$
$$ \begin{align*} J_{M}^{\xi}(\gamma)=\left\lvert\mathscr{X}_{\gamma}^{0,\xi}\left(\mathbf{F}_{q}\right)\right\rvert, \end{align*} $$
and so
 $$ \begin{align*} J_{M}(\gamma)=\mathrm{vol}\left(\mathfrak{a}_{M_{\textrm{SL}_{3}}}^{\textrm{SL}_{3}}\middle/X_{*}\left(M_{\textrm{SL}_{3}}\right)\right) \cdot\left\lvert\mathscr{X}_{\gamma}^{0,\xi}\left(\mathbf{F}_{q}\right)\right\rvert \end{align*} $$
$$ \begin{align*} J_{M}(\gamma)=\mathrm{vol}\left(\mathfrak{a}_{M_{\textrm{SL}_{3}}}^{\textrm{SL}_{3}}\middle/X_{*}\left(M_{\textrm{SL}_{3}}\right)\right) \cdot\left\lvert\mathscr{X}_{\gamma}^{0,\xi}\left(\mathbf{F}_{q}\right)\right\rvert \end{align*} $$
by Theorem 2.8 and Remark 2.3.
In this section, we restrict ourselves to the split case. After conjugation, we take T to be the maximal torus of G of the diagonal matrices. Then
![]() $M_{0}=T$
and the other proper Levi subgroups in
$M_{0}=T$
and the other proper Levi subgroups in
![]() $\mathcal {L}(T)$
can be parametrized as follows: for a nonempty subset
$\mathcal {L}(T)$
can be parametrized as follows: for a nonempty subset
![]() $I\subsetneq \{1,2,3\}$
, let
$I\subsetneq \{1,2,3\}$
, let
![]() $P_{I}$
be the parabolic subgroup of G which stabilizes the flag
$P_{I}$
be the parabolic subgroup of G which stabilizes the flag
 $$ \begin{align*} \bigoplus_{i=1}^{3}\mathbf{F}_{q} e_{i}\supsetneq \bigoplus_{i\notin I}\mathbf{F}_{q} e_{i}\supsetneq \emptyset. \end{align*} $$
$$ \begin{align*} \bigoplus_{i=1}^{3}\mathbf{F}_{q} e_{i}\supsetneq \bigoplus_{i\notin I}\mathbf{F}_{q} e_{i}\supsetneq \emptyset. \end{align*} $$
Let
![]() $P_{I}=M_{I}N_{I}$
be the standard Levi factorization. We have
$P_{I}=M_{I}N_{I}$
be the standard Levi factorization. We have
![]() $M_{I}\cong \textrm {GL}_{2}\times \textrm {GL}_{1}$
. As
$M_{I}\cong \textrm {GL}_{2}\times \textrm {GL}_{1}$
. As
![]() $M_{I}=M_{I^{c}}$
, with
$M_{I}=M_{I^{c}}$
, with
![]() $I^{c}$
the complement of I, it is enough to calculate
$I^{c}$
the complement of I, it is enough to calculate
![]() $J_{T}(\gamma )$
and
$J_{T}(\gamma )$
and
![]() $J_{M_{\{i\}}}(\gamma )$
,
$J_{M_{\{i\}}}(\gamma )$
,
![]() $i=1,2,3$
.
$i=1,2,3$
.
Let
![]() $\gamma \in \mathfrak {t}(\mathcal {O})$
be a regular element. As we show in the appendix of [Reference Chen9], up to conjugation by the Weyl group we can suppose that
$\gamma \in \mathfrak {t}(\mathcal {O})$
be a regular element. As we show in the appendix of [Reference Chen9], up to conjugation by the Weyl group we can suppose that
In this case,
![]() $\gamma $
is said to be in minimal form, and we call
$\gamma $
is said to be in minimal form, and we call
 $$ \begin{align*} (n_{1},n_{2})=\big(\mathrm{val}(\alpha_{12}(\gamma)),\mathrm{val}(\alpha_{23}(\gamma))\big) \end{align*} $$
$$ \begin{align*} (n_{1},n_{2})=\big(\mathrm{val}(\alpha_{12}(\gamma)),\mathrm{val}(\alpha_{23}(\gamma))\big) \end{align*} $$
the root valuation of
![]() $\gamma $
. The dimension of the affine Springer fiber
$\gamma $
. The dimension of the affine Springer fiber
![]() $\mathscr {X}_{\gamma }$
is known to be
$\mathscr {X}_{\gamma }$
is known to be
In the remainder of the section, we assume that
![]() $n_{1}\geq 1$
, as the case
$n_{1}\geq 1$
, as the case
![]() $n_{1}=0$
reduces to the group
$n_{1}=0$
reduces to the group
![]() $\textrm {GL}_{2}$
. Recall that we have calculated the Poincaré polynomial of
$\textrm {GL}_{2}$
. Recall that we have calculated the Poincaré polynomial of
![]() $F_{\gamma }$
in [Reference Chaudouard and Laumon11].
$F_{\gamma }$
in [Reference Chaudouard and Laumon11].
Proposition 6.1. The fundamental domain
![]() $F_{\gamma }$
admits an affine paving. Its Poincaré polynomial, which depends only on the root valuation
$F_{\gamma }$
admits an affine paving. Its Poincaré polynomial, which depends only on the root valuation
![]() $(n_{1},n_{2})$
, is
$(n_{1},n_{2})$
, is
 $$ \begin{align*} P_{\left(n_{1},n_{2}\right)}(t)&=\sum_{i=1}^{n_{1}}i\left(t^{4i-2}+t^{4i-4}\right)+\sum_{i=2n_{1}}^{n_{1}+n_{2}-1}(2n_{1}+1)t^{2i}\\ & \quad +\sum_{i=n_{1}+n_{2}}^{2n_{1}+n_{2}-1}4(2n_{1}+n_{2}-i)t^{2i}+t^{4n_{1}+2n_{2}}. \end{align*} $$
$$ \begin{align*} P_{\left(n_{1},n_{2}\right)}(t)&=\sum_{i=1}^{n_{1}}i\left(t^{4i-2}+t^{4i-4}\right)+\sum_{i=2n_{1}}^{n_{1}+n_{2}-1}(2n_{1}+1)t^{2i}\\ & \quad +\sum_{i=n_{1}+n_{2}}^{2n_{1}+n_{2}-1}4(2n_{1}+n_{2}-i)t^{2i}+t^{4n_{1}+2n_{2}}. \end{align*} $$
In particular,
 $ \left \lvert F_{\gamma }\left (\mathbf{F}_{q}\right )\right \rvert =P_{\left (n_{1},n_{2}\right )}\left (q^{1/2}\right ).$
$ \left \lvert F_{\gamma }\left (\mathbf{F}_{q}\right )\right \rvert =P_{\left (n_{1},n_{2}\right )}\left (q^{1/2}\right ).$
6.1. Calculation of
 $J_{T}(\gamma )$
$J_{T}(\gamma )$
Set
![]() $(a_{1},a_{2})\in \textbf {N}^{2}$
, and let
$(a_{1},a_{2})\in \textbf {N}^{2}$
, and let
![]() $\Pi $
be the positive
$\Pi $
be the positive
![]() $(G,T)$
-orthogonal family defined by
$(G,T)$
-orthogonal family defined by
 $$ \begin{align*} \lambda_{w}(\Pi)=\lambda_{w}\left(\Sigma_{\gamma}\right)+ w\sum_{i=1}^{2}a_{i}\alpha_{i}^{\vee},\qquad \forall w\in W. \end{align*} $$
$$ \begin{align*} \lambda_{w}(\Pi)=\lambda_{w}\left(\Sigma_{\gamma}\right)+ w\sum_{i=1}^{2}a_{i}\alpha_{i}^{\vee},\qquad \forall w\in W. \end{align*} $$
Assume that
![]() $\Pi $
is sufficiently regular in the sense of §4.2, which means that
$\Pi $
is sufficiently regular in the sense of §4.2, which means that
![]() $a_{1}, a_{2}\gg 0$
and
$a_{1}, a_{2}\gg 0$
and
We will calculate
 $$ \begin{align*} Q_{\gamma}^{0}(a_{1},a_{2}):=\left\lvert\mathscr{X}_{\gamma}^{0}(\Pi)\left(\mathbf{F}_{q}\right)\right\rvert \end{align*} $$
$$ \begin{align*} Q_{\gamma}^{0}(a_{1},a_{2}):=\left\lvert\mathscr{X}_{\gamma}^{0}(\Pi)\left(\mathbf{F}_{q}\right)\right\rvert \end{align*} $$
following the two approaches that we have explained, and draw conclusions on Arthur’s weighted orbital integral.
6.1.1. Counting points by Arthur–Kottwitz reduction
We will work out each term in Corollary 3.7. Look at the summands indexed by the Borel subgroups. Each stratum contributes
![]() $q^{2n_{1}+n_{2}}$
, so it remains to count the number of lattice points
$q^{2n_{1}+n_{2}}$
, so it remains to count the number of lattice points
 $$ \begin{align*} \sum_{B\in \mathcal{P}(T)}\left\lvert\Lambda_{T}^{0}\cap R_{B}\cap \Pi\right\rvert=6\left\lvert\Lambda_{T}^{0}\cap R_{B_{0}}\cap \Pi\right\rvert, \end{align*} $$
$$ \begin{align*} \sum_{B\in \mathcal{P}(T)}\left\lvert\Lambda_{T}^{0}\cap R_{B}\cap \Pi\right\rvert=6\left\lvert\Lambda_{T}^{0}\cap R_{B_{0}}\cap \Pi\right\rvert, \end{align*} $$
where the equality is due to the symmetry of
![]() $\Pi $
with respect to
$\Pi $
with respect to
![]() $\Sigma _{\gamma }$
. We identify
$\Sigma _{\gamma }$
. We identify
 $$ \begin{align*} \Lambda_{T}^{0}\cong \left\{(m_{1},m_{2},m_{3})\in \textbf{Z}^{3}\mid m_{1}+m_{2}+m_{3}=0\right\} \end{align*} $$
$$ \begin{align*} \Lambda_{T}^{0}\cong \left\{(m_{1},m_{2},m_{3})\in \textbf{Z}^{3}\mid m_{1}+m_{2}+m_{3}=0\right\} \end{align*} $$
in the usual way. Let
 $\overline {\mathfrak {a}}_{B_{0}}^{G}=\left \{a\in \mathfrak {a}_{T}^{G}\mid \alpha _{1}(a)\geq 0, \ \alpha _{2}(a)\geq 0\right \}$
, and let
$\overline {\mathfrak {a}}_{B_{0}}^{G}=\left \{a\in \mathfrak {a}_{T}^{G}\mid \alpha _{1}(a)\geq 0, \ \alpha _{2}(a)\geq 0\right \}$
, and let
 $$ \begin{align*} R_{0}=\left\{a\in \overline{\mathfrak{a}}_{B_{0}}^{G}\mid \varpi_{1}(a)\leq a_{1}-1, \ \varpi_{2}(a)\leq a_{2}-1\right\}. \end{align*} $$
$$ \begin{align*} R_{0}=\left\{a\in \overline{\mathfrak{a}}_{B_{0}}^{G}\mid \varpi_{1}(a)\leq a_{1}-1, \ \varpi_{2}(a)\leq a_{2}-1\right\}. \end{align*} $$
Up to a suitable translation, we have
 $$ \begin{align*} \left\lvert\Lambda_{T}^{0}\cap R_{B_{0}}\cap \Pi\right\rvert=\left\lvert \Lambda_{T}^{0}\cap R_{0}\right\rvert. \end{align*} $$
$$ \begin{align*} \left\lvert\Lambda_{T}^{0}\cap R_{B_{0}}\cap \Pi\right\rvert=\left\lvert \Lambda_{T}^{0}\cap R_{0}\right\rvert. \end{align*} $$
We can express it as the difference of two lattice point-counting problems. Let
 $$ \begin{align*} R_{1} &= \left\{a\in \overline{\mathfrak{a}}_{B_{0}}^{G}\mid\varpi_{1}(a)\leq a_{1}-1, \ \varpi_{2}(a)\leq 2(a_{1}-1)\right\},\\ R_{2} &= \left\{a\in \overline{\mathfrak{a}}_{B_{0}}^{G}\mid\varpi_{1}(a)\leq a_{1}-1, \ \varpi_{2}(a)\geq a_{2}\right\}. \end{align*} $$
$$ \begin{align*} R_{1} &= \left\{a\in \overline{\mathfrak{a}}_{B_{0}}^{G}\mid\varpi_{1}(a)\leq a_{1}-1, \ \varpi_{2}(a)\leq 2(a_{1}-1)\right\},\\ R_{2} &= \left\{a\in \overline{\mathfrak{a}}_{B_{0}}^{G}\mid\varpi_{1}(a)\leq a_{1}-1, \ \varpi_{2}(a)\geq a_{2}\right\}. \end{align*} $$
Then we have
 $$ \begin{align*} \left\lvert \Lambda_{T}^{0}\cap R_{0}\right\rvert=\left\lvert \Lambda_{T}^{0}\cap R_{1}\right\rvert-\left\lvert \Lambda_{T}^{0}\cap R_{2}\right\rvert.\end{align*} $$
$$ \begin{align*} \left\lvert \Lambda_{T}^{0}\cap R_{0}\right\rvert=\left\lvert \Lambda_{T}^{0}\cap R_{1}\right\rvert-\left\lvert \Lambda_{T}^{0}\cap R_{2}\right\rvert.\end{align*} $$
We count
 $\left \lvert \Lambda _{T}^{0}\cap R_{1}\right \rvert $
as follows:
$\left \lvert \Lambda _{T}^{0}\cap R_{1}\right \rvert $
as follows:
 $$ \begin{align*} \left\lvert\Lambda_{T}^{0}\cap R_{1}\right\rvert &= \sum_{n=0}^{+\infty} \left\lvert R_{1}\cap \left\{\mu\in \Lambda_{T}^{0}\mid\varpi_{1}(\mu)=n\right\}\right\rvert\\ &= \sum_{i=1}^{\left\lfloor \frac {a_{1}}{2}\right\rfloor}[(3i-2)+(3i-1)]+\frac{1-(-1)^{a_{1}}}{2}\left(1+\frac{3(a_{1}-1)}{2}\right)\\ &= 3\left\lfloor \frac {a_{1}}{2}\right\rfloor^{2}+\frac{1}{4}(1-(-1)^{a_{1}})(3a_{1}-1), \end{align*} $$
$$ \begin{align*} \left\lvert\Lambda_{T}^{0}\cap R_{1}\right\rvert &= \sum_{n=0}^{+\infty} \left\lvert R_{1}\cap \left\{\mu\in \Lambda_{T}^{0}\mid\varpi_{1}(\mu)=n\right\}\right\rvert\\ &= \sum_{i=1}^{\left\lfloor \frac {a_{1}}{2}\right\rfloor}[(3i-2)+(3i-1)]+\frac{1-(-1)^{a_{1}}}{2}\left(1+\frac{3(a_{1}-1)}{2}\right)\\ &= 3\left\lfloor \frac {a_{1}}{2}\right\rfloor^{2}+\frac{1}{4}(1-(-1)^{a_{1}})(3a_{1}-1), \end{align*} $$
where
![]() $\lfloor x \rfloor $
means the largest integer that is less than or equal to x. Similarly, we have
$\lfloor x \rfloor $
means the largest integer that is less than or equal to x. Similarly, we have
 $$ \begin{align*} \left\lvert \Lambda_{T}^{0}\cap R_{2}\right\rvert &= \sum_{n=2\left(a_{1}-1\right)}^{-\infty} \left\lvert R_{2}\cap \left\{\mu\in \Lambda_{T}^{0}\mid\varpi_{2}(\mu)=n\right\}\right\rvert\\ &= \sum_{i=1}^{\left\lfloor \frac {2a_{1}-a_{2}-1}{2}\right\rfloor}(i+i)+\frac{1+(-1)^{2a_{1}-a_{2}}}{2}\cdot \frac{2a_{1}-a_{2}}{2}\\ &= \left\lfloor \frac {2a_{1}-a_{2}-1}{2}\right\rfloor\left(\left\lfloor \frac {2a_{1}-a_{2}-1}{2}\right\rfloor+1\right)+\frac{1}{4}\left(1+(-1)^{2a_{1}-a_{2}}\right)(2a_{1}-a_{2}). \end{align*} $$
$$ \begin{align*} \left\lvert \Lambda_{T}^{0}\cap R_{2}\right\rvert &= \sum_{n=2\left(a_{1}-1\right)}^{-\infty} \left\lvert R_{2}\cap \left\{\mu\in \Lambda_{T}^{0}\mid\varpi_{2}(\mu)=n\right\}\right\rvert\\ &= \sum_{i=1}^{\left\lfloor \frac {2a_{1}-a_{2}-1}{2}\right\rfloor}(i+i)+\frac{1+(-1)^{2a_{1}-a_{2}}}{2}\cdot \frac{2a_{1}-a_{2}}{2}\\ &= \left\lfloor \frac {2a_{1}-a_{2}-1}{2}\right\rfloor\left(\left\lfloor \frac {2a_{1}-a_{2}-1}{2}\right\rfloor+1\right)+\frac{1}{4}\left(1+(-1)^{2a_{1}-a_{2}}\right)(2a_{1}-a_{2}). \end{align*} $$
In summary, the summands in Corollary 3.7 indexed by the Borel subgroups contribute
 $$ \begin{align} &6q^{2n_{1}+n_{2}}\left[ 3\left\lfloor \frac {a_{1}}{2}\right\rfloor^{2} -\left\lfloor \frac {2a_{1}-a_{2}-1}{2}\right\rfloor\left(\left\lfloor \frac {2a_{1}-a_{2}-1}{2}\right\rfloor+1\right)\right. \nonumber\\ &\qquad\qquad\qquad\qquad\quad\left. +\frac{1}{4}(1-(-1)^{a_{1}})(3a_{1}-1)-\frac{1}{4}\left(1+(-1)^{2a_{1}-a_{2}}\right)(2a_{1}-a_{2}) \right]. \end{align} $$
$$ \begin{align} &6q^{2n_{1}+n_{2}}\left[ 3\left\lfloor \frac {a_{1}}{2}\right\rfloor^{2} -\left\lfloor \frac {2a_{1}-a_{2}-1}{2}\right\rfloor\left(\left\lfloor \frac {2a_{1}-a_{2}-1}{2}\right\rfloor+1\right)\right. \nonumber\\ &\qquad\qquad\qquad\qquad\quad\left. +\frac{1}{4}(1-(-1)^{a_{1}})(3a_{1}-1)-\frac{1}{4}\left(1+(-1)^{2a_{1}-a_{2}}\right)(2a_{1}-a_{2}) \right]. \end{align} $$
Now we calculate the contributions of the summands indexed by the maximal parabolic subgroups. They are parametrized at the beginning of the section by nonempty subsets
![]() $I\subsetneq \{1,2,3\}$
. For
$I\subsetneq \{1,2,3\}$
. For
 $\mu \in \Lambda _{M_{I}^{\mathrm{ad}}}\cong \textbf {Z}/2$
, let
$\mu \in \Lambda _{M_{I}^{\mathrm{ad}}}\cong \textbf {Z}/2$
, let
 $q_{I}^{\mu }=\left \lvert F_{\gamma }^{M_{I},\nu }\left (\mathbf{F}_{q}\right )\right \rvert $
, for any
$q_{I}^{\mu }=\left \lvert F_{\gamma }^{M_{I},\nu }\left (\mathbf{F}_{q}\right )\right \rvert $
, for any
![]() $\nu \in \Lambda _{M_{I}}$
which projects to
$\nu \in \Lambda _{M_{I}}$
which projects to
 $\mu \in \Lambda _{M_{I}^{\mathrm{ad}}}$
. Let
$\mu \in \Lambda _{M_{I}^{\mathrm{ad}}}$
. Let
![]() $\alpha _{I}$
be the unique element in
$\alpha _{I}$
be the unique element in
![]() $\Phi _{B_{0}\cap M_{I}}(M_{I},T)$
. A simple calculation with the affine Springer fibers for the group
$\Phi _{B_{0}\cap M_{I}}(M_{I},T)$
. A simple calculation with the affine Springer fibers for the group
![]() $\textrm {GL}_{2}$
shows that
$\textrm {GL}_{2}$
shows that
 $$ \begin{align*} q_{I}^{(0)}=\sum_{i=0}^{\mathrm{val}\left(\alpha_{I}(\gamma)\right)}q^{i},\qquad q_{I}^{(1)}=\sum_{i=0}^{\mathrm{val}\left(\alpha_{I}(\gamma)\right)-1}q^{i}. \end{align*} $$
$$ \begin{align*} q_{I}^{(0)}=\sum_{i=0}^{\mathrm{val}\left(\alpha_{I}(\gamma)\right)}q^{i},\qquad q_{I}^{(1)}=\sum_{i=0}^{\mathrm{val}\left(\alpha_{I}(\gamma)\right)-1}q^{i}. \end{align*} $$
For
![]() $I=\{i\}$
,
$I=\{i\}$
,
![]() $i=1,2,3$
, it is easy to see that
$i=1,2,3$
, it is easy to see that
 $$ \begin{align*} \left\lvert \Lambda_{M_{I}}^{0}\cap \pi_{M_{I}}\left(R_{P_{I}}\right)\cap \pi_{M_{I}}(\Pi)\cap c_{M}^{-1}(0)\right\rvert &= \left\lfloor \frac{a_{1}}{2}\right\rfloor,\\ \left\lvert \Lambda_{M_{I}}^{0}\cap \pi_{M_{I}}\left(R_{P_{I}}\right)\cap \pi_{M_{I}}(\Pi)\cap c_{M}^{-1}(1)\right\rvert&=\left\lfloor \frac{a_{1}+1}{2}\right\rfloor.\end{align*} $$
$$ \begin{align*} \left\lvert \Lambda_{M_{I}}^{0}\cap \pi_{M_{I}}\left(R_{P_{I}}\right)\cap \pi_{M_{I}}(\Pi)\cap c_{M}^{-1}(0)\right\rvert &= \left\lfloor \frac{a_{1}}{2}\right\rfloor,\\ \left\lvert \Lambda_{M_{I}}^{0}\cap \pi_{M_{I}}\left(R_{P_{I}}\right)\cap \pi_{M_{I}}(\Pi)\cap c_{M}^{-1}(1)\right\rvert&=\left\lfloor \frac{a_{1}+1}{2}\right\rfloor.\end{align*} $$
The summands indexed by
![]() $P_{I}$
in Corollary 3.7 with
$P_{I}$
in Corollary 3.7 with
![]() $\lvert I\rvert =1$
contribute in total
$\lvert I\rvert =1$
contribute in total
 $$ \begin{align} \left\lfloor \frac{a_{1}}{2}\right\rfloor\left(q^{2n_{1}}\sum_{i=0}^{n_{2}}q^{i}+2q^{n_{1}+n_{2}}\sum_{i=0}^{n_{1}}q^{i} \right)+ \left\lfloor \frac{a_{1}+1}{2}\right\rfloor\left(q^{2n_{1}}\sum_{i=0}^{n_{2}-1}q^{i}+2q^{n_{1}+n_{2}}\sum_{i=0}^{n_{1}-1}q^{i} \right). \end{align} $$
$$ \begin{align} \left\lfloor \frac{a_{1}}{2}\right\rfloor\left(q^{2n_{1}}\sum_{i=0}^{n_{2}}q^{i}+2q^{n_{1}+n_{2}}\sum_{i=0}^{n_{1}}q^{i} \right)+ \left\lfloor \frac{a_{1}+1}{2}\right\rfloor\left(q^{2n_{1}}\sum_{i=0}^{n_{2}-1}q^{i}+2q^{n_{1}+n_{2}}\sum_{i=0}^{n_{1}-1}q^{i} \right). \end{align} $$
Similarly, the summands indexed by
![]() $P_{I}$
with
$P_{I}$
with
![]() $\lvert I\rvert =2$
contribute in total
$\lvert I\rvert =2$
contribute in total
 $$ \begin{align} \left\lfloor \frac{a_{2}}{2}\right\rfloor\left(q^{2n_{1}}\sum_{i=0}^{n_{2}}q^{i}+2q^{n_{1}+n_{2}}\sum_{i=0}^{n_{1}}q^{i} \right) + \left\lfloor \frac{a_{2}+1}{2}\right\rfloor\left(q^{2n_{1}}\sum_{i=0}^{n_{2}-1}q^{i}+2q^{n_{1}+n_{2}}\sum_{i=0}^{n_{1}-1}q^{i} \right). \end{align} $$
$$ \begin{align} \left\lfloor \frac{a_{2}}{2}\right\rfloor\left(q^{2n_{1}}\sum_{i=0}^{n_{2}}q^{i}+2q^{n_{1}+n_{2}}\sum_{i=0}^{n_{1}}q^{i} \right) + \left\lfloor \frac{a_{2}+1}{2}\right\rfloor\left(q^{2n_{1}}\sum_{i=0}^{n_{2}-1}q^{i}+2q^{n_{1}+n_{2}}\sum_{i=0}^{n_{1}-1}q^{i} \right). \end{align} $$
Summing up the contributions from formulas (6.1), (6.2), and (6.3), we obtain the following:
Proposition 6.2. We have
 $$ \begin{align*} Q_{\gamma}^{0}(a_{1},a_{2})&=\sum_{i=1}^{n_{1}}i\left(q^{2i-1}+q^{2i-2}\right)+\sum_{i=2n_{1}}^{n_{1}+n_{2}-1}(2n_{1}+1)q^{i}\\ &\quad +\sum_{i=n_{1}+n_{2}}^{2n_{1}+n_{2}-1}4(2n_{1}+n_{2}-i)q^{i}+q^{2n_{1}+n_{2}}\\ &\quad +6q^{2n_{1}+n_{2}}\left[ 3\left\lfloor \frac {a_{1}}{2}\right\rfloor^{2} -\left\lfloor \frac {2a_{1}-a_{2}-1}{2}\right\rfloor\left(\left\lfloor \frac {2a_{1}-a_{2}-1}{2}\right\rfloor+1\right) \right. \\ & \quad\left. +\,\frac{1}{4}(1-(-1)^{a_{1}})(3a_{1}-1)-\frac{1}{4}\left(1+(-1)^{2a_{1}-a_{2}}\right)(2a_{1}-a_{2}) \right]\\ &\quad +\left(\left\lfloor \frac{a_{1}}{2}\right\rfloor+\left\lfloor \frac{a_{2}}{2}\right\rfloor\right)\left(q^{2n_{1}}\sum_{i=0}^{n_{2}}q^{i}+2q^{n_{1}+n_{2}}\sum_{i=0}^{n_{1}}q^{i} \right)\\ &\quad+ \left(\left\lfloor \frac{a_{1}+1}{2}\right\rfloor+\left\lfloor \frac{a_{2}+1}{2}\right\rfloor\right)\left(q^{2n_{1}}\sum_{i=0}^{n_{2}-1}q^{i}+2q^{n_{1}+n_{2}}\sum_{i=0}^{n_{1}-1}q^{i} \right). \end{align*} $$
$$ \begin{align*} Q_{\gamma}^{0}(a_{1},a_{2})&=\sum_{i=1}^{n_{1}}i\left(q^{2i-1}+q^{2i-2}\right)+\sum_{i=2n_{1}}^{n_{1}+n_{2}-1}(2n_{1}+1)q^{i}\\ &\quad +\sum_{i=n_{1}+n_{2}}^{2n_{1}+n_{2}-1}4(2n_{1}+n_{2}-i)q^{i}+q^{2n_{1}+n_{2}}\\ &\quad +6q^{2n_{1}+n_{2}}\left[ 3\left\lfloor \frac {a_{1}}{2}\right\rfloor^{2} -\left\lfloor \frac {2a_{1}-a_{2}-1}{2}\right\rfloor\left(\left\lfloor \frac {2a_{1}-a_{2}-1}{2}\right\rfloor+1\right) \right. \\ & \quad\left. +\,\frac{1}{4}(1-(-1)^{a_{1}})(3a_{1}-1)-\frac{1}{4}\left(1+(-1)^{2a_{1}-a_{2}}\right)(2a_{1}-a_{2}) \right]\\ &\quad +\left(\left\lfloor \frac{a_{1}}{2}\right\rfloor+\left\lfloor \frac{a_{2}}{2}\right\rfloor\right)\left(q^{2n_{1}}\sum_{i=0}^{n_{2}}q^{i}+2q^{n_{1}+n_{2}}\sum_{i=0}^{n_{1}}q^{i} \right)\\ &\quad+ \left(\left\lfloor \frac{a_{1}+1}{2}\right\rfloor+\left\lfloor \frac{a_{2}+1}{2}\right\rfloor\right)\left(q^{2n_{1}}\sum_{i=0}^{n_{2}-1}q^{i}+2q^{n_{1}+n_{2}}\sum_{i=0}^{n_{1}-1}q^{i} \right). \end{align*} $$
In particular, it depends quasi-polynomially on
![]() $(a_{1},a_{2})$
.
$(a_{1},a_{2})$
.
6.1.2. Counting points by Harder–Narasimhan reduction
We begin by counting points on the main body; we need to work out each term in Theorem 4.8. For
![]() $L=T$
, it is easy to see that
$L=T$
, it is easy to see that
 $\left \lvert \mathscr {X}_{\gamma }^{T,0,\xi ^{T}}\left (\mathbf{F}_{q}\right )\right \rvert =1$
, and we need to count the number of lattice points in
$\left \lvert \mathscr {X}_{\gamma }^{T,0,\xi ^{T}}\left (\mathbf{F}_{q}\right )\right \rvert =1$
, and we need to count the number of lattice points in
![]() $ \Lambda _{T}^{0}\cap \Pi _{0}. $
Notice that for this we can shrink
$ \Lambda _{T}^{0}\cap \Pi _{0}. $
Notice that for this we can shrink
![]() $\Pi _{0}$
to the convex hull of
$\Pi _{0}$
to the convex hull of
![]() $ \Lambda _{T}^{0}\cap \Pi _{0} $
. We conserve the notation
$ \Lambda _{T}^{0}\cap \Pi _{0} $
. We conserve the notation
![]() $\Pi _{0}$
for the shrunken polytope. In [Reference Chaudouard and Laumon11, §6], we calculate
$\Pi _{0}$
for the shrunken polytope. In [Reference Chaudouard and Laumon11, §6], we calculate
![]() $\mathrm{Ec}(x_{0})$
for a particular choice of regular point
$\mathrm{Ec}(x_{0})$
for a particular choice of regular point
![]() $x_{0}\in \mathscr {X}^{\mathrm{reg}}_{\gamma }$
; we can adapt the result to our current setting. Let
$x_{0}\in \mathscr {X}^{\mathrm{reg}}_{\gamma }$
; we can adapt the result to our current setting. Let
![]() $(\sigma _{1}\sigma _{2}\sigma _{3})$
be the permutation sending
$(\sigma _{1}\sigma _{2}\sigma _{3})$
be the permutation sending
![]() $(123)$
to
$(123)$
to
![]() $(\sigma _{1}\sigma _{2}\sigma _{3})$
. The vertices of
$(\sigma _{1}\sigma _{2}\sigma _{3})$
. The vertices of
![]() $\Sigma _{\gamma }$
are
$\Sigma _{\gamma }$
are
 $$ \begin{align*} \lambda_{123}\left(\Sigma_{\gamma}\right)&=(0,0,0), & \lambda_{321}\left(\Sigma_{\gamma}\right)&=(-2n_{1},n_{1}-n_{2},n_{1}+n_{2}),\\ \lambda_{213}\left(\Sigma_{\gamma}\right)&=(-n_{1},n_{1},0), & \lambda_{312}\left(\Sigma_{\gamma}\right)&=(-n_{1},-n_{2},n_{1}+n_{2}),\\ \lambda_{132}\left(\Sigma_{\gamma}\right)&=(0,-n_{2},n_{2}), & \lambda_{231}\left(\Sigma_{\gamma}\right)&=(-2n_{1},n_{1},n_{1}). \end{align*} $$
$$ \begin{align*} \lambda_{123}\left(\Sigma_{\gamma}\right)&=(0,0,0), & \lambda_{321}\left(\Sigma_{\gamma}\right)&=(-2n_{1},n_{1}-n_{2},n_{1}+n_{2}),\\ \lambda_{213}\left(\Sigma_{\gamma}\right)&=(-n_{1},n_{1},0), & \lambda_{312}\left(\Sigma_{\gamma}\right)&=(-n_{1},-n_{2},n_{1}+n_{2}),\\ \lambda_{132}\left(\Sigma_{\gamma}\right)&=(0,-n_{2},n_{2}), & \lambda_{231}\left(\Sigma_{\gamma}\right)&=(-2n_{1},n_{1},n_{1}). \end{align*} $$
The vertices of
![]() $\Pi _{0}$
can be calculated to be
$\Pi _{0}$
can be calculated to be
 $$ \begin{align*} \lambda_{123}(\Pi_{0})&=(a_{1}-2n_{1}-1, a_{2}-a_{1}+n_{1}-n_{2}, -a_{2}+n_{1}+n_{2}+1),\\ \lambda_{321}(\Pi_{0})&=(-a_{2}+1, a_{2}-a_{1},a_{1}-1),\\ \lambda_{213}(\Pi_{0})&=(a_{2}-a_{1}-n_{1},a_{1}-n_{2}-1, -a_{2}+n_{1}+n_{2}+1),\\ \lambda_{312}(\Pi_{0})&=(a_{2}-a_{1}-n_{1}, -a_{2}+n_{1}+1,a_{1}-1),\\ \lambda_{132}(\Pi_{0})&=(a_{1}-2n_{1}-1, -a_{2}+n_{1}+1, a_{2}-a_{1}+n_{1}), \\ \lambda_{231}(\Pi_{0})&=(-a_{2}+1, a_{1}-n_{2}-1, a_{2}-a_{1}+n_{2}). \end{align*} $$
$$ \begin{align*} \lambda_{123}(\Pi_{0})&=(a_{1}-2n_{1}-1, a_{2}-a_{1}+n_{1}-n_{2}, -a_{2}+n_{1}+n_{2}+1),\\ \lambda_{321}(\Pi_{0})&=(-a_{2}+1, a_{2}-a_{1},a_{1}-1),\\ \lambda_{213}(\Pi_{0})&=(a_{2}-a_{1}-n_{1},a_{1}-n_{2}-1, -a_{2}+n_{1}+n_{2}+1),\\ \lambda_{312}(\Pi_{0})&=(a_{2}-a_{1}-n_{1}, -a_{2}+n_{1}+1,a_{1}-1),\\ \lambda_{132}(\Pi_{0})&=(a_{1}-2n_{1}-1, -a_{2}+n_{1}+1, a_{2}-a_{1}+n_{1}), \\ \lambda_{231}(\Pi_{0})&=(-a_{2}+1, a_{1}-n_{2}-1, a_{2}-a_{1}+n_{2}). \end{align*} $$
We will count the lattice points in
![]() $\Pi _{0}$
indirectly. We complete the hexagon
$\Pi _{0}$
indirectly. We complete the hexagon
![]() $\Pi _{0}$
to a triangle
$\Pi _{0}$
to a triangle
![]() $T_{0}$
, whose vertices are
$T_{0}$
, whose vertices are
 $$ \begin{align*} \lambda_{123}(T_{0})&= \lambda_{132}(T_{0}) =(2a_{2}-2n_{1}-n_{2}-2, -a_{2}+n_{1}+1, -a_{2}+n_{1}+n_{2}+1),\\ \lambda_{321}(T_{0})&=\lambda_{312}(T_{0}) =(-a_{2}+1, -a_{2}+n_{1}+1, 2a_{2}-n_{1}-2),\\ \lambda_{213}(T_{0})&=\lambda_{231}(T_{0}) =(-a_{2}+1,2a_{2}-2-n_{1}-n_{2},-a_{2}+n_{1}+n_{2}+1). \end{align*} $$
$$ \begin{align*} \lambda_{123}(T_{0})&= \lambda_{132}(T_{0}) =(2a_{2}-2n_{1}-n_{2}-2, -a_{2}+n_{1}+1, -a_{2}+n_{1}+n_{2}+1),\\ \lambda_{321}(T_{0})&=\lambda_{312}(T_{0}) =(-a_{2}+1, -a_{2}+n_{1}+1, 2a_{2}-n_{1}-2),\\ \lambda_{213}(T_{0})&=\lambda_{231}(T_{0}) =(-a_{2}+1,2a_{2}-2-n_{1}-n_{2},-a_{2}+n_{1}+n_{2}+1). \end{align*} $$
Let
![]() $T_{1}\cup T_{2}\cup T_{3}$
be the complement of
$T_{1}\cup T_{2}\cup T_{3}$
be the complement of
![]() $\Pi _{0}$
in
$\Pi _{0}$
in
![]() $T_{0}$
, as shown in Figure 4. Notice that the
$T_{0}$
, as shown in Figure 4. Notice that the
![]() $T_{i}$
s do not contain their common boundary with
$T_{i}$
s do not contain their common boundary with
![]() $\Pi _{0}$
, so
$\Pi _{0}$
, so
 $$ \begin{align*} \left\lvert \Lambda_{T}^{0}\cap \Pi_{0}\right\rvert =\left\lvert \Lambda_{T}^{0}\cap T_{0}\right\rvert -\sum_{i=1}^{3}\left\lvert \Lambda_{T}^{0}\cap T_{i}\right\rvert. \end{align*} $$
$$ \begin{align*} \left\lvert \Lambda_{T}^{0}\cap \Pi_{0}\right\rvert =\left\lvert \Lambda_{T}^{0}\cap T_{0}\right\rvert -\sum_{i=1}^{3}\left\lvert \Lambda_{T}^{0}\cap T_{i}\right\rvert. \end{align*} $$
The right-hand side is much easier to calculate.

Figure 4 Completing the hexagon to a triangle.
The length of the edges of
![]() $T_{0}$
is
$T_{0}$
is
![]() $3a_{2}-3-2n_{1}-n_{2}$
, so
$3a_{2}-3-2n_{1}-n_{2}$
, so
 $$ \begin{align*} \left\lvert \Lambda_{T}^{0}\cap T_{0}\right\rvert&= \sum_{i=1}^{3a_{2}-3-2n_{1}-n_{2}+1} i\\ &= \frac{1}{2}(3a_{2}-2-2n_{1}-n_{2})(3a_{2}-1-2n_{1}-n_{2}). \end{align*} $$
$$ \begin{align*} \left\lvert \Lambda_{T}^{0}\cap T_{0}\right\rvert&= \sum_{i=1}^{3a_{2}-3-2n_{1}-n_{2}+1} i\\ &= \frac{1}{2}(3a_{2}-2-2n_{1}-n_{2})(3a_{2}-1-2n_{1}-n_{2}). \end{align*} $$
The length of the edges of
![]() $T_{1}$
is
$T_{1}$
is
![]() $2a_{2}-a_{1}-n_{1}-1$
. As we do not count the lattice points on the common boundary of
$2a_{2}-a_{1}-n_{1}-1$
. As we do not count the lattice points on the common boundary of
![]() $T_{1}$
and
$T_{1}$
and
![]() $\Pi _{0}$
, we have
$\Pi _{0}$
, we have
 $$ \begin{align*} \left\lvert \Lambda_{T}^{0}\cap T_{1}\right\rvert &= \sum_{i=1}^{2a_{2}-a_{1}-n_{1}-1} i\\ &= \frac{1}{2}(2a_{2}-a_{1}-n_{1}-1)(2a_{2}-a_{1}-n_{1}). \end{align*} $$
$$ \begin{align*} \left\lvert \Lambda_{T}^{0}\cap T_{1}\right\rvert &= \sum_{i=1}^{2a_{2}-a_{1}-n_{1}-1} i\\ &= \frac{1}{2}(2a_{2}-a_{1}-n_{1}-1)(2a_{2}-a_{1}-n_{1}). \end{align*} $$
Similarly, the length of the edges of
![]() $T_{2}$
is
$T_{2}$
is
![]() $2a_{2}-a_{1}-n_{2}-1$
and we have
$2a_{2}-a_{1}-n_{2}-1$
and we have
 $$ \begin{align*} \left\lvert \Lambda_{T}^{0}\cap T_{2}\right\rvert = \frac{1}{2}(2a_{2}-a_{1}-n_{2}-1)(2a_{2}-a_{1}-n_{2}). \end{align*} $$
$$ \begin{align*} \left\lvert \Lambda_{T}^{0}\cap T_{2}\right\rvert = \frac{1}{2}(2a_{2}-a_{1}-n_{2}-1)(2a_{2}-a_{1}-n_{2}). \end{align*} $$
The triangle
![]() $T_{3}$
is of the same size as
$T_{3}$
is of the same size as
![]() $T_{1}$
, so
$T_{1}$
, so
 $$ \begin{align*} \left\lvert \Lambda_{T}^{0}\cap T_{3}\right\rvert = \frac{1}{2}(2a_{2}-a_{1}-n_{1}-1)(2a_{2}-a_{1}-n_{1}). \end{align*} $$
$$ \begin{align*} \left\lvert \Lambda_{T}^{0}\cap T_{3}\right\rvert = \frac{1}{2}(2a_{2}-a_{1}-n_{1}-1)(2a_{2}-a_{1}-n_{1}). \end{align*} $$
Finally,
 $$ \begin{align} \left\lvert \Lambda_{T}^{0}\cap \Pi_{0}\right\rvert &= \left\lvert \Lambda_{T}^{0}\cap T_{0}\right\rvert -\sum_{i=1}^{3}\left\lvert \Lambda_{T}^{0}\cap T_{i}\right\rvert\\ &=\frac{1}{2}(3a_{2}-2-2n_{1}-n_{2})(3a_{2}-1-2n_{1}-n_{2})\nonumber\\ & \quad -(2a_{2}-a_{1}-n_{1}-1)(2a_{2}-a_{1}-n_{1})\nonumber\\ & \quad -\frac{1}{2}(2a_{2}-a_{1}-n_{2}-1)(2a_{2}-a_{1}-n_{2}).\nonumber \end{align} $$
$$ \begin{align} \left\lvert \Lambda_{T}^{0}\cap \Pi_{0}\right\rvert &= \left\lvert \Lambda_{T}^{0}\cap T_{0}\right\rvert -\sum_{i=1}^{3}\left\lvert \Lambda_{T}^{0}\cap T_{i}\right\rvert\\ &=\frac{1}{2}(3a_{2}-2-2n_{1}-n_{2})(3a_{2}-1-2n_{1}-n_{2})\nonumber\\ & \quad -(2a_{2}-a_{1}-n_{1}-1)(2a_{2}-a_{1}-n_{1})\nonumber\\ & \quad -\frac{1}{2}(2a_{2}-a_{1}-n_{2}-1)(2a_{2}-a_{1}-n_{2}).\nonumber \end{align} $$
We go on to calculate
 $\left \lvert \Lambda _{L}^{0}\cap \pi _{L}(\Pi _{0})\right \rvert $
for the other Levi subgroups
$\left \lvert \Lambda _{L}^{0}\cap \pi _{L}(\Pi _{0})\right \rvert $
for the other Levi subgroups
![]() $L\in \mathcal {L}(T)$
. Let
$L\in \mathcal {L}(T)$
. Let
![]() $d_{L}$
be the distance between the facets
$d_{L}$
be the distance between the facets
 $\Pi _{0}^{Q}$
and
$\Pi _{0}^{Q}$
and
 $\Pi _{0}^{Q^{-}}$
, where
$\Pi _{0}^{Q^{-}}$
, where
![]() $\mathcal {P}(L)=\{Q,Q^{-}\}$
. It is easy to see that
$\mathcal {P}(L)=\{Q,Q^{-}\}$
. It is easy to see that
 $$ \begin{align*} \left\lvert \Lambda_{L}^{0}\cap \pi_{L}(\Pi_{0})\right\rvert =d_{L}+1. \end{align*} $$
$$ \begin{align*} \left\lvert \Lambda_{L}^{0}\cap \pi_{L}(\Pi_{0})\right\rvert =d_{L}+1. \end{align*} $$
The set
![]() $\mathcal {L}(T)\backslash \{T,G\}$
consists of three elements, Levi factors
$\mathcal {L}(T)\backslash \{T,G\}$
consists of three elements, Levi factors
![]() $M_{\{i\}}$
of the parabolic subgroups
$M_{\{i\}}$
of the parabolic subgroups
![]() $P_{\{i\}}$
,
$P_{\{i\}}$
,
![]() $i=1,2,3$
. Using the explicit expression of the vertices of
$i=1,2,3$
. Using the explicit expression of the vertices of
![]() $\Pi _{0}$
, we can calculate
$\Pi _{0}$
, we can calculate
 $$ \begin{align} \hspace{-15pt}\left\lvert \Lambda_{M_{\{1\}}}^{0}\cap \pi_{M_{\{1\}}}(\Pi_{0})\right\rvert &= d_{M_{\{1\}}}+1=a_{1}+a_{2}-2n_{1}-1, \end{align} $$
$$ \begin{align} \hspace{-15pt}\left\lvert \Lambda_{M_{\{1\}}}^{0}\cap \pi_{M_{\{1\}}}(\Pi_{0})\right\rvert &= d_{M_{\{1\}}}+1=a_{1}+a_{2}-2n_{1}-1, \end{align} $$
 $$ \begin{align} \left\lvert \Lambda_{M_{\{2\}}}^{0}\cap \pi_{M_{\{2\}}}(\Pi_{0})\right\rvert &= d_{M_{\{2\}}}+1=a_{1}+a_{2}-n_{1}-n_{2}-1, \end{align} $$
$$ \begin{align} \left\lvert \Lambda_{M_{\{2\}}}^{0}\cap \pi_{M_{\{2\}}}(\Pi_{0})\right\rvert &= d_{M_{\{2\}}}+1=a_{1}+a_{2}-n_{1}-n_{2}-1, \end{align} $$
 $$ \begin{align} \left\lvert \Lambda_{M_{\{3\}}}^{0}\cap \pi_{M_{\{3\}}}(\Pi_{0})\right\rvert &= d_{M_{\{3\}}}+1=a_{1}+a_{2}-n_{1}-n_{2}-1. \end{align} $$
$$ \begin{align} \left\lvert \Lambda_{M_{\{3\}}}^{0}\cap \pi_{M_{\{3\}}}(\Pi_{0})\right\rvert &= d_{M_{\{3\}}}+1=a_{1}+a_{2}-n_{1}-n_{2}-1. \end{align} $$
Now that
 $\left \lvert \mathscr {X}_{\gamma }^{L,0,\xi ^{L}}\left (\mathbf{F}_{q}\right )\right \rvert $
has been calculated in equation (5.1), we can insert equations (6.4)–(6.7) into the equation in Theorem 4.8 to get the following:
$\left \lvert \mathscr {X}_{\gamma }^{L,0,\xi ^{L}}\left (\mathbf{F}_{q}\right )\right \rvert $
has been calculated in equation (5.1), we can insert equations (6.4)–(6.7) into the equation in Theorem 4.8 to get the following:
Proposition 6.3. The number of rational points on the main body is
 $$ \begin{align*} \left\lvert {}^{m}\mathscr{X}_{\gamma}^{0}(\Pi)\left(\mathbf{F}_{q}\right)\right\rvert &= \left\lvert\mathscr{X}_{\gamma}^{0,\xi}\left(\mathbf{F}_{q}\right)\right\rvert+ q^{2n_{1}+n_{2}} \left[\frac{1}{2}(3a_{2}-2-2n_{1}-n_{2})(3a_{2}-1-2n_{1}-n_{2}) \right. \\& \vphantom{\frac{1}{2}} \quad -(2a_{2}-a_{1}-n_{1}-1)(2a_{2}-a_{1}-n_{1})\\& \quad \left. -\frac{1}{2}(2a_{2}-a_{1}-n_{2}-1)(2a_{2}-a_{1}-n_{2})\right ]\\&\quad +q^{2n_{1}} (a_{1}+a_{2}-2n_{1}-1) \left(n_{2}q^{n_{2}}-\sum_{i=0}^{n_{2}-1}q^{i}\right)\\ &\quad+2q^{n_{1}+n_{2}}(a_{1}+a_{2}-n_{1}-n_{2}-1) \left(n_{1}q^{n_{1}}-\sum_{i=0}^{n_{1}-1}q^{i}\right). \end{align*} $$
$$ \begin{align*} \left\lvert {}^{m}\mathscr{X}_{\gamma}^{0}(\Pi)\left(\mathbf{F}_{q}\right)\right\rvert &= \left\lvert\mathscr{X}_{\gamma}^{0,\xi}\left(\mathbf{F}_{q}\right)\right\rvert+ q^{2n_{1}+n_{2}} \left[\frac{1}{2}(3a_{2}-2-2n_{1}-n_{2})(3a_{2}-1-2n_{1}-n_{2}) \right. \\& \vphantom{\frac{1}{2}} \quad -(2a_{2}-a_{1}-n_{1}-1)(2a_{2}-a_{1}-n_{1})\\& \quad \left. -\frac{1}{2}(2a_{2}-a_{1}-n_{2}-1)(2a_{2}-a_{1}-n_{2})\right ]\\&\quad +q^{2n_{1}} (a_{1}+a_{2}-2n_{1}-1) \left(n_{2}q^{n_{2}}-\sum_{i=0}^{n_{2}-1}q^{i}\right)\\ &\quad+2q^{n_{1}+n_{2}}(a_{1}+a_{2}-n_{1}-n_{2}-1) \left(n_{1}q^{n_{1}}-\sum_{i=0}^{n_{1}-1}q^{i}\right). \end{align*} $$
Now we proceed to counting points on the tail. To begin with, we write down the vertices of
![]() $\Pi $
:
$\Pi $
:
 $$ \begin{align*} \lambda_{123}(\Pi)&=(a_{1}, a_{2}-a_{1}, -a_{2}),\\ \lambda_{321}(\Pi)&=(-a_{2}-2n_{1}, a_{2}-a_{1}+n_{1}-n_{2},a_{1}+n_{1}+n_{2}),\\ \lambda_{213}(\Pi)&=(a_{2}-a_{1}-n_{1},a_{1}+n_{1}, -a_{2}),\\ \lambda_{312}(\Pi)&=(a_{2}-a_{1}-n_{1}, -a_{2}-n_{2},a_{1}+n_{1}+n_{2}),\\ \lambda_{132}(\Pi)&=(a_{1}, -a_{2}-n_{2}, a_{2}-a_{1}+n_{2}), \\ \lambda_{231}(\Pi)&=(-a_{2}-2n_{1}, a_{1}+n_{1}, a_{2}-a_{1}+n_{1}). \end{align*} $$
$$ \begin{align*} \lambda_{123}(\Pi)&=(a_{1}, a_{2}-a_{1}, -a_{2}),\\ \lambda_{321}(\Pi)&=(-a_{2}-2n_{1}, a_{2}-a_{1}+n_{1}-n_{2},a_{1}+n_{1}+n_{2}),\\ \lambda_{213}(\Pi)&=(a_{2}-a_{1}-n_{1},a_{1}+n_{1}, -a_{2}),\\ \lambda_{312}(\Pi)&=(a_{2}-a_{1}-n_{1}, -a_{2}-n_{2},a_{1}+n_{1}+n_{2}),\\ \lambda_{132}(\Pi)&=(a_{1}, -a_{2}-n_{2}, a_{2}-a_{1}+n_{2}), \\ \lambda_{231}(\Pi)&=(-a_{2}-2n_{1}, a_{1}+n_{1}, a_{2}-a_{1}+n_{1}). \end{align*} $$
For nonempty subsets
![]() $I\subsetneq \{1,2,3\}$
, we simplify the notation
$I\subsetneq \{1,2,3\}$
, we simplify the notation
![]() $E_{P_{I}}(\Pi )$
to
$E_{P_{I}}(\Pi )$
to
![]() $E_{I}(\Pi )$
. Using the coordinates of vertices of
$E_{I}(\Pi )$
. Using the coordinates of vertices of
![]() $\Pi $
, we can calculate the lengths of the edges of
$\Pi $
, we can calculate the lengths of the edges of
![]() $\Pi $
and find the following expression for
$\Pi $
and find the following expression for
![]() $E_{I}(\Pi )$
: when
$E_{I}(\Pi )$
: when
![]() $\lvert I\rvert =1$
, we have
$\lvert I\rvert =1$
, we have
 $$ \begin{align} E_{I}(\Pi)=\left(A_{\alpha_{I}}^{G,M_{I}}\right)^{2a_{2}-a_{1}}\left(\Sigma_{\gamma}\right). \end{align} $$
$$ \begin{align} E_{I}(\Pi)=\left(A_{\alpha_{I}}^{G,M_{I}}\right)^{2a_{2}-a_{1}}\left(\Sigma_{\gamma}\right). \end{align} $$
When
![]() $\lvert I\rvert =2$
, we have
$\lvert I\rvert =2$
, we have
 $$ \begin{align} E_{I}(\Pi)=\left(A_{\alpha_{I}}^{G,M_{I}}\right)^{2a_{1}-a_{2}}\left(\Sigma_{\gamma}\right). \end{align} $$
$$ \begin{align} E_{I}(\Pi)=\left(A_{\alpha_{I}}^{G,M_{I}}\right)^{2a_{1}-a_{2}}\left(\Sigma_{\gamma}\right). \end{align} $$
As explained before, we can use the Arthur–Kottwitz reduction inductively to count the number of rational points on
 $\mathscr {X}_{\gamma }^{0}(E_{I}(\Pi ))$
. We give the details for
$\mathscr {X}_{\gamma }^{0}(E_{I}(\Pi ))$
. We give the details for
![]() $I=\{3\}$
; the others can be calculated in the same way.
$I=\{3\}$
; the others can be calculated in the same way.
Applying Arthur–Kottwitz reduction to pass from
 $\left (\!\! A_{\alpha _{\{3\}}}^{G,M_{\{3\}}} \!\!\right )^{a}(\Sigma _{\gamma })$
to
$\left (\!\! A_{\alpha _{\{3\}}}^{G,M_{\{3\}}} \!\!\right )^{a}(\Sigma _{\gamma })$
to
 $\left(\!\! A_{\alpha _{\{3\}}}^{G,M_{\{3\}}} \!\!\right)^{a+1}(\Sigma _{\gamma })$
, the picture is similar to Figure 2. We obtain
$\left(\!\! A_{\alpha _{\{3\}}}^{G,M_{\{3\}}} \!\!\right)^{a+1}(\Sigma _{\gamma })$
, the picture is similar to Figure 2. We obtain
 $$ \begin{align*} \left\lvert\mathscr{X}_{\gamma}^{0}\left(\left(A_{\alpha_{\{3\}}}^{G,M_{\{3\}}}\right)^{a+1}\left(\Sigma_{\gamma}\right)\right)\left(\mathbf{F}_{q}\right)\right\rvert &= \left\lvert\mathscr{X}_{\gamma}^{0}\left(\left(A_{\alpha_{\{3\}}}^{G,M_{\{3\}}}\right)^{a}\left(\Sigma_{\gamma}\right)\right)\left(\mathbf{F}_{q}\right)\right\rvert +q^{2n_{1}}\left\lvert F_{\gamma}^{M_{\{1\}},1}\left(\mathbf{F}_{q}\right)\right\rvert\\ & \quad +q^{n_{1}+n_{2}}\left\lvert F_{\gamma}^{M_{\{13\}},1}\left(\mathbf{F}_{q}\right)\right\rvert +q^{2n_{1}+n_{2}}\\ &= \left\lvert\mathscr{X}_{\gamma}^{0}\left(\left(A_{\alpha_{\{3\}}}^{G,M_{\{3\}}}\right)^{a}\left(\Sigma_{\gamma}\right)\right)\left(\mathbf{F}_{q}\right)\right\rvert +q^{2n_{1}}\sum_{i=0}^{n_{2}-1}q^{i}\\ & \quad +q^{n_{1}+n_{2}}\sum_{i=0}^{n_{1}-1}q^{i}+q^{2n_{1}+n_{2}}. \end{align*} $$
$$ \begin{align*} \left\lvert\mathscr{X}_{\gamma}^{0}\left(\left(A_{\alpha_{\{3\}}}^{G,M_{\{3\}}}\right)^{a+1}\left(\Sigma_{\gamma}\right)\right)\left(\mathbf{F}_{q}\right)\right\rvert &= \left\lvert\mathscr{X}_{\gamma}^{0}\left(\left(A_{\alpha_{\{3\}}}^{G,M_{\{3\}}}\right)^{a}\left(\Sigma_{\gamma}\right)\right)\left(\mathbf{F}_{q}\right)\right\rvert +q^{2n_{1}}\left\lvert F_{\gamma}^{M_{\{1\}},1}\left(\mathbf{F}_{q}\right)\right\rvert\\ & \quad +q^{n_{1}+n_{2}}\left\lvert F_{\gamma}^{M_{\{13\}},1}\left(\mathbf{F}_{q}\right)\right\rvert +q^{2n_{1}+n_{2}}\\ &= \left\lvert\mathscr{X}_{\gamma}^{0}\left(\left(A_{\alpha_{\{3\}}}^{G,M_{\{3\}}}\right)^{a}\left(\Sigma_{\gamma}\right)\right)\left(\mathbf{F}_{q}\right)\right\rvert +q^{2n_{1}}\sum_{i=0}^{n_{2}-1}q^{i}\\ & \quad +q^{n_{1}+n_{2}}\sum_{i=0}^{n_{1}-1}q^{i}+q^{2n_{1}+n_{2}}. \end{align*} $$
From this relation and equation (6.8), we deduce that
 $$ \begin{align} \left\lvert \mathscr{X}_{\gamma}^{0}\left(E_{\{3\}}(\Pi)\right)\left(\mathbf{F}_{q}\right)\right\rvert &=\left\lvert F_{\gamma}\left(\mathbf{F}_{q}\right)\right\rvert+(2a_{2}-a_{1})\left(q^{2n_{1}}\sum_{i=0}^{n_{2}-1}q^{i} \right. \\ & \quad \left. +q^{n_{1}+n_{2}}\sum_{i=0}^{n_{1}-1}q^{i}+q^{2n_{1}+n_{2}}\right). \nonumber \end{align} $$
$$ \begin{align} \left\lvert \mathscr{X}_{\gamma}^{0}\left(E_{\{3\}}(\Pi)\right)\left(\mathbf{F}_{q}\right)\right\rvert &=\left\lvert F_{\gamma}\left(\mathbf{F}_{q}\right)\right\rvert+(2a_{2}-a_{1})\left(q^{2n_{1}}\sum_{i=0}^{n_{2}-1}q^{i} \right. \\ & \quad \left. +q^{n_{1}+n_{2}}\sum_{i=0}^{n_{1}-1}q^{i}+q^{2n_{1}+n_{2}}\right). \nonumber \end{align} $$
Similarly, we have
 $$ \begin{align} \hspace{8pt}\left\lvert \mathscr{X}_{\gamma}^{0}\left(E_{\{1\}}(\Pi)\right)\left(\mathbf{F}_{q}\right)\right\rvert&=\left\lvert F_{\gamma}\left(\mathbf{F}_{q}\right)\right\rvert+(2a_{2}-a_{1})\left( 2q^{n_{1}+n_{2}}\sum_{i=0}^{n_{1}-1}q^{i} +q^{2n_{1}+n_{2}}\right), \end{align} $$
$$ \begin{align} \hspace{8pt}\left\lvert \mathscr{X}_{\gamma}^{0}\left(E_{\{1\}}(\Pi)\right)\left(\mathbf{F}_{q}\right)\right\rvert&=\left\lvert F_{\gamma}\left(\mathbf{F}_{q}\right)\right\rvert+(2a_{2}-a_{1})\left( 2q^{n_{1}+n_{2}}\sum_{i=0}^{n_{1}-1}q^{i} +q^{2n_{1}+n_{2}}\right), \end{align} $$
 $$ \begin{align} \hspace{-100pt}\left\lvert \mathscr{X}_{\gamma}^{0}\left(E_{\{2\}}(\Pi)\right)\left(\mathbf{F}_{q}\right)\right\rvert &=\left\lvert F_{\gamma}\left(\mathbf{F}_{q}\right)\right\rvert +(2a_{2}-a_{1})\left(q^{2n_{1}}\sum_{i=0}^{n_{2}-1}q^{i} \right.\\& \quad \left. +q^{n_{1}+n_{2}}\sum_{i=0}^{n_{1}-1}q^{i}+q^{2n_{1}+n_{2}}\right), \nonumber \end{align} $$
$$ \begin{align} \hspace{-100pt}\left\lvert \mathscr{X}_{\gamma}^{0}\left(E_{\{2\}}(\Pi)\right)\left(\mathbf{F}_{q}\right)\right\rvert &=\left\lvert F_{\gamma}\left(\mathbf{F}_{q}\right)\right\rvert +(2a_{2}-a_{1})\left(q^{2n_{1}}\sum_{i=0}^{n_{2}-1}q^{i} \right.\\& \quad \left. +q^{n_{1}+n_{2}}\sum_{i=0}^{n_{1}-1}q^{i}+q^{2n_{1}+n_{2}}\right), \nonumber \end{align} $$
 $$ \begin{align} \hspace{-100pt}\left\lvert \mathscr{X}_{\gamma}^{0}\left(E_{\{12\}}(\Pi)\right)\left(\mathbf{F}_{q}\right)\right\rvert &=\left\lvert F_{\gamma}\left(\mathbf{F}_{q}\right)\right\rvert +(2a_{1}-a_{2})\left(q^{2n_{1}}\sum_{i=0}^{n_{2}-1}q^{i} \right.\\& \quad \left. +q^{n_{1}+n_{2}}\sum_{i=0}^{n_{1}-1}q^{i}+q^{2n_{1}+n_{2}}\right), \nonumber \end{align} $$
$$ \begin{align} \hspace{-100pt}\left\lvert \mathscr{X}_{\gamma}^{0}\left(E_{\{12\}}(\Pi)\right)\left(\mathbf{F}_{q}\right)\right\rvert &=\left\lvert F_{\gamma}\left(\mathbf{F}_{q}\right)\right\rvert +(2a_{1}-a_{2})\left(q^{2n_{1}}\sum_{i=0}^{n_{2}-1}q^{i} \right.\\& \quad \left. +q^{n_{1}+n_{2}}\sum_{i=0}^{n_{1}-1}q^{i}+q^{2n_{1}+n_{2}}\right), \nonumber \end{align} $$
 $$ \begin{align} \hspace{2pt}\left\lvert \mathscr{X}_{\gamma}^{0}\left(E_{\{23\}}(\Pi)\right)\left(\mathbf{F}_{q}\right)\right\rvert &=\left\lvert F_{\gamma}\left(\mathbf{F}_{q}\right)\right\rvert+(2a_{1}-a_{2})\left( 2q^{n_{1}+n_{2}}\sum_{i=0}^{n_{1}-1}q^{i}+q^{2n_{1}+n_{2}}\right), \end{align} $$
$$ \begin{align} \hspace{2pt}\left\lvert \mathscr{X}_{\gamma}^{0}\left(E_{\{23\}}(\Pi)\right)\left(\mathbf{F}_{q}\right)\right\rvert &=\left\lvert F_{\gamma}\left(\mathbf{F}_{q}\right)\right\rvert+(2a_{1}-a_{2})\left( 2q^{n_{1}+n_{2}}\sum_{i=0}^{n_{1}-1}q^{i}+q^{2n_{1}+n_{2}}\right), \end{align} $$
 $$ \begin{align} \hspace{-100pt}\left\lvert \mathscr{X}_{\gamma}^{0}\left(E_{\{13\}}(\Pi)\right)\left(\mathbf{F}_{q}\right)\right\rvert &=\left\lvert F_{\gamma}\left(\mathbf{F}_{q}\right)\right\rvert+(2a_{1}-a_{2})\left(q^{2n_{1}}\sum_{i=0}^{n_{2}-1}q^{i} \right. \nonumber\\& \quad \left. +q^{n_{1}+n_{2}}\sum_{i=0}^{n_{1}-1}q^{i}+q^{2n_{1}+n_{2}}\right). \end{align} $$
$$ \begin{align} \hspace{-100pt}\left\lvert \mathscr{X}_{\gamma}^{0}\left(E_{\{13\}}(\Pi)\right)\left(\mathbf{F}_{q}\right)\right\rvert &=\left\lvert F_{\gamma}\left(\mathbf{F}_{q}\right)\right\rvert+(2a_{1}-a_{2})\left(q^{2n_{1}}\sum_{i=0}^{n_{2}-1}q^{i} \right. \nonumber\\& \quad \left. +q^{n_{1}+n_{2}}\sum_{i=0}^{n_{1}-1}q^{i}+q^{2n_{1}+n_{2}}\right). \end{align} $$
Inserting equations (6.10)–(6.15) into equation (4.6), we get the following:
Proposition 6.4. The number of rational points on the tail equals
 $$ \begin{align*} \left\lvert {}^{t}\mathscr{X}_{\gamma}^{0}(\Pi)\left(\mathbf{F}_{q}\right)\right\rvert=(a_{1}+a_{2})\left(2q^{2n_{1}}\sum_{i=0}^{n_{2}-1}q^{i} +4q^{n_{1}+n_{2}}\sum_{i=0}^{n_{1}-1}q^{i}+3q^{2n_{1}+n_{2}} \right). \end{align*} $$
$$ \begin{align*} \left\lvert {}^{t}\mathscr{X}_{\gamma}^{0}(\Pi)\left(\mathbf{F}_{q}\right)\right\rvert=(a_{1}+a_{2})\left(2q^{2n_{1}}\sum_{i=0}^{n_{2}-1}q^{i} +4q^{n_{1}+n_{2}}\sum_{i=0}^{n_{1}-1}q^{i}+3q^{2n_{1}+n_{2}} \right). \end{align*} $$
The sum of results in Propositions 6.3 and 6.4 gives us another expression for
 $Q_{\gamma }^{0}(a_{1},a_{2})$
:
$Q_{\gamma }^{0}(a_{1},a_{2})$
:
Corollary 6.5.
 $$ \begin{align*} Q_{\gamma}^{0}(a_{1},a_{2}) &= \left\lvert \mathscr{X}_{\gamma}^{0,\xi}\left(\mathbf{F}_{q}\right)\right\rvert+ q^{2n_{1}+n_{2}} \left[\frac{1}{2}(3a_{2}-2-2n_{1}-n_{2})(3a_{2}-1-2n_{1}-n_{2}) \right.\\& \qquad -(2a_{2}-a_{1}-n_{1}-1)(2a_{2}-a_{1}-n_{1})\\& \left. \qquad -\frac{1}{2}(2a_{2}-a_{1}-n_{2}-1)(2a_{2}-a_{1}-n_{2})\right ]\\& \qquad + q^{2n_{1}} (a_{1}+a_{2}-2n_{1}-1) \left(n_{2}q^{n_{2}}-\sum_{i=0}^{n_{2}-1}q^{i}\right)\\& \qquad +2q^{n_{1}+n_{2}}(a_{1}+a_{2}-n_{1}-n_{2}-1) \left(n_{1}q^{n_{1}}-\sum_{i=0}^{n_{1}-1}q^{i}\right)\\& \qquad +(a_{1}+a_{2})\left(2q^{2n_{1}}\sum_{i=0}^{n_{2}-1}q^{i} +4q^{n_{1}+n_{2}}\sum_{i=0}^{n_{1}-1}q^{i}+3q^{2n_{1}+n_{2}}\right). \end{align*} $$
$$ \begin{align*} Q_{\gamma}^{0}(a_{1},a_{2}) &= \left\lvert \mathscr{X}_{\gamma}^{0,\xi}\left(\mathbf{F}_{q}\right)\right\rvert+ q^{2n_{1}+n_{2}} \left[\frac{1}{2}(3a_{2}-2-2n_{1}-n_{2})(3a_{2}-1-2n_{1}-n_{2}) \right.\\& \qquad -(2a_{2}-a_{1}-n_{1}-1)(2a_{2}-a_{1}-n_{1})\\& \left. \qquad -\frac{1}{2}(2a_{2}-a_{1}-n_{2}-1)(2a_{2}-a_{1}-n_{2})\right ]\\& \qquad + q^{2n_{1}} (a_{1}+a_{2}-2n_{1}-1) \left(n_{2}q^{n_{2}}-\sum_{i=0}^{n_{2}-1}q^{i}\right)\\& \qquad +2q^{n_{1}+n_{2}}(a_{1}+a_{2}-n_{1}-n_{2}-1) \left(n_{1}q^{n_{1}}-\sum_{i=0}^{n_{1}-1}q^{i}\right)\\& \qquad +(a_{1}+a_{2})\left(2q^{2n_{1}}\sum_{i=0}^{n_{2}-1}q^{i} +4q^{n_{1}+n_{2}}\sum_{i=0}^{n_{1}-1}q^{i}+3q^{2n_{1}+n_{2}}\right). \end{align*} $$
In particular, this shows that
 $Q_{\gamma }^{0}(a_{1},a_{2})$
depends polynomially on
$Q_{\gamma }^{0}(a_{1},a_{2})$
depends polynomially on
![]() $(a_{1},a_{2})\in \textbf {N}^{2}$
. As a corollary, the expression for
$(a_{1},a_{2})\in \textbf {N}^{2}$
. As a corollary, the expression for
 $Q_{\gamma }^{0}(a_{1},a_{2})$
in Proposition 6.2 is also a polynomial in
$Q_{\gamma }^{0}(a_{1},a_{2})$
in Proposition 6.2 is also a polynomial in
![]() $(a_{1},a_{2})$
, although it does not seem to be so.
$(a_{1},a_{2})$
, although it does not seem to be so.
6.1.3. Arthur’s weighted orbital integral
Now we can compare the two expressions in Proposition 6.2 and Corollary 6.5 for
 $Q_{\gamma }^{0}(a_{1},a_{2})$
. Look at their constant terms
$Q_{\gamma }^{0}(a_{1},a_{2})$
. Look at their constant terms
 $Q_{\gamma }^{0}(0,0)$
. As
$Q_{\gamma }^{0}(0,0)$
. As
 $J_{T}^{\xi }(\gamma )=\left \lvert \mathscr {X}_{\gamma }^{0,\xi }\left (\mathbf{F}_{q}\right )\right \rvert $
in this case, we obtain the following:
$J_{T}^{\xi }(\gamma )=\left \lvert \mathscr {X}_{\gamma }^{0,\xi }\left (\mathbf{F}_{q}\right )\right \rvert $
in this case, we obtain the following:
Theorem 6.6. Chaudouard and Laumon’s weighted orbital integral for
![]() $\gamma $
equals
$\gamma $
equals
 $$ \begin{align*} J_{T}^{\xi}(\gamma)=\sum_{i=1}^{n_{1}}i\left(q^{2i-1}+q^{2i-2}\right) +\sum_{i=n_{1}+n_{2}}^{2n_{1}+n_{2}-1} (4n_{1}+2n_{2}-4i-3)q^{i} +\left(n_{1}^{2}+2n_{1}n_{2}\right)q^{2n_{1}+n_{2}}. \end{align*} $$
$$ \begin{align*} J_{T}^{\xi}(\gamma)=\sum_{i=1}^{n_{1}}i\left(q^{2i-1}+q^{2i-2}\right) +\sum_{i=n_{1}+n_{2}}^{2n_{1}+n_{2}-1} (4n_{1}+2n_{2}-4i-3)q^{i} +\left(n_{1}^{2}+2n_{1}n_{2}\right)q^{2n_{1}+n_{2}}. \end{align*} $$
By Theorem 2.8 and Remark 2.3, we get Arthur’s weighted orbital integral as well. For the orbital integral
![]() $I^{G}_{\gamma }$
, as T is split, we can calculate it easily by equation (2.4):
$I^{G}_{\gamma }$
, as T is split, we can calculate it easily by equation (2.4):
 $$ \begin{align*} I^{G}_{\gamma}=q^{2n_{1}+n_{2}}. \end{align*} $$
$$ \begin{align*} I^{G}_{\gamma}=q^{2n_{1}+n_{2}}. \end{align*} $$
6.2. Calculation of
 $J_{M_{1}}(\gamma )$
$J_{M_{1}}(\gamma )$
We parametrize the Levi groups as before, with the further simplification
![]() $M_{i}:=M_{\{i\}}$
. Let
$M_{i}:=M_{\{i\}}$
. Let
![]() $\gamma =\textrm {diag}(\gamma _{1},\gamma _{2},\gamma _{3})$
and
$\gamma =\textrm {diag}(\gamma _{1},\gamma _{2},\gamma _{3})$
and
![]() $\gamma '=\textrm {diag}(\gamma _{1},\gamma _{3},\gamma _{2})$
; notice that
$\gamma '=\textrm {diag}(\gamma _{1},\gamma _{3},\gamma _{2})$
; notice that
Moreover,
![]() $\mathscr {X}_{\gamma }$
and
$\mathscr {X}_{\gamma }$
and
![]() $\mathscr {X}_{\gamma '}$
have the same geometry, as they have the same root valuation (indeed, they have the same affine paving), which implies that
$\mathscr {X}_{\gamma '}$
have the same geometry, as they have the same root valuation (indeed, they have the same affine paving), which implies that
Hence it is enough to calculate
![]() $J_{M_{1}}(\gamma )$
and
$J_{M_{1}}(\gamma )$
and
![]() $J_{M_{3}}(\gamma )$
. Notice that
$J_{M_{3}}(\gamma )$
. Notice that
![]() $M_{1}$
corresponds to the root
$M_{1}$
corresponds to the root
![]() $\alpha _{2}$
and
$\alpha _{2}$
and
![]() $M_{3}$
to the root
$M_{3}$
to the root
![]() $\alpha _{1}$
.
$\alpha _{1}$
.
As usual, we identify
![]() $X_{*}(T)\cong \textbf {Z}^{3}$
and
$X_{*}(T)\cong \textbf {Z}^{3}$
and
![]() $\mathfrak {a}_{T}^{G}$
with the hyperplane
$\mathfrak {a}_{T}^{G}$
with the hyperplane
![]() $x_{1}+x_{2}+x_{3}=0$
of
$x_{1}+x_{2}+x_{3}=0$
of
![]() $\mathfrak {a}_{T}=X_{*}(T)\otimes \textbf {R}\cong \textbf {R}^{3}$
. The subspace
$\mathfrak {a}_{T}=X_{*}(T)\otimes \textbf {R}\cong \textbf {R}^{3}$
. The subspace
 $\mathfrak {a}_{T}^{M_{1}}\subset \mathfrak {a}_{T}^{G}$
becomes the line
$\mathfrak {a}_{T}^{M_{1}}\subset \mathfrak {a}_{T}^{G}$
becomes the line
![]() $\{(0,x,-x)\}$
, and the subspace
$\{(0,x,-x)\}$
, and the subspace
 $\mathfrak {a}_{M_{1}}^{G}\subset \mathfrak {a}_{T}^{G}$
becomes
$\mathfrak {a}_{M_{1}}^{G}\subset \mathfrak {a}_{T}^{G}$
becomes
![]() $\{(-x,x/2,x/2)\}$
. The lattice
$\{(-x,x/2,x/2)\}$
. The lattice
 $\Lambda _{M_{1}}^{0}$
is identified with
$\Lambda _{M_{1}}^{0}$
is identified with
![]() $\textbf {Z}$
by the mapping
$\textbf {Z}$
by the mapping
 $$ \begin{align*} \Lambda_{M_{1}}^{0}\to \textbf{Z}: (-(a+b),a,b)\mapsto a+b. \end{align*} $$
$$ \begin{align*} \Lambda_{M_{1}}^{0}\to \textbf{Z}: (-(a+b),a,b)\mapsto a+b. \end{align*} $$
Its inclusion in
 $\mathfrak {a}_{M_{1}}^{G}$
is described by the mapping
$\mathfrak {a}_{M_{1}}^{G}$
is described by the mapping
 $$ \begin{align*} \Lambda_{M_{1}}^{0}\to \mathfrak{a}_{M_{1}}^{G}: (-(a+b),a,b)\mapsto (-(a+b),(a+b)/2, (a+b)/2). \end{align*} $$
$$ \begin{align*} \Lambda_{M_{1}}^{0}\to \mathfrak{a}_{M_{1}}^{G}: (-(a+b),a,b)\mapsto (-(a+b),(a+b)/2, (a+b)/2). \end{align*} $$
We identify
 $\mathfrak {a}_{M_{1}}^{G}$
with
$\mathfrak {a}_{M_{1}}^{G}$
with
![]() $\textbf {R}$
by identifying
$\textbf {R}$
by identifying
![]() $(-x,x/2,x/2)$
with x; the inclusion
$(-x,x/2,x/2)$
with x; the inclusion
 $\Lambda _{M_{1}}^{0}\subset \mathfrak {a}_{M_{1}}^{G}$
becomes the natural embedding
$\Lambda _{M_{1}}^{0}\subset \mathfrak {a}_{M_{1}}^{G}$
becomes the natural embedding
![]() $\textbf {Z}\subset \textbf {R}$
. On the other hand, the discrete free abelian group
$\textbf {Z}\subset \textbf {R}$
. On the other hand, the discrete free abelian group
![]() $\Lambda \cong X_{*}(T)$
is naturally identified with
$\Lambda \cong X_{*}(T)$
is naturally identified with
![]() $\textbf {Z}^{3}$
, and the morphism
$\textbf {Z}^{3}$
, and the morphism
![]() $H_{M_{1}}:\Lambda \to \mathfrak {a}_{M_{1}}$
can be calculated to be
$H_{M_{1}}:\Lambda \to \mathfrak {a}_{M_{1}}$
can be calculated to be
 $$ \begin{align*} H_{M_{1}}(a_{1},a_{2},a_{3})=\left(a_{1}, \frac{a_{2}+a_{3}}{2}, \frac{a_{2}+a_{3}}{2} \right). \end{align*} $$
$$ \begin{align*} H_{M_{1}}(a_{1},a_{2},a_{3})=\left(a_{1}, \frac{a_{2}+a_{3}}{2}, \frac{a_{2}+a_{3}}{2} \right). \end{align*} $$
Hence
![]() $\Lambda ^{H_{M_{1}}}$
is freely generated by the element
$\Lambda ^{H_{M_{1}}}$
is freely generated by the element
 $\textrm {diag}\left (1,\epsilon ,\epsilon ^{-1}\right )$
.
$\textrm {diag}\left (1,\epsilon ,\epsilon ^{-1}\right )$
.
According to Proposition 3.1, we can take
 $\Sigma _{\gamma }^{G,M_{1}}$
to be the interval
$\Sigma _{\gamma }^{G,M_{1}}$
to be the interval
![]() $[0,2n_{1}]$
in
$[0,2n_{1}]$
in
 $\mathfrak {a}_{M_{1}}^{G}\cong \textbf {R}$
. For
$\mathfrak {a}_{M_{1}}^{G}\cong \textbf {R}$
. For
![]() $N\in \textbf {N}$
,
$N\in \textbf {N}$
,
![]() $N\gg 0$
, let
$N\gg 0$
, let
![]() $\Pi _{N}$
be the interval
$\Pi _{N}$
be the interval
![]() $[-N,2n_{1}+N]$
, regarded as a
$[-N,2n_{1}+N]$
, regarded as a
![]() $(G,M_{1})$
-orthogonal family in
$(G,M_{1})$
-orthogonal family in
 $\mathfrak {a}_{M_{1}}^{G}$
. We are going to calculate
$\mathfrak {a}_{M_{1}}^{G}$
. We are going to calculate
 $\left (\Lambda ^{H_{M_{1}}}\middle \backslash \mathscr {X}_{\gamma }(\Pi _{N})\right )\left (\mathbf{F}_{q}\right )$
by the two approaches we have described.
$\left (\Lambda ^{H_{M_{1}}}\middle \backslash \mathscr {X}_{\gamma }(\Pi _{N})\right )\left (\mathbf{F}_{q}\right )$
by the two approaches we have described.
In the Arthur–Kottwitz approach, we need to calculate
 $$ \begin{align*} \left\lvert\left(\Lambda^{H_{M_{1}}}\middle\backslash F_{\gamma}^{G,M_{1}}\right)\left(\mathbf{F}_{q}\right)\right\rvert \quad \text{and} \quad \left\lvert\left(\Lambda^{H_{M_{1}}}\middle\backslash F_{\gamma}^{M_{1},M_{1}}\right)\left(\mathbf{F}_{q}\right)\right\rvert. \end{align*} $$
$$ \begin{align*} \left\lvert\left(\Lambda^{H_{M_{1}}}\middle\backslash F_{\gamma}^{G,M_{1}}\right)\left(\mathbf{F}_{q}\right)\right\rvert \quad \text{and} \quad \left\lvert\left(\Lambda^{H_{M_{1}}}\middle\backslash F_{\gamma}^{M_{1},M_{1}}\right)\left(\mathbf{F}_{q}\right)\right\rvert. \end{align*} $$
Combining Proposition 3.8 and Corollary 3.10, we get
 $$ \begin{align*} \left\lvert\left(\Lambda^{H_{M_{1}}}\middle\backslash F_{\gamma}^{G,M_{1}}\right)\left(\mathbf{F}_{q}\right)\right\rvert=\left\lvert F_{\gamma,\mu}^{G,M_{1}}\left(\mathbf{F}_{q}\right)\right\rvert=q^{2n_{1}+n_{2}}+2q^{n_{1}+n_{2}}\left(1+q+\dotsb+q^{n_{1}-1}\right). \end{align*} $$
$$ \begin{align*} \left\lvert\left(\Lambda^{H_{M_{1}}}\middle\backslash F_{\gamma}^{G,M_{1}}\right)\left(\mathbf{F}_{q}\right)\right\rvert=\left\lvert F_{\gamma,\mu}^{G,M_{1}}\left(\mathbf{F}_{q}\right)\right\rvert=q^{2n_{1}+n_{2}}+2q^{n_{1}+n_{2}}\left(1+q+\dotsb+q^{n_{1}-1}\right). \end{align*} $$
For the second calculation, since
 $F_{\gamma }^{M_{1},M_{1}}=\mathscr {X}_{\gamma }^{M_{1},(0)}$
and
$F_{\gamma }^{M_{1},M_{1}}=\mathscr {X}_{\gamma }^{M_{1},(0)}$
and
![]() $\Lambda ^{H_{M_{1}}}=\Lambda ^{M_{1}}$
, we have
$\Lambda ^{H_{M_{1}}}=\Lambda ^{M_{1}}$
, we have
 $$ \begin{align*} \left\lvert\left(\Lambda^{H_{M_{1}}}\middle\backslash F_{\gamma}^{M_{1},M_{1}}\right)\left(\mathbf{F}_{q}\right)\right\rvert=\left\lvert\left(\Lambda^{M_{1}}\middle\backslash \mathscr{X}_{\gamma}^{M_{1},0}\right)\left(\mathbf{F}_{q}\right)\right\rvert=q^{n_{2}}.\end{align*} $$
$$ \begin{align*} \left\lvert\left(\Lambda^{H_{M_{1}}}\middle\backslash F_{\gamma}^{M_{1},M_{1}}\right)\left(\mathbf{F}_{q}\right)\right\rvert=\left\lvert\left(\Lambda^{M_{1}}\middle\backslash \mathscr{X}_{\gamma}^{M_{1},0}\right)\left(\mathbf{F}_{q}\right)\right\rvert=q^{n_{2}}.\end{align*} $$
The reduction process is illustrated by a figure similar to Figure 2. By Corollary 3.7, we have the following:
Proposition 6.7.
 $$ \begin{align*} \left\lvert\left(\Lambda^{H_{M_{1}}}\middle\backslash \mathscr{X}_{\gamma}^{0}(\Pi_{N})\right)\left(\mathbf{F}_{q}\right)\right\rvert&=\left\lvert\left(\Lambda^{H_{M_{1}}}\middle\backslash F_{\gamma}^{G,M_{1}}\right)\left(\mathbf{F}_{q}\right)\right\rvert+2Nq^{2n_{1}}\left\lvert\left(\Lambda^{H_{M_{1}}}\middle\backslash F_{\gamma}^{M_{1},M_{1}}\right)\left(\mathbf{F}_{q}\right)\right\rvert \nonumber \\ &= q^{2n_{1}+n_{2}}+2q^{n_{1}+n_{2}}\left(1+q+\dotsb+q^{n_{1}-1}\right)+2Nq^{2n_{1}+n_{2}} \nonumber \\ &=(2N+1)q^{2n_{1}+n_{2}}+2q^{n_{1}+n_{2}}\left(1+q+\dotsb+q^{n_{1}-1}\right). \end{align*} $$
$$ \begin{align*} \left\lvert\left(\Lambda^{H_{M_{1}}}\middle\backslash \mathscr{X}_{\gamma}^{0}(\Pi_{N})\right)\left(\mathbf{F}_{q}\right)\right\rvert&=\left\lvert\left(\Lambda^{H_{M_{1}}}\middle\backslash F_{\gamma}^{G,M_{1}}\right)\left(\mathbf{F}_{q}\right)\right\rvert+2Nq^{2n_{1}}\left\lvert\left(\Lambda^{H_{M_{1}}}\middle\backslash F_{\gamma}^{M_{1},M_{1}}\right)\left(\mathbf{F}_{q}\right)\right\rvert \nonumber \\ &= q^{2n_{1}+n_{2}}+2q^{n_{1}+n_{2}}\left(1+q+\dotsb+q^{n_{1}-1}\right)+2Nq^{2n_{1}+n_{2}} \nonumber \\ &=(2N+1)q^{2n_{1}+n_{2}}+2q^{n_{1}+n_{2}}\left(1+q+\dotsb+q^{n_{1}-1}\right). \end{align*} $$
In the Harder–Narasimhan approach, we begin with counting points on the tail. By construction,
 $$ \begin{align} \left\lvert\left(\Lambda^{H_{M_{1}}}\middle\backslash ^{t}\mathscr{X}_{\gamma}^{0}(\Pi_{N})\right)\left(\mathbf{F}_{q}\right)\right\rvert &=2\left\lvert\left(\Lambda^{H_{M_{1}}}\middle\backslash F_{\gamma}^{G,M_{1}}\right)\left(\mathbf{F}_{q}\right)\right\rvert \nonumber\\ &= 2\left[q^{2n_{1}+n_{2}}+2q^{n_{1}+n_{2}}\left(1+q+\dotsb+q^{n_{1}-1}\right)\right]. \end{align} $$
$$ \begin{align} \left\lvert\left(\Lambda^{H_{M_{1}}}\middle\backslash ^{t}\mathscr{X}_{\gamma}^{0}(\Pi_{N})\right)\left(\mathbf{F}_{q}\right)\right\rvert &=2\left\lvert\left(\Lambda^{H_{M_{1}}}\middle\backslash F_{\gamma}^{G,M_{1}}\right)\left(\mathbf{F}_{q}\right)\right\rvert \nonumber\\ &= 2\left[q^{2n_{1}+n_{2}}+2q^{n_{1}+n_{2}}\left(1+q+\dotsb+q^{n_{1}-1}\right)\right]. \end{align} $$
Then we calculate
 $$ \begin{align*} \left\lvert\left(\Lambda^{H_{M_{1}}}\middle\backslash \mathscr{X}_{\gamma}^{M_{1},0,\xi^{M_{1}}}\right)\left(\mathbf{F}_{q}\right)\right\rvert=\left\lvert\left(\Lambda^{H_{M_{1}}}\middle\backslash \mathscr{X}_{\gamma}^{M_{1},0}\right)\left(\mathbf{F}_{q}\right)\right\rvert=q^{n_{2}}. \end{align*} $$
$$ \begin{align*} \left\lvert\left(\Lambda^{H_{M_{1}}}\middle\backslash \mathscr{X}_{\gamma}^{M_{1},0,\xi^{M_{1}}}\right)\left(\mathbf{F}_{q}\right)\right\rvert=\left\lvert\left(\Lambda^{H_{M_{1}}}\middle\backslash \mathscr{X}_{\gamma}^{M_{1},0}\right)\left(\mathbf{F}_{q}\right)\right\rvert=q^{n_{2}}. \end{align*} $$
By Theorem 4.8, this implies
 $$ \begin{align} \left\lvert\left(\Lambda^{H_{M_{1}}}\middle\backslash {}^{m}\mathscr{X}_{\gamma}^{0}(\Pi_{N})\right)\left(\mathbf{F}_{q}\right)\right\rvert&=\left\lvert\left(\Lambda^{H_{M_{1}}}\middle\backslash \mathscr{X}_{\gamma}^{\xi,0}\right)\left(\mathbf{F}_{q}\right)\right\rvert+[2N-(2n_{1}+1)]\cdot q^{2n_{1}} \nonumber\\ & \quad \cdot \left\lvert\left(\Lambda^{H_{M_{1}}}\middle\backslash \mathscr{X}_{\gamma}^{M_{1},0,\xi^{M_{1}}}\right)\left(\mathbf{F}_{q}\right)\right\rvert \nonumber \\ &= \left\lvert\left(\Lambda^{H_{M_{1}}}\middle\backslash \mathscr{X}_{\gamma}^{\xi,0}\right)\left(\mathbf{F}_{q}\right)\right\rvert+[2N-(2n_{1}+1)]\cdot q^{2n_{1}+n_{2}}. \end{align} $$
$$ \begin{align} \left\lvert\left(\Lambda^{H_{M_{1}}}\middle\backslash {}^{m}\mathscr{X}_{\gamma}^{0}(\Pi_{N})\right)\left(\mathbf{F}_{q}\right)\right\rvert&=\left\lvert\left(\Lambda^{H_{M_{1}}}\middle\backslash \mathscr{X}_{\gamma}^{\xi,0}\right)\left(\mathbf{F}_{q}\right)\right\rvert+[2N-(2n_{1}+1)]\cdot q^{2n_{1}} \nonumber\\ & \quad \cdot \left\lvert\left(\Lambda^{H_{M_{1}}}\middle\backslash \mathscr{X}_{\gamma}^{M_{1},0,\xi^{M_{1}}}\right)\left(\mathbf{F}_{q}\right)\right\rvert \nonumber \\ &= \left\lvert\left(\Lambda^{H_{M_{1}}}\middle\backslash \mathscr{X}_{\gamma}^{\xi,0}\right)\left(\mathbf{F}_{q}\right)\right\rvert+[2N-(2n_{1}+1)]\cdot q^{2n_{1}+n_{2}}. \end{align} $$
Combining equations (6.16) and (6.17), we obtain the following:
Proposition 6.8.
 $$ \begin{align*} \left\lvert\left(\Lambda^{H_{M_{1}}}\middle\backslash \mathscr{X}_{\gamma}^{0}(\Pi_{N})\right)\left(\mathbf{F}_{q}\right)\right\rvert&=\left\lvert\left(\Lambda^{H_{M_{1}}}\middle\backslash \mathscr{X}_{\gamma}^{\xi,0}\right)\left(\mathbf{F}_{q}\right)\right\rvert+[2N-(2n_{1}+1)]\cdot q^{2n_{1}+n_{2}} \nonumber \\ & \quad +2\left[q^{2n_{1}+n_{2}}+2q^{n_{1}+n_{2}}\left(1+q+\dotsb+q^{n_{1}-1}\right)\right]. \end{align*} $$
$$ \begin{align*} \left\lvert\left(\Lambda^{H_{M_{1}}}\middle\backslash \mathscr{X}_{\gamma}^{0}(\Pi_{N})\right)\left(\mathbf{F}_{q}\right)\right\rvert&=\left\lvert\left(\Lambda^{H_{M_{1}}}\middle\backslash \mathscr{X}_{\gamma}^{\xi,0}\right)\left(\mathbf{F}_{q}\right)\right\rvert+[2N-(2n_{1}+1)]\cdot q^{2n_{1}+n_{2}} \nonumber \\ & \quad +2\left[q^{2n_{1}+n_{2}}+2q^{n_{1}+n_{2}}\left(1+q+\dotsb+q^{n_{1}-1}\right)\right]. \end{align*} $$
Comparing Propositions 6.7 and 6.8, we get the following:
Proposition 6.9.
 $$ \begin{align*} \left\lvert\left(\Lambda^{H_{M_{1}}}\middle\backslash \mathscr{X}_{\gamma}^{\xi,0}\right)\left(\mathbf{F}_{q}\right)\right\rvert= 2n_{1}q^{2n_{1}+n_{2}}-2q^{n_{1}+n_{2}}\left(1+q+\dotsb+q^{n_{1}-1}\right). \end{align*} $$
$$ \begin{align*} \left\lvert\left(\Lambda^{H_{M_{1}}}\middle\backslash \mathscr{X}_{\gamma}^{\xi,0}\right)\left(\mathbf{F}_{q}\right)\right\rvert= 2n_{1}q^{2n_{1}+n_{2}}-2q^{n_{1}+n_{2}}\left(1+q+\dotsb+q^{n_{1}-1}\right). \end{align*} $$
It remains to calculate the volume factor
 $\textrm {vol}_{dt}\left (\Lambda ^{H_{M_{1}}}\middle \backslash T(F)_{M_{1}}^{1}\right )$
. By equation (2.5), it equals
$\textrm {vol}_{dt}\left (\Lambda ^{H_{M_{1}}}\middle \backslash T(F)_{M_{1}}^{1}\right )$
. By equation (2.5), it equals
![]() $1$
because
$1$
because
![]() $S=T$
and the morphism
$S=T$
and the morphism
![]() $H_{M_{1}}: X_{*}(T)\to X_{*}(M)$
is surjective. The foregoing calculations can be summarized as follows:
$H_{M_{1}}: X_{*}(T)\to X_{*}(M)$
is surjective. The foregoing calculations can be summarized as follows:
Theorem 6.10. We have
 $$ \begin{align*} J_{M_{1}}^{\xi}(\gamma)=\left\lvert\left(\Lambda^{H_{M_{1}}}\middle\backslash \mathscr{X}_{\gamma}^{\xi,0}\right)\left(\mathbf{F}_{q}\right)\right\rvert= 2n_{1}q^{2n_{1}+n_{2}}-2q^{n_{1}+n_{2}}\left(1+q+\dotsb+q^{n_{1}-1}\right).\end{align*} $$
$$ \begin{align*} J_{M_{1}}^{\xi}(\gamma)=\left\lvert\left(\Lambda^{H_{M_{1}}}\middle\backslash \mathscr{X}_{\gamma}^{\xi,0}\right)\left(\mathbf{F}_{q}\right)\right\rvert= 2n_{1}q^{2n_{1}+n_{2}}-2q^{n_{1}+n_{2}}\left(1+q+\dotsb+q^{n_{1}-1}\right).\end{align*} $$
6.3. Calculation of
 $J_{M_{3}}(\gamma )$
$J_{M_{3}}(\gamma )$
We make identifications as before. The subspace
 $\mathfrak {a}_{T}^{M_{3}}\subset \mathfrak {a}_{T}^{G}$
becomes the line
$\mathfrak {a}_{T}^{M_{3}}\subset \mathfrak {a}_{T}^{G}$
becomes the line
![]() $\{(x,-x,0)\}$
, and the subspace
$\{(x,-x,0)\}$
, and the subspace
 $\mathfrak {a}_{M_{3}}^{G}\subset \mathfrak {a}_{T}^{G}$
becomes
$\mathfrak {a}_{M_{3}}^{G}\subset \mathfrak {a}_{T}^{G}$
becomes
![]() $\{(x/2,x/2,-x)\}$
; they are identified with
$\{(x/2,x/2,-x)\}$
; they are identified with
![]() $\textbf {R}$
as before. The lattice
$\textbf {R}$
as before. The lattice
 $\Lambda _{M_{3}}^{0}$
is identified with
$\Lambda _{M_{3}}^{0}$
is identified with
![]() $\textbf {Z}$
by the mapping
$\textbf {Z}$
by the mapping
 $$ \begin{align*} \Lambda_{M_{3}}^{0}\to \textbf{Z}: (a,b,-(a+b))\mapsto a+b. \end{align*} $$
$$ \begin{align*} \Lambda_{M_{3}}^{0}\to \textbf{Z}: (a,b,-(a+b))\mapsto a+b. \end{align*} $$
The inclusion
 $\Lambda _{M_{3}}^{0}\subset \mathfrak {a}_{M_{3}}^{G}$
becomes again the natural embedding
$\Lambda _{M_{3}}^{0}\subset \mathfrak {a}_{M_{3}}^{G}$
becomes again the natural embedding
![]() $\textbf {Z}\subset \textbf {R}$
. Similarly, the group
$\textbf {Z}\subset \textbf {R}$
. Similarly, the group
![]() $\Lambda ^{H_{M_{3}}}$
is freely generated by the element
$\Lambda ^{H_{M_{3}}}$
is freely generated by the element
 $\textrm {diag}\left (\epsilon ,\epsilon ^{-1},1\right )$
.
$\textrm {diag}\left (\epsilon ,\epsilon ^{-1},1\right )$
.
By Proposition 3.1, we can take
 $\Sigma _{\gamma }^{G,M_{3}}$
to be the interval
$\Sigma _{\gamma }^{G,M_{3}}$
to be the interval
![]() $[0,n_{1}+n_{2}]$
in
$[0,n_{1}+n_{2}]$
in
 $\mathfrak {a}_{M_{3}}^{G}\cong \textbf {R}$
. For
$\mathfrak {a}_{M_{3}}^{G}\cong \textbf {R}$
. For
![]() $N\in \textbf {N}$
,
$N\in \textbf {N}$
,
![]() $N\gg 0$
, let
$N\gg 0$
, let
![]() $\Pi _{N}$
be the interval
$\Pi _{N}$
be the interval
![]() $[-N,n_{1}+n_{2}+N]$
, regarded as a
$[-N,n_{1}+n_{2}+N]$
, regarded as a
![]() $(G,M_{3})$
-orthogonal family in
$(G,M_{3})$
-orthogonal family in
 $\mathfrak {a}_{M_{3}}^{G}$
. We calculate
$\mathfrak {a}_{M_{3}}^{G}$
. We calculate
 $\left (\Lambda ^{H_{M_{3}}}\middle \backslash \mathscr {X}_{\gamma }(\Pi _{N})\right )\left (\mathbf{F}_{q}\right )$
in two ways as before.
$\left (\Lambda ^{H_{M_{3}}}\middle \backslash \mathscr {X}_{\gamma }(\Pi _{N})\right )\left (\mathbf{F}_{q}\right )$
in two ways as before.
Using similar calculations as before, we get
 $$ \begin{align*} \left\lvert\left(\Lambda^{H_{M_{3}}}\middle\backslash F_{\gamma}^{M_{3},M_{3}}\right)\left(\mathbf{F}_{q}\right)\right\rvert=\left\lvert\left(\Lambda^{M_{3}}\middle\backslash \mathscr{X}_{\gamma}^{M_{3},0}\right)\left(\mathbf{F}_{q}\right)\right\rvert=q^{n_{1}} \end{align*} $$
$$ \begin{align*} \left\lvert\left(\Lambda^{H_{M_{3}}}\middle\backslash F_{\gamma}^{M_{3},M_{3}}\right)\left(\mathbf{F}_{q}\right)\right\rvert=\left\lvert\left(\Lambda^{M_{3}}\middle\backslash \mathscr{X}_{\gamma}^{M_{3},0}\right)\left(\mathbf{F}_{q}\right)\right\rvert=q^{n_{1}} \end{align*} $$
and
 $$ \begin{align*} \left\lvert\left(\Lambda^{H_{M_{3}}}\middle\backslash F_{\gamma}^{G,M_{3}}\right)\left(\mathbf{F}_{q}\right)\right\rvert&=\left\lvert F_{\gamma,\mu}^{G,M_{3}}\left(\mathbf{F}_{q}\right)\right\rvert=q^{2n_{1}+n_{2}}+q^{n_{1}+n_{2}}\left(1+q+\dotsb+q^{n_{1}-1}\right) \nonumber\\ & \quad +q^{2n_{1}}\left(1+q+\dotsb +q^{n_{2}-1}\right). \end{align*} $$
$$ \begin{align*} \left\lvert\left(\Lambda^{H_{M_{3}}}\middle\backslash F_{\gamma}^{G,M_{3}}\right)\left(\mathbf{F}_{q}\right)\right\rvert&=\left\lvert F_{\gamma,\mu}^{G,M_{3}}\left(\mathbf{F}_{q}\right)\right\rvert=q^{2n_{1}+n_{2}}+q^{n_{1}+n_{2}}\left(1+q+\dotsb+q^{n_{1}-1}\right) \nonumber\\ & \quad +q^{2n_{1}}\left(1+q+\dotsb +q^{n_{2}-1}\right). \end{align*} $$
With Arthur–Kottwitz reduction, we obtain the following:
Proposition 6.11.
 $$ \begin{align*} \left\lvert\left(\Lambda^{H_{M_{3}}}\middle\backslash \mathscr{X}_{\gamma}^{0}(\Pi_{N})\right)\left(\mathbf{F}_{q}\right)\right\rvert &=\left\lvert\left(\Lambda^{H_{M_{3}}}\middle\backslash F_{\gamma}^{G,M_{3}}\right)\left(\mathbf{F}_{q}\right)\right\rvert+2Nq^{n_{1}+n_{2}}\left\lvert\left(\Lambda^{H_{M_{3}}}\middle\backslash F_{\gamma}^{M_{3},M_{3}}\right)\left(\mathbf{F}_{q}\right)\right\rvert \\ &= q^{2n_{1}+n_{2}}+q^{n_{1}+n_{2}}\left(1+q+\dotsb+q^{n_{1}-1}\right) \\ & \quad +q^{2n_{1}}\left(1+q+\dotsb +q^{n_{2}-1}\right)+2Nq^{2n_{1}+n_{2}} \\ &=(2N+1)q^{2n_{1}+n_{2}}+q^{n_{1}+n_{2}}\left(1+q+\dotsb+q^{n_{1}-1}\right) \\ & \quad +q^{2n_{1}}\left(1+q+\dotsb +q^{n_{2}-1}\right). \end{align*} $$
$$ \begin{align*} \left\lvert\left(\Lambda^{H_{M_{3}}}\middle\backslash \mathscr{X}_{\gamma}^{0}(\Pi_{N})\right)\left(\mathbf{F}_{q}\right)\right\rvert &=\left\lvert\left(\Lambda^{H_{M_{3}}}\middle\backslash F_{\gamma}^{G,M_{3}}\right)\left(\mathbf{F}_{q}\right)\right\rvert+2Nq^{n_{1}+n_{2}}\left\lvert\left(\Lambda^{H_{M_{3}}}\middle\backslash F_{\gamma}^{M_{3},M_{3}}\right)\left(\mathbf{F}_{q}\right)\right\rvert \\ &= q^{2n_{1}+n_{2}}+q^{n_{1}+n_{2}}\left(1+q+\dotsb+q^{n_{1}-1}\right) \\ & \quad +q^{2n_{1}}\left(1+q+\dotsb +q^{n_{2}-1}\right)+2Nq^{2n_{1}+n_{2}} \\ &=(2N+1)q^{2n_{1}+n_{2}}+q^{n_{1}+n_{2}}\left(1+q+\dotsb+q^{n_{1}-1}\right) \\ & \quad +q^{2n_{1}}\left(1+q+\dotsb +q^{n_{2}-1}\right). \end{align*} $$
For the Harder–Narasimhan reduction, we count the points on the tail
 $$ \begin{align*} \left\lvert\left(\Lambda^{H_{M_{3}}}\middle\backslash ^{t}\mathscr{X}_{\gamma}^{0}(\Pi_{N})\right)\left(\mathbf{F}_{q}\right)\right\rvert&=2\left\lvert\left(\Lambda^{H_{M_{3}}}\middle\backslash F_{\gamma}^{G,M_{3}}\right)\left(\mathbf{F}_{q}\right)\right\rvert \\ &= 2\left[q^{2n_{1}+n_{2}}+q^{n_{1}+n_{2}}\left(1+q+\dotsb+q^{n_{1}-1}\right) \right. \\ & \qquad \left. +q^{2n_{1}}\left(1+q+\dotsb+q^{n_{2}-1}\right)\right] \end{align*} $$
$$ \begin{align*} \left\lvert\left(\Lambda^{H_{M_{3}}}\middle\backslash ^{t}\mathscr{X}_{\gamma}^{0}(\Pi_{N})\right)\left(\mathbf{F}_{q}\right)\right\rvert&=2\left\lvert\left(\Lambda^{H_{M_{3}}}\middle\backslash F_{\gamma}^{G,M_{3}}\right)\left(\mathbf{F}_{q}\right)\right\rvert \\ &= 2\left[q^{2n_{1}+n_{2}}+q^{n_{1}+n_{2}}\left(1+q+\dotsb+q^{n_{1}-1}\right) \right. \\ & \qquad \left. +q^{2n_{1}}\left(1+q+\dotsb+q^{n_{2}-1}\right)\right] \end{align*} $$
and the
![]() $\xi $
-stable points
$\xi $
-stable points
 $$ \begin{align*} \left\lvert\left(\Lambda^{H_{M_{3}}}\middle\backslash \mathscr{X}_{\gamma}^{M_{3},0,\xi^{M_{3}}}\right)\left(\mathbf{F}_{q}\right)\right\rvert=\left\lvert\left(\Lambda^{H_{M_{3}}}\middle\backslash \mathscr{X}_{\gamma}^{M_{3},0}\right)\left(\mathbf{F}_{q}\right)\right\rvert=q^{n_{1}}. \end{align*} $$
$$ \begin{align*} \left\lvert\left(\Lambda^{H_{M_{3}}}\middle\backslash \mathscr{X}_{\gamma}^{M_{3},0,\xi^{M_{3}}}\right)\left(\mathbf{F}_{q}\right)\right\rvert=\left\lvert\left(\Lambda^{H_{M_{3}}}\middle\backslash \mathscr{X}_{\gamma}^{M_{3},0}\right)\left(\mathbf{F}_{q}\right)\right\rvert=q^{n_{1}}. \end{align*} $$
Hence the points in the main body are
 $$ \begin{align*} \left\lvert\left(\Lambda^{H_{M_{3}}}\middle\backslash {}^{m}\mathscr{X}_{\gamma}^{0}(\Pi_{N})\right)\left(\mathbf{F}_{q}\right)\right\rvert&=\left\lvert\left(\Lambda^{H_{M_{3}}}\middle\backslash \mathscr{X}_{\gamma}^{\xi,0}\right)\left(\mathbf{F}_{q}\right)\right\rvert+[2N-(n_{1}+n_{2}+1)]\cdot q^{n_{1}+n_{2}} \\ & \quad \cdot \left\lvert\left(\Lambda^{H_{M_{3}}}\middle\backslash \mathscr{X}_{\gamma}^{M_{3},0,\xi^{M_{3}}}\right)\left(\mathbf{F}_{q}\right)\right\rvert \\ &= \left\lvert\left(\Lambda^{H_{M_{3}}}\middle\backslash \mathscr{X}_{\gamma}^{\xi,0}\right)\left(\mathbf{F}_{q}\right)\right\rvert+[2N-(n_{1}+n_{2}+1)]\cdot q^{2n_{1}+n_{2}}.\end{align*} $$
$$ \begin{align*} \left\lvert\left(\Lambda^{H_{M_{3}}}\middle\backslash {}^{m}\mathscr{X}_{\gamma}^{0}(\Pi_{N})\right)\left(\mathbf{F}_{q}\right)\right\rvert&=\left\lvert\left(\Lambda^{H_{M_{3}}}\middle\backslash \mathscr{X}_{\gamma}^{\xi,0}\right)\left(\mathbf{F}_{q}\right)\right\rvert+[2N-(n_{1}+n_{2}+1)]\cdot q^{n_{1}+n_{2}} \\ & \quad \cdot \left\lvert\left(\Lambda^{H_{M_{3}}}\middle\backslash \mathscr{X}_{\gamma}^{M_{3},0,\xi^{M_{3}}}\right)\left(\mathbf{F}_{q}\right)\right\rvert \\ &= \left\lvert\left(\Lambda^{H_{M_{3}}}\middle\backslash \mathscr{X}_{\gamma}^{\xi,0}\right)\left(\mathbf{F}_{q}\right)\right\rvert+[2N-(n_{1}+n_{2}+1)]\cdot q^{2n_{1}+n_{2}}.\end{align*} $$
Combining them gives us the following:
Proposition 6.12.
 $$ \begin{align*} \left\lvert\left(\Lambda^{H_{M_{3}}}\middle\backslash \mathscr{X}_{\gamma}^{0}(\Pi_{N})\right)\left(\mathbf{F}_{q}\right)\right\rvert&=\left\lvert\left(\Lambda^{H_{M_{3}}}\middle\backslash {}^{m}\mathscr{X}_{\gamma}^{0}(\Pi_{N})\right)\left(\mathbf{F}_{q}\right)\right\rvert+\left\lvert\left(\Lambda^{H_{M_{3}}}\middle\backslash {}^{t}\mathscr{X}_{\gamma}^{0}(\Pi_{N})\right)\left(\mathbf{F}_{q}\right)\right\rvert \\ &= \left\lvert\left(\Lambda^{H_{M_{3}}}\middle\backslash \mathscr{X}_{\gamma}^{\xi,0}\right)\left(\mathbf{F}_{q}\right)\right\rvert+[2N-(n_{1}+n_{2}+1)]\cdot q^{2n_{1}+n_{2}} \\ & \quad +2\left[q^{2n_{1}+n_{2}}+q^{n_{1}+n_{2}}\left(1+q+\dotsb+q^{n_{1}-1}\right) \right. \\ & \qquad \quad \left. +q^{2n_{1}}\left(1+q+\dotsb+q^{n_{2}-1}\right)\right]. \end{align*} $$
$$ \begin{align*} \left\lvert\left(\Lambda^{H_{M_{3}}}\middle\backslash \mathscr{X}_{\gamma}^{0}(\Pi_{N})\right)\left(\mathbf{F}_{q}\right)\right\rvert&=\left\lvert\left(\Lambda^{H_{M_{3}}}\middle\backslash {}^{m}\mathscr{X}_{\gamma}^{0}(\Pi_{N})\right)\left(\mathbf{F}_{q}\right)\right\rvert+\left\lvert\left(\Lambda^{H_{M_{3}}}\middle\backslash {}^{t}\mathscr{X}_{\gamma}^{0}(\Pi_{N})\right)\left(\mathbf{F}_{q}\right)\right\rvert \\ &= \left\lvert\left(\Lambda^{H_{M_{3}}}\middle\backslash \mathscr{X}_{\gamma}^{\xi,0}\right)\left(\mathbf{F}_{q}\right)\right\rvert+[2N-(n_{1}+n_{2}+1)]\cdot q^{2n_{1}+n_{2}} \\ & \quad +2\left[q^{2n_{1}+n_{2}}+q^{n_{1}+n_{2}}\left(1+q+\dotsb+q^{n_{1}-1}\right) \right. \\ & \qquad \quad \left. +q^{2n_{1}}\left(1+q+\dotsb+q^{n_{2}-1}\right)\right]. \end{align*} $$
Comparing Propositions 6.11 and 6.12, we get the following:
Proposition 6.13.
 $$ \begin{align*} \left\lvert\left(\Lambda^{H_{M_{3}}}\middle\backslash \mathscr{X}_{\gamma}^{\xi,0}\right)\left(\mathbf{F}_{q}\right)\right\rvert &= (n_{1}+n_{2})q^{2n_{1}+n_{2}}-q^{n_{1}+n_{2}}\left(1+q+\dotsb+q^{n_{1}-1}\right) \\ & \quad -q^{2n_{1}}\left(1+q+\dotsb+q^{n_{2}-1}\right). \end{align*} $$
$$ \begin{align*} \left\lvert\left(\Lambda^{H_{M_{3}}}\middle\backslash \mathscr{X}_{\gamma}^{\xi,0}\right)\left(\mathbf{F}_{q}\right)\right\rvert &= (n_{1}+n_{2})q^{2n_{1}+n_{2}}-q^{n_{1}+n_{2}}\left(1+q+\dotsb+q^{n_{1}-1}\right) \\ & \quad -q^{2n_{1}}\left(1+q+\dotsb+q^{n_{2}-1}\right). \end{align*} $$
As before, the volume factor
 $\textrm {vol}_{dt}\left (\Lambda ^{H_{M_{3}}}\middle \backslash T(F)_{M_{3}}^{1}\right )$
equals
$\textrm {vol}_{dt}\left (\Lambda ^{H_{M_{3}}}\middle \backslash T(F)_{M_{3}}^{1}\right )$
equals
![]() $1$
, and so we have the following:
$1$
, and so we have the following:
Theorem 6.14. We have
 $$ \begin{align*} J_{M_{3}}^{\xi}(\gamma)=\left\lvert\left(\Lambda^{H_{M_{3}}}\middle\backslash \mathscr{X}_{\gamma}^{\xi,0}\right)\left(\mathbf{F}_{q}\right)\right\rvert&=(n_{1}+n_{2})q^{2n_{1}+n_{2}}-q^{n_{1}+n_{2}}\left(1+q+\dotsb+q^{n_{1}-1}\right)\\ & \quad -q^{2n_{1}}\left(1+q+\dotsb+q^{n_{2}-1}\right). \end{align*} $$
$$ \begin{align*} J_{M_{3}}^{\xi}(\gamma)=\left\lvert\left(\Lambda^{H_{M_{3}}}\middle\backslash \mathscr{X}_{\gamma}^{\xi,0}\right)\left(\mathbf{F}_{q}\right)\right\rvert&=(n_{1}+n_{2})q^{2n_{1}+n_{2}}-q^{n_{1}+n_{2}}\left(1+q+\dotsb+q^{n_{1}-1}\right)\\ & \quad -q^{2n_{1}}\left(1+q+\dotsb+q^{n_{2}-1}\right). \end{align*} $$
7. Calculations for
 $\textrm {GL}_{3}$
-mixed case
$\textrm {GL}_{3}$
-mixed case
Let
![]() $G=\textrm {GL}_{3}$
and let
$G=\textrm {GL}_{3}$
and let
![]() $\gamma \in \mathfrak {gl}_{3}(F)$
be a regular semisimple integral element. Assume that
$\gamma \in \mathfrak {gl}_{3}(F)$
be a regular semisimple integral element. Assume that
![]() $T\cong F^{\times }\times \textrm {Res}_{E_{2}/F}E_{2}^{\times }$
, with
$T\cong F^{\times }\times \textrm {Res}_{E_{2}/F}E_{2}^{\times }$
, with
![]() $E_{2}$
a separable totally ramified field extension over F of degree
$E_{2}$
a separable totally ramified field extension over F of degree
![]() $2$
. As before, we can reduce to the case in which
$2$
. As before, we can reduce to the case in which
![]() $\gamma $
is a matrix of the form
$\gamma $
is a matrix of the form
 $$ \begin{align} \gamma=\begin{bmatrix} a&&\\ &&b_{0}\epsilon^{n}\\ &b_{0}\epsilon^{n+1}& \end{bmatrix}, \end{align} $$
$$ \begin{align} \gamma=\begin{bmatrix} a&&\\ &&b_{0}\epsilon^{n}\\ &b_{0}\epsilon^{n+1}& \end{bmatrix}, \end{align} $$
with
![]() $a\in \mathcal {O}, b_{0}\in \mathcal {O}^{\times }$
. Let
$a\in \mathcal {O}, b_{0}\in \mathcal {O}^{\times }$
. Let
![]() $m=\mathrm{val}(a)$
.
$m=\mathrm{val}(a)$
.
Let P be the parabolic subgroup
![]() $P=B_{0}\cup B_{0}s_{2}B_{0}$
, and let
$P=B_{0}\cup B_{0}s_{2}B_{0}$
, and let
![]() $P=MN$
be the standard Levi decomposition. We identify
$P=MN$
be the standard Levi decomposition. We identify
![]() $X_{*}(A)\cong \textbf {Z}^{3}$
in the usual way. This gives us an identification
$X_{*}(A)\cong \textbf {Z}^{3}$
in the usual way. This gives us an identification
![]() $\Lambda _{M}\cong \textbf {Z}^{2}$
and hence
$\Lambda _{M}\cong \textbf {Z}^{2}$
and hence
![]() $\Lambda _{M}\otimes \textbf {R}\cong \textbf {R}^{2}$
. We also identify
$\Lambda _{M}\otimes \textbf {R}\cong \textbf {R}^{2}$
. We also identify
![]() $\mathfrak {a}_{M}^{G}$
with the line
$\mathfrak {a}_{M}^{G}$
with the line
![]() $x+y=0$
in
$x+y=0$
in
![]() $\textbf {R}^{2}$
, which can be further identified with
$\textbf {R}^{2}$
, which can be further identified with
![]() $\textbf {R}$
by taking the coordinate x. Under these identifications, the moment polytope
$\textbf {R}$
by taking the coordinate x. Under these identifications, the moment polytope
![]() $\Sigma _{\gamma }$
of the fundamental domain
$\Sigma _{\gamma }$
of the fundamental domain
![]() $F_{\gamma }$
can be taken to be the closed interval
$F_{\gamma }$
can be taken to be the closed interval
 $$ \begin{align*} \Sigma_{\gamma}=[-n(\gamma, P,P^{-}),0]\subset \textbf{R}\cong \mathfrak{a}_{M}^{G}. \end{align*} $$
$$ \begin{align*} \Sigma_{\gamma}=[-n(\gamma, P,P^{-}),0]\subset \textbf{R}\cong \mathfrak{a}_{M}^{G}. \end{align*} $$
To simplify the notation, we abbreviate
![]() $n(\gamma , P,P^{-})$
to
$n(\gamma , P,P^{-})$
to
![]() $n_{\gamma }$
. We have
$n_{\gamma }$
. We have
By definition, we can take
 $$ \begin{align*} F_{\gamma}=\mathscr{X}_{\gamma}\cap \mathscr{X}^{n+1}\left(\Sigma_{\gamma}\right). \end{align*} $$
$$ \begin{align*} F_{\gamma}=\mathscr{X}_{\gamma}\cap \mathscr{X}^{n+1}\left(\Sigma_{\gamma}\right). \end{align*} $$
This can be refined a little bit. For
![]() $(n_{1},n_{2})\in \textbf {N}^{2}$
, let
$(n_{1},n_{2})\in \textbf {N}^{2}$
, let
![]() $\Pi _{n_{1},n_{2}}$
be the positive
$\Pi _{n_{1},n_{2}}$
be the positive
![]() $(G,A)$
-orthogonal family as indicated in Figure 5 (excluding the dashed part).
$(G,A)$
-orthogonal family as indicated in Figure 5 (excluding the dashed part).

Figure 5 The
![]() $(G,A)$
-orthogonal family
$(G,A)$
-orthogonal family
![]() $\Pi _{n_{1},n_{2}}$
and its extension to a triangle.
$\Pi _{n_{1},n_{2}}$
and its extension to a triangle.
Consider the positive
![]() $(G,A)$
-orthogonal families
$(G,A)$
-orthogonal families
![]() $\Pi _{n_{\gamma },n+1}$
. For
$\Pi _{n_{\gamma },n+1}$
. For
![]() $i\in \textbf {Z}$
,
$i\in \textbf {Z}$
,
![]() $-n_{\gamma }\leq i\leq 0$
, let
$-n_{\gamma }\leq i\leq 0$
, let
 $$ \begin{align*} \Pi_{n_{\gamma},n+1}^{i}=\Pi_{n_{\gamma},n+1}\cap \pi_{M}^{-1}(i), \end{align*} $$
$$ \begin{align*} \Pi_{n_{\gamma},n+1}^{i}=\Pi_{n_{\gamma},n+1}\cap \pi_{M}^{-1}(i), \end{align*} $$
where
![]() $i\in \textbf {Z}$
is considered as an element of
$i\in \textbf {Z}$
is considered as an element of
![]() $\mathfrak {a}_{M}^{G}$
by the identification
$\mathfrak {a}_{M}^{G}$
by the identification
![]() $\textbf {R}\cong \mathfrak {a}_{M}^{G}$
. By Theorem 5.2, we have
$\textbf {R}\cong \mathfrak {a}_{M}^{G}$
. By Theorem 5.2, we have
 $$ \begin{align*} \mathscr{X}_{\gamma}^{M,(i,n+1-i)}\subset \mathscr{X}^{M,(i,n+1-i)}\left(\Pi_{n_{\gamma},n+1}^{i}\right),\qquad \text{for } i=-n_{\gamma},\dotsc, 0. \end{align*} $$
$$ \begin{align*} \mathscr{X}_{\gamma}^{M,(i,n+1-i)}\subset \mathscr{X}^{M,(i,n+1-i)}\left(\Pi_{n_{\gamma},n+1}^{i}\right),\qquad \text{for } i=-n_{\gamma},\dotsc, 0. \end{align*} $$
This implies that
 $$ \begin{align*} F_{\gamma}=\mathscr{X}_{\gamma}\cap \mathscr{X}^{n+1}\left(\Sigma_{\gamma}\right)=\mathscr{X}_{\gamma}\cap \mathscr{X}^{n+1}\left(\Pi_{n_{\gamma},n+1}\right). \end{align*} $$
$$ \begin{align*} F_{\gamma}=\mathscr{X}_{\gamma}\cap \mathscr{X}^{n+1}\left(\Sigma_{\gamma}\right)=\mathscr{X}_{\gamma}\cap \mathscr{X}^{n+1}\left(\Pi_{n_{\gamma},n+1}\right). \end{align*} $$
It is possible, but quite hard, to construct an affine paving of
![]() $F_{\gamma }$
and count the number of rational points with it. Instead, we take an indirect route. Let
$F_{\gamma }$
and count the number of rational points with it. Instead, we take an indirect route. Let
![]() $\Delta _{n_{\gamma },n+1}$
be the completion of
$\Delta _{n_{\gamma },n+1}$
be the completion of
![]() $\Pi _{n_{\gamma },n+1}$
into a triangle, as indicated in Figure 5. We can count the number of rational points on
$\Pi _{n_{\gamma },n+1}$
into a triangle, as indicated in Figure 5. We can count the number of rational points on
 $\mathscr {X}_{\gamma }^{n+1}\left (\Delta _{n_{\gamma },n+1}\right )$
quite easily, using the affine pavings in [Reference Chen9, Proposition 3.6]. The complementary
$\mathscr {X}_{\gamma }^{n+1}\left (\Delta _{n_{\gamma },n+1}\right )$
quite easily, using the affine pavings in [Reference Chen9, Proposition 3.6]. The complementary
 $\mathscr {X}_{\gamma }^{n+1}\left (\Delta _{n_{\gamma },n+1}\right )\Big \backslash F_{\gamma }$
can be treated by the Arthur–Kottwitz reduction. Taking their difference, we find
$\mathscr {X}_{\gamma }^{n+1}\left (\Delta _{n_{\gamma },n+1}\right )\Big \backslash F_{\gamma }$
can be treated by the Arthur–Kottwitz reduction. Taking their difference, we find
![]() $\left \lvert F_{\gamma }\left (\mathbf{F}_{q}\right )\right \rvert $
.
$\left \lvert F_{\gamma }\left (\mathbf{F}_{q}\right )\right \rvert $
.
We calculate the number of rational points on
 $\mathscr {X}_{\gamma }^{n+1}\left (\Delta _{n_{\gamma },n+1}\right )$
. For
$\mathscr {X}_{\gamma }^{n+1}\left (\Delta _{n_{\gamma },n+1}\right )$
. For
![]() $N\in \textbf {N}$
, let
$N\in \textbf {N}$
, let
 $$ \begin{align*} I_{N}=\textrm{Ad}\left(\textrm{diag}\left(\epsilon^{N},1,1\right)\right) I. \end{align*} $$
$$ \begin{align*} I_{N}=\textrm{Ad}\left(\textrm{diag}\left(\epsilon^{N},1,1\right)\right) I. \end{align*} $$
According to [Reference Chen9, Proposition 3.6], when
![]() $N\gg 0$
, we have an affine paving
$N\gg 0$
, we have an affine paving
 $$ \begin{align*} \mathscr{X}_{\gamma}^{n+1}\left(\Delta_{n_{\gamma},n+1}\right)=\bigcup_{\epsilon^{\textbf{a}}\in \mathscr{X}_{\gamma}^{n+1}\left(\Delta_{n_{\gamma},n+1}\right)^{A}} \mathscr{X}_{\gamma}^{n+1}\left(\Delta_{n_{\gamma},n+1}\right)\cap I_{N}\epsilon^{\textbf{a}}K/K. \end{align*} $$
$$ \begin{align*} \mathscr{X}_{\gamma}^{n+1}\left(\Delta_{n_{\gamma},n+1}\right)=\bigcup_{\epsilon^{\textbf{a}}\in \mathscr{X}_{\gamma}^{n+1}\left(\Delta_{n_{\gamma},n+1}\right)^{A}} \mathscr{X}_{\gamma}^{n+1}\left(\Delta_{n_{\gamma},n+1}\right)\cap I_{N}\epsilon^{\textbf{a}}K/K. \end{align*} $$
The dimension of the affine paving can be calculated using [Reference Chen9, Lemma 3.1], together with Theorem 5.2. When
![]() $m\leq n$
– that is,
$m\leq n$
– that is,
![]() $\gamma $
is not equivalued – the dimension of the paving is
$\gamma $
is not equivalued – the dimension of the paving is
 $$ \begin{align*} \min\{a_{2},m\}+\min\{a_{3},m\}+ \begin{cases} a_{2}-a_{3}& \text{if } 0\leq a_{2}-a_{3}\leq n,\\ a_{3}-a_{2}-1 &\text{if } 1\leq a_{3}-a_{2}\leq n+1. \end{cases} \end{align*} $$
$$ \begin{align*} \min\{a_{2},m\}+\min\{a_{3},m\}+ \begin{cases} a_{2}-a_{3}& \text{if } 0\leq a_{2}-a_{3}\leq n,\\ a_{3}-a_{2}-1 &\text{if } 1\leq a_{3}-a_{2}\leq n+1. \end{cases} \end{align*} $$
Otherwise, the intersection is empty. When
![]() $m\geq n+1$
– that is,
$m\geq n+1$
– that is,
![]() $\gamma $
is equivalued – the dimension of the paving is
$\gamma $
is equivalued – the dimension of the paving is
 $$ \begin{align*} \min\{a_{2},n\}+\min\{a_{3},n+1\}+ \begin{cases} a_{2}-a_{3}& \text{if } 0\leq a_{2}-a_{3}\leq n,\\ a_{3}-a_{2}-1 &\text{if } 1\leq a_{3}-a_{2}\leq n+1. \end{cases} \end{align*} $$
$$ \begin{align*} \min\{a_{2},n\}+\min\{a_{3},n+1\}+ \begin{cases} a_{2}-a_{3}& \text{if } 0\leq a_{2}-a_{3}\leq n,\\ a_{3}-a_{2}-1 &\text{if } 1\leq a_{3}-a_{2}\leq n+1. \end{cases} \end{align*} $$
Otherwise, the intersection is empty. We summarize the situation in Figures 6 and 7. The triangle is cut into four parts by the two long red lines, and the dimension of the fibration
![]() $f_{P}$
restricted to the affine pavings in different parts are given by different formulas. The two dashed lines bound the region where
$f_{P}$
restricted to the affine pavings in different parts are given by different formulas. The two dashed lines bound the region where
 $\mathscr {X}_{\gamma }^{M}\cap I_{N}\epsilon ^{\textbf {a}}K/K$
is nonempty.
$\mathscr {X}_{\gamma }^{M}\cap I_{N}\epsilon ^{\textbf {a}}K/K$
is nonempty.

Figure 6 Counting points in the nonequivalued case.

Figure 7 Counting points in the equivalued case.
Proposition 7.1. Let
![]() $\gamma $
be a matrix in the form of equation (7.1). When
$\gamma $
be a matrix in the form of equation (7.1). When
![]() $\mathrm{val}(a)=m\leq n$
, we have
$\mathrm{val}(a)=m\leq n$
, we have
 $$ \begin{align*} \left\lvert\mathscr{X}_{\gamma}^{n+1}\left(\Delta_{2m,n+1}\right)\left(\mathbf{F}_{q}\right)\right\rvert&= \sum_{j=0}^{2m-1}\left(\left\lfloor \frac{j}{2} \right\rfloor+1\right) q^{j} +(2m+n+1)q^{2m}\\ & \quad +\sum_{j=2m+1}^{m+n}(4m+n+1-j)q^{j} +\sum_{j=m+n+1}^{2m+n}\big(3(2m+n-j)+1\big)q^{j}\\ & \quad +q^{2m}\sum_{j=0}^{n}q^{j}. \end{align*} $$
$$ \begin{align*} \left\lvert\mathscr{X}_{\gamma}^{n+1}\left(\Delta_{2m,n+1}\right)\left(\mathbf{F}_{q}\right)\right\rvert&= \sum_{j=0}^{2m-1}\left(\left\lfloor \frac{j}{2} \right\rfloor+1\right) q^{j} +(2m+n+1)q^{2m}\\ & \quad +\sum_{j=2m+1}^{m+n}(4m+n+1-j)q^{j} +\sum_{j=m+n+1}^{2m+n}\big(3(2m+n-j)+1\big)q^{j}\\ & \quad +q^{2m}\sum_{j=0}^{n}q^{j}. \end{align*} $$
In the summation, we use the convention that a summand is empty if its subscript is greater than its superscript.
Proof. Summing along the dotted blue lines in the four regions of Figure 6, we get
 $$ \begin{align*} \left\lvert\mathscr{X}_{\gamma}^{n+1}\left(\Delta_{2m,n+1}\right)\left(\mathbf{F}_{q}\right)\right\rvert&= \sum_{i=0}^{m}q^{i}\left(1+q+\dotsb+q^{i}\right)+ \sum_{i=m+1}^{2m}q^{i}\left(1+q+\dotsb+q^{2m-i}\right)\\ & \quad +\sum_{i=0}^{m-1}q^{i+m}\left(q^{m+1-i}+\dotsb+q^{n}\right) +\sum_{i=0}^{m-1}q^{i+m}\left(q^{m-i}+\dotsb+q^{n}\right)\\ & \quad + q^{2m}\sum_{i=2m+1}^{2m+n}\left(1+q+\dotsb+q^{i-2m}\right)+q^{2m}\sum_{i=0}^{n}q^{i}. \end{align*} $$
$$ \begin{align*} \left\lvert\mathscr{X}_{\gamma}^{n+1}\left(\Delta_{2m,n+1}\right)\left(\mathbf{F}_{q}\right)\right\rvert&= \sum_{i=0}^{m}q^{i}\left(1+q+\dotsb+q^{i}\right)+ \sum_{i=m+1}^{2m}q^{i}\left(1+q+\dotsb+q^{2m-i}\right)\\ & \quad +\sum_{i=0}^{m-1}q^{i+m}\left(q^{m+1-i}+\dotsb+q^{n}\right) +\sum_{i=0}^{m-1}q^{i+m}\left(q^{m-i}+\dotsb+q^{n}\right)\\ & \quad + q^{2m}\sum_{i=2m+1}^{2m+n}\left(1+q+\dotsb+q^{i-2m}\right)+q^{2m}\sum_{i=0}^{n}q^{i}. \end{align*} $$
After rearranging the summand, we get the proposition.
Proposition 7.2. Let
![]() $\gamma $
be a matrix in the form of equation (7.1). When
$\gamma $
be a matrix in the form of equation (7.1). When
![]() $\mathrm{val}(a)=m> n$
, we have
$\mathrm{val}(a)=m> n$
, we have
 $$ \begin{align*} \left\lvert\mathscr{X}_{\gamma}^{n+1}\left(\Delta_{2n+1,n+1}\right)\left(\mathbf{F}_{q}\right)\right\rvert= \sum_{j=0}^{2n}\left(\left\lfloor \frac{j}{2} \right\rfloor+1\right) q^{j} +\sum_{j=2n+1}^{3n+1}(3(3n-j+1)+1)q^{j} +q^{2n+1}\sum_{j=0}^{n}q^{j}. \end{align*} $$
$$ \begin{align*} \left\lvert\mathscr{X}_{\gamma}^{n+1}\left(\Delta_{2n+1,n+1}\right)\left(\mathbf{F}_{q}\right)\right\rvert= \sum_{j=0}^{2n}\left(\left\lfloor \frac{j}{2} \right\rfloor+1\right) q^{j} +\sum_{j=2n+1}^{3n+1}(3(3n-j+1)+1)q^{j} +q^{2n+1}\sum_{j=0}^{n}q^{j}. \end{align*} $$
Proof. Summing along the dotted blue lines in the four regions of Figure 7, we get
 $$ \begin{align*} \left\lvert\mathscr{X}_{\gamma}^{n+1}\left(\Delta_{2n+1,n+1}\right)\left(\mathbf{F}_{q}\right)\right\rvert&= \sum_{i=0}^{n}q^{i}\left(1+q+\dotsb+q^{i}\right)+ \sum_{i=n+1}^{2n+1}q^{i}\left(1+q+\dotsb+q^{2n+1-i}\right)\\ & \quad +\sum_{i=1}^{n}q^{i+n}\left(q^{n+1-i}+\dotsb+q^{n}\right) +\sum_{i=1}^{n-1}q^{i+n+1}\left(q^{n+1-i}+\dotsb+q^{n}\right)\\ & \quad + q^{2n+1}\sum_{i=2n+2}^{3n+1}\left(1+q+\dotsb+q^{i-(2n+1)}\right)+q^{2n+1}\sum_{i=0}^{n}q^{i}. \end{align*} $$
$$ \begin{align*} \left\lvert\mathscr{X}_{\gamma}^{n+1}\left(\Delta_{2n+1,n+1}\right)\left(\mathbf{F}_{q}\right)\right\rvert&= \sum_{i=0}^{n}q^{i}\left(1+q+\dotsb+q^{i}\right)+ \sum_{i=n+1}^{2n+1}q^{i}\left(1+q+\dotsb+q^{2n+1-i}\right)\\ & \quad +\sum_{i=1}^{n}q^{i+n}\left(q^{n+1-i}+\dotsb+q^{n}\right) +\sum_{i=1}^{n-1}q^{i+n+1}\left(q^{n+1-i}+\dotsb+q^{n}\right)\\ & \quad + q^{2n+1}\sum_{i=2n+2}^{3n+1}\left(1+q+\dotsb+q^{i-(2n+1)}\right)+q^{2n+1}\sum_{i=0}^{n}q^{i}. \end{align*} $$
After rearranging the summand, we get the proposition.
Now we calculate the number of rational points on the complement
 $\mathscr {X}_{\gamma }^{n+1}\left (\Delta _{n_{\gamma },n+1}\right )\backslash F_{\gamma }$
. For
$\mathscr {X}_{\gamma }^{n+1}\left (\Delta _{n_{\gamma },n+1}\right )\backslash F_{\gamma }$
. For
![]() $i\in \textbf {Z}$
,
$i\in \textbf {Z}$
,
![]() $1\leq i\leq n+1$
, let
$1\leq i\leq n+1$
, let
 $$ \begin{align*} \Delta_{n_{\gamma},n+1}^{i}=\Delta_{n_{\gamma},n+1}\cap \pi_{M}^{-1}(i), \end{align*} $$
$$ \begin{align*} \Delta_{n_{\gamma},n+1}^{i}=\Delta_{n_{\gamma},n+1}\cap \pi_{M}^{-1}(i), \end{align*} $$
where
![]() $i\in \textbf {Z}$
is considered as an element of
$i\in \textbf {Z}$
is considered as an element of
![]() $\mathfrak {a}_{M}^{G}$
by the identification
$\mathfrak {a}_{M}^{G}$
by the identification
![]() $\textbf {R}\cong \mathfrak {a}_{M}^{G}$
.
$\textbf {R}\cong \mathfrak {a}_{M}^{G}$
.
Proposition 7.3. Let
![]() $\gamma $
be a matrix in the form of equation (7.1). We have
$\gamma $
be a matrix in the form of equation (7.1). We have
 $$ \begin{align*} \mathscr{X}_{\gamma}^{n+1}\left(\Delta_{n_{\gamma},n+1}\right)\Big\backslash F_{\gamma} = \bigcup_{i=1}^{n+1}f_{P}^{-1}\left(\mathscr{X}_{\gamma}^{M,(i,n+1-i)}\left(\Delta^{i}_{n_{\gamma},n+1}\right)\right)\cap \mathscr{X}_{\gamma}, \end{align*} $$
$$ \begin{align*} \mathscr{X}_{\gamma}^{n+1}\left(\Delta_{n_{\gamma},n+1}\right)\Big\backslash F_{\gamma} = \bigcup_{i=1}^{n+1}f_{P}^{-1}\left(\mathscr{X}_{\gamma}^{M,(i,n+1-i)}\left(\Delta^{i}_{n_{\gamma},n+1}\right)\right)\cap \mathscr{X}_{\gamma}, \end{align*} $$
where
![]() $(i,n+1-i)\in \textbf {Z}^{2}$
is regarded as an element in
$(i,n+1-i)\in \textbf {Z}^{2}$
is regarded as an element in
![]() $\Lambda _{M}$
by the identification
$\Lambda _{M}$
by the identification
![]() $\textbf {Z}^{2}\cong \Lambda _{M}$
. Its number of rational points over
$\textbf {Z}^{2}\cong \Lambda _{M}$
. Its number of rational points over
![]() $\mathbf{F}_{q}$
equals
$\mathbf{F}_{q}$
equals
 $$ \begin{align*} q^{n_{\gamma}}\sum_{j=0}^{n}\left(1+q+\dotsb+q^{j}\right). \end{align*} $$
$$ \begin{align*} q^{n_{\gamma}}\sum_{j=0}^{n}\left(1+q+\dotsb+q^{j}\right). \end{align*} $$
Proof. Observe that the second assertion is a direct consequence of the first one by Proposition 2.4. It is thus enough to show the first assertion.
Set
 $x\in \mathscr {X}_{\gamma }^{n+1}\left (\Delta _{n_{\gamma },n+1}\right )$
, and notice that it does not belong to
$x\in \mathscr {X}_{\gamma }^{n+1}\left (\Delta _{n_{\gamma },n+1}\right )$
, and notice that it does not belong to
![]() $F_{\gamma }$
if and only if
$F_{\gamma }$
if and only if
because
![]() $H_{P^{-}}(x)\leq H_{P}(x)$
. This implies that
$H_{P^{-}}(x)\leq H_{P}(x)$
. This implies that
 $$ \begin{align*} \mathscr{X}_{\gamma}^{n+1}\left(\Delta_{n_{\gamma},n+1}\right)\Big\backslash F_{\gamma} = \bigcup_{i=1}^{n+1}f_{P}^{-1}\left(\mathscr{X}_{\gamma}^{M,(i,n+1-i)}\left(\Delta^{i}_{n_{\gamma},n+1}\right)\right)\cap \mathscr{X}_{\gamma}\left(\Delta_{n_{\gamma},n+1}\right). \end{align*} $$
$$ \begin{align*} \mathscr{X}_{\gamma}^{n+1}\left(\Delta_{n_{\gamma},n+1}\right)\Big\backslash F_{\gamma} = \bigcup_{i=1}^{n+1}f_{P}^{-1}\left(\mathscr{X}_{\gamma}^{M,(i,n+1-i)}\left(\Delta^{i}_{n_{\gamma},n+1}\right)\right)\cap \mathscr{X}_{\gamma}\left(\Delta_{n_{\gamma},n+1}\right). \end{align*} $$
To finish the proof, we only need to show that
 $$ \begin{align*} f_{P}^{-1}\left(\mathscr{X}_{\gamma}^{M,(i,n+1-i)}\left(\Delta^{i}_{n_{\gamma},n+1}\right)\right)\cap \mathscr{X}_{\gamma}\left(\Delta_{n_{\gamma},n+1}\right)=f_{P}^{-1}\left(\mathscr{X}_{\gamma}^{M,(i,n+1-i)}\left(\Delta^{i}_{n_{\gamma},n+1}\right)\right)\cap \mathscr{X}_{\gamma}, \end{align*} $$
$$ \begin{align*} f_{P}^{-1}\left(\mathscr{X}_{\gamma}^{M,(i,n+1-i)}\left(\Delta^{i}_{n_{\gamma},n+1}\right)\right)\cap \mathscr{X}_{\gamma}\left(\Delta_{n_{\gamma},n+1}\right)=f_{P}^{-1}\left(\mathscr{X}_{\gamma}^{M,(i,n+1-i)}\left(\Delta^{i}_{n_{\gamma},n+1}\right)\right)\cap \mathscr{X}_{\gamma}, \end{align*} $$
for
![]() $i=1,\dotsc , n+1$
. The inclusion ‘
$i=1,\dotsc , n+1$
. The inclusion ‘
![]() $\subset $
’ is obvious; we only need to show its inverse. For any point
$\subset $
’ is obvious; we only need to show its inverse. For any point
 $x\in f_{P}^{-1}\left (\mathscr {X}_{\gamma }^{M,(i,n+1-i)}\left (\Delta ^{i}_{n_{\gamma },n+1}\right )\right )\cap \mathscr {X}_{\gamma }$
, the inclusion (7.2) holds. By Proposition 3.1, together with the fact that
$x\in f_{P}^{-1}\left (\mathscr {X}_{\gamma }^{M,(i,n+1-i)}\left (\Delta ^{i}_{n_{\gamma },n+1}\right )\right )\cap \mathscr {X}_{\gamma }$
, the inclusion (7.2) holds. By Proposition 3.1, together with the fact that
![]() $\mathrm{Ec}(x)$
is a positive
$\mathrm{Ec}(x)$
is a positive
![]() $(G,A)$
-orthogonal family, we have
$(G,A)$
-orthogonal family, we have
whence the equality we want.
Summarizing all the foregoing discussions, we get the following:
Theorem 7.4. Let
![]() $\gamma $
be a matrix in the form of equation (7.1). When
$\gamma $
be a matrix in the form of equation (7.1). When
![]() $\mathrm{val}(a)=m\leq n$
, we have
$\mathrm{val}(a)=m\leq n$
, we have
 $$ \begin{align*} \left\lvert F_{\gamma}\left(\mathbf{F}_{q}\right)\right\rvert&= \sum_{j=0}^{2m-1}\left(\left\lfloor \frac{j}{2} \right\rfloor+1\right) q^{j} +(2m+1)\sum_{j=2m}^{m+n} q^{j}\\ & \quad +\sum_{j=m+n+1}^{2m+n-1}(2(2m+n-j)+1)q^{j} +q^{2m+n}. \end{align*} $$
$$ \begin{align*} \left\lvert F_{\gamma}\left(\mathbf{F}_{q}\right)\right\rvert&= \sum_{j=0}^{2m-1}\left(\left\lfloor \frac{j}{2} \right\rfloor+1\right) q^{j} +(2m+1)\sum_{j=2m}^{m+n} q^{j}\\ & \quad +\sum_{j=m+n+1}^{2m+n-1}(2(2m+n-j)+1)q^{j} +q^{2m+n}. \end{align*} $$
When
![]() $\mathrm{val}(a)=m> n$
, we have
$\mathrm{val}(a)=m> n$
, we have
 $$ \begin{align*} \left\lvert F_{\gamma}\left(\mathbf{F}_{q}\right)\right\rvert= \sum_{j=0}^{2n}\left(\left\lfloor \frac{j}{2} \right\rfloor+1\right) q^{j} +\sum_{j=2n+1}^{3n}(2(3n+1-j)+1)q^{j} +q^{3n+1}. \end{align*} $$
$$ \begin{align*} \left\lvert F_{\gamma}\left(\mathbf{F}_{q}\right)\right\rvert= \sum_{j=0}^{2n}\left(\left\lfloor \frac{j}{2} \right\rfloor+1\right) q^{j} +\sum_{j=2n+1}^{3n}(2(3n+1-j)+1)q^{j} +q^{3n+1}. \end{align*} $$
Now it is easy to deduce the weighted orbital integral
 $J_{M}^{\xi }(\gamma )$
. For
$J_{M}^{\xi }(\gamma )$
. For
![]() $N\in \textbf {N}$
,
$N\in \textbf {N}$
,
![]() $N\gg 0$
, let
$N\gg 0$
, let
 $$ \begin{align*} \Pi_{N}=\left[-n_{\gamma}-N, N\right]\subset \textbf{R}\cong \mathfrak{a}_{M}^{G}. \end{align*} $$
$$ \begin{align*} \Pi_{N}=\left[-n_{\gamma}-N, N\right]\subset \textbf{R}\cong \mathfrak{a}_{M}^{G}. \end{align*} $$
We can count the number of rational points
 $\left \lvert \mathscr {X}_{\gamma }^{n+1}(\Pi _{N})\left (\mathbf{F}_{q}\right )\right \rvert $
in two ways. By the Arthur–Kottwitz reduction, we have
$\left \lvert \mathscr {X}_{\gamma }^{n+1}(\Pi _{N})\left (\mathbf{F}_{q}\right )\right \rvert $
in two ways. By the Arthur–Kottwitz reduction, we have
 $$ \begin{align*} \left\lvert \mathscr{X}_{\gamma}^{n+1}(\Pi_{N})\left(\mathbf{F}_{q}\right)\right\rvert=\left\lvert F_{\gamma}\left(\mathbf{F}_{q}\right)\right\rvert+2N q^{n_{\gamma}}\cdot \left\lvert F_{\gamma}^{M}\left(\mathbf{F}_{q}\right)\right\rvert. \end{align*} $$
$$ \begin{align*} \left\lvert \mathscr{X}_{\gamma}^{n+1}(\Pi_{N})\left(\mathbf{F}_{q}\right)\right\rvert=\left\lvert F_{\gamma}\left(\mathbf{F}_{q}\right)\right\rvert+2N q^{n_{\gamma}}\cdot \left\lvert F_{\gamma}^{M}\left(\mathbf{F}_{q}\right)\right\rvert. \end{align*} $$
By the Harder–Narasimhan reduction, we have
 $$ \begin{align*} \left\lvert \mathscr{X}_{\gamma}^{n+1}(\Pi_{N})\left(\mathbf{F}_{q}\right)\right\rvert&=2\left\lvert F_{\gamma}\left(\mathbf{F}_{q}\right)\right\rvert+\left\lvert\mathscr{X}_{\gamma}^{n+1,\xi}\left(\mathbf{F}_{q}\right)\right\rvert\\ & \quad +\left(2N-n_{\gamma}-1\right) q^{n_{\gamma}}\cdot \left\lvert F_{\gamma}^{M}\left(\mathbf{F}_{q}\right)\right\rvert, \end{align*} $$
$$ \begin{align*} \left\lvert \mathscr{X}_{\gamma}^{n+1}(\Pi_{N})\left(\mathbf{F}_{q}\right)\right\rvert&=2\left\lvert F_{\gamma}\left(\mathbf{F}_{q}\right)\right\rvert+\left\lvert\mathscr{X}_{\gamma}^{n+1,\xi}\left(\mathbf{F}_{q}\right)\right\rvert\\ & \quad +\left(2N-n_{\gamma}-1\right) q^{n_{\gamma}}\cdot \left\lvert F_{\gamma}^{M}\left(\mathbf{F}_{q}\right)\right\rvert, \end{align*} $$
where we use the fact that
 $\mathscr {X}_{\gamma }^{M,\nu ,\xi }=F_{\gamma }^{M}$
for any
$\mathscr {X}_{\gamma }^{M,\nu ,\xi }=F_{\gamma }^{M}$
for any
![]() $\nu \in \Lambda _{M}$
because
$\nu \in \Lambda _{M}$
because
![]() $\gamma $
is anisotropic in
$\gamma $
is anisotropic in
![]() $\mathfrak {m}(F)$
. The comparison of the two expressions implies
$\mathfrak {m}(F)$
. The comparison of the two expressions implies
 $$ \begin{align*} \left\lvert\mathscr{X}_{\gamma}^{n+1,\xi}\left(\mathbf{F}_{q}\right)\right\rvert=\left(n_{\gamma}+1\right)q^{n_{\gamma}} \cdot \left\lvert F_{\gamma}^{M}\left(\mathbf{F}_{q}\right)\right\rvert-\left\lvert F_{\gamma}\left(\mathbf{F}_{q}\right)\right\rvert. \end{align*} $$
$$ \begin{align*} \left\lvert\mathscr{X}_{\gamma}^{n+1,\xi}\left(\mathbf{F}_{q}\right)\right\rvert=\left(n_{\gamma}+1\right)q^{n_{\gamma}} \cdot \left\lvert F_{\gamma}^{M}\left(\mathbf{F}_{q}\right)\right\rvert-\left\lvert F_{\gamma}\left(\mathbf{F}_{q}\right)\right\rvert. \end{align*} $$
By Theorems 7.4 and 5.2, we have the following:
Theorem 7.5. Let
![]() $\gamma $
be a matrix in the form of equation (7.1). When
$\gamma $
be a matrix in the form of equation (7.1). When
![]() $\mathrm{val}(a)=m\leq n$
, we have
$\mathrm{val}(a)=m\leq n$
, we have
 $$ \begin{align*} J_{M}^{\xi}(\gamma)=\left\lvert\mathscr{X}_{\gamma}^{n+1,\xi}\left(\mathbf{F}_{q}\right)\right\rvert &= 2mq^{2m+n}+\sum_{j=m+n+1}^{2m+n-1}2(j-m-n)q^{j} -\sum_{j=0}^{2m-1}\left(\left\lfloor \frac{j}{2} \right\rfloor+1\right) q^{j}. \end{align*} $$
$$ \begin{align*} J_{M}^{\xi}(\gamma)=\left\lvert\mathscr{X}_{\gamma}^{n+1,\xi}\left(\mathbf{F}_{q}\right)\right\rvert &= 2mq^{2m+n}+\sum_{j=m+n+1}^{2m+n-1}2(j-m-n)q^{j} -\sum_{j=0}^{2m-1}\left(\left\lfloor \frac{j}{2} \right\rfloor+1\right) q^{j}. \end{align*} $$
When
![]() $\mathrm{val}(a)=m> n$
, we have
$\mathrm{val}(a)=m> n$
, we have
 $$ \begin{align*} J_{M}^{\xi}(\gamma)=\left\lvert\mathscr{X}_{\gamma}^{n+1,\xi}\left(\mathbf{F}_{q}\right)\right\rvert &= (2n+1)q^{3n+1}+\sum_{j=2n+1}^{3n}(2j-4n-1)q^{j} -\sum_{j=0}^{2n}\left(\left\lfloor \frac{j}{2} \right\rfloor+1\right) q^{j}. \end{align*} $$
$$ \begin{align*} J_{M}^{\xi}(\gamma)=\left\lvert\mathscr{X}_{\gamma}^{n+1,\xi}\left(\mathbf{F}_{q}\right)\right\rvert &= (2n+1)q^{3n+1}+\sum_{j=2n+1}^{3n}(2j-4n-1)q^{j} -\sum_{j=0}^{2n}\left(\left\lfloor \frac{j}{2} \right\rfloor+1\right) q^{j}. \end{align*} $$
By Theorem 2.8 and Remark 2.3, we get Arthur’s weighted orbital integral. As before, the orbital integral
![]() $I^{G}_{\gamma }$
can be calculated by equation (2.4):
$I^{G}_{\gamma }$
can be calculated by equation (2.4):
 $$ \begin{align*} I_{\gamma}^{G}=q^{n_{\gamma}}\sum_{i=0}^{n}q^{i}= \begin{cases} q^{2m}\sum_{i=0}^{n}q^{i}&\text{if }m\leq n,\\ q^{2n+1}\sum_{i=0}^{n}q^{i}&\text{if }m>n. \end{cases} \end{align*} $$
$$ \begin{align*} I_{\gamma}^{G}=q^{n_{\gamma}}\sum_{i=0}^{n}q^{i}= \begin{cases} q^{2m}\sum_{i=0}^{n}q^{i}&\text{if }m\leq n,\\ q^{2n+1}\sum_{i=0}^{n}q^{i}&\text{if }m>n. \end{cases} \end{align*} $$
8. Calculations for
 $\textrm {GL}_{3}$
-anisotropic case
$\textrm {GL}_{3}$
-anisotropic case
Let
![]() $G=\textrm {GL}_{3}$
and
$G=\textrm {GL}_{3}$
and
![]() $\gamma \in \mathfrak {gl}_{3}(F)$
be a regular semisimple integral element. Assume that
$\gamma \in \mathfrak {gl}_{3}(F)$
be a regular semisimple integral element. Assume that
![]() $\text {char}(k)>3$
and
$\text {char}(k)>3$
and
![]() $T\cong \textrm {Res}_{E_{3}/F}E_{3}^{\times }$
, with
$T\cong \textrm {Res}_{E_{3}/F}E_{3}^{\times }$
, with
 $E_{3}=\mathbf{F}_{q} (\! (\epsilon ^{\frac {1}{3}} )\! )$
. As before, take the basis
$E_{3}=\mathbf{F}_{q} (\! (\epsilon ^{\frac {1}{3}} )\! )$
. As before, take the basis
 $\left \{\epsilon ^{\frac {2}{3}}, \epsilon ^{\frac {1}{3}},1\right \}$
of
$\left \{\epsilon ^{\frac {2}{3}}, \epsilon ^{\frac {1}{3}},1\right \}$
of
![]() $E_{3}$
over F. We can assume that
$E_{3}$
over F. We can assume that
![]() $\gamma $
is of the form
$\gamma $
is of the form
 $$ \begin{align} \gamma=\begin{bmatrix} &b_{0}\epsilon^{n_{1}}&c_{0}\epsilon^{n_{2}}\\ c_{0}\epsilon^{n_{2}+1} &&b_{0}\epsilon^{n_{1}}\\ b_{0}\epsilon^{n_{1}+1}&c_{0}\epsilon^{n_{2}+1}& \end{bmatrix}, \end{align} $$
$$ \begin{align} \gamma=\begin{bmatrix} &b_{0}\epsilon^{n_{1}}&c_{0}\epsilon^{n_{2}}\\ c_{0}\epsilon^{n_{2}+1} &&b_{0}\epsilon^{n_{1}}\\ b_{0}\epsilon^{n_{1}+1}&c_{0}\epsilon^{n_{2}+1}& \end{bmatrix}, \end{align} $$
with
![]() $b_{0},c_{0}\in \mathcal {O}^{\times }$
and
$b_{0},c_{0}\in \mathcal {O}^{\times }$
and
![]() $n_{1},n_{2}\in \textbf {N}$
. In this case, Arthur’s weighted orbital integral is the same as the orbital integral, and both are equal to
$n_{1},n_{2}\in \textbf {N}$
. In this case, Arthur’s weighted orbital integral is the same as the orbital integral, and both are equal to
 $\left \lvert \mathscr {X}_{\gamma }^{0}\left (\mathbf{F}_{q}\right )\right \rvert $
. The matrix
$\left \lvert \mathscr {X}_{\gamma }^{0}\left (\mathbf{F}_{q}\right )\right \rvert $
. The matrix
![]() $\gamma $
is equivalued of valuation
$\gamma $
is equivalued of valuation
 $n_{1}+\frac {1}{3}$
if
$n_{1}+\frac {1}{3}$
if
![]() $n_{1}\leq n_{2}$
, and equivalued of valuation
$n_{1}\leq n_{2}$
, and equivalued of valuation
 $n_{2}+\frac {2}{3}$
if
$n_{2}+\frac {2}{3}$
if
![]() $n_{2}< n_{1}$
. According to Goresky, Kottwitz, and MacPherson [Reference Goresky, Kottwitz and MacPherson16], the affine Springer fiber
$n_{2}< n_{1}$
. According to Goresky, Kottwitz, and MacPherson [Reference Goresky, Kottwitz and MacPherson16], the affine Springer fiber
![]() $\mathscr {X}_{\gamma }$
admits affine paving
$\mathscr {X}_{\gamma }$
admits affine paving
 $$ \begin{align*} \mathscr{X}_{\gamma}=\bigcup_{\textbf{a}=(a_{1},a_{2},a_{3})\in \textbf{Z}^{3}} \mathscr{X}_{\gamma} \cap I\epsilon^{\textbf{a}}K/K. \end{align*} $$
$$ \begin{align*} \mathscr{X}_{\gamma}=\bigcup_{\textbf{a}=(a_{1},a_{2},a_{3})\in \textbf{Z}^{3}} \mathscr{X}_{\gamma} \cap I\epsilon^{\textbf{a}}K/K. \end{align*} $$
Let
![]() $S_{\textbf {a}}$
be the cell
$S_{\textbf {a}}$
be the cell
![]() $\mathscr {X}_{\gamma } \cap I\epsilon ^{\textbf {a}}K/K$
. Restricted to the connected component
$\mathscr {X}_{\gamma } \cap I\epsilon ^{\textbf {a}}K/K$
. Restricted to the connected component
 $\mathscr {X}_{\gamma }^{0}$
, we can calculate that
$\mathscr {X}_{\gamma }^{0}$
, we can calculate that
![]() $S_{\textbf {a}}$
is nonempty if and only if
$S_{\textbf {a}}$
is nonempty if and only if
and that it is of dimension
 $$ \begin{align*} \left\lvert\left\{(m,\alpha)\in \textbf{Z}\times \Phi(G,A)\mid 0\leq m+\alpha(x)<n_{1}+\frac{1}{3}, \ m+\alpha(y_{\textbf{a}})<0\right\}\right\rvert, \end{align*} $$
$$ \begin{align*} \left\lvert\left\{(m,\alpha)\in \textbf{Z}\times \Phi(G,A)\mid 0\leq m+\alpha(x)<n_{1}+\frac{1}{3}, \ m+\alpha(y_{\textbf{a}})<0\right\}\right\rvert, \end{align*} $$
with
![]() $x=(1,2/3,1/3), y_{\textbf {a}}=(-a_{1},-a_{2},-a_{3})\in X_{*}(A)\otimes \textbf {R}$
. The results are summarized in Figure 8. Summing up, we get the following:
$x=(1,2/3,1/3), y_{\textbf {a}}=(-a_{1},-a_{2},-a_{3})\in X_{*}(A)\otimes \textbf {R}$
. The results are summarized in Figure 8. Summing up, we get the following:

Figure 8 Counting points for ramified anisotropic
![]() $\gamma \in \mathfrak {gl}_{3}(\mathcal {O})$
: First case.
$\gamma \in \mathfrak {gl}_{3}(\mathcal {O})$
: First case.
Theorem 8.1. Let
![]() $\gamma \in \mathfrak {gl}_{3}(\mathcal {O})$
be the matrix in equation (8.1). Suppose that
$\gamma \in \mathfrak {gl}_{3}(\mathcal {O})$
be the matrix in equation (8.1). Suppose that
![]() $n_{1}\leq n_{2}$
; it is then equivalued of valuation
$n_{1}\leq n_{2}$
; it is then equivalued of valuation
 $n_{1}+\frac {1}{3}$
. The orbital integral associated to
$n_{1}+\frac {1}{3}$
. The orbital integral associated to
![]() $\gamma $
equals
$\gamma $
equals
 $$ \begin{align*} I_{\gamma}^{G}&=\left\lvert \mathscr{X}_{\gamma}^{0}\left(\mathbf{F}_{q}\right)\right\rvert =1+2\sum_{i=1}^{\left\lfloor \frac{n_{1}}{3}\right\rfloor} q^{2(3i-1)}\left(q^{2}+q+1\right)\\ & \quad +\sum_{i=1}^{n_{1}} \left(i-2 \left\lfloor \frac{i}{3} \right\rfloor -1 \right) q^{2i-3}\left(q^{3}+2q^{2}+2q+1\right)\\ & \quad +\sum_{i=n_{1}+1}^{2n_{1}}\left(2n_{1}-i-2 \left\lceil \frac{2n_{1}-i}{3} \right\rceil+1\right)q^{i+n_{1}-1}(q+2)\\ & \quad +q^{2n_{1}-1}\left(\left\lceil \frac{2n_{1}-1}{3} \right\rceil-\left\lfloor \frac{n_{1}-2}{3} \right\rfloor -1\right) +2\sum_{i=\left\lceil \frac{2n_{1}-1}{3} \right\rceil}^{n_{1}-1}q^{3i+1}, \end{align*} $$
$$ \begin{align*} I_{\gamma}^{G}&=\left\lvert \mathscr{X}_{\gamma}^{0}\left(\mathbf{F}_{q}\right)\right\rvert =1+2\sum_{i=1}^{\left\lfloor \frac{n_{1}}{3}\right\rfloor} q^{2(3i-1)}\left(q^{2}+q+1\right)\\ & \quad +\sum_{i=1}^{n_{1}} \left(i-2 \left\lfloor \frac{i}{3} \right\rfloor -1 \right) q^{2i-3}\left(q^{3}+2q^{2}+2q+1\right)\\ & \quad +\sum_{i=n_{1}+1}^{2n_{1}}\left(2n_{1}-i-2 \left\lceil \frac{2n_{1}-i}{3} \right\rceil+1\right)q^{i+n_{1}-1}(q+2)\\ & \quad +q^{2n_{1}-1}\left(\left\lceil \frac{2n_{1}-1}{3} \right\rceil-\left\lfloor \frac{n_{1}-2}{3} \right\rfloor -1\right) +2\sum_{i=\left\lceil \frac{2n_{1}-1}{3} \right\rceil}^{n_{1}-1}q^{3i+1}, \end{align*} $$
where
![]() $\lfloor x\rfloor $
denotes the largest integer less than or equal to x, and
$\lfloor x\rfloor $
denotes the largest integer less than or equal to x, and
![]() $\lceil x\rceil $
denotes the smallest integer greater than or equal to x.
$\lceil x\rceil $
denotes the smallest integer greater than or equal to x.
The same calculations apply for
![]() $n_{2}< n_{1}$
, with the differences that
$n_{2}< n_{1}$
, with the differences that
![]() $S_{\textbf {a}}$
is nonempty if and only if
$S_{\textbf {a}}$
is nonempty if and only if
and that it is isomorphic to an affine space of dimension
 $$ \begin{align*} \left\lvert\left\{(m,\alpha)\in \textbf{Z}\times \Phi(G,A)\mid 0\leq m+\alpha(x)<n_{2}+\frac{2}{3}, \ m+\alpha(y_{\textbf{a}})<0\right\}\right\rvert. \end{align*} $$
$$ \begin{align*} \left\lvert\left\{(m,\alpha)\in \textbf{Z}\times \Phi(G,A)\mid 0\leq m+\alpha(x)<n_{2}+\frac{2}{3}, \ m+\alpha(y_{\textbf{a}})<0\right\}\right\rvert. \end{align*} $$
These are summarized schematically in Figure 9. Summing up, we get the following:

Figure 9 Counting points for ramified anisotropic
![]() $\gamma \in \mathfrak {gl}_{3}(\mathcal {O})$
: Second case.
$\gamma \in \mathfrak {gl}_{3}(\mathcal {O})$
: Second case.
Theorem 8.2. Let
![]() $\gamma \in \mathfrak {gl}_{3}(\mathcal {O})$
be the matrix in equation (8.1). Suppose that
$\gamma \in \mathfrak {gl}_{3}(\mathcal {O})$
be the matrix in equation (8.1). Suppose that
![]() $n_{2}< n_{1}$
; it is then equivalued of valuation
$n_{2}< n_{1}$
; it is then equivalued of valuation
 $n_{2}+\frac {2}{3}$
. The orbital integral associated to
$n_{2}+\frac {2}{3}$
. The orbital integral associated to
![]() $\gamma $
equals
$\gamma $
equals
 $$ \begin{align*} I_{\gamma}^{G}&=\left\lvert \mathscr{X}_{\gamma}^{0}\left(\mathbf{F}_{q}\right)\right\rvert =1+2\sum_{i=1}^{\left\lfloor \frac{n_{2}}{3}\right\rfloor} q^{2(3i-1)}\left(q^{2}+q+1\right)\\ & \quad +\sum_{i=1}^{n_{2}} \left(i-2 \left\lfloor \frac{i}{3} \right\rfloor -1 \right) q^{2i-3}\left(q^{3}+2q^{2}+2q+1\right) +\left(n_{2}-2 \left\lceil \frac{n_{2}-1}{3} \right\rceil \right) q^{2n_{2}-1}\left(1+2q^{2}\right)\\ & \quad +\sum_{i=n_{2}+2}^{2n_{2}}\left(2n_{2}-i-2 \left\lceil \frac{2n_{2}-i}{3} \right\rceil+1\right)q^{i+n_{2}-1}(1+2q)\\ & \quad +2\sum_{i=0}^{\left\lfloor \frac{n_{2}-2}{3} \right\rfloor} q^{3(n_{2}-i)-2}(1+q) +2q^{2n_{2}}\left(\left\lceil \frac{2n_{2}-1}{3} \right\rceil-\left\lfloor \frac{n_{2}-2}{3} \right\rfloor -1\right) +q^{3n_{2}+1}. \end{align*} $$
$$ \begin{align*} I_{\gamma}^{G}&=\left\lvert \mathscr{X}_{\gamma}^{0}\left(\mathbf{F}_{q}\right)\right\rvert =1+2\sum_{i=1}^{\left\lfloor \frac{n_{2}}{3}\right\rfloor} q^{2(3i-1)}\left(q^{2}+q+1\right)\\ & \quad +\sum_{i=1}^{n_{2}} \left(i-2 \left\lfloor \frac{i}{3} \right\rfloor -1 \right) q^{2i-3}\left(q^{3}+2q^{2}+2q+1\right) +\left(n_{2}-2 \left\lceil \frac{n_{2}-1}{3} \right\rceil \right) q^{2n_{2}-1}\left(1+2q^{2}\right)\\ & \quad +\sum_{i=n_{2}+2}^{2n_{2}}\left(2n_{2}-i-2 \left\lceil \frac{2n_{2}-i}{3} \right\rceil+1\right)q^{i+n_{2}-1}(1+2q)\\ & \quad +2\sum_{i=0}^{\left\lfloor \frac{n_{2}-2}{3} \right\rfloor} q^{3(n_{2}-i)-2}(1+q) +2q^{2n_{2}}\left(\left\lceil \frac{2n_{2}-1}{3} \right\rceil-\left\lfloor \frac{n_{2}-2}{3} \right\rfloor -1\right) +q^{3n_{2}+1}. \end{align*} $$
Acknowledgments
We want to thank Gérard Laumon for the discussions which led to this work, and we want to thank the anonymous referee for the careful reading and very helpful suggestions.
Competing Interest
The author(s) declare none.