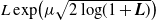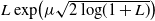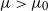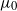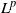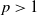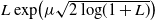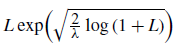1. Introduction
The notion of g-expectation was first introduced by Peng [Reference Peng19]. It is a kind of dynamically consistent nonlinear expectation induced by backward stochastic differential equations (BSDEs). More precisely, the g-expectation operator
![]() $\mathcal E_{0,T}^g[\!\cdot\!]\colon L(\mathcal F_T)\to \mathbb R$
is defined by
$\mathcal E_{0,T}^g[\!\cdot\!]\colon L(\mathcal F_T)\to \mathbb R$
is defined by
![]() $\mathcal E_{0,T}^g[\xi]=y_0$
, where
$\mathcal E_{0,T}^g[\xi]=y_0$
, where
![]() $(y,z)\;:\!=\; (y_t,z_t)_{t\in [0,T]}$
is a solution of the BSDE with terminal condition
$(y,z)\;:\!=\; (y_t,z_t)_{t\in [0,T]}$
is a solution of the BSDE with terminal condition
![]() $\xi$
and generator g. It is by now well known that the g-expectation has a wide application in economic and financial problems under uncertainty (see e.g. [Reference Chen and Epstein5], [Reference Delbaen, Peng and Rosazza Gianin6], [Reference Duffie and Epstein7], and [Reference Rosazza Gianin21]). Among such works, we are concerned with the optimal stopping problem under g-expectation, namely,
$\xi$
and generator g. It is by now well known that the g-expectation has a wide application in economic and financial problems under uncertainty (see e.g. [Reference Chen and Epstein5], [Reference Delbaen, Peng and Rosazza Gianin6], [Reference Duffie and Epstein7], and [Reference Rosazza Gianin21]). Among such works, we are concerned with the optimal stopping problem under g-expectation, namely,
Here
![]() $\widetilde L_t\;:\!=\; L_t\textbf 1_{t<T}+\xi\textbf 1_{t=T}$
is a reward process, where the continuous process L is a running reward and
$\widetilde L_t\;:\!=\; L_t\textbf 1_{t<T}+\xi\textbf 1_{t=T}$
is a reward process, where the continuous process L is a running reward and
![]() $\xi$
is a final reward. The classical linear optimal stopping problem corresponds to the case where
$\xi$
is a final reward. The classical linear optimal stopping problem corresponds to the case where
![]() $g=0$
or more generally g is linear (see e.g. El Karoui [Reference El Karoui8] for a systematic study).
$g=0$
or more generally g is linear (see e.g. El Karoui [Reference El Karoui8] for a systematic study).
There are numerous works on the nonlinear optimal stopping problem (1) under g-expectation (see e.g. [Reference Bayraktar and Yao1], [Reference Bayraktar, Karatzas and Yao3], and [Reference Wu23]). In those papers, the reward process is assumed to be, as usual, square-integrable or uniformly bounded. On the other hand, the theory of reflected backward stochastic differential equations (RBSDEs) introduced by El Karoui et al. [Reference El Karoui, Kapoudjian, Pardoux, Peng and Quenez9] opened up a promising perspective on optimal stopping problems under g-expectation. The RBSDE is a kind of BSDE with constraints. More precisely, the solution Y of the BSDE is constrained to stay above a given barrier process L. In order to achieve this, a non-decreasing process K is added to the solution
 \begin{equation}\begin{cases}Y_t=\xi+\int_t^T g(s,Y_s,Z_s) \,{\mathrm{d}} s-\int_t^T Z_s \,{\mathrm{d}} B_s+K_T-K_t,\\[5pt]Y_t\ge L_t, \quad \int_0^T (Y_t-L_t)\,{\mathrm{d}} K_t=0,\end{cases}\end{equation}
\begin{equation}\begin{cases}Y_t=\xi+\int_t^T g(s,Y_s,Z_s) \,{\mathrm{d}} s-\int_t^T Z_s \,{\mathrm{d}} B_s+K_T-K_t,\\[5pt]Y_t\ge L_t, \quad \int_0^T (Y_t-L_t)\,{\mathrm{d}} K_t=0,\end{cases}\end{equation}
where the second condition is called the Skorokhod minimality condition. It means that the process K only increases when Y reaches the barrier L. By a solution of RBSDE (2), we mean a triple
![]() $\{(Y_t,Z_t,K_t),\ 0\le t\le T\}$
of predictable processes with values in
$\{(Y_t,Z_t,K_t),\ 0\le t\le T\}$
of predictable processes with values in
![]() $\mathbb R\times\mathbb R^{1\times d}\times \mathbb R$
such that
$\mathbb R\times\mathbb R^{1\times d}\times \mathbb R$
such that
![]() ${\mathbb P}$
-a.s.,
${\mathbb P}$
-a.s.,
![]() $t\mapsto Y_t$
is continuous,
$t\mapsto Y_t$
is continuous,
![]() $t\mapsto Z_t$
belongs to
$t\mapsto Z_t$
belongs to
![]() $L^2(0,T)$
,
$L^2(0,T)$
,
![]() $t\mapsto K_t$
is non-decreasing, continuous and
$t\mapsto K_t$
is non-decreasing, continuous and
![]() $t\mapsto g(t,Y_t,Z_t)$
is integrable, and
$t\mapsto g(t,Y_t,Z_t)$
is integrable, and
![]() ${\mathbb P}$
-a.s., (Y, Z, K) verifies (2). An important result is that the value process of nonlinear optimal stopping problem can be completely characterized by the first component of the unique solution of the corresponding RBSDE (see [Reference Bayraktar and Yao2], [Reference El Karoui, Pardoux and Quenez10], or [Reference Quenez and Sulem20]):
${\mathbb P}$
-a.s., (Y, Z, K) verifies (2). An important result is that the value process of nonlinear optimal stopping problem can be completely characterized by the first component of the unique solution of the corresponding RBSDE (see [Reference Bayraktar and Yao2], [Reference El Karoui, Pardoux and Quenez10], or [Reference Quenez and Sulem20]):
Moreover, the first time process Y reaches process L after
![]() $t=0$
is an optimal stopping time for (1). With the theory of RBSDEs, the investigation of nonlinear optimal stopping problem is sufficiently rich. Hence El Karoui et al. [Reference El Karoui, Kapoudjian, Pardoux, Peng and Quenez9] first proved the existence and uniqueness of solutions to RBSDEs with
$t=0$
is an optimal stopping time for (1). With the theory of RBSDEs, the investigation of nonlinear optimal stopping problem is sufficiently rich. Hence El Karoui et al. [Reference El Karoui, Kapoudjian, Pardoux, Peng and Quenez9] first proved the existence and uniqueness of solutions to RBSDEs with
![]() $L^2$
-data under Lipschitz-type assumptions on the generator. Lepeltier, Matoussi, and Xu [Reference Lepeltier, Matoussi and Xu18] improved this result under monotonicity as well as general growth conditions. The RBSDE with
$L^2$
-data under Lipschitz-type assumptions on the generator. Lepeltier, Matoussi, and Xu [Reference Lepeltier, Matoussi and Xu18] improved this result under monotonicity as well as general growth conditions. The RBSDE with
![]() $L^p$
-data (
$L^p$
-data (
![]() $p\in (1,2]$
) was first studied by Hamadene and Popier [Reference Hamadène and Popier12] under Lipschitz conditions. Rozkosz and Slomiński [Reference Rozkosz and Slomiński22] and Klimsiak [Reference Klimsiak15] improved this result under monotonicity condition on generator. Moreover, they also studied the case of
$p\in (1,2]$
) was first studied by Hamadene and Popier [Reference Hamadène and Popier12] under Lipschitz conditions. Rozkosz and Slomiński [Reference Rozkosz and Slomiński22] and Klimsiak [Reference Klimsiak15] improved this result under monotonicity condition on generator. Moreover, they also studied the case of
![]() $p=1$
[Reference Klimsiak15, Reference Rozkosz and Slomiński22], which is of particular interest. It means the terminal payoff and reward process is only integrable. However, in this case one needs to restrict the generator g to grow sublinearly with respect to the third variable, that is, for some
$p=1$
[Reference Klimsiak15, Reference Rozkosz and Slomiński22], which is of particular interest. It means the terminal payoff and reward process is only integrable. However, in this case one needs to restrict the generator g to grow sublinearly with respect to the third variable, that is, for some
![]() $q\in [0,1)$
,
$q\in [0,1)$
,
for RBSDE (2) to have a unique solution [Reference Klimsiak15, Reference Rozkosz and Slomiński22]. The sublinear growth condition is somewhat restrictive and not convenient for various applications.
In this paper we aim to study the optimal stopping problem (1) under weak integrability assumptions on data (at least, weaker than
![]() $L^p$
-integrability for any
$L^p$
-integrability for any
![]() $p>1$
), but without assuming the sublinear growth condition (3). Then it is a natural question to ask: What is the optimal integrability assumption under which the RBSDE with standard generator has a unique solution? The recent work of Hu and Tang [Reference Hu and Tang13] gives us a partial resolution to this problem for the standard BSDE. They introduced a class of BSDEs with
$p>1$
), but without assuming the sublinear growth condition (3). Then it is a natural question to ask: What is the optimal integrability assumption under which the RBSDE with standard generator has a unique solution? The recent work of Hu and Tang [Reference Hu and Tang13] gives us a partial resolution to this problem for the standard BSDE. They introduced a class of BSDEs with
![]() $L\exp\bigl(\mu\sqrt{2\log\!(1+L)}\bigr)$
-integrable data with
$L\exp\bigl(\mu\sqrt{2\log\!(1+L)}\bigr)$
-integrable data with
![]() $\mu>\mu_0$
for some critical value
$\mu>\mu_0$
for some critical value
![]() $\mu_0>0$
. This integrability is weaker than
$\mu_0>0$
. This integrability is weaker than
![]() $L^p$
-integrability for any
$L^p$
-integrability for any
![]() $p>1$
and stronger than
$p>1$
and stronger than
![]() $L\log L$
-integrability. They showed that this BSDE has a solution without sublinear growth condition (3). They also showed that the existence result fails in the case of
$L\log L$
-integrability. They showed that this BSDE has a solution without sublinear growth condition (3). They also showed that the existence result fails in the case of
![]() $\mu<\mu_0$
. Subsequently, Buckdahn, Hu and Tang [Reference Buckdahn, Hu and Tang4] gave the uniqueness result for this BSDE, which was missing from [Reference Hu and Tang13]. Fan and Hu [Reference Fan and Hu11] studied the critical case of
$\mu<\mu_0$
. Subsequently, Buckdahn, Hu and Tang [Reference Buckdahn, Hu and Tang4] gave the uniqueness result for this BSDE, which was missing from [Reference Hu and Tang13]. Fan and Hu [Reference Fan and Hu11] studied the critical case of
![]() $\mu=\mu_0$
.
$\mu=\mu_0$
.
Motivated by [Reference Buckdahn, Hu and Tang4] and [Reference Hu and Tang13], we study a class of RBSDEs with
![]() $L\exp\bigl(\mu\sqrt{2\log\!(1+L)}\bigr)$
-integrable data. In Section 2 we establish the main existence and uniqueness result for these RBSDEs. We then give comparison theorems for these RBSDEs in Section 3. The existence argument is similar to that of [Reference Hu and Tang13] with some modifications when deriving a priori bounds on the solution. However, the uniqueness and comparison arguments are different from those of [Reference Buckdahn, Hu and Tang4]. We argue by transforming the original equation into a new one with integrable parameters with the help of the Girsanov theorem. Our approach may be more useful for future development (see Remark 2 for details). As we mentioned above, we can use our results to characterize the value process of the nonlinear optimal stopping problem under g-expectation with an
$L\exp\bigl(\mu\sqrt{2\log\!(1+L)}\bigr)$
-integrable data. In Section 2 we establish the main existence and uniqueness result for these RBSDEs. We then give comparison theorems for these RBSDEs in Section 3. The existence argument is similar to that of [Reference Hu and Tang13] with some modifications when deriving a priori bounds on the solution. However, the uniqueness and comparison arguments are different from those of [Reference Buckdahn, Hu and Tang4]. We argue by transforming the original equation into a new one with integrable parameters with the help of the Girsanov theorem. Our approach may be more useful for future development (see Remark 2 for details). As we mentioned above, we can use our results to characterize the value process of the nonlinear optimal stopping problem under g-expectation with an
![]() $L\exp\bigl(\mu\sqrt{2\log\!(1+L)}\bigr)$
-integrable reward process, by following the standard arguments as in [Reference Bayraktar and Yao2], [Reference El Karoui, Pardoux and Quenez10], and [Reference Quenez and Sulem20]. Finally, in Section 4, we briefly describe the main difficulties in the critical case.
$L\exp\bigl(\mu\sqrt{2\log\!(1+L)}\bigr)$
-integrable reward process, by following the standard arguments as in [Reference Bayraktar and Yao2], [Reference El Karoui, Pardoux and Quenez10], and [Reference Quenez and Sulem20]. Finally, in Section 4, we briefly describe the main difficulties in the critical case.
1.1. Notation
We are given a complete probability space
![]() $(\Omega,\mathcal F,\mathbb P)$
on which a d-dimensional Brownian motion B is defined. We let
$(\Omega,\mathcal F,\mathbb P)$
on which a d-dimensional Brownian motion B is defined. We let
![]() $\mathbb F\;:\!=\; \{\mathcal F_t\}_{t\in [0,T]}$
denote the natural filtration generated by B. Let
$\mathbb F\;:\!=\; \{\mathcal F_t\}_{t\in [0,T]}$
denote the natural filtration generated by B. Let
![]() $p\ge 1$
.
$p\ge 1$
.
-
•
 $L^p$
denotes the space of all
$L^p$
denotes the space of all
 $\mathcal F_T$
-measurable scalar random variables
$\mathcal F_T$
-measurable scalar random variables
 $\xi$
with
$\xi$
with  \begin{equation*}\|\xi\|_{L^p}^p\;:\!=\; \mathbb E[|\xi|^p]<+\infty.\end{equation*}
\begin{equation*}\|\xi\|_{L^p}^p\;:\!=\; \mathbb E[|\xi|^p]<+\infty.\end{equation*}
-
•
 $\mathbb S^p$
denotes the space of
$\mathbb S^p$
denotes the space of
 $\mathbb R$
-valued,
$\mathbb R$
-valued,
 $\mathbb F$
-adapted processes Y, with continuous paths, such that
$\mathbb F$
-adapted processes Y, with continuous paths, such that  \begin{equation*}\|Y\|_{\mathbb S^p}^p\;:\!=\; \mathbb E\biggl[\sup_{0\le t\le T}|Y_t|^p\biggr]<+\infty.\end{equation*}
\begin{equation*}\|Y\|_{\mathbb S^p}^p\;:\!=\; \mathbb E\biggl[\sup_{0\le t\le T}|Y_t|^p\biggr]<+\infty.\end{equation*}
-
•
 $\mathbb H^p$
denotes the space of all predictable
$\mathbb H^p$
denotes the space of all predictable
 $\mathbb R^{1\times d}$
-valued processes Z with
$\mathbb R^{1\times d}$
-valued processes Z with  \begin{equation*}\|Z\|_{\mathbb H^p}^p\;:\!=\; \mathbb E\Biggl[\biggl(\int_0^T|Z_t|^2 \,{\mathrm{d}} t\biggr)^{p/2}\Biggr]<+\infty.\end{equation*}
\begin{equation*}\|Z\|_{\mathbb H^p}^p\;:\!=\; \mathbb E\Biggl[\biggl(\int_0^T|Z_t|^2 \,{\mathrm{d}} t\biggr)^{p/2}\Biggr]<+\infty.\end{equation*}
-
•
 $\mathbb I^p$
denotes the space of
$\mathbb I^p$
denotes the space of
 $\mathbb R$
-valued, adapted processes K, with continuous, non-decreasing paths such that
$\mathbb R$
-valued, adapted processes K, with continuous, non-decreasing paths such that
 $K_0=0$
and
$K_0=0$
and  \begin{equation*}\|K\|_{\mathbb I^p}^p\;:\!=\; \mathbb E[(K_T)^p]<+\infty.\end{equation*}
\begin{equation*}\|K\|_{\mathbb I^p}^p\;:\!=\; \mathbb E[(K_T)^p]<+\infty.\end{equation*}
-
• The
 $\sigma$
-field of predictable subsets of
$\sigma$
-field of predictable subsets of
 $\Omega\times [0,T]$
is denoted by
$\Omega\times [0,T]$
is denoted by
 $\mathcal P$
.
$\mathcal P$
. -
• For any
 $t\in [0,T]$
,
$t\in [0,T]$
,
 $\mathbb T^{t,T}$
denotes the space of all stopping times taking values in [t, T].
$\mathbb T^{t,T}$
denotes the space of all stopping times taking values in [t, T]. -
•
 $a^+\;:\!=\; \max\{a,0\}$
,
$a^+\;:\!=\; \max\{a,0\}$
,
 $X_t^*\;:\!=\; \sup_{0\le s \le t}|X_s|$
, and
$X_t^*\;:\!=\; \sup_{0\le s \le t}|X_s|$
, and
 $\mathbb E_t[\!\cdot\!]\;:\!=\; \mathbb E[\!\cdot\!|\mathcal F_t]$
,
$\mathbb E_t[\!\cdot\!]\;:\!=\; \mathbb E[\!\cdot\!|\mathcal F_t]$
,
 $t\in [0,T]$
.
$t\in [0,T]$
. -
• Throughout the paper,
 $\psi$
denotes a function defined by
$\psi$
denotes a function defined by  \begin{equation*}\psi(x,\mu)\;:\!=\; x\exp\bigl(\mu\sqrt{2\log (1+x)}\bigr),\quad (x,\mu)\in [0,+\infty)\times (0,+\infty).\end{equation*}
\begin{equation*}\psi(x,\mu)\;:\!=\; x\exp\bigl(\mu\sqrt{2\log (1+x)}\bigr),\quad (x,\mu)\in [0,+\infty)\times (0,+\infty).\end{equation*}
2. Main existence and uniqueness result
Consider the following RBSDE:
 \begin{equation}\begin{cases}Y_t=\xi+\int_t^T g(s,Y_s,Z_s)\,{\mathrm{d}} s-\int_t^T Z_s \,{\mathrm{d}} B_s+K_T-K_t,\\[5pt]Y_t\ge L_t,\quad \int_0^T (Y_t-L_t)\,{\mathrm{d}} K_t=0,\end{cases}\end{equation}
\begin{equation}\begin{cases}Y_t=\xi+\int_t^T g(s,Y_s,Z_s)\,{\mathrm{d}} s-\int_t^T Z_s \,{\mathrm{d}} B_s+K_T-K_t,\\[5pt]Y_t\ge L_t,\quad \int_0^T (Y_t-L_t)\,{\mathrm{d}} K_t=0,\end{cases}\end{equation}
where
![]() $\xi\ge L_T$
and
$\xi\ge L_T$
and
![]() $g\colon \Omega\times [0,T]\times \mathbb R\times\mathbb R^{1\times d}\to\mathbb R$
is measurable with respect to
$g\colon \Omega\times [0,T]\times \mathbb R\times\mathbb R^{1\times d}\to\mathbb R$
is measurable with respect to
![]() $\mathcal P\otimes\mathcal B(\mathbb R)\otimes\mathcal B(\mathbb R^{1\times d})$
. We assume that the generator g satisfies the standard Lipschitz assumption, that is, for any
$\mathcal P\otimes\mathcal B(\mathbb R)\otimes\mathcal B(\mathbb R^{1\times d})$
. We assume that the generator g satisfies the standard Lipschitz assumption, that is, for any
![]() $(y^i,z^i)\in\mathbb R\times\mathbb R^{1\times d}$
,
$(y^i,z^i)\in\mathbb R\times\mathbb R^{1\times d}$
,
![]() $i=1,2$
,
$i=1,2$
,
with
![]() $\beta\ge 0$
and
$\beta\ge 0$
and
![]() $\gamma\ge0$
. We set
$\gamma\ge0$
. We set
![]() $g_0\;:\!=\; g(\cdot,0,0)$
for simplicity.
$g_0\;:\!=\; g(\cdot,0,0)$
for simplicity.
Theorem 1. Let the generator g verify the Lipschitz condition (5). Let us suppose that there exists
![]() $\mu>\gamma\sqrt{T}$
such that
$\mu>\gamma\sqrt{T}$
such that
Then the RBSDE (4) admits a unique solution (Y, Z, K) such that
![]() $\psi (|Y|,a)$
belongs to class (D) for some
$\psi (|Y|,a)$
belongs to class (D) for some
![]() $a>0$
.
$a>0$
.
Proof. We first prove the existence result. We shall follow the arguments of [Reference Hu and Tang13, Theorem 3.1]. Let us fix
![]() $n\in N^*$
and
$n\in N^*$
and
![]() $p\in N^*$
. Set
$p\in N^*$
. Set
 \begin{alignat*}{3}\xi^{n,p} & \;:\!=\; \xi^+\wedge n-\xi^-\wedge p, &\quad L^{n,p} &\;:\!=\; L^+\wedge n-L^-\wedge p,\\[5pt] g_0^{n,p} &\;:\!=\; g_0^+\wedge n-g_0^-\wedge p, &\quad g^{n,p} &\;:\!=\; g-g_0+g_0^{n,p}.\end{alignat*}
\begin{alignat*}{3}\xi^{n,p} & \;:\!=\; \xi^+\wedge n-\xi^-\wedge p, &\quad L^{n,p} &\;:\!=\; L^+\wedge n-L^-\wedge p,\\[5pt] g_0^{n,p} &\;:\!=\; g_0^+\wedge n-g_0^-\wedge p, &\quad g^{n,p} &\;:\!=\; g-g_0+g_0^{n,p}.\end{alignat*}
As the terminal value
![]() $\xi^{n,p}$
, the barrier
$\xi^{n,p}$
, the barrier
![]() $L^{n,p}$
and
$L^{n,p}$
and
![]() $g^{n,p}(\cdot,0,0)$
are bounded (hence square-integrable) and
$g^{n,p}(\cdot,0,0)$
are bounded (hence square-integrable) and
![]() $g^{n,p}$
is Lipschitz-continuous, in view of the existence result in [Reference El Karoui, Kapoudjian, Pardoux, Peng and Quenez9], the RBSDE
$g^{n,p}$
is Lipschitz-continuous, in view of the existence result in [Reference El Karoui, Kapoudjian, Pardoux, Peng and Quenez9], the RBSDE
![]() $(\xi^{n,p},L^{n,p},g^{n,p})$
has a unique solution
$(\xi^{n,p},L^{n,p},g^{n,p})$
has a unique solution
![]() $(Y^{n,p},Z^{n,p},K^{n,p})$
in
$(Y^{n,p},Z^{n,p},K^{n,p})$
in
![]() $\mathbb S^2\times \mathbb H^2\times\mathbb I^2$
. In particular, there exists a
$\mathbb S^2\times \mathbb H^2\times\mathbb I^2$
. In particular, there exists a
![]() $\mathbb R$
-valued (resp.
$\mathbb R$
-valued (resp.
![]() $\mathbb R^d$
-valued) adapted process
$\mathbb R^d$
-valued) adapted process
![]() $\beta_s^{n,p}$
(resp.
$\beta_s^{n,p}$
(resp.
![]() $\gamma_s^{n,p}$
), with
$\gamma_s^{n,p}$
), with
![]() $|\beta_s^{n,p}|\le \beta$
(resp.
$|\beta_s^{n,p}|\le \beta$
(resp.
![]() $|\gamma_s^{n,p}|\le\gamma$
) such that
$|\gamma_s^{n,p}|\le\gamma$
) such that
Let us define
 \begin{align*}X_t^{n,p} & \;:\!=\; \exp\biggl(\int_0^t \beta_r^{n,p}\,{\mathrm{d}} r\biggr),\\[5pt] \dfrac{{\mathrm{d}}\mathbb P^{n,p}}{{\mathrm{d}}\mathbb P} & \;:\!=\; \exp\biggl(\int_0^{T}\gamma_s^{n,p}\cdot {\mathrm{d}} B_s-\dfrac{1}{2}\int_0^T |\gamma_s^{n,p}|^2 \,{\mathrm{d}} s\biggr),\\[5pt] B^{\mathbb P^{n,p}} & =B_{\cdot}-\int_0^{\cdot}\gamma_s^{n,p}\,{\mathrm{d}} s.\end{align*}
\begin{align*}X_t^{n,p} & \;:\!=\; \exp\biggl(\int_0^t \beta_r^{n,p}\,{\mathrm{d}} r\biggr),\\[5pt] \dfrac{{\mathrm{d}}\mathbb P^{n,p}}{{\mathrm{d}}\mathbb P} & \;:\!=\; \exp\biggl(\int_0^{T}\gamma_s^{n,p}\cdot {\mathrm{d}} B_s-\dfrac{1}{2}\int_0^T |\gamma_s^{n,p}|^2 \,{\mathrm{d}} s\biggr),\\[5pt] B^{\mathbb P^{n,p}} & =B_{\cdot}-\int_0^{\cdot}\gamma_s^{n,p}\,{\mathrm{d}} s.\end{align*}
Then, by the Girsanov theorem,
![]() $B^{\mathbb P^{n,p}}$
is a
$B^{\mathbb P^{n,p}}$
is a
![]() $\mathbb P^{n,p}$
-Brownian motion, and we can rewrite the solution of RBSDE
$\mathbb P^{n,p}$
-Brownian motion, and we can rewrite the solution of RBSDE
![]() $(\xi^{n,p},L^{n,p},g^{n,p})$
as
$(\xi^{n,p},L^{n,p},g^{n,p})$
as
 \begin{equation*} \begin{cases}X_t^{n,p}Y_t^{n,p}=X_T^{n,p}\xi^{n,p}+\int_t^T X_s^{n,p}g_0^{n,p}(s)\,{\mathrm{d}} s-\int_t^T X_s^{n,p}Z_s^{n,p}\,{\mathrm{d}} B_s^{\mathbb P^{n,p}}+\int_t^T X_s^{n,p}\,{\mathrm{d}} K_s^{n,p},\\[5pt] X_t^{n,p}Y_t^{n,p}\ge X_t^{n,p}L_t^{n,p},\quad \int_0^T X_s^{n,p}(Y_s^{n,p}-L_s^{n,p})\,{\mathrm{d}} K_s^{n,p}=0.\end{cases}\end{equation*}
\begin{equation*} \begin{cases}X_t^{n,p}Y_t^{n,p}=X_T^{n,p}\xi^{n,p}+\int_t^T X_s^{n,p}g_0^{n,p}(s)\,{\mathrm{d}} s-\int_t^T X_s^{n,p}Z_s^{n,p}\,{\mathrm{d}} B_s^{\mathbb P^{n,p}}+\int_t^T X_s^{n,p}\,{\mathrm{d}} K_s^{n,p},\\[5pt] X_t^{n,p}Y_t^{n,p}\ge X_t^{n,p}L_t^{n,p},\quad \int_0^T X_s^{n,p}(Y_s^{n,p}-L_s^{n,p})\,{\mathrm{d}} K_s^{n,p}=0.\end{cases}\end{equation*}
Using the Snell envelope representation of solutions to RBSDEs (see e.g. [Reference El Karoui, Kapoudjian, Pardoux, Peng and Quenez9, Proposition 2.3]), we have
Then we deduce that
 \begin{align*}&\mathbb E_t^{\mathbb P^{n,p}}\biggl[\int_t^T X_s^{n,p}g_0^{n,p}(s)\,{\mathrm{d}} s+X_T^{n,p}\xi^{n,p}\biggr]\le X_t^{n,p}Y_t^{n,p}\\[5pt] &\quad \le \mathop{\mathrm{ess\sup}}_{\tau\in\mathbb T^{t,T}}\mathbb E_t^{\mathbb P^{n,p}}\biggl[\int_t^{\tau}X_s^{n,p}g_0^{n,p}(s)\,{\mathrm{d}} s+X_{\tau}^{n,p}(L_{\tau}^{n,p})^+\textbf 1_{\tau<T}+X_{T}^{n,p}\xi^{n,p}\textbf 1_{\tau=T}\biggr].\end{align*}
\begin{align*}&\mathbb E_t^{\mathbb P^{n,p}}\biggl[\int_t^T X_s^{n,p}g_0^{n,p}(s)\,{\mathrm{d}} s+X_T^{n,p}\xi^{n,p}\biggr]\le X_t^{n,p}Y_t^{n,p}\\[5pt] &\quad \le \mathop{\mathrm{ess\sup}}_{\tau\in\mathbb T^{t,T}}\mathbb E_t^{\mathbb P^{n,p}}\biggl[\int_t^{\tau}X_s^{n,p}g_0^{n,p}(s)\,{\mathrm{d}} s+X_{\tau}^{n,p}(L_{\tau}^{n,p})^+\textbf 1_{\tau<T}+X_{T}^{n,p}\xi^{n,p}\textbf 1_{\tau=T}\biggr].\end{align*}
This inequality leads to
 \begin{align*}|Y_t^{n,p}|&\le \mathop{\mathrm{ess\sup}}_{\tau\in\mathbb T^{t,T}}\mathbb E_t^{\mathbb P^{n,p}}\biggl[\int_t^{\tau}|g_0^{n,p}(s)|\,{\mathrm{e}}^{\beta (s-t)}\,{\mathrm{d}} s+{\mathrm{e}}^{\beta (\tau-t)}(L_{\tau}^{n,p})^+\textbf 1_{\tau<T}+{\mathrm{e}}^{\beta (T-t)}|\xi^{n,p}|\textbf 1_{\tau=T}\biggr]\\[5pt] &\le {\mathrm{e}}^{\beta (T-t)}\mathbb E_t^{\mathbb P^{n,p}}\biggl[\int_t^T |g_0^{n,p}(s)|\,{\mathrm{d}} s+(L_T^{n,p})^{+,*}+|\xi^{n,p}|\biggr]\\[5pt] &\le {\mathrm{e}}^{\beta (T-t)}\mathbb E_t^{\mathbb P^{n,p}}\biggl[\int_t^T |g_0(s)|\,{\mathrm{d}} s+L_T^{+,*}+|\xi|\biggr].\end{align*}
\begin{align*}|Y_t^{n,p}|&\le \mathop{\mathrm{ess\sup}}_{\tau\in\mathbb T^{t,T}}\mathbb E_t^{\mathbb P^{n,p}}\biggl[\int_t^{\tau}|g_0^{n,p}(s)|\,{\mathrm{e}}^{\beta (s-t)}\,{\mathrm{d}} s+{\mathrm{e}}^{\beta (\tau-t)}(L_{\tau}^{n,p})^+\textbf 1_{\tau<T}+{\mathrm{e}}^{\beta (T-t)}|\xi^{n,p}|\textbf 1_{\tau=T}\biggr]\\[5pt] &\le {\mathrm{e}}^{\beta (T-t)}\mathbb E_t^{\mathbb P^{n,p}}\biggl[\int_t^T |g_0^{n,p}(s)|\,{\mathrm{d}} s+(L_T^{n,p})^{+,*}+|\xi^{n,p}|\biggr]\\[5pt] &\le {\mathrm{e}}^{\beta (T-t)}\mathbb E_t^{\mathbb P^{n,p}}\biggl[\int_t^T |g_0(s)|\,{\mathrm{d}} s+L_T^{+,*}+|\xi|\biggr].\end{align*}
Using Lemmas 2.4 and 2.6 of [Reference Hu and Tang13] and the fact that
![]() $\mu>\gamma\sqrt T$
, we deduce that
$\mu>\gamma\sqrt T$
, we deduce that
 \begin{align} |Y_t^{n,p}| &\le\bar Y_t \notag \\[5pt] & \;:\!=\; \dfrac{1}{\sqrt{1-({\gamma^2}/{\mu^2})(T-t)}}\,{\mathrm{e}}^{\beta (T-t)}+{\mathrm{e}}^{2\mu^2+\beta (T-t)}\cdot \mathbb E_t\biggl[\psi(|\xi|+L_T^{+,*}+\int_t^T |g_0(s)|\,{\mathrm{d}} s,\mu)\biggr].\end{align}
\begin{align} |Y_t^{n,p}| &\le\bar Y_t \notag \\[5pt] & \;:\!=\; \dfrac{1}{\sqrt{1-({\gamma^2}/{\mu^2})(T-t)}}\,{\mathrm{e}}^{\beta (T-t)}+{\mathrm{e}}^{2\mu^2+\beta (T-t)}\cdot \mathbb E_t\biggl[\psi(|\xi|+L_T^{+,*}+\int_t^T |g_0(s)|\,{\mathrm{d}} s,\mu)\biggr].\end{align}
This estimate, together with the monotone stability theorem (see [Reference Bayraktar and Yao2, Theorem 3.1] or [Reference Kobylanski, Lepeltier, Quenez and Torres16, Theorem 4]) is fundamental to proving our existence result. Since
![]() $Y^{n,p}$
is non-decreasing in n and non-increasing in p thanks to the comparison theorem (see [Reference El Karoui, Kapoudjian, Pardoux, Peng and Quenez9, Theorem 4.1]), by the localization method in [Reference Bayraktar and Yao2] and [Reference Lepeltier and Xu17] there exists some process
$Y^{n,p}$
is non-decreasing in n and non-increasing in p thanks to the comparison theorem (see [Reference El Karoui, Kapoudjian, Pardoux, Peng and Quenez9, Theorem 4.1]), by the localization method in [Reference Bayraktar and Yao2] and [Reference Lepeltier and Xu17] there exists some process
![]() $Z\in L^2(0,T)$
such that
$Z\in L^2(0,T)$
such that
![]() $(Y\;:\!=\; \inf_p\sup_n Y^{n,p},Z,K\;:\!=\; \sup_p\inf_n K^{n,p})$
is an adapted solution. The fact that
$(Y\;:\!=\; \inf_p\sup_n Y^{n,p},Z,K\;:\!=\; \sup_p\inf_n K^{n,p})$
is an adapted solution. The fact that
![]() $\psi(|Y|,a)$
belongs to class (D) for some
$\psi(|Y|,a)$
belongs to class (D) for some
![]() $a>0$
can be proved by following exactly the same method as in [Reference Buckdahn, Hu and Tang4], thanks to (6). Since
$a>0$
can be proved by following exactly the same method as in [Reference Buckdahn, Hu and Tang4], thanks to (6). Since
![]() $\mu>b\sqrt{t}$
, we can choose
$\mu>b\sqrt{t}$
, we can choose
![]() $a>0$
,
$a>0$
,
![]() $b>\gamma\sqrt{T}$
, and
$b>\gamma\sqrt{T}$
, and
![]() $c>0$
such that
$c>0$
such that
![]() $a+b+c=\mu$
. For such a constant a,
$a+b+c=\mu$
. For such a constant a,
![]() $\psi(|Y|,a)$
belongs to class (D) (see the proof of Theorem 2.4 of [Reference Buckdahn, Hu and Tang4]).
$\psi(|Y|,a)$
belongs to class (D) (see the proof of Theorem 2.4 of [Reference Buckdahn, Hu and Tang4]).
We now prove the uniqueness of the solution. For
![]() $i=1,2$
, let
$i=1,2$
, let
![]() $(Y^i,Z^i,K^i)$
be a solution to RBSDE (4) such that
$(Y^i,Z^i,K^i)$
be a solution to RBSDE (4) such that
![]() $\psi (|Y^i|,a^i)$
belongs to class (D) for some
$\psi (|Y^i|,a^i)$
belongs to class (D) for some
![]() $a^i>0$
. Define
$a^i>0$
. Define
Then both
![]() $\psi (|Y^1|,a)$
and
$\psi (|Y^1|,a)$
and
![]() $\psi (|Y^2|,a)$
belong to class (D), since
$\psi (|Y^2|,a)$
belong to class (D), since
![]() $\psi (x,\mu)$
is non-decreasing in
$\psi (x,\mu)$
is non-decreasing in
![]() $\mu$
. Moreover, in view of Proposition 2.3 of [Reference Buckdahn, Hu and Tang4], we have
$\mu$
. Moreover, in view of Proposition 2.3 of [Reference Buckdahn, Hu and Tang4], we have
 \begin{align*} \psi(|\delta Y_t|,a)&\le \psi(|Y_t^1|+|Y_t^2|,a)\\[5pt] &=\psi\biggl(\dfrac{1}{2}\times 2|Y_t^1|+\dfrac{1}{2}\times 2|Y_t^2|,a\biggr)\\[5pt] &\le \dfrac{1}{2}\psi(2|Y_t^1|,a)+\dfrac{1}{2}\psi(2|Y_t^2|,a)\\[5pt] &\le \dfrac{1}{2}\psi(2,a)[\psi(|Y_t^1|,a)+\psi(|Y_t^2|,a)],\end{align*}
\begin{align*} \psi(|\delta Y_t|,a)&\le \psi(|Y_t^1|+|Y_t^2|,a)\\[5pt] &=\psi\biggl(\dfrac{1}{2}\times 2|Y_t^1|+\dfrac{1}{2}\times 2|Y_t^2|,a\biggr)\\[5pt] &\le \dfrac{1}{2}\psi(2|Y_t^1|,a)+\dfrac{1}{2}\psi(2|Y_t^2|,a)\\[5pt] &\le \dfrac{1}{2}\psi(2,a)[\psi(|Y_t^1|,a)+\psi(|Y_t^2|,a)],\end{align*}
from which we deduce that
![]() $\psi(|\delta Y|,a)$
belongs to class (D).
$\psi(|\delta Y|,a)$
belongs to class (D).
By a standard linearization argument, we see that there exist two adapted processes u and v such that
![]() $|u_s|\le \beta$
,
$|u_s|\le \beta$
,
![]() $|v_s|\le\gamma$
, and
$|v_s|\le\gamma$
, and
![]() $g(s,Y_s^1,Z_s^1)-g(s,Y_s^2,Z_s^2)=u_s\delta Y_s+\delta Z_s v_s$
and the triple
$g(s,Y_s^1,Z_s^1)-g(s,Y_s^2,Z_s^2)=u_s\delta Y_s+\delta Z_s v_s$
and the triple
![]() $(\delta Y,\delta Z,\delta K)$
satisfies
$(\delta Y,\delta Z,\delta K)$
satisfies
Set
![]() $\theta\;:\!=\; {a^2}/{(4\gamma^2)}$
. Let us define
$\theta\;:\!=\; {a^2}/{(4\gamma^2)}$
. Let us define
Then, by the Girsanov theorem,
![]() $B^{\mathbb Q}$
is a
$B^{\mathbb Q}$
is a
![]() $\mathbb Q$
-Brownian motion on
$\mathbb Q$
-Brownian motion on
![]() $[T-\theta,T]$
. Therefore we have
$[T-\theta,T]$
. Therefore we have
![]() $\mathbb Q$
-a.s.
$\mathbb Q$
-a.s.
We now show that
![]() $\{\delta Y_t,t\in[T-\theta,T]\}$
belongs to class (D) under
$\{\delta Y_t,t\in[T-\theta,T]\}$
belongs to class (D) under
![]() $\mathbb Q$
. To do this, we note that
$\mathbb Q$
. To do this, we note that
![]() $\psi(|\delta Y|,a)$
belongs to class (D). Using Lemmas 2.4 and 2.6 of [Reference Hu and Tang13], we have for any
$\psi(|\delta Y|,a)$
belongs to class (D). Using Lemmas 2.4 and 2.6 of [Reference Hu and Tang13], we have for any
![]() $\tau\in\mathbb T^{T-\theta,T}$
and
$\tau\in\mathbb T^{T-\theta,T}$
and
![]() $A\in\mathcal F_T$
,
$A\in\mathcal F_T$
,
 \begin{align*}\mathbb E^{\mathbb Q}[\textbf 1_A|\delta Y_{\tau}|]&\le \mathbb E\biggl[\textbf 1_A |\delta Y_{\tau}|\exp\biggl(\int_{T-\theta}^T v_s\cdot \,{\mathrm{d}} B_s\biggr)\biggr]\\[5pt] &\le \mathbb E\biggl[\textbf 1_A\exp\biggl( \dfrac{\bigl|\int_{T-\theta}^T v_s\cdot {\mathrm{d}} B_s\bigr|^2}{2a^2} \biggr)\biggr]+\mathbb E\bigl[{\mathrm{e}}^{2a^2}\textbf 1_A\psi (|\delta Y_{\tau}|,a)\bigr]\\[5pt] &\le \mathbb E\biggl[\exp\biggl( \dfrac{\bigl|\int_{T-\theta}^T \sqrt 2 v_s\cdot {\mathrm{d}} B_s\bigr|^2}{2a^2} \biggr)\biggr]^{1/2}\cdot \mathbb P(A)^{1/2}+\mathbb E\bigl[{\mathrm{e}}^{2a^2}\textbf 1_A\psi (|\delta Y_{\tau}|,a)\bigr]\\[5pt] &\le \biggl(1-\dfrac{2\gamma^2}{a^2}\theta\biggr)^{-1/4}\cdot \mathbb P(A)^{1/2}+{\mathrm{e}}^{2a^2}\mathbb E[\textbf 1_A\psi (|\delta Y_{\tau}|,a)]\\[5pt] &= 2^{1/4}\cdot\mathbb P(A)^{1/2} +{\mathrm{e}}^{2a^2}\mathbb E[\textbf 1_A\psi (|\delta Y_{\tau}|,a)].\end{align*}
\begin{align*}\mathbb E^{\mathbb Q}[\textbf 1_A|\delta Y_{\tau}|]&\le \mathbb E\biggl[\textbf 1_A |\delta Y_{\tau}|\exp\biggl(\int_{T-\theta}^T v_s\cdot \,{\mathrm{d}} B_s\biggr)\biggr]\\[5pt] &\le \mathbb E\biggl[\textbf 1_A\exp\biggl( \dfrac{\bigl|\int_{T-\theta}^T v_s\cdot {\mathrm{d}} B_s\bigr|^2}{2a^2} \biggr)\biggr]+\mathbb E\bigl[{\mathrm{e}}^{2a^2}\textbf 1_A\psi (|\delta Y_{\tau}|,a)\bigr]\\[5pt] &\le \mathbb E\biggl[\exp\biggl( \dfrac{\bigl|\int_{T-\theta}^T \sqrt 2 v_s\cdot {\mathrm{d}} B_s\bigr|^2}{2a^2} \biggr)\biggr]^{1/2}\cdot \mathbb P(A)^{1/2}+\mathbb E\bigl[{\mathrm{e}}^{2a^2}\textbf 1_A\psi (|\delta Y_{\tau}|,a)\bigr]\\[5pt] &\le \biggl(1-\dfrac{2\gamma^2}{a^2}\theta\biggr)^{-1/4}\cdot \mathbb P(A)^{1/2}+{\mathrm{e}}^{2a^2}\mathbb E[\textbf 1_A\psi (|\delta Y_{\tau}|,a)]\\[5pt] &= 2^{1/4}\cdot\mathbb P(A)^{1/2} +{\mathrm{e}}^{2a^2}\mathbb E[\textbf 1_A\psi (|\delta Y_{\tau}|,a)].\end{align*}
We then have
On the other hand, for any
![]() $\varepsilon>0$
, there exists
$\varepsilon>0$
, there exists
![]() $ \vartheta_1>0$
such that, for all
$ \vartheta_1>0$
such that, for all
![]() $ A\in\mathcal F_T$
$ A\in\mathcal F_T$
![]() $(\mathbb P(A)<\vartheta_1)$
, we have
$(\mathbb P(A)<\vartheta_1)$
, we have
Since
![]() $\mathbb Q$
is equivalent to
$\mathbb Q$
is equivalent to
![]() $\mathbb P$
,
$\mathbb P$
,
![]() $\mathbb P$
is totally continuous with respect to
$\mathbb P$
is totally continuous with respect to
![]() $\mathbb Q$
(see e.g. [Reference Klenke14, Definition 7.35 and Theorem 7.37]). Thus there exists
$\mathbb Q$
(see e.g. [Reference Klenke14, Definition 7.35 and Theorem 7.37]). Thus there exists
![]() $ \vartheta_2>0$
such that, for any A
$ \vartheta_2>0$
such that, for any A
![]() $(\mathbb Q(A)<\vartheta_2)$
, we have
$(\mathbb Q(A)<\vartheta_2)$
, we have
Consequently we deduce that, for any
![]() $ \varepsilon>0$
, there exists
$ \varepsilon>0$
, there exists
![]() $\vartheta_2>0$
such that, for any A
$\vartheta_2>0$
such that, for any A
![]() $(\mathbb Q(A)<\vartheta_2)$
, we have
$(\mathbb Q(A)<\vartheta_2)$
, we have
In view of (8) and (9), we deduce that
![]() $\{\delta Y_t,t\in [T-\theta, T]\}$
belongs to class (D) under
$\{\delta Y_t,t\in [T-\theta, T]\}$
belongs to class (D) under
![]() $\mathbb Q$
. We define the stopping times
$\mathbb Q$
. We define the stopping times
with the convention that
![]() $\inf\phi=+\infty$
. Applying Itô’s formula to
$\inf\phi=+\infty$
. Applying Itô’s formula to
![]() $|\delta Y_t|$
(see e.g. [Reference Hamadène and Popier12, Corollary 1]), we obtain for any
$|\delta Y_t|$
(see e.g. [Reference Hamadène and Popier12, Corollary 1]), we obtain for any
![]() $t\in [T-\theta,T]$
$t\in [T-\theta,T]$
 \begin{align*}|\delta Y_{t\wedge\tau_n}|&\le |\delta Y_{\tau_n}|+\int_{t\wedge\tau_n}^{\tau_n} \text{sgn}(\delta Y_s)u_s\delta Y_s\,{\mathrm{d}} s-\int_{t\wedge\tau_n}^{\tau_n}\text{sgn}(\delta Y_s)\delta Z_s \,{\mathrm{d}} B_s^{\mathbb Q}+\int_{t\wedge\tau_n}^{\tau_n}\text{sgn}(\delta Y_s)\,{\mathrm{d}}\delta K_s\\[5pt] &\le |\delta Y_{\tau_n}|+\int_{t\wedge\tau_n}^{\tau_n} \beta |\delta Y_s|\,{\mathrm{d}} s-\int_{t\wedge\tau_n}^{\tau_n}\text{sgn}(\delta Y_s)\delta Z_s \,{\mathrm{d}} B_s^{\mathbb Q}+\int_{t\wedge\tau_n}^{\tau_n}\text{sgn}(\delta Y_s)\,{\mathrm{d}}\delta K_s.\end{align*}
\begin{align*}|\delta Y_{t\wedge\tau_n}|&\le |\delta Y_{\tau_n}|+\int_{t\wedge\tau_n}^{\tau_n} \text{sgn}(\delta Y_s)u_s\delta Y_s\,{\mathrm{d}} s-\int_{t\wedge\tau_n}^{\tau_n}\text{sgn}(\delta Y_s)\delta Z_s \,{\mathrm{d}} B_s^{\mathbb Q}+\int_{t\wedge\tau_n}^{\tau_n}\text{sgn}(\delta Y_s)\,{\mathrm{d}}\delta K_s\\[5pt] &\le |\delta Y_{\tau_n}|+\int_{t\wedge\tau_n}^{\tau_n} \beta |\delta Y_s|\,{\mathrm{d}} s-\int_{t\wedge\tau_n}^{\tau_n}\text{sgn}(\delta Y_s)\delta Z_s \,{\mathrm{d}} B_s^{\mathbb Q}+\int_{t\wedge\tau_n}^{\tau_n}\text{sgn}(\delta Y_s)\,{\mathrm{d}}\delta K_s.\end{align*}
Observe that
 \begin{align*}\text{sgn}(\delta Y_s)\,{\mathrm{d}}(\delta K)_s&=\textbf 1_{\delta Y_s\neq 0}\dfrac{\delta Y_s}{|\delta Y_s|}\,{\mathrm{d}}(\delta K)_s\\[5pt] &=\textbf 1_{\delta Y_s\neq 0}\dfrac{Y_s^1-L_s}{|\delta Y_s|}\,{\mathrm{d}}(\delta K)_s-\textbf 1_{\delta Y_s\neq 0}\dfrac{Y_s^2-L_s}{|\delta Y_s|}\,{\mathrm{d}}(\delta K)_s\\[5pt] &=-\textbf 1_{\delta Y_s\neq 0}\dfrac{Y_s^1-L_s}{|\delta Y_s|}\,{\mathrm{d}} K_s^2-\textbf 1_{\delta Y_s\neq 0}\dfrac{Y_s^2-L_s}{|\delta Y_s|}\,{\mathrm{d}} K_s^1\\[5pt] &\le 0,\quad s\in [T-\theta,T].\end{align*}
\begin{align*}\text{sgn}(\delta Y_s)\,{\mathrm{d}}(\delta K)_s&=\textbf 1_{\delta Y_s\neq 0}\dfrac{\delta Y_s}{|\delta Y_s|}\,{\mathrm{d}}(\delta K)_s\\[5pt] &=\textbf 1_{\delta Y_s\neq 0}\dfrac{Y_s^1-L_s}{|\delta Y_s|}\,{\mathrm{d}}(\delta K)_s-\textbf 1_{\delta Y_s\neq 0}\dfrac{Y_s^2-L_s}{|\delta Y_s|}\,{\mathrm{d}}(\delta K)_s\\[5pt] &=-\textbf 1_{\delta Y_s\neq 0}\dfrac{Y_s^1-L_s}{|\delta Y_s|}\,{\mathrm{d}} K_s^2-\textbf 1_{\delta Y_s\neq 0}\dfrac{Y_s^2-L_s}{|\delta Y_s|}\,{\mathrm{d}} K_s^1\\[5pt] &\le 0,\quad s\in [T-\theta,T].\end{align*}
Therefore, for any
![]() $T-\theta\le u\le t\le T$
,
$T-\theta\le u\le t\le T$
,
Observe that
![]() $\delta Y_{\tau_n}\to \delta Y_T=0$
and
$\delta Y_{\tau_n}\to \delta Y_T=0$
and
![]() $\delta Y_{t\wedge\tau_n}\to \delta Y_{t}$
. Since
$\delta Y_{t\wedge\tau_n}\to \delta Y_{t}$
. Since
![]() $\{\delta Y_t,t\in [T-\theta,T]\}$
belongs to class (D) under
$\{\delta Y_t,t\in [T-\theta,T]\}$
belongs to class (D) under
![]() $\mathbb Q$
, by sending
$\mathbb Q$
, by sending
![]() $n\to\infty$
in the above inequality and taking a subsequence if necessary, we get
$n\to\infty$
in the above inequality and taking a subsequence if necessary, we get
By virtue of Gronwall’s inequality, we obtain for all
![]() $T-\theta\le u\le t\le T $
$T-\theta\le u\le t\le T $
In particular, we have at
![]() $u=t$
,
$u=t$
,
![]() $\delta Y_t=0$
,
$\delta Y_t=0$
,
![]() $\mathbb Q$
-a.s. Since
$\mathbb Q$
-a.s. Since
![]() $\mathbb Q$
is equivalent to
$\mathbb Q$
is equivalent to
![]() $\mathbb P$
, this holds up to a set of
$\mathbb P$
, this holds up to a set of
![]() $\mathbb P$
-measure zero. It is then clear that
$\mathbb P$
-measure zero. It is then clear that
![]() $\delta Z_t=0$
and
$\delta Z_t=0$
and
![]() $\delta K_t=0$
for all
$\delta K_t=0$
for all
![]() $t\in [T-\theta,T]$
. The uniqueness is obtained on the interval
$t\in [T-\theta,T]$
. The uniqueness is obtained on the interval
![]() $[T-\theta,T]$
. In an identical way, we have the uniqueness of the solution on the interval
$[T-\theta,T]$
. In an identical way, we have the uniqueness of the solution on the interval
![]() $[T-2\theta,T-\theta]$
. By a finite number of steps, we cover in this way the whole interval [0, T], and we conclude the uniqueness of the solution on the interval [0, T].
$[T-2\theta,T-\theta]$
. By a finite number of steps, we cover in this way the whole interval [0, T], and we conclude the uniqueness of the solution on the interval [0, T].
Remark 1. Our approach to the uniqueness consists in transforming the original equation into a new one (7) with integrable parameters. Moreover, the generator of (7) does not depend on z. Hence the original problem is transformed into an
![]() $L^1$
-solution problem, which is much easier to handle. In [Reference Buckdahn, Hu and Tang4], Buckdahn, Hu, and Tang proved the uniqueness by showing the uniform integrability of
$L^1$
-solution problem, which is much easier to handle. In [Reference Buckdahn, Hu and Tang4], Buckdahn, Hu, and Tang proved the uniqueness by showing the uniform integrability of
whereas we argue by showing that
![]() $\delta Y$
belongs to class (D) under a new probability measure. We would like to mention that our method may be more flexible for future development (e.g. RBSDEs with possibly non-Lipschitz generators).
$\delta Y$
belongs to class (D) under a new probability measure. We would like to mention that our method may be more flexible for future development (e.g. RBSDEs with possibly non-Lipschitz generators).
3. Comparison theorems
We first prove a general comparison theorem for supersolutions of BSDEs for which the data are
![]() $L\exp\bigl(\mu\sqrt{2\log\!(1+L)}\bigr)$
-integrable.
$L\exp\bigl(\mu\sqrt{2\log\!(1+L)}\bigr)$
-integrable.
Theorem 2. Suppose that
![]() $g^1(s,y,z)$
and
$g^1(s,y,z)$
and
![]() $g^2(s,y,z)$
are two Lipschitz generators and
$g^2(s,y,z)$
are two Lipschitz generators and
![]() $\xi^1$
,
$\xi^1$
,
![]() $\xi^2$
are two terminal conditions, and
$\xi^2$
are two terminal conditions, and
![]() $K^1$
and
$K^1$
and
![]() $K^2$
are two continuous, non-decreasing processes. Suppose that we have pairs
$K^2$
are two continuous, non-decreasing processes. Suppose that we have pairs
![]() $(Y_t^i,Z_t^i)_{t\in [0,T]}$
,
$(Y_t^i,Z_t^i)_{t\in [0,T]}$
,
![]() $i=1,2$
, satisfying
$i=1,2$
, satisfying
If
![]() $\psi (|Y^1|,a^1)$
and
$\psi (|Y^1|,a^1)$
and
![]() $\psi(|Y^2|,a^2)$
belong to class (D) for some
$\psi(|Y^2|,a^2)$
belong to class (D) for some
![]() $a^1,a^2>0$
and, moreover, if for any
$a^1,a^2>0$
and, moreover, if for any
![]() $0\le t\le T$
$0\le t\le T$
and
![]() $K^2-K^1$
is a non-decreasing process, then
$K^2-K^1$
is a non-decreasing process, then
![]() $Y_t^1\le Y_t^2$
,
$Y_t^1\le Y_t^2$
,
![]() $0\le t\le T$
, almost surely.
$0\le t\le T$
, almost surely.
Proof. Set
![]() $a\;:\!=\; a^1\wedge a^2$
. Then both
$a\;:\!=\; a^1\wedge a^2$
. Then both
![]() $\psi (|Y^1|,a)$
and
$\psi (|Y^1|,a)$
and
![]() $\psi (|Y^2|,a)$
belong to class (D). We also define
$\psi (|Y^2|,a)$
belong to class (D). We also define
By the Lipschitz assumption, we have two adapted processes
![]() $u_s$
and
$u_s$
and
![]() $v_s$
such that
$v_s$
such that
![]() $|u_s|\le\beta$
,
$|u_s|\le\beta$
,
![]() $|v_s|\le\gamma$
, and
$|v_s|\le\gamma$
, and
![]() $g^2(s,Y_s^1,Z_s^1)-g^2(s,Y_s^2,Z_s^2)=u_s\delta Y_s+\delta Z_s v_s$
. We define the stopping times
$g^2(s,Y_s^1,Z_s^1)-g^2(s,Y_s^2,Z_s^2)=u_s\delta Y_s+\delta Z_s v_s$
. We define the stopping times
with the convention that
![]() $\inf \phi=\infty$
. Since
$\inf \phi=\infty$
. Since
![]() $(\delta Y,\delta Z)$
satisfies the linear BSDE
$(\delta Y,\delta Z)$
satisfies the linear BSDE
we have
where
Since
![]() $\delta g_r\le 0$
and
$\delta g_r\le 0$
and
![]() ${\mathrm{d}}(\delta K)_r\le 0$
,
${\mathrm{d}}(\delta K)_r\le 0$
,
Note that thanks to Lemmas 2.4 and 2.6 of [Reference Hu and Tang13],
and for
![]() $t\in [T-{a^2}/{(4\gamma^2)},T]$
,
$t\in [T-{a^2}/{(4\gamma^2)},T]$
,
 \begin{align} \mathbb E\biggl[\biggl|\exp\biggl(\frac{1}{2a^2}\biggl(\int_{t\wedge\tau_n}^{\tau_n}v_s\cdot {\mathrm{d}} B_s\biggr)^2\biggr)\biggr|^2\biggr] & =\mathbb E\biggl[\exp\biggl(\frac{1}{a^2}\biggl(\int_{t\wedge\tau_n}^{\tau_n}v_s\cdot {\mathrm{d}} B_s\biggr)^2\biggr)\biggr] \notag \\[5pt] &\le \biggl[1-\dfrac{2\gamma^2}{a^2}(T-t)\biggr]^{-1/2} \notag \\[5pt] &\le \sqrt 2.\end{align}
\begin{align} \mathbb E\biggl[\biggl|\exp\biggl(\frac{1}{2a^2}\biggl(\int_{t\wedge\tau_n}^{\tau_n}v_s\cdot {\mathrm{d}} B_s\biggr)^2\biggr)\biggr|^2\biggr] & =\mathbb E\biggl[\exp\biggl(\frac{1}{a^2}\biggl(\int_{t\wedge\tau_n}^{\tau_n}v_s\cdot {\mathrm{d}} B_s\biggr)^2\biggr)\biggr] \notag \\[5pt] &\le \biggl[1-\dfrac{2\gamma^2}{a^2}(T-t)\biggr]^{-1/2} \notag \\[5pt] &\le \sqrt 2.\end{align}
Moreover, we have
From (12) and (13), it follows that for
![]() $t\in [T-{a^2}/{(4\gamma^2)},T]$
, the family of random variables
$t\in [T-{a^2}/{(4\gamma^2)},T]$
, the family of random variables
is uniformly integrable. Finally, letting
![]() $n\to \infty$
in inequality (11), in view of
$n\to \infty$
in inequality (11), in view of
![]() $\delta\xi\le 0$
, we have
$\delta\xi\le 0$
, we have
![]() $\delta Y_t\le 0$
on the interval
$\delta Y_t\le 0$
on the interval
![]() $[T-{a^2}/{(4\gamma^2)},T]$
. In an identical way, we have
$[T-{a^2}/{(4\gamma^2)},T]$
. In an identical way, we have
![]() $\delta Y_t\le 0$
on the interval
$\delta Y_t\le 0$
on the interval
![]() $[T-{a^2}/{(2\gamma^2)},T-{a^2}/{(4\gamma^2)}]$
. By a finite number of steps, we have the comparison principle on the whole interval [0, T].
$[T-{a^2}/{(2\gamma^2)},T-{a^2}/{(4\gamma^2)}]$
. By a finite number of steps, we have the comparison principle on the whole interval [0, T].
We now state the main result of this section.
Theorem 3. Suppose that we have two parameters
![]() $(\xi^{1},g^{1},L^{1})$
and
$(\xi^{1},g^{1},L^{1})$
and
![]() $(\xi^2,g^2,L^2)$
. Let
$(\xi^2,g^2,L^2)$
. Let
![]() $(Y^i,Z^i,K^i)$
be the solution of the RBSDE
$(Y^i,Z^i,K^i)$
be the solution of the RBSDE
![]() $(\xi^i,g^i,L^i)$
,
$(\xi^i,g^i,L^i)$
,
![]() $i=1,2$
. Assume that
$i=1,2$
. Assume that
![]() $\psi(|Y^i|,a^i)$
belongs to class (D) for some
$\psi(|Y^i|,a^i)$
belongs to class (D) for some
![]() $a^i>0$
with
$a^i>0$
with
![]() $i=1,2$
, and
$i=1,2$
, and
![]() $g^2$
satisfies the Lipschitz condition (5). We further assume that
$g^2$
satisfies the Lipschitz condition (5). We further assume that
Then
![]() $Y_t^1\le Y_t^2$
for all
$Y_t^1\le Y_t^2$
for all
![]() $t\in [0,T]$
, almost surely.
$t\in [0,T]$
, almost surely.
Proof. Define
 \begin{gather*} a\;:\!=\; a^1\wedge a^2,\quad \delta Y\;:\!=\; Y^1-Y^2,\quad \delta Z\;:\!=\; Z^1-Z^2, \\[5pt] \delta K\;:\!=\; K^1-K^2,\quad \delta\xi\;:\!=\; \xi^1-\xi^2,\quad \delta g_t\;:\!=\; g^1(t,Y_t^1,Z_t^1)-g^2(t,Y_t^1,Z_t^1). \end{gather*}
\begin{gather*} a\;:\!=\; a^1\wedge a^2,\quad \delta Y\;:\!=\; Y^1-Y^2,\quad \delta Z\;:\!=\; Z^1-Z^2, \\[5pt] \delta K\;:\!=\; K^1-K^2,\quad \delta\xi\;:\!=\; \xi^1-\xi^2,\quad \delta g_t\;:\!=\; g^1(t,Y_t^1,Z_t^1)-g^2(t,Y_t^1,Z_t^1). \end{gather*}
By the Lipschitz assumption, there are two processes u and v such that
![]() $|u|\le \beta$
,
$|u|\le \beta$
,
![]() $|v|\le \gamma$
, and
$|v|\le \gamma$
, and
Obviously,
![]() $(\delta Y,\delta Z,\delta K)$
satisfies the following equation:
$(\delta Y,\delta Z,\delta K)$
satisfies the following equation:
Define
![]() $\theta\;:\!=\; {a^2}/{(4\gamma^2)}$
. By following the same arguments as we did before (more precisely, the uniqueness part of the proof of Theorem 1),
$\theta\;:\!=\; {a^2}/{(4\gamma^2)}$
. By following the same arguments as we did before (more precisely, the uniqueness part of the proof of Theorem 1),
![]() $\psi (|\delta Y|,a)$
belongs to class (D) and there exists a probability measure
$\psi (|\delta Y|,a)$
belongs to class (D) and there exists a probability measure
![]() $\mathbb Q$
equivalent to
$\mathbb Q$
equivalent to
![]() $\mathbb P$
such that
$\mathbb P$
such that
![]() $(\delta Y,\delta Z,\delta K)$
satisfies
$(\delta Y,\delta Z,\delta K)$
satisfies
![]() $\mathbb Q$
-a.s.
$\mathbb Q$
-a.s.
where
![]() $B^{\mathbb Q}$
is a
$B^{\mathbb Q}$
is a
![]() $\mathbb Q$
-Brownian motion on
$\mathbb Q$
-Brownian motion on
![]() $[T-\theta,T]$
. In particular, the process
$[T-\theta,T]$
. In particular, the process
![]() $\{\delta Y_t,t\in [T-\theta,T]\}$
belongs to class (D) under
$\{\delta Y_t,t\in [T-\theta,T]\}$
belongs to class (D) under
![]() $\mathbb Q$
. We define the stopping times
$\mathbb Q$
. We define the stopping times
![]() $\tau_n$
as in (10). Applying the Itô–Tanaka formula to
$\tau_n$
as in (10). Applying the Itô–Tanaka formula to
![]() $\delta Y_t^+$
, we obtain for any
$\delta Y_t^+$
, we obtain for any
![]() $t\in [T-\theta,T]$
$t\in [T-\theta,T]$
 \begin{align} &\delta Y_{t\wedge\tau_n}^+\notag\\[5pt] &\le \delta Y_{\tau_n}^++\int_{t\wedge\tau_n}^{\tau_n} \textbf 1_{\delta Y_s>0}[\delta g_s+u_s\delta Y_s]\,{\mathrm{d}} s-\int_{t\wedge\tau_n}^{\tau_n}\textbf 1_{\delta Y_s>0}\delta Z_s \,{\mathrm{d}} B_s^{\mathbb Q}+\int_{t\wedge\tau_n}^{\tau_n}\textbf 1_{\delta Y_s>0}\,{\mathrm{d}} (\delta K)_s.\end{align}
\begin{align} &\delta Y_{t\wedge\tau_n}^+\notag\\[5pt] &\le \delta Y_{\tau_n}^++\int_{t\wedge\tau_n}^{\tau_n} \textbf 1_{\delta Y_s>0}[\delta g_s+u_s\delta Y_s]\,{\mathrm{d}} s-\int_{t\wedge\tau_n}^{\tau_n}\textbf 1_{\delta Y_s>0}\delta Z_s \,{\mathrm{d}} B_s^{\mathbb Q}+\int_{t\wedge\tau_n}^{\tau_n}\textbf 1_{\delta Y_s>0}\,{\mathrm{d}} (\delta K)_s.\end{align}
Using
![]() $L_t^1\le L_t^2$
, we have
$L_t^1\le L_t^2$
, we have
![]() $L_t^1\le Y_t^1\wedge Y_t^2\le Y_t^1$
and
$L_t^1\le Y_t^1\wedge Y_t^2\le Y_t^1$
and
Therefore we have for all
![]() $s\in [T-\theta,T]$
$s\in [T-\theta,T]$
Using this and the fact that
![]() $\delta g_s\le 0$
, we deduce from (14) that for all
$\delta g_s\le 0$
, we deduce from (14) that for all
![]() $T-\theta\le u\le t\le T$
$T-\theta\le u\le t\le T$
Since
![]() $\{\delta Y_t,t\in [T-\theta,T]\}$
belongs to class (D) under
$\{\delta Y_t,t\in [T-\theta,T]\}$
belongs to class (D) under
![]() $\mathbb Q$
, so do
$\mathbb Q$
, so do
![]() $\{\delta Y_t^+,t\in [T-\theta,T]\}$
. We also know hat
$\{\delta Y_t^+,t\in [T-\theta,T]\}$
. We also know hat
![]() $\delta Y_{t\wedge\tau_n}^+\to \delta Y_t^+$
and
$\delta Y_{t\wedge\tau_n}^+\to \delta Y_t^+$
and
![]() $\delta Y_{\tau_n}^+\to \delta Y_T^+=\delta \xi^+=0$
. By sending n to
$\delta Y_{\tau_n}^+\to \delta Y_T^+=\delta \xi^+=0$
. By sending n to
![]() $\infty$
in the above inequality, we obtain for all
$\infty$
in the above inequality, we obtain for all
![]() $T-\theta\le u\le t\le T$
$T-\theta\le u\le t\le T$
Gronwall’s inequality implies that
![]() $\delta Y_t^+=0$
for all
$\delta Y_t^+=0$
for all
![]() $t\in [T-\theta,T]$
,
$t\in [T-\theta,T]$
,
![]() $\mathbb Q$
-a.s. Since
$\mathbb Q$
-a.s. Since
![]() $\mathbb Q$
is equivalent to
$\mathbb Q$
is equivalent to
![]() $\mathbb P$
, we see that
$\mathbb P$
, we see that
![]() $\delta Y_t^+=0$
(i.e.
$\delta Y_t^+=0$
(i.e.
![]() $Y_t^1\le Y_t^2$
) for all
$Y_t^1\le Y_t^2$
) for all
![]() $t\in [T-\theta,T]$
,
$t\in [T-\theta,T]$
,
![]() ${\mathbb P}$
-a.s. In an identical way, we obtain the comparison on the interval
${\mathbb P}$
-a.s. In an identical way, we obtain the comparison on the interval
![]() $[T-2\theta,T-\theta]$
. In a finite number of steps, we have the comparison on the whole interval [0, T]. The proof is then complete.
$[T-2\theta,T-\theta]$
. In a finite number of steps, we have the comparison on the whole interval [0, T]. The proof is then complete.
4. About the critical case
The assumption that
![]() $\mu>\gamma\sqrt{T}$
is a key ingredient in our procedure. Fan and Hu [Reference Fan and Hu11] considered the critical case
$\mu>\gamma\sqrt{T}$
is a key ingredient in our procedure. Fan and Hu [Reference Fan and Hu11] considered the critical case
![]() $\mu=\gamma\sqrt T$
for the standard BSDE. In this critical case the main difficulty comes from the fact that one cannot use the dual representation method (hence the Snell envelope representation and the Girsanov theorem in our reflected case). To overcome this difficulty, Fan and Hu [Reference Fan and Hu11] introduced an approximate function
$\mu=\gamma\sqrt T$
for the standard BSDE. In this critical case the main difficulty comes from the fact that one cannot use the dual representation method (hence the Snell envelope representation and the Girsanov theorem in our reflected case). To overcome this difficulty, Fan and Hu [Reference Fan and Hu11] introduced an approximate function
![]() $\phi(s,x;\;t)$
which has some similarity to
$\phi(s,x;\;t)$
which has some similarity to
![]() $\psi (x,\mu)$
. Then they directly applied Itô’s formula to
$\psi (x,\mu)$
. Then they directly applied Itô’s formula to
![]() $\phi(s,Y_s;\;t)$
in order to get an a priori estimate for
$\phi(s,Y_s;\;t)$
in order to get an a priori estimate for
![]() $Y_t$
as well as
$Y_t$
as well as
![]() $\psi(|Y_t|,\gamma\sqrt t)$
. However, this approach does not work well for our reflected dynamics. If we apply Itô’s formula to
$\psi(|Y_t|,\gamma\sqrt t)$
. However, this approach does not work well for our reflected dynamics. If we apply Itô’s formula to
![]() $\phi(s,Y_s;\;t)$
as in [Reference Fan and Hu11], we have the influence of the non-decreasing component, which can never be removed. Hence we cannot get the estimate for
$\phi(s,Y_s;\;t)$
as in [Reference Fan and Hu11], we have the influence of the non-decreasing component, which can never be removed. Hence we cannot get the estimate for
![]() $\psi(|Y_t|,\gamma\sqrt t)$
. At this point the proof of uniqueness in the critical case would be extremely difficult. We leave this interesting problem for future work.
$\psi(|Y_t|,\gamma\sqrt t)$
. At this point the proof of uniqueness in the critical case would be extremely difficult. We leave this interesting problem for future work.
Acknowledgements
We are sincerely grateful to the editors and two anonymous referees for their insightful comments and useful suggestions to improve the manuscript.
Funding information
There are no funding bodies to thank relating to this creation of this article.
Competing interests
There were no competing interests to declare which arose during the preparation or publication process of this article.