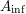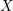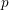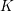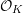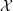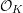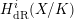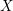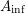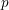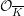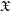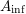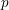1 Introduction
1.1 Integral relations between
 $p$
-adic cohomology theories
$p$
-adic cohomology theories
For a proper, smooth scheme
![]() $X$
over a complete, discretely valued extension
$X$
over a complete, discretely valued extension
![]() $K$
of
$K$
of
![]() $\mathbb{Q}_{p}$
with a perfect residue field
$\mathbb{Q}_{p}$
with a perfect residue field
![]() $k$
, comparison isomorphisms of
$k$
, comparison isomorphisms of
![]() $p$
-adic Hodge theory relate the
$p$
-adic Hodge theory relate the
![]() $p$
-adic étale, de Rham, and, in the case of semistable reduction, also crystalline cohomologies of
$p$
-adic étale, de Rham, and, in the case of semistable reduction, also crystalline cohomologies of
![]() $X$
. For instance, they show that for
$X$
. For instance, they show that for
![]() $i\in \mathbb{Z}$
, the
$i\in \mathbb{Z}$
, the
![]() $\operatorname{Gal}(\overline{K}/K)$
-representation
$\operatorname{Gal}(\overline{K}/K)$
-representation
![]() $H_{\acute{\text{e}}\text{t}}^{i}(X_{\overline{K}},\mathbb{Q}_{p})$
functorially determines the filtered
$H_{\acute{\text{e}}\text{t}}^{i}(X_{\overline{K}},\mathbb{Q}_{p})$
functorially determines the filtered
![]() $K$
-vector space
$K$
-vector space
![]() $H_{\text{dR}}^{i}(X/K)$
. Even though the integral analogues of these isomorphisms are known to fail in general, one may still consider their hypothetical consequences, for instance, one may ask the following.
$H_{\text{dR}}^{i}(X/K)$
. Even though the integral analogues of these isomorphisms are known to fail in general, one may still consider their hypothetical consequences, for instance, one may ask the following.
∙ For proper, flat, semistable
 ${\mathcal{O}}_{K}$
-models
${\mathcal{O}}_{K}$
-models
 ${\mathcal{X}}$
and
${\mathcal{X}}$
and
 ${\mathcal{X}}^{\prime }$
of
${\mathcal{X}}^{\prime }$
of
 $X$
endowed with their standard log structures, do the images of
$X$
endowed with their standard log structures, do the images of
 $H_{\log \text{dR}}^{i}({\mathcal{X}}/{\mathcal{O}}_{K})$
and
$H_{\log \text{dR}}^{i}({\mathcal{X}}/{\mathcal{O}}_{K})$
and
 $H_{\log \text{dR}}^{i}({\mathcal{X}}^{\prime }/{\mathcal{O}}_{K})$
in
$H_{\log \text{dR}}^{i}({\mathcal{X}}^{\prime }/{\mathcal{O}}_{K})$
in
 $H_{\text{dR}}^{i}(X/K)$
agree?
$H_{\text{dR}}^{i}(X/K)$
agree?
One of the goals of the present paper is to show that the answer is positive if the logarithmic de Rham cohomology of the models
![]() ${\mathcal{X}}$
and
${\mathcal{X}}$
and
![]() ${\mathcal{X}}^{\prime }$
is torsion free (see (8.6.2) and Theorem 8.7): in this case, both
${\mathcal{X}}^{\prime }$
is torsion free (see (8.6.2) and Theorem 8.7): in this case, both
![]() $H_{\log \text{dR}}^{i}({\mathcal{X}}/{\mathcal{O}}_{K})$
and
$H_{\log \text{dR}}^{i}({\mathcal{X}}/{\mathcal{O}}_{K})$
and
![]() $H_{\log \text{dR}}^{i}({\mathcal{X}}^{\prime }/{\mathcal{O}}_{K})$
agree with the
$H_{\log \text{dR}}^{i}({\mathcal{X}}^{\prime }/{\mathcal{O}}_{K})$
agree with the
![]() ${\mathcal{O}}_{K}$
-lattice in
${\mathcal{O}}_{K}$
-lattice in
![]() $H_{\text{dR}}^{i}(X/K)$
that is functorially determined by
$H_{\text{dR}}^{i}(X/K)$
that is functorially determined by
![]() $H_{\acute{\text{e}}\text{t}}^{i}(X_{\overline{K}},\mathbb{Z}_{p})$
. The good reduction case of this result may be derived from the work of Bhatt–Morrow–Scholze [Reference Bhatt, Morrow and ScholzeBMS18] on integral
$H_{\acute{\text{e}}\text{t}}^{i}(X_{\overline{K}},\mathbb{Z}_{p})$
. The good reduction case of this result may be derived from the work of Bhatt–Morrow–Scholze [Reference Bhatt, Morrow and ScholzeBMS18] on integral
![]() $p$
-adic Hodge theory, and our approach, as well as the bulk of this paper, is concerned with extending the framework of [Reference Bhatt, Morrow and ScholzeBMS18] to the semistable case.
$p$
-adic Hodge theory, and our approach, as well as the bulk of this paper, is concerned with extending the framework of [Reference Bhatt, Morrow and ScholzeBMS18] to the semistable case.
1.2 The
 $A_{\text{inf}}$
-cohomology in the semistable case
$A_{\text{inf}}$
-cohomology in the semistable case
To approach the question above, we set
![]() $C:=\widehat{\overline{K}}$
, let
$C:=\widehat{\overline{K}}$
, let
![]() $A_{\text{inf}}:=W({\mathcal{O}}_{C}^{\flat })$
be the basic period ring of Fontaine, and, for a semistable
$A_{\text{inf}}:=W({\mathcal{O}}_{C}^{\flat })$
be the basic period ring of Fontaine, and, for a semistable
![]() ${\mathcal{O}}_{K}$
-model
${\mathcal{O}}_{K}$
-model
![]() ${\mathcal{X}}$
of
${\mathcal{X}}$
of
![]() $X$
, similarly to the smooth case treated in [Reference Bhatt, Morrow and ScholzeBMS18], construct the
$X$
, similarly to the smooth case treated in [Reference Bhatt, Morrow and ScholzeBMS18], construct the
![]() $A_{\text{inf}}$
-cohomology object
$A_{\text{inf}}$
-cohomology object
that is quasi-isomorphic to a bounded complex of finite free
![]() $A_{\text{inf}}$
-modules and has finitely presented cohomology
$A_{\text{inf}}$
-modules and has finitely presented cohomology
![]() $H_{A_{\text{inf}}}^{i}({\mathcal{X}})$
. We show that base changes of
$H_{A_{\text{inf}}}^{i}({\mathcal{X}})$
. We show that base changes of
![]() $R\unicode[STIX]{x1D6E4}_{A_{\text{inf}}}({\mathcal{X}})$
recover other cohomology theories:
$R\unicode[STIX]{x1D6E4}_{A_{\text{inf}}}({\mathcal{X}})$
recover other cohomology theories:
 $$\begin{eqnarray}\begin{array}{@{}rcl@{}}\textstyle R\unicode[STIX]{x1D6E4}_{A_{\text{inf}}}({\mathcal{X}})\otimes _{A_{\text{inf}}}^{\mathbb{L}}W(C^{\flat })\ & \cong \ & \textstyle R\unicode[STIX]{x1D6E4}_{\acute{\text{e}}\text{t}}(X_{\overline{K}},\mathbb{Z}_{p})\otimes _{\mathbb{Z}_{p}}^{\mathbb{L}}W(C^{\flat }),\\ R\unicode[STIX]{x1D6E4}_{A_{\text{inf}}}({\mathcal{X}})\otimes _{A_{\text{inf}},\,\unicode[STIX]{x1D703}}^{\mathbb{L}}{\mathcal{O}}_{C}\ & \cong \ & R\unicode[STIX]{x1D6E4}_{\log \text{dR}}({\mathcal{X}}/{\mathcal{O}}_{K})\otimes _{{\mathcal{O}}_{K}}^{\mathbb{L}}{\mathcal{O}}_{C},\\ R\unicode[STIX]{x1D6E4}_{A_{\text{inf}}}({\mathcal{X}})\otimes _{A_{\text{inf}}}^{\mathbb{L}}W(\overline{k})\ & \cong \ & R\unicode[STIX]{x1D6E4}_{\log \text{cris}}({\mathcal{X}}_{k}/W(k))\otimes _{W(k)}^{\mathbb{L}}W(\overline{k}),\end{array}\end{eqnarray}$$
$$\begin{eqnarray}\begin{array}{@{}rcl@{}}\textstyle R\unicode[STIX]{x1D6E4}_{A_{\text{inf}}}({\mathcal{X}})\otimes _{A_{\text{inf}}}^{\mathbb{L}}W(C^{\flat })\ & \cong \ & \textstyle R\unicode[STIX]{x1D6E4}_{\acute{\text{e}}\text{t}}(X_{\overline{K}},\mathbb{Z}_{p})\otimes _{\mathbb{Z}_{p}}^{\mathbb{L}}W(C^{\flat }),\\ R\unicode[STIX]{x1D6E4}_{A_{\text{inf}}}({\mathcal{X}})\otimes _{A_{\text{inf}},\,\unicode[STIX]{x1D703}}^{\mathbb{L}}{\mathcal{O}}_{C}\ & \cong \ & R\unicode[STIX]{x1D6E4}_{\log \text{dR}}({\mathcal{X}}/{\mathcal{O}}_{K})\otimes _{{\mathcal{O}}_{K}}^{\mathbb{L}}{\mathcal{O}}_{C},\\ R\unicode[STIX]{x1D6E4}_{A_{\text{inf}}}({\mathcal{X}})\otimes _{A_{\text{inf}}}^{\mathbb{L}}W(\overline{k})\ & \cong \ & R\unicode[STIX]{x1D6E4}_{\log \text{cris}}({\mathcal{X}}_{k}/W(k))\otimes _{W(k)}^{\mathbb{L}}W(\overline{k}),\end{array}\end{eqnarray}$$
see §7.2; here
![]() $R\unicode[STIX]{x1D6E4}_{\log \text{cris}}$
denotes the logarithmic crystalline (that is, Hyodo–Kato) cohomology,
$R\unicode[STIX]{x1D6E4}_{\log \text{cris}}$
denotes the logarithmic crystalline (that is, Hyodo–Kato) cohomology,
![]() $W(k)$
(respectively,
$W(k)$
(respectively,
![]() ${\mathcal{O}}_{K}$
) carries the log structure associated to
${\mathcal{O}}_{K}$
) carries the log structure associated to
![]() $\mathbb{N}_{{\geqslant}0}\xrightarrow[{}]{1\,\mapsto \,0,\,0\,\mapsto \,1}W(k)$
(respectively,
$\mathbb{N}_{{\geqslant}0}\xrightarrow[{}]{1\,\mapsto \,0,\,0\,\mapsto \,1}W(k)$
(respectively,
![]() ${\mathcal{O}}_{K}\setminus \{0\}{\hookrightarrow}{\mathcal{O}}_{K}$
), and
${\mathcal{O}}_{K}\setminus \{0\}{\hookrightarrow}{\mathcal{O}}_{K}$
), and
![]() ${\mathcal{X}}_{k}$
is endowed with the base change of the standard log structure
${\mathcal{X}}_{k}$
is endowed with the base change of the standard log structure
![]() ${\mathcal{O}}_{{\mathcal{X}},\,\acute{\text{e}}\text{t}}\cap ({\mathcal{O}}_{{\mathcal{X}},\,\acute{\text{e}}\text{t}}[\frac{1}{p}])^{\times }$
of
${\mathcal{O}}_{{\mathcal{X}},\,\acute{\text{e}}\text{t}}\cap ({\mathcal{O}}_{{\mathcal{X}},\,\acute{\text{e}}\text{t}}[\frac{1}{p}])^{\times }$
of
![]() ${\mathcal{X}}$
.
${\mathcal{X}}$
.
If the cohomology of
![]() $R\unicode[STIX]{x1D6E4}_{\log \text{dR}}({\mathcal{X}}/{\mathcal{O}}_{K})$
is torsion free, then each
$R\unicode[STIX]{x1D6E4}_{\log \text{dR}}({\mathcal{X}}/{\mathcal{O}}_{K})$
is torsion free, then each
![]() $H_{A_{\text{inf}}}^{i}({\mathcal{X}})$
is
$H_{A_{\text{inf}}}^{i}({\mathcal{X}})$
is
![]() $A_{\text{inf}}$
-free and the base changes (1.2.1) hold in each individual cohomological degree (see §7.6 and Proposition 7.7). In this case, the Fargues equivalence for Breuil–Kisin–Fargues
$A_{\text{inf}}$
-free and the base changes (1.2.1) hold in each individual cohomological degree (see §7.6 and Proposition 7.7). In this case, the Fargues equivalence for Breuil–Kisin–Fargues
![]() $\operatorname{Gal}(\overline{K}/K)$
-modules allows us to prove that
$\operatorname{Gal}(\overline{K}/K)$
-modules allows us to prove that
(see Theorem 8.7). Then
![]() $H_{\acute{\text{e}}\text{t}}^{i}(X_{\overline{K}},\mathbb{Z}_{p})$
also determinesFootnote
1
$H_{\acute{\text{e}}\text{t}}^{i}(X_{\overline{K}},\mathbb{Z}_{p})$
also determinesFootnote
1
![]() $H_{\log \text{dR}}^{i}({\mathcal{X}}/{\mathcal{O}}_{K})$
(and
$H_{\log \text{dR}}^{i}({\mathcal{X}}/{\mathcal{O}}_{K})$
(and
![]() $H_{\log \text{cris}}^{i}({\mathcal{X}}_{k}/W(k))$
) and, since the same reasoning applies to another model
$H_{\log \text{cris}}^{i}({\mathcal{X}}_{k}/W(k))$
) and, since the same reasoning applies to another model
![]() ${\mathcal{X}}^{\prime }$
, the result claimed in §1.1 follows.
${\mathcal{X}}^{\prime }$
, the result claimed in §1.1 follows.
The base changes (1.2.1) also allow us to extend the cohomology specialization results obtained in the good reduction case in [Reference Bhatt, Morrow and ScholzeBMS18]. Qualitatively, in Proposition 7.7 we show that
![]() $H_{\log \text{dR}}^{i}({\mathcal{X}}/{\mathcal{O}}_{K})$
is torsion free if and only if
$H_{\log \text{dR}}^{i}({\mathcal{X}}/{\mathcal{O}}_{K})$
is torsion free if and only if
![]() $H_{\log \text{cris}}^{i}({\mathcal{X}}_{k}/W(k))$
is torsion free, in which case
$H_{\log \text{cris}}^{i}({\mathcal{X}}_{k}/W(k))$
is torsion free, in which case
![]() $H_{\acute{\text{e}}\text{t}}^{i}(X_{\overline{K}},\mathbb{Z}_{p})$
is torsion free. Quantitatively, in Theorems 7.9 and 7.12 we show that for every
$H_{\acute{\text{e}}\text{t}}^{i}(X_{\overline{K}},\mathbb{Z}_{p})$
is torsion free. Quantitatively, in Theorems 7.9 and 7.12 we show that for every
![]() $n\geqslant 0$
, we have
$n\geqslant 0$
, we have
 $$\begin{eqnarray}\begin{array}{@{}rcl@{}}\operatorname{length}_{\mathbb{Z}_{p}}((H_{\acute{\text{e}}\text{t}}^{i}(X_{\overline{K}},\mathbb{Z}_{p})_{\text{tors}})/p^{n})\ & {\leqslant}\ & \displaystyle \operatorname{length}_{W(k)}((H_{\log \text{cris}}^{i}({\mathcal{X}}_{k}/W(k))_{\text{tors}})/p^{n}),\\ \operatorname{length}_{\mathbb{Z}_{p}}((H_{\acute{\text{e}}\text{t}}^{i}(X_{\overline{K}},\mathbb{Z}_{p})_{\text{tors}})/p^{n})\ & {\leqslant}\ & \displaystyle \frac{1}{\operatorname{length}_{{\mathcal{O}}_{K}}({\mathcal{O}}_{K}/p)}\,\cdot \,\operatorname{length}_{{\mathcal{O}}_{K}}((H_{\log \text{dR}}^{i}({\mathcal{X}}/{\mathcal{O}}_{K})_{\text{tors}})/p^{n}).\end{array}\end{eqnarray}$$
$$\begin{eqnarray}\begin{array}{@{}rcl@{}}\operatorname{length}_{\mathbb{Z}_{p}}((H_{\acute{\text{e}}\text{t}}^{i}(X_{\overline{K}},\mathbb{Z}_{p})_{\text{tors}})/p^{n})\ & {\leqslant}\ & \displaystyle \operatorname{length}_{W(k)}((H_{\log \text{cris}}^{i}({\mathcal{X}}_{k}/W(k))_{\text{tors}})/p^{n}),\\ \operatorname{length}_{\mathbb{Z}_{p}}((H_{\acute{\text{e}}\text{t}}^{i}(X_{\overline{K}},\mathbb{Z}_{p})_{\text{tors}})/p^{n})\ & {\leqslant}\ & \displaystyle \frac{1}{\operatorname{length}_{{\mathcal{O}}_{K}}({\mathcal{O}}_{K}/p)}\,\cdot \,\operatorname{length}_{{\mathcal{O}}_{K}}((H_{\log \text{dR}}^{i}({\mathcal{X}}/{\mathcal{O}}_{K})_{\text{tors}})/p^{n}).\end{array}\end{eqnarray}$$
1.3 The semistable comparison isomorphism
The analysis of
![]() $R\unicode[STIX]{x1D6E4}_{A_{\text{inf}}}({\mathcal{X}})$
, specifically, its relation to the
$R\unicode[STIX]{x1D6E4}_{A_{\text{inf}}}({\mathcal{X}})$
, specifically, its relation to the
![]() $p$
-adic étale and the logarithmic crystalline cohomologies, permits us to reprove in Theorem 9.5 the semistable conjecture of Fontaine–Jansen [Reference KatoKat94a, Conjecture 1.1]:
$p$
-adic étale and the logarithmic crystalline cohomologies, permits us to reprove in Theorem 9.5 the semistable conjecture of Fontaine–Jansen [Reference KatoKat94a, Conjecture 1.1]:
Other proofs of this conjecture have been given in [Reference TsujiTsu99], [Reference FaltingsFal02], [Reference NiziołNiz08], [Reference BhattBha12], [Reference BeilinsonBei13a], and [Reference Colmez and NiziołCN17], whereas [Reference Bhatt, Morrow and ScholzeBMS18] used
![]() $R\unicode[STIX]{x1D6E4}_{A_{\text{inf}}}({\mathcal{X}})$
to reprove the crystalline conjecture. Similarly to [Reference Colmez and NiziołCN17], we establish (1.3.1) for
$R\unicode[STIX]{x1D6E4}_{A_{\text{inf}}}({\mathcal{X}})$
to reprove the crystalline conjecture. Similarly to [Reference Colmez and NiziołCN17], we establish (1.3.1) for
![]() $p$
-adic formal
$p$
-adic formal
![]() ${\mathcal{O}}_{K}$
-schemes
${\mathcal{O}}_{K}$
-schemes
![]() ${\mathcal{X}}$
that are proper, flat, and ‘semistable’.
${\mathcal{X}}$
that are proper, flat, and ‘semistable’.
A key result that leads to (1.3.1) is the absolute crystalline comparison isomorphism
of Corollary 5.43, whose construction in §5 forms the technical core of this paper. This construction is based on an ‘all possible coordinates’ technique that is a variant of its analogue used to establish (1.3.2) in the smooth case in [Reference Bhatt, Morrow and ScholzeBMS18, §12]. The presence of singularities and log structures creates additional complications that do not appear in the smooth case and are examined in §5.
Using the absolute crystalline comparison isomorphism, in Theorem 6.6 we compare the
![]() $A_{\text{inf}}$
-cohomology of
$A_{\text{inf}}$
-cohomology of
![]() ${\mathcal{X}}$
with the
${\mathcal{X}}$
with the
![]() $B_{\text{dR}}^{+}$
-cohomology of
$B_{\text{dR}}^{+}$
-cohomology of
![]() $X$
defined by Bhatt–Morrow–Scholze in [Reference Bhatt, Morrow and ScholzeBMS18, §13]:
$X$
defined by Bhatt–Morrow–Scholze in [Reference Bhatt, Morrow and ScholzeBMS18, §13]:
The identification (1.3.3) is important for ensuring that the semistable comparison (1.3.1) is compatible with the de Rham comparison proved in [Reference ScholzeSch13a], and hence that it respects filtrations.
As for the question posed in §1.1, even though it only involves the étale and the de Rham cohomologies, the resolution of its torsion-free case outlined in §1.2 uses both (1.3.2) and (1.3.3) (so also the bulk of the material of this paper). This is because we need to ensure that the determination of
![]() $H_{\text{dR}}^{i}(X/K)$
by
$H_{\text{dR}}^{i}(X/K)$
by
![]() $H_{\acute{\text{e}}\text{t}}^{i}(X_{\overline{K}},\mathbb{Q}_{p})$
via the de Rham comparison of
$H_{\acute{\text{e}}\text{t}}^{i}(X_{\overline{K}},\mathbb{Q}_{p})$
via the de Rham comparison of
![]() $p$
-adic Hodge theory is compatible with the determination of
$p$
-adic Hodge theory is compatible with the determination of
![]() $H_{\log \text{dR}}^{i}({\mathcal{X}}/{\mathcal{O}}_{K})$
and
$H_{\log \text{dR}}^{i}({\mathcal{X}}/{\mathcal{O}}_{K})$
and
![]() $H_{\log \text{dR}}^{i}({\mathcal{X}}^{\prime }/{\mathcal{O}}_{K})$
by
$H_{\log \text{dR}}^{i}({\mathcal{X}}^{\prime }/{\mathcal{O}}_{K})$
by
![]() $H_{\acute{\text{e}}\text{t}}^{i}(X_{\overline{K}},\mathbb{Z}_{p})$
via
$H_{\acute{\text{e}}\text{t}}^{i}(X_{\overline{K}},\mathbb{Z}_{p})$
via
![]() $A_{\text{inf}}$
-cohomology and Breuil–Kisin–Fargues modules. In fact, to show that the cohomology modules of
$A_{\text{inf}}$
-cohomology and Breuil–Kisin–Fargues modules. In fact, to show that the cohomology modules of
![]() $R\unicode[STIX]{x1D6E4}_{A_{\text{inf}}}({\mathcal{X}})$
are Breuil–Kisin–Fargues, we already use the absolute crystalline comparison (1.3.2).
$R\unicode[STIX]{x1D6E4}_{A_{\text{inf}}}({\mathcal{X}})$
are Breuil–Kisin–Fargues, we already use the absolute crystalline comparison (1.3.2).
1.4 The object
 $A\unicode[STIX]{x1D6FA}_{\mathfrak{X}}$
and its base changes
$A\unicode[STIX]{x1D6FA}_{\mathfrak{X}}$
and its base changes
Even though we have so far focused on schemes, the construction and the analysis of
![]() $R\unicode[STIX]{x1D6E4}_{A_{\text{inf}}}(-)$
works for any
$R\unicode[STIX]{x1D6E4}_{A_{\text{inf}}}(-)$
works for any
![]() $p$
-adic formal
$p$
-adic formal
![]() ${\mathcal{O}}_{C}$
-scheme
${\mathcal{O}}_{C}$
-scheme
![]() $\mathfrak{X}$
that is semistable in the sense described in §1.5 (see (1.5.1)) and that, whenever needed, is assumed to be proper. Specifically, for such an
$\mathfrak{X}$
that is semistable in the sense described in §1.5 (see (1.5.1)) and that, whenever needed, is assumed to be proper. Specifically, for such an
![]() $\mathfrak{X}$
, in §2.2 we use the (variant for the étale topology of the) definition of Bhatt–Morrow–Scholze from [Reference Bhatt, Morrow and ScholzeBMS18] to build an object
$\mathfrak{X}$
, in §2.2 we use the (variant for the étale topology of the) definition of Bhatt–Morrow–Scholze from [Reference Bhatt, Morrow and ScholzeBMS18] to build an object
As in the smooth case of [Reference Bhatt, Morrow and ScholzeBMS18], the relation of
![]() $R\unicode[STIX]{x1D6E4}_{A_{\text{inf}}}(\mathfrak{X})$
to the
$R\unicode[STIX]{x1D6E4}_{A_{\text{inf}}}(\mathfrak{X})$
to the
![]() $p$
-adic étale cohomology of the adic generic fiber
$p$
-adic étale cohomology of the adic generic fiber
![]() $\mathfrak{X}_{C}^{\text{ad}}$
of
$\mathfrak{X}_{C}^{\text{ad}}$
of
![]() $\mathfrak{X}$
follows from the results of [Reference ScholzeSch13a] (see §2). In turn, the relations to the logarithmic de Rham and crystalline cohomologies are the subjects of §§4 and 5, respectively, and rest on the following identifications established in Theorems 4.17 and 5.4:
$\mathfrak{X}$
follows from the results of [Reference ScholzeSch13a] (see §2). In turn, the relations to the logarithmic de Rham and crystalline cohomologies are the subjects of §§4 and 5, respectively, and rest on the following identifications established in Theorems 4.17 and 5.4:
where
![]() $u:(\mathfrak{X}_{{\mathcal{O}}_{C}/p}/A_{\text{cris}})_{\log \text{cris}}\rightarrow \mathfrak{X}_{\acute{\text{e}}\text{t}}$
is the forgetful map of topoi. The arguments for (1.4.1) build on the same general skeleton as in [Reference Bhatt, Morrow and ScholzeBMS18] but differ, among other aspects, in how they handle the interaction of the Deligne–Berthelot–Ogus décalage functor
$u:(\mathfrak{X}_{{\mathcal{O}}_{C}/p}/A_{\text{cris}})_{\log \text{cris}}\rightarrow \mathfrak{X}_{\acute{\text{e}}\text{t}}$
is the forgetful map of topoi. The arguments for (1.4.1) build on the same general skeleton as in [Reference Bhatt, Morrow and ScholzeBMS18] but differ, among other aspects, in how they handle the interaction of the Deligne–Berthelot–Ogus décalage functor
![]() $L\unicode[STIX]{x1D702}$
used in the definition of
$L\unicode[STIX]{x1D702}$
used in the definition of
![]() $A\unicode[STIX]{x1D6FA}_{\mathfrak{X}}$
with the intervening base changes and with the almost isomorphisms supplied by the almost purity theorem. Namely, for this, the nonflatness over the singular points of
$A\unicode[STIX]{x1D6FA}_{\mathfrak{X}}$
with the intervening base changes and with the almost isomorphisms supplied by the almost purity theorem. Namely, for this, the nonflatness over the singular points of
![]() $\mathfrak{X}$
of the explicit perfectoid proétale covers that we construct makes it difficult to directly adapt the arguments from [Reference Bhatt, Morrow and ScholzeBMS18]. Instead, we take advantage of several general results about
$\mathfrak{X}$
of the explicit perfectoid proétale covers that we construct makes it difficult to directly adapt the arguments from [Reference Bhatt, Morrow and ScholzeBMS18]. Instead, we take advantage of several general results about
![]() $L\unicode[STIX]{x1D702}$
from [Reference BhattBha18]. Verifying their assumptions in our case amounts to the analysis in §3 of continuous group cohomology modules built using the aforementioned perfectoid cover. The typical conclusion of this analysis is that these modules have no nonzero ‘almost torsion’ and that the element
$L\unicode[STIX]{x1D702}$
from [Reference BhattBha18]. Verifying their assumptions in our case amounts to the analysis in §3 of continuous group cohomology modules built using the aforementioned perfectoid cover. The typical conclusion of this analysis is that these modules have no nonzero ‘almost torsion’ and that the element
![]() $\unicode[STIX]{x1D707}\in A_{\text{inf}}$
kills their ‘nonintegral parts’.
$\unicode[STIX]{x1D707}\in A_{\text{inf}}$
kills their ‘nonintegral parts’.
Further and more specific overviews of our arguments are given in the beginning of each section that follows. In the rest of this introduction, we fix the precise notational setup for the remainder of the paper (see §1.5), discuss the logarithmic structure on
![]() $\mathfrak{X}$
that we later use without notational explication (see §1.6), and review the relevant general notational conventions (see §1.7).
$\mathfrak{X}$
that we later use without notational explication (see §1.6), and review the relevant general notational conventions (see §1.7).
1.5 The setup
In what follows, we fix the notational setup.
∙ We fix an algebraically closed field
 $k$
of characteristic
$k$
of characteristic
 $p>0$
, let
$p>0$
, let
 $C$
be the completed algebraic closure of
$C$
be the completed algebraic closure of
 $W(k)[\frac{1}{p}]$
, and let
$W(k)[\frac{1}{p}]$
, and let
 $\mathfrak{m}\subset {\mathcal{O}}_{C}$
be the maximal ideal in the valuation ring of
$\mathfrak{m}\subset {\mathcal{O}}_{C}$
be the maximal ideal in the valuation ring of
 $C$
.
$C$
.∙ For convenience, we fix an embedding
 $p^{\mathbb{Q}}\subset C$
, that is, for every prime
$p^{\mathbb{Q}}\subset C$
, that is, for every prime
 $\ell$
, we fix a system of compatible
$\ell$
, we fix a system of compatible
 $\ell ^{n}$
-power roots
$\ell ^{n}$
-power roots
 $p^{1/\ell ^{\infty }}:=(p^{1/\ell ^{n}})_{n\geqslant 0}$
of
$p^{1/\ell ^{\infty }}:=(p^{1/\ell ^{n}})_{n\geqslant 0}$
of
 $p$
in
$p$
in
 ${\mathcal{O}}_{C}$
.
${\mathcal{O}}_{C}$
.∙ We fix a
 $p$
-adic formal scheme
$p$
-adic formal scheme
 $\mathfrak{X}$
over
$\mathfrak{X}$
over
 ${\mathcal{O}}_{C}$
that in the étale topology may be covered by open affines
${\mathcal{O}}_{C}$
that in the étale topology may be covered by open affines
 $\mathfrak{U}$
which admit an étale
$\mathfrak{U}$
which admit an étale
 ${\mathcal{O}}_{C}$
-morphism (1.5.1)for some
${\mathcal{O}}_{C}$
-morphism (1.5.1)for some $$\begin{eqnarray}\mathfrak{U}=\operatorname{Spf}(R)\rightarrow \operatorname{Spf}(R^{\Box })\quad \text{with}\quad R^{\Box }:={\mathcal{O}}_{C}\{t_{0},\ldots ,t_{r},t_{r+1}^{\pm 1},\ldots ,t_{d}^{\pm 1}\}/(t_{0}\cdots t_{r}-p^{q})\end{eqnarray}$$
$$\begin{eqnarray}\mathfrak{U}=\operatorname{Spf}(R)\rightarrow \operatorname{Spf}(R^{\Box })\quad \text{with}\quad R^{\Box }:={\mathcal{O}}_{C}\{t_{0},\ldots ,t_{r},t_{r+1}^{\pm 1},\ldots ,t_{d}^{\pm 1}\}/(t_{0}\cdots t_{r}-p^{q})\end{eqnarray}$$
 $d\geqslant 0$
, some
$d\geqslant 0$
, some
 $0\leqslant r\leqslant d$
, and some
$0\leqslant r\leqslant d$
, and some
 $q\in \mathbb{Q}_{{>}0}$
(where
$q\in \mathbb{Q}_{{>}0}$
(where
 $d$
,
$d$
,
 $r$
, and
$r$
, and
 $q$
may depend on
$q$
may depend on
 $\mathfrak{U}$
).
$\mathfrak{U}$
).
For example,
![]() $C$
could be the completed algebraic closure of any discretely valued field
$C$
could be the completed algebraic closure of any discretely valued field
![]() $K$
of mixed characteristic
$K$
of mixed characteristic
![]() $(0,p)$
with a perfect residue field. In addition, no generality is gained by allowing
$(0,p)$
with a perfect residue field. In addition, no generality is gained by allowing
![]() $p^{q}$
in (1.5.1) to be any nonunit
$p^{q}$
in (1.5.1) to be any nonunit
![]() $\unicode[STIX]{x1D70B}\in {\mathcal{O}}_{C}\setminus \{0\}$
. The role of the embedding
$\unicode[STIX]{x1D70B}\in {\mathcal{O}}_{C}\setminus \{0\}$
. The role of the embedding
![]() $p^{\mathbb{Q}}\subset C$
is to simplify arguments with explicit charts for the log structure on
$p^{\mathbb{Q}}\subset C$
is to simplify arguments with explicit charts for the log structure on
![]() $\mathfrak{X}$
(defined in §1.6); this is particularly useful in §5, especially in §§5.25–5.26. Our
$\mathfrak{X}$
(defined in §1.6); this is particularly useful in §5, especially in §§5.25–5.26. Our
![]() $C$
is less general than in [Reference Bhatt, Morrow and ScholzeBMS18], where any complete algebraically closed nonarchimedean extension of
$C$
is less general than in [Reference Bhatt, Morrow and ScholzeBMS18], where any complete algebraically closed nonarchimedean extension of
![]() $\mathbb{Q}_{p}$
is typically allowed. One of the main reasons for this is that we want to be able to apply, especially in §5, certain auxiliary results from [Reference BeilinsonBei13a] (in any event, relations
$\mathbb{Q}_{p}$
is typically allowed. One of the main reasons for this is that we want to be able to apply, especially in §5, certain auxiliary results from [Reference BeilinsonBei13a] (in any event, relations
![]() $t_{0}\cdots t_{r}-\unicode[STIX]{x1D70B}$
in which
$t_{0}\cdots t_{r}-\unicode[STIX]{x1D70B}$
in which
![]() $\unicode[STIX]{x1D70B}$
has a nonrational valuation go beyond ‘semistable reduction’).
$\unicode[STIX]{x1D70B}$
has a nonrational valuation go beyond ‘semistable reduction’).
The existence of étale local semistable coordinates (1.5.1) implies that each
![]() $\mathfrak{X}_{{\mathcal{O}}_{C}/p^{n}}$
is flat and locally of finite presentation over
$\mathfrak{X}_{{\mathcal{O}}_{C}/p^{n}}$
is flat and locally of finite presentation over
![]() ${\mathcal{O}}_{C}/p^{n}$
and
${\mathcal{O}}_{C}/p^{n}$
and
![]() $\mathfrak{X}_{{\mathcal{O}}_{C}/p^{n}}^{\text{sm}}$
is dense in
$\mathfrak{X}_{{\mathcal{O}}_{C}/p^{n}}^{\text{sm}}$
is dense in
![]() $\mathfrak{X}_{{\mathcal{O}}_{C}/p^{n}}$
. By [SP, 04D1] and limit arguments, equation (1.5.1) is the formal
$\mathfrak{X}_{{\mathcal{O}}_{C}/p^{n}}$
. By [SP, 04D1] and limit arguments, equation (1.5.1) is the formal
![]() $p$
-adic completion of the
$p$
-adic completion of the
![]() $\overline{W(k)}$
-base change of an étale
$\overline{W(k)}$
-base change of an étale
![]() ${\mathcal{O}}$
-morphism
${\mathcal{O}}$
-morphism
for some discrete valuation subring
![]() ${\mathcal{O}}\subset \overline{W(k)}$
that contains
${\mathcal{O}}\subset \overline{W(k)}$
that contains
![]() $p^{q}$
. The references [SP, 04D1] and [Reference Gabber and RameroGR03, 7.1.6(i)] also imply that
$p^{q}$
. The references [SP, 04D1] and [Reference Gabber and RameroGR03, 7.1.6(i)] also imply that
![]() $R$
is
$R$
is
![]() $R^{\Box }$
-flat. In addition, if
$R^{\Box }$
-flat. In addition, if
![]() $R\otimes _{{\mathcal{O}}_{C}}k$
is not
$R\otimes _{{\mathcal{O}}_{C}}k$
is not
![]() $k$
-smooth, then
$k$
-smooth, then
![]() $R$
determines
$R$
determines
![]() $q$
.Footnote
2
$q$
.Footnote
2
Any smooth
![]() $p$
-adic formal
$p$
-adic formal
![]() ${\mathcal{O}}_{C}$
-scheme
${\mathcal{O}}_{C}$
-scheme
![]() $\mathfrak{X}$
meets the requirements above: indeed, then the cover
$\mathfrak{X}$
meets the requirements above: indeed, then the cover
![]() $\{\mathfrak{U}\}$
exists already for the Zariski topology with
$\{\mathfrak{U}\}$
exists already for the Zariski topology with
![]() $r=0$
and
$r=0$
and
![]() $q=1$
for all
$q=1$
for all
![]() $\mathfrak{U}$
, see [Reference Fujiwara and KatoFK18, I.5.3.18]. Another key example is
$\mathfrak{U}$
, see [Reference Fujiwara and KatoFK18, I.5.3.18]. Another key example is
for some discrete valuation subring
![]() ${\mathcal{O}}\subset {\mathcal{O}}_{C}$
with a perfect residue field and a uniformizer
${\mathcal{O}}\subset {\mathcal{O}}_{C}$
with a perfect residue field and a uniformizer
![]() $\unicode[STIX]{x1D70B}\in {\mathcal{O}}$
and a locally of finite type, flat
$\unicode[STIX]{x1D70B}\in {\mathcal{O}}$
and a locally of finite type, flat
![]() ${\mathcal{O}}$
-scheme
${\mathcal{O}}$
-scheme
![]() ${\mathcal{X}}$
that is semistable in the sense that
${\mathcal{X}}$
that is semistable in the sense that
![]() ${\mathcal{X}}_{{\mathcal{O}}/\unicode[STIX]{x1D70B}}$
is a normal crossings divisor in
${\mathcal{X}}_{{\mathcal{O}}/\unicode[STIX]{x1D70B}}$
is a normal crossings divisor in
![]() ${\mathcal{X}}$
(as defined in [SP, 0BSF]), so that, in particular,
${\mathcal{X}}$
(as defined in [SP, 0BSF]), so that, in particular,
![]() ${\mathcal{X}}$
is regular at every point of
${\mathcal{X}}$
is regular at every point of
![]() ${\mathcal{X}}_{{\mathcal{O}}/\unicode[STIX]{x1D70B}}$
.Footnote
3
Moreover, if
${\mathcal{X}}_{{\mathcal{O}}/\unicode[STIX]{x1D70B}}$
.Footnote
3
Moreover, if
![]() ${\mathcal{X}}$
is even strictly semistable in the sense that
${\mathcal{X}}$
is even strictly semistable in the sense that
![]() ${\mathcal{X}}_{{\mathcal{O}}/\unicode[STIX]{x1D70B}}$
is even a strict normal crossings divisor in
${\mathcal{X}}_{{\mathcal{O}}/\unicode[STIX]{x1D70B}}$
is even a strict normal crossings divisor in
![]() ${\mathcal{X}}$
(as defined in [SP, 0BI9]), then the étale maps (1.5.4) exist even Zariski locally on
${\mathcal{X}}$
(as defined in [SP, 0BI9]), then the étale maps (1.5.4) exist even Zariski locally on
![]() ${\mathcal{X}}$
, and so the cover
${\mathcal{X}}$
, and so the cover
![]() $\{\mathfrak{U}\}$
also exists already for the Zariski topology of
$\{\mathfrak{U}\}$
also exists already for the Zariski topology of
![]() $\mathfrak{X}$
.
$\mathfrak{X}$
.
∙ We let
 $\mathfrak{X}_{C}^{\text{ad}}$
denote the adic generic fiber of
$\mathfrak{X}_{C}^{\text{ad}}$
denote the adic generic fiber of
 $\mathfrak{X}$
. By (1.5.1) and [Reference HuberHub96, 3.5.1], the adic space
$\mathfrak{X}$
. By (1.5.1) and [Reference HuberHub96, 3.5.1], the adic space
 $\mathfrak{X}_{C}^{\text{ad}}$
is smooth over
$\mathfrak{X}_{C}^{\text{ad}}$
is smooth over
 $C$
; by [Reference HuberHub96, 1.3.18 ii)], if
$C$
; by [Reference HuberHub96, 1.3.18 ii)], if
 $\mathfrak{X}$
is
$\mathfrak{X}$
is
 ${\mathcal{O}}_{C}$
-proper, then
${\mathcal{O}}_{C}$
-proper, then
 $\mathfrak{X}_{C}^{\text{ad}}$
is
$\mathfrak{X}_{C}^{\text{ad}}$
is
 $C$
-proper.
$C$
-proper.∙ We let
 $(\mathfrak{X}_{C}^{\text{ad}})_{\text{pro}\acute{\text{e}}\text{t}}$
denote the proétale site of
$(\mathfrak{X}_{C}^{\text{ad}})_{\text{pro}\acute{\text{e}}\text{t}}$
denote the proétale site of
 $\mathfrak{X}_{C}^{\text{ad}}$
(reviewed in [Reference Bhatt, Morrow and ScholzeBMS18, §5.1] and defined in [Reference ScholzeSch13a, 3.9] and [Reference ScholzeSch16, (1)]) and let (1.5.5)be the morphism to the étale site of
$\mathfrak{X}_{C}^{\text{ad}}$
(reviewed in [Reference Bhatt, Morrow and ScholzeBMS18, §5.1] and defined in [Reference ScholzeSch13a, 3.9] and [Reference ScholzeSch16, (1)]) and let (1.5.5)be the morphism to the étale site of $$\begin{eqnarray}\unicode[STIX]{x1D708}:(\mathfrak{X}_{C}^{\text{ad}})_{\text{pro}\acute{\text{e}}\text{t}}\rightarrow \mathfrak{X}_{\acute{\text{e}}\text{t}}\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D708}:(\mathfrak{X}_{C}^{\text{ad}})_{\text{pro}\acute{\text{e}}\text{t}}\rightarrow \mathfrak{X}_{\acute{\text{e}}\text{t}}\end{eqnarray}$$
 $\mathfrak{X}$
that sends any étale
$\mathfrak{X}$
that sends any étale
 $\mathfrak{U}\rightarrow \mathfrak{X}$
to the constant pro-system associated to its adic generic fiber. By [SP, 00X6], this functor indeed defines a morphism of sites: by [Reference HuberHub96, 3.5.1], it preserves coverings, commutes with fiber products, and respects final objects. Thus,
$\mathfrak{U}\rightarrow \mathfrak{X}$
to the constant pro-system associated to its adic generic fiber. By [SP, 00X6], this functor indeed defines a morphism of sites: by [Reference HuberHub96, 3.5.1], it preserves coverings, commutes with fiber products, and respects final objects. Thus,
 $\unicode[STIX]{x1D708}$
induces a morphism of topoi
$\unicode[STIX]{x1D708}$
induces a morphism of topoi
 $(\unicode[STIX]{x1D708}^{-1},\unicode[STIX]{x1D708}_{\ast })$
(see [SP, 00XC]).
$(\unicode[STIX]{x1D708}^{-1},\unicode[STIX]{x1D708}_{\ast })$
(see [SP, 00XC]).
1.6 The logarithmic structure on
 $\mathfrak{X}$
$\mathfrak{X}$
Unless noted otherwise, we always equip
(1) the ring
 ${\mathcal{O}}_{C}$
(respectively,
${\mathcal{O}}_{C}$
(respectively,
 ${\mathcal{O}}_{C}/p^{n}$
or
${\mathcal{O}}_{C}/p^{n}$
or
 $k$
) with the log structure
$k$
) with the log structure
 ${\mathcal{O}}_{C}\setminus \{0\}{\hookrightarrow}{\mathcal{O}}_{C}$
(respectively, its pullback);
${\mathcal{O}}_{C}\setminus \{0\}{\hookrightarrow}{\mathcal{O}}_{C}$
(respectively, its pullback);(2) the formal scheme
 $\mathfrak{X}$
(respectively,
$\mathfrak{X}$
(respectively,
 $\mathfrak{X}_{{\mathcal{O}}_{C}/p^{n}}$
or
$\mathfrak{X}_{{\mathcal{O}}_{C}/p^{n}}$
or
 $\mathfrak{X}_{k}$
) with the log structure given by the subsheaf associated to the subpresheafFootnote
4
$\mathfrak{X}_{k}$
) with the log structure given by the subsheaf associated to the subpresheafFootnote
4
 ${\mathcal{O}}_{\mathfrak{X},\,\acute{\text{e}}\text{t}}\cap ({\mathcal{O}}_{\mathfrak{X},\,\acute{\text{e}}\text{t}}[\frac{1}{p}])^{\times }{\hookrightarrow}{\mathcal{O}}_{\mathfrak{ X},\,\acute{\text{e}}\text{t}}$
(respectively, its pullback log structure).
${\mathcal{O}}_{\mathfrak{X},\,\acute{\text{e}}\text{t}}\cap ({\mathcal{O}}_{\mathfrak{X},\,\acute{\text{e}}\text{t}}[\frac{1}{p}])^{\times }{\hookrightarrow}{\mathcal{O}}_{\mathfrak{ X},\,\acute{\text{e}}\text{t}}$
(respectively, its pullback log structure).
Both (1) and (2) determine the same log structure on
![]() $\operatorname{Spf}({\mathcal{O}}_{C})$
, so the map
$\operatorname{Spf}({\mathcal{O}}_{C})$
, so the map
![]() $\mathfrak{X}\rightarrow \operatorname{Spf}({\mathcal{O}}_{C})$
is that of log formal schemes. Moreover, étale locally on
$\mathfrak{X}\rightarrow \operatorname{Spf}({\mathcal{O}}_{C})$
is that of log formal schemes. Moreover, étale locally on
![]() $\mathfrak{X}$
, the log structure may be made explicit: in the presence of a coordinate morphism (1.5.1), Claims 1.6.1 and 1.6.3 below give an explicit chart for the log structure of
$\mathfrak{X}$
, the log structure may be made explicit: in the presence of a coordinate morphism (1.5.1), Claims 1.6.1 and 1.6.3 below give an explicit chart for the log structure of
![]() $\mathfrak{U}$
, namely, the chart (1.6.2) in which we replace
$\mathfrak{U}$
, namely, the chart (1.6.2) in which we replace
![]() ${\mathcal{O}}$
by
${\mathcal{O}}$
by
![]() ${\mathcal{O}}_{C}$
, replace
${\mathcal{O}}_{C}$
, replace
![]() $U$
by
$U$
by
![]() $\mathfrak{U}$
, and set
$\mathfrak{U}$
, and set
![]() $\unicode[STIX]{x1D70B}:=p^{q}$
. This chart shows, in particular, that
$\unicode[STIX]{x1D70B}:=p^{q}$
. This chart shows, in particular, that
![]() $\mathfrak{U}$
and
$\mathfrak{U}$
and
![]() ${\mathcal{O}}_{C}$
may be endowed with fine log structures whose base changes along a ‘change of log structure’ self-map of
${\mathcal{O}}_{C}$
may be endowed with fine log structures whose base changes along a ‘change of log structure’ self-map of
![]() ${\mathcal{O}}_{C}$
recover the log structures described in (1)–(2) (for example, the fine log structure on
${\mathcal{O}}_{C}$
recover the log structures described in (1)–(2) (for example, the fine log structure on
![]() ${\mathcal{O}}_{C}$
could be that determined by the chart
${\mathcal{O}}_{C}$
could be that determined by the chart
![]() $\mathbb{N}_{{\geqslant}0}\xrightarrow[{}]{a\,\mapsto (p^{q})^{a}}{\mathcal{O}}_{C}$
, in which case the ‘change of log structure’ self-map of
$\mathbb{N}_{{\geqslant}0}\xrightarrow[{}]{a\,\mapsto (p^{q})^{a}}{\mathcal{O}}_{C}$
, in which case the ‘change of log structure’ self-map of
![]() ${\mathcal{O}}_{C}$
is the identity on the underlying scheme
${\mathcal{O}}_{C}$
is the identity on the underlying scheme
![]() $\operatorname{Spec}({\mathcal{O}}_{C})$
and is determined on the log structures by the map of charts
$\operatorname{Spec}({\mathcal{O}}_{C})$
and is determined on the log structures by the map of charts
![]() $\mathbb{N}_{{\geqslant}0}\xrightarrow[{}]{a\,\mapsto (p^{q})^{a}}{\mathcal{O}}_{C}\setminus \{0\}$
). Since many common properties of maps of log schemes are stable under base change, in practice this means that we may often deal with the log structures in (1)–(2) as if they were fine and, in particular, we may cite [Reference KatoKat89] for certain purposes.
$\mathbb{N}_{{\geqslant}0}\xrightarrow[{}]{a\,\mapsto (p^{q})^{a}}{\mathcal{O}}_{C}\setminus \{0\}$
). Since many common properties of maps of log schemes are stable under base change, in practice this means that we may often deal with the log structures in (1)–(2) as if they were fine and, in particular, we may cite [Reference KatoKat89] for certain purposes.
By the preceding discussion, all the log structures above are quasi-coherent and integral. Moreover, by [Reference KatoKat89, 3.7(2)], each
![]() $\mathfrak{X}_{{\mathcal{O}}_{C}/p^{n}}$
is log smooth over
$\mathfrak{X}_{{\mathcal{O}}_{C}/p^{n}}$
is log smooth over
![]() ${\mathcal{O}}_{C}/p^{n}$
, so that, by [Reference KatoKat89, 3.10], the
${\mathcal{O}}_{C}/p^{n}$
, so that, by [Reference KatoKat89, 3.10], the
![]() ${\mathcal{O}}_{\mathfrak{X}}$
-module
${\mathcal{O}}_{\mathfrak{X}}$
-module
![]() $\unicode[STIX]{x1D6FA}_{\mathfrak{X}/{\mathcal{O}}_{C},\,\log }^{1}$
of logarithmic differentials is finite locally free. We set
$\unicode[STIX]{x1D6FA}_{\mathfrak{X}/{\mathcal{O}}_{C},\,\log }^{1}$
of logarithmic differentials is finite locally free. We set
let
![]() $\unicode[STIX]{x1D6FA}_{\mathfrak{X}/{\mathcal{O}}_{C},\,\log }^{\bullet }$
denote the logarithmic de Rham complex, and set
$\unicode[STIX]{x1D6FA}_{\mathfrak{X}/{\mathcal{O}}_{C},\,\log }^{\bullet }$
denote the logarithmic de Rham complex, and set
Claim 1.6.1. For a valuation subring
![]() ${\mathcal{O}}\subset \overline{W(k)}$
and an
${\mathcal{O}}\subset \overline{W(k)}$
and an
![]() ${\mathcal{O}}$
-scheme
${\mathcal{O}}$
-scheme
![]() $U$
that has an étale morphism
$U$
that has an étale morphism
the log structure on
![]() $U$
associated to
$U$
associated to
![]() ${\mathcal{O}}_{U,\,\acute{\text{e}}\text{t}}\cap ({\mathcal{O}}_{U,\,\acute{\text{e}}\text{t}}[\frac{1}{p}])^{\times }$
has the chart
${\mathcal{O}}_{U,\,\acute{\text{e}}\text{t}}\cap ({\mathcal{O}}_{U,\,\acute{\text{e}}\text{t}}[\frac{1}{p}])^{\times }$
has the chart
given by
![]() $(a_{i})_{0\leqslant i\leqslant r}\mapsto \prod _{0\leqslant i\leqslant r}t_{i}^{a_{i}}$
on
$(a_{i})_{0\leqslant i\leqslant r}\mapsto \prod _{0\leqslant i\leqslant r}t_{i}^{a_{i}}$
on
![]() $\mathbb{N}_{{\geqslant}0}^{r+1}$
, the diagonal
$\mathbb{N}_{{\geqslant}0}^{r+1}$
, the diagonal
![]() $\mathbb{N}_{{\geqslant}0}\rightarrow \mathbb{N}_{{\geqslant}0}^{r+1}$
and
$\mathbb{N}_{{\geqslant}0}\rightarrow \mathbb{N}_{{\geqslant}0}^{r+1}$
and
![]() $\mathbb{N}_{{\geqslant}0}\xrightarrow[{}]{a\,\mapsto \unicode[STIX]{x1D70B}^{a}}({\mathcal{O}}\setminus \{0\})$
on
$\mathbb{N}_{{\geqslant}0}\xrightarrow[{}]{a\,\mapsto \unicode[STIX]{x1D70B}^{a}}({\mathcal{O}}\setminus \{0\})$
on
![]() $\mathbb{N}_{{\geqslant}0}$
, and the structure map
$\mathbb{N}_{{\geqslant}0}$
, and the structure map
![]() $({\mathcal{O}}\setminus \{0\})\rightarrow \unicode[STIX]{x1D6E4}(U,{\mathcal{O}}_{U})$
on
$({\mathcal{O}}\setminus \{0\})\rightarrow \unicode[STIX]{x1D6E4}(U,{\mathcal{O}}_{U})$
on
![]() ${\mathcal{O}}\setminus \{0\}$
.
${\mathcal{O}}\setminus \{0\}$
.
Proof. Without loss of generality,
![]() $U$
is affine, so, by a limit argument, we may assume that
$U$
is affine, so, by a limit argument, we may assume that
![]() ${\mathcal{O}}$
is discretely valued. Then
${\mathcal{O}}$
is discretely valued. Then
![]() $U$
, endowed with the log structure associated to (1.6.2), is logarithmically regular in the sense of [Reference KatoKat94b, 2.1] (compare with [Reference BeilinsonBei12, §4.1, proof of Lemma]). Therefore, since the locus of triviality of this log structure is
$U$
, endowed with the log structure associated to (1.6.2), is logarithmically regular in the sense of [Reference KatoKat94b, 2.1] (compare with [Reference BeilinsonBei12, §4.1, proof of Lemma]). Therefore, since the locus of triviality of this log structure is
![]() $U[\frac{1}{p}]$
, the claim follows from [Reference KatoKat94b, 11.6].◻
$U[\frac{1}{p}]$
, the claim follows from [Reference KatoKat94b, 11.6].◻
Claim 1.6.3. For
![]() ${\mathcal{O}}$
as in Claim 1.6.1, a flat
${\mathcal{O}}$
as in Claim 1.6.1, a flat
![]() ${\mathcal{O}}$
-scheme
${\mathcal{O}}$
-scheme
![]() $U$
(respectively, and its formal
$U$
(respectively, and its formal
![]() $p$
-adic completion
$p$
-adic completion
![]() $\mathfrak{U}$
) endowed with the log structure associated to
$\mathfrak{U}$
) endowed with the log structure associated to
![]() ${\mathcal{O}}_{U,\,\acute{\text{e}}\text{t}}\cap ({\mathcal{O}}_{U,\,\acute{\text{e}}\text{t}}[\frac{1}{p}])^{\times }$
(respectively,
${\mathcal{O}}_{U,\,\acute{\text{e}}\text{t}}\cap ({\mathcal{O}}_{U,\,\acute{\text{e}}\text{t}}[\frac{1}{p}])^{\times }$
(respectively,
![]() ${\mathcal{O}}_{\mathfrak{U},\,\acute{\text{e}}\text{t}}\cap ({\mathcal{O}}_{\mathfrak{U},\,\acute{\text{e}}\text{t}}[\frac{1}{p}])^{\times }$
),
${\mathcal{O}}_{\mathfrak{U},\,\acute{\text{e}}\text{t}}\cap ({\mathcal{O}}_{\mathfrak{U},\,\acute{\text{e}}\text{t}}[\frac{1}{p}])^{\times }$
),
Proof. For a geometric point
![]() $\overline{u}$
of
$\overline{u}$
of
![]() $\mathfrak{U}$
, due to [SP, 04D1], the stalk map
$\mathfrak{U}$
, due to [SP, 04D1], the stalk map
![]() ${\mathcal{O}}_{U,\,\overline{u}}\cong j^{-1}({\mathcal{O}}_{U,\,\overline{u}})\rightarrow {\mathcal{O}}_{\mathfrak{U},\,\overline{u}}$
induces an isomorphism
${\mathcal{O}}_{U,\,\overline{u}}\cong j^{-1}({\mathcal{O}}_{U,\,\overline{u}})\rightarrow {\mathcal{O}}_{\mathfrak{U},\,\overline{u}}$
induces an isomorphism
![]() ${\mathcal{O}}_{U,\,\overline{u}}/p^{n}\cong {\mathcal{O}}_{\mathfrak{U},\,\overline{u}}/p^{n}$
for every
${\mathcal{O}}_{U,\,\overline{u}}/p^{n}\cong {\mathcal{O}}_{\mathfrak{U},\,\overline{u}}/p^{n}$
for every
![]() $n>0$
. We consider the stalk map
$n>0$
. We consider the stalk map
Every element
![]() $x$
of the target of (1.6.5) satisfies the equation
$x$
of the target of (1.6.5) satisfies the equation
![]() $xy=p^{n}$
for some
$xy=p^{n}$
for some
![]() $n>0$
. We choose an
$n>0$
. We choose an
![]() $\widetilde{x}\in {\mathcal{O}}_{U,\,\overline{u}}$
congruent to
$\widetilde{x}\in {\mathcal{O}}_{U,\,\overline{u}}$
congruent to
![]() $x$
modulo
$x$
modulo
![]() $p^{n+1}$
, so that
$p^{n+1}$
, so that
![]() $\widetilde{x}\widetilde{y}=p^{n}+p^{n+1}\widetilde{z}$
for some
$\widetilde{x}\widetilde{y}=p^{n}+p^{n+1}\widetilde{z}$
for some
![]() $\widetilde{y},\widetilde{z}\in {\mathcal{O}}_{U,\,\overline{u}}$
. Since
$\widetilde{y},\widetilde{z}\in {\mathcal{O}}_{U,\,\overline{u}}$
. Since
![]() $1+p\widetilde{z}\in {\mathcal{O}}_{U,\,\overline{u}}^{\times }$
, we adjust
$1+p\widetilde{z}\in {\mathcal{O}}_{U,\,\overline{u}}^{\times }$
, we adjust
![]() $\widetilde{y}$
to get
$\widetilde{y}$
to get
![]() $\widetilde{x}\widetilde{y}=p^{n}$
, which shows that
$\widetilde{x}\widetilde{y}=p^{n}$
, which shows that
![]() $\widetilde{x}\in {\mathcal{O}}_{U,\,\overline{u}}\cap ({\mathcal{O}}_{U,\,\overline{u}}[\frac{1}{p}])^{\times }$
and
$\widetilde{x}\in {\mathcal{O}}_{U,\,\overline{u}}\cap ({\mathcal{O}}_{U,\,\overline{u}}[\frac{1}{p}])^{\times }$
and
![]() $(p^{n})\subset (\widetilde{x})$
. Thus, the image of
$(p^{n})\subset (\widetilde{x})$
. Thus, the image of
![]() $\widetilde{x}$
in
$\widetilde{x}$
in
![]() ${\mathcal{O}}_{\mathfrak{U},\,\overline{u}}$
and
${\mathcal{O}}_{\mathfrak{U},\,\overline{u}}$
and
![]() $x$
generate the same ideal, and hence are unit multiples of each other. Conversely, if
$x$
generate the same ideal, and hence are unit multiples of each other. Conversely, if
![]() $\widetilde{x}_{1},\widetilde{x}_{2}\in {\mathcal{O}}_{U,\,\overline{u}}\cap ({\mathcal{O}}_{U,\,\overline{u}}[\frac{1}{p}])^{\times }$
are unit multiples of each other in
$\widetilde{x}_{1},\widetilde{x}_{2}\in {\mathcal{O}}_{U,\,\overline{u}}\cap ({\mathcal{O}}_{U,\,\overline{u}}[\frac{1}{p}])^{\times }$
are unit multiples of each other in
![]() ${\mathcal{O}}_{\mathfrak{U},\,\overline{u}}$
, then, by reducing modulo
${\mathcal{O}}_{\mathfrak{U},\,\overline{u}}$
, then, by reducing modulo
![]() $p^{n}$
for a large enough
$p^{n}$
for a large enough
![]() $n$
, we see that they generate the same ideal in
$n$
, we see that they generate the same ideal in
![]() ${\mathcal{O}}_{U,\,\overline{u}}$
, so are unit multiples of each other already in
${\mathcal{O}}_{U,\,\overline{u}}$
, so are unit multiples of each other already in
![]() ${\mathcal{O}}_{U,\,\overline{u}}$
. In conclusion, the map (1.6.5) induces an isomorphism
${\mathcal{O}}_{U,\,\overline{u}}$
. In conclusion, the map (1.6.5) induces an isomorphism
to the effect that the map (1.6.4) is indeed strict, as claimed. ◻
1.7 Conventions and additional notation
For a field
![]() $K$
, we let
$K$
, we let
![]() $\overline{K}$
be its algebraic closure (taken inside
$\overline{K}$
be its algebraic closure (taken inside
![]() $C$
if
$C$
if
![]() $K$
is given as a subfield of
$K$
is given as a subfield of
![]() $C$
). If
$C$
). If
![]() $K$
has a valuation, we let
$K$
has a valuation, we let
![]() ${\mathcal{O}}_{K}$
be its valuation subring and write
${\mathcal{O}}_{K}$
be its valuation subring and write
![]() $\overline{{\mathcal{O}}}_{K}$
for the integral closure of
$\overline{{\mathcal{O}}}_{K}$
for the integral closure of
![]() ${\mathcal{O}}_{K}$
in
${\mathcal{O}}_{K}$
in
![]() $\overline{K}$
. In mixed characteristic, we normalize the valuations by requiring that
$\overline{K}$
. In mixed characteristic, we normalize the valuations by requiring that
![]() $v(p)=1$
. We let
$v(p)=1$
. We let
![]() $(-)^{\text{sm}}$
denote the smooth locus of a (formal) scheme over an implicitly understood base. For power series rings, we use
$(-)^{\text{sm}}$
denote the smooth locus of a (formal) scheme over an implicitly understood base. For power series rings, we use
![]() $\{-\}$
to indicate decaying coefficients. For a topological ring
$\{-\}$
to indicate decaying coefficients. For a topological ring
![]() $R$
, we let
$R$
, we let
![]() $R^{\circ }$
denote the subset of powerbounded elements.
$R^{\circ }$
denote the subset of powerbounded elements.
We let
![]() $W(-)$
(respectively
$W(-)$
(respectively
![]() $W_{n}(-)$
) denote
$W_{n}(-)$
) denote
![]() $p$
-typical Witt vectors (respectively, their length
$p$
-typical Witt vectors (respectively, their length
![]() $n$
truncation), and let
$n$
truncation), and let
![]() $[-]$
denote Teichmüller representatives. We let
$[-]$
denote Teichmüller representatives. We let
![]() $\mathbb{Z}_{(p)}$
be the localization of
$\mathbb{Z}_{(p)}$
be the localization of
![]() $\mathbb{Z}$
at
$\mathbb{Z}$
at
![]() $p$
, let
$p$
, let
![]() $\unicode[STIX]{x1D707}_{p^{n}}$
be the group scheme of
$\unicode[STIX]{x1D707}_{p^{n}}$
be the group scheme of
![]() $p^{n}$
th roots of unity, and let
$p^{n}$
th roots of unity, and let
![]() $\unicode[STIX]{x1D701}_{p^{n}}$
denote a primitive
$\unicode[STIX]{x1D701}_{p^{n}}$
denote a primitive
![]() $p^{n}$
th root of unity. For brevity, we set
$p^{n}$
th root of unity. For brevity, we set
![]() $\mathbb{Z}_{p}(1):=\varprojlim (\unicode[STIX]{x1D707}_{p^{n}}(C))$
. We let
$\mathbb{Z}_{p}(1):=\varprojlim (\unicode[STIX]{x1D707}_{p^{n}}(C))$
. We let
![]() $\widehat{M}$
denote the (by default,
$\widehat{M}$
denote the (by default,
![]() $p$
-adic) completion of a module
$p$
-adic) completion of a module
![]() $M$
and, similarly, let
$M$
and, similarly, let
![]() $\widehat{\bigoplus }$
denote the completion of a direct sum. Unless specified otherwise, we endow a
$\widehat{\bigoplus }$
denote the completion of a direct sum. Unless specified otherwise, we endow a
![]() $p$
-adically complete module with the inverse limit of the discrete topologies.
$p$
-adically complete module with the inverse limit of the discrete topologies.
We use the definition of a perfectoid ring given in [Reference Bhatt, Morrow and ScholzeBMS18, 3.5] (the compatibility with prior definitions is discussed in [Reference Bhatt, Morrow and ScholzeBMS18, 3.20]). Explicitly, by [Reference Bhatt, Morrow and ScholzeBMS18, 3.9 and 3.10], a
![]() $p$
-torsion-free ring
$p$
-torsion-free ring
![]() $S$
is perfectoid if and only if
$S$
is perfectoid if and only if
![]() $S$
is
$S$
is
![]() $p$
-adically complete and the divisor
$p$
-adically complete and the divisor
![]() $(p)\subset S$
has a
$(p)\subset S$
has a
![]() $p$
-power root in the sense that there is a
$p$
-power root in the sense that there is a
![]() $\unicode[STIX]{x1D71B}\in S$
with
$\unicode[STIX]{x1D71B}\in S$
with
![]() $(\unicode[STIX]{x1D71B}^{p})=(p)$
and
$(\unicode[STIX]{x1D71B}^{p})=(p)$
and![]() In particular, for such an
In particular, for such an
![]() $S$
, any
$S$
, any
![]() $p$
-adically formally étale
$p$
-adically formally étale
![]() $S$
-algebra
$S$
-algebra
![]() $S^{\prime }$
that is
$S^{\prime }$
that is
![]() $p$
-adically complete is also perfectoid.
$p$
-adically complete is also perfectoid.
For a ring object
![]() $R$
of a topos
$R$
of a topos
![]() $\mathscr{T}$
, we write
$\mathscr{T}$
, we write
![]() $D(\mathscr{T},R)$
, or simply
$D(\mathscr{T},R)$
, or simply
![]() $D(R)$
, for the derived category of
$D(R)$
, for the derived category of
![]() $R$
-modules. For an object
$R$
-modules. For an object
![]() $M$
of a derived category, we denote its derived
$M$
of a derived category, we denote its derived
![]() $p$
-adic completion by
$p$
-adic completion by
(see [SP, 0940] for the definition of
![]() $R\lim$
). For a morphism
$R\lim$
). For a morphism
![]() $f$
of ringed topoi, we use the commutativity of the functor
$f$
of ringed topoi, we use the commutativity of the functor
![]() $Rf_{\ast }$
with derived limits and derived completions, see [SP, 0A07 and 0944].
$Rf_{\ast }$
with derived limits and derived completions, see [SP, 0A07 and 0944].
For a profinite group
![]() $H$
and a continuous
$H$
and a continuous
![]() $H$
-module
$H$
-module
![]() $M$
, we write
$M$
, we write
![]() $R\unicode[STIX]{x1D6E4}_{\text{cont}}(H,M)$
for the continuous cochain complex. Whenever convenient, we also view
$R\unicode[STIX]{x1D6E4}_{\text{cont}}(H,M)$
for the continuous cochain complex. Whenever convenient, we also view
![]() $R\unicode[STIX]{x1D6E4}_{\text{cont}}(H,-)$
as the derived global sections functor of the site of profinite
$R\unicode[STIX]{x1D6E4}_{\text{cont}}(H,-)$
as the derived global sections functor of the site of profinite
![]() $H$
-sets (see [Reference ScholzeSch13a, 3.7(iii)] and [Reference ScholzeSch16, (1)]).
$H$
-sets (see [Reference ScholzeSch13a, 3.7(iii)] and [Reference ScholzeSch16, (1)]).
For commuting endomorphisms
![]() $f_{1},\ldots ,f_{n}$
of an abelian group
$f_{1},\ldots ,f_{n}$
of an abelian group
![]() $A$
, we recall the Koszul complex:
$A$
, we recall the Koszul complex:
where
![]() $A$
is regarded as a
$A$
is regarded as a
![]() $\mathbb{Z}[x_{1},\ldots ,x_{n}]$
-module by letting
$\mathbb{Z}[x_{1},\ldots ,x_{n}]$
-module by letting
![]() $x_{j}$
act as
$x_{j}$
act as
![]() $f_{j}$
, the tensor products are over
$f_{j}$
, the tensor products are over
![]() $\mathbb{Z}[x_{1},\ldots ,x_{n}]$
, and the factor complexes are concentrated in degrees
$\mathbb{Z}[x_{1},\ldots ,x_{n}]$
, and the factor complexes are concentrated in degrees
![]() $0$
and
$0$
and
![]() $1$
.
$1$
.
For an ideal
![]() $I$
of a ring
$I$
of a ring
![]() $R$
and an
$R$
and an
![]() $R$
-module complex
$R$
-module complex
![]() $(M^{\bullet },d^{\bullet })$
with
$(M^{\bullet },d^{\bullet })$
with
![]() $M^{j}\cong 0$
for
$M^{j}\cong 0$
for
![]() $j<0$
, the subcomplex
$j<0$
, the subcomplex
We will mostly (but a priori not always, see Proposition 5.34) use
![]() $\unicode[STIX]{x1D702}_{I}(M^{\bullet })$
as in [Reference Bhatt, Morrow and ScholzeBMS18, 6.2], namely, when
$\unicode[STIX]{x1D702}_{I}(M^{\bullet })$
as in [Reference Bhatt, Morrow and ScholzeBMS18, 6.2], namely, when
![]() $I$
is generated by a nonzero-divisor and the
$I$
is generated by a nonzero-divisor and the
![]() $M^{j}$
have no nonzero
$M^{j}$
have no nonzero
![]() $I$
-torsion.
$I$
-torsion.
A logarithmic divided power thickening (or, for brevity, a log PD thickening) is an exact closed immersion of logarithmic (often abbreviated to log) schemes equipped with a divided power structure on the quasi-coherent sheaf of ideals that defines the underlying closed immersion of schemes.
2 The object
 $A\unicode[STIX]{x1D6FA}_{\mathfrak{X}}$
and the
$A\unicode[STIX]{x1D6FA}_{\mathfrak{X}}$
and the
 $p$
-adic étale cohomology of
$p$
-adic étale cohomology of
 $\mathfrak{X}$
$\mathfrak{X}$
As in the case when
![]() $\mathfrak{X}$
is smooth treated in [Reference Bhatt, Morrow and ScholzeBMS18], the eventual construction of the
$\mathfrak{X}$
is smooth treated in [Reference Bhatt, Morrow and ScholzeBMS18], the eventual construction of the
![]() $A_{\text{inf}}$
-cohomology modules of
$A_{\text{inf}}$
-cohomology modules of
![]() $\mathfrak{X}$
rests on the object
$\mathfrak{X}$
rests on the object
![]() $A\unicode[STIX]{x1D6FA}_{\mathfrak{X}}$
that lives in a derived category of
$A\unicode[STIX]{x1D6FA}_{\mathfrak{X}}$
that lives in a derived category of
![]() $A_{\text{inf}}$
-module sheaves on
$A_{\text{inf}}$
-module sheaves on
![]() $\mathfrak{X}$
. In this short section, we review the definition of
$\mathfrak{X}$
. In this short section, we review the definition of
![]() $A\unicode[STIX]{x1D6FA}_{\mathfrak{X}}$
in §2.2 and then, in the case when
$A\unicode[STIX]{x1D6FA}_{\mathfrak{X}}$
in §2.2 and then, in the case when
![]() $\mathfrak{X}$
is proper, review the connection between
$\mathfrak{X}$
is proper, review the connection between
![]() $A\unicode[STIX]{x1D6FA}_{\mathfrak{X}}$
and the integral
$A\unicode[STIX]{x1D6FA}_{\mathfrak{X}}$
and the integral
![]() $p$
-adic étale cohomology of
$p$
-adic étale cohomology of
![]() $\mathfrak{X}_{C}^{\text{ad}}$
in Theorem 2.3. We begin by fixing the basic notation that concerns the ring
$\mathfrak{X}_{C}^{\text{ad}}$
in Theorem 2.3. We begin by fixing the basic notation that concerns the ring
![]() $A_{\text{inf}}$
of integral
$A_{\text{inf}}$
of integral
![]() $p$
-adic Hodge theory. The setup of §§2.1–2.2 will be used freely in the rest of the paper.
$p$
-adic Hodge theory. The setup of §§2.1–2.2 will be used freely in the rest of the paper.
2.1 The ring
 $A_{\text{inf}}$
$A_{\text{inf}}$
We denote the tilt of
![]() ${\mathcal{O}}_{C}$
by
${\mathcal{O}}_{C}$
by
as multiplicative monoids (see [Reference ScholzeSch12, 3.4(i)]). We regard
![]() $p^{1/p^{\infty }}$
fixed in §1.5 as an element of
$p^{1/p^{\infty }}$
fixed in §1.5 as an element of
![]() ${\mathcal{O}}_{C}^{\flat }$
. Due to the fixed embedding
${\mathcal{O}}_{C}^{\flat }$
. Due to the fixed embedding
![]() $p^{\mathbb{Q}_{{\geqslant}0}}\subset {\mathcal{O}}_{C}$
, this element comes equipped with well-defined powers
$p^{\mathbb{Q}_{{\geqslant}0}}\subset {\mathcal{O}}_{C}$
, this element comes equipped with well-defined powers
![]() $(p^{1/p^{\infty }})^{q}\in {\mathcal{O}}_{C}^{\flat }$
for
$(p^{1/p^{\infty }})^{q}\in {\mathcal{O}}_{C}^{\flat }$
for
![]() $q\in \mathbb{Q}_{{\geqslant}0}$
. For each
$q\in \mathbb{Q}_{{\geqslant}0}$
. For each
![]() $x\in {\mathcal{O}}_{C}^{\flat }$
, we let
$x\in {\mathcal{O}}_{C}^{\flat }$
, we let
![]() $(\ldots ,x^{(1)},x^{(0)})$
denote its preimage in
$(\ldots ,x^{(1)},x^{(0)})$
denote its preimage in
![]() $\mathop{\varprojlim }\nolimits_{y\mapsto y^{p}}{\mathcal{O}}_{C}$
. The map
$\mathop{\varprojlim }\nolimits_{y\mapsto y^{p}}{\mathcal{O}}_{C}$
. The map
![]() $x\mapsto \text{val}_{{\mathcal{O}}_{C}}(x^{(0)})$
makes
$x\mapsto \text{val}_{{\mathcal{O}}_{C}}(x^{(0)})$
makes
![]() ${\mathcal{O}}_{C}^{\flat }$
a complete valuation ring of height
${\mathcal{O}}_{C}^{\flat }$
a complete valuation ring of height
![]() $1$
whose fraction field
$1$
whose fraction field
![]() $C^{\flat }:=\operatorname{Frac}({\mathcal{O}}_{C}^{\flat })$
is algebraically closed (see [Reference ScholzeSch12, 3.4(iii), 3.7(ii)]). We let
$C^{\flat }:=\operatorname{Frac}({\mathcal{O}}_{C}^{\flat })$
is algebraically closed (see [Reference ScholzeSch12, 3.4(iii), 3.7(ii)]). We let
![]() $\mathfrak{m}^{\flat }$
denote the maximal ideal of
$\mathfrak{m}^{\flat }$
denote the maximal ideal of
![]() ${\mathcal{O}}_{C}^{\flat }$
.
${\mathcal{O}}_{C}^{\flat }$
.
The basic period ring
![]() $A_{\text{inf}}$
of Fontaine is defined by
$A_{\text{inf}}$
of Fontaine is defined by
We equip the local domain
![]() $A_{\text{inf}}$
with the product of the valuation topologies via the Witt coordinate bijection
$A_{\text{inf}}$
with the product of the valuation topologies via the Witt coordinate bijection
![]() $W({\mathcal{O}}_{C}^{\flat })\cong \prod _{n=1}^{\infty }{\mathcal{O}}_{C}^{\flat }$
. Then
$W({\mathcal{O}}_{C}^{\flat })\cong \prod _{n=1}^{\infty }{\mathcal{O}}_{C}^{\flat }$
. Then
![]() $A_{\text{inf}}$
is complete and its topology agrees with the
$A_{\text{inf}}$
is complete and its topology agrees with the
![]() $(p,[x])$
-adic topology for any nonzero nonunit
$(p,[x])$
-adic topology for any nonzero nonunit
![]() $x\in {\mathcal{O}}_{C}^{\flat }$
. We fix (once and for all) a compatible system
$x\in {\mathcal{O}}_{C}^{\flat }$
. We fix (once and for all) a compatible system
![]() $\unicode[STIX]{x1D716}=(\ldots ,\unicode[STIX]{x1D701}_{p^{2}},\unicode[STIX]{x1D701}_{p},1)$
of
$\unicode[STIX]{x1D716}=(\ldots ,\unicode[STIX]{x1D701}_{p^{2}},\unicode[STIX]{x1D701}_{p},1)$
of
![]() $p$
-power roots of unity in
$p$
-power roots of unity in
![]() ${\mathcal{O}}_{C}$
, so that
${\mathcal{O}}_{C}$
, so that
![]() $\unicode[STIX]{x1D716}\in {\mathcal{O}}_{C}^{\flat }$
, and set
$\unicode[STIX]{x1D716}\in {\mathcal{O}}_{C}^{\flat }$
, and set
Since
![]() $(p,\unicode[STIX]{x1D707})=(p,[\unicode[STIX]{x1D716}-1])$
, the topology of
$(p,\unicode[STIX]{x1D707})=(p,[\unicode[STIX]{x1D716}-1])$
, the topology of
![]() $A_{\text{inf}}$
is
$A_{\text{inf}}$
is
![]() $(p,\unicode[STIX]{x1D707})$
-adic. By forming the limit of the sequences
$(p,\unicode[STIX]{x1D707})$
-adic. By forming the limit of the sequences
we see that
![]() $A_{\text{inf}}/\unicode[STIX]{x1D707}$
is
$A_{\text{inf}}/\unicode[STIX]{x1D707}$
is
![]() $p$
-adically complete and that the ideal
$p$
-adically complete and that the ideal
![]() $(\unicode[STIX]{x1D707})\subset A_{\text{inf}}$
does not depend on the choice of
$(\unicode[STIX]{x1D707})\subset A_{\text{inf}}$
does not depend on the choice of
![]() $\unicode[STIX]{x1D716}$
(use the fact that the valuation of
$\unicode[STIX]{x1D716}$
(use the fact that the valuation of
![]() $\unicode[STIX]{x1D701}_{p}-1$
does not depend on
$\unicode[STIX]{x1D701}_{p}-1$
does not depend on
![]() $\unicode[STIX]{x1D701}_{p}$
).
$\unicode[STIX]{x1D701}_{p}$
).
The assignment
![]() $[x]\mapsto x^{(0)}$
extends uniquely to a ring homomorphism
$[x]\mapsto x^{(0)}$
extends uniquely to a ring homomorphism
which is surjective, as indicated, and intertwines the Frobenius
![]() $\unicode[STIX]{x1D711}$
of
$\unicode[STIX]{x1D711}$
of
![]() $A_{\text{inf}}$
with the absolute Frobenius of
$A_{\text{inf}}$
with the absolute Frobenius of
![]() ${\mathcal{O}}_{C}/p$
. Its kernel
${\mathcal{O}}_{C}/p$
. Its kernel
![]() $\operatorname{Ker}(\unicode[STIX]{x1D703})\subset A_{\text{inf}}$
is principal and generated by the element
$\operatorname{Ker}(\unicode[STIX]{x1D703})\subset A_{\text{inf}}$
is principal and generated by the element
(see [Reference Bhatt, Morrow and ScholzeBMS18, 3.16]). Analogues of the sequences (2.1.2) show that each
![]() $A_{\text{inf}}/\unicode[STIX]{x1D709}^{n}$
is
$A_{\text{inf}}/\unicode[STIX]{x1D709}^{n}$
is
![]() $p$
-adically complete. In fact, the map
$p$
-adically complete. In fact, the map
![]() $\unicode[STIX]{x1D703}$
identifies
$\unicode[STIX]{x1D703}$
identifies
![]() $A_{\text{inf}}/\unicode[STIX]{x1D709}^{n}$
with the initial
$A_{\text{inf}}/\unicode[STIX]{x1D709}^{n}$
with the initial
![]() $p$
-adically complete infinitesimal thickening of
$p$
-adically complete infinitesimal thickening of
![]() ${\mathcal{O}}_{C}$
of order
${\mathcal{O}}_{C}$
of order
![]() $n-1$
, see [Reference Szamuely and ZábrádiSZ18, 3.13]. The composition
$n-1$
, see [Reference Szamuely and ZábrádiSZ18, 3.13]. The composition
and its kernel is generated by the element
![]() $\unicode[STIX]{x1D711}(\unicode[STIX]{x1D709})=\sum _{i=0}^{p-1}[\unicode[STIX]{x1D716}^{i}]$
.
$\unicode[STIX]{x1D711}(\unicode[STIX]{x1D709})=\sum _{i=0}^{p-1}[\unicode[STIX]{x1D716}^{i}]$
.
Due to the nature of our
![]() $C$
(see §1.5), the ring
$C$
(see §1.5), the ring
![]() ${\mathcal{O}}_{C}/p$
is a
${\mathcal{O}}_{C}/p$
is a
![]() $k$
-algebra, so
$k$
-algebra, so
![]() $A_{\text{inf}}$
is a
$A_{\text{inf}}$
is a
![]() $W(k)$
-algebra.
$W(k)$
-algebra.
2.2 The object
 $A\unicode[STIX]{x1D6FA}_{\mathfrak{X}}$
$A\unicode[STIX]{x1D6FA}_{\mathfrak{X}}$
The operations that define
![]() ${\mathcal{O}}_{C}^{\flat }$
and
${\mathcal{O}}_{C}^{\flat }$
and
![]() $A_{\text{inf}}$
make sense on the proétale site
$A_{\text{inf}}$
make sense on the proétale site
![]() $(\mathfrak{X}_{C}^{\text{ad}})_{\text{pro}\acute{\text{e}}\text{t}}$
: namely, as in [Reference ScholzeSch13a, 4.1, 5.10, and 6.1], we have the integral completed structure sheaf
$(\mathfrak{X}_{C}^{\text{ad}})_{\text{pro}\acute{\text{e}}\text{t}}$
: namely, as in [Reference ScholzeSch13a, 4.1, 5.10, and 6.1], we have the integral completed structure sheaf
and the basic period sheaf
For brevity, we often denote these sheaves simply by
![]() $\widehat{{\mathcal{O}}}^{+}$
,
$\widehat{{\mathcal{O}}}^{+}$
,
![]() $\widehat{{\mathcal{O}}}^{+,\,\flat }$
, and
$\widehat{{\mathcal{O}}}^{+,\,\flat }$
, and
![]() $\mathbb{A}_{\text{inf}}$
. Affinoid perfectoids form a basis for
$\mathbb{A}_{\text{inf}}$
. Affinoid perfectoids form a basis for
![]() $(\mathfrak{X}_{C}^{\text{ad}})_{\text{pro}\acute{\text{e}}\text{t}}$
(see [Reference ScholzeSch13a, 4.7]) and the construction of the map
$(\mathfrak{X}_{C}^{\text{ad}})_{\text{pro}\acute{\text{e}}\text{t}}$
(see [Reference ScholzeSch13a, 4.7]) and the construction of the map
![]() $\unicode[STIX]{x1D703}$
of (2.1.3) makes sense for any perfectoid
$\unicode[STIX]{x1D703}$
of (2.1.3) makes sense for any perfectoid
![]() ${\mathcal{O}}_{C}$
-algebra (see [Reference Bhatt, Morrow and ScholzeBMS18, §3]). In particular,
${\mathcal{O}}_{C}$
-algebra (see [Reference Bhatt, Morrow and ScholzeBMS18, §3]). In particular,
![]() $\mathbb{A}_{\text{inf},\,\mathfrak{X}_{C}^{\text{ad}}}$
comes equipped with the map
$\mathbb{A}_{\text{inf},\,\mathfrak{X}_{C}^{\text{ad}}}$
comes equipped with the map
which, by construction, is compatible with the map
![]() $\unicode[STIX]{x1D703}:A_{\text{inf}}\rightarrow {\mathcal{O}}_{C}$
, intertwines the Witt vector Frobenius
$\unicode[STIX]{x1D703}:A_{\text{inf}}\rightarrow {\mathcal{O}}_{C}$
, intertwines the Witt vector Frobenius
![]() $\unicode[STIX]{x1D711}$
of
$\unicode[STIX]{x1D711}$
of
![]() $\mathbb{A}_{ inf,\,\mathfrak{X}_{C}^{\text{ad}}}$
with the absolute Frobenius of
$\mathbb{A}_{ inf,\,\mathfrak{X}_{C}^{\text{ad}}}$
with the absolute Frobenius of
![]() $\widehat{{\mathcal{O}}}_{\mathfrak{ X}_{C}^{\text{ad}}}^{+}/p$
, and, by [Reference ScholzeSch13a, 6.3 and 6.5], is surjective with
$\widehat{{\mathcal{O}}}_{\mathfrak{ X}_{C}^{\text{ad}}}^{+}/p$
, and, by [Reference ScholzeSch13a, 6.3 and 6.5], is surjective with
![]() $\operatorname{Ker}(\unicode[STIX]{x1D703}_{\mathfrak{ X}_{C}^{\text{ad}}})=\unicode[STIX]{x1D709}\,\cdot \,\mathbb{A}_{\text{inf},\,\mathfrak{X}_{C}^{\text{ad}}}$
(in addition,
$\operatorname{Ker}(\unicode[STIX]{x1D703}_{\mathfrak{ X}_{C}^{\text{ad}}})=\unicode[STIX]{x1D709}\,\cdot \,\mathbb{A}_{\text{inf},\,\mathfrak{X}_{C}^{\text{ad}}}$
(in addition,
![]() $\unicode[STIX]{x1D709}$
is not a zero divisor in
$\unicode[STIX]{x1D709}$
is not a zero divisor in
![]() $\mathbb{A}_{\text{inf},\,\mathfrak{X}_{C}^{\text{ad}}}$
).
$\mathbb{A}_{\text{inf},\,\mathfrak{X}_{C}^{\text{ad}}}$
).
The key object that we are going to study in this paper is
where the décalage functor
![]() $L\unicode[STIX]{x1D702}$
of [Reference Bhatt, Morrow and ScholzeBMS18, §6] is formed with respect to the ideal
$L\unicode[STIX]{x1D702}$
of [Reference Bhatt, Morrow and ScholzeBMS18, §6] is formed with respect to the ideal
![]() $(\unicode[STIX]{x1D707})$
of the constant sheaf
$(\unicode[STIX]{x1D707})$
of the constant sheaf
![]() $A_{\text{inf}}$
of
$A_{\text{inf}}$
of
![]() $\mathfrak{X}_{\acute{\text{e}}\text{t}}$
(the definition of
$\mathfrak{X}_{\acute{\text{e}}\text{t}}$
(the definition of
![]() $L\unicode[STIX]{x1D702}_{(\unicode[STIX]{x1D707})}$
builds on the formula (1.7.3) for
$L\unicode[STIX]{x1D702}_{(\unicode[STIX]{x1D707})}$
builds on the formula (1.7.3) for
![]() $\unicode[STIX]{x1D702}_{(\unicode[STIX]{x1D707})}$
). The formula (2.2.3) may also be executed with the Zariski site
$\unicode[STIX]{x1D702}_{(\unicode[STIX]{x1D707})}$
). The formula (2.2.3) may also be executed with the Zariski site
![]() $\mathfrak{X}_{\text{Zar}}$
as the target of
$\mathfrak{X}_{\text{Zar}}$
as the target of
![]() $\unicode[STIX]{x1D708}$
, and it then defines the object
$\unicode[STIX]{x1D708}$
, and it then defines the object
which is the
![]() $A\unicode[STIX]{x1D6FA}_{\mathfrak{X}}$
that was used in [Reference Bhatt, Morrow and ScholzeBMS18]. We will only use
$A\unicode[STIX]{x1D6FA}_{\mathfrak{X}}$
that was used in [Reference Bhatt, Morrow and ScholzeBMS18]. We will only use
![]() $A\unicode[STIX]{x1D6FA}_{\mathfrak{X}_{\text{Zar}}}$
in Corollary 4.21 (and in some results that lead to it) for comparison with
$A\unicode[STIX]{x1D6FA}_{\mathfrak{X}_{\text{Zar}}}$
in Corollary 4.21 (and in some results that lead to it) for comparison with
![]() $A\unicode[STIX]{x1D6FA}_{\mathfrak{X}}$
.
$A\unicode[STIX]{x1D6FA}_{\mathfrak{X}}$
.
Since
![]() $\unicode[STIX]{x1D711}(\unicode[STIX]{x1D707})=\unicode[STIX]{x1D711}(\unicode[STIX]{x1D709})\unicode[STIX]{x1D707}$
, by [Reference Bhatt, Morrow and ScholzeBMS18, 6.11], we have
$\unicode[STIX]{x1D711}(\unicode[STIX]{x1D707})=\unicode[STIX]{x1D711}(\unicode[STIX]{x1D709})\unicode[STIX]{x1D707}$
, by [Reference Bhatt, Morrow and ScholzeBMS18, 6.11], we have
![]() $L\unicode[STIX]{x1D702}_{(\unicode[STIX]{x1D711}(\unicode[STIX]{x1D707}))}\cong L\unicode[STIX]{x1D702}_{(\unicode[STIX]{x1D711}(\unicode[STIX]{x1D709}))}\circ L\unicode[STIX]{x1D702}_{(\unicode[STIX]{x1D707})}$
, so the Frobenius automorphism of
$L\unicode[STIX]{x1D702}_{(\unicode[STIX]{x1D711}(\unicode[STIX]{x1D707}))}\cong L\unicode[STIX]{x1D702}_{(\unicode[STIX]{x1D711}(\unicode[STIX]{x1D709}))}\circ L\unicode[STIX]{x1D702}_{(\unicode[STIX]{x1D707})}$
, so the Frobenius automorphism of
![]() $\mathbb{A}_{\text{inf},\,\mathfrak{X}_{C}^{\text{ad}}}$
gives the Frobenius morphism
$\mathbb{A}_{\text{inf},\,\mathfrak{X}_{C}^{\text{ad}}}$
gives the Frobenius morphism
which, by [Reference Bhatt, Morrow and ScholzeBMS18, 6.14], induces an isomorphism
In addition, by loc. cit., we also have
so a result of Scholze [Reference Bhatt, Morrow and ScholzeBMS18, 5.6] supplies the following relation to integral
![]() $p$
-adic étale cohomology.
$p$
-adic étale cohomology.
Theorem 2.3. If
![]() $\mathfrak{X}$
is proper over
$\mathfrak{X}$
is proper over
![]() ${\mathcal{O}}_{C}$
, then there is an identification
${\mathcal{O}}_{C}$
, then there is an identification
In broad strokes, the proof of Theorem 2.3 given in [Reference Bhatt, Morrow and ScholzeBMS18, 5.6] goes as follows: one considers the map
induced by the inclusion
![]() $A_{\text{inf}}{\hookrightarrow}\mathbb{A}_{\text{inf},\,\mathfrak{X}_{C}^{\text{ad}}}$
and deduces from the almost purity theorem with, for instance, Lemma 3.17 below that the ideal
$A_{\text{inf}}{\hookrightarrow}\mathbb{A}_{\text{inf},\,\mathfrak{X}_{C}^{\text{ad}}}$
and deduces from the almost purity theorem with, for instance, Lemma 3.17 below that the ideal
kills the cohomology of its cone. Since
![]() $\unicode[STIX]{x1D707}$
lies in
$\unicode[STIX]{x1D707}$
lies in
![]() $W(\mathfrak{m}^{\flat })$
and we have the identification (2.2.7), it follows that the map (2.3.2) induces the identification (2.3.1).
$W(\mathfrak{m}^{\flat })$
and we have the identification (2.2.7), it follows that the map (2.3.2) induces the identification (2.3.1).
Remark 2.4. In practice,
![]() $\mathfrak{X}$
often arises as the formal
$\mathfrak{X}$
often arises as the formal
![]() $p$
-adic completion of a proper, finitely presented
$p$
-adic completion of a proper, finitely presented
![]() ${\mathcal{O}}_{C}$
-scheme
${\mathcal{O}}_{C}$
-scheme
![]() ${\mathcal{X}}$
. In this situation,
${\mathcal{X}}$
. In this situation,
![]() $\mathfrak{X}_{C}^{\text{ad}}$
agrees with the adic space associated to
$\mathfrak{X}_{C}^{\text{ad}}$
agrees with the adic space associated to
![]() ${\mathcal{X}}_{C}$
(see [Reference ConradCon99, 5.3.1 4.], [Reference HuberHub94, 4.6(i)], and [Reference HuberHub96, 1.9.2 ii)]) and, by [Reference HuberHub96, 3.7.2], we have
${\mathcal{X}}_{C}$
(see [Reference ConradCon99, 5.3.1 4.], [Reference HuberHub94, 4.6(i)], and [Reference HuberHub96, 1.9.2 ii)]) and, by [Reference HuberHub96, 3.7.2], we have
3 The local analysis of
 $A\unicode[STIX]{x1D6FA}_{\mathfrak{X}}$
$A\unicode[STIX]{x1D6FA}_{\mathfrak{X}}$
Even though the definition of the object
![]() $A\unicode[STIX]{x1D6FA}_{\mathfrak{X}}$
given in (2.2.3) is global, the key computations that will eventually relate it to the logarithmic de Rham and crystalline cohomologies are local and are presented in this section. Under the assumption that
$A\unicode[STIX]{x1D6FA}_{\mathfrak{X}}$
given in (2.2.3) is global, the key computations that will eventually relate it to the logarithmic de Rham and crystalline cohomologies are local and are presented in this section. Under the assumption that
![]() $\mathfrak{X}$
has a coordinate morphism as in (1.5.1) (or (3.1.1) below), their basic goal is to express the cohomology of the proétale sheaf
$\mathfrak{X}$
has a coordinate morphism as in (1.5.1) (or (3.1.1) below), their basic goal is to express the cohomology of the proétale sheaf
![]() $\mathbb{A}_{ inf,\,\mathfrak{X}_{C}^{\text{ad}}}$
, at least after applying
$\mathbb{A}_{ inf,\,\mathfrak{X}_{C}^{\text{ad}}}$
, at least after applying
![]() $L\unicode[STIX]{x1D702}_{(\unicode[STIX]{x1D707})}$
, in terms of continuous group cohomology formed using an explicit perfectoid proétale cover
$L\unicode[STIX]{x1D702}_{(\unicode[STIX]{x1D707})}$
, in terms of continuous group cohomology formed using an explicit perfectoid proétale cover
![]() $\mathfrak{X}_{C,\,\infty }^{\text{ad}}$
of
$\mathfrak{X}_{C,\,\infty }^{\text{ad}}$
of
![]() $\mathfrak{X}_{C}^{\text{ad}}$
(see Theorem 3.20). The basic relation of this sort is supplied by the almost purity theorem, so the key point is to explicate the appearing group cohomology modules well enough in order to eliminate the ‘almost’ ambiguities inherent in this theorem with the help of Lemma 3.18 below that comes from [Reference BhattBha18]. We first carry out this program for the simpler sheaf
$\mathfrak{X}_{C}^{\text{ad}}$
(see Theorem 3.20). The basic relation of this sort is supplied by the almost purity theorem, so the key point is to explicate the appearing group cohomology modules well enough in order to eliminate the ‘almost’ ambiguities inherent in this theorem with the help of Lemma 3.18 below that comes from [Reference BhattBha18]. We first carry out this program for the simpler sheaf
![]() $\widehat{{\mathcal{O}}}_{\mathfrak{ X}_{C}^{\text{ad}}}^{+}$
, and then build on this case to address
$\widehat{{\mathcal{O}}}_{\mathfrak{ X}_{C}^{\text{ad}}}^{+}$
, and then build on this case to address
![]() $\mathbb{A}_{ inf,\,\mathfrak{X}_{C}^{\text{ad}}}$
.
$\mathbb{A}_{ inf,\,\mathfrak{X}_{C}^{\text{ad}}}$
.
In comparison with the local analysis carried out in the smooth case in [Reference Bhatt, Morrow and ScholzeBMS18], one complication is that the perfectoid cover of
![]() $\mathfrak{X}$
that gives rise to
$\mathfrak{X}$
that gives rise to
![]() $\mathfrak{X}_{C,\,\infty }^{\text{ad}}$
is not flat over the singular points of
$\mathfrak{X}_{C,\,\infty }^{\text{ad}}$
is not flat over the singular points of
![]() $\mathfrak{X}_{k}$
. This makes it difficult to transfer various arguments with ‘
$\mathfrak{X}_{k}$
. This makes it difficult to transfer various arguments with ‘
![]() $q$
-de Rham complexes’ across the coordinate morphism (3.1.1). In fact, we avoid
$q$
-de Rham complexes’ across the coordinate morphism (3.1.1). In fact, we avoid
![]() $q$
-de Rham complexes altogether and instead phrase the intermediate steps of the local analysis purely in terms of continuous group cohomology modules.
$q$
-de Rham complexes altogether and instead phrase the intermediate steps of the local analysis purely in terms of continuous group cohomology modules.
3.1 The local setup
We assume throughout §3 that
![]() $\mathfrak{X}=\operatorname{Spf}(R)$
and for some
$\mathfrak{X}=\operatorname{Spf}(R)$
and for some
![]() $d\geqslant 0$
, some
$d\geqslant 0$
, some
![]() $0\leqslant r\leqslant d$
, and some
$0\leqslant r\leqslant d$
, and some
![]() $q\in \mathbb{Q}_{{>}0}$
, there is an étale
$q\in \mathbb{Q}_{{>}0}$
, there is an étale
![]() $\operatorname{Spf}({\mathcal{O}}_{C})$
-morphism as in (1.5.1):
$\operatorname{Spf}({\mathcal{O}}_{C})$
-morphism as in (1.5.1):
Due to our assumptions from §1.5, a general
![]() $\mathfrak{X}$
is of this form on a basis for its étale topology.
$\mathfrak{X}$
is of this form on a basis for its étale topology.
3.2 The perfectoid cover
 $\mathfrak{X}_{C,\,\infty }^{\text{ad}}$
$\mathfrak{X}_{C,\,\infty }^{\text{ad}}$
For each
![]() $m\geqslant 0$
, we consider the
$m\geqslant 0$
, we consider the
![]() $R^{\Box }$
-algebra
$R^{\Box }$
-algebra
where, as always unless mentioned otherwise (see §1.7), the completion is
![]() $p$
-adic. Explicitly, we have the
$p$
-adic. Explicitly, we have the
![]() $p$
-adically completed direct sum decomposition
$p$
-adically completed direct sum decomposition
which shows that
![]() $R_{\infty }^{\Box }$
is perfectoid (see §1.7) and that, for each
$R_{\infty }^{\Box }$
is perfectoid (see §1.7) and that, for each
![]() $m\geqslant 0$
, the map
$m\geqslant 0$
, the map
![]() $R_{m}^{\Box }\rightarrow R_{\infty }^{\Box }$
is an inclusion of an
$R_{m}^{\Box }\rightarrow R_{\infty }^{\Box }$
is an inclusion of an
![]() $R_{m}^{\Box }$
-module direct summand composed of those summands
$R_{m}^{\Box }$
-module direct summand composed of those summands
![]() ${\mathcal{O}}_{C}\,\cdot \,t_{0}^{a_{0}}\cdots t_{d}^{a_{d}}$
of (3.2.1) for which
${\mathcal{O}}_{C}\,\cdot \,t_{0}^{a_{0}}\cdots t_{d}^{a_{d}}$
of (3.2.1) for which
![]() $p^{m}a_{j}\in \mathbb{Z}$
for all
$p^{m}a_{j}\in \mathbb{Z}$
for all
![]() $j$
.
$j$
.
The corresponding
![]() $R$
-algebras are
$R$
-algebras are
Each
![]() $R_{m}$
(respectively,
$R_{m}$
(respectively,
![]() $R_{\infty }$
) is a
$R_{\infty }$
) is a
![]() $p$
-torsion-free
$p$
-torsion-free
![]() $p$
-adically formally étale
$p$
-adically formally étale
![]() $R_{m}^{\Box }$
-algebra (respectively,
$R_{m}^{\Box }$
-algebra (respectively,
![]() $R_{\infty }^{\Box }$
-algebra). In particular,
$R_{\infty }^{\Box }$
-algebra). In particular,
![]() $R_{\infty }$
is perfectoid (see §1.7). By [Reference Gabber and RameroGR03, 7.1.6(ii)], each
$R_{\infty }$
is perfectoid (see §1.7). By [Reference Gabber and RameroGR03, 7.1.6(ii)], each
![]() $R_{m}$
is
$R_{m}$
is
![]() $p$
-adically complete.
$p$
-adically complete.
The summands in (3.2.1) with
![]() $a_{j}\not \in \mathbb{Z}$
for some
$a_{j}\not \in \mathbb{Z}$
for some
![]() $0\leqslant j\leqslant d$
comprise an
$0\leqslant j\leqslant d$
comprise an
![]() $R^{\Box }$
-submodule
$R^{\Box }$
-submodule
![]() $M_{\infty }^{\Box }$
of
$M_{\infty }^{\Box }$
of
![]() $R_{\infty }^{\Box }$
, and we set
$R_{\infty }^{\Box }$
, and we set
![]() $M_{\infty }:=R\,\widehat{\otimes }_{R^{\Box }}\,M_{\infty }^{\Box }$
. Thus, we have the
$M_{\infty }:=R\,\widehat{\otimes }_{R^{\Box }}\,M_{\infty }^{\Box }$
. Thus, we have the
![]() $R^{\Box }$
-module (respectively,
$R^{\Box }$
-module (respectively,
![]() $R$
-module) decomposition
$R$
-module) decomposition
The profinite group
acts
![]() $R^{\Box }$
-linearly on
$R^{\Box }$
-linearly on
![]() $R_{m}^{\Box }$
by scaling each
$R_{m}^{\Box }$
by scaling each
![]() $t_{j}^{1/p^{m}}$
by the
$t_{j}^{1/p^{m}}$
by the
![]() $\unicode[STIX]{x1D707}_{p^{m}}$
-component of
$\unicode[STIX]{x1D707}_{p^{m}}$
-component of
![]() $\unicode[STIX]{x1D716}_{j}$
. The induced actions of
$\unicode[STIX]{x1D716}_{j}$
. The induced actions of
![]() $\unicode[STIX]{x1D6E5}$
on
$\unicode[STIX]{x1D6E5}$
on
![]() $R_{\infty }^{\Box }$
and
$R_{\infty }^{\Box }$
and
![]() $R_{\infty }$
are continuous, compatible, and preserve the decompositions (3.2.1) and (3.2.2). In terms of the element
$R_{\infty }$
are continuous, compatible, and preserve the decompositions (3.2.1) and (3.2.2). In terms of the element
![]() $\unicode[STIX]{x1D716}$
fixed in §2.1,
$\unicode[STIX]{x1D716}$
fixed in §2.1,
![]() $\unicode[STIX]{x1D6E5}$
is topologically freely generated by the following
$\unicode[STIX]{x1D6E5}$
is topologically freely generated by the following
![]() $d$
elements:
$d$
elements:
After inverting
![]() $p$
, for each
$p$
, for each
![]() $m\geqslant 0$
, we have
$m\geqslant 0$
, we have
so
![]() $R_{m}^{\Box }[\frac{1}{p}]$
is the
$R_{m}^{\Box }[\frac{1}{p}]$
is the
![]() $R^{\Box }[\frac{1}{p}]$
-algebra obtained by adjoining the
$R^{\Box }[\frac{1}{p}]$
-algebra obtained by adjoining the
![]() $(p^{m})^{\text{th}}$
roots of
$(p^{m})^{\text{th}}$
roots of
![]() $t_{1},\ldots ,t_{d}\in (R^{\Box }[\frac{1}{p}])^{\times }$
, and hence is finite étale over
$t_{1},\ldots ,t_{d}\in (R^{\Box }[\frac{1}{p}])^{\times }$
, and hence is finite étale over
![]() $R^{\Box }[\frac{1}{p}]$
. Therefore,
$R^{\Box }[\frac{1}{p}]$
. Therefore,
![]() $\mathop{\varinjlim }\nolimits_{m}(R_{m}^{\Box }[\frac{1}{p}])$
is a pro-(finite étale)
$\mathop{\varinjlim }\nolimits_{m}(R_{m}^{\Box }[\frac{1}{p}])$
is a pro-(finite étale)
![]() $\unicode[STIX]{x1D6E5}$
-cover of
$\unicode[STIX]{x1D6E5}$
-cover of
![]() $R^{\Box }[\frac{1}{p}]$
. The explicit description (3.2.1) implies that
$R^{\Box }[\frac{1}{p}]$
. The explicit description (3.2.1) implies that
![]() $R_{m}^{\Box }=(R_{m}^{\Box }[\frac{1}{p}])^{\circ }$
, so the pro-object
$R_{m}^{\Box }=(R_{m}^{\Box }[\frac{1}{p}])^{\circ }$
, so the pro-object
is an affinoid perfectoid pro-(finite étale)
![]() $\unicode[STIX]{x1D6E5}$
-cover of the adic generic fiber
$\unicode[STIX]{x1D6E5}$
-cover of the adic generic fiber
![]() $(\mathfrak{X}^{\Box })_{C}^{\text{ad}}$
of
$(\mathfrak{X}^{\Box })_{C}^{\text{ad}}$
of
![]() $\operatorname{Spf}(R^{\Box })$
; in particular,
$\operatorname{Spf}(R^{\Box })$
; in particular,
![]() $(\mathfrak{X}^{\Box })_{C,\,\infty }^{\text{ad}}$
is an affinoid perfectoid object of the proétale site
$(\mathfrak{X}^{\Box })_{C,\,\infty }^{\text{ad}}$
is an affinoid perfectoid object of the proétale site
![]() $((\mathfrak{X}^{\Box })_{C}^{\text{ad}})_{\text{pro}\acute{\text{e}}\text{t}}$
. Consequently, the
$((\mathfrak{X}^{\Box })_{C}^{\text{ad}})_{\text{pro}\acute{\text{e}}\text{t}}$
. Consequently, the
![]() $\mathfrak{X}_{C}^{\text{ad}}$
-base change of
$\mathfrak{X}_{C}^{\text{ad}}$
-base change of
![]() $(\mathfrak{X}^{\Box })_{C,\,\infty }^{\text{ad}}$
, namely, the tower
$(\mathfrak{X}^{\Box })_{C,\,\infty }^{\text{ad}}$
, namely, the tower
is an affinoid perfectoid pro-(finite étale)
![]() $\unicode[STIX]{x1D6E5}$
-cover of
$\unicode[STIX]{x1D6E5}$
-cover of
![]() $\mathfrak{X}_{C}^{\text{ad}}$
, so, in particular, is an affinoid perfectoid object of
$\mathfrak{X}_{C}^{\text{ad}}$
, so, in particular, is an affinoid perfectoid object of
![]() $(\mathfrak{X}_{C}^{\text{ad}})_{\text{pro}\acute{\text{e}}\text{t}}$
.
$(\mathfrak{X}_{C}^{\text{ad}})_{\text{pro}\acute{\text{e}}\text{t}}$
.
By [Reference ScholzeSch13a, 4.10(iii)], the value on
![]() $\mathfrak{X}_{C,\,\infty }^{\text{ad}}$
of the sheaf
$\mathfrak{X}_{C,\,\infty }^{\text{ad}}$
of the sheaf
![]() $\widehat{{\mathcal{O}}}_{\mathfrak{ X}_{C}^{\text{ad}}}^{+}$
reviewed in (2.2.1) is
$\widehat{{\mathcal{O}}}_{\mathfrak{ X}_{C}^{\text{ad}}}^{+}$
reviewed in (2.2.1) is
![]() $R_{\infty }$
.
$R_{\infty }$
.
3.3 The cohomology of
 $\widehat{{\mathcal{O}}}^{+}$
and continuous group cohomology
$\widehat{{\mathcal{O}}}^{+}$
and continuous group cohomology
By [Reference ScholzeSch13a, 3.5, 3.7(iii) and its proof, 6.6] (see also [Reference ScholzeSch16]), the Čech complex of the sheaf
![]() $\widehat{{\mathcal{O}}}_{\mathfrak{ X}_{C}^{\text{ad}}}^{+}$
with respect to the pro-(finite étale) affinoid perfectoid cover
$\widehat{{\mathcal{O}}}_{\mathfrak{ X}_{C}^{\text{ad}}}^{+}$
with respect to the pro-(finite étale) affinoid perfectoid cover
is identified with the continuous cochain complex
![]() $R\unicode[STIX]{x1D6E4}_{\text{cont}}(\unicode[STIX]{x1D6E5},R_{\infty })$
. In particular, by using [SP, 01GY], we obtain the edge map to the proétale cohomology of
$R\unicode[STIX]{x1D6E4}_{\text{cont}}(\unicode[STIX]{x1D6E5},R_{\infty })$
. In particular, by using [SP, 01GY], we obtain the edge map to the proétale cohomology of
![]() $\widehat{{\mathcal{O}}}_{\mathfrak{ X}_{C}^{\text{ad}}}^{+}$
:
$\widehat{{\mathcal{O}}}_{\mathfrak{ X}_{C}^{\text{ad}}}^{+}$
:
which on the level of cohomology is described by the Cartan–Leray spectral sequence (see [SP, 01GY] or [Reference Artin, Grothendieck and VerdierSGA 4II
, V.3.3]). By the almost purity theorem [Reference ScholzeSch13a, 4.10 (v)], the maximal ideal
![]() $\mathfrak{m}\subset {\mathcal{O}}_{C}$
kills the cohomology groups of
$\mathfrak{m}\subset {\mathcal{O}}_{C}$
kills the cohomology groups of
![]() $\operatorname{Cone}(e)$
.
$\operatorname{Cone}(e)$
.
We will show in Theorem 3.9 that
![]() $L\unicode[STIX]{x1D702}_{(\unicode[STIX]{x1D701}_{p}-1)}(e)$
is an isomorphism, so that
$L\unicode[STIX]{x1D702}_{(\unicode[STIX]{x1D701}_{p}-1)}(e)$
is an isomorphism, so that
is computed in terms of continuous group cohomology. For this, we will use the following lemma.
Lemma 3.4 [Reference Bhatt, Morrow and ScholzeBMS18, 8.11(i)].
An
![]() ${\mathcal{O}}_{C}$
-module map
${\mathcal{O}}_{C}$
-module map
![]() $f:M\rightarrow M^{\prime }$
with
$f:M\rightarrow M^{\prime }$
with
and both
![]() $\operatorname{Ker}f$
and
$\operatorname{Ker}f$
and
![]() $\operatorname{Coker}f$
killed by
$\operatorname{Coker}f$
killed by
![]() $\mathfrak{m}$
induces an isomorphism
$\mathfrak{m}$
induces an isomorphism
In order to apply Lemma 3.4, we will check in Proposition 3.8 that the cohomology modules
![]() $H_{\text{cont}}^{i}(\unicode[STIX]{x1D6E5},R_{\infty })$
have no nonzero
$H_{\text{cont}}^{i}(\unicode[STIX]{x1D6E5},R_{\infty })$
have no nonzero
![]() $\mathfrak{m}$
-torsion. This will use the following general lemmas.
$\mathfrak{m}$
-torsion. This will use the following general lemmas.
Lemma 3.5. For an inclusion
![]() $\mathfrak{o}\subset \mathfrak{O}$
of a discrete valuation ring into a nondiscrete valuation ring of rank
$\mathfrak{o}\subset \mathfrak{O}$
of a discrete valuation ring into a nondiscrete valuation ring of rank
![]() $1$
, if
$1$
, if
![]() $N$
is an
$N$
is an
![]() $\mathfrak{o}$
-module and
$\mathfrak{o}$
-module and
![]() $\mathfrak{M}\subset \mathfrak{O}$
denotes the maximal ideal, then
$\mathfrak{M}\subset \mathfrak{O}$
denotes the maximal ideal, then
![]() $(N\otimes _{\mathfrak{o}}\mathfrak{O})[\mathfrak{M}]=0$
.
$(N\otimes _{\mathfrak{o}}\mathfrak{O})[\mathfrak{M}]=0$
.
Proof. The
![]() $\mathfrak{o}$
-flatness of
$\mathfrak{o}$
-flatness of
![]() $\mathfrak{O}$
reduces us to the case when
$\mathfrak{O}$
reduces us to the case when
![]() $N$
is finitely generated, so it suffices to observe that
$N$
is finitely generated, so it suffices to observe that
![]() $(\mathfrak{O}/(a))[\mathfrak{M}]=0$
whenever
$(\mathfrak{O}/(a))[\mathfrak{M}]=0$
whenever
![]() $a\in \mathfrak{O}$
.◻
$a\in \mathfrak{O}$
.◻
Lemma 3.6. Fix an
![]() $i\in \mathbb{Z}_{{\geqslant}0}$
, let
$i\in \mathbb{Z}_{{\geqslant}0}$
, let
![]() $H$
be a profinite group, let
$H$
be a profinite group, let
![]() $\{M_{j}\}\text{}_{j\in J}$
be
$\{M_{j}\}\text{}_{j\in J}$
be
![]() $p$
-adically complete,
$p$
-adically complete,
![]() $p$
-torsion-free, continuous
$p$
-torsion-free, continuous
![]() $H$
-modules, and suppose that either:
$H$
-modules, and suppose that either:
(i) the group
 $H_{\text{cont}}^{i}(H,M_{j})$
is
$H_{\text{cont}}^{i}(H,M_{j})$
is
 $p$
-torsion free for every
$p$
-torsion free for every
 $j$
; or
$j$
; or(ii) some
 $p^{n}$
kills
$p^{n}$
kills
 $H_{\text{cont}}^{i}(H,M_{j})$
for every
$H_{\text{cont}}^{i}(H,M_{j})$
for every
 $j$
.
$j$
.
Then the following map is injective:
In particular, in the case (i) (respectively, (ii)),
![]() $H_{\text{cont}}^{i}(H,\widehat{\bigoplus }_{j\in J}M_{j})$
is
$H_{\text{cont}}^{i}(H,\widehat{\bigoplus }_{j\in J}M_{j})$
is
![]() $p$
-torsion free (respectively, killed by
$p$
-torsion free (respectively, killed by
![]() $p^{n}$
).
$p^{n}$
).
Proof. Let
![]() $c$
be a continuous
$c$
be a continuous
![]() $(\widehat{\bigoplus }_{j\in J}M_{j})$
-valued
$(\widehat{\bigoplus }_{j\in J}M_{j})$
-valued
![]() $i$
-cocycle that represents an element of the kernel. For each
$i$
-cocycle that represents an element of the kernel. For each
![]() $j$
, let
$j$
, let
![]() $c_{j}$
be the ‘
$c_{j}$
be the ‘
![]() $j$
th coordinate’ of
$j$
th coordinate’ of
![]() $c$
. We discard the
$c$
. We discard the
![]() $j$
with
$j$
with
![]() $c_{j}=0$
and, for each remaining
$c_{j}=0$
and, for each remaining
![]() $j$
, we choose the maximal
$j$
, we choose the maximal
![]() $n_{j}\in \mathbb{Z}_{{\geqslant}0}$
such that
$n_{j}\in \mathbb{Z}_{{\geqslant}0}$
such that
![]() $c_{j}$
is
$c_{j}$
is
![]() $(p^{n_{j}}M_{j})$
-valued, so that the function
$(p^{n_{j}}M_{j})$
-valued, so that the function
![]() $j\mapsto n_{j}$
is finite-to-one. Since each
$j\mapsto n_{j}$
is finite-to-one. Since each
![]() $M_{j}$
is
$M_{j}$
is
![]() $p$
-torsion free, each
$p$
-torsion free, each
![]() $p^{-n_{j}}c_{j}$
is an
$p^{-n_{j}}c_{j}$
is an
![]() $M_{j}$
-valued continuous
$M_{j}$
-valued continuous
![]() $i$
-cocycle.
$i$
-cocycle.
In the case (i), the class of
![]() $p^{-n_{j}}c_{j}$
in
$p^{-n_{j}}c_{j}$
in
![]() $H_{\text{cont}}^{i}(H,M_{j})$
vanishes, so each
$H_{\text{cont}}^{i}(H,M_{j})$
vanishes, so each
![]() $c_{j}$
is the coboundary of a
$c_{j}$
is the coboundary of a
![]() $(p^{n_{j}}M_{j})$
-valued continuous
$(p^{n_{j}}M_{j})$
-valued continuous
![]() $(i-1)$
-cochain
$(i-1)$
-cochain
![]() $b_{j}$
. In the case (ii),
$b_{j}$
. In the case (ii),
![]() $p^{n}$
kills
$p^{n}$
kills
![]() $H_{\text{cont}}^{i}(H,M_{j})$
, so
$H_{\text{cont}}^{i}(H,M_{j})$
, so
![]() $c_{j}$
is the coboundary of a
$c_{j}$
is the coboundary of a
![]() $(p^{n_{j}-n}M_{j})$
-valued continuous
$(p^{n_{j}-n}M_{j})$
-valued continuous
![]() $(i-1)$
-cochain
$(i-1)$
-cochain
![]() $b_{j}$
whenever
$b_{j}$
whenever
![]() $n_{j}\geqslant n$
.
$n_{j}\geqslant n$
.
In both cases, the
![]() $b_{j}$
exhibit
$b_{j}$
exhibit
![]() $c$
as a continuous coboundary.◻
$c$
as a continuous coboundary.◻
Lemma 3.7 [Reference Bhatt, Morrow and ScholzeBMS18, 7.3(ii)].
Let
![]() $H$
be a profinite group isomorphic to
$H$
be a profinite group isomorphic to
![]() $\mathbb{Z}_{p}^{\oplus d}$
for some
$\mathbb{Z}_{p}^{\oplus d}$
for some
![]() $d>0$
, and let
$d>0$
, and let
![]() $M\cong \mathop{\varprojlim }\nolimits_{n\geqslant 1}M_{n}$
be a continuous
$M\cong \mathop{\varprojlim }\nolimits_{n\geqslant 1}M_{n}$
be a continuous
![]() $H$
-module with each
$H$
-module with each
![]() $M_{n}$
a discrete,
$M_{n}$
a discrete,
![]() $p^{n}$
-torsion, continuous
$p^{n}$
-torsion, continuous
![]() $H$
-module. For any
$H$
-module. For any
![]() $\unicode[STIX]{x1D6FE}_{1},\ldots ,\unicode[STIX]{x1D6FE}_{d}\in H$
that topologically freely generate
$\unicode[STIX]{x1D6FE}_{1},\ldots ,\unicode[STIX]{x1D6FE}_{d}\in H$
that topologically freely generate
![]() $H$
, there is a natural identification
$H$
, there is a natural identification
in the derived category (see §1.7 for the notation).◻
Proposition 3.8. The element
![]() $\unicode[STIX]{x1D701}_{p}-1$
kills the
$\unicode[STIX]{x1D701}_{p}-1$
kills the
![]() ${\mathcal{O}}_{C}$
-modules
${\mathcal{O}}_{C}$
-modules
![]() $H_{\text{cont}}^{i}(\unicode[STIX]{x1D6E5},M_{\infty })$
. Moreover, for each
$H_{\text{cont}}^{i}(\unicode[STIX]{x1D6E5},M_{\infty })$
. Moreover, for each
![]() $b\in {\mathcal{O}}_{C}$
, the
$b\in {\mathcal{O}}_{C}$
, the
![]() ${\mathcal{O}}_{C}$
-modules
${\mathcal{O}}_{C}$
-modules
![]() $R_{\infty }/b$
and
$R_{\infty }/b$
and
![]() $H_{\text{cont}}^{i}(\unicode[STIX]{x1D6E5},R_{\infty }/b)$
have no nonzero
$H_{\text{cont}}^{i}(\unicode[STIX]{x1D6E5},R_{\infty }/b)$
have no nonzero
![]() $\mathfrak{m}$
-torsion.
$\mathfrak{m}$
-torsion.
Proof. Let
![]() $S:={\mathcal{O}}_{C}\,\cdot \,t_{0}^{a_{0}}\cdots t_{d}^{a_{d}}$
be a summand of (3.2.1). By Lemma 3.7, the
$S:={\mathcal{O}}_{C}\,\cdot \,t_{0}^{a_{0}}\cdots t_{d}^{a_{d}}$
be a summand of (3.2.1). By Lemma 3.7, the
![]() ${\mathcal{O}}_{C}$
-module
${\mathcal{O}}_{C}$
-module
![]() $H_{\text{cont}}^{i}(\unicode[STIX]{x1D6E5},S)$
is the
$H_{\text{cont}}^{i}(\unicode[STIX]{x1D6E5},S)$
is the
![]() $i$
th cohomology of the
$i$
th cohomology of the
![]() ${\mathcal{O}}_{C}$
-tensor product of
${\mathcal{O}}_{C}$
-tensor product of
![]() $d$
complexes of the form
$d$
complexes of the form
![]() ${\mathcal{O}}_{C}\xrightarrow[{}]{\unicode[STIX]{x1D701}-1}{\mathcal{O}}_{C}$
for suitable
${\mathcal{O}}_{C}\xrightarrow[{}]{\unicode[STIX]{x1D701}-1}{\mathcal{O}}_{C}$
for suitable
![]() $p$
-power roots of unity
$p$
-power roots of unity
![]() $\unicode[STIX]{x1D701}$
. Moreover, since the
$\unicode[STIX]{x1D701}$
. Moreover, since the
![]() $d$
complexes may be defined over some discrete valuation subring of
$d$
complexes may be defined over some discrete valuation subring of
![]() ${\mathcal{O}}_{C}$
, Lemma 3.5 ensures that
${\mathcal{O}}_{C}$
, Lemma 3.5 ensures that
If
![]() $S$
contributes to
$S$
contributes to
![]() $M_{\infty }$
, that is, if
$M_{\infty }$
, that is, if
![]() $a_{j}\not \in \mathbb{Z}$
for some
$a_{j}\not \in \mathbb{Z}$
for some
![]() $j$
, then some
$j$
, then some
![]() $\unicode[STIX]{x1D701}$
is not
$\unicode[STIX]{x1D701}$
is not
![]() $1$
, and the corresponding factor complex is quasi-isomorphic to
$1$
, and the corresponding factor complex is quasi-isomorphic to
![]() ${\mathcal{O}}_{C}/(\unicode[STIX]{x1D701}-1)$
. Thus, in this case,
${\mathcal{O}}_{C}/(\unicode[STIX]{x1D701}-1)$
. Thus, in this case,
For
![]() $m>0$
, let
$m>0$
, let
![]() $M_{m}^{\Box }$
denote the
$M_{m}^{\Box }$
denote the
![]() $p$
-adically completed direct sum of those summands
$p$
-adically completed direct sum of those summands
![]() ${\mathcal{O}}_{C}\,\cdot \,t_{0}^{a_{0}}\cdots t_{d}^{a_{d}}$
of (3.2.1) for which
${\mathcal{O}}_{C}\,\cdot \,t_{0}^{a_{0}}\cdots t_{d}^{a_{d}}$
of (3.2.1) for which
![]() $m$
is the smallest nonnegative integer with
$m$
is the smallest nonnegative integer with
![]() $p^{m}\,\cdot \,(a_{0},\ldots ,a_{d})\in \mathbb{Z}^{\oplus (d+1)}$
. Lemma 3.6 and (3.8.1)–(3.8.2) imply that the
$p^{m}\,\cdot \,(a_{0},\ldots ,a_{d})\in \mathbb{Z}^{\oplus (d+1)}$
. Lemma 3.6 and (3.8.1)–(3.8.2) imply that the
![]() ${\mathcal{O}}_{C}$
-module
${\mathcal{O}}_{C}$
-module
Since
![]() $R$
is
$R$
is
![]() $R^{\Box }$
-flat and
$R^{\Box }$
-flat and
![]() $R\otimes _{R^{\Box }}M_{m}^{\Box }$
is
$R\otimes _{R^{\Box }}M_{m}^{\Box }$
is
![]() $p$
-adically complete (see §§1.5 and 3.2), Lemma 3.7 gives
$p$
-adically complete (see §§1.5 and 3.2), Lemma 3.7 gives
Since
![]() $M_{\infty }\cong \widehat{\bigoplus }_{m}(R\otimes _{R^{\Box }}M_{m}^{\Box })$
, equations (3.8.3)–(3.8.4) and Lemma 3.6 imply that
$M_{\infty }\cong \widehat{\bigoplus }_{m}(R\otimes _{R^{\Box }}M_{m}^{\Box })$
, equations (3.8.3)–(3.8.4) and Lemma 3.6 imply that
![]() $\unicode[STIX]{x1D701}_{p}-1$
kills
$\unicode[STIX]{x1D701}_{p}-1$
kills
![]() $H_{\text{cont}}^{i}(\unicode[STIX]{x1D6E5},M_{\infty })$
.
$H_{\text{cont}}^{i}(\unicode[STIX]{x1D6E5},M_{\infty })$
.
Since
![]() $R_{\infty }/b$
is
$R_{\infty }/b$
is
![]() $p$
-adically complete and each of the summands of the decomposition
$p$
-adically complete and each of the summands of the decomposition
may be defined over a suitably large discrete valuation subring of
![]() ${\mathcal{O}}_{C}$
, Lemma 3.5 ensures that
${\mathcal{O}}_{C}$
, Lemma 3.5 ensures that
![]() $R_{\infty }/b$
has no nonzero
$R_{\infty }/b$
has no nonzero
![]() $\mathfrak{m}$
-torsion. In addition, the
$\mathfrak{m}$
-torsion. In addition, the
![]() $\unicode[STIX]{x1D6E5}$
-action on each summand may be defined over a possibly larger such subring, so, by Lemmas 3.5 and 3.7, in the case
$\unicode[STIX]{x1D6E5}$
-action on each summand may be defined over a possibly larger such subring, so, by Lemmas 3.5 and 3.7, in the case
![]() $b\neq 0$
each
$b\neq 0$
each
This conclusion extends to the case
![]() $b=0$
because the
$b=0$
because the
![]() $(\unicode[STIX]{x1D701}_{p}-1)$
-annihilation of
$(\unicode[STIX]{x1D701}_{p}-1)$
-annihilation of
![]() $H_{\text{cont}}^{i}(\unicode[STIX]{x1D6E5},M_{\infty })$
supplies the injection
$H_{\text{cont}}^{i}(\unicode[STIX]{x1D6E5},M_{\infty })$
supplies the injection
![]() $H_{\text{cont}}^{i}(\unicode[STIX]{x1D6E5},M_{\infty }){\hookrightarrow}H_{\text{cont}}^{i}(\unicode[STIX]{x1D6E5},M_{\infty }/(\unicode[STIX]{x1D701}_{p}-1))$
. It remains to observe that the
$H_{\text{cont}}^{i}(\unicode[STIX]{x1D6E5},M_{\infty }){\hookrightarrow}H_{\text{cont}}^{i}(\unicode[STIX]{x1D6E5},M_{\infty }/(\unicode[STIX]{x1D701}_{p}-1))$
. It remains to observe that the
![]() ${\mathcal{O}}_{C}$
-module
${\mathcal{O}}_{C}$
-module
![]() $H_{\text{cont}}^{i}(\unicode[STIX]{x1D6E5},R/b)$
also has no nonzero
$H_{\text{cont}}^{i}(\unicode[STIX]{x1D6E5},R/b)$
also has no nonzero
![]() $\mathfrak{m}$
-torsion:
$\mathfrak{m}$
-torsion:
![]() $\unicode[STIX]{x1D6E5}$
acts trivially on
$\unicode[STIX]{x1D6E5}$
acts trivially on
![]() $R/b$
, so Lemma 3.7 ensures that
$R/b$
, so Lemma 3.7 ensures that
![]() $H_{\text{cont}}^{i}(\unicode[STIX]{x1D6E5},R/b)$
is a direct sum of copies of
$H_{\text{cont}}^{i}(\unicode[STIX]{x1D6E5},R/b)$
is a direct sum of copies of
![]() $R/b$
.◻
$R/b$
.◻
Theorem 3.9. The edge map
![]() $e$
defined in (3.3.1) induces the isomorphism
$e$
defined in (3.3.1) induces the isomorphism
Proof. Proposition 3.8 ensures that the
![]() ${\mathcal{O}}_{C}$
-modules
${\mathcal{O}}_{C}$
-modules
![]() $H_{\text{cont}}^{i}(\unicode[STIX]{x1D6E5},R_{\infty })$
have no nonzero
$H_{\text{cont}}^{i}(\unicode[STIX]{x1D6E5},R_{\infty })$
have no nonzero
![]() $\mathfrak{m}$
-torsion and that
$\mathfrak{m}$
-torsion and that
Since
![]() $\unicode[STIX]{x1D6E5}$
acts trivially on
$\unicode[STIX]{x1D6E5}$
acts trivially on
![]() $R$
, this last quotient is a finite direct sum of copies of
$R$
, this last quotient is a finite direct sum of copies of
![]() $R$
(see Lemma 3.7), so, by Proposition 3.8, it has no nonzero
$R$
(see Lemma 3.7), so, by Proposition 3.8, it has no nonzero
![]() $\mathfrak{m}$
-torsion. Consequently, since
$\mathfrak{m}$
-torsion. Consequently, since
![]() $\mathfrak{m}$
kills the kernel and the cokernel of each map
$\mathfrak{m}$
kills the kernel and the cokernel of each map
(see §3.3), Lemma 3.4 applies to these maps and gives the desired conclusion. ◻
Remark 3.10. Theorem 3.9 extends as follows: for any profinite group
![]() $\unicode[STIX]{x1D6E5}^{\prime }$
equipped with a continuous surjection
$\unicode[STIX]{x1D6E5}^{\prime }$
equipped with a continuous surjection
![]() $\unicode[STIX]{x1D6E5}^{\prime }{\twoheadrightarrow}\unicode[STIX]{x1D6E5}$
and any pro-(finite étale) affinoid perfectoid
$\unicode[STIX]{x1D6E5}^{\prime }{\twoheadrightarrow}\unicode[STIX]{x1D6E5}$
and any pro-(finite étale) affinoid perfectoid
![]() $\unicode[STIX]{x1D6E5}^{\prime }$
-cover
$\unicode[STIX]{x1D6E5}^{\prime }$
-cover
compatibly with the surjection
![]() $\unicode[STIX]{x1D6E5}^{\prime }{\twoheadrightarrow}\unicode[STIX]{x1D6E5}$
, the edge map
$\unicode[STIX]{x1D6E5}^{\prime }{\twoheadrightarrow}\unicode[STIX]{x1D6E5}$
, the edge map
![]() $e^{\prime }$
defined analogously to (3.3.1) induces the isomorphism
$e^{\prime }$
defined analogously to (3.3.1) induces the isomorphism
Indeed, by the almost purity theorem [Reference ScholzeSch13a, 4.10(v)], the ideal
![]() $\mathfrak{m}$
kills the cohomology of
$\mathfrak{m}$
kills the cohomology of
![]() $\operatorname{Cone}(e^{\prime })$
(in addition to that of
$\operatorname{Cone}(e^{\prime })$
(in addition to that of
![]() $\operatorname{Cone}(e)$
), so the octahedral axiom (see [Reference Beilinson, Bernstein and DeligneBBD82, 1.1.7.1]) ensures that it also kills the cohomology of the cone of the map
$\operatorname{Cone}(e)$
), so the octahedral axiom (see [Reference Beilinson, Bernstein and DeligneBBD82, 1.1.7.1]) ensures that it also kills the cohomology of the cone of the map
![]() $R\unicode[STIX]{x1D6E4}_{\text{cont}}(\unicode[STIX]{x1D6E5},R_{\infty })\rightarrow R\unicode[STIX]{x1D6E4}_{\text{cont}}(\unicode[STIX]{x1D6E5}^{\prime },R_{\infty }^{\prime })$
; Lemma 3.4 then applies to this map and combines with Theorem 3.9 to give the claim.
$R\unicode[STIX]{x1D6E4}_{\text{cont}}(\unicode[STIX]{x1D6E5},R_{\infty })\rightarrow R\unicode[STIX]{x1D6E4}_{\text{cont}}(\unicode[STIX]{x1D6E5}^{\prime },R_{\infty }^{\prime })$
; Lemma 3.4 then applies to this map and combines with Theorem 3.9 to give the claim.
The main goal of this section is an analogue of Theorem 3.9 for the sheaf
![]() $\mathbb{A}_{\text{inf},\,\mathfrak{X}_{C}^{\text{ad}}}$
(see Theorem 3.20). To prepare for it, in §§3.11 and 3.14 we describe the values of the sheaves
$\mathbb{A}_{\text{inf},\,\mathfrak{X}_{C}^{\text{ad}}}$
(see Theorem 3.20). To prepare for it, in §§3.11 and 3.14 we describe the values of the sheaves
![]() $\widehat{{\mathcal{O}}}_{\mathfrak{ X}_{C}^{\text{ad}}}^{+,\,\flat }$
and
$\widehat{{\mathcal{O}}}_{\mathfrak{ X}_{C}^{\text{ad}}}^{+,\,\flat }$
and
![]() $\mathbb{A}_{\text{inf},\,\mathfrak{X}_{C}^{\text{ad}}}$
on
$\mathbb{A}_{\text{inf},\,\mathfrak{X}_{C}^{\text{ad}}}$
on
![]() $\mathfrak{X}_{C,\,\infty }^{\text{ad}}$
.
$\mathfrak{X}_{C,\,\infty }^{\text{ad}}$
.
3.11 The tilt
 $R_{\infty }^{\flat }$
$R_{\infty }^{\flat }$
Thanks to the explicit description (3.2.1) of the perfectoid ring
![]() $R_{\infty }^{\Box }$
, its tilt
$R_{\infty }^{\Box }$
, its tilt
is described explicitly by the identification

where
![]() $x_{i}^{1/p^{m}}$
corresponds to the
$x_{i}^{1/p^{m}}$
corresponds to the
![]() $p$
-power compatible sequence
$p$
-power compatible sequence
![]() $(\ldots ,t_{i}^{1/p^{m+1}},t_{i}^{1/p^{m}})$
of elements of
$(\ldots ,t_{i}^{1/p^{m+1}},t_{i}^{1/p^{m}})$
of elements of
![]() $R_{\infty }^{\Box }$
, the completions are
$R_{\infty }^{\Box }$
, the completions are
![]() $p^{1/p^{\infty }}$
-adic, and the decomposition is as
$p^{1/p^{\infty }}$
-adic, and the decomposition is as
![]() ${\mathcal{O}}_{C}^{\flat }$
-modules. Thus,
${\mathcal{O}}_{C}^{\flat }$
-modules. Thus,
is identified with the
![]() $p^{1/p^{\infty }}$
-adic completion of any lift of the étale
$p^{1/p^{\infty }}$
-adic completion of any lift of the étale
![]() $R_{\infty }^{\Box }/p$
-algebra
$R_{\infty }^{\Box }/p$
-algebra
![]() $R_{\infty }/p$
to an étale
$R_{\infty }/p$
to an étale
![]() $(R_{\infty }^{\Box })^{\flat }$
-algebra (such a lift exists, see [SP, 04D1]). By [Reference ScholzeSch13a, 5.11(i)], the value on
$(R_{\infty }^{\Box })^{\flat }$
-algebra (such a lift exists, see [SP, 04D1]). By [Reference ScholzeSch13a, 5.11(i)], the value on
![]() $\mathfrak{X}_{C,\,\infty }^{\text{ad}}$
of the sheaf
$\mathfrak{X}_{C,\,\infty }^{\text{ad}}$
of the sheaf
![]() $\widehat{{\mathcal{O}}}_{\mathfrak{ X}_{C}^{\text{ad}}}^{+,\,\flat }$
reviewed in (2.2.1) is the ring
$\widehat{{\mathcal{O}}}_{\mathfrak{ X}_{C}^{\text{ad}}}^{+,\,\flat }$
reviewed in (2.2.1) is the ring
![]() $R_{\infty }^{\flat }$
.
$R_{\infty }^{\flat }$
.
By functoriality, the group
![]() $\unicode[STIX]{x1D6E5}$
acts continuously and
$\unicode[STIX]{x1D6E5}$
acts continuously and
![]() ${\mathcal{O}}_{C}^{\flat }$
-linearly on
${\mathcal{O}}_{C}^{\flat }$
-linearly on
![]() $(R_{\infty }^{\Box })^{\flat }$
and
$(R_{\infty }^{\Box })^{\flat }$
and
![]() $R_{\infty }^{\flat }$
. Explicitly,
$R_{\infty }^{\flat }$
. Explicitly,
![]() $\unicode[STIX]{x1D6E5}$
respects the completed direct sum decomposition and an
$\unicode[STIX]{x1D6E5}$
respects the completed direct sum decomposition and an
![]() $(\unicode[STIX]{x1D716}_{0},\ldots ,\unicode[STIX]{x1D716}_{d})\in \unicode[STIX]{x1D6E5}$
scales
$(\unicode[STIX]{x1D716}_{0},\ldots ,\unicode[STIX]{x1D716}_{d})\in \unicode[STIX]{x1D6E5}$
scales
![]() $x_{j}^{a_{j}}$
by
$x_{j}^{a_{j}}$
by
![]() $\unicode[STIX]{x1D716}_{j}^{a_{j}}\in {\mathcal{O}}_{C}^{\flat }$
.
$\unicode[STIX]{x1D716}_{j}^{a_{j}}\in {\mathcal{O}}_{C}^{\flat }$
.
Our analysis in §3.14 of the value on
![]() $\mathfrak{X}_{C,\,\infty }^{\text{ad}}$
of the sheaf
$\mathfrak{X}_{C,\,\infty }^{\text{ad}}$
of the sheaf
![]() $\mathbb{A}_{\text{inf},\,\mathfrak{X}_{C}^{\text{ad}}}$
will hinge on the following lemmas.
$\mathbb{A}_{\text{inf},\,\mathfrak{X}_{C}^{\text{ad}}}$
will hinge on the following lemmas.
Lemma 3.12. Both
![]() $R_{\infty }^{\flat }/b$
and
$R_{\infty }^{\flat }/b$
and
![]() $H_{\text{cont}}^{i}(\unicode[STIX]{x1D6E5},R_{\infty }^{\flat }/b)$
for each
$H_{\text{cont}}^{i}(\unicode[STIX]{x1D6E5},R_{\infty }^{\flat }/b)$
for each
![]() $b\in {\mathcal{O}}_{C}^{\flat }\setminus \{0\}$
have no nonzero
$b\in {\mathcal{O}}_{C}^{\flat }\setminus \{0\}$
have no nonzero
![]() $\mathfrak{m}^{\flat }$
-torsion.
$\mathfrak{m}^{\flat }$
-torsion.
Proof. We may assume that
![]() $b\in \mathfrak{m}^{\flat }$
, so, by using Frobenius, that
$b\in \mathfrak{m}^{\flat }$
, so, by using Frobenius, that
![]() $b\,\mid \,p^{1/p^{\infty }}$
in
$b\,\mid \,p^{1/p^{\infty }}$
in
![]() ${\mathcal{O}}_{C}^{\flat }$
. Then Proposition 3.8 and the
${\mathcal{O}}_{C}^{\flat }$
. Then Proposition 3.8 and the
![]() $\unicode[STIX]{x1D6E5}$
-isomorphism
$\unicode[STIX]{x1D6E5}$
-isomorphism
![]() $R_{\infty }^{\flat }/b\cong R_{\infty }/b^{\sharp }$
for some
$R_{\infty }^{\flat }/b\cong R_{\infty }/b^{\sharp }$
for some
![]() $b^{\sharp }\in {\mathcal{O}}_{C}$
gives the claim.◻
$b^{\sharp }\in {\mathcal{O}}_{C}$
gives the claim.◻
Lemma 3.13. For any affinoid perfectoid
![]() $\operatorname{Spa}(R_{\infty }^{\prime }[\frac{1}{p}],R_{\infty }^{\prime })$
over
$\operatorname{Spa}(R_{\infty }^{\prime }[\frac{1}{p}],R_{\infty }^{\prime })$
over
![]() $\operatorname{Spa}(C,{\mathcal{O}}_{C})$
, the ring
$\operatorname{Spa}(C,{\mathcal{O}}_{C})$
, the ring
is
![]() $(p,\unicode[STIX]{x1D707})$
-adically complete (respectively,
$(p,\unicode[STIX]{x1D707})$
-adically complete (respectively,
![]() $p$
-adically complete). Moreover, for any
$p$
-adically complete). Moreover, for any
![]() $n,n^{\prime }>0$
, the sequence
$n,n^{\prime }>0$
, the sequence
![]() $(p^{n},\unicode[STIX]{x1D707}^{n^{\prime }})$
is
$(p^{n},\unicode[STIX]{x1D707}^{n^{\prime }})$
is
![]() $\mathbb{A}_{\text{inf}}(R_{\infty }^{\prime })$
-regular and the
$\mathbb{A}_{\text{inf}}(R_{\infty }^{\prime })$
-regular and the
![]() $A_{\text{inf}}/(p^{n},\unicode[STIX]{x1D707}^{n^{\prime }})$
-algebra
$A_{\text{inf}}/(p^{n},\unicode[STIX]{x1D707}^{n^{\prime }})$
-algebra
![]() $\mathbb{A}_{\text{inf}}(R_{\infty }^{\prime })/(p^{n},\unicode[STIX]{x1D707}^{n^{\prime }})$
is flat.
$\mathbb{A}_{\text{inf}}(R_{\infty }^{\prime })/(p^{n},\unicode[STIX]{x1D707}^{n^{\prime }})$
is flat.
Proof. By its definition, the perfect
![]() ${\mathcal{O}}_{C}^{\flat }$
-algebra
${\mathcal{O}}_{C}^{\flat }$
-algebra
![]() $(R_{\infty }^{\prime })^{\flat }:=\mathop{\varprojlim }\nolimits_{y\mapsto y^{p}}(R_{\infty }^{\prime }/p)$
has no nonzero
$(R_{\infty }^{\prime })^{\flat }:=\mathop{\varprojlim }\nolimits_{y\mapsto y^{p}}(R_{\infty }^{\prime }/p)$
has no nonzero
![]() $p^{1/p^{\infty }}$
-torsion (that is, it is
$p^{1/p^{\infty }}$
-torsion (that is, it is
![]() ${\mathcal{O}}_{C}^{\flat }$
-flat), so the regular sequence claim follows from [SP, 07DV]. The formal criterion of flatness [Reference BourbakiBou, Ch. III, §5.2, Theorem 1(i)
${\mathcal{O}}_{C}^{\flat }$
-flat), so the regular sequence claim follows from [SP, 07DV]. The formal criterion of flatness [Reference BourbakiBou, Ch. III, §5.2, Theorem 1(i)
![]() $\Leftrightarrow$
(iv)] then implies the
$\Leftrightarrow$
(iv)] then implies the
![]() $A_{\text{inf}}/(p^{n},\unicode[STIX]{x1D707}^{n^{\prime }})$
-flatness of
$A_{\text{inf}}/(p^{n},\unicode[STIX]{x1D707}^{n^{\prime }})$
-flatness of
![]() $\mathbb{A}_{\text{inf}}(R_{\infty }^{\prime })/(p^{n},\unicode[STIX]{x1D707}^{n^{\prime }})$
(even with
$\mathbb{A}_{\text{inf}}(R_{\infty }^{\prime })/(p^{n},\unicode[STIX]{x1D707}^{n^{\prime }})$
(even with
![]() $n^{\prime }=0$
). In addition, the short exact sequences (2.1.2) with
$n^{\prime }=0$
). In addition, the short exact sequences (2.1.2) with
![]() $(R_{\infty }^{\prime })^{\flat }$
in place of
$(R_{\infty }^{\prime })^{\flat }$
in place of
![]() ${\mathcal{O}}_{C}^{\flat }$
imply the
${\mathcal{O}}_{C}^{\flat }$
imply the
![]() $p$
-adic completeness of
$p$
-adic completeness of
![]() $\mathbb{A}_{\text{inf}}(R_{\infty }^{\prime })/\unicode[STIX]{x1D707}$
.
$\mathbb{A}_{\text{inf}}(R_{\infty }^{\prime })/\unicode[STIX]{x1D707}$
.
Analogously to the case of
![]() $A_{\text{inf}}$
discussed in §2.1, we use the Witt coordinate bijection and the
$A_{\text{inf}}$
discussed in §2.1, we use the Witt coordinate bijection and the
![]() $\unicode[STIX]{x1D707}$
-adic topology on
$\unicode[STIX]{x1D707}$
-adic topology on
![]() $(R_{\infty }^{\prime })^{\flat }$
to topologize
$(R_{\infty }^{\prime })^{\flat }$
to topologize
![]() $\mathbb{A}_{\text{inf}}(R_{\infty }^{\prime })\cong \prod _{n=1}^{\infty }(R_{\infty }^{\prime })^{\flat }$
and we see that this topology agrees with the
$\mathbb{A}_{\text{inf}}(R_{\infty }^{\prime })\cong \prod _{n=1}^{\infty }(R_{\infty }^{\prime })^{\flat }$
and we see that this topology agrees with the
![]() $(p,\unicode[STIX]{x1D707})$
-adic topology. Thus,
$(p,\unicode[STIX]{x1D707})$
-adic topology. Thus,
![]() $\mathbb{A}_{\text{inf}}(R_{\infty }^{\prime })$
is
$\mathbb{A}_{\text{inf}}(R_{\infty }^{\prime })$
is
![]() $(p,\unicode[STIX]{x1D707})$
-adically complete.◻
$(p,\unicode[STIX]{x1D707})$
-adically complete.◻
3.14 The ring
 $\mathbb{A}_{\text{inf}}(R_{\infty })$
$\mathbb{A}_{\text{inf}}(R_{\infty })$
By [Reference ScholzeSch13a, 6.5(i)], the value on
![]() $\mathfrak{X}_{C,\,\infty }^{\text{ad}}$
of the sheaf
$\mathfrak{X}_{C,\,\infty }^{\text{ad}}$
of the sheaf
![]() $\mathbb{A}_{\text{inf},\,\mathfrak{X}_{C}^{\text{ad}}}$
is the ring
$\mathbb{A}_{\text{inf},\,\mathfrak{X}_{C}^{\text{ad}}}$
is the ring
By Lemma 3.13 and the formal criterion of flatness,
![]() $\mathbb{A}_{\text{inf}}(R_{\infty })$
is
$\mathbb{A}_{\text{inf}}(R_{\infty })$
is
![]() $(p,\unicode[STIX]{x1D707})$
-adically formally flat as an
$(p,\unicode[STIX]{x1D707})$
-adically formally flat as an
![]() $A_{\text{inf}}$
-algebra and
$A_{\text{inf}}$
-algebra and
![]() $(p,\unicode[STIX]{x1D707})$
-adically formally étale as an
$(p,\unicode[STIX]{x1D707})$
-adically formally étale as an
![]() $\mathbb{A}_{\text{inf}}(R_{\infty }^{\Box })$
-algebra. By using, in addition, Lemma 3.12, we see that each quotient
$\mathbb{A}_{\text{inf}}(R_{\infty }^{\Box })$
-algebra. By using, in addition, Lemma 3.12, we see that each quotient
In general, for a perfect
![]() $\mathbb{F}_{p}$
-algebra
$\mathbb{F}_{p}$
-algebra
![]() $A$
, the Witt ring
$A$
, the Witt ring
![]() $W(A)$
is the unique
$W(A)$
is the unique
![]() $p$
-adically complete
$p$
-adically complete
![]() $p$
-torsion-free
$p$
-torsion-free
![]() $\mathbb{Z}_{p}$
-algebra
$\mathbb{Z}_{p}$
-algebra
![]() $\widetilde{A}$
equipped with an isomorphism
$\widetilde{A}$
equipped with an isomorphism
![]() $\widetilde{A}/p\simeq A$
(see [Reference BhattBha18, 2.5]). For an
$\widetilde{A}/p\simeq A$
(see [Reference BhattBha18, 2.5]). For an
![]() $a\in A$
, the Teichmüller
$a\in A$
, the Teichmüller
![]() $[a]\in \widetilde{A}$
is
$[a]\in \widetilde{A}$
is
![]() $\displaystyle \lim _{n\rightarrow \infty }(\widetilde{a}_{n}^{p^{n}})$
where
$\displaystyle \lim _{n\rightarrow \infty }(\widetilde{a}_{n}^{p^{n}})$
where
![]() $\widetilde{a}_{n}\in \widetilde{A}$
is any lift of
$\widetilde{a}_{n}\in \widetilde{A}$
is any lift of
![]() $a^{1/p^{n}}$
(see [Reference BhattBha18, 2.4]). Therefore,
$a^{1/p^{n}}$
(see [Reference BhattBha18, 2.4]). Therefore,

where the completions are
![]() $(p,\unicode[STIX]{x1D707})$
-adic, the decomposition is as
$(p,\unicode[STIX]{x1D707})$
-adic, the decomposition is as
![]() $A_{\text{inf}}$
-modules, and, in terms of §3.11, we have
$A_{\text{inf}}$
-modules, and, in terms of §3.11, we have
![]() $X_{i}^{1/p^{m}}=[x_{i}^{1/p^{m}}]$
. The summands for which
$X_{i}^{1/p^{m}}=[x_{i}^{1/p^{m}}]$
. The summands for which
![]() $a_{i}\in \mathbb{Z}$
for all
$a_{i}\in \mathbb{Z}$
for all
![]() $i$
comprise a subring
$i$
comprise a subring
where the convergence is
![]() $(p,\unicode[STIX]{x1D707})$
-adic. The remaining summands, that is, those for which
$(p,\unicode[STIX]{x1D707})$
-adic. The remaining summands, that is, those for which
![]() $a_{i}\not \in \mathbb{Z}$
for some
$a_{i}\not \in \mathbb{Z}$
for some
![]() $i$
, comprise an
$i$
, comprise an
![]() $A(R^{\Box })$
-submodule
$A(R^{\Box })$
-submodule
![]() $N_{\infty }^{\Box }\subset \mathbb{A}_{\text{inf}}(R_{\infty }^{\Box })$
.
$N_{\infty }^{\Box }\subset \mathbb{A}_{\text{inf}}(R_{\infty }^{\Box })$
.
On sections over
![]() $\mathfrak{X}_{C,\,\infty }^{\text{ad}}$
, the map
$\mathfrak{X}_{C,\,\infty }^{\text{ad}}$
, the map
![]() $\unicode[STIX]{x1D703}$
from (2.2.2) is identified with the unique ring homomorphism
$\unicode[STIX]{x1D703}$
from (2.2.2) is identified with the unique ring homomorphism
is surjective with the kernel generated by the regular element
![]() $\unicode[STIX]{x1D709}$
(see [Reference Bhatt, Morrow and ScholzeBMS18, 3.10, 3.11]), and intertwines the Witt vector Frobenius of
$\unicode[STIX]{x1D709}$
(see [Reference Bhatt, Morrow and ScholzeBMS18, 3.10, 3.11]), and intertwines the Witt vector Frobenius of
![]() $\mathbb{A}_{\text{inf}}(R_{\infty })$
with the absolute Frobenius of
$\mathbb{A}_{\text{inf}}(R_{\infty })$
with the absolute Frobenius of
![]() $R_{\infty }/p$
. Thus,
$R_{\infty }/p$
. Thus,
We use the surjection (3.14.3) to uniquely lift the étale
![]() $R^{\Box }/p$
-algebra
$R^{\Box }/p$
-algebra
![]() $R/p$
to a
$R/p$
to a
![]() $(p,\unicode[STIX]{x1D707})$
-adically complete, formally étale
$(p,\unicode[STIX]{x1D707})$
-adically complete, formally étale
![]() $A(R^{\Box })$
-algebra
$A(R^{\Box })$
-algebra
![]() $A(R)$
. By construction, we have the identification
$A(R)$
. By construction, we have the identification
where the completion is
![]() $(p,\unicode[STIX]{x1D707})$
-adic. Therefore, by setting
$(p,\unicode[STIX]{x1D707})$
-adic. Therefore, by setting
![]() $N_{\infty }:=N_{\infty }^{\Box }\,\widehat{\otimes }_{A(R^{\Box })}\,A(R)$
, we arrive at the decompositions of
$N_{\infty }:=N_{\infty }^{\Box }\,\widehat{\otimes }_{A(R^{\Box })}\,A(R)$
, we arrive at the decompositions of
![]() $\mathbb{A}_{\text{inf}}(R_{\infty }^{\Box })$
and
$\mathbb{A}_{\text{inf}}(R_{\infty }^{\Box })$
and
![]() $\mathbb{A}_{\text{inf}}(R_{\infty })$
into ‘integral’ and ‘nonintegral’ parts:
$\mathbb{A}_{\text{inf}}(R_{\infty })$
into ‘integral’ and ‘nonintegral’ parts:
Modulo
![]() $\operatorname{Ker}\unicode[STIX]{x1D703}$
(that is, modulo
$\operatorname{Ker}\unicode[STIX]{x1D703}$
(that is, modulo
![]() $\unicode[STIX]{x1D709}$
), these decompositions reduce to the decompositions (3.2.2).
$\unicode[STIX]{x1D709}$
), these decompositions reduce to the decompositions (3.2.2).
The Witt vector Frobenius of
![]() $\mathbb{A}_{\text{inf}}(R_{\infty }^{\Box })$
preserves
$\mathbb{A}_{\text{inf}}(R_{\infty }^{\Box })$
preserves
![]() $A(R^{\Box })$
; explicitly: it is semilinear with respect to the Frobenius of
$A(R^{\Box })$
; explicitly: it is semilinear with respect to the Frobenius of
![]() $A_{\text{inf}}$
and raises each
$A_{\text{inf}}$
and raises each
![]() $X_{i}^{1/p^{m}}$
to the
$X_{i}^{1/p^{m}}$
to the
![]() $p$
th power. By construction,
$p$
th power. By construction,
![]() $A(R)$
inherits a Frobenius ring endomorphism from
$A(R)$
inherits a Frobenius ring endomorphism from
![]() $A(R^{\Box })$
, and the identification (3.14.4) is Frobenius-equivariant.
$A(R^{\Box })$
, and the identification (3.14.4) is Frobenius-equivariant.
The natural
![]() $\unicode[STIX]{x1D6E5}$
-action on
$\unicode[STIX]{x1D6E5}$
-action on
![]() $\mathbb{A}_{\text{inf}}(R_{\infty })$
is continuous and commutes with the Frobenius. Explicitly,
$\mathbb{A}_{\text{inf}}(R_{\infty })$
is continuous and commutes with the Frobenius. Explicitly,
![]() $\unicode[STIX]{x1D6E5}$
respects the completed direct sum decomposition and an
$\unicode[STIX]{x1D6E5}$
respects the completed direct sum decomposition and an
![]() $(\unicode[STIX]{x1D716}_{0},\ldots ,\unicode[STIX]{x1D716}_{d})\in \unicode[STIX]{x1D6E5}$
scales
$(\unicode[STIX]{x1D716}_{0},\ldots ,\unicode[STIX]{x1D716}_{d})\in \unicode[STIX]{x1D6E5}$
scales
![]() $X_{j}^{a_{j}}$
by
$X_{j}^{a_{j}}$
by
![]() $[\unicode[STIX]{x1D716}_{j}^{a_{j}}]\in A_{\text{inf}}$
. The
$[\unicode[STIX]{x1D716}_{j}^{a_{j}}]\in A_{\text{inf}}$
. The
![]() $\unicode[STIX]{x1D6E5}$
-action on
$\unicode[STIX]{x1D6E5}$
-action on
![]() $A(R^{\Box })$
lifts uniquely to a necessarily Frobenius-equivariant
$A(R^{\Box })$
lifts uniquely to a necessarily Frobenius-equivariant
![]() $\unicode[STIX]{x1D6E5}$
-action on
$\unicode[STIX]{x1D6E5}$
-action on
![]() $A(R)$
. In particular,
$A(R)$
. In particular,
![]() $\unicode[STIX]{x1D6E5}$
acts trivially on
$\unicode[STIX]{x1D6E5}$
acts trivially on
![]() $A(R)/\unicode[STIX]{x1D707}$
. The identifications (3.14.4) and (3.14.5) are
$A(R)/\unicode[STIX]{x1D707}$
. The identifications (3.14.4) and (3.14.5) are
![]() $\unicode[STIX]{x1D6E5}$
-equivariant.
$\unicode[STIX]{x1D6E5}$
-equivariant.
3.15 The cohomology of
 $\mathbb{A}_{\text{inf}}$
and continuous group cohomology
$\mathbb{A}_{\text{inf}}$
and continuous group cohomology
Similarly to §3.3, the Čech complex of the sheaf
![]() $\mathbb{A}_{\text{inf},\,\mathfrak{X}_{C}^{\text{ad}}}$
with respect to the pro-(finite étale) affinoid perfectoid cover
$\mathbb{A}_{\text{inf},\,\mathfrak{X}_{C}^{\text{ad}}}$
with respect to the pro-(finite étale) affinoid perfectoid cover
![]() $\mathfrak{X}_{C,\,\infty }^{\text{ad}}\rightarrow \mathfrak{X}_{C}^{\text{ad}}$
is identified with the continuous cochain complex
$\mathfrak{X}_{C,\,\infty }^{\text{ad}}\rightarrow \mathfrak{X}_{C}^{\text{ad}}$
is identified with the continuous cochain complex
![]() $R\unicode[STIX]{x1D6E4}_{\text{cont}}(\unicode[STIX]{x1D6E5},\mathbb{A}_{\text{inf}}(R_{\infty }))$
. Thus, by using [SP, 01GY], we obtain the edge map to the proétale cohomology of
$R\unicode[STIX]{x1D6E4}_{\text{cont}}(\unicode[STIX]{x1D6E5},\mathbb{A}_{\text{inf}}(R_{\infty }))$
. Thus, by using [SP, 01GY], we obtain the edge map to the proétale cohomology of
![]() $\mathbb{A}_{\text{inf},\,\mathfrak{X}_{C}^{\text{ad}}}$
:
$\mathbb{A}_{\text{inf},\,\mathfrak{X}_{C}^{\text{ad}}}$
:
By the almost purity theorem, more precisely, by [Reference ScholzeSch13a, 6.5(ii)], the subset
![]() $[\mathfrak{m}^{\flat }]\subset A_{\text{inf}}$
that consists of the Teichmüller lifts of the elements in the maximal ideal
$[\mathfrak{m}^{\flat }]\subset A_{\text{inf}}$
that consists of the Teichmüller lifts of the elements in the maximal ideal
![]() $\mathfrak{m}^{\flat }\subset {\mathcal{O}}_{C}^{\flat }$
kills all the cohomology groups of
$\mathfrak{m}^{\flat }\subset {\mathcal{O}}_{C}^{\flat }$
kills all the cohomology groups of
![]() $\operatorname{Cone}(e)$
. Since
$\operatorname{Cone}(e)$
. Since
![]() $\unicode[STIX]{x1D707}\in W(\mathfrak{m}^{\flat })$
(see (2.3.3)), it will be useful to strengthen this annihilation as follows.
$\unicode[STIX]{x1D707}\in W(\mathfrak{m}^{\flat })$
(see (2.3.3)), it will be useful to strengthen this annihilation as follows.
Lemma 3.16. The ideal
![]() $W(\mathfrak{m}^{\flat })\subset A_{\text{inf}}$
defined in (2.3.3) kills each
$W(\mathfrak{m}^{\flat })\subset A_{\text{inf}}$
defined in (2.3.3) kills each
![]() $H^{i}(\operatorname{Cone}(e))$
.
$H^{i}(\operatorname{Cone}(e))$
.
Proof. We argue similarly to [Reference Bhatt, Morrow and ScholzeBMS18, proof of Theorem 5.6]. Both the source and the target of
![]() $e$
are derived
$e$
are derived
![]() $p$
-adically complete (see §1.7), so, by [Reference Bhatt and ScholzeBS15, 3.4.4 and 3.4.14], each
$p$
-adically complete (see §1.7), so, by [Reference Bhatt and ScholzeBS15, 3.4.4 and 3.4.14], each
![]() $H^{i}(\operatorname{Cone}(e))$
is also derived
$H^{i}(\operatorname{Cone}(e))$
is also derived
![]() $p$
-adically complete. Thus, the desired conclusion follows from the following lemma.◻
$p$
-adically complete. Thus, the desired conclusion follows from the following lemma.◻
Lemma 3.17. If
![]() $[\mathfrak{m}^{\flat }]A_{\text{inf}}$
kills a derived
$[\mathfrak{m}^{\flat }]A_{\text{inf}}$
kills a derived
![]() $p$
-adically complete
$p$
-adically complete
![]() $A_{\text{inf}}$
-module
$A_{\text{inf}}$
-module
![]() $H$
, then so does
$H$
, then so does
![]() $W(\mathfrak{m}^{\flat })$
.
$W(\mathfrak{m}^{\flat })$
.
Proof. By the derived
![]() $p$
-adic completeness, any free
$p$
-adic completeness, any free
![]() $A_{\text{inf}}$
-module resolution
$A_{\text{inf}}$
-module resolution
![]() $F^{\bullet }$
of
$F^{\bullet }$
of
![]() $H$
satisfies
$H$
satisfies
Moreover, for every
![]() $n\geqslant 1$
the ideals
$n\geqslant 1$
the ideals
![]() $[\mathfrak{m}^{\flat }]\cdot W_{n}({\mathcal{O}}_{C}^{\flat })$
and
$[\mathfrak{m}^{\flat }]\cdot W_{n}({\mathcal{O}}_{C}^{\flat })$
and
![]() $W_{n}(\mathfrak{m}^{\flat }):=\operatorname{Ker}(W_{n}({\mathcal{O}}_{C}^{\flat })\rightarrow W_{n}(k))$
of
$W_{n}(\mathfrak{m}^{\flat }):=\operatorname{Ker}(W_{n}({\mathcal{O}}_{C}^{\flat })\rightarrow W_{n}(k))$
of
![]() $W_{n}({\mathcal{O}}_{C}^{\flat })$
agree. Thus, the
$W_{n}({\mathcal{O}}_{C}^{\flat })$
agree. Thus, the
![]() $([\mathfrak{m}^{\flat }]A_{\text{inf}})$
-annihilation of
$([\mathfrak{m}^{\flat }]A_{\text{inf}})$
-annihilation of
![]() $H$
implies that
$H$
implies that
![]() $W_{n}(\mathfrak{m}^{\flat })$
kills both
$W_{n}(\mathfrak{m}^{\flat })$
kills both
Thus, since
![]() $[\mathfrak{m}^{\flat }]^{2}=[\mathfrak{m}^{\flat }]$
and
$[\mathfrak{m}^{\flat }]^{2}=[\mathfrak{m}^{\flat }]$
and
![]() $F_{0}/p^{n}$
has no nonzero
$F_{0}/p^{n}$
has no nonzero
![]() $m$
-torsion for every nonzero
$m$
-torsion for every nonzero
![]() $m\in [\mathfrak{m}^{\flat }]$
, any element
$m\in [\mathfrak{m}^{\flat }]$
, any element
![]() $x\in W_{n+1}(\mathfrak{m}^{\flat })\,\cdot \,(F_{0}/p^{n+1})$
may be lifted to
$x\in W_{n+1}(\mathfrak{m}^{\flat })\,\cdot \,(F_{0}/p^{n+1})$
may be lifted to
![]() $W_{n+1}(\mathfrak{m}^{\flat })\,\cdot \,(F_{-1}/p^{n+1})$
, compatibly with a specified lift of its image
$W_{n+1}(\mathfrak{m}^{\flat })\,\cdot \,(F_{-1}/p^{n+1})$
, compatibly with a specified lift of its image
![]() $\overline{x}\in W_{n}(\mathfrak{m}^{\flat })\,\cdot \,(F_{0}/p^{n})$
to
$\overline{x}\in W_{n}(\mathfrak{m}^{\flat })\,\cdot \,(F_{0}/p^{n})$
to
![]() $W_{n}(\mathfrak{m}^{\flat })\,\cdot \,(F_{-1}/p^{n})$
. In particular,
$W_{n}(\mathfrak{m}^{\flat })\,\cdot \,(F_{-1}/p^{n})$
. In particular,
![]() $W(\mathfrak{m}^{\flat })\,\cdot \,(\mathop{\varprojlim }\nolimits_{n}(F^{0}/p^{n}))$
lies in the image of
$W(\mathfrak{m}^{\flat })\,\cdot \,(\mathop{\varprojlim }\nolimits_{n}(F^{0}/p^{n}))$
lies in the image of
![]() $\mathop{\varprojlim }\nolimits_{n}(F^{-1}/p^{n})$
, that is,
$\mathop{\varprojlim }\nolimits_{n}(F^{-1}/p^{n})$
, that is,
![]() $W(\mathfrak{m}^{\flat })$
kills
$W(\mathfrak{m}^{\flat })$
kills
![]() $H$
, as desired.◻
$H$
, as desired.◻
We will show in Theorem 3.20 that
![]() $L\unicode[STIX]{x1D702}_{(\unicode[STIX]{x1D707})}(e)$
is an isomorphism, so that continuous group cohomology computes
$L\unicode[STIX]{x1D702}_{(\unicode[STIX]{x1D707})}(e)$
is an isomorphism, so that continuous group cohomology computes
![]() $L\unicode[STIX]{x1D702}_{(\unicode[STIX]{x1D707})}(R\unicode[STIX]{x1D6E4}_{\text{pro}\acute{\text{e}}\text{t}}(\mathfrak{X}_{C}^{\text{ad}},\mathbb{A}_{\text{inf}}))$
. For this, we will use the following lemma.
$L\unicode[STIX]{x1D702}_{(\unicode[STIX]{x1D707})}(R\unicode[STIX]{x1D6E4}_{\text{pro}\acute{\text{e}}\text{t}}(\mathfrak{X}_{C}^{\text{ad}},\mathbb{A}_{\text{inf}}))$
. For this, we will use the following lemma.
Lemma 3.18. If
![]() $B\xrightarrow[{}]{b}B^{\prime }$
is a morphism in
$B\xrightarrow[{}]{b}B^{\prime }$
is a morphism in
![]() $D(A_{\text{inf}})$
such that each
$D(A_{\text{inf}})$
such that each
![]() $H^{i}(B\otimes _{A_{\text{inf}}}^{\mathbb{L}}A_{\text{inf}}/\unicode[STIX]{x1D707})$
has no nonzero
$H^{i}(B\otimes _{A_{\text{inf}}}^{\mathbb{L}}A_{\text{inf}}/\unicode[STIX]{x1D707})$
has no nonzero
![]() $W(\mathfrak{m}^{\flat })$
-torsion and
$W(\mathfrak{m}^{\flat })$
-torsion and
![]() $W(\mathfrak{m}^{\flat })$
kills each
$W(\mathfrak{m}^{\flat })$
kills each
![]() $H^{i}(\operatorname{Cone}(b))$
, then
$H^{i}(\operatorname{Cone}(b))$
, then
![]() $L\unicode[STIX]{x1D702}_{(\unicode[STIX]{x1D707})}(b)$
is an isomorphism.
$L\unicode[STIX]{x1D702}_{(\unicode[STIX]{x1D707})}(b)$
is an isomorphism.
Proof. Since
![]() $L\unicode[STIX]{x1D702}$
is not a triangulated functor, the fact that
$L\unicode[STIX]{x1D702}$
is not a triangulated functor, the fact that
![]() $L\unicode[STIX]{x1D702}_{(\unicode[STIX]{x1D707})}(\operatorname{Cone}(b))\cong 0$
does not a priori suffice. Instead, the ideal
$L\unicode[STIX]{x1D702}_{(\unicode[STIX]{x1D707})}(\operatorname{Cone}(b))\cong 0$
does not a priori suffice. Instead, the ideal
![]() $(W(\mathfrak{m}^{\flat }))^{2}$
kills the cohomology of
$(W(\mathfrak{m}^{\flat }))^{2}$
kills the cohomology of
![]() $\operatorname{Cone}(b)\otimes _{A_{\text{inf}}}^{\mathbb{L}}A_{\text{inf}}/\unicode[STIX]{x1D707}$
, so the sequences
$\operatorname{Cone}(b)\otimes _{A_{\text{inf}}}^{\mathbb{L}}A_{\text{inf}}/\unicode[STIX]{x1D707}$
, so the sequences
are short exact. By the Bockstein construction (see [Reference Bhatt, Morrow and ScholzeBMS18, 6.12]), as
![]() $i$
varies, they comprise a short exact sequence whose terms are complexes that compute
$i$
varies, they comprise a short exact sequence whose terms are complexes that compute
![]() $L\unicode[STIX]{x1D702}_{(\unicode[STIX]{x1D707})}(B)\otimes _{A_{\text{inf}}}^{\mathbb{L}}A_{\text{inf}}/\unicode[STIX]{x1D707}$
, etc. Thus, the vanishing of
$L\unicode[STIX]{x1D702}_{(\unicode[STIX]{x1D707})}(B)\otimes _{A_{\text{inf}}}^{\mathbb{L}}A_{\text{inf}}/\unicode[STIX]{x1D707}$
, etc. Thus, the vanishing of
![]() $L\unicode[STIX]{x1D702}_{(\unicode[STIX]{x1D707})}(\operatorname{Cone}(b))$
implies that
$L\unicode[STIX]{x1D702}_{(\unicode[STIX]{x1D707})}(\operatorname{Cone}(b))$
implies that
![]() $(L\unicode[STIX]{x1D702}_{(\unicode[STIX]{x1D707})}(b))\otimes _{A_{\text{inf}}}^{\mathbb{L}}A_{\text{inf}}/\unicode[STIX]{x1D707}$
is an isomorphism. It follows that
$(L\unicode[STIX]{x1D702}_{(\unicode[STIX]{x1D707})}(b))\otimes _{A_{\text{inf}}}^{\mathbb{L}}A_{\text{inf}}/\unicode[STIX]{x1D707}$
is an isomorphism. It follows that
![]() $\operatorname{Cone}(L\unicode[STIX]{x1D702}_{(\unicode[STIX]{x1D707})}(b))\otimes _{A_{\text{inf}}}^{\mathbb{L}}A_{\text{inf}}/\unicode[STIX]{x1D707}\cong 0$
, so
$\operatorname{Cone}(L\unicode[STIX]{x1D702}_{(\unicode[STIX]{x1D707})}(b))\otimes _{A_{\text{inf}}}^{\mathbb{L}}A_{\text{inf}}/\unicode[STIX]{x1D707}\cong 0$
, so
![]() $\unicode[STIX]{x1D707}$
acts invertibly on the cohomology of
$\unicode[STIX]{x1D707}$
acts invertibly on the cohomology of
![]() $\operatorname{Cone}(L\unicode[STIX]{x1D702}_{(\unicode[STIX]{x1D707})}(b))$
. But then, as we see after applying
$\operatorname{Cone}(L\unicode[STIX]{x1D702}_{(\unicode[STIX]{x1D707})}(b))$
. But then, as we see after applying
![]() $-\otimes _{A_{\text{inf}}}^{\mathbb{L}}A_{\text{inf}}[\frac{1}{\unicode[STIX]{x1D707}}]$
, this cohomology vanishes.◻
$-\otimes _{A_{\text{inf}}}^{\mathbb{L}}A_{\text{inf}}[\frac{1}{\unicode[STIX]{x1D707}}]$
, this cohomology vanishes.◻
We now verify that the edge map
![]() $e$
defined in (3.15.1) also meets the first assumption of Lemma 3.18.
$e$
defined in (3.15.1) also meets the first assumption of Lemma 3.18.
Proposition 3.19. For each
![]() $i\in \mathbb{Z}$
, the
$i\in \mathbb{Z}$
, the
![]() $A_{\text{inf}}$
-module
$A_{\text{inf}}$
-module
![]() $H_{\text{cont}}^{i}(\unicode[STIX]{x1D6E5},\mathbb{A}_{\text{inf}}(R_{\infty })/\unicode[STIX]{x1D707})$
is
$H_{\text{cont}}^{i}(\unicode[STIX]{x1D6E5},\mathbb{A}_{\text{inf}}(R_{\infty })/\unicode[STIX]{x1D707})$
is
![]() $p$
-torsion free and
$p$
-torsion free and
![]() $p$
-adically complete; moreover, the following natural maps are isomorphisms:
$p$
-adically complete; moreover, the following natural maps are isomorphisms:
and
In addition,
![]() $H_{\text{cont}}^{i}(\unicode[STIX]{x1D6E5},\mathbb{A}_{\text{inf}}(R_{\infty })/(\unicode[STIX]{x1D707},p^{n}))$
and
$H_{\text{cont}}^{i}(\unicode[STIX]{x1D6E5},\mathbb{A}_{\text{inf}}(R_{\infty })/(\unicode[STIX]{x1D707},p^{n}))$
and
![]() $H_{\text{cont}}^{i}(\unicode[STIX]{x1D6E5},\mathbb{A}_{\text{inf}}(R_{\infty })/\unicode[STIX]{x1D707})$
have no nonzero
$H_{\text{cont}}^{i}(\unicode[STIX]{x1D6E5},\mathbb{A}_{\text{inf}}(R_{\infty })/\unicode[STIX]{x1D707})$
have no nonzero
![]() $W(\mathfrak{m}^{\flat })$
-torsion.
$W(\mathfrak{m}^{\flat })$
-torsion.
Proof. Since
![]() $A(R)/\unicode[STIX]{x1D707}$
is
$A(R)/\unicode[STIX]{x1D707}$
is
![]() $p$
-adically complete and has a trivial
$p$
-adically complete and has a trivial
![]() $\unicode[STIX]{x1D6E5}$
-action (see Lemma 3.13 and §3.14), Lemma 3.7 implies that
$\unicode[STIX]{x1D6E5}$
-action (see Lemma 3.13 and §3.14), Lemma 3.7 implies that
![]() $H_{\text{cont}}^{i}(\unicode[STIX]{x1D6E5},A(R)/\unicode[STIX]{x1D707})$
is a direct sum of copies of
$H_{\text{cont}}^{i}(\unicode[STIX]{x1D6E5},A(R)/\unicode[STIX]{x1D707})$
is a direct sum of copies of
![]() $A(R)/\unicode[STIX]{x1D707}$
, and likewise for
$A(R)/\unicode[STIX]{x1D707}$
, and likewise for
![]() $H_{\text{cont}}^{i}(\unicode[STIX]{x1D6E5},A(R)/(\unicode[STIX]{x1D707},p^{n}))$
. Consequently, since, by (3.14.1), the rings
$H_{\text{cont}}^{i}(\unicode[STIX]{x1D6E5},A(R)/(\unicode[STIX]{x1D707},p^{n}))$
. Consequently, since, by (3.14.1), the rings
![]() $A(R)/(\unicode[STIX]{x1D707},p^{n})$
and
$A(R)/(\unicode[STIX]{x1D707},p^{n})$
and
![]() $A(R)/\unicode[STIX]{x1D707}$
have no nonzero
$A(R)/\unicode[STIX]{x1D707}$
have no nonzero
![]() $W(\mathfrak{m}^{\flat })$
-torsion, the analogues of all the claims with
$W(\mathfrak{m}^{\flat })$
-torsion, the analogues of all the claims with
![]() $A(R)$
in place of
$A(R)$
in place of
![]() $\mathbb{A}_{\text{inf}}(R_{\infty })$
follow. Thus, due to (3.14.5), we only need to establish these analogues with
$\mathbb{A}_{\text{inf}}(R_{\infty })$
follow. Thus, due to (3.14.5), we only need to establish these analogues with
![]() $N_{\infty }$
in place of
$N_{\infty }$
in place of
![]() $\mathbb{A}_{\text{inf}}(R_{\infty })$
.
$\mathbb{A}_{\text{inf}}(R_{\infty })$
.
To prepare for treating
![]() $N_{\infty }$
, we start by building on the ideas of [Reference BhattBha18, proof of Lemma 4.6] to analyze a single summand
$N_{\infty }$
, we start by building on the ideas of [Reference BhattBha18, proof of Lemma 4.6] to analyze a single summand
![]() $S:=A_{\text{inf}}\,\cdot \,X_{0}^{a_{0}}\cdots X_{d}^{a_{d}}$
that, as in §3.14, contributes to
$S:=A_{\text{inf}}\,\cdot \,X_{0}^{a_{0}}\cdots X_{d}^{a_{d}}$
that, as in §3.14, contributes to
![]() $N_{\infty }^{\Box }$
. We set
$N_{\infty }^{\Box }$
. We set
and let
![]() $m\in \mathbb{Z}_{{>}0}$
be the minimal such that
$m\in \mathbb{Z}_{{>}0}$
be the minimal such that
![]() $p^{m}b_{j}\in \mathbb{Z}$
for all
$p^{m}b_{j}\in \mathbb{Z}$
for all
![]() $j$
. Lemma 3.7 applied with the topological generators
$j$
. Lemma 3.7 applied with the topological generators
![]() $\unicode[STIX]{x1D6FF}_{1},\ldots ,\unicode[STIX]{x1D6FF}_{d}$
of
$\unicode[STIX]{x1D6FF}_{1},\ldots ,\unicode[STIX]{x1D6FF}_{d}$
of
![]() $\unicode[STIX]{x1D6E5}$
defined in §3.2 gives an
$\unicode[STIX]{x1D6E5}$
defined in §3.2 gives an
![]() $A_{\text{inf}}$
-isomorphism
$A_{\text{inf}}$
-isomorphism
where
![]() $C^{\bullet }$
is the
$C^{\bullet }$
is the
![]() $(A_{\text{inf}}/\unicode[STIX]{x1D707})$
-tensor product of the
$(A_{\text{inf}}/\unicode[STIX]{x1D707})$
-tensor product of the
![]() $d$
complexes
$d$
complexes
By reordering the
![]() $b_{j}$
, we may assume that for all
$b_{j}$
, we may assume that for all
![]() $j$
we have
$j$
we have
![]() $b_{j}/b_{1}\in \mathbb{Z}_{(p)}$
, so that
$b_{j}/b_{1}\in \mathbb{Z}_{(p)}$
, so that
![]() $b_{1}\not \in \mathbb{Z}$
and both
$b_{1}\not \in \mathbb{Z}$
and both
![]() $[\unicode[STIX]{x1D716}^{b_{1}}]-1\,\mid \,[\unicode[STIX]{x1D716}^{b_{j}}]-1$
and
$[\unicode[STIX]{x1D716}^{b_{1}}]-1\,\mid \,[\unicode[STIX]{x1D716}^{b_{j}}]-1$
and
![]() $[\unicode[STIX]{x1D716}^{b_{1}}]-1\,\mid \,\unicode[STIX]{x1D707}$
. Then the object (3.19.4) with
$[\unicode[STIX]{x1D716}^{b_{1}}]-1\,\mid \,\unicode[STIX]{x1D707}$
. Then the object (3.19.4) with
![]() $j=1$
is given by the complex
$j=1$
is given by the complex
![]() $[A_{\text{inf}}/([\unicode[STIX]{x1D716}^{b_{1}}]-1)\xrightarrow[{}]{0}A_{\text{inf}}/([\unicode[STIX]{x1D716}^{b_{1}}]-1)]$
and, by using the left-hand sides of (3.19.4) for the factors with
$[A_{\text{inf}}/([\unicode[STIX]{x1D716}^{b_{1}}]-1)\xrightarrow[{}]{0}A_{\text{inf}}/([\unicode[STIX]{x1D716}^{b_{1}}]-1)]$
and, by using the left-hand sides of (3.19.4) for the factors with
![]() $j\neq 1$
, we see that
$j\neq 1$
, we see that
![]() $C^{\bullet }$
is quasi-isomorphic to a direct sum of shifts of
$C^{\bullet }$
is quasi-isomorphic to a direct sum of shifts of
Thus, for
![]() $i\in \mathbb{Z}$
,
$i\in \mathbb{Z}$
,
By Lemma 3.7 and [SP, 061Z, 0662], this implies that
We now analyze
![]() $N_{\infty }^{\Box }$
. Since
$N_{\infty }^{\Box }$
. Since
![]() $\mathbb{A}_{\text{inf}}(R_{\infty }^{\Box })/\unicode[STIX]{x1D707}$
is
$\mathbb{A}_{\text{inf}}(R_{\infty }^{\Box })/\unicode[STIX]{x1D707}$
is
![]() $p$
-adically complete, §3.14 gives the
$p$
-adically complete, §3.14 gives the
![]() $\unicode[STIX]{x1D6E5}$
-decomposition
$\unicode[STIX]{x1D6E5}$
-decomposition
in which the completion is
![]() $p$
-adic. Lemma 3.6 (i) then combines with (3.19.5) to prove that
$p$
-adic. Lemma 3.6 (i) then combines with (3.19.5) to prove that
Analogously to (3.19.6), this, in turn, implies that
Finally, we analyze
![]() $N_{\infty }$
. The identification
$N_{\infty }$
. The identification
is
![]() $\unicode[STIX]{x1D6E5}$
-equivariant and
$\unicode[STIX]{x1D6E5}$
-equivariant and
![]() $A(R)/(\unicode[STIX]{x1D707},p^{n})$
is
$A(R)/(\unicode[STIX]{x1D707},p^{n})$
is
![]() $(A(R^{\Box })/(\unicode[STIX]{x1D707},p^{n}))$
-flat, so Lemma 3.7 gives the identifications
$(A(R^{\Box })/(\unicode[STIX]{x1D707},p^{n}))$
-flat, so Lemma 3.7 gives the identifications
which are compatible as
![]() $n$
varies. Consequently, for
$n$
varies. Consequently, for
![]() $n>1$
, the sequences
$n>1$
, the sequences
are short exact because, by (3.19.5) and (3.19.7), so are their analogues with
![]() $N_{\infty }^{\Box }$
in place of
$N_{\infty }^{\Box }$
in place of
![]() $N_{\infty }$
. By taking the inverse limit of these sequences for varying
$N_{\infty }$
. By taking the inverse limit of these sequences for varying
![]() $n$
and using [SP, 0D6K], we obtain
$n$
and using [SP, 0D6K], we obtain
which is the sought analogue of (3.19.2). The
![]() $p$
-torsion-freeness of
$p$
-torsion-freeness of
![]() $H_{\text{cont}}^{i}(\unicode[STIX]{x1D6E5},N_{\infty }/\unicode[STIX]{x1D707})$
follows from (3.19.9)–(3.19.10) and, as in (3.19.6), it implies that
$H_{\text{cont}}^{i}(\unicode[STIX]{x1D6E5},N_{\infty }/\unicode[STIX]{x1D707})$
follows from (3.19.9)–(3.19.10) and, as in (3.19.6), it implies that
It remains to show that each
![]() $H_{\text{cont}}^{i}(\unicode[STIX]{x1D6E5},N_{\infty }/(\unicode[STIX]{x1D707},p^{n}))$
has no nonzero
$H_{\text{cont}}^{i}(\unicode[STIX]{x1D6E5},N_{\infty }/(\unicode[STIX]{x1D707},p^{n}))$
has no nonzero
![]() $W(\mathfrak{m}^{\flat })$
-torsion.
$W(\mathfrak{m}^{\flat })$
-torsion.
The surjectivity aspect of the short exact sequences (3.19.9) implies that the sequences
remain short exact after applying
![]() $H_{\text{cont}}^{i}(\unicode[STIX]{x1D6E5},-)$
. Thus,
$H_{\text{cont}}^{i}(\unicode[STIX]{x1D6E5},-)$
. Thus,
![]() $H_{\text{cont}}^{i}(\unicode[STIX]{x1D6E5},N_{\infty }/(\unicode[STIX]{x1D707},p^{n}))$
is a successive extension of copies of
$H_{\text{cont}}^{i}(\unicode[STIX]{x1D6E5},N_{\infty }/(\unicode[STIX]{x1D707},p^{n}))$
is a successive extension of copies of
![]() $H_{\text{cont}}^{i}(\unicode[STIX]{x1D6E5},N_{\infty }/(\unicode[STIX]{x1D707},p))$
. Consequently, it has no nonzero
$H_{\text{cont}}^{i}(\unicode[STIX]{x1D6E5},N_{\infty }/(\unicode[STIX]{x1D707},p))$
. Consequently, it has no nonzero
![]() $W(\mathfrak{m}^{\flat })$
-torsion because, by Lemma 3.12, neither does
$W(\mathfrak{m}^{\flat })$
-torsion because, by Lemma 3.12, neither does
![]() $H_{\text{cont}}^{i}(\unicode[STIX]{x1D6E5},N_{\infty }/(\unicode[STIX]{x1D707},p))$
(note that
$H_{\text{cont}}^{i}(\unicode[STIX]{x1D6E5},N_{\infty }/(\unicode[STIX]{x1D707},p))$
(note that
![]() $N_{\infty }/(\unicode[STIX]{x1D707},p)$
is a direct summand of
$N_{\infty }/(\unicode[STIX]{x1D707},p)$
is a direct summand of
![]() $\mathbb{A}_{\text{inf}}(R_{\infty })/(\unicode[STIX]{x1D707},p)\cong R_{\infty }^{\flat }/\unicode[STIX]{x1D707}$
).◻
$\mathbb{A}_{\text{inf}}(R_{\infty })/(\unicode[STIX]{x1D707},p)\cong R_{\infty }^{\flat }/\unicode[STIX]{x1D707}$
).◻
Theorem 3.20. The edge map
![]() $e$
defined in (3.15.1) induces the isomorphism
$e$
defined in (3.15.1) induces the isomorphism
Proof. By the projection formula [SP, 0944],
so Proposition 3.19 implies that the cohomology modules of
![]() $R\unicode[STIX]{x1D6E4}_{\text{cont}}(\unicode[STIX]{x1D6E5},\mathbb{A}_{\text{inf}}(R_{\infty }))\otimes _{A_{\text{inf}}}^{\mathbb{L}}A_{\text{inf}}/\unicode[STIX]{x1D707}$
have no nonzero
$R\unicode[STIX]{x1D6E4}_{\text{cont}}(\unicode[STIX]{x1D6E5},\mathbb{A}_{\text{inf}}(R_{\infty }))\otimes _{A_{\text{inf}}}^{\mathbb{L}}A_{\text{inf}}/\unicode[STIX]{x1D707}$
have no nonzero
![]() $W(\mathfrak{m}^{\flat })$
-torsion. Thus, the claim follows from Lemmas 3.16 and 3.18.◻
$W(\mathfrak{m}^{\flat })$
-torsion. Thus, the claim follows from Lemmas 3.16 and 3.18.◻
Remark 3.21. Analogously to Remark 3.10, Theorem 3.20 extends as follows: for any pro-(finite étale) affinoid perfectoid
![]() $\unicode[STIX]{x1D6E5}^{\prime }$
-cover
$\unicode[STIX]{x1D6E5}^{\prime }$
-cover
subject to the same conditions as in Remark 3.10, the edge map
![]() $e^{\prime }$
defined analogously to (3.15.1) induces the isomorphism
$e^{\prime }$
defined analogously to (3.15.1) induces the isomorphism
Indeed, as in Remark 3.10, by the almost purity theorem and the octahedral axiom,
![]() $[\mathfrak{m}^{\flat }]A_{\text{inf}}$
kills the cohomology modules of the cone of the map
$[\mathfrak{m}^{\flat }]A_{\text{inf}}$
kills the cohomology modules of the cone of the map
and, by [Reference Bhatt and ScholzeBS15, 3.4.4 and 3.4.14], these modules are derived
![]() $p$
-adically complete; thus, by Lemma 3.17, even
$p$
-adically complete; thus, by Lemma 3.17, even
![]() $W(\mathfrak{m}^{\flat })$
kills them, to the effect that Lemma 3.18 applies to the map
$W(\mathfrak{m}^{\flat })$
kills them, to the effect that Lemma 3.18 applies to the map
![]() $e_{0}$
and proves the claim.
$e_{0}$
and proves the claim.
As a final goal of §3, we wish to show in Theorem 3.34 that even the maps
![]() $L\unicode[STIX]{x1D702}_{(\unicode[STIX]{x1D707})}(e\,\widehat{\otimes }_{A_{\text{inf}}}^{\mathbb{L}}\,A_{\text{cris}}^{(m)})$
are isomorphisms for
$L\unicode[STIX]{x1D702}_{(\unicode[STIX]{x1D707})}(e\,\widehat{\otimes }_{A_{\text{inf}}}^{\mathbb{L}}\,A_{\text{cris}}^{(m)})$
are isomorphisms for
![]() $A_{\text{inf}}$
-algebras
$A_{\text{inf}}$
-algebras
![]() $A_{\text{cris}}^{(m)}$
reviewed in §3.26 below. This extension of Theorem 3.20 will be important for relating
$A_{\text{cris}}^{(m)}$
reviewed in §3.26 below. This extension of Theorem 3.20 will be important for relating
![]() $A\unicode[STIX]{x1D6FA}_{\mathfrak{X}}$
to logarithmic crystalline cohomology in §5. Our analysis of
$A\unicode[STIX]{x1D6FA}_{\mathfrak{X}}$
to logarithmic crystalline cohomology in §5. Our analysis of
![]() $L\unicode[STIX]{x1D702}_{(\unicode[STIX]{x1D707})}(e\,\widehat{\otimes }_{A_{\text{inf}}}^{\mathbb{L}}\,A_{\text{cris}}^{(m)})$
will use the following further consequences of the proof of Proposition 3.19.
$L\unicode[STIX]{x1D702}_{(\unicode[STIX]{x1D707})}(e\,\widehat{\otimes }_{A_{\text{inf}}}^{\mathbb{L}}\,A_{\text{cris}}^{(m)})$
will use the following further consequences of the proof of Proposition 3.19.
3.22 The decomposition of
 $N_{\infty }$
$N_{\infty }$
For
![]() $m\geqslant 0$
, let
$m\geqslant 0$
, let
![]() $N_{m}^{\Box }$
be the
$N_{m}^{\Box }$
be the
![]() $(p,\unicode[STIX]{x1D707})$
-adically completed direct sum of those summands
$(p,\unicode[STIX]{x1D707})$
-adically completed direct sum of those summands
![]() $A_{\text{inf}}\,\cdot \,X_{0}^{a_{0}}\cdots X_{d}^{a_{d}}$
that contribute to
$A_{\text{inf}}\,\cdot \,X_{0}^{a_{0}}\cdots X_{d}^{a_{d}}$
that contribute to
![]() $\mathbb{A}_{\text{inf}}(R_{\infty }^{\Box })$
in §3.14 for which
$\mathbb{A}_{\text{inf}}(R_{\infty }^{\Box })$
in §3.14 for which
![]() $m$
is the smallest nonnegative integer such that
$m$
is the smallest nonnegative integer such that
![]() $p^{m}a_{j}\in \mathbb{Z}$
for all
$p^{m}a_{j}\in \mathbb{Z}$
for all
![]() $j$
(equivalently, in the notation of (3.19.3), such that
$j$
(equivalently, in the notation of (3.19.3), such that
![]() $p^{m}b_{j}\in \mathbb{Z}$
for all
$p^{m}b_{j}\in \mathbb{Z}$
for all
![]() $j$
). For varying
$j$
). For varying
![]() $m>0$
, the
$m>0$
, the
![]() $A(R^{\Box })$
-modules
$A(R^{\Box })$
-modules
![]() $N_{m}^{\Box }$
and the
$N_{m}^{\Box }$
and the
![]() $A(R)$
-modules
$A(R)$
-modules
![]() $N_{m}:=N_{m}^{\Box }\,\widehat{\otimes }_{A(R^{\Box })}\,A(R)$
comprise the
$N_{m}:=N_{m}^{\Box }\,\widehat{\otimes }_{A(R^{\Box })}\,A(R)$
comprise the
![]() $(p,\unicode[STIX]{x1D707})$
-adically completed direct sum decompositions
$(p,\unicode[STIX]{x1D707})$
-adically completed direct sum decompositions
For a fixed
![]() $i$
, Lemma 3.7 and (3.19.5)–(3.19.6) imply that
$i$
, Lemma 3.7 and (3.19.5)–(3.19.6) imply that
Corollary 3.23. For all
![]() $i$
and
$i$
and
![]() $n,m\geqslant 0$
,
$n,m\geqslant 0$
,
Proof. If
![]() $R=R^{\Box }$
, then (3.22.2) suffices. In addition, by Lazard’s theorem,
$R=R^{\Box }$
, then (3.22.2) suffices. In addition, by Lazard’s theorem,
![]() $A(R)/(\unicode[STIX]{x1D707},p^{n})$
is a filtered direct limit of finite free
$A(R)/(\unicode[STIX]{x1D707},p^{n})$
is a filtered direct limit of finite free
![]() $A(R^{\Box })/(\unicode[STIX]{x1D707},p^{n})$
-modules. Thus, the general case of the claim follows by using (3.19.8) and its analogue for
$A(R^{\Box })/(\unicode[STIX]{x1D707},p^{n})$
-modules. Thus, the general case of the claim follows by using (3.19.8) and its analogue for
![]() $N_{0}$
and
$N_{0}$
and
![]() $N_{0}^{\Box }$
.◻
$N_{0}^{\Box }$
.◻
We wish to supplement Proposition 3.19 with Proposition 3.25 that analyzes the cohomology of
![]() $N_{\infty }$
without reducing modulo
$N_{\infty }$
without reducing modulo
![]() $\unicode[STIX]{x1D707}$
. Its proof will use the following base change result for
$\unicode[STIX]{x1D707}$
. Its proof will use the following base change result for
![]() $L\unicode[STIX]{x1D702}$
.
$L\unicode[STIX]{x1D702}$
.
Lemma 3.24 [Reference BhattBha18, 5.16].
For a ring
![]() $A$
, elements
$A$
, elements
![]() $f,g\in A$
with
$f,g\in A$
with
![]() $g$
a nonzero-divisor, and a
$g$
a nonzero-divisor, and a
![]() $K\in D(A)$
, if the modules
$K\in D(A)$
, if the modules
![]() $H^{i}(K\otimes _{A}^{\mathbb{L}}A/f)$
have no nonzero
$H^{i}(K\otimes _{A}^{\mathbb{L}}A/f)$
have no nonzero
![]() $g$
-torsion, then the natural map
$g$
-torsion, then the natural map
is an isomorphism.◻
Proposition 3.25. The element
![]() $\unicode[STIX]{x1D707}$
kills every
$\unicode[STIX]{x1D707}$
kills every
![]() $H_{\text{cont}}^{i}(\unicode[STIX]{x1D6E5},N_{\infty })$
.
$H_{\text{cont}}^{i}(\unicode[STIX]{x1D6E5},N_{\infty })$
.
Proof. Let
![]() $\unicode[STIX]{x1D6FF}_{1},\ldots ,\unicode[STIX]{x1D6FF}_{d}$
be the free generators of
$\unicode[STIX]{x1D6FF}_{1},\ldots ,\unicode[STIX]{x1D6FF}_{d}$
be the free generators of
![]() $\unicode[STIX]{x1D6E5}$
fixed in §3.2. By Lemma 3.7, we need to prove that
$\unicode[STIX]{x1D6E5}$
fixed in §3.2. By Lemma 3.7, we need to prove that
The key point, with which we start, is to prove the vanishing (3.25.1) modulo
![]() $\unicode[STIX]{x1D711}(\unicode[STIX]{x1D709})$
. The isomorphism
$\unicode[STIX]{x1D711}(\unicode[STIX]{x1D709})$
. The isomorphism
Lemma 3.7, and Proposition 3.19 show that the cohomology of
![]() $K_{N_{\infty }}(\unicode[STIX]{x1D6FF}_{1}-1,\ldots ,\unicode[STIX]{x1D6FF}_{d}-1)\otimes _{A_{\text{inf}}}^{\mathbb{L}}A_{\text{inf}}/\unicode[STIX]{x1D707}$
is
$K_{N_{\infty }}(\unicode[STIX]{x1D6FF}_{1}-1,\ldots ,\unicode[STIX]{x1D6FF}_{d}-1)\otimes _{A_{\text{inf}}}^{\mathbb{L}}A_{\text{inf}}/\unicode[STIX]{x1D707}$
is
![]() $p$
-torsion free. Therefore, Lemma 3.24 supplies the identification
$p$
-torsion free. Therefore, Lemma 3.24 supplies the identification
The inverse Frobenius
![]() $\unicode[STIX]{x1D711}^{-1}$
maps
$\unicode[STIX]{x1D711}^{-1}$
maps
![]() $N_{\infty }^{\Box }$
isomorphically onto a direct summand of
$N_{\infty }^{\Box }$
isomorphically onto a direct summand of
![]() $N_{\infty }^{\Box }$
, so it maps
$N_{\infty }^{\Box }$
, so it maps
![]() $N_{\infty }$
isomorphically onto a direct summand of
$N_{\infty }$
isomorphically onto a direct summand of
![]() $N_{\infty }$
. Thus,
$N_{\infty }$
. Thus,
![]() $\unicode[STIX]{x1D711}^{-1}$
maps
$\unicode[STIX]{x1D711}^{-1}$
maps
![]() $N_{\infty }/\unicode[STIX]{x1D711}(\unicode[STIX]{x1D709})$
isomorphically onto a direct summand of
$N_{\infty }/\unicode[STIX]{x1D711}(\unicode[STIX]{x1D709})$
isomorphically onto a direct summand of
![]() $N_{\infty }/\unicode[STIX]{x1D709}\cong M_{\infty }$
(see (3.14.5)). In particular, by Lemma 3.7 and Proposition 3.8,
$N_{\infty }/\unicode[STIX]{x1D709}\cong M_{\infty }$
(see (3.14.5)). In particular, by Lemma 3.7 and Proposition 3.8,
![]() $\unicode[STIX]{x1D701}_{p}-1$
kills the cohomology of
$\unicode[STIX]{x1D701}_{p}-1$
kills the cohomology of
![]() $K_{N_{\infty }/\unicode[STIX]{x1D711}(\unicode[STIX]{x1D709})}(\unicode[STIX]{x1D6FF}_{1}-1,\ldots ,\unicode[STIX]{x1D6FF}_{d}-1)$
, so both sides of (3.25.2) are acyclic.
$K_{N_{\infty }/\unicode[STIX]{x1D711}(\unicode[STIX]{x1D709})}(\unicode[STIX]{x1D6FF}_{1}-1,\ldots ,\unicode[STIX]{x1D6FF}_{d}-1)$
, so both sides of (3.25.2) are acyclic.
Since
![]() $N_{\infty }$
is
$N_{\infty }$
is
![]() $(p,\unicode[STIX]{x1D707})$
-adically complete, it is also
$(p,\unicode[STIX]{x1D707})$
-adically complete, it is also
![]() $\unicode[STIX]{x1D711}(\unicode[STIX]{x1D709})$
-adically complete (see [SP, 090T]). Thus,
$\unicode[STIX]{x1D711}(\unicode[STIX]{x1D709})$
-adically complete (see [SP, 090T]). Thus,
![]() $K_{N_{\infty }}(\unicode[STIX]{x1D6FF}_{1}-1,\ldots ,\unicode[STIX]{x1D6FF}_{d}-1)$
is derived
$K_{N_{\infty }}(\unicode[STIX]{x1D6FF}_{1}-1,\ldots ,\unicode[STIX]{x1D6FF}_{d}-1)$
is derived
![]() $\unicode[STIX]{x1D711}(\unicode[STIX]{x1D709})$
-adically complete, and [Reference Bhatt, Morrow and ScholzeBMS18, 6.19] implies the same for
$\unicode[STIX]{x1D711}(\unicode[STIX]{x1D709})$
-adically complete, and [Reference Bhatt, Morrow and ScholzeBMS18, 6.19] implies the same for
![]() $L\unicode[STIX]{x1D702}_{(\unicode[STIX]{x1D707})}(K_{N_{\infty }}(\unicode[STIX]{x1D6FF}_{1}-1,\ldots ,\unicode[STIX]{x1D6FF}_{d}-1))$
. The established acyclicity of the left-hand side of (3.25.2) therefore implies the desired vanishing (3.25.1).◻
$L\unicode[STIX]{x1D702}_{(\unicode[STIX]{x1D707})}(K_{N_{\infty }}(\unicode[STIX]{x1D6FF}_{1}-1,\ldots ,\unicode[STIX]{x1D6FF}_{d}-1))$
. The established acyclicity of the left-hand side of (3.25.2) therefore implies the desired vanishing (3.25.1).◻
3.26 The
 $A_{\text{inf}}$
-algebras
$A_{\text{inf}}$
-algebras
 $A_{\text{cris}}^{(m)}$
$A_{\text{cris}}^{(m)}$
For
![]() $m\in \mathbb{Z}_{{\geqslant}1}$
, we let
$m\in \mathbb{Z}_{{\geqslant}1}$
, we let
![]() $A_{\text{cris}}^{(m)}$
be the
$A_{\text{cris}}^{(m)}$
be the
![]() $p$
-adic completion of the
$p$
-adic completion of the
![]() $A_{\text{inf}}$
-subalgebra
$A_{\text{inf}}$
-subalgebra
![]() $A_{\text{cris}}^{0,\,(m)}$
of
$A_{\text{cris}}^{0,\,(m)}$
of
![]() $A_{\text{inf}}[\frac{1}{p}]$
generated by the elements
$A_{\text{inf}}[\frac{1}{p}]$
generated by the elements
![]() $\unicode[STIX]{x1D709}^{s}/s!$
with
$\unicode[STIX]{x1D709}^{s}/s!$
with
![]() $s\leqslant m$
. In particular,
$s\leqslant m$
. In particular,
![]() $A_{\text{cris}}^{(m)}\cong A_{\text{inf}}$
for
$A_{\text{cris}}^{(m)}\cong A_{\text{inf}}$
for
![]() $m<p$
. In contrast, if
$m<p$
. In contrast, if
![]() $m\geqslant p$
, then, since
$m\geqslant p$
, then, since
![]() $\unicode[STIX]{x1D707}^{p}/p!\in A_{\text{cris}}^{(m)}$
, the
$\unicode[STIX]{x1D707}^{p}/p!\in A_{\text{cris}}^{(m)}$
, the
![]() $p$
-adic and
$p$
-adic and
![]() $(p,\unicode[STIX]{x1D707})$
-adic topologies of
$(p,\unicode[STIX]{x1D707})$
-adic topologies of
![]() $A_{\text{cris}}^{(m)}$
agree. By its definition,
$A_{\text{cris}}^{(m)}$
agree. By its definition,
![]() $A_{\text{cris}}^{(m)}$
is
$A_{\text{cris}}^{(m)}$
is
![]() $p$
-torsion free; in fact, although we will not use this, Proposition 5.36 below implies that
$p$
-torsion free; in fact, although we will not use this, Proposition 5.36 below implies that
![]() $A_{\text{cris}}^{(m)}$
is even a domain. The map
$A_{\text{cris}}^{(m)}$
is even a domain. The map
![]() $\unicode[STIX]{x1D703}$
of (2.1.3) extends to
$\unicode[STIX]{x1D703}$
of (2.1.3) extends to
![]() $A_{\text{cris}}^{(m)}$
:
$A_{\text{cris}}^{(m)}$
:
Due to the ‘finite-type nature’ of the
![]() $A_{\text{inf}}$
-algebra
$A_{\text{inf}}$
-algebra
![]() $A_{\text{cris}}^{(m)}$
, more precisely, due to [Reference Bhatt, Morrow and ScholzeBMS18, 12.8(ii)], the systems of ideals
$A_{\text{cris}}^{(m)}$
, more precisely, due to [Reference Bhatt, Morrow and ScholzeBMS18, 12.8(ii)], the systems of ideals
Equivalently,
Therefore, by taking the inverse limit over
![]() $n$
of the sequences
$n$
of the sequences
we conclude that
The Frobenius automorphism of
![]() $A_{\text{inf}}$
preserves the subring
$A_{\text{inf}}$
preserves the subring
![]() $A_{\text{cris}}^{0,\,(m)}\subset A_{\text{inf}}[\frac{1}{p}]$
: indeed, for
$A_{\text{cris}}^{0,\,(m)}\subset A_{\text{inf}}[\frac{1}{p}]$
: indeed, for
![]() $m\geqslant p$
, since
$m\geqslant p$
, since
![]() $\unicode[STIX]{x1D709}=\sum _{i=0}^{p-1}[\unicode[STIX]{x1D716}^{i/p}]$
and
$\unicode[STIX]{x1D709}=\sum _{i=0}^{p-1}[\unicode[STIX]{x1D716}^{i/p}]$
and
![]() $\unicode[STIX]{x1D709}^{p}\in pA_{\text{cris}}^{0,\,(m)}$
, we have
$\unicode[STIX]{x1D709}^{p}\in pA_{\text{cris}}^{0,\,(m)}$
, we have
![]() $\unicode[STIX]{x1D711}(\unicode[STIX]{x1D709})=\sum _{i=0}^{p-1}[\unicode[STIX]{x1D716}^{i}]$
and
$\unicode[STIX]{x1D711}(\unicode[STIX]{x1D709})=\sum _{i=0}^{p-1}[\unicode[STIX]{x1D716}^{i}]$
and
![]() $\unicode[STIX]{x1D711}(\unicode[STIX]{x1D709})\in pA_{\text{cris}}^{0,\,(m)}$
. Thus, the Frobenius induces a ring endomorphism
$\unicode[STIX]{x1D711}(\unicode[STIX]{x1D709})\in pA_{\text{cris}}^{0,\,(m)}$
. Thus, the Frobenius induces a ring endomorphism
which, via the map
![]() $\unicode[STIX]{x1D703}$
, intertwines the absolute Frobenius of
$\unicode[STIX]{x1D703}$
, intertwines the absolute Frobenius of
![]() ${\mathcal{O}}_{C}/p$
(compare with (2.1.3)).
${\mathcal{O}}_{C}/p$
(compare with (2.1.3)).
3.27 The
 $A(R)$
-algebras
$A(R)$
-algebras
 $A_{\text{cris}}^{(m)}(R)$
$A_{\text{cris}}^{(m)}(R)$
The ‘relative version’ of
![]() $A_{\text{cris}}^{(m)}$
(respectively, a ‘highly ramified cover’ of this relative version) is the
$A_{\text{cris}}^{(m)}$
(respectively, a ‘highly ramified cover’ of this relative version) is the
![]() $A(R)$
-algebra (respectively,
$A(R)$
-algebra (respectively,
![]() $\mathbb{A}_{\text{inf}}(R_{\infty })$
-algebra)
$\mathbb{A}_{\text{inf}}(R_{\infty })$
-algebra)
where the completion is
![]() $(p,\unicode[STIX]{x1D707})$
-adic (equivalently,
$(p,\unicode[STIX]{x1D707})$
-adic (equivalently,
![]() $p$
-adic if
$p$
-adic if
![]() $m\geqslant p$
). In the case
$m\geqslant p$
). In the case
![]() $m<p$
, due to Lemma 3.13 and §3.26, we have
$m<p$
, due to Lemma 3.13 and §3.26, we have
![]() $A_{\text{cris}}^{(m)}(R)\cong A(R)$
and
$A_{\text{cris}}^{(m)}(R)\cong A(R)$
and
![]() $\mathbb{A}_{\text{cris}}^{(m)}(R_{\infty })\cong \mathbb{A}_{\text{inf}}(R_{\infty })$
.
$\mathbb{A}_{\text{cris}}^{(m)}(R_{\infty })\cong \mathbb{A}_{\text{inf}}(R_{\infty })$
.
Due to the decomposition (3.14.5), the subring
![]() $A_{\text{cris}}^{(m)}(R)\subset \mathbb{A}_{\text{cris}}^{(m)}(R_{\infty })$
is an
$A_{\text{cris}}^{(m)}(R)\subset \mathbb{A}_{\text{cris}}^{(m)}(R_{\infty })$
is an
![]() $A_{\text{cris}}^{(m)}(R)$
-module direct summand. Explicitly, the decomposition of
$A_{\text{cris}}^{(m)}(R)$
-module direct summand. Explicitly, the decomposition of
![]() $\mathbb{A}_{\text{inf}}(R_{\infty }^{\Box })$
described in §3.14 gives the decomposition
$\mathbb{A}_{\text{inf}}(R_{\infty }^{\Box })$
described in §3.14 gives the decomposition
where the completion is
![]() $(p,\unicode[STIX]{x1D707})$
-adic (equivalently,
$(p,\unicode[STIX]{x1D707})$
-adic (equivalently,
![]() $p$
-adic if
$p$
-adic if
![]() $m\geqslant p$
), and
$m\geqslant p$
), and
![]() $\mathbb{A}_{\text{cris}}^{(m)}(R_{\infty })$
is
$\mathbb{A}_{\text{cris}}^{(m)}(R_{\infty })$
is
![]() $(p,\unicode[STIX]{x1D707})$
-adically formally étale over
$(p,\unicode[STIX]{x1D707})$
-adically formally étale over
![]() $\mathbb{A}_{\text{cris}}^{(m)}(R_{\infty }^{\Box })$
(see §3.14). In particular, (3.26.2) holds with
$\mathbb{A}_{\text{cris}}^{(m)}(R_{\infty }^{\Box })$
(see §3.14). In particular, (3.26.2) holds with
![]() $A_{\text{cris}}^{(m)}$
replaced by
$A_{\text{cris}}^{(m)}$
replaced by
![]() $\mathbb{A}_{\text{cris}}^{(m)}(R_{\infty }^{\Box })$
, and hence also by
$\mathbb{A}_{\text{cris}}^{(m)}(R_{\infty }^{\Box })$
, and hence also by
![]() $\mathbb{A}_{\text{cris}}^{(m)}(R_{\infty })$
. Consequently, the generalization of (3.26.4) holds too:
$\mathbb{A}_{\text{cris}}^{(m)}(R_{\infty })$
. Consequently, the generalization of (3.26.4) holds too:
In addition, by (3.27.1) and the formal étaleness, each
![]() $\mathbb{A}_{\text{cris}}^{(m)}(R_{\infty })$
is
$\mathbb{A}_{\text{cris}}^{(m)}(R_{\infty })$
is
![]() $p$
-torsion free. By §§3.14 and 3.26, the rings
$p$
-torsion free. By §§3.14 and 3.26, the rings
![]() $A_{\text{cris}}^{(m)}(R)$
and
$A_{\text{cris}}^{(m)}(R)$
and
![]() $\mathbb{A}_{\text{cris}}^{(m)}(R_{\infty })$
come equipped with compatible
$\mathbb{A}_{\text{cris}}^{(m)}(R_{\infty })$
come equipped with compatible
![]() $A_{\text{cris}}^{(m)}$
-semilinear Frobenius endomorphisms that are compatible as
$A_{\text{cris}}^{(m)}$
-semilinear Frobenius endomorphisms that are compatible as
![]() $m$
varies.
$m$
varies.
The group
![]() $\unicode[STIX]{x1D6E5}$
acts continuously, Frobenius-equivariantly, and
$\unicode[STIX]{x1D6E5}$
acts continuously, Frobenius-equivariantly, and
![]() $A_{\text{cris}}^{(m)}$
-linearly on
$A_{\text{cris}}^{(m)}$
-linearly on
![]() $A_{\text{cris}}^{(m)}(R)$
and
$A_{\text{cris}}^{(m)}(R)$
and
![]() $\mathbb{A}_{\text{cris}}^{(m)}(R_{\infty })$
. For each
$\mathbb{A}_{\text{cris}}^{(m)}(R_{\infty })$
. For each
![]() $\unicode[STIX]{x1D6FF}\in \unicode[STIX]{x1D6E5}$
, the
$\unicode[STIX]{x1D6FF}\in \unicode[STIX]{x1D6E5}$
, the
![]() $A_{\text{inf}}$
-module endomorphism
$A_{\text{inf}}$
-module endomorphism
![]() $\frac{\unicode[STIX]{x1D6FF}-1}{\unicode[STIX]{x1D707}}$
of
$\frac{\unicode[STIX]{x1D6FF}-1}{\unicode[STIX]{x1D707}}$
of
![]() $A(R)$
induces an
$A(R)$
induces an
![]() $A_{\text{cris}}^{(m)}$
-module endomorphism
$A_{\text{cris}}^{(m)}$
-module endomorphism
![]() $\frac{\unicode[STIX]{x1D6FF}-1}{\unicode[STIX]{x1D707}}$
of
$\frac{\unicode[STIX]{x1D6FF}-1}{\unicode[STIX]{x1D707}}$
of
![]() $A_{\text{cris}}^{(m)}(R)$
that satisfies
$A_{\text{cris}}^{(m)}(R)$
that satisfies
![]() $\unicode[STIX]{x1D6FF}=1+\unicode[STIX]{x1D707}\,\cdot \,\frac{\unicode[STIX]{x1D6FF}-1}{\unicode[STIX]{x1D707}}$
. In particular,
$\unicode[STIX]{x1D6FF}=1+\unicode[STIX]{x1D707}\,\cdot \,\frac{\unicode[STIX]{x1D6FF}-1}{\unicode[STIX]{x1D707}}$
. In particular,
![]() $\unicode[STIX]{x1D6E5}$
acts trivially on
$\unicode[STIX]{x1D6E5}$
acts trivially on
![]() $A_{\text{cris}}^{(m)}(R)/\unicode[STIX]{x1D707}$
.
$A_{\text{cris}}^{(m)}(R)/\unicode[STIX]{x1D707}$
.
3.28 The
 $A_{\text{cris}}^{(m)}$
-base change of the edge map
$A_{\text{cris}}^{(m)}$
-base change of the edge map
Since
![]() $A_{\text{cris}}^{(m)}\cong A_{\text{inf}}$
for
$A_{\text{cris}}^{(m)}\cong A_{\text{inf}}$
for
![]() $m<p$
, for the sake of analyzing the map
$m<p$
, for the sake of analyzing the map
![]() $e\,\widehat{\otimes }_{A_{\text{inf}}}^{\mathbb{L}}\,A_{\text{cris}}^{(m)}$
, where
$e\,\widehat{\otimes }_{A_{\text{inf}}}^{\mathbb{L}}\,A_{\text{cris}}^{(m)}$
, where
![]() $e$
is as in (3.15.1), we suppose that
$e$
is as in (3.15.1), we suppose that
![]() $m\geqslant p$
. Then, for each
$m\geqslant p$
. Then, for each
![]() $n>0$
, we have
$n>0$
, we have
![]() $A_{\text{cris}}^{(m)}/p^{n}\cong A_{\text{cris}}^{(m)}/(p^{n},\unicode[STIX]{x1D707}^{n^{\prime }})$
for every large enough
$A_{\text{cris}}^{(m)}/p^{n}\cong A_{\text{cris}}^{(m)}/(p^{n},\unicode[STIX]{x1D707}^{n^{\prime }})$
for every large enough
![]() $n^{\prime }>0$
(see §3.26). Consequently, since
$n^{\prime }>0$
(see §3.26). Consequently, since
![]() $(p^{n},\unicode[STIX]{x1D707}^{n^{\prime }})$
is an
$(p^{n},\unicode[STIX]{x1D707}^{n^{\prime }})$
is an
![]() $\mathbb{A}_{\text{inf}}(R_{\infty })$
-regular sequence with
$\mathbb{A}_{\text{inf}}(R_{\infty })$
-regular sequence with
![]() $\mathbb{A}_{\text{inf}}(R_{\infty })/(p^{n},\unicode[STIX]{x1D707}^{n^{\prime }})$
flat over
$\mathbb{A}_{\text{inf}}(R_{\infty })/(p^{n},\unicode[STIX]{x1D707}^{n^{\prime }})$
flat over
![]() $A_{\text{inf}}/(p^{n},\unicode[STIX]{x1D707}^{n^{\prime }})$
(see Lemma 3.13), the projection formula [SP, 0944] and Lemma 3.7 imply that
$A_{\text{inf}}/(p^{n},\unicode[STIX]{x1D707}^{n^{\prime }})$
(see Lemma 3.13), the projection formula [SP, 0944] and Lemma 3.7 imply that
Consequently, the edge map
![]() $e$
defined in (3.15.1) gives rise to the map
$e$
defined in (3.15.1) gives rise to the map
Since
![]() $[\mathfrak{m}^{\flat }]$
kills each
$[\mathfrak{m}^{\flat }]$
kills each
![]() $H^{i}(\operatorname{Cone}(e))$
(see §3.15) and
$H^{i}(\operatorname{Cone}(e))$
(see §3.15) and
![]() $[\mathfrak{m}^{\flat }]^{2}=[\mathfrak{m}^{\flat }]$
, by using a free
$[\mathfrak{m}^{\flat }]^{2}=[\mathfrak{m}^{\flat }]$
, by using a free
![]() $A_{\text{inf}}$
-module resolution of
$A_{\text{inf}}$
-module resolution of
![]() $A_{\text{cris}}^{(m)}/p^{n}$
and the definition [SP, 064M], we see that
$A_{\text{cris}}^{(m)}/p^{n}$
and the definition [SP, 064M], we see that
![]() $[\mathfrak{m}^{\flat }]$
also kills each
$[\mathfrak{m}^{\flat }]$
also kills each
![]() $H^{i}(\operatorname{Cone}(e)\otimes _{A_{\text{inf}}}^{\mathbb{L}}A_{\text{cris}}^{(m)}/p^{n})$
. Consequently, by [SP, 0D6K], the ideal
$H^{i}(\operatorname{Cone}(e)\otimes _{A_{\text{inf}}}^{\mathbb{L}}A_{\text{cris}}^{(m)}/p^{n})$
. Consequently, by [SP, 0D6K], the ideal
![]() $[\mathfrak{m}^{\flat }]A_{\text{inf}}$
kills each
$[\mathfrak{m}^{\flat }]A_{\text{inf}}$
kills each
![]() $H^{i}(\operatorname{Cone}(e)\,\widehat{\otimes }_{A_{\text{inf}}}^{\mathbb{L}}\,A_{\text{cris}}^{(m)})$
, to the effect that, by Lemma 3.17 (and [Reference Bhatt and ScholzeBS15, 3.4.4 and 3.4.14]), so does
$H^{i}(\operatorname{Cone}(e)\,\widehat{\otimes }_{A_{\text{inf}}}^{\mathbb{L}}\,A_{\text{cris}}^{(m)})$
, to the effect that, by Lemma 3.17 (and [Reference Bhatt and ScholzeBS15, 3.4.4 and 3.4.14]), so does
![]() $W(\mathfrak{m}^{\flat })$
. In conclusion,
$W(\mathfrak{m}^{\flat })$
. In conclusion,
By applying Lemma 3.18, we will show in Theorem 3.34 that
![]() $L\unicode[STIX]{x1D702}_{(\unicode[STIX]{x1D707})}(e\,\widehat{\otimes }_{A_{\text{inf}}}^{\mathbb{L}}\,A_{\text{cris}}^{(m)})$
is an isomorphism. Thus, we need to know that the
$L\unicode[STIX]{x1D702}_{(\unicode[STIX]{x1D707})}(e\,\widehat{\otimes }_{A_{\text{inf}}}^{\mathbb{L}}\,A_{\text{cris}}^{(m)})$
is an isomorphism. Thus, we need to know that the
![]() $A_{\text{inf}}$
-modules
$A_{\text{inf}}$
-modules
![]() $H_{\text{cont}}^{i}(\unicode[STIX]{x1D6E5},\mathbb{A}_{\text{cris}}^{(m)}(R_{\infty })/\unicode[STIX]{x1D707})$
have no nonzero
$H_{\text{cont}}^{i}(\unicode[STIX]{x1D6E5},\mathbb{A}_{\text{cris}}^{(m)}(R_{\infty })/\unicode[STIX]{x1D707})$
have no nonzero
![]() $W(\mathfrak{m}^{\flat })$
-torsion (compare with Proposition 3.19 for
$W(\mathfrak{m}^{\flat })$
-torsion (compare with Proposition 3.19 for
![]() $\mathbb{A}_{\text{inf}}(R_{\infty })/\unicode[STIX]{x1D707}$
). The following result is a step in that direction.
$\mathbb{A}_{\text{inf}}(R_{\infty })/\unicode[STIX]{x1D707}$
). The following result is a step in that direction.
Proposition 3.29. Each
![]() $\mathbb{A}_{\text{cris}}^{(m)}(R_{\infty })/(\unicode[STIX]{x1D707},p^{n})$
and also
$\mathbb{A}_{\text{cris}}^{(m)}(R_{\infty })/(\unicode[STIX]{x1D707},p^{n})$
and also
![]() $\mathbb{A}_{\text{cris}}^{(m)}(R_{\infty })/\unicode[STIX]{x1D707}$
have no nonzero
$\mathbb{A}_{\text{cris}}^{(m)}(R_{\infty })/\unicode[STIX]{x1D707}$
have no nonzero
![]() $W(\mathfrak{m}^{\flat })$
-torsion.
$W(\mathfrak{m}^{\flat })$
-torsion.
Proof. By the
![]() $p$
-adic completeness of
$p$
-adic completeness of
![]() $\mathbb{A}_{\text{cris}}^{(m)}(R_{\infty })/\unicode[STIX]{x1D707}$
(see (3.27.2)), we may focus on the rings
$\mathbb{A}_{\text{cris}}^{(m)}(R_{\infty })/\unicode[STIX]{x1D707}$
(see (3.27.2)), we may focus on the rings
![]() $\mathbb{A}_{\text{cris}}^{(m)}(R_{\infty })/(\unicode[STIX]{x1D707},p^{n})$
. The argument for the latter is similar to that of [Reference Bhatt, Morrow and ScholzeBMS18, 12.8(iii)] and uses approximation by Noetherian rings. Namely, by the
$\mathbb{A}_{\text{cris}}^{(m)}(R_{\infty })/(\unicode[STIX]{x1D707},p^{n})$
. The argument for the latter is similar to that of [Reference Bhatt, Morrow and ScholzeBMS18, 12.8(iii)] and uses approximation by Noetherian rings. Namely, by the
![]() $(p,\unicode[STIX]{x1D711}^{-1}(\unicode[STIX]{x1D707}))$
-adic completeness of
$(p,\unicode[STIX]{x1D711}^{-1}(\unicode[STIX]{x1D707}))$
-adic completeness of
![]() $A_{\text{inf}}$
, the assignment
$A_{\text{inf}}$
, the assignment
By [Reference Bhatt, Morrow and ScholzeBMS18, 4.31], this makes
![]() $A_{\text{inf}}$
a faithfully flat
$A_{\text{inf}}$
a faithfully flat
![]() $\mathbb{Z}_{p}\unicode[STIX]{x27E6}T\unicode[STIX]{x27E7}$
-algebra. Thus, letting
$\mathbb{Z}_{p}\unicode[STIX]{x27E6}T\unicode[STIX]{x27E7}$
-algebra. Thus, letting
![]() $M$
be the mod
$M$
be the mod
![]() $((T+1)^{p}-1,p^{n})$
reduction of the
$((T+1)^{p}-1,p^{n})$
reduction of the
![]() $\mathbb{Z}_{p}\unicode[STIX]{x27E6}T\unicode[STIX]{x27E7}$
-subalgebra of
$\mathbb{Z}_{p}\unicode[STIX]{x27E6}T\unicode[STIX]{x27E7}$
-subalgebra of
![]() $\mathbb{Z}_{p}\unicode[STIX]{x27E6}T\unicode[STIX]{x27E7}[\frac{1}{p}]$
generated by the
$\mathbb{Z}_{p}\unicode[STIX]{x27E6}T\unicode[STIX]{x27E7}[\frac{1}{p}]$
generated by the
![]() $\frac{1}{s!}(\sum _{i=0}^{p-1}(T+1)^{i})^{s}$
with
$\frac{1}{s!}(\sum _{i=0}^{p-1}(T+1)^{i})^{s}$
with
![]() $s\leqslant m$
, we have the identification
$s\leqslant m$
, we have the identification
The
![]() $(\mathbb{Z}_{p}\unicode[STIX]{x27E6}T\unicode[STIX]{x27E7}/((T+1)^{p}-1,p^{n}))$
-flatness of
$(\mathbb{Z}_{p}\unicode[STIX]{x27E6}T\unicode[STIX]{x27E7}/((T+1)^{p}-1,p^{n}))$
-flatness of
![]() $\mathbb{A}_{\text{inf}}(R_{\infty })/(\unicode[STIX]{x1D707},p^{n})$
ensures that the
$\mathbb{A}_{\text{inf}}(R_{\infty })/(\unicode[STIX]{x1D707},p^{n})$
ensures that the
![]() $\unicode[STIX]{x1D711}^{-1}(\unicode[STIX]{x1D707})$
-torsion submodule of
$\unicode[STIX]{x1D711}^{-1}(\unicode[STIX]{x1D707})$
-torsion submodule of
![]() $\mathbb{A}_{\text{cris}}^{(m)}(R_{\infty })/(\unicode[STIX]{x1D707},p^{n})$
is the base change of the
$\mathbb{A}_{\text{cris}}^{(m)}(R_{\infty })/(\unicode[STIX]{x1D707},p^{n})$
is the base change of the
![]() $T$
-torsion submodule
$T$
-torsion submodule
![]() $M[T]\subset M$
. Consequently, since
$M[T]\subset M$
. Consequently, since
![]() $\unicode[STIX]{x1D711}^{-1}(\unicode[STIX]{x1D707})\in W(\mathfrak{m}^{\flat })$
, the consideration of the
$\unicode[STIX]{x1D711}^{-1}(\unicode[STIX]{x1D707})\in W(\mathfrak{m}^{\flat })$
, the consideration of the
![]() $p$
-adic filtration of
$p$
-adic filtration of
![]() $M[T]$
reduces us to proving that
$M[T]$
reduces us to proving that
which follows from Lemma 3.12. ◻
To relate
![]() $H_{\text{cont}}^{i}(\unicode[STIX]{x1D6E5},\mathbb{A}_{\text{cris}}^{(m)}(R_{\infty })/\unicode[STIX]{x1D707})$
to
$H_{\text{cont}}^{i}(\unicode[STIX]{x1D6E5},\mathbb{A}_{\text{cris}}^{(m)}(R_{\infty })/\unicode[STIX]{x1D707})$
to
![]() $H_{\text{cont}}^{i}(\unicode[STIX]{x1D6E5},\mathbb{A}_{\text{inf}}(R_{\infty })/\unicode[STIX]{x1D707})$
in Proposition 3.33, we will use the following general result about exactness properties of
$H_{\text{cont}}^{i}(\unicode[STIX]{x1D6E5},\mathbb{A}_{\text{inf}}(R_{\infty })/\unicode[STIX]{x1D707})$
in Proposition 3.33, we will use the following general result about exactness properties of
![]() $p$
-adically completed tensor products. For concreteness, we state it for
$p$
-adically completed tensor products. For concreteness, we state it for
![]() $A_{\text{inf}}$
and its algebra
$A_{\text{inf}}$
and its algebra
![]() $A_{\text{cris}}^{(m)}$
, but the proof is not specific to these choices.
$A_{\text{cris}}^{(m)}$
, but the proof is not specific to these choices.
Lemma 3.30. For a fixed
![]() $m\geqslant p$
, consider the following condition on an
$m\geqslant p$
, consider the following condition on an
![]() $A_{\text{inf}}$
-module
$A_{\text{inf}}$
-module
![]() $L$
:
$L$
:
which means that for every
![]() $j,n$
, the map
$j,n$
, the map
![]() $\operatorname{Tor}_{j}^{A_{\text{inf}}}(L,A_{\text{cris}}^{(m)}/p^{n^{\prime }})\rightarrow \operatorname{Tor}_{j}^{A_{\text{inf}}}(L,A_{\text{cris}}^{(m)}/p^{n})$
vanishes for some
$\operatorname{Tor}_{j}^{A_{\text{inf}}}(L,A_{\text{cris}}^{(m)}/p^{n^{\prime }})\rightarrow \operatorname{Tor}_{j}^{A_{\text{inf}}}(L,A_{\text{cris}}^{(m)}/p^{n})$
vanishes for some
![]() $n^{\prime }>n$
. For a bounded complex
$n^{\prime }>n$
. For a bounded complex
of
![]() $A_{\text{inf}}$
-modules, if each
$A_{\text{inf}}$
-modules, if each
![]() $M^{i}$
and each
$M^{i}$
and each
![]() $H^{i}(M^{\bullet })$
satisfy (
$H^{i}(M^{\bullet })$
satisfy (
![]() $\star$
), then, for every
$\star$
), then, for every
![]() $i$
, we have
$i$
, we have
Proof. For an inverse system
![]() $\{0\rightarrow I_{n}^{\prime }\rightarrow I_{n}\rightarrow I_{n}^{\prime \prime }\rightarrow 0\}\text{}_{n>0}$
of short exact sequences of abelian groups,
$\{0\rightarrow I_{n}^{\prime }\rightarrow I_{n}\rightarrow I_{n}^{\prime \prime }\rightarrow 0\}\text{}_{n>0}$
of short exact sequences of abelian groups,
![]() $\{I_{n}\}\text{}_{n>0}$
is Mittag–Leffler with vanishing eventual images if and only if so are both
$\{I_{n}\}\text{}_{n>0}$
is Mittag–Leffler with vanishing eventual images if and only if so are both
![]() $\{I_{n}^{\prime }\}\text{}_{n>0}$
and
$\{I_{n}^{\prime }\}\text{}_{n>0}$
and
![]() $\{I_{n}^{\prime \prime }\}\text{}_{n>0}$
. Therefore, the short exact sequences
$\{I_{n}^{\prime \prime }\}\text{}_{n>0}$
. Therefore, the short exact sequences
imply, by descending induction on
![]() $i$
, that each
$i$
, that each
![]() $\operatorname{Ker}(d^{i})$
and each
$\operatorname{Ker}(d^{i})$
and each
![]() $\operatorname{Im}(d^{i})$
satisfy (
$\operatorname{Im}(d^{i})$
satisfy (
![]() $\star$
). Consequently, these sequences remain short exact after applying
$\star$
). Consequently, these sequences remain short exact after applying
![]() $-\,\widehat{\otimes }_{A_{\text{inf}}}\,A_{\text{cris}}^{(m)}$
, to the effect that the flanking terms of (3.30.1) get identified. By construction, this identification is compatible with the canonical maps to
$-\,\widehat{\otimes }_{A_{\text{inf}}}\,A_{\text{cris}}^{(m)}$
, to the effect that the flanking terms of (3.30.1) get identified. By construction, this identification is compatible with the canonical maps to
![]() $\mathop{\varprojlim }\nolimits_{n}(H^{i}(M^{\bullet }\otimes _{A_{\text{inf}}}A_{\text{cris}}^{(m)}/p^{n}))$
, so it remains to establish the second identification in (3.30.1).
$\mathop{\varprojlim }\nolimits_{n}(H^{i}(M^{\bullet }\otimes _{A_{\text{inf}}}A_{\text{cris}}^{(m)}/p^{n}))$
, so it remains to establish the second identification in (3.30.1).
By [SP, 0662 and 0130], the spectral sequences associated to a double complex give the following spectral sequences that converge to
![]() $H^{i+j}(M^{\bullet }\otimes _{A_{\text{inf}}}^{\mathbb{L}}A_{\text{cris}}^{(m)}/p^{n})$
:
$H^{i+j}(M^{\bullet }\otimes _{A_{\text{inf}}}^{\mathbb{L}}A_{\text{cris}}^{(m)}/p^{n})$
:
where the differential on the
![]() $\vphantom{E}^{(n)\prime }E_{1}$
-page is
$\vphantom{E}^{(n)\prime }E_{1}$
-page is
![]() $H^{j}(d^{i}\otimes _{A_{\text{inf}}}^{\mathbb{L}}A_{\text{cris}}^{(m)}/p^{n})$
. As
$H^{j}(d^{i}\otimes _{A_{\text{inf}}}^{\mathbb{L}}A_{\text{cris}}^{(m)}/p^{n})$
. As
![]() $n$
varies, both families of spectral sequences form inverse systems. Moreover, by assumption, the systems
$n$
varies, both families of spectral sequences form inverse systems. Moreover, by assumption, the systems
![]() $\{\vphantom{E}^{(n)}E_{2}^{ij}\}\text{}_{n>0}$
with
$\{\vphantom{E}^{(n)}E_{2}^{ij}\}\text{}_{n>0}$
with
![]() $i\neq 0$
and
$i\neq 0$
and
![]() $\{\vphantom{E}^{(n)\prime }E_{1}^{ij}\}\text{}_{n>0}$
with
$\{\vphantom{E}^{(n)\prime }E_{1}^{ij}\}\text{}_{n>0}$
with
![]() $j\neq 0$
are Mittag–Leffler with vanishing eventual images. This persists to the subsequent pages: namely, by the first sentence of the proof, to the systems
$j\neq 0$
are Mittag–Leffler with vanishing eventual images. This persists to the subsequent pages: namely, by the first sentence of the proof, to the systems
![]() $\{\vphantom{E}^{(n)}E_{s}^{ij}\}\text{}_{n>0}$
with
$\{\vphantom{E}^{(n)}E_{s}^{ij}\}\text{}_{n>0}$
with
![]() $i\neq 0$
and
$i\neq 0$
and
![]() $\{\vphantom{E}^{(n)\prime }E_{s}^{ij}\}\text{}_{n>0}$
with
$\{\vphantom{E}^{(n)\prime }E_{s}^{ij}\}\text{}_{n>0}$
with
![]() $j\neq 0$
for any
$j\neq 0$
for any
![]() $s\leqslant \infty$
. Consequently, the edge maps
$s\leqslant \infty$
. Consequently, the edge maps
become isomorphisms after applying the functor
![]() $\mathop{\varprojlim }\nolimits_{n}$
. It remains to note that then so does their composition, which is the canonical map
$\mathop{\varprojlim }\nolimits_{n}$
. It remains to note that then so does their composition, which is the canonical map
![]() $H^{i}(M^{\bullet })\otimes _{A_{\text{inf}}}A_{\text{cris}}^{(m)}/p^{n}\rightarrow H^{i}(M^{\bullet }\otimes _{A_{\text{inf}}}A_{\text{cris}}^{(m)}/p^{n})$
.◻
$H^{i}(M^{\bullet })\otimes _{A_{\text{inf}}}A_{\text{cris}}^{(m)}/p^{n}\rightarrow H^{i}(M^{\bullet }\otimes _{A_{\text{inf}}}A_{\text{cris}}^{(m)}/p^{n})$
.◻
To make Lemma 3.30 practical, we now establish its condition (
![]() $\star$
) in several keycases.
$\star$
) in several keycases.
Lemma 3.31. For a fixed
![]() $m\geqslant p$
, the condition (
$m\geqslant p$
, the condition (
![]() $\star$
) holds in any of the following cases:
$\star$
) holds in any of the following cases:
(i) for any
 $n,n^{\prime }>0$
, the sequence
$n,n^{\prime }>0$
, the sequence
 $(p^{n},\unicode[STIX]{x1D707}^{n^{\prime }})$
is
$(p^{n},\unicode[STIX]{x1D707}^{n^{\prime }})$
is
 $L$
-regular and
$L$
-regular and
 $L/(p^{n},\unicode[STIX]{x1D707}^{n^{\prime }})$
is
$L/(p^{n},\unicode[STIX]{x1D707}^{n^{\prime }})$
is
 $A_{\text{inf}}/(p^{n},\unicode[STIX]{x1D707}^{n^{\prime }})$
-flat;
$A_{\text{inf}}/(p^{n},\unicode[STIX]{x1D707}^{n^{\prime }})$
-flat;(ii) the module
 $L$
has no nonzero
$L$
has no nonzero
 $p$
-torsion and each
$p$
-torsion and each
 $L/p^{n}$
is a filtered direct limit of direct sums of
$L/p^{n}$
is a filtered direct limit of direct sums of
 $A_{\text{inf}}$
-modules of the form
$A_{\text{inf}}$
-modules of the form
 $A_{\text{inf}}/(\unicode[STIX]{x1D711}^{-s}(\unicode[STIX]{x1D707}),p^{n})$
for variable
$A_{\text{inf}}/(\unicode[STIX]{x1D711}^{-s}(\unicode[STIX]{x1D707}),p^{n})$
for variable
 $s\geqslant 0$
.
$s\geqslant 0$
.
Thus, (
![]() $\star$
) holds for
$\star$
) holds for
![]() $\mathbb{A}_{\text{inf}}(R_{\infty })$
and
$\mathbb{A}_{\text{inf}}(R_{\infty })$
and
![]() $\mathbb{A}_{\text{inf}}(R_{\infty })/\unicode[STIX]{x1D707}$
, and for each
$\mathbb{A}_{\text{inf}}(R_{\infty })/\unicode[STIX]{x1D707}$
, and for each
![]() $H_{\text{cont}}^{i}(\unicode[STIX]{x1D6E5},N_{\infty })$
and
$H_{\text{cont}}^{i}(\unicode[STIX]{x1D6E5},N_{\infty })$
and
![]() $H_{\text{cont}}^{i}(\unicode[STIX]{x1D6E5},\mathbb{A}_{\text{inf}}(R_{\infty })/\unicode[STIX]{x1D707})$
.
$H_{\text{cont}}^{i}(\unicode[STIX]{x1D6E5},\mathbb{A}_{\text{inf}}(R_{\infty })/\unicode[STIX]{x1D707})$
.
Proof. If (i) holds, then, by the regular sequence aspect,
![]() $L\otimes _{A_{\text{inf}}}^{\mathbb{L}}A_{\text{inf}}/(p^{n},\unicode[STIX]{x1D707}^{n^{\prime }})\cong L/(p^{n},\unicode[STIX]{x1D707}^{n^{\prime }})$
, so, by the flatness aspect,
$L\otimes _{A_{\text{inf}}}^{\mathbb{L}}A_{\text{inf}}/(p^{n},\unicode[STIX]{x1D707}^{n^{\prime }})\cong L/(p^{n},\unicode[STIX]{x1D707}^{n^{\prime }})$
, so, by the flatness aspect,
![]() $L\otimes _{A_{\text{inf}}}^{\mathbb{L}}A_{\text{cris}}^{(m)}/p^{n}$
is concentrated in degree
$L\otimes _{A_{\text{inf}}}^{\mathbb{L}}A_{\text{cris}}^{(m)}/p^{n}$
is concentrated in degree
![]() $0$
. Thus, in the case (i), the inverse systems in (
$0$
. Thus, in the case (i), the inverse systems in (
![]() $\star$
) vanish termwise.
$\star$
) vanish termwise.
If (ii) holds, then each
![]() $L\otimes _{A_{\text{inf}}}^{\mathbb{L}}A_{\text{inf}}/p^{n}$
is concentrated in degree
$L\otimes _{A_{\text{inf}}}^{\mathbb{L}}A_{\text{inf}}/p^{n}$
is concentrated in degree
![]() $0$
, so
$0$
, so
for every
![]() $j\geqslant 0$
. In addition, since
$j\geqslant 0$
. In addition, since
![]() $\unicode[STIX]{x1D711}^{-s}(\unicode[STIX]{x1D707})\,\mid \,\unicode[STIX]{x1D707}$
for
$\unicode[STIX]{x1D711}^{-s}(\unicode[STIX]{x1D707})\,\mid \,\unicode[STIX]{x1D707}$
for
![]() $s\geqslant 0$
and each
$s\geqslant 0$
and each
![]() $A_{\text{inf}}/p^{n}$
has no nonzero
$A_{\text{inf}}/p^{n}$
has no nonzero
![]() $\unicode[STIX]{x1D707}$
-torsion, the assumption on
$\unicode[STIX]{x1D707}$
-torsion, the assumption on
![]() $L/p^{n}$
in (ii) ensures that the right-hand side of (3.31.1) vanishes termwise for
$L/p^{n}$
in (ii) ensures that the right-hand side of (3.31.1) vanishes termwise for
![]() $j>1$
. In contrast, for
$j>1$
. In contrast, for
![]() $j=1$
and every
$j=1$
and every
![]() $n>0$
, there is an
$n>0$
, there is an
![]() $n^{\prime }>n$
such that the transition map between positions
$n^{\prime }>n$
such that the transition map between positions
![]() $n^{\prime }$
and
$n^{\prime }$
and
![]() $n$
in the right-hand side system of (3.31.1) vanishes: this follows from the identification
$n$
in the right-hand side system of (3.31.1) vanishes: this follows from the identification
and (3.26.2). Consequently, (ii) implies (
![]() $\star$
), as claimed.
$\star$
), as claimed.
By Lemma 3.13, (i) holds for
![]() $\mathbb{A}_{\text{inf}}(R_{\infty })$
and then, by Lazard’s theorem, (ii) holds for
$\mathbb{A}_{\text{inf}}(R_{\infty })$
and then, by Lazard’s theorem, (ii) holds for
![]() $\mathbb{A}_{\text{inf}}(R_{\infty })/\unicode[STIX]{x1D707}$
. Likewise, Proposition 3.19, Corollary 3.23, and Lazard’s theorem imply that (ii) holds for each
$\mathbb{A}_{\text{inf}}(R_{\infty })/\unicode[STIX]{x1D707}$
. Likewise, Proposition 3.19, Corollary 3.23, and Lazard’s theorem imply that (ii) holds for each
![]() $H_{\text{cont}}^{i}(\unicode[STIX]{x1D6E5},\mathbb{A}_{\text{inf}}(R_{\infty })/\unicode[STIX]{x1D707})$
. By Lemma 3.7,
$H_{\text{cont}}^{i}(\unicode[STIX]{x1D6E5},\mathbb{A}_{\text{inf}}(R_{\infty })/\unicode[STIX]{x1D707})$
. By Lemma 3.7,
![]() $H_{\text{cont}}^{i}(\unicode[STIX]{x1D6E5},N_{\infty })$
vanishes for large
$H_{\text{cont}}^{i}(\unicode[STIX]{x1D6E5},N_{\infty })$
vanishes for large
![]() $i$
and, by Proposition 3.25, we have the short exact sequences
$i$
and, by Proposition 3.25, we have the short exact sequences
Therefore, due to the first sentence of the proof of Lemma 3.30, descending induction on
![]() $i$
shows that (
$i$
shows that (
![]() $\star$
) for
$\star$
) for
![]() $H_{\text{cont}}^{i}(\unicode[STIX]{x1D6E5},\mathbb{A}_{\text{inf}}(R_{\infty })/\unicode[STIX]{x1D707})$
implies (
$H_{\text{cont}}^{i}(\unicode[STIX]{x1D6E5},\mathbb{A}_{\text{inf}}(R_{\infty })/\unicode[STIX]{x1D707})$
implies (
![]() $\star$
) for
$\star$
) for
![]() $H_{\text{cont}}^{i}(\unicode[STIX]{x1D6E5},N_{\infty })$
.◻
$H_{\text{cont}}^{i}(\unicode[STIX]{x1D6E5},N_{\infty })$
.◻
Thanks to Lemma 3.31, we may draw the following concrete consequences from Lemma 3.30.
Proposition 3.32. For every
![]() $m\geqslant p$
and
$m\geqslant p$
and
![]() $i\in \mathbb{Z}$
, we have the identifications
$i\in \mathbb{Z}$
, we have the identifications
In particular,
![]() $\unicode[STIX]{x1D707}$
kills every
$\unicode[STIX]{x1D707}$
kills every
![]() $H_{\text{cont}}^{i}(\unicode[STIX]{x1D6E5},N_{\infty }\,\widehat{\otimes }_{A_{\text{inf}}}\,A_{\text{cris}}^{(m)})$
.
$H_{\text{cont}}^{i}(\unicode[STIX]{x1D6E5},N_{\infty }\,\widehat{\otimes }_{A_{\text{inf}}}\,A_{\text{cris}}^{(m)})$
.
Proof. By Lemma 3.7, the Koszul complex
![]() $M^{\bullet }$
of
$M^{\bullet }$
of
![]() $N_{\infty }$
with respect to
$N_{\infty }$
with respect to
![]() $\unicode[STIX]{x1D6FF}_{1},\ldots ,\unicode[STIX]{x1D6FF}_{d}$
satisfies
$\unicode[STIX]{x1D6FF}_{1},\ldots ,\unicode[STIX]{x1D6FF}_{d}$
satisfies
as well as
for every
![]() $n>0$
. Moreover, by Lemma 3.31, each
$n>0$
. Moreover, by Lemma 3.31, each
![]() $M^{i}$
and each
$M^{i}$
and each
![]() $H^{i}(M^{\bullet })$
satisfy (
$H^{i}(M^{\bullet })$
satisfy (
![]() $\star$
). Thus, (3.32.1) is a special case of (3.30.1). By Proposition 3.25,
$\star$
). Thus, (3.32.1) is a special case of (3.30.1). By Proposition 3.25,
![]() $\unicode[STIX]{x1D707}$
kills every
$\unicode[STIX]{x1D707}$
kills every
![]() $H_{\text{cont}}^{i}(\unicode[STIX]{x1D6E5},N_{\infty })$
, so, by (3.32.1), it also kills every
$H_{\text{cont}}^{i}(\unicode[STIX]{x1D6E5},N_{\infty })$
, so, by (3.32.1), it also kills every
![]() $H_{\text{cont}}^{i}(\unicode[STIX]{x1D6E5},N_{\infty }\,\widehat{\otimes }_{A_{\text{inf}}}\,A_{\text{cris}}^{(m)})$
.◻
$H_{\text{cont}}^{i}(\unicode[STIX]{x1D6E5},N_{\infty }\,\widehat{\otimes }_{A_{\text{inf}}}\,A_{\text{cris}}^{(m)})$
.◻
Proposition 3.33. For every
![]() $m\geqslant p$
and
$m\geqslant p$
and
![]() $i\in \mathbb{Z}$
, we have the identifications
$i\in \mathbb{Z}$
, we have the identifications
Moreover, the
![]() $A_{\text{inf}}$
-module
$A_{\text{inf}}$
-module
![]() $H_{\text{cont}}^{i}(\unicode[STIX]{x1D6E5},\mathbb{A}_{\text{cris}}^{(m)}(R_{\infty })/\unicode[STIX]{x1D707})$
has no nonzero
$H_{\text{cont}}^{i}(\unicode[STIX]{x1D6E5},\mathbb{A}_{\text{cris}}^{(m)}(R_{\infty })/\unicode[STIX]{x1D707})$
has no nonzero
![]() $W(\mathfrak{m}^{\flat })$
-torsion.
$W(\mathfrak{m}^{\flat })$
-torsion.
Proof. Similarly to the proof of Proposition 3.32, Lemma 3.30 applies to the Koszul complex of
![]() $\mathbb{A}_{\text{inf}}(R_{\infty })/\unicode[STIX]{x1D707}$
and, due to (3.27.2), gives the identifications. Thus, it suffices to show that each
$\mathbb{A}_{\text{inf}}(R_{\infty })/\unicode[STIX]{x1D707}$
and, due to (3.27.2), gives the identifications. Thus, it suffices to show that each
has no nonzero
![]() $W(\mathfrak{m}^{\flat })$
-torsion. Since
$W(\mathfrak{m}^{\flat })$
-torsion. Since
![]() $\unicode[STIX]{x1D6E5}$
acts trivially on
$\unicode[STIX]{x1D6E5}$
acts trivially on
![]() $A(R)/(\unicode[STIX]{x1D707},p^{n})$
, Lemma 3.7 and Proposition 3.29 imply that each
$A(R)/(\unicode[STIX]{x1D707},p^{n})$
, Lemma 3.7 and Proposition 3.29 imply that each
![]() $H_{\text{cont}}^{i}(\unicode[STIX]{x1D6E5},A(R)/(\unicode[STIX]{x1D707},p^{n}))\otimes _{A_{\text{inf}}/p^{n}}A_{\text{cris}}^{(m)}/p^{n}$
has no nonzero
$H_{\text{cont}}^{i}(\unicode[STIX]{x1D6E5},A(R)/(\unicode[STIX]{x1D707},p^{n}))\otimes _{A_{\text{inf}}/p^{n}}A_{\text{cris}}^{(m)}/p^{n}$
has no nonzero
![]() $W(\mathfrak{m}^{\flat })$
-torsion. Consequently, due to the decomposition (3.22.1), it suffices to show that for
$W(\mathfrak{m}^{\flat })$
-torsion. Consequently, due to the decomposition (3.22.1), it suffices to show that for
![]() $j>0$
, the module
$j>0$
, the module
has no nonzero
![]() $W(\mathfrak{m}^{\flat })$
-torsion. For this, similarly to the proof of Proposition 3.29, we will approximate by Noetherian rings. More precisely, similarly to (3.29.1), the assignment
$W(\mathfrak{m}^{\flat })$
-torsion. For this, similarly to the proof of Proposition 3.29, we will approximate by Noetherian rings. More precisely, similarly to (3.29.1), the assignment
for which
![]() $A_{\text{inf}}$
is
$A_{\text{inf}}$
is
![]() $\mathbb{Z}\unicode[STIX]{x27E6}T\unicode[STIX]{x27E7}$
-flat. In terms of this morphism, the
$\mathbb{Z}\unicode[STIX]{x27E6}T\unicode[STIX]{x27E7}$
-flat. In terms of this morphism, the
![]() $A_{\text{inf}}$
-algebra
$A_{\text{inf}}$
-algebra
![]() $A_{\text{cris}}^{(m)}/(\unicode[STIX]{x1D711}^{-j}(\unicode[STIX]{x1D707}),p^{n})$
is the
$A_{\text{cris}}^{(m)}/(\unicode[STIX]{x1D711}^{-j}(\unicode[STIX]{x1D707}),p^{n})$
is the
![]() $A_{\text{inf}}/(\unicode[STIX]{x1D711}^{-j}(\unicode[STIX]{x1D707}),p^{n})$
-base change of the mod
$A_{\text{inf}}/(\unicode[STIX]{x1D711}^{-j}(\unicode[STIX]{x1D707}),p^{n})$
-base change of the mod
![]() $(T,p^{n})$
reduction
$(T,p^{n})$
reduction
![]() $M$
of the
$M$
of the
![]() $\mathbb{Z}_{p}\unicode[STIX]{x27E6}T\unicode[STIX]{x27E7}$
-subalgebra of
$\mathbb{Z}_{p}\unicode[STIX]{x27E6}T\unicode[STIX]{x27E7}$
-subalgebra of
![]() $\mathbb{Z}_{p}\unicode[STIX]{x27E6}T\unicode[STIX]{x27E7}[\frac{1}{p}]$
generated by the elements
$\mathbb{Z}_{p}\unicode[STIX]{x27E6}T\unicode[STIX]{x27E7}[\frac{1}{p}]$
generated by the elements
![]() $\frac{1}{s!}(\sum _{i=0}^{p-1}(T+1)^{p^{j-1}\,\cdot \,i})^{s}$
with
$\frac{1}{s!}(\sum _{i=0}^{p-1}(T+1)^{p^{j-1}\,\cdot \,i})^{s}$
with
![]() $s\leqslant m$
. Consequently, we need to show that
$s\leqslant m$
. Consequently, we need to show that
has no nonzero
![]() $W(\mathfrak{m}^{\flat })$
-torsion. By Corollary 3.23, the module
$W(\mathfrak{m}^{\flat })$
-torsion. By Corollary 3.23, the module
Thus, by
![]() $p$
-adically filtering
$p$
-adically filtering
![]() $M$
, we reduce to showing that
$M$
, we reduce to showing that
![]() $H_{\text{cont}}^{i}(\unicode[STIX]{x1D6E5},N_{j}/(\unicode[STIX]{x1D707},p^{n}))/p$
has no nonzero
$H_{\text{cont}}^{i}(\unicode[STIX]{x1D6E5},N_{j}/(\unicode[STIX]{x1D707},p^{n}))/p$
has no nonzero
![]() $W(\mathfrak{m}^{\flat })$
-torsion. This, in turn, follows from Proposition 3.19 and Lemma 3.12.◻
$W(\mathfrak{m}^{\flat })$
-torsion. This, in turn, follows from Proposition 3.19 and Lemma 3.12.◻
With Proposition 3.33 in hand, we are ready for the promised claim about
![]() $L\unicode[STIX]{x1D702}_{(\unicode[STIX]{x1D707})}(e\,\widehat{\otimes }_{A_{\text{inf}}}^{\mathbb{L}}\,A_{\text{cris}}^{(m)})$
.
$L\unicode[STIX]{x1D702}_{(\unicode[STIX]{x1D707})}(e\,\widehat{\otimes }_{A_{\text{inf}}}^{\mathbb{L}}\,A_{\text{cris}}^{(m)})$
.
Theorem 3.34. For each
![]() $m\geqslant p$
, the map
$m\geqslant p$
, the map
![]() $e\,\widehat{\otimes }_{A_{\text{inf}}}^{\mathbb{L}}\,A_{\text{cris}}^{(m)}$
from (3.28.1) induces the isomorphism
$e\,\widehat{\otimes }_{A_{\text{inf}}}^{\mathbb{L}}\,A_{\text{cris}}^{(m)}$
from (3.28.1) induces the isomorphism
Proof. By (3.28.2), the ideal
![]() $W(\mathfrak{m}^{\flat })\subset A_{\text{inf}}$
kills the cohomology of
$W(\mathfrak{m}^{\flat })\subset A_{\text{inf}}$
kills the cohomology of
![]() $\operatorname{Cone}(e\,\widehat{\otimes }_{A_{\text{inf}}}^{\mathbb{L}}\,A_{\text{cris}}^{(m)})$
. By Proposition 3.33 (and the projection formula [SP, 0944] with (3.27.2)), the cohomology modules of
$\operatorname{Cone}(e\,\widehat{\otimes }_{A_{\text{inf}}}^{\mathbb{L}}\,A_{\text{cris}}^{(m)})$
. By Proposition 3.33 (and the projection formula [SP, 0944] with (3.27.2)), the cohomology modules of
have no nonzero
![]() $W(\mathfrak{m}^{\flat })$
-torsion. Thus, Lemma 3.18 applies and gives the desired conclusion.◻
$W(\mathfrak{m}^{\flat })$
-torsion. Thus, Lemma 3.18 applies and gives the desired conclusion.◻
Remark 3.35. Analogously to Remark 3.21, we may extend Theorem 3.34 to any affinoid perfectoid
![]() $\unicode[STIX]{x1D6E5}^{\prime }$
-cover that refines
$\unicode[STIX]{x1D6E5}^{\prime }$
-cover that refines
![]() $\mathfrak{X}_{C,\,\infty }^{\text{ad}}\rightarrow \mathfrak{X}_{C}^{\text{ad}}$
and is subject to the same conditions as in Remark 3.10: more precisely, with the notation used there, we have
$\mathfrak{X}_{C,\,\infty }^{\text{ad}}\rightarrow \mathfrak{X}_{C}^{\text{ad}}$
and is subject to the same conditions as in Remark 3.10: more precisely, with the notation used there, we have
where
![]() $\mathbb{A}_{\text{cris}}^{(m)}(R_{\infty }^{\prime }):=\mathbb{A}_{\text{inf}}(R_{\infty }^{\prime })\,\widehat{\otimes }_{A_{\text{inf}}}\,A_{\text{cris}}^{(m)}$
. Indeed, as there (see also §3.28), the ideal
$\mathbb{A}_{\text{cris}}^{(m)}(R_{\infty }^{\prime }):=\mathbb{A}_{\text{inf}}(R_{\infty }^{\prime })\,\widehat{\otimes }_{A_{\text{inf}}}\,A_{\text{cris}}^{(m)}$
. Indeed, as there (see also §3.28), the ideal
![]() $W(\mathfrak{m}^{\flat })$
kills the cohomology of the cone of the map
$W(\mathfrak{m}^{\flat })$
kills the cohomology of the cone of the map
![]() $R\unicode[STIX]{x1D6E4}_{\text{cont}}(\unicode[STIX]{x1D6E5},\mathbb{A}_{\text{cris}}^{(m)}(R_{\infty }))\rightarrow R\unicode[STIX]{x1D6E4}_{\text{cont}}(\unicode[STIX]{x1D6E5}^{\prime },\mathbb{A}_{\text{cris}}^{(m)}(R_{\infty }^{\prime }))$
, so Lemma 3.18 applies to this map and gives the claim.
$R\unicode[STIX]{x1D6E4}_{\text{cont}}(\unicode[STIX]{x1D6E5},\mathbb{A}_{\text{cris}}^{(m)}(R_{\infty }))\rightarrow R\unicode[STIX]{x1D6E4}_{\text{cont}}(\unicode[STIX]{x1D6E5}^{\prime },\mathbb{A}_{\text{cris}}^{(m)}(R_{\infty }^{\prime }))$
, so Lemma 3.18 applies to this map and gives the claim.
4 The de Rham specialization of
 $A\unicode[STIX]{x1D6FA}_{\mathfrak{X}}$
$A\unicode[STIX]{x1D6FA}_{\mathfrak{X}}$
With the local analysis of §3 at our disposal, we turn to relating
![]() $A\unicode[STIX]{x1D6FA}_{\mathfrak{X}}$
to the logarithmic de Rham complex of
$A\unicode[STIX]{x1D6FA}_{\mathfrak{X}}$
to the logarithmic de Rham complex of
![]() $\mathfrak{X}$
in Theorem 4.17. The key steps for this are the identification and the analysis of the Hodge–Tate specialization of
$\mathfrak{X}$
in Theorem 4.17. The key steps for this are the identification and the analysis of the Hodge–Tate specialization of
![]() $A\unicode[STIX]{x1D6FA}_{\mathfrak{X}}$
in Theorems 4.2 and 4.11. These steps were also used in the smooth case in [Reference Bhatt, Morrow and ScholzeBMS18, §§8 and 9] but, due to the difficulties mentioned in the beginning of §3, we carry them out differently. Namely, we rely on the analysis of group cohomology presented in §3 and, in the identification step, we use Lemma 3.24 (which comes from [Reference BhattBha18]). Nevertheless, similarly to [Reference Bhatt, Morrow and ScholzeBMS18, §9.2], we will take advantage of the following formalism of presheaves.
$A\unicode[STIX]{x1D6FA}_{\mathfrak{X}}$
in Theorems 4.2 and 4.11. These steps were also used in the smooth case in [Reference Bhatt, Morrow and ScholzeBMS18, §§8 and 9] but, due to the difficulties mentioned in the beginning of §3, we carry them out differently. Namely, we rely on the analysis of group cohomology presented in §3 and, in the identification step, we use Lemma 3.24 (which comes from [Reference BhattBha18]). Nevertheless, similarly to [Reference Bhatt, Morrow and ScholzeBMS18, §9.2], we will take advantage of the following formalism of presheaves.
4.1 The presheaf version
 $A\unicode[STIX]{x1D6FA}_{\mathfrak{X}}^{\text{psh}}$
$A\unicode[STIX]{x1D6FA}_{\mathfrak{X}}^{\text{psh}}$
In addition to the étale site
![]() $\mathfrak{X}_{\acute{\text{e}}\text{t}}$
, we consider the site
$\mathfrak{X}_{\acute{\text{e}}\text{t}}$
, we consider the site
![]() $\mathfrak{X}_{\acute{\text{e}}\text{t}}^{\text{psh}}$
whose objects are those connected affine opens of
$\mathfrak{X}_{\acute{\text{e}}\text{t}}^{\text{psh}}$
whose objects are those connected affine opens of
![]() $\mathfrak{X}_{\acute{\text{e}}\text{t}}$
that have an étale coordinate map (1.5.1) and coverings are the isomorphisms. Thus, the topology of
$\mathfrak{X}_{\acute{\text{e}}\text{t}}$
that have an étale coordinate map (1.5.1) and coverings are the isomorphisms. Thus, the topology of
![]() $\mathfrak{X}_{\acute{\text{e}}\text{t}}^{\text{psh}}$
is the coarsest possible and any presheaf is already a sheaf. Since the objects of
$\mathfrak{X}_{\acute{\text{e}}\text{t}}^{\text{psh}}$
is the coarsest possible and any presheaf is already a sheaf. Since the objects of
![]() $\mathfrak{X}_{\acute{\text{e}}\text{t}}^{\text{psh}}$
form a basis of
$\mathfrak{X}_{\acute{\text{e}}\text{t}}^{\text{psh}}$
form a basis of
![]() $\mathfrak{X}_{\acute{\text{e}}\text{t}}$
, there is a morphism of topoi
$\mathfrak{X}_{\acute{\text{e}}\text{t}}$
, there is a morphism of topoi
for which
![]() $\unicode[STIX]{x1D719}_{\ast }$
is given by restricting sheaves on
$\unicode[STIX]{x1D719}_{\ast }$
is given by restricting sheaves on
![]() $\mathfrak{X}_{\acute{\text{e}}\text{t}}$
to
$\mathfrak{X}_{\acute{\text{e}}\text{t}}$
to
![]() $\mathfrak{X}_{\acute{\text{e}}\text{t}}^{\text{psh}}$
and
$\mathfrak{X}_{\acute{\text{e}}\text{t}}^{\text{psh}}$
and
![]() $\unicode[STIX]{x1D719}^{-1}$
is given by sheafifying. In particular, since any sheaf is the sheafification of its associated presheaf,
$\unicode[STIX]{x1D719}^{-1}$
is given by sheafifying. In particular, since any sheaf is the sheafification of its associated presheaf,
![]() $\unicode[STIX]{x1D719}^{-1}\circ \unicode[STIX]{x1D719}_{\ast }\cong \operatorname{id}$
. We let
$\unicode[STIX]{x1D719}^{-1}\circ \unicode[STIX]{x1D719}_{\ast }\cong \operatorname{id}$
. We let
be the indicated composition of morphisms of topoi (with
![]() $\unicode[STIX]{x1D708}$
defined in (1.5.5)) and set
$\unicode[STIX]{x1D708}$
defined in (1.5.5)) and set
Since
![]() $L\unicode[STIX]{x1D702}$
commutes with pullback under flat morphisms of ringed topoi (see [Reference Bhatt, Morrow and ScholzeBMS18, 6.14]),
$L\unicode[STIX]{x1D702}$
commutes with pullback under flat morphisms of ringed topoi (see [Reference Bhatt, Morrow and ScholzeBMS18, 6.14]),
Moreover,
![]() $A\unicode[STIX]{x1D6FA}_{\mathfrak{X}}^{\text{psh}}$
may be described explicitly: for every object
$A\unicode[STIX]{x1D6FA}_{\mathfrak{X}}^{\text{psh}}$
may be described explicitly: for every object
![]() $\mathfrak{U}$
of
$\mathfrak{U}$
of
![]() $\mathfrak{X}_{\acute{\text{e}}\text{t}}^{\text{psh}}$
, we have
$\mathfrak{X}_{\acute{\text{e}}\text{t}}^{\text{psh}}$
, we have
In particular, since, by [Reference Bhatt, Morrow and ScholzeBMS18, 6.19], the functor
![]() $L\unicode[STIX]{x1D702}$
preserves derived completeness when used in the context of a replete topos (such as that of sets), we see from (4.1.3) that
$L\unicode[STIX]{x1D702}$
preserves derived completeness when used in the context of a replete topos (such as that of sets), we see from (4.1.3) that
![]() $A\unicode[STIX]{x1D6FA}_{\mathfrak{X}}^{\text{psh}}$
is derived
$A\unicode[STIX]{x1D6FA}_{\mathfrak{X}}^{\text{psh}}$
is derived
![]() $\unicode[STIX]{x1D709}$
-adically (and also
$\unicode[STIX]{x1D709}$
-adically (and also
![]() $\unicode[STIX]{x1D711}(\unicode[STIX]{x1D709})$
-adically) complete (compare with Corollary 4.6 below).
$\unicode[STIX]{x1D711}(\unicode[STIX]{x1D709})$
-adically) complete (compare with Corollary 4.6 below).
Armed with the formalism of §4.1, we now identify the Hodge–Tate specialization of
![]() $A\unicode[STIX]{x1D6FA}_{\mathfrak{X}}$
.
$A\unicode[STIX]{x1D6FA}_{\mathfrak{X}}$
.
Theorem 4.2. We have the identification
where in the target
![]() $L\unicode[STIX]{x1D702}$
is with respect to the ideal sheaf
$L\unicode[STIX]{x1D702}$
is with respect to the ideal sheaf
![]() $(\unicode[STIX]{x1D701}_{p}-1){\mathcal{O}}_{\mathfrak{X},\,\acute{\text{e}}\text{t}}\subset {\mathcal{O}}_{\mathfrak{X},\,\acute{\text{e}}\text{t}}$
. If the coordinate morphisms (1.5.1) exist Zariski locally on
$(\unicode[STIX]{x1D701}_{p}-1){\mathcal{O}}_{\mathfrak{X},\,\acute{\text{e}}\text{t}}\subset {\mathcal{O}}_{\mathfrak{X},\,\acute{\text{e}}\text{t}}$
. If the coordinate morphisms (1.5.1) exist Zariski locally on
![]() $\mathfrak{X}$
, then (4.2.1) also holds for
$\mathfrak{X}$
, then (4.2.1) also holds for
![]() $A\unicode[STIX]{x1D6FA}_{\mathfrak{X}_{\text{Zar}}}$
(defined in (2.2.4)).
$A\unicode[STIX]{x1D6FA}_{\mathfrak{X}_{\text{Zar}}}$
(defined in (2.2.4)).
Proof. The kernel of
![]() $\unicode[STIX]{x1D703}_{\mathfrak{ X}_{C}^{\text{ad}}}\circ \unicode[STIX]{x1D711}^{-1}:\mathbb{A}_{\text{inf},\,\mathfrak{X}_{C}^{\text{ad}}}{\twoheadrightarrow}\widehat{{\mathcal{O}}}_{\mathfrak{ X}_{C}^{\text{ad}}}^{+}$
is generated by the nonzero-divisor
$\unicode[STIX]{x1D703}_{\mathfrak{ X}_{C}^{\text{ad}}}\circ \unicode[STIX]{x1D711}^{-1}:\mathbb{A}_{\text{inf},\,\mathfrak{X}_{C}^{\text{ad}}}{\twoheadrightarrow}\widehat{{\mathcal{O}}}_{\mathfrak{ X}_{C}^{\text{ad}}}^{+}$
is generated by the nonzero-divisor
![]() $\unicode[STIX]{x1D711}(\unicode[STIX]{x1D709})$
(see §2.2), so the projection formula [SP, 0944] provides the identification
$\unicode[STIX]{x1D711}(\unicode[STIX]{x1D709})$
(see §2.2), so the projection formula [SP, 0944] provides the identification
Since
![]() $(\unicode[STIX]{x1D703}\circ \unicode[STIX]{x1D711}^{-1})(\unicode[STIX]{x1D707})=\unicode[STIX]{x1D701}_{p}-1$
, this induces the map (4.2.1) and, likewise, also its presheaf version
$(\unicode[STIX]{x1D703}\circ \unicode[STIX]{x1D711}^{-1})(\unicode[STIX]{x1D707})=\unicode[STIX]{x1D701}_{p}-1$
, this induces the map (4.2.1) and, likewise, also its presheaf version
Due to (4.1.2), the map
![]() $\unicode[STIX]{x1D719}^{-1}$
brings (4.2.2) to (4.2.1), so we seek to show that (4.2.2) is an isomorphism.
$\unicode[STIX]{x1D719}^{-1}$
brings (4.2.2) to (4.2.1), so we seek to show that (4.2.2) is an isomorphism.
For every object
![]() $\mathfrak{U}\cong \operatorname{Spf}(R)$
of
$\mathfrak{U}\cong \operatorname{Spf}(R)$
of
![]() $\mathfrak{X}_{\acute{\text{e}}\text{t}}^{\text{psh}}$
equipped with an étale morphism as in (1.5.1), the discussion and the notation of §3 apply. In particular, Proposition 3.19 and (3.20.1) ensure that the cohomology of
$\mathfrak{X}_{\acute{\text{e}}\text{t}}^{\text{psh}}$
equipped with an étale morphism as in (1.5.1), the discussion and the notation of §3 apply. In particular, Proposition 3.19 and (3.20.1) ensure that the cohomology of
![]() $R\unicode[STIX]{x1D6E4}_{\text{cont}}(\unicode[STIX]{x1D6E5},\mathbb{A}_{\text{inf}}(R_{\infty }))\otimes _{A_{\text{inf}}}^{\mathbb{L}}A_{\text{inf}}/\unicode[STIX]{x1D707}$
is
$R\unicode[STIX]{x1D6E4}_{\text{cont}}(\unicode[STIX]{x1D6E5},\mathbb{A}_{\text{inf}}(R_{\infty }))\otimes _{A_{\text{inf}}}^{\mathbb{L}}A_{\text{inf}}/\unicode[STIX]{x1D707}$
is
![]() $p$
-torsion free. Thus, since we have
$p$
-torsion free. Thus, since we have
![]() $\unicode[STIX]{x1D711}(\unicode[STIX]{x1D709})\equiv p\hspace{0.2em}{\rm mod}\hspace{0.2em}(\unicode[STIX]{x1D707})$
(see §2.1), Lemma 3.24 implies that
$\unicode[STIX]{x1D711}(\unicode[STIX]{x1D709})\equiv p\hspace{0.2em}{\rm mod}\hspace{0.2em}(\unicode[STIX]{x1D707})$
(see §2.1), Lemma 3.24 implies that
Since the edge maps (3.3.1) and (3.15.1) are compatible, Theorems 3.9 and 3.20 then imply that
Consequently, (4.2.2) is an isomorphism on every
![]() $\mathfrak{U}$
, as desired.◻
$\mathfrak{U}$
, as desired.◻
4.3 The object
 $\widetilde{\unicode[STIX]{x1D6FA}}_{\mathfrak{X}}$
$\widetilde{\unicode[STIX]{x1D6FA}}_{\mathfrak{X}}$
To proceed further, we need to analyze the right-hand side of (4.2.1), namely,
where, as in Theorem 4.2, the functor
![]() $L\unicode[STIX]{x1D702}$
is formed with respect to the ideal sheaf
$L\unicode[STIX]{x1D702}$
is formed with respect to the ideal sheaf
![]() $(\unicode[STIX]{x1D701}_{p}-1){\mathcal{O}}_{\mathfrak{X},\,\acute{\text{e}}\text{t}}$
.
$(\unicode[STIX]{x1D701}_{p}-1){\mathcal{O}}_{\mathfrak{X},\,\acute{\text{e}}\text{t}}$
.
Proposition 4.4. For
![]() $i\geqslant 0$
, the
$i\geqslant 0$
, the
![]() ${\mathcal{O}}_{\mathfrak{X},\,\acute{\text{e}}\text{t}}$
-module
${\mathcal{O}}_{\mathfrak{X},\,\acute{\text{e}}\text{t}}$
-module
![]() $H^{i}(\widetilde{\unicode[STIX]{x1D6FA}}_{\mathfrak{X}})$
is locally free of rank
$H^{i}(\widetilde{\unicode[STIX]{x1D6FA}}_{\mathfrak{X}})$
is locally free of rank
![]() $\binom{\dim _{x}(\mathfrak{X}_{k})}{i}$
at a variable closed point
$\binom{\dim _{x}(\mathfrak{X}_{k})}{i}$
at a variable closed point
![]() $x$
of
$x$
of
![]() $\mathfrak{X}_{k}$
(in particular, each
$\mathfrak{X}_{k}$
(in particular, each
![]() $H^{i}(\widetilde{\unicode[STIX]{x1D6FA}}_{\mathfrak{X}})/p^{n}$
is a quasi-coherent
$H^{i}(\widetilde{\unicode[STIX]{x1D6FA}}_{\mathfrak{X}})/p^{n}$
is a quasi-coherent
![]() ${\mathcal{O}}_{\mathfrak{X},\,\acute{\text{e}}\text{t}}/p^{n}$
-module). Moreover,
${\mathcal{O}}_{\mathfrak{X},\,\acute{\text{e}}\text{t}}/p^{n}$
-module). Moreover,
Proof. The claims are étale local (see [SP, 058S]), so we assume that
![]() $\mathfrak{X}=\operatorname{Spf}(R)$
, that
$\mathfrak{X}=\operatorname{Spf}(R)$
, that
![]() $\mathfrak{X}$
is connected, and that there is an étale
$\mathfrak{X}$
is connected, and that there is an étale
![]() $\operatorname{Spf}({\mathcal{O}}_{C})$
-morphism as in (1.5.1):
$\operatorname{Spf}({\mathcal{O}}_{C})$
-morphism as in (1.5.1):
so that the discussion and the notation of §3 apply. In particular, since
![]() $R$
is
$R$
is
![]() $R^{\Box }$
-flat (see §1.5) and
$R^{\Box }$
-flat (see §1.5) and
![]() $\unicode[STIX]{x1D6E5}$
acts trivially on
$\unicode[STIX]{x1D6E5}$
acts trivially on
![]() $R^{\Box }$
and
$R^{\Box }$
and
![]() $R$
, Lemma 3.7 and Proposition 3.8 imply that
$R$
, Lemma 3.7 and Proposition 3.8 imply that
Thus, since the edge maps
![]() $e$
of (3.3.1) are compatible for
$e$
of (3.3.1) are compatible for
![]() $R$
and
$R$
and
![]() $R^{\Box }$
, Theorem 3.9 shows that
$R^{\Box }$
, Theorem 3.9 shows that
is an isomorphism of free
![]() $R$
-modules of rank
$R$
-modules of rank
![]() $\binom{d}{i}$
. Consequently,
$\binom{d}{i}$
. Consequently,
to the effect that
![]() $H^{i}(\widetilde{\unicode[STIX]{x1D6FA}}_{\mathfrak{X}})$
is free of rank
$H^{i}(\widetilde{\unicode[STIX]{x1D6FA}}_{\mathfrak{X}})$
is free of rank
![]() $\binom{d}{i}$
, as desired. For (4.4.1), by §3.3, we need to show that
$\binom{d}{i}$
, as desired. For (4.4.1), by §3.3, we need to show that
![]() $R\overset{{\sim}}{\longrightarrow }(R_{\infty })^{\unicode[STIX]{x1D6E5}}$
. This map is an inclusion of a direct summand whose complementary summand
$R\overset{{\sim}}{\longrightarrow }(R_{\infty })^{\unicode[STIX]{x1D6E5}}$
. This map is an inclusion of a direct summand whose complementary summand
![]() $M_{\infty }^{\unicode[STIX]{x1D6E5}}$
is both
$M_{\infty }^{\unicode[STIX]{x1D6E5}}$
is both
![]() $p$
-torsion free and, by Proposition 3.8, killed by
$p$
-torsion free and, by Proposition 3.8, killed by
![]() $\unicode[STIX]{x1D701}_{p}-1$
, so the claim follows.◻
$\unicode[STIX]{x1D701}_{p}-1$
, so the claim follows.◻
Remark 4.5. The proof of Proposition 4.4, specifically, (4.4.4) and (4.4.5), shows that if
![]() $\mathfrak{X}$
is affine, connected, and admits a coordinate map as in (1.5.1), then the presheaf assigning
$\mathfrak{X}$
is affine, connected, and admits a coordinate map as in (1.5.1), then the presheaf assigning ![]() to a variable
to a variable
![]() $\mathfrak{X}$
-étale affine
$\mathfrak{X}$
-étale affine
![]() $\mathfrak{X}^{\prime }$
is already a sheaf. In particular, if the coordinate maps (1.5.1) exist Zariski locally on
$\mathfrak{X}^{\prime }$
is already a sheaf. In particular, if the coordinate maps (1.5.1) exist Zariski locally on
![]() $\mathfrak{X}$
(for instance, if
$\mathfrak{X}$
(for instance, if
![]() $\mathfrak{X}$
is
$\mathfrak{X}$
is
![]() ${\mathcal{O}}_{C}$
-smooth or arises as in (1.5.3) from a strictly semistable
${\mathcal{O}}_{C}$
-smooth or arises as in (1.5.3) from a strictly semistable
![]() ${\mathcal{X}}$
), then the sheaves
${\mathcal{X}}$
), then the sheaves
![]() $H^{i}(\widetilde{\unicode[STIX]{x1D6FA}}_{\mathfrak{X}})$
may be computed using the Zariski topology: more precisely, then the object
$H^{i}(\widetilde{\unicode[STIX]{x1D6FA}}_{\mathfrak{X}})$
may be computed using the Zariski topology: more precisely, then the object
![]() $\widetilde{\unicode[STIX]{x1D6FA}}_{\mathfrak{X}_{\text{Zar}}}$
defined by the formula (4.3.1) using the Zariski topology of
$\widetilde{\unicode[STIX]{x1D6FA}}_{\mathfrak{X}_{\text{Zar}}}$
defined by the formula (4.3.1) using the Zariski topology of
![]() $\mathfrak{X}$
satisfies
$\mathfrak{X}$
satisfies
Corollary 4.6. The object
![]() $A\unicode[STIX]{x1D6FA}_{\mathfrak{X}}$
is derived
$A\unicode[STIX]{x1D6FA}_{\mathfrak{X}}$
is derived
![]() $\unicode[STIX]{x1D709}$
-adically complete and
$\unicode[STIX]{x1D709}$
-adically complete and
Proof. For the derived
![]() $\unicode[STIX]{x1D709}$
-adic completeness, since
$\unicode[STIX]{x1D709}$
-adic completeness, since
![]() $\unicode[STIX]{x1D719}^{-1}\circ R\unicode[STIX]{x1D719}_{\ast }\cong \operatorname{id}$
, it suffices to show that the map
$\unicode[STIX]{x1D719}^{-1}\circ R\unicode[STIX]{x1D719}_{\ast }\cong \operatorname{id}$
, it suffices to show that the map
becomes an isomorphism after applying
![]() $R\unicode[STIX]{x1D719}_{\ast }$
. Thus, since
$R\unicode[STIX]{x1D719}_{\ast }$
. Thus, since
![]() $A\unicode[STIX]{x1D6FA}_{\mathfrak{X}}^{\text{psh}}$
is derived
$A\unicode[STIX]{x1D6FA}_{\mathfrak{X}}^{\text{psh}}$
is derived
![]() $\unicode[STIX]{x1D709}$
-adically complete (see §4.1), it suffices to establish the adjunction isomorphism (4.6.1). For this, by the definition of
$\unicode[STIX]{x1D709}$
-adically complete (see §4.1), it suffices to establish the adjunction isomorphism (4.6.1). For this, by the definition of
![]() $\mathfrak{X}_{\acute{\text{e}}\text{t}}^{\text{psh}}$
given in §4.1, we may assume that
$\mathfrak{X}_{\acute{\text{e}}\text{t}}^{\text{psh}}$
given in §4.1, we may assume that
![]() $\mathfrak{X}$
is affine, connected, and admits an étale morphism (1.5.1). In addition, since
$\mathfrak{X}$
is affine, connected, and admits an étale morphism (1.5.1). In addition, since
![]() $A\unicode[STIX]{x1D6FA}_{\mathfrak{X}}^{\text{psh}}$
is derived
$A\unicode[STIX]{x1D6FA}_{\mathfrak{X}}^{\text{psh}}$
is derived
![]() $\unicode[STIX]{x1D711}(\unicode[STIX]{x1D709})$
-adically complete, the
$\unicode[STIX]{x1D711}(\unicode[STIX]{x1D709})$
-adically complete, the
![]() $\mathfrak{X}_{\acute{\text{e}}\text{t}}^{\text{psh}}$
-analogue of [Reference Bhatt, Morrow and ScholzeBMS18, 9.15] reduces us to proving that
$\mathfrak{X}_{\acute{\text{e}}\text{t}}^{\text{psh}}$
-analogue of [Reference Bhatt, Morrow and ScholzeBMS18, 9.15] reduces us to proving that
By the five lemmas, we may assume that
![]() $n=1$
and, by the proof of Theorem 4.2,
$n=1$
and, by the proof of Theorem 4.2,
It remains to recall from Remark 4.5 that the cohomology presheaves of
![]() $\unicode[STIX]{x1D6FA}_{\mathfrak{X}}^{\text{psh}}$
are sheaves.◻
$\unicode[STIX]{x1D6FA}_{\mathfrak{X}}^{\text{psh}}$
are sheaves.◻
Our next task is to identify the vector bundles
![]() $H^{i}(\widetilde{\unicode[STIX]{x1D6FA}}_{\mathfrak{X}})$
with the twists of the bundles given by logarithmic differentials (see Theorem 4.11). For this, in Proposition 4.8, we first express
$H^{i}(\widetilde{\unicode[STIX]{x1D6FA}}_{\mathfrak{X}})$
with the twists of the bundles given by logarithmic differentials (see Theorem 4.11). For this, in Proposition 4.8, we first express
![]() $H^{i}(\widetilde{\unicode[STIX]{x1D6FA}}_{\mathfrak{X}})$
as
$H^{i}(\widetilde{\unicode[STIX]{x1D6FA}}_{\mathfrak{X}})$
as
![]() $\bigwedge ^{i}H^{1}(\widetilde{\unicode[STIX]{x1D6FA}}_{\mathfrak{X}})$
, and then, in (4.10.2), construct a map that relates
$\bigwedge ^{i}H^{1}(\widetilde{\unicode[STIX]{x1D6FA}}_{\mathfrak{X}})$
, and then, in (4.10.2), construct a map that relates
![]() $H^{1}(\widetilde{\unicode[STIX]{x1D6FA}}_{\mathfrak{X}})$
to Kähler differentials.
$H^{1}(\widetilde{\unicode[STIX]{x1D6FA}}_{\mathfrak{X}})$
to Kähler differentials.
4.7 The cup product maps
By the same arguments as in [SP, 068G], there are product maps
that satisfy
![]() $x\cup y=(-1)^{jj^{\prime }}y\cup x$
(see [SP, 0BYI]). By [SP, 0B6C], there is a cup product map
$x\cup y=(-1)^{jj^{\prime }}y\cup x$
(see [SP, 0BYI]). By [SP, 0B6C], there is a cup product map
These maps combine to give the ‘cup product map’ (where the tensor product is over
![]() ${\mathcal{O}}_{\mathfrak{X},\,\acute{\text{e}}\text{t}}$
)
${\mathcal{O}}_{\mathfrak{X},\,\acute{\text{e}}\text{t}}$
)
Proposition 4.8. For each
![]() $i>0$
, the map (4.7.1) induces the isomorphism
$i>0$
, the map (4.7.1) induces the isomorphism
Proof. By Proposition 4.4, each
![]() $H^{i}(\widetilde{\unicode[STIX]{x1D6FA}}_{\mathfrak{X}})$
has no nontrivial
$H^{i}(\widetilde{\unicode[STIX]{x1D6FA}}_{\mathfrak{X}})$
has no nontrivial
![]() $2$
-torsion, so the antisymmetry of the map (4.7.1) in each pair of variables indeed induces the
$2$
-torsion, so the antisymmetry of the map (4.7.1) in each pair of variables indeed induces the
![]() ${\mathcal{O}}_{\mathfrak{X},\,\acute{\text{e}}\text{t}}$
-module map (4.8.1). For the isomorphism claim, we may work étale locally, so we put ourselves in the situation (4.4.2). The edge maps
${\mathcal{O}}_{\mathfrak{X},\,\acute{\text{e}}\text{t}}$
-module map (4.8.1). For the isomorphism claim, we may work étale locally, so we put ourselves in the situation (4.4.2). The edge maps
of (3.3.1) are compatible with cup products: to check this, one identifies
![]() $H^{i}(\mathfrak{X}_{C}^{\text{ad}},\widehat{{\mathcal{O}}}^{+})$
with the direct limit of the
$H^{i}(\mathfrak{X}_{C}^{\text{ad}},\widehat{{\mathcal{O}}}^{+})$
with the direct limit of the
![]() $i$
th Čech cohomology groups of
$i$
th Čech cohomology groups of
![]() $\widehat{{\mathcal{O}}}^{+}$
with respect to a variable proétale hypercovering of
$\widehat{{\mathcal{O}}}^{+}$
with respect to a variable proétale hypercovering of
![]() $\mathfrak{X}_{C}^{\text{ad}}$
(see [SP, 01H0]) and uses the hypercovering construction of the cup product (see [SP, 01FP]). Due to Theorem 3.9 and (4.4.3), it then remains to argue that via the cup product the identification
$\mathfrak{X}_{C}^{\text{ad}}$
(see [SP, 01H0]) and uses the hypercovering construction of the cup product (see [SP, 01FP]). Due to Theorem 3.9 and (4.4.3), it then remains to argue that via the cup product the identification
which follows from [Reference Bhatt, Morrow and ScholzeBMS18, 7.3 and 7.5]. ◻
To relate
![]() $H^{1}(\widetilde{\unicode[STIX]{x1D6FA}}_{\mathfrak{X}})$
to Kähler differentials, we now review the needed material on cotangent complexes.
$H^{1}(\widetilde{\unicode[STIX]{x1D6FA}}_{\mathfrak{X}})$
to Kähler differentials, we now review the needed material on cotangent complexes.
4.9 The completed cotangent complex
 $\widehat{\mathbb{L}}_{\widehat{{\mathcal{O}}}^{+}/\mathbb{Z}_{p}}$
$\widehat{\mathbb{L}}_{\widehat{{\mathcal{O}}}^{+}/\mathbb{Z}_{p}}$
Affinoid perfectoids form a basis of
![]() $(\mathfrak{X}_{C}^{\text{ad}})_{\text{pro}\acute{\text{e}}\text{t}}$
(see [Reference ScholzeSch13a, 4.7]). Therefore, [Reference Bhatt, Morrow and ScholzeBMS18, 3.14] ensures that for the sheaf of rings
$(\mathfrak{X}_{C}^{\text{ad}})_{\text{pro}\acute{\text{e}}\text{t}}$
(see [Reference ScholzeSch13a, 4.7]). Therefore, [Reference Bhatt, Morrow and ScholzeBMS18, 3.14] ensures that for the sheaf of rings
![]() $\widehat{{\mathcal{O}}}_{\mathfrak{ X}_{C}^{\text{ad}}}^{+}$
, the cotangent complex
$\widehat{{\mathcal{O}}}_{\mathfrak{ X}_{C}^{\text{ad}}}^{+}$
, the cotangent complex
![]() $\mathbb{L}_{\widehat{{\mathcal{O}}}^{+}/{\mathcal{O}}_{C}}$
, whose terms are
$\mathbb{L}_{\widehat{{\mathcal{O}}}^{+}/{\mathcal{O}}_{C}}$
, whose terms are
![]() $\widehat{{\mathcal{O}}}_{\mathfrak{ X}_{C}^{\text{ad}}}^{+}$
-flat and which gives an object of
$\widehat{{\mathcal{O}}}_{\mathfrak{ X}_{C}^{\text{ad}}}^{+}$
-flat and which gives an object of
![]() $D^{{\leqslant}0}(\widehat{{\mathcal{O}}}_{\mathfrak{ X}_{C}^{\text{ad}}}^{+})$
, satisfies
$D^{{\leqslant}0}(\widehat{{\mathcal{O}}}_{\mathfrak{ X}_{C}^{\text{ad}}}^{+})$
, satisfies
Consequently, the derived
![]() $p$
-adic completion turns the canonical morphism
$p$
-adic completion turns the canonical morphism
in the derived category. By [Reference Gabber and RameroGR03, 6.5.12(ii)], the complex
![]() $\mathbb{L}_{{\mathcal{O}}_{C}/\mathbb{Z}_{p}}$
is quasi-isomorphic to
$\mathbb{L}_{{\mathcal{O}}_{C}/\mathbb{Z}_{p}}$
is quasi-isomorphic to
![]() $\unicode[STIX]{x1D6FA}_{{\mathcal{O}}_{C}/\mathbb{Z}_{p}}^{1}$
placed in degree
$\unicode[STIX]{x1D6FA}_{{\mathcal{O}}_{C}/\mathbb{Z}_{p}}^{1}$
placed in degree
![]() $0$
. The
$0$
. The
![]() $p$
-divisibility of
$p$
-divisibility of
![]() $\unicode[STIX]{x1D6FA}_{{\mathcal{O}}_{C}/\mathbb{Z}_{p}}^{1}$
then ensures that for every
$\unicode[STIX]{x1D6FA}_{{\mathcal{O}}_{C}/\mathbb{Z}_{p}}^{1}$
then ensures that for every
![]() $n>0$
we have
$n>0$
we have
where
![]() ${\mathcal{O}}^{+}$
abbreviates the integral structure sheaf
${\mathcal{O}}^{+}$
abbreviates the integral structure sheaf
![]() ${\mathcal{O}}_{\mathfrak{ X}_{C}^{\text{ad}}}^{+}$
. Moreover, by [Reference FontaineFon82, Theorem 1
${\mathcal{O}}_{\mathfrak{ X}_{C}^{\text{ad}}}^{+}$
. Moreover, by [Reference FontaineFon82, Theorem 1
![]() $^{\prime }$
(ii)],Footnote
5
$^{\prime }$
(ii)],Footnote
5
In conclusion, letting
![]() $\{1\}$
abbreviate the
$\{1\}$
abbreviate the
![]() ${\mathcal{O}}_{C}$
-tensor product with
${\mathcal{O}}_{C}$
-tensor product with
![]() ${\mathcal{O}}_{C}\{1\}$
, we obtain an isomorphism
${\mathcal{O}}_{C}\{1\}$
, we obtain an isomorphism
4.10 The relation between
 $\widetilde{\unicode[STIX]{x1D6FA}}_{\mathfrak{X}}$
and Kähler differentials
$\widetilde{\unicode[STIX]{x1D6FA}}_{\mathfrak{X}}$
and Kähler differentials
The functoriality of the cotangent complex supplies the pullback morphism
To explicate its source, we note that, as in §4.9, the explicit description of
![]() $\mathbb{L}_{{\mathcal{O}}_{C}/\mathbb{Z}_{p}}$
gives
$\mathbb{L}_{{\mathcal{O}}_{C}/\mathbb{Z}_{p}}$
gives
Moreover, the short exact sequence [SP, 0D6K] leads to the identification
(the
![]() $R^{1}\lim$
term vanishes due to the description [Reference IllusieIll71, III.3.2.7]: each
$R^{1}\lim$
term vanishes due to the description [Reference IllusieIll71, III.3.2.7]: each
![]() $\mathfrak{X}_{{\mathcal{O}}_{C}/p^{n}}$
is a local complete intersection over
$\mathfrak{X}_{{\mathcal{O}}_{C}/p^{n}}$
is a local complete intersection over
![]() ${\mathcal{O}}_{C}/p^{n}$
and, as may be seen using (1.5.1), no nonzero local section of a vector bundle on
${\mathcal{O}}_{C}/p^{n}$
and, as may be seen using (1.5.1), no nonzero local section of a vector bundle on
![]() $\mathfrak{X}_{{\mathcal{O}}_{C}/p^{n}}$
vanishes on
$\mathfrak{X}_{{\mathcal{O}}_{C}/p^{n}}$
vanishes on
![]() $\mathfrak{X}_{{\mathcal{O}}_{C}/p^{n}}^{\text{sm}}$
). By [Reference IllusieIll71, III.3.1.2], over
$\mathfrak{X}_{{\mathcal{O}}_{C}/p^{n}}^{\text{sm}}$
). By [Reference IllusieIll71, III.3.1.2], over
![]() $\mathfrak{X}^{\text{sm}}$
, this identification gives a quasi-isomorphism between
$\mathfrak{X}^{\text{sm}}$
, this identification gives a quasi-isomorphism between
Consequently, by applying
![]() $H^{0}(-)$
to the map (4.10.1) and twisting by
$H^{0}(-)$
to the map (4.10.1) and twisting by
![]() ${\mathcal{O}}_{C}\{-1\}$
we obtain the first map in the following composition of
${\mathcal{O}}_{C}\{-1\}$
we obtain the first map in the following composition of
![]() ${\mathcal{O}}_{\mathfrak{X},\,\acute{\text{e}}\text{t}}$
-module morphisms:
${\mathcal{O}}_{\mathfrak{X},\,\acute{\text{e}}\text{t}}$
-module morphisms:
By [Reference Bhatt, Morrow and ScholzeBMS18, 8.15 and its proof], the restriction of this composition to
![]() $\mathfrak{X}^{\text{sm}}$
is an isomorphism onto
$\mathfrak{X}^{\text{sm}}$
is an isomorphism onto
![]() $((\unicode[STIX]{x1D701}_{p}-1)\cdot H^{1}(\widetilde{\unicode[STIX]{x1D6FA}}_{\mathfrak{X}}))|_{\mathfrak{X}^{\text{sm}}}$
. Moreover, by Proposition 4.4, the
$((\unicode[STIX]{x1D701}_{p}-1)\cdot H^{1}(\widetilde{\unicode[STIX]{x1D6FA}}_{\mathfrak{X}}))|_{\mathfrak{X}^{\text{sm}}}$
. Moreover, by Proposition 4.4, the
![]() ${\mathcal{O}}_{\mathfrak{X},\,\acute{\text{e}}\text{t}}$
-module
${\mathcal{O}}_{\mathfrak{X},\,\acute{\text{e}}\text{t}}$
-module
![]() $H^{1}(\widetilde{\unicode[STIX]{x1D6FA}}_{\mathfrak{X}})$
is a vector bundle, so it has no nonzero
$H^{1}(\widetilde{\unicode[STIX]{x1D6FA}}_{\mathfrak{X}})$
is a vector bundle, so it has no nonzero
![]() $(\unicode[STIX]{x1D701}_{p}-1)$
-torsion and
$(\unicode[STIX]{x1D701}_{p}-1)$
-torsion and
![]() $(H^{1}(\widetilde{\unicode[STIX]{x1D6FA}}_{\mathfrak{X}}))/(\unicode[STIX]{x1D701}_{p}-1)$
has no nonzero local sections that vanish on
$(H^{1}(\widetilde{\unicode[STIX]{x1D6FA}}_{\mathfrak{X}}))/(\unicode[STIX]{x1D701}_{p}-1)$
has no nonzero local sections that vanish on
![]() $\mathfrak{X}_{{\mathcal{O}}_{C}/(\unicode[STIX]{x1D701}_{p}-1)}^{\text{sm}}$
. In conclusion, we may divide the composition (4.10.2) by
$\mathfrak{X}_{{\mathcal{O}}_{C}/(\unicode[STIX]{x1D701}_{p}-1)}^{\text{sm}}$
. In conclusion, we may divide the composition (4.10.2) by
![]() $\unicode[STIX]{x1D701}_{p}-1$
to obtain a map
$\unicode[STIX]{x1D701}_{p}-1$
to obtain a map
Theorem 4.11. The restriction of the map (4.10.3) to
![]() $\mathfrak{X}^{\text{sm}}$
extends uniquely to an
$\mathfrak{X}^{\text{sm}}$
extends uniquely to an
![]() ${\mathcal{O}}_{\mathfrak{X},\,\acute{\text{e}}\text{t}}$
-isomorphism
${\mathcal{O}}_{\mathfrak{X},\,\acute{\text{e}}\text{t}}$
-isomorphism
which, by (4.4.1) and Proposition 4.8, induces an
![]() ${\mathcal{O}}_{\mathfrak{X},\,\acute{\text{e}}\text{t}}$
-module identification
${\mathcal{O}}_{\mathfrak{X},\,\acute{\text{e}}\text{t}}$
-module identification
The proof of Theorem 4.11 will use the formal GAGA and Grothendieck existence theorems. The Noetherian cases of these theorems proved in [Reference Grothendieck and DieudonnéEGA III1 , §5] have been extended to suitable non-Noetherian settings by K. Fujiwara and F. Kato (with important inputs by O. Gabber). The following theorem summarizes the relevant to our aims special case of this extension.
Theorem 4.12 (Fujiwara–Kato).
For a valuation ring
![]() $V$
of height
$V$
of height
![]() $1$
, a nonzero nonunit
$1$
, a nonzero nonunit
![]() $a\in V$
such that
$a\in V$
such that
![]() $V$
is
$V$
is
![]() $a$
-adically complete, and a proper, finitely presented
$a$
-adically complete, and a proper, finitely presented
![]() $V$
-scheme
$V$
-scheme
![]() $Y$
, the functor
$Y$
, the functor
is an equivalence from the category of finitely presented
![]() ${\mathcal{O}}_{Y}$
-modules
${\mathcal{O}}_{Y}$
-modules
![]() ${\mathcal{F}}$
to that of sequences
${\mathcal{F}}$
to that of sequences
![]() $({\mathcal{F}}_{n})_{n>0}$
of finitely presented
$({\mathcal{F}}_{n})_{n>0}$
of finitely presented
![]() ${\mathcal{O}}_{Y_{V/a^{n}}}$
-modules
${\mathcal{O}}_{Y_{V/a^{n}}}$
-modules
![]() ${\mathcal{F}}_{n}$
equipped with isomorphisms
${\mathcal{F}}_{n}$
equipped with isomorphisms
![]() ${\mathcal{F}}_{n+1}|_{Y_{V/a^{n}}}\simeq {\mathcal{F}}_{n}$
.
${\mathcal{F}}_{n+1}|_{Y_{V/a^{n}}}\simeq {\mathcal{F}}_{n}$
.
Proof. The claim is a special case of [Reference Fujiwara and KatoFK18, I.10.1.2]. In order to explain why [Reference Fujiwara and KatoFK18, I.10.1.2] implies our assertion, we first reinterpret our source and target categories.
By a result of Gabber [Reference Fujiwara and KatoFK18, 0.9.2.7], the ring
![]() $V$
is ‘
$V$
is ‘
![]() $a$
-adically topologically universally adhesive’, so, by [Reference Fujiwara and KatoFK18, 0.8.5.25(2)], it is also ‘topologically universally coherent with respect to
$a$
-adically topologically universally adhesive’, so, by [Reference Fujiwara and KatoFK18, 0.8.5.25(2)], it is also ‘topologically universally coherent with respect to
![]() $(a)$
’. In particular, by [Reference Fujiwara and KatoFK18, 0.8.5.24], every finitely presented
$(a)$
’. In particular, by [Reference Fujiwara and KatoFK18, 0.8.5.24], every finitely presented
![]() $V$
-algebra is a coherent ring and, hence, by [Reference Fujiwara and KatoFK18, 0.5.1.2], the
$V$
-algebra is a coherent ring and, hence, by [Reference Fujiwara and KatoFK18, 0.5.1.2], the
![]() ${\mathcal{O}}_{Y}$
-module
${\mathcal{O}}_{Y}$
-module
![]() ${\mathcal{O}}_{Y}$
is coherent (in the sense of [Reference Fujiwara and KatoFK18, 0.4.1.4(2)] or [Reference Grothendieck and DieudonnéEGA I, 0.5.3.1]). In particular, by [Reference Fujiwara and KatoFK18, 0.4.1.8], an
${\mathcal{O}}_{Y}$
is coherent (in the sense of [Reference Fujiwara and KatoFK18, 0.4.1.4(2)] or [Reference Grothendieck and DieudonnéEGA I, 0.5.3.1]). In particular, by [Reference Fujiwara and KatoFK18, 0.4.1.8], an
![]() ${\mathcal{O}}_{Y}$
-module
${\mathcal{O}}_{Y}$
-module
![]() ${\mathcal{F}}$
is finitely presented if and only if
${\mathcal{F}}$
is finitely presented if and only if
![]() ${\mathcal{F}}$
is coherent, and likewise for
${\mathcal{F}}$
is coherent, and likewise for
![]() ${\mathcal{O}}_{Y_{V/a^{n}}}$
-modules for
${\mathcal{O}}_{Y_{V/a^{n}}}$
-modules for
![]() $n>0$
.
$n>0$
.
By [Reference Fujiwara and KatoFK18, 0.8.4.2 and 0.8.5.19(3)], the formal
![]() $a$
-adic completion
$a$
-adic completion
![]() $\widehat{Y}$
of
$\widehat{Y}$
of
![]() $Y$
is covered by open affines whose coordinate rings are ‘topologically universally adhesive’ and, hence, by [Reference Fujiwara and KatoFK18, 0.8.5.18], also ‘topologically universally Noetherian outside
$Y$
is covered by open affines whose coordinate rings are ‘topologically universally adhesive’ and, hence, by [Reference Fujiwara and KatoFK18, 0.8.5.18], also ‘topologically universally Noetherian outside
![]() $(a)$
’. In particular, by [Reference Fujiwara and KatoFK18, I.2.1.1(1) and I.2.1.7], the topological ring
$(a)$
’. In particular, by [Reference Fujiwara and KatoFK18, I.2.1.1(1) and I.2.1.7], the topological ring
![]() $V$
is ‘topologically universally rigid-Noetherian’ and the formal scheme
$V$
is ‘topologically universally rigid-Noetherian’ and the formal scheme
![]() $\widehat{Y}$
is ‘universally rigid-Noetherian’. In addition, by [Reference Fujiwara and KatoFK18, 0.8.4.5], the formal scheme
$\widehat{Y}$
is ‘universally rigid-Noetherian’. In addition, by [Reference Fujiwara and KatoFK18, 0.8.4.5], the formal scheme
![]() $\widehat{Y}$
is locally of finite presentation over
$\widehat{Y}$
is locally of finite presentation over
![]() $\operatorname{Spf}(V)$
. Thus, [Reference Fujiwara and KatoFK18, I.7.2.2] applied with
$\operatorname{Spf}(V)$
. Thus, [Reference Fujiwara and KatoFK18, I.7.2.2] applied with
![]() $A=V$
and [Reference Fujiwara and KatoFK18, I.7.2.1] imply that
$A=V$
and [Reference Fujiwara and KatoFK18, I.7.2.1] imply that
![]() $\widehat{Y}$
is ‘universally cohesive’. Then, by [Reference Fujiwara and KatoFK18, I.7.2.4 and I.3.4.1], the functor
$\widehat{Y}$
is ‘universally cohesive’. Then, by [Reference Fujiwara and KatoFK18, I.7.2.4 and I.3.4.1], the functor
![]() $({\mathcal{F}}_{n})\mapsto \varprojlim {\mathcal{F}}_{n}$
is an equivalence from the target category of (4.12.1) to the category of coherent
$({\mathcal{F}}_{n})\mapsto \varprojlim {\mathcal{F}}_{n}$
is an equivalence from the target category of (4.12.1) to the category of coherent
![]() ${\mathcal{O}}_{\widehat{Y}}$
-modules.
${\mathcal{O}}_{\widehat{Y}}$
-modules.
In conclusion, our claim is that the quasi-coherent pullback
![]() $i^{\ast }$
along the morphism
$i^{\ast }$
along the morphism
![]() $i:\widehat{Y}\rightarrow Y$
of locally ringed spaces induces an equivalence between the category of coherent
$i:\widehat{Y}\rightarrow Y$
of locally ringed spaces induces an equivalence between the category of coherent
![]() ${\mathcal{O}}_{Y}$
-modules and that of coherent
${\mathcal{O}}_{Y}$
-modules and that of coherent
![]() ${\mathcal{O}}_{\widehat{Y}}$
-modules. This is a special case of [Reference Fujiwara and KatoFK18, I.10.1.2] (see also [Reference Fujiwara and KatoFK18, I.§9.1]).◻
${\mathcal{O}}_{\widehat{Y}}$
-modules. This is a special case of [Reference Fujiwara and KatoFK18, I.10.1.2] (see also [Reference Fujiwara and KatoFK18, I.§9.1]).◻
Remarks.
4.13. In Theorem 4.12, if each
 ${\mathcal{F}}_{n}$
is locally free, then the
${\mathcal{F}}_{n}$
is locally free, then the
 ${\mathcal{O}}_{Y}$
-module
${\mathcal{O}}_{Y}$
-module
 ${\mathcal{F}}$
that algebraizes the sequence
${\mathcal{F}}$
that algebraizes the sequence
 $({\mathcal{F}}_{n})_{n>0}$
is also locally free. Indeed, it is enough to argue that the stalks of
$({\mathcal{F}}_{n})_{n>0}$
is also locally free. Indeed, it is enough to argue that the stalks of
 ${\mathcal{F}}$
at the points of
${\mathcal{F}}$
at the points of
 $Y_{V/a}$
are flat, so, since
$Y_{V/a}$
are flat, so, since
 $i$
is flat by [Reference Fujiwara and KatoFK18, I.1.4.7(2), 0.8.5.8(2), 0.8.5.17], it suffices to note that the
$i$
is flat by [Reference Fujiwara and KatoFK18, I.1.4.7(2), 0.8.5.8(2), 0.8.5.17], it suffices to note that the
 ${\mathcal{O}}_{\widehat{Y}}$
-module
${\mathcal{O}}_{\widehat{Y}}$
-module
 $i^{\ast }{\mathcal{F}}\cong \varprojlim {\mathcal{F}}_{n}$
is locally free because the Nakayama lemma ensures that
$i^{\ast }{\mathcal{F}}\cong \varprojlim {\mathcal{F}}_{n}$
is locally free because the Nakayama lemma ensures that
 ${\mathcal{F}}_{n+1}$
is locally trivialized by any lifts of local sections that trivialize
${\mathcal{F}}_{n+1}$
is locally trivialized by any lifts of local sections that trivialize
 ${\mathcal{F}}_{n}$
.
${\mathcal{F}}_{n}$
.4.14. Remark 4.13. and the proof of Theorem 4.12 also show that
 $i$
is flat and that the functor
$i$
is flat and that the functor
 $({\mathcal{F}}_{n})\mapsto \varprojlim {\mathcal{F}}_{n}$
is an equivalence to the category of finitely presented
$({\mathcal{F}}_{n})\mapsto \varprojlim {\mathcal{F}}_{n}$
is an equivalence to the category of finitely presented
 ${\mathcal{O}}_{\widehat{Y}}$
-modules.
${\mathcal{O}}_{\widehat{Y}}$
-modules.
4.15 Proof of Theorem 4.11
As we observed in §4.10, no nonzero local section of a vector bundle on
![]() $\mathfrak{X}$
vanishes on
$\mathfrak{X}$
vanishes on
![]() $\mathfrak{X}^{\text{sm}}$
. Thus, the desired isomorphism (4.11.1) is unique if it exists. Consequently, we may assume that
$\mathfrak{X}^{\text{sm}}$
. Thus, the desired isomorphism (4.11.1) is unique if it exists. Consequently, we may assume that
![]() $\mathfrak{X}=\operatorname{Spf}({\mathcal{O}}_{C}\{t_{0},\ldots ,t_{r},t_{r+1}^{\pm 1},\ldots ,t_{d}^{\pm 1}\}/(t_{0}\cdots t_{r}-p^{q}))$
with
$\mathfrak{X}=\operatorname{Spf}({\mathcal{O}}_{C}\{t_{0},\ldots ,t_{r},t_{r+1}^{\pm 1},\ldots ,t_{d}^{\pm 1}\}/(t_{0}\cdots t_{r}-p^{q}))$
with
![]() $r$
,
$r$
,
![]() $d$
, and
$d$
, and
![]() $q$
as in (1.5.1). In this case,
$q$
as in (1.5.1). In this case,
![]() $\mathfrak{X}$
is an open subscheme of the formal
$\mathfrak{X}$
is an open subscheme of the formal
![]() $p$
-adic completion of some proper, flat
$p$
-adic completion of some proper, flat
![]() $\overline{W(k)}$
-scheme
$\overline{W(k)}$
-scheme
![]() ${\mathcal{X}}$
that Zariski locally has étale ‘coordinate morphisms’ as in (1.5.2) with
${\mathcal{X}}$
that Zariski locally has étale ‘coordinate morphisms’ as in (1.5.2) with
![]() ${\mathcal{O}}$
there replaced by
${\mathcal{O}}$
there replaced by
![]() $\overline{W(k)}$
. Thus, finally, we may drop the previous assumptions and assume instead that
$\overline{W(k)}$
. Thus, finally, we may drop the previous assumptions and assume instead that
![]() $\mathfrak{X}=\widehat{{\mathcal{X}}}$
with
$\mathfrak{X}=\widehat{{\mathcal{X}}}$
with
![]() ${\mathcal{X}}$
as above. We equip
${\mathcal{X}}$
as above. We equip
![]() ${\mathcal{X}}$
with the log structure
${\mathcal{X}}$
with the log structure
![]() ${\mathcal{O}}_{{\mathcal{X}}}\cap ({\mathcal{O}}_{{\mathcal{X}}}[\frac{1}{p}])^{\times }$
, so that
${\mathcal{O}}_{{\mathcal{X}}}\cap ({\mathcal{O}}_{{\mathcal{X}}}[\frac{1}{p}])^{\times }$
, so that
![]() ${\mathcal{X}}$
is log smooth over
${\mathcal{X}}$
is log smooth over
![]() $\overline{W(k)}$
(see §1.6, especially, Claim 1.6.1) and the map
$\overline{W(k)}$
(see §1.6, especially, Claim 1.6.1) and the map
![]() $\mathfrak{X}\rightarrow {\mathcal{X}}$
of log ringed étale sites is strict (see Claim 1.6.3). By Theorem 4.12, the map (4.10.3) algebraizes to an
$\mathfrak{X}\rightarrow {\mathcal{X}}$
of log ringed étale sites is strict (see Claim 1.6.3). By Theorem 4.12, the map (4.10.3) algebraizes to an
![]() ${\mathcal{O}}_{{\mathcal{X}}}$
-module map
${\mathcal{O}}_{{\mathcal{X}}}$
-module map
By Proposition 4.4 and Remark 4.13., the
![]() ${\mathcal{O}}_{{\mathcal{X}}}$
-module
${\mathcal{O}}_{{\mathcal{X}}}$
-module
![]() ${\mathcal{H}}$
is locally free. By (4.10.3) and the Nakayama lemma,
${\mathcal{H}}$
is locally free. By (4.10.3) and the Nakayama lemma,
![]() $f$
is surjective at every point of
$f$
is surjective at every point of
![]() ${\mathcal{X}}_{k}^{\text{sm}}$
.
${\mathcal{X}}_{k}^{\text{sm}}$
.
Claim 4.15.1. There is an isomorphism
![]() ${\mathcal{H}}_{C}\simeq \unicode[STIX]{x1D6FA}_{{\mathcal{X}}_{C}/C}^{1}$
.
${\mathcal{H}}_{C}\simeq \unicode[STIX]{x1D6FA}_{{\mathcal{X}}_{C}/C}^{1}$
.
Proof. By the adic GAGA (see [Reference ScholzeSch13a, 9.1(i)]), it suffices to find an analogous isomorphism after pullback to
![]() $({\mathcal{X}}_{C})^{\text{ad}}\cong \mathfrak{X}_{C}^{\text{ad}}$
. On the one hand, such a pullback of
$({\mathcal{X}}_{C})^{\text{ad}}\cong \mathfrak{X}_{C}^{\text{ad}}$
. On the one hand, such a pullback of
![]() ${\mathcal{H}}_{C}$
is isomorphic to
${\mathcal{H}}_{C}$
is isomorphic to
![]() $(R^{1}\unicode[STIX]{x1D708}_{\ast }(\widehat{{\mathcal{O}}}_{\mathfrak{ X}_{C}^{\text{ad}}}^{+}))[\frac{1}{p}]$
. On the other hand, [Reference ScholzeSch13b, 3.23–3.24 and their proofs] supply an isomorphism between
$(R^{1}\unicode[STIX]{x1D708}_{\ast }(\widehat{{\mathcal{O}}}_{\mathfrak{ X}_{C}^{\text{ad}}}^{+}))[\frac{1}{p}]$
. On the other hand, [Reference ScholzeSch13b, 3.23–3.24 and their proofs] supply an isomorphism between
![]() $(R^{1}\unicode[STIX]{x1D708}_{\ast }(\widehat{{\mathcal{O}}}_{\mathfrak{ X}_{C}^{\text{ad}}}^{+}))[\frac{1}{p}]$
and the pullback of
$(R^{1}\unicode[STIX]{x1D708}_{\ast }(\widehat{{\mathcal{O}}}_{\mathfrak{ X}_{C}^{\text{ad}}}^{+}))[\frac{1}{p}]$
and the pullback of
![]() $\unicode[STIX]{x1D6FA}_{{\mathcal{X}}_{C}/C}^{1}$
to
$\unicode[STIX]{x1D6FA}_{{\mathcal{X}}_{C}/C}^{1}$
to
![]() $({\mathcal{X}}_{C})^{\text{ad}}$
.◻
$({\mathcal{X}}_{C})^{\text{ad}}$
.◻
Claim 4.15.1 ensures that
![]() $f_{C}$
is a generically surjective morphism between isomorphic vector bundles on
$f_{C}$
is a generically surjective morphism between isomorphic vector bundles on
![]() ${\mathcal{X}}_{C}$
. Since
${\mathcal{X}}_{C}$
. Since
![]() ${\mathcal{X}}_{C}$
is proper and smooth, every global section of the structure sheaf of each connected component of
${\mathcal{X}}_{C}$
is proper and smooth, every global section of the structure sheaf of each connected component of
![]() ${\mathcal{X}}_{C}$
is constant, so
${\mathcal{X}}_{C}$
is constant, so
![]() $\det (f_{C})$
is an isomorphism, and hence
$\det (f_{C})$
is an isomorphism, and hence
![]() $f_{C}$
is also an isomorphism. In conclusion,
$f_{C}$
is also an isomorphism. In conclusion,
![]() $f|_{{\mathcal{X}}^{\text{sm}}}$
is a surjection between vector bundles of the same rank, so
$f|_{{\mathcal{X}}^{\text{sm}}}$
is a surjection between vector bundles of the same rank, so
Since
![]() ${\mathcal{X}}\setminus {\mathcal{X}}^{\text{sm}}$
is of codimension
${\mathcal{X}}\setminus {\mathcal{X}}^{\text{sm}}$
is of codimension
![]() ${\geqslant}2$
in
${\geqslant}2$
in
![]() ${\mathcal{X}}$
, limit arguments and [Reference Grothendieck and DieudonnéEGA IV2
, 5.10.5] ensure that
${\mathcal{X}}$
, limit arguments and [Reference Grothendieck and DieudonnéEGA IV2
, 5.10.5] ensure that
![]() ${\mathcal{H}}$
is the unique vector bundle extension of
${\mathcal{H}}$
is the unique vector bundle extension of
![]() ${\mathcal{H}}|_{{\mathcal{X}}^{\text{sm}}}$
to
${\mathcal{H}}|_{{\mathcal{X}}^{\text{sm}}}$
to
![]() ${\mathcal{X}}$
. The isomorphism (4.15.2) then leads to an isomorphism
${\mathcal{X}}$
. The isomorphism (4.15.2) then leads to an isomorphism
![]() $\unicode[STIX]{x1D6FA}_{{\mathcal{X}}/{\mathcal{O}}_{C},\,\log }^{1}\{-1\}\simeq {\mathcal{H}}$
whose formal
$\unicode[STIX]{x1D6FA}_{{\mathcal{X}}/{\mathcal{O}}_{C},\,\log }^{1}\{-1\}\simeq {\mathcal{H}}$
whose formal
![]() $p$
-adic completion gives the desired (4.11.1).◻
$p$
-adic completion gives the desired (4.11.1).◻
Remark 4.16. If the coordinate morphisms (1.5.1) exist Zariski locally on
![]() $\mathfrak{X}$
, then, by (4.5.1), the identifications of Theorem 4.11 hold already for the Zariski topology; more precisely, then
$\mathfrak{X}$
, then, by (4.5.1), the identifications of Theorem 4.11 hold already for the Zariski topology; more precisely, then
We are ready to relate the de Rham specialization of
![]() $A\unicode[STIX]{x1D6FA}_{\mathfrak{X}}$
to differential forms by combining the results above with the argument from the proof of [Reference Bhatt, Morrow and ScholzeBMS18, 14.1].
$A\unicode[STIX]{x1D6FA}_{\mathfrak{X}}$
to differential forms by combining the results above with the argument from the proof of [Reference Bhatt, Morrow and ScholzeBMS18, 14.1].
Theorem 4.17. There is an identification
If the coordinate morphisms (1.5.1) exist Zariski locally on
![]() $\mathfrak{X}$
, then (4.17.1) also holds for
$\mathfrak{X}$
, then (4.17.1) also holds for
![]() $A\unicode[STIX]{x1D6FA}_{\mathfrak{X}_{\text{Zar}}}$
.
$A\unicode[STIX]{x1D6FA}_{\mathfrak{X}_{\text{Zar}}}$
.
Proof. Since
![]() $\unicode[STIX]{x1D711}(\unicode[STIX]{x1D707})=\unicode[STIX]{x1D711}(\unicode[STIX]{x1D709})\unicode[STIX]{x1D707}$
(see §2.1), [Reference Bhatt, Morrow and ScholzeBMS18, 6.11] gives the second identification in
$\unicode[STIX]{x1D711}(\unicode[STIX]{x1D707})=\unicode[STIX]{x1D711}(\unicode[STIX]{x1D709})\unicode[STIX]{x1D707}$
(see §2.1), [Reference Bhatt, Morrow and ScholzeBMS18, 6.11] gives the second identification in
By [Reference Bhatt, Morrow and ScholzeBMS18, 6.12], since
![]() $A_{\text{inf}}/(\unicode[STIX]{x1D711}(\unicode[STIX]{x1D709}))\cong {\mathcal{O}}_{C}$
via
$A_{\text{inf}}/(\unicode[STIX]{x1D711}(\unicode[STIX]{x1D709}))\cong {\mathcal{O}}_{C}$
via
![]() $\unicode[STIX]{x1D703}\circ \unicode[STIX]{x1D711}^{-1}$
, the object
$\unicode[STIX]{x1D703}\circ \unicode[STIX]{x1D711}^{-1}$
, the object
![]() $(L\unicode[STIX]{x1D702}_{(\unicode[STIX]{x1D711}(\unicode[STIX]{x1D709}))}(A\unicode[STIX]{x1D6FA}_{\mathfrak{X}}))\otimes _{A_{\text{inf}},\,\unicode[STIX]{x1D703}\circ \unicode[STIX]{x1D711}^{-1}}^{\mathbb{L}}{\mathcal{O}}_{C}$
is identified with the complex whose
$(L\unicode[STIX]{x1D702}_{(\unicode[STIX]{x1D711}(\unicode[STIX]{x1D709}))}(A\unicode[STIX]{x1D6FA}_{\mathfrak{X}}))\otimes _{A_{\text{inf}},\,\unicode[STIX]{x1D703}\circ \unicode[STIX]{x1D711}^{-1}}^{\mathbb{L}}{\mathcal{O}}_{C}$
is identified with the complex whose
![]() $i$
th degree term is
$i$
th degree term is
and the differentials are given by Bockstein homomorphisms.
Since
![]() ${\mathcal{O}}_{C}^{\flat }$
is perfect,
${\mathcal{O}}_{C}^{\flat }$
is perfect,
![]() $\widehat{\mathbb{L}}_{A_{\text{inf}}/\mathbb{Z}_{p}}\cong 0$
. Moreover, (4.9.1) applied with
$\widehat{\mathbb{L}}_{A_{\text{inf}}/\mathbb{Z}_{p}}\cong 0$
. Moreover, (4.9.1) applied with
![]() $\mathfrak{X}=\operatorname{Spf}({\mathcal{O}}_{C})$
implies that
$\mathfrak{X}=\operatorname{Spf}({\mathcal{O}}_{C})$
implies that
![]() $\widehat{\mathbb{L}}_{{\mathcal{O}}_{C}/\mathbb{Z}_{p}}\cong ({\mathcal{O}}_{C}\{1\})[1]$
. Thus,
$\widehat{\mathbb{L}}_{{\mathcal{O}}_{C}/\mathbb{Z}_{p}}\cong ({\mathcal{O}}_{C}\{1\})[1]$
. Thus,
![]() $\widehat{\mathbb{L}}_{{\mathcal{O}}_{C}/A_{\text{inf}}}\cong ({\mathcal{O}}_{C}\{1\})[1]$
, where
$\widehat{\mathbb{L}}_{{\mathcal{O}}_{C}/A_{\text{inf}}}\cong ({\mathcal{O}}_{C}\{1\})[1]$
, where
![]() ${\mathcal{O}}_{C}$
is an
${\mathcal{O}}_{C}$
is an
![]() $A_{\text{inf}}$
-algebra via
$A_{\text{inf}}$
-algebra via
![]() $\unicode[STIX]{x1D703}\circ \unicode[STIX]{x1D711}^{-1}$
. In particular, due to [Reference IllusieIll71, III.3.2.4(iii)], we have
$\unicode[STIX]{x1D703}\circ \unicode[STIX]{x1D711}^{-1}$
. In particular, due to [Reference IllusieIll71, III.3.2.4(iii)], we have
![]() $\operatorname{Ker}(\unicode[STIX]{x1D703}\,\circ \,\unicode[STIX]{x1D711}^{-1})/(\operatorname{Ker}(\unicode[STIX]{x1D703}\,\circ \,\unicode[STIX]{x1D711}^{-1}))^{2}\cong {\mathcal{O}}_{C}\{1\}$
.
$\operatorname{Ker}(\unicode[STIX]{x1D703}\,\circ \,\unicode[STIX]{x1D711}^{-1})/(\operatorname{Ker}(\unicode[STIX]{x1D703}\,\circ \,\unicode[STIX]{x1D711}^{-1}))^{2}\cong {\mathcal{O}}_{C}\{1\}$
.
In conclusion, by (4.11.2) and the preceding discussion,
![]() $A\unicode[STIX]{x1D6FA}_{\mathfrak{X}}\otimes _{A_{\text{inf}},\,\unicode[STIX]{x1D703}}^{\mathbb{L}}{\mathcal{O}}_{C}$
is identified with the complex whose
$A\unicode[STIX]{x1D6FA}_{\mathfrak{X}}\otimes _{A_{\text{inf}},\,\unicode[STIX]{x1D703}}^{\mathbb{L}}{\mathcal{O}}_{C}$
is identified with the complex whose
![]() $i$
th degree term is
$i$
th degree term is
![]() $\unicode[STIX]{x1D6FA}_{\mathfrak{X}/{\mathcal{O}}_{C},\,\log }^{i}$
and the differentials are certain Bockstein homomorphisms. Each
$\unicode[STIX]{x1D6FA}_{\mathfrak{X}/{\mathcal{O}}_{C},\,\log }^{i}$
and the differentials are certain Bockstein homomorphisms. Each
![]() $\unicode[STIX]{x1D6FA}_{\mathfrak{X}/{\mathcal{O}}_{C},\,\log }^{i}$
is a vector bundle, so the agreement of the Bockstein differentials with those of
$\unicode[STIX]{x1D6FA}_{\mathfrak{X}/{\mathcal{O}}_{C},\,\log }^{i}$
is a vector bundle, so the agreement of the Bockstein differentials with those of
![]() $\unicode[STIX]{x1D6FA}_{\mathfrak{X}/{\mathcal{O}}_{C},\,\log }^{\bullet }$
may be checked over
$\unicode[STIX]{x1D6FA}_{\mathfrak{X}/{\mathcal{O}}_{C},\,\log }^{\bullet }$
may be checked over
![]() $\mathfrak{X}^{\text{sm}}$
(compare with the argument for (4.10.3)), where it follows from [Reference Bhatt, Morrow and ScholzeBMS18, 14.1(ii)] (or [Reference BhattBha18, proof of Proposition 7.9]).
$\mathfrak{X}^{\text{sm}}$
(compare with the argument for (4.10.3)), where it follows from [Reference Bhatt, Morrow and ScholzeBMS18, 14.1(ii)] (or [Reference BhattBha18, proof of Proposition 7.9]).
Due to Remark 4.16, the proof for
![]() $A\unicode[STIX]{x1D6FA}_{\mathfrak{X}_{\text{Zar}}}$
is the same.◻
$A\unicode[STIX]{x1D6FA}_{\mathfrak{X}_{\text{Zar}}}$
is the same.◻
Corollary 4.18. The de Rham specialization of
![]() $R\unicode[STIX]{x1D6E4}(\mathfrak{X}_{\acute{\text{e}}\text{t}},A\unicode[STIX]{x1D6FA}_{\mathfrak{X}})$
may be identified as follows:
$R\unicode[STIX]{x1D6E4}(\mathfrak{X}_{\acute{\text{e}}\text{t}},A\unicode[STIX]{x1D6FA}_{\mathfrak{X}})$
may be identified as follows:
Remark 4.19. In the case when
![]() $\mathfrak{X}\cong \widehat{{\mathcal{X}}}$
for a proper, flat
$\mathfrak{X}\cong \widehat{{\mathcal{X}}}$
for a proper, flat
![]() $\overline{W(k)}$
-scheme
$\overline{W(k)}$
-scheme
![]() ${\mathcal{X}}$
that étale locally has étale coordinate morphisms (1.5.2) with
${\mathcal{X}}$
that étale locally has étale coordinate morphisms (1.5.2) with
![]() ${\mathcal{O}}$
there replaced by
${\mathcal{O}}$
there replaced by
![]() $\overline{W(k)}$
, we have the further identification
$\overline{W(k)}$
, we have the further identification
where
![]() ${\mathcal{X}}$
is endowed with the log structure
${\mathcal{X}}$
is endowed with the log structure
![]() ${\mathcal{O}}_{{\mathcal{X}},\,\acute{\text{e}}\text{t}}\cap ({\mathcal{O}}_{{\mathcal{X}},\,\acute{\text{e}}\text{t}}[\frac{1}{p}])^{\times }$
(whose pullback to
${\mathcal{O}}_{{\mathcal{X}},\,\acute{\text{e}}\text{t}}\cap ({\mathcal{O}}_{{\mathcal{X}},\,\acute{\text{e}}\text{t}}[\frac{1}{p}])^{\times }$
(whose pullback to
![]() $\mathfrak{X}$
is the log structure
$\mathfrak{X}$
is the log structure
![]() ${\mathcal{O}}_{\mathfrak{X},\,\acute{\text{e}}\text{t}}\cap ({\mathcal{O}}_{\mathfrak{X},\,\acute{\text{e}}\text{t}}[\frac{1}{p}])^{\times }$
of
${\mathcal{O}}_{\mathfrak{X},\,\acute{\text{e}}\text{t}}\cap ({\mathcal{O}}_{\mathfrak{X},\,\acute{\text{e}}\text{t}}[\frac{1}{p}])^{\times }$
of
![]() $\mathfrak{X}$
, see Claim 1.6.3) and
$\mathfrak{X}$
, see Claim 1.6.3) and
![]() $\overline{W(k)}$
is endowed with the log structure associated to
$\overline{W(k)}$
is endowed with the log structure associated to
![]() $\overline{W(k)}\setminus \{0\}{\hookrightarrow}\overline{W(k)}$
. Indeed, the pullback map between the
$\overline{W(k)}\setminus \{0\}{\hookrightarrow}\overline{W(k)}$
. Indeed, the pullback map between the
![]() $E_{1}$
-spectral sequences
$E_{1}$
-spectral sequences
 $$\begin{eqnarray}\begin{array}{@{}rcl@{}}H^{j}({\mathcal{X}}_{{\mathcal{O}}_{C}},\unicode[STIX]{x1D6FA}_{{\mathcal{X}}_{{\mathcal{O}}_{C}}/{\mathcal{O}}_{C},\,\log }^{i})\ & \Rightarrow \ & \displaystyle H^{i+j}(R\unicode[STIX]{x1D6E4}({\mathcal{X}}_{\acute{\text{e}}\text{t}},\unicode[STIX]{x1D6FA}_{{\mathcal{X}}_{{\mathcal{O}}_{C}}/{\mathcal{O}}_{C},\,\log }^{\bullet })),\\ H^{j}(\mathfrak{X},\unicode[STIX]{x1D6FA}_{\mathfrak{X}/{\mathcal{O}}_{C},\,\log }^{i})\ & \Rightarrow \ & \displaystyle H^{i+j}(R\unicode[STIX]{x1D6E4}_{\log \text{dR}}(\mathfrak{X}/{\mathcal{O}}_{C}))\end{array}\end{eqnarray}$$
$$\begin{eqnarray}\begin{array}{@{}rcl@{}}H^{j}({\mathcal{X}}_{{\mathcal{O}}_{C}},\unicode[STIX]{x1D6FA}_{{\mathcal{X}}_{{\mathcal{O}}_{C}}/{\mathcal{O}}_{C},\,\log }^{i})\ & \Rightarrow \ & \displaystyle H^{i+j}(R\unicode[STIX]{x1D6E4}({\mathcal{X}}_{\acute{\text{e}}\text{t}},\unicode[STIX]{x1D6FA}_{{\mathcal{X}}_{{\mathcal{O}}_{C}}/{\mathcal{O}}_{C},\,\log }^{\bullet })),\\ H^{j}(\mathfrak{X},\unicode[STIX]{x1D6FA}_{\mathfrak{X}/{\mathcal{O}}_{C},\,\log }^{i})\ & \Rightarrow \ & \displaystyle H^{i+j}(R\unicode[STIX]{x1D6E4}_{\log \text{dR}}(\mathfrak{X}/{\mathcal{O}}_{C}))\end{array}\end{eqnarray}$$
is an isomorphism because, by the Grothendieck finiteness and comparison theorems [Reference Grothendieck and DieudonnéEGA III1
, 3.2.1 and 4.1.7] (combined with limit arguments, which use Claim 1.6.1 and the fact that
![]() ${\mathcal{X}}$
is necessarily finitely presented, see [SP, 053E]; alternatively, directly by [Reference Fujiwara and KatoFK18, I.9.2.1]),
${\mathcal{X}}$
is necessarily finitely presented, see [SP, 053E]; alternatively, directly by [Reference Fujiwara and KatoFK18, I.9.2.1]),
Corollary 4.20. If
![]() $\mathfrak{X}$
is proper over
$\mathfrak{X}$
is proper over
![]() ${\mathcal{O}}_{C}$
, then
${\mathcal{O}}_{C}$
, then
![]() $R\unicode[STIX]{x1D6E4}(\mathfrak{X}_{\acute{\text{e}}\text{t}},A\unicode[STIX]{x1D6FA}_{\mathfrak{X}})$
is a perfect object of
$R\unicode[STIX]{x1D6E4}(\mathfrak{X}_{\acute{\text{e}}\text{t}},A\unicode[STIX]{x1D6FA}_{\mathfrak{X}})$
is a perfect object of
![]() $D^{{\geqslant}0}(A_{\text{inf}})$
; in other words, then
$D^{{\geqslant}0}(A_{\text{inf}})$
; in other words, then
![]() $R\unicode[STIX]{x1D6E4}(\mathfrak{X}_{\acute{\text{e}}\text{t}},A\unicode[STIX]{x1D6FA}_{\mathfrak{X}})$
is quasi-isomorphic to a bounded complex of finite free
$R\unicode[STIX]{x1D6E4}(\mathfrak{X}_{\acute{\text{e}}\text{t}},A\unicode[STIX]{x1D6FA}_{\mathfrak{X}})$
is quasi-isomorphic to a bounded complex of finite free
![]() $A_{\text{inf}}$
-modules.
$A_{\text{inf}}$
-modules.
Proof. By the Grothendieck finiteness theorem [Reference UllrichUll95, 5.3] and the spectral sequence as in Remark 4.19, the
![]() ${\mathcal{O}}_{C}$
-modules
${\mathcal{O}}_{C}$
-modules
![]() $H^{j}(R\unicode[STIX]{x1D6E4}_{\log \text{dR}}(\mathfrak{X}/{\mathcal{O}}_{C}))$
are finitely presented and, hence, also perfect (see [SP, 0ASP]). Thus, by Corollary 4.18 and [SP, 066U], the object
$H^{j}(R\unicode[STIX]{x1D6E4}_{\log \text{dR}}(\mathfrak{X}/{\mathcal{O}}_{C}))$
are finitely presented and, hence, also perfect (see [SP, 0ASP]). Thus, by Corollary 4.18 and [SP, 066U], the object
of
![]() $D^{{\geqslant}0}({\mathcal{O}}_{C})$
is perfect. Moreover, by Corollary 4.6, the object
$D^{{\geqslant}0}({\mathcal{O}}_{C})$
is perfect. Moreover, by Corollary 4.6, the object
![]() $R\unicode[STIX]{x1D6E4}(\mathfrak{X}_{\acute{\text{e}}\text{t}},A\unicode[STIX]{x1D6FA}_{\mathfrak{X}})$
is derived
$R\unicode[STIX]{x1D6E4}(\mathfrak{X}_{\acute{\text{e}}\text{t}},A\unicode[STIX]{x1D6FA}_{\mathfrak{X}})$
is derived
![]() $\unicode[STIX]{x1D709}$
-adically complete. Therefore, by [SP, 09AW], it is perfect as well, as desired.◻
$\unicode[STIX]{x1D709}$
-adically complete. Therefore, by [SP, 09AW], it is perfect as well, as desired.◻
We close the section by comparing
![]() $R\unicode[STIX]{x1D6E4}(\mathfrak{X}_{\acute{\text{e}}\text{t}},A\unicode[STIX]{x1D6FA}_{\mathfrak{X}})$
with its analogue defined using the Zariski topology.
$R\unicode[STIX]{x1D6E4}(\mathfrak{X}_{\acute{\text{e}}\text{t}},A\unicode[STIX]{x1D6FA}_{\mathfrak{X}})$
with its analogue defined using the Zariski topology.
Corollary 4.21. If the coordinate morphisms (1.5.1) exist Zariski locally on
![]() $\mathfrak{X}$
, then the cohomology
$\mathfrak{X}$
, then the cohomology
![]() $R\unicode[STIX]{x1D6E4}(\mathfrak{X}_{\acute{\text{e}}\text{t}},A\unicode[STIX]{x1D6FA}_{\mathfrak{X}})$
may be computed using the Zariski topology of
$R\unicode[STIX]{x1D6E4}(\mathfrak{X}_{\acute{\text{e}}\text{t}},A\unicode[STIX]{x1D6FA}_{\mathfrak{X}})$
may be computed using the Zariski topology of
![]() $\mathfrak{X}$
; more precisely, then
$\mathfrak{X}$
; more precisely, then
Proof. By Theorem 4.17 and Corollary 4.18, the reduction of (4.21.1) modulo
![]() $\unicode[STIX]{x1D709}$
is identified with
$\unicode[STIX]{x1D709}$
is identified with
and, hence, is an isomorphism as indicated. Thus, since, by Corollary 4.6 (and its Zariski analogue),
![]() $R\unicode[STIX]{x1D6E4}(\mathfrak{X}_{\text{Zar}},A\unicode[STIX]{x1D6FA}_{\mathfrak{X}_{\text{Zar}}})$
and
$R\unicode[STIX]{x1D6E4}(\mathfrak{X}_{\text{Zar}},A\unicode[STIX]{x1D6FA}_{\mathfrak{X}_{\text{Zar}}})$
and
![]() $R\unicode[STIX]{x1D6E4}(\mathfrak{X}_{\acute{\text{e}}\text{t}},A\unicode[STIX]{x1D6FA}_{\mathfrak{X}})$
are derived
$R\unicode[STIX]{x1D6E4}(\mathfrak{X}_{\acute{\text{e}}\text{t}},A\unicode[STIX]{x1D6FA}_{\mathfrak{X}})$
are derived
![]() $\unicode[STIX]{x1D709}$
-adic complete, (4.21.1) is an isomorphism.◻
$\unicode[STIX]{x1D709}$
-adic complete, (4.21.1) is an isomorphism.◻
5 The absolute crystalline comparison isomorphism
In Theorem 4.17, we identified the
![]() ${\mathcal{O}}_{C}$
-base change along
${\mathcal{O}}_{C}$
-base change along
![]() $\unicode[STIX]{x1D703}$
of the object
$\unicode[STIX]{x1D703}$
of the object
![]() $A\unicode[STIX]{x1D6FA}_{\mathfrak{X}}$
with
$A\unicode[STIX]{x1D6FA}_{\mathfrak{X}}$
with
![]() $\unicode[STIX]{x1D6FA}_{\mathfrak{X}/{\mathcal{O}}_{C},\,\log }^{\bullet }$
. The goal of this section is to similarly identify the
$\unicode[STIX]{x1D6FA}_{\mathfrak{X}/{\mathcal{O}}_{C},\,\log }^{\bullet }$
. The goal of this section is to similarly identify the
![]() $A_{\text{cris}}$
-base change of
$A_{\text{cris}}$
-base change of
![]() $A\unicode[STIX]{x1D6FA}_{\mathfrak{X}}$
with an object that computes the logarithmic crystalline (that is, Hyodo–Kato) cohomology of
$A\unicode[STIX]{x1D6FA}_{\mathfrak{X}}$
with an object that computes the logarithmic crystalline (that is, Hyodo–Kato) cohomology of
![]() $\mathfrak{X}_{{\mathcal{O}}_{C}/p}$
over
$\mathfrak{X}_{{\mathcal{O}}_{C}/p}$
over
![]() $A_{\text{cris}}$
(see Theorem 5.4). This is more general because, on the one hand,
$A_{\text{cris}}$
(see Theorem 5.4). This is more general because, on the one hand,
![]() $\unicode[STIX]{x1D703}$
factors through the morphism
$\unicode[STIX]{x1D703}$
factors through the morphism
![]() $A_{\text{inf}}\rightarrow A_{\text{cris}}$
, while, on the other hand,
$A_{\text{inf}}\rightarrow A_{\text{cris}}$
, while, on the other hand,
![]() $\unicode[STIX]{x1D6FA}_{\mathfrak{X}/{\mathcal{O}}_{C},\,\log }^{\bullet }$
computes the log crystalline cohomology of
$\unicode[STIX]{x1D6FA}_{\mathfrak{X}/{\mathcal{O}}_{C},\,\log }^{\bullet }$
computes the log crystalline cohomology of
![]() $\mathfrak{X}_{{\mathcal{O}}_{C}/p}$
over
$\mathfrak{X}_{{\mathcal{O}}_{C}/p}$
over
![]() ${\mathcal{O}}_{C}$
. In fact, even the map
${\mathcal{O}}_{C}$
. In fact, even the map
![]() $A_{\text{inf}}{\twoheadrightarrow}A_{\text{inf}}/\unicode[STIX]{x1D707}$
factors through
$A_{\text{inf}}{\twoheadrightarrow}A_{\text{inf}}/\unicode[STIX]{x1D707}$
factors through
![]() $A_{\text{inf}}\rightarrow A_{\text{cris}}$
, so the identification of the
$A_{\text{inf}}\rightarrow A_{\text{cris}}$
, so the identification of the
![]() $A_{\text{cris}}$
-base change of
$A_{\text{cris}}$
-base change of
![]() $A\unicode[STIX]{x1D6FA}_{\mathfrak{X}}$
will capture the entire
$A\unicode[STIX]{x1D6FA}_{\mathfrak{X}}$
will capture the entire
![]() $\unicode[STIX]{x1D707}=0$
locus of
$\unicode[STIX]{x1D707}=0$
locus of
![]() $A_{\text{inf}}$
(in contrast, the comparison with the
$A_{\text{inf}}$
(in contrast, the comparison with the
![]() $p$
-adic étale cohomology captured the
$p$
-adic étale cohomology captured the
![]() $\unicode[STIX]{x1D707}\neq 0$
locus, see Theorem 2.3).
$\unicode[STIX]{x1D707}\neq 0$
locus, see Theorem 2.3).
In comparison with the case when
![]() $\mathfrak{X}$
is smooth treated in [Reference Bhatt, Morrow and ScholzeBMS18, §12], controlling the interaction of the functor
$\mathfrak{X}$
is smooth treated in [Reference Bhatt, Morrow and ScholzeBMS18, §12], controlling the interaction of the functor
![]() $L\unicode[STIX]{x1D702}_{(\unicode[STIX]{x1D707})}$
with the relevant base changes seems more subtle. To overcome this, we resort to the analysis of continuous group cohomology carried out in §3. Another major complication is the presence of log structures. Specifically, not knowing the existence of logarithmic divided power envelopes of certain nonexact logarithmic closed immersions in mixed characteristic, we are forced to devise slightly indirect arguments when analyzing the relevant divided power envelopes. For this, we rely on the results and arguments from [Reference KatoKat89] and [Reference BeilinsonBei13b];Footnote
6
the latter reference is especially useful for us because some log structures that we use are not coherent (only quasi-coherent).
$L\unicode[STIX]{x1D702}_{(\unicode[STIX]{x1D707})}$
with the relevant base changes seems more subtle. To overcome this, we resort to the analysis of continuous group cohomology carried out in §3. Another major complication is the presence of log structures. Specifically, not knowing the existence of logarithmic divided power envelopes of certain nonexact logarithmic closed immersions in mixed characteristic, we are forced to devise slightly indirect arguments when analyzing the relevant divided power envelopes. For this, we rely on the results and arguments from [Reference KatoKat89] and [Reference BeilinsonBei13b];Footnote
6
the latter reference is especially useful for us because some log structures that we use are not coherent (only quasi-coherent).
5.1 The ring
 $A_{\text{cris}}$
$A_{\text{cris}}$
Using the generator
![]() $\unicode[STIX]{x1D709}$
of the kernel of
$\unicode[STIX]{x1D709}$
of the kernel of
![]() $\unicode[STIX]{x1D703}:A_{\text{inf}}{\twoheadrightarrow}{\mathcal{O}}_{C}$
, we let
$\unicode[STIX]{x1D703}:A_{\text{inf}}{\twoheadrightarrow}{\mathcal{O}}_{C}$
, we let
![]() $A_{\text{cris}}^{0}$
be the
$A_{\text{cris}}^{0}$
be the
![]() $A_{\text{inf}}$
-subalgebra of
$A_{\text{inf}}$
-subalgebra of
![]() $A_{\text{inf}}[\frac{1}{p}]$
generated by the divided powers
$A_{\text{inf}}[\frac{1}{p}]$
generated by the divided powers
![]() $\frac{\unicode[STIX]{x1D709}^{n}}{n!}$
for
$\frac{\unicode[STIX]{x1D709}^{n}}{n!}$
for
![]() $n\geqslant 1$
. The induced map
$n\geqslant 1$
. The induced map
![]() $\unicode[STIX]{x1D703}:A_{\text{cris}}^{0}{\twoheadrightarrow}{\mathcal{O}}_{C}$
identifies
$\unicode[STIX]{x1D703}:A_{\text{cris}}^{0}{\twoheadrightarrow}{\mathcal{O}}_{C}$
identifies
![]() $A_{\text{cris}}^{0}$
with the divided power envelope of
$A_{\text{cris}}^{0}$
with the divided power envelope of
![]() $\unicode[STIX]{x1D703}:A_{\text{inf}}{\twoheadrightarrow}{\mathcal{O}}_{C}/p$
over
$\unicode[STIX]{x1D703}:A_{\text{inf}}{\twoheadrightarrow}{\mathcal{O}}_{C}/p$
over
![]() $(\mathbb{Z}_{p},p\mathbb{Z}_{p})$
equipped with the unique divided powers on
$(\mathbb{Z}_{p},p\mathbb{Z}_{p})$
equipped with the unique divided powers on
![]() $p\mathbb{Z}_{p}$
, see [Reference TsujiTsu99, A2.8]. Since
$p\mathbb{Z}_{p}$
, see [Reference TsujiTsu99, A2.8]. Since
![]() $\unicode[STIX]{x1D703}(\unicode[STIX]{x1D707})=0$
, we have
$\unicode[STIX]{x1D703}(\unicode[STIX]{x1D707})=0$
, we have
![]() $\unicode[STIX]{x1D707}^{p}\in pA_{\text{cris}}^{0}$
, so the
$\unicode[STIX]{x1D707}^{p}\in pA_{\text{cris}}^{0}$
, so the
![]() $p$
-adic topology of
$p$
-adic topology of
![]() $A_{\text{cris}}^{0}$
agrees with the
$A_{\text{cris}}^{0}$
agrees with the
![]() $(p,\unicode[STIX]{x1D707})$
-adic topology. We set
$(p,\unicode[STIX]{x1D707})$
-adic topology. We set
The induced map
![]() $\unicode[STIX]{x1D703}:A_{\text{cris}}{\twoheadrightarrow}{\mathcal{O}}_{C}$
identifies
$\unicode[STIX]{x1D703}:A_{\text{cris}}{\twoheadrightarrow}{\mathcal{O}}_{C}$
identifies
![]() $A_{\text{cris}}$
with the initial
$A_{\text{cris}}$
with the initial
![]() $p$
-adically complete divided power thickening of
$p$
-adically complete divided power thickening of
![]() ${\mathcal{O}}_{C}$
over
${\mathcal{O}}_{C}$
over
![]() $\mathbb{Z}_{p}$
(see [Reference TsujiTsu99, A1.3 and A1.5]). By Proposition 5.36 below (or by [Reference TsujiTsu99, A2.13] and [Reference BrinonBri06, 2.33]), the map
$\mathbb{Z}_{p}$
(see [Reference TsujiTsu99, A1.3 and A1.5]). By Proposition 5.36 below (or by [Reference TsujiTsu99, A2.13] and [Reference BrinonBri06, 2.33]), the map
![]() $A_{\text{cris}}^{0}\rightarrow A_{\text{cris}}$
is an injection into an integral domain.
$A_{\text{cris}}^{0}\rightarrow A_{\text{cris}}$
is an injection into an integral domain.
Analogously to §3.26, the ring
![]() $A_{\text{cris}}$
comes equipped with the Frobenius endomorphism
$A_{\text{cris}}$
comes equipped with the Frobenius endomorphism
![]() $\unicode[STIX]{x1D711}$
that intertwines the absolute Frobenius endomorphism of
$\unicode[STIX]{x1D711}$
that intertwines the absolute Frobenius endomorphism of
![]() ${\mathcal{O}}_{C}/p$
via the map
${\mathcal{O}}_{C}/p$
via the map
![]() $\unicode[STIX]{x1D703}$
. The identification
$\unicode[STIX]{x1D703}$
. The identification
is Frobenius equivariant and compatible with the maps
![]() $\unicode[STIX]{x1D703}$
.
$\unicode[STIX]{x1D703}$
.
5.2 The log structure on
 $A_{\text{cris}}$
$A_{\text{cris}}$
For each
![]() $n>0$
, the ring
$n>0$
, the ring
![]() $A_{\text{cris}}/p^{n}$
is a divided power thickening of
$A_{\text{cris}}/p^{n}$
is a divided power thickening of
![]() ${\mathcal{O}}_{C}/p$
over
${\mathcal{O}}_{C}/p$
over
![]() $\mathbb{Z}/p^{n}$
. Therefore, by [Reference BeilinsonBei13b, §1.17, Lemma], every quasi-coherent, integral log structure
$\mathbb{Z}/p^{n}$
. Therefore, by [Reference BeilinsonBei13b, §1.17, Lemma], every quasi-coherent, integral log structure
![]() ${\mathcal{N}}$
on
${\mathcal{N}}$
on
![]() ${\mathcal{O}}_{C}/p$
for which
${\mathcal{O}}_{C}/p$
for which
![]() ${\mathcal{N}}/({\mathcal{O}}_{C}/p)^{\times }$
is uniquely
${\mathcal{N}}/({\mathcal{O}}_{C}/p)^{\times }$
is uniquely
![]() $p$
-divisible lifts uniquely to a quasi-coherent, integral log structure on
$p$
-divisible lifts uniquely to a quasi-coherent, integral log structure on
![]() $A_{\text{cris}}/p^{n}$
. Thus, letting
$A_{\text{cris}}/p^{n}$
. Thus, letting
![]() ${\mathcal{N}}$
be the default log structure §1.6 (1) on
${\mathcal{N}}$
be the default log structure §1.6 (1) on
![]() ${\mathcal{O}}_{C}/p$
, for which
${\mathcal{O}}_{C}/p$
, for which
we obtain compatible, quasi-coherent, integral log structures on the rings
![]() $A_{\text{cris}}/p^{n}$
, to the effect that each
$A_{\text{cris}}/p^{n}$
, to the effect that each
![]() $A_{\text{cris}}/p^{n}$
becomes a log PD thickening of
$A_{\text{cris}}/p^{n}$
becomes a log PD thickening of
![]() ${\mathcal{O}}_{C}/p$
. Explicitly, these log structures are the pullbacks of the log structure on
${\mathcal{O}}_{C}/p$
. Explicitly, these log structures are the pullbacks of the log structure on
![]() $A_{\text{cris}}$
associated to the prelog structure
$A_{\text{cris}}$
associated to the prelog structure
In what follows, we always equip:
∙ each
 $A_{\text{cris}}/p^{n}$
, as well as
$A_{\text{cris}}/p^{n}$
, as well as
 $A_{\text{cris}}$
, with the log structure described above;
$A_{\text{cris}}$
, with the log structure described above;∙ each
 $\mathbb{Z}/p^{n}\mathbb{Z}$
with the standard divided powers on
$\mathbb{Z}/p^{n}\mathbb{Z}$
with the standard divided powers on
 $p\mathbb{Z}/p^{n}\mathbb{Z}$
and the trivial log structure.
$p\mathbb{Z}/p^{n}\mathbb{Z}$
and the trivial log structure.
For every divided power thickening
![]() $\widetilde{Z}$
over
$\widetilde{Z}$
over
![]() $\mathbb{Z}/p^{n}\mathbb{Z}$
of an
$\mathbb{Z}/p^{n}\mathbb{Z}$
of an
![]() ${\mathcal{O}}_{C}/p$
-scheme
${\mathcal{O}}_{C}/p$
-scheme
![]() $Z$
, the morphism
$Z$
, the morphism
![]() $Z\xrightarrow[{}]{z}\operatorname{Spec}({\mathcal{O}}_{C}/p)$
extends uniquely to a PD morphism
$Z\xrightarrow[{}]{z}\operatorname{Spec}({\mathcal{O}}_{C}/p)$
extends uniquely to a PD morphism
![]() $\widetilde{Z}\xrightarrow[{}]{\widetilde{z}}\operatorname{Spec}(A_{\text{cris}}/p^{n})$
(see the proof of [Reference TsujiTsu99, A1.5]). If, in addition,
$\widetilde{Z}\xrightarrow[{}]{\widetilde{z}}\operatorname{Spec}(A_{\text{cris}}/p^{n})$
(see the proof of [Reference TsujiTsu99, A1.5]). If, in addition,
![]() $\widetilde{Z}$
is equipped with a quasi-coherent, integral log structure for which
$\widetilde{Z}$
is equipped with a quasi-coherent, integral log structure for which
![]() $z$
is enhanced to a morphism
$z$
is enhanced to a morphism
![]() $z^{\sharp }$
of log schemes, then, by [Reference BeilinsonBei13b, §1.17, Exercise], the morphism
$z^{\sharp }$
of log schemes, then, by [Reference BeilinsonBei13b, §1.17, Exercise], the morphism
![]() $z^{\sharp }$
extends uniquely to a PD morphism
$z^{\sharp }$
extends uniquely to a PD morphism
![]() $\widetilde{z}^{\sharp }:\widetilde{Z}\rightarrow \operatorname{Spec}(A_{\text{cris}}/p^{n})$
of log schemes.
$\widetilde{z}^{\sharp }:\widetilde{Z}\rightarrow \operatorname{Spec}(A_{\text{cris}}/p^{n})$
of log schemes.
5.3 The absolute crystalline cohomology of
 $\mathfrak{X}_{{\mathcal{O}}_{C}/p}$
$\mathfrak{X}_{{\mathcal{O}}_{C}/p}$
We let
be the log crystalline site of
![]() $\mathfrak{X}_{{\mathcal{O}}_{C}/p}$
over
$\mathfrak{X}_{{\mathcal{O}}_{C}/p}$
over
![]() $\mathbb{Z}_{p}$
defined as in [Reference BeilinsonBei13b, §1.12]: the objects are the étale
$\mathbb{Z}_{p}$
defined as in [Reference BeilinsonBei13b, §1.12]: the objects are the étale
![]() $\mathfrak{X}_{{\mathcal{O}}_{C}/p}$
-schemes
$\mathfrak{X}_{{\mathcal{O}}_{C}/p}$
-schemes
![]() $Z$
equipped with a divided power thickening
$Z$
equipped with a divided power thickening
![]() $\widetilde{Z}$
over some
$\widetilde{Z}$
over some
![]() $\mathbb{Z}/p^{n}\mathbb{Z}$
such that
$\mathbb{Z}/p^{n}\mathbb{Z}$
such that
![]() $\widetilde{Z}$
is, in turn, equipped with a quasi-coherent, integral log structure whose pullback to
$\widetilde{Z}$
is, in turn, equipped with a quasi-coherent, integral log structure whose pullback to
![]() $Z$
is identified with the pullback of the log structure of
$Z$
is identified with the pullback of the log structure of
![]() $\mathfrak{X}_{{\mathcal{O}}_{C}/p}$
(which is defined in §1.6 (2)); the coverings are the jointly surjective étale log PD morphisms. The universal property of
$\mathfrak{X}_{{\mathcal{O}}_{C}/p}$
(which is defined in §1.6 (2)); the coverings are the jointly surjective étale log PD morphisms. The universal property of
![]() $A_{\text{cris}}$
reviewed in the last paragraph of §5.2 gives the following identification of sites:
$A_{\text{cris}}$
reviewed in the last paragraph of §5.2 gives the following identification of sites:
where
![]() $(\mathfrak{X}_{{\mathcal{O}}_{C}/p}/A_{\text{cris}})_{\log \text{cris}}$
is the log crystalline site of
$(\mathfrak{X}_{{\mathcal{O}}_{C}/p}/A_{\text{cris}})_{\log \text{cris}}$
is the log crystalline site of
![]() $\mathfrak{X}_{{\mathcal{O}}_{C}/p}$
over
$\mathfrak{X}_{{\mathcal{O}}_{C}/p}$
over
![]() $A_{\text{cris}}$
defined analogously to the site
$A_{\text{cris}}$
defined analogously to the site
![]() $(\mathfrak{X}_{{\mathcal{O}}_{C}/p}/\mathbb{Z}_{p})_{\log \text{cris}}$
reviewed above (simply replace
$(\mathfrak{X}_{{\mathcal{O}}_{C}/p}/\mathbb{Z}_{p})_{\log \text{cris}}$
reviewed above (simply replace
![]() $\mathbb{Z}/p^{n}\mathbb{Z}$
by
$\mathbb{Z}/p^{n}\mathbb{Z}$
by
![]() $A_{\text{cris}}/p^{n}$
). The absolute logarithmic crystalline cohomology of
$A_{\text{cris}}/p^{n}$
). The absolute logarithmic crystalline cohomology of
![]() $\mathfrak{X}_{{\mathcal{O}}_{C}/p}$
is the cohomology of the structure sheaf:
$\mathfrak{X}_{{\mathcal{O}}_{C}/p}$
is the cohomology of the structure sheaf:
We consider the morphism of topoi
that ‘forgets the thickenings
![]() $\widetilde{Z}$
’ (see [Reference BeilinsonBei13b, §1.5]), and we use it to obtain the identification
$\widetilde{Z}$
’ (see [Reference BeilinsonBei13b, §1.5]), and we use it to obtain the identification
By the functoriality discussed in [Reference BeilinsonBei13b, §1.5, Corollary], the absolute Frobenius of
![]() $\mathfrak{X}_{{\mathcal{O}}_{C}/p}$
(which is the multiplication by
$\mathfrak{X}_{{\mathcal{O}}_{C}/p}$
(which is the multiplication by
![]() $p$
on log structures) and the Frobenius of
$p$
on log structures) and the Frobenius of
![]() $A_{\text{cris}}$
induce the
$A_{\text{cris}}$
induce the
![]() $A_{\text{cris}}$
-semilinear Frobenius endomorphisms of
$A_{\text{cris}}$
-semilinear Frobenius endomorphisms of
![]() $Ru_{\ast }({\mathcal{O}}_{\mathfrak{X}_{{\mathcal{O}}_{C}/p}/A_{\text{cris}}})$
and
$Ru_{\ast }({\mathcal{O}}_{\mathfrak{X}_{{\mathcal{O}}_{C}/p}/A_{\text{cris}}})$
and
![]() $R\unicode[STIX]{x1D6E4}_{\log \text{cris}}(\mathfrak{X}_{{\mathcal{O}}_{C}/p}/A_{\text{cris}})$
.
$R\unicode[STIX]{x1D6E4}_{\log \text{cris}}(\mathfrak{X}_{{\mathcal{O}}_{C}/p}/A_{\text{cris}})$
.
The main goal of this section is the following identification of the
![]() $A_{\text{cris}}$
-base change of
$A_{\text{cris}}$
-base change of
![]() $A\unicode[STIX]{x1D6FA}_{\mathfrak{X}}$
.
$A\unicode[STIX]{x1D6FA}_{\mathfrak{X}}$
.
Theorem 5.4. There is a Frobenius-equivariant identification
where the Frobenii result from those discussed in §§2.1, 2.2, 5.1, and 5.3 and, consistently with the notation (1.7.1), we have
![]() $A\unicode[STIX]{x1D6FA}_{\mathfrak{X}}\,\widehat{\otimes }_{A_{\text{inf}}}^{\mathbb{L}}\,A_{\text{cris}}=R\lim _{n}(A\unicode[STIX]{x1D6FA}_{\mathfrak{X}}\otimes _{A_{\text{inf}}}^{\mathbb{L}}A_{\text{cris}}/p^{n})$
.
$A\unicode[STIX]{x1D6FA}_{\mathfrak{X}}\,\widehat{\otimes }_{A_{\text{inf}}}^{\mathbb{L}}\,A_{\text{cris}}=R\lim _{n}(A\unicode[STIX]{x1D6FA}_{\mathfrak{X}}\otimes _{A_{\text{inf}}}^{\mathbb{L}}A_{\text{cris}}/p^{n})$
.
We will first prove a version of Theorem 5.4 in the presence of fixed semistable coordinates. We will then complete the proof by using ‘all possible coordinates’ to globalize the argument. This overall strategy is similar to that used in [Reference Bhatt, Morrow and ScholzeBMS18, §12] in the smooth case.
5.5 The local setup
For the local argument, we assume until §5.17 that
![]() $\mathfrak{X}=\operatorname{Spf}(R)$
, that
$\mathfrak{X}=\operatorname{Spf}(R)$
, that
![]() $\mathfrak{X}$
is connected, and that for some
$\mathfrak{X}$
is connected, and that for some
![]() $0\leqslant r\leqslant d$
and
$0\leqslant r\leqslant d$
and
![]() $q\in \mathbb{Q}_{{>}0}$
there is an étale
$q\in \mathbb{Q}_{{>}0}$
there is an étale
![]() ${\mathcal{O}}_{C}$
-morphism
${\mathcal{O}}_{C}$
-morphism
We use the rings
![]() $R_{\infty }^{\Box }$
and
$R_{\infty }^{\Box }$
and
![]() $R_{\infty }$
, the group
$R_{\infty }$
, the group
![]() $\unicode[STIX]{x1D6E5}$
, and its generators
$\unicode[STIX]{x1D6E5}$
, and its generators
![]() $\unicode[STIX]{x1D6FF}_{i}$
introduced in §3.2, the rings
$\unicode[STIX]{x1D6FF}_{i}$
introduced in §3.2, the rings
![]() $\mathbb{A}_{\text{inf}}(R_{\infty }^{\Box })$
,
$\mathbb{A}_{\text{inf}}(R_{\infty }^{\Box })$
,
![]() $\mathbb{A}_{\text{inf}}(R_{\infty })$
,
$\mathbb{A}_{\text{inf}}(R_{\infty })$
,
![]() $A(R^{\Box })$
, and
$A(R^{\Box })$
, and
![]() $A(R)$
and the modules
$A(R)$
and the modules
![]() $N_{\infty }^{\Box }$
and
$N_{\infty }^{\Box }$
and
![]() $N_{\infty }$
introduced in §3.14, the rings
$N_{\infty }$
introduced in §3.14, the rings
![]() $\mathbb{A}_{\text{cris}}^{(m)}(R_{\infty })$
and
$\mathbb{A}_{\text{cris}}^{(m)}(R_{\infty })$
and
![]() $A_{\text{cris}}^{(m)}(R)$
introduced in §3.27, and the object
$A_{\text{cris}}^{(m)}(R)$
introduced in §3.27, and the object
![]() $A\unicode[STIX]{x1D6FA}_{\mathfrak{X}}^{\text{psh}}$
introduced in §4.1.
$A\unicode[STIX]{x1D6FA}_{\mathfrak{X}}^{\text{psh}}$
introduced in §4.1.
Roughly speaking, with the coordinates above, we will access the right-hand side of (5.4.1) through the logarithmic de Rham complex of an explicit log smooth lift
![]() $\operatorname{Spf}(A_{\text{cris}}(R))$
over
$\operatorname{Spf}(A_{\text{cris}}(R))$
over
![]() $\operatorname{Spf}(A_{\text{cris}})$
of
$\operatorname{Spf}(A_{\text{cris}})$
of
![]() $\mathfrak{X}_{{\mathcal{O}}_{C}/p}$
over
$\mathfrak{X}_{{\mathcal{O}}_{C}/p}$
over
![]() $\operatorname{Spec}({\mathcal{O}}_{C}/p)$
(see Proposition 5.13). This complex may be made explicit by expressing its differentials in terms of the
$\operatorname{Spec}({\mathcal{O}}_{C}/p)$
(see Proposition 5.13). This complex may be made explicit by expressing its differentials in terms of the
![]() $\unicode[STIX]{x1D6E5}$
-action on
$\unicode[STIX]{x1D6E5}$
-action on
![]() $A_{\text{cris}}(R)$
(see Lemma 5.15). In contrast, results from §3, namely, Theorem 3.20 and (3.25.1), make the left-hand side of (5.4.1) explicit. Once both sides are explicit, one identifies them and establishes (the presheaf version of) the local case of Theorem 5.4.
$A_{\text{cris}}(R)$
(see Lemma 5.15). In contrast, results from §3, namely, Theorem 3.20 and (3.25.1), make the left-hand side of (5.4.1) explicit. Once both sides are explicit, one identifies them and establishes (the presheaf version of) the local case of Theorem 5.4.
However, this relatively short local proof, whose detailed version in the good reduction case is given in [Reference Bhatt, Morrow and ScholzeBMS18, 12.5], is ill-suited for globalization. This is because it appears difficult to extend the implicit exchange of the order of the functors
![]() $L\unicode[STIX]{x1D702}_{(\unicode[STIX]{x1D707})}$
and
$L\unicode[STIX]{x1D702}_{(\unicode[STIX]{x1D707})}$
and
![]() $-\,\widehat{\otimes }_{A_{\text{inf}}}^{\mathbb{L}}\,A_{\text{cris}}$
in this argument to general perfectoid covers that appear in the ‘all possible coordinates’ technique. For instance, one may attempt to use the almost purity theorem and Lemma 3.18 to reduce such commutativity to the ‘base case’ of
$-\,\widehat{\otimes }_{A_{\text{inf}}}^{\mathbb{L}}\,A_{\text{cris}}$
in this argument to general perfectoid covers that appear in the ‘all possible coordinates’ technique. For instance, one may attempt to use the almost purity theorem and Lemma 3.18 to reduce such commutativity to the ‘base case’ of
![]() $R_{\infty }$
, but this requires understanding the
$R_{\infty }$
, but this requires understanding the
![]() $W(\mathfrak{m}^{\flat })$
-torsion in the groups
$W(\mathfrak{m}^{\flat })$
-torsion in the groups
that seem difficult to access due to pathologies of the ring
![]() $A_{\text{cris}}/\unicode[STIX]{x1D707}$
.
$A_{\text{cris}}/\unicode[STIX]{x1D707}$
.
Similarly to [Reference Bhatt, Morrow and ScholzeBMS18, §12.2], to overcome this difficulty we will use the rings
![]() $A_{\text{cris}}^{(m)}$
reviewed in §3.26 that retain better finite-type properties over
$A_{\text{cris}}^{(m)}$
reviewed in §3.26 that retain better finite-type properties over
![]() $A_{\text{inf}}$
than
$A_{\text{inf}}$
than
![]() $A_{\text{cris}}$
. In particular, we use the work of §3 to commute the functors
$A_{\text{cris}}$
. In particular, we use the work of §3 to commute the functors
![]() $L\unicode[STIX]{x1D702}_{(\unicode[STIX]{x1D707})}$
and
$L\unicode[STIX]{x1D702}_{(\unicode[STIX]{x1D707})}$
and
![]() $-\,\widehat{\otimes }_{A_{\text{inf}}}^{\mathbb{L}}\,A_{\text{cris}}^{(m)}$
in the following proposition.
$-\,\widehat{\otimes }_{A_{\text{inf}}}^{\mathbb{L}}\,A_{\text{cris}}^{(m)}$
in the following proposition.
Proposition 5.6. In the local setting of §5.5, for every
![]() $m\geqslant p$
, we have
$m\geqslant p$
, we have
Proof. The map (5.6.1) exists because its target is derived
![]() $p$
-adically complete (see [Reference Bhatt, Morrow and ScholzeBMS18, 6.19]). Moreover, by Theorems 3.20 and 3.34, it suffices to prove that
$p$
-adically complete (see [Reference Bhatt, Morrow and ScholzeBMS18, 6.19]). Moreover, by Theorems 3.20 and 3.34, it suffices to prove that
By Propositions 3.25 and 3.32, the ‘nonintegral’ part
![]() $N_{\infty }$
does not contribute, so it suffices to show:
$N_{\infty }$
does not contribute, so it suffices to show:
In turn, (5.6.2) follows from the triviality of the
![]() $\unicode[STIX]{x1D6E5}$
-action on
$\unicode[STIX]{x1D6E5}$
-action on
![]() $A(R)/\unicode[STIX]{x1D707}$
and
$A(R)/\unicode[STIX]{x1D707}$
and
![]() $A_{\text{cris}}^{(m)}(R)/\unicode[STIX]{x1D707}$
(see §§3.14 and 3.27): namely, due to Lemma 3.7 and this triviality, the left-hand (respectively, right-hand) side of (5.6.2) becomes
$A_{\text{cris}}^{(m)}(R)/\unicode[STIX]{x1D707}$
(see §§3.14 and 3.27): namely, due to Lemma 3.7 and this triviality, the left-hand (respectively, right-hand) side of (5.6.2) becomes
where the completed tensor product is nonderived (that is, termwise) because each
![]() $p^{n}$
,
$p^{n}$
,
![]() $\unicode[STIX]{x1D707}^{n^{\prime }}$
is an
$\unicode[STIX]{x1D707}^{n^{\prime }}$
is an
![]() $A(R)$
-regular sequence with
$A(R)$
-regular sequence with
![]() $A(R)/(p^{n},\unicode[STIX]{x1D707}^{n^{\prime }})$
flat over
$A(R)/(p^{n},\unicode[STIX]{x1D707}^{n^{\prime }})$
flat over
![]() $A_{\text{inf}}/(p^{n},\unicode[STIX]{x1D707}^{n^{\prime }})$
(see Lemma 3.13); the two Koszul complexes may then be identified termwise (see §3.27).◻
$A_{\text{inf}}/(p^{n},\unicode[STIX]{x1D707}^{n^{\prime }})$
(see Lemma 3.13); the two Koszul complexes may then be identified termwise (see §3.27).◻
Continuing to work in the local setting, we now express the (presheaf version of the) left-hand side of (5.4.1) in the form that will be convenient for the ‘all possible coordinates’ technique.
Corollary 5.7. In the local setting of §5.5, there is a Frobenius-equivariant identification
(see (4.1.1) for
![]() $A\unicode[STIX]{x1D6FA}_{\mathfrak{X}}^{\text{psh}}$
) where, on the right-hand side, the direct limit and the
$A\unicode[STIX]{x1D6FA}_{\mathfrak{X}}^{\text{psh}}$
) where, on the right-hand side, the direct limit and the
![]() $p$
-adic completion are termwise.
$p$
-adic completion are termwise.
Proof. The
![]() $\unicode[STIX]{x1D6E5}$
-equivariant Frobenii of the rings
$\unicode[STIX]{x1D6E5}$
-equivariant Frobenii of the rings
![]() $\mathbb{A}_{\text{cris}}^{(m)}(R_{\infty })$
are compatible as
$\mathbb{A}_{\text{cris}}^{(m)}(R_{\infty })$
are compatible as
![]() $m$
varies (see §3.27), so, due to the divisibility
$m$
varies (see §3.27), so, due to the divisibility
![]() $\unicode[STIX]{x1D707}\,\mid \,\unicode[STIX]{x1D711}(\unicode[STIX]{x1D707})$
, they induce the Frobenius on the right-hand side of (5.7.1). Proposition 5.6 and Theorem 3.34 give the Frobenius-equivariant identification
$\unicode[STIX]{x1D707}\,\mid \,\unicode[STIX]{x1D711}(\unicode[STIX]{x1D707})$
, they induce the Frobenius on the right-hand side of (5.7.1). Proposition 5.6 and Theorem 3.34 give the Frobenius-equivariant identification
so it remains to pass to the direct limit and to form the
![]() $p$
-adic completion.◻
$p$
-adic completion.◻
We turn to the right-hand side of (5.4.1) and begin by constructing a log smooth lift
![]() $A_{\text{cris}}(R)$
of
$A_{\text{cris}}(R)$
of
![]() $R/p$
.
$R/p$
.
5.8 The ring
 $A_{\text{cris}}(R)$
$A_{\text{cris}}(R)$
The ‘relative version’ of
![]() $A_{\text{cris}}$
(respectively, a ‘highly ramified cover’ of this relative version) is the
$A_{\text{cris}}$
(respectively, a ‘highly ramified cover’ of this relative version) is the
![]() $A(R)$
-algebra (respectively,
$A(R)$
-algebra (respectively,
![]() $\mathbb{A}_{\text{inf}}(R_{\infty })$
-algebra)
$\mathbb{A}_{\text{inf}}(R_{\infty })$
-algebra)
where the completion is
![]() $p$
-adic (equivalently,
$p$
-adic (equivalently,
![]() $(p,\unicode[STIX]{x1D707})$
-adic, see §5.1). Due to the decomposition (3.14.5), the subring
$(p,\unicode[STIX]{x1D707})$
-adic, see §5.1). Due to the decomposition (3.14.5), the subring
![]() $A_{\text{cris}}(R)\subset \mathbb{A}_{\text{cris}}(R_{\infty })$
is an
$A_{\text{cris}}(R)\subset \mathbb{A}_{\text{cris}}(R_{\infty })$
is an
![]() $A_{\text{cris}}(R)$
-module direct summand. The maps
$A_{\text{cris}}(R)$
-module direct summand. The maps
![]() $\unicode[STIX]{x1D703}$
from §§3.14 and 5.1 induce compatible surjections
$\unicode[STIX]{x1D703}$
from §§3.14 and 5.1 induce compatible surjections
We let
![]() $\mathbb{A}_{\text{cris}}^{0}(R_{\infty })$
be the
$\mathbb{A}_{\text{cris}}^{0}(R_{\infty })$
be the
![]() $\mathbb{A}_{\text{inf}}(R_{\infty })$
-subalgebra of
$\mathbb{A}_{\text{inf}}(R_{\infty })$
-subalgebra of
![]() $\mathbb{A}_{\text{inf}}(R_{\infty })[\frac{1}{p}]$
generated by the elements
$\mathbb{A}_{\text{inf}}(R_{\infty })[\frac{1}{p}]$
generated by the elements
![]() $\unicode[STIX]{x1D709}^{n}/n!$
for
$\unicode[STIX]{x1D709}^{n}/n!$
for
![]() $n\geqslant 1$
. By [Reference TsujiTsu99, proof of A2.8], letting
$n\geqslant 1$
. By [Reference TsujiTsu99, proof of A2.8], letting
![]() $\mathbb{A}_{\text{inf}}(R_{\infty })[\frac{T^{n}}{n!}]_{n\geqslant 1}$
denote the divided power polynomial algebra over
$\mathbb{A}_{\text{inf}}(R_{\infty })[\frac{T^{n}}{n!}]_{n\geqslant 1}$
denote the divided power polynomial algebra over
![]() $\mathbb{A}_{\text{inf}}(R_{\infty })$
in one variable, we have
$\mathbb{A}_{\text{inf}}(R_{\infty })$
in one variable, we have
Consequently, since
![]() $\unicode[STIX]{x1D709}$
generates
$\unicode[STIX]{x1D709}$
generates
![]() $\operatorname{Ker}(\unicode[STIX]{x1D703})\subset \mathbb{A}_{\text{inf}}(R_{\infty })$
, the ring
$\operatorname{Ker}(\unicode[STIX]{x1D703})\subset \mathbb{A}_{\text{inf}}(R_{\infty })$
, the ring
![]() $\mathbb{A}_{\text{cris}}^{0}(R_{\infty })$
is identified with the divided power envelope of
$\mathbb{A}_{\text{cris}}^{0}(R_{\infty })$
is identified with the divided power envelope of
![]() $(\mathbb{A}_{\text{inf}}(R_{\infty }),\operatorname{Ker}(\unicode[STIX]{x1D703})+p\mathbb{A}_{\text{inf}}(R_{\infty }))$
over
$(\mathbb{A}_{\text{inf}}(R_{\infty }),\operatorname{Ker}(\unicode[STIX]{x1D703})+p\mathbb{A}_{\text{inf}}(R_{\infty }))$
over
![]() $(\mathbb{Z}_{p},p\mathbb{Z}_{p})$
. By the previous display,
$(\mathbb{Z}_{p},p\mathbb{Z}_{p})$
. By the previous display,
By §3.14, the ring
![]() $\mathbb{A}_{\text{cris}}(R_{\infty })$
(respectively,
$\mathbb{A}_{\text{cris}}(R_{\infty })$
(respectively,
![]() $A_{\text{cris}}(R)$
) is
$A_{\text{cris}}(R)$
) is
![]() $p$
-adically formally étale as an
$p$
-adically formally étale as an
![]() $\mathbb{A}_{\text{cris}}(R_{\infty }^{\Box })$
-algebra (respectively,
$\mathbb{A}_{\text{cris}}(R_{\infty }^{\Box })$
-algebra (respectively,
![]() $A_{\text{cris}}(R^{\Box })$
-algebra) and
$A_{\text{cris}}(R^{\Box })$
-algebra) and
![]() $p$
-adically formally flat as an
$p$
-adically formally flat as an
![]() $A_{\text{cris}}$
-algebra. In particular,
$A_{\text{cris}}$
-algebra. In particular,
![]() $\mathbb{A}_{\text{cris}}(R_{\infty })$
inherits
$\mathbb{A}_{\text{cris}}(R_{\infty })$
inherits
![]() $p$
-torsion freeness from
$p$
-torsion freeness from
![]() $A_{\text{cris}}$
. Moreover, even though we will not use this,
$A_{\text{cris}}$
. Moreover, even though we will not use this,
![]() $\mathbb{A}_{\text{cris}}(R_{\infty })$
is also
$\mathbb{A}_{\text{cris}}(R_{\infty })$
is also
![]() $\unicode[STIX]{x1D707}$
-torsion free, as follows from Proposition 5.36 below (contrast this with an argument for (3.27.2)).
$\unicode[STIX]{x1D707}$
-torsion free, as follows from Proposition 5.36 below (contrast this with an argument for (3.27.2)).
The rings
![]() $A_{\text{cris}}(R)$
and
$A_{\text{cris}}(R)$
and
![]() $\mathbb{A}_{\text{cris}}(R_{\infty })$
come equipped with
$\mathbb{A}_{\text{cris}}(R_{\infty })$
come equipped with
![]() $A_{\text{cris}}$
-semilinear Frobenius endomorphisms that are compatible with their counterparts for
$A_{\text{cris}}$
-semilinear Frobenius endomorphisms that are compatible with their counterparts for
![]() $A_{\text{cris}}^{(m)}(R)$
and
$A_{\text{cris}}^{(m)}(R)$
and
![]() $\mathbb{A}_{\text{cris}}^{(m)}(R_{\infty })$
discussed in §3.27. The profinite group
$\mathbb{A}_{\text{cris}}^{(m)}(R_{\infty })$
discussed in §3.27. The profinite group
![]() $\unicode[STIX]{x1D6E5}$
acts continuously, Frobenius-equivariantly, and
$\unicode[STIX]{x1D6E5}$
acts continuously, Frobenius-equivariantly, and
![]() $A_{\text{cris}}$
-linearly on
$A_{\text{cris}}$
-linearly on
![]() $A_{\text{cris}}(R)$
and
$A_{\text{cris}}(R)$
and
![]() $\mathbb{A}_{\text{cris}}(R_{\infty })$
. As in §3.27, the induced
$\mathbb{A}_{\text{cris}}(R_{\infty })$
. As in §3.27, the induced
![]() $\unicode[STIX]{x1D6E5}$
-action on
$\unicode[STIX]{x1D6E5}$
-action on
![]() $A_{\text{cris}}(R)/\unicode[STIX]{x1D707}$
is trivial.
$A_{\text{cris}}(R)/\unicode[STIX]{x1D707}$
is trivial.
We will endow
![]() $A_{\text{cris}}(R)$
with a log structure, which will, in fact, come from
$A_{\text{cris}}(R)$
with a log structure, which will, in fact, come from
![]() $A(R)$
.
$A(R)$
.
5.9 The log structure on
 $A(R)$
$A(R)$
Provisionally, we consider the (fine) log structures on
![]() $A_{\text{inf}}$
and
$A_{\text{inf}}$
and
![]() $A(R)$
associated to the prelog structures
$A(R)$
associated to the prelog structures
Then, under the diagonal map
![]() $\mathbb{N}_{{\geqslant}0}\rightarrow \mathbb{N}_{{\geqslant}0}^{r+1}$
, the ring
$\mathbb{N}_{{\geqslant}0}\rightarrow \mathbb{N}_{{\geqslant}0}^{r+1}$
, the ring
![]() $A(R)$
is a
$A(R)$
is a
![]() $(p,\unicode[STIX]{x1D707})$
-adically formally log smooth
$(p,\unicode[STIX]{x1D707})$
-adically formally log smooth
![]() $A_{\text{inf}}$
-algebra (see (3.14.2) and [Reference KatoKat89, 3.5–3.6]). To eliminate the dependence on
$A_{\text{inf}}$
-algebra (see (3.14.2) and [Reference KatoKat89, 3.5–3.6]). To eliminate the dependence on
![]() $q$
, we always, unless noted otherwise, equip
$q$
, we always, unless noted otherwise, equip
![]() $A_{\text{inf}}$
with the log structure associated to the prelog structure
$A_{\text{inf}}$
with the log structure associated to the prelog structure
Likewise, we always equip
![]() $A(R)$
with the log structure that is the base change of the fine log structure on
$A(R)$
with the log structure that is the base change of the fine log structure on
![]() $A(R)$
described above along the ‘change of log structure’ self-map of
$A(R)$
described above along the ‘change of log structure’ self-map of
![]() $A_{\text{inf}}$
determined by
$A_{\text{inf}}$
determined by
![]() $\mathbb{N}_{{\geqslant}0}\xrightarrow[{}]{a\,\mapsto \,((p^{1/p^{\infty }})^{q})^{a}}{\mathcal{O}}_{C}^{\flat }\setminus \{0\}$
. Explicitly, this log structure is associated to the prelog structure
$\mathbb{N}_{{\geqslant}0}\xrightarrow[{}]{a\,\mapsto \,((p^{1/p^{\infty }})^{q})^{a}}{\mathcal{O}}_{C}^{\flat }\setminus \{0\}$
. Explicitly, this log structure is associated to the prelog structure
that embeds
![]() $\mathbb{N}_{{\geqslant}0}$
diagonally into
$\mathbb{N}_{{\geqslant}0}$
diagonally into
![]() $\mathbb{N}_{{\geqslant}0}^{r+1}$
, sends an
$\mathbb{N}_{{\geqslant}0}^{r+1}$
, sends an
![]() $a\in \mathbb{N}_{{\geqslant}0}$
to
$a\in \mathbb{N}_{{\geqslant}0}$
to
![]() $((p^{1/p^{\infty }})^{q})^{a}$
, and sends the
$((p^{1/p^{\infty }})^{q})^{a}$
, and sends the
![]() $i$
th standard basis vector of
$i$
th standard basis vector of
![]() $\mathbb{N}_{{\geqslant}0}^{r+1}$
(respectively, an
$\mathbb{N}_{{\geqslant}0}^{r+1}$
(respectively, an
![]() $x\in {\mathcal{O}}_{C}^{\flat }\setminus \{0\}$
) to
$x\in {\mathcal{O}}_{C}^{\flat }\setminus \{0\}$
) to
![]() $X_{i}$
(respectively, to
$X_{i}$
(respectively, to
![]() $[x]$
).
$[x]$
).
These latter ‘default’ log structures on
![]() $A_{\text{inf}}$
and
$A_{\text{inf}}$
and
![]() $A(R)$
are quasi-coherent and integral and, by base change, with them
$A(R)$
are quasi-coherent and integral and, by base change, with them
![]() $A(R)$
is
$A(R)$
is
![]() $(p,\unicode[STIX]{x1D707})$
-adically formally log smooth over
$(p,\unicode[STIX]{x1D707})$
-adically formally log smooth over
![]() $A_{\text{inf}}$
. In fact, via the map
$A_{\text{inf}}$
. In fact, via the map
![]() $\unicode[STIX]{x1D703}$
, the ring
$\unicode[STIX]{x1D703}$
, the ring
![]() $A(R)$
over
$A(R)$
over
![]() $A_{\text{inf}}$
becomes a
$A_{\text{inf}}$
becomes a
![]() $(p,\unicode[STIX]{x1D707})$
-adically formally log smooth thickening of
$(p,\unicode[STIX]{x1D707})$
-adically formally log smooth thickening of
![]() $R/p$
over
$R/p$
over
![]() ${\mathcal{O}}_{C}/p$
(where
${\mathcal{O}}_{C}/p$
(where
![]() $R/p$
is endowed with the log structure discussed in §1.6).
$R/p$
is endowed with the log structure discussed in §1.6).
The Frobenii of
![]() $A_{\text{inf}}$
and
$A_{\text{inf}}$
and
![]() $A(R)$
extend to the log structures by letting them act as multiplication by
$A(R)$
extend to the log structures by letting them act as multiplication by
![]() $p$
on
$p$
on
![]() $\mathbb{N}_{{\geqslant}0}^{r+1}$
and
$\mathbb{N}_{{\geqslant}0}^{r+1}$
and
![]() $\mathbb{N}_{{\geqslant}0}$
and as the
$\mathbb{N}_{{\geqslant}0}$
and as the
![]() $p$
th power map on
$p$
th power map on
![]() ${\mathcal{O}}_{C}^{\flat }\setminus \{0\}$
. Consequently, the Frobenius of the log
${\mathcal{O}}_{C}^{\flat }\setminus \{0\}$
. Consequently, the Frobenius of the log
![]() $A_{\text{inf}}$
-algebra
$A_{\text{inf}}$
-algebra
![]() $A(R)$
lifts the absolute Frobenius of the log
$A(R)$
lifts the absolute Frobenius of the log
![]() ${\mathcal{O}}_{C}/p$
-algebra
${\mathcal{O}}_{C}/p$
-algebra
![]() $R/p$
.
$R/p$
.
The Frobenius-equivariant
![]() $\unicode[STIX]{x1D6E5}$
-action on the
$\unicode[STIX]{x1D6E5}$
-action on the
![]() $A_{\text{inf}}$
-algebra
$A_{\text{inf}}$
-algebra
![]() $A(R)$
(see §3.14) extends to a Frobenius-equivariant
$A(R)$
(see §3.14) extends to a Frobenius-equivariant
![]() $\unicode[STIX]{x1D6E5}$
-action on the log
$\unicode[STIX]{x1D6E5}$
-action on the log
![]() $A_{\text{inf}}$
-scheme
$A_{\text{inf}}$
-scheme
![]() $\operatorname{Spec}(A(R))$
: indeed, a
$\operatorname{Spec}(A(R))$
: indeed, a
![]() $\unicode[STIX]{x1D6FF}\in \unicode[STIX]{x1D6E5}$
sends each
$\unicode[STIX]{x1D6FF}\in \unicode[STIX]{x1D6E5}$
sends each
![]() $X_{i}$
with
$X_{i}$
with
![]() $0\leqslant i\leqslant r$
to
$0\leqslant i\leqslant r$
to
![]() $u_{\unicode[STIX]{x1D6FF},\,i}\,\cdot \,X_{i}$
for some Teichmüller unit
$u_{\unicode[STIX]{x1D6FF},\,i}\,\cdot \,X_{i}$
for some Teichmüller unit
![]() $u_{\unicode[STIX]{x1D6FF},\,i}\in A(R)^{\times }$
(see §3.14) and the prelog structures
$u_{\unicode[STIX]{x1D6FF},\,i}\in A(R)^{\times }$
(see §3.14) and the prelog structures
determine the same log structure on
![]() $\operatorname{Spec}(A(R))$
, namely, the one associated to the prelog structure
$\operatorname{Spec}(A(R))$
, namely, the one associated to the prelog structure
5.10 The logarithmic de Rham complex
With a slight abuse of notation, we let
be the (global section complex of the) logarithmic de Rham complex of
![]() $\operatorname{Spf}(A(R))$
over
$\operatorname{Spf}(A(R))$
over
![]() $\operatorname{Spf}(A_{\text{inf}})$
. More precisely,
$\operatorname{Spf}(A_{\text{inf}})$
. More precisely,
![]() $\unicode[STIX]{x1D6FA}_{A(R)/A_{\text{inf}},\,\log }^{\bullet }$
is the (termwise) inverse limit over
$\unicode[STIX]{x1D6FA}_{A(R)/A_{\text{inf}},\,\log }^{\bullet }$
is the (termwise) inverse limit over
![]() $n,n^{\prime }>0$
of the logarithmic de Rham complexes of
$n,n^{\prime }>0$
of the logarithmic de Rham complexes of
![]() $A(R)/(p^{n},\unicode[STIX]{x1D707}^{n^{\prime }})$
over
$A(R)/(p^{n},\unicode[STIX]{x1D707}^{n^{\prime }})$
over
![]() $A_{\text{inf}}/(p^{n},\unicode[STIX]{x1D707}^{n^{\prime }})$
(described, for instance, in [Reference OgusOgu18, V.2.1.1]). Due to the formal log smoothness of
$A_{\text{inf}}/(p^{n},\unicode[STIX]{x1D707}^{n^{\prime }})$
(described, for instance, in [Reference OgusOgu18, V.2.1.1]). Due to the formal log smoothness of
![]() $A(R)$
over
$A(R)$
over
![]() $A_{\text{inf}}$
, each
$A_{\text{inf}}$
, each
![]() $\unicode[STIX]{x1D6FA}_{A(R)/A_{\text{inf}},\,\log }^{i}$
is a free
$\unicode[STIX]{x1D6FA}_{A(R)/A_{\text{inf}},\,\log }^{i}$
is a free
![]() $A(R)$
-module: indeed, the logarithmic differentials
$A(R)$
-module: indeed, the logarithmic differentials
form an
![]() $A(R)$
-basis of
$A(R)$
-basis of
![]() $\unicode[STIX]{x1D6FA}_{A(R)/A_{\text{inf}},\,\log }^{1}$
. We let
$\unicode[STIX]{x1D6FA}_{A(R)/A_{\text{inf}},\,\log }^{1}$
. We let
denote the dual basis of log
![]() $A_{\text{inf}}$
-derivations (we do not notationally explicate the accompanying homomorphisms from the log structure to
$A_{\text{inf}}$
-derivations (we do not notationally explicate the accompanying homomorphisms from the log structure to
![]() $A(R)$
). These satisfy the following explicit formulas that are derived using the relation
$A(R)$
). These satisfy the following explicit formulas that are derived using the relation
![]() $d\log (X_{0})+\cdots +d\log (X_{r})=0$
:
$d\log (X_{0})+\cdots +d\log (X_{r})=0$
:
The
![]() $\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\log (X_{i})}$
also define an isomorphism
$\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\log (X_{i})}$
also define an isomorphism
![]() $\unicode[STIX]{x1D6FA}_{A(R)/A_{\text{inf}},\,\log }^{1}\cong A(R)^{\oplus d}$
, which extends to an isomorphism
$\unicode[STIX]{x1D6FA}_{A(R)/A_{\text{inf}},\,\log }^{1}\cong A(R)^{\oplus d}$
, which extends to an isomorphism
that may be considered canonical because its construction only uses data determined by the local coordinate map (5.5.1). The Frobenius of the log
![]() $A_{\text{inf}}$
-algebra
$A_{\text{inf}}$
-algebra
![]() $A(R)$
multiplies each
$A(R)$
multiplies each
![]() $d\log (X_{i})$
by
$d\log (X_{i})$
by
![]() $p$
, so its effect on the right-hand side of (5.10.3) is given in each degree
$p$
, so its effect on the right-hand side of (5.10.3) is given in each degree
![]() $j$
by
$j$
by
![]() $p^{j}$
times the Frobenius of
$p^{j}$
times the Frobenius of
![]() $A(R)$
.
$A(R)$
.
5.11 The log structure on
 $A_{\text{cris}}(R)$
$A_{\text{cris}}(R)$
Unless specified otherwise, we equip the
![]() $A(R)$
-algebras
$A(R)$
-algebras
![]() $A_{\text{cris}}(R)$
and
$A_{\text{cris}}(R)$
and
![]() $A_{\text{cris}}(R)/p^{n}$
for
$A_{\text{cris}}(R)/p^{n}$
for
![]() $n>0$
with the pullback of the log structure on
$n>0$
with the pullback of the log structure on
![]() $A(R)$
determined by (5.9.2). Thus, since the log structures (5.9.1) on
$A(R)$
determined by (5.9.2). Thus, since the log structures (5.9.1) on
![]() $A_{\text{inf}}$
and (5.2.1) on
$A_{\text{inf}}$
and (5.2.1) on
![]() $A_{\text{cris}}$
agree,
$A_{\text{cris}}$
agree,
![]() $A_{\text{cris}}(R)$
is
$A_{\text{cris}}(R)$
is
![]() $p$
-adically formally log smooth over
$p$
-adically formally log smooth over
![]() $A_{\text{cris}}$
. Letting the completion be
$A_{\text{cris}}$
. Letting the completion be
![]() $p$
-adic, we set
$p$
-adic, we set
which is the (global sections of the) logarithmic de Rham complex of
![]() $\operatorname{Spf}(A_{\text{cris}}(R))$
over
$\operatorname{Spf}(A_{\text{cris}}(R))$
over
![]() $\operatorname{Spf}(A_{\text{cris}})$
.
$\operatorname{Spf}(A_{\text{cris}})$
.
We use the
![]() $p$
-adic completeness of
$p$
-adic completeness of
![]() $A_{\text{cris}}(R)$
and its
$A_{\text{cris}}(R)$
and its
![]() $p$
-adic formal flatness over
$p$
-adic formal flatness over
![]() $A_{\text{cris}}$
(see §5.8) to extend the divided power structure of
$A_{\text{cris}}$
(see §5.8) to extend the divided power structure of
![]() $A_{\text{cris}}$
to
$A_{\text{cris}}$
to
![]() $A_{\text{cris}}(R)$
(see [SP, 07H1]). In effect,
$A_{\text{cris}}(R)$
(see [SP, 07H1]). In effect,
![]() $A_{\text{cris}}(R)$
over
$A_{\text{cris}}(R)$
over
![]() $A_{\text{cris}}$
becomes a
$A_{\text{cris}}$
becomes a
![]() $p$
-adically formally log smooth log PD thickening of
$p$
-adically formally log smooth log PD thickening of
![]() $R/p$
over
$R/p$
over
![]() ${\mathcal{O}}_{C}/p$
(compare with §5.9).
${\mathcal{O}}_{C}/p$
(compare with §5.9).
Through results of [Reference BeilinsonBei13b], the following lemma will be key for relating the right-hand side of (5.4.1) to the logarithmic de Rham cohomology of
![]() $\operatorname{Spf}(A_{\text{cris}}(R))$
over
$\operatorname{Spf}(A_{\text{cris}}(R))$
over
![]() $\operatorname{Spf}(A_{\text{cris}})$
in Proposition 5.13.
$\operatorname{Spf}(A_{\text{cris}})$
in Proposition 5.13.
Lemma 5.12. For each
![]() $n\geqslant 1$
, the log smooth log PD thickening
$n\geqslant 1$
, the log smooth log PD thickening
![]() $A_{\text{cris}}(R)/p^{n}$
over
$A_{\text{cris}}(R)/p^{n}$
over
![]() $A_{\text{cris}}/p^{n}$
of
$A_{\text{cris}}/p^{n}$
of
![]() $R/p$
over
$R/p$
over
![]() ${\mathcal{O}}_{C}/p$
is PD smooth in the sense of [Reference BeilinsonBei13b, §1.4] (see the proof for the definition).
${\mathcal{O}}_{C}/p$
is PD smooth in the sense of [Reference BeilinsonBei13b, §1.4] (see the proof for the definition).
Proof. The PD smoothness is the claim that for every log PD thickening
![]() $U{\hookrightarrow}\widetilde{U}$
over the log PD scheme
$U{\hookrightarrow}\widetilde{U}$
over the log PD scheme
![]() $A_{\text{cris}}/p^{n}$
such that
$A_{\text{cris}}/p^{n}$
such that
![]() $U$
is affine and the log structure of
$U$
is affine and the log structure of
![]() $\widetilde{U}$
(and, hence, also of
$\widetilde{U}$
(and, hence, also of
![]() $U$
) is integral and quasi-coherent, the indicated diagonal log PD morphism exists in every commutative diagram
$U$
) is integral and quasi-coherent, the indicated diagonal log PD morphism exists in every commutative diagram

of log schemes and log (or log PD where indicated) scheme morphisms over
![]() $A_{\text{cris}}/p^{n}$
(see [Reference BeilinsonBei13a, §1.4]).
$A_{\text{cris}}/p^{n}$
(see [Reference BeilinsonBei13a, §1.4]).
This sought property of
![]() $A_{\text{cris}}(R)/p^{n}$
is invariant under base change that changes the log structure on
$A_{\text{cris}}(R)/p^{n}$
is invariant under base change that changes the log structure on
![]() $A_{\text{cris}}/p^{n}$
, so we may assume that
$A_{\text{cris}}/p^{n}$
, so we may assume that
![]() $A_{\text{cris}}/p^{n}$
and
$A_{\text{cris}}/p^{n}$
and
![]() $A_{\text{cris}}(R)/p^{n}$
are instead equipped with the pullbacks of the ‘provisional’ fine log structures defined in §5.9. Moreover, since the PD structure of
$A_{\text{cris}}(R)/p^{n}$
are instead equipped with the pullbacks of the ‘provisional’ fine log structures defined in §5.9. Moreover, since the PD structure of
![]() $A_{\text{cris}}(R)/p^{n}$
is extended from
$A_{\text{cris}}(R)/p^{n}$
is extended from
![]() $A_{\text{cris}}/p^{n}$
, the log PD thickening
$A_{\text{cris}}/p^{n}$
, the log PD thickening
over
![]() $A_{\text{cris}}/p^{n}$
is its own log PD-envelope over
$A_{\text{cris}}/p^{n}$
is its own log PD-envelope over
![]() $A_{\text{cris}}/p^{n}$
(in the sense of [Reference BeilinsonBei13b, §1.3]). Thus, the log smoothness of
$A_{\text{cris}}/p^{n}$
(in the sense of [Reference BeilinsonBei13b, §1.3]). Thus, the log smoothness of
![]() $A_{\text{cris}}(R)/p^{n}$
over
$A_{\text{cris}}(R)/p^{n}$
over
![]() $A_{\text{cris}}/p^{n}$
and [Reference BeilinsonBei13b, §1.4, Remarks (ii)] give the claimed PD smoothness.◻
$A_{\text{cris}}/p^{n}$
and [Reference BeilinsonBei13b, §1.4, Remarks (ii)] give the claimed PD smoothness.◻
Proposition 5.13. In the local setting of §5.5, letting
![]() $\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\log (X_{i})}:A_{\text{cris}}^{(m)}(R)\rightarrow A_{\text{cris}}^{(m)}(R)$
denote the
$\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\log (X_{i})}:A_{\text{cris}}^{(m)}(R)\rightarrow A_{\text{cris}}^{(m)}(R)$
denote the
![]() $A_{\text{cris}}^{(m)}$
-derivations induced from (5.10.1) by base change, we have Frobenius-equivariant identifications
$A_{\text{cris}}^{(m)}$
-derivations induced from (5.10.1) by base change, we have Frobenius-equivariant identifications
(the Frobenius action on the last term is analogous to that described after (5.10.3)).
Proof. By Lemma 5.12, each
![]() $A_{\text{cris}}(R)/p^{n}$
over
$A_{\text{cris}}(R)/p^{n}$
over
![]() $A_{\text{cris}}/p^{n}$
is a PD smooth thickening of
$A_{\text{cris}}/p^{n}$
is a PD smooth thickening of
![]() $R/p$
over
$R/p$
over
![]() ${\mathcal{O}}_{C}/p$
, so [Reference BeilinsonBei13b, (1.8.1)] gives the Frobenius-equivariant identificationFootnote
7
${\mathcal{O}}_{C}/p$
, so [Reference BeilinsonBei13b, (1.8.1)] gives the Frobenius-equivariant identificationFootnote
7
Since the sheaves
![]() $\unicode[STIX]{x1D6FA}_{\operatorname{Spf}(A_{\text{cris}}(R))/\operatorname{Spf}(A_{\text{cris}}),\,\log }^{i}$
are locally free and, in particular, quasi-coherent, they are acyclic for
$\unicode[STIX]{x1D6FA}_{\operatorname{Spf}(A_{\text{cris}}(R))/\operatorname{Spf}(A_{\text{cris}}),\,\log }^{i}$
are locally free and, in particular, quasi-coherent, they are acyclic for
![]() $\unicode[STIX]{x1D6E4}_{\acute{\text{e}}\text{t}}(\operatorname{Spf}(A_{\text{cris}}(R)),-)$
(see [Reference Fujiwara and KatoFK18, I.1.1.23(2)]), so we have
$\unicode[STIX]{x1D6E4}_{\acute{\text{e}}\text{t}}(\operatorname{Spf}(A_{\text{cris}}(R)),-)$
(see [Reference Fujiwara and KatoFK18, I.1.1.23(2)]), so we have
It remains to observe that the latter complex is identified with
![]() $\unicode[STIX]{x1D6FA}_{A_{\text{cris}}(R)/A_{\text{cris}},\,\log }^{\bullet }$
.◻
$\unicode[STIX]{x1D6FA}_{A_{\text{cris}}(R)/A_{\text{cris}},\,\log }^{\bullet }$
.◻
Having expressed the presheaf versions of both sides of (5.4.1) in the desired forms in Corollary 5.7 and Proposition 5.13, we now seek to exhibit an isomorphism between them in Proposition 5.16.
5.14 The element
 $\log ([\unicode[STIX]{x1D716}])$
$\log ([\unicode[STIX]{x1D716}])$
Fix an
![]() $m\geqslant p^{2}$
. By the proof of [Reference Bhatt, Morrow and ScholzeBMS18, 12.2],Footnote
8
each
$m\geqslant p^{2}$
. By the proof of [Reference Bhatt, Morrow and ScholzeBMS18, 12.2],Footnote
8
each
![]() $\unicode[STIX]{x1D707}^{n}/(n+1)!\in A_{\text{cris}}^{(m)}[\frac{1}{p}]$
with
$\unicode[STIX]{x1D707}^{n}/(n+1)!\in A_{\text{cris}}^{(m)}[\frac{1}{p}]$
with
![]() $n\geqslant 1$
lies in
$n\geqslant 1$
lies in
![]() $A_{\text{cris}}^{(m)}$
, is
$A_{\text{cris}}^{(m)}$
, is
![]() $p$
-adically topologically nilpotent there, and
$p$
-adically topologically nilpotent there, and
![]() $p$
-adically tends to
$p$
-adically tends to
![]() $0$
as
$0$
as
![]() $n\rightarrow \infty$
. Consequently, recalling that
$n\rightarrow \infty$
. Consequently, recalling that
![]() $\unicode[STIX]{x1D707}=[\unicode[STIX]{x1D716}]-1$
, we may define
$\unicode[STIX]{x1D707}=[\unicode[STIX]{x1D716}]-1$
, we may define
so that the Frobenius maps
![]() $\log ([\unicode[STIX]{x1D716}])$
to
$\log ([\unicode[STIX]{x1D716}])$
to
![]() $p\cdot \log ([\unicode[STIX]{x1D716}])$
. By [Reference Bhatt, Morrow and ScholzeBMS18, 12.2],Footnote
9
the elements
$p\cdot \log ([\unicode[STIX]{x1D716}])$
. By [Reference Bhatt, Morrow and ScholzeBMS18, 12.2],Footnote
9
the elements
![]() $\log ([\unicode[STIX]{x1D716}])$
and
$\log ([\unicode[STIX]{x1D716}])$
and
![]() $\unicode[STIX]{x1D707}$
are unit multiples of each other in
$\unicode[STIX]{x1D707}$
are unit multiples of each other in
![]() $A_{\text{cris}}^{(m)}$
, so
$A_{\text{cris}}^{(m)}$
, so
![]() $\frac{(\log ([\unicode[STIX]{x1D716}]))^{n}}{\unicode[STIX]{x1D707}\,\cdot \,n!}$
lies in
$\frac{(\log ([\unicode[STIX]{x1D716}]))^{n}}{\unicode[STIX]{x1D707}\,\cdot \,n!}$
lies in
![]() $A_{\text{cris}}^{(m)}$
, is topologically nilpotent if
$A_{\text{cris}}^{(m)}$
, is topologically nilpotent if
![]() $n>1$
, and
$n>1$
, and
![]() $p$
-adically tends to
$p$
-adically tends to
![]() $0$
in
$0$
in
![]() $A_{\text{cris}}^{(m)}$
as
$A_{\text{cris}}^{(m)}$
as
![]() $n\rightarrow \infty$
.
$n\rightarrow \infty$
.
The following lemma describes the
![]() $\unicode[STIX]{x1D6E5}$
-action on
$\unicode[STIX]{x1D6E5}$
-action on
![]() $A_{\text{cris}}^{(m)}(R)$
in terms of the derivations
$A_{\text{cris}}^{(m)}(R)$
in terms of the derivations
![]() $\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\log (X_{i})}$
induced on
$\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\log (X_{i})}$
induced on
![]() $A_{\text{cris}}^{(m)}(R)$
by base change from the derivations (5.10.1).
$A_{\text{cris}}^{(m)}(R)$
by base change from the derivations (5.10.1).
Lemma 5.15. For
![]() $m\geqslant p^{2}$
, a
$m\geqslant p^{2}$
, a
![]() $\unicode[STIX]{x1D6FF}_{i}\in \unicode[STIX]{x1D6E5}$
with
$\unicode[STIX]{x1D6FF}_{i}\in \unicode[STIX]{x1D6E5}$
with
![]() $i=1,\ldots ,d$
(see §3.2) acts on
$i=1,\ldots ,d$
(see §3.2) acts on
![]() $A_{\text{cris}}^{(m)}(R)$
as the series
$A_{\text{cris}}^{(m)}(R)$
as the series
In particular, for
![]() $m$
and
$m$
and
![]() $i$
as above, we have the following description of the ‘
$i$
as above, we have the following description of the ‘
![]() $q$
-derivative’
$q$
-derivative’
![]() $\frac{\unicode[STIX]{x1D6FF}_{i}-1}{\unicode[STIX]{x1D707}}$
:
$\frac{\unicode[STIX]{x1D6FF}_{i}-1}{\unicode[STIX]{x1D707}}$
:
where the parenthetical factor defines an
![]() $A_{\text{cris}}^{(m)}$
-linear additive automorphism of
$A_{\text{cris}}^{(m)}$
-linear additive automorphism of
![]() $A_{\text{cris}}^{(m)}(R)$
.
$A_{\text{cris}}^{(m)}(R)$
.
Proof. The argument is similar to that of [Reference Bhatt, Morrow and ScholzeBMS18, 12.4]. First,
![]() $\frac{(\log ([\unicode[STIX]{x1D716}]))^{n}}{n!}$
tends to
$\frac{(\log ([\unicode[STIX]{x1D716}]))^{n}}{n!}$
tends to
![]() $0$
in the
$0$
in the
![]() $p$
-adic topology of
$p$
-adic topology of
![]() $A_{\text{cris}}^{(m)}$
(see §5.14), so the series (5.15.1) does define an
$A_{\text{cris}}^{(m)}$
(see §5.14), so the series (5.15.1) does define an
![]() $A_{\text{cris}}^{(m)}$
-linear additive endomorphism of
$A_{\text{cris}}^{(m)}$
-linear additive endomorphism of
![]() $A_{\text{cris}}^{(m)}(R)$
. This endomorphism is also multiplicative because, by the Leibniz rule,
$A_{\text{cris}}^{(m)}(R)$
. This endomorphism is also multiplicative because, by the Leibniz rule,
Therefore, in the case
![]() $R=R^{\Box }$
, the desired equality
$R=R^{\Box }$
, the desired equality
follows by noting that both of its sides agree on every
![]() $X_{j}$
: indeed, due to the formulas (5.10.2), they send
$X_{j}$
: indeed, due to the formulas (5.10.2), they send
![]() $X_{i}$
to
$X_{i}$
to
![]() $[\unicode[STIX]{x1D716}]X_{i}$
, fix each
$[\unicode[STIX]{x1D716}]X_{i}$
, fix each
![]() $X_{j}$
with
$X_{j}$
with
![]() $0<j\neq i$
, and send
$0<j\neq i$
, and send
![]() $X_{0}$
to
$X_{0}$
to
![]() $[\unicode[STIX]{x1D716}^{-1}]X_{0}$
if
$[\unicode[STIX]{x1D716}^{-1}]X_{0}$
if
![]() $i\leqslant r$
and to
$i\leqslant r$
and to
![]() $X_{0}$
if
$X_{0}$
if
![]() $r<i$
.
$r<i$
.
In the general case, since
![]() $\unicode[STIX]{x1D707}$
, and hence also
$\unicode[STIX]{x1D707}$
, and hence also
![]() $\unicode[STIX]{x1D709}$
, divides each
$\unicode[STIX]{x1D709}$
, divides each
![]() $\frac{(\log ([\unicode[STIX]{x1D716}]))^{n}}{n!}$
with
$\frac{(\log ([\unicode[STIX]{x1D716}]))^{n}}{n!}$
with
![]() $n\geqslant 1$
(see §5.14), both sides of the equality (5.15.3) induce the trivial action modulo
$n\geqslant 1$
(see §5.14), both sides of the equality (5.15.3) induce the trivial action modulo
![]() $(p,\unicode[STIX]{x1D709})$
(see §3.27). Therefore, due to the formal étaleness of
$(p,\unicode[STIX]{x1D709})$
(see §3.27). Therefore, due to the formal étaleness of
![]() $A_{\text{cris}}^{(m)}(R)$
over
$A_{\text{cris}}^{(m)}(R)$
over
![]() $A_{\text{cris}}^{(m)}(R^{\Box })$
and the settled
$A_{\text{cris}}^{(m)}(R^{\Box })$
and the settled
![]() $R=R^{\Box }$
case, the sides agree.
$R=R^{\Box }$
case, the sides agree.
Since
![]() $A_{\text{cris}}^{(m)}(R)$
is
$A_{\text{cris}}^{(m)}(R)$
is
![]() $\unicode[STIX]{x1D707}$
-torsion free (see (3.27.2)) and
$\unicode[STIX]{x1D707}$
-torsion free (see (3.27.2)) and
![]() $\unicode[STIX]{x1D707}\,\mid \,\frac{(\log ([\unicode[STIX]{x1D716}]))^{n}}{n!}$
in
$\unicode[STIX]{x1D707}\,\mid \,\frac{(\log ([\unicode[STIX]{x1D716}]))^{n}}{n!}$
in
![]() $A_{\text{cris}}^{(m)}$
, the equality (5.15.2) follows from (5.15.3). Since
$A_{\text{cris}}^{(m)}$
, the equality (5.15.2) follows from (5.15.3). Since
![]() $\frac{(\log ([\unicode[STIX]{x1D716}]))^{n}}{\unicode[STIX]{x1D707}\,\cdot \,n!}$
is a unit for
$\frac{(\log ([\unicode[STIX]{x1D716}]))^{n}}{\unicode[STIX]{x1D707}\,\cdot \,n!}$
is a unit for
![]() $n=1$
, is topologically nilpotent for
$n=1$
, is topologically nilpotent for
![]() $n>1$
(see §5.14), and
$n>1$
(see §5.14), and
![]() $p$
-adically tends to
$p$
-adically tends to
![]() $0$
as
$0$
as
![]() $n\rightarrow \infty$
, the parenthetical factor of (5.15.2) is indeed an automorphism.◻
$n\rightarrow \infty$
, the parenthetical factor of (5.15.2) is indeed an automorphism.◻
We are ready to settle the (presheaf version of the) local case of Theorem 5.4.
Proposition 5.16. In the local setting of §5.5, for
![]() $m\geqslant p^{2}$
and
$m\geqslant p^{2}$
and
![]() $i=1,\ldots ,d$
, the morphism
$i=1,\ldots ,d$
, the morphism
of complexes in degrees
![]() $0$
and
$0$
and
![]() $1$
is Frobenius equivariant, granted that the usual Frobenius action on the copy of
$1$
is Frobenius equivariant, granted that the usual Frobenius action on the copy of
![]() $A_{\text{cris}}^{(m)}(R)$
in degree
$A_{\text{cris}}^{(m)}(R)$
in degree
![]() $1$
of the source is multiplied by
$1$
of the source is multiplied by
![]() $p$
(compare with the description after (5.10.3)). For
$p$
(compare with the description after (5.10.3)). For
![]() $m\geqslant p^{2}$
, these morphisms induce a Frobenius-equivariant quasi-isomorphism
$m\geqslant p^{2}$
, these morphisms induce a Frobenius-equivariant quasi-isomorphism
which, as
![]() $m$
varies, induces the Frobenius-equivariant identification (a local version of (5.4.1)):
$m$
varies, induces the Frobenius-equivariant identification (a local version of (5.4.1)):
Proof. The Frobenius-equivariance of (5.16.1) follows from the equations
(see §§5.10 and 5.14). Since
![]() $\unicode[STIX]{x1D6E5}$
acts trivially on
$\unicode[STIX]{x1D6E5}$
acts trivially on
![]() $A_{\text{cris}}^{(m)}(R)/\unicode[STIX]{x1D707}$
(see §3.27), the subcomplex
$A_{\text{cris}}^{(m)}(R)/\unicode[STIX]{x1D707}$
(see §3.27), the subcomplex
is obtained by letting its
![]() $j$
th term be the submodule of the
$j$
th term be the submodule of the
![]() $j$
th term of
$j$
th term of
composed of the
![]() $\unicode[STIX]{x1D707}^{j}$
-multiples (see (1.7.2) and (1.7.3)); since
$\unicode[STIX]{x1D707}^{j}$
-multiples (see (1.7.2) and (1.7.3)); since
![]() $\unicode[STIX]{x1D707}\,\mid \,\unicode[STIX]{x1D711}(\unicode[STIX]{x1D707})$
, this subcomplex is Frobenius-stable. Thus, Lemma 5.15 implies that the morphisms (5.16.1) induce an isomorphism
$\unicode[STIX]{x1D707}\,\mid \,\unicode[STIX]{x1D711}(\unicode[STIX]{x1D707})$
, this subcomplex is Frobenius-stable. Thus, Lemma 5.15 implies that the morphisms (5.16.1) induce an isomorphism
Proposition 3.32 (with Lemma 3.7) implies that the natural inclusion of the target of (5.16.4) into the target of (5.16.2) is a quasi-isomorphism, and (5.16.2) follows. The maps (5.16.2) are compatible as
![]() $m$
varies, so, by passing to their limit over
$m$
varies, so, by passing to their limit over
![]() $m$
, forming the termwise
$m$
, forming the termwise
![]() $p$
-adic completions, and applying Corollary 5.7 and Proposition 5.13, we obtain the desired identification (5.16.3).◻
$p$
-adic completions, and applying Corollary 5.7 and Proposition 5.13, we obtain the desired identification (5.16.3).◻
Proposition 5.16 concludes the ‘single coordinate patch’ part of the proof of Theorem 5.4, so we turn to the ‘all possible coordinates’ technique that will globalize the argument. For this, the key steps are, for a small enough affine
![]() $\mathfrak{X}$
, to build in §5.21 a functorial in
$\mathfrak{X}$
, to build in §5.21 a functorial in
![]() $\mathfrak{X}$
explicit complex that computes the presheaf version of the left-hand side of (5.4.1), to then build in §5.32 such a complex for the right-hand side of (5.4.1), and, finally, to build in §5.38 and Proposition 5.39 a natural quasi-isomorphism between these complexes. Each of these steps will use our work in the setting of §5.5 discussed so far.
$\mathfrak{X}$
explicit complex that computes the presheaf version of the left-hand side of (5.4.1), to then build in §5.32 such a complex for the right-hand side of (5.4.1), and, finally, to build in §5.38 and Proposition 5.39 a natural quasi-isomorphism between these complexes. Each of these steps will use our work in the setting of §5.5 discussed so far.
5.17 More general coordinates
Continuing to work locally, we now assume until the final part of the proof of Theorem 5.4 given in §5.40 that
![]() $\mathfrak{X}=\operatorname{Spf}(R)$
is affine and nonempty, that every two irreducible components of
$\mathfrak{X}=\operatorname{Spf}(R)$
is affine and nonempty, that every two irreducible components of
![]() $\operatorname{Spec}(R\otimes _{{\mathcal{O}}_{C}}k)$
meet (so that
$\operatorname{Spec}(R\otimes _{{\mathcal{O}}_{C}}k)$
meet (so that
![]() $\mathfrak{X}$
is connected), and that we have:
$\mathfrak{X}$
is connected), and that we have:
∙ a finite set
 $\unicode[STIX]{x1D6F4}$
that indexes the coordinates of the formal
$\unicode[STIX]{x1D6F4}$
that indexes the coordinates of the formal
 ${\mathcal{O}}_{C}$
-torus
${\mathcal{O}}_{C}$
-torus  $$\begin{eqnarray}R_{\unicode[STIX]{x1D6F4}}^{\Box }:={\mathcal{O}}_{C}\{t_{\unicode[STIX]{x1D70E}}^{\pm 1}\,|\,\unicode[STIX]{x1D70E}\in \unicode[STIX]{x1D6F4}\};\end{eqnarray}$$
$$\begin{eqnarray}R_{\unicode[STIX]{x1D6F4}}^{\Box }:={\mathcal{O}}_{C}\{t_{\unicode[STIX]{x1D70E}}^{\pm 1}\,|\,\unicode[STIX]{x1D70E}\in \unicode[STIX]{x1D6F4}\};\end{eqnarray}$$
∙ a nonempty finite set
 $\unicode[STIX]{x1D6EC}$
and, for each
$\unicode[STIX]{x1D6EC}$
and, for each
 $\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}$
, an
$\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}$
, an
 ${\mathcal{O}}_{C}$
-algebra
${\mathcal{O}}_{C}$
-algebra  $$\begin{eqnarray}\quad R_{\unicode[STIX]{x1D706}}^{\Box }:={\mathcal{O}}_{C}\{t_{\unicode[STIX]{x1D706},\,0},\ldots ,t_{\unicode[STIX]{x1D706},\,r_{\unicode[STIX]{x1D706}}},t_{\unicode[STIX]{x1D706},\,r_{\unicode[STIX]{x1D706}}+1}^{\pm 1},\ldots ,t_{\unicode[STIX]{x1D706},\,d}^{\pm 1}\}/(t_{\unicode[STIX]{x1D706},\,0}\cdots t_{\unicode[STIX]{x1D706},\,r_{\unicode[STIX]{x1D706}}}-p^{q_{\unicode[STIX]{x1D706}}})\quad \text{with}\quad q_{\unicode[STIX]{x1D706}}\in \mathbb{Q}_{{>}0};\end{eqnarray}$$
$$\begin{eqnarray}\quad R_{\unicode[STIX]{x1D706}}^{\Box }:={\mathcal{O}}_{C}\{t_{\unicode[STIX]{x1D706},\,0},\ldots ,t_{\unicode[STIX]{x1D706},\,r_{\unicode[STIX]{x1D706}}},t_{\unicode[STIX]{x1D706},\,r_{\unicode[STIX]{x1D706}}+1}^{\pm 1},\ldots ,t_{\unicode[STIX]{x1D706},\,d}^{\pm 1}\}/(t_{\unicode[STIX]{x1D706},\,0}\cdots t_{\unicode[STIX]{x1D706},\,r_{\unicode[STIX]{x1D706}}}-p^{q_{\unicode[STIX]{x1D706}}})\quad \text{with}\quad q_{\unicode[STIX]{x1D706}}\in \mathbb{Q}_{{>}0};\end{eqnarray}$$
∙ a closed immersion
(5.17.1)where the products are formed over $$\begin{eqnarray}\textstyle \mathfrak{X}=\operatorname{Spf}(R)\rightarrow \operatorname{Spf}(R_{\unicode[STIX]{x1D6F4}}^{\Box })\times \mathop{\prod }_{\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}}\operatorname{Spf}(R_{\unicode[STIX]{x1D706}}^{\Box }),\end{eqnarray}$$
$$\begin{eqnarray}\textstyle \mathfrak{X}=\operatorname{Spf}(R)\rightarrow \operatorname{Spf}(R_{\unicode[STIX]{x1D6F4}}^{\Box })\times \mathop{\prod }_{\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}}\operatorname{Spf}(R_{\unicode[STIX]{x1D706}}^{\Box }),\end{eqnarray}$$
 $\operatorname{Spf}({\mathcal{O}}_{C})$
, subject to the requirements that already (5.17.2)and, for each
$\operatorname{Spf}({\mathcal{O}}_{C})$
, subject to the requirements that already (5.17.2)and, for each $$\begin{eqnarray}\mathfrak{X}=\operatorname{Spf}(R)\rightarrow \operatorname{Spf}(R_{\unicode[STIX]{x1D6F4}}^{\Box })\quad \text{is a closed immersion}\end{eqnarray}$$
$$\begin{eqnarray}\mathfrak{X}=\operatorname{Spf}(R)\rightarrow \operatorname{Spf}(R_{\unicode[STIX]{x1D6F4}}^{\Box })\quad \text{is a closed immersion}\end{eqnarray}$$
 $\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}$
, the induced map(5.17.3)
$\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}$
, the induced map(5.17.3)
By (5.17.3), for each
![]() $\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}$
, the irreducible components of
$\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}$
, the irreducible components of
![]() $\operatorname{Spec}(R\otimes _{{\mathcal{O}}_{C}}k)$
are a priori identified with the connected components of
$\operatorname{Spec}(R\otimes _{{\mathcal{O}}_{C}}k)$
are a priori identified with the connected components of
![]() $\bigsqcup _{i}\operatorname{Spec}((R\otimes _{{\mathcal{O}}_{C}}k)/(t_{\unicode[STIX]{x1D706},\,i}))$
. Thus, our assumption on
$\bigsqcup _{i}\operatorname{Spec}((R\otimes _{{\mathcal{O}}_{C}}k)/(t_{\unicode[STIX]{x1D706},\,i}))$
. Thus, our assumption on
![]() $\operatorname{Spec}(R\otimes _{{\mathcal{O}}_{C}}k)$
implies that each irreducible component of
$\operatorname{Spec}(R\otimes _{{\mathcal{O}}_{C}}k)$
implies that each irreducible component of
![]() $\operatorname{Spec}(R\otimes _{{\mathcal{O}}_{C}}k)$
is cut out by a unique
$\operatorname{Spec}(R\otimes _{{\mathcal{O}}_{C}}k)$
is cut out by a unique
![]() $t_{\unicode[STIX]{x1D706},\,i}$
with
$t_{\unicode[STIX]{x1D706},\,i}$
with
![]() $0\leqslant i\leqslant r_{\unicode[STIX]{x1D706}}$
.
$0\leqslant i\leqslant r_{\unicode[STIX]{x1D706}}$
.
By §1.5, if
![]() $R\otimes _{{\mathcal{O}}_{C}}k$
is not
$R\otimes _{{\mathcal{O}}_{C}}k$
is not
![]() $k$
-smooth, then
$k$
-smooth, then
![]() $R$
determines
$R$
determines
![]() $q_{\unicode[STIX]{x1D706}}$
, which therefore does not depend on
$q_{\unicode[STIX]{x1D706}}$
, which therefore does not depend on
![]() $\unicode[STIX]{x1D706}$
. On the other hand, if
$\unicode[STIX]{x1D706}$
. On the other hand, if
![]() $R\otimes _{{\mathcal{O}}_{C}}k$
is
$R\otimes _{{\mathcal{O}}_{C}}k$
is
![]() $k$
-smooth, then
$k$
-smooth, then
![]() $q_{\unicode[STIX]{x1D706}}$
may depend on
$q_{\unicode[STIX]{x1D706}}$
may depend on
![]() $\unicode[STIX]{x1D706}$
. This, together with the possibility that
$\unicode[STIX]{x1D706}$
. This, together with the possibility that
![]() $r_{\unicode[STIX]{x1D706}}>0$
, complicates matters in the ‘simpler’ smooth case but is crucial to allow in order for the eventual ‘all possible coordinates’ constructions to be functorial in
$r_{\unicode[STIX]{x1D706}}>0$
, complicates matters in the ‘simpler’ smooth case but is crucial to allow in order for the eventual ‘all possible coordinates’ constructions to be functorial in
![]() $R$
.
$R$
.
For any
![]() $\mathfrak{X}$
, the data above exist on a basis for
$\mathfrak{X}$
, the data above exist on a basis for
![]() $\mathfrak{X}_{\acute{\text{e}}\text{t}}$
: indeed, a coordinate map (5.17.3) exists étale locally on
$\mathfrak{X}_{\acute{\text{e}}\text{t}}$
: indeed, a coordinate map (5.17.3) exists étale locally on
![]() $\mathfrak{X}$
(see §1.5), and then
$\mathfrak{X}$
(see §1.5), and then
![]() $R$
is the
$R$
is the
![]() $p$
-adic completion of a finite-type
$p$
-adic completion of a finite-type
![]() ${\mathcal{O}}_{C}$
-algebra, so the Zariski topology of
${\mathcal{O}}_{C}$
-algebra, so the Zariski topology of
![]() $\operatorname{Spf}(R)$
has a basis whose elements embed into some (variable)
$\operatorname{Spf}(R)$
has a basis whose elements embed into some (variable)
![]() $\widehat{\mathbb{G}}_{m}^{\unicode[STIX]{x1D6F4}}$
.
$\widehat{\mathbb{G}}_{m}^{\unicode[STIX]{x1D6F4}}$
.
Each (5.17.3) is an instance of the local setting of §5.5, so the discussion between §5.5 and the present section applies to it. Another instance is the identity map
![]() $\operatorname{Spf}(R_{\unicode[STIX]{x1D6F4}}^{\Box })\xrightarrow[{}]{=}\operatorname{Spf}(R_{\unicode[STIX]{x1D6F4}}^{\Box })$
(with
$\operatorname{Spf}(R_{\unicode[STIX]{x1D6F4}}^{\Box })\xrightarrow[{}]{=}\operatorname{Spf}(R_{\unicode[STIX]{x1D6F4}}^{\Box })$
(with
![]() $r=0$
and
$r=0$
and
![]() $d=\#\unicode[STIX]{x1D6F4}$
), so the indicated discussion also applies to the ring
$d=\#\unicode[STIX]{x1D6F4}$
), so the indicated discussion also applies to the ring
![]() $R_{\unicode[STIX]{x1D6F4}}^{\Box }$
in place of
$R_{\unicode[STIX]{x1D6F4}}^{\Box }$
in place of
![]() $R^{\Box }$
.
$R^{\Box }$
.
Our first aim in this setup is to reexpress the (presheaf version of the) left-hand side of (5.4.1) in §5.21.
5.18 The perfectoid
 $R_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC},\,\infty }$
$R_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC},\,\infty }$
For each
![]() $\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}$
, we set
$\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}$
, we set
and let
be the affinoid perfectoid pro-(finite étale)
![]() $\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D706}}$
-covers defined as in §3.2 using the coordinate map
$\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D706}}$
-covers defined as in §3.2 using the coordinate map ![]() . Similarly, we set
. Similarly, we set
and let
be the affinoid perfectoid pro-(finite étale)
![]() $\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D6F4}}$
-cover defined as in §3.2 using the coordinate map
$\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D6F4}}$
-cover defined as in §3.2 using the coordinate map
![]() $\operatorname{Spf}(R_{\unicode[STIX]{x1D6F4}}^{\Box })\xrightarrow[{}]{=}\operatorname{Spf}(R_{\unicode[STIX]{x1D6F4}}^{\Box })$
, so that, explicitly,
$\operatorname{Spf}(R_{\unicode[STIX]{x1D6F4}}^{\Box })\xrightarrow[{}]{=}\operatorname{Spf}(R_{\unicode[STIX]{x1D6F4}}^{\Box })$
, so that, explicitly,
By forming products over
![]() $\operatorname{Spa}({\mathcal{O}}_{C}[\frac{1}{p}],{\mathcal{O}}_{C})$
and setting
$\operatorname{Spa}({\mathcal{O}}_{C}[\frac{1}{p}],{\mathcal{O}}_{C})$
and setting
we obtain the affinoid perfectoid pro-(finite étale)
![]() $\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}$
-cover
$\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}$
-cover
which we abbreviate as
Its base change along the generic fiber of (5.17.1) is the pro-(finite étale)
![]() $\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}$
-cover
$\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}$
-cover
which contains each
![]() $\operatorname{Spa}(R_{\unicode[STIX]{x1D706},\,\infty }[\frac{1}{p}],R_{\unicode[STIX]{x1D706},\,\infty })\rightarrow \operatorname{Spa}(R[\frac{1}{p}],R)$
as a subcover. Thus, by the almost purity theorem [Reference ScholzeSch12, 7.9(iii)], the
$\operatorname{Spa}(R_{\unicode[STIX]{x1D706},\,\infty }[\frac{1}{p}],R_{\unicode[STIX]{x1D706},\,\infty })\rightarrow \operatorname{Spa}(R[\frac{1}{p}],R)$
as a subcover. Thus, by the almost purity theorem [Reference ScholzeSch12, 7.9(iii)], the
![]() ${\mathcal{O}}_{C}$
-algebra
${\mathcal{O}}_{C}$
-algebra
![]() $R_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC},\,\infty }$
defined by (5.18.1) is perfectoid (the notions of ‘perfectoid’ used here and in [Reference ScholzeSch12] agree by [Reference Bhatt, Morrow and ScholzeBMS18, 3.20]).
$R_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC},\,\infty }$
defined by (5.18.1) is perfectoid (the notions of ‘perfectoid’ used here and in [Reference ScholzeSch12] agree by [Reference Bhatt, Morrow and ScholzeBMS18, 3.20]).
The topological generators for
![]() $\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D6F4}}$
and
$\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D6F4}}$
and
![]() $\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D706}}$
fixed in §3.2 are
$\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D706}}$
fixed in §3.2 are
and
Jointly, the
![]() $\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D70E}}$
and
$\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D70E}}$
and
![]() $\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D706},\,i}$
topologically freely generate
$\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D706},\,i}$
topologically freely generate
![]() $\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}$
.
$\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}$
.
5.19 The rings
 $\mathbb{A}_{\text{inf}}(R_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC},\,\infty })$
and
$\mathbb{A}_{\text{inf}}(R_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC},\,\infty })$
and
 $\mathbb{A}_{\text{cris}}^{(m)}(R_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC},\,\infty })$
$\mathbb{A}_{\text{cris}}^{(m)}(R_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC},\,\infty })$
Similarly to §3.14, we set
By Lemma 3.13, for
![]() $n,n^{\prime }>0$
, the sequence
$n,n^{\prime }>0$
, the sequence
![]() $(p^{n},\unicode[STIX]{x1D707}^{n^{\prime }})$
is
$(p^{n},\unicode[STIX]{x1D707}^{n^{\prime }})$
is
![]() $\mathbb{A}_{\text{inf}}(R_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC},\,\infty })$
-regular,
$\mathbb{A}_{\text{inf}}(R_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC},\,\infty })$
-regular,
is
![]() $A_{\text{inf}}/(p^{n},\unicode[STIX]{x1D707}^{n^{\prime }})$
-flat, and
$A_{\text{inf}}/(p^{n},\unicode[STIX]{x1D707}^{n^{\prime }})$
-flat, and
![]() $\mathbb{A}_{\text{inf}}(R_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC},\,\infty })/\unicode[STIX]{x1D707}$
is
$\mathbb{A}_{\text{inf}}(R_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC},\,\infty })/\unicode[STIX]{x1D707}$
is
![]() $p$
-adically complete. As in §3.14, we have the surjection
$p$
-adically complete. As in §3.14, we have the surjection
that intertwines the Witt vector Frobenius of
![]() $\mathbb{A}_{\text{inf}}(R_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC},\,\infty })$
with the absolute Frobenius of
$\mathbb{A}_{\text{inf}}(R_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC},\,\infty })$
with the absolute Frobenius of
![]() $R_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC},\,\infty }/p$
and whose kernel is generated by the regular element
$R_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC},\,\infty }/p$
and whose kernel is generated by the regular element
![]() $\unicode[STIX]{x1D709}$
. To fix further notation, we let
$\unicode[STIX]{x1D709}$
. To fix further notation, we let
be the isomorphisms (3.14.2) for
![]() $R_{\unicode[STIX]{x1D6F4}}^{\Box }$
and
$R_{\unicode[STIX]{x1D6F4}}^{\Box }$
and
![]() $R_{\unicode[STIX]{x1D706}}^{\Box }$
. Similarly to §3.27, for an
$R_{\unicode[STIX]{x1D706}}^{\Box }$
. Similarly to §3.27, for an
![]() $m\in \mathbb{Z}_{{\geqslant}1}$
, we set
$m\in \mathbb{Z}_{{\geqslant}1}$
, we set
where the completion is
![]() $(p,\unicode[STIX]{x1D707})$
-adic (equivalently,
$(p,\unicode[STIX]{x1D707})$
-adic (equivalently,
![]() $p$
-adic if
$p$
-adic if
![]() $m\geqslant p$
). Since
$m\geqslant p$
). Since
![]() $\mathbb{A}_{\text{inf}}(R_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC},\,\infty })$
is
$\mathbb{A}_{\text{inf}}(R_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC},\,\infty })$
is
![]() $(p,\unicode[STIX]{x1D707})$
-adically formally flat over
$(p,\unicode[STIX]{x1D707})$
-adically formally flat over
![]() $A_{\text{inf}}$
, the ring
$A_{\text{inf}}$
, the ring
![]() $\mathbb{A}_{\text{cris}}^{(m)}(R_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC},\,\infty })$
inherits
$\mathbb{A}_{\text{cris}}^{(m)}(R_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC},\,\infty })$
inherits
![]() $p$
-torsion freeness from
$p$
-torsion freeness from
![]() $A_{\text{cris}}^{(m)}$
. By also using the short exact sequences (3.26.3) and the vanishing (3.26.2), we see that
$A_{\text{cris}}^{(m)}$
. By also using the short exact sequences (3.26.3) and the vanishing (3.26.2), we see that
As in §3.27, the rings
![]() $\mathbb{A}_{\text{cris}}^{(m)}(R_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC},\,\infty })$
come equipped with
$\mathbb{A}_{\text{cris}}^{(m)}(R_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC},\,\infty })$
come equipped with
![]() $A_{\text{cris}}^{(m)}$
-semilinear Frobenius endomorphisms that are compatible as
$A_{\text{cris}}^{(m)}$
-semilinear Frobenius endomorphisms that are compatible as
![]() $m$
varies. The maps (3.26.1) and (5.19.1) give rise to the surjection
$m$
varies. The maps (3.26.1) and (5.19.1) give rise to the surjection
The actions of the profinite group
![]() $\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}$
on
$\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}$
on
![]() $\mathbb{A}_{\text{inf}}(R_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC},\,\infty })$
and
$\mathbb{A}_{\text{inf}}(R_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC},\,\infty })$
and
![]() $\mathbb{A}_{\text{cris}}^{(m)}(R_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC},\,\infty })$
are compatible, continuous, and Frobenius-equivariant.
$\mathbb{A}_{\text{cris}}^{(m)}(R_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC},\,\infty })$
are compatible, continuous, and Frobenius-equivariant.
The following consequence of Remark 3.35 will help us build a desired functorial complex in §5.21.
Proposition 5.20. In the local setting of §5.17, for every
![]() $m\geqslant p$
, the analogue for
$m\geqslant p$
, the analogue for
![]() $R_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC},\,\infty }$
of the edge map (3.15.1) induces the Frobenius-equivariant identification
$R_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC},\,\infty }$
of the edge map (3.15.1) induces the Frobenius-equivariant identification
In particular, we have the following Frobenius-equivariant identification in the derived category:
where the direct limit and the
![]() $p$
-adic completion of the complexes in the source are formed termwise.
$p$
-adic completion of the complexes in the source are formed termwise.
Proof. Proposition 5.6 gives the Frobenius-equivariant identification
Therefore, since the pro-(finite étale) affinoid perfectoid
![]() $\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}$
-cover
$\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}$
-cover
![]() $\operatorname{Spa}(R_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC},\,\infty }[\frac{1}{p}],R_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC},\,\infty })$
of
$\operatorname{Spa}(R_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC},\,\infty }[\frac{1}{p}],R_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC},\,\infty })$
of
![]() $\operatorname{Spa}(R[\frac{1}{p}],R)$
contains
$\operatorname{Spa}(R[\frac{1}{p}],R)$
contains
![]() $\operatorname{Spa}(R_{\unicode[STIX]{x1D706},\,\infty }[\frac{1}{p}],R_{\unicode[STIX]{x1D706},\,\infty })$
as a subcover (see §5.18), Remark 3.35 applies and (with Lemma 3.7) gives (5.20.1). The remaining assertion follows: each
$\operatorname{Spa}(R_{\unicode[STIX]{x1D706},\,\infty }[\frac{1}{p}],R_{\unicode[STIX]{x1D706},\,\infty })$
as a subcover (see §5.18), Remark 3.35 applies and (with Lemma 3.7) gives (5.20.1). The remaining assertion follows: each
![]() $\mathbb{A}_{\text{cris}}^{(m)}(R_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC},\,\infty })$
is
$\mathbb{A}_{\text{cris}}^{(m)}(R_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC},\,\infty })$
is
![]() $p$
-torsion free, so the termwise
$p$
-torsion free, so the termwise
![]() $p$
-adic completion of the source there agrees with the derived
$p$
-adic completion of the source there agrees with the derived
![]() $p$
-adic completion.◻
$p$
-adic completion.◻
5.21 A functorial complex that computes
 $R\unicode[STIX]{x1D6E4}(\mathfrak{X}_{\acute{\text{e}}\text{t}}^{\text{psh}},A\unicode[STIX]{x1D6FA}_{\mathfrak{X}}^{\text{psh}})\,\widehat{\otimes }_{A_{\text{inf}}}^{\mathbb{L}}\,A_{\text{cris}}$
$R\unicode[STIX]{x1D6E4}(\mathfrak{X}_{\acute{\text{e}}\text{t}}^{\text{psh}},A\unicode[STIX]{x1D6FA}_{\mathfrak{X}}^{\text{psh}})\,\widehat{\otimes }_{A_{\text{inf}}}^{\mathbb{L}}\,A_{\text{cris}}$
For a fixed
![]() $R$
, we form the filtered direct limit over the closed immersions (5.17.1) for varying
$R$
, we form the filtered direct limit over the closed immersions (5.17.1) for varying
![]() $\unicode[STIX]{x1D6F4}$
and
$\unicode[STIX]{x1D6F4}$
and
![]() $\unicode[STIX]{x1D6EC}$
to build the complex
$\unicode[STIX]{x1D6EC}$
to build the complex
where the direct limits and the
![]() $p$
-adic completion are termwise. By its construction, this complex comes equipped with an
$p$
-adic completion are termwise. By its construction, this complex comes equipped with an
![]() $A_{\text{cris}}$
-semilinear Frobenius endomorphism. The isomorphisms of Proposition 5.20 are compatible with enlarging
$A_{\text{cris}}$
-semilinear Frobenius endomorphism. The isomorphisms of Proposition 5.20 are compatible with enlarging
![]() $\unicode[STIX]{x1D6F4}$
and
$\unicode[STIX]{x1D6F4}$
and
![]() $\unicode[STIX]{x1D6EC}$
, so they show that in the derived category the complex (5.21.1) is canonically and Frobenius-equivariantly identified with
$\unicode[STIX]{x1D6EC}$
, so they show that in the derived category the complex (5.21.1) is canonically and Frobenius-equivariantly identified with
Moreover, if
![]() $R^{\prime }$
is a
$R^{\prime }$
is a
![]() $p$
-adically formally étale
$p$
-adically formally étale
![]() $R$
-algebra equipped with data as in §5.17 for some sets
$R$
-algebra equipped with data as in §5.17 for some sets
![]() $\unicode[STIX]{x1D6F4}^{\prime }$
and
$\unicode[STIX]{x1D6F4}^{\prime }$
and
![]() $\unicode[STIX]{x1D6EC}^{\prime }$
, then the term indexed by
$\unicode[STIX]{x1D6EC}^{\prime }$
, then the term indexed by
![]() $\unicode[STIX]{x1D6F4}$
,
$\unicode[STIX]{x1D6F4}$
,
![]() $\unicode[STIX]{x1D6EC}$
(and by the closed immersion (5.17.1)) of the direct limit (5.21.1) maps to the term indexed by
$\unicode[STIX]{x1D6EC}$
(and by the closed immersion (5.17.1)) of the direct limit (5.21.1) maps to the term indexed by
![]() $\unicode[STIX]{x1D6F4}\cup \unicode[STIX]{x1D6F4}^{\prime }$
,
$\unicode[STIX]{x1D6F4}\cup \unicode[STIX]{x1D6F4}^{\prime }$
,
![]() $\unicode[STIX]{x1D6EC}\cup \unicode[STIX]{x1D6EC}^{\prime }$
(and by a closed immersion of
$\unicode[STIX]{x1D6EC}\cup \unicode[STIX]{x1D6EC}^{\prime }$
(and by a closed immersion of
![]() $\operatorname{Spf}(R^{\prime })$
) of the analogous direct limit for
$\operatorname{Spf}(R^{\prime })$
) of the analogous direct limit for
![]() $R^{\prime }$
, compatibly with the transition maps in (5.21.1) and with the Frobenius. Thus, the complex (5.21.1) equipped with its Frobenius is functorial in
$R^{\prime }$
, compatibly with the transition maps in (5.21.1) and with the Frobenius. Thus, the complex (5.21.1) equipped with its Frobenius is functorial in
![]() $R$
, and so is its identification with
$R$
, and so is its identification with
![]() $R\unicode[STIX]{x1D6E4}(\mathfrak{X}_{\acute{\text{e}}\text{t}}^{\text{psh}},A\unicode[STIX]{x1D6FA}_{\mathfrak{X}}^{\text{psh}})\,\widehat{\otimes }_{A_{\text{inf}}}^{\mathbb{L}}\,A_{\text{cris}}$
.
$R\unicode[STIX]{x1D6E4}(\mathfrak{X}_{\acute{\text{e}}\text{t}}^{\text{psh}},A\unicode[STIX]{x1D6FA}_{\mathfrak{X}}^{\text{psh}})\,\widehat{\otimes }_{A_{\text{inf}}}^{\mathbb{L}}\,A_{\text{cris}}$
.
Our next aim is to similarly reexpress the (presheaf version of the) right-hand side of (5.4.1) in §5.32.
5.22 The completed log PD envelope
 $D_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}$
$D_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}$
By §5.9, the maps
![]() $\unicode[STIX]{x1D703}:A(R_{\unicode[STIX]{x1D706}}^{\Box }){\twoheadrightarrow}R_{\unicode[STIX]{x1D706}}^{\Box }$
of (3.14.3) are compatible with log structures. Thus, they give rise to a Frobenius-equivariant closed immersion
$\unicode[STIX]{x1D703}:A(R_{\unicode[STIX]{x1D706}}^{\Box }){\twoheadrightarrow}R_{\unicode[STIX]{x1D706}}^{\Box }$
of (3.14.3) are compatible with log structures. Thus, they give rise to a Frobenius-equivariant closed immersion
of
![]() $(p,\unicode[STIX]{x1D707})$
-adic formal log schemes, where the products are over the
$(p,\unicode[STIX]{x1D707})$
-adic formal log schemes, where the products are over the
![]() $(p,\unicode[STIX]{x1D707})$
-adic formal log scheme
$(p,\unicode[STIX]{x1D707})$
-adic formal log scheme
![]() $\operatorname{Spf}(A_{\text{inf}})$
. By [Reference KatoKat89, 4.1, 4.4], for
$\operatorname{Spf}(A_{\text{inf}})$
. By [Reference KatoKat89, 4.1, 4.4], for
![]() $n,n^{\prime }>0$
, the quasi-coherent log structure of
$n,n^{\prime }>0$
, the quasi-coherent log structure of
and the log scheme map
are integral.
For
![]() $n,n^{\prime }>0$
, by [Reference BeilinsonBei13b, 1.3, Theorem], the
$n,n^{\prime }>0$
, by [Reference BeilinsonBei13b, 1.3, Theorem], the
![]() $A_{\text{inf}}/(p^{n},\unicode[STIX]{x1D707}^{n^{\prime }})$
-base change of the closed immersion (5.22.1) has a log PD envelope
$A_{\text{inf}}/(p^{n},\unicode[STIX]{x1D707}^{n^{\prime }})$
-base change of the closed immersion (5.22.1) has a log PD envelope
which, in particular, is a nil thickening of
![]() $\operatorname{Spec}(R/p)$
, so is affine as indicated (see [SP, 01ZT]). In fact,
$\operatorname{Spec}(R/p)$
, so is affine as indicated (see [SP, 01ZT]). In fact,
![]() $D_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC},\,n,\,n^{\prime }}$
is supplied already by [Reference KatoKat89, 5.4] because the closed immersion (5.22.1) is the base change of a similar closed immersion of fine formal log schemes along a ‘change of log structure’ self-map of
$D_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC},\,n,\,n^{\prime }}$
is supplied already by [Reference KatoKat89, 5.4] because the closed immersion (5.22.1) is the base change of a similar closed immersion of fine formal log schemes along a ‘change of log structure’ self-map of
![]() $A_{\text{inf}}$
(see §5.9).Footnote
10
$A_{\text{inf}}$
(see §5.9).Footnote
10
If
![]() $n^{\prime }$
is large enough relative to
$n^{\prime }$
is large enough relative to
![]() $n$
, so that
$n$
, so that
![]() $\unicode[STIX]{x1D707}^{n^{\prime }}\in p^{n}A_{\text{cris}}$
, then, by §§5.1–5.2,
$\unicode[STIX]{x1D707}^{n^{\prime }}\in p^{n}A_{\text{cris}}$
, then, by §§5.1–5.2,
![]() $\operatorname{Spec}(A_{\text{cris}}/p^{n})$
is identified with the log PD envelope of the exact log closed immersion
$\operatorname{Spec}(A_{\text{cris}}/p^{n})$
is identified with the log PD envelope of the exact log closed immersion
Thus, for such
![]() $n$
,
$n$
,
![]() $n^{\prime }$
, the envelope
$n^{\prime }$
, the envelope
![]() $\operatorname{Spec}(D_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC},\,n,\,n^{\prime }})$
comes equipped with a canonical log PD morphism to
$\operatorname{Spec}(D_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC},\,n,\,n^{\prime }})$
comes equipped with a canonical log PD morphism to
![]() $\operatorname{Spec}(A_{\text{cris}}/p^{n})$
that identifies it with the log PD envelope of
$\operatorname{Spec}(A_{\text{cris}}/p^{n})$
that identifies it with the log PD envelope of
Thus, letting
![]() $D_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC},\,n}$
be this log PD envelope, that is, the common
$D_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC},\,n}$
be this log PD envelope, that is, the common
![]() $D_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC},\,n,\,n^{\prime }}$
for large
$D_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC},\,n,\,n^{\prime }}$
for large
![]() $n^{\prime }$
, we have
$n^{\prime }$
, we have
![]() $D_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC},\,n}/p^{n-1}\cong D_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC},\,n-1}$
for
$D_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC},\,n}/p^{n-1}\cong D_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC},\,n-1}$
for
![]() $n>1$
and obtain a
$n>1$
and obtain a
![]() $p$
-adic formal log
$p$
-adic formal log
![]() $\operatorname{Spf}(A_{\text{cris}})$
-scheme
$\operatorname{Spf}(A_{\text{cris}})$
-scheme
![]() $\operatorname{Spf}(D_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}})$
that fits into a factorization
$\operatorname{Spf}(D_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}})$
that fits into a factorization
where the products are formed over the
![]() $p$
-adic formal log scheme
$p$
-adic formal log scheme
![]() $\operatorname{Spf}(A_{\text{cris}})$
and we have
$\operatorname{Spf}(A_{\text{cris}})$
and we have
By functoriality,
![]() $\operatorname{Spf}(D_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}})$
comes equipped with an
$\operatorname{Spf}(D_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}})$
comes equipped with an
![]() $A_{\text{cris}}$
-semilinear Frobenius. In addition, since, for each
$A_{\text{cris}}$
-semilinear Frobenius. In addition, since, for each
![]() $n>0$
, the ideal defining the exact closed immersion
$n>0$
, the ideal defining the exact closed immersion
![]() $\operatorname{Spec}(R/p){\hookrightarrow}\operatorname{Spec}(R/p^{n})$
inherits divided powers from
$\operatorname{Spec}(R/p){\hookrightarrow}\operatorname{Spec}(R/p^{n})$
inherits divided powers from
![]() $\mathbb{Z}/p^{n}$
, the universal property of
$\mathbb{Z}/p^{n}$
, the universal property of
![]() $D_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}$
supplies the factorization
$D_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}$
supplies the factorization
The profinite group
![]() $\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}$
acts continuously and Frobenius-equivariantly on
$\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}$
acts continuously and Frobenius-equivariantly on
![]() $A_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}^{\Box }$
over
$A_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}^{\Box }$
over
![]() $A_{\text{inf}}$
(see §3.14) and, due to the last paragraph of §5.9, this action extends to a
$A_{\text{inf}}$
(see §3.14) and, due to the last paragraph of §5.9, this action extends to a
![]() $\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}$
-action on the
$\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}$
-action on the
![]() $(p,\unicode[STIX]{x1D707})$
-adic formal log scheme
$(p,\unicode[STIX]{x1D707})$
-adic formal log scheme
![]() $\operatorname{Spf}(A_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}^{\Box })$
. Thus, since the closed immersion (5.22.1) is
$\operatorname{Spf}(A_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}^{\Box })$
. Thus, since the closed immersion (5.22.1) is
![]() $\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}$
-equivariant,
$\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}$
-equivariant,
![]() $\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}$
acts
$\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}$
acts
![]() $A_{\text{cris}}$
-linearly and Frobenius-equivariantly on each
$A_{\text{cris}}$
-linearly and Frobenius-equivariantly on each
![]() $D_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC},\,n}$
and also on
$D_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC},\,n}$
and also on
![]() $D_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}$
.
$D_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}$
.
The main practical deficiency of
![]() $D_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}$
is its inexplicit nature, for instance, we do not know whether
$D_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}$
is its inexplicit nature, for instance, we do not know whether
![]() $D_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}$
is
$D_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}$
is
![]() $p$
-torsion free. In contrast, its utility for us manifests itself through the following proposition.
$p$
-torsion free. In contrast, its utility for us manifests itself through the following proposition.
Proposition 5.23. In the local setting of §5.17, the complex (where the inverse limit is termwise)
is canonically and Frobenius-equivariantly identified in the derived category as follows:
Under this identification, the map
In particular, we have a Frobenius-equivariant identification
where the
![]() $\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\log (X_{\unicode[STIX]{x1D70E}})}$
(respectively,
$\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\log (X_{\unicode[STIX]{x1D70E}})}$
(respectively,
![]() $\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\log (X_{\unicode[STIX]{x1D706},\,i})}$
) are as in (5.10.1) with
$\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\log (X_{\unicode[STIX]{x1D706},\,i})}$
) are as in (5.10.1) with
![]() $R_{\unicode[STIX]{x1D6F4}}^{\Box }$
(respectively,
$R_{\unicode[STIX]{x1D6F4}}^{\Box }$
(respectively,
![]() $R_{\unicode[STIX]{x1D706}}^{\Box }$
) in place of
$R_{\unicode[STIX]{x1D706}}^{\Box }$
) in place of
![]() $R$
and the Frobenius acts in degree
$R$
and the Frobenius acts in degree
![]() $j$
on the right-hand side as
$j$
on the right-hand side as
![]() $p^{j}$
times the Frobenius of
$p^{j}$
times the Frobenius of
![]() $D_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}$
(compare with §5.10).
$D_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}$
(compare with §5.10).
Proof. By §5.11, each
![]() $A_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC},\,\text{cris}}^{\Box }/p^{n}$
is a log smooth thickening of
$A_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC},\,\text{cris}}^{\Box }/p^{n}$
is a log smooth thickening of
![]() $R/p$
over
$R/p$
over
![]() $A_{\text{cris}}/p^{n}$
. Therefore, by [Reference BeilinsonBei13a, 1.4, Remarks (ii)] (and the second paragraph of §5.22), the log PD thickening
$A_{\text{cris}}/p^{n}$
. Therefore, by [Reference BeilinsonBei13a, 1.4, Remarks (ii)] (and the second paragraph of §5.22), the log PD thickening
![]() $D_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC},\,n}$
of
$D_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC},\,n}$
of
![]() $R/p$
is PD smooth over
$R/p$
is PD smooth over
![]() $A_{\text{cris}}/p^{n}$
(see the proof of Lemma 5.12). Thus, as in the proof of Proposition 5.13 above, [Reference BeilinsonBei13a, (1.8.1)] ensures that the logarithmic PD de Rham complex
$A_{\text{cris}}/p^{n}$
(see the proof of Lemma 5.12). Thus, as in the proof of Proposition 5.13 above, [Reference BeilinsonBei13a, (1.8.1)] ensures that the logarithmic PD de Rham complex
![]() $\unicode[STIX]{x1D6FA}_{D_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC},\,n}/(A_{\text{cris}}/p^{n}),\,\log ,\,\text{PD}}^{\bullet }$
Frobenius-equivariantly computes
$\unicode[STIX]{x1D6FA}_{D_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC},\,n}/(A_{\text{cris}}/p^{n}),\,\log ,\,\text{PD}}^{\bullet }$
Frobenius-equivariantly computes
![]() $R\unicode[STIX]{x1D6E4}_{\log \text{cris}}({\mathcal{O}}_{\mathfrak{X}_{{\mathcal{O}}_{C}/p}/(A_{\text{cris}}/p^{n})})$
. By [Reference BeilinsonBei13a, 1.7, Exercises, (i)],
$R\unicode[STIX]{x1D6E4}_{\log \text{cris}}({\mathcal{O}}_{\mathfrak{X}_{{\mathcal{O}}_{C}/p}/(A_{\text{cris}}/p^{n})})$
. By [Reference BeilinsonBei13a, 1.7, Exercises, (i)],
so (5.23.1) follows. Then, since each
![]() $R/p^{n}$
is a log smooth log PD thickening of
$R/p^{n}$
is a log smooth log PD thickening of
![]() $R/p$
over
$R/p$
over
![]() ${\mathcal{O}}_{C}/p^{n}$
, analogous reasoning applies to
${\mathcal{O}}_{C}/p^{n}$
, analogous reasoning applies to
(compare with the proof of Proposition 5.13) and gives (5.23.2).
Finally, the identification (5.23.3) results from (5.23.1) and the Frobenius-equivariant identifications
supplied by (5.10.3). ◻
Remark 5.24. By [Reference BeilinsonBei13a, (1.11.1)], the first map in (5.23.2) induces the identification
in the derived category, so the same holds for the second map:
To make the identification (5.23.3) analogous to the identification in Proposition 5.20, we will express
![]() $D_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}$
as a completed direct limit of rings
$D_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}$
as a completed direct limit of rings
![]() $D_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}^{(m)}$
that ‘are generated by divided powers of degree at most
$D_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}^{(m)}$
that ‘are generated by divided powers of degree at most
![]() $m$
’, see (5.30.1). For this, we will build on the ideas from the proof of [Reference KatoKat89, 4.10(1)] to identify
$m$
’, see (5.30.1). For this, we will build on the ideas from the proof of [Reference KatoKat89, 4.10(1)] to identify
![]() $D_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}$
with the
$D_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}$
with the
![]() $p$
-adic completion of the (nonlog) divided power envelope of an exact closed immersion in Lemma 5.29.Footnote
11
This will also make
$p$
-adic completion of the (nonlog) divided power envelope of an exact closed immersion in Lemma 5.29.Footnote
11
This will also make
![]() $D_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}$
more explicit and easier to analyze.
$D_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}$
more explicit and easier to analyze.
5.25 A chart for
 $A_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}^{\Box }$
$A_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}^{\Box }$
To express
![]() $D_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}$
as the
$D_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}$
as the
![]() $p$
-adic completion of a usual (nonlog) divided power envelope, in §§5.25–5.27 we build a chart for the (fine version) of the log closed immersion
$p$
-adic completion of a usual (nonlog) divided power envelope, in §§5.25–5.27 we build a chart for the (fine version) of the log closed immersion
For this, we fix the unique
![]() $q\in \mathbb{Q}_{{>}0}$
for which
$q\in \mathbb{Q}_{{>}0}$
for which
so that
![]() $q_{\unicode[STIX]{x1D706}}/q\in \mathbb{Z}_{{>}0}$
for every
$q_{\unicode[STIX]{x1D706}}/q\in \mathbb{Z}_{{>}0}$
for every
![]() $\unicode[STIX]{x1D706}$
(and even
$\unicode[STIX]{x1D706}$
(and even
![]() $q_{\unicode[STIX]{x1D706}}=q$
in the case when
$q_{\unicode[STIX]{x1D706}}=q$
in the case when
![]() $R\otimes _{{\mathcal{O}}_{C}}k$
is not
$R\otimes _{{\mathcal{O}}_{C}}k$
is not
![]() $k$
-smooth, see §5.17). We endow
$k$
-smooth, see §5.17). We endow
![]() ${\mathcal{O}}_{C}/p$
and
${\mathcal{O}}_{C}/p$
and
![]() $A_{\text{inf}}$
with the compatible via
$A_{\text{inf}}$
with the compatible via
![]() $\unicode[STIX]{x1D703}$
fine log structures determined by
$\unicode[STIX]{x1D703}$
fine log structures determined by
For each
![]() $\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}$
, we consider the submonoid
$\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}$
, we consider the submonoid
so that the chart
makes
![]() $\operatorname{Spec}(A(R_{\unicode[STIX]{x1D706}}^{\Box }))$
a fine log
$\operatorname{Spec}(A(R_{\unicode[STIX]{x1D706}}^{\Box }))$
a fine log
![]() $\operatorname{Spec}(A_{\text{inf}})$
-scheme. We let
$\operatorname{Spec}(A_{\text{inf}})$
-scheme. We let
be the quotient monoid obtained by identifying the diagonal elements
![]() $(q/q_{\unicode[STIX]{x1D706}},\ldots ,q/q_{\unicode[STIX]{x1D706}})$
, so that the map
$(q/q_{\unicode[STIX]{x1D706}},\ldots ,q/q_{\unicode[STIX]{x1D706}})$
, so that the map
is a chart for the target
![]() $\operatorname{Spec}(A_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}^{\Box })$
of a fine version of the log closed immersion (5.25.1). In terms of this chart, the Frobenius of
$\operatorname{Spec}(A_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}^{\Box })$
of a fine version of the log closed immersion (5.25.1). In terms of this chart, the Frobenius of
![]() $A_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}^{\Box }$
multiplies each element of
$A_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}^{\Box }$
multiplies each element of
![]() $Q$
by
$Q$
by
![]() $p$
(see §5.9).
$p$
(see §5.9).
5.26 A convenient chart in the smooth case
We consider the case when
![]() $R\otimes _{{\mathcal{O}}_{C}}k$
is
$R\otimes _{{\mathcal{O}}_{C}}k$
is
![]() $k$
-smooth, so that for each
$k$
-smooth, so that for each
![]() $\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}$
there is a unique
$\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}$
there is a unique
![]() $0\leqslant i_{\unicode[STIX]{x1D706}}\leqslant r_{\unicode[STIX]{x1D706}}$
with
$0\leqslant i_{\unicode[STIX]{x1D706}}\leqslant r_{\unicode[STIX]{x1D706}}$
with
![]() $t_{\unicode[STIX]{x1D706},\,i_{\unicode[STIX]{x1D706}}}\not \in R^{\times }$
, and build the monoids
$t_{\unicode[STIX]{x1D706},\,i_{\unicode[STIX]{x1D706}}}\not \in R^{\times }$
, and build the monoids
where each
![]() $\mathbb{Z}$
by which we quotient is embedded diagonally. For each
$\mathbb{Z}$
by which we quotient is embedded diagonally. For each
![]() $(\unicode[STIX]{x1D706},i)$
with
$(\unicode[STIX]{x1D706},i)$
with
![]() $0\leqslant i\leqslant r_{\unicode[STIX]{x1D706}}$
,
$0\leqslant i\leqslant r_{\unicode[STIX]{x1D706}}$
,
explicitly,
![]() $n_{\unicode[STIX]{x1D706},\,i_{\unicode[STIX]{x1D706}}}=\frac{q_{\unicode[STIX]{x1D706}}}{q}$
and
$n_{\unicode[STIX]{x1D706},\,i_{\unicode[STIX]{x1D706}}}=\frac{q_{\unicode[STIX]{x1D706}}}{q}$
and
![]() $n_{\unicode[STIX]{x1D706},\,i}=0$
for
$n_{\unicode[STIX]{x1D706},\,i}=0$
for
![]() $i\neq i_{\unicode[STIX]{x1D706}}$
. In particular,
$i\neq i_{\unicode[STIX]{x1D706}}$
. In particular,
![]() $\prod _{0\leqslant i\leqslant r_{\unicode[STIX]{x1D706}}}v_{\unicode[STIX]{x1D706},\,i}=1$
for each
$\prod _{0\leqslant i\leqslant r_{\unicode[STIX]{x1D706}}}v_{\unicode[STIX]{x1D706},\,i}=1$
for each
![]() $\unicode[STIX]{x1D706}$
. The map
$\unicode[STIX]{x1D706}$
. The map
where the subscript
![]() $(\unicode[STIX]{x1D706},i)$
indicates the factor
$(\unicode[STIX]{x1D706},i)$
indicates the factor
![]() $\mathbb{Z}$
of (5.26.1) being considered, is a chart for the source
$\mathbb{Z}$
of (5.26.1) being considered, is a chart for the source
![]() $\operatorname{Spec}(R/p)$
of a fine version of the log closed immersion (5.25.1). In terms of this chart, the Frobenius of
$\operatorname{Spec}(R/p)$
of a fine version of the log closed immersion (5.25.1). In terms of this chart, the Frobenius of
![]() $R/p$
multiplies each element of
$R/p$
multiplies each element of
![]() $P_{\unicode[STIX]{x1D706}_{0}}$
by
$P_{\unicode[STIX]{x1D706}_{0}}$
by
![]() $p$
.
$p$
.
Due to (5.26.2), knowing the indices
![]() $i_{\unicode[STIX]{x1D706}}$
, we may evidently express the image of every generator of
$i_{\unicode[STIX]{x1D706}}$
, we may evidently express the image of every generator of
![]() $Q$
under
$Q$
under
![]() $Q\rightarrow A_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}^{\Box }{\twoheadrightarrow}R/p$
in terms of the images of elements of
$Q\rightarrow A_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}^{\Box }{\twoheadrightarrow}R/p$
in terms of the images of elements of
![]() $P_{\unicode[STIX]{x1D706}_{0}}$
without knowing the ‘values’ of these images. Thus, the log closed immersion (5.25.1) has a natural Frobenius-equivariant chart
$P_{\unicode[STIX]{x1D706}_{0}}$
without knowing the ‘values’ of these images. Thus, the log closed immersion (5.25.1) has a natural Frobenius-equivariant chart
that, for instance, sends
![]() $1\in (\mathbb{N}_{{\geqslant}0})_{(\unicode[STIX]{x1D706}_{0},\,i_{\unicode[STIX]{x1D706}_{0}})}$
to the element
$1\in (\mathbb{N}_{{\geqslant}0})_{(\unicode[STIX]{x1D706}_{0},\,i_{\unicode[STIX]{x1D706}_{0}})}$
to the element
![]() $(q_{\unicode[STIX]{x1D706}_{0}}/q,-1,\ldots ,-1)$
of
$(q_{\unicode[STIX]{x1D706}_{0}}/q,-1,\ldots ,-1)$
of
each
![]() $(q/q_{\unicode[STIX]{x1D706}},\ldots ,q/q_{\unicode[STIX]{x1D706}})$
to
$(q/q_{\unicode[STIX]{x1D706}},\ldots ,q/q_{\unicode[STIX]{x1D706}})$
to
![]() $1\in \mathbb{N}_{{\geqslant}0}$
, each
$1\in \mathbb{N}_{{\geqslant}0}$
, each
![]() $1\in (\mathbb{N}_{{\geqslant}0})_{(\unicode[STIX]{x1D706},i)}$
with
$1\in (\mathbb{N}_{{\geqslant}0})_{(\unicode[STIX]{x1D706},i)}$
with
![]() $i\neq i_{\unicode[STIX]{x1D706}}$
to
$i\neq i_{\unicode[STIX]{x1D706}}$
to
![]() $1\in \mathbb{Z}_{(\unicode[STIX]{x1D706},i)}$
, etc.
$1\in \mathbb{Z}_{(\unicode[STIX]{x1D706},i)}$
, etc.
More precisely, the resulting
![]() $A_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}^{\Box }$
-algebra
$A_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}^{\Box }$
-algebra
comes equipped with an
![]() $A_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}^{\Box }$
-semilinear Frobenius and is initial among the
$A_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}^{\Box }$
-semilinear Frobenius and is initial among the
![]() $A_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}^{\Box }$
-algebras
$A_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}^{\Box }$
-algebras
![]() $B$
equipped with a unit
$B$
equipped with a unit
![]() $V_{\unicode[STIX]{x1D706},\,i}\in B^{\times }$
for each
$V_{\unicode[STIX]{x1D706},\,i}\in B^{\times }$
for each
![]() $(\unicode[STIX]{x1D706},i)$
with
$(\unicode[STIX]{x1D706},i)$
with
![]() $0\leqslant i\leqslant r_{\unicode[STIX]{x1D706}}$
subject to the relations
$0\leqslant i\leqslant r_{\unicode[STIX]{x1D706}}$
subject to the relations
In particular,
A fine version of the log closed immersion (5.25.1) factors Frobenius-equivariantly as follows:
where
![]() $\operatorname{Spec}(A_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}^{\Box }\otimes _{\mathbb{Z}[Q]}\mathbb{Z}[P_{\unicode[STIX]{x1D706}_{0}}])$
is equipped with the log structure determined by
$\operatorname{Spec}(A_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}^{\Box }\otimes _{\mathbb{Z}[Q]}\mathbb{Z}[P_{\unicode[STIX]{x1D706}_{0}}])$
is equipped with the log structure determined by
![]() $P_{\unicode[STIX]{x1D706}_{0}}$
. By construction,
$P_{\unicode[STIX]{x1D706}_{0}}$
. By construction,
![]() $j_{\unicode[STIX]{x1D706}_{0}}$
is an exact closed immersion and, by [Reference KatoKat89, 3.5], the projection
$j_{\unicode[STIX]{x1D706}_{0}}$
is an exact closed immersion and, by [Reference KatoKat89, 3.5], the projection
![]() $q_{\unicode[STIX]{x1D706}_{0}}$
is log étale.
$q_{\unicode[STIX]{x1D706}_{0}}$
is log étale.
The relations (5.26.3) do not depend on the choice of
![]() $\unicode[STIX]{x1D706}_{0}$
, so neither does the factorization (5.26.5). More precisely, for another
$\unicode[STIX]{x1D706}_{0}$
, so neither does the factorization (5.26.5). More precisely, for another
![]() $\unicode[STIX]{x1D706}_{0}^{\prime }\in \unicode[STIX]{x1D6EC}$
, we have a natural isomorphism over
$\unicode[STIX]{x1D706}_{0}^{\prime }\in \unicode[STIX]{x1D6EC}$
, we have a natural isomorphism over
![]() $Q$
of charts for
$Q$
of charts for
![]() $R/p$
:
$R/p$
:
which gives rise to the vertical Frobenius-equivariant isomorphism in the following commutative diagram.

5.27 A convenient chart in the nonsmooth case
We now consider the case when
![]() $R\otimes _{{\mathcal{O}}_{C}}k$
is not
$R\otimes _{{\mathcal{O}}_{C}}k$
is not
![]() $k$
-smooth, so that
$k$
-smooth, so that
![]() $q_{\unicode[STIX]{x1D706}}=q$
and
$q_{\unicode[STIX]{x1D706}}=q$
and
![]() $Q_{\unicode[STIX]{x1D706}}\cong \prod _{0\leqslant i\leqslant r_{\unicode[STIX]{x1D706}}}\mathbb{N}_{{\geqslant}0}$
for every
$Q_{\unicode[STIX]{x1D706}}\cong \prod _{0\leqslant i\leqslant r_{\unicode[STIX]{x1D706}}}\mathbb{N}_{{\geqslant}0}$
for every
![]() $\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}$
. Letting
$\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}$
. Letting
![]() $\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D706}}\subset Q_{\unicode[STIX]{x1D706}}$
be the diagonal copy of
$\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D706}}\subset Q_{\unicode[STIX]{x1D706}}$
be the diagonal copy of
![]() $\mathbb{N}_{{\geqslant}0}$
, we can then describe the chart
$\mathbb{N}_{{\geqslant}0}$
, we can then describe the chart
![]() $Q$
for a fine version of
$Q$
for a fine version of
![]() $\operatorname{Spec}(A_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}^{\Box })$
as follows:
$\operatorname{Spec}(A_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}^{\Box })$
as follows:
By §5.17, each
![]() $t_{\unicode[STIX]{x1D706},\,i}\not \in R^{\times }$
cuts out a unique irreducible component
$t_{\unicode[STIX]{x1D706},\,i}\not \in R^{\times }$
cuts out a unique irreducible component
![]() $\overline{\{y_{\unicode[STIX]{x1D706},\,i}\}}$
of
$\overline{\{y_{\unicode[STIX]{x1D706},\,i}\}}$
of
![]() $\operatorname{Spec}(R\otimes _{{\mathcal{O}}_{C}}k)$
. Its generic point
$\operatorname{Spec}(R\otimes _{{\mathcal{O}}_{C}}k)$
. Its generic point
![]() $y_{\unicode[STIX]{x1D706},\,i}$
determines the ideal
$y_{\unicode[STIX]{x1D706},\,i}$
determines the ideal
![]() $(t_{\unicode[STIX]{x1D706},\,i})\subset R$
: indeed,
$(t_{\unicode[STIX]{x1D706},\,i})\subset R$
: indeed,
![]() $(p^{q})\subset (t_{\unicode[STIX]{x1D706},\,i})$
in
$(p^{q})\subset (t_{\unicode[STIX]{x1D706},\,i})$
in
![]() $R$
and the ideal
$R$
and the ideal
![]() $(t_{\unicode[STIX]{x1D706},\,i})/(p^{q})\subset R/(p^{q})$
is the kernel of the localization map
$(t_{\unicode[STIX]{x1D706},\,i})/(p^{q})\subset R/(p^{q})$
is the kernel of the localization map
![]() $R/(p^{q})\rightarrow (R/(p^{q}))_{y_{\unicode[STIX]{x1D706},\,i}}$
, as may be seen over
$R/(p^{q})\rightarrow (R/(p^{q}))_{y_{\unicode[STIX]{x1D706},\,i}}$
, as may be seen over
![]() $R_{\unicode[STIX]{x1D706}}^{\Box }$
. Conversely, for each generic point
$R_{\unicode[STIX]{x1D706}}^{\Box }$
. Conversely, for each generic point
![]() $y$
of
$y$
of
![]() $\operatorname{Spec}(R\otimes _{{\mathcal{O}}_{C}}k)$
and
$\operatorname{Spec}(R\otimes _{{\mathcal{O}}_{C}}k)$
and
![]() $\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}$
, a unique
$\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}$
, a unique
![]() $t_{\unicode[STIX]{x1D706},\,i_{\unicode[STIX]{x1D706}}(y)}$
with
$t_{\unicode[STIX]{x1D706},\,i_{\unicode[STIX]{x1D706}}(y)}$
with
![]() $0\leqslant i_{\unicode[STIX]{x1D706}}(y)\leqslant r_{\unicode[STIX]{x1D706}}$
cuts out
$0\leqslant i_{\unicode[STIX]{x1D706}}(y)\leqslant r_{\unicode[STIX]{x1D706}}$
cuts out
![]() $\overline{\{y\}}$
(see §5.17). Consequently, for each
$\overline{\{y\}}$
(see §5.17). Consequently, for each
![]() $y$
and
$y$
and
![]() $\unicode[STIX]{x1D706},\unicode[STIX]{x1D706}_{0}\in \unicode[STIX]{x1D6EC}$
,
$\unicode[STIX]{x1D706},\unicode[STIX]{x1D706}_{0}\in \unicode[STIX]{x1D6EC}$
,
Letting
![]() ${\mathcal{Y}}$
denote the set of the generic points of
${\mathcal{Y}}$
denote the set of the generic points of
![]() $\operatorname{Spec}(R\otimes _{{\mathcal{O}}_{C}}k)$
, for
$\operatorname{Spec}(R\otimes _{{\mathcal{O}}_{C}}k)$
, for
![]() $\unicode[STIX]{x1D706}_{0}\in \unicode[STIX]{x1D6EC}$
we build the monoid
$\unicode[STIX]{x1D706}_{0}\in \unicode[STIX]{x1D6EC}$
we build the monoid
where the quotient means that for every
![]() $\unicode[STIX]{x1D706}\neq \unicode[STIX]{x1D706}_{0}$
we are identifying every diagonal element of
$\unicode[STIX]{x1D706}\neq \unicode[STIX]{x1D706}_{0}$
we are identifying every diagonal element of
![]() $\prod _{0\leqslant i\leqslant r_{\unicode[STIX]{x1D706}}}\mathbb{Z}$
with the corresponding diagonal element of
$\prod _{0\leqslant i\leqslant r_{\unicode[STIX]{x1D706}}}\mathbb{Z}$
with the corresponding diagonal element of
![]() $\prod _{\{0\leqslant i\leqslant r_{\unicode[STIX]{x1D706}_{0}}\}\setminus i_{\unicode[STIX]{x1D706}_{0}}({\mathcal{Y}})}\mathbb{Z}$
(interpreted to be
$\prod _{\{0\leqslant i\leqslant r_{\unicode[STIX]{x1D706}_{0}}\}\setminus i_{\unicode[STIX]{x1D706}_{0}}({\mathcal{Y}})}\mathbb{Z}$
(interpreted to be
![]() $0$
if the indexing set is empty). The assignment (as in §5.26, subscripts indicate factors in (5.27.2))
$0$
if the indexing set is empty). The assignment (as in §5.26, subscripts indicate factors in (5.27.2))
determines a chart
for the source
![]() $\operatorname{Spec}(R/p)$
of a fine version of the log closed immersion (5.25.1). In terms of this chart, the Frobenius of
$\operatorname{Spec}(R/p)$
of a fine version of the log closed immersion (5.25.1). In terms of this chart, the Frobenius of
![]() $R/p$
multiplies each element of
$R/p$
multiplies each element of
![]() $P_{\unicode[STIX]{x1D706}_{0}}$
by
$P_{\unicode[STIX]{x1D706}_{0}}$
by
![]() $p$
.
$p$
.
Due to the relation (5.27.1), the images in
![]() $R/p$
of the generators of
$R/p$
of the generators of
![]() $Q$
are evidently expressible in terms of the images of the elements of
$Q$
are evidently expressible in terms of the images of the elements of
![]() $P_{\unicode[STIX]{x1D706}_{0}}$
(without knowing the ‘values’ of these images), so, as in the smooth case, there is a natural Frobenius-equivariant chart for a fine version of (5.25.1):
$P_{\unicode[STIX]{x1D706}_{0}}$
(without knowing the ‘values’ of these images), so, as in the smooth case, there is a natural Frobenius-equivariant chart for a fine version of (5.25.1):
that, for instance, for
![]() $\unicode[STIX]{x1D706}\neq \unicode[STIX]{x1D706}_{0}$
and
$\unicode[STIX]{x1D706}\neq \unicode[STIX]{x1D706}_{0}$
and
![]() $y\in {\mathcal{Y}}$
, sends
$y\in {\mathcal{Y}}$
, sends
![]() $1\in (\mathbb{N}_{{\geqslant}0})_{(\unicode[STIX]{x1D706},\,i_{\unicode[STIX]{x1D706}}(y))}$
to
$1\in (\mathbb{N}_{{\geqslant}0})_{(\unicode[STIX]{x1D706},\,i_{\unicode[STIX]{x1D706}}(y))}$
to
![]() $(1,1)\in (\mathbb{N}_{{\geqslant}0})_{y}\times \mathbb{Z}_{(\unicode[STIX]{x1D706},\,i_{\unicode[STIX]{x1D706}}(y))}$
.
$(1,1)\in (\mathbb{N}_{{\geqslant}0})_{y}\times \mathbb{Z}_{(\unicode[STIX]{x1D706},\,i_{\unicode[STIX]{x1D706}}(y))}$
.
The resulting
![]() $A_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}^{\Box }$
-algebra
$A_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}^{\Box }$
-algebra
comes equipped with an
![]() $A_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}^{\Box }$
-semilinear Frobenius endomorphism and is initial among the
$A_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}^{\Box }$
-semilinear Frobenius endomorphism and is initial among the
![]() $A_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}^{\Box }$
-algebras
$A_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}^{\Box }$
-algebras
![]() $B$
for which
$B$
for which
![]() $X_{\unicode[STIX]{x1D706},\,i}\in B^{\times }$
when
$X_{\unicode[STIX]{x1D706},\,i}\in B^{\times }$
when
![]() $i\not \in i_{\unicode[STIX]{x1D706}}({\mathcal{Y}})$
and that are equipped with, for each
$i\not \in i_{\unicode[STIX]{x1D706}}({\mathcal{Y}})$
and that are equipped with, for each
![]() $y\in {\mathcal{Y}}$
and
$y\in {\mathcal{Y}}$
and
![]() $\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}$
, a unit
$\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}$
, a unit
![]() $U_{\unicode[STIX]{x1D706},\,\unicode[STIX]{x1D706}_{0},\,y}\in B^{\times }$
subject to the relations
$U_{\unicode[STIX]{x1D706},\,\unicode[STIX]{x1D706}_{0},\,y}\in B^{\times }$
subject to the relations
For a
![]() $\unicode[STIX]{x1D706}_{0}^{\prime }\in \unicode[STIX]{x1D6EC}$
, we may set
$\unicode[STIX]{x1D706}_{0}^{\prime }\in \unicode[STIX]{x1D6EC}$
, we may set
![]() $U_{\unicode[STIX]{x1D706},\,\unicode[STIX]{x1D706}_{0}^{\prime },\,y}=U_{\unicode[STIX]{x1D706},\,\unicode[STIX]{x1D706}_{0},\,y}\,\cdot \,U_{\unicode[STIX]{x1D706}_{0}^{\prime },\,\unicode[STIX]{x1D706}_{0},\,y}^{-1}$
to express the
$U_{\unicode[STIX]{x1D706},\,\unicode[STIX]{x1D706}_{0}^{\prime },\,y}=U_{\unicode[STIX]{x1D706},\,\unicode[STIX]{x1D706}_{0},\,y}\,\cdot \,U_{\unicode[STIX]{x1D706}_{0}^{\prime },\,\unicode[STIX]{x1D706}_{0},\,y}^{-1}$
to express the
![]() $U_{\unicode[STIX]{x1D706},\,\unicode[STIX]{x1D706}_{0}^{\prime },\,y}$
in terms of the
$U_{\unicode[STIX]{x1D706},\,\unicode[STIX]{x1D706}_{0}^{\prime },\,y}$
in terms of the
![]() $U_{\unicode[STIX]{x1D706},\,\unicode[STIX]{x1D706}_{0},\,y}$
, so, up to a canonical
$U_{\unicode[STIX]{x1D706},\,\unicode[STIX]{x1D706}_{0},\,y}$
, so, up to a canonical
![]() $A_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}^{\Box }$
-isomorphism,
$A_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}^{\Box }$
-isomorphism,
![]() $A_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}^{\Box }\otimes _{\mathbb{Z}[Q]}\mathbb{Z}[P_{\unicode[STIX]{x1D706}_{0}}]$
does not depend on
$A_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}^{\Box }\otimes _{\mathbb{Z}[Q]}\mathbb{Z}[P_{\unicode[STIX]{x1D706}_{0}}]$
does not depend on
![]() $\unicode[STIX]{x1D706}_{0}$
. Moreover,
$\unicode[STIX]{x1D706}_{0}$
. Moreover,
As in the smooth case, we equip
![]() $\operatorname{Spec}(A_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}^{\Box }\otimes _{\mathbb{Z}[Q]}\mathbb{Z}[P_{\unicode[STIX]{x1D706}_{0}}])$
with the log structure determined by
$\operatorname{Spec}(A_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}^{\Box }\otimes _{\mathbb{Z}[Q]}\mathbb{Z}[P_{\unicode[STIX]{x1D706}_{0}}])$
with the log structure determined by
![]() $P_{\unicode[STIX]{x1D706}_{0}}$
, so a fine version of the log closed immersion (5.25.1) factors Frobenius-equivariantly as follows:
$P_{\unicode[STIX]{x1D706}_{0}}$
, so a fine version of the log closed immersion (5.25.1) factors Frobenius-equivariantly as follows:
where
![]() $j_{\unicode[STIX]{x1D706}_{0}}$
is an exact closed immersion and, by [Reference KatoKat89, 3.5], the projection
$j_{\unicode[STIX]{x1D706}_{0}}$
is an exact closed immersion and, by [Reference KatoKat89, 3.5], the projection
![]() $q_{\unicode[STIX]{x1D706}_{0}}$
is log étale. As in §5.26, we have natural isomorphisms
$q_{\unicode[STIX]{x1D706}_{0}}$
is log étale. As in §5.26, we have natural isomorphisms
![]() $P_{\unicode[STIX]{x1D706}_{0}}\simeq P_{\unicode[STIX]{x1D706}_{0}^{\prime }}$
over
$P_{\unicode[STIX]{x1D706}_{0}}\simeq P_{\unicode[STIX]{x1D706}_{0}^{\prime }}$
over
![]() $Q$
and the compatibility diagram (5.26.7).
$Q$
and the compatibility diagram (5.26.7).
We now use the charts
![]() $Q\rightarrow P_{\unicode[STIX]{x1D706}_{0}}$
to build a (nonlog) PD envelope whose
$Q\rightarrow P_{\unicode[STIX]{x1D706}_{0}}$
to build a (nonlog) PD envelope whose
![]() $p$
-adic completion is
$p$
-adic completion is
![]() $D_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}$
.
$D_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}$
.
5.28 The divided power envelope of
 $j_{\unicode[STIX]{x1D706}_{0}}$
$j_{\unicode[STIX]{x1D706}_{0}}$
For
![]() $\unicode[STIX]{x1D706}_{0}\in \unicode[STIX]{x1D6EC}$
, we let
$\unicode[STIX]{x1D706}_{0}\in \unicode[STIX]{x1D6EC}$
, we let
![]() $D_{j_{\unicode[STIX]{x1D706}_{0}}}$
be the divided power envelope over
$D_{j_{\unicode[STIX]{x1D706}_{0}}}$
be the divided power envelope over
![]() $(\mathbb{Z}_{p},p\mathbb{Z}_{p})$
of the closed immersion
$(\mathbb{Z}_{p},p\mathbb{Z}_{p})$
of the closed immersion
![]() $j_{\unicode[STIX]{x1D706}_{0}}$
defined in (5.26.5) and (5.27.5). The universal property of
$j_{\unicode[STIX]{x1D706}_{0}}$
defined in (5.26.5) and (5.27.5). The universal property of
![]() $A_{\text{cris}}^{0}$
(see §5.1) identifies
$A_{\text{cris}}^{0}$
(see §5.1) identifies
![]() $D_{j_{\unicode[STIX]{x1D706}_{0}}}$
with the divided power envelope of the closed immersion
$D_{j_{\unicode[STIX]{x1D706}_{0}}}$
with the divided power envelope of the closed immersion
(compare with §5.22). Since
![]() $j_{\unicode[STIX]{x1D706}_{0}}$
underlies an exact closed immersion of log schemes, we may, in addition, identify
$j_{\unicode[STIX]{x1D706}_{0}}$
underlies an exact closed immersion of log schemes, we may, in addition, identify
![]() $D_{j_{\unicode[STIX]{x1D706}_{0}}}$
endowed with the log structure determined by
$D_{j_{\unicode[STIX]{x1D706}_{0}}}$
endowed with the log structure determined by
![]() $P_{\unicode[STIX]{x1D706}_{0}}$
with the log PD envelope of
$P_{\unicode[STIX]{x1D706}_{0}}$
with the log PD envelope of
![]() $j_{\unicode[STIX]{x1D706}_{0}}$
over
$j_{\unicode[STIX]{x1D706}_{0}}$
over
![]() $\mathbb{Z}_{p}$
, or of
$\mathbb{Z}_{p}$
, or of
![]() $j_{\unicode[STIX]{x1D706}_{0},\,\text{cris}}$
over
$j_{\unicode[STIX]{x1D706}_{0},\,\text{cris}}$
over
![]() $A_{\text{cris}}^{0}$
(compare with [Reference KatoKat89, 5.5.1]). For
$A_{\text{cris}}^{0}$
(compare with [Reference KatoKat89, 5.5.1]). For
![]() $\unicode[STIX]{x1D706}_{0}^{\prime }\in \unicode[STIX]{x1D6EC}$
, the vertical isomorphism in (5.26.7) induces an isomorphism
$\unicode[STIX]{x1D706}_{0}^{\prime }\in \unicode[STIX]{x1D6EC}$
, the vertical isomorphism in (5.26.7) induces an isomorphism
By functoriality,
![]() $D_{j_{\unicode[STIX]{x1D706}_{0}}}$
comes equipped with an
$D_{j_{\unicode[STIX]{x1D706}_{0}}}$
comes equipped with an
![]() $A_{\text{cris}}^{0}$
-semilinear Frobenius endomorphism, and the isomorphisms (5.28.1) are Frobenius equivariant. Due to (5.26.4) and (5.27.4), there is a map
$A_{\text{cris}}^{0}$
-semilinear Frobenius endomorphism, and the isomorphisms (5.28.1) are Frobenius equivariant. Due to (5.26.4) and (5.27.4), there is a map
its formation is compatible with the isomorphisms (5.28.1).
By the universal property of
![]() $A_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}^{\Box }\otimes _{\mathbb{Z}[Q]}\mathbb{Z}[P_{\unicode[STIX]{x1D706}_{0}}]$
(see (5.26.3) and (5.27.3)), the continuous
$A_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}^{\Box }\otimes _{\mathbb{Z}[Q]}\mathbb{Z}[P_{\unicode[STIX]{x1D706}_{0}}]$
(see (5.26.3) and (5.27.3)), the continuous
![]() $\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}$
-action on
$\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}$
-action on
![]() $A_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}^{\Box }$
extends to a
$A_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}^{\Box }$
extends to a
![]() $(p,\unicode[STIX]{x1D707})$
-adically continuous
$(p,\unicode[STIX]{x1D707})$
-adically continuous
![]() $\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}$
-action on
$\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}$
-action on
![]() $A_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}^{\Box }\otimes _{\mathbb{Z}[Q]}\mathbb{Z}[P_{\unicode[STIX]{x1D706}_{0}}]$
, so it induces an
$A_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}^{\Box }\otimes _{\mathbb{Z}[Q]}\mathbb{Z}[P_{\unicode[STIX]{x1D706}_{0}}]$
, so it induces an
![]() $A_{\text{cris}}^{0}$
-linear
$A_{\text{cris}}^{0}$
-linear
![]() $\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}$
-action on
$\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}$
-action on
![]() $D_{j_{\unicode[STIX]{x1D706}_{0}}}$
. As an
$D_{j_{\unicode[STIX]{x1D706}_{0}}}$
. As an
![]() $(A_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}^{\Box }\otimes _{\mathbb{Z}[Q]}\mathbb{Z}[P_{\unicode[STIX]{x1D706}_{0}}])$
-algebra,
$(A_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}^{\Box }\otimes _{\mathbb{Z}[Q]}\mathbb{Z}[P_{\unicode[STIX]{x1D706}_{0}}])$
-algebra,
![]() $D_{j_{\unicode[STIX]{x1D706}_{0}}}$
is generated by the divided powers of the elements of the ideal of
$D_{j_{\unicode[STIX]{x1D706}_{0}}}$
is generated by the divided powers of the elements of the ideal of
![]() $j_{\unicode[STIX]{x1D706}_{0}}$
, so this action is
$j_{\unicode[STIX]{x1D706}_{0}}$
, so this action is
![]() $p$
-adically continuous.
$p$
-adically continuous.
Lemma 5.29. For
![]() $\unicode[STIX]{x1D706}_{0}\in \unicode[STIX]{x1D6EC}$
, the map
$\unicode[STIX]{x1D706}_{0}\in \unicode[STIX]{x1D6EC}$
, the map
![]() $q_{\unicode[STIX]{x1D706}_{0}}$
induces Frobenius- and
$q_{\unicode[STIX]{x1D706}_{0}}$
induces Frobenius- and
![]() $\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}$
-equivariant isomorphisms
$\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}$
-equivariant isomorphisms
that are
![]() $A_{\text{cris}}$
-linear and compatible with divided powers, maps to
$A_{\text{cris}}$
-linear and compatible with divided powers, maps to
![]() $R/p^{n}$
(respectively,
$R/p^{n}$
(respectively,
![]() $R$
; see (5.22.3) and (5.28.2)), and the isomorphisms (5.28.1). In particular,
$R$
; see (5.22.3) and (5.28.2)), and the isomorphisms (5.28.1). In particular,
![]() $D_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}$
is
$D_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}$
is
![]() $p$
-adically complete,
$p$
-adically complete,
and the
![]() $\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}$
-action on
$\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}$
-action on
![]() $D_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}$
is
$D_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}$
is
![]() $p$
-adically continuous.
$p$
-adically continuous.
Proof. We may identify
![]() $D_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC},\,n}$
with the log PD envelope of
$D_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC},\,n}$
with the log PD envelope of
defined using fine log structures (see §5.22). On the other hand, we may identify
![]() $D_{j_{\unicode[STIX]{x1D706}_{0}}}/p^{n}$
with the (log) divided power envelope of
$D_{j_{\unicode[STIX]{x1D706}_{0}}}/p^{n}$
with the (log) divided power envelope of
![]() $j_{\unicode[STIX]{x1D706}_{0},\,\text{cris}}\otimes _{A_{\text{cris}}^{0}}A_{\text{cris}}^{0}/p^{n}$
, that is, of
$j_{\unicode[STIX]{x1D706}_{0},\,\text{cris}}\otimes _{A_{\text{cris}}^{0}}A_{\text{cris}}^{0}/p^{n}$
, that is, of
(see §5.28 and [SP, 07HB]). Consider a commutative square

of log schemes over
![]() $A_{\text{cris}}/p^{n}$
in which
$A_{\text{cris}}/p^{n}$
in which
![]() $T_{0}{\hookrightarrow}T$
is a log PD thickening such that the log structure
$T_{0}{\hookrightarrow}T$
is a log PD thickening such that the log structure
![]() ${\mathcal{N}}_{T}$
of
${\mathcal{N}}_{T}$
of
![]() $T$
(and, hence, also
$T$
(and, hence, also
![]() ${\mathcal{N}}_{T_{0}}$
of
${\mathcal{N}}_{T_{0}}$
of
![]() $T_{0}$
) is integral and quasi-coherent and the log structures of
$T_{0}$
) is integral and quasi-coherent and the log structures of
![]() $\operatorname{Spec}((A_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC},\,\text{cris}}^{\Box }/p^{n})\otimes _{\mathbb{Z}[Q]}\mathbb{Z}[P_{\unicode[STIX]{x1D706}_{0}}])$
and
$\operatorname{Spec}((A_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC},\,\text{cris}}^{\Box }/p^{n})\otimes _{\mathbb{Z}[Q]}\mathbb{Z}[P_{\unicode[STIX]{x1D706}_{0}}])$
and
![]() $\operatorname{Spec}(A_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC},\,\text{cris}}^{\Box }/p^{n})$
are determined by the charts
$\operatorname{Spec}(A_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC},\,\text{cris}}^{\Box }/p^{n})$
are determined by the charts
![]() $P_{\unicode[STIX]{x1D706}_{0}}$
and
$P_{\unicode[STIX]{x1D706}_{0}}$
and
![]() $Q$
, respectively (see §§5.25–5.27). By [Reference BeilinsonBei13a, 1.1 Exercises (iii)], for any
$Q$
, respectively (see §§5.25–5.27). By [Reference BeilinsonBei13a, 1.1 Exercises (iii)], for any
![]() $t,t^{\prime }\in \unicode[STIX]{x1D6E4}(T,{\mathcal{N}}_{T})$
and
$t,t^{\prime }\in \unicode[STIX]{x1D6E4}(T,{\mathcal{N}}_{T})$
and
![]() $u_{0}\in {\mathcal{O}}_{T_{0}}^{\times }$
with
$u_{0}\in {\mathcal{O}}_{T_{0}}^{\times }$
with
![]() $t|_{T_{0}}=u_{0}\cdot t^{\prime }|_{T_{0}}$
, there exists a unique lift
$t|_{T_{0}}=u_{0}\cdot t^{\prime }|_{T_{0}}$
, there exists a unique lift
![]() $u\in {\mathcal{O}}_{T}^{\times }$
of
$u\in {\mathcal{O}}_{T}^{\times }$
of
![]() $u_{0}$
such that
$u_{0}$
such that
![]() $t=ut^{\prime }$
. Thus, by the construction of
$t=ut^{\prime }$
. Thus, by the construction of
![]() $P_{\unicode[STIX]{x1D706}_{0}}$
and the universal property described by (5.26.3) and (5.27.3), there is a unique log morphism indicated by the dashed arrow in (5.29.2) that makes the diagram commute. Consequently,
$P_{\unicode[STIX]{x1D706}_{0}}$
and the universal property described by (5.26.3) and (5.27.3), there is a unique log morphism indicated by the dashed arrow in (5.29.2) that makes the diagram commute. Consequently,
![]() $q_{\unicode[STIX]{x1D706}_{0}}$
induces an isomorphism between the log PD envelopes:
$q_{\unicode[STIX]{x1D706}_{0}}$
induces an isomorphism between the log PD envelopes:
Functoriality implies the claimed compatibilities, and (5.29.1) implies the ‘in particular’ assertion. ◻
We now use Lemma 5.29 to define the rings
![]() $D_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}^{(m)}$
that are analogous to the rings
$D_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}^{(m)}$
that are analogous to the rings
![]() $A_{\text{cris}}^{(m)}(R)$
of §3.27.
$A_{\text{cris}}^{(m)}(R)$
of §3.27.
5.30 The rings
 $D_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}^{(m)}$
$D_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}^{(m)}$
For
![]() $\unicode[STIX]{x1D706}_{0}\in \unicode[STIX]{x1D6EC}$
, the divided powers of the elements of the ideal of
$\unicode[STIX]{x1D706}_{0}\in \unicode[STIX]{x1D6EC}$
, the divided powers of the elements of the ideal of
![]() $j_{\unicode[STIX]{x1D706}_{0}}$
generate
$j_{\unicode[STIX]{x1D706}_{0}}$
generate
![]() $D_{j_{\unicode[STIX]{x1D706}_{0}}}$
as an algebra over
$D_{j_{\unicode[STIX]{x1D706}_{0}}}$
as an algebra over
![]() $A_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}^{\Box }\otimes _{\mathbb{Z}[Q]}\mathbb{Z}[P_{\unicode[STIX]{x1D706}_{0}}]$
. In turn, for a fixed
$A_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}^{\Box }\otimes _{\mathbb{Z}[Q]}\mathbb{Z}[P_{\unicode[STIX]{x1D706}_{0}}]$
. In turn, for a fixed
![]() $m\in \mathbb{Z}_{{\geqslant}1}$
, the divided powers of degree at most
$m\in \mathbb{Z}_{{\geqslant}1}$
, the divided powers of degree at most
![]() $m$
generate a Frobenius-stable
$m$
generate a Frobenius-stable
![]() $(A_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}^{\Box }\otimes _{\mathbb{Z}[Q]}\mathbb{Z}[P_{\unicode[STIX]{x1D706}_{0}}])$
-subalgebra
$(A_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}^{\Box }\otimes _{\mathbb{Z}[Q]}\mathbb{Z}[P_{\unicode[STIX]{x1D706}_{0}}])$
-subalgebra
Since
![]() $D_{j_{\unicode[STIX]{x1D706}_{0}}}$
is naturally and Frobenius-semilinearly an
$D_{j_{\unicode[STIX]{x1D706}_{0}}}$
is naturally and Frobenius-semilinearly an
![]() $A_{\text{cris}}^{0}$
-algebra (see §5.28),
$A_{\text{cris}}^{0}$
-algebra (see §5.28),
![]() $D_{j_{\unicode[STIX]{x1D706}_{0}}}^{(m)}$
is naturally and Frobenius-semilinearly an algebra over the subring
$D_{j_{\unicode[STIX]{x1D706}_{0}}}^{(m)}$
is naturally and Frobenius-semilinearly an algebra over the subring
![]() $A_{\text{cris}}^{0,\,(m)}\subset A_{\text{cris}}^{0}$
defined in §3.26. By Lemma 5.29,
$A_{\text{cris}}^{0,\,(m)}\subset A_{\text{cris}}^{0}$
defined in §3.26. By Lemma 5.29,
and the same holds for the image
![]() $D_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}^{0,\,(m)}\subset D_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}^{0}$
of
$D_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}^{0,\,(m)}\subset D_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}^{0}$
of
![]() $D_{j_{\unicode[STIX]{x1D706}_{0}}}^{(m)}$
in
$D_{j_{\unicode[STIX]{x1D706}_{0}}}^{(m)}$
in
![]() $D_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}$
. For
$D_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}$
. For
![]() $m\geqslant p$
, the
$m\geqslant p$
, the
![]() $p$
-adic completion
$p$
-adic completion
and comes equipped with an
![]() $A_{\text{cris}}^{(m)}$
-semilinear Frobenius.
$A_{\text{cris}}^{(m)}$
-semilinear Frobenius.
By Lemma 5.29, the composition
![]() $D_{j_{\unicode[STIX]{x1D706}_{0}}}{\twoheadrightarrow}D_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}^{0}{\hookrightarrow}D_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}$
induces an isomorphism modulo
$D_{j_{\unicode[STIX]{x1D706}_{0}}}{\twoheadrightarrow}D_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}^{0}{\hookrightarrow}D_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}$
induces an isomorphism modulo
![]() $p^{n}$
and, hence, so do both maps that comprise it. Thus, since
$p^{n}$
and, hence, so do both maps that comprise it. Thus, since
![]() $D_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}^{0}=\bigcup _{m\geqslant p}D_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}^{0,\,(m)}$
, we have
$D_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}^{0}=\bigcup _{m\geqslant p}D_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}^{0,\,(m)}$
, we have
compatibly with the Frobenii. In what follows,
![]() $D_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}^{0}$
plays the role of the ring that underlies the hypothetical log PD envelope of the log closed immersion (5.25.1) (see footnote 11).
$D_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}^{0}$
plays the role of the ring that underlies the hypothetical log PD envelope of the log closed immersion (5.25.1) (see footnote 11).
By Lemma 5.29, the
![]() $\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}$
-action on
$\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}$
-action on
![]() $D_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}$
respects the subrings
$D_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}$
respects the subrings
![]() $D_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}^{0,\,(m)}\subset D_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}$
. The induced
$D_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}^{0,\,(m)}\subset D_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}$
. The induced
![]() $A_{\text{cris}}^{(m)}$
-linear
$A_{\text{cris}}^{(m)}$
-linear
![]() $\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}$
-action on
$\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}$
-action on
![]() $D_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}^{(m)}$
is
$D_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}^{(m)}$
is
![]() $p$
-adically continuous and compatible as
$p$
-adically continuous and compatible as
![]() $m$
varies. The identifications in (5.30.1) are
$m$
varies. The identifications in (5.30.1) are
![]() $\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}$
-equivariant.
$\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}$
-equivariant.
5.31 The derivations
 $\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\log (X_{\unicode[STIX]{x1D70F}})}$
$\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\log (X_{\unicode[STIX]{x1D70F}})}$
For brevity, let
![]() $\unicode[STIX]{x1D70F}$
denote either the index ‘
$\unicode[STIX]{x1D70F}$
denote either the index ‘
![]() $\unicode[STIX]{x1D70E}$
’ for some
$\unicode[STIX]{x1D70E}$
’ for some
![]() $\unicode[STIX]{x1D70E}\in \unicode[STIX]{x1D6F4}$
or the index ‘
$\unicode[STIX]{x1D70E}\in \unicode[STIX]{x1D6F4}$
or the index ‘
![]() $\unicode[STIX]{x1D706},i$
’ for some
$\unicode[STIX]{x1D706},i$
’ for some
![]() $\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}$
and
$\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}$
and
![]() $i=1,\ldots ,d$
. The log derivations
$i=1,\ldots ,d$
. The log derivations
![]() $\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\log (X_{\unicode[STIX]{x1D70F}})}$
defined in (5.10.1) with
$\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\log (X_{\unicode[STIX]{x1D70F}})}$
defined in (5.10.1) with
![]() $R_{\unicode[STIX]{x1D6F4}}^{\Box }$
or
$R_{\unicode[STIX]{x1D6F4}}^{\Box }$
or
![]() $R_{\unicode[STIX]{x1D706}}^{\Box }$
in place of
$R_{\unicode[STIX]{x1D706}}^{\Box }$
in place of
![]() $R$
give rise to the log
$R$
give rise to the log
![]() $A_{\text{inf}}$
-derivations
$A_{\text{inf}}$
-derivations
(as in §5.10, we do not explicate the accompanying homomorphisms from the log structure). These, in turn, induce the divided power
![]() $A_{\text{cris}}$
-derivations
$A_{\text{cris}}$
-derivations
(compare with Proposition 5.23 and its proof, especially (5.23.4)), where a divided power
![]() $A_{\text{cris}}$
-derivation
$A_{\text{cris}}$
-derivation
![]() $\unicode[STIX]{x2202}$
is required to satisfy
$\unicode[STIX]{x2202}$
is required to satisfy
![]() $\unicode[STIX]{x2202}(x^{[m]})=x^{[m-1]}\unicode[STIX]{x2202}(x)$
for divided powers
$\unicode[STIX]{x2202}(x^{[m]})=x^{[m-1]}\unicode[STIX]{x2202}(x)$
for divided powers
![]() $x^{[m]}$
with
$x^{[m]}$
with
![]() $m\geqslant 1$
, in addition to the
$m\geqslant 1$
, in addition to the
![]() $A_{\text{cris}}$
-linearity and the Leibniz rule.
$A_{\text{cris}}$
-linearity and the Leibniz rule.
Since
![]() $q_{\unicode[STIX]{x1D706}_{0}}$
is log étale (see §§5.26–5.27), the derivations (5.31.1) uniquely extend to log
$q_{\unicode[STIX]{x1D706}_{0}}$
is log étale (see §§5.26–5.27), the derivations (5.31.1) uniquely extend to log
![]() $A_{\text{inf}}$
-derivations
$A_{\text{inf}}$
-derivations
These, in turn, induce divided power
![]() $A_{\text{cris}}^{0}$
-derivations (see [SP, 07HW])
$A_{\text{cris}}^{0}$
-derivations (see [SP, 07HW])
By construction, the derivations (5.31.2) and (5.31.4) are compatible, so they induce
![]() $A_{\text{cris}}^{(m)}$
-derivations
$A_{\text{cris}}^{(m)}$
-derivations
that are compatible as
![]() $m$
varies and recover (5.31.2) under the identification
$m$
varies and recover (5.31.2) under the identification
Consequently, we may reexpress the identification (5.23.3) as the Frobenius-equivariant identification
where in degree
![]() $j$
of
$j$
of
![]() $K_{D_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}^{(m)}}((\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\log (X_{\unicode[STIX]{x1D70F}})})_{\unicode[STIX]{x1D70F}})$
the Frobenius acts as
$K_{D_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}^{(m)}}((\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\log (X_{\unicode[STIX]{x1D70F}})})_{\unicode[STIX]{x1D70F}})$
the Frobenius acts as
![]() $p^{j}$
times the Frobenius of
$p^{j}$
times the Frobenius of
![]() $D_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}^{(m)}$
.
$D_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}^{(m)}$
.
5.32 A functorial complex that computes
 $R\unicode[STIX]{x1D6E4}_{\log \text{cris}}(\mathfrak{X}_{{\mathcal{O}}_{C}/p}/A_{\text{cris}})$
$R\unicode[STIX]{x1D6E4}_{\log \text{cris}}(\mathfrak{X}_{{\mathcal{O}}_{C}/p}/A_{\text{cris}})$
For a fixed
![]() $R$
, the formation of the rings
$R$
, the formation of the rings
![]() $D_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}$
,
$D_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}$
,
![]() $D_{j_{\unicode[STIX]{x1D706}_{0}}}$
,
$D_{j_{\unicode[STIX]{x1D706}_{0}}}$
,
![]() $D_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}^{0}$
, and
$D_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}^{0}$
, and
![]() $D_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}^{(m)}$
and the morphisms
$D_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}^{(m)}$
and the morphisms
![]() $j_{\unicode[STIX]{x1D706}_{0}}$
and
$j_{\unicode[STIX]{x1D706}_{0}}$
and
![]() $q_{\unicode[STIX]{x1D706}_{0}}$
is compatible with enlarging
$q_{\unicode[STIX]{x1D706}_{0}}$
is compatible with enlarging
![]() $\unicode[STIX]{x1D6F4}$
and
$\unicode[STIX]{x1D6F4}$
and
![]() $\unicode[STIX]{x1D6EC}$
, and the same holds for the identification (5.31.5). Thus, we may form the filtered direct limit over all the closed immersions (5.17.1) for varying
$\unicode[STIX]{x1D6EC}$
, and the same holds for the identification (5.31.5). Thus, we may form the filtered direct limit over all the closed immersions (5.17.1) for varying
![]() $\unicode[STIX]{x1D6F4}$
and
$\unicode[STIX]{x1D6F4}$
and
![]() $\unicode[STIX]{x1D6EC}$
to build the complex
$\unicode[STIX]{x1D6EC}$
to build the complex
where the direct limits and the
![]() $p$
-adic completion are termwise. By construction, this complex comes equipped with an
$p$
-adic completion are termwise. By construction, this complex comes equipped with an
![]() $A_{\text{cris}}$
-semilinear Frobenius endomorphism (see the end of §5.31) and, by (5.31.5), in the derived category it is canonically and Frobenius-equivariantly identified with
$A_{\text{cris}}$
-semilinear Frobenius endomorphism (see the end of §5.31) and, by (5.31.5), in the derived category it is canonically and Frobenius-equivariantly identified with
Moreover, if
![]() $R^{\prime }$
is a
$R^{\prime }$
is a
![]() $p$
-adically formally étale
$p$
-adically formally étale
![]() $R$
-algebra equipped with data as in §5.17 for some sets
$R$
-algebra equipped with data as in §5.17 for some sets
![]() $\unicode[STIX]{x1D6F4}^{\prime }$
and
$\unicode[STIX]{x1D6F4}^{\prime }$
and
![]() $\unicode[STIX]{x1D6EC}^{\prime }$
, then the term indexed by
$\unicode[STIX]{x1D6EC}^{\prime }$
, then the term indexed by
![]() $\unicode[STIX]{x1D6F4}$
,
$\unicode[STIX]{x1D6F4}$
,
![]() $\unicode[STIX]{x1D6EC}$
(and by the closed immersion (5.17.1)) of the direct limit (5.32.1) maps toFootnote
12
the term indexed by
$\unicode[STIX]{x1D6EC}$
(and by the closed immersion (5.17.1)) of the direct limit (5.32.1) maps toFootnote
12
the term indexed by
![]() $\unicode[STIX]{x1D6F4}\cup \unicode[STIX]{x1D6F4}^{\prime }$
,
$\unicode[STIX]{x1D6F4}\cup \unicode[STIX]{x1D6F4}^{\prime }$
,
![]() $\unicode[STIX]{x1D6EC}\cup \unicode[STIX]{x1D6EC}^{\prime }$
(and by a closed immersion of
$\unicode[STIX]{x1D6EC}\cup \unicode[STIX]{x1D6EC}^{\prime }$
(and by a closed immersion of
![]() $\operatorname{Spf}(R^{\prime })$
) of the analogous direct limit for
$\operatorname{Spf}(R^{\prime })$
) of the analogous direct limit for
![]() $R^{\prime }$
, compatibly with the transition maps in (5.32.1) and with the Frobenius. Thus, the complex (5.32.1) equipped with its Frobenius is functorial in
$R^{\prime }$
, compatibly with the transition maps in (5.32.1) and with the Frobenius. Thus, the complex (5.32.1) equipped with its Frobenius is functorial in
![]() $R$
, and so is its identification with
$R$
, and so is its identification with
![]() $R\unicode[STIX]{x1D6E4}_{\log \text{cris}}({\mathcal{O}}_{\mathfrak{X}_{{\mathcal{O}}_{C}/p}/A_{\text{cris}}})$
.
$R\unicode[STIX]{x1D6E4}_{\log \text{cris}}({\mathcal{O}}_{\mathfrak{X}_{{\mathcal{O}}_{C}/p}/A_{\text{cris}}})$
.
Since the formation of the maps (5.23.2) is compatible with enlarging
![]() $\unicode[STIX]{x1D6F4}$
and
$\unicode[STIX]{x1D6F4}$
and
![]() $\unicode[STIX]{x1D6EC}$
, and then also with replacing
$\unicode[STIX]{x1D6EC}$
, and then also with replacing
![]() $R$
by
$R$
by
![]() $R^{\prime }$
, the map
$R^{\prime }$
, the map
![]() $R\unicode[STIX]{x1D6E4}_{\log \text{cris}}({\mathcal{O}}_{\mathfrak{X}_{{\mathcal{O}}_{C}/p}/A_{\text{cris}}})\rightarrow R\unicode[STIX]{x1D6E4}_{\log \text{dR}}(\mathfrak{X}/{\mathcal{O}}_{C})$
is identified with a map
$R\unicode[STIX]{x1D6E4}_{\log \text{cris}}({\mathcal{O}}_{\mathfrak{X}_{{\mathcal{O}}_{C}/p}/A_{\text{cris}}})\rightarrow R\unicode[STIX]{x1D6E4}_{\log \text{dR}}(\mathfrak{X}/{\mathcal{O}}_{C})$
is identified with a map
whose formation is compatible with replacing
![]() $R$
by
$R$
by
![]() $R^{\prime }$
.
$R^{\prime }$
.
Having constructed the functorial complexes (5.21.1) and (5.32.1), we seek to exhibit a natural map between them and to prove that it is an isomorphism. These tasks, which will be completed in §5.38 and Proposition 5.39, are the last stepping stones to the proof of Theorem 5.4 given in §5.40. We begin with the following variants of Lemma 5.15 and Proposition 5.16.
Lemma 5.33. For
![]() $m\geqslant p^{2}$
, the element
$m\geqslant p^{2}$
, the element
![]() $\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D70F}}\in \unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}$
, where the index
$\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D70F}}\in \unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}$
, where the index
![]() $\unicode[STIX]{x1D70F}$
is either ‘
$\unicode[STIX]{x1D70F}$
is either ‘
![]() $\unicode[STIX]{x1D70E}$
’ for some
$\unicode[STIX]{x1D70E}$
’ for some
![]() $\unicode[STIX]{x1D70E}\in \unicode[STIX]{x1D6F4}$
or ‘
$\unicode[STIX]{x1D70E}\in \unicode[STIX]{x1D6F4}$
or ‘
![]() $\unicode[STIX]{x1D706},i$
’ for some
$\unicode[STIX]{x1D706},i$
’ for some
![]() $\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}$
and
$\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}$
and
![]() $i=1,\ldots ,d$
(see §5.18), acts on
$i=1,\ldots ,d$
(see §5.18), acts on
![]() $D_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}^{(m)}$
as the endomorphism
$D_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}^{(m)}$
as the endomorphism
where
![]() $\frac{(\log ([\unicode[STIX]{x1D716}]))^{n}}{n!}$
lies in
$\frac{(\log ([\unicode[STIX]{x1D716}]))^{n}}{n!}$
lies in
![]() $A_{\text{cris}}^{(m)}$
and
$A_{\text{cris}}^{(m)}$
and
![]() $p$
-adically tends to
$p$
-adically tends to
![]() $0$
(see §5.14).
$0$
(see §5.14).
Proof. Analogously to the proof of Lemma 5.15, the series (5.33.1) a priori defines an
![]() $A_{\text{cris}}$
-algebra endomorphism of
$A_{\text{cris}}$
-algebra endomorphism of
![]() $D_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}$
. Moreover, by Lemma 5.15, the action of
$D_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}$
. Moreover, by Lemma 5.15, the action of
![]() $\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D70F}}$
on the ring
$\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D70F}}$
on the ring
![]() $A_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC},\,\text{cris}}^{\Box }$
defined in (5.22.2) is given by (5.33.1). Thus, due to the universal properties (5.26.3) and (5.27.3), the same holds for the action of
$A_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC},\,\text{cris}}^{\Box }$
defined in (5.22.2) is given by (5.33.1). Thus, due to the universal properties (5.26.3) and (5.27.3), the same holds for the action of
![]() $\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D70F}}$
on
$\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D70F}}$
on
(see (5.31.3)), where the completion is
![]() $p$
-adic. Then, by the universal property of
$p$
-adic. Then, by the universal property of
![]() $D_{j_{\unicode[STIX]{x1D706}_{0}}}$
(see §5.28) and (5.29.1), the element
$D_{j_{\unicode[STIX]{x1D706}_{0}}}$
(see §5.28) and (5.29.1), the element
![]() $\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D70F}}$
acts on
$\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D70F}}$
acts on
![]() $D_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}$
, and hence also on
$D_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}$
, and hence also on
![]() $D_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}^{0,\,(m)}$
and
$D_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}^{0,\,(m)}$
and
![]() $D_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}^{(m)}$
, by the series (5.33.1).◻
$D_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}^{(m)}$
, by the series (5.33.1).◻
Proposition 5.34. In the local setting of §5.17, for
![]() $m\geqslant p^{2}$
, the additive morphisms
$m\geqslant p^{2}$
, the additive morphisms
of complexes in degree
![]() $0$
and
$0$
and
![]() $1$
, where the index
$1$
, where the index
![]() $\unicode[STIX]{x1D70F}$
ranges over ‘
$\unicode[STIX]{x1D70F}$
ranges over ‘
![]() $\unicode[STIX]{x1D70E}$
’ for
$\unicode[STIX]{x1D70E}$
’ for
![]() $\unicode[STIX]{x1D70E}\in \unicode[STIX]{x1D6F4}$
and ‘
$\unicode[STIX]{x1D70E}\in \unicode[STIX]{x1D6F4}$
and ‘
![]() $\unicode[STIX]{x1D706},i$
’ for
$\unicode[STIX]{x1D706},i$
’ for
![]() $\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}$
and
$\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}$
and
![]() $i=1,\ldots ,d$
, define a Frobenius-equivariant morphism (whose target is defined as in (1.7.3))
$i=1,\ldots ,d$
, define a Frobenius-equivariant morphism (whose target is defined as in (1.7.3))
where in each degree
![]() $j$
of the source the Frobenius acts as
$j$
of the source the Frobenius acts as
![]() $p^{j}$
times the Frobenius of
$p^{j}$
times the Frobenius of
![]() $D_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}^{(m)}$
.
$D_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}^{(m)}$
.
Proof. By Lemma 5.33, the morphism (5.34.1) is well defined. Moreover, the image of its degree
![]() $1$
component lies in
$1$
component lies in
![]() $\unicode[STIX]{x1D707}\cdot D_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}^{(m)}$
because, by §5.14, the element
$\unicode[STIX]{x1D707}\cdot D_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}^{(m)}$
because, by §5.14, the element
![]() $\frac{(\log ([\unicode[STIX]{x1D716}]))^{n}}{\unicode[STIX]{x1D707}\,\cdot \,n!}$
lies in
$\frac{(\log ([\unicode[STIX]{x1D716}]))^{n}}{\unicode[STIX]{x1D707}\,\cdot \,n!}$
lies in
![]() $A_{\text{cris}}^{(m)}$
and
$A_{\text{cris}}^{(m)}$
and
![]() $p$
-adically tends to
$p$
-adically tends to
![]() $0$
. The rest of the claim then follows from the definitions (1.7.2) and (1.7.3), granted that one argues the Frobenius-equivariance as in the proof of Proposition 5.16.◻
$0$
. The rest of the claim then follows from the definitions (1.7.2) and (1.7.3), granted that one argues the Frobenius-equivariance as in the proof of Proposition 5.16.◻
Proposition 5.34 reduces the task of exhibiting a natural map from the complex (5.32.1) to the complex (5.21.1) to exhibiting a natural
![]() $\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}$
-equivariant ring morphism
$\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}$
-equivariant ring morphism
To build the latter, we will realize
![]() $\mathbb{A}_{\text{cris}}^{(m)}(R_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC},\,\infty })$
inside the following ring
$\mathbb{A}_{\text{cris}}^{(m)}(R_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC},\,\infty })$
inside the following ring
![]() $\mathbb{A}_{\text{cris}}(R_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC},\,\infty })$
.
$\mathbb{A}_{\text{cris}}(R_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC},\,\infty })$
.
5.35 The ring
 $\mathbb{A}_{\text{cris}}(R_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC},\,\infty })$
$\mathbb{A}_{\text{cris}}(R_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC},\,\infty })$
For an affinoid perfectoid
![]() $\operatorname{Spa}(R_{\infty }^{\prime }[\frac{1}{p}],R_{\infty }^{\prime })$
over
$\operatorname{Spa}(R_{\infty }^{\prime }[\frac{1}{p}],R_{\infty }^{\prime })$
over
![]() $\operatorname{Spa}(C,{\mathcal{O}}_{C})$
(such as that with
$\operatorname{Spa}(C,{\mathcal{O}}_{C})$
(such as that with
![]() $R_{\infty }^{\prime }=R_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC},\,\infty }$
), we consider the
$R_{\infty }^{\prime }=R_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC},\,\infty }$
), we consider the
![]() $\mathbb{A}_{\text{inf}}(R_{\infty }^{\prime })$
-subalgebra
$\mathbb{A}_{\text{inf}}(R_{\infty }^{\prime })$
-subalgebra
generated by the elements
![]() $\unicode[STIX]{x1D709}^{n}/n!$
for
$\unicode[STIX]{x1D709}^{n}/n!$
for
![]() $n\geqslant 1$
. Analogously to §5.8, by [Reference TsujiTsu99, proof of A2.8], we have
$n\geqslant 1$
. Analogously to §5.8, by [Reference TsujiTsu99, proof of A2.8], we have
Thus, analogously to §5.8, the ring
![]() $\mathbb{A}_{\text{cris}}^{0}(R_{\infty }^{\prime })$
is identified with the divided power envelope of
$\mathbb{A}_{\text{cris}}^{0}(R_{\infty }^{\prime })$
is identified with the divided power envelope of
![]() $(\mathbb{A}_{\text{inf}}(R_{\infty }^{\prime }),\operatorname{Ker}(\unicode[STIX]{x1D703})+p\,\cdot \,\mathbb{A}_{\text{inf}}(R_{\infty }^{\prime }))$
over
$(\mathbb{A}_{\text{inf}}(R_{\infty }^{\prime }),\operatorname{Ker}(\unicode[STIX]{x1D703})+p\,\cdot \,\mathbb{A}_{\text{inf}}(R_{\infty }^{\prime }))$
over
![]() $(\mathbb{Z}_{p},p\mathbb{Z}_{p})$
, and
$(\mathbb{Z}_{p},p\mathbb{Z}_{p})$
, and
For an
![]() $m\in \mathbb{Z}_{{\geqslant}1}$
, we let
$m\in \mathbb{Z}_{{\geqslant}1}$
, we let
![]() $\mathbb{A}_{\text{cris}}^{0,\,(m)}(R_{\infty }^{\prime })\subset \mathbb{A}_{\text{cris}}^{0}(R_{\infty }^{\prime })$
be the
$\mathbb{A}_{\text{cris}}^{0,\,(m)}(R_{\infty }^{\prime })\subset \mathbb{A}_{\text{cris}}^{0}(R_{\infty }^{\prime })$
be the
![]() $\mathbb{A}_{\text{inf}}(R_{\infty }^{\prime })$
-subalgebra generated by the elements
$\mathbb{A}_{\text{inf}}(R_{\infty }^{\prime })$
-subalgebra generated by the elements
![]() $\unicode[STIX]{x1D709}^{n}/n!$
with
$\unicode[STIX]{x1D709}^{n}/n!$
with
![]() $n\leqslant m$
(compare with §3.26). For a fixed
$n\leqslant m$
(compare with §3.26). For a fixed
![]() $m$
, the subalgebra
$m$
, the subalgebra
is described by explicit lower bounds on the ‘
![]() $p$
-adic valuations’ of the coefficients of
$p$
-adic valuations’ of the coefficients of
![]() $T^{N}$
for
$T^{N}$
for
![]() $N\geqslant 1$
. Thus, since the sequence
$N\geqslant 1$
. Thus, since the sequence
![]() $(p,\unicode[STIX]{x1D709})$
is
$(p,\unicode[STIX]{x1D709})$
is
![]() $\mathbb{A}_{\text{inf}}(R_{\infty }^{\prime })$
-regular (compare with Lemma 3.13), the quotient of
$\mathbb{A}_{\text{inf}}(R_{\infty }^{\prime })$
-regular (compare with Lemma 3.13), the quotient of
![]() $\mathbb{A}_{\text{inf}}(R_{\infty }^{\prime })[\frac{T^{n}}{n!}]_{n\geqslant 1}$
by
$\mathbb{A}_{\text{inf}}(R_{\infty }^{\prime })[\frac{T^{n}}{n!}]_{n\geqslant 1}$
by
![]() $\mathbb{A}_{\text{inf}}(R_{\infty }^{\prime })[\frac{T^{n}}{n!}]_{m\geqslant n\geqslant 1}$
has no nonzero
$\mathbb{A}_{\text{inf}}(R_{\infty }^{\prime })[\frac{T^{n}}{n!}]_{m\geqslant n\geqslant 1}$
has no nonzero
![]() $(T-\unicode[STIX]{x1D709})$
-torsion. Consequently,
$(T-\unicode[STIX]{x1D709})$
-torsion. Consequently,
to the effect that
Thus, by letting the completion be
![]() $p$
-adic if
$p$
-adic if
![]() $m\geqslant p$
and
$m\geqslant p$
and
![]() $(p,\unicode[STIX]{x1D707})$
-adic if
$(p,\unicode[STIX]{x1D707})$
-adic if
![]() $m<p$
, we obtain the following identification with the
$m<p$
, we obtain the following identification with the
![]() $A_{\text{cris}}^{(m)}$
-algebra
$A_{\text{cris}}^{(m)}$
-algebra
![]() $\mathbb{A}_{\text{cris}}^{(m)}(R_{\infty }^{\prime })$
defined as in (5.19.3):
$\mathbb{A}_{\text{cris}}^{(m)}(R_{\infty }^{\prime })$
defined as in (5.19.3):
Proposition 5.36. For an affinoid perfectoid
![]() $\operatorname{Spa}(R_{\infty }^{\prime }[\frac{1}{p}],R_{\infty }^{\prime })$
over
$\operatorname{Spa}(R_{\infty }^{\prime }[\frac{1}{p}],R_{\infty }^{\prime })$
over
![]() $\operatorname{Spa}(C,{\mathcal{O}}_{C})$
and an
$\operatorname{Spa}(C,{\mathcal{O}}_{C})$
and an
![]() $m\geqslant 1$
, the following ring homomorphisms are injective:
$m\geqslant 1$
, the following ring homomorphisms are injective:
where the completion is
![]() $\unicode[STIX]{x1D709}$
-adic and the definition of the last map is explained in the proof. In particular, the
$\unicode[STIX]{x1D709}$
-adic and the definition of the last map is explained in the proof. In particular, the
![]() $A_{\text{inf}}$
-algebras in (5.36.1) have no nonzero
$A_{\text{inf}}$
-algebras in (5.36.1) have no nonzero
![]() $\unicode[STIX]{x1D707}$
-torsion.
$\unicode[STIX]{x1D707}$
-torsion.
Proof. The assertion about the
![]() $\unicode[STIX]{x1D707}$
-torsion follows from the rest because
$\unicode[STIX]{x1D707}$
-torsion follows from the rest because
![]() $\unicode[STIX]{x1D707}/\unicode[STIX]{x1D709}$
is a unit in
$\unicode[STIX]{x1D707}/\unicode[STIX]{x1D709}$
is a unit in
![]() $\mathbb{B}_{\text{dR}}^{+}(R_{\infty }^{\prime })$
(see (2.1.1)–(2.1.4)) and
$\mathbb{B}_{\text{dR}}^{+}(R_{\infty }^{\prime })$
(see (2.1.1)–(2.1.4)) and
![]() $\mathbb{B}_{\text{dR}}^{+}(R_{\infty }^{\prime })$
inherits
$\mathbb{B}_{\text{dR}}^{+}(R_{\infty }^{\prime })$
inherits
![]() $\unicode[STIX]{x1D709}$
-torsion freeness from
$\unicode[STIX]{x1D709}$
-torsion freeness from
![]() $\mathbb{A}_{\text{inf}}(R_{\infty }^{\prime })$
.
$\mathbb{A}_{\text{inf}}(R_{\infty }^{\prime })$
.
The sequence
![]() $(p,\unicode[STIX]{x1D709})$
is
$(p,\unicode[STIX]{x1D709})$
is
![]() $\mathbb{A}_{\text{inf}}(R_{\infty }^{\prime })$
-regular and
$\mathbb{A}_{\text{inf}}(R_{\infty }^{\prime })$
-regular and
![]() $\mathbb{A}_{\text{inf}}(R_{\infty }^{\prime })$
is
$\mathbb{A}_{\text{inf}}(R_{\infty }^{\prime })$
is
![]() $\unicode[STIX]{x1D709}$
-adically separated (see [SP, 090T]), so the ring
$\unicode[STIX]{x1D709}$
-adically separated (see [SP, 090T]), so the ring
![]() $\mathbb{A}_{\text{inf}}(R_{\infty }^{\prime })[\frac{1}{p}]$
is also
$\mathbb{A}_{\text{inf}}(R_{\infty }^{\prime })[\frac{1}{p}]$
is also
![]() $\unicode[STIX]{x1D709}$
-adically separated. Thus, we obtain the injection
$\unicode[STIX]{x1D709}$
-adically separated. Thus, we obtain the injection
which, in particular, allows us to assume that
![]() $m\geqslant p$
. For varying
$m\geqslant p$
. For varying
![]() $n\geqslant 0$
, the
$n\geqslant 0$
, the
![]() $\mathbb{A}_{\text{inf}}(R_{\infty }^{\prime })$
-submodules
$\mathbb{A}_{\text{inf}}(R_{\infty }^{\prime })$
-submodules
form a decreasing filtration of
![]() $\mathbb{A}_{\text{cris}}^{0}(R_{\infty }^{\prime })$
by ideals. By [Reference TsujiTsu99, A2.9(2)],Footnote
13
each
$\mathbb{A}_{\text{cris}}^{0}(R_{\infty }^{\prime })$
by ideals. By [Reference TsujiTsu99, A2.9(2)],Footnote
13
each
Thus, the
![]() $p$
-adic completions
$p$
-adic completions
![]() $\operatorname{Fil}_{n}:=(\operatorname{Fil}_{n}^{0})\widehat{~~}$
form a decreasing filtration of
$\operatorname{Fil}_{n}:=(\operatorname{Fil}_{n}^{0})\widehat{~~}$
form a decreasing filtration of
![]() $\mathbb{A}_{\text{cris}}(R_{\infty }^{\prime })$
by ideals with
$\mathbb{A}_{\text{cris}}(R_{\infty }^{\prime })$
by ideals with
The
![]() $p$
-torsion freeness also supplies a decreasing filtration modulo
$p$
-torsion freeness also supplies a decreasing filtration modulo
![]() $p$
:
$p$
:
The isomorphism
![]() $\mathbb{A}_{\text{cris}}^{0}(R_{\infty }^{\prime })\cong (\mathbb{A}_{\text{inf}}(R_{\infty }^{\prime })[T^{n}/n!]_{n\geqslant 1})/(T-\unicode[STIX]{x1D709})$
gives the explicit description
$\mathbb{A}_{\text{cris}}^{0}(R_{\infty }^{\prime })\cong (\mathbb{A}_{\text{inf}}(R_{\infty }^{\prime })[T^{n}/n!]_{n\geqslant 1})/(T-\unicode[STIX]{x1D709})$
gives the explicit description
(compare with [Reference Brinon and ConradBC09, 9.4.1(3)]), so the filtration
![]() $\{\operatorname{Fil}_{n}^{0}/p\operatorname{Fil}_{n}^{0}\}\text{}_{n\geqslant 0}$
is separated. Thus, since
$\{\operatorname{Fil}_{n}^{0}/p\operatorname{Fil}_{n}^{0}\}\text{}_{n\geqslant 0}$
is separated. Thus, since
the
![]() $p$
-adic separatedness of
$p$
-adic separatedness of
![]() $\mathbb{A}_{\text{cris}}(R_{\infty }^{\prime })$
and (5.36.2) force the filtration
$\mathbb{A}_{\text{cris}}(R_{\infty }^{\prime })$
and (5.36.2) force the filtration
![]() $\{\operatorname{Fil}_{n}\}\text{}_{n\geqslant 0}$
to be separated too:
$\{\operatorname{Fil}_{n}\}\text{}_{n\geqslant 0}$
to be separated too:
Moreover, we have the injection
![]() $\mathop{\varprojlim }\nolimits_{n}\,(\mathbb{A}_{\text{cris}}^{0}(R_{\infty }^{\prime })/\operatorname{Fil}_{n}^{0}){\hookrightarrow}\mathbb{B}_{\text{dR}}^{+}(R_{\infty }^{\prime })$
that results from the injections
$\mathop{\varprojlim }\nolimits_{n}\,(\mathbb{A}_{\text{cris}}^{0}(R_{\infty }^{\prime })/\operatorname{Fil}_{n}^{0}){\hookrightarrow}\mathbb{B}_{\text{dR}}^{+}(R_{\infty }^{\prime })$
that results from the injections
Thus, we obtain the desired natural injection
![]() $\mathbb{A}_{\text{cris}}(R_{\infty }^{\prime }){\hookrightarrow}\mathbb{B}_{\text{dR}}^{+}(R_{\infty }^{\prime })$
of
$\mathbb{A}_{\text{cris}}(R_{\infty }^{\prime }){\hookrightarrow}\mathbb{B}_{\text{dR}}^{+}(R_{\infty }^{\prime })$
of
![]() $\mathbb{A}_{\text{cris}}^{0}(R_{\infty }^{\prime })$
-algebras.
$\mathbb{A}_{\text{cris}}^{0}(R_{\infty }^{\prime })$
-algebras.
We turn to the remaining injection
![]() $\mathbb{A}_{\text{cris}}^{(m)}(R_{\infty }^{\prime }){\hookrightarrow}\mathbb{A}_{\text{cris}}(R_{\infty }^{\prime })$
. For
$\mathbb{A}_{\text{cris}}^{(m)}(R_{\infty }^{\prime }){\hookrightarrow}\mathbb{A}_{\text{cris}}(R_{\infty }^{\prime })$
. For
![]() $n\geqslant 0$
, we consider the ideal
$n\geqslant 0$
, we consider the ideal
so that
![]() $\{\operatorname{Fil}_{n}^{0,\,(m)}\}\text{}_{n\geqslant 0}$
forms a filtration of
$\{\operatorname{Fil}_{n}^{0,\,(m)}\}\text{}_{n\geqslant 0}$
forms a filtration of
![]() $\mathbb{A}_{\text{cris}}^{0,\,(m)}(R_{\infty }^{\prime })$
. Explicitly, as an
$\mathbb{A}_{\text{cris}}^{0,\,(m)}(R_{\infty }^{\prime })$
. Explicitly, as an
![]() $\mathbb{A}_{\text{inf}}(R_{\infty }^{\prime })$
-module,
$\mathbb{A}_{\text{inf}}(R_{\infty }^{\prime })$
-module,
![]() $\operatorname{Fil}_{n}^{0,\,(m)}$
is generated by the products
$\operatorname{Fil}_{n}^{0,\,(m)}$
is generated by the products
![]() $\unicode[STIX]{x1D709}^{n_{1}}/n_{1}!\cdots \unicode[STIX]{x1D709}^{n_{s}}/n_{s}!$
with
$\unicode[STIX]{x1D709}^{n_{1}}/n_{1}!\cdots \unicode[STIX]{x1D709}^{n_{s}}/n_{s}!$
with
![]() $n_{1}+\cdots +n_{s}\geqslant n$
and
$n_{1}+\cdots +n_{s}\geqslant n$
and
![]() $0\leqslant n_{i}\leqslant m$
. By (5.36.2), each
$0\leqslant n_{i}\leqslant m$
. By (5.36.2), each
so we again get the induced filtration modulo
![]() $p$
:
$p$
:
As in the case of
![]() $\{\operatorname{Fil}_{n}^{0}/p\operatorname{Fil}_{n}^{0}\}\text{}_{n\geqslant 0}$
, the analogous to (5.36.4) description of
$\{\operatorname{Fil}_{n}^{0}/p\operatorname{Fil}_{n}^{0}\}\text{}_{n\geqslant 0}$
, the analogous to (5.36.4) description of
supplied by the isomorphism (5.35.1) shows that the filtration
![]() $\{\operatorname{Fil}_{n}^{0,\,(m)}\!/p\operatorname{Fil}_{n}^{0,\,(m)}\}\text{}_{n\geqslant 0}$
is separated.
$\{\operatorname{Fil}_{n}^{0,\,(m)}\!/p\operatorname{Fil}_{n}^{0,\,(m)}\}\text{}_{n\geqslant 0}$
is separated.
For each
![]() $n>0$
, there is a
$n>0$
, there is a
![]() $j_{n}>0$
such that
$j_{n}>0$
such that
![]() $p^{j_{n}}$
kills
$p^{j_{n}}$
kills
(for instance,
![]() $j_{n}:=\operatorname{ord}_{p}(n!)$
has this property). Consequently,
$j_{n}:=\operatorname{ord}_{p}(n!)$
has this property). Consequently,
![]() $p^{j_{n}}$
kills the kernel of the map
$p^{j_{n}}$
kills the kernel of the map
so, for
![]() $j>j_{n}$
, every element of this kernel is a multiple of
$j>j_{n}$
, every element of this kernel is a multiple of
![]() $p^{j-j_{n}}$
. The short exact sequences
$p^{j-j_{n}}$
. The short exact sequences
then show that for each
![]() $n>0$
, every element of the kernel
$n>0$
, every element of the kernel
lies in
![]() $\mathop{\varprojlim }\nolimits_{j>0}(\operatorname{Fil}_{n}^{0,\,(m)}/p^{j}\operatorname{Fil}_{n}^{0,\,(m)})$
. In particular, this kernel maps to
$\mathop{\varprojlim }\nolimits_{j>0}(\operatorname{Fil}_{n}^{0,\,(m)}/p^{j}\operatorname{Fil}_{n}^{0,\,(m)})$
. In particular, this kernel maps to
![]() $\operatorname{Fil}_{n}^{0,\,(m)}/p\subset \mathbb{A}_{\text{cris}}^{0,\,(m)}(R_{\infty }^{\prime })/p$
for each
$\operatorname{Fil}_{n}^{0,\,(m)}/p\subset \mathbb{A}_{\text{cris}}^{0,\,(m)}(R_{\infty }^{\prime })/p$
for each
![]() $n>0$
. However, by the previous paragraph,
$n>0$
. However, by the previous paragraph,
![]() $\bigcap _{n>0}\,(\operatorname{Fil}_{n}^{0,\,(m)}/p)=0$
, so the kernel (5.36.6) lies in
$\bigcap _{n>0}\,(\operatorname{Fil}_{n}^{0,\,(m)}/p)=0$
, so the kernel (5.36.6) lies in
![]() $p\cdot \mathbb{A}_{\text{cris}}^{(m)}(R_{\infty }^{\prime })$
. Since
$p\cdot \mathbb{A}_{\text{cris}}^{(m)}(R_{\infty }^{\prime })$
. Since
![]() $\mathbb{A}_{\text{cris}}(R_{\infty }^{\prime })$
has no nonzero
$\mathbb{A}_{\text{cris}}(R_{\infty }^{\prime })$
has no nonzero
![]() $p$
-torsion and
$p$
-torsion and
![]() $\mathbb{A}_{\text{cris}}^{(m)}(R_{\infty }^{\prime })$
is
$\mathbb{A}_{\text{cris}}^{(m)}(R_{\infty }^{\prime })$
is
![]() $p$
-adically separated, this implies that the map
$p$
-adically separated, this implies that the map
![]() $\mathbb{A}_{\text{cris}}^{(m)}(R_{\infty }^{\prime })\rightarrow \mathbb{A}_{\text{cris}}(R_{\infty }^{\prime })$
is injective, as desired.◻
$\mathbb{A}_{\text{cris}}^{(m)}(R_{\infty }^{\prime })\rightarrow \mathbb{A}_{\text{cris}}(R_{\infty }^{\prime })$
is injective, as desired.◻
The following lemma is the final step to building the desired map
![]() $D_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}^{(m)}\rightarrow \mathbb{A}_{\text{cris}}^{(m)}(R_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC},\,\infty })$
in §5.38.
$D_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}^{(m)}\rightarrow \mathbb{A}_{\text{cris}}^{(m)}(R_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC},\,\infty })$
in §5.38.
Lemma 5.37. For
![]() $\unicode[STIX]{x1D706}_{0}\in \unicode[STIX]{x1D6EC}$
, there is a
$\unicode[STIX]{x1D706}_{0}\in \unicode[STIX]{x1D6EC}$
, there is a
![]() $\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}$
-equivariant divided power morphism
$\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}$
-equivariant divided power morphism
that is compatible with the isomorphisms
![]() $D_{j_{\unicode[STIX]{x1D706}_{0}}}\cong D_{j_{\unicode[STIX]{x1D706}_{0}^{\prime }}}$
of (5.28.1) and is Frobenius-equivariant.
$D_{j_{\unicode[STIX]{x1D706}_{0}}}\cong D_{j_{\unicode[STIX]{x1D706}_{0}^{\prime }}}$
of (5.28.1) and is Frobenius-equivariant.
Proof. By construction,
![]() $\mathbb{A}_{\text{inf}}(R_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC},\,\infty })$
is an
$\mathbb{A}_{\text{inf}}(R_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC},\,\infty })$
is an
![]() $A_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}^{\Box }$
-algebra. Moreover, since
$A_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}^{\Box }$
-algebra. Moreover, since
![]() $\mathbb{A}_{\text{inf}}(R_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC},\,\infty })$
is
$\mathbb{A}_{\text{inf}}(R_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC},\,\infty })$
is
![]() $\unicode[STIX]{x1D709}$
-adically complete with
$\unicode[STIX]{x1D709}$
-adically complete with
![]() $\mathbb{A}_{\text{inf}}(R_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC},\,\infty })/\unicode[STIX]{x1D709}\cong R_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC},\,\infty }$
(see §5.19), if
$\mathbb{A}_{\text{inf}}(R_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC},\,\infty })/\unicode[STIX]{x1D709}\cong R_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC},\,\infty }$
(see §5.19), if
![]() $t_{\unicode[STIX]{x1D706},\,i}$
is a unit in
$t_{\unicode[STIX]{x1D706},\,i}$
is a unit in
![]() $R\subset R_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC},\,\infty }$
, then
$R\subset R_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC},\,\infty }$
, then
![]() $X_{\unicode[STIX]{x1D706},\,i}$
is a unit in
$X_{\unicode[STIX]{x1D706},\,i}$
is a unit in
![]() $\mathbb{A}_{\text{inf}}(R_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC},\,\infty })$
(see (3.14.3)). Thus, if
$\mathbb{A}_{\text{inf}}(R_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC},\,\infty })$
(see (3.14.3)). Thus, if
![]() $R\otimes _{{\mathcal{O}}_{C}}k$
is
$R\otimes _{{\mathcal{O}}_{C}}k$
is
![]() $k$
-smooth, then equations (5.26.3) have a unique solution in
$k$
-smooth, then equations (5.26.3) have a unique solution in
![]() $\mathbb{A}_{\text{inf}}(R_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC},\,\infty })$
, to the effect that, in this case,
$\mathbb{A}_{\text{inf}}(R_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC},\,\infty })$
, to the effect that, in this case,
![]() $\mathbb{A}_{\text{inf}}(R_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC},\,\infty })$
is naturally and
$\mathbb{A}_{\text{inf}}(R_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC},\,\infty })$
is naturally and
![]() $\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}$
-equivariantly an
$\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}$
-equivariantly an
![]() $(A_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}^{\Box }\otimes _{\mathbb{Z}[Q]}\mathbb{Z}[P_{\unicode[STIX]{x1D706}_{0}}])$
-algebra, compatibly with the ‘change of
$(A_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}^{\Box }\otimes _{\mathbb{Z}[Q]}\mathbb{Z}[P_{\unicode[STIX]{x1D706}_{0}}])$
-algebra, compatibly with the ‘change of
![]() $\unicode[STIX]{x1D706}_{0}$
’ isomorphisms of (5.26.7), the maps (5.26.4) and (5.19.1) to
$\unicode[STIX]{x1D706}_{0}$
’ isomorphisms of (5.26.7), the maps (5.26.4) and (5.19.1) to
![]() $R$
and
$R$
and
![]() $R_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC},\,\infty }$
, and the Frobenii.
$R_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC},\,\infty }$
, and the Frobenii.
If
![]() $R\otimes _{{\mathcal{O}}_{C}}k$
is not
$R\otimes _{{\mathcal{O}}_{C}}k$
is not
![]() $k$
-smooth, then, in the notation of §5.27, for each
$k$
-smooth, then, in the notation of §5.27, for each
![]() $m\geqslant 0$
and a generic point
$m\geqslant 0$
and a generic point
![]() $y\in {\mathcal{Y}}$
of
$y\in {\mathcal{Y}}$
of
![]() $\operatorname{Spec}(R\otimes _{{\mathcal{O}}_{C}}k)$
, the element
$\operatorname{Spec}(R\otimes _{{\mathcal{O}}_{C}}k)$
, the element
![]() $t_{\unicode[STIX]{x1D706}_{0},\,i_{\unicode[STIX]{x1D706}_{0}}(y)}^{1/p^{m}}$
is not a zero divisor in
$t_{\unicode[STIX]{x1D706}_{0},\,i_{\unicode[STIX]{x1D706}_{0}}(y)}^{1/p^{m}}$
is not a zero divisor in
![]() $R_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC},\,\infty }$
and is a unit in
$R_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC},\,\infty }$
and is a unit in
![]() $R_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC},\,\infty }[\frac{1}{p}]$
. Thus, since
$R_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC},\,\infty }[\frac{1}{p}]$
. Thus, since
![]() $R_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC},\,\infty }$
is integrally closed in
$R_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC},\,\infty }$
is integrally closed in
![]() $R_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC},\,\infty }[\frac{1}{p}]$
, we conclude from (5.27.1) that
$R_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC},\,\infty }[\frac{1}{p}]$
, we conclude from (5.27.1) that
In other words,
By the uniqueness,
![]() $(u_{\unicode[STIX]{x1D706},\,\unicode[STIX]{x1D706}_{0},\,y}^{(m+1)})^{p}=u_{\unicode[STIX]{x1D706},\,\unicode[STIX]{x1D706}_{0},\,y}^{(m)}$
, so
$(u_{\unicode[STIX]{x1D706},\,\unicode[STIX]{x1D706}_{0},\,y}^{(m+1)})^{p}=u_{\unicode[STIX]{x1D706},\,\unicode[STIX]{x1D706}_{0},\,y}^{(m)}$
, so
![]() $u_{\unicode[STIX]{x1D706},\,\unicode[STIX]{x1D706}_{0},\,y}^{\flat }:=(u_{\unicode[STIX]{x1D706},\,\unicode[STIX]{x1D706}_{0},\,y}^{(m)})_{m\geqslant 0}\in (R_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC},\,\infty }^{\flat })^{\times }$
satisfies
$u_{\unicode[STIX]{x1D706},\,\unicode[STIX]{x1D706}_{0},\,y}^{\flat }:=(u_{\unicode[STIX]{x1D706},\,\unicode[STIX]{x1D706}_{0},\,y}^{(m)})_{m\geqslant 0}\in (R_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC},\,\infty }^{\flat })^{\times }$
satisfies
(see §§3.11 and 3.14). Thus, since each
![]() $X_{\unicode[STIX]{x1D706},\,i}$
is a nonzero-divisor in
$X_{\unicode[STIX]{x1D706},\,i}$
is a nonzero-divisor in
![]() $\mathbb{A}_{\text{inf}}(R_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC},\,\infty })$
, the
$\mathbb{A}_{\text{inf}}(R_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC},\,\infty })$
, the
![]() $[u_{\unicode[STIX]{x1D706},\,\unicode[STIX]{x1D706}_{0},\,y}^{\flat }]$
solve the equations (5.27.3) in
$[u_{\unicode[STIX]{x1D706},\,\unicode[STIX]{x1D706}_{0},\,y}^{\flat }]$
solve the equations (5.27.3) in
![]() $\mathbb{A}_{\text{inf}}(R_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC},\,\infty })$
, compatibly with the solution in
$\mathbb{A}_{\text{inf}}(R_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC},\,\infty })$
, compatibly with the solution in
![]() $R\subset R_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC},\,\infty }$
of (5.27.4). Thus, in the nonsmooth case as well,
$R\subset R_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC},\,\infty }$
of (5.27.4). Thus, in the nonsmooth case as well,
![]() $\mathbb{A}_{\text{inf}}(R_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC},\,\infty })$
is
$\mathbb{A}_{\text{inf}}(R_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC},\,\infty })$
is
![]() $\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}$
-equivariantly an algebra over
$\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}$
-equivariantly an algebra over
![]() $A_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}^{\Box }\otimes _{\mathbb{Z}[Q]}\mathbb{Z}[P_{\unicode[STIX]{x1D706}_{0}}]$
, compatibly with the change of
$A_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}^{\Box }\otimes _{\mathbb{Z}[Q]}\mathbb{Z}[P_{\unicode[STIX]{x1D706}_{0}}]$
, compatibly with the change of
![]() $\unicode[STIX]{x1D706}_{0}$
, the maps (5.27.4) and (5.19.1) to
$\unicode[STIX]{x1D706}_{0}$
, the maps (5.27.4) and (5.19.1) to
![]() $R$
and
$R$
and
![]() $R_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC},\,\infty }$
, and the Frobenii.
$R_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC},\,\infty }$
, and the Frobenii.
In conclusion, in all the cases we obtain a commutative square which is compatible with the change of
![]() $\unicode[STIX]{x1D706}_{0}$
:
$\unicode[STIX]{x1D706}_{0}$
:

The universal property of
![]() $D_{j_{\unicode[STIX]{x1D706}_{0}}}$
then supplies the desired divided power morphism (5.37.1).◻
$D_{j_{\unicode[STIX]{x1D706}_{0}}}$
then supplies the desired divided power morphism (5.37.1).◻
5.38 The comparison map
The
![]() $p$
-adic completion of the morphism (5.37.1) is the morphism
$p$
-adic completion of the morphism (5.37.1) is the morphism
(see Lemma 5.29), which does not depend on
![]() $\unicode[STIX]{x1D706}_{0}$
. By construction, it makes the following diagram commute.
$\unicode[STIX]{x1D706}_{0}$
. By construction, it makes the following diagram commute.

Its restriction to
![]() $D_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}^{0,\,(m)}$
of §5.30 lands in the subring
$D_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}^{0,\,(m)}$
of §5.30 lands in the subring ![]() , so, by passing to
, so, by passing to
![]() $p$
-adic completions and using (5.35.2), we obtain the compatible morphisms
$p$
-adic completions and using (5.35.2), we obtain the compatible morphisms
that recover (5.38.1) via the identifications (5.30.1) and (5.1.1). By construction and Lemma 5.37, the morphisms (5.38.3) are
![]() $\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}$
-equivariant and Frobenius-equivariant, so they give rise to the Frobenius-equivariant morphisms of complexes
$\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}$
-equivariant and Frobenius-equivariant, so they give rise to the Frobenius-equivariant morphisms of complexes
After applying the functor
![]() $\unicode[STIX]{x1D702}_{(\unicode[STIX]{x1D707})}$
, these morphisms compose with those constructed in Proposition 5.34 to give rise to the desired Frobenius-equivariant comparison map of complexes:
$\unicode[STIX]{x1D702}_{(\unicode[STIX]{x1D707})}$
, these morphisms compose with those constructed in Proposition 5.34 to give rise to the desired Frobenius-equivariant comparison map of complexes:
where the direct limits and the
![]() $p$
-adic completions are formed termwise and, for brevity, we let
$p$
-adic completions are formed termwise and, for brevity, we let
![]() $\unicode[STIX]{x1D70F}$
range over the indices ‘
$\unicode[STIX]{x1D70F}$
range over the indices ‘
![]() $\unicode[STIX]{x1D70E}$
’ for
$\unicode[STIX]{x1D70E}$
’ for
![]() $\unicode[STIX]{x1D70E}\in \unicode[STIX]{x1D6F4}$
and ‘
$\unicode[STIX]{x1D70E}\in \unicode[STIX]{x1D6F4}$
and ‘
![]() $(\unicode[STIX]{x1D706},i)$
’ for
$(\unicode[STIX]{x1D706},i)$
’ for
![]() $\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}$
and
$\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}$
and
![]() $i=1,\ldots ,d$
.
$i=1,\ldots ,d$
.
The source (respectively, the target) of the map (5.38.4) is a term of the direct limit (5.32.1) (respectively, (5.21.1)) and the formation of this map is compatible with enlarging
![]() $\unicode[STIX]{x1D6F4}$
and
$\unicode[STIX]{x1D6F4}$
and
![]() $\unicode[STIX]{x1D6EC}$
, that is, with the transition maps of the direct limits (5.32.1) and (5.21.1). Moreover, if
$\unicode[STIX]{x1D6EC}$
, that is, with the transition maps of the direct limits (5.32.1) and (5.21.1). Moreover, if
![]() $R^{\prime }$
is a
$R^{\prime }$
is a
![]() $p$
-adically formally étale
$p$
-adically formally étale
![]() $R$
-algebra equipped with data as in (5.17.1) for some sets
$R$
-algebra equipped with data as in (5.17.1) for some sets
![]() $\unicode[STIX]{x1D6F4}^{\prime }$
and
$\unicode[STIX]{x1D6F4}^{\prime }$
and
![]() $\unicode[STIX]{x1D6EC}^{\prime }$
, then the map (5.38.4) and its analogue for
$\unicode[STIX]{x1D6EC}^{\prime }$
, then the map (5.38.4) and its analogue for
![]() $R^{\prime }$
and the sets
$R^{\prime }$
and the sets
![]() $\unicode[STIX]{x1D6F4}\cup \unicode[STIX]{x1D6F4}^{\prime }$
,
$\unicode[STIX]{x1D6F4}\cup \unicode[STIX]{x1D6F4}^{\prime }$
,
![]() $\unicode[STIX]{x1D6EC}\cup \unicode[STIX]{x1D6EC}^{\prime }$
(and the induced closed immersion (5.17.1)) are compatible with the maps between their sources (respectively, targets) discussed in §§5.21 and 5.32.
$\unicode[STIX]{x1D6EC}\cup \unicode[STIX]{x1D6EC}^{\prime }$
(and the induced closed immersion (5.17.1)) are compatible with the maps between their sources (respectively, targets) discussed in §§5.21 and 5.32.
In conclusion, by taking the filtered direct limit of the maps (5.38.4) over all the closed immersions (5.17.1) for varying
![]() $\unicode[STIX]{x1D6F4}$
and
$\unicode[STIX]{x1D6F4}$
and
![]() $\unicode[STIX]{x1D6EC}$
(but a fixed
$\unicode[STIX]{x1D6EC}$
(but a fixed
![]() $R$
), we obtain a comparison map from the complex (5.32.1) to the complex (5.21.1), and the formation of this map is compatible with replacing
$R$
), we obtain a comparison map from the complex (5.32.1) to the complex (5.21.1), and the formation of this map is compatible with replacing
![]() $R$
by a formally étale
$R$
by a formally étale
![]() $R$
-algebra
$R$
-algebra
![]() $R^{\prime }$
. The following proposition implies that this map is a quasi-isomorphism.
$R^{\prime }$
. The following proposition implies that this map is a quasi-isomorphism.
Proposition 5.39. The Frobenius-equivariant comparison map (5.38.4) is a quasi-isomorphism.
Proof. The proof is similar to that of [Reference Bhatt, Morrow and ScholzeBMS18, 12.9], and the idea is to reduce to the case of a single coordinate morphism settled in Proposition 5.16. More precisely, for
![]() $m\geqslant p$
, let
$m\geqslant p$
, let
be the closed immersion induced by its analogue for
![]() $D_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}$
, that is, by the first map in (5.22.2). For each
$D_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}$
, that is, by the first map in (5.22.2). For each
![]() $\unicode[STIX]{x1D706}_{0}\in \unicode[STIX]{x1D6EC}$
, the ideal of
$\unicode[STIX]{x1D706}_{0}\in \unicode[STIX]{x1D6EC}$
, the ideal of
![]() $A_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}^{\Box }\otimes _{\mathbb{Z}[Q]}\mathbb{Z}[P_{\unicode[STIX]{x1D706}_{0}}]$
that cuts out
$A_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}^{\Box }\otimes _{\mathbb{Z}[Q]}\mathbb{Z}[P_{\unicode[STIX]{x1D706}_{0}}]$
that cuts out
![]() $R/p$
(see (5.27.5)) is finitely generated. Consequently, for each
$R/p$
(see (5.27.5)) is finitely generated. Consequently, for each
![]() $m\geqslant p$
, the ideal of
$m\geqslant p$
, the ideal of
![]() $D_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}^{(m)}$
that cuts out
$D_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}^{(m)}$
that cuts out
![]() $R/p$
is also finitely generated and, hence, due to divided powers, it is also
$R/p$
is also finitely generated and, hence, due to divided powers, it is also
![]() $p$
-adically topologically nilpotent. Thus, fixing a
$p$
-adically topologically nilpotent. Thus, fixing a
![]() $\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}$
and, for
$\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}$
and, for
![]() $m\geqslant p$
, letting
$m\geqslant p$
, letting
![]() $A_{\text{cris}}^{(m)}(R)_{\unicode[STIX]{x1D706}}$
denote the ring
$A_{\text{cris}}^{(m)}(R)_{\unicode[STIX]{x1D706}}$
denote the ring
![]() $A_{\text{cris}}^{(m)}(R)$
of §3.27 constructed using the coordinate morphism
$A_{\text{cris}}^{(m)}(R)$
of §3.27 constructed using the coordinate morphism
![]() $R_{\unicode[STIX]{x1D706}}^{\Box }\rightarrow R$
, we may use the
$R_{\unicode[STIX]{x1D706}}^{\Box }\rightarrow R$
, we may use the
![]() $p$
-adic formal étaleness of
$p$
-adic formal étaleness of
![]() $A_{\text{cris}}^{(m)}(R_{\unicode[STIX]{x1D706}}^{\Box })\rightarrow A_{\text{cris}}^{(m)}(R)_{\unicode[STIX]{x1D706}}$
(see §3.14) to obtain the unique indicated lifts in the commutative diagram
$A_{\text{cris}}^{(m)}(R_{\unicode[STIX]{x1D706}}^{\Box })\rightarrow A_{\text{cris}}^{(m)}(R)_{\unicode[STIX]{x1D706}}$
(see §3.14) to obtain the unique indicated lifts in the commutative diagram

in which the bottom right horizontal map results from the fact that, by construction, each
![]() $D_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}^{(m)}$
is both an
$D_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}^{(m)}$
is both an
![]() $A(R_{\unicode[STIX]{x1D706}}^{\Box })$
-algebra and an
$A(R_{\unicode[STIX]{x1D706}}^{\Box })$
-algebra and an
![]() $A_{\text{cris}}^{(m)}$
-algebra. By the uniqueness of such lifts, the resulting maps
$A_{\text{cris}}^{(m)}$
-algebra. By the uniqueness of such lifts, the resulting maps
are compatible as
![]() $m$
varies,
$m$
varies,
![]() $\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}$
-equivariant, where
$\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}$
-equivariant, where
![]() $\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}$
acts on
$\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}$
acts on
![]() $A_{\text{cris}}^{(m)}(R)_{\unicode[STIX]{x1D706}}$
through the projection
$A_{\text{cris}}^{(m)}(R)_{\unicode[STIX]{x1D706}}$
through the projection
![]() $\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}{\twoheadrightarrow}\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D706}}$
, and are compatible with the maps from its source and target to
$\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}{\twoheadrightarrow}\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D706}}$
, and are compatible with the maps from its source and target to
![]() $\mathbb{A}_{\text{cris}}^{(m)}(R_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC},\,\infty })$
. By construction, the maps (5.39.1) are also compatible with the derivations
$\mathbb{A}_{\text{cris}}^{(m)}(R_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC},\,\infty })$
. By construction, the maps (5.39.1) are also compatible with the derivations
![]() $\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\log (X_{\unicode[STIX]{x1D706},\,i})}$
for
$\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\log (X_{\unicode[STIX]{x1D706},\,i})}$
for
![]() $i=1,\ldots ,d$
discussed in §§5.10 and 5.31. Consequently, the diagram
$i=1,\ldots ,d$
discussed in §§5.10 and 5.31. Consequently, the diagram

commutes, where the index
![]() $\unicode[STIX]{x1D70F}$
ranges over ‘
$\unicode[STIX]{x1D70F}$
ranges over ‘
![]() $\unicode[STIX]{x1D70E}$
’ for
$\unicode[STIX]{x1D70E}$
’ for
![]() $\unicode[STIX]{x1D70E}\in \unicode[STIX]{x1D6F4}$
and ‘
$\unicode[STIX]{x1D70E}\in \unicode[STIX]{x1D6F4}$
and ‘
![]() $(\unicode[STIX]{x1D706}^{\prime },i)$
’ for
$(\unicode[STIX]{x1D706}^{\prime },i)$
’ for
![]() $\unicode[STIX]{x1D706}^{\prime }\in \unicode[STIX]{x1D6EC}$
and
$\unicode[STIX]{x1D706}^{\prime }\in \unicode[STIX]{x1D6EC}$
and
![]() $i=1,\ldots ,d$
. By Proposition 5.16, for
$i=1,\ldots ,d$
. By Proposition 5.16, for
![]() $m\geqslant p^{2}$
, the top horizontal map in (5.39.2) is a quasi-isomorphism and, by Lemma 3.7 and Remark 3.35, so is the right vertical map. By Proposition 5.13 and (5.31.5), the left vertical map in (5.39.2) becomes a quasi-isomorphism after applying
$m\geqslant p^{2}$
, the top horizontal map in (5.39.2) is a quasi-isomorphism and, by Lemma 3.7 and Remark 3.35, so is the right vertical map. By Proposition 5.13 and (5.31.5), the left vertical map in (5.39.2) becomes a quasi-isomorphism after applying
![]() $\mathop{\varinjlim }\nolimits_{m\geqslant p}$
and forming the termwise
$\mathop{\varinjlim }\nolimits_{m\geqslant p}$
and forming the termwise
![]() $p$
-adic completion. These operations turn the bottom horizontal map in (5.39.2) into the comparison map (5.38.4), so we conclude that the latter is also a quasi-isomorphism, as desired.◻
$p$
-adic completion. These operations turn the bottom horizontal map in (5.39.2) into the comparison map (5.38.4), so we conclude that the latter is also a quasi-isomorphism, as desired.◻
5.40 Proof of Theorem 5.4
By §5.38 and Proposition 5.39, the functorial in
![]() $R$
complexes (5.21.1) and (5.32.1) define canonically and Frobenius-equivariantly quasi-isomorphic complexes of presheaves on a basis for the topology of
$R$
complexes (5.21.1) and (5.32.1) define canonically and Frobenius-equivariantly quasi-isomorphic complexes of presheaves on a basis for the topology of
![]() $\mathfrak{X}_{\acute{\text{e}}\text{t}}$
. Their associated complexes of sheaves on
$\mathfrak{X}_{\acute{\text{e}}\text{t}}$
. Their associated complexes of sheaves on
![]() $\mathfrak{X}_{\acute{\text{e}}\text{t}}$
are then also canonically and Frobenius-equivariantly quasi-isomorphic. By §§5.21 and 5.32, these complexes of sheaves Frobenius-compatibly represent
$\mathfrak{X}_{\acute{\text{e}}\text{t}}$
are then also canonically and Frobenius-equivariantly quasi-isomorphic. By §§5.21 and 5.32, these complexes of sheaves Frobenius-compatibly represent
![]() $A\unicode[STIX]{x1D6FA}_{\mathfrak{X}}\,\widehat{\otimes }_{A_{\text{inf}}}^{\mathbb{L}}\,A_{\text{cris}}$
and
$A\unicode[STIX]{x1D6FA}_{\mathfrak{X}}\,\widehat{\otimes }_{A_{\text{inf}}}^{\mathbb{L}}\,A_{\text{cris}}$
and
![]() $Ru_{\ast }({\mathcal{O}}_{\mathfrak{X}_{{\mathcal{O}}_{C}/p}/A_{\text{cris}}})$
, respectively, so that, in conclusion, Proposition 5.39 supplies a Frobenius-equivariant isomorphism
$Ru_{\ast }({\mathcal{O}}_{\mathfrak{X}_{{\mathcal{O}}_{C}/p}/A_{\text{cris}}})$
, respectively, so that, in conclusion, Proposition 5.39 supplies a Frobenius-equivariant isomorphism
which gives the desired identification (5.4.1). ◻
We have obtained two ways to identify the de Rham specialization of
![]() $A\unicode[STIX]{x1D6FA}_{\mathfrak{X}}$
: we may either use (4.17.1) or combine (5.40.1) with the fact that the logarithmic crystalline cohomology of
$A\unicode[STIX]{x1D6FA}_{\mathfrak{X}}$
: we may either use (4.17.1) or combine (5.40.1) with the fact that the logarithmic crystalline cohomology of
![]() $\mathfrak{X}_{{\mathcal{O}}_{C}/p}$
over
$\mathfrak{X}_{{\mathcal{O}}_{C}/p}$
over
![]() ${\mathcal{O}}_{C}$
is computed by
${\mathcal{O}}_{C}$
is computed by
![]() $\unicode[STIX]{x1D6FA}_{\mathfrak{X}/{\mathcal{O}}_{C},\,\log }^{\bullet }$
. For use in §8, we now check that these two identifications agree.
$\unicode[STIX]{x1D6FA}_{\mathfrak{X}/{\mathcal{O}}_{C},\,\log }^{\bullet }$
. For use in §8, we now check that these two identifications agree.
Proposition 5.41. The following diagram commutes:

where the unlabeled map results from the identification
of [Reference BeilinsonBei13a, (1.8.1) and (1.11.1)] (compare with Remark 5.24).
Proof. The overall argument is similar to that given in the smooth case in [Reference Bhatt, Morrow and ScholzeBMS18, proof of 14.1].
The claim is local, so we assume the setup of §5.17. Then
![]() $d\log (X_{\unicode[STIX]{x1D70E}})$
and
$d\log (X_{\unicode[STIX]{x1D70E}})$
and
![]() $d\log (X_{\unicode[STIX]{x1D706},\,i})$
generate the differential graded algebra
$d\log (X_{\unicode[STIX]{x1D706},\,i})$
generate the differential graded algebra
![]() $\unicode[STIX]{x1D6FA}_{D_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}/A_{\text{cris}},\,\log ,\,\text{PD}}^{\bullet }$
over
$\unicode[STIX]{x1D6FA}_{D_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}/A_{\text{cris}},\,\log ,\,\text{PD}}^{\bullet }$
over
![]() $D_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}$
(see Proposition 5.23), so, since the terms of
$D_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}$
(see Proposition 5.23), so, since the terms of
![]() $\unicode[STIX]{x1D6FA}_{\operatorname{Spf}(R)/{\mathcal{O}}_{C},\,\log }^{\bullet }$
are
$\unicode[STIX]{x1D6FA}_{\operatorname{Spf}(R)/{\mathcal{O}}_{C},\,\log }^{\bullet }$
are
![]() $p$
-torsion free and each
$p$
-torsion free and each
![]() $t_{\unicode[STIX]{x1D70E}}$
and
$t_{\unicode[STIX]{x1D70E}}$
and
![]() $t_{\unicode[STIX]{x1D706},\,i}$
is a unit in
$t_{\unicode[STIX]{x1D706},\,i}$
is a unit in
![]() $R[\frac{1}{p}]$
, there is at most one map of differential graded algebras
$R[\frac{1}{p}]$
, there is at most one map of differential graded algebras
By Proposition 5.23, the unlabeled map of (5.41.1) is identified with this unique map, so we need to show that so is the composition in (5.41.1).
We recall from the proof of Theorem 4.17 that the right diagonal map in (5.41.1) is defined by composing the Frobenius of
![]() $A\unicode[STIX]{x1D6FA}_{\mathfrak{X}}$
, the reduction modulo
$A\unicode[STIX]{x1D6FA}_{\mathfrak{X}}$
, the reduction modulo
![]() $\unicode[STIX]{x1D711}(\unicode[STIX]{x1D709})$
, and the canonical identification supplied by [Reference Bhatt, Morrow and ScholzeBMS18, 6.12] of
$\unicode[STIX]{x1D711}(\unicode[STIX]{x1D709})$
, and the canonical identification supplied by [Reference Bhatt, Morrow and ScholzeBMS18, 6.12] of
![]() $(L\unicode[STIX]{x1D702}_{(\unicode[STIX]{x1D711}(\unicode[STIX]{x1D709}))}(A\unicode[STIX]{x1D6FA}_{\mathfrak{X}}))/\unicode[STIX]{x1D711}(\unicode[STIX]{x1D709})$
with the complexFootnote
14
$(L\unicode[STIX]{x1D702}_{(\unicode[STIX]{x1D711}(\unicode[STIX]{x1D709}))}(A\unicode[STIX]{x1D6FA}_{\mathfrak{X}}))/\unicode[STIX]{x1D711}(\unicode[STIX]{x1D709})$
with the complexFootnote
14
![]() $H^{\bullet }(A\unicode[STIX]{x1D6FA}_{\mathfrak{X}}/\unicode[STIX]{x1D711}(\unicode[STIX]{x1D709}))$
that is a posteriori identified with
$H^{\bullet }(A\unicode[STIX]{x1D6FA}_{\mathfrak{X}}/\unicode[STIX]{x1D711}(\unicode[STIX]{x1D709}))$
that is a posteriori identified with
![]() $\unicode[STIX]{x1D6FA}_{\operatorname{Spf}(R)/{\mathcal{O}}_{C},\,\log }^{\bullet }$
and whose differentials are a priori given by Bockstein homomorphisms (defined in [Reference Bhatt, Morrow and ScholzeBMS18, 6.12] using
$\unicode[STIX]{x1D6FA}_{\operatorname{Spf}(R)/{\mathcal{O}}_{C},\,\log }^{\bullet }$
and whose differentials are a priori given by Bockstein homomorphisms (defined in [Reference Bhatt, Morrow and ScholzeBMS18, 6.12] using
![]() $A\unicode[STIX]{x1D6FA}_{\mathfrak{X}}/(\unicode[STIX]{x1D711}(\unicode[STIX]{x1D709}))^{2}$
). Letting
$A\unicode[STIX]{x1D6FA}_{\mathfrak{X}}/(\unicode[STIX]{x1D711}(\unicode[STIX]{x1D709}))^{2}$
). Letting
![]() $\unicode[STIX]{x1D70F}$
range over the usual indices (see §5.31), we may also apply this construction to the complex
$\unicode[STIX]{x1D70F}$
range over the usual indices (see §5.31), we may also apply this construction to the complex
Frobenius maps it isomorphically to
![]() $\unicode[STIX]{x1D702}_{(\unicode[STIX]{x1D711}(\unicode[STIX]{x1D707}))}(K_{\mathbb{A}_{\text{inf}}(R_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC},\,\infty })}((\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D70F}}-1)_{\unicode[STIX]{x1D70F}}))$
, for which the reduction modulo
$\unicode[STIX]{x1D702}_{(\unicode[STIX]{x1D711}(\unicode[STIX]{x1D707}))}(K_{\mathbb{A}_{\text{inf}}(R_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC},\,\infty })}((\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D70F}}-1)_{\unicode[STIX]{x1D70F}}))$
, for which the reduction modulo
![]() $\unicode[STIX]{x1D711}(\unicode[STIX]{x1D709})$
map is
$\unicode[STIX]{x1D711}(\unicode[STIX]{x1D709})$
map is
Moreover, due to the isomorphism (4.2.2) and Remarks 3.10 and 3.21,
The cited remarks and Theorem 4.11 (with Remark 4.5) imply that this describes the de Rham specialization map
![]() $A\unicode[STIX]{x1D6FA}_{\mathfrak{X}}\rightarrow \unicode[STIX]{x1D6FA}_{\mathfrak{X}/{\mathcal{O}}_{C},\,\log }^{\bullet }$
in terms of the complex
$A\unicode[STIX]{x1D6FA}_{\mathfrak{X}}\rightarrow \unicode[STIX]{x1D6FA}_{\mathfrak{X}/{\mathcal{O}}_{C},\,\log }^{\bullet }$
in terms of the complex
![]() $\unicode[STIX]{x1D702}_{(\unicode[STIX]{x1D707})}(K_{\mathbb{A}_{\text{inf}}(R_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC},\,\infty })}((\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D70F}}-1)_{\unicode[STIX]{x1D70F}}))$
.
$\unicode[STIX]{x1D702}_{(\unicode[STIX]{x1D707})}(K_{\mathbb{A}_{\text{inf}}(R_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC},\,\infty })}((\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D70F}}-1)_{\unicode[STIX]{x1D70F}}))$
.
We now describe the right diagonal map of (5.41.1) in terms of
![]() $\unicode[STIX]{x1D702}_{(\unicode[STIX]{x1D707})}(K_{\mathbb{A}_{\text{cris}}^{(m)}(R_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC},\,\infty })}((\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D70F}}-1)_{\unicode[STIX]{x1D70F}}))$
, which is a variable term that comprises the target of the comparison map (5.38.4). Namely, we first let
$\unicode[STIX]{x1D702}_{(\unicode[STIX]{x1D707})}(K_{\mathbb{A}_{\text{cris}}^{(m)}(R_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC},\,\infty })}((\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D70F}}-1)_{\unicode[STIX]{x1D70F}}))$
, which is a variable term that comprises the target of the comparison map (5.38.4). Namely, we first let
![]() $\unicode[STIX]{x1D711}(\mathbb{A}_{\text{cris}}^{(m)}(R_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC},\,\infty }))$
be the analogue of the ring
$\unicode[STIX]{x1D711}(\mathbb{A}_{\text{cris}}^{(m)}(R_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC},\,\infty }))$
be the analogue of the ring
![]() $\mathbb{A}_{\text{cris}}^{(m)}(R_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC},\,\infty })$
built using the element
$\mathbb{A}_{\text{cris}}^{(m)}(R_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC},\,\infty })$
built using the element
![]() $\unicode[STIX]{x1D711}(\unicode[STIX]{x1D709})$
instead of
$\unicode[STIX]{x1D711}(\unicode[STIX]{x1D709})$
instead of
![]() $\unicode[STIX]{x1D709}$
, so that the Frobenius gives the isomorphism
$\unicode[STIX]{x1D709}$
, so that the Frobenius gives the isomorphism
![]() $\mathbb{A}_{\text{cris}}^{(m)}(R_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC},\,\infty })\overset{{\sim}}{\longrightarrow }\unicode[STIX]{x1D711}(\mathbb{A}_{\text{cris}}^{(m)}(R_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC},\,\infty }))$
.Footnote
15
Then the Frobenius maps the complex
$\mathbb{A}_{\text{cris}}^{(m)}(R_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC},\,\infty })\overset{{\sim}}{\longrightarrow }\unicode[STIX]{x1D711}(\mathbb{A}_{\text{cris}}^{(m)}(R_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC},\,\infty }))$
.Footnote
15
Then the Frobenius maps the complex
![]() $\unicode[STIX]{x1D702}_{(\unicode[STIX]{x1D707})}(K_{\mathbb{A}_{\text{cris}}^{(m)}(R_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC},\,\infty })}((\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D70F}}-1)_{\unicode[STIX]{x1D70F}}))$
isomorphically to the complex
$\unicode[STIX]{x1D702}_{(\unicode[STIX]{x1D707})}(K_{\mathbb{A}_{\text{cris}}^{(m)}(R_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC},\,\infty })}((\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D70F}}-1)_{\unicode[STIX]{x1D70F}}))$
isomorphically to the complex
![]() $\unicode[STIX]{x1D702}_{(\unicode[STIX]{x1D711}(\unicode[STIX]{x1D707}))}(K_{\unicode[STIX]{x1D711}(\mathbb{A}_{\text{cris}}^{(m)}(R_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC},\,\infty }))}((\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D70F}}-1)_{\unicode[STIX]{x1D70F}}))$
, for which the reduction modulo
$\unicode[STIX]{x1D702}_{(\unicode[STIX]{x1D711}(\unicode[STIX]{x1D707}))}(K_{\unicode[STIX]{x1D711}(\mathbb{A}_{\text{cris}}^{(m)}(R_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC},\,\infty }))}((\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D70F}}-1)_{\unicode[STIX]{x1D70F}}))$
, for which the reduction modulo
![]() $\unicode[STIX]{x1D711}(\unicode[STIX]{x1D709})$
map is
$\unicode[STIX]{x1D711}(\unicode[STIX]{x1D709})$
map is
Via a morphism induced by
![]() $\unicode[STIX]{x1D703}\circ \unicode[STIX]{x1D711}^{-1}:\unicode[STIX]{x1D711}(\mathbb{A}_{\text{cris}}^{(m)}(R_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC},\,\infty })){\twoheadrightarrow}R_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC},\,\infty }$
, the target of (5.41.3) maps to
$\unicode[STIX]{x1D703}\circ \unicode[STIX]{x1D711}^{-1}:\unicode[STIX]{x1D711}(\mathbb{A}_{\text{cris}}^{(m)}(R_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC},\,\infty })){\twoheadrightarrow}R_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC},\,\infty }$
, the target of (5.41.3) maps to
because, since each
![]() $H^{i}(\unicode[STIX]{x1D702}_{(\unicode[STIX]{x1D701}_{p}-1)}(K_{R_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC},\,\infty }}((\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D70F}}-1)_{\unicode[STIX]{x1D70F}})))$
is
$H^{i}(\unicode[STIX]{x1D702}_{(\unicode[STIX]{x1D701}_{p}-1)}(K_{R_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC},\,\infty }}((\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D70F}}-1)_{\unicode[STIX]{x1D70F}})))$
is
![]() $p$
-torsion free, the agreement of the Bockstein differentials may be checked after inverting
$p$
-torsion free, the agreement of the Bockstein differentials may be checked after inverting
![]() $p$
by using the fact that
$p$
by using the fact that
![]() $(\mathbb{A}_{\text{inf}}(R_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC},\,\infty })/\unicode[STIX]{x1D711}(\unicode[STIX]{x1D709})^{2})[\frac{1}{p}]$
is an algebra over
$(\mathbb{A}_{\text{inf}}(R_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC},\,\infty })/\unicode[STIX]{x1D711}(\unicode[STIX]{x1D709})^{2})[\frac{1}{p}]$
is an algebra over
![]() $\unicode[STIX]{x1D711}(\mathbb{A}_{\text{cris}}^{(m)}(R_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC},\,\infty }))$
via a map that lifts
$\unicode[STIX]{x1D711}(\mathbb{A}_{\text{cris}}^{(m)}(R_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC},\,\infty }))$
via a map that lifts
![]() $\unicode[STIX]{x1D703}\circ \unicode[STIX]{x1D711}^{-1}$
. The resulting composition
$\unicode[STIX]{x1D703}\circ \unicode[STIX]{x1D711}^{-1}$
. The resulting composition
is the promised description of the right diagonal map of (5.41.1). In addition, by construction and [Reference Bhatt, Morrow and ScholzeBMS18, 6.13], this composition is a morphism of differential graded algebrasFootnote
16
that in degree
![]() $0$
is given by the map
$0$
is given by the map
![]() $\unicode[STIX]{x1D703}$
of (5.19.4).
$\unicode[STIX]{x1D703}$
of (5.19.4).
On the other hand, the comparison map
would be a map of differential graded algebras if in the formula
that describes the morphism (5.34.1) in degree
![]() $1$
we could disregard the terms with
$1$
we could disregard the terms with
![]() $n\geqslant 1$
. However,
$n\geqslant 1$
. However,
![]() $\log ([\unicode[STIX]{x1D716}])$
and
$\log ([\unicode[STIX]{x1D716}])$
and
![]() $\unicode[STIX]{x1D707}$
are unit multiples of each other (see §5.14) and
$\unicode[STIX]{x1D707}$
are unit multiples of each other (see §5.14) and
![]() $\unicode[STIX]{x1D703}(\unicode[STIX]{x1D707}^{n}/(n+1)!)=0$
in
$\unicode[STIX]{x1D703}(\unicode[STIX]{x1D707}^{n}/(n+1)!)=0$
in
![]() ${\mathcal{O}}_{C}$
for
${\mathcal{O}}_{C}$
for
![]() $n\geqslant 1$
, so we can indeed ignore these terms if we are only interested in the composition
$n\geqslant 1$
, so we can indeed ignore these terms if we are only interested in the composition
that describes the composition in (5.41.1). In conclusion, this composition is a morphism of differential graded algebras that, due to (5.38.2), in degree
![]() $0$
is the map
$0$
is the map
![]() $D_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}{\twoheadrightarrow}R$
from (5.22.3). Therefore, as desired, it is the unique morphism (5.41.2).◻
$D_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}{\twoheadrightarrow}R$
from (5.22.3). Therefore, as desired, it is the unique morphism (5.41.2).◻
We now use Theorem 5.4 to analyze the crystalline specialization of
![]() $R\unicode[STIX]{x1D6E4}(\mathfrak{X}_{\acute{\text{e}}\text{t}},A\unicode[STIX]{x1D6FA}_{\mathfrak{X}})$
.
$R\unicode[STIX]{x1D6E4}(\mathfrak{X}_{\acute{\text{e}}\text{t}},A\unicode[STIX]{x1D6FA}_{\mathfrak{X}})$
.
5.42 The crystalline specialization map
The Witt vector functoriality gives the surjection
Since
![]() $\unicode[STIX]{x1D709}$
maps to
$\unicode[STIX]{x1D709}$
maps to
![]() $p$
in
$p$
in
![]() $W(k)$
, this surjection factors through
$W(k)$
, this surjection factors through
![]() $A_{\text{cris}}$
as follows:
$A_{\text{cris}}$
as follows:
![]() $A_{\text{inf}}{\hookrightarrow}A_{\text{cris}}{\twoheadrightarrow}W(k)$
. We equip
$A_{\text{inf}}{\hookrightarrow}A_{\text{cris}}{\twoheadrightarrow}W(k)$
. We equip
![]() $W(k)$
with the pullback of the log structure (5.2.1) on
$W(k)$
with the pullback of the log structure (5.2.1) on
![]() $A_{\text{cris}}$
. Explicitly, the resulting log structure on
$A_{\text{cris}}$
. Explicitly, the resulting log structure on
![]() $W(k)$
is associated to the prelog structure
$W(k)$
is associated to the prelog structure
![]() $\mathbb{Q}_{{\geqslant}0}\xrightarrow[{}]{0\,\neq \,q\,\mapsto \,0,\,0\,\mapsto \,1}W(k)$
.
$\mathbb{Q}_{{\geqslant}0}\xrightarrow[{}]{0\,\neq \,q\,\mapsto \,0,\,0\,\mapsto \,1}W(k)$
.
Corollary 5.43. For quasi-compact and quasi-separated
![]() $\mathfrak{X}$
, we have Frobenius-equivariant identifications
$\mathfrak{X}$
, we have Frobenius-equivariant identifications
For
![]() ${\mathcal{O}}_{C}$
-proper
${\mathcal{O}}_{C}$
-proper
![]() $\mathfrak{X}$
, we have Frobenius-equivariant identifications
$\mathfrak{X}$
, we have Frobenius-equivariant identifications
and the cohomology modules of
![]() $R\unicode[STIX]{x1D6E4}(\mathfrak{X}_{\acute{\text{e}}\text{t}},A\unicode[STIX]{x1D6FA}_{\mathfrak{X}})\otimes _{A_{\text{inf}}}^{\mathbb{L}}A_{\text{cris}}[\frac{1}{p}]$
are finite free over
$R\unicode[STIX]{x1D6E4}(\mathfrak{X}_{\acute{\text{e}}\text{t}},A\unicode[STIX]{x1D6FA}_{\mathfrak{X}})\otimes _{A_{\text{inf}}}^{\mathbb{L}}A_{\text{cris}}[\frac{1}{p}]$
are finite free over
![]() $A_{\text{cris}}[\frac{1}{p}]$
.
$A_{\text{cris}}[\frac{1}{p}]$
.
Proof. By [Reference Bhatt, Morrow and ScholzeBMS18, 4.9(i)], a finitely presented
![]() $A_{\text{inf}}/p^{n}$
-module is perfect as an
$A_{\text{inf}}/p^{n}$
-module is perfect as an
![]() $A_{\text{inf}}$
-module. Consequently, any
$A_{\text{inf}}$
-module. Consequently, any
![]() $A_{\text{inf}}/p^{n}$
-module
$A_{\text{inf}}/p^{n}$
-module
![]() $M$
is a filtered direct limit of perfect
$M$
is a filtered direct limit of perfect
![]() $A_{\text{inf}}$
-modules, so, by [SP, 0739],
$A_{\text{inf}}$
-modules, so, by [SP, 0739],
This applies to
![]() $M=A_{\text{cris}}/p^{n}$
, so the first identification in (5.43.1) follows from Theorem 5.4.
$M=A_{\text{cris}}/p^{n}$
, so the first identification in (5.43.1) follows from Theorem 5.4.
For each finite subextension of
![]() $C/(W(k)[\frac{1}{p}])$
, we consider its ring of integers
$C/(W(k)[\frac{1}{p}])$
, we consider its ring of integers
![]() ${\mathcal{O}}\subset {\mathcal{O}}_{C}$
equipped with the (fine) log structure associated to
${\mathcal{O}}\subset {\mathcal{O}}_{C}$
equipped with the (fine) log structure associated to
![]() ${\mathcal{O}}\cap ({\mathcal{O}}[\frac{1}{p}])^{\times }{\hookrightarrow}{\mathcal{O}}$
. By using étale local semistable coordinates (1.5.1) and Claims 1.6.1 and 1.6.3, we employ limit arguments to find such an
${\mathcal{O}}\cap ({\mathcal{O}}[\frac{1}{p}])^{\times }{\hookrightarrow}{\mathcal{O}}$
. By using étale local semistable coordinates (1.5.1) and Claims 1.6.1 and 1.6.3, we employ limit arguments to find such an
![]() ${\mathcal{O}}$
and a quasi-compact and quasi-separated, fine, log smooth log scheme
${\mathcal{O}}$
and a quasi-compact and quasi-separated, fine, log smooth log scheme
![]() ${\mathcal{X}}$
over
${\mathcal{X}}$
over
![]() ${\mathcal{O}}/p$
that descends
${\mathcal{O}}/p$
that descends
![]() $\mathfrak{X}_{{\mathcal{O}}_{C}/p}$
and is of Cartier type (see [Reference KatoKat89, 4.8]). Then the base change theorem [Reference BeilinsonBei13a, (1.11.1)] appliesFootnote
17
and shows that
$\mathfrak{X}_{{\mathcal{O}}_{C}/p}$
and is of Cartier type (see [Reference KatoKat89, 4.8]). Then the base change theorem [Reference BeilinsonBei13a, (1.11.1)] appliesFootnote
17
and shows that
so the second identification in (5.43.1) follows from the first.
If
![]() $\mathfrak{X}$
is
$\mathfrak{X}$
is
![]() ${\mathcal{O}}_{C}$
-proper, then, by Corollary 4.20, the object
${\mathcal{O}}_{C}$
-proper, then, by Corollary 4.20, the object
![]() $R\unicode[STIX]{x1D6E4}(\mathfrak{X}_{\acute{\text{e}}\text{t}},A\unicode[STIX]{x1D6FA}_{\mathfrak{X}})$
is quasi-isomorphic to a bounded complex of finite free
$R\unicode[STIX]{x1D6E4}(\mathfrak{X}_{\acute{\text{e}}\text{t}},A\unicode[STIX]{x1D6FA}_{\mathfrak{X}})$
is quasi-isomorphic to a bounded complex of finite free
![]() $A_{\text{inf}}$
-modules, so the identifications in (5.43.2) follow from those in (5.43.1). Moreover, then
$A_{\text{inf}}$
-modules, so the identifications in (5.43.2) follow from those in (5.43.1). Moreover, then
![]() ${\mathcal{X}}$
is
${\mathcal{X}}$
is
![]() ${\mathcal{O}}$
-proper and [Reference BeilinsonBei13a, 1.18, Theorem] proves that the cohomology groups of
${\mathcal{O}}$
-proper and [Reference BeilinsonBei13a, 1.18, Theorem] proves that the cohomology groups of
are finite free
![]() $A_{\text{cris}}[\frac{1}{p}]$
-modules.◻
$A_{\text{cris}}[\frac{1}{p}]$
-modules.◻
Remarks.
5.44. In the preceding proof, the special fiber
 ${\mathcal{X}}_{k}$
is a descent of
${\mathcal{X}}_{k}$
is a descent of
 $\mathfrak{X}_{k}$
to a fine, log smooth log scheme of Cartier type over
$\mathfrak{X}_{k}$
to a fine, log smooth log scheme of Cartier type over
 $k$
equipped with the log structure associated to (the base change map is a ‘change of log structure’ self-map of
$k$
equipped with the log structure associated to (the base change map is a ‘change of log structure’ self-map of $$\begin{eqnarray}\mathbb{N}_{{\geqslant}0}\xrightarrow[{}]{1\,\mapsto \,0,\,0\,\mapsto \,1}k\end{eqnarray}$$
$$\begin{eqnarray}\mathbb{N}_{{\geqslant}0}\xrightarrow[{}]{1\,\mapsto \,0,\,0\,\mapsto \,1}k\end{eqnarray}$$
 $k$
determined by the map
$k$
determined by the map
 $\mathbb{N}_{{\geqslant}0}\rightarrow \mathbb{Q}_{{\geqslant}0}$
that sends
$\mathbb{N}_{{\geqslant}0}\rightarrow \mathbb{Q}_{{\geqslant}0}$
that sends
 $1$
to the valuation of a uniformizer of
$1$
to the valuation of a uniformizer of
 ${\mathcal{O}}$
). Given such a descent, the base change theorem [Reference BeilinsonBei13a, (1.11.1)] gives the further Frobenius-equivariant identification (5.44.1)where the
${\mathcal{O}}$
). Given such a descent, the base change theorem [Reference BeilinsonBei13a, (1.11.1)] gives the further Frobenius-equivariant identification (5.44.1)where the $$\begin{eqnarray}\quad R\unicode[STIX]{x1D6E4}_{\log \text{cris}}(\mathfrak{X}_{k}/W(k))\cong R\unicode[STIX]{x1D6E4}_{\log \text{cris}}({\mathcal{X}}_{k}/W(k)),\end{eqnarray}$$
$$\begin{eqnarray}\quad R\unicode[STIX]{x1D6E4}_{\log \text{cris}}(\mathfrak{X}_{k}/W(k))\cong R\unicode[STIX]{x1D6E4}_{\log \text{cris}}({\mathcal{X}}_{k}/W(k)),\end{eqnarray}$$
 $W(k)$
on the left (respectively, right) is equipped with the log structure associated to
$W(k)$
on the left (respectively, right) is equipped with the log structure associated to
 $\mathbb{Q}_{{\geqslant}0}\xrightarrow[{}]{0\,\neq \,q\,\mapsto \,0,\,0\,\mapsto \,1}W(k)$
(respectively,
$\mathbb{Q}_{{\geqslant}0}\xrightarrow[{}]{0\,\neq \,q\,\mapsto \,0,\,0\,\mapsto \,1}W(k)$
(respectively,
 $\mathbb{N}_{{\geqslant}0}\xrightarrow[{}]{1\,\mapsto \,0,\,0\,\mapsto \,1}W(k)$
). Likewise, if
$\mathbb{N}_{{\geqslant}0}\xrightarrow[{}]{1\,\mapsto \,0,\,0\,\mapsto \,1}W(k)$
). Likewise, if
 $\mathfrak{X}_{k}$
is
$\mathfrak{X}_{k}$
is
 $k$
-smooth, then [Reference BeilinsonBei13a, (1.11.1)] gives the Frobenius-equivariant identification (5.44.2)
$k$
-smooth, then [Reference BeilinsonBei13a, (1.11.1)] gives the Frobenius-equivariant identification (5.44.2) $$\begin{eqnarray}\quad R\unicode[STIX]{x1D6E4}_{\log \text{cris}}(\mathfrak{X}_{k}/W(k))\cong R\unicode[STIX]{x1D6E4}_{\text{cris}}(\mathfrak{X}_{k}/W(k)).\end{eqnarray}$$
$$\begin{eqnarray}\quad R\unicode[STIX]{x1D6E4}_{\log \text{cris}}(\mathfrak{X}_{k}/W(k))\cong R\unicode[STIX]{x1D6E4}_{\text{cris}}(\mathfrak{X}_{k}/W(k)).\end{eqnarray}$$
5.45. The identification (5.43.3) expresses
 $R\unicode[STIX]{x1D6E4}_{\log \text{cris}}(\mathfrak{X}_{k}/W(k))$
in terms of
$R\unicode[STIX]{x1D6E4}_{\log \text{cris}}(\mathfrak{X}_{k}/W(k))$
in terms of
 $R\unicode[STIX]{x1D6E4}_{\log \text{cris}}(\mathfrak{X}_{{\mathcal{O}}_{C}/p}/A_{\text{cris}})$
. Further results from [Reference BeilinsonBei13a] imply a converse for proper
$R\unicode[STIX]{x1D6E4}_{\log \text{cris}}(\mathfrak{X}_{{\mathcal{O}}_{C}/p}/A_{\text{cris}})$
. Further results from [Reference BeilinsonBei13a] imply a converse for proper
 $\mathfrak{X}$
after extending coefficients to
$\mathfrak{X}$
after extending coefficients to
 $B_{\text{st}}^{+}$
, see (9.2.2) below (when
$B_{\text{st}}^{+}$
, see (9.2.2) below (when
 $\mathfrak{X}_{k}$
is
$\mathfrak{X}_{k}$
is
 $k$
-smooth,
$k$
-smooth,
 $A_{\text{cris}}[\frac{1}{p}]$
in place of
$A_{\text{cris}}[\frac{1}{p}]$
in place of
 $B_{\text{st}}^{+}$
suffices, see [Reference Bhatt, Morrow and ScholzeBMS18, 13.21]).
$B_{\text{st}}^{+}$
suffices, see [Reference Bhatt, Morrow and ScholzeBMS18, 13.21]).
6 The comparison to the
 $B_{\text{dR}}^{+}$
-cohomology
$B_{\text{dR}}^{+}$
-cohomology
The main goal of this section is to prove in Theorem 6.6 that for
![]() ${\mathcal{O}}_{C}$
-proper
${\mathcal{O}}_{C}$
-proper
![]() $\mathfrak{X}$
, we have
$\mathfrak{X}$
, we have
where the definition of
![]() $R\unicode[STIX]{x1D6E4}_{\text{cris}}(\mathfrak{X}_{C}^{\text{ad}}/B_{\text{dR}}^{+})$
, the ‘crystalline cohomology of
$R\unicode[STIX]{x1D6E4}_{\text{cris}}(\mathfrak{X}_{C}^{\text{ad}}/B_{\text{dR}}^{+})$
, the ‘crystalline cohomology of
![]() $\mathfrak{X}_{C}^{\text{ad}}$
over
$\mathfrak{X}_{C}^{\text{ad}}$
over
![]() $B_{\text{dR}}^{+}$
’, was given in [Reference Bhatt, Morrow and ScholzeBMS18, §13] (see §6.2 for a brief review). This definition is purely in terms of
$B_{\text{dR}}^{+}$
’, was given in [Reference Bhatt, Morrow and ScholzeBMS18, §13] (see §6.2 for a brief review). This definition is purely in terms of
![]() $\mathfrak{X}_{C}^{\text{ad}}$
and was engineered in [Reference Bhatt, Morrow and ScholzeBMS18, §13] to be compatible with
$\mathfrak{X}_{C}^{\text{ad}}$
and was engineered in [Reference Bhatt, Morrow and ScholzeBMS18, §13] to be compatible with
![]() $R\unicode[STIX]{x1D6E4}_{\log \text{cris}}(\mathfrak{X}_{{\mathcal{O}}_{C}/p}/A_{\text{cris}})$
when
$R\unicode[STIX]{x1D6E4}_{\log \text{cris}}(\mathfrak{X}_{{\mathcal{O}}_{C}/p}/A_{\text{cris}})$
when
![]() $\mathfrak{X}$
is smooth. Thus, for (6.0.1), we only need to check that a slightly more general definition that uses the étale topology and more general embeddings than those furnished by annuli leads to the same cohomology (see §§6.2–6.3). For this, we adapt the arguments of [Reference Bhatt, Morrow and ScholzeBMS18, §13]; in fact, our
$\mathfrak{X}$
is smooth. Thus, for (6.0.1), we only need to check that a slightly more general definition that uses the étale topology and more general embeddings than those furnished by annuli leads to the same cohomology (see §§6.2–6.3). For this, we adapt the arguments of [Reference Bhatt, Morrow and ScholzeBMS18, §13]; in fact, our
![]() $C$
is
$C$
is
![]() $(\overline{W(k)}[\frac{1}{p}])\,\widehat{~}$
(see §1.5), so we may simplify the descent to a discretely valued base aspects of these arguments by taking advantage of a result of Huber on the local structure of étale maps of adic spaces (see §6.3).
$(\overline{W(k)}[\frac{1}{p}])\,\widehat{~}$
(see §1.5), so we may simplify the descent to a discretely valued base aspects of these arguments by taking advantage of a result of Huber on the local structure of étale maps of adic spaces (see §6.3).
6.1 The ring
 $B_{\text{dR}}^{+}$
$B_{\text{dR}}^{+}$
Since
![]() $\unicode[STIX]{x1D709}$
is not a zero divisor in
$\unicode[STIX]{x1D709}$
is not a zero divisor in
![]() $A_{\text{inf}}[\frac{1}{p}]$
and generates
$A_{\text{inf}}[\frac{1}{p}]$
and generates
![]() $\operatorname{Ker}(\unicode[STIX]{x1D703}[\frac{1}{p}])$
, the
$\operatorname{Ker}(\unicode[STIX]{x1D703}[\frac{1}{p}])$
, the
![]() $(\operatorname{Ker}(\unicode[STIX]{x1D703}[\frac{1}{p}]))$
-adic completion of
$(\operatorname{Ker}(\unicode[STIX]{x1D703}[\frac{1}{p}]))$
-adic completion of
![]() $A_{\text{inf}}[\frac{1}{p}]$
is a complete discrete valuation ring
$A_{\text{inf}}[\frac{1}{p}]$
is a complete discrete valuation ring
![]() $B_{\text{dR}}^{+}$
with
$B_{\text{dR}}^{+}$
with
![]() $\unicode[STIX]{x1D709}$
as a uniformizer and
$\unicode[STIX]{x1D709}$
as a uniformizer and
![]() $C$
as the residue field. By Proposition 5.36, both
$C$
as the residue field. By Proposition 5.36, both
![]() $A_{\text{inf}}$
and
$A_{\text{inf}}$
and
![]() $A_{\text{cris}}$
are subalgebras of
$A_{\text{cris}}$
are subalgebras of
![]() $B_{\text{dR}}^{+}$
. By the ‘glueing of flatness’ [Reference Raynaud and GrusonRG71, II.1.4.2.1], the ring
$B_{\text{dR}}^{+}$
. By the ‘glueing of flatness’ [Reference Raynaud and GrusonRG71, II.1.4.2.1], the ring
![]() $B_{\text{dR}}^{+}$
is flat as an
$B_{\text{dR}}^{+}$
is flat as an
![]() $A_{\text{inf}}$
-algebra. We set
$A_{\text{inf}}$
-algebra. We set
Our
![]() $A_{\text{inf}}$
is a
$A_{\text{inf}}$
is a
![]() $W(k)$
-algebra (see §2.1), so, by the infinitesimal lifting,
$W(k)$
-algebra (see §2.1), so, by the infinitesimal lifting,
![]() $B_{\text{dR}}^{+}$
is a
$B_{\text{dR}}^{+}$
is a
![]() $\overline{W(k)}[\frac{1}{p}]$
-algebra.
$\overline{W(k)}[\frac{1}{p}]$
-algebra.
6.2 The
 $B_{\text{dR}}^{+}$
-cohomology using the étale topology
$B_{\text{dR}}^{+}$
-cohomology using the étale topology
In [Reference Bhatt, Morrow and ScholzeBMS18, §13], Bhatt–Morrow–Scholze used the analytic topology of a smooth adic
![]() $C$
-space
$C$
-space
![]() $X$
to define the ‘
$X$
to define the ‘
![]() $B_{\text{dR}}^{+}$
-cohomology’ of
$B_{\text{dR}}^{+}$
-cohomology’ of
![]() $X$
,
$X$
,
We now review their construction and show that it may also be carried out in the étale topology.
By [Reference HuberHub96, 1.6.10, 2.2.8], the analytic (respectively, étale) topology of
![]() $X$
has a basis of affinoids
$X$
has a basis of affinoids
![]() $\operatorname{Spa}(A,A^{\circ })$
each of which admits a map
$\operatorname{Spa}(A,A^{\circ })$
each of which admits a map
that is a composition of a rational embedding, a finite étale map, and a rational embedding. By localizing further, we refine the basis to consist of those
![]() $\operatorname{Spa}(A,A^{\circ })$
as above for which there is a finite subset
$\operatorname{Spa}(A,A^{\circ })$
as above for which there is a finite subset
![]() $\unicode[STIX]{x1D6F9}\subset (A^{\circ })^{\times }$
such that the following map is surjective:
$\unicode[STIX]{x1D6F9}\subset (A^{\circ })^{\times }$
such that the following map is surjective:
Then, by endowing each
![]() $A_{\text{inf}}/\unicode[STIX]{x1D709}^{n}$
with the
$A_{\text{inf}}/\unicode[STIX]{x1D709}^{n}$
with the
![]() $p$
-adic topology, each
$p$
-adic topology, each
![]() $(A_{\text{inf}}/\unicode[STIX]{x1D709}^{n})[\frac{1}{p}]$
with the unique ring topology for which
$(A_{\text{inf}}/\unicode[STIX]{x1D709}^{n})[\frac{1}{p}]$
with the unique ring topology for which
![]() $A_{\text{inf}}/\unicode[STIX]{x1D709}^{n}$
is an open subring, setting
$A_{\text{inf}}/\unicode[STIX]{x1D709}^{n}$
is an open subring, setting
and composing the projection onto the
![]() $n=1$
term with (6.2.2), we obtain the surjection
$n=1$
term with (6.2.2), we obtain the surjection
By the Leibniz rule, any
![]() $(B_{\text{dR}}^{+}\langle (X_{u}^{\pm 1})_{u\in \unicode[STIX]{x1D6F9}}\rangle )$
-valued derivation of
$(B_{\text{dR}}^{+}\langle (X_{u}^{\pm 1})_{u\in \unicode[STIX]{x1D6F9}}\rangle )$
-valued derivation of
![]() $B_{\text{dR}}^{+}\langle (X_{u}^{\pm 1})_{u\in \unicode[STIX]{x1D6F9}}\rangle$
induces a
$B_{\text{dR}}^{+}\langle (X_{u}^{\pm 1})_{u\in \unicode[STIX]{x1D6F9}}\rangle$
induces a
![]() $D_{\unicode[STIX]{x1D6F9}}(A)$
-valued derivation of
$D_{\unicode[STIX]{x1D6F9}}(A)$
-valued derivation of
![]() $D_{\unicode[STIX]{x1D6F9}}(A)$
. Thus, the commuting derivations
$D_{\unicode[STIX]{x1D6F9}}(A)$
. Thus, the commuting derivations
![]() $\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\log (X_{u})}:=X_{u}\cdot \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}X_{u}}$
give rise to the Koszul complex
$\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\log (X_{u})}:=X_{u}\cdot \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}X_{u}}$
give rise to the Koszul complex
that is functorial in enlarging
![]() $\unicode[STIX]{x1D6F9}$
. The resulting complex
$\unicode[STIX]{x1D6F9}$
. The resulting complex
is contravariantly functorial in
![]() $\operatorname{Spa}(A,A^{\circ })$
. Consequently, by varying
$\operatorname{Spa}(A,A^{\circ })$
. Consequently, by varying
![]() $\operatorname{Spa}(A,A^{\circ })$
, we obtain a complex of presheaves on the basis described above for the analytic (respectively, étale) topology of
$\operatorname{Spa}(A,A^{\circ })$
, we obtain a complex of presheaves on the basis described above for the analytic (respectively, étale) topology of
![]() $X$
. The hypercohomology of the associated complex of sheaves is, by definition, the
$X$
. The hypercohomology of the associated complex of sheaves is, by definition, the
![]() $B_{\text{dR}}^{+}$
-cohomology of
$B_{\text{dR}}^{+}$
-cohomology of
![]() $X$
:
$X$
:
By [Reference Bhatt, Morrow and ScholzeBMS18, 13.12(ii), 13.13], if
![]() $\operatorname{Spa}(A,A^{\circ })$
is fixed and
$\operatorname{Spa}(A,A^{\circ })$
is fixed and
![]() $\unicode[STIX]{x1D6F9}$
is sufficiently large, then
$\unicode[STIX]{x1D6F9}$
is sufficiently large, then
![]() $D_{\unicode[STIX]{x1D6F9}}(A)$
is
$D_{\unicode[STIX]{x1D6F9}}(A)$
is
![]() $\unicode[STIX]{x1D709}$
-torsion free and
$\unicode[STIX]{x1D709}$
-torsion free and
![]() $\unicode[STIX]{x1D709}$
-adically complete,
$\unicode[STIX]{x1D709}$
-adically complete,
![]() $\unicode[STIX]{x1D6FA}_{D_{\unicode[STIX]{x1D6F9}}(A)/B_{\text{dR}}^{+}}^{\bullet }$
maps quasi-isomorphically to
$\unicode[STIX]{x1D6FA}_{D_{\unicode[STIX]{x1D6F9}}(A)/B_{\text{dR}}^{+}}^{\bullet }$
maps quasi-isomorphically to
![]() $\unicode[STIX]{x1D6FA}_{A/B_{\text{dR}}^{+}}^{\bullet }$
, and, in the derived category, we have a canonical identification
$\unicode[STIX]{x1D6FA}_{A/B_{\text{dR}}^{+}}^{\bullet }$
, and, in the derived category, we have a canonical identification
Consequently, by [Reference Bhatt, Morrow and ScholzeBMS18, 9.15] (which we also used for proving Corollary 4.6), our definition of
![]() $R\unicode[STIX]{x1D6E4}_{\text{cris}}(X/B_{\text{dR}}^{+})$
agrees with that of [Reference Bhatt, Morrow and ScholzeBMS18, §13] (where one skips the sheafification step),
$R\unicode[STIX]{x1D6E4}_{\text{cris}}(X/B_{\text{dR}}^{+})$
agrees with that of [Reference Bhatt, Morrow and ScholzeBMS18, §13] (where one skips the sheafification step),
and their (derived) reductions modulo
![]() $\unicode[STIX]{x1D709}$
are canonically and compatibly identified with the de Rham cohomology objects
$\unicode[STIX]{x1D709}$
are canonically and compatibly identified with the de Rham cohomology objects
![]() $R\unicode[STIX]{x1D6E4}(X,\unicode[STIX]{x1D6FA}_{X/C}^{\bullet ,\,\text{cont}})$
and
$R\unicode[STIX]{x1D6E4}(X,\unicode[STIX]{x1D6FA}_{X/C}^{\bullet ,\,\text{cont}})$
and
![]() $R\unicode[STIX]{x1D6E4}(X_{\acute{\text{e}}\text{t}},\unicode[STIX]{x1D6FA}_{X/C}^{\bullet ,\,\text{cont}})$
, respectively, for instance:
$R\unicode[STIX]{x1D6E4}(X_{\acute{\text{e}}\text{t}},\unicode[STIX]{x1D6FA}_{X/C}^{\bullet ,\,\text{cont}})$
, respectively, for instance:
Thus, since, by the Hodge-to-de Rham spectral sequence and [Reference ScholzeSch13a, 9.2(ii)], the formation of the de Rham cohomology is insensitive to passage to the étale topology, we have
via pullback. In addition, if
![]() $X$
is proper over
$X$
is proper over
![]() $C$
and there is a complete, discretely valued subfield
$C$
and there is a complete, discretely valued subfield
![]() $K\subset C$
with a perfect residue field and a proper, smooth adic space
$K\subset C$
with a perfect residue field and a proper, smooth adic space
![]() $X_{0}$
over
$X_{0}$
over
![]() $K$
equipped with an isomorphism
$K$
equipped with an isomorphism
![]() $X\cong X_{0}\widehat{\otimes }_{K}C$
, then, by [Reference Bhatt, Morrow and ScholzeBMS18, 13.20], there is a canonical identification
$X\cong X_{0}\widehat{\otimes }_{K}C$
, then, by [Reference Bhatt, Morrow and ScholzeBMS18, 13.20], there is a canonical identification
In this situation, by the proof of [Reference Bhatt, Morrow and ScholzeBMS18, 13.20], the reduction modulo
![]() $\unicode[STIX]{x1D709}$
of the identification (6.2.8) recovers the identification (6.2.6) under the base change identification
$\unicode[STIX]{x1D709}$
of the identification (6.2.8) recovers the identification (6.2.6) under the base change identification
6.3 The
 $B_{\text{dR}}^{+}$
-cohomology using more general embeddings
$B_{\text{dR}}^{+}$
-cohomology using more general embeddings
To relate
![]() $R\unicode[STIX]{x1D6E4}_{\text{cris}}(X_{\acute{\text{e}}\text{t}}/B_{\text{dR}}^{+})$
to the absolute crystalline cohomology of §5.3, we now mildly generalize the construction of the former.
$R\unicode[STIX]{x1D6E4}_{\text{cris}}(X_{\acute{\text{e}}\text{t}}/B_{\text{dR}}^{+})$
to the absolute crystalline cohomology of §5.3, we now mildly generalize the construction of the former.
The étale topology of
![]() $X$
has a basis of affinoids
$X$
has a basis of affinoids
![]() $\operatorname{Spa}(A,A^{\circ })$
each of which admits an étale map
$\operatorname{Spa}(A,A^{\circ })$
each of which admits an étale map
for some
![]() $d\geqslant r\geqslant 0$
and
$d\geqslant r\geqslant 0$
and
![]() $q\in \mathbb{Q}_{{>}0}$
(we have seen in §6.2 that even those with
$q\in \mathbb{Q}_{{>}0}$
(we have seen in §6.2 that even those with
![]() $r=0$
would suffice). By [Reference HuberHub96, 1.7.3(iii)]Footnote
18
and limit arguments, there is a finite subextension
$r=0$
would suffice). By [Reference HuberHub96, 1.7.3(iii)]Footnote
18
and limit arguments, there is a finite subextension
![]() $W(k)[\frac{1}{p}]\subset K\subset C$
with the ring of integers
$W(k)[\frac{1}{p}]\subset K\subset C$
with the ring of integers
![]() ${\mathcal{O}}$
containing
${\mathcal{O}}$
containing
![]() $p^{q}$
and a finite-type
$p^{q}$
and a finite-type
![]() $({\mathcal{O}}[T_{0},\ldots ,T_{r},T_{r+1}^{\pm 1},\ldots ,T_{d}^{\pm 1}]/(T_{0}\cdots T_{r}-p^{q}))$
-algebra
$({\mathcal{O}}[T_{0},\ldots ,T_{r},T_{r+1}^{\pm 1},\ldots ,T_{d}^{\pm 1}]/(T_{0}\cdots T_{r}-p^{q}))$
-algebra
![]() $A_{0}$
that is étale after inverting
$A_{0}$
that is étale after inverting
![]() $p$
, flat over
$p$
, flat over
![]() ${\mathcal{O}}$
, normal, and such that the morphism (6.3.1) is the
${\mathcal{O}}$
, normal, and such that the morphism (6.3.1) is the
![]() $C$
-base change of an étale
$C$
-base change of an étale
![]() $\operatorname{Spa}(K,{\mathcal{O}})$
-morphism
$\operatorname{Spa}(K,{\mathcal{O}})$
-morphism
By also using the reduced fiber theorem [SP, 09IL], we enlarge
![]() $K$
to ensure that, in addition,
$K$
to ensure that, in addition,
The connected components of
![]() $\operatorname{Spec}(A_{0})$
on which
$\operatorname{Spec}(A_{0})$
on which
![]() $p$
is a unit do not contribute to
$p$
is a unit do not contribute to
![]() $\widehat{A_{0}}$
, so we lose no generality by assuming that
$\widehat{A_{0}}$
, so we lose no generality by assuming that
![]() $\operatorname{Spec}(A_{0})$
has no such components.
$\operatorname{Spec}(A_{0})$
has no such components.
By working locally on
![]() $\operatorname{Spa}(\widehat{A_{0}}[\frac{1}{p}],\widehat{A_{0}})$
, we refine the basis above to consist of those
$\operatorname{Spa}(\widehat{A_{0}}[\frac{1}{p}],\widehat{A_{0}})$
, we refine the basis above to consist of those
![]() $\operatorname{Spa}(A,A^{\circ })$
for which, in addition, there are finite subsets
$\operatorname{Spa}(A,A^{\circ })$
for which, in addition, there are finite subsets
![]() $\unicode[STIX]{x1D6F9}_{0}\subset (\widehat{A_{0}})^{\times }$
and
$\unicode[STIX]{x1D6F9}_{0}\subset (\widehat{A_{0}})^{\times }$
and
![]() $\unicode[STIX]{x1D6EF}_{0}\subset \widehat{A_{0}}\cap (\widehat{A_{0}}[\frac{1}{p}])^{\times }$
such that the map
$\unicode[STIX]{x1D6EF}_{0}\subset \widehat{A_{0}}\cap (\widehat{A_{0}}[\frac{1}{p}])^{\times }$
such that the map
is surjective. Then there are finite subsets
![]() $\unicode[STIX]{x1D6F9}\subset (A^{\circ })^{\times }$
and
$\unicode[STIX]{x1D6F9}\subset (A^{\circ })^{\times }$
and
![]() $\unicode[STIX]{x1D6EF}\subset A^{\circ }\cap A^{\times }$
such that the map
$\unicode[STIX]{x1D6EF}\subset A^{\circ }\cap A^{\times }$
such that the map
is also surjective. Defining the ring
![]() $B_{\text{dR}}^{+}\langle (X_{u}^{\pm 1})_{u\in \unicode[STIX]{x1D6F9}},\,(X_{a})_{a\in \unicode[STIX]{x1D6EF}}\rangle$
analogously to (6.2.3), so that the map (6.3.5) gives rise to the surjection
$B_{\text{dR}}^{+}\langle (X_{u}^{\pm 1})_{u\in \unicode[STIX]{x1D6F9}},\,(X_{a})_{a\in \unicode[STIX]{x1D6EF}}\rangle$
analogously to (6.2.3), so that the map (6.3.5) gives rise to the surjection
we set
By [Reference Bhatt, Morrow and ScholzeBMS18, 13.4(ii)], each
![]() $D_{\unicode[STIX]{x1D6F9},\,\unicode[STIX]{x1D6EF},\,n}(A)$
is a complete, strongly Noetherian Tate ring (in the sense of [Reference HuberHub93, §1]), with the image of
$D_{\unicode[STIX]{x1D6F9},\,\unicode[STIX]{x1D6EF},\,n}(A)$
is a complete, strongly Noetherian Tate ring (in the sense of [Reference HuberHub93, §1]), with the image of
![]() $(A_{\text{inf}}/\unicode[STIX]{x1D709}^{n})\langle (X_{u}^{\pm 1})_{u\in \unicode[STIX]{x1D6F4}},(X_{a})_{a\in \unicode[STIX]{x1D6EF}}\rangle$
endowed with its
$(A_{\text{inf}}/\unicode[STIX]{x1D709}^{n})\langle (X_{u}^{\pm 1})_{u\in \unicode[STIX]{x1D6F4}},(X_{a})_{a\in \unicode[STIX]{x1D6EF}}\rangle$
endowed with its
![]() $p$
-adic topology as a ring of definition. By construction,
$p$
-adic topology as a ring of definition. By construction,
![]() $D_{\unicode[STIX]{x1D6F9},\,\unicode[STIX]{x1D6EF},\,n}(A)$
is a nilpotent thickening of
$D_{\unicode[STIX]{x1D6F9},\,\unicode[STIX]{x1D6EF},\,n}(A)$
is a nilpotent thickening of
![]() $D_{\unicode[STIX]{x1D6F9},\,\unicode[STIX]{x1D6EF},\,1}(A)\cong A$
.
$D_{\unicode[STIX]{x1D6F9},\,\unicode[STIX]{x1D6EF},\,1}(A)\cong A$
.
The ring
![]() $B_{\text{dR}}^{+}$
is a
$B_{\text{dR}}^{+}$
is a
![]() $K$
-algebra (see §6.1), so we let
$K$
-algebra (see §6.1), so we let
![]() $(B_{\text{dR}}^{+}/\unicode[STIX]{x1D709}^{n})_{0}\subset B_{\text{dR}}^{+}/\unicode[STIX]{x1D709}^{n}$
for
$(B_{\text{dR}}^{+}/\unicode[STIX]{x1D709}^{n})_{0}\subset B_{\text{dR}}^{+}/\unicode[STIX]{x1D709}^{n}$
for
![]() $n>0$
be the (module-finite)
$n>0$
be the (module-finite)
![]() $A_{\text{inf}}/\unicode[STIX]{x1D709}^{n}$
-subalgebra generated by the image of
$A_{\text{inf}}/\unicode[STIX]{x1D709}^{n}$
-subalgebra generated by the image of
![]() ${\mathcal{O}}$
. The proof of [Reference Bhatt, Morrow and ScholzeBMS18, 13.11] shows (with
${\mathcal{O}}$
. The proof of [Reference Bhatt, Morrow and ScholzeBMS18, 13.11] shows (with
![]() $R_{A}$
there replaced by our
$R_{A}$
there replaced by our
![]() $\widehat{A_{0}}[\frac{1}{p}]$
)Footnote
19
that the
$\widehat{A_{0}}[\frac{1}{p}]$
)Footnote
19
that the
![]() $B_{\text{dR}}^{+}$
-algebra
$B_{\text{dR}}^{+}$
-algebra
has no nonzero
![]() $\unicode[STIX]{x1D709}$
-torsion and is
$\unicode[STIX]{x1D709}$
-torsion and is
![]() $\unicode[STIX]{x1D709}$
-adically complete with
$\unicode[STIX]{x1D709}$
-adically complete with
The argument of footnote 19 shows that the map
![]() $(B_{\text{dR}}^{+}/\unicode[STIX]{x1D709}^{n+1})_{0}\widehat{\otimes }_{{\mathcal{O}}}A_{0}\rightarrow (B_{\text{dR}}^{+}/\unicode[STIX]{x1D709}^{n})_{0}\widehat{\otimes }_{{\mathcal{O}}}A_{0}$
is surjective for
$(B_{\text{dR}}^{+}/\unicode[STIX]{x1D709}^{n+1})_{0}\widehat{\otimes }_{{\mathcal{O}}}A_{0}\rightarrow (B_{\text{dR}}^{+}/\unicode[STIX]{x1D709}^{n})_{0}\widehat{\otimes }_{{\mathcal{O}}}A_{0}$
is surjective for
![]() $n>0$
(with the kernel of square zero, as may be seen after inverting
$n>0$
(with the kernel of square zero, as may be seen after inverting
![]() $p$
), so the subring
$p$
), so the subring
Moreover, we have the following analogue of [Reference Bhatt, Morrow and ScholzeBMS18, 13.12(ii)] whose proof will be given in §6.4.
Lemma 6.3.8. If
![]() $\operatorname{Spa}(A,A^{\circ })$
is an element of the refined basis for
$\operatorname{Spa}(A,A^{\circ })$
is an element of the refined basis for
![]() $X_{\acute{\text{e}}\text{t}}$
described above,
$X_{\acute{\text{e}}\text{t}}$
described above,
![]() $\unicode[STIX]{x1D6F9}\subset (A^{\circ })^{\times }$
(respectively,
$\unicode[STIX]{x1D6F9}\subset (A^{\circ })^{\times }$
(respectively,
![]() $\unicode[STIX]{x1D6EF}\subset A^{\circ }\cap A^{\times }$
) contains the images of the
$\unicode[STIX]{x1D6EF}\subset A^{\circ }\cap A^{\times }$
) contains the images of the
![]() $T_{i}$
for
$T_{i}$
for
![]() $r+1\leqslant i\leqslant d$
(respectively,
$r+1\leqslant i\leqslant d$
(respectively,
![]() $1\leqslant i\leqslant r$
) under a coordinate morphism as in (6.3.1), and
$1\leqslant i\leqslant r$
) under a coordinate morphism as in (6.3.1), and
![]() $\unicode[STIX]{x1D6F9}$
and
$\unicode[STIX]{x1D6F9}$
and
![]() $\unicode[STIX]{x1D6EF}$
are large enough (see the proof for the precise meaning), then
$\unicode[STIX]{x1D6EF}$
are large enough (see the proof for the precise meaning), then
where
![]() $\widetilde{a}\in \mathop{\varprojlim }\nolimits_{n>0}((B_{\text{dR}}^{+}/\unicode[STIX]{x1D709}^{n})_{0}\widehat{\otimes }_{{\mathcal{O}}}A_{0})\subset B_{\text{dR}}^{+}\widehat{\otimes }_{K}(A_{0}[\frac{1}{p}])$
is a fixed lift of
$\widetilde{a}\in \mathop{\varprojlim }\nolimits_{n>0}((B_{\text{dR}}^{+}/\unicode[STIX]{x1D709}^{n})_{0}\widehat{\otimes }_{{\mathcal{O}}}A_{0})\subset B_{\text{dR}}^{+}\widehat{\otimes }_{K}(A_{0}[\frac{1}{p}])$
is a fixed lift of
![]() $a$
(see (6.3.7)). In particular, for large
$a$
(see (6.3.7)). In particular, for large
![]() $\unicode[STIX]{x1D6F9}$
and
$\unicode[STIX]{x1D6F9}$
and
![]() $\unicode[STIX]{x1D6EF}$
, the
$\unicode[STIX]{x1D6EF}$
, the
![]() $B_{\text{dR}}^{+}$
-algebra
$B_{\text{dR}}^{+}$
-algebra
![]() $D_{\unicode[STIX]{x1D6F9},\,\unicode[STIX]{x1D6EF}}(A)$
has no nonzero
$D_{\unicode[STIX]{x1D6F9},\,\unicode[STIX]{x1D6EF}}(A)$
has no nonzero
![]() $\unicode[STIX]{x1D709}$
-torsion and is
$\unicode[STIX]{x1D709}$
-torsion and is
![]() $\unicode[STIX]{x1D709}$
-adically complete.
$\unicode[STIX]{x1D709}$
-adically complete.
Similarly to §6.2, for any
![]() $\unicode[STIX]{x1D6F9}$
and
$\unicode[STIX]{x1D6F9}$
and
![]() $\unicode[STIX]{x1D6EF}$
as in (6.3.5), the derivations
$\unicode[STIX]{x1D6EF}$
as in (6.3.5), the derivations
![]() $\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\log (X_{a})}:=X_{a}\,\cdot \,\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}X_{a}}$
with
$\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\log (X_{a})}:=X_{a}\,\cdot \,\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}X_{a}}$
with
![]() $a\in \unicode[STIX]{x1D6F9}\cup \unicode[STIX]{x1D6EF}$
extend to
$a\in \unicode[STIX]{x1D6F9}\cup \unicode[STIX]{x1D6EF}$
extend to
![]() $D_{\unicode[STIX]{x1D6F9},\,\unicode[STIX]{x1D6EF}}(A)$
, and we may define the Koszul complex
$D_{\unicode[STIX]{x1D6F9},\,\unicode[STIX]{x1D6EF}}(A)$
, and we may define the Koszul complex
that is functorial in replacing
![]() $\unicode[STIX]{x1D6F9}$
and
$\unicode[STIX]{x1D6F9}$
and
![]() $\unicode[STIX]{x1D6EF}$
by larger
$\unicode[STIX]{x1D6EF}$
by larger
![]() $\unicode[STIX]{x1D6F9}^{\prime }$
and
$\unicode[STIX]{x1D6F9}^{\prime }$
and
![]() $\unicode[STIX]{x1D6EF}^{\prime }$
. Since
$\unicode[STIX]{x1D6EF}^{\prime }$
. Since
![]() $a\in A^{\times }$
for
$a\in A^{\times }$
for
![]() $a\in \unicode[STIX]{x1D6F9}\cup \unicode[STIX]{x1D6EF}$
, the proof of [Reference Bhatt, Morrow and ScholzeBMS18, 13.13] shows that for
$a\in \unicode[STIX]{x1D6F9}\cup \unicode[STIX]{x1D6EF}$
, the proof of [Reference Bhatt, Morrow and ScholzeBMS18, 13.13] shows that for
![]() $\unicode[STIX]{x1D6F9}$
and
$\unicode[STIX]{x1D6F9}$
and
![]() $\unicode[STIX]{x1D6EF}$
to which Lemma 6.3.8 applies,
$\unicode[STIX]{x1D6EF}$
to which Lemma 6.3.8 applies,
compatibly with enlarging
![]() $\unicode[STIX]{x1D6F9}$
and
$\unicode[STIX]{x1D6F9}$
and
![]() $\unicode[STIX]{x1D6EF}$
. In particular, due to the derived
$\unicode[STIX]{x1D6EF}$
. In particular, due to the derived
![]() $\unicode[STIX]{x1D709}$
-adic completeness supplied by Lemma 6.3.8, for such large enough
$\unicode[STIX]{x1D709}$
-adic completeness supplied by Lemma 6.3.8, for such large enough
![]() $\unicode[STIX]{x1D6F9}$
and
$\unicode[STIX]{x1D6F9}$
and
![]() $\unicode[STIX]{x1D6EF}$
, the map
$\unicode[STIX]{x1D6EF}$
, the map
Thus, if the element
![]() $\operatorname{Spa}(A,A^{\circ })$
of the refined basis above also belongs to the basis considered in §6.2, that is, if it has an étale coordinate map as in (6.2.1) and a surjection (6.2.2), then we obtain the functorial in
$\operatorname{Spa}(A,A^{\circ })$
of the refined basis above also belongs to the basis considered in §6.2, that is, if it has an étale coordinate map as in (6.2.1) and a surjection (6.2.2), then we obtain the functorial in
![]() $\operatorname{Spa}(A,A^{\circ })$
quasi-isomorphism with the complex
$\operatorname{Spa}(A,A^{\circ })$
quasi-isomorphism with the complex
![]() $\unicode[STIX]{x1D6FA}_{A/B_{\text{dR}}^{+}}^{\bullet }$
of (6.2.4):
$\unicode[STIX]{x1D6FA}_{A/B_{\text{dR}}^{+}}^{\bullet }$
of (6.2.4):
Such
![]() $\operatorname{Spa}(A,A^{\circ })$
still form a basis for
$\operatorname{Spa}(A,A^{\circ })$
still form a basis for
![]() $X_{\acute{\text{e}}\text{t}}$
(see the parenthetical remark after (6.3.1)), so we conclude that the hypercohomology of the sheafification of the complex of presheaves furnished by the target of (6.3.11) is identified with
$X_{\acute{\text{e}}\text{t}}$
(see the parenthetical remark after (6.3.1)), so we conclude that the hypercohomology of the sheafification of the complex of presheaves furnished by the target of (6.3.11) is identified with
![]() $R\unicode[STIX]{x1D6E4}_{\text{cris}}(X_{\acute{\text{e}}\text{t}}/B_{\text{dR}}^{+})$
. In conclusion, we may summarize informally:
$R\unicode[STIX]{x1D6E4}_{\text{cris}}(X_{\acute{\text{e}}\text{t}}/B_{\text{dR}}^{+})$
. In conclusion, we may summarize informally:
6.4 Proof of Lemma 6.3.8
We adapt the proof of [Reference Bhatt, Morrow and ScholzeBMS18, 13.12(ii)] as follows. In addition to the coordinate morphism (6.3.1) and its descent (6.3.2) used in the statement, we fix subsets
such that, as in (6.3.4), the map
is surjective and
![]() $\unicode[STIX]{x1D6F9}_{0}$
(respectively,
$\unicode[STIX]{x1D6F9}_{0}$
(respectively,
![]() $\unicode[STIX]{x1D6EF}_{0}$
) contains the images of the
$\unicode[STIX]{x1D6EF}_{0}$
) contains the images of the
![]() $T_{i}$
for
$T_{i}$
for
![]() $r+1\leqslant i\leqslant d$
(respectively,
$r+1\leqslant i\leqslant d$
(respectively,
![]() $1\leqslant i\leqslant r$
) under the map (6.3.2). We require that
$1\leqslant i\leqslant r$
) under the map (6.3.2). We require that
![]() $\unicode[STIX]{x1D6F9}$
(respectively,
$\unicode[STIX]{x1D6F9}$
(respectively,
![]() $\unicode[STIX]{x1D6EF}$
) contains the image of this
$\unicode[STIX]{x1D6EF}$
) contains the image of this
![]() $\unicode[STIX]{x1D6F9}_{0}$
(respectively,
$\unicode[STIX]{x1D6F9}_{0}$
(respectively,
![]() $\unicode[STIX]{x1D6EF}_{0}$
) in
$\unicode[STIX]{x1D6EF}_{0}$
) in
![]() $A^{\circ }$
; this is the meaning of ‘large enough’ in the statement. We set
$A^{\circ }$
; this is the meaning of ‘large enough’ in the statement. We set
The continuous map
![]() $K\rightarrow B_{\text{dR}}^{+}$
(see §6.1) gives a continuous map compatible with
$K\rightarrow B_{\text{dR}}^{+}$
(see §6.1) gives a continuous map compatible with
![]() $s_{0}$
and
$s_{0}$
and
![]() $s$
:
$s$
:
By the
![]() $K[T_{1},\ldots ,T_{r},T_{r+1}^{\pm 1},\ldots ,T_{d}^{\pm 1}]$
-étaleness of
$K[T_{1},\ldots ,T_{r},T_{r+1}^{\pm 1},\ldots ,T_{d}^{\pm 1}]$
-étaleness of
![]() $A_{0}[\frac{1}{p}]$
, the map
$A_{0}[\frac{1}{p}]$
, the map
By [Reference Gabber and RameroGR03, 7.3.15], for each
![]() $n>0$
, the subring
$n>0$
, the subring
![]() $D_{0,\,n}^{\circ }\subset D_{0,\,n}$
of powerbounded elements is the preimage of its counterpart
$D_{0,\,n}^{\circ }\subset D_{0,\,n}$
of powerbounded elements is the preimage of its counterpart
![]() $(\widehat{A_{0}}[\frac{1}{p}])^{\circ }\subset \widehat{A_{0}}[\frac{1}{p}]$
. Thus, the lift (6.4.1) maps
$(\widehat{A_{0}}[\frac{1}{p}])^{\circ }\subset \widehat{A_{0}}[\frac{1}{p}]$
. Thus, the lift (6.4.1) maps
![]() $A_{0}$
to
$A_{0}$
to
![]() $D_{0,\,n}^{\circ }$
, so also to some ring of definition of
$D_{0,\,n}^{\circ }$
, so also to some ring of definition of
![]() $D_{0,\,n}$
. By composing with the map
$D_{0,\,n}$
. By composing with the map
![]() $D_{0,\,n}\rightarrow D_{\unicode[STIX]{x1D6F9},\,\unicode[STIX]{x1D6EF},\,n}(A)$
, we obtain the map
$D_{0,\,n}\rightarrow D_{\unicode[STIX]{x1D6F9},\,\unicode[STIX]{x1D6EF},\,n}(A)$
, we obtain the map
![]() $A_{0}\rightarrow D_{\unicode[STIX]{x1D6F9},\,\unicode[STIX]{x1D6EF},\,n}(A)$
whose image lies in some ring of definition, so, as
$A_{0}\rightarrow D_{\unicode[STIX]{x1D6F9},\,\unicode[STIX]{x1D6EF},\,n}(A)$
whose image lies in some ring of definition, so, as
![]() $n$
varies, also the map
$n$
varies, also the map
This gives rise to the continuous map
![]() $y$
in the diagram
$y$
in the diagram

whose maps ‘
![]() $X_{T_{i}}\mapsto T_{i}$
’ and
$X_{T_{i}}\mapsto T_{i}$
’ and
![]() $z$
are defined as follows.
$z$
are defined as follows.
∙ To define the map ‘
 $X_{T_{i}}\mapsto T_{i}$
’, one first forms the inverse limit over
$X_{T_{i}}\mapsto T_{i}$
’, one first forms the inverse limit over
 $N$
of the maps defined by using the fact that each
$N$
of the maps defined by using the fact that each $$\begin{eqnarray}\textstyle \quad (A_{\text{inf}}/\unicode[STIX]{x1D709}^{n})\langle (X_{u}^{\pm 1})_{u\in \unicode[STIX]{x1D6F9}},(X_{a})_{a\in \unicode[STIX]{x1D6EF}}\rangle \xrightarrow[{}]{X_{T_{i}}\mapsto T_{i}}((B_{\text{dR}}^{+}/\unicode[STIX]{x1D709}^{n})_{0}\otimes _{{\mathcal{O}}}A_{0}/p^{N})\unicode[STIX]{x27E6}(X_{a}-\widetilde{a})_{a\in (\unicode[STIX]{x1D6F9}\cup \unicode[STIX]{x1D6EF})\setminus \{T_{1},\ldots ,T_{d}\}}\unicode[STIX]{x27E7}\end{eqnarray}$$
$$\begin{eqnarray}\textstyle \quad (A_{\text{inf}}/\unicode[STIX]{x1D709}^{n})\langle (X_{u}^{\pm 1})_{u\in \unicode[STIX]{x1D6F9}},(X_{a})_{a\in \unicode[STIX]{x1D6EF}}\rangle \xrightarrow[{}]{X_{T_{i}}\mapsto T_{i}}((B_{\text{dR}}^{+}/\unicode[STIX]{x1D709}^{n})_{0}\otimes _{{\mathcal{O}}}A_{0}/p^{N})\unicode[STIX]{x27E6}(X_{a}-\widetilde{a})_{a\in (\unicode[STIX]{x1D6F9}\cup \unicode[STIX]{x1D6EF})\setminus \{T_{1},\ldots ,T_{d}\}}\unicode[STIX]{x27E7}\end{eqnarray}$$
 $\widetilde{u}$
with
$\widetilde{u}$
with
 $u\in \unicode[STIX]{x1D6F9}$
is a unit in
$u\in \unicode[STIX]{x1D6F9}$
is a unit in
 $(B_{\text{dR}}^{+}/\unicode[STIX]{x1D709}^{n})_{0}\widehat{\otimes }_{{\mathcal{O}}}A_{0}$
(see the sentence around (6.3.7)) and the identity
$(B_{\text{dR}}^{+}/\unicode[STIX]{x1D709}^{n})_{0}\widehat{\otimes }_{{\mathcal{O}}}A_{0}$
(see the sentence around (6.3.7)) and the identity  . Then one inverts
. Then one inverts
 $p$
and forms the inverse limit over
$p$
and forms the inverse limit over
 $n$
.
$n$
.∙ The continuous map
 $z$
is defined by combining the top part of the diagram, the
$z$
is defined by combining the top part of the diagram, the
 $\unicode[STIX]{x1D709}$
-adic completeness of
$\unicode[STIX]{x1D709}$
-adic completeness of
 $B_{\text{dR}}^{+}\widehat{\otimes }_{K}(A_{0}[\frac{1}{p}])$
(see §6.3), and the definition of
$B_{\text{dR}}^{+}\widehat{\otimes }_{K}(A_{0}[\frac{1}{p}])$
(see §6.3), and the definition of
 $D_{\unicode[STIX]{x1D6F9},\,\unicode[STIX]{x1D6EF}}(A)$
.
$D_{\unicode[STIX]{x1D6F9},\,\unicode[STIX]{x1D6EF}}(A)$
.
By construction, the diagram commutes, so
![]() $y\circ z=\operatorname{id}$
. By
$y\circ z=\operatorname{id}$
. By
![]() $K[T_{1},\ldots ,T_{r},T_{r+1}^{\pm 1},\ldots ,T_{d}^{\pm 1}]$
-étaleness of
$K[T_{1},\ldots ,T_{r},T_{r+1}^{\pm 1},\ldots ,T_{d}^{\pm 1}]$
-étaleness of
![]() $A_{0}[\frac{1}{p}]$
, the
$A_{0}[\frac{1}{p}]$
, the
![]() $K[T_{1},\ldots ,T_{r},T_{r+1}^{\pm 1},\ldots ,T_{d}^{\pm 1}]$
-algebra endomorphism
$K[T_{1},\ldots ,T_{r},T_{r+1}^{\pm 1},\ldots ,T_{d}^{\pm 1}]$
-algebra endomorphism
![]() $z\circ y$
of the pro-thickening
$z\circ y$
of the pro-thickening
![]() $(B_{\text{dR}}^{+}\widehat{\otimes }_{K}(A_{0}[\frac{1}{p}]))\unicode[STIX]{x27E6}(X_{a}-\widetilde{a})_{a\in (\unicode[STIX]{x1D6F9}\cup \unicode[STIX]{x1D6EF})\setminus \{T_{1},\ldots ,T_{d}\}}\unicode[STIX]{x27E7}$
of
$(B_{\text{dR}}^{+}\widehat{\otimes }_{K}(A_{0}[\frac{1}{p}]))\unicode[STIX]{x27E6}(X_{a}-\widetilde{a})_{a\in (\unicode[STIX]{x1D6F9}\cup \unicode[STIX]{x1D6EF})\setminus \{T_{1},\ldots ,T_{d}\}}\unicode[STIX]{x27E7}$
of
![]() $A$
is the identity on
$A$
is the identity on
![]() $A_{0}[\frac{1}{p}]$
, so also on
$A_{0}[\frac{1}{p}]$
, so also on
![]() $(B_{\text{dR}}^{+}\widehat{\otimes }_{K}(A_{0}[\frac{1}{p}]))$
. It also fixes every
$(B_{\text{dR}}^{+}\widehat{\otimes }_{K}(A_{0}[\frac{1}{p}]))$
. It also fixes every
![]() $X_{a}$
, so it must be the identity. Thus,
$X_{a}$
, so it must be the identity. Thus,
![]() $z$
is the desired isomorphism (6.3.9).☐
$z$
is the desired isomorphism (6.3.9).☐
6.5 The map from the absolute crystalline cohomology
Returning to the
![]() $\mathfrak{X}$
of §1.5, our next goal is to use the preceding discussion to exhibit a map
$\mathfrak{X}$
of §1.5, our next goal is to use the preceding discussion to exhibit a map
For this, we use the basis of
![]() $\mathfrak{X}_{\acute{\text{e}}\text{t}}$
consisting of the affine opens
$\mathfrak{X}_{\acute{\text{e}}\text{t}}$
consisting of the affine opens
![]() $\operatorname{Spf}(R)$
as in the ‘all possible coordinates’ setting of §5.17 and adopt the subsequent notation of §§5.17–5.40. To relate to §6.3, we set
$\operatorname{Spf}(R)$
as in the ‘all possible coordinates’ setting of §5.17 and adopt the subsequent notation of §§5.17–5.40. To relate to §6.3, we set
(so that
![]() $A^{\circ }\cong R$
and
$A^{\circ }\cong R$
and
![]() $t_{\unicode[STIX]{x1D706},\,0}$
are omitted). We may descend the étale map (5.17.3) for
$t_{\unicode[STIX]{x1D706},\,0}$
are omitted). We may descend the étale map (5.17.3) for
![]() $\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}$
to the ring of integers of a finite subextension
$\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}$
to the ring of integers of a finite subextension
![]() $W(k)[\frac{1}{p}]\subset K\subset C$
(see (1.5.2)) and then obtain the descended coordinate map (6.3.2) on the generic fiber. In addition, by enlarging
$W(k)[\frac{1}{p}]\subset K\subset C$
(see (1.5.2)) and then obtain the descended coordinate map (6.3.2) on the generic fiber. In addition, by enlarging
![]() $K$
and using the closed immersion (5.17.2), we may ensure that the descent has a closed immersion (6.3.4) (with
$K$
and using the closed immersion (5.17.2), we may ensure that the descent has a closed immersion (6.3.4) (with
![]() $\unicode[STIX]{x1D6EF}_{0}=\emptyset$
); we then enlarge
$\unicode[STIX]{x1D6EF}_{0}=\emptyset$
); we then enlarge
![]() $\unicode[STIX]{x1D6F9}$
by adjoining the image in
$\unicode[STIX]{x1D6F9}$
by adjoining the image in
![]() $(A^{\circ })^{\times }$
of the resulting
$(A^{\circ })^{\times }$
of the resulting
![]() $\unicode[STIX]{x1D6F9}_{0}$
. Thus, the above choices of
$\unicode[STIX]{x1D6F9}_{0}$
. Thus, the above choices of
![]() $A$
, the enlarged
$A$
, the enlarged
![]() $\unicode[STIX]{x1D6F9}$
, and
$\unicode[STIX]{x1D6F9}$
, and
![]() $\unicode[STIX]{x1D6EF}$
satisfy the assumptions of §6.3: specifically,
$\unicode[STIX]{x1D6EF}$
satisfy the assumptions of §6.3: specifically,
![]() $\operatorname{Spa}(A,A^{\circ })$
is an element of the (refined) basis of
$\operatorname{Spa}(A,A^{\circ })$
is an element of the (refined) basis of
![]() $(\mathfrak{X}_{C}^{\text{ad}})_{\acute{\text{e}}\text{t}}$
considered there,
$(\mathfrak{X}_{C}^{\text{ad}})_{\acute{\text{e}}\text{t}}$
considered there,
![]() $\unicode[STIX]{x1D6F9}$
(respectively,
$\unicode[STIX]{x1D6F9}$
(respectively,
![]() $\unicode[STIX]{x1D6EF}$
) contains
$\unicode[STIX]{x1D6EF}$
) contains
![]() $t_{\unicode[STIX]{x1D706},\,i}$
for
$t_{\unicode[STIX]{x1D706},\,i}$
for
![]() $r_{\unicode[STIX]{x1D706}}+1\leqslant i\leqslant d$
(respectively,
$r_{\unicode[STIX]{x1D706}}+1\leqslant i\leqslant d$
(respectively,
![]() $1\leqslant i\leqslant r_{\unicode[STIX]{x1D706}}$
), and Lemma 6.3.8 applies to (the enlarged)
$1\leqslant i\leqslant r_{\unicode[STIX]{x1D706}}$
), and Lemma 6.3.8 applies to (the enlarged)
![]() $\unicode[STIX]{x1D6F9}$
and
$\unicode[STIX]{x1D6F9}$
and
![]() $\unicode[STIX]{x1D6EF}$
. In conclusion, with these choices, the entire §6.3 applies.
$\unicode[STIX]{x1D6EF}$
. In conclusion, with these choices, the entire §6.3 applies.
By using descents and [Reference Gabber and RameroGR03, 7.3.15] as in the proof of Lemma 6.3.8, we see that the elements
![]() $[(p^{1/p^{\infty }})^{q_{\unicode[STIX]{x1D706}}}]/(X_{t_{\unicode[STIX]{x1D706},\,1}}\cdots X_{t_{\unicode[STIX]{x1D706},\,r_{\unicode[STIX]{x1D706}}}})$
of
$[(p^{1/p^{\infty }})^{q_{\unicode[STIX]{x1D706}}}]/(X_{t_{\unicode[STIX]{x1D706},\,1}}\cdots X_{t_{\unicode[STIX]{x1D706},\,r_{\unicode[STIX]{x1D706}}}})$
of
![]() $D_{\unicode[STIX]{x1D6F9},\,\unicode[STIX]{x1D6EF},\,n}(A)$
lie in
$D_{\unicode[STIX]{x1D6F9},\,\unicode[STIX]{x1D6EF},\,n}(A)$
lie in
![]() $(D_{\unicode[STIX]{x1D6F9},\,\unicode[STIX]{x1D6EF},\,n}(A))^{\circ }$
. Thus, each
$(D_{\unicode[STIX]{x1D6F9},\,\unicode[STIX]{x1D6EF},\,n}(A))^{\circ }$
. Thus, each
![]() $(D_{\unicode[STIX]{x1D6F9},\,\unicode[STIX]{x1D6EF},\,n}(A))^{\circ }$
, so also
$(D_{\unicode[STIX]{x1D6F9},\,\unicode[STIX]{x1D6EF},\,n}(A))^{\circ }$
, so also
![]() $D_{\unicode[STIX]{x1D6F9},\,\unicode[STIX]{x1D6EF}}(A)$
, is naturally an algebra over the ring
$D_{\unicode[STIX]{x1D6F9},\,\unicode[STIX]{x1D6EF}}(A)$
, is naturally an algebra over the ring
![]() $A_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}^{\Box }$
defined in (5.22.1). In fact, since each
$A_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}^{\Box }$
defined in (5.22.1). In fact, since each
![]() $D_{\unicode[STIX]{x1D6F9},\,\unicode[STIX]{x1D6EF},\,n}(A)$
is a
$D_{\unicode[STIX]{x1D6F9},\,\unicode[STIX]{x1D6EF},\,n}(A)$
is a
![]() $\mathbb{Q}$
-algebra in which
$\mathbb{Q}$
-algebra in which
![]() $\unicode[STIX]{x1D709}^{m}$
vanishes for
$\unicode[STIX]{x1D709}^{m}$
vanishes for
![]() $m\geqslant n$
and each
$m\geqslant n$
and each
![]() $X_{a}$
is a unit in
$X_{a}$
is a unit in
![]() $D_{\unicode[STIX]{x1D6F9},\,\unicode[STIX]{x1D6EF}}(A)$
, the universal relations (5.26.3) and (5.27.3) imply that each
$D_{\unicode[STIX]{x1D6F9},\,\unicode[STIX]{x1D6EF}}(A)$
, the universal relations (5.26.3) and (5.27.3) imply that each
![]() $(D_{\unicode[STIX]{x1D6F9},\,\unicode[STIX]{x1D6EF},\,n}(A))^{\circ }$
, so also
$(D_{\unicode[STIX]{x1D6F9},\,\unicode[STIX]{x1D6EF},\,n}(A))^{\circ }$
, so also
![]() $D_{\unicode[STIX]{x1D6F9},\,\unicode[STIX]{x1D6EF}}(A)$
, is naturally an algebra over
$D_{\unicode[STIX]{x1D6F9},\,\unicode[STIX]{x1D6EF}}(A)$
, is naturally an algebra over
compatibly with the maps
and the ‘change of
![]() $\unicode[STIX]{x1D706}_{0}$
’ isomorphisms (5.26.7). The resulting algebra structure map factors through some (necessarily
$\unicode[STIX]{x1D706}_{0}$
’ isomorphisms (5.26.7). The resulting algebra structure map factors through some (necessarily
![]() $p$
-adically complete) ring of definition
$p$
-adically complete) ring of definition
![]() $(D_{\unicode[STIX]{x1D6F9},\,\unicode[STIX]{x1D6EF},\,n}(A))_{0}$
:
$(D_{\unicode[STIX]{x1D6F9},\,\unicode[STIX]{x1D6EF},\,n}(A))_{0}$
:
so the map
![]() $(D_{\unicode[STIX]{x1D6F9},\,\unicode[STIX]{x1D6EF},\,n}(A))_{0}\rightarrow R$
is surjective. In addition, by [SP, 07GM], the kernel of the map
$(D_{\unicode[STIX]{x1D6F9},\,\unicode[STIX]{x1D6EF},\,n}(A))_{0}\rightarrow R$
is surjective. In addition, by [SP, 07GM], the kernel of the map
![]() $(D_{\unicode[STIX]{x1D6F9},\,\unicode[STIX]{x1D6EF},\,n}(A))^{\circ }{\twoheadrightarrow}R/p$
has a unique divided power structure, so we obtain a map
$(D_{\unicode[STIX]{x1D6F9},\,\unicode[STIX]{x1D6EF},\,n}(A))^{\circ }{\twoheadrightarrow}R/p$
has a unique divided power structure, so we obtain a map
from the divided power envelope
![]() $D_{j_{\unicode[STIX]{x1D706}_{0}}}$
defined in §5.28. For a fixed
$D_{j_{\unicode[STIX]{x1D706}_{0}}}$
defined in §5.28. For a fixed
![]() $n$
and modulo the
$n$
and modulo the
![]() $\unicode[STIX]{x1D709}^{m}/m!$
with
$\unicode[STIX]{x1D709}^{m}/m!$
with
![]() $m\geqslant n$
, the kernel of the map
$m\geqslant n$
, the kernel of the map
![]() $(A_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}^{\Box }\otimes _{A_{\text{inf}}}A_{\text{cris}}^{0})\otimes _{\mathbb{Z}[Q]}\mathbb{Z}[P_{\unicode[STIX]{x1D706}_{0}}]{\twoheadrightarrow}R/p$
is finitely generated and, due to the surjectivity of
$(A_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}^{\Box }\otimes _{A_{\text{inf}}}A_{\text{cris}}^{0})\otimes _{\mathbb{Z}[Q]}\mathbb{Z}[P_{\unicode[STIX]{x1D706}_{0}}]{\twoheadrightarrow}R/p$
is finitely generated and, due to the surjectivity of
![]() $(A_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}^{\Box }\otimes _{A_{\text{inf}}}A_{\text{cris}}^{0})\otimes _{\mathbb{Z}[Q]}\mathbb{Z}[P_{\unicode[STIX]{x1D706}_{0}}]{\twoheadrightarrow}R$
, the generating set may be arranged to consist of
$(A_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}^{\Box }\otimes _{A_{\text{inf}}}A_{\text{cris}}^{0})\otimes _{\mathbb{Z}[Q]}\mathbb{Z}[P_{\unicode[STIX]{x1D706}_{0}}]{\twoheadrightarrow}R$
, the generating set may be arranged to consist of
![]() $p$
and a finite set of elements that vanish already in
$p$
and a finite set of elements that vanish already in
![]() $R$
. Thus, since
$R$
. Thus, since
![]() $D_{j_{\unicode[STIX]{x1D706}_{0}}}$
is generated as an
$D_{j_{\unicode[STIX]{x1D706}_{0}}}$
is generated as an
![]() $((A_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}^{\Box }\otimes _{A_{\text{inf}}}A_{\text{cris}}^{0})\otimes _{\mathbb{Z}[Q]}\mathbb{Z}[P_{\unicode[STIX]{x1D706}_{0}}])$
-algebra by the divided powers of the elements of this kernel, by enlarging
$((A_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}^{\Box }\otimes _{A_{\text{inf}}}A_{\text{cris}}^{0})\otimes _{\mathbb{Z}[Q]}\mathbb{Z}[P_{\unicode[STIX]{x1D706}_{0}}])$
-algebra by the divided powers of the elements of this kernel, by enlarging
![]() $(D_{\unicode[STIX]{x1D6F9},\,\unicode[STIX]{x1D6EF},\,n}(A))_{0}$
we may factor the map (6.5.4) as follows:
$(D_{\unicode[STIX]{x1D6F9},\,\unicode[STIX]{x1D6EF},\,n}(A))_{0}$
we may factor the map (6.5.4) as follows:
Consequently, we obtain continuous maps that are independent of
![]() $\unicode[STIX]{x1D706}_{0}$
and compatible as
$\unicode[STIX]{x1D706}_{0}$
and compatible as
![]() $n$
varies:
$n$
varies:
Via the last map, the
![]() $D_{j_{\unicode[STIX]{x1D706}_{0}}}$
-valued derivations
$D_{j_{\unicode[STIX]{x1D706}_{0}}}$
-valued derivations
![]() $\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\log (X_{\unicode[STIX]{x1D70E}})}$
for
$\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\log (X_{\unicode[STIX]{x1D70E}})}$
for
![]() $\unicode[STIX]{x1D70E}\in \unicode[STIX]{x1D6F4}$
and
$\unicode[STIX]{x1D70E}\in \unicode[STIX]{x1D6F4}$
and
![]() $\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\log (X_{\unicode[STIX]{x1D706},\,i})}$
for
$\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\log (X_{\unicode[STIX]{x1D706},\,i})}$
for
![]() $\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}$
and
$\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}$
and
![]() $1\leqslant i\leqslant d$
of
$1\leqslant i\leqslant d$
of
![]() $D_{j_{\unicode[STIX]{x1D706}_{0}}}$
are compatible with the corresponding
$D_{j_{\unicode[STIX]{x1D706}_{0}}}$
are compatible with the corresponding
![]() $D_{\unicode[STIX]{x1D6F9},\,\unicode[STIX]{x1D6EF}}(A)$
-valued derivations of
$D_{\unicode[STIX]{x1D6F9},\,\unicode[STIX]{x1D6EF}}(A)$
-valued derivations of
![]() $D_{\unicode[STIX]{x1D6F9},\,\unicode[STIX]{x1D6EF}}(A)$
(see (6.5.2) and §§5.31 and 6.3). Thus, due to the density of
$D_{\unicode[STIX]{x1D6F9},\,\unicode[STIX]{x1D6EF}}(A)$
(see (6.5.2) and §§5.31 and 6.3). Thus, due to the density of
![]() $D_{j_{\unicode[STIX]{x1D706}_{0}}}$
in
$D_{j_{\unicode[STIX]{x1D706}_{0}}}$
in
![]() $D_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}$
, the same compatibility holds for the map
$D_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}$
, the same compatibility holds for the map
![]() $D_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}\rightarrow D_{\unicode[STIX]{x1D6F9},\,\unicode[STIX]{x1D6EF}}(A)$
, to the effect that we obtain a map of complexes
$D_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}\rightarrow D_{\unicode[STIX]{x1D6F9},\,\unicode[STIX]{x1D6EF}}(A)$
, to the effect that we obtain a map of complexes
Its formation commutes with enlarging
![]() $\unicode[STIX]{x1D6F4}$
and
$\unicode[STIX]{x1D6F4}$
and
![]() $\unicode[STIX]{x1D6EC}$
(and, respectively,
$\unicode[STIX]{x1D6EC}$
(and, respectively,
![]() $\unicode[STIX]{x1D6F9}$
and
$\unicode[STIX]{x1D6F9}$
and
![]() $\unicode[STIX]{x1D6EF}$
), so we obtain the map
$\unicode[STIX]{x1D6EF}$
), so we obtain the map
The formation of this map is compatible with replacing
![]() $R$
by a
$R$
by a
![]() $p$
-adically formally étale
$p$
-adically formally étale
![]() $R$
-algebra
$R$
-algebra
![]() $R^{\prime }$
equipped with data as in §5.17. The resulting map of complexes of presheaves gives rise to the map of complexes of sheaves on
$R^{\prime }$
equipped with data as in §5.17. The resulting map of complexes of presheaves gives rise to the map of complexes of sheaves on
![]() $\mathfrak{X}_{\acute{\text{e}}\text{t}}$
from the complex whose
$\mathfrak{X}_{\acute{\text{e}}\text{t}}$
from the complex whose
![]() $R\unicode[STIX]{x1D6E4}(\mathfrak{X}_{\acute{\text{e}}\text{t}},-)$
is identified with
$R\unicode[STIX]{x1D6E4}(\mathfrak{X}_{\acute{\text{e}}\text{t}},-)$
is identified with
![]() $R\unicode[STIX]{x1D6E4}_{\log \text{cris}}(\mathfrak{X}_{{\mathcal{O}}_{C}/p}/A_{\text{cris}})$
(see (5.23.3) and §5.32) to the pushforward of the complex whose
$R\unicode[STIX]{x1D6E4}_{\log \text{cris}}(\mathfrak{X}_{{\mathcal{O}}_{C}/p}/A_{\text{cris}})$
(see (5.23.3) and §5.32) to the pushforward of the complex whose
![]() $R\unicode[STIX]{x1D6E4}((\mathfrak{X}_{C}^{\text{ad}})_{\acute{\text{e}}\text{t}},-)$
is identified with
$R\unicode[STIX]{x1D6E4}((\mathfrak{X}_{C}^{\text{ad}})_{\acute{\text{e}}\text{t}},-)$
is identified with
![]() $R\unicode[STIX]{x1D6E4}_{\text{cris}}(\mathfrak{X}_{C}^{\text{ad}}/B_{\text{dR}}^{+})$
(see §6.3 and (6.3.12)). Thus, by applying
$R\unicode[STIX]{x1D6E4}_{\text{cris}}(\mathfrak{X}_{C}^{\text{ad}}/B_{\text{dR}}^{+})$
(see §6.3 and (6.3.12)). Thus, by applying
![]() $R\unicode[STIX]{x1D6E4}(\mathfrak{X}_{\acute{\text{e}}\text{t}},-)$
, we obtain the desired map (6.5.1):
$R\unicode[STIX]{x1D6E4}(\mathfrak{X}_{\acute{\text{e}}\text{t}},-)$
, we obtain the desired map (6.5.1):
In addition, by its construction and Lemma 5.29, the map
![]() $D_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}\rightarrow D_{\unicode[STIX]{x1D6F9},\,\unicode[STIX]{x1D6EF}}(R[\frac{1}{p}])$
of (6.5.5) is compatible with the maps to
$D_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}\rightarrow D_{\unicode[STIX]{x1D6F9},\,\unicode[STIX]{x1D6EF}}(R[\frac{1}{p}])$
of (6.5.5) is compatible with the maps to
![]() $R[\frac{1}{p}]$
(see (6.5.3)). Thus, [Reference Bhatt, Morrow and ScholzeBMS18, 13.13] used to obtain (6.3.10) implies that the map (6.5.6) is compatible with the maps in the derived category to
$R[\frac{1}{p}]$
(see (6.5.3)). Thus, [Reference Bhatt, Morrow and ScholzeBMS18, 13.13] used to obtain (6.3.10) implies that the map (6.5.6) is compatible with the maps in the derived category to
![]() $\unicode[STIX]{x1D6FA}_{R[\frac{1}{p}]/C}^{\bullet ,\,\text{cont}}$
described in the last display of §5.32 and (6.3.10). In conclusion, the map (6.5.1) fits into the following commutative square.
$\unicode[STIX]{x1D6FA}_{R[\frac{1}{p}]/C}^{\bullet ,\,\text{cont}}$
described in the last display of §5.32 and (6.3.10). In conclusion, the map (6.5.1) fits into the following commutative square.

Having constructed the map (6.5.1), we are ready for the following extension of [Reference Bhatt, Morrow and ScholzeBMS18, 13.23].
Theorem 6.6. If
![]() $\mathfrak{X}$
is
$\mathfrak{X}$
is
![]() ${\mathcal{O}}_{C}$
-proper, then the map (6.5.1) induces the identification
${\mathcal{O}}_{C}$
-proper, then the map (6.5.1) induces the identification
and the cohomology modules of
![]() $R\unicode[STIX]{x1D6E4}_{\text{cris}}(\mathfrak{X}_{C}^{\text{ad}}/B_{\text{dR}}^{+})$
are finite free over
$R\unicode[STIX]{x1D6E4}_{\text{cris}}(\mathfrak{X}_{C}^{\text{ad}}/B_{\text{dR}}^{+})$
are finite free over
![]() $B_{\text{dR}}^{+}$
. In particular, then
$B_{\text{dR}}^{+}$
. In particular, then
compatibly with the identifications modulo
![]() $\unicode[STIX]{x1D709}$
with
$\unicode[STIX]{x1D709}$
with
![]() $R\unicode[STIX]{x1D6E4}_{\text{dR}}(\mathfrak{X}_{C}^{\text{ad}}/C)$
given by (4.18.1) and (6.2.6).
$R\unicode[STIX]{x1D6E4}_{\text{dR}}(\mathfrak{X}_{C}^{\text{ad}}/C)$
given by (4.18.1) and (6.2.6).
Proof. By Corollaries 4.20 and 5.43, the object
![]() $R\unicode[STIX]{x1D6E4}_{\log \text{cris}}(\mathfrak{X}_{{\mathcal{O}}_{C}/p}/A_{\text{cris}})$
of
$R\unicode[STIX]{x1D6E4}_{\log \text{cris}}(\mathfrak{X}_{{\mathcal{O}}_{C}/p}/A_{\text{cris}})$
of
![]() $D(A_{\text{cris}})$
is perfect and its cohomology modules become finite free after inverting
$D(A_{\text{cris}})$
is perfect and its cohomology modules become finite free after inverting
![]() $p$
. Therefore, due to (5.24.1) and the derived
$p$
. Therefore, due to (5.24.1) and the derived
![]() $p$
-adic completeness, we have the identification
$p$
-adic completeness, we have the identification
Consequently, both sides of (6.6.1) are derived
![]() $\unicode[STIX]{x1D709}$
-adically complete (see (6.2.5)) and, due to (6.2.6) and the commutativity of the diagram (6.5.7), the map (6.5.1) identifies their reductions modulo
$\unicode[STIX]{x1D709}$
-adically complete (see (6.2.5)) and, due to (6.2.6) and the commutativity of the diagram (6.5.7), the map (6.5.1) identifies their reductions modulo
![]() $\unicode[STIX]{x1D709}$
. In conclusion, (6.5.1) induces the desired identification (6.6.1) and the
$\unicode[STIX]{x1D709}$
. In conclusion, (6.5.1) induces the desired identification (6.6.1) and the
![]() $B_{\text{dR}}^{+}$
-freeness claim follows from the first sentence of the proof. The combination of (5.43.2) and (6.6.1) gives (6.6.2) and the asserted compatibility follows from Proposition 5.41 and the commutativity of (6.5.7). ◻
$B_{\text{dR}}^{+}$
-freeness claim follows from the first sentence of the proof. The combination of (5.43.2) and (6.6.1) gives (6.6.2) and the asserted compatibility follows from Proposition 5.41 and the commutativity of (6.5.7). ◻
6.7 The
 $B_{\text{dR}}^{+}$
-cohomology and the étale cohomology
$B_{\text{dR}}^{+}$
-cohomology and the étale cohomology
For any proper, smooth adic space
![]() $X$
over
$X$
over
![]() $C$
, in [Reference Bhatt, Morrow and ScholzeBMS18, 13.1] Bhatt–Morrow–Scholze constructed the functorial in
$C$
, in [Reference Bhatt, Morrow and ScholzeBMS18, 13.1] Bhatt–Morrow–Scholze constructed the functorial in
![]() $X$
identification
$X$
identification
Due to the identification (6.2.8), when
![]() $X\cong X_{0}\widehat{\otimes }_{K}C$
for a proper, smooth adic space
$X\cong X_{0}\widehat{\otimes }_{K}C$
for a proper, smooth adic space
![]() $X_{0}$
defined over a complete, discretely valued subfield
$X_{0}$
defined over a complete, discretely valued subfield
![]() $K\subset C$
that has a perfect residue field, the inverse of (6.7.1) supplies the functorial in
$K\subset C$
that has a perfect residue field, the inverse of (6.7.1) supplies the functorial in
![]() $X_{0}$
de Rham comparison isomorphism
$X_{0}$
de Rham comparison isomorphism
If
![]() $C\cong \widehat{\overline{K}}$
, then, by transport of structure, the identification (6.7.2) is
$C\cong \widehat{\overline{K}}$
, then, by transport of structure, the identification (6.7.2) is
![]() $\operatorname{Gal}(\overline{K}/K)$
-equivariant (with
$\operatorname{Gal}(\overline{K}/K)$
-equivariant (with
![]() $\operatorname{Gal}(\overline{K}/K)$
acting trivially on
$\operatorname{Gal}(\overline{K}/K)$
acting trivially on
![]() $R\unicode[STIX]{x1D6E4}_{\text{dR}}(X_{0}/K)$
) and, by [Reference Bhatt, Morrow and ScholzeBMS18, 13.1], it recovers the isomorphism constructed in [Reference ScholzeSch13a, 8.4]. In particular, in this case, (6.7.2) is compatible with filtrations, where
$R\unicode[STIX]{x1D6E4}_{\text{dR}}(X_{0}/K)$
) and, by [Reference Bhatt, Morrow and ScholzeBMS18, 13.1], it recovers the isomorphism constructed in [Reference ScholzeSch13a, 8.4]. In particular, in this case, (6.7.2) is compatible with filtrations, where
![]() $B_{\text{dR}}$
is filtered by its discrete valuation and
$B_{\text{dR}}$
is filtered by its discrete valuation and
![]() $R\unicode[STIX]{x1D6E4}_{\text{dR}}(X_{0}/K)$
(respectively,
$R\unicode[STIX]{x1D6E4}_{\text{dR}}(X_{0}/K)$
(respectively,
![]() $R\unicode[STIX]{x1D6E4}_{\acute{\text{e}}\text{t}}(X_{0}\widehat{\otimes }_{K}C,\mathbb{Z}_{p})$
) is equipped with the Hodge (respectively, trivial) filtration.
$R\unicode[STIX]{x1D6E4}_{\acute{\text{e}}\text{t}}(X_{0}\widehat{\otimes }_{K}C,\mathbb{Z}_{p})$
) is equipped with the Hodge (respectively, trivial) filtration.
For proper
![]() $\mathfrak{X}$
, we now have two ways to identify
$\mathfrak{X}$
, we now have two ways to identify
we can either base change (2.3.1) to
![]() $B_{\text{dR}}$
or combine (6.6.2) and (6.7.1). We now prove that the two ways give the same identification; this will be important in the proof of Theorem 8.7.
$B_{\text{dR}}$
or combine (6.6.2) and (6.7.1). We now prove that the two ways give the same identification; this will be important in the proof of Theorem 8.7.
Proposition 6.8. If
![]() $\mathfrak{X}$
is
$\mathfrak{X}$
is
![]() ${\mathcal{O}}_{C}$
-proper, then the map
${\mathcal{O}}_{C}$
-proper, then the map
![]() $R\unicode[STIX]{x1D6E4}_{\text{cris}}(\mathfrak{X}_{C}^{\text{ad}}/B_{\text{dR}}^{+})\rightarrow R\unicode[STIX]{x1D6E4}(\mathfrak{X}_{C}^{\text{ad}},\mathbb{Z}_{p})\otimes _{\mathbb{Z}_{p}}B_{\text{dR}}^{+}$
of [Reference Bhatt, Morrow and ScholzeBMS18, proof of 13.1] that underlies the identification (6.7.1) for
$R\unicode[STIX]{x1D6E4}_{\text{cris}}(\mathfrak{X}_{C}^{\text{ad}}/B_{\text{dR}}^{+})\rightarrow R\unicode[STIX]{x1D6E4}(\mathfrak{X}_{C}^{\text{ad}},\mathbb{Z}_{p})\otimes _{\mathbb{Z}_{p}}B_{\text{dR}}^{+}$
of [Reference Bhatt, Morrow and ScholzeBMS18, proof of 13.1] that underlies the identification (6.7.1) for
![]() $X=\mathfrak{X}_{C}^{\text{ad}}$
makes the diagram
$X=\mathfrak{X}_{C}^{\text{ad}}$
makes the diagram

commute; in particular, the identification of
![]() $R\unicode[STIX]{x1D6E4}(\mathfrak{X}_{\acute{\text{e}}\text{t}},A\unicode[STIX]{x1D6FA}_{\mathfrak{X}})\otimes _{A_{\text{inf}}}^{\mathbb{L}}B_{\text{dR}}$
with
$R\unicode[STIX]{x1D6E4}(\mathfrak{X}_{\acute{\text{e}}\text{t}},A\unicode[STIX]{x1D6FA}_{\mathfrak{X}})\otimes _{A_{\text{inf}}}^{\mathbb{L}}B_{\text{dR}}$
with
![]() $R\unicode[STIX]{x1D6E4}_{\acute{\text{e}}\text{t}}(\mathfrak{X}_{C}^{\text{ad}},\mathbb{Z}_{p})\otimes _{\mathbb{Z}_{p}}^{\mathbb{L}}B_{\text{dR}}$
that results from (2.3.1) (and is encoded by the bottom part of the above diagram) agrees with the identification that results from (6.6.2) and (6.7.1) (and is encoded by the top part of the diagram).
$R\unicode[STIX]{x1D6E4}_{\acute{\text{e}}\text{t}}(\mathfrak{X}_{C}^{\text{ad}},\mathbb{Z}_{p})\otimes _{\mathbb{Z}_{p}}^{\mathbb{L}}B_{\text{dR}}$
that results from (2.3.1) (and is encoded by the bottom part of the above diagram) agrees with the identification that results from (6.6.2) and (6.7.1) (and is encoded by the top part of the diagram).
Proof. Since
![]() $\unicode[STIX]{x1D711}^{-1}(\unicode[STIX]{x1D707})$
lies in
$\unicode[STIX]{x1D711}^{-1}(\unicode[STIX]{x1D707})$
lies in
![]() $W(\mathfrak{m}^{\flat })$
and is a unit in
$W(\mathfrak{m}^{\flat })$
and is a unit in
![]() $B_{\text{dR}}^{+}$
, the discussion after Theorem 2.3 implies that the map labeled ‘(2.3.2)’ in the diagram is an isomorphism. In particular, due to [Reference ScholzeSch13a, 5.1], the object
$B_{\text{dR}}^{+}$
, the discussion after Theorem 2.3 implies that the map labeled ‘(2.3.2)’ in the diagram is an isomorphism. In particular, due to [Reference ScholzeSch13a, 5.1], the object
![]() $R\unicode[STIX]{x1D6E4}_{\acute{\text{e}}\text{t}}(\mathfrak{X}_{C}^{\text{ad}},\mathbb{A}_{\text{inf},\,\mathfrak{X}_{C}^{\text{ad}}})\otimes _{A_{\text{inf}}}^{\mathbb{L}}B_{\text{dR}}^{+}$
of
$R\unicode[STIX]{x1D6E4}_{\acute{\text{e}}\text{t}}(\mathfrak{X}_{C}^{\text{ad}},\mathbb{A}_{\text{inf},\,\mathfrak{X}_{C}^{\text{ad}}})\otimes _{A_{\text{inf}}}^{\mathbb{L}}B_{\text{dR}}^{+}$
of
![]() $D(B_{\text{dR}}^{+})$
is perfect. We will now review the definition given in [Reference Bhatt, Morrow and ScholzeBMS18, proof of 13.1] of the composition
$D(B_{\text{dR}}^{+})$
is perfect. We will now review the definition given in [Reference Bhatt, Morrow and ScholzeBMS18, proof of 13.1] of the composition
![]() $f$
of the right vertical map with this map ‘(2.3.2)’.
$f$
of the right vertical map with this map ‘(2.3.2)’.
Let
![]() $\operatorname{Spa}(A,A^{\circ })$
be an element of the basis for the analytic topology of
$\operatorname{Spa}(A,A^{\circ })$
be an element of the basis for the analytic topology of
![]() $\mathfrak{X}_{C}^{\text{ad}}$
discussed in §6.2. For a large enough set
$\mathfrak{X}_{C}^{\text{ad}}$
discussed in §6.2. For a large enough set
![]() $\unicode[STIX]{x1D6F9}$
as in §6.2, we consider the surjection
$\unicode[STIX]{x1D6F9}$
as in §6.2, we consider the surjection
![]() $C\langle (X_{u}^{\pm 1})_{u\in \unicode[STIX]{x1D6F9}}\rangle \xrightarrow[{}]{X_{u}\mapsto u\,}A$
from (6.2.2), as well as the perfectoid
$C\langle (X_{u}^{\pm 1})_{u\in \unicode[STIX]{x1D6F9}}\rangle \xrightarrow[{}]{X_{u}\mapsto u\,}A$
from (6.2.2), as well as the perfectoid
![]() $(\prod _{\unicode[STIX]{x1D6F9}}\mathbb{Z}_{p}(1))$
-cover
$(\prod _{\unicode[STIX]{x1D6F9}}\mathbb{Z}_{p}(1))$
-cover
![]() $C\langle (X_{u}^{\pm 1/p^{\infty }})_{u\in \unicode[STIX]{x1D6F9}}\rangle$
of
$C\langle (X_{u}^{\pm 1/p^{\infty }})_{u\in \unicode[STIX]{x1D6F9}}\rangle$
of
![]() $C\langle (X_{u}^{\pm 1})_{u\in \unicode[STIX]{x1D6F9}}\rangle$
. Granted that
$C\langle (X_{u}^{\pm 1})_{u\in \unicode[STIX]{x1D6F9}}\rangle$
. Granted that
![]() $\unicode[STIX]{x1D6F9}$
contains the images of the
$\unicode[STIX]{x1D6F9}$
contains the images of the
![]() $T_{i}$
under some étale coordinate map (6.2.1), the base change of this cover to
$T_{i}$
under some étale coordinate map (6.2.1), the base change of this cover to
![]() $\operatorname{Spa}(A,A^{\circ })$
is a perfectoid
$\operatorname{Spa}(A,A^{\circ })$
is a perfectoid
![]() $(\prod _{\unicode[STIX]{x1D6F9}}\mathbb{Z}_{p}(1))$
-cover
$(\prod _{\unicode[STIX]{x1D6F9}}\mathbb{Z}_{p}(1))$
-cover
Each
![]() $u\in \unicode[STIX]{x1D6F9}$
has a canonical system
$u\in \unicode[STIX]{x1D6F9}$
has a canonical system
![]() $u^{1/p^{\infty }}$
of
$u^{1/p^{\infty }}$
of
![]() $p$
-power roots in
$p$
-power roots in
![]() $A_{\unicode[STIX]{x1D6F9},\,\infty }^{+}$
, which gives the unit
$A_{\unicode[STIX]{x1D6F9},\,\infty }^{+}$
, which gives the unit
![]() $[u^{1/p^{\infty }}]$
in the
$[u^{1/p^{\infty }}]$
in the
![]() $B_{\text{dR}}^{+}$
-algebra
$B_{\text{dR}}^{+}$
-algebra
![]() $\mathbb{B}_{\text{dR}}^{+}(A_{\unicode[STIX]{x1D6F9},\,\infty }^{+})$
(see Proposition 5.36). Since
$\mathbb{B}_{\text{dR}}^{+}(A_{\unicode[STIX]{x1D6F9},\,\infty }^{+})$
(see Proposition 5.36). Since
![]() $\mathbb{B}_{\text{dR}}^{+}(A_{\unicode[STIX]{x1D6F9},\,\infty }^{+})$
may be viewed as a pro-(infinitesimal thickening) of
$\mathbb{B}_{\text{dR}}^{+}(A_{\unicode[STIX]{x1D6F9},\,\infty }^{+})$
may be viewed as a pro-(infinitesimal thickening) of
![]() $A_{\unicode[STIX]{x1D6F9},\,\infty }$
, the map
$A_{\unicode[STIX]{x1D6F9},\,\infty }$
, the map
![]() $X_{u}\mapsto [u^{1/p^{\infty }}]$
extends to a continuous
$X_{u}\mapsto [u^{1/p^{\infty }}]$
extends to a continuous
![]() $B_{\text{dR}}^{+}$
-morphism
$B_{\text{dR}}^{+}$
-morphism
By construction, for each
![]() $u\in \unicode[STIX]{x1D6F9}$
, this morphism intertwines
$u\in \unicode[STIX]{x1D6F9}$
, this morphism intertwines
![]() $\exp \Bigl(\log ([\unicode[STIX]{x1D716}])\,\cdot \,\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\log (X_{u})}\Bigr)$
defined by the formula (5.15.1) and viewed as a ring endomorphism of
$\exp \Bigl(\log ([\unicode[STIX]{x1D716}])\,\cdot \,\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\log (X_{u})}\Bigr)$
defined by the formula (5.15.1) and viewed as a ring endomorphism of
![]() $D_{\unicode[STIX]{x1D6F9}}(A)$
with the action of the generator
$D_{\unicode[STIX]{x1D6F9}}(A)$
with the action of the generator
![]() $[\unicode[STIX]{x1D716}]$
of the
$[\unicode[STIX]{x1D716}]$
of the
![]() $u$
th copy of
$u$
th copy of
![]() $\mathbb{Z}_{p}(1)$
on
$\mathbb{Z}_{p}(1)$
on
![]() $\mathbb{B}_{\text{dR}}^{+}(A_{\unicode[STIX]{x1D6F9},\,\infty }^{+})$
. In particular, letting
$\mathbb{B}_{\text{dR}}^{+}(A_{\unicode[STIX]{x1D6F9},\,\infty }^{+})$
. In particular, letting
![]() $\unicode[STIX]{x1D6FE}_{u}$
denote this generator, we may use the same formula as in (5.16.1) to define the morphism of complexes
$\unicode[STIX]{x1D6FE}_{u}$
denote this generator, we may use the same formula as in (5.16.1) to define the morphism of complexes
whose formation is functorial in
![]() $\unicode[STIX]{x1D6F9}$
and, after passing to the direct limit over all
$\unicode[STIX]{x1D6F9}$
and, after passing to the direct limit over all
![]() $\unicode[STIX]{x1D6F9}$
, also in
$\unicode[STIX]{x1D6F9}$
, also in
![]() $\operatorname{Spa}(A,A^{\circ })$
. The almost purity theorem identifies the cohomology of the sheaf of complexes determined by the target of (6.8.3) with
$\operatorname{Spa}(A,A^{\circ })$
. The almost purity theorem identifies the cohomology of the sheaf of complexes determined by the target of (6.8.3) with
![]() $R\unicode[STIX]{x1D6E4}_{\acute{\text{e}}\text{t}}(\mathfrak{X}_{C}^{\text{ad}},\mathbb{A}_{\text{inf},\,\mathfrak{X}_{C}^{\text{ad}}})\otimes _{A_{\text{inf}}}^{\mathbb{L}}B_{\text{dR}}^{+}$
(see [Reference Bhatt, Morrow and ScholzeBMS18, proof of 13.1]). The cohomology of the sheaf of complexes determined by the source of (6.8.3) is, by definition,
$R\unicode[STIX]{x1D6E4}_{\acute{\text{e}}\text{t}}(\mathfrak{X}_{C}^{\text{ad}},\mathbb{A}_{\text{inf},\,\mathfrak{X}_{C}^{\text{ad}}})\otimes _{A_{\text{inf}}}^{\mathbb{L}}B_{\text{dR}}^{+}$
(see [Reference Bhatt, Morrow and ScholzeBMS18, proof of 13.1]). The cohomology of the sheaf of complexes determined by the source of (6.8.3) is, by definition,
![]() $R\unicode[STIX]{x1D6E4}_{\text{cris}}(\mathfrak{X}_{C}^{\text{ad}}/B_{\text{dR}}^{+})$
(see §6.2). Therefore, by passing to the direct limit over all
$R\unicode[STIX]{x1D6E4}_{\text{cris}}(\mathfrak{X}_{C}^{\text{ad}}/B_{\text{dR}}^{+})$
(see §6.2). Therefore, by passing to the direct limit over all
![]() $\unicode[STIX]{x1D6F9}$
, sheafifying, and forming cohomology, the maps (6.8.3) produce the aforementioned composition
$\unicode[STIX]{x1D6F9}$
, sheafifying, and forming cohomology, the maps (6.8.3) produce the aforementioned composition
![]() $f$
defined in [Reference Bhatt, Morrow and ScholzeBMS18, proof of 13.1].
$f$
defined in [Reference Bhatt, Morrow and ScholzeBMS18, proof of 13.1].
The same construction gives the morphisms (6.8.3) for the objects
![]() $\operatorname{Spa}(A,A^{\circ })$
of the basis of the étale topology of
$\operatorname{Spa}(A,A^{\circ })$
of the basis of the étale topology of
![]() $\mathfrak{X}_{C}^{\text{ad}}$
considered in §6.2. Due to (6.2.7), this leads to the same map
$\mathfrak{X}_{C}^{\text{ad}}$
considered in §6.2. Due to (6.2.7), this leads to the same map
![]() $f$
. In addition, we may generalize the construction of the morphisms (6.8.3) further by using the basis for the étale topology of
$f$
. In addition, we may generalize the construction of the morphisms (6.8.3) further by using the basis for the étale topology of
![]() $\mathfrak{X}_{C}^{\text{ad}}$
considered in §6.3: the cover (6.8.1) gets replaced by the cover
$\mathfrak{X}_{C}^{\text{ad}}$
considered in §6.3: the cover (6.8.1) gets replaced by the cover
that is the base change of the perfectoid
for large enough
![]() $\unicode[STIX]{x1D6F9}\subset (A^{\circ })^{\times }$
and
$\unicode[STIX]{x1D6F9}\subset (A^{\circ })^{\times }$
and
![]() $\unicode[STIX]{x1D6EF}\subset A^{\circ }\cap A^{\times }$
, and the rest is (mildly) modified accordingly. Due to (6.3.12), this variant of the construction gives the same map
$\unicode[STIX]{x1D6EF}\subset A^{\circ }\cap A^{\times }$
, and the rest is (mildly) modified accordingly. Due to (6.3.12), this variant of the construction gives the same map
![]() $f$
.
$f$
.
In conclusion, since the construction of
![]() $f$
may be carried out in the setting of §6.3 and follows the same pattern as the construction of the map (5.40.1), namely, is based on the map as in (5.16.1), all we need to check is that, in the notation of §6.5, the following diagram commutes.
$f$
may be carried out in the setting of §6.3 and follows the same pattern as the construction of the map (5.40.1), namely, is based on the map as in (5.16.1), all we need to check is that, in the notation of §6.5, the following diagram commutes.

For this desired commutativity, we may first replace
![]() $\mathbb{B}_{\text{dR}}^{+}(A_{\unicode[STIX]{x1D6F9},\,\unicode[STIX]{x1D6EF},\,\infty }^{+})$
by
$\mathbb{B}_{\text{dR}}^{+}(A_{\unicode[STIX]{x1D6F9},\,\unicode[STIX]{x1D6EF},\,\infty }^{+})$
by
![]() $\mathbb{B}_{\text{dR}}^{+}(A_{\unicode[STIX]{x1D6F9},\,\unicode[STIX]{x1D6EF},\,\infty }^{+})/\unicode[STIX]{x1D709}^{n}$
for a variable
$\mathbb{B}_{\text{dR}}^{+}(A_{\unicode[STIX]{x1D6F9},\,\unicode[STIX]{x1D6EF},\,\infty }^{+})/\unicode[STIX]{x1D709}^{n}$
for a variable
![]() $n>0$
, then replace
$n>0$
, then replace
![]() $D_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}$
by
$D_{\unicode[STIX]{x1D6F4},\,\unicode[STIX]{x1D6EC}}$
by
![]() $D_{j_{\unicode[STIX]{x1D706}_{0}}}$
for some
$D_{j_{\unicode[STIX]{x1D706}_{0}}}$
for some
![]() $\unicode[STIX]{x1D706}_{0}\in \unicode[STIX]{x1D6EC}$
, and, finally, since
$\unicode[STIX]{x1D706}_{0}\in \unicode[STIX]{x1D6EC}$
, and, finally, since
![]() $\mathbb{B}_{\text{dR}}^{+}(A_{\unicode[STIX]{x1D6F9},\,\unicode[STIX]{x1D6EF},\,\infty }^{+})/\unicode[STIX]{x1D709}^{n}$
is a
$\mathbb{B}_{\text{dR}}^{+}(A_{\unicode[STIX]{x1D6F9},\,\unicode[STIX]{x1D6EF},\,\infty }^{+})/\unicode[STIX]{x1D709}^{n}$
is a
![]() $\mathbb{Q}$
-algebra and
$\mathbb{Q}$
-algebra and
![]() $D_{j_{\unicode[STIX]{x1D706}_{0}}}$
is generated by divided powers, replace
$D_{j_{\unicode[STIX]{x1D706}_{0}}}$
is generated by divided powers, replace
![]() $D_{j_{\unicode[STIX]{x1D706}_{0}}}$
by
$D_{j_{\unicode[STIX]{x1D706}_{0}}}$
by
However, each
![]() $X_{\unicode[STIX]{x1D70F}}$
of (5.19.2) with either
$X_{\unicode[STIX]{x1D70F}}$
of (5.19.2) with either
![]() $\unicode[STIX]{x1D70F}=\unicode[STIX]{x1D70E}$
for
$\unicode[STIX]{x1D70F}=\unicode[STIX]{x1D70E}$
for
![]() $\unicode[STIX]{x1D70E}\in \unicode[STIX]{x1D6F4}$
or
$\unicode[STIX]{x1D70E}\in \unicode[STIX]{x1D6F4}$
or
![]() $\unicode[STIX]{x1D70F}=(\unicode[STIX]{x1D706},i)$
for
$\unicode[STIX]{x1D70F}=(\unicode[STIX]{x1D706},i)$
for
![]() $\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}$
and
$\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}$
and
![]() $1\leqslant i\leqslant d$
maps to the unit
$1\leqslant i\leqslant d$
maps to the unit
![]() $[X_{\unicode[STIX]{x1D70F}}^{1/p^{\infty }}]\in (\mathbb{B}_{\text{dR}}^{+}(A_{\unicode[STIX]{x1D6F9},\,\unicode[STIX]{x1D6EF},\,\infty }^{+}))^{\times }$
under either of the two maps from
$[X_{\unicode[STIX]{x1D70F}}^{1/p^{\infty }}]\in (\mathbb{B}_{\text{dR}}^{+}(A_{\unicode[STIX]{x1D6F9},\,\unicode[STIX]{x1D6EF},\,\infty }^{+}))^{\times }$
under either of the two maps from
supplied by the diagram (6.8.4), so these two maps indeed agree, as desired. ◻
7 The
 $A_{\text{inf}}$
-cohomology modules
$A_{\text{inf}}$
-cohomology modules
 $H_{A_{\text{inf}}}^{i}(\mathfrak{X})$
and their specializations
$H_{A_{\text{inf}}}^{i}(\mathfrak{X})$
and their specializations
In this section, we define and analyze the
![]() $A_{\text{inf}}$
-cohomology groups
$A_{\text{inf}}$
-cohomology groups
![]() $H_{A_{\text{inf}}}^{i}(\mathfrak{X})$
of an
$H_{A_{\text{inf}}}^{i}(\mathfrak{X})$
of an
![]() ${\mathcal{O}}_{C}$
-proper
${\mathcal{O}}_{C}$
-proper
![]() $\mathfrak{X}$
. We show that each
$\mathfrak{X}$
. We show that each
![]() $H_{A_{\text{inf}}}^{i}(\mathfrak{X})$
is a Breuil–Kisin–Fargues module (see Theorem 7.4) and deduce that, loosely speaking, the
$H_{A_{\text{inf}}}^{i}(\mathfrak{X})$
is a Breuil–Kisin–Fargues module (see Theorem 7.4) and deduce that, loosely speaking, the
![]() $p$
-adic étale cohomology of
$p$
-adic étale cohomology of
![]() $\mathfrak{X}_{C}^{\text{ad}}$
has at most the amount of torsion contained in the logarithmic crystalline cohomology of
$\mathfrak{X}_{C}^{\text{ad}}$
has at most the amount of torsion contained in the logarithmic crystalline cohomology of
![]() $\mathfrak{X}_{k}$
or the logarithmic de Rham cohomology of
$\mathfrak{X}_{k}$
or the logarithmic de Rham cohomology of
![]() $\mathfrak{X}$
(see Theorems 7.9 and 7.12). Most of these results are variants of their analogues established in the smooth case in [Reference Bhatt, Morrow and ScholzeBMS18]. Their proofs, granted inputs from §2 and §§4–5, are generally similar to those of [Reference Bhatt, Morrow and ScholzeBMS18] and in large part rely on commutative algebra over
$\mathfrak{X}$
(see Theorems 7.9 and 7.12). Most of these results are variants of their analogues established in the smooth case in [Reference Bhatt, Morrow and ScholzeBMS18]. Their proofs, granted inputs from §2 and §§4–5, are generally similar to those of [Reference Bhatt, Morrow and ScholzeBMS18] and in large part rely on commutative algebra over
![]() $A_{\text{inf}}$
.
$A_{\text{inf}}$
.
7.1 Properness of
 $\mathfrak{X}$
$\mathfrak{X}$
Throughout §7, we assume that
![]() $\mathfrak{X}$
is proper and
$\mathfrak{X}$
is proper and
![]() $\mathfrak{X}_{k}$
is purely
$\mathfrak{X}_{k}$
is purely
![]() $d$
-dimensional.
$d$
-dimensional.
7.2 The
 $A_{\text{inf}}$
-cohomology
$A_{\text{inf}}$
-cohomology
 $R\unicode[STIX]{x1D6E4}_{A_{\text{inf}}}(\mathfrak{X})$
$R\unicode[STIX]{x1D6E4}_{A_{\text{inf}}}(\mathfrak{X})$
We use the object
![]() $A\unicode[STIX]{x1D6FA}_{\mathfrak{X}}\in D^{{\geqslant}0}(\mathfrak{X}_{\acute{\text{e}}\text{t}},A_{\text{inf}})$
of §2.2 to set
$A\unicode[STIX]{x1D6FA}_{\mathfrak{X}}\in D^{{\geqslant}0}(\mathfrak{X}_{\acute{\text{e}}\text{t}},A_{\text{inf}})$
of §2.2 to set
Since
![]() $L\unicode[STIX]{x1D702}$
commutes with pullback along a flat morphism of ringed topoi (see [Reference Bhatt, Morrow and ScholzeBMS18, 6.14]), the object
$L\unicode[STIX]{x1D702}$
commutes with pullback along a flat morphism of ringed topoi (see [Reference Bhatt, Morrow and ScholzeBMS18, 6.14]), the object
![]() $R\unicode[STIX]{x1D6E4}_{A_{\text{inf}}}(\mathfrak{X})$
is contravariantly functorial in
$R\unicode[STIX]{x1D6E4}_{A_{\text{inf}}}(\mathfrak{X})$
is contravariantly functorial in
![]() $\mathfrak{X}$
: an
$\mathfrak{X}$
: an
![]() ${\mathcal{O}}_{C}$
-morphism
${\mathcal{O}}_{C}$
-morphism
![]() $\mathfrak{X}^{\prime }\rightarrow \mathfrak{X}$
induces a morphism
$\mathfrak{X}^{\prime }\rightarrow \mathfrak{X}$
induces a morphism
Corollary 4.20 ensures that
![]() $R\unicode[STIX]{x1D6E4}_{A_{\text{inf}}}(\mathfrak{X})$
is perfect, that is, isomorphic to a bounded complex of finite free
$R\unicode[STIX]{x1D6E4}_{A_{\text{inf}}}(\mathfrak{X})$
is perfect, that is, isomorphic to a bounded complex of finite free
![]() $A_{\text{inf}}$
-modules. Moreover, by (2.3), (4.18.1), and (5.43.2), we have the following identifications:
$A_{\text{inf}}$
-modules. Moreover, by (2.3), (4.18.1), and (5.43.2), we have the following identifications:
 $$\begin{eqnarray}\begin{array}{@{}rcl@{}}\displaystyle \textstyle R\unicode[STIX]{x1D6E4}_{A_{\text{inf}}}(\mathfrak{X})\otimes _{A_{\text{inf}}}^{\mathbb{L}}A_{\text{inf}}[\frac{1}{\unicode[STIX]{x1D707}}]\ & \cong \ & \displaystyle \textstyle R\unicode[STIX]{x1D6E4}_{\acute{\text{e}}\text{t}}(\mathfrak{X}_{C}^{\text{ad}},\mathbb{Z}_{p})\otimes _{\mathbb{Z}_{p}}^{\mathbb{L}}A_{\text{inf}}[\frac{1}{\unicode[STIX]{x1D707}}];\\ \displaystyle R\unicode[STIX]{x1D6E4}_{A_{\text{inf}}}(\mathfrak{X})\otimes _{A_{\text{inf}},\,\unicode[STIX]{x1D703}}^{\mathbb{L}}{\mathcal{O}}_{C}\ & \cong \ & \displaystyle R\unicode[STIX]{x1D6E4}_{\log \text{dR}}(\mathfrak{X}/{\mathcal{O}}_{C});\\ \displaystyle R\unicode[STIX]{x1D6E4}_{A_{\text{inf}}}(\mathfrak{X})\otimes _{A_{\text{inf}}}^{\mathbb{L}}W(k)\ & \cong \ & \displaystyle R\unicode[STIX]{x1D6E4}_{\log \text{cris}}(\mathfrak{X}_{k}/W(k)).\end{array}\end{eqnarray}$$
$$\begin{eqnarray}\begin{array}{@{}rcl@{}}\displaystyle \textstyle R\unicode[STIX]{x1D6E4}_{A_{\text{inf}}}(\mathfrak{X})\otimes _{A_{\text{inf}}}^{\mathbb{L}}A_{\text{inf}}[\frac{1}{\unicode[STIX]{x1D707}}]\ & \cong \ & \displaystyle \textstyle R\unicode[STIX]{x1D6E4}_{\acute{\text{e}}\text{t}}(\mathfrak{X}_{C}^{\text{ad}},\mathbb{Z}_{p})\otimes _{\mathbb{Z}_{p}}^{\mathbb{L}}A_{\text{inf}}[\frac{1}{\unicode[STIX]{x1D707}}];\\ \displaystyle R\unicode[STIX]{x1D6E4}_{A_{\text{inf}}}(\mathfrak{X})\otimes _{A_{\text{inf}},\,\unicode[STIX]{x1D703}}^{\mathbb{L}}{\mathcal{O}}_{C}\ & \cong \ & \displaystyle R\unicode[STIX]{x1D6E4}_{\log \text{dR}}(\mathfrak{X}/{\mathcal{O}}_{C});\\ \displaystyle R\unicode[STIX]{x1D6E4}_{A_{\text{inf}}}(\mathfrak{X})\otimes _{A_{\text{inf}}}^{\mathbb{L}}W(k)\ & \cong \ & \displaystyle R\unicode[STIX]{x1D6E4}_{\log \text{cris}}(\mathfrak{X}_{k}/W(k)).\end{array}\end{eqnarray}$$
If
![]() $\mathfrak{X}_{k}$
is
$\mathfrak{X}_{k}$
is
![]() $k$
-smooth, then we may drop ‘
$k$
-smooth, then we may drop ‘
![]() $\log$
’ from the subscripts (compare with (5.44.2)).
$\log$
’ from the subscripts (compare with (5.44.2)).
The Frobenius morphism (2.2.5) gives rise to the Frobenius morphism
that becomes an isomorphism after inverting
![]() $\unicode[STIX]{x1D711}(\unicode[STIX]{x1D709})$
(see (2.2.6)). Consequently the cohomology modules
$\unicode[STIX]{x1D711}(\unicode[STIX]{x1D709})$
(see (2.2.6)). Consequently the cohomology modules
![]() $H_{A_{\text{inf}}}^{i}(\mathfrak{X})$
come equipped with the
$H_{A_{\text{inf}}}^{i}(\mathfrak{X})$
come equipped with the
![]() $A_{\text{inf}}$
-module morphism
$A_{\text{inf}}$
-module morphism
that becomes an isomorphism after inverting
![]() $\unicode[STIX]{x1D711}(\unicode[STIX]{x1D709})$
. We will prove in Theorem 7.4 that these morphisms make each
$\unicode[STIX]{x1D711}(\unicode[STIX]{x1D709})$
. We will prove in Theorem 7.4 that these morphisms make each
![]() $H_{A_{\text{inf}}}^{i}(\mathfrak{X})$
a Breuil–Kisin–Fargues module in the following sense of [Reference Bhatt, Morrow and ScholzeBMS18, 4.22].
$H_{A_{\text{inf}}}^{i}(\mathfrak{X})$
a Breuil–Kisin–Fargues module in the following sense of [Reference Bhatt, Morrow and ScholzeBMS18, 4.22].
7.3 Breuil–Kisin–Fargues modules
A Breuil–Kisin–Fargues module is a finitely presented
![]() $A_{\text{inf}}$
-module
$A_{\text{inf}}$
-module
![]() $M$
equipped with an
$M$
equipped with an
![]() $A_{\text{inf}}[\frac{1}{\unicode[STIX]{x1D711}(\unicode[STIX]{x1D709})}]$
-module isomorphism
$A_{\text{inf}}[\frac{1}{\unicode[STIX]{x1D711}(\unicode[STIX]{x1D709})}]$
-module isomorphism
such that
![]() $M[\frac{1}{p}]$
is
$M[\frac{1}{p}]$
is
![]() $A_{\text{inf}}[\frac{1}{p}]$
-free. By [Reference Bhatt, Morrow and ScholzeBMS18, 4.9(i)], any such
$A_{\text{inf}}[\frac{1}{p}]$
-free. By [Reference Bhatt, Morrow and ScholzeBMS18, 4.9(i)], any such
![]() $M$
is perfect as an
$M$
is perfect as an
![]() $A_{\text{inf}}$
-module, that is,
$A_{\text{inf}}$
-module, that is,
![]() $M$
has a finite resolution by finite free
$M$
has a finite resolution by finite free
![]() $A_{\text{inf}}$
-modules. A morphism of Breuil–Kisin–Fargues modules is an
$A_{\text{inf}}$
-modules. A morphism of Breuil–Kisin–Fargues modules is an
![]() $A_{\text{inf}}$
-module morphism that commutes with the isomorphisms
$A_{\text{inf}}$
-module morphism that commutes with the isomorphisms
![]() $\unicode[STIX]{x1D711}_{M}$
.
$\unicode[STIX]{x1D711}_{M}$
.
Theorem 7.4. Each
![]() $(H_{A_{\text{inf}}}^{i}(\mathfrak{X}),\unicode[STIX]{x1D711})$
is a Breuil–Kisin–Fargues module which vanishes unless
$(H_{A_{\text{inf}}}^{i}(\mathfrak{X}),\unicode[STIX]{x1D711})$
is a Breuil–Kisin–Fargues module which vanishes unless
![]() $i\in [0,2d]$
. In particular, each
$i\in [0,2d]$
. In particular, each
![]() $H_{A_{\text{inf}}}^{i}(\mathfrak{X})$
is perfect as an
$H_{A_{\text{inf}}}^{i}(\mathfrak{X})$
is perfect as an
![]() $A_{\text{inf}}$
-module and each
$A_{\text{inf}}$
-module and each
![]() $(H_{A_{\text{inf}}}^{i}(\mathfrak{X}))[\frac{1}{p}]$
is
$(H_{A_{\text{inf}}}^{i}(\mathfrak{X}))[\frac{1}{p}]$
is
![]() $A_{\text{inf}}[\frac{1}{p}]$
-free.
$A_{\text{inf}}[\frac{1}{p}]$
-free.
Proof. Due to the relation with
![]() $R\unicode[STIX]{x1D6E4}_{\acute{\text{e}}\text{t}}(\mathfrak{X}_{C}^{\text{ad}},\mathbb{Z}_{p})$
, each
$R\unicode[STIX]{x1D6E4}_{\acute{\text{e}}\text{t}}(\mathfrak{X}_{C}^{\text{ad}},\mathbb{Z}_{p})$
, each
![]() $(H_{A_{\text{inf}}}^{i}(\mathfrak{X}))[\frac{1}{p\unicode[STIX]{x1D707}}]$
is a free
$(H_{A_{\text{inf}}}^{i}(\mathfrak{X}))[\frac{1}{p\unicode[STIX]{x1D707}}]$
is a free
![]() $A_{\text{inf}}[\frac{1}{p\unicode[STIX]{x1D707}}]$
-module. Moreover, by Corollary 5.43, the cohomology modules of
$A_{\text{inf}}[\frac{1}{p\unicode[STIX]{x1D707}}]$
-module. Moreover, by Corollary 5.43, the cohomology modules of
![]() $R\unicode[STIX]{x1D6E4}_{A_{\text{inf}}}(\mathfrak{X})\otimes _{A_{\text{inf}}}^{\mathbb{L}}A_{\text{cris}}[\frac{1}{p}]$
are free over
$R\unicode[STIX]{x1D6E4}_{A_{\text{inf}}}(\mathfrak{X})\otimes _{A_{\text{inf}}}^{\mathbb{L}}A_{\text{cris}}[\frac{1}{p}]$
are free over
![]() $A_{\text{cris}}[\frac{1}{p}]$
. Therefore, [Reference Bhatt, Morrow and ScholzeBMS18, 4.20] applies and proves that each
$A_{\text{cris}}[\frac{1}{p}]$
. Therefore, [Reference Bhatt, Morrow and ScholzeBMS18, 4.20] applies and proves that each
![]() $H_{A_{\text{inf}}}^{i}(\mathfrak{X})$
is a finitely presented
$H_{A_{\text{inf}}}^{i}(\mathfrak{X})$
is a finitely presented
![]() $A_{\text{inf}}$
-module that becomes free after inverting
$A_{\text{inf}}$
-module that becomes free after inverting
![]() $p$
, so
$p$
, so
![]() $(H_{A_{\text{inf}}}^{i}(\mathfrak{X}),\unicode[STIX]{x1D711})$
is a Breuil–Kisin–Fargues module.
$(H_{A_{\text{inf}}}^{i}(\mathfrak{X}),\unicode[STIX]{x1D711})$
is a Breuil–Kisin–Fargues module.
Since
![]() $R\unicode[STIX]{x1D6E4}_{A_{\text{inf}}}(\mathfrak{X})$
is perfect, its top degree cohomology is finitely presented and of formation compatible with base change. Thus, by the de Rham specialization of (7.2.1) and the Nakayama lemma,
$R\unicode[STIX]{x1D6E4}_{A_{\text{inf}}}(\mathfrak{X})$
is perfect, its top degree cohomology is finitely presented and of formation compatible with base change. Thus, by the de Rham specialization of (7.2.1) and the Nakayama lemma,
![]() $H_{A_{\text{inf}}}^{i}(\mathfrak{X})=0$
for
$H_{A_{\text{inf}}}^{i}(\mathfrak{X})=0$
for
![]() $i>2d$
. The same holds for
$i>2d$
. The same holds for
![]() $i<0$
because
$i<0$
because
![]() $R\unicode[STIX]{x1D6E4}_{A_{\text{inf}}}(\mathfrak{X})\in D^{{\geqslant}0}(A_{\text{inf}})$
.◻
$R\unicode[STIX]{x1D6E4}_{A_{\text{inf}}}(\mathfrak{X})\in D^{{\geqslant}0}(A_{\text{inf}})$
.◻
For completeness sake, we mention the following corollary, which may also be proved more directly.
Corollary 7.5. For each
![]() $i\in \mathbb{Z}$
, the rank of the finitely presented
$i\in \mathbb{Z}$
, the rank of the finitely presented
![]() $\mathbb{Z}_{p}$
-module
$\mathbb{Z}_{p}$
-module
![]() $H_{\acute{\text{e}}\text{t}}^{i}(\mathfrak{X}_{C}^{\text{ad}},\mathbb{Z}_{p})$
is equal to the rank of the finitely presented
$H_{\acute{\text{e}}\text{t}}^{i}(\mathfrak{X}_{C}^{\text{ad}},\mathbb{Z}_{p})$
is equal to the rank of the finitely presented
![]() $W(k)$
-module
$W(k)$
-module
![]() $H_{\log \text{cris}}^{i}(\mathfrak{X}_{k}/W(k))$
, and is also equal to the rank of the finitely presented
$H_{\log \text{cris}}^{i}(\mathfrak{X}_{k}/W(k))$
, and is also equal to the rank of the finitely presented
![]() ${\mathcal{O}}_{C}$
-module
${\mathcal{O}}_{C}$
-module
![]() $H_{\log \text{dR}}^{i}(\mathfrak{X}/{\mathcal{O}}_{C}):=R^{i}\unicode[STIX]{x1D6E4}(\mathfrak{X}_{\acute{\text{e}}\text{t}},\unicode[STIX]{x1D6FA}_{\mathfrak{X}/{\mathcal{O}}_{C},\,\log }^{\bullet })$
(see also (7.10.1) below).
$H_{\log \text{dR}}^{i}(\mathfrak{X}/{\mathcal{O}}_{C}):=R^{i}\unicode[STIX]{x1D6E4}(\mathfrak{X}_{\acute{\text{e}}\text{t}},\unicode[STIX]{x1D6FA}_{\mathfrak{X}/{\mathcal{O}}_{C},\,\log }^{\bullet })$
(see also (7.10.1) below).
Proof. The finite presentation assertions follow, for instance, from the perfectness of
![]() $R\unicode[STIX]{x1D6E4}_{A_{\text{inf}}}(\mathfrak{X})$
, the comparisons (7.2.1), and the coherence of the ring
$R\unicode[STIX]{x1D6E4}_{A_{\text{inf}}}(\mathfrak{X})$
, the comparisons (7.2.1), and the coherence of the ring
![]() ${\mathcal{O}}_{C}$
. Due to Theorem 7.4 and the comparisons (7.2.1), all the ranks in question are equal to the rank of the free
${\mathcal{O}}_{C}$
. Due to Theorem 7.4 and the comparisons (7.2.1), all the ranks in question are equal to the rank of the free
![]() $A_{\text{inf}}[\frac{1}{p}]$
-module
$A_{\text{inf}}[\frac{1}{p}]$
-module
![]() $(H_{A_{\text{inf}}}^{i}(\mathfrak{X}))[\frac{1}{p}]$
.◻
$(H_{A_{\text{inf}}}^{i}(\mathfrak{X}))[\frac{1}{p}]$
.◻
7.6 Base change for individual
 $H_{A_{\text{inf}}}^{i}(\mathfrak{X})$
$H_{A_{\text{inf}}}^{i}(\mathfrak{X})$
Since
![]() $A_{\text{inf}}[\frac{1}{\unicode[STIX]{x1D707}}]$
is
$A_{\text{inf}}[\frac{1}{\unicode[STIX]{x1D707}}]$
is
![]() $A_{\text{inf}}$
-flat, equation (7.2.1) implies that
$A_{\text{inf}}$
-flat, equation (7.2.1) implies that
In particular, since
![]() $\unicode[STIX]{x1D707}$
is a unit in
$\unicode[STIX]{x1D707}$
is a unit in
![]() $W(C^{\flat })$
and
$W(C^{\flat })$
and
![]() $W(C^{\flat })$
is
$W(C^{\flat })$
is
![]() $A_{\text{inf}}$
-flat (the localization of
$A_{\text{inf}}$
-flat (the localization of
![]() $A_{\text{inf}}$
at the prime ideal
$A_{\text{inf}}$
at the prime ideal
![]() $(p)$
is a discrete valuation ring whose completion is
$(p)$
is a discrete valuation ring whose completion is
![]() $W(C^{\flat })$
)
$W(C^{\flat })$
)
A similar de Rham comparison consists of the following exact sequences that result from (7.2.1) and [SP, 0662]:
Similarly, by Theorem 7.4 and [Reference Bhatt, Morrow and ScholzeBMS18, 4.9], we have a Frobenius-equivariant exact sequence
for each
![]() $i\in \mathbb{Z}$
. In particular, we have the top degree base changes
$i\in \mathbb{Z}$
. In particular, we have the top degree base changes
Due to Theorem 7.4, the injections in the sequences (7.6.3)–(7.6.4) become isomorphisms after inverting
![]() $p$
. The same holds without inverting
$p$
. The same holds without inverting
![]() $p$
in the case when
$p$
in the case when
![]() $H_{A_{\text{inf}}}^{i+1}(\mathfrak{X})$
is
$H_{A_{\text{inf}}}^{i+1}(\mathfrak{X})$
is
![]() $A_{\text{inf}}$
-free. For such freeness, we have the following consequence of Theorem 7.4 and [Reference Bhatt, Morrow and ScholzeBMS18, §4.2].
$A_{\text{inf}}$
-free. For such freeness, we have the following consequence of Theorem 7.4 and [Reference Bhatt, Morrow and ScholzeBMS18, §4.2].
Proposition 7.7. For each
![]() $i\in \mathbb{Z}$
, the
$i\in \mathbb{Z}$
, the
![]() ${\mathcal{O}}_{C}$
-module
${\mathcal{O}}_{C}$
-module
![]() $H_{\log \text{dR}}^{i}(\mathfrak{X}/{\mathcal{O}}_{C})$
is
$H_{\log \text{dR}}^{i}(\mathfrak{X}/{\mathcal{O}}_{C})$
is
![]() $p$
-torsion free (equivalently, free) if and only if the
$p$
-torsion free (equivalently, free) if and only if the
![]() $W(k)$
-module
$W(k)$
-module
![]() $H_{\log \text{cris}}^{i}(\mathfrak{X}_{k}/W(k))$
is
$H_{\log \text{cris}}^{i}(\mathfrak{X}_{k}/W(k))$
is
![]() $p$
-torsion free (equivalently, free), in which case
$p$
-torsion free (equivalently, free), in which case
![]() $H_{A_{\text{inf}}}^{i}(\mathfrak{X})$
is free as an
$H_{A_{\text{inf}}}^{i}(\mathfrak{X})$
is free as an
![]() $A_{\text{inf}}$
-module and
$A_{\text{inf}}$
-module and
![]() $H_{\acute{\text{e}}\text{t}}^{i}(\mathfrak{X}_{C}^{\text{ad}},\mathbb{Z}_{p})$
is free as a
$H_{\acute{\text{e}}\text{t}}^{i}(\mathfrak{X}_{C}^{\text{ad}},\mathbb{Z}_{p})$
is free as a
![]() $\mathbb{Z}_{p}$
-module.
$\mathbb{Z}_{p}$
-module.
Proof. Due to Theorem 7.4, we may apply [Reference Bhatt, Morrow and ScholzeBMS18, 4.18] and combine it with (7.2.1) to conclude that
![]() $H_{\log \text{dR}}^{i}(\mathfrak{X}/{\mathcal{O}}_{C})$
is
$H_{\log \text{dR}}^{i}(\mathfrak{X}/{\mathcal{O}}_{C})$
is
![]() $p$
-torsion free if and only if so is
$p$
-torsion free if and only if so is
![]() $H_{\log \text{cris}}^{i}(\mathfrak{X}_{k}/W(k))$
. When these conditions hold, the freeness of
$H_{\log \text{cris}}^{i}(\mathfrak{X}_{k}/W(k))$
. When these conditions hold, the freeness of
![]() $H_{A_{\text{inf}}}^{i}(\mathfrak{X})$
and
$H_{A_{\text{inf}}}^{i}(\mathfrak{X})$
and
![]() $H_{\acute{\text{e}}\text{t}}^{i}(\mathfrak{X}_{C}^{\text{ad}},\mathbb{Z}_{p})$
follows from [Reference Bhatt, Morrow and ScholzeBMS18, 4.17] and (7.6.1).◻
$H_{\acute{\text{e}}\text{t}}^{i}(\mathfrak{X}_{C}^{\text{ad}},\mathbb{Z}_{p})$
follows from [Reference Bhatt, Morrow and ScholzeBMS18, 4.17] and (7.6.1).◻
Remark 7.8. As was observed by Jesse Silliman and Ravi Fernando during the Arizona Winter School 2017, the first assertion of Proposition 7.7 may be strengthened as follows: for each
![]() $i\in \mathbb{Z}$
,
$i\in \mathbb{Z}$
,
that is,
![]() $H_{\log \text{dR}}^{i}(\mathfrak{X}/{\mathcal{O}}_{C})$
and
$H_{\log \text{dR}}^{i}(\mathfrak{X}/{\mathcal{O}}_{C})$
and
![]() $H_{\log \text{cris}}^{i}(\mathfrak{X}_{k}/W(k))$
have the same number of cyclic summands (in the sense of (7.10.1) below). Indeed, by Corollary 7.5, the ranks of
$H_{\log \text{cris}}^{i}(\mathfrak{X}_{k}/W(k))$
have the same number of cyclic summands (in the sense of (7.10.1) below). Indeed, by Corollary 7.5, the ranks of
![]() $H_{\log \text{dR}}^{i}(\mathfrak{X}/{\mathcal{O}}_{C})$
and
$H_{\log \text{dR}}^{i}(\mathfrak{X}/{\mathcal{O}}_{C})$
and
![]() $H_{\log \text{cris}}^{i}(\mathfrak{X}_{k}/W(k))$
agree and, by [Reference BeilinsonBei13a, (1.8.1)], so do the
$H_{\log \text{cris}}^{i}(\mathfrak{X}_{k}/W(k))$
agree and, by [Reference BeilinsonBei13a, (1.8.1)], so do the
![]() $k$
-fibers of
$k$
-fibers of
![]() $R\unicode[STIX]{x1D6E4}_{\log \text{dR}}(\mathfrak{X}/{\mathcal{O}}_{C})$
and
$R\unicode[STIX]{x1D6E4}_{\log \text{dR}}(\mathfrak{X}/{\mathcal{O}}_{C})$
and
![]() $R\unicode[STIX]{x1D6E4}_{\log \text{cris}}(\mathfrak{X}_{k}/W(k))$
, so the claim follows by descending induction on
$R\unicode[STIX]{x1D6E4}_{\log \text{cris}}(\mathfrak{X}_{k}/W(k))$
, so the claim follows by descending induction on
![]() $i$
from the following exact sequences supplied by [SP, 0662]:
$i$
from the following exact sequences supplied by [SP, 0662]:
The following variant of [Reference Bhatt, Morrow and ScholzeBMS18, 14.5(ii)] strengthens the relationship between the freeness of
![]() $H_{\acute{\text{e}}\text{t}}^{i}(\mathfrak{X}_{C}^{\text{ad}},\mathbb{Z}_{p})$
and that of
$H_{\acute{\text{e}}\text{t}}^{i}(\mathfrak{X}_{C}^{\text{ad}},\mathbb{Z}_{p})$
and that of
![]() $H_{\log \text{cris}}^{i}(\mathfrak{X}_{k}/W(k))$
supplied by Proposition 7.7.
$H_{\log \text{cris}}^{i}(\mathfrak{X}_{k}/W(k))$
supplied by Proposition 7.7.
Theorem 7.9. For every
![]() $i\in \mathbb{Z}$
and
$i\in \mathbb{Z}$
and
![]() $n\in \mathbb{Z}_{{\geqslant}0}$
, we have
$n\in \mathbb{Z}_{{\geqslant}0}$
, we have
Proof. The proof of the first inequality is analogous to the proof of [Reference Bhatt, Morrow and ScholzeBMS18, 14.5(ii)]. Namely, by Corollary 7.5, we may drop the subscripts ‘
![]() $\text{tors}$
’ and, by Theorem 7.4, (7.6.2), and [Reference Bhatt, Morrow and ScholzeBMS18, 4.15(ii)], we have
$\text{tors}$
’ and, by Theorem 7.4, (7.6.2), and [Reference Bhatt, Morrow and ScholzeBMS18, 4.15(ii)], we have
Since
![]() $\operatorname{length}_{W(k)}(Q/p^{n})=\operatorname{length}_{W(k)}(\operatorname{Tor}_{1}^{W(k)}(Q,W(k)/p^{n}))$
for every
$\operatorname{length}_{W(k)}(Q/p^{n})=\operatorname{length}_{W(k)}(\operatorname{Tor}_{1}^{W(k)}(Q,W(k)/p^{n}))$
for every
![]() $W(k)$
-module
$W(k)$
-module
![]() $Q$
that is finite and torsion, the short exact sequence (7.6.4) yields the inequality
$Q$
that is finite and torsion, the short exact sequence (7.6.4) yields the inequality
and the first inequality in (7.9.1) follows. Due to the short exact sequences
that result from [SP, 0662], the second inequality in (7.9.1) follows from the first. ◻
The de Rham analogue of Theorem 7.9 is Theorem 7.12 below and uses the following formalism.
7.10 The normalized length
Let
![]() $\mathfrak{o}$
be a valuation ring of rank
$\mathfrak{o}$
be a valuation ring of rank
![]() $1$
and mixed characteristic
$1$
and mixed characteristic
![]() $(0,p)$
. We normalize its valuation
$(0,p)$
. We normalize its valuation
![]() $\text{val}_{\mathfrak{o}}$
by requiring that
$\text{val}_{\mathfrak{o}}$
by requiring that
![]() $\text{val}_{\mathfrak{o}}(p)=1$
. By the structure theorem [SP, 0ASP] (see also [Reference Gabber and RameroGR03, 6.1.14]), every finitely presented
$\text{val}_{\mathfrak{o}}(p)=1$
. By the structure theorem [SP, 0ASP] (see also [Reference Gabber and RameroGR03, 6.1.14]), every finitely presented
![]() $\mathfrak{o}$
-module
$\mathfrak{o}$
-module
![]() $M$
is of the form
$M$
is of the form
If
![]() $M$
is, in addition, torsion, to the effect that the
$M$
is, in addition, torsion, to the effect that the
![]() $a_{i}$
are nonzero, then we set
$a_{i}$
are nonzero, then we set
More intrinsically,
![]() $\text{val}_{\mathfrak{o}}(M)$
is the valuation of any generator of the 0th Fitting ideal
$\text{val}_{\mathfrak{o}}(M)$
is the valuation of any generator of the 0th Fitting ideal
![]() $\operatorname{Fitt}_{0}(M)\subset \mathfrak{o}$
of
$\operatorname{Fitt}_{0}(M)\subset \mathfrak{o}$
of
![]() $M$
, so it depends only on
$M$
, so it depends only on
![]() $M$
. If
$M$
. If
![]() $\mathfrak{o}$
is a discrete valuation ring for which
$\mathfrak{o}$
is a discrete valuation ring for which
![]() $p$
is a uniformizer, then
$p$
is a uniformizer, then
![]() $\text{val}_{\mathfrak{o}}(M)=\operatorname{length}_{\mathfrak{o}}(M)$
. In general,
$\text{val}_{\mathfrak{o}}(M)=\operatorname{length}_{\mathfrak{o}}(M)$
. In general,
![]() $\text{val}_{\mathfrak{o}}$
has the advantage of being invariant under the extension of scalars to a larger
$\text{val}_{\mathfrak{o}}$
has the advantage of being invariant under the extension of scalars to a larger
![]() $\mathfrak{o}$
. Any short exact sequence
$\mathfrak{o}$
. Any short exact sequence
of finitely presented, torsion
![]() $\mathfrak{o}$
-modules gives rise to the equality
$\mathfrak{o}$
-modules gives rise to the equality
![]() $\operatorname{Fitt}_{0}(M_{2})=\operatorname{Fitt}_{0}(M_{1})\operatorname{Fitt}_{0}(M_{3})$
(see [Reference Gabber and RameroGR03, 6.3.1 and 6.3.5(i)]), so the assignment
$\operatorname{Fitt}_{0}(M_{2})=\operatorname{Fitt}_{0}(M_{1})\operatorname{Fitt}_{0}(M_{3})$
(see [Reference Gabber and RameroGR03, 6.3.1 and 6.3.5(i)]), so the assignment
![]() $\text{val}_{\mathfrak{o}}(-)$
satisfies
$\text{val}_{\mathfrak{o}}(-)$
satisfies
The following lemma is the de Rham version of [Reference Bhatt, Morrow and ScholzeBMS18, 4.14], which gave the inequality (7.9.2).
Lemma 7.11. For a finitely presented
![]() $W_{n}({\mathcal{O}}_{C}^{\flat })$
-module
$W_{n}({\mathcal{O}}_{C}^{\flat })$
-module
![]() $M$
for some
$M$
for some
![]() $n\geqslant 1$
, we have
$n\geqslant 1$
, we have
Proof. Since the ring
![]() $W_{n}({\mathcal{O}}_{C}^{\flat })$
is coherent (see [Reference Bhatt, Morrow and ScholzeBMS18, 3.24]), the
$W_{n}({\mathcal{O}}_{C}^{\flat })$
is coherent (see [Reference Bhatt, Morrow and ScholzeBMS18, 3.24]), the
![]() $W_{n}({\mathcal{O}}_{C}^{\flat })$
-module
$W_{n}({\mathcal{O}}_{C}^{\flat })$
-module
![]() $M[\unicode[STIX]{x1D709}]$
is finitely presented. Moreover, due to (7.10.2), the flatness of
$M[\unicode[STIX]{x1D709}]$
is finitely presented. Moreover, due to (7.10.2), the flatness of
![]() $A_{\text{inf}}\rightarrow W(C^{\flat })$
(see §7.6), and the snake lemma, both sides of (7.11.1) are additive in short exact sequences. Therefore, we may assume that
$A_{\text{inf}}\rightarrow W(C^{\flat })$
(see §7.6), and the snake lemma, both sides of (7.11.1) are additive in short exact sequences. Therefore, we may assume that
![]() $n=1$
and, due to the structure theorem [SP, 0ASP], that
$n=1$
and, due to the structure theorem [SP, 0ASP], that
![]() $M={\mathcal{O}}_{C}^{\flat }/(x)$
for some
$M={\mathcal{O}}_{C}^{\flat }/(x)$
for some
![]() $x\in {\mathcal{O}}_{C}^{\flat }$
.
$x\in {\mathcal{O}}_{C}^{\flat }$
.
If
![]() $x=0$
, then both sides of (7.11.1) are equal to
$x=0$
, then both sides of (7.11.1) are equal to
![]() $1$
. If
$1$
. If
![]() $x\neq 0$
, then the left-hand side vanishes, and so does the right-hand side because
$x\neq 0$
, then the left-hand side vanishes, and so does the right-hand side because
![]() $M[\unicode[STIX]{x1D709}]\cong \operatorname{Tor}_{{\mathcal{O}}_{C}^{\flat }}^{1}(M,{\mathcal{O}}_{C}/p)$
and the following sequence is exact:
$M[\unicode[STIX]{x1D709}]\cong \operatorname{Tor}_{{\mathcal{O}}_{C}^{\flat }}^{1}(M,{\mathcal{O}}_{C}/p)$
and the following sequence is exact:
Theorem 7.12. For every
![]() $i\in \mathbb{Z}$
and
$i\in \mathbb{Z}$
and
![]() $n\in \mathbb{Z}_{{\geqslant}0}$
, we have (recall from §7.10 that
$n\in \mathbb{Z}_{{\geqslant}0}$
, we have (recall from §7.10 that
![]() $\text{val}_{\mathbb{Z}_{p}}=\operatorname{length}_{\mathbb{Z}_{p}}$
)
$\text{val}_{\mathbb{Z}_{p}}=\operatorname{length}_{\mathbb{Z}_{p}}$
)
 $$\begin{eqnarray}\begin{array}{@{}rcl@{}}\text{val}_{\mathbb{Z}_{p}}((H_{\acute{\text{e}}\text{t}}^{i}(\mathfrak{X}_{C}^{\text{ad}},\mathbb{Z}_{p})_{\text{tors}})/p^{n})\ & {\leqslant}\ & \text{val}_{{\mathcal{O}}_{C}}((H_{\log \text{dR}}^{i}(\mathfrak{X}/{\mathcal{O}}_{C})_{\text{tors}})/p^{n}),\\ \text{val}_{\mathbb{Z}_{p}}(H_{\acute{\text{e}}\text{t}}^{i}(\mathfrak{X}_{C}^{\text{ad}},\mathbb{Z}/p^{n}\mathbb{Z}))\ & {\leqslant}\ & \text{val}_{{\mathcal{O}}_{C}}(R^{i}\unicode[STIX]{x1D6E4}(\mathfrak{X}_{{\mathcal{O}}_{C}/p^{n},\,\acute{\text{e}}\text{t}},\unicode[STIX]{x1D6FA}_{\mathfrak{X}_{{\mathcal{O}}_{C}/p^{n}}/({\mathcal{O}}_{C}/p^{n}),\,\log }^{\bullet })).\end{array}\end{eqnarray}$$
$$\begin{eqnarray}\begin{array}{@{}rcl@{}}\text{val}_{\mathbb{Z}_{p}}((H_{\acute{\text{e}}\text{t}}^{i}(\mathfrak{X}_{C}^{\text{ad}},\mathbb{Z}_{p})_{\text{tors}})/p^{n})\ & {\leqslant}\ & \text{val}_{{\mathcal{O}}_{C}}((H_{\log \text{dR}}^{i}(\mathfrak{X}/{\mathcal{O}}_{C})_{\text{tors}})/p^{n}),\\ \text{val}_{\mathbb{Z}_{p}}(H_{\acute{\text{e}}\text{t}}^{i}(\mathfrak{X}_{C}^{\text{ad}},\mathbb{Z}/p^{n}\mathbb{Z}))\ & {\leqslant}\ & \text{val}_{{\mathcal{O}}_{C}}(R^{i}\unicode[STIX]{x1D6E4}(\mathfrak{X}_{{\mathcal{O}}_{C}/p^{n},\,\acute{\text{e}}\text{t}},\unicode[STIX]{x1D6FA}_{\mathfrak{X}_{{\mathcal{O}}_{C}/p^{n}}/({\mathcal{O}}_{C}/p^{n}),\,\log }^{\bullet })).\end{array}\end{eqnarray}$$
Proof. The proof is analogous to that of Theorem 7.9. Namely, by Corollary 7.5, we may drop the subscripts ‘
![]() $\text{tors}$
’ and, by Theorem 7.4, (7.6.2), and Lemma 7.11, we have
$\text{tors}$
’ and, by Theorem 7.4, (7.6.2), and Lemma 7.11, we have
The presentation (7.10.1) implies that
![]() $\text{val}_{{\mathcal{O}}_{C}}(Q/p^{n})=\text{val}_{{\mathcal{O}}_{C}}(\operatorname{Tor}_{1}^{{\mathcal{O}}_{C}}(Q,{\mathcal{O}}_{C}/p^{n}))$
for every finitely presented, torsion
$\text{val}_{{\mathcal{O}}_{C}}(Q/p^{n})=\text{val}_{{\mathcal{O}}_{C}}(\operatorname{Tor}_{1}^{{\mathcal{O}}_{C}}(Q,{\mathcal{O}}_{C}/p^{n}))$
for every finitely presented, torsion
![]() ${\mathcal{O}}_{C}$
-module
${\mathcal{O}}_{C}$
-module
![]() $Q$
, so the short exact sequence (7.6.3) yields the inequality
$Q$
, so the short exact sequence (7.6.3) yields the inequality
This proves the first inequality in (7.12.1) and, analogously to the proof of Theorem 7.9, the second inequality follows from the first. ◻
The results above, specifically, (7.8.1) and Theorems 7.9 and 7.12 prompt the following question.
Question 7.13. Are there examples of
![]() ${\mathcal{O}}_{C}$
-proper
${\mathcal{O}}_{C}$
-proper
![]() $\mathfrak{X}$
satisfying the assumptions of §1.5 for which
$\mathfrak{X}$
satisfying the assumptions of §1.5 for which
8 A functorial lattice inside the de Rham cohomology
To a proper, smooth scheme
![]() $X$
over a complete, discretely valued extension
$X$
over a complete, discretely valued extension
![]() $K$
of
$K$
of
![]() $\mathbb{Q}_{p}$
with a perfect residue field, in Example 8.6 we functorially associate an
$\mathbb{Q}_{p}$
with a perfect residue field, in Example 8.6 we functorially associate an
![]() ${\mathcal{O}}_{K}$
-lattice
${\mathcal{O}}_{K}$
-lattice
In fact,
![]() $L_{\text{dR}}^{i}(X)$
functorially depends only on
$L_{\text{dR}}^{i}(X)$
functorially depends only on
![]() $H_{\acute{\text{e}}\text{t}}^{i}(X_{\overline{K}},\mathbb{Z}_{p})$
and its construction, which relies on the theory of Breuil–Kisin–Fargues modules, proceeds along familiar lines of integral
$H_{\acute{\text{e}}\text{t}}^{i}(X_{\overline{K}},\mathbb{Z}_{p})$
and its construction, which relies on the theory of Breuil–Kisin–Fargues modules, proceeds along familiar lines of integral
![]() $p$
-adic Hodge theory; compare, for instance, with [Reference LiuLiu18, §4]. The work of the preceding sections allows us to interpret
$p$
-adic Hodge theory; compare, for instance, with [Reference LiuLiu18, §4]. The work of the preceding sections allows us to interpret
![]() $L_{\text{dR}}^{i}(X)$
geometrically: we show in Theorem 8.7 that if
$L_{\text{dR}}^{i}(X)$
geometrically: we show in Theorem 8.7 that if
![]() $X$
has a proper, flat, semistable
$X$
has a proper, flat, semistable
![]() ${\mathcal{O}}_{K}$
-model
${\mathcal{O}}_{K}$
-model
![]() ${\mathcal{X}}$
for which
${\mathcal{X}}$
for which
![]() $H_{\log \text{dR}}^{i}({\mathcal{X}}/{\mathcal{O}}_{K})$
and
$H_{\log \text{dR}}^{i}({\mathcal{X}}/{\mathcal{O}}_{K})$
and
![]() $H_{\log \text{dR}}^{i+1}({\mathcal{X}}/{\mathcal{O}}_{K})$
are
$H_{\log \text{dR}}^{i+1}({\mathcal{X}}/{\mathcal{O}}_{K})$
are
![]() ${\mathcal{O}}_{K}$
-free, then
${\mathcal{O}}_{K}$
-free, then
We do not know whether the same holds ‘modulo torsion’ if one drops the
![]() ${\mathcal{O}}_{K}$
-freeness assumption.
${\mathcal{O}}_{K}$
-freeness assumption.
8.1 The base field
 $K$
$K$
Throughout §8, we assume that
![]() $C\cong \widehat{\overline{K}}$
for a fixed complete, discretely valued field
$C\cong \widehat{\overline{K}}$
for a fixed complete, discretely valued field
![]() $K$
that is of mixed characteristic
$K$
that is of mixed characteristic
![]() $(0,p)$
and has a perfect residue field
$(0,p)$
and has a perfect residue field
![]() $k_{0}$
. We set
$k_{0}$
. We set
so that
![]() $G$
acts continuously on
$G$
acts continuously on
![]() $C$
, and hence also on
$C$
, and hence also on
![]() $A_{\text{inf}}$
. The continuous maps
$A_{\text{inf}}$
. The continuous maps
![]() $\unicode[STIX]{x1D711}$
and
$\unicode[STIX]{x1D711}$
and
![]() $\unicode[STIX]{x1D703}$
are
$\unicode[STIX]{x1D703}$
are
![]() $G$
-equivariant, and the ideals
$G$
-equivariant, and the ideals
![]() $(\unicode[STIX]{x1D709})$
,
$(\unicode[STIX]{x1D709})$
,
![]() $(\unicode[STIX]{x1D711}(\unicode[STIX]{x1D709}))$
, and
$(\unicode[STIX]{x1D711}(\unicode[STIX]{x1D709}))$
, and
![]() $(\unicode[STIX]{x1D707})$
of
$(\unicode[STIX]{x1D707})$
of
![]() $A_{\text{inf}}$
are
$A_{\text{inf}}$
are
![]() $G$
-stable (see §2.1).
$G$
-stable (see §2.1).
If
![]() ${\mathcal{X}}$
is a
${\mathcal{X}}$
is a
![]() $p$
-adic formal
$p$
-adic formal
![]() ${\mathcal{O}}_{K}$
-scheme for which
${\mathcal{O}}_{K}$
-scheme for which
![]() $\mathfrak{X}:={\mathcal{X}}\widehat{\otimes }_{{\mathcal{O}}_{K}}{\mathcal{O}}_{C}$
satisfies the assumptions of §1.5, then, by the functoriality of
$\mathfrak{X}:={\mathcal{X}}\widehat{\otimes }_{{\mathcal{O}}_{K}}{\mathcal{O}}_{C}$
satisfies the assumptions of §1.5, then, by the functoriality of
![]() $R\unicode[STIX]{x1D6E4}_{A_{\text{inf}}}(\mathfrak{X})$
(see §7.2),
$R\unicode[STIX]{x1D6E4}_{A_{\text{inf}}}(\mathfrak{X})$
(see §7.2),
![]() $G$
acts
$G$
acts
![]() $A_{\text{inf}}$
-semilinearly on each
$A_{\text{inf}}$
-semilinearly on each
![]() $H_{A_{\text{inf}}}^{i}(\mathfrak{X})$
.
$H_{A_{\text{inf}}}^{i}(\mathfrak{X})$
.
8.2 The Fargues equivalence
By [Reference Bhatt, Morrow and ScholzeBMS18, 4.26], for any Breuil–Kisin–Fargues module
![]() $(M,\unicode[STIX]{x1D711}_{M})$
(see §7.3), its étale realization, namely,
$(M,\unicode[STIX]{x1D711}_{M})$
(see §7.3), its étale realization, namely,
is a finitely generated
![]() $\mathbb{Z}_{p}$
-module that comes equipped with an identification
$\mathbb{Z}_{p}$
-module that comes equipped with an identification
Thus,
![]() $M_{\acute{\text{e}}\text{t}}$
is
$M_{\acute{\text{e}}\text{t}}$
is
![]() $\mathbb{Z}_{p}$
-free if
$\mathbb{Z}_{p}$
-free if
![]() $M$
is
$M$
is
![]() $A_{\text{inf}}$
-free and, for any
$A_{\text{inf}}$
-free and, for any
![]() $(M,\unicode[STIX]{x1D711}_{M})$
, we have
$(M,\unicode[STIX]{x1D711}_{M})$
, we have
![]() $M\otimes _{A_{\text{inf}}}B_{\text{dR}}\cong M_{\acute{\text{e}}\text{t}}\otimes _{\mathbb{Z}_{p}}B_{\text{dR}}$
, so that
$M\otimes _{A_{\text{inf}}}B_{\text{dR}}\cong M_{\acute{\text{e}}\text{t}}\otimes _{\mathbb{Z}_{p}}B_{\text{dR}}$
, so that
![]() $M_{\acute{\text{e}}\text{t}}$
comes equipped with a
$M_{\acute{\text{e}}\text{t}}$
comes equipped with a
![]() $B_{\text{dR}}^{+}$
-sublattice (recall that
$B_{\text{dR}}^{+}$
-sublattice (recall that
![]() $M[\frac{1}{p}]$
is
$M[\frac{1}{p}]$
is
![]() $A_{\text{inf}}[\frac{1}{p}]$
-free, see §7.3)
$A_{\text{inf}}[\frac{1}{p}]$
-free, see §7.3)
By a theorem of Fargues [Reference Bhatt, Morrow and ScholzeBMS18, 4.28], the category of
![]() $A_{\text{inf}}$
-free Breuil–Kisin–Fargues modules
$A_{\text{inf}}$
-free Breuil–Kisin–Fargues modules
![]() $(M,\unicode[STIX]{x1D711}_{M})$
is equivalent to that of pairs
$(M,\unicode[STIX]{x1D711}_{M})$
is equivalent to that of pairs
![]() $(T,\unicode[STIX]{x1D6EF})$
consisting of a finite free
$(T,\unicode[STIX]{x1D6EF})$
consisting of a finite free
![]() $\mathbb{Z}_{p}$
-module
$\mathbb{Z}_{p}$
-module
![]() $T$
and a
$T$
and a
![]() $B_{\text{dR}}^{+}$
-lattice
$B_{\text{dR}}^{+}$
-lattice
![]() $\unicode[STIX]{x1D6EF}\subset T\otimes _{\mathbb{Z}_{p}}B_{\text{dR}}$
via the functor
$\unicode[STIX]{x1D6EF}\subset T\otimes _{\mathbb{Z}_{p}}B_{\text{dR}}$
via the functor
8.3 Breuil–Kisin–Fargues
 $G$
-modules
$G$
-modules
Due to the origin of our
![]() $C$
(see §8.1), we may consider Breuil–Kisin–Fargues
$C$
(see §8.1), we may consider Breuil–Kisin–Fargues
![]() $G$
-modules, that is, Breuil–Kisin–Fargues modules
$G$
-modules, that is, Breuil–Kisin–Fargues modules
![]() $(M,\unicode[STIX]{x1D711}_{M})$
equipped with an
$(M,\unicode[STIX]{x1D711}_{M})$
equipped with an
![]() $A_{\text{inf}}$
-semilinear
$A_{\text{inf}}$
-semilinear
![]() $G$
-action on
$G$
-action on
![]() $M$
for which
$M$
for which
![]() $\unicode[STIX]{x1D711}_{M}$
is
$\unicode[STIX]{x1D711}_{M}$
is
![]() $G$
-equivariant. A morphism of Breuil–Kisin–Fargues
$G$
-equivariant. A morphism of Breuil–Kisin–Fargues
![]() $G$
-modules is a
$G$
-modules is a
![]() $G$
-equivariant
$G$
-equivariant
![]() $A_{\text{inf}}$
-module morphism that commutes with the isomorphisms
$A_{\text{inf}}$
-module morphism that commutes with the isomorphisms
![]() $\unicode[STIX]{x1D711}_{M}$
.
$\unicode[STIX]{x1D711}_{M}$
.
For instance, if an
![]() ${\mathcal{X}}$
as in §8.1 is proper, then each
${\mathcal{X}}$
as in §8.1 is proper, then each
![]() $H_{A_{\text{inf}}}^{i}(\mathfrak{X})$
is a Breuil–Kisin–Fargues
$H_{A_{\text{inf}}}^{i}(\mathfrak{X})$
is a Breuil–Kisin–Fargues
![]() $G$
-module (see Theorem 7.4). The étale realization
$G$
-module (see Theorem 7.4). The étale realization
![]() $M_{\acute{\text{e}}\text{t}}$
of a Breuil–Kisin–Fargues
$M_{\acute{\text{e}}\text{t}}$
of a Breuil–Kisin–Fargues
![]() $G$
-module
$G$
-module
![]() $(M,\unicode[STIX]{x1D711}_{M})$
carries the induced
$(M,\unicode[STIX]{x1D711}_{M})$
carries the induced
![]() $\mathbb{Z}_{p}$
-linear
$\mathbb{Z}_{p}$
-linear
![]() $G$
-action.
$G$
-action.
Proposition 8.4. The category of
![]() $A_{\text{inf}}$
-free Breuil–Kisin–Fargues
$A_{\text{inf}}$
-free Breuil–Kisin–Fargues
![]() $G$
-modules
$G$
-modules
![]() $(M,\unicode[STIX]{x1D711}_{M})$
is equivalent to that of pairs
$(M,\unicode[STIX]{x1D711}_{M})$
is equivalent to that of pairs
![]() $(T,\unicode[STIX]{x1D6EF})$
consisting of a finite free
$(T,\unicode[STIX]{x1D6EF})$
consisting of a finite free
![]() $\mathbb{Z}_{p}$
-module
$\mathbb{Z}_{p}$
-module
![]() $T$
equipped with a
$T$
equipped with a
![]() $G$
-action and a
$G$
-action and a
![]() $G$
-stable
$G$
-stable
![]() $B_{\text{dR}}^{+}$
-lattice
$B_{\text{dR}}^{+}$
-lattice
![]() $\unicode[STIX]{x1D6EF}\subset T\otimes _{\mathbb{Z}_{p}}B_{\text{dR}}$
via the functor
$\unicode[STIX]{x1D6EF}\subset T\otimes _{\mathbb{Z}_{p}}B_{\text{dR}}$
via the functor
Proof. The claim follows from the Fargues equivalence reviewed in §8.2. ◻
8.5 An étale lattice determines a de Rham lattice
Let
![]() $T$
be a finite free
$T$
be a finite free
![]() $\mathbb{Z}_{p}$
-module endowed with a continuous
$\mathbb{Z}_{p}$
-module endowed with a continuous
![]() $G$
-action for which the
$G$
-action for which the
![]() $G$
-representation
$G$
-representation
![]() $T[\frac{1}{p}]$
is de Rham, so that there is a
$T[\frac{1}{p}]$
is de Rham, so that there is a
![]() $G$
-equivariant identification
$G$
-equivariant identification
For such
![]() $T$
, the
$T$
, the
![]() $B_{\text{dR}}^{+}$
-lattice
$B_{\text{dR}}^{+}$
-lattice
![]() $D_{\text{dR}}(T)\otimes _{K}B_{\text{dR}}^{+}$
is evidently
$D_{\text{dR}}(T)\otimes _{K}B_{\text{dR}}^{+}$
is evidently
![]() $G$
-stable in
$G$
-stable in
![]() $T\otimes _{\mathbb{Z}_{p}}B_{\text{dR}}$
. Thus, by Proposition 8.4, the pair
$T\otimes _{\mathbb{Z}_{p}}B_{\text{dR}}$
. Thus, by Proposition 8.4, the pair
![]() $(T,D_{\text{dR}}(T)\otimes _{K}B_{\text{dR}}^{+})$
, so
$(T,D_{\text{dR}}(T)\otimes _{K}B_{\text{dR}}^{+})$
, so
![]() $T$
, determines an
$T$
, determines an
![]() $A_{\text{inf}}$
-free Breuil–Kisin–Fargues
$A_{\text{inf}}$
-free Breuil–Kisin–Fargues
![]() $G$
-module
$G$
-module
that depends functorially on
![]() $T$
. The de Rham realization
$T$
. The de Rham realization
is an
![]() ${\mathcal{O}}_{C}$
-lattice in
${\mathcal{O}}_{C}$
-lattice in
Therefore, functorially in
![]() $T$
, we obtain the
$T$
, we obtain the
![]() ${\mathcal{O}}_{K}$
-lattice
${\mathcal{O}}_{K}$
-lattice
Example 8.6. We fix a
![]() $K$
-scheme
$K$
-scheme
![]() $X$
(or even a
$X$
(or even a
![]() $K$
-rigid space, which we view as an adic space, see [Reference HuberHub96, 1.1.11(d)]) that is proper and smooth, and set
$K$
-rigid space, which we view as an adic space, see [Reference HuberHub96, 1.1.11(d)]) that is proper and smooth, and set
As is well known and follows from (6.7.2), the
![]() $G$
-representation
$G$
-representation
![]() $(L_{\acute{\text{e}}\text{t}}^{i}(X))[\frac{1}{p}]$
is de Rham and
$(L_{\acute{\text{e}}\text{t}}^{i}(X))[\frac{1}{p}]$
is de Rham and
functorially in
![]() $X$
. Thus, using the discussion of §8.5, we obtain the
$X$
. Thus, using the discussion of §8.5, we obtain the
![]() ${\mathcal{O}}_{K}$
-lattice
${\mathcal{O}}_{K}$
-lattice
that is functorial in
![]() $X$
(even in
$X$
(even in
![]() $L_{\acute{\text{e}}\text{t}}^{i}(X)$
). Its definition implies that for a finite Galois extension
$L_{\acute{\text{e}}\text{t}}^{i}(X)$
). Its definition implies that for a finite Galois extension
![]() $K^{\prime }/K$
,
$K^{\prime }/K$
,
If
![]() $X$
extends to a proper, flat, semistable
$X$
extends to a proper, flat, semistable
![]() ${\mathcal{O}}_{K}$
-scheme
${\mathcal{O}}_{K}$
-scheme
![]() ${\mathcal{X}}$
such that
${\mathcal{X}}$
such that
![]() $H_{\log \text{dR}}^{i}({\mathcal{X}}/{\mathcal{O}}_{K})$
and
$H_{\log \text{dR}}^{i}({\mathcal{X}}/{\mathcal{O}}_{K})$
and
![]() $H_{\log \text{dR}}^{i+1}({\mathcal{X}}/{\mathcal{O}}_{K})$
are
$H_{\log \text{dR}}^{i+1}({\mathcal{X}}/{\mathcal{O}}_{K})$
are
![]() ${\mathcal{O}}_{K}$
-free (where
${\mathcal{O}}_{K}$
-free (where
![]() ${\mathcal{X}}$
is endowed with the log structure
${\mathcal{X}}$
is endowed with the log structure
![]() ${\mathcal{O}}_{{\mathcal{X}},\,\acute{\text{e}}\text{t}}\cap ({\mathcal{O}}_{{\mathcal{X}},\,\acute{\text{e}}\text{t}}[\frac{1}{p}])^{\times }$
), then, by the following Theorem 8.7 (and GAGA techniques, similarly to Remark 4.19),
${\mathcal{O}}_{{\mathcal{X}},\,\acute{\text{e}}\text{t}}\cap ({\mathcal{O}}_{{\mathcal{X}},\,\acute{\text{e}}\text{t}}[\frac{1}{p}])^{\times }$
), then, by the following Theorem 8.7 (and GAGA techniques, similarly to Remark 4.19),
in particular, if
![]() ${\mathcal{X}}^{\prime }$
is another such
${\mathcal{X}}^{\prime }$
is another such
![]() ${\mathcal{O}}_{K}$
-model of
${\mathcal{O}}_{K}$
-model of
![]() $X$
, then
$X$
, then
Theorem 8.7. Let
![]() ${\mathcal{X}}$
be a proper, flat
${\mathcal{X}}$
be a proper, flat
![]() $p$
-adic formal
$p$
-adic formal
![]() ${\mathcal{O}}_{K}$
-scheme endowed with the log structure
${\mathcal{O}}_{K}$
-scheme endowed with the log structure
![]() ${\mathcal{O}}_{{\mathcal{X}},\,\acute{\text{e}}\text{t}}\cap ({\mathcal{O}}_{{\mathcal{X}},\,\acute{\text{e}}\text{t}}[\frac{1}{p}])^{\times }$
such that
${\mathcal{O}}_{{\mathcal{X}},\,\acute{\text{e}}\text{t}}\cap ({\mathcal{O}}_{{\mathcal{X}},\,\acute{\text{e}}\text{t}}[\frac{1}{p}])^{\times }$
such that
![]() ${\mathcal{X}}$
has an étale cover by affines
${\mathcal{X}}$
has an étale cover by affines
![]() ${\mathcal{U}}$
each of which has an étale morphism
${\mathcal{U}}$
each of which has an étale morphism
(where
![]() $d$
,
$d$
,
![]() $r$
, and
$r$
, and
![]() $\unicode[STIX]{x1D70B}$
depend on
$\unicode[STIX]{x1D70B}$
depend on
![]() ${\mathcal{U}}$
). If
${\mathcal{U}}$
). If
![]() $H_{\log \text{dR}}^{i}({\mathcal{X}}/{\mathcal{O}}_{K})$
and
$H_{\log \text{dR}}^{i}({\mathcal{X}}/{\mathcal{O}}_{K})$
and
![]() $H_{\log \text{dR}}^{i+1}({\mathcal{X}}/{\mathcal{O}}_{K})$
are
$H_{\log \text{dR}}^{i+1}({\mathcal{X}}/{\mathcal{O}}_{K})$
are
![]() ${\mathcal{O}}_{K}$
-free, then
${\mathcal{O}}_{K}$
-free, then
in fact, then, setting
![]() $\mathfrak{X}:={\mathcal{X}}\widehat{\otimes }_{{\mathcal{O}}_{K}}{\mathcal{O}}_{C}$
, we have the identification
$\mathfrak{X}:={\mathcal{X}}\widehat{\otimes }_{{\mathcal{O}}_{K}}{\mathcal{O}}_{C}$
, we have the identification
of Breuil–Kisin–Fargues
![]() $G$
-modules.
$G$
-modules.
Proof. By working locally on
![]() ${\mathcal{U}}$
, in the target of (8.7.1) we may replace each
${\mathcal{U}}$
, in the target of (8.7.1) we may replace each
![]() $t_{i}$
by
$t_{i}$
by
![]() $t_{i}^{\pm 1}$
for
$t_{i}^{\pm 1}$
for
![]() $r+1\leqslant i\leqslant d$
, so
$r+1\leqslant i\leqslant d$
, so
![]() $\mathfrak{X}$
satisfies the assumptions of §1.5. Moreover, by the Grothendieck comparison theorem and flat base change (compare with Remark 4.19), for
$\mathfrak{X}$
satisfies the assumptions of §1.5. Moreover, by the Grothendieck comparison theorem and flat base change (compare with Remark 4.19), for
![]() $j=i$
and
$j=i$
and
![]() $j=i+1$
, we have
$j=i+1$
, we have
Thus, by Proposition 7.7, the Breuil–Kisin–Fargues
![]() $G$
-modules
$G$
-modules
![]() $H_{A_{\text{inf}}}^{i}(\mathfrak{X})$
and
$H_{A_{\text{inf}}}^{i}(\mathfrak{X})$
and
![]() $H_{A_{\text{inf}}}^{i+1}(\mathfrak{X})$
(see §8.3) are
$H_{A_{\text{inf}}}^{i+1}(\mathfrak{X})$
(see §8.3) are
![]() $A_{\text{inf}}$
-free. By (7.6.2), we have the
$A_{\text{inf}}$
-free. By (7.6.2), we have the
![]() $G$
-equivariant identification of the étale realization:
$G$
-equivariant identification of the étale realization:
which, consequently, is
![]() $\mathbb{Z}_{p}$
-free. By Proposition 6.8, the
$\mathbb{Z}_{p}$
-free. By Proposition 6.8, the
![]() $B_{\text{dR}}$
-base change of this identification agrees with the identification
$B_{\text{dR}}$
-base change of this identification agrees with the identification
![]() $H_{A_{\text{inf}}}^{i}(\mathfrak{X})\otimes _{A_{\text{inf}}}B_{\text{dR}}\cong H_{\acute{\text{e}}\text{t}}^{i}({\mathcal{X}}_{C}^{\text{ad}},\mathbb{Z}_{p})\otimes _{\mathbb{Z}_{p}}B_{\text{dR}}$
that results by combining
$H_{A_{\text{inf}}}^{i}(\mathfrak{X})\otimes _{A_{\text{inf}}}B_{\text{dR}}\cong H_{\acute{\text{e}}\text{t}}^{i}({\mathcal{X}}_{C}^{\text{ad}},\mathbb{Z}_{p})\otimes _{\mathbb{Z}_{p}}B_{\text{dR}}$
that results by combining
and
This compatibility and §8.5 (see also (8.6.1)) supply the desired
![]() $G$
-equivariant identification (8.7.3):
$G$
-equivariant identification (8.7.3):
Under this identification, by Theorem 6.6 and the sentence after (6.2.8), the identifications
agree. Thus, (7.6.3) implies the following equality inside
![]() $H_{\text{dR}}^{i}({\mathcal{X}}_{C}^{\text{ad}}/C)$
:
$H_{\text{dR}}^{i}({\mathcal{X}}_{C}^{\text{ad}}/C)$
:
which, together with the second identification in (8.7.4), gives the desired (8.7.2). ◻
Remark 8.8. In the proof above, we have seen that both
![]() $H_{A_{\text{inf}}}^{i}(\mathfrak{X})$
and
$H_{A_{\text{inf}}}^{i}(\mathfrak{X})$
and
![]() $H_{A_{\text{inf}}}^{i+1}(\mathfrak{X})$
are
$H_{A_{\text{inf}}}^{i+1}(\mathfrak{X})$
are
![]() $A_{\text{inf}}$
-free, so, by (7.6.4), we have the
$A_{\text{inf}}$
-free, so, by (7.6.4), we have the
![]() $G$
-equivariant and Frobenius-equivariant identifications
$G$
-equivariant and Frobenius-equivariant identifications
and hence also the Frobenius-equivariant identification
In particular, (8.7.3) and (8.8.1) show that, under the assumptions of Theorem 8.7, the integral
![]() $p$
-adic étale cohomology
$p$
-adic étale cohomology
![]() $H_{\acute{\text{e}}\text{t}}^{i}({\mathcal{X}}_{C}^{\text{ad}},\mathbb{Z}_{p})$
endowed with its Galois action functorially determines the integral logarithmic crystalline cohomology
$H_{\acute{\text{e}}\text{t}}^{i}({\mathcal{X}}_{C}^{\text{ad}},\mathbb{Z}_{p})$
endowed with its Galois action functorially determines the integral logarithmic crystalline cohomology
![]() $H_{\log \text{cris}}^{i}({\mathcal{X}}_{k_{0}}/W(k_{0}))$
endowed with its Frobenius.
$H_{\log \text{cris}}^{i}({\mathcal{X}}_{k_{0}}/W(k_{0}))$
endowed with its Frobenius.
9 The semistable comparison isomorphism
Our final goal is to deduce the semistable comparison isomorphism for suitable proper, ‘semistable’ formal schemes (see Theorem 9.5). This extends [Reference Bhatt, Morrow and ScholzeBMS18, 1.1(i)], which treated the good reduction case (see also [Reference Tan and TongTT15, 1.2] for a result ‘with coefficients’ over an absolutely unramified base), and is similar to the semistable comparison established by Colmez–Niziol [Reference Colmez and NiziołCN17, 5.26]. More precisely, [Reference Colmez and NiziołCN17, 5.26] also includes cases in which the log structures are not ‘vertical’.
9.1 The ring
 $B_{\text{st}}$
$B_{\text{st}}$
We consider the log PD thickenings
![]() $A_{\text{cris}}/p^{n}$
of
$A_{\text{cris}}/p^{n}$
of
![]() ${\mathcal{O}}_{C}/p$
(see §5.2) and set
${\mathcal{O}}_{C}/p$
(see §5.2) and set
The element
![]() $p\in {\mathcal{O}}_{C}\setminus \{0\}$
belongs to the log structure of
$p\in {\mathcal{O}}_{C}\setminus \{0\}$
belongs to the log structure of
![]() ${\mathcal{O}}_{C}/p$
(see §1.6 (1)), so its preimage in the log structure of
${\mathcal{O}}_{C}/p$
(see §1.6 (1)), so its preimage in the log structure of
![]() $A_{\text{cris}}/p^{n}$
is a
$A_{\text{cris}}/p^{n}$
is a
![]() $(1+J_{n},\times )$
-torsor, which is necessarily trivialFootnote
20
(compare with [Reference BeilinsonBei13a, §1.1, Exercises, (iii)]). Consequently, as
$(1+J_{n},\times )$
-torsor, which is necessarily trivialFootnote
20
(compare with [Reference BeilinsonBei13a, §1.1, Exercises, (iii)]). Consequently, as
![]() $n$
varies, these torsors comprise a trivial
$n$
varies, these torsors comprise a trivial
![]() $(1+J,\times )$
-torsor
$(1+J,\times )$
-torsor
![]() $\unicode[STIX]{x1D70F}_{0}$
, whose base change along the logarithm map
$\unicode[STIX]{x1D70F}_{0}$
, whose base change along the logarithm map
![]() $(1+J,\times )\rightarrow (J,+)\subset (A_{\text{cris}},+)$
furnished by the divided power structure on
$(1+J,\times )\rightarrow (J,+)\subset (A_{\text{cris}},+)$
furnished by the divided power structure on
![]() $J$
is a trivial
$J$
is a trivial
![]() $(A_{\text{cris}},+)$
-torsor
$(A_{\text{cris}},+)$
-torsor
![]() $\unicode[STIX]{x1D70F}$
, the Fontaine–Hyodo–Kato torsor (compare with [Reference BeilinsonBei13a, §1.15, p. 23]). The functor which to an
$\unicode[STIX]{x1D70F}$
, the Fontaine–Hyodo–Kato torsor (compare with [Reference BeilinsonBei13a, §1.15, p. 23]). The functor which to an
![]() $A_{\text{cris}}$
-algebra
$A_{\text{cris}}$
-algebra
![]() $A$
assigns the underlying set of the
$A$
assigns the underlying set of the
![]() $(A,+)$
-torsor
$(A,+)$
-torsor
![]() $\unicode[STIX]{x1D70F}\times _{(A_{\text{cris}},+)}(A,+)$
is represented by the
$\unicode[STIX]{x1D70F}\times _{(A_{\text{cris}},+)}(A,+)$
is represented by the
![]() $A_{\text{cris}}$
-algebra
$A_{\text{cris}}$
-algebra
![]() $A_{\text{st}}$
, so
$A_{\text{st}}$
, so
![]() $A_{\text{st}}$
is the initial
$A_{\text{st}}$
is the initial
![]() $A_{\text{cris}}$
-algebra over which the Fontaine–Hyodo–Kato torsor is canonically trivialized.
$A_{\text{cris}}$
-algebra over which the Fontaine–Hyodo–Kato torsor is canonically trivialized.
We may noncanonically trivialize
![]() $\unicode[STIX]{x1D70F}_{0}$
(for instance,
$\unicode[STIX]{x1D70F}_{0}$
(for instance,
![]() $[p^{1/p^{\infty }}]$
is a trivialization, see (5.2.1)) to obtain an isomorphism
$[p^{1/p^{\infty }}]$
is a trivialization, see (5.2.1)) to obtain an isomorphism
![]() $A_{\text{st}}\simeq A_{\text{cris}}[T]$
, which, upon adjusting the trivialization by an
$A_{\text{st}}\simeq A_{\text{cris}}[T]$
, which, upon adjusting the trivialization by an
![]() $a\in 1+J$
, gets postcomposed with the
$a\in 1+J$
, gets postcomposed with the
![]() $A_{\text{cris}}$
-automorphism
$A_{\text{cris}}$
-automorphism
![]() $A_{\text{cris}}[T]\xrightarrow[{}]{T\mapsto T+\log (a)}A_{\text{cris}}[T]$
. The
$A_{\text{cris}}[T]\xrightarrow[{}]{T\mapsto T+\log (a)}A_{\text{cris}}[T]$
. The
![]() $A_{\text{cris}}$
-derivation
$A_{\text{cris}}$
-derivation
![]() $-d/dT$
respects these automorphisms, so it induces a canonical
$-d/dT$
respects these automorphisms, so it induces a canonical
![]() $A_{\text{cris}}$
-derivation, the monodromy operator,
$A_{\text{cris}}$
-derivation, the monodromy operator,
(our
![]() $N$
agrees with that of [Reference BeilinsonBei13a], see [Reference BeilinsonBei13a, §1.15, Remarks (i)]; compare also with [Reference TsujiTsu99, 4.1.1]).
$N$
agrees with that of [Reference BeilinsonBei13a], see [Reference BeilinsonBei13a, §1.15, Remarks (i)]; compare also with [Reference TsujiTsu99, 4.1.1]).
By [Reference BeilinsonBei13a, (1.15.2)], the Frobenius pullback of
![]() $\unicode[STIX]{x1D70F}_{0}$
is isomorphic to the
$\unicode[STIX]{x1D70F}_{0}$
is isomorphic to the
![]() $p$
-fold self-product of
$p$
-fold self-product of
![]() $\unicode[STIX]{x1D70F}_{0}$
, and hence likewise for the base change
$\unicode[STIX]{x1D70F}_{0}$
, and hence likewise for the base change
![]() $\unicode[STIX]{x1D70F}$
of
$\unicode[STIX]{x1D70F}$
of
![]() $\unicode[STIX]{x1D70F}_{0}$
to
$\unicode[STIX]{x1D70F}_{0}$
to
![]() $(A_{\text{cris}},+)$
. Thus, we have an
$(A_{\text{cris}},+)$
. Thus, we have an
![]() $A_{\text{cris}}$
-semilinear Frobenius
$A_{\text{cris}}$
-semilinear Frobenius
that in terms of an isomorphism
![]() $A_{\text{st}}\simeq A_{\text{cris}}[T]$
obtained by trivializing
$A_{\text{st}}\simeq A_{\text{cris}}[T]$
obtained by trivializing
![]() $\unicode[STIX]{x1D70F}_{0}$
is described by
$\unicode[STIX]{x1D70F}_{0}$
is described by
![]() $T\mapsto pT$
. The interaction of
$T\mapsto pT$
. The interaction of
![]() $\unicode[STIX]{x1D711}$
and
$\unicode[STIX]{x1D711}$
and
![]() $N$
is described by the formula
$N$
is described by the formula
![]() $N\unicode[STIX]{x1D711}=p\unicode[STIX]{x1D711}N$
.
$N\unicode[STIX]{x1D711}=p\unicode[STIX]{x1D711}N$
.
Since
![]() $\unicode[STIX]{x1D707}$
and
$\unicode[STIX]{x1D707}$
and
![]() $\log ([\unicode[STIX]{x1D716}])$
are unit multiples of each other in
$\log ([\unicode[STIX]{x1D716}])$
are unit multiples of each other in
![]() $A_{\text{cris}}$
(see §5.14) and
$A_{\text{cris}}$
(see §5.14) and
the Frobenius (9.1.1) and, evidently, also the derivation
![]() $N$
induce their counterparts on
$N$
induce their counterparts on
The relation
![]() $N\unicode[STIX]{x1D711}=p\unicode[STIX]{x1D711}N$
continues to hold for
$N\unicode[STIX]{x1D711}=p\unicode[STIX]{x1D711}N$
continues to hold for
![]() $B_{\text{st}}^{+}$
and
$B_{\text{st}}^{+}$
and
![]() $B_{\text{st}}$
. As is explained in [Reference BeilinsonBei13a, §1.17], the
$B_{\text{st}}$
. As is explained in [Reference BeilinsonBei13a, §1.17], the
![]() $A_{\text{cris}}$
-algebras
$A_{\text{cris}}$
-algebras
![]() $B_{\text{st}}^{+}$
and
$B_{\text{st}}^{+}$
and
![]() $B_{\text{st}}$
reviewed above agree with those constructed in [Reference FontaineFon94, §3].
$B_{\text{st}}$
reviewed above agree with those constructed in [Reference FontaineFon94, §3].
For us, the significance of the period ring
![]() $B_{\text{st}}^{+}$
lies in the following comparison between the logarithmic crystalline cohomology of
$B_{\text{st}}^{+}$
lies in the following comparison between the logarithmic crystalline cohomology of
![]() $\mathfrak{X}_{k}$
over
$\mathfrak{X}_{k}$
over
![]() $W(k)$
and of
$W(k)$
and of
![]() $\mathfrak{X}_{{\mathcal{O}}_{C}/p}$
over
$\mathfrak{X}_{{\mathcal{O}}_{C}/p}$
over
![]() $A_{\text{cris}}$
(compare with [Reference Bhatt, Morrow and ScholzeBMS18, 13.21]).
$A_{\text{cris}}$
(compare with [Reference Bhatt, Morrow and ScholzeBMS18, 13.21]).
Proposition 9.2. If
![]() $\mathfrak{X}$
is
$\mathfrak{X}$
is
![]() ${\mathcal{O}}_{C}$
-proper, then
${\mathcal{O}}_{C}$
-proper, then
where the log structures are those of §§1.6 (2), 5.2, and 5.42. In particular, if
![]() $\mathfrak{X}$
is
$\mathfrak{X}$
is
![]() ${\mathcal{O}}_{C}$
-proper and
${\mathcal{O}}_{C}$
-proper and
![]() ${\mathcal{Y}}$
is a descent of
${\mathcal{Y}}$
is a descent of
![]() $\mathfrak{X}_{{\mathcal{O}}_{C}/p}$
to a proper, log smooth, fine log
$\mathfrak{X}_{{\mathcal{O}}_{C}/p}$
to a proper, log smooth, fine log
![]() ${\mathcal{O}}/p$
-scheme of Cartier type for some discrete valuation subring
${\mathcal{O}}/p$
-scheme of Cartier type for some discrete valuation subring
![]() ${\mathcal{O}}\subset {\mathcal{O}}_{C}$
with a perfect residue field
${\mathcal{O}}\subset {\mathcal{O}}_{C}$
with a perfect residue field
![]() $k_{0}$
and
$k_{0}$
and ![]() (where
(where
![]() ${\mathcal{O}}/p$
is equipped with the log structure associated to the chart
${\mathcal{O}}/p$
is equipped with the log structure associated to the chart
![]() ${\mathcal{O}}\setminus \{0\}\rightarrow {\mathcal{O}}/p$
), then we have the following identification that is compatible with the actions of
${\mathcal{O}}\setminus \{0\}\rightarrow {\mathcal{O}}/p$
), then we have the following identification that is compatible with the actions of
![]() $\unicode[STIX]{x1D711}$
and
$\unicode[STIX]{x1D711}$
and
![]() $N$
(described in the proof):
$N$
(described in the proof):
where
![]() $W(k_{0})$
is endowed with the log structure associated to
$W(k_{0})$
is endowed with the log structure associated to
![]() $\mathbb{N}_{{\geqslant}0}\xrightarrow[{}]{1\,\mapsto \,0,\,0\,\mapsto \,1}W(k_{0})$
.
$\mathbb{N}_{{\geqslant}0}\xrightarrow[{}]{1\,\mapsto \,0,\,0\,\mapsto \,1}W(k_{0})$
.
Proof. A descent
![]() ${\mathcal{Y}}$
exists (see the proof of Corollary 5.43), so (9.2.2) follows from [Reference BeilinsonBei13a, (1.16.2) and (1.18.5)] and, due to (5.44.1), it implies (9.2.1). On the left-hand side of (9.2.2), the operator
${\mathcal{Y}}$
exists (see the proof of Corollary 5.43), so (9.2.2) follows from [Reference BeilinsonBei13a, (1.16.2) and (1.18.5)] and, due to (5.44.1), it implies (9.2.1). On the left-hand side of (9.2.2), the operator
![]() $N$
combines the monodromy of
$N$
combines the monodromy of
![]() $R\unicode[STIX]{x1D6E4}_{\log \text{cris}}({\mathcal{X}}_{k_{0}}/W(k_{0}))$
and
$R\unicode[STIX]{x1D6E4}_{\log \text{cris}}({\mathcal{X}}_{k_{0}}/W(k_{0}))$
and
![]() $B_{\text{st}}^{+}$
, so is ‘
$B_{\text{st}}^{+}$
, so is ‘
![]() $N\otimes 1+1\otimes N$
’; on the right-hand side,
$N\otimes 1+1\otimes N$
’; on the right-hand side,
![]() $N$
is the monodromy of
$N$
is the monodromy of
![]() $B_{\text{st}}^{+}$
. On both sides of (9.2.2), the Frobenius
$B_{\text{st}}^{+}$
. On both sides of (9.2.2), the Frobenius
![]() $\unicode[STIX]{x1D711}$
acts on both factors.◻
$\unicode[STIX]{x1D711}$
acts on both factors.◻
Remark 9.3. One may eliminate the dependence of (9.2.2) on the choice of
![]() ${\mathcal{Y}}$
by forming a direct limit over all the possible
${\mathcal{Y}}$
by forming a direct limit over all the possible
![]() ${\mathcal{Y}}$
, see [Reference BeilinsonBei13a, §1.18, Remarks (i)].
${\mathcal{Y}}$
, see [Reference BeilinsonBei13a, §1.18, Remarks (i)].
9.4 The base field
 $K$
$K$
For the rest of §9, we assume that
![]() $C=\widehat{\overline{K}}$
for a fixed complete, discretely valued subfield
$C=\widehat{\overline{K}}$
for a fixed complete, discretely valued subfield
![]() $K\subset C$
with a perfect residue field
$K\subset C$
with a perfect residue field
![]() $k_{0}$
, set
$k_{0}$
, set
![]() $G:=\operatorname{Gal}(\overline{K}/K)$
, and endow
$G:=\operatorname{Gal}(\overline{K}/K)$
, and endow
![]() ${\mathcal{O}}_{K}$
(respectively,
${\mathcal{O}}_{K}$
(respectively,
![]() ${\mathcal{O}}_{K}/p$
) with the log structure associated to the chart
${\mathcal{O}}_{K}/p$
) with the log structure associated to the chart
![]() ${\mathcal{O}}_{K}\setminus \{0\}{\hookrightarrow}{\mathcal{O}}_{K}$
(respectively, its base change). By functoriality,
${\mathcal{O}}_{K}\setminus \{0\}{\hookrightarrow}{\mathcal{O}}_{K}$
(respectively, its base change). By functoriality,
![]() $G$
acts on
$G$
acts on
![]() $A_{\text{cris}}$
,
$A_{\text{cris}}$
,
![]() $A_{\text{st}}$
,
$A_{\text{st}}$
,
![]() $B_{\text{st}}^{+}$
, and, since the ideal
$B_{\text{st}}^{+}$
, and, since the ideal
![]() $(\unicode[STIX]{x1D707})$
does not depend on the choice of
$(\unicode[STIX]{x1D707})$
does not depend on the choice of
![]() $\unicode[STIX]{x1D716}$
(see §2.1), also on
$\unicode[STIX]{x1D716}$
(see §2.1), also on
![]() $B_{\text{st}}$
. These
$B_{\text{st}}$
. These
![]() $G$
-actions commute with
$G$
-actions commute with
![]() $\unicode[STIX]{x1D711}$
and
$\unicode[STIX]{x1D711}$
and
![]() $N$
. When
$N$
. When
![]() ${\mathcal{O}}$
of Proposition 9.2 is our
${\mathcal{O}}$
of Proposition 9.2 is our
![]() ${\mathcal{O}}_{K}$
, the identification (9.2.2) is
${\mathcal{O}}_{K}$
, the identification (9.2.2) is
![]() $G$
-equivariant granted that
$G$
-equivariant granted that
![]() $G$
acts on both sides by functoriality.
$G$
acts on both sides by functoriality.
Theorem 9.5. Let
![]() ${\mathcal{X}}$
be a proper
${\mathcal{X}}$
be a proper
![]() $p$
-adic formal
$p$
-adic formal
![]() ${\mathcal{O}}_{K}$
-scheme that has an étale cover by affines
${\mathcal{O}}_{K}$
-scheme that has an étale cover by affines
![]() ${\mathcal{U}}$
each of which has an étale
${\mathcal{U}}$
each of which has an étale
![]() ${\mathcal{O}}_{K}$
-morphism
${\mathcal{O}}_{K}$
-morphism
(where
![]() $d$
,
$d$
,
![]() $r$
, and
$r$
, and
![]() $\unicode[STIX]{x1D70B}$
depend on
$\unicode[STIX]{x1D70B}$
depend on
![]() ${\mathcal{U}}$
) and endow
${\mathcal{U}}$
) and endow
![]() ${\mathcal{X}}$
with the log structure
${\mathcal{X}}$
with the log structure
![]() ${\mathcal{O}}_{{\mathcal{X}},\,\acute{\text{e}}\text{t}}\cap ({\mathcal{O}}_{{\mathcal{X}},\,\acute{\text{e}}\text{t}}[\frac{1}{p}])^{\times }$
. There is the following natural,
${\mathcal{O}}_{{\mathcal{X}},\,\acute{\text{e}}\text{t}}\cap ({\mathcal{O}}_{{\mathcal{X}},\,\acute{\text{e}}\text{t}}[\frac{1}{p}])^{\times }$
. There is the following natural,
![]() $G$
-equivariant isomorphism compatible with the actions of
$G$
-equivariant isomorphism compatible with the actions of
![]() $\unicode[STIX]{x1D711}$
and
$\unicode[STIX]{x1D711}$
and
![]() $N$
:
$N$
:
where
![]() $W(k_{0})$
is endowed with the log structure associated to
$W(k_{0})$
is endowed with the log structure associated to
![]() $\mathbb{N}_{{\geqslant}0}\xrightarrow[{}]{1\,\mapsto \,0,\,0\,\mapsto \,1}W(k_{0})$
. In particular,
$\mathbb{N}_{{\geqslant}0}\xrightarrow[{}]{1\,\mapsto \,0,\,0\,\mapsto \,1}W(k_{0})$
. In particular,
Proof. We set
![]() $\mathfrak{X}:={\mathcal{X}}\widehat{\otimes }_{{\mathcal{O}}_{K}}{\mathcal{O}}_{C}$
, so that
$\mathfrak{X}:={\mathcal{X}}\widehat{\otimes }_{{\mathcal{O}}_{K}}{\mathcal{O}}_{C}$
, so that
![]() $\mathfrak{X}$
meets the requirements of §1.5. By Claims 1.6.1 and 1.6.3 and [Reference KatoKat89, 4.8], the base change
$\mathfrak{X}$
meets the requirements of §1.5. By Claims 1.6.1 and 1.6.3 and [Reference KatoKat89, 4.8], the base change
![]() ${\mathcal{X}}_{{\mathcal{O}}_{K}/p}$
is fine, log smooth, and of Cartier type over
${\mathcal{X}}_{{\mathcal{O}}_{K}/p}$
is fine, log smooth, and of Cartier type over
![]() ${\mathcal{O}}_{K}/p$
, so Proposition 9.2 applies to it and gives the
${\mathcal{O}}_{K}/p$
, so Proposition 9.2 applies to it and gives the
![]() $G$
-equivariant (see §9.4) identification
$G$
-equivariant (see §9.4) identification
that is compatible with
![]() $\unicode[STIX]{x1D711}$
and
$\unicode[STIX]{x1D711}$
and
![]() $N$
. In addition, by (2.3.1), we have the
$N$
. In addition, by (2.3.1), we have the
![]() $G$
-equivariant identification
$G$
-equivariant identification
that is trivially compatible with
![]() $N$
and is compatible with
$N$
and is compatible with
![]() $\unicode[STIX]{x1D711}$
by the discussion after Theorem 2.3. The desired (9.5.1) follows by combining the displayed identifications.◻
$\unicode[STIX]{x1D711}$
by the discussion after Theorem 2.3. The desired (9.5.1) follows by combining the displayed identifications.◻
Remark 9.6. The isomorphism (9.5.1) is compatible with filtrations in the following sense: by [Reference FontaineFon94, §4.2], there is a (noncanonical)
![]() $A_{\text{cris}}$
-algebra homomorphism
$A_{\text{cris}}$
-algebra homomorphism
![]() $B_{\text{st}}\rightarrow B_{\text{dR}}$
and, by the proof above and Proposition 6.8, the
$B_{\text{st}}\rightarrow B_{\text{dR}}$
and, by the proof above and Proposition 6.8, the
![]() $B_{\text{dR}}$
-base change of the isomorphism (9.5.1) is identified with the de Rham comparison isomorphism (6.7.2) (with
$B_{\text{dR}}$
-base change of the isomorphism (9.5.1) is identified with the de Rham comparison isomorphism (6.7.2) (with
![]() $X_{0}={\mathcal{X}}_{K}^{\text{ad}}$
) that is compatible with filtrations.
$X_{0}={\mathcal{X}}_{K}^{\text{ad}}$
) that is compatible with filtrations.
Acknowledgements
We thank Bhargav Bhatt and Matthew Morrow for writing the surveys [Reference BhattBha18] and [Reference MorrowMor16], which have been useful for preparing this paper. We thank the referee for helpful comments and suggestions. We thank Bhargav Bhatt, Pierre Colmez, Ravi Fernando, Luc Illusie, Arthur-César Le Bras, Matthew Morrow, Wiesława Nizioł, Arthur Ogus, Peter Scholze, Joseph Stahl, Jakob Stix, Jan Vonk, and Olivier Wittenberg for helpful conversations or correspondence. We thank the Kyoto Top Global University program for providing the framework in which this collaboration started. We thank the Miller Institute at the University of California Berkeley, the Research Institute for Mathematical Sciences at Kyoto University, and the University of Bonn for their support during the preparation of this article.