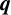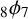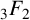1 Introduction
India’s great mathematician Ramanujan mentioned the formula
 $$ \begin{align} \sum_{k=0}^{\infty} (-1)^{k}(4k+1)\frac{(\tfrac{1}{2})_{k}^{5}}{k!^{5}}= \frac{2}{\Gamma(\tfrac{3}{4})^{4}} \end{align} $$
$$ \begin{align} \sum_{k=0}^{\infty} (-1)^{k}(4k+1)\frac{(\tfrac{1}{2})_{k}^{5}}{k!^{5}}= \frac{2}{\Gamma(\tfrac{3}{4})^{4}} \end{align} $$
in his second letter to Hardy on February 27, 1913. Here
![]() $\Gamma (x)$
stands for the Gamma function and
$\Gamma (x)$
stands for the Gamma function and
![]() $(a)_{k}=a(a+1)\cdots (a+k-1)$
is the rising factorial. In 1997, Van Hamme [Reference Van Hamme15] observed that thirteen Ramanujan-type formulae possess neat p-adic analogues. For instance, the formula (1.1) corresponds to the supercongruence
$(a)_{k}=a(a+1)\cdots (a+k-1)$
is the rising factorial. In 1997, Van Hamme [Reference Van Hamme15] observed that thirteen Ramanujan-type formulae possess neat p-adic analogues. For instance, the formula (1.1) corresponds to the supercongruence
 $$ \begin{align} \sum_{k=0}^{(p-1)/2} (-1)^{k}(4k+1)\frac{(\tfrac{1}{2})_{k}^{5}}{k!^{5}} \equiv \begin{cases} -\dfrac{p}{\Gamma_{p}(\tfrac{3}{4})^{4}} \pmod{p^{3}} &\text{if }p\equiv 1\pmod 4\text{,}\\ 0\pmod{p^{3}} &\text{if }p\equiv 3\pmod 4\text{,} \end{cases} \end{align} $$
$$ \begin{align} \sum_{k=0}^{(p-1)/2} (-1)^{k}(4k+1)\frac{(\tfrac{1}{2})_{k}^{5}}{k!^{5}} \equiv \begin{cases} -\dfrac{p}{\Gamma_{p}(\tfrac{3}{4})^{4}} \pmod{p^{3}} &\text{if }p\equiv 1\pmod 4\text{,}\\ 0\pmod{p^{3}} &\text{if }p\equiv 3\pmod 4\text{,} \end{cases} \end{align} $$
(tagged as (A.2) in [Reference Van Hamme15]). Here and in what follows, p always denotes an odd prime and
![]() $\Gamma _{p}(x)$
is Morita’s p-adic Gamma function (see, for example, [Reference Robert12, Ch. 7]). The supercongruence (1.2) was first confirmed by McCarthy and Osburn [Reference McCarthy and Osburn11]. Swisher [Reference Swisher13] further proved that (1.2) is true modulo
$\Gamma _{p}(x)$
is Morita’s p-adic Gamma function (see, for example, [Reference Robert12, Ch. 7]). The supercongruence (1.2) was first confirmed by McCarthy and Osburn [Reference McCarthy and Osburn11]. Swisher [Reference Swisher13] further proved that (1.2) is true modulo
![]() $p^{5}$
for
$p^{5}$
for
![]() $p\equiv 1\pmod {4}$
and
$p\equiv 1\pmod {4}$
and
![]() $p>5$
. Liu [Reference Liu10] extended (1.2) for
$p>5$
. Liu [Reference Liu10] extended (1.2) for
![]() $p\equiv 3\pmod {4}$
to a congruence modulo
$p\equiv 3\pmod {4}$
to a congruence modulo
![]() $p^{4}$
. Recently, among other things, Wei [Reference Wei18] gave the following generalisation of the second case of (1.2):
$p^{4}$
. Recently, among other things, Wei [Reference Wei18] gave the following generalisation of the second case of (1.2):
 $$ \begin{align*} \sum_{k=0}^{(p-1)/2} (-1)^{k}(4k+1)\frac{(\tfrac{1}{2})_{k}^{5}}{k!^{5}} \equiv p^{2}\frac{(\tfrac{3}{4})_{(p-1)/2}}{(\tfrac{5}{4})_{(p-1)/2}}\pmod{p^{5}} \quad\text{for }p\equiv 3\pmod 4\text{.} \end{align*} $$
$$ \begin{align*} \sum_{k=0}^{(p-1)/2} (-1)^{k}(4k+1)\frac{(\tfrac{1}{2})_{k}^{5}}{k!^{5}} \equiv p^{2}\frac{(\tfrac{3}{4})_{(p-1)/2}}{(\tfrac{5}{4})_{(p-1)/2}}\pmod{p^{5}} \quad\text{for }p\equiv 3\pmod 4\text{.} \end{align*} $$
During the past few years, there has been considerable interest in q-analogues of supercongruences. In particular, using the creative microscoping method introduced by the author and Zudilin [Reference Guo and Zudilin7], Wang and Yue [Reference Wang and Yue16], together with the author [Reference Guo5], gave a q-analogue of (1.2): modulo
![]() $[n]\Phi _{n}(q)^{2}$
,
$[n]\Phi _{n}(q)^{2}$
,
 $$ \begin{align} \sum_{k=0}^{M} (-1)^{k}[4k+1]\frac{(q;q^{2})_{k}^{4}(q^{2};q^{4})_{k}}{(q^{2};q^{2})_{k}^{4}(q^{4};q^{4})_{k}}q^{k} \equiv \begin{cases} \dfrac{(q^{2};q^{4})_{(n-1)/4}^{2}}{(q^{4};q^{4})_{(n-1)/4}^{2}}[n] &\text{if }n\equiv 1\pmod 4\text{,}\\ 0 &\text{if }n\equiv 3\pmod 4\text{,} \end{cases} \end{align} $$
$$ \begin{align} \sum_{k=0}^{M} (-1)^{k}[4k+1]\frac{(q;q^{2})_{k}^{4}(q^{2};q^{4})_{k}}{(q^{2};q^{2})_{k}^{4}(q^{4};q^{4})_{k}}q^{k} \equiv \begin{cases} \dfrac{(q^{2};q^{4})_{(n-1)/4}^{2}}{(q^{4};q^{4})_{(n-1)/4}^{2}}[n] &\text{if }n\equiv 1\pmod 4\text{,}\\ 0 &\text{if }n\equiv 3\pmod 4\text{,} \end{cases} \end{align} $$
where
![]() $M=(n-1)/2$
or
$M=(n-1)/2$
or
![]() $n-1$
. Wei [Reference Wei17, Reference Wei18] further generalised (1.3) to the moduli
$n-1$
. Wei [Reference Wei17, Reference Wei18] further generalised (1.3) to the moduli
![]() $[n]\Phi _{n}(q)^{3}$
and
$[n]\Phi _{n}(q)^{3}$
and
![]() $[n]\Phi _{n}(q)^{4}$
.
$[n]\Phi _{n}(q)^{4}$
.
We now need to familiarise ourselves with the standard q-notation. The q-shifted factorial is defined by
![]() $(a;q)_{n}=(1-a)(1-aq)\cdots (1-aq^{n-1})$
for
$(a;q)_{n}=(1-a)(1-aq)\cdots (1-aq^{n-1})$
for
![]() $n\geqslant 1$
and
$n\geqslant 1$
and
![]() $(a;q)_{0}=1$
. For simplicity, we also use the abbreviated notation
$(a;q)_{0}=1$
. For simplicity, we also use the abbreviated notation
![]() $(a_{1},a_{2},\ldots ,a_{m};q)_{n}=(a_{1};q)_{n} (a_{2};q)_{n}\cdots (a_{m};q)_{n}$
for
$(a_{1},a_{2},\ldots ,a_{m};q)_{n}=(a_{1};q)_{n} (a_{2};q)_{n}\cdots (a_{m};q)_{n}$
for
![]() $n\geqslant 0$
. The q-integer is
$n\geqslant 0$
. The q-integer is
![]() $[n]=[n]_{q}=(1-q^{n})/(1-q^{n})$
. The nth cyclotomic polynomial
$[n]=[n]_{q}=(1-q^{n})/(1-q^{n})$
. The nth cyclotomic polynomial
![]() $\Phi _{n}(q)$
is given by
$\Phi _{n}(q)$
is given by
 $$ \begin{align*} \Phi_{n}(q)=\prod_{\substack{1\leqslant k\leqslant n\\ \gcd(k,n)=1}}(q-\zeta^{k}), \end{align*} $$
$$ \begin{align*} \Phi_{n}(q)=\prod_{\substack{1\leqslant k\leqslant n\\ \gcd(k,n)=1}}(q-\zeta^{k}), \end{align*} $$
where
![]() $\zeta $
is a primitive nth root of unity.
$\zeta $
is a primitive nth root of unity.
Letting
![]() $n=p\equiv 1\pmod 4$
and taking
$n=p\equiv 1\pmod 4$
and taking
![]() $q\to 1$
in (1.3), we obtain
$q\to 1$
in (1.3), we obtain
 $$ \begin{align} \sum_{k=0}^{(p-1)/2} (-1)^{k}(4k+1)\frac{(\tfrac{1}{2})_{k}^{5}}{k!^{5}} \equiv \frac{(\tfrac{1}{2})_{(p-1)/4}^{2}}{(1)_{(p-1)/4}^{2}}p={-1/2 \choose (p-1)/4}^{2} p \pmod{p^{3}}. \end{align} $$
$$ \begin{align} \sum_{k=0}^{(p-1)/2} (-1)^{k}(4k+1)\frac{(\tfrac{1}{2})_{k}^{5}}{k!^{5}} \equiv \frac{(\tfrac{1}{2})_{(p-1)/4}^{2}}{(1)_{(p-1)/4}^{2}}p={-1/2 \choose (p-1)/4}^{2} p \pmod{p^{3}}. \end{align} $$
From [Reference Van Hamme14, Theorem 3], we know that
 $$ \begin{align*}{-1/2 \choose (p-1)/4}\equiv \frac{\Gamma_{p}(\tfrac{1}{4})^{2}}{\Gamma_{p}(\tfrac{1}{2})}\pmod{p^{2}}. \end{align*} $$
$$ \begin{align*}{-1/2 \choose (p-1)/4}\equiv \frac{\Gamma_{p}(\tfrac{1}{4})^{2}}{\Gamma_{p}(\tfrac{1}{2})}\pmod{p^{2}}. \end{align*} $$
Since
![]() $\Gamma _{p}(\tfrac 12)^{2}=-1$
for
$\Gamma _{p}(\tfrac 12)^{2}=-1$
for
![]() $p\equiv 1\pmod {4}$
, by the identity
$p\equiv 1\pmod {4}$
, by the identity
![]() $\Gamma _{p}(\tfrac 14)^{4} \Gamma _{p}(\tfrac 34)^{4}=1$
, we see that the supercongruence (1.4) is just (1.2) for
$\Gamma _{p}(\tfrac 14)^{4} \Gamma _{p}(\tfrac 34)^{4}=1$
, we see that the supercongruence (1.4) is just (1.2) for
![]() $p\equiv 1\pmod {4}$
. This implies that (1.3) for
$p\equiv 1\pmod {4}$
. This implies that (1.3) for
![]() $M=(n-1)/2$
really is a q-analogue of the (A.2) supercongruence of Van Hamme.
$M=(n-1)/2$
really is a q-analogue of the (A.2) supercongruence of Van Hamme.
Note that supercongruences may have different q-analogues. See [Reference Guo and Zudilin8] for such examples. In this note, we shall give the following new q-analogue of (1.2).
Theorem 1.1. Let
![]() $n>1$
be an odd integer. Then, modulo
$n>1$
be an odd integer. Then, modulo
![]() $[n]_{q^{2}}\Phi _{n}(q^{2})^{2}$
,
$[n]_{q^{2}}\Phi _{n}(q^{2})^{2}$
,
 $$ \begin{align} &\sum_{k=0}^{M} (-1)^{k}[4k+1]_{q^{2}}[4k+1]^{2}\frac{(q^{2};q^{4})_{k}^{4}(q^{4};q^{8})_{k}} {(q^{4};q^{4})_{k}^{4}(q^{8};q^{8})_{k}}q^{-2k} \notag\\ &\quad\equiv \begin{cases} -\dfrac{2q(q^{4};q^{8})_{(n-1)/4}^{2}}{(1+q^{2})(q^{8};q^{8})_{(n-1)/4}^{2}}[n]_{q^{2}}&\text{if }n\equiv 1\pmod{4}\text{,}\\[10pt] \dfrac{(1+q)^{2}(q^{4},q^{12}; q^{8})_{(n-3)/4}} {(1+q^{2})(1+q^{4})(q^{8},q^{16}; q^{8})_{(n-3)/4}}[n]_{q^{2}}& \text{if }n\equiv 3\pmod{4}\text{,} \end{cases} \end{align} $$
$$ \begin{align} &\sum_{k=0}^{M} (-1)^{k}[4k+1]_{q^{2}}[4k+1]^{2}\frac{(q^{2};q^{4})_{k}^{4}(q^{4};q^{8})_{k}} {(q^{4};q^{4})_{k}^{4}(q^{8};q^{8})_{k}}q^{-2k} \notag\\ &\quad\equiv \begin{cases} -\dfrac{2q(q^{4};q^{8})_{(n-1)/4}^{2}}{(1+q^{2})(q^{8};q^{8})_{(n-1)/4}^{2}}[n]_{q^{2}}&\text{if }n\equiv 1\pmod{4}\text{,}\\[10pt] \dfrac{(1+q)^{2}(q^{4},q^{12}; q^{8})_{(n-3)/4}} {(1+q^{2})(1+q^{4})(q^{8},q^{16}; q^{8})_{(n-3)/4}}[n]_{q^{2}}& \text{if }n\equiv 3\pmod{4}\text{,} \end{cases} \end{align} $$
where
![]() $M=(n-1)/2$
or
$M=(n-1)/2$
or
![]() $n-1$
.
$n-1$
.
For n prime, letting
![]() $q\to -1$
in Theorem 1.1, we get (1.2). However, for n prime and
$q\to -1$
in Theorem 1.1, we get (1.2). However, for n prime and
![]() $q\to 1$
in Theorem 1.1, we arrive at
$q\to 1$
in Theorem 1.1, we arrive at
 $$ \begin{align} \sum_{k=0}^{(p-1)/2} (-1)^{k}(4k+1)^{3}\frac{(\tfrac{1}{2})_{k}^{5}}{k!^{5}} \equiv \begin{cases} \dfrac{p}{\Gamma_{p}(\tfrac{3}{4})^{4}} \pmod{p^{3}} &\text{if }p\equiv 1\pmod 4\text{,}\\[10pt] \dfrac{(\tfrac{1}{2})_{(p-3)/4}(\tfrac{3}{2})_{(p-3)/4}p}{(\frac{p-3}{4})!(\frac{p+1}{4})!}\pmod{p^{3}} &\text{if }p\equiv 3\pmod 4\text{.} \end{cases} \end{align} $$
$$ \begin{align} \sum_{k=0}^{(p-1)/2} (-1)^{k}(4k+1)^{3}\frac{(\tfrac{1}{2})_{k}^{5}}{k!^{5}} \equiv \begin{cases} \dfrac{p}{\Gamma_{p}(\tfrac{3}{4})^{4}} \pmod{p^{3}} &\text{if }p\equiv 1\pmod 4\text{,}\\[10pt] \dfrac{(\tfrac{1}{2})_{(p-3)/4}(\tfrac{3}{2})_{(p-3)/4}p}{(\frac{p-3}{4})!(\frac{p+1}{4})!}\pmod{p^{3}} &\text{if }p\equiv 3\pmod 4\text{.} \end{cases} \end{align} $$
Thus, Theorem 1.1 may be considered as a common q-analogue of (1.2) and (1.6).
Letting n be an odd prime power and
![]() $q\to 1$
in (1.3) and (1.5), we are led to the following results. If
$q\to 1$
in (1.3) and (1.5), we are led to the following results. If
![]() $p^{r}\equiv 1\pmod {4}$
, then
$p^{r}\equiv 1\pmod {4}$
, then
 $$ \begin{align} \sum_{k=0}^{(p^{r}-1)/d} (-1)^{k}(4k+1)\frac{(\tfrac{1}{2})_{k}^{5}}{k!^{5}} &\equiv {(p^{r}-1)/2\choose (p^{r}-1)/4}^{2}\frac{p^{r}}{2^{p^{r}-1}} \pmod{p^{r+2}}, \end{align} $$
$$ \begin{align} \sum_{k=0}^{(p^{r}-1)/d} (-1)^{k}(4k+1)\frac{(\tfrac{1}{2})_{k}^{5}}{k!^{5}} &\equiv {(p^{r}-1)/2\choose (p^{r}-1)/4}^{2}\frac{p^{r}}{2^{p^{r}-1}} \pmod{p^{r+2}}, \end{align} $$
 $$ \begin{align} \sum_{k=0}^{(p^{r}-1)/d} (-1)^{k}(4k+1)^{3}\frac{(\tfrac{1}{2})_{k}^{5}}{k!^{5}} &\equiv -{(p^{r}-1)/2\choose (p^{r}-1)/4}^{2}\frac{p^{r}}{2^{p^{r}-1}} \pmod{p^{r+2}}, \end{align} $$
$$ \begin{align} \sum_{k=0}^{(p^{r}-1)/d} (-1)^{k}(4k+1)^{3}\frac{(\tfrac{1}{2})_{k}^{5}}{k!^{5}} &\equiv -{(p^{r}-1)/2\choose (p^{r}-1)/4}^{2}\frac{p^{r}}{2^{p^{r}-1}} \pmod{p^{r+2}}, \end{align} $$
where
![]() $d=1$
or
$d=1$
or
![]() $2$
. Since
$2$
. Since
![]() $4+1+(4k+1)^{3}=2(4k+1)(8k^{2}+4k+1)$
, combining (1.7) and (1.8), we obtain the following conclusion.
$4+1+(4k+1)^{3}=2(4k+1)(8k^{2}+4k+1)$
, combining (1.7) and (1.8), we obtain the following conclusion.
Corollary 1.2. If
![]() $p^{r}\equiv 1\pmod {4}$
, then
$p^{r}\equiv 1\pmod {4}$
, then
 $$ \begin{align} \sum_{k=0}^{(p^{r}-1)/d} (-1)^{k}(4k+1)(8k^{2}+4k+1) \frac{(\tfrac{1}{2})_{k}^{5}}{k!^{5}} &\equiv 0\pmod{p^{r+2}}, \end{align} $$
$$ \begin{align} \sum_{k=0}^{(p^{r}-1)/d} (-1)^{k}(4k+1)(8k^{2}+4k+1) \frac{(\tfrac{1}{2})_{k}^{5}}{k!^{5}} &\equiv 0\pmod{p^{r+2}}, \end{align} $$
where
![]() $d=1$
or
$d=1$
or
![]() $2$
.
$2$
.
Note that the author [Reference Guo4, Conjecture 4.5] conjectured that (1.9) is true modulo
![]() $p^{3r}$
for
$p^{3r}$
for
![]() $p\equiv 1\pmod {4}$
.
$p\equiv 1\pmod {4}$
.
We shall prove Theorem 1.1 in the next section. In Section 3, we raise two related conjectures on supercongruences.
2 Proof of Theorem 1.1
We first give the following q-congruence. See [Reference Guo and Schlosser6, Lemma 3.1] for a short proof.
Lemma 2.1. Let n be a positive odd integer. Then, for
![]() $0\leqslant k\leqslant (n-1)/2$
,
$0\leqslant k\leqslant (n-1)/2$
,
 $$ \begin{align*} \frac{(aq;q^{2})_{(n-1)/2-k}}{(q^{2}/a;q^{2})_{(n-1)/2-k}} \equiv (-a)^{(n-1)/2-2k}\frac{(aq;q^{2})_{k}}{(q^{2}/a;q^{2})_{k}} q^{(n-1)^{2}/4+k} \pmod{\Phi_{n}(q)}. \end{align*} $$
$$ \begin{align*} \frac{(aq;q^{2})_{(n-1)/2-k}}{(q^{2}/a;q^{2})_{(n-1)/2-k}} \equiv (-a)^{(n-1)/2-2k}\frac{(aq;q^{2})_{k}}{(q^{2}/a;q^{2})_{k}} q^{(n-1)^{2}/4+k} \pmod{\Phi_{n}(q)}. \end{align*} $$
We will use a powerful transformation of Andrews (see [Reference Andrews and Askey1, Theorem 4]), which can be stated as follows:
 $$ \begin{align} &\sum_{k\geqslant 0}\frac{(a,q\sqrt{a},-q\sqrt{a},b_{1},c_{1},\ldots,b_{m},c_{m},q^{-N};q)_{k}} {(q,\!\sqrt{a},-\sqrt{a},aq/b_{1},aq/c_{1},\ldots,aq/b_{m},aq/c_{m},aq^{N+1};q)_{k}} \bigg(\frac{a^{m}q^{m+N}}{b_{1}c_{1}\cdots b_{m}c_{m}}\bigg)^{k} \notag\\ &\quad=\frac{(aq,aq/b_{m}c_{m};q)_{N}}{(aq/b_{m},aq/c_{m};q)_{N}} \sum_{j_{1},\ldots,j_{m-1}\geqslant 0} \frac{(aq/b_{1}c_{1};q)_{j_{1}}\cdots(aq/b_{m-1}c_{m-1};q)_{j_{m-1}}} {(q;q)_{j_{1}}\cdots(q;q)_{j_{m-1}}} \notag\\ &\qquad\times\frac{(b_{2},c_{2};q)_{j_{1}}\cdots(b_{m},c_{m};q)_{j_{1}+\cdots+j_{m-1}}} {(aq/b_{1},aq/c_{1};q)_{j_{1}} \cdots(aq/b_{m-1},aq/c_{m-1};q)_{j_{1}+\cdots+j_{m-1}}} \notag\\ &\qquad\times\frac{(q^{-N};q)_{j_{1}+\cdots+j_{m-1}}} {(b_{m}c_{m}q^{-N}/a;q)_{j_{1}+\cdots+j_{m-1}}} \frac{(aq)^{\,j_{m-2}+\cdots+(m-2)j_{1}} q^{j_{1}+\cdots+j_{m-1}}} {(b_{2}c_{2})^{\,j_{1}}\cdots(b_{m-1}c_{m-1})^{j_{1}+\cdots+j_{m-2}}}. \end{align} $$
$$ \begin{align} &\sum_{k\geqslant 0}\frac{(a,q\sqrt{a},-q\sqrt{a},b_{1},c_{1},\ldots,b_{m},c_{m},q^{-N};q)_{k}} {(q,\!\sqrt{a},-\sqrt{a},aq/b_{1},aq/c_{1},\ldots,aq/b_{m},aq/c_{m},aq^{N+1};q)_{k}} \bigg(\frac{a^{m}q^{m+N}}{b_{1}c_{1}\cdots b_{m}c_{m}}\bigg)^{k} \notag\\ &\quad=\frac{(aq,aq/b_{m}c_{m};q)_{N}}{(aq/b_{m},aq/c_{m};q)_{N}} \sum_{j_{1},\ldots,j_{m-1}\geqslant 0} \frac{(aq/b_{1}c_{1};q)_{j_{1}}\cdots(aq/b_{m-1}c_{m-1};q)_{j_{m-1}}} {(q;q)_{j_{1}}\cdots(q;q)_{j_{m-1}}} \notag\\ &\qquad\times\frac{(b_{2},c_{2};q)_{j_{1}}\cdots(b_{m},c_{m};q)_{j_{1}+\cdots+j_{m-1}}} {(aq/b_{1},aq/c_{1};q)_{j_{1}} \cdots(aq/b_{m-1},aq/c_{m-1};q)_{j_{1}+\cdots+j_{m-1}}} \notag\\ &\qquad\times\frac{(q^{-N};q)_{j_{1}+\cdots+j_{m-1}}} {(b_{m}c_{m}q^{-N}/a;q)_{j_{1}+\cdots+j_{m-1}}} \frac{(aq)^{\,j_{m-2}+\cdots+(m-2)j_{1}} q^{j_{1}+\cdots+j_{m-1}}} {(b_{2}c_{2})^{\,j_{1}}\cdots(b_{m-1}c_{m-1})^{j_{1}+\cdots+j_{m-2}}}. \end{align} $$
It should be pointed out that Andrews’ transformation is a multiseries generalisation of Watson’s
![]() $_{8}\phi _{7}$
transformation:
$_{8}\phi _{7}$
transformation:
 $$ \begin{align*} & {}_{8}\phi_{7}\!\left[\begin{array}{@{}cccccccc@{}} a,& qa^{{1}/{2}},& -qa^{{1}/{2}}, & b, & c, & d, & e, & q^{-n} \\ & a^{{1}/{2}}, & -a^{{1}/{2}}, & aq/b, & aq/c, & aq/d, & aq/e, & aq^{n+1} \end{array};\, q,\, \frac{a^{2}q^{n+2}}{bcde} \right] \notag\\[5pt] &\quad =\frac{(aq, aq/de;q)_{n}} {(aq/d, aq/e;q)_{n}} \,{}_{4}\phi_{3}\!\left[\begin{array}{@{}c@{}} aq/bc,\ d,\ e,\ q^{-n} \\ aq/b,\, aq/c,\, deq^{-n}/a \end{array};\, q,\, q \right] \end{align*} $$
$$ \begin{align*} & {}_{8}\phi_{7}\!\left[\begin{array}{@{}cccccccc@{}} a,& qa^{{1}/{2}},& -qa^{{1}/{2}}, & b, & c, & d, & e, & q^{-n} \\ & a^{{1}/{2}}, & -a^{{1}/{2}}, & aq/b, & aq/c, & aq/d, & aq/e, & aq^{n+1} \end{array};\, q,\, \frac{a^{2}q^{n+2}}{bcde} \right] \notag\\[5pt] &\quad =\frac{(aq, aq/de;q)_{n}} {(aq/d, aq/e;q)_{n}} \,{}_{4}\phi_{3}\!\left[\begin{array}{@{}c@{}} aq/bc,\ d,\ e,\ q^{-n} \\ aq/b,\, aq/c,\, deq^{-n}/a \end{array};\, q,\, q \right] \end{align*} $$
(see [Reference Gasper and Rahman3, Appendix (III.18)]), where the basic hypergeometric series
![]() $_{r+1}\phi _{r}$
is defined as
$_{r+1}\phi _{r}$
is defined as
 $$ \begin{align*}_{r+1}\phi_{r}\left[\begin{array}{@{}c@{}} a_{1},a_{2},\ldots,a_{r+1}\\ b_{1},b_{2},\ldots,b_{r} \end{array};\,q,\, z \right] =\sum_{k=0}^{\infty}\frac{(a_{1},a_{2},\ldots, a_{r+1};q)_{k} } {(q,b_{1},\ldots,b_{r};q)_{k}} z^{k}. \end{align*} $$
$$ \begin{align*}_{r+1}\phi_{r}\left[\begin{array}{@{}c@{}} a_{1},a_{2},\ldots,a_{r+1}\\ b_{1},b_{2},\ldots,b_{r} \end{array};\,q,\, z \right] =\sum_{k=0}^{\infty}\frac{(a_{1},a_{2},\ldots, a_{r+1};q)_{k} } {(q,b_{1},\ldots,b_{r};q)_{k}} z^{k}. \end{align*} $$
We shall also use Andrews’ terminating q-analogue of Watson’s
![]() $_{3}F_{2}$
summation (see [Reference Andrews2] or [Reference Gasper and Rahman3, (II.17)]):
$_{3}F_{2}$
summation (see [Reference Andrews2] or [Reference Gasper and Rahman3, (II.17)]):
 $$ \begin{align} {}_{4}\phi_{3}\left[\begin{array}{@{}c@{}} q^{-n},\, a^{2}q^{n+1},\,c,\, -c \\ aq,\, -aq,\, c^{2}\end{array};\,q,q\right] =\begin{cases} 0&\text{if }\textit{n}\text{ is odd},\\ \dfrac{c^{n}(q, a^{2}q^{2}/c^{2}; q^{2})_{n/2}} {(a^{2}q^{2},\, c^{2}q; q^{2})_{n/2}}& \text{if }\textit{n}\text{ is even,} \end{cases} \end{align} $$
$$ \begin{align} {}_{4}\phi_{3}\left[\begin{array}{@{}c@{}} q^{-n},\, a^{2}q^{n+1},\,c,\, -c \\ aq,\, -aq,\, c^{2}\end{array};\,q,q\right] =\begin{cases} 0&\text{if }\textit{n}\text{ is odd},\\ \dfrac{c^{n}(q, a^{2}q^{2}/c^{2}; q^{2})_{n/2}} {(a^{2}q^{2},\, c^{2}q; q^{2})_{n/2}}& \text{if }\textit{n}\text{ is even,} \end{cases} \end{align} $$
and the following q-Watson-type summation due to Wei et al. [Reference Wei, Gong and Li19, Corollary 5]:
 $$ \begin{align} {}_{4}\phi_{3}\bigg[\begin{array}{@{}c@{}} q^{-n},\, a^{2}q^{n+1},\,c,\, -cq \\ aq,\, -aq,\, c^{2}q\end{array};\,q,q\bigg] =\begin{cases} \dfrac{c^{n}(q;q^{2})_{(n+1)/2}(a^{2}q^{2}/c^{2}; q^{2})_{(n-1)/2}} {(a^{2}q^{2};q^{2})_{(n-1)/2}(c^{2}q; q^{2})_{(n+1)/2}}&\text{if }\textit{n}\text{ is odd},\\[10pt] \dfrac{c^{n}(q, a^{2}q^{2}/c^{2}; q^{2})_{n/2}} {(a^{2}q^{2},\, c^{2}q; q^{2})_{n/2}}& \text{if }\textit{n}\text{ is even.} \end{cases} \end{align} $$
$$ \begin{align} {}_{4}\phi_{3}\bigg[\begin{array}{@{}c@{}} q^{-n},\, a^{2}q^{n+1},\,c,\, -cq \\ aq,\, -aq,\, c^{2}q\end{array};\,q,q\bigg] =\begin{cases} \dfrac{c^{n}(q;q^{2})_{(n+1)/2}(a^{2}q^{2}/c^{2}; q^{2})_{(n-1)/2}} {(a^{2}q^{2};q^{2})_{(n-1)/2}(c^{2}q; q^{2})_{(n+1)/2}}&\text{if }\textit{n}\text{ is odd},\\[10pt] \dfrac{c^{n}(q, a^{2}q^{2}/c^{2}; q^{2})_{n/2}} {(a^{2}q^{2},\, c^{2}q; q^{2})_{n/2}}& \text{if }\textit{n}\text{ is even.} \end{cases} \end{align} $$
We first prove the following parametric version of Theorem 1.1.
Theorem 2.2. Let
![]() $n>1$
be an odd integer. Then, modulo
$n>1$
be an odd integer. Then, modulo
![]() $\Phi _{n}(q^{2})(1-aq^{2n})(a-q^{2n})$
,
$\Phi _{n}(q^{2})(1-aq^{2n})(a-q^{2n})$
,
 $$ \begin{align} &\sum_{k=0}^{(n-1)/2} (-1)^{k}[4k+1]_{q^{2}}[4k+1]^{2}\frac{(aq^{2},q^{2}/a;q^{4})_{k} (q^{2};q^{4})_{k}^{2}(q^{4};q^{8})_{k}} {(aq^{4},q^{4}/a;q^{4})_{k}(q^{4};q^{4})_{k}^{2}(q^{8};q^{8})_{k}}q^{-2k} \notag\\ &\quad\equiv \begin{cases} \bigg(1-\dfrac{(1+q)(1-aq^{2})(1-q^{2}/a)}{(1-q)(1-q^{4})}\bigg) \dfrac{(q^{4};q^{8})_{(n-1)/4}^{2}}{(q^{8};q^{8})_{(n-1)/4}^{2}}[n]_{q^{2}}&\text{if }n\equiv 1\pmod{4}\text{,}\\[10pt] \dfrac{(1+q)(1-aq^{2})(1-q^{2}/a)(q^{4},q^{12}; q^{8})_{(n-3)/4}} {(1-q)(1-q^{8})(q^{8},q^{16}; q^{8})_{(n-3)/4}}[n]_{q^{2}}& \text{if }n\equiv 3\pmod{4}\text{.} \end{cases} \end{align} $$
$$ \begin{align} &\sum_{k=0}^{(n-1)/2} (-1)^{k}[4k+1]_{q^{2}}[4k+1]^{2}\frac{(aq^{2},q^{2}/a;q^{4})_{k} (q^{2};q^{4})_{k}^{2}(q^{4};q^{8})_{k}} {(aq^{4},q^{4}/a;q^{4})_{k}(q^{4};q^{4})_{k}^{2}(q^{8};q^{8})_{k}}q^{-2k} \notag\\ &\quad\equiv \begin{cases} \bigg(1-\dfrac{(1+q)(1-aq^{2})(1-q^{2}/a)}{(1-q)(1-q^{4})}\bigg) \dfrac{(q^{4};q^{8})_{(n-1)/4}^{2}}{(q^{8};q^{8})_{(n-1)/4}^{2}}[n]_{q^{2}}&\text{if }n\equiv 1\pmod{4}\text{,}\\[10pt] \dfrac{(1+q)(1-aq^{2})(1-q^{2}/a)(q^{4},q^{12}; q^{8})_{(n-3)/4}} {(1-q)(1-q^{8})(q^{8},q^{16}; q^{8})_{(n-3)/4}}[n]_{q^{2}}& \text{if }n\equiv 3\pmod{4}\text{.} \end{cases} \end{align} $$
Proof. For
![]() $a=q^{-2n}$
or
$a=q^{-2n}$
or
![]() $a=q^{2n}$
, the left-hand side of (2.4) may be written as
$a=q^{2n}$
, the left-hand side of (2.4) may be written as
 $$ \begin{align*} &\sum_{k=0}^{(n-1)/2} (-1)^{k}[4k+1]_{q^{2}}[4k+1]^{2}\frac{(q^{2-2n},q^{2+2n};q^{4})_{k} (q^{2};q^{4})_{k}^{2}(q^{4};q^{8})_{k}} {(q^{4-2n},q^{4+2n};q^{4})_{k}(q^{4};q^{4})_{k}^{2}(q^{8};q^{8})_{k}}q^{-2k}. \end{align*} $$
$$ \begin{align*} &\sum_{k=0}^{(n-1)/2} (-1)^{k}[4k+1]_{q^{2}}[4k+1]^{2}\frac{(q^{2-2n},q^{2+2n};q^{4})_{k} (q^{2};q^{4})_{k}^{2}(q^{4};q^{8})_{k}} {(q^{4-2n},q^{4+2n};q^{4})_{k}(q^{4};q^{4})_{k}^{2}(q^{8};q^{8})_{k}}q^{-2k}. \end{align*} $$
Letting
![]() $m=3$
,
$m=3$
,
![]() $q\mapsto q^{4}$
,
$q\mapsto q^{4}$
,
![]() $a=q^{2}$
,
$a=q^{2}$
,
![]() $b_{1}=c_{1}=q^{5}$
,
$b_{1}=c_{1}=q^{5}$
,
![]() $b_{2}=c_{2}=q^{2}$
,
$b_{2}=c_{2}=q^{2}$
,
![]() $b_{3}=-q^{2}$
,
$b_{3}=-q^{2}$
,
![]() $c_{3}=q^{2+2n}$
and
$c_{3}=q^{2+2n}$
and
![]() $N=(n-1)/2$
in (2.1), we see that the above summation is equal to
$N=(n-1)/2$
in (2.1), we see that the above summation is equal to
 $$ \begin{align} &\frac{(q^{6},-q^{2-2n};q^{4})_{(n-1)/2}}{(-q^{4},q^{4-2n};q^{4})_{(n-1)/2}} \notag\\ &\quad\times \sum_{j_{1},j_{2}\geqslant 0} \frac{(q^{-4};q^{4})_{j_{1}}(q^{2};q^{4})_{j_{2}}(q^{2},q^{2};q^{4})_{j_{1}}(-q^{2},q^{2+2n},q^{2-2n};q^{4})_{j_{1}+j_{2}}}{(q^{4};q^{4})_{j_{1}} (q^{4};q^{4})_{j_{2}}(q,q;q^{4})_{j_{1}} (q^{4},q^{4},-q^{4};q^{4})_{j_{1}+j_{2}}}q^{6j_{1}+4j_{2}} \notag\\ &=(-1)^{(n-1)/2}q^{1-n}[n]_{q^{2}} \sum_{j_{2}=0}^{(n-1)/2}\frac{(q^{2},-q^{2},q^{2+2n},q^{2-2n};q^{4})_{j_{2}}}{(q^{4},q^{4},q^{4},-q^{4};q^{4})_{j_{2}}}q^{4j_{2}} \notag\\ &\quad+(-1)^{(n+1)/2}q^{3-n}[n]_{q^{2}} (1+q)^{2}\sum_{j_{2}=0}^{(n-3)/2}\frac{(q^{2};q^{4})_{j_{2}}(-q^{2},q^{2+2n},q^{2-2n};q^{4})_{j_{2}+1}}{(q^{4};q^{4}){j_{2}}(q^{4},q^{4},-q^{4};q^{4})_{j_{2}+1}}q^{4j_{2}}, \end{align} $$
$$ \begin{align} &\frac{(q^{6},-q^{2-2n};q^{4})_{(n-1)/2}}{(-q^{4},q^{4-2n};q^{4})_{(n-1)/2}} \notag\\ &\quad\times \sum_{j_{1},j_{2}\geqslant 0} \frac{(q^{-4};q^{4})_{j_{1}}(q^{2};q^{4})_{j_{2}}(q^{2},q^{2};q^{4})_{j_{1}}(-q^{2},q^{2+2n},q^{2-2n};q^{4})_{j_{1}+j_{2}}}{(q^{4};q^{4})_{j_{1}} (q^{4};q^{4})_{j_{2}}(q,q;q^{4})_{j_{1}} (q^{4},q^{4},-q^{4};q^{4})_{j_{1}+j_{2}}}q^{6j_{1}+4j_{2}} \notag\\ &=(-1)^{(n-1)/2}q^{1-n}[n]_{q^{2}} \sum_{j_{2}=0}^{(n-1)/2}\frac{(q^{2},-q^{2},q^{2+2n},q^{2-2n};q^{4})_{j_{2}}}{(q^{4},q^{4},q^{4},-q^{4};q^{4})_{j_{2}}}q^{4j_{2}} \notag\\ &\quad+(-1)^{(n+1)/2}q^{3-n}[n]_{q^{2}} (1+q)^{2}\sum_{j_{2}=0}^{(n-3)/2}\frac{(q^{2};q^{4})_{j_{2}}(-q^{2},q^{2+2n},q^{2-2n};q^{4})_{j_{2}+1}}{(q^{4};q^{4}){j_{2}}(q^{4},q^{4},-q^{4};q^{4})_{j_{2}+1}}q^{4j_{2}}, \end{align} $$
where we have used the fact that
![]() $(q^{-4};q^{4})_{j_{1}}=0$
for
$(q^{-4};q^{4})_{j_{1}}=0$
for
![]() $j_{1}>1$
.
$j_{1}>1$
.
Taking
![]() $q\mapsto q^{4}$
,
$q\mapsto q^{4}$
,
![]() $a=1$
,
$a=1$
,
![]() $c=q^{2}$
and
$c=q^{2}$
and
![]() $n\mapsto (n-1)/2$
in (2.2), we have
$n\mapsto (n-1)/2$
in (2.2), we have
 $$ \begin{align*} \sum_{j_{2}=0}^{(n-1)/2}\frac{(q^{2},-q^{2},q^{2+2n},q^{2-2n};q^{4})_{j_{2}}}{(q^{4},q^{4},q^{4},-q^{4};q^{4})_{j_{2}}}q^{4j_{2}} =\begin{cases} q^{n-1}\dfrac{(q^{4}; q^{8})_{(n-1)/4}^{2}} {(q^{8}; q^{8})_{(n-1)/4}^{2}}&\text{if }n\equiv 1\pmod{4}\text{,}\\[5pt] 0& \text{if }n\equiv 3\pmod{4}\text{.} \end{cases} \end{align*} $$
$$ \begin{align*} \sum_{j_{2}=0}^{(n-1)/2}\frac{(q^{2},-q^{2},q^{2+2n},q^{2-2n};q^{4})_{j_{2}}}{(q^{4},q^{4},q^{4},-q^{4};q^{4})_{j_{2}}}q^{4j_{2}} =\begin{cases} q^{n-1}\dfrac{(q^{4}; q^{8})_{(n-1)/4}^{2}} {(q^{8}; q^{8})_{(n-1)/4}^{2}}&\text{if }n\equiv 1\pmod{4}\text{,}\\[5pt] 0& \text{if }n\equiv 3\pmod{4}\text{.} \end{cases} \end{align*} $$
Similarly, taking
![]() $q\mapsto q^{4}$
,
$q\mapsto q^{4}$
,
![]() $a=q^{4}$
,
$a=q^{4}$
,
![]() $c=q^{2}$
and
$c=q^{2}$
and
![]() $n\mapsto (n-3)/2$
in (2.3), we get
$n\mapsto (n-3)/2$
in (2.3), we get
 $$ \begin{align*} &\sum_{j_{2}=0}^{(n-3)/2}\frac{(q^{2};q^{4})_{j_{2}}(-q^{2},q^{2+2n},q^{2-2n};q^{4})_{j_{2}+1}}{(q^{4};q^{4}){j_{2}}(q^{4},q^{4},-q^{4};q^{4})_{j_{2}+1}}q^{4j_{2}} \\ &\quad=\frac{(1+q^{2})(1-q^{2+2n})(1-q^{2-2n})}{(1-q^{4})^{2}(1+q^{4})} \sum_{j_{2}=0}^{(n-3)/2}\frac{(q^{2},-q^{6},q^{6+2n},q^{6-2n};q^{4})_{j_{2}}}{(q^{4},q^{8},q^{8},-q^{8};q^{4})_{j_{2}}}q^{4j_{2}}\\ &\quad=\begin{cases} q^{n-3}\dfrac{(1+q^{2})(1-q^{2+2n})(1-q^{2-2n})(q^{4}; q^{8})_{(n-1)/4}^{2}} {(1-q^{4})^{2}(q^{8}; q^{8})_{(n-1)/4}^{2}}&\text{if }n\equiv 1\pmod{4}\text{,}\\[10pt] q^{n-3}\dfrac{(1+q^{2})(1-q^{2+2n})(1-q^{2-2n})(q^{4},q^{12}; q^{8})_{(n-3)/4}} {(1-q^{4})^{2}(1+q^{4})(q^{8},q^{16}; q^{8})_{(n-3)/4}}& \text{if }n\equiv 3\pmod{4}\text{.} \end{cases} \end{align*} $$
$$ \begin{align*} &\sum_{j_{2}=0}^{(n-3)/2}\frac{(q^{2};q^{4})_{j_{2}}(-q^{2},q^{2+2n},q^{2-2n};q^{4})_{j_{2}+1}}{(q^{4};q^{4}){j_{2}}(q^{4},q^{4},-q^{4};q^{4})_{j_{2}+1}}q^{4j_{2}} \\ &\quad=\frac{(1+q^{2})(1-q^{2+2n})(1-q^{2-2n})}{(1-q^{4})^{2}(1+q^{4})} \sum_{j_{2}=0}^{(n-3)/2}\frac{(q^{2},-q^{6},q^{6+2n},q^{6-2n};q^{4})_{j_{2}}}{(q^{4},q^{8},q^{8},-q^{8};q^{4})_{j_{2}}}q^{4j_{2}}\\ &\quad=\begin{cases} q^{n-3}\dfrac{(1+q^{2})(1-q^{2+2n})(1-q^{2-2n})(q^{4}; q^{8})_{(n-1)/4}^{2}} {(1-q^{4})^{2}(q^{8}; q^{8})_{(n-1)/4}^{2}}&\text{if }n\equiv 1\pmod{4}\text{,}\\[10pt] q^{n-3}\dfrac{(1+q^{2})(1-q^{2+2n})(1-q^{2-2n})(q^{4},q^{12}; q^{8})_{(n-3)/4}} {(1-q^{4})^{2}(1+q^{4})(q^{8},q^{16}; q^{8})_{(n-3)/4}}& \text{if }n\equiv 3\pmod{4}\text{.} \end{cases} \end{align*} $$
Substituting the above two identities into (2.5), we obtain
 $$ \begin{align*} &\sum_{k=0}^{(n-1)/2} (-1)^{k}[4k+1]_{q^{2}}[4k+1]^{2}\frac{(q^{2-2n},q^{2+2n};q^{4})_{k} (q^{2};q^{4})_{k}^{2}(q^{4};q^{8})_{k}} {(q^{4-2n},q^{4+2n};q^{4})_{k}(q^{4};q^{4})_{k}^{2}(q^{8};q^{8})_{k}}q^{-2k}\\ &\quad= \begin{cases} \bigg(1-\dfrac{(1+q)(1-q^{2+2n})(1-q^{2-2n})}{(1-q)(1-q^{4})}\bigg) \dfrac{(q^{4};q^{8})_{(n-1)/4}^{2}}{(q^{8};q^{8})_{(n-1)/4}^{2}}[n]_{q^{2}}&\text{if }n\equiv 1\pmod{4}\text{,}\\[10pt] \dfrac{(1+q)(1-q^{2+2n})(1-q^{2-2n})(q^{4},q^{12}; q^{8})_{(n-3)/4}} {(1-q)(1-q^{8})(q^{8},q^{16}; q^{8})_{(n-3)/4}}[n]_{q^{2}}& \text{if }n\equiv 3\pmod{4}\text{.} \end{cases} \end{align*} $$
$$ \begin{align*} &\sum_{k=0}^{(n-1)/2} (-1)^{k}[4k+1]_{q^{2}}[4k+1]^{2}\frac{(q^{2-2n},q^{2+2n};q^{4})_{k} (q^{2};q^{4})_{k}^{2}(q^{4};q^{8})_{k}} {(q^{4-2n},q^{4+2n};q^{4})_{k}(q^{4};q^{4})_{k}^{2}(q^{8};q^{8})_{k}}q^{-2k}\\ &\quad= \begin{cases} \bigg(1-\dfrac{(1+q)(1-q^{2+2n})(1-q^{2-2n})}{(1-q)(1-q^{4})}\bigg) \dfrac{(q^{4};q^{8})_{(n-1)/4}^{2}}{(q^{8};q^{8})_{(n-1)/4}^{2}}[n]_{q^{2}}&\text{if }n\equiv 1\pmod{4}\text{,}\\[10pt] \dfrac{(1+q)(1-q^{2+2n})(1-q^{2-2n})(q^{4},q^{12}; q^{8})_{(n-3)/4}} {(1-q)(1-q^{8})(q^{8},q^{16}; q^{8})_{(n-3)/4}}[n]_{q^{2}}& \text{if }n\equiv 3\pmod{4}\text{.} \end{cases} \end{align*} $$
This proves that both sides of (2.4) are equal when
![]() $a=q^{\pm 2n}$
. Namely, the q-congruence (2.4) holds modulo
$a=q^{\pm 2n}$
. Namely, the q-congruence (2.4) holds modulo
![]() $1-aq^{2n}$
or
$1-aq^{2n}$
or
![]() $a-q^{2n}$
.
$a-q^{2n}$
.
Moreover, in view of Lemma 2.1, we can verify that the kth and
![]() $((n-1)/2-k)$
th summands cancel each other modulo
$((n-1)/2-k)$
th summands cancel each other modulo
![]() $\Phi _{n}(q^{2})$
for any positive odd integer n. It follows that
$\Phi _{n}(q^{2})$
for any positive odd integer n. It follows that
 $$ \begin{align} \sum_{k=0}^{(n-1)/2} (-1)^{k}[4k+1]_{q^{2}}[4k+1]^{2}\frac{(aq^{2},q^{2}/a;q^{4})_{k} (q^{2};q^{4})_{k}^{2}(q^{4};q^{8})_{k}} {(aq^{4},q^{4}/a;q^{4})_{k}(q^{4};q^{4})_{k}^{2}(q^{8};q^{8})_{k}}q^{-2k} \equiv 0 \pmod{\Phi_{n}(q^{2})}. \end{align} $$
$$ \begin{align} \sum_{k=0}^{(n-1)/2} (-1)^{k}[4k+1]_{q^{2}}[4k+1]^{2}\frac{(aq^{2},q^{2}/a;q^{4})_{k} (q^{2};q^{4})_{k}^{2}(q^{4};q^{8})_{k}} {(aq^{4},q^{4}/a;q^{4})_{k}(q^{4};q^{4})_{k}^{2}(q^{8};q^{8})_{k}}q^{-2k} \equiv 0 \pmod{\Phi_{n}(q^{2})}. \end{align} $$
Noticing that
![]() $[n]_{q^{2}}\equiv 0\pmod {\Phi _{n}(q^{2})}$
for
$[n]_{q^{2}}\equiv 0\pmod {\Phi _{n}(q^{2})}$
for
![]() $n>1$
, we conclude that the q-congruence (2.4) also holds modulo
$n>1$
, we conclude that the q-congruence (2.4) also holds modulo
![]() $\Phi _{n}(q)$
.
$\Phi _{n}(q)$
.
Since
![]() $1-aq^{2n}$
,
$1-aq^{2n}$
,
![]() $a-q^{2n}$
and
$a-q^{2n}$
and
![]() $\Phi _{n}(q^{2})$
are pairwise relatively prime polynomials in q, we complete the proof of the theorem.
$\Phi _{n}(q^{2})$
are pairwise relatively prime polynomials in q, we complete the proof of the theorem.
Proof of Theorem 1.1.
It is easy to see that the denominators on both sides of (2.4) when
![]() $a=1$
are relatively prime to
$a=1$
are relatively prime to
![]() $\Phi _{n}(q^{2})$
. However, when
$\Phi _{n}(q^{2})$
. However, when
![]() $a=1$
, the polynomial
$a=1$
, the polynomial
![]() $(1-aq^{2n})(a-q^{2n})$
contains the factor
$(1-aq^{2n})(a-q^{2n})$
contains the factor
![]() $\Phi _{n}(q^{2})^{2}$
. Therefore, the
$\Phi _{n}(q^{2})^{2}$
. Therefore, the
![]() $a=1$
case of (2.4) implies that (1.5) is true modulo
$a=1$
case of (2.4) implies that (1.5) is true modulo
![]() $\Phi _{n}(q^{2})^{3}$
for
$\Phi _{n}(q^{2})^{3}$
for
![]() $M=(n-1)/2$
. Furthermore, since
$M=(n-1)/2$
. Furthermore, since
![]() $(q^{2};q^{4})_{k}^{4}(q^{4};q^{8})_{k}/((q^{4};q^{4})_{k}^{4}(q^{8};q^{8})_{k})\equiv 0\pmod {\Phi _{n}(q^{2})^{5}}$
for
$(q^{2};q^{4})_{k}^{4}(q^{4};q^{8})_{k}/((q^{4};q^{4})_{k}^{4}(q^{8};q^{8})_{k})\equiv 0\pmod {\Phi _{n}(q^{2})^{5}}$
for
![]() $(n-1)/2<k\leqslant n-1$
, we see that (1.5) is also true modulo
$(n-1)/2<k\leqslant n-1$
, we see that (1.5) is also true modulo
![]() $\Phi _{n}(q^{2})^{3}$
for
$\Phi _{n}(q^{2})^{3}$
for
![]() $M=n-1$
.
$M=n-1$
.
It remains to prove the following two q-congruences:
 $$ \begin{align} \sum_{k=0}^{(n-1)/2} (-1)^{k}[4k+1]_{q^{2}}[4k+1]^{2}\frac{(q^{2};q^{4})_{k}^{4}(q^{4};q^{8})_{k}}{(q^{4};q^{4})_{k}^{4}(q^{8};q^{8})_{k}}q^{-2k} \equiv 0\pmod{[n]_{q^{2}}}, \end{align} $$
$$ \begin{align} \sum_{k=0}^{(n-1)/2} (-1)^{k}[4k+1]_{q^{2}}[4k+1]^{2}\frac{(q^{2};q^{4})_{k}^{4}(q^{4};q^{8})_{k}}{(q^{4};q^{4})_{k}^{4}(q^{8};q^{8})_{k}}q^{-2k} \equiv 0\pmod{[n]_{q^{2}}}, \end{align} $$
 $$ \begin{align} \hspace{-10pt}\sum_{k=0}^{n-1} (-1)^{k}[4k+1]_{q^{2}}[4k+1]^{2}\frac{(q^{2};q^{4})_{k}^{4}(q^{4};q^{8})_{k}} {(q^{4};q^{4})_{k}^{4}(q^{8};q^{8})_{k}}q^{-2k} \equiv 0\pmod{[n]_{q^{2}}}. \end{align} $$
$$ \begin{align} \hspace{-10pt}\sum_{k=0}^{n-1} (-1)^{k}[4k+1]_{q^{2}}[4k+1]^{2}\frac{(q^{2};q^{4})_{k}^{4}(q^{4};q^{8})_{k}} {(q^{4};q^{4})_{k}^{4}(q^{8};q^{8})_{k}}q^{-2k} \equiv 0\pmod{[n]_{q^{2}}}. \end{align} $$
For
![]() $n>1$
, let
$n>1$
, let
![]() $\zeta \ne 1$
be an nth root of unity, possibly not primitive. Suppose
$\zeta \ne 1$
be an nth root of unity, possibly not primitive. Suppose
![]() $\zeta $
is a primitive root of unity of odd degree d satisfying
$\zeta $
is a primitive root of unity of odd degree d satisfying
![]() $d\mid n$
. Let
$d\mid n$
. Let
![]() $c_{q}(k)$
be the kth term on the left-hand side of the congruences (2.7) and (2.8). Then
$c_{q}(k)$
be the kth term on the left-hand side of the congruences (2.7) and (2.8). Then
 $$ \begin{align*} c_{q}(k)=(-1)^{k}[4k+1]_{q^{2}}[4k+1]^{2}\frac{(q^{2};q^{4})_{k}^{4}(q^{4};q^{8})_{k}}{(q^{4};q^{4})_{k}^{4}(q^{8};q^{8})_{k}}q^{-2k}. \end{align*} $$
$$ \begin{align*} c_{q}(k)=(-1)^{k}[4k+1]_{q^{2}}[4k+1]^{2}\frac{(q^{2};q^{4})_{k}^{4}(q^{4};q^{8})_{k}}{(q^{4};q^{4})_{k}^{4}(q^{8};q^{8})_{k}}q^{-2k}. \end{align*} $$
Observe that (2.6) is true for any odd
![]() $n>1$
. Thus, letting
$n>1$
. Thus, letting
![]() $a=1$
and
$a=1$
and
![]() $n=d$
in (2.6), we obtain
$n=d$
in (2.6), we obtain
 $$ \begin{align*} \sum_{k=0}^{(d-1)/2}c_{\zeta}(k)=\sum_{k=0}^{d-1}c_{\zeta}(k)=0 \quad\text{and}\quad\sum_{k=0}^{(d-1)/2}c_{-\zeta}(k)=\sum_{k=0}^{d-1}c_{-\zeta}(k)=0. \end{align*} $$
$$ \begin{align*} \sum_{k=0}^{(d-1)/2}c_{\zeta}(k)=\sum_{k=0}^{d-1}c_{\zeta}(k)=0 \quad\text{and}\quad\sum_{k=0}^{(d-1)/2}c_{-\zeta}(k)=\sum_{k=0}^{d-1}c_{-\zeta}(k)=0. \end{align*} $$
Noticing that
 $$ \begin{align*} \frac{c_{\zeta}(\ell d+k)}{c_{\zeta}(\ell d)} =\lim_{q\to\zeta}\frac{c_{q}(\ell d+k)}{c_{q}(\ell d)} =c_{\zeta}(k), \end{align*} $$
$$ \begin{align*} \frac{c_{\zeta}(\ell d+k)}{c_{\zeta}(\ell d)} =\lim_{q\to\zeta}\frac{c_{q}(\ell d+k)}{c_{q}(\ell d)} =c_{\zeta}(k), \end{align*} $$
we have
 $$ \begin{align*} \sum_{k=0}^{n-1}c_{\zeta}(k)=\sum_{\ell=0}^{n/d-1}\sum_{k=0}^{d-1}c_{\zeta}(\ell d+k) =\sum_{\ell=0}^{n/d-1}c_{\zeta}(\ell d) \sum_{k=0}^{d-1}c_{\zeta}(k)=0, \end{align*} $$
$$ \begin{align*} \sum_{k=0}^{n-1}c_{\zeta}(k)=\sum_{\ell=0}^{n/d-1}\sum_{k=0}^{d-1}c_{\zeta}(\ell d+k) =\sum_{\ell=0}^{n/d-1}c_{\zeta}(\ell d) \sum_{k=0}^{d-1}c_{\zeta}(k)=0, \end{align*} $$
and
 $$ \begin{align*} \sum_{k=0}^{(n-1)/2}c_{\zeta}(k) =\sum_{\ell=0}^{(n/d-3)/2} c_{\zeta}(\ell d) \sum_{k=0}^{d-1}c_{\zeta}(k)+\sum_{k=0}^{(d-1)/2}c_{\zeta}((n-d)/2+k)=0. \end{align*} $$
$$ \begin{align*} \sum_{k=0}^{(n-1)/2}c_{\zeta}(k) =\sum_{\ell=0}^{(n/d-3)/2} c_{\zeta}(\ell d) \sum_{k=0}^{d-1}c_{\zeta}(k)+\sum_{k=0}^{(d-1)/2}c_{\zeta}((n-d)/2+k)=0. \end{align*} $$
This means that both the sums
![]() $\sum _{k=0}^{n-1}c_{q}(k)$
and
$\sum _{k=0}^{n-1}c_{q}(k)$
and
![]() $\sum _{k=0}^{(n-1)/2}c_{q}(k)$
are divisible by
$\sum _{k=0}^{(n-1)/2}c_{q}(k)$
are divisible by
![]() $\Phi _{d}(q)$
. Similarly, we can show that they are also divisible by
$\Phi _{d}(q)$
. Similarly, we can show that they are also divisible by
![]() $\Phi _{d}(-q)$
. Since d can be any divisor of n larger than
$\Phi _{d}(-q)$
. Since d can be any divisor of n larger than
![]() $1$
, we deduce that each of them is congruent to
$1$
, we deduce that each of them is congruent to
![]() $0$
modulo
$0$
modulo
 $$ \begin{align*} \prod_{d\mid n,\, d>1}\Phi_{d}(q) \Phi_{d}(-q)=[n]_{q^{2}}, \end{align*} $$
$$ \begin{align*} \prod_{d\mid n,\, d>1}\Phi_{d}(q) \Phi_{d}(-q)=[n]_{q^{2}}, \end{align*} $$
3 Two open problems
Swisher [Reference Swisher13] proposed many interesting conjectures on generalisations of Van Hamme’s supercongruences (A.2)–(L.2). Recently, the author and Zudilin [Reference Guo and Zudilin9] have proved some conjectures of Swisher by establishing their q-analogues. Here we would like to propose a similar conjecture.
Conjecture 3.1. Let
![]() $p\equiv 1\pmod {4}$
and let
$p\equiv 1\pmod {4}$
and let
![]() $r,s\geqslant 1$
. Then
$r,s\geqslant 1$
. Then
 $$ \begin{align} \sum_{k=0}^{(p^{r}-1)/d} (-1)^{k}(4k+1)^{2s+1}\frac{(\tfrac{1}{2})_{k}^{5}}{k!^{5}} \equiv -p\Gamma_{p}(\tfrac{1}{4})^{4}\, \sum_{k=0}^{(p^{r-1}-1)/d} (-1)^{k}(4k+1)^{2s+1}\frac{(\tfrac{1}{2})_{k}^{5}}{k!^{5}} \pmod{p^{3r-2}}, \end{align} $$
$$ \begin{align} \sum_{k=0}^{(p^{r}-1)/d} (-1)^{k}(4k+1)^{2s+1}\frac{(\tfrac{1}{2})_{k}^{5}}{k!^{5}} \equiv -p\Gamma_{p}(\tfrac{1}{4})^{4}\, \sum_{k=0}^{(p^{r-1}-1)/d} (-1)^{k}(4k+1)^{2s+1}\frac{(\tfrac{1}{2})_{k}^{5}}{k!^{5}} \pmod{p^{3r-2}}, \end{align} $$
where
![]() $d=1$
or
$d=1$
or
![]() $2$
.
$2$
.
For
![]() $s=0$
, Swisher [Reference Swisher13, (A.3)] and the author [Reference Guo5, Conjecture 4.1] conjectured that (3.1) holds modulo
$s=0$
, Swisher [Reference Swisher13, (A.3)] and the author [Reference Guo5, Conjecture 4.1] conjectured that (3.1) holds modulo
![]() $p^{5r}$
for
$p^{5r}$
for
![]() $p>5$
. From (1.8), we can easily see that (3.1) is true modulo
$p>5$
. From (1.8), we can easily see that (3.1) is true modulo
![]() $p^{r}$
for
$p^{r}$
for
![]() $s=1$
.
$s=1$
.
Finally, motivated by [Reference Guo4, Conjecture 4.5], we believe that the following generalisation of Corollary 1.2 for p of the form
![]() $4k+3$
should be true.
$4k+3$
should be true.
Conjecture 3.2. Let
![]() $p\equiv 3\pmod {4}$
and let
$p\equiv 3\pmod {4}$
and let
![]() $r\geqslant 2$
be even. Then
$r\geqslant 2$
be even. Then
 $$ \begin{align*} \sum_{k=0}^{(p^{r}-1)/d} (-1)^{k}(4k+1)(8k^{2}+4k+1) \frac{(\tfrac{1}{2})_{k}^{5}}{k!^{5}} &\equiv 0\pmod{p^{2r}}, \end{align*} $$
$$ \begin{align*} \sum_{k=0}^{(p^{r}-1)/d} (-1)^{k}(4k+1)(8k^{2}+4k+1) \frac{(\tfrac{1}{2})_{k}^{5}}{k!^{5}} &\equiv 0\pmod{p^{2r}}, \end{align*} $$
where
![]() $d=1$
or
$d=1$
or
![]() $2$
.
$2$
.