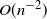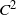On Markov chain approximations for computing boundary crossing probabilities of diffusion processes

Abstract

We propose a discrete-time discrete-space Markov chain approximation with a Brownian bridge correction for computing curvilinear boundary crossing probabilities of a general diffusion process on a finite time interval. For broad classes of curvilinear boundaries and diffusion processes, we prove the convergence of the constructed approximations in the form of products of the respective substochastic matrices to the boundary crossing probabilities for the process as the time grid used to construct the Markov chains is getting finer. Numerical results indicate that the convergence rate for the proposed approximation with the Brownian bridge correction is $O(n^{-2})$ in the case of $C^2$ boundaries and a uniform time grid with n steps.

1. Introduction

We consider the problem of approximating the probability for a general diffusion process to stay between two curvilinear boundaries. Mathematically, the problem is solved: the non-crossing probability can be expressed as a solution to the respective boundary value problem for the backward Kolmogorov partial differential equation (this result goes back to the 1930s [34, 36, 37]). However, simple explicit analytic expressions are confined to the case of the Wiener process using the method of images [38], and most of the results for diffusion processes rely on verifying Cherkasov’s conditions [12, 51, 53] and then transforming the problem to that for the Wiener process by using a monotone transformation. Outside this class of special cases, we should mostly rely on computing numerical approximations to the desired probabilities.

One popular approach to finding expressions for the first-passage-time density is through the use of Volterra integral equations. Much work was done on the method of integral equations for approximating the first-passage-time density for general diffusion processes [10, 11, 20, 32, 52, 53, 55], culminating with [24], which expressed the first-passage-time density of a general diffusion process in terms of the solution to a Volterra integral equation of the second kind. Volterra integral equations of the first kind for the first-passage time for Brownian motion were derived in [41, 47]. Although the method of integral equations is quite efficient for computational purposes, a drawback of the method is that the kernel of the integral equation is expressed in terms of the transition probabilities of the diffusion process. Therefore, for this method to work, we have to first compute these transition probabilities for all times on the time grid used. The method proposed in this paper only requires knowledge of the drift and diffusion coefficients, allowing it to be easily used in the general case. For further details on the connection between Volterra integral equations and the first-passage-time density, we refer the reader to [49]. Other computational techniques include Monte Carlo [21, 31], including exact simulation methods [4, 5, 27, 28] and continuity corrections employing boundary shifting to compensate for the ‘discrete monitoring bias’ [9, 22, 58], and numerical solving of partial differential equations (see, e.g., [48] and references therein).

The classical probabilistic approach to the boundary-crossing problem is the method of weak approximation, which involves proving that a sequence of simpler processes $X_n$ weakly converges to the desired diffusion process in a suitable functional space, which entails the convergence of the corresponding non-crossing probabilities. Along with the already mentioned [34, 36, 37], one can say that this approach was effectively used in [17] in the case of ‘flat boundaries’ (see also [6, Chapter 2, 11]). More recently, the authors in [19] approximated the Wiener process with a sequence of discrete Markov chains with absorbing states and expressed the non-crossing probability as a product of transition matrices. The authors in [33] extended the results in [19] by approximating a general diffusion with a sequence of Markov chains and similarly expressed the non-crossing probability as a product of transition matrices. However, the convergence rates of these approximations were proved to be $O(n^{-1/2})$ , which leaves much to be desired in practical applications.

Another standard approach is to approximate the true boundary with one for which the crossing probability is easier to compute. In the one-sided boundary case, [50, 61] used piecewise-linear approximations and the well-known formula for a one-sided linear boundary crossing probability for the Brownian bridge process to express the non-crossing probability in terms of a multiple Gaussian integral. This was generalised to the case of two-sided boundaries in [45] and to diffusion processes set up in that case in [62]. In the case of Brownian motion, a sharp explicit error bound for the approximation of the corresponding boundary crossing probabilities was obtained in [8] and extended to general diffusion processes in [15].

The present paper combines piecewise-linear boundary approximations, limit theorems on convergence of Markov chains to diffusions, and a modification of the matrix multiplication scheme from [19] to create an efficient and tractable numerical method for computing the boundary crossing probabilities for time-inhomogeneous diffusion processes in both one- and two-sided boundary cases. The approach in the paper consists of the following steps:

1. (i) Transform the original general diffusion process into one with unit diffusion coefficient, applying the same transformation to the boundaries.

2. (ii) Approximate the transformed diffusion process with a discrete-time Gaussian Markov process using a weak Taylor expansion.

3. (iii) Approximate the discrete-time process from step (ii) with a discrete Markov chain in discrete time, whose transition probabilities are given by the normalised values of the transition density of the process from step (ii). The state spaces of the discrete Markov chain are constructed in such a way that the Markov chain does not overshoot or undershoot the boundaries when hitting them.

4. (iv) Construct a continuous-time process that interpolates the Markov chain from step (iii) with a collection of Brownian bridges.

5. (v) Approximate the transformed boundaries with piecewise linear ones and compute the piecewise linear boundary crossing probability of the interpolated process constructed in step (iv) using matrix multiplication.

The paper is structured as follows. In Section 2 we describe in detail the above steps. Section 3 states the main results of the paper. These include convergence in distribution of our approximating discrete schemes with Brownian bridge interpolations to the original process and, as a corollary, convergence of the respective boundary crossing probabilities as well. That section also contains a sketch of a possible argument showing that the convergence rate of the boundary crossing probability approximations is $O(n^{-2})$ provided that the nth time interval partition has rank $O(n^{-1})$ as $n\to\infty$ . In Section 4 we present the proofs of these results. Section 5 contains numerical examples and a brief discussion of the performance of our method compared to some existing alternative approaches.

2. Markov chain approximation of a diffusion

2.1. Step (i)

We are interested in the boundary crossing probability of a one-dimensional diffusion process Y, whose dynamics are governed by the following stochastic differential equation:

(1) \begin{equation} \begin{cases} \mathrm{d} Y(t) = \mu_Y(t,Y(t))\,\mathrm{d} t + \sigma_Y(t,Y(t))\,\mathrm{d} W(t), & t\in (0,1],\\ Y(0) = y_0, \end{cases}\end{equation}

where $\{W_t\}_{t\geq 0}$ is a standard Brownian motion process defined on a stochastic basis $(\Omega,\mathcal{F},(\mathcal{F}_{t})_{t\geq 0},\mathbb{P})$ and $y_0$ is constant. We assume that $\mu_Y\colon[0,1] \times \mathbb{R} \to \mathbb{R}$ and $\sigma_Y \colon [0,1] \times \mathbb{R} \to (0,\infty)$ satisfy the following conditions sufficient for the uniqueness and existence of a strong solution to (1) [18, pp. 297–298]:

Condition 1. The functions $\mu_Y$ and $\sigma_Y$ are continuous in both variables and such that, for some $K < \infty$ , $x \mu_Y(t,x) \leq K(1 +x^2)$ and $\sigma_Y^2(t,x) \leq K(1 + x^2)$ for all $(t,x)\in [0,1]\times \mathbb{R}$ and, for any bounded open set $U \subset \mathbb{R}$ , there exists a $K_U < \infty$ such that

\begin{equation*} \lvert\mu_Y(t,x) - \mu_Y(t,y)\rvert + \lvert\sigma_Y^2(t,x) - \sigma_Y^2(t,y)\rvert \leq K_U\lvert x - y\rvert \end{equation*}

for all $t\in [0,1]$ , $x,y\in U$ .

For the unit-diffusion transformation ${\psi}_t(y) \,:\!=\, \int_0^y\sigma_Y(t,u)^{-1}\,\mathrm{d} u$ to be well defined, we will also assume the following.

Condition 2. The function $\sigma_Y$ is continuously differentiable with respect to (t, x) with bounded partial derivatives, and $\inf_{(t,x) \in [0,1]\times \mathbb{R}}\sigma_Y(t,x)>0$ .

By Itô’s lemma, the transformed process $X =\{X(t) \,:\!=\, {\psi}_t(Y(t))\}_{t\in[0,1]}$ is a diffusion process with a unit diffusion coefficient (see, e.g., [35, Section 4.7] or [54]),

(2) \begin{equation} \begin{cases} \mathrm{d} X(t) = {\mu_X}(t,X(t))\,\mathrm{d} t + \mathrm{d} W(t),&t\in (0,1], \\ X(0) = x_0 \,:\!=\, {\psi}_0(y_0), \end{cases}\end{equation}

where ${\mu_X}(t,x) = (\partial_t {\psi}_t + {\mu_Y}/{\sigma_Y} - \tfrac12 \partial_x\sigma_Y)\circ {\psi}_t^{-1}(x)$ and ${\psi}_t^{-1}(z)$ is the inverse of $z = {\psi}_t(y)$ in y.

Denote by ${C}=C([0,1])$ the space of continuous functions $x \colon [0,1]\to\mathbb{R}$ equipped with the uniform norm $\|{x}\|_{\infty} \,:\!=\, \sup_{t\in[0,1]}\lvert x(t)\rvert$ . For a fixed $x_0 \in \mathbb{R}$ , consider the class

\begin{equation*} \mathcal{G}\,:\!=\, \{(\,f^-,f^{+})\colon f^{\pm} \in {C},\,f^-(0) < x_0 < f^+(0),\, \inf_{0 \leq t \leq 1}(\,f^+(t) - f^-(t)) > 0\}\end{equation*}

of pairs of functions from C and introduce the notation

\begin{equation*} S(\,f^-,f^{+})\,:\!=\, \{x \in {C}\colon f^-(t) < x(t) < f^+(t),\,t\in [0,1] \},\qquad (\,f^-,f^{+}) \in \mathcal{G}.\end{equation*}

The problem we deal with in this paper is how to compute the probability of the form $\mathbb{P}(Y \in S(g_0^-,g_0^{+}))$ for $(g_0^-,g_0^{+}) \in \mathcal{G}$ . Clearly, the desired probability coincides with $\mathbb{P}(X \in G)$ , $G\,:\!=\, S(g^-,g^{+})$ , where $g^{\pm}(t) \,:\!=\, {\psi}_t(g_0^{\pm}(t))$ , $t\in[0,1]$ . It is also clear that $(g^{-},g^{+}) \in \mathcal{G}$ due to Condition 2. Henceforth, we work exclusively with the process X and the boundaries $g^{\pm}$ .

2.2. Step (ii)

In the context of curvilinear boundary crossing probabilities, [19] approximated the Wiener process by discrete Markov chains with transition probabilities computed by first taking the values of the Wiener process transition densities on a lattice and then normalising these to obtain a probability distribution on that lattice (there is also a small adjustment of that distribution to perfectly match the first two moments of the original transition probabilities and the ‘discretised’ ones).

In the general diffusion case, due to the absence of closed-form expressions for the transition density of X, we use transition probabilities of the weak Taylor approximations of X to construct the approximating discrete process. As the second-order expansion is to be used, we further require that the following condition is met.

Condition 3. For any fixed $x \in \mathbb{R}$ , ${\mu_X}(\,\cdot\,,x) \in C^1([0,1])$ , and for any fixed $t \in [0,1]$ , ${\mu_X}(t,\,\cdot\,) \in C^2(\mathbb{R})$ . Moreover, for any $r>0$ , there exists a $K_r <\infty$ such that

\begin{equation*} \lvert {\mu_X}(t,x)\rvert + \lvert \partial_t {\mu_X}(t,x)\rvert + \lvert \partial_{x} {\mu_X}(t,x) \rvert + \lvert \partial_{xx} {\mu_X}(t,x) \rvert \leq K_r , \qquad t\in[0,1], \,\lvert x \rvert \leq r. \end{equation*}

Next, for any $n \geq 1$ , let $t_{n,k}\,:\!=\, k/n$ , $k=0,1,\ldots, n$ , be the uniform partition of [0,1] of rank $\Delta_{n}\,:\!=\,1/n$ . Introduce discrete scheme drift ${\beta}_{n,k}$ and diffusion ${\alpha}_{n,k}^{1/2}$ coefficients by setting, for $k=1,2,\ldots, n$ ,

(3) \begin{align} {\beta}_{n,k}(x) & \,:\!=\, \big({\mu_X} + \tfrac12\Delta_{n}(\partial_t{\mu_X} + {\mu_X}\partial_x{\mu_X} + \tfrac12\partial_{xx}{\mu_X})\big)(t_{n,k-1},x), \end{align}

(4) \begin{align} {\alpha}_{n,k}^{1/2}(x) & \,:\!=\, 1 + \tfrac12\Delta_{n}\partial_x {\mu_X} (t_{n,k-1},x). \end{align}

For each fixed $n \geq 1$ , the nth second-order weak Taylor approximation of the diffusion (2) is defined as the discrete-time process $\zeta_n \,:\!=\,\{\zeta_{n,k}\}_{k=0}^n$ , specified by $\zeta_{n,0} = x_0$ and

\begin{equation*} \zeta_{n,k}= \zeta_{n,k-1} + {\beta}_{n,k}(\zeta_{n,k-1})\Delta_{n} + \alpha_{n,k}^{1/2}(\zeta_{n,k-1}) \Delta_{n}^{1/2} Z_{n,k}, \qquad k=1,\ldots,n, \end{equation*}

where $\{Z_{n,k}\}_{k=1}^n$ is a triangular array of independent standard normal random variables. For more detail on weak Taylor approximations to solutions of stochastic differential equations, see, e.g., [35, Chapter 14]. Clearly, the conditional distributions of the increments $\zeta_{n,k}- \zeta_{n,k-1}$ given $\zeta_{n,k-1}$ are Gaussian, and so the transition probabilities of the discrete-time process $\zeta_{n}$ can be easily obtained.

2.3. Step (iii)

Next, we further approximate the discrete-time continuous state space process $\zeta_n$ with a discrete-time discrete-state-space Markov chain $\xi_n\,:\!=\,\{\xi_{n,k}\}_{k=0}^n$ , whose transition probabilities are based on the normalised values of the transition density of $\zeta_n$ .

To improve the convergence rate for our approximations to $\mathbb{P}(X \in G)$ , we construct our Markov chains $\xi_n$ choosing, generally speaking, different state spaces for each time step. Namely, the state space $E_{n,k}$ for $\xi_{n,k}$ , $k=0,1,\ldots,n$ , is chosen to be a lattice such that $g^{\pm}(t_{n,k}) \in E_{n,k}$ . This modification improves upon the Markov chain approximation suggested in [19], and is widely used for accelerating the convergence rate of numerical schemes in barrier option pricing [13]. More precisely, the spaces $E_{n,k}$ are constructed as follows. Let $g_{n,k}^{\pm} \,:\!=\, g^{\pm}(t_{n,k})$ , $k=1,\ldots,n$ , and, for fixed $\delta\in (0,\tfrac12]$ and $\gamma>0$ , set

\begin{equation*} {w}_{n,k} \,:\!=\, \begin{cases} \dfrac{(g_{n,k}^+ -g_{n,k}^{-})/\Delta_{n}^{1/2 +\delta} }{\lfloor{\gamma(g_{n,k}^+ -g_{n,k}^{-})/\Delta_{n}^{1/2 +\delta}}\rfloor}, & 1 \leq k<n, \\ \dfrac{(g^+(1) -g^-(1))/\Delta_{n} }{\lfloor{\gamma(g^+(1) -g^-(1))/\Delta_{n} }\rfloor}, & k=n, \end{cases}\end{equation*}

assuming that n is large enough that the integer parts in all the denominators are non-zero. We set the time-dependent space lattice step sizes to be

(5) \begin{equation} h_{n,k} \,:\!=\, \begin{cases} {w}_{n,k}\Delta_{n}^{1/2 +\delta}, & 1 \leq k < n, \\ {w}_{n,n}\Delta_{n}, & k = n. \end{cases}\end{equation}

The state space for $\xi_{n,k}$ is the $h_{n,k}$ -spaced lattice

(6) \begin{equation} E_{n,k}\,:\!=\, \{ g_{n,k}^+ - j h_{n,k} \colon j \in \mathbb{Z}\}, \qquad k = 1,\ldots,n.\end{equation}

We also put $E_{n,0}\,:\!=\,\{x_0\}$ and $E_{n}\,:\!=\, E_{n,0}\times E_{n,1} \times \cdots \times E_{n,n}$ . Note that

(7) \begin{equation} \max_{1\leq k\leq n}\lvert {w}_{n,k} - \gamma^{-1}\rvert \to 0\quad \mbox{ as $n\to\infty$} ,\end{equation}

and $\gamma^{-1}\leq {w}_{n,k}\leq 2\gamma^{-1}$ for all $1\leq k\leq n$ (assuming, as above, that n is large enough).

Further, for $k=1,\ldots,n,$ recalling (3) and (4), we let

(8) \begin{equation} {\mu}_{n,k}(x) \,:\!=\, {\beta}_{n,k}(x)\Delta_{n}, \qquad \sigma^{2}_{n,k}(x)\,:\!=\, {\alpha}_{n,k}(x)\Delta_{n},\end{equation}

and define $\xi_{n,k}$ , $k=1,\ldots,n$ , $n\geq 1$ , as a triangular array of random variables, where each row forms a Markov chain with one-step transition probabilities given by

\begin{equation*} p_{n,k}(x,y) \,:\!=\, \mathbb{P}(\xi_{n,k} = y \mid \xi_{n,k-1}=x) = \varphi(y \mid x + {\mu}_{n,k}(x),\, \sigma^{2}_{n,k}(x))\frac{h_{n,k}}{{C_{n,k}}(x)}\end{equation*}

for $(x,y) \in E_{n,k-1}\times E_{n,k}$ , where $\varphi(x\mid\mu,\sigma^2)\,:\!=\, (2\pi \sigma^2)^{-1/2}\mathrm{e}^{-(x -\mu)^2/(2\sigma^2) }$ , $x\in\mathbb R$ , denotes the Gaussian density with mean $\mu$ and variance $\sigma^2$ , and

(9) \begin{equation} {C_{n,k}}(x) \,:\!=\, \sum_{y \in E_{n,k}}\varphi(y \mid x + {\mu}_{n,k}(x),\sigma^{2}_{n,k}(x))h_{n,k}, \qquad x \in \mathbb{R}.\end{equation}

2.4. Step (iv)

As an initial approximation for $\mathbb{P}(X \in G )$ we could take $\mathbb{P}(g_{n,k}^- < X(t_{n,k}) < g_{n,k}^+, k = 1,\ldots,n)$ , which can in turn be approximated using the Chapman–Kolmogorov equations by

\begin{equation*} \mathbb{P}(g_{n,k}^- < \xi_{n,k} < g_{n,k}^+, \, k = 1,\ldots,n) = \sum_{\boldsymbol{{x}}\in E_n^G} \prod_{k=1}^n p_{n,k}(x_{k-1},x_k),\end{equation*}

where $\boldsymbol{{x}} = (x_0,x_1,\ldots,x_n)$ and $E_{n}^G\,:\!=\, E_{n,0}\times E_{n,1}^G \times \cdots \times E_{n,n}^G$ ,

\begin{equation*} E_{n,k}^G\,:\!=\, \{x \in E_{n,k} \colon g^-_{n,k} < x < g^+_{n,k}\},\qquad k = 1,\ldots,n.\end{equation*}

Without loss of generality, we can assume that n is large enough that none of $E_{n,k}^G$ is empty.

An approximation of this kind was used in [19] to approximate the boundary crossing probability of the Brownian motion. Such discrete-time approximations of boundary crossing probabilities are well known to converge slowly to the respective probability in the ‘continuously monitored’ case since they fail to account for the probability of boundary crossing by the continuous-time process at an epoch inside a time interval between consecutive points on the time grid used.

In order to correct for this, so-called ‘continuity corrections’ have been studied in the context of sequential analysis [58] and, more recently, in the context of barrier option pricing [9]. These types of corrections have also been used in [50] to correct for discrete-time monitoring bias in Monte Carlo estimates of the boundary crossing probabilities of the Brownian motion. Without such a correction, using the classical result from [43, 44], the convergence rate of the approximation from [19] was shown to be $O(n^{-1/2})$ . However, as our numerical experiments demonstrate, using our more accurate approximations of the transition probabilities in conjunction with the Brownian bridge correction greatly improves it from $O(n^{-1/2})$ to $O(n^{-2})$ .

In the case of standard Brownian motion, the correction consists of simply multiplying the one-step transition probabilities by the non-crossing probability of a suitably pinned Brownian bridge. Due to the local Brownian nature of a diffusion process, it was shown in [3] that the leading-order term of the diffusion bridge crossing probability is given by an expression close to that of the Brownian bridge. Thus, to account for the possibility of the process X crossing the boundary inside time intervals $[t_{n,k-1},t_{n,k}]$ , we define a process ${\widetilde{X}_{n}} \,:\!=\, \{{\widetilde{X}_{n}}(t)\}_{t\in[0,1]}$ which interpolates between the subsequent nodes $(t_{n,k}, \xi_{n,k})$ with a collection of independent Brownian bridges:

(10) \begin{equation} {\widetilde{X}_{n}}(t) \,:\!=\, B_{n,k}^{ \xi_{n,k-1}, \xi_{n,k} }(t), \qquad t \in [t_{n,k-1},t_{n,k}], \ k=1,\ldots,n,\end{equation}

where $B_{n,k}^{x,y}(t) \,:\!=\, B_{n,k}^{\circ}(t) + x + n(t-t_{n,k-1})(y-x)$ , $x,y\in\mathbb R$ , and $B_{n,k}^{\circ}(t)$ , $t\in [t_{n,k-1},t_{n,k}]$ , are independent Brownian motions ‘pinned’ at the time–space points $(t_{n,k-1},0)$ and $(t_{n,k},0)$ , these Brownian bridges being independent of $\xi_n$ . Analogous to [45, Theorem 1], using the Chapman–Kolmogorov equations, the non-crossing probability of the boundaries $g^{\pm}$ for ${\widetilde{X}_{n}}$ can be expressed as

(11) \begin{equation} \mathbb{P}({\widetilde{X}_{n}} \in G)= \mathbb{E}\prod_{k=1}^{n}\left(1-{\pi}_{n,k}(g^-,g^+\mid \xi_{n,k-1},\xi_{n,k})\right),\end{equation}

where

\[ {\pi}_{n,k}(g^-,g^+\mid x,y) \,:\!=\, \mathbb{P} \bigg(\sup_{t\in [t_{n,k-1},t_{n,k}]} (B_{n,k}^{x,y}(t) -g^+(t))(B_{n,k}^{x,y}(t) -g^-(t))\ge 0 \bigg)\]

is the probability that the trajectory of a Brownian motion process pinned at the points $(t_{n,k-1},x)$ and $(t_{n,k},y)$ will be outside of the ‘corridor’ between the boundaries $g^{\pm}(t)$ at some point during the time interval $[t_{n,k-1},t_{n,k}]$ .

2.5. Step (v)

The above representation can be equivalently written as a matrix product:

(12) \begin{equation} \mathbb{P}( {\widetilde{X}_{n}} \in G ) = \textbf{T}_{n,1}\textbf{T}_{n,2}\cdots \textbf{T}_{n,n} \textbf{1}^\top,\end{equation}

where $\textbf{1}=(1,\ldots,1)$ is a row vector of length $\lvert E_{n,n}^G \rvert$ , and the sub-stochastic matrices $\textbf{T}_{n,k}$ of dimensions $\lvert E_{n,k-1}^G \rvert \times \lvert E_{n,k}^G \rvert$ have entries equal to the respective taboo transition probabilities

\begin{equation*} (1-{\pi}_{n,k}(g^-,g^+ \mid x,y))p_{n,k}(x,y), \qquad (x,y) \in E_{n,k-1}^G \times E_{n,k}^G.\end{equation*}

Unfortunately, closed-form expressions for curvilinear boundary Brownian bridge crossing probabilities ${\pi}_{n,k}(g^-,g^+\mid x,y)$ are known in a few special cases only, so we approximate the original boundaries $g^{\pm}$ with piecewise linear functions $f_n^{\pm}$ , which linearly interpolate between the subsequent nodes $(t_{n,k},g_{n,k}^{\pm})$ for $k=0,\ldots,n$ . In the special case of a one-sided boundary (when $g^-=-\infty$ ), the expression for the linear boundary crossing probability of the Brownian bridge is well known [7, p. 63]:

\begin{equation*} {\pi}_{n,k}({-}\infty ,f_n^+ \mid x,y) = \exp\bigg\{\frac{-2}{\Delta_{n}}(g_{n,k-1}^+ - x)(g_{n,k}^+ - y)\bigg\}, \qquad x<g_{n,k-1}^+,y<g_{n,k}^+.\end{equation*}

In the case when both the upper and lower boundaries $f_n^{\pm}$ are linear, if the time interval $\Delta_{n}$ is sufficiently small, we can approximate the Brownian bridge crossing probability with the sum of one-sided crossing probabilities:

\begin{equation*} {\pi}_{n,k}(\,f_n^-,f_n^+\mid x,y) = {\pi}_{n,k}(\,f_{n}^-,\infty \mid x,y) + {\pi}_{n,k}({-}\infty,f_{n}^+ \mid x,y) - \vartheta(x,y,\Delta_{n}),\end{equation*}

where the positive error term $\vartheta$ admits the obvious upper bound

\begin{align*} \vartheta(x,y,{\Delta_n}) & \leq \pi_{n,k}(\,f_n^-,\infty\mid x,y)\max_{t\in[t_{n,k-1},t_{n,k}]}P_{t,f_n^-(t);t_{n,k},y} \biggl(\sup_{s\in [t,t_{n,k}]}(W(s)-f_n^+(s))\geq 0\biggr) \\ & \quad + \pi_{n,k}({-}\infty,f_n^+\mid x,y)\max_{t\in[t_{n,k-1},t_{n,k}]}P_{t,f_n^+(t);t_{n,k},y} \biggl(\inf_{s\in [t,t_{n,k}]}(W(s)-f_n^-(s))\leq 0\biggr),\end{align*}

where $P_{s,a;t,b}(\cdot) \,:\!=\, \mathbb{P}(\,\cdot\mid W(s)=a,W(t)=b)$ . An infinite series expression for ${\pi}_{n,k}(\,f_n^-,f_n^+\mid x,y)$ can be found, e.g., in [2, 25].

We can further apply our method to approximate probabilities of the form $\mathbb{P}(X \in G, X(1) \in [a,b])$ for some $[a,b] \subseteq [g^-(1), g^+(1)]$ . We first replace the final space grid $E_{n,n}^G$ with

\begin{equation*} E_{n,n}^{[a,b]} \,:\!=\, \bigg\{a \leq x \leq b \colon x = b - j\frac{b-a}{\lfloor{\gamma (b-a)/{\Delta_n}}\rfloor}, j\in \mathbb{Z}\bigg\}.\end{equation*}

Then, instead of (12) we have $\mathbb{P}({\widetilde{X}_{n}} \in G,{\widetilde{X}_{n}}(1) \in [a,b]) = \textbf{T}_{n,1}\textbf{T}_{n,2} \cdots \textbf{T}_{n,n}\textbf{1}_{[a,b]}^{\top}$ , where $\textbf{T}_{n,n}$ is now of dimension $\lvert E_{n,n-1}^G\rvert \times \lvert E_{n,n}^{[a,b]}\rvert$ and $\textbf{1}_{[a,b]} = (1,\ldots,1)$ is a row vector of length $\lvert E_{n,n}^{[a,b]}\rvert$ .

2.6. Remarks

We conclude this section with several remarks aimed at clarifying the choices we made in our construction and the connections of our method with existing approaches in the literature.

Remark 1. Our main results actually hold in a more general setting where, instead of using uniform partitions, we employ general ones $0 = t_{n,0} < t_{n,1} <\cdots < t_{n,n} = 1$ subject to the condition that, for some constants ${\eta_2} \geq {\eta_1} > 0$ and all $n\ge 1$ ,

(13) \begin{equation} \frac{{\eta_1}}{n} \leq t_{n,k} - t_{n,k-1} \leq \frac{{\eta_2}}{n}, \qquad k=1,2,\ldots,n. \end{equation}

All the proofs extend to this case in a straightforward way.

Using a more general sequence of partitions satisfying (13) helps to improve convergence rates by choosing a higher frequency of partition nodes on time intervals where the second derivatives of the boundaries $g^{\pm}$ are large.

Remark 2. Note that the fact that the transition probabilities of the ‘time-discretised’ process $\zeta$ are Gaussian is important. High-order approximation of transition semigroups is achieved by matching sufficiently many moments for one-step transition probabilities (see, e.g., [29, Theorem 11.6.3] and [1]), and in the case of Gaussian distributions, the moments are available. When the transition kernels are Gaussian, for the discrete-space approximation used in our paper, convergence is extremely fast (cf. Lemma 3).

Observe also that directly using a weak Taylor expansion for a general diffusion process with a space-dependent diffusion coefficient results in a non-central $\chi^2$ distribution for the transition probabilities [16], which artificially limits the domain of the approximating process.

For other approaches to approximating the transition density of a general diffusion process, see, e.g., [30, 39] and the references therein.

Remark 3. The choice of the lattice spans in (5) can be explained as follows. Our approximation scheme involves replacing the original boundaries with piecewise linear ones (in Step (v)), which introduces an error of the order $O(n^{-2})$ (under assumption (13) and given that the functions $g^{\pm}$ are twice continuously differentiable). Therefore, there is no point in using $h_{n,k}$ smaller than necessary to achieve the above precision. At the end of Section 3 we present a sketch of an argument indicating that the convergence rate for the boundary crossing probabilities is $O(n^{-2})$ . It shows that it suffices to choose $h_{n,n}\asymp n^{-1}$ , whereas $h_{n,k} \asymp n^{-{1}/{2}-\delta}$ , $k < n$ , can be much larger. This is so because our Markov chain computational algorithm can be viewed as repeated trapezoidal quadrature and the partial derivative in y of the taboo (on boundary crossing) joint density of $(X(t_{n,k-1}),X(t_{n,k+1}))$ given $X(t_{n,k})=y$ at the boundary $y = g(t_{n,k})$ at all time steps before the terminal time is zero, ensuring a higher approximation rate at these steps compared to the terminal one (cf. the Euler–Maclaurin formula).

Remark 4. If we used $\delta = 0$ in (5), there would be no convergence of the sequence of processes $\{\xi_n\}_{n \geq 1}$ to the desired diffusion limit. This is because there would be no convergence of the moments of the increments (cf. Lemma 3). Note also that, instead of using the power function (5), we could take $h_{n,k}\,:\!=\, w_{n,k}({\Delta_n})^{1/2}\psi({\Delta_n})$ for some $\psi(x) \to 0$ as $x \downarrow 0$ , with $w_{n,k} \,:\!=\, v_{n,k}/\lfloor{v_{n,k}}\rfloor$ , where

\begin{equation*} v_{n,k} \,:\!=\, \frac{g_{n,k}^+ -g_{n,k}^-}{(\Delta_{n} )^{1/2}\psi(\Delta_{n} )}, \end{equation*}

(in our case, $\psi(x) = x^{\delta}/\gamma$ ). We chose the power function for simplicity’s sake.

Remark 5. Choosing suitable $\delta < \frac{1}{2}$ and $\gamma>0$ in the definition of $h_{n,k}$ for $k < n$ can be used to reduce the computational burden. In our numerical experiments, we found that reducing the value of $\delta \in \big(0,\frac{1}{2}\big)$ did not negatively affect the empirical convergence rates for boundary crossing probabilities if $\gamma$ is sufficiently large ( $\gamma \geq 1.5$ ). In the case $\delta = 0$ , our proposed scheme no longer converges since the infinitesimal moments do not converge (cf. Lemma 3). To restore convergence, we could use the adjusted transition probabilities suggested in [19]. However, we would not be able to apply the shifting state space methodology above since the approximation in [19] relies on adjusting the transition probabilities on a state space that is not changing each time step.

Remark 6. In the standard Brownian motion case, the matrix multiplication scheme in (12) can be seen as recursive numerical integration using the trapezoidal rule (cf. [45, Remark 3]). We may be tempted to employ higher-order quadrature methods instead. However, constructing a Markov chain approximation based on numerical integration techniques that use variable node positioning (e.g. Gauss–Legendre quadrature) would require interpolation of the resulting evolved transition density, causing the matrix multiplication in (11) to lose its probabilistic meaning. An alternative approach using efficient numerical integration techniques based on analytic mappings (e.g. double-exponential quadrature [60]) that maintain the positions of nodes is numerically feasible. However, verifying theoretical weak convergence for the resulting sequence of Markov chains is more difficult. Furthermore, using the trapezoidal rule allows us to use the Euler–Maclaurin summation formula to improve the convergence rate. From our numerical experimentation, the one-dimensional trapezoidal rule that we propose in this paper strikes a good balance between simplicity, flexibility, and numerical efficiency.

3. Main results

Set $\nu_n(t) \,:\!=\, \max\{k\geq 0 \colon t \geq t_{n,k}\}$ , $t\in [0,1]$ , and introduce an auxiliary pure jump process

(14) \begin{equation} {X_n}(t) \,:\!=\, \xi_{n,\nu_n(t)}, \qquad t \in [0,1].\end{equation}

Clearly, the trajectories of the process ${X_n}$ belong to the Skorokhod space ${D} = {D}([0,1])$ , which we will endow with the first Skorokhod metric,

\begin{equation*} d(x,y) = \inf_{\lambda \in \Lambda}\bigg\{\varepsilon\geq 0\colon \sup_{t\in[0,1]} \lvert x(t) - y(\lambda(t)) \rvert \leq \varepsilon, \sup_{t\in[0,1]}\lvert\lambda(t)-t \rvert \leq \varepsilon\bigg\}, \qquad x,y\in{D},\end{equation*}

where $\Lambda$ denotes the class of strictly increasing continuous mappings of [0, 1] onto itself [6, Chapter 3]. We will use ${\Rightarrow}$ to denote convergence in distribution of random elements of (D, d).

Theorem 1. Under Condition [3], $X_n {\Rightarrow} X$ as $n\to \infty$ .

Due to the small amplitude of the interpolating Brownian bridges’ oscillations, it is unsurprising that the sequence of processes $\{{\widetilde{X}_{n}}\}$ also converges weakly to X.

Corollary 1. ${\widetilde{X}_{n}} {\Rightarrow} X$ as $n\to\infty$ .

The following result is a theoretical justification of the Markov chain approximation method proposed in this paper.

Corollary 2. Let $(g^-,g^{+})$ , $(g_n^-,g_n^{+})$ , $n\geq 1$ , be elements of $\mathcal{G}$ such that $\|{g_n^{\pm} - g^{\pm}}\|_{\infty} \to 0$ as $n\to \infty$ , $G_n \,:\!=\, S(g_n^-,g_n^{+})$ . Then, for any Borel set B with $\partial B$ of zero Lebesgue measure,

(15) \begin{equation} \lim_{n\to\infty}\mathbb{P}({\widetilde{X}_{n}} \in G_n,\, {\widetilde{X}_{n}}(1) \in B) = \mathbb{P}(X \in G, X(1) \in B). \end{equation}

It immediately follows from this corollary that, for any piecewise continuous $f \colon [g^-(1)$ , $g^+(1)] \to \mathbb{R}$ , $\lim_{n \to \infty}\mathbb{E} f({\widetilde{X}_{n}}(1))\textbf{1}\{{\widetilde{X}_{n}} \in G_n\} = \mathbb{E} f(X(1))\textbf{1}\{X \in G\}$ . This relation can be used, for instance, for computing risk-neutral prices of barrier options [8].

The above results establish the validity of the proposed approximation scheme. However, numerical studies strongly suggest that, under suitable conditions (including $g^\pm \in C^2$ ), the convergence rate in (15) is $O(n^{-2})$ (cf. the classical much slower convergence rate $O(n^{-1/2})$ in the boundary crossing problem in the invariance principle from [43, 44], establishing which required a very technical lengthy argument). Unsurprisingly, proving such a sharp result turned out to be a very challenging task that requires making quite a few difficult steps and is still a work in progress even in the simplest standard Brownian motion process case. To provide some insight into why such a high convergence rate holds true for our scheme for diffusions (2), we now give a sketch of a possible argument leading to the desired bound. To simplify the argument, we assume that closed-form expressions for the ‘taboo transition densities’

\[ \phi_{n,k} (x,y) \,:\!=\, \partial_y \mathbb{P} \big(g^-(t) < X(t) <g^+ (t),\, t\in [t_{n,k-1}, t_{n,k} ];\, \ X_{t_{n,k }}\le y \mid X_{t_{n,k-1}}=x\big)\]

are available (note that, say, $\phi_{n,k} (x,y) = 0$ if $x\not\in (g^-(t_{n,k-1}), g^+ (t_{n,k-1}))$ ). Therefore, we can and do skip approximation of these densities.

Recalling the definition (6) of the grids $E_{n,k}$ , denote the ‘taboo transition semigroup’ for the discrete-time ‘skeleton’ of our process X and its discrete approximation by

\begin{equation*} (T_{n,k}\,f)(x) \,:\!=\, \int_{g^-(t_{n,k})}^{g^+(t_{n,k})} \phi_{n,k} (x,y)\,f(y)\,\mathrm{d} y, \qquad (S_{n,k}\,f)(x) \,:\!=\, \sum_{y \in E_{n,k}} \phi_{n,k} (x,y)\,f(y)h_{n,k},\end{equation*}

respectively.

Conjecture 1. Assume that $g^\pm\in C^2([0,1])$ . Then, for any bounded continuous function $f \colon \mathbb R \to \mathbb R$ and any $x\in (g^-(0), g^+(0))$ , as $n\to \infty$ ,

\begin{equation*} ( S_{n,1}\cdots S_{n,n}-T_{n,1}\cdots T_{n,n})\,f(x) = O(n^{-2}). \end{equation*}

$f\equiv 1$ yields the desired convergence rate for the boundary crossing probabilities.

A possible approach to proving the above conjecture can be outlined as follows. First, without loss of generality, we can assume that $x=0$ in this argument. Second, using the bound from [8], we replace the original boundaries $g^\pm$ with their polygonal approximations $\widehat g^\pm$ with nodes at the points $(t_{n,k}, g^\pm (t_{n,k}))$ , $k=0,1,\ldots, n$ , which introduces an error of the order $O(n^{-2})$ . Next, using the method of compositions approach [56], we get

(16) \begin{equation} S_{n,1}\cdots S_{n,n}\, f - T_{n,1}\cdots T_{n,n}\,f = \sum_{k=1}^n f_{n,k} + \varepsilon_n,\end{equation}

where

\begin{align*} f_{n,k} & \,:\!=\, T_{n,1}\cdots T_{n,k-1} (S_{n,k}-T_{n,k}) T_{n,k+1}\cdots T_{n,n}\,f, \\ \varepsilon_n & \,:\!=\, \sum_{k=2}^n (S_{n,1}\cdots S_{n,k-1}- T_{n,1}\cdots T_{n,k-1}) (S_{n,k}-T_{n,k}) T_{n,k+1}\cdots T_{n,n}\,f.\end{align*}

As $\varepsilon_n$ is a sum of terms involving compositions of the ‘small operator differences’ $S_{n,1}\cdots S_{n,k-1} -T_{n,1}\cdots T_{n,k-1}$ and $S_{n,k}-T_{n,k}$ , we can expect that its order of magnitude is higher than that of $f_{n,k}$ . Unfortunately, a formal proof of that claim appears to be a rather difficult technical task. For the rest of this semi-formal argument, we will ignore the term $\varepsilon_n$ .

Now set $\phi_{n,k;z}(y) \,:\!=\, \phi_{n,k}(y,z)$ , and let $u_{n,k}(z) \,:\!=\, (T_{n,1}\cdots T_{n,k-1} \phi_{n,k;z})(0)$ , $v_{n,k}(z) \,:\!=\, (T_{n,k+1}\cdots T_{n,n}\, f)(z)$ . Using the Euler–Maclaurin summation formula [46, Section 8.1], we get, for $1\le k\le n-1$ ,

\begin{equation*} ((S_{n,k} - T_{n,k}) v_{n,k} )(x) \approx h_{ n,k}^4\frac{B_4}{4!} \partial_{zzz}(\phi_{n,k}(x,z)v_{n,k}(z)) \big|_{z=g^-(t_{n,k} )}^{z=g^+ (t_{n,k} )},\end{equation*}

where $B_j$ denotes the jth Bernoulli number, and we used the boundary conditions

(17) \begin{equation} u_{n,k} (g^\pm (t_{n,k} )) = v_{n,k} (g^\pm (t_{n,k} )) =0 , \qquad k \leq n-1,\end{equation}

assumed the existence of the limits of the third derivatives in the above formula, and retained the first term in the asymptotic expansion.

By the linearity of the operators $S_{n,k}$ and $T_{n,k}$ , changing the order of integration and differentiation, we have, for $k \leq n-1$ ,

(18) \begin{equation} (T_{n,1}\cdots T_{n,k-1}(S_{n,k}-T_{n,k}) v_{n,k} )(0) \approx h_{n,k}^4 \frac{B_4}{4!} (u_{n,k} (z)v_{n,k} (z))''' \big|_{z=g^-(t_{n,k} )}^{z=g^+(t_{n,k} )}.\end{equation}

Using the product rule and the boundary conditions (17) yields, for $1\le k \le n-1$ ,

(19) \begin{equation} (u_{n,k} (z)v_{n,k} (z))'''\big|_{z=g^\pm(t_{n,k} )} = 3u^{\prime\prime}_{n,k}(g^\pm(t_{n,k} ))v^{\prime}_{n,k} (g^\pm(t_{n,k} )) +3u^{\prime}_{n,k} (g^\pm(t_{n,k} ))v^{\prime\prime}_{n,k} (g^\pm(t_{n,k} )).\end{equation}

From classical diffusion theory, the functions $u_{n,k} (z)$ and $v_{n,k} (z)$ coincide with $u(t_{n,k} ,z)$ and $v(t_{n,k} ,z)$ , respectively, where u(t,z) and v(t,z) are solutions of the following boundary value problems for Kolmogorov equations in the domain $D\,:\!=\,\{(t,z)\colon t\in (0,1), z\in (\widehat g^-(t), \widehat g^+ (t)) \}$ :

(20) \begin{align} (\partial_t + L)v & = 0, & v(t,\widehat g^{\pm}(t)) & = 0, & v(1,z) & = f(z), \end{align}

(21) \begin{align} (\partial_t -L^*) u & = 0, \qquad & u(t,\widehat g^{\pm}(t)) & = 0, \qquad & u(0,z) & = \delta_0(z), \end{align}

where

\begin{align*} (L w)(t,z) & \,:\!=\, \mu(t,z)\partial_z w(t,z) + \tfrac{1}{2} \partial_{zz}w(t,z), \\ (L^* w)(t,z) & \,:\!=\, -\partial_z (\mu(t,z) w (t,z)) + \tfrac{1}{2}\partial_{zz} w (t,z).\end{align*}

Using the boundary conditions on u and v on $\widehat g=\widehat g^\pm$ and the chain rule, we can show that, for both $\Psi (t)\,:\!=\, v(t, \widehat g(t))$ and $\Psi^* (t)\,:\!=\, u(t, \widehat g(t))$ ,

\begin{align*} 0 & = \frac{\mathrm{d}}{\mathrm{d} t}\Psi(t{+}) = \partial_t v(t,\widehat g(t)) + \widehat g'(t{+})\partial_z v(t,\widehat g(t)), \\ 0 & = \frac{\mathrm{d}}{\mathrm{d} t}\Psi^*(t{-}) = \partial_t u(t,\widehat g(t )) + \widehat g'(t{-})\partial_z u(t,\widehat g(t)).\end{align*}

Here and in what follows, we use notation conventions of the form $\partial_t v(t,\widehat g^+(t ))=\lim_{z\uparrow \widehat g^+(t)}\partial_t v(t,z)$ , etc. With this in mind, we now get, from (20) and (21), the relations

(22) \begin{align} -(Lv)(t,\widehat g(t)) + \widehat g'(t{+}) \partial_z v(t,\widehat g(t) ) & = 0, \end{align}

(23) \begin{align} (L^*u)(t,\widehat g(t)) + \widehat g'(t{-})\partial_z u (t,\widehat g(t)) & = 0. \end{align}

Rearranging (23), using the product rule and the boundary condition $u(t,\widehat g(t))=0$ ,

(24) \begin{align} \tfrac{1}{2} \partial_{zz}u(t,\widehat g(t)) & = \partial_z(\mu u) (t, \widehat g(t)) - \widehat g'(t{-})\partial_z u(t,\widehat g(t)) \nonumber \\ & = ((\partial_z \mu) u + \mu \partial_z u -\widehat g'(t{-})\partial_z u) (t,\widehat g(t)) \nonumber \\ & = (\mu(t,\widehat g(t)) - \widehat g'(t{-}))\partial_z u(t,\widehat g(t)). \end{align}

Similarly, using (22),

(25) \begin{equation} \tfrac{1}{2} \partial_{zz}v(t,\widehat g(t)) = -(\mu(t,\widehat g(t)) - \widehat g'(t{+}))\partial_z v(t,\widehat g(t)).\end{equation}

Substituting (24) and (25) into (19), since g is twice continuously differentiable,

\begin{align*} (u_{n,k}(z) v_{n,k} (z))'''\big|_{z = g (t_{n,k}) } & = 6\big[(\mu(t_{n,k}, z) - \widehat g'(t{-}))u^{\prime}_{n,k} (z)v^{\prime}_{n,k} (z) \\ & \quad - (\mu (t_{n,k},z) - \widehat g'(t_{n,k}{+}))u^{\prime}_{n,k} (z) v^{\prime}_{n,k} (z)\big]_{z= g(t_{n,k})} \\ & = 6(\widehat g'(t_{n,k} {+}) - \widehat g'(t_{n,k} {-})) u^{\prime}_{n,k} (g(t_{n,k} ))v^{\prime}_{n,k} (g(t_{n,k} )) \\ & = 6g''(\theta_{n,k} ) u^{\prime}_{n,k} (g(t_{n,k} ))v^{\prime}_{n,k} (g(t_{n,k} )){\Delta_n}\end{align*}

for some $\theta_{n,k} \in [t_{n,k-1},t_{n,k+1}]$ . Substituting the above expression into (18) and letting, for convenience of summation, $g_1 (t) \,:\!=\, g^- (t)$ and $g_2 (t) \,:\!=\, g^+ (t)$ , we have, for $k\leq n-1$ ,

\begin{equation*} f_{n,k} \approx \frac{ B_4}{4 }h_{n,k}^4 \sum_{i=1}^2({-}1)^ig^{\prime\prime}_i(\theta_{n,k} )u^{\prime}_{n,k} (g_i(t_{n,k} ))v^{\prime}_{n,k} (g_i(t_{n,k} )){\Delta_n},\end{equation*}

where we can replace $h_{n,k}$ on the right-hand side with $h_{n,1}$ in view of (5) and (7). Substituting the resulting expression for $f_{n,k}$ into (16), and assuming that the emerging Riemann sums converge as $n \to \infty$ and that, when $t_{n,k}\to t$ ,

\[ u^{\prime}_{n,k}(g_i(t_{n,k})) = \partial_z\widetilde u(t_{n,k},g_i(t_{n,k})) \to \partial_z\widetilde u(t,g_i(t)),\]

where $\widetilde u$ is the solution to the boundary value problem (21) with $\widehat g^\pm$ replaced with $g^\pm$ , and that similar convergence holds for $v^{\prime}_{n,k}$ and $\widetilde v$ (the latter solving (20) with $g^\pm$ instead of $\widehat g^\pm$ ), we have

\begin{equation*} \sum_{k=1}^{n-1}\,f_{n,k} \approx \frac{B_4}{4 }h_{n,1}^4\sum_{i=1}^{2}({-}1)^i \int_0^1 g^{\prime\prime}_i(t)\partial_z\widetilde u(t,g_i(t)) \partial_z \widetilde v(t,g_i(t))\,\mathrm{d} t.\end{equation*}

We can show that the integrals on the right-hand side are finite using the observations that $\partial_z \widetilde v(t,g(t)) =O((1-t)^{-1/2})$ as $t\to 1$ and that $\partial_z \widetilde u(t,g(t))$ is uniformly bounded. Our numerical computations indicate that the above conjecture on the behaviour of the Riemann sums is correct.

For $k=n$ , since $u_{n,n}(g(1)) = 0$ , using the Euler–Maclaurin summation formula we have

\begin{equation*} T_{n,1} \cdots T_{n,n-1} (S_{n,n}-T_{n,n})\,f \approx \frac{B_2}{2!}h_{n,n}^2 (u_{n,n}(z)\,f(z))'\big|_{z=g_1(1)}^{z=g_2(1)} = \frac{h_{n,n}^2}{12}u^{\prime}_{n,n} (z)\,f(z)\big|_{z=g_1(1)}^{z = g_2(1)}.\end{equation*}

It now follows from (16) that $(S_{n,1} \cdots S_{n,n } - T_{n,1} \cdots T_{n,n })\,f \approx C_1h_{n,1}^4 + C_2h_{n,n}^2$ , with the constants

$$C_1\,:\!=\, \frac{-1}{120}\sum_{i=1}^2({-}1)^i\int_0^1 g^{\prime\prime}_i(t)\partial_z\widetilde u(t,g_i(t))\partial_z \widetilde v(t,g_i(t))\,\mathrm{d} t, \qquad C_2\,:\!=\, \frac{1}{12}u^{\prime}_{n,n}(z)\,f(z)\big|_{z=g_1(1)}^{z=g_2(1)}.$$

Since $h_{n,1} = o(n^{-1/2})$ and $h_{n,n} = O(n^{-1})$ , we have obtained the claimed convergence rate.

Remark 7. To accelerate the numerical evaluation of $\mathbb{P}({\widetilde{X}_{n}} \in G_n)$ , we can ignore the normalising factors ${C_{n,k}}(x)$ as they are very close to 1. Indeed, let $\widehat{\textbf{T}}_{n,k}$ be $\lvert E_{n,k-1}^G\rvert \times \lvert E_{n,k}^G\rvert$ matrices with entries

(26) \begin{equation} q_{n,k}(x,y) \,:\!=\, (1 - {\pi}_{n,k}(\,f_n^-,f_n^+\mid x,y)) \varphi(y\mid x + {\mu}_{n,k}(x), \sigma^{2}_{n,k}(x))h_{n,k} \end{equation}

for $(x,y) \in E_{n,k-1}^G\times E_{n,k}^G$ . These matrices differ from the $\textbf{T}_{n,k}$ from (12) in that they do not involve the factors $C_{n,k}(x)$ . For M and $c_0$ defined in Lemma 2, we show below that

(27) \begin{equation} \big\lvert \mathbb{P}({\widetilde{X}_{n}} \in G_n) - \widehat{\textbf{T}}_{n,1}\widehat{\textbf{T}}_{n,2}\cdots \widehat{\textbf{T}}_{n,n}\textbf{1}^{\top} \big\rvert \leq c_0n\rho_n^{n-1}\exp\{-Mn^{2\delta}\} , \end{equation}

where $\rho_n \,:\!=\, 1 \vee \max_{1\leq j\leq n}\sup_{\lvert x\rvert \leq r} C_{n,j}(x)$ . Note that some care must be exercised when choosing $\gamma$ and $\delta$ . Using small values of $\gamma$ and $\delta$ will result in the error from replacing the normalising factors with 1 becoming non-negligible. It will be seen from the derivation of (3.3) that when $\delta = 0$ the leading term of the error of the left-hand side is equal to $2n\mathrm{e}^{-2\pi^2\gamma^2}$ . Figure 1 illustrates this observation numerically in the case of the standard Brownian motion process and boundaries

(28) \begin{equation} g^{\pm}(t) = \pm \frac{t}{3} \cosh^{-1}(2\mathrm{e}^{9/(2t)}), \qquad t\ge 0. \end{equation}

Figure 1. On this log–log plot, the bullets $\bullet$ show the absolute errors between Markov chain approximations with $\gamma =1$ , $\delta =0$ and normalising factors $C_{n,k}(x)$ replaced with 1, and the true boundary crossing probability of the standard Brownian motion process of boundaries (28). The dashed line corresponds to the straight line $2n\mathrm{e}^{-2\pi^2\gamma^2}$ .

4. Proofs

The proof of Theorem 1 is based on several auxiliary results. For the reader’s convenience, we will first state them as separate lemmata. Recall the quantity $K_r$ that appeared in Condition 3, and also ${\beta}$ and $\alpha^{1/2}$ from (3) and (4).

Lemma 1. For $r>\lvert x_0\rvert $ , $\max_{1\leq k\leq n} \sup_{\lvert x\rvert\leq r} \big(\lvert {\beta}_{n,k}(x) \rvert \vee {\alpha}_{n,k}(x) \big) \leq K^{\prime}_r$ , where $K^{\prime}_r \,:\!=\, \big(K_r + \frac{1}{2}K_r\big(\frac{3}{2} + K_r\big)\big) \vee \big(1 + \frac{1}{2}K_r\big)^2$ .

The result is directly obtained by substituting the upper bound on the partial derivatives of ${\mu_X}$ from Condition 3 into the definitions of ${\beta}$ and ${\alpha}$ in (3) and (4), respectively.

Lemma 2. For any $r>\lvert x_0 \rvert $ and $n > 1 + 2K_r$ , for the normalising factors $C_{n,k}(x)$ from (9) we have $\max_{1\leq k \leq n}\sup_{x \in E_{n,k}(r)}\lvert C_{n,k}(x) - 1 \rvert \leq c_0\mathrm{e}^{-Mn^{2\delta}}$ , where

(29) \begin{equation} E_{n,k}(r) \,:\!=\, E_{n,k-1} \cap [-r,r], \qquad r >0,\end{equation}

$\delta$ is the quantity appearing in (5), $M = M(\gamma ) \,:\!=\, \gamma^2\pi^2/ 4$ , and $c_0 \,:\!=\, 2/(1 - \mathrm{e}^{-M})$ .

Proof of Lemma 2. For brevity, let $\mu \,:\!=\, {\mu}_{n,k}(x)$ and $\sigma^2 \,:\!=\, \sigma^{2}_{n,k}(x)$ . Set

(30) \begin{equation} \widehat{\varphi}_{\sigma}(s) \,:\!=\, \int_{-\infty}^{+\infty}\varphi(x\mid 0,\sigma^2)\mathrm{e}^{-2\pi i s x}\,\mathrm{d} x = \mathrm{e}^{-2\pi^2 s^2\sigma^2} , \qquad s\in \mathbb{R}. \end{equation}

Since both $\varphi(\,\cdot\,\mid 0,\sigma^2)$ and $\widehat{\varphi}_{\sigma}(\,\cdot\,)$ decay at infinity faster than any power function, we can apply the Poisson summation formula [59, p. 252] to obtain

\begin{align*} C_{n,k}(x) & = \sum_{j\in\mathbb{Z}}\varphi(jh_{n,k}+g^+ (t_{n,k})\mid x +\mu,\sigma^2)h_{n,k} \\ & = 1 + \sum_{\ell\in\mathbb{Z}\setminus \{0\}} \widehat{\varphi}_{\sigma}(\ell/h_{n,k}) \mathrm{e}^{-2\pi i (x + \mu -g^+ (t_{n,k}))\ell/h_{n,k}} \\ & = 1 + 2\sum_{\ell=1}^{\infty} \widehat{\varphi}_{\sigma}(\ell/h_{n,k}) \cos(2\pi(x + \mu - g^+(t_{n,k})) \ell/h_{n,k}), \qquad x \in E_{n,k-1}, \end{align*}

since $\widehat{\varphi}_{\sigma }(0) = 1$ . It follows that $|C_{n,k}(x) - 1| \leq 2\sum_{\ell=1}^{\infty}\lvert \widehat{\varphi}_{\sigma}(\ell/h_{n,k})\rvert$ . Using (30) and the elementary inequality $\mathrm{e}^{-a\ell^2} \leq \mathrm{e}^{-a\ell}$ , $\ell\geq 1$ , $a>0$ , we obtain

(31) \begin{equation} |C_{n,k}(x) - 1| \leq 2\sum_{\ell=1}^{\infty}\mathrm{e}^{-2\pi^2 \ell \sigma^2 /h_{n,k}^2} = \frac{2\mathrm{e}^{-2\pi^2 \sigma^2 /h_{n,k}^2}}{1-\mathrm{e}^{-2\pi^2\sigma^2/h_{n,k}^2}}. \end{equation}

By Condition 3, for $n > 2K_r$ we have

(32) \begin{align} \inf_{\lvert x\rvert \leq r}{\alpha}_{n,k}(x) & = \inf_{\lvert x\rvert \leq r}\big(1 + \tfrac12\Delta_{n}\partial_x {\mu_X}(t_{n,k-1},x)\big)^2 \nonumber \\ & \geq 1 - \Delta_{n}\sup_{\lvert x\rvert \leq r}\lvert \partial_x {\mu_X}(t_{n,k-1},x) \rvert \geq 1 - K_r/n \geq \tfrac12. \end{align}

Substituting $\sigma^2 ={\sigma}_{n,k}^2(x) = {\alpha}_{n,k}(x)\Delta_{n}\geq {\Delta_n}/2$ into (31) and using the inequality

(33) \begin{equation} \min_{1\leq k\leq n}\frac{\Delta_{n} }{h_{n,k}^{2}} = \frac{1}{{w}_{n,n}^2\Delta_{n} } \wedge \min_{1\leq k\leq n-1}\frac{1}{{w}_{n,k}^2 \Delta_{n}^{2\delta}} \geq \frac{\gamma^2}{4} ( n \wedge n ^{2\delta} ) = \frac{\gamma^2n^{2\delta}}{4 }, \end{equation}

which holds since $\max_{1\leq k\leq n}\lvert {w}_{n,k}\rvert \leq 2\gamma^{-1}$ , $\delta < \frac12$ , we obtain

\begin{equation*} \max_{1\leq k \leq n }\sup_{\lvert x\rvert\leq r}|C_{n,k}(x) - 1| \leq \frac{2\mathrm{e}^{-Mn^{2\delta}}}{1 - \mathrm{e}^{-Mn^{2\delta}}} \leq c_0 \mathrm{e}^{-Mn^{2\delta}}. \end{equation*}

Lemma 3. Let Z be a standard normal random variable independent of $\{\xi_{n,k}\}_{k=1}^n$ . Set

(34) \begin{equation} Z_{n,k}(x) \,:\!=\, {\mu}_{n,k}(x) + {\sigma}_{n,k}(x)Z, \qquad k=1,\ldots,n, \ x \in \mathbb{R}, \end{equation}

and let $\Delta\xi_{n,k}\,:\!=\,\xi_{n,k}-\xi_{n,k-1}$ . Denote by $\mathbb{E}_{k,x}$ the conditional expectation given $\xi_{n,k-1}=x$ , and set, for $r>\lvert x_0\rvert$ and sub-grids $E_{n,k}(r)$ from (29),

(35) \begin{equation} e_{n,k}(m,r) \,:\!=\, \sup_{x \in E_{n,k}(r)}\lvert \mathbb{E}_{k,x}(\Delta \xi_{n,k})^m - \mathbb{E}Z_{n,k}^m(x)\rvert , \qquad m= 1,2,\ldots \end{equation}

Then $\max_{1\leq k\leq n} e_{n,k}(m,r) \leq c_m\mathrm{e}^{-Mn^{2\delta}}$ for $n > (1+2 K_r) \vee M^{-1/(2\delta)}$ , where $c_m\in (0,\infty)$ is a constant whose explicit value is given in (40).

Proof of Lemma 3. For brevity, we will often supress dependence on m, n, k, and x. This should cause no confusion. Set $C = C_{n,k}(x)$ , ${\lambda} \,:\!=\, \mathbb{E}_{k,x}({\Delta\xi}_{n,k})^m$ , ${\widetilde{\lambda}} \,:\!=\, \mathbb{E} Z_{n,k}^m(x)$ , for $m= 1,2,\ldots$ Using the triangle inequality,

(36) \begin{equation} \lvert {\lambda} - {\widetilde{\lambda}} \rvert = \bigg\lvert \frac{1-C}{C}{\widetilde{\lambda}} + \frac{1}{C}(C {\lambda} - {\widetilde{\lambda}}) \bigg\rvert \leq \bigg\lvert\frac{C-1}{C}\bigg\rvert\lvert {\widetilde{\lambda}}\rvert + \frac{1}{C}\lvert C{\lambda} - {\widetilde{\lambda}}\rvert. \end{equation}

The term $C{\lambda} = C \mathbb{E}_{k,x} ({\Delta\xi}_{n,k})^m$ can be viewed as a trapezoidal approximation of ${\widetilde{\lambda}}=\mathbb{E} Z_{n,k}^m(x)$ , so after rewriting ${\widetilde{\lambda}}$ as an integral, we can express $C{\lambda} - {\widetilde{\lambda}}$ as the quadrature error

\begin{align*} \varepsilon_{k}(x) \,:\!=\, C{\lambda} - {\widetilde{\lambda}} & = \sum_{j \in \mathbb{Z}} (jh_{n,k} + g^+ (t_{n,k}) - x)^m \varphi(jh_{n,k} + g^+ (t_{n,k})- x\mid \mu, \sigma^2) h_{n,k} \\ & \quad - \int_{-\infty}^{+\infty}(u + g^+ (t_{n,k})-x)^m\varphi(u+g^+(t_{n,k}) - x\mid\mu,\sigma^2)\,\mathrm{d} u, \end{align*}

where $\mu = {\mu}_{n,k}(x)$ and $\sigma^2 = {\sigma}_{n,k}^2(x)$ . We further note that, due to (4), the condition $n \geq 2 K_r$ ensures that $\sigma^2 > 0$ . For $s\in \mathbb{R}$ , set

(37) \begin{align} {\widehat{p}}(s) \,:\!=\, \int_{-\infty}^{+\infty}(v + \mu)^m\varphi(v\mid 0, \sigma^2)\mathrm{e}^{-2\pi i s v}\,\mathrm{d} v & = \sum_{l=0}^m\binom{m}{l}\mu^{m-l}\int_{-\infty}^{+\infty}v^l \varphi(v\mid0,\sigma^2)\mathrm{e}^{-2\pi isv}\,\mathrm{d} v \nonumber \\ & = \sum_{l=0}^m\binom{m}{l}\mu^{m-l}({-}i\sigma)^lH_l(2\pi s\sigma)\mathrm{e}^{-2\pi^2 s^2 \sigma^2}, \end{align}

where $H_l(x) \,:\!=\,({-}1)^l\mathrm{e}^{x^2/2}({\mathrm{d}^l}/{\mathrm{d} x^l})\mathrm{e}^{-x^2/2}$ , $x\in \mathbb{R}$ , $l \geq 1$ , is the lth Chebyshev–Hermite polynomial. Since both $(\,\cdot\,-x)^m \varphi(\,\cdot\, - x\mid\mu,\sigma^2)$ and ${\widehat{p}}(\,\cdot\,)$ decay at infinity faster than any power function, using the Poisson summation formula [59, p. 252] and the change of variables $v = u h_{n,k} + g^+ (t_{n,k}) -x $ in (37), we obtain

\begin{align*} \varepsilon_{k}(x) & = \sum_{\ell\in\mathbb{Z}\backslash \{0\}} {\widehat{p}}(\ell/h_{n,k}) \exp\{-2\pi i({-}g^+(t_{n,k}) + x + \mu)\ell/h_{n,k}\} \\ & = 2\sum_{\ell= 1}^{\infty} {\operatorname{Re}}\bigl[{\widehat{p}}(\ell/h_{n,k}) \exp\{-2\pi i({-}g^+ (t_{n,k}) + x +\mu)\ell/h_{n,k}\}\bigr]. \end{align*}

Since $\lvert {\operatorname{Re}} z \rvert\leq \lvert z\rvert$ , $z \in \mathbb{C}$ , and $\lvert \mathrm{e}^{is}\rvert\leq 1$ , $s \in \mathbb{R}$ , we obtain $\lvert \varepsilon_{k}(x)\rvert \leq 2\sum_{\ell= 1}^{\infty}\lvert{\widehat{p}}(\ell/h_{n,k})\rvert$ . Note that $\lvert H_l(u) \rvert \leq C^{\prime}_l(\lvert u\rvert^{\ell} + 1)$ , $u \in \mathbb{R}$ , $l =1,2,\ldots$ , where $C^{\prime}_l$ is a constant that depends on l only and we can assume without loss of generality that $\{C^{\prime}_l \}_{l\geq 1}$ is a non-decreasing sequence. Therefore, we have $\lvert ({-}i \sigma )^l H_l(2 \pi s \sigma )\rvert \leq C_l( s^l \sigma^{2l} +\sigma^l)$ , $s \geq 1$ , where $C_l\,:\!=\, (2\pi)^lC^{\prime}_l$ . Using $\mu^{m-l}(\ell\sigma^2/h_{n,k})^l=\beta_{n,k}^{m-l}(x)\alpha_{n,k}^l(x)\ell^m{\Delta_n}^m/(h_{n,k}^l\ell^{m-l})$ , and the fact that $h_{n,k}^{-l}\ell^{-(m-l)}\leq h_{n,k}^{-m}$ for $l\leq m$ as $h_{n,k}<1$ , we obtain from (37) that

\begin{align*} \lvert \varepsilon_{k}(x) \rvert & \leq 2\sum_{\ell =1}^{\infty}\sum_{l=0}^m \binom{m}{l} C_l \lvert \mu\rvert ^{m-l} \bigg(\bigg(\frac{\ell\sigma^2}{h_{n,k}}\bigg)^l + \sigma^l\bigg)\mathrm{e}^{-2\pi^2 \sigma^2 \ell^2/h_{n,k}^2} \\ & \leq 2 \sum_{\ell=1}^{\infty}\sum_{l=0}^m \binom{m}{l}C_l \bigg(\bigg(\frac{{\Delta_n}}{h_{n,k}}\bigg)^m\lvert{\beta}_{n,k}^{m-l}(x)\rvert{\alpha}_{n,k}^{l}(x)\ell^m \\ &\quad + \lvert {\beta}_{n,k}^{m-l}(x)\rvert {\alpha}_{n,k}^{l/2}(x) \Delta_{n}^{m-l/2}\bigg) \mathrm{e}^{-2\pi^2 \sigma^2 \ell^2 /h_{n,k}^2}. \end{align*}

Since $C_l$ is non-decreasing in l,

\begin{equation*} \sup_{x \in E_{n,k}(r)}\sum_{l=0}^m\binom{m}{l}C_l\bigg(\frac{\Delta_{n} }{h_{n,k}}\bigg)^m \lvert \beta_{n,k}^{m-l}(x)\rvert \alpha_{n,k}^l(x)\leq 2^mC_m ( 2K^{\prime}_r )^m \,=\!:\,L_{m,r}, \end{equation*}

where we used Lemma 1 and the inequality $\max_{1\leq k\leq n}\Delta_{n}/h_{n,k} \leq 2$ , which follows from $\min_{1\leq k\leq n}h_{n,k}\geq \min\{ (1/n)^{1/2 + \delta},1/n\}/2 = 1/2n$ . Again using Lemma 1 and the trivial bound $\Delta_{n}^{m-l/2}\leq 1$ , $0\leq l\leq m$ , we have

\begin{equation*} \sup_{x \in E_{n,k}(r)}\sum_{l=0}^{m}\binom{m}{l}C_l \lvert \beta_{n,k}^{m-l}(x)\rvert \alpha_{n,k}^{l/2}(x)(\Delta_{n})^{m-l/2} \leq 2^m C_m(K^{\prime}_r)^m \leq L_{m,r}. \end{equation*}

Hence,

\begin{equation*} \sup_{x \in E_{n,k}(r)}\lvert\varepsilon_k(x) \rvert \leq 2L_{m,r}\sum_{\ell =1}^{\infty} (\ell^m + 1)\mathrm{e}^{-2\pi^2\sigma^2 \ell^2/h_{n,k}^2} \leq 4L_{m,r}\sum_{\ell =1}^{\infty} \ell^m \mathrm{e}^{-\ell M n^{2\delta}}, \end{equation*}

where we used (32), (33) and the bound $\mathrm{e}^{-a\ell^2} \leq \mathrm{e}^{-a\ell}$ , $\ell \geq 1$ , $a>0$ , in the second inequality. Note that $\sum_{\ell=1}^{\infty}\ell^mz^{\ell}\leq a_mz$ , $z \in [0,\mathrm{e}^{-1}]$ , where $a_m\,:\!=\, \sum_{\ell =1}^{\infty}\ell^m \mathrm{e}^{-\ell +1} <\infty$ . As $Mn^{2\delta}>1$ , we obtain from here that

(38) \begin{equation} \max_{1\leq k \leq n }\sup_{x \in E_{n,k}(r)}\lvert \varepsilon_{k}(x)\rvert \leq 4a_mL_{m,r} \mathrm{e}^{-Mn^{2\delta}}. \end{equation}

From Lemma 2,

(39) \begin{equation} \sup_{x \in E_{n,k}(r)}\bigg|\frac{ C_{n,k}(x) -1}{C_{n,k}(x)} \bigg| \leq \frac{c_0\mathrm{e}^{-Mn^{2\delta}}}{1-c_0}. \end{equation}

Using inequalities (38) and (39) in (36), we get

\begin{equation*} \max_{1\leq k\leq n}\sup_{x \in E_{n,k}(r)}\lvert\mathrm{e}_{n,k}(m,r)\rvert \leq c_m\mathrm{e}^{-Mn^{2\delta}}, \end{equation*}

where

(40) \begin{equation} c_m \,:\!=\, \frac{c_0}{1-c_0}\max_{1\leq k\leq n}\sup_{x \in E_{n,k}(r)} \lvert\mathbb{E}Z_{n,k}^m(x)\rvert + \frac{4a_mL_{m,r}}{1-c_0}. \end{equation}

The boundedness of $\max_{1\leq k\leq n}\sup_{x \in E_{n,k}(r)}\lvert \mathbb{E} Z_{n,k}^m(x)\rvert$ can be proved by applying the inequality $\lvert x +y \rvert^m \leq 2^{m-1}(\lvert x \rvert^m + \lvert y\rvert^m)$ , $x,y \in\mathbb{R}$ , $m\geq 1$ , to obtain

\begin{align*} \sup_{x \in E_{n,k}(r)}\lvert\mathbb{E} Z_{n,k}^m(x)\rvert & \leq 2^{m-1} \sup_{\lvert x\rvert \leq r}(\lvert {\beta}_{n,k}(x)\Delta_{n} \rvert^m + \lvert {\alpha}_{n,k}(x)\Delta_{n} \rvert^{m/2} \mathbb{E} \lvert Z\rvert^m ) \\ & \leq 2^{m-1}\bigg((K^{\prime}_r)^m + (2K^{\prime}_{r})^{m/2}\pi^{-1/2}\Gamma\bigg(\frac{m+1}{2}\bigg)\bigg) < \infty, \end{align*}

where $\Gamma$ is the gamma function. Lemma 3 is proved.

To prove the convergence stated in Theorem 1 we will use the martingale characterisation method, verifying the sufficient conditions for convergence from [18, Theorem 4.1 in Chapter 7] (to be referred to as the EK theorem in what follows). For $x \in E_{n,k-1}$ , let

\begin{equation*} b_{n,k}(x) \,:\!=\, \frac{1}{\Delta_{n}}\mathbb{E}[\Delta\xi_{n,k}\mid \xi_{n,k-1} =x ], \qquad {a}_{n,k}(x) \,:\!=\, \frac{1}{\Delta_{n}}\textrm{var}[\Delta\xi_{n,k}\mid \xi_{n,k-1} =x].\end{equation*}

Using the standard semimartingale decomposition of $X_n$ (see (14)), we set

\begin{equation*} B_n(t) \,:\!=\, \sum_{k=1}^{\nu_n(t)}b_{n,k}(\xi_{n,k-1})\Delta_{n}, \qquad A_n(t) \,:\!=\, \sum_{k=1}^{\nu_n(t)}{a}_{n,k}(\xi_{n,k-1})\Delta_{n},\end{equation*}

and let $M_n\,:\!=\, X_n - B_n$ . With respect to the natural filtration

\begin{equation*} \textbf{F}^n\,:\!=\, \{ \sigma(X_n(s),B_n(s),A_n(s) \colon s\leq t) \colon t\geq 0\} = \{\sigma(\xi_{n,k} \colon k \leq \nu_n(t),t\geq 0 )\},\end{equation*}

our $B_n$ , $A_n$ , and $M_n$ are the predictable drift, angle bracket, and martingale component, respectively, of the process ${X_n}$ .

The EK theorem is stated for time-homogeneous processes. To use it in our case, we consider the vector-valued processes $\boldsymbol{{X}}_n(t) \,:\!=\, (t,X_n(t))$ and, for a fixed $r>0$ , let $\tau_n^r$ be localising $\textbf{F}^n$ -stopping times, $\tau_n^r \,:\!=\, \inf\{t \colon \|{\boldsymbol{{X}}_n(t)}\| \vee \|{\boldsymbol{{X}}_n(t{-}) }\|\geq r \}$ , $\|{\boldsymbol{{u}}}\| = \lvert u_1\rvert \vee \lvert u_2 \rvert$ being the maximum norm of $\boldsymbol{{u}} =(u_1,u_2)$ .

Lemma 4. For each fixed $r>\lvert x_0\rvert $ , as $n\to\infty$ ,

\begin{equation*} \sup_{t \leq 1 \wedge \tau_n^r}\bigg\lvert B_n(t) - \int_0^t{\mu_X}(s,X_n(s))\,\mathrm{d} s\bigg\rvert \xrightarrow{\mathrm{a.s.}} 0, \qquad \sup_{t \leq 1 \wedge \tau_n^r}\lvert A_n(t) - t\rvert \xrightarrow{\mathrm{a.s.}} 0. \end{equation*}

Proof of Lemma 4. Since on each of the time intervals $[t_{n,k-1},t_{n,k})$ , $k=1,\ldots,n$ , the process $X_n$ is equal to $\xi_{n,k-1}$ , we have the following decomposition:

(41) \begin{align} & B_n(t) - \int_0^t {\mu_X}(s,X_n(s))\,\mathrm{d} s \nonumber \\ & = \sum_{k=1}^{\nu_n(t)}\biggl[ {b}_{n,k}(\xi_{n,k-1})\Delta_{n}- \int_{t_{n,k-1}}^{t_{n,k}} {\mu_X}(s,{X_n}(s))\,\mathrm{d} s\biggr] - \int_{t_{n,\nu_n(t)}}^{t}{\mu_X}(s,{X_n}(s))\,\mathrm{d} s \nonumber \\ & = \sum_{k=1}^{\nu_n(t)}({b}{n,k}(\xi_{n,k-1}) - {\beta}_{n,k}(\xi_{n,k-1}))\Delta_{n}+ \sum_{k=1}^{\nu_n(t)}({\beta}_{n,k}(\xi_{n,k-1}) - {\mu_X}(t_{n,k-1},\xi_{n,k-1}))\Delta_{n}\nonumber \\ & \quad + \sum_{k=1}^{\nu_n(t)}\int_{t_{n,k-1}}^{t_{n,k}} [{\mu_X}(t_{n,k-1},X_n(s))-{\mu_X}(s,X_n(s))]\,\mathrm{d} s - \int_{t_{n,\nu_n(t)}}^{t}{\mu_X}(s,\xi_{n,\nu_n(t)})\,\mathrm{d} s. \end{align}

Due to the stopping-time localisation, the first term on the right-hand side of (41) has the following upper bound (see (8), (34), and (35)):

(42) \begin{align} \sup_{t \leq 1 \wedge \tau_n^r} & \Bigg\lvert\sum_{k=1}^{\nu_n(t)}({b}_{n,k}(\xi_{n,k-1}) - {\beta}_{n,k}(\xi_{n,k-1}))\Delta_{n}\Bigg\rvert \nonumber \\ & = \sup_{t \leq 1\wedge \tau_n^r}\Bigg\lvert\sum_{k=1}^{\nu_n(t)}(\mathbb{E}[\Delta\xi_{n,k}\mid \xi_{n,k-1}] - \mathbb{E}[Z_{n,k}(\xi_{n,k-1})\mid\xi_{n,k-1}])\Bigg\rvert \nonumber \\ & \leq \sum_{k=1}^n\sup_{x \in E_{n,k}(r)}\lvert \mathbb{E}_{k,x}\Delta \xi_{n,k}-\mathbb{E} {Z_{n,k}}(x)\rvert \leq \sum_{k=1}^n e_{n,k}(1,r). \end{align}

To bound the second term on the right-hand side of (41), we use the definition of $\beta_{n,k}$ in (3) and Condition 3 to get following inequality:

(43) \begin{align} \sup_{x \in E_{n,k}(r)}\lvert{\beta}_{n,k}(x) - {\mu_X}(t_{n,k-1},x)\rvert & \leq \tfrac12\Delta_{n}\sup_{\lvert x\rvert \leq r}\big\lvert\big(\partial_t{\mu_X} + {\mu_X}\partial_x{\mu_X} + \tfrac12\partial_{xx}{\mu_X}\big)(t_{n,k-1},x)\big\rvert \nonumber \\ & \leq \tfrac12\Delta_{n}K_r\big(K_r + \tfrac{3}{2}\big). \end{align}

The second-last term in (41) can be bounded from above by using the bound for $\partial_t {\mu_X}$ from Condition 3:

(44) \begin{equation} \sup_{t \leq 1\wedge \tau_n^r}\sum_{k=1}^{\nu_n(t)}\bigg\lvert\int_{t_{n,k-1}}^{t_{n,k}} [{\mu_X}(t_{n,k-1},X_n(s))-{\mu_X}(s,X_n(s))]\,\mathrm{d} s\bigg\rvert \leq K_r\Delta_{n}. \end{equation}

Again using Condition 3, the last term in (41) is bounded as follows:

(45) \begin{equation} \sup_{t\leq 1 \wedge \tau_n^r}\bigg\lvert\int_{t_{n,\nu_n(t)}}^t{\mu_X}(s,X_{n,\nu_n(t)})\,\mathrm{d} s\bigg\rvert \leq K_r\Delta_{n} . \end{equation}

Using inequalities (42)–(45) in the decomposition (41), we obtain

\begin{align*} \sup_{t \leq 1 \wedge \tau_n^r}\bigg\lvert B_n(t) - \int_0^t{\mu_X}(s,X_n(s))\,\mathrm{d} s \bigg\rvert \leq \sum_{k=1}^n e_{n,k}(1,r) + K_r\big(\tfrac12 K_r + \tfrac{11}{4}\big)\Delta_{n}. \end{align*}

Since $ \Delta_{n}\to 0$ as $n\to \infty$ , the first half of the lemma follows after applying Lemma 3 with $m=1$ .

Similarly,

(46) \begin{equation} A_n(t) - t = \sum_{k=1}^{\nu_n(t)}({a}_{n,k}(\xi_{n,k-1}) - {\alpha}_{n,k}(\xi_{n,k-1}))\Delta_{n} + \sum_{k=1}^{\nu_n(t)}({\alpha}_{n,k}(\xi_{n,k-1}) - 1) \Delta_{n}- \int_{t_{n,\nu_n(t)}}^{t} \,\mathrm{d} s. \end{equation}

To bound the first term on the right-hand side of (46), we use ${\text{Var}} [Y \mid X] = \mathbb{E}[Y^2\mid X] - (\mathbb{E}[Y\mid X])^2$ for a square-integrable random variable Y to obtain

(47) \begin{align} \sup_{t \leq 1 \wedge \tau_n^r} & \Bigg\lvert\sum_{k=1}^{\nu_n(t)}({a}_{n,k}(\xi_{n,k-1}) - {\alpha}_{n,k}(\xi_{n,k-1}))\Delta_{n}\Bigg\rvert \nonumber \\ & = \sup_{t \leq 1 \wedge \tau_n^r}\Bigg\lvert\sum_{k=1}^{\nu_n(t)}({\text{Var}}[\Delta \xi_{n,k}\mid \xi_{n,k-1}] - {\text{Var}}[{Z_{n,k}}(\xi_{n,k-1}) \mid \xi_{n,k-1}]) \Bigg\rvert \nonumber \\ & \leq \sup_{t \leq 1 \wedge \tau_n^r} \sum_{k=1}^{\nu_n(t)}\bigl\lvert \mathbb{E}[(\Delta \xi_{n,k})^2\mid \xi_{n,k-1}] - \mathbb{E}[{Z_{n,k}}^2(\xi_{n,k-1})\mid\xi_{n,k-1}]\bigr\rvert \nonumber \\ & \quad + \sup_{t \leq 1 \wedge \tau_n^r}\sum_{k=1}^{\nu_n(t)}\bigl\lvert(\mathbb{E}[\Delta\xi_{n,k}\mid\xi_{n,k-1}])^2 - (\mathbb{E}[{Z_{n,k}}(\xi_{n,k-1})\mid\xi_{n,k-1}])^2\bigr\rvert \nonumber \\ & \leq \sum_{k=1}^{n} e_{n,k}(2,r) + 2\sum_{k=1}^ne_{n,k}(1,r) \biggl(e_{n,k}(1,r) + \sup_{x \in E_{n,k}(r) }\lvert \mathbb{E} {Z_{n,k}}(x)\rvert\biggr) , \end{align}

where we used the elementary bound

(48) \begin{equation} \lvert x^2 -y^2 \rvert \leq \lvert x - y\rvert (\lvert x-y\rvert + 2\lvert y\rvert) \end{equation}

in the final inequality. Furthermore,

\begin{equation*} \max_{1\leq k \leq n}\sup_{x\in E_{n,k}(r)}\lvert \mathbb{E} {Z_{n,k}}(x)\rvert \leq \max_{1\leq k \leq n}\sup_{\lvert x\rvert\leq r}\lvert {\beta}_{n,k}(x)\rvert\Delta_{n} \leq K^{\prime}_r . \end{equation*}

Lemma 3 with $m=1$ and $m=2$ implies that the expression in the last line of (47) vanishes as $n\to\infty$ . The second term on the right-hand side of (46) is bounded from above using (4), Lemma 1, and Condition 3:

(49) \begin{align} \sup_{t\leq 1 \wedge \tau_n^r} \sum_{k=1}^{\nu_n(t)}\lvert {\alpha}_{n,k}(\xi_{n,k-1}) - 1\rvert\Delta_{n} & \leq \max_{1\leq k\leq n}\sup_{x\in E_{n,k}(r)} \big\lvert \alpha^{1/2}_{n,k}(x) - 1\big\rvert\big(\alpha^{1/2}_{n,k}(x) + 1\big) \nonumber \\ & \leq \tfrac{1}{2} \Delta_{n}K_r (\sqrt{K^{\prime}_r} + 1). \end{align}

For the last term in (46) we have

(50) \begin{equation} \sup_{t\leq 1 \wedge \tau_n^r}\bigg\lvert \int_{t_{n,\nu_n}(t)}^t \,\mathrm{d} s\bigg\rvert \leq \Delta_{n}. \end{equation}

Applying inequalities (47)–(50) to (46), we complete the proof of Lemma 4.

Lemma 5. For each fixed $r>\lvert x_0\rvert $ ,

(51) \begin{align} \lim_{n\to\infty}\mathbb{E} \sup_{t\leq 1 \wedge \tau_n^r} \lvert B_n(t) - B_n(t{-}) \rvert^2 & = 0, \end{align}

(52) \begin{align} \lim_{n\to\infty}\mathbb{E} \sup_{t\leq 1 \wedge \tau_n^r} \lvert A_n(t) - A_n(t{-}) \rvert & = 0, \end{align}

(53) \begin{align} \lim_{n\to\infty}\mathbb{E} \sup_{t\leq 1 \wedge \tau_n^r} \lvert X_n(t) - X_n(t{-}) \rvert^2 & = 0. \end{align}

Proof of Lemma 5. Set $\overline{\xi}_n \,:\!=\, \max_{1\leq k\leq n}\lvert \xi_{n,k}\rvert$ and

\begin{equation*} \chi_n^r \,:\!=\, \min\{k \leq n \colon \lvert \xi_{n,k}\rvert \geq r\}\textbf{1}\{\overline{\xi}_n \geq r\} + n\textbf{1}\{\overline{\xi}_n <r\}. \end{equation*}

The jumps of $B_n$ are given by the conditional means of the increments, so

\begin{equation*} \mathbb{E} \sup_{t\leq 1 \wedge \tau_n^r} \lvert B_n(t) - B_n(t{-}) \rvert^2 = \mathbb{E} \max_{ k \leq \chi_n^r }(\mathbb{E}[{\Delta\xi}_{n,k}\mid\xi_{n,k-1}])^2 \leq \mathbb{E} \max_{1\leq k \leq n }\sup_{x \in E_{n,k}(r)}(\mathbb{E}_{k,x}\Delta \xi_{n,k})^2. \end{equation*}

By the triangle inequality, for $x \in E_{n,k}(r)$ ,

\begin{equation*} \lvert\mathbb{E}_{k,x}\Delta \xi_{n,k}\rvert \leq \lvert\mathbb{E}_{k,x}\Delta\xi_{n,k} - \mathbb{E}{Z_{n,k}}(x)\rvert + \lvert \mathbb{E} {Z_{n,k}}(x) \rvert \leq e_{n,k}(1,r) + \lvert {\beta}_{n,k}(x)\rvert\Delta_{n}. \end{equation*}

By inequality (13) and Lemmata 1 and 3, we obtain (51). The jumps of $A_n$ are given by the conditional variances of the increments, so

\begin{equation*} \mathbb{E} \sup_{t\leq 1 \wedge \tau_n^r} \lvert A_n(t) - A_n(t{-}) \rvert = \mathbb{E} \max_{k\leq \chi_n^r}{\text{Var}}[{\Delta\xi}_{n,k}\mid\xi_{n,k-1}] \leq \mathbb{E} \max_{1\leq k \leq n }\sup_{x\in E_{n,k}(r)}{\text{Var}}_{k,x}\Delta\xi_{n,k}, \end{equation*}

where ${\text{Var}}_{k,x}[\,\cdot\,]\,:\!=\,{\text{Var}}[\,\cdot\mid \xi_{n,k-1}=x]$ . Using (48), we obtain, for $x \in E_{n,k}(r)$ ,

\begin{align*} \lvert {\text{Var}}_{k,x} \Delta \xi_{n,k}\rvert & \leq \lvert {\text{Var}}_{k,x} \Delta \xi_{n,k} - {\text{Var}} {Z_{n,k}}(x)\rvert +{\text{Var}} {Z_{n,k}}(x) \\ & \leq \lvert \mathbb{E}_{k,x} (\Delta \xi_{n,k})^2 - \mathbb{E} Z_{n,k}^2(x)\rvert + \lvert (\mathbb{E}_{k,x} \Delta \xi_{n,k})^2 - (\mathbb{E} Z_{n,k}(x))^2\rvert + \sigma^{2}_{n,k}(x) \\ & \leq e_{n,k}(2,r) + e_{n,k}(1,r)( e_{n,k}(1,r) + 2\lvert {\beta}_{n,k}(x) \rvert \Delta_{n} ) + {\alpha}_{n,k}(x)\Delta_{n}. \end{align*}

By the local boundedness of ${\beta}_{n,k}$ and ${\alpha}_{n,k}$ , from Lemma 1 we obtain (52). Further,

\begin{equation*} \mathbb{E} \sup_{t\leq 1 \wedge \tau_n^r} \lvert X_n(t) - X_n(t{-}) \rvert^2 = \mathbb{E} \max_{k\leq \chi_n^r}({\Delta\xi}_{n,k})^2. \end{equation*}

Using Lyapunov’s inequality, we obtain

\begin{align*} \mathbb{E} \max_{k\leq \chi_n^r}({\Delta\xi}_{n,k})^2 \leq \Big(\mathbb{E} \max_{k\leq \chi_n^r}( {\Delta\xi}_{n,k})^{4}\Big)^{1/2} & \leq \Bigg(\mathbb{E} \sum_{k \leq \chi_n^r} ({\Delta\xi}_{n,k})^4 \Bigg)^{1/2} \\ & \leq \Bigg(\sum_{k=1}^n\sup_{x\in E_{n,k}(r)}\mathbb{E}_{k,x}( \Delta \xi_{n,k} )^{4}\Bigg)^{1/2}. \end{align*}

By the triangle inequality, we have

\begin{align*} \lvert \mathbb{E}_{k,x} (\Delta \xi_{n,k})^{4} \rvert & \leq \lvert \mathbb{E}_{k,x} (\Delta \xi_{n,k})^4 - \mathbb{E} Z_{n,k}^4(x)\rvert + \mathbb{E} Z_{n,k}^4(x) \\ & \leq e_{n,k}(4,r) + ({\beta}_{n,k}(x)\Delta_{n} )^4 + 6({\beta}_{n,k}(x)\Delta_{n} )^2{\alpha}_{n,k}(x)\Delta_{n}+ 3( {\alpha}_{n,k}(x)\Delta_{n} )^2. \end{align*}

Using Lemmata 1 and 3 we obtain (53). Lemma 5 is proved.

Proof of Theorem 1. We verify the conditions of the EK theorem. Denote by L the generator of the bivariate process $\boldsymbol{{X}} \,:\!=\, \{\boldsymbol{{X}}(t) = (t,X(t))\}_{t\in [0,1]}$ ,

\begin{equation*} Lf = \partial_t f + \mu \partial_xf + \tfrac12 \partial_{xx}\,f, \qquad f\in C_\mathrm{c}^{\infty}(\mathbb{R}^2), \end{equation*}

where $C_\mathrm{c}^{\infty}(\mathbb{R}^2)$ is the space of infinitely many times differentiable functions with compact support. The distribution of $\boldsymbol{{X}}$ is the solution to the martingale problem for L, i.e., for $f \in C_\mathrm{c}^{\infty}(\mathbb{R}^2)$ ,

\begin{equation*} f(\boldsymbol{{X}}(t)) - f(\boldsymbol{{X}}(0)) - \int_0^t Lf(\boldsymbol{{X}}(s))\,\mathrm{d} s , \qquad t\in[0,1], \end{equation*}

is a martingale. Using Condition 3, by [18, Proposition 3.5 in Chapter 5] the martingale problem for L is well posed since the solution for the stochastic differential equation (2) exists and is unique. Therefore, the first condition in the EK theorem is met.

The martingale characteristics of $\boldsymbol{{X}}_n = (t,{X_n}(t))$ are given by

\begin{equation*} \boldsymbol{{B}}_n(t) \,:\!=\, (t,B_n(t)), \qquad \boldsymbol{{A}}_n(t) \,:\!=\, \left(\begin{array}{} 0 \hphantom{dd} &0\\ 0 \hphantom{dd} & A_n(t)\end{array}\right), \qquad \boldsymbol{{M}}_n(t) \,:\!=\, (0,M_n(t)). \end{equation*}

A simple calculation shows that $\boldsymbol{{M}}_n$ and $\boldsymbol{{M}}_n^{\top}\boldsymbol{{M}}_n - \boldsymbol{{A}}_n$ are $\textbf{F}^n$ -martingales. It follows from Lemmata 4 and 5 that conditions (4.3)–(4.7) in the EK theorem are satisfied, which means that all the conditions of that theorem are met. Theorem 1 is proved.

Proof of Corollary 1. Denote the process whose trajectories are polygons with nodes $(t_{n,k}, \xi_{n,k})$ by ${\widehat{X}_n}$ . By the triangle inequality,

\begin{equation*} \|{{\widetilde{X}_{n}}-{X_n}}\|_{\infty} \leq \|{{\widetilde{X}_{n}}-{\widehat{X}_n}}\|_{\infty} + \|{{\widehat{X}_n}-{X_n}}\|_{\infty}, \end{equation*}

where ${\widetilde{X}_{n}}$ was defined in (10). Using the distribution of the maximum of the standard Brownian bridge $B^{\circ}$ [7, p. 63], for any $\varepsilon>0$ we obtain

\begin{align*} \mathbb{P}(\|{{\widetilde{X}_{n}}-{\widehat{X}_n}}\|_{\infty} \geq \varepsilon) &= \mathbb{P}\biggl(\max_{1\leq k \leq n} \sup_{s \in[t_{n,k-1},t_{n,k}]} \lvert {B^{\circ}}_{n,k}(s)\rvert \geq \varepsilon\biggr) \\ & \leq \sum_{k=1}^n\mathbb{P}\biggl(\sup_{t\in[0,1]}\lvert{B^{\circ}}(t)\rvert \geq \varepsilon/\sqrt{\Delta_{n}} \biggr) \leq 2 n \exp\bigl\{-2\varepsilon^2/ \Delta_{n} \bigr\}. \end{align*}

Hence, $\|{{\widetilde{X}_{n}}-{\widehat{X}_n}}\|_{\infty} \xrightarrow{\mathrm{p}} 0$ since $\Delta_{n}= 1/n$ . Further, $\|{{\widehat{X}_n}-{X_n}}\|_{\infty} = \sup_{t \in (0,1]}\lvert X_n(t) - X_n(t{-})\rvert\xrightarrow{\mathrm{p}} 0$ since ${X_n} {\Rightarrow} X$ and X is almost surely continuous. Therefore, $d({\widetilde{X}_{n}},{X_n}) \leq \|{{\widetilde{X}_{n}} - {X_n}}\|_{\infty} \xrightarrow{\mathrm{p}} 0$ . It follows from [6, Theorem 4.1] that ${\widetilde{X}_{n}} {\Rightarrow} X$ as $n\to\infty$ .

Proof of Corollary 2. For sets $A \subset {C}$ and $B \subseteq \mathbb{R}$ , set $A[B] \,:\!=\, A \cap \{ x \in {C} \colon x(1) \in B\}$ . Recall that, for $(g^-,g^{+})\in \mathcal{G}$ , $\inf_{t\in [0,1]}(g^+(t) - g^-(t) ) >0$ . For any $\varepsilon \in (0, \varepsilon')$ , $\varepsilon'\,:\!=\,[ \inf_{t\in [0,1]}(g^+(t) - g^-(t) )/2] \wedge ( g^+(0) -x_0) \wedge (x_0 -g^-(0))$ , and all sufficiently large n (such that $\|{g_n^{\pm} - g^{\pm}}\|_{\infty} < \varepsilon'$ ), the ‘strips’ $G^{\pm \varepsilon} \,:\!=\, S(g^-\mp \varepsilon, g^{+}\pm \varepsilon)$ are non-empty and

\begin{equation*} \mathbb{P}({\widetilde{X}_{n}} \in G^{-\varepsilon}[B]) \leq \mathbb{P}({\widetilde{X}_{n}} \in G_n[B]) \leq \mathbb{P}({\widetilde{X}_{n}} \in G^{+\varepsilon}[B]). \end{equation*}

Note that $\mathbb{P}(X \in \partial (G^{\pm \varepsilon})) = 0$ (the boundary is taken with respect to the uniform topology) due to the continuity of the distributions of $\sup_{0\leq t\leq 1} (X(t) - g^+(t))$ and $\inf_{0\leq t\leq 1}(X(t) - g^-(t))$ [6, p. 232]. Furthermore, due to X(1) having a continuous density, it is clear that $\mathbb{P}( X(1) \in \partial B ) = 0$ for any Borel set B with $\partial B$ of Lebesgue measure zero. By subadditivity and the fact that $\partial (A_1\cap A_2) \subseteq \partial A_1 \cup \partial A_2$ for arbitrary sets $A_1$ and $A_2$ , it follows that

\begin{equation*} \mathbb{P}(X \in \partial (G[B]) ) \leq \mathbb{P}(X \in \partial G) + \mathbb{P}(X(1) \in \partial B) = 0. \end{equation*}

Hence, from Corollary 1,

\begin{equation*} \liminf_{n\to \infty} \mathbb{P}({\widetilde{X}_{n}} \in G_n[B]) \geq \mathbb{P}(X \in G^{-\varepsilon}[B]), \qquad \limsup_{n\to \infty }\mathbb{P}({\widetilde{X}_{n}} \in G_n[B]) \leq \mathbb{P}(X \in G^{+\varepsilon}[B]). \end{equation*}

As $\mathbb{P}(X \in \partial (G[B])) = 0$ , we also have

\begin{equation*} \mathbb{P}(X \in G^{+\varepsilon}[B]) - \mathbb{P}(X \in G^{-\varepsilon}[B] ) = \mathbb{P}(X \in (\partial G)^{(\varepsilon)}[B]) \to 0 \quad \text{as } \varepsilon \downarrow 0, \end{equation*}

where $(\partial G)^{(\varepsilon)}$ is the $\varepsilon$ -neighbourhood of $\partial G$ (also in the uniform norm). The result follows.

Proof of relation (27). Let $r \,:\!=\, \|{g^-}\|_{\infty} \vee \|{g^+}\|_{\infty} $ . Using the elementary inequality

\begin{equation*} \Biggl\lvert 1 - \prod_{j=1}^n a_j\Biggr\rvert \leq \Biggl(\max_{i < n}\prod_{k=1}^i \lvert a_k \rvert\Biggr) \sum_{j=1}^{n}\lvert 1 - a_j \rvert \leq \Bigl(1 \vee \max_{k \leq n}\lvert a_k \rvert\Bigr)^{n-1}\sum_{j=1}^n \lvert 1-a_j \rvert, \end{equation*}

we have

\begin{align*} \lvert \mathbb{P}({\widetilde{X}_{n}} \in G_n) - \widehat{\textbf{T}}_{n,1}\widehat{\textbf{T}}_{n,2}\cdots \widehat{\textbf{T}}_{n,n}\textbf{1}^{\top} \rvert & = \Bigg| \sum_{\boldsymbol{{x}} \in E_n^G}\prod_{k=1}^n \frac{q_{n,k}(x_{k-1},x_k)}{C_{n,k}(x_{k-1})} -\sum_{\boldsymbol{{x}} \in E_n^G}\prod_{k=1}^n q_{n,k}(x_{k-1},x_k) \Bigg| \\ & = \Bigg|\sum_{\boldsymbol{{x}} \in E_n^G}\prod_{k=1}^n \frac{q_{n,k}(x_{k-1},x_k)}{C_{n,k}(x_{k-1})} \Bigg(1 -\prod_{i=1}^{n} C_{n,i}(x_{i-1}) \Bigg)\Bigg| \\ & \leq \mathbb{P}({\widetilde{X}_{n}} \in G_n) \rho_n^{n-1}\sum_{i=1}^n \sup_{x \in E_{n,k}(r)}\lvert 1 - C_{n,i}(x) \rvert, \end{align*}

where $\rho_n \,:\!=\, 1 \vee \max_{1\leq j\leq n}\sup_{\lvert x\rvert \leq r} C_{n,j}(x)$ . Using Lemma 2, we obtain (27).

5. Numerical examples

To illustrate the efficiency of our approximation scheme (12), we implemented it in the programming language Julia run on a MacBook Pro 2020 laptop computer with an Intel Core i5 processor (2 GHz, 16 RAM). We used the package HyperDualNumbers.jl to evaluate the partial derivatives of ${\mu_X}$ in (3).

It is well known in the numerical analysis literature that trapezoidal quadrature is extremely accurate for analytic functions [23]. In light of (27), for numerical illustration purposes we drop the normalising constants $C_{n,k}(x)$ and use $\widehat{\textbf{T}}_{n,1}\widehat{\textbf{T}}_{n,2}\cdots \widehat{\textbf{T}}_{n,n}\textbf{1}^{\top}$ instead of $\mathbb{P}({\widetilde{X}_{n}} \in G_n)$ to approximate $\mathbb{P}(X \in G)$ .

5.1. The Wiener process with one-sided boundary

Using the method of images, [14] obtained a closed-form expression for the crossing probability of the boundary

\begin{equation*} g_\mathrm{D}(t) \,:\!=\, \tfrac12 - t \ln \big(\tfrac{1}{4}(1 + \sqrt{1 + 8\mathrm{e}^{-1/t}})\big), \qquad t>0,\end{equation*}

for the standard Wiener process $W\,:\!=\,\{W(t) \colon t\geq 0\}$ .

In order to make the state space $E_{n}^G$ finite in the case of the one-sided boundary where $g^-(t) = -\infty$ , we insert an absorbing lower boundary at a low enough fixed level $L<x_0$ and replace $E_{n,k}^G$ with

\begin{align*} E_{n,k}^{G,L} & \,:\!=\, \{x \in E_{n,k} \colon L < x < g_{n,k}^+ \}, \qquad k=1,\ldots,n, \\ E_{n}^{G,L} & \,:\!=\, E_{n,0} \times E_{n,1}^{G,L} \times \cdots \times E_{n,n}^{G,L}.\end{align*}

We approximate $\mathbb{P}(W(t) < g_\mathrm{D}(t),\, t\in [0,1])$ with $\big(\prod_{k=1}^n\textbf{T}_{n,k}^L\big)\textbf{1}^\top$ , where $\textbf{T}_{n,k}^L$ are substochastic matrices of dimensions $\big(\big\lvert E_{n,k-1}^{G,L}\big\rvert + 1\big) \times \big(\big\lvert E_{n,k}^{G,L}\big\rvert + 1\big)$ with entries equal to the respective transition probabilities

\begin{equation*} \begin{cases} q_{n,k}(x,y), & (x,y) \in E_{n,k-1}^{G,L} \times E_{n,k}^{G,L}, \\ \sum_{z\in E_{n,k}\cap({-}\infty,L]}q_{n,k}(x,z), & x \in E_{n,k-1}^{G,L},\, y = L,\\ 1, & x = L,\,y = L,\\ 0, & \text{otherwise}, \end{cases}\end{equation*}

where we put $f_n^-(t) = -\infty$ in the definition of $q_{n,k}$ in (26). This approximation assumes that the lower auxiliary boundary L is sufficiently far away from the initial point $x_0$ and the upper boundary, such that after a sample path crosses the lower boundary it is highly unlikely that it will cross the upper boundary in the remaining time. In our example, we took $L=-3$ . The probability of the Wiener process first hitting this level and then crossing $g_\mathrm{D}$ prior to time $t=1$ is less than $1.26\times 10^{-6}$ . Further, we chose $x_0 =0$ , $\delta = 0$ , and $\gamma = 2$ . To guarantee convergence of the scheme, $\delta$ must be strictly positive; however, for the values of n we are interested in and the larger value of $\gamma$ compared to the one in the example from Fig. 1, the error is negligible.

Figure 2. Approximation of the boundary $g_\mathrm{D}$ non-crossing probabilities for the Wiener process. The exact Daniels boundary crossing probability in this case is $0.479\,749\,35\ldots$ The left pane shows a log–log plot of the absolute approximation error as a function of n. The right pane shows the time evolution of the taboo transition density using the Markov chain approximation ${\widetilde{X}_{n}}$ with $n = 20$ .

The left pane in Fig. 2 shows a log–log plot of the absolute approximation error as a function of n. The crosses $\times$ show the absolute error of the Markov chain approximation without the Brownian bridge correction, while the bullets $\bullet$ show the error when using the Brownian bridge correction. The upper and lower dashed lines correspond to $C_1n^{-1/2}$ and $C_2n^{-2}$ respectively, where $C_1$ and $C_2$ are fitted constants. We see that the convergence rate $\lvert \mathbb{P}(W\in G) - \mathbb{P}({\widetilde{X}_{n}} \in G_n)\rvert$ is of the order $O(n^{-2})$ , which is the same as the boundary approximation order of the error $\lvert \mathbb{P}(W \in G) - \mathbb{P}(W \in G_n)\rvert = O(n^{-2})$ proved in [8] in the case of twice continuously differentiable boundaries. It appears that, due to the high accuracy of approximation of the increments’ moments (Lemma 3) and the Brownian bridge correction applied to the transition probabilities, we achieve a much faster convergence rate compared to the convergence rate $O(n^{-1/2})$ achieved in [19].

The right pane in Fig. 2 shows the time evolution of the taboo transition density using the Markov chain approximation ${\widetilde{X}_{n}}$ with $n = 20$ . The positions of the nodes on the surface correspond to the points from the respective $E_{n,k}^{G,-3}$ . Note from (5) that the spacing between the nodes at the final time step $t = 1$ is finer compared to earlier time steps. This is crucial for the observed improved convergence rate.

5.2. The Ornstein–Uhlenbeck process

Let X be the Ornstein–Uhlenbeck (OU) process satisfying the stochastic differential equation

\begin{equation*} \begin{cases} \mathrm{d} X(t) = -X(t)\,\mathrm{d} t + \mathrm{d} W(t), \qquad t \in (0,1], \\ X(0) = 0. \end{cases}\end{equation*}

The usual approach for computing the boundary crossing probability of the OU process is to express the process in terms of a time-changed Brownian motion. This is achieved by using the time substitution $\theta(t) \,:\!=\, (\mathrm{e}^{2 t}-1)/2$ , so that we can write $X(t) = \mathrm{e}^{-t}W(\theta(t))$ .

To illustrate the effectiveness of our approximation, we consider the following two-sided boundary for which explicit boundary crossing probabilities are available for the OU process:

\begin{equation*} g_{\psi}^{\pm}(t) \,:\!=\, \mathrm{e}^{-t}\psi_{\pm}(\theta(t)), \quad \mbox{where } \psi_{\pm}(t) = \pm \tfrac12 t \cosh^{-1}(\mathrm{e}^{4/t}), \qquad t>0.\end{equation*}

Letting $t \,:\!=\, \theta(s)$ , we obtain

\begin{align*} P_{\psi}(T) & \,:\!=\, \mathbb{P}(\psi_{-}(t) < W(t) < \psi_{+}(t), \, 0 \leq t \leq T) \\ & = \mathbb{P}(\mathrm{e}^{-s}\psi_{-}(\theta(s)) < \mathrm{e}^{-s}W(\theta(s)) < \mathrm{e}^{-s}\psi_{\pm}(\theta(s)), \, 0 \leq s \leq \theta^{-1}(T)) \\ & = \mathbb{P}(g_{\psi}^{-}(s) < X(s) < g_{\psi}^{+}(s), \, s \in [0,\theta^{-1}(T)]),\end{align*}

where we set $T \,:\!=\, \theta(1)$ so that $s\in[0,1]$ . A closed-form expression for $P_{\psi}(T)$ can be found [38, p. 28]. The exact boundary crossing probability in this case is $0.750\,502\,88\ldots$

Using (3) and (4), the approximate drift and diffusion coefficients of the weak second-order Itô–Taylor expansion for the OU process are given by ${\beta}_{n,k}(x) = - x + \tfrac12\Delta_{n}x$ , $\alpha^{1/2}_{n,k}(x) = 1 - \tfrac12\Delta_{n}$ . From the numerical results below, it appears that it is sufficient to use the weak second-order Itô–Taylor expansion of transition densities instead of the true transition density of the OU process for our Markov chain approximation to maintain a $O(n^{-2})$ convergence rate of the boundary crossing probabilities.

In the log–log plot in the left pane of Fig. 3, the crosses $\times$ show the absolute error of the Markov chain approximation without the Brownian bridge correction, while the bullets $\bullet$ show the error with the Brownian bridge correction. The markers $\bigtriangleup$ and $\circ$ show the absolute error of the Markov chain approximation using the exact transition density of the OU process and the Euler–Maruyama approximation instead of the transition density from the Itô–Taylor expansion, respectively. From this plot, we empirically observe that the convergence rate $\lvert \mathbb{P}(X\in G) - \mathbb{P}({\widetilde{X}_{n}} \in G_n)\rvert$ is of the order $O(n^{-2})$ , which is the same as the boundary approximation order of error $\lvert \mathbb{P}(X \in G) - \mathbb{P}(X \in G_n)\rvert = O(n^{-2})$ proved in [15] in the case of twice continuously differentiable boundaries. It appears that, at this level of accuracy, we might ignore the higher-order terms in the diffusion bridge crossing probability derived in [3].

Figure 3. Approximation of non-crossing probabilities of the OU process with boundaries $g_{\psi}^{\pm}$ . The left pane shows a log–log plot of the absolute approximation error as a function of n. The upper and lower dashed lines correspond to $C_1n^{-1/2}$ , $C_2n^{-1}$ , and $C_3n^{-2}$ respectively, where $C_1$ , $C_2$ , and $C_3$ are fitted constants. The right pane depicts the time evolution of the taboo transition density using the Markov chain approximation ${\widetilde{X}_{n}}$ with $n = 20$ .

5.3. The Bessel process

To test our method on a non–Gaussian diffusion process, we chose the Bessel process, due to the availability of a closed-form expression for its transition density. Note also that the Cox–Ingersoll–Ross (CIR) process popular in mathematical finance is a suitably time–space-transformed Bessel process, and hence boundary crossing probabilities for the CIR process can be immediately obtained from those for the Bessel case.

For $\nu \geq 0$ , the Bessel process of order $\nu$ can be defined as the (strong) solution of the stochastic differential equation [7, p. 66]

\begin{equation*} \mathrm{d} X(t) = \frac{2\nu + 1}{2X(t)}\,\mathrm{d} t + \mathrm{d} W(t), \qquad t >0; \quad X(0) = x_0 >0.\end{equation*}

The approximate drift and diffusion coefficients of the weak second-order Itô–Taylor expansion for the Bessel process are given by

\begin{equation*} \beta_{n,k}(x) = \frac{2\nu + 1}{2 x} + \frac{1-4\nu^2}{8x^3}\Delta_n, \qquad \alpha^{1/2}_{n,k} (x) = 1 - \frac{2 \nu +1}{4x^2}\Delta_n.\end{equation*}

For numerical illustration purposes, we tested our algorithm in the case when $\nu = \frac12$ , $x_0 = 1$ , $g^{-}(t) = 0.7$ and $g^+(t) = +\infty$ , for which a closed-form expression is available for benchmarking [26, Theorem 2.2]). The results of the numerical calculations are shown in Fig. 4. The left pane presents a log–log plot of the absolute approximation error. The $\times$ markers show the Markov chain approximation error without the Brownian bridge correction. The markers $\circ$ , $\bullet$ , and $\Delta$ show the error of the Markov chain approximation with the Brownian bridge correction when using the Euler–Maruyama approximation, the Itô–Taylor approximation, and the exact transition density respectively. We can see that the observed convergence rate is the same, $O(n^{-2})$ , whether one uses the Itô–Taylor approximation or the exact transition densities, but the rate drops to $O(n^{-1})$ when using the Euler–Maruyama approximation. The right pane shows the time evolution of the taboo transition density using the Markov chain approximation ${\widetilde{X}_{n}}$ with $n = 20$ . An artificial absorbing boundary has been inserted at $x = 7$ to ensure that probability mass is not lost.

Figure 4. Approximation of the boundary crossing probabilities for the Bessel process with initial condition $X(0) = 1$ , starting above the boundary $g^-(t) = 0.7$ . The exact boundary crossing probability in this case is $0.534\,924\ldots$ The left pane shows a log–log plot of the absolute approximation error as a function of n. The dashed lines correspond to $C_1n^{-1/2}$ , $C_2n^{-1}$ , $C_3n^{-2}$ , and $C_4n^{-2}$ from top to bottom, where $C_1$ , $C_2$ , $C_3$ , and $C_4$ are fitted constants. The right pane depicts the time evolution of the taboo transition density using the Markov chain approximation ${\widetilde{X}_{n}}$ with $n = 20$ .

5.4. Comparison with other methods

In this subsection we will comment on the relative performance of our approach compared to the previously proposed ones in the special basic case of one-sided boundary g for the Brownian motion process.

Based on the results of our numerical experiments, one of the most efficient methods for numerical computation of the boundary crossing probability of the Brownian motion is the method of integral equations [49]. The method proposed in [41, 47] is based on numerically solving (using ‘midpoint’ quadratures) a Volterra integral equation of the first kind with the kernel $K (t,s): = \overline{\Phi}((g(t)-g(s))/\sqrt{t-s})$ , $0<s<t$ , where $\overline{\Phi}$ is the standard normal ‘tail’. Unfortunately, the convergence rate for that method was discussed in neither [47] nor [41]. If the above kernel K had no end-point singularity, it would follow from the proof of [40, Theorem 9.1] that the convergence rate is $O(n^{-2})$ , n being the number of steps on the uniform time grid used, since that rate is essentially determined by the quadrature error. In view of the results of [42, Section 7], the proof of the above-mentioned theorem from [40] indicates that, in the case of our kernel K, the convergence rate will be $O(n^{-3/2})$ . And indeed, our numerical experiments show that the convergence rate for that method is of that order and, moreover, that the error may have the form $C_0 n^{-3/2} + C_0 n^{- 2} + C_0 n^{-5/2} + \cdots$ . Hence, in our comparison, when comparing the results of different methods after applying Richardson’s extrapolation [57, p. 27], we assumed that the error dependence on the small parameter $n^{-1}$ for the above-mentioned integral equation method is of that form.

In [52] the first-passage-time density of the boundary g was shown to satisfy a Volterra integral equation of the second type. Its solution was approximated using the trapezoidal rule in [11]; however, the convergence rates where not discussed in that paper. In [55], the authors obtained a series expansion for the solution to the integral equation using the method of successive approximations, with each term in the series containing an integral. Error analysis was done on the truncation of the series expansion. However, the integrals in the series expansion were obtained numerically using quadratures, and there was no mention of the convergence rate for the quadratures.

Note that both Volterra integral equations mentioned above are special cases of the spectrum of integral equations given in [49, Theorem 6.1]. Our numerical experiments showed that the approximation from [47] performs better, and hence we chose it to be the benchmark for the comparison in this subsection.

In Fig. 5 we show a comparison between the Markov chain approximation and the integral equation method proposed in [41], which is a version of the approach from [47] (labeled ‘IE’). The label ‘MC (No BB)’ refers to the Markov chain approximation results obtained without using the Brownian bridge correction, whereas just ‘MC’ corresponds to the Markov chain method with that correction.

Figure 5. Log–log plot of the absolute approximation errors versus the computational time for our Markov chain approximation and the integral equation method applied to the standard Brownian motion crossing Daniels’ boundary before time $T=1$ . Labels ending with R $(p_1,p_2,\ldots,p_k)$ indicate the use of Richardson’s extrapolation applied repeatedly to the respective sequence A(h) with an error of the form $a_1 h^{p_1} + a_2 h^{p_2} + \cdots + a_kh^{p_k} + o(h^{p_k})$ , h being the appropriate small parameter in the scheme used.

We see from Fig. 5 that applying the Brownian bridge correction dramatically improves the efficiency of our scheme. Pre-Richardson’s extrapolation, the computational times for the integral equation method are generally lower, which is unsurprising since our method discretises both space and time variables, while the integral equation method only discretises time. However, our scheme becomes competitive once we apply Richardson’s extrapolation. Furthermore, and most importantly, our method works for general diffusion processes whereas the method of integral equations requires an explicit expression for the transition density.

Another important advantage of our approach is that it can easily be modified to calculate expressions that involve the space variable, because our scheme essentially approximates taboo transition probabilities.