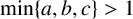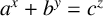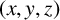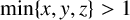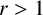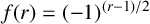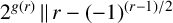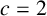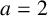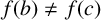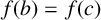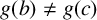1 Introduction
Let
![]() $\mathbb {N}$
be the set of all positive integers. Let a, b, c be fixed coprime positive integers with
$\mathbb {N}$
be the set of all positive integers. Let a, b, c be fixed coprime positive integers with
![]() $\min \{a,b,c\}>1$
. We assume without loss of generality that a, b and c are not perfect powers. The purely exponential Diophantine equation
$\min \{a,b,c\}>1$
. We assume without loss of generality that a, b and c are not perfect powers. The purely exponential Diophantine equation
has been studied deeply (see [Reference Le, Scott and Styer17] for a survey of the results). In 1933, Mahler [Reference Mahler18] used his p-adic analogue of the Diophantine approximation method of Thue–Siegel to prove that (1.1) has only finitely many solutions
![]() $(x,y,z)$
, but his method is ineffective. Let
$(x,y,z)$
, but his method is ineffective. Let
![]() $N(a,b,c)$
denote the number of solutions
$N(a,b,c)$
denote the number of solutions
![]() $(x,y,z)$
of (1.1). An effective upper bound for
$(x,y,z)$
of (1.1). An effective upper bound for
![]() $N(a,b,c)$
was first given by Gel’fond [Reference Gel’fond7], using his new method in transcendental number theory. Subsequently, as a straightforward consequence of an upper bound for the number of solutions of binary S-unit equations due to Beukers and Schlickewei [Reference Beukers and Schlickewei2], the bound was improved to
$N(a,b,c)$
was first given by Gel’fond [Reference Gel’fond7], using his new method in transcendental number theory. Subsequently, as a straightforward consequence of an upper bound for the number of solutions of binary S-unit equations due to Beukers and Schlickewei [Reference Beukers and Schlickewei2], the bound was improved to
![]() $N(a,b,c)\le 2^{36}$
. More accurate upper bounds for
$N(a,b,c)\le 2^{36}$
. More accurate upper bounds for
![]() $N(a,b,c)$
have been obtained under certain conditions:
$N(a,b,c)$
have been obtained under certain conditions:
-
(i) if
 $2 \nmid c$
, then
$2 \nmid c$
, then
 $N(a,b,c) \le 2$
(Scott and Styer [Reference Scott and Styer21]);
$N(a,b,c) \le 2$
(Scott and Styer [Reference Scott and Styer21]); -
(ii) if
 $\max \{a,b,c\}>5\times 10^{27}$
, then
$\max \{a,b,c\}>5\times 10^{27}$
, then
 $N(a,b,c) \le 3$
(Hu and Le [Reference Hu and Le10]);
$N(a,b,c) \le 3$
(Hu and Le [Reference Hu and Le10]); -
(iii) if
 $2 \mid c$
and
$2 \mid c$
and
 $\max \{a,b,c\}>10^{62}$
, then
$\max \{a,b,c\}>10^{62}$
, then
 $N(a,b,c) \le 2$
(Hu and Le [Reference Hu and Le11]);
$N(a,b,c) \le 2$
(Hu and Le [Reference Hu and Le11]); -
(iv) if
 $2\mid c$
and
$2\mid c$
and
 $a<b<10^{62}$
, then
$a<b<10^{62}$
, then
 $N(a,b,c) \le 2$
, except for
$N(a,b,c) \le 2$
, except for
 $N(3,5,2)=3$
(Miyazaki and Pink [Reference Miyazaki and Pink19]).
$N(3,5,2)=3$
(Miyazaki and Pink [Reference Miyazaki and Pink19]).
Nevertheless, deeper problems about the number of solutions of (1.1) remain unresolved. Let
![]() $N^{\prime }(a,b,c)$
denote the number of solutions
$N^{\prime }(a,b,c)$
denote the number of solutions
![]() $(x,y,z)$
of (1.1) with
$(x,y,z)$
of (1.1) with
![]() $\min \{x,y,z\}>1$
. In this paper, we will discuss the following conjecture.
$\min \{x,y,z\}>1$
. In this paper, we will discuss the following conjecture.
Conjecture 1.1 (Terai–Jeśmanowicz conjecture).
For any triple
![]() $(a,b,c)$
of positive integers with
$(a,b,c)$
of positive integers with
![]() $\min\{a,b,c\}>1$
, we have
$\min\{a,b,c\}>1$
, we have
![]() $N^{\prime }(a,b,c)\le 1$
.
$N^{\prime }(a,b,c)\le 1$
.
This conjecture contains the famous Jeśmanowicz conjecture concerning Pythagorean triples (see [Reference Jeśmanowicz12]) and its original form was put forward by Terai [Reference Terai22]. It is related to the generalised Fermat conjecture (see Problems B19 and D2 of [Reference Guy8]) and seems very difficult. In 2015, Hu and Le [Reference Hu and Le9] gave a general criterion to judge whether Conjecture 1.1 is true, but this criterion is difficult to apply because it involves some unsolved problems such as the existence of Wieferich primes (see Problem A3 of [Reference Guy8]).
We now discuss Conjecture 1.1 for
![]() $2 \in \{a,b,c\}$
using a different approach from the one in [Reference Hu and Le9]. First, by means of the results of [Reference Le14, Reference Scott20], we can directly prove the following result.
$2 \in \{a,b,c\}$
using a different approach from the one in [Reference Hu and Le9]. First, by means of the results of [Reference Le14, Reference Scott20], we can directly prove the following result.
Theorem 1.2. If
![]() $c=2$
or a, b and c are distinct primes, then Conjecture 1.1 is true.
$c=2$
or a, b and c are distinct primes, then Conjecture 1.1 is true.
For any odd positive integer r with
![]() $r>1$
, we define
$r>1$
, we define
![]() $f(r)=(-1)^{(r-1)/2}$
and
$f(r)=(-1)^{(r-1)/2}$
and
![]() $2^{g(r)}\,\|\, r-(-1)^{(r-1)/2}$
. Obviously,
$2^{g(r)}\,\|\, r-(-1)^{(r-1)/2}$
. Obviously,
![]() $f(r) \in \{-1,1\}$
and
$f(r) \in \{-1,1\}$
and
![]() $g(r)$
is a positive integer with
$g(r)$
is a positive integer with
![]() $g(r) \ge 2$
. Using a combination of various methods including Baker’s method and known results on exponential Diophantine equations, we prove the following result.
$g(r) \ge 2$
. Using a combination of various methods including Baker’s method and known results on exponential Diophantine equations, we prove the following result.
Theorem 1.3. If
![]() $a=2$
and either
$a=2$
and either
![]() $f(b)\ne f(c)$
, or
$f(b)\ne f(c)$
, or
![]() $f(b)=f(c)$
and
$f(b)=f(c)$
and
![]() $g(b)\ne g(c)$
, then Conjecture 1.1 is true.
$g(b)\ne g(c)$
, then Conjecture 1.1 is true.
2 Preliminaries
For any positive integer s, let
![]() ${\mathop{\mathrm{ord}}\nolimits}_{2}(s)$
denote the order of
${\mathop{\mathrm{ord}}\nolimits}_{2}(s)$
denote the order of
![]() $2$
in s, namely,
$2$
in s, namely,
![]() $2^{{\mathop{\mathrm{ord}}\nolimits}_{2}(s)}\,\|\,s$
.
$2^{{\mathop{\mathrm{ord}}\nolimits}_{2}(s)}\,\|\,s$
.
Lemma 2.1. For any positive integers r and s such that
![]() $r>1$
,
$r>1$
,
![]() $2 \nmid r$
and
$2 \nmid r$
and
![]() $2\mid s$
, we have
$2\mid s$
, we have
Proof. Since
![]() $2\mid s$
and
$2\mid s$
and
![]() $r=2^{g(r)}r_{1}+f(r)$
, where
$r=2^{g(r)}r_{1}+f(r)$
, where
![]() $r_{1}$
is an odd positive integer,
$r_{1}$
is an odd positive integer,
 $$ \begin{align} r^{s}-1&=(2^{g(r)}r_{1}+f(r))^{s}-1\notag\\ &=((f(r))^{s}-1)+2^{g(r)}r_{1}s(f(r))^{s-1}+\sum_{i=2}^{s}\binom{s}{i}(2^{g(r)}r_{1})^{i}(f(r))^{s-i}\notag\\ &=2^{g(r)}r_{1}sf(r)+\sum_{i=2}^{s}\binom{s}{i}(2^{g(r)}r_{1}f(r))^{i}. \end{align} $$
$$ \begin{align} r^{s}-1&=(2^{g(r)}r_{1}+f(r))^{s}-1\notag\\ &=((f(r))^{s}-1)+2^{g(r)}r_{1}s(f(r))^{s-1}+\sum_{i=2}^{s}\binom{s}{i}(2^{g(r)}r_{1})^{i}(f(r))^{s-i}\notag\\ &=2^{g(r)}r_{1}sf(r)+\sum_{i=2}^{s}\binom{s}{i}(2^{g(r)}r_{1}f(r))^{i}. \end{align} $$
Further, since
![]() $g(r) \ge 2$
and
$g(r) \ge 2$
and
![]() $2\nmid r_{1}f(r)$
, we see that
$2\nmid r_{1}f(r)$
, we see that
![]() $2^{g(r)+{\mathop{\mathrm{ord}}\nolimits}_{2}(s)}\,\|\; 2^{g(r)}r_{1}sf(r)$
and
$2^{g(r)+{\mathop{\mathrm{ord}}\nolimits}_{2}(s)}\,\|\; 2^{g(r)}r_{1}sf(r)$
and
 $$ \begin{align*} \binom{s}{i}(2^{g(r)}r_{1}f(r))^{i} \equiv 2^{g(r)}s\binom{s-1}{i-1}\frac{2^{g(r)(i-1)}}{i}(r_{1}f(r))^{i} \equiv 0 \pmod{2^{g(r)+{\mathop{\mathrm{ord}}\nolimits}_{2}(s)+1}},\quad i \ge 2. \end{align*} $$
$$ \begin{align*} \binom{s}{i}(2^{g(r)}r_{1}f(r))^{i} \equiv 2^{g(r)}s\binom{s-1}{i-1}\frac{2^{g(r)(i-1)}}{i}(r_{1}f(r))^{i} \equiv 0 \pmod{2^{g(r)+{\mathop{\mathrm{ord}}\nolimits}_{2}(s)+1}},\quad i \ge 2. \end{align*} $$
For any real number
![]() $\alpha $
, let
$\alpha $
, let
![]() $\log \alpha $
denote the natural logarithm of
$\log \alpha $
denote the natural logarithm of
![]() $\alpha $
.
$\alpha $
.
Lemma 2.2. Let
![]() $\alpha _{1}$
,
$\alpha _{1}$
,
![]() $\alpha _{2}$
,
$\alpha _{2}$
,
![]() $\beta _{1}$
,
$\beta _{1}$
,
![]() $\beta _{2}$
be positive integers with
$\beta _{2}$
be positive integers with
![]() $\min \{\alpha _{1},\alpha _{2}\}>1$
. Further, let
$\min \{\alpha _{1},\alpha _{2}\}>1$
. Further, let
![]() $\Lambda =\beta _{1} \log \alpha _{1}-\beta _{2}\log \alpha _{2}$
. If
$\Lambda =\beta _{1} \log \alpha _{1}-\beta _{2}\log \alpha _{2}$
. If
![]() $\Lambda \ne 0$
, then
$\Lambda \ne 0$
, then
 $$ \begin{align*} \log|\Lambda|>-25.2(\log \alpha_{1})(\log \alpha_{2})\bigg(\max\bigg\{10,0.38+\log \bigg(\frac{\beta_{1}}{\log \alpha_{2}}+\frac{\beta_{2}}{\log \alpha_{1}}\bigg)\bigg\}\bigg)^{2}. \end{align*} $$
$$ \begin{align*} \log|\Lambda|>-25.2(\log \alpha_{1})(\log \alpha_{2})\bigg(\max\bigg\{10,0.38+\log \bigg(\frac{\beta_{1}}{\log \alpha_{2}}+\frac{\beta_{2}}{\log \alpha_{1}}\bigg)\bigg\}\bigg)^{2}. \end{align*} $$
Proof. This is the special case of [Reference Laurent13, Corollary 2] for
![]() $m=10$
.
$m=10$
.
Lemma 2.3. Let
![]() $\alpha _{1}$
,
$\alpha _{1}$
,
![]() $\alpha _{2}$
be odd integers with
$\alpha _{2}$
be odd integers with
![]() $\min \{|\alpha _{1}|,|\alpha _{2}|\}\ge 3$
and let
$\min \{|\alpha _{1}|,|\alpha _{2}|\}\ge 3$
and let
![]() $\beta _{1}$
,
$\beta _{1}$
,
![]() $\beta _{2}$
be positive integers. Further, let
$\beta _{2}$
be positive integers. Further, let
![]() $\Lambda ^{\prime }=\alpha _{1}^{\,\beta _{1}}-\alpha _{2}^{\,\beta _{2}}$
. If
$\Lambda ^{\prime }=\alpha _{1}^{\,\beta _{1}}-\alpha _{2}^{\,\beta _{2}}$
. If
![]() $\Lambda ^{\prime }\ne 0$
and
$\Lambda ^{\prime }\ne 0$
and
![]() $\alpha _{1}\equiv \alpha _{2}\equiv 1 \pmod {4}$
, then
$\alpha _{1}\equiv \alpha _{2}\equiv 1 \pmod {4}$
, then
 $$ \begin{align*} {\mathop{\mathrm{ord}}\nolimits}_{2}(|\Lambda^{\prime}|)&<19.55(\log|\alpha_{1}|)(\log|\alpha_{2}|)\\ &\quad \times \bigg(\max\bigg\{12\log 2,0.\,4+\log(2\log 2)+\log\bigg(\frac{\beta_{1}}{\log|\alpha_{2}|}+\frac{\beta_{2}}{\log|\alpha_{1}|}\bigg)\bigg\}\bigg)^{2}. \end{align*} $$
$$ \begin{align*} {\mathop{\mathrm{ord}}\nolimits}_{2}(|\Lambda^{\prime}|)&<19.55(\log|\alpha_{1}|)(\log|\alpha_{2}|)\\ &\quad \times \bigg(\max\bigg\{12\log 2,0.\,4+\log(2\log 2)+\log\bigg(\frac{\beta_{1}}{\log|\alpha_{2}|}+\frac{\beta_{2}}{\log|\alpha_{1}|}\bigg)\bigg\}\bigg)^{2}. \end{align*} $$
Proof. This is the special case of [Reference Bugeaud4, Theorem 2] for
![]() $p=2$
,
$p=2$
,
![]() $y_{1}=y_{2}=1$
,
$y_{1}=y_{2}=1$
,
![]() $\alpha _{1}\equiv \alpha _{2}\equiv 1 \pmod 4$
,
$\alpha _{1}\equiv \alpha _{2}\equiv 1 \pmod 4$
,
![]() $g=1$
and
$g=1$
and
![]() $E=2$
.
$E=2$
.
Lemma 2.4 [Reference Cohn6, Reference Le16].
The equation
has only the solutions
![]() $(X,Y,m,n)=(5,3,1,3), (7,3,5,4)$
and
$(X,Y,m,n)=(5,3,1,3), (7,3,5,4)$
and
![]() $(11,5,2,3)$
.
$(11,5,2,3)$
.
Lemma 2.5 [Reference Bennett and Skinner1, Theorem 8.4].
The equation
has only the solution
![]() $(X,Y,m,n)=(71,17,7,3)$
.
$(X,Y,m,n)=(71,17,7,3)$
.
Lemma 2.6 [Reference Cao5].
If
![]() $a=2$
and b and c are distinct odd primes with
$a=2$
and b and c are distinct odd primes with
![]() $\max \{b,c\}<100$
, then
$\max \{b,c\}<100$
, then
![]() $N^{\prime }(a,b,c)\le 1$
.
$N^{\prime }(a,b,c)\le 1$
.
Lemma 2.7 [Reference Scott and Styer21].
If
![]() $2 \nmid c$
, then
$2 \nmid c$
, then
![]() $N(a,b,c) \le 2$
.
$N(a,b,c) \le 2$
.
Lemma 2.8 [Reference Scott20, Theorem 6].
![]() $N^{\prime }(a,b,2)\le 1$
.
$N^{\prime }(a,b,2)\le 1$
.
According to Theorems 1, 2 and 3 of [Reference Le14] and the proof of them, we can obtain the following lemma.
Lemma 2.9. Let p and q be fixed odd primes with
![]() $p \ne q$
.
$p \ne q$
.
-
(i) The equation
(2.3)has at most one solution $$ \begin{align} 2^{x}+p^{y}=q^{z},\quad x,y,z \in \mathbb{N} \end{align} $$
$$ \begin{align} 2^{x}+p^{y}=q^{z},\quad x,y,z \in \mathbb{N} \end{align} $$
 $(x,y,z)$
with
$(x,y,z)$
with
 $2\mid y$
and this solution has
$2\mid y$
and this solution has
 $z=1$
, except for
$z=1$
, except for
 $(p,q,x,y,z)=(3,5,4,2,2),~(5,3,1,2,3),~(7,3,5,2,4)$
and
$(p,q,x,y,z)=(3,5,4,2,2),~(5,3,1,2,3),~(7,3,5,2,4)$
and
 $(11,5,2,2,3)$
.
$(11,5,2,2,3)$
.
-
(ii) Equation (2.3) has at most one solution
 $(x,y,z)$
with
$(x,y,z)$
with
 $2 \mid x$
and
$2 \mid x$
and
 $2\nmid y$
.
$2\nmid y$
. -
(iii) Equation (2.3) has at most one solution
 $(x,y,z)$
with
$(x,y,z)$
with
 $2 \nmid xy$
.
$2 \nmid xy$
.
Remark 2.10. The reference [Reference Le14] is written in Chinese and the proof of the theorems mentioned is rather complicated. In the present case, this lemma can be easily obtained using the tools in [Reference Bilu, Hanrot and Voutier3, Reference Le15, Reference Voutier24].
3 Further lemmas on (1.1) for
 $a=2$
$a=2$
Let
![]() $a=2$
and let b and c be fixed coprime odd positive integers with
$a=2$
and let b and c be fixed coprime odd positive integers with
![]() $\min \{b,c\}\ge 3$
. In this section, we give some results on the solutions
$\min \{b,c\}\ge 3$
. In this section, we give some results on the solutions
![]() $(x,y,z)$
of the equation
$(x,y,z)$
of the equation
Lemma 3.1.
Proof. Let
![]() $(x,y,z)$
be a solution of (3.1) with
$(x,y,z)$
be a solution of (3.1) with
![]() $2 \nmid yz$
.
$2 \nmid yz$
.
(i) Note that
![]() $f(b) \ne f(c)$
is equivalent to
$f(b) \ne f(c)$
is equivalent to
![]() $b \not \equiv c \pmod 4$
. Since
$b \not \equiv c \pmod 4$
. Since
![]() $2 \nmid yz$
, by (3.1), we have
$2 \nmid yz$
, by (3.1), we have
![]() $2^{x}=c^{z}-b^{y} \equiv 2 \pmod 4$
. This means
$2^{x}=c^{z}-b^{y} \equiv 2 \pmod 4$
. This means
![]() $x=1$
, which contradicts
$x=1$
, which contradicts
![]() $x>1$
. Therefore, we obtain the conclusion (i).
$x>1$
. Therefore, we obtain the conclusion (i).
(ii) Since
![]() $2 \nmid bc$
, we may write
$2 \nmid bc$
, we may write
Assume that
![]() $f(b)=f(c)$
. Since
$f(b)=f(c)$
. Since
![]() $2 \nmid yz$
and
$2 \nmid yz$
and
![]() $f(b)=f(c)\in \{-1,1\}$
, we see from (3.1) and (3.2) that
$f(b)=f(c)\in \{-1,1\}$
, we see from (3.1) and (3.2) that
 $$ \begin{align} 2^{x}&=(2^{g(c)}c_{1}+f(c))^{z}-(2^{g(b)}b_{1}+f(b))^{y}\notag\\ &=\sum_{i=1}^{\max\{y,z\}}\bigg(\binom{z}{i}(2^{g(c)}c_{1})^{i}(f(c))^{z-i}-\binom{y}{i}(2^{g(b)}b_{1})^{i}(f(b))^{y-i}\bigg)\notag\\ &=(2^{g(c)}c_{1}z-2^{g(b)}b_{1}y)+\sum_{i=2}^{\max\{y,z\}}\bigg(\binom{z}{i}(2^{g(c)}c_{1})^{i}-\binom{y}{i}(2^{g(b)}b_{1})^{i}\bigg)(f(c))^{i+1}. \end{align} $$
$$ \begin{align} 2^{x}&=(2^{g(c)}c_{1}+f(c))^{z}-(2^{g(b)}b_{1}+f(b))^{y}\notag\\ &=\sum_{i=1}^{\max\{y,z\}}\bigg(\binom{z}{i}(2^{g(c)}c_{1})^{i}(f(c))^{z-i}-\binom{y}{i}(2^{g(b)}b_{1})^{i}(f(b))^{y-i}\bigg)\notag\\ &=(2^{g(c)}c_{1}z-2^{g(b)}b_{1}y)+\sum_{i=2}^{\max\{y,z\}}\bigg(\binom{z}{i}(2^{g(c)}c_{1})^{i}-\binom{y}{i}(2^{g(b)}b_{1})^{i}\bigg)(f(c))^{i+1}. \end{align} $$
When
![]() $g(b)\ne g(c)$
, since
$g(b)\ne g(c)$
, since
![]() $2 \nmid b_{1}c_{1}yz$
, we have
$2 \nmid b_{1}c_{1}yz$
, we have
and
 $$ \begin{align*} \sum_{i=2}^{\max\{y,z\}}\bigg(\binom{z}{i}(2^{g(c)}c_{1})^{i}-\binom{y}{i}(2^{g(b)}b_{1})^{i}\bigg)(f(c))^{i+1} \equiv 0 \pmod{2^{\min\{g(b),g(c)\}+1}}. \end{align*} $$
$$ \begin{align*} \sum_{i=2}^{\max\{y,z\}}\bigg(\binom{z}{i}(2^{g(c)}c_{1})^{i}-\binom{y}{i}(2^{g(b)}b_{1})^{i}\bigg)(f(c))^{i+1} \equiv 0 \pmod{2^{\min\{g(b),g(c)\}+1}}. \end{align*} $$
Since
![]() $\min \{g(b),g(c)\}\ge 2$
, we see from (3.3) that
$\min \{g(b),g(c)\}\ge 2$
, we see from (3.3) that
![]() $x=\min \{g(b),g(c)\}$
and the conclusion (ii) is obtained.
$x=\min \{g(b),g(c)\}$
and the conclusion (ii) is obtained.
Lemma 3.2. All solutions
![]() $(x,y,z)$
of (3.1) with
$(x,y,z)$
of (3.1) with
![]() $\max \{b,c\}> 100$
satisfy
$\max \{b,c\}> 100$
satisfy
and
Proof. We first consider the case
![]() $2^{x}<c^{0.8z}$
. By (3.1) with
$2^{x}<c^{0.8z}$
. By (3.1) with
![]() $\max \{b,c\}> 100$
, we have
$\max \{b,c\}> 100$
, we have
![]() $b^{y}>2^{x}$
and
$b^{y}>2^{x}$
and
 $$ \begin{align} z \log c &=\log(b^{y}+2^{x})=y\log b+\log \bigg(1+\frac{2^{x}}{b^{y}}\bigg)\notag\\ &<y \log b + \frac{2^{x}}{b^{y}}=y\log b+\frac{2^{x+1}}{2b^{y}}<y\log b+\frac{2c^{0.8z}}{c^{z}} =y\log b+\frac{2}{c^{z/5}}. \end{align} $$
$$ \begin{align} z \log c &=\log(b^{y}+2^{x})=y\log b+\log \bigg(1+\frac{2^{x}}{b^{y}}\bigg)\notag\\ &<y \log b + \frac{2^{x}}{b^{y}}=y\log b+\frac{2^{x+1}}{2b^{y}}<y\log b+\frac{2c^{0.8z}}{c^{z}} =y\log b+\frac{2}{c^{z/5}}. \end{align} $$
Let
![]() $(\alpha _{1},\alpha _{2},\beta _{1},\beta _{2})=(c,b,z,y)$
and
$(\alpha _{1},\alpha _{2},\beta _{1},\beta _{2})=(c,b,z,y)$
and
![]() $\Lambda =z\log c - y\log b$
. By (3.6),
$\Lambda =z\log c - y\log b$
. By (3.6),
![]() $0<\Lambda <2/c^{z/5}$
and
$0<\Lambda <2/c^{z/5}$
and
Since
![]() $\min \{b,c\}\ge 3$
, using Lemma 2.2, we have
$\min \{b,c\}\ge 3$
, using Lemma 2.2, we have
 $$ \begin{align} \log|\Lambda|>-25.2(\log c)(\log b)\bigg(\max\bigg\{10,0.38+\log\bigg(\frac{z}{\log b}+\frac{y}{\log c}\bigg)\bigg\}\bigg)^{2}. \end{align} $$
$$ \begin{align} \log|\Lambda|>-25.2(\log c)(\log b)\bigg(\max\bigg\{10,0.38+\log\bigg(\frac{z}{\log b}+\frac{y}{\log c}\bigg)\bigg\}\bigg)^{2}. \end{align} $$
When
![]() $10 \ge 0.38+\log (z/\!\log b+y/\!\log c)$
, by (3.7) and (3.8), we have
$10 \ge 0.38+\log (z/\!\log b+y/\!\log c)$
, by (3.7) and (3.8), we have
which gives
When
![]() $10<0.38+\log (z/\!\log b+y/\!\log c)$
, by (3.6), (3.7) and (3.8), we have
$10<0.38+\log (z/\!\log b+y/\!\log c)$
, by (3.6), (3.7) and (3.8), we have
 $$ \begin{align*} &\log 2 +25.2(\log c)(\log b)\bigg(0.38+\log\bigg(\frac{2z}{\log b}\bigg)\bigg)^{2}\\ &\quad>\log 2+25.2(\log c)(\log b)\bigg(0.38+\log \bigg(\frac{z}{\log b}+\frac{y}{\log c}\bigg)\bigg)^{2} >\frac{z}{5}\log c, \end{align*} $$
$$ \begin{align*} &\log 2 +25.2(\log c)(\log b)\bigg(0.38+\log\bigg(\frac{2z}{\log b}\bigg)\bigg)^{2}\\ &\quad>\log 2+25.2(\log c)(\log b)\bigg(0.38+\log \bigg(\frac{z}{\log b}+\frac{y}{\log c}\bigg)\bigg)^{2} >\frac{z}{5}\log c, \end{align*} $$
which gives
 $$ \begin{align} \frac{5\log 2}{(\log b)(\log c)}+126\bigg(0.38+\log 2+\log \bigg(\frac{z}{\log b}\bigg)\bigg)^{2}>\frac{z}{\log b}. \end{align} $$
$$ \begin{align} \frac{5\log 2}{(\log b)(\log c)}+126\bigg(0.38+\log 2+\log \bigg(\frac{z}{\log b}\bigg)\bigg)^{2}>\frac{z}{\log b}. \end{align} $$
Since
![]() $(\log b)(\log c)> (\log 3)(\log 100)$
, we can calculate from (3.10) that z satisfies
$(\log b)(\log c)> (\log 3)(\log 100)$
, we can calculate from (3.10) that z satisfies
Therefore, since
![]() $y \log b<z \log c$
and
$y \log b<z \log c$
and
![]() $x \log 2<(4z \log c)/5$
, by (3.9) and (3.11), we obtain (3.4).
$x \log 2<(4z \log c)/5$
, by (3.9) and (3.11), we obtain (3.4).
Next, we consider the case
![]() $2^{x}>c^{0.8z}$
. Let
$2^{x}>c^{0.8z}$
. Let
![]() $(\alpha _{1},\alpha _{2},\beta _{1},\beta _{2})=(cf(c),bf(b),z,y)$
and
$(\alpha _{1},\alpha _{2},\beta _{1},\beta _{2})=(cf(c),bf(b),z,y)$
and
![]() $\Lambda ^{\prime }=(cf(c))^{z}-(bf(b))^{y}$
. Since
$\Lambda ^{\prime }=(cf(c))^{z}-(bf(b))^{y}$
. Since
![]() $x \ge 2$
, by (3.1) and (3.2), we have
$x \ge 2$
, by (3.1) and (3.2), we have
![]() $|\Lambda ^{\prime }|=2^{x}$
, that is,
$|\Lambda ^{\prime }|=2^{x}$
, that is,
![]() ${\mathop{\mathrm{ord}}\nolimits}_{2}(|\Lambda ^{\prime }|)=x$
. Since
${\mathop{\mathrm{ord}}\nolimits}_{2}(|\Lambda ^{\prime }|)=x$
. Since
![]() $\min \{|cf(c)|,|b(f(b)|\}=\min \{b,c\}\ge 3$
and
$\min \{|cf(c)|,|b(f(b)|\}=\min \{b,c\}\ge 3$
and
![]() $cf(c)\equiv bf(b)\equiv 1 \pmod 4$
, by Lemma 2.3,
$cf(c)\equiv bf(b)\equiv 1 \pmod 4$
, by Lemma 2.3,
 $$ \begin{align} x<19.55(\log c)(\log b) \bigg(\max\bigg\{12\log 2,0.4+\log(2\log2)+\log\bigg(\frac{z}{\log b}+\frac{y}{\log c}\bigg)\bigg\}\bigg)^{2}. \end{align} $$
$$ \begin{align} x<19.55(\log c)(\log b) \bigg(\max\bigg\{12\log 2,0.4+\log(2\log2)+\log\bigg(\frac{z}{\log b}+\frac{y}{\log c}\bigg)\bigg\}\bigg)^{2}. \end{align} $$
However, since
![]() $2^{x}>c^{0.8z}$
,
$2^{x}>c^{0.8z}$
,
 $$ \begin{align} x>\frac{0.8z\log c}{\log 2}. \end{align} $$
$$ \begin{align} x>\frac{0.8z\log c}{\log 2}. \end{align} $$
The combination of (3.12) and (3.13) yields
 $$ \begin{align} z <16.94(\log b) \bigg(\max\bigg\{12\log 2,0.4+\log(2\log 2)+\log\bigg(\frac{z}{\log b}+\frac{y}{\log c}\bigg)\bigg\}\bigg)^{2}. \end{align} $$
$$ \begin{align} z <16.94(\log b) \bigg(\max\bigg\{12\log 2,0.4+\log(2\log 2)+\log\bigg(\frac{z}{\log b}+\frac{y}{\log c}\bigg)\bigg\}\bigg)^{2}. \end{align} $$
When
![]() $12\log 2 \ge 0.4+\log (2\log 2)+\log (z/\!\log b+y/\!\log c)$
, by (3.14), we get
$12\log 2 \ge 0.4+\log (2\log 2)+\log (z/\!\log b+y/\!\log c)$
, by (3.14), we get
![]() $z<1172\log b$
. When
$z<1172\log b$
. When
![]() $12\log 2<0.4+\log (2\log 2)+\log (z/\!\log b+y/\!\log c)$
, by (3.6) and (3.14), we have
$12\log 2<0.4+\log (2\log 2)+\log (z/\!\log b+y/\!\log c)$
, by (3.6) and (3.14), we have
 $$ \begin{align*} \frac{z}{\log b}&<16.94\bigg(0.4+\log(2\log2)+\log\bigg(\frac{z}{\log b}+\frac{y}{\log c}\bigg)\bigg)^{2}\\ &<16.94\bigg(0.4+\log(2\log2)+\log\bigg(\frac{2z}{\log b}\bigg)\bigg)^{2}, \end{align*} $$
$$ \begin{align*} \frac{z}{\log b}&<16.94\bigg(0.4+\log(2\log2)+\log\bigg(\frac{z}{\log b}+\frac{y}{\log c}\bigg)\bigg)^{2}\\ &<16.94\bigg(0.4+\log(2\log2)+\log\bigg(\frac{2z}{\log b}\bigg)\bigg)^{2}, \end{align*} $$
whence
Hence, if
![]() $2^{x}>c^{0.8z}$
, then all the solutions
$2^{x}>c^{0.8z}$
, then all the solutions
![]() $(x,y,z)$
of (3.1) satisfy (3.15). Therefore, since
$(x,y,z)$
of (3.1) satisfy (3.15). Therefore, since
![]() $y \log b<z \log c$
and
$y \log b<z \log c$
and
![]() $x \log 2<z \log c$
, by (3.15), we obtain (3.5).
$x \log 2<z \log c$
, by (3.15), we obtain (3.5).
Lemma 3.3. Assume that
![]() $x=\min \{g(b),g(c)\}\le 23$
. Then, all solutions
$x=\min \{g(b),g(c)\}\le 23$
. Then, all solutions
![]() $(x,y,z)$
of (3.1) satisfy
$(x,y,z)$
of (3.1) satisfy
Proof. The proof proceeds along the same lines as that of the first half of Lemma 3.2. Since
![]() $2^{x} \le 2^{g(b)}\le b+1 < b^{y}$
, we see from (3.1) that
$2^{x} \le 2^{g(b)}\le b+1 < b^{y}$
, we see from (3.1) that
which, together with the assumption
![]() $x \le 23$
, implies that
$x \le 23$
, implies that
We know by Lemma 2.2 that (3.8) holds.
When
![]() $10 \ge 0.38+\log (z/\!\log b+y/\!\log c)$
, by (3.8) and (3.17),
$10 \ge 0.38+\log (z/\!\log b+y/\!\log c)$
, by (3.8) and (3.17),
whence
When
![]() $10<0.38+\log (z/\!\log b+y/\!\log c)$
, by (3.8) and (3.17),
$10<0.38+\log (z/\!\log b+y/\!\log c)$
, by (3.8) and (3.17),
 $$ \begin{align*} 24\log 2+25.2(\log c)(\log b)\bigg(0.38+\log \bigg(\frac{2z}{\log b}\bigg)\bigg)^{2}> z \log c, \end{align*} $$
$$ \begin{align*} 24\log 2+25.2(\log c)(\log b)\bigg(0.38+\log \bigg(\frac{2z}{\log b}\bigg)\bigg)^{2}> z \log c, \end{align*} $$
which together with
![]() $(\log b)(\log c) \ge (\log 3)(\log 5)$
yields
$(\log b)(\log c) \ge (\log 3)(\log 5)$
yields
The inequalities in the lemma now follow from (3.18), (3.19) and
![]() $y \log b < z \log c$
.
$y \log b < z \log c$
.
Lemma 3.4. If
![]() $(x,y,z)$
is a solution of (3.1) with
$(x,y,z)$
is a solution of (3.1) with
![]() $2 \nmid yz$
, then
$2 \nmid yz$
, then
![]() $\gcd (y,z)=1$
.
$\gcd (y,z)=1$
.
Proof. Let
![]() $d=\gcd (y,z)$
. Then we have
$d=\gcd (y,z)$
. Then we have
Since
![]() $2 \nmid yz$
, we have
$2 \nmid yz$
, we have
![]() $2 \nmid d$
. Since
$2 \nmid d$
. Since
![]() $2 \nmid bc$
, if
$2 \nmid bc$
, if
![]() $d>1$
, then
$d>1$
, then
![]() $c^{Z(d-1)}+\cdots +b^{Y(d-1)}$
is an odd positive integer greater than
$c^{Z(d-1)}+\cdots +b^{Y(d-1)}$
is an odd positive integer greater than
![]() $1$
contradicting (3.21). So we must have
$1$
contradicting (3.21). So we must have
![]() $d=1$
.
$d=1$
.
By Lemmas 2.4 and 2.5, we can directly obtain the next two lemmas.
Lemma 3.5. Equation (3.1) has only the solution
![]() $(b,c,x,y,z)=(11,5,2,2,3)$
satisfying
$(b,c,x,y,z)=(11,5,2,2,3)$
satisfying
![]() $2 \mid y$
and
$2 \mid y$
and
![]() $2 \nmid z$
.
$2 \nmid z$
.
Lemma 3.6. Equation (3.1) has only the solution
![]() $(b,c,x,y,z)=(17,71,7,3,2)$
satisfying
$(b,c,x,y,z)=(17,71,7,3,2)$
satisfying
![]() $2 \nmid y$
and
$2 \nmid y$
and
![]() $2 \mid z$
.
$2 \mid z$
.
Lemma 3.7. Equation (3.1) has only the solutions
and
satisfying
![]() $2 \mid y$
and
$2 \mid y$
and
![]() $2 \mid z$
.
$2 \mid z$
.
Proof. Let
![]() $(x,y,z)$
be a solution of (3.1) with
$(x,y,z)$
be a solution of (3.1) with
![]() $2 \mid y$
and
$2 \mid y$
and
![]() $2 \mid z$
. Then,
$2 \mid z$
. Then,
![]() $2^{x}=c^{z}-b^{y}=(c^{z/2}+b^{y/2})(c^{z/2}-b^{y/2})$
. Further, since
$2^{x}=c^{z}-b^{y}=(c^{z/2}+b^{y/2})(c^{z/2}-b^{y/2})$
. Further, since
![]() $\gcd (c^{z/2}+b^{y/2},c^{z/2}-b^{y/2})=2$
,
$\gcd (c^{z/2}+b^{y/2},c^{z/2}-b^{y/2})=2$
,
which gives
Since
![]() $b>1$
, we see from the second equality of (3.24) that
$b>1$
, we see from the second equality of (3.24) that
![]() $y/2$
is odd. If
$y/2$
is odd. If
![]() ${y/2>1}$
, then
${y/2>1}$
, then
![]() $2^{x-2}=b^{y/2}+1=(b+1)(b^{y/2-1}-b^{y/2-2}+\cdots -b+1)$
, where
$2^{x-2}=b^{y/2}+1=(b+1)(b^{y/2-1}-b^{y/2-2}+\cdots -b+1)$
, where
![]() $b^{y/2-1}-b^{y/2-2}+\cdots -b+1$
is an odd positive integer greater than
$b^{y/2-1}-b^{y/2-2}+\cdots -b+1$
is an odd positive integer greater than
![]() $1$
, a contradiction. So we have
$1$
, a contradiction. So we have
Similarly, if
![]() $z/2$
is odd, then from the first equality of (3.24),
$z/2$
is odd, then from the first equality of (3.24),
Hence, by (3.25) and (3.26), we obtain (3.23).
If
![]() $z/2$
is even, then
$z/2$
is even, then
![]() $2^{x-2}=c^{z/2}-1=(c^{z/4}+1)(c^{z/4}-1)$
, whence
$2^{x-2}=c^{z/2}-1=(c^{z/4}+1)(c^{z/4}-1)$
, whence
Therefore, by (3.25) and (3.27), we obtain (3.22). The lemma is proved.
Here and below, we assume that
![]() $(x_{1},y_{1},z_{1})$
and
$(x_{1},y_{1},z_{1})$
and
![]() $(x_{2},y_{2},z_{2})$
are two distinct solutions of (3.1). We can further assume without loss of generality that
$(x_{2},y_{2},z_{2})$
are two distinct solutions of (3.1). We can further assume without loss of generality that
![]() $x_{1} \le x_{2}$
.
$x_{1} \le x_{2}$
.
Lemma 3.8. We have
![]() $2 \nmid y_{1}y_{2}z_{1}z_{2}$
.
$2 \nmid y_{1}y_{2}z_{1}z_{2}$
.
Proof. By Lemmas 3.5, 3.6 and 3.7, if
![]() $2 \mid y_{1}y_{2}z_{1}z_{2}$
, then
$2 \mid y_{1}y_{2}z_{1}z_{2}$
, then
However, by Lemma 2.6, we can eliminate the cases
![]() $(b,c)=(11,5)$
,
$(b,c)=(11,5)$
,
![]() $(17,71)$
and
$(17,71)$
and
![]() $(7,3)$
. Alternatively, by Lemma 2.7, if
$(7,3)$
. Alternatively, by Lemma 2.7, if
![]() $(a,b,c)=(2,2^{t}-1,2^{t}+1)$
, then (1.1) has only two solutions
$(a,b,c)=(2,2^{t}-1,2^{t}+1)$
, then (1.1) has only two solutions
![]() $(x,y,z)=(1,1,1)$
and
$(x,y,z)=(1,1,1)$
and
![]() $(t+2,2,2)$
. Therefore, we can eliminate the cases
$(t+2,2,2)$
. Therefore, we can eliminate the cases
![]() $(b,c)=(2^{t}-1,2^{t}+1) (t=2,3,\ldots )$
in (3.28). Thus, the lemma is proved.
$(b,c)=(2^{t}-1,2^{t}+1) (t=2,3,\ldots )$
in (3.28). Thus, the lemma is proved.
Lemma 3.9. We have
![]() $y_{1}z_{2} \ne y_{2}z_{1}$
.
$y_{1}z_{2} \ne y_{2}z_{1}$
.
Proof. By Lemmas 3.4 and 3.8,
![]() $\gcd (y_{1},z_{1})=\gcd (y_{2},z_{2})=1$
. Hence, if
$\gcd (y_{1},z_{1})=\gcd (y_{2},z_{2})=1$
. Hence, if
![]() $y_{1}z_{2}=y_{2}z_{1}$
, then
$y_{1}z_{2}=y_{2}z_{1}$
, then
![]() $y_{1}\mid y_{2}$
and
$y_{1}\mid y_{2}$
and
![]() $y_{2}\mid y_{1}$
. This implies that
$y_{2}\mid y_{1}$
. This implies that
![]() $y_{1}=y_{2}$
,
$y_{1}=y_{2}$
,
![]() $z_{1}=z_{2}$
and
$z_{1}=z_{2}$
and
![]() $(x_{1},y_{1},z_{1})=(x_{2},y_{2},z_{2})$
, a contradiction. The lemma is proved.
$(x_{1},y_{1},z_{1})=(x_{2},y_{2},z_{2})$
, a contradiction. The lemma is proved.
Lemma 3.10. If
![]() $\max \{b,c\}>8\times 10^{6}$
, then
$\max \{b,c\}>8\times 10^{6}$
, then
![]() $2^{x_{1}}<c^{0.8z_{1}}$
.
$2^{x_{1}}<c^{0.8z_{1}}$
.
Proof. By (3.1),
![]() $b^{y_{1}}\equiv c^{z_{1}}\pmod {2^{x_{1}}}$
and
$b^{y_{1}}\equiv c^{z_{1}}\pmod {2^{x_{1}}}$
and
![]() $b^{y_{2}}\equiv c^{z_{2}}\pmod {2^{x_{2}}}$
. Since
$b^{y_{2}}\equiv c^{z_{2}}\pmod {2^{x_{2}}}$
. Since
![]() $x_{1} \le x_{2}$
, we get
$x_{1} \le x_{2}$
, we get
![]() $b^{y_{1}y_{2}}\equiv c^{z_{1}y_{2}}\equiv c^{z_{2}y_{1}}\pmod {2^{x_{1}}}$
and
$b^{y_{1}y_{2}}\equiv c^{z_{1}y_{2}}\equiv c^{z_{2}y_{1}}\pmod {2^{x_{1}}}$
and
![]() $c^{z_{1}z_{2}}\equiv b^{y_{1}z_{2}}\equiv b^{y_{2}z_{1}}\pmod {2^{x_{1}}}$
. Consequently,
$c^{z_{1}z_{2}}\equiv b^{y_{1}z_{2}}\equiv b^{y_{2}z_{1}}\pmod {2^{x_{1}}}$
. Consequently,
![]() $b^{|y_{1}z_{2}-y_{2}z_{1}|}\equiv c^{|y_{1}z_{2}-y_{2}z_{1}|}\equiv 1 \pmod {2^{x_{1}}}$
. Let
$b^{|y_{1}z_{2}-y_{2}z_{1}|}\equiv c^{|y_{1}z_{2}-y_{2}z_{1}|}\equiv 1 \pmod {2^{x_{1}}}$
. Let
![]() $m =\max \{b,c\}$
. We have
$m =\max \{b,c\}$
. We have
By Lemmas 3.8 and 3.9,
![]() $|y_{1}z_{2}-y_{2}z_{1}|$
is an even positive integer. Since
$|y_{1}z_{2}-y_{2}z_{1}|$
is an even positive integer. Since
![]() $2 \nmid m$
, by Lemma 2.1,
$2 \nmid m$
, by Lemma 2.1,
Further, since
![]() $2^{g(m)}\le m+1$
and
$2^{g(m)}\le m+1$
and
![]() $2^{{\mathop{\mathrm{ord}}\nolimits}_{2}|y_{1}z_{2}-y_{2}z_{1}|}\le |y_{1}z_{2}-y_{2}z_{1}|$
, by (3.31),
$2^{{\mathop{\mathrm{ord}}\nolimits}_{2}|y_{1}z_{2}-y_{2}z_{1}|}\le |y_{1}z_{2}-y_{2}z_{1}|$
, by (3.31),
Furthermore, by Lemma 3.2, if
![]() $2^{x_{1}}>c^{0.8z_{1}}$
, then
$2^{x_{1}}>c^{0.8z_{1}}$
, then
Recall that
![]() $c^{z_{1}}>b^{y_{1}}$
,
$c^{z_{1}}>b^{y_{1}}$
,
![]() $2\nmid y_{1}z_{1}$
and
$2\nmid y_{1}z_{1}$
and
![]() $\min \{y_{1},z_{1}\}\ge 3$
. We have
$\min \{y_{1},z_{1}\}\ge 3$
. We have
![]() $c^{z_{1}} \ge m^{3}$
. Therefore, if
$c^{z_{1}} \ge m^{3}$
. Therefore, if
![]() $2^{x_{1}}>c^{0.8z_{1}}$
, then from (3.34), we get
$2^{x_{1}}>c^{0.8z_{1}}$
, then from (3.34), we get
whence
![]() $m < 8\times 10^{6}$
. Thus, if
$m < 8\times 10^{6}$
. Thus, if
![]() $m>8\times 10^{6}$
, then
$m>8\times 10^{6}$
, then
![]() $2^{x_{1}}<c^{0.8z_{1}}$
.
$2^{x_{1}}<c^{0.8z_{1}}$
.
4 Proof of Theorem 1.2
Obviously, by Lemma 2.8, the theorem holds for
![]() $c=2$
. Moreover, in case a, b and c are distinct primes, we only have to consider
$c=2$
. Moreover, in case a, b and c are distinct primes, we only have to consider
![]() $(a,b,c)=(2,p,q)$
, where p and q are odd primes with
$(a,b,c)=(2,p,q)$
, where p and q are odd primes with
![]() $p \ne q$
. Then, (1.1) can be rewritten as (2.3). Further, by Lemma 2.6, the theorem holds for
$p \ne q$
. Then, (1.1) can be rewritten as (2.3). Further, by Lemma 2.6, the theorem holds for
![]() $(p,q)=(3,5),~(5,3),~(7,3)$
and
$(p,q)=(3,5),~(5,3),~(7,3)$
and
![]() $(11,5)$
.
$(11,5)$
.
We now assume that
![]() $N^{\prime }(2,p,q)>1$
. It follows that (2.3) has two solutions
$N^{\prime }(2,p,q)>1$
. It follows that (2.3) has two solutions
![]() $(x_{1},y_{1},z_{1})$
and
$(x_{1},y_{1},z_{1})$
and
![]() $(x_{2},y_{2},z_{2})$
with
$(x_{2},y_{2},z_{2})$
with
![]() $\min \{x_{j},y_{j},z_{j}\}>1$
for
$\min \{x_{j},y_{j},z_{j}\}>1$
for
![]() $j=1,2$
. Since we have excluded the cases
$j=1,2$
. Since we have excluded the cases
![]() $(p,q)=(3,5),~(5,3),~(7,3)$
and
$(p,q)=(3,5),~(5,3),~(7,3)$
and
![]() $(11,5)$
, by Lemma 2.9, we can assume without loss of generality that
$(11,5)$
, by Lemma 2.9, we can assume without loss of generality that
![]() $2 \mid x_{1}$
,
$2 \mid x_{1}$
,
![]() $2\nmid x_{2}$
and
$2\nmid x_{2}$
and
![]() $2\nmid y_{1}y_{2}$
. Then
$2\nmid y_{1}y_{2}$
. Then
If
![]() $p\ne 3$
, since
$p\ne 3$
, since
![]() $2\nmid y_{1}y_{2}$
and
$2\nmid y_{1}y_{2}$
and
![]() $p^{y_{1}}\equiv p^{y_{2}}\equiv p \pmod 3$
, then from (4.1),
$p^{y_{1}}\equiv p^{y_{2}}\equiv p \pmod 3$
, then from (4.1),
However, since
![]() $p \ne 3$
,
$p \ne 3$
,
![]() $1+p\not \equiv 2+p\pmod 3$
and
$1+p\not \equiv 2+p\pmod 3$
and
![]() $3 \mid (1+p)(2+p)$
, (4.2) is false.
$3 \mid (1+p)(2+p)$
, (4.2) is false.
If
![]() $p=3$
, by (4.1), then we have
$p=3$
, by (4.1), then we have
![]() $q^{z_{1}}\equiv 1 \pmod 3$
and
$q^{z_{1}}\equiv 1 \pmod 3$
and
![]() $q^{z_{2}} \equiv 2 \pmod 3$
, whence
$q^{z_{2}} \equiv 2 \pmod 3$
, whence
![]() $q \equiv 2 \pmod 3$
,
$q \equiv 2 \pmod 3$
,
![]() $2\mid z_{1}$
and
$2\mid z_{1}$
and
![]() $2 \nmid z_{2}$
. Hence, by the first equality of (4.1),
$2 \nmid z_{2}$
. Hence, by the first equality of (4.1),
Eliminating
![]() $q^{z_{1}/2}$
from (4.3), we have
$q^{z_{1}/2}$
from (4.3), we have
However, since
![]() $x_{1}/2+1 \ge 2$
and
$x_{1}/2+1 \ge 2$
and
![]() $2\nmid y_{1}$
, we get from (4.4) that
$2\nmid y_{1}$
, we get from (4.4) that
![]() $0 \equiv 2^{x_{1}/2+1}\equiv 3^{y_{1}}-1\equiv 3-1\equiv 2 \pmod 4$
, a contradiction. Thus, the theorem is proved.
$0 \equiv 2^{x_{1}/2+1}\equiv 3^{y_{1}}-1\equiv 3-1\equiv 2 \pmod 4$
, a contradiction. Thus, the theorem is proved.
5 Proof of Theorem 1.3
To show Theorem 1.3, we need the following lemma.
Lemma 5.1. If
![]() $a=2$
,
$a=2$
,
![]() $f(b)=f(c)$
,
$f(b)=f(c)$
,
![]() $g(b)\ne g(c)$
and
$g(b)\ne g(c)$
and
![]() $\max \{b,c\}>8.4\times 10^{6}$
, then Conjecture 1.1 is true.
$\max \{b,c\}>8.4\times 10^{6}$
, then Conjecture 1.1 is true.
Proof. Assume that
![]() $a=2$
,
$a=2$
,
![]() $f(b)=f(c)$
,
$f(b)=f(c)$
,
![]() $g(b)\ne g(c)$
,
$g(b)\ne g(c)$
,
![]() $\max \{b,c\}>8.4\times 10^{6}$
and
$\max \{b,c\}>8.4\times 10^{6}$
and
![]() $N^{\prime }(a,b,c)>1$
. Then, by the conclusions of Lemma 3.8 and of Lemma 3.1(ii), (3.1) has two distinct solutions
$N^{\prime }(a,b,c)>1$
. Then, by the conclusions of Lemma 3.8 and of Lemma 3.1(ii), (3.1) has two distinct solutions
![]() $(x_{1},y_{1},z_{1})$
and
$(x_{1},y_{1},z_{1})$
and
![]() $(x_{2},y_{2},z_{2})$
with
$(x_{2},y_{2},z_{2})$
with
Since
![]() $(x_{1},y_{1},z_{1})\ne (x_{2},y_{2},z_{2})$
, by (5.1), we may assume without loss of generality that
$(x_{1},y_{1},z_{1})\ne (x_{2},y_{2},z_{2})$
, by (5.1), we may assume without loss of generality that
Let
We see from (3.6) and (5.3) that
Further, by (5.1), (5.2) and (5.4),
Furthermore, by Lemma 3.10, we have
![]() $2^{x_{1}}<c^{0.8z_{1}}$
. Hence, by (3.6) and (5.5),
$2^{x_{1}}<c^{0.8z_{1}}$
. Hence, by (3.6) and (5.5),
However, by Lemmas 3.8 and 3.9,
![]() $|y_{1}z_{2}-y_{2}z_{1}|$
is an even positive integer. So,
$|y_{1}z_{2}-y_{2}z_{1}|$
is an even positive integer. So,
By (5.3),
 $$ \begin{align} |y_{1}z_{2}-y_{2}z_{1}|&=\frac{1}{\log c}|y_{1}(z_{2}\log c)-y_{2}(z_{1}\log c)|\notag\\ &=\frac{1}{\log c}|y_{1}(y_{2}\log b+\Lambda_{2})-y_{2}(y_{1}\log b+\Lambda_{1})|\notag\\ &=\frac{1}{\log c}|y_{1}\Lambda_{2}-y_{2}\Lambda_{1}|. \end{align} $$
$$ \begin{align} |y_{1}z_{2}-y_{2}z_{1}|&=\frac{1}{\log c}|y_{1}(z_{2}\log c)-y_{2}(z_{1}\log c)|\notag\\ &=\frac{1}{\log c}|y_{1}(y_{2}\log b+\Lambda_{2})-y_{2}(y_{1}\log b+\Lambda_{1})|\notag\\ &=\frac{1}{\log c}|y_{1}\Lambda_{2}-y_{2}\Lambda_{1}|. \end{align} $$
Since
![]() $y_{1} \Lambda _{2}>0$
and
$y_{1} \Lambda _{2}>0$
and
![]() $y_{2}\Lambda _{1}>0$
by (5.4), we see from (5.8) that
$y_{2}\Lambda _{1}>0$
by (5.4), we see from (5.8) that
 $$ \begin{align} |y_{1}z_{2}-y_{2}z_{1}|<\max\bigg\{\frac{y_{1}\Lambda_{2}}{\log c},\frac{y_{2}\Lambda_{1}}{\log c}\bigg\}. \end{align} $$
$$ \begin{align} |y_{1}z_{2}-y_{2}z_{1}|<\max\bigg\{\frac{y_{1}\Lambda_{2}}{\log c},\frac{y_{2}\Lambda_{1}}{\log c}\bigg\}. \end{align} $$
Further, by (5.2) and Lemma 3.2,
Hence, by (5.6), (5.7), (5.9) and (5.10),
whence we obtain
However, since
![]() $\max \{b,c\}>8.4\times 10^{6}$
and
$\max \{b,c\}>8.4\times 10^{6}$
and
![]() $c^{z_{1}}\ge (\max \{b,c\})^{3}$
, (5.11) is false. Thus, we have
$c^{z_{1}}\ge (\max \{b,c\})^{3}$
, (5.11) is false. Thus, we have
![]() $N^{\prime }(a,b,c)\le 1$
if
$N^{\prime }(a,b,c)\le 1$
if
![]() $a=2$
,
$a=2$
,
![]() $f(b)=f(c)$
,
$f(b)=f(c)$
,
![]() $g(b)\ne g(c)$
and
$g(b)\ne g(c)$
and
![]() $\max \{b,c\}>8.4\times 10^{6}$
.
$\max \{b,c\}>8.4\times 10^{6}$
.
We are now ready to prove Theorem 1.3.
Proof of Theorem 1.3.
Obviously, by the conclusion of Lemma 3.1(i), Conjecture 1.1 is true if
![]() $a=2$
and
$a=2$
and
![]() $f(b)\ne f(c)$
. We now assume that
$f(b)\ne f(c)$
. We now assume that
![]() $a=2$
,
$a=2$
,
![]() $f(b)=f(c)$
,
$f(b)=f(c)$
,
![]() $g(b)\ne g(c)$
and
$g(b)\ne g(c)$
and
![]() $N^{\prime }(a,b,c)>1$
. Moreover, by Lemma 5.1, we may assume that
$N^{\prime }(a,b,c)>1$
. Moreover, by Lemma 5.1, we may assume that
Then, by the conclusion of Lemma 3.1(ii), (3.1) has two distinct solutions
![]() $(x_{1},y_{1},z_{1})$
and
$(x_{1},y_{1},z_{1})$
and
![]() $(x_{2},y_{2},z_{2})$
with
$(x_{2},y_{2},z_{2})$
with
and we may assume that
![]() $y_{1}<y_{2}$
and
$y_{1}<y_{2}$
and
![]() $z_{1}<z_{2}$
. Further, by (5.12), we have
$z_{1}<z_{2}$
. Further, by (5.12), we have
![]() $2^{g(b)}\le b+1 \le 8.4\times 10^{6}$
, which together with (5.13) implies that
$2^{g(b)}\le b+1 \le 8.4\times 10^{6}$
, which together with (5.13) implies that
It follows from Lemma 3.3 that
Furthermore, by (3.16) and (5.14),
Thus, by the same argument as the proof of Lemma 5.1, we see from (5.15) and (5.16) that
whence we obtain
Consequently, it only remains to show that (3.1) has no solutions if
with
![]() $2 \nmid bcy_{1}z_{1}$
(by Lemma 3.8). We checked that the above claim is true by a simple program in PARI/GP [23] with precision
$2 \nmid bcy_{1}z_{1}$
(by Lemma 3.8). We checked that the above claim is true by a simple program in PARI/GP [23] with precision
![]() $100$
. Indeed, the result showed that for any c,
$100$
. Indeed, the result showed that for any c,
![]() $x_{1}$
,
$x_{1}$
,
![]() $y_{1}$
,
$y_{1}$
,
![]() $z_{1}$
in the above ranges, the fractional part of
$z_{1}$
in the above ranges, the fractional part of
![]() $(c^{z_{1}}-2^{x_{1}})^{1/y_{1}}$
is greater than
$(c^{z_{1}}-2^{x_{1}})^{1/y_{1}}$
is greater than
![]() $10^{-6}$
. The computation time was within
$10^{-6}$
. The computation time was within
![]() $1$
minute. Thus, the theorem is proved.
$1$
minute. Thus, the theorem is proved.
Acknowledgement
The authors thank the referee for reading the draft very carefully and putting forward some valuable suggestions.