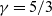1 Introduction
Compressible flows constitute a majority of the naturally occurring fluid flows in the universe and exhibit intricate physics. In the incompressible regime, pressure acts as a Lagrange multiplier that enforces the velocity field to be solenoidal. The role of pressure is significantly altered in the compressible regime, where pressure is governed by internal energy dynamics. The non-zero dilatation in compressible turbulence facilitates the internal kinetic energy exchange across the scales, which is interspersed with nonlinear energy transfer between scales. Consequently, the thermodynamic quantities such as density, pressure and temperature exhibit significant fluctuations and necessitate statistical treatment, in addition to the velocity field.
To investigate compressible turbulence statistics, we utilise the following governing equations of the compressible fluid, assuming an ideal gas:
Here,
![]() $\rho$
,
$\rho$
,
![]() ${\boldsymbol{u}}$
, p, T and
${\boldsymbol{u}}$
, p, T and
![]() $\boldsymbol{\tau}$
denote density, velocity, pressure, temperature and viscous stress tensor, respectively. Einstein summation convention is followed. The coefficient of viscosity is denoted by
$\boldsymbol{\tau}$
denote density, velocity, pressure, temperature and viscous stress tensor, respectively. Einstein summation convention is followed. The coefficient of viscosity is denoted by
![]() $\mu$
and bulk viscosity is taken to be zero. The ratio of specific heats (
$\mu$
and bulk viscosity is taken to be zero. The ratio of specific heats (
![]() $C_p/C_v$
) is denoted by
$C_p/C_v$
) is denoted by
![]() $\gamma$
. The equations are normalised with respect to the reference quantities (represented with a subscript 0), leading to three dimensionless parameters: (i) Reynolds number (Re), (ii) Mach number (M) and (iii) Prandtl number (Pr), defined as:
$\gamma$
. The equations are normalised with respect to the reference quantities (represented with a subscript 0), leading to three dimensionless parameters: (i) Reynolds number (Re), (ii) Mach number (M) and (iii) Prandtl number (Pr), defined as:
A straightforward way to obtain the statistics would be to analyse governing equations (1.1), upon averaging. However, a quick examination would reveal the closure problem, with each term in the continuity, momentum and energy equations requiring its own infinite hierarchy of equations. As a result, the moment hierarchy in compressible turbulence is more involved than its incompressible counterpart. Probability density function (PDF) approach has been utilised to examine statistics of compressible non-reacting and reacting flows [Reference Fox5, Reference Farshchi4, Reference Kollmann7, Reference Praturi, Plümacher and Oberlack16]. The PDF approach circumvents the issue of multiple hierarchies and gives rise to a single hierarchy of multi-point PDF equations [Reference Praturi, Plümacher and Oberlack16]. In a similar manner, characteristic function (CF), the Fourier transform of the PDF, gives rise to an alternate hierarchy of infinite multi-point CF equations [Reference Praturi, Plümacher and Oberlack16]. Characteristic functional can also be utilized for the examination of statistics, and the resulting equation is a functional differential equation [Reference Kollmann7].
Lie group theory has been successfully applied to several areas of physics, including turbulence. In the incompressible regime, symmetry methods have been applied to glean insights in (i) the multi-point moment [Reference Oberlack and Rosteck12] and (ii) the PDF approaches [Reference Wacławczyk, Grebenev and Oberlack20]. In the symmetry analysis of the statistical approaches, it is seen that the symmetries of the instantaneous equations are retained; and two additional symmetries, namely the ‘shape’ and ‘intermittency’ symmetries, are admitted. All of the symmetry groups derived have been instrumental in obtaining scaling laws for various canonical flows and have been verified against direct numerical simulations and/or experimental data [Reference Avsarkisov, Oberlack and Hoyas1, Reference Sadeghi, Oberlack and Gauding17, Reference Sadeghi and Oberlack18, Reference Sadeghi, Oberlack and Gauding19, Reference Oberlack, Hoyas, Kraheberger, Alcántara-Ávila and Laux11]. The goal of this study is to investigate the behaviour of statistics in compressible turbulence, by performing Lie symmetry analysis on the CF hierarchy. The advantages of performing the analysis on CF hierarchy will be discussed in the next section, where the governing CF equations are introduced.
This paper is organised as follows. We introduce the governing equations of the CF hierarchy and the additional conditions/constraints imposed on CFs in Section 2. In Section 3, the symmetries of CF hierarchy are derived. The global form of each of the symmetry transformations and their physical significance are presented in Section 4. The resulting global moment transformations are discussed in Section 5. The key findings of this study are summarised in Section 6.
2 CF hierarchy in compressible turbulence
For a random variable, ‘U’, its CF (
![]() $\varphi$
) is defined as follows [Reference Pope15, Reference Lumley8]:
$\varphi$
) is defined as follows [Reference Pope15, Reference Lumley8]:
where s is the spectral parameter and f(U) is the PDF of U. In other words, CF represents the expectation of
![]() $\exp{ (\mathrm{i} s U)}$
and is complex in nature. Like the PDF, CF contains all of the information about the statistics of the random variable, U. The moments of U can be evaluated from the CF by computing its derivatives, that is,
$\exp{ (\mathrm{i} s U)}$
and is complex in nature. Like the PDF, CF contains all of the information about the statistics of the random variable, U. The moments of U can be evaluated from the CF by computing its derivatives, that is,
Compared to the PDF approach, the reconstruction of the CF from the moments is also more straightforward. Let us consider the Taylor series expansion of CF about
![]() $s=0$
[Reference Wacławczyk, Staffolani, Oberlack, Rosteck, Wilczek and Friedrich21]:
$s=0$
[Reference Wacławczyk, Staffolani, Oberlack, Rosteck, Wilczek and Friedrich21]:
This implies that all the moments of U can be pieced together to form the CF.
In compressible turbulence, as it is critical to examine density, pressure and temperature statistics in addition to velocity, we utilise the following definition for the multi-point CF [Reference Praturi, Plümacher and Oberlack16]:
 \begin{equation}\begin{aligned} &\varphi_n\!\left({}^{(1)}\underline{\varrho}, {}^{(1)}\underline{{\boldsymbol{v}}}, {}^{(1)}\underline{\theta},{}^{(2)}\underline{\varrho}, {}^{(2)}\underline{{\boldsymbol{v}}}, {}^{(2)}\underline{\theta}, ... , {}^{(n)}\underline{\varrho}, {}^{(n)}\underline{{\boldsymbol{v}}}, {}^{(n)}\underline{\theta}; t, {\boldsymbol{x}}^{(1)}, {\boldsymbol{x}}^{(2)}, ... , {\boldsymbol{x}}^{(n)}\right) = \\[5pt] & \quad \left\langle \exp \left[ \mathrm{i} \sum_{k=1}^n \!\left( {}^{(k)}\underline{\varrho} \rho({\boldsymbol{x}}^{(k)}, t) + {}^{(k)}\underline{v}_i u_i({\boldsymbol{x}}^{(k)}, t) + {}^{(k)}\underline{\theta} T({\boldsymbol{x}}^{(k)}, t) \right) \right] \right\rangle.\end{aligned}\end{equation}
\begin{equation}\begin{aligned} &\varphi_n\!\left({}^{(1)}\underline{\varrho}, {}^{(1)}\underline{{\boldsymbol{v}}}, {}^{(1)}\underline{\theta},{}^{(2)}\underline{\varrho}, {}^{(2)}\underline{{\boldsymbol{v}}}, {}^{(2)}\underline{\theta}, ... , {}^{(n)}\underline{\varrho}, {}^{(n)}\underline{{\boldsymbol{v}}}, {}^{(n)}\underline{\theta}; t, {\boldsymbol{x}}^{(1)}, {\boldsymbol{x}}^{(2)}, ... , {\boldsymbol{x}}^{(n)}\right) = \\[5pt] & \quad \left\langle \exp \left[ \mathrm{i} \sum_{k=1}^n \!\left( {}^{(k)}\underline{\varrho} \rho({\boldsymbol{x}}^{(k)}, t) + {}^{(k)}\underline{v}_i u_i({\boldsymbol{x}}^{(k)}, t) + {}^{(k)}\underline{\theta} T({\boldsymbol{x}}^{(k)}, t) \right) \right] \right\rangle.\end{aligned}\end{equation}
where
![]() $\varphi_n$
represents the n-point CF.
$\varphi_n$
represents the n-point CF.
![]() ${}^{(k)}\underline{\varrho}$
,
${}^{(k)}\underline{\varrho}$
,
![]() ${}^{(k)}\underline{{\boldsymbol{v}}}$
and
${}^{(k)}\underline{{\boldsymbol{v}}}$
and
![]() ${}^{(k)}\underline{\theta}$
are the spectral parameters of density, velocity and temperature, respectively, at point
${}^{(k)}\underline{\theta}$
are the spectral parameters of density, velocity and temperature, respectively, at point
![]() ${\boldsymbol{x}}^{(k)}$
and k takes values from 1 to n. Going forward, we simplify the notation for spectral parameters by dropping the underline and represent them as
${\boldsymbol{x}}^{(k)}$
and k takes values from 1 to n. Going forward, we simplify the notation for spectral parameters by dropping the underline and represent them as
![]() ${}^{(k)}\varrho$
,
${}^{(k)}\varrho$
,
![]() ${}^{(k)}{\boldsymbol{v}}$
and
${}^{(k)}{\boldsymbol{v}}$
and
![]() ${}^{(k)}\theta$
. The governing equation for
${}^{(k)}\theta$
. The governing equation for
![]() $\varphi_n$
, derived in [Reference Praturi, Plümacher and Oberlack16], is given below:
$\varphi_n$
, derived in [Reference Praturi, Plümacher and Oberlack16], is given below:
 \begin{equation} \begin{aligned} &\left[ \frac{\partial}{\partial t} + \frac{1}{\mathrm{i}} \sum_{k=1}^n \frac{\partial^2}{\partial x_j^{(k)} \partial \> {}^{(k)}v_j } \right] \prod_{l=1}^n \frac{\partial}{\partial {}^{(l)}\varrho} \varphi_n \\[5pt] & \quad = - \sum_{k=1}^n \frac{\> {}^{(k)}\varrho}{\mathrm{i}} \left[\frac{\partial }{\partial x_j^{(n+1)}}\left. \prod_{l=1}^n \frac{\partial}{\partial {}^{(l)}\varrho} \frac{\partial^{2} \varphi_{n+1}}{\partial \>{}^{(n+1)}v_j \> \partial \>{}^{(k)}\varrho }\right|_{{}^{(n+1)}\varrho, {}^{(n+1)}{\boldsymbol{v}}, {}^{(n+1)}\theta = 0} \right]_{{\boldsymbol{x}}^{n+1}={\boldsymbol{x}}^{(k)}}\\[5pt] & \quad -\sum_{k=1}^n \frac{{}^{(k)}v_i}{\gamma M^2} \left[ \frac{\partial }{\partial x_i^{(n+1)}}\left. \prod_{l=1, l\neq k}^n \frac{\partial}{\partial {}^{(l)}\varrho} \frac{\partial^{2} \varphi_{n+1}}{\partial \>{}^{(n+1)}\varrho \> \partial \>{}^{(n+1)}\theta}\right|_{{}^{(n+1)}\varrho, {}^{(n+1)}{\boldsymbol{v}}, {}^{(n+1)}\theta = 0} \right]_{{\boldsymbol{x}}^{(n+1)}={\boldsymbol{x}}^{(k)}} \\[5pt] & \quad - \sum_{k=1}^n \frac{\gamma-1}{\mathrm{i}} {}^{(k)}\theta \left[ \frac{\partial}{\partial x_j^{(n+1)}} \left. \prod_{l=1}^n \frac{\partial}{\partial {}^{(l)}\varrho} \frac{\partial^{2} \varphi_{n+1}}{\partial \>{}^{(k)}\theta \partial \>{}^{(n+1)}v_j} \right|_{{}^{(n+1)}\varrho, {}^{(n+1)}{\boldsymbol{v}}, {}^{(n+1)}\theta = 0} \right]_{{\boldsymbol{x}}^{(n+1)} = {\boldsymbol{x}}^{(k)}} \end{aligned}.\end{equation}
\begin{equation} \begin{aligned} &\left[ \frac{\partial}{\partial t} + \frac{1}{\mathrm{i}} \sum_{k=1}^n \frac{\partial^2}{\partial x_j^{(k)} \partial \> {}^{(k)}v_j } \right] \prod_{l=1}^n \frac{\partial}{\partial {}^{(l)}\varrho} \varphi_n \\[5pt] & \quad = - \sum_{k=1}^n \frac{\> {}^{(k)}\varrho}{\mathrm{i}} \left[\frac{\partial }{\partial x_j^{(n+1)}}\left. \prod_{l=1}^n \frac{\partial}{\partial {}^{(l)}\varrho} \frac{\partial^{2} \varphi_{n+1}}{\partial \>{}^{(n+1)}v_j \> \partial \>{}^{(k)}\varrho }\right|_{{}^{(n+1)}\varrho, {}^{(n+1)}{\boldsymbol{v}}, {}^{(n+1)}\theta = 0} \right]_{{\boldsymbol{x}}^{n+1}={\boldsymbol{x}}^{(k)}}\\[5pt] & \quad -\sum_{k=1}^n \frac{{}^{(k)}v_i}{\gamma M^2} \left[ \frac{\partial }{\partial x_i^{(n+1)}}\left. \prod_{l=1, l\neq k}^n \frac{\partial}{\partial {}^{(l)}\varrho} \frac{\partial^{2} \varphi_{n+1}}{\partial \>{}^{(n+1)}\varrho \> \partial \>{}^{(n+1)}\theta}\right|_{{}^{(n+1)}\varrho, {}^{(n+1)}{\boldsymbol{v}}, {}^{(n+1)}\theta = 0} \right]_{{\boldsymbol{x}}^{(n+1)}={\boldsymbol{x}}^{(k)}} \\[5pt] & \quad - \sum_{k=1}^n \frac{\gamma-1}{\mathrm{i}} {}^{(k)}\theta \left[ \frac{\partial}{\partial x_j^{(n+1)}} \left. \prod_{l=1}^n \frac{\partial}{\partial {}^{(l)}\varrho} \frac{\partial^{2} \varphi_{n+1}}{\partial \>{}^{(k)}\theta \partial \>{}^{(n+1)}v_j} \right|_{{}^{(n+1)}\varrho, {}^{(n+1)}{\boldsymbol{v}}, {}^{(n+1)}\theta = 0} \right]_{{\boldsymbol{x}}^{(n+1)} = {\boldsymbol{x}}^{(k)}} \end{aligned}.\end{equation}
In the above multi-point CF equation, we ignore the terms arising due to viscosity and heat conductivity. As the viscous and heat conductivity terms are symmetry breaking, these terms are not considered in this study. For the complete equation, the reader is referred to [Reference Praturi, Plümacher and Oberlack16]. As the CF is a probability measure, additional conditions also need to be imposed [Reference Lundgren9]. These restrictions, called the ‘side conditions’, are listed below:
-
(1) Reduction: The order of the CF is reduced, when we set the spectral parameters to zero, that is,
(2.6a)In the above equation, we demonstrate that the \begin{equation}\begin{aligned} &\varphi_{n+1} \!\left({}^{(1)}\varrho, {}^{(1)}{\boldsymbol{v}}, {}^{(1)}\theta, .. , {}^{(n)}\varrho, {}^{(n)}{\boldsymbol{v}}, {}^{(n)}\theta, 0, \textbf{0}, 0; t, {\boldsymbol{x}}^{(1)}, .. , {\boldsymbol{x}}^{(n)}, {\boldsymbol{x}}^{(n+1)}\right) = \\[4pt] & \quad \varphi_{n} \!\left({}^{(1)}\varrho, {}^{(1)}{\boldsymbol{v}}, {}^{(1)}\theta, .. , {}^{(n)}\varrho, {}^{(n)}{\boldsymbol{v}}, {}^{(n)}\theta; t, {\boldsymbol{x}}^{(1)}, .. , {\boldsymbol{x}}^{(n)}\right).\end{aligned}\end{equation}
\begin{equation}\begin{aligned} &\varphi_{n+1} \!\left({}^{(1)}\varrho, {}^{(1)}{\boldsymbol{v}}, {}^{(1)}\theta, .. , {}^{(n)}\varrho, {}^{(n)}{\boldsymbol{v}}, {}^{(n)}\theta, 0, \textbf{0}, 0; t, {\boldsymbol{x}}^{(1)}, .. , {\boldsymbol{x}}^{(n)}, {\boldsymbol{x}}^{(n+1)}\right) = \\[4pt] & \quad \varphi_{n} \!\left({}^{(1)}\varrho, {}^{(1)}{\boldsymbol{v}}, {}^{(1)}\theta, .. , {}^{(n)}\varrho, {}^{(n)}{\boldsymbol{v}}, {}^{(n)}\theta; t, {\boldsymbol{x}}^{(1)}, .. , {\boldsymbol{x}}^{(n)}\right).\end{aligned}\end{equation}
 $(n+1)-$
point CF reduces to
$(n+1)-$
point CF reduces to
 $n-$
point CF, when the spectral parameters corresponding to
$n-$
point CF, when the spectral parameters corresponding to
 ${\boldsymbol{x}}^{(n+1)}$
, that is,
${\boldsymbol{x}}^{(n+1)}$
, that is,
 ${}^{(n+1)}\varrho, {}^{(n+1)}{\boldsymbol{v}}$
and
${}^{(n+1)}\varrho, {}^{(n+1)}{\boldsymbol{v}}$
and
 ${}^{(n+1)}\theta$
, are set to be zero. For the case of a single-point CF, reduction condition implies that: (2.6b)
${}^{(n+1)}\theta$
, are set to be zero. For the case of a single-point CF, reduction condition implies that: (2.6b) \begin{equation}\varphi_1\!\left({}^{(1)}\varrho = 0, {}^{(1)}{\boldsymbol{v}} = \textbf{0}, {}^{(1)}\theta = 0; t, {\boldsymbol{x}}^{(1)}\right) = 1.\end{equation}
\begin{equation}\varphi_1\!\left({}^{(1)}\varrho = 0, {}^{(1)}{\boldsymbol{v}} = \textbf{0}, {}^{(1)}\theta = 0; t, {\boldsymbol{x}}^{(1)}\right) = 1.\end{equation}
-
(2) Coincidence: When two points considered in the CF are infinitesimally closer to one another,
(2.7)the order of CF is effectively reduced and the spectral parameters at those points are added to one another. \begin{equation}\begin{aligned} \lim_{|{\boldsymbol{x}}^{(n+1)}-{\boldsymbol{x}}^{(n)}|\to 0} &\varphi_{n+1} \!\left(.. , {}^{(n)}\varrho, {}^{(n)}{\boldsymbol{v}}, {}^{(n)}\theta, {}^{(n+1)}\varrho, {}^{(n+1)}{\boldsymbol{v}}, {}^{(n+1)}\theta; t, {\boldsymbol{x}}^{(1)}, .. , {\boldsymbol{x}}^{(n)}, {\boldsymbol{x}}^{(n+1)}\right) \\ & \quad = \varphi_{n} \!\left(.. , {}^{(n)}\varrho+{}^{(n+1)}\varrho, {}^{(n)}{\boldsymbol{v}}+{}^{(n+1)}{\boldsymbol{v}}, {}^{(n)}\theta+{}^{(n+1)}\theta; t, {\boldsymbol{x}}^{(1)}, .. , {\boldsymbol{x}}^{(n)}\right),\end{aligned}\end{equation}
\begin{equation}\begin{aligned} \lim_{|{\boldsymbol{x}}^{(n+1)}-{\boldsymbol{x}}^{(n)}|\to 0} &\varphi_{n+1} \!\left(.. , {}^{(n)}\varrho, {}^{(n)}{\boldsymbol{v}}, {}^{(n)}\theta, {}^{(n+1)}\varrho, {}^{(n+1)}{\boldsymbol{v}}, {}^{(n+1)}\theta; t, {\boldsymbol{x}}^{(1)}, .. , {\boldsymbol{x}}^{(n)}, {\boldsymbol{x}}^{(n+1)}\right) \\ & \quad = \varphi_{n} \!\left(.. , {}^{(n)}\varrho+{}^{(n+1)}\varrho, {}^{(n)}{\boldsymbol{v}}+{}^{(n+1)}{\boldsymbol{v}}, {}^{(n)}\theta+{}^{(n+1)}\theta; t, {\boldsymbol{x}}^{(1)}, .. , {\boldsymbol{x}}^{(n)}\right),\end{aligned}\end{equation}
-
(3) Permutation: The order in which the points in the multi-point CF are considered has no effect on the value of
 $\varphi_n$
. This is expressed as: (2.8)
$\varphi_n$
. This is expressed as: (2.8) \begin{equation}\begin{aligned} &\varphi_{n} \!\left(... , {}^{(l)}\varrho, {}^{(l)}{\boldsymbol{v}}, {}^{(l)}\theta, ..., {}^{(k)}\varrho, {}^{(k)}{\boldsymbol{v}}, {}^{(k)}\theta; t, ... , {\boldsymbol{x}}^{(l)}, ..., {\boldsymbol{x}}^{(k)}, ...\right) \\[3pt] &\quad = \varphi_{n} \!\left(... , {}^{(k)}\varrho, {}^{(k)}{\boldsymbol{v}}, {}^{(k)}\theta, ..., {}^{(l)}\varrho, {}^{(l)}{\boldsymbol{v}}, {}^{(l)}\theta; t, ... , {\boldsymbol{x}}^{(k)}, ..., {\boldsymbol{x}}^{(l)}, ...\right).\end{aligned}\end{equation}
\begin{equation}\begin{aligned} &\varphi_{n} \!\left(... , {}^{(l)}\varrho, {}^{(l)}{\boldsymbol{v}}, {}^{(l)}\theta, ..., {}^{(k)}\varrho, {}^{(k)}{\boldsymbol{v}}, {}^{(k)}\theta; t, ... , {\boldsymbol{x}}^{(l)}, ..., {\boldsymbol{x}}^{(k)}, ...\right) \\[3pt] &\quad = \varphi_{n} \!\left(... , {}^{(k)}\varrho, {}^{(k)}{\boldsymbol{v}}, {}^{(k)}\theta, ..., {}^{(l)}\varrho, {}^{(l)}{\boldsymbol{v}}, {}^{(l)}\theta; t, ... , {\boldsymbol{x}}^{(k)}, ..., {\boldsymbol{x}}^{(l)}, ...\right).\end{aligned}\end{equation}
-
(4) Separation: When one of the points is infinitely separated from all other points considered in the multi-point CF, then,
(2.9)the statistics at the infinitely separated point are independent from all other points, and as a result, multiplication ensues. \begin{equation} \lim_{|{\boldsymbol{x}}^{(n+1)}-{\boldsymbol{x}}^{(k)}| \to \infty} \varphi_{n+1} = \varphi_1 \!\left({}^{(n+1)}\varrho, {}^{(n+1)}{\boldsymbol{v}}, {}^{(n+1)}\theta; t, {\boldsymbol{x}}^{(n+1)}\right) \varphi_n, \quad \forall k = 1-n\end{equation}
\begin{equation} \lim_{|{\boldsymbol{x}}^{(n+1)}-{\boldsymbol{x}}^{(k)}| \to \infty} \varphi_{n+1} = \varphi_1 \!\left({}^{(n+1)}\varrho, {}^{(n+1)}{\boldsymbol{v}}, {}^{(n+1)}\theta; t, {\boldsymbol{x}}^{(n+1)}\right) \varphi_n, \quad \forall k = 1-n\end{equation}
All of the above ‘side conditions’ will also be included as a part of the symmetry analysis, in the subsequent sections, in addition to the governing equation (2.5).
3 Symmetry analysis
In this section, we first demonstrate the symmetry groups exhibited by the compressible Euler equations. Then, we perform Lie group analysis on the compressible multi-point CF hierarchy. To this end, we first compute the symmetry groups of single- and two-point CF equations, while imposing the side conditions. The resulting infinitesimals are generalised for a multi-point CF.
3.1 Lie groups of the compressible Euler equation
Euler equations can be obtained from the set of equations (1.1) upon neglecting the effects of viscosity and heat conductivity, that is, by setting
![]() $\mu = \kappa = 0$
:
$\mu = \kappa = 0$
:
For an arbitrary value of the specific heat ratio (
![]() $\gamma$
), the following are the symmetry transformations of Euler equations [Reference Ibragimov6, Reference Ovsiannikov14]:
$\gamma$
), the following are the symmetry transformations of Euler equations [Reference Ibragimov6, Reference Ovsiannikov14]:
-
(1) Time translation symmetry
 $\left(T_{a_t}\right)$
: The equations (3.1) are invariant, when time is translated by an arbitrary constant,
$\left(T_{a_t}\right)$
: The equations (3.1) are invariant, when time is translated by an arbitrary constant,
 $a_t \in \mathbb{R}$
. The global form of symmetry transformation,
$a_t \in \mathbb{R}$
. The global form of symmetry transformation,
 $T_{a_t}$
, is (3.2a)with the symmetry operator:
$T_{a_t}$
, is (3.2a)with the symmetry operator: \begin{equation} T_{a_t}\,:\, \quad t^* = t + a_t, \quad {\boldsymbol{x}}^* = {\boldsymbol{x}}, \quad \rho^* = \rho, \quad {\boldsymbol{u}}^* = {\boldsymbol{u}}, \quad T^* = T, \quad p^* = p \end{equation}
(3.2b)
\begin{equation} T_{a_t}\,:\, \quad t^* = t + a_t, \quad {\boldsymbol{x}}^* = {\boldsymbol{x}}, \quad \rho^* = \rho, \quad {\boldsymbol{u}}^* = {\boldsymbol{u}}, \quad T^* = T, \quad p^* = p \end{equation}
(3.2b) \begin{equation} X = \frac{\partial}{\partial t}. \end{equation}
\begin{equation} X = \frac{\partial}{\partial t}. \end{equation}
-
(2) Spatial translation symmetry
 $\left(T_{a_{x,i}}\right)$
: The three symmetry groups represented by
$\left(T_{a_{x,i}}\right)$
: The three symmetry groups represented by
 $T_{a_{x,i}},$
$T_{a_{x,i}},$
 $i = 1, 2, 3$
indicate the invariance of the system (3.1) with respect to arbitrary spatial translation by
$i = 1, 2, 3$
indicate the invariance of the system (3.1) with respect to arbitrary spatial translation by
 $a_{x,i} \in \mathbb{R}, i = 1,2, 3$
. The global transformation is (3.2c)and the symmetry operator is
$a_{x,i} \in \mathbb{R}, i = 1,2, 3$
. The global transformation is (3.2c)and the symmetry operator is \begin{equation} T_{a_{x,i}}\,: \quad t^* = t, \quad x_i^* = x_i + a_{x,i}, \quad \rho^* = \rho, \quad {\boldsymbol{u}}^*={\boldsymbol{u}}, \quad T^* = T, \quad p^* = p , \end{equation}
(3.2d)for
\begin{equation} T_{a_{x,i}}\,: \quad t^* = t, \quad x_i^* = x_i + a_{x,i}, \quad \rho^* = \rho, \quad {\boldsymbol{u}}^*={\boldsymbol{u}}, \quad T^* = T, \quad p^* = p , \end{equation}
(3.2d)for \begin{equation} X = \frac{\partial}{\partial x_1}, \quad X = \frac{\partial}{\partial x_2}, \quad X = \frac{\partial}{\partial x_3}, \end{equation}
\begin{equation} X = \frac{\partial}{\partial x_1}, \quad X = \frac{\partial}{\partial x_2}, \quad X = \frac{\partial}{\partial x_3}, \end{equation}
 $a_{x,1}, a_{x,2}$
and
$a_{x,1}, a_{x,2}$
and
 $a_{x,3}$
, respectively.
$a_{x,3}$
, respectively.
-
(3) Galilean symmetry
 $\left(T_{a_{g,i}}\right)$
: The Euler equations are invariant in a coordinate frame that is moving at constant velocity,
$\left(T_{a_{g,i}}\right)$
: The Euler equations are invariant in a coordinate frame that is moving at constant velocity,
 $a_{g,i} \in \mathbb{R}, i = 1, 2, 3$
: (3.2e)with the symmetry operators given by:
$a_{g,i} \in \mathbb{R}, i = 1, 2, 3$
: (3.2e)with the symmetry operators given by: \begin{equation} T_{a_{g,i}}\,: \quad t^* = t, \> x_i^* = x_i + a_{g,i}t, \> \rho^* = \rho, \> u_i^* = u_i + a_{g,i}, \> T^* = T, \> p^* = p , \end{equation}
(3.2f)for
\begin{equation} T_{a_{g,i}}\,: \quad t^* = t, \> x_i^* = x_i + a_{g,i}t, \> \rho^* = \rho, \> u_i^* = u_i + a_{g,i}, \> T^* = T, \> p^* = p , \end{equation}
(3.2f)for \begin{equation} X = t \frac{\partial}{\partial x_1} + \frac{\partial}{\partial u_1}, \quad X = t \frac{\partial}{\partial x_2} + \frac{\partial}{\partial u_2}, \quad X = X = t \frac{\partial}{\partial x_3} + \frac{\partial}{\partial u_3},\end{equation}
\begin{equation} X = t \frac{\partial}{\partial x_1} + \frac{\partial}{\partial u_1}, \quad X = t \frac{\partial}{\partial x_2} + \frac{\partial}{\partial u_2}, \quad X = X = t \frac{\partial}{\partial x_3} + \frac{\partial}{\partial u_3},\end{equation}
 $a_{g,1}, a_{g,2}$
and
$a_{g,1}, a_{g,2}$
and
 $a_{g,3}$
, respectively.
$a_{g,3}$
, respectively.
-
(4) Rotational symmetry
 $\left(T_{a_{r,i}}\right)$
: This symmetry signifies the invariance of Euler equations (3.1) under rotation, represented by three symmetry groups,
$\left(T_{a_{r,i}}\right)$
: This symmetry signifies the invariance of Euler equations (3.1) under rotation, represented by three symmetry groups,
 $a_{r,i} \in \mathbb{R}, i = 1, 2, 3$
. For example, rotation about
$a_{r,i} \in \mathbb{R}, i = 1, 2, 3$
. For example, rotation about
 $x_1$
axis, written in terms of the group parameter,
$x_1$
axis, written in terms of the group parameter,
 $a_{r,1}$
, is given by: (3.2g)with
$a_{r,1}$
, is given by: (3.2g)with \begin{equation} \begin{aligned} T_{a_{r,1}}\,:\quad &t^* = t, x_2^* = \left(\cos{a_{r,1}}\right) x_2 - \left(\sin{a_{r,1}}\right) x_3, x_3^* = \left(\sin{a_{r,1}}\right) x_2 + \left(\cos{a_{r,1}}\right) x_3, \\ &\rho^* = \rho, u_2^* = \left(\cos{a_{r,1}}\right) u_2 - \left(\sin{a_{r,1}}\right) u_3, u_3^* = \left(\sin{a_{r,1}}\right) u_2 + \left(\cos{a_{r,1}}\right) u_3, \\ &x_1^* = x_1,\quad u_1^* = u_1,\quad T^* = T,\quad p^* = p, \end{aligned}\end{equation}
(3.2h)Similarly, the rotation about
\begin{equation} \begin{aligned} T_{a_{r,1}}\,:\quad &t^* = t, x_2^* = \left(\cos{a_{r,1}}\right) x_2 - \left(\sin{a_{r,1}}\right) x_3, x_3^* = \left(\sin{a_{r,1}}\right) x_2 + \left(\cos{a_{r,1}}\right) x_3, \\ &\rho^* = \rho, u_2^* = \left(\cos{a_{r,1}}\right) u_2 - \left(\sin{a_{r,1}}\right) u_3, u_3^* = \left(\sin{a_{r,1}}\right) u_2 + \left(\cos{a_{r,1}}\right) u_3, \\ &x_1^* = x_1,\quad u_1^* = u_1,\quad T^* = T,\quad p^* = p, \end{aligned}\end{equation}
(3.2h)Similarly, the rotation about \begin{equation} X = x_2 \frac{\partial}{\partial x_3} - x_3 \frac{\partial}{\partial x_2} + u_2 \frac{\partial}{\partial u_3} - u_3 \frac{\partial}{\partial u_2}.\end{equation}
\begin{equation} X = x_2 \frac{\partial}{\partial x_3} - x_3 \frac{\partial}{\partial x_2} + u_2 \frac{\partial}{\partial u_3} - u_3 \frac{\partial}{\partial u_2}.\end{equation}
 $x_2$
axis, represented by
$x_2$
axis, represented by
 $a_{r,2}$
, is given by: (3.2i)with
$a_{r,2}$
, is given by: (3.2i)with \begin{equation} \begin{aligned} T_{a_{r,2}}\,:\quad &t^* = t, x_1^* = \left(\cos{a_{r,2}}\right) x_1 - \left(\sin{a_{r,2}}\right) x_3, x_3^* = \left(\sin{a_{r,2}}\right) x_1 + \left(\cos{a_{r,2}}\right) x_3, \\ &\rho^* = \rho, u_1^* = \left(\cos{a_{r,2}}\right) u_1 - \left(\sin{a_{r,2}}\right) u_3, u_3^* = \left(\sin{a_{r,2}}\right) u_1 + \left(\cos{a_{r,2}}\right) u_3, \\ &x_2^* = x_2,\quad u_2^* = u_2,\quad T^* = T,\quad p^* = p, \end{aligned}\end{equation}
(3.2j)Finally, rotation about
\begin{equation} \begin{aligned} T_{a_{r,2}}\,:\quad &t^* = t, x_1^* = \left(\cos{a_{r,2}}\right) x_1 - \left(\sin{a_{r,2}}\right) x_3, x_3^* = \left(\sin{a_{r,2}}\right) x_1 + \left(\cos{a_{r,2}}\right) x_3, \\ &\rho^* = \rho, u_1^* = \left(\cos{a_{r,2}}\right) u_1 - \left(\sin{a_{r,2}}\right) u_3, u_3^* = \left(\sin{a_{r,2}}\right) u_1 + \left(\cos{a_{r,2}}\right) u_3, \\ &x_2^* = x_2,\quad u_2^* = u_2,\quad T^* = T,\quad p^* = p, \end{aligned}\end{equation}
(3.2j)Finally, rotation about \begin{equation} X = - x_3 \frac{\partial}{\partial x_1} + x_1 \frac{\partial}{\partial x_3} - u_3 \frac{\partial}{\partial u_1} + u_1 \frac{\partial}{\partial u_3}.\end{equation}
\begin{equation} X = - x_3 \frac{\partial}{\partial x_1} + x_1 \frac{\partial}{\partial x_3} - u_3 \frac{\partial}{\partial u_1} + u_1 \frac{\partial}{\partial u_3}.\end{equation}
 $x_3$
axis can be written, using the group parameter
$x_3$
axis can be written, using the group parameter
 $a_{r,3}$
, as: (3.2k)and the symmetry operator is
$a_{r,3}$
, as: (3.2k)and the symmetry operator is \begin{equation} \begin{aligned} T_{a_{r,3}}\,: \quad &t^* = t, x_1^* = \left(\cos{a_{r,3}}\right) x_1 - \left(\sin{a_{r,3}}\right) x_2, x_2^* = \left(\sin{a_{r,3}}\right) x_1 + \left(\cos{a_{r,3}}\right) x_2, \\ &\rho^* = \rho, u_1^* = \left(\cos{a_{r,3}}\right) u_1 - \left(\sin{a_{r,3}}\right) u_2, u_2^* = \left(\sin{a_{r,3}}\right) u_1 + \left(\cos{a_{r,3}}\right) u_2, \\ &x_3^* = x_3,\quad u_3^* = u_3,\quad T^* = T,\quad p^* = p, \end{aligned} \end{equation}
(3.2l)Consequently, the Euler equations are invariant under any linear combination of the above three rotation groups, leaving the equations invariant under arbitrary rotation.
\begin{equation} \begin{aligned} T_{a_{r,3}}\,: \quad &t^* = t, x_1^* = \left(\cos{a_{r,3}}\right) x_1 - \left(\sin{a_{r,3}}\right) x_2, x_2^* = \left(\sin{a_{r,3}}\right) x_1 + \left(\cos{a_{r,3}}\right) x_2, \\ &\rho^* = \rho, u_1^* = \left(\cos{a_{r,3}}\right) u_1 - \left(\sin{a_{r,3}}\right) u_2, u_2^* = \left(\sin{a_{r,3}}\right) u_1 + \left(\cos{a_{r,3}}\right) u_2, \\ &x_3^* = x_3,\quad u_3^* = u_3,\quad T^* = T,\quad p^* = p, \end{aligned} \end{equation}
(3.2l)Consequently, the Euler equations are invariant under any linear combination of the above three rotation groups, leaving the equations invariant under arbitrary rotation. \begin{equation} X = - x_2 \frac{\partial}{\partial x_1} + x_1 \frac{\partial}{\partial x_2} - u_2 \frac{\partial}{\partial u_1} + u_1 \frac{\partial}{\partial u_2}. \end{equation}
\begin{equation} X = - x_2 \frac{\partial}{\partial x_1} + x_1 \frac{\partial}{\partial x_2} - u_2 \frac{\partial}{\partial u_1} + u_1 \frac{\partial}{\partial u_2}. \end{equation}
-
(5) Scaling of time (
 $T_{a_{s,t}}$
): When time, velocity, temperature and pressure are scaled as shown below, the Euler equations are invariant: (3.2m)where, the group parameter,
$T_{a_{s,t}}$
): When time, velocity, temperature and pressure are scaled as shown below, the Euler equations are invariant: (3.2m)where, the group parameter, \begin{equation} T_{a_{s,t}}\,:\, t^* = e^{a_{s,t}} t, x_i^* = x_i, \rho^* = \rho, u_i^* = e^{-a_{s,t}} u_i, T^* = e^{-2a_{s,t}} T, p^* = e^{-2a_{s,t}} p, \end{equation}
\begin{equation} T_{a_{s,t}}\,:\, t^* = e^{a_{s,t}} t, x_i^* = x_i, \rho^* = \rho, u_i^* = e^{-a_{s,t}} u_i, T^* = e^{-2a_{s,t}} T, p^* = e^{-2a_{s,t}} p, \end{equation}
 $a_{s,t} \in \mathbb{R}$
, and the corresponding symmetry operator is (3.2n)
$a_{s,t} \in \mathbb{R}$
, and the corresponding symmetry operator is (3.2n) \begin{equation} X = t \frac{\partial}{\partial t} - u_i \frac{\partial}{\partial u_i} - 2T \frac{\partial}{\partial T} - 2p \frac{\partial}{\partial p}. \end{equation}
\begin{equation} X = t \frac{\partial}{\partial t} - u_i \frac{\partial}{\partial u_i} - 2T \frac{\partial}{\partial T} - 2p \frac{\partial}{\partial p}. \end{equation}
-
(6) Scaling of space (
 $T_{a_{s,x}}$
): Similarly, the following scaling transformation of space and dependent variables leaves the Euler equations invariant: (3.2o)with
$T_{a_{s,x}}$
): Similarly, the following scaling transformation of space and dependent variables leaves the Euler equations invariant: (3.2o)with \begin{equation} T_{a_{s,x}}\,:\, t^* = t, x_i^* = e^{a_{s,x}} x_i, \rho^* = \rho, u_i^* = e^{a_{s,x}} u_i, T^* = e^{2a_{s,x}} T, p^* = e^{2a_{s,x}} p, \end{equation}
\begin{equation} T_{a_{s,x}}\,:\, t^* = t, x_i^* = e^{a_{s,x}} x_i, \rho^* = \rho, u_i^* = e^{a_{s,x}} u_i, T^* = e^{2a_{s,x}} T, p^* = e^{2a_{s,x}} p, \end{equation}
 $a_{s,x} \in \mathbb{R}$
. The symmetry operator is given by: (3.2p)
$a_{s,x} \in \mathbb{R}$
. The symmetry operator is given by: (3.2p) \begin{equation} X = x_i \frac{\partial}{\partial x_i} + u_i \frac{\partial}{\partial u_i} + 2T \frac{\partial}{\partial T} + 2p \frac{\partial}{\partial p}. \end{equation}
\begin{equation} X = x_i \frac{\partial}{\partial x_i} + u_i \frac{\partial}{\partial u_i} + 2T \frac{\partial}{\partial T} + 2p \frac{\partial}{\partial p}. \end{equation}
-
(7) Scaling of density
 $\left(T_{a_{s,\rho}}\right)$
: The scaling symmetry that is unique to compressible flows is the scaling of density and pressure, represented by the group parameter,
$\left(T_{a_{s,\rho}}\right)$
: The scaling symmetry that is unique to compressible flows is the scaling of density and pressure, represented by the group parameter,
 $a_{s,\rho} \in \mathbb{R}$
: (3.2q)whose symmetry operator is
$a_{s,\rho} \in \mathbb{R}$
: (3.2q)whose symmetry operator is \begin{equation} T_{a_{s,\rho}}\,:\quad t^* = t, x_i^* = x_i, \rho^* = e^{a_{s,\rho}} \rho, u_i^* = u_i, T^* = T, p^* = e^{a_{s,\rho}} p \end{equation}
(3.2r)
\begin{equation} T_{a_{s,\rho}}\,:\quad t^* = t, x_i^* = x_i, \rho^* = e^{a_{s,\rho}} \rho, u_i^* = u_i, T^* = T, p^* = e^{a_{s,\rho}} p \end{equation}
(3.2r) \begin{equation} X = \rho \frac{\partial}{\partial \rho} + p \frac{\partial}{\partial p}. \end{equation}
\begin{equation} X = \rho \frac{\partial}{\partial \rho} + p \frac{\partial}{\partial p}. \end{equation}
In addition to the above symmetry groups, monatomic gases, that is, gases with specific heat ratio
![]() $\gamma = 5/3$
, satisfy an additional ‘projective’ symmetry transformation
$\gamma = 5/3$
, satisfy an additional ‘projective’ symmetry transformation
![]() $\left(T_{a_{pr}}\right)$
:
$\left(T_{a_{pr}}\right)$
:
 \begin{equation}\begin{aligned} T_{a_{pr}}\,: \quad &t^* = \frac{t}{1-a_{pr}t}, x_i^* = \frac{x_i}{1-a_{pr}t}, \rho^* = \rho \!\left(1 - a_{pr}t\right)^3, T^* = T\!\left(1-a_{pr}t\right)^2 \\ &p^* = p \!\left(1-a_{pr}t\right)^5, u_i^* = a_{pr} x_i + u_i \!\left(1 - a_{pr}t\right),\end{aligned}\end{equation}
\begin{equation}\begin{aligned} T_{a_{pr}}\,: \quad &t^* = \frac{t}{1-a_{pr}t}, x_i^* = \frac{x_i}{1-a_{pr}t}, \rho^* = \rho \!\left(1 - a_{pr}t\right)^3, T^* = T\!\left(1-a_{pr}t\right)^2 \\ &p^* = p \!\left(1-a_{pr}t\right)^5, u_i^* = a_{pr} x_i + u_i \!\left(1 - a_{pr}t\right),\end{aligned}\end{equation}
where,
![]() $a_{pr} \in \mathbb{R}$
, and the resulting symmetry operator is
$a_{pr} \in \mathbb{R}$
, and the resulting symmetry operator is
The projective group is demonstrative of the power of Lie group analysis in identifying the relevant physics exhibited by the differential equations. For more discussion on this group, the reader is referred to Chapter 12 of [Reference Cantwell3].
When viscosity and heat conductivity are considered, the scaling of space and time groups merge into a single scaling group. As a result, in compressible flows with constant viscosity and heat conductivity, there are two scaling groups, as opposed to Euler equations with three scaling groups. In compressible flows,
![]() $\mu$
and
$\mu$
and
![]() $\kappa$
are functions of temperature, leading to more symmetry breaking. Therefore, in this paper, we perform symmetry analysis of CF hierarchy upon neglecting the viscosity and heat conduction terms. In turbulent flows, in the limit of zero viscosity (
$\kappa$
are functions of temperature, leading to more symmetry breaking. Therefore, in this paper, we perform symmetry analysis of CF hierarchy upon neglecting the viscosity and heat conduction terms. In turbulent flows, in the limit of zero viscosity (
![]() $\mu \to 0$
), the assumption is not too restrictive. When
$\mu \to 0$
), the assumption is not too restrictive. When
![]() $\mu \to 0$
, the action of viscosity is limited to the smallest scales, thus justifying inviscid consideration for the rest of the scales. Furthermore, viscosity and heat conductivity also break projection symmetry.
$\mu \to 0$
, the action of viscosity is limited to the smallest scales, thus justifying inviscid consideration for the rest of the scales. Furthermore, viscosity and heat conductivity also break projection symmetry.
3.2 Lie group analysis of the CF hierarchy
Let us begin our investigation of the CF hierarchy by looking at the single-point CF equation. The equation for single-point CF, obtained from equation (2.5) by substituting
![]() $n=1$
, is given below:
$n=1$
, is given below:
 \begin{equation} \begin{aligned} \left[\mathrm{i} \frac{\partial}{\partial t} + \frac{\partial^2}{\partial x_j^{(1)} \partial \> {}^{(1)}v_j } \right] \frac{\partial}{\partial {}^{(1)}\varrho} \varphi_1 = & - {}^{(1)}\varrho \left[\frac{\partial }{\partial x_j^{(2)}}\left. \frac{\partial^{3} \varphi_{2}}{\partial \>{}^{(2)}v_j \> \partial \>{}^{(1)}\varrho^2 }\right|_{{}^{(2)}\varrho, {}^{(2)}{\boldsymbol{v}}, {}^{(2)}\theta = 0} \right]_{{\boldsymbol{x}}^{(2)}={\boldsymbol{x}}^{(1)}}\\[4pt] & -\mathrm{i}\frac{{}^{(1)}v_i}{\gamma M^2} \left[ \frac{\partial }{\partial x_i^{(2)}}\left. \frac{\partial^{2} \varphi_{2}}{\partial \>{}^{(2)}\varrho \> \partial \>{}^{(2)}\theta}\right|_{{}^{(2)}\varrho, {}^{(2)}{\boldsymbol{v}}, {}^{(2)}\theta = 0} \right]_{{\boldsymbol{x}}^{(2)}={\boldsymbol{x}}^{(1)}}\\[4pt] & -(\gamma-1) {}^{(k)}\theta \left[ \frac{\partial}{\partial x_j^{(2)}} \left. \frac{\partial^{3} \varphi_{2}}{\partial {}^{(1)}\varrho \> \partial \>{}^{(1)}\theta \> \partial \>{}^{(2)}v_j} \right|_{{}^{(2)}\varrho, {}^{(2)}{\boldsymbol{v}}, {}^{(2)}\theta = 0} \right]_{{\boldsymbol{x}}^{(2)}={\boldsymbol{x}}^{(1)}}. \end{aligned}\end{equation}
\begin{equation} \begin{aligned} \left[\mathrm{i} \frac{\partial}{\partial t} + \frac{\partial^2}{\partial x_j^{(1)} \partial \> {}^{(1)}v_j } \right] \frac{\partial}{\partial {}^{(1)}\varrho} \varphi_1 = & - {}^{(1)}\varrho \left[\frac{\partial }{\partial x_j^{(2)}}\left. \frac{\partial^{3} \varphi_{2}}{\partial \>{}^{(2)}v_j \> \partial \>{}^{(1)}\varrho^2 }\right|_{{}^{(2)}\varrho, {}^{(2)}{\boldsymbol{v}}, {}^{(2)}\theta = 0} \right]_{{\boldsymbol{x}}^{(2)}={\boldsymbol{x}}^{(1)}}\\[4pt] & -\mathrm{i}\frac{{}^{(1)}v_i}{\gamma M^2} \left[ \frac{\partial }{\partial x_i^{(2)}}\left. \frac{\partial^{2} \varphi_{2}}{\partial \>{}^{(2)}\varrho \> \partial \>{}^{(2)}\theta}\right|_{{}^{(2)}\varrho, {}^{(2)}{\boldsymbol{v}}, {}^{(2)}\theta = 0} \right]_{{\boldsymbol{x}}^{(2)}={\boldsymbol{x}}^{(1)}}\\[4pt] & -(\gamma-1) {}^{(k)}\theta \left[ \frac{\partial}{\partial x_j^{(2)}} \left. \frac{\partial^{3} \varphi_{2}}{\partial {}^{(1)}\varrho \> \partial \>{}^{(1)}\theta \> \partial \>{}^{(2)}v_j} \right|_{{}^{(2)}\varrho, {}^{(2)}{\boldsymbol{v}}, {}^{(2)}\theta = 0} \right]_{{\boldsymbol{x}}^{(2)}={\boldsymbol{x}}^{(1)}}. \end{aligned}\end{equation}
The advantage of using the CF formulation, over the conventional PDF formulation [Reference Praturi, Plümacher and Oberlack16], can easily be seen in the above equation. The equation (3.4) is local, where as the PDF hierarchy is non-local as it includes integral terms. In equation (3.4),
![]() $\varphi_1$
and
$\varphi_1$
and
![]() $\varphi_2$
are the dependent variables and
$\varphi_2$
are the dependent variables and
![]() $t, {\boldsymbol{x}}^{(1)}, {\boldsymbol{x}}^{(2)}, {}^{(1)}\varrho, {}^{(2)}\varrho, {}^{(1)}{\boldsymbol{v}}, {}^{(2)}{\boldsymbol{v}}, {}^{(1)}\theta$
and
$t, {\boldsymbol{x}}^{(1)}, {\boldsymbol{x}}^{(2)}, {}^{(1)}\varrho, {}^{(2)}\varrho, {}^{(1)}{\boldsymbol{v}}, {}^{(2)}{\boldsymbol{v}}, {}^{(1)}\theta$
and
![]() ${}^{(2)}\theta$
are the independent variables.
${}^{(2)}\theta$
are the independent variables.
To compute the symmetries, we make use of one of the infinite classes of the ‘generalised form of the symmetry operators’ that are equivalent to Lie point groups [Reference Olver13]. We specifically consider the ‘evolutionary’ form of the generalised symmetry operators in which the infinitesimals for the independent variables are zero. This precludes us from considering the transformation of independent variables explicitly. Specifically, the infinitesimal transformation of the CFs,
![]() $\varphi_1^*$
and
$\varphi_1^*$
and
![]() $\varphi_2^*$
, are represented as:
$\varphi_2^*$
, are represented as:
where, a is the group parameter and,
 \begin{equation}\begin{aligned} \tilde{\eta}^{\varphi_1} =\ &\eta^{\varphi_1} - \xi^t \frac{\partial \varphi_1}{\partial t} - \xi^{x^{(1)}_1} \frac{\partial \varphi_1}{\partial x^{(1)}_1} - \xi^{x^{(1)}_2} \frac{\partial \varphi_1}{\partial x^{(1)}_2} - \xi^{x^{(1)}_3} \frac{\partial \varphi_1}{\partial x^{(1)}_3} - \xi^{{}^{(1)}\varrho} \frac{\partial \varphi_1}{\partial \> {}^{(1)}\varrho} \\ &- \xi^{{}^{(1)}v_1} \frac{\partial \varphi_1}{\partial \> {}^{(1)}v_1} - \xi^{{}^{(1)}v_2} \frac{\partial \varphi_1}{\partial \> {}^{(1)}v_2} - \xi^{{}^{(1)}v_3} \frac{\partial \varphi_1}{\partial \> {}^{(1)}v_3} - \xi^{{}^{(1)}\theta} \frac{\partial \varphi_1}{\partial \> {}^{(1)}\theta},\end{aligned}\end{equation}
\begin{equation}\begin{aligned} \tilde{\eta}^{\varphi_1} =\ &\eta^{\varphi_1} - \xi^t \frac{\partial \varphi_1}{\partial t} - \xi^{x^{(1)}_1} \frac{\partial \varphi_1}{\partial x^{(1)}_1} - \xi^{x^{(1)}_2} \frac{\partial \varphi_1}{\partial x^{(1)}_2} - \xi^{x^{(1)}_3} \frac{\partial \varphi_1}{\partial x^{(1)}_3} - \xi^{{}^{(1)}\varrho} \frac{\partial \varphi_1}{\partial \> {}^{(1)}\varrho} \\ &- \xi^{{}^{(1)}v_1} \frac{\partial \varphi_1}{\partial \> {}^{(1)}v_1} - \xi^{{}^{(1)}v_2} \frac{\partial \varphi_1}{\partial \> {}^{(1)}v_2} - \xi^{{}^{(1)}v_3} \frac{\partial \varphi_1}{\partial \> {}^{(1)}v_3} - \xi^{{}^{(1)}\theta} \frac{\partial \varphi_1}{\partial \> {}^{(1)}\theta},\end{aligned}\end{equation}
and
 \begin{equation}\begin{aligned} \tilde{\eta}^{\varphi_2} =\ & \eta^{\varphi_2} - \xi^t \frac{\partial \varphi_2}{\partial t} - \xi^{x^{(1)}_1} \frac{\partial \varphi_2}{\partial x^{(1)}_1} - \xi^{x^{(1)}_2} \frac{\partial \varphi_2}{\partial x^{(1)}_2} - \xi^{x^{(1)}_3} \frac{\partial \varphi_2}{\partial x^{(1)}_3} - \xi^{{}^{(1)}\varrho} \frac{\partial \varphi_2}{\partial \> {}^{(1)}\varrho} \\ &- \xi^{{}^{(1)}v_1} \frac{\partial \varphi_2}{\partial \> {}^{(1)}v_1} - \xi^{{}^{(1)}v_2} \frac{\partial \varphi_2}{\partial \> {}^{(1)}v_2} - \xi^{{}^{(1)}v_3} \frac{\partial \varphi_2}{\partial \> {}^{(1)}v_3} - \xi^{{}^{(1)}\theta} \frac{\partial \varphi_2}{\partial \> {}^{(1)}\theta} \\ &- \xi^{x^{(2)}_1} \frac{\partial \varphi_2}{\partial x^{(2)}_1} - \xi^{x^{(2)}_2} \frac{\partial \varphi_2}{\partial x^{(2)}_2} - \xi^{x^{(2)}_3} \frac{\partial \varphi_2}{\partial x^{(2)}_3} - \xi^{{}^{(2)}\varrho} \frac{\partial \varphi_2}{\partial \> {}^{(2)}\varrho} \\ &- \xi^{{}^{(2)}v_1} \frac{\partial \varphi_2}{\partial \> {}^{(2)}v_1} - \xi^{{}^{(2)}v_2} \frac{\partial \varphi_2}{\partial \> {}^{(2)}v_2} - \xi^{{}^{(2)}v_3} \frac{\partial \varphi_2}{\partial \> {}^{(2)}v_3} - \xi^{{}^{(2)}\theta} \frac{\partial \varphi_2}{\partial \> {}^{(2)}\theta}\end{aligned}\end{equation}
\begin{equation}\begin{aligned} \tilde{\eta}^{\varphi_2} =\ & \eta^{\varphi_2} - \xi^t \frac{\partial \varphi_2}{\partial t} - \xi^{x^{(1)}_1} \frac{\partial \varphi_2}{\partial x^{(1)}_1} - \xi^{x^{(1)}_2} \frac{\partial \varphi_2}{\partial x^{(1)}_2} - \xi^{x^{(1)}_3} \frac{\partial \varphi_2}{\partial x^{(1)}_3} - \xi^{{}^{(1)}\varrho} \frac{\partial \varphi_2}{\partial \> {}^{(1)}\varrho} \\ &- \xi^{{}^{(1)}v_1} \frac{\partial \varphi_2}{\partial \> {}^{(1)}v_1} - \xi^{{}^{(1)}v_2} \frac{\partial \varphi_2}{\partial \> {}^{(1)}v_2} - \xi^{{}^{(1)}v_3} \frac{\partial \varphi_2}{\partial \> {}^{(1)}v_3} - \xi^{{}^{(1)}\theta} \frac{\partial \varphi_2}{\partial \> {}^{(1)}\theta} \\ &- \xi^{x^{(2)}_1} \frac{\partial \varphi_2}{\partial x^{(2)}_1} - \xi^{x^{(2)}_2} \frac{\partial \varphi_2}{\partial x^{(2)}_2} - \xi^{x^{(2)}_3} \frac{\partial \varphi_2}{\partial x^{(2)}_3} - \xi^{{}^{(2)}\varrho} \frac{\partial \varphi_2}{\partial \> {}^{(2)}\varrho} \\ &- \xi^{{}^{(2)}v_1} \frac{\partial \varphi_2}{\partial \> {}^{(2)}v_1} - \xi^{{}^{(2)}v_2} \frac{\partial \varphi_2}{\partial \> {}^{(2)}v_2} - \xi^{{}^{(2)}v_3} \frac{\partial \varphi_2}{\partial \> {}^{(2)}v_3} - \xi^{{}^{(2)}\theta} \frac{\partial \varphi_2}{\partial \> {}^{(2)}\theta}\end{aligned}\end{equation}
are the characteristics of the symmetry transformation [Reference Olver13]. Here,
![]() $\eta^{\varphi_1}$
and
$\eta^{\varphi_1}$
and
![]() $\eta^{\varphi_2}$
are the infinitesimals for
$\eta^{\varphi_2}$
are the infinitesimals for
![]() $\varphi_1, \varphi_2$
; and
$\varphi_1, \varphi_2$
; and
![]() $\xi^t$
,
$\xi^t$
,
![]() $\xi^{x^{(k)}_i}, \xi^{{}^{(k)}\varrho}, \xi^{{}^{(k)}v_i}$
and
$\xi^{x^{(k)}_i}, \xi^{{}^{(k)}\varrho}, \xi^{{}^{(k)}v_i}$
and
![]() $\xi^{{}^{(k)}\theta}$
are the infinitesimals for time, space and spectral parameters for density, velocity and temperature, respectively; and
$\xi^{{}^{(k)}\theta}$
are the infinitesimals for time, space and spectral parameters for density, velocity and temperature, respectively; and
![]() $i=1-3$
,
$i=1-3$
,
![]() $k = 1, 2$
. It should be noted that all of the infinitesimals,
$k = 1, 2$
. It should be noted that all of the infinitesimals,
![]() $\eta^{\varphi_1}, \eta^{\varphi_2}, \xi^t, \xi^{x^{(k)}_i}, \xi^{{}^{(k)}\varrho}, \xi^{{}^{(k)}v_i}$
and
$\eta^{\varphi_1}, \eta^{\varphi_2}, \xi^t, \xi^{x^{(k)}_i}, \xi^{{}^{(k)}\varrho}, \xi^{{}^{(k)}v_i}$
and
![]() $\xi^{{}^{(k)}\theta}$
are explicit functions of
$\xi^{{}^{(k)}\theta}$
are explicit functions of
![]() $t, x_i$
and the dependent variables. This implies that we do not consider the infinitesimals to depend on the derivatives of the dependent variables,
$t, x_i$
and the dependent variables. This implies that we do not consider the infinitesimals to depend on the derivatives of the dependent variables,
![]() $\varphi_n$
, for all n. In the evolutionary form of generalised symmetries, the derivatives of
$\varphi_n$
, for all n. In the evolutionary form of generalised symmetries, the derivatives of
![]() $\varphi_1$
and
$\varphi_1$
and
![]() $\varphi_2$
transform as:
$\varphi_2$
transform as:
and
etc. This implies that the infinitesimals for the derivatives of the dependent variables (say time derivative of
![]() $\varphi_1$
) in the evolutionary form of the generalised symmetry formulation can be obtained by taking the total derivatives (here, with respect to time) of the infinitesimal of the dependent variable (
$\varphi_1$
) in the evolutionary form of the generalised symmetry formulation can be obtained by taking the total derivatives (here, with respect to time) of the infinitesimal of the dependent variable (
![]() $\tilde{\eta}^{\varphi_1}$
). As the CF equations contain high-order derivatives (the order of the highest derivative increases as the order of CF is increased), the handling of derivatives is simplified in the evolutionary form of symmetry operators. This operator has also been used to derive the symmetries of integro-differential equations [Reference Wacławczyk, Grebenev and Oberlack20], as the limits on the integral do not undergo any transformation.
$\tilde{\eta}^{\varphi_1}$
). As the CF equations contain high-order derivatives (the order of the highest derivative increases as the order of CF is increased), the handling of derivatives is simplified in the evolutionary form of symmetry operators. This operator has also been used to derive the symmetries of integro-differential equations [Reference Wacławczyk, Grebenev and Oberlack20], as the limits on the integral do not undergo any transformation.
To compute the symmetries of CF equation (3.4), we apply the evolutionary form of the symmetry operator with the infinitesimals as defined above. Thus, the obtained determining equation is of the form:
 \begin{equation} \begin{aligned} \mathrm{i} \frac{D^2 \tilde{\eta}^{\varphi_1}}{D t D \> {}^{(1)}\varrho} &+ \frac{D^3 \tilde{\eta}^{\varphi_1}}{D \>{}^{(1)}v_j D x^{(1)}_j D \> {}^{(1)}\varrho} = - {}^{(1)}\varrho \left[ \frac{D}{D x^{(2)}_j} \!\left( \frac{D^3 \tilde{\eta}^{\varphi_2}}{D \> {}^{(2)}v_j D \> {}^{(1)}\varrho^2} \right)_{{}^{(2)}\varrho, {}^{(2)}{\boldsymbol{v}}, {}^{(2)}\theta = 0} \right]_{{\boldsymbol{x}}^{(2)}={\boldsymbol{x}}^{(1)}} \\[4pt] &- \mathrm{i}\frac{{}^{(1)}v_i}{\gamma M^2} \left[ \frac{D}{D x^{(2)}_i} \!\left( \frac{D^2 \tilde{\eta}^{\varphi_2}}{D \> {}^{(2)}\varrho D \> {}^{(2)}\theta} \right)_{{}^{(2)}\varrho, {}^{(2)}{\boldsymbol{v}}, {}^{(2)}\theta = 0} \right]_{{\boldsymbol{x}}^{(2)}={\boldsymbol{x}}^{(1)}} \\[4pt] &- {}^{(1)}\theta (\gamma - 1) \left[ \frac{D}{D x^{(2)}_j} \!\left( \frac{D^3 \tilde{\eta}^{\varphi_2}}{D \> {}^{(2)}v_j D \> {}^{(1)}\varrho D \> {}^{(1)}\theta} \right)_{{}^{(2)}\varrho, {}^{(2)}{\boldsymbol{v}}, {}^{(2)}\theta = 0} \right]_{{\boldsymbol{x}}^{(2)}={\boldsymbol{x}}^{(1)}}. \end{aligned}\end{equation}
\begin{equation} \begin{aligned} \mathrm{i} \frac{D^2 \tilde{\eta}^{\varphi_1}}{D t D \> {}^{(1)}\varrho} &+ \frac{D^3 \tilde{\eta}^{\varphi_1}}{D \>{}^{(1)}v_j D x^{(1)}_j D \> {}^{(1)}\varrho} = - {}^{(1)}\varrho \left[ \frac{D}{D x^{(2)}_j} \!\left( \frac{D^3 \tilde{\eta}^{\varphi_2}}{D \> {}^{(2)}v_j D \> {}^{(1)}\varrho^2} \right)_{{}^{(2)}\varrho, {}^{(2)}{\boldsymbol{v}}, {}^{(2)}\theta = 0} \right]_{{\boldsymbol{x}}^{(2)}={\boldsymbol{x}}^{(1)}} \\[4pt] &- \mathrm{i}\frac{{}^{(1)}v_i}{\gamma M^2} \left[ \frac{D}{D x^{(2)}_i} \!\left( \frac{D^2 \tilde{\eta}^{\varphi_2}}{D \> {}^{(2)}\varrho D \> {}^{(2)}\theta} \right)_{{}^{(2)}\varrho, {}^{(2)}{\boldsymbol{v}}, {}^{(2)}\theta = 0} \right]_{{\boldsymbol{x}}^{(2)}={\boldsymbol{x}}^{(1)}} \\[4pt] &- {}^{(1)}\theta (\gamma - 1) \left[ \frac{D}{D x^{(2)}_j} \!\left( \frac{D^3 \tilde{\eta}^{\varphi_2}}{D \> {}^{(2)}v_j D \> {}^{(1)}\varrho D \> {}^{(1)}\theta} \right)_{{}^{(2)}\varrho, {}^{(2)}{\boldsymbol{v}}, {}^{(2)}\theta = 0} \right]_{{\boldsymbol{x}}^{(2)}={\boldsymbol{x}}^{(1)}}. \end{aligned}\end{equation}
The point evaluations such as
![]() ${}^{(2)}\varrho, {}^{(2)}{\boldsymbol{v}}, {}^{(2)}\theta = 0$
and
${}^{(2)}\varrho, {}^{(2)}{\boldsymbol{v}}, {}^{(2)}\theta = 0$
and
![]() ${\boldsymbol{x}}^{(2)}={\boldsymbol{x}}^{(1)}$
do not need to be transformed as we utilise the evolutionary form of the symmetry operator. Similarly, the determining equation for the governing equation of two-point CF can also be derived.
${\boldsymbol{x}}^{(2)}={\boldsymbol{x}}^{(1)}$
do not need to be transformed as we utilise the evolutionary form of the symmetry operator. Similarly, the determining equation for the governing equation of two-point CF can also be derived.
Finally, upon utilising the computer algebra system, Maple [Reference Maple10], for part of the symmetry calculations, the following are the infinitesimals of the symmetries admitted by the single-point CF equation (3.4):
and
 \begin{equation}\begin{aligned} \eta^{\varphi_1} = & F_1\!\left(t, {\boldsymbol{x}}^{(1)}, {}^{(1)}\varrho, {}^{(1)}{\boldsymbol{v}}, {}^{(1)}\theta\right) + \mathrm{i} \varphi_1 \bigg[\frac{a_{pr}}{2} {}^{(1)}v_i x^{(1)}_i + a_{g,1} {}^{(1)}v_1 + a_{g,2} {}^{(1)}v_2 \\ &\left. + a_{g,3} {}^{(1)}v_3 + \frac{a_{\varphi}}{\mathrm{i}} + \frac{5-3\gamma}{2\mathrm{i} (\gamma - 1)} a_{pr} t \right].\end{aligned}\end{equation}
\begin{equation}\begin{aligned} \eta^{\varphi_1} = & F_1\!\left(t, {\boldsymbol{x}}^{(1)}, {}^{(1)}\varrho, {}^{(1)}{\boldsymbol{v}}, {}^{(1)}\theta\right) + \mathrm{i} \varphi_1 \bigg[\frac{a_{pr}}{2} {}^{(1)}v_i x^{(1)}_i + a_{g,1} {}^{(1)}v_1 + a_{g,2} {}^{(1)}v_2 \\ &\left. + a_{g,3} {}^{(1)}v_3 + \frac{a_{\varphi}}{\mathrm{i}} + \frac{5-3\gamma}{2\mathrm{i} (\gamma - 1)} a_{pr} t \right].\end{aligned}\end{equation}
In the above infinitesimals for independent (3.8) and dependent (3.9) variables, it can be seen that the Euler equation symmetries are replicated. These are represented by the same group parameters as Section 3.1, that is,
![]() $a_t$
for time translation,
$a_t$
for time translation,
![]() $a_{x,i}$
for space translation,
$a_{x,i}$
for space translation,
![]() $a_{g,i}$
for Galilean symmetry,
$a_{g,i}$
for Galilean symmetry,
![]() $a_{s,t}$
for scaling of time,
$a_{s,t}$
for scaling of time,
![]() $a_{s,x}$
for scaling of space and
$a_{s,x}$
for scaling of space and
![]() $a_{s,\rho}$
for scaling of density and
$a_{s,\rho}$
for scaling of density and
![]() $a_{pr}$
for projective symmetries. We also notice two additional groups, denoted by
$a_{pr}$
for projective symmetries. We also notice two additional groups, denoted by
![]() $F_1$
and
$F_1$
and
![]() $a_{\varphi}$
, that appear in the statistical CF equations. These are as a result named, ‘statistical symmetries’, a convention that is adopted in incompressible turbulence as well [Reference Oberlack and Rosteck12, Reference Wacławczyk, Staffolani, Oberlack, Rosteck, Wilczek and Friedrich21]. The function
$a_{\varphi}$
, that appear in the statistical CF equations. These are as a result named, ‘statistical symmetries’, a convention that is adopted in incompressible turbulence as well [Reference Oberlack and Rosteck12, Reference Wacławczyk, Staffolani, Oberlack, Rosteck, Wilczek and Friedrich21]. The function
![]() $F_1$
appears in the infinitesimal,
$F_1$
appears in the infinitesimal,
![]() $\eta^{\varphi_1}$
due to principle of superposition, as single-point CF equation (3.4) is a linear differential equation.
$\eta^{\varphi_1}$
due to principle of superposition, as single-point CF equation (3.4) is a linear differential equation.
![]() $F_1$
is an arbitrary function of the independent variables (in the CF formulation), which could lead to a translation type of symmetry in the single-point CF,
$F_1$
is an arbitrary function of the independent variables (in the CF formulation), which could lead to a translation type of symmetry in the single-point CF,
![]() $\varphi_1$
. On the other hand,
$\varphi_1$
. On the other hand,
![]() $a_{\varphi}$
is a dilation/scaling symmetry group, which will lead to the scaling of
$a_{\varphi}$
is a dilation/scaling symmetry group, which will lead to the scaling of
![]() $\varphi_1$
.
$\varphi_1$
.
It is interesting to note that the single-point CF equation (3.4) admits the projection symmetry group for all values of
![]() $\gamma$
. However, as seen in the previous section, the CFs, including the transformed ones (
$\gamma$
. However, as seen in the previous section, the CFs, including the transformed ones (
![]() $\varphi_1^*$
), need to satisfy additional constraints (2.6a)–(2.9). In the following section, the side conditions are enforced on the transformed CFs (
$\varphi_1^*$
), need to satisfy additional constraints (2.6a)–(2.9). In the following section, the side conditions are enforced on the transformed CFs (
![]() $\varphi_n^*$
) by imposing restrictions on their infinitesimals (
$\varphi_n^*$
) by imposing restrictions on their infinitesimals (
![]() $\eta^{\varphi_n}$
).
$\eta^{\varphi_n}$
).
3.2.1 Imposing side conditions on the infinitesimals
Let us now consider the restrictions on the infinitesimals that are imposed as a result of side conditions. We apply the evolutionary form of the generalised symmetry operator on the reduction side condition (2.6b). This results in:
implying,
 \begin{equation} \begin{aligned} &\left[ \eta^{\varphi_1} - \xi^t \frac{\partial \varphi_1}{\partial t} - \xi^{x^{(1)}_1} \frac{\partial \varphi_1}{\partial x^{(1)}_1} - \xi^{x^{(1)}_2} \frac{\partial \varphi_1}{\partial x^{(1)}_2} - \xi^{x^{(1)}_3} \frac{\partial \varphi_1}{\partial x^{(1)}_3} - \xi^{{}^{(1)}\varrho} \frac{\partial \varphi_1}{\partial \> {}^{(1)}\varrho} \right. \\ &\qquad \left.- \xi^{{}^{(1)}v_1} \frac{\partial \varphi_1}{\partial \> {}^{(1)}v_1} - \xi^{{}^{(1)}v_2} \frac{\partial \varphi_1}{\partial \> {}^{(1)}v_2} - \xi^{{}^{(1)}v_3} \frac{\partial \varphi_1}{\partial \> {}^{(1)}v_3} - \xi^{{}^{(1)}\theta} \frac{\partial \varphi_1}{\partial \> {}^{(1)}\theta} \right]_{{}^{(1)}\varrho = 0, {}^{(1)}{\boldsymbol{v}}=\textbf{0}, {}^{(1)}\theta = 0} = 0 \end{aligned}\end{equation}
\begin{equation} \begin{aligned} &\left[ \eta^{\varphi_1} - \xi^t \frac{\partial \varphi_1}{\partial t} - \xi^{x^{(1)}_1} \frac{\partial \varphi_1}{\partial x^{(1)}_1} - \xi^{x^{(1)}_2} \frac{\partial \varphi_1}{\partial x^{(1)}_2} - \xi^{x^{(1)}_3} \frac{\partial \varphi_1}{\partial x^{(1)}_3} - \xi^{{}^{(1)}\varrho} \frac{\partial \varphi_1}{\partial \> {}^{(1)}\varrho} \right. \\ &\qquad \left.- \xi^{{}^{(1)}v_1} \frac{\partial \varphi_1}{\partial \> {}^{(1)}v_1} - \xi^{{}^{(1)}v_2} \frac{\partial \varphi_1}{\partial \> {}^{(1)}v_2} - \xi^{{}^{(1)}v_3} \frac{\partial \varphi_1}{\partial \> {}^{(1)}v_3} - \xi^{{}^{(1)}\theta} \frac{\partial \varphi_1}{\partial \> {}^{(1)}\theta} \right]_{{}^{(1)}\varrho = 0, {}^{(1)}{\boldsymbol{v}}=\textbf{0}, {}^{(1)}\theta = 0} = 0 \end{aligned}\end{equation}
that is,
As
![]() $\eta^{\varphi_1}, \xi^{{}^{(1)}\varrho}, \xi^{{}^{(1)}v_i}$
and
$\eta^{\varphi_1}, \xi^{{}^{(1)}\varrho}, \xi^{{}^{(1)}v_i}$
and
![]() $\xi^{{}^{(1)}\theta}$
do not depend on
$\xi^{{}^{(1)}\theta}$
do not depend on
![]() $\langle \rho \rangle, \langle {\boldsymbol{u}} \rangle$
and
$\langle \rho \rangle, \langle {\boldsymbol{u}} \rangle$
and
![]() $\langle T \rangle$
, this implies
$\langle T \rangle$
, this implies
 \begin{equation}\begin{aligned} &\left. \eta^{\varphi_1} \right|_{{}^{(1)}\varrho={}^{(1)}{\boldsymbol{v}} = {}^{(1)}\theta = 0} = 0, \quad \left. \xi^{{}^{(1)}\varrho} \right|_{{}^{(1)}\varrho = 0, {}^{(1)}{\boldsymbol{v}}=\textbf{0}, {}^{(1)}\theta = 0} = 0, \\ &\left. \xi^{{}^{(1)}v_i} \right|_{{}^{(1)}\varrho = 0, {}^{(1)}{\boldsymbol{v}}=\textbf{0}, {}^{(1)}\theta = 0} = 0, \quad \left. \xi^{{}^{(1)}\theta} \right|_{{}^{(1)}\varrho = 0, {}^{(1)}{\boldsymbol{v}}=\textbf{0}, {}^{(1)}\theta = 0} = 0, \quad i = 1 - 3.\end{aligned}\end{equation}
\begin{equation}\begin{aligned} &\left. \eta^{\varphi_1} \right|_{{}^{(1)}\varrho={}^{(1)}{\boldsymbol{v}} = {}^{(1)}\theta = 0} = 0, \quad \left. \xi^{{}^{(1)}\varrho} \right|_{{}^{(1)}\varrho = 0, {}^{(1)}{\boldsymbol{v}}=\textbf{0}, {}^{(1)}\theta = 0} = 0, \\ &\left. \xi^{{}^{(1)}v_i} \right|_{{}^{(1)}\varrho = 0, {}^{(1)}{\boldsymbol{v}}=\textbf{0}, {}^{(1)}\theta = 0} = 0, \quad \left. \xi^{{}^{(1)}\theta} \right|_{{}^{(1)}\varrho = 0, {}^{(1)}{\boldsymbol{v}}=\textbf{0}, {}^{(1)}\theta = 0} = 0, \quad i = 1 - 3.\end{aligned}\end{equation}
Applying similar techniques on the coincidence condition (2.7), we obtain
Substituting the expressions for
![]() $\tilde{\eta}^{\varphi_n}$
and
$\tilde{\eta}^{\varphi_n}$
and
![]() $\tilde{\eta}^{\varphi_{n+1}}$
in the above equation (2.7) in terms of
$\tilde{\eta}^{\varphi_{n+1}}$
in the above equation (2.7) in terms of
![]() $\eta^{\varphi_n}, \xi^t, \xi^{x^{(k)}_i}, \xi^{{}^{(k)}\varrho}, \xi^{{}^{(k)}v_i}$
and
$\eta^{\varphi_n}, \xi^t, \xi^{x^{(k)}_i}, \xi^{{}^{(k)}\varrho}, \xi^{{}^{(k)}v_i}$
and
![]() $\xi^{{}^{(k)}\theta}$
, we obtain:
$\xi^{{}^{(k)}\theta}$
, we obtain:
 \begin{equation}\begin{aligned} \lim_{|{\boldsymbol{x}}^{(n+1)}-{\boldsymbol{x}}^{(n)}|\to 0} &\eta^{\varphi_{n+1}} \!\left(t, {\boldsymbol{x}}^{(1)}, {}^{(1)}\varrho, {}^{(1)}{\boldsymbol{v}}, {}^{(1)}\theta, ..., {\boldsymbol{x}}^{(n+1)}, {}^{(n+1)}\varrho, {}^{(n+1)}{\boldsymbol{v}}, {}^{(n+1)}\theta, ...\right) \\ &= \eta^{\varphi_n} \!\left(.., {}^{(n+1)}\varrho+{}^{(n)}\varrho, {}^{(n+1)}{\boldsymbol{v}}+{}^{(n)}{\boldsymbol{v}}, {}^{(n+1)}\theta+{}^{(n)}\theta, ... \right).\end{aligned}\end{equation}
\begin{equation}\begin{aligned} \lim_{|{\boldsymbol{x}}^{(n+1)}-{\boldsymbol{x}}^{(n)}|\to 0} &\eta^{\varphi_{n+1}} \!\left(t, {\boldsymbol{x}}^{(1)}, {}^{(1)}\varrho, {}^{(1)}{\boldsymbol{v}}, {}^{(1)}\theta, ..., {\boldsymbol{x}}^{(n+1)}, {}^{(n+1)}\varrho, {}^{(n+1)}{\boldsymbol{v}}, {}^{(n+1)}\theta, ...\right) \\ &= \eta^{\varphi_n} \!\left(.., {}^{(n+1)}\varrho+{}^{(n)}\varrho, {}^{(n+1)}{\boldsymbol{v}}+{}^{(n)}{\boldsymbol{v}}, {}^{(n+1)}\theta+{}^{(n)}\theta, ... \right).\end{aligned}\end{equation}
The permutation side condition (2.8) results in:
implying that
![]() $\tilde{\eta}^{\varphi_n}$
does not change regardless of order in which spatial locations and their corresponding spectral parameters are considered. The above equation, upon simplification, results in:
$\tilde{\eta}^{\varphi_n}$
does not change regardless of order in which spatial locations and their corresponding spectral parameters are considered. The above equation, upon simplification, results in:
The separation side condition (2.9) leads to the following restrictions on the infinitesimals:
The separation side condition is not applied in the previous studies on incompressible turbulence [Reference Oberlack and Rosteck12, Reference Wacławczyk, Staffolani, Oberlack, Rosteck, Wilczek and Friedrich21], and the current study. We consider a arbitrarily large domain that is not infinite in extent, in this study. As a result, the above separation condition does not need to be strictly enforced. In addition, in most practical turbulence applications, where scaling laws are derived using symmetry principles, infinite domains are not considered.
Let us now impose the reduction side condition (3.11) on the infinitesimals in (3.8) and (3.9). It is seen that the infinitesimals
![]() $\xi^{{}^{(1)}\varrho}, \xi^{{}^{(1)}v_i}$
and
$\xi^{{}^{(1)}\varrho}, \xi^{{}^{(1)}v_i}$
and
![]() $\xi^{{}^{(1)}\theta}$
automatically satisfy the reduction side condition (3.11), as
$\xi^{{}^{(1)}\theta}$
automatically satisfy the reduction side condition (3.11), as
![]() $\xi^{{}^{(1)}\varrho} = \xi^{{}^{(1)}v_i} = \xi^{{}^{(1)}\theta} = 0$
when
$\xi^{{}^{(1)}\varrho} = \xi^{{}^{(1)}v_i} = \xi^{{}^{(1)}\theta} = 0$
when
![]() ${}^{(1)}\varrho = {}^{(1)}{\boldsymbol{v}} = {}^{(1)}\theta = 0$
. Hence, we turn our attention to
${}^{(1)}\varrho = {}^{(1)}{\boldsymbol{v}} = {}^{(1)}\theta = 0$
. Hence, we turn our attention to
![]() $\eta^{\varphi_1}$
:
$\eta^{\varphi_1}$
:
It can be seen that the only symmetry groups that remain after imposing
![]() ${}^{(1)}\varrho = {}^{(1)}v_i = {}^{(1)}\theta = 0$
are the projection (
${}^{(1)}\varrho = {}^{(1)}v_i = {}^{(1)}\theta = 0$
are the projection (
![]() $a_{pr}$
) group, superposition group (
$a_{pr}$
) group, superposition group (
![]() $F_1$
) and the dilation group (
$F_1$
) and the dilation group (
![]() $a_{\varphi}$
). In the above equation, we consider one group at a time, as they are single-parameter symmetry transformations. We begin with the projective group,
$a_{\varphi}$
). In the above equation, we consider one group at a time, as they are single-parameter symmetry transformations. We begin with the projective group,
![]() $a_{pr}$
:
$a_{pr}$
:
implying that the reduction side condition is satisfied by the projective group only for the case of monatomic gases. This is consistent with what is seen in the Euler equations. In CF formulation, however, the restriction to monatomic gases is imposed by the reduction side condition. The imposition of reduction side condition on the
![]() $F_1$
group results in
$F_1$
group results in
implying that
![]() $F_1$
must reduce to zero, when spectral parameters are zero. This also implies that
$F_1$
must reduce to zero, when spectral parameters are zero. This also implies that
![]() $F_1$
cannot be a constant (other than zero), as it would violate reduction condition. Finally, the reduction condition on the dilation group,
$F_1$
cannot be a constant (other than zero), as it would violate reduction condition. Finally, the reduction condition on the dilation group,
![]() $a_{\varphi}$
, leads to the restriction that
$a_{\varphi}$
, leads to the restriction that
![]() $a_{\varphi} = 0$
. However, one could conceive the following transformation for
$a_{\varphi} = 0$
. However, one could conceive the following transformation for
![]() $\varphi_1$
, by combining
$\varphi_1$
, by combining
![]() $F_1$
and
$F_1$
and
![]() $a_{\varphi}$
groups:
$a_{\varphi}$
groups:
In this case, we consider
![]() $F_1 = - a_{\varphi}$
and as a result, the reduction condition is automatically satisfied. The groups,
$F_1 = - a_{\varphi}$
and as a result, the reduction condition is automatically satisfied. The groups,
![]() $a_{\varphi}$
and
$a_{\varphi}$
and
![]() $F_1 = -a_{\varphi}$
(as seen above, that
$F_1 = -a_{\varphi}$
(as seen above, that
![]() $F_1$
cannot be a constant), each considered separately do not satisfy the reduction side condition. However, when considered together as shown in equation (3.20), the reduction constraint is upheld. The final form for the single-point CF infinitesimal is
$F_1$
cannot be a constant), each considered separately do not satisfy the reduction side condition. However, when considered together as shown in equation (3.20), the reduction constraint is upheld. The final form for the single-point CF infinitesimal is
Similarly, utilising MAPLE [Reference Maple10] for part of the analysis of the two-point CF (upon imposing the reduction side condition) results in:
 \begin{align} \eta^{\varphi_2} =\, & F_2\!\left(t, {\boldsymbol{x}}^{(1)}, {\boldsymbol{x}}^{(2)}, {}^{(1)}\varrho, {}^{(1)}{\boldsymbol{v}}, {}^{(1)}\theta, {}^{(2)}\varrho, {}^{(2)}{\boldsymbol{v}}, {}^{(2)}\theta\right) - a_{\varphi}\nonumber\\[4pt]& + \mathrm{i} \varphi_2 \left[ \frac{a_{\varphi}}{\mathrm{i}} + \frac{a_{pr}}{2} \!\left( {}^{(1)}v_i x^{(1)}_i + {}^{(2)}v_i x^{(2}_i \right) + a_{g,1} \!\left( {}^{(1)}v_1 + {}^{(2)}v_1 \right)\right. \\[4pt] & + a_{g,2} \!\left( {}^{(1)}v_2 + {}^{(2)}v_2 \right) + a_{g,3} \!\left( {}^{(1)}v_3 + {}^{(2)}v_3 \right) \Big].\nonumber\end{align}
\begin{align} \eta^{\varphi_2} =\, & F_2\!\left(t, {\boldsymbol{x}}^{(1)}, {\boldsymbol{x}}^{(2)}, {}^{(1)}\varrho, {}^{(1)}{\boldsymbol{v}}, {}^{(1)}\theta, {}^{(2)}\varrho, {}^{(2)}{\boldsymbol{v}}, {}^{(2)}\theta\right) - a_{\varphi}\nonumber\\[4pt]& + \mathrm{i} \varphi_2 \left[ \frac{a_{\varphi}}{\mathrm{i}} + \frac{a_{pr}}{2} \!\left( {}^{(1)}v_i x^{(1)}_i + {}^{(2)}v_i x^{(2}_i \right) + a_{g,1} \!\left( {}^{(1)}v_1 + {}^{(2)}v_1 \right)\right. \\[4pt] & + a_{g,2} \!\left( {}^{(1)}v_2 + {}^{(2)}v_2 \right) + a_{g,3} \!\left( {}^{(1)}v_3 + {}^{(2)}v_3 \right) \Big].\nonumber\end{align}
Finally, using one- and two-point CF infinitesimals, we generalise the expression for an
![]() $n-$
point CF infinitesimal, which is given by:
$n-$
point CF infinitesimal, which is given by:
 \begin{equation} \begin{aligned} \eta^{\varphi_n} =\, & F_n\!\left(t, {\boldsymbol{x}}^{(1)},..., {\boldsymbol{x}}^{(n)}, {}^{(1)}\varrho, {}^{(1)}{\boldsymbol{v}}, {}^{(1)}\theta,..., {}^{(n)}\varrho, {}^{(n)}{\boldsymbol{v}}, {}^{(n)}\theta\right) - a_{\varphi} \\[4pt] & + \mathrm{i} \varphi_n \left[ \frac{a_{\varphi}}{\mathrm{i}} +\frac{a_{pr}}{2} \sum_{k=1}^n {}^{(k)}v_i x^{(k)}_i+ a_{g,1} \sum_{k=1}^n {}^{(k)}v_1 + a_{g,2} \sum_{k=1}^n {}^{(k)}v_2 + a_{g,3} \sum_{k=1}^n {}^{(k)}v_3 \right]. \end{aligned}\end{equation}
\begin{equation} \begin{aligned} \eta^{\varphi_n} =\, & F_n\!\left(t, {\boldsymbol{x}}^{(1)},..., {\boldsymbol{x}}^{(n)}, {}^{(1)}\varrho, {}^{(1)}{\boldsymbol{v}}, {}^{(1)}\theta,..., {}^{(n)}\varrho, {}^{(n)}{\boldsymbol{v}}, {}^{(n)}\theta\right) - a_{\varphi} \\[4pt] & + \mathrm{i} \varphi_n \left[ \frac{a_{\varphi}}{\mathrm{i}} +\frac{a_{pr}}{2} \sum_{k=1}^n {}^{(k)}v_i x^{(k)}_i+ a_{g,1} \sum_{k=1}^n {}^{(k)}v_1 + a_{g,2} \sum_{k=1}^n {}^{(k)}v_2 + a_{g,3} \sum_{k=1}^n {}^{(k)}v_3 \right]. \end{aligned}\end{equation}
In the above equations (3.22) and (3.23), the functions
![]() $F_2$
and
$F_2$
and
![]() $F_n$
appear as a result of the superposition principle. It is important to note that in equations (3.8), (3.21), (3.22) and (3.23),
$F_n$
appear as a result of the superposition principle. It is important to note that in equations (3.8), (3.21), (3.22) and (3.23),
![]() $a_{pr}$
is non-zero only for monatomic gases, that is, when
$a_{pr}$
is non-zero only for monatomic gases, that is, when
![]() $\gamma \neq 5/3$
,
$\gamma \neq 5/3$
,
![]() $a_{pr} = 0$
. All the other Euler symmetry groups uphold the side conditions without any restrictions. We impose the coincidence (2.7) and permutation (2.8) side conditions on statistical groups in the next section.
$a_{pr} = 0$
. All the other Euler symmetry groups uphold the side conditions without any restrictions. We impose the coincidence (2.7) and permutation (2.8) side conditions on statistical groups in the next section.
4 Physics represented by each of the groups
In this section, we will derive the global forms each of the symmetry transformations and discuss their relevant physics. The kinematic symmetries – namely space translation (
![]() $a_{x,i}$
), time translation (
$a_{x,i}$
), time translation (
![]() $a_{t}$
) and rotation groups (
$a_{t}$
) and rotation groups (
![]() $a_{r,i}$
) – which pertain to coordinate system independence are not discussed in this section.
$a_{r,i}$
) – which pertain to coordinate system independence are not discussed in this section.
4.1 Projective group
We begin with the projective transformation represented by the group parameter,
![]() $a_{pr}$
. This transformation is a symmetry of CF hierarchy only for monatomic gases,
$a_{pr}$
. This transformation is a symmetry of CF hierarchy only for monatomic gases,
![]() $\gamma = 5/3$
. Under this group, the infinitesimals for the dependent and independent variables are given by:
$\gamma = 5/3$
. Under this group, the infinitesimals for the dependent and independent variables are given by:
 \begin{equation} \begin{aligned} &\xi^t = t^2, \quad \xi^{x^{(1)}_1} = x^{(1)}_1 t , \quad \xi^{x^{(1)}_2} = x^{(1)}_2 t , \quad \xi^{x^{(1)}_3} = x^{(1)}_3 t, \quad \xi^{{}^{(1)}\varrho} = 3{}^{(1)}\varrho t, \\ &\xi^{{}^{(1)}v_1} = {}^{(1)}v_1 t, \quad \xi^{{}^{(1)}v_2} = {}^{(1)}v_2 t, \quad \xi^{{}^{(1)}v_3} = {}^{(1)}v_3 t, \quad \xi^{{}^{(1)}\theta} = 2 \> {}^{(1)}\theta t \\ &\eta^{\varphi_1} = \varphi_1 \left[ \mathrm{i} x^{(1)}_i \> {}^{(1)}v_i \right]. \end{aligned}\end{equation}
\begin{equation} \begin{aligned} &\xi^t = t^2, \quad \xi^{x^{(1)}_1} = x^{(1)}_1 t , \quad \xi^{x^{(1)}_2} = x^{(1)}_2 t , \quad \xi^{x^{(1)}_3} = x^{(1)}_3 t, \quad \xi^{{}^{(1)}\varrho} = 3{}^{(1)}\varrho t, \\ &\xi^{{}^{(1)}v_1} = {}^{(1)}v_1 t, \quad \xi^{{}^{(1)}v_2} = {}^{(1)}v_2 t, \quad \xi^{{}^{(1)}v_3} = {}^{(1)}v_3 t, \quad \xi^{{}^{(1)}\theta} = 2 \> {}^{(1)}\theta t \\ &\eta^{\varphi_1} = \varphi_1 \left[ \mathrm{i} x^{(1)}_i \> {}^{(1)}v_i \right]. \end{aligned}\end{equation}
Below is the global transformation, that is obtained utilising Lie’s first theorem [Reference Bluman and Kumei2]:
 \begin{equation} \varphi_1^* = \varphi_1 \exp \!\left( \mathrm{i} a_{pr} \frac{ {}^{(1)}v_i x^{(1)}_i}{1-a_{pr} t} \right).\end{equation}
\begin{equation} \varphi_1^* = \varphi_1 \exp \!\left( \mathrm{i} a_{pr} \frac{ {}^{(1)}v_i x^{(1)}_i}{1-a_{pr} t} \right).\end{equation}
For a general multi-point CF, the infinitesimal and the global transformation take the form:
 \begin{equation} \eta^{\varphi_n} = \mathrm{i} \varphi_n \left[ x^{(1)}_i \> {}^{(1)}v_i + .. + x^{(n)}_i \> {}^{(n)}v_i \right] , \varphi_n^* = \varphi_n \exp \!\left(\mathrm{i} a_{pr} \frac{ {}^{(1)}v_i x^{(1)}_i + ... + {}^{(n)}v_i x^{(n)}_i}{1-a_{pr} t} \right).\end{equation}
\begin{equation} \eta^{\varphi_n} = \mathrm{i} \varphi_n \left[ x^{(1)}_i \> {}^{(1)}v_i + .. + x^{(n)}_i \> {}^{(n)}v_i \right] , \varphi_n^* = \varphi_n \exp \!\left(\mathrm{i} a_{pr} \frac{ {}^{(1)}v_i x^{(1)}_i + ... + {}^{(n)}v_i x^{(n)}_i}{1-a_{pr} t} \right).\end{equation}
4.2 Dilation groups
Let us now investigate the dilation group,
![]() $a_{s,t}$
, also known as ‘scaling in time’. The non-trivial infinitesimals resulting from this symmetry transformation are
$a_{s,t}$
, also known as ‘scaling in time’. The non-trivial infinitesimals resulting from this symmetry transformation are
All other dependent and independent variables do not transform under this symmetry group. The global form of the transformation is given by:
For ‘scaling in space’ group,
![]() $a_{s,x}$
, the infinitesimals and global form of the symmetry transformation are given below:
$a_{s,x}$
, the infinitesimals and global form of the symmetry transformation are given below:
The third dilation group that exists only in compressible fluids is ‘scaling of density’, represented by the parameter,
![]() $a_{s,\rho}$
. The only non-trivial infinitesimal in the CF formulation is that of density spectral parameter, that is,
$a_{s,\rho}$
. The only non-trivial infinitesimal in the CF formulation is that of density spectral parameter, that is,
![]() $\xi^{{}^{(1)}\varrho}$
. The expressions for the infinitesimal and the corresponding global transformation are given below:
$\xi^{{}^{(1)}\varrho}$
. The expressions for the infinitesimal and the corresponding global transformation are given below:
4.3 Galilean invariance
For the case of the Galilean invariance groups,
![]() $a_{g,\alpha}$
, where
$a_{g,\alpha}$
, where
![]() $\alpha=1 - 3$
, the non-zero infinitesimals are
$\alpha=1 - 3$
, the non-zero infinitesimals are
The global transformation takes the form:
In the above equation, repeated
![]() $\alpha$
indices do not imply summation.
$\alpha$
indices do not imply summation.
4.4 Statistical groups
We now turn our attention to the new symmetry groups in the CF formulation that are not seen in the Euler equations. We begin with the function,
![]() $F_1$
, seen in the
$F_1$
, seen in the
![]() $\eta^{\varphi_1}$
equation (3.21):
$\eta^{\varphi_1}$
equation (3.21):
and all other infinitesimals are trivial in nature. As a result, the global form of this symmetry takes the form:
For the multi-point CF, the global transformation due to superposition principle (from equation (3.23)), takes the form:
To establish how the infinite hierarchy of functions
![]() $F_1, ..., F_n$
are related to one another, we impose the reduction side condition, that is, we set the spectral parameters at
$F_1, ..., F_n$
are related to one another, we impose the reduction side condition, that is, we set the spectral parameters at
![]() ${\boldsymbol{x}}^{(n)}$
to zero. The equation then becomes
${\boldsymbol{x}}^{(n)}$
to zero. The equation then becomes
As the dependence on
![]() ${\boldsymbol{x}}^{(n)}$
is not exhibited by
${\boldsymbol{x}}^{(n)}$
is not exhibited by
![]() $\varphi_{n-1}^*$
and
$\varphi_{n-1}^*$
and
![]() $\varphi_{n-1}$
, the reduction condition implies that
$\varphi_{n-1}$
, the reduction condition implies that
![]() $F_n$
at
$F_n$
at
![]() ${}^{(n)}\varrho = {}^{(n)}{\boldsymbol{v}} = {}^{(n)}\theta = 0$
does not depend on
${}^{(n)}\varrho = {}^{(n)}{\boldsymbol{v}} = {}^{(n)}\theta = 0$
does not depend on
![]() ${\boldsymbol{x}}^{(n)}$
too. In addition
${\boldsymbol{x}}^{(n)}$
too. In addition
![]() $F_n (... {}^{(n)}\varrho = {}^{(n)}{\boldsymbol{v}} = {}^{(n)}\theta = 0)$
should also identically satisfy the governing equation for
$F_n (... {}^{(n)}\varrho = {}^{(n)}{\boldsymbol{v}} = {}^{(n)}\theta = 0)$
should also identically satisfy the governing equation for
![]() $(n-1)-$
point CF. Therefore,
$(n-1)-$
point CF. Therefore,
![]() $F_n (... {}^{(n)}\varrho = {}^{(n)}{\boldsymbol{v}} = {}^{(n)}\theta = 0)$
reduces to the same family of functions that are represented by
$F_n (... {}^{(n)}\varrho = {}^{(n)}{\boldsymbol{v}} = {}^{(n)}\theta = 0)$
reduces to the same family of functions that are represented by
![]() $F_{n-1}$
. The set of functions,
$F_{n-1}$
. The set of functions,
![]() $F_n$
, to satisfy the permutation side condition (2.8), when:
$F_n$
, to satisfy the permutation side condition (2.8), when:
that is, the function value remains unchanged regardless of the order in which the spatial points are considered. Coincidence side condition (2.7) is upheld when:
In the case of separation side condition (2.9),
 \begin{equation}\begin{aligned} \lim_{|{\boldsymbol{x}}^{(n+1)}-{\boldsymbol{x}}^{(k)}| \to \infty} F_{n+1} &= \varphi_1\!\left({}^{(n+1)}\varrho, {}^{(n+1)}{\boldsymbol{v}}, {}^{(n+1)}\theta; t, {\boldsymbol{x}}^{(n+1)}\right) F_n \\ & \quad + \varphi_n F_1 \!\left( t, {\boldsymbol{x}}^{(n+1)}, {}^{(n+1)}\varrho, {}^{(n+1)}{\boldsymbol{v}}, {}^{(n+1)}\theta\right)\end{aligned}\end{equation}
\begin{equation}\begin{aligned} \lim_{|{\boldsymbol{x}}^{(n+1)}-{\boldsymbol{x}}^{(k)}| \to \infty} F_{n+1} &= \varphi_1\!\left({}^{(n+1)}\varrho, {}^{(n+1)}{\boldsymbol{v}}, {}^{(n+1)}\theta; t, {\boldsymbol{x}}^{(n+1)}\right) F_n \\ & \quad + \varphi_n F_1 \!\left( t, {\boldsymbol{x}}^{(n+1)}, {}^{(n+1)}\varrho, {}^{(n+1)}{\boldsymbol{v}}, {}^{(n+1)}\theta\right)\end{aligned}\end{equation}
needs to be satisfied. As discussed previously, the separation side condition (2.9) is not imposed in this study.
As an example, let us consider a set of functions
![]() $F_n$
that do not have any spatial and temporal dependence, that is,
$F_n$
that do not have any spatial and temporal dependence, that is,
The transformed CFs,
![]() $\varphi_n^*$
, given by:
$\varphi_n^*$
, given by:
automatically satisfy the CF hierarchy. This symmetry is a more general compressible analogue of the ‘shape’ symmetry demonstrated in [Reference Wacławczyk, Staffolani, Oberlack, Rosteck, Wilczek and Friedrich21]. As established in the previous section, the functions
![]() $F_n$
cannot be constants as they would then violate the reduction side condition. As evidenced in the case of shape symmetry in incompressible flows [Reference Wacławczyk, Staffolani, Oberlack, Rosteck, Wilczek and Friedrich21], the separation side condition is not satisfied. The discussion pertinent to not strictly enforcing this side condition is presented in Section 3.2.1.
$F_n$
cannot be constants as they would then violate the reduction side condition. As evidenced in the case of shape symmetry in incompressible flows [Reference Wacławczyk, Staffolani, Oberlack, Rosteck, Wilczek and Friedrich21], the separation side condition is not satisfied. The discussion pertinent to not strictly enforcing this side condition is presented in Section 3.2.1.
Finally, we investigate the symmetry group
![]() $a_{\varphi}$
. The resulting infinitesimals and the global transformation are
$a_{\varphi}$
. The resulting infinitesimals and the global transformation are
The above global form of the transformation satisfies all the required conditions, except for the separation side condition (2.9). This symmetry is the compressible counterpart of the ‘intermittency’ symmetry, representing the external intermittency seen in turbulent flows [Reference Wacławczyk, Staffolani, Oberlack, Rosteck, Wilczek and Friedrich21]. The implications of the both of the above statistical symmetries is investigated in detail in the next section.
5 Global symmetry transformations of compressible turbulence moments
One of the major advantages of computing the symmetries of the CF hierarchy is the ease with which these symmetries could be translated to any velocity and thermodynamics moments. In this section, we explore the symmetry transformations of various key statistics in compressible turbulence, such as kinetic and internal energies, various order moments of velocity, density, temperature and pressure. The advantage of utilising the CF formulation for symmetry investigation becomes clearly evident in this section. Eventually, this will also have important implications on the development of statistical turbulence models for compressible flows.
5.1 Averaged kinetic energy
We begin our investigation with averaged kinetic energy (k), which in compressible turbulence is defined as:
As discussed in the introduction, the moments can be obtained from the CF, upon taking derivatives. In the case of kinetic energy, this would imply that we compute
Computing the transformation of k in equation (5.1) under the projective group (4.2) is a bit involved. We first look at the above triple derivative of CF in transformed variables, that is,
 \begin{equation} \frac{\partial^3 \varphi_1^*}{ \partial \> {}^{(1)}\varrho^* \partial \> {}^{(1)}v_i^* \partial \> {}^{(1)}v_i^*} = \frac{\partial^3}{ \partial \> {}^{(1)}\varrho^* \partial \> {}^{(1)}v_i^* \partial \> {}^{(1)}v_i^*} \left[ \varphi_1 \exp \!\left( \mathrm{i} a_{pr}\frac{ {}^{(1)}v_i x^{(1)}_i}{1-a_{pr} t} \right) \right].\end{equation}
\begin{equation} \frac{\partial^3 \varphi_1^*}{ \partial \> {}^{(1)}\varrho^* \partial \> {}^{(1)}v_i^* \partial \> {}^{(1)}v_i^*} = \frac{\partial^3}{ \partial \> {}^{(1)}\varrho^* \partial \> {}^{(1)}v_i^* \partial \> {}^{(1)}v_i^*} \left[ \varphi_1 \exp \!\left( \mathrm{i} a_{pr}\frac{ {}^{(1)}v_i x^{(1)}_i}{1-a_{pr} t} \right) \right].\end{equation}
We now obtain the expressions for each of the derivatives with respect to the transformed variables in terms of original variables:
 \begin{equation}\begin{aligned} \frac{\partial}{\partial \> {}^{(1)}\varrho^*} &= \frac{\partial t}{\partial \> {}^{(1)}\varrho^*} \frac{\partial}{\partial t} + \frac{\partial x^{(1)}_i}{\partial \> {}^{(1)}\varrho^*} \frac{\partial}{\partial x^{(i)}_i} + \frac{\partial \>{}^{(1)}\varrho }{\partial \> {}^{(1)}\varrho^*} \frac{\partial}{\partial \>{}^{(1)}\varrho} + \frac{\partial \>{}^{(1)}v_i }{\partial \> {}^{(1)}\varrho^*} \frac{\partial}{\partial \>{}^{(1)}v_i} + \frac{\partial \>{}^{(1)}\theta }{\partial \> {}^{(1)}\varrho^*} \frac{\partial}{\partial \>{}^{(1)}\theta} \\ &= \frac{1}{\left(1+a_{pr} t^*\right)^3} \frac{\partial}{\partial \>{}^{(1)}\varrho} = \left(1 - a_{pr} t\right)^3 \frac{\partial}{\partial \>{}^{(1)}\varrho}\end{aligned}\end{equation}
\begin{equation}\begin{aligned} \frac{\partial}{\partial \> {}^{(1)}\varrho^*} &= \frac{\partial t}{\partial \> {}^{(1)}\varrho^*} \frac{\partial}{\partial t} + \frac{\partial x^{(1)}_i}{\partial \> {}^{(1)}\varrho^*} \frac{\partial}{\partial x^{(i)}_i} + \frac{\partial \>{}^{(1)}\varrho }{\partial \> {}^{(1)}\varrho^*} \frac{\partial}{\partial \>{}^{(1)}\varrho} + \frac{\partial \>{}^{(1)}v_i }{\partial \> {}^{(1)}\varrho^*} \frac{\partial}{\partial \>{}^{(1)}v_i} + \frac{\partial \>{}^{(1)}\theta }{\partial \> {}^{(1)}\varrho^*} \frac{\partial}{\partial \>{}^{(1)}\theta} \\ &= \frac{1}{\left(1+a_{pr} t^*\right)^3} \frac{\partial}{\partial \>{}^{(1)}\varrho} = \left(1 - a_{pr} t\right)^3 \frac{\partial}{\partial \>{}^{(1)}\varrho}\end{aligned}\end{equation}
and
 \begin{equation}\begin{aligned} \frac{\partial}{\partial \> {}^{(1)}v_j^*} &= \frac{\partial t}{\partial \> {}^{(1)}v_j^*} \frac{\partial}{\partial t} + \frac{\partial x^{(1)}_i}{\partial \> {}^{(1)}v_j^*} \frac{\partial}{\partial x^{(i)}_i} + \frac{\partial \>{}^{(1)}\varrho }{\partial \> {}^{(1)}v_j^*} \frac{\partial}{\partial \>{}^{(1)}\varrho} + \frac{\partial \>{}^{(1)}v_i }{\partial \> {}^{(1)}v_j^*} \frac{\partial}{\partial \>{}^{(1)}v_i} + \frac{\partial \>{}^{(1)}\theta }{\partial \> {}^{(1)}v_j^*} \frac{\partial}{\partial \>{}^{(1)}\theta} \\ &= \frac{1}{1+ a_{pr} t^*} \frac{\partial}{\partial \>{}^{(1)}v_j} = \left(1 - a_{pr} t\right) \frac{\partial}{\partial \>{}^{(1)}v_j}.\end{aligned}\end{equation}
\begin{equation}\begin{aligned} \frac{\partial}{\partial \> {}^{(1)}v_j^*} &= \frac{\partial t}{\partial \> {}^{(1)}v_j^*} \frac{\partial}{\partial t} + \frac{\partial x^{(1)}_i}{\partial \> {}^{(1)}v_j^*} \frac{\partial}{\partial x^{(i)}_i} + \frac{\partial \>{}^{(1)}\varrho }{\partial \> {}^{(1)}v_j^*} \frac{\partial}{\partial \>{}^{(1)}\varrho} + \frac{\partial \>{}^{(1)}v_i }{\partial \> {}^{(1)}v_j^*} \frac{\partial}{\partial \>{}^{(1)}v_i} + \frac{\partial \>{}^{(1)}\theta }{\partial \> {}^{(1)}v_j^*} \frac{\partial}{\partial \>{}^{(1)}\theta} \\ &= \frac{1}{1+ a_{pr} t^*} \frac{\partial}{\partial \>{}^{(1)}v_j} = \left(1 - a_{pr} t\right) \frac{\partial}{\partial \>{}^{(1)}v_j}.\end{aligned}\end{equation}
As a result, we obtain
 \begin{equation} \begin{aligned} \frac{\partial^3 \varphi_1^*}{ \partial \> {}^{(1)}\varrho^* \partial \> {}^{(1)}v_i^* \partial \> {}^{(1)}v_i^*} & = \left(1-a_{pr} t\right)^5 \frac{\partial^3 \varphi_1^*}{ \partial \> {}^{(1)}\varrho \partial \> {}^{(1)}v_i \partial \> {}^{(1)}v_i} \\[3pt] &= \left(1- a_{pr} t\right)^5 \frac{\partial^3 }{ \partial \> {}^{(1)}\varrho \partial \> {}^{(1)}v_i \partial \> {}^{(1)}v_i} \left[ \varphi_1 \exp \!\left( \mathrm{i} a_{pr} \frac{ {}^{(1)}v_i x^{(1)}_i}{1- a_{pr} t} \right) \right] \\[3pt] &= \left(1- a_{pr} t\right)^5 \left[ \frac{\partial^3 \varphi_1}{\partial \>{}^{(1)}\varrho \partial \> {}^{(1)}v_i \partial \> {}^{(1)}v_i} + \frac{2\mathrm{i} a_{pr} \> x^{(1)}_i}{1- a_{pr} t} \frac{\partial^2 \varphi_1}{\partial \>{}^{(1)}\varrho \partial \> {}^{(1)}v_i } \right. \\[3pt] &\left. - \frac{x^{(1)}_i x^{(1)}_i a_{pr}^2 }{\left(1- a_{pr} t\right)^2} \frac{\partial \varphi_1}{\partial \>{}^{(1)}\varrho } \right] \exp \!\left(\mathrm{i} a_{pr} \frac{ {}^{(1)}v_i x^{(1)}_i}{1- a_{pr} t} \right). \end{aligned}\end{equation}
\begin{equation} \begin{aligned} \frac{\partial^3 \varphi_1^*}{ \partial \> {}^{(1)}\varrho^* \partial \> {}^{(1)}v_i^* \partial \> {}^{(1)}v_i^*} & = \left(1-a_{pr} t\right)^5 \frac{\partial^3 \varphi_1^*}{ \partial \> {}^{(1)}\varrho \partial \> {}^{(1)}v_i \partial \> {}^{(1)}v_i} \\[3pt] &= \left(1- a_{pr} t\right)^5 \frac{\partial^3 }{ \partial \> {}^{(1)}\varrho \partial \> {}^{(1)}v_i \partial \> {}^{(1)}v_i} \left[ \varphi_1 \exp \!\left( \mathrm{i} a_{pr} \frac{ {}^{(1)}v_i x^{(1)}_i}{1- a_{pr} t} \right) \right] \\[3pt] &= \left(1- a_{pr} t\right)^5 \left[ \frac{\partial^3 \varphi_1}{\partial \>{}^{(1)}\varrho \partial \> {}^{(1)}v_i \partial \> {}^{(1)}v_i} + \frac{2\mathrm{i} a_{pr} \> x^{(1)}_i}{1- a_{pr} t} \frac{\partial^2 \varphi_1}{\partial \>{}^{(1)}\varrho \partial \> {}^{(1)}v_i } \right. \\[3pt] &\left. - \frac{x^{(1)}_i x^{(1)}_i a_{pr}^2 }{\left(1- a_{pr} t\right)^2} \frac{\partial \varphi_1}{\partial \>{}^{(1)}\varrho } \right] \exp \!\left(\mathrm{i} a_{pr} \frac{ {}^{(1)}v_i x^{(1)}_i}{1- a_{pr} t} \right). \end{aligned}\end{equation}
Finally, the transformed kinetic energy under the projective group is given by:
In all of the scaling groups, the global transformation for k is straightforward, as these groups lead to the scaling of kinetic energy. For ‘scaling of time’ group (4.4), the global symmetry transformation of k looks like:
For the ‘scaling of space’ group (4.5):
Finally, the ‘scaling of density’ group (4.6):
We now shift our focus to two statistical symmetries that are present specifically in the case of CF hierarchy and not seen in Euler equations: shape and intermittency groups ((4.17) and (4.18)). For the shape symmetry (4.17), the global transformation of k, takes the form:
 \begin{equation}\begin{aligned} \left\langle \frac{1}{2} \rho u_i u_i \right\rangle^* &= \left\langle \frac{1}{2} \rho u_i u_i \right\rangle + \frac{\mathrm{i}}{2} a \left. \frac{\partial^3 F_1}{\partial \> {}^{(1)}\varrho \partial \> {}^{(1)}v_i \partial \> {}^{(1)}v_i} \right|_{{}^{(1)}\varrho = {}^{(1)}v_i = {}^{(1)}\theta = 0} \\ &= \left\langle \frac{1}{2} \rho u_i u_i \right\rangle + a_k,\end{aligned}\end{equation}
\begin{equation}\begin{aligned} \left\langle \frac{1}{2} \rho u_i u_i \right\rangle^* &= \left\langle \frac{1}{2} \rho u_i u_i \right\rangle + \frac{\mathrm{i}}{2} a \left. \frac{\partial^3 F_1}{\partial \> {}^{(1)}\varrho \partial \> {}^{(1)}v_i \partial \> {}^{(1)}v_i} \right|_{{}^{(1)}\varrho = {}^{(1)}v_i = {}^{(1)}\theta = 0} \\ &= \left\langle \frac{1}{2} \rho u_i u_i \right\rangle + a_k,\end{aligned}\end{equation}
where
![]() $a_k$
is a constant. Therefore, the addition of a constant to averaged kinetic energy in compressible turbulence leaves its governing equation invariant. In the case of the intermittency group (4.18), the kinetic energy transforms as:
$a_k$
is a constant. Therefore, the addition of a constant to averaged kinetic energy in compressible turbulence leaves its governing equation invariant. In the case of the intermittency group (4.18), the kinetic energy transforms as:
5.2 Averaged internal energy
The second measure of considerable importance in compressible turbulence is the averaged internal energy (e), defined as:
As the ratio,
![]() $1/(\gamma - 1)$
remains a constant for a given gas, we focus on the average pressure,
$1/(\gamma - 1)$
remains a constant for a given gas, we focus on the average pressure,
![]() $\langle p \rangle$
in the remainder of the paper, when we are investigating averaged internal energy. Based on our definition of CF,
$\langle p \rangle$
in the remainder of the paper, when we are investigating averaged internal energy. Based on our definition of CF,
![]() $\langle p \rangle$
can be obtained by:
$\langle p \rangle$
can be obtained by:
where, we have used ideal gas law,
![]() $p = \rho T$
, in its non-dimensional form. As a result,
$p = \rho T$
, in its non-dimensional form. As a result,
![]() $\langle p \rangle$
is obtained by taking derivatives of
$\langle p \rangle$
is obtained by taking derivatives of
![]() $\varphi_1$
with respect to
$\varphi_1$
with respect to
![]() ${}^{(1)}\varrho$
and
${}^{(1)}\varrho$
and
![]() ${}^{(1)}\theta$
.
${}^{(1)}\theta$
.
Let us now begin our investigation of transformation of internal energy under symmetries of CF. For the projective group (4.2), we obtain
We perform similar calculations as shown for k in the previous Subsection 5.1, to obtain the transformed e:
 \begin{equation}\begin{aligned} \frac{\partial}{\partial \> {}^{(1)}\theta^*} &= \frac{\partial t}{\partial \> {}^{(1)}\theta^*} \frac{\partial}{\partial t} + \frac{\partial x^{(1)}_i}{\partial \> {}^{(1)}\theta^*} \frac{\partial}{\partial x^{(1)}_i} + \frac{\partial \> {}^{(1)}\varrho}{\partial \> {}^{(1)}\theta^*} \frac{\partial}{\partial \> {}^{(1)}\varrho} + \frac{\partial \> {}^{(1)}v_i}{\partial \> {}^{(1)}\theta^*} \frac{\partial}{\partial \> {}^{(1)}v_i} + \frac{\partial \> {}^{(1)}\theta}{\partial \> {}^{(1)}\theta^*} \frac{\partial}{\partial \> {}^{(1)}\theta} \\ &= \left(1- a_{pr} t\right)^2 \frac{\partial}{\partial \> {}^{(1)}\theta},\end{aligned}\end{equation}
\begin{equation}\begin{aligned} \frac{\partial}{\partial \> {}^{(1)}\theta^*} &= \frac{\partial t}{\partial \> {}^{(1)}\theta^*} \frac{\partial}{\partial t} + \frac{\partial x^{(1)}_i}{\partial \> {}^{(1)}\theta^*} \frac{\partial}{\partial x^{(1)}_i} + \frac{\partial \> {}^{(1)}\varrho}{\partial \> {}^{(1)}\theta^*} \frac{\partial}{\partial \> {}^{(1)}\varrho} + \frac{\partial \> {}^{(1)}v_i}{\partial \> {}^{(1)}\theta^*} \frac{\partial}{\partial \> {}^{(1)}v_i} + \frac{\partial \> {}^{(1)}\theta}{\partial \> {}^{(1)}\theta^*} \frac{\partial}{\partial \> {}^{(1)}\theta} \\ &= \left(1- a_{pr} t\right)^2 \frac{\partial}{\partial \> {}^{(1)}\theta},\end{aligned}\end{equation}
leading to,
 \begin{equation} \begin{aligned} \frac{\partial^2 \varphi_1^*}{\partial \> {}^{(1)}\varrho^* \partial \> {}^{(1)}\theta^*} &= \left(1- a_{pr} t\right)^5 \frac{\partial^2 }{\partial \> {}^{(1)}\varrho \partial \> {}^{(1)}\theta} \left[ \varphi_1 \exp \!\left( \mathrm{i} a_{pr} \frac{{}^{(1)}v_i x^{(1)}_i}{1- a_{pr} t} \right) \right] \\ &= \left(1- a_{pr} t\right)^5 \frac{\partial^2 \varphi_1}{\partial \> {}^{(1)}\varrho \partial \> {}^{(1)}\theta} \exp \!\left( \mathrm{i} a_{pr} \frac{{}^{(1)}v_i x^{(1)}_i}{1- a_{pr} t} \right), \end{aligned}\end{equation}
\begin{equation} \begin{aligned} \frac{\partial^2 \varphi_1^*}{\partial \> {}^{(1)}\varrho^* \partial \> {}^{(1)}\theta^*} &= \left(1- a_{pr} t\right)^5 \frac{\partial^2 }{\partial \> {}^{(1)}\varrho \partial \> {}^{(1)}\theta} \left[ \varphi_1 \exp \!\left( \mathrm{i} a_{pr} \frac{{}^{(1)}v_i x^{(1)}_i}{1- a_{pr} t} \right) \right] \\ &= \left(1- a_{pr} t\right)^5 \frac{\partial^2 \varphi_1}{\partial \> {}^{(1)}\varrho \partial \> {}^{(1)}\theta} \exp \!\left( \mathrm{i} a_{pr} \frac{{}^{(1)}v_i x^{(1)}_i}{1- a_{pr} t} \right), \end{aligned}\end{equation}
and finally,
In the case of ‘scaling of time’ symmetry (4.4), the global transformation of averaged internal energy is
In ‘scaling of space’ (4.5),
‘Scaling of density’ (4.6) leads to:
The global transformation of e, in the case of shape symmetry (4.17), is given by:
Finally, the intermittency group (4.18) leads to:
5.3 Higher-order velocity and thermodynamic moments
We now investigate the higher-order moments of density, temperature, pressure and velocity. Since we are interested in multi-point moments, we need to consider the derivatives of the multi-point CF. For example, the multi-point density moments are obtained from the CF as follows:
 \begin{equation} \left\langle \prod_{l = 1}^n \rho({\boldsymbol{x}}^{(l)}, t) \right\rangle = \frac{1}{\mathrm{i}^n} \left[ \prod_{l = 1}^n \frac{\partial}{\partial \> {}^{(l)}\varrho} \varphi_n \right]_{{}^{(1)}\varrho = {}^{(1)}v_i = {}^{(1)}\theta = ... {}^{(n)}\varrho = {}^{(n)}v_i = {}^{(n)}\theta = 0 }\end{equation}
\begin{equation} \left\langle \prod_{l = 1}^n \rho({\boldsymbol{x}}^{(l)}, t) \right\rangle = \frac{1}{\mathrm{i}^n} \left[ \prod_{l = 1}^n \frac{\partial}{\partial \> {}^{(l)}\varrho} \varphi_n \right]_{{}^{(1)}\varrho = {}^{(1)}v_i = {}^{(1)}\theta = ... {}^{(n)}\varrho = {}^{(n)}v_i = {}^{(n)}\theta = 0 }\end{equation}
We now write down the global transformations of each of the higher-order moments with respect to the symmetry transformations of the CF hierarchy given in Section 3.2, starting with the nth-order moment of density:
 \begin{equation} a_{pr}\,: \quad \left\langle \prod_{l = 1}^n \rho({\boldsymbol{x}}^{(l)}, t) \right\rangle^* = \left(1- a_{pr} t\right)^{3n } \left\langle \prod_{l = 1}^n \rho({\boldsymbol{x}}^{(l)}, t) \right\rangle\end{equation}
\begin{equation} a_{pr}\,: \quad \left\langle \prod_{l = 1}^n \rho({\boldsymbol{x}}^{(l)}, t) \right\rangle^* = \left(1- a_{pr} t\right)^{3n } \left\langle \prod_{l = 1}^n \rho({\boldsymbol{x}}^{(l)}, t) \right\rangle\end{equation}
 \begin{equation} a_{s,\rho}\,: \quad \left\langle \prod_{l = 1}^n \rho({\boldsymbol{x}}^{(l)}, t) \right\rangle^* = e^{ n a_{s,\rho}} \left\langle \prod_{l = 1}^n \rho({\boldsymbol{x}}^{(l)}, t) \right\rangle\end{equation}
\begin{equation} a_{s,\rho}\,: \quad \left\langle \prod_{l = 1}^n \rho({\boldsymbol{x}}^{(l)}, t) \right\rangle^* = e^{ n a_{s,\rho}} \left\langle \prod_{l = 1}^n \rho({\boldsymbol{x}}^{(l)}, t) \right\rangle\end{equation}
 \begin{equation} F_n\,: \quad \left\langle \prod_{l = 1}^n \rho({\boldsymbol{x}}^{(l)}, t) \right\rangle^* = \left\langle \prod_{l = 1}^n \rho({\boldsymbol{x}}^{(l)}, t) \right\rangle + a_{\rho, n}\end{equation}
\begin{equation} F_n\,: \quad \left\langle \prod_{l = 1}^n \rho({\boldsymbol{x}}^{(l)}, t) \right\rangle^* = \left\langle \prod_{l = 1}^n \rho({\boldsymbol{x}}^{(l)}, t) \right\rangle + a_{\rho, n}\end{equation}
 \begin{equation} a_{\varphi}\,: \left\langle \prod_{l = 1}^n \rho({\boldsymbol{x}}^{(l)}, t) \right\rangle^* = e^{a_{\varphi}} \left\langle \prod_{l = 1}^n \rho({\boldsymbol{x}}^{(l)}, t) \right\rangle\end{equation}
\begin{equation} a_{\varphi}\,: \left\langle \prod_{l = 1}^n \rho({\boldsymbol{x}}^{(l)}, t) \right\rangle^* = e^{a_{\varphi}} \left\langle \prod_{l = 1}^n \rho({\boldsymbol{x}}^{(l)}, t) \right\rangle\end{equation}
Now the multi-point temperature moments transform as:
 \begin{equation} a_{pr}\,: \quad \left\langle \prod_{l = 1}^n T({\boldsymbol{x}}^{(l)}, t) \right\rangle^* = \left(1- a_{pr} t\right)^{2n } \left\langle \prod_{l = 1}^n T({\boldsymbol{x}}^{(l)}, t) \right\rangle\end{equation}
\begin{equation} a_{pr}\,: \quad \left\langle \prod_{l = 1}^n T({\boldsymbol{x}}^{(l)}, t) \right\rangle^* = \left(1- a_{pr} t\right)^{2n } \left\langle \prod_{l = 1}^n T({\boldsymbol{x}}^{(l)}, t) \right\rangle\end{equation}
 \begin{equation} a_{s,t}\,: \quad \left\langle \prod_{l = 1}^n T({\boldsymbol{x}}^{(l)}, t) \right\rangle^* = e^{-2 n a_{s,t}} \left\langle \prod_{l = 1}^n T({\boldsymbol{x}}^{(l)}, t) \right\rangle\end{equation}
\begin{equation} a_{s,t}\,: \quad \left\langle \prod_{l = 1}^n T({\boldsymbol{x}}^{(l)}, t) \right\rangle^* = e^{-2 n a_{s,t}} \left\langle \prod_{l = 1}^n T({\boldsymbol{x}}^{(l)}, t) \right\rangle\end{equation}
 \begin{equation} a_{s,x}\,: \quad \left\langle \prod_{l = 1}^n T({\boldsymbol{x}}^{(l)}, t) \right\rangle^* = e^{2 n a_{s,x}} \left\langle \prod_{l = 1}^n T({\boldsymbol{x}}^{(l)}, t) \right\rangle\end{equation}
\begin{equation} a_{s,x}\,: \quad \left\langle \prod_{l = 1}^n T({\boldsymbol{x}}^{(l)}, t) \right\rangle^* = e^{2 n a_{s,x}} \left\langle \prod_{l = 1}^n T({\boldsymbol{x}}^{(l)}, t) \right\rangle\end{equation}
 \begin{equation} F_n \,: \left\langle \prod_{l = 1}^n T({\boldsymbol{x}}^{(l)}, t) \right\rangle^* = \left\langle \prod_{l = 1}^n T({\boldsymbol{x}}^{(l)}, t) \right\rangle + a_{T, n}\end{equation}
\begin{equation} F_n \,: \left\langle \prod_{l = 1}^n T({\boldsymbol{x}}^{(l)}, t) \right\rangle^* = \left\langle \prod_{l = 1}^n T({\boldsymbol{x}}^{(l)}, t) \right\rangle + a_{T, n}\end{equation}
 \begin{equation} a_{\varphi}\,: \quad \left\langle \prod_{l = 1}^n T({\boldsymbol{x}}^{(l)}, t) \right\rangle^* = e^{a_{\varphi}} \left\langle \prod_{l = 1}^n T({\boldsymbol{x}}^{(l)}, t) \right\rangle\end{equation}
\begin{equation} a_{\varphi}\,: \quad \left\langle \prod_{l = 1}^n T({\boldsymbol{x}}^{(l)}, t) \right\rangle^* = e^{a_{\varphi}} \left\langle \prod_{l = 1}^n T({\boldsymbol{x}}^{(l)}, t) \right\rangle\end{equation}
In the case of pressure,
 \begin{equation} a_{pr}\,: \quad \left\langle \prod_{l = 1}^n p({\boldsymbol{x}}^{(l)}, t) \right\rangle^* = \left(1- a_{pr} t\right)^{5n } \left\langle \prod_{l = 1}^n p({\boldsymbol{x}}^{(l)}, t) \right\rangle\end{equation}
\begin{equation} a_{pr}\,: \quad \left\langle \prod_{l = 1}^n p({\boldsymbol{x}}^{(l)}, t) \right\rangle^* = \left(1- a_{pr} t\right)^{5n } \left\langle \prod_{l = 1}^n p({\boldsymbol{x}}^{(l)}, t) \right\rangle\end{equation}
 \begin{equation} a_{s,t}\,: \quad \left\langle \prod_{l = 1}^n p({\boldsymbol{x}}^{(l)}, t) \right\rangle^* = e^{-2 n a_{s,t}} \left\langle \prod_{l = 1}^n p({\boldsymbol{x}}^{(l)}, t) \right\rangle\end{equation}
\begin{equation} a_{s,t}\,: \quad \left\langle \prod_{l = 1}^n p({\boldsymbol{x}}^{(l)}, t) \right\rangle^* = e^{-2 n a_{s,t}} \left\langle \prod_{l = 1}^n p({\boldsymbol{x}}^{(l)}, t) \right\rangle\end{equation}
 \begin{equation} a_{s,x}\,: \quad \left\langle \prod_{l = 1}^n p({\boldsymbol{x}}^{(l)}, t) \right\rangle^* = e^{2 n a_{s,x}} \left\langle \prod_{l = 1}^n p({\boldsymbol{x}}^{(l)}, t) \right\rangle\end{equation}
\begin{equation} a_{s,x}\,: \quad \left\langle \prod_{l = 1}^n p({\boldsymbol{x}}^{(l)}, t) \right\rangle^* = e^{2 n a_{s,x}} \left\langle \prod_{l = 1}^n p({\boldsymbol{x}}^{(l)}, t) \right\rangle\end{equation}
 \begin{equation} a_{s,\rho}\,: \quad \left\langle \prod_{l = 1}^n p({\boldsymbol{x}}^{(l)}, t) \right\rangle^* = e^{ n a_{s,\rho}} \left\langle \prod_{l = 1}^n p({\boldsymbol{x}}^{(l)}, t) \right\rangle\end{equation}
\begin{equation} a_{s,\rho}\,: \quad \left\langle \prod_{l = 1}^n p({\boldsymbol{x}}^{(l)}, t) \right\rangle^* = e^{ n a_{s,\rho}} \left\langle \prod_{l = 1}^n p({\boldsymbol{x}}^{(l)}, t) \right\rangle\end{equation}
 \begin{equation} F_n\,: \quad \left\langle \prod_{l = 1}^n p({\boldsymbol{x}}^{(l)}, t) \right\rangle^* = \left\langle \prod_{l = 1}^n p({\boldsymbol{x}}^{(l)}, t) \right\rangle + a_{p, n}\end{equation}
\begin{equation} F_n\,: \quad \left\langle \prod_{l = 1}^n p({\boldsymbol{x}}^{(l)}, t) \right\rangle^* = \left\langle \prod_{l = 1}^n p({\boldsymbol{x}}^{(l)}, t) \right\rangle + a_{p, n}\end{equation}
 \begin{equation} a_{\varphi}\,: \quad \left\langle \prod_{l = 1}^n p({\boldsymbol{x}}^{(l)}, t) \right\rangle^* = e^{a_{\varphi}} \left\langle \prod_{l = 1}^n p({\boldsymbol{x}}^{(l)}, t) \right\rangle\end{equation}
\begin{equation} a_{\varphi}\,: \quad \left\langle \prod_{l = 1}^n p({\boldsymbol{x}}^{(l)}, t) \right\rangle^* = e^{a_{\varphi}} \left\langle \prod_{l = 1}^n p({\boldsymbol{x}}^{(l)}, t) \right\rangle\end{equation}
The multi-point velocity moments constitute an nth-order tensor that can be obtained from the CF as:
where
![]() $i_1, i_2, ... , i_n$
are indices of the multi-point velocity moment tensor taking values from 1 to 3. The global transformations of the multi-point velocity moment tensor under the CF symmetries are given below:
$i_1, i_2, ... , i_n$
are indices of the multi-point velocity moment tensor taking values from 1 to 3. The global transformations of the multi-point velocity moment tensor under the CF symmetries are given below:
 \begin{equation}\begin{aligned} a_{pr}\,: \left\langle \prod_{l = 1}^n u_{i_l} \left({\boldsymbol{x}}^{(l)}, t\right) \right\rangle^* =& \left(1-a_{pr} t\right)^n \left\langle \prod_{l = 1}^n u_{i_l} \left({\boldsymbol{x}}^{(l)}, t\right) \right\rangle \\ & + \left(1- a_{pr} t\right)^{n-1} \sum_{k = 1}^n \left[ a_{pr} \> x^{(k)}_{i_k} \left\langle \prod_{l = 1, l \neq k}^n u_{i_l} \left({\boldsymbol{x}}^{(l)}, t\right) \right\rangle \right] \\ & + \cdots + \left(1- a_{pr} t\right) \sum_{k = 1}^n \left[ a_{pr}^{n-1} \left\langle u_{i_k} \left({\boldsymbol{x}}^{(k)}, t\right) \right\rangle \prod_{l = 1, l \neq k}^n x^{(l)}_{i_l} \right] \\ &+ a_{pr}^n x^{(1)}_{i_1} x^{(2)}_{i_2} ... x^{(n)}_{i_{n}}\end{aligned}\end{equation}
\begin{equation}\begin{aligned} a_{pr}\,: \left\langle \prod_{l = 1}^n u_{i_l} \left({\boldsymbol{x}}^{(l)}, t\right) \right\rangle^* =& \left(1-a_{pr} t\right)^n \left\langle \prod_{l = 1}^n u_{i_l} \left({\boldsymbol{x}}^{(l)}, t\right) \right\rangle \\ & + \left(1- a_{pr} t\right)^{n-1} \sum_{k = 1}^n \left[ a_{pr} \> x^{(k)}_{i_k} \left\langle \prod_{l = 1, l \neq k}^n u_{i_l} \left({\boldsymbol{x}}^{(l)}, t\right) \right\rangle \right] \\ & + \cdots + \left(1- a_{pr} t\right) \sum_{k = 1}^n \left[ a_{pr}^{n-1} \left\langle u_{i_k} \left({\boldsymbol{x}}^{(k)}, t\right) \right\rangle \prod_{l = 1, l \neq k}^n x^{(l)}_{i_l} \right] \\ &+ a_{pr}^n x^{(1)}_{i_1} x^{(2)}_{i_2} ... x^{(n)}_{i_{n}}\end{aligned}\end{equation}
 \begin{equation} a_{s,t}\,: \quad \left\langle \prod_{l = 1}^n u_{i_l} ({\boldsymbol{x}}^{(l)}, t) \right\rangle^* = e^{-n a_{s,t}} \left\langle \prod_{l = 1}^n u_{i_l} ({\boldsymbol{x}}^{(l)}, t) \right\rangle\end{equation}
\begin{equation} a_{s,t}\,: \quad \left\langle \prod_{l = 1}^n u_{i_l} ({\boldsymbol{x}}^{(l)}, t) \right\rangle^* = e^{-n a_{s,t}} \left\langle \prod_{l = 1}^n u_{i_l} ({\boldsymbol{x}}^{(l)}, t) \right\rangle\end{equation}
 \begin{equation} a_{s,x}\,: \quad \left\langle \prod_{l = 1}^n u_{i_l} ({\boldsymbol{x}}^{(l)}, t) \right\rangle^* = e^{n a_{s,x}} \left\langle \prod_{l = 1}^n u_{i_l} ({\boldsymbol{x}}^{(l)}, t) \right\rangle\end{equation}
\begin{equation} a_{s,x}\,: \quad \left\langle \prod_{l = 1}^n u_{i_l} ({\boldsymbol{x}}^{(l)}, t) \right\rangle^* = e^{n a_{s,x}} \left\langle \prod_{l = 1}^n u_{i_l} ({\boldsymbol{x}}^{(l)}, t) \right\rangle\end{equation}
 \begin{equation} F_n\,: \quad \left\langle \prod_{l = 1}^n u_{i_l} ({\boldsymbol{x}}^{(l)}, t) \right\rangle^* = \left\langle \prod_{l = 1}^n u_{i_l} ({\boldsymbol{x}}^{(l)}, t) \right\rangle + a_{i_1 i_2 .. i_n}\end{equation}
\begin{equation} F_n\,: \quad \left\langle \prod_{l = 1}^n u_{i_l} ({\boldsymbol{x}}^{(l)}, t) \right\rangle^* = \left\langle \prod_{l = 1}^n u_{i_l} ({\boldsymbol{x}}^{(l)}, t) \right\rangle + a_{i_1 i_2 .. i_n}\end{equation}
 \begin{equation} a_{\varphi}\,: \quad \left\langle \prod_{l = 1}^n u_{i_l} ({\boldsymbol{x}}^{(l)}, t) \right\rangle^* = e^{a_{\varphi}} \left\langle \prod_{l = 1}^n u_{i_l} ({\boldsymbol{x}}^{(l)}, t) \right\rangle.\end{equation}
\begin{equation} a_{\varphi}\,: \quad \left\langle \prod_{l = 1}^n u_{i_l} ({\boldsymbol{x}}^{(l)}, t) \right\rangle^* = e^{a_{\varphi}} \left\langle \prod_{l = 1}^n u_{i_l} ({\boldsymbol{x}}^{(l)}, t) \right\rangle.\end{equation}
Thus, all the flow and thermodynamics moments can be obtained from the CF hierarchy and as a result, the process of finding scaling laws via Lie group analysis is considerably simplified.
6 Conclusions
We derive the symmetries of the CF hierarchy of compressible turbulence. As the infinite set of CF equations encompasses all the flow and thermodynamic moment hierarchies, it is an effective framework, in the next step, for obtaining scaling laws for compressible statistics. The effects of viscosity and heat conductivity are neglected, as they lead to symmetry breaking in the instantaneous equations. The symmetry groups of the CF hierarchy obtained can be broadly classified into two groups:
-
(1) Euler symmetries: The symmetries exhibited by the compressible Euler equations are replicated in the CF framework, as anticipated. These include (i) the three dilation groups: scaling in time, space and density; (ii) groups corresponding to invariance with respect to coordinate system; and (iii) projective group which is solely restricted to monatomic gases (
 $\gamma = 5/3$
), that is, gases with only translational degrees of freedom, due to the imposition of reduction side condition.
$\gamma = 5/3$
), that is, gases with only translational degrees of freedom, due to the imposition of reduction side condition. -
(2) Statistical symmetries: In additional to the Euler symmetries that are replicated in the CF hierarchy, additional symmetries – the so called ‘statistical’ symmetries – manifest, mainly as a result of the linearity of the governing equations. Due to the principle of superposition, a general infinite set of functions,
 $F_n$
, could be added to the CF hierarchy, subject to additional constraints. Depending on the form of
$F_n$
, could be added to the CF hierarchy, subject to additional constraints. Depending on the form of
 $F_n$
, two types of statistical symmetry groups emerge that are also evident in the moment and PDF hierarchies in incompressible turbulence:
$F_n$
, two types of statistical symmetry groups emerge that are also evident in the moment and PDF hierarchies in incompressible turbulence:-
(a) Shape symmetry: When the functions,
 $F_n$
, do not exhibit any spatial and temporal dependence, then the symmetry analogous to that of the ‘shape’ symmetry in incompressible turbulence results. Just like its incompressible counterpart, shape symmetry in the compressible CF hierarchy implies the invariance of the moments to translation.
$F_n$
, do not exhibit any spatial and temporal dependence, then the symmetry analogous to that of the ‘shape’ symmetry in incompressible turbulence results. Just like its incompressible counterpart, shape symmetry in the compressible CF hierarchy implies the invariance of the moments to translation. -
(b) Intermittency symmetry: Like its counterpart in incompressible turbulence, this symmetry indicates the external intermittency seen in turbulent flows. This symmetry group results in the scaling of compressible moments by an arbitrary constant.
-
The findings of this paper will be helpful in deriving scaling laws for compressible turbulence statistics in various canonical flows. They are also useful in invariant modelling of compressible turbulence.
Acknowledgements
The first author is supported by ‘Humboldt Research Fellowship for Postdoctoral Researchers’ from Alexander von Humboldt Foundation. D. P. is funded by DFG (German Research Foundation) under grant No. ‘OB 96/48-1’.
Conflict of interest
None.