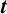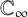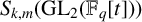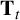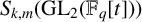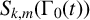1 Introduction
Let
![]() $S_k(\mathrm {{SL}}_2(\mathbb {Z}))$
be the space of weight k cusp forms of level one. It is well known that this space admits a basis of Hecke eigenforms, that is, normalised eigenfunctions for all the Hecke operators
$S_k(\mathrm {{SL}}_2(\mathbb {Z}))$
be the space of weight k cusp forms of level one. It is well known that this space admits a basis of Hecke eigenforms, that is, normalised eigenfunctions for all the Hecke operators
![]() $T_n$
. The space
$T_n$
. The space
![]() $S_k(\Gamma _0(N))$
still admits a basis of Hecke eigenforms, but only for those
$S_k(\Gamma _0(N))$
still admits a basis of Hecke eigenforms, but only for those
![]() $T_n$
such that
$T_n$
such that
![]() $(n,N)=1$
. To find a basis of eigenforms for all the
$(n,N)=1$
. To find a basis of eigenforms for all the
![]() $T_n$
, we have to focus on forms that are genuinely of level N and also to consider the operator
$T_n$
, we have to focus on forms that are genuinely of level N and also to consider the operator
![]() $U_p$
if
$U_p$
if
![]() $p\mid N$
, as Atkin and Lehner realised [Reference Atkin and Lehner1]. More precisely, we have to distinguish between oldforms, that is, forms coming from lower levels
$p\mid N$
, as Atkin and Lehner realised [Reference Atkin and Lehner1]. More precisely, we have to distinguish between oldforms, that is, forms coming from lower levels
![]() $M\mid N$
, and newforms, which are defined as the orthogonal complement of oldforms with respect to the Petersson inner product (see [Reference Diamond and Shurman10, Ch. 5]).
$M\mid N$
, and newforms, which are defined as the orthogonal complement of oldforms with respect to the Petersson inner product (see [Reference Diamond and Shurman10, Ch. 5]).
The present paper mainly deals with a function field counterpart of the above results. It comes after a series of papers [Reference Bandini and Valentino3, Reference Bandini and Valentino4, Reference Bandini and Valentino6, Reference Valentino13], in which we investigated:
-
(1) diagonalisability of Hecke operators;
-
(2) injectivity of Hecke operators;
-
(3) newforms and oldforms,
for the Drinfeld modular forms. Let
![]() $S_{k,m}(\mathrm {{GL}}_2(\mathbb {F}_q[t]))$
, respectively
$S_{k,m}(\mathrm {{GL}}_2(\mathbb {F}_q[t]))$
, respectively
![]() $S_{k,m}(\Gamma _0(\mathfrak {p}))$
, be the space of Drinfeld cusp forms of weight k, type m and level one, respectively level
$S_{k,m}(\Gamma _0(\mathfrak {p}))$
, be the space of Drinfeld cusp forms of weight k, type m and level one, respectively level
![]() $\mathfrak {p}$
, where
$\mathfrak {p}$
, where
![]() $\mathfrak {p}=(P)$
is a prime ideal of
$\mathfrak {p}=(P)$
is a prime ideal of
![]() $\mathcal {O}:=\mathbb {F}_q[t]$
and q a power of a fixed prime
$\mathcal {O}:=\mathbb {F}_q[t]$
and q a power of a fixed prime
![]() $p\in \mathbb {Z}$
(see Section 2 for details of the definitions and notation appearing in this introduction). Denote by
$p\in \mathbb {Z}$
(see Section 2 for details of the definitions and notation appearing in this introduction). Denote by
![]() $\mathbf {T}_{\mathfrak {p}}$
and
$\mathbf {T}_{\mathfrak {p}}$
and
![]() $\mathbf {U}_{\mathfrak {p}}$
respectively the Hecke and Atkin–Lehner operators acting on
$\mathbf {U}_{\mathfrak {p}}$
respectively the Hecke and Atkin–Lehner operators acting on
![]() $S_{k,m}(\mathrm {{GL}}_2(\mathcal {O}))$
and
$S_{k,m}(\mathrm {{GL}}_2(\mathcal {O}))$
and
![]() $S_{k,m}(\Gamma _0(\mathfrak {p}))$
.
$S_{k,m}(\Gamma _0(\mathfrak {p}))$
.
One of the challenges in the positive characteristic setting comes from the lack of a suitable analogue of the Petersson inner product. In [Reference Bandini and Valentino3, Reference Bandini and Valentino4], we overcame this using a combination of a combinatorial argument, that is, Teitelbaum interpretation of cusp forms as harmonic cocycles (see [Reference Teitelbaum12]), and of twisted trace maps to describe what we identify as newforms. The combinatorial method allowed us to describe explicitly the matrix associated to the
![]() $\mathbf {U}_{\mathfrak {p}}$
-operator acting on
$\mathbf {U}_{\mathfrak {p}}$
-operator acting on
![]() $S_{k,m}(\Gamma _0(\mathfrak {p}))$
, when
$S_{k,m}(\Gamma _0(\mathfrak {p}))$
, when
![]() $\mathfrak {p}$
is prime generated by a degree-one polynomial, and to formulate a series of conjectures, supported by numerical search, on the distribution of slopes, that is,
$\mathfrak {p}$
is prime generated by a degree-one polynomial, and to formulate a series of conjectures, supported by numerical search, on the distribution of slopes, that is,
![]() $\mathfrak {p}$
-adic valuations of eigenvalues of
$\mathfrak {p}$
-adic valuations of eigenvalues of
![]() $\mathbf {U}_{\mathfrak {p}}$
, as the weight varies. In [Reference Bandini and Valentino4], among other things, we gave the following conjecture.
$\mathbf {U}_{\mathfrak {p}}$
, as the weight varies. In [Reference Bandini and Valentino4], among other things, we gave the following conjecture.
Conjecture 1.1 [Reference Bandini and Valentino4, Conjecture 1.1].
With the notation as above,
-
(1)
 $\mathbf {T}_{\mathfrak {p}}$
is injective;
$\mathbf {T}_{\mathfrak {p}}$
is injective; -
(2)
 $S_{k,m}(\Gamma _0(\mathfrak {p}))$
is the direct sum of oldforms
$S_{k,m}(\Gamma _0(\mathfrak {p}))$
is the direct sum of oldforms
 $S^{\mathrm {old}}_{k,m}(\Gamma _0(\mathfrak {p}))$
and newforms
$S^{\mathrm {old}}_{k,m}(\Gamma _0(\mathfrak {p}))$
and newforms
 $S^{\mathrm {new}}_{k,m}(\Gamma _0(\mathfrak {p}))$
.
$S^{\mathrm {new}}_{k,m}(\Gamma _0(\mathfrak {p}))$
.
We provided some evidence: in particular,
-
(a) for the case
 $\deg (P)=1$
and
$\deg (P)=1$
and
 $\dim _{\mathbb {C}_\infty }(S_{k,m}(\mathrm {{GL}}_2(\mathcal {O})))=0$
, in [Reference Bandini and Valentino4, Section 5];
$\dim _{\mathbb {C}_\infty }(S_{k,m}(\mathrm {{GL}}_2(\mathcal {O})))=0$
, in [Reference Bandini and Valentino4, Section 5]; -
(b) for the case
 $\deg (P)=1$
and
$\deg (P)=1$
and
 $\dim _{\mathbb {C}_\infty }(S_{k,m}(\mathrm {{GL}}_2(\mathcal {O})))=1$
, in the (unpublished) Section 3 of [Reference Bandini and Valentino5].
$\dim _{\mathbb {C}_\infty }(S_{k,m}(\mathrm {{GL}}_2(\mathcal {O})))=1$
, in the (unpublished) Section 3 of [Reference Bandini and Valentino5].
Recently, Dalal and Kumar [Reference Dalal and Kumar9, Theorem 4.6] provided a new proof for case (b): their method is based on the analysis of the Fourier coefficients of the image of a generator via the Hecke operator
![]() $\mathbf {T}_{\mathfrak {p}}$
and, hopefully, it is suitable for more generalisations. Since there seems to be quite some interest in results of this type, we decided to present here our original proof of this fact based on the linear algebra interpretation of the Hecke operators
$\mathbf {T}_{\mathfrak {p}}$
and, hopefully, it is suitable for more generalisations. Since there seems to be quite some interest in results of this type, we decided to present here our original proof of this fact based on the linear algebra interpretation of the Hecke operators
![]() ${\textbf {T}}_{\mathfrak {p}}$
and
${\textbf {T}}_{\mathfrak {p}}$
and
![]() ${\textbf {U}}_{\mathfrak {p}}$
and of the trace maps
${\textbf {U}}_{\mathfrak {p}}$
and of the trace maps
![]() ${\textit {Tr}}$
and
${\textit {Tr}}$
and
![]() ${\textit {Tr}}'$
[Reference Bandini and Valentino3, Reference Bandini and Valentino4]. The proof is via direct computation, exploiting the symmetries of the matrices representing these operators. We believe that such symmetries are the key to improve the results but, to go further, we probably need a deeper understanding of how they reflect on the action on oldforms, that is, to find the counterpart for oldforms of the antidiagonal action on newforms (see [Reference Bandini and Valentino4, Section 5.2]). The statement and an explicit example already appeared in [Reference Bandini and Valentino6, Example 2.19].
${\textit {Tr}}'$
[Reference Bandini and Valentino3, Reference Bandini and Valentino4]. The proof is via direct computation, exploiting the symmetries of the matrices representing these operators. We believe that such symmetries are the key to improve the results but, to go further, we probably need a deeper understanding of how they reflect on the action on oldforms, that is, to find the counterpart for oldforms of the antidiagonal action on newforms (see [Reference Bandini and Valentino4, Section 5.2]). The statement and an explicit example already appeared in [Reference Bandini and Valentino6, Example 2.19].
The paper is organised as follows. In Section 2, we recall the objects we shall work with: Drinfeld modular forms, Hecke operators, degeneracy and trace maps, which will enable us to define oldforms and newforms despite the absence of an appropriate inner product. In Section 3, we specialise at
![]() $\mathfrak {p}=(t)$
and, as in [Reference Bandini and Valentino3], we associate explicit matrices to all operators. In particular, we describe a matrix M (see (3.2)) that is involved in the description of
$\mathfrak {p}=(t)$
and, as in [Reference Bandini and Valentino3], we associate explicit matrices to all operators. In particular, we describe a matrix M (see (3.2)) that is involved in the description of
![]() $\mathbf {U}_t$
and has many peculiar symmetries. After that, we briefly deal with the diagonalisability of M and then prove our main results.
$\mathbf {U}_t$
and has many peculiar symmetries. After that, we briefly deal with the diagonalisability of M and then prove our main results.
2 Setting and notation
Let K be the global function field
![]() $\mathbb {F}_q(t)$
, where q is a power of a fixed prime
$\mathbb {F}_q(t)$
, where q is a power of a fixed prime
![]() $p\in \mathbb {Z}$
. Fix the prime
$p\in \mathbb {Z}$
. Fix the prime
![]() ${1}/{t}$
at
${1}/{t}$
at
![]() $\infty $
and denote by
$\infty $
and denote by
![]() $\mathcal {O}:=\mathbb {F}_q[t]$
its ring of integers (that is, the ring of functions regular outside
$\mathcal {O}:=\mathbb {F}_q[t]$
its ring of integers (that is, the ring of functions regular outside
![]() $\infty $
). Let
$\infty $
). Let
![]() $K_\infty =\mathbb {F}_q(({1}/{t}))$
be the completion of K at
$K_\infty =\mathbb {F}_q(({1}/{t}))$
be the completion of K at
![]() ${1}/{t}$
and denote by
${1}/{t}$
and denote by
![]() $\mathbb {C}_\infty $
the completion of an algebraic closure of
$\mathbb {C}_\infty $
the completion of an algebraic closure of
![]() $K_\infty $
.
$K_\infty $
.
2.1 Drinfeld modular forms
We work on the Drinfeld upper half-plane, the set
![]() $\Omega :=\mathbb {P}^1(\mathbb {C}_\infty ) - \mathbb {P}^1(K_\infty )$
together with a structure of rigid analytic space (see [Reference Fresnel and van der Put11]). The group
$\Omega :=\mathbb {P}^1(\mathbb {C}_\infty ) - \mathbb {P}^1(K_\infty )$
together with a structure of rigid analytic space (see [Reference Fresnel and van der Put11]). The group
![]() $\text {GL}_2(K_\infty )$
acts on
$\text {GL}_2(K_\infty )$
acts on
![]() $\Omega $
via Möbius transformations
$\Omega $
via Möbius transformations
![]() $(\begin {smallmatrix} {a} & {b} \\ {c} & {d} \end {smallmatrix})(z)= ({az+b})/({cz+d})$
. Let
$(\begin {smallmatrix} {a} & {b} \\ {c} & {d} \end {smallmatrix})(z)= ({az+b})/({cz+d})$
. Let
![]() $\Gamma $
be an arithmetic subgroup of
$\Gamma $
be an arithmetic subgroup of
![]() $\text {GL}_2(\mathcal {O})$
:
$\text {GL}_2(\mathcal {O})$
:
![]() $\Gamma $
has finitely many cusps, represented by
$\Gamma $
has finitely many cusps, represented by
![]() $\Gamma \backslash \mathbb {P}^1(K)$
. For
$\Gamma \backslash \mathbb {P}^1(K)$
. For
![]() $\gamma =(\begin {smallmatrix} {a} & {b} \\ {c} & {d} \end {smallmatrix})\in \text {GL}_2(K_\infty )$
,
$\gamma =(\begin {smallmatrix} {a} & {b} \\ {c} & {d} \end {smallmatrix})\in \text {GL}_2(K_\infty )$
,
![]() $k,m \in \mathbb {Z}$
and
$k,m \in \mathbb {Z}$
and
![]() $\varphi :\Omega \to \mathbb {C}_\infty $
, we define
$\varphi :\Omega \to \mathbb {C}_\infty $
, we define
Definition 2.1. A rigid analytic function
![]() $\varphi :\Omega \to \mathbb {C}_\infty $
is called a Drinfeld modular function of weight k and type
$\varphi :\Omega \to \mathbb {C}_\infty $
is called a Drinfeld modular function of weight k and type
![]() $\ m\in \mathbb {Z}/o(\Gamma )\mathbb {Z}\ {}$
for
$\ m\in \mathbb {Z}/o(\Gamma )\mathbb {Z}\ {}$
for
![]() $\ \Gamma $
if
$\ \Gamma $
if
where
![]() $o(\Gamma )$
is the number of scalar matrices in
$o(\Gamma )$
is the number of scalar matrices in
![]() $\Gamma $
. A Drinfeld modular function
$\Gamma $
. A Drinfeld modular function
![]() $\varphi $
of weight
$\varphi $
of weight
![]() $k\geqslant 0$
and type m for
$k\geqslant 0$
and type m for
![]() $\Gamma $
is called a Drinfeld modular form if
$\Gamma $
is called a Drinfeld modular form if
![]() $\varphi $
is holomorphic at all cusps and it is called a cusp form if it vanishes at all cusps. The space of Drinfeld modular forms of weight k and type m for
$\varphi $
is holomorphic at all cusps and it is called a cusp form if it vanishes at all cusps. The space of Drinfeld modular forms of weight k and type m for
![]() $\Gamma $
will be denoted by
$\Gamma $
will be denoted by
![]() $M_{k,m}(\Gamma )$
. The subspace of cuspidal modular forms is denoted by
$M_{k,m}(\Gamma )$
. The subspace of cuspidal modular forms is denoted by
![]() $S_{k,m}(\Gamma )$
.
$S_{k,m}(\Gamma )$
.
This definition coincides with [Reference Böckle7, Definition 5.1]. Other authors require the function to be meromorphic (in the sense of rigid analysis, see for example, [Reference Cornelissen, Gekeler, van der Put, Reversat and van Geel8, Definition 1.4]) and would call our functions weakly modular.
Let
![]() $\mathfrak {p}=(P)\subset \mathcal {O}$
be a prime with P irreducible of degree one. We shall work only with the arithmetic subgroup
$\mathfrak {p}=(P)\subset \mathcal {O}$
be a prime with P irreducible of degree one. We shall work only with the arithmetic subgroup
![]() $\Gamma _0(\mathfrak {p})$
of upper triangular matrices modulo
$\Gamma _0(\mathfrak {p})$
of upper triangular matrices modulo
![]() $\mathfrak {p}$
and the spaces
$\mathfrak {p}$
and the spaces
![]() $S_{k,m}(\text {GL}_2(\mathcal {O}))$
and
$S_{k,m}(\text {GL}_2(\mathcal {O}))$
and
![]() $S_{k,m}(\Gamma _0(\mathfrak {p}))$
which we call respectively cusp forms of level one and of level
$S_{k,m}(\Gamma _0(\mathfrak {p}))$
which we call respectively cusp forms of level one and of level
![]() $\mathfrak {p}$
. Note that in both cases,
$\mathfrak {p}$
. Note that in both cases,
![]() $o(\Gamma )=q-1$
. To have nontrivial forms, the weight and type must satisfy
$o(\Gamma )=q-1$
. To have nontrivial forms, the weight and type must satisfy
![]() $k\equiv 2m\pmod {q-1}$
.
$k\equiv 2m\pmod {q-1}$
.
2.2 Hecke operators
We have the Hecke operators:
 $$ \begin{align*} \mathbf{T}_{\mathfrak{p}}(\varphi)(z):=P^{k-m}\Big(\varphi \,|_{k,m} \left(\begin{smallmatrix} {P} & {0} \\ {0} & {1} \end{smallmatrix}\right)\Big)(z)+ P^{k-m}\sum_{Q\in \mathbb{F}_q} \Big(\varphi \,|_{k,m} \left(\begin{smallmatrix} {1} & {Q} \\ {0} & {P} \end{smallmatrix}\right)\Big)(z), \quad \text{on } S_{k,m}(\text{GL}_2(\mathcal{O}));\end{align*} $$
$$ \begin{align*} \mathbf{T}_{\mathfrak{p}}(\varphi)(z):=P^{k-m}\Big(\varphi \,|_{k,m} \left(\begin{smallmatrix} {P} & {0} \\ {0} & {1} \end{smallmatrix}\right)\Big)(z)+ P^{k-m}\sum_{Q\in \mathbb{F}_q} \Big(\varphi \,|_{k,m} \left(\begin{smallmatrix} {1} & {Q} \\ {0} & {P} \end{smallmatrix}\right)\Big)(z), \quad \text{on } S_{k,m}(\text{GL}_2(\mathcal{O}));\end{align*} $$
 $$ \begin{align*} \mathbf{U}_{\mathfrak{p}}(\varphi)(z):=P^{k-m} \sum_{Q\in \mathbb{F}_q} \Big(\varphi\,|_{k,m} \left(\begin{smallmatrix} {1} & {Q} \\ {0} & {P} \end{smallmatrix}\right)\Big)(z), \quad \text{on } S_{k,m}(\Gamma_0(\mathfrak{p})).\end{align*} $$
$$ \begin{align*} \mathbf{U}_{\mathfrak{p}}(\varphi)(z):=P^{k-m} \sum_{Q\in \mathbb{F}_q} \Big(\varphi\,|_{k,m} \left(\begin{smallmatrix} {1} & {Q} \\ {0} & {P} \end{smallmatrix}\right)\Big)(z), \quad \text{on } S_{k,m}(\Gamma_0(\mathfrak{p})).\end{align*} $$
2.3 Newforms and oldforms
As already mentioned in the introduction, in the positive characteristic setting, we do not have an analogue of the Petersson inner product; therefore, we need a different approach. In [Reference Bandini and Valentino4, Section 3], we defined oldforms and newforms of level t. The definition has been generalised in [Reference Bandini and Valentino6, Reference Valentino13], but Dalal and Kumar in [Reference Dalal and Kumar9, Section 4.3] pointed out the existence of a twisted Eisenstein form both new and old (for our definition) when the level is
![]() $\mathfrak {p}\mathfrak {q}$
(
$\mathfrak {p}\mathfrak {q}$
(
![]() $\mathfrak {q}$
another prime different from
$\mathfrak {q}$
another prime different from
![]() $\mathfrak {p}$
). Since we shall only work with levels one and
$\mathfrak {p}$
). Since we shall only work with levels one and
![]() $\mathfrak {p}$
, we can still rely on our original definition, which we now recall.
$\mathfrak {p}$
, we can still rely on our original definition, which we now recall.
We have an injective map
 $$ \begin{align*} (\delta_1,\delta_{\mathfrak{p}}) & : S_{k,m}(\text{GL}_2(\mathcal{O}))^2 \longrightarrow S_{k,m}(\Gamma_0(\mathfrak{p}))\\[3pt] (\delta_1,\delta_{\mathfrak{p}})(\varphi,\psi) & =\varphi(z) + \Big(\psi\,|_{k,m} \left(\begin{smallmatrix} {P} & {0} \\ {0} & {1} \end{smallmatrix}\right)\Big)(z)=\varphi(z)+P^m\psi(P z). \end{align*} $$
$$ \begin{align*} (\delta_1,\delta_{\mathfrak{p}}) & : S_{k,m}(\text{GL}_2(\mathcal{O}))^2 \longrightarrow S_{k,m}(\Gamma_0(\mathfrak{p}))\\[3pt] (\delta_1,\delta_{\mathfrak{p}})(\varphi,\psi) & =\varphi(z) + \Big(\psi\,|_{k,m} \left(\begin{smallmatrix} {P} & {0} \\ {0} & {1} \end{smallmatrix}\right)\Big)(z)=\varphi(z)+P^m\psi(P z). \end{align*} $$
Definition 2.2. The space of oldforms of level
![]() $\ \mathfrak {p}$
, denoted by
$\ \mathfrak {p}$
, denoted by
![]() $S^{\mathrm {old}}_{k,m}(\Gamma _0(\mathfrak {p}))$
, is the subspace of
$S^{\mathrm {old}}_{k,m}(\Gamma _0(\mathfrak {p}))$
, is the subspace of
![]() $S_{k,m}(\Gamma _0(\mathfrak {p}))$
generated by
$S_{k,m}(\Gamma _0(\mathfrak {p}))$
generated by
![]() $\mathrm {Im}(\delta _1,\delta _{\mathfrak {p}})$
.
$\mathrm {Im}(\delta _1,\delta _{\mathfrak {p}})$
.
We recall that
![]() $R=\{ \mathrm {Id}, (\begin {smallmatrix} {0} & {-1} \\ {1} & {Q} \end {smallmatrix})\,:\,Q\in \mathbb {F}_q\}$
is a system of coset representatives for
$R=\{ \mathrm {Id}, (\begin {smallmatrix} {0} & {-1} \\ {1} & {Q} \end {smallmatrix})\,:\,Q\in \mathbb {F}_q\}$
is a system of coset representatives for
![]() $\Gamma _0(\mathfrak {p})\backslash \text {GL}_2(\mathcal {O})$
.
$\Gamma _0(\mathfrak {p})\backslash \text {GL}_2(\mathcal {O})$
.
Definition 2.3. We have the following maps defined on
![]() $S_{k,m}(\Gamma _0(\mathfrak {p}))$
:
$S_{k,m}(\Gamma _0(\mathfrak {p}))$
:
-
• the Fricke involution, which preserves the space
 $S_{k,m}(\Gamma _0(\mathfrak {p}))$
, represented by the matrix
$S_{k,m}(\Gamma _0(\mathfrak {p}))$
, represented by the matrix
 $\gamma _{\mathfrak {p}}:= (\begin {smallmatrix} {0} & {-1} \\ {P} & {0} \end {smallmatrix})$
and defined by
$\gamma _{\mathfrak {p}}:= (\begin {smallmatrix} {0} & {-1} \\ {P} & {0} \end {smallmatrix})$
and defined by
 $\varphi ^{{\textit {Fr}}}=( \varphi \,|_{k,m} \gamma _{\mathfrak {p}})$
;
$\varphi ^{{\textit {Fr}}}=( \varphi \,|_{k,m} \gamma _{\mathfrak {p}})$
; -
• the trace map, defined by
 $$ \begin{align*} {\textit{Tr}}: S_{k,m}(\Gamma_0(\mathfrak{p})) & \to S_{k,m}({\mathrm{{GL}}}_2(\mathcal{O})) \\[2pt] \varphi &\mapsto \sum_{\gamma\in R} (\varphi\,|_{k,m} \gamma)(z); \end{align*} $$
$$ \begin{align*} {\textit{Tr}}: S_{k,m}(\Gamma_0(\mathfrak{p})) & \to S_{k,m}({\mathrm{{GL}}}_2(\mathcal{O})) \\[2pt] \varphi &\mapsto \sum_{\gamma\in R} (\varphi\,|_{k,m} \gamma)(z); \end{align*} $$
-
• the twisted trace map, defined by
 $$ \begin{align*} {\textit{Tr}}':S_{k,m}(\Gamma_0(\mathfrak{p})) & \to S_{k,m}({\mathrm{{GL}}}_2(\mathcal{O})) \\[2pt] \varphi &\mapsto {\textit{Tr}}(\varphi^{Fr}). \end{align*} $$
$$ \begin{align*} {\textit{Tr}}':S_{k,m}(\Gamma_0(\mathfrak{p})) & \to S_{k,m}({\mathrm{{GL}}}_2(\mathcal{O})) \\[2pt] \varphi &\mapsto {\textit{Tr}}(\varphi^{Fr}). \end{align*} $$
Definition 2.4. The space of newforms of level
![]() $\,\mathfrak {p}$
is
$\,\mathfrak {p}$
is
![]() ${S^{\mathrm {new}}_{k,m}(\Gamma _0(\mathfrak {p})) = \mathrm {Ker}({\textit {Tr}})\cap \mathrm {Ker}({\textit {Tr}}')}$
.
${S^{\mathrm {new}}_{k,m}(\Gamma _0(\mathfrak {p})) = \mathrm {Ker}({\textit {Tr}})\cap \mathrm {Ker}({\textit {Tr}}')}$
.
The following important criterion is [Reference Bandini and Valentino6, Theorem 2.8 and Corollary 2.10].
Theorem 2.5. We have a direct sum decomposition
![]() $S_{k,m}(\Gamma _0(\mathfrak {p}))=S^{\mathrm {old}}_{k,m}(\Gamma _0(\mathfrak {p})) \oplus S^{\mathrm {new}}_{k,m}(\Gamma _0(\mathfrak {p}))$
if and only if the map
$S_{k,m}(\Gamma _0(\mathfrak {p}))=S^{\mathrm {old}}_{k,m}(\Gamma _0(\mathfrak {p})) \oplus S^{\mathrm {new}}_{k,m}(\Gamma _0(\mathfrak {p}))$
if and only if the map
![]() $\mathcal {D}:=Id-P^{k-2m}({\textit {Tr}}')^2$
is bijective. Moreover,
$\mathcal {D}:=Id-P^{k-2m}({\textit {Tr}}')^2$
is bijective. Moreover,
3 Main results
For the level t (actually for any prime of degree one), we computed the matrix associated to the operator
![]() $\mathbf {U}_t$
acting on
$\mathbf {U}_t$
acting on
![]() $S_{k,m}(\Gamma _0(t))$
(using Teitelbaum’s interpretation with harmonic cocycles in [Reference Bandini and Valentino3, Section 4] and [Reference Bandini and Valentino4, Sections 3 and 4]). For the convenience of the reader, we recall the matrices involved in our computations.
$S_{k,m}(\Gamma _0(t))$
(using Teitelbaum’s interpretation with harmonic cocycles in [Reference Bandini and Valentino3, Section 4] and [Reference Bandini and Valentino4, Sections 3 and 4]). For the convenience of the reader, we recall the matrices involved in our computations.
To have
![]() $S_{k,m}(\Gamma _0(t))\neq 0$
, we need
$S_{k,m}(\Gamma _0(t))\neq 0$
, we need
![]() $k\equiv 2m\pmod {q-1}$
, and hence there exists a unique
$k\equiv 2m\pmod {q-1}$
, and hence there exists a unique
![]() $d\in \mathbb {N}$
such that
$d\in \mathbb {N}$
such that
![]() $k=2m+(d-1)(q-1)$
. For notational reasons, we put
$k=2m+(d-1)(q-1)$
. For notational reasons, we put
![]() $j+1\equiv m\pmod {q-1}$
with
$j+1\equiv m\pmod {q-1}$
with
![]() $0\leqslant j\leqslant q-2$
: the letters j and d provide the type m and the dimension of the matrix U associated to the action of
$0\leqslant j\leqslant q-2$
: the letters j and d provide the type m and the dimension of the matrix U associated to the action of
![]() $\mathbf {U}_t$
on
$\mathbf {U}_t$
on
![]() $S_{k,m}(\Gamma _0(t))$
. The crucial ingredient is the following matrix. For even
$S_{k,m}(\Gamma _0(t))$
. The crucial ingredient is the following matrix. For even
![]() $d=2n$
, put
$d=2n$
, put
 $$ \begin{align*} \small{T:= \left(\begin{array}{@{}cccccccc@{}} m_{1,1} & m_{1,2} & \cdots & m_{1,n} & (-1)^{\,j+1}m_{1,n} & \cdots & (-1)^{\,j+1}m_{1,2} & (-1)^{\,j+1}m_{1,1}\\ m_{2,1} & m_{2,2} & \cdots & m_{2,n} & (-1)^{\,j+1}m_{2,n} & \cdots & (-1)^{\,j+1}m_{2,2} & (-1)^{\,j+1}m_{2,1}\\ \vdots & \vdots & & \vdots & \vdots & & \vdots & \vdots\\ m_{n,1} & m_{n,2} & \cdots & m_{n,n} & (-1)^{\,j+1}m_{n,n} & \cdots & (-1)^{\,j+1}m_{n,2} & (-1)^{\,j+1}m_{n,1}\\ m_{n+1,1} & m_{n+1,2} & \cdots & 0 & 0 & \cdots & (-1)^{\,j+1}m_{n+1,2} & (-1)^{\,j+1}m_{n+1,1}\\ \vdots & \vdots & \unicode{x22F0} & \vdots & \vdots & \ddots & \vdots & \vdots\\ m_{2n-1,1} & 0 & \cdots & 0 & 0 & \cdots & 0 & (-1)^{\,j+1}m_{2n-1,1}\\ 0 & 0 & \cdots & 0 & 0 & \cdots & 0 & 0 \end{array} \right).} \end{align*} $$
$$ \begin{align*} \small{T:= \left(\begin{array}{@{}cccccccc@{}} m_{1,1} & m_{1,2} & \cdots & m_{1,n} & (-1)^{\,j+1}m_{1,n} & \cdots & (-1)^{\,j+1}m_{1,2} & (-1)^{\,j+1}m_{1,1}\\ m_{2,1} & m_{2,2} & \cdots & m_{2,n} & (-1)^{\,j+1}m_{2,n} & \cdots & (-1)^{\,j+1}m_{2,2} & (-1)^{\,j+1}m_{2,1}\\ \vdots & \vdots & & \vdots & \vdots & & \vdots & \vdots\\ m_{n,1} & m_{n,2} & \cdots & m_{n,n} & (-1)^{\,j+1}m_{n,n} & \cdots & (-1)^{\,j+1}m_{n,2} & (-1)^{\,j+1}m_{n,1}\\ m_{n+1,1} & m_{n+1,2} & \cdots & 0 & 0 & \cdots & (-1)^{\,j+1}m_{n+1,2} & (-1)^{\,j+1}m_{n+1,1}\\ \vdots & \vdots & \unicode{x22F0} & \vdots & \vdots & \ddots & \vdots & \vdots\\ m_{2n-1,1} & 0 & \cdots & 0 & 0 & \cdots & 0 & (-1)^{\,j+1}m_{2n-1,1}\\ 0 & 0 & \cdots & 0 & 0 & \cdots & 0 & 0 \end{array} \right).} \end{align*} $$
(The reason to denote it by T will become apparent shortly.) For odd
![]() $d=2n-1$
, one just needs to modify the indices and add the central nth column
$d=2n-1$
, one just needs to modify the indices and add the central nth column
The entries of T are the binomial coefficients in
![]() $\mathbb {F}_p$
,
$\mathbb {F}_p$
,
 $$ \begin{align} \displaystyle{ m_{a,b}= \begin{cases} \displaystyle{-\left[\binom{\,j+(d-a)(q-1)}{\,j+(d-b)(q-1)} + (-1)^{\,j+1} \binom{\,j+(d-a)(q-1)}{\,j+(b-1)(q-1)}\right]} & \mathrm{if}\ a\neq b, \\[8pt] \displaystyle{(-1)^{\,j}\binom{\,j+(d-a)(q-1)}{\,j+(a-1)(q-1)}} & \mathrm{if}\ a=b. \end{cases}} \end{align} $$
$$ \begin{align} \displaystyle{ m_{a,b}= \begin{cases} \displaystyle{-\left[\binom{\,j+(d-a)(q-1)}{\,j+(d-b)(q-1)} + (-1)^{\,j+1} \binom{\,j+(d-a)(q-1)}{\,j+(b-1)(q-1)}\right]} & \mathrm{if}\ a\neq b, \\[8pt] \displaystyle{(-1)^{\,j}\binom{\,j+(d-a)(q-1)}{\,j+(a-1)(q-1)}} & \mathrm{if}\ a=b. \end{cases}} \end{align} $$
Let A be the antidiagonal matrix
 $$ \begin{align*} A= \left( \begin{array}{@{}ccc@{}} 0 & & (-1)^{\,j+1} \\ & \unicode{x22F0} & \\ (-1)^{\,j+1} & & 0 \end{array}\right). \end{align*} $$
$$ \begin{align*} A= \left( \begin{array}{@{}ccc@{}} 0 & & (-1)^{\,j+1} \\ & \unicode{x22F0} & \\ (-1)^{\,j+1} & & 0 \end{array}\right). \end{align*} $$
Then
![]() $A^2=I$
(the identity matrix of dimension d) and the main symmetry of T can be expressed as
$A^2=I$
(the identity matrix of dimension d) and the main symmetry of T can be expressed as
![]() $TA=T$
. This is clear for even d. For odd d and even j, note that the central column is identically 0 by (3.1), while for odd j, one is simply multiplying the central column by one. Finally, let
$TA=T$
. This is clear for even d. For odd d and even j, note that the central column is identically 0 by (3.1), while for odd j, one is simply multiplying the central column by one. Finally, let
We list here the matrices associated to the maps involved in our computations.
-
• The action of
 $\mathbf {U}_t$
on
$\mathbf {U}_t$
on
 $S_{k,m}(\Gamma _0(t))$
is described by where for
$S_{k,m}(\Gamma _0(t))$
is described by where for $$ \begin{align*} U= M D:= M \left(\begin{array}{@{}ccc@{}} t^{s_1} & & 0\\ & \ddots & \\ 0 & & t^{s_d} \end{array}\right), \end{align*} $$
$$ \begin{align*} U= M D:= M \left(\begin{array}{@{}ccc@{}} t^{s_1} & & 0\\ & \ddots & \\ 0 & & t^{s_d} \end{array}\right), \end{align*} $$
 $1\leqslant i\leqslant d$
, we put
$1\leqslant i\leqslant d$
, we put
 $s_i=j+1+(i-1)(q-1)$
(so that
$s_i=j+1+(i-1)(q-1)$
(so that
 $s_i+s_{d+1-i}=k$
for
$s_i+s_{d+1-i}=k$
for
 $1\leqslant i\leqslant {d}/{2}$
or
$1\leqslant i\leqslant {d}/{2}$
or
 $1\leqslant i\leqslant {(d+1)}/{2}$
accordingly as d is even or odd).
$1\leqslant i\leqslant {(d+1)}/{2}$
accordingly as d is even or odd).
-
• The matrix for the Fricke involution
 ${\textit {Fr}}(t)$
is Note that
${\textit {Fr}}(t)$
is Note that $$ \begin{align*} t^{m-k}F=t^{m-k}\left( \begin{array}{@{}ccc@{}} 0 & & (-t)^{s_d} \\ & \unicode{x22F0} & \\ (-t)^{s_1} & & 0 \end{array}\right) = t^{m-k} \left( \begin{array}{@{}ccc@{}} 0 & & (-1)^{\,j+1}t^{s_d} \\ & \unicode{x22F0} & \\ (-1)^{\,j+1}t^{s_1} & & 0 \end{array}\right). \end{align*} $$
$$ \begin{align*} t^{m-k}F=t^{m-k}\left( \begin{array}{@{}ccc@{}} 0 & & (-t)^{s_d} \\ & \unicode{x22F0} & \\ (-t)^{s_1} & & 0 \end{array}\right) = t^{m-k} \left( \begin{array}{@{}ccc@{}} 0 & & (-1)^{\,j+1}t^{s_d} \\ & \unicode{x22F0} & \\ (-1)^{\,j+1}t^{s_1} & & 0 \end{array}\right). \end{align*} $$
 $F^2=t^k I$
and
$F^2=t^k I$
and
 $AF=D$
.
$AF=D$
.
-
• Direct computation (see [Reference Bandini and Valentino3, Section 3.3]) provides the equation
(3.3)Its immediate translation in matrix form is $$ \begin{align} {\textit{Tr}}(\varphi)=\varphi+t^{-m}{\textbf{U}}_t(\varphi^{Fr}). \end{align} $$
$$ \begin{align} {\textit{Tr}}(\varphi)=\varphi+t^{-m}{\textbf{U}}_t(\varphi^{Fr}). \end{align} $$
 $$ \begin{align*} I+t^{-m}MD(t^{m-k}F) & =I+t^{-k}MAF^2 = I+MA \nonumber \\ & = A^2+(T-A)A = (A+T-A)A = TA = T. \end{align*} $$
$$ \begin{align*} I+t^{-m}MD(t^{m-k}F) & =I+t^{-k}MAF^2 = I+MA \nonumber \\ & = A^2+(T-A)A = (A+T-A)A = TA = T. \end{align*} $$
-
• The matrix for the twisted trace follows directly:
 $$ \begin{align*} T' = t^{m-k}TF = \begin{cases} t^{m-k}(M+A)F = t^{m-k}(MF+D) \\ t^{m-k}TAF = t^{m-k}TD \\ t^{m-k}TAF = t^{m-k}(I+MA)F = t^{m-k}(F+ MD ). \end{cases} \end{align*} $$
$$ \begin{align*} T' = t^{m-k}TF = \begin{cases} t^{m-k}(M+A)F = t^{m-k}(MF+D) \\ t^{m-k}TAF = t^{m-k}TD \\ t^{m-k}TAF = t^{m-k}(I+MA)F = t^{m-k}(F+ MD ). \end{cases} \end{align*} $$
-
• Finally, since the trace acts trivially on
 $\mathrm {Im}(\delta _1)$
, it is easy to see that
$\mathrm {Im}(\delta _1)$
, it is easy to see that
 $\mathrm {Ker}({\textit {Tr}}-Id)=\mathrm {Im}(\delta _1)$
, that is, in terms of matrices,
$\mathrm {Ker}({\textit {Tr}}-Id)=\mathrm {Im}(\delta _1)$
, that is, in terms of matrices,
 $\mathrm {Im}(\delta _1)=\mathrm {Ker}(T-I)=\mathrm {Ker}(MA)$
.
$\mathrm {Im}(\delta _1)=\mathrm {Ker}(T-I)=\mathrm {Ker}(MA)$
.
3.1 Diagonalisability of M
As seen above, the matrices M and T satisfy a number of equations. We mention a few more, leading to the diagonalisability of M (unfortunately not equivalent to the diagonalisability of
![]() $U=MD$
, which is included in [Reference Bandini and Valentino4, Conjecture 1.1] and is related to the conjectures treated in this paper), but we shall not pursue this topic further here.
$U=MD$
, which is included in [Reference Bandini and Valentino4, Conjecture 1.1] and is related to the conjectures treated in this paper), but we shall not pursue this topic further here.
-
(i) Like all trace maps
 $T^2=T$
and T is diagonalisable. This obviously leads to
$T^2=T$
and T is diagonalisable. This obviously leads to
 $d^2$
equations in the entries
$d^2$
equations in the entries
 $m_{i,j}$
which are still difficult to handle for a generic d.
$m_{i,j}$
which are still difficult to handle for a generic d. -
(ii) Let
 $\underline {v}=M\underline {w} \in \mathrm {Im}(M)$
. Then
$\underline {v}=M\underline {w} \in \mathrm {Im}(M)$
. Then
 $T\underline {v}=TM\underline {w}=T(T-A)\underline {w}=(T^2-TA)\underline {w} = 0$
, that is,
$T\underline {v}=TM\underline {w}=T(T-A)\underline {w}=(T^2-TA)\underline {w} = 0$
, that is,
 $\mathrm {Im}(M)\subseteq \mathrm {Ker}(T)$
. Conversely, let
$\mathrm {Im}(M)\subseteq \mathrm {Ker}(T)$
. Conversely, let
 $\underline {v}\in \mathrm {Ker} (T)$
. Then, writing
$\underline {v}\in \mathrm {Ker} (T)$
. Then, writing
 $\underline {v}=-A\underline {w}$
, we get
$\underline {v}=-A\underline {w}$
, we get
 $0=T\underline {v}= -TA\underline {w}=-T\underline {w}$
, that is,
$0=T\underline {v}= -TA\underline {w}=-T\underline {w}$
, that is,
 $\underline {w}\in \mathrm {Ker} (T)$
as well. Therefore,
$\underline {w}\in \mathrm {Ker} (T)$
as well. Therefore,
 $M\underline {w}=(T-A)\underline {w}= -A\underline {w}=\underline {v}\in \mathrm {Im} (M)$
. Hence,
$M\underline {w}=(T-A)\underline {w}= -A\underline {w}=\underline {v}\in \mathrm {Im} (M)$
. Hence,
 $\mathrm {Im} (M)=\mathrm {Ker} (T)$
.
$\mathrm {Im} (M)=\mathrm {Ker} (T)$
. -
(iii) Finally,
 $$ \begin{align*} M^3 & = (T-A)^3=(T^2-AT-TA+I)(T-A) \\ \ & = (-AT+I)(T-A)=-AT^2+T+ATA-A \\ \ & = T-A =M. \end{align*} $$
$$ \begin{align*} M^3 & = (T-A)^3=(T^2-AT-TA+I)(T-A) \\ \ & = (-AT+I)(T-A)=-AT^2+T+ATA-A \\ \ & = T-A =M. \end{align*} $$
Therefore, for any
![]() $p\neq 2$
, the matrix M is diagonalisable and we can write
$p\neq 2$
, the matrix M is diagonalisable and we can write
where each
![]() $\underline {v}_\alpha $
is in the M-eigenspace of the eigenvalue
$\underline {v}_\alpha $
is in the M-eigenspace of the eigenvalue
![]() $\alpha \in \{0,1,-1\}$
. This reflects the results of [Reference Bandini and Valentino2], where we found examples of nondiagonalisability of
$\alpha \in \{0,1,-1\}$
. This reflects the results of [Reference Bandini and Valentino2], where we found examples of nondiagonalisability of
![]() $\mathbf {U}_t$
in characteristic two, due to the presence of inseparable eigenvalues associated to newforms.
$\mathbf {U}_t$
in characteristic two, due to the presence of inseparable eigenvalues associated to newforms.
3.2 Injectivity of
 $\mathbf {T}_t$
$\mathbf {T}_t$
In [Reference Bandini and Valentino4], we proved some special cases of Conjecture 1.1 building on the analogue of Theorem 3.2 and on the above matrices/formulae (which are not available for
![]() $\deg P\geqslant 2$
). In particular, in [Reference Bandini and Valentino4, Theorem 5.5], we proved that when
$\deg P\geqslant 2$
). In particular, in [Reference Bandini and Valentino4, Theorem 5.5], we proved that when
![]() $\dim _{\mathbb {C}_\infty }(S_{k,m}({{\mathrm {GL}}}_2(\mathcal {O}))=0$
, that is, there are no oldforms, the matrix M is antidiagonal and the conjectures hold. We shall now approach the case
$\dim _{\mathbb {C}_\infty }(S_{k,m}({{\mathrm {GL}}}_2(\mathcal {O}))=0$
, that is, there are no oldforms, the matrix M is antidiagonal and the conjectures hold. We shall now approach the case
![]() $\dim _{\mathbb {C}_\infty }(S_{k,m}({{\mathrm {GL}}}_2(\mathcal {O}))=1$
. This will include many more cases since, for example,
$\dim _{\mathbb {C}_\infty }(S_{k,m}({{\mathrm {GL}}}_2(\mathcal {O}))=1$
. This will include many more cases since, for example,
![]() $\dim _{\mathbb {C}_\infty }(S_{k,0}({{\mathrm {GL}}}_2(\mathcal {O}))=1$
if and only if
$\dim _{\mathbb {C}_\infty }(S_{k,0}({{\mathrm {GL}}}_2(\mathcal {O}))=1$
if and only if
![]() $q\leqslant d <2q-1$
, by [Reference Dalal and Kumar9, Proposition 4.3] (compare with the bounds of [Reference Bandini and Valentino4, Theorems 5.8, 5.9, 5.12 and 5.14]).
$q\leqslant d <2q-1$
, by [Reference Dalal and Kumar9, Proposition 4.3] (compare with the bounds of [Reference Bandini and Valentino4, Theorems 5.8, 5.9, 5.12 and 5.14]).
Theorem 3.1. Assume
![]() $\dim _{\mathbb {C}_\infty }\mathrm {Im} (\delta _1)=1$
. Then
$\dim _{\mathbb {C}_\infty }\mathrm {Im} (\delta _1)=1$
. Then
![]() $\mathbf {T}_t$
is injective.
$\mathbf {T}_t$
is injective.
Proof. Observe that, by [Reference Bandini and Valentino6, Proposition 2.5],
![]() $\mathrm {Ker}(\mathbf {T}_t)=\mathrm {Ker}(MA)\cap \mathrm {Ker}(MDMD)$
. Thanks to our assumption on the dimension of
$\mathrm {Ker}(\mathbf {T}_t)=\mathrm {Ker}(MA)\cap \mathrm {Ker}(MDMD)$
. Thanks to our assumption on the dimension of
![]() $\mathrm {Im}(\delta _1)=\mathrm {Ker}(MA)$
and because the entries of
$\mathrm {Im}(\delta _1)=\mathrm {Ker}(MA)$
and because the entries of
![]() $MA$
are in
$MA$
are in
![]() $\mathbb {F}_p$
, we have
$\mathbb {F}_p$
, we have
![]() $\dim _{\mathbb {C}_\infty }( \mathrm {Ker}(MA)\cap \mathrm {Ker}(MDMD))\leqslant 1$
and we can fix a generator
$\dim _{\mathbb {C}_\infty }( \mathrm {Ker}(MA)\cap \mathrm {Ker}(MDMD))\leqslant 1$
and we can fix a generator
![]() $\underline {a}=(a_1,\ldots ,a_d)\in \mathbb {F}_p^d$
. To avoid adding the transpose symbol to the several indices we shall need in the computations, with a little abuse of notation, we shall write
$\underline {a}=(a_1,\ldots ,a_d)\in \mathbb {F}_p^d$
. To avoid adding the transpose symbol to the several indices we shall need in the computations, with a little abuse of notation, we shall write
![]() $\underline {a}$
both for the row vector and for its transpose, the context will clarify which one we are using. Our goal is to prove
$\underline {a}$
both for the row vector and for its transpose, the context will clarify which one we are using. Our goal is to prove
![]() $\underline {a}=0$
.
$\underline {a}=0$
.
We prove the case of even dimension
![]() $d=2n$
; for odd d, the argument is exactly the same. The vector
$d=2n$
; for odd d, the argument is exactly the same. The vector
![]() $\underline {a}$
satisfies the following equations coming from
$\underline {a}$
satisfies the following equations coming from
![]() $MA\underline {a}=0$
:
$MA\underline {a}=0$
:
 $$ \begin{align} \begin{cases} (m_{1,1}-1)a_1+m_{1,2}a_2+\cdots + m_{1,n}a_n+(-1)^{\,j+1}m_{1,n}a_{n+1}+\cdots + (-1)^{\,j+1}m_{1,1}a_{2n}=0\\ m_{2,1}a_1+(m_{2,2}-1)a_2+\cdots + m_{2,n}a_n+(-1)^{\,j+1}m_{2,n}a_{n+1}+\cdots + (-1)^{\,j+1}m_{2,1}a_{2n}=0\\ \vdots \\ m_{n,1}a_1+m_{n,2}a_2+\cdots + (m_{n,n}-1)a_n+(-1)^{\,j+1}m_{n,n}a_{n+1}+\cdots + (-1)^{\,j+1}m_{n,1}a_{2n}=0\\ m_{n+1,1}a_1+m_{n+1,2}a_2+\cdots +m_{n+1,n-1}a_{n-1}-a_{n+1}+\cdots +(-1)^{\,j+1}m_{n+1,1}a_{2n}=0\\ \vdots \\ m_{2n-1,1}a_1-a_{2n-1}+(-1)^{\,j+1}m_{2n-1,1}a_{2n}=0\\ -a_{2n}=0. \end{cases} \end{align} $$
$$ \begin{align} \begin{cases} (m_{1,1}-1)a_1+m_{1,2}a_2+\cdots + m_{1,n}a_n+(-1)^{\,j+1}m_{1,n}a_{n+1}+\cdots + (-1)^{\,j+1}m_{1,1}a_{2n}=0\\ m_{2,1}a_1+(m_{2,2}-1)a_2+\cdots + m_{2,n}a_n+(-1)^{\,j+1}m_{2,n}a_{n+1}+\cdots + (-1)^{\,j+1}m_{2,1}a_{2n}=0\\ \vdots \\ m_{n,1}a_1+m_{n,2}a_2+\cdots + (m_{n,n}-1)a_n+(-1)^{\,j+1}m_{n,n}a_{n+1}+\cdots + (-1)^{\,j+1}m_{n,1}a_{2n}=0\\ m_{n+1,1}a_1+m_{n+1,2}a_2+\cdots +m_{n+1,n-1}a_{n-1}-a_{n+1}+\cdots +(-1)^{\,j+1}m_{n+1,1}a_{2n}=0\\ \vdots \\ m_{2n-1,1}a_1-a_{2n-1}+(-1)^{\,j+1}m_{2n-1,1}a_{2n}=0\\ -a_{2n}=0. \end{cases} \end{align} $$
Now put
![]() $\underline {p(t)}:=MD\underline {a}\in \mathbb {F}_p[t]^{2n}$
, with coordinates
$\underline {p(t)}:=MD\underline {a}\in \mathbb {F}_p[t]^{2n}$
, with coordinates
![]() $p_i(t)$
. Then (with
$p_i(t)$
. Then (with
![]() $a_{2n}=0$
),
$a_{2n}=0$
),
![]() $\underline {p}(t)$
is equal to
$\underline {p}(t)$
is equal to
 $$ \begin{align} \left(\!\!\! \begin{array}{c} m_{1,1} a_1t^{s_1}+ \cdots + m_{1,n}a_n t^{s_n}+ (-1)^{\,j+1}m_{1,n}a_{n+1}t^{s_{n+1}}+ \cdots + (-1)^{\,j+1}m_{1,2}a_{2n-1}t^{s_{2n-1}}\\ m_{2,1} a_1t^{s_1}+ \cdots + m_{2,n} a_n t^{s_n}+ (-1)^{\,j+1}m_{2,n}a_{n+1}t^{s_{n+1}}+ \cdots +(-1)^{\,j+1}(m_{2,2}-1)a_{2n-1}t^{s_{2n-1}}\\ \vdots \\ m_{n,1} a_1t^{s_1}+\cdots + + (-1)^{\,j+1}(m_{n,n}-1)a_{n+1}t^{s_{n+1}}+ \cdots + (-1)^{\,j+1}m_{n,2}a_{2n-1}t^{s_{2n-1}}\\ m_{n+1,1} a_1t^{s_1}+\cdots +(-1)^ja_n t^{s_n}+ m_{n+1,n-1}a_{n+2}t^{s_{n+2}} + \cdots +(-1)^{\,j+1}m_{n+1,2}a_{2n-1}t^{s_{2n-1}}\\ \vdots \\ m_{2n-1,1} a_1t^{s_1}+ (-1)^{{\kern2pt}j} a_2t^{s_2}\\ (-1)^{{\kern2pt}j} a_1t^{s_1} \end{array}\!\!\!\right)\!. \end{align} $$
$$ \begin{align} \left(\!\!\! \begin{array}{c} m_{1,1} a_1t^{s_1}+ \cdots + m_{1,n}a_n t^{s_n}+ (-1)^{\,j+1}m_{1,n}a_{n+1}t^{s_{n+1}}+ \cdots + (-1)^{\,j+1}m_{1,2}a_{2n-1}t^{s_{2n-1}}\\ m_{2,1} a_1t^{s_1}+ \cdots + m_{2,n} a_n t^{s_n}+ (-1)^{\,j+1}m_{2,n}a_{n+1}t^{s_{n+1}}+ \cdots +(-1)^{\,j+1}(m_{2,2}-1)a_{2n-1}t^{s_{2n-1}}\\ \vdots \\ m_{n,1} a_1t^{s_1}+\cdots + + (-1)^{\,j+1}(m_{n,n}-1)a_{n+1}t^{s_{n+1}}+ \cdots + (-1)^{\,j+1}m_{n,2}a_{2n-1}t^{s_{2n-1}}\\ m_{n+1,1} a_1t^{s_1}+\cdots +(-1)^ja_n t^{s_n}+ m_{n+1,n-1}a_{n+2}t^{s_{n+2}} + \cdots +(-1)^{\,j+1}m_{n+1,2}a_{2n-1}t^{s_{2n-1}}\\ \vdots \\ m_{2n-1,1} a_1t^{s_1}+ (-1)^{{\kern2pt}j} a_2t^{s_2}\\ (-1)^{{\kern2pt}j} a_1t^{s_1} \end{array}\!\!\!\right)\!. \end{align} $$
Since
![]() $MD\underline {p(t)}=0$
, we also have the equations:
$MD\underline {p(t)}=0$
, we also have the equations:
 $$ \begin{align} {\begin{cases} m_{1,1}t^{s_1}p_1(t)+ \cdots + m_{1,n}t^{s_n}p_n (t)+ (-1)^{\,j+1}m_{1,n}t^{s_{n+1}}p_{n+1}(t)+ \cdots + (-1)^{\,j+1}(m_{1,1}-1)t^{s_{2n}}p_{2n}(t)=0\\ m_{2,1}t^{s_1}p_1(t)+ \cdots + m_{2,n} t^{s_n}p_n (t)+ (-1)^{\,j+1}m_{2,n}t^{s_{n+1}}p_{n+1}(t)+ \cdots + (-1)^{\,j+1}m_{2,1}t^{s_{2n}}p_{2n}(t)=0\\ \vdots \\ m_{n,1}t^{s_1}p_1(t)+\cdots + m_{n,n}t^{s_n}p_n(t)+ (-1)^{\,j+1}(m_{n,n}-1)t^{s_{n+1}}p_{n+1}(t)+ \cdots + (-1)^{\,j+1}m_{n,1}t^{s_{2n}}p_{2n}(t)=0\\ \vdots \\ m_{2n-1,1}t^{s_1}p_1(t)+ (-1)^{{\kern2pt}j} t^{s_2}p_2(t)+ (-1)^{\,j+1}m_{2n-1,1}t^{s_{2n}}p_{2n}(t)=0\\ (-1)^jt^{s_1}p_1(t)=0. \end{cases}} \end{align} $$
$$ \begin{align} {\begin{cases} m_{1,1}t^{s_1}p_1(t)+ \cdots + m_{1,n}t^{s_n}p_n (t)+ (-1)^{\,j+1}m_{1,n}t^{s_{n+1}}p_{n+1}(t)+ \cdots + (-1)^{\,j+1}(m_{1,1}-1)t^{s_{2n}}p_{2n}(t)=0\\ m_{2,1}t^{s_1}p_1(t)+ \cdots + m_{2,n} t^{s_n}p_n (t)+ (-1)^{\,j+1}m_{2,n}t^{s_{n+1}}p_{n+1}(t)+ \cdots + (-1)^{\,j+1}m_{2,1}t^{s_{2n}}p_{2n}(t)=0\\ \vdots \\ m_{n,1}t^{s_1}p_1(t)+\cdots + m_{n,n}t^{s_n}p_n(t)+ (-1)^{\,j+1}(m_{n,n}-1)t^{s_{n+1}}p_{n+1}(t)+ \cdots + (-1)^{\,j+1}m_{n,1}t^{s_{2n}}p_{2n}(t)=0\\ \vdots \\ m_{2n-1,1}t^{s_1}p_1(t)+ (-1)^{{\kern2pt}j} t^{s_2}p_2(t)+ (-1)^{\,j+1}m_{2n-1,1}t^{s_{2n}}p_{2n}(t)=0\\ (-1)^jt^{s_1}p_1(t)=0. \end{cases}} \end{align} $$
Note that in (3.6), we have polynomials in
![]() $\mathbb {F}_p[t]$
. From now on, we shall use the identity principle for polynomials to solve the equations in the
$\mathbb {F}_p[t]$
. From now on, we shall use the identity principle for polynomials to solve the equations in the
![]() $a_i$
. From the last row in (3.6), we get
$a_i$
. From the last row in (3.6), we get
![]() $p_1(t)=0$
, and comparing with (3.5) and recalling the
$p_1(t)=0$
, and comparing with (3.5) and recalling the
![]() $s_i$
are distinct,
$s_i$
are distinct,
Substituting in the first and second-last equations in (3.4), we obtain
which also means that
![]() $p_{2n}(t)=0$
. We can rewrite (3.4), (3.5) and (3.6) as
$p_{2n}(t)=0$
. We can rewrite (3.4), (3.5) and (3.6) as
 $$ \begin{align} \begin{cases} (m_{2,2}-1)a_2+\cdots + m_{2,n}a_n+(-1)^{\,j+1}m_{2,n}a_{n+1}+\cdots + (-1)^{\,j+1}m_{2,3}a_{2n-2}=0\\ \vdots \\ m_{n,2}a_2+\cdots + (m_{n,n}-1)a_n+(-1)^{\,j+1}m_{n,n}a_{n+1}+\cdots + (-1)^{\,j+1}m_{n,3}a_{2n-2}=0\\ m_{n+1,2}a_2+\cdots+m_{n+1,n-1}a_{n-1}-a_{n+1}+\cdots +(-1)^{\,j+1}m_{n+1,3}a_{2n-2}=0\\ \vdots \\ m_{2n-2,2}a_2-a_{2n-2}=0\\ a_1=a_{2n-1}=a_{2n}=0, \end{cases} \end{align} $$
$$ \begin{align} \begin{cases} (m_{2,2}-1)a_2+\cdots + m_{2,n}a_n+(-1)^{\,j+1}m_{2,n}a_{n+1}+\cdots + (-1)^{\,j+1}m_{2,3}a_{2n-2}=0\\ \vdots \\ m_{n,2}a_2+\cdots + (m_{n,n}-1)a_n+(-1)^{\,j+1}m_{n,n}a_{n+1}+\cdots + (-1)^{\,j+1}m_{n,3}a_{2n-2}=0\\ m_{n+1,2}a_2+\cdots+m_{n+1,n-1}a_{n-1}-a_{n+1}+\cdots +(-1)^{\,j+1}m_{n+1,3}a_{2n-2}=0\\ \vdots \\ m_{2n-2,2}a_2-a_{2n-2}=0\\ a_1=a_{2n-1}=a_{2n}=0, \end{cases} \end{align} $$
 $$ \begin{align} \small{\underline{p(t)}=\left( \hspace{-0.5em}\begin{array}{c} 0\\ m_{2,2}a_2t^{s_2}+ \cdots + m_{2,n} a_n t^{s_n}+ (-1)^{\,j+1}m_{2,n}a_{n+1}t^{s_{n+1}}+ \cdots +(-1)^{\,j+1}m_{2,3}a_{2n-2}t^{s_{2n-2}}\\ \vdots \\ m_{n,2} a_2t^{s_2}+\cdots + m_{n,n}a_n t^{s_n}+ (-1)^{\,j+1}(m_{n,n}-1)a_{n+1}t^{s_{n+1}}+ \cdots + (-1)^{\,j+1}m_{n,3}a_{2n-2}t^{s_{2n-2}}\\ m_{n+1,2} a_2t^{s_2}+\cdots +(-1)^ja_n t^{s_n}+ m_{n+1,n-1}a_{n+2}t^{s_{n+2}} + \cdots +(-1)^{\,j+1}m_{n+1,3}a_{2n-2}t^{s_{2n-2}}\\ \vdots \\ (-1)^{{\kern2pt}j} a_2t^{s_2}\\ 0 \end{array}\hspace{-0.5em}\right)} \end{align} $$
$$ \begin{align} \small{\underline{p(t)}=\left( \hspace{-0.5em}\begin{array}{c} 0\\ m_{2,2}a_2t^{s_2}+ \cdots + m_{2,n} a_n t^{s_n}+ (-1)^{\,j+1}m_{2,n}a_{n+1}t^{s_{n+1}}+ \cdots +(-1)^{\,j+1}m_{2,3}a_{2n-2}t^{s_{2n-2}}\\ \vdots \\ m_{n,2} a_2t^{s_2}+\cdots + m_{n,n}a_n t^{s_n}+ (-1)^{\,j+1}(m_{n,n}-1)a_{n+1}t^{s_{n+1}}+ \cdots + (-1)^{\,j+1}m_{n,3}a_{2n-2}t^{s_{2n-2}}\\ m_{n+1,2} a_2t^{s_2}+\cdots +(-1)^ja_n t^{s_n}+ m_{n+1,n-1}a_{n+2}t^{s_{n+2}} + \cdots +(-1)^{\,j+1}m_{n+1,3}a_{2n-2}t^{s_{2n-2}}\\ \vdots \\ (-1)^{{\kern2pt}j} a_2t^{s_2}\\ 0 \end{array}\hspace{-0.5em}\right)} \end{align} $$
and
 $$ \begin{align} \small\begin{cases} m_{1,2}t^{s_2}p_2(t)+ \cdots + m_{1,n}t^{s_n}p_n(t)+ (-1)^{\,j+1}m_{1,n}t^{s_{n+1}}p_{n+1}(t)+ \cdots (-1)^{\,j+1}m_{1,2}t^{s_{2n-1}}p_{2n-1}(t)=0\\ m_{2,2}t^{s_2}p_2(t)+ \cdots + m_{2,n} t^{s_n}p_n(t)+ (-1)^{\,j+1}m_{2,n}t^{s_{n+1}}p_{n+1}(t)+ \cdots + (-1)^{\,j+1}(m_{2,2}-1)t^{s_{2n-1}}p_{2n-1}(t)=0\\ \vdots \\ m_{n,2} t^{s_2}p_2(t)+\cdots + m_{n,n}t^{s_n}p_n(t)+ (-1)^{\,j+1}(m_{n,n}-1)t^{s_{n+1}}p_{n+1}(t)+ \cdots + (-1)^{\,j+1}m_{n,2}t^{s_{2n-1}}p_{2n-1}(t)=0\\ \vdots \\ (-1)^{{\kern2pt}j} t^{s_2}p_2(t)=0\\ p_1(t)=p_{2n}(t)=0. \end{cases} \end{align} $$
$$ \begin{align} \small\begin{cases} m_{1,2}t^{s_2}p_2(t)+ \cdots + m_{1,n}t^{s_n}p_n(t)+ (-1)^{\,j+1}m_{1,n}t^{s_{n+1}}p_{n+1}(t)+ \cdots (-1)^{\,j+1}m_{1,2}t^{s_{2n-1}}p_{2n-1}(t)=0\\ m_{2,2}t^{s_2}p_2(t)+ \cdots + m_{2,n} t^{s_n}p_n(t)+ (-1)^{\,j+1}m_{2,n}t^{s_{n+1}}p_{n+1}(t)+ \cdots + (-1)^{\,j+1}(m_{2,2}-1)t^{s_{2n-1}}p_{2n-1}(t)=0\\ \vdots \\ m_{n,2} t^{s_2}p_2(t)+\cdots + m_{n,n}t^{s_n}p_n(t)+ (-1)^{\,j+1}(m_{n,n}-1)t^{s_{n+1}}p_{n+1}(t)+ \cdots + (-1)^{\,j+1}m_{n,2}t^{s_{2n-1}}p_{2n-1}(t)=0\\ \vdots \\ (-1)^{{\kern2pt}j} t^{s_2}p_2(t)=0\\ p_1(t)=p_{2n}(t)=0. \end{cases} \end{align} $$
We repeat the same argument starting now from the second-last equation in (3.9), which yields
![]() $p_2(t)=0$
. This means
$p_2(t)=0$
. This means
which, substituted in the first equation of (3.7), gives
![]() $a_2=0$
. From the second-last equations in (3.7) and (3.8),
$a_2=0$
. From the second-last equations in (3.7) and (3.8),
![]() $a_{2n-2}=0$
and
$a_{2n-2}=0$
and
![]() $p_{2n-1}(t)=0$
as well. Iterating the process, we see that the specular symmetries between
$p_{2n-1}(t)=0$
as well. Iterating the process, we see that the specular symmetries between
![]() $MD$
(
$MD$
(
![]() $(-1)^{{\kern2pt}j}$
on the antidiagonal) and
$(-1)^{{\kern2pt}j}$
on the antidiagonal) and
![]() $MA$
(
$MA$
(
![]() $-1$
on the diagonal) and the positions of the
$-1$
on the diagonal) and the positions of the
![]() $m_{i,i}-1$
lead to
$m_{i,i}-1$
lead to
![]() $\underline {a}=0$
.
$\underline {a}=0$
.
3.3 Direct sum
We use the criterion of Theorem 2.5 to show that
![]() ${\mathrm {Ker}(\mathcal {D})=0}$
. Note that
${\mathrm {Ker}(\mathcal {D})=0}$
. Note that
![]() $\varphi \in \mathrm {Ker}(\mathcal {D})$
yields
$\varphi \in \mathrm {Ker}(\mathcal {D})$
yields
![]() $\varphi -t^{k-2m}(Tr')^2(\varphi )=0$
, that is,
$\varphi -t^{k-2m}(Tr')^2(\varphi )=0$
, that is,
![]() $\varphi =t^{k-2m}(Tr')^2(\varphi )\in S_{k,m}({\mathrm {{GL}}}_2(\mathcal {O}))$
; and hence
$\varphi =t^{k-2m}(Tr')^2(\varphi )\in S_{k,m}({\mathrm {{GL}}}_2(\mathcal {O}))$
; and hence
![]() $\varphi $
is old and, in particular, belongs to
$\varphi $
is old and, in particular, belongs to
![]() $\mathrm {Im}(\delta _1)=\mathrm {Ker}(MA)$
. So we write
$\mathrm {Im}(\delta _1)=\mathrm {Ker}(MA)$
. So we write
![]() $\varphi =\delta _1\psi $
and, by [Reference Bandini and Valentino3, (3.2)],
$\varphi =\delta _1\psi $
and, by [Reference Bandini and Valentino3, (3.2)],
![]() ${\textbf {U}}_t(\delta _1\psi )=\delta _1{\textbf {T}}_t\psi -t^{k-m}\delta _t\psi $
is old as well. Moreover,
${\textbf {U}}_t(\delta _1\psi )=\delta _1{\textbf {T}}_t\psi -t^{k-m}\delta _t\psi $
is old as well. Moreover,
 $$ \begin{align*} t^{2m-k}\delta_1\psi & = ({\textit{Tr}}')^2(\delta_1\psi)=({\textit{Tr}}')({\textit{Tr}}'(\delta_1\psi)) \\[3pt] \ & = {\textit{Tr}}'((\delta_1\psi)^{{\textit{Fr}}}+t^{m-k}{\textbf{U}}_t(\delta_1\psi)) \quad \mathrm{(use\ the\ twisted\ version\ of\ (3.3))} \\[3pt] \ & = {\textit{Tr}}(((\delta_1\psi)^{{\textit{Fr}}})^{{\textit{Fr}}}) + t^{m-k}{\textit{Tr}}'({\textbf{U}}_t(\delta_1\psi)) \\[3pt] \ & = t^{2m-k}{\textit{Tr}}(\delta_1\psi) + t^{m-k}{\textit{Tr}}'({\textbf{U}}_t(\delta_1\psi)) \\[3pt] \ & = t^{2m-k}\delta_1\psi + t^{m-k}{\textit{Tr}}'({\textbf{U}}_t(\delta_1\psi)), \end{align*} $$
$$ \begin{align*} t^{2m-k}\delta_1\psi & = ({\textit{Tr}}')^2(\delta_1\psi)=({\textit{Tr}}')({\textit{Tr}}'(\delta_1\psi)) \\[3pt] \ & = {\textit{Tr}}'((\delta_1\psi)^{{\textit{Fr}}}+t^{m-k}{\textbf{U}}_t(\delta_1\psi)) \quad \mathrm{(use\ the\ twisted\ version\ of\ (3.3))} \\[3pt] \ & = {\textit{Tr}}(((\delta_1\psi)^{{\textit{Fr}}})^{{\textit{Fr}}}) + t^{m-k}{\textit{Tr}}'({\textbf{U}}_t(\delta_1\psi)) \\[3pt] \ & = t^{2m-k}{\textit{Tr}}(\delta_1\psi) + t^{m-k}{\textit{Tr}}'({\textbf{U}}_t(\delta_1\psi)) \\[3pt] \ & = t^{2m-k}\delta_1\psi + t^{m-k}{\textit{Tr}}'({\textbf{U}}_t(\delta_1\psi)), \end{align*} $$
that is,
![]() ${\textit {Tr}}'({\textbf {U}}_t(\delta _1\psi ))=0$
. We can similarly prove that
${\textit {Tr}}'({\textbf {U}}_t(\delta _1\psi ))=0$
. We can similarly prove that
![]() ${\textit {Tr}}({\textbf {U}}_t(\delta _1\psi ))=0$
(that is,
${\textit {Tr}}({\textbf {U}}_t(\delta _1\psi ))=0$
(that is,
![]() ${\textbf {U}}_t(\delta _1\psi )$
is old and new), but the equations coming from
${\textbf {U}}_t(\delta _1\psi )$
is old and new), but the equations coming from
![]() $MA$
and
$MA$
and
![]() $T'U$
will be enough for our purposes.
$T'U$
will be enough for our purposes.
Theorem 3.2. If
![]() $\dim _{\mathbb {C}_\infty }\mathrm {Im} (\delta _1)=1$
, then
$\dim _{\mathbb {C}_\infty }\mathrm {Im} (\delta _1)=1$
, then
![]() $S_{k,m}(\Gamma _0(t))=S^{\mathrm {old}}_{k,m}(\Gamma _0(t))\oplus S^{\mathrm {new}}_{k,m}(\Gamma _0(t))$
.
$S_{k,m}(\Gamma _0(t))=S^{\mathrm {old}}_{k,m}(\Gamma _0(t))\oplus S^{\mathrm {new}}_{k,m}(\Gamma _0(t))$
.
Proof. Take
![]() $\underline {a}\in \mathbb {F}_p^d$
satisfying
$\underline {a}\in \mathbb {F}_p^d$
satisfying
![]() $MA\underline {a}=0$
and representing an element
$MA\underline {a}=0$
and representing an element
![]() $\eta =\delta _1\varphi \in \mathrm {Ker}(\mathcal {D})$
, so that, as seen above,
$\eta =\delta _1\varphi \in \mathrm {Ker}(\mathcal {D})$
, so that, as seen above,
![]() $TF(MD\underline {a})=0$
. We prove that these two relations yield
$TF(MD\underline {a})=0$
. We prove that these two relations yield
![]() $\underline {a}=0$
, so that
$\underline {a}=0$
, so that
![]() $\mathrm {Ker}(\mathcal {D})=0$
and
$\mathrm {Ker}(\mathcal {D})=0$
and
![]() $\mathcal {D}$
is invertible. As before, we only treat the case of even
$\mathcal {D}$
is invertible. As before, we only treat the case of even
![]() $d=2n$
.
$d=2n$
.
The equation
![]() $MA\underline {a}=0$
gives again the system (3.4) (in particular,
$MA\underline {a}=0$
gives again the system (3.4) (in particular,
![]() $a_{2n}=0$
). Writing
$a_{2n}=0$
). Writing
![]() $\underline {p(t)}=MD\underline {a}$
as in (3.5), from
$\underline {p(t)}=MD\underline {a}$
as in (3.5), from
![]() $TF(MD\underline {a})=0$
,
$TF(MD\underline {a})=0$
,
 $$ \begin{align} \begin{cases} m_{1,1}t^{s_1}p_1(t)+ \cdots + m_{1,n}t^{s_n}p_n(t)+ m_{1,n}(-t)^{s_{n+1}}p_{n+1}(t)+ \cdots + m_{1,1}(-t)^{s_{2n}}p_{2n}(t)=0\\ m_{2,1}t^{s_1}p_1(t)+ \cdots + m_{2,n} t^{s_n}p_n(t)+ m_{2,n}(-t)^{s_{n+1}}p_{n+1}(t)+ \cdots + m_{2,1}(-t)^{s_{2n}}p_{2n}(t)=0\\ \vdots \\ m_{n,1}t^{s_1}p_1(t)+\cdots + m_{n,n}t^{s_n}p_n(t)+ m_{n,n}(-t)^{s_{n+1}}p_{n+1}(t)+ \cdots + m_{n,1}(-t)^{s_{2n}}p_{2n}(t)=0\\ m_{n+1,1}t^{s_1}p_1(t)+\cdots +m_{n+1,1}(-t)^{s_{2n}}p_{2n}(t)=0\\ \vdots \\ m_{2n-2,1}t^{s_1}p_1(t)+ m_{2n-2,2}t^{s_2}p_2(t)+ m_{2n-2,2}(-t)^{s_{2n-1}}p_{2n-1}(t)+m_{2n-2,1}(-t)^{s_{2n}}p_{2n}(t)\!=\!0\\ m_{2n-1,1}t^{s_1}p_1(t)+ m_{2n-1,1}(-t)^{s_{2n}}p_{2n}(t)=0. \end{cases} \end{align} $$
$$ \begin{align} \begin{cases} m_{1,1}t^{s_1}p_1(t)+ \cdots + m_{1,n}t^{s_n}p_n(t)+ m_{1,n}(-t)^{s_{n+1}}p_{n+1}(t)+ \cdots + m_{1,1}(-t)^{s_{2n}}p_{2n}(t)=0\\ m_{2,1}t^{s_1}p_1(t)+ \cdots + m_{2,n} t^{s_n}p_n(t)+ m_{2,n}(-t)^{s_{n+1}}p_{n+1}(t)+ \cdots + m_{2,1}(-t)^{s_{2n}}p_{2n}(t)=0\\ \vdots \\ m_{n,1}t^{s_1}p_1(t)+\cdots + m_{n,n}t^{s_n}p_n(t)+ m_{n,n}(-t)^{s_{n+1}}p_{n+1}(t)+ \cdots + m_{n,1}(-t)^{s_{2n}}p_{2n}(t)=0\\ m_{n+1,1}t^{s_1}p_1(t)+\cdots +m_{n+1,1}(-t)^{s_{2n}}p_{2n}(t)=0\\ \vdots \\ m_{2n-2,1}t^{s_1}p_1(t)+ m_{2n-2,2}t^{s_2}p_2(t)+ m_{2n-2,2}(-t)^{s_{2n-1}}p_{2n-1}(t)+m_{2n-2,1}(-t)^{s_{2n}}p_{2n}(t)\!=\!0\\ m_{2n-1,1}t^{s_1}p_1(t)+ m_{2n-1,1}(-t)^{s_{2n}}p_{2n}(t)=0. \end{cases} \end{align} $$
In the last equation of (3.10), the term of highest degree is
![]() $m_{2n-1,1}(-t)^{s_{2n}}(-1)^ja_1t^{s_1}= -m_{2n-1,1}a_1t^k$
(note that
$m_{2n-1,1}(-t)^{s_{2n}}(-1)^ja_1t^{s_1}= -m_{2n-1,1}a_1t^k$
(note that
![]() $p_1(t)$
has degree at most
$p_1(t)$
has degree at most
![]() $s_{2n-1}$
because
$s_{2n-1}$
because
![]() $a_{2n}=0$
); therefore,
$a_{2n}=0$
); therefore,
![]() $m_{2n-1,1}a_1=0$
and the second-last equation in (3.4) tells us that
$m_{2n-1,1}a_1=0$
and the second-last equation in (3.4) tells us that
![]() $a_{2n-1}=0$
. Now, (3.4) and (3.5) turn into
$a_{2n-1}=0$
. Now, (3.4) and (3.5) turn into
 $$ \begin{align} \begin{cases} (m_{1,1}-1)a_1+m_{1,2}a_2+\cdots + m_{1,n}a_n+(-1)^{\,j+1}m_{1,n}a_{n+1}+\cdots + (-1)^{\,j+1}m_{1,3}a_{2n-2}\!=\!0\\ m_{2,1}a_1+(m_{2,2}-1)a_2+\cdots + m_{2,n}a_n+(-1)^{\,j+1}m_{2,n}a_{n+1}+\cdots + (-1)^{\,j+1}m_{2,3}a_{2n-2}\!=\!0\\ \vdots \\ m_{n,1}a_1+m_{n,2}a_2+\cdots + (m_{n,n}-1)a_n+(-1)^{\,j+1}m_{n,n}a_{n+1}+\cdots + (-1)^{\,j+1}m_{n,3}a_{2n-2}\!=\!0\\ m_{n+1,1}a_1+m_{n+1,2}a_2+\cdots +m_{n+1,n-1}a_{n-1}-a_{n+1}+\cdots +(-1)^{\,j+1}m_{n+1,3}a_{2n-2}=0\\ \vdots \\ m_{2n-2,1}a_1+m_{2n-2,2}a_2-a_{2n-2}=0\\ m_{2n-1,1}a_1=0\\ a_{2n-1}=a_{2n}=0 \end{cases} \end{align} $$
$$ \begin{align} \begin{cases} (m_{1,1}-1)a_1+m_{1,2}a_2+\cdots + m_{1,n}a_n+(-1)^{\,j+1}m_{1,n}a_{n+1}+\cdots + (-1)^{\,j+1}m_{1,3}a_{2n-2}\!=\!0\\ m_{2,1}a_1+(m_{2,2}-1)a_2+\cdots + m_{2,n}a_n+(-1)^{\,j+1}m_{2,n}a_{n+1}+\cdots + (-1)^{\,j+1}m_{2,3}a_{2n-2}\!=\!0\\ \vdots \\ m_{n,1}a_1+m_{n,2}a_2+\cdots + (m_{n,n}-1)a_n+(-1)^{\,j+1}m_{n,n}a_{n+1}+\cdots + (-1)^{\,j+1}m_{n,3}a_{2n-2}\!=\!0\\ m_{n+1,1}a_1+m_{n+1,2}a_2+\cdots +m_{n+1,n-1}a_{n-1}-a_{n+1}+\cdots +(-1)^{\,j+1}m_{n+1,3}a_{2n-2}=0\\ \vdots \\ m_{2n-2,1}a_1+m_{2n-2,2}a_2-a_{2n-2}=0\\ m_{2n-1,1}a_1=0\\ a_{2n-1}=a_{2n}=0 \end{cases} \end{align} $$
and
 $$ \begin{align*} \small{\underline{p(t)}\! = \! \left(\!\!\! \begin{array}{c} m_{1,1} a_1t^{s_1}+ \cdots + m_{1,n}a_nt^{s_n}+ (-1)^{\,j+1}m_{1,n}a_{n+1}t^{s_{n+1}}+ \cdots + (-1)^{\,j+1}m_{1,3}a_{2n-2}t^{s_{2n-2}}\\ m_{2,1} a_1t^{s_1}+ \cdots + m_{2,n} a_nt^{s_n}+ (-1)^{\,j+1}m_{2,n}a_{n+1}t^{s_{n+1}}+ \cdots +(-1)^{\,j+1}m_{2,3}a_{2n-2}t^{s_{2n-2}}\\ \vdots \\ m_{n,1} a_1t^{s_1}+\cdots + m_{n,n}a_nt^{s_n}+ (-1)^{\,j+1}(m_{n,n}-1)a_{n+1}t^{s_{n+1}}+ \cdots + (-1)^{\,j+1}m_{n,3}a_{2n-2}t^{s_{2n-2}}\\ m_{n+1,1} a_1t^{s_1}+\cdots +(-1)^ja_nt^{s_n}+ m_{n+1,n-1}a_{n+2}t^{s_{n+2}} + \cdots +(-1)^{\,j+1}m_{n+1,3}a_{2n-2}t^{s_{2n-2}}\\ \vdots \\ (-1)^{{\kern2pt}j} a_2t^{s_2}\\ (-1)^{{\kern2pt}j} a_1t^{s_1} \end{array}\!\!\!\right).} \end{align*} $$
$$ \begin{align*} \small{\underline{p(t)}\! = \! \left(\!\!\! \begin{array}{c} m_{1,1} a_1t^{s_1}+ \cdots + m_{1,n}a_nt^{s_n}+ (-1)^{\,j+1}m_{1,n}a_{n+1}t^{s_{n+1}}+ \cdots + (-1)^{\,j+1}m_{1,3}a_{2n-2}t^{s_{2n-2}}\\ m_{2,1} a_1t^{s_1}+ \cdots + m_{2,n} a_nt^{s_n}+ (-1)^{\,j+1}m_{2,n}a_{n+1}t^{s_{n+1}}+ \cdots +(-1)^{\,j+1}m_{2,3}a_{2n-2}t^{s_{2n-2}}\\ \vdots \\ m_{n,1} a_1t^{s_1}+\cdots + m_{n,n}a_nt^{s_n}+ (-1)^{\,j+1}(m_{n,n}-1)a_{n+1}t^{s_{n+1}}+ \cdots + (-1)^{\,j+1}m_{n,3}a_{2n-2}t^{s_{2n-2}}\\ m_{n+1,1} a_1t^{s_1}+\cdots +(-1)^ja_nt^{s_n}+ m_{n+1,n-1}a_{n+2}t^{s_{n+2}} + \cdots +(-1)^{\,j+1}m_{n+1,3}a_{2n-2}t^{s_{2n-2}}\\ \vdots \\ (-1)^{{\kern2pt}j} a_2t^{s_2}\\ (-1)^{{\kern2pt}j} a_1t^{s_1} \end{array}\!\!\!\right).} \end{align*} $$
Consider the second-last equation in (3.10):
The term with the highest possible degree
![]() $s_1+s_{2n}=s_2+s_{2n-1}=k$
is
$s_1+s_{2n}=s_2+s_{2n-1}=k$
is
and hence
![]() $m_{2n-2,1}a_1+m_{2n-2,2}a_2=0$
. Looking at the system (3.11), we obtain
$m_{2n-2,1}a_1+m_{2n-2,2}a_2=0$
. Looking at the system (3.11), we obtain
![]() $a_{2n-2}=0$
; and hence the degree of
$a_{2n-2}=0$
; and hence the degree of
![]() $p_i(t)$
is bounded by
$p_i(t)$
is bounded by
![]() $ s_{2n-3}$
for all i.
$ s_{2n-3}$
for all i.
The proof goes on in the same way. It may be less evident than the one for Theorem 3.1 (where the
![]() $a_i$
vanished in pairs), but looking always at the terms of degree k of the
$a_i$
vanished in pairs), but looking always at the terms of degree k of the
![]() $(2n-i)$
th equation of (3.10) and substituting in (3.11), we are able to prove that
$(2n-i)$
th equation of (3.10) and substituting in (3.11), we are able to prove that
![]() $a_{2n-i}=0$
and, as an immediate consequence from (3.5), that all the
$a_{2n-i}=0$
and, as an immediate consequence from (3.5), that all the
![]() $p_{i}(t)$
have degree at most
$p_{i}(t)$
have degree at most
![]() $s_{2n-i-1}$
. For example, midway through the proof we get
$s_{2n-i-1}$
. For example, midway through the proof we get
 $$ \begin{align*} \underline{a}=\left(\begin{array}{@{}c@{}} a_1\\ \vdots \\ a_n\\ 0\\ \vdots \\ 0 \end{array} \right)\quad \mathrm{and} \quad \underline{p(t)}=\left(\begin{array}{@{}c@{}} m_{1,1} a_1t^{s_1}+ \cdots + m_{1,n}a_nt^{s_n}\\ \vdots\\ m_{n,1} a_1t^{s_1}+\cdots + m_{n,n}a_nt^{s_n}\\ m_{n+1,1} a_1t^{s_1}+\cdots + (-1)^ja_nt^{s_n}\\ m_{n+2,1} a_1t^{s_1}+\cdots + (-1)^ja_{n-1}t^{s_{n-1}}\\ \vdots\\ (-1)^ja_1t^{s_1} \end{array} \right). \end{align*} $$
$$ \begin{align*} \underline{a}=\left(\begin{array}{@{}c@{}} a_1\\ \vdots \\ a_n\\ 0\\ \vdots \\ 0 \end{array} \right)\quad \mathrm{and} \quad \underline{p(t)}=\left(\begin{array}{@{}c@{}} m_{1,1} a_1t^{s_1}+ \cdots + m_{1,n}a_nt^{s_n}\\ \vdots\\ m_{n,1} a_1t^{s_1}+\cdots + m_{n,n}a_nt^{s_n}\\ m_{n+1,1} a_1t^{s_1}+\cdots + (-1)^ja_nt^{s_n}\\ m_{n+2,1} a_1t^{s_1}+\cdots + (-1)^ja_{n-1}t^{s_{n-1}}\\ \vdots\\ (-1)^ja_1t^{s_1} \end{array} \right). \end{align*} $$
Therefore, what remains of (3.4) is
 $$ \begin{align} \begin{cases} (m_{1,1}-1)a_1+m_{1,2}a_2+\cdots + m_{1,n}a_n=0\\ m_{2,1}a_1+(m_{2,2}-1)a_2+\cdots + m_{2,n}a_n=0\\ \vdots \\ m_{n,1}a_1+m_{n,2}a_2+\cdots + (m_{n,n}-1)a_n=0\\ a_{n+1}=\cdots =a_{2n}=0. \end{cases} \end{align} $$
$$ \begin{align} \begin{cases} (m_{1,1}-1)a_1+m_{1,2}a_2+\cdots + m_{1,n}a_n=0\\ m_{2,1}a_1+(m_{2,2}-1)a_2+\cdots + m_{2,n}a_n=0\\ \vdots \\ m_{n,1}a_1+m_{n,2}a_2+\cdots + (m_{n,n}-1)a_n=0\\ a_{n+1}=\cdots =a_{2n}=0. \end{cases} \end{align} $$
Finally, we observe that the nth equation of (3.10) is
As before, the term of degree k must have coefficient 0 and it appears only in the final terms starting from
![]() $m_{n,n}(-t)^{s_{n+1}}p_{n+1}(t)$
. So we get
$m_{n,n}(-t)^{s_{n+1}}p_{n+1}(t)$
. So we get
and, by (3.12),
![]() $a_n=0$
as well. Iterating we get
$a_n=0$
as well. Iterating we get
![]() $\underline {a}=0$
and so our claim.
$\underline {a}=0$
and so our claim.