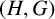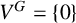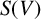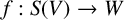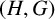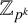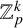1 Introduction
Let G be a finite group which acts on a space X and let
![]() $f: X \to Y$
be a continuous map from X into another space Y. If H is a subgroup of G, then H acts on the right on each orbit
$f: X \to Y$
be a continuous map from X into another space Y. If H is a subgroup of G, then H acts on the right on each orbit
![]() $Gx$
of G as follows: if
$Gx$
of G as follows: if
![]() $y \in Gx$
and
$y \in Gx$
and
![]() $y = gx$
, with
$y = gx$
, with
![]() $g \in G$
, then
$g \in G$
, then
![]() $h \cdot y = g h^{-1} x$
. A point
$h \cdot y = g h^{-1} x$
. A point
![]() $x\in X$
is said to be an
$x\in X$
is said to be an
![]() $(H, G)$
-coincidence point of f (as introduced by Gonçalves et al. in [Reference Gonçalves, Jaworowski and Pergher6]) if f sends every orbit of the action of H on the G-orbit of x to a single point. Of course, if H is the trivial subgroup, then every point of X is an
$(H, G)$
-coincidence point of f (as introduced by Gonçalves et al. in [Reference Gonçalves, Jaworowski and Pergher6]) if f sends every orbit of the action of H on the G-orbit of x to a single point. Of course, if H is the trivial subgroup, then every point of X is an
![]() $(H, G)$
-coincidence. If
$(H, G)$
-coincidence. If
![]() $H = G$
, this is the usual definition of a G-coincidence point, that is,
$H = G$
, this is the usual definition of a G-coincidence point, that is,
![]() $f(x) = f(g x )$
for all
$f(x) = f(g x )$
for all
![]() $g\in G$
. Let us denote by
$g\in G$
. Let us denote by
![]() $A(f, H, G)$
the set of all
$A(f, H, G)$
the set of all
![]() $(H, G)$
-coincidence points. Borsuk–Ulam theorems estimate the size of the set
$(H, G)$
-coincidence points. Borsuk–Ulam theorems estimate the size of the set
![]() $A(f, H, G)$
. For the case when the target space Y is a CW-complex, this problem was considered by Gonçalves et al. [Reference Gonçalves, Jaworowski and Pergher6] (for the subgroup
$A(f, H, G)$
. For the case when the target space Y is a CW-complex, this problem was considered by Gonçalves et al. [Reference Gonçalves, Jaworowski and Pergher6] (for the subgroup
![]() $H= \mathbb {Z}_p$
of a finite group G, X a homotopy sphere and Y a CW-complex) and Gonçalves et al. [Reference Gonçalves, Jaworowski, Pergher and Volovikov7] (for the subgroup
$H= \mathbb {Z}_p$
of a finite group G, X a homotopy sphere and Y a CW-complex) and Gonçalves et al. [Reference Gonçalves, Jaworowski, Pergher and Volovikov7] (for the subgroup
![]() $H= \mathbb {Z}_p$
of a finite group G, X under certain (co)homological assumptions and Y a CW-complex). In [Reference de Mattos, dos Santos and Souza5], by considering the target space
$H= \mathbb {Z}_p$
of a finite group G, X under certain (co)homological assumptions and Y a CW-complex). In [Reference de Mattos, dos Santos and Souza5], by considering the target space
![]() $Y=M$
a manifold and H a proper nontrivial subgroup of G, we proved a formulation of the Borsuk–Ulam theorem for manifolds in terms of
$Y=M$
a manifold and H a proper nontrivial subgroup of G, we proved a formulation of the Borsuk–Ulam theorem for manifolds in terms of
![]() $(H,G)$
-coincidences which has applications to the famous topological Tverberg problem (see for example, [Reference Blagojević, Frick and Ziegler1]).
$(H,G)$
-coincidences which has applications to the famous topological Tverberg problem (see for example, [Reference Blagojević, Frick and Ziegler1]).
Let W be a real vector space and let V be an orthogonal representation of a group G with
![]() $V^{G} = \{0\}$
. Let
$V^{G} = \{0\}$
. Let
![]() $S(V)$
be the sphere of V and suppose that
$S(V)$
be the sphere of V and suppose that
![]() $f: S(V) \to W$
is a continuous map. We estimate the size of
$f: S(V) \to W$
is a continuous map. We estimate the size of
![]() $A(f, H, G)$
if G is a cyclic group of prime power order
$A(f, H, G)$
if G is a cyclic group of prime power order
![]() $\mathbb {Z}_{p^k}$
or a p-torus
$\mathbb {Z}_{p^k}$
or a p-torus
![]() $\mathbb {Z}_p^k$
(Theorems 3.1, 3.2 and 3.5).
$\mathbb {Z}_p^k$
(Theorems 3.1, 3.2 and 3.5).
2 Bourgin–Yang versions of the Borsuk–Ulam theorem for
 $\mathbb {Z}_{p^k}$
and
$\mathbb {Z}_{p^k}$
and
 $\mathbb {Z}_p^k$
$\mathbb {Z}_p^k$
Let
![]() $G = \mathbb {Z}_{p^k}$
be a cyclic group of prime power order,
$G = \mathbb {Z}_{p^k}$
be a cyclic group of prime power order,
![]() $k\geq 1$
. Given two powers
$k\geq 1$
. Given two powers
![]() $p^m, p^n$
of p with
$p^m, p^n$
of p with
![]() $ 1 \leq m\leq n\leq k-1$
, we set
$ 1 \leq m\leq n\leq k-1$
, we set
where
![]() $\vert H\vert $
is the cardinality of H. We write
$\vert H\vert $
is the cardinality of H. We write
![]() $\mathcal {A}_X$
for a set of all the G-orbits of a space X (up to a homeomorphism and thus up to an isomorphism of finite G-sets).
$\mathcal {A}_X$
for a set of all the G-orbits of a space X (up to a homeomorphism and thus up to an isomorphism of finite G-sets).
Let V be an orthogonal representation of
![]() $G = \mathbb {Z}_{p^k}$
, p prime,
$G = \mathbb {Z}_{p^k}$
, p prime,
![]() $k\geq 1$
, such that
$k\geq 1$
, such that
![]() $V^G=\{0\}$
(for the set of fixed points of G). For
$V^G=\{0\}$
(for the set of fixed points of G). For
![]() $G=\mathbb {Z}_{p^k}$
, with p odd, every nontrivial irreducible orthogonal representation is even dimensional and admits a complex structure [Reference Serre10], so V also admits such a structure. We write
$G=\mathbb {Z}_{p^k}$
, with p odd, every nontrivial irreducible orthogonal representation is even dimensional and admits a complex structure [Reference Serre10], so V also admits such a structure. We write
![]() $d(V)=\dim _{\mathbb {C}} V =\tfrac 12 \dim _{\mathbb {R}} V $
, an integral numerical invariant of V.
$d(V)=\dim _{\mathbb {C}} V =\tfrac 12 \dim _{\mathbb {R}} V $
, an integral numerical invariant of V.
The following Bourgin–Yang versions of the Borsuk–Ulam theorem for complex orthogonal representations of
![]() $G=\mathbb {Z}_{p^{k}}$
, p prime,
$G=\mathbb {Z}_{p^{k}}$
, p prime,
![]() $k\geq 1$
and for real orthogonal representations of
$k\geq 1$
and for real orthogonal representations of
![]() $G=\mathbb {Z}_{2^{k}}$
,
$G=\mathbb {Z}_{2^{k}}$
,
![]() $k\geq 1$
are from [Reference Marzantowicz, de Mattos and dos Santos8].
$k\geq 1$
are from [Reference Marzantowicz, de Mattos and dos Santos8].
Theorem 2.1 [Reference Marzantowicz, de Mattos and dos Santos8, Theorem 3.6]
Let V, W be two complex orthogonal representations of the cyclic group
![]() $G=\mathbb {Z}_{p^k}$
,
$G=\mathbb {Z}_{p^k}$
,
![]() $p> 2 $
prime,
$p> 2 $
prime,
![]() $k\geq 1$
, such that
$k\geq 1$
, such that
![]() $V^G=W^G=\{0\}$
. Let
$V^G=W^G=\{0\}$
. Let
![]() $f: S(V)\,\,{\overset {G}\to }\,\, W$
be an equivariant map and
$f: S(V)\,\,{\overset {G}\to }\,\, W$
be an equivariant map and
![]() $Z_f :=f^{-1}(0)=\{v\in S(V) \mid f(v)=0\}$
. Suppose
$Z_f :=f^{-1}(0)=\{v\in S(V) \mid f(v)=0\}$
. Suppose
![]() $\mathcal {A}_{S(V)} \subset \mathcal {A}_{m,n}$
and
$\mathcal {A}_{S(V)} \subset \mathcal {A}_{m,n}$
and
![]() $\mathcal {A}_{S(W)} \subset \mathcal {A}_{{m},{n}}$
. Then
$\mathcal {A}_{S(W)} \subset \mathcal {A}_{{m},{n}}$
. Then
Theorem 2.2 [Reference Marzantowicz, de Mattos and dos Santos8, Theorem 3.9]
Let V, W be two real orthogonal representations of the cyclic group
![]() $G=\mathbb {Z}_{2^k}$
,
$G=\mathbb {Z}_{2^k}$
,
![]() $k\geq 1$
, such that
$k\geq 1$
, such that
![]() $V^G=W^G=\{0\}$
. Let
$V^G=W^G=\{0\}$
. Let
![]() $f: S(V)\,\,{\overset {G}\to }\,\, W$
be an equivariant map and
$f: S(V)\,\,{\overset {G}\to }\,\, W$
be an equivariant map and
![]() $Z_f=f^{-1}(0)$
. Suppose that
$Z_f=f^{-1}(0)$
. Suppose that
![]() $\mathcal {A}_{S(V)} \subset \mathcal {A}_{m,n}$
and
$\mathcal {A}_{S(V)} \subset \mathcal {A}_{m,n}$
and
![]() $\mathcal {A}_{S(W)} \subset \mathcal {A}_{{m},{n}}$
. Then
$\mathcal {A}_{S(W)} \subset \mathcal {A}_{{m},{n}}$
. Then
The next result is the classical version of the Bourgin–Yang theorem for a p-torus
![]() $\mathbb {Z}_p^k = \mathbb {Z}_p \times \mathbb {Z}_p\times \cdots \times \mathbb {Z}_p$
(k times).
$\mathbb {Z}_p^k = \mathbb {Z}_p \times \mathbb {Z}_p\times \cdots \times \mathbb {Z}_p$
(k times).
Theorem 2.3 [Reference Marzantowicz, de Mattos and dos Santos9, Theorem 2.1]
Let V and W be two orthogonal representations of the group
![]() $G = \mathbb {Z}_p^k$
such that
$G = \mathbb {Z}_p^k$
such that
![]() $V^{G} = W^{G} = \{ 0 \}$
. Let
$V^{G} = W^{G} = \{ 0 \}$
. Let
![]() $f: S(V) \to W$
be a continuous map. Then
$f: S(V) \to W$
be a continuous map. Then
For further recent extensions of the Bourgin–Yang theorem, see [Reference Błaszczyk, Marzantowicz and Singh2, Reference Błaszczyk, Marzantowicz and Singh3].
3 Estimating the size of the
 $(H, G)$
-coincidences set
$(H, G)$
-coincidences set
Let
![]() $W^{\prime }$
be a real vector space and
$W^{\prime }$
be a real vector space and
![]() $f:S(V)\to W^{\prime }$
a continuous map. In this section, we estimate the size of the set
$f:S(V)\to W^{\prime }$
a continuous map. In this section, we estimate the size of the set
![]() $A(f,\mathbb {Z}_{p^i}, \mathbb {Z}_{p^k})$
under various assumptions.
$A(f,\mathbb {Z}_{p^i}, \mathbb {Z}_{p^k})$
under various assumptions.
Theorem 3.1. Let V be a complex orthogonal representation of the cyclic group
![]() $G=\mathbb {Z}_{p^k}$
,
$G=\mathbb {Z}_{p^k}$
,
![]() $p \geq 3$
prime and
$p \geq 3$
prime and
![]() $k\geq 1$
, such that
$k\geq 1$
, such that
![]() $V^G=\{0\}$
and let
$V^G=\{0\}$
and let
![]() $W^{\prime }$
be a real vector space. Let
$W^{\prime }$
be a real vector space. Let
![]() $f:S(V)\to W^{\prime }$
be a continuous map.
$f:S(V)\to W^{\prime }$
be a continuous map.
-
(1) If
 $\mathcal {A}_{S(V)} \subset \mathcal {A}_{1,p^{k-1}}$
, then for all i with
$\mathcal {A}_{S(V)} \subset \mathcal {A}_{1,p^{k-1}}$
, then for all i with
 $1\leq i \leq k$
,
$1\leq i \leq k$
,  $$ \begin{align*} \dim A(f,\mathbb{Z}_{p^i}, \mathbb{Z}_{p^k})\geq 2\bigg \lceil\frac{d(V)-1}{p^{k-1}}\bigg \rceil-(p^{k} - p^{k-i})\,dW^{\prime}. \end{align*} $$
$$ \begin{align*} \dim A(f,\mathbb{Z}_{p^i}, \mathbb{Z}_{p^k})\geq 2\bigg \lceil\frac{d(V)-1}{p^{k-1}}\bigg \rceil-(p^{k} - p^{k-i})\,dW^{\prime}. \end{align*} $$
-
(2) If
 $\mathcal {A}_{S(V)} \subset \mathcal {A}_{1,p^{i-1}}$
for some i with
$\mathcal {A}_{S(V)} \subset \mathcal {A}_{1,p^{i-1}}$
for some i with
 $1\leq i \leq k$
, then
$1\leq i \leq k$
, then  $$ \begin{align*} \dim A(f,\mathbb{Z}_{p^i}, \mathbb{Z}_{p^k})\geq 2\bigg \lceil\frac{d(V)-1}{p^{i-1}}\bigg \rceil-(p^{k} - p^{k-i})\,dW^{\prime}. \end{align*} $$
$$ \begin{align*} \dim A(f,\mathbb{Z}_{p^i}, \mathbb{Z}_{p^k})\geq 2\bigg \lceil\frac{d(V)-1}{p^{i-1}}\bigg \rceil-(p^{k} - p^{k-i})\,dW^{\prime}. \end{align*} $$
Proof. Let i be fixed with
![]() $1\leq i\leq k$
. Consider the real vector space
$1\leq i\leq k$
. Consider the real vector space
![]() $\oplus _{j=1}^{p^k} W^{\prime }$
, which is the direct sum of
$\oplus _{j=1}^{p^k} W^{\prime }$
, which is the direct sum of
![]() $p^{k}$
copies of
$p^{k}$
copies of
![]() $W^{\prime }$
. The space
$W^{\prime }$
. The space
![]() $\oplus _{j=1}^{p^k} W^{\prime }$
admits an action of the cyclic group
$\oplus _{j=1}^{p^k} W^{\prime }$
admits an action of the cyclic group
![]() $G=\mathbb {Z}_{p^{k}}$
, given by
$G=\mathbb {Z}_{p^{k}}$
, given by
for a fixed generator
![]() $g \in G$
and for each
$g \in G$
and for each
![]() $(w_{1},\ldots ,w_{p^{k}})\in \oplus _{j=1}^{p^k} W^{\prime }$
.
$(w_{1},\ldots ,w_{p^{k}})\in \oplus _{j=1}^{p^k} W^{\prime }$
.
Denote by
![]() $\Delta ({W^{\prime }}^{p^{k-i}})$
the diagonal of
$\Delta ({W^{\prime }}^{p^{k-i}})$
the diagonal of
![]() $ \oplus _{j=1}^{p^k} W^{\prime } = {W^{\prime }}^{p^{k-i}} \oplus \cdots \oplus {W^{\prime }}^{p^{k-i}}$
. Then
$ \oplus _{j=1}^{p^k} W^{\prime } = {W^{\prime }}^{p^{k-i}} \oplus \cdots \oplus {W^{\prime }}^{p^{k-i}}$
. Then
 $$ \begin{align*} {\underset{j=1}{\overset{p^k}\bigoplus}} W^{\prime}= \Delta ({W^{\prime}}^{p^{k-i}})\oplus (\Delta ({W^{\prime}}^{p^{k-i}}))^{\bot}, \end{align*} $$
$$ \begin{align*} {\underset{j=1}{\overset{p^k}\bigoplus}} W^{\prime}= \Delta ({W^{\prime}}^{p^{k-i}})\oplus (\Delta ({W^{\prime}}^{p^{k-i}}))^{\bot}, \end{align*} $$
where
![]() $\Delta ({W^{\prime }}^{p^{k-i}})^{\bot }$
is the orthogonal complement of
$\Delta ({W^{\prime }}^{p^{k-i}})^{\bot }$
is the orthogonal complement of
![]() $\Delta ({W^{\prime }}^{p^{k-i}})$
. Now
$\Delta ({W^{\prime }}^{p^{k-i}})$
. Now
![]() $\Delta ({W^{\prime }}^{p^{k-i}})$
is a G-subspace of
$\Delta ({W^{\prime }}^{p^{k-i}})$
is a G-subspace of
![]() $\oplus _{j=1}^{p^k} W^{\prime }$
of dimension
$\oplus _{j=1}^{p^k} W^{\prime }$
of dimension
![]() $p^{k-i}\dim W^{\prime } $
, so
$p^{k-i}\dim W^{\prime } $
, so
![]() $\Delta (W^{p^{k-i}})^{\bot }$
is a G-subrepresentation of
$\Delta (W^{p^{k-i}})^{\bot }$
is a G-subrepresentation of
![]() $\oplus _{j=1}^{p^k} W^{\prime }$
of dimension
$\oplus _{j=1}^{p^k} W^{\prime }$
of dimension
![]() $(p^{k}- p^{k-i})\dim W^{\prime }$
for which
$(p^{k}- p^{k-i})\dim W^{\prime }$
for which
![]() $({\Delta ({W^{\prime }}^{p^{k-i}})^{\bot }})^G=\{0\}$
.
$({\Delta ({W^{\prime }}^{p^{k-i}})^{\bot }})^G=\{0\}$
.
Denote by
![]() $a_1, \ldots , a_r$
a set of representatives of the left lateral classes of
$a_1, \ldots , a_r$
a set of representatives of the left lateral classes of
![]() $G/\mathbb {Z}_{p^i}$
, where
$G/\mathbb {Z}_{p^i}$
, where
![]() $r = p^{k-i}$
. Consider the map
$r = p^{k-i}$
. Consider the map
defined by
where
![]() $F_{j} (x) = (f(a_1 h^j x), \ldots , f(a_r h^j x))$
,
$F_{j} (x) = (f(a_1 h^j x), \ldots , f(a_r h^j x))$
,
![]() $j = 0, 1, \ldots , p^i - 1$
, for a fixed generator
$j = 0, 1, \ldots , p^i - 1$
, for a fixed generator
![]() $h \in \mathbb {Z}_{p^i}.$
The linear orthogonal projection along the diagonal
$h \in \mathbb {Z}_{p^i}.$
The linear orthogonal projection along the diagonal
![]() $\Delta ({W^{\prime }}^{p^{k-i}})$
defines a G-equivariant map
$\Delta ({W^{\prime }}^{p^{k-i}})$
defines a G-equivariant map
![]() $\rho :\Delta ({W^{\prime }}^{p^{k-i}})\oplus \Delta ({W^{\prime }}^{p^{k-i}})^{\bot }\to \Delta ({W^{\prime }}^{p^{k-i}})^{\bot }$
. Let us denote by l the composition
$\rho :\Delta ({W^{\prime }}^{p^{k-i}})\oplus \Delta ({W^{\prime }}^{p^{k-i}})^{\bot }\to \Delta ({W^{\prime }}^{p^{k-i}})^{\bot }$
. Let us denote by l the composition
with
For a fixed generator
![]() $g\in G$
, we can take
$g\in G$
, we can take
![]() $h = g^{p^{k-i}}, a_1\, {=}\ e, a_2 = g, \ldots , a_r\, {=}\ g^{p^{k-i} - 1},$
and then F is a G-equivariant map. Moreover,
$h = g^{p^{k-i}}, a_1\, {=}\ e, a_2 = g, \ldots , a_r\, {=}\ g^{p^{k-i} - 1},$
and then F is a G-equivariant map. Moreover,
To check the validity of the inclusion
![]() $\mathcal {A}_{S(\Delta ({W^{\prime }}^{p^{k-i}})^\bot )}\subset \mathcal {A}_{1,p^{i-1}}$
, it suffices to prove that the cardinality of the orbit
$\mathcal {A}_{S(\Delta ({W^{\prime }}^{p^{k-i}})^\bot )}\subset \mathcal {A}_{1,p^{i-1}}$
, it suffices to prove that the cardinality of the orbit
![]() $\mathbb {Z}_{p^k} w$
belongs to the set
$\mathbb {Z}_{p^k} w$
belongs to the set
![]() $\{p^k, p^{k-1}, \ldots , p^{k-i+1} \}$
for any
$\{p^k, p^{k-1}, \ldots , p^{k-i+1} \}$
for any
![]() $w=(w_1, \ldots , w_{p^k}) \in S(\Delta ({W^{\prime }}^{p^{k-i}})^\bot )$
. From [Reference Bredon4, Ch. 1, Proposition 4.1], the cardinality of the orbit
$w=(w_1, \ldots , w_{p^k}) \in S(\Delta ({W^{\prime }}^{p^{k-i}})^\bot )$
. From [Reference Bredon4, Ch. 1, Proposition 4.1], the cardinality of the orbit
![]() $\mathbb {Z}_{p^k} w$
belongs to the set
$\mathbb {Z}_{p^k} w$
belongs to the set
![]() $\{p^{k}, p^{k-1}, \ldots , p, p^{0}=1 \}$
. Let
$\{p^{k}, p^{k-1}, \ldots , p, p^{0}=1 \}$
. Let
![]() $w=(w_1, \ldots , w_{p^k})$
be an element in
$w=(w_1, \ldots , w_{p^k})$
be an element in
![]() $S(\Delta ({W^{\prime }}^{p^{k-i}})^\bot )$
and suppose that
$S(\Delta ({W^{\prime }}^{p^{k-i}})^\bot )$
and suppose that
![]() $|\mathbb {Z}_{p^k} w|\in \{p^{k-i}, p^{k-i-1}, \ldots , p^{0}=1 \},$
that is,
$|\mathbb {Z}_{p^k} w|\in \{p^{k-i}, p^{k-i-1}, \ldots , p^{0}=1 \},$
that is,
![]() $|\mathbb {Z}_{p^k} w|=p^{\,j}$
for some j with
$|\mathbb {Z}_{p^k} w|=p^{\,j}$
for some j with
![]() $0\leq j\leq k-i$
.
$0\leq j\leq k-i$
.
Assertion. We have
![]() $\mathbb {Z}_{p^k} w =\{w, gw,\ldots ,g^{p^{\,j} -1} w\}$
, for a fixed generator g of
$\mathbb {Z}_{p^k} w =\{w, gw,\ldots ,g^{p^{\,j} -1} w\}$
, for a fixed generator g of
![]() $\mathbb {Z}_{p^{k}}$
.
$\mathbb {Z}_{p^{k}}$
.
In fact, consider a cyclic group G,
![]() $g\in G$
a fixed generator and
$g\in G$
a fixed generator and
![]() $\{w, gw,\ldots ,g^{s-1}w\}$
the maximum set of the first s elements of the orbit
$\{w, gw,\ldots ,g^{s-1}w\}$
the maximum set of the first s elements of the orbit
![]() $Gw$
that are distinct from each other. From this definition,
$Gw$
that are distinct from each other. From this definition,
![]() $g^{s}w\in \{w, gw,\ldots ,g^{s-1}w\}.$
Suppose that
$g^{s}w\in \{w, gw,\ldots ,g^{s-1}w\}.$
Suppose that
Then
However, this contradicts the definition of the set
![]() $\{w, gw,\ldots ,g^{s-1}w\}$
.
$\{w, gw,\ldots ,g^{s-1}w\}$
.
Now, if
![]() $g^{t}w \in Gw$
, for some
$g^{t}w \in Gw$
, for some
![]() $t\in \mathbb {N}$
, we have
$t\in \mathbb {N}$
, we have
![]() $t=ns+r$
with
$t=ns+r$
with
![]() $0\leq r\leq s-1$
. Therefore,
$0\leq r\leq s-1$
. Therefore,
since
![]() $g^{ns} w = (g^{s}\cdots g^{s})w=w$
and
$g^{ns} w = (g^{s}\cdots g^{s})w=w$
and
![]() $0\leq r\leq s-1$
.
$0\leq r\leq s-1$
.
Thus, for a fixed generator g of
![]() $\mathbb {Z}_{p^{k}}$
,
$\mathbb {Z}_{p^{k}}$
,
 $$ \begin{align*} w = g^{p^{\,j}}w & = g^{p^{\,j}}(w_{1},\ldots,w_{p^{\,j}},\ldots,w_{(p^{k-j}-1) p^{\,j}+1},\ldots, w_{p^{k}}) \\ & = (w_{p^{\,j}+1},\ldots, w_{2p^{\,j}}, \ldots,w_{(p^{k-j}-1) p^{\,j}+1},\ldots, w_{p^{k}},w_{1},\ldots,w_{p^{\,j}}) \end{align*} $$
$$ \begin{align*} w = g^{p^{\,j}}w & = g^{p^{\,j}}(w_{1},\ldots,w_{p^{\,j}},\ldots,w_{(p^{k-j}-1) p^{\,j}+1},\ldots, w_{p^{k}}) \\ & = (w_{p^{\,j}+1},\ldots, w_{2p^{\,j}}, \ldots,w_{(p^{k-j}-1) p^{\,j}+1},\ldots, w_{p^{k}},w_{1},\ldots,w_{p^{\,j}}) \end{align*} $$
and so
![]() $w\in \Delta ({W^{\prime }}^{p^{\,j}})$
. Since
$w\in \Delta ({W^{\prime }}^{p^{\,j}})$
. Since
and
![]() $j\in \{0,1,\ldots ,k-i\}$
, we conclude that
$j\in \{0,1,\ldots ,k-i\}$
, we conclude that
![]() $w\in \Delta ({W^{\prime }}^{p^{\,j}})\subset \Delta ({W^{\prime }}^{p^{k-i}}),$
which is a contradiction since
$w\in \Delta ({W^{\prime }}^{p^{\,j}})\subset \Delta ({W^{\prime }}^{p^{k-i}}),$
which is a contradiction since
![]() $\Delta ({W^{\prime }}^{p^{k-i}})\cap S(\Delta ({W^{\prime }}^{p^{k-i}})^{\bot })=\emptyset .$
$\Delta ({W^{\prime }}^{p^{k-i}})\cap S(\Delta ({W^{\prime }}^{p^{k-i}})^{\bot })=\emptyset .$
This proves the assertion and the theorem follows from Theorem 2.1.
We also have the following estimate for the size of
![]() $A(f,\mathbb {Z}_{2^i}, \mathbb {Z}_{2^k})$
.
$A(f,\mathbb {Z}_{2^i}, \mathbb {Z}_{2^k})$
.
Theorem 3.2. Let V be a real orthogonal representation of the cyclic group
![]() $G=\mathbb {Z}_{2^k}$
,
$G=\mathbb {Z}_{2^k}$
,
![]() $k\geq 1$
, such that
$k\geq 1$
, such that
![]() $V^G=\{0\}$
and let
$V^G=\{0\}$
and let
![]() $W^{\prime }$
be a real vector space. Let
$W^{\prime }$
be a real vector space. Let
![]() $f:S(V)\to W^{\prime }$
be a continuous map.
$f:S(V)\to W^{\prime }$
be a continuous map.
-
(1) If
 $\mathcal {A}_{S(V)} \subset \mathcal {A}_{1,2^{k-1}}$
, then for all i with
$\mathcal {A}_{S(V)} \subset \mathcal {A}_{1,2^{k-1}}$
, then for all i with
 $1\leq i \leq k$
,
$1\leq i \leq k$
,  $$ \begin{align*} \dim \, A(f,\mathbb{Z}_{2^i}, \mathbb{Z}_{2^k})\geq \bigg\lceil\frac{d(V)-1}{2^{k-1}}\bigg\rceil-(2^{k-1} - 2^{k-i})\,dW^{\prime}. \end{align*} $$
$$ \begin{align*} \dim \, A(f,\mathbb{Z}_{2^i}, \mathbb{Z}_{2^k})\geq \bigg\lceil\frac{d(V)-1}{2^{k-1}}\bigg\rceil-(2^{k-1} - 2^{k-i})\,dW^{\prime}. \end{align*} $$
-
(2) If
 $\mathcal {A}_{S(V)} \subset \mathcal {A}_{1,2^{i-1}}$
, then for some i with
$\mathcal {A}_{S(V)} \subset \mathcal {A}_{1,2^{i-1}}$
, then for some i with
 $1\leq i \leq k$
,
$1\leq i \leq k$
,  $$ \begin{align*} \dim A(f,\mathbb{Z}_{2^i}, \mathbb{Z}_{2^k})\geq \bigg \lceil\frac{d(V)-1}{2^{i-1}}\bigg\rceil-(2^{k-1} - 2^{k-i})\,dW^{\prime}. \end{align*} $$
$$ \begin{align*} \dim A(f,\mathbb{Z}_{2^i}, \mathbb{Z}_{2^k})\geq \bigg \lceil\frac{d(V)-1}{2^{i-1}}\bigg\rceil-(2^{k-1} - 2^{k-i})\,dW^{\prime}. \end{align*} $$
Proof. For
![]() $G=\mathbb {Z}_{2^k}$
,
$G=\mathbb {Z}_{2^k}$
,
![]() $k\geq 1$
, using the same steps as in the proof of Theorem 3.1 and applying Theorem 2.2 gives the result.
$k\geq 1$
, using the same steps as in the proof of Theorem 3.1 and applying Theorem 2.2 gives the result.
Remark 3.3. We observe that Theorems 3.1 and 3.2 have peculiar characteristics that differentiate them from the classic results on
![]() $(H, G)$
-coincidences. The first is that the action of the group G on the sphere
$(H, G)$
-coincidences. The first is that the action of the group G on the sphere
![]() $S(V)$
is not necessarily free. The second is that the theorems provide an estimate for the dimension of the set of
$S(V)$
is not necessarily free. The second is that the theorems provide an estimate for the dimension of the set of
![]() $(H, G)$
-coincidences of a continuous function
$(H, G)$
-coincidences of a continuous function
![]() $f: S(V) \to W^{\prime }$
, for all subgroups
$f: S(V) \to W^{\prime }$
, for all subgroups
![]() $H = \mathbb {Z}_{p^i}$
of
$H = \mathbb {Z}_{p^i}$
of
![]() $G = \mathbb {Z}_{p^k}$
.
$G = \mathbb {Z}_{p^k}$
.
Example 3.4. Let G and
![]() $W^{\prime }$
be
$W^{\prime }$
be
![]() $\mathbb {Z}_4$
and
$\mathbb {Z}_4$
and
![]() $\mathbb {R}$
, respectively. Let
$\mathbb {R}$
, respectively. Let
![]() $\pi : S^1 \to \mathbb {R}$
be the projection on the first factor and
$\pi : S^1 \to \mathbb {R}$
be the projection on the first factor and
![]() $p: \mathbb {R} \to \mathbb {R}$
be the polynomial function
$p: \mathbb {R} \to \mathbb {R}$
be the polynomial function
![]() $p(x)= x (x-1)(x+1)$
. Consider the action of
$p(x)= x (x-1)(x+1)$
. Consider the action of
![]() $\mathbb {Z}_4$
on
$\mathbb {Z}_4$
on
![]() $S^1$
as the rotation of
$S^1$
as the rotation of
![]() $\pi /4$
. Then
$\pi /4$
. Then
![]() $f = p \circ \pi $
is such that
$f = p \circ \pi $
is such that
![]() $A(f, \mathbb {Z}_2, \mathbb {Z}_4) = \{ (1,0), (0,1), (-1,0), (0, -1)\}$
and therefore
$A(f, \mathbb {Z}_2, \mathbb {Z}_4) = \{ (1,0), (0,1), (-1,0), (0, -1)\}$
and therefore
![]() $\dim A(f, \mathbb {Z}_2, \mathbb {Z}_4) = 0$
. In this case, we have the equality
$\dim A(f, \mathbb {Z}_2, \mathbb {Z}_4) = 0$
. In this case, we have the equality
where
![]() $V = \mathbb {R}^2$
,
$V = \mathbb {R}^2$
,
![]() $k=2$
and
$k=2$
and
![]() $i=1$
.
$i=1$
.
If we take
![]() $p(x) = x^2 (x - 1)(x + 1)$
and
$p(x) = x^2 (x - 1)(x + 1)$
and
![]() $f = p \circ \pi $
, then all points of
$f = p \circ \pi $
, then all points of
![]() $S^1$
are
$S^1$
are
![]() $(\mathbb {Z}_2, \mathbb {Z}_4)$
-coincidence points of f, that is,
$(\mathbb {Z}_2, \mathbb {Z}_4)$
-coincidence points of f, that is,
![]() $A(f, \mathbb {Z}_2, \mathbb {Z}_4) = S^1$
and therefore,
$A(f, \mathbb {Z}_2, \mathbb {Z}_4) = S^1$
and therefore,
![]() $\dim A(f, \mathbb {Z}_2, \mathbb {Z}_4) = 1$
.
$\dim A(f, \mathbb {Z}_2, \mathbb {Z}_4) = 1$
.
The next result is an
![]() $(H, G)$
-coincidence version of the Bourgin–Yang theorem for p-torus
$(H, G)$
-coincidence version of the Bourgin–Yang theorem for p-torus
![]() $\mathbb {Z}_p^k$
.
$\mathbb {Z}_p^k$
.
Theorem 3.5. Let V and
![]() $W^{\prime }$
be two orthogonal representations of the group
$W^{\prime }$
be two orthogonal representations of the group
![]() $G = \mathbb {Z}_p^k$
such that
$G = \mathbb {Z}_p^k$
such that
![]() $V^{G} = {W^{\prime }}^{G} = \{ 0 \}$
. Let
$V^{G} = {W^{\prime }}^{G} = \{ 0 \}$
. Let
![]() $f: S(V) \to W^{\prime }$
be a continuous map. Then
$f: S(V) \to W^{\prime }$
be a continuous map. Then
Proof. Let
![]() $a_1, \ldots , a_r$
be a set of representatives of the left lateral classes of
$a_1, \ldots , a_r$
be a set of representatives of the left lateral classes of
![]() $G/\mathbb {Z}_p^i$
, where
$G/\mathbb {Z}_p^i$
, where
![]() $r = p^{k-i}$
. Let
$r = p^{k-i}$
. Let
![]() $\mathbb {Z}_p^i = \{h_1, \ldots , h_{p^i}\}$
be a fixed enumeration of elements of
$\mathbb {Z}_p^i = \{h_1, \ldots , h_{p^i}\}$
be a fixed enumeration of elements of
![]() $\mathbb {Z}_p^i$
. Consider the map
$\mathbb {Z}_p^i$
. Consider the map
defined by
where
![]() $F_j (x) = (f(a_1 h_j x), \ldots , f(a_r h_j x))$
,
$F_j (x) = (f(a_1 h_j x), \ldots , f(a_r h_j x))$
,
![]() $j = 1, \ldots , p^i$
.
$j = 1, \ldots , p^i$
.
For a fixed enumeration
![]() $\mathbb {Z}_p^k = \{ g_1, \ldots , g_{p^k}\}$
of the elements of
$\mathbb {Z}_p^k = \{ g_1, \ldots , g_{p^k}\}$
of the elements of
![]() $\mathbb {Z}_p^k$
, we define a
$\mathbb {Z}_p^k$
, we define a
![]() $\mathbb {Z}_p^k$
-action on
$\mathbb {Z}_p^k$
-action on
![]() $\Delta ({W^{\prime }}^{p^{k-i}})\oplus \Delta ({W^{\prime }}^{p^{k-i}})^{\bot }$
as follows: for each
$\Delta ({W^{\prime }}^{p^{k-i}})\oplus \Delta ({W^{\prime }}^{p^{k-i}})^{\bot }$
as follows: for each
![]() $g_j \in \mathbb {Z}_p^k$
and for each
$g_j \in \mathbb {Z}_p^k$
and for each
![]() $(y_1, \ldots , y_{p^k}) \in \Delta ({W^{\prime }}^{p^{k-i}})\oplus \Delta ({W^{\prime }}^{p^{k-i}})^{\bot }$
, set
$(y_1, \ldots , y_{p^k}) \in \Delta ({W^{\prime }}^{p^{k-i}})\oplus \Delta ({W^{\prime }}^{p^{k-i}})^{\bot }$
, set
where the permutation
![]() $\sigma _{g_j}$
is defined by
$\sigma _{g_j}$
is defined by
![]() $\sigma _{g_j} (k) = u$
,
$\sigma _{g_j} (k) = u$
,
![]() $g_k g_j = g_u$
. Then F becomes
$g_k g_j = g_u$
. Then F becomes
![]() $\mathbb {Z}_p^k$
-equivariant.
$\mathbb {Z}_p^k$
-equivariant.
The linear orthogonal projection along the diagonal
![]() $\Delta ({W^{\prime }}^{p^{k-i}})$
defines a G-equivariant map
$\Delta ({W^{\prime }}^{p^{k-i}})$
defines a G-equivariant map
Let us denote by l the composition
with
![]() $Z_{l}=l^{-1}(0)=(\,\rho \circ F)^{-1}(0)=F^{-1}(\Delta ({W^{\prime }}^{p^{k-i}}))= A(f,\mathbb {Z}_p^i, \mathbb {Z}_p^k).$
From Theorem 2.3,
$Z_{l}=l^{-1}(0)=(\,\rho \circ F)^{-1}(0)=F^{-1}(\Delta ({W^{\prime }}^{p^{k-i}}))= A(f,\mathbb {Z}_p^i, \mathbb {Z}_p^k).$
From Theorem 2.3,
![]() $\dim Z_l \geq \dim _{\mathbb {R}} V + \dim _{\mathbb {R}} \Delta ({W^{\prime }}^{p^{k-i}})^{\bot } - 1$
, that is,
$\dim Z_l \geq \dim _{\mathbb {R}} V + \dim _{\mathbb {R}} \Delta ({W^{\prime }}^{p^{k-i}})^{\bot } - 1$
, that is,