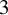1 Introduction
The goal of this article is to analyze whether certain geometric conditions imply that a one-dimensional foliation in a
![]() $3$
-manifold is the foliation by flow lines of a topological Anosov flow. We do this analysis for one-dimensional foliations whose leaves lie inside leaves of two-dimensional foliations and whose leaves are quasigeodesics in these two-dimensional foliations. In other words, the goal of this article is to analyze whether some strictly geometric behavior implies strong dynamical systems behavior in this setting. This has important connections with partial hyperbolicity in dimension three.
$3$
-manifold is the foliation by flow lines of a topological Anosov flow. We do this analysis for one-dimensional foliations whose leaves lie inside leaves of two-dimensional foliations and whose leaves are quasigeodesics in these two-dimensional foliations. In other words, the goal of this article is to analyze whether some strictly geometric behavior implies strong dynamical systems behavior in this setting. This has important connections with partial hyperbolicity in dimension three.
A foliation
![]() $\mathcal {G}$
subfoliates a foliation
$\mathcal {G}$
subfoliates a foliation
![]() $\mathcal {F}$
if each leaf of
$\mathcal {F}$
if each leaf of
![]() $\mathcal {F}$
has a foliation made up of leaves of
$\mathcal {F}$
has a foliation made up of leaves of
![]() $\mathcal {G}$
. We call
$\mathcal {G}$
. We call
![]() $\mathcal {G}$
the subfoliation and
$\mathcal {G}$
the subfoliation and
![]() $\mathcal {F}$
the super foliation. This situation is very common, for example, if
$\mathcal {F}$
the super foliation. This situation is very common, for example, if
![]() $\mathcal {F}_1$
and
$\mathcal {F}_1$
and
![]() $\mathcal {F}_2$
are two foliations which are transverse to each other everywhere, then their intersection forms a subfoliation of each of them. This article aims to study geometric properties of leaves of subfoliations inside the leaves of the super foliation.
$\mathcal {F}_2$
are two foliations which are transverse to each other everywhere, then their intersection forms a subfoliation of each of them. This article aims to study geometric properties of leaves of subfoliations inside the leaves of the super foliation.
One very common and extremely important example is the following: let
![]() $\Phi $
be an Anosov flow and let
$\Phi $
be an Anosov flow and let
![]() $\mathcal {F}^{ws}, \mathcal {F}^{wu}$
be the weak stable and weak unstable foliations of
$\mathcal {F}^{ws}, \mathcal {F}^{wu}$
be the weak stable and weak unstable foliations of
![]() $\Phi $
respectively [Reference AnosovAno63, Reference Katok and HasselblattKH95]. Then
$\Phi $
respectively [Reference AnosovAno63, Reference Katok and HasselblattKH95]. Then
![]() $\mathcal {F}^{ws}, \mathcal {F}^{wu}$
are transverse to each other—the intersection is the foliation by flow lines of
$\mathcal {F}^{ws}, \mathcal {F}^{wu}$
are transverse to each other—the intersection is the foliation by flow lines of
![]() $\Phi $
which is a subfoliation of each of them. This example has connections with geometry or large-scale geometry: the leaves of
$\Phi $
which is a subfoliation of each of them. This example has connections with geometry or large-scale geometry: the leaves of
![]() $\mathcal {F}^{ws}, \mathcal {F}^{wu}$
are Gromov hyperbolic. In rough terms, this means that they are negatively curved. The subfoliation by flow lines in, say,
$\mathcal {F}^{ws}, \mathcal {F}^{wu}$
are Gromov hyperbolic. In rough terms, this means that they are negatively curved. The subfoliation by flow lines in, say,
![]() $\mathcal {F}^{ws}$
satisfies an additional strong geometric property: in each leaf of
$\mathcal {F}^{ws}$
satisfies an additional strong geometric property: in each leaf of
![]() $\mathcal {F}^{ws}$
, the flow lines are quasigeodesics. This means that when lifted to the universal cover of the leaves, the flow lines are uniformly efficient up to a bounded multiplicative distortion in measuring length in the weak stable leaves. In other words, the flow lines are quasi-isometrically embedded in these weak stable leaves. The quasigeodesic property has many important consequences, for example, the flow lines are within a bounded distance from length minimizing geodesics when lifted to the universal cover of their respective weak stable leaves [Reference GromovGro87, Reference ThurstonThu82, Reference ThurstonThu97]. Hence the flow lines have well-defined distinct ideal points in the Gromov boundary of the weak stable leaves in both directions. These properties and others are very strong and useful in many contexts. Obviously, this also works for the flow subfoliation of the weak unstable foliation.
$\mathcal {F}^{ws}$
, the flow lines are quasigeodesics. This means that when lifted to the universal cover of the leaves, the flow lines are uniformly efficient up to a bounded multiplicative distortion in measuring length in the weak stable leaves. In other words, the flow lines are quasi-isometrically embedded in these weak stable leaves. The quasigeodesic property has many important consequences, for example, the flow lines are within a bounded distance from length minimizing geodesics when lifted to the universal cover of their respective weak stable leaves [Reference GromovGro87, Reference ThurstonThu82, Reference ThurstonThu97]. Hence the flow lines have well-defined distinct ideal points in the Gromov boundary of the weak stable leaves in both directions. These properties and others are very strong and useful in many contexts. Obviously, this also works for the flow subfoliation of the weak unstable foliation.
A (one-dimensional) subfoliation made of quasigeodesics in the leaves of a super foliation by Gromov hyperbolic leaves is called a leafwise quasigeodesic foliation.
The Anosov case has an additional geometric property: in (say) a weak stable leaf, all flow lines are forward asymptotic, which is a defining property of the weak stable foliation. In particular, all flow lines in a given weak stable leaf have the same forward ideal point in the ideal boundary of the weak stable leaf (when lifted to the universal cover).
When all leaves of a leafwise quasigeodesic subfoliation in a leaf of the super foliation have a common ideal point, we call that leaf a funnel leaf. If all leaves of the super foliation are funnel leaves, then the leafwise quasigeodesic foliation is said to have the funnel property.
The motivation for this article is the following question: is the funnel property an additional property or is it a consequence of the leafwise quasigeodesic property? The importance of this is the following: in dimension three, we have a much stronger connection between some of these properties as follows. Suppose that
![]() $\mathcal {G}$
is a leafwise quasigeodesic foliation (which is a one-dimensional subfoliation of a two-dimensional foliation) which has the funnel property. The ambient manifold is three-dimensional. Suppose that the foliation
$\mathcal {G}$
is a leafwise quasigeodesic foliation (which is a one-dimensional subfoliation of a two-dimensional foliation) which has the funnel property. The ambient manifold is three-dimensional. Suppose that the foliation
![]() $\mathcal {G}$
is orientable or, in other words, it is the foliation of a non-singular flow. Then one can prove that the flow in question is expansive. (We refer to [Reference Barthelmé, Fenley and PotrieBFP20] for definitions of the terms used here and for detailed proofs.) This implies that the flow is a topological Anosov flow [Reference Inaba and MatsumotoIM90, Theorem 15], [Reference PaternainPat93, Lemma 7]. If the flow is transitive (the union of periodic orbits is dense), then the topological Anosov flow is in addition orbitally equivalent to a (smooth) Anosov flow [Reference ShannonSha20]. This means that if the leafwise quasigeodesic property implies the funnel property, then this purely geometric condition implies a very strong dynamical systems property: the foliation is the flow foliation of an Anosov flow, up to topological equivalence.
$\mathcal {G}$
is orientable or, in other words, it is the foliation of a non-singular flow. Then one can prove that the flow in question is expansive. (We refer to [Reference Barthelmé, Fenley and PotrieBFP20] for definitions of the terms used here and for detailed proofs.) This implies that the flow is a topological Anosov flow [Reference Inaba and MatsumotoIM90, Theorem 15], [Reference PaternainPat93, Lemma 7]. If the flow is transitive (the union of periodic orbits is dense), then the topological Anosov flow is in addition orbitally equivalent to a (smooth) Anosov flow [Reference ShannonSha20]. This means that if the leafwise quasigeodesic property implies the funnel property, then this purely geometric condition implies a very strong dynamical systems property: the foliation is the flow foliation of an Anosov flow, up to topological equivalence.
In this article, we prove that the funnel property is not a consequence of leafwise quasigeodesic behavior.
Theorem 1.1. There are examples of leafwise quasigeodesic foliations in dimension three which do not have the funnel property. In these examples, the two-dimensional foliations are
![]() $C^0$
with
$C^0$
with
![]() $C^1$
leaves and the subfoliation is by
$C^1$
leaves and the subfoliation is by
![]() $C^1$
curves in the two-dimensional leaves.
$C^1$
curves in the two-dimensional leaves.
We now briefly explain one class of examples: start with the Franks–Williams example of a non-transitive Anosov flow
![]() $\Phi $
. This is obtained as follows: start with a suspension Anosov flow and do a DA (derived from Anosov) blow up of a periodic orbit transforming it into (say) a repelling orbit
$\Phi $
. This is obtained as follows: start with a suspension Anosov flow and do a DA (derived from Anosov) blow up of a periodic orbit transforming it into (say) a repelling orbit
![]() $\alpha $
. Remove a tubular neighborhood of
$\alpha $
. Remove a tubular neighborhood of
![]() $\alpha $
so that the resulting semiflow is incoming in the complement of the removed tubular neighborhood of
$\alpha $
so that the resulting semiflow is incoming in the complement of the removed tubular neighborhood of
![]() $\alpha $
. Glue this manifold with boundary with a copy of it which has a reversed flow. One fundamental result is that the ensuing flow
$\alpha $
. Glue this manifold with boundary with a copy of it which has a reversed flow. One fundamental result is that the ensuing flow
![]() $\Phi $
in the final manifold
$\Phi $
in the final manifold
![]() $\mathcal {M}$
is Anosov [Reference Béguin, Bonatti and YuBBY17, Reference Franks and WilliamsFW80]. This holds for certain isotopy classes of gluings and certain gluing maps satisfying transversality conditions. These were the first examples of non-transitive Anosov flows in dimension three. Our examples use this flow. There is a smooth torus T in
$\mathcal {M}$
is Anosov [Reference Béguin, Bonatti and YuBBY17, Reference Franks and WilliamsFW80]. This holds for certain isotopy classes of gluings and certain gluing maps satisfying transversality conditions. These were the first examples of non-transitive Anosov flows in dimension three. Our examples use this flow. There is a smooth torus T in
![]() $\mathcal {M}$
transverse to the flow. There is a single two-dimensional attractor and a single two-dimensional repeller of the flow
$\mathcal {M}$
transverse to the flow. There is a single two-dimensional attractor and a single two-dimensional repeller of the flow
![]() $\Phi $
in M. Start with a one-dimensional foliation Z in T which is transverse to the intersections of both the weak stable and the weak unstable foliations of
$\Phi $
in M. Start with a one-dimensional foliation Z in T which is transverse to the intersections of both the weak stable and the weak unstable foliations of
![]() $\Phi $
with T. Saturate Z by the flow producing a collection of two-dimensional sets embedded in
$\Phi $
with T. Saturate Z by the flow producing a collection of two-dimensional sets embedded in
![]() $\mathcal {M}$
. The flow saturation of T is an open subset V of M, and the collection of the two-dimensional subsets described is a two-dimensional foliation in V. In addition, V is exactly the complement of the union of the attractor and the repeller of
$\mathcal {M}$
. The flow saturation of T is an open subset V of M, and the collection of the two-dimensional subsets described is a two-dimensional foliation in V. In addition, V is exactly the complement of the union of the attractor and the repeller of
![]() $\Phi $
. Complete the foliation in V to a foliation
$\Phi $
. Complete the foliation in V to a foliation
![]() $\mathcal {F}$
in
$\mathcal {F}$
in
![]() $\mathcal {M}$
which is the weak unstable foliation of
$\mathcal {M}$
which is the weak unstable foliation of
![]() $\Phi $
in the attractor of
$\Phi $
in the attractor of
![]() $\Phi $
and the weak stable foliation in the repeller of
$\Phi $
and the weak stable foliation in the repeller of
![]() $\Phi $
. The proof that this is in fact a foliation of
$\Phi $
. The proof that this is in fact a foliation of
![]() $\mathcal {M}$
depends on a careful choice of the one-dimensional foliation Z in T. There is a subtle point here in that if one chooses an arbitrary foliation Z in T, then when lifting to
$\mathcal {M}$
depends on a careful choice of the one-dimensional foliation Z in T. There is a subtle point here in that if one chooses an arbitrary foliation Z in T, then when lifting to
![]() $\widetilde {\mathcal {M}}$
, the lifted sets may not be properly embedded in
$\widetilde {\mathcal {M}}$
, the lifted sets may not be properly embedded in
![]() $\widetilde {\mathcal {M}}$
and so
$\widetilde {\mathcal {M}}$
and so
![]() $\mathcal {F}$
would not be a foliation in
$\mathcal {F}$
would not be a foliation in
![]() $\mathcal {M}$
. This is carefully analyzed in §3 and there we prove that for appropriate choices of Z, the object
$\mathcal {M}$
. This is carefully analyzed in §3 and there we prove that for appropriate choices of Z, the object
![]() $\mathcal {F}$
we construct is a foliation. The super foliation is this two-dimensional foliation
$\mathcal {F}$
we construct is a foliation. The super foliation is this two-dimensional foliation
![]() $\mathcal {F}$
. The subfoliation
$\mathcal {F}$
. The subfoliation
![]() $\mathcal {G}$
of
$\mathcal {G}$
of
![]() $\mathcal {F}$
is the foliation by flow lines of
$\mathcal {F}$
is the foliation by flow lines of
![]() $\Phi $
. Each leaf of
$\Phi $
. Each leaf of
![]() $\mathcal {F}$
is saturated by flow lines. We prove that
$\mathcal {F}$
is saturated by flow lines. We prove that
![]() $\mathcal {G}$
is a leafwise quasigeodesic subfoliation of
$\mathcal {G}$
is a leafwise quasigeodesic subfoliation of
![]() $\mathcal {F}$
, but
$\mathcal {F}$
, but
![]() $\mathcal {G}$
does not have the funnel property. There is an Anosov flow
$\mathcal {G}$
does not have the funnel property. There is an Anosov flow
![]() $\Phi $
in this example; however, notice that the super foliation
$\Phi $
in this example; however, notice that the super foliation
![]() $\mathcal {F}$
is neither the weak stable nor the weak unstable foliation of
$\mathcal {F}$
is neither the weak stable nor the weak unstable foliation of
![]() $\Phi $
, but rather a different foliation. In fact in the same way, one can construct an infinite number of inequivalent examples with the same starting flow
$\Phi $
, but rather a different foliation. In fact in the same way, one can construct an infinite number of inequivalent examples with the same starting flow
![]() $\Phi $
. The foliations are pairwise distinguished because of how they intersect the torus T in foliations which are not equivalent.
$\Phi $
. The foliations are pairwise distinguished because of how they intersect the torus T in foliations which are not equivalent.
In this article, we consider more general examples. We prove that one can construct examples starting with any non-transitive Anosov flow
![]() $\Phi $
in dimension three so that all the basic sets have dimension two. As in the case of the Franks–Williams example, we construct super foliations which have Gromov hyperbolic leaves and whose leaves are saturated by flow lines of
$\Phi $
in dimension three so that all the basic sets have dimension two. As in the case of the Franks–Williams example, we construct super foliations which have Gromov hyperbolic leaves and whose leaves are saturated by flow lines of
![]() $\Phi $
. We show that the subfoliation
$\Phi $
. We show that the subfoliation
![]() $\mathcal {G}$
by flow lines of
$\mathcal {G}$
by flow lines of
![]() $\Phi $
is by quasigeodesics in each leaf of the super foliation
$\Phi $
is by quasigeodesics in each leaf of the super foliation
![]() $\mathcal {F}$
. This is the hardest step to prove. This involves a very careful analysis of the geometry in these examples. The proof that
$\mathcal {F}$
. This is the hardest step to prove. This involves a very careful analysis of the geometry in these examples. The proof that
![]() $\mathcal {G}$
is not funnel is simpler than proving it is leafwise quasigeodesic as a subfoliation of
$\mathcal {G}$
is not funnel is simpler than proving it is leafwise quasigeodesic as a subfoliation of
![]() $\mathcal {F}$
.
$\mathcal {F}$
.
In the course of the proof of Theorem 1.1, we prove another independent result which can be used in other contexts. In Definition 6.1, we define the notion of continuity properties for a pair of foliations
![]() $(\mathcal {F}, \mathcal {G})$
on
$(\mathcal {F}, \mathcal {G})$
on
![]() $\mathcal {M}$
where
$\mathcal {M}$
where
![]() $\mathcal {F}$
is a two-dimensional foliation sub-foliated by a one-dimensional foliation
$\mathcal {F}$
is a two-dimensional foliation sub-foliated by a one-dimensional foliation
![]() $\mathcal {G}$
. We can show that the continuity property implies leafwise quasigeodisity.
$\mathcal {G}$
. We can show that the continuity property implies leafwise quasigeodisity.
Theorem 1.2. Suppose
![]() $\mathcal {F}$
is a two-dimensional foliation on a 3-manifold
$\mathcal {F}$
is a two-dimensional foliation on a 3-manifold
![]() $\mathcal {M}$
and
$\mathcal {M}$
and
![]() $\mathcal {F}$
is subfoliated by a one-dimensional foliation
$\mathcal {F}$
is subfoliated by a one-dimensional foliation
![]() $\mathcal {G}$
. If the pair
$\mathcal {G}$
. If the pair
![]() $(\mathcal {F},\mathcal {G})$
satisfies the continuity properties as defined in Definition 6.1, then
$(\mathcal {F},\mathcal {G})$
satisfies the continuity properties as defined in Definition 6.1, then
![]() $\mathcal {G}$
is leafwise quasigeodesic on
$\mathcal {G}$
is leafwise quasigeodesic on
![]() $\mathcal {F}$
.
$\mathcal {F}$
.
We finish this introduction mentioning another reason why we analyzed this question: this comes from partially hyperbolic dynamics. Let f be a partially hyperbolic diffeomorphism in a closed
![]() $3$
-manifold M (we refer to [Reference Barthelmé, Fenley and PotrieBFP20] for definitions and properties of partially hyperbolic diffeomorphisms). Under very general orientability conditions, there is a pair of transverse two- dimensional branching foliations (center stable and center unstable foliations) associated with the partially hyperbolic diffeomorphism which intersect in an one-dimensional branching foliation, called the center foliation [Reference Burago and IvanovBI08]. The center foliation subfoliates both the center stable and center unstable foliations. In some situations [Reference Barthelmé, Fenley and PotrieBFP20], it is shown that the center foliation is a leafwise quasigeodesic subfoliation of both the center stable and center unstable foliations. However, in [Reference Barthelmé, Fenley and PotrieBFP20], it is proved that in the partially hyperbolic setting the leafwise quasigeodesic property implies that the center foliation has the funnel property (as a subfoliation of both super foliations). The proof of this also uses dynamical system properties, namely partial hyperbolicity. An open question from the article [Reference Barthelmé, Fenley and PotrieBFP20] was to whether the funnel property could be derived strictly from the leafwise quasigeodesic property in (say) the center stable foliation. In this article, we prove that this is not the case by constructing counterexamples for general foliations.
$3$
-manifold M (we refer to [Reference Barthelmé, Fenley and PotrieBFP20] for definitions and properties of partially hyperbolic diffeomorphisms). Under very general orientability conditions, there is a pair of transverse two- dimensional branching foliations (center stable and center unstable foliations) associated with the partially hyperbolic diffeomorphism which intersect in an one-dimensional branching foliation, called the center foliation [Reference Burago and IvanovBI08]. The center foliation subfoliates both the center stable and center unstable foliations. In some situations [Reference Barthelmé, Fenley and PotrieBFP20], it is shown that the center foliation is a leafwise quasigeodesic subfoliation of both the center stable and center unstable foliations. However, in [Reference Barthelmé, Fenley and PotrieBFP20], it is proved that in the partially hyperbolic setting the leafwise quasigeodesic property implies that the center foliation has the funnel property (as a subfoliation of both super foliations). The proof of this also uses dynamical system properties, namely partial hyperbolicity. An open question from the article [Reference Barthelmé, Fenley and PotrieBFP20] was to whether the funnel property could be derived strictly from the leafwise quasigeodesic property in (say) the center stable foliation. In this article, we prove that this is not the case by constructing counterexamples for general foliations.
2 Preliminaries
A
![]() $C^1$
-flow
$C^1$
-flow
![]() $\Phi _t:\mathcal {M}\rightarrow \mathcal {M}$
on a Riemannian manifold
$\Phi _t:\mathcal {M}\rightarrow \mathcal {M}$
on a Riemannian manifold
![]() $\mathcal {M}$
is
$\mathcal {M}$
is
![]() $Anosov$
if the tangent bundle
$Anosov$
if the tangent bundle
![]() $T\mathcal {M}$
splits into three
$T\mathcal {M}$
splits into three
![]() $D\Phi _{t}$
-invariant sub-bundles
$D\Phi _{t}$
-invariant sub-bundles
![]() $T\mathcal {M}=E^{s}\oplus E^{0} \oplus E^u$
and there exists two constants
$T\mathcal {M}=E^{s}\oplus E^{0} \oplus E^u$
and there exists two constants
![]() $C,\unicode{x3bb}>0$
such that:
$C,\unicode{x3bb}>0$
such that:
-
•
 $E^0$
is generated by the non-zero vector field defined by the flow
$E^0$
is generated by the non-zero vector field defined by the flow
 $\Phi _t$
;
$\Phi _t$
; -
• for any
 $v\in E^s$
and
$v\in E^s$
and
 $t>0$
,
$t>0$
,  $$ \begin{align*}\|D\Phi_{t}(v)\|\leq Ce^{-\unicode{x3bb} t}\|v\|;\end{align*} $$
$$ \begin{align*}\|D\Phi_{t}(v)\|\leq Ce^{-\unicode{x3bb} t}\|v\|;\end{align*} $$
-
• for any
 $w\in E^u$
and
$w\in E^u$
and
 $t>0$
,
$t>0$
,  $$ \begin{align*}\|D\Phi_{t}(w)\|\geq Ce^{\unicode{x3bb} t}\|w\|.\end{align*} $$
$$ \begin{align*}\|D\Phi_{t}(w)\|\geq Ce^{\unicode{x3bb} t}\|w\|.\end{align*} $$
The definition is independent of the choice of the Riemannian metric
![]() $\|.\|$
as the underlying manifold
$\|.\|$
as the underlying manifold
![]() $\mathcal {M}$
is compact. For a point
$\mathcal {M}$
is compact. For a point
![]() $x\in \mathcal {M}$
, the set
$x\in \mathcal {M}$
, the set
![]() $\gamma _x=\{\Phi _t(x)|t\in \mathbb {R}\}$
is called the flow line of x. The collection of all flow lines of a flow defines a one-dimensional foliation on
$\gamma _x=\{\Phi _t(x)|t\in \mathbb {R}\}$
is called the flow line of x. The collection of all flow lines of a flow defines a one-dimensional foliation on
![]() $\mathcal {M}$
. For an Anosov flow, there are several flow invariant foliations associated with the flow and these foliations play a key role in the study of Anosov flows.
$\mathcal {M}$
. For an Anosov flow, there are several flow invariant foliations associated with the flow and these foliations play a key role in the study of Anosov flows.
Property 2.1. [Reference AnosovAno63]
For an Anosov flow
![]() $\Phi _t$
on
$\Phi _t$
on
![]() $\mathcal {M}$
, the distributions
$\mathcal {M}$
, the distributions
![]() $E^u$
,
$E^u$
,
![]() $E^s$
,
$E^s$
,
![]() $E^{0}\oplus E^{u}$
, and
$E^{0}\oplus E^{u}$
, and
![]() $E^{0}\oplus E^{s}$
are uniquely integrable. The associated foliations are denoted by
$E^{0}\oplus E^{s}$
are uniquely integrable. The associated foliations are denoted by
![]() $\mathcal {F}^u$
,
$\mathcal {F}^u$
,
![]() $\mathcal {F}^s$
,
$\mathcal {F}^s$
,
![]() $\mathcal {F}^{wu}$
, and
$\mathcal {F}^{wu}$
, and
![]() $\mathcal {F}^{ws}$
respectively and they are called the strong unstable, strong stable, weak unstable, and weak stable foliation on
$\mathcal {F}^{ws}$
respectively and they are called the strong unstable, strong stable, weak unstable, and weak stable foliation on
![]() $\mathcal {M}$
.
$\mathcal {M}$
.
For the remainder of this article, we will assume that
![]() $\mathcal {M}$
is a closed three-dimensional Riemannian manifold.
$\mathcal {M}$
is a closed three-dimensional Riemannian manifold.
We also assume that
![]() $\mathcal {M}$
is equipped with an Anosov flow
$\mathcal {M}$
is equipped with an Anosov flow
![]() $\Phi _t$
and
$\Phi _t$
and
![]() $\widetilde {\Phi }_t$
is the lift of the flow
$\widetilde {\Phi }_t$
is the lift of the flow
![]() $\Phi _t$
in
$\Phi _t$
in
![]() $\widetilde {\mathcal {M}}$
, the universal cover of
$\widetilde {\mathcal {M}}$
, the universal cover of
![]() $\mathcal {M}$
. The strong unstable, strong stable, weak unstable, and weak stable foliations of
$\mathcal {M}$
. The strong unstable, strong stable, weak unstable, and weak stable foliations of
![]() $\widetilde {\Phi }$
are the lifts of the foliations
$\widetilde {\Phi }$
are the lifts of the foliations
![]() $\mathcal {F}^u$
,
$\mathcal {F}^u$
,
![]() $\mathcal {F}^s$
,
$\mathcal {F}^s$
,
![]() $\mathcal {F}^{wu}$
, and
$\mathcal {F}^{wu}$
, and
![]() $\mathcal {F}^{ws}$
in the universal cover
$\mathcal {F}^{ws}$
in the universal cover
![]() $\widetilde {\mathcal {M}}$
, and these foliations in
$\widetilde {\mathcal {M}}$
, and these foliations in
![]() $\widetilde {\mathcal {M}}$
are denoted by
$\widetilde {\mathcal {M}}$
are denoted by
![]() $\widetilde {\mathcal {F}}^u$
,
$\widetilde {\mathcal {F}}^u$
,
![]() $\widetilde {\mathcal {F}}^s$
,
$\widetilde {\mathcal {F}}^s$
,
![]() $\widetilde {\mathcal {F}}^{wu}$
, and
$\widetilde {\mathcal {F}}^{wu}$
, and
![]() $\widetilde {\mathcal {F}}^{ws}$
respectively.
$\widetilde {\mathcal {F}}^{ws}$
respectively.
A map
![]() $f:(X_1,d_1)\rightarrow (X_2,d_2)$
is called a
$f:(X_1,d_1)\rightarrow (X_2,d_2)$
is called a
![]() $(K,s)$
-quasi-isometric embedding if there exits
$(K,s)$
-quasi-isometric embedding if there exits
![]() $K>1$
and
$K>1$
and
![]() $s>0$
such that for all
$s>0$
such that for all
![]() $x,y\in X_1$
,
$x,y\in X_1$
,
A
![]() $(K,s)$
-quasigeodesic in X is the image of a
$(K,s)$
-quasigeodesic in X is the image of a
![]() $(K,s)$
-quasi-isometric embedding
$(K,s)$
-quasi-isometric embedding
![]() $\gamma :[a,b]\rightarrow X$
, where
$\gamma :[a,b]\rightarrow X$
, where
![]() $[a,b]$
is a closed interval on
$[a,b]$
is a closed interval on
![]() $\mathbb {R}$
with the Euclidean metric. The interval could be infinite (that is,
$\mathbb {R}$
with the Euclidean metric. The interval could be infinite (that is,
![]() $a = -\infty $
,
$a = -\infty $
,
![]() $b = \infty $
, or both), in which case the notation would be of a half open or open interval. If we have a map
$b = \infty $
, or both), in which case the notation would be of a half open or open interval. If we have a map
![]() $\mathbb {R} \rightarrow X$
with rectifiable image, we consider the arclength metric in the domain
$\mathbb {R} \rightarrow X$
with rectifiable image, we consider the arclength metric in the domain
![]() $\mathbb {R}$
.
$\mathbb {R}$
.
Lemma 2.2. Flow lines on the leaves in
![]() $\widetilde {\mathcal {F}}^{ws}$
and
$\widetilde {\mathcal {F}}^{ws}$
and
![]() $\widetilde {\mathcal {F}}^{wu}$
are quasigeodesics with respect to the induced path metric from
$\widetilde {\mathcal {F}}^{wu}$
are quasigeodesics with respect to the induced path metric from
![]() $\widetilde {\mathcal {M}}$
in their respective leaves.
$\widetilde {\mathcal {M}}$
in their respective leaves.
Proof. Reparameterize the flow to have unit speed. The new flow is still Anosov with the same flow lines and the same weak stable and weak unstable foliations; however, the strong stable and strong unstable leaves may change [Reference AnosovAno63, Reference Anosov and SinaıAS67].
Any leaf L of
![]() $\widetilde {\mathcal {F}}^{wu}$
is subfoliated by
$\widetilde {\mathcal {F}}^{wu}$
is subfoliated by
![]() $\widetilde {\mathcal {F}}^{u}$
and by the flow lines, these two foliations are transversal to each other. We can define a metric
$\widetilde {\mathcal {F}}^{u}$
and by the flow lines, these two foliations are transversal to each other. We can define a metric
![]() $ds'$
on L by
$ds'$
on L by
![]() $ds'=dw+dy$
, where
$ds'=dw+dy$
, where
![]() $dw$
measures length along flow lines and
$dw$
measures length along flow lines and
![]() $dy$
measures length along unstable curves. Suppose
$dy$
measures length along unstable curves. Suppose
![]() $ds$
is the Riemannian metric induced on
$ds$
is the Riemannian metric induced on
![]() $L^{wu}$
from
$L^{wu}$
from
![]() $\widetilde {\mathcal {M}}$
. The two path metrics induced in L from
$\widetilde {\mathcal {M}}$
. The two path metrics induced in L from
![]() $ds'$
and
$ds'$
and
![]() $ds$
are uniformly quasi-isometric to each other [Reference FenleyFen94]. Moreover, each flow line in the leaf L is a length-minimizing curve in the
$ds$
are uniformly quasi-isometric to each other [Reference FenleyFen94]. Moreover, each flow line in the leaf L is a length-minimizing curve in the
![]() $ds'$
metric, and hence flow lines are uniform quasigeodesics with respect to the metric induced by
$ds'$
metric, and hence flow lines are uniform quasigeodesics with respect to the metric induced by
![]() $ds$
. Similarly, it can be shown that flow lines on leaves in
$ds$
. Similarly, it can be shown that flow lines on leaves in
![]() $\widetilde {\mathcal {F}}^{ws}$
are quasigeodesic with respect to the induced metric on their respective leaves.
$\widetilde {\mathcal {F}}^{ws}$
are quasigeodesic with respect to the induced metric on their respective leaves.
Definition 2.3. Suppose
![]() $\mathcal {F}$
is a two-dimensional foliation on
$\mathcal {F}$
is a two-dimensional foliation on
![]() $\mathcal {M}$
with Gromov hyperbolic leaves when lifted to the universal cover. Suppose that
$\mathcal {M}$
with Gromov hyperbolic leaves when lifted to the universal cover. Suppose that
![]() $\mathcal {G}$
is a one-dimensional foliation on
$\mathcal {G}$
is a one-dimensional foliation on
![]() $\mathcal {M}$
which subfoliates
$\mathcal {M}$
which subfoliates
![]() $\mathcal {F}$
. In this situation, we say that leaves of
$\mathcal {F}$
. In this situation, we say that leaves of
![]() $\mathcal {G}$
are leafwise quasigeodesic in
$\mathcal {G}$
are leafwise quasigeodesic in
![]() $\mathcal {F}$
if every leaf of
$\mathcal {F}$
if every leaf of
![]() $\mathcal {G}$
is a quasigeodesic in the respective leaf of
$\mathcal {G}$
is a quasigeodesic in the respective leaf of
![]() $\mathcal {F}$
containing it when lifted to the universal cover of the leaf. In that case, we say that
$\mathcal {F}$
containing it when lifted to the universal cover of the leaf. In that case, we say that
![]() $\mathcal {G}$
is a leafwise quasigeodesic subfoliation of
$\mathcal {G}$
is a leafwise quasigeodesic subfoliation of
![]() $\mathcal {F}$
.
$\mathcal {F}$
.
In Lemma 2.2, the flow lines of
![]() $\Phi _t$
are shown to be leafwise quasigeodesics in the leaves of
$\Phi _t$
are shown to be leafwise quasigeodesics in the leaves of
![]() $\mathcal {F}^{ws}$
and
$\mathcal {F}^{ws}$
and
![]() $\mathcal {F}^{wu}$
.
$\mathcal {F}^{wu}$
.
The leaves in
![]() $\widetilde {\mathcal {F}}^{ws}$
and
$\widetilde {\mathcal {F}}^{ws}$
and
![]() $\widetilde {\mathcal {F}}^{wu}$
are Gromov hyperbolic with respect to the Riemannian metric on the leaves induced from the metric on
$\widetilde {\mathcal {F}}^{wu}$
are Gromov hyperbolic with respect to the Riemannian metric on the leaves induced from the metric on
![]() $\widetilde {\mathcal {M}}$
[Reference FenleyFen94]. Suppose that L is a leaf either in
$\widetilde {\mathcal {M}}$
[Reference FenleyFen94]. Suppose that L is a leaf either in
![]() $\widetilde {\mathcal {F}}^{ws}$
or in
$\widetilde {\mathcal {F}}^{ws}$
or in
![]() $\widetilde {\mathcal {F}}^{wu}$
. As the leaves are Gromov hyperbolic, we can define the ideal boundary of L which is homeomorphic to the circle and we denote it as
$\widetilde {\mathcal {F}}^{wu}$
. As the leaves are Gromov hyperbolic, we can define the ideal boundary of L which is homeomorphic to the circle and we denote it as
![]() $S^1(L)$
. The compactification
$S^1(L)$
. The compactification
![]() $L \cup S^1(L)$
is homeomorphic to a closed disk. As the flow lines are quasigeodesics in L, they define two distinct ideal points on
$L \cup S^1(L)$
is homeomorphic to a closed disk. As the flow lines are quasigeodesics in L, they define two distinct ideal points on
![]() $S^1(L)$
: if
$S^1(L)$
: if
![]() $\gamma $
is a flow line in L, then the forward ray of
$\gamma $
is a flow line in L, then the forward ray of
![]() $\gamma $
defines an unique ideal point on
$\gamma $
defines an unique ideal point on
![]() $S^1(L)$
as
$S^1(L)$
as
![]() $\gamma $
is a quasigeodesic, which is called the forward or positive ideal point of
$\gamma $
is a quasigeodesic, which is called the forward or positive ideal point of
![]() $\gamma $
. Similarly, we define the backward or negative ideal point as the limit of the ray in the backward direction. The following statement describes the equivalence between the forward and backward flow rays in the leaves of
$\gamma $
. Similarly, we define the backward or negative ideal point as the limit of the ray in the backward direction. The following statement describes the equivalence between the forward and backward flow rays in the leaves of
![]() $\widetilde {\mathcal {F}}^{ws}$
and
$\widetilde {\mathcal {F}}^{ws}$
and
![]() $\widetilde {\mathcal {F}}^{wu}$
, and the points on their ideal boundaries.
$\widetilde {\mathcal {F}}^{wu}$
, and the points on their ideal boundaries.
Property 2.4. [Reference FenleyFen94]
For a leaf L either in
![]() $\widetilde {\mathcal {F}}^{ws}$
or
$\widetilde {\mathcal {F}}^{ws}$
or
![]() $\widetilde {\mathcal {F}}^{wu}$
, all the points on
$\widetilde {\mathcal {F}}^{wu}$
, all the points on
![]() $S^1(L)$
correspond to forward or backward flow rays on L. If
$S^1(L)$
correspond to forward or backward flow rays on L. If
![]() $L\in \widetilde {\mathcal {F}}^{ws}$
, then all the flow lines on L have a common forward ideal point and all the other ideal points are backward ideal points on
$L\in \widetilde {\mathcal {F}}^{ws}$
, then all the flow lines on L have a common forward ideal point and all the other ideal points are backward ideal points on
![]() $S^1(L)$
of the flow lines. No two different flow lines define a common negative or backward ideal point.
$S^1(L)$
of the flow lines. No two different flow lines define a common negative or backward ideal point.
If
![]() $L\in \widetilde {\mathcal {F}}^{wu}$
, then all the flow lines have a common backward ideal point and all the forward flow lines define all the other ideal points on
$L\in \widetilde {\mathcal {F}}^{wu}$
, then all the flow lines have a common backward ideal point and all the forward flow lines define all the other ideal points on
![]() $S^1(L)$
. No two different flow lines define the same positive or forward ideal point.
$S^1(L)$
. No two different flow lines define the same positive or forward ideal point.
The property for forward ideal points in
![]() $\widetilde {\mathcal {F}}^{ws}$
is immediate as these flow lines are forward asymptotic, a direct consequence of the definitions. The property for backward ideal points in leaves of
$\widetilde {\mathcal {F}}^{ws}$
is immediate as these flow lines are forward asymptotic, a direct consequence of the definitions. The property for backward ideal points in leaves of
![]() $\widetilde {\mathcal {F}}^{ws}$
is not as immediate and is proved in [Reference FenleyFen94].
$\widetilde {\mathcal {F}}^{ws}$
is not as immediate and is proved in [Reference FenleyFen94].
Definition 2.5. Suppose that
![]() $\mathcal {G}$
is a leafwise quasigeodesic subfoliation of
$\mathcal {G}$
is a leafwise quasigeodesic subfoliation of
![]() $\mathcal {F}$
. If a leaf L of
$\mathcal {F}$
. If a leaf L of
![]() $\widetilde {\mathcal {F}}$
has all leaves of
$\widetilde {\mathcal {F}}$
has all leaves of
![]() $\widetilde {\mathcal {G}}$
in it sharing a common ideal point, then the projected leaf
$\widetilde {\mathcal {G}}$
in it sharing a common ideal point, then the projected leaf
![]() $\pi (L)$
of
$\pi (L)$
of
![]() $\mathcal {F}$
in
$\mathcal {F}$
in
![]() $\mathcal {M}$
is called a funnel leaf. In this case, the common ideal point shared by all the flow lines in L is called the funnel point of L.
$\mathcal {M}$
is called a funnel leaf. In this case, the common ideal point shared by all the flow lines in L is called the funnel point of L.
Corollary 2.6. By Property 2.4, for an Anosov flow
![]() $\Phi _t$
on a 3-manifold
$\Phi _t$
on a 3-manifold
![]() $\mathcal {M}$
, with the flow foliation a leafwise quasigeodesic subfoliaton of both
$\mathcal {M}$
, with the flow foliation a leafwise quasigeodesic subfoliaton of both
![]() $\mathcal {F}^{ws}$
and
$\mathcal {F}^{ws}$
and
![]() $\mathcal {F}^{wu}$
, the following happens: all the leaves in weak stable foliation
$\mathcal {F}^{wu}$
, the following happens: all the leaves in weak stable foliation
![]() $\mathcal {F}^{ws}$
and weak unstable foliation
$\mathcal {F}^{ws}$
and weak unstable foliation
![]() $\mathcal {F}^{wu}$
are funnel leaves, as shown in Figure 1.
$\mathcal {F}^{wu}$
are funnel leaves, as shown in Figure 1.

Figure 1 Geometry of flow lines on the leaves in
![]() $\widetilde {\mathcal {F}}^{\,wu}$
(a) and
$\widetilde {\mathcal {F}}^{\,wu}$
(a) and
![]() $\widetilde {\mathcal {F}}^{\,ws}$
(b).
$\widetilde {\mathcal {F}}^{\,ws}$
(b).
2.1 Basic sets of Anosov flows on 3-manifolds
The Anosov flow
![]() $\Phi $
is called
$\Phi $
is called
![]() $\textit{transitive}$
if there exists a flow line
$\textit{transitive}$
if there exists a flow line
![]() $\gamma $
dense in
$\gamma $
dense in
![]() $\mathcal {M}$
, otherwise the flow is non-transitive. The first example of a non-transitive Anosov flow was constructed by John Franks and Bob Williams in their 1980’s article [Reference Franks and WilliamsFW80].
$\mathcal {M}$
, otherwise the flow is non-transitive. The first example of a non-transitive Anosov flow was constructed by John Franks and Bob Williams in their 1980’s article [Reference Franks and WilliamsFW80].
A point
![]() $x\in \mathcal {M}$
is called non-wandering if for any open neighborhood U of x and any
$x\in \mathcal {M}$
is called non-wandering if for any open neighborhood U of x and any
![]() $t_0> 0$
, there exists
$t_0> 0$
, there exists
![]() $t> t_0$
such that
$t> t_0$
such that
![]() $\Phi _{t}(U)\cap U\neq \emptyset $
, the set of all non-wandering points is denoted by
$\Phi _{t}(U)\cap U\neq \emptyset $
, the set of all non-wandering points is denoted by
![]() $\Omega (\Phi )$
. For a non-transitive Anosov flow
$\Omega (\Phi )$
. For a non-transitive Anosov flow
![]() $\Phi _t$
, the non-wandering set
$\Phi _t$
, the non-wandering set
![]() $\Omega (\Phi )$
is not equal to the whole manifold
$\Omega (\Phi )$
is not equal to the whole manifold
![]() $\mathcal {M}$
and according to spectral decomposition theorem [Reference SmaleSma67],
$\mathcal {M}$
and according to spectral decomposition theorem [Reference SmaleSma67],
![]() $\Omega (\Phi )$
is decomposed into finitely many closed, disjoint,
$\Omega (\Phi )$
is decomposed into finitely many closed, disjoint,
![]() $\Phi _t$
-invariant, and transitive
$\Phi _t$
-invariant, and transitive
![]() $basic$
sets
$basic$
sets
![]() $\{ \Lambda _i, i = 1, \ldots , n\}$
, so
$\{ \Lambda _i, i = 1, \ldots , n\}$
, so
![]() $\Omega (\Phi )=\bigsqcup \nolimits _{i=1}^{n} \Lambda _i$
.
$\Omega (\Phi )=\bigsqcup \nolimits _{i=1}^{n} \Lambda _i$
.
Suppose
![]() $\Lambda $
is a basic set of a non-transitive Anosov flow
$\Lambda $
is a basic set of a non-transitive Anosov flow
![]() $\Phi _t$
on a 3-manifold. Then
$\Phi _t$
on a 3-manifold. Then
![]() $\Lambda $
can be characterized into four different types [Reference BrunellaBru93, Reference SmaleSma67]:
$\Lambda $
can be characterized into four different types [Reference BrunellaBru93, Reference SmaleSma67]:
-
•
 $\mathrm{dim}(\Lambda )=2$
, and the basic set
$\mathrm{dim}(\Lambda )=2$
, and the basic set
 $\Lambda $
is an attractor, i.e. there exists an open set U containing
$\Lambda $
is an attractor, i.e. there exists an open set U containing
 $\Lambda $
such that
$\Lambda $
such that
 $\bigcap \nolimits _{t>0}\Phi _t(U)=\Lambda $
;
$\bigcap \nolimits _{t>0}\Phi _t(U)=\Lambda $
; -
•
 $\mathrm{dim}(\Lambda )=2$
, and the basic set
$\mathrm{dim}(\Lambda )=2$
, and the basic set
 $\Lambda $
is a repeller, i.e
$\Lambda $
is a repeller, i.e
 $\Lambda $
is an attractor for the reversed flow
$\Lambda $
is an attractor for the reversed flow
 $\Psi _t=\Phi _{-t}$
;
$\Psi _t=\Phi _{-t}$
; -
•
 $\mathrm{dim}(\Lambda )=1$
, and
$\mathrm{dim}(\Lambda )=1$
, and
 $\Lambda $
is a saddle with local cross section a Cantor set;
$\Lambda $
is a saddle with local cross section a Cantor set; -
•
 $\mathrm{dim}(\Lambda )=1$
, and
$\mathrm{dim}(\Lambda )=1$
, and
 $\unicode{x3bb} $
is a hyperbolic periodic orbit.
$\unicode{x3bb} $
is a hyperbolic periodic orbit.
Property 2.7. If
![]() $\Lambda $
is an
$\Lambda $
is an
![]() $\textit{attractor}$
, then
$\textit{attractor}$
, then
![]() $\Lambda $
is saturated by weak unstable leaves. If
$\Lambda $
is saturated by weak unstable leaves. If
![]() $\Lambda $
is a
$\Lambda $
is a
![]() $\textit{repeller}$
, then
$\textit{repeller}$
, then
![]() $\Lambda $
is saturated by weak stable leaves.
$\Lambda $
is saturated by weak stable leaves.
From now on we assume the following.
Assumption 2.8. We assume throughout that the Anosov flow
![]() $\Phi $
on
$\Phi $
on
![]() $\mathcal {M}$
is non-transitive and its non-wandering set
$\mathcal {M}$
is non-transitive and its non-wandering set
![]() $\Omega $
consists of two-dimensional basic sets only.
$\Omega $
consists of two-dimensional basic sets only.
In other words, we assume that
![]() $\Phi $
has no one-dimensional basic set. As
$\Phi $
has no one-dimensional basic set. As
![]() $\mathcal {M}$
is compact, there exits at least one attracting basic set and one repelling basic set. Suppose
$\mathcal {M}$
is compact, there exits at least one attracting basic set and one repelling basic set. Suppose
![]() $\mathcal {A}$
denotes the union of all attracting basic sets and
$\mathcal {A}$
denotes the union of all attracting basic sets and
![]() $\mathcal {R}$
denotes the the union of all repelling basic sets. We will denote the collection of all lifts of
$\mathcal {R}$
denotes the the union of all repelling basic sets. We will denote the collection of all lifts of
![]() $\mathcal {A}$
in
$\mathcal {A}$
in
![]() $\widetilde {\mathcal {M}}$
by
$\widetilde {\mathcal {M}}$
by
![]() $\widetilde {\mathcal {A}}$
. Here,
$\widetilde {\mathcal {A}}$
. Here,
![]() $\widetilde {\mathcal {A}}$
is the the attracting set for
$\widetilde {\mathcal {A}}$
is the the attracting set for
![]() $\widetilde {\Phi }_{t}$
defined on
$\widetilde {\Phi }_{t}$
defined on
![]() $\widetilde {\mathcal {M}}$
. The union of all lifts of
$\widetilde {\mathcal {M}}$
. The union of all lifts of
![]() $\mathcal {R}$
is denoted by
$\mathcal {R}$
is denoted by
![]() $\widetilde {\mathcal {R}}$
similarly.
$\widetilde {\mathcal {R}}$
similarly.
Property 2.9. [Reference Katok and HasselblattKH95]
Suppose
![]() $\gamma $
is a flow line not contained in
$\gamma $
is a flow line not contained in
![]() $\mathcal {A}$
or
$\mathcal {A}$
or
![]() $\mathcal {R}$
. Then there exists a flow line in
$\mathcal {R}$
. Then there exists a flow line in
![]() $\mathcal {A}$
, say
$\mathcal {A}$
, say
![]() $\alpha $
, such that the forward rays of
$\alpha $
, such that the forward rays of
![]() $\gamma $
and
$\gamma $
and
![]() $\alpha $
are asymptotic in
$\alpha $
are asymptotic in
![]() $\mathcal {M}$
. Similarly, there exits a flow line
$\mathcal {M}$
. Similarly, there exits a flow line
![]() $\beta $
in
$\beta $
in
![]() $\mathcal {R}$
such that the backward rays of
$\mathcal {R}$
such that the backward rays of
![]() $\gamma $
and
$\gamma $
and
![]() $\beta $
are asymptotic in
$\beta $
are asymptotic in
![]() $\mathcal {M}$
.
$\mathcal {M}$
.
Proof. This is classical [Reference Katok and HasselblattKH95], we explain briefly. Given the orbit
![]() $\gamma $
, it gets closer and closer to the attractor
$\gamma $
, it gets closer and closer to the attractor
![]() $\mathcal {A}$
in future time. Fix x in
$\mathcal {A}$
in future time. Fix x in
![]() $\gamma $
. Every point in the attractor has a local product structure, see, for example, Proposition 6.4.21 of [Reference Katok and HasselblattKH95]. Hence for a t sufficiently big,
$\gamma $
. Every point in the attractor has a local product structure, see, for example, Proposition 6.4.21 of [Reference Katok and HasselblattKH95]. Hence for a t sufficiently big,
![]() $\Phi _t(x)$
is
$\Phi _t(x)$
is
![]() $\epsilon $
near the attractor where
$\epsilon $
near the attractor where
![]() $\epsilon $
is smaller than the size of product boxes of the hyperbolic set
$\epsilon $
is smaller than the size of product boxes of the hyperbolic set
![]() $\mathcal {A}$
. Hence,
$\mathcal {A}$
. Hence,
![]() $\Phi _t(x)$
is
$\Phi _t(x)$
is
![]() $\epsilon $
near some point z in
$\epsilon $
near some point z in
![]() $\mathcal {A}$
and there is w in
$\mathcal {A}$
and there is w in
![]() $\mathcal {A}$
near z so that
$\mathcal {A}$
near z so that
![]() $\Phi _t(x)$
is in the stable manifold of w because of the local product structure in sets of size
$\Phi _t(x)$
is in the stable manifold of w because of the local product structure in sets of size
![]() $\epsilon $
. This proves the result.
$\epsilon $
. This proves the result.
The attractor is saturated by leaves of
![]() $\mathcal {F}^{wu}$
and the repeller saturated by leaves of
$\mathcal {F}^{wu}$
and the repeller saturated by leaves of
![]() $\mathcal {F}^{ws}$
. In the property above, one can choose the flow line
$\mathcal {F}^{ws}$
. In the property above, one can choose the flow line
![]() $\alpha $
in the attractor
$\alpha $
in the attractor
![]() $\mathcal {A}$
to be contained in the boundary of the attractor. This means the following: let
$\mathcal {A}$
to be contained in the boundary of the attractor. This means the following: let
![]() $x \in \alpha $
and L the
$x \in \alpha $
and L the
![]() $\mathcal {F}^{ws}$
leaf through x. Let D be a small disk in L with x in the interior. The local flow line of x cuts D into two components
$\mathcal {F}^{ws}$
leaf through x. Let D be a small disk in L with x in the interior. The local flow line of x cuts D into two components
![]() $D_1, D_2$
(which are also disks). The condition is that one of
$D_1, D_2$
(which are also disks). The condition is that one of
![]() $D_1$
or
$D_1$
or
![]() $D_2$
does not intersect the attractor
$D_2$
does not intersect the attractor
![]() $\mathcal {A}$
. Suppose it is
$\mathcal {A}$
. Suppose it is
![]() $D_1$
. The ‘
$D_1$
. The ‘
![]() $D_1$
side’ of
$D_1$
side’ of
![]() $\alpha $
in L is the side so that
$\alpha $
in L is the side so that
![]() $\gamma $
is getting increasingly closer to
$\gamma $
is getting increasingly closer to
![]() $\alpha $
.
$\alpha $
.
3 The foliation
 $\mathcal {F}$
$\mathcal {F}$
Throughout the article, we will fix a non-transitive Anosov flow
![]() $\Phi $
as in the previous section, that is,
$\Phi $
as in the previous section, that is,
![]() $\Phi $
has only two-dimensional basic sets.
$\Phi $
has only two-dimensional basic sets.
To prove our results, we will consider a two-dimensional foliation
![]() $\mathcal {F}$
in
$\mathcal {F}$
in
![]() $\mathcal {M}$
such that:
$\mathcal {M}$
such that:
-
• on the attractor
 $\mathcal {A}$
,
$\mathcal {A}$
,
 $\mathcal {F}|_{\mathcal {A}}=\mathcal {F}^{wu}|_{\mathcal {A}}$
;
$\mathcal {F}|_{\mathcal {A}}=\mathcal {F}^{wu}|_{\mathcal {A}}$
; -
• on the repeller
 $\mathcal {R}$
,
$\mathcal {R}$
,
 $\mathcal {F}|_{\mathcal {R}}=\mathcal {F}^{ws}|_{\mathcal {R}}$
;
$\mathcal {F}|_{\mathcal {R}}=\mathcal {F}^{ws}|_{\mathcal {R}}$
; -
• on
 $\mathcal {M}\setminus \{\mathcal {A}\cup \mathcal {R}\}$
,
$\mathcal {M}\setminus \{\mathcal {A}\cup \mathcal {R}\}$
,
 $\mathcal {F}$
is transversal to both
$\mathcal {F}$
is transversal to both
 $\mathcal {F}^{ws}$
and
$\mathcal {F}^{ws}$
and
 $\mathcal {F}^{wu}$
;
$\mathcal {F}^{wu}$
; -
• every leaf
 $L\in \mathcal {F}$
is subfoliated by the flow lines of
$L\in \mathcal {F}$
is subfoliated by the flow lines of
 $\Phi $
, i.e. every leaf L is
$\Phi $
, i.e. every leaf L is
 $\Phi _{\mathbb {R}}$
-invariant.
$\Phi _{\mathbb {R}}$
-invariant.
We will denote the lift of
![]() $\mathcal {F}$
in the universal cover
$\mathcal {F}$
in the universal cover
![]() $\widetilde {\mathcal {M}}$
by
$\widetilde {\mathcal {M}}$
by
![]() $\widetilde {\mathcal {F}}$
. Leaves of
$\widetilde {\mathcal {F}}$
. Leaves of
![]() $\widetilde {\mathcal {F}}$
in
$\widetilde {\mathcal {F}}$
in
![]() $\widetilde {\mathcal {A}}$
and
$\widetilde {\mathcal {A}}$
and
![]() $\widetilde {\mathcal {R}}$
look like the leaves in Figure 1. Leaves in
$\widetilde {\mathcal {R}}$
look like the leaves in Figure 1. Leaves in
![]() $\widetilde {\mathcal {M}}\setminus (\widetilde {\mathcal {A}}\cup \widetilde {\mathcal {R}})$
are described in Figure 2. It is not immediate from the definition why the leaves not contained in
$\widetilde {\mathcal {M}}\setminus (\widetilde {\mathcal {A}}\cup \widetilde {\mathcal {R}})$
are described in Figure 2. It is not immediate from the definition why the leaves not contained in
![]() $\widetilde {\mathcal {A}}$
and
$\widetilde {\mathcal {A}}$
and
![]() $\widetilde {\mathcal {R}}$
are as described in Figure 2, but we will prove this later in this article.
$\widetilde {\mathcal {R}}$
are as described in Figure 2, but we will prove this later in this article.
Theorem 3.1. There exists foliations
![]() $\mathcal {F}$
with the properties described above.
$\mathcal {F}$
with the properties described above.

Figure 2 An example of a leaf
![]() $L\in \widetilde {\mathcal {F}}$
not contained in
$L\in \widetilde {\mathcal {F}}$
not contained in
![]() $\widetilde {\mathcal {A}}$
or
$\widetilde {\mathcal {A}}$
or
![]() $\widetilde {\mathcal {R}}$
. In
$\widetilde {\mathcal {R}}$
. In
![]() $R_1$
, forward rays are asymptotic to
$R_1$
, forward rays are asymptotic to
![]() $\widetilde {\mathcal {A}}$
; in
$\widetilde {\mathcal {A}}$
; in
![]() $R_3$
, backward rays are asymptotic to
$R_3$
, backward rays are asymptotic to
![]() $\widetilde {\mathcal {R}}$
;
$\widetilde {\mathcal {R}}$
;
![]() $R_2$
, the blue line, represents the intersection of L with some lift
$R_2$
, the blue line, represents the intersection of L with some lift
![]() $\widetilde T_i$
of some torus
$\widetilde T_i$
of some torus
![]() $T_i$
.
$T_i$
.
Start of the proof of Theorem 3.1. We start with an Anosov flow as described above. For simplicity, assume that M is orientable as well. There is a finite collection of disjoint tori
![]() $\{ T_i \}$
transverse to the flow
$\{ T_i \}$
transverse to the flow
![]() $\Phi $
which separate the basic sets [Reference BrunellaBru93, Reference SmaleSma67]. We choose
$\Phi $
which separate the basic sets [Reference BrunellaBru93, Reference SmaleSma67]. We choose
![]() $T_i$
to be smooth. The collection of tori is supposed to be minimal respective to the property that if an orbit is not in
$T_i$
to be smooth. The collection of tori is supposed to be minimal respective to the property that if an orbit is not in
![]() $\mathcal {R}$
or
$\mathcal {R}$
or
![]() $\mathcal {A}$
, then it intersects one of the
$\mathcal {A}$
, then it intersects one of the
![]() $\{ T_i \}$
. Let
$\{ T_i \}$
. Let
![]() $\gamma $
be such an orbit intersecting a specific
$\gamma $
be such an orbit intersecting a specific
![]() $T_i$
, let x be a point in the intersection. Then the forward orbit of x is asymptotic to a component A of the attractor
$T_i$
, let x be a point in the intersection. Then the forward orbit of x is asymptotic to a component A of the attractor
![]() $\mathcal {A}$
—this uses the important fact that there are no one-dimensional components of the non-wandering set of
$\mathcal {A}$
—this uses the important fact that there are no one-dimensional components of the non-wandering set of
![]() $\Phi $
by assumption. The set of such x so that the forward ray of x is asymptotic to A is open in
$\Phi $
by assumption. The set of such x so that the forward ray of x is asymptotic to A is open in
![]() $T_i$
. This holds for any component A of the attractor
$T_i$
. This holds for any component A of the attractor
![]() $\mathcal {A}$
. Since the union over such components of
$\mathcal {A}$
. Since the union over such components of
![]() $\mathcal {A}$
is all of
$\mathcal {A}$
is all of
![]() $T_i$
and
$T_i$
and
![]() $T_i$
is connected, it follows that all orbits in
$T_i$
is connected, it follows that all orbits in
![]() $T_i$
are forward asymptotic to a single component A of
$T_i$
are forward asymptotic to a single component A of
![]() $\mathcal {A}$
.
$\mathcal {A}$
.
In a similar way, one proves that if
![]() $T_1, T_2$
are tori contained in the complement of the union of the attractor and repeller, and
$T_1, T_2$
are tori contained in the complement of the union of the attractor and repeller, and
![]() $T_1, T_2$
intersect a common orbit of
$T_1, T_2$
intersect a common orbit of
![]() $\Phi $
, then
$\Phi $
, then
![]() $T_1, T_2$
intersect exactly the same set of orbits of
$T_1, T_2$
intersect exactly the same set of orbits of
![]() $\Phi $
. In other words, if B is a component of
$\Phi $
. In other words, if B is a component of
![]() $\mathcal {M} - (\mathcal {A} \cup \mathcal {R})$
, then there is a torus T contained in B, transverse to
$\mathcal {M} - (\mathcal {A} \cup \mathcal {R})$
, then there is a torus T contained in B, transverse to
![]() $\Phi $
so that B is the flow saturation of T. Hence, we can choose a minimal collection
$\Phi $
so that B is the flow saturation of T. Hence, we can choose a minimal collection
![]() $\{ T_i \}$
of tori transverse to
$\{ T_i \}$
of tori transverse to
![]() $\Phi $
and intersecting all orbits in the complement of
$\Phi $
and intersecting all orbits in the complement of
![]() $\mathcal {A} \cup \mathcal {R}$
, and any such orbit intersects a unique
$\mathcal {A} \cup \mathcal {R}$
, and any such orbit intersects a unique
![]() $T_i$
and only once.
$T_i$
and only once.
3.1 Construction of
 $\mathcal {F}$
$\mathcal {F}$
Now we construct
![]() $\mathcal {F}$
. The foliations
$\mathcal {F}$
. The foliations
![]() $\mathcal {F}^{ws}, \mathcal {F}^{wu}$
are
$\mathcal {F}^{ws}, \mathcal {F}^{wu}$
are
![]() $C^0$
with
$C^0$
with
![]() $C^1$
leaves [Reference Katok and HasselblattKH95], and so are the intersections with each
$C^1$
leaves [Reference Katok and HasselblattKH95], and so are the intersections with each
![]() $T_i$
. On each
$T_i$
. On each
![]() $T_i$
, choose a one-dimensional
$T_i$
, choose a one-dimensional
![]() $C^1$
foliation
$C^1$
foliation
![]() $F_i$
transverse to both
$F_i$
transverse to both
Saturate
![]() $F_i$
by the flow to produce a two-dimensional foliation in the flow saturation of
$F_i$
by the flow to produce a two-dimensional foliation in the flow saturation of
![]() $T_i$
. Note that the leaves in the flow saturation are either a plane or an infinite annulus. Let
$T_i$
. Note that the leaves in the flow saturation are either a plane or an infinite annulus. Let
![]() $\mathcal {F}$
be this foliation in the complement of the attractor union the repellor. Figure 2 describes a possible leaf in the lift
$\mathcal {F}$
be this foliation in the complement of the attractor union the repellor. Figure 2 describes a possible leaf in the lift
![]() $\widetilde {\mathcal {F}}$
of
$\widetilde {\mathcal {F}}$
of
![]() $\mathcal {F}$
to
$\mathcal {F}$
to
![]() $\widetilde {\mathcal {M}}$
, where
$\widetilde {\mathcal {M}}$
, where
![]() $R_2$
, the blue line, represents its intersection with some lift of
$R_2$
, the blue line, represents its intersection with some lift of
![]() $T_i$
. The figure depicts the following several properties that we are going to prove later and that are essential to the results of this article: (1) we will show later that leaves of
$T_i$
. The figure depicts the following several properties that we are going to prove later and that are essential to the results of this article: (1) we will show later that leaves of
![]() $\widetilde {\mathcal {F}}$
are Gromov hyperbolic; (2) we will also show that for
$\widetilde {\mathcal {F}}$
are Gromov hyperbolic; (2) we will also show that for
![]() $L \in \widetilde {\mathcal {F}}$
not in the lift of the attractor or repeller, each flow ray in L converges to a single point in
$L \in \widetilde {\mathcal {F}}$
not in the lift of the attractor or repeller, each flow ray in L converges to a single point in
![]() $S^1(L)$
and distinct flow rays do not forward converge to the same ideal point in
$S^1(L)$
and distinct flow rays do not forward converge to the same ideal point in
![]() $S^1(L)$
. Similarly for backward flow rays.
$S^1(L)$
. Similarly for backward flow rays.
A flow line that does not intersect any
![]() $T_i$
has to lie either in the attractor (
$T_i$
has to lie either in the attractor (
![]() $\mathcal {A}$
) or in the repeller (
$\mathcal {A}$
) or in the repeller (
![]() $\mathcal {R}$
). We define
$\mathcal {R}$
). We define
![]() $\mathcal {F}$
to be
$\mathcal {F}$
to be
![]() $\mathcal {F}^{wu}$
in the attractor,
$\mathcal {F}^{wu}$
in the attractor,
![]() $\mathcal {F}^{ws}$
in the repeller, and the saturation of the
$\mathcal {F}^{ws}$
in the repeller, and the saturation of the
![]() $F_i$
everywhere else.
$F_i$
everywhere else.
3.2 Properties of
 $\mathcal {F}$
$\mathcal {F}$
At this point,
![]() $\mathcal {F}$
is just a collection of two-dimensional subsets of
$\mathcal {F}$
is just a collection of two-dimensional subsets of
![]() $\mathcal {M}$
. We will prove that
$\mathcal {M}$
. We will prove that
![]() $\mathcal {F}$
is a foliation of
$\mathcal {F}$
is a foliation of
![]() $\mathcal {M}$
. Clearly,
$\mathcal {M}$
. Clearly,
![]() $\mathcal {F}$
is a foliation in the complement of the union of the attractor and the repeller, because this is an open set and because of the definition of
$\mathcal {F}$
is a foliation in the complement of the union of the attractor and the repeller, because this is an open set and because of the definition of
![]() $\mathcal {F}$
: each component
$\mathcal {F}$
: each component
![]() $\mathcal {C}$
of
$\mathcal {C}$
of
![]() $\mathcal {M} \setminus (\mathcal {A} \cup \mathcal {R})$
is equal to
$\mathcal {M} \setminus (\mathcal {A} \cup \mathcal {R})$
is equal to
![]() $\Phi _{\mathbb {R}}(T_i)$
for some
$\Phi _{\mathbb {R}}(T_i)$
for some
![]() $T_i$
and this is homeomorphic to
$T_i$
and this is homeomorphic to
![]() $T_i \times \mathbb {R}$
with the product topology (the topology in
$T_i \times \mathbb {R}$
with the product topology (the topology in
![]() $T_i$
is induced from
$T_i$
is induced from
![]() $\mathcal {M}$
). The foliation
$\mathcal {M}$
). The foliation
![]() $\mathcal {F}$
in
$\mathcal {F}$
in
![]() $\mathcal {C}$
is equivalent to the foliation
$\mathcal {C}$
is equivalent to the foliation
![]() $F_i \times \mathbb {R}$
in
$F_i \times \mathbb {R}$
in
![]() $T_i \times \mathbb {R}$
.
$T_i \times \mathbb {R}$
.
The interaction between
![]() $\mathcal {F}$
in
$\mathcal {F}$
in
![]() $\mathcal {M} - (\mathcal {A} \cup \mathcal {R})$
and
$\mathcal {M} - (\mathcal {A} \cup \mathcal {R})$
and
![]() $\mathcal {F}$
in
$\mathcal {F}$
in
![]() $\mathcal {A} \cup \mathcal {R}$
is more complex. There is a subtle point here, which we now explain. Let
$\mathcal {A} \cup \mathcal {R}$
is more complex. There is a subtle point here, which we now explain. Let
![]() $\widetilde {\mathcal {F}}$
be the lift of
$\widetilde {\mathcal {F}}$
be the lift of
![]() $\mathcal {F}$
to
$\mathcal {F}$
to
![]() $\widetilde {\mathcal {M}}$
. If
$\widetilde {\mathcal {M}}$
. If
![]() $\mathcal {F}$
is a foliation, then it will follow that
$\mathcal {F}$
is a foliation, then it will follow that
![]() $\widetilde {\mathcal {F}}$
is a foliation of
$\widetilde {\mathcal {F}}$
is a foliation of
![]() $\widetilde {\mathcal {M}}$
by properly embedded planes. By construction, the ‘leaves’ of
$\widetilde {\mathcal {M}}$
by properly embedded planes. By construction, the ‘leaves’ of
![]() $\mathcal {F}$
intersecting the attractor are contained in the attractor and similarly for the repeller. Therefore, the leaves of
$\mathcal {F}$
intersecting the attractor are contained in the attractor and similarly for the repeller. Therefore, the leaves of
![]() $\mathcal {F}$
in the complement of
$\mathcal {F}$
in the complement of
![]() $\mathcal {A} \cup \mathcal {R}$
are entirely contained in the complement of
$\mathcal {A} \cup \mathcal {R}$
are entirely contained in the complement of
![]() $\mathcal {A} \cup \mathcal {R}$
as well. In particular, if L is a lift of a leaf of
$\mathcal {A} \cup \mathcal {R}$
as well. In particular, if L is a lift of a leaf of
![]() $\mathcal {F}$
in the complement of the attractor and repeller, then it should be properly embedded when lifted to
$\mathcal {F}$
in the complement of the attractor and repeller, then it should be properly embedded when lifted to
![]() $\widetilde {\mathcal {M}}$
. As it turns out, this property is not true if one starts with an arbitrary foliation
$\widetilde {\mathcal {M}}$
. As it turns out, this property is not true if one starts with an arbitrary foliation
![]() $F_i$
in
$F_i$
in
![]() $T_i$
. Let us review the construction: we start with a foliation
$T_i$
. Let us review the construction: we start with a foliation
![]() $F_i$
in
$F_i$
in
![]() $T_i$
and saturate it by the flow to produce a foliation in an open set in
$T_i$
and saturate it by the flow to produce a foliation in an open set in
![]() $\mathcal {M}$
. Then consider a lift L of a leaf of this foliation to the universal cover. Is L always properly embedded in
$\mathcal {M}$
. Then consider a lift L of a leaf of this foliation to the universal cover. Is L always properly embedded in
![]() $\widetilde {\mathcal {M}}$
? In general, this is not true. For example, start with the Franks–Williams non-transitive flow [Reference Franks and WilliamsFW80], consider a smooth torus T which separates the attractor and repeller, and start with say the intersection of the stable foliation of
$\widetilde {\mathcal {M}}$
? In general, this is not true. For example, start with the Franks–Williams non-transitive flow [Reference Franks and WilliamsFW80], consider a smooth torus T which separates the attractor and repeller, and start with say the intersection of the stable foliation of
![]() $\Phi $
with T, which we call F. Then for some of the leaves of F, it follows that if L is a lift of the flow saturation to
$\Phi $
with T, which we call F. Then for some of the leaves of F, it follows that if L is a lift of the flow saturation to
![]() $\widetilde {\mathcal {M}}$
, then L is not properly embedded in
$\widetilde {\mathcal {M}}$
, then L is not properly embedded in
![]() $\mathcal {M}$
. For example, [Reference Franks and WilliamsFW80, Fig. 3, p. 164] depicts the foliations induced by the weak stable and unstable foliations in T for the Franks–Williams flow. Each has two Reeb components. Take
$\mathcal {M}$
. For example, [Reference Franks and WilliamsFW80, Fig. 3, p. 164] depicts the foliations induced by the weak stable and unstable foliations in T for the Franks–Williams flow. Each has two Reeb components. Take
![]() $\alpha $
to be a leaf of the stable foliation which is not in the interior of a Reeb component, that is, a horizontal line in the figure, and also that
$\alpha $
to be a leaf of the stable foliation which is not in the interior of a Reeb component, that is, a horizontal line in the figure, and also that
![]() $\alpha $
is a closed curve. Lift it to
$\alpha $
is a closed curve. Lift it to
![]() $\widetilde \alpha $
in
$\widetilde \alpha $
in
![]() $\widetilde {\mathcal {M}}$
. If C is the flow saturation of
$\widetilde {\mathcal {M}}$
. If C is the flow saturation of
![]() $\widetilde \alpha $
, then C is not properly embedded in
$\widetilde \alpha $
, then C is not properly embedded in
![]() $\widetilde {\mathcal {M}}$
: there is an orbit
$\widetilde {\mathcal {M}}$
: there is an orbit
![]() $\gamma $
of
$\gamma $
of
![]() $\widetilde \Phi $
which is not in C but is contained in the closure of C. This orbit
$\widetilde \Phi $
which is not in C but is contained in the closure of C. This orbit
![]() $\gamma $
is the lift of a periodic orbit contained in the attractor of the Franks–Williams flow. The same would happen if we took F to be the intersection of the unstable foliation with T,
$\gamma $
is the lift of a periodic orbit contained in the attractor of the Franks–Williams flow. The same would happen if we took F to be the intersection of the unstable foliation with T,
![]() $\alpha $
a closed leaf of F, and considering the repeller of
$\alpha $
a closed leaf of F, and considering the repeller of
![]() $\Phi $
instead of the attractor.
$\Phi $
instead of the attractor.
The reason why our construction of
![]() $\mathcal {F}$
as above produces a foliation is because we start with a foliation
$\mathcal {F}$
as above produces a foliation is because we start with a foliation
![]() $F_i$
in
$F_i$
in
![]() $T_i$
which is transverse to both the stable and unstable foliations in
$T_i$
which is transverse to both the stable and unstable foliations in
![]() $T_i$
. We first prove the following result.
$T_i$
. We first prove the following result.
Lemma 3.2. Let
![]() $\ell $
be a leaf of
$\ell $
be a leaf of
![]() $F_i$
and let E be the flow saturation of
$F_i$
and let E be the flow saturation of
![]() $\ell $
. Then, with the induced path metric from
$\ell $
. Then, with the induced path metric from
![]() $\mathcal {M}$
, it follows that E is complete.
$\mathcal {M}$
, it follows that E is complete.
Proof. Let E be the flow saturation of
![]() $\ell $
. Since
$\ell $
. Since
![]() $\ell $
is smooth and the flow is
$\ell $
is smooth and the flow is
![]() $C^1$
it follows that E is
$C^1$
it follows that E is
![]() $C^1$
. For any
$C^1$
. For any
![]() $x, y$
in
$x, y$
in
![]() $\ell $
if
$\ell $
if
then
![]() $x = y$
and
$x = y$
and
![]() $t = s$
, since the component of
$t = s$
, since the component of
![]() $\mathcal {M} - (\mathcal {A} \cup \mathcal {R})$
containing
$\mathcal {M} - (\mathcal {A} \cup \mathcal {R})$
containing
![]() $\ell $
is homeomorphic to
$\ell $
is homeomorphic to
![]() $T \times \mathbb {R}$
and
$T \times \mathbb {R}$
and
![]() $\ell $
is injectively immersed in T. Hence, E is parameterized as
$\ell $
is injectively immersed in T. Hence, E is parameterized as
![]() $\ell \times \mathbb {R}$
, that is, every point p in E can be represented as
$\ell \times \mathbb {R}$
, that is, every point p in E can be represented as
![]() $(x,t)$
where
$(x,t)$
where
![]() $x\in \ell $
and
$x\in \ell $
and
![]() $t\in \mathbb {R}$
.
$t\in \mathbb {R}$
.
The Riemannian metric in
![]() $\mathcal {M}$
induces a Riemannian metric in E and a path metric in E. What we prove is the following.
$\mathcal {M}$
induces a Riemannian metric in E and a path metric in E. What we prove is the following.
Claim 1. There is
![]() $a_0> 0$
so that any point
$a_0> 0$
so that any point
![]() $p = (x, t)$
in E is the center of a metric disk of radius
$p = (x, t)$
in E is the center of a metric disk of radius
![]() $a_0$
in E.
$a_0$
in E.
Proof. This is obvious for any point p in
![]() $\ell $
or, in other words, if
$\ell $
or, in other words, if
![]() $t = 0$
.
$t = 0$
.
We now prove the claim for
![]() $t> 0$
using the unstable foliation. The analogous proof shows the result for
$t> 0$
using the unstable foliation. The analogous proof shows the result for
![]() $t < 0$
using the stable foliation. The foliation
$t < 0$
using the stable foliation. The foliation
![]() $F_i$
is transverse to both the stable and unstable foliations induced in
$F_i$
is transverse to both the stable and unstable foliations induced in
![]() $T_i$
, hence uniformly transverse to these foliations (which means the angles between
$T_i$
, hence uniformly transverse to these foliations (which means the angles between
![]() $F_i$
and
$F_i$
and
![]() $\mathcal {F}^{wu}\cap T_i$
or
$\mathcal {F}^{wu}\cap T_i$
or
![]() $\mathcal {F}^cs\cap T_i$
are uniformly bounded away from 0 on
$\mathcal {F}^cs\cap T_i$
are uniformly bounded away from 0 on
![]() $T_i$
). Given any smoothly embedded curve
$T_i$
). Given any smoothly embedded curve
![]() $\alpha $
in M, let
$\alpha $
in M, let
![]() $l_u(\alpha )$
be its unstable length: we integrate only the component of the tangent vector in the direction of the unstable bundle. For example, if
$l_u(\alpha )$
be its unstable length: we integrate only the component of the tangent vector in the direction of the unstable bundle. For example, if
![]() $\alpha $
is contained in a weak stable leaf, then
$\alpha $
is contained in a weak stable leaf, then
![]() $l_u(\alpha )$
is zero, while if
$l_u(\alpha )$
is zero, while if
![]() $\alpha $
is contained in a strong unstable leaf, then
$\alpha $
is contained in a strong unstable leaf, then
![]() $l_u(\alpha )$
is the same as its length under the Riemannian metric of
$l_u(\alpha )$
is the same as its length under the Riemannian metric of
![]() $\mathcal {M}$
. In particular, if
$\mathcal {M}$
. In particular, if
![]() $\alpha $
is a curve not contained in a strong stable or unstable leaf, then the original length
$\alpha $
is a curve not contained in a strong stable or unstable leaf, then the original length
![]() $l(\alpha )$
is always strictly greater than the unstable length
$l(\alpha )$
is always strictly greater than the unstable length
![]() $l_u(\alpha )$
.
$l_u(\alpha )$
.
By the definition of an Anosov flow, there exist constants
![]() $C> 0,\unicode{x3bb} >1$
such that if we flow forward a segment with t amount of time, the new unstable length is at least
$C> 0,\unicode{x3bb} >1$
such that if we flow forward a segment with t amount of time, the new unstable length is at least
![]() $C\unicode{x3bb} ^t$
times the original unstable length. Hence if we let
$C\unicode{x3bb} ^t$
times the original unstable length. Hence if we let
![]() $a_1 = C$
, then for any smooth segment, any flow forward of that segment has unstable length which is at least
$a_1 = C$
, then for any smooth segment, any flow forward of that segment has unstable length which is at least
![]() $a_1$
times the original unstable length.
$a_1$
times the original unstable length.
Since
![]() $F_i$
is uniformly transverse to
$F_i$
is uniformly transverse to
![]() $\mathcal {F}^{ws}\cap T_i$
by our construction, it follows that any point x in
$\mathcal {F}^{ws}\cap T_i$
by our construction, it follows that any point x in
![]() $T_i$
is the midpoint of a segment
$T_i$
is the midpoint of a segment
![]() $\beta $
in its leaf of
$\beta $
in its leaf of
![]() $F_i$
of unstable length
$F_i$
of unstable length
![]() $2$
. For any
$2$
. For any
![]() $t \geq 0$
, the unstable length of
$t \geq 0$
, the unstable length of
![]() $\Phi _t(\beta )$
is at least
$\Phi _t(\beta )$
is at least
![]() $2 a_1$
. This constant
$2 a_1$
. This constant
![]() $a_1$
is defined globally. In addition, if v is a non-zero vector tangent to
$a_1$
is defined globally. In addition, if v is a non-zero vector tangent to
![]() $\beta $
, then v makes a definite positive angle with the flow direction. Since flowing forward increases the size of unstable vectors more than the size of tangent vectors (where
$\beta $
, then v makes a definite positive angle with the flow direction. Since flowing forward increases the size of unstable vectors more than the size of tangent vectors (where
![]() $t> t_0 > 0$
for some
$t> t_0 > 0$
for some
![]() $t_0$
big enough), it follows that there is a global constant
$t_0$
big enough), it follows that there is a global constant
![]() $\theta> 0$
so that
$\theta> 0$
so that
![]() $D\Phi _t v$
also makes an angle
$D\Phi _t v$
also makes an angle
![]() $> \theta $
with the tangent to the flow. Consider the infinitesimal arclengths
$> \theta $
with the tangent to the flow. Consider the infinitesimal arclengths
![]() $dt, ds, du$
along the flow, stable, and unstable bundles. The (non-Riemannian) metric
$dt, ds, du$
along the flow, stable, and unstable bundles. The (non-Riemannian) metric
is quasicomparable (this means Lipschitz equivalent) with the Riemannian metric in M: there is
![]() $a_2> 0$
so that the Riemannian length is at least
$a_2> 0$
so that the Riemannian length is at least
![]() $a_2$
times the length in this metric. Consider the following set:
$a_2$
times the length in this metric. Consider the following set:
for
![]() $t \geq 0$
. The segment
$t \geq 0$
. The segment
![]() $\beta $
of
$\beta $
of
![]() $F_i$
is contained in the leaf E of
$F_i$
is contained in the leaf E of
![]() $\mathcal {F}$
. From any point in the boundary of A to
$\mathcal {F}$
. From any point in the boundary of A to
![]() $\Phi _t(x)$
along E, one has to have at least
$\Phi _t(x)$
along E, one has to have at least
![]() $a_1$
unstable length and flow length of at least
$a_1$
unstable length and flow length of at least
![]() $1$
. It follows that there is a global constant
$1$
. It follows that there is a global constant
![]() $a_0$
(depending only on
$a_0$
(depending only on
![]() $a_1$
) so that A contains a disk in the Riemannian metric of radius
$a_1$
) so that A contains a disk in the Riemannian metric of radius
![]() $a_0$
and centered at
$a_0$
and centered at
![]() $\Phi _t(x)$
.
$\Phi _t(x)$
.
For
![]() $t < 0$
, we use the stable foliation and flow backward instead of forward. This finishes the proof of the claim.
$t < 0$
, we use the stable foliation and flow backward instead of forward. This finishes the proof of the claim.
The claim shows that E is complete and finishes the proof of the lemma.
Continuation of the proof of Theorem 3.1
We consider the collection
![]() $\mathcal {F}$
as constructed in the beginning of this section. This object
$\mathcal {F}$
as constructed in the beginning of this section. This object
![]() $\mathcal {F}$
is a foliation restricted to
$\mathcal {F}$
is a foliation restricted to
![]() $\mathcal {M} - (\mathcal {A} \cup \mathcal {R})$
and this is an open set.
$\mathcal {M} - (\mathcal {A} \cup \mathcal {R})$
and this is an open set.
The only remaining thing to prove is that if a sequence
![]() $x_n$
in
$x_n$
in
![]() $\mathcal {M} - (\mathcal {A} \cup \mathcal {R})$
converges to x in
$\mathcal {M} - (\mathcal {A} \cup \mathcal {R})$
converges to x in
![]() $\mathcal {A} \cup \mathcal {R}$
, then the leaves of
$\mathcal {A} \cup \mathcal {R}$
, then the leaves of
![]() $\mathcal {F}$
through
$\mathcal {F}$
through
![]() $x_n$
converge to the leaf of
$x_n$
converge to the leaf of
![]() $\mathcal {F}$
through x. Without loss of generality, we may assume that x is in an attractor.
$\mathcal {F}$
through x. Without loss of generality, we may assume that x is in an attractor.
Let
![]() $p_n \in T_i$
so that
$p_n \in T_i$
so that
![]() $x_n$
are in
$x_n$
are in
![]() $\Phi _{\mathbb {R}}(p_n)$
. There are
$\Phi _{\mathbb {R}}(p_n)$
. There are
![]() $t_n \in \mathbb {R}$
with
$t_n \in \mathbb {R}$
with
![]() $x_n = \Phi _{t_n}(p_n)$
. Since x is in the attractor, then
$x_n = \Phi _{t_n}(p_n)$
. Since x is in the attractor, then
![]() $t_n$
converges to positive
$t_n$
converges to positive
![]() $\infty $
. The leaf of
$\infty $
. The leaf of
![]() $\mathcal {F}$
through
$\mathcal {F}$
through
![]() $p_n$
is the
$p_n$
is the
![]() $\Phi $
flow saturation of the leaf of
$\Phi $
flow saturation of the leaf of
![]() $F_i$
through
$F_i$
through
![]() $p_n$
. The tangent to this two-dimensional set through
$p_n$
. The tangent to this two-dimensional set through
![]() $p_n$
is generated by the Anosov vector field generating
$p_n$
is generated by the Anosov vector field generating
![]() $\Phi $
and a tangent vector v to
$\Phi $
and a tangent vector v to
![]() $F_i$
at
$F_i$
at
![]() $p_n$
. The leaf of
$p_n$
. The leaf of
![]() $\mathcal {F}$
is
$\mathcal {F}$
is
![]() $\Phi $
-flow invariant. Flowing forward, the flow vector remains invariant. The vector v is transverse to the weak stable foliation and hence it flows increasingly more (does not matter how fast) to the weak unstable direction. So flowing forward, these leaves become increasingly more tangent to the
$\Phi $
-flow invariant. Flowing forward, the flow vector remains invariant. The vector v is transverse to the weak stable foliation and hence it flows increasingly more (does not matter how fast) to the weak unstable direction. So flowing forward, these leaves become increasingly more tangent to the
![]() $E^0 \oplus E^u$
bundle and limit to leaves of
$E^0 \oplus E^u$
bundle and limit to leaves of
![]() $\mathcal {F}^{wu}$
. Since flowing forward limits to the attractor, this shows that the leaves of
$\mathcal {F}^{wu}$
. Since flowing forward limits to the attractor, this shows that the leaves of
![]() $\mathcal {F}$
through
$\mathcal {F}$
through
![]() $x_n$
converge to the leaf of
$x_n$
converge to the leaf of
![]() $\mathcal {F}$
through x.
$\mathcal {F}$
through x.
In addition, the previous lemma shows that the leaves of
![]() $\mathcal {F}$
through
$\mathcal {F}$
through
![]() $x_n$
are complete in their path metrics. This shows that
$x_n$
are complete in their path metrics. This shows that
![]() $\mathcal {F}$
defines a foliation. We stress that Lemma 3.2 is needed to ensure that
$\mathcal {F}$
defines a foliation. We stress that Lemma 3.2 is needed to ensure that
![]() $\mathcal {F}$
is a foliation. Otherwise, even if the tangent directions of
$\mathcal {F}$
is a foliation. Otherwise, even if the tangent directions of
![]() $\mathcal {F}$
in
$\mathcal {F}$
in
![]() $\mathcal {M} - (\mathcal {A} \cup \mathcal {R})$
and
$\mathcal {M} - (\mathcal {A} \cup \mathcal {R})$
and
![]() $\mathcal {F}$
in
$\mathcal {F}$
in
![]() $\mathcal {A} \cup \mathcal {R}$
match continuously, one would have that leaves of the first set ‘arrive’ at leaves of the second set in finite distance. In other words, the union of a leaf in
$\mathcal {A} \cup \mathcal {R}$
match continuously, one would have that leaves of the first set ‘arrive’ at leaves of the second set in finite distance. In other words, the union of a leaf in
![]() $\mathcal {M} - (\mathcal {A} \cup \mathcal {R})$
and a leaf in
$\mathcal {M} - (\mathcal {A} \cup \mathcal {R})$
and a leaf in
![]() $(\mathcal {A} \cup \mathcal {R})$
would form a branched surface. This would produce a branching foliation, instead of a foliation.
$(\mathcal {A} \cup \mathcal {R})$
would form a branched surface. This would produce a branching foliation, instead of a foliation.
This finishes the proof of Theorem 3.1.□
We remark that the construction of
![]() $\mathcal {F}$
highlights why our methods do not work when there are one-dimensional basic sets. For simplicity, suppose that there is a basic set which is a periodic orbit
$\mathcal {F}$
highlights why our methods do not work when there are one-dimensional basic sets. For simplicity, suppose that there is a basic set which is a periodic orbit
![]() $\gamma $
. There is a torus T so that negative saturation limits on
$\gamma $
. There is a torus T so that negative saturation limits on
![]() $\gamma $
. If we start with F in T transverse to both
$\gamma $
. If we start with F in T transverse to both
![]() $\mathcal {F}^{ws} \cap T$
and
$\mathcal {F}^{ws} \cap T$
and
![]() $\mathcal {F}^{wu} \cap T$
, then flowing backward will make it limit to the weak stable leaf of
$\mathcal {F}^{wu} \cap T$
, then flowing backward will make it limit to the weak stable leaf of
![]() $\gamma $
. So the weak stable leaf of
$\gamma $
. So the weak stable leaf of
![]() $\gamma $
is in the collection
$\gamma $
is in the collection
![]() $\mathcal {F}$
so constructed. However, there is also a torus
$\mathcal {F}$
so constructed. However, there is also a torus
![]() $T'$
so that the forward flow saturation limits on
$T'$
so that the forward flow saturation limits on
![]() $\gamma $
. The similar argument shows that the weak unstable foliation of
$\gamma $
. The similar argument shows that the weak unstable foliation of
![]() $\gamma $
also has to lie in the collection
$\gamma $
also has to lie in the collection
![]() $\mathcal {F}$
. Hence the collection
$\mathcal {F}$
. Hence the collection
![]() $\mathcal {F}$
has sets which intersect transversely and cannot be a foliation.
$\mathcal {F}$
has sets which intersect transversely and cannot be a foliation.
Remark 3.3. By construction, the foliation
![]() $\mathcal {F}$
does not have compact leaves: any leaf in
$\mathcal {F}$
does not have compact leaves: any leaf in
![]() $\mathcal {R} \cup \mathcal {A}$
is not compact as they are weak stable leaves of an Anosov flow. Each leaf in
$\mathcal {R} \cup \mathcal {A}$
is not compact as they are weak stable leaves of an Anosov flow. Each leaf in
![]() $\mathcal {M} - (\mathcal {R} \cup \mathcal {A})$
limits on
$\mathcal {M} - (\mathcal {R} \cup \mathcal {A})$
limits on
![]() $\mathcal {R}$
and hence cannot be compact. Since
$\mathcal {R}$
and hence cannot be compact. Since
![]() $\mathcal {F}$
does not have compact leaves, it follows from Novikov’s theorem [Reference CalegariCal01] that leaves of
$\mathcal {F}$
does not have compact leaves, it follows from Novikov’s theorem [Reference CalegariCal01] that leaves of
![]() $\widetilde {\mathcal {F}}$
are properly embedded planes in
$\widetilde {\mathcal {F}}$
are properly embedded planes in
![]() $\widetilde {\mathcal {M}}$
.
$\widetilde {\mathcal {M}}$
.
To prove Theorem 1.1, we will prove the following properties for such a foliation
![]() $\mathcal {F}$
:
$\mathcal {F}$
:
-
(1) the flow lines are leafwise quasigeodesics in leaves of
 $\mathcal {F}$
;
$\mathcal {F}$
; -
(2) every leaf of
 $\mathcal {F}$
not contained in
$\mathcal {F}$
not contained in
 $\mathcal {A}$
or
$\mathcal {A}$
or
 $\mathcal {R}$
is a non-funnel leaf, as in Figure 2.
$\mathcal {R}$
is a non-funnel leaf, as in Figure 2.
4 Gromov hyperbolicity of the leaves of
 $\mathcal {F}$
$\mathcal {F}$
We will consider a foliation
![]() $\mathcal {F}$
as constructed in the previous section.
$\mathcal {F}$
as constructed in the previous section.
In this section, we will show that there exists a metric g such that every leaf of the foliation
![]() $\mathcal {F}$
is Gromov hyperbolic. By Candel’s uniformization theorem, this condition is equivalent to the fact that every holonomy invariant non-trivial measure
$\mathcal {F}$
is Gromov hyperbolic. By Candel’s uniformization theorem, this condition is equivalent to the fact that every holonomy invariant non-trivial measure
![]() $\mu $
on
$\mu $
on
![]() $\mathcal {M}$
has Euler characteristic
$\mathcal {M}$
has Euler characteristic
![]() $\chi _{\mu }(\mathcal {M},\mathcal {F})<0$
, which includes the case when there exists no invariant measure. For more details about the Euler characteristic, see [Reference CandelCan93] or [Reference Candel and ConlonCC00]. In our context, we will prove that there is no holonomy invariant transverse measure to
$\chi _{\mu }(\mathcal {M},\mathcal {F})<0$
, which includes the case when there exists no invariant measure. For more details about the Euler characteristic, see [Reference CandelCan93] or [Reference Candel and ConlonCC00]. In our context, we will prove that there is no holonomy invariant transverse measure to
![]() $\mathcal {F}$
. Candel’s theorem requires that the foliation has
$\mathcal {F}$
. Candel’s theorem requires that the foliation has
![]() $C^{\infty }$
leaves. To obtain that, we use Calegari’s result [Reference CalegariCal01b] which implies that
$C^{\infty }$
leaves. To obtain that, we use Calegari’s result [Reference CalegariCal01b] which implies that
![]() $\mathcal {F}$
is isotopic to a foliation with
$\mathcal {F}$
is isotopic to a foliation with
![]() $C^{\infty }$
leaves. This does not change the property that
$C^{\infty }$
leaves. This does not change the property that
![]() $\mathcal {F}$
has or does not have holonomy invariant transverse measures. Once this is obtained, Candel proved that there is a metric in
$\mathcal {F}$
has or does not have holonomy invariant transverse measures. Once this is obtained, Candel proved that there is a metric in
![]() $\mathcal {M}$
inducing a smooth Riemannian metric in the leaves so that curvature in each leaf of
$\mathcal {M}$
inducing a smooth Riemannian metric in the leaves so that curvature in each leaf of
![]() $\mathcal {F}$
is constant equal to
$\mathcal {F}$
is constant equal to
![]() $-1$
. A precise statement can be found in [Reference CandelCan93], [Reference Candel and ConlonCC00], or [Reference CalegariCal01]. We call such a metric a Candel metric. This Candel metric is not smooth in the transverse direction.
$-1$
. A precise statement can be found in [Reference CandelCan93], [Reference Candel and ConlonCC00], or [Reference CalegariCal01]. We call such a metric a Candel metric. This Candel metric is not smooth in the transverse direction.
Here is the precise statement on the equivalence of Gromov hyperbolicity of leaves of a foliation and negative Euler characteristic of a positive invariant measure.
Proposition 4.1. [Reference CandelCan93]
Let
![]() $(M,F)$
be a compact oriented surface lamination with a Riemannian metric g. Then
$(M,F)$
be a compact oriented surface lamination with a Riemannian metric g. Then
![]() $\chi (M,\mu )<0$
for every positive invariant transverse measure
$\chi (M,\mu )<0$
for every positive invariant transverse measure
![]() $\mu $
if and only if there is a metric in M which induces a metric in each leaf of F which makes it into a hyperbolic surface. In particular, this holds true if M has no invariant measure.
$\mu $
if and only if there is a metric in M which induces a metric in each leaf of F which makes it into a hyperbolic surface. In particular, this holds true if M has no invariant measure.
To prove that all the leaves of
![]() $\mathcal {F}$
are Gromov hyperbolic, we will show that there does not exist any invariant measure. We will argue by contradiction, we assume that there exists a invariant measure
$\mathcal {F}$
are Gromov hyperbolic, we will show that there does not exist any invariant measure. We will argue by contradiction, we assume that there exists a invariant measure
![]() $\mu $
, and we will attain a contradiction.
$\mu $
, and we will attain a contradiction.
The
![]() $support$
of
$support$
of
![]() $\mu $
on
$\mu $
on
![]() $\mathcal {M}$
, denoted by
$\mathcal {M}$
, denoted by
![]() $\textit{supp}(\mu )$
, is defined as the collection of all points
$\textit{supp}(\mu )$
, is defined as the collection of all points
![]() $x\in \mathcal {M}$
such that if
$x\in \mathcal {M}$
such that if
![]() $\tau $
is a one-dimensional manifold transverse to
$\tau $
is a one-dimensional manifold transverse to
![]() $\mathcal {F}$
which contains x in its interior, then
$\mathcal {F}$
which contains x in its interior, then
![]() $\mu (\tau )>0$
. The support of a holonomy invariant transverse measure is a closed set and it is saturated by
$\mu (\tau )>0$
. The support of a holonomy invariant transverse measure is a closed set and it is saturated by
![]() $\mathcal {F}$
, which means
$\mathcal {F}$
, which means
![]() $\textit{supp}(\mu )$
is a union of leaves of
$\textit{supp}(\mu )$
is a union of leaves of
![]() $\mathcal {F}$
. The orientation hypothesis is not essential as it can be achieved by a double cover. The double cover does not change the conformal type of any leaf.
$\mathcal {F}$
. The orientation hypothesis is not essential as it can be achieved by a double cover. The double cover does not change the conformal type of any leaf.
Lemma 4.2. The support of
![]() $\mu $
on
$\mu $
on
![]() $\mathcal {M}$
contains at least one leaf from the attractor
$\mathcal {M}$
contains at least one leaf from the attractor
![]() $\mathcal {A}$
or the repeller
$\mathcal {A}$
or the repeller
![]() $\mathcal {R}$
.
$\mathcal {R}$
.
Proof. Consider a point
![]() $x\in \textit{supp}(\mu )$
and suppose
$x\in \textit{supp}(\mu )$
and suppose
![]() $L_x$
is the leaf in
$L_x$
is the leaf in
![]() $\mathcal {F}$
which contains x, then
$\mathcal {F}$
which contains x, then
![]() $L_x\subset \textit{supp}(\mu )$
as
$L_x\subset \textit{supp}(\mu )$
as
![]() $\textit{supp}(\mu )$
is
$\textit{supp}(\mu )$
is
![]() $\mathcal {F}$
-saturated. If
$\mathcal {F}$
-saturated. If
![]() $x\in \mathcal {A}$
, then
$x\in \mathcal {A}$
, then
![]() $L_{x}\subset \mathcal {A}$
and the claim is true. Similarly if x is in
$L_{x}\subset \mathcal {A}$
and the claim is true. Similarly if x is in
![]() $\mathcal {R}$
, then its leaf is contained in
$\mathcal {R}$
, then its leaf is contained in
![]() $\textit{supp}(\mu )$
. Finally suppose that
$\textit{supp}(\mu )$
. Finally suppose that
![]() $x\notin (\mathcal {A} \cup \mathcal {R})$
. Then consider the sequence
$x\notin (\mathcal {A} \cup \mathcal {R})$
. Then consider the sequence
![]() $\{\Phi _{n}(x)\}$
as
$\{\Phi _{n}(x)\}$
as
![]() $n \rightarrow \infty $
. Let z be an accumulation point of
$n \rightarrow \infty $
. Let z be an accumulation point of
![]() $\{\Phi _{n}(x)\}$
. As
$\{\Phi _{n}(x)\}$
. As
![]() $\textit{supp}(\mu )$
is closed, z is in
$\textit{supp}(\mu )$
is closed, z is in
![]() $\textit{supp}(\mu )$
and hence
$\textit{supp}(\mu )$
and hence
![]() $L_{z}\subset \textit{supp}(\mu )$
. Since z is an accumulation point of
$L_{z}\subset \textit{supp}(\mu )$
. Since z is an accumulation point of
![]() $\Phi _n(x)$
, it implies that z is a non-wandering point, and hence
$\Phi _n(x)$
, it implies that z is a non-wandering point, and hence
![]() $z\in \mathcal {A}\cup \mathcal {R}$
and
$z\in \mathcal {A}\cup \mathcal {R}$
and
![]() $L_z\subset (\mathcal {A}\cup \mathcal {R})\cap \textit{supp}(\mu )$
. In fact, since
$L_z\subset (\mathcal {A}\cup \mathcal {R})\cap \textit{supp}(\mu )$
. In fact, since
![]() $n \rightarrow \infty $
, it follows that z is in the attractor, so
$n \rightarrow \infty $
, it follows that z is in the attractor, so
![]() $L_z \subset \mathcal {A}$
.
$L_z \subset \mathcal {A}$
.
Suppose L is a leaf in
![]() $\textit{supp}(\mu )$
which is contained in
$\textit{supp}(\mu )$
which is contained in
![]() $\mathcal {A}$
(assume in
$\mathcal {A}$
(assume in
![]() $\mathcal {A}$
without loss of generality). By [Reference PlantePla75, Theorem 6.3], we know that if
$\mathcal {A}$
without loss of generality). By [Reference PlantePla75, Theorem 6.3], we know that if
![]() $\mu $
is a holonomy invariant transverse measure on a compact manifold foliated by a codimension-one foliation
$\mu $
is a holonomy invariant transverse measure on a compact manifold foliated by a codimension-one foliation
![]() $\mathcal {F}$
, then any leaf contained in
$\mathcal {F}$
, then any leaf contained in
![]() $\textit{supp}(\mu )$
has polynomial growth. Then the leaf
$\textit{supp}(\mu )$
has polynomial growth. Then the leaf
![]() $L_z$
in the attractor
$L_z$
in the attractor
![]() $\mathcal {A}$
, as obtained in the previous paragraph, has polynomial growth. Recall that the leaves of
$\mathcal {A}$
, as obtained in the previous paragraph, has polynomial growth. Recall that the leaves of
![]() $\mathcal {F}$
are either planes or annuli. At the same time,
$\mathcal {F}$
are either planes or annuli. At the same time,
![]() $L_z$
is contained in the attractor and each leaf in the attractor belongs to the weak unstable foliation of the Anosov flow
$L_z$
is contained in the attractor and each leaf in the attractor belongs to the weak unstable foliation of the Anosov flow
![]() $\Phi $
. However, weak stable and weak unstable leaves of Anosov flows have exponential growth, a contradiction.
$\Phi $
. However, weak stable and weak unstable leaves of Anosov flows have exponential growth, a contradiction.
As each leaf
![]() $L\in \widetilde {\mathcal {F}}$
is Gromov hyperbolic with respect to the path metric from the induced Riemannian metric from
$L\in \widetilde {\mathcal {F}}$
is Gromov hyperbolic with respect to the path metric from the induced Riemannian metric from
![]() $\widetilde {\mathcal {M}}$
, we can define the circle at infinity or the ideal boundary
$\widetilde {\mathcal {M}}$
, we can define the circle at infinity or the ideal boundary
![]() $S^1(L)$
of each leaf L.
$S^1(L)$
of each leaf L.
Next we will describe the topology we will use on the spaces
 $$ \begin{align*}S^{1}(\widetilde{\mathcal{M}})=\bigcup\limits_{L\in\widetilde{\mathcal{F}}}S^{1}(L)\quad\text{and}\end{align*} $$
$$ \begin{align*}S^{1}(\widetilde{\mathcal{M}})=\bigcup\limits_{L\in\widetilde{\mathcal{F}}}S^{1}(L)\quad\text{and}\end{align*} $$
 $$ \begin{align*}\widetilde{\mathcal{M}} \cup S^{1}(\widetilde{\mathcal{M}})=\bigcup\limits_{L\in\widetilde{\mathcal{F}}}(L\cup S^{1}(L)).\end{align*} $$
$$ \begin{align*}\widetilde{\mathcal{M}} \cup S^{1}(\widetilde{\mathcal{M}})=\bigcup\limits_{L\in\widetilde{\mathcal{F}}}(L\cup S^{1}(L)).\end{align*} $$
For this, we will assume first that
![]() $\mathcal {M}$
has a Candel metric.
$\mathcal {M}$
has a Candel metric.
Suppose
![]() $\tau $
is an open segment homeomorphic to (0,1) and transversal to
$\tau $
is an open segment homeomorphic to (0,1) and transversal to
![]() $\widetilde {\mathcal {F}}$
. We define the the following sets
$\widetilde {\mathcal {F}}$
. We define the the following sets
If
![]() $T^{1}(\tau )$
denotes the unit tangent bundle of
$T^{1}(\tau )$
denotes the unit tangent bundle of
![]() $\widetilde {\mathcal {F}}$
restricted to
$\widetilde {\mathcal {F}}$
restricted to
![]() $\tau $
, then
$\tau $
, then
![]() $T^{1}(\tau )$
is naturally homeomorphic to the standard cylinder. The natural identification between
$T^{1}(\tau )$
is naturally homeomorphic to the standard cylinder. The natural identification between
![]() $T^{1}(\tau )$
and
$T^{1}(\tau )$
and
![]() $\mathcal {P}_{\tau }$
induces the topology on
$\mathcal {P}_{\tau }$
induces the topology on
![]() $\mathcal {P}_{\tau }$
homeomorphic to the standard annulus. In [Reference FenleyFen02], it is proved that this topology is independent of the particular transversal
$\mathcal {P}_{\tau }$
homeomorphic to the standard annulus. In [Reference FenleyFen02], it is proved that this topology is independent of the particular transversal
![]() $\tau $
that is chosen intersecting the same sets of leaves of
$\tau $
that is chosen intersecting the same sets of leaves of
![]() $\widetilde {\mathcal {F}}$
. This is because the metrics induced in
$\widetilde {\mathcal {F}}$
. This is because the metrics induced in
![]() $S^1(L)$
from the visual metric in any point are Hölder equivalent.
$S^1(L)$
from the visual metric in any point are Hölder equivalent.
Similarly,
![]() $\mathcal {Q}_{\tau }$
has a natural topology homeomorphic to the standard solid cylinder.
$\mathcal {Q}_{\tau }$
has a natural topology homeomorphic to the standard solid cylinder.
The collection of all
![]() $\mathcal {P}_{\tau }$
sets over a
$\mathcal {P}_{\tau }$
sets over a
![]() $\pi _1(\mathcal {M})$
-invariant discrete collection of transversals defines a topology on
$\pi _1(\mathcal {M})$
-invariant discrete collection of transversals defines a topology on
![]() $S^{1}(\widetilde {\mathcal {M}})$
. Similarly, the collection of
$S^{1}(\widetilde {\mathcal {M}})$
. Similarly, the collection of
![]() $\mathcal {Q}_{\tau }$
sets over the same collection of transversals defines a topology on
$\mathcal {Q}_{\tau }$
sets over the same collection of transversals defines a topology on
![]() $\widetilde {\mathcal {M}} \cup S^{1}(\widetilde {\mathcal {M}})$
. Deck transformations act by homeomorphisms on both sets. For more details, see [Reference FenleyFen02], [Reference CalegariCal00], or [Reference CalegariCal01].
$\widetilde {\mathcal {M}} \cup S^{1}(\widetilde {\mathcal {M}})$
. Deck transformations act by homeomorphisms on both sets. For more details, see [Reference FenleyFen02], [Reference CalegariCal00], or [Reference CalegariCal01].
After the fact, it is easy to see that the topologies described are independent of the specific metric in
![]() $\mathcal {M}$
chosen and also work for any Riemannian metric in
$\mathcal {M}$
chosen and also work for any Riemannian metric in
![]() $\mathcal {M}$
.
$\mathcal {M}$
.
5 Properties of flow lines
This section describes the behavior of forward rays of flow lines, in particular their asymptotic behavior toward the the boundary at infinity
![]() $\bigcup \{S^{1}(L)|L\in \widetilde {\mathcal {F}}\}$
. In particular, we will prove that the rays are quasigeodesics in their respective leaves of
$\bigcup \{S^{1}(L)|L\in \widetilde {\mathcal {F}}\}$
. In particular, we will prove that the rays are quasigeodesics in their respective leaves of
![]() $\widetilde {\mathcal {F}}$
. Notice that this is definitely much weaker than saying that full flow lines are quasigeodesics in their respective leaves. We will also show that in some leaves, the forward ideal points are pairwise distinct and the negative ideal points are also pairwise distinct. In particular, even if the flow foliation is a leafwise quasigeodesic subfoliation of
$\widetilde {\mathcal {F}}$
. Notice that this is definitely much weaker than saying that full flow lines are quasigeodesics in their respective leaves. We will also show that in some leaves, the forward ideal points are pairwise distinct and the negative ideal points are also pairwise distinct. In particular, even if the flow foliation is a leafwise quasigeodesic subfoliation of
![]() $\mathcal {F}$
, it will not have the funnel property.
$\mathcal {F}$
, it will not have the funnel property.
We now introduce a family of sets in
![]() $\widetilde {\mathcal {M}}$
which will be extremely useful for us.
$\widetilde {\mathcal {M}}$
which will be extremely useful for us.
5.1 The sets
 $\mathcal {U}$
$\mathcal {U}$
Consider an arbitrary point
![]() $x\in \widetilde {\mathcal {A}}\subset \widetilde {\mathcal {M}}$
and the forward ray from x which is denoted by
$x\in \widetilde {\mathcal {A}}\subset \widetilde {\mathcal {M}}$
and the forward ray from x which is denoted by
starting at x, and let
![]() $L_x\subset \widetilde {\mathcal {A}}$
be the leaf containing
$L_x\subset \widetilde {\mathcal {A}}$
be the leaf containing
![]() $\gamma ^{+}_{x}$
. Recall that in the attractor
$\gamma ^{+}_{x}$
. Recall that in the attractor
![]() $\mathcal {A}$
, the foliation
$\mathcal {A}$
, the foliation
![]() $\mathcal {F}$
is equal to
$\mathcal {F}$
is equal to
![]() $\mathcal {F}^{wu}$
, and hence transverse to
$\mathcal {F}^{wu}$
, and hence transverse to
![]() $\mathcal {F}^{ws}$
. Therefore, the foliations
$\mathcal {F}^{ws}$
. Therefore, the foliations
![]() $\widetilde {\mathcal {F}}$
and
$\widetilde {\mathcal {F}}$
and
![]() $\widetilde {\mathcal {F}}^{ws}$
are transversal to each other near
$\widetilde {\mathcal {F}}^{ws}$
are transversal to each other near
![]() $\widetilde {\mathcal {A}}$
.
$\widetilde {\mathcal {A}}$
.
Let U be a compact rectangle transverse to the flow and with x in the interior of U. We assume that U is contained in the foliation boxes of all foliations
![]() $\widetilde {\mathcal {F}},\ \widetilde {\mathcal {F}}^s, \text { and } \widetilde {\mathcal {F}}^{ws}$
such that U is made up of a union of stable segments, every one of which intersects the local strong unstable segment through x. Consider the set
$\widetilde {\mathcal {F}},\ \widetilde {\mathcal {F}}^s, \text { and } \widetilde {\mathcal {F}}^{ws}$
such that U is made up of a union of stable segments, every one of which intersects the local strong unstable segment through x. Consider the set
The set
![]() $\mathcal {U}$
is a neighborhood of the forward ray
$\mathcal {U}$
is a neighborhood of the forward ray
![]() $\widetilde {\Phi }_{[0,\infty )}(x)$
. We can assume that
$\widetilde {\Phi }_{[0,\infty )}(x)$
. We can assume that
![]() $\mathcal {U}$
is homeomorphic to
$\mathcal {U}$
is homeomorphic to
![]() $[-1,1]\times [-1,1]\times [0,\infty )$
with
$[-1,1]\times [-1,1]\times [0,\infty )$
with
![]() $x=(0,0,0)$
and we can define coordinates on
$x=(0,0,0)$
and we can define coordinates on
![]() $\mathcal {U}$
such that the following hold.
$\mathcal {U}$
such that the following hold.
-
• U is identified with
 $[-1,1]\times [-1,1]\times \{0\}$
and points on U are represented as
$[-1,1]\times [-1,1]\times \{0\}$
and points on U are represented as
 $(r,s,0)$
for
$(r,s,0)$
for
 $r,s\in [-1,1]$
. In particular,
$r,s\in [-1,1]$
. In particular,
 $x=(0,0,0)$
.
$x=(0,0,0)$
. -
• For a point
 $y=(r,s,0)$
,
$y=(r,s,0)$
,
 $\widetilde {\Phi }_t(y)$
has coordinates
$\widetilde {\Phi }_t(y)$
has coordinates
 $(r,s,t)$
, that is, the ray
$(r,s,t)$
, that is, the ray
 $\{(r,s,t)|t\in [0,\infty )\}$
represents the ray
$\{(r,s,t)|t\in [0,\infty )\}$
represents the ray
 $\Phi _{[0,\infty )}(y)$
.
$\Phi _{[0,\infty )}(y)$
. -
• For a point
 $y'=(r',s,t')\in \mathcal {U}$
,
$y'=(r',s,t')\in \mathcal {U}$
,
 ${P_{y'}}$
denotes the horizontal infinite strip The infinite strip
${P_{y'}}$
denotes the horizontal infinite strip The infinite strip $$ \begin{align*}P_{y'}=\{(r,s,t)|r\in[-1,1],t\in[0,\infty)\}.\end{align*} $$
$$ \begin{align*}P_{y'}=\{(r,s,t)|r\in[-1,1],t\in[0,\infty)\}.\end{align*} $$
 $P_{y'}$
is contained in the leaf
$P_{y'}$
is contained in the leaf
 $L_{y'}\in \widetilde {\mathcal {F}}$
which contains
$L_{y'}\in \widetilde {\mathcal {F}}$
which contains
 $y'$
.
$y'$
.
-
• For a point
 $y'=(r,s',t')\in \mathcal {U}$
,
$y'=(r,s',t')\in \mathcal {U}$
,
 ${Q_{y'}}$
denotes the vertical infinite strip The infinite strip
${Q_{y'}}$
denotes the vertical infinite strip The infinite strip $$ \begin{align*}Q_{y'}=\{(r,s,t)|s\in[-1,1],t\in[0,\infty)\}.\end{align*} $$
$$ \begin{align*}Q_{y'}=\{(r,s,t)|s\in[-1,1],t\in[0,\infty)\}.\end{align*} $$
 $Q_{y'}$
is contained in the leaf
$Q_{y'}$
is contained in the leaf
 $E_{y'}\in \widetilde {\mathcal {F}}^{ws}$
which contains
$E_{y'}\in \widetilde {\mathcal {F}}^{ws}$
which contains
 $y'$
.
$y'$
.
As
![]() $x=(0,0,0)\in \widetilde {\mathcal {A}}$
, the leaf of
$x=(0,0,0)\in \widetilde {\mathcal {A}}$
, the leaf of
![]() $\widetilde {\mathcal {F}}$
through x is actually the weak unstable leaf of
$\widetilde {\mathcal {F}}$
through x is actually the weak unstable leaf of
![]() $\widetilde \Phi $
through x, and hence
$\widetilde \Phi $
through x, and hence
![]() $P_{x}$
is contained in the
$P_{x}$
is contained in the
![]() $\widetilde {\mathcal {F}}^{wu}$
leaf through x.
$\widetilde {\mathcal {F}}^{wu}$
leaf through x.
The sets
![]() $\mathcal {U}$
will be used throughout this section. Any such particular set
$\mathcal {U}$
will be used throughout this section. Any such particular set
![]() $\mathcal {U}$
is completely determined by the rectangle U.
$\mathcal {U}$
is completely determined by the rectangle U.
We can define a projection map
![]() $\Pi : \mathcal {U} \rightarrow P_x$
by the formula
$\Pi : \mathcal {U} \rightarrow P_x$
by the formula
![]() $\Pi (y)=S_{y} \cap P_{x}$
, where
$\Pi (y)=S_{y} \cap P_{x}$
, where
![]() $S_{y}$
is the one-dimensional leaf of the strong stable foliation
$S_{y}$
is the one-dimensional leaf of the strong stable foliation
![]() $\widetilde {\mathcal {F}}^{s}$
containing y. This is possible because one can do that in the original rectangle U as it is a union of strong stable segments, and then
$\widetilde {\mathcal {F}}^{s}$
containing y. This is possible because one can do that in the original rectangle U as it is a union of strong stable segments, and then
![]() $\mathcal {U}$
is the flow forward saturation of U and the maps
$\mathcal {U}$
is the flow forward saturation of U and the maps
![]() $\widetilde \Phi _t$
preserve the strong stable foliation in
$\widetilde \Phi _t$
preserve the strong stable foliation in
![]() $\widetilde {\mathcal {M}}$
. These projection maps are well defined and continuous because of the foliation structures on
$\widetilde {\mathcal {M}}$
. These projection maps are well defined and continuous because of the foliation structures on
![]() $\mathcal {U}$
.
$\mathcal {U}$
.
Observation 5.1. Here we list out all of the important observations from the above construction of
![]() $\mathcal {U}$
which we need in the rest of the article.
$\mathcal {U}$
which we need in the rest of the article.
-
(1) For any
 $y\in \mathcal {U}$
, the rays
$y\in \mathcal {U}$
, the rays
 $\widetilde {\Phi }_{[0,\infty )}(y)$
and
$\widetilde {\Phi }_{[0,\infty )}(y)$
and
 $\widetilde {\Phi }_{[0,\infty )}(\Pi (y))$
are asymptotic as they lie on the same weak stable leaf.
$\widetilde {\Phi }_{[0,\infty )}(\Pi (y))$
are asymptotic as they lie on the same weak stable leaf. -
(2) We can assume that lengths of all the line segments
 $\{(r,s,0)|s\in [-1,1]\}$
are less than a fixed
$\{(r,s,0)|s\in [-1,1]\}$
are less than a fixed
 $\epsilon>0$
in
$\epsilon>0$
in
 $\widetilde {\mathcal {M}}$
. Without loss of generality, we assume
$\widetilde {\mathcal {M}}$
. Without loss of generality, we assume
 $\epsilon $
is small enough that for any point
$\epsilon $
is small enough that for any point
 $p\in \mathcal {M}$
, the
$p\in \mathcal {M}$
, the
 $\epsilon -$
neighborhood of p is contained in a covering neighborhood of all the foliations
$\epsilon -$
neighborhood of p is contained in a covering neighborhood of all the foliations
 $\mathcal {F}, \mathcal {F}^u, \mathcal {F}^s, \mathcal {F}^{wu}, \mathcal {F}^{ws}$
.
$\mathcal {F}, \mathcal {F}^u, \mathcal {F}^s, \mathcal {F}^{wu}, \mathcal {F}^{ws}$
. -
(3) We have considered a Candel metric on the leaves of
 $\widetilde {\mathcal {F}}$
in
$\widetilde {\mathcal {F}}$
in
 $\widetilde {\mathcal {M}}$
and the Candel metric varies continuously on the leaves transversally.
$\widetilde {\mathcal {M}}$
and the Candel metric varies continuously on the leaves transversally.
The line segment
![]() $\unicode{x3bb} =\{(0,s,0)|s\in [-1,1]\}$
is transversal to
$\unicode{x3bb} =\{(0,s,0)|s\in [-1,1]\}$
is transversal to
![]() $\widetilde {\mathcal {F}}$
. Consider the open sets
$\widetilde {\mathcal {F}}$
. Consider the open sets
![]() $\mathcal {V}=\bigcup \nolimits _{x'\in \unicode{x3bb} }S^{1}(L_{x'})$
and
$\mathcal {V}=\bigcup \nolimits _{x'\in \unicode{x3bb} }S^{1}(L_{x'})$
and
![]() $\mathcal {W}=\bigcup \nolimits _{x'\in \unicode{x3bb} }(L_{x'}\cup S^{1}(L_{x'}))$
.
$\mathcal {W}=\bigcup \nolimits _{x'\in \unicode{x3bb} }(L_{x'}\cup S^{1}(L_{x'}))$
.
Definition 5.2. Let
![]() $\gamma $
be a flow line of
$\gamma $
be a flow line of
![]() $\widetilde \Phi $
contained in a leaf L of
$\widetilde \Phi $
contained in a leaf L of
![]() $\widetilde {\mathcal {F}}$
. Given z in
$\widetilde {\mathcal {F}}$
. Given z in
![]() $\gamma $
, if the forward ray of
$\gamma $
, if the forward ray of
![]() $\gamma $
converges to a single point of
$\gamma $
converges to a single point of
![]() $S^1(L)$
, we let this be
$S^1(L)$
, we let this be
![]() $\eta ^+(z)$
. Similarly define
$\eta ^+(z)$
. Similarly define
![]() $\eta ^-(z)$
. In addition, given a point a in
$\eta ^-(z)$
. In addition, given a point a in
![]() $\widetilde {\mathcal {M}}$
, let
$\widetilde {\mathcal {M}}$
, let
![]() $\gamma _a$
be the flow line of
$\gamma _a$
be the flow line of
![]() $\widetilde \Phi $
containing a.
$\widetilde \Phi $
containing a.
At this point, we only know that flow lines on
![]() $\widetilde {\mathcal {A}}\cup \widetilde {R}$
are leafwise quasigeodesics (by Lemma 2.2). Hence for
$\widetilde {\mathcal {A}}\cup \widetilde {R}$
are leafwise quasigeodesics (by Lemma 2.2). Hence for
![]() $x\in \widetilde {\mathcal {A}}\cup \widetilde {R}$
, both
$x\in \widetilde {\mathcal {A}}\cup \widetilde {R}$
, both
![]() $\eta ^+(x)$
and
$\eta ^+(x)$
and
![]() $\eta ^-(x)$
are well-defined points in
$\eta ^-(x)$
are well-defined points in
![]() $S^1(L)$
. The next lemma shows that every flow ray on
$S^1(L)$
. The next lemma shows that every flow ray on
![]() $\widetilde {\mathcal {M}}$
is leafwise quasigeodesic (in the respective leaf of
$\widetilde {\mathcal {M}}$
is leafwise quasigeodesic (in the respective leaf of
![]() $\widetilde {\mathcal {F}}$
), and hence
$\widetilde {\mathcal {F}}$
), and hence
![]() $\eta ^+(x)$
and
$\eta ^+(x)$
and
![]() $\eta ^-(x)$
are well defined for any arbitrary
$\eta ^-(x)$
are well defined for any arbitrary
![]() $x\in \widetilde {\mathcal {M}}$
. The proof of this lemma is quite involved.
$x\in \widetilde {\mathcal {M}}$
. The proof of this lemma is quite involved.
Lemma 5.3. For any
![]() $w\in \widetilde {\mathcal {M}}$
, the forward and the backward rays of the flow line
$w\in \widetilde {\mathcal {M}}$
, the forward and the backward rays of the flow line
![]() $\gamma _{w}= \widetilde \Phi _{\mathbb {R}}(w)$
are quasigeodesics on the leaf
$\gamma _{w}= \widetilde \Phi _{\mathbb {R}}(w)$
are quasigeodesics on the leaf
![]() $L_w$
in
$L_w$
in
![]() $\widetilde {\mathcal {F}}$
which contains the flow line.
$\widetilde {\mathcal {F}}$
which contains the flow line.
Proof. In §4, we proved that
![]() $\mathcal {F}$
does not admit any holonomy invariant transverse measure, so by Candel’s theorem,
$\mathcal {F}$
does not admit any holonomy invariant transverse measure, so by Candel’s theorem,
![]() $\mathcal {M}$
admits a Candel metric. To prove the current lemma, we assume a Candel metric in
$\mathcal {M}$
admits a Candel metric. To prove the current lemma, we assume a Candel metric in
![]() $\mathcal {M}$
so that leaves of
$\mathcal {M}$
so that leaves of
![]() $\mathcal {F}$
are hyperbolic surfaces. This metric is not Riemannian, but the result is independent of the metric.
$\mathcal {F}$
are hyperbolic surfaces. This metric is not Riemannian, but the result is independent of the metric.
By Lemma 2.2, every forward or backward ray in a leaf in
![]() $\widetilde {\mathcal {F}}^{wu}$
or
$\widetilde {\mathcal {F}}^{wu}$
or
![]() $\widetilde {\mathcal {F}}^{ws}$
is quasigeodesic in its respective leaf. In particular, every flow line is a quasigeodesic in the respective leaf of
$\widetilde {\mathcal {F}}^{ws}$
is quasigeodesic in its respective leaf. In particular, every flow line is a quasigeodesic in the respective leaf of
![]() $\mathcal {F}$
if contained in the attractor or repeller.
$\mathcal {F}$
if contained in the attractor or repeller.
So we may assume that the ray is in a leaf not in the attractor or repeller. Property 2.9 shows that every forward (respectively backward) ray is asymptotic with a ray in the attractor (respectively repeller). We will prove the result for a forward ray and the backward case is similar. Suppose
![]() $\gamma $
denotes a forward ray not contained in the attractor. By taking a subray, we may assume that the ray
$\gamma $
denotes a forward ray not contained in the attractor. By taking a subray, we may assume that the ray
![]() $\gamma $
is in the weak stable leaf of a point x in the attractor and the initial point w of the ray
$\gamma $
is in the weak stable leaf of a point x in the attractor and the initial point w of the ray
![]() $\gamma $
is very near x and contained in the strong stable segment of x. Hence we may assume that the initial point is contained in a local cross section U to
$\gamma $
is very near x and contained in the strong stable segment of x. Hence we may assume that the initial point is contained in a local cross section U to
![]() $\widetilde \Phi $
which is a rectangle centered at x, as described in the construction of the set
$\widetilde \Phi $
which is a rectangle centered at x, as described in the construction of the set
![]() $\mathcal {U}$
in the beginning of this section. Let
$\mathcal {U}$
in the beginning of this section. Let
![]() $L_x$
be the leaf of
$L_x$
be the leaf of
![]() $\widetilde {\mathcal {F}}$
containing x, and similarly define
$\widetilde {\mathcal {F}}$
containing x, and similarly define
![]() $L_w$
.
$L_w$
.
Recall that
![]() $L_x$
is also the weak unstable leaf of
$L_x$
is also the weak unstable leaf of
![]() $\widetilde \Phi $
containing x.
$\widetilde \Phi $
containing x.
Therefore, it is sufficient to show that every forward ray in the set
![]() $\mathcal {U}$
described above is quasigeodesic in its respective leaf of
$\mathcal {U}$
described above is quasigeodesic in its respective leaf of
![]() $\widetilde {\mathcal {F}}$
. In the leaf
$\widetilde {\mathcal {F}}$
. In the leaf
![]() $L_x$
through x, we consider a curve c as follows.
$L_x$
through x, we consider a curve c as follows.
Let I be the compact unstable segment
![]() $U \cap L_x$
which has endpoints
$U \cap L_x$
which has endpoints
![]() $z, y$
. Let
$z, y$
. Let
![]() $r_1=\widetilde \Phi _{[0,\infty )}(z)$
and
$r_1=\widetilde \Phi _{[0,\infty )}(z)$
and
![]() $r_2=\widetilde \Phi _{[0,\infty )}(y)$
be the forward rays of
$r_2=\widetilde \Phi _{[0,\infty )}(y)$
be the forward rays of
![]() $\widetilde \Phi $
through z and y. Then
$\widetilde \Phi $
through z and y. Then
![]() $c := r_1 \cup I \cup r_2$
is the bi-infinite curve on
$c := r_1 \cup I \cup r_2$
is the bi-infinite curve on
![]() $L_x$
, as shown in Figure 3.
$L_x$
, as shown in Figure 3.

Figure 3 The region
![]() $A_x$
in
$A_x$
in
![]() $L_x$
and the half-space
$L_x$
and the half-space
![]() $P_x$
. The region
$P_x$
. The region
![]() $A_x$
is the region bounded by the curve
$A_x$
is the region bounded by the curve
![]() $c = r_1 \cup I \cup r_2$
.
$c = r_1 \cup I \cup r_2$
.
The two rays
![]() $r_1$
and
$r_1$
and
![]() $r_2$
are quasigeodesics in
$r_2$
are quasigeodesics in
![]() $L_x$
by Lemma 2.2 as
$L_x$
by Lemma 2.2 as
![]() $L_x$
is a weak unstable leaf of
$L_x$
is a weak unstable leaf of
![]() $\widetilde \Phi $
. Moreover, they converge to distinct ideal points in
$\widetilde \Phi $
. Moreover, they converge to distinct ideal points in
![]() $S^1(L_x)$
. Let
$S^1(L_x)$
. Let
![]() $\nu $
be the interval in
$\nu $
be the interval in
![]() $S^1(L_x)$
bounded by these ideal points and containing the ideal point of
$S^1(L_x)$
bounded by these ideal points and containing the ideal point of
![]() $\widetilde \Phi _{[0,\infty )}(x)$
.
$\widetilde \Phi _{[0,\infty )}(x)$
.
The curve c bounds a region
![]() $A_x$
in
$A_x$
in
![]() $L_x$
(as in Figure 3) which is exactly
$L_x$
(as in Figure 3) which is exactly
![]() $\widetilde \Phi _{[0,\infty )}(I)$
. The region
$\widetilde \Phi _{[0,\infty )}(I)$
. The region
![]() $A_x$
is contained in
$A_x$
is contained in
![]() $\mathcal {U}$
, in fact,
$\mathcal {U}$
, in fact,
This region contains a half plane in
![]() $L_x$
, which we denote as
$L_x$
, which we denote as
![]() $P_x$
, as shown in Figure 3.
$P_x$
, as shown in Figure 3.
Recall that we are considering w, a point in
![]() $U \cap \widetilde {\mathcal {F}}^s(x)$
, where
$U \cap \widetilde {\mathcal {F}}^s(x)$
, where
![]() $\widetilde {\mathcal {F}}^s(x)$
is the strong stable leaf of x, in other words,
$\widetilde {\mathcal {F}}^s(x)$
is the strong stable leaf of x, in other words,
![]() $\Pi (w)=x$
in
$\Pi (w)=x$
in
![]() $\mathcal {U}$
according to the definition of the map
$\mathcal {U}$
according to the definition of the map
![]() $\Pi $
above. Let J be the intersection of
$\Pi $
above. Let J be the intersection of
![]() $L_w \cap U$
, where
$L_w \cap U$
, where
![]() $L_w$
is the leaf of
$L_w$
is the leaf of
![]() $\widetilde {\mathcal {F}}$
through w. Then
$\widetilde {\mathcal {F}}$
through w. Then
![]() $B_w := \widetilde \Phi _{[0,\infty )}(J)$
is contained in
$B_w := \widetilde \Phi _{[0,\infty )}(J)$
is contained in
![]() $L_w$
and contained in
$L_w$
and contained in
![]() $\mathcal {U}$
. In addition,
$\mathcal {U}$
. In addition,
![]() $\Pi (B_w)=A_x$
.
$\Pi (B_w)=A_x$
.
Since every point in J is in the strong stable leaf of a point in I, it follows that every flow ray in
![]() $B_w$
is asymptotic to a flow ray in
$B_w$
is asymptotic to a flow ray in
![]() $A_x$
by Observation 5.1(2). In fact, as points leave compact sets in
$A_x$
by Observation 5.1(2). In fact, as points leave compact sets in
![]() $B_w$
, they become closer and closer to
$B_w$
, they become closer and closer to
![]() $A_x$
.
$A_x$
.
The flow ray
![]() $r_x=\widetilde \Phi _{[0,\infty )}(x)$
is quasigeodesic on
$r_x=\widetilde \Phi _{[0,\infty )}(x)$
is quasigeodesic on
![]() $L_x$
by Lemma 2.2 as
$L_x$
by Lemma 2.2 as
![]() $L_x$
is a weak unstable leaf of
$L_x$
is a weak unstable leaf of
![]() $\widetilde \Phi $
. We want to show that
$\widetilde \Phi $
. We want to show that
![]() $r_w=\widetilde \Phi _{[0,\infty )}(w)$
is also quasigeodesic with respect to the induced path metric on
$r_w=\widetilde \Phi _{[0,\infty )}(w)$
is also quasigeodesic with respect to the induced path metric on
![]() $L_w$
. The key idea of the proof is as follows: the induced metrics on the leaves
$L_w$
. The key idea of the proof is as follows: the induced metrics on the leaves
![]() $\widetilde {\mathcal {F}}$
vary continuously and the region
$\widetilde {\mathcal {F}}$
vary continuously and the region
![]() $A_x\subset L_x$
is very close to
$A_x\subset L_x$
is very close to
![]() $B_w\subset L_w$
. As
$B_w\subset L_w$
. As
![]() $r_x$
is quasigeodesic in its leaf and asymptotic to the ray
$r_x$
is quasigeodesic in its leaf and asymptotic to the ray
![]() $r_w = \widetilde \Phi _{[0,\infty })(w)$
, it follows that the other ray is also a quasigeodesic in its
$r_w = \widetilde \Phi _{[0,\infty })(w)$
, it follows that the other ray is also a quasigeodesic in its
![]() $\widetilde {\mathcal {F}}$
leaf.
$\widetilde {\mathcal {F}}$
leaf.
Next we provide more specific details. In the leaf
![]() $L_x$
, choose two points
$L_x$
, choose two points
![]() $x_1, x_2$
in I with x in between them so that the geodesic
$x_1, x_2$
in I with x in between them so that the geodesic
![]() $\beta _x$
in
$\beta _x$
in
![]() $L_x$
with ideal points
$L_x$
with ideal points
![]() $\eta ^+(x_1), \eta ^+(x_2)$
is contained in the interior of
$\eta ^+(x_1), \eta ^+(x_2)$
is contained in the interior of
![]() $A_x$
. This is possible since the flow lines in
$A_x$
. This is possible since the flow lines in
![]() $L_x$
are uniform quasigeodesics and they spread out in the forward direction. We stress that, in general, it is not possible to choose
$L_x$
are uniform quasigeodesics and they spread out in the forward direction. We stress that, in general, it is not possible to choose
![]() $x_1, x_2$
as the endpoints of
$x_1, x_2$
as the endpoints of
![]() $\nu $
as the flow lines are only quasigeodesics and not geodesics in
$\nu $
as the flow lines are only quasigeodesics and not geodesics in
![]() $L_x$
. Recall that
$L_x$
. Recall that
![]() $\nu $
is the interval of
$\nu $
is the interval of
![]() $S^1(L_x)$
defined previously. Let
$S^1(L_x)$
defined previously. Let
![]() $P_x$
be the half plane of
$P_x$
be the half plane of
![]() $L_x$
bounded by
$L_x$
bounded by
![]() $\beta _x$
and containing a forward ray from x. We also may assume that every point in
$\beta _x$
and containing a forward ray from x. We also may assume that every point in
![]() $P_x$
is
$P_x$
is
![]() $\epsilon _1$
close to
$\epsilon _1$
close to
![]() $L_w$
with
$L_w$
with
![]() $\epsilon _1$
very close to zero. Then
$\epsilon _1$
very close to zero. Then
![]() $\beta _x$
is
$\beta _x$
is
![]() $\epsilon _1$
close to a curve
$\epsilon _1$
close to a curve
![]() $\beta '$
in
$\beta '$
in
![]() $L_w$
which has geodesic curvature in
$L_w$
which has geodesic curvature in
![]() $L_w$
very close to zero. To obtain this property of
$L_w$
very close to zero. To obtain this property of
![]() $\beta '$
with small geodesic curvature in
$\beta '$
with small geodesic curvature in
![]() $L_w$
was one of the reasons to choose a Candel metric with hyperbolic leaves varying continuously, and hence uniformly continuously, since
$L_w$
was one of the reasons to choose a Candel metric with hyperbolic leaves varying continuously, and hence uniformly continuously, since
![]() $\mathcal {M}$
is compact. Notice that using this continuity only gives us a curve
$\mathcal {M}$
is compact. Notice that using this continuity only gives us a curve
![]() $\beta '$
with small geodesic curvature, but not necessarily one which has zero geodesic curvature. However, since the induced path metric in
$\beta '$
with small geodesic curvature, but not necessarily one which has zero geodesic curvature. However, since the induced path metric in
![]() $L_w$
is hyperbolic, it now follows that this curve
$L_w$
is hyperbolic, it now follows that this curve
![]() $\beta '$
with very small geodesic curvature is very close in
$\beta '$
with very small geodesic curvature is very close in
![]() $L_w$
to an actual geodesic in
$L_w$
to an actual geodesic in
![]() $L_w$
. This geodesic is denoted by
$L_w$
. This geodesic is denoted by
![]() $\beta _w$
. Let
$\beta _w$
. Let
![]() $P_w$
be the union of the size-
$P_w$
be the union of the size-
![]() $1$
neighborhood of
$1$
neighborhood of
![]() $\beta _w$
in
$\beta _w$
in
![]() $L_w$
and the half plane of
$L_w$
and the half plane of
![]() $L_w$
which is very close to
$L_w$
which is very close to
![]() $P_x$
, as shown in Figure 4.
$P_x$
, as shown in Figure 4.

Figure 4
![]() $P_x$
in
$P_x$
in
![]() $L_x$
is asymptotic to
$L_x$
is asymptotic to
![]() $P_w$
in
$P_w$
in
![]() $L_w$
.
$L_w$
.
Note that
![]() $\Pi ^{-1}(r_x)=r_w$
. We choose
$\Pi ^{-1}(r_x)=r_w$
. We choose
![]() $\epsilon _1$
small enough so that
$\epsilon _1$
small enough so that
![]() $\Pi ^{-1}$
is defined in
$\Pi ^{-1}$
is defined in
![]() $P_x$
and
$P_x$
and
![]() $\Pi ^{-1}(L_x) \subset P_w$
. This is the reason to include a neighborhood of
$\Pi ^{-1}(L_x) \subset P_w$
. This is the reason to include a neighborhood of
![]() $\beta _w$
in
$\beta _w$
in
![]() $L_w$
.
$L_w$
.
We will now show that the map
![]() $\Pi ^{-1}:P_x\rightarrow P_w$
is a quasi-isometry. Using the fact that
$\Pi ^{-1}:P_x\rightarrow P_w$
is a quasi-isometry. Using the fact that
![]() $P_w$
is very close to
$P_w$
is very close to
![]() $L_x$
, continuity of leafwise Riemannian metric on
$L_x$
, continuity of leafwise Riemannian metric on
![]() $\mathcal {M}$
, and the compactness of
$\mathcal {M}$
, and the compactness of
![]() $\mathcal {M}$
, we obtain the following: given
$\mathcal {M}$
, we obtain the following: given
![]() $\epsilon> 0$
, we can consider
$\epsilon> 0$
, we can consider
![]() $\epsilon _1>0$
small enough, such that
$\epsilon _1>0$
small enough, such that
Next consider
![]() $a_0$
and
$a_0$
and
![]() $b_0$
on
$b_0$
on
![]() $P_x$
and let
$P_x$
and let
![]() $\rho $
be the geodesic connecting them on
$\rho $
be the geodesic connecting them on
![]() $P_x$
. Partition
$P_x$
. Partition
![]() $\rho $
in n subintervals
$\rho $
in n subintervals
![]() $a_0, a_1,a_2,\ldots ,a_{n+1}=b_0$
such that
$a_0, a_1,a_2,\ldots ,a_{n+1}=b_0$
such that
![]() $d_{L_x}(a_i,a_{i+1})= 1$
for all
$d_{L_x}(a_i,a_{i+1})= 1$
for all
![]() $0\leq i<n-1$
and
$0\leq i<n-1$
and
![]() $0 < d_{L_x}(a_{n},b_0)\leq 1$
. As
$0 < d_{L_x}(a_{n},b_0)\leq 1$
. As
![]() $d(a_i,a_{i+1})\leq 1$
for all i,
$d(a_i,a_{i+1})\leq 1$
for all i,
 $$ \begin{align*}d_{L_w}(\Pi^{-1}(a_0),\Pi^{-1}(b_0))&\leq \sum_{i=0}^{n}d_{L_w}(\Pi^{-1}(a_i),\Pi^{-1}(a_{i+1}))\\&\leq (n+1)(1+\epsilon) = n(1 + \epsilon) + (1+\epsilon).\end{align*} $$
$$ \begin{align*}d_{L_w}(\Pi^{-1}(a_0),\Pi^{-1}(b_0))&\leq \sum_{i=0}^{n}d_{L_w}(\Pi^{-1}(a_i),\Pi^{-1}(a_{i+1}))\\&\leq (n+1)(1+\epsilon) = n(1 + \epsilon) + (1+\epsilon).\end{align*} $$
By construction,
![]() $n < d_{L_x}(a_0,b_0)$
. Hence, we conclude
$n < d_{L_x}(a_0,b_0)$
. Hence, we conclude
where
![]() $C_0 = (1 +\epsilon )$
is a fixed constant. Similarly, if
$C_0 = (1 +\epsilon )$
is a fixed constant. Similarly, if
![]() $a_0, b_0$
are in
$a_0, b_0$
are in
![]() $\Pi ^{-1}(P_x)$
, we get that
$\Pi ^{-1}(P_x)$
, we get that
![]() $d_{L_x}(\Pi (a_0), \Pi (b_0)) < C_1 d_{L_w}(a_0,b_0) + C_2$
for some globally fixed constants
$d_{L_x}(\Pi (a_0), \Pi (b_0)) < C_1 d_{L_w}(a_0,b_0) + C_2$
for some globally fixed constants
![]() $C_1, C_2$
. Since
$C_1, C_2$
. Since
![]() $\Pi ^{-1}(P_x)$
is
$\Pi ^{-1}(P_x)$
is
![]() $2$
-dense in
$2$
-dense in
![]() $P_w$
, it follows that
$P_w$
, it follows that
![]() $\Pi ^{-1}$
is a quasi-isometry from
$\Pi ^{-1}$
is a quasi-isometry from
![]() $P_x$
to
$P_x$
to
![]() $P_w$
.
$P_w$
.
Finally, as we know that
![]() $r_x$
is a quasigeodesic on
$r_x$
is a quasigeodesic on
![]() $P_x$
, then its image via the quasi-isometry
$P_x$
, then its image via the quasi-isometry
![]() $\Pi ^{-1}$
,
$\Pi ^{-1}$
,
![]() $r_w=\Pi ^{-1}(r_x)$
is a quasigeodesic on
$r_w=\Pi ^{-1}(r_x)$
is a quasigeodesic on
![]() $P_w\subset L_w$
with respect to the metric
$P_w\subset L_w$
with respect to the metric
![]() $d_{L_w}$
. Since
$d_{L_w}$
. Since
![]() $P_w$
is a quasi-isometrically embedded in
$P_w$
is a quasi-isometrically embedded in
![]() $L_w$
, it now follows that
$L_w$
, it now follows that
![]() $r_w$
is a quasigeodesic in
$r_w$
is a quasigeodesic in
![]() $L_w$
.
$L_w$
.
If we reverse the flow, every backward ray becomes a forward ray, and hence leafwise quasigeodesic.
This finally finishes the proof of Lemma 5.3.
By compactness and continuity, there is global
![]() $K_0,s_0>0$
so that given any flow line
$K_0,s_0>0$
so that given any flow line
![]() $\gamma $
, there is a forward ray
$\gamma $
, there is a forward ray
![]() $\gamma ^+$
and a backward ray
$\gamma ^+$
and a backward ray
![]() $\gamma ^-$
of
$\gamma ^-$
of
![]() $\gamma $
which are
$\gamma $
which are
![]() $(K_0,s_0)$
quasigeodesics in leaf
$(K_0,s_0)$
quasigeodesics in leaf
![]() $L_{\gamma }$
, the leaf of
$L_{\gamma }$
, the leaf of
![]() $\widetilde {\mathcal {F}}$
containing
$\widetilde {\mathcal {F}}$
containing
![]() $\gamma $
. Note that all the leaves
$\gamma $
. Note that all the leaves
![]() $L\in \widetilde {\mathcal {F}}$
are hyperbolic and we can define their boundary at infinity
$L\in \widetilde {\mathcal {F}}$
are hyperbolic and we can define their boundary at infinity
![]() $S^1(L)$
. As the flow rays
$S^1(L)$
. As the flow rays
![]() $\gamma ^+$
and
$\gamma ^+$
and
![]() $\gamma ^-$
are quasigeodesics on
$\gamma ^-$
are quasigeodesics on
![]() $F_{\gamma }$
, they define unique points on the ideal boundary
$F_{\gamma }$
, they define unique points on the ideal boundary
![]() $S^1(L_{\gamma })$
. Hence for all
$S^1(L_{\gamma })$
. Hence for all
![]() $a\in \gamma \subset \widetilde {\mathcal {M}}$
, the forward subray
$a\in \gamma \subset \widetilde {\mathcal {M}}$
, the forward subray
![]() $\gamma ^+_a$
limits on a single point in
$\gamma ^+_a$
limits on a single point in
![]() $S^1(L_{\gamma })$
and
$S^1(L_{\gamma })$
and
![]() $\eta ^+(a)$
is well defined as in Definition 5.2. Similarly,
$\eta ^+(a)$
is well defined as in Definition 5.2. Similarly,
![]() $\eta ^-(a)$
is also well defined by the backward subray
$\eta ^-(a)$
is also well defined by the backward subray
![]() $\gamma ^-_a$
.
$\gamma ^-_a$
.
In the next proposition, we consider the sets
![]() $P_y$
contained in
$P_y$
contained in
![]() $\mathcal {U}$
.
$\mathcal {U}$
.
Proposition 5.4. Suppose
![]() $a,b\in P_y\subset L_y$
but
$a,b\in P_y\subset L_y$
but
![]() $\gamma _{a}\neq \gamma _{b}$
, then
$\gamma _{a}\neq \gamma _{b}$
, then
![]() $\eta ^{+}(a)\neq \eta ^{+}(b)$
in
$\eta ^{+}(a)\neq \eta ^{+}(b)$
in
![]() $S^1(L_y)$
.
$S^1(L_y)$
.
Proof. By the previous Lemma 5.3, we already know that all rays are quasigeodesics in their respective leaves. We do the proof by contradiction and assume that
![]() $\eta ^+(a) = \eta ^+(b)$
on
$\eta ^+(a) = \eta ^+(b)$
on
![]() $S^1(L_y)$
. Since the rays
$S^1(L_y)$
. Since the rays
![]() $\widetilde \Phi _{[0,\infty )}(a), \widetilde \Phi _{[0,\infty )}(b)$
are quasigeodesics in
$\widetilde \Phi _{[0,\infty )}(a), \widetilde \Phi _{[0,\infty )}(b)$
are quasigeodesics in
![]() $L_y$
and by assumption they have the same ideal point in
$L_y$
and by assumption they have the same ideal point in
![]() $S^1(L_y)$
, the following happens: there is
$S^1(L_y)$
, the following happens: there is
![]() $d_0> 0$
and points
$d_0> 0$
and points
![]() $p_i, q_i$
in
$p_i, q_i$
in
![]() $\widetilde \Phi _{[0,\infty )}(a), \widetilde \Phi _{[0,\infty )}(b)$
respectively, escaping in the rays so that
$\widetilde \Phi _{[0,\infty )}(a), \widetilde \Phi _{[0,\infty )}(b)$
respectively, escaping in the rays so that
![]() $d_{L_y}(p_i,q_i) < d_0$
. Consider the points
$d_{L_y}(p_i,q_i) < d_0$
. Consider the points
![]() $\Pi (a)$
and
$\Pi (a)$
and
![]() $\Pi (b)$
on
$\Pi (b)$
on
![]() $P_x$
. Since
$P_x$
. Since
are asymptotic in the weak stable leaf of
![]() $\widetilde \Phi $
in
$\widetilde \Phi $
in
![]() $\widetilde {\mathcal {M}}$
, there are
$\widetilde {\mathcal {M}}$
, there are
![]() $p^{\prime }_i$
in
$p^{\prime }_i$
in
![]() $\widetilde \Phi _{[0,\infty )}(\Pi (a))$
with
$\widetilde \Phi _{[0,\infty )}(\Pi (a))$
with
![]() $d(p_i,p^{\prime }_i) \rightarrow 0$
. Here d is the ambient distance in
$d(p_i,p^{\prime }_i) \rightarrow 0$
. Here d is the ambient distance in
![]() $\widetilde {\mathcal {M}}$
. Similarly, there are
$\widetilde {\mathcal {M}}$
. Similarly, there are
![]() $q^{\prime }_i$
in
$q^{\prime }_i$
in
![]() $\widetilde \Phi _{[0,\infty )}(\Pi (b))$
with
$\widetilde \Phi _{[0,\infty )}(\Pi (b))$
with
![]() $d(q_i,q^{\prime }_i) \rightarrow 0$
. By the local product structure of the foliation
$d(q_i,q^{\prime }_i) \rightarrow 0$
. By the local product structure of the foliation
![]() $\mathcal {F}$
, it follows that
$\mathcal {F}$
, it follows that
![]() $d_{L_x}(p^{\prime }_i,q^{\prime }_i) < d_0 + 1$
for i sufficiently big.
$d_{L_x}(p^{\prime }_i,q^{\prime }_i) < d_0 + 1$
for i sufficiently big.
We explain this in more detail. We choose a finite cover of M by foliated boxes of
![]() $\mathcal {F}$
, each of which contains a ball of radius
$\mathcal {F}$
, each of which contains a ball of radius
![]() $2/m$
, where m is a fixed integer. Any disk in a leaf of
$2/m$
, where m is a fixed integer. Any disk in a leaf of
![]() $\mathcal {F}$
which has diameter less than
$\mathcal {F}$
which has diameter less than
![]() $1/m$
which is product foliated and any path in the disk is approximated by a path in another leaf with length very close to the length of the original path. Let n be the smallest positive integer bigger than
$1/m$
which is product foliated and any path in the disk is approximated by a path in another leaf with length very close to the length of the original path. Let n be the smallest positive integer bigger than
![]() $d_0$
. Using compactness of
$d_0$
. Using compactness of
![]() $\mathcal {M}$
, it follows that any connected union of at most
$\mathcal {M}$
, it follows that any connected union of at most
![]() $nm$
such disks in a leaf has a transversal neighborhood of fixed size which is product foliated and has the property above on lengths of paths. Therefore, the paths from
$nm$
such disks in a leaf has a transversal neighborhood of fixed size which is product foliated and has the property above on lengths of paths. Therefore, the paths from
![]() $p_i$
to
$p_i$
to
![]() $q_i$
in
$q_i$
in
![]() $L_y$
can be approximated by paths from
$L_y$
can be approximated by paths from
![]() $p^{\prime }_i$
to
$p^{\prime }_i$
to
![]() $q^{\prime }_i$
in
$q^{\prime }_i$
in
![]() $L_x$
with length very close, resulting in
$L_x$
with length very close, resulting in
![]() $d_{L_x}(p^{\prime }_i,q^{\prime }_i) < d_0 + 1$
for i sufficiently big.
$d_{L_x}(p^{\prime }_i,q^{\prime }_i) < d_0 + 1$
for i sufficiently big.
Therefore, the rays
![]() $\widetilde \Phi _{[0,\infty )}(\Pi (a))$
,
$\widetilde \Phi _{[0,\infty )}(\Pi (a))$
,
![]() $\widetilde \Phi _{[0,\infty )}(\Pi (b))$
converge to the same ideal point in
$\widetilde \Phi _{[0,\infty )}(\Pi (b))$
converge to the same ideal point in
![]() $S^1(L_x)$
. However,
$S^1(L_x)$
. However,
![]() $L_x$
is also a weak unstable leaf of
$L_x$
is also a weak unstable leaf of
![]() $\widetilde \Phi $
and as the flow lines
$\widetilde \Phi $
and as the flow lines
![]() $\widetilde \Phi _{\mathbb {R}}(\Pi (a))$
and
$\widetilde \Phi _{\mathbb {R}}(\Pi (a))$
and
![]() $\widetilde \Phi _{\mathbb {R}}(\Pi (b))$
are distinct flow lines in
$\widetilde \Phi _{\mathbb {R}}(\Pi (b))$
are distinct flow lines in
![]() $L_x$
, by the description of ideal points of flow lines in weak unstable leaves as in Property 2.4, the forward limit points are distinct, that is,
$L_x$
, by the description of ideal points of flow lines in weak unstable leaves as in Property 2.4, the forward limit points are distinct, that is,
This is a contradiction and shows that
![]() $\eta ^+(a) \neq \eta ^+(b)$
in
$\eta ^+(a) \neq \eta ^+(b)$
in
![]() $S^1(L_y)$
.
$S^1(L_y)$
.
Lemma 5.5. In each leaf L of
![]() $\widetilde {\mathcal {F}}$
, the leaf space of the flow foliation is Hausdorff and homeomorphic to the real line
$\widetilde {\mathcal {F}}$
, the leaf space of the flow foliation is Hausdorff and homeomorphic to the real line
![]() $\mathbb {R}$
.
$\mathbb {R}$
.
Proof. For the leaves of
![]() $\widetilde {\mathcal {F}}$
in lifts
$\widetilde {\mathcal {F}}$
in lifts
![]() $\widetilde {\mathcal {A}}$
and
$\widetilde {\mathcal {A}}$
and
![]() $\widetilde {\mathcal {R}}$
of the attractor and repeller, the result is obvious, since the foliation by flow lines satisfies this property in weak stable and weak unstable leaves of Anosov flows [Reference FenleyFen94]. Any other leaf L of
$\widetilde {\mathcal {R}}$
of the attractor and repeller, the result is obvious, since the foliation by flow lines satisfies this property in weak stable and weak unstable leaves of Anosov flows [Reference FenleyFen94]. Any other leaf L of
![]() $\widetilde {\mathcal {F}}$
is the lift of a leaf of
$\widetilde {\mathcal {F}}$
is the lift of a leaf of
![]() $\mathcal {F}$
which intersects a torus T from the collection of tori
$\mathcal {F}$
which intersects a torus T from the collection of tori
![]() $\{T_i\}$
which separates
$\{T_i\}$
which separates
![]() $\mathcal {A}$
and
$\mathcal {A}$
and
![]() $\mathcal {R}$
. Hence L intersects a lift
$\mathcal {R}$
. Hence L intersects a lift
![]() $\widetilde T$
of T in a curve
$\widetilde T$
of T in a curve
![]() $\beta $
. The flow saturation of
$\beta $
. The flow saturation of
![]() $\beta $
is exactly L, since every flow line in M is either in the attractor or repeller; or intersects a torus in
$\beta $
is exactly L, since every flow line in M is either in the attractor or repeller; or intersects a torus in
![]() $\{T_i\}$
. The curve
$\{T_i\}$
. The curve
![]() $\beta $
is transverse to the weak stable and weak unstable foliations, and hence intersects a flow line exactly once. Hence
$\beta $
is transverse to the weak stable and weak unstable foliations, and hence intersects a flow line exactly once. Hence
![]() $\beta $
parameterizes the flowlines in L. This proves the result.
$\beta $
parameterizes the flowlines in L. This proves the result.
For each L of
![]() $\widetilde {\mathcal {F}}$
, the map
$\widetilde {\mathcal {F}}$
, the map
![]() $\eta ^+$
induces a map from the flow foliation leaf space in L (which is
$\eta ^+$
induces a map from the flow foliation leaf space in L (which is
![]() $\cong \mathbb {R}$
) to
$\cong \mathbb {R}$
) to
![]() $S^1(L)$
. Since flow lines are disjoint, this map is weakly monotone.
$S^1(L)$
. Since flow lines are disjoint, this map is weakly monotone.
Corollary 5.6. For all
![]() $y\in \mathcal {U}$
,
$y\in \mathcal {U}$
,
![]() $\eta ^{+}(y)\neq \eta ^{-}(y)$
in
$\eta ^{+}(y)\neq \eta ^{-}(y)$
in
![]() $S^1(L_y)$
.
$S^1(L_y)$
.
Proof. If
![]() $\eta ^{+}(y)=\eta ^{-}(y)$
, then the flow line
$\eta ^{+}(y)=\eta ^{-}(y)$
, then the flow line
![]() $\gamma _{y}$
bounds a disk
$\gamma _{y}$
bounds a disk
![]() $\mathcal {D}$
on
$\mathcal {D}$
on
![]() $L_y\cup S^{1}(L_y)$
such that the closure of
$L_y\cup S^{1}(L_y)$
such that the closure of
![]() $\mathcal {D}$
in
$\mathcal {D}$
in
![]() $L \cup S^1(L)$
intersects
$L \cup S^1(L)$
intersects
![]() $S^1(L)$
only in
$S^1(L)$
only in
![]() $\eta ^{+}(y)=\eta ^{-}(y)$
. For any z in the interior of
$\eta ^{+}(y)=\eta ^{-}(y)$
. For any z in the interior of
![]() $\mathcal {D}$
, the flow line
$\mathcal {D}$
, the flow line
![]() $\gamma _{z}$
is contained in
$\gamma _{z}$
is contained in
![]() $\mathcal {D}$
, and hence
$\mathcal {D}$
, and hence
![]() $\eta ^{+}(z)=\eta ^{-}(z)=\eta ^{+}(y)=\eta ^{-}(y)$
. This contradicts Proposition 5.4, because if z,
$\eta ^{+}(z)=\eta ^{-}(z)=\eta ^{+}(y)=\eta ^{-}(y)$
. This contradicts Proposition 5.4, because if z,
![]() $y\in \mathcal {U}$
, and
$y\in \mathcal {U}$
, and
![]() $\gamma _z \neq \gamma _y$
, then
$\gamma _z \neq \gamma _y$
, then
![]() $\eta ^+(z) \neq \eta ^+(y)$
.
$\eta ^+(z) \neq \eta ^+(y)$
.
We now extend the map
![]() $\eta ^+$
to a map from
$\eta ^+$
to a map from
![]() $\widetilde {\mathcal {M}}$
to
$\widetilde {\mathcal {M}}$
to
![]() $S^{1}(\widetilde {\mathcal {M}})$
. For each x in
$S^{1}(\widetilde {\mathcal {M}})$
. For each x in
![]() $\widetilde {\mathcal {M}}$
,
$\widetilde {\mathcal {M}}$
,
![]() $\eta ^+(x)$
is in
$\eta ^+(x)$
is in
![]() $S^1(L_x) \subset S^{1}(\widetilde {\mathcal {M}})$
.
$S^1(L_x) \subset S^{1}(\widetilde {\mathcal {M}})$
.
Proposition 5.7.
![]() $\eta ^{+}$
and
$\eta ^{+}$
and
![]() $\eta ^{-}$
are continuous on
$\eta ^{-}$
are continuous on
![]() $\widetilde {\mathcal {M}}$
.
$\widetilde {\mathcal {M}}$
.
Proof. In this proof, we again use a Candel metric in M.
Suppose
![]() $x_i\rightarrow x_0$
in
$x_i\rightarrow x_0$
in
![]() $\widetilde {\mathcal {M}}$
. We will show that
$\widetilde {\mathcal {M}}$
. We will show that
![]() $\eta ^{+}(x_i)\rightarrow \eta ^{+}(x_0)$
in
$\eta ^{+}(x_i)\rightarrow \eta ^{+}(x_0)$
in
![]() $S^{1}(\widetilde {\mathcal {M}})$
. There are two different cases depending on whether
$S^{1}(\widetilde {\mathcal {M}})$
. There are two different cases depending on whether
![]() $x_0\in \widetilde {\mathcal {R}}$
or
$x_0\in \widetilde {\mathcal {R}}$
or
![]() $x_0\notin \widetilde {\mathcal {R}}$
.
$x_0\notin \widetilde {\mathcal {R}}$
.
We first prove the result for
![]() $x_0\notin \widetilde {\mathcal {R}}$
. As
$x_0\notin \widetilde {\mathcal {R}}$
. As
![]() $x_0\notin \widetilde {\mathcal {R}}$
, the forward ray starting at
$x_0\notin \widetilde {\mathcal {R}}$
, the forward ray starting at
![]() $x_0$
is asymptotic to a forward flow ray in
$x_0$
is asymptotic to a forward flow ray in
![]() $\widetilde {\mathcal {A}}$
. Therefore, it is enough to assume that
$\widetilde {\mathcal {A}}$
. Therefore, it is enough to assume that
![]() $\{x_i\}$
and
$\{x_i\}$
and
![]() $x_0$
belong to a neighborhood
$x_0$
belong to a neighborhood
![]() $\mathcal {U}$
as constructed above, since this is true for every ray asymptoptic to
$\mathcal {U}$
as constructed above, since this is true for every ray asymptoptic to
![]() $\widetilde {\mathcal {A}}$
.
$\widetilde {\mathcal {A}}$
.
For z in
![]() $\widetilde {\mathcal {M}}$
, let
$\widetilde {\mathcal {M}}$
, let
![]() $L_z$
be the leaf of
$L_z$
be the leaf of
![]() $\widetilde {\mathcal {F}}$
containing z.
$\widetilde {\mathcal {F}}$
containing z.
For
![]() $i\in \mathbb {N}\cup \{0\}$
, let
$i\in \mathbb {N}\cup \{0\}$
, let
![]() $\gamma ^{+}_i$
denote the forward flow ray starting from
$\gamma ^{+}_i$
denote the forward flow ray starting from
![]() $x_i$
and let
$x_i$
and let
![]() $\zeta _{i}$
denote the geodesic ray on
$\zeta _{i}$
denote the geodesic ray on
![]() $L_{x_i}$
starting at
$L_{x_i}$
starting at
![]() $x_i$
and with ideal point
$x_i$
and with ideal point
![]() $\eta ^{+}(x_i)$
in
$\eta ^{+}(x_i)$
in
![]() $S^1(L_{x_i})$
. Each
$S^1(L_{x_i})$
. Each
![]() $\zeta _i$
defines the ideal point
$\zeta _i$
defines the ideal point
![]() $\eta ^{+}(x_i)$
on
$\eta ^{+}(x_i)$
on
![]() $S^1(L_{x_i})$
, therefore it is enough to show that any convergent subsequence of
$S^1(L_{x_i})$
, therefore it is enough to show that any convergent subsequence of
![]() $(\zeta _{i})$
converges to
$(\zeta _{i})$
converges to
![]() $\zeta _0$
in the compact open topology. Since all
$\zeta _0$
in the compact open topology. Since all
![]() $x_i$
are contained in a compact subset of
$x_i$
are contained in a compact subset of
![]() $\widetilde {\mathcal {M}}$
, existence of convergent subsequences of
$\widetilde {\mathcal {M}}$
, existence of convergent subsequences of
![]() $\{\zeta _i\}$
is assured.
$\{\zeta _i\}$
is assured.
Suppose that a subsequence
![]() $(\zeta _{i(k)})$
converges to
$(\zeta _{i(k)})$
converges to
![]() $\zeta '$
. We have to prove that
$\zeta '$
. We have to prove that
![]() $\zeta '=\zeta _0$
. We assume that the neighborhood
$\zeta '=\zeta _0$
. We assume that the neighborhood
![]() $\mathcal {U}$
constructed above has a point
$\mathcal {U}$
constructed above has a point
![]() $x \in \widetilde {\mathcal {A}}$
, as in the construction of
$x \in \widetilde {\mathcal {A}}$
, as in the construction of
![]() $\mathcal {U}$
. Then all flow rays in
$\mathcal {U}$
. Then all flow rays in
![]() $L_x \cap \mathcal {U}$
are
$L_x \cap \mathcal {U}$
are
![]() $(K,s)$
-quasigeodesics in
$(K,s)$
-quasigeodesics in
![]() $L_x$
for some fixed
$L_x$
for some fixed
![]() $K, s$
. Since all flow rays in
$K, s$
. Since all flow rays in
![]() $\mathcal {U}$
are forward asymptotic to flow rays in
$\mathcal {U}$
are forward asymptotic to flow rays in
![]() $L_x$
, there are
$L_x$
, there are
![]() $K',s'$
so that all flow rays in
$K',s'$
so that all flow rays in
![]() $\mathcal {U}$
are
$\mathcal {U}$
are
![]() $(K',s')$
-quasigeodesics in their respective
$(K',s')$
-quasigeodesics in their respective
![]() $\widetilde {\mathcal {F}}$
leaves. It follows that there exists a constant
$\widetilde {\mathcal {F}}$
leaves. It follows that there exists a constant
![]() $d'> 0$
such that
$d'> 0$
such that
where
![]() $\mathcal {N}_{d'}$
denotes the neighborhood of radius d in the respective leaf of
$\mathcal {N}_{d'}$
denotes the neighborhood of radius d in the respective leaf of
![]() $\widetilde {\mathcal {F}}$
. For any
$\widetilde {\mathcal {F}}$
. For any
![]() $d_1> 0$
, the segment of length
$d_1> 0$
, the segment of length
![]() $d_1$
on
$d_1$
on
![]() $\gamma ^{+}_{i(k)}$
starting at
$\gamma ^{+}_{i(k)}$
starting at
![]() $x_{i(k)}$
is within
$x_{i(k)}$
is within
![]() $d'$
-distance from
$d'$
-distance from
![]() $\zeta _{i(k)}$
. Therefore in the limit, the segment of
$\zeta _{i(k)}$
. Therefore in the limit, the segment of
![]() $\gamma ^+_0$
of length
$\gamma ^+_0$
of length
![]() $d_1$
starting from
$d_1$
starting from
![]() $x_0$
is contained in
$x_0$
is contained in
![]() $\mathcal {N}_{d'}(\zeta ')$
in the respective leaf. This is true for all
$\mathcal {N}_{d'}(\zeta ')$
in the respective leaf. This is true for all
![]() $d_1$
, so
$d_1$
, so
![]() $\zeta '$
is at Hausdorff distance
$\zeta '$
is at Hausdorff distance
![]() $d'$
from
$d'$
from
![]() $\gamma ^{+}_0$
on
$\gamma ^{+}_0$
on
![]() $L_{x_0}$
. However,
$L_{x_0}$
. However,
![]() $\gamma ^{+}_0$
is also at a bounded distance from
$\gamma ^{+}_0$
is also at a bounded distance from
![]() $\zeta _0$
on
$\zeta _0$
on
![]() $L_{x_0}$
; therefore,
$L_{x_0}$
; therefore,
![]() $\zeta '$
and
$\zeta '$
and
![]() $\zeta _0$
are at a finite Hausdorff distance from each other on
$\zeta _0$
are at a finite Hausdorff distance from each other on
![]() $L_{x_0}$
. Hence
$L_{x_0}$
. Hence
![]() $\zeta '=\zeta _0$
, because they have the same starting point. As this is true for all convergent subsequences of
$\zeta '=\zeta _0$
, because they have the same starting point. As this is true for all convergent subsequences of
![]() $(\zeta _i)$
, we get our result for
$(\zeta _i)$
, we get our result for
![]() $x_0$
not in
$x_0$
not in
![]() $\widetilde {\mathcal {R}}$
.
$\widetilde {\mathcal {R}}$
.
Before dealing with the remaining case, let us note the following.
Observation 5.8. By the construction of
![]() $\mathcal {U}$
starting with x in
$\mathcal {U}$
starting with x in
![]() $\widetilde {\mathcal {A}}$
and continuity of
$\widetilde {\mathcal {A}}$
and continuity of
![]() $\eta ^{+}$
near
$\eta ^{+}$
near
![]() $\widetilde {\mathcal {A}}$
, we observe that the set
$\widetilde {\mathcal {A}}$
, we observe that the set
![]() $\mathcal {U}\cup \{\eta ^{+}(z)|z\in \mathcal {U}\}$
is homeomorphic to
$\mathcal {U}\cup \{\eta ^{+}(z)|z\in \mathcal {U}\}$
is homeomorphic to
![]() $[0,1]\times [0,1]\times [0,1]$
inside
$[0,1]\times [0,1]\times [0,1]$
inside
![]() $\mathcal {W}=\bigcup \nolimits _{y\in \unicode{x3bb} }(L_y\cup S^1(L_y))$
, which is homeomorphic to a compact solid cylinder
$\mathcal {W}=\bigcup \nolimits _{y\in \unicode{x3bb} }(L_y\cup S^1(L_y))$
, which is homeomorphic to a compact solid cylinder
![]() $[0,1]\times \{ \mathrm {the closed unit disc} \mathbb {D}\}$
.
$[0,1]\times \{ \mathrm {the closed unit disc} \mathbb {D}\}$
.
The set
![]() $\mathcal {U}\cup \{\eta ^{+}(z)|z\in \mathcal {U}\}$
above is saturated by forward flow lines and all the ideal points contained in this neighborhood are defined by forward flow rays. Hence, we conclude the following.
$\mathcal {U}\cup \{\eta ^{+}(z)|z\in \mathcal {U}\}$
above is saturated by forward flow lines and all the ideal points contained in this neighborhood are defined by forward flow rays. Hence, we conclude the following.
-
(1) If
 $L\in \widetilde {\mathcal {F}}|_{\widetilde {\mathcal {A}}}$
and
$L\in \widetilde {\mathcal {F}}|_{\widetilde {\mathcal {A}}}$
and
 $p\in L$
, then there exists a neighborhood
$p\in L$
, then there exists a neighborhood
 $N_p$
of
$N_p$
of
 $\eta ^+(p)$
in
$\eta ^+(p)$
in
 $\bigcup _{L\in \widetilde {\mathcal {F}}} S^1(L)$
such that
$\bigcup _{L\in \widetilde {\mathcal {F}}} S^1(L)$
such that
 $N_p\subset \eta ^+(\widetilde {\mathcal {M}})$
and
$N_p\subset \eta ^+(\widetilde {\mathcal {M}})$
and
 $N_p\cap \eta ^-(\widetilde {\mathcal {M}})=\emptyset $
.
$N_p\cap \eta ^-(\widetilde {\mathcal {M}})=\emptyset $
. -
(2) Similarly, for
 $q\in L_q\in \widetilde {\mathcal {R}}$
, there exists a neighborhood
$q\in L_q\in \widetilde {\mathcal {R}}$
, there exists a neighborhood
 $N_q$
of
$N_q$
of
 $\eta ^-(q)$
in
$\eta ^-(q)$
in
 $\bigcup _{L\in \widetilde {\mathcal {F}}} S^1(L)$
such that
$\bigcup _{L\in \widetilde {\mathcal {F}}} S^1(L)$
such that
 $N_q\subset \eta ^-(\widetilde {\mathcal {M}})$
and
$N_q\subset \eta ^-(\widetilde {\mathcal {M}})$
and
 $N_p\cap \eta ^+(\widetilde {\mathcal {M}})=\emptyset $
. Moreover, the backward ray
$N_p\cap \eta ^+(\widetilde {\mathcal {M}})=\emptyset $
. Moreover, the backward ray
 $\gamma ^-_q$
starting from q is contained in an infinite cubical neighborhood in
$\gamma ^-_q$
starting from q is contained in an infinite cubical neighborhood in
 $\widetilde {\mathcal {M}}$
saturated by backward flow rays.
$\widetilde {\mathcal {M}}$
saturated by backward flow rays.
To continue the proof of Proposition 5.7, we next assume that
![]() $x_0\in \widetilde {\mathcal {R}}$
. Suppose that a subsequence
$x_0\in \widetilde {\mathcal {R}}$
. Suppose that a subsequence
![]() $(\eta ^{+}(x_{i(k)}))$
converges to q where q is not
$(\eta ^{+}(x_{i(k)}))$
converges to q where q is not
![]() $\eta ^+(x_0)$
. As
$\eta ^+(x_0)$
. As
![]() $x_0$
is in
$x_0$
is in
![]() $\widetilde {\mathcal {R}}$
, then
$\widetilde {\mathcal {R}}$
, then
![]() $L_{x_0}$
is a leaf of the weak stable foliation
$L_{x_0}$
is a leaf of the weak stable foliation
![]() $\widetilde {\mathcal {F}}^{ws}$
. Hence by Property 2.4 on
$\widetilde {\mathcal {F}}^{ws}$
. Hence by Property 2.4 on
![]() $L_{x_0}$
, all the forward flow rays converge to a single ideal point in
$L_{x_0}$
, all the forward flow rays converge to a single ideal point in
![]() $S^1(L_{x_0})$
and all the other ideal points in
$S^1(L_{x_0})$
and all the other ideal points in
![]() $S^1(L_{x_0})$
are ideal points of backward flow rays. As
$S^1(L_{x_0})$
are ideal points of backward flow rays. As
![]() $q\neq \eta ^{+}(x_0)$
, q is defined by a backward ray, that is,
$q\neq \eta ^{+}(x_0)$
, q is defined by a backward ray, that is,
![]() $q = \eta ^-(z)$
for some z in
$q = \eta ^-(z)$
for some z in
![]() $L_{x_0}$
. By Observation 5.8(2) starting with z in
$L_{x_0}$
. By Observation 5.8(2) starting with z in
![]() $\widetilde {\mathcal {R}}$
(notice that z is in the repeller, not the attractor), there exits a neighborhood
$\widetilde {\mathcal {R}}$
(notice that z is in the repeller, not the attractor), there exits a neighborhood
![]() $\mathcal {V}$
saturated by backward flow rays around z in
$\mathcal {V}$
saturated by backward flow rays around z in
![]() $\bigcup \{L_y\cup S^1(L_y)|y\in \unicode{x3bb} '\}$
for some transversal
$\bigcup \{L_y\cup S^1(L_y)|y\in \unicode{x3bb} '\}$
for some transversal
![]() $\unicode{x3bb} '$
. By Observation 5.8(2), all limit points are backward ideal points in
$\unicode{x3bb} '$
. By Observation 5.8(2), all limit points are backward ideal points in
![]() $\mathcal {V}$
and no limit point is a forward ideal point. This contradicts the fact that the forward rays
$\mathcal {V}$
and no limit point is a forward ideal point. This contradicts the fact that the forward rays
![]() $\gamma ^{+}_{i(k)}$
have ideal points in these intervals of ideal points for k big enough by construction. This contradiction shows that a subsequence
$\gamma ^{+}_{i(k)}$
have ideal points in these intervals of ideal points for k big enough by construction. This contradiction shows that a subsequence
![]() $(\eta ^+(x_{i(k)}))$
converging to
$(\eta ^+(x_{i(k)}))$
converging to
![]() $q \neq \eta ^+(x_0)$
is not possible, and hence
$q \neq \eta ^+(x_0)$
is not possible, and hence
![]() $q=\eta ^+(x_0)$
.
$q=\eta ^+(x_0)$
.
Hence
![]() $\eta ^{+}$
is continuous on
$\eta ^{+}$
is continuous on
![]() $\widetilde {\mathcal {M}}$
. If we consider the flow
$\widetilde {\mathcal {M}}$
. If we consider the flow
![]() $\Psi _t=\Phi _{-t}$
, then backward ideal points of
$\Psi _t=\Phi _{-t}$
, then backward ideal points of
![]() $\Phi _t$
are forward ideal points of
$\Phi _t$
are forward ideal points of
![]() $\Psi _{-t}$
and the continuity of
$\Psi _{-t}$
and the continuity of
![]() $\eta ^{-}$
follows. This completes the proof of Proposition 5.7.
$\eta ^{-}$
follows. This completes the proof of Proposition 5.7.
6 Flow lines are leafwise quasigeodesic
In this section, we prove a general result of quasigeodesic behavior of some subfoliations. This result will imply that in the examples we constructed associated with non-transitive Anosov flows, the flow lines are uniform quasigeodesics in their respective two-dimensional leaves. We first consider some general continuity properties.
Definition 6.1. (Continuity properties)
Let
![]() $\mathcal {G}$
be a one-dimensional oriented subfoliation of a two-dimensional foliation
$\mathcal {G}$
be a one-dimensional oriented subfoliation of a two-dimensional foliation
![]() $\mathcal {F}$
with Gromov hyperbolic leaves on a 3-manifold
$\mathcal {F}$
with Gromov hyperbolic leaves on a 3-manifold
![]() $\mathcal {M}$
. Suppose that leaves of
$\mathcal {M}$
. Suppose that leaves of
![]() $\mathcal {G}$
are
$\mathcal {G}$
are
![]() $C^1$
curves in leaves of
$C^1$
curves in leaves of
![]() $\mathcal {F}$
. Suppose that the following three properties are satisfied.
$\mathcal {F}$
. Suppose that the following three properties are satisfied.
-
(1) For each x in
 $\widetilde M$
, let
$\widetilde M$
, let
 $\ell $
be the leaf of
$\ell $
be the leaf of
 $\widetilde {\mathcal {G}}$
containing it, and L the leaf of
$\widetilde {\mathcal {G}}$
containing it, and L the leaf of
 $\widetilde {\mathcal {F}}$
containing x. Then in the forward direction (given by the orientation of
$\widetilde {\mathcal {F}}$
containing x. Then in the forward direction (given by the orientation of
 $\widetilde {\mathcal {G}}$
), the leaf
$\widetilde {\mathcal {G}}$
), the leaf
 $\ell $
has a unique limiting point in
$\ell $
has a unique limiting point in
 $S^1(L)$
and this is denoted by
$S^1(L)$
and this is denoted by
 $\eta ^+(x)$
. Similarly, in the negative direction, there is a unique limiting point in
$\eta ^+(x)$
. Similarly, in the negative direction, there is a unique limiting point in
 $S^1(L)$
denoted by
$S^1(L)$
denoted by
 $\eta ^-(x)$
.
$\eta ^-(x)$
. -
(2) For each x in
 $\widetilde M$
, the points
$\widetilde M$
, the points
 $\eta ^+(x), \eta ^-(x)$
are distinct points in
$\eta ^+(x), \eta ^-(x)$
are distinct points in
 $S^1(L)$
(L the leaf of
$S^1(L)$
(L the leaf of
 $\widetilde {\mathcal {F}}$
containing x).
$\widetilde {\mathcal {F}}$
containing x). -
(3) The functions
 $\eta ^+, \eta ^-: \widetilde {\mathcal {M}} \rightarrow \bigcup _{L\in \widetilde {\mathcal {F}}}S^{1}(L) $
are continuous.
$\eta ^+, \eta ^-: \widetilde {\mathcal {M}} \rightarrow \bigcup _{L\in \widetilde {\mathcal {F}}}S^{1}(L) $
are continuous.
Then we say that
![]() $(\mathcal {F},\mathcal {G})$
has the continuity properties.
$(\mathcal {F},\mathcal {G})$
has the continuity properties.
From the foliation
![]() $\mathcal {G}$
, we can produce a flow with flow lines which are the leaves of
$\mathcal {G}$
, we can produce a flow with flow lines which are the leaves of
![]() $\mathcal {G}$
: for example, just flow forward along leaves of
$\mathcal {G}$
: for example, just flow forward along leaves of
![]() $\mathcal {G}$
with speed
$\mathcal {G}$
with speed
![]() $1$
in the positive direction. Any reparameterization of the flow produces a time parameter which is quasi-isometric with this one, so the result on the quasigeodesic behavior of flow lines depends only on
$1$
in the positive direction. Any reparameterization of the flow produces a time parameter which is quasi-isometric with this one, so the result on the quasigeodesic behavior of flow lines depends only on
![]() $\mathcal {G}$
and not the particular parameterization, or description of
$\mathcal {G}$
and not the particular parameterization, or description of
![]() $\mathcal {G}$
as the flow foliation of a flow.
$\mathcal {G}$
as the flow foliation of a flow.
Notice that the two-dimensional foliation
![]() $\mathcal {F}$
constructed in §3 with the one-dimensional subfoliation
$\mathcal {F}$
constructed in §3 with the one-dimensional subfoliation
![]() $\mathcal {G}$
by the flow lines of
$\mathcal {G}$
by the flow lines of
![]() $\Phi _t$
satisfies the continuity properties as follows. In the previous section, we proved the pair
$\Phi _t$
satisfies the continuity properties as follows. In the previous section, we proved the pair
![]() $(\mathcal {F},\mathcal {G})$
satisfies the properties (1), (2), and (3) of Definition 6.1: property (1) was proved in Lemma 5.3, property (2) was proved in Corollary 5.6, and property (3) was proved in Proposition 5.7.
$(\mathcal {F},\mathcal {G})$
satisfies the properties (1), (2), and (3) of Definition 6.1: property (1) was proved in Lemma 5.3, property (2) was proved in Corollary 5.6, and property (3) was proved in Proposition 5.7.
The next result is a general result that will imply that the foliations we constructed in §3 are leafwise quasigeodesic foliations.
Theorem 6.2. Suppose that
![]() $\widetilde {\mathcal {G}}$
is a one-dimensional subfoliation of a two-dimensional foliation
$\widetilde {\mathcal {G}}$
is a one-dimensional subfoliation of a two-dimensional foliation
![]() $\widetilde {\mathcal {F}}$
satisfying the continuity properties of Definition 6.1. Then
$\widetilde {\mathcal {F}}$
satisfying the continuity properties of Definition 6.1. Then
![]() $\widetilde {\mathcal {G}}$
is a leafwise quasigeodesic foliation.
$\widetilde {\mathcal {G}}$
is a leafwise quasigeodesic foliation.
The proof will be attained by the following three results. In the next lemma, we combine all the results of the previous section to obtain a key property that will be used to show that all the flow lines are quasigeodesic on their respective leaves of
![]() $\widetilde {\mathcal {F}}$
.
$\widetilde {\mathcal {F}}$
.
We stress that the quasigeodesic behavior is proved using only the continuity properties, irrespective of how these continuity properties are obtained. Therefore, Theorem 6.2 is applicable not only to the examples constructed in §3, but theoretically to many other situations as well.
To prove Theorem 6.2, again we use a Candel metric. Given x in
![]() $\widetilde {\mathcal {M}}$
, let
$\widetilde {\mathcal {M}}$
, let
![]() $\gamma _x$
be the leaf of
$\gamma _x$
be the leaf of
![]() $\widetilde {\mathcal {G}}$
through it. In addition, let
$\widetilde {\mathcal {G}}$
through it. In addition, let
![]() $L_x$
be the leaf of
$L_x$
be the leaf of
![]() $\widetilde {\mathcal {F}}$
containing x. Using property (i) of Definition 6.1, we let
$\widetilde {\mathcal {F}}$
containing x. Using property (i) of Definition 6.1, we let
![]() $\eta ^+(x), \eta ^-(x)$
be the unique limiting points of the two rays of
$\eta ^+(x), \eta ^-(x)$
be the unique limiting points of the two rays of
![]() $\gamma _x$
in
$\gamma _x$
in
![]() $S^1(L_x)$
. Notice that they are distinct points in
$S^1(L_x)$
. Notice that they are distinct points in
![]() $S^1(L_x)$
by property (ii) of Definition 6.1. Since
$S^1(L_x)$
by property (ii) of Definition 6.1. Since
![]() $L_x$
has a hyperbolic metric, there is a unique geodesic in
$L_x$
has a hyperbolic metric, there is a unique geodesic in
![]() $L_x$
, denoted by
$L_x$
, denoted by
![]() $g_x$
, whose ideal points in
$g_x$
, whose ideal points in
![]() $S^1(L_x)$
are
$S^1(L_x)$
are
![]() $\eta ^+(x), \eta ^-(x)$
.
$\eta ^+(x), \eta ^-(x)$
.
Lemma 6.3. There exists
![]() $\delta>0$
such that for all
$\delta>0$
such that for all
![]() $x\in \widetilde {\mathcal {M}}$
, we have that
$x\in \widetilde {\mathcal {M}}$
, we have that
where
![]() $g_x$
is the geodesic on
$g_x$
is the geodesic on
![]() $L_x$
connecting
$L_x$
connecting
![]() $\eta ^{+}(x)$
and
$\eta ^{+}(x)$
and
![]() $\eta ^{-}(x)$
and
$\eta ^{-}(x)$
and
![]() $\mathcal {N}_{\delta }(g_x)$
is the
$\mathcal {N}_{\delta }(g_x)$
is the
![]() $\delta $
-neighborhood of
$\delta $
-neighborhood of
![]() $g_x$
on
$g_x$
on
![]() $L_x$
.
$L_x$
.
Proof. Suppose that there does not exist any such
![]() $\delta $
. Then there exists a sequence
$\delta $
. Then there exists a sequence
![]() $(x_i)$
in
$(x_i)$
in
![]() $\widetilde {\mathcal {M}}$
with
$\widetilde {\mathcal {M}}$
with
![]() $x_i$
in leaves
$x_i$
in leaves
![]() $L_{x_i}$
of
$L_{x_i}$
of
![]() $\widetilde {\mathcal {F}}$
such that
$\widetilde {\mathcal {F}}$
such that
![]() $d_{L_{x_i}}(x_i, g_{x_i})>i$
. Up to deck transformations, there exists a convergent subsequence of
$d_{L_{x_i}}(x_i, g_{x_i})>i$
. Up to deck transformations, there exists a convergent subsequence of
![]() $(x_i)$
which we assume is the original sequence, and we assume
$(x_i)$
which we assume is the original sequence, and we assume
![]() $x_i\rightarrow x$
. By property (iii) of Definition 6.1, we know that
$x_i\rightarrow x$
. By property (iii) of Definition 6.1, we know that
Since
![]() $x_i$
converges to x, we assume that all
$x_i$
converges to x, we assume that all
![]() $x_i$
are in leaves of
$x_i$
are in leaves of
![]() $\widetilde {\mathcal {F}}$
which intersect a fixed transveral
$\widetilde {\mathcal {F}}$
which intersect a fixed transveral
![]() $\unicode{x3bb} $
to
$\unicode{x3bb} $
to
![]() $\widetilde {\mathcal {F}}$
.
$\widetilde {\mathcal {F}}$
.
Since
![]() $\eta ^+(x_i)$
converges to
$\eta ^+(x_i)$
converges to
![]() $\eta ^+(x)$
,
$\eta ^+(x)$
,
![]() $\eta ^-(x_i)$
converges to
$\eta ^-(x_i)$
converges to
![]() $\eta ^-(x)$
, and
$\eta ^-(x)$
, and
![]() $\eta ^+(x) \neq \eta ^-(x)$
, it follows that
$\eta ^+(x) \neq \eta ^-(x)$
, it follows that
![]() $\{g_{x_i}\}$
converges to
$\{g_{x_i}\}$
converges to
![]() $g_x$
. This uses that the topology defined on
$g_x$
. This uses that the topology defined on
![]() $\bigcup \nolimits _{y\in \unicode{x3bb} }(S^1(L_y))$
is given by the trivialization of the unit tangent bundle to
$\bigcup \nolimits _{y\in \unicode{x3bb} }(S^1(L_y))$
is given by the trivialization of the unit tangent bundle to
![]() $\widetilde {\mathcal {F}}$
along
$\widetilde {\mathcal {F}}$
along
![]() $\unicode{x3bb} $
. By convergence we mean convergence in the compact open topology. However, this contradicts that
$\unicode{x3bb} $
. By convergence we mean convergence in the compact open topology. However, this contradicts that
![]() $d_{L_{x_i}}(x_i,g_{x_i})$
converges to infinity, since
$d_{L_{x_i}}(x_i,g_{x_i})$
converges to infinity, since
![]() $d_{L_x}(x,g_x)$
is finite and the sequence
$d_{L_x}(x,g_x)$
is finite and the sequence
![]() $d_{L_{x_i}}(x_i, g_{x_i})$
converges to it. This finishes the proof.
$d_{L_{x_i}}(x_i, g_{x_i})$
converges to it. This finishes the proof.
We now prove a weak quasigeodesic property of the leaves of
![]() $\widetilde {\mathcal {G}}$
in the leaves of
$\widetilde {\mathcal {G}}$
in the leaves of
![]() $\widetilde {\mathcal {F}}$
containing them.
$\widetilde {\mathcal {F}}$
containing them.
Proposition 6.4. For any
![]() $b>0$
, there exists a
$b>0$
, there exists a
![]() $c_b>0$
such that if
$c_b>0$
such that if
![]() $\gamma $
is the segment in a leaf of
$\gamma $
is the segment in a leaf of
![]() $\widetilde {\mathcal {G}}$
connecting x and y with
$\widetilde {\mathcal {G}}$
connecting x and y with
![]() $length(\gamma )>c_b$
, then
$length(\gamma )>c_b$
, then
![]() $d_{L_x}(x,y)>b$
, where
$d_{L_x}(x,y)>b$
, where
![]() $L_x$
is the leaf of
$L_x$
is the leaf of
![]() $\widetilde {\mathcal {F}}$
which contains x.
$\widetilde {\mathcal {F}}$
which contains x.
Proof. Fix
![]() $b>0$
. We do the proof by contradiction. Suppose the statement is not true for some
$b>0$
. We do the proof by contradiction. Suppose the statement is not true for some
![]() $b>0$
. Then for all
$b>0$
. Then for all
![]() $i\in \mathbb {N}$
, there exists two points
$i\in \mathbb {N}$
, there exists two points
![]() $x_i$
and
$x_i$
and
![]() $y_i$
in leaves
$y_i$
in leaves
![]() $L_i$
of
$L_i$
of
![]() $\widetilde {\mathcal {F}}$
, with
$\widetilde {\mathcal {F}}$
, with
![]() $x_i, y_i$
in the same flow line defining a flow line segment
$x_i, y_i$
in the same flow line defining a flow line segment
![]() $\gamma _i$
satisfying
$\gamma _i$
satisfying
![]() $length(\gamma _i)>i$
but
$length(\gamma _i)>i$
but
![]() $d_{L_i}(x_i, y_i)<b$
. Up to deck transformations and a subsequence, we assume that
$d_{L_i}(x_i, y_i)<b$
. Up to deck transformations and a subsequence, we assume that
![]() $(x_i)$
is convergent and
$(x_i)$
is convergent and
![]() $x_{i}\rightarrow x_0$
. Since
$x_{i}\rightarrow x_0$
. Since
![]() $d_{L_i}(x_i,y_i) < b$
, we can similarly assume that
$d_{L_i}(x_i,y_i) < b$
, we can similarly assume that
![]() $( y_i )$
is convergent and let
$( y_i )$
is convergent and let
![]() $y_i\rightarrow y_0$
.
$y_i\rightarrow y_0$
.
Claim 2.
![]() $x_0$
and
$x_0$
and
![]() $y_0$
are on the same leaf
$y_0$
are on the same leaf
![]() $L_0$
of
$L_0$
of
![]() $\widetilde {\mathcal {F}}$
.
$\widetilde {\mathcal {F}}$
.
Proof. If we consider a compact ball
![]() $B_{x_0}$
on
$B_{x_0}$
on
![]() $L_0$
containing
$L_0$
containing
![]() $x_0$
and a product neighborhood
$x_0$
and a product neighborhood
![]() $N(B_{x_0})$
with respect to
$N(B_{x_0})$
with respect to
![]() $\widetilde {\mathcal {F}}$
, then for all large i,
$\widetilde {\mathcal {F}}$
, then for all large i,
![]() $L_i$
intersects
$L_i$
intersects
![]() $N(B_{x_0})$
and
$N(B_{x_0})$
and
![]() $x_i\in L_i\cap N(B_{x_0})$
. If we consider
$x_i\in L_i\cap N(B_{x_0})$
. If we consider
![]() $B_{x_0}$
sufficiently large, the assumption
$B_{x_0}$
sufficiently large, the assumption
![]() $d_{L_i}(x_i,y_i)<b$
for all i forces that
$d_{L_i}(x_i,y_i)<b$
for all i forces that
![]() $y_i$
has to be contained in
$y_i$
has to be contained in
![]() $N(B_{x_0})$
. Hence by the product structure on
$N(B_{x_0})$
. Hence by the product structure on
![]() $N(B_{x_0})$
,
$N(B_{x_0})$
,
![]() $y_0$
also has to lie on
$y_0$
also has to lie on
![]() $L_0$
as
$L_0$
as
![]() $y_i\rightarrow y_0$
.
$y_i\rightarrow y_0$
.
Claim 3.
![]() $x_0$
and
$x_0$
and
![]() $y_0$
cannot be on the same flow line in
$y_0$
cannot be on the same flow line in
![]() $L_0$
.
$L_0$
.
Proof. If not, then there exists a flow line segment
![]() $\gamma $
connecting
$\gamma $
connecting
![]() $x_0$
and
$x_0$
and
![]() $y_0$
and consider a compact neighborhood
$y_0$
and consider a compact neighborhood
![]() $\mathcal {N}$
around
$\mathcal {N}$
around
![]() $\gamma $
which has a product structure with respect to the flow lines. As
$\gamma $
which has a product structure with respect to the flow lines. As
![]() $x_i\rightarrow x_0$
and
$x_i\rightarrow x_0$
and
![]() $y_i\rightarrow y_0$
, the flow segments
$y_i\rightarrow y_0$
, the flow segments
![]() $\gamma _i$
are contained in
$\gamma _i$
are contained in
![]() $\mathcal {N}$
for all large i. By continuity of length of flow lines,
$\mathcal {N}$
for all large i. By continuity of length of flow lines,
![]() $\textit{length}(\gamma _i)\rightarrow \textit{length}(\gamma )$
. However, that is not possible as
$\textit{length}(\gamma _i)\rightarrow \textit{length}(\gamma )$
. However, that is not possible as
![]() $length(\gamma _i)\rightarrow \infty $
and
$length(\gamma _i)\rightarrow \infty $
and
![]() $\gamma $
is compact, a contradiction.
$\gamma $
is compact, a contradiction.
Claim 4.
![]() $x_0$
and
$x_0$
and
![]() $y_0$
cannot be connected by a curve on
$y_0$
cannot be connected by a curve on
![]() $L_0$
everywhere transversal to the flow lines in
$L_0$
everywhere transversal to the flow lines in
![]() $L_0$
.
$L_0$
.
Proof. Suppose that there exists a line segment
![]() $\sigma $
on
$\sigma $
on
![]() $L_0$
everywhere transversal to the flow lines on
$L_0$
everywhere transversal to the flow lines on
![]() $L_0$
and connecting
$L_0$
and connecting
![]() $x_0$
and
$x_0$
and
![]() $y_0$
. By the local product structure of
$y_0$
. By the local product structure of
![]() $\widetilde {\mathcal {F}}$
near
$\widetilde {\mathcal {F}}$
near
![]() $\sigma \in L_0$
, there should be a segment
$\sigma \in L_0$
, there should be a segment
![]() $\sigma _i$
in
$\sigma _i$
in
![]() $L_i$
connecting
$L_i$
connecting
![]() $x_i$
and
$x_i$
and
![]() $y_i$
, and everywhere transversal to flow lines on
$y_i$
, and everywhere transversal to flow lines on
![]() $L_i$
. Up to taking a sub-segment of
$L_i$
. Up to taking a sub-segment of
![]() $\gamma _i$
if necessary and then a sub-segment of
$\gamma _i$
if necessary and then a sub-segment of
![]() $\sigma _i$
, we may assume that
$\sigma _i$
, we may assume that
![]() $\gamma _i$
does not intersect the interior of
$\gamma _i$
does not intersect the interior of
![]() $\sigma _i$
. It follows that the union of
$\sigma _i$
. It follows that the union of
![]() $\sigma _i$
and
$\sigma _i$
and
![]() $\gamma _i$
bounds a disk
$\gamma _i$
bounds a disk
![]() $\mathcal {D}_i$
on
$\mathcal {D}_i$
on
![]() $L_i$
as their end points are the same. All the flow lines which enter
$L_i$
as their end points are the same. All the flow lines which enter
![]() $\mathcal {D}_i$
transversally intersecting
$\mathcal {D}_i$
transversally intersecting
![]() $\sigma _i$
have to exit
$\sigma _i$
have to exit
![]() $\mathcal {D}_i$
transversally intersecting
$\mathcal {D}_i$
transversally intersecting
![]() $\sigma _i$
. The Poincaré–Hopf theorem says that there exists at least one flow line tangent to
$\sigma _i$
. The Poincaré–Hopf theorem says that there exists at least one flow line tangent to
![]() $\sigma _i$
, a contradiction.
$\sigma _i$
, a contradiction.
By Lemma 5.5, the leaf space of the flow foliation in
![]() $L_0$
is homeomorphic to the reals. Hence any two distinct flow lines in
$L_0$
is homeomorphic to the reals. Hence any two distinct flow lines in
![]() $L_0$
are connected by a transversal.
$L_0$
are connected by a transversal.
This contradiction proves Proposition 6.4.
Now we are ready to prove our final claim.
Proposition 6.5. The leaves of
![]() $\widetilde {\mathcal {G}}$
are uniformly quasigeodesics in their respective leaves of
$\widetilde {\mathcal {G}}$
are uniformly quasigeodesics in their respective leaves of
![]() $\widetilde {\mathcal {F}}$
.
$\widetilde {\mathcal {F}}$
.
Proof. We prove the theorem by contradiction. Recall that we are using a Candel metric in leaves of
![]() $\mathcal {F}$
. We assume that the leaves of
$\mathcal {F}$
. We assume that the leaves of
![]() $\widetilde {\mathcal {G}}$
are not uniform quasigeodesic on their leaves. From this assumption, we will construct a sequence of pairs
$\widetilde {\mathcal {G}}$
are not uniform quasigeodesic on their leaves. From this assumption, we will construct a sequence of pairs
![]() $\{(x_i,y_i)\}$
such that
$\{(x_i,y_i)\}$
such that
![]() $x_i$
and
$x_i$
and
![]() $y_i$
are connected by a flow segment
$y_i$
are connected by a flow segment
![]() $\gamma _i$
, where
$\gamma _i$
, where
![]() $\text { length}(\gamma _i)\rightarrow \infty $
but
$\text { length}(\gamma _i)\rightarrow \infty $
but
![]() $d_{L_i}(x_i, y_i)$
is bounded. Here
$d_{L_i}(x_i, y_i)$
is bounded. Here
![]() $L_i$
is the
$L_i$
is the
![]() $\widetilde {\mathcal {F}}$
leaf containing both
$\widetilde {\mathcal {F}}$
leaf containing both
![]() $x_i, y_i$
. However, this will contradict Proposition 6.4. A very similar result was proved in [Reference Fenley and MosherFM01], we reconstruct the same arguments in our specific case.
$x_i, y_i$
. However, this will contradict Proposition 6.4. A very similar result was proved in [Reference Fenley and MosherFM01], we reconstruct the same arguments in our specific case.
By our assumption, the leaves of
![]() $\widetilde {\mathcal {G}}$
are not uniform quasigeodesics. We get that for any
$\widetilde {\mathcal {G}}$
are not uniform quasigeodesics. We get that for any
![]() $K>0$
, there exists a segment of a leaf of
$K>0$
, there exists a segment of a leaf of
![]() $\widetilde {\mathcal {G}}$
with endpoints
$\widetilde {\mathcal {G}}$
with endpoints
![]() $x, y$
denoted by
$x, y$
denoted by
![]() $\gamma _{[x,y]}$
, contained in a leaf of
$\gamma _{[x,y]}$
, contained in a leaf of
![]() $\widetilde {\mathcal {F}}$
denoted by
$\widetilde {\mathcal {F}}$
denoted by
![]() $L_x$
, and such that
$L_x$
, and such that
For each K, one can find such
![]() $x, y, L_x$
, which obviously depend on K, but we omit the explicit dependence on K for notational simplicity. Consider the geodesic
$x, y, L_x$
, which obviously depend on K, but we omit the explicit dependence on K for notational simplicity. Consider the geodesic
![]() $g_x=g_y$
on
$g_x=g_y$
on
![]() $L_x$
with ideal points
$L_x$
with ideal points
By Lemma 6.3, there exists
![]() $\delta>0$
such that
$\delta>0$
such that
![]() $\gamma \subset \mathcal {N}_{\delta }(g_x)$
, where the neighborhood is in
$\gamma \subset \mathcal {N}_{\delta }(g_x)$
, where the neighborhood is in
![]() $L_x$
. This
$L_x$
. This
![]() $\delta $
is global, it works for any segment in a leaf of
$\delta $
is global, it works for any segment in a leaf of
![]() $\widetilde {\mathcal {G}}$
in its respective leaf of
$\widetilde {\mathcal {G}}$
in its respective leaf of
![]() $\widetilde {\mathcal {F}}$
. Let
$\widetilde {\mathcal {F}}$
. Let
![]() $\rho :L_{x}\rightarrow g_x$
be the ‘closest point map projection’, which means
$\rho :L_{x}\rightarrow g_x$
be the ‘closest point map projection’, which means
![]() $\rho (p)$
is the orthogonal projection in
$\rho (p)$
is the orthogonal projection in
![]() $L_x$
to
$L_x$
to
![]() $g_x$
, a bi-infinite length-minimizing geodesic on
$g_x$
, a bi-infinite length-minimizing geodesic on
![]() $L_x$
. The map is well defined as the leaves
$L_x$
. The map is well defined as the leaves
![]() $L_x$
are of constant curvature
$L_x$
are of constant curvature
![]() $-1$
and so isometric to the hyperbolic plane: the ‘closest point map’ on to a length-minimizing geodesic is well defined in the hyperbolic plane. It follows that:
$-1$
and so isometric to the hyperbolic plane: the ‘closest point map’ on to a length-minimizing geodesic is well defined in the hyperbolic plane. It follows that:
Let us assume that
![]() $d_{L_x}(x,y)>1+2\delta $
. Hence,
$d_{L_x}(x,y)>1+2\delta $
. Hence,
![]() $d_{L_{x}}(\rho (x),\rho (y))> 1$
by equation (6.1) and
$d_{L_{x}}(\rho (x),\rho (y))> 1$
by equation (6.1) and
 $$ \begin{align*}\frac{\text{ length}(\gamma_{[x,y]})}{d_{L_x}(\rho(x),\rho(y))}\geq\frac{\text{ length}(\gamma_{[x,y]})}{d_{L_x}(x,y)}\geq 2K>K+\frac{K}{d_{L_x}(\rho(x),\rho(y))}. \end{align*} $$
$$ \begin{align*}\frac{\text{ length}(\gamma_{[x,y]})}{d_{L_x}(\rho(x),\rho(y))}\geq\frac{\text{ length}(\gamma_{[x,y]})}{d_{L_x}(x,y)}\geq 2K>K+\frac{K}{d_{L_x}(\rho(x),\rho(y))}. \end{align*} $$
Therefore,
where
![]() $\lceil a \rceil $
denotes the integer n such that
$\lceil a \rceil $
denotes the integer n such that
![]() $n-1<a\leq n$
.
$n-1<a\leq n$
.
Suppose
![]() $n_0=\lceil d_{L_x}(\rho (x),\rho (y))\rceil $
, then
$n_0=\lceil d_{L_x}(\rho (x),\rho (y))\rceil $
, then
![]() $\text {length}(\gamma _{[x,y]})>n_0 K$
. Also,
$\text {length}(\gamma _{[x,y]})>n_0 K$
. Also,
and hence we can construct a sequence
![]() $\{\rho (x)=z_0,z_1,\ldots ,z_n=\rho (y)\}$
of points in
$\{\rho (x)=z_0,z_1,\ldots ,z_n=\rho (y)\}$
of points in
![]() $g_x$
, such that
$g_x$
, such that
![]() $d_{L_x}(z_{i-1},z_i)=1$
for all
$d_{L_x}(z_{i-1},z_i)=1$
for all
![]() $i<n_0$
and
$i<n_0$
and
![]() $d_{L_x}(z_{n_0-1},z_{n_0})\leq 1$
. Next we consider the sequence
$d_{L_x}(z_{n_0-1},z_{n_0})\leq 1$
. Next we consider the sequence
![]() $x=x_0,x_1,\ldots ,x_{n_0}$
, where
$x=x_0,x_1,\ldots ,x_{n_0}$
, where
![]() $x_i$
is the last point on
$x_i$
is the last point on
![]() $\gamma _{[x,y]}$
such that
$\gamma _{[x,y]}$
such that
![]() $\rho (x_i)=z_i$
.
$\rho (x_i)=z_i$
.
If
![]() $\gamma _i$
denotes the flow segment joining
$\gamma _i$
denotes the flow segment joining
![]() $x_{i-1}$
and
$x_{i-1}$
and
![]() $x_i$
, we have
$x_i$
, we have
![]() $\gamma _{[x,y]}=\gamma _1 * \gamma _2 *\cdots *\gamma _{n_0}$
. Hence,
$\gamma _{[x,y]}=\gamma _1 * \gamma _2 *\cdots *\gamma _{n_0}$
. Hence,
 $$ \begin{align*}\sum_{n=1}^{n_0}\text{length}(\gamma_i)=\text{length}(\gamma_{[x,y]})>n_0K.\end{align*} $$
$$ \begin{align*}\sum_{n=1}^{n_0}\text{length}(\gamma_i)=\text{length}(\gamma_{[x,y]})>n_0K.\end{align*} $$
By the pigeonhole principle, there exists
![]() $x_{i-1}$
and
$x_{i-1}$
and
![]() $x_{i}$
such that
$x_{i}$
such that
![]() $\text { length}(\gamma _{[x_{i-1},x_i]})>K$
. However, from
$\text { length}(\gamma _{[x_{i-1},x_i]})>K$
. However, from
![]() $(*)$
, we get that for all i,
$(*)$
, we get that for all i,
As the choice of
![]() $K>0$
was arbitrary, this proves that the ‘weak quasigeodesic property’ in Lemma 6.4 is not true for
$K>0$
was arbitrary, this proves that the ‘weak quasigeodesic property’ in Lemma 6.4 is not true for
![]() $b=1+2\delta $
, a contradiction. We conclude that leaves of
$b=1+2\delta $
, a contradiction. We conclude that leaves of
![]() $\widetilde {\mathcal {G}}$
are uniformly quasigeodesic on their respective leaves of
$\widetilde {\mathcal {G}}$
are uniformly quasigeodesic on their respective leaves of
![]() $\widetilde {\mathcal {F}}$
.
$\widetilde {\mathcal {F}}$
.
This finishes the proof of Proposition 6.5.
7 Conclusion
We now apply the results of this section to the two-dimensional foliation
![]() $\mathcal {F}$
with a subfoliation
$\mathcal {F}$
with a subfoliation
![]() $\mathcal {G}$
as constructed in §3. Section 4 shows that every leaf in
$\mathcal {G}$
as constructed in §3. Section 4 shows that every leaf in
![]() $\mathcal {F}$
is Gromov hyperbolic when lifted to the universal cover. Proposition 6.5 proves that the flow foliation (that is, the foliation
$\mathcal {F}$
is Gromov hyperbolic when lifted to the universal cover. Proposition 6.5 proves that the flow foliation (that is, the foliation
![]() $\mathcal {G}$
) is a leafwise quasigeodesic subfoliation of
$\mathcal {G}$
) is a leafwise quasigeodesic subfoliation of
![]() $\mathcal {F}$
. Moreover, Proposition 5.4 proves that all leaves of
$\mathcal {F}$
. Moreover, Proposition 5.4 proves that all leaves of
![]() $\mathcal {F}$
which are not contained in
$\mathcal {F}$
which are not contained in
![]() $\mathcal {A}$
or
$\mathcal {A}$
or
![]() $\mathcal {R}$
are non-funnel. This is because of the following: if
$\mathcal {R}$
are non-funnel. This is because of the following: if
![]() $\gamma _a, \gamma _b$
are distinct flow lines in some leaf L of
$\gamma _a, \gamma _b$
are distinct flow lines in some leaf L of
![]() $\widetilde {\mathcal {F}}$
which are not in the lift of the attractor or the repeller, then Proposition 5.4 shows that
$\widetilde {\mathcal {F}}$
which are not in the lift of the attractor or the repeller, then Proposition 5.4 shows that
![]() $\eta ^+(a) \not = \eta ^+(b)$
in
$\eta ^+(a) \not = \eta ^+(b)$
in
![]() $S^1(L)$
. Applying the same result to negative flow rays, one obtains that
$S^1(L)$
. Applying the same result to negative flow rays, one obtains that
![]() $\eta ^-(a) \not = \eta ^-(b)$
in
$\eta ^-(a) \not = \eta ^-(b)$
in
![]() $S^1(L)$
. Hence L cannot be a funnel leaf. However, all leaves in
$S^1(L)$
. Hence L cannot be a funnel leaf. However, all leaves in
![]() $\mathcal {A}$
or
$\mathcal {A}$
or
![]() $\mathcal {R}$
are funnel by Corollary 2.6. This completes the proof of the Theorem 1.1.
$\mathcal {R}$
are funnel by Corollary 2.6. This completes the proof of the Theorem 1.1.
Acknowledgement
We thank Rafael Potrie for providing a crucial idea which greatly simplified the proof of Lemma 3.2.