A sinusoidal travelling wave-train is at normal incidence upon a two-dimensional finite dock fixed on the surface of a body of water of great depth, and the problem investigated herein is that of finding the limiting form of the induced velocity potential for short waves. Of particular interest are the amplitudes of the wave-trains reflected and transmitted towards infinity by such an obstacle. The potential is expressed as a sum of coupled semi-infinite dock potentials, whence results a pair of weakly coupled integral equations for the solution. This formulation of the problem is shown to be amenable to an approximate solution for large wave-numbers, and the first few terms are derived in formal expansions for the reflection and transmission coefficients.

Sears and Titchmarsh (1) have formulated an expansion in eigenfunctions which requires a knowledge of the s-zeros of the equation

Here ka > 0 is supposed given and β is a real constant such that 0 ≤ β < π. The above equation is encountered when one seeks the eigenfunctions of the differential equation

on the interval 0 < α ≤ r < ∞ subject to the condition of vanishing at r = α. Solutions of (2) are the Bessel functions J±is(kr) and every solution w of (2) is such that r−½w(r) belongs to L2 (α, ∞). Since the problem is of the limit circle type at infinity it is necessary to prescribe a suitable asymptotic condition there to make the eigenfunctions determinate. In the present instance this condition is

The electron avalanche that takes place within an internally amplifying semiconductor radiation detector has been analysed statistically, treating the process as an example of multi-dimensional branching processes. By extending the result obtained from Good's theorem to the case of continuous variable, an integral equation is derived for the generating function of the probability that a single primary electron-hole pair, formed at a depth x, induces an avalanche consisting of n pairs. On the basis of this equation, expressions are deduced for the mean value and the standard deviation σ of the total number n of pairs in an avalanche induced by n0 primary pairs produced at x, as well as the probability w(x, n0, n) of getting an avalanche of ‘size’ n. In particular cases these expressions lead to various simple relations of practical importance.

It is shown that Huygens's principle holds for the solutions of Maxwell's equations for p-forms of all degrees in a gravitational plane wave space, while the solutions of the wave equation for 1, 2, and 3-forms, however, may have tails.

The quantum-mechanical energy-level density g(E) is given as a functional of the quantum-mechanical kernel K(q″, q′, t″ −t′). On taking the kernel K in the Feynman's form, one obtains the function g(E), without solving a Schrödinger equation. As an example, the embedding of a particle in the one-dimensional square well with infinitely high walls is analysed. The functions K(x″, x′, t−t′) and g(E) are represented as sums of terms corresponding to classical paths of different types. By an adequate choice of some terms due to the ‘most important’ paths, one may construct partial sums giving approximations of the function g(E). The utilization of such approximations for estimation of energy levels is demonstrated.

Eringen's theory(1) of homogeneous, isotropic, hyperelastic dielectric is applied to consider the effects of polarization on the surface tractions when a hollow cylindrical reinforced dielectric carrying a uniform surface charge at its inner surface is subjected to simultaneous large extension, inflation and torsion. New effects due to reinforcement and polarization have been observed separately. For vanishing charge, the results reduce to those of classical finite strain theory (2).

A study is made of a problem in acoustic radiation, with the object of developing a rigorous theory of short-wave asymptotic solutions of the Helmholtz wave equation. The particular example under consideration is that of the radiation of sound waves by a smooth convex cylinder pulsating with prescribed normal velocity V(s) exp (−iωt), where s denotes arc length of the curve C bounding the cylinder cross-section, and ω is the radian frequency.

It is shown that a singular integral equation, arising in the theory of neutron streaming in cylindrical channels, can be solved by the Wiener-Hopf technique. The singular equation is converted into a non-singular Fredholm one, which may be solved very simply by finite difference methods and matrix inversion.

The front from the expansion into a vacuum of an infinite wedge of polytropic gas initially at rest at constant pressure is studied in detail. It is shown how the shape of that part of the gas-vacuum interface resulting from the presence of the sharp corner changes with the wedge angle and the adiabatic index of the gas. In addition to analytic results for wedges of arbitrary angle, numerical results substantiating the analysis are given for the special case of 90°. Finally, explicit formulae for the path of a particle initially part of a 60° wedge of water allowed to collapse at time t = 0 are derived from an exact linear solution obtained by Suchkov and interpreted through the hydraulic analogy for adiabatic index 2.

Following Heading (4) a systematic search is made for useful refractive index profiles in spherically stratified isotropic media which are capable of yielding wave functions expressed in terms of the standard transcendental functions. Previously known profiles are shown to emerge as special cases of the analysis. Subject to the criteria adopted all possible profiles are derived.

The dimer problem, which in the three-dimensional case is one of the classical unsolved problems of solid-state chemistry, can be formulated mathematically as follows. We define a brick to be a d-dimensional (d ≥ 2) rectangular parallelopiped with sides whose lengths are integers. An n-brick is a brick whose volume is n; and a dimer is a 2-brick. The problem is to determine the number of ways of dissecting an n-brick into dimers; and since this is only possible when n is even we confine attention hereafter to n-bricks with n even. Consider an n-brick with sides of length a1, a2, …, ad, where n = a1a2 … ad, and write a = (a1, a2, …, ad). Let fa denote the number of ways of dissecting this brick into ½n dimers. On the basis of physical and heuristic arguments chemists have known for many years that fa increases more or less exponentially with n; and recently a rigorous proof (1) of this fact has been given in the following form: if ai → ∞ for all i = 1, 2, …, d, then n−1 logfa tends to a finite limit, which we denote by λd. The principal outstanding problem for chemists is to determine the numerical value of λ3, or failing an exact determination to estimate λ3 or to find upper and lower bounds for it.

In this paper the effect of surface tension is included in a well-known problem in the theory of two-dimensional infinitesimal water waves. The problem is that of the reflection of waves from a fixed vertical barrier immersed to a depth a into deep water. It is shown how the solution for the velocity potential may be determined uniquely when simple assumptions are made concerning the behaviour of the free surface near the barrier. In particular, expressions are derived for the reflection coefficient, defined as the ratio of the amplitude of the reflected wave to that of the incident wave, at infinity, and the transmission coefficient, defined similarly. It is shown how these coefficients, for small values of the surface tension force, tend to the values obtained by Ursell (4) when surface tension is ignored. The related problem of a completely immersed vertical barrier extending to a distance a from the surface may be solved in a similar manner. Expressions for the reflection and transmission coefficients for this case are given.

A mathematical analogue between a special class of problems in steady magnetohydrodynamics and appropriate problems in the theory of the scattering of sound pulses is established and exploited. Rigorous asymptotic expansions for large Hartmann number M are obtained for the exact solution of the prototype problem, the circular cylinder. Asymptotic expansions for large M in the case of a cylinder whose cross-section is an arbitrary closed convex curve are obtained as a straightforward application of the theory of geometrical optics and Keller's geometrical theory of diffraction.

The problem of the diffraction of axisymmetric harmonic elastic waves by a rigid circular disc is reduced to finding the solution of a pair of integral equations of the second kind suitable for iteration at low frequencies. Using the principle of contraction mapping, the rate of convergence of the iteration procedure is discussed and the error caused by stopping at any particular stage estimated. Detailed calculations are given for plane compressional waves at normal incidence.

The wave function φ(x, y) satisfies the equation

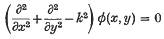
in the infinite region

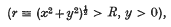
and satisfies the boundary condition Kφ + φy = 0 on the two line segments (y = 0, −∞ < x < −R) and (y = 0, R < x < ∞). We are not concerned with the properties of φ(x, y) inside the circle r = R. It is shown that outside the circle r = R the wave function φ(x, y) can be written as the sum of a wave source, a wave dipole, regular waves and wave-free potentials. (These basic functions are defined in section 2.) The proof makes use of analytic continuation into the image region (r > R, y ≤ 0) cut along the negative y-axis.

Two methods are given for this step. The first method uses Schwarz's symmetry principle to define the auxiliary wave function Φ = Kφ + φy throughout r > R, and φ can then be found by solving differential equations in the y or x direction. The second method uses Green's theorem. Applications in the theory of water waves are suggested.

In a recent paper (1), the author has discussed how certain ergodic properties of a doubly infinite non-negative matrix T = {tij} are related to those of its finite (n × n) corner truncations, (n)T = {(n)tij}.

In considering the problem of waves on a sloping beach, little regard seems to have been given to the effect of surface tension. Wehausen and Laitone (7) tend to attribute this to the fact that the additional force is small. This does not, of course, preclude the possibility that the effect may be appreciable in certain regions, and Longuet-Higgins (3), for example, has shown this to be the case near the crests for waves on the point of breaking. They also add, which is probably rather more pertinent, that difficulties arise when a solid boundary pierces the surface, since an additional boundary condition is required at the intersection, but give no indication as to what the boundary condition should be.

This paper is a sequel to a recent paper (1) in which the author discussed gravity waves on a horizontal layer of conducting fluid with a normal electrostatic field at the free surface. In this work results are given for waves in an incompressible dielectric fluid, in a similar configuration. Treating the dielectric as an inviscid fluid the stability of the system is first described in terms of the changes in potential energy in a small static displacement. The result so obtained is then confirmed by a normal mode analysis in which a dispersion relation is obtained for the inviscid model. The paper gives finally a discussion of the results for a viscous dielectric fluid, the main point of which is that, as in (1), in the transition from stable to unstable disturbances viscosity plays no part, and that the stability characteristics are the same as those for an inviscid dielectric fluid.

The goodness of fit of hypothetical discriminant functions has been discussed by Bartlett(1), Kshirsagar(2, 3), Radcliffe(4) and Williams (5–8). The associated problem of obtaining confidence intervals for the coefficients of a single discriminant function or canonical variable has been dealt with by Bartlett (1).