In a previous paper (3), to which this is a sequel, a central limit theorem was presented for the homogeneous additive processes defined on a finite Markov chain, a class of processes treated extensively by Miller (4). A typical homogeneous process {R(t), X(t)} takes its values in the space
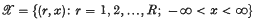
and is described by a vector distribution F(x, t) with components
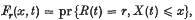
and an increment matrix distribution B(x) governing the transitions. The present paper treats the motion of the process in the same space when its homogeneity is modified by the presence of a set of boundary states in x. Such bounded processes have many applications to the theory of queues, dams, and inventories. Indeed, this paper and its predecessor were motivated initially by a desire to discuss queuing systems with many servers and many service phases. We will treat both absorbing boundaries and associated passage time densities, and reflecting boundaries. For the latter our main objective is an asymptotic discussion of the tails of the ergodic distribution.
 wave functions
wave functions