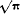It is very desirable when teaching mathematics not merely to state definitions and prove theorems, but also to show the train of thought that would lead us naturally to these definitions and theorems. Students are thus enabled to see mathematics as an alive, continuously developing subject. They are reminded of the interdependence of the various branches of mathematics; the memory of each branch is kept alive in the students’ minds, because it is continually being revisited, and the student finds it easier to remember results when he understands the thinking that produced them. This approach also encourages a student to try to carry the train of thought further and to make his own discoveries.

Notation: Functions which are to be elements of a group will be indicated by small letters, e.g., z′ = f(z), z′ = d(z) etc., the identity-function being denoted by z′ = e(z); z and z′ will be used for the variables. Small letters may also be used for constants (real or complex), with no fear of ambiguity. Groups will be abbreviated: Cn (cyclic group of order n); Dn (dihedral group of order 2n); Sn (symmetric group of order n!); An (alternating group of order .

who arrived at the result through discussions in an undergraduate class at the University of Southampton.

Of the various metrics which can be placed on the co-ordinate plane R×R, the Euclidean metric is universally known, and two others are becoming more widely known in schools. With the co-ordinate notation for points x = (x1, x2), these metrics are

Vector geometry is often developed as a subsection of a geometrical structure, much of which is unrelated to the vector properties deduced. The basic results depend on the law which may be stated in the form AB + BC = AC. This requires only that the equality of two vectors is meaningful, and that if AB = XY and BC = YZ, then AC = XZ (if “equals” are added to “equals” the results are equal). We need not assume that A, B, C,… represent points—they could be for example lines in a plane, planes in space or even elements of a group. A vector may be thought of as a “direction” for changing from one element to another: thus AB = CD means that the way of changing from C to D is essentially the same as the way of changing from A to B. We develop a structure which has these properties.

There seems to be doubt about the meaning of the word “function.” Roughly speaking applied mathematicians tend to use it in its old meaning as a synonym for “dependent variable”, while some pure mathematicians use it to mean a mapping in which no element of the domain can have more than one image.

Generalization of the ellipse to

is credited to Gabriel Lamé, the 19th-century French physicist and the eponym of this family of curves. Lamé curves have recently been taken out of mathematical limbo due to their appeal to certain designers and architects. Particularly to be mentioned is Piet Hein, the contemporary Danish poet-designer-scientist (and inventor of mathematical games) who rediscovered the curves and has been using “superellipses” (Lamé curves with n > 2, and therefore oval) in objets d’art, furniture, pottery, fabric patterns, and so on. His major achievement to date is a sunken oval shopping plaza, promenade, and pool in the centre of Stockholm; its shape is a superellipse with 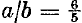and 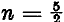. Derivatively, Gerald Robinson, a Toronto architect, has incorporated a superelliptic parking garage into a shopping complex (called a Superblock) in downtown Peterborough, Ontario; the parameters are 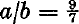and n = 2.71828 … (the exponential coefficient). In such urban contexts the two-parameter super-ellipse is efficiently tailorable to the dimensions of the site. It is said to be very elegant.

In a recent paper (1) P. Holgate obtains the following equations for pk(t) [k = 1,2,…, n], the probability that, at time t, the n animals in a given area are grouped into k herds.

“It is clear that desk machines will increasingly be used in schools at all levels”

Some Lessons in Mathematics, 1964

“Machines can illuminate the idea of place value”

Nuffield Project Desk Calculators, 1967

“A realisation that the use of machines has arrived in order to ease any necessary burdens of computation”

Examinations Bulletin No. 1 1963