Integer triangles with integer circumradii

Extract

When studying properties of the circumcircle of an integer triangle, it quickly becomes evident that the radius of such a circle (circumradius) need not itself be an integer. When it is not an integer, the circumradius can still be rational but it can also be irrational, as exemplified in the following examples. It is left to the reader to verify that the triangle with sides 10, 24, 26 has circumradius 13, and that the corresponding values for the triangles with sides 13, 14, 15 and 1, 1, 1 are 65/8 and 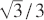respectively. It is shown in Theorem 1 below that a necessary condition for the circumradius to be an integer is that the area of the triangle is itself an integer (Heronian triangle) but this condition is not in itself sufficient. A simple counterexample is given by the 13, 14, 15 triangle above which has area 84. However, as a consequence of Theorem 1, we can restrict ourselves to consideringHeronian triangles, and relevant properties of such triangles, proved in [1], are given in Theorems 2 and 3 below. We also need to quote some well-known results involving the sums of two squares (see e.g. [2]) and these are listed in Lemma 3. In all that follows, we will use the convention that if T is a triangle with sides a, b, c and z > 0, then zT will denote the triangle, similar to T, with sides za, zb, zc.