Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-11-28T20:17:02.152Z Has data issue: false hasContentIssue false
  • English
  • Français

Some undecidability results in strong algebraic languages

Published online by Cambridge University Press:  12 March 2014

Cornelia Kalfa
Cornelia Kalfa*
Affiliation:
Aristotle University, Thessaloniki, Greece
Get access Rights & Permissions [Opens in a new window]

Extract

The recursively unsolvable halting problem for Turing machines is reduced to the problem of the existence or not of an algorithm for deciding whether a field is finite. The latter problem is further reduced to the decision problem of each of properties

for recursive sets Σ of equations of strong algebraic languages with infinitely many operation symbols.

Decision problems concerning properties of sets of equations were first raised by Tarski [9] and subsequently examined by Perkins [6], McKenzie [4], McNulty [5] and Pigozzi [7]. Perkins is the only one who studied recursive sets; the others investigated finite sets. Since the undecidability of properties Pi for recursive sets of equations does not imply any answer to the corresponding decision problems for finite sets, the latter problems remain open.

The work presented here is part of my Ph.D. thesis [2]. I thank Wilfrid Hodges, who supervised it.

An algebraic language is a first-order language with equality but without relation symbols. It is here denoted by 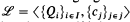, where Qi is an operation symbol and cj, is a constant symbol.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 49 , Issue 3 , September 1984 , pp. 951 - 954
Copyright
Copyright © Association for Symbolic Logic 1984

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Chang, C. C. and Keisler, H. J., Model theory, North-Holland, Amsterdam, 1973.Google Scholar
[2]Kalfa, C., Decision problems concerning sets of equations, Ph.D. Thesis, Bedford College, University of London, London, 1980.Google Scholar
[3]Kalfa, C., Undecidable properties of recursive sets of equations, Abstracts of Papers Presented to the American Mathematical Society, vol. 1 (1980), p. 239 (abstract 80T-E20).Google Scholar
[4]McKenzie, R., On spectra, and the negative solution of the decision problem for identities having a finite nontrivial model, this Journal, vol. 40 (1975), pp. 186–196.Google Scholar
[5]McNulty, G. F., Undecidable properties of finite sets of equations, this Journal, vol. 41 (1976), pp. 589–604.Google Scholar
[6]Perkins, P., Unsolvable problems for equational theories, Notre Dame Journal of Formal Logic, vol. 8 (1967), pp. 175–185.CrossRefGoogle Scholar
[7]Pigozzi, D., Base-undecidable properties of universal varieties, Algebra Universalis, vol. 6 (1976), pp. 193–223.CrossRefGoogle Scholar
[8]Rogers, H. Jr., Theory of recursive Junctions and effective computability, McGraw-Hill, New York, 1967.Google Scholar
[9]Tarski, A., Equational logic and equational theories of algebras, Contributions to Mathematical Logic (Colloquium, Hannover, 1966; Schmidt, H. A., Schütte, K. and Thiele, H.-J., editors), North-Holland, Amsterdam, 1968, pp. 275–288.Google Scholar