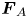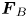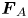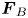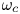Lane formation in 3D driven pair-ion plasmas: I Parallel External Forcing

Abstract

Lane formation dynamics of driven three-dimensional pair-ion plasmas (PIP) is investigated. Extensive Langevin dynamics simulation is performed to study the influence of an external electric field on the behaviour of the PIP system. In our model, one half of the particles are pushed into the field direction by an external force $\boldsymbol {F}_{A}$ while the other half are pulled into the opposite direction by an external force $\boldsymbol {F}_{B}$. We show that if $\boldsymbol {F}_{A}$ and $\boldsymbol {F}_{B}$ are parallel, the system undergoes a non-equilibrium phase transition from a disordered state to a lane formation state parallel to the field direction with increasing field strength. The lanes are formed by the same kind of particles moving collectively with the field. The lane order parameter has been implemented to detect phase transition. Further, we show the lane formation in the presence of a time-varying external electric field. In particular, the effect of parallel forces are investigated. Unlike the previously reported two-dimensional case (Sarma, et al., Phys. Plasmas, vol. 27, 2020, p. 012106; Baruah, et al., J. Plasma Phys., vol. 87, issue 2, 2021, p. 905870202), for the time-varying electric field case, spontaneous formation and the breaking of lanes are not observed for all values of applied frequencies; however, the orderness varies and spontaneous formation and breaking of lanes is observed for values close to a critical frequency $\omega _c$. Further, some aspects of the lane formation dynamics of a PIP system are also studied in the presence of an external magnetic field, which reveals that the presence of an external magnetic field accelerates the lane formation process and introduces a drift of the lanes in a direction perpendicular to both electric and magnetic fields.

1. Introduction

When driven out of equilibrium, many physical systems may spontaneously exhibit many different kinds of pattern formation which are much richer than traditional phase transitions in equilibrium systems. The detailed behaviour of non-equilibrium systems that form patterns may be extremely challenging to predict, and as such is therefore a very interesting field of research. Lane formation is one of the representative examples of non-equilibrium phase transitions. Lane formation has been extensively studied not only in pedestrian dynamics (see, Helbing & Molnár 1995; Helbing, Farkas & Vicsek 2000), but also for various physical particles, such as charged colloids (Tarama, Egelhaaf & Löwen 2019), microswimmers (Kogler & Klapp 2015) and in Langevin dynamics (LD) simulation of oppositely driven plasma particles (Sarma, Baruah & Ganesh 2020; Baruah, Sarma & Ganesh 2021). Local lane formation has also been found in real-space experiments of oppositely charged colloids in an electric field (Vissers et al. 2011b) and in an alternating electric field (Vissers, van Blaaderen & Imhof 2011a), as well as in binary plasma (Sütterlin et al. 2009). Phase diagrams of oppositely charged particles in an electric field have been calculated with Brownian dynamic simulation (Rex & Löwen 2007; Sarma et al. 2020), where lane formation phenomena have been found. Recently, lane formation was also discovered in complex plasma experiments performed under microgravity conditions onboard the International Space Station (Sütterlin et al. 2009) and the first experimental realization on lane formation in binary complex plasmas under microgravity conditions has also been performed (Du et al. 2012), which provides an ideal model system for comparison with numerical experiments and observations in colloidal suspensions. In a recent study, the formation of imposed patterns was also studied by placing a wide-wire mesh (waffle) in a strongly magnetized plasma both experimentally and numerically (Menati et al. 2020). Patterns were formed due to plasma being trapped beneath the edges of the wide-wire mesh which are also very different from the patterns formed while using a narrow-wire mesh (Hall 2019).

A fundamental understanding of non-equilibrium phenomena requires resolving the underlying dynamical processes on the scale of the individual particles. For this pair-ion plasmas (PIP) (Sarma et al. 2020; Baruah et al. 2021) is excellent model system, which is a two ion components system with opposite charges and equal masses. Their dynamical time scale is different from electron–ion plasmas and electron–hole plasmas which leads to distinct thermodynamical behaviour. Criteria to define the pure PIP were presented in 2007 (Saleem 2007). Since PIP is a collection of both matter and antimatter particles, it represents a paradigm for the study of basic plasma science, and many open questions exist regarding these unique systems. It represents a new state of matter with unique thermodynamic properties drastically different from those of ordinary electron–ion plasmas and can be brought out of equilibrium by applying external fields; the trajectories of the individual particles can be tracked (Sarma et al. 2020; Baruah et al. 2021). Pair-ion plasmas are found in many astrophysical settings, such as gamma-ray bursts (Rees 2000), and have recently also been produced in carefully designed laboratory experiments (Oohara & Hatakeyama 2003, 2007). The PIP in a magnetic field are unique in that both species are equally and strongly magnetized. The behaviour of such a kind of plasma system both in the absence and presence of the external magnetic field in three dimensions is largely unexplored.

We have addressed the lane formation dynamics and the effect of both constant and oscillatory external parallel forces in Part 1 of the work for a strongly coupled pair-ion plasma system. The effect of an external magnetic field is also studied. Importantly the above-mentioned effects were not previously investigated in the presence of non-parallel forces for a three-dimensional (3-D) PIP system, which is presented in Part 2 (Prajapati, Baruah & Ganesh 2023) of our work. Hence, the present work is arranged as two companion papers – Part 1 and Part 2 (Prajapati et al. 2023). In the first part (i.e. Part 1) of the work, we present an extensive study of lane formation dynamics in the presence of parallel forces using extensive LD simulation of a 3-D PIP system. In the second part of the companion paper (i.e. Part 2; Prajapati et al. (2023)) we address the behaviour of the system in the presence of external non-parallel forces using extensive LD simulation in a strongly coupled 3-D PIP system.

The rest of the paper (Part 1) is organized as follows. In § 2, we define the model used. The simulation technique along with the lane formation order parameter and $XZ$ averaged charge profile are discussed in § 3. In § 4, the results for parallel forces are presented both in the presence and absence of an external magnetic field and discussed in detail. Finally, we finish with conclusions in § 5.

2. The model

In our model, we consider a PIP system comprising of $N$ charged particles of the same magnitude $|Q|$ and of equal masses in a cubic box having size $L_{x} = L_{y} = L_{z} = L$. Half of the particles carry a positive charge and the other half carry a negative charge, with partial number densities $\rho _{1}=\rho _{2}$ taking $\rho _{1}+\rho _{2}=\rho$, where, $\rho ={N}/{L_{x}L_{y}L_{z}}$ is the number density of the system. To minimize effects of the boundaries, we impose the periodic boundary conditions for $X$, $Y$ and $Z$-directions.

The interaction potential reads as:

(2.1)\begin{equation} U(r_{ij})=\left(\frac{Q_{A}Q_{B}}{4{\rm \pi}\epsilon_{0}r_{ij}}\right) \exp\left({-\kappa\left(\frac{r_{ij}}{a}-1\right)}\right) \end{equation}

where, $r_{ij}$ is the distance between the $i$th and $j$th pair; $\kappa ={a}/{\lambda _{D}}$ is the screening parameter resulting from the shielding dynamics of ‘background’ charged particles (Oohara, Date & Hatakeyama 2005), it governs the range of interaction. Here, $\lambda _{D}$ is the Debye length; ‘$a$’ is the Wigner–Seitz radius; $Q_{A, B}$ is the charge of particle $A$ $(B)$, such that $Q_{A}Q_{B}=-1$ and $Q_{A}Q_{A} = Q_{B}Q_{B} = +1$. This is a valid model for charge-stabilized suspensions in three (Löwen & Kramposthuber 1993) and two (Lowen 1992) spatial dimensions as well as for the system under study (Leunissen et al. 2005; Royall et al. 2006).

The particle trajectories are governed by the LD equation,

(2.2)\begin{equation} m_{i}\frac{{\rm d}^{2}\boldsymbol{r}_{i}}{{\rm d} t^{2}}={-}\gamma \frac{{\rm d}\boldsymbol{r}_{i}}{{\rm d} t}-\sum_{i < j}^{}\boldsymbol{\nabla} U\left(r_{ij}\right)+\boldsymbol{F}_{{\rm ext}}+\boldsymbol{F}^{(R)}_{i}, \end{equation}

where $i=1,\ldots \ldots \ldots,N$; $m_{i}$, $r_{i}$ are, respectively, the number of PIP particles, the mass and position of the $i$th particle; $-\sum _{i < j}^{}\boldsymbol {\nabla } U(r_{ij})$ is the force comprised of interparticle interactions. Here, the summation is done for $(i < j)$ to account for all unique pairs of the particles as well as to avoid double calculations of the same interaction and improve computation efficiency. As is well known, in Langevin model, each PIP particle experiences two forces arising from the background ‘heat bath’ namely: a dampening force $-\gamma ({{\rm d}\boldsymbol {r}_{i}}/{{\rm d} t})$ which represents a dynamical friction experienced by the PIP particles; and a fluctuating force $\boldsymbol {F}^{(R)}_{i}$. These two forces, in combination, are the reason that keeps the Brownian motion in the system ‘alive’. This Brownian motion from the heat bath due to background interactions, results in dissipation of PIP particles via $-\gamma ({{\rm d}\boldsymbol {r}_{i}}/{{\rm d} t})$, where, $\gamma$ is the friction constant. Here,

(2.3)\begin{equation} \boldsymbol{F}_{{\rm ext}}=\boldsymbol{F}_{E}+\boldsymbol{F}_{{\rm mag}}, \end{equation}

is the force comprised of the external force fields. In our model, $\boldsymbol {F}_{E}$ is the space-independent homogeneous external electric force acting on the PIP particles along the $Z$-direction. Under the influence of this external forcing half of the particles (say, positively charged) will drift along the positive $Z$-direction, while, the other half of the particles (say, negatively charged) will drift along the negative $Z$-direction, leading to the satisfaction of the criteria of ‘oppositely driven’. These forces experienced by positively and negatively charged particles are termed as $\boldsymbol {F}_{A}$ and $\boldsymbol {F}_{B}$, respectively. First, we study the case where the two external forces $\boldsymbol {F}_{A}$ and $\boldsymbol {F}_{B}$ are parallel, i.e. $\boldsymbol {F}_{A} = -\boldsymbol {F}_{B} = |\boldsymbol {F}_{E}|$, the $\boldsymbol {F}_{E}$ is the force acting on the $i$th particle and is considered to point in the $Z$-direction which is modelled as:

(2.4)\begin{equation} \boldsymbol{F}_{E}(t)=\hat z E_{0}\cos(\omega t), \end{equation}

where, $E_{0}$ is the strength or amplitude of the external electric field, $\omega$ is the frequency of the external electric field (with $\omega = 0$ leading to the constant-field case) and $\hat z$ is the unit vector along the $Z$-direction. Here,

(2.5)\begin{equation} \boldsymbol{F}_{{\rm mag}}=\frac{Q_{A,B}\boldsymbol{B}}{m_{i}c}\dot{r}_{i}\times\hat{e}_{y} \end{equation}

is the force due to the external magnetic field applied along the $Y$-direction, $c$ is the speed of light. In our simulation, the strength of the magnetic field $\boldsymbol {B}$ is incorporated by a factor $\beta ={\omega _{c}}/{\omega _{{\rm pd}}}\propto |\boldsymbol {B}|$, i.e. the ratio of the cyclotron frequency $\omega _{c}={Q_{A,B}B}/{m_{i}c}$ and the plasma frequency $\omega _{{\rm pd}}=[{2Q_{A,B}^{2}}/{4{\rm \pi} \epsilon _{0}a^{3}m_{i}}]^{1/2}$. Here, simulations are performed with $\beta$ values varying from $0.001$ to $1.0$. In real units, $\beta =1.0$ is equivalent to a magnetic field strength $B=14.958~{\rm T}$ for the PIP system as created in the $C^{\pm }_{60}$ experiment (Oohara et al. 2005) can be considered as reasonable enough to describe this problem.

The force $\boldsymbol {F}^{(R)}_{i}$ describes random kicks of the background acting on the $i$th PIP particle by the ‘bath’. Here $\boldsymbol {F}^{(R)}_{i}$ is a rapidly fluctuating force, which is due to the impacts of the particles of the ‘bath’ and the particles in the plasma system (also called ‘noise’). These impacts or collisions are represented as ‘random kicks of the background’. These kicks are mimicked by Gaussian random numbers with zero mean, $\overline {\boldsymbol {F}^{(R)}_{i}}=0$, and variance:

(2.6)\begin{equation} \overline{\left(\boldsymbol{F}^{(R)}_{i}\right)_{\alpha}(t) \left(\boldsymbol{F}^{(R)}_{j}\right)_{\eta}(t^{'})}=2k_{B}T\gamma \delta_{\alpha \eta}\delta_{ij}\delta\left(t-t^{'}\right). \end{equation}

The subscripts $\alpha$ and $\eta$ stand for two Cartesian components; $i$ and $j$ stands for $i$th and $j$th particles; $t$ and $t^{'}$ for two distinct times, where, $\delta _{\alpha \eta }$ and $\delta _{ij}$ are Kronecker deltas; the third $\delta$ stand for the Dirac delta function; and $k_{B}T$ is the thermal energy of the bath.

Here, the length, time, energy, density and electric fields are normalizedby $a$, $\omega _{{\rm pd}}^{-1}$, $k_BT$, $a^{3}$ and ${Q}/{4{\rm \pi} \epsilon _{0}a^{2}}$, respectively. In these units the Coulomb coupling parameter is defined as $\varGamma$ where $\varGamma ={Q_{A,B}^{2}}/{4{\rm \pi} \epsilon _{0}ak_{B}T}$; here, $k_{B}T$ denotes the thermal energy. For this study, the stochastic Langevin normalized equations for the particle trajectories $\boldsymbol {r}_{i}(t)$ $(i = 1,\ldots, N)$ read as:

(2.7)\begin{equation} \frac{{\rm d}^{2}\boldsymbol{r}_{i}}{{\rm d} t^{2}}={-}\gamma\frac{{\rm d}\boldsymbol{r}_{i}}{{\rm d} t} +\sum_{i< j}\frac{\varGamma}{r_{ij}}\left(\kappa+\frac{1}{r_{ij}}\right) \exp[-\kappa(r_{ij}-1)]+\boldsymbol{F}_{{\rm ext}}(t)+\boldsymbol{F}^{(R)}_{i}(t). \end{equation}

3. Simulation procedure

Extensive LD simulations using the OpenMP parallel program are carried out to analyse the non-equilibrium phase transition which is associated with lane formation on the 3-D PIP system having a periodic boundary condition along all three directions, both in the presence and absence of the external magnetic field. Our investigations are carried out for $\kappa = 0.0001$, $N=1000$ particles and encompass a measurement time $t\omega _{{\rm pd}}=8\times 10^{5} \Delta t$ which is preceded by an equilibration period. After equilibration with the desired temperature $\varGamma ^{-1}$, using the Langevin equation, the force due to the external electric field $\boldsymbol {F_{E}}$ is applied to the particles at $t=2\times 10^{5}\Delta t$ time steps. The data collection is obtained for the last $2\times 10^{5}\Delta t$ steps after the system has reached a far-from-equilibrium quasisteady state. Here, the external magnetic field is applied from the beginning of the simulation and the entire study has been performed. Scaling studies have been performed with $N$ and ‘volume’ $V$ ($=L_{x}\times L_{y} \times L_{z}$) which suggests that $N=1000$ is enough to describe the problem and to minimize finite size effects. To begin with, each particle is assigned an initial velocity which is random in direction such that the average kinetic energy corresponds to the chosen temperature. We discretize (2.7) with the time step $\Delta t$, and integrate it by using the velocity Verlet method. To ensure a sufficient numerical accuracy, we choose $\Delta t=0.003$.

The simulation chamber being cubic in nature and having periodic boundaries along all three directions requires caution while calculating interaction potential in cases of small $\kappa$ or a small $N$. In such cases Ewald sums (Salin & Caillol 2000) are employed to handle the long-range interactions and limit the absolute uncertainties required for the thermal averages of the energy. The Ewald sums method eliminates the uncertainties that arise due to simple truncation of interaction potential. For the system under study, it is observed that the Ewald contribution towards potential energy is almost $1.41\,\%$ of the potential energy calculated using truncation of interaction potential. This indicates that the system size is sufficiently large to neglect Ewald sums and a simple truncation along with minimum image convention will be a reliable method to numerically simulate the PIP system with few uncertainties.

3.1. Order parameter

An order parameter is a measure of the degree of order in a system undergoing some sort of phase transition. Following Ikeda & Kim (2017) and Sarma et al. (2020), we define the following as the order parameter of lane formation. The simulation system is divided into $n_{{\rm div}}$ number of identical strips along the driven direction (say, along $\hat z$ for the case of parallel forces). Thus, the width of each strip along the $X$-direction is given by $l_{{\rm div}} = L/n_{{\rm div}}$. Following the work by Dzubiella, Hoffmann & Löwen (2002), the value of $l_{{\rm div}}$ is chosen by defining a ‘suitable length scale’ as $l_{{\rm div}} > \frac {1}{2}\rho ^{1/d}$. Here, $\rho$ is the particle number density and $d = 3$ is the dimensions of the simulation performed. The order parameter for the lane formation, say, in the $k$th strip is defined as

(3.1)\begin{equation} \phi_{k}=\frac{n^{+}_{k}-n^{-}_{k}}{n^{+}_{k}+n^{-}_{k}}, \end{equation}

where $n^{\pm }_{k}$ represents the number of ‘$\pm$’ species in the $k$th strip. The order parameter $\phi$ for the total system is then defined as

(3.2)\begin{equation} \phi=\left\langle\frac{1}{n_{{\rm div}}}\sum^{n_{{\rm div}}}_{k=1}|\phi_{k}|\right\rangle , \end{equation}

where the brackets denote a time average. The order parameter $\phi$ begins at around $0$ at the initial state since oppositely charged particles are found inside the system, and finally reaches $1$ when the system exhibits the lane formation in the steady state. The former corresponds to the randomly mixed state, whereas the latter corresponds to the lane formation structure by the particles of the same species along the driven direction. In this study, the order parameter is evaluated for various values of applied electric field strength $E_0$ and as shown earlier (Sarma et al. 2020), here also it is found that the critical value of the field strength $E_{c}$ is determined by setting $\phi =0.5$, where the system just started to form lanes.

3.2. Charge profile

Charge profile is used to study the geometric properties of the lane structure formed. The charge profile is measured similar to the concept of order parameter defined in § 3.1. For a 3-D system the simulation chamber is divided into $n_{{\rm div}}$ number of divisions along the driven direction (say the $y$-direction) having thickness $l_{{\rm div}} = L/n_{{\rm div}}$. For any $k$th strip we measure the total charge and plot it against the position of the strip. The total charge $Q_{XZ}$ in a strip is the numerical sum of the charges of all the particles in that strip averaged over the $X$ and $Z$-directions.

Thus, plotting this quantity $Q_{XZ}$ versus $L_y$ gives us the charge profile. A positive spike indicates the presence of a lane of positive particles and similarly a lane of negatively charged particles is represented by a negative spike in the profile plot.

4. Results and discussions: lane formation in presence of parallel external forces

In this subsection, we mainly focus on the results obtained for the study of non-equilibrium lane formation dynamics in a 3-D PIP system for the inertial (or finite mass ‘$m$’) or underdamped case with parallel external forces. Here, the effect of both constant ($\omega =0$) and oscillatory ($\omega \neq 0$) external electric field forces are observed in the presence ($\beta \neq 0$) and absence ($\beta =0$) of the external magnetic field.

4.1. Constant electric field

Simulation snapshots for the 3-D PIP system associated with a situation where the external forces $\boldsymbol {F}_{A}$ and $\boldsymbol {F}_{B}$ are parallel to each other are shown in figures 1(a), 1(b), 1(c) and 1(d). In all snapshots, the labels on the $X$, $Y$ and $Z$-axes are labelled as $L_x$, $L_y$ and $L_z$, respectively, to represent the simulation domain, i.e. the dimensions of the simulation box along all three directions. Here, a constant external electric field of strength $E_{0}=30 > E_{c}$ is applied along the $Z$-direction. One clearly sees lane formation parallel to the external field in figure 1. Of course, due to the presence of an additional dimension, the lane structure is more complicated in three dimensions than in two dimensions (Sarma et al. 2020). Here, no external magnetic field ($\beta =0$) is applied and other parameters are used as $\varGamma =2.5$, $\rho =0.245$ and $\omega =0$. Figure 1(a) represents a 3-D view of the simulation chamber showing lane configurations, the view on the ($Y,Z$) plane demonstrates a structure reminiscent of the two-dimensional (2-D) phase separation (see, figure 1b), figure 1(c) indicates the view on the ($X,Z$) plane parallel to the field direction $Z$ and a top 3-D view of the simulation chamber is shown in figure 1(d).

Figure 1. Typical simulation snapshots of the 3-D PIP system with parallel fields $\boldsymbol {F}_{A} = - \boldsymbol {F}_{B}$, in the absence of an external magnetic field ($\beta =0$) and lanes parallel to the field: (a) 3-D view; (b) view on the ($Y, Z$) plane; (c) view on the ($X, Z$) plane parallel to the field direction $Z$; (d) top 3-D view of the simulation chamber. The particles are rendered as spheres. For these snapshots we simulated $N=1000$ PIP particles. The parameters are $E_{0}=30 > E_{c}$, $\varGamma =2.5$, $\rho =0.245$ and $\omega =0$.

In figure 2, the instantaneous positions of the particles are plotted at different simulation times for an external electric field having strength $E_0 = 30 > E_c$, frequency $\omega = 0, \varGamma = 2.5,\ \rho = 0.245$ and $\beta = 0$. The initial snapshot at $t\omega _{{\rm pd}} = 1$ indicates a completely random mixed state with the order parameter value $\phi = 0.3383$. The next snapshot at $t\omega _{{\rm pd}} = 380$, taken before the external electric field is switched on at $t\omega _{{\rm pd}} = 600$, is indicating a structure with row-like arrangement of particles where each row has a random mixture of both species of particles with $\phi = 0.1732$ and at $t\omega _{{\rm pd}} = 614$ the system reaches the transition point where the row-like structure was disrupted and particles exhibited a motion in response to the applied external field, the $\phi$ value is recorded as $0.4017$. The last snapshot is taken at $t\omega _{{\rm pd}} = 1640$ with $\phi = 0.7315$, where a lane-like formation is seen. The system thus goes through different phases throughout the simulation run. The above-mentioned four distinct phases were seen for all the simulations performed for this case.

Figure 2. Typical simulation snapshots of the 3-D PIP system with parallel fields $\boldsymbol {F}_{A} = - \boldsymbol {F}_{B}$, taken at (a) $t\omega _{{\rm pd}} = 1$, (b) $t\omega _{{\rm pd}} = 380$, (c) $t\omega _{{\rm pd}} = 614$, (d) $t\omega _{{\rm pd}} =1640$. The particles are rendered as spheres. For these snapshots we simulated $N=1000$ PIP particles. The parameters are $E_{0}=30$, $\varGamma =2.5$, $\rho =0.245$, $\beta = 0.0$ and $\omega =0$.

Simulation snapshots for both in the absence ($\beta =0$) and presence of different external magnetic field strengths are shown in figure 3(a–d). For all the cases the external electric forces $\boldsymbol {F}_{A}$ and $\boldsymbol {F}_{B}$ are parallel: $\boldsymbol {F}_{A} = - \boldsymbol {F}_{B}$ and applied in the $Z$-direction. The model parameters are fixed to $E_{0}=30 > E_{c}$, $\varGamma =2.5$, $\rho =0.245$ and $\omega =0$. In figure 3(a), $\beta =0.0$ is applied and the lane phase is visible. In figure 3(b–d), on the other hand, simulation snapshots for lane formation dynamics investigated with $\beta =0.01, 0.1, 1.0$, respectively, are shown. The formation of planes, each consisting of similar types of particles are observed. For a lower value of $\beta$, individual lanes consist of a good mixture of positively charged (black) and negatively charged (red) PIP particles. With increasing $\beta$ value the system gradually forms planes consisting of more of the same types of PIP particles is observed. The planes tend to become more and more saturated with the same species of particles with increasing $\beta$ which indicates the increase in orderness in each plane. When the lanes are fully saturated, it means that the individual lanes are composed of only one species of particle. It is also observed that a drift is associated with the lanes, where the lanes drift in a direction perpendicular to both electric and magnetic fields which is discussed later in the study. The dependence of the increase in the orderness of these planes on the external magnetic field can also be further verified from the corresponding time variation of the order parameter ($\phi$) plot as shown in figure 4. While $\phi$ is small before the application of the external electric field, it grows when an electric field strength $E_{0}$ greater than critical field strength $E_{c}$ is applied at $t\omega _{{\rm pd}}=600$ time steps. The critical value of the electric field strength $E_{c}$ is determined at the electric field strength value where the lane formation has just started, the corresponding value of the order parameter is recorded as $\phi =0.5$ for the simulation runs with increasing field strength. The plot shows that in the presence of a magnetic field $(\beta \neq 0)$ the $\phi$ value increases with increasing $\beta$, which indicates that increasing the value of magnetic field strength accelerates the lane formation dynamics. As a comparative study, the time variation of $\phi$ in the absence of a magnetic field $(\beta = 0)$ is also indicated in figure 4.

Figure 3. Typical simulation snapshots of the 3-D PIP system with parallel fields $\boldsymbol {F}_{A} = - \boldsymbol {F}_{B}$, in the presence of different values of the external magnetic field ($\beta \neq 0$) and planes parallel to the field: (a) 3-D view with $\beta =0.001$; (b) 3-D view with $\beta =0.01$;(c) 3-D view with $\beta =0.1$, (d) 3-D view with $\beta =1.0$. There is $E \times B$ drift associated with the lanes formed in the presence of both electric and magnetic fields. We have tried to visualize the drift in figure 6. The particles are rendered as spheres. For these snapshots we simulated $N=1000$ PIP particles. The parameters are $E_{0}=30$, $\varGamma =2.5$, $\rho =0.245$ and $\omega =0$. External electric field is applied in the $Z$-direction and the magnetic field is applied in the $Y$-direction.

Figure 4. Time variation of order parameter ($\phi$) plot for the external magnetic field strength values $\beta =0, 0.01, 0.1, 1.0$, for a PIP system with parallel fields $\boldsymbol {F}_{A} = - \boldsymbol {F}_{B}$. The plot shows the $\phi$ value increases with increasing $\beta$, which indicates that the system moves towards a highly self-organized state. The parameters are $E_{0}=30$, $\varGamma =2.5$, $\rho =0.245$ and $\omega =0$. An external electric field is applied in the $Z$-direction and a magnetic field is applied in the $Y$-direction.

The non-equilibrium phase diagram in three spatial dimensions is presented in figure 5, plotted both in the presence ($\beta =1.0$) and absence ($\beta =0$) of the external magnetic field. This phase diagram is obtained for constant ($\omega =0$) external electric forces applied parallel to each other. The location of the phase transition is estimated via the behaviour of the order parameter $\phi$. As mentioned above, the critical electric field strength $E_{c}$ is obtained by setting $\phi =0.5$ for the set of runs with increasing field strength $E_{0}$. The plot clearly shows that with the application of the external magnetic field ($\beta =1.0$) the PIP system enters into the ordered lane phase for comparatively lower value of the electric field strength than that in the absence ($\beta =0$) of the magnetic field. In conclusion, the higher the magnetic field strength, the lower is the strength of the external electric field required to reach the transition point.

Figure 5. Critical field strength $E_{c}$ for the 3-D PIP system versus $\kappa$ for both in the presence ($\beta =1.0$) and absence ($\beta =0$) of the external magnetic field as obtained from the LD simulation. By increasing the field strength $E_{c}$, the system shows a phase transition from disordered state to a state characterized by lane formation. The transition is indicated by the symbols, the lines are a guide to the eye. The presence of an external magnetic field accelerates the lane formation at comparatively lower value of electric field strength. The other parameters are $\varGamma =2.5$, $\rho =0.245$ and $\omega =0$.

In figure 6(a), a series of simulation snapshots is taken for the 3-D PIP system in the presence of a magnetic field $(\beta =1)$. The snapshots are taken at $t\omega _{{\rm pd}} = 1080, 1090, 1101, 1112, 1123$ and $1134$, respectively, with parameters $E_{0}=30$, $\varGamma =2.5$, $\rho =0.245$ and $\omega =0$. The plots reveal that in the presence of both external electric and magnetic fields, a drift of lanes in the direction perpendicular to electric and magnetic field directions is observed. This drift is visualized in figure 6(a) where a random lane of negative particles is selected and its evolution with time is depicted. Here the lane under consideration is highlighted with a green rectangular box. A corresponding $XZ$-average charge profile is also plotted as shown in figure 6(b) for all the snapshots taken in figure 6(a). The positive peaks in the charge profile indicate a presence of a lane composed of positively charged particles and similarly a negative peak shows a lane of negatively charged particles. The red dashed line is drawn at $Q_{XZ} = 0$ to separate the positive lane peaks from the negative lane peaks. At the start of recording, the snapshot of the selected lane (highlighted with green box) is located at $L_y = -5.85$ at $t\omega _{{\rm pd}} = 1080$. In the next snapshot at $t\omega _{{\rm pd}} = 1090$ the lane is found to drift in the positive $Y$-direction to $L_y = -4.26$. In all the consecutive snapshots the lane continues drifting towards the positive $Y$-direction. In the last snapshot the lane reaches $L_y = 1.86$ when $t\omega _{{\rm pd}} = 1134$ and the drift continues for the whole simulation time. On calculating this velocity of the drifting lanes one obtains

(4.1)\begin{equation} v_d = \frac{\Delta L_y}{\Delta t\omega_{{\rm pd}}} = \frac{1.86 + 5.85}{1134 - 1080} = 0.142, \end{equation}

where, $\Delta L_y$ is the displacement covered by drifting lanes in time interval of $\Delta t\omega _{{\rm pd}}$. For the given $E_0 = 30$ and $\beta = 1.0$, the $E\times B$ drift velocity of particles is observed to be $E_0/\beta = 30$ which is greater than the calculated value of $v_d$ for the lanes. It could be assumed that some additional forces are arising when the individual particles form a lane. As a consequence of which the drift velocity of the lane is reduced.

Figure 6. (a) Typical simulation snapshots of the 3-D PIP system with parallel fields $\boldsymbol {F}_{A} = - \boldsymbol {F}_{B}$, in the presence of an external magnetic field ($\beta =1.0$) taken at $t\omega _{{\rm pd}} = 1080, 1090, 1101, 1112, 1123$ and $1134$ and lanes parallel to the field are seen. The parameters used are $E_{0}=30$, $\varGamma =2.5$, $\rho =0.245$ and $\omega =0$. Motion of one particular lane is highlighted by a green box. (b) The $XZ$-average charge profile is plotted for the simulation snapshots taken at ‘(a)’ and the motion of same lane under green box is also highlighted. The number $Q_{XZ}$ is the numerical sum of all charges (positive and negative) in a respective grid.

4.2. Oscillatory electric field

We now focus on a time dependent external electric field with non-vanishing frequency. In particular, the lane formation dynamics of a PIP system in the presence of such forces applied parallelly (i.e. along the $Z$-direction) is studied by simulating LD. The whole study is performed for various values of the frequency of the external oscillatory field ranging from $\omega = 0.001$ to 3.0 (only a few results are presented here), taking $\varGamma = 2.5$ and $\rho = 0.245$. Here, we have also examined the effect of an external magnetic field on lane formation.

For oscillatory external electric forces $\boldsymbol {F}_{A}= - \boldsymbol {F}_{B}$, data for the order parameter $\phi$ obtained from the simulations for electric field strengths $E_{0} = 20, 30, 40, 50, 80, 100$, field frequency $\omega =0.001$ plotted versus time are shown in figure 7(a). The location of the lane phase is estimated via the behaviour of the order parameter $\phi$. However, when the field strength is sufficiently high enough, the system moves towards a self-organized lane state which is clear from the fact that $\phi > 0.5$ for $E_0 = 50, 80$ and $100$. It is noted that a lane state is not observed when $E_0$ reaches 30, upon application of an oscillatory field, although in the application of constant parallel electric field forces the system reaches the critical field strength value at $E_{0}=E_{c}=23$ for $\kappa =0.0001$. The plot clearly shows that an enhanced critical field strength $E_{c}$ is necessary to drive a transition towards lane formation in the presence of time-varying external electric forces. Additionally, for $E_0 = 40$, initially it is observed that there is an increase in $\phi$ above $0.5$ which gradually decreases with time below $\phi = 0.5$. Indicating that upon application of external time-varying forces, lanes were initially formed ($\phi > 0$) and later spontaneously broke ($\phi < 0$) with time. This phenomenon is observed for field strength values close to $E_c$ and is also discussed later in the study. Simulation snapshots of the system associated with this situation are shown in figure 7(b). The first snapshot is taken for $E_0 = 20 < E_c$, and clearly, no self-organization of particles is observed. For higher values of $E_0 = 50, 80$ and $100$, the system gradually enters a highly self-organized state with orderness increasing with increasing field strength. No significant change is seen on the geometry of the lanes with $E_0$ variation. As discussed in our previous study (Sarma et al. 2020) on a 2-D PIP system in the presence of an oscillating external field, here, in the 3-D case also the critical frequency $\omega _{c}$ exists upon which a transition back to the disordered state occurs. In our previous study (Sarma et al. 2020) it is also reported that in the presence of an oscillatory external electric field in a 2-D PIP system, the system oscillates between ordered and disordered states (which is estimated via the behaviour of the order parameter $\phi$) for lower frequency values. However, in our study it is observed that the oscillation in $\phi$ exists, but this oscillation is not sufficient enough to break the self-organized lane state and bring the system to a disordered state. This indicates that the external field frequency $\omega = 0.001 < \omega _c$ for the 3-D PIP system under study.

Figure 7. (a) Time variation of order parameter ($\phi$) plot. (b) Typical simulation snapshots of the 3-D PIP system in the presence of parallel oscillatory fields $\boldsymbol {F}_{A} = - \boldsymbol {F}_{B}$, for different values of $E_0 = 20, 30, 40, 50, 80$ and $100$ in the absence of an external magnetic field ($\beta =0$). The parameters used are $\omega = 0.001$, $\varGamma =2.5$ and $\rho =0.245$.

To study the effect of the external field frequency on lane dynamics, $\phi$ is plotted versus $t\omega _{{\rm pd}}$ for different values of field frequency $\omega = 0.001, 0.01, 0.1, 0.2, 0.5, 0.8, 1.0$ and $1.2$ taking $E_{0} = 50 > E_{c}$, $\varGamma =2.5$, $\rho =0.245$ and $\beta =0$, as shown in figure 8. It is evident from the figure that if a time-varying field with amplitude $E_{0} > E_{c}$ is present then with gradual increase of field frequency $\omega$, the $\phi$ value decreases. For lower values of frequency the system remains in the lane state, while above critical frequency value $\omega _{c}$ where $\phi = 0.5$, the system goes back to a disordered state. With this concept, $\omega _{c}$ is found as shown in figure 9(a) both in the presence ($\beta =1.0$) and absence ($\beta =0$) of the external magnetic field, and subsequently, the phase diagram for 3-D PIP system is also obtained as shown in figure 9(b).

Figure 8. Time variation of order parameter ($\phi$) plot in the presence of parallel oscillatory fields $\boldsymbol {F}_{A} = - \boldsymbol {F}_{B}$ with $E_0 = 50 > E_c$ for different values of $\omega = 0.001, 0.01, 0.1, 0.2, 0.5, 0.8, 1.0$ and $1.2$. The parameters used are $\varGamma =2.5$, $\rho =0.245$ and $\beta = 0.0$.

Figure 9. (a) The $\phi$ versus $\omega$ plot for both in the presence ($\beta =1.0$) and absence ($\beta =0$) of the external magnetic field. (b) The $E_c$ versus $\omega$ plot for the 3-D PIP system as obtained from the LD simulation. The other parameters are $\varGamma =2.5$ and $\rho =0.245$.

In figure 9(a), $\phi$ is plotted versus field frequency $\omega$ for a 3-D PIP system in the presence of an external oscillatory parallel field both in the presence (indicated by red coloured line) and absence (indicated by blue line) of the external magnetic field. Initially it is seen that at lower values of $\omega$ the system stays in a lane state with $\phi \geq 0.5$; however, as $\omega$ increases the curve takes a downward trend and at higher values of $\omega$ no lane state is observed with $\phi < 0.5$. An horizontal line at $\phi = 0.5$ is drawn to separate lane and no lane zone. The point of intersection of the frequency variation of the $\phi$ curve with this horizontal line gives us the critical value of frequency ‘$\omega _c$’ of the system. A similar trend is also observed in the presence of a magnetic field. However, the presence of a magnetic field has introduced a positive shift in the curve and an increase in $\omega _c$ is noted in the presence of a magnetic field. For $\beta = 0$ case $\omega _{c}$ is recorded as 1.05, however, $\omega _{c}$ is recorded as 1.75 for $\beta = 1.0$. Thus, the presence of a magnetic field contributed to a lane state and a higher value of critical frequency is now required to transit the 3-D PIP system back to a disordered state.

By doing extensive LD simulations for different parameters of electric field strength and frequency values, we concluded with a phase plot shown in figure 9(b). In figure 9(b), critical electric field strength is plotted against frequency value in the presence of oscillatory parallel external forces. It is noted that as frequency is increased $E_c$ also increases. The blue line in figure 9(b) acts as a phase separation boundary in the presence of oscillatory external forces. Parameters below this phase separation line are not able to transit the system to a lane state. However, parameters above the phase separation line are able to transit the system to a lane state. It is also noted that the presence of oscillatory field results in an oscillation of order parameter which is shown in figure 8, however, spontaneous breaking and formation of lanes is observed only for parameters on the blue line or parameters in very close proximity of the blue line indicated in figure 9(b). For parameters above blue line, oscillation in the order parameter is observed, however, no spontaneous breaking and formation is observed. It is also important to mention that as reported by Sarma et al. (2020), in a 2-D PIP system spontaneous formation and breaking of lanes is observed for all $E_0 \geq E_c$. However, in our present study, it is observed that such effect is seen only for $E_0$ very close to $E_c$, which is also shown in figure 7(a). In the figure, the system is unable to transit to lane state for $E_0 < E_c$, whereas, for $E_0 > > E_c$ the system remains in a lane state throughout simulation. However, for $E_0 = 40$, i.e. $E_0$ close to $E_c$, a typical behaviour of spontaneous formation and breaking of lanes is observed evident by a decrease in $\phi$ below $0.5$. Results similar to the study performed by Sarma et al. (2020) are obtained in the presence of non-parallel external forces which is shown in case 2 of § 3.2 in Part 2 (Prajapati et al. 2023) of the companion paper, where, a spontaneous formation and breaking of lane is observed for all $E_0 \geq E_c$.

The friction constant $\gamma$ also plays a major role in the dynamics of lane formation. The friction ($\gamma$), if sufficiently large, encourages the collapse of the lane which can be understood using figure 10. In figure 10, the time variation of order parameter $(\phi )$ is plotted for different values of $\gamma$ in the presence of constant parallel external forcing. The other parameters used are $E_0 = 40,\ \omega = 0.0$ and $\varGamma = 2.5$. It is clear from the figure that for a fixed electric field strength value, as expected, with increasing $\gamma$, $\phi$ decreases. Further, increase in $\gamma$ would lead to breaking or collapse of lanes. This in turn indicates that a stronger electric field is needed to transit the same system towards a lane state at high $\gamma$. Thus, an increase in critical field strength is observed with increasing $\gamma$.

Figure 10. Time variation of order parameter ($\phi$) plot in the presence of parallel forcing $\boldsymbol {F}_{A} = - \boldsymbol {F}_{B}$ with $E_0 = 40$ for different values of $\gamma = 5, 7, 10, 15$ and $20$. The parameters used are $\varGamma =2.5$, $\rho =0.245$ and $\beta = 0.0$.

5. Conclusions

We have studied the influence of parallel external fields on non-equilibrium lane formation dynamics in a 3-D PIP system performing LD simulation both in the presence and absence of an external magnetic field. From the study we make the following conclusions.

1. (i) We observe that the pattern formation in a PIP system is a general effect, which is independent of the dimensionality of the model.

2. (ii) As a principal observation, formation of parallel lanes are observed on application of parallel forces. Our set-up of parallel electric fields is realized by two crossing pedestrian lanes in which pedestrians are only moving in one direction.

3. (iii) A critical value of the electric field above which self-organization takes place exists both in the presence and absence of the external magnetic field.

4. (iv) Using a suitable order parameter, a lane formation phase is identified.

5. (v) The process of lane formation prevails for oscillating electric field forces both in the presence and absence of the magnetic field, which shows an interesting oscillatory behaviour in the order parameter. However, spontaneous breaking and reformation of lanes is not observed throughout the simulation time. Rather, a spontaneous formation and breaking of lanes is observed for frequency values close to critical frequency $\omega _c$.

6. (vi) A critical value of frequency was also observed above which no lane state is observed for $\omega _0 > \omega _c$. However, an increase in critical frequency was observed in the presence of a magnetic field.

7. (vii) The effect of external magnetic field strength on the lane formation dynamics was systematically analysed. In particular, lanes saturate with increasing magnetic field which also increases the orderness in the system.

8. (viii) In the presence of a magnetic field, a drift of lanes in a direction perpendicular to parallel forces and magnetic field is observed.

In the following companion paper, i.e. Part 2 (Prajapati et al. 2023), we will present our study on lane formation dynamics in the presence of a non-parallel external forces both in the presence and absence of a magnetic field. We will bring out the effect of various parameters on the dynamics of the lanes formed and the contribution in a 3-D PIP system.