Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-19T17:04:18.840Z Has data issue: false hasContentIssue false
  • English
  • Français

Resolved and subgrid dynamics of Rayleigh–Bénard convection

Published online by Cambridge University Press:  28 March 2019

Riccardo Togni ,
Andrea Cimarelli Open the ORCID record for Andrea Cimarelli [Opens in a new window]  and
Elisabetta De Angelis Open the ORCID record for Elisabetta De Angelis [Opens in a new window]
Riccardo Togni
Affiliation:
DIN, Università di Bologna, Via Fontanelle 40, 47121 Forlì, Italy
Andrea Cimarelli
Affiliation:
School of Engineering, Cardiff University, Queen’s Buildings, The Parade, Cardiff CF243AA, UK
Elisabetta De Angelis*
Affiliation:
DIN, Università di Bologna, Via Fontanelle 40, 47121 Forlì, Italy School of Engineering, Cardiff University, Queen’s Buildings, The Parade, Cardiff CF243AA, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In this work we present and demonstrate the reliability of a theoretical framework for the study of thermally driven turbulence. It consists of scale-by-scale budget equations for the second-order velocity and temperature structure functions and their limiting cases, represented by the turbulent kinetic energy and temperature variance budgets. This framework represents an extension of the classical Kolmogorov and Yaglom equations to inhomogeneous and anisotropic flows, and allows for a novel assessment of the turbulent processes occurring at different scales and locations in the fluid domain. Two relevant characteristic scales, 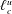$\ell _{c}^{u}$ for the velocity field and 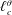$\ell _{c}^{\unicode[STIX]{x1D703}}$ for the temperature field, are identified. These variables separate the space of scales into a quasi-homogeneous range, characterized by turbulent kinetic energy and temperature variance cascades towards dissipation, and an inhomogeneity-dominated range, where the production and the transport in physical space are important. This theoretical framework is then extended to the context of large-eddy simulation to quantify the effect of a low-pass filtering operation on both resolved and subgrid dynamics of turbulent Rayleigh–Bénard convection. It consists of single-point and scale-by-scale budget equations for the filtered velocity and temperature fields. To evaluate the effect of the filter length 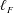$\ell _{F}$ on the resolved and subgrid dynamics, the velocity and temperature fields obtained from a direct numerical simulation are split into filtered and residual components using a spectral cutoff filter. It is found that when 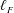$\ell _{F}$ is smaller than the minimum values of the cross-over scales given by 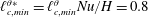$\ell _{c,min}^{\unicode[STIX]{x1D703}\ast }=\ell _{c,min}^{\unicode[STIX]{x1D703}}Nu/H=0.8$, the resolved processes correspond to the exact ones, except for a depletion of viscous and thermal dissipations, and the only role of the subgrid scales is to drain turbulent kinetic energy and temperature variance to dissipate them. On the other hand, the resolved dynamics is much poorer in the near-wall region and the effects of the subgrid scales are more complex for filter lengths of the order of 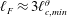$\ell _{F}\approx 3\ell _{c,min}^{\unicode[STIX]{x1D703}}$ or larger. This study suggests that classic eddy-viscosity/diffusivity models employed in large-eddy simulation may suffer from some limitations for large filter lengths, and that alternative closures should be considered to account for the inhomogeneous processes at subgrid level. Moreover, the theoretical framework based on the filtered Kolmogorov and Yaglom equations may represent a valuable tool for future assessments of the subgrid-scale models.

JFM classification

Turbulent Flows: Turbulent convection Turbulent Flows: Turbulence modelling Turbulent Flows: Turbulence theory
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 867 , 25 May 2019 , pp. 906 - 933
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ahlers, G., Bodenschatz, E., Funfschilling, D., Grossmann, S., He, X., Lohse, D., Stevens, R. J. A. M. & Verzicco, R. 2012 Logarithmic temperature profiles in turbulent Rayleigh–Bénard convection. Phys. Rev. Lett. 109 (11), 114501.Google Scholar
Antonia, R. A. & Orlandi, P. 2003 Effect of Schmidt number on small-scale passive scalar turbulence. Appl. Mech. Rev. 56 (6), 615–632.Google Scholar
Bryan, G. H., Wyngaard, J. C. & Fritsch, J. M. 2003 Resolution requirements for the simulation of deep moist convection. Mon. Weath. Rev. 131 (10), 2394–2416.Google Scholar
Burattini, P., Antonia, R. A. & Danaila, L. 2005 Scale-by-scale energy budget on the axis of a turbulent round jet. J. Turbul. (6), N19.Google Scholar
Cabot, W. H. 1993 Large eddy simulations of time-dependent and buoyancy-driven channel flows. Annual Research Briefs 1992. pp. 45–60. CTR Annual Research Briefs (Center for Turbulence Research, Stanford University/NASA Ames).Google Scholar
Chillà, F. & Schumacher, J. 2012 New perspectives in turbulent Rayleigh–Bénard convection. Eur. Phys. J. E 35 (7), 1–25.Google Scholar
Cimarelli, A. & De Angelis, E. 2011 Analysis of the Kolmogorov equation for filtered wall-turbulent flows. J. Fluid Mech. 676, 376–395.Google Scholar
Cimarelli, A. & De Angelis, E. 2012 Anisotropic dynamics and sub-grid energy transfer in wall-turbulence. Phys. Fluids 24 (1), 015102.Google Scholar
Cimarelli, A. & De Angelis, E. 2014 The physics of energy transfer toward improved subgrid-scale models. Phys. Fluids 26 (5), 055103.Google Scholar
Cimarelli, A., De Angelis, E. & Casciola, C. M. 2013 Paths of energy in turbulent channel flows. J. Fluid Mech. 715, 436–451.Google Scholar
Cimarelli, A., De Angelis, E., Jiménez, J. & Casciola, C. M. 2016 Cascades and wall-normal fluxes in turbulent channel flows. J. Fluid Mech. 796, 417–436.Google Scholar
Corrsin, S. 1951 On the spectrum of isotropic temperature fluctuations in an isotropic turbulence. J. Appl. Phys. 22 (4), 469–473.Google Scholar
Dabbagh, F., Trias, F. X., Gorobets, A. & Oliva, A. 2016 New subgrid-scale models for large-eddy simulation of Rayleigh–Bénard convection. J. Phys. Conf. Ser. 745 (3), 032041.Google Scholar
Dabbagh, F., Trias, F. X., Gorobets, A. & Oliva, A. 2017 A priori study of subgrid-scale features in turbulent Rayleigh–Bénard convection. Phys. Fluids 29 (10), 105103.Google Scholar
Danaila, L., Anselmet, F., Zhou, T. & Antonia, R. A. 2001 Turbulent energy scale budget equations in a fully developed channel flow. J. Fluid Mech. 430, 87–109.Google Scholar
Danaila, L., Krawczynski, J. F., Thiesset, F. & Renou, B. 2012 Yaglom-like equation in axisymmetric anisotropic turbulence. Physica D 241 (3), 216–223.Google Scholar
Davidson, P. A., Pearson, B. R. & Staplehurst, P. 2004 How to describe turbulent energy distributions without the Fourier transform. In Proceedings of the AFMC 15, Sydney, Australia. University of Sydney.Google Scholar
Deardorff, J. W. 1974 Three-dimensional numerical study of the height and mean structure of a heated planetary boundary layer. Boundary-Layer Meteorol. 7 (1), 81–106.Google Scholar
Domaradzki, J. A., Liu, W., Härtel, C. & Kleiser, L. 1994 Energy transfer in numerically simulated wall-bounded turbulent flows. Phys. Fluids 6, 1583–1599.Google Scholar
Dupuy, D., Toutant, A. & Bataille, F. 2018 Turbulence kinetic energy exchanges in flows with highly variable fluid properties. J. Fluid Mech. 834, 5–54.Google Scholar
Gauding, M., Wick, A., Pitsch, H. & Peters, N. 2014 Generalised scale-by-scale energy-budget equations and large-eddy simulations of anisotropic scalar turbulence at various Schmidt numbers. J. Turbul. 15 (12), 857–882.Google Scholar
Gayen, B., Hughes, G. O. & Griffiths, R. W. 2013 Completing the mechanical energy pathways in turbulent Rayleigh–Benard convection. Phys. Rev. Lett. 111 (12), 124301.Google Scholar
Grossmann, S. & Lohse, D. 2000 Scaling in thermal convection: a unifying theory. J. Fluid Mech. 407, 27–56.Google Scholar
Härtel, C., Kleiser, L., Unger, F. & Friedrich, R. 1994 Subgrid-scale energy transfer in the near-wall region of turbulent flows. Phys. Fluids 6 (9), 3130–3143.Google Scholar
Hill, R. J. 2002 Exact second-order structure–function relationships. J. Fluid Mech. 468, 317–326.Google Scholar
Kimmel, S. J. & Domaradzki, J. A. 2000 Large eddy simulations of Rayleigh–Bénard convection using subgrid scale estimation model. Phys. Fluids 12 (1), 169–184.Google Scholar
Kolmogorov, A. N. 1941a Dissipation of energy in locally isotropic turbulence. Dokl. Akad. Nauk SSSR 32, 16–18.Google Scholar
Kolmogorov, A. N. 1941b The local structure of turbulence in incompressible viscous fluid for very large Reynolds numbers. In Dokl. Akad. Nauk SSSR, vol. 30, pp. 301–305. JSTOR.Google Scholar
Lilly, D. K. 1962 On the numerical simulation of buoyant convection. Tellus 14 (2), 148–172.Google Scholar
Lilly, D. K. 1967 The representation of small scale turbulence in numerical simulation experiments. In Proceedings of the IBM Scientific Computing Symposium on Environmental Science, pp. 195–210. IBM.Google Scholar
Liu, S., Meneveau, C. & Katz, J. 1994 On the properties of similarity subgrid-scale models as deduced from measurements in a turbulent jet. J. Fluid Mech. 275, 83–119.Google Scholar
Lohse, D. & Xia, K.-Q. 2010 Small-scale properties of turbulent Rayleigh–Bénard convection. Annu. Rev. Fluid Mech. 42, 335–364.Google Scholar
Marati, N., Casciola, C. M. & Piva, R. 2004 Energy cascade and spatial fluxes in wall turbulence. J. Fluid Mech. 521, 191–215.Google Scholar
Mason, P. J. 1989 Large-eddy simulation of the convective atmospheric boundary layer. J. Atmos. Sci. 46 (11), 1492–1516.Google Scholar
Obukhov, A. M.1968 Structure of the temperature field in turbulent flow. Tech. Rep. DTIC Document.Google Scholar
Piomelli, U. 1999 Large-eddy simulation: achievements and challenges. Prog. Aerosp. Sci. 35 (4), 335–362.Google Scholar
Piomelli, U. & Balaras, E. 2002 Wall-layer models for large-eddy simulations. Annu. Rev. Fluid Mech. 34 (1), 349–374.Google Scholar
Piomelli, U., Cabot, W. H., Moin, P. & Lee, S. 1991 Subgrid-scale backscatter in turbulent and transitional flows. Phys. Fluids A 3 (7), 1766–1771.Google Scholar
Pope, S. B.2001 Turbulent Flows. Cambridge University Press.Google Scholar
Porté-Agel, F., Parlange, M. B., Meneveau, C. & Eichinger, W. E. 2001 A priori field study of the subgrid-scale heat fluxes and dissipation in the atmospheric surface layer. J. Atmos. Sci. 58 (18), 2673–2698.Google Scholar
Sergent, A., Joubert, P. & Le Quéré, P. 2006 Large-eddy simulation of turbulent thermal convection using a mixed scale diffusivity model. Prog. Comput. Fluid Dyn. 6 (1-3), 40–49.Google Scholar
Siggia, E. D. 1994 High Rayleigh number convection. Annu. Rev. Fluid Mech. 26 (1), 137–168.Google Scholar
Smagorinsky, J. 1963 General circulation experiments with the primitive equations. 1. The basic experiment. Mon. Weath. Rev. 91 (3), 99–164.Google Scholar
Togni, R., Cimarelli, A. & De Angelis, E. 2015 Physical and scale-by-scale analysis of Rayleigh–Bénard convection. J. Fluid Mech. 782, 380–404.Google Scholar
Valente, P. C. & Vassilicos, J. C. 2015 The energy cascade in grid-generated non-equilibrium decaying turbulence. Phys. Fluids 27 (4), 045103.Google Scholar
Van Reeuwijk, M., Jonker, H. J. J. & Hanjalić, K. 2005 Identification of the wind in Rayleigh–Bénard convection. Phys. Fluids 17 (5), 051704.Google Scholar
Yaglom, A. M. 1949 On the local structure of a temperature field in a turbulent flow. Dokl. Akad. Nauk SSSR 69 (6), 743.Google Scholar