Published online by Cambridge University Press: 14 June 2019
In this paper, we investigate the receptivity of a supersonic boundary layer to impinging acoustic waves. Unlike previous studies of acoustic receptivity, where the sound waves have phase speeds comparable with or larger than the free-stream velocity 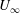 $U_{\infty }$, the acoustic waves here have much slower (
$U_{\infty }$, the acoustic waves here have much slower (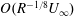 $O(R^{-1/8}U_{\infty })$) phase velocity, and their characteristic wavelength and frequency are of
$O(R^{-1/8}U_{\infty })$) phase velocity, and their characteristic wavelength and frequency are of 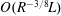 $O(R^{-3/8}L)$ and
$O(R^{-3/8}L)$ and 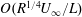 $O(R^{1/4}U_{\infty }/L)$ respectively, compatible with the triple-deck structure, where
$O(R^{1/4}U_{\infty }/L)$ respectively, compatible with the triple-deck structure, where 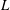 $L$ is the distance to the leading edge and
$L$ is the distance to the leading edge and 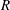 $R$ the Reynolds number based on
$R$ the Reynolds number based on 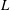 $L$ and
$L$ and 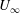 $U_{\infty }$. A significant feature of a sound wave on the triple-deck scale is that an
$U_{\infty }$. A significant feature of a sound wave on the triple-deck scale is that an 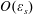 $O(\unicode[STIX]{x1D700}_{s})$ perturbation in the free stream generates much stronger (
$O(\unicode[STIX]{x1D700}_{s})$ perturbation in the free stream generates much stronger (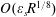 $O(\unicode[STIX]{x1D700}_{s}R^{1/8})$) velocity fluctuations in the boundary layer. Two receptivity mechanisms are considered. The first is new, involving the interaction of two such acoustic waves and operating in a boundary layer over a smooth wall. The second involves the interaction between an acoustic wave and the steady perturbation induced by a wavy wall. The sound–sound, or sound–roughness, interactions generate a forcing in resonance with a neutral Tollmien–Schlichting (T–S) wave. The latter is thus excited near the lower branch of the neutral curve, and subsequently undergoes exponential amplification. The excitation through sound–sound interaction may offer a possible explanation for the appearance of instability modes downstream of their neutral locations as was observed in a supersonic boundary layer over a smooth wall. The triple-deck formalism is adopted to describe impingement and reflection of the acoustic waves, and ensuing receptivity, allowing the coupling coefficient to be calculated. The two receptivity processes with the acoustic waves on the triple-deck scale are much more effective compared with those involving usual sound waves, with the coupling coefficient being greater by a factor of
$O(\unicode[STIX]{x1D700}_{s}R^{1/8})$) velocity fluctuations in the boundary layer. Two receptivity mechanisms are considered. The first is new, involving the interaction of two such acoustic waves and operating in a boundary layer over a smooth wall. The second involves the interaction between an acoustic wave and the steady perturbation induced by a wavy wall. The sound–sound, or sound–roughness, interactions generate a forcing in resonance with a neutral Tollmien–Schlichting (T–S) wave. The latter is thus excited near the lower branch of the neutral curve, and subsequently undergoes exponential amplification. The excitation through sound–sound interaction may offer a possible explanation for the appearance of instability modes downstream of their neutral locations as was observed in a supersonic boundary layer over a smooth wall. The triple-deck formalism is adopted to describe impingement and reflection of the acoustic waves, and ensuing receptivity, allowing the coupling coefficient to be calculated. The two receptivity processes with the acoustic waves on the triple-deck scale are much more effective compared with those involving usual sound waves, with the coupling coefficient being greater by a factor of 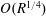 $O(R^{1/4})$ and
$O(R^{1/4})$ and 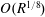 $O(R^{1/8})$ in the sound–sound and sound–roughness interactions, respectively. A parametric study for both the reflection and coupling coefficients is conducted for representative T–S waves, to assess the influence of the streamwise and spanwise wavenumbers, and the phase speed (or frequency) of the acoustic wave.
$O(R^{1/8})$ in the sound–sound and sound–roughness interactions, respectively. A parametric study for both the reflection and coupling coefficients is conducted for representative T–S waves, to assess the influence of the streamwise and spanwise wavenumbers, and the phase speed (or frequency) of the acoustic wave.