Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-19T16:50:55.308Z Has data issue: false hasContentIssue false
  • English
  • Français

Decomposition of wake dynamics in fluid–structure interaction via low-dimensional models

Published online by Cambridge University Press:  28 March 2019

T. P. Miyanawala Open the ORCID record for T. P. Miyanawala [Opens in a new window]  and
R. K. Jaiman Open the ORCID record for R. K. Jaiman [Opens in a new window]
T. P. Miyanawala
Affiliation:
Department of Mechanical Engineering, National University of Singapore, 117575 Singapore
R. K. Jaiman*
Affiliation:
Department of Mechanical Engineering, University of British Columbia, Vancouver, BC V6T 1Z4, Canada
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We present a dynamic decomposition analysis of the wake flow in fluid–structure interaction (FSI) systems under both laminar and turbulent flow conditions. Of particular interest is to provide the significance of low-dimensional wake flow features and their interaction dynamics to sustain the free vibration of a square cylinder at a relatively low mass ratio. To obtain the high-dimensional data, we employ a body-conforming variational FSI solver based on the recently developed partitioned iterative scheme and the dynamic subgrid-scale turbulence model for a moderate Reynolds number (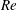$Re$). The snapshot data from high-dimensional FSI simulations are projected to a low-dimensional subspace using the proper orthogonal decomposition (POD). We utilize each corresponding POD mode to detect features of the organized motions, namely, the vortex street, the shear layer and the near-wake bubble. We find that the vortex shedding modes contribute solely to the lift force, while the near-wake and shear layer modes play a dominant role in the drag force. We further examine the fundamental mechanism of this dynamical behaviour and propose a force decomposition technique via low-dimensional approximation. To elucidate the frequency lock-in, we systematically analyse the decomposed modes and their dynamical contributions to the force fluctuations for a range of reduced velocity at low Reynolds number laminar flow. These quantitative mode energy contributions demonstrate that the shear layer feeds the vorticity flux to the wake vortices and the near-wake bubble during the wake–body synchronization. Based on the decomposition of wake dynamics, we suggest an interaction cycle for the frequency lock-in during the wake–body interaction, which provides the interrelationship between the high-amplitude motion and the dominating wake features. Through our investigation of wake–body synchronization below critical 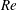$Re$ range, we discover that the bluff body can undergo a synchronized high-amplitude vibration due to flexibility-induced unsteadiness. Owing to the wake turbulence at a moderate Reynolds number of 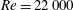$Re=22\,000$, a distorted set of POD modes and the broadband energy distribution are observed, while the interaction cycle for the wake synchronization is found to be valid for the turbulent wake flow.

JFM classification

Nonlinear Dynamical Systems: Low-dimensional models Wakes/Jets: Vortex streets
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 867 , 25 May 2019 , pp. 723 - 764
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bearman, P. W. 1997 Near wake flows behind two-and three-dimensional bluff bodies. J. Wind Engng Ind. Aerodyn. 69, 33–54.Google Scholar
Braza, M., Chassaing, P. H. H. M. & Minh, H. H. 1986 Numerical study and physical analysis of the pressure and velocity fields in the near wake of a circular cylinder. J. Fluid Mech. 165, 79–130.Google Scholar
Cantwell, B. & Coles, D. 1983 An experimental study of entrainment and transport in the turbulent near wake of a circular cylinder. J. Fluid Mech. 136, 321–374.Google Scholar
Chaturantabut, S. & Sorensen, D. C. 2009 Discrete empirical interpolation for nonlinear model reduction. In Proceedings of the 48th IEEE Conference on Decision and Control 2009, held jointly with the 2009 28th Chinese Control Conference, pp. 4316–4321. IEEE.Google Scholar
Deane, A. E., Kevrekidis, I. G., Karniadakis, G. E. & Orszag, S. A. 1991 Low-dimensional models for complex geometry flows: application to grooved channels and circular cylinders. Phys. Fluids A 3 (10), 2337–2354.Google Scholar
Dong, S., Karniadakis, G. E., Ekmekci, A. & Rockwell, D. 2006 A combined direct numerical simulation–particle image velocimetry study of the turbulent near wake. J. Fluid Mech. 569, 185–207.Google Scholar
Guan, M. Z., Narendran, K., Miyanawala, T. P., Ma, P. F. & Jaiman, R. K. 2017 Control of flow-induced motion in multi-column offshore platform by near-wake jets. In ASME 2017 36th International Conference on Ocean, Offshore and Arctic Engineering. American Society of Mechanical Engineers.Google Scholar
Holmes, P. 2012 Turbulence, Coherent Structures, Dynamical Systems and Symmetry. Cambridge University Press.Google Scholar
Jaiman, R. K., Guan, M. Z. & Miyanawala, T. P. 2016a Partitioned iterative and dynamic subgrid-scale methods for freely vibrating square-section structures at subcritical Reynolds number. Comput. Fluids 133, 68–89.Google Scholar
Jaiman, R. K., Pillalamarri, N. R. & Guan, M. Z.2016b A stable second-order partitioned iterative scheme for freely vibrating low-mass bluff bodies in a uniform flow. Comput. Meth. Appl. Mech. Eng. 301, pp. 187–215.Google Scholar
Jauvtis, N. & Williamson, C. H. K. 2004 The effect of two degrees of freedom on vortex-induced vibration at low mass and damping. J. Fluid Mech. 509, 23–62.Google Scholar
Khalak, A & Williamson, C. H. 1999 Motions, forces and mode transitions in vortex-induced vibrations at low mass-damping. J. Fluids Struct. 13 (7–8), 813–851.Google Scholar
Law, Y. Z. & Jaiman, R. K. 2017 Wake stabilization mechanism of low-drag suppression devices for vortex-induced vibration. J. Fluids Struct. 70, 428–449.Google Scholar
Liberge, E. & Hamdouni, A. 2010 Reduced order modelling method via proper orthogonal decomposition (POD) for flow around an oscillating cylinder. J. Fluids Struct. 26 (2), 292–311.Google Scholar
Lighthill, J. 1986 Fundamentals concerning wave loading on offshore structures. J. Fluid Mech. 173, 667–681.Google Scholar
Lumley, J. L. 1967 The structure of inhomogeneous turbulent flows. In Atmospheric Turbulence and Radio Wave Propagation (ed. Yaglom, A. M. & Tatarsky, V. I.), pp. 166–178. Nauka.Google Scholar
Ma, X. & Karniadakis, G. E. 2002 A low-dimensional model for simulating three-dimensional cylinder flow. J. Fluid Mech. 458, 181–190.Google Scholar
Meliga, P. & Chomaz, J. M. 2011 An asymptotic expansion for the vortex-induced vibrations of a circular cylinder. J. Fluid Mech. 671, 137–167.Google Scholar
Miyanawala, T. P., Guan, M. Z. & Jaiman, R. K. 2016 Flow-induced vibrations of a square cylinder with combined translational and rotational oscillations. In ASME 2016 35th International Conference on Ocean, Offshore and Arctic Engineering. American Society of Mechanical Engineers.Google Scholar
Miyanawala, T. P. & Jaiman, R. K.2017 An efficient deep learning technique for the Navier–Stokes equations: application to unsteady wake flow dynamics. arXiv:1710.09099.Google Scholar
Miyanawala, T. P. & Jaiman, R. K. 2018 Self-sustaining turbulent wake characteristics in fluid–structure interaction of a square cylinder. J. Fluids Struct. 77, 80–101.Google Scholar
Morison, J. R., Johnson, J. W. & Schaaf, S. A. 1950 The force exerted by surface waves on piles. J. Petrol. Tech. 2 (05), 149–154.Google Scholar
Narendran, K., Guan, M. Z., Ma, P. F., Choudhary, A., Hussain, A. A. & Jaiman, R. K. 2018 Control of vortex-induced motion in multi-column offshore platform by near-wake jets. Comput. Fluids 167, 111–128.Google Scholar
Noack, B. R., Afanasiev, K., Morzyński, M., Tadmor, G. & Thiele, F. 2003 A hierarchy of low-dimensional models for the transient and post-transient cylinder wake. J. Fluid Mech. 497, 335–363.Google Scholar
Park, D. & Yang, K. S. 2016 Flow instabilities in the wake of a rounded square cylinder. J. Fluid Mech. 793, 915–932.Google Scholar
Rempfer, D. 2003 Low-dimensional modeling and numerical simulation of transition in simple shear flows. Annu. Rev. Fluid Mech. 35 (1), 229–265.Google Scholar
Rowley, C. W. & Dawson, S. T. M. 2017 Model reduction for flow analysis and control. Annu. Rev. Fluid Mech. 49, 387–417.Google Scholar
Sarpkaya, T. 2001 On the force decompositions of Lighthill and Morison. J. Fluids Struct. 15 (2), 227–233.Google Scholar
Sirovich, L. 1987 Turbulence and the dynamics of coherent structures. I. Coherent structures. Q. Appl. Maths 45 (3), 561–571.Google Scholar
Taira, K., Brunton, S. L., Dawson, S. T. M., Rowley, C. W., Colonius, T., Mckeon, B. J., Schmidt, O. T., Gordeyev, S., Theofilis, V. & Ukeiley, L. S. 2017 Modal analysis of fluid flows: an overview. AIAA J. 55, 4013–4041.Google Scholar
Williamson, C. H. K. 1996 Vortex dynamics in the cylinder wake. Annu. Rev. Fluid Mech. 28 (1), 477–539.Google Scholar
Yao, W. & Jaiman, R. K. 2017 Model reduction and mechanism for the vortex-induced vibrations of bluff bodies. J. Fluid Mech. 827, 357–393.Google Scholar