Hostname: page-component-7bb8b95d7b-dvmhs Total loading time: 0 Render date: 2024-09-20T10:42:21.722Z Has data issue: false hasContentIssue false
  • English
  • Français

Efficiency of reversible MCMC methods: elementary derivations and applications to composite methods

Part of: Markov processes

Published online by Cambridge University Press:  18 September 2024

Radford M. Neal  and
Jeffrey S. Rosenthal Open the ORCID record for Jeffrey S. Rosenthal [Opens in a new window]
Radford M. Neal*
Affiliation:
University of Toronto
Jeffrey S. Rosenthal*
Affiliation:
University of Toronto
*
*Postal address: Department of Statistical Sciences, University of Toronto.
*Postal address: Department of Statistical Sciences, University of Toronto.
Get access Rights & Permissions [Opens in a new window]

Abstract

We review criteria for comparing the efficiency of Markov chain Monte Carlo (MCMC) methods with respect to the asymptotic variance of estimates of expectations of functions of state, and show how such criteria can justify ways of combining improvements to MCMC methods. We say that a chain on a finite state space with transition matrix P efficiency-dominates one with transition matrix Q if for every function of state it has lower (or equal) asymptotic variance. We give elementary proofs of some previous results regarding efficiency dominance, leading to a self-contained demonstration that a reversible chain with transition matrix P efficiency-dominates a reversible chain with transition matrix Q if and only if none of the eigenvalues of 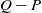$Q-P$ are negative. This allows us to conclude that modifying a reversible MCMC method to improve its efficiency will also improve the efficiency of a method that randomly chooses either this or some other reversible method, and to conclude that improving the efficiency of a reversible update for one component of state (as in Gibbs sampling) will improve the overall efficiency of a reversible method that combines this and other updates. It also explains how antithetic MCMC can be more efficient than independent and identically distributed sampling. We also establish conditions that can guarantee that a method is not efficiency-dominated by any other method.

Keywords

Markov chainasymptotic varianceefficiency dominationPeskun ordering

MSC classification

Primary: 60J10: Markov chains (discrete-time Markov processes on discrete state spaces)
Secondary: 60J22: Computational methods in Markov chains
Type
Original Article
Information
Journal of Applied Probability , First View , pp. 1 - 21
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press on behalf of Applied Probability Trust.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Andrieu, C. and Livingstone, S. (2021). Peskun–Tierney ordering for Markovian Monte Carlo: Beyond the reversible scenario. Ann. Stat. 49, 1958–1981.CrossRefGoogle Scholar
Bartlett, M. S. (1946). On the theoretical specification and sampling properties of autocorrelated time-series. Suppl. J. Roy. Stat. Soc. 8, 27–41.CrossRefGoogle Scholar
Bendat, J. and Sherman, S. (1955). Monotone and convex operator functions. Trans. Amer. Math. Soc. 79, 58–71.CrossRefGoogle Scholar
Bhatia, R. (1997). Matrix Analysis (Graduate Texts in Mathematics 169). Springer, New York.Google Scholar
Billingsley, P. (1968). Convergence of Probability Measures. Wiley, New York.Google Scholar
Brooks, S., Gelman, A., Jones, G. and Meng, X.-L. (eds) (2011). Handbook of Markov Chain Monte Carlo. Chapman & Hall, New York.CrossRefGoogle Scholar
Chan, K. S. and Geyer, C. J. (1994). Discussion: Markov chains for exploring posterior distributions. Ann. Stat. 22, 1747–1758.CrossRefGoogle Scholar
Frigessi, A., Hwang, C.-R. and Younes, L. (1992). Optimal spectral structure of reversible stochastic matrices, Monte Carlo methods and the simulation of Markov random fields. Ann. Appl. Prob. 2, 610–628.CrossRefGoogle Scholar
Gagnon, P. and Maire, F. (2023). An asymptotic Peskun ordering and its application to lifted samplers. Bernoulli 30, 2301–2325.Google Scholar
Geyer, C. (1992). Practical Markov chain Monte Carlo. Stat. Sci. 7. 473–483.Google Scholar
Green, P. J. and Han, X.-L. (1992). Metropolis methods, Gaussian proposals, and antithetic variables. In Stochastic Models, Statistical Methods and Algorithms in Image Analysis, eds P. Barone, A. Frigessi and M. Piccione. Springer, Berlin.CrossRefGoogle Scholar
Häggström, O. and Rosenthal, J. S. (2007). On variance conditions for Markov chain CLTs. Electron. Commun. Prob. 12, 454–464.CrossRefGoogle Scholar
Horn, R. A. and Johnson, C. R. (2013). Matrix Analysis, 2nd edn. Cambridge University Press.Google Scholar
Huang, L.-J. and Mao, Y.-H. (2023). Variational formulas for asymptotic variance of general discrete-time Markov chains. Bernoulli 29, 300–322.CrossRefGoogle Scholar
Kipnis, C. and Varadhan, S. R. S. (1986). Central limit theorem for additive functionals of reversible Markov processes and applications to simple exclusions. Commun. Math. Phys. 104, 1–19.CrossRefGoogle Scholar
Li, G., Smith, A. and Zhou, Q. (2023). Importance is important: A guide to informed importance tempering methods. Preprint, arXiv:2304.06251.Google Scholar
Löwner, K. (1934). Über monotone Matrixfunktionen. Math. Z. 38, 177–216.CrossRefGoogle Scholar
Mira, A. (2001). Ordering and improving the performance of Monte Carlo Markov chains. Stat. Sci. 16, 340–350.CrossRefGoogle Scholar
Mira, A. and Geyer, C. J. (1999). Ordering Monte Carlo Markov chains. Technical Report No. 632, School of Statistics, University of Minnesota.Google Scholar
Neal, R. M. (2004). Improving asymptotic variance of MCMC estimators: Non-reversible chains are better. Preprint, arXiv:math/0407281.Google Scholar
Neal, R. M. (2024). Modifying Gibbs sampling to avoid self transitions. Preprint, arXiv:2403.18054.Google Scholar
Peskun, P. H. (1973). Optimum Monte Carlo sampling using Markov chains. Biometrika 60, 607–612.CrossRefGoogle Scholar
Roberts, G. O. and Rosenthal, J. S. (2008). Variance bounding Markov chains. Ann. Appl. Prob. 18, 1201–1214.CrossRefGoogle Scholar
Suwa, H. (2022). Reducing rejection exponentially improves Markov chain Monte Carlo sampling. Preprint, arxiv:2208.03935.Google Scholar
Tierney, L. (1994). Markov chains for exploring posterior distributions. Ann. Stat. 22, 1701–1762.Google Scholar
Tierney, L. (1998). A note on Metropolis–Hastings kernels for general state spaces. Ann. Appl. Prob. 8, 1–9.CrossRefGoogle Scholar
Zanella, G. (2019). Informed proposals for local MCMC in discrete spaces. J. Amer. Stat. Assoc. 115, 852–865.CrossRefGoogle Scholar