Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-28T05:21:34.612Z Has data issue: false hasContentIssue false
  • English
  • Français

G-GRAPHS AND SPECIAL REPRESENTATIONS FOR BINARY DIHEDRAL GROUPS IN GL(2,ℂ)

Published online by Cambridge University Press:  06 August 2012

ALVARO NOLLA DE CELIS
ALVARO NOLLA DE CELIS*
Affiliation:
Graduate School of Mathematics, Nagoya University, Chikusa-ku, Nagoya 464-8602, Japan e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Given a finite subgroup G⊂GL(2,ℂ), it is known that the minimal resolution of singularity ℂ2/G is the moduli space Y=G-Hilb(ℂ2) of G-clusters 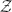⊂ℂ2. The explicit description of Y can be obtained by calculating every possible distinguished basis for as vector spaces. These basis are the so-called G-graphs. In this paper we classify G-graphs for any small binary dihedral subgroup G in GL(2,ℂ), and in the context of the special McKay correspondence we use this classification to give a combinatorial description of special representations of G appearing in Y in terms of its maximal normal cyclic subgroup H ⊴ G.

Keywords

Primary 14E16Secondary 14C0514E15
Type
Research Article
Information
Glasgow Mathematical Journal , Volume 55 , Issue 1 , January 2013 , pp. 23 - 57
Copyright
Copyright © Glasgow Mathematical Journal Trust 2012

References

REFERENCES

1.Bridgeland, T., King, A. and Reid, M., The McKay correspondence as an equivalence of derived categories, J. Amer. Math. Soc. 14 (3) (2001), 535–554 (electronic).CrossRefGoogle Scholar
2.Brieskorn, E., Rationale Singularitäten komplexer Flächen, Invent. Math. 4 (1967/1968), 336–358.CrossRefGoogle Scholar
3.Craw, A. and Reid, M., How to calculate A-Hilb ℂ3, in Geometry of toric varieties, vol. 6 of Seminaires et Congres (Societe Mathematique de France, Paris, 2002), 129–154.Google Scholar
4.Ishii, A., On the McKay correspondence for a finite small subgroup of GL(2, ℂ), J. Reine Angew. Math., 549 (2002), 221–233.Google Scholar
5.Ito, Y., Special McKay correspondence, in Geometry of toric varieties, vol. 6 of Seminaires et Congres (Societe Mathematique de France, Paris, 2002), 213–225.Google Scholar
6.Ito, Y. and Nakamura, I., McKay correspondence and Hilbert schemes, Proc. Japan Acad. Ser. A Math. Sci. 72 (7) (1996), 135–138.Google Scholar
7.Iyama, O. and Wemyss, M., The classification of special CM modules, Math. Z. 265 (1) (2010), 41–83.Google Scholar
8.Kidoh, R., Hilbert schemes and cyclic quotient surface singularities, Hokkaido Math. J. 30 (1) (2001), 91–103.Google Scholar
9.Leng, B., The Mckay correspondence and orbifold Riemann-Roch, PhD Thesis (University of Warwick, 2002).Google Scholar
10.McKay, J., Graphs, singularities, and finite groups, The Santa Cruz Conference on Finite Groups (University of California, Santa Cruz, CA, 1979), Proc. Sympos. Pure Math. 37 (1980), 183–186 (American Mathematical Society Providence, RI, 1980).Google Scholar
11.Nakamura, I., Hilbert schemes of abelian group orbits, J. Algebraic Geom. 10 (4) (2001), 757–779.Google Scholar
12.Nolla de Celis, A., Dihedral groups and G-Hilbert schemes. PhD Thesis (University of Warwick, 2008), 112 pp.Google Scholar
13.Nolla de Celis, A., Dihedral G-Hilb via representations of the Mckay quiver. Proc. Japan Acad. Ser. A, 88 (5) (2012), 78–83.Google Scholar
14.Reid, M., Surface cyclic quotient singularities and Hirzebruch–Jung resolutions, available at http://homepages.warwick.ac.uk/~masda/surf/more/cyclic.pdf, accessed 20 June 2012.Google Scholar
15.Reid, M., La correspondance de McKay, Astérisque 276 (2002), 53–72 (Séminaire Bourbaki, 1999 (2000)).Google Scholar
16.Riemenschneider, O., Deformationen von Quotientensingularitäten (nach zyklischen Gruppen), Math. Ann. 209 (1974), 211–248.Google Scholar
17.Riemenschneider, O., Special representations and the two-dimensional McKay correspondence, Hokkaido Math. J. 32 (2) (2003), 317–333.Google Scholar
18.Sebestean, M., Correspondance de McKay et équivalences dérivés. PhD Thesis (Université Paris 7, 2005).Google Scholar
19.Shephard, G. C. and Todd, J. A., Finite unitary reflection groups, Canadian J. Math. 6 (1954), 274–304.CrossRefGoogle Scholar
20.Wunram, J., Reflexive modules on quotient surface singularities, Math. Ann. 279 (4) (1988), 583–598.Google Scholar
21.Yoshino, Y., Cohen-Macaulay modules over Cohen–Macaulay rings, London Mathematical Society Lecture Note Series, vol. 146 (Cambridge University Press, Cambridge, UK, 1990).Google Scholar