Hostname: page-component-586b7cd67f-t7fkt Total loading time: 0 Render date: 2024-11-24T00:06:19.236Z Has data issue: false hasContentIssue false
  • English
  • Français

Quantum Symmetries of Graph C*-algebras

Published online by Cambridge University Press:  20 November 2018

Simon Schmidt  and
Moritz Weber
Simon Schmidt
Affiliation:
Saarland University, Fachbereich Mathematik, 66041 Saarbrücken, Germany, e-mail : [email protected], [email protected]
Moritz Weber
Affiliation:
Saarland University, Fachbereich Mathematik, 66041 Saarbrücken, Germany, e-mail : [email protected], [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

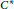The study of graph ${{C}^{*}}$-algebras has a long history in operator algebras. Surprisingly, their quantum symmetries have not yet been computed. We close this gap by proving that the quantum automorphism group of a finite, directed graph without multiple edges acts maximally on the corresponding graph 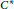${{C}^{*}}$-algebra. This shows that the quantum symmetry of a graph coincides with the quantum symmetry of the graph 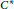${{C}^{*}}$-algebra. In our result, we use the definition of quantum automorphism groups of graphs as given by Banica in 2005. Note that Bichon gave a different definition in 2003; our action is inspired from his work. We review and compare these two definitions and we give a complete table of quantum automorphism groups (with respect to either of the two definitions) for undirected graphs on four vertices.

Keywords

46LXX05CXX20B25finite graphgraph automorphismautomorphism groupquantum automorphismgraph C*-algebraquantum groupquantum symmetry
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 61 , Issue 4 , 01 December 2018 , pp. 848 - 864
Copyright
Copyright © Canadian Mathematical Society 2018

References

[1] Banica, T., Quantum automorphism groups of homogeneous graphs. J. Funct. Anal. 224 (2005), 243–280. http://dx.doi.org/!0.1016/j.jfa.2004.11.002Google Scholar
[2] Banica, T. and Bichon, J., Quantum automorphism groups of vertex-transitive graphs of order ≤ 11. J. Algebraic Combin. 26 (2007), no. 1, 83-105. http://dx.doi.org/10.1007/s10801-006-0049-9Google Scholar
[3] Banica, T., Bichon, J., and Chenevier, G., Graphs having no quantum symmetry. Ann. Inst. Fourier (Grenoble) 57 (2007), 955–971. http://dx.doi.org/10.5802/aif.2282Google Scholar
[4] Bhowmick, J., Goswami, D., and Skalski, A., Quantum isometry groups of 0-dimensional manifolds. Trans. Amer. Math. Soc. 363 (2011), no. 2, 901-921. http://dx.doi.Org/10.1090/S0002-9947-2010-05141-4Google Scholar
[5] Bichon, J., Quantum automorphism groups of finite graphs. Proc. Amer. Math. Soc. 131 (2003), 665–673. http://dx.doi.Org/10.1090/S0002-9939-02-06798-9Google Scholar
[6] Bichon, J., Free wreath product by the quantum permutation group. Algebr. Represent. Theory 7 (2004), 343–362. http://dx.doi.Org/10.1023/B:ALCE.0000042148.97035.caGoogle Scholar
[7] Chassaniol, A., Quantum automorphism group of the lexicographic product of finite regular graphs. J. Algebra 456 (2016), 23–45. http://dx.doi.Org/10.1016/j.jalgebra.2O16.01.036Google Scholar
[8] Cuntz, J. and Krieger, W., A class of C*-algebras and topological Markov chains. Invent. Math. 56 (1980), no. 3, 251-268. http://dx.doi.org/10.1007/BF01390048Google Scholar
[9] Eilers, S., Restorff, G., Ruiz, E., and Sorensen, A., The complete classification of unital graph C*-algebras: Geometric and strong. arxiv:1611.07120Google Scholar
[10] Fulton, M. B., The quantum automorphism group and undirected trees. Ph.D. Thesis, Virginia Polytechnic Institute and State University, 2006.Google Scholar
[11] Goswami, D. and Bhowmick, J., Quantum isometry groups. Infosys Science Foundation Series in Mathematical Science, Springer, New Delhi, 2016. http://dx.doi.Org/10.1007/978-81-322-3667-2Google Scholar
[12] Joardar, S. and Mandai, A., Quantum symmetry of graph C* -algebras associated with connected graphs. 2017. arxiv:1 711.04253Google Scholar
[13] Neshveyev, S. and Tuset, L., Compact quantum groups and their representation categories. Cours Specialises, 20, Société Mathématique de France, Paris, 2013.Google Scholar
[14] Podles, P., Symmetries of quantum spaces. Subgroups and quotient spaces of quantum SU(2) and SO(3) groups. Comm. Math. Phys. 170 (1995), 1–20. http://dx.doi.Org/10.1007/BF02099436Google Scholar
[15] Raeburn, I., Graph algebras. CBMS Regional Conference Series in Mathematics, 103, Published for the Conference Board of the Mathematical Sciences, Washington, DC; by the American Mathematical Society, Providence, RI, 2005. http://dx.doi.Org/10.1090/cbms/103Google Scholar
[16] Speicher, R. and Weber, M., Quantum groups with partial commutation relations. arxiv:1603.09192Google Scholar
[17] Timmermann, T., An invitation to quantum groups and duality. From Hopf algebras to multiplicative unitaries and beyond. EMS Textbooks in Mathematics, European Mathematical Society (EMS), Zurich, 2008. http://dx.doi.Org/10.4171/043Google Scholar
[18] Wang, S., Quantum symmetry groups of finite spaces. Comm. Math. Phys. 195 (1998), 195–211. http://dx.doi.Org/10.1OO7/sOO22OOO5O385Google Scholar
[19] Woronowicz, S. L., Compact matrix pseudogroups. Comm. Math. Phys. 111 (1987), 613–665. http://dx.doi.Org/10.1007/BF01219077Google Scholar
[20] Woronowicz, S. L., A remark on compact matrix quantum groups. Lett. Math. Phys. 21 (1991), no. 1, 35-39. http://dx.doi.Org/10.1007/BF00414633Google Scholar