No CrossRef data available.
Article contents
On Spectral Synthesis for One Point
Published online by Cambridge University Press: 20 November 2018
Extract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
In [2, page 3831], Varopoulos proves that for any ∈ > 0 there exists a function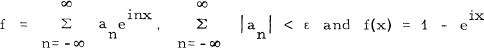 
on a neighbourhood of 0. Indeed, if 0 < ∈ < π/2, then f(x) defined to be equal to 1 - e when -eix
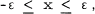, linear on [∈, 2π - ∈] and of period 2π, is an example of such a function.
The above result can be used to give a direct proof of the following result without reference to the L2 theory [1, Theorem 2.6.4].
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1969
References
2.
Varopoulos, N. Th., Sur les ensembles parfaits et les séries trigonométriques. C.R. Acad. Se. Paris
260 (1965) 4668–4670, 5165–5168, 5997–6000.Google Scholar
You have
Access