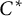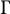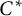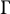1 Introduction
Let X be a compact metric space and T be a set of probability Borel measures on
![]() $X.$
For each open subset O of X, we consider its measure
$X.$
For each open subset O of X, we consider its measure
![]() $\mu (O).$
This gives a function
$\mu (O).$
This gives a function
![]() $\widehat {O}(\mu )=\mu (O)$
(
$\widehat {O}(\mu )=\mu (O)$
(
![]() $\mu \in T$
) on
$\mu \in T$
) on
![]() $T.$
This function is lower-semicontinuous on T if we endow T with the weak*-topology. Let
$T.$
This function is lower-semicontinuous on T if we endow T with the weak*-topology. Let
![]() ${\alpha }: X\to X$
be a homeomorphism on X and T be the set of
${\alpha }: X\to X$
be a homeomorphism on X and T be the set of
![]() ${\alpha }$
-invariant probability Borel measures. One considers the case that there are sufficiently many open sets O for which
${\alpha }$
-invariant probability Borel measures. One considers the case that there are sufficiently many open sets O for which
![]() $\widehat {O}$
is continuous on
$\widehat {O}$
is continuous on
![]() $T.$
This is certainly the case when the action is uniquely ergodic. The small boundary condition, or the condition of mean dimension zero, requires that in any neighborhood
$T.$
This is certainly the case when the action is uniquely ergodic. The small boundary condition, or the condition of mean dimension zero, requires that in any neighborhood
![]() $N(x)$
of each point
$N(x)$
of each point
![]() $x\in X,$
there is a neighborhood
$x\in X,$
there is a neighborhood
![]() $O(x)\subset N(x)$
such that
$O(x)\subset N(x)$
such that
![]() $\widehat {O(x)}$
is continuous. Let
$\widehat {O(x)}$
is continuous. Let
![]() $\omega (\widehat {O})$
be the oscillation of the function
$\omega (\widehat {O})$
be the oscillation of the function
![]() $\widehat {O}.$
If
$\widehat {O}.$
If
![]() $\widehat {O}$
is continuous, then
$\widehat {O}$
is continuous, then
![]() $\omega (\widehat {O})=0.$
$\omega (\widehat {O})=0.$
Let A be a
![]() $C^*$
-algebra with tracial state space
$C^*$
-algebra with tracial state space
![]() $T(A).$
For each
$T(A).$
For each
![]() $a\in A_+,$
one defines the rank function of a by
$a\in A_+,$
one defines the rank function of a by
![]() $\widehat {[a]}(\tau )=\lim _{n\to \infty }\tau (a^{1/n})$
for
$\widehat {[a]}(\tau )=\lim _{n\to \infty }\tau (a^{1/n})$
for
![]() $\tau \in T(A).$
When
$\tau \in T(A).$
When
![]() $A=M_n,$
i.e., A is the
$A=M_n,$
i.e., A is the
![]() $n\times n$
matrix algebra,
$n\times n$
matrix algebra,
![]() $\widehat {[a]}$
is just the normalized rank of
$\widehat {[a]}$
is just the normalized rank of
![]() $a.$
We study the oscillation of the function
$a.$
We study the oscillation of the function
![]() $\widehat {[a]}.$
It is called tracial oscillation of the element
$\widehat {[a]}.$
It is called tracial oscillation of the element
![]() $a.$
This notion of tracial oscillation has been studied in [Reference Elliott, Gong, Lin and Niu11, Reference Lin26] in connection with the augmented Cuntz semigroups. We introduce the notion of tracial approximate oscillation zero for
$a.$
This notion of tracial oscillation has been studied in [Reference Elliott, Gong, Lin and Niu11, Reference Lin26] in connection with the augmented Cuntz semigroups. We introduce the notion of tracial approximate oscillation zero for
![]() $C^*$
-algebras. Roughly speaking, a unital
$C^*$
-algebras. Roughly speaking, a unital
![]() $C^*$
-algebra A has tracial approximate oscillation zero, if each positive element a is approximated (tracially) by elements in the hereditary
$C^*$
-algebra A has tracial approximate oscillation zero, if each positive element a is approximated (tracially) by elements in the hereditary
![]() $C^*$
-subalgebra generated by a with small tracial oscillation (see Definition 5.1). If
$C^*$
-subalgebra generated by a with small tracial oscillation (see Definition 5.1). If
![]() ${\alpha }$
is a minimal homeomorphism on X and
${\alpha }$
is a minimal homeomorphism on X and
![]() $(X, {\alpha })$
has mean dimension zero, it is shown in [Reference Elliott and Niu12] that the crossed product
$(X, {\alpha })$
has mean dimension zero, it is shown in [Reference Elliott and Niu12] that the crossed product
![]() $C^*$
-algebra
$C^*$
-algebra
![]() $C(X)\rtimes _{\alpha } \mathbb {Z}$
is
$C(X)\rtimes _{\alpha } \mathbb {Z}$
is
![]() ${\cal Z}$
-stable. As a consequence,
${\cal Z}$
-stable. As a consequence,
![]() $C(X)\rtimes _{\alpha } \mathbb {Z}$
has tracial approximate oscillation zero (see Theorem 1.1 below).
$C(X)\rtimes _{\alpha } \mathbb {Z}$
has tracial approximate oscillation zero (see Theorem 1.1 below).
The notion of stable rank was introduced to
![]() $C^*$
-algebra theory by Rieffel in [Reference Rieffel36]. A unital
$C^*$
-algebra theory by Rieffel in [Reference Rieffel36]. A unital
![]() $C^*$
-algebra has stable rank one if its invertible elements are dense in
$C^*$
-algebra has stable rank one if its invertible elements are dense in
![]() $A.$
The notion plays an important role in the study of simple
$A.$
The notion plays an important role in the study of simple
![]() $C^*$
-algebras (see some earlier work, for example, [Reference Dădărlat, Nagy, Némethi and Pasnicu9, Reference Putnam35]). It is proved by Rørdam [Reference Rørdam41] that if A is a unital finite separable simple
$C^*$
-algebras (see some earlier work, for example, [Reference Dădărlat, Nagy, Némethi and Pasnicu9, Reference Putnam35]). It is proved by Rørdam [Reference Rørdam41] that if A is a unital finite separable simple
![]() ${\cal Z}$
-stable
${\cal Z}$
-stable
![]() $C^*$
-algebra, then A has stable rank one. Robert in [Reference Robert38] introduced the notion of almost stable rank one, which is also a very useful notion, and showed that every stably projectionless
$C^*$
-algebra, then A has stable rank one. Robert in [Reference Robert38] introduced the notion of almost stable rank one, which is also a very useful notion, and showed that every stably projectionless
![]() ${\cal Z}$
-stable simple
${\cal Z}$
-stable simple
![]() $C^*$
-algebra has almost stable rank one. A question remains open, however, whether a separable simple
$C^*$
-algebra has almost stable rank one. A question remains open, however, whether a separable simple
![]() $C^*$
-algebra with almost stable rank one actually has stable rank one.
$C^*$
-algebra with almost stable rank one actually has stable rank one.
There is a canonical map
![]() $\Gamma $
from the Cuntz semigroup of
$\Gamma $
from the Cuntz semigroup of
![]() $A,$
denoted by
$A,$
denoted by
![]() $\mathrm {Cu}(A),$
to
$\mathrm {Cu}(A),$
to
![]() $\mathrm {LAff}_+(\widetilde {QT}(A)),$
the set of strictly positive lower semi-continuous affine functions (vanishing at zero) on the cone of 2-quasitraces on
$\mathrm {LAff}_+(\widetilde {QT}(A)),$
the set of strictly positive lower semi-continuous affine functions (vanishing at zero) on the cone of 2-quasitraces on
![]() $A,$
defined by
$A,$
defined by
![]() $\Gamma ([a])(\tau )=d_\tau (a)$
(for
$\Gamma ([a])(\tau )=d_\tau (a)$
(for
![]() $\tau \in {\widetilde {QT}}(A)$
). A question posed by N. Brown (see the remark after Question 1.1 of [Reference Thiel42]) asked whether this map is surjective, i.e., whether every strictly positive lower semi-continuous affine function on
$\tau \in {\widetilde {QT}}(A)$
). A question posed by N. Brown (see the remark after Question 1.1 of [Reference Thiel42]) asked whether this map is surjective, i.e., whether every strictly positive lower semi-continuous affine function on
![]() ${\widetilde {QT}}(A)$
is a rank function for some positive element in
${\widetilde {QT}}(A)$
is a rank function for some positive element in
![]() $A\otimes {\cal K}.$
It is of course an important question. In fact, the strict comparison and surjectivity of
$A\otimes {\cal K}.$
It is of course an important question. In fact, the strict comparison and surjectivity of
![]() $\Gamma $
are perhaps equally important when one studies Cuntz semigroups. If we denote by
$\Gamma $
are perhaps equally important when one studies Cuntz semigroups. If we denote by
![]() $\mathrm {Cu}(A)_+$
the set of purely non-compact elements in the Cuntz semigroup of a separable stably finite simple
$\mathrm {Cu}(A)_+$
the set of purely non-compact elements in the Cuntz semigroup of a separable stably finite simple
![]() $C^*$
-algebra
$C^*$
-algebra
![]() $A,$
then strict comparison is the condition that
$A,$
then strict comparison is the condition that
![]() $\Gamma $
restricted on
$\Gamma $
restricted on
![]() $\mathrm {Cu}(A)_+$
is injective. If
$\mathrm {Cu}(A)_+$
is injective. If
![]() $\Gamma $
is also surjective, then the map
$\Gamma $
is also surjective, then the map
![]() $\Gamma $
gives an isomorphism from
$\Gamma $
gives an isomorphism from
![]() $\mathrm {Cu}(A)_+$
onto
$\mathrm {Cu}(A)_+$
onto
![]() $\mathrm {LAff}_+(\widetilde {QT}(A)).$
In [Reference Elliott, Robert and Santiago13], it is shown that if A is
$\mathrm {LAff}_+(\widetilde {QT}(A)).$
In [Reference Elliott, Robert and Santiago13], it is shown that if A is
![]() ${\cal Z}$
-stable, then the map
${\cal Z}$
-stable, then the map
![]() $\Gamma $
is indeed surjective, which extends an earlier result of [Reference Brown, Perera and Toms7]. More recently, it is proved in [Reference Antoine, Perera, Robert and Thiel1, Reference Thiel42] that when A has stable rank one,
$\Gamma $
is indeed surjective, which extends an earlier result of [Reference Brown, Perera and Toms7]. More recently, it is proved in [Reference Antoine, Perera, Robert and Thiel1, Reference Thiel42] that when A has stable rank one,
![]() $\Gamma $
is surjective. We show that if A is a
$\Gamma $
is surjective. We show that if A is a
![]() $\sigma $
-unital simple
$\sigma $
-unital simple
![]() $C^*$
-algebra which has strict comparison and tracial approximate oscillation zero, then the map
$C^*$
-algebra which has strict comparison and tracial approximate oscillation zero, then the map
![]() $\Gamma $
is surjective. On the other hand, if A is a
$\Gamma $
is surjective. On the other hand, if A is a
![]() $\sigma $
-unital stably finite simple
$\sigma $
-unital stably finite simple
![]() $C^*$
-algebra with strict comparison which has almost stable rank one and
$C^*$
-algebra with strict comparison which has almost stable rank one and
![]() $\Gamma $
is surjective, then A has tracial approximate oscillation zero.
$\Gamma $
is surjective, then A has tracial approximate oscillation zero.
Let A be a
![]() $\sigma $
-unital simple
$\sigma $
-unital simple
![]() $C^*$
-algebra. We also found that if A has tracial approximate oscillation zero, then A has a nice matricial structure, a property that we call (TM) (see Definition 8.1). We prove that if A has strict comparison and has property (TM), then A has stable rank one. As a by-product, we show that, if A has strict comparison and
$C^*$
-algebra. We also found that if A has tracial approximate oscillation zero, then A has a nice matricial structure, a property that we call (TM) (see Definition 8.1). We prove that if A has strict comparison and has property (TM), then A has stable rank one. As a by-product, we show that, if A has strict comparison and
![]() $\Gamma $
is surjective, then the condition that A has almost stable rank one implies that A actually has stable rank one.
$\Gamma $
is surjective, then the condition that A has almost stable rank one implies that A actually has stable rank one.
Our main result may be stated as follows:
Theorem 1.1 Let A be a separable simple
![]() $C^*$
-algebra which admits at least one densely defined non-trivial 2-quasitrace and has strict comparison.
$C^*$
-algebra which admits at least one densely defined non-trivial 2-quasitrace and has strict comparison.
Then the following are equivalent:
(1) A has tracial approximate oscillation zero;
(2)
![]() $\Gamma $
is surjective (see Definition 2.13) and A has stable rank one;
$\Gamma $
is surjective (see Definition 2.13) and A has stable rank one;
(3) A has stable rank one;
(4)
![]() $\Gamma $
is surjective and A has almost stable rank one;
$\Gamma $
is surjective and A has almost stable rank one;
(5) A has property (TM).
The technical terms in the statement above will be discussed in detail in the process and some examples of simple
![]() $C^*$
-algebras which satisfy (1) will be given (e.g., Proposition 5.8 and Theorem 5.9). The condition that A has a non-trivial densely defined 2-quasitrace could be replaced by that A is stably finite (see Remark 9.10). Note that Theorem 1.1 is stated without assuming that A is nuclear or exact. Related to the Toms–Winter conjecture, Thiel in [Reference Thiel42] shows that under the same assumption as that of Theorem 1.1, if A is unital and has stable rank one, then
$C^*$
-algebras which satisfy (1) will be given (e.g., Proposition 5.8 and Theorem 5.9). The condition that A has a non-trivial densely defined 2-quasitrace could be replaced by that A is stably finite (see Remark 9.10). Note that Theorem 1.1 is stated without assuming that A is nuclear or exact. Related to the Toms–Winter conjecture, Thiel in [Reference Thiel42] shows that under the same assumption as that of Theorem 1.1, if A is unital and has stable rank one, then
![]() $\Gamma $
is surjective, and, if, in addition, A has local finite nuclear dimension, then A is
$\Gamma $
is surjective, and, if, in addition, A has local finite nuclear dimension, then A is
![]() ${\cal Z}$
-stable. With the same spirit, Corollary 9.8 below states that, under the same assumption as in Theorem 1.1, if (1) in the theorem above also holds and A has local finite nuclear dimension, then A is
${\cal Z}$
-stable. With the same spirit, Corollary 9.8 below states that, under the same assumption as in Theorem 1.1, if (1) in the theorem above also holds and A has local finite nuclear dimension, then A is
![]() ${\cal Z}$
-stable (see also Remark 9.9 for an even weaker hypothesis). In fact, the idea of tracial oscillation zero can also be directly used in the study of Toms–Winter conjecture (see [Reference Lin25]).
${\cal Z}$
-stable (see also Remark 9.9 for an even weaker hypothesis). In fact, the idea of tracial oscillation zero can also be directly used in the study of Toms–Winter conjecture (see [Reference Lin25]).
The paper is organized as follows. Section 2 is a preliminary that lists a number of notations and definitions that are used in the paper. It also includes some known facts which may not be stated explicitly in the literature. Section 3 discusses some preliminary cancellation properties that will be used later. In Section 4, we recall the notion of tracial oscillation and introduce the notion of tracial approximate oscillation for positive elements. In Section 5, we introduce the notion of tracial approximate oscillation zero for
![]() $C^*$
-algebras and give some examples of separable
$C^*$
-algebras and give some examples of separable
![]() $C^*$
-algebras which have positive tracial approximate oscillation and examples which have tracial approximate oscillation zero. In particular, we show that, if the cone of 2-quasitraces of A has a basis S which has countably many extremal points, then A has tracial approximate oscillation zero. In Section 6, we study sequence algebras and its quotients for compact
$C^*$
-algebras which have positive tracial approximate oscillation and examples which have tracial approximate oscillation zero. In particular, we show that, if the cone of 2-quasitraces of A has a basis S which has countably many extremal points, then A has tracial approximate oscillation zero. In Section 6, we study sequence algebras and its quotients for compact
![]() $C^*$
-algebras A. We find that
$C^*$
-algebras A. We find that
![]() $l^\infty (A)/I_{_{\overline {QT(A)}^w}},$
where
$l^\infty (A)/I_{_{\overline {QT(A)}^w}},$
where
![]() $I_{_{\overline {QT(A)}^w}}$
is the quasitrace kernel ideal, is a SAW*-algebra and has real rank zero and stable rank one, provided A has tracial approximate oscillation zero. Section 7 contains one of the main results: if A has strict comparison and tracial approximate oscillation zero, then
$I_{_{\overline {QT(A)}^w}}$
is the quasitrace kernel ideal, is a SAW*-algebra and has real rank zero and stable rank one, provided A has tracial approximate oscillation zero. Section 7 contains one of the main results: if A has strict comparison and tracial approximate oscillation zero, then
![]() $\Gamma $
is surjective. In Section 8, we introduce the property (TM), a property of tracial matricial structure. We show that, under the assumption of strict comparison, the property (TM) is equivalent to the property of tracial approximate oscillation zero. The last section is devoted to the proof of Theorem 1.1 mentioned above, in particular, (1)
$\Gamma $
is surjective. In Section 8, we introduce the property (TM), a property of tracial matricial structure. We show that, under the assumption of strict comparison, the property (TM) is equivalent to the property of tracial approximate oscillation zero. The last section is devoted to the proof of Theorem 1.1 mentioned above, in particular, (1)
![]() $\Rightarrow $
(2) without assuming that A is separable (but
$\Rightarrow $
(2) without assuming that A is separable (but
![]() $\sigma $
-unital).
$\sigma $
-unital).
2 Preliminary
In this section, we will give a list of basic notations and a number of definitions which will be used throughout this paper. Most of them are familiar to experts. It also includes some basic facts about Cuntz semigroups and 2-quasitraces, as well as some ad hoc but more or less known facts. Readers are encouraged to skip them until they are needed.
2.1 Some basic notations and definitions
Notation 2.1 In this paper, the set of all positive integers is denoted by
![]() $\mathbb {N}.$
The set of all compact operators on a separable infinite-dimensional Hilbert space is denoted by
$\mathbb {N}.$
The set of all compact operators on a separable infinite-dimensional Hilbert space is denoted by
![]() ${\cal K}.$
${\cal K}.$
Let A be a normed space and
![]() ${\cal F}\subset A$
a subset. Let
${\cal F}\subset A$
a subset. Let
![]() $\epsilon>0$
. For any pair
$\epsilon>0$
. For any pair
![]() $a,b\in A,$
we write
$a,b\in A,$
we write
![]() $a\approx _{\epsilon }b$
if
$a\approx _{\epsilon }b$
if
![]() $\|a-b\|< \epsilon $
. We write
$\|a-b\|< \epsilon $
. We write
![]() $a\in _\varepsilon {\cal F}$
if there is
$a\in _\varepsilon {\cal F}$
if there is
![]() $x\in {\cal F}$
such that
$x\in {\cal F}$
such that
![]() $a\approx _\varepsilon x.$
$a\approx _\varepsilon x.$
Let A be a
![]() $C^*$
-algebra and
$C^*$
-algebra and
![]() $x\in A.$
Let
$x\in A.$
Let
![]() $|x|:=(x^*x)^{1/2}.$
If
$|x|:=(x^*x)^{1/2}.$
If
![]() $a, b\in A$
and
$a, b\in A$
and
![]() $ab=ba=a^*b=ba^*=0,$
we often write
$ab=ba=a^*b=ba^*=0,$
we often write
![]() $a\perp b.$
$a\perp b.$
Notation 2.2 Let A be a
![]() $C^*$
-algebra and
$C^*$
-algebra and
![]() $S\subset A$
a subset of
$S\subset A$
a subset of
![]() $A.$
Denote by
$A.$
Denote by
![]() $\mathrm {Her}_A(S)$
(or just
$\mathrm {Her}_A(S)$
(or just
![]() $\mathrm {Her}(S),$
when A is clear) the hereditary
$\mathrm {Her}(S),$
when A is clear) the hereditary
![]() $C^*$
-subalgebra of A generated by
$C^*$
-subalgebra of A generated by
![]() $S.$
Denote by
$S.$
Denote by
![]() $A^{\mathbf {1}}$
the unit ball of
$A^{\mathbf {1}}$
the unit ball of
![]() $A,$
and by
$A,$
and by
![]() $A_+$
the set of all positive elements in
$A_+$
the set of all positive elements in
![]() $A.$
Put
$A.$
Put
![]() $A_+^{\mathbf {1}}:=A_+\cap A^{\mathbf {1}}.$
Denote by
$A_+^{\mathbf {1}}:=A_+\cap A^{\mathbf {1}}.$
Denote by
![]() $\widetilde A$
the minimal unitization of
$\widetilde A$
the minimal unitization of
![]() $A.$
When A is unital, denote by
$A.$
When A is unital, denote by
![]() $GL(A)$
the group of invertible elements of
$GL(A)$
the group of invertible elements of
![]() $A,$
and by
$A,$
and by
![]() $U(A)$
the unitary group of
$U(A)$
the unitary group of
![]() $A.$
Let
$A.$
Let
![]() $\mathrm {Ped}(A)$
denote the Pedersen ideal of
$\mathrm {Ped}(A)$
denote the Pedersen ideal of
![]() $A, \mathrm {Ped}(A)_+= \mathrm {Ped}(A)\cap A_+, \mathrm {Ped}(A)^{\mathbf {1}}=A^{\mathbf {1}}\cap \mathrm {Ped}(A)$
, and
$A, \mathrm {Ped}(A)_+= \mathrm {Ped}(A)\cap A_+, \mathrm {Ped}(A)^{\mathbf {1}}=A^{\mathbf {1}}\cap \mathrm {Ped}(A)$
, and
![]() $\mathrm {Ped}(A)_+^{\mathbf {1}}=\mathrm {Ped}(A)_+\cap \mathrm {Ped}(A)^{\mathbf {1}}.$
Denote by
$\mathrm {Ped}(A)_+^{\mathbf {1}}=\mathrm {Ped}(A)_+\cap \mathrm {Ped}(A)^{\mathbf {1}}.$
Denote by
![]() $T(A)$
the tracial state space of
$T(A)$
the tracial state space of
![]() $A.$
Except the Pedersen ideal, all other ideals mentioned in this paper are closed two-sided ideals.
$A.$
Except the Pedersen ideal, all other ideals mentioned in this paper are closed two-sided ideals.
Definition 2.3 Let A and B be
![]() $C^*$
-algebras and
$C^*$
-algebras and
![]() $\phi : A\rightarrow B$
a linear map. The map
$\phi : A\rightarrow B$
a linear map. The map
![]() $\phi $
is said to be positive if
$\phi $
is said to be positive if
![]() $\phi (A_+)\subset B_+.$
The map
$\phi (A_+)\subset B_+.$
The map
![]() $\phi $
is said to be completely positive contractive, abbreviated to c.p.c., if
$\phi $
is said to be completely positive contractive, abbreviated to c.p.c., if
![]() $\|\phi \|\leq 1$
and
$\|\phi \|\leq 1$
and
![]() $\phi \otimes \mathrm {id}: A\otimes M_n\rightarrow B\otimes M_n$
are positive for all
$\phi \otimes \mathrm {id}: A\otimes M_n\rightarrow B\otimes M_n$
are positive for all
![]() $n\in \mathbb {N}.$
A c.p.c. map
$n\in \mathbb {N}.$
A c.p.c. map
![]() $\phi : A\to B$
is called order zero, if for any
$\phi : A\to B$
is called order zero, if for any
![]() $x,y\in A_+, xy=0$
implies
$x,y\in A_+, xy=0$
implies
![]() $\phi (x)\phi (y)=0$
(see Definition 2.3 of [Reference Winter and Zacharias45]).
$\phi (x)\phi (y)=0$
(see Definition 2.3 of [Reference Winter and Zacharias45]).
In what follows,
![]() $\{e_{i,j}\}_{i,j=1}^n$
(or just
$\{e_{i,j}\}_{i,j=1}^n$
(or just
![]() $\{e_{i,j}\},$
if there is no confusion) stands for a system of matrix units for
$\{e_{i,j}\},$
if there is no confusion) stands for a system of matrix units for
![]() $M_n, 1_n$
for the identity of
$M_n, 1_n$
for the identity of
![]() $M_n, \iota \in C_0((0,1])$
for the identity function on
$M_n, \iota \in C_0((0,1])$
for the identity function on
![]() $(0,1],$
i.e.,
$(0,1],$
i.e.,
![]() $\iota (t)=t$
for all
$\iota (t)=t$
for all
![]() $t\in (0,1].$
We also write
$t\in (0,1].$
We also write
![]() $\{e_{i,j}\}$
for a system of matrix units for
$\{e_{i,j}\}$
for a system of matrix units for
![]() ${\cal K}.$
${\cal K}.$
Definition 2.4 A
![]() $C^*$
-algebra A is said to have stable rank one [Reference Rieffel36] if
$C^*$
-algebra A is said to have stable rank one [Reference Rieffel36] if
![]() $\widetilde A=\overline {GL(\widetilde A)},$
i.e.,
$\widetilde A=\overline {GL(\widetilde A)},$
i.e.,
![]() $GL(\widetilde A)$
is dense in
$GL(\widetilde A)$
is dense in
![]() $\widetilde A.$
A
$\widetilde A.$
A
![]() $C^*$
-algebra A is said to have almost stable rank one [Reference Robert38] if, for any hereditary
$C^*$
-algebra A is said to have almost stable rank one [Reference Robert38] if, for any hereditary
![]() $C^*$
-subalgebra
$C^*$
-subalgebra
![]() $B\subset A, B\subset \overline {GL(\widetilde B)}.$
$B\subset A, B\subset \overline {GL(\widetilde B)}.$
Notation 2.5 Let
![]() $\epsilon , \delta>0.$
Define continuous functions
$\epsilon , \delta>0.$
Define continuous functions
![]() $f_{\epsilon }, g_\delta : [0,+\infty ) \rightarrow [0,1]$
by
$f_{\epsilon }, g_\delta : [0,+\infty ) \rightarrow [0,1]$
by
 $$ \begin{align*} f_{\epsilon}(t)= \begin{cases} 0, &t\in [0,\epsilon/2],\\ 1, &t\in [\epsilon,\infty),\\ \mathrm{linear, } &{t\in[\epsilon/2, \epsilon],} \end{cases}\,\,\,\mathrm{and}\,\,\, g_\delta(t)=\begin{cases} 0, &t\in \{0\}\cup [\delta, \infty),\\ 1, &{t\in[\delta/8, \delta/2]},\\ \mathrm{linear,} &t\in [0,\delta/8]\cup [\delta/2, \delta]. \end{cases} \end{align*} $$
$$ \begin{align*} f_{\epsilon}(t)= \begin{cases} 0, &t\in [0,\epsilon/2],\\ 1, &t\in [\epsilon,\infty),\\ \mathrm{linear, } &{t\in[\epsilon/2, \epsilon],} \end{cases}\,\,\,\mathrm{and}\,\,\, g_\delta(t)=\begin{cases} 0, &t\in \{0\}\cup [\delta, \infty),\\ 1, &{t\in[\delta/8, \delta/2]},\\ \mathrm{linear,} &t\in [0,\delta/8]\cup [\delta/2, \delta]. \end{cases} \end{align*} $$
(Note that
![]() $(t-\delta /2)_+$
and
$(t-\delta /2)_+$
and
![]() $f_{\delta }$
have the same support.)
$f_{\delta }$
have the same support.)
2.2 Cuntz semigroup and quasitraces
Definition 2.6 Let A be a
![]() $C^*$
-algebra, and let
$C^*$
-algebra, and let
![]() $a,\, b\in (A\otimes {\cal K})_+.$
We write
$a,\, b\in (A\otimes {\cal K})_+.$
We write
![]() $a \lesssim b$
if there are
$a \lesssim b$
if there are
![]() $x_k\in A\otimes {\cal K}$
such that
$x_k\in A\otimes {\cal K}$
such that
![]() $\lim _{k\rightarrow \infty }\|a-x_k^*bx_k\|=0$
. We write
$\lim _{k\rightarrow \infty }\|a-x_k^*bx_k\|=0$
. We write
![]() $a \sim b$
if
$a \sim b$
if
![]() $a \lesssim b$
and
$a \lesssim b$
and
![]() $b \lesssim a$
both hold [Reference Cuntz8]. The Cuntz relation
$b \lesssim a$
both hold [Reference Cuntz8]. The Cuntz relation
![]() $\sim $
is an equivalence relation. Set
$\sim $
is an equivalence relation. Set
![]() $\mathrm {Cu}(A)=(A\otimes {\cal K})_+/\sim .$
Denote by
$\mathrm {Cu}(A)=(A\otimes {\cal K})_+/\sim .$
Denote by
![]() $V(A)$
the subset of those elements in
$V(A)$
the subset of those elements in
![]() $ \mathrm {Cu}(A)$
which are represented by projections.
$ \mathrm {Cu}(A)$
which are represented by projections.
Definition 2.7 Let A be a
![]() $C^*$
-algebra. A densely defined 2-quasitrace is a 2-quasitrace defined on
$C^*$
-algebra. A densely defined 2-quasitrace is a 2-quasitrace defined on
![]() $\mathrm {Ped}(A\otimes {\cal K})$
(see Definition II.1.1 of [Reference Blackadar and Handelman2]). Denote by
$\mathrm {Ped}(A\otimes {\cal K})$
(see Definition II.1.1 of [Reference Blackadar and Handelman2]). Denote by
![]() ${\widetilde {QT}}(A)$
the set of densely defined 2-quasitraces on
${\widetilde {QT}}(A)$
the set of densely defined 2-quasitraces on
![]() $A\otimes {\cal K}.$
In what follows, we will identify A with
$A\otimes {\cal K}.$
In what follows, we will identify A with
![]() $A\otimes e_{1,1}$
whenever it is convenient. Note that we require that a 2-quasitrace has finite value on
$A\otimes e_{1,1}$
whenever it is convenient. Note that we require that a 2-quasitrace has finite value on
![]() $\mathrm {Ped}(A\otimes {\cal K}).$
In particular, we exclude the function on
$\mathrm {Ped}(A\otimes {\cal K}).$
In particular, we exclude the function on
![]() $\mathrm {Ped}( {{A\otimes {\cal K}}})$
with only
$\mathrm {Ped}( {{A\otimes {\cal K}}})$
with only
![]() $\infty $
value from the consideration.
$\infty $
value from the consideration.
We endow
![]() ${\widetilde {QT}}(A)$
with the topology in which a net
${\widetilde {QT}}(A)$
with the topology in which a net
![]() ${{\{}}\tau _i{{\}}}$
converges to
${{\{}}\tau _i{{\}}}$
converges to
![]() $\tau $
if
$\tau $
if
![]() ${{\{}}\tau _i(a){{\}}}$
converges to
${{\{}}\tau _i(a){{\}}}$
converges to
![]() $\tau (a)$
for all
$\tau (a)$
for all
![]() $a\in \mathrm {Ped}(A\otimes {\cal K})$
(see also (4.1) on page 985 of [Reference Elliott, Robert and Santiago13]).
$a\in \mathrm {Ped}(A\otimes {\cal K})$
(see also (4.1) on page 985 of [Reference Elliott, Robert and Santiago13]).
Note that, for each
![]() $a\in ({{A}} \otimes {\cal K})_+$
and
$a\in ({{A}} \otimes {\cal K})_+$
and
![]() $\varepsilon>0, f_\varepsilon (a)\in \mathrm {Ped}(A\otimes {\cal K})_+.$
Define, for each
$\varepsilon>0, f_\varepsilon (a)\in \mathrm {Ped}(A\otimes {\cal K})_+.$
Define, for each
![]() $\tau \in {\widetilde {QT}}(A),$
$\tau \in {\widetilde {QT}}(A),$
We will use properties of 2-quasitraces discussed in [Reference Blackadar and Handelman2, Reference Elliott, Robert and Santiago13] (see, in particular, Section 4.1 and Theorem 4.4 of [Reference Elliott, Robert and Santiago13]). Denote by
![]() ${\widetilde T}(A)$
the subset of
${\widetilde T}(A)$
the subset of
![]() $\widetilde {QT}(A)$
consisting of traces.
$\widetilde {QT}(A)$
consisting of traces.
Definition 2.8 Recall (Theorem 4.7 of [Reference Elliott, Gong, Lin and Niu10]) that a
![]() $\sigma $
-unital
$\sigma $
-unital
![]() $C^*$
-algebra A is compact if and only if
$C^*$
-algebra A is compact if and only if
![]() $A=\mathrm {Ped}(A).$
Every unital
$A=\mathrm {Ped}(A).$
Every unital
![]() $C^*$
-algebra is compact. Let A be a compact
$C^*$
-algebra is compact. Let A be a compact
![]() $C^*$
-algebra. Since
$C^*$
-algebra. Since
![]() $A=\mathrm {Ped}(A),$
every (densely defined) 2-quasitrace is actually defined on
$A=\mathrm {Ped}(A),$
every (densely defined) 2-quasitrace is actually defined on
![]() $A.$
By II 2.3 of [Reference Blackadar and Handelman2], every 2-quasitrace on A is bounded. Put
$A.$
By II 2.3 of [Reference Blackadar and Handelman2], every 2-quasitrace on A is bounded. Put
![]() $QT_{[0,1]}(A)=\{\tau \in {\widetilde {QT}}(A): \| \tau {|_A}\|\le 1\}.$
Then
$QT_{[0,1]}(A)=\{\tau \in {\widetilde {QT}}(A): \| \tau {|_A}\|\le 1\}.$
Then
![]() $QT_{[0,1]}(A)$
is a compact convex subset of
$QT_{[0,1]}(A)$
is a compact convex subset of
![]() ${\widetilde {QT}}(A)$
(see [Reference Elliott, Robert and Santiago13, Theorem 4.4]). Denote by
${\widetilde {QT}}(A)$
(see [Reference Elliott, Robert and Santiago13, Theorem 4.4]). Denote by
![]() $QT(A)$
the set of 2-quasitraces
$QT(A)$
the set of 2-quasitraces
![]() $\tau $
with
$\tau $
with
![]() $\|\tau {|_A}\|=1.$
It is a convex subset of
$\|\tau {|_A}\|=1.$
It is a convex subset of
![]() ${\widetilde {QT}}(A).$
Denote by
${\widetilde {QT}}(A).$
Denote by
![]() $\overline {QT(A)}^w$
the (weak*) closure of
$\overline {QT(A)}^w$
the (weak*) closure of
![]() $QT(A).$
Then, in the case that A is compact and
$QT(A).$
Then, in the case that A is compact and
![]() $\widetilde {QT}(A)\setminus \{0\}\not =\emptyset ,$
$\widetilde {QT}(A)\setminus \{0\}\not =\emptyset ,$
![]() $\mathbb {R}_+ \cdot \overline {QT(A)}^w={\widetilde {QT}}(A)$
(if
$\mathbb {R}_+ \cdot \overline {QT(A)}^w={\widetilde {QT}}(A)$
(if
![]() $QT(A)=\emptyset ,$
then
$QT(A)=\emptyset ,$
then
![]() $\overline {QT(A)}^w=\emptyset $
).
$\overline {QT(A)}^w=\emptyset $
).
Let
![]() $I\subset A$
be an ideal and
$I\subset A$
be an ideal and
![]() $\{e_\lambda \}$
be a quasi-central approximate identity for
$\{e_\lambda \}$
be a quasi-central approximate identity for
![]() $I.$
Suppose that
$I.$
Suppose that
![]() $\tau \in \widetilde {QT}(I).$
Then
$\tau \in \widetilde {QT}(I).$
Then
![]() $\tau (a)=\lim _\lambda \tau (ae_\lambda )$
(for
$\tau (a)=\lim _\lambda \tau (ae_\lambda )$
(for
![]() $a\in A$
) defines a (densely defined) 2-quasitrace of
$a\in A$
) defines a (densely defined) 2-quasitrace of
![]() $A.$
Note that
$A.$
Note that
![]() $\|\tau |_A\|=\|\tau |_I\|.$
If
$\|\tau |_A\|=\|\tau |_I\|.$
If
![]() $\tau \in \widetilde {QT}(A),$
then
$\tau \in \widetilde {QT}(A),$
then
![]() $\tau _I(a)=\lim _{\lambda } \tau (ae_\lambda )$
also densely defines a 2-quasitrace of A with
$\tau _I(a)=\lim _{\lambda } \tau (ae_\lambda )$
also densely defines a 2-quasitrace of A with
![]() $\|\tau _I|_{A}\|\le \|\tau \|$
(see Definition 2.5 of [Reference Lin23]). Let
$\|\tau _I|_{A}\|\le \|\tau \|$
(see Definition 2.5 of [Reference Lin23]). Let
![]() $a\in \mathrm {Ped}(A\otimes {\cal K})_+$
and
$a\in \mathrm {Ped}(A\otimes {\cal K})_+$
and
![]() $I_a$
be the ideal generated by
$I_a$
be the ideal generated by
![]() $a.$
By [Reference Blackadar and Handelman2, II.4.2], every
$a.$
By [Reference Blackadar and Handelman2, II.4.2], every
![]() $\tau $
in
$\tau $
in
![]() $\widetilde {QT}(\mathrm {Her}(a))$
can be uniquely extended to a 2-quasitrace
$\widetilde {QT}(\mathrm {Her}(a))$
can be uniquely extended to a 2-quasitrace
![]() $\tau $
in
$\tau $
in
![]() $\widetilde {QT}(I_a).$
In what follows, we will identify
$\widetilde {QT}(I_a).$
In what follows, we will identify
![]() $\widetilde {QT}(\mathrm {Her}(a))$
with
$\widetilde {QT}(\mathrm {Her}(a))$
with
![]() $\{\tau _{I_a}: \tau \in \widetilde {QT}(\mathrm {Her}(a))\}.$
$\{\tau _{I_a}: \tau \in \widetilde {QT}(\mathrm {Her}(a))\}.$
The following is a quasitrace version of Lemma 4.5 of [Reference Elliott, Gong, Lin and Niu10].
Proposition 2.9 (Lemma 4.5 of [Reference Elliott, Gong, Lin and Niu10])
Let A be a
![]() $\sigma $
-unital compact
$\sigma $
-unital compact
![]() $C^*$
-algebra. Then
$C^*$
-algebra. Then
![]() $0\not \in \overline {QT(A)}^w$
and
$0\not \in \overline {QT(A)}^w$
and
![]() $\overline {QT(A)}^w$
is compact.
$\overline {QT(A)}^w$
is compact.
Proof We may assume that
![]() $QT(A)\not =\emptyset .$
By Lemma 4.4 of [Reference Elliott, Gong, Lin and Niu10], there is
$QT(A)\not =\emptyset .$
By Lemma 4.4 of [Reference Elliott, Gong, Lin and Niu10], there is
![]() $e_1\in M_n(A)$
with
$e_1\in M_n(A)$
with
![]() $0\le e_1\le 1$
and
$0\le e_1\le 1$
and
![]() $x\in M_n(A)$
such that
$x\in M_n(A)$
such that
![]() $e_1x^*x=x^*xe_1=x^*x$
and
$e_1x^*x=x^*xe_1=x^*x$
and
![]() $a_0=xx^*$
is a strictly positive element of A (for some
$a_0=xx^*$
is a strictly positive element of A (for some
![]() $n\in \mathbb {N}$
). Note that
$n\in \mathbb {N}$
). Note that
![]() $\tau (e_1)\ge d_\tau (a_0)=1$
for all
$\tau (e_1)\ge d_\tau (a_0)=1$
for all
![]() $\tau \in QT(A).$
Note also that
$\tau \in QT(A).$
Note also that
Put
![]() $S=\{\tau \in QT_{[0,1]}(A): \tau (e_1)\ge 1\}.$
Then S is compact and
$S=\{\tau \in QT_{[0,1]}(A): \tau (e_1)\ge 1\}.$
Then S is compact and
![]() $0\not \in S.$
Since
$0\not \in S.$
Since
![]() $\tau (e_1)\ge d_\tau (a_0)=1, QT(A)\subset S.$
So
$\tau (e_1)\ge d_\tau (a_0)=1, QT(A)\subset S.$
So
![]() $\overline {QT(A)}^w\subset S$
and
$\overline {QT(A)}^w\subset S$
and
![]() $0\not \in \overline {QT(A)}^w.$
This also implies that
$0\not \in \overline {QT(A)}^w.$
This also implies that
![]() $\overline {QT(A)}^w$
is compact.
$\overline {QT(A)}^w$
is compact.
Proposition 2.10 Let A be a
![]() $\sigma $
-unital
$\sigma $
-unital
![]() $C^*$
-algebra and
$C^*$
-algebra and
![]() $S_1, S_2\subset {\widetilde {QT}}(A)$
nonempty compact subsets. Then one has the following (with
$S_1, S_2\subset {\widetilde {QT}}(A)$
nonempty compact subsets. Then one has the following (with
![]() $\|\tau \|=\|\tau |_A\|$
):
$\|\tau \|=\|\tau |_A\|$
):
(1) If
![]() $\mathbb {R}_+\cdot S_1= \widetilde {QT}(A)$
and
$\mathbb {R}_+\cdot S_1= \widetilde {QT}(A)$
and
![]() $0\not \in S_1,$
then there exists
$0\not \in S_1,$
then there exists
![]() $L_1\in \mathbb {R}_+$
such that
$L_1\in \mathbb {R}_+$
such that
(2) If
![]() $a\in \mathrm {Ped}(A\otimes {\cal K})_+^{\mathbf {1}},$
then
$a\in \mathrm {Ped}(A\otimes {\cal K})_+^{\mathbf {1}},$
then
![]() $ {{d=\sup \{\|\tau |_{\mathrm {Her}(a)}\|: \tau \in S_1\}}}<\infty. $
$ {{d=\sup \{\|\tau |_{\mathrm {Her}(a)}\|: \tau \in S_1\}}}<\infty. $
(3) If A is compact, then
![]() $M_1=\sup \{\|\tau \|: \tau \in S_1\}<\infty .$
$M_1=\sup \{\|\tau \|: \tau \in S_1\}<\infty .$
(4) If a is as in (2), and
![]() $S_1$
is as in (1), then
$S_1$
is as in (1), then
![]() $\overline {QT(\mathrm {Her}(a))}^w \subset \{r\cdot \tau : \tau \in S_1, r\in [0, L]\}$
for some
$\overline {QT(\mathrm {Her}(a))}^w \subset \{r\cdot \tau : \tau \in S_1, r\in [0, L]\}$
for some
![]() $L\in \mathbb {R}_+$
(see the last paragraph of Definition 2.8).
$L\in \mathbb {R}_+$
(see the last paragraph of Definition 2.8).
Proof To see (1) holds, let us assume otherwise. Then there exist sequences
![]() $r_n\in \mathbb {R}_+, s_n\in S_1$
and
$r_n\in \mathbb {R}_+, s_n\in S_1$
and
![]() $t_n\in S_2$
such that
$t_n\in S_2$
such that
![]() $r_ns_n=t_n, n\in \mathbb {N}$
and
$r_ns_n=t_n, n\in \mathbb {N}$
and
![]() $\lim _{n\to \infty } r_n=\infty .$
Since both
$\lim _{n\to \infty } r_n=\infty .$
Since both
![]() $S_1, S_2$
are compact, without loss of generality, we may assume that
$S_1, S_2$
are compact, without loss of generality, we may assume that
![]() $s_n\to s\in S_1$
and
$s_n\to s\in S_1$
and
![]() $t_n\to t\in S_2.$
$t_n\to t\in S_2.$
Since
![]() $s\not =0,$
choose
$s\not =0,$
choose
![]() $ c\in \mathrm {Ped}(A)_+^{\mathbf {1}}$
such that
$ c\in \mathrm {Ped}(A)_+^{\mathbf {1}}$
such that
![]() $s(c)>0.$
It follows that there exists
$s(c)>0.$
It follows that there exists
![]() $n_0\in \mathbb {N}$
such that
$n_0\in \mathbb {N}$
such that
![]() $s_n(c)>s(c)/2>0$
for all
$s_n(c)>s(c)/2>0$
for all
![]() $n\ge n_0.$
Consequently,
$n\ge n_0.$
Consequently,
Hence,
![]() $t(c)=\infty .$
However,
$t(c)=\infty .$
However,
![]() $c\in \mathrm {Ped}(A)_+.$
A contradiction.
$c\in \mathrm {Ped}(A)_+.$
A contradiction.
For (2), since
![]() $a\in \mathrm {Ped}(A\otimes {\cal K})_+,$
there are
$a\in \mathrm {Ped}(A\otimes {\cal K})_+,$
there are
![]() $b_i\in (A\otimes {\cal K})_+$
and
$b_i\in (A\otimes {\cal K})_+$
and
![]() $f_i\in C_{c}((0, \infty ))_+$
(
$f_i\in C_{c}((0, \infty ))_+$
(
![]() $1\le i\le m$
), the set of continuous functions with compact supports, such that
$1\le i\le m$
), the set of continuous functions with compact supports, such that
![]() $ a\le \sum _{i=1}^m f_i(b_i) $
(see [Reference Pedersen30, Theorem 5.6.1]). It follows that
$ a\le \sum _{i=1}^m f_i(b_i) $
(see [Reference Pedersen30, Theorem 5.6.1]). It follows that
![]() $a\lesssim \mathrm {diag}(f_1(b_1), f_2(b_2),...,f_m(b_m)).$
One can choose
$a\lesssim \mathrm {diag}(f_1(b_1), f_2(b_2),...,f_m(b_m)).$
One can choose
![]() $f\in C_{c}((0, \infty ))_+$
with
$f\in C_{c}((0, \infty ))_+$
with
![]() $0\le f\le 1$
such that
$0\le f\le 1$
such that
![]() $ff_i=f_i, 1\le i\le m.$
Put
$ff_i=f_i, 1\le i\le m.$
Put
![]() $b=\mathrm {diag}(f(b_1), f(b_2),...,f(b_m))).$
Then
$b=\mathrm {diag}(f(b_1), f(b_2),...,f(b_m))).$
Then
But
![]() $\widehat {b}$
is bounded on the compact subset
$\widehat {b}$
is bounded on the compact subset
![]() $S_1.$
Put
$S_1.$
Put
![]() $M=\sup \{\tau (b): \tau \in {{S_1}}\}.$
Then
$M=\sup \{\tau (b): \tau \in {{S_1}}\}.$
Then
![]() $M<\infty $
and
$M<\infty $
and
To see (3), let
![]() $a\in A$
be a strictly positive element. Since
$a\in A$
be a strictly positive element. Since
![]() $A=\mathrm {Ped}(A), a\in \mathrm {Ped}(A)_+$
and
$A=\mathrm {Ped}(A), a\in \mathrm {Ped}(A)_+$
and
![]() $\mathrm {Her}(a)=A.$
Thus, (3) follows from (2).
$\mathrm {Her}(a)=A.$
Thus, (3) follows from (2).
For (4), let
![]() $I_a$
be the (closed) ideal of
$I_a$
be the (closed) ideal of
![]() $A\otimes {\cal K}$
generated by
$A\otimes {\cal K}$
generated by
![]() $a.$
Then
$a.$
Then
![]() $\{\tau _I: \tau \in {\overline {QT(\mathrm {Her}(a))}}^w\}$
is a compact subset of
$\{\tau _I: \tau \in {\overline {QT(\mathrm {Her}(a))}}^w\}$
is a compact subset of
![]() $\widetilde {QT}_{[0, 1]}(A)$
(see the last paragraph of Definition 2.8). Hence, part (4) of the lemma then follows from (1).
$\widetilde {QT}_{[0, 1]}(A)$
(see the last paragraph of Definition 2.8). Hence, part (4) of the lemma then follows from (1).
2.3 Comparison and canonical map
 $\Gamma $
$\Gamma $
Definition 2.11 A simple
![]() $C^*$
-algebra A is said to have (Blackadar’s) strict comparison, if, for any
$C^*$
-algebra A is said to have (Blackadar’s) strict comparison, if, for any
![]() $a, b\in (A\otimes {\cal K})_+,$
one has
$a, b\in (A\otimes {\cal K})_+,$
one has
![]() $a\lesssim b,$
provided
$a\lesssim b,$
provided
2.12 Let A be a
![]() $\sigma $
-unital
$\sigma $
-unital
![]() $C^*$
-algebra and
$C^*$
-algebra and
![]() $e\in \mathrm {Ped}(A\otimes {\cal K})_+\setminus \{0\}.$
If e is a full element, put
$e\in \mathrm {Ped}(A\otimes {\cal K})_+\setminus \{0\}.$
If e is a full element, put
![]() $T_e=\{\tau \in \widetilde {QT}(A): \tau (e)=1\}.$
Then
$T_e=\{\tau \in \widetilde {QT}(A): \tau (e)=1\}.$
Then
![]() $T_e$
is a compact convex subset and is a basis for the cone
$T_e$
is a compact convex subset and is a basis for the cone
![]() $\widetilde {QT}(A)$
(see Proposition 3.4 of [Reference Tikuisis43]). If, in addition, A is simple, then e is always full. Put
$\widetilde {QT}(A)$
(see Proposition 3.4 of [Reference Tikuisis43]). If, in addition, A is simple, then e is always full. Put
![]() $A_1=\mathrm {Her}(e).$
By Brown’s stable isomorphism theorem (see [Reference Brown4]),
$A_1=\mathrm {Her}(e).$
By Brown’s stable isomorphism theorem (see [Reference Brown4]),
![]() $A\otimes {\cal K}\cong A_1\otimes {\cal K}.$
So
$A\otimes {\cal K}\cong A_1\otimes {\cal K}.$
So
![]() $e\in \mathrm {Ped}(A_1\otimes {\cal K})_+.$
Then
$e\in \mathrm {Ped}(A_1\otimes {\cal K})_+.$
Then
![]() $A_1=\mathrm {Ped}(A_1)$
(see, for example, Theorem 2.1(iii) of [Reference Tikuisis43]); in other words,
$A_1=\mathrm {Ped}(A_1)$
(see, for example, Theorem 2.1(iii) of [Reference Tikuisis43]); in other words,
![]() $A_1$
is algebraically simple. Therefore, instead of studying
$A_1$
is algebraically simple. Therefore, instead of studying
![]() $A\otimes {\cal K},$
we will study
$A\otimes {\cal K},$
we will study
![]() $A_1\otimes {\cal K}.$
Throughout the paper, we often consider
$A_1\otimes {\cal K}.$
Throughout the paper, we often consider
![]() $\sigma $
-unital simple
$\sigma $
-unital simple
![]() $C^*$
-algebras A with
$C^*$
-algebras A with
![]() $\mathrm {Ped}(A)=A$
(in other words, algebraically simple
$\mathrm {Ped}(A)=A$
(in other words, algebraically simple
![]() $C^*$
-algebras).
$C^*$
-algebras).
Definition 2.13 Let A be a
![]() $C^*$
-algebra with
$C^*$
-algebra with
![]() ${\widetilde {QT}}(A)\setminus \{0\}\not =\emptyset .$
Denote by
${\widetilde {QT}}(A)\setminus \{0\}\not =\emptyset .$
Denote by
![]() $L(\widetilde {QT}(A))$
the family of continuous real-valued functions f on
$L(\widetilde {QT}(A))$
the family of continuous real-valued functions f on
![]() $\widetilde {QT}(A)$
such that
$\widetilde {QT}(A)$
such that
![]() $f({\alpha } \tau )={\alpha } f(\tau )$
for all
$f({\alpha } \tau )={\alpha } f(\tau )$
for all
![]() ${\alpha }\in \mathbb {R}_+$
and
${\alpha }\in \mathbb {R}_+$
and
![]() $\tau \in \widetilde {QT}(A)$
and
$\tau \in \widetilde {QT}(A)$
and
![]() $f(\tau +t)=f(\tau )+f(t)$
for all
$f(\tau +t)=f(\tau )+f(t)$
for all
![]() $\tau , t\in \widetilde {QT}(A).$
Let
$\tau , t\in \widetilde {QT}(A).$
Let
![]() $S\subset {\widetilde {QT}}(A)$
be a convex subset. Set
$S\subset {\widetilde {QT}}(A)$
be a convex subset. Set
Note that if
![]() $0\in S,$
then
$0\in S,$
then
![]() $f(0)=0$
for all
$f(0)=0$
for all
![]() $f\in \mathrm {LAff}_+(S).$
For a simple
$f\in \mathrm {LAff}_+(S).$
For a simple
![]() $C^*$
-algebra A and
$C^*$
-algebra A and
![]() $a\in (A\otimes {\cal K})_+,$
the function
$a\in (A\otimes {\cal K})_+,$
the function
![]() $\hat {a}(\tau )=\tau (a)$
(
$\hat {a}(\tau )=\tau (a)$
(
![]() $\tau \in S$
) is in general in
$\tau \in S$
) is in general in
![]() $\mathrm {LAff}_+(S).$
If
$\mathrm {LAff}_+(S).$
If
![]() $a\in \mathrm {Ped}(A\otimes {\cal K})_+,$
then
$a\in \mathrm {Ped}(A\otimes {\cal K})_+,$
then
![]() $\widehat {a}\in \operatorname {Aff}_+(S).$
Recall that
$\widehat {a}\in \operatorname {Aff}_+(S).$
Recall that
![]() $\widehat {[a]}(\tau )=d_\tau (a)$
for
$\widehat {[a]}(\tau )=d_\tau (a)$
for
![]() $\tau \in {\widetilde {QT}}(A).$
So
$\tau \in {\widetilde {QT}}(A).$
So
![]() $\widehat {[a]}\in \mathrm {LAff}_+(\widetilde {QT}(A)).$
Caution:
$\widehat {[a]}\in \mathrm {LAff}_+(\widetilde {QT}(A)).$
Caution:
![]() $\widehat {a}$
and
$\widehat {a}$
and
![]() $\widehat {[a]}$
are not the same in general.
$\widehat {[a]}$
are not the same in general.
We will write
![]() $\Gamma : \mathrm {Cu}(A)\to \mathrm {LAff}_+({\widetilde {QT}}(A))$
for the canonical map defined by
$\Gamma : \mathrm {Cu}(A)\to \mathrm {LAff}_+({\widetilde {QT}}(A))$
for the canonical map defined by
![]() $\Gamma ([a])(\tau )=\widehat {[a]}(\tau )=d_\tau (a)$
for all
$\Gamma ([a])(\tau )=\widehat {[a]}(\tau )=d_\tau (a)$
for all
![]() $\tau \in {\widetilde {QT}}(A).$
$\tau \in {\widetilde {QT}}(A).$
(1) In the case that A is simple and
![]() $A=\mathrm {Ped}(A), \Gamma $
also induces a canonical map
$A=\mathrm {Ped}(A), \Gamma $
also induces a canonical map
![]() $\Gamma _1: \mathrm {Cu}(A)\to \mathrm {LAff}_+(\overline {QT(A)}^w).$
Since, in this case,
$\Gamma _1: \mathrm {Cu}(A)\to \mathrm {LAff}_+(\overline {QT(A)}^w).$
Since, in this case,
![]() $\mathbb {R}_+\overline {QT(A)}^w={\widetilde {QT}}(A),$
the map
$\mathbb {R}_+\overline {QT(A)}^w={\widetilde {QT}}(A),$
the map
![]() $\Gamma $
is surjective if and only if
$\Gamma $
is surjective if and only if
![]() $\Gamma _1$
is surjective.
$\Gamma _1$
is surjective.
(2) In the case that A is stably finite and simple, denote by
![]() $\mathrm {Cu}(A)_+$
the set of purely non-compact elements (see Proposition 6.4 of [Reference Elliott, Robert and Santiago13]). Suppose that
$\mathrm {Cu}(A)_+$
the set of purely non-compact elements (see Proposition 6.4 of [Reference Elliott, Robert and Santiago13]). Suppose that
![]() $\Gamma $
is surjective. Let
$\Gamma $
is surjective. Let
![]() $p\in (A\otimes {\cal K})_+$
be a projection (so
$p\in (A\otimes {\cal K})_+$
be a projection (so
![]() $p\in \mathrm {Ped}(A\otimes {\cal K})$
). There are
$p\in \mathrm {Ped}(A\otimes {\cal K})$
). There are
![]() $a_n\in (A\otimes {\cal K})_+$
with
$a_n\in (A\otimes {\cal K})_+$
with
![]() $0\le a_n\le 1$
such that
$0\le a_n\le 1$
such that
![]() $\widehat {[a_n]}=(1/2^n)\widehat {[p]}, n\in \mathbb {N}.$
Define
$\widehat {[a_n]}=(1/2^n)\widehat {[p]}, n\in \mathbb {N}.$
Define
![]() $b=\mathrm {diag}(a_1/2, a_2/2^2,...,a_n/2^n,...)\in A\otimes {\cal K}.$
Then
$b=\mathrm {diag}(a_1/2, a_2/2^2,...,a_n/2^n,...)\in A\otimes {\cal K}.$
Then
![]() $0$
is a limit point of
$0$
is a limit point of
![]() $\mathrm {sp}(b).$
Therefore,
$\mathrm {sp}(b).$
Therefore,
![]() $[b]$
cannot be represented by a projection. In other words,
$[b]$
cannot be represented by a projection. In other words,
![]() $[b]\in \mathrm {Cu}(A)_+.$
We compute that
$[b]\in \mathrm {Cu}(A)_+.$
We compute that
![]() ${\widehat {[b]}}={{\widehat {[p]}}}.$
It then follows that
${\widehat {[b]}}={{\widehat {[p]}}}.$
It then follows that
![]() $\Gamma |_{\mathrm {Cu}(A)_+}$
is surjective.
$\Gamma |_{\mathrm {Cu}(A)_+}$
is surjective.
Suppose that A is simple and a is a purely non-compact element and
Then, for any
![]() $\varepsilon>0$
(recall that
$\varepsilon>0$
(recall that
![]() $f_\varepsilon (a)\in \mathrm {Ped}(A)$
),
$f_\varepsilon (a)\in \mathrm {Ped}(A)$
),
If A has strict comparison, then
![]() $f_\varepsilon (a)\lesssim b.$
Since this holds for all
$f_\varepsilon (a)\lesssim b.$
Since this holds for all
![]() $\varepsilon>0,$
we conclude that
$\varepsilon>0,$
we conclude that
![]() $a\lesssim b.$
$a\lesssim b.$
The reader should be reminded that when A is exact, every 2-quasitrace is a trace (see [Reference Haagerup17]). These facts will be used without further explanation.
2.4 Cuntz null sequences and the ideal generated by Cuntz null sequences
Definition 2.14 Let A be a separable non-elementary simple
![]() $C^*$
-algebra. Then A contains a sequence of nonzero elements
$C^*$
-algebra. Then A contains a sequence of nonzero elements
![]() $e_n\in \mathrm {Ped}(A)$
with
$e_n\in \mathrm {Ped}(A)$
with
![]() $0\le e_n\le 1$
such that
$0\le e_n\le 1$
such that
![]() $e_{n+1}\lesssim e_n$
for all
$e_{n+1}\lesssim e_n$
for all
![]() $n\in \mathbb {N},$
and for any finite subset
$n\in \mathbb {N},$
and for any finite subset
![]() ${\cal F}\subset A_+\setminus \{0\},$
there exists
${\cal F}\subset A_+\setminus \{0\},$
there exists
![]() $n_0\in \mathbb {N}$
such that, for all
$n_0\in \mathbb {N}$
such that, for all
![]() $n\ge n_0,$
$n\ge n_0,$
(see Lemma 4.3 of [Reference Fu and Lin15]).
For general
![]() $C^*$
-algebra
$C^*$
-algebra
![]() $A,$
a sequence
$A,$
a sequence
![]() $\{ a_n\}\subset A_+$
is said to be truly Cuntz-null and written
$\{ a_n\}\subset A_+$
is said to be truly Cuntz-null and written
![]() $a_n\stackrel {c.}{\to } 0$
if, for any finite subset
$a_n\stackrel {c.}{\to } 0$
if, for any finite subset
![]() ${\cal F}\subset A_+{{\backslash \{0\}}},$
there exists
${\cal F}\subset A_+{{\backslash \{0\}}},$
there exists
![]() $n_0\in \mathbb {N}$
such that, for all
$n_0\in \mathbb {N}$
such that, for all
![]() $n\ge n_0,$
$n\ge n_0,$
This is equivalent to saying that, for any
![]() $d\in A_+\setminus \{0\},$
there exists
$d\in A_+\setminus \{0\},$
there exists
![]() $n_0\in \mathbb {N}$
such that, for all
$n_0\in \mathbb {N}$
such that, for all
![]() $n\ge n_0, a_n\lesssim d. $
We also write
$n\ge n_0, a_n\lesssim d. $
We also write
![]() $a_n\stackrel {c.}{\searrow } 0$
if
$a_n\stackrel {c.}{\searrow } 0$
if
![]() $a_{n+1}\lesssim a_n$
for all
$a_{n+1}\lesssim a_n$
for all
![]() $n\in \mathbb {N}$
and
$n\in \mathbb {N}$
and
![]() $a_n\stackrel {c.}{\to } 0.$
$a_n\stackrel {c.}{\to } 0.$
A sequence
![]() $\{x_n\}\subset A\otimes {\cal K}$
is said to be Cuntz-null if, for any
$\{x_n\}\subset A\otimes {\cal K}$
is said to be Cuntz-null if, for any
![]() $\varepsilon>0, f_\varepsilon (x_n^*x_n)\stackrel {c.}{\to } 0.$
$\varepsilon>0, f_\varepsilon (x_n^*x_n)\stackrel {c.}{\to } 0.$
Definition 2.15 Let X be a normed space, and let
![]() $l^\infty (X)$
denote the space of bounded sequences of
$l^\infty (X)$
denote the space of bounded sequences of
![]() $X.$
When A is a
$X.$
When A is a
![]() $C^*$
-algebra,
$C^*$
-algebra,
![]() $l^\infty (A)$
is also a
$l^\infty (A)$
is also a
![]() $C^*$
-algebra, and
$C^*$
-algebra, and
![]() $c_0(A)=\{\{a_n\}\in l^\infty (A): \lim _{n\to \infty }\|a_n\|=0\}$
is an ideal of
$c_0(A)=\{\{a_n\}\in l^\infty (A): \lim _{n\to \infty }\|a_n\|=0\}$
is an ideal of
![]() $l^\infty (A).$
Let
$l^\infty (A).$
Let
![]() $A_\infty =l^{\infty }(A)/c_0(A)$
and
$A_\infty =l^{\infty }(A)/c_0(A)$
and
![]() $\pi _\infty : l^\infty (A)\to A_\infty $
be the quotient map. We view A as a
$\pi _\infty : l^\infty (A)\to A_\infty $
be the quotient map. We view A as a
![]() $C^*$
-subalgebra of
$C^*$
-subalgebra of
![]() $l^\infty (A)$
via the canonical map
$l^\infty (A)$
via the canonical map
![]() $\iota : a\mapsto \{a,a,...\}$
for all
$\iota : a\mapsto \{a,a,...\}$
for all
![]() $a\in A.$
In what follows, we may identify a with the constant sequence
$a\in A.$
In what follows, we may identify a with the constant sequence
![]() $\{a,a,...\}$
in
$\{a,a,...\}$
in
![]() $l^\infty (A)$
without further warning. Let
$l^\infty (A)$
without further warning. Let
![]() $\{C_n\}$
be a sequence of
$\{C_n\}$
be a sequence of
![]() $C^*$
-subalgebra s of
$C^*$
-subalgebra s of
![]() $A.$
We may also use notation
$A.$
We may also use notation
![]() $l^\infty (\{C_n\})=\{\{c_n\}\in l^\infty (A): c_n\in C_n\}$
for the infinite product of
$l^\infty (\{C_n\})=\{\{c_n\}\in l^\infty (A): c_n\in C_n\}$
for the infinite product of
![]() $\{C_n\}.$
$\{C_n\}.$
Denote by
![]() $ N_{cu}(A) $
(or just
$ N_{cu}(A) $
(or just
![]() $N_{cu}$
) the set of all Cuntz-null sequences in
$N_{cu}$
) the set of all Cuntz-null sequences in
![]() $l^\infty (A).$
$l^\infty (A).$
It follows from Proposition 3.5 of [Reference Fu, Li and Lin14] that, if A has no one-dimensional hereditary
![]() $C^*$
-subalgebra s, then
$C^*$
-subalgebra s, then
![]() $N_{cu}(A)$
is an ideal of
$N_{cu}(A)$
is an ideal of
![]() $l^\infty (A).$
Moreover, if A is non-elementary and simple,
$l^\infty (A).$
Moreover, if A is non-elementary and simple,
![]() $c_0(A)\subsetneqq N_{cu}(A).$
Denote by
$c_0(A)\subsetneqq N_{cu}(A).$
Denote by
![]() $\Pi _{cu}: l^\infty (A)\to l^\infty (A)/N_{cu}(A)$
the quotient map and
$\Pi _{cu}: l^\infty (A)\to l^\infty (A)/N_{cu}(A)$
the quotient map and
![]() $\Pi _{cu}(A)^\perp =\{b\in l^\infty (A)/N_{cu}: b\Pi _{cu}(a)=\Pi _{cu}(a)b=0 \mbox { for all } a\in A\}.$
$\Pi _{cu}(A)^\perp =\{b\in l^\infty (A)/N_{cu}: b\Pi _{cu}(a)=\Pi _{cu}(a)b=0 \mbox { for all } a\in A\}.$
Definition 2.16 Let A be a
![]() $C^*$
-algebra with
$C^*$
-algebra with
![]() ${{\widetilde {QT}(A)\not =\emptyset .}}$
Fix a compact subset
${{\widetilde {QT}(A)\not =\emptyset .}}$
Fix a compact subset
![]() $T\subset {{\widetilde {QT}(A).}}$
For each
$T\subset {{\widetilde {QT}(A).}}$
For each
![]() $x\in A,$
define
$x\in A,$
define
Then
![]() $\|x^*\|_{_{2, T}}=\|x\|_{_{2, T}}.$
$\|x^*\|_{_{2, T}}=\|x\|_{_{2, T}}.$
By Lemma 3.5 of [Reference Haagerup17] (one does not need to assume that A is unital),
Then
In other words,
We also have
It follows that
![]() $\{a\in A: \|a\|_{_{2,T}}=0\}$
is a (closed two-sided) ideal of
$\{a\in A: \|a\|_{_{2,T}}=0\}$
is a (closed two-sided) ideal of
![]() $A.$
$A.$
We also have the following inequality for
![]() $a\in \mathrm {Ped}(A\otimes {\cal K})_+:$
$a\in \mathrm {Ped}(A\otimes {\cal K})_+:$
In fact, for all
![]() $n\in \mathbb {N},$
we have
$n\in \mathbb {N},$
we have
![]() $\tau (a^2)=\tau (a^{1/2n}a^{2-(1/n)}a^{1/2n})\le \|a^{2-(1/n)}\|\tau (a^{1/n}).$
Let
$\tau (a^2)=\tau (a^{1/2n}a^{2-(1/n)}a^{1/2n})\le \|a^{2-(1/n)}\|\tau (a^{1/n}).$
Let
![]() $n\to \infty .$
We obtain
$n\to \infty .$
We obtain
![]() $\tau (a^2)\le \|a\|^2d_\tau (a).$
So (e2.19) holds.
$\tau (a^2)\le \|a\|^2d_\tau (a).$
So (e2.19) holds.
Definition 2.17 Suppose that A is a
![]() $\sigma $
-unital
$\sigma $
-unital
![]() $C^*$
-algebra with
$C^*$
-algebra with
![]() ${\widetilde {QT}}(A)\setminus \{0\}\not =\emptyset ,$
and
${\widetilde {QT}}(A)\setminus \{0\}\not =\emptyset ,$
and
![]() $T\subset {\widetilde {QT}}(A)$
is a compact subset with
$T\subset {\widetilde {QT}}(A)$
is a compact subset with
![]() $T\not =\{0\}.$
Define
$T\not =\{0\}.$
Define
Then
![]() $I_{T}$
is an ideal of
$I_{T}$
is an ideal of
![]() $l^\infty (A).$
$l^\infty (A).$
Suppose that A is a simple non-elementary
![]() $C^*$
-algebra. Then it is clear that
$C^*$
-algebra. Then it is clear that
It follows from the proof of Proposition 3.8 of [Reference Fu, Li and Lin14] that
![]() $I_{_{\overline {QT(A)}^w}}=N_{cu}(A)$
if
$I_{_{\overline {QT(A)}^w}}=N_{cu}(A)$
if
![]() $A=\mathrm {Ped}(A)$
and A has strict comparison. Denote by
$A=\mathrm {Ped}(A)$
and A has strict comparison. Denote by
![]() $\Pi : l^\infty (A)\to l^\infty (A)/I_{{{_{\overline {QT(A)}^w}}}}$
the quotient map.
$\Pi : l^\infty (A)\to l^\infty (A)/I_{{{_{\overline {QT(A)}^w}}}}$
the quotient map.
Proposition 2.18 Let A be a
![]() $\sigma $
-unital algebraically simple
$\sigma $
-unital algebraically simple
![]() $C^*$
-algebra such that
$C^*$
-algebra such that
![]() $QT(A)\not =\emptyset .$
Let
$QT(A)\not =\emptyset .$
Let
![]() $S \subset {\widetilde {QT}}(A)\setminus \{0\}$
be a compact subset such that
$S \subset {\widetilde {QT}}(A)\setminus \{0\}$
be a compact subset such that
![]() $QT(A)\subset \mathbb {R}_+ \cdot S.$
Then
$QT(A)\subset \mathbb {R}_+ \cdot S.$
Then
Moreover, if A has strict comparison, then
![]() $I_{_{\overline {QT(A)}^w}}=N_{cu}.$
$I_{_{\overline {QT(A)}^w}}=N_{cu}.$
Proof By Proposition 2.10,
![]() $0<s_1=\sup \{\|\tau {{|_A}}\|: \tau \in S\}<\infty .$
Since
$0<s_1=\sup \{\|\tau {{|_A}}\|: \tau \in S\}<\infty .$
Since
![]() $S\subset {\widetilde {QT}}(A)\setminus \{0\}$
and is compact,
$S\subset {\widetilde {QT}}(A)\setminus \{0\}$
and is compact,
Suppose that
![]() $\{a_n\} \in (I_{_{\overline {QT(A)}^w}})_+^{\mathbf {1}}.$
Then, for any
$\{a_n\} \in (I_{_{\overline {QT(A)}^w}})_+^{\mathbf {1}}.$
Then, for any
![]() $\varepsilon>0,$
there exists
$\varepsilon>0,$
there exists
![]() $n_0\in \mathbb {N}$
such that, if
$n_0\in \mathbb {N}$
such that, if
![]() $n\ge n_0,$
$n\ge n_0,$
Thus, if
![]() $n\ge n_0,$
for any
$n\ge n_0,$
for any
![]() $t\in S,$
$t\in S,$
This implies that
![]() $\{a_n\}\in I_{_S}.$
It follows that
$\{a_n\}\in I_{_S}.$
It follows that
![]() $I_{_{\overline {QT(A)}^w}} \subset I_{_S}.$
$I_{_{\overline {QT(A)}^w}} \subset I_{_S}.$
Conversely, if
![]() $\{a_n\}\in I_S,$
there exists
$\{a_n\}\in I_S,$
there exists
![]() $n_1\in \mathbb {N}$
such that, if
$n_1\in \mathbb {N}$
such that, if
![]() $n\ge n_1,$
$n\ge n_1,$
Note that, for all
![]() $\tau \in QT(A),$
there are
$\tau \in QT(A),$
there are
![]() $r_\tau \in \mathbb {R}_+$
and
$r_\tau \in \mathbb {R}_+$
and
![]() $t_\tau \in S$
such that
$t_\tau \in S$
such that
![]() $\tau =r_\tau t_\tau .$
Since
$\tau =r_\tau t_\tau .$
Since
![]() $r_\tau \|t_\tau \|\le 1,$
we have
$r_\tau \|t_\tau \|\le 1,$
we have
![]() $ r_\tau \le 1/\|t_\tau \|\le 1/s_2. $
Suppose
$ r_\tau \le 1/\|t_\tau \|\le 1/s_2. $
Suppose
![]() $\tau \in \overline {QT(A)}^w.$
Then there are
$\tau \in \overline {QT(A)}^w.$
Then there are
![]() $t_n\in S$
and
$t_n\in S$
and
![]() $r_n>0$
such that
$r_n>0$
such that
![]() $r_n t_n\in QT(A)$
and
$r_n t_n\in QT(A)$
and
![]() $r_nt_n\to \tau .$
As mentioned above, we have
$r_nt_n\to \tau .$
As mentioned above, we have
![]() $r_n\le 1/s_2$
for all
$r_n\le 1/s_2$
for all
![]() $n\in \mathbb {N}.$
Since S is compact (and
$n\in \mathbb {N}.$
Since S is compact (and
![]() $\{r_n\}$
is bounded), by choosing a subsequence, we may assume that
$\{r_n\}$
is bounded), by choosing a subsequence, we may assume that
![]() $t_n\to t_\tau \in S$
and
$t_n\to t_\tau \in S$
and
![]() $r_n\to r_\tau .$
In other words,
$r_n\to r_\tau .$
In other words,
![]() $\tau =r_\tau t_\tau .$
Note that
$\tau =r_\tau t_\tau .$
Note that
![]() $\|\tau \|\le 1.$
So we also have
$\|\tau \|\le 1.$
So we also have
![]() $r_\tau \le 1/s_2.$
Therefore, for any
$r_\tau \le 1/s_2.$
Therefore, for any
![]() $n\ge n_1,$
if
$n\ge n_1,$
if
![]() $\tau \in \overline {QT(A)}^w,$
$\tau \in \overline {QT(A)}^w,$
Thus,
![]() $\{a_n\}\in I_{_{\overline {QT(A)}^w}}.$
$\{a_n\}\in I_{_{\overline {QT(A)}^w}}.$
To see the last part of the statement, choose
![]() $b\in \mathrm {Ped}(A)_+^{\mathbf {1}}\setminus \{0\}.$
Let
$b\in \mathrm {Ped}(A)_+^{\mathbf {1}}\setminus \{0\}.$
Let
![]() $S=\{\tau \in \widetilde {QT}(A): \tau (b)=1\}.$
Then
$S=\{\tau \in \widetilde {QT}(A): \tau (b)=1\}.$
Then
![]() $S\subset \widetilde {QT}(A)\setminus \{0\}$
is a compact subset and,
$S\subset \widetilde {QT}(A)\setminus \{0\}$
is a compact subset and,
![]() $\widetilde {QT}(A)=\mathbb {R} \cdot S.$
By (the “Moreover” part of) Proposition 3.8 of [Reference Fu, Li and Lin14],
$\widetilde {QT}(A)=\mathbb {R} \cdot S.$
By (the “Moreover” part of) Proposition 3.8 of [Reference Fu, Li and Lin14],
![]() $N_{cu}=I_S=I_{_{\overline {QT(A)}^w}}.$
$N_{cu}=I_S=I_{_{\overline {QT(A)}^w}}.$
Let A be a
![]() $\sigma $
-unital simple
$\sigma $
-unital simple
![]() $C^*$
-algebra and
$C^*$
-algebra and
![]() $\{e_n\}$
be an approximate identity with
$\{e_n\}$
be an approximate identity with
![]() $e_{n+1}e_n=e_ne_{n+1}$
(
$e_{n+1}e_n=e_ne_{n+1}$
(
![]() $n\in \mathbb {N}$
). Recall that A is said to have continuous scale, if, for any
$n\in \mathbb {N}$
). Recall that A is said to have continuous scale, if, for any
![]() $a\in A_+\setminus \{0\},$
there is
$a\in A_+\setminus \{0\},$
there is
![]() $n_0\in \mathbb {N}$
such that
$n_0\in \mathbb {N}$
such that
This definition does not depend on the choice of
![]() $\{e_n\}$
(see [Reference Lin22, Definition 2.1] and [Reference Lin19, Definition 2.5]). With terminology of Definition 2.14, A has continuous scale if and only if, for any
$\{e_n\}$
(see [Reference Lin22, Definition 2.1] and [Reference Lin19, Definition 2.5]). With terminology of Definition 2.14, A has continuous scale if and only if, for any
![]() $m(n)>n, e_{m(n)}-e_n\stackrel {c.}{\to } 0$
for any
$m(n)>n, e_{m(n)}-e_n\stackrel {c.}{\to } 0$
for any
![]() $\{e_n\}$
for which
$\{e_n\}$
for which
![]() $e_{n+1}e_n=e_ne_{n+1}=e_n$
(
$e_{n+1}e_n=e_ne_{n+1}=e_n$
(
![]() $n\in \mathbb {N}$
).
$n\in \mathbb {N}$
).
The following is known. The proof of it is exactly the same as that of the case
![]() $T(A)=QT(A)$
(see [Reference Elliott, Gong, Lin and Niu10, Definition 5.1, Remark 5.2, Theorem 5.3, and Proposition 5.4] for details, and also see the remark after Definition 6.3 of [Reference Fu, Li and Lin14]).
$T(A)=QT(A)$
(see [Reference Elliott, Gong, Lin and Niu10, Definition 5.1, Remark 5.2, Theorem 5.3, and Proposition 5.4] for details, and also see the remark after Definition 6.3 of [Reference Fu, Li and Lin14]).
Theorem 2.19 (cf. Theorem 5.3 and Proposition 5.4 of [Reference Elliott, Gong, Lin and Niu10], also [Reference Lin19])
Let A be a
![]() $\sigma $
-unital simple
$\sigma $
-unital simple
![]() $C^*$
-algebra with a strict positive element
$C^*$
-algebra with a strict positive element
![]() $e_A,$
continuous scale and
$e_A,$
continuous scale and
![]() $QT(A)\not =\emptyset .$
Then
$QT(A)\not =\emptyset .$
Then
![]() $QT(A)$
is compact and
$QT(A)$
is compact and
![]() $\widehat {[e_A]}$
is continuous on
$\widehat {[e_A]}$
is continuous on
![]() ${\widetilde {QT}}(A).$
Assuming A has strict comparison, then A has continuous scale if and only if
${\widetilde {QT}}(A).$
Assuming A has strict comparison, then A has continuous scale if and only if
![]() $\widehat {[ e_A]}$
is continuous on
$\widehat {[ e_A]}$
is continuous on
![]() ${\widetilde {QT}}(A).$
${\widetilde {QT}}(A).$
Proposition 2.20 Let A be a separable non-elementary simple
![]() $C^*$
-algebra. Then A has continuous scale if and only if
$C^*$
-algebra. Then A has continuous scale if and only if
![]() $\Pi _{cu}(A)^\perp =\{0\}.$
$\Pi _{cu}(A)^\perp =\{0\}.$
Proof Suppose that A has continuous scale. Let
![]() $\{b_n\}\in l^\infty (A)_+^{\mathbf {1}}$
be such that
$\{b_n\}\in l^\infty (A)_+^{\mathbf {1}}$
be such that
![]() $b=\Pi _{cu}(\{b_n\})\in \Pi _{cu}(A)^\perp .$
Fix a truly Cuntz-null sequence of
$b=\Pi _{cu}(\{b_n\})\in \Pi _{cu}(A)^\perp .$
Fix a truly Cuntz-null sequence of
![]() $\{a_n\}$
in the unit ball of
$\{a_n\}$
in the unit ball of
![]() $A_+$
such that
$A_+$
such that
![]() $a_n\not =0$
for all
$a_n\not =0$
for all
![]() $n\in \mathbb {N}$
(see Definition 2.14). Let
$n\in \mathbb {N}$
(see Definition 2.14). Let
![]() $e\in A_+^{\mathbf {1}}$
be a strictly positive element. Note that, for each
$e\in A_+^{\mathbf {1}}$
be a strictly positive element. Note that, for each
![]() $k\in \mathbb {N}, \{f_{1/2k}(e)b_n\}_{n\in \mathbb {N}}$
is a Cuntz-null sequence. For each
$k\in \mathbb {N}, \{f_{1/2k}(e)b_n\}_{n\in \mathbb {N}}$
is a Cuntz-null sequence. For each
![]() $k\in \mathbb {N},$
there are
$k\in \mathbb {N},$
there are
![]() $l(k), n(k)\in \mathbb {N}$
such that
$l(k), n(k)\in \mathbb {N}$
such that
We may assume that
![]() $l(k+1)>l(k)\ge k$
and
$l(k+1)>l(k)\ge k$
and
![]() $n(k)>{{2}}k$
for all
$n(k)>{{2}}k$
for all
![]() $k\in \mathbb {N}.$
Define
$k\in \mathbb {N}.$
Define
![]() $c_{0,i}=c_{1,i}=0$
if
$c_{0,i}=c_{1,i}=0$
if
![]() $1\le i<l(1),$
and, if
$1\le i<l(1),$
and, if
![]() $l(k)\le i<l(k+1),$
define
$l(k)\le i<l(k+1),$
define
Put
![]() ${\bar b}_i=b_i-c_{0,i}-c_{1,i}, i\in \mathbb {N}.$
Note that, if
${\bar b}_i=b_i-c_{0,i}-c_{1,i}, i\in \mathbb {N}.$
Note that, if
![]() $l(k)\le i {{<}} l(k+1), {\bar b_i}=(f_{1/n(i)}(e)-f_{1/2k}(e))b_i$
(
$l(k)\le i {{<}} l(k+1), {\bar b_i}=(f_{1/n(i)}(e)-f_{1/2k}(e))b_i$
(
![]() $k>1$
). By (e2.29), one verifies that
$k>1$
). By (e2.29), one verifies that
![]() $\{c_{0,n}\}\in N_{cu}(A).$
In fact, for a fixed
$\{c_{0,n}\}\in N_{cu}(A).$
In fact, for a fixed
![]() $1/2>\varepsilon >0,$
choose
$1/2>\varepsilon >0,$
choose
![]() $k_0$
such that
$k_0$
such that
![]() $1/k_0<\varepsilon .$
For any finite subset
$1/k_0<\varepsilon .$
For any finite subset
![]() ${\cal F}\subset A_+\setminus \{0\},$
choose
${\cal F}\subset A_+\setminus \{0\},$
choose
![]() $J\in \mathbb {N}$
such that
$J\in \mathbb {N}$
such that
![]() $a_i\lesssim b$
for all
$a_i\lesssim b$
for all
![]() $b\in {\cal F}$
and for all
$b\in {\cal F}$
and for all
![]() $i\ge J.$
It follows that, if
$i\ge J.$
It follows that, if
![]() $k_1\ge J,$
by (e2.29), for all
$k_1\ge J,$
by (e2.29), for all
![]() $l(k)\le i<l(k+1)$
and
$l(k)\le i<l(k+1)$
and
![]() $k\ge \max \{k_0, k_1\},$
$k\ge \max \{k_0, k_1\},$
for all
![]() $b\in {\cal F}.$
Hence,
$b\in {\cal F}.$
Hence,
![]() $\{c_{0,n}\}\in N_{cu}(A).$
Also, by (e2.30),
$\{c_{0,n}\}\in N_{cu}(A).$
Also, by (e2.30),
![]() $\{c_{1,i}\}\in c_0(A).$
It follows that
$\{c_{1,i}\}\in c_0(A).$
It follows that
It suffices to show that
![]() $\{{\bar b}_n\}\in N_{cu}.$
In fact, for all
$\{{\bar b}_n\}\in N_{cu}.$
In fact, for all
![]() $l(k)\le i <l(k+1),$
$l(k)\le i <l(k+1),$
Since A has continuous scale, then
![]() $f_{1/2n(l(k+1))}(e)-f_{1/2k}(e)\stackrel {c.}{\to } 0$
(see [Reference Lin22, Definition 2.1] and [Reference Lin19, Definition 2.5], for example). It follows that
$f_{1/2n(l(k+1))}(e)-f_{1/2k}(e)\stackrel {c.}{\to } 0$
(see [Reference Lin22, Definition 2.1] and [Reference Lin19, Definition 2.5], for example). It follows that
![]() $\{{\bar b}_n\}\in N_{cu}(A).$
This implies that
$\{{\bar b}_n\}\in N_{cu}(A).$
This implies that
![]() $\{b_n\}\in N_{cu}(A).$
Consequently,
$\{b_n\}\in N_{cu}(A).$
Consequently,
![]() $\Pi _{cu}(A)^\perp =\{0\}.$
$\Pi _{cu}(A)^\perp =\{0\}.$
Conversely, suppose that
![]() $\Pi _{cu}(A)^\perp =\{0\}.$
Let
$\Pi _{cu}(A)^\perp =\{0\}.$
Let
![]() $e_n=f_{1/2n}(e), n\in \mathbb {N}.$
Choose any
$e_n=f_{1/2n}(e), n\in \mathbb {N}.$
Choose any
![]() $m(n)>n.$
Define
$m(n)>n.$
Define
![]() $d_n=e_{4m(n)}-f_{1/n}(e).$
Then, for any
$d_n=e_{4m(n)}-f_{1/n}(e).$
Then, for any
![]() $a\in A, \lim _{n\to \infty }ad_n=0.$
It follows that
$a\in A, \lim _{n\to \infty }ad_n=0.$
It follows that
![]() $\Pi _{cu}(\{d_n\})\in \Pi _{cu}(A)^\perp =\{0\}.$
In other words,
$\Pi _{cu}(\{d_n\})\in \Pi _{cu}(A)^\perp =\{0\}.$
In other words,
![]() $\{d_n\}\in N_{cu}(A).$
Therefore, for any
$\{d_n\}\in N_{cu}(A).$
Therefore, for any
![]() $0<\delta <1/4,$
$0<\delta <1/4,$
Note that, for all
![]() $n\in \mathbb {N},$
$n\in \mathbb {N},$
Thus,
It follows that
![]() $(e_{2m(n)}-e_{n})\stackrel {c.}{\to } 0.$
Hence, A has continuous scale.
$(e_{2m(n)}-e_{n})\stackrel {c.}{\to } 0.$
Hence, A has continuous scale.
3 Comparison and cancellation of projections
Lemma 3.1 Let A be a
![]() $C^*$
-algebra and
$C^*$
-algebra and
![]() $\tau \in {{\widetilde {QT}}}(A)\setminus \{0\}.$
Let
$\tau \in {{\widetilde {QT}}}(A)\setminus \{0\}.$
Let
![]() $e\in A_+$
and
$e\in A_+$
and
![]() $a\in A$
such that
$a\in A$
such that
![]() $ea=a=ae.$
Suppose that
$ea=a=ae.$
Suppose that
![]() $\tau (e)<\infty .$
Then, for any
$\tau (e)<\infty .$
Then, for any
![]() $f\in C_0({\mathbb {R}}),$
it holds that
$f\in C_0({\mathbb {R}}),$
it holds that
![]() $\tau (f(e-a^*a))=\tau (f(e-aa^*)).$
In particular,
$\tau (f(e-a^*a))=\tau (f(e-aa^*)).$
In particular,
![]() $\|e-a^*a\|_{2,\tau }=\|e-aa^*\|_{2,\tau }.$
Moreover,
$\|e-a^*a\|_{2,\tau }=\|e-aa^*\|_{2,\tau }.$
Moreover,
![]() $d_\tau (g(e-a^*a))=d_\tau (g(e-aa^*))$
for any
$d_\tau (g(e-a^*a))=d_\tau (g(e-aa^*))$
for any
![]() $g\in C_0(\mathbb {R}),$
assuming
$g\in C_0(\mathbb {R}),$
assuming
![]() $g(e-a^*a)$
and
$g(e-a^*a)$
and
![]() $g(e-aa^*)$
are positive.
$g(e-aa^*)$
are positive.
Proof Note that since
![]() $C^*(e,a^*a)$
and
$C^*(e,a^*a)$
and
![]() $C^*(e,aa^*)$
are commutative, the restrictions of
$C^*(e,aa^*)$
are commutative, the restrictions of
![]() $\tau $
on them are linear. Let
$\tau $
on them are linear. Let
![]() $n\in \mathbb {N}.$
Then
$n\in \mathbb {N}.$
Then
 $$ \begin{align}\nonumber \tau((e-a^*a)^n) &=\tau\left(e^n+\sum_{m=1}^n\frac{n!}{m!(n-m)!}({{-}}a^*a)^m\right)\\\nonumber &= \tau(e^n)+\sum_{m=1}^n\frac{n!}{m!(n-m)!}\tau( ({{-}}a^*a)^m) \\\nonumber &= \tau(e^n)+\sum_{m=1}^n\frac{n!}{m!(n-m)!}\tau( ({-}aa^*)^m) \\&=\tau\left(e^n+\sum_{m=1}^n\frac{n!}{m!(n-m)!} ({{-}}aa^*)^m\right) =\tau((e-aa^*)^n). \end{align} $$
$$ \begin{align}\nonumber \tau((e-a^*a)^n) &=\tau\left(e^n+\sum_{m=1}^n\frac{n!}{m!(n-m)!}({{-}}a^*a)^m\right)\\\nonumber &= \tau(e^n)+\sum_{m=1}^n\frac{n!}{m!(n-m)!}\tau( ({{-}}a^*a)^m) \\\nonumber &= \tau(e^n)+\sum_{m=1}^n\frac{n!}{m!(n-m)!}\tau( ({-}aa^*)^m) \\&=\tau\left(e^n+\sum_{m=1}^n\frac{n!}{m!(n-m)!} ({{-}}aa^*)^m\right) =\tau((e-aa^*)^n). \end{align} $$
Thus, for any polynomial
![]() $P, \tau (P(e-a^*a))=\tau (P(e-aa^*)).$
In particular,
$P, \tau (P(e-a^*a))=\tau (P(e-aa^*)).$
In particular,
![]() $\|e-a^*a\|_{2,\tau }=\|e-aa^*\|_{2,\tau }.$
Therefore, by the continuity of 2-quasitraces (see [Reference Blackadar and Handelman2, Corollary II.2.5]), and the Stone–Weierstrass theorem,
$\|e-a^*a\|_{2,\tau }=\|e-aa^*\|_{2,\tau }.$
Therefore, by the continuity of 2-quasitraces (see [Reference Blackadar and Handelman2, Corollary II.2.5]), and the Stone–Weierstrass theorem,
![]() $\tau (f(e-a^*a))=\tau (f(e-aa^*))$
for all
$\tau (f(e-a^*a))=\tau (f(e-aa^*))$
for all
![]() $f\in C_0({\mathbb {R}}).$
Moreover, for any
$f\in C_0({\mathbb {R}}).$
Moreover, for any
![]() $g\in C_0(\mathbb {R}),$
assuming
$g\in C_0(\mathbb {R}),$
assuming
![]() $g(e-a^*a)$
and
$g(e-a^*a)$
and
![]() ${{g}}(e-aa^*)$
are positive,
${{g}}(e-aa^*)$
are positive,
Lemma 3.2 Let
![]() $A,B$
be
$A,B$
be
![]() $C^*$
-algebras and
$C^*$
-algebras and
![]() $\pi :A\to B$
be a surjective homomorphism. Assume
$\pi :A\to B$
be a surjective homomorphism. Assume
![]() $p,q\in B$
are projections, and
$p,q\in B$
are projections, and
![]() $x\in B$
satisfies
$x\in B$
satisfies
![]() $px=x=xq.$
Then there are
$px=x=xq.$
Then there are
![]() $\tilde p,\tilde q\in A_+^{\mathbf {1}}$
and
$\tilde p,\tilde q\in A_+^{\mathbf {1}}$
and
![]() $\tilde x\in A,$
such that
$\tilde x\in A,$
such that
![]() $\pi (\tilde p)=p, \pi (\tilde q)=q, \pi (\tilde x)=x,$
and
$\pi (\tilde p)=p, \pi (\tilde q)=q, \pi (\tilde x)=x,$
and
![]() $\tilde p\tilde x=\tilde x=\tilde x\tilde q.$
Moreover, if
$\tilde p\tilde x=\tilde x=\tilde x\tilde q.$
Moreover, if
![]() $p=q,$
we can take
$p=q,$
we can take
![]() $\tilde p=\tilde q.$
$\tilde p=\tilde q.$
Proof We may assume that
![]() $\|x\|\leq 1.$
Let
$\|x\|\leq 1.$
Let
![]() $p_1,q_1\in A_+^{\mathbf {1}}$
such that
$p_1,q_1\in A_+^{\mathbf {1}}$
such that
![]() $\pi (p_1)=p, \pi (q_1)=q.$
Since
$\pi (p_1)=p, \pi (q_1)=q.$
Since
![]() $p,q$
are projections, we also have
$p,q$
are projections, we also have
![]() $\pi (f_{1/2}(p_1)) =f_{1/2}(\pi (p_1)) =p,$
and
$\pi (f_{1/2}(p_1)) =f_{1/2}(\pi (p_1)) =p,$
and
![]() $\pi ({{f_{1/2}}}(q_1)) =f_{1/2}(\pi (q_1))=q.$
Note
$\pi ({{f_{1/2}}}(q_1)) =f_{1/2}(\pi (q_1))=q.$
Note
![]() $x^*x\leq q.$
By [Reference Pedersen30, Proposition 1.5.10], there exists
$x^*x\leq q.$
By [Reference Pedersen30, Proposition 1.5.10], there exists
![]() $y\in A^{\mathbf {1}}$
such that
$y\in A^{\mathbf {1}}$
such that
![]() $\pi (y)=x$
and
$\pi (y)=x$
and
![]() $y^*y\le f_{1/2}(q_1).$
Put
$y^*y\le f_{1/2}(q_1).$
Put
![]() $\tilde x=f_{1/2}(p_1)y.$
Then
$\tilde x=f_{1/2}(p_1)y.$
Then
and
![]() $\tilde x^*\tilde x\le y^*y\le f_{1/2}(q_1).$
Set
$\tilde x^*\tilde x\le y^*y\le f_{1/2}(q_1).$
Set
![]() $\tilde p=f_{1/8}(p_1)$
and
$\tilde p=f_{1/8}(p_1)$
and
![]() $\tilde q=f_{1/8}(q_1).$
Then
$\tilde q=f_{1/8}(q_1).$
Then
![]() $\pi (\tilde p)=p, \pi (\tilde q)=q.$
The facts that
$\pi (\tilde p)=p, \pi (\tilde q)=q.$
The facts that
![]() $f_{1/8}(p_1)f_{1/4}(p_1)=f_{1/4}(p_1)$
and
$f_{1/8}(p_1)f_{1/4}(p_1)=f_{1/4}(p_1)$
and
![]() $f_{1/8}(q_1)f_{1/4}(q_1)=f_{1/4}(q_1)$
imply that
$f_{1/8}(q_1)f_{1/4}(q_1)=f_{1/4}(q_1)$
imply that
![]() $\tilde p\tilde x=\tilde x=\tilde x\tilde q.$
Moreover, if
$\tilde p\tilde x=\tilde x=\tilde x\tilde q.$
Moreover, if
![]() $p=q,$
we can take
$p=q,$
we can take
![]() $p_1=q_1,$
and hence
$p_1=q_1,$
and hence
![]() $\tilde p=\tilde q.$
$\tilde p=\tilde q.$
Proposition 3.3 Let A be a
![]() $C^*$
-algebra with
$C^*$
-algebra with
![]() ${\widetilde {QT}}(A)\setminus \{0\}\not =\emptyset .$
Suppose that
${\widetilde {QT}}(A)\setminus \{0\}\not =\emptyset .$
Suppose that
![]() $T\subset {\widetilde {QT}}(A)\setminus \{0\}$
is a compact subset. Then every projection in
$T\subset {\widetilde {QT}}(A)\setminus \{0\}$
is a compact subset. Then every projection in
![]() $l^\infty (A)/I_{T}(A)$
is finite (see Definition 2.17).
$l^\infty (A)/I_{T}(A)$
is finite (see Definition 2.17).
Proof Let
![]() $B=l^\infty (A)/I_T(A)$
and
$B=l^\infty (A)/I_T(A)$
and
![]() $\pi :l^\infty (A)\to B$
be the quotient map. Assume
$\pi :l^\infty (A)\to B$
be the quotient map. Assume
![]() $p\in B$
is a projection,
$p\in B$
is a projection,
![]() $u\in B$
satisfies
$u\in B$
satisfies
![]() $u^*u=p$
, and
$u^*u=p$
, and
![]() $uu^*\leq p.$
We need to show
$uu^*\leq p.$
We need to show
![]() $uu^*=p.$
$uu^*=p.$
By Lemma 3.2, there are
![]() $a=\{a_1,a_2,...\}\in l^\infty (A)_+^{\mathbf {1}}$
and
$a=\{a_1,a_2,...\}\in l^\infty (A)_+^{\mathbf {1}}$
and
![]() $v=\{v_1,v_2,...\}\in l^\infty (A)$
such that
$v=\{v_1,v_2,...\}\in l^\infty (A)$
such that
![]() $\pi (a)=p, \pi (v)=u,$
and
$\pi (a)=p, \pi (v)=u,$
and
![]() $av=v=va.$
Since
$av=v=va.$
Since
![]() $\pi (a) = p=\pi (v^*v),$
we have
$\pi (a) = p=\pi (v^*v),$
we have
![]() $\lim _{n\to \infty }\|a_n-v_n^*v_n\|_{_{2,T}}=0.$
By Lemma 3.1,
$\lim _{n\to \infty }\|a_n-v_n^*v_n\|_{_{2,T}}=0.$
By Lemma 3.1,
![]() $\|a_n-v_nv_n^*\|_{_{2,T}}=\|a_n-v_n^*v_n\|_{_{2,T}}\to 0 (n\to \infty ).$
Hence,
$\|a_n-v_nv_n^*\|_{_{2,T}}=\|a_n-v_n^*v_n\|_{_{2,T}}\to 0 (n\to \infty ).$
Hence,
which shows p is a finite projection.
Proposition 3.4 Let A be a non-elementary simple
![]() $C^*$
-algebra with
$C^*$
-algebra with
![]() ${\widetilde {QT}}(A)\setminus \{0\}\not =\emptyset .$
Let
${\widetilde {QT}}(A)\setminus \{0\}\not =\emptyset .$
Let
![]() $T\subset {\widetilde {QT}}_{[0,1]}(A)\setminus \{0\}.$
Then, for any
$T\subset {\widetilde {QT}}_{[0,1]}(A)\setminus \{0\}.$
Then, for any
![]() $a\in \mathrm {Ped}(A)_+^{\mathbf {1}}\backslash \{0\},$
any
$a\in \mathrm {Ped}(A)_+^{\mathbf {1}}\backslash \{0\},$
any
![]() $\varepsilon>0,$
there is
$\varepsilon>0,$
there is
![]() $b\in \mathrm {Her}(a)_+$
such that
$b\in \mathrm {Her}(a)_+$
such that
![]() $b\le a,$
$b\le a,$
![]() $\|a-b\|_{_{2, T}}<\varepsilon ,$
and
$\|a-b\|_{_{2, T}}<\varepsilon ,$
and
![]() $d_\tau (b)<d_\tau (a)$
for all
$d_\tau (b)<d_\tau (a)$
for all
![]() $\tau \in T.$
$\tau \in T.$
Proof It follows from the first paragraph of Definition 2.14 that there exists
![]() $c\in \mathrm {Her}(a)_+$
with
$c\in \mathrm {Her}(a)_+$
with
![]() $\|c\|=1$
such that
$\|c\|=1$
such that
![]() $d_\tau (c)<\varepsilon ^2$
for all
$d_\tau (c)<\varepsilon ^2$
for all
![]() $\tau \in T.$
Define
$\tau \in T.$
Define
![]() $b=a^{1/2}(1-f_{1/4}(c))a^{1/2}.$
Then
$b=a^{1/2}(1-f_{1/4}(c))a^{1/2}.$
Then
![]() $0\le b\le a.$
It follows from (e2.17) that
$0\le b\le a.$
It follows from (e2.17) that
For all
![]() $\tau \in T,$
$\tau \in T,$
 $$ \begin{align*}\kern-6pt\begin{array}{lll} d_\tau(b)\!\!\!\! &\qquad\ =&\!\! d_{\tau}(a^{1/2}(1-f_{1/4}(c))a^{1/2}) = d_{\tau}((1-f_{1/4}(c){\kern-1pt})^{1/2} a (1-f_{1/4}(c){\kern-1pt})^{1/2}) \\\!\!\!\! &\qquad\ <&\!\! d_{\tau}((1-f_{1/4}(c))^{1/2} a (1-f_{1/4}(c))^{1/2})+ d_\tau(f_{1/2}(c)) \\\!\!\!\! &\overset{\mathrm{(orthogonality)}}{=}&\!\! d_{\tau}((1-f_{1/4}(c))^{1/2} a (1-f_{1/4}(c))^{1/2} +f_{1/2}(c)) \le d_\tau(a). \end{array}\end{align*} $$
$$ \begin{align*}\kern-6pt\begin{array}{lll} d_\tau(b)\!\!\!\! &\qquad\ =&\!\! d_{\tau}(a^{1/2}(1-f_{1/4}(c))a^{1/2}) = d_{\tau}((1-f_{1/4}(c){\kern-1pt})^{1/2} a (1-f_{1/4}(c){\kern-1pt})^{1/2}) \\\!\!\!\! &\qquad\ <&\!\! d_{\tau}((1-f_{1/4}(c))^{1/2} a (1-f_{1/4}(c))^{1/2})+ d_\tau(f_{1/2}(c)) \\\!\!\!\! &\overset{\mathrm{(orthogonality)}}{=}&\!\! d_{\tau}((1-f_{1/4}(c))^{1/2} a (1-f_{1/4}(c))^{1/2} +f_{1/2}(c)) \le d_\tau(a). \end{array}\end{align*} $$
Theorem 3.5 Let A be a non-elementary algebraically simple
![]() $C^*$
-algebra with
$C^*$
-algebra with
![]() $QT(A)\not =\emptyset .$
Assume that A has strict comparison. Then
$QT(A)\not =\emptyset .$
Assume that A has strict comparison. Then
![]() $l^\infty (A)/I_{\overline {QT(A)}^w}$
has cancellation of projections, i.e., for any projections
$l^\infty (A)/I_{\overline {QT(A)}^w}$
has cancellation of projections, i.e., for any projections
![]() $p,q,r\in l^\infty (A)/I_{\overline {QT(A)}^w},$
if
$p,q,r\in l^\infty (A)/I_{\overline {QT(A)}^w},$
if
![]() $p,q\leq r$
and
$p,q\leq r$
and
![]() $p\sim q,$
then
$p\sim q,$
then
![]() $r-p\sim r-q.$
$r-p\sim r-q.$
Proof Set
![]() $B:=l^\infty (A)/I_{_{\overline {QT(A)}^w}}$
and let
$B:=l^\infty (A)/I_{_{\overline {QT(A)}^w}}$
and let
![]() $\Pi :l^\infty (A)\to B$
denote the quotient map.
$\Pi :l^\infty (A)\to B$
denote the quotient map.
Let
![]() $p,q,r\in B$
be projections with
$p,q,r\in B$
be projections with
![]() $p,q\leq r,$
and assume that there is a partial isometry
$p,q\leq r,$
and assume that there is a partial isometry
![]() $v{\kern-1pt}\in{\kern-1pt} B$
such that
$v{\kern-1pt}\in{\kern-1pt} B$
such that
![]() $v^*v{\kern-1pt}={\kern-1pt}p, vv^*{\kern-1pt}={\kern-1pt}q.$
By Lemma 3.2, there are
$v^*v{\kern-1pt}={\kern-1pt}p, vv^*{\kern-1pt}={\kern-1pt}q.$
By Lemma 3.2, there are
![]() $e{\kern-1pt}={\kern-1pt}\{e_1,e_2,...\}{\kern-1pt}\in{\kern-1pt} l^\infty (A)_+^{\mathbf {1}}$
and
$e{\kern-1pt}={\kern-1pt}\{e_1,e_2,...\}{\kern-1pt}\in{\kern-1pt} l^\infty (A)_+^{\mathbf {1}}$
and
![]() $w=\{w_1,w_2,...\}\in l^\infty (A)$
such that
$w=\{w_1,w_2,...\}\in l^\infty (A)$
such that
![]() $\pi (e)=r, \pi (w)=v,$
and
$\pi (e)=r, \pi (w)=v,$
and
![]() $ew=w=we.$
Then, by Lemma 3.1, we have
$ew=w=we.$
Then, by Lemma 3.1, we have
![]() $ d_\tau (f_{1/4}(e_n-w^*_nw_n))= d_\tau (f_{1/4}(e_n-w_nw_n^*)) $
for all
$ d_\tau (f_{1/4}(e_n-w^*_nw_n))= d_\tau (f_{1/4}(e_n-w_nw_n^*)) $
for all
![]() $\tau \in \overline {QT(A)}^w$
and
$\tau \in \overline {QT(A)}^w$
and
![]() $n\in \mathbb {N}.$
By Proposition 3.4, for each
$n\in \mathbb {N}.$
By Proposition 3.4, for each
![]() $n\in \mathbb {N},$
there is
$n\in \mathbb {N},$
there is
![]() $b_n\in A_+^{\mathbf {1}}$
such that
$b_n\in A_+^{\mathbf {1}}$
such that
Since A has strict comparison, we have
![]() $b_n\lesssim f_{1/4}(e_n-w_nw_n^*).$
By [Reference Rørdam40, Proposition 2.4(iv)], for each
$b_n\lesssim f_{1/4}(e_n-w_nw_n^*).$
By [Reference Rørdam40, Proposition 2.4(iv)], for each
![]() $n\in \mathbb {N},$
there is
$n\in \mathbb {N},$
there is
![]() $x_n'\in A$
such that
$x_n'\in A$
such that
Note that
![]() $f_{1/n}(b)(b-1/n)_+=(b-1/n)_+.$
Choose
$f_{1/n}(b)(b-1/n)_+=(b-1/n)_+.$
Choose
![]() $x_n=x_n'(b-1/n)_+^{1/2}.$
Then
$x_n=x_n'(b-1/n)_+^{1/2}.$
Then
Note
![]() $\|x_n\|^2=\|x_n^*x_n\|=\|(b_n-1/n)_+\|\leq 1.$
The second part of (e3.6) implies
$\|x_n\|^2=\|x_n^*x_n\|=\|(b_n-1/n)_+\|\leq 1.$
The second part of (e3.6) implies
Let
![]() $c_n=e_n-w^*_nw_n$
and
$c_n=e_n-w^*_nw_n$
and
![]() $d_n=e_n-w_nw_n^*$
(
$d_n=e_n-w_nw_n^*$
(
![]() $n\in \mathbb {N}$
). Let
$n\in \mathbb {N}$
). Let
![]() $x=\{x_1,x_2,...\}, b= \{b_1,b_2,...\}, c=\{c_1,c_2,...\},$
and
$x=\{x_1,x_2,...\}, b= \{b_1,b_2,...\}, c=\{c_1,c_2,...\},$
and
![]() $d=\{d_1,d_2,...\}\in l^\infty (A).$
Then
$d=\{d_1,d_2,...\}\in l^\infty (A).$
Then
and
Let
![]() $y=v+\Pi (x).$
Note that
$y=v+\Pi (x).$
Note that
![]() $v\Pi (x)^*=vp(r-p)\Pi (x)^*=0$
and
$v\Pi (x)^*=vp(r-p)\Pi (x)^*=0$
and
![]() $\Pi (x)v^*=(v\Pi (x)^*)^*=0.$
Also, note that
$\Pi (x)v^*=(v\Pi (x)^*)^*=0.$
Also, note that
![]() $v^*\Pi (x)=v^*q(r-q)\Pi (x)=0$
and
$v^*\Pi (x)=v^*q(r-q)\Pi (x)=0$
and
![]() $\Pi (x)^*v=(v^*\Pi (x))^*=0.$
Then we compute (using also (e3.8) and (e3.9)) that
$\Pi (x)^*v=(v^*\Pi (x))^*=0.$
Then we compute (using also (e3.8) and (e3.9)) that
By Proposition 3.3, r is a finite projection. Hence,
![]() $\Pi (x)\Pi (x)^*+q=r.$
Consequently,
$\Pi (x)\Pi (x)^*+q=r.$
Consequently,
![]() $\Pi (x)\Pi (x)^*=r-q.$
Together with (e3.8), we obtain
$\Pi (x)\Pi (x)^*=r-q.$
Together with (e3.8), we obtain
![]() $r-p\sim r-q.$
The theorem then follows.
$r-p\sim r-q.$
The theorem then follows.
4 Tracial oscillations
In this section, we will introduce the notion of tracial approximate oscillation for positive elements in a
![]() $C^*$
-algebra and present some basics around the notion.
$C^*$
-algebra and present some basics around the notion.
Definition 4.1 Let A be a
![]() $C^*$
-algebra with
$C^*$
-algebra with
![]() ${\widetilde {QT}}(A)\setminus \{0\}\not =\emptyset .$
Let
${\widetilde {QT}}(A)\setminus \{0\}\not =\emptyset .$
Let
![]() $S\subset {\widetilde {QT}}(A)$
be a compact subset. Define, for each
$S\subset {\widetilde {QT}}(A)$
be a compact subset. Define, for each
![]() $a\in (A\otimes {\cal K})_+,$
$a\in (A\otimes {\cal K})_+,$
(see A1 of [Reference Elliott, Gong, Lin and Niu11]). The number
![]() $\omega (a)|_S$
is called the (tracial) oscillation of a on
$\omega (a)|_S$
is called the (tracial) oscillation of a on
![]() $S.$
$S.$
If
![]() $a\in \mathrm {Ped}(A\otimes {\cal K})_+,$
then
$a\in \mathrm {Ped}(A\otimes {\cal K})_+,$
then
![]() $\omega (a)|_S<\infty $
(see (2) of Proposition 2.10). Since
$\omega (a)|_S<\infty $
(see (2) of Proposition 2.10). Since
![]() $\tau (f_{1/n}(a))\nearrow d_\tau (a)$
(point-wisely) and
$\tau (f_{1/n}(a))\nearrow d_\tau (a)$
(point-wisely) and
![]() $\widehat {c}$
is continuous on compact set S for each
$\widehat {c}$
is continuous on compact set S for each
![]() $c\in \mathrm {Ped}(\overline {a(A\otimes {\cal K})a})_+,$
one has
$c\in \mathrm {Ped}(\overline {a(A\otimes {\cal K})a})_+,$
one has
Note that, exactly as in A1 of [Reference Elliott, Gong, Lin and Niu11], if
![]() $a, b\in (A\otimes {\cal K})_+^{\mathbf {1}}$
and
$a, b\in (A\otimes {\cal K})_+^{\mathbf {1}}$
and
![]() $a\sim b,$
then
$a\sim b,$
then
![]() $\omega (a)|_S=\omega (b)|_S$
(cf. Proposition 4.2 below). For each
$\omega (a)|_S=\omega (b)|_S$
(cf. Proposition 4.2 below). For each
![]() $h\in \mathrm {LAff}_+(\widetilde {QT}(A)),$
define
$h\in \mathrm {LAff}_+(\widetilde {QT}(A)),$
define
Recall that, in general, for any real function f defined on
![]() $S,$
the oscillation of f at
$S,$
the oscillation of f at
![]() $s\in S$
is defined as
$s\in S$
is defined as
where
![]() $O(s)$
is an open neighborhood of s and the infimum above is taken among all such
$O(s)$
is an open neighborhood of s and the infimum above is taken among all such
![]() $O(s).$
Denote by
$O(s).$
Denote by
![]() $\omega (f)|_S=\sup \{\omega (f)(s): s\in S\}.$
Then (recall that S is compact)
$\omega (f)|_S=\sup \{\omega (f)(s): s\in S\}.$
Then (recall that S is compact)
Let
![]() $a\in (A\otimes {\cal K})_+.$
For each
$a\in (A\otimes {\cal K})_+.$
For each
![]() $\tau \in S,$
and its neighborhood
$\tau \in S,$
and its neighborhood
![]() $O(\tau ),$
define
$O(\tau ),$
define
One may note that, if
![]() $O_1(\tau )\subset O_2(\tau ),$
then
$O_1(\tau )\subset O_2(\tau ),$
then
![]() $\omega _{O_1(\tau )}(a)|_S\le \omega _{O_2(\tau )}(a)|_S.$
Define
$\omega _{O_1(\tau )}(a)|_S\le \omega _{O_2(\tau )}(a)|_S.$
Define
(the infimum is taken among all neighborhood
![]() $O(\tau )$
of
$O(\tau )$
of
![]() $\tau $
in S). In other words, when S is fixed,
$\tau $
in S). In other words, when S is fixed,
![]() $\omega (a)(\tau )|_S$
is the oscillation of the lower-semicontinuous function
$\omega (a)(\tau )|_S$
is the oscillation of the lower-semicontinuous function
![]() $\widehat {[a]}$
at
$\widehat {[a]}$
at
![]() $\tau .$
In particular,
$\tau .$
In particular,
![]() $\widehat {[a]}$
is continuous on S if and only if
$\widehat {[a]}$
is continuous on S if and only if
![]() $\omega (a)(\tau )|_S=0$
for all
$\omega (a)(\tau )|_S=0$
for all
![]() $\tau \in S.$
$\tau \in S.$
(1) If
![]() $c_n\in {{\mathrm {Her}(a)_+^{\mathbf {1}}}}$
and
$c_n\in {{\mathrm {Her}(a)_+^{\mathbf {1}}}}$
and
![]() $\tau (c_n)\nearrow d_\tau (a)$
for all
$\tau (c_n)\nearrow d_\tau (a)$
for all
![]() $\tau \in S,$
then
$\tau \in S,$
then
In general, one checks that
(2) For most of the time, we will assume that A is simple and S is a compact subset of
![]() ${\widetilde {QT}}(A)\setminus \{0\}$
such that
${\widetilde {QT}}(A)\setminus \{0\}$
such that
![]() ${{\mathbb {R}_+\cdot S}}={\widetilde {QT}}(A),$
for example,
${{\mathbb {R}_+\cdot S}}={\widetilde {QT}}(A),$
for example,
![]() $S=T_b$
for some
$S=T_b$
for some
![]() $b\in \mathrm {Ped}(A)_+\setminus \{0\}.$
Or, in the case that
$b\in \mathrm {Ped}(A)_+\setminus \{0\}.$
Or, in the case that
![]() $A=\mathrm {Ped}(A), S=\overline {QT(A)}^w.$
When S is understood, we may omit S in the notation. In fact, when A is compact, we may write
$A=\mathrm {Ped}(A), S=\overline {QT(A)}^w.$
When S is understood, we may omit S in the notation. In fact, when A is compact, we may write
![]() $\omega (a)$
instead of
$\omega (a)$
instead of
![]() $\omega (a)|_{\overline {QT(A)}^w}.$
$\omega (a)|_{\overline {QT(A)}^w}.$
(3) Let
![]() $S_1, S_2\subset \widetilde {QT}(A)\setminus \{0\}$
be compact subsets such that
$S_1, S_2\subset \widetilde {QT}(A)\setminus \{0\}$
be compact subsets such that
![]() $\mathbb {R}_+\cdot S_i=\widetilde {QT}(A),$
$\mathbb {R}_+\cdot S_i=\widetilde {QT}(A),$
![]() $i=1,2.$
If
$i=1,2.$
If
![]() $\omega (a)|_{S_1}=0,$
then
$\omega (a)|_{S_1}=0,$
then
![]() $\omega (a)|_{S_2}=0$
(see also Proposition 2.10). In what follows, we write
$\omega (a)|_{S_2}=0$
(see also Proposition 2.10). In what follows, we write
![]() $\omega (a)=0$
if
$\omega (a)=0$
if
![]() $\omega (a)|_{S}=0$
for one compact subset of
$\omega (a)|_{S}=0$
for one compact subset of
![]() $\widetilde {QT}(A)$
such that
$\widetilde {QT}(A)$
such that
![]() $\mathbb {R}_+\cdot S=\widetilde {QT}(A).$
$\mathbb {R}_+\cdot S=\widetilde {QT}(A).$
Proposition 4.2 [Reference Elliott, Gong, Lin and Niu11, A1] Let
![]() $a,b\in (A\otimes {\cal K})_+.$
Let
$a,b\in (A\otimes {\cal K})_+.$
Let
![]() $S\subset \widetilde {QT}(A)$
be a compact subset. If
$S\subset \widetilde {QT}(A)$
be a compact subset. If
![]() $a\sim b,$
then
$a\sim b,$
then
![]() $\omega (a)(\tau )|_S=\omega (b)(\tau )|_S$
for all
$\omega (a)(\tau )|_S=\omega (b)(\tau )|_S$
for all
![]() $\tau \in S,$
and
$\tau \in S,$
and
![]() $\omega (a)|_S=\omega (b)|_S.$
$\omega (a)|_S=\omega (b)|_S.$
Proof Let
![]() $\tau \in S.$
Let
$\tau \in S.$
Let
![]() $O(\tau )$
be any open neighborhood of
$O(\tau )$
be any open neighborhood of
![]() $\tau .$
For any
$\tau .$
For any
![]() $\varepsilon>0,$
there is
$\varepsilon>0,$
there is
![]() $\delta>0$
such that
$\delta>0$
such that
Since
![]() $a\sim b,$
there exists a sequence
$a\sim b,$
there exists a sequence
![]() $x_n\in A\otimes {\cal K}$
such that
$x_n\in A\otimes {\cal K}$
such that
![]() $x_nx_n^*\to a$
and
$x_nx_n^*\to a$
and
![]() $x_n^*x_n\in \mathrm {Her}(b)=\overline {b(A\otimes {\cal K})b}.$
Since
$x_n^*x_n\in \mathrm {Her}(b)=\overline {b(A\otimes {\cal K})b}.$
Since
![]() $a^{1/m}aa^{1/m}\to a$
as
$a^{1/m}aa^{1/m}\to a$
as
![]() $m\to \infty ,$
replacing
$m\to \infty ,$
replacing
![]() $x_n$
by
$x_n$
by
![]() $a^{1/m(n)}x_n$
for some subsequence
$a^{1/m(n)}x_n$
for some subsequence
![]() $\{m(n)\},$
we may assume that
$\{m(n)\},$
we may assume that
![]() $x_nx_n^*\in \mathrm {Her}(a).$
Note that, for any
$x_nx_n^*\in \mathrm {Her}(a).$
Note that, for any
![]() $\delta>0,$
$\delta>0,$
Since S is compact, by (2) of Proposition 2.10,
![]() $\sup \{\|t|_{\mathrm {Her}(a)}\|:t\in S\}<\infty .$
It follows that there is
$\sup \{\|t|_{\mathrm {Her}(a)}\|:t\in S\}<\infty .$
It follows that there is
![]() $m\in \mathbb {N}$
such that
$m\in \mathbb {N}$
such that
Note that
![]() $d_t(a)=d_t(b)$
for all
$d_t(a)=d_t(b)$
for all
![]() $t\in S$
because of
$t\in S$
because of
![]() $a\sim b.$
Also, note that
$a\sim b.$
Also, note that
![]() $t(f_\delta (x_mx_m^*))=t(f_\delta (x_m^*x_m))$
for all
$t(f_\delta (x_mx_m^*))=t(f_\delta (x_m^*x_m))$
for all
![]() $t\in S.$
Then
$t\in S.$
Then
Since
![]() $\varepsilon $
is arbitrary, we have
$\varepsilon $
is arbitrary, we have
![]() $\omega _{O(\tau )}(b){{|_S}}\leq \omega _{O(\tau )}(a){{|_S}}.$
Exactly the same argument shows that
$\omega _{O(\tau )}(b){{|_S}}\leq \omega _{O(\tau )}(a){{|_S}}.$
Exactly the same argument shows that
![]() $\omega _{O(\tau )}(a)|_S\leq \omega _{O(\tau )}(b){{|_S}}.$
Hence,
$\omega _{O(\tau )}(a)|_S\leq \omega _{O(\tau )}(b){{|_S}}.$
Hence,
![]() $\omega _{O(\tau )}(a)|_S=\omega _{O(\tau )}(b){{|_S}}.$
Since
$\omega _{O(\tau )}(a)|_S=\omega _{O(\tau )}(b){{|_S}}.$
Since
![]() $O(\tau )$
is an arbitrary open neighborhood of
$O(\tau )$
is an arbitrary open neighborhood of
![]() $\tau ,$
we have
$\tau ,$
we have
For the last identity in the proposition, we note that, by (e4.9),
Definition 4.3 In the case that A does not have strict comparison, we may still want to consider elements with zero tracial oscillation. We write
![]() $\omega ^c(a)=0$
if
$\omega ^c(a)=0$
if
![]() $g_{1/n}(a)\stackrel {c.}{\to } 0$
(recall Definition 2.5 for
$g_{1/n}(a)\stackrel {c.}{\to } 0$
(recall Definition 2.5 for
![]() $g_\delta ,$
and also see Definition 2.14). Let
$g_\delta ,$
and also see Definition 2.14). Let
![]() $\{a_n\}\in l^\infty (A)_+.$
We write
$\{a_n\}\in l^\infty (A)_+.$
We write
![]() $\lim _{n\to \infty } \omega ^c(a_n)=0,$
if there exists
$\lim _{n\to \infty } \omega ^c(a_n)=0,$
if there exists
![]() $\delta _n\in (0, 1/2)$
such that
$\delta _n\in (0, 1/2)$
such that
![]() $g_{\delta _n}(a_n)\stackrel {c.}{\to } 0.$
$g_{\delta _n}(a_n)\stackrel {c.}{\to } 0.$
Note that, by Proposition 2.10, if A is compact, then the number s in part (1) of the next proposition is always finite. Let
![]() $\tau \in S.$
In the next lemma, we write
$\tau \in S.$
In the next lemma, we write
![]() $O(\tau )$
for an open neighborhood of
$O(\tau )$
for an open neighborhood of
![]() $\tau $
in
$\tau $
in
![]() $S.$
$S.$
Proposition 4.4 Let A be a
![]() $\sigma $
-unital
$\sigma $
-unital
![]() $C^*$
-algebra. Let
$C^*$
-algebra. Let
![]() $S\subset {\widetilde {QT}}(A)\setminus \{0\}\not =\emptyset $
be a compact subset.
$S\subset {\widetilde {QT}}(A)\setminus \{0\}\not =\emptyset $
be a compact subset.
(1) Suppose that
![]() $s:=\{\|\tau |_A\|: \tau \in S\}<\infty .$
If
$s:=\{\|\tau |_A\|: \tau \in S\}<\infty .$
If
![]() $a, b\in (A\otimes {\cal K})_+^{\mathbf {1}},$
then
$a, b\in (A\otimes {\cal K})_+^{\mathbf {1}},$
then
where
![]() $\overline {d_\tau }(b)|_S:= \inf \{\sup \{d_t(b):t\in O(\tau )\}: O(\tau )\,\, \mbox {open neighborhoods of}\,\, \tau \,\, {\mbox {in}} \,\,S\}.$
$\overline {d_\tau }(b)|_S:= \inf \{\sup \{d_t(b):t\in O(\tau )\}: O(\tau )\,\, \mbox {open neighborhoods of}\,\, \tau \,\, {\mbox {in}} \,\,S\}.$
(2) If
![]() $a\perp b,$
then
$a\perp b,$
then
Moreover,
(3) For
![]() $\sigma $
-unital simple
$\sigma $
-unital simple
![]() $C^*$
-algebra
$C^*$
-algebra
![]() $A, \omega ^c(a)=0$
if and only if
$A, \omega ^c(a)=0$
if and only if
![]() $\mathrm {Her}(a)$
has continuous scale.
$\mathrm {Her}(a)$
has continuous scale.
Proof (1) For the inequality on the left, let
![]() $\varepsilon>0.$
Fix
$\varepsilon>0.$
Fix
![]() $\tau \in S.$
Choose an open neighborhood
$\tau \in S.$
Choose an open neighborhood
![]() $O(\tau )$
of
$O(\tau )$
of
![]() $\tau $
in S such that
$\tau $
in S such that
Note that there is
![]() $\delta>0$
such that
$\delta>0$
such that
Note that
![]() $a+b\approx _{\delta /2} (a-\delta /2)_++b.$
By [Reference Rørdam40, Proposition 2.2], we have
$a+b\approx _{\delta /2} (a-\delta /2)_++b.$
By [Reference Rørdam40, Proposition 2.2], we have
![]() $f_{\delta }(a+b)\lesssim (a-\delta /2)_++b.$
Then, for any
$f_{\delta }(a+b)\lesssim (a-\delta /2)_++b.$
Then, for any
![]() $t\in {{O(\tau )}},$
we have
$t\in {{O(\tau )}},$
we have
Then, for
![]() $t\in O(\tau ),$
$t\in O(\tau ),$
![]() $d_t(a)+t(f_{\delta }(a+b)) \leq d_t(a+b)+t(f_{\delta /2}(a))+\overline {d_\tau }(b)|_S+\varepsilon .$
It follows that
$d_t(a)+t(f_{\delta }(a+b)) \leq d_t(a+b)+t(f_{\delta /2}(a))+\overline {d_\tau }(b)|_S+\varepsilon .$
It follows that
Hence,
Let
![]() $\varepsilon \to 0,$
then we have the desired inequality.
$\varepsilon \to 0,$
then we have the desired inequality.
Now we turn to the inequality on the right. By definition, for any
![]() $\varepsilon>0,$
there are open neighborhood
$\varepsilon>0,$
there are open neighborhood
![]() $O(\tau )$
of
$O(\tau )$
of
![]() $\tau $
in
$\tau $
in
![]() $S,$
and
$S,$
and
![]() $\delta>0$
such that
$\delta>0$
such that
Note that
![]() $a\in \mathrm {Her}(a+b),$
then there is
$a\in \mathrm {Her}(a+b),$
then there is
![]() $\eta>0$
such that
$\eta>0$
such that
![]() $f_\delta (a)\approx _{\varepsilon /(s+1)} f_\eta (a+b)f_\delta (a) f_\eta (a+b).$
Hence, for any
$f_\delta (a)\approx _{\varepsilon /(s+1)} f_\eta (a+b)f_\delta (a) f_\eta (a+b).$
Hence, for any
![]() $t\in O(\tau ),$
by [Reference Blackadar and Handelman2, Corollary II.2.5(iii)],
$t\in O(\tau ),$
by [Reference Blackadar and Handelman2, Corollary II.2.5(iii)],
 $$ \begin{align} d_t(a+b)-t(f_\eta(a+b)) &\leq d_t(b)+d_t(a)-t(f_\eta(a+b)f_\delta(a) f_\eta(a+b)) \nonumber\\ &\leq d_t(b)+d_t(a)-t(f_\delta(a))+\varepsilon \end{align} $$
$$ \begin{align} d_t(a+b)-t(f_\eta(a+b)) &\leq d_t(b)+d_t(a)-t(f_\eta(a+b)f_\delta(a) f_\eta(a+b)) \nonumber\\ &\leq d_t(b)+d_t(a)-t(f_\delta(a))+\varepsilon \end{align} $$
Hence,
 $$ \begin{align}\nonumber \omega(a+b)(\tau)|_S &\leq \sup\{d_t(a+b)-t(f_\eta(a+b)):t\in O(\tau)\}\\ &\leq \overline{d_\tau}(b)+\omega(a)(\tau)|_S+3\varepsilon. \end{align} $$
$$ \begin{align}\nonumber \omega(a+b)(\tau)|_S &\leq \sup\{d_t(a+b)-t(f_\eta(a+b)):t\in O(\tau)\}\\ &\leq \overline{d_\tau}(b)+\omega(a)(\tau)|_S+3\varepsilon. \end{align} $$
Let
![]() $\varepsilon \to 0,$
(1) then follows.
$\varepsilon \to 0,$
(1) then follows.
For (2), we have, for any
![]() $1/2>\varepsilon >0,$
since
$1/2>\varepsilon >0,$
since
![]() $a\perp b,$
$a\perp b,$
for all
![]() $\tau \in S.$
Thus,
$\tau \in S.$
Thus,
Hence, the inequality on the right in (e4.18) holds.
Now we turn to the inequality on the left of (e4.18). Since
![]() $a\bot b,$
for all
$a\bot b,$
for all
![]() $\tau \in S$
and all
$\tau \in S$
and all
![]() $\eta>0,$
$\eta>0,$
Thus,
![]() $ \omega (a)|_S \leq \sup \{d_\tau (a)-f_{\eta }(a): \tau \in S\} \leq \sup \{d_\tau (a+b)-f_{\eta }(a+b): \tau \in S\}. $
Since
$ \omega (a)|_S \leq \sup \{d_\tau (a)-f_{\eta }(a): \tau \in S\} \leq \sup \{d_\tau (a+b)-f_{\eta }(a+b): \tau \in S\}. $
Since
![]() $\eta $
can be arbitrary small, we have
$\eta $
can be arbitrary small, we have
Similarly,
![]() $\omega (b)|_S\le \omega (a+b)|_S.$
Thus, the inequality on the left of (e4.18) holds. The estimates (e4.19) can be checked similarly.
$\omega (b)|_S\le \omega (a+b)|_S.$
Thus, the inequality on the left of (e4.18) holds. The estimates (e4.19) can be checked similarly.
For (3), recall that
![]() $\mathrm {Her}(a)$
has continuous scale if and only if
$\mathrm {Her}(a)$
has continuous scale if and only if
![]() $e_{m(n)}-e_n\stackrel {c.}{\to } 0$
for any
$e_{m(n)}-e_n\stackrel {c.}{\to } 0$
for any
![]() $m(n)>n,$
where
$m(n)>n,$
where
![]() $e_n=f_{1/2^n}(a), n\in \mathbb {N}.$
Suppose that
$e_n=f_{1/2^n}(a), n\in \mathbb {N}.$
Suppose that
![]() $\omega ^c(a)=0.$
Then, for each
$\omega ^c(a)=0.$
Then, for each
![]() $n\in \mathbb {N}$
and any
$n\in \mathbb {N}$
and any
![]() $m(n)\ge n,$
$m(n)\ge n,$
It follows that
![]() $\mathrm {Her}(a)$
has continuous scale.
$\mathrm {Her}(a)$
has continuous scale.
Conversely, suppose that
![]() $\mathrm {Her}(a)$
has continuous scale. For any
$\mathrm {Her}(a)$
has continuous scale. For any
![]() $d\in A_+\setminus \{0\},$
choose
$d\in A_+\setminus \{0\},$
choose
![]() $n_0\in \mathbb {N}$
such that, for any
$n_0\in \mathbb {N}$
such that, for any
![]() $m(n)>n\ge n_0,$
$m(n)>n\ge n_0,$
Suppose that
![]() $k_0>2^{n_0}.$
Fix
$k_0>2^{n_0}.$
Fix
![]() $k\ge k_0.$
For any
$k\ge k_0.$
For any
![]() $\varepsilon \in (0,1/4),$
there is
$\varepsilon \in (0,1/4),$
there is
![]() $m(n)>n_0$
such that
$m(n)>n_0$
such that
In other words, for any
![]() $\varepsilon \in (0, 1/4), f_\varepsilon (g_{1/k}(a))\lesssim d.$
It follows that
$\varepsilon \in (0, 1/4), f_\varepsilon (g_{1/k}(a))\lesssim d.$
It follows that
![]() $g_{1/k}(a)\lesssim d$
(for any
$g_{1/k}(a)\lesssim d$
(for any
![]() $k\ge k_0$
). This proves (3).
$k\ge k_0$
). This proves (3).
Lemma 4.5 Let A be a
![]() $C^*$
-algebra with a nonempty compact subset
$C^*$
-algebra with a nonempty compact subset
![]() $S\subset \widetilde {QT}(A)$
, and let
$S\subset \widetilde {QT}(A)$
, and let
![]() $a\in {{(A\otimes {\cal K})_+.}}$
Then, for any
$a\in {{(A\otimes {\cal K})_+.}}$
Then, for any
![]() $\varepsilon>0,$
there exists
$\varepsilon>0,$
there exists
![]() $\delta _0>0$
such that
$\delta _0>0$
such that
Proof We may assume that
![]() $\omega (a)|_S<\infty .$
There exists
$\omega (a)|_S<\infty .$
There exists
![]() $\delta _0>0$
such that, for all
$\delta _0>0$
such that, for all
![]() $0<\eta \le 2\delta _0,$
$0<\eta \le 2\delta _0,$
Then, there exists
![]() $\sigma _0>0$
such that, if
$\sigma _0>0$
such that, if
![]() $0<\delta <\delta _0,$
$0<\delta <\delta _0,$
for all
![]() $\tau \in S.$
Note that
$\tau \in S.$
Note that
![]() $d_\tau (f_\delta (a))\le \tau (f_{\delta /2}(a))$
for all
$d_\tau (f_\delta (a))\le \tau (f_{\delta /2}(a))$
for all
![]() $\tau \in \widetilde {QT}(A).$
It follows that (see (2) of Proposition 2.10)
$\tau \in \widetilde {QT}(A).$
It follows that (see (2) of Proposition 2.10)
Proposition 4.6 Let A be a
![]() $C^*$
-algebra with a nonempty compact subset
$C^*$
-algebra with a nonempty compact subset
![]() $S\subset \widetilde {QT}(A)$
and
$S\subset \widetilde {QT}(A)$
and
![]() $a\in {{(A\otimes {\cal K})_+^{\mathbf {1}}}}$
with
$a\in {{(A\otimes {\cal K})_+^{\mathbf {1}}}}$
with
![]() $\omega (a)<\infty ,$
and
$\omega (a)<\infty ,$
and
![]() $0<\delta <1/2.$
Then, for any
$0<\delta <1/2.$
Then, for any
![]() $\varepsilon>0,$
there is
$\varepsilon>0,$
there is
![]() $0<\eta <\delta /2$
and
$0<\eta <\delta /2$
and
![]() $n_0\in \mathbb {N}$
such that
$n_0\in \mathbb {N}$
such that
Proof Fix
![]() $0<\delta <1/2.$
For any
$0<\delta <1/2.$
For any
![]() $\varepsilon>0,$
there exists
$\varepsilon>0,$
there exists
![]() $\tau _0\in S$
such that
$\tau _0\in S$
such that
For this
![]() $\tau _0,$
choose
$\tau _0,$
choose
![]() $0<\eta <\delta /2$
such that
$0<\eta <\delta /2$
such that
![]() $ d_{\tau _0}(a)-\tau _0(f_\eta (a))<\varepsilon /4. $
Then
$ d_{\tau _0}(a)-\tau _0(f_\eta (a))<\varepsilon /4. $
Then
Hence,
To see the second inequality, choose
![]() $n_0\in \mathbb {N}$
such that
$n_0\in \mathbb {N}$
such that
It follows that, for all
![]() $\tau \in S,$
$\tau \in S,$
Therefore, by (e4.51),
![]() $ \sup \{\tau (a^{1/n_0})-d_\tau (f_\delta (a)): \tau \in S \}\ge \omega (a)|_S-\varepsilon. $
$ \sup \{\tau (a^{1/n_0})-d_\tau (f_\delta (a)): \tau \in S \}\ge \omega (a)|_S-\varepsilon. $
Definition 4.7 Let A be a
![]() $C^*$
-algebra, let
$C^*$
-algebra, let
![]() $S\subset {\widetilde {QT}}(A) $
be a compact subset, and let
$S\subset {\widetilde {QT}}(A) $
be a compact subset, and let
![]() $a\in {{(A\otimes {\cal K})_+.}}$
Put
$a\in {{(A\otimes {\cal K})_+.}}$
Put
![]() $B=\mathrm {Her}(a)$
and
$B=\mathrm {Her}(a)$
and
![]() $I_{_{S,B}}=\{\{b_n\}\in l^\infty (B): \lim _{n\to \infty }\|b_n\|_{_{2, S}} =0\}.$
Denote by
$I_{_{S,B}}=\{\{b_n\}\in l^\infty (B): \lim _{n\to \infty }\|b_n\|_{_{2, S}} =0\}.$
Denote by
![]() $\Pi _S: l^\infty (B)\to l^\infty (B)/I_{_{S,B}}$
and
$\Pi _S: l^\infty (B)\to l^\infty (B)/I_{_{S,B}}$
and
![]() $\Pi _{cu}: l^\infty (B)\to l^\infty (B)/N_{cu}(B)$
(in the case that B has no one-dimensional hereditary
$\Pi _{cu}: l^\infty (B)\to l^\infty (B)/N_{cu}(B)$
(in the case that B has no one-dimensional hereditary
![]() $C^*$
-subalgebra) the quotient maps, respectively.
$C^*$
-subalgebra) the quotient maps, respectively.
Let A be a
![]() $\sigma $
-unital
$\sigma $
-unital
![]() $C^*$
-algebra and
$C^*$
-algebra and
![]() $a\in (A\otimes {\cal K})_+$
with
$a\in (A\otimes {\cal K})_+$
with
![]() $\|a\|_{_{2, S}}<\infty .$
Define (here we assume that
$\|a\|_{_{2, S}}<\infty .$
Define (here we assume that
![]() $b_n\in \mathrm {Ped}(A\otimes {\cal K})_+$
and
$b_n\in \mathrm {Ped}(A\otimes {\cal K})_+$
and
![]() $\mathrm {Her}(a)=\overline {a(A\otimes {\cal K})a}$
)
$\mathrm {Her}(a)=\overline {a(A\otimes {\cal K})a}$
)
 $$ \begin{align}\nonumber \Omega^T(a)|_S&= \inf\{\|\Pi_S(\iota(a)-\{b_n\})\|: \{b_n\}\in l^\infty(\mathrm{Her}(a))_+, \|b_n\|\le \|a\|, \,\, \lim_{n\to\infty}\omega(b_n)|_S=0\},\nonumber\\ \Omega^T_{T}(a)|_S&= \inf\{\limsup_{n}\|a-b_n\|_{_{2, S}}: b_n\in \mathrm{Her}(a)_+, \|b_n\|\le \|a\|, \lim_{n\to\infty}\omega(b_n)|_S=0\},\nonumber\\ \Omega_C^T(a)|_S&=\inf\{\|\Pi_{cu}(\iota(a)-\{b_n\}{{)}}\|: \{b_n\}\in l^\infty(\mathrm{Her}(a))_+, \|b_n\|\le \|a\|, \lim_{n\to\infty} \omega(b_n)|_S=0\}, \nonumber\\ \Omega^{C}(a)&=\inf\{\|\Pi_{cu}(\iota(a)-\{b_n\}{{)}}\|: \{b_n\}\in l^\infty(\mathrm{Her}(a))_+, \,\, \|b_n\|\le \|a\|,\,\,\lim_{n\to\infty} \omega^c(b_n)=0\}\,\,\,\mathrm{and}\,\,\,\nonumber\\ \Omega^N(a)|_S&=\inf \{\|\pi_\infty(\iota(a)-\{b_n\})\|: b_n\in l^\infty(\mathrm{Her}(a))_+, \lim_{n\to\infty} \omega(b_n)|_S=0\}.\nonumber\\ \end{align} $$
$$ \begin{align}\nonumber \Omega^T(a)|_S&= \inf\{\|\Pi_S(\iota(a)-\{b_n\})\|: \{b_n\}\in l^\infty(\mathrm{Her}(a))_+, \|b_n\|\le \|a\|, \,\, \lim_{n\to\infty}\omega(b_n)|_S=0\},\nonumber\\ \Omega^T_{T}(a)|_S&= \inf\{\limsup_{n}\|a-b_n\|_{_{2, S}}: b_n\in \mathrm{Her}(a)_+, \|b_n\|\le \|a\|, \lim_{n\to\infty}\omega(b_n)|_S=0\},\nonumber\\ \Omega_C^T(a)|_S&=\inf\{\|\Pi_{cu}(\iota(a)-\{b_n\}{{)}}\|: \{b_n\}\in l^\infty(\mathrm{Her}(a))_+, \|b_n\|\le \|a\|, \lim_{n\to\infty} \omega(b_n)|_S=0\}, \nonumber\\ \Omega^{C}(a)&=\inf\{\|\Pi_{cu}(\iota(a)-\{b_n\}{{)}}\|: \{b_n\}\in l^\infty(\mathrm{Her}(a))_+, \,\, \|b_n\|\le \|a\|,\,\,\lim_{n\to\infty} \omega^c(b_n)=0\}\,\,\,\mathrm{and}\,\,\,\nonumber\\ \Omega^N(a)|_S&=\inf \{\|\pi_\infty(\iota(a)-\{b_n\})\|: b_n\in l^\infty(\mathrm{Her}(a))_+, \lim_{n\to\infty} \omega(b_n)|_S=0\}.\nonumber\\ \end{align} $$
We will focus on
![]() $\Omega ^T(a).$
$\Omega ^T(a).$
(1) Note, for the convenience, in the definition above, we always assume that
![]() $\|a\|_{_{2, S}}<\infty .$
$\|a\|_{_{2, S}}<\infty .$
(2) Note also that
![]() $\lim _{n\to \infty }\|af_{1/n}(a)-a\|=0$
and
$\lim _{n\to \infty }\|af_{1/n}(a)-a\|=0$
and
Hence, if
![]() $\omega (a)|_S=0,$
by Lemma 4.5, then
$\omega (a)|_S=0,$
by Lemma 4.5, then
![]() $\Omega ^N(a)|_S=\Omega ^T(a)|_S={{\Omega ^T_T(a)|_S}}=0.$
$\Omega ^N(a)|_S=\Omega ^T(a)|_S={{\Omega ^T_T(a)|_S}}=0.$
One may call
![]() $\Omega ^T(a)|_S$
the tracial approximate oscillation of a (on S). If
$\Omega ^T(a)|_S$
the tracial approximate oscillation of a (on S). If
![]() $\Omega ^T(a)|_S=0,$
we say a has approximately tracial oscillation zero (on S). Often, when S is understood, we may omit S in notation above. In particular, when A is algebraically simple, we write
$\Omega ^T(a)|_S=0,$
we say a has approximately tracial oscillation zero (on S). Often, when S is understood, we may omit S in notation above. In particular, when A is algebraically simple, we write
![]() $\Omega ^T(a):=\Omega ^T(a)|_{_{\overline {QT(A)}^w}}.$
$\Omega ^T(a):=\Omega ^T(a)|_{_{\overline {QT(A)}^w}}.$
(3) It is, perhaps, convenient to use (1) and (2) of Proposition 4.8 for the definition of
![]() $\Omega ^T(a)|_S=0.$
We would like to mention that, for the definition of
$\Omega ^T(a)|_S=0.$
We would like to mention that, for the definition of
![]() $\Omega ^T_C(a)$
and
$\Omega ^T_C(a)$
and
![]() $\Omega ^C(a),$
we also require that
$\Omega ^C(a),$
we also require that
![]() $C^*$
-algebra A has no one-dimensional hereditary
$C^*$
-algebra A has no one-dimensional hereditary
![]() $C^*$
-subalgebra s (see Definition 2.15).
$C^*$
-subalgebra s (see Definition 2.15).
(4) Moreover, since
![]() $\omega (0){{|_S}}=0,$
we have
$\omega (0){{|_S}}=0,$
we have
When A is unital,
![]() $\Omega ^T(a){{|_S}}=0$
for any
$\Omega ^T(a){{|_S}}=0$
for any
![]() $a\in GL(A)\cap A_+,$
since
$a\in GL(A)\cap A_+,$
since
![]() $\omega (1_A)=0.$
$\omega (1_A)=0.$
(5) In the case that A is a
![]() $\sigma $
-unital algebraically simple
$\sigma $
-unital algebraically simple
![]() $C^*$
-algebra with strict comparison, if
$C^*$
-algebra with strict comparison, if
![]() $S=\overline {QT(A)}^w$
and
$S=\overline {QT(A)}^w$
and
![]() $\Omega ^T_T(a)|_S=0,$
then
$\Omega ^T_T(a)|_S=0,$
then
![]() $\Omega ^T(a)|_S=\Omega ^N(a)|_S=\Omega ^T_C(a)|_S=\Omega ^C(a)=0$
(see (2) of Proposition 4.8, (2) after Definition 5.1, and Proposition 5.7).
$\Omega ^T(a)|_S=\Omega ^N(a)|_S=\Omega ^T_C(a)|_S=\Omega ^C(a)=0$
(see (2) of Proposition 4.8, (2) after Definition 5.1, and Proposition 5.7).
Proposition 4.8 Let A be a
![]() $C^*$
-algebra,
$C^*$
-algebra,
![]() ${{a\in ( A\otimes {\cal K})_+^{\mathbf {1}}}}$
, and
${{a\in ( A\otimes {\cal K})_+^{\mathbf {1}}}}$
, and
![]() $S\subset \widetilde {QT}(A)$
a compact subset such that
$S\subset \widetilde {QT}(A)$
a compact subset such that
![]() $\|a\|_{_{2, S}}<\infty .$
$\|a\|_{_{2, S}}<\infty .$
(1) If
![]() $\Omega ^T(a)|_S=0,$
then there exists a sequence
$\Omega ^T(a)|_S=0,$
then there exists a sequence
![]() $\{b_n\}\subset \ {{\mathrm {Ped}(\mathrm {Her}(a))_+^{\mathbf {1}}}}$
such that
$\{b_n\}\subset \ {{\mathrm {Ped}(\mathrm {Her}(a))_+^{\mathbf {1}}}}$
such that
and, if
![]() $\Omega ^T_T(a)|_S=0,$
there exists
$\Omega ^T_T(a)|_S=0,$
there exists
![]() $b_n\in \mathrm {Ped}(\mathrm {Her}(a))_+^{\mathbf {1}}, n\in \mathbb {N},$
such that
$b_n\in \mathrm {Ped}(\mathrm {Her}(a))_+^{\mathbf {1}}, n\in \mathbb {N},$
such that
(2)
![]() $\Omega ^T(a)|_S=0$
if and only if
$\Omega ^T(a)|_S=0$
if and only if
![]() $\Omega _T^T(a)|_S=0.$
$\Omega _T^T(a)|_S=0.$
(3) If there exists
![]() $M\ge 1$
such that
$M\ge 1$
such that
then
![]() $\Omega ^T(a)|_S=0.$
$\Omega ^T(a)|_S=0.$
(4) If
![]() $\{a_n\}\in (I_{_{S}})_+^{\mathbf {1}},$
then there is
$\{a_n\}\in (I_{_{S}})_+^{\mathbf {1}},$
then there is
![]() $\{b_n\}\in (I_{_{S}})^{\mathbf {1}}_+, n\in \mathbb {N},$
such that
$\{b_n\}\in (I_{_{S}})^{\mathbf {1}}_+, n\in \mathbb {N},$
such that
Proof Recall that
![]() $B={{\mathrm {Her}(a)}}$
and
$B={{\mathrm {Her}(a)}}$
and
![]() $\Pi _S: l^\infty (B)\to l^\infty (B)/I_{_{S,B}}$
is the quotient map.
$\Pi _S: l^\infty (B)\to l^\infty (B)/I_{_{S,B}}$
is the quotient map.
For (1), there is, for each
![]() $k\in \mathbb {N},$
a sequence
$k\in \mathbb {N},$
a sequence
![]() $\{c_n^{(k)}\}\in l^\infty ({{\mathrm {Ped}(\mathrm {Her}(a))}})$
with
$\{c_n^{(k)}\}\in l^\infty ({{\mathrm {Ped}(\mathrm {Her}(a))}})$
with
![]() $0\le c_n^{(k)}\le 1$
and
$0\le c_n^{(k)}\le 1$
and
![]() $\lim _{n\to \infty }\omega (c_n^{(k)})|_S=0$
such that
$\lim _{n\to \infty }\omega (c_n^{(k)})|_S=0$
such that
Therefore, for each
![]() $k\in \mathbb {N},$
there is
$k\in \mathbb {N},$
there is
![]() $n(k)\in \mathbb {N}$
such that
$n(k)\in \mathbb {N}$
such that
Define
![]() $b_k=c_{n(k)}^{(k)},\,\, k\in \mathbb {N}.$
Then
$b_k=c_{n(k)}^{(k)},\,\, k\in \mathbb {N}.$
Then
![]() $0\le b_k\le 1, b_k\in {{\mathrm {Ped}(\mathrm {Her}(a))}}$
and
$0\le b_k\le 1, b_k\in {{\mathrm {Ped}(\mathrm {Her}(a))}}$
and
![]() $\lim _{n\to \infty } \omega (b_n)|_S=0.$
Moreover,
$\lim _{n\to \infty } \omega (b_n)|_S=0.$
Moreover,
It follows that
![]() ${{\|}}\Pi _S(\iota (a)-\{b_n\})\|=0,$
and (e4.58) holds. A similar proof above shows that, if
${{\|}}\Pi _S(\iota (a)-\{b_n\})\|=0,$
and (e4.58) holds. A similar proof above shows that, if
![]() $\Omega ^T_T(a)=0$
implies that there is
$\Omega ^T_T(a)=0$
implies that there is
![]() $b_n\in \mathrm {Ped}(\mathrm {Her}(a))_+^{\mathbf {1}}$
such that (e4.58) holds.
$b_n\in \mathrm {Ped}(\mathrm {Her}(a))_+^{\mathbf {1}}$
such that (e4.58) holds.
For (2), we note that (e4.58) implies that
![]() $\iota (a)-\{b_n\}\in I_{_{S}}.$
So, if
$\iota (a)-\{b_n\}\in I_{_{S}}.$
So, if
![]() $\Omega ^T_T(a)|_S=0,$
then
$\Omega ^T_T(a)|_S=0,$
then
![]() $\|\Pi _S(\iota (a)-\{b_n\})\|=0.$
Hence,
$\|\Pi _S(\iota (a)-\{b_n\})\|=0.$
Hence,
![]() $\Omega ^T(a)|_S=0.$
The converse also holds.
$\Omega ^T(a)|_S=0.$
The converse also holds.
To show (3) holds, suppose that there are
![]() $c_n^{(k)}\in {{\mathrm {Ped}}}(\mathrm {Her}(a))$
such that
$c_n^{(k)}\in {{\mathrm {Ped}}}(\mathrm {Her}(a))$
such that
![]() $0\le c_n^{(k)}\le M, \lim _{n\to \infty }\omega (c_n^{(k)}){{|_S}}=0$
and
$0\le c_n^{(k)}\le M, \lim _{n\to \infty }\omega (c_n^{(k)}){{|_S}}=0$
and
By the proof of (1), one obtains
![]() $b_n\in {{\mathrm {Ped}}}(\mathrm {Her}(a))_+$
with
$b_n\in {{\mathrm {Ped}}}(\mathrm {Her}(a))_+$
with
![]() $0\le b_n\le M$
such that
$0\le b_n\le M$
such that
Define
![]() $g\in C_0((0, \|a\|+M])$
by
$g\in C_0((0, \|a\|+M])$
by
![]() $g(t)=\|a\|$
if
$g(t)=\|a\|$
if
![]() $t\in [\|a\|, \|a\|+M]$
and
$t\in [\|a\|, \|a\|+M]$
and
![]() $g(t)=t$
if
$g(t)=t$
if
![]() $t\in [0,\|a\|].$
Since M is fixed and
$t\in [0,\|a\|].$
Since M is fixed and
![]() $g(a)=a,$
we have
$g(a)=a,$
we have
Put
![]() $c_n=g(b_n).$
Then
$c_n=g(b_n).$
Then
![]() $c_n\in {{\mathrm {Ped}}}(\mathrm {Her}(a))_+$
and
$c_n\in {{\mathrm {Ped}}}(\mathrm {Her}(a))_+$
and
![]() $\|c_n\|\le \|a\|.$
Since
$\|c_n\|\le \|a\|.$
Since
![]() $c_n=g(b_n)\sim b_n,$
then
$c_n=g(b_n)\sim b_n,$
then
![]() $\lim _{n\to \infty }\omega (c_n){|_{S}}=0.$
Therefore, by (e4.65),
$\lim _{n\to \infty }\omega (c_n){|_{S}}=0.$
Therefore, by (e4.65),
![]() $\Omega ^T(a){{|_S}}=0.$
$\Omega ^T(a){{|_S}}=0.$
(4) Since
![]() $\{a_n\}\in (I_{_{S}})_+^{\mathbf {1}}, \lim _{n\to \infty }\|a_n\|_{_{2, S}}=0.$
Choose
$\{a_n\}\in (I_{_{S}})_+^{\mathbf {1}}, \lim _{n\to \infty }\|a_n\|_{_{2, S}}=0.$
Choose
![]() $\delta _n:=\sqrt {\|a_n\|_{2,S}+1/n}$
and
$\delta _n:=\sqrt {\|a_n\|_{2,S}+1/n}$
and
![]() $b_n=(a_n-\delta _n)_+, n\in \mathbb {N}.$
Then
$b_n=(a_n-\delta _n)_+, n\in \mathbb {N}.$
Then
![]() $\|b_n\|\le 1, n\in \mathbb {N}, \|b_n\|_{_{2, S}}\le \|a_n\|_{_{2, S}}\to 0$
and
$\|b_n\|\le 1, n\in \mathbb {N}, \|b_n\|_{_{2, S}}\le \|a_n\|_{_{2, S}}\to 0$
and
![]() $\lim _{n\to \infty } \|a_n-b_n\|=0.$
$\lim _{n\to \infty } \|a_n-b_n\|=0.$
Note that
where
![]() $\eta \in (0,1)$
and
$\eta \in (0,1)$
and
![]() $\chi _{[\delta _n,+\infty )}$
is the characteristic function of
$\chi _{[\delta _n,+\infty )}$
is the characteristic function of
![]() $[\delta _n,+\infty ).$
Then, for all
$[\delta _n,+\infty ).$
Then, for all
![]() $\tau \in S,$
$\tau \in S,$
It follows that
![]() $\lim _{n\to \infty }\sup \{d_\tau (b_n):\tau \in S\}=0.$
$\lim _{n\to \infty }\sup \{d_\tau (b_n):\tau \in S\}=0.$
The next proposition also justifies that we often write
![]() $\Omega ^T(a)=0$
instead of
$\Omega ^T(a)=0$
instead of
![]() $\Omega ^T(a)|_S$
for some compact set
$\Omega ^T(a)|_S$
for some compact set
![]() $S\subset \widetilde {QT}(A)\setminus \{0\}$
such that
$S\subset \widetilde {QT}(A)\setminus \{0\}$
such that
![]() $\mathbb {R}_+\cdot S=\widetilde {QT}(A).$
$\mathbb {R}_+\cdot S=\widetilde {QT}(A).$
Proposition 4.9 Let A be a
![]() $C^*$
-algebra and
$C^*$
-algebra and
![]() $S_1, S_2\subset \widetilde {QT}(A)\setminus \{0\}$
be nonempty compact subsets such that
$S_1, S_2\subset \widetilde {QT}(A)\setminus \{0\}$
be nonempty compact subsets such that
![]() $\mathbb {R}_+\cdot S_1=\mathbb {R}_+ \cdot S_2=\widetilde {QT}(A).$
Suppose that
$\mathbb {R}_+\cdot S_1=\mathbb {R}_+ \cdot S_2=\widetilde {QT}(A).$
Suppose that
![]() $a \in {{(A\otimes {\cal K})_+^{\mathbf {1}}}}.$
Then
$a \in {{(A\otimes {\cal K})_+^{\mathbf {1}}}}.$
Then
![]() $\Omega ^T(a)|_{S_1}=0$
(
$\Omega ^T(a)|_{S_1}=0$
(
![]() $\Omega ^T_C(a)|_{S_1}=0,$
or
$\Omega ^T_C(a)|_{S_1}=0,$
or
![]() $\Omega ^N(a)|_{S_1}=0$
) if and only if
$\Omega ^N(a)|_{S_1}=0$
) if and only if
![]() $\Omega ^T(a)|_{S_2}=0$
(
$\Omega ^T(a)|_{S_2}=0$
(
![]() $\Omega ^T_C(a)|_{S_2}=0,$
or
$\Omega ^T_C(a)|_{S_2}=0,$
or
![]() $\Omega ^N(a)|_{S_2}=0$
). Moreover, if
$\Omega ^N(a)|_{S_2}=0$
). Moreover, if
![]() ${{a\in \mathrm {Ped}(A\otimes {\cal K})_+}}$
and
${{a\in \mathrm {Ped}(A\otimes {\cal K})_+}}$
and
![]() $\Omega ^T(a)|_{S_a}=0,$
where
$\Omega ^T(a)|_{S_a}=0,$
where
![]() $S_a=\overline {\{\tau \in \widetilde {QT}(A): \|\tau |_{\mathrm {Her}(a)}\|=1\}}^w,$
then
$S_a=\overline {\{\tau \in \widetilde {QT}(A): \|\tau |_{\mathrm {Her}(a)}\|=1\}}^w,$
then
![]() $\Omega ^T(a)|_{S_1}=0.$
$\Omega ^T(a)|_{S_1}=0.$
Proof It follows from (1) of Proposition 2.10 that there is
![]() $L\in \mathbb {R}_+$
such that
$L\in \mathbb {R}_+$
such that
If
![]() $\Omega ^T(a)|_{S_1}=0,$
then, by Proposition 4.8, there exists a sequence
$\Omega ^T(a)|_{S_1}=0,$
then, by Proposition 4.8, there exists a sequence
![]() $b_n\in {{\mathrm {Ped}(\mathrm {Her}(a))}}$
with
$b_n\in {{\mathrm {Ped}(\mathrm {Her}(a))}}$
with
![]() $\|b_n\|\le \|a\|$
such that
$\|b_n\|\le \|a\|$
such that
![]() $\lim _{n\to \infty }\omega (b_n)|_{S_1}=0$
and
$\lim _{n\to \infty }\omega (b_n)|_{S_1}=0$
and
![]() $\lim _{n\to \infty }\|a-b_n\|_{_{2, S_1}}=0.$
It follows that
$\lim _{n\to \infty }\|a-b_n\|_{_{2, S_1}}=0.$
It follows that
Then
![]() $\Omega ^T(a)|_{S_2}=0.$
Exactly the same argument shows that if
$\Omega ^T(a)|_{S_2}=0.$
Exactly the same argument shows that if
![]() $\Omega _C^T(a)|_{S_1}=0$
(or
$\Omega _C^T(a)|_{S_1}=0$
(or
![]() $\Omega ^N(a)|_{S_1}=0$
), then
$\Omega ^N(a)|_{S_1}=0$
), then
![]() $\Omega _C^T(a)|_{S_2}=0$
(or
$\Omega _C^T(a)|_{S_2}=0$
(or
![]() $\Omega ^N(a)|_{S_2}=0$
).
$\Omega ^N(a)|_{S_2}=0$
).
To see the last statement, we note that
![]() $(S_1)|_{\mathrm {Her}(a)}$
is bounded (see (2) of Proposition 2.10). In other words, there is
$(S_1)|_{\mathrm {Her}(a)}$
is bounded (see (2) of Proposition 2.10). In other words, there is
![]() $L>0$
such that
$L>0$
such that
![]() $(S_1)|_{\mathrm {Her}(a)}\subset \{r\cdot \tau : \tau \in S_a, r\in [0, L]\}.$
$(S_1)|_{\mathrm {Her}(a)}\subset \{r\cdot \tau : \tau \in S_a, r\in [0, L]\}.$
Lemma 4.10 Let A be a
![]() $C^*$
-algebra,
$C^*$
-algebra,
![]() $a\in (A\otimes {\cal K})_+$
, and
$a\in (A\otimes {\cal K})_+$
, and
![]() $S\subset {{{\widetilde {QT}}(A)}}$
a compact subset. Suppose
$S\subset {{{\widetilde {QT}}(A)}}$
a compact subset. Suppose
![]() ${{e\in \mathrm {Her}(a)_+}}.$
Then
${{e\in \mathrm {Her}(a)_+}}.$
Then
![]() $e\sim a^{1/2}ea^{1/2}\sim e^{1/2}ae^{1/2},$
and
$e\sim a^{1/2}ea^{1/2}\sim e^{1/2}ae^{1/2},$
and
Proof Since
![]() $e\in \mathrm {Her}(a)_+^{\mathbf {1}},$
we compute that
$e\in \mathrm {Her}(a)_+^{\mathbf {1}},$
we compute that
It follows that
![]() $e\sim a^{1/2}ea^{1/2}\sim e^{1/2}ae^{1/2}\le e.$
Therefore, by Proposition 4.2, (e4.68) and (e4.69) hold.
$e\sim a^{1/2}ea^{1/2}\sim e^{1/2}ae^{1/2}\le e.$
Therefore, by Proposition 4.2, (e4.68) and (e4.69) hold.
Let us end this section with the following fact. The proof could be simplified when
![]() $QT(A)=T(A).$
Recall that when
$QT(A)=T(A).$
Recall that when
![]() $A=\mathrm {Ped}(A),$
we write
$A=\mathrm {Ped}(A),$
we write
![]() $\omega (a)=\omega (a)|_{_{\overline {QT(A)}^w}}$
and
$\omega (a)=\omega (a)|_{_{\overline {QT(A)}^w}}$
and
![]() $\Omega ^T_T(a)=\Omega ^T_T(a)|_{_{\overline {QT(A)}^w}}.$
$\Omega ^T_T(a)=\Omega ^T_T(a)|_{_{\overline {QT(A)}^w}}.$
Proposition 4.11 Let A be an algebraically simple
![]() $C^*$
-algebra with
$C^*$
-algebra with
![]() $QT(A)\not =\emptyset .$
Suppose that A has strict comparison and
$QT(A)\not =\emptyset .$
Suppose that A has strict comparison and
![]() $\Gamma $
is surjective (see Definition 2.13). Then, for any
$\Gamma $
is surjective (see Definition 2.13). Then, for any
![]() $a\in \mathrm {Ped}(A\otimes {\cal K})_+,$
$a\in \mathrm {Ped}(A\otimes {\cal K})_+,$
Proof Fix
![]() $a\in \mathrm {Ped}(A\otimes {\cal K})_+\setminus \{0\}.$
Let
$a\in \mathrm {Ped}(A\otimes {\cal K})_+\setminus \{0\}.$
Let
![]() $\varepsilon>0.$
If there is a subsequence
$\varepsilon>0.$
If there is a subsequence
![]() $\{n_k\}\subset \mathbb {N}$
such that
$\{n_k\}\subset \mathbb {N}$
such that
![]() $f_{1/4n_k}(a)-f_{{{1/}}n_k}(a)=0,$
then
$f_{1/4n_k}(a)-f_{{{1/}}n_k}(a)=0,$
then
![]() $f_{1/4n_k}(a)$
is a projection. Consequently,
$f_{1/4n_k}(a)$
is a projection. Consequently,
![]() $\omega (f_{1/4n_k}(a))=0$
for all
$\omega (f_{1/4n_k}(a))=0$
for all
![]() $k\in \mathbb {N}.$
Note that
$k\in \mathbb {N}.$
Note that
![]() $af_{1/4n_k}(a)\sim f_{1/4n_k}(a).$
It follows that
$af_{1/4n_k}(a)\sim f_{1/4n_k}(a).$
It follows that
![]() $\omega (af_{1/4n_k}(a))=0, k\in \mathbb {N}.$
Since
$\omega (af_{1/4n_k}(a))=0, k\in \mathbb {N}.$
Since
![]() $\lim _{k\to \infty }\|a-af_{1/4n_k}(a)\|=0, \Omega ^T(a)=0.$
Hence, (e4.71) holds.
$\lim _{k\to \infty }\|a-af_{1/4n_k}(a)\|=0, \Omega ^T(a)=0.$
Hence, (e4.71) holds.
Next, we assume that for some
![]() $n_0\in \mathbb {N}, f_{1/4n}(a)-f_{{1/n}}(a)\not =0$
for all
$n_0\in \mathbb {N}, f_{1/4n}(a)-f_{{1/n}}(a)\not =0$
for all
![]() $n\ge n_0.$
Moreover,
$n\ge n_0.$
Moreover,
For the rest of this proof, we will assume
![]() $n\geq n_0.$
Since the map
$n\geq n_0.$
Since the map
![]() $\Gamma $
is surjective, there is
$\Gamma $
is surjective, there is
![]() $c_n\in (A\otimes {\cal K})_+^{\mathbf {1}}$
such that
$c_n\in (A\otimes {\cal K})_+^{\mathbf {1}}$
such that
![]() $d_\tau (c_n)=\tau (f_{1/n}(a))$
for all
$d_\tau (c_n)=\tau (f_{1/n}(a))$
for all
![]() $\tau \in \overline {QT(A)}^w.$
Since
$\tau \in \overline {QT(A)}^w.$
Since
![]() $\widehat {f_{1/n}(a)}$
is continuous on
$\widehat {f_{1/n}(a)}$
is continuous on
![]() $\overline {QT(A)}^w, \omega (c_n)=0.$
Choose
$\overline {QT(A)}^w, \omega (c_n)=0.$
Choose
![]() $0<\delta _n<1$
such that (by also Lemma 4.5),
$0<\delta _n<1$
such that (by also Lemma 4.5),
Note that we have
Since A has strict comparison,
![]() $c_n\lesssim f_{1/4n}(a).$
By Proposition 2.4 of [Reference Rørdam40], there is
$c_n\lesssim f_{1/4n}(a).$
By Proposition 2.4 of [Reference Rørdam40], there is
![]() $x_n\in A\otimes {\cal K}$
such that
$x_n\in A\otimes {\cal K}$
such that
Put
![]() $b_n=a^{1/2}x_nx_n^*a^{1/2}.$
Then
$b_n=a^{1/2}x_nx_n^*a^{1/2}.$
Then
![]() $\|b_n\| \le \|a\|$
and
$\|b_n\| \le \|a\|$
and
![]() $b_n\in \mathrm {Her}(f_{1/4n}(a)).$
By Lemma 4.10 and (e4.73),
$b_n\in \mathrm {Her}(f_{1/4n}(a)).$
By Lemma 4.10 and (e4.73),
![]() $\omega (b_n)=\omega (x_nx_n^*)=\omega (x_n^*x_n)=\omega (f_{\delta _n}(c_n))\leq 1/2^n\to 0.$
Note that
$\omega (b_n)=\omega (x_nx_n^*)=\omega (x_n^*x_n)=\omega (f_{\delta _n}(c_n))\leq 1/2^n\to 0.$
Note that
Put
![]() $a_n=a^{1/2}{{f_{1/8n}(a)}} a^{1/2}$
and
$a_n=a^{1/2}{{f_{1/8n}(a)}} a^{1/2}$
and
![]() $d_n= {{f_{1/8n}(a)}}-x_nx_n^*.$
Then
$d_n= {{f_{1/8n}(a)}}-x_nx_n^*.$
Then
![]() $0\le d_n\le 1$
and
$0\le d_n\le 1$
and
![]() $0\le a_n-b_n, n\in \mathbb {N}.$
For all
$0\le a_n-b_n, n\in \mathbb {N}.$
For all
![]() $\tau \in \overline {QT(A)}^w,$
we compute that
$\tau \in \overline {QT(A)}^w,$
we compute that
Note that
![]() $\|a-a_n\|<1/n.$
It follows that, by (e2.17), (e2.19), and (e4.82),
$\|a-a_n\|<1/n.$
It follows that, by (e2.17), (e2.19), and (e4.82),
Hence (by also (2) of Proposition 2.10),
Let
![]() $\varepsilon \to 0.$
We then obtain (e4.71) (recall that
$\varepsilon \to 0.$
We then obtain (e4.71) (recall that
![]() $\lim _{n\to \infty }\omega (b_n)=0$
).
$\lim _{n\to \infty }\omega (b_n)=0$
).
5
 $C^*$
-algebras with tracial approximate oscillation zero
$C^*$
-algebras with tracial approximate oscillation zero
In this section, we will introduce the notion of T-tracial approximate oscillation zero for
![]() $C^*$
-algebras with non-trivial 2-quasitraces. We also present some examples of simple
$C^*$
-algebras with non-trivial 2-quasitraces. We also present some examples of simple
![]() $C^*$
-algebras with tracial approximate oscillation zero (see Proposition 5.8 and Theorems 5.9 and 5.10).
$C^*$
-algebras with tracial approximate oscillation zero (see Proposition 5.8 and Theorems 5.9 and 5.10).
Definition 5.1 Let A be a
![]() $C^*$
-algebra with
$C^*$
-algebra with
![]() ${\widetilde {QT}}(A)\setminus \{0\}\not =\emptyset $
and
${\widetilde {QT}}(A)\setminus \{0\}\not =\emptyset $
and
![]() $S\subset \widetilde {QT}(A)\setminus \{0\}$
a compact convex subset of A such that
$S\subset \widetilde {QT}(A)\setminus \{0\}$
a compact convex subset of A such that
![]() $\mathbb {R}_+ \cdot S={\widetilde {QT}}(A). C^*$
-algebra A is said to have norm approximate oscillation zero (relative to S) if for any
$\mathbb {R}_+ \cdot S={\widetilde {QT}}(A). C^*$
-algebra A is said to have norm approximate oscillation zero (relative to S) if for any
![]() $a\in \mathrm {Ped}(A\otimes {\cal K})_+, \Omega ^N(a)|_S=0.$
It is said to have tracial approximate oscillation zero (relative to S), if for any
$a\in \mathrm {Ped}(A\otimes {\cal K})_+, \Omega ^N(a)|_S=0.$
It is said to have tracial approximate oscillation zero (relative to S), if for any
![]() $a\in \mathrm {Ped}(A\otimes {\cal K})_+, \Omega ^T_C(a)|_S=0.$
We say that A has T-tracial approximate oscillation zero (relative to S) if
$a\in \mathrm {Ped}(A\otimes {\cal K})_+, \Omega ^T_C(a)|_S=0.$
We say that A has T-tracial approximate oscillation zero (relative to S) if
![]() $\Omega ^T(a)|_S=0$
for all
$\Omega ^T(a)|_S=0$
for all
![]() $a\in \mathrm {Ped}(A\otimes {\cal K})_+.$
We say that A has C-tracial approximate oscillation zero if
$a\in \mathrm {Ped}(A\otimes {\cal K})_+.$
We say that A has C-tracial approximate oscillation zero if
![]() $\Omega ^C(a)=0$
for all
$\Omega ^C(a)=0$
for all
![]() $a\in \mathrm {Ped}(A\otimes {\cal K})_+.$
$a\in \mathrm {Ped}(A\otimes {\cal K})_+.$
Note that, by Proposition 4.9, these definitions do not depend on the choices of
![]() $S.$
Therefore, we often omit S in the notation.
$S.$
Therefore, we often omit S in the notation.
(1) If A is a
![]() $\sigma $
-unital simple
$\sigma $
-unital simple
![]() $C^*$
-algebra and
$C^*$
-algebra and
![]() $a\in \mathrm {Ped}(A\otimes {\cal K})_+^{\mathbf {1}},$
then
$a\in \mathrm {Ped}(A\otimes {\cal K})_+^{\mathbf {1}},$
then
![]() $QT(\mathrm {Her}(a))$
may be viewed as a convex subset of
$QT(\mathrm {Her}(a))$
may be viewed as a convex subset of
![]() $\widetilde {QT}(A).$
Put
$\widetilde {QT}(A).$
Put
![]() $S_1=\overline {QT(\mathrm {Her}(a))}^w.$
Therefore (see also Proposition 2.9),
$S_1=\overline {QT(\mathrm {Her}(a))}^w.$
Therefore (see also Proposition 2.9),
![]() $\Omega ^T(a)|_S=0$
if and only if
$\Omega ^T(a)|_S=0$
if and only if
![]() $\Omega ^T(a)|_{S_1}=0.$
$\Omega ^T(a)|_{S_1}=0.$
(2) By Proposition 4.8,
![]() $\Omega ^T_T(a)|_S=0$
if and only if
$\Omega ^T_T(a)|_S=0$
if and only if
![]() $\Omega ^T(a)|_S=0$
for all
$\Omega ^T(a)|_S=0$
for all
![]() $a\in (A\otimes {\cal K})_+$
with
$a\in (A\otimes {\cal K})_+$
with
![]() $\|a\|_{_{2, S}}<\infty .$
By Proposition 5.7 below, that A has norm approximate oscillation zero is the same as that A has T-tracial approximate oscillation zero.
$\|a\|_{_{2, S}}<\infty .$
By Proposition 5.7 below, that A has norm approximate oscillation zero is the same as that A has T-tracial approximate oscillation zero.
If A is
![]() $\sigma $
-unital, non-elementary, and simple and has strict comparison, then, by Proposition 2.18, for any nonzero
$\sigma $
-unital, non-elementary, and simple and has strict comparison, then, by Proposition 2.18, for any nonzero
![]() $a\in \mathrm {Ped}(A\otimes {\cal K})_+,$
one has
$a\in \mathrm {Ped}(A\otimes {\cal K})_+,$
one has
![]() $I_{_{\overline {QT(A_a)}^w}}=N_{cu}(A_a),$
where
$I_{_{\overline {QT(A_a)}^w}}=N_{cu}(A_a),$
where
![]() $A_a=\mathrm {Her}(a).$
It follows that, in this case, the notion of tracial approximate oscillation zero, the notion of T-tracial approximate oscillation zero, the notion of C-tracial approximate oscillation zero, and that of norm approximate oscillation zero all coincide (see also Proposition 5.7).
$A_a=\mathrm {Her}(a).$
It follows that, in this case, the notion of tracial approximate oscillation zero, the notion of T-tracial approximate oscillation zero, the notion of C-tracial approximate oscillation zero, and that of norm approximate oscillation zero all coincide (see also Proposition 5.7).
(3) Note also that, if A has (T-) tracial approximate oscillation zero, then
![]() $M_n(A)$
also has (T-) tracial approximate oscillation zero.
$M_n(A)$
also has (T-) tracial approximate oscillation zero.
If we view
![]() $\|\cdot \|_{_{2, \overline {QT(A)}^w}}$
as an
$\|\cdot \|_{_{2, \overline {QT(A)}^w}}$
as an
![]() $L^2$
-norm, then that A has T-tracial approximate oscillation zero has an analogue to that “almost” continuous functions are dense in the
$L^2$
-norm, then that A has T-tracial approximate oscillation zero has an analogue to that “almost” continuous functions are dense in the
![]() $L^2$
-norm. It is worth mentioning that a
$L^2$
-norm. It is worth mentioning that a
![]() $\sigma $
-unital simple
$\sigma $
-unital simple
![]() $C^*$
-algebra has (T-) tracial approximate oscillation zero, if, for some
$C^*$
-algebra has (T-) tracial approximate oscillation zero, if, for some
![]() $e\in \mathrm {Ped}(A)_+\setminus \{0\}, \mathrm {Her}(e)$
has (T-) tracial approximate oscillation zero.
$e\in \mathrm {Ped}(A)_+\setminus \{0\}, \mathrm {Her}(e)$
has (T-) tracial approximate oscillation zero.
Definition 5.2 Let A be a
![]() $\sigma $
-unital
$\sigma $
-unital
![]() $C^*$
-algebra with
$C^*$
-algebra with
![]() $\widetilde {QT}\setminus \{0\}\not =\emptyset .$
Define
$\widetilde {QT}\setminus \{0\}\not =\emptyset .$
Define
where
![]() $S_a=\overline {QT(\mathrm {Her}(a))}^w$
(see the last paragraph of Definition 2.8). Note that, since
$S_a=\overline {QT(\mathrm {Her}(a))}^w$
(see the last paragraph of Definition 2.8). Note that, since
![]() $\Omega ^T(a)|_{_{S_a}}\le \|a\|$
for any
$\Omega ^T(a)|_{_{S_a}}\le \|a\|$
for any
![]() $a\in \mathrm {Ped}(A\otimes {\cal K})_+^{\mathbf {1}}$
and for any
$a\in \mathrm {Ped}(A\otimes {\cal K})_+^{\mathbf {1}}$
and for any
![]() $C^*$
-algebra
$C^*$
-algebra
![]() $A,$
one has that
$A,$
one has that
![]() $0\le \mathbb {O}(A)\le 1.$
The number
$0\le \mathbb {O}(A)\le 1.$
The number
![]() $\mathbb {O}(A)$
is called T-tracial approximate oscillation of
$\mathbb {O}(A)$
is called T-tracial approximate oscillation of
![]() $A.$
$A.$
Suppose that
![]() $S\subset \widetilde {QT}(A)\setminus \{0\}$
is a compact convex set such that
$S\subset \widetilde {QT}(A)\setminus \{0\}$
is a compact convex set such that
![]() $\mathbb {R}_+\cdot S=\widetilde {QT}(A).$
By (the “Moreover” part of) Proposition 4.9, if
$\mathbb {R}_+\cdot S=\widetilde {QT}(A).$
By (the “Moreover” part of) Proposition 4.9, if
![]() $\mathbb {O}(A)=0,$
then A has T-tracial approximate oscillation zero. Conversely, if A has T-tracial approximate oscillation zero, then
$\mathbb {O}(A)=0,$
then A has T-tracial approximate oscillation zero. Conversely, if A has T-tracial approximate oscillation zero, then
![]() $\mathbb {O}(A)=0$
(see (4) of Proposition 2.10).
$\mathbb {O}(A)=0$
(see (4) of Proposition 2.10).
The next example shows that there are (commutative)
![]() $C^*$
-algebras A of stable rank one such that
$C^*$
-algebras A of stable rank one such that
![]() $\mathbb {O}(A)>0.$
By Theorem 1.1, if A is a separable simple
$\mathbb {O}(A)>0.$
By Theorem 1.1, if A is a separable simple
![]() $C^*$
-algebra which has strict comparison but does not have stable rank one, then
$C^*$
-algebra which has strict comparison but does not have stable rank one, then
![]() $\mathbb {O}(A)>0.$
However, we do not have any such examples.
$\mathbb {O}(A)>0.$
However, we do not have any such examples.
Example 5.3 Let
![]() $A=C([0,1]).$
Then
$A=C([0,1]).$
Then
![]() $T(A)$
is compact and
$T(A)$
is compact and
![]() ${\widetilde {QT}}(A)=\widetilde {T}(A).$
Let
${\widetilde {QT}}(A)=\widetilde {T}(A).$
Let
![]() ${{a\in }} A_+\setminus \{0\}$
be such that
${{a\in }} A_+\setminus \{0\}$
be such that
![]() $0\le a\le 1$
that is not invertible. Let
$0\le a\le 1$
that is not invertible. Let
![]() $G=\{t\in [0,1]: a(t)>0\}.$
Then G is an open subset. Note
$G=\{t\in [0,1]: a(t)>0\}.$
Then G is an open subset. Note
![]() $0\in \mathrm {sp}(a).$
Since A has no nontrivial projection, there are
$0\in \mathrm {sp}(a).$
Since A has no nontrivial projection, there are
![]() $t_n\in \mathrm {sp}(a)$
with
$t_n\in \mathrm {sp}(a)$
with
![]() $\lim _{n\to \infty }t_n=0.$
For any
$\lim _{n\to \infty }t_n=0.$
For any
![]() $0<\delta <1/2,$
let
$0<\delta <1/2,$
let
![]() $b=f_\delta (a).$
Let
$b=f_\delta (a).$
Let
![]() $s_n\in G$
such that
$s_n\in G$
such that
![]() $a(s_n)=t_n, n\in \mathbb {N}.$
Then, for some
$a(s_n)=t_n, n\in \mathbb {N}.$
Then, for some
![]() $0<\eta <\delta /2,$
there is
$0<\eta <\delta /2,$
there is
![]() $s_n$
in the support of
$s_n$
in the support of
![]() $c=f_\eta (a)-f_{\delta /2}(a).$
There is a Borel probability measure
$c=f_\eta (a)-f_{\delta /2}(a).$
There is a Borel probability measure
![]() $\mu _n$
on
$\mu _n$
on
![]() $[0,1]$
such that
$[0,1]$
such that
![]() $\mu ({{\{s_n\}}})=1.$
Let
$\mu ({{\{s_n\}}})=1.$
Let
![]() $\tau _{\mu _n}$
be the tracial state induced by
$\tau _{\mu _n}$
be the tracial state induced by
![]() $\mu _n,$
then
$\mu _n,$
then
![]() $\tau _{\mu _n}(f_{\eta /2}(a)-b)=1.$
This implies that
$\tau _{\mu _n}(f_{\eta /2}(a)-b)=1.$
This implies that
![]() $\omega (a)|_{S_a}=1.$
This also holds for any nonzero
$\omega (a)|_{S_a}=1.$
This also holds for any nonzero
![]() $g\in \mathrm {Her}(a)_+\subset A_+.$
In other words, for any
$g\in \mathrm {Her}(a)_+\subset A_+.$
In other words, for any
![]() $g\in \mathrm {Her}(a)_+, \omega (g)|_{S_a}=1.$
Therefore,
$g\in \mathrm {Her}(a)_+, \omega (g)|_{S_a}=1.$
Therefore,
![]() $\Omega ^T(a)=1.$
It follows
$\Omega ^T(a)=1.$
It follows
![]() $\mathbb {O}(A)=1.$
Recall that A has stable rank one.
$\mathbb {O}(A)=1.$
Recall that A has stable rank one.
Proposition 5.4 If A is a simple
![]() $C^*$
-algebra which has (T-) tracial approximate oscillation zero, then every hereditary
$C^*$
-algebra which has (T-) tracial approximate oscillation zero, then every hereditary
![]() $C^*$
-subalgebra of A also has (T-) tracial approximate oscillation zero.
$C^*$
-subalgebra of A also has (T-) tracial approximate oscillation zero.
Proof This follows from the definition immediately.
Definition 5.5 Let S be a compact subset of
![]() ${{{\widetilde {QT}}}}(A)\setminus \{0\}$
such that
${{{\widetilde {QT}}}}(A)\setminus \{0\}$
such that
![]() $\widetilde {QT}(A)={{\mathbb {R}_+}}\cdot S$
and
$\widetilde {QT}(A)={{\mathbb {R}_+}}\cdot S$
and
![]() $B\subset A$
be a hereditary
$B\subset A$
be a hereditary
![]() $C^*$
-subalgebra. A sequence of elements
$C^*$
-subalgebra. A sequence of elements
![]() $\{e_n\}\subset \mathrm {Ped}(B)_+^{\mathbf {1}}$
is said to be tracial approximate identity for
$\{e_n\}\subset \mathrm {Ped}(B)_+^{\mathbf {1}}$
is said to be tracial approximate identity for
![]() $B,$
if, for any
$B,$
if, for any
![]() $b\in B,$
$b\in B,$
and
![]() $\{e_n\}$
is said to be T-tracial approximate identity for B (relative to S), if, for any
$\{e_n\}$
is said to be T-tracial approximate identity for B (relative to S), if, for any
![]() $b\in B$
with
$b\in B$
with
![]() $\|b\|_{_{2, S}}<\infty ,$
$\|b\|_{_{2, S}}<\infty ,$
We do not require that
![]() $\{e_n\}$
is increasing.
$\{e_n\}$
is increasing.
Proposition 5.6 Let A be a
![]() $C^*$
-algebra,
$C^*$
-algebra,
![]() $a\in (A\otimes {\cal K})_+$
with
$a\in (A\otimes {\cal K})_+$
with
![]() $\|a\|_{_{2, S}}<\infty $
, and
$\|a\|_{_{2, S}}<\infty $
, and
![]() $S\subset {\widetilde {QT}}(A)\setminus \{0\}$
be a compact subset.
$S\subset {\widetilde {QT}}(A)\setminus \{0\}$
be a compact subset.
(1) Then
![]() $\Omega ^N(a)|_S=0$
if and only if
$\Omega ^N(a)|_S=0$
if and only if
![]() $\mathrm {Her}(a)$
has a (not necessarily increasing) approximate identity
$\mathrm {Her}(a)$
has a (not necessarily increasing) approximate identity
![]() $\{e_n\}$
such that
$\{e_n\}$
such that
![]() $\lim _{n\to \infty }\omega _n(e_n)|{{_S}}=0.$
$\lim _{n\to \infty }\omega _n(e_n)|{{_S}}=0.$
(2) Moreover,
![]() $\Omega ^T(a)|_S=0$
(or
$\Omega ^T(a)|_S=0$
(or
![]() $\Omega ^T_C(a)|_S=0$
) if and only if
$\Omega ^T_C(a)|_S=0$
) if and only if
![]() $\mathrm {Her}(a)$
admits a T-tracial (or tracial) approximate identity (relative to S)
$\mathrm {Her}(a)$
admits a T-tracial (or tracial) approximate identity (relative to S)
![]() $\{e_n\}$
with
$\{e_n\}$
with
![]() $\lim _{n\to \infty }\omega (e_n)|_S=0.$
$\lim _{n\to \infty }\omega (e_n)|_S=0.$
Proof For (1), let us assume that
![]() $\{e_n\}$
is a (not necessarily increasing) approximate identity for
$\{e_n\}$
is a (not necessarily increasing) approximate identity for
![]() $\mathrm {Her}(a)$
such that
$\mathrm {Her}(a)$
such that
![]() $\lim _{n\to \infty }\omega (e_n)=0.$
Then
$\lim _{n\to \infty }\omega (e_n)=0.$
Then
By Lemma 4.10,
![]() $ \omega (e_n^{1/2}ae_n^{1/2})|_S\le \omega (e_n)|_S\to 0. $
Thus,
$ \omega (e_n^{1/2}ae_n^{1/2})|_S\le \omega (e_n)|_S\to 0. $
Thus,
![]() $\Omega ^N(a)|_S=0.$
$\Omega ^N(a)|_S=0.$
Conversely, suppose that
![]() $a\in (A\otimes {\cal K})_+^{\mathbf {1}}$
and
$a\in (A\otimes {\cal K})_+^{\mathbf {1}}$
and
![]() $\{b_n\}\in l^\infty (\mathrm {Her}(a))_+$
such that
$\{b_n\}\in l^\infty (\mathrm {Her}(a))_+$
such that
Note that
![]() $\lim _{n\to \infty }\|b_n\|=\|a\|\le 1.$
Let
$\lim _{n\to \infty }\|b_n\|=\|a\|\le 1.$
Let
![]() $g\in C([0,\infty ))_+^{\mathbf {1}}$
such that
$g\in C([0,\infty ))_+^{\mathbf {1}}$
such that
![]() $g(t)=t$
if
$g(t)=t$
if
![]() $t\in [0, 1]$
and
$t\in [0, 1]$
and
![]() $g(t)=1$
if
$g(t)=1$
if
![]() $t>1.$
Then, for any
$t>1.$
Then, for any
![]() $n\in \mathbb {N}, g(b_n)\sim b_n.$
We also have
$n\in \mathbb {N}, g(b_n)\sim b_n.$
We also have
![]() $\lim _{n\to \infty }\|g(a)-g(b_n)\|=0.$
But
$\lim _{n\to \infty }\|g(a)-g(b_n)\|=0.$
But
![]() $g(a)=a.$
Then, replacing
$g(a)=a.$
Then, replacing
![]() $b_n$
by
$b_n$
by
![]() $g(b_n),$
we may assume that
$g(b_n),$
we may assume that
![]() $\|b_n\|\le 1.$
For each
$\|b_n\|\le 1.$
For each
![]() $k\in \mathbb {N},$
choose
$k\in \mathbb {N},$
choose
![]() $ {{n_k}}$
such that
$ {{n_k}}$
such that
Put
![]() $e_k=b_{n_k}^{1/k},\,k\in \mathbb {N}.$
Then, for any
$e_k=b_{n_k}^{1/k},\,k\in \mathbb {N}.$
Then, for any
![]() $x\in \mathrm {Her}(a),$
$x\in \mathrm {Her}(a),$
This shows that
![]() $\{e_k\}$
is a (not necessarily increasing) approximate identity for
$\{e_k\}$
is a (not necessarily increasing) approximate identity for
![]() $\mathrm {Her}(a).$
Since
$\mathrm {Her}(a).$
Since
![]() $e_k=b_{n_k}^{1/k},$
we have that
$e_k=b_{n_k}^{1/k},$
we have that
![]() $\omega (e_k)=\omega (b_{n_k})$
and
$\omega (e_k)=\omega (b_{n_k})$
and
For (2), let us prove one case.
Fix
![]() $a\in \mathrm {Ped}(A\otimes {\cal K})_+.$
Without loss of generality, we may assume that
$a\in \mathrm {Ped}(A\otimes {\cal K})_+.$
Without loss of generality, we may assume that
![]() $0\le a\le 1.$
Suppose that
$0\le a\le 1.$
Suppose that
![]() $\{e_n\}$
is a T-tracial approximate identity of
$\{e_n\}$
is a T-tracial approximate identity of
![]() $\mathrm {Her}(a)$
relative to
$\mathrm {Her}(a)$
relative to
![]() $S.$
Then
$S.$
Then
 $$ \begin{align*}\nonumber \lim_{n\to\infty}\| a-e_na\|_{_{2, S}}&=\lim_{n\to\infty}\| a-ae_n\|_{_{2, S}}=0\,\,\,\mathrm{and}\,\,\,\\\nonumber \lim_{n\to \infty}\| a-e_nae_n\|^{2/3}_{_{2, S}} &\le \lim_{n\to\infty}(\|a-e_na\|^{2/3}_{_{2, S}}+\|e_na-e_nae_n\|^{2/3}_{_{2, S}})\\\nonumber &\le\lim_{n\to\infty}\|e_n(a-ae_n)\|_{_{2,S}}^{2/3}\le \lim_{n\to\infty}(\|e_n^2\|^{{{1/3}}}\| a-ae_n\|_{_{2, S}}^{2/3})=0. \end{align*} $$
$$ \begin{align*}\nonumber \lim_{n\to\infty}\| a-e_na\|_{_{2, S}}&=\lim_{n\to\infty}\| a-ae_n\|_{_{2, S}}=0\,\,\,\mathrm{and}\,\,\,\\\nonumber \lim_{n\to \infty}\| a-e_nae_n\|^{2/3}_{_{2, S}} &\le \lim_{n\to\infty}(\|a-e_na\|^{2/3}_{_{2, S}}+\|e_na-e_nae_n\|^{2/3}_{_{2, S}})\\\nonumber &\le\lim_{n\to\infty}\|e_n(a-ae_n)\|_{_{2,S}}^{2/3}\le \lim_{n\to\infty}(\|e_n^2\|^{{{1/3}}}\| a-ae_n\|_{_{2, S}}^{2/3})=0. \end{align*} $$
By Lemma 4.10,
![]() $\omega (e_nae_n)|_S\le \omega (e_n^2)|_S=\omega (e_n)|_S\to 0.$
Thus,
$\omega (e_nae_n)|_S\le \omega (e_n^2)|_S=\omega (e_n)|_S\to 0.$
Thus,
![]() $\Omega ^T(a)|_S=0.$
$\Omega ^T(a)|_S=0.$
Conversely, suppose that
![]() $\Omega ^T(a)|_S=0.$
Then, by Proposition 4.8, there exists
$\Omega ^T(a)|_S=0.$
Then, by Proposition 4.8, there exists
![]() $\{b_n\}\subset {{\mathrm {Ped}(\mathrm {Her}(a))}}_+^{\mathbf {1}}$
such that
$\{b_n\}\subset {{\mathrm {Ped}(\mathrm {Her}(a))}}_+^{\mathbf {1}}$
such that
Let
![]() $B=\mathrm {Her}(a)$
and
$B=\mathrm {Her}(a)$
and
![]() $\Pi _S: l^\infty (B)\to l^\infty (B)/I_{_{S,B}}$
be the quotient map (see Definition 4.7 for
$\Pi _S: l^\infty (B)\to l^\infty (B)/I_{_{S,B}}$
be the quotient map (see Definition 4.7 for
![]() $I_{_{S,B}}$
). Then
$I_{_{S,B}}$
). Then
For each
![]() $k\in \mathbb {N},$
we have
$k\in \mathbb {N},$
we have
It follows that, for each
![]() $k\in \mathbb {N},$
there exists
$k\in \mathbb {N},$
there exists
![]() $n(k)\in \mathbb {N}$
such that
$n(k)\in \mathbb {N}$
such that
Choose
![]() $e_k=b_{n(k)}^{1/k}, k\in \mathbb {N}.$
Then, for any
$e_k=b_{n(k)}^{1/k}, k\in \mathbb {N}.$
Then, for any
![]() $c\in \mathrm {Her}(a),$
$c\in \mathrm {Her}(a),$
Since
![]() $b_{n(k)}\sim e_k,$
$b_{n(k)}\sim e_k,$
The proposition then follows.
Proposition 5.7 Let A be a
![]() $\sigma $
-unital
$\sigma $
-unital
![]() $C^*$
-algebra, let
$C^*$
-algebra, let
![]() $S\subset \widetilde {QT}(A)$
be a compact subset, and let
$S\subset \widetilde {QT}(A)$
be a compact subset, and let
![]() $a\in {{\mathrm {Ped}(A\otimes {\cal K})_+.}}$
Then
$a\in {{\mathrm {Ped}(A\otimes {\cal K})_+.}}$
Then
![]() $\Omega ^T(a)|_S=0$
if and only if
$\Omega ^T(a)|_S=0$
if and only if
![]() $\Omega ^N(a)|_S=0.$
$\Omega ^N(a)|_S=0.$
Proof For the “if” part, let us assume
![]() $ \Omega ^N(a)|_S=0.$
By the definition there is
$ \Omega ^N(a)|_S=0.$
By the definition there is
![]() $\{b_n\}\in l^\infty (\mathrm {Her}(a))_+$
such that
$\{b_n\}\in l^\infty (\mathrm {Her}(a))_+$
such that
![]() $ \omega (b_n)|_S<1/n$
and
$ \omega (b_n)|_S<1/n$
and
![]() $\|a-b_n\|< 1/n.$
Let
$\|a-b_n\|< 1/n.$
Let
![]() $b_n'=\frac {\|a\|b_n}{\|b_n\|+1/n}.$
Then
$b_n'=\frac {\|a\|b_n}{\|b_n\|+1/n}.$
Then
![]() $\|b_n'\|\leq \|a\|,$
$\|b_n'\|\leq \|a\|,$
For the “only if” part, let us assume that
![]() $\Omega ^T(a)|_S=0.$
Then, by Proposition 5.6, there are
$\Omega ^T(a)|_S=0.$
Then, by Proposition 5.6, there are
![]() $e_n\in {{\mathrm {Her}(a)}}_+^{\mathbf {1}}$
such that
$e_n\in {{\mathrm {Her}(a)}}_+^{\mathbf {1}}$
such that
It follows that
![]() $\{b_n\}=\{a-a^{1/2}e_na^{1/2}\}\in {{(I_{_{S}})_+}}$
(see Definition 2.16 for the definition of
$\{b_n\}=\{a-a^{1/2}e_na^{1/2}\}\in {{(I_{_{S}})_+}}$
(see Definition 2.16 for the definition of
![]() $I_{_{S}}$
). By (4) of Proposition 4.8, there exists
$I_{_{S}}$
). By (4) of Proposition 4.8, there exists
![]() $\{c_n\}\in (I_{_{S}})_{{+}}$
such that
$\{c_n\}\in (I_{_{S}})_{{+}}$
such that
Put
![]() $d_n=a^{1/2}e_na^{1/2}+c_n, n\in \mathbb {N}.$
Then
$d_n=a^{1/2}e_na^{1/2}+c_n, n\in \mathbb {N}.$
Then
![]() $d_n\ge 0.$
Put
$d_n\ge 0.$
Put
![]() ${\bar {d_n}}={\|a\| d_n\over {\|d_n\|+1/n}}, n\in \mathbb {N}.$
Then
${\bar {d_n}}={\|a\| d_n\over {\|d_n\|+1/n}}, n\in \mathbb {N}.$
Then
![]() $\|{\bar d}_n\|\le \|a\|$
for all
$\|{\bar d}_n\|\le \|a\|$
for all
![]() $n\in \mathbb {N}.$
Since
$n\in \mathbb {N}.$
Since
![]() $\lim _{n\to \infty }\|a-d_n\|=0,$
we have
$\lim _{n\to \infty }\|a-d_n\|=0,$
we have
![]() $\lim _{n\to \infty }\|d_n\|=\|a\|.$
It follows that
$\lim _{n\to \infty }\|d_n\|=\|a\|.$
It follows that
On the other hand, by Proposition 4.4(1) (see also (2) of Proposition 2.10) for all
![]() $\tau \in S$
,
$\tau \in S$
,
for all
![]() $n\in \mathbb {N}.$
By Lemma 4.10,
$n\in \mathbb {N}.$
By Lemma 4.10,
![]() $\lim _{n\to \infty }\omega (a^{1/2}e_na^{1/2}) =\lim _{n\to \infty }\omega (e_n)=0.$
By the fact that
$\lim _{n\to \infty }\omega (a^{1/2}e_na^{1/2}) =\lim _{n\to \infty }\omega (e_n)=0.$
By the fact that
![]() $\bar d_n\sim d_n$
and Proposition 4.2, we have
$\bar d_n\sim d_n$
and Proposition 4.2, we have
 $$ \begin{align} \lim_{n\to\infty}\omega({\bar d}_n) &= \lim_{n\to\infty}\omega(d_n) \overset{(4.9)}{=} \lim_{n\to\infty}\sup_{\tau\in S}\{ \omega(d_n)(\tau)|_S\}\nonumber \\&\overset{(5.19)}{\leq} \lim_{n\to\infty}\omega(a^{1/2}e_na^{1/2} )|_S+ \lim_{n\to\infty}\sup\{d_\tau(c_n): \tau\in S\}=0. \end{align} $$
$$ \begin{align} \lim_{n\to\infty}\omega({\bar d}_n) &= \lim_{n\to\infty}\omega(d_n) \overset{(4.9)}{=} \lim_{n\to\infty}\sup_{\tau\in S}\{ \omega(d_n)(\tau)|_S\}\nonumber \\&\overset{(5.19)}{\leq} \lim_{n\to\infty}\omega(a^{1/2}e_na^{1/2} )|_S+ \lim_{n\to\infty}\sup\{d_\tau(c_n): \tau\in S\}=0. \end{align} $$
Let us present some examples of
![]() $C^*$
-algebras which have norm approximate oscillation zero.
$C^*$
-algebras which have norm approximate oscillation zero.
Proposition 5.8 Let A be a
![]() $C^*$
-algebra of real rank zero. Then A has norm approximate oscillation zero.
$C^*$
-algebra of real rank zero. Then A has norm approximate oscillation zero.
Proof Let
![]() $a\in \mathrm {Ped}(A)$
with
$a\in \mathrm {Ped}(A)$
with
![]() $0\le a \le 1.$
Put
$0\le a \le 1.$
Put
![]() $B=\mathrm {Her}(a).$
Then B has an approximate identity
$B=\mathrm {Her}(a).$
Then B has an approximate identity
![]() $\{e_n\}$
consisting of projections. Note that, since
$\{e_n\}$
consisting of projections. Note that, since
![]() $e_n$
is a projection,
$e_n$
is a projection,
![]() $\widehat {[ e_n]}=\widehat {e_n}$
is continuous on
$\widehat {[ e_n]}=\widehat {e_n}$
is continuous on
![]() $S.$
The proposition follows from Proposition 5.6.
$S.$
The proposition follows from Proposition 5.6.
Let
![]() $T_b=\{s\in {\widetilde {QT}}(A): s(b)=1\}$
for some nonzero
$T_b=\{s\in {\widetilde {QT}}(A): s(b)=1\}$
for some nonzero
![]() $b\in (\mathrm {Ped}(A\otimes {\cal K}))_+.$
It is a compact convex subset and
$b\in (\mathrm {Ped}(A\otimes {\cal K}))_+.$
It is a compact convex subset and
![]() $T_b$
is a basis for the cone
$T_b$
is a basis for the cone
![]() ${{\widetilde {QT}}}(A)$
if A is simple. The proof of the following is taken from Lemma 4.8 of [Reference Lin20] (see also Remark 4.7 of [Reference Lin20]).
${{\widetilde {QT}}}(A)$
if A is simple. The proof of the following is taken from Lemma 4.8 of [Reference Lin20] (see also Remark 4.7 of [Reference Lin20]).
Theorem 5.9 Let A be a
![]() $C^*$
-algebra with countable
$C^*$
-algebra with countable
![]() $\partial _e(T_b)$
(for some
$\partial _e(T_b)$
(for some
![]() $b\in \mathrm {Ped}(A)_+\setminus \{0\}$
), where
$b\in \mathrm {Ped}(A)_+\setminus \{0\}$
), where
![]() $\partial _e(T_b)$
is the set of extremal points of
$\partial _e(T_b)$
is the set of extremal points of
![]() $T_b.$
Then
$T_b.$
Then
In particular, A has norm approximate oscillation zero.
Proof We may assume that
![]() $a\in \mathrm {Ped}(A\otimes {\cal K})_+\setminus \{0\}$
and
$a\in \mathrm {Ped}(A\otimes {\cal K})_+\setminus \{0\}$
and
![]() $0\le a\le 1.$
If
$0\le a\le 1.$
If
![]() $0\in \overline {{{\mathbb {R}_+}}\setminus \mathrm {sp}(a)},$
then
$0\in \overline {{{\mathbb {R}_+}}\setminus \mathrm {sp}(a)},$
then
![]() $\Omega ^N(a)=0.$
To see this, let
$\Omega ^N(a)=0.$
To see this, let
![]() $s_n\in \mathbb {R}_+\setminus \mathrm {sp}(a)$
such that
$s_n\in \mathbb {R}_+\setminus \mathrm {sp}(a)$
such that
![]() $s_n\searrow 0.$
Then the characteristic function
$s_n\searrow 0.$
Then the characteristic function
![]() $\chi _{[s_n, 1]}$
is continuous on
$\chi _{[s_n, 1]}$
is continuous on
![]() $\mathrm {sp}(a).$
Therefore,
$\mathrm {sp}(a).$
Therefore,
![]() $p_n=\chi _{[s_n, 1]}(a)\in C^*(a)\subset \mathrm {Her}(a)$
is a projection. Note that
$p_n=\chi _{[s_n, 1]}(a)\in C^*(a)\subset \mathrm {Her}(a)$
is a projection. Note that
![]() $p_n\le p_{n+1}$
for all
$p_n\le p_{n+1}$
for all
![]() $n\in \mathbb {N}.$
Then
$n\in \mathbb {N}.$
Then
In other words,
![]() $\{p_n\}$
is an approximate identity for
$\{p_n\}$
is an approximate identity for
![]() $\mathrm {Her}(a).$
Moreover,
$\mathrm {Her}(a).$
Moreover,
![]() $\omega (p_n)=0.$
So this case follows from Proposition 5.6.
$\omega (p_n)=0.$
So this case follows from Proposition 5.6.
Therefore, without loss of generality, we may assume that
![]() $[0,r]\subset \mathrm {sp}(a)$
for some
$[0,r]\subset \mathrm {sp}(a)$
for some
![]() $0<r<1.$
Let
$0<r<1.$
Let
![]() $r/2>\eta >0.$
$r/2>\eta >0.$
Note that, since
![]() $a\in \mathrm {Ped}(A\otimes {\cal K})_+, \sup \{d_\tau (a): \tau \in T_b\}=M<\infty $
(see Proposition 2.10). For each
$a\in \mathrm {Ped}(A\otimes {\cal K})_+, \sup \{d_\tau (a): \tau \in T_b\}=M<\infty $
(see Proposition 2.10). For each
![]() $\tau \in \partial _e(T_b), \tau $
induces a Borel measure
$\tau \in \partial _e(T_b), \tau $
induces a Borel measure
![]() $\mu _\tau $
on
$\mu _\tau $
on
![]() $\mathrm {sp}(a)$
which is bounded by
$\mathrm {sp}(a)$
which is bounded by
![]() $M.$
$M.$
We claim that there is
![]() $s\in ( r-\eta , r]$
such that
$s\in ( r-\eta , r]$
such that
To see this, write
![]() $\partial _e(T_b)=\{\tau _n\}_{n\in \mathbb {N}'},$
where
$\partial _e(T_b)=\{\tau _n\}_{n\in \mathbb {N}'},$
where
![]() $\mathbb {N}'$
is a subset of
$\mathbb {N}'$
is a subset of
![]() $\mathbb {N}.$
For each
$\mathbb {N}.$
For each
![]() $k\in \mathbb {N}',$
and
$k\in \mathbb {N}',$
and
![]() $n\in \mathbb {N},$
define
$n\in \mathbb {N},$
define
Since
![]() $\mu _{\tau _k}(\mathrm {sp}(a))\le M, S_{k,n}$
must be finite. It follows that
$\mu _{\tau _k}(\mathrm {sp}(a))\le M, S_{k,n}$
must be finite. It follows that
![]() $S_k=\cup _{n=1}^\infty S_{k,n}$
is countable. Thus,
$S_k=\cup _{n=1}^\infty S_{k,n}$
is countable. Thus,
![]() $S=\cup _{k\in \mathbb {N}'}S_k$
is countable. Therefore, there must be
$S=\cup _{k\in \mathbb {N}'}S_k$
is countable. Therefore, there must be
![]() $s\in (r-\eta , r]$
such that
$s\in (r-\eta , r]$
such that
![]() $s\not \in S.$
In other words, there must be
$s\not \in S.$
In other words, there must be
![]() $s\in (r-\eta ,r]$
such that
$s\in (r-\eta ,r]$
such that
Since
![]() $T_b$
is compact, by the Krein–Milman theorem, this implies that
$T_b$
is compact, by the Krein–Milman theorem, this implies that
This proves the claim.
By the claim, for each integer
![]() $n\in \mathbb {N},$
there is
$n\in \mathbb {N},$
there is
![]() $\delta>0$
such that
$\delta>0$
such that
![]() $1/2^{n+1}<\delta <1/2^n$
and
$1/2^{n+1}<\delta <1/2^n$
and
Note that
is a lower semi-continuous function. By Portmanteau Theorem, the function
![]() $h: T_b\to \mathbb {R}_+$
given by
$h: T_b\to \mathbb {R}_+$
given by
is an upper semi-continuous function.Footnote 1
By (e5.27),
It follows that
![]() $d_\tau ({{(a-\delta )_+}})$
is continuous.
$d_\tau ({{(a-\delta )_+}})$
is continuous.
To prove the lemma, let
![]() $\varepsilon>0.$
Choose
$\varepsilon>0.$
Choose
![]() $n\in \mathbb {N}$
such that
$n\in \mathbb {N}$
such that
![]() $1/2^n<\varepsilon .$
Choose
$1/2^n<\varepsilon .$
Choose
![]() $1/2^{n+1}<\delta _n<1/2^n$
such that
$1/2^{n+1}<\delta _n<1/2^n$
such that
![]() $\mu _\tau (\{\delta _n\})=0$
for all
$\mu _\tau (\{\delta _n\})=0$
for all
![]() $\tau \in S$
as above. Put
$\tau \in S$
as above. Put
![]() $d_n={{(a-\delta _n)_+.}}$
Then
$d_n={{(a-\delta _n)_+.}}$
Then
Since
![]() $d_\tau (d_n)=d_\tau ({{(a-\delta _n)_+}}),$
we have that
$d_\tau (d_n)=d_\tau ({{(a-\delta _n)_+}}),$
we have that
![]() $\omega ({{d_n}})(\tau )|_{T_b}=0$
for all
$\omega ({{d_n}})(\tau )|_{T_b}=0$
for all
![]() $\tau \in T_b.$
The lemma follows.
$\tau \in T_b.$
The lemma follows.
The following is a restatement of Lemma 7.2 of [Reference Elliott, Gong, Lin and Niu10] with the same proof (and with some necessary modification and correcting a typo).
Theorem 5.10 Let A be a
![]() $\sigma $
-unital simple
$\sigma $
-unital simple
![]() $C^*$
-algebra which has strict comparison and almost stable rank one. Suppose that the canonical map
$C^*$
-algebra which has strict comparison and almost stable rank one. Suppose that the canonical map
![]() $\Gamma : \mathrm {Cu}(A)\to \mathrm {LAff}_+({\widetilde {QT}}(A))$
is surjective (see Definition 2.13). Then A has norm approximate oscillation zero.
$\Gamma : \mathrm {Cu}(A)\to \mathrm {LAff}_+({\widetilde {QT}}(A))$
is surjective (see Definition 2.13). Then A has norm approximate oscillation zero.
Proof Let
![]() $e_A\in \mathrm {Ped}(A)_+\setminus \{0\}$
and
$e_A\in \mathrm {Ped}(A)_+\setminus \{0\}$
and
![]() $A_1=\mathrm {Her}(e_A).$
Then
$A_1=\mathrm {Her}(e_A).$
Then
![]() $\mathrm {Ped}(A_1)=A_1.$
Since A is
$\mathrm {Ped}(A_1)=A_1.$
Since A is
![]() $\sigma $
-unital,
$\sigma $
-unital,
![]() $A\otimes {\cal K}\cong A_1\otimes {\cal K}$
by Brown’s stable isomorphism theorem [Reference Brown4]. Therefore, it suffices to show that
$A\otimes {\cal K}\cong A_1\otimes {\cal K}$
by Brown’s stable isomorphism theorem [Reference Brown4]. Therefore, it suffices to show that
![]() $A_1$
has norm approximate oscillation zero. To simplify notation, we may assume that
$A_1$
has norm approximate oscillation zero. To simplify notation, we may assume that
![]() $A=A_1$
(and
$A=A_1$
(and
![]() $A=\mathrm {Ped}(A)$
).
$A=\mathrm {Ped}(A)$
).
Let
![]() $a\in \mathrm {Ped}(A\otimes {\cal K})_+^{\mathbf {1}}.$
It follows from the proof of Lemma 7.2 of [Reference Elliott, Gong, Lin and Niu10] that, since
$a\in \mathrm {Ped}(A\otimes {\cal K})_+^{\mathbf {1}}.$
It follows from the proof of Lemma 7.2 of [Reference Elliott, Gong, Lin and Niu10] that, since
![]() $\mathrm {Her}(a)$
also has strict comparison, almost stable rank one, and
$\mathrm {Her}(a)$
also has strict comparison, almost stable rank one, and
![]() $\Gamma $
is surjective,
$\Gamma $
is surjective,
![]() $\mathrm {Her}(a)$
has an approximate identity consisting of elements
$\mathrm {Her}(a)$
has an approximate identity consisting of elements
![]() $\{e_n\}$
such that
$\{e_n\}$
such that
![]() $\widehat {e_n}$
is continuous on
$\widehat {e_n}$
is continuous on
![]() $\overline {QT(A)}^w.$
Then the theorem follows from Proposition 5.6. Since we do not assume that
$\overline {QT(A)}^w.$
Then the theorem follows from Proposition 5.6. Since we do not assume that
![]() $QT(A)=T(A),$
to be complete, let us repeat some of the argument in the proof of Lemma 7.2 of [Reference Elliott, Gong, Lin and Niu10] which will be, again, used in the proof of Lemma 8.9.
$QT(A)=T(A),$
to be complete, let us repeat some of the argument in the proof of Lemma 7.2 of [Reference Elliott, Gong, Lin and Niu10] which will be, again, used in the proof of Lemma 8.9.
By Proposition 5.6, it suffices to show that, for any
![]() $\varepsilon \in (0, 1/2),$
there is
$\varepsilon \in (0, 1/2),$
there is
![]() $e\in \mathrm {Her}(a)_+^{\mathbf {1}}$
such that
$e\in \mathrm {Her}(a)_+^{\mathbf {1}}$
such that
![]() $f_\varepsilon (a)\le e$
and
$f_\varepsilon (a)\le e$
and
![]() $\widehat {[e]}$
is continuous. By the first part of the proof of Theorem 5.9, we may assume that
$\widehat {[e]}$
is continuous. By the first part of the proof of Theorem 5.9, we may assume that
![]() $[0,\varepsilon _0)\subset \mathrm {sp}(a)$
for some
$[0,\varepsilon _0)\subset \mathrm {sp}(a)$
for some
![]() $\varepsilon _0\in (0, \varepsilon ).$
$\varepsilon _0\in (0, \varepsilon ).$
Note that, without loss of generality, we may assume that
where
![]() $\varepsilon /4>\delta _1, \delta _1/2>\eta _1, \eta _1/2>\delta _2,$
and
$\varepsilon /4>\delta _1, \delta _1/2>\eta _1, \eta _1/2>\delta _2,$
and
![]() $\delta _2/2>\eta >0.$
Put
$\delta _2/2>\eta >0.$
Put
![]() $h_i(\tau )=\tau (f_{\delta _i}(a))\,\,\,\mathrm {for\,\,\,all}\,\,\, \tau \in {{\overline {QT(A)}^w}} , i=1,2.$
Then
$h_i(\tau )=\tau (f_{\delta _i}(a))\,\,\,\mathrm {for\,\,\,all}\,\,\, \tau \in {{\overline {QT(A)}^w}} , i=1,2.$
Then
![]() $h_i\in \operatorname {Aff}_+(\overline {QT(A)}^w).$
Since
$h_i\in \operatorname {Aff}_+(\overline {QT(A)}^w).$
Since
![]() $\Gamma $
is surjective, there is
$\Gamma $
is surjective, there is
![]() $c\in (A\otimes {\cal K})_+^{{\mathbf {1}}}$
such that
$c\in (A\otimes {\cal K})_+^{{\mathbf {1}}}$
such that
![]() $d_\tau (c)=h_2(\tau )$
for all
$d_\tau (c)=h_2(\tau )$
for all
![]() $\tau \in \overline {QT(A)}^w.$
Since A has strict comparison, (e5.32) and the choice of c implies
$\tau \in \overline {QT(A)}^w.$
Since A has strict comparison, (e5.32) and the choice of c implies
![]() $c\lesssim f_{\eta }(a).$
Since A has almost stable rank one, by Lemma 3.2 of [Reference Elliott, Gong, Lin and Niu10] and (e5.32), there is
$c\lesssim f_{\eta }(a).$
Since A has almost stable rank one, by Lemma 3.2 of [Reference Elliott, Gong, Lin and Niu10] and (e5.32), there is
![]() $x\in A\otimes {\cal K}$
such that
$x\in A\otimes {\cal K}$
such that
Put
![]() $c_0=xx^*.$
Then
$c_0=xx^*.$
Then
![]() $0\le c_0\le 1.$
Note that
$0\le c_0\le 1.$
Note that
![]() $d_\tau (c_0)=d_\tau (c)$
for all
$d_\tau (c_0)=d_\tau (c)$
for all
![]() $\tau \in \overline {QT(A)}^w.$
Since
$\tau \in \overline {QT(A)}^w.$
Since
![]() $h_1$
is continuous,
$h_1$
is continuous,
![]() $h_1(\tau )<h_2(\tau )= d_\tau (c)=d_\tau (c_0)=\lim _{n\to \infty }\tau (f_{1/n}(c_0))$
for all
$h_1(\tau )<h_2(\tau )= d_\tau (c)=d_\tau (c_0)=\lim _{n\to \infty }\tau (f_{1/n}(c_0))$
for all
![]() $\tau \in \overline {QT(A)}^w,$
and
$\tau \in \overline {QT(A)}^w,$
and
![]() $\overline {QT(A)}^w$
is compact, there is an integer
$\overline {QT(A)}^w$
is compact, there is an integer
![]() $m>2$
such that
$m>2$
such that
By (e5.32) and Lemma 3.2 of [Reference Elliott, Gong, Lin and Niu10], there is a unitary u in the unitization of
![]() $\mathrm {Her}(f_{\eta }(a))$
such that
$\mathrm {Her}(f_{\eta }(a))$
such that
Set
![]() $c_1=uc_0u^*.$
Then
$c_1=uc_0u^*.$
Then
There is
![]() $g\in C_0((0,1])$
such that
$g\in C_0((0,1])$
such that
![]() $0\le g\le 1, g(t)>0$
for all
$0\le g\le 1, g(t)>0$
for all
![]() $t\in (0,1],$
and
$t\in (0,1],$
and
Put
![]() $e=g(c_1).$
Then
$e=g(c_1).$
Then
![]() $[e]=[ c_1]=[ c_0] = [ c].$
In particular,
$[e]=[ c_1]=[ c_0] = [ c].$
In particular,
![]() $d_\tau (e)$
is continuous on
$d_\tau (e)$
is continuous on
![]() $\overline {QT(A)}^w.$
But we also have, by (e5.36),
$\overline {QT(A)}^w.$
But we also have, by (e5.36),
This completes the proof.
6
 $C^*$
-algebra
$C^*$
-algebra
 $l^\infty (A)/I_{_{\overline {QT(A)}^w}}$
$l^\infty (A)/I_{_{\overline {QT(A)}^w}}$
Definition 6.1 Let A be a compact
![]() $C^*$
-algebra, and let
$C^*$
-algebra, and let
![]() $p\in l^\infty (A)/I_{_{\overline {QT(A)}^w}}$
(or in
$p\in l^\infty (A)/I_{_{\overline {QT(A)}^w}}$
(or in
![]() $l^\infty (A)/N_{cu}(A)$
) be a projection and
$l^\infty (A)/N_{cu}(A)$
) be a projection and
![]() $\{e_n\}\in l^\infty (A)_+^{\mathbf {1}}$
such that
$\{e_n\}\in l^\infty (A)_+^{\mathbf {1}}$
such that
![]() $\Pi (\{e_n\})=p$
(recall that
$\Pi (\{e_n\})=p$
(recall that
![]() $\Pi : l^\infty (A)\to l^\infty (A)/I_{_{\overline {QT(A)}^w}}$
is the quotient map). The sequence
$\Pi : l^\infty (A)\to l^\infty (A)/I_{_{\overline {QT(A)}^w}}$
is the quotient map). The sequence
![]() $\{e_n\}$
is said to be a permanent projection lifting, if for any sequence of positive integers
$\{e_n\}$
is said to be a permanent projection lifting, if for any sequence of positive integers
![]() $\{m(n)\},$
$\{m(n)\},$
Proposition 6.2 Let A be a compact
![]() $C^*$
-algebra with
$C^*$
-algebra with
![]() ${\widetilde {QT}}(A)\setminus \{0\}\not =\emptyset $
and
${\widetilde {QT}}(A)\setminus \{0\}\not =\emptyset $
and
![]() $\{e_n\}\in l^\infty (A)_+^{\mathbf {1}}.$
$\{e_n\}\in l^\infty (A)_+^{\mathbf {1}}.$
(1) Let
![]() $p=\Pi (\{e_n\})$
(or
$p=\Pi (\{e_n\})$
(or
![]() $p=\Pi _{cu}(\{e_n\})$
) be a projection. Then
$p=\Pi _{cu}(\{e_n\})$
) be a projection. Then
![]() $\{f_{\delta }(e_n)\}$
is a permanent projection lifting of p for any
$\{f_{\delta }(e_n)\}$
is a permanent projection lifting of p for any
![]() $0<\delta <1/2$
(for both cases) and
$0<\delta <1/2$
(for both cases) and
(2) If
![]() $\{e_n\}$
is a permanent projection lifting, then
$\{e_n\}$
is a permanent projection lifting, then
![]() $\lim _{n\to \infty }\omega (e_n)=0.$
Moreover, an element
$\lim _{n\to \infty }\omega (e_n)=0.$
Moreover, an element
![]() $\{e_n\}$
is a permanent projection lifting (from
$\{e_n\}$
is a permanent projection lifting (from
![]() $l ^\infty (A)/I_{_{\overline {QT(A)}^w}}$
) if and only if
$l ^\infty (A)/I_{_{\overline {QT(A)}^w}}$
) if and only if
(3) If
![]() $\{e_n\}\in l^\infty (A)_+^{\mathbf {1}}$
and
$\{e_n\}\in l^\infty (A)_+^{\mathbf {1}}$
and
![]() $\lim _{n\to \infty }\omega (e_n)=0$
, then for some
$\lim _{n\to \infty }\omega (e_n)=0$
, then for some
![]() $l(k)\in \mathbb {N}, p=\Pi (\{e_k^{{{1/l(k)}}}\})$
is a projection, and
$l(k)\in \mathbb {N}, p=\Pi (\{e_k^{{{1/l(k)}}}\})$
is a projection, and
![]() $\{e_k^{{{1/{l(k)}}}}\}$
is a permanent projection lifting of
$\{e_k^{{{1/{l(k)}}}}\}$
is a permanent projection lifting of
![]() $p.$
$p.$
(4) Suppose that
![]() ${{p=}}\Pi _{{{cu}}}(\{e_n\})$
is a projection for some
${{p=}}\Pi _{{{cu}}}(\{e_n\})$
is a projection for some
![]() $\{e_n\}\in l^\infty (A)_+^{\mathbf {1}}.$
Then
$\{e_n\}\in l^\infty (A)_+^{\mathbf {1}}.$
Then
![]() $\{e_n\}$
is a permanent projection lifting (from
$\{e_n\}$
is a permanent projection lifting (from
![]() $l ^\infty (A)/N_{cu}$
) if
$l ^\infty (A)/N_{cu}$
) if
![]() $g_\delta (e_n)\stackrel {c.}{\to } 0$
for some
$g_\delta (e_n)\stackrel {c.}{\to } 0$
for some
![]() $\delta \in (0,1/4).$
$\delta \in (0,1/4).$
(5) If
![]() $\{e_n\}$
is a permanent projection lifting of
$\{e_n\}$
is a permanent projection lifting of
![]() $p \in l^\infty (A)/I_{_{\overline {QT(A)}^w}},$
then
$p \in l^\infty (A)/I_{_{\overline {QT(A)}^w}},$
then
(see Definition 2.15 for
![]() $l^\infty (\{\mathrm {Her}(e_n)\})$
).
$l^\infty (\{\mathrm {Her}(e_n)\})$
).
(6) If A is algebraically simple and
![]() $QT(A)\not =\emptyset $
and
$QT(A)\not =\emptyset $
and
![]() $e\in A_+^{\mathbf {1}}$
is a strictly positive element such that
$e\in A_+^{\mathbf {1}}$
is a strictly positive element such that
![]() $\widehat {{{[e]}}}$
is continuous on
$\widehat {{{[e]}}}$
is continuous on
![]() $\overline {QT(A)}^w,$
then
$\overline {QT(A)}^w,$
then
![]() $l^\infty (A)/I_{_{\overline {QT(A)}^w}}$
is unital.
$l^\infty (A)/I_{_{\overline {QT(A)}^w}}$
is unital.
(7) A
![]() $\sigma $
-unital simple
$\sigma $
-unital simple
![]() $C^*$
-algebra A has continuous scale if and only if
$C^*$
-algebra A has continuous scale if and only if
![]() $l^\infty (A)/N_{cu}$
is unital.
$l^\infty (A)/N_{cu}$
is unital.
Proof (1) Note that
![]() $\Pi (f_\delta (\{e_n\}))=f_\delta (\Pi (\{e_n\}))=p$
for any
$\Pi (f_\delta (\{e_n\}))=f_\delta (\Pi (\{e_n\}))=p$
for any
![]() $0<\delta <1/2.$
Therefore,
$0<\delta <1/2.$
Therefore,
![]() $\Pi (f_{\delta /2}(\{e_n\}))=p.$
Put
$\Pi (f_{\delta /2}(\{e_n\}))=p.$
Put
![]() $b_n=f_\delta (e_n), n\in \mathbb {N}.$
For any integers
$b_n=f_\delta (e_n), n\in \mathbb {N}.$
For any integers
![]() $\{m(n)\},$
we have
$\{m(n)\},$
we have
It follows that
This proves the first part of (1) (the proof for
![]() $p=\Pi _{cu}(\{f_\delta (e_n)\})$
is similar).
$p=\Pi _{cu}(\{f_\delta (e_n)\})$
is similar).
Since
![]() $\Pi (\{f_{\delta }(e_n)\})=p$
(or
$\Pi (\{f_{\delta }(e_n)\})=p$
(or
![]() $\Pi _{cu}(\{f_\delta (e_n)\})=p$
), we have
$\Pi _{cu}(\{f_\delta (e_n)\})=p$
), we have
Part (1) follows.
(2) If
then, for any
![]() $\{m(n)\}{{\ \subset \mathbb {N}}},$
$\{m(n)\}{{\ \subset \mathbb {N}}},$
It follows that
![]() $\{e_n^{1/m(n)}-e_n^2\}\in I_{_{\overline {QT(A)}^w}}.$
Since
$\{e_n^{1/m(n)}-e_n^2\}\in I_{_{\overline {QT(A)}^w}}.$
Since
![]() $e_n^2\le e_n$
for all
$e_n^2\le e_n$
for all
![]() $n\in \mathbb {N},$
this also implies that
$n\in \mathbb {N},$
this also implies that
![]() $\{e_n-e_n^2\}\in I_{_{\overline {QT(A)}^w}}.$
Hence,
$\{e_n-e_n^2\}\in I_{_{\overline {QT(A)}^w}}.$
Hence,
![]() $\Pi (\{e_n\})$
is a projection and
$\Pi (\{e_n\})$
is a projection and
![]() $\{e_n\}$
is a permanent projection lifting.
$\{e_n\}$
is a permanent projection lifting.
Now suppose that
![]() $\{e_n\}$
is a permanent projection lifting of
$\{e_n\}$
is a permanent projection lifting of
![]() $p=\Pi (\{e_n\}).$
Let us show first that
$p=\Pi (\{e_n\}).$
Let us show first that
![]() $\lim _{n\to \infty }\omega (e_n)=0.$
Otherwise, there exists a subsequence
$\lim _{n\to \infty }\omega (e_n)=0.$
Otherwise, there exists a subsequence
![]() $\{l(k)\}$
such that
$\{l(k)\}$
such that
![]() $\omega (e_{l(k)})>\sigma $
for some
$\omega (e_{l(k)})>\sigma $
for some
![]() $\sigma>0.$
Fix any
$\sigma>0.$
Fix any
![]() $\delta \in (0,1/4).$
By Proposition 4.6, for each of these
$\delta \in (0,1/4).$
By Proposition 4.6, for each of these
![]() $l(k),$
there are
$l(k),$
there are
![]() $m(l(k))$
such that
$m(l(k))$
such that
Choose a sequence
![]() $m(n)$
of integers which extends
$m(n)$
of integers which extends
![]() $m(l(k)).$
Then
$m(l(k)).$
Then
Therefore,
![]() $\Pi (\{e_n^{1/m(n)}\})\not =\Pi (f_\delta (\{e_n\}))=p.$
A contradiction. Hence,
$\Pi (\{e_n^{1/m(n)}\})\not =\Pi (f_\delta (\{e_n\}))=p.$
A contradiction. Hence,
![]() $\lim _{n\to \infty }\omega (e_n)=0.$
$\lim _{n\to \infty }\omega (e_n)=0.$
Therefore, there exists a sequence
![]() $\{m(n)\}$
such that
$\{m(n)\}$
such that
Then, since
![]() $\{(e_n^{1/m(n)}-e_n^2)^{1/2}\}\in I_{_{\overline {QT(A)}^w}}$
(for any
$\{(e_n^{1/m(n)}-e_n^2)^{1/2}\}\in I_{_{\overline {QT(A)}^w}}$
(for any
![]() $\{m(n)\}$
), we also have that
$\{m(n)\}$
), we also have that
 $$ \begin{align}\nonumber &\sup\{d_\tau(e_n)-\tau(e_n^2): \tau\in \overline{QT(A)}^w\}\\\nonumber &\le \sup\{d_\tau(e_n)-\tau(e_n^{1/m(n)}): \tau\in \overline{QT(A)}^w\}+\sup\{\tau(e_n^{1/m(n)}-e_n^2):\tau\in \overline{QT(A)}^w\}\nonumber\\&<1/n+\|(e_n^{1/m(n)}-e_n^2)^{1/2}\|_{_{2, \overline{QT(A)}^w}}\,\,\to 0 \,\,\,\, \mathrm{as\,\,{{n}}\to\infty}.\nonumber\\ \end{align} $$
$$ \begin{align}\nonumber &\sup\{d_\tau(e_n)-\tau(e_n^2): \tau\in \overline{QT(A)}^w\}\\\nonumber &\le \sup\{d_\tau(e_n)-\tau(e_n^{1/m(n)}): \tau\in \overline{QT(A)}^w\}+\sup\{\tau(e_n^{1/m(n)}-e_n^2):\tau\in \overline{QT(A)}^w\}\nonumber\\&<1/n+\|(e_n^{1/m(n)}-e_n^2)^{1/2}\|_{_{2, \overline{QT(A)}^w}}\,\,\to 0 \,\,\,\, \mathrm{as\,\,{{n}}\to\infty}.\nonumber\\ \end{align} $$
(3) In this case, since
![]() $\lim _{n\to \infty }\omega (e_n)=0,$
there are
$\lim _{n\to \infty }\omega (e_n)=0,$
there are
![]() $l({{n}})\in \mathbb {N}$
such that
$l({{n}})\in \mathbb {N}$
such that
It follows that
for any integers
![]() $m(n)\ge l({{n}}).$
Since
$m(n)\ge l({{n}}).$
Since
as
![]() ${{n}}\to \infty , \Pi (\{e_n^{1/2{{l}}(n)}\})=p$
is a projection. By (e6.13), for any integers
${{n}}\to \infty , \Pi (\{e_n^{1/2{{l}}(n)}\})=p$
is a projection. By (e6.13), for any integers
![]() ${{m(n)}}\ge l({{n}}),$
${{m(n)}}\ge l({{n}}),$
It follows that
![]() $\{e_n^{{{1/l(n)}}}\}$
is a permanent projection lifting of
$\{e_n^{{{1/l(n)}}}\}$
is a permanent projection lifting of
![]() $p.$
$p.$
(4) Suppose that
![]() $g_\delta (e_n)\stackrel {c.}{\to } 0$
for some
$g_\delta (e_n)\stackrel {c.}{\to } 0$
for some
![]() $0<\delta <1/4.$
We have, for any
$0<\delta <1/4.$
We have, for any
![]() $m(n)\in \mathbb {N},$
$m(n)\in \mathbb {N},$
It follows that
![]() $\{e_n^{1/m(n)}-f_{\delta /2}(e_n)e{{_n^{1/m(n)}}}\}\in N_{cu}.$
One then checks that
$\{e_n^{1/m(n)}-f_{\delta /2}(e_n)e{{_n^{1/m(n)}}}\}\in N_{cu}.$
One then checks that
Thus, (4) follows.
For (5), let
![]() $B=l^\infty (A)/I_{_{\overline {QT(A)}^w}}.$
It is clear that
$B=l^\infty (A)/I_{_{\overline {QT(A)}^w}}.$
It is clear that
![]() $pBp\subset \Pi (l^\infty ( {{\{}}\mathrm {Her}(e_n){{\}}})).$
Suppose that
$pBp\subset \Pi (l^\infty ( {{\{}}\mathrm {Her}(e_n){{\}}})).$
Suppose that
![]() ${{g\in }}\Pi (l^\infty ( {{\{}}\mathrm {Her}(e_n){{\}}}){{)_+^{\mathbf {1}}}}.$
Then we may write
${{g\in }}\Pi (l^\infty ( {{\{}}\mathrm {Her}(e_n){{\}}}){{)_+^{\mathbf {1}}}}.$
Then we may write
![]() $g=\Pi (\{g_n\})$
such that
$g=\Pi (\{g_n\})$
such that
![]() $g_n\in (\mathrm {Her}(e_n))^{\mathbf {1}}_+,$
$g_n\in (\mathrm {Her}(e_n))^{\mathbf {1}}_+,$
![]() $n\in \mathbb {N}.$
For any
$n\in \mathbb {N}.$
For any
![]() $\varepsilon>0,$
there exists
$\varepsilon>0,$
there exists
![]() $m(n)\in \mathbb {N}$
such that
$m(n)\in \mathbb {N}$
such that
Thus,
However, since
![]() $\{e_n\}$
is a permanent projection lifting of
$\{e_n\}$
is a permanent projection lifting of
![]() $p, \Pi (\{e_n^{1/m(n)}\})=p.$
Thus,
$p, \Pi (\{e_n^{1/m(n)}\})=p.$
Thus,
It follows
![]() $g\in pBp.$
This shows that
$g\in pBp.$
This shows that
![]() $C=pBp=\Pi (l^\infty ({{\{}}\mathrm {Her}(e_n){{\}}})).$
$C=pBp=\Pi (l^\infty ({{\{}}\mathrm {Her}(e_n){{\}}})).$
(6) In this case,
![]() $\omega (e)=0.$
Therefore, by (3),
$\omega (e)=0.$
Therefore, by (3),
![]() $\{e^{{{1/l(n)}}}\}$
is a permanent projection lifting for
$\{e^{{{1/l(n)}}}\}$
is a permanent projection lifting for
![]() $p=\Pi (\{e^{{{1/l(n)}}}\})$
(for some
$p=\Pi (\{e^{{{1/l(n)}}}\})$
(for some
![]() $l({{n}})\in \mathbb {N}$
).
$l({{n}})\in \mathbb {N}$
).
For any
![]() $\{x_n\}\in l^\infty (A),$
there is a sequence
$\{x_n\}\in l^\infty (A),$
there is a sequence
![]() $\{m(n)\}$
of integers such that
$\{m(n)\}$
of integers such that
Hence
![]() $p\{x_n\}=\{x_n\}p=\{x_n\}.$
So p is the unit of
$p\{x_n\}=\{x_n\}p=\{x_n\}.$
So p is the unit of
![]() $l^\infty (A)/I_{_{\overline {QT(A)}^w}}.$
$l^\infty (A)/I_{_{\overline {QT(A)}^w}}.$
For (7), suppose that A has continuous scale. Let
![]() $e\in A_+^{\mathbf {1}}$
be a strictly positive element. By (3) of Proposition 4.4,
$e\in A_+^{\mathbf {1}}$
be a strictly positive element. By (3) of Proposition 4.4,
![]() $\omega ^c(e)=0.$
Then, for any
$\omega ^c(e)=0.$
Then, for any
![]() $\varepsilon>0$
and
$\varepsilon>0$
and
![]() $n\in \mathbb {N},$
there exists an integer
$n\in \mathbb {N},$
there exists an integer
![]() $l(n)\in \mathbb {N}$
such that
$l(n)\in \mathbb {N}$
such that
Since
![]() $g_{1/n}(e)\stackrel {c.}{\to } 0$
(see Definition 4.3), we conclude that
$g_{1/n}(e)\stackrel {c.}{\to } 0$
(see Definition 4.3), we conclude that
![]() $\{e^{1/(m(n)}-e^{1/l(n)}\}, \{ e^{1/2l(n)}-e^{1/l(n)}\}\in N_{cu}.$
It follows that
$\{e^{1/(m(n)}-e^{1/l(n)}\}, \{ e^{1/2l(n)}-e^{1/l(n)}\}\in N_{cu}.$
It follows that
![]() $p=\Pi (\{e^{1/l(n)}\})$
is a projection and
$p=\Pi (\{e^{1/l(n)}\})$
is a projection and
![]() $\{e^{1/l(n)}\}$
is a permanent projection lifting.
$\{e^{1/l(n)}\}$
is a permanent projection lifting.
Let
![]() $\{b_n\}\in l^\infty (A).$
Then, for each
$\{b_n\}\in l^\infty (A).$
Then, for each
![]() $n\in \mathbb {N},$
there is
$n\in \mathbb {N},$
there is
![]() $m(n)\in \mathbb {N}$
with
$m(n)\in \mathbb {N}$
with
![]() $m(n)\ge l(n)$
such that
$m(n)\ge l(n)$
such that
![]() $\|e^{1/m(n)}b_n-b_n\|<1/n.$
Recall that
$\|e^{1/m(n)}b_n-b_n\|<1/n.$
Recall that
![]() $p=\Pi (\{e^{1/m(n)}\}).$
Thus,
$p=\Pi (\{e^{1/m(n)}\}).$
Thus,
![]() $p\Pi (\{b_n\})=\Pi (\{b_n\}).$
It follows
$p\Pi (\{b_n\})=\Pi (\{b_n\}).$
It follows
![]() $l^\infty (A)/{{N_{cu}}}$
is unital.
$l^\infty (A)/{{N_{cu}}}$
is unital.
Conversely, let
![]() $p\in l^\infty (A)/{{N_{cu}}}$
be the unit. Let
$p\in l^\infty (A)/{{N_{cu}}}$
be the unit. Let
![]() $\{e_n\}\in l^\infty (A)_+^{\mathbf {1}}$
such that
$\{e_n\}\in l^\infty (A)_+^{\mathbf {1}}$
such that
![]() $\Pi (\{e_n\})=p.$
We claim that
$\Pi (\{e_n\})=p.$
We claim that
![]() $\Pi (A)^\perp =\{0\}.$
Otherwise, for each
$\Pi (A)^\perp =\{0\}.$
Otherwise, for each
![]() $n,$
there exists
$n,$
there exists
![]() $b_n\in A_+$
with
$b_n\in A_+$
with
![]() $\|b_n\|=1$
such that
$\|b_n\|=1$
such that
![]() $\|e_nb_n\|<1/n.$
Then
$\|e_nb_n\|<1/n.$
Then
![]() $p\Pi (\{b_n\})=0.$
Impossible. Thus,
$p\Pi (\{b_n\})=0.$
Impossible. Thus,
![]() $\Pi (A)^\perp =\{0\}.$
By Proposition 2.20, A has continuous scale.
$\Pi (A)^\perp =\{0\}.$
By Proposition 2.20, A has continuous scale.
Lemma 6.3 Let A be a compact
![]() $C^*$
-algebra with
$C^*$
-algebra with
![]() $QT(A)\not =\emptyset .$
If A has T-tracial approximate oscillation zero, then, for any
$QT(A)\not =\emptyset .$
If A has T-tracial approximate oscillation zero, then, for any
![]() $x\in (l^\infty (A)/I_{_{\overline {QT(A)}^w}})_+,$
there is a projection
$x\in (l^\infty (A)/I_{_{\overline {QT(A)}^w}})_+,$
there is a projection
![]() $p\in {{l^\infty (A)/I_{_{\overline {QT(A)}^w}}}}$
such that
$p\in {{l^\infty (A)/I_{_{\overline {QT(A)}^w}}}}$
such that
![]() $px=x=xp.$
$px=x=xp.$
Proof Let
![]() $B=l^\infty (A)/I_{_{\overline {QT(A)}^w}}$
and
$B=l^\infty (A)/I_{_{\overline {QT(A)}^w}}$
and
![]() $\Pi : l^\infty (A)\to B$
be the quotient map. Let
$\Pi : l^\infty (A)\to B$
be the quotient map. Let
![]() $x\in B_+.$
Without loss of generality, we may assume that
$x\in B_+.$
Without loss of generality, we may assume that
![]() $0\le x\le 1.$
$0\le x\le 1.$
Let
![]() $y=\{y_n\}\in l^\infty (A)$
with
$y=\{y_n\}\in l^\infty (A)$
with
![]() $0\le y\le 1$
such that
$0\le y\le 1$
such that
![]() $\Pi (y)=x.$
Since A has T-tracial approximate oscillation zero, there are
$\Pi (y)=x.$
Since A has T-tracial approximate oscillation zero, there are
![]() $d_n\in \mathrm {Her}(y_n)_+^{\mathbf {1}}$
and
$d_n\in \mathrm {Her}(y_n)_+^{\mathbf {1}}$
and
![]() $\delta _n {{\in (0,1/4n)}} $
such that
$\delta _n {{\in (0,1/4n)}} $
such that
Define
![]() $d=\{d_n\}\in l^\infty (A).$
Then
$d=\{d_n\}\in l^\infty (A).$
Then
![]() $\Pi (d) =\Pi ({{y}} )=x.$
Put
$\Pi (d) =\Pi ({{y}} )=x.$
Put
![]() $e_n=f_{\delta _n/2}(d_n),\,\, n\in \mathbb {N}$
and
$e_n=f_{\delta _n/2}(d_n),\,\, n\in \mathbb {N}$
and
![]() $e=\{e_n\}.$
Then
$e=\{e_n\}.$
Then
![]() $e\in {{l^\infty (A{)_+^{\mathbf {1}}}.}}$
Moreover,
$e\in {{l^\infty (A{)_+^{\mathbf {1}}}.}}$
Moreover,
It follows that
It remains to show that
![]() $p:=\Pi (e)$
is a projection. To do this, we compute that
$p:=\Pi (e)$
is a projection. To do this, we compute that
It follows that
Thus,
![]() $p=\Pi (e)=\Pi (e)^2,$
or
$p=\Pi (e)=\Pi (e)^2,$
or
![]() $p\in B$
is a projection.
$p\in B$
is a projection.
Theorem 6.4 Let A be a compact
![]() $C^*$
-algebra with non-empty
$C^*$
-algebra with non-empty
![]() $QT(A).$
If A has T-tracial approximate oscillation zero, then
$QT(A).$
If A has T-tracial approximate oscillation zero, then
![]() $l^\infty (A)/I_{\overline {QT(A)}^w}(A)$
has real rank zero.
$l^\infty (A)/I_{\overline {QT(A)}^w}(A)$
has real rank zero.
Proof Let
![]() $B=l^\infty (A)/I_{_{\overline {QT(A)}^w}}(A)$
and
$B=l^\infty (A)/I_{_{\overline {QT(A)}^w}}(A)$
and
![]() $\Pi : l^\infty (A)\to B$
be the quotient map.
$\Pi : l^\infty (A)\to B$
be the quotient map.
We claim that, if
![]() $p\in B$
is a nonzero projection, then
$p\in B$
is a nonzero projection, then
![]() $C:=p{{\widetilde B}}p=pBp$
has real rank zero.
$C:=p{{\widetilde B}}p=pBp$
has real rank zero.
Let
![]() $\{e_n\}\in l^\infty (A)_+^{\mathbf {1}}$
such that
$\{e_n\}\in l^\infty (A)_+^{\mathbf {1}}$
such that
![]() $\Pi (\{e_n\})=p.$
Upon replacing
$\Pi (\{e_n\})=p.$
Upon replacing
![]() $e_n$
by
$e_n$
by
![]() $f_{1/4}(e_n),$
by Lemma 6.2, we may assume that
$f_{1/4}(e_n),$
by Lemma 6.2, we may assume that
![]() $\{e_n\}$
is a permanent projection lifting of
$\{e_n\}$
is a permanent projection lifting of
![]() $p.$
By (5) of Proposition 6.2,
$p.$
By (5) of Proposition 6.2,
![]() $C=pBp=\Pi (l^\infty ( {{\{}}\mathrm {Her}(e_n) {{\}}})).$
$C=pBp=\Pi (l^\infty ( {{\{}}\mathrm {Her}(e_n) {{\}}})).$
Let
![]() $a, b\in C_+$
be such that
$a, b\in C_+$
be such that
![]() $ab=0.$
We may assume that
$ab=0.$
We may assume that
![]() $\|a\|, \|b\|\le 1.$
$\|a\|, \|b\|\le 1.$
Then, by Proposition 10.1.10 of [Reference Loring28], for example, we may assume that
![]() $a=\Pi (\{a_n\})$
and
$a=\Pi (\{a_n\})$
and
![]() $b=\Pi (\{b_n\}),$
where
$b=\Pi (\{b_n\}),$
where
![]() $a_n, b_n\in \mathrm {Her}(e_n)_+$
and
$a_n, b_n\in \mathrm {Her}(e_n)_+$
and
![]() $\{a_n\},\,\{b_n\}\in l^\infty ({{\{}}\mathrm {Her}(e_n){{\}}})$
such that
$\{a_n\},\,\{b_n\}\in l^\infty ({{\{}}\mathrm {Her}(e_n){{\}}})$
such that
![]() $a_nb_n=b_na_n=0$
for all
$a_nb_n=b_na_n=0$
for all
![]() $n\in \mathbb {N}.$
Since A has T-tracial approximate oscillation zero, there are
$n\in \mathbb {N}.$
Since A has T-tracial approximate oscillation zero, there are
![]() $d_n\in \mathrm {Her}(a_n)_+^{\mathbf {1}}$
and
$d_n\in \mathrm {Her}(a_n)_+^{\mathbf {1}}$
and
![]() $\delta _n {{\in (0,1/4n)}} $
such that
$\delta _n {{\in (0,1/4n)}} $
such that
Define
![]() $d=\{d_n\}\in l^\infty ({{\{}}\mathrm {Her}(a_n){{\}}}).$
Then
$d=\{d_n\}\in l^\infty ({{\{}}\mathrm {Her}(a_n){{\}}}).$
Then
![]() $a=\Pi (\{a_n\})=\Pi (d).$
Put
$a=\Pi (\{a_n\})=\Pi (d).$
Put
Put
![]() ${{g=\Pi (g')}}.$
Recall that
${{g=\Pi (g')}}.$
Recall that
![]() $l^\infty ({{\{}}\mathrm {Her}(e_n){{\}}})=pBp.$
Thus,
$l^\infty ({{\{}}\mathrm {Her}(e_n){{\}}})=pBp.$
Thus,
![]() $g\in pBp_+.$
Since
$g\in pBp_+.$
Since
![]() $d_n\in \mathrm {Her}(a_n),$
we have
$d_n\in \mathrm {Her}(a_n),$
we have
![]() $g_nb_n=b_ng_n=0.$
In other words,
$g_nb_n=b_ng_n=0.$
In other words,
Note that
![]() $f_{\delta _n}(d_n)g_n=f_{\delta _n}(d_n)$
for all
$f_{\delta _n}(d_n)g_n=f_{\delta _n}(d_n)$
for all
![]() $n\in \mathbb {N}.$
It follows that
$n\in \mathbb {N}.$
It follows that
We compute that
It follows that
Thus,
![]() ${{g=g^2}},$
or
${{g=g^2}},$
or
![]() $g\in pBp$
is a projection. Recall that
$g\in pBp$
is a projection. Recall that
In other words,
This and (e6.32) imply that
![]() $pBp$
has real rank zero and the claim is proved.
$pBp$
has real rank zero and the claim is proved.
To show that B has real rank zero, let
![]() $x\in B_{s.a.}$
and let
$x\in B_{s.a.}$
and let
![]() $\varepsilon>0.$
Put
$\varepsilon>0.$
Put
![]() $z=x^2.$
Then, by Lemma 6.3, there is a projection
$z=x^2.$
Then, by Lemma 6.3, there is a projection
![]() $p\in B$
such that
$p\in B$
such that
![]() $pz=z=zp.$
Hence,
$pz=z=zp.$
Hence,
![]() $x\in pBp.$
By the claim that we have just shown,
$x\in pBp.$
By the claim that we have just shown,
![]() $pBp$
has real rank zero. Then there is
$pBp$
has real rank zero. Then there is
![]() $y\in (pBp)_{s.a.}$
with finite spectrum such that
$y\in (pBp)_{s.a.}$
with finite spectrum such that
![]() $\|x-y\|<\varepsilon .$
By Theorem 2.9 of [Reference Brown and Pedersen6], B has real rank zero.
$\|x-y\|<\varepsilon .$
By Theorem 2.9 of [Reference Brown and Pedersen6], B has real rank zero.
If A is unital, then
![]() $l^\infty (A)$
is the multiplier algebra of
$l^\infty (A)$
is the multiplier algebra of
![]() $c_0(A).$
Thus,
$c_0(A).$
Thus,
![]() $l^\infty (A)/c_0(A)$
is a corona algebra. Therefore,
$l^\infty (A)/c_0(A)$
is a corona algebra. Therefore,
![]() $l^\infty (A)/I_{_{\overline {QT(A)}^w}}$
is an SSAW*-algebra (see Proposition 3 of [Reference Pedersen31] and Section 3 of [Reference Pedersen33]). The above theorem also implies that, for non-unital case, we also have the next corollary. (One may also compare Corollaries 6.5 and 6.7 (at least in unital case) with those of Lemma 1.8, Theorem 1.9, and Corollary 1.10 of [Reference Lin21].)
$l^\infty (A)/I_{_{\overline {QT(A)}^w}}$
is an SSAW*-algebra (see Proposition 3 of [Reference Pedersen31] and Section 3 of [Reference Pedersen33]). The above theorem also implies that, for non-unital case, we also have the next corollary. (One may also compare Corollaries 6.5 and 6.7 (at least in unital case) with those of Lemma 1.8, Theorem 1.9, and Corollary 1.10 of [Reference Lin21].)
Corollary 6.5 Let A be a
![]() $\sigma $
-unital compact
$\sigma $
-unital compact
![]() $C^*$
-algebra with
$C^*$
-algebra with
![]() $QT(A)\not =\emptyset .$
Suppose that A has T-tracial approximate oscillation zero. Then
$QT(A)\not =\emptyset .$
Suppose that A has T-tracial approximate oscillation zero. Then
![]() $l^\infty (A)/I_{_{\overline {QT(A)}^w}}$
is an SSAW*-algebra with real rank zero.
$l^\infty (A)/I_{_{\overline {QT(A)}^w}}$
is an SSAW*-algebra with real rank zero.
Proof This is contained in the proof of Lemma 6.4. Since
![]() $M_n(A)$
also has T-tracial approximate oscillation zero, it suffices to show that
$M_n(A)$
also has T-tracial approximate oscillation zero, it suffices to show that
![]() $B:=l^\infty (A)/I_{\overline {QT(A)}^w}$
is an SAW*-algebra. Consider elements
$B:=l^\infty (A)/I_{\overline {QT(A)}^w}$
is an SAW*-algebra. Consider elements
![]() $a, b\in B_+$
such that
$a, b\in B_+$
such that
![]() $ab=ba=0.$
By Lemma 6.4, there is a projection
$ab=ba=0.$
By Lemma 6.4, there is a projection
![]() $p\in B$
such that
$p\in B$
such that
Then the first part of the proof of Theorem 6.4 provides a projection
![]() ${{g}}\in B$
such that
${{g}}\in B$
such that
![]() ${{g}}a=a$
and
${{g}}a=a$
and
![]() ${{g}}b=0.$
Consequently, B is an SAW*-algebra of real rank zero.
${{g}}b=0.$
Consequently, B is an SAW*-algebra of real rank zero.
Theorem 6.6 Let A be an algebraically simple
![]() $C^*$
-algebra with
$C^*$
-algebra with
![]() $QT(A)\not =\emptyset .$
Suppose that A has strict comparison and T-tracial approximate oscillation zero. Then
$QT(A)\not =\emptyset .$
Suppose that A has strict comparison and T-tracial approximate oscillation zero. Then
![]() $l^\infty (A)/I_{\overline {QT(A)}^w}$
has stable rank one.
$l^\infty (A)/I_{\overline {QT(A)}^w}$
has stable rank one.
Proof Put
![]() $B=l^\infty (A)/I_{{{_{\overline {QT(A)}^w}}}}.$
We first show that
$B=l^\infty (A)/I_{{{_{\overline {QT(A)}^w}}}}.$
We first show that
![]() $pBp$
has stable rank one if p is a nonzero projection. By Theorem 6.4,
$pBp$
has stable rank one if p is a nonzero projection. By Theorem 6.4,
![]() $pBp$
has real rank zero. Let
$pBp$
has real rank zero. Let
![]() $q, f\in pBp$
be projections such that
$q, f\in pBp$
be projections such that
![]() $q\sim f.$
Then, by Theorem 3.5,
$q\sim f.$
Then, by Theorem 3.5,
![]() $p-q\sim p-f.$
By Proposition 2.4(III) of [Reference Blackadar and Handelman2] and Theorem 2.6 of [Reference Brown and Pedersen6],
$p-q\sim p-f.$
By Proposition 2.4(III) of [Reference Blackadar and Handelman2] and Theorem 2.6 of [Reference Brown and Pedersen6],
![]() $pBp$
has stable rank one.
$pBp$
has stable rank one.
To show B has stable rank one, let
![]() $x\in {{\widetilde B}}$
and
$x\in {{\widetilde B}}$
and
![]() $\varepsilon>0.$
Write
$\varepsilon>0.$
Write
![]() $x=\lambda +y,$
where
$x=\lambda +y,$
where
![]() $\lambda \in \mathbb {C}$
and
$\lambda \in \mathbb {C}$
and
![]() $y\in B.$
By Lemma 6.3, there is a projection
$y\in B.$
By Lemma 6.3, there is a projection
![]() $p\in B$
such that
$p\in B$
such that
![]() $p(y^*y+yy^*)=(y^*y+yy^*).$
It follows that
$p(y^*y+yy^*)=(y^*y+yy^*).$
It follows that
![]() $y\in pBp.$
From what has been shown,
$y\in pBp.$
From what has been shown,
![]() $pBp$
has stable rank one. Choose
$pBp$
has stable rank one. Choose
![]() $z_1\in GL(pBp)$
such that
$z_1\in GL(pBp)$
such that
Define
![]() $z_2=z_1+\lambda (1-p),$
if
$z_2=z_1+\lambda (1-p),$
if
![]() $\lambda \not =0,$
and
$\lambda \not =0,$
and
![]() $z_2=z_1+\varepsilon (1-p),$
if
$z_2=z_1+\varepsilon (1-p),$
if
![]() $\lambda =0.$
Then
$\lambda =0.$
Then
![]() $z_2\in GL({{\widetilde B}})$
and
$z_2\in GL({{\widetilde B}})$
and
Corollary 6.7 Let A be an algebraically simple
![]() $C^*$
-algebra with
$C^*$
-algebra with
![]() $QT(A)\not =\emptyset .$
Suppose that A has strict comparison and T-tracial approximate oscillation zero. Then
$QT(A)\not =\emptyset .$
Suppose that A has strict comparison and T-tracial approximate oscillation zero. Then
![]() $l^\infty (A)/I_{_{\overline {QT(A)}^w}}$
has unitary polar decomposition.
$l^\infty (A)/I_{_{\overline {QT(A)}^w}}$
has unitary polar decomposition.
Proof This follows from Corollary 6.5 above and Theorem 3.5 of [Reference Pedersen33].
7 Range of dimension functions
In this section, we will show that if A has T-tracial approximate oscillation zero, then the image of
![]() $\Gamma $
is “dense,” and if, in addition, A has strict comparison, then
$\Gamma $
is “dense,” and if, in addition, A has strict comparison, then
![]() $\Gamma $
is surjective.
$\Gamma $
is surjective.
Lemma 7.1 Let
![]() $0\le a\le 1, b, c\in A^{\mathbf {1}}$
be such that
$0\le a\le 1, b, c\in A^{\mathbf {1}}$
be such that
(or
![]() $a\le b+c, b, c\in A_+^{\mathbf {1}}$
). Then, for any
$a\le b+c, b, c\in A_+^{\mathbf {1}}$
). Then, for any
![]() $\delta \in (0, 1/2),$
$\delta \in (0, 1/2),$
(or
![]() $[f_\delta (a)]\le [f_{\delta /4}(b)]+[f_{\delta /4}(c)]$
).
$[f_\delta (a)]\le [f_{\delta /4}(b)]+[f_{\delta /4}(c)]$
).
Proof Note that
Let
![]() $0<\eta <1/4.$
Then, by Lemma 1.7 of [Reference Phillips34],
$0<\eta <1/4.$
Then, by Lemma 1.7 of [Reference Phillips34],
(recall Notation 2.5). Put
 $ z=\begin {pmatrix} b & 0\\ c & 0\end {pmatrix}.$
Then
$ z=\begin {pmatrix} b & 0\\ c & 0\end {pmatrix}.$
Then
Hence (see Lemma 1.7 of [Reference Phillips34], for example, for the first “
![]() $\lesssim$
” sign below),
$\lesssim$
” sign below),
We then have (see also (e7.4))
For the case that
![]() $a\le b+c,$
as computed above, there is
$a\le b+c,$
as computed above, there is
![]() $z\in M_2(A)$
such that
$z\in M_2(A)$
such that
One then sees the proof of the second part is exactly the same as that of the first part.
Lemma 7.2 Let A be a non-elementary simple
![]() $C^*$
-algebra with
$C^*$
-algebra with
![]() $\mathrm {Ped}(A)=A$
and with
$\mathrm {Ped}(A)=A$
and with
![]() $QT(A)\not =\emptyset .$
Let
$QT(A)\not =\emptyset .$
Let
![]() $\{e_n\}, \{b_n\}\in l^\infty (\mathrm {Ped}(A){{_+^{\mathbf {1}}}}).$
Recall that
$\{e_n\}, \{b_n\}\in l^\infty (\mathrm {Ped}(A){{_+^{\mathbf {1}}}}).$
Recall that
![]() $\Pi : l^\infty (A)\to l^\infty (A)/I_{_{\overline {QT(A)}^w}}$
is the quotient map.
$\Pi : l^\infty (A)\to l^\infty (A)/I_{_{\overline {QT(A)}^w}}$
is the quotient map.
(1) Suppose that
![]() $\Pi (\{e_n\})\le \Pi (\{b_n\})$
(or
$\Pi (\{e_n\})\le \Pi (\{b_n\})$
(or
![]() $\Pi _{cu}(\{e_n\})\le \Pi _{cu}(\{b_n\})$
). Then, any integer
$\Pi _{cu}(\{e_n\})\le \Pi _{cu}(\{b_n\})$
). Then, any integer
![]() $m\in \mathbb {N}$
and
$m\in \mathbb {N}$
and
![]() $\varepsilon>0,$
(any
$\varepsilon>0,$
(any
![]() $d\in \mathrm {Ped}(A)_+^{\mathbf {1}}\setminus \{0\}$
), there exists
$d\in \mathrm {Ped}(A)_+^{\mathbf {1}}\setminus \{0\}$
), there exists
![]() $k_0\in \mathbb {N}$
such that, for all
$k_0\in \mathbb {N}$
such that, for all
![]() $k\ge k_0,$
$k\ge k_0,$
where
![]() $d_k\in A_+$
and
$d_k\in A_+$
and
![]() $\sup \{d_\tau (d_k):\tau \in \overline {QT(A)}^w\}<1/m$
(or
$\sup \{d_\tau (d_k):\tau \in \overline {QT(A)}^w\}<1/m$
(or
![]() $d_k\lesssim d$
and
$d_k\lesssim d$
and
![]() $\sup \{d_\tau (d_k):\tau \in \overline {QT(A)}^w\}<1/m$
).
$\sup \{d_\tau (d_k):\tau \in \overline {QT(A)}^w\}<1/m$
).
(2) Suppose that
![]() $p=\Pi (\{e_n\})$
is a projection (or
$p=\Pi (\{e_n\})$
is a projection (or
![]() $p=\Pi _{cu}(\{e_n\})$
is a projection and
$p=\Pi _{cu}(\{e_n\})$
is a projection and
![]() $\omega ^c(e_n)\to 0$
),
$\omega ^c(e_n)\to 0$
),
![]() $\{e_n\}$
is a permanent projection lifting of p and
$\{e_n\}$
is a permanent projection lifting of p and
Then, any integer
![]() $m\in \mathbb {N},$
and
$m\in \mathbb {N},$
and
![]() $\varepsilon \in (0,1)$
(and any nonzero
$\varepsilon \in (0,1)$
(and any nonzero
![]() $d\in \mathrm {Ped}(A)_+$
), there exists
$d\in \mathrm {Ped}(A)_+$
), there exists
![]() $k_0\ge \mathbb {N}$
such that, for all
$k_0\ge \mathbb {N}$
such that, for all
![]() $k\ge k_0,$
$k\ge k_0,$
where
![]() $0\le d_k\le 1, d_k\in (A\otimes {\cal K})_+$
and
$0\le d_k\le 1, d_k\in (A\otimes {\cal K})_+$
and
where
![]() $\sup \{d_\tau (d_k):\tau \in \overline {QT(A)}^w\}<1/m$
(or,
$\sup \{d_\tau (d_k):\tau \in \overline {QT(A)}^w\}<1/m$
(or,
![]() $d_k\lesssim d$
and
$d_k\lesssim d$
and
![]() $\sup \{d_\tau (d_k):\tau \in \overline {QT(A)}^w\}<1/m$
).
$\sup \{d_\tau (d_k):\tau \in \overline {QT(A)}^w\}<1/m$
).
Proof We will use the following easy claim: If B is a
![]() $C^*$
-algebra and
$C^*$
-algebra and
![]() $I\subset B$
is a (closed two-sided) ideal, and, if
$I\subset B$
is a (closed two-sided) ideal, and, if
![]() $x, y\in B_+$
such that
$x, y\in B_+$
such that
![]() $\pi (x)\le \pi (y),$
then there exists
$\pi (x)\le \pi (y),$
then there exists
![]() $j\in I_+$
such that
$j\in I_+$
such that
![]() $x\le y+j.$
In fact, there is
$x\le y+j.$
In fact, there is
![]() $z\in A_+$
such that
$z\in A_+$
such that
![]() $(y-x)-z\in I.$
Put
$(y-x)-z\in I.$
Put
![]() $c=-y+x+z\in I.$
Then
$c=-y+x+z\in I.$
Then
Choose
![]() $j=c_+\in I_+.$
This proves the claim.
$j=c_+\in I_+.$
This proves the claim.
Since A is a non-elementary simple
![]() $C^*$
-algebra, one may choose
$C^*$
-algebra, one may choose
![]() $d_0\in \mathrm {Her}(d)_+^{\mathbf {1}} {{\setminus \{0\}}}$
such that
$d_0\in \mathrm {Her}(d)_+^{\mathbf {1}} {{\setminus \{0\}}}$
such that
![]() $2(m+1)[d_0]\le [d].$
By the easy claim above, there is
$2(m+1)[d_0]\le [d].$
By the easy claim above, there is
![]() $\{h_n\}\in ( I_{_{\overline {QT(A)}^w}})_+^{\mathbf {1}}$
(or
$\{h_n\}\in ( I_{_{\overline {QT(A)}^w}})_+^{\mathbf {1}}$
(or
![]() $\{h_n\}\in N_{cu}(A)_+^{\mathbf {1}}$
) such that, in all cases,
$\{h_n\}\in N_{cu}(A)_+^{\mathbf {1}}$
) such that, in all cases,
To show (1), we apply Lemma 7.1 to obtain
Since
![]() $h_n$
is in
$h_n$
is in
![]() $(I_{_{\overline {QT(A)}^w}})_+$
(or in
$(I_{_{\overline {QT(A)}^w}})_+$
(or in
![]() $(N_{cu})_+$
), there exists
$(N_{cu})_+$
), there exists
![]() $k_0\in \mathbb {N}$
such that, for all
$k_0\in \mathbb {N}$
such that, for all
![]() $k\ge k_0,$
$k\ge k_0,$
(or
![]() $ f_{\varepsilon /8}((h_k)_+)\lesssim d_0 $
). Therefore, with
$ f_{\varepsilon /8}((h_k)_+)\lesssim d_0 $
). Therefore, with
![]() $d_k=f_{\varepsilon /8}(h_k),$
for all
$d_k=f_{\varepsilon /8}(h_k),$
for all
![]() $k\ge k_0,$
$k\ge k_0,$
Part (1) follows.
For (2), we keep the same
![]() $d_k$
and
$d_k$
and
![]() $h_k$
as described above. Since now
$h_k$
as described above. Since now
![]() $\{e_n\}$
is a permanent projection lifting, we may assume that
$\{e_n\}$
is a permanent projection lifting, we may assume that
![]() $\lim _{n\to \infty }\omega (e_n)=0,$
by (2) of Proposition 6.2. Thus, we may assume that there exists
$\lim _{n\to \infty }\omega (e_n)=0,$
by (2) of Proposition 6.2. Thus, we may assume that there exists
![]() $\eta _0>0$
and
$\eta _0>0$
and
![]() $n_1\in \mathbb {N}$
such that
$n_1\in \mathbb {N}$
such that
(see Notation 2.5) for all
![]() $n\ge n_0\,\,\,\mathrm {and}\,\,\, 0<\eta \le \eta _0$
(or we assume that
$n\ge n_0\,\,\,\mathrm {and}\,\,\, 0<\eta \le \eta _0$
(or we assume that
![]() $\omega ^c(e_n)\to 0,$
and then
$\omega ^c(e_n)\to 0,$
and then
for all
![]() $n\ge n_0\,\,\,\mathrm {and}\,\,\, 0<\eta \le \eta _0$
).
$n\ge n_0\,\,\,\mathrm {and}\,\,\, 0<\eta \le \eta _0$
).
There exists
![]() $n_2\in \mathbb {N}$
such that (recall that
$n_2\in \mathbb {N}$
such that (recall that
![]() $h_n\in (I_{_{\overline {QT(A)}^w}})^{\mathbf {1}}_+$
) (or
$h_n\in (I_{_{\overline {QT(A)}^w}})^{\mathbf {1}}_+$
) (or
![]() $h_n\in (N_{cu})^{\mathbf {1}}_+$
)
$h_n\in (N_{cu})^{\mathbf {1}}_+$
)
(or
![]() $ f_{\eta _0/8}((h_n))\lesssim d_0 $
for
$ f_{\eta _0/8}((h_n))\lesssim d_0 $
for
![]() $n\ge n_2$
). We have, by Lemma 7.1,
$n\ge n_2$
). We have, by Lemma 7.1,
Put
![]() $k_0=\max \{n_1, n_2\}.$
Then, if
$k_0=\max \{n_1, n_2\}.$
Then, if
![]() $n\ge k_0,$
we have
$n\ge k_0,$
we have
where
![]() $d_n=\mathrm {diag}(g_{\eta _0}(e_n), f_{\eta _0/8}((h_n))), n\in \mathbb {N}.$
Recall (by (e7.17) and (e7.19)) that
$d_n=\mathrm {diag}(g_{\eta _0}(e_n), f_{\eta _0/8}((h_n))), n\in \mathbb {N}.$
Recall (by (e7.17) and (e7.19)) that
![]() $d_\tau (d_n)<1/m$
for all
$d_\tau (d_n)<1/m$
for all
![]() $\tau \in \overline {QT(A)}^w $
(or, in the second case,
$\tau \in \overline {QT(A)}^w $
(or, in the second case,
![]() $[d_k]\le 2[d_0]\le [d]$
). Part (2) then follows.
$[d_k]\le 2[d_0]\le [d]$
). Part (2) then follows.
Lemma 7.3 Let A be a non-elementary algebraically simple
![]() $C^*$
-algebra with
$C^*$
-algebra with
![]() $QT(A)\not =\emptyset .$
$QT(A)\not =\emptyset .$
(1) Suppose that A has tracial approximate oscillation zero. Then, for any
![]() $a\in A_+^{\mathbf {1}}\setminus \{0\},$
there exists a sequence
$a\in A_+^{\mathbf {1}}\setminus \{0\},$
there exists a sequence
![]() $0\le e_{n}\le 1$
in
$0\le e_{n}\le 1$
in
![]() $\mathrm {Her}(a)$
such that
$\mathrm {Her}(a)$
such that
![]() $\Pi _{cu}(\{e_{n}\})$
is full in
$\Pi _{cu}(\{e_{n}\})$
is full in
![]() $l^\infty (A)/N_{cu}(A)$
and
$l^\infty (A)/N_{cu}(A)$
and
(2) Suppose that A has T-tracial approximate oscillation zero. Then, for any
![]() $a\in A_+^{\mathbf {1}}\setminus \{0\},$
there exists a sequence
$a\in A_+^{\mathbf {1}}\setminus \{0\},$
there exists a sequence
![]() $0\le e_{n}\le 1$
in
$0\le e_{n}\le 1$
in
![]() $\mathrm {Her}(a)$
such that
$\mathrm {Her}(a)$
such that
![]() $\Pi _{cu}(\{e_{n}\})$
is full in
$\Pi _{cu}(\{e_{n}\})$
is full in
![]() $l^\infty (A)/N_{cu}(A)$
and
$l^\infty (A)/N_{cu}(A)$
and
Proof (1) Since A has tracial approximate oscillation zero, by Proposition 5.6, there exists a tracial approximate identity
![]() $\{e_n\}$
for
$\{e_n\}$
for
![]() $\mathrm {Her}(a)$
(with
$\mathrm {Her}(a)$
(with
![]() $\|e_n\|\le 1$
) such that
$\|e_n\|\le 1$
) such that
![]() $\lim _{n\to \infty }\omega (e_n)=0.$
Note that
$\lim _{n\to \infty }\omega (e_n)=0.$
Note that
Since
![]() $A=\mathrm {Ped}(A),$
by Proposition 5.6 of [Reference Elliott, Gong, Lin and Niu10],
$A=\mathrm {Ped}(A),$
by Proposition 5.6 of [Reference Elliott, Gong, Lin and Niu10],
![]() $\iota (a)$
is full in
$\iota (a)$
is full in
![]() $l^\infty (A).$
Hence,
$l^\infty (A).$
Hence,
![]() $\Pi _{cu}(\iota (a))$
is full in
$\Pi _{cu}(\iota (a))$
is full in
![]() $l^\infty (A)/N_{cu}(A),$
and so is
$l^\infty (A)/N_{cu}(A),$
and so is
![]() $\Pi (\{e_n\}).$
$\Pi (\{e_n\}).$
The proof of (2) is exactly the same. We omit it.
Lemma 7.4 Let A be a non-elementary algebraically simple
![]() $C^*$
-algebra with
$C^*$
-algebra with
![]() $QT(A)\not =\emptyset .$
Suppose that A has T-tracial approximate oscillation zero. Then, for any
$QT(A)\not =\emptyset .$
Suppose that A has T-tracial approximate oscillation zero. Then, for any
![]() $n\in \mathbb {N},$
there is a full projection
$n\in \mathbb {N},$
there is a full projection
![]() $p\in l^\infty (A)/I_{_{\overline {QT(A)}^w}}$
with
$p\in l^\infty (A)/I_{_{\overline {QT(A)}^w}}$
with
![]() $p=\Pi (\{e_j\})$
for some
$p=\Pi (\{e_j\})$
for some
![]() $e_j\in A_+^{\mathbf {1}}$
(
$e_j\in A_+^{\mathbf {1}}$
(
![]() $j\in \mathbb {N}$
) such that
$j\in \mathbb {N}$
) such that
and there is a sequence of mutually orthogonal full projections
![]() $p_1,p_2,...,p_k,...$
in
$p_1,p_2,...,p_k,...$
in
![]() $l^\infty (A)/I_{_{\overline {QT(A)}^w}}$
such that
$l^\infty (A)/I_{_{\overline {QT(A)}^w}}$
such that
![]() $pp_j=0, j\in \mathbb {N}$
and
$pp_j=0, j\in \mathbb {N}$
and
Moreover, for each
![]() $k\in \mathbb {N},$
there are mutually orthogonal and mutually equivalent full projections
$k\in \mathbb {N},$
there are mutually orthogonal and mutually equivalent full projections
![]() $p_{k,1},p_{k,2},...,p_{k,2^{k+1}}$
in
$p_{k,1},p_{k,2},...,p_{k,2^{k+1}}$
in
![]() $p_k(l^\infty (A)/I_{\overline {QT(A)}^w})p_k.$
$p_k(l^\infty (A)/I_{\overline {QT(A)}^w})p_k.$
Proof Fix
![]() $n\in \mathbb {N}.$
Since A is a non-elementary simple
$n\in \mathbb {N}.$
Since A is a non-elementary simple
![]() $C^*$
-algebra, we may choose two mutually orthogonal elements
$C^*$
-algebra, we may choose two mutually orthogonal elements
![]() $a_1, a_2\in \mathrm {Ped}(A)_+^{\mathbf {1}}\setminus \{0\}$
and
$a_1, a_2\in \mathrm {Ped}(A)_+^{\mathbf {1}}\setminus \{0\}$
and
![]() $x\in A_+$
such that
$x\in A_+$
such that
Find four mutually orthogonal and mutually Cuntz equivalent elements
![]() $a_{2,1}, ...,a_{2,4}\in \mathrm {Her}(a_2)_+^{\mathbf {1}}\setminus \{0\}.$
By Lemma 7.3, there exists a sequence
$a_{2,1}, ...,a_{2,4}\in \mathrm {Her}(a_2)_+^{\mathbf {1}}\setminus \{0\}.$
By Lemma 7.3, there exists a sequence
![]() $\{e_n'\}$
in
$\{e_n'\}$
in
![]() $\mathrm {Her}(a_1)^{\mathbf {1}}$
such that
$\mathrm {Her}(a_1)^{\mathbf {1}}$
such that
![]() $\Pi (\{e_n'\})$
is full and
$\Pi (\{e_n'\})$
is full and
![]() $\lim _{n\to \infty }\omega (e_n')=0.$
There exists, by (3) of Lemma 6.2, a sequence of integers
$\lim _{n\to \infty }\omega (e_n')=0.$
There exists, by (3) of Lemma 6.2, a sequence of integers
![]() $m(j)$
such that
$m(j)$
such that
![]() $p=\Pi (\{e_j')^{1/m(j)}\})$
is a full projection. Note that
$p=\Pi (\{e_j')^{1/m(j)}\})$
is a full projection. Note that
where
![]() $e_j=(e_j')^{1/m(j)}, j\in \mathbb {N}.$
$e_j=(e_j')^{1/m(j)}, j\in \mathbb {N}.$
In
![]() $B=\mathrm {Her}(a_{2,1}),$
one finds a sequence of mutually orthogonal nonzero positive elements
$B=\mathrm {Her}(a_{2,1}),$
one finds a sequence of mutually orthogonal nonzero positive elements
![]() $\{y_n\}$
such that
$\{y_n\}$
such that
To see this, choose mutually orthogonal nonzero elements
![]() $b_1, b_1'\in B_+^{\mathbf {1}}$
and
$b_1, b_1'\in B_+^{\mathbf {1}}$
and
![]() $c_1\in B$
such that
$c_1\in B$
such that
![]() $c_1^*c_1=b_1$
and
$c_1^*c_1=b_1$
and
![]() $c_1c_1^*=b_1'.$
Choose
$c_1c_1^*=b_1'.$
Choose
![]() $y_1=b_1.$
There are mutually orthogonal and mutually Cuntz equivalent nonzero elements
$y_1=b_1.$
There are mutually orthogonal and mutually Cuntz equivalent nonzero elements
![]() $b_{2,i}\in \mathrm {Her}(b_1')$
(
$b_{2,i}\in \mathrm {Her}(b_1')$
(
![]() $1\le i\le 2^2$
). Choose
$1\le i\le 2^2$
). Choose
![]() $y_2=b_{2,1}.$
We then proceed to divide
$y_2=b_{2,1}.$
We then proceed to divide
![]() $b_{2,4}.$
A standard induction argument produces the desired sequence
$b_{2,4}.$
A standard induction argument produces the desired sequence
![]() $\{y_k\}.$
$\{y_k\}.$
For each
![]() $k,$
there are
$k,$
there are
![]() $2^{k+1}$
mutually orthogonal nonzero elements
$2^{k+1}$
mutually orthogonal nonzero elements
![]() $y_{k,1},y_{k,2},...,y_{k,2^{k+1}}$
in
$y_{k,1},y_{k,2},...,y_{k,2^{k+1}}$
in
![]() $\mathrm {Her}(y_k)$
and elements
$\mathrm {Her}(y_k)$
and elements
![]() $z_{k,1},z_{k,2},...,z_{k,2^{k+1}}$
in
$z_{k,1},z_{k,2},...,z_{k,2^{k+1}}$
in
![]() $\mathrm {Her}(y_k)$
such that
$\mathrm {Her}(y_k)$
such that
Applying Lemma 7.3, one obtains, for each
![]() $k\in \mathbb {N},$
a sequence
$k\in \mathbb {N},$
a sequence
![]() $\{e_{k,1, n}\}\subset \mathrm {Her}(y_{k,1})_+^{\mathbf {1}}$
such that
$\{e_{k,1, n}\}\subset \mathrm {Her}(y_{k,1})_+^{\mathbf {1}}$
such that
![]() $\Pi (\{e_{k,1,n}\}_{n\in \mathbb {N}})$
is full in
$\Pi (\{e_{k,1,n}\}_{n\in \mathbb {N}})$
is full in
![]() $l^\infty (A)/I_{_{\overline {QT(A)}^w}}$
and
$l^\infty (A)/I_{_{\overline {QT(A)}^w}}$
and
![]() $\lim _{n\to \infty }\omega (e_{k,1,n})=0.$
$\lim _{n\to \infty }\omega (e_{k,1,n})=0.$
Since
![]() $\lim _{n\to \infty }\omega (e_{k,1, n})=0,$
by (3) of Lemma 6.2, there is also, for each
$\lim _{n\to \infty }\omega (e_{k,1, n})=0,$
by (3) of Lemma 6.2, there is also, for each
![]() $k,$
a sequence
$k,$
a sequence
![]() $m(n,k)\in \mathbb {N}$
such that
$m(n,k)\in \mathbb {N}$
such that
is a full projection in
![]() $l^\infty (A)/I_{S,0}.$
Write
$l^\infty (A)/I_{S,0}.$
Write
![]() $z_{k,j}=u_{k,j}|z_{k,j}|$
as polar decomposition of
$z_{k,j}=u_{k,j}|z_{k,j}|$
as polar decomposition of
![]() $z_{k,j}$
in
$z_{k,j}$
in
![]() $A^{**},$
(
$A^{**},$
(
![]() $1\le j\le 2^{k+1}$
). Put
$1\le j\le 2^{k+1}$
). Put
Then
![]() $v_{k,j}^*v_{k,j}=p_{k,1}$
(see (e7.31)). Thus, we obtain mutually orthogonal and mutually equivalent full projections
$v_{k,j}^*v_{k,j}=p_{k,1}$
(see (e7.31)). Thus, we obtain mutually orthogonal and mutually equivalent full projections
![]() $p_{k,j}, j=1,2,...,2^{k+1}.$
By the construction, we also have
$p_{k,j}, j=1,2,...,2^{k+1}.$
By the construction, we also have
![]() $p_{k,j}p_{k',j'}=0,$
if
$p_{k,j}p_{k',j'}=0,$
if
![]() $k\not =k',$
as well as
$k\not =k',$
as well as
![]() $pp_{k,j}=0$
for all
$pp_{k,j}=0$
for all
![]() $k, j\in N.$
Put
$k, j\in N.$
Put
![]() $p_k:=\sum _{j=1}^{2^{k+1}}p_{k,j}.$
Note also
$p_k:=\sum _{j=1}^{2^{k+1}}p_{k,j}.$
Note also
The following two lemmas are variations of S. Zhang’s halving projection lemma. We need some modification as we do not assume the
![]() $C^*$
-algebra is simple.
$C^*$
-algebra is simple.
Lemma 7.5 (Zhang [Reference Zhang48, Theorem I(i)])
Let A be a
![]() $C^*$
-algebra of real rank zero and r a full projection of
$C^*$
-algebra of real rank zero and r a full projection of
![]() $A.$
Suppose that
$A.$
Suppose that
![]() $p\in A$
is a nonzero projection such that
$p\in A$
is a nonzero projection such that
![]() $[p]\not \le [r].$
Then, there are mutually orthogonal projections
$[p]\not \le [r].$
Then, there are mutually orthogonal projections
![]() $p_1,p_2, p_3\in A$
such that
$p_1,p_2, p_3\in A$
such that
Proof We begin with the following claim which is extracted from the proof of [Reference Zhang48, Theorem I(i)].
Claim: Let C be a
![]() $C^*$
-algebra, and let
$C^*$
-algebra, and let
![]() $v_1,...,v_{2^m}\in C$
be partial isometries such that
$v_1,...,v_{2^m}\in C$
be partial isometries such that
![]() $v_iv_i^*\perp v_jv_j^*$
(
$v_iv_i^*\perp v_jv_j^*$
(
![]() $i\neq j$
) and
$i\neq j$
) and
![]() $v_i^*v_i\ge v_{i+1}^*v_{i+1}$
(
$v_i^*v_i\ge v_{i+1}^*v_{i+1}$
(
![]() $1\le i\le 2^m-1$
). Then there is a partial isometry
$1\le i\le 2^m-1$
). Then there is a partial isometry
![]() $v\in C$
such that
$v\in C$
such that
![]() $v^*v\perp vv^*$
and
$v^*v\perp vv^*$
and
![]() $0\le \sum _{i=1}^{2^m} v_iv_i^*-(v^*v+vv^*)\le v_1v_1^*.$
$0\le \sum _{i=1}^{2^m} v_iv_i^*-(v^*v+vv^*)\le v_1v_1^*.$
Proof of the claim: We use induction on
![]() $m.$
When
$m.$
When
![]() $m=1,$
let
$m=1,$
let
![]() $v:=v_1v_2^*.$
Then
$v:=v_1v_2^*.$
Then
![]() $v^*v\perp vv^*$
because
$v^*v\perp vv^*$
because
![]() $v_1v_1^*\perp v_2v_2^*,$
and
$v_1v_1^*\perp v_2v_2^*,$
and
![]() $v^*v=v_2v_1^*v_1v_2^*=v_2v_2^*$
because
$v^*v=v_2v_1^*v_1v_2^*=v_2v_2^*$
because
![]() $v_1^*v_1\ge v_2^*v_2.$
Note that
$v_1^*v_1\ge v_2^*v_2.$
Note that
![]() $vv^*=v_1v_2^*v_2v_1^*.$
Thus,
$vv^*=v_1v_2^*v_2v_1^*.$
Thus,
The last equation above also shows that
![]() $v_1v_1^*+v_2v_2^*-(v^*v+vv^*)$
is positive. Hence, the claim holds for
$v_1v_1^*+v_2v_2^*-(v^*v+vv^*)$
is positive. Hence, the claim holds for
![]() $m=1.$
$m=1.$
Assume that the claim holds for
![]() $m\ge 1.$
Let
$m\ge 1.$
Let
![]() $v_1,...,v_{2^{m+1}}$
be partial isometries such that
$v_1,...,v_{2^{m+1}}$
be partial isometries such that
![]() $v_iv_i^*\perp v_jv_j^*$
(
$v_iv_i^*\perp v_jv_j^*$
(
![]() $i\neq j$
) and
$i\neq j$
) and
![]() $v_i^*v_i\ge v_{i+1}^*v_{i+1}$
(
$v_i^*v_i\ge v_{i+1}^*v_{i+1}$
(
![]() $1\le i\le 2^{m+1}-1$
). Define
$1\le i\le 2^{m+1}-1$
). Define
![]() $e_i:=v_i^*v_i$
and
$e_i:=v_i^*v_i$
and
![]() $w_i=v_i(e_i-e_{2^{m+1}-i+1}), i=1,...,2^m.$
For
$w_i=v_i(e_i-e_{2^{m+1}-i+1}), i=1,...,2^m.$
For
![]() $i=1,...,2^m-1,$
we have
$i=1,...,2^m-1,$
we have
Note that the above also shows that
![]() $w_i^*w_i$
are projections for all
$w_i^*w_i$
are projections for all
![]() $i.$
Since
$i.$
Since
![]() $w_iw_i^*\le v_iv_i^*,$
we have that
$w_iw_i^*\le v_iv_i^*,$
we have that
![]() $w_iw_i^*$
are mutually orthogonal.
$w_iw_i^*$
are mutually orthogonal.
Consider
![]() $w_i, 1\le i\le 2^m.$
By induction, there is a partial isometry
$w_i, 1\le i\le 2^m.$
By induction, there is a partial isometry
![]() $w\in C$
such that
$w\in C$
such that
![]() $w^*w\perp ww^*$
and
$w^*w\perp ww^*$
and
 $$ \begin{align} 0\le \sum_{i=1}^{2^m} w_iw_i^*-(w^*w+ww^*) \le w_1w_1^*\ (\le v_1v_1^*). \end{align} $$
$$ \begin{align} 0\le \sum_{i=1}^{2^m} w_iw_i^*-(w^*w+ww^*) \le w_1w_1^*\ (\le v_1v_1^*). \end{align} $$
Hence,
![]() $ww=0.$
Note that
$ww=0.$
Note that
 $$ \begin{align} &w^*w+ww^* \le \sum_{i=1}^{2^m} w_iw_i^* =\sum_{i=1}^{2^m} v_i (e_i-e_{2^{m+1}-i+1})v_i^* \\\nonumber &\quad= \sum_{i=1}^{2^m} v_iv_i^*-v_ie_{2^{m+1}-i+1}v_i^* \in \left(\sum_{i=1}^{2^m} v_ie_{2^{m+1}-i+1}v_i^*\right)^\perp\cap \left(\sum_{i=1}^{2^m}v_{2^{m+1}-i+1}v_{2^{m+1}-i+1}^* \right)^\perp, \end{align} $$
$$ \begin{align} &w^*w+ww^* \le \sum_{i=1}^{2^m} w_iw_i^* =\sum_{i=1}^{2^m} v_i (e_i-e_{2^{m+1}-i+1})v_i^* \\\nonumber &\quad= \sum_{i=1}^{2^m} v_iv_i^*-v_ie_{2^{m+1}-i+1}v_i^* \in \left(\sum_{i=1}^{2^m} v_ie_{2^{m+1}-i+1}v_i^*\right)^\perp\cap \left(\sum_{i=1}^{2^m}v_{2^{m+1}-i+1}v_{2^{m+1}-i+1}^* \right)^\perp, \end{align} $$
where
![]() $b^\perp =\{a\in A: ab=ba=0\}.$
Recall that
$b^\perp =\{a\in A: ab=ba=0\}.$
Recall that
![]() $v_{2^{m+1}-i+1}^*v_{2^{m+1}-i+1}=e_{2^{m+1}-i+1}$
(
$v_{2^{m+1}-i+1}^*v_{2^{m+1}-i+1}=e_{2^{m+1}-i+1}$
(
![]() $1\le i\le 2^m$
) and
$1\le i\le 2^m$
) and
![]() $v_i^*v_i\ge v_{i+1}^*v_{i+1}$
(
$v_i^*v_i\ge v_{i+1}^*v_{i+1}$
(
![]() $1\le i\le 2^{m+1}-1$
). Hence,
$1\le i\le 2^{m+1}-1$
). Hence,
 $$ \begin{align} &\sum_{i=1}^{2^m} v_ie_{2^{m+1}-i+1}v_i^*=\sum_{i=1}^{2^m}v_iv_{2^{m+1}-i+1}^*( v_iv_{2^{m+1}-i+1}^*)^*\,\,\,\mathrm{and}\,\,\, \end{align} $$
$$ \begin{align} &\sum_{i=1}^{2^m} v_ie_{2^{m+1}-i+1}v_i^*=\sum_{i=1}^{2^m}v_iv_{2^{m+1}-i+1}^*( v_iv_{2^{m+1}-i+1}^*)^*\,\,\,\mathrm{and}\,\,\, \end{align} $$
 $$ \begin{align} & \kern-5pt \sum_{i=1}^{2^m}v_{2^{m+1}-i+1}v_{2^{m+1}-i+1}^*=\sum_{i=1}^{2^m}( v_iv_{2^{m+1}-i+1}^*)^*v_iv_{2^{m+1}-i+1}^*. \end{align} $$
$$ \begin{align} & \kern-5pt \sum_{i=1}^{2^m}v_{2^{m+1}-i+1}v_{2^{m+1}-i+1}^*=\sum_{i=1}^{2^m}( v_iv_{2^{m+1}-i+1}^*)^*v_iv_{2^{m+1}-i+1}^*. \end{align} $$
Thus,
 $$ \begin{align*}\nonumber ww^*+w^*w\in \left( \sum_{i=1}^{2^m}v_iv_{2^{m+1}-i+1}^*( v_iv_{2^{m+1}-i+1}^*)^*\right)^\perp \cap \left(\sum_{i=1}^{2^m}( v_iv_{2^{m+1}-i+1}^*)^*v_iv_{2^{m+1}-i+1}^* \right)^\perp. \end{align*} $$
$$ \begin{align*}\nonumber ww^*+w^*w\in \left( \sum_{i=1}^{2^m}v_iv_{2^{m+1}-i+1}^*( v_iv_{2^{m+1}-i+1}^*)^*\right)^\perp \cap \left(\sum_{i=1}^{2^m}( v_iv_{2^{m+1}-i+1}^*)^*v_iv_{2^{m+1}-i+1}^* \right)^\perp. \end{align*} $$
It follows that, for
![]() $1\le i\le 2^m,$
$1\le i\le 2^m,$
Define
![]() $v:=w+\sum _{i=1}^{2^m}v_iv_{2^{m+1}-i+1}^*.$
By (e7.42) and the fact that
$v:=w+\sum _{i=1}^{2^m}v_iv_{2^{m+1}-i+1}^*.$
By (e7.42) and the fact that
![]() $w^2=0$
together with
$w^2=0$
together with
![]() $v_iv_i^*\perp v_jv_j^*$
(
$v_iv_i^*\perp v_jv_j^*$
(
![]() $i\neq j$
), we compute that
$i\neq j$
), we compute that
 $$ \begin{align} v^2&=\left(w+\sum_{i=1}^{2^m}v_iv_{2^{m+1}-i+1}^*\right)\left(w+\sum_{i=1}^{2^m}v_iv_{2^{m+1}-i+1}^*\right)=0,\end{align} $$
$$ \begin{align} v^2&=\left(w+\sum_{i=1}^{2^m}v_iv_{2^{m+1}-i+1}^*\right)\left(w+\sum_{i=1}^{2^m}v_iv_{2^{m+1}-i+1}^*\right)=0,\end{align} $$
 $$ \begin{align} v^*v&=w^*w+ \sum_{i=1}^{2^m}v_{2^{m+1}-i+1}v_i^*v_iv_{2^{m+1}-i+1}^* =w^*w+ \sum_{i=1}^{2^m}v_{2^{m+1}-i+1}v_{2^{m+1}-i+1}^*,\,\,\,\mathrm{and}\,\,\, \end{align} $$
$$ \begin{align} v^*v&=w^*w+ \sum_{i=1}^{2^m}v_{2^{m+1}-i+1}v_i^*v_iv_{2^{m+1}-i+1}^* =w^*w+ \sum_{i=1}^{2^m}v_{2^{m+1}-i+1}v_{2^{m+1}-i+1}^*,\,\,\,\mathrm{and}\,\,\, \end{align} $$
 $$ \begin{align} vv^*&=ww^*+ \sum_{i=1}^{2^m}v_iv_{2^{m+1}-i+1}^*v_{2^{m+1}-i+1}v_i^* =ww^*+ \sum_{i=1}^{2^m}v_ie_{2^{m+1}-i+1}v_i^*. \end{align} $$
$$ \begin{align} vv^*&=ww^*+ \sum_{i=1}^{2^m}v_iv_{2^{m+1}-i+1}^*v_{2^{m+1}-i+1}v_i^* =ww^*+ \sum_{i=1}^{2^m}v_ie_{2^{m+1}-i+1}v_i^*. \end{align} $$
Then
 $$ \begin{align} \sum_{i=1}^{2^{m+1}}v_iv_i^*-(v^*v+vv^*) &= \sum_{i=1}^{2^{m}}v_iv_i^*-\left(w^*w+ww^*+ \sum_{i=1}^{2^m}v_ie_{2^{m+1}-i+1}v_i^*\right)\end{align} $$
$$ \begin{align} \sum_{i=1}^{2^{m+1}}v_iv_i^*-(v^*v+vv^*) &= \sum_{i=1}^{2^{m}}v_iv_i^*-\left(w^*w+ww^*+ \sum_{i=1}^{2^m}v_ie_{2^{m+1}-i+1}v_i^*\right)\end{align} $$
 $$ \begin{align} &= \sum_{i=1}^{2^{m}} \left(v_iv_i^*- v_ie_{2^{m+1}-i+1}v_i^*\right) -\left(w^*w+ww^*\right) \end{align} $$
$$ \begin{align} &= \sum_{i=1}^{2^{m}} \left(v_iv_i^*- v_ie_{2^{m+1}-i+1}v_i^*\right) -\left(w^*w+ww^*\right) \end{align} $$
 $$ \begin{align} &\overset{(7.39)}{=} \sum_{i=1}^{2^m} w_iw_i^*- \left(w^*w+ww^*\right) \end{align} $$
$$ \begin{align} &\overset{(7.39)}{=} \sum_{i=1}^{2^m} w_iw_i^*- \left(w^*w+ww^*\right) \end{align} $$
By induction, the claim holds for all
![]() $m\in \mathbb {N}.$
$m\in \mathbb {N}.$
For the proof of the lemma, applying Lemma 1.1 of [Reference Zhang47], we obtain partial isometries
![]() $v_1, v_2,...,v_n\in A$
such that
$v_1, v_2,...,v_n\in A$
such that
Since
![]() $[p]\not \le [r], n\ge 2.$
By adding
$[p]\not \le [r], n\ge 2.$
By adding
![]() $0$
if necessary, we may assume that
$0$
if necessary, we may assume that
![]() $n=2^m$
for some
$n=2^m$
for some
![]() $m\in \mathbb {N}.$
Then, by (e7.50), (e7.51), and the claim, there is a partial isometry
$m\in \mathbb {N}.$
Then, by (e7.50), (e7.51), and the claim, there is a partial isometry
![]() $v\in A$
such that
$v\in A$
such that
![]() $v^*v\perp vv^*, 0\le p-(v^*v+vv^*)\le v_1v_1^*\lesssim r.$
Then the lemma holds (by choosing
$v^*v\perp vv^*, 0\le p-(v^*v+vv^*)\le v_1v_1^*\lesssim r.$
Then the lemma holds (by choosing
![]() $p_1=vv^*$
and
$p_1=vv^*$
and
![]() $p_2=v^*v$
).
$p_2=v^*v$
).
Lemma 7.6 (S. Zhang)
Let A be a
![]() $C^*$
-algebra of real rank zero and r be a full projection of A such that
$C^*$
-algebra of real rank zero and r be a full projection of A such that
![]() $B=(1-r)A(1-r)$
contains, for each
$B=(1-r)A(1-r)$
contains, for each
![]() $k\in \mathbb {N},$
a sequence of mutually orthogonal full projections
$k\in \mathbb {N},$
a sequence of mutually orthogonal full projections
![]() $\{r_{n,j}': 1\le j\le 2^{n+1}, n\in \mathbb {N}\}$
such that
$\{r_{n,j}': 1\le j\le 2^{n+1}, n\in \mathbb {N}\}$
such that
![]() $2^{k+n}[r_n']\le [r],$
where
$2^{k+n}[r_n']\le [r],$
where
![]() $r_n'=\sum _{j=1}^{2^{n+1}} r_{n,j}',$
and
$r_n'=\sum _{j=1}^{2^{n+1}} r_{n,j}',$
and
![]() $r_{n,1}', r_{n,2}',...,r_{n,2^{n+1}}'$
are mutually equivalent (
$r_{n,1}', r_{n,2}',...,r_{n,2^{n+1}}'$
are mutually equivalent (
![]() $n\in \mathbb {N}$
). Suppose that
$n\in \mathbb {N}$
). Suppose that
![]() $p\in A$
is a nonzero projection such that
$p\in A$
is a nonzero projection such that
![]() $[p]\not \le [r] .$
Then, for any
$[p]\not \le [r] .$
Then, for any
![]() $m\in \mathbb {N},$
there are mutually orthogonal projections
$m\in \mathbb {N},$
there are mutually orthogonal projections
![]() $p_{_{1}},p_{_{2}}, ..., p_{_{2^m}}, p_{_{2^m+1}}\in A$
such that
$p_{_{1}},p_{_{2}}, ..., p_{_{2^m}}, p_{_{2^m+1}}\in A$
such that
 $$ \begin{align} p=\sum_{j=1}^{2^m} p_j+p_{_{2^m+1}},\,\, p_{_{j}}\sim p_{_{1}}, 1\le j\le 2^m, \,\,\,\mathrm{and}\,\,\, p_{_{2^m+1}}\lesssim r+r', \end{align} $$
$$ \begin{align} p=\sum_{j=1}^{2^m} p_j+p_{_{2^m+1}},\,\, p_{_{j}}\sim p_{_{1}}, 1\le j\le 2^m, \,\,\,\mathrm{and}\,\,\, p_{_{2^m+1}}\lesssim r+r', \end{align} $$
where
![]() $r'$
is a finite sum of
$r'$
is a finite sum of
![]() $r_{n,j}' s$
and
$r_{n,j}' s$
and
![]() $2[r']<r.$
$2[r']<r.$
Proof We use the induction on
![]() $m.$
If
$m.$
If
![]() $m=1,$
the lemma follows from Lemma 7.5.
$m=1,$
the lemma follows from Lemma 7.5.
Suppose that the lemma holds for
![]() $m{{\geq 1}}.$
Then there are mutually orthogonal projections
$m{{\geq 1}}.$
Then there are mutually orthogonal projections
![]() $p_{_{1}},p_{_{2}}, ..., p_{_{2^m}}, p_{_{2^m+1}}\in A$
such that
$p_{_{1}},p_{_{2}}, ..., p_{_{2^m}}, p_{_{2^m+1}}\in A$
such that
 $$ \begin{align} p=\sum_{j=1}^{2^m} p_j+p_{_{2^m+1}},\,\, p_j\sim p_1, 1\le j\le 2^m, \,\,\,\mathrm{and}\,\,\, p_{2^m+1}\lesssim r+r", \end{align} $$
$$ \begin{align} p=\sum_{j=1}^{2^m} p_j+p_{_{2^m+1}},\,\, p_j\sim p_1, 1\le j\le 2^m, \,\,\,\mathrm{and}\,\,\, p_{2^m+1}\lesssim r+r", \end{align} $$
where
![]() $r"$
is a finite sum of
$r"$
is a finite sum of
![]() $r_{n,i}'s$
and
$r_{n,i}'s$
and
![]() $2[r"]<[r].$
Choose
$2[r"]<[r].$
Choose
![]() $r_{K,1}'$
among
$r_{K,1}'$
among
![]() $\{r_{n,j}'\}$
but not those which have been used for the sum of
$\{r_{n,j}'\}$
but not those which have been used for the sum of
![]() $ r".$
We choose K such that
$ r".$
We choose K such that
![]() $K>2m.$
Note that
$K>2m.$
Note that
We also note that
![]() $[p_1]\not \le [r_{K,1}'].$
(Otherwise,
$[p_1]\not \le [r_{K,1}'].$
(Otherwise,
![]() $[p]\le 2^m[r_{K,1}']\le 2^K[r_{K,1}]\le [r],$
a contradiction.) Applying Lemma 7.5 to
$[p]\le 2^m[r_{K,1}']\le 2^K[r_{K,1}]\le [r],$
a contradiction.) Applying Lemma 7.5 to
![]() $p_1$
(as p) and the full projection
$p_1$
(as p) and the full projection
![]() $r_{K,1}'$
, we may write
$r_{K,1}'$
, we may write
Since
![]() $p_j\sim p_1,$
we also have mutually orthogonal projections
$p_j\sim p_1,$
we also have mutually orthogonal projections
![]() $p_{j,1}, p_{j,2},p_{j,3}$
such that
$p_{j,1}, p_{j,2},p_{j,3}$
such that
Note that
Put
![]() $s:=\sum _{j=1}^{{{2^m}}}p_{_{j,3}}.$
Then
$s:=\sum _{j=1}^{{{2^m}}}p_{_{j,3}}.$
Then
 $$ \begin{align} s\lesssim r+r"+\sum_{j=1}^{2^{{m}}} r_{K,j}', \,\,2\left[r"+\sum_{j=1}^{2^{{m}}}r^{\prime}_{K,j}\right]\le [r] \,\,\,\mathrm{and}\,\,\, p=\sum_{j=1}^{2^m} (p_{j,1}+p_{j,2}) +s. \end{align} $$
$$ \begin{align} s\lesssim r+r"+\sum_{j=1}^{2^{{m}}} r_{K,j}', \,\,2\left[r"+\sum_{j=1}^{2^{{m}}}r^{\prime}_{K,j}\right]\le [r] \,\,\,\mathrm{and}\,\,\, p=\sum_{j=1}^{2^m} (p_{j,1}+p_{j,2}) +s. \end{align} $$
This completes the induction.
Recall that, if
![]() $C_n\subset A$
(
$C_n\subset A$
(
![]() $n\in \mathbb {N}$
), then
$n\in \mathbb {N}$
), then
![]() $l^\infty (\{C_n\})=\{\{c_n\}\in l^\infty (A): c_n\in C_n\}.$
$l^\infty (\{C_n\})=\{\{c_n\}\in l^\infty (A): c_n\in C_n\}.$
Lemma 7.7 Let A be a non-elementary,
![]() $\sigma $
-unital, and algebraically simple
$\sigma $
-unital, and algebraically simple
![]() $C^*$
-algebra with
$C^*$
-algebra with
![]() $QT(A)\not =\emptyset $
and with T-tracial approximate oscillation zero. Let
$QT(A)\not =\emptyset $
and with T-tracial approximate oscillation zero. Let
![]() $\{e_k\}$
be a sequence in
$\{e_k\}$
be a sequence in
![]() $A_+^{\mathbf {1}}\setminus \{0\}$
such that
$A_+^{\mathbf {1}}\setminus \{0\}$
such that
![]() $\{e_k\}\not \in I_{_{\overline {QT(A)}^w}},$
and
$\{e_k\}\not \in I_{_{\overline {QT(A)}^w}},$
and
![]() $\{e_k\}$
is a permanent projection lifting of the projection
$\{e_k\}$
is a permanent projection lifting of the projection
![]() $p=\Pi (\{e_k\}),$
and let
$p=\Pi (\{e_k\}),$
and let
![]() $n>1$
be an integer and
$n>1$
be an integer and
![]() $\varepsilon>0.$
$\varepsilon>0.$
Then, there are mutually orthogonal and mutually (Cuntz) equivalent elements
for
![]() $k\ge k_0$
(for some
$k\ge k_0$
(for some
![]() $k_0$
),
$k_0$
),
Proof Let
![]() $m\ge 1$
be an integer, and let
$m\ge 1$
be an integer, and let
![]() $\varepsilon>0.$
Put
$\varepsilon>0.$
Put
![]() $B=l^\infty (A)/I_{_{\overline {QT(A)}^w}}.$
Since A has T-tracial oscillation zero, by Theorem 6.4, B has real rank zero. Since
$B=l^\infty (A)/I_{_{\overline {QT(A)}^w}}.$
Since A has T-tracial oscillation zero, by Theorem 6.4, B has real rank zero. Since
![]() $\{e_k\}\not \in I_{_{\overline {QT(A)}^w}},$
$\{e_k\}\not \in I_{_{\overline {QT(A)}^w}},$
If
![]() $r=\Pi (\{r_n\})$
(is full) and
$r=\Pi (\{r_n\})$
(is full) and
![]() $r_n\in A_+^{\mathbf {1}},$
and
$r_n\in A_+^{\mathbf {1}},$
and
then
![]() $[\Pi (\{e_k\})]\not \le [r].$
It then follows from Lemmas 7.4 and 7.6 that, there are
$[\Pi (\{e_k\})]\not \le [r].$
It then follows from Lemmas 7.4 and 7.6 that, there are
![]() $2^{m}+1$
mutually orthogonal projections
$2^{m}+1$
mutually orthogonal projections
![]() $p_1, p_2,...,p_{2^m}, s\in B$
such that s is full,
$p_1, p_2,...,p_{2^m}, s\in B$
such that s is full,
![]() $s=\Pi (\{s_n\}),$
where
$s=\Pi (\{s_n\}),$
where
![]() $s_n\in A_+^{\mathbf {1}},$
$s_n\in A_+^{\mathbf {1}},$
 $$ \begin{align} &p=\sum_{i=1}^{2^m}p_i+s,\,\, p_1\sim p_j, 1\le j\le 2^m\,\,\,\mathrm{and}\,\,\, \end{align} $$
$$ \begin{align} &p=\sum_{i=1}^{2^m}p_i+s,\,\, p_1\sim p_j, 1\le j\le 2^m\,\,\,\mathrm{and}\,\,\, \end{align} $$
Recall that
![]() $\{e_{{k}}\}$
is a permanent projection lifting of
$\{e_{{k}}\}$
is a permanent projection lifting of
![]() $p.$
Then, by (5) of Proposition 6.2,
$p.$
Then, by (5) of Proposition 6.2,
![]() $pBp= l^\infty (\{\mathrm {Her}(e_{{k}})\})/I_{_{\overline {QT(A)}^w}} .$
Define a homomorphism
$pBp= l^\infty (\{\mathrm {Her}(e_{{k}})\})/I_{_{\overline {QT(A)}^w}} .$
Define a homomorphism
![]() $\phi : C_0((0,1])\otimes M_{2^m}\to pBp$
such that
$\phi : C_0((0,1])\otimes M_{2^m}\to pBp$
such that
Since
![]() $C_0((0,1])\otimes M_{2^m}$
is semiprojective, there is a homomorphism
$C_0((0,1])\otimes M_{2^m}$
is semiprojective, there is a homomorphism
Write
![]() $\psi =\{\Psi _k\},$
where
$\psi =\{\Psi _k\},$
where
![]() $\Psi _k: C_0((0,1])\otimes M_{2^m}\to \mathrm {Her}(e_{{k}})$
is a homomorphism. Put
$\Psi _k: C_0((0,1])\otimes M_{2^m}\to \mathrm {Her}(e_{{k}})$
is a homomorphism. Put
Then
![]() $\{g_{k,1}\},\{g_{k,2}\},...,\{g_{k,2^m}\}$
are mutually orthogonal and mutually equivalent. Note that
$\{g_{k,1}\},\{g_{k,2}\},...,\{g_{k,2^m}\}$
are mutually orthogonal and mutually equivalent. Note that
![]() $\Pi (g_{k,i})\}=p_i$
and
$\Pi (g_{k,i})\}=p_i$
and
![]() $\{g_{k,i}\}$
is a permanent projection lifting of
$\{g_{k,i}\}$
is a permanent projection lifting of
![]() $p_i,$
and by (2) of Lemma 6.2,
$p_i,$
and by (2) of Lemma 6.2,
![]() $\lim _{k\to \infty }\omega (g_{k,i})=0.$
$\lim _{k\to \infty }\omega (g_{k,i})=0.$
Then, by Lemma 7.2, there is
![]() $k_1\in \mathbb {N},$
such that, for all
$k_1\in \mathbb {N},$
such that, for all
![]() $k\ge k_1,$
$k\ge k_1,$
 $$ \begin{align} \kern6pt d_\tau(e_k)< d_\tau\left(\sum_{j=1}^{2^m}g_{k,j}\right)+d_\tau({{s_k}})+\varepsilon/2\le 2^md_\tau(g_{k,1})+\varepsilon \,\,\,\mathrm{for\,\,\,all}\,\,\, \tau\in \overline{QT(A)}^w. \end{align} $$
$$ \begin{align} \kern6pt d_\tau(e_k)< d_\tau\left(\sum_{j=1}^{2^m}g_{k,j}\right)+d_\tau({{s_k}})+\varepsilon/2\le 2^md_\tau(g_{k,1})+\varepsilon \,\,\,\mathrm{for\,\,\,all}\,\,\, \tau\in \overline{QT(A)}^w. \end{align} $$
Also, by Lemma 7.2, we may assume that, for all
![]() $k\ge k_1,$
$k\ge k_1,$
 $$ \begin{align} 2^md_\tau(g_{k,1}) \le d_\tau\left(\sum_{j=1}^{2^m}g_{k,j}+{{s_k}}\right)\le d_\tau(e_k)+\varepsilon\,\,\,\mathrm{for\,\,\,all}\,\,\, \tau\in \overline{QT(A)}^w. \end{align} $$
$$ \begin{align} 2^md_\tau(g_{k,1}) \le d_\tau\left(\sum_{j=1}^{2^m}g_{k,j}+{{s_k}}\right)\le d_\tau(e_k)+\varepsilon\,\,\,\mathrm{for\,\,\,all}\,\,\, \tau\in \overline{QT(A)}^w. \end{align} $$
We choose a large m such that
![]() $2^m=ln+m_0,$
where
$2^m=ln+m_0,$
where
![]() $l\in \mathbb {N}$
and
$l\in \mathbb {N}$
and
![]() $m_0\in {{\mathbb {N}\cup \{0\}}}$
such that
$m_0\in {{\mathbb {N}\cup \{0\}}}$
such that
![]() $m_0/2^m<\varepsilon /4.$
Note that, since
$m_0/2^m<\varepsilon /4.$
Note that, since
![]() $\{g_{k,1}\}, \{g_{k,2}\},...,\{g_{k,2^m}\}$
are mutually orthogonal, for any sum
$\{g_{k,1}\}, \{g_{k,2}\},...,\{g_{k,2^m}\}$
are mutually orthogonal, for any sum
![]() $f_{k,j}$
of some l many
$f_{k,j}$
of some l many
![]() $\{g_{k, i}\}'s, \lim _{k\to \infty } \omega (f_{k,j})=0.$
For each
$\{g_{k, i}\}'s, \lim _{k\to \infty } \omega (f_{k,j})=0.$
For each
![]() $1\le j\le n,$
by (e7.66) and (e7.67), and by choosing
$1\le j\le n,$
by (e7.66) and (e7.67), and by choosing
![]() $f_{k,j}$
to be a sum of l many (different)
$f_{k,j}$
to be a sum of l many (different)
![]() $g_{k,i}'s,$
we see (e7.58) and (e7.59) hold.
$g_{k,i}'s,$
we see (e7.58) and (e7.59) hold.
Corollary 7.8 Let A be a non-elementary,
![]() $\sigma $
-unital, and algebraically simple
$\sigma $
-unital, and algebraically simple
![]() $C^*$
-algebra with
$C^*$
-algebra with
![]() $QT(A)\not =\emptyset $
and T-tracial approximate oscillation zero. Let
$QT(A)\not =\emptyset $
and T-tracial approximate oscillation zero. Let
![]() $e_k\in A_+^{\mathbf {1}}\setminus \{0\}$
(
$e_k\in A_+^{\mathbf {1}}\setminus \{0\}$
(
![]() $k\in \mathbb {N}$
) be such that
$k\in \mathbb {N}$
) be such that
![]() $\{e_k\}\not \in I_{\overline {QT(A)}^w}$
and
$\{e_k\}\not \in I_{\overline {QT(A)}^w}$
and
![]() $\{e_k\}$
is a permanent projection lifting of
$\{e_k\}$
is a permanent projection lifting of
![]() $p=\Pi (\{e_k \}),$
and let
$p=\Pi (\{e_k \}),$
and let
![]() $n>1$
be an integer and
$n>1$
be an integer and
![]() $\varepsilon>0.$
$\varepsilon>0.$
Then, there is
![]() $k_0\in \mathbb {N}$
such that, for any
$k_0\in \mathbb {N}$
such that, for any
![]() $k\ge k_0$
and for any
$k\ge k_0$
and for any
![]() $1\le i\le n,$
there exists
$1\le i\le n,$
there exists
![]() ${{h}}_{k,i}\in {{\mathrm {Her}(e_k)_+}}$
such that
${{h}}_{k,i}\in {{\mathrm {Her}(e_k)_+}}$
such that
Proof By the proof of Lemma 7.7, for
![]() $k\ge k_0,$
$k\ge k_0,$
So, for any
![]() $1\le i\le n,$
choose
$1\le i\le n,$
choose
![]() ${{h_{k,i}}}=\sum _{j=1}^i f_{k,j}.$
Then
${{h_{k,i}}}=\sum _{j=1}^i f_{k,j}.$
Then
Definition 7.9 Let A be a
![]() $C^*$
-algebra with
$C^*$
-algebra with
![]() ${\widetilde {QT}}(A)\setminus \{0\}\not =\emptyset .$
Define
${\widetilde {QT}}(A)\setminus \{0\}\not =\emptyset .$
Define
Lemma 7.10 Let A be a non-elementary,
![]() $\sigma $
-unital, and simple
$\sigma $
-unital, and simple
![]() $C^*$
-algebra with
$C^*$
-algebra with
![]() ${\widetilde {QT}}(A)\setminus \{0\}\not =\emptyset .$
Suppose that A has T-tracial approximate oscillation zero. Then the image of the canonical map
${\widetilde {QT}}(A)\setminus \{0\}\not =\emptyset .$
Suppose that A has T-tracial approximate oscillation zero. Then the image of the canonical map
![]() $\Gamma $
(see Definition 2.13) is dense in
$\Gamma $
(see Definition 2.13) is dense in
![]() $R_{\tau , f}(A).$
$R_{\tau , f}(A).$
Proof Fix a nonzero element
![]() $0\le e\le 1$
in
$0\le e\le 1$
in
![]() $\mathrm {Ped}(A)_+.$
Let
$\mathrm {Ped}(A)_+.$
Let
![]() $A_1=\mathrm {Her}(e).$
Then
$A_1=\mathrm {Her}(e).$
Then
![]() $A_1=\mathrm {Ped}(A_1).$
By Brown’s stable isomorphism theorem [Reference Brown4],
$A_1=\mathrm {Ped}(A_1).$
By Brown’s stable isomorphism theorem [Reference Brown4],
![]() $A_1\otimes {\cal K}\cong A\otimes {\cal K}.$
It suffices to show that the image of the map
$A_1\otimes {\cal K}\cong A\otimes {\cal K}.$
It suffices to show that the image of the map
![]() $\Gamma _1: \mathrm {Cu}(A_1)=\mathrm {Cu}(A)\to \mathrm {LAff}_+(\overline {QT(A_1)}^w)$
is dense in
$\Gamma _1: \mathrm {Cu}(A_1)=\mathrm {Cu}(A)\to \mathrm {LAff}_+(\overline {QT(A_1)}^w)$
is dense in
Fix
![]() $a\in \mathrm {Ped}(A_1\otimes {\cal K})_+.$
Let
$a\in \mathrm {Ped}(A_1\otimes {\cal K})_+.$
Let
![]() $\varepsilon>0.$
It suffices to show that there is
$\varepsilon>0.$
It suffices to show that there is
![]() $f\in \mathrm {Cu}(A_1)$
such that
$f\in \mathrm {Cu}(A_1)$
such that
Without loss of generality, we may assume that
![]() $0\le a\le 1.$
Since
$0\le a\le 1.$
Since
![]() $a\in \mathrm {Ped}(A_1\otimes {\cal K})_+,$
there exists
$a\in \mathrm {Ped}(A_1\otimes {\cal K})_+,$
there exists
![]() $r\ge 1$
such that
$r\ge 1$
such that
![]() $r[f_{\delta }(e)]\ge [a]$
for some
$r[f_{\delta }(e)]\ge [a]$
for some
![]() $\delta \in (0,1/4).$
Therefore, we may assume that
$\delta \in (0,1/4).$
Therefore, we may assume that
![]() $a\in M_r(A_1)$
for some integer
$a\in M_r(A_1)$
for some integer
![]() $r\ge 1.$
$r\ge 1.$
Put
![]() $B:=l^\infty (A_1)/I_{_{\overline {QT(A_1)}^w}}.$
Then, by Theorem 6.4, B has real rank zero.
$B:=l^\infty (A_1)/I_{_{\overline {QT(A_1)}^w}}.$
Then, by Theorem 6.4, B has real rank zero.
Therefore, for any
![]() $\varepsilon>0,$
there are mutually orthogonal projections
$\varepsilon>0,$
there are mutually orthogonal projections
![]() $p_1, p_2,...,p_m\in M_r(B)$
and
$p_1, p_2,...,p_m\in M_r(B)$
and
![]() $\lambda _1, \lambda _2,...,\lambda _m\in (0, 1)$
such that
$\lambda _1, \lambda _2,...,\lambda _m\in (0, 1)$
such that
 $$ \begin{align} \left\|\Pi(\iota(a))-\sum_{i=1}^m\lambda_i p_i\right\|<\varepsilon/16. \end{align} $$
$$ \begin{align} \left\|\Pi(\iota(a))-\sum_{i=1}^m\lambda_i p_i\right\|<\varepsilon/16. \end{align} $$
We may assume that
![]() $\lambda _i\in (0,1)\cap \mathbb {Q}.$
There are mutually orthogonal elements
$\lambda _i\in (0,1)\cap \mathbb {Q}.$
There are mutually orthogonal elements
![]() $\{e_{n,i}\}\in l^\infty ( M_r(A_1) )$
(
$\{e_{n,i}\}\in l^\infty ( M_r(A_1) )$
(
![]() $i=1,2,...,m$
) such that
$i=1,2,...,m$
) such that
![]() $\Pi (\{e_{n,i}\})=p_i, i=1,2,...,m.$
By Proposition 6.2, we may assume that
$\Pi (\{e_{n,i}\})=p_i, i=1,2,...,m.$
By Proposition 6.2, we may assume that
![]() $\{e_{n,i}\}$
is a permanent projection lifting. By (2) of Proposition 6.2,
$\{e_{n,i}\}$
is a permanent projection lifting. By (2) of Proposition 6.2,
![]() $\lim _{n\to \infty }\omega (e_{n,i})=0.$
Without loss of generality, we may assume that, for all
$\lim _{n\to \infty }\omega (e_{n,i})=0.$
Without loss of generality, we may assume that, for all
![]() $n\in \mathbb {N},$
$n\in \mathbb {N},$
Applying Corollary 7.8, without loss of generality, we may also assume that, there are permanent projection liftings
![]() $\{f_{n,i}\}$
such that
$\{f_{n,i}\}$
such that
By (e7.72), there exists
![]() $\{c_n\}\in I_{_{\overline {QT(A_1)}^w}}$
and
$\{c_n\}\in I_{_{\overline {QT(A_1)}^w}}$
and
![]() $n_1\in \mathbb {N}$
such that, for all
$n_1\in \mathbb {N}$
such that, for all
![]() $n\ge n_1,$
$n\ge n_1,$
 $$ \begin{align} \left\|a-\sum_{i=1}^m \lambda_ie_{i,n}+c_n\right\|<\varepsilon/8. \end{align} $$
$$ \begin{align} \left\|a-\sum_{i=1}^m \lambda_ie_{i,n}+c_n\right\|<\varepsilon/8. \end{align} $$
Then, for
![]() $n\ge n_1,$
$n\ge n_1,$
 $$ \begin{align*}{{\sup\left\{\left|\tau\left(a-\sum_{i=1}^m \lambda_ie_{n,i}+c_n\right)\right|:\tau\in \overline{QT(A_1)}^w\right\}<\varepsilon/8.}}\end{align*} $$
$$ \begin{align*}{{\sup\left\{\left|\tau\left(a-\sum_{i=1}^m \lambda_ie_{n,i}+c_n\right)\right|:\tau\in \overline{QT(A_1)}^w\right\}<\varepsilon/8.}}\end{align*} $$
Since
![]() $\{c_n\} \in I_{_{\overline {QT(A_1)}^w}},$
we have
$\{c_n\} \in I_{_{\overline {QT(A_1)}^w}},$
we have
![]() $\{|c_n|^{1/2}\}\in I_{{_{\overline {QT(A_1)}^w}}}.$
It follows that
$\{|c_n|^{1/2}\}\in I_{{_{\overline {QT(A_1)}^w}}}.$
It follows that
Therefore, there exists
![]() $n_2\ge n_1$
such that
$n_2\ge n_1$
such that
 $$ \begin{align} \left|\tau\left(a-\sum_{i=1}^m \lambda_ie_{n,i}\right)|<|\tau(c_n)\right|+\varepsilon/8<\varepsilon/4\,\,\,\mathrm{for\,\,\,all}\,\,\, \tau\in \overline{QT(A_1)}^w\,\,\mathrm{and} \,\,\,\mathrm{for\,\,\,all}\,\,\, n\ge n_2. \end{align} $$
$$ \begin{align} \left|\tau\left(a-\sum_{i=1}^m \lambda_ie_{n,i}\right)|<|\tau(c_n)\right|+\varepsilon/8<\varepsilon/4\,\,\,\mathrm{for\,\,\,all}\,\,\, \tau\in \overline{QT(A_1)}^w\,\,\mathrm{and} \,\,\,\mathrm{for\,\,\,all}\,\,\, n\ge n_2. \end{align} $$
Thus, by (e7.73) and (e7.74), for
![]() $n\ge n_2,$
$n\ge n_2,$
 $$ \begin{align} \left|\tau(a)-\sum_{i=1}^m d_\tau(f_{n,i})\right|<\varepsilon/2\,\,\,\mathrm{for\,\,\,all}\,\,\, \tau\in \overline{QT(A_1)}^w. \end{align} $$
$$ \begin{align} \left|\tau(a)-\sum_{i=1}^m d_\tau(f_{n,i})\right|<\varepsilon/2\,\,\,\mathrm{for\,\,\,all}\,\,\, \tau\in \overline{QT(A_1)}^w. \end{align} $$
Put
![]() $e=\mathrm {diag}(f_{n,1}, f_{n,2},...,f_{n,m}).$
Then
$e=\mathrm {diag}(f_{n,1}, f_{n,2},...,f_{n,m}).$
Then
This completes the proof.
Theorem 7.11 Let A be a non-elementary and
![]() $\sigma $
-unital simple
$\sigma $
-unital simple
![]() $C^*$
-algebra with
$C^*$
-algebra with
![]() $\widetilde {QT}(A)\setminus \{0\}\not =\emptyset $
and strict comparison. Suppose that A has T-tracial approximate oscillation zero. Then
$\widetilde {QT}(A)\setminus \{0\}\not =\emptyset $
and strict comparison. Suppose that A has T-tracial approximate oscillation zero. Then
![]() $\Gamma $
is surjective (see Definition 2.13).
$\Gamma $
is surjective (see Definition 2.13).
Proof We keep the same setting as in the proof of Theorem 7.10.
Let
![]() $b\in \mathrm {Ped}(A_1\otimes {\cal K})_+$
with
$b\in \mathrm {Ped}(A_1\otimes {\cal K})_+$
with
![]() $0\le b\le 1.$
Choose
$0\le b\le 1.$
Choose
![]() $b_n=(1-1/(n+1))b.$
Then
$b_n=(1-1/(n+1))b.$
Then
![]() $h_n:=b_{n+1}-b_n\in \mathrm {Ped}(A_1\otimes {\cal K})_+\setminus \{0\}.$
Put
$h_n:=b_{n+1}-b_n\in \mathrm {Ped}(A_1\otimes {\cal K})_+\setminus \{0\}.$
Put
Applying Theorem 7.10, for each
![]() $n\in \mathbb {N},$
we obtain
$n\in \mathbb {N},$
we obtain
![]() $f_n\in \mathrm {Ped}(A_1\otimes {\cal K})_+$
such that
$f_n\in \mathrm {Ped}(A_1\otimes {\cal K})_+$
such that
In particular, for all
![]() $n\in \mathbb {N},$
$n\in \mathbb {N},$
Then, for all
![]() $\tau \in \overline {QT(A_1)}^w$
(note that
$\tau \in \overline {QT(A_1)}^w$
(note that
![]() $b_nb_{n+1}=b_{n+1}b_n$
),
$b_nb_{n+1}=b_{n+1}b_n$
),
It follows from the strict comparison that
![]() $[f_n]$
is an increasing sequence in
$[f_n]$
is an increasing sequence in
![]() $\mathrm {Cu}(A).$
Let f be the supremum of
$\mathrm {Cu}(A).$
Let f be the supremum of
![]() $\{[f_n]\}$
in
$\{[f_n]\}$
in
![]() $\mathrm {Cu}(A).$
We also have, for all
$\mathrm {Cu}(A).$
We also have, for all
![]() $\tau \in \overline {QT(A_1)}^w,$
$\tau \in \overline {QT(A_1)}^w,$
It follows that
![]() $\widehat {f}(\tau )\ge \tau (b_n)$
for all
$\widehat {f}(\tau )\ge \tau (b_n)$
for all
![]() $\tau \in \overline {QT(A_1)}^w$
and for each
$\tau \in \overline {QT(A_1)}^w$
and for each
![]() $n\in \mathbb {N}.$
Hence,
$n\in \mathbb {N}.$
Hence,
Let
![]() $\varepsilon>0.$
By Theorem 7.10, there is
$\varepsilon>0.$
By Theorem 7.10, there is
![]() $c_\varepsilon \in \mathrm {Cu}( A_1 )$
such that
$c_\varepsilon \in \mathrm {Cu}( A_1 )$
such that
Then, for all
![]() $n\in \mathbb {N}$
(see also (e7.81)),
$n\in \mathbb {N}$
(see also (e7.81)),
Hence,
![]() $[f]\le [c_\varepsilon ].$
It follows that
$[f]\le [c_\varepsilon ].$
It follows that
Let
![]() $\varepsilon \to 0.$
We conclude that
$\varepsilon \to 0.$
We conclude that
![]() $\widehat {f}(\tau )=\tau (b)$
for all
$\widehat {f}(\tau )=\tau (b)$
for all
![]() $\tau \in \overline {QT(A_1)}^w.$
$\tau \in \overline {QT(A_1)}^w.$
So far we have shown that, for any
![]() $b\in \mathrm {Ped}(A\otimes {\cal K})_+,$
there is
$b\in \mathrm {Ped}(A\otimes {\cal K})_+,$
there is
![]() $f\in \mathrm {Cu}(A)$
such that
$f\in \mathrm {Cu}(A)$
such that
![]() $\widehat {f}(\tau )=\tau (b)$
for all
$\widehat {f}(\tau )=\tau (b)$
for all
![]() $\tau \in \overline {QT(A)}^w.$
Note that, for any
$\tau \in \overline {QT(A)}^w.$
Note that, for any
![]() $a\in (A\otimes {\cal K})_+, (a-\|a\|/n)_+\in \mathrm {Ped}(A\otimes {\cal K}).$
Thus, there are
$a\in (A\otimes {\cal K})_+, (a-\|a\|/n)_+\in \mathrm {Ped}(A\otimes {\cal K}).$
Thus, there are
![]() $f_n\in \mathrm {Cu}(A)$
such that
$f_n\in \mathrm {Cu}(A)$
such that
![]() $\widehat {f_n}(\tau )=\tau ((a-\|a\|/n)_+)$
for all
$\widehat {f_n}(\tau )=\tau ((a-\|a\|/n)_+)$
for all
![]() $\tau \in \overline {QT(A)}^w.$
Since
$\tau \in \overline {QT(A)}^w.$
Since
![]() $(a-\|a\|/n)_+\nearrow a,$
we conclude, using the similar argument used above, that there is
$(a-\|a\|/n)_+\nearrow a,$
we conclude, using the similar argument used above, that there is
![]() $f\in \mathrm {Cu}(A)$
such that
$f\in \mathrm {Cu}(A)$
such that
![]() $\widehat {f}(\tau )=\tau (a)$
for all
$\widehat {f}(\tau )=\tau (a)$
for all
![]() $\tau \in \overline {QT(A)}^w.$
Applying Theorem 5.7 of [Reference Elliott, Robert and Santiago13] and repeating the argument above, we conclude that
$\tau \in \overline {QT(A)}^w.$
Applying Theorem 5.7 of [Reference Elliott, Robert and Santiago13] and repeating the argument above, we conclude that
![]() $\Gamma $
is surjective.
$\Gamma $
is surjective.
8 Tracially matricial property
Definition 8.1 Let A be a
![]() $C^*$
-algebra and
$C^*$
-algebra and
![]() $S\subset \widetilde {QT}(A)\setminus \{0\}$
be a nonempty compact subset.
$S\subset \widetilde {QT}(A)\setminus \{0\}$
be a nonempty compact subset.
![]() $C^*$
-algebra A is said to have property (TM) relative to
$C^*$
-algebra A is said to have property (TM) relative to
![]() $S,$
if for any
$S,$
if for any
![]() $a\in \mathrm {Ped}(A\otimes {\cal K})_+,$
any
$a\in \mathrm {Ped}(A\otimes {\cal K})_+,$
any
![]() $\varepsilon>0,$
any
$\varepsilon>0,$
any
![]() $n\in \mathbb {N},$
there is a c.p.c. order zero map
$n\in \mathbb {N},$
there is a c.p.c. order zero map
![]() $\phi : M_n\to \mathrm {Her}(a)$
such that
$\phi : M_n\to \mathrm {Her}(a)$
such that
![]() $\|a-\phi (1_n)a\|_{_{2,S}}<\varepsilon .$
$\|a-\phi (1_n)a\|_{_{2,S}}<\varepsilon .$
A
![]() $\sigma $
-unital simple
$\sigma $
-unital simple
![]() $C^*$
-algebra A with
$C^*$
-algebra A with
![]() $\widetilde {QT}(A)\setminus \{0\}\not =\emptyset $
is said to have property (TM), if for some
$\widetilde {QT}(A)\setminus \{0\}\not =\emptyset $
is said to have property (TM), if for some
![]() $e\in \mathrm {Ped}(A)_+^{\mathbf {1}}\setminus \{0\}, \mathrm {Her}(e)$
has property (TM) relative to
$e\in \mathrm {Ped}(A)_+^{\mathbf {1}}\setminus \{0\}, \mathrm {Her}(e)$
has property (TM) relative to
![]() $\overline {QT(A)}^w.$
$\overline {QT(A)}^w.$
From the definition, it is clear that, if A is a
![]() $\sigma $
-unital simple
$\sigma $
-unital simple
![]() $C^*$
-algebra which has property (TM), then
$C^*$
-algebra which has property (TM), then
![]() $A\otimes {\cal K}$
has property (TM), and by Brown’s stable isomorphism theorem [Reference Brown4], every
$A\otimes {\cal K}$
has property (TM), and by Brown’s stable isomorphism theorem [Reference Brown4], every
![]() $\sigma $
-unital hereditary
$\sigma $
-unital hereditary
![]() $C^*$
-subalgebra has property (TM). Since we only need to consider
$C^*$
-subalgebra has property (TM). Since we only need to consider
![]() $\mathrm {Her}(a)$
for each
$\mathrm {Her}(a)$
for each
![]() $a\in \mathrm {Ped}(A\otimes {\cal K})_+^{\mathbf {1}},$
it follows that every hereditary
$a\in \mathrm {Ped}(A\otimes {\cal K})_+^{\mathbf {1}},$
it follows that every hereditary
![]() $C^*$
-subalgebra has property (TM).
$C^*$
-subalgebra has property (TM).
In the absence of strict comparison, one may also define the following:
A
![]() $C^*$
-algebra A is said to have property (CM), if, for any
$C^*$
-algebra A is said to have property (CM), if, for any
![]() $n\in \mathbb {N}$
and any
$n\in \mathbb {N}$
and any
![]() $a\in \mathrm {Ped}(A\otimes {\cal K})_+^{\mathbf {1}},$
there is a c.p.c. order zero map
$a\in \mathrm {Ped}(A\otimes {\cal K})_+^{\mathbf {1}},$
there is a c.p.c. order zero map
![]() $\phi : M_n\to l^\infty (C)/N_{cu}(C)$
such that
$\phi : M_n\to l^\infty (C)/N_{cu}(C)$
such that
where
![]() $C=\overline {a(A\otimes {\cal K})a}.$
$C=\overline {a(A\otimes {\cal K})a}.$
Remark 8.2 In Definition 8.1, let
![]() $\psi : C_0((0,1])\otimes M_n\to \mathrm {Her}(a)$
be the homomorphism induced by
$\psi : C_0((0,1])\otimes M_n\to \mathrm {Her}(a)$
be the homomorphism induced by
![]() $\phi ,$
i.e.,
$\phi ,$
i.e.,
![]() $\psi (\iota \otimes e_{i,j})=\phi (e_{i,j})$
(
$\psi (\iota \otimes e_{i,j})=\phi (e_{i,j})$
(
![]() $1\le i, j\le n$
). Then
$1\le i, j\le n$
). Then
![]() $\mathrm {Her}(a)$
has some “tracially large” matricial structure (see Proposition 8.3).
$\mathrm {Her}(a)$
has some “tracially large” matricial structure (see Proposition 8.3).
Let
![]() $x\in \mathrm {Ped}(A\otimes {\cal K}).$
Then
$x\in \mathrm {Ped}(A\otimes {\cal K}).$
Then
![]() $a_0=x^*x+xx^*\in \mathrm {Ped}(A\otimes {\cal K})_+.$
Note
$a_0=x^*x+xx^*\in \mathrm {Ped}(A\otimes {\cal K})_+.$
Note
![]() $x\in \mathrm {Her}(a_0).$
Let
$x\in \mathrm {Her}(a_0).$
Let
![]() ${\cal F\subset } \mathrm {Her}(a_0)^{\mathbf {1}}$
be a finite set. For any
${\cal F\subset } \mathrm {Her}(a_0)^{\mathbf {1}}$
be a finite set. For any
![]() $1>\varepsilon >0,$
there is
$1>\varepsilon >0,$
there is
![]() $a\in \mathrm {Her}(a_0)_+^{\mathbf {1}}$
such that
$a\in \mathrm {Her}(a_0)_+^{\mathbf {1}}$
such that
If A has property (TM) relative to S such that
![]() $\|\tau \|\le 1$
for all
$\|\tau \|\le 1$
for all
![]() $\tau \in S,$
then there is a c.p.c. order zero map
$\tau \in S,$
then there is a c.p.c. order zero map
![]() $\phi : M_n\to \mathrm {Her}(a_0)$
such that
$\phi : M_n\to \mathrm {Her}(a_0)$
such that
![]() $ \|a-\phi (1_n)a\|_{_{2, S} }<(\varepsilon /2)^3. $
Then, for all
$ \|a-\phi (1_n)a\|_{_{2, S} }<(\varepsilon /2)^3. $
Then, for all
![]() $y\in {\cal F},$
$y\in {\cal F},$
Similarly,
The following fact is well known. For completeness, we include a proof here.
Proposition 8.3 Let A be a
![]() $C^*$
-algebra,
$C^*$
-algebra,
![]() $n\in \mathbb {N},$
and
$n\in \mathbb {N},$
and
![]() $\phi :M_n\to A$
be a c.p.c. order zero map. Then
$\phi :M_n\to A$
be a c.p.c. order zero map. Then
![]() $\mathrm {Her}(\phi (1_n))\cong \mathrm {Her}(\phi (e_{1,1}))\otimes M_n.$
$\mathrm {Her}(\phi (1_n))\cong \mathrm {Her}(\phi (e_{1,1}))\otimes M_n.$
Proof Let
![]() $\psi : C_0((0,1])\otimes M_n\to A$
be the homomorphism defined by
$\psi : C_0((0,1])\otimes M_n\to A$
be the homomorphism defined by
![]() $\psi (\imath \otimes e_{ij})=\phi (e_{i,j}),$
where
$\psi (\imath \otimes e_{ij})=\phi (e_{i,j}),$
where
![]() $\imath $
is the identity function on
$\imath $
is the identity function on
![]() $(0,1], i,j\le n.$
In particular,
$(0,1], i,j\le n.$
In particular,
![]() $\psi (\imath \otimes 1_n)=\phi (1_n).$
Write
$\psi (\imath \otimes 1_n)=\phi (1_n).$
Write
![]() $\psi (\imath \otimes e_{i,j})=u_{i,j}r_{{j}}$
as a polar decomposition of
$\psi (\imath \otimes e_{i,j})=u_{i,j}r_{{j}}$
as a polar decomposition of
![]() $\phi (\imath \otimes e_{i,j})$
in
$\phi (\imath \otimes e_{i,j})$
in
![]() $A^{**}.$
Hence,
$A^{**}.$
Hence,
![]() $r_{{j}}=|{{\psi }}(\imath \otimes e_{i,j})|$
and
$r_{{j}}=|{{\psi }}(\imath \otimes e_{i,j})|$
and
![]() $u_{i,j}$
is a partial isometry in
$u_{i,j}$
is a partial isometry in
![]() $A^{**}.$
Note that
$A^{**}.$
Note that
![]() $au_{i,j}b\in A$
for all
$au_{i,j}b\in A$
for all
![]() $a\in p_iA^{**}p_i\cap A$
and
$a\in p_iA^{**}p_i\cap A$
and
![]() $b\in p_jA^{**}p_j\cap A,$
where
$b\in p_jA^{**}p_j\cap A,$
where
![]() $p_i$
is the open projection of
$p_i$
is the open projection of
![]() $r_i, i,j=1,2,...,n.$
Since
$r_i, i,j=1,2,...,n.$
Since
![]() $\psi $
is a homomorphism, we compute that
$\psi $
is a homomorphism, we compute that
![]() $p_i=u_{i,i}, i=1,2,...,n,$
and
$p_i=u_{i,i}, i=1,2,...,n,$
and
![]() $\{u_{i,j}\}_{1\le i,j\le n}$
forms a system of matrix units for
$\{u_{i,j}\}_{1\le i,j\le n}$
forms a system of matrix units for
![]() $M_n.$
$M_n.$
Define
![]() $\Phi : M_n(\mathrm {Her}({{\varphi }}(e_{1,1})))\cong \mathrm {Her}(\phi (e_{1,1}))\otimes M_n\to \mathrm {Her}(\phi (1_n))$
by defining
$\Phi : M_n(\mathrm {Her}({{\varphi }}(e_{1,1})))\cong \mathrm {Her}(\phi (e_{1,1}))\otimes M_n\to \mathrm {Her}(\phi (1_n))$
by defining
![]() $\Phi (a\otimes e_{i,j})=u_{i,1}au_{1,j}$
for all
$\Phi (a\otimes e_{i,j})=u_{i,1}au_{1,j}$
for all
![]() $a\in \mathrm {Her}({{\varphi }}(e_{1,1})), i,j=1,2,...,n.$
Then
$a\in \mathrm {Her}({{\varphi }}(e_{1,1})), i,j=1,2,...,n.$
Then
![]() $\Phi $
is a homomorphism. Since
$\Phi $
is a homomorphism. Since
![]() $\Phi $
is the identity map on
$\Phi $
is the identity map on
![]() $\mathrm {Her}{{(\phi (e_{1,1}))}}$
and
$\mathrm {Her}{{(\phi (e_{1,1}))}}$
and
![]() $M_n$
is simple, the map
$M_n$
is simple, the map
![]() $\Phi $
is injective. Put
$\Phi $
is injective. Put
![]() $B=\Phi (M_n(\mathrm {Her}({{\varphi }}(e_{1,1})))).$
To see
$B=\Phi (M_n(\mathrm {Her}({{\varphi }}(e_{1,1})))).$
To see
![]() $\Phi $
is surjective, let
$\Phi $
is surjective, let
![]() $x\in A,$
then, for any
$x\in A,$
then, for any
![]() $i,j=1,2,...,n, b_{i,j}=u_{1,i}r_ixr_ju_{j,1}\in \mathrm {Her}(\phi (e_{1,1}){{)}}.$
Therefore,
$i,j=1,2,...,n, b_{i,j}=u_{1,i}r_ixr_ju_{j,1}\in \mathrm {Her}(\phi (e_{1,1}){{)}}.$
Therefore,
It follows that
![]() $\mathrm {Her}(\phi (1_n))=B.$
The lemma follows.
$\mathrm {Her}(\phi (1_n))=B.$
The lemma follows.
Lemma 8.4 Let A be a simple
![]() $C^*$
-algebra with
$C^*$
-algebra with
![]() ${\widetilde {QT}}(A)\setminus \{0\}\not =\emptyset .$
Suppose that
${\widetilde {QT}}(A)\setminus \{0\}\not =\emptyset .$
Suppose that
![]() $A=\mathrm {Ped}(A), A$
has strict comparison and
$A=\mathrm {Ped}(A), A$
has strict comparison and
![]() $\Gamma $
is surjective. Suppose that
$\Gamma $
is surjective. Suppose that
![]() $b\in \mathrm {Ped}(A\otimes {\cal K})_+^{\mathbf {1}}.$
Then, for any
$b\in \mathrm {Ped}(A\otimes {\cal K})_+^{\mathbf {1}}.$
Then, for any
![]() $\varepsilon>0$
and any integer
$\varepsilon>0$
and any integer
![]() $n\ge 1,$
there is a c.p.c. order zero map
$n\ge 1,$
there is a c.p.c. order zero map
![]() $\phi : M_n\to \mathrm {Her}(b)$
such that
$\phi : M_n\to \mathrm {Her}(b)$
such that
Moreover, if
![]() $QT(A)=T(A),$
then
$QT(A)=T(A),$
then
Proof Fix
![]() $\varepsilon \in (0,1/2)$
and
$\varepsilon \in (0,1/2)$
and
![]() $n\in \mathbb {N}.$
Since
$n\in \mathbb {N}.$
Since
![]() $\Gamma : \mathrm {Cu}(A)\to \mathrm {LAff}_+(\overline {QT(A)}^w)$
is surjective,
$\Gamma : \mathrm {Cu}(A)\to \mathrm {LAff}_+(\overline {QT(A)}^w)$
is surjective,
![]() $\Gamma |_{\mathrm {Cu}(A)_+}$
is also surjective (see (2.13)). Note that
$\Gamma |_{\mathrm {Cu}(A)_+}$
is also surjective (see (2.13)). Note that
![]() $(1/n)\widehat {[b]}\in \mathrm {LAff}_+(\overline {QT(A)}^w).$
We may choose
$(1/n)\widehat {[b]}\in \mathrm {LAff}_+(\overline {QT(A)}^w).$
We may choose
![]() $b_1\in (A\otimes {\cal K})_+^{\mathbf {1}}$
such that
$b_1\in (A\otimes {\cal K})_+^{\mathbf {1}}$
such that
![]() $d_\tau (b_1)=(1/n)d_\tau (b)$
for all
$d_\tau (b_1)=(1/n)d_\tau (b)$
for all
![]() $\tau \in \overline {QT(A)}^w$
and
$\tau \in \overline {QT(A)}^w$
and
![]() $b_1$
is not Cuntz equivalent to a projection. We compute that
$b_1$
is not Cuntz equivalent to a projection. We compute that
![]() $\omega (b_1)=(1/n)\omega (b)$
(see (e4.5)). Choose
$\omega (b_1)=(1/n)\omega (b)$
(see (e4.5)). Choose
![]() $\delta>0$
such that
$\delta>0$
such that
Put
![]() $b_2=f_\delta (b_1)$
and
$b_2=f_\delta (b_1)$
and
![]() $ d_1=\mathrm {diag}(\overbrace {b_1, b_1,...,b_1}^n)\in A\otimes {\cal K}. $
Then
$ d_1=\mathrm {diag}(\overbrace {b_1, b_1,...,b_1}^n)\in A\otimes {\cal K}. $
Then
Since
![]() $b_1$
is not Cuntz equivalent to a projection, for any
$b_1$
is not Cuntz equivalent to a projection, for any
![]() $0<\eta <\delta /2, d_\tau (f_\eta (d_1))<d_\tau (b)$
for all
$0<\eta <\delta /2, d_\tau (f_\eta (d_1))<d_\tau (b)$
for all
![]() $\tau \in \overline {QT(A)}^w.$
Since A has strict comparison, by [Reference Rørdam40, Proposition 2.4(iv)], there is
$\tau \in \overline {QT(A)}^w.$
Since A has strict comparison, by [Reference Rørdam40, Proposition 2.4(iv)], there is
![]() $x\in A\otimes {\cal K}$
such that
$x\in A\otimes {\cal K}$
such that
Then one obtains an isomorphism
 $$ \begin{align*}\psi: \mathrm{Her}(x^*x)&\to \mathrm{Her}(xx^*)\subset \mathrm{Her}(b) \,\,\, \mathrm{{such\,\, that}} \,\,\, \psi(f(x^*x))\\& =f(xx^*)\,\,\,\mathrm{for\,\,\,all}\,\,\, f\in C_0((0, \|x\|^2]). \end{align*} $$
$$ \begin{align*}\psi: \mathrm{Her}(x^*x)&\to \mathrm{Her}(xx^*)\subset \mathrm{Her}(b) \,\,\, \mathrm{{such\,\, that}} \,\,\, \psi(f(x^*x))\\& =f(xx^*)\,\,\,\mathrm{for\,\,\,all}\,\,\, f\in C_0((0, \|x\|^2]). \end{align*} $$
It induces a homomorphism
![]() $\phi _c: C_0(\mathrm {sp}(f_\delta ({{b_1}})))\otimes M_n\to \mathrm {Her}(b)$
such that
$\phi _c: C_0(\mathrm {sp}(f_\delta ({{b_1}})))\otimes M_n\to \mathrm {Her}(b)$
such that
![]() $\phi _c(\imath \otimes 1_n)=xx^*,$
where
$\phi _c(\imath \otimes 1_n)=xx^*,$
where
![]() $\imath \in C_0(f_\delta ({{b_1}}))$
is the identity function on
$\imath \in C_0(f_\delta ({{b_1}}))$
is the identity function on
![]() $\mathrm {sp}({{f_{\delta }(b_1)}}).$
Define a c.p.c. order zero map
$\mathrm {sp}({{f_{\delta }(b_1)}}).$
Define a c.p.c. order zero map
![]() $\phi : M_n\to \mathrm {Her}(b)$
by
$\phi : M_n\to \mathrm {Her}(b)$
by
![]() $\phi (e_{i,j})=\phi _c(\imath \otimes {{e_{i,j}}})$
(
$\phi (e_{i,j})=\phi _c(\imath \otimes {{e_{i,j}}})$
(
![]() $1\le i,j\le 1$
).
$1\le i,j\le 1$
).
Let p be the open projection in
![]() $A^{**}$
corresponding to b which may be identified with the identity of
$A^{**}$
corresponding to b which may be identified with the identity of
![]() $\widetilde {\mathrm {Her}(b)}.$
We extend each
$\widetilde {\mathrm {Her}(b)}.$
We extend each
![]() $\tau \in \overline {QT(A)}^w$
to a 2-quasitrace on
$\tau \in \overline {QT(A)}^w$
to a 2-quasitrace on
![]() $\widetilde {\mathrm {Her}(b)}$
(see II.2.5 of [Reference Blackadar and Handelman2]) such that
$\widetilde {\mathrm {Her}(b)}$
(see II.2.5 of [Reference Blackadar and Handelman2]) such that
![]() $\tau (p)=\|\tau |_{\mathrm {Her}(b)}\|=d_\tau (b).$
Then, we have, for all
$\tau (p)=\|\tau |_{\mathrm {Her}(b)}\|=d_\tau (b).$
Then, we have, for all
![]() $\tau \in \overline {QT(A)}^w,$
$\tau \in \overline {QT(A)}^w,$
It follows that
In the case that
![]() $QT(A)=T(A),$
one can also apply Cauchy–Bunyakovsky–Schwarz inequality (and (e8.14)) to obtain (e8.9).
$QT(A)=T(A),$
one can also apply Cauchy–Bunyakovsky–Schwarz inequality (and (e8.14)) to obtain (e8.9).
Theorem 8.5 Let A be a
![]() $\sigma $
-unital simple non-elementary
$\sigma $
-unital simple non-elementary
![]() $C^*$
-algebra with
$C^*$
-algebra with
![]() $QT(A)\setminus \{0\}\not =\emptyset .$
Suppose that A has strict comparison and T-tracial approximate oscillation zero. Then A has property (TM).
$QT(A)\setminus \{0\}\not =\emptyset .$
Suppose that A has strict comparison and T-tracial approximate oscillation zero. Then A has property (TM).
Proof Choose
![]() $e\in \mathrm {Ped}(A)_+\setminus \{0\}$
and define
$e\in \mathrm {Ped}(A)_+\setminus \{0\}$
and define
![]() $A_1=\mathrm {Her}(e).$
By Brown’s stable isomorphism theorem [Reference Brown4],
$A_1=\mathrm {Her}(e).$
By Brown’s stable isomorphism theorem [Reference Brown4],
![]() $A_1\otimes {\cal K}\cong A\otimes {\cal K}.$
To show that A has property (TM), it suffices to show that
$A_1\otimes {\cal K}\cong A\otimes {\cal K}.$
To show that A has property (TM), it suffices to show that
![]() $A_1$
has property (TM). To simplify notation, without loss of generality, we may assume that
$A_1$
has property (TM). To simplify notation, without loss of generality, we may assume that
![]() $A=\mathrm {Ped}(A).$
$A=\mathrm {Ped}(A).$
Fix
![]() $a\in \mathrm {Ped}(A\otimes {\cal K})$
such that
$a\in \mathrm {Ped}(A\otimes {\cal K})$
such that
![]() $0\le a\le 1.$
Since A has T-tracial approximate oscillation zero,
$0\le a\le 1.$
Since A has T-tracial approximate oscillation zero,
![]() $\Omega ^T(a)=0.$
It follows that there is a sequence
$\Omega ^T(a)=0.$
It follows that there is a sequence
![]() $c_k\in \mathrm {Her}(a)$
with
$c_k\in \mathrm {Her}(a)$
with
![]() $0\le c_k\le 1$
such that
$0\le c_k\le 1$
such that
where
![]() $c=\{c_k\}$
and
$c=\{c_k\}$
and
![]() $\Pi : l^\infty (A)\to l^\infty (A)/I_{_{\overline {QT(A)}^w}}$
is the quotient map. By Theorem 7.11,
$\Pi : l^\infty (A)\to l^\infty (A)/I_{_{\overline {QT(A)}^w}}$
is the quotient map. By Theorem 7.11,
![]() $\Gamma $
is surjective. Then, applying Lemma 8.4, we obtain a c.p.c. order zero map
$\Gamma $
is surjective. Then, applying Lemma 8.4, we obtain a c.p.c. order zero map
![]() $\phi _k: M_n\to \mathrm {Her}( c_k )\subset \mathrm {Her}(a)$
such that
$\phi _k: M_n\to \mathrm {Her}( c_k )\subset \mathrm {Her}(a)$
such that
Fix
![]() $1>\varepsilon >0.$
Choose
$1>\varepsilon >0.$
Choose
![]() $k_0\ge 1$
such that
$k_0\ge 1$
such that
Since
![]() $\Pi (\iota (a))=\Pi (c),$
there exists
$\Pi (\iota (a))=\Pi (c),$
there exists
![]() $k_1\ge k_0$
such that
$k_1\ge k_0$
such that
Choose
![]() $b=c_{k_1+1}.$
Then, for
$b=c_{k_1+1}.$
Then, for
![]() $k\ge k_1,$
$k\ge k_1,$
 $$ \begin{align*}\nonumber \|a-\phi_k(1_n)a\|_{_{2, \overline{QT(A)}^w}}^{2/3} &\le \|a-b\|_{_{2, \overline{QT(A)}^w}}^{2/3} +\|b-\phi_k(1_n)b\|_{_{2, \overline{QT(A)}^w}}^{2/3}\\\nonumber &+\|\phi_k(1_n)(b-a)\|_{_{2, \overline{QT(A)}^w}}^{2/3}\\\nonumber &< \varepsilon/3+\varepsilon/3+\varepsilon/3<\varepsilon.\\[-34pt] \end{align*} $$
$$ \begin{align*}\nonumber \|a-\phi_k(1_n)a\|_{_{2, \overline{QT(A)}^w}}^{2/3} &\le \|a-b\|_{_{2, \overline{QT(A)}^w}}^{2/3} +\|b-\phi_k(1_n)b\|_{_{2, \overline{QT(A)}^w}}^{2/3}\\\nonumber &+\|\phi_k(1_n)(b-a)\|_{_{2, \overline{QT(A)}^w}}^{2/3}\\\nonumber &< \varepsilon/3+\varepsilon/3+\varepsilon/3<\varepsilon.\\[-34pt] \end{align*} $$
Lemma 8.6 Let A be a
![]() $\sigma $
-unital algebraically simple
$\sigma $
-unital algebraically simple
![]() $C^*$
-algebra with
$C^*$
-algebra with
![]() $QT(A){\kern-1.2pt}\not ={\kern-1.2pt}\emptyset .$
Suppose that A has property (TM) and
$QT(A){\kern-1.2pt}\not ={\kern-1.2pt}\emptyset .$
Suppose that A has property (TM) and
![]() $a\in \mathrm {Ped}(A\otimes {\cal K})_+^{\mathbf {1}}\setminus \{0\}.$
Then, for any integer
$a\in \mathrm {Ped}(A\otimes {\cal K})_+^{\mathbf {1}}\setminus \{0\}.$
Then, for any integer
![]() $n, r\in \mathbb {N},$
any
$n, r\in \mathbb {N},$
any
![]() $k\in \mathbb {N}$
(
$k\in \mathbb {N}$
(
![]() $k\ge 2$
) and
$k\ge 2$
) and
![]() $\varepsilon>0,$
there exist an integer
$\varepsilon>0,$
there exist an integer
![]() $m_k\geq r\in \mathbb {N}$
and mutually orthogonal elements
$m_k\geq r\in \mathbb {N}$
and mutually orthogonal elements
![]() $b_{k,1}, b_{k,2},...,b_{k,n}\in \mathrm {Her}(a)_+^{\mathbf {1}}$
such that
$b_{k,1}, b_{k,2},...,b_{k,n}\in \mathrm {Her}(a)_+^{\mathbf {1}}$
such that
![]() $[b_{k,i}]=[b_{k,1}], i=1,2,...,n,$
$[b_{k,i}]=[b_{k,1}], i=1,2,...,n,$
and an integer
![]() $ l(k) \in \mathbb {N}$
such that
$ l(k) \in \mathbb {N}$
such that
Proof Fix
![]() $n\in \mathbb {N}.$
Since A has property (TM), for each
$n\in \mathbb {N}.$
Since A has property (TM), for each
![]() $m\in \mathbb {N},$
there exists a c.p.c. order zero map
$m\in \mathbb {N},$
there exists a c.p.c. order zero map
![]() $ \phi _m : M_n\to \mathrm {Her}(a)$
such that
$ \phi _m : M_n\to \mathrm {Her}(a)$
such that
Define
![]() $c:=\Pi (\{a^{1/m}\}{{_{m\in \mathbb {N}}}})$
and
$c:=\Pi (\{a^{1/m}\}{{_{m\in \mathbb {N}}}})$
and
![]() $\phi : M_n\to l^\infty (A)/I_{_{\overline {QT(A)}^w}}$
such that
$\phi : M_n\to l^\infty (A)/I_{_{\overline {QT(A)}^w}}$
such that
![]() $\phi (f)=\Pi (\{\phi _m(f)\})$
for all
$\phi (f)=\Pi (\{\phi _m(f)\})$
for all
![]() $f\in M_n.$
Then
$f\in M_n.$
Then
It follows that
![]() $c=cf_{1/2}(\phi (1_n))=f_{1/2}(\phi (1_n))c=c.$
Thus,
$c=cf_{1/2}(\phi (1_n))=f_{1/2}(\phi (1_n))c=c.$
Thus,
![]() $c\le f_{1/2}(\phi (1_n)).$
$c\le f_{1/2}(\phi (1_n)).$
Let
![]() $\varepsilon>0.$
By (1) of Lemma 7.2, for each integer
$\varepsilon>0.$
By (1) of Lemma 7.2, for each integer
![]() $k\ge 2,$
there exists
$k\ge 2,$
there exists
![]() $m_k{{\geq r}}\in \mathbb {N}$
such that, for all
$m_k{{\geq r}}\in \mathbb {N}$
such that, for all
![]() $m\ge m_k,$
$m\ge m_k,$
where
![]() $\sup \{d_\tau (d_m): \tau \in \overline {QT(A)}^w\}<\varepsilon /2.$
Put
$\sup \{d_\tau (d_m): \tau \in \overline {QT(A)}^w\}<\varepsilon /2.$
Put
![]() $b_{k,i}=\phi _{m_k}(e_{i,i}) 1\le i\le n$
and
$b_{k,i}=\phi _{m_k}(e_{i,i}) 1\le i\le n$
and
![]() $k\in \mathbb {N}.$
Then (e8.20) holds. On the other hand, since
$k\in \mathbb {N}.$
Then (e8.20) holds. On the other hand, since
![]() $\phi _{m_k}(1_n)\in \mathrm {Her}(a),$
for each
$\phi _{m_k}(1_n)\in \mathrm {Her}(a),$
for each
![]() $k,$
there is
$k,$
there is
![]() $l(k)\in \mathbb {N}$
such that
$l(k)\in \mathbb {N}$
such that
It follows that (see Proposition 2.2 of [Reference Rørdam40]), for
![]() $k\ge 2,$
$k\ge 2,$
Then (e8.21) holds.
Theorem 8.7 Let A be a
![]() $\sigma $
-unital simple
$\sigma $
-unital simple
![]() $C^*$
-algebra with
$C^*$
-algebra with
![]() $QT(A)\not =\{0\}.$
If A has strict comparison and property (TM), then
$QT(A)\not =\{0\}.$
If A has strict comparison and property (TM), then
![]() $\Gamma $
is surjective (see Definition 2.13).
$\Gamma $
is surjective (see Definition 2.13).
Proof It suffices to prove the proposition for the case that
![]() $A=\mathrm {Ped}(A).$
$A=\mathrm {Ped}(A).$
We claim that, for any
![]() $a\in \mathrm {Ped}(A\otimes {\cal K})_+^{\mathbf {1}}\setminus \{0\}$
and any integer
$a\in \mathrm {Ped}(A\otimes {\cal K})_+^{\mathbf {1}}\setminus \{0\}$
and any integer
![]() $n\in \mathbb {N},$
there exists
$n\in \mathbb {N},$
there exists
![]() $b\in (A\otimes {\cal K})_+$
such that
$b\in (A\otimes {\cal K})_+$
such that
Case (1):
![]() $0$
is an isolated point of
$0$
is an isolated point of
![]() $\mathrm {sp}(a).$
In this case, we may assume that
$\mathrm {sp}(a).$
In this case, we may assume that
![]() $a=p$
for some projection
$a=p$
for some projection
![]() $p.$
Choose
$p.$
Choose
 $$ \begin{align} \eta:=\left({1\over{(n+1)^2}}\right)\inf\{\tau(p): \tau\in \overline{QT(A)}^w\}>0. \end{align} $$
$$ \begin{align} \eta:=\left({1\over{(n+1)^2}}\right)\inf\{\tau(p): \tau\in \overline{QT(A)}^w\}>0. \end{align} $$
Note that
![]() $f_{1/k}(p)=p$
for all
$f_{1/k}(p)=p$
for all
![]() $k>1.$
Applying Lemma 8.6, we obtain
$k>1.$
Applying Lemma 8.6, we obtain
![]() $b\in \mathrm {Her}(a)_+$
such that
$b\in \mathrm {Her}(a)_+$
such that
Then we compute that
Case (2):
![]() $0$
is not an isolated point of
$0$
is not an isolated point of
![]() $\mathrm {sp}(a).$
We will use Lemma 8.6 for an induction argument. Put
$\mathrm {sp}(a).$
We will use Lemma 8.6 for an induction argument. Put
Fix
![]() $n\in N.$
Since
$n\in N.$
Since
![]() $0$
is a not an isolated point of
$0$
is a not an isolated point of
![]() $\mathrm {sp}(a),$
for each integer
$\mathrm {sp}(a),$
for each integer
![]() $k,$
there is a smallest integer
$k,$
there is a smallest integer
![]() ${{J}}(k)>k$
such that
${{J}}(k)>k$
such that
Define, for each
![]() $k,$
$k,$
Applying Lemma 8.6, there are mutually orthogonal elements
![]() $b_{1,1}, b_{1,2},...,b_{1,n}\in \mathrm {Her}(a)_+^{\mathbf {1}}$
such that
$b_{1,1}, b_{1,2},...,b_{1,n}\in \mathrm {Her}(a)_+^{\mathbf {1}}$
such that
![]() $[b_{1,i}]=[b_{1,1}], i=1,2,...,n,$
and, for some
$[b_{1,i}]=[b_{1,1}], i=1,2,...,n,$
and, for some
![]() $m_1\in \mathbb {N},$
$m_1\in \mathbb {N},$
and an integer
![]() $l(1)\in \mathbb {N}$
such that
$l(1)\in \mathbb {N}$
such that
Put
![]() $c_1:=f_{1/2}(b_{1,1}).$
Then, for all
$c_1:=f_{1/2}(b_{1,1}).$
Then, for all
![]() $\tau \in \overline {QT(A)}^w,$
$\tau \in \overline {QT(A)}^w,$
Choose
![]() $k_2>l(1)$
such that
$k_2>l(1)$
such that
![]() $k_2\ge J(l(1)).$
Applying Lemma 8.6, we obtain
$k_2\ge J(l(1)).$
Applying Lemma 8.6, we obtain
![]() $m_2\ge m_1$
and mutually orthogonal
$m_2\ge m_1$
and mutually orthogonal
![]() $b_{2,1},b_{2,2},...,b_{2,n}\in \mathrm {Her}(a)_+^{\mathbf {1}}$
with
$b_{2,1},b_{2,2},...,b_{2,n}\in \mathrm {Her}(a)_+^{\mathbf {1}}$
with
![]() $b_{2,j}\sim b_{2,1}$
(
$b_{2,j}\sim b_{2,1}$
(
![]() $1\le j\le n$
) and
$1\le j\le n$
) and
![]() $l(k_2)\in \mathbb {N}$
such that
$l(k_2)\in \mathbb {N}$
such that
Put
![]() $c_2=f_{1/k_2}(b_{2,1}).$
Then, for all
$c_2=f_{1/k_2}(b_{2,1}).$
Then, for all
![]() $\tau \in \overline {QT(A)}^w,$
$\tau \in \overline {QT(A)}^w,$
We compute that, for all
![]() $\tau \in \overline {QT(A)}^w,$
by (e8.39), (e8.37), and (e8.34) (recall that
$\tau \in \overline {QT(A)}^w,$
by (e8.39), (e8.37), and (e8.34) (recall that
![]() $k_2>J(l(1))$
),
$k_2>J(l(1))$
),
Since A has strict comparison, we obtain
Suppose that we have constructed integers
![]() $k_i, m_i, l(i)\in \mathbb {N}$
and
$k_i, m_i, l(i)\in \mathbb {N}$
and
![]() $b_{i,1}\in \mathrm {Her}(a)_+^{\mathbf {1}}, 1\le i\le I$
such that, for all
$b_{i,1}\in \mathrm {Her}(a)_+^{\mathbf {1}}, 1\le i\le I$
such that, for all
![]() $2\le i\le I$
and
$2\le i\le I$
and
![]() $\tau \in \overline {QT(A)}^w$
(with
$\tau \in \overline {QT(A)}^w$
(with
![]() $l(0)=1$
and
$l(0)=1$
and
![]() $\eta _{l(0)}=\eta _1$
),
$\eta _{l(0)}=\eta _1$
),
and verified that
![]() $ [f_{1/k_i}(b_{i,1}) ] \le [f_{1/k_{i+1}}(b_{i+1,1})], 1\le i\le I-1.$
$ [f_{1/k_i}(b_{i,1}) ] \le [f_{1/k_{i+1}}(b_{i+1,1})], 1\le i\le I-1.$
Define
![]() $c_i=f_{1/k_i}(b_{i,1}), 1\le i\le I.$
By applying Lemma 8.6, there is
$c_i=f_{1/k_i}(b_{i,1}), 1\le i\le I.$
By applying Lemma 8.6, there is
![]() $k_{I+1}>J(l(i))>l(i), l(I+1)\ge k_{I+1}, m_{I+1}\ge m_I,$
and
$k_{I+1}>J(l(i))>l(i), l(I+1)\ge k_{I+1}, m_{I+1}\ge m_I,$
and
![]() $b_{I+1,1}\in \mathrm {Her}(a)_+^{\mathbf {1}}$
such that, for all
$b_{I+1,1}\in \mathrm {Her}(a)_+^{\mathbf {1}}$
such that, for all
![]() $\tau \in \overline {QT(A)}^w,$
$\tau \in \overline {QT(A)}^w,$
Then, for all
![]() $\tau \in \overline {QT(A)}^w,$
$\tau \in \overline {QT(A)}^w,$
 $$ \begin{align}\nonumber nd_\tau(f_{1/k_{I+1}}(b_{I+1,1}))&>d_\tau(f_{1/k_{I+1}}(a^{1/m_{I+1}}))-\eta_{l(I)}\\\nonumber &=d_\tau(f_{1/l(I)}(a)) +(d_\tau(f_{1/k_{I+1}}(a^{1/m_{I+1}}))-d_\tau(f_{1/l(I)}(a)))-\eta_{l(I)}\\\nonumber &\ge nd_\tau(f_{1/k_I}(b_{I,1})) +(d_\tau(f_{1/k_{I+1}}(a^{1/m_{I+1}}))-d_\tau(f_{1/l(I)}(a)))-\eta_{l(I)} \\ &>nd_\tau(f_{1/k_I}(b_{I,1}))+\sigma_{l(I)}-\eta_{l(I)}>nd_\tau(f_{1/k_I}(b_{I,1})). \end{align} $$
$$ \begin{align}\nonumber nd_\tau(f_{1/k_{I+1}}(b_{I+1,1}))&>d_\tau(f_{1/k_{I+1}}(a^{1/m_{I+1}}))-\eta_{l(I)}\\\nonumber &=d_\tau(f_{1/l(I)}(a)) +(d_\tau(f_{1/k_{I+1}}(a^{1/m_{I+1}}))-d_\tau(f_{1/l(I)}(a)))-\eta_{l(I)}\\\nonumber &\ge nd_\tau(f_{1/k_I}(b_{I,1})) +(d_\tau(f_{1/k_{I+1}}(a^{1/m_{I+1}}))-d_\tau(f_{1/l(I)}(a)))-\eta_{l(I)} \\ &>nd_\tau(f_{1/k_I}(b_{I,1}))+\sigma_{l(I)}-\eta_{l(I)}>nd_\tau(f_{1/k_I}(b_{I,1})). \end{align} $$
Put
![]() $c_{I+1}=f_{1/k_{I+1}}(b_{I+1,1}).$
Then, by the strict comparison, estimates above imply that
$c_{I+1}=f_{1/k_{I+1}}(b_{I+1,1}).$
Then, by the strict comparison, estimates above imply that
Thus, by induction, we obtain an increasing sequence
![]() $c_i\in \mathrm {Her}(a)_+^{\mathbf {1}}$
such that, for all
$c_i\in \mathrm {Her}(a)_+^{\mathbf {1}}$
such that, for all
![]() $\tau \in \overline {QT(A)}^w,$
$\tau \in \overline {QT(A)}^w,$
Let
![]() $c\in (A\otimes {\cal K})_+$
be such that
$c\in (A\otimes {\cal K})_+$
be such that
![]() $[c]$
is the supremum of
$[c]$
is the supremum of
![]() $\{[c_i]\}.$
Then, by (e8.54), for all
$\{[c_i]\}.$
Then, by (e8.54), for all
![]() $i,$
$i,$
Thus (recall that A is simple), for all sufficiently large
![]() $i,$
$i,$
It follows that (let
![]() $i\to \infty $
)
$i\to \infty $
)
On the other hand, by (e8.55),
For any
![]() $\varepsilon>0,$
choose a nonzero element
$\varepsilon>0,$
choose a nonzero element
![]() $e\in A_+$
such that
$e\in A_+$
such that
![]() $d_\tau (e)<\varepsilon /2$
for all
$d_\tau (e)<\varepsilon /2$
for all
![]() $\tau \in \overline {QT(A)}^w.$
Then, by the strict comparison,
$\tau \in \overline {QT(A)}^w.$
Then, by the strict comparison,
If follows that
![]() $n[c]\le [a]+[e].$
Hence,
$n[c]\le [a]+[e].$
Hence,
Let
![]() $\varepsilon \to 0.$
We also obtain
$\varepsilon \to 0.$
We also obtain
Combining (e8.62) and (e8.58), the claim also holds for Case (2).
We now show that the proved claim implies that
![]() $\mathrm {Cu}(A)$
has the property D stated in the proof of Proposition 6.21 of [Reference Robert37]. Let
$\mathrm {Cu}(A)$
has the property D stated in the proof of Proposition 6.21 of [Reference Robert37]. Let
![]() $x'\ll x,$
where
$x'\ll x,$
where
![]() $x=[a]$
for some
$x=[a]$
for some
![]() $a\in ( A\otimes {\cal K} )_+ .$
Since
$a\in ( A\otimes {\cal K} )_+ .$
Since
then
Note
![]() $(a-\|a\|/k)_+\in \mathrm {Ped}(A\otimes {\cal K})_+.$
Then the claim implies that there is
$(a-\|a\|/k)_+\in \mathrm {Ped}(A\otimes {\cal K})_+.$
Then the claim implies that there is
![]() $y\in \mathrm {Cu}(A)$
such that
$y\in \mathrm {Cu}(A)$
such that
Therefore, as observed by L. Robert (see Property D in the proof of Proposition 6.21 of [Reference Robert37]), following Corollary 5.8 of [Reference Elliott, Robert and Santiago13],
![]() $\Gamma $
is surjective.
$\Gamma $
is surjective.
Lemma 8.8 Let A be a
![]() $C^*$
-algebra and
$C^*$
-algebra and
![]() $a, b\in A_+^{\mathbf {1}}.$
Suppose that there is
$a, b\in A_+^{\mathbf {1}}.$
Suppose that there is
![]() $x\in A$
such that
$x\in A$
such that
Then, for any
![]() $\varepsilon>0,$
there exists a unitary
$\varepsilon>0,$
there exists a unitary
![]() $U\in M_2 ({{\widetilde A}})$
such that
$U\in M_2 ({{\widetilde A}})$
such that
Proof First, we claim that, for any
![]() $y\in A, \mathrm {dist}(\mathrm {diag}(y, 0), GL(M_2({{\widetilde A}})))=0.$
To see this, let
$y\in A, \mathrm {dist}(\mathrm {diag}(y, 0), GL(M_2({{\widetilde A}})))=0.$
To see this, let
![]() $\varepsilon>0.$
Choose
$\varepsilon>0.$
Choose
 $V=\begin {pmatrix} 0& 1\\ 1 & 0\end {pmatrix}$
which is a unitary in
$V=\begin {pmatrix} 0& 1\\ 1 & 0\end {pmatrix}$
which is a unitary in
![]() $M_2(\mathbb {C}).$
Then
$M_2(\mathbb {C}).$
Then
 $$ \begin{align*}Y:=\begin{pmatrix} 0& 1\\ 1 & 0\end{pmatrix} \begin{pmatrix} y & 0\\ 0 & 0\end{pmatrix}=\begin{pmatrix} 0 & 0\\ y & 0\end{pmatrix}, \end{align*} $$
$$ \begin{align*}Y:=\begin{pmatrix} 0& 1\\ 1 & 0\end{pmatrix} \begin{pmatrix} y & 0\\ 0 & 0\end{pmatrix}=\begin{pmatrix} 0 & 0\\ y & 0\end{pmatrix}, \end{align*} $$
which is a nilpotent. Therefore,
![]() $Y+\varepsilon \cdot 1_2\in GL(M_2({{\widetilde A}})).$
Then
$Y+\varepsilon \cdot 1_2\in GL(M_2({{\widetilde A}})).$
Then
This proves the claim.
To prove the lemma, we will combine the claim with an argument of Rørdam. By Proposition 2.4 of [Reference Rørdam40], for any
![]() $\varepsilon>0,$
there exist
$\varepsilon>0,$
there exist
![]() $\delta>0$
and
$\delta>0$
and
![]() $r\in A$
such that
$r\in A$
such that
Put
![]() $z=rf_\delta (b)^{1/2}$
and
$z=rf_\delta (b)^{1/2}$
and
![]() $Z=\mathrm {diag}(z, 0).$
By the claim and Theorem 5 of [Reference Pedersen32], there is a unitary
$Z=\mathrm {diag}(z, 0).$
By the claim and Theorem 5 of [Reference Pedersen32], there is a unitary
![]() $U\in M_2({{\widetilde A}})$
such that
$U\in M_2({{\widetilde A}})$
such that
Note that
![]() $Z^*Z\in \mathrm {Her}({\bar b}),$
where
$Z^*Z\in \mathrm {Her}({\bar b}),$
where
![]() ${\bar b}=\mathrm {diag}(b,0).$
Moreover (with
${\bar b}=\mathrm {diag}(b,0).$
Moreover (with
![]() ${\bar a}=\mathrm {diag}(a, 0)$
),
${\bar a}=\mathrm {diag}(a, 0)$
),
Lemma 8.9 Let A be an algebraically simple
![]() $C^*$
-algebra which has strict comparison. Suppose that
$C^*$
-algebra which has strict comparison. Suppose that
![]() $QT(A)\not =\emptyset $
and the canonical map
$QT(A)\not =\emptyset $
and the canonical map
![]() $\Gamma $
is surjective.
$\Gamma $
is surjective.
Suppose that
![]() $a, a'\in \mathrm {Ped}(A)^{\mathbf {1}}\setminus \{0\}$
with
$a, a'\in \mathrm {Ped}(A)^{\mathbf {1}}\setminus \{0\}$
with
![]() $a\in \mathrm {Her}(a').$
Then, there exists
$a\in \mathrm {Her}(a').$
Then, there exists
![]() $1/2>\varepsilon _0$
satisfying the following: For any
$1/2>\varepsilon _0$
satisfying the following: For any
![]() $0<\eta <\varepsilon <\varepsilon _0,$
any
$0<\eta <\varepsilon <\varepsilon _0,$
any
![]() $\sigma>0,$
there exist
$\sigma>0,$
there exist
![]() $c\in \mathrm {Her}(f_{\eta }(a))_+^{\mathbf {1}}$
with
$c\in \mathrm {Her}(f_{\eta }(a))_+^{\mathbf {1}}$
with
![]() $\|c\|\le \|a\|$
and unitary
$\|c\|\le \|a\|$
and unitary
![]() $U\in M_2(\mathrm {Her}(a')^\sim )$
such that (with
$U\in M_2(\mathrm {Her}(a')^\sim )$
such that (with
![]() $b=U^*\mathrm {diag}(c, 0)U$
)
$b=U^*\mathrm {diag}(c, 0)U$
)
and, for some
![]() $1>\delta >0,$
$1>\delta >0,$
Moreover,
where
![]() $B:=\mathrm {Her}(b)^\perp \cap \mathrm {Her}(\mathrm {diag}(a,a'))$
and
$B:=\mathrm {Her}(b)^\perp \cap \mathrm {Her}(\mathrm {diag}(a,a'))$
and
![]() $g_\eta (t)\in C_0((0, 1])$
is defined as in Notation 2.5.
$g_\eta (t)\in C_0((0, 1])$
is defined as in Notation 2.5.
Consequently, if e is a strictly positive element in
![]() $(\mathrm {Her}(b)^\perp \cap \mathrm {Her}(\mathrm {diag}(a,a'))),$
then
$(\mathrm {Her}(b)^\perp \cap \mathrm {Her}(\mathrm {diag}(a,a'))),$
then
Proof Without loss of generality, we may assume that
![]() $\|a\|\le 1.$
Let us first assume that
$\|a\|\le 1.$
Let us first assume that
![]() $[0,\varepsilon _0)\subset \mathrm {sp}(a)$
for some
$[0,\varepsilon _0)\subset \mathrm {sp}(a)$
for some
![]() $\varepsilon _0>0.$
$\varepsilon _0>0.$
Fix
![]() $0<\varepsilon <\varepsilon _0.$
Note that, without loss of generality, we may assume that
$0<\varepsilon <\varepsilon _0.$
Note that, without loss of generality, we may assume that
where
![]() $\varepsilon /2>\delta _1, \delta _1/2>\eta _1, \eta _1/2>\delta _2, \delta _2/2>\eta .$
Put
$\varepsilon /2>\delta _1, \delta _1/2>\eta _1, \eta _1/2>\delta _2, \delta _2/2>\eta .$
Put
![]() $h_i(\tau )=\tau (f_{\delta _i}(a))\,\,\,\mathrm {for\,\,\,all} \tau \in \overline {QT(A)}^w, i=1,2.$
Then
$h_i(\tau )=\tau (f_{\delta _i}(a))\,\,\,\mathrm {for\,\,\,all} \tau \in \overline {QT(A)}^w, i=1,2.$
Then
![]() $h_i\in \operatorname {Aff}_+(\overline {QT(A)}^w), i=1,2.$
$h_i\in \operatorname {Aff}_+(\overline {QT(A)}^w), i=1,2.$
Since
![]() $\Gamma $
is surjective, there is
$\Gamma $
is surjective, there is
![]() $c_0\in (A\otimes {\cal K})_+$
such that
$c_0\in (A\otimes {\cal K})_+$
such that
![]() $d_\tau (c_0)=h_2(\tau )$
for all
$d_\tau (c_0)=h_2(\tau )$
for all
![]() $\tau \in {{\overline {QT(A)}^w.}}$
Choose
$\tau \in {{\overline {QT(A)}^w.}}$
Choose
![]() $\delta _0>0$
such that (as
$\delta _0>0$
such that (as
![]() $h_2$
is continuous)
$h_2$
is continuous)
Since
![]() $h_1<h_2$
are continuous, we may also assume, by choosing smaller
$h_1<h_2$
are continuous, we may also assume, by choosing smaller
![]() $\delta _0$
, that
$\delta _0$
, that
Since A has strict comparison, by (e8.73), there is
![]() $x\in A\otimes {\cal K}$
such that
$x\in A\otimes {\cal K}$
such that
Choose
![]() $c=xx^*.$
Then
$c=xx^*.$
Then
![]() $0\le c\le 1$
and
$0\le c\le 1$
and
![]() $d_\tau (c)=d_\tau (f_{\delta _0/4}(c_0))$
for all
$d_\tau (c)=d_\tau (f_{\delta _0/4}(c_0))$
for all
![]() $\overline {QT(A)}^w.$
Let
$\overline {QT(A)}^w.$
Let
![]() $C=\mathrm {Her}(f_{\eta }(a)).$
By (e8.75), the strict comparison and Lemma 8.8, we obtain a unitary
$C=\mathrm {Her}(f_{\eta }(a)).$
By (e8.75), the strict comparison and Lemma 8.8, we obtain a unitary
![]() $U\in M_2(\widetilde C)$
such that
$U\in M_2(\widetilde C)$
such that
where
![]() ${\bar c}=\mathrm {diag}(c,0).$
Let
${\bar c}=\mathrm {diag}(c,0).$
Let
![]() $b=U^*{\bar c}U.$
Then
$b=U^*{\bar c}U.$
Then
(so (1) holds). Moreover,
![]() $d_\tau (b)=d_\tau (c)$
for all
$d_\tau (b)=d_\tau (c)$
for all
![]() $\tau \in \overline {T(A)}^w.$
Consequently,
$\tau \in \overline {T(A)}^w.$
Consequently,
(so (2) holds). Moreover, there is
![]() $1>\delta >0$
such that
$1>\delta >0$
such that
It then follows from (e8.74) that
(so (3) holds). To show the “Moreover” part, put
Since
![]() $g_{\eta /2}(a)\perp f_\eta (a),$
we have
$g_{\eta /2}(a)\perp f_\eta (a),$
we have
It follows that
![]() $U^*\mathrm {diag}(g_{\eta /2}(a), a')U\in B.$
If e is a strictly positive element in
$U^*\mathrm {diag}(g_{\eta /2}(a), a')U\in B.$
If e is a strictly positive element in
![]() $\mathrm {Her}(b)^{\perp }\cap \mathrm {Her}(\mathrm {diag}(a, a')),$
then
$\mathrm {Her}(b)^{\perp }\cap \mathrm {Her}(\mathrm {diag}(a, a')),$
then
This proves the case that
![]() $[0, \varepsilon _0]\subset \mathrm {sp}(a).$
$[0, \varepsilon _0]\subset \mathrm {sp}(a).$
If there exists
![]() $r_n\in (0,1]$
with
$r_n\in (0,1]$
with
then
![]() $b_n=f_{2r_n}(a)$
has the property that
$b_n=f_{2r_n}(a)$
has the property that
![]() $\omega (b_n)=0.$
Then the lemma follows by choosing
$\omega (b_n)=0.$
Then the lemma follows by choosing
![]() $U=\mathrm {diag}(1,1)$
and
$U=\mathrm {diag}(1,1)$
and
![]() $b=b_n$
for some sufficiently large
$b=b_n$
for some sufficiently large
![]() $n.$
$n.$
Lemma 8.10 Let A be a
![]() $\sigma $
-unital algebraically simple
$\sigma $
-unital algebraically simple
![]() $C^*$
-algebra with
$C^*$
-algebra with
![]() $QT(A){{\not =}}\emptyset .$
Suppose that A has strict comparison and
$QT(A){{\not =}}\emptyset .$
Suppose that A has strict comparison and
![]() $\Gamma $
is surjective. Suppose that
$\Gamma $
is surjective. Suppose that
![]() $a=\mathrm {diag}(0, a_1, a_2,...,a_n)$
in
$a=\mathrm {diag}(0, a_1, a_2,...,a_n)$
in
![]() $M_{n+1}(A){{^{\mathbf {1}}_+}}$
for some integer
$M_{n+1}(A){{^{\mathbf {1}}_+}}$
for some integer
![]() $n\ge 1.$
Then, for any
$n\ge 1.$
Then, for any
![]() $1/2>\varepsilon >0$
and
$1/2>\varepsilon >0$
and
![]() $1/2>\sigma >0,$
there exists
$1/2>\sigma >0,$
there exists
![]() $d\in M_{n+1}(A){{^{\mathbf {1}}_+}}$
such that
$d\in M_{n+1}(A){{^{\mathbf {1}}_+}}$
such that
Proof For
![]() $n=1,$
this follows immediately from Lemma 8.9.
$n=1,$
this follows immediately from Lemma 8.9.
Assume that the lemma holds for
![]() $n\ge 1.$
$n\ge 1.$
Let
![]() $0\le e_A\le 1$
be a strictly positive element of
$0\le e_A\le 1$
be a strictly positive element of
![]() $A.$
Fix
$A.$
Fix
![]() $1/2>\varepsilon >0.$
Choose
$1/2>\varepsilon >0.$
Choose
![]() $\eta =\varepsilon /4(n+2)$
and
$\eta =\varepsilon /4(n+2)$
and
![]() $\sigma _0:=\sigma /2(n+2).$
We will apply Lemma 8.9 with
$\sigma _0:=\sigma /2(n+2).$
We will apply Lemma 8.9 with
![]() $a_j\in \mathrm {Her}(e_A)$
(
$a_j\in \mathrm {Her}(e_A)$
(
![]() $1\le j\le n+1$
),
$1\le j\le n+1$
),
![]() $\eta $
as above, and
$\eta $
as above, and
![]() $\sigma _0$
(in place of
$\sigma _0$
(in place of
![]() $\sigma $
).
$\sigma $
).
By Lemma 8.9, there is
![]() $c_1\in \mathrm {Her}(f_\eta (a_1))_+^{\mathbf {1}},$
a unitary
$c_1\in \mathrm {Her}(f_\eta (a_1))_+^{\mathbf {1}},$
a unitary
![]() $U_1\in M_2({{\widetilde A}})$
, and
$U_1\in M_2({{\widetilde A}})$
, and
![]() ${{b_1'}}=U_1^*\mathrm {diag}(0,c_1)U_1$
such that
${{b_1'}}=U_1^*\mathrm {diag}(0,c_1)U_1$
such that
where
![]() $B_1:=(\mathrm {Her}({{b_1'}})^\perp \cap \mathrm {Her}(\mathrm {diag}(a_1,e_A)))_+.$
Put
$B_1:=(\mathrm {Her}({{b_1'}})^\perp \cap \mathrm {Her}(\mathrm {diag}(a_1,e_A)))_+.$
Put
 $$ \begin{align} &V_1=\mathrm{diag}(U_1, \overbrace{1_{{{\widetilde A}}},..., 1_{{{\widetilde A}}}}^{n-1}),\,\, {\alpha}_2=V_1^*\mathrm{diag}(0, 0, a_2,...,a_{n+1})V_1\,\,\,\mathrm{and}\,\,\, \end{align} $$
$$ \begin{align} &V_1=\mathrm{diag}(U_1, \overbrace{1_{{{\widetilde A}}},..., 1_{{{\widetilde A}}}}^{n-1}),\,\, {\alpha}_2=V_1^*\mathrm{diag}(0, 0, a_2,...,a_{n+1})V_1\,\,\,\mathrm{and}\,\,\, \end{align} $$
Define
![]() $C_1=\mathrm {Her}(V_1^*(e_A, 0, e_A,...,e_A)V_1).$
Then
$C_1=\mathrm {Her}(V_1^*(e_A, 0, e_A,...,e_A)V_1).$
Then
In
![]() $C_1,$
we may write
$C_1,$
we may write
![]() ${\alpha }_2=\mathrm {diag}(0, a_2,a_3,...,a_{n+1})$
(the number of possible nonzero elements is now reduced to n).
${\alpha }_2=\mathrm {diag}(0, a_2,a_3,...,a_{n+1})$
(the number of possible nonzero elements is now reduced to n).
By the induction assumption, there is
![]() $b_2\in C_1$
with
$b_2\in C_1$
with
![]() $0\le b_2\le 1$
such that
$0\le b_2\le 1$
such that
Define
![]() $d:=b_1+b_2.$
Note that
$d:=b_1+b_2.$
Note that
![]() $b_1\perp b_2.$
Then
$b_1\perp b_2.$
Then
and (by (2) of 4.4)
This completes the induction. The lemma follows.
Theorem 8.11 Let A be a
![]() $\sigma $
-unital simple
$\sigma $
-unital simple
![]() $C^*$
-algebra with
$C^*$
-algebra with
![]() $ \widetilde {QT} (A)\setminus \{0\}\not =\emptyset .$
Suppose that A has strict comparison and property (TM). Then A has T-tracial approximate oscillation zero.
$ \widetilde {QT} (A)\setminus \{0\}\not =\emptyset .$
Suppose that A has strict comparison and property (TM). Then A has T-tracial approximate oscillation zero.
Proof Choose
![]() $e\in \mathrm {Ped}(A)_+\setminus \{0\}$
and
$e\in \mathrm {Ped}(A)_+\setminus \{0\}$
and
![]() $A_1=\mathrm {Her}(e).$
Then
$A_1=\mathrm {Her}(e).$
Then
![]() $\mathrm {Ped}(A_1)=A_1.$
To prove the theorem, without loss of generality, we may assume that
$\mathrm {Ped}(A_1)=A_1.$
To prove the theorem, without loss of generality, we may assume that
![]() $A=\mathrm {Ped}(A).$
By Theorem 8.7,
$A=\mathrm {Ped}(A).$
By Theorem 8.7,
![]() $\Gamma $
is surjective.
$\Gamma $
is surjective.
Fix
![]() $a\in \mathrm {Ped}(A\otimes {\cal K} )_+^{\mathbf {1}}.$
We claim that
$a\in \mathrm {Ped}(A\otimes {\cal K} )_+^{\mathbf {1}}.$
We claim that
![]() $\mathrm {Her}(a)$
has a T-tracial approximate identity
$\mathrm {Her}(a)$
has a T-tracial approximate identity
![]() $\{d_n\}$
such that
$\{d_n\}$
such that
![]() $\lim _{n\to \infty }\omega (d_n)=0.$
$\lim _{n\to \infty }\omega (d_n)=0.$
Put
![]() $B=\mathrm {Her}(a).$
Then
$B=\mathrm {Her}(a).$
Then
![]() $\mathrm {Ped}(B)=B$
and
$\mathrm {Ped}(B)=B$
and
![]() $B\otimes {\cal K}\cong A\otimes {\cal K}.$
Therefore, to simplify notation, without loss of generality, we may also assume that
$B\otimes {\cal K}\cong A\otimes {\cal K}.$
Therefore, to simplify notation, without loss of generality, we may also assume that
![]() $a\in A.$
$a\in A.$
Let
![]() $\varepsilon>0$
and let
$\varepsilon>0$
and let
![]() $n\in \mathbb {N}$
such that
$n\in \mathbb {N}$
such that
![]() $1/n<(\varepsilon /8)^2.$
Since A has property (TM), there is a c.p.c. order zero map
$1/n<(\varepsilon /8)^2.$
Since A has property (TM), there is a c.p.c. order zero map
![]() $\phi : M_{n+1}\to \mathrm {Her}(a)$
such that
$\phi : M_{n+1}\to \mathrm {Her}(a)$
such that
By Proposition 8.3, let
![]() ${{C}}=\mathrm {Her}(\phi (1_{n+1}))\cong M_{n+1}((\mathrm {Her}(\phi (e_{1,1}))).$
Write
${{C}}=\mathrm {Her}(\phi (1_{n+1}))\cong M_{n+1}((\mathrm {Her}(\phi (e_{1,1}))).$
Write
Choose
![]() $0<\eta <(\varepsilon /16)^2.$
Put
$0<\eta <(\varepsilon /16)^2.$
Put
![]() $c_n=\mathrm {diag}(0, c,c,...,c).$
It follows from Lemma 8.10 that there exists
$c_n=\mathrm {diag}(0, c,c,...,c).$
It follows from Lemma 8.10 that there exists
![]() $d\in {{C}}_+^{\mathbf {1}}$
such that
$d\in {{C}}_+^{\mathbf {1}}$
such that
Hence,
Hence,
![]() $d(c_n-2\eta )_+=(c_n-2\eta )_+=(c_n-2\eta )_+d.$
It follows that (we now working in a commutative
$d(c_n-2\eta )_+=(c_n-2\eta )_+=(c_n-2\eta )_+d.$
It follows that (we now working in a commutative
![]() $C^*$
-subalgebra)
$C^*$
-subalgebra)
Note that
Then (see also (2.16)), by (e8.97), (e8.98), and (e8.93),
 $$ \begin{align}\nonumber \|a-da\|^{2/3}_{_{2, \overline{QT(A)}^w}}&=(\sup\,_{_{ \tau\in \overline{QT(A)}^w}}\{\tau(a(1-d)^2a)\})^{1/3}\\\nonumber &\le \sup\,_{_{ \tau\in \overline{QT(A)}^w}}\{\tau(a(1-(c_n-2\eta)_+)^2a)\})^{1/3} =\|a-(c_n-2\eta)_+a\|^{2/3}_{_{2, \overline{QT(A)}^w}}\\\nonumber &\le \|a-c_na\|^{2/3}_{_{2, \overline{QT(A)}^w}} +\|(c_n-({c_n-2\eta})_+)a\|^{2/3}_{_{2, \overline{QT(A)}^w}}\\&< \|a-\phi(1_{n+1})a\|^{2/3}_{_{2,\overline{QT(A)}^w}}+\left({1\over{n+1}}\right)^{2/3}+(2\eta)^{2/3}\end{align} $$
$$ \begin{align}\nonumber \|a-da\|^{2/3}_{_{2, \overline{QT(A)}^w}}&=(\sup\,_{_{ \tau\in \overline{QT(A)}^w}}\{\tau(a(1-d)^2a)\})^{1/3}\\\nonumber &\le \sup\,_{_{ \tau\in \overline{QT(A)}^w}}\{\tau(a(1-(c_n-2\eta)_+)^2a)\})^{1/3} =\|a-(c_n-2\eta)_+a\|^{2/3}_{_{2, \overline{QT(A)}^w}}\\\nonumber &\le \|a-c_na\|^{2/3}_{_{2, \overline{QT(A)}^w}} +\|(c_n-({c_n-2\eta})_+)a\|^{2/3}_{_{2, \overline{QT(A)}^w}}\\&< \|a-\phi(1_{n+1})a\|^{2/3}_{_{2,\overline{QT(A)}^w}}+\left({1\over{n+1}}\right)^{2/3}+(2\eta)^{2/3}\end{align} $$
Since
![]() $\omega (d)<1/2^n,$
this proves the claim. The theorem then follows from the claim and Lemma 5.6.
$\omega (d)<1/2^n,$
this proves the claim. The theorem then follows from the claim and Lemma 5.6.
9 Stable rank one
Let A be a
![]() $C^*$
-algebra and
$C^*$
-algebra and
![]() $n\in \mathbb {N}.$
Recall that we view
$n\in \mathbb {N}.$
Recall that we view
![]() $M_n(A)$
as a
$M_n(A)$
as a
![]() $C^*$
-subalgebra of
$C^*$
-subalgebra of
![]() $M_{n+1}(A)$
in the canonical way, i.e.,
$M_{n+1}(A)$
in the canonical way, i.e.,
![]() $M_n(A)$
is the upper left block of
$M_n(A)$
is the upper left block of
![]() $M_{n+1}(A).$
$M_{n+1}(A).$
Recall an element
![]() $a=(a_{i,j})_{n\times n}$
in
$a=(a_{i,j})_{n\times n}$
in
![]() $M_n(A)$
is called upper (resp. lower) triangular, if
$M_n(A)$
is called upper (resp. lower) triangular, if
![]() $a_{i,j}=0$
whenever
$a_{i,j}=0$
whenever
![]() $i<j$
(resp.
$i<j$
(resp.
![]() $i>j$
), and a is called strictly upper (resp. lower) triangular, if
$i>j$
), and a is called strictly upper (resp. lower) triangular, if
![]() $a_{i,j}=0$
whenever
$a_{i,j}=0$
whenever
![]() $i\le j$
(resp.
$i\le j$
(resp.
![]() $i\ge j$
).
$i\ge j$
).
The following proposition is a generalization of an elementary fact in linear algebra.
Proposition 9.1 Let A be a
![]() $C^*$
-algebra such that
$C^*$
-algebra such that
![]() $A\subset \overline {GL( {{\widetilde A}})}.$
Then, for any
$A\subset \overline {GL( {{\widetilde A}})}.$
Then, for any
![]() $n\in \mathbb {N},$
any
$n\in \mathbb {N},$
any
![]() $a\in M_n(A),$
and any
$a\in M_n(A),$
and any
![]() $\varepsilon>0,$
there is an upper triangular matrix
$\varepsilon>0,$
there is an upper triangular matrix
![]() $x\in M_n(A)$
and a lower triangular matrix
$x\in M_n(A)$
and a lower triangular matrix
![]() $y\in M_n(A)$
such that
$y\in M_n(A)$
such that
![]() $a\approx _\varepsilon xy.$
$a\approx _\varepsilon xy.$
Proof We prove this by induction on
![]() $n.$
For
$n.$
For
![]() $n=1,$
let
$n=1,$
let
![]() $a\in M_n(A)=A$
and
$a\in M_n(A)=A$
and
![]() $\varepsilon>0.$
By the existence of approximate identity, there is
$\varepsilon>0.$
By the existence of approximate identity, there is
![]() $e\in A_+$
such that
$e\in A_+$
such that
![]() $a\approx _\varepsilon ae.$
Note that a and e are triangular matrices in
$a\approx _\varepsilon ae.$
Note that a and e are triangular matrices in
![]() $M_n(A).$
Thus, the proposition holds for
$M_n(A).$
Thus, the proposition holds for
![]() $n=1.$
$n=1.$
Assume the proposition holds for
![]() $n\geq 1.$
Let
$n\geq 1.$
Let
![]() $a=\sum _{i,j=1}^{n+1}a_{i,j}\otimes e_{i,j} \in A\otimes M_{n+1},$
where
$a=\sum _{i,j=1}^{n+1}a_{i,j}\otimes e_{i,j} \in A\otimes M_{n+1},$
where
![]() $a_{i,j}\in A$
and
$a_{i,j}\in A$
and
![]() $\{e_{i,j}\}$
is the matrix units of
$\{e_{i,j}\}$
is the matrix units of
![]() $M_{n+1}, i,j=1,...,n+1.$
Let
$M_{n+1}, i,j=1,...,n+1.$
Let
![]() $\varepsilon>0.$
Since
$\varepsilon>0.$
Since
![]() $A\subset \overline {GL({{\widetilde A}})},$
there is
$A\subset \overline {GL({{\widetilde A}})},$
there is
![]() $\tilde a\in GL(\widetilde A)$
such that
$\tilde a\in GL(\widetilde A)$
such that
In what follows in this proof,
![]() $1$
is the identity of
$1$
is the identity of
![]() ${{\widetilde A}}$
and
${{\widetilde A}}$
and
![]() $1_{n+1}$
is the identity of
$1_{n+1}$
is the identity of
![]() $M_{n+1}({{\widetilde A}}).$
$M_{n+1}({{\widetilde A}}).$
Let
![]() $b^{(0)}:=\sum _{i=1}^{n}a_{i,n+1}\tilde a^{-1}\otimes e_{i,n+1}$
and
$b^{(0)}:=\sum _{i=1}^{n}a_{i,n+1}\tilde a^{-1}\otimes e_{i,n+1}$
and
![]() $c^{(0)}:=\sum _{j=1}^{n}\tilde a^{-1}a_{n+1,j}\otimes e_{n+1,j}.$
Then
$c^{(0)}:=\sum _{j=1}^{n}\tilde a^{-1}a_{n+1,j}\otimes e_{n+1,j}.$
Then
![]() $b^{(0)}$
and
$b^{(0)}$
and
![]() $c^{(0)}$
are nilpotents. Put
$c^{(0)}$
are nilpotents. Put
Let
![]() $s:=ba'c.$
Note that
$s:=ba'c.$
Note that
![]() $a',b,c, s$
are in
$a',b,c, s$
are in
![]() $M_{n+1}(\widetilde A).$
Let
$M_{n+1}(\widetilde A).$
Let
![]() $a^{\prime }_{i,j}$
(resp.
$a^{\prime }_{i,j}$
(resp.
![]() $b_{i,j},c_{i,j}, s_{i,j}$
) be the
$b_{i,j},c_{i,j}, s_{i,j}$
) be the
![]() $(i,j)$
th entry of
$(i,j)$
th entry of
![]() $a'$
(resp.
$a'$
(resp.
![]() $b,c, s$
),
$b,c, s$
),
![]() $1\leq i,j\leq n+1.$
Note that
$1\leq i,j\leq n+1.$
Note that
 $$ \begin{align} s_{i,j}=\sum_{m=1}^{n+1}\left(\sum_{k=1}^{n+1} b_{i,k}a^{\prime}_{k,m}c_{m,j} \right) \quad (1\leq i,j\leq n+1). \end{align} $$
$$ \begin{align} s_{i,j}=\sum_{m=1}^{n+1}\left(\sum_{k=1}^{n+1} b_{i,k}a^{\prime}_{k,m}c_{m,j} \right) \quad (1\leq i,j\leq n+1). \end{align} $$
If
![]() $A=\widetilde A,$
then
$A=\widetilde A,$
then
![]() $s_{i,j}\in A.$
Otherwise, denote by
$s_{i,j}\in A.$
Otherwise, denote by
![]() $\pi : M_{n+1}({{\widetilde A}})\to M_{n+1}$
the quotient map. Then
$\pi : M_{n+1}({{\widetilde A}})\to M_{n+1}$
the quotient map. Then
It follows that
![]() $\pi (s)=\pi (\tilde a\otimes e_{n+1,n+1}).$
Thus,
$\pi (s)=\pi (\tilde a\otimes e_{n+1,n+1}).$
Thus,
Note that
![]() $b_{n+1,k}=0$
for
$b_{n+1,k}=0$
for
![]() $1\leq k \leq n$
and
$1\leq k \leq n$
and
![]() $c_{m,j}=0$
for
$c_{m,j}=0$
for
![]() $m\notin \{j,n+1\},$
if
$m\notin \{j,n+1\},$
if
![]() $1\le j\le n.$
By (e9.3), we have, for
$1\le j\le n.$
By (e9.3), we have, for
![]() $1\le j\le n,$
$1\le j\le n,$
If
![]() $1\leq i\leq n,$
then
$1\leq i\leq n,$
then
![]() $b_{i,k}=0$
for
$b_{i,k}=0$
for
![]() $k\notin \{i,n+1\}$
and
$k\notin \{i,n+1\}$
and
![]() $c_{m,n+1}=0$
for
$c_{m,n+1}=0$
for
![]() $1\leq m \leq n.$
By (e9.3), we compute
$1\leq m \leq n.$
By (e9.3), we compute
We also have
 $$ \begin{align} s_{n+1,n+1}=\sum_{m=1}^{n+1}\left(\sum_{k=1}^{n+1} b_{n+1,k}a^{\prime}_{k,m}c_{m,n+1} \right) = b_{n+1,n+1}a^{\prime}_{n+1,n+1}c_{n+1,n+1} =\tilde a. \end{align} $$
$$ \begin{align} s_{n+1,n+1}=\sum_{m=1}^{n+1}\left(\sum_{k=1}^{n+1} b_{n+1,k}a^{\prime}_{k,m}c_{m,n+1} \right) = b_{n+1,n+1}a^{\prime}_{n+1,n+1}c_{n+1,n+1} =\tilde a. \end{align} $$
Therefore (e9.4), (e9.6), (e9.7), and (e9.9) show that
where
![]() $d\in M_n(A).$
Note that b and c are invertible in
$d\in M_n(A).$
Note that b and c are invertible in
![]() $M_{n+1}(\widetilde A),$
as both
$M_{n+1}(\widetilde A),$
as both
![]() $b^{(0)}$
and
$b^{(0)}$
and
![]() $c^{(0)}$
are nilpotents. Let
$c^{(0)}$
are nilpotents. Let
![]() $\varepsilon _1= \frac {\varepsilon }{4(1+\|b^{-1}\| \cdot \|c^{-1}\|)}.$
By our assumption, there is an upper triangular matrix
$\varepsilon _1= \frac {\varepsilon }{4(1+\|b^{-1}\| \cdot \|c^{-1}\|)}.$
By our assumption, there is an upper triangular matrix
![]() $x_1$
and a lower triangular matrix
$x_1$
and a lower triangular matrix
![]() $y_1$
in
$y_1$
in
![]() $M_n(A)$
such that
$M_n(A)$
such that
Let
![]() $e\in M_{n+1}(A)_+^{\mathbf {1}}$
be a diagonal matrix such that
$e\in M_{n+1}(A)_+^{\mathbf {1}}$
be a diagonal matrix such that
![]() $a\approx _{\varepsilon /4}eae.$
$a\approx _{\varepsilon /4}eae.$
Note that
![]() $b^{-1}=1_{n+1}+b^{(0)}$
and
$b^{-1}=1_{n+1}+b^{(0)}$
and
![]() $x{{:}}=eb^{-1}(x_1+\tilde a\otimes e_{n+1,n+1})$
are upper triangular matrix in
$x{{:}}=eb^{-1}(x_1+\tilde a\otimes e_{n+1,n+1})$
are upper triangular matrix in
![]() $M_{n+1}(A).$
Similarly,
$M_{n+1}(A).$
Similarly,
![]() $c^{-1}{{=1_{n+1}+c^{(0)}}}$
is a lower triangular matrix in
$c^{-1}{{=1_{n+1}+c^{(0)}}}$
is a lower triangular matrix in
![]() $M_{n+1}(\widetilde A),$
and
$M_{n+1}(\widetilde A),$
and
is a lower triangular matrix in
![]() $M_{n+1}(A).$
Then
$M_{n+1}(A).$
Then
Thus, the proposition holds for
![]() $n+1.$
By induction, the proposition holds.
$n+1.$
By induction, the proposition holds.
Proposition 9.2 Let A be a
![]() $C^*$
-algebra such that
$C^*$
-algebra such that
![]() $A\subset \overline {GL({{\widetilde A}})}$
and let
$A\subset \overline {GL({{\widetilde A}})}$
and let
![]() $n\in \mathbb {N}.$
Then, for any
$n\in \mathbb {N}.$
Then, for any
![]() $a\in M_n(A)$
and any
$a\in M_n(A)$
and any
![]() $\varepsilon>0,$
there is a strictly upper triangular matrix
$\varepsilon>0,$
there is a strictly upper triangular matrix
![]() $x\in M_{n+1}(A)$
and a strictly lower triangular matrix
$x\in M_{n+1}(A)$
and a strictly lower triangular matrix
![]() $y\in M_{n+1}(A)$
such that
$y\in M_{n+1}(A)$
such that
![]() $a\approx _{\varepsilon }xy.$
$a\approx _{\varepsilon }xy.$
In particular, any element in
![]() $M_n(A)$
can be approximated in norm by product of two nilpotent elements in
$M_n(A)$
can be approximated in norm by product of two nilpotent elements in
![]() $M_{n+1}(A).$
$M_{n+1}(A).$
Proof By Proposition 9.1, there is an upper triangular matrix
![]() $x_1\in M_n(A)$
and a lower triangular matrix
$x_1\in M_n(A)$
and a lower triangular matrix
![]() $y_1\in M_n(A)$
such that
$y_1\in M_n(A)$
such that
![]() $a\approx _\varepsilon x_1y_1.$
Let
$a\approx _\varepsilon x_1y_1.$
Let
![]() $v=\sum _{i=1}^n1_{\widetilde A} \otimes e_{i,i+1}\in M_{n+1}(\widetilde A).$
Then
$v=\sum _{i=1}^n1_{\widetilde A} \otimes e_{i,i+1}\in M_{n+1}(\widetilde A).$
Then
![]() $x=x_1v\in M_{n+1}(A)$
is a strict upper triangular matrix and
$x=x_1v\in M_{n+1}(A)$
is a strict upper triangular matrix and
![]() $y=v^*y_1\in M_{n+1}(A)$
is a strict lower triangular matrix, and
$y=v^*y_1\in M_{n+1}(A)$
is a strict lower triangular matrix, and
![]() $xy=x_1vv^*y_1=x_1y_1\approx _\varepsilon a$
. (Recall that we identify
$xy=x_1vv^*y_1=x_1y_1\approx _\varepsilon a$
. (Recall that we identify
![]() $M_n(A)$
with the upper left
$M_n(A)$
with the upper left
![]() $n\times n$
corner of
$n\times n$
corner of
![]() $M_{n+1}(A)$
.)
$M_{n+1}(A)$
.)
The last part of the proposition follows from the fact that strictly triangular matrices are nilpotents.
Lemma 9.3 Let A be a
![]() $\sigma $
-unital algebraically simple non-elementary
$\sigma $
-unital algebraically simple non-elementary
![]() $C^*$
-algebra with
$C^*$
-algebra with
![]() $QT(A)\not =\emptyset $
which has strict comparison. Suppose that A also has the property (TM). Let
$QT(A)\not =\emptyset $
which has strict comparison. Suppose that A also has the property (TM). Let
![]() $a\in A.$
If there are
$a\in A.$
If there are
![]() $b_1,b_2\in A_+\setminus \{0\}$
such that
$b_1,b_2\in A_+\setminus \{0\}$
such that
![]() $a^*a+aa^*, b_1, b_2$
are mutually orthogonal, then, for any
$a^*a+aa^*, b_1, b_2$
are mutually orthogonal, then, for any
![]() $\varepsilon>0,$
there are two nilpotents
$\varepsilon>0,$
there are two nilpotents
![]() $x,y\in A$
such that
$x,y\in A$
such that
![]() $\|a-xy\|<\varepsilon .$
$\|a-xy\|<\varepsilon .$
Proof Let
![]() $B=l^\infty (A)/I_{_{\overline {QT(A)}^w}}.$
Recall that
$B=l^\infty (A)/I_{_{\overline {QT(A)}^w}}.$
Recall that
![]() $\Pi :l^\infty (A)\to B$
is the quotient map and
$\Pi :l^\infty (A)\to B$
is the quotient map and
![]() $\iota :A\to l^\infty (A)$
is the canonical embedding. Denote
$\iota :A\to l^\infty (A)$
is the canonical embedding. Denote
![]() ${\bar \iota }:=\Pi \circ \iota .$
Fix
${\bar \iota }:=\Pi \circ \iota .$
Fix
![]() $a\in A.$
Without loss of generality, we may assume
$a\in A.$
Without loss of generality, we may assume
![]() $\|a\|\leq 1.$
Put
$\|a\|\leq 1.$
Put
![]() $a_0=a^*a+aa^*.$
Assume that there are
$a_0=a^*a+aa^*.$
Assume that there are
![]() $b_1,b_2\in A_+$
such that
$b_1,b_2\in A_+$
such that
![]() $0=b_1b_2=ab_1=b_1a=ab_2=b_2a{{}} .$
Let
$0=b_1b_2=ab_1=b_1a=ab_2=b_2a{{}} .$
Let
![]() $\varepsilon>0.$
Since A is simple and non-elementary, one can choose
$\varepsilon>0.$
Since A is simple and non-elementary, one can choose
![]() $n\in \mathbb {N}$
such that
$n\in \mathbb {N}$
such that
Since A has property (TM), by Theorem 8.11, A has T-tracial approximate oscillation zero. Then, by Theorem 6.6, B has stable rank one. Also, by the last part of Remark 8.2, for each
![]() $m\in \mathbb {N},$
there is a c.p.c. order zero map
$m\in \mathbb {N},$
there is a c.p.c. order zero map
![]() $\phi _m: M_n\to \mathrm {Her}({{a_0}})$
such that
$\phi _m: M_n\to \mathrm {Her}({{a_0}})$
such that
Let
![]() $\phi :M_n\to l^\infty (A)$
be the map induced by
$\phi :M_n\to l^\infty (A)$
be the map induced by
![]() $\{\phi _m\}_{m\in \mathbb {N}}$
and
$\{\phi _m\}_{m\in \mathbb {N}}$
and
![]() ${\bar \phi }:=\Pi \circ \phi .$
Then (e9.14) shows that
${\bar \phi }:=\Pi \circ \phi .$
Then (e9.14) shows that
Denote by
![]() $\{e_{i,j}: 1{\kern-1pt}\le{\kern-1pt} i,j{\kern-1pt}\le{\kern-1pt} n\}$
a system of matrix units for
$\{e_{i,j}: 1{\kern-1pt}\le{\kern-1pt} i,j{\kern-1pt}\le{\kern-1pt} n\}$
a system of matrix units for
![]() $M_n$
and
$M_n$
and
![]() $\{e_{i,j}: 1{\kern-1pt}\le{\kern-1pt} {{i}},j{\kern-1pt}\le{\kern-1pt} n{\kern-1pt}+{\kern-1pt}1\}$
an expanded system of matrix units for
$\{e_{i,j}: 1{\kern-1pt}\le{\kern-1pt} {{i}},j{\kern-1pt}\le{\kern-1pt} n{\kern-1pt}+{\kern-1pt}1\}$
an expanded system of matrix units for
![]() $M_{n+1}.$
In particular, we view
$M_{n+1}.$
In particular, we view
![]() $M_n$
generated by
$M_n$
generated by
![]() $ \{e_{i,j}: 1\le i,j\le 1\}$
as a
$ \{e_{i,j}: 1\le i,j\le 1\}$
as a
![]() $C^*$
-subalgebra of
$C^*$
-subalgebra of
![]() $M_{n+1}$
generated by
$M_{n+1}$
generated by
![]() $\{e_{i,j}:1\le i,j\le n+1\}.$
$\{e_{i,j}:1\le i,j\le n+1\}.$
Since A has strict comparison, and for all
![]() $m\in \mathbb {N},$
$m\in \mathbb {N},$
we have
![]() $\phi _m(e_{1,1})\lesssim b_2$
for all
$\phi _m(e_{1,1})\lesssim b_2$
for all
![]() $m\in \mathbb {N}.$
By [Reference Rørdam40, Proposition 2.4(iv)], there are
$m\in \mathbb {N}.$
By [Reference Rørdam40, Proposition 2.4(iv)], there are
![]() ${v_m}\in A$
${v_m}\in A$
(see (e3.5)) and (e3.6)). Note that
Let
![]() $v=\{v_1,v_2,...\}\in l^\infty (A).$
Since
$v=\{v_1,v_2,...\}\in l^\infty (A).$
Since
![]() $\|(\phi _m(e_{1,1})-1/m)_+-\phi _m(e_{1,1})\|\leq 1/m$
(
$\|(\phi _m(e_{1,1})-1/m)_+-\phi _m(e_{1,1})\|\leq 1/m$
(
![]() $m\in \mathbb {N}$
), we have
$m\in \mathbb {N}$
), we have
The facts that
![]() $\phi _m(1_n)\in \mathrm {Her}({{a_0}}), \mathrm {Her}({{a_0}})\bot \mathrm {Her}(b_2),$
and
$\phi _m(1_n)\in \mathrm {Her}({{a_0}}), \mathrm {Her}({{a_0}})\bot \mathrm {Her}(b_2),$
and
![]() $v_mv_m^*\in \mathrm {Her}(b_2)$
show that
$v_mv_m^*\in \mathrm {Her}(b_2)$
show that
![]() $\phi _m(1_n)\bot v_mv_m^*$
for all
$\phi _m(1_n)\bot v_mv_m^*$
for all
![]() $m\in \mathbb {N}.$
Hence,
$m\in \mathbb {N}.$
Hence,
Let
![]() $h: C_0((0,1])\otimes M_n\to B$
be the homomorphism defined by
$h: C_0((0,1])\otimes M_n\to B$
be the homomorphism defined by
![]() $h(\imath \otimes e_{i,j})={\bar \phi }(e_{i,j})$
(
$h(\imath \otimes e_{i,j})={\bar \phi }(e_{i,j})$
(
![]() $1\le i,j\le n$
). Extend
$1\le i,j\le n$
). Extend
![]() ${\widetilde h}: C_0((0,1])\otimes M_{n+1}\to B$
by
${\widetilde h}: C_0((0,1])\otimes M_{n+1}\to B$
by
![]() $\widetilde h(\imath \otimes e_{i,j})=h({{\imath \otimes e_{i,j}}})$
and
$\widetilde h(\imath \otimes e_{i,j})=h({{\imath \otimes e_{i,j}}})$
and
![]() $\widetilde h(\imath \otimes e_{1, n+1})=v^*.$
By (e9.18) and (e9.19),
$\widetilde h(\imath \otimes e_{1, n+1})=v^*.$
By (e9.18) and (e9.19),
![]() $\widetilde h$
is indeed a homomorphism. Define
$\widetilde h$
is indeed a homomorphism. Define
![]() $\widetilde \phi (e_{i,j})=\widetilde h({{\imath \otimes e_{i,j}}})$
for
$\widetilde \phi (e_{i,j})=\widetilde h({{\imath \otimes e_{i,j}}})$
for
![]() $1\le i,j\le n+1.$
$1\le i,j\le n+1.$
As we view
![]() $M_n$
as a
$M_n$
as a
![]() $C^*$
-subalgebra of
$C^*$
-subalgebra of
![]() $M_{n+1},$
$M_{n+1},$
![]() $\widetilde \phi $
is an extension of
$\widetilde \phi $
is an extension of
![]() ${\bar \phi },$
i.e.,
${\bar \phi },$
i.e.,
![]() $\widetilde \phi |_{M_n}={\bar \phi }.$
By Proposition 8.3,
$\widetilde \phi |_{M_n}={\bar \phi }.$
By Proposition 8.3,
and
Moreover, as
![]() $\{e_{i,j}: 1\le i,j\le n\}\subset \{e_{i,j}:1\le i,j\le n+1\},$
we also write
$\{e_{i,j}: 1\le i,j\le n\}\subset \{e_{i,j}:1\le i,j\le n+1\},$
we also write
Since B has stable rank one, by [Reference Brown and Pedersen5, Corollary 3.6],
![]() $\mathrm {Her}_B(\widetilde \phi (1_{n+1}))$
also has stable rank one. Note, by (e9.15),
$\mathrm {Her}_B(\widetilde \phi (1_{n+1}))$
also has stable rank one. Note, by (e9.15),
![]() ${\bar \iota }(a)\in \mathrm {Her}_B({\bar \phi }(1_n)) \cong \mathrm {Her}_B({\bar \phi }(e_{1,1}))\otimes M_{n},$
Then, by Proposition 9.2, there are nilpotents
${\bar \iota }(a)\in \mathrm {Her}_B({\bar \phi }(1_n)) \cong \mathrm {Her}_B({\bar \phi }(e_{1,1}))\otimes M_{n},$
Then, by Proposition 9.2, there are nilpotents
Recall that
![]() $\Pi (vv^*+\phi (1_n))=\widetilde \phi (1_{n+1}).$
Thus,
$\Pi (vv^*+\phi (1_n))=\widetilde \phi (1_{n+1}).$
Thus,
Also, note that
![]() $(vv^*+\phi (1_n))\bot \iota (b_1).$
Thus,
$(vv^*+\phi (1_n))\bot \iota (b_1).$
Thus,
By (e9.22) and the fact that nilpotents can be lifted (see [Reference Olsen and Pedersen29, Theorem 6.7]), there are nilpotents
![]() $x_2,y_2\in \mathrm {Her}_{l^\infty (A)}(vv^*+\phi (1_n))$
such that
$x_2,y_2\in \mathrm {Her}_{l^\infty (A)}(vv^*+\phi (1_n))$
such that
It follows from (e9.23) that we also have
Since
![]() $\|{\bar \iota }(a)-x_1y_1\|<\varepsilon /8, $
there is
$\|{\bar \iota }(a)-x_1y_1\|<\varepsilon /8, $
there is
![]() $\bar z\in I_{\overline {QT(A)}^w}$
such that
$\bar z\in I_{\overline {QT(A)}^w}$
such that
Note that
![]() $\iota (a)-x_2y_2\in \{\iota (b_1)\}^\bot .$
Hence, there is
$\iota (a)-x_2y_2\in \{\iota (b_1)\}^\bot .$
Hence, there is
![]() $d\in \{\iota (b_1)\}^\bot $
such that
$d\in \{\iota (b_1)\}^\bot $
such that
Let
Then
Choose
![]() $\delta>0$
such that
$\delta>0$
such that
![]() $\|zf_\delta (|z|)-z\|<\varepsilon /8.$
Then
$\|zf_\delta (|z|)-z\|<\varepsilon /8.$
Then
Write
![]() $z=\{z_1,z_2,...\}$
with
$z=\{z_1,z_2,...\}$
with
![]() $z_i\perp b_1$
$z_i\perp b_1$
![]() $(i\in \mathbb {N}).$
Since
$(i\in \mathbb {N}).$
Since
![]() $z\in {{I_{_{\overline {QT(A)}^w}}}},$
there is
$z\in {{I_{_{\overline {QT(A)}^w}}}},$
there is
![]() $i\in \mathbb {N}$
such that (note that the first inequality of the following always holds)
$i\in \mathbb {N}$
such that (note that the first inequality of the following always holds)
 $$ \begin{align} \sup_{\tau\in {{\overline{QT(A)}^w}}}\{d_\tau(f_{\delta/2}(|z_i|))\} \leq \frac{{4}}{\delta}\sup_{\tau\in {{\overline{QT(A)}^w}}}\tau(|z_i|) <{{\inf_{\tau\in \overline{QT(A)}^w}\{d_\tau(b_1)\}.}} \end{align} $$
$$ \begin{align} \sup_{\tau\in {{\overline{QT(A)}^w}}}\{d_\tau(f_{\delta/2}(|z_i|))\} \leq \frac{{4}}{\delta}\sup_{\tau\in {{\overline{QT(A)}^w}}}\tau(|z_i|) <{{\inf_{\tau\in \overline{QT(A)}^w}\{d_\tau(b_1)\}.}} \end{align} $$
Since A has strict comparison,
![]() $f_{\delta /2}(|z_i|)\lesssim b_1.$
By [Reference Rørdam40, Proposition 2.4(iv)], there is
$f_{\delta /2}(|z_i|)\lesssim b_1.$
By [Reference Rørdam40, Proposition 2.4(iv)], there is
![]() $r\in A$
such that
$r\in A$
such that
Write
![]() $x_2=\{x_{2, j}\}_{j\in \mathbb {N}}$
and
$x_2=\{x_{2, j}\}_{j\in \mathbb {N}}$
and
![]() $y_2=\{y_{2, j}\}_{j\in \mathbb {N}}.$
By (e9.25),
$y_2=\{y_{2, j}\}_{j\in \mathbb {N}}.$
By (e9.25),
![]() $x_{2,i}\bot b_1$
and
$x_{2,i}\bot b_1$
and
![]() $y_{2,i}\bot b_1.$
Together with (e9.29), we have
$y_{2,i}\bot b_1.$
Together with (e9.29), we have
Thus,
Since
![]() $x_2$
and
$x_2$
and
![]() $y_2$
are nilpotents, so are
$y_2$
are nilpotents, so are
![]() $x_{2,i},y_{2,i}.$
By (e9.26) and (e9.29),
$x_{2,i},y_{2,i}.$
By (e9.26) and (e9.29),
![]() $r^*z_i=0.$
Hence,
$r^*z_i=0.$
Hence,
By (e9.29),
![]() $r^2=0.$
By (e9.30),
$r^2=0.$
By (e9.30),
Let
![]() ${\alpha }_1:=x_{2,i}, {\alpha }_2:=z_ir^*, {\beta }_1:=y_{2,i},$
and
${\alpha }_1:=x_{2,i}, {\alpha }_2:=z_ir^*, {\beta }_1:=y_{2,i},$
and
![]() ${\beta }_2:=r.$
Then the last paragraph shows that
${\beta }_2:=r.$
Then the last paragraph shows that
![]() ${\alpha }_1,{\alpha }_2,{\beta }_1,{\beta }_2$
are all nilpotents, and
${\alpha }_1,{\alpha }_2,{\beta }_1,{\beta }_2$
are all nilpotents, and
![]() ${\alpha }_2{\alpha }_1={\beta }_1{\beta }_2=0.$
Then it is standard to conclude that
${\alpha }_2{\alpha }_1={\beta }_1{\beta }_2=0.$
Then it is standard to conclude that
![]() $x:={\alpha }_1+{\alpha }_2$
and
$x:={\alpha }_1+{\alpha }_2$
and
![]() ${y:=}{\beta }_1+{\beta }_2$
are nilpotents (see the proof of Claim 1 in the proof of [Reference Fu and Lin16, Lemma 5.6]).
${y:=}{\beta }_1+{\beta }_2$
are nilpotents (see the proof of Claim 1 in the proof of [Reference Fu and Lin16, Lemma 5.6]).
The lemma follows.
Theorem 9.4 Let A be a
![]() $\sigma $
-unital simple
$\sigma $
-unital simple
![]() $C^*$
-algebra with
$C^*$
-algebra with
![]() ${\widetilde {QT}}(A)\setminus \{0\}\not =\emptyset .$
If A has strict comparison and has T-tracial approximate oscillation zero, then A has stable rank one.
${\widetilde {QT}}(A)\setminus \{0\}\not =\emptyset .$
If A has strict comparison and has T-tracial approximate oscillation zero, then A has stable rank one.
Proof We may assume that A is non-elementary. There are two cases.
Case 1. A has a nonzero projection p.
Set
![]() $A_1:=pAp.$
Then
$A_1:=pAp.$
Then
![]() $A_1$
is unital, simple, has nonempty
$A_1$
is unital, simple, has nonempty
![]() ${{QT(A_1)}},$
and has strict comparison as well as T-tracial approximate oscillation zero. Hence,
${{QT(A_1)}},$
and has strict comparison as well as T-tracial approximate oscillation zero. Hence,
![]() $l^\infty (A_1)/I_{_{\overline {QT(A_1)}}}$
has stable rank one (see Theorem 6.6). Let
$l^\infty (A_1)/I_{_{\overline {QT(A_1)}}}$
has stable rank one (see Theorem 6.6). Let
![]() $a\in A_1$
be a non-invertible element, and let
$a\in A_1$
be a non-invertible element, and let
![]() $\varepsilon>0.$
Since
$\varepsilon>0.$
Since
![]() $A_1$
is simple and finite, by [Reference Rørdam39, Proposition 3.2 and Lemma 3.5], there is a unitary
$A_1$
is simple and finite, by [Reference Rørdam39, Proposition 3.2 and Lemma 3.5], there is a unitary
![]() $u\in U(A_1),$
an element
$u\in U(A_1),$
an element
![]() $\bar a\in A_1,$
and a positive element
$\bar a\in A_1,$
and a positive element
![]() $b\in (A_1)_+\backslash \{0\}$
such that
$b\in (A_1)_+\backslash \{0\}$
such that
![]() $\|a-\bar a\|<\varepsilon /4$
and
$\|a-\bar a\|<\varepsilon /4$
and
![]() $b(u\bar a)=(u\bar a)b=0.$
Note that
$b(u\bar a)=(u\bar a)b=0.$
Note that
![]() $\mathrm {Her}(b)$
is also infinite-dimensional. Hence, there are two nonzero orthogonal positive elements
$\mathrm {Her}(b)$
is also infinite-dimensional. Hence, there are two nonzero orthogonal positive elements
![]() $b_1,b_2\in \mathrm {Her}(b).$
$b_1,b_2\in \mathrm {Her}(b).$
By Theorem 8.5, A has property (TM). We then apply Lemma 9.3 to obtain two nilpotent elements
![]() $x,y$
such that
$x,y$
such that
Let
![]() $\delta>0$
be such that
$\delta>0$
be such that
Note that
![]() $x+\delta $
and
$x+\delta $
and
![]() $y+\delta $
are invertible since
$y+\delta $
are invertible since
![]() $x,y$
are nilpotents. Then that
$x,y$
are nilpotents. Then that
shows that a can be approximated by an invertible element
![]() $u^* (x+\delta )(y+\delta )$
up to the tolerance
$u^* (x+\delta )(y+\delta )$
up to the tolerance
![]() $\varepsilon .$
Hence,
$\varepsilon .$
Hence,
![]() $A_1$
has stable rank one. It follows that A also has stable rank one.
$A_1$
has stable rank one. It follows that A also has stable rank one.
Case 2. A has no nonzero projections. By Theorem 7.11, the canonical map
![]() $\Gamma $
is surjective. Choose
$\Gamma $
is surjective. Choose
![]() $e\in (A\otimes {\cal K})_+$
with
$e\in (A\otimes {\cal K})_+$
with
![]() $0\le e\le 1$
such that
$0\le e\le 1$
such that
![]() $\widehat {[e]}$
is continuous on
$\widehat {[e]}$
is continuous on
![]() $\widetilde {QT}(A).$
By Theorem 2.19,
$\widetilde {QT}(A).$
By Theorem 2.19,
![]() $C=\mathrm {Her}(e)$
has continuous scale. By Brown’s stable isomorphism theorem [Reference Brown4],
$C=\mathrm {Her}(e)$
has continuous scale. By Brown’s stable isomorphism theorem [Reference Brown4],
![]() $C\otimes {\cal K}\cong A\otimes {\cal K}.$
Therefore, it suffices to show that C has stable rank one (see [Reference Rieffel36, Theorem 6.4]). Hence, without loss of generality, we may assume that A has continuous scale (and
$C\otimes {\cal K}\cong A\otimes {\cal K}.$
Therefore, it suffices to show that C has stable rank one (see [Reference Rieffel36, Theorem 6.4]). Hence, without loss of generality, we may assume that A has continuous scale (and
![]() $QT(A)\not =\emptyset $
).
$QT(A)\not =\emptyset $
).
Let
![]() $A_1$
be a
$A_1$
be a
![]() $\sigma $
-unital hereditary
$\sigma $
-unital hereditary
![]() $C^*$
-subalgebra of
$C^*$
-subalgebra of
![]() $A.$
Let
$A.$
Let
![]() $a\in A_1^{\mathbf {1}}$
and let
$a\in A_1^{\mathbf {1}}$
and let
![]() $\varepsilon>0.$
Let
$\varepsilon>0.$
Let
![]() $a_1:=a^*a+aa^*.$
Then there is
$a_1:=a^*a+aa^*.$
Then there is
![]() $\delta>0$
such that
$\delta>0$
such that
Let
![]() $\bar a:=f_{\delta }({{a_1}})af_\delta ({{a_1}}).$
Since
$\bar a:=f_{\delta }({{a_1}})af_\delta ({{a_1}}).$
Since
![]() $A_1$
has no nonzero projections, we may assume that
$A_1$
has no nonzero projections, we may assume that
![]() $[0, \delta ]\subset \mathrm {sp}({{a_1}}).$
Let
$[0, \delta ]\subset \mathrm {sp}({{a_1}}).$
Let
![]() $g\in C_0((0,1])_+$
with
$g\in C_0((0,1])_+$
with
![]() $\mathrm {supp}(g)\subset [\delta /4,\delta /2],$
then
$\mathrm {supp}(g)\subset [\delta /4,\delta /2],$
then
Let us consider
![]() $A_2=\mathrm {Her}_{A_1}(f_{\delta /8}({{a_1}})).$
Note that
$A_2=\mathrm {Her}_{A_1}(f_{\delta /8}({{a_1}})).$
Note that
![]() $A_2$
is simple,
$A_2$
is simple,
![]() $A_2=\mathrm {Ped}(A_2)$
and
$A_2=\mathrm {Ped}(A_2)$
and
![]() $QT(A_2)\not =\emptyset $
and has strict comparison. Moreover, by Proposition 5.4,
$QT(A_2)\not =\emptyset $
and has strict comparison. Moreover, by Proposition 5.4,
![]() $A_2$
has T-tracial approximate oscillation zero. Hence, by Theorem 6.6,
$A_2$
has T-tracial approximate oscillation zero. Hence, by Theorem 6.6,
![]() $l^\infty (A_2)/I_{_{{\overline {QT(A_2)}^w}}}$
has stable rank one. Note that
$l^\infty (A_2)/I_{_{{\overline {QT(A_2)}^w}}}$
has stable rank one. Note that
![]() $\bar a, b\in A_2.$
Note also that, since A is non-elementary,
$\bar a, b\in A_2.$
Note also that, since A is non-elementary,
![]() $\mathrm {Her}_{A_2}(b)$
is infinite-dimensional. It follows that there are
$\mathrm {Her}_{A_2}(b)$
is infinite-dimensional. It follows that there are
![]() $b_1,b_2\in {{\mathrm {Her}_{A_2}(b)_+\setminus \{0\}}}$
such that
$b_1,b_2\in {{\mathrm {Her}_{A_2}(b)_+\setminus \{0\}}}$
such that
![]() $b_1\bot b_2.$
Since
$b_1\bot b_2.$
Since
![]() $\bar a^*\bar a+\bar a\bar a^*, b_1, b_2$
are mutually orthogonal, applying Lemma 9.3, we get two nilpotents
$\bar a^*\bar a+\bar a\bar a^*, b_1, b_2$
are mutually orthogonal, applying Lemma 9.3, we get two nilpotents
![]() $x,y\in A_2\subset A_1$
such that
$x,y\in A_2\subset A_1$
such that
![]() $\|\bar a-xy\|<\varepsilon /2.$
It follows that
$\|\bar a-xy\|<\varepsilon /2.$
It follows that
![]() $\|a-xy\|<\varepsilon .$
$\|a-xy\|<\varepsilon .$
Therefore, for any
![]() $\sigma $
-unital hereditary
$\sigma $
-unital hereditary
![]() $C^*$
-subalgebra
$C^*$
-subalgebra
![]() $A_1\subset A,$
any
$A_1\subset A,$
any
![]() $a\in A_1,$
and any
$a\in A_1,$
and any
![]() $\varepsilon>0,$
there are nilpotents
$\varepsilon>0,$
there are nilpotents
![]() $x,y\in A_1$
such that
$x,y\in A_1$
such that
![]() $\|a-xy\|<\varepsilon .$
Together with the facts that A is projectionless and assumed to have continuous scale, applying [Reference Fu, Li and Lin14, Theorem 6.4], we conclude that A has stable rank one.
$\|a-xy\|<\varepsilon .$
Together with the facts that A is projectionless and assumed to have continuous scale, applying [Reference Fu, Li and Lin14, Theorem 6.4], we conclude that A has stable rank one.
The proof of Theorem 1.1
Proof For (1)
![]() $\Rightarrow $
(2), applying Theorem 7.11, we know that
$\Rightarrow $
(2), applying Theorem 7.11, we know that
![]() $\Gamma $
is surjective. Then (2) follows from Theorem 9.4.
$\Gamma $
is surjective. Then (2) follows from Theorem 9.4.
Both (2)
![]() $\Rightarrow $
(3) and (2)
$\Rightarrow $
(3) and (2)
![]() $\Rightarrow $
(4) are obvious. That (3)
$\Rightarrow $
(4) are obvious. That (3)
![]() $\Rightarrow $
(2) follows from [Reference Antoine, Perera, Robert and Thiel1].
$\Rightarrow $
(2) follows from [Reference Antoine, Perera, Robert and Thiel1].
For (4)
![]() $\Rightarrow $
(1), we apply Theorem 5.10. That (1)
$\Rightarrow $
(1), we apply Theorem 5.10. That (1)
![]() $\Leftrightarrow $
(5) follows from Theorems 8.5 and 8.11. This ends the proof of Theorem 1.1.
$\Leftrightarrow $
(5) follows from Theorems 8.5 and 8.11. This ends the proof of Theorem 1.1.
Note that the separability condition is only used in the implication of (3)
![]() $\Rightarrow $
(2).
$\Rightarrow $
(2).
We learned that the following is also obtained by S. Geffen and W. Winter.
Corollary 9.5 Let A be a
![]() $\sigma $
-unital stably finite simple
$\sigma $
-unital stably finite simple
![]() $C^*$
-algebra of real rank zero which has strict comparison. Then
$C^*$
-algebra of real rank zero which has strict comparison. Then
![]() $\Gamma $
is surjective and A has stable rank one.
$\Gamma $
is surjective and A has stable rank one.
Proof Let
![]() $p\in A$
be a nonzero projection and
$p\in A$
be a nonzero projection and
![]() $B=pAp.$
It suffices to show the statement holds for
$B=pAp.$
It suffices to show the statement holds for
![]() $B.$
Note that B is unital and stably finite. By the paragraph right after the proof of Theorem 3.3 of [Reference Blackadar and Rørdam3], B has a 2-quasitrace (see also 1.3(III) of [Reference Blackadar and Handelman2]). By Proposition 5.8, A has tracial approximate oscillation zero. Then the corollary follows from Theorem 9.4.
$B.$
Note that B is unital and stably finite. By the paragraph right after the proof of Theorem 3.3 of [Reference Blackadar and Rørdam3], B has a 2-quasitrace (see also 1.3(III) of [Reference Blackadar and Handelman2]). By Proposition 5.8, A has tracial approximate oscillation zero. Then the corollary follows from Theorem 9.4.
Let A be a separable simple
![]() $C^*$
-algebra with
$C^*$
-algebra with
![]() ${\widetilde {QT}}(A)\setminus \{0\}\not =\emptyset .$
Let
${\widetilde {QT}}(A)\setminus \{0\}\not =\emptyset .$
Let
![]() $e\in \mathrm {Ped}(A)_+\setminus \{0\}.$
Recall that
$e\in \mathrm {Ped}(A)_+\setminus \{0\}.$
Recall that
![]() $T_e=\{\tau \in {\widetilde {QT}}(A): \tau (e)=1\}$
is a compact convex set which is also a basis for the cone
$T_e=\{\tau \in {\widetilde {QT}}(A): \tau (e)=1\}$
is a compact convex set which is also a basis for the cone
![]() $\widetilde {QT}(A).$
$\widetilde {QT}(A).$
Corollary 9.6 Let A be a
![]() $\sigma $
-unital simple
$\sigma $
-unital simple
![]() $C^*$
-algebra with
$C^*$
-algebra with
![]() $QT(A)\not =\emptyset $
which has strict comparison. Suppose that, for some
$QT(A)\not =\emptyset $
which has strict comparison. Suppose that, for some
![]() $e\in \mathrm {Ped}(A)_+^{\mathbf {1}}\setminus \{0\}$
,
$e\in \mathrm {Ped}(A)_+^{\mathbf {1}}\setminus \{0\}$
,
![]() $\partial _e(T_e)$
has countably many points. Then
$\partial _e(T_e)$
has countably many points. Then
![]() $\Gamma $
is surjective, A has stable rank one, property (TM) and T-tracial approximate oscillation zero.
$\Gamma $
is surjective, A has stable rank one, property (TM) and T-tracial approximate oscillation zero.
Proof It follows from Theorem 5.9 that A has norm approximate oscillation zero. Thus, the corollary follows from Theorem 9.4 immediately.
The following is perhaps known, but we are not able to locate it in the literature.
Proposition 9.7 Let A be a separable
![]() $C^*$
-algebra which has local finite nuclear dimension. Then every hereditary
$C^*$
-algebra which has local finite nuclear dimension. Then every hereditary
![]() $C^*$
-subalgebra
$C^*$
-subalgebra
![]() $B\subset A$
also has local finite nuclear dimension.
$B\subset A$
also has local finite nuclear dimension.
Proof Let B be a hereditary
![]() $C^*$
-subalgebra of A. Let
$C^*$
-subalgebra of A. Let
![]() $\varepsilon>0$
and
$\varepsilon>0$
and
![]() ${\cal F}\subset B$
be a finite subset. To simplify notation, without loss of generality, we may assume that
${\cal F}\subset B$
be a finite subset. To simplify notation, without loss of generality, we may assume that
![]() ${\cal F}\subset B^{\mathbf {1}}$
and there is
${\cal F}\subset B^{\mathbf {1}}$
and there is
![]() $e_B\in B_+^{\mathbf {1}}$
such that
$e_B\in B_+^{\mathbf {1}}$
such that
![]() $e_Bx=xe_B=x$
for all
$e_Bx=xe_B=x$
for all
![]() $x\in {\cal F}.$
$x\in {\cal F}.$
Choose
![]() $\delta>0$
as in Lemma 3.3 of [Reference Elliott, Gong, Lin and Niu10] associated with
$\delta>0$
as in Lemma 3.3 of [Reference Elliott, Gong, Lin and Niu10] associated with
![]() $\varepsilon /4$
(in place of
$\varepsilon /4$
(in place of
![]() $\varepsilon $
) and
$\varepsilon $
) and
![]() $\sigma =\varepsilon /4.$
We may assume that
$\sigma =\varepsilon /4.$
We may assume that
![]() $\delta <\varepsilon /4.$
$\delta <\varepsilon /4.$
Since A has local finite nuclear dimension, there is a
![]() $C^*$
-subalgebra
$C^*$
-subalgebra
![]() $C\subset A$
with finite nuclear dimension, say k (
$C\subset A$
with finite nuclear dimension, say k (
![]() $k\in \mathbb {N}{{\cup \{0\}}}$
), such that
$k\in \mathbb {N}{{\cup \{0\}}}$
), such that
Choose
![]() $d\in C_+^{\mathbf {1}}$
such that
$d\in C_+^{\mathbf {1}}$
such that
![]() $\|e_B-d\|<\delta .$
Then, by Lemma 3.3 of [Reference Elliott, Gong, Lin and Niu10], there is a partial isometry
$\|e_B-d\|<\delta .$
Then, by Lemma 3.3 of [Reference Elliott, Gong, Lin and Niu10], there is a partial isometry
![]() $w\in A^{**}$
such that
$w\in A^{**}$
such that
Set
![]() $C_1=w^*\overline {f_{\varepsilon /4}(d)Cf_{\varepsilon /4}(d)}w\subset B.$
By Proposition 2.5 of [Reference Winter and Zacharias46],
$C_1=w^*\overline {f_{\varepsilon /4}(d)Cf_{\varepsilon /4}(d)}w\subset B.$
By Proposition 2.5 of [Reference Winter and Zacharias46],
![]() $\overline {f_{\varepsilon /4}(d)Cf_{\varepsilon /4}(d)}$
has nuclear dimension
$\overline {f_{\varepsilon /4}(d)Cf_{\varepsilon /4}(d)}$
has nuclear dimension
![]() $k.$
Since
$k.$
Since
![]() $C_1\cong \overline {f_{\varepsilon /4}(d)Cf_{\varepsilon /4}(d)}, C_1$
has nuclear dimension
$C_1\cong \overline {f_{\varepsilon /4}(d)Cf_{\varepsilon /4}(d)}, C_1$
has nuclear dimension
![]() $k.$
We then estimate that
$k.$
We then estimate that
Thus, B has local finite nuclear dimension.
As in [Reference Thiel42], we have the following (note that, by [Reference Haagerup17], since A is exact,
![]() $\widetilde {T}(A)=\widetilde {QT}(A)$
).
$\widetilde {T}(A)=\widetilde {QT}(A)$
).
Corollary 9.8 Let A be a separable exact simple
![]() $C^*$
-algebra with
$C^*$
-algebra with
![]() $ {\widetilde {T}}(A) {{\setminus \{0\}}}\not =\emptyset .$
Suppose that A has strict comparison, T-tracial approximate oscillation zero and has local finite nuclear dimension. Then
$ {\widetilde {T}}(A) {{\setminus \{0\}}}\not =\emptyset .$
Suppose that A has strict comparison, T-tracial approximate oscillation zero and has local finite nuclear dimension. Then
![]() $A\otimes {\cal Z}\cong A.$
$A\otimes {\cal Z}\cong A.$
Proof Choose
![]() $e\in \mathrm {Ped}(A)_+^{\mathbf {1}}\setminus \{0\}$
and
$e\in \mathrm {Ped}(A)_+^{\mathbf {1}}\setminus \{0\}$
and
![]() $B=\mathrm {Her}(e),$
Then
$B=\mathrm {Her}(e),$
Then
![]() $\mathrm {Ped}(B)=B.$
It suffices to show (see Corollary 3.1 of [Reference Toms and Winter44]) that B is
$\mathrm {Ped}(B)=B.$
It suffices to show (see Corollary 3.1 of [Reference Toms and Winter44]) that B is
![]() ${\cal Z}$
-stable. Note that B has strict comparison, and, by Proposition 9.7, has local finite nuclear dimension. Since B also has T-tracial approximate oscillation zero (see Proposition 5.4), by Theorem 7.11,
${\cal Z}$
-stable. Note that B has strict comparison, and, by Proposition 9.7, has local finite nuclear dimension. Since B also has T-tracial approximate oscillation zero (see Proposition 5.4), by Theorem 7.11,
![]() $\Gamma $
is surjective. It follows that B has m-almost divisibility for some m (in fact m can be zero). By [Reference Tikuisis43, Theorem 8.5(iii)], B is
$\Gamma $
is surjective. It follows that B has m-almost divisibility for some m (in fact m can be zero). By [Reference Tikuisis43, Theorem 8.5(iii)], B is
![]() ${\cal Z}$
-stable.
${\cal Z}$
-stable.
Remark 9.9 At least in the unital case, the condition that A has local finite nuclear dimension in Corollary 9.8 can be further weakened to that A is amenable and has weak tracial finite nuclear dimension (see Definition 8.1 and Theorem 8.3 of [Reference Lin24]).
Remark 9.10 (1) Note that, in Theorem 1.1 and Corollary 9.6, we do not assume that A is amenable or even exact.
(2) Usually, the condition that A has strict comparison implies that A has at least one densely defined nonzero 2-quasitrace. However, one may insist that the condition that A has strict comparison means that, if A has no nonzero 2-quasitraces, A is purely infinite. In that case, the assumption in Theorem 1.1 (part of the assumption of Corollary 9.8) may be replaced by that A is finite and has strict comparison.
(3) On the other hand, if one assumes that
![]() $\mathrm {Cu}(A)$
is almost unperforated and A is not purely infinite, then, by [Reference Rørdam41], A has strict comparison (in the usual sense) (see also Remark 2.5 and Proposition 4.9 of [Reference Fu and Lin16]). Conversely, if A has strict comparison (in usual sense),
$\mathrm {Cu}(A)$
is almost unperforated and A is not purely infinite, then, by [Reference Rørdam41], A has strict comparison (in the usual sense) (see also Remark 2.5 and Proposition 4.9 of [Reference Fu and Lin16]). Conversely, if A has strict comparison (in usual sense),
![]() $\mathrm {Cu}(A)$
is almost unperforated. Therefore, if one prefers not to mention 2-quasitraces in Theorem 1.1, one could use the condition that A is finite and
$\mathrm {Cu}(A)$
is almost unperforated. Therefore, if one prefers not to mention 2-quasitraces in Theorem 1.1, one could use the condition that A is finite and
![]() $\mathrm {Cu}(A)$
is almost unperforated.
$\mathrm {Cu}(A)$
is almost unperforated.
(4) If A is a unital stably finite simple
![]() $C^*$
-algebra, then, by [Reference Rørdam40, Theorem 6.1] (see also [Reference Cuntz8, Corollary 4.7] and [Reference Blackadar and Handelman2, Theorem II.2.2]), A has at least one nontrivial 2-quasitrace. So, in the unital case, we may assume that A is stably finite instead assume that A has a nontrivial 2-quasitrace. This also works for the case that A is not unital but
$C^*$
-algebra, then, by [Reference Rørdam40, Theorem 6.1] (see also [Reference Cuntz8, Corollary 4.7] and [Reference Blackadar and Handelman2, Theorem II.2.2]), A has at least one nontrivial 2-quasitrace. So, in the unital case, we may assume that A is stably finite instead assume that A has a nontrivial 2-quasitrace. This also works for the case that A is not unital but
![]() $K_0(A)_+\not =\{0\}.$
However, when A is stably projectionless, the situation is somewhat different. Nevertheless, we may proceed this as follows:
$K_0(A)_+\not =\{0\}.$
However, when A is stably projectionless, the situation is somewhat different. Nevertheless, we may proceed this as follows:
We assume that A is a separable simple
![]() $C^*$
-algebra. Recall that an element
$C^*$
-algebra. Recall that an element
![]() $a\in \mathrm {Ped}(A)_+$
is infinite, if there are nonzero elements
$a\in \mathrm {Ped}(A)_+$
is infinite, if there are nonzero elements
![]() ${{b,\ }}c\in \mathrm {Ped}(A)_+$
such that
${{b,\ }}c\in \mathrm {Ped}(A)_+$
such that
![]() $ bc=0, b+c\lesssim c$
and
$ bc=0, b+c\lesssim c$
and
![]() $c\lesssim a. A$
is said to be finite, if there are no infinite elements in
$c\lesssim a. A$
is said to be finite, if there are no infinite elements in
![]() $\mathrm {Ped}(A)_+. A$
is said to be stably finite, if
$\mathrm {Ped}(A)_+. A$
is said to be stably finite, if
![]() $M_n(A)$
is finite for each n (see Definition 1.1 of [Reference Lin and Zhang27] and Definition 4.7 of [Reference Fu and Lin16], for example).
$M_n(A)$
is finite for each n (see Definition 1.1 of [Reference Lin and Zhang27] and Definition 4.7 of [Reference Fu and Lin16], for example).
Choose
![]() $e\in \mathrm {Ped}(A)_+\setminus \{0\}$
and consider
$e\in \mathrm {Ped}(A)_+\setminus \{0\}$
and consider
![]() $B=\mathrm {Her}(e).$
Without loss of generality, we may well assume that
$B=\mathrm {Her}(e).$
Without loss of generality, we may well assume that
![]() $A=B$
for convenience. Define
$A=B$
for convenience. Define
![]() $K_0^*(A)$
(using
$K_0^*(A)$
(using
![]() $W(A)$
not
$W(A)$
not
![]() $\mathrm {Cu}(A)$
) exactly the same way as in Section 4 of [Reference Cuntz8]. Note that Lemma 4.1 of [Reference Cuntz8] holds automatically with the definition above. The same definition of order there (before Proposition 4.2 of [Reference Cuntz8]) also works in this case. In other words, so defined
$\mathrm {Cu}(A)$
) exactly the same way as in Section 4 of [Reference Cuntz8]. Note that Lemma 4.1 of [Reference Cuntz8] holds automatically with the definition above. The same definition of order there (before Proposition 4.2 of [Reference Cuntz8]) also works in this case. In other words, so defined
![]() $K_0^*(A)$
is a (directed) ordered group and the stably finiteness ensures that
$K_0^*(A)$
is a (directed) ordered group and the stably finiteness ensures that
![]() $K_0^*(A)$
is not zero. Since A is simple, Proposition 4.2 of [Reference Cuntz8] still holds. We now return to the paragraph right after the proof Theorem 3.3 of [Reference Blackadar and Rørdam3]. Note that
$K_0^*(A)$
is not zero. Since A is simple, Proposition 4.2 of [Reference Cuntz8] still holds. We now return to the paragraph right after the proof Theorem 3.3 of [Reference Blackadar and Rørdam3]. Note that
![]() $(K_0^*(A), K_0^*(A)_+, [e])$
is a scaled ordered group which has a state, and which gives a dimension function. By [Reference Blackadar and Handelman2, II.2.2], the dimension function just mentioned gives a 2-quasitrace on
$(K_0^*(A), K_0^*(A)_+, [e])$
is a scaled ordered group which has a state, and which gives a dimension function. By [Reference Blackadar and Handelman2, II.2.2], the dimension function just mentioned gives a 2-quasitrace on
![]() $A.$
Therefore, we may replace the condition that
$A.$
Therefore, we may replace the condition that
![]() ${\widetilde {QT}}(A)\setminus \{0\}\not =\emptyset $
by the condition that A is stably finite (recall that we assume that A is simple) in Theorem 1.1 (see also [Reference Kirchberg18] for the case that A is exact).
${\widetilde {QT}}(A)\setminus \{0\}\not =\emptyset $
by the condition that A is stably finite (recall that we assume that A is simple) in Theorem 1.1 (see also [Reference Kirchberg18] for the case that A is exact).
(5) One may notice that the condition that A has strict comparison and
![]() $\Gamma $
is surjective implies that there is an isomorphism
$\Gamma $
is surjective implies that there is an isomorphism
![]() $\Gamma ^\sim : \mathrm {Cu}(A)\to V(A)\sqcup (\mathrm {LAff}_+(\widetilde {QT}(A))\setminus \{0\})$
(see also Definition 2.13).
$\Gamma ^\sim : \mathrm {Cu}(A)\to V(A)\sqcup (\mathrm {LAff}_+(\widetilde {QT}(A))\setminus \{0\})$
(see also Definition 2.13).