Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Gutierrez-Castillo, Paloma
Kagel, Adam
and
Thomases, Becca
2020.
Three-dimensional viscoelastic instabilities in a four-roll mill geometry at the Stokes limit.
Physics of Fluids,
Vol. 32,
Issue. 2,
Xia, H. M.
Wu, J. W.
Zheng, J. J.
Zhang, J.
and
Wang, Z. P.
2021.
Nonlinear microfluidics: device physics, functions, and applications.
Lab on a Chip,
Vol. 21,
Issue. 7,
p.
1241.
Castillo, Ernesto
Moreno, Laura
Baiges, Joan
and
Codina, Ramon
2021.
Stabilised Variational Multi-scale Finite Element Formulations for Viscoelastic Fluids.
Archives of Computational Methods in Engineering,
Vol. 28,
Issue. 3,
p.
1987.
Nieto Simavilla, David
and
Ellero, Marco
2022.
Mesoscopic simulations of inertial drag enhancement and polymer migration in viscoelastic solutions flowing around a confined array of cylinders.
Journal of Non-Newtonian Fluid Mechanics,
Vol. 305,
Issue. ,
p.
104811.
Datta, Sujit S.
Ardekani, Arezoo M.
Arratia, Paulo E.
Beris, Antony N.
Bischofberger, Irmgard
McKinley, Gareth H.
Eggers, Jens G.
López-Aguilar, J. Esteban
Fielding, Suzanne M.
Frishman, Anna
Graham, Michael D.
Guasto, Jeffrey S.
Haward, Simon J.
Shen, Amy Q.
Hormozi, Sarah
Morozov, Alexander
Poole, Robert J.
Shankar, V.
Shaqfeh, Eric S. G.
Stark, Holger
Steinberg, Victor
Subramanian, Ganesh
and
Stone, Howard A.
2022.
Perspectives on viscoelastic flow instabilities and elastic turbulence.
Physical Review Fluids,
Vol. 7,
Issue. 8,
Davoodi, Mahdi
Zografos, Konstantinos
and
Poole, Robert J.
2022.
On the similarities of the sPTT and FENE-P models for polymeric fluids.
Science Talks,
Vol. 2,
Issue. ,
p.
100015.
Castillo Sánchez, Hugo A.
Jovanović, Mihailo R.
Kumar, Satish
Morozov, Alexander
Shankar, V.
Subramanian, Ganesh
and
Wilson, Helen J.
2022.
Understanding viscoelastic flow instabilities: Oldroyd-B and beyond.
Journal of Non-Newtonian Fluid Mechanics,
Vol. 302,
Issue. ,
p.
104742.
Davoodi, M.
Zografos, K.
Oliveira, P. J.
and
Poole, R. J.
2022.
On the similarities between the simplified Phan-Thien–Tanner model and the finitely extensible nonlinear elastic dumbbell (Peterlin closure) model in simple and complex flows.
Physics of Fluids,
Vol. 34,
Issue. 3,
Lacassagne, Tom
Cagney, Neil
Boulafentis, Theofilos
and
Balabani, Stavroula
2023.
Elasto inertia transitions in Taylor Couette flows.
Science Talks,
Vol. 5,
Issue. ,
p.
100115.
Peng, Sai
Tang, Tingting
Li, Jianhui
Zhang, Mengqi
and
Yu, Peng
2023.
Numerical study of viscoelastic upstream instability.
Journal of Fluid Mechanics,
Vol. 959,
Issue. ,
Li, Mengqi
Boulafentis, Theofilos
Stathoulopoulos, Antonios
Liu, Zhaomiao
and
Balabani, Stavroula
2023.
Flows inside polymer microfluidic droplets: Role of elasticity.
Chemical Engineering Science,
Vol. 278,
Issue. ,
p.
118887.
Jung, Michael
Shakeri, Pegah
and
Seemann, Ralf
2023.
Effect of viscoelasticity on displacement processes in porous media.
Frontiers in Physics,
Vol. 11,
Issue. ,
Chun, Byoungjin
and
Jung, Hyun Wook
2023.
Universal flow-induced orientational ordering of colloidal rods in planar shear and extensional flows: Dilute and semidilute concentrations.
Journal of Rheology,
Vol. 67,
Issue. 2,
p.
315.
Mokhtari, Omar
Quintard, Michel
and
Davit, Yohan
2024.
A web of sticky strands: how localized stress controls spatio-temporal fluctuations in viscoelastic flows through a lattice of obstacles.
Journal of Fluid Mechanics,
Vol. 980,
Issue. ,
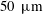 $50~\unicode[STIX]{x03BC}\text{m}$ cylinder (in a
$50~\unicode[STIX]{x03BC}\text{m}$ cylinder (in a 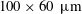 $100\times 60~\unicode[STIX]{x03BC}\text{m}$ channel), a novel 3-D holographic particle velocimetry technique reveals the underlying complexity of the flow, including inherent three-dimensionality and symmetry breaking as well as strong upstream propagation effects via elastic waves.
$100\times 60~\unicode[STIX]{x03BC}\text{m}$ channel), a novel 3-D holographic particle velocimetry technique reveals the underlying complexity of the flow, including inherent three-dimensionality and symmetry breaking as well as strong upstream propagation effects via elastic waves.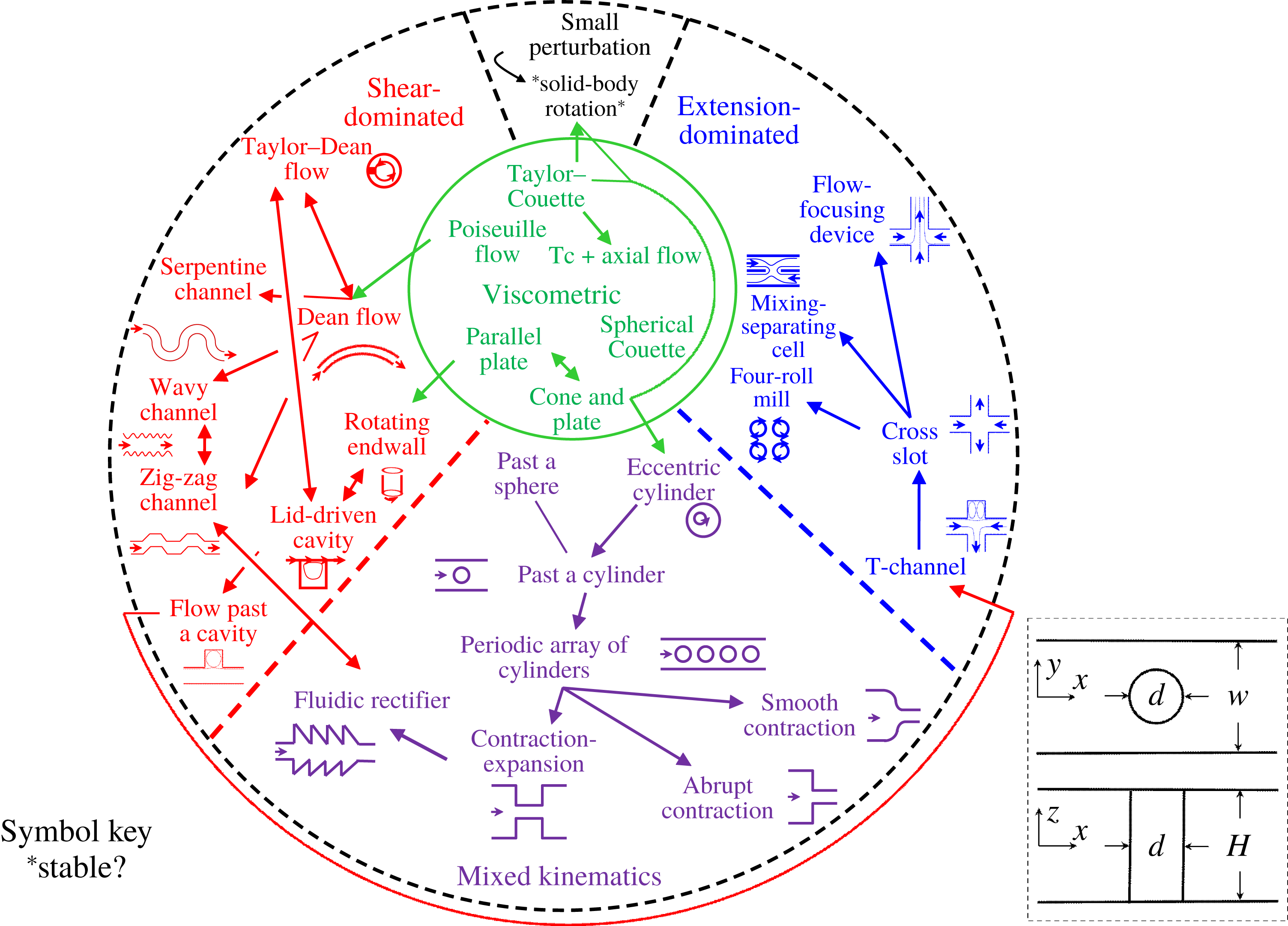
1 Introduction
Purely elastic instabilities (Shaqfeh Reference Shaqfeh1996) driven by elastic normal stresses have been widely observed in the absence of significant inertial effects, in both viscometric flows, that imparts steady shearing motion on each fluid particle (Larson, Shaqfeh & Muller Reference Larson, Shaqfeh and Muller1990), and more general non-viscometric flow geometries (Pakdel & McKinley Reference Pakdel and McKinley1996). In addition to the usual material properties of density $\unicode[STIX]{x1D70C}$
and dynamic viscosity
$\unicode[STIX]{x1D70C}$
and dynamic viscosity
 $\unicode[STIX]{x1D702}$
which characterise single-phase Newtonian flows, dilute polymeric solutions, like those used by Qin et al. (Reference Qin, Salipante, Hudson and Arratia2019) and most other studies in this area, are also characterised by a ‘relaxation’ time (Bird, Armstrong & Hassager Reference Bird, Armstrong and Hassager1987). The Deborah number
$\unicode[STIX]{x1D702}$
which characterise single-phase Newtonian flows, dilute polymeric solutions, like those used by Qin et al. (Reference Qin, Salipante, Hudson and Arratia2019) and most other studies in this area, are also characterised by a ‘relaxation’ time (Bird, Armstrong & Hassager Reference Bird, Armstrong and Hassager1987). The Deborah number
 $De$
, which is a measure of this relaxation time relative to a characteristic residence time of the flow, must become unimportant in fully developed, steady viscometric flows as the characteristic residence time tends to infinity. The second parameter governing the flow of single-phase viscoelastic fluids in the inertialess limit is the Weissenberg number
$De$
, which is a measure of this relaxation time relative to a characteristic residence time of the flow, must become unimportant in fully developed, steady viscometric flows as the characteristic residence time tends to infinity. The second parameter governing the flow of single-phase viscoelastic fluids in the inertialess limit is the Weissenberg number
 $Wi$
, the ratio of elastic to viscous stresses. These two parameters are often thought of as essentially interchangeable although, in general, they represent subtly different properties of the flow: one quantifying inherently Lagrangian unsteady effects (
$Wi$
, the ratio of elastic to viscous stresses. These two parameters are often thought of as essentially interchangeable although, in general, they represent subtly different properties of the flow: one quantifying inherently Lagrangian unsteady effects (
 $De$
) and the other the ‘strength’ of the flow (
$De$
) and the other the ‘strength’ of the flow (
 $Wi$
). In the problem studied by Qin et al. (Reference Qin, Salipante, Hudson and Arratia2019) of flow past a cylinder of diameter
$Wi$
). In the problem studied by Qin et al. (Reference Qin, Salipante, Hudson and Arratia2019) of flow past a cylinder of diameter
 $d$
in an approximately square channel of height
$d$
in an approximately square channel of height
 $H$
, the characteristic time scale of the flow can be estimated as the time taken for a fluid particle to circumvent half the cylinder (i.e.
$H$
, the characteristic time scale of the flow can be estimated as the time taken for a fluid particle to circumvent half the cylinder (i.e.
 $\unicode[STIX]{x03C0}d/2U\sim d/U\sim H/U$
as
$\unicode[STIX]{x03C0}d/2U\sim d/U\sim H/U$
as
 $d\sim H$
). The Deborah number is then
$d\sim H$
). The Deborah number is then
 $De\sim \unicode[STIX]{x1D706}U/H$
. The Weissenberg number in Qin et al. (Reference Qin, Salipante, Hudson and Arratia2019) is
$De\sim \unicode[STIX]{x1D706}U/H$
. The Weissenberg number in Qin et al. (Reference Qin, Salipante, Hudson and Arratia2019) is
 $Wi=N_{1}/2\unicode[STIX]{x1D70F}=N_{1}/(2\dot{\unicode[STIX]{x1D6FE}}\unicode[STIX]{x1D702})$
, where
$Wi=N_{1}/2\unicode[STIX]{x1D70F}=N_{1}/(2\dot{\unicode[STIX]{x1D6FE}}\unicode[STIX]{x1D702})$
, where
 $N_{1}$
is the first-normal stress difference (the ‘elastic’ stress),
$N_{1}$
is the first-normal stress difference (the ‘elastic’ stress),
 $\unicode[STIX]{x1D70F}$
the shear stress and
$\unicode[STIX]{x1D70F}$
the shear stress and
 $\dot{\unicode[STIX]{x1D6FE}}$
the shear rate. Only for an upper-convected Maxwell model (Bird et al.
Reference Bird, Armstrong and Hassager1987), where
$\dot{\unicode[STIX]{x1D6FE}}$
the shear rate. Only for an upper-convected Maxwell model (Bird et al.
Reference Bird, Armstrong and Hassager1987), where
 $N_{1}=2\unicode[STIX]{x1D706}\unicode[STIX]{x1D702}\dot{\unicode[STIX]{x1D6FE}}^{2}$
and
$N_{1}=2\unicode[STIX]{x1D706}\unicode[STIX]{x1D702}\dot{\unicode[STIX]{x1D6FE}}^{2}$
and
 $\unicode[STIX]{x1D70F}=\unicode[STIX]{x1D702}\dot{\unicode[STIX]{x1D6FE}}$
in steady simple shear, does this yield
$\unicode[STIX]{x1D70F}=\unicode[STIX]{x1D702}\dot{\unicode[STIX]{x1D6FE}}$
in steady simple shear, does this yield
 $Wi=\unicode[STIX]{x1D706}\dot{\unicode[STIX]{x1D6FE}}\sim \unicode[STIX]{x1D706}U/H$
and hence
$Wi=\unicode[STIX]{x1D706}\dot{\unicode[STIX]{x1D6FE}}\sim \unicode[STIX]{x1D706}U/H$
and hence
 $Wi=De$
. However,
$Wi=De$
. However,
 $De$
and
$De$
and
 $Wi$
both increase with decreasing characteristic length scale(s). Hence, the microfluidic environment, which typically minimises inertial effects due to its small length scales, also enhances elastic effects. As a result, microfluidic experiments have been widely exploited to probe purely elastic instabilities in viscoelastic fluids, which usually arise from the combination of elastic stresses and streamline curvature. This mechanism is captured in the phenomenological criterion due to Pakdel & McKinley (Reference Pakdel and McKinley1996), which states that instability may arise when the product of a ‘local’
$Wi$
both increase with decreasing characteristic length scale(s). Hence, the microfluidic environment, which typically minimises inertial effects due to its small length scales, also enhances elastic effects. As a result, microfluidic experiments have been widely exploited to probe purely elastic instabilities in viscoelastic fluids, which usually arise from the combination of elastic stresses and streamline curvature. This mechanism is captured in the phenomenological criterion due to Pakdel & McKinley (Reference Pakdel and McKinley1996), which states that instability may arise when the product of a ‘local’
 $De$
based on a length scale involving the local streamline curvature (
$De$
based on a length scale involving the local streamline curvature (
 $\mathfrak{R}$
) and a ‘local’
$\mathfrak{R}$
) and a ‘local’
 $Wi$
based on local shear rate and local tensile (normal) stress along the streamline exceeds a critical parameter (
$Wi$
based on local shear rate and local tensile (normal) stress along the streamline exceeds a critical parameter (
 $M_{CR}^{2}$
) (i.e.
$M_{CR}^{2}$
) (i.e.
 $(N_{1}/\unicode[STIX]{x1D70F})(\unicode[STIX]{x1D706}U/\mathfrak{R})>M_{CR}^{2}$
).
$(N_{1}/\unicode[STIX]{x1D70F})(\unicode[STIX]{x1D706}U/\mathfrak{R})>M_{CR}^{2}$
).
Purely elastic instabilities and, at higher flow rates, even highly disordered flows termed ‘elastic turbulence’ have been observed in a wide range of different geometries. One way of categorising these flows is via a schematic representation – a ‘map’ – demarcating these flows into: viscometric, shear-dominated, extension-dominated and those of mixed kinematics, as shown in figure 1. The map highlights the interrelation between flows of apparently differing character – between the ‘cross-slot’ and the ‘mixing-separating’ geometry, for example, or the similarity between flow past a cylinder and into a contraction. The flow past a cylinder in a channel studied by Qin et al. (Reference Qin, Salipante, Hudson and Arratia2019), shown schematically as an inset in figure 1, falls into the island of ‘mixed kinematics’.
2 Overview
Following on from earlier seminal work in the same group by Pan et al. (Reference Pan, Morozov, Wagner and Arratia2013), where an array of cylinders in a microfluidic channel was used to show that a sustained elastic instability leading to elastic turbulence could also be achieved in the absence of streamline curvature far downstream of the array, the recent study of Qin et al. (Reference Qin, Salipante, Hudson and Arratia2019) looks in detail at the instability around a single cylinder. It is precisely these ‘finite amplitude’ perturbations (Morozov & van Saarloos Reference Morozov and van Saarloos2007) which – when combined in an array of cylinders – were able to drive a self-sustaining turbulent motion far downstream ( ${\sim}400$
channel widths) in the straight channel. Hence an understanding of the underlying instability mechanisms around an isolated cylinder is potentially of broad interest. The significant advance of Qin et al. (Reference Qin, Salipante, Hudson and Arratia2019) on most previous studies of purely elastic instabilities (with limited exceptions such as the study by Afik & Steinberg Reference Afik and Steinberg2017) is in the use of a novel in-line three-dimensional (3-D) holographic particle tracking technique. The technique, detailed in Salipante, Little & Hudson (Reference Salipante, Little and Hudson2017), involves recording using a high-speed camera of the flow seeded with tracer particles and illuminated by a laser mounted on an inverted microscope. In this manner, the positions of the particles are determined using back-scattering reconstruction and a fully 3-D velocity field can be reconstructed by differentiating Lagrangian particle trajectories. These 3-D velocity fields reveal much more complex flow transitions as the flow rate (and hence
${\sim}400$
channel widths) in the straight channel. Hence an understanding of the underlying instability mechanisms around an isolated cylinder is potentially of broad interest. The significant advance of Qin et al. (Reference Qin, Salipante, Hudson and Arratia2019) on most previous studies of purely elastic instabilities (with limited exceptions such as the study by Afik & Steinberg Reference Afik and Steinberg2017) is in the use of a novel in-line three-dimensional (3-D) holographic particle tracking technique. The technique, detailed in Salipante, Little & Hudson (Reference Salipante, Little and Hudson2017), involves recording using a high-speed camera of the flow seeded with tracer particles and illuminated by a laser mounted on an inverted microscope. In this manner, the positions of the particles are determined using back-scattering reconstruction and a fully 3-D velocity field can be reconstructed by differentiating Lagrangian particle trajectories. These 3-D velocity fields reveal much more complex flow transitions as the flow rate (and hence
 $Wi$
) is increased than could previously be inferred from two-dimensional measurements. In particular, the findings of Qin et al. (Reference Qin, Salipante, Hudson and Arratia2019) of strong three-dimensionality at higher flow rates are significant in that they are likely to be systemic to most microfluidic flows studied to date because most microfluidic channels have finite depth, with an approximately square cross-section (as in Qin et al.
Reference Qin, Salipante, Hudson and Arratia2019).
$Wi$
) is increased than could previously be inferred from two-dimensional measurements. In particular, the findings of Qin et al. (Reference Qin, Salipante, Hudson and Arratia2019) of strong three-dimensionality at higher flow rates are significant in that they are likely to be systemic to most microfluidic flows studied to date because most microfluidic channels have finite depth, with an approximately square cross-section (as in Qin et al.
Reference Qin, Salipante, Hudson and Arratia2019).
Figure 1. Purely elastic flow instability map (‘PEFIM’): a taxonomy for purely elastic instabilities based on flow type, including potential relationships between different prototype geometries. Inset in bottom right-hand corner defines axes for the situation studied by Qin et al. (Reference Qin, Salipante, Hudson and Arratia2019).
Two-dimensional measurements in the $xy$
-centreplane (see inset of figure 1 for axis definition) of Qin et al. (Reference Qin, Salipante, Hudson and Arratia2019) reveal that an upstream vortex develops immediately in front of the cylinder as
$xy$
-centreplane (see inset of figure 1 for axis definition) of Qin et al. (Reference Qin, Salipante, Hudson and Arratia2019) reveal that an upstream vortex develops immediately in front of the cylinder as
 $Wi$
is increased. Beyond a critical
$Wi$
is increased. Beyond a critical
 $Wi\sim 4$
, the vortex begins to fluctuate weakly in time although it retains its symmetry about the midline of the
$Wi\sim 4$
, the vortex begins to fluctuate weakly in time although it retains its symmetry about the midline of the
 $xy$
-centreplane. This symmetry is lost beyond
$xy$
-centreplane. This symmetry is lost beyond
 $Wi\sim 8$
, and for
$Wi\sim 8$
, and for
 $Wi>9$
the flow enters a stronger time-dependent regime where the length of the upstream vortex frequently collapses to
$Wi>9$
the flow enters a stronger time-dependent regime where the length of the upstream vortex frequently collapses to
 ${\sim}2d$
and then regenerates (up to
${\sim}2d$
and then regenerates (up to
 $6d$
).
$6d$
).
The novel 3-D measurements reveal that the ‘top’ and ‘bottom’ walls play a fundamental role in the dynamics as the flow at high $Wi$
is revealed to be made up of a pair of separate recirculation zones, each originating between the ‘corner’ of the cylinder and the top/bottom walls. These zones are anticorrelated in that as one grows the other decays – and vice versa. Thus symmetry breaking first noted across the midline of the
$Wi$
is revealed to be made up of a pair of separate recirculation zones, each originating between the ‘corner’ of the cylinder and the top/bottom walls. These zones are anticorrelated in that as one grows the other decays – and vice versa. Thus symmetry breaking first noted across the midline of the
 $xy$
-centreplane is followed by symmetry breaking across the midline of the
$xy$
-centreplane is followed by symmetry breaking across the midline of the
 $xz$
-centreplane, and the flow is strongly 3-D, something which is only fully revealed by these new measurements. Finally, the results also suggest the presence of apparently different instability mechanisms upstream and downstream of the cylinder. The upstream propagation of disturbances suggests that perturbations may be transmitted against the primary flow direction via an ‘elastic wave’, but with a wave speed which does not simply scale with
$xz$
-centreplane, and the flow is strongly 3-D, something which is only fully revealed by these new measurements. Finally, the results also suggest the presence of apparently different instability mechanisms upstream and downstream of the cylinder. The upstream propagation of disturbances suggests that perturbations may be transmitted against the primary flow direction via an ‘elastic wave’, but with a wave speed which does not simply scale with
 $\unicode[STIX]{x1D706}$
. For a viscoelastic shear wave, based on a Maxwell type model with constant polymeric viscosity
$\unicode[STIX]{x1D706}$
. For a viscoelastic shear wave, based on a Maxwell type model with constant polymeric viscosity
 $\unicode[STIX]{x1D702}_{p}$
and relaxation time
$\unicode[STIX]{x1D702}_{p}$
and relaxation time
 $\unicode[STIX]{x1D706}$
, the wave speed is constant
$\unicode[STIX]{x1D706}$
, the wave speed is constant
 $c_{s}=\sqrt{(\unicode[STIX]{x1D702}_{p}/\unicode[STIX]{x1D70C}\unicode[STIX]{x1D706})}$
and this leaves open precisely what is the physical interpretation of the wave (see also Varshney & Steinberg Reference Varshney and Steinberg2019).
$c_{s}=\sqrt{(\unicode[STIX]{x1D702}_{p}/\unicode[STIX]{x1D70C}\unicode[STIX]{x1D706})}$
and this leaves open precisely what is the physical interpretation of the wave (see also Varshney & Steinberg Reference Varshney and Steinberg2019).
3 Future
Given that the results of Qin et al. (Reference Qin, Salipante, Hudson and Arratia2019) reveal the potentially strong influence of the walls on the time-dependent flow which develops, an obvious next step would be to investigate the effect of varying the depth aspect ratio of the channel to determine if this instability always arises at the same preferential location or if new mechanisms arise when the channel is deeper. Novel fabrication methods which allow much higher aspect ratios (for example, Haward, Toda-Peters & Shen Reference Haward, Toda-Peters and Shen2018) than conventional PDMS microchannels may prove fruitful in this regard. Studies which can probe systematically the effect of varying the viscoelastic shear wave speed, perhaps by changing the polymeric viscosity contribution whilst holding the density and relaxation time approximately constant, may shed more light on the upstream propagation mechanisms. In this vein, and given the rich dynamics observed, fully resolved 3-D time-dependent numerical simulations using viscoelastic constitutive equations would also seem like an interesting avenue to pursue. In this latter case, the simulations have the ability to fully ‘turn off’ inertia, something that a real experiment can never truly do. However, the very complicated flow patterns and dynamics observed experimentally present a significant challenge for numerical simulations and a stringent test of existing viscoelastic constitutive equations.