We study the two-dimensional, irrotational flow of an inviscid, incompressible fluid injected from a line source moving at constant speed along a horizontal boundary, into a second, immiscible, inviscid fluid of lower density. A semi-infinite, horizontal layer sustained by the moving source has previously been studied as a simple model for a powder snow avalanche, an example of an eruption current, Carroll et al. (Phys. Fluids, vol. 24, 2012, 066603). We show that with fluids of unequal densities, in a frame of reference moving with the source, no steady solution exists, and formulate an initial/boundary value problem that allows us to study the evolution of the flow. After considering the limit of small density difference, we study the fully nonlinear initial/boundary value problem and find that the flow at the head of the layer is effectively a dam break for the initial conditions that we have used. We study the dynamics of this in detail for small times using the method of matched asymptotic expansions. Finally, we solve the fully nonlinear free boundary problem numerically using an adaptive vortex blob method, after regularising the flow by modifying the initial interface to include a thin layer of the denser fluid that extends to infinity ahead of the source. We find that the disturbance of the interface in the linear theory develops into a dispersive shock in the fully nonlinear initial/boundary value problem, which then overturns. For sufficiently large Richardson number, overturning can also occur at the head of the layer.
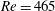 $Re=465$
$Re=465$