We start with an overview of what is accepted as good practice. We will review several general ethical guidelines. These guidelines can be used to appreciate good research and to indicate where and how research does not adhere to these guidelines. Good practice is “what we all say we (should) adhere to.” In the second part of this chapter, the focus is more on specific ethical guidelines for statistical analysis. Of course, there is overlap with the more general guidelines, but there are also a few specifically relevant for statistics. In that case one can think of misinterpreting p values, malpractice such as p hacking and harking.
1.1 What Is Good Practice?
Before we can learn something about bad practice and how to recognize it, we must establish what good practice is. Good practice is what we hope happens most of the time. However, interviews, literature studies, and individual cases tell us that various degrees of sloppy science happen frequently and that questionable research practices (QRPs) are around.Footnote 1 Before we turn to general ethical guidelines, consider the following principles:Footnote 2
Respect
People who participate in research, as informants or otherwise, shall be treated with respect.
Good Consequences
Researchers shall seek to ensure that their activities produce good consequences and that any adverse consequences are within the limits of acceptability.
Fairness
All research projects shall be designed and implemented fairly.
Integrity
Researchers shall comply with recognized norms and behave responsibly, openly, and honestly towards their colleagues and the public.
These four principles translate into fourteen guidelines:Footnote 3
1 Quest for truth:
Being honest, open, and systematic, and documenting clearly
2 Academic freedom:
Choice of topic and methodology, implementation of research, and publication of results.
3 Quality:
Possessing the necessary competence, designing relevant research questions, undertaking suitable choices of methodology, and ensuring sound and appropriate project implementation in terms of data collection, data processing, and safekeeping/storage of the material.
4 Voluntary informed consent:Footnote 4
Explicit, voluntary, and documentable.
5 Confidentiality:
No damage to individuals who are the subjects of research.
6 Impartiality:
No conflicts of interest. Openness to colleagues, research participants, sources of finance, and other relevant parties.
7 Integrity:
Trustworthiness of research. No fabrication, falsification, or (self-)plagiarism.Footnote 5
We need a few more insights here.
Self-plagiarism is well defined. Indeed, “Self-plagiarism is defined as a type of plagiarism in which the writer republishes a work in its entirety or reuses portions of a previously written text while authoring a new work.”Footnote 6 Some people believe that self-plagiarism is a consequence of what is called the “publish or perish” culture at academic institutions. Wikipedia says:
When people are pushed to produce many publications, it can be tempting to incorporate, for example, parts of previous papers into a new paper, without telling the reader. Quoting one’s own work is not a problem, however, at least if one tells the reader that it occurs.Footnote 8“Publish or perish” is an aphorism describing the pressure to publish academic work in order to succeed in an academic career. Such institutional pressure is generally strongest at research universities. Some researchers have identified the publish or perish environment as a contributing factor to the replication crisis.Footnote 7
So far, we have reviewed seven guidelines, but there are seven more.Footnote 9
8 Good reference practice:Footnote 10
Verifiability (meaning that one should be able to find the references).
9 Collegiality:
Data ownership and sharing, authorship, publication, peer review, and cooperation.
Indeed, these days, various journals include statements such as:
Conceptualization, P.H.F. and M.W.; methodology, P.H.F.; software, M.W.; validation, P.H.F. and M.W.; formal analysis, P.H.F. and M.W.; investigation, P.H.F. and M.W.; resources, P.H.F.; data curation, P.H.F.; writing – original draft preparation, P.H.F. and M.W.; writing – review and editing, P.H.F.; visualization, P.H.F. and M.W.; supervision, P.H.F.; project administration, P.H.F. and M.W. All authors have read and agreed to the published version of the manuscript.Footnote 11
10 Institutional responsibilities:
Ensure compliance with good academic practice and with establishing mechanisms that can address cases of suspected violations of ethical research norms.
11 Availability of results:Footnote 12
Openness, verifiability, returning benefit to research participants and society in general.
12 Social responsibility:
Research will benefit research participants, relevant groups, or society in general, and prevent from causing harm. Distinction between being an expert and having an opinion. Refrain from abusing authority.
13 Global responsibilities:
Research should help counteract global injustice and preserve biological diversity.
14 Laws and regulations:Footnote 13
To be abided by.
1.2 Ethical Guidelines for Statistical Practice
The American Statistical Association publishes a list of ethical guidelines for statistical practice.Footnote 14 The general guidelines address the following items:
professional integrity and accountability
integrity of data and methods
responsibilities to research subjects
responsibilities to research team colleagues
responsibilities to other statisticians or statistics practitioners
responsibilities regarding allegations of misconduct
responsibilities of employers, including organizations, individuals, attorneys, or other clients employing statistical practitioners
Each item is detailed on their website. There are guidelines for statistical practice that go beyond the more general guidelines noted here. There is a knowledge asymmetry between the statistical practitioner and, for example, a client or funder. Clients receive statistical advice and may not be able to reproduce how the statistician created the advice. This requires “extra” ethical behavior from statisticians.
Let us zoom in on even more specific features that hold for statistics, and as such also for econometrics. There are a few concepts in statistics that are commonly used, but it may happen that people misunderstand these. We will see in Chapter 2 that simple statistical tools can highlight fabricated data, for example because the results are simply too good to be true.
In the remainder of this chapter, we will address asking for the source of the data, the notion to abstain from drawing suggestive graphs, what p values mean,Footnote 15 why p hacking is malpractice, why harking (after defining it) is even worse, and we present some basic insights concerning multiple testing. The last issue concerns the notion that when you run enough statistical tests, you will always find something.
1.3 Where Do the Data Come From? And What Do they Look Like?
A first question that one could ask is: What is the source of the data? Who compiled the data and for which purpose? Does the data provider have an interest in the outcomes?Footnote 16
On page 95 of Calling Bullshit, we read:
If you are looking at quantitative indicators that others have compiled, ask yourself: Are these numbers measuring what they are intended to measure? Or are people gaming the system and rendering this measure useless?Footnote 17
This notion is particularly relevant in the case of bid books for large events or infrastructural projects. Think of the situation when the mayor of a city asks for insights into whether it could be beneficial to attract the Olympic Games to her city. The mayor does not want to hear that organizing such an event could be a financial disaster. So, most often bid books excel in providing tables and graphs where returns are exaggerated. Bid book compilers will always find sources that can support their enthusiastic projections in terms of income and their downward-sized cost projections. In the end, it is well known and widely documented that hosting the Olympic Games rarely leads to profits.Footnote 18
An interesting recent case study on closely looking at data is a beautifully written paper that has been cited hundreds of times; it is on a fascinating topic: surveys.Footnote 19 People are sometimes asked to complete a survey in which one of the last items asks them to indicate whether they filled in the questionnaire honestly. The authors of this paper decided to discover if not ending the survey with this statement but beginning with it would lead to more honest behavior. To do this, they decided to study the miles that people report they drive when they are asked this by an insurance company.
The study has been summarized as follows:
Our focus here is on Study 3 in the 2012 paper, a field experiment (N = 13,488) conducted by an auto insurance company in the southeastern United States under the supervision of the fourth author. Customers were asked to report the current odometer reading of up to four cars covered by their policy. They were randomly assigned to sign a statement indicating, “I promise that the information I am providing is true” either at the top or bottom of the form. Customers assigned to the “sign-at-the-top” condition reported driving 2,400 more miles (10.3%) than those assigned to the “sign-at-the-bottom” condition.
It continues:
Let’s first think about what the distribution of miles driven should look like. If there were about a year separating the Time 1 and Time 2 mileages, we might expect something like the figure below, taken from the UK Department of Transportation based on similar data (two consecutive odometer readings) collected in 2010.Footnote 20
Now before the reader turns to Figure 1.1, what would we think a histogram of mileages would look like? Some people drive frequently, some drive rarely, and a large group will report mileages around some mean or median value. The data would not reflect a Gaussian distribution, as there might be some skewness to the right where there are people who really drive many miles for their work. Indeed, one could imagine that the data would look like those in Figure 1.1.
Indeed, the histogram in Figure 1.1 mimics a nonsymmetric right-skewed distribution with a few large outlying observations in the right tail. However, when we look at the data that were analyzed in the study of Shu et al.,Footnote 21 we have the data as in Figure 1.2. These data look like data from a uniform distribution, where all mileages have an equal probability of being observed. And that is not the only thing. Beyond 50,000 miles there are no observations. There seems to be a cut-off point. This case provides an example where it pays off to first imagine how the data could look before you analyze any data. You would never have imagined a uniform distribution in the first place, given the type of variable that you are considering.

Figure 1.2 Data analyzed in Shu et al.
Lisa L. Shu, Nina Mazar, Francesca Gino, Dan Ariely, and Max H. Bazerman 2012), Signing at the beginning makes ethics salient and decreases dishonest self-reports in comparison to signing at the end, Proceedings of the National Academy of Sciences of the United States of America, 109 (38), 15197–15200; https://doi.org/10.1073/pnas.1209746109
1.4 No Suggestive Graphs
Statistical data analysis may start with visualizations of the data. This can be done via histograms, as mentioned earlier, but also line graphs and pie charts, and there are various other ways to visually present or summarize data. Making useful graphs is an art,Footnote 22 and the graphs should be informative. Look at Figure 1.3, which puts the number of flat stages in the Tour de France and the number of mass sprints at the finish, over the years, in one graph. The headline of the associated article in a Dutch newspaper was “Do more flat stages in the Tour de France lead to more mass sprints at the finish?” with, of course, the emphasis being on the word “lead.” If you casually looked at the graph, given that you had seen the headline, you would be tempted to answer the question with a “no,” even though no formal analysis has been conducted.

Figure 1.3 The number of flat stages in the Tour de France and the number of mass sprints at the finish, 1947–2020.
As another example, Figure 1.4 depicts the number of unfree countries in the world, when observed over a thirteen-year period. Indeed, if you look at the graph, you would be tempted to fully agree with the title of the report, that “democracy is under siege.” Obviously, the line goes up, and from 2008 to 2020 the number of unfree countries increases from forty-two to fifty-four. We shall not doubt that there is an increase in the number of unfree countries, nor shall we question how “democracy” is measured, but it is insightful to consider a longer period of data, as is done in Figure 1.5.

Figure 1.4 Number of unfree countries in the world, 2008–2020.
When we look at the same variable since 1972, we see that the year 2008 is the lowest point in the graph since 1993, and thus to start the graph in 2008 as in Figure 1.4 makes the steepness of the line the greatest. Overall, from 1972, the number of unfree countries shows a downward trend, with, admittedly, a recent increase. As the number of countries in the world is not fixed, with new countries in Eastern Europe, in former Yugoslavia, and in Africa, we can also illustrate the fraction of countries that can be labeled as unfree, as is done in Figure 1.6.
From this, we see that the downward trend that was visible in Figure 1.5 is now even steeper when we look at the fraction of unfree countries. Again, there is no doubt that in recent years there has been an increase in unfree countries, but the extent of this increase can be visualized in diverse ways.Footnote 23

Figure 1.5 Number of unfree countries in the world, 1972–2020.

Figure 1.6 Fraction of unfree countries in the world, 1972–2020.
1.5 p Value
The most often used metric in (classical) statistical analysis is the so-called p value. Looking at assorted studies,Footnote 24 it is also the most misunderstood metric or even the most misused.
Wikipedia says:
In null hypothesis significance testing, the p-value is the probability of obtaining test results at least as extreme as the results actually observed, under the assumption that the null hypothesis is correct. A very small p-value means that such an extreme observed outcome would be very unlikely under the null hypothesis.Footnote 25
The p value is associated with the Type 1 error (![]() ) in hypothesis testing. This is defined as the case when you reject the null hypothesis
) in hypothesis testing. This is defined as the case when you reject the null hypothesis ![]() if
if ![]() is true. You preferably want this error to be small. Note that the Type 1 error will never be exactly equal to zero. There is always some risk that a wrong decision will be made.Footnote 26
is true. You preferably want this error to be small. Note that the Type 1 error will never be exactly equal to zero. There is always some risk that a wrong decision will be made.Footnote 26
Now, in much research we see that a small p value is interpreted as that the alternative hypothesis ![]() is correct.Footnote 27 We see that researchers claim to have found “an effect” when they reject the null hypothesis. We also see studies where people have made the decision for you, that is, which p value is relevant.Footnote 28 You then find tables with labels such as ***, which means a p value smaller than 0.01, **, meaning a p value smaller than 0.05, and *, meaning the p value is smaller than 0.10, or something like that. Often, these cut-off points are arbitrary choices, where 0.05 is often conveniently chosen as 0.05 matches with t values larger than 2 or more negative than −2, for a standard normal distribution. A t value measures the number of standard deviations that a number or estimate is away from the mean, where this mean is often equal to 0 in case of hypothesis testing.
is correct.Footnote 27 We see that researchers claim to have found “an effect” when they reject the null hypothesis. We also see studies where people have made the decision for you, that is, which p value is relevant.Footnote 28 You then find tables with labels such as ***, which means a p value smaller than 0.01, **, meaning a p value smaller than 0.05, and *, meaning the p value is smaller than 0.10, or something like that. Often, these cut-off points are arbitrary choices, where 0.05 is often conveniently chosen as 0.05 matches with t values larger than 2 or more negative than −2, for a standard normal distribution. A t value measures the number of standard deviations that a number or estimate is away from the mean, where this mean is often equal to 0 in case of hypothesis testing.
In contrast to using asterisks, we would recommend allowing readers of a study to make their own choice of which value they deem large or small, and hence one should better just report the obtained p value itself. Some argue that a small p value, suggesting the rejection of a null hypothesis, could be seen as meaning that more research is needed.Footnote 29
1.6 p Hacking
The misuse of p values on purpose is called p hacking, and indeed, it is something we should not do.
Wikipedia says:
Data dredging (also known as data snooping or p hacking), is the misuse of data analysis to find patterns in data that can be presented as statistically significant, thus dramatically increasing and understating the risk of false positives. This is done by performing many statistical tests on the data and only reporting those that come back with significant results.Footnote 30
If you read this quote, you would immediately feel that p hacking is malpractice. p hacking is also associated with false positives, which can occur if you run many tests, as we will see in Section 1.8.Footnote 31
1.7 Harking
Another “do not do this” in statistics is called harking.
Wikipedia says:
HARKing is an acronym coined by social psychologist Norbert Kerr that refers to the questionable research practice of Hypothesizing After the Results are Known. Kerr defined HARKing as “presenting a post hoc hypothesis in the introduction of a research report as if it were an a priori hypothesis.”Footnote 32 HARKing may occur when a researcher tests an a priori hypothesis but then omits that hypothesis from their research report after they find out the results of their test; inappropriate forms of post hoc analysis and/or post hoc theorizing then may lead to a post hoc hypothesis.Footnote 33
This behavior goes against a main principle in statistics, which is that you first formulate a hypothesis and then collect data to see if there is evidence against or in favor of that hypothesis. Pretending that you already knew the outcome in advance by shifting the order of actions leads to no sound addition to the knowledge base. Harking does not bring science any further, and in fact may even obstruct progress.
Obviously, when you read about the misuse of p values, p hacking, and harking, you would think that nobody would do this. But still, there are plenty of examples around, and therefore it is important that you are clear about your research design, your hypothesis, and your data collection before you begin.Footnote 34
1.8 Size and Power
To see what happens when multiple tests are conducted, and how false inference can occur, consider again three basic aspects of statistical testing. We have already mentioned the Type 1 error (![]() ), which is that you reject
), which is that you reject ![]() if
if ![]() is true (which is preferably small but will never be exactly zero). There is also a Type 2 error (
is true (which is preferably small but will never be exactly zero). There is also a Type 2 error (![]() ), which is that you do not reject
), which is that you do not reject ![]() if
if ![]() is not true (and this is also preferably small), and its mirror concept called the power of a test (
is not true (and this is also preferably small), and its mirror concept called the power of a test (![]() ), which is that you reject
), which is that you reject ![]() if
if ![]() is false indeed (which is preferably large, and is of course never exactly equal to 1). Even though
is false indeed (which is preferably large, and is of course never exactly equal to 1). Even though ![]() and
and ![]() can be small. they will never be exactly zero as there is always a positive chance of making a wrong decision. If you run just a single test, then the chance of making a wrong decision is of the size of
can be small. they will never be exactly zero as there is always a positive chance of making a wrong decision. If you run just a single test, then the chance of making a wrong decision is of the size of ![]() and
and ![]() . However, if you run a test many times, then the size of the overall chance can become quite large. Here are two illustrations of this phenomenon.
. However, if you run a test many times, then the size of the overall chance can become quite large. Here are two illustrations of this phenomenon.
Suppose there is a test on fraud with power 0.80, so the test finds fraud in 80 percent of the cases when fraud occurs. The same test incorrectly indicates fraud in 0.02 of the cases when people do not commit fraud. Hence, 0.02 is probability of the Type 1 error. In a two-by-two table, this hypothetical situation looks like
| True fraud | |||
| yes | no | ||
| Test says | yes | 80 | 2 |
| No | 20 | 98 |
Suppose now that 1 percent of the people truly do commit fraud. And suppose further that you examine 10,000 individuals, which thus means that 100 of those commit fraud. The test finds 80 of the 100 individuals. But what happens to the others? Of the 9,900 individuals who do not commit fraud, 2 percent (Type 1 error) will be marked as committing fraud, which gives 198 additional hits. Taking the 80 and 198 together, we thus have the percentage of innocent individuals over all individuals for which the test gives a signal as
The probability went from 0.02 (![]() ) and 0.20 (
) and 0.20 (![]() ) to 0.71.
) to 0.71.
Here is another example that shows the impact of multiple testing. At a crime scene, a DNA sample is taken. The sample is compared with DNA profiles of 20,000 men. Suppose the DNA test erroneously gives a match in 1 of any 10,000 comparisons. This means there is a small error of type 1, namely 0.0001. Suppose that there is a match found for one man. Is the man guilty because the test makes no mistakes in 9,999 of the 10,000 cases? Well, not really!
Suppose that in reality no one of the 20,000 men in the database has ever been at the crime scene. What is now the probability of still finding at least one match?
The probability of a match by pure chance is
The probability of no match by pure chance is therefore
The probability of no match when trying 20,000 times (independent cases) is

The probability of at least one match by pure chance after trying 20,000 times is then

You will see that the probability of making an incorrect judgment has increased from 0.01 percent to 86.5 percent. This is called a false positive, and this frequently happens in statistical practice. If you run enough tests, there is virtually always a test result with a hit.
In these examples, the 10,000 and 20,000 cases could be viewed as independent cases. But in many settings, cases are not independent, and then the chance of getting false positives becomes even larger. Indeed, you do not need so many cases then, as with a small number of cases you will already obtain false inference. Similarly, searching many variables to see which ones have significant parameters in a regression model will virtually always lead to significant results, at least if you keep the p value cut off point constant as you proceed. We return to this in Chapter 4.
1.9 Correlation and Causality
Correlation and causality do not mean the same thing. When there is causality, there is likely correlation, but when there is correlation there does not need to be a causal link. Yet it is tempting to mix the two concepts – even more so when graphs show suggestive common features and when there is an underlying variable that drives the variables.
Look at the two lines in Figure 1.7, which correspond with the number of thefts from a military complex and the number of thefts of animals, both on an annual basis.Footnote 35 To make it even more suggestive, look at the scatter plot in Figure 1.8.

Figure 1.7 Thefts from a military complex and thefts of animals, the Netherlands, yearly data for 2010–2019.
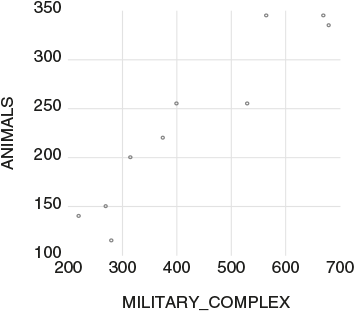
Figure 1.8 Thefts of animals against thefts from a military complex, the Netherlands, yearly data for 2010–2019.
By plotting one variable against the other and by making the choice of putting one variable on the x axis and the other on the y axis, one could be framed to believe that the variable on the x axis is causing (or leading) the variable on the y axis. When a graph as in Figure 1.8 is presented, you could be inclined to consider the regression model:
where ![]() , and where
, and where ![]() is an error term. Application of Ordinary Least Squares (OLS) to estimate
is an error term. Application of Ordinary Least Squares (OLS) to estimate ![]() and
and ![]() results in
results in

where standard errors are presented in parentheses. The t value for the hypothesis ![]() is 8.049, and this is beyond the 5 percent critical value of 2. The
is 8.049, and this is beyond the 5 percent critical value of 2. The ![]() of this regression is 0.890, which is quite close to 1. Hence, one could be tempted to believe that there is a strong link between the two variables, and even that thefts from a military complex is leading or causing the thefts of animals.
of this regression is 0.890, which is quite close to 1. Hence, one could be tempted to believe that there is a strong link between the two variables, and even that thefts from a military complex is leading or causing the thefts of animals.
Looking back at Figure 1.7, we see that both variables show a downward trending. pattern. Could it be that behind the two patterns there is a downward trend because of better precautionary measures or more surveillance? If the latter effects are proxied by a variable ![]() , which takes the values 0, 1, 2, …, 9, and when we consider the regression model
, which takes the values 0, 1, 2, …, 9, and when we consider the regression model

then the following OLS based estimates are obtained:

We can see now that the t value for the null hypothesis ![]() is 0.894, and hence the suggestive relation between the two variables is just driven by a previously omitted variable, where the trend can also measure an increase in precautionary rules. The correlation between the two variables is a spurious correlation. In Chapter 7, we return to the phenomenon of spurious correlations.Footnote 36
is 0.894, and hence the suggestive relation between the two variables is just driven by a previously omitted variable, where the trend can also measure an increase in precautionary rules. The correlation between the two variables is a spurious correlation. In Chapter 7, we return to the phenomenon of spurious correlations.Footnote 36
1.10 What to Do?
A good starting point for your own research is to try to replicate earlier studies.Footnote 37 You contact the original authors, ask for the data that they used, or retrieve the data from a publicly available database, then you use the same methods of analysis and the same estimation methods. In the case of data obtained from experiments, you can run a similar experiment to see if you end up with the same conclusions.
This is nicely put by Aarts et al.: “Innovation points out paths that are possible; replication points out paths that are likely; progress relies on both.”Footnote 38
1.11 What Makes Us Deviate from Ethical Guidelines?
Even though the various guidelines in this chapter make sense and have obvious face value, as we will also see in Chapter 2, it does happen that these guidelines are not met. What could be the reason that this happens?Footnote 39
One reason can be ignorance. If you are not aware of multiple testing problems, then you may just run many tests or regressions without being aware that the results are most likely flawed. Hence, solid knowledge of the ins and outs of the methods and techniques that you use is important.
Some people claim that the editors of journals make people misbehave. Journals like to publish significant results,Footnote 40 results that attract readership and citations. Journals with more citations have more impact; they climb up the ladder and gain high esteem. Editors of top journals at the same time increase their recognition.Footnote 41
Not following ethical guidelines can be motivated by the fact that many universities want academics to have impact. This can be obtained if mainstream or social media pick up research results, and they like results that attract attention and sell. Some academics have become media stars, and some sell thousands of copies of popularized versions of their academic work.
It may also be that university boards follow the “publish or perish” rule, mentioned earlier, which can make people hastily draft many papers, thereby perhaps falling into the self-plagiarism trap.
Finally, clients of econometricians’ advice may wish to hear certain outcomes that are convenient to them and suit their managerial purposes.
Anyway, whatever the reasons are, it is mandatory for valid science to follow the ethical guidelines. Be aware that there is judgment at all stages of the model building and forecasting process. There is always something to decide. The ethics part comes in when you know what the consequences of the choices are and when you do not know these. And one simple strategy, to make sure that others can be convinced that you are indeed behaving ethically, is to write everything down. Report all choices that you have made.Footnote 42 In the next chapters, we will see that this may be easier said than done.










