We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
Putnam [‘On the non-periodicity of the zeros of the Riemann zeta-function’,
Amer. J. Math.76 (1954), 97–99] proved that
the sequence of consecutive positive zeros of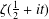 
$\unicode[STIX]{x1D701}(\frac{1}{2}+it)$ does not contain any infinite arithmetic progression. We
extend this result to a certain class of zeta functions.
