We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We give a generalisation of the Cartan decomposition for connected compact Lie groups of type B motivated by the work on visible actions of Kobayashi [‘A generalized Cartan decomposition for the double coset space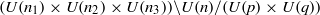 
$(U(n_{1})\times U(n_{2})\times U(n_{3})) \backslash U(n)/ (U(p)\times U(q))$’, J. Math. Soc. Japan59 (2007), 669–691] for type A groups. Suppose that 
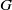$G$ is a connected compact Lie group of type B, 
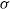$\sigma $ is a Chevalley–Weyl involution and 
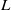$L$,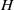 
$H$ are Levi subgroups. First, we prove that 
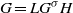$G=LG^{\sigma }H$ holds if and only if either (I) both 
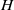$H$ and 
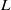$L$ are maximal and of type A, or (II) 
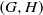$(G,H)$ is symmetric and 
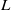$L$ is the Levi subgroup of an arbitrary maximal parabolic subgroup up to switching 
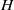$H$ and 
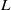$L$. This classification gives a visible action of 
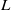$L$ on the generalised flag variety 
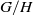$G/H$, as well as that of the 
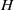$H$-action on 
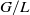$G/L$ and of the 
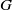$G$-action on 
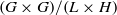$(G\times G)/(L\times H)$. Second, we find an explicit ‘slice’ 
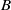$B$ with 
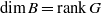$\dim B=\mathrm {rank}\, G$ in case I, and 
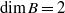$\dim B=2$ or 
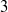$3$ in case II, such that a generalised Cartan decomposition 
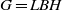$G=LBH$holds. An application to multiplicity-free theorems of representations is also discussed.
