We analyze the elementary theory of certain fields 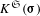 $K^{\mathfrak{S}}(\boldsymbol{\unicode[STIX]{x1D70E}})$ of totally
$K^{\mathfrak{S}}(\boldsymbol{\unicode[STIX]{x1D70E}})$ of totally 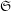 $\mathfrak{S}$ -adic algebraic numbers that were introduced and studied by Geyer and Jarden and by Haran, Jarden, and Pop. In particular, we provide an axiomatization of these theories and prove their decidability, thereby giving a common generalization of classical decidability results of Jarden and Kiehne, Fried, Haran, and Völklein, and Ershov.
$\mathfrak{S}$ -adic algebraic numbers that were introduced and studied by Geyer and Jarden and by Haran, Jarden, and Pop. In particular, we provide an axiomatization of these theories and prove their decidability, thereby giving a common generalization of classical decidability results of Jarden and Kiehne, Fried, Haran, and Völklein, and Ershov.
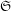 $\mathfrak{S}$ -ADIC NUMBERS
$\mathfrak{S}$ -ADIC NUMBERS