1 results
The Thickness of the Cartesian Product of Two Graphs
-
- Journal:
- Canadian Mathematical Bulletin / Volume 59 / Issue 4 / 01 December 2016
- Published online by Cambridge University Press:
- 20 November 2018, pp. 705-720
- Print publication:
- 01 December 2016
-
- Article
-
- You have access
- Export citation
-
The thickness of a graph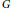
$G$ is the minimum number of planar subgraphs whose union is 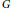$G$. A 
$t$-minimal graph is a graph of thickness $t$ that contains no proper subgraph of thickness $t$. In this paper, upper and lower bounds are obtained for the thickness,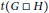 
$t\left( G\,\square \,H \right)$, of the Cartesian product of two graphs 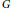$G$ and 
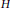$H$, in terms of the thickness 
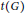$t\left( G \right)$ and 
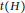$t\left( H \right)$. Furthermore, the thickness of the Cartesian product of two planar graphs and of a $t$-minimal graph and a planar graph are determined. By using a new planar decomposition of the complete bipartite graph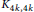 
${{K}_{4k,\,4k}}$, the thickness of the Cartesian product of two complete bipartite graphs 
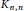${{K}_{n,n}}$ and 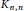${{K}_{n,n}}$ is also given for 
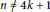$n\,\ne \,4k\,+\,1$.
