We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
The n-dimensional cyclic system of second-order nonlinear differential equations
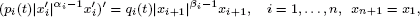
is analysed in the framework of regular variation. Under the assumption that αi and βi are positive constants such that α1 … αn > β1 … βn and pi and qi are regularly varying functions, it is shown that the situation in which the system possesses decreasing regularly varying solutions of negative indices can be completely characterized, and moreover that the asymptotic behaviour of such solutions is governed by a unique formula describing their order of decay precisely. Examples are presented to demonstrate that the main results for the system can be applied effectively to some classes of partial differential equations with radial symmetry to provide new accurate information about the existence and the asymptotic behaviour of their radial positive strongly decreasing solutions.
