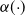We consider an (R, Q) inventory model with two types of orders, normal orders and emergency orders, which are issued at different inventory levels. These orders are delivered after exponentially distributed lead times. In between deliveries, the inventory level decreases in a state-dependent way, according to a release rate function 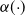$\alpha({\cdot})$ . This function represents the fluid demand rate; it could be controlled by a system manager via price adaptations. We determine the mean number of downcrossings $\theta(x)$ of any level x in one regenerative cycle, and use it to obtain the steady-state density f (x) of the inventory level. We also derive the rates of occurrence of normal deliveries and of emergency deliveries, and the steady-state probability of having zero inventory.